一元线性回归论文
统计预测与决策课程论文---范文1 - 副本

统计预测和决策课程论文-------------------安徽省人口总数的预测学院:班级:学生姓名:指导教师:完成时间:目录摘要 (2)一绪论 (3)二数据来源 (3)三模型及预测方法的介绍 (3)四模型建立、求解及检验 (6)1.移动平均法预测 (6)2.指数平滑法预测 (7)3.一元线性回归预测 (7)五模型评价 (9)六参考文献 (11)摘要近几年来,就业问题一直是各严峻而艰巨的任务,关系到国家未来的前途命运,然而,导致这个问题难以解决的最主要原因便是应届毕业生的总数高居不下,甚至有上涨的趋势。
研究毕业生总数的变动趋势,有利于掌握未来几年的岗位需求,从而可以沉着应对。
本论文通过运用移动平均法、指数平滑法,一元线性回归方程等,拟合总数变动趋势等分析方法,通过建模求解我们可以预测到未来五年我国应届毕业生总人数的变动趋势[键词]:移动平均法;指数平滑法;线性回归;excel一、绪论由于毕业生就业情况和国家未来的前途命运紧密相关,现行中国推进全面深化改革,这各艰巨的任务理所当然的落在当代当学生发身上,所以,发展经济的前提便是是毕业生能够充分毕业,给他们用武之地。
二、数据来源从中国统计年鉴上得到的安徽省2000到2012年总人口数的数据,如下 (单位:万人)年份 总数2001 114 2002 145 2003 212 2004 280 2005 338 2006 413 2007 495 2008 559 2009 611 2010 631 2011 660 2012 680 2013 700 2014 727三、模型及预测方法的介绍 1.移动平均法:移动平均法是根据时间序列资料逐项推移,依次计算包含一定项数的时序平均数,以反映长期趋势的方法。
当时间序列的数值由于受周期变动和不规则变动的影响,起伏较大,不易显示出发展趋势时,可用移动平均法,消除这些因素的影响,来分析、预测序列的长期趋势。
移动平均法有简单的平均法、加权平均法和趋势移动平均法 (1)简单移动平均法设时间序列为:12t y y y ; 简单移动平均法的计算公式为:11t t t N t y y y M N--+++=,t N ≤式中:t M —t 期移动平均数 N — 移动平均项数 预测公式为:1t t M yΛ+=即以第t 期移动平均数作为第t+1期的预期值。
对“一元线性回归方程在标准曲线上的应用”的补充研究

防水, 2 010 ( 2) : 41- 42 .
� � � � � � � � � � � � � � � � 2 黄海 , 罗友丰 , 陈志 英, 等. 10.0 统计 分 � � � 析 .北京: 人民邮电出版社, 2001 , 2.
验误差为 0;=0 �1 时, 与
性, 值愈接近 1, 与 之间线性关系愈好 � 利用三 次曲线相关系数为 =0.999 04 , 而该文中的相关系数 才为 0.997 9,因而三次曲线的相关系数 更接近于
� � 2
述数据进行三次拟合 , 可得回归方程:
-5 2 -8 3
� � � � � =16 6 .021+ 0. 001 76 -1.424 10 + 9.701 10 关系该文仅介绍了一元线性回归的方法, 一元线性回
� � � 10 16 中 国建筑防水
39
检测技术
根据回归方程可得其拟合曲线, 见图 1 �
� � � 中在 (23 0.6 ) � 相对湿度 (90 2 ) % 时, 水蒸气通过 Z L
A : A
某中空玻璃用丁基热熔密封胶进入干燥剂的速度数
� , -� � 据见表 1, 其中横坐标 为时间/ , 纵坐标 为质量 /
.B �A � , -
, 作散点图, 经分析, 其变化趋势应服从三次曲线分 布, 方程为:
检测技术
对 "一 元 线 性 回 归 方 程 在 标 准 曲 线 上 的应用" 的补充研究
范加冬, 张令刚
( 中国矿业大学力学与建ቤተ መጻሕፍቲ ባይዱ工程学院土木工程系, 江苏 徐州 221006)
摘要: 变量间的相互关系有时较为复杂, 一元线性 回归仅能描 述很少的一种情况�在 �一元线性回归方程在标准曲线上的应 用� 一文 的基础上 , 运用 曲线拟合 对数据进行 重新回 归, 结果 显示曲线拟合比一元线性回归精 度更高� 应用范围更广, 更适 用于在材料性能检测与试验研 究过程中准确寻找 变量间的相 关关系� 关键词: 一元线性回归; 曲线拟合; 标准曲线; 相互关系 文章编号: 1007-497X(2010 ) -16 -0039-02 中图分类号: TU 502+ . 4 文献标识码: A �A � / / F J ,
一元线性回归模型案例分析

一元线性回归模型案例分析一元线性回归是最基本的回归分析方法,它的主要目的是寻找一个函数能够描述因变量对于自变量的依赖关系。
在一元线性回归中,我们假定存在满足线性关系的自变量与因变量之间的函数关系,即因变量y与单个自变量x之间存在着线性关系,可表达为:y=β0+ β1x (1)其中,β0和β1分别为常量,也称为回归系数,它们是要由样本数据来拟合出来的。
因此,一元线性回归的主要任务就是求出最优回归系数和平方和最小平方根函数,从而评价模型的合理性。
下面我们来介绍如何使用一元线性回归模型进行案例分析。
数据收集:首先,研究者需要收集自变量和因变量之间关系的相关数据。
这些数据应该有足够多的样本观测值,以使统计分析结果具有足够的统计力量,表示研究者所研究的关系的强度。
此外,这些数据的收集方法也需要正确严格,以避免因相关数据缺乏准确性而影响到结果的准确性。
模型构建:其次,研究者需要利用所收集的数据来构建一元线性回归模型。
即建立公式(1),求出最优回归系数β0和β1,即最小二乘法拟合出模型方程式。
模型验证:接下来,研究者需要对所构建的一元线性回归模型进行验证,以确定模型精度及其包含的统计意义。
可以使用F检验和t检验,以检验回归系数β0和β1是否具有统计显著性。
另外,研究者还可以利用R2等有效的拟合检验统计指标来衡量模型精度,从而对模型的拟合水平进行评价,从而使研究者能够准确无误地判断其研究的相关系数的统计显著性及包含的统计意义。
另外,研究者还可以利用偏回归方差分析(PRF),这是一种多元线性回归分析技术,用于计算每一个自变量对相应因变量的贡献率,使研究者能够对拟合模型中每一个自变量的影响程度进行详细的分析。
模型应用:最后,研究者可以利用一元线性回归模型进行应用,以实现实际问题的求解以及数据挖掘等功能。
例如我们可以使用这一模型来预测某一物品价格及销量、研究公司收益及投资、检测影响某一地区经济发展的因素等。
综上所述,一元线性回归是一种利用单变量因变量之间存在着线性关系来拟合出回归系数的回归分析方法,它可以应用于许多不同的问题,是一种非常实用的有效的统计分析方法。
一元线性回归案例分析

ˆ 0 135 .31 是样本回归方程的截距,它表示不受可支 配收入的影响的自发消费行为。
参数估计量的符号和大小,均符合经济理论及南通市的 实际情况。
第三步 评价模型——统计检验
r2=0.98,说明总离差平方和的98%被样本回归直线解 释,仅有2%违背解释。因此,样本回归直线对样本点 的拟合优度是很好的。 F=786.13﹥F0.05(1,17)=4.45,总体线性显著。 给出显著水平α=0.05,查自由度ν =19-2=17的t分布, 得临界值t0.025(17)=2.11, t0=5.47﹥t0.025(17), t1=28.04 ﹥t0.025(17), 故回归系数均显著不为零,回归模型中应包含常数项, X对Y有显著影响。
¥849.8 ¥1,035.3 ¥974.7 ¥1,200.9
82 ¥488.1 ¥566.8 89 ¥718.4 ¥821.0 95 ¥1,041.0 ¥1,289.8 83 ¥509.6 ¥591.2 90 ¥767.2 ¥884.2 96 ¥1,099.3 ¥1,432.9 84 ¥576.4 ¥700.0 91 ¥759.5 ¥903.7 97 ¥1,186.1 ¥1,539.0 85 ¥654.7 ¥744.1 92 ¥820.3 ¥984.1 98 ¥1,252.5 ¥1,663.6 86 ¥755.6 ¥851.2
ห้องสมุดไป่ตู้
从以上的评价可以看出,此模型是比较好的
第四步 预测应用
1.
2.
假如给出1999年、2000年南通的人均可支 配收入(1980年不变价格)分别为 X99=1763元,X00=1863元,求1999年、 2000年人均消费性支出预测值? 假如2001——2004年的人均可支配收入未 知,你能预测2001——2004年的人均消费 性支出吗?如何预测?
【文献综述】一元线性回归在经济预测中的应用

文献综述信息与计算科学一元线性回归在经济预测中的应用经济预测是指用可靠的方法进行对未来经济的分析,是与未来有关的旨在减少不确定性对经济活动影响的一种经济分析.它是对将来经济发展的科学认识活动.经济预测是以科学的理论和方法、可靠的资料、精密的计算及对客观规律性的认识所作出的分析和判断。
这样的预测是一种分析的程序,它可以重复地连续进行下去。
目的是为未来问题的经济决策服务.为了提高决策的正确性,需要由预测提供有关未来的情报,使决策者增加对未来的了解,把不确定性或无知程度降到最低限度,并有可能从各种备选方案中作出最优决策.因此,经济预测是各级领导机关和经济管理工作者展望经济发展前景,制定政策,编制计划,做出决策,以及进行科学管理的重要依据,在计划经济中有着重要的作用.预测是一门实用学科,它有科学基础,包括理论、资料、方法、计算等因素,依赖于对客观经济规律的认识和掌握。
它还依赖于预测者提出假设、选择方法、利用资料的技巧,和运用他自己的学识、经验、获得的情报进行判断的能力.经济预测有它的哲学基础、经济学基础、统计学基础,同时在多数情况下还以经济数学模型的建立与运用为基础。
一种实用模型根据一定的理论和事实,考虑到种种条件的假设和政策变化的影响,就可以用来预测经济的发展.经济预测的方法一般分为质的预测方法与量的预测方法两大类。
第一类方法,如专家调查法、民意调查法等.后一种方法是向消费者、生产者调查他们对未来发展的意见或意向,考虑他们的心理因素的预测方法.它适用于了解居民的消费需求和购买意图、市场的动向以及投资的趋向等问题.第二类方法,如时间数列法、指标分析法、因素分析法等。
时间数列法是通过分析时间数列的组成要素来研究其变化形态,把过去的发展趋势延续下去和外推未来的预测方法.它的主要方法有移动平均法、加权移动平均法、指数平滑法、最小平方法等等。
指标分析法是通过分析反映经济变动的互有联系的指标或指标组,研究那些预示经济转折的“动向”指标和预报经济可能出现严重问题的“警戒”指标,来确定经济形势变化的迹象的预测方法。
一元线性回归模型案例分析

一元线性回归模型案例分析一、研究的目的要求居民消费在社会经济的持续发展中有着重要的作用。
居民合理的消费模式和居民适度的消费规模有利于经济持续健康的增长,而且这也是人民生活水平的具体体现。
改革开放以来随着中国经济的快速发展,人民生活水平不断提高,居民的消费水平也不断增长。
但是在看到这个整体趋势的同时,还应看到全国各地区经济发展速度不同,居民消费水平也有明显差异。
例如,2002年全国城市居民家庭平均每人每年消费支出为6029.88元, 最低的黑龙江省仅为人均4462.08元,最高的上海市达人均10464元,上海是黑龙江的2.35倍。
为了研究全国居民消费水平及其变动的原因,需要作具体的分析。
影响各地区居民消费支出有明显差异的因素可能很多,例如,居民的收入水平、就业状况、零售物价指数、利率、居民财产、购物环境等等都可能对居民消费有影响。
为了分析什么是影响各地区居民消费支出有明显差异的最主要因素,并分析影响因素与消费水平的数量关系,可以建立相应的计量经济模型去研究。
二、模型设定我们研究的对象是各地区居民消费的差异。
居民消费可分为城市居民消费和农村居民消费,由于各地区的城市与农村人口比例及经济结构有较大差异,最具有直接对比可比性的是城市居民消费。
而且,由于各地区人口和经济总量不同,只能用“城市居民每人每年的平均消费支出”来比较,而这正是可从统计年鉴中获得数据的变量。
所以模型的被解释变量Y 选定为“城市居民每人每年的平均消费支出”。
因为研究的目的是各地区城市居民消费的差异,并不是城市居民消费在不同时间的变动,所以应选择同一时期各地区城市居民的消费支出来建立模型。
因此建立的是2002年截面数据模型。
影响各地区城市居民人均消费支出有明显差异的因素有多种,但从理论和经验分析,最主要的影响因素应是居民收入,其他因素虽然对居民消费也有影响,但有的不易取得数据,如“居民财产”和“购物环境”;有的与居民收入可能高度相关,如“就业状况”、“居民财产”;还有的因素在运用截面数据时在地区间的差异并不大,如“零售物价指数”、“利率”。
基于一元线性回归数学模型的简单应用方法之欧阳学创编

基于一元线性回归数学模型的简单应用方法刘亚阳(天津医科大学生物医学工程学院09级生医二班,天津 300070)摘要:人们经常用已知系统实测数据对数据进行拟合,并找出最佳拟合直线,对数据进行更为精准的估测。
回归分析方法是寻求统计规律的重要方法之一,本文针对一元线性回归模型进行研究,用最小二乘法对参数进行估计。
同时,根据已给出的24组纤维样品的拉伸长度和强度数据建立模型,从拉伸倍数预测强度,并运用MATLAB对已建立的一元线性回归数学模型进行检验,剔除异常点,用剩余的点重新计算,用经过检验的数学模型预测,使所得到结果更加符合真实数据的估计值。
关键词:一元线性回归模型;最小二乘法;预测;拟合直线引言随着现今的发展,人们需要对各个行业的各种发展和变化趋势做出预测,这时需要建立一个准确简练数学回归模型,有助于对将发生的变化进行准确预测。
本论文主要向大家介绍较为简单的一元线性回归数学模型,以某种合成纤维的强度和拉伸倍数之间的关系为例,建立一元线性回归数学模型,并运用MATLAB对已建立的模型进行检验,剔除异常点重新计算,最终得到更为精准的数学模型。
1实验对象及方法1.1实验对象某种合成纤维的强度与其拉伸倍数之间有一定关系,下表是实测24个纤维样品的强度y与相应的拉伸倍数x的数据记录.1.2实验方法1.2.1观测数据对这24组数据进行观察,可以发现y有随着x增加而增加的趋势,但它们之间的具体关系又是不确定的。
1.2.2绘制散点图以拉伸倍数X为横坐标,强度Y为纵坐标,绘制散点图1.2.3构建数学模型散点图有助于我们粗略地了解两个变量之间大致上存在怎样的相关关系。
根据对散点图的观察,发现图中的散点在一定范围可以近似为线性关系,所以将其构建为一元线性回归数学模型。
变量y对x的回归方程的形式为1-2-1根据样本数据去寻求未知参数a与b的估计值aˆ和bˆ,使得回归直线方程1-2-2与所有的观测点拟合得最好.对任一给定iiyx,的估计值为:()nibxayi,...,2,1ˆ=+=这些估计值同实际观测值之间的离差(或随机误差)为:1-2-3离差平方和为:根据最小二乘法准则,当离差平方和最小时,直线与观测点拟合的最好,所以可以根据微积分的极值求法得到预估值()()021=+--=∂∂∑=niiiixbxaybQ1-2-4 通过整理得到a与b的线性方程组1-2-5将∑==niixnx11和∑-=niiyny11代入上式可得到a与b的估计值bxay+=x bayˆˆˆ+=()()n,…,2,1,=iyxiiiiiiibxayyy--=-=ˆε()()∑∑==+-==niiiniibxayQ1212ε()0)(21=+--=∂∂∑=niiibxayaQ∑∑===+niniyixibna11∑∑∑====+niniiiiniiyxxbxa1121x b y ax n x yx n yx bni ini ii -=--=∑∑==ˆˆ12211-2-61.2.4用MATLAB 对所得结果进行检验,剔除异常点得到更加符合真实值的拟合直线2结果2.1计算实验所需数据代入公式得到回归直线方程用excel 计算24组xy y x y x ,,,,22的和及所需数据∑∑∑∑∑=============2412412412224124160.731,93.650,61.8297125.4,3125.510.113,50.127,24i i i i i i ii i i i y x y xy x y x n代入b a ˆ,ˆ的公式中可得1505.0ˆ8587.0ˆ1221=-==--=∑∑==x b y ax n xyx n yx bni ini ii图1 用excel 计算24组xy y x y x ,,,,22的和 所求回归直线方程为:x y 8587.01505.0ˆ+=2.2用MATLAB 对本题进行求解建立一元线性回归模型,绘制散点图,得出y 的系数根据所求出系数做出拟合直线。
关于一元线性回归分析的一些思考

第19卷第4期重庆电子工程职业学院学报Vol.19No.42010年7月Journal of Chongqing College of Electronic EngineeringJul.20101一元线性回归分析设因变量y 和自变量x 满足如下线性关系:y=β0+β1x+ε,E(ε)=0,0<Var(ε)=σ2<∞(1)其中ε是期望为0,方差为σ2的随机误差;除特别声明外,均假定x 是一非随机变量;y 是随机变量;β0,β1,σ2为未知参数,其中β0,β1又称为回归系数。
(1)式为一元线性回归的理论模型。
对(x,y)数据作n 次观察,得到(x 1,y 1),(x 2,y 2),…,(x n ,y n );并作出散点图,用方程表示:yi=β0+β1x i +εi ,i=1,2,…n 。
(2)对ε作如下假设:10正态性,即εi ~N(0,σ2),i=1,2,…n ;20不相关性,即Cov(εi ,εj )=0,i ≠j;i,j=1,2,…n 。
这种模型称为正态线性模型,以下的讨论都是围绕此情形展开。
1.1回归方程的估计使用最小二乘法寻求回归系数的估计量β赞0、β赞1,使得关于β赞0、β赞1的函数Q=(β赞0+β赞1)=nj =1Σ(y j -β赞0-β赞1x j )2最小,由数学分析的极值理论可知,β赞0、β赞1应满足鄣Q 鄣β赞0=0,鄣Q 鄣β赞1=0由此可得β赞0=y 軃-β赞1x 軃,β赞1=ni =1Σ(x i -x軃)y ini =1Σ(x i-x軃)2;其中x 軃=1n ni =1Σx i ,y=1n ni =1Σy i ,而且一般情况下,x i 不会完全相等。
从而得到经验回归方程:y赞=β赞0+β赞1x (3)1.2回归效果的评价1.2.1判定系数R 2检验法在对回归效果进行检验之前,给出几个记号:Q T =ni =1Σ(y i -y軃)2———总的离差平方和;Q R =ni =1Σ(y赞i -y 軃)2———回归平方和;Q e =ni =1Σ(y i -y軃i )2———残差平方和;显然,Q T =Q R +Q e (4)两边同时除以Q T ,记R 2=Q R T =1-Q e T,称之为判定系数,其衡量的是回归效果的优良程度;其值越靠近1(或0),说明“回归的比重”越大(越小),拟合数据的效果越好(越差)。
一元线性回归分析

一元线性回归分析摘要:一元线性回归分析是一种常用的预测和建模技术,广泛应用于各个领域,如经济学、统计学、金融学等。
本文将详细介绍一元线性回归分析的基本概念、模型建立、参数估计和模型检验等方面内容,并通过一个具体的案例来说明如何应用一元线性回归分析进行数据分析和预测。
1. 引言1.1 背景一元线性回归分析是通过建立一个线性模型,来描述自变量和因变量之间的关系。
通过分析模型的拟合程度和参数估计值,我们可以了解自变量对因变量的影响,并进行预测和决策。
1.2 目的本文的目的是介绍一元线性回归分析的基本原理、建模过程和应用方法,帮助读者了解和应用这一常用的数据分析技术。
2. 一元线性回归模型2.1 模型表达式一元线性回归模型的基本形式为:Y = β0 + β1X + ε其中,Y是因变量,X是自变量,β0和β1是回归系数,ε是误差项。
2.2 模型假设一元线性回归模型的基本假设包括:- 线性关系假设:自变量X与因变量Y之间存在线性关系。
- 独立性假设:每个观测值之间相互独立。
- 正态性假设:误差项ε服从正态分布。
- 同方差性假设:每个自变量取值下的误差项具有相同的方差。
3. 一元线性回归分析步骤3.1 数据收集和整理在进行一元线性回归分析之前,需要收集相关的自变量和因变量数据,并对数据进行整理和清洗,以保证数据的准确性和可用性。
3.2 模型建立通过将数据代入一元线性回归模型的表达式,可以得到回归方程的具体形式。
根据实际需求和数据特点,选择适当的变量和函数形式,建立最优的回归模型。
3.3 参数估计利用最小二乘法或最大似然法等统计方法,估计回归模型中的参数。
通过最小化观测值与回归模型预测值之间的差异,找到最优的参数估计值。
3.4 模型检验通过对回归模型的拟合程度进行检验,评估模型的准确性和可靠性。
常用的检验方法包括:残差分析、显著性检验、回归系数的显著性检验等。
4. 一元线性回归分析实例为了更好地理解一元线性回归分析的应用,我们以房价和房屋面积之间的关系为例进行分析。
一元线性回归分析

∑
1)模 型 回归系数的估计
6
为 了估计 回归系数 ,假定试验得到两个变量= 与 Y的 n个
数据对 xf,Yf l’ 1,2,3…,l,我们将这 对观测∑值代 人式 (1),
得
Yf= a-4-bxi-I- ,i=1,2,3… ,n
少 = a+bx
这里 G1,占2… …。, 互独-, er ̄随机变量 ,军服从正态分布 ,
[3]金 成龙.高职新 生校 园环境 适应性调 查与研 究. 经济 研究导刊 ,2011(4)287-288
[4】杨维杰.云南 高职院校新生 心理适应性调 查及 新生心理
健康教育对策.大科技 ,201i(4):I 91—193
【5]周治.高职 院校 新生适应 性 问题及对 策研 究. 职教论 坛 201 3 (17): 62—64 ’
速度 的测试 中,对 时间间隔为 30/h的刀具厚度进行预测 ,得 到
厂
1
, 刀具的厚度预测区间简化为l 一“l一 , +“1一 l,
输入计算指令
(4)用 Excel“分析工具库 ”提供的 “回归”工具 ,找出 线性 回归方程 ,并检验其显著性。
(上接 第 42页 )[2】刘艳坤 .普通 高校 高职新生适应性障碍分析 及对策研 究.重庆职业技术 学院学报 ,2008(1):23-25
设 计 原 理 在实际问题 中,经常会 出现两个变 量之间的相关关系不是
线性的 (即直线型 ),而是非线性 的 (即曲线 型 )。设其 中有两
个 变量 与Y,我们 可以用一个确定 函数关 系式 日: =.y(x)
大致的描述 Y与 之间的相关关 系 ,函数 U(x)称 为 Y关
于 X的回归 函数 ,
一元线性回归分析研究实验报告

一元线性回归分析研究实验报告一元线性回归分析研究实验报告一、引言一元线性回归分析是一种基本的统计学方法,用于研究一个因变量和一个自变量之间的线性关系。
本实验旨在通过一元线性回归模型,探讨两个变量之间的关系,并对所得数据进行统计分析和解读。
二、实验目的本实验的主要目的是:1.学习和掌握一元线性回归分析的基本原理和方法;2.分析两个变量之间的线性关系;3.对所得数据进行统计推断,为后续研究提供参考。
三、实验原理一元线性回归分析是一种基于最小二乘法的统计方法,通过拟合一条直线来描述两个变量之间的线性关系。
该直线通过使实际数据点和拟合直线之间的残差平方和最小化来获得。
在数学模型中,假设因变量y和自变量x之间的关系可以用一条直线表示,即y = β0 + β1x + ε。
其中,β0和β1是模型的参数,ε是误差项。
四、实验步骤1.数据收集:收集包含两个变量的数据集,确保数据的准确性和可靠性;2.数据预处理:对数据进行清洗、整理和标准化;3.绘制散点图:通过散点图观察两个变量之间的趋势和关系;4.模型建立:使用最小二乘法拟合一元线性回归模型,计算模型的参数;5.模型评估:通过统计指标(如R2、p值等)对模型进行评估;6.误差分析:分析误差项ε,了解模型的可靠性和预测能力;7.结果解释:根据统计指标和误差分析结果,对所得数据进行解释和解读。
五、实验结果假设我们收集到的数据集如下:经过数据预处理和散点图绘制,我们发现因变量y和自变量x之间存在明显的线性关系。
以下是使用最小二乘法拟合的回归模型:y = 1.2 + 0.8x模型的R2值为0.91,说明该模型能够解释因变量y的91%的变异。
此外,p 值小于0.05,说明我们可以在95%的置信水平下认为该模型是显著的。
误差项ε的方差为0.4,说明模型的预测误差为0.4。
这表明模型具有一定的可靠性和预测能力。
六、实验总结通过本实验,我们掌握了一元线性回归分析的基本原理和方法,并对两个变量之间的关系进行了探讨。
一元线性回归方程在安全中的应用论文

一元线性回归方程在安全中的应用摘要:在安全领域,有相当多的一部分计算需要通过一元线性回归方程进行初步的分析检测,本文通过实例证明与理论分析,解释一元线性回归方程在安全中的应用在建筑安全,桥梁安全,生产安全等现实环境中,大量存在的变量之间有着非确定性的统计相关关系。
这种关系的特点是变量之间不能给出精确的函数表达式,即不是一一对应关系,但在一定条件下变量之间有着某种规律性的关系。
例如在其他条件不变下地基深度与建筑物抗震度的关系,又如工厂消毒程度与产品合格率的关系。
而回归分析是研究变量之间不确定的统计相关关系的经典方法之一在建筑安全,桥梁安全,生产安全等现实环境中,大量存在的变量之间有着非确定性的统计相关关系。
这种关系的特点是变量之间不能给出精确的函数表达式,即不是一一对应关系,但在一定条件下变量之间有着某种规律性的关系。
例如在其他条件不变下地基深度与建筑物抗震度的关系,又如工厂消毒程度与产品合格率的关系。
而回归分析是研究变量之间不确定的统计相关关系的经典方法之一一元线性回归模型是最简单的线性回归模型,在模型中只有一个自变量,其参数估计方法普通最小二乘法也是最普遍使用的,虽然就某一方面的安全因素存在多个相关的因变量,但通过一元线性回归模型,可以以最简单快速的方法计算算出其主要变量的规律关系,并对其进行预测。
一元线性回归模型的一般形式是=——被解释变量————解释变量————随机误差——回归系数,其中.——样本实际值样本取值:首先确定所研究的2个变量X,Y,其中X以适当的梯度差进行调查,并得出对应的Y的实际值,再将统计的X,Y代入式子中,便得得出回归系数,并得出回归方程,以此对未知的Y进行预测与推断。
例:已知,某柱子内钢筋总质量为X,钢筋可承受张力为Y,在编号1-12的柱子样本数据见表求:编号13的柱子内钢筋质量为2099,预测该柱子可承受张力为多少(将年份改编号,人均国民收入改为钢筋质量,人均消费金额改为可承受张力)实际上,13号柱子的可承受张力为1148,相对误差为1.77%由以上实例可以证明,在一些的安全检验领域,通过可靠的样本数据,利用一元线性回归方程可以有效预测其结果,效果好,计算简单实用,且迅速,为安全检测人员在进行安全鉴定中时提供一个相对可靠的数据。
一元线性回归论文

一元线性回归分析论文专业:姓名:学号:摘要回归分析是数理统计中处理变量之间一种较为成熟、实用和有效的办法。
它可以简便有效地利用调查的统计资料,对经济现象进行事先预计和推断,为此引出一元线性回归分析数学模型和解决问题的方法。
本文回顾了描述变量相关关系和回归分析方面的基本知识,系统阐述了一元线性回归模型的基本原理,并将所学的知识与实际生产生活相结合,解决实际问题。
目录第一章回归分析概述 (1)1.1相关关系基本知识: (1)1.2回归分析基本知识回顾: (2)1.2.1回归分析的定义 (2)1.2.2.回归模型的分类 (2)1.2.3.回归分析的步骤 (3)1.2.4.回归分析的任务 (3)第二章一元线性回归的基本理论 (4)2.1一元线性关系的判断 (4)2.2一元线性回归模型的建立 (4)2.3模型回归效果的显著性检验 (5)2.3.1线性假设的显著性检验(T检验) (5)2.3.2线性回归的方差分析(F检验) (6)2.4利用回归方程进行预测 (9)2.4.一元线性回归模型的使用条件和特点 (11)2.4.1一元线性回归模型的使用条件 (11)2.4.2.一元线性回归模型的特点 (12)第三章一元线性回归分析方法的实际应用 (13)3.1.典型实际问题 (13)3.2应用MATLAB与EXCEL软件对验数据进行分析 (14)3.2.1应用MATLAB分析 (14)3.2.2应用Excel软件分析 (18)第四章总结 (25)第一章回归分析概述随着科技的迅速发展,数学的应用不仅在它的传统领域——经济建设、工程技术等方面发挥着越来越重要的作用,而且不断向一些新的领域渗透,形成了许多交叉科学,如计量经济学、人口控制论、生物数学等。
数学模型成为人们认识和研究这些学科的一种重要的工具,如何利用所学知识,建立与实际生活背景更贴切的数学模型来解决我们经济生活中存在的问题是摆在人们面前的重要课题!本文回顾了描述变量相关关系和回归分析方面的基本知识,系统阐述了一元线性回归模型的基本原理,并将其应用于实际生活中。
一元线性回归

· · ·· ·· · · ·· ·
2 4 6 8 10
o线附 近, 这告诉我们变量x和y之间大致可看作线 性关系. 从图中还看到, 这些点又不完全在 一条直线上, 这表明x和y的关系并没有确切 到给定x就可以唯一确定y的程度.
其原因在于人有较大的个体差异, 因而身高 和体重的关系, 是既密切但又不能完全确定 的函数关系.
类似的变量间的关系在大自然和社会中 屡见不鲜.
例如 , 小麦的穗长与穗重的关系 ; 某班学生最 后一次考试分数与第一次考试分数的关系;温 度、降雨量与农作物产量间的关系;人的年龄 与血压的关系;最大积雪深度与灌溉面积间的 关系;家庭收入与支出的关系等等.
这种大量存在的变量间既互相联系但又不 是完全确定的关系,称为相关关系. 从数量的角度去研究这种关系,是数 理统计的一个任务. 这包括通过观察和试 验数据去判断变量之间有无关系,对其关 系大小作出数量上的估计 , 对互有关系的 变量通过其一去推断和预测其它,等等. 回归分析就是研究相关关系的一种重 要的数理统计方法.
V=I. R
以上两例的共同点在于,三个量中任意 两个已知,其余一个就可以完全确定. 也就 是说,变量之间存在着确定性的关系,并且 可以用数学表达式来表示这种关系. 然而,在大量的实际问题中,变量之 间虽有某种关系,但这种关系很难找到一 种精确的表示方法来描述.
例如,人的身高与体重之间有一定的关系, 知道一个人的身高可以大致估计出他的体重, 但并不能算出体重的精确值.
y=a+bx+ε, ε ~N(0, )
2
(1)
现对模型(1)中的变量x , y进行了n次独 立观察, 得样本 (x1,y1),…,(xn,yn) (3)
一元线性回归分析论文

一元线性回归分析的应用——以微生物生长与温度关系为例摘要:一元线性回归预测法是分析一个因变量与一个自变量之间的线性关系的预测方法。
应用最小二乘法确定直线,进而运用直线进行预测。
本文运用一元线性回归分析的方法,构建模型并求出模型参数,对分析结果的显著性进行了假设检验,从而了微生物生长与温度间的关系。
关键词:一元线性回归分析;最小二乘法;假设检验;微生物;温度回归分析是研究变量之间相关关系的统计学方法,它描述的是变量间不完全确定的关系。
回归分析通过建立模型来研究变量间的这种关系,既可以用于分析和解释变量间的关系,又可用于预测和控制,进而广泛应用于自然科学、工程技术、经济管理等领域。
本文尝试用一元线性回归分析方法为微生物生长与温度之间的关系建模,并对之后几年的情况进行分析和预测。
1 一元线性回归分析法原理1.1 问题及其数学模型一元线性回归分析主要应用于两个变量之间线性关系的研究,回归模型模型为εββ++=x Y 10,其中10,ββ为待定系数。
实际问题中,通过观测得到n 组数据(X i ,Y i )(i=1,2,…,n ),它们满足模型i i i x y εββ++=10(i=1,2,…,n )并且通常假定E(εi )=0,V ar (εi )=σ2各εi 相互独立且服从正态分布。
回归分析就是根据样本观察值寻求10,ββ的估计10ˆ,ˆββ,对于给定x 值, 取x Y 10ˆˆˆββ+=,作为x Y E 10)(ββ+=的估计,利用最小二乘法得到10,ββ的估计10ˆ,ˆββ,其中⎪⎪⎩⎪⎪⎨⎧⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛-=-=∑∑==n i i ni i i x n x xy n y x x y 1221110ˆˆˆβββ。
1.2 相关系数上述回归方程存在一些计算相关系数。
设L XX =∑∑==-=-=ni i ni i defxx x n x x x L 12212)(,称为关于X 的离差平方和;L yy =21)(∑=-=ni i y y S 总称为关于Y 的离差平方和,L xy =∑∑==-=-=ni i n i i defxx x n x x x L 12212)(1)(∑=-=ni i y y S 总称为关于X 与Y 的离差积和。
一元线性回归分析和有效应用

TECHNICS ·APPLICATION技术·应用文 李会芳一元线性回归分析和有效应用一、一元线性回归分析基本原理一元线性回归的数学模型为y=β0+β1x+ε。
其中,变量x对因变量y的影响可以用(β0+β1x)表示出来,β0和β1是待定参数,ε则表示其他不确定因素对y造成的影响,通常来说ε是无法确定的,一般将ε假设为方差为σ2,期望是0的正态分布。
回归分析在实际中的应用其实就是一个求解未知数的过程。
它通过给出的一系列样本数值对待定参数β0和β1进行精确估计,并将估计值用β0'和β1'来表示。
在计算时采用最小二乘法对估计值进行计算:计算所给出样本值的平均值,再将相关数据带入上述公式,就可以利用最小二乘法计算出β0'和β1'的值,最后将得出的数值带入一元线性回归的数学模型即可。
二、一元线性回归分析的有效应用(一)一元线性回归分析在经济中的应用利用一元线性回归分析可以对生活中的一些经济关系进行分析,它是经济预测中常用的方法之一。
本文以财政收入和GDP之间的线性关系分析为例来对一元线性回归分析在实际中的应用情况进行探讨。
下面是某十年国家财政收入占国内生产总值的比重图:财政收入和国内经济生产总值之间有直接的关系。
下面以财政收入为自变量x,国内生产总值为因变量y,建立一元线性回归模型来对两者之间的关系进行具体的分析。
假设财政收入x和国内生产总值y的方程为:y=β+β1x1,将上表中的数据输入电脑中,利用SSPS软件进行线性回归分析得出下表。
由上表可以得出β1'=5.110,β0'=19044.809,拟合度为0.944,所以财政收入和国内生产总值的线性方程可以写为:y=19044.809+5.110x1从拟合度就可知线性显著,所以上述方程成立。
可以看出,财政收入和GDP之间成正比,这说明GDP能够迅速增长和财政收入的增加有很大的关系。
(二)一元线性回归分析在工程预测进度中的应用将一元线性回归分析应用于进度控制当中,可以有效地对工程进度进行预测,从而实现有效的事前控制。
第二节 一元线性回归范文

第二节 一元线性回归在客观世界中, 普遍存在着变量之间的关系.数学的一个重要作用就是从数量上来揭示、表达和分析这些关系。
而变量之间关系, 一般可分为确定的和非确定的两类. 确定性关系可用函数关系表示, 而非确定性关系则不然.例如, 人的身高和体重的关系、人的血压和年龄的关系、某产品的广告投入与销售额间的关系等, 它们之间是有关联的,但是它们之间的关系又不能用普通函数来表示。
我们称这类非确定性关系为相关关系。
具有相关关系的变量虽然不具有确定的函数关系,但是可以借助函数关系来表示它们之间的统计规律,这种近似地表示它们之间的相关关系的函数被称为回归函数。
回归分析是研究两个或两个以上变量相关关系的一种重要的统计方法。
在实际中最简单的情形是由两个变量组成的关系。
考虑用下列模型表示)(x f Y =. 但是,由于两个变量之间不存在确定的函数关系,因此必须把随机波动考虑进去,故引入模型如下ε+=)(x f Y其中Y 是随机变量,x 是普通变量,ε是随机变量(称为随机误差)。
回归分析就是根据已得的试验结果以及以往的经验来建立统计模型,并研究变量间的相关关系,建立起变量之间关系的近似表达式,即经验公式,并由此对相应的变量进行预测和控制等。
本节主要介绍一元线性回归模型估计、检验以及相应的预测和控制等问题。
分布图示★ 引言 ★ 引例★ 一元线性回归模型 ★ 最小二乘估计★ 例1 ★ 例2★ 最小二乘估计的性质 ★ 回归方程的检验假设 ★ 总偏差平方和的分解 ★ 回归方程的检验方法★ 例3 ★ 例4★ 预测问题 ★ 例5 ★ 控制问题★ 可化一元线性回归的情形 ★ 例6★ 内容小结 ★ 课堂练习★ 习题8-2内容要点一、引例为了研究某一化学反应过程中温度x 对产品得率Y 的影响. 测得数据如下:89857874706661545145%/190180170160150140130120110100/i i y C x 温度温度试研究这些数据所蕴藏的规律性.二、一元线性回归模型一般地,当随机变量Y 与普通变量x 之间有线性关系时, 可设εββ++=x Y 10, (1)),,0(~2σεN 其中10,ββ为待定系数。
《统计学》实验报告(一元线性回归分析)
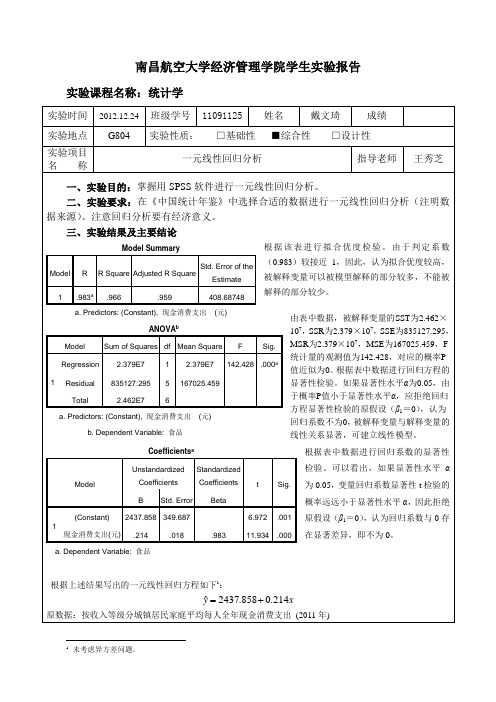
南昌航空大学经济管理学院学生实验报告实验课程名称:统计学实验时间 2012.12.24 班级学号 11091125 姓名戴文琦成绩实验地点 G804实验性质: □基础性 ■综合性 □设计性实验项目名 称一元线性回归分析指导老师王秀芝一、实验目的:掌握用SPSS 软件进行一元线性回归分析。
二、实验要求:在《中国统计年鉴》中选择合适的数据进行一元线性回归分析(注明数据来源)。
注意回归分析要有经济意义。
三、实验结果及主要结论根据该表进行拟合优度检验。
由于判定系数(0.983)较接近1,因此,认为拟合优度较高,被解释变量可以被模型解释的部分较多,不能被解释的部分较少。
由表中数据,被解释变量的SST 为2.462×107,SSR 为2.379×107,SSE 为835127.295,MSR 为2.379×107,MSE 为167025.459,F 统计量的观测值为142.428,对应的概率P 值近似为0。
根据表中数据进行回归方程的显著性检验。
如果显著性水平α为0.05,由于概率P 值小于显著性水平α,应拒绝回归方程显著性检验的原假设(β1=0),认为回归系数不为0,被解释变量与解释变量的线性关系显著,可建立线性模型。
根据表中数据进行回归系数的显著性检验。
可以看出,如果显著性水平α为0.05,变量回归系数显著性t 检验的概率远远小于显著性水平α,因此拒绝原假设(β1=0),认为回归系数与0存在显著差异,即不为0。
根据上述结果写出的一元线性回归方程如下1:x y214.0858.2437ˆ+= 原数据:按收入等级分城镇居民家庭平均每人全年现金消费支出 (2011年)Model SummaryModel R R Square Adjusted R Square Std. Error of theEstimate 1.983a.966.959408.68748a. Predictors: (Constant), 现金消费支出 (元)ANOVA bModel Sum of Squares df Mean Square F Sig.1 Regression 2.379E7 1 2.379E7 142.428 .000aResidual 835127.295 5 167025.459 Total 2.462E7 6a. Predictors: (Constant), 现金消费支出 (元)b. Dependent Variable: 食品 Coefficients aModelUnstandardizedCoefficients Standardized CoefficientstSig.BStd. ErrorBeta1(Constant) 2437.858 349.6876.972.001现金消费支出(元).214.018.98311.934 .000a. Dependent Variable: 食品1未考虑异方差问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一元线性回归分析论文专业:姓名:学号:摘要回归分析是数理统计中处理变量之间一种较为成熟、实用和有效的办法。
它可以简便有效地利用调查的统计资料,对经济现象进行事先预计和推断,为此引出一元线性回归分析数学模型和解决问题的方法。
本文回顾了描述变量相关关系和回归分析方面的基本知识,系统阐述了一元线性回归模型的基本原理,并将所学的知识与实际生产生活相结合,解决实际问题。
目录第一章回归分析概述 (1)1.1相关关系基本知识: (1)1.2回归分析基本知识回顾: (2)1.2.1回归分析的定义 (2)1.2.2.回归模型的分类 (2)1.2.3.回归分析的步骤 (3)1.2.4.回归分析的任务 (3)第二章一元线性回归的基本理论 (4)2.1一元线性关系的判断 (4)2.2一元线性回归模型的建立 (4)2.3模型回归效果的显著性检验 (5)2.3.1线性假设的显著性检验(T检验) (5)2.3.2线性回归的方差分析(F检验) (6)2.4利用回归方程进行预测 (9)2.4.一元线性回归模型的使用条件和特点 (11)2.4.1一元线性回归模型的使用条件 (11)2.4.2.一元线性回归模型的特点 (12)第三章一元线性回归分析方法的实际应用 (13)3.1.典型实际问题 (13)3.2应用MATLAB与EXCEL软件对验数据进行分析 (14)3.2.1应用MATLAB分析 (14)3.2.2应用Excel软件分析 (18)第四章总结 (25)第一章回归分析概述随着科技的迅速发展,数学的应用不仅在它的传统领域——经济建设、工程技术等方面发挥着越来越重要的作用,而且不断向一些新的领域渗透,形成了许多交叉科学,如计量经济学、人口控制论、生物数学等。
数学模型成为人们认识和研究这些学科的一种重要的工具,如何利用所学知识,建立与实际生活背景更贴切的数学模型来解决我们经济生活中存在的问题是摆在人们面前的重要课题!本文回顾了描述变量相关关系和回归分析方面的基本知识,系统阐述了一元线性回归模型的基本原理,并将其应用于实际生活中。
1.1相关关系基本知识:在生产实践和科学实验中,经常会遇到一些相互关联、相互制约的变量,它们之间客观上存在着一定的关系,为了揭示其内在联系,往往需要确定这些变量的关系程度。
变量之间的关系大致可分为两类,一类是确定性的关系,变量之间按照确定的函数关系发生关联,也称函数关系,如物理学中速度与加速度之间的关系;另一类是不确定性的关系,这种关系无法用一个数学公式来精确描述。
当一个变量(称因变量或可控变量)的取值确定后,若另一个变量(称因变量或依变量)的取值虽无确定值,但以一确定的条件概率分布与之对应,这种变量间的不确定性关系称为相关关系,如人的血压与年龄,身高与体重之间的关系,存在相关关系的变量称为相关变量。
统计学中研究相关关系的理论模型有相关模型和回归模型两种;相关模型指的是变量间具有平行变化关系,相应的统计分析方法称为相关分析,研究的是多个变量在数量关系上的密切程度和性质;回归模型指的是变量间具有因果变化关系,相关的统计分析方法称为回归分析,研究的是一个随机变量与一个或多个可控变量之间的变化关系。
相关分析是回归分析的基础和前提,回归分析则是相关分析的深入和继续。
相关分析需要依靠回归分析来表现变量之间数量相关的具体形式,而回归分析则需要依靠相关分析来表现变量之间数量变化的相关程度;相关分析研究变量之间相关的方向和程度,不能推断变量之间相互关系的具体形式,也无法从一个变量的变化来推测另一个变量的变化情况;回归分析可以推断变量之间相互关系的具体形式,能够从一个变量的变化来推测另一个变量的变化情况。
1.2回归分析基本知识回顾:1.2.1回归分析的定义在研究某一社会经济现象的发展变化规律时,所研究的现象或对象称为被解释变量,它是分析的对象;把引起这一现象变化的因素称为解释变量,它是引起这一现象变化的原因,被解释变量反映了解释变量变化的结果。
回归分析是研究某一被解释变量(因变量)与另一个或多个解释变量(自变量)间的依存关系,其目的在于根据已知的解释变量值或固定的解释变量值(重复抽样)来估计和预测被解释变量的总体平均值。
1.2.2.回归模型的分类(1)按模型中自变量的多少,分为一元回归模型和多元回归模型;(2)按模型中参数与被解释变量之间是否线性,分为线性回归模型和非线性回归模型;(3)按模型中方程数目的多少,分为单一方程模型和联立方程模型;1.2.3.回归分析的步骤(1)数据的收集与选取;(2)回归模型参数的估计、模型的确定检验与修正;(3)回归模型应用与推广。
1.2.4.回归分析的任务找出相关变量间的回归方程,并利用其进行预测和控制。
(1)依据一组实验数据,判断变量间是否存在相关关系,若有则建立相关变量间的数学关系式(回归方程),并对所获得的回归方程的可信度作统计检验;(2)判断各变标考核变量(随机变量)影响的显著性,并做出统计选择;(3)利用最终获得的回归方程对生产和试验进行预测和控制。
回归分析是一种传统意义上的应用性较强的科学方法之一,在各个领域都得到了广泛的应用,它不仅可以提取大量数据中的重要信息,掌握这些数据的特点及规律,进而得出变量间相关关系的数学表达式,对这些关系进行分析;还可以利用这些关系式,有一些变量去预测和控制另一个因变量的取值,进而知道这种预测和控制所到达的程度,并分析得出结论。
第二章 一元线性回归的基本理论2.1一元线性关系的判断一元线性回归模型的使用条件是两个变量之间存在线性关系,通过相关系数的来判定两个变量之间存在线性相关。
1nnni i i i x y x y r -=∑∑∑1r ≤,r 越大,线性相关越密切;当0.51r ≤≤为线性相关,可以用一元线性回归分析预测。
2.2一元线性回归模型的建立设随机变量y 与变量x 之间存在着直线相关关系,(,)i i x y 可用模型表示为:01(1,2,...,)i i i y x i n ββε=++=,0β与1β为未知参数,(1,2,...)i i n ε=相互独立且服从2(0,)N σ的正态分布,求得0β与1β的估计值0b 和1b ,对 于x ,()E y 的估计值01b b x +,记为y ∧,则方程01y b b x ∧=+称为y 对x 的一 元线性回归模型。
利用最小二乘法估计参数:若能使回归直线01y b b x ∧=+尽可能地靠近散点(,)i i x y ,即应使总的离回归平方和:22010111(,)()()nni i i i i i Q b b y y y b b x ∧===-=--∑∑达到最小,欲使二元函数01(,)Q b b 最小,即2011001112()02()0ni i i ni i ii Q y b b x bQ y b b x x b ==∂⎧=---=⎪∂⎪⎨∂⎪=---=⎪∂⎩∑∑ 整理得:0111201111n n i i i i n n ni i i i i i i nb b x y bx b x x y =====⎧+=⎪⎪⎨⎪+=⎪⎩∑∑∑∑∑ 其解0b ,1b 称为0β与1β的最小二乘估计。
令11n i i x x n -==∑,11ni i y y n -==∑进一步表示为:011121()()()n i i i ni i b y b x x x y y b x x ----=-=⎧=-⎪⎪⎪--⎨=⎪⎪-⎪⎩∑∑ 即求出y 对x 的一元线性回归模型01y b b x ∧=+。
2.3模型回归效果的显著性检验对于一元线性回归模型来说,我们常用的检验方法有以下几种:线性假设的显著性检验、线性回归的方差分析、相关系数的显著性检验、拟合优度……下面我们重点介绍一下线性假设的显著性检验和线性回归的方差分析。
2.3.1线性假设的显著性检验(T 检验)1、t 统计量回归系数估计量服从正态分布:222001122ˆˆ~, ~, i i i X N N n x x σββσββ⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭∑∑∑, 用2σ的无偏估计量2ˆ22-=∑n e iσ来代替2σ时,可以构造t 统计量:1111ˆˆˆ()e t S βββ-==0000ˆˆˆ()e t S βββββ--==所构造的t 统计量服从自由度为n-2的t 分布。
即t ~ t (n-2) 1、回归系数估计量的t 检验步骤下面以估计量1ˆβ为例,介绍t 检验的步骤。
1> 提出假设原假设H 0:β1=0 备择假设H 1:β1≠02>给定显著性水平,查t 分布表获得临界值)2(2-n t α,对于例2-1,在显著性水平α=0.05,n-2=8时,查t 分布表,得到:306.2)2(2=-n t α。
3>根据下式利用样本数据计算检验统计量t 的值1111ˆˆˆ()e t S βββ-==4>进行比较,做出判断若2(2)t t n α>-,差异显著,拒绝原假设,接收备择假设。
若2(2)t t n α<-,差异不显著,接受原假设。
2.3.2线性回归的方差分析(F 检验)1、方差分析F 检验是根据平方和分解式,直接从回归效果检验回归方程的检验性。
平方和分解式为:()222111nnnii i i i i i y y y y y y ∧∧-==⎛⎫⎛⎫-=-+- ⎪ ⎪⎝⎭⎝⎭∑∑∑其中()21nii y y --∑称为总平方和,简记为SST 或者S 总或yy L ,SST 表示 sum ofsquare for total 。
21nii y y ∧=⎛⎫- ⎪⎝⎭∑称为回归平方和,简记为SSR 或者S 回,R 表示regression 。
21ni i i y y ∧=⎛⎫- ⎪⎝⎭∑称为残差平方和,简记为SSE 或者S 残,E 表示error 。
因而平方和分解式可以简写为:SST=SSR+SSE对总平方和(SST )的这两个分量进行研究,就称为从回归角度进行的方差分析每个平方和都具有相应的自由度,假定给n 个变量赋予数值,在计算平方和时,总有k 个变量可以自由取值,即是这k 个变量线性独立,我们说这个平方和的自由度为k 。
与每一个平方和相联系的是它们的自由度。
对于一元线性回归模型,SST 有n -1个自由度;SSE 有1个自由度;SSR 有n -2个自由度。
平方和与自由度之比即为平均平方和。
将平方和、自由度及平均平方和列成一个表,该表称为方差分析表。
一元线性回归方差分析表2、F 检验统计量定义从方差分析的角度进行的回归模型整体性检验所采用的检验统计量是F 统计量。
检验统计量F 反映平均回归平方和与平均剩余平方和的比较。
2121SSR11SSE22ni i ni i i y y F n y y n ∧=∧=⎛⎫- ⎪⎝⎭==⎛⎫-- ⎪⎝⎭-∑∑且F 服从自由度为1和n-2的F 分布。
