案例分析报告(一元线性回归模型)
一元线性回归模型案例分析

一元线性回归模型案例分析一元线性回归是最基本的回归分析方法,它的主要目的是寻找一个函数能够描述因变量对于自变量的依赖关系。
在一元线性回归中,我们假定存在满足线性关系的自变量与因变量之间的函数关系,即因变量y与单个自变量x之间存在着线性关系,可表达为:y=β0+ β1x (1)其中,β0和β1分别为常量,也称为回归系数,它们是要由样本数据来拟合出来的。
因此,一元线性回归的主要任务就是求出最优回归系数和平方和最小平方根函数,从而评价模型的合理性。
下面我们来介绍如何使用一元线性回归模型进行案例分析。
数据收集:首先,研究者需要收集自变量和因变量之间关系的相关数据。
这些数据应该有足够多的样本观测值,以使统计分析结果具有足够的统计力量,表示研究者所研究的关系的强度。
此外,这些数据的收集方法也需要正确严格,以避免因相关数据缺乏准确性而影响到结果的准确性。
模型构建:其次,研究者需要利用所收集的数据来构建一元线性回归模型。
即建立公式(1),求出最优回归系数β0和β1,即最小二乘法拟合出模型方程式。
模型验证:接下来,研究者需要对所构建的一元线性回归模型进行验证,以确定模型精度及其包含的统计意义。
可以使用F检验和t检验,以检验回归系数β0和β1是否具有统计显著性。
另外,研究者还可以利用R2等有效的拟合检验统计指标来衡量模型精度,从而对模型的拟合水平进行评价,从而使研究者能够准确无误地判断其研究的相关系数的统计显著性及包含的统计意义。
另外,研究者还可以利用偏回归方差分析(PRF),这是一种多元线性回归分析技术,用于计算每一个自变量对相应因变量的贡献率,使研究者能够对拟合模型中每一个自变量的影响程度进行详细的分析。
模型应用:最后,研究者可以利用一元线性回归模型进行应用,以实现实际问题的求解以及数据挖掘等功能。
例如我们可以使用这一模型来预测某一物品价格及销量、研究公司收益及投资、检测影响某一地区经济发展的因素等。
综上所述,一元线性回归是一种利用单变量因变量之间存在着线性关系来拟合出回归系数的回归分析方法,它可以应用于许多不同的问题,是一种非常实用的有效的统计分析方法。
eviews实验报告一元线形回归模型
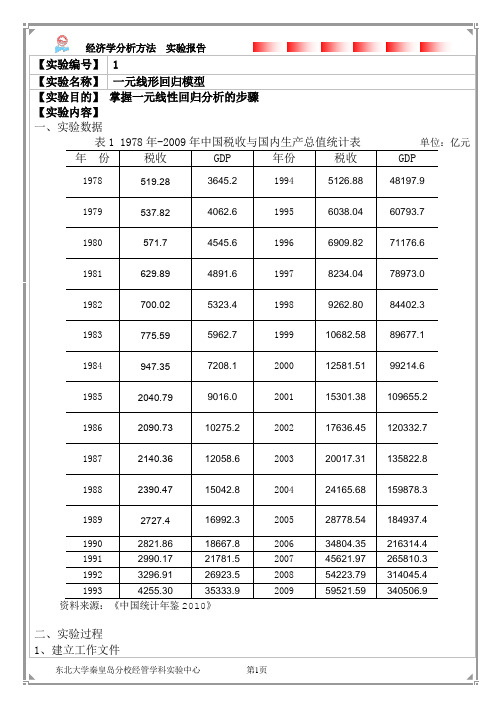
【实验编号】 1【实验名称】一元线形回归模型【实验目的】掌握一元线性回归分析的步骤【实验内容】一、实验数据表1 1978年-2009年中国税收与国内生产总值统计表单位:亿元年份税收GDP 年份税收GDP1978 519.28 3645.2 1994 5126.88 48197.91979 537.82 4062.6 1995 6038.04 60793.71980 571.7 4545.6 1996 6909.82 71176.61981 629.89 4891.6 1997 8234.04 78973.01982 700.02 5323.4 1998 9262.80 84402.31983 775.59 5962.7 1999 10682.58 89677.11984 947.35 7208.1 2000 12581.51 99214.61985 2040.79 9016.0 2001 15301.38 109655.21986 2090.73 10275.2 2002 17636.45 120332.71987 2140.36 12058.6 2003 20017.31 135822.81988 2390.47 15042.8 2004 24165.68 159878.31989 2727.4 16992.3 2005 28778.54 184937.41990 2821.86 18667.8 2006 34804.35 216314.41991 2990.17 21781.5 2007 45621.97 265810.31992 3296.91 26923.5 2008 54223.79 314045.41993 4255.30 35333.9 2009 59521.59 340506.9 资料来源:《中国统计年鉴2010》二、实验过程1、建立工作文件(1)点击桌面Eviews5.0图标,运行Eviews软件。
一元线性回归模型典型例题分析

第二章 一元线性回归模型典型例题分析例1、令kids 表示一名妇女生育孩子的数目,educ 表示该妇女接受过教育的年数.生育率对教育年数的简单回归模型为μββ++=educ kids 10(1)随机扰动项μ包含什么样的因素?它们可能与教育水平相关吗?(2)上述简单回归分析能够揭示教育对生育率在其他条件不变下的影响吗?请解释.例2.已知回归模型μβα++=N E ,式中E 为某类公司一名新员工的起始薪金(元),N 为所受教育水平(年).随机扰动项μ的分布未知,其他所有假设都满足。
如果被解释变量新员工起始薪金的计量单位由元改为100元,估计的截距项与斜率项有无变化?如果解释变量所受教育水平的度量单位由年改为月,估计的截距项与斜率项有无变化?例3.对于人均存款与人均收入之间的关系式t t t Y S μβα++=使用美国36年的年度数据得如下估计模型,括号内为标准差:)011.0()105.151(067.0105.384ˆtt Y S +=2R =0.538 023.199ˆ=σ(1)β的经济解释是什么?(2)α和β的符号是什么?为什么?实际的符号与你的直觉一致吗?如果有冲突的话,你可以给出可能的原因吗?(3)对于拟合优度你有什么看法吗? (4)检验统计值?例4.下列方程哪些是正确的?哪些是错误的?为什么?⑴ y x t n t t =+=αβ12,,, ⑵ y x t n t t t =++=αβμ12,,,⑶ y x t n t t t=++= ,,,αβμ12⑷ ,,,y x t n t t t =++=αβμ12 ⑸ y x t n t t =+= ,,,αβ12 ⑹ ,,,y x t n t t =+=αβ12⑺ y x t n t t t =++= ,,,αβμ12 ⑻ ,,,y x t n t tt =++=αβμ12其中带“^”者表示“估计值”.例5.对于过原点回归模型i i i u X Y +=1β ,试证明∑=∧221)(iu XVar σβ例6、对没有截距项的一元回归模型i i i X Y μβ+=1称之为过原点回归(regression through the origin )。
一元线性回归案例

例8. 集装箱吞吐量与外贸额
2001-2006年中国集装箱吞吐量增长与外贸 额增长的弹性分析.以Y表示集装箱吞吐量 (百万标准箱),X表示外贸额(百亿美元). OLS回归方程为 Y=3.7667+0.509X (2.06) (31.78) t (5)=2.776 n=6 R^2=0.996
0.1
例8. 集装箱吞吐量与外贸额
例8. 集装箱吞吐量与外贸额
2001-2007年中国集装箱吞吐量增长与外贸 额增长的弹性分析.以Y表示集装箱吞吐量 增长率(%),X表示外贸额增长率(%). OLS回归方程为 Y=18.449+0.3155X (2.3982) (1.078) t (5)=2.015 n=7 R^2=0.1887
0.1
例4. 考试分数与出勤率
假如期末考试的分数(score)取决于出勤率 (attend)和影响考试成绩的其他无法观测因素 (如学生能力等): score= β1+β2 attend+u 许多不加分析的回归发现: 这一回归中β2 〈0,即分数与出勤率负相关. 这一模型在什么情况下满足均值独立条件? 除非学生学习能力、学习攻击、年龄及其他因素与 出勤率无关,但这几乎不可能.
例3. 静态菲利普斯曲线
时间序列数据 令inf(t)表示年通货膨胀率,unem(t)表示事业率, 下 列菲利普斯曲线假定了一个不变的自然失业率和 固定的通货膨胀率预期. Inf(t)=β1+β2 unem(t)+u 依据1948-1996年美国经济数据, OLS回归方程为 Inf(t)=1.42+0.468 unem(t) (1.72) (0.289) n=49 R^2=0.053
例5. 学校的数学成绩与学校午餐项目
一元线性回归分析案例

数学3——统计内容
再冷的石头,坐上三年也会暖 !
1. 画散点图
2. 了解最小二乘法的思想
3. 求回归直线方程
y=bx+a
4. 用回归直线方程解决应用问题
课题:选修2-3 8.5 回归分析案例
复习 变量之间的两种关系
再冷的石头,坐上三年也会暖 !
问题1:正方形的面积y与正方形的边长x之间
选修2-3——统计案例
5. 引入线性回归模型
y=bx+a+e
6. 了解模型中随机误差项e产 生的原因
7. 了解相关指数 R2 和模型拟 合的效果之间的关系
8. 了解残差图的作用 9. 利用线性回归模型解决一类
非线性回归问题 10. 正确理解分析方法与结果
课题:选修2-3 8.5 回归分析案例
再冷的石头,坐上三年也会暖 !
课题:选修2-3 8.5 回归分析案例
解:(1)列出下表,并计算
再冷的石头,坐上三年也会暖 !
i
1
2
3
4
5
6
7
8
9
10
xi 104 180 190 177 147 134 150 191 204 121 yi 100 200 210 185 155 135 170 205 235 125 xiyi 10400 36000 39900 32745 22785 18090 25500 39155 47940 15125
现实生活中存在着大量的相关关系。 如:人的身高与年龄; 产品的成本与生产数量; 商品的销售额与广告费; 家庭的支出与收入。等等
探索:水稻产量y与施肥量x之间大致有何规 律?
课题:选修2-3 8.5 回归分析案例
数据分析线性回归报告(3篇)

第1篇一、引言线性回归分析是统计学中一种常用的数据分析方法,主要用于研究两个或多个变量之间的线性关系。
本文以某城市房价数据为例,通过线性回归模型对房价的影响因素进行分析,以期为房地产市场的决策提供数据支持。
二、数据来源与处理1. 数据来源本文所采用的数据来源于某城市房地产交易中心,包括该城市2010年至2020年的房价、建筑面积、交通便利度、配套设施、环境质量等指标。
2. 数据处理(1)数据清洗:对原始数据进行清洗,去除缺失值、异常值等。
(2)数据转换:对部分指标进行转换,如交通便利度、配套设施、环境质量等指标采用五分制评分。
(3)变量选择:根据研究目的,选取建筑面积、交通便利度、配套设施、环境质量等指标作为自变量,房价作为因变量。
三、线性回归模型构建1. 模型假设(1)因变量与自变量之间存在线性关系;(2)自变量之间不存在多重共线性;(3)误差项服从正态分布。
2. 模型建立(1)选择合适的线性回归模型:根据研究目的和数据特点,采用多元线性回归模型。
(2)计算回归系数:使用最小二乘法计算回归系数。
(3)检验模型:对模型进行显著性检验、方差分析等。
四、结果分析1. 模型检验(1)显著性检验:F检验结果为0.000,P值小于0.05,说明模型整体显著。
(2)回归系数检验:t检验结果显示,所有自变量的回归系数均显著,符合模型假设。
2. 模型结果(1)回归系数:建筑面积、交通便利度、配套设施、环境质量的回归系数分别为0.345、0.456、0.678、0.523,说明这些因素对房价有显著的正向影响。
(2)R²:模型的R²为0.876,说明模型可以解释约87.6%的房价变异。
3. 影响因素分析(1)建筑面积:建筑面积对房价的影响最大,说明在房价构成中,建筑面积所占的比重较大。
(2)交通便利度:交通便利度对房价的影响较大,说明在购房时,消费者对交通便利性的需求较高。
(3)配套设施:配套设施对房价的影响较大,说明在购房时,消费者对生活配套设施的需求较高。
一元线性回归分析研究实验报告

一元线性回归分析研究实验报告一元线性回归分析研究实验报告一、引言一元线性回归分析是一种基本的统计学方法,用于研究一个因变量和一个自变量之间的线性关系。
本实验旨在通过一元线性回归模型,探讨两个变量之间的关系,并对所得数据进行统计分析和解读。
二、实验目的本实验的主要目的是:1.学习和掌握一元线性回归分析的基本原理和方法;2.分析两个变量之间的线性关系;3.对所得数据进行统计推断,为后续研究提供参考。
三、实验原理一元线性回归分析是一种基于最小二乘法的统计方法,通过拟合一条直线来描述两个变量之间的线性关系。
该直线通过使实际数据点和拟合直线之间的残差平方和最小化来获得。
在数学模型中,假设因变量y和自变量x之间的关系可以用一条直线表示,即y = β0 + β1x + ε。
其中,β0和β1是模型的参数,ε是误差项。
四、实验步骤1.数据收集:收集包含两个变量的数据集,确保数据的准确性和可靠性;2.数据预处理:对数据进行清洗、整理和标准化;3.绘制散点图:通过散点图观察两个变量之间的趋势和关系;4.模型建立:使用最小二乘法拟合一元线性回归模型,计算模型的参数;5.模型评估:通过统计指标(如R2、p值等)对模型进行评估;6.误差分析:分析误差项ε,了解模型的可靠性和预测能力;7.结果解释:根据统计指标和误差分析结果,对所得数据进行解释和解读。
五、实验结果假设我们收集到的数据集如下:经过数据预处理和散点图绘制,我们发现因变量y和自变量x之间存在明显的线性关系。
以下是使用最小二乘法拟合的回归模型:y = 1.2 + 0.8x模型的R2值为0.91,说明该模型能够解释因变量y的91%的变异。
此外,p 值小于0.05,说明我们可以在95%的置信水平下认为该模型是显著的。
误差项ε的方差为0.4,说明模型的预测误差为0.4。
这表明模型具有一定的可靠性和预测能力。
六、实验总结通过本实验,我们掌握了一元线性回归分析的基本原理和方法,并对两个变量之间的关系进行了探讨。
一元线性回归模型实验报告

一元线性回归模型实验报告——以中国1985~2009年财政收入Y 和国内生产总值(和国内生产总值(GDP GDP GDP)为例)为例以GDP 为横轴,Y 为纵轴的散点图为纵轴的散点图以GDP 为解释变量,Y 为被解释变量,建立一元线性回归方程:为被解释变量,建立一元线性回归方程:Y i =β0+β1·GDP iDependent Variable: Y Method: Least Squares Date: 11/06/11 Time: 22:35 Sample: 1985 2009 Included observations: 25Variable Coefficient Std. Error t-Statistic Prob. C -3225.757 787.7145 -4.095084 0.0004 GDP0.1973980.00565734.894270.0000R-squared0.981461 Mean dependent var 16899.30 Adjusted R-squared 0.980655 S.D. dependent var 19287.38 S.E. of regression 2682.632 Akaike info criterion 18.70360 Sum squared resid1.66E+08Schwarz criterion 18.80111Log likelihood -231.7950 F-statistic 1217.610 Durbin-Watson stat0.118499Prob(F-statistic) 0.000000图3:回归分析结果:回归分析结果可得出β^0=-3225.757 β^1=0.197398财政收入随国内生产总值变化的一元线性回归方程为:财政收入随国内生产总值变化的一元线性回归方程为:Y ^=-3225.757+0.197398·GDPR 2=0.981461斜率的经济意义是:在1985~2009年间,GDP 每增加一单位,财政收入平均增加0.197398单位。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
案例分析报告(2014——2015学年第一学期)
课程名称:预测与决策
专业班级:电子商务1202 学号: 02
学生姓名:陈维维
2014 年 11月
案例分析(一元线性回归模型)
我国城镇居民家庭人均消费支出预测
一、研究目的与要求
居民消费在社会经济的持续发展中有着重要的作用,居民合理的消费模式和居民适度的消费规模有利于经济持续健康的增长,而且这也是人民生活水平的具体体现。
从理论角度讲,消费需求的具体内容主要体现在消费结构上,要增加居民消费,就要从研究居民消费结构入手,只有了解居民消费结构变化的趋势和规律,掌握消费需求的热点和发展方向,才能为消费者提供良好的政策环境,引导消费者合理扩大消费,才能促进产业结构调整与消费结构优化升级相协调,才能推动国民经济平稳、健康发展。
例如,2008年全国城镇居民家庭平均每人每年消费支出为元,最低的青海省仅为人均元,最高的上海市达人均元,上海是黑龙江的倍。
为了研究全国居民消费水平及其变动的原因,需要作具体的分析。
影响各地区居民消费支出有明显差异的因素可能很多,例如,零售物价指数、利率、居民财产、购物环境等等都可能对居民消费有影响。
为了分析什么是影响各地区居民消费支出有明显差异的最主要因素,并分析影响因素与消费水平的数量关系,可以建立相应的计量经济模型去研究。
二、模型设定
我研究的对象是各地区居民消费的差异。
居民消费可分为城镇居民消费和农村居民消费,由于各地区的城镇与农村人口比例及经济结构有较大差异,最具有直接对比可比性的是城市居民消费。
而且,由于各地区人口和经济总量不同,只能用“城镇居民每人每年的平均消费支出”来比较,而这正是可从统计年鉴中获得数据的变量。
所以模型的被解释变量Y选定为“城镇居民每人每年的平均消费支出”。
因为研究的目的是各地区城镇居民消费的差异,并不是城镇居民消费在
不同时间的变动,所以应选择同一时期各地区城镇居民的消费支出来建立模型。
因此建立的是2008年截面数据模型。
影响各地区城镇居民人均消费支出有明显差异的因素有多种,但从理论和经验分析,最主要的影响因素应是居民收入,其他因素虽然对居民消费也有影响,但有的不易取得数据,如“居民财产”和“购物环境”;有的与居民收入可能高度相关,如“就业状况”、“居民财产”;还有的因素在运用截面数据时在地区间的差异并不大,如“零售物价指数”、“利率”。
因此这些其他因素可以不列入模型,即便它们对居民消费有某些影响也可归入随即扰动项中。
为了与“城镇居民人均消费支出”相对应,选择在统计年鉴中可以获得的“城市居民每人每年可支配收入”作为解释变量X。
以下是2008年各地区城镇居民人均年消费支出和可支配收入表
数据来源:作城镇居民家庭平均每人每年消费支出(Y)和城市居民人均年可支配收入(X)的散点图,如图
从散点图可以看出居民家庭平均每人每年消费支出(Y)和城市居民人均年可支配收入(X)大体呈现为线性关系,所以建立的计量经济模型为如下线性模型: Yi=a+bXi+εi i=1,2,···n
一元线性回归预测法,是指两个具有线性关系的变量,配合线性回归模型,根据自变量的变动来预测因变量平均发展趋势的方法。
三、OLS估计
采用OLS法估计其模型的回归系数
最小平方法的中心思想,是通过数学模型,配合一条较为理想的趋势线。
这条趋势线必须满足以下两点要求:
(1)原数列的观察值与模型的估计值的离差平方和为最小;
(2)原数列的观察值与模型的估计值的离差总和为零。
1、首先进入Excel程序,建立工作薄,接下来进行一元线性回归的输入形式。
2、计算2x、2y及xy,分别在“D2、E2、F2”单元格通过相对引用输入计算公式并向下复制。
3、计算∑x 、∑y 、∑2x 、∑2y 及∑xy 。
4、一元线性回归系数的计算:
x
b y a x x n y
x xy n b -=--=
∑∑∑∑∑22)(
所以b=
a=
5、按bX a Y
+=ˆ计算估计值:
四、相关系数
相关系数是一元线性回归中用来衡量两个变量之间相关程度的重要指标。
主要有两种定义方法:根据总变差定义以及根据积差法定义,由于根据积差法定义的相关系数不需要先求回归模型的剩余变差,可以直接从样本数据中计算得到,所以在本案例中比较适合使用。
其定义为
相关系数2
2
2
2
y y n x x n y
x xy n r )
()
(∑∑∑∑∑∑∑---=
;
五、模型检验
1、经济意义检验
所估计的参数,说明城镇居民人均年可支配收入每相差1元,可导致居民消费支出相差元,这与经济学中边际消费倾向的意义相符。
2、显著性检验
本案例中可决系数为(可决系数R 2
的大小表明了在y 的总变差中自由量x 变动所引起的百分比,它是评价两个变量之间线性相关关系强弱的一个重要指标。
),说明所建模型整体上对样本数据拟合较好,即解释变量“城镇居民人均年可支配收入”对被解释变量“城镇居民人均年消费支出”的绝大部分差异作出了
解释。
对回归系数的t 检验:当显著性水平取α=,自由度为n-2=31-2=29 查相关系数临界值表,得(29)=。
因为R=>(29)=。
故在α=显著性水平之上,检验通过,说明两个变量之间相关关系显著,也就是表明,城镇人均年可支配收入对人均年消费支出有显著影响。
六、回归预测
1、计算估计标准误差。
2
n bx a y 2
n y y 2n SSE S 2
2
y ---=--=
-=∑∑)
()ˆ(
查表确定)(2/2n t -α。
在Excel 中输入=POWER((E34-K8*C34-K6*F34)/(G33-2), 即可得到s
y =
由图表中可以看出来,黑龙江省、贵州省、甘肃省、青海省、新疆省等地可支配收入以及消费支出都排名靠后。
还有其他部分省虽然可支配收入高于其他省,但是消费支出却少于其他,例如,山西省,江西省,河南省等(我选择的可支配收入的临界值是12000,消费水平的临界值是9000)。
其中大部分都是西部地区。
在西部大开发的推动下,如果西部地区的城市居民人均年可支配收入第一步争取达到2000美元(按现有汇率即人命币12245元),第二步再争取达到2500美元(即人民币元),利用所估计的模型可预测这时城市居民可能达到的人均年消费支出水平。
可以注意到,这里的预测是利用所示数据模型对被解释变量在不同空间状况的空间预测。
接下来进行预测:首先
按n
x x x x n 11S t y 2220y
20)()(∑∑--++±α确定预测区间。
所谓预测区间就是指在一定的显著性水平上,依据数理统计方法计算出的包含预测目标未来真实值的某一区间范围。
根据公式可以求得:
当显著性水平取α=,自由度n-m=31-2=29时,查t 分布表得: (29)=
第一步达到12245元的时候,预测区间为: 输入公式=H35-K29*K33,=H35+K29*K33,得:
预测区间为(,)
第二步达到元的时候,预测区间为:
输入公式=H36-K29*K33,=H36+K29*K33,得:
预测区间为(,)
七、总结
消费需求主要来源于居民的可支配收入,而居民的可支配收入又来自于居民的人均收入即狭义上的居民的固定工资,它是形成当期购买力最主要的来源,同
样也是影响消费需求的最直接最重要的因素。
此次案例分析我以2008年全国各地可支配收入和消费支出数据资料为基础,假设人均年可支配收入为自变量X(单位:元),人均年消费支出为因变量y(单位:元),并做出可支配收入和消费支出的相关关系图。
从这两个变量的相关关系图可观测到两者之间的大体趋势,发现它们基本上呈现出一种直线的统计关系,所以我进一步进行回归分析,并进行线性相关系数R的显著性检验。
若|R|=1表示完全线性相关;0<|R|<1表示存在不同程度线性相关;|R|<为低度线性相关,<|R|<为中度线性相关,|R|>为高度线性相关。
|R|越接近于I,说明两个变量的相关程度越密切。
通过公式,利用Excel数字处理功能,进行数据处理和简单的线性相关分析,我得出2008年全国城镇居民可支配收入和消费需求的回归方程式:y=+。
相关系数为:R= ,R2=,说明2008年全国城镇居民可支配收入和消费支出之间存在着显著的相关关系。
居民可支配收入每增加1000元,消费支出将增加大约元。
可以这么说,居民可支配收入与消费需求状况紧密相关,可支配收入会对消费需求产生重要影响,即可支配收入的扩大或缩小会导致消费需求的相应的变化。
最后通过线性相关性的检验,证实前面得出的结论:居民的可支配收入对消费需求的影响十分显著。
居民可支配收入的稳定提高,使居民的消费需求有了最坚实的基础,进而提高居民的消费需求和消费支出,拥有一个稳定舒心的生活,高水平的居民可支配收入,是影响消费需求的决定性的因素。
