第11章外排序第2讲-磁盘排序-生成初始归并段
数据结构 试题(A)-答案

3.建立平衡二叉树过程如图2所示(图中加阴影的结点表示要调整的结点)。
图2构造平衡二叉树过程
评分标准:每次调整占1分。
4.答:不能。因为在这里,二分查找只减少了关键字间的比较次数,而记录的移动次数不变,时间的复杂度仍为O(n2)。
评分标准:答对“不能”占3分,说明理由占5分。
A.872B.860
C.868D.864
8.一个具有1025个结点的二叉树的高h为。
A.11B.10
C.11~1025D.12~1024
9.一棵二叉树的后序遍历序列为DABEC,中序遍历序列为DEBAC,则先序遍历序列为。
A.ACBEDB.DECAB
C.DEABCD.CEDBA
10.对图1所示的无向图,从顶点1开始进行深度优先遍历;可得到顶点访问序列。
2.给出如下各种情况下求任意一个顶点的度的过程(只需文字描述):(8分)
(1)含n个顶点的无向图采用邻接矩阵存储;
(2)含n个顶点的无向图采用邻接表存储;
(3)含n个顶点的有向图采用邻接矩阵存储;
(4)含n个顶点的有向图采用邻接表存储。
3.将整数序列{4,5,7,2,1,3,6}中的数依次插入到一棵空的平衡二叉树中,试构造相应的平衡二叉树。(要求画出每个元素插入过程,若需调整,还需给出调整后的结果,并指出是什么类型的调整,12分)
A.输出第i(1≤i≤n)个元素值
B.交换第1个元素与第2个元素的值
C.顺序输出这n个元素的值
D.输出与给定值x相等的元素在线性表中的序号
4.设n个元素进栈序列是p1,p2,p3,…,pn,其输出序列是1,2,3,…,n,若p3=3,则p1的值。
A.可能是2B.一定是2
C++排序讲义

j j
j
j
ji
ij
ij
ij
i
i
i
二趟排序: 13 4 48 38 27 49 55 65 97 76 Ch8_3.c
希尔排序特点
子序列的构成不是简单的“逐段分割”,而是将相隔某个增 量的记录组成一个子序列 希尔排序可提高排序速度,因为 分组后n值减小,n² 更小,而T(n)=O(n² ),所以T(n)从总体 上看是减小了 关键字较小的记录跳跃式前移,在进行最后一趟增量为1 的插入排序时,序列已基本有序 增量序列取法 无除1以外的公因子 最后一个增量值必须为1
j j j j j j 排序结果:(13 27 38 49 65 76 97)
算法评价
时间复杂度 若待排序记录按关键字从小到大排列(正序) 关键字比较次数: n
1 n 1
i 2
记录移动次数:
2 2(n 1)
i 2
n
若待排序记录按关键字从大到小排列(逆序) n (n 2)(n 1) 关键字比较次数: i
§8.2 交换排序
冒泡排序
排序过程
将第一个记录的关键字与第二个记录的关键字进行比较,若 为逆序r[1].key>r[2].key,则交换;然后比较第二个记录与第 三个记录;依次类推,直至第n-1个记录和第n个记录比较为 止——第一趟冒泡排序,结果关键字最大的记录被安置在最 后一个记录上 对前n-1个记录进行第二趟冒泡排序,结果使关键字次大的记 录被安置在第n-1个记录位置 重复上述过程,直到“在一趟排序过程中没有进行过交换记 录的操作”为止
输出:13 27 38 49 50 65
76 97 50 49 38 65 27 13 输出:13 27 38 49 50 65 97 50
2023年研究生全国统考计算机试题——数据结构与操作系统试题解析

一、单项选择题1. 下列对顺序存储的有序表(长度为n)实现给定操作的算法中平均时间复杂度为O(1)的是()。
A、查找包含指定值元素的值B、插入包含指定值元素的算法C、删除第i(1≤i≤n)个元素的算法D、获取第i(1≤i≤n)个值的算法2、现有非空双向链表L,其结点结构为,prev是指向直接前驱结点的指针,next是指向直接后继结点的指针。
若要在L中指针p 所指向的结点(非尾结点)之后插入指针s指向的新结点,则在执行了语句序列:“s->next=p->next;p->next=s;”,后,还要执行()。
A、s->next->prev=p;s->prev=p;B、p->next->prev=s;s->prev=p;C、s->prev=s->next->prev; s->next->prev=s;D、p->next->prev=s->prev;s->next->prev=p;3、若采用三元组表存储结构存储稀疏矩阵M,则除三元组外,下列数据中还需要保存的是()。
I. M的行数;II.M中包含非零元素的行数;III.M的列数;IV.M中包含非零元素的列数。
A、仅I、IIIB、仅I、IIC、仅III、IVD、I、II、III、IV4、在由6个字符组成的字符集S中,各个字符出现的频次分别为3,4,5,6,8,10,为S构造的哈夫曼树的加权平均长度为()。
A、2.4B、2.5C、2.67D、2.75注:每个关键字的查找长度为:图片加权平均长度为:(3×3+3×4+3×5+3×6+2×8+2×10)/(3+4+5+6+8+10)=2.5。
如果不考虑权重,会错误计算为(3+3+3+3+2+2)/6≈2.67,从而误选C。
5、已知一棵二叉树的树形如下图所示,若其后序遍历为fdbeca,则其先序列为()。
外部排序

2 外部排序的方法
例如:假设有一个含10,000个记录的磁盘文件,而当前所用的计算机一次只能 对1,000个记录进行内部排序,则首先利用内部排序的方法得到10个初始归并 段,然后进行逐趟归并。
假设进行2 路归并(即两两归并),则第一趟由10个归并段得到5个归并段;
tIO值取决于外存,远远大于tIS和tmg。 外部排序的时间取决于读写外存的次数d。
2 外部排序的方法
例如:若对上述例子采用2 路归并,则只需进行4趟归并, 外排所需总的时间: 10*tIS+500*tIO+4*1000*tmg
若对上述例子采用5 路归并,则只需进行2趟归并,总的访问外存的次数为 100+2 100=300次
一般情况下,假设待排记录序列含 m 个初始归并段,外排时 采用 k 路归并,则归并趟数s= logkm ,显然,随着k的增大 或m的减小,归并的趟数将减少,因此对外排而言,通常采用 多路归并。k 的大小可选,但需综合考虑各种因素。
3 多路平衡归并的实现
一、多路平衡归并ቤተ መጻሕፍቲ ባይዱ性质:
•分析: m 个初始归并段,外排时采用 k 路归并,则归并趟数为 logkm , K 大, 趟数减少,读写记录的总数将减少。但 K 大,会使内部归并时间tmg增大?。
• 改进:采用胜者树或者败者树,从 K 个元素中挑选一个最小的元素仅需 log2k 次 比较,这时总的时间耗费将下降为: log2m × ( n - 1 ) × tmg
•磁带信息的表示:
一种磁化方向、代表1 另一种磁化方向,代表0
01001001 10101111
•磁带文件的组织:
外排序

外排所需总的时间为: 外排所需总的时间为:
m*tIS + d*tIO + S*u*tmg = 10*tIS + 500*tIO + 4*10000*tmg
示例: 示例:
• 设有一个包含4500个对象的输入文件。现 设有一个包含4500个对象的输入文件。 个对象的输入文件 用一台其内存至多可容纳750个对象 内存至多可容纳 个对象的计 用一台其内存至多可容纳750个对象的计 算机对该文件进行排序。输入文件放在磁 算机对该文件进行排序。 盘上,磁盘每个页块可容纳250个对象 每个页块可容纳 个对象, 盘上,磁盘每个页块可容纳250个对象, 250= 这样全部对象可存储在 4500 / 250=18 个 页块中。输出文件也放在磁盘上,用以存 页块中。输出文件也放在磁盘上, 放归并结果。 放归并结果。
一、外排序的基本过程
• 当对象以文件形式存放于磁盘上的时候,通常 当对象以文件形式存放于磁盘上的时候, 是按物理块存储的。 是按物理块存储的。 • 物理块也叫做页块,是磁盘存取的基本单位。 物理块也叫做页块,是磁盘存取的基本单位。
• 每个页块可以存放几个对象。操作系统按 每个页块可以存放几个对象。 页块对磁盘上的信息进行读写。 页块对磁盘上的信息进行读写。 • 本节所指的磁盘是由若干片磁盘组成的磁 盘组, 盘组,各个盘片安装在同一主轴上高速旋 转。各个盘面上半径相同的磁道构成了柱 各盘面设置一个读写磁头, 面。各盘面设置一个读写磁头,它们装在 同一动臂上, 同一动臂上,可以径向从一个柱面移到另 一个柱面上。 一个柱面上。
硬盘简介 磁盘的主要技术指标 柱面:多个盘片的同一磁道。 柱面:多个盘片的同一磁道。 目前常见的硬盘容量有 6.2GB、10GB、20GB、 、 、 、 40GB、60GB、80GB等等。 、 等等。 、 等等
归并排序PPT课件

.
12
10.6 基数排序
❖ “花色”优先
先分成4堆; 然后,每堆再按“面值”排; 最后,收成一堆。
扑克牌 “排序” 为例
.
13
10.6 基数排序
❖ “面值”优先
先分成13堆; 每堆再按“花色”排;
扑克牌 “排序” 为例
.
14
10.6 基数排序
❖ 多关键码排序
假设有n个记录……的序列 { R1, R2, …,Rn}
.
24
10.6.2 链式基数排序
分配 算法
.
25
10.6.2 链式基数排序
收集 算法
.
26
10.6.2 链式基数排序
❖ 性能分析
若每个关键码有d 位,需要重复执行d 趟“分配” 与“收集”。而每趟对n 个对象进行“分配”, 对r 个队列进行“收集”。总时间复杂度为O(d (n+r))。
若基数r相同,对于数据个数较多而关键码位数
.
5
初始关键字: [49] [38] [65] [97] [76] [13] [27] 一趟归并后: [38 49] [65 97] [13 76] [27] 二趟归并后: [38 49 65 97] [13 27 76] 三趟归并后: [13 27 38 49 65 76 97]
.
6
10.5 归并排序
每个记录Ri中含有d个关键字(Ki0, Ki1, …,Kid-1)。则 有序是指:对于序列中任意两个记录Ri和Rj(1≤i<j≤n) 都满足下列(词典)有序关系:
(Ki0, Ki1, …,Kid-1)< (Kj0, Kj1, …,Kjd-1) 其中K0被称为“最高”位关键字,Kd-1被称为 “最低” 位关键字。
第11章外排序第3讲-磁盘排序-多路平衡归并
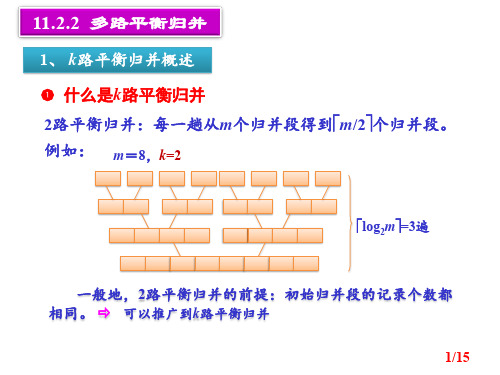
2、 利用败者树实现k路平衡归并过程 败者树用于在k个记录中选取最小关键字的记录。败者
树类似于堆排序中的堆。 利用败者树实现k路平衡归并的过程是:
先建立败者树。 然后对k个输入有序段进行k路平衡归并。
7/15
【例11-2】 设有5个初始归并段,它们中各记录的关键字
分别是:
F0:{17,21,∞} F1:{5,44,∞} F2:{10,12,∞} F3:{29,32,∞} F4:{15,56,∞}
5/15
总共需要的关键字比较次数:
(k-1)/log2k在k增大时会增大
log2m × (u-1) × (k-1)/log2k
在初始归并段个数m与记录个数u确定时是常量
结论:增大归并路数k,读写磁盘次数减少,而关键字比较 次数会增大。若k增大到一定的程度,就会抵消掉由于减少读写磁 盘次数而赢得的时间。
11.2.2 多路平衡归并
1、 k路平衡归并概述 什么是k路平衡归并 2路平衡归并:每一趟从m个归并段得到m/2个归并段。 例如: m=8,k=2
log2m=3遍
一般地,2路平衡归并的前提:初始归并段的记录个数都 相同。 可以推广到k路平衡归并
1/15
影响k路平衡归并的因素 影响k路平衡归并的效率 的因素:
结论:关键字比较次数与k无关 总的内部归并时间不 会随k的增大而增大。
利用败者树实现k路平衡归并
只要内存空间允许,尽可能增大归并路数k。
12/15
13/15
采用败者树,置换-选择排序中关键字比较次数分析 共有n个记录,内存工作区WA的容量为w:
若在w个记录中选取最小关键字的采用败者树方法,每次 需要log2w次比较。 总的时间复杂度为O(n log2w)。
【外排序】外排序算法(磁盘排序、磁带排序)
【外排序】外排序算法(磁盘排序、磁带排序) 外存设备结构分析 败者树多路归并 最佳归并树白话讲解列队猫2020-06-20 21:15:46外排序外排序概述外排序的基本方法是归并排序法例子总结存储设备(可忽略)磁带磁带结构磁盘硬盘结构块硬盘上的数据定位磁盘排序磁盘排序过程1.生成初始顺串方法1(常规方法):方法2:置换-选择排序方法2.处理顺串形成有序文件1.多路平衡归并2.利用败者树实现k路平衡归并过程利用败者树实现k路平衡归并的过程是:最佳归并树最佳归并树概念存在的问题当进行k路归并时最后进行归并的归并段小于k个构造步骤磁带排序磁带多路平衡归并排序磁带多阶段归并排序外排序概述(本章设计内容后续会具体讲解)外排序是指数据存放在外存中,数据排序时涉及内、外存数据交换的排序方法。
存储在外存上的数据以文件为基本单位,由文件系统进行读写操作,读写操作的基本单位为物理块外排序的基本方法是归并排序法一、生成若干初始归并段(顺串):这一过程也称为文件预处理。
一种常规的方法如下:1. 把含有n个记录的文件,按内存大小w分成若干长度为w的子文件(归并段);2. 分别将各子文件(归并段)调入内存,采用有效的内排序方法排序后送回外存。
产生m=[n/w]个初始归并段。
此时产生的若干子文件称为顺串二、多路归并:(所谓多路归并,具体使用几路归并是看计算机内存大小的,如计算机内存为2则只能使用2路归并) 对这些初始归并段进行多遍归并,使得有序的归并段逐渐扩大,最后在外存上形成整个文件的单一归并段,也就完成了这个文件的外排序。
例子1. 将一个大文件分成M个小文件,每个小文件是有序的2. 然后我们从M个子文件中各取一个数字进入内存处理(将该数字打上队列编号标记方便后续处理)3. 比较中转站中的数据,当从中转站出来的最小数字(升序排列)就是我们最后要排序的数字之一,将其写入到归并结果文件 因为该数字打上了队列编号,所以方便我们通知对应的编号队列继续出数字进入中转站队列(保证从中转站中取出的数据是所有文件中最小的),可以看出中转站一直保存了M个记录,当中转站中的所有数字都出队完毕,则本次归并结束。
Sorting

:桶排序、计数排序、基数排序
简单选择排序
相对于冒泡排序: 交换次数相当少
例如: { 2, 2, 1}, 第一次选的时候变成 { 1, 2, 2 }, 两个2的次序就变了
不稳定排序
时间复杂度分析
最好 O(n^2) 最坏 O(n^2) 平均 O(n^2)
1.交换排序: 冒泡排序、快速排序
2.插入排序: 直接插入排序、希尔排序
4.归并排序
非基于比较的排序
:桶排序、计数排序、基数排序
3.基数排序(又叫鸽巢排序)
在计数排序中,当k很大时,时间和空间的开销都会增大(可以想一下对 序列{8888,1234,9999}用计数排序,此时不但浪费很多空间,而且时间 方面还不如比较排序.
基数排序时间T(n)=d*(2k+3n),其中d是记录值的位数, (2k+3n)是每一趟计数排序时间,上文分析过了,k不超 过9,d的值一般也很小,k、d都可以看成是一个很小的 常数,所以时间复杂度o(n)。最坏最佳情况并不改变 时间复杂度。基数排序是稳定的。辅助空间同计数排序 k+n.
维护一个k大小的堆 时间复杂度: O(n * log k)
1.交换排序: 冒泡排序、快速排序
2.插入排序: 直接插入排序、希尔排序
基于比较的排序
O ( N * log N )
3.选择排序: 简单选择排序、堆排序
4.归并排序
非基于比较的排序
:桶排序、计数排序、基数排序
每一趟归并都需要扫描一遍所有记录,耗时 O(n)
最好 O(n)
最坏 O(n^2)
平均 O(n^2)
1. 求冒泡排序总共需要交换的次数 50, 40, 95, 20, 15, 70, 60, 45,
归并排序的详细过程

归并排序的详细过程归并排序是一种常见的排序算法,它通过将待排序序列分成若干个子序列,分别对每个子序列进行排序,然后再将排好序的子序列合并成最终的有序序列。
下面将详细介绍归并排序的过程。
1. 分解阶段:将待排序的序列不断二分,直到每个子序列只剩下一个元素为止。
这个过程可以使用递归来实现。
例如,对于序列[8, 4, 2, 5, 1, 3, 6, 7],先将其二分为[8, 4, 2, 5]和[1, 3, 6, 7]两个子序列,再将这两个子序列继续二分,直到每个子序列只剩下一个元素。
2. 合并阶段:将相邻的两个子序列合并成一个有序序列。
具体的合并过程如下:- 创建一个临时数组来存放合并后的序列。
- 初始化两个指针,分别指向两个子序列的起始位置。
- 依次比较两个子序列中的元素,将较小的元素放入临时数组中,并将指向该元素的指针后移一位。
- 当其中一个子序列的指针移到末尾时,将另一个子序列中剩余的元素依次放入临时数组中。
- 将临时数组中的元素复制回原始序列的对应位置。
以序列[8, 4, 2, 5, 1, 3, 6, 7]为例,将其分解为[8, 4, 2, 5]和[1, 3, 6, 7]两个子序列,然后对这两个子序列进行合并。
首先比较两个子序列的第一个元素,4小于8,将4放入临时数组中,并将指向4的指针后移一位。
接着比较2和8,2小于8,将2放入临时数组中,并将指向2的指针后移一位。
继续比较5和8,5小于8,将5放入临时数组中,并将指向5的指针后移一位。
此时第一个子序列中的元素已经全部放入临时数组中。
接下来比较两个子序列的第一个元素,3小于1,将3放入临时数组中,并将指向3的指针后移一位。
继续比较6和1,6大于1,将1放入临时数组中,并将指向1的指针后移一位。
接着比较6和3,6大于3,将3放入临时数组中,并将指向3的指针后移一位。
最后比较6和7,7小于6,将7放入临时数组中,并将指向7的指针后移一位。
此时第二个子序列中的元素已经全部放入临时数组中。
数据结构11-外部排序

例: 5 - 路平衡归
并的败者树:
[0] 531 [1] 510
[2] 5304
[3] 52
[4] 543
b0 12 b1 1805 b2 30
b3 b4 253 16
12 1805 30 14 12059 38
253 16 17 128598 56
b5
2334
0 3448
28 31
初始归并段
5
8 10 …
磁盘是在一片塑料薄膜上涂有磁性材料用以记 录数据的存储介质。它分成多个磁道(柱面),每 个磁道又分为多个扇区,多个磁盘组成的磁盘组还 涉及到盘片号(磁头号),磁盘绕轴高速旋转,读 写头则沿其一条半径作直线运动以寻道。它也不是
连续运转的设备,读写信息只能在旋转稳定时进行, 且找到要读写的记录也需要一定的寻道、寻扇区时 间,因此,在磁盘上读写信息所需的时间由三部分 组成:TI/O = tseek + tla + n tw,其中 tseek 为寻道时间 (seek time), tla 为寻扇区时间(latency time time), tw 为传输时间(transmission time)。磁盘 是一种随机存储设备。
§11.6 最佳归并树
用置换-选择排序得到的初始归并段长度各不相 同,那应如何进行 k 路平衡归并呢?这实际上是建立 k 叉霍夫曼树的问题:当初始归并段总数不足( ( m 1 ) MOD ( k - 1 ) ≠ 0 )时,需附加 k - ( m - 1 ) MOD ( k - 1 ) -1 个长度为零的虚段,亦即第一次归并时只 对 ( m - 1 ) MOD ( k - 1 ) + 1 个初始归并段归并。建 立 k 叉霍夫曼树每次仍是选择记录数相对少的初始归 并段先进行归并。最佳归并树不适合磁带归并排序。
内排序 数据结构讲义

3. 选择类
从记录的无序子序列中“选择”关键字最小 或最大的记录,并将它加入到有序子序列中,以 此方法增加记录的有序子序列的长度。
直接选择排序 堆排序
4. 归并类
通过“归并”两个或两个以上的记录有序子 序列,逐步增加记录有序序列的长度。
5. 其它方法 如:基数排序
11.2 插入排序 基本思想:
将 R[i].key 和 枢轴的关键字进行比较,要求R[i].key ≤ 枢轴的关键字temp.key
void QuickSort(RecType R[],int s,i行快速排序*/
{ int i=s,j=t; RecType temp;
if (s<t)
第11章 内 排 序
11.1 排序的基本概念 11.2 插入排序
11.3 交换排序 11.4 选择排序 11.5 归并排序 11.6 基数排序 11.7 各种内排序方法的比较和选择
本章小结
11.1 排序的基本概念
所谓排序,就是要整理表中的记录,使之按关键字 递增(或递减)有序排列。
其确切定义如下:
i=0 0 9 8 7 6 5 4 3 2 1 i=1 0 1 9 8 7 6 5 4 3 2 i=2 0 1 2 9 8 7 6 5 4 3 i=3 0 1 2 3 9 8 7 6 5 4 i=4 0 1 2 3 4 9 8 7 6 5 i=5 0 1 2 3 4 5 9 8 7 6 i=6 0 1 2 3 4 5 6 9 8 7 i=7 0 1 2 3 4 5 6 7 9 8 i=8 0 1 2 3 4 5 6 7 8 9
在有些情况下,在第i(i<n-1)趟时已排好序了,但仍执行后 面几趟的比较。实际上,一旦算法中某一趟比较时不出现记录 交换,说明已排好序了,就可以结束本算法。
第14周外排序第1讲-外排序概述

第11章外排序1、什么是外排序外排序是指数据存放在外存中,数据排序时涉及内、外存数据交换的排序方法。
内存数据交换文件存储在外存上的数据以文件为基本单位。
(1)生成若干初始归并段(顺串):这一过程也称为文件预处理。
一种常规的方法如下:❶把含有n 个记录的文件,按内存大小w 分成若干长度为w 的子文件(归并段);❷分别将各子文件(归并段)调入内存,采用有效的内排序方法排序后送回外存。
产生⎡n /w ⎤个初始归并段。
外排序的基本方法是归并排序法。
它分为以下两个步骤:2、外排序的基本方法内存abc.databc 1.dat abc 2.dat …abc n .dat均有序某内排序算法(2)多路归并:对这些初始归并段进行多遍归并,使得有序的归并段逐渐扩大,最后在外存上形成整个文件的单一归并段,也就完成了这个文件的外排序。
内存abc 1.dat abc 2.dat …abc n .databc.dat有序采用归并算法示例文件abc.dat:5,6,3,4,9,8,1,7,10,2递增排序应用程序可用的内存空间大小w=2。
5,6,3,4,9,8,1,7,10,2外排序过程:w =2内存abc.dat(1)生成5个初始归并段①abc1.dat :5,6②abc2.dat :3,4③abc3.dat :8,9④abc4.dat :1,7⑤abc5.dat :2,10外排序过程:k =2内存abc1.dat abc2.databc12.dat :3,4,5,6(2)多路归并:w =2 2路归并(k =2)abc1.dat :5,6abc2.dat :3,4abc1.dat :abc2.dat :5634比较abc12.dat :内存∞ ∞u (u =4)个记录需要进行u -1次操作(不考虑∞ )k (k =2)路归并每次需要k -1次关键字比较大致分析总的关键字比较次数:(u -1)(k -1)段1记录段2记录结果段内存abc3.databc4.dat abc34.dat:1,7,8,9abc3.dat:8,9abc4.dat:1,7w =2内存abc12.databc34.dat abc1234.dat:1,3,4,5,6,7,8,9abc12.dat:3,4,5,6abc34.dat:1,7,8,9k =2内存abc1234.databc5.dat abc.dat:1,2,3,4,5,6,7,8,9,10abc1234.dat:1,3,4,5,6,7,8,9abc5.dat:2,10k =2归并过程对应的归并树5,6abc1.dat 3,4abc2.dat 3,4,5,6abc12.dat 8,9abc3.dat 1,7abc4.dat 1,7,8,9abc34.dat 1,3,4,5,6,7,8,9abc1234.dat 1,2,3,4,5,6,7,8,9,10abc.dat2,10abc5.dat 归并过程的性能:记录读写次数。
排序算法所用的辅助空间

排序算法所用的辅助空间一、引言在计算机科学中,排序算法是数据处理的基本技术之一。
排序算法可以分为内部排序和外部排序两大类。
内部排序是指待排序数据全部加载到内存中进行排序,而外部排序则是针对大规模数据,需要借助外部存储设备进行排序。
本文将重点讨论排序算法中所使用的辅助空间。
二、排序算法概述1.内部排序内部排序算法是指待排序数据可以完全加载到内存中进行排序的算法,如快速排序、归并排序、堆排序等。
这些算法的特点是时间复杂度较低,但在处理大规模数据时,空间复杂度成为瓶颈。
2.外部排序外部排序算法针对的是大规模数据,其特点是数据规模超过内存容量。
外部排序需要借助外部存储设备,如磁盘等,进行排序。
常见的外部排序算法有归并排序、快速排序等。
三、辅助空间的作用1.空间复杂度辅助空间是指在排序过程中,除待排序数据外,还需要使用的额外空间。
辅助空间的大小直接影响到排序算法的性能。
一般来说,我们希望辅助空间尽量小,以提高排序效率。
2.实例分析以归并排序为例,归并排序需要使用额外的空间存储中间结果。
当待排序数据规模较大时,辅助空间的需求也随之增加。
此时,可以考虑使用外部排序算法,将数据分块,依次加载到内存中进行排序,最后合并排序结果。
四、常见排序算法的辅助空间使用1.快速排序快速排序算法采用递归策略,其辅助空间主要用于存储子序列。
在递归过程中,快速排序会创建一个新的序列,将原序列分为两个子序列。
这个过程会递归进行,直到序列长度为1。
快速排序的辅助空间与递归深度成正比。
2.归并排序归并排序算法的辅助空间主要用于存储临时数据。
在归并过程中,需要将两个已排序的序列合并成一个有序序列。
这个过程需要额外的空间存储临时数据,以便进行合并操作。
归并排序的辅助空间与序列数量成正比。
3.堆排序堆排序算法在排序过程中,需要构建最大堆或最小堆。
堆排序的辅助空间主要用于存储堆结构的数据。
堆排序的辅助空间与堆的大小成正比。
4.计数排序计数排序是一种非比较排序算法,其原理是根据键值统计每个键值出现的次数,然后将计数结果存储在辅助空间中。
数据结构-排序PPT课件

O(nlogn),归并排序的平均时间复杂度为O(nlogn)。其中,n为待排序序列的长度。
06
基数排序
基数排序是一种非比较型整数排序算法,其原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。
分配和收集
基数排序是一种稳定的排序算法,即相同的元素在排序后仍保持原有的顺序。
文件系统需要对文件和目录进行排序,以便用户可以更方便地浏览和管理文件。
数据挖掘和分析中需要对数据进行排序,以便发现数据中的模式和趋势。
计算机图形学中需要对图形数据进行排序,以便进行高效的渲染和操作。
数据库系统
文件系统
数据挖掘和分析
计算机图形学
02
插入排序
将待排序的元素按其排序码的大小,逐个插入到已经排好序的有序序列中,直到所有元素插入完毕。
简单选择排序
基本思想:将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了。 时间复杂度:堆排序的时间复杂度为O(nlogn),其中n为待排序元素的个数。 稳定性:堆排序是不稳定的排序算法。 优点:堆排序在最坏的情况下也能保证时间复杂度为O(nlogn),并且其空间复杂度为O(1),是一种效率较高的排序算法。
基数排序的实现过程
空间复杂度
基数排序的空间复杂度为O(n+k),其中n为待排序数组的长度,k为计数数组的长度。
时间复杂度
基数排序的时间复杂度为O(d(n+k)),其中d为最大位数,n为待排序数组的长度,k为计数数组的长度。
适用场景
当待排序数组的元素位数较少且范围较小时,基数排序具有较高的效率。然而,当元素位数较多或范围较大时,基数排序可能不是最优选择。
归并排序算法图文详解(模版使用)

归并排序算法图⽂详解(模版使⽤)算法介绍引⽤百度百科的介绍。
归并排序(Merge Sort)是建⽴在操作上的⼀种有效,稳定的排序算法,该算法是采⽤(Divide and Conquer)的⼀个⾮常典型的应⽤。
将已有序的⼦合并,得到完全有序的序列;即先使每个⼦序列有序,再使⼦序列段间有序。
若将两个有序表合并成⼀个有序表,称为⼆路归并。
算法描述归并排序,采⽤是分治法,先将数组分成⼦序列,让⼦序列有序,再将⼦序列间有序,合并成有序数组。
算法描述:(1)把长度为n的输⼊序列分成长度 n/2的⼦序列;(2)对两个⼦序列采⽤归并排序;(3)合并所有⼦序列。
算法实现void mergeSortInOrder(int[] arr,int bgn,int mid, int end){int l = bgn, m = mid +1, e = end;//相当于对⼀个数组的前半部分和后半部分进⾏排序排序,从开始的只有两个数,到后⾯//因为基本有序,所以只需要进⾏合并就⾏int[] arrs = new int[end - bgn + 1];int k = 0;//进⾏有序合并while(l <= mid && m <= e){if(arr[l] < arr[m]){arrs[k++] = arr[l++];}else{arrs[k++] = arr[m++];}}//如果前半部分⼤的⽐较多,直接接在后⾯while(l <= mid){arrs[k++] = arr[l++];}//如果后半部分⼤的⽐较多,直接接在后⾯while(m <= e){arrs[k++] = arr[m++];}//对我们原来的数组进⾏值的覆盖for(int i = 0; i < arrs.length; i++){arr[i + bgn] = arrs[i];}}void mergeSort(int[] arr, int bgn, int end){//如果开始指针⼤于结束指针,结束if(bgn >= end){return;}//通过分治将我们的数组分成多个⼩数组int mid = (bgn + end) >> 1;mergeSort(arr,bgn,mid);mergeSort(arr,mid + 1, end);//对我们的⼩数组进⾏排序mergeSortInOrder(arr,bgn,mid,end);}算法分析稳定排序外排序(需要消耗额外的内存)时间复杂度O(nlogn),空间复杂度为O(1)。
数据结构-外部排序

11-11
3 多路平衡归并的实现
• 对于2路归并, 令两个归并段上有u个记录, 每得到 归并后的一个记录, 仅需一次比较即可, 因此得到 含u个记录的归并段需进行u-1次比较。 • 对于k路归并, 令u个记录分布在k个归并段上, 显 然, 归并后的第一个记录应是k个归并段中关键字 最小的记录, 这需要进行k-1次比较, 得到u个记录 的归并段, 共需(u-1)(k-1)次比较。由此, 对n个记录的 文件进行外排序时, 在内部归并过程中进行的总的 比较次数为s(k-1)(n-1)。假设所得初始归并段为m个, 则 归并过程中进行比较的总的时间为:
结果:采用胜者树后, 从 k 个元素中挑选一个最小的元素仅需 log2k 次比较, 这时总的比较次数下降为:
logkm × log2k × ( n - 1 ) × tmg = log2m × ( n - 1 ) × tmg
该结果和 k 无关, 这是通过多用空间换来的。 • 改进:采用胜者树, k个元素中最小的元素输出之后, 从根结点到 它的相应的叶子结点路径上的结点都需要进行修改, 为了加快程 序运行的速度产生了败者树。
11-16
3 多路平衡归并的实现
• 败者树 在父节点中记下刚进行完的比赛中的败者, 但同样让胜者去参加下一轮的竞赛, 便得 到一棵“败者树”。
11-17
3 多路平衡归并的实现
• 下图即为一棵实现5-路归并的败者树ls[0…4], 图 中方形结点表示叶子结点(也可看成是外结点), 分 别为5个归并段中当前参加归并的待选择记录的关 键码;败者树中根结点ls[1]的双亲结点ls[0]为 “冠军”, 在此指示各归并段中的最小关键码记录 为第三段中的记录;结点ls[3]指示b1和b2两个叶 子结点中的败者即是b2, 而胜者b1和b3(b3是叶子 结点b3、b4和b0经过两场比赛后选出的获胜者)进 行比较, 结点ls[1]则指示它们中的败者为b1。
数据结构教程李春葆课后答案第11章外排序

第11章外排序教材中练习题及参考答案1. 外排序中两个相对独立的阶段是什么?答:外排序中两个相对独立的阶段是产生初始归并段和多路归并排序。
2.给出一组关键字T=(12,2,16,30,8,28,4,10,20,6,18),设内存工作区可容纳4个记录,给出用置换-选择排序算法得到的全部初始归并段。
答:置换-选择排序算法的执行过程如表11.1所示。
共产生两个初始归并段,归并段1为(2,8,12,16,28,30),归并段2为(4,6,10,18,20)。
表11.1 初始归并段的生成过程3. 设输入的关键字满足k1>k2>…>k n,缓冲区大小为m,用置换-选择排序方法可产生多少个初始归并段?答:可产生⎡n/m⎤个初始归并段。
设记录R i的关键字为k i(1≤i≤n),先读入m个记录R1、R2、…、R m,采用败者树选择最小记录R m,将其输出到到归并段1,R min=k m,在该位置上读入R m+1,采用败者树选择最小记录R m-1,将其输出到到归并段1,R min=k m-1,在该位置上读入R m+2,采用败者树选择最小记录R m-2,将其输出到到归并段1,R min=k m-2,…,以此类推,产生归并段1:(R m,R m-1,…,R1)。
同样产生其他归并段(R2m,R2m-1,…,R m+1),(R3m,R3m-1,…,R2m+1),…,一共有⎡n/m⎤个初始归并段。
4. 什么是多路平衡归并,多路平衡归并的目的是什么?答:归并过程可以用一棵归并树来表示。
多路平衡归并对应的归并树中,每个结点都是平衡的,即每个结点的所有子树的高度相差不超过1。
k路平衡归并的过程是:第一趟归并将m个初始归并段归并为⎡m/k⎤个归并段,以后每一趟归并将l个初始归并段归并为⎡l/k⎤个归并段,直到最后形成一个大的归并段为止。
m个归并段采用k路平衡归并,总的归并趟数s=⎡log k m⎤。
其趟数是所有归并方案中最少的,所以多路平衡归并的目的是减少归并趟数。
数据结构课程设计--二路归并排序说明书

前言1.1排序的重要性生活中,无时不刻不充满这排序,比如:班级同学的成绩排名问题,公司产值高低的问题等等,解决这些问题的过程中,都涉及到了一个数据结构的构造思想过程。
数据结构中的排序,也有很多种,如:插入排序、交换排序、选择排序等等,此时我们就要注意选择具有优解的算法,将一个数据元素(或记录)的任意序列,重新排列成一个有序的排列,便于我们查找。
假设含有n个记录的序列为{R1,R2,Rn},其相应的关键字序列为{K1,K2,…,Kn}需确定1,2…n的一种排序P1,P2…Pn,使其相应的关键字满足如下的非递减的关系:Kp1≤Kp2≤…≤Kpn,即按关键字{Rp1,Rp2,…,Rpn}有序的排列,这样的一种操作称为排序。
一般情况下,排序又分为内部排序和外部排序。
而在内部排序中又含有很多排序方法,就其全面性能而言,很难提出一种被认为是最好的方法,因为每一种方法都有它的优缺点,适合在不同的环境下使用。
我们学习的排序有:直接插入排序、折半插入排序、希尔排序、快速排序、基数排序、归并排序等。
本次课题研究中,我主要进行了二路归并排序的研究和学习。
1.2设计的背景和意义排序是计算机领域的一类非常重要的问题,计算机在出来数据的过程中,有25%的时间花在了排序上,有许多的计算机设备,排序用去计算机处理数据时间的一半以上,这对于提高计算机的运行速度有一定的影响。
此时排序算法的高效率显得尤为重要。
在排序算法汇中,归并排序(Merging sort)是与插入排序、交换排序、选择排序不同的另一类排序方法。
归并的含义是将两个或两个以上的有序表组合成一个新的有序表。
归并排序可分为多路归并排序,两路归并排序,既可用于内排序,也可以用于外排序。
这里仅对内排序的两路归并排序进行讨论。
而我们这里所探究学习的二路归并排序,设计思路更加清晰、明了,程序本身也不像堆结构那样复杂,同时时间复杂度仅为0(N),同时在处理大规模归并排序的时候,排序速度也明显优于冒泡法等一些排序算法,提高排序算法的效率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
写
F1文件
读
读
Fin文件
内存
写 F2文件
读
写…
读
写
内存
Fout文件
Fm文件
生成若干初始归并段
归并成一个有序文件
1/14
磁盘排序示例演示
设有一个文件Fin.dat,内含4500个记录:A1,A2,…, A4500,现在要对该文件进行排序,结果放在Fout.dat文件中。 可占用的内存空间至多只能对750个记录进行排序。
4/14
归并方案1:二路归并1
F1
F2
F3
F4
F5
F6
F7
F8
F9
F10
Fout
注意:
① 内存大小为750个记录,但任意大小的两个归并段都可以进行归并。 ② 每归并一次,参与归并的每个记录都要读一次和写一次。
5/14
方案1的读写记录数计算
F1
F2
F3
F4
F5
F6
F7
F1和F2中 每个记录
F8
F9
10/14
【例11-1】 设磁盘文件中共有18个记录,记录的关键字
分别为: {15,4,97,64,17,32,108,44,76,9,39,82,
56,31,80,73,255,68} 若内存工作区可容纳5个记录,用置换-选择排序可产生
几个初始归并段,每个初始归并段包含哪些记录?
11/14
置换-选择排序示例演示 18个记录(w=5): 15 4 97 64 17 32 108 44 76 9 39 82 56 31 80 73 255 68 ∞
读3次、
F10
写3次
Fout
总的读记录数(写记录数与之相同):
[(F1+F2+F3+F4的记录数) ×3+(F5+F6的记录数) ×2] =12000=8/3遍
该数越大,效率越差 等于哈夫曼树的WPL
6/14
归并方案2:二路归并2
F1
F2
F3
F4
F5
F6
F7
F8 F9
F10
Fout
方案2:总的读记录数WPL=15000。 方案1更好
abc.dat
某内排序算法
内存
abc1.dat abc2.dat
…
abcn.dat
均有序
另一种方法:采用一种称为置换-选择排序方法用于 生成初始归并段。
可以减少生成的初始归并段个数
9/14
置换-选择排序方法
(1)从待排文件Fin中按内存工作区WA的容量w读入w个记录。设归并 段编号i=1。
(2)使用败者树从WA中选出关键字最小的记录Rmin。 (3)将Rmin记录输出到Fout中,作为当前归并段的一个成员。 (4)若Fin不空,则从Fin中读入下一个记录x放在Rmin所在的工作区位置 代替Rmin。 (5)在工作区中所有≥Rmin的记录中选择出最小记录作为新的Rmin,转 (3),直到选不出这样的Rmin。 (6)设i=i+1,开始一个新的归并段。 (7)若工作区已空,则初始归并段已全部产生;否则转(2)。
方案1:总的读记录数WPL=12000。
7/14
归并方案3:三路归并
F7
F8
Fout
总的读记录数(写记录数与之相同):
方案3 :WPL=(750+750+750) ×2+ (750+750+750) ×2=9000
不同的归并方案所需要的读写记录数是不同的!
8/14
11.2.1 生成初始归并段
生成前面的初始归并段的方法
Fin.dat文件放在磁盘上。存 (750)
Fout.dat文件
2/14
第1阶段:产生初始归并段
文件Fin.dat (含4500个记录)
某种内排序方法
容量为750个记录
产生6个长度为 750个记录的有序 文件F1~F6。
3/14
第2阶段:多路归并
可用内存空间大小为750个记录 可以使用多种归并方案来完成
内存工作区w=5
Rmin=4113467895097246278
归并段1: 归并段2: 依次类推,产生归并段2:9,31,39,56,68,73,80,255
12/14
置换-选择排序中关键字比较次数分析 共有n个记录,内存工作区WA的容量为w:
若在w个记录中选取最小关键字的采用简单比较方法,每 次需要w-1次比较。 总的时间复杂度为O(nw)。
13/14
━━本讲完━━
14/14
