[西安电子科大通信原理讲义]07通信原理第七讲(可编辑)
通信原理讲义

通信原理讲义第一章绪论1.1 通信系统的组成1.1.1 通信一般系统模型点对点通信模型:反映了通信系统的共性。
1.1.2 模拟通信与数字通信●消息可以分成两类ﻩﻩ离散消息:消息的状态是可数的或离散型的(如符号、文字等),也称为数字消息。
连续消息:状态连续变化的消息(如语音、图像),也称为模拟消息。
●消息与电信号之间必须建立单一的对应关系。
通常,消息被载荷在电信号的某以参量上。
ﻩﻩ数字信号:电信号的参量携带离散消息,该参量离散取值。
模拟信号:电信号的参量携带连续消息,参量连续取值。
●相应的通信系统分成两类ﻩ数字通信系统ﻩﻩ模拟通信系统●模拟信号与数字信号之间可以相互转换在信息源中使用模-数(数-模)转换器,接受端使用数-模(模-数)转换器。
●数字通信比模拟通信更能适应对通信技术越来越高的要求(1)数字传输的抗干扰能力强,中继时可以消除噪声的积累;(2)传输差错可以控制;(3)便于使用现代数字信号处理技术对信息进行处理;(4) 易于加密处理;(5) 可以综合传递各种消息,增强系统功能。
● 模拟通信系统模型(点对点)基带信号:携带信息,但具有频率很低的频谱分量,不适宜传输的原始电信号。
已调信号:基带信号经过调之后转换成其频带适合信道传输的信号,也称频带信号。
调制器:将基带信号转变为频带信号的设备。
解调器:将频带信号转变为基带信号的设备。
模拟通信强调变换的线性特性,既已调参量与基带信号成比例。
● 数字通信系统模型(点对点) 强调已调参量与基带信号之间的一一对应。
数字通信需要解决的问题:(2) 编码与解码:通过差错控制编码消除噪声或干扰造成的差错; (3) 加密和解密:对基带信号进行人为“搅乱”;(4) 同步:发送和接收节拍一致,包括:位同步(码元同步)和群同步、帧同步、句同步或码组同步。
数字通信模型:同步环节的位置不固定,图中没有出现。
消息消息数字基带传输模型:● 数字通信的缺点 比模拟通信占据更宽的频带。
国防科大通信原理

DSB
Ps 1 1 00% PDSB
39
3.1 线性调制(幅度调制)原理
3.1.2 双边带调幅DSB
(2) DSB的解调 sDSB (t )
t
M ( )
H
H
t
SDSB ()
t
c
0
c
DSB包络已不能直接反映原调制信号的波形, 因此DSB的解调过程必须利用载波的相位信息— —相干解调。
27
3.1 线性调制(幅度调制)原理
(2) AM已调信号频谱
co sct 1 2[(c)( c)]
m(t)M()
A02A0()
则 : sAM(t) [A 0m (t)]cosct A 0cosctm (t)cosct
A 0 [ ( c ) ( c ) ] 1 2 [ M ( c ) M ( c ) ]
测量、建模 无线通信的发展也是随着对无线信道不断
认识、不断提出新的更能准确描述信道自然 特性的模型而迅速发展的
5
常用的信道模型
① 瑞利(Rayleigh)分布衰落
当电磁波经过反射、折射、散射等丰富路径传 播至接收端时,接收信号包络服从Rayleigh分布。 假设r为接收信号包络,其概率密度函数为:
将调制信号(基带信号)转换成适合于信道传输 的已调信号(频带信号);
实现信道的多路复用,提高信道利用率; 扩展信号带宽,提高系统抗干扰、抗衰落能力; 实现传输带宽与信噪比之间的互换。
21
引言
调制的定义:
调制就是把信号转换成适合在信道中传输 的形式的过程。
广义调制分为基带调制和载波调制。载波 调制是用调制信号(原始信号)控制载波 的某个(或几个)参数的过程。
B
Receiver
通信原理樊昌信课件

信息“1”变化,遇到“0”则不变。
16
第7章数字带通传输系统
2DPSK信号调制器原理方框图
开关电路
c o ωs ct
0
π
e2D P S K(t)
1 8 00移 相
s(t)
码变换
差分码可取传号差分码或空号差分码。其中,传号差分码的
编码规则为
bn = an ⊕ bn−1
式中,⊕为模2加,bn-1为bn的前一码元,最初的bn-1可任意 设定。
1
0
1
1
0
1
1
0
1
t
t
t
振幅键控
频移键控
相移键控
数字调制可分为二进制调制和多进制调制。
3
第7章数字带通传输系统
z 7.1 二进制数字调制原理
7.1.1 二进制相移键控(2PSK)
2PSK信号的表达式:
在“2P0S”K。中因,此通e,2P常S2KP用(St初)K=信始A号相c的位os时(0ω和域ctπ表分+ 达ϕ别n式表) 为示二进制“1”和
功率谱密度曲线
( ) P2PSK f
" − fc
"
fc − fs
fc
fc + fs
f
从以上分析可见,二进制相移键控信号的频谱特性与2ASK 的十分相似,带宽也是基带信号带宽的两倍。区别仅在
于当P=1/2时,其谱中无离散谱(即载波分量),此时 2PSK信号实际上相当于抑制载波的双边带信号。因此, 它可以看作是双极性基带信号作用下的调幅信号。
上式的逆过程称为差分译码(码反变换),即
an = bn ⊕ bn−1
17
第7章数字带通传输系统
通信原理 (完整)精选全文

数字通信的主要优点:
(a) 失真的数字信号
(b) 恢复的数字信号
数字信号波形的失真和恢复
数字通信的主要缺点:
➢ 占用带宽大 ➢ 设备复杂 ➢ 同步要求高
宽带通信、压缩编码 VLSI、SOC、ASIC 信号处理技术
应用实例:
➢ 数字传输技术:电话、电视、计算机数据等 信号的远距离传输。
➢ 模拟传输技术:有线电话环路、无线电广 播、电视广播等。
狭义信道
有线信道 无线信道
中长波地波 短波电离层反射 超短波、微波视距传输 超短波、微波对流层散射 卫星中继
编码信道 调制信道
信 源
加 密 器
编 码 器
调 制 器
发 转 换 器
信 道
收 转 换 器
解 调 器
解解 码密 器器
信 宿
发送设备
噪 声
接收设备
广义信道
广义信道
调制信道:
调制器输出端到解调器输入端的所有设备和媒介。 研究调制和解调时,常用调制信道。 连续信道/模拟信道。
eo(t)
e0t htei t nt e0t kt ei t nt
n(t)
n(t): 加性干扰 k(t): 乘性干扰
k t 依赖于网络的特性,k t 反映网络特性对 ei t 的作用。
干扰
加性干扰:本地噪声
始终存在
乘性干扰:非理理想信道 与信号共存
sR t sT tht nt
乘性 加性
增量调制DM
军用、 民用电话
Hale Waihona Puke 差分脉码调制DPCM电视电话、 图像编码
其 他 语 言 编 码 方 式 中低速数字电话 ADPCM、 APC、 LPC
按信号复用方式分类
电子科技大学 通信原理课件 李晓峰 考研

39/52
1.5 频带与电波传播
电子科技大学通信学院
40/52
1.5 频带与电波传播
电子科技大学通信学院
41/52
1.5 频带与电波传播
电子科技大学通信学院
42/52
1.5 频带与电波传播
电子科技大学通信学院
43/52
1.5 频带与电波传播
电子科技大学通信学院
44/52
1.5 频带与电波传播
50/52
1.6 数字与模拟通信系统
电子科技大学通信学院
51/52
1.6 数字与模拟通信系统
电子科技大学通信学院
52/52
1.6 数字与模拟通信系统
电子科技大学通信学院
53/52
1.6 数字与模拟通信系统
电子科技大学通信学院
54/52
1.6 数字与模拟通信系统
电子科技大学通信学院
55/52
电子科技大学通信学院 13/52
1.3 信源与常见的消息
量纲:1/s
电子科技大学通信学院
14/52
1.3 信源与常见的消息
电子科技大学通信学院
15/52
1.3 信源与常见的消息
可以用确定的函数形式表达的信号。 信号的波形可以由有限时间上的值确定。
电子科技大学通信学院
16/52
1.3 信源与常见的消息
电子科技大学通信学院
8/52
1.2 历史回顾
电子科技大学通信学院
9/52
1.2 历史回顾
电子科技大学通信学院
10/52
1.3 信源与常见的消息
电子科技大学通信学院
11/52
1.3 信源与常见的消息
信号与消息存在某种对应关系(映射)
通信原理教学大纲

通信原理教学大纲第一篇:通信原理教学大纲《通信原理》教学大纲(Principles of Communication)(电子、通信专业适用)学时:64学分:4(授课:52学时,实验:12学时)一、教育目标(性质与任务)本课程是为电子信息工程专业和通信工程专业学生开设的一门通信主干课程。
它既是通信专业知识的入门课又是重要的通信的专业基础课。
本课程的主要任务是通过讲课、练习,使学生掌握通信原理的基础知识,掌握通信系统的一般问题的解决方法。
二、课程内容与基本要求通信系统概述掌握通信系统的基本组成,通信系统分类及通信方式。
掌握信息及其度量方法。
掌握模拟和数字通信系统的主要性能指标。
2 随机信号分析理解随机过程的一般描述;掌握随机过程的数字特征;掌握维纳一欣钦定理,即平稳随机过程的相关函数与功率谱密度是傅立叶变换对;掌握高斯过程的数字特征以及一维密度函数;掌握窄带随机过程的包络和相位分别为瑞利分布和均匀分布;掌握正弦波如窄带随机过程的包络满足莱斯分布;掌握平稳随机过程通过线性系统还是平稳随机过程。
3 信道掌握信道定义、分类和信道数字模型。
掌握恒参信道及随参信道的定义。
了解分集接收方法。
掌握数字信道和模拟信道的容量计算方法,尤其是要理解香农公式的含义及应用条件等。
模拟调制系统掌握幅度调制中AM、DSB、SSB和VSB的基本原理、调制与解调框图、数学描述、以及抗噪性能;掌握模拟调频的基本原理、调制与解调框图以及数学描述;掌握频分复用的概念;了解复合调制和多级调制。
5 数字基带传输系统掌握数字基带信号及其频谱特性;基带传输的常用码型;深入理解数字基带传输中码间干扰和噪声;熟练掌握无码间干扰的基带传输特性以及噪声对传输性能的影响;掌握改善传输性能的重要措施:部分响应系统和时域均衡。
6 数字调制系统掌握2ASK、2FSK、2PSK和2DPSK数字调制的基本原理、调制和解调框图及系统的抗噪声性能并进行比较;掌握多进制数字调制系统中的QPSK、QDPSK和16QAM的基本原理及系统抗噪声性能。
通信原理西安电子科技大学黄葆华PPT学习教案

2.2 周期信号的频谱分析
思考
为什么要进行频谱分析?
第3页/共44页
2.2 周期信号的频谱分析
周期信号的三种傅氏级数表示法
1.
f (t) A0 [ An cos 2πnf0t Bn sin 2πnf0t]0
T0 2 f (t)dt 是周期信号f(t)的平均值(直流分量)
(2-12)
Vn 2
P( f )df
n
(2-13)
第34页/共44页
∵
f (t) (t
t0 )dt
f
(t0 )
(t
t0 )dt
f
(t0 )
∴
Vn
2 f
nf0 df
Vn
2
则
Vn 2
Vn 2
f nf0 df
n
n
(2-14)
由(2-13)、(2-14)式推出:
P( f ) Vn 2 f nf0 n
第36页/共44页
例2.3 求信号x(t)=Acos2πf 0t的功率谱及功率。
解:
∵
x(t)
Acos 2
f0t
A e j2 f0t 2
A e j2 f0t 2
∴
V1
V1
A 2
故 P( f ) V1 2 ( f f0 ) V1 2 ( f f0 )
A2 4
[ (
f
f0) (
f
f 0 )]
2.5 波形相关
2.5.1 相关函数
1. 互相关函数的定义
对于两个能量信号f 1(t)和f 2(t),其互相关函数定义为
R12 ( ) f1(t) f2 (t )dt
对于一般的功率信号f1(t)和f 2(t),其互相关函数定义为
西安电子科技大学通信原理-PPT精品文档

无线 有记忆 编码信道 无记忆 广义 设备 媒质 恒参信道 调制信道 随参信道
2.1 信道定义、分类、模型
3.模型 1〉调制信道模型:时变线性网络
编码器 调 制 输 入 器 发转 换器 信道 收转 换器 解 编码器 调 输 出 器
2.4 随机信号及噪声
2>广义:数学期望、方差与t无关,自相关函数 只与时间 间隔有关 a (t ) a 2 2 ( t ) R ( t , t ) R ( ) 3〉性质:各态历经性,时间平均代替统计平均
a a ______ 2 2 ________ R ( ) R ( )
( w ) ( w )
2.3 随参信道特性及其对所传信号的影响
1.随参信道特性: K(t)〜t 变化快 2.随参信道的传输媒质的三个特点: (1)对信号的帅耗随时间而变; (2)传输的时延随时间而变; (3)多径传播。 3.多径传播对信号传输的影响 (1)产生瑞利型衰落; (2)引起频率弥散; (3)发生频率选择性衰落。 4.改进措施:分集接收
2 包络: 一维瑞利分布 f( ) 2exp 0 2 2 1 f( ) 0 2 均匀分布 2
2.4 随机信号及噪声
(6)正弦波加窄带高斯过程
r ( t ) s ( t ) n ( t ) A cos( t ) n ( t ) c
2 2
2.4 随机信号及噪声
标准正态: 误差函数:
a 0
erf (x ) 2
1
2
e
0
x
z2
dz
(4)白噪声 1〉理想白噪声:功率谱密度在整个频域内都是 均匀分布
通信原理第7章(樊昌信第七版)PPT课件

B 方式
225° 315° 45° 135°
矢量图
10
11
01
A方式
00 参考相位
01 a(0)
00
B方式
第15页/共46页
b(1) 11 a(1)
10 b(0)
双比特码元 ab
a 0(−1) 1(+1) 1(+1) 0(−1)
b 0(−1) 0(−1) 1(+1) 1(+1)
波形
10
11
00
输入 滤波器
sin ct
x
载波 恢复
低通 x1(t) 抽样
滤波器
判决
位定时
低通
抽样
滤波器 x2 (t) 判决
a
并/串 变换 输出
b
存在问题:存在900的相位模糊(0, 90, 180, 270)
解决方案:采用四相相对相位调制,即QDPSK。
第19页/共46页
QPSK 特点:
01
相位跳变:0°,± 90°,± 180°
MFSK信号占用较宽的频带,信道频带利用率不高。
B
fM
f1
2 TB
MFSK一般用于 调制速率(1/TB) 不高的衰落信道 传输场合。
第11页/共46页
§7.4.3 多进制相移键控 (MPSK) 1 基本概念
利用载波的M种不同相位表示数字信息。 信号矢量图(星座图):
第12页/共46页
随着M的增加,多相制信号可以在相同的带宽中传输 更多比特的信息,从而提高频带利用率。
Pe
M 1 er/2 2
Pe
rb r / log2 M
——每比特的信噪功率比
第40页/共46页
通信原理第7版第7章PPT课件(樊昌信版)

实验二:数字调制与解调实验
实验目的
掌握数字调制与解调的基本原理和实现方法。
实验内容
设计并实现一个数字调制与解调系统,包括调制器、解调器和信道等部分。
实验二:数字调制与解调实验
01
实验步骤
02
1. 选择合适的数字调制方式,如2ASK、2FSK、2PSK等。
03
2. 设计并实现调制器,将数字基带信号转换为已调信号。
循环码
编码原理
01
循环码是一种具有循环特性的线性分组码,其任意码字的循环
移位仍然是该码的码字。
生成多项式与校验多项式
02
生成多项式用于描述循环码的编码规则,而校验多项式则用于
检测接收码字中的错误。
编码效率与纠错能力
03
循环码的编码效率与线性分组码相当,但纠错能力更强,可以
纠正多个错误。
卷积码
编码原理
06
同步原理与技术
载波同步技术
载波同步的定义
在通信系统中,使本地产生的载波频率和相位与接收到的信号载波保持一致的过程。
载波同步的方法
包括直接法、插入导频法和同步法。直接法利用接收信号中的载波分量进行同步;插入导频法在发送端插入一个导频 信号,接收端利用导频信号进行同步;同步法则是通过特定的同步信号或同步头来实现同步。
归零码(RZ)
在码元间隔内电平回归到零,有利于时钟提取。
差分码(Differential Cod…
利用相邻码元电平的相对变化来表示信息,抗干扰能力强。
眼图与误码率分析
眼图概念
通过示波器观察到的数字基带信号的一种图形表示,可以 直观地反映信号的质量和传输性能。
眼图参数
包括眼睛张开度、眼睛高度、眼睛宽度和交叉点位置等, 用于评估信号的定时误差、幅度失真和噪声影响等。
通信原理(第7版)复习资料讲解
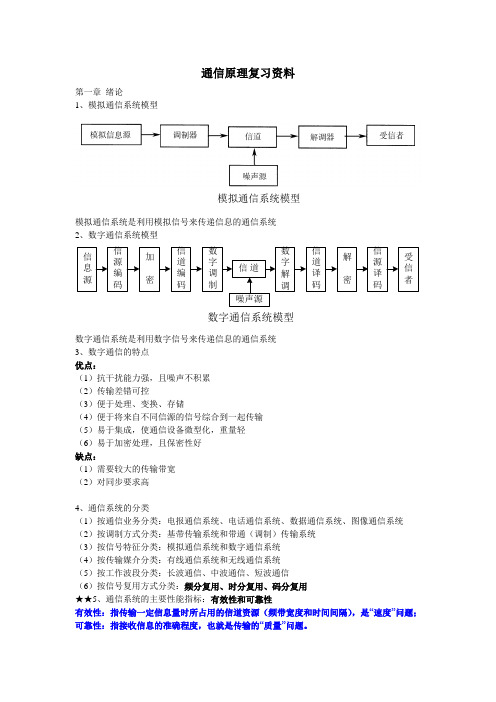
通信原理复习资料第一章 绪论1、模拟通信系统模型模拟通信系统是利用模拟信号来传递信息的通信系统 2、数字通信系统模型数字通信系统是利用数字信号来传递信息的通信系统 3、数字通信的特点 优点:(1)抗干扰能力强,且噪声不积累 (2)传输差错可控(3)便于处理、变换、存储(4)便于将来自不同信源的信号综合到一起传输 (5)易于集成,使通信设备微型化,重量轻 (6)易于加密处理,且保密性好 缺点:(1)需要较大的传输带宽 (2)对同步要求高4、通信系统的分类(1)按通信业务分类:电报通信系统、电话通信系统、数据通信系统、图像通信系统 (2)按调制方式分类:基带传输系统和带通(调制)传输系统 (3)按信号特征分类:模拟通信系统和数字通信系统 (4)按传输媒介分类:有线通信系统和无线通信系统 (5)按工作波段分类:长波通信、中波通信、短波通信(6)按信号复用方式分类:频分复用、时分复用、码分复用 ★★5、通信系统的主要性能指标:有效性和可靠性有效性:指传输一定信息量时所占用的信道资源(频带宽度和时间间隔),是“速度”问题; 可靠性:指接收信息的准确程度,也就是传输的“质量”问题。
模拟通信系统模型数字通信系统模型(1)模拟通信系统:有效性:可用有效传输频带来度量。
可靠性:可用接收端解调器输出信噪比来度量。
(2)数字通信系统:有效性:用传输速率和频带利用率来衡量。
可靠性:常用误码率和误信率表示。
码元传输速率R B :定义为单位时间(每秒)传送码元的数目,单位为波特(Baud ); 信息传输速率R b :定义为单位时间内传递的平均信息量或比特数,单位为比特/秒。
6、通信的目的:传递消息中所包含的信息。
7、通信方式可分为:单工、半双工和全双工通信★8、信息量是对信息发生的概率(不确定性)的度量。
一个二进制码元含1b 的信息量;一个M 进制码元含有log 2M 比特的信息量。
9、信息源的熵,即每个符号的平均信息量:)x (p log )x(p I i 2n1i i∑=-=结论:等概率发送时,信息源的熵有最大值。
通信原理--绪论 ppt课件

➢模拟信号: 信号参量取值连续
➢数字信号: 信号参量取值离散
信息
:消息中蕴含的有效内容。
ppt课件
9
三者关系
内涵
信息
传输
消息 载体
表现形式
信号
模拟信号 数字信号
Q&A
ppt课件
10
① 模拟信号 和 数字信号:
ppt课件
11
② 消息 ~ 电信号的转换:
t
➢ 话筒(声音传感器)把声音转变成音频信号; ➢ 数字终端把符号转变成数字信号; ➢ 摄像机把图像转变成视频信号; ➢ 热敏电阻(温度传感器)把温度转变成电信号。
ppt课件
43
配套辅导教材:
➢ 整理知识 ➢ 梳理关系 ➢ 剖析难点 ➢ 强化重点
归纳结论 引导主线 解惑疑点 点击考点
曹丽娜 编著
樊昌信 国防工业出版社
ppt课件
44
谢谢!
ppt课件
45
曹丽娜可靠性?headline?headlinetext有效性性能指标模拟通信数字通信?传输带宽?输出信噪比?频带利用率?差错概率矛盾关联互换36ppt课件西安电子科技大学通信工程学院课件制作
课件
ppt课件
1
第1章
绪论
通信原理(第7版)
樊昌信 曹丽娜 编著
ppt课件
2
精品资料
• 你怎么称呼老师? • 如果老师最后没有总结一节课的重点的难点,你
ppt课件
38
1.5.1 数字通信系统的有效性指标
与进制数 有关吗 ?
RB
1 Ts
与信源统计 特性有关吗 ?
例如:1秒内传输1000个码元,则 RB =1000 Baud
西电通信原理大纲

《通信原理》教学大纲适用专业:通信工程、电子信息工程、信息安全、空间信息与数字技术等--------------------------------------------------------------------------------一、课程基本要求以及在教学计划中的地位与作用本课程是通信与信息系统专业的一门必修主课,既是通信专业的基础理论课,又是一门专业性的课程。
通过学习,可使学生打下良好的理论基础,并可初步培养对通信系统进行分析和设计的能力。
本课程的要求是:掌握现代通信,尤其是数字通信的基本概念、基本理论以及基本的分析方法;熟悉通信系统的组成和工作原理;了解通信系统主要组成部分的实现方法。
二、课程内容和基本要求第1章绪论掌握内容:通信系统的基本问题与主要性能指标;模拟通信与数字通信;信息量、平均信息量、信息速率。
熟悉内容:通信系统的分类;通信方式。
了解内容:通信的概念与发展;第2章随机过程掌握内容:平稳随机过程的数字特征与概率密度函数;平稳随机过程的相关函数与功率谱密度;高斯过程与窄带高斯过程;熟悉内容:平稳随机过程;平稳随机过程的各态历经性;正弦波加窄带高斯过程;随机过程通过线性系统。
了解内容:随机信号与随机过程;n维联合概率密度函数。
第3章信道与噪声掌握内容:调制信道模型;编码信道模型;恒参信道对信号传输的影响;加性高斯白噪声;Shannon信道容量公式。
熟悉内容:信道的定义与模型;恒参信道实例;随参信道实例;随参信道对信号传输的影响;起伏噪声;噪声等效带宽;连续信道的信道容量“三要素”。
了解内容:随参信道特性的改善。
第4章模拟调制系统掌握内容:AM、DSB、SSB信号调制与解调;AM、DSB、SSB信号抗噪声性能。
熟悉内容:VSB、FM、PM信号的调制原理;频分复用的概念。
了解内容:FM信号的解调原理;复合调制及多级调制的概念。
第5章数字基带传输系统掌握内容:数字基带信号;AMI码、HDB3码、PST码、双相码的编码原理和主要优缺点;无码间干扰的基带传输特性;无码间干扰时的基带系统抗噪声性能。
西安电子科技大学通信原理真题答案详解

西安电子科技大学 通信工程学院 考研资料第一部分 通信原理一、填空题 1. 瑞利2. 99.7kbps 【解析】香农公式3. 10 10 01 01 10 10 01 014. ()d 0.5tf K m ττ−∞∫5. 见“通信原理必背”。
6. 2DPSK ;2FSK 。
【解析】有效性最差即频带最宽。
7. 32kHz 【解析】同2007.三.4。
8. 896【解析】12×32+5129. 2【解析】0521d t ==+,∴2t =。
10. 正交频分复用二、简答题1. 见“通信原理必背”。
2. 见“通信原理必背”。
3. ①见“通信原理必背”;②1.001MHz ,0.999MHz 。
4. ①见“通信原理必背”;②存在180 相位模糊,采用2DPSK 。
5. ()()()o S t s t h t =∗,波形如图11-1,()o S t 出现最大值的时刻为T ,最大值为2TA 。
三、综合题1. (1) 见“通信原理必背”;(2)d j 0()e t H K ωω−=;(3) 125【解析】3210W i S −=×,352()2410 3.210W i n N P f −=⋅××=×,DSB 2G =,∴2125o i o iS SN N ==。
2. (1) 见“通信原理必背”;(2)T R ()()G G ωω==;(3) 32进制,107η=。
3. (1) 见“通信原理必背”;(2) 参见2004.三.5(1) (信码不一样,但原理一样)。
4. (1)H 210MHz s f f ==,每个抽样值用8个二进制数字表示,∴信息速率7810bps b R =×。
(2) 传输带宽60MHz ,频带利用率2B/Hz 9η=图 11-12225. (1)[]110100011010101001⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦H PI ;[]100101010110001011⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦G IQ 。
通信原理樊昌信课件

不同(an不同),前者为单极性,后者为双极性。因此, 我们可以直接引用2ASK信号功率谱密度的公式来表述
2PSK信号的功率谱,即
P2PSK (
f
)
=
1 4
[Ps
(
f
+
fc) +
Ps ( f
−
fc )]
应当注意,这里的Ps(f)是双极性矩形脉冲序列的功率谱。
10
第7章数字带通传输系统
由第6章知,双极性全占空矩形随机脉冲序列的功率谱密度
2DPSK信号相位:(0) π 0 0 π π π 0 π π
或
(π ) 0 π π 0 0 0 π 0 0
相应的2DPSK信号的波形如下:
(a)绝对码
1
1
0
1
0
(b)相对码
0
1
0
0
1
1
参考
(c)2DPSK t
由此例可知,对于相同的基带信号,由于初始相位不同,2DPSK信 号的相位可以不同。
即:2DPSK信号的相位并不直接代表基带信号,而前后码元的相对
式中
e2PSK (t) = s(t )cosωct
∑ s(t) = an g(t − nTs )
n
这里,g(t)是脉宽为Ts的单个矩形脉冲,而an的统计特性为
an =
1, − 1,
概率为 P 概率为1 − P
5
第7章数字带通传输系统
即发送二进制符号“0”时(an取+1),e2PSK(t)取0相位; 发送二进制符号“1”时( an取 -1), e2PSK(t)取π相位。 这种以载波的不同相位直接去表示相应二进制数字信 号的调制方式,称为二进制绝对相移方式。 典型波形
通信原理(全套1162页PPT课件)

2.4 信號通過線性時不變系統
109/104
2.4 信號通過線性時不變系統
110/104
2.4 信號通過線性時不變系統
111/104
2.4 信號通過線性時不變系統
112/104
2.4 信號通過線性時不變系統
113/104
2.4 信號通過線性時不變系統
114/104
2.4 信號通過線性時不變系統
201/128
3.2 模擬角度調製
202/128
3.2 模擬角度調製
203/128
3.2 模擬角度調製
204/128
3.2 模擬角度調製
205/128
3.2 模擬角度調製
206/128
3.2 模擬角度調製
207/128
3.2 模擬角度調製
208/128
3.2 模擬角度調製
209/128
249/128
3.4 *角度調製系統的抗雜訊性能
250/128
3.4 *角度調製系統的抗雜訊性能
251/128
3.4 *角度調製系統的抗雜訊性能
252/128
3.4 *角度調製系統的抗雜訊性能
253/128
3.4 *角度調製系統的抗雜訊性能
254/128
3.4 *角度調製系統的抗雜訊性能
62/104
2.1 確知信號
63/104
2.1 確知信號
64/104
2.1 確知信號
65/104
2.1 確知信號
66/104
2.1 確知信號
67/104
2.1 確知信號
68/104
2.1 確知信號
69/104
2.1 確知信號
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《通信原理》第七讲
§2.4 随机过程通过线性系统
通信系统中的信号或噪声一般都是随机的,因此在以后的讨论中我们必然会
遇到这样的问题:随机过程通过系统(或网络)后,输出过程将是什么样的过程?
v t 等于输入信号v t 与系统的单位冲击响应h t 的卷
线性系统的响应 0 i 积,即
∞
v t v t ?h t v τ h t ?τ dτ(2.4-1 )
0 i ∫?∞ i
若h t ?H ω
v t ?V ω,v t ?V ω,,则有
0 0 i i
V ωH ωV ω(2.4-2 )
0 i
若线性系统是物理可实现的,则
t
v t v τh t ?τdτ
(2.4-3 )
0 ∫?∞ i
或
∞
v t h τv t ?τdτ
(2.4-4 )
0 ∫0 i
如果把v t 看作是输入随机过程的一个样本,则v t 可看作
是输出随机过
i
程的一个样本。
显然,输入过程ξ t 的每个样本与输出过程ξ t 的
相应样本之
i
间都满足式(2.4-4 )的关系。
这样,就整个过程而言,便有
∞
ξt h τξt ?τdτ
(2.4-5)
0 ∫0 i
假定输入ξ t 是平稳随机过程,现在来分析系统的输出过程ξ
t 的统计特
i
性。
ξ t
一、输出过程 0 的数学期望
∞∞
∞
E [ξ t ] E [ h τ ξ t ?τ dτ ] h τ E [ξ
t ?τ ]dτ a ? h τ dτ
0 ∫0 i ∫0 i ∫0
因为
∞
H ω∫0 h t ej ωt dt
求得
∞
H 0 ∫0 h t dt
所以
E [ξ t ] a ?H 0 (2.4-6)
由此可见, 输出过程的数学期望等于输入过程的数学期望与直流传递函数
H 0
的乘积,且E[ξ t ]与t无关。
ξ t
二、输出过程 0 的自相关函数
R t ,t E [ t t ]
+τ ξ ξ +τ
0 1 1 0 1 0 1
[ ∞
∞ ]
E h α ξ t ?α dα h β ξ t
+τ?β dβ
∫ i 1 ∫ i
1
0 0
∞∞
h α h β E [ξ t ?α ξ t
+τ?β ]dαdβ
∫∫ i 1 i 1
0 0
根据平稳性
E [ξ t ?α ξ t +τ?β ] R τ+α?β
i 1 i 1 i
于是
∞∞
R t ,t +τ h α h β R τ+α?β dαdβ
R τ(2.4-7)
0 1 1 ∫∫i 0
0 0
可见, ξ t 的自相关函数只依赖时间间隔τ而与时间起点t 无关。
由以上(1)
1
及(2)证明,若线性系统的输入过程是平稳的,那么输出过程也是平稳。
ξ t
三、输出过程 0 的功率谱密度
∞
P ω R τ e?j ωτdτ
0 ∫?∞ 0
∞∞∞
[ h α h β R τ+α?β dαdβ]e?j ωτdτ
∫∫∫ i ?∞ 0 0
'
令ττ+α?β,。
