高考数学常考的100个基础知识点
高考数学必考点《数学文化》精选100题

第 1 页 共 75 页高考数学必考点《数学文化》精选100题1.密位制是度量角的一种方法.把一周角等分为6000份,每一份叫做1密位的角.以密位作为角的度量单位,这种度量角的单位制,叫做角的密位制.在角的密位制中,采用四个数码表示角的大小,单位名称密位二字可以省去不写.密位的写法是在百位数与十位数字之间画一条短线,如密位7写成“007-”,478密位写成“478-”,1周角等于6000密位,记作1周角6000=-,1直角1500=-.如果一个半径为2的扇形,它的面积为76π,则其圆心角用密位制表示为( ) A .1250-B .1750-C .2100-D .3500-2.天干地支纪年法源于中国,中国自古便有十天干与十二地支,十天干即甲、乙、丙、丁、戊、己、庚、辛、壬、癸;十二地支即子、丑、寅、卯、辰、已、午、未、申、酉、戌、亥.天干地支纪年法是按顺序以一个天干和一个地支相配,排列起来,天干在前,地支在后,天干由“甲”起,地支由“子”起,例如,第一年为“甲子”,第二年为“乙丑”,第三年为“丙寅”,以此类推,排列到“癸酉”后,天干回到“甲”重新开始,即“甲戌”,“乙亥”,然后地支回到“子”重新开始,即“丙子”,以此类推.今年是辛丑年,也是伟大、光荣、正确的中国共产党成立100周年,则中国共产党成立的那一年是( )A .辛酉年B .辛戊年C .壬酉年D .壬戊年3.九连环是我国从古至今广泛流传的一种益智游戏,它用九个圆环相连成串,以解开为胜.据明代杨慎《丹铅总录》记载:“两环互相贯为一,得其关捩,解之为二,又合面为一”.在某种玩法中,用n a 表示解下()9,n n n *≤∈N个圆环所需的移动最少次数,若11a =,且1121,22,n n n a n a a n ---⎧=⎨+⎩为偶数为奇数,则解下5个环所需的最少移动次数为( ) A .7B .13C .16D .224.《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积12=(弦+矢)⨯矢,弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心高中数学资料共享群(734924357) 第 2 页 共 75 页角为 23π,半径等于20米的弧田,按照上述经验公式计算所得弧田面积约是( )(参考数据: 3.14π≈1.73≈)A .220平方米B .246平方米C .223平方米D .250平方米5.我国南北朝数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法,其理论依据是:设实数x 的不足近似值和过剩近似值分别为b a 和dc (,,,a b cd N +∈),则b d a c++是x 的更为精确的不足近似值或过剩近似值.我们知道 2.71828e =⋅⋅⋅,若令2714105e <<,则第一次用“调日法”后得4115是e 的更为精确的过剩近似值,即27411015e <<,若每次都取最简分数,那么第二次用“调日法”后可得e 的近似分数为( )A .6825 B .4115 C .2710 D .1456.如图,洛书(古称龟书),是阴阳五行术数之源.在古代传说中有神龟出于洛水,其甲壳上有此图像,结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,五方白圈皆阳数,四角黑点为阴数.若从四个阴数和五个阳数中随机选取3个数,则选取的3个数之和为奇数的方法数为( )A .30B .40C .44D .707.《掷铁饼者》取材于希腊的现实生活中的体育竞技活动,刻画的是一名强健的男子在掷铁饼过程中最具有表现力的瞬间.现在把掷铁饼者张开的双臂近似看成一张拉满弦的第 3 页 共 75 页 “弓”,掷铁饼者的手臂长约4π米,肩宽约为8π米,“弓”所在圆的半径约为1.25米,你估测一下掷铁饼者双手之间的距离约为(参考数据1.414≈,1.732≈)( )A .1.012米B .2.043米C .1.768米D .2.945米8.在地球公转过程中,太阳直射点的纬度随时间周而复始不断变化,太阳直射点回归运动的一个周期就是一个回归年.某科研小组以某年春分(太阳直射赤道且随后太阳直射点逐渐北移的时间)为初始时间,统计了连续400天太阳直射点的纬度值(太阳直射北半球时取正值,直射南半球时取负值).设第x 天时太阳直射点的纬度值为,y 该科研小组通过对数据的整理和分析.得到y 与x 近似满足23.43929110.01720279y sin x =.则每400年中,要使这400年与400个回归年所含的天数最为接近.应设定闰年的个数为(精确到1)( ) 参考数据182.62110.01720279π≈ A .95B .96C .97D .989.“中国剩余定理”又称“孙子定理”,讲的是关于整除的问题.现有这样一个整除问题:将1到2021这2021个正整数中能被3除余1且被5除余1的数按从小到大的顺序排成一列,构成数列{}n a ,则数列{}n a 各项的和为( )A .137835B .137836C .135809D .13581010.我国古代以天为主,以地为从,天和干相连叫天干,地和支相连叫地支,合起来叫天干地支.天干有十个,就是甲、乙、丙、丁、戊、己、庚、辛、壬、癸,地支有十二个,依次是子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥.古人把它们按照甲子、乙丑、丙寅……的顺序而不重复地搭配起来,从甲子到癸亥共六十对,叫做一甲子.我国古人用这六十对干支来表示年、月、日、时的序号,周而复始,不断循环,这就是干支纪年法(即农历).干支纪年历法,是屹立于世界民族之林的科学历法之一.今年(2020高中数学资料共享群(734924357) 第 4 页 共 75 页年)是庚子年,小华的爸爸今年6月6日是56周岁生日,小华爸爸出生那年的农历是( )A .庚子B .甲辰C .癸卯D .丙申11.《周髀算经》是中国最古老的天文学和数学著作,书中提到:冬至、小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种这十二个节气的日影子长依次成等差数列.若冬至、大寒、雨水的日影子长的和是40.5尺,芒种的日影子长为4.5尺,则冬至的日影子长为( )A .6.5尺B .13.5尺C .14.5尺D .15.5尺12.英国数学家泰勒(B . Taylor ,1685-1731)以发现泰勒公式和泰勒级数闻名于世。由泰勒公式,我们能得到111111!2!3!!(1)!e e n n θ=+++++++(其中e 为自然对数的底数,()()01,!12...21n n n n θ<<=⨯-⨯-⨯⨯⨯),其拉格朗日余项是.(1)!n e R n θ=+可以看出,右边的项用得越多,计算得到的e 的近似值也就越精确。若3(1)!n +近似地表示e 的泰勒公式的拉格朗日余项,n R n R 不超过11000时,正整数n 的最小值是( ) A .5B .6C .7D .813.攒尖是古代中国建筑中屋顶的一种结构形式依其平面有圆形攒尖、三角攒尖、四角攒尖、六角攒尖等,多见于亭阁式建筑如图所示,某园林建筑为六角攒尖,它的主要部分的轮廓可近似看作一个正六棱锥,设正六棱锥的侧面等腰三角形的顶角为2θ,则侧棱与底面内切圆半径的比为( )第 5 页 共 75 页A.3sin θ B.3cos θ C .12sin θ D .12cos θ14.“瓦当”是中国古建筑装饰檐头的附件,是中国特有的文化艺术遗产,为探究下面“瓦当”图案的面积,向半径为10的圆内投入1000粒芝麻,落入阴影部分的有400粒.则估计“瓦当”图案的面积是( )A .40B .40πC .4D .4π15.明朝早期,郑和在七下西洋的过程中,将中国古代天体测量方面所取得的成就创造性应用于航海,形成了一套自成体系且行之有效的先进航海技术——“过洋牵星术”.简单地说,就是通过观测不同季节、时辰的日月星辰在天空运行的位置和测量星辰在海面以上的高度来判断方位,其采用的主要工具为牵星板,由12块正方形木板组成,最小的一块边长约为2厘米(称一指).观测时,将木板立起,一手拿着木板,手臂垂直,眼睛到木板的距离大约为72厘米,使牵星板与海平面垂直,让板的下边缘与海平面重合,上边缘对着所观测的星辰,与其相切,依高低不同替换、调整木板,木板上边缘与被观测星辰重合时所用的是几指板,观测的星辰离海平面的高度就是几指,然后就可以推算出船在海中的地理纬度.如图所示,若在一次观测中,所用的牵星板为九指板,则sin 2α=( )A .1235 B.17 C .817 D .81516.古代数学著作《九章算术》有如下问题:“今有女子善织,日自倍,五日织五尺,高中数学资料共享群(734924357) 第 6 页 共 75 页问日织几何?”意思是:“一女子善于织布,每天织的布都是前一天的2倍,已知她5天共织布5尺,问这女子每天分别织布多少?”根据上题的已知条件,可求得该女子第2天所织布的尺数为( )A .2031 B .531 C .1031 D .403117.筒车是我国古代发明的一种水利灌溉工具,既经济又环保,明代科学家徐光启在《农政全书》中用图1描绘了筒车的工作原理.假定在水流稳定的情况下,筒车上的每一个盛水筒都做匀速圆周运动.将筒车抽象为一个几何图形(圆),筒车的半径为2m ,筒车的轴心O 到水面的距离为1m ,筒车每分钟按逆时针转动2圈.规定:盛水筒M 对应的点P 从水中浮现(即0P 时的位置)时开始计算时间,设盛水筒M 从0P 运动到点P 时所用时间为t (单位:s ),且此时点P 距离水面的高度为h (单位:m ).若以筒车的轴心O 为坐标原点,过点O 的水平直线为x 轴建立平面直角坐标系xOy (如图2),则h 与t 的函数关系式为( )A .2sin 1156h t ππ⎛⎫=-+ ⎪⎝⎭,[)0,t ∈+∞B .2sin 1156h t ππ⎛⎫=++ ⎪⎝⎭,[)0,t ∈+∞ C .2sin 16h t ππ⎛⎫=-+ ⎪⎝⎭,[)0,t ∈+∞ D .2sin 16h t ππ⎛⎫=++ ⎪⎝⎭,[)0,t ∈+∞ 18.我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,即在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,则ABC的面积S =根据此公式,若cos (2)cos 0a B b c A +-=,且2224b c a ,则ABC的面积为()AB.CD.19.我国古代数学论著中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯二百五十四,请问底层几盏灯?意思是:一座7层塔共挂了254盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的底层共有灯()A.32盏B.64盏C.128盏D.196盏20.我国古代数学名著《九章算术》中有如下“两鼠穿墙”问题:有两只老鼠同时从墙的两面相对着打洞穿墙.大老鼠第一天打进11尺,以后每天进度是前一天的2倍.小老鼠第一天也打进1尺,以后每天进度是前一天的一半.如果墙的厚度为10尺,则两鼠穿透此墙至少在第()A.3天B.4天C.5天D.6天21.中国古代重要的数学著作《孙子算经》下卷有题:今有物,不知其数.三三数之,剩二;五五数之,剩三;七七数之,剩二.问:物几何?现有如下表示:已知{}32,A x x n n N*==+∈,{}53,B x x n n N*==+∈,{}72,C x x n n N*==+∈,若x A B C∈⋂⋂,则下列选项中符合题意的整数x为()A.8B.127C.37D.2322.刘徽(约公元225年-295年),魏晋期间伟大的数学家,中国古典数学理论的奠基人之一.他在割圆术中提出的“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”,这可视为中国古代极限观念的佳作.割圆术的核心思想是将一个圆的内接正n边形等分成n个等腰三角形(如图所示),当n变得很大时,这n个等腰三角形的面积之和近似等于圆的面积,运用割圆术的思想得到6sin的近似值为()第7页共75页高中数学资料共享群(734924357) 第 8 页 共 75 页A .30πB .60πC .90π D .180π 23.电影《刘三姐》中有一个“舟妹分狗”的片段.其中,罗秀才唱道:三百条狗交给你,一少三多四下分,不要双数要单数,看你怎样分得匀舟妹唱道;九十九条圩上卖,九十九条腊起来,九十九条赶羊走,剩下三条,财主请来当奴才(讽刺财主请来对歌的三个奴才).事实上,电影中罗秀才提出了一个数学问题:把300条狗分成4群,每群都是单数,1群少,3群多,数量多的三群必须都是一样的,否则就不是一少三多,问你怎样分?舟妹已唱出其中一种分法,即{}3,99,99,99,那么,所有分法的种数为( ) A .6B .9C .10D .1224.我国古代数学家著作《九章算术》有如下问题:“今有人持金出五关,前关二而税一,次关三而税一,次关四而税一,次关五而税一,次关六而税一,并五关所税,适重一斤.问本持金几何.”,其意思是“今有人持金出五关,第一关收税金为持金的12,第2关收税金为剩余的13,第3关收税金为剩余税金的14,第4关收税金为剩余税金的15,第5关收税金为剩余税金的16”5关所税金之和,恰好重1斤.则在此问题中,第3关收税金为( )斤A .110 B .310 C .13 D .91025.朱世杰是历史上最伟大的数学家之一,他所著的《四元玉鉴》卷中“如像招数”五问第 9 页 共 75 页 中有如下问题:“今有官司差夫一千八百六十四人筑堤,只云初日差六十四人,次日转多七人,每人日支米三升.”其大意为“官府陆续派遣1864人前往修筑堤坝,第一天派出64人,从第二天开始每天派出的人数比前一天多7人,修筑堤坝的每人每天分发大米3升.”在该问题中前5天共分发多少升大米?( )A .1170B .1440C .1512D .177226.中国的少数民族有不少具有鲜明特色的建筑,如图①所示的建筑为坐落于广西三江林溪河上的程阳永济桥,是典型的侗族建筑,该类建筑由桥、塔、亭组成,其中塔、亭建在石桥上,具有多层结构,被称为世界十大最不可思议桥梁之一,因为行人过往能够躲避风雨,故名“风雨桥”.已知程阳永济桥上的塔从上往下看,其边界构成的曲线可以看作正六边形结构,如图①所示,且各层的六边形的边长均为整数,从内往外依次成等差数列.若这四层六边形的周长之和为156,且图①,则最外层六边形的周长为( )A .54B .48C .42D .3027.如图是隋唐天坛,古叫圜丘,它位于唐长安城明德门遗址东约950米,即今西安市雁塔区陕西师范大学以南.天坛初建于隋而废弃于唐末,比北京明清天坛早1000多年,是隋唐王朝近三百年里的皇家祭天之处.某数学兴趣小组为了测得天坛的直径,在天坛外围测得60AB =米,60BC =米,40CD =米,60ABC ∠=︒,120BCD ∠=︒,据此可以估计天坛的最下面一层的直径AD 大约为( ).(结果精确到1米)1.414≈1.732≈2.236≈2.646≈)A .39米B .43米C .49米D .53米高中数学资料共享群(734924357) 第 10 页 共 75 页28.《孙子算经》记载,中国古代诸侯的等级从低到高分为:男、子、伯、侯、公,一共五级.现每个级别的诸侯分别有1,2,3,4,5人,按照如下规则给他们分发一批苹果:同一等级的诸侯所得苹果数依次为1a ,2a ,3a ,…,且满足()*1k k a a k k N +=+∈;任一等级诸侯所得苹果数量最多的比高一级的诸侯所得苹果数最少的少一个.现已知等级为男的诸侯所得苹果数为1,则这批苹果共有( )个.A .158B .159C .160D .16129.祖暅(公元5-6世纪,祖冲之之子,是我国齐梁时代的数学家.他提出了一条原理:“幂势既同,则积不容异.”这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现,比祖暅晚一千一百多年.椭球体是椭圆绕其轴旋转所成的旋转体.如图将底面直径皆为2b ,高皆为a 的椭半球体及已被挖去了圆锥体的圆柱体放置于同一平面β上.以平行于平面β的平面于距平面β任意高d 处可横截得到S 圆及S 环两截面,可以证明S S =环圆总成立.据此,短轴长为6cm ,长轴为8cm 的椭球体的体积是( )3cmA .24πB .48πC .192πD .384π30.蹴鞠,又名蹴球,蹴圆,筑球,踢圆等,蹴有用脚蹴、踢、蹋的含义,鞠最早系外包皮革、内实米糠的球.因而蹴鞠就是指古人以脚蹴,蹋、踢皮球的活动,类似今日的足球.2006年5月20日,蹴鞠已作为非物质文化遗产经国务院批准列入第一批国家非物质文化遗产名录.3D打印属于快速成形技术的一种,它是一种以数字模型文件为基础,运用粉末状金属或塑料等可粘合材料,通过逐层堆叠累积的方式来构造物体的技术(即“积层造型法”).过去常在模具制造、工业设计等领域被用于制造模型,现正用于一些产品的直接制造,特别是一些高价值应用(比如髋关节、牙齿或一些飞机零部件等).已知某鞠的表面上有四个点A 、B 、C 、D ,满足任意两点间的直线距离为,现在利用3D 打印技术制作模型,该模型是由鞠的内部挖去由ABCD 组成的几何体后剩余的部分,打印所用原料密度为31g/cm ,不考虑打印损耗,制作该模型所需原料的质量约为( )(参考数据:取 3.14π= 1.41= 1.73=,精确到0.1) A .113.0gB .267.9gC .99.2gD .13.8g31.我国古代著名的数学专著《九章算术》里有一段叙述:今有良马和驽马发长安至齐,良马初日行一百零三里,日增十三里;驽马初日行九十七里,日减半里;良马先至齐,复还迎驽马,九日后二马相逢.问:齐去长安多少里?( )A .1125B .1250C .2250D .250032.数学著作《孙子算经》中有这样一个问题:“今有物不知其数,三三数之剩二(除以3余2),五五数之剩三(除以5余3),问物几何?”现将1到2020共2020个整数中,同时满足“三三数之剩二,五五数之剩三”的数按从小到大的顺序排成一列,构成数列{},n a 则该数列共有( )A .132项B .133项C .134项D .135项33.1750年,欧拉在给哥德巴赫的一封信中列举了多面体的一些性质,其中一条是:如果用V 、E 和F 表示闭的凸多面体的顶点数、棱数和面数,则有如下关系:2V E F -+=.已知正十二面体有20个顶点,则正十二面体有( )条棱 A .30B .14C .20D .2634.龙马负图、神龟载书图像如图甲所示,数千年来被认为是中华传统文化的源头;其中洛书有云,神龟出于洛水,甲壳上的图像如图乙所示,其结构是戴九履一,左三右七,二四为肩,六八为足u ,以五居中,五方白圈皆阳数,四角黑点为阴数;若从阳数和阴数中分别随机抽出2个和1个,则被抽到的3个数的数字之和超过16的概率为( )A.1340B.720C.14D.31035.降雨量是气象部门观测的重要数据,日降雨量是指一天内降落在地面单位面积雨水层的深度(单位:毫米)。我国古代就有关于降雨量测量方法的记载,古代数学名著《数书九章》中有“天池盆测雨”题:天池盆(圆台形状)盆口直径二尺八寸,盆底直径为一尺二寸,盆深一尺八寸。若盆中积水深九寸,则平地降雨量是几寸(注:一尺等于十寸,一寸等于10厘米)?已知某隧道的积水程度与日降水量的关系如下表所示:如果某天该隧道的日降水量按照“天池盆测雨”题中数据计算,则该隧道的积水程度为()A.一级B.二级C.三级D.四级36.攒尖是古代中国建筑中屋顶的一种结构形式.宋代称为撮尖,清代称攒尖.依其平面有圆形攒尖、三角攒尖、四角攒尖、六角攒尖等,也有单檐和重檐之分,多见于亭阁式建筑.如图所示,某园林建筑为六角攒尖,它的主要部分的轮廓可近似看作一个正六棱锥,若此正六棱锥的侧面等腰三角形的底角为 ,则侧棱与底面外接圆半径的比为()A .12cos αB .12sin αC .sin 3πsin 8αD .cos 3πcos 8α37.描金又称泥金画漆,是一种传统工艺美术技艺.起源于战国时期,在漆器表面,用金色描绘花纹的装饰方法,常以黑漆作底,也有少数以朱漆为底.描金工作分为两道工序,第一道工序是上漆,第二道工序是描绘花纹.现甲,乙两位工匠要完成A ,B ,C 三件原料的描金工作,每件原料先由甲上漆,再由乙描绘花纹.每道工序所需的时间(单位:h )如下:则完成这三件原料的描金工作最少需要( )A .43hB.46h C .47h D .49h38.德国著名的天文学家开普勒说过:“几何学里有两件宝,一个是勾股定理,另一个是黄金分割.如果把勾股定理比作黄金矿的话,那么可以把黄金分割比作钻石矿.”黄金三角形有两种,其中底与腰之比为黄金分割比的黄金三角形被认为是最美的三角形,它是一个顶角为36的等腰三角形(另一种是顶角为108的等腰三角形).例如,五角星由五个黄金三角形与一个正五边形组成,如图所示,在其中一个黄金ABC 中,12BC AC =.根据这些信息,可得sin126=( )A B C D39.“九天揽月”是中华民族的伟大梦想,我国探月工程的进展与实力举世瞩目.近期,“嫦娥四号”探测器实现历史上的首次月背着陆,月球上“嫦娥四号”的着陆点,被命名为天河基地,如图是“嫦娥四号”运行轨道示意图.圆形轨道距月球表面100千米,椭圆形轨道的一个焦点是月球球心,一个长轴顶点位于两轨道相切的变轨处,另一个长轴顶点距月球表面15千米,则椭圆形轨道的焦距为()A.85km B.42.5km C.50km D.100km40.《九章算术》是我国古代内容极为丰富的数学名著.书中有如下问题:“今有委米依垣内角,下周四尺. 高三尺.何积及为米几何?”其意思为:“ 在屋内墙角处堆放米,米堆底部的弧长为4尺.米堆的高为3尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放斛的米约有()A.7斛B.3斛C.9斛D.12斛41.我国南宋数学家杨辉1261年所著的《详解九章算法》就给出了著名的杨辉三角,由此可见我国古代数学的成就是非常值得中华民族自豪的.以下关于杨辉三角的猜想中错误的是()A .由“与首末两端‘等距离’的两个二项式系数相等”猜想:C n m =C n n -mB .由“在相邻的两行中,除1以外的每一个数都等于它‘肩上’两个数的和”猜想:11r r r n nn C C C -+=+ C .由“第n 行所有数之和为2n ”猜想:C n 0+C n 1+C n 2+…+C n n =2nD .由“111=11,112=121,113=1331”猜想:115=1510105142.阿波罗尼斯(约公元前262-190年)证明过这样一个命题:平面内到两定点距离之比为常数(0,1)k k k >≠的点的轨迹是圆,后人将这个圆称为阿氏圆.若平面内两定点A B 、间的距离为4,动点P 满足PA PB=P A B 、、不共线时,PAB △面积的最大值是( )A .3 B C .D .343.古希腊时期,的矩形称为黄金矩形,称为黄金分割比例.下图为希腊的一古建筑.其中部分廊、檐、顶的连接点为图中所示相关对应点,图中的矩形ABCD ,EBCF ,FGHC ,FGJI ,LGJK ,MNJK 均近似为黄金矩形.若A 与D 间的距离大于18.7m ,C 与F 间的距离小于12m .则该古建筑中A 与B 间的距离可能是( )(参考数据:10.6182≈,70.6180.38≈,30.6180.236≈)A .29mB .29.8mC .30.8mD .32.8m44.《几何原本》第二卷中的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,通过这一原理,很多代数的定理都能够通过图形实现证明,并称之为无字证明.现有如图所示的图形,点F 在半圆O 上,且OF AB ⊥,点C 在直径AB 上运动.设AC a =,BC b =,则由FC OF ≥可以直接证明的不等式为( )A .)0,02a b a b +≥>>B .()2220,0a b ab a b +≥>>C .)20,0ab a b a b≤>>+ D .)0,02a b a b +≤>> 45.我国明代著名乐律学家、明宗室王子朱载堉在《律学新说》中提出的十二平均律,即是现代在钢琴的键盘上,一个八度音程从一个c 键到下一个1c 键的8个白键与5个黑键(如图)的音频恰成一个公比为1c 的频率正好是中音c 的2倍.已知标准音1a 的频率为440Hz ,那么频率为的音名是( )A .dB .fC .eD .#d46.刘徽是中国魏晋时期杰出的数学家,他提出“割圆求周”方法:当n很大时,用圆内接正n边形的周长近似等于圆周长,并计算出精确度很高的圆周率π31416≈..在《九章算术注》中总结出“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”的极限思想.运用此思想,当π取3.1416时可得sin1︒的近似值为()A.0.00873B.0.01745C.0.02618D.0.03491 47.3D打印属于快速成形技术的一种,它是一种以数字模型文件为基础,运用粉末状金属或塑料等可粘合材料,通过逐层堆叠累积的方式来构造物体的技术(即“积层造型法”).过去常在模具制造、工业设计等领域被用于制造模型,现正用于一些产品的直接制造,特别是一些高价值应用(比如髋关节、牙齿或一些飞机零部件等).已知利用3D 打印技术制作如图所示的模型.该模型为在圆锥底内挖去一个正方体后的剩余部分(正方体四个顶点在圆锥母线上,四个顶点在圆锥底面上),圆锥底面直径为,母.打印所用原料密度为31 g/cm,不考虑打印损耗,制作该模型所需原料的质量约为()(取π 3.14=,精确到0.1)A.609.4g B.447.3g C.398.3g D.357.3g 48.《九章算术》中《方田》章有弧田面积计算问题,术日:以弦乘矢,矢又自乘,并之,二而一.其大意是弧田面积计算公式为:弧田面积=12(弦×矢+矢×矢),弧田是由圆弧(弧田弧)和以圆弧的端点为端点的线段(弧田弦)围成的平面图形,公式中的“弦”指的是弧田弦的长,“矢”指的是弧田所在圆的半径与圆心到弧田弧的距离之差,现有一弧田,其弧田弦AB等于6米,其弧田弧所在圆为圆O,若用上述弧田面积计算公式算得该弧田的面积为72平方米,则cos①AOB=()A.125B.325C.15D.72549.我国天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气的晷。
高三数学球体体积知识点大全

高三数学球体体积知识点大全高三数学-球体体积知识点大全一、引言球体是数学几何学中的重要概念,其体积计算是数学高考中的常见题型。
本文将详细介绍高三数学中与球体体积有关的知识点,包括基本公式、推导过程以及解题技巧。
二、基本公式1. 球体体积公式球体体积公式是数学中最基本的公式之一,其表达方式如下:V = 4/3πr³其中,V代表球体的体积,r代表球的半径,π约等于3.14159。
2. 球体的直径和半径关系球体的直径是通过球心的两个点,直径长等于半径的两倍。
即d = 2r。
3. 球面积公式球面积公式是求解球面表面积的重要公式,其表达方式如下:A = 4πr²其中,A代表球面的表面积,r代表球的半径,π约等于3.14159。
三、推导过程1. 推导球体体积公式为了更好地理解球体体积公式的推导过程,我们可以运用积分的方法进行推导。
首先,将球体沿x轴旋转一周,形成旋转曲面。
然后,将该旋转曲面划分成无穷多的小圆环。
通过计算每个小圆环的面积,并将其进行累加,即可求得球体体积。
2. 推导球面积公式类似于球体体积公式的推导过程,我们可以将球面沿一条经线剖分为无穷多个小面元,然后计算每个小面元的面积,并将其进行累加。
最终,就可以得到球面积公式。
四、解题技巧1. 分析题目要求在解题过程中,首先要仔细分析题目给出的条件和要求。
明确已知信息,确定需要求解的未知量,有助于选择适当的解题方法。
2. 应用公式灵活当遇到计算球体体积的题目时,可根据题目给出的已知条件,选择合适的体积公式计算。
同时,要熟练运用化简和换元等技巧,简化计算过程。
3. 结合实际情境在解题过程中,可以结合实际情境进行分析。
例如,计算某物体的体积时,可以通过给出的半径或直径进行换算,进一步帮助理解题目以及解题思路。
五、例题分析1. 一个半径为5cm的球体的体积是多少?解析:根据球体体积公式V = 4/3πr³,代入半径r=5cm,计算得V = 4/3π(5)³ ≈ 523.6cm³。
高考数学100热点题型精讲:极坐标与直角坐标的简单互换

【变式实践 3】
将下列点的极坐标与直角坐标进行互化,并判断在第几现象
4π
2
(1)(2, 3 ); (2)(2,3π) (3)(-2,2 3); (4)( 6,- 2
知识运用 3
将直线的极坐标与直角坐标的互换
【例 4】
(1)(2015 春•会宁县校级期中)化极坐标方程 ρ2cosθ﹣ρ=0 为直角坐标方程
A.2
B.
2 4+
9
C.
2 4+
9
D. 3
5.直线 = 和直线 sin( − ) = 1的位置关系(
) A. 垂直
B. 平行
C. 相交但不垂直 D.
重合
6.在极坐标系中,定点 A(2,0),点 B 在直线 ρcosθ+ρsinθ=0 上运动,当线段 AB 最短时,点 B 的极坐标为 . 7.在极坐标系中,曲线 C1 和 C2 的方程分别为 2 cos2 = sin 和 cos = 1,以极点 为平面直角坐标系的原点,极轴为 x 轴正半轴,建立平面直角坐标系,则曲线 C1 和
【知识运用】
知识运用 1
平面直角坐标系中的伸缩变换
类型一 根据变换 φ:xy′′==λμ··xy((λμ>>00))求出变化前或后的点或曲线方程
【例 1】(1).在同一平面直角坐标系中,已知伸缩变换 φ:x2′y′==3xy,. 求点
A13,-2经过 φ 变换所得的点 A′的坐标.
(2)(2015 秋•南关区校级月考)曲线 x2+y2=1 经过 φ: 新曲线的方程为 .
【圆与圆相交弦】(5) (2015·湖南长沙一模,12)在极坐标系中,已知两圆 C1: ρ=2cos θ和 C2:ρ=2sin θ,则过两圆圆心的直线的极坐标方程是________. 【解题知识提醒】 1、两点间距离公式:
高中数学各题型详细方法总结+100个核心考点全汇总!

高中数学各题型详细方法总结+100个核心考点全汇总!学好数学有三点需要强调:学习知识,把握题型,提取方法。
关于基础知识,就不过多一一列举,主要是通过具体实例,来让同学们感受一下学习数学的核心思想:不同题型对应不同方法;学习数学,就是一个归纳题型和解题方法的过程。
一般情况下,高考数学后几道大题分别是:三角函数,立体几何,数列,圆锥曲线,函数与导数。
每个题型都有对应的出题套路,每一种套路都有对应的解题方法。
三角函数这个题型有两种考法,大概10%~20%的概率考解三角形,80%~90%的概率考三角函数本身。
(一)解三角形不管题目是什么,作为被考察者,你要明白关于解三角形,你只学了三个公式——正弦定理,余弦定理和面积公式。
所以,解三角形的题目,求面积的话肯定用面积公式。
至于什么时候用正弦,什么时候用余弦,如果你不能迅速判断,都尝试一下也未尝不可。
(二)三角函数三角函数,套路一般是给出一个比较复杂的式子,问函数的定义域、值域、周期频率和单调性等问题。
解决方法就是首先利用“和差倍半”对式子进行化简,化简成掌握以上公式,关于题型见下图。
立体几何相比于前面的三角函数,立体几何题型要稍微复杂一些,可能会卡住一些人。
该题通常有2-3问,第一问求某条线的大小或证明某个线/面与另外一个线/面平行或垂直,最后一问求二面角。
这类题解题方法主要有两种,传统法和空间向量法,其中各有利弊。
(一)向量法:使用向量法的好处在于没有任何思维含量,肯定能解出最终答案。
缺点是计算量大,且容易出错。
应用空间向量法,首先应该建立空间直角坐标系。
建系结束后,根据已知条件可用向量确定每条直线。
其形式为AB=(a,b,c)然后进行后续证明与求解。
(二)传统法:学习立体几何章节,虽然学了很多性质定理和判定定理,但针对高考立体几何大题而言,解题方法基本是唯一的,除了上图6和8有两种解题方法以外,其他都是有唯一的方法。
所以,熟练掌握解题模型,拿到题目直接按照标准解法去求解便可。
高考数学常考的100个基础知识点

高考数学常考的100个基础知识点
一、数据处理
1、用直线和曲线表示简单的函数关系;
2、求方程的根,包括一元二次方程、一元三次方程;
3、极限的概念及求极限的方法;
4、利用大致数量关系求微分;
5、抽样定理及其推广;
二、几何
1、角的三种度数制;
2、角平分线的性质;
3、对称中心及其对称性;
4、多边形几何关系;
5、曲线的斜率;
6、空间几何关系;
7、证明的方法;
三、排列组合数
1、概念及其性质;
2、组合数的运算;
3、二项式定理及其推广;
4、抽屉原理;
5、幂集的运算;
四、计算
1、分数的运算;
2、两次方程的求解;
3、直角坐标系的使用;
4、根式的运算及其化简;
5、三次根式的求解;
6、不等式的解法;
7、指数函数及其运用;
五、三角函数
1、三角函数的基本性质;
2、正弦定理及其运用;
3、余弦定理及其换元;
4、正切定理及其反函数;
5、正余弦的平面坐标表示;
六、统计
1、概率的概念及性质;
2、离散随机变量的计算;
3、独立性及独立性的性质;
4、条件概率与期望;
5、相关与相关系数;
七、函数
1、函数的定义及其性质;
2、函数的图形表示;
3、函数的单调性;
4、函数的综合应用;
5、函数的最值及其导数;
八、数列
1、数列的极限及性质;
2、常用数列的求和;
3、等差、等比数列的性质;
4、数列的通项公式;。
高中数学基本知识点汇总

高中数学基本知识点汇总高中数学基本知识点汇总高中数学基本知识点:第一:函数与导数(1)三阶段:1)学习函数概念、图象、性质。
以指对函数为例,重点学习函数与反函数及单调性2)以三角函数为例,重点学习奇偶性与周期性3)学习函数极限、连续性、导数。
最终落在导数应用注:(文科)解析式选用多项式函数。
(理科)指、对、三角函数为载体选择、填空多考查图象、反函数、奇偶性、极限、连续性、导数的几何意义第二:数列:在高考中占重要地位(1)重点研究等差数列、等比数列,主要是通项公式及前n项和公式(2)通过比较抽象数列入手,进行严格的逻辑推证(3)通项与前n项和的重要关系注:选择、填空多突出函数与方程思想、数形结合、特殊与一般、有限与无限的考查。
第三:不等式:(1)学习不等式性质、简单不等式解法、不等式证明、不等式应用(2)删去无理不等式、保留二次不等式、分式不等式、含绝对值简单不等式、简单指对不等式,均值定理只考虑两个正数注:选择、填空多考查解不等式的同解变形、数形结合、特殊化思想、均值定理,解答题多考查解不等式、不等式证明、含参数不等式、与函数导数数列相结合(知识网络交汇)第四:三角函数同角公式由8个删为3个,删去余切诱导公式,删去半角公式、积化和差公式,删去反三角函数与简单三角方程绝大部分内容,只保留反正弦、反余弦、反正切意义与符号表示新增内容:平面向量、极限与导数作了替代突出考查三角函数图象与性质第五:立体几何新增空间向量方法,开拓了高考命题思路,删去圆柱、圆台。
只保留了球,删去了棱台,保留了棱柱、棱锥空间向量将几何元素数量化,显现解题优势第六:解析几何(1)着重考查解析几何基本思想,利用代数工具研究几何题目是解析几何基本特点和性质(3)在解题过程中计算占了很大比例,对运算能力有较高要求(4)曲线定义和性质是解题基础(5)突出考查函数与方程思想、数形结合、特殊与一般第七:概率与统计(1)在工农业和社会生活中有广泛应用(2)是重要的处理问题方法与重要数学工具之一(3)必修方面:随机事件的概率、等可能性事件的概率、互斥事件有一个发生的概率、相互独立事件概率、独立重复试验。
高考数学基础知识汇总

高考数学常用结论1.德摩根公式 ();()U U U U U U C A B C A C B C A B C A C B == .2U U A B A A B B A B C B C A =⇔=⇔⊆⇔⊆ U A C B ⇔=Φ U C A B R ⇔= 3. 若A={123,,n a a a a },则A的子集有2n 个,真子集有(2n -1)个,非空真子集有(2n-2)个4.二次函数的解析式的三种形式 ①一般式2()(0)f x ax bx c a =++≠;② 顶点式 2()()(0)f x a x h k a =-+≠;③零点式12()()()(0)f x a x x x x a =--≠.三次函数的解析式的三种形式①一般式32()(0)f x ax bx cx d a =+++≠ ②零点式123()()()()(0)f x a x x x x x x a =---≠ 5.设[]2121,,x x b a x x ≠∈⋅那么[]1212()()()0x x f x f x -->⇔[]1212()()0(),f x f x f x a b x x ->⇔-在上是增函数;[]1212()()()0x x f x f x --<⇔[]1212()()0(),f x f x f x a b x x -<⇔-在上是减函数.设函数)(x f y =在某个区间内可导,如果0)(>'x f ,则)(x f 为增函数;如果0)(<'x f ,则)(x f 为减函数. 6.函数()y f x =的图象的对称性:①函数()y f x =的图象关于直线x a =对称()()f a x f a x ⇔+=-(2)()f a x f x ⇔-= ②函数()y f x =的图象关于直2a b x +=对称()()f a x f b x ⇔+=-()()f a b x f x ⇔+-=.③函数()y f x =的图象关于点(,0)a 对称()(2)f x f a x ⇔=-- 函数()y f x =的图象关于点(,)a b 对称()2(2)f x b f a x ⇔=--7.两个函数图象的对称性:①函数()y f x =与函数()y f x =-的图象关于直线0x =(即y 轴)对称. ②函数()y f m x a =-与函数()y f b m x =-的图象关于直线2a b x m+=对称.特殊地: ()y f x a =-与函数()y f a x =-的图象关于直线x a =对称 ③函数()y f x =的图象关于直线x a =对称的解析式为(2)y f a x =- ④函数()y f x =的图象关于点(,0)a 对称的解析式为(2)y f a x =-- ⑤函数)(x f y =和)(1x fy -=的图象关于直线y=x 对称.8.分数指数幂mna=0,,a m n N *>∈,且1n >).1m nmnaa-=(0,,a m n N *>∈,且1n >).9. log (0,1,0)ba Nb a N a a N =⇔=>≠>.log log log a a a M N M N +=(0.1,0,0)a a M N >≠>> log log log a a aM M N N-=(0.1,0,0)a a M N >≠>>10.对数的换底公式 log log log m a m N N a=.推论 loglog mna an b b m=.对数恒等式log a NaN =(0,1a a >≠)11.11,1,2n nn s n a s s n -=⎧=⎨-≥⎩( 数列{}n a 的前n 项的和为12n n s a a a =+++ ).12.等差数列{}n a 的通项公式*11(1)()n a a n d dn a d n N =+-=+-∈;13.等差数列{}n a 的变通项公式d m n a a m n )(-+=对于等差数列{}n a ,若q p m n +=+,(m,n,p,q 为正整数)则q p m n a a a a +=+。
高考数学100个高频考点---4.23

高考数学100个高频考点1.集合的性质:①任何一个集合是它本身的子集,记为A A ⊆;②空集是任何集合的子集,记为A ⊆φ;③空集是任何非空集合的真子集;2.四种命题的形式及相互关系:原命题:若P 则q;逆命题:若q 则p;否命题:若┑P 则┑q;逆否命题:若┑q 则┑p。
①、原命题为真,它的逆命题不一定为真。
②、原命题为真,它的否命题不一定为真。
③、原命题为真,它的逆否命题一定为真。
3.函数的性质(1)定义域:(2)值域:(3)奇偶性:(在整个定义域内考虑)①定义:①偶函数:)()(x f x f =-,②奇函数:)()(x f x f -=-②判断方法步骤:a.求出定义域;b.判断定义域是否关于原点对称;c.求)(x f -;d.比较)()(x f x f 与-或)()(x f x f --与的关系。
(4)函数的单调性定义:对于函数f(x)的定义域I 内某个区间上的任意两个自变量的值x 1,x 2,⑴若当x 1<x 2时,都有f(x 1)<f(x 2),则说f(x)在这个区间上是增函数;⑵若当x 1<x 2时,都有f(x 1)>f(x 2),则说f(x)在这个区间上是减函数.4.二次函数的解析式的三种形式①一般式f (x )=ax 2+bx +c (a ≠0);②顶点式f (x )=a (x -h )2+k (a ≠0);③零点式f (x )=a (x -x 1)(x -x 2)(a ≠0)。
5.设x 1,x 2∈[a ,b ],x 1≠x 2那么⇔>--⇔>--0)()(0)]()()[(21212121x x x f x f x f x f x x f (x )在[a ,b ]上是增函数;⇔<--⇔<--0)()(0)]()()[(21212121x x x f x f x f x f x x f (x )在[a ,b ]上是减函数。
设函数y =f (x )在某个区间内可导,如果f ′(x )>0,则f (x )为增函数;如果f ′(x )<0,则f (x )为减函数。
千锤百炼-高考数学100个热点问题——第90炼 取球问题

第90炼 取球问题一、基础知识:在很多随机变量的题目中,常以“取球”作为故事背景,通过对“取球”提出不同的要求,来考察不同的模型,常见的模型及处理方式如下:1、独立重复试验模型:关键词“可放回的抽取”,即下一次的取球试验与上一次的相同。
2、超几何分布模型:关键词“不放回的抽取”3、与条件概率相关:此类问题通常包含一个抽球的规则,并一次次的抽取,要注意前一次的结果对后一步抽球的影响4、古典概型:要注意虽然题目中会说明“相同的”小球,但是为了能使用古典概型(保证基本事件为等可能事件),通常要将“相同的”小球视为“不同的”元素,在利用排列组合知识进行分子分母的计数。
5、数字问题:在小球上标注数字,所涉及的问题与数字相关(奇,偶,最大,最小等),在解决此类问题时,要将数字模型转化为“怎样取球”的问题,从而转化为前几个类型进行求解。
二、典型例题:例1:一袋中有6个黑球,4个白球(1)不放回地依次取出3个球,已知第一次取出的是白球,求第三次取到黑球的概率 (2)有放回地依次取出3个球,已知第一次取出的是白球,求第三次取到黑球的概率 (3)有放回的依次取出3个球,求取到白球个数X 的分布列,期望和方差(1)思路:因为是不放回的取球,所以后面取球的情况受到前面的影响,要使用条件概率相关公式进行计算。
第一次已经取到白球,所以剩下6个黑球,3个白球;若第二次取到黑球,则第三次取到黑球的概率为6598⋅,若第二次取到白球,则第三次取到黑球的概率为3698⋅,从而能够得到第三次取到黑球的概率解:设事件A 为“不放回取球,第一次取出白球时,第三次取到黑球”()65364829898723P A ∴=⋅+⋅== (2)思路:因为是有放回的取球,所以每次取球的结果互不影响,属于独立重复试验模型,所以第三次取球时依然是6个黑球,3个白球,取得黑球的概率为69解:设事件B 为“有放回取球,第一次取出白球时,第三次取到黑球”()23P B ∴=(3)思路:本问依然属于独立重复试验模型,X 的取值为0,1,2,3,则X 符合二项分布,即23,5XB ⎛⎫⎪⎝⎭,所以可通过二项分布的概率计算公式求得概率,得到分布列 解:X 的取值为0,1,2,3,依题意可得:23,5XB ⎛⎫ ⎪⎝⎭()30332705125P X C ⎛⎫∴=== ⎪⎝⎭ ()2133254155125P X C ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭ ()12233236255125P X C ⎛⎫⎛⎫=== ⎪⎪⎝⎭⎝⎭ ()3332835125P X C ⎛⎫=== ⎪⎝⎭23,5XB ⎛⎫ ⎪⎝⎭26355EX ∴=⋅= 231835525DX =⋅⋅= 例2:已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的3个红球和3个黑球,现从甲,乙两个盒内各任取2个球 (1)求取出的4个球中没有红球的概率 (2)求取出的4个球中恰有1个红球的概率(3)设ξ为取出的4个球中红球的个数,求ξ的分布列和数学期望思路:本题这三问的关键在于所取球中红球的个数,考虑红球个数来自于两个盒内拿出红球个数的总和,所以可将红球总数进行分配,从而得到每个盒中出红球的情况,进而计算出概率(1)设事件i A 为“甲盒中取出i 个红球”,事件j B 为“乙盒中取出j 个红球”则()()2213332246,i i j ji j C C C C P A P B C C --== 设事件A 为“4个球中没有红球”则()()()0202133300224633161510C C C C P A P A P B C C =⋅=⋅=⋅= (2)设事件B 为“4个球中恰有1个红球”()()()0211110213331333011022224646393326156155C C C C C C C C P B P A B P A B C C C C ∴=+=⋅+⋅=⋅+⋅= (3)ξ可取的值为0,1,2,3()()1010P P A ξ∴===()()215P P B ξ===()()()0220111113331333021122224646225C C C C C C C C P P A B P A B C C C C ξ==+=⋅+⋅= ()()11021333122246331361510C C C C P P A B C C ξ===⋅=⋅=ξ∴的分布列为:01231055102E ξ∴=⨯+⨯+⨯+⨯=例3:甲、乙两袋中各装有大小相同的小球9个,其中甲袋中红色、黑色、白色小球的个数分别为2、3、4,乙袋中红色、黑色、白色小球的个数均为3,某人用左右手分别从甲、乙两袋中取球.(1)若左右手各取一球,求两只手中所取的球颜色不同的概率;(2)若左右手依次各取两球,称同一手中两球颜色相同的取法为成功取法,记成功取法次数为随机变量X ,求X 的分布列和数学期望.解:(1)设事件A 为“两只手中所取的球颜色不同”,则A 为“两只手中所取的球颜色相同”()()2333432119999993P A P A ⎛⎫=-=-⋅+⋅+⋅= ⎪⎝⎭(2)X 可取的值为0,1,2左手取球成功的概率222234129518C C C P C ++==右手取球成功的概率22233322914C C C P C ++== ()511301118424P X ⎛⎫⎛⎫∴==-⋅-=⎪ ⎪⎝⎭⎝⎭ ()5151711118418418P X ⎛⎫⎛⎫==-⋅+⋅-= ⎪ ⎪⎝⎭⎝⎭()515218472P X ==⋅= X ∴的分布列为01224187236EX ∴=⨯+⨯+⨯= 例4:袋中装有若干个质地均匀大小相同的红球和白球,白球数量是红球数量的两倍,每次从袋中摸出一个球,然后放回,若累计3次摸到红球则停止摸球,否则继续摸球直到第5次摸球后结束(1)求摸球四次就停止的事件发生的概率(2)记摸到红球的次数为ξ,求随机变量ξ的分布列及其期望(1)思路:本题为有放回摸球,可理解为独立重复试验,如果摸球四次就停止,说明在这四次中一共摸到3次红球,且前三次有两次摸到红球,第四次又摸到红球。
2024年成人高考数学知识点

2024年成人高考数学知识点一、函数。
1. 函数的概念。
- 设A、B是非空的数集,如果按照某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数,记作y = f(x),x∈A。
其中,x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y值叫做函数值,函数值的集合{f(x)x∈A}叫做函数的值域。
- 例如,y = x²,定义域为R,当x = 1时,y = 1;当x=-1时,y = 1,对于定义域内的每一个x都有唯一的y与之对应。
2. 函数的性质。
- 单调性。
- 设函数y = f(x)的定义域为I,如果对于定义域I内的某个区间D内的任意两个自变量x₁,x₂,当x₁<x₂时,都有f(x₁)<f(x₂)(或f(x₁)>f(x₂)),那么就说函数y = f(x)在区间D上是增函数(或减函数)。
- 例如,y = 2x在R上是增函数,因为对于任意的x₁<x₂,都有2x₁<2x₂。
- 奇偶性。
- 对于函数y = f(x)的定义域内的任意一个x,如果f(-x)= - f(x),那么函数y = f(x)就叫做奇函数;如果f(-x)=f(x),那么函数y = f(x)就叫做偶函数。
- 例如,y = x³是奇函数,因为f(-x)=(-x)³=-x³ = - f(x);y = x²是偶函数,因为f(-x)=(-x)²=x²=f(x)。
二、数列。
1. 数列的概念。
- 按照一定次序排列的一列数称为数列,数列中的每一个数都叫做这个数列的项。
数列可以看作一个定义域为正整数集N*(或它的有限子集{1,2,3,…,n})的函数,当自变量从小到大依次取值时对应的一列函数值。
- 例如,数列1,3,5,7,…,通项公式为an = 2n - 1(n∈N*)。
高考数学基础知识大全(ppt 147页)

91、微软离破产永远只有18个月 ——世界首富比尔?盖茨
92、预防是解决危机的最好方法 ——英国危机管理专家迈克尔?里杰斯 特 93、21世纪,没有危机感是最大的危 机
——哈佛商学院教授理查德?帕斯卡尔 第十四章 奖励什么,就会得到什么 P223 管理者必须在工作与奖励之间建立恰 当的联 系。想 要什么 就应该 奖励什 么,奖 励什么 ,你就 会得到 什么, 有效的 奖励可 以引导 员工努 力工作 。
<<返回目录
<<返回目录
<<返回目录
<<返回目录
<<返回目录
要点3 立体几何初步
<<返回目录;<返回目录
<<返回目录
<<返回目录
要点4 平面解析几何初步
<<返回目录
<<返回目录
<<返回目录
<<返回目录
<<返回目录
<<返回目录
<<返回目录
<<返回目录
<<返回目录
94、奖励什么,就会得到什么 ——管理专家米契尔?拉伯福 95、我们宣布讲究实绩、注重实效, 却往往 奖励了 那些专 会做表 面文章 、投机 取巧的 人。 ——管理专家米契尔?拉伯福 96、不能搞平均主义,平均主义惩罚 表现好 的,鼓 励表现 差的, 得来的 只是一 支坏的 职工队 伍
——管理学者史蒂格 97、 不只奖励成功,而且奖励失败 ——通用电器公司总裁杰克?韦尔奇
98、无法评估,就无法管理 ——管理学家琼?玛格丽塔 99、你不能衡量它,就不能管理它 ——管理大师彼得?杜拉克 100、如果强调什么,你就检查什么“ 不耻最 后。”即 使慢, 驰而不 息,纵 令落后 ,纵令 失败, 但一定 可以达 到他所 向往的 目标。 ——鲁 迅 2、不经一翻彻骨寒,怎得梅花扑鼻香 。—— 宋帆 3、不要失去信心,只要坚持不懈,就 终会有 成果的 。—— 钱学森 4、常常是最后一把钥匙打开了门。— —彦语 5、成大事不在于力量的大小,而在于 能坚持 多久。 ——约 翰生 6、达到重要目标有两个途径——努力 及毅力 。努力 只有少 数人所 有,但 坚韧不 拔的毅 力则多 数人均 可实行 。—拿 破仑 7、点点滴滴的藏,集成了一大仓。— —德国 谚语 8、读不在三更五鼓,功只怕一曝十寒 。—— 郭沫若 9、告诉你使我达到目标的奥秘吧,我 惟一的 力量就 是我的 坚持精 神。— —巴斯 德 10、革命道德不是从天上掉下来的。 它是从 日常的 坚持不 懈的斗 争和锻 炼中发 展和巩 固起来 的,正 如玉石 越磨越 亮,黄 金越炼 越纯一 样。— —胡志 明 11、苟有恒,何必三更起五更眠;最 无益, 只怕一 日曝十 日寒。 ——毛 泽东 12、古今之成大事业、大学问者,必 经过三 种之境 界:“昨 夜西风 凋碧树 ,独上 高楼, 望尽天 涯路” ,此第 一境界 也;“衣 带渐宽 终不悔 ,为伊 消得人 憔悴” ,此第 三境界 也。— —王国 维 13、古人学问无遗力,少壮工夫老始 成。— —陆游 14、故天将降大任于是人也,必先苦 其心志 ,劳其 筋骨, 饿其体 肤,空 乏其身 ,行拂 乱其所 为,所 以动心 忍性, 增益其 所不能 。—— 孟轲 15、贵有恒,何必三更起五更眠。最 无益, 只怕一 日曝十 日寒。 ——毛 泽东 16、坚持对于勇气,正如轮子对于杠 杆,那 是支点 的永恒 更新。 ——[法]雨果 17、进锐退速。——孟珂《孟子》 18、精诚所至,金石为开。——蔡锷 19、涓滴之水终可以磨损大石,不是 由于它 力量强 大,而 是由于 昼夜不 舍的滴 坠。— —贝多 芬 20、科学的永恒性就在于坚持不懈地 寻求之 中,科 学就其 容量而 言,是 不枯竭 的,就 其目标 而言, 是永远 不可企 及的。 ——卡·冯·伯 尔 21、逆水行舟用力撑,一篙松劲退千 寻。— —董必 武 22、骐骥一跃,不能十步;驽马十驾 ,功在 不舍。 (骐骥 :俊马 。驽马 :跑不 快的马 。驾 ,马行一日为一驾。——先秦《荀子 ·劝学 》 ;你不检查,就等于不重视 ——IBM公司总裁郭士纳
2020高考数学100个必考知识点详解14 函数的切线问题

第14 函数的切线问题一、基础知识: (一)与切线相关的定义1、切线的定义:在曲线的某点A 附近取点B ,并使B 沿曲线不断接近A 。
这样直线AB 的极限位置就是曲线在点A 的切线。
(1)此为切线的确切定义,一方面在图像上可定性的理解为直线刚好与曲线相碰,另一方面也可理解为一个动态的过程,让切点A 附近的点向A 不断接近,当与A 距离非常小时,观察直线AB 是否稳定在一个位置上(2)判断一条直线是否为曲线的切线,不再能用公共点的个数来判定。
例如函数3y x =在()1,1--处的切线,与曲线有两个公共点。
(3)在定义中,点B 不断接近A 包含两个方向,A 点右边的点向左接近,左边的点向右接近,只有无论从哪个方向接近,直线AB 的极限位置唯一时,这个极限位置才能够成为在点A 处的切线。
对于一个函数,并不能保证在每一个点处均有切线。
例如y x =在()0,0处,通过观察图像可知,当0x =左边的点向其无限接近时,割线的极限位置为y x =-,而当0x =右边的点向其无限接近时,割线的极限位置为y x =,两个不同的方向极限位置不相同,故y x =在()0,0处不含切线(4)由于点B 沿函数曲线不断向A 接近,所以若()f x 在A 处有切线,那么必须在A 点及其附近有定义(包括左边与右边)2、切线与导数:设函数()y f x =上点()()00,,A x f x ()f x 在A 附近有定义且附近的点()()00,B x x f x x +∆+∆,则割线AB 斜率为: ()()()()()000000AB f x x f x f x x f x k x x x x +∆-+∆-==+∆-∆ 当B 无限接近A 时,即x ∆接近于零,∴直线AB 到达极限位置时的斜率表示为:()()000limx f x x f x k x∆→+∆-=∆,即切线斜率,由导数定义可知:()()()'0000lim x f x x f x k f x x∆→+∆-==∆。
高考数学常用公式及结论&会考复习必背知识点
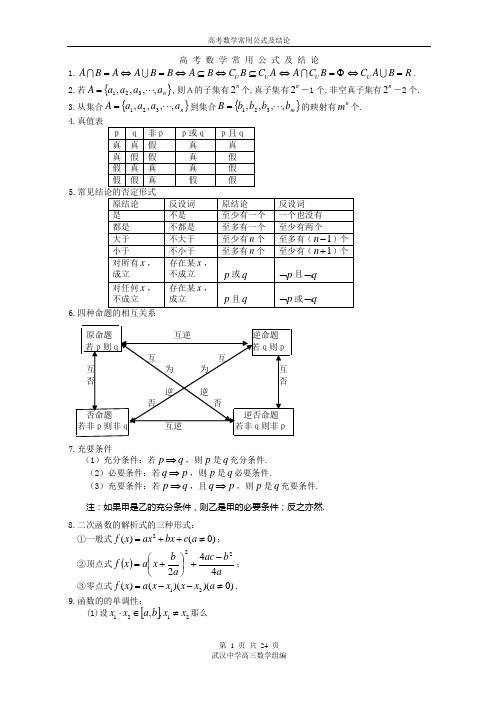
高 考 数 学 常 用 公 式 及 结 论1.U U AB A A B B A BC B C A =⇔=⇔⊆⇔⊆U A C B ⇔=ΦU C A B R ⇔=.2.若{}n a a a a A ,,,,321⋅⋅⋅=,则A的子集有2n 个,真子集有2n -1个,非空真子集有2n -2个.3.从集合{}n a a a a A ,,,,321⋅⋅⋅=到集合{}m b b b b B ,,,,321⋅⋅⋅=的映射有nm 个.4.真值表5.6.7.充要条件(1)充分条件:若p q ⇒,则p 是q 充分条件.(2)必要条件:若q p ⇒,则p 是q 必要条件.(3)充要条件:若p q ⇒,且q p ⇒,则p 是q 充要条件.注:如果甲是乙的充分条件,则乙是甲的必要条件;反之亦然. 8.二次函数的解析式的三种形式: ①一般式2()(0)f x ax bx c a =++≠;②顶点式()a b ac a b x a x f 44222-+⎪⎭⎫ ⎝⎛+=; ③零点式12()()()(0)f x a x x x x a =--≠.9.函数的的单调性:(1)设[]2121,,x x b a x x ≠∈⋅那么[]1212()()()0x x f x f x -->⇔[]b a x f x x x f x f ,)(0)()(2121在⇔>--上是增函数;[]1212()()()0x x f x f x --<⇔[]b a x f x x x f x f ,)(0)()(2121在⇔<--上是减函数. (2)设函数)(x f y =在某个区间内可导,如果0)(>'x f ,则)(x f 为增函数; 如果0)(<'x f ,则)(x f 为减函数.10.函数()y f x =的图象的对称性:①()y f x =的图象关于直线x a =对称()()f a x f a x ⇔+=-(2)()f a x f x ⇔-=;②()y f x =的图象关于直线2a bx +=对称()()f a x f b x ⇔+=-()()f a b x f x ⇔+-=;③()y f x =的图象关于点(,0)a 对称()()()()02=-++⇔--=⇔x a f x a f x a f x f ,()y f x =的图象关于点(,)a b 对称⇔()()()()b x a f x a f x a f b x f 222=-++⇔--=.11.两个函数的图象的对称性:①函数()y f x =与函数()y f x =-的图象关于直线0x =(即y 轴)对称; ②函数()y f x a =-与函数()y f a x =-的图象关于直线x a =对称; ③函数()y f x =的图象关于直线x a =对称的解析式为(2)y f a x =-; ④函数()y f x =的图象关于点(,0)a 对称的解析式为(2)y f a x =--; ⑤函数)(x f y =和函数)(1x fy -=的图象关于直线x y =对称.12.奇偶函数的图象特征奇函数的图象关于原点对称,偶函数的图象关于y 轴对称;反过来,如果一个函数的图象关于原点对称,那么这个函数是奇函数;如果一个函数的图象关于y 轴对称,那么这个函数是偶函数.13.多项式函数110()n n n n P x a x a x a --=+++的奇偶性多项式函数()P x 是奇函数⇔()P x 的偶次项(即奇数项)的系数全为零. 多项式函数()P x 是偶函数⇔()P x 的奇次项(即偶数项)的系数全为零.14.若将函数)(x f y =的图象右移a 、上移b 个单位,得到函数b a x f y +-=)(的图象;若将曲线0),(=y x f 的图象右移a 、上移b 个单位,得到曲线0),(=--b y a x f 的图象. 15.几个常见的函数方程(1)正比例函数()f x cx =,()()(),(1)f x y f x f y f c +=+=. (2)指数函数()xf x a =,()()(),(1)0f x y f x f y f a +==≠.(3)对数函数()log a f x x =,()()(),()1(0,1)f xy f x f y f a a a =+=>≠.(4)幂函数()f x x α=,'()()(),(1)f xy f x f y f α==.(5)余弦函数()cos f x x =,正弦函数()sin g x x =,()()()()()f x y f x f y g x g y -=+,()(0)1,lim1x g x f x→==. 16.几个函数方程的周期(约定a>0)(1))()(a x f x f +=,则)(x f 的周期T=a ;(2)0)()(=+=a x f x f ,或)0)(()(1)(≠=+x f x f a x f , 或1()()f x a f x +=-(()0)f x ≠,或[]1(),(()0,1)2f x a f x =+∈,则)(x f 的周期T=2a ;(3))0)(()(11)(≠+-=x f a x f x f ,则)(x f 的周期T=3a ;(4))()(1)()()(212121x f x f x f x f x x f -+=+且1212()1(()()1,0||2)f a f x f x x x a =⋅≠<-<,则)(x f 的周期T=4a ;(5)()()(2)(3)(4)f x f x a f x a f x a f x a +++++++()()(2)(3)(4)f x f x a f x a f x a f x a =++++,则)(x f 的周期T=5a ; (6))()()(a x f x f a x f +-=+,则)(x f 的周期T=6a.17.分数指数幂:m na=1m nm naa-=(以上0,,a m n N *>∈,且1n >).18.①b N N a a b=⇔=log ; ②()N M MN a a a log log log +=;③N M N M a a alog log log -=; ④log log m n a a nb b m=. 19.对数的换底公式:log log log m a m N N a=.对数恒等式:log a Na N =.20.数列{}n a 的前n 项和为12n n s a a a =+++,则11,1,2n n n s n a s s n -=⎧=⎨-≥⎩.21.①等差数列{}n a 的通项公式:()d n a a n 11-+=,或d m n a a m n )(-+=mn a a d mn --=⇔.②前n 项和公式: 1()2n n n a a s +=1(1)2n n na d -=+211()22d n a d n =+-. 22.对于等差数列{}n a ,若q p m n +=+(m 、n 、p 、q 为正整数),则q p m n a a a a +=+.23.若数列{}n a 是等差数列,n S 是其前n 项和,*N k ∈,那么k S ,k k S S -2,k k S S 23-成等差数列,其公差d k D 2=,如下图所示:kkk kk S S S k k S S k k k a a a a a a a a 3232k31221S 321-+-+++++++++++. 24.数列{}n a 是等差数列⇔n a kn b =+;数列{}n a 是等差数列⇔n S =2An Bn +.25.设数列{}n a 是等差数列,奇S 是奇数项的和,偶S 是偶数项的和,n S 是前n 项的和,则 ①前n 项的和偶奇S S S n +=; ②当n 为偶数时,d 2nS =-奇偶S ,其中d 为公差; ③当n 为奇数时,则中偶奇a S =-S ,中奇a 21n S +=,中偶a 21n S -=,11S S -+=n n 偶奇,n =-+=-偶奇偶奇偶奇S S S S S S S n(其中中a 是等差数列的中间一项)26.若等差数列{}n a 和{}n b 的前12-n 项的和分别为12-n S 和 12-n T ,则1212--=n n n n T S b a .27.①等比数列{}n a 的通项公式:nn n q qa qa a ⋅==-111;或m n m n m n m n a a q q a a =⇔=--.②前n 项和公式:11(1),11,1n n a q q s q na q ⎧-≠⎪=-⎨⎪=⎩,或11,11,1n n a a qq q s na q -⎧≠⎪-=⎨⎪=⎩.28.对于等比数列{}n a ,若v u m n +=+(n 、m 、u 、v 为正整数),则v u m n a a a a ⋅=⋅. 29.数列{}n a 是等比数列,n S 是其前n 项的和,*N k ∈,那么k S ,k k S S -2,k k S S 23-成等比数列,其公比为kq Q =.30.分期付款(按揭贷款)每次还款(1)(1)1nn ab b x b +=+-元(贷款a 元,n 次还清,每期利率为b ).31.裂项法:①()11111+-=+n n n n ; ②()()⎪⎭⎫ ⎝⎛+--⋅=+-1211212112121n n n n ;③()11b a b a ba --=+ ;④()()! 11! 1! 1+-=+n n n n .32.常见三角不等式 (1)若(0,)2x π∈,则sin tan x x x <<. (2) 若(0,)2x π∈,则1sin cos x x <+≤(3) |sin ||cos |1x x +≥.33.同角三角函数的基本关系式:①22sin cos 1θθ+=,αα22sec tan 1=+,αα22csc cot 1=+; ②tan θ=θθcos sin ; ③tan 1cot θθ⋅=. 34.正弦、余弦的诱导公式:212(1)sin ,sin()2(1)s ,n n n n co n απαα-⎧-⎪+=⎨⎪-⎩为偶数为奇数;212(1)s ,s()2(1)sin ,nn co n n co n απαα+⎧-⎪+=⎨⎪-⎩为偶数为奇数. 即:“奇变偶不变,符号看象限”.如απαsin 2cos -=⎪⎭⎫⎝⎛+,()ααπcos cos -=-. 35.和角与差角公式①sin()sin cos cos sin αβαβαβ±=±;cos()cos cos sin sin αβαβαβ±=;tan tan tan()1tan tan αβαβαβ±±=.②22sin()sin()sin sin αβαβαβ+-=-;22cos()cos()cos sin αβαβαβ+-=-. ③sin cos a b αα+)αϕ+(其中,辅助角ϕ所在象限由点(,)a b 所在的象限决定,tan baϕ=). 36.二倍角公式:①αααcos sin 22sin =.②2222cos 2cos sin 2cos 112sin ααααα=-=-=-(升幂公式).221cos 21cos 2cos ,sin 22αααα+-==(降幂公式). 37.万能公式:22tan sin 21tan ααα=+;221tan cos 21tan ααα-=+;22tan tan 21tan ααα=-(正切倍角公式). 38.半角公式:sin 1cos tan 21cos sin ααααα-==+. 39.三函数的周期公式:①函数sin()y A x ωϕ=+及cos()y A x ωϕ=+的周期ωπ2=T (A 、ω、ϕ为常数,且A ≠0).②函数()φω+=x A y tan 的周期ωπ=T (A 、ω、ϕ为常数,且A ≠0). 40.sin y x =的单调递增区间为2,222k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦,单调递减区间为32,222k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦,对称轴为()2x k k Z ππ=+∈,对称中心为(),0k π()k Z ∈. 41.cos y x =的单调递增区间为[]2,2k k k Z πππ-∈,单调递减区间为[]2,2k k k Z πππ+∈,对称轴为()x k k Z π=∈,对称中心为,02k ππ⎛⎫+ ⎪⎝⎭()k Z ∈. 42.tan y x =的单调递增区间为,22k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭,对称中心为⎪⎭⎫⎝⎛0,2πk ()Z k ∈. 43.三角函数变换:①相位变换:x y sin =的图象()()−−−−−−−−−→−<>个单位平移或向右向左φφφ00()φ+=x y sin 的图象;②周期变换:x y sin =的图象()()−−−−−−−−−−−−→−><<倍到原来的或缩短横坐标伸长ωωω1110x y ωsin =的图象; ③振幅变换:x y sin =的图象()()−−−−−−−−−−−→−<<>倍到原来的或缩短纵坐标伸长A A A 101x A y sin =的图象.44.①正弦定理 2sin sin sin a b cR A B C ===(R 为ABC ∆的外接圆的半径); ②余弦定理2222cos a b c bc A =+-;2222cos b c a ca B =+-;2222cos c a b ab C =+-.45.三角形面积公式:①111222a b c S ah bh ch ===(a b c h h h 、、分别表示a 、b 、c 边上的高);②111sin sin sin 222S ab C bc A ca B ===.46.在△ABC 中,有①()222C A BA B C C A B πππ+++=⇔=-+⇔=-222()C A B π⇔=-+; ②B A b a sin sin >⇔>(注意是在ABC ∆中).47.平面上两点间的距离公式:,A B d =A 11(,)x y ,B 22(,)x y . 48.向量的平行与垂直: 设a =11(,)x y ,b =22(,)x y ,且b ≠0,则①a ∥b ⇔b =λa 12210x y x y ⇔-=;② a ⊥b (a ≠0)⇔a ·b =012120x x y y ⇔+=.49.线段的定比分点公式:设111(,)P x y ,222(,)P x y ,(,)P x y 是线段12P P 的分点,λ是实数,且12PP PP λ=,则121211x x x y y y λλλλ+⎧=⎪⎪+⎨+⎪=⎪+⎩⇔121OP OP OP λλ+=+⇔12(1)OP tOP t OP =+-(其中11t λ=+). 50.若OA xOB yOB =+,则A 、B 、C 共线的充要条件是1=+y x .51.三角形的重心坐标公式: △ABC 三个顶点的坐标分别为11A(x ,y )、22B(x ,y )、33C(x ,y ),则其重心的坐标是123123(,)33x x x y y y G ++++. 52.①点的平移公式 ''''x x h x x h y y k y y k⎧⎧=+=-⎪⎪⇔⎨⎨=+=-⎪⎪⎩⎩''OP OP PP ⇔=+ (图形F 上的任意一点P(x ,y)在平移后的图形'F 上的对应点为'''(,)P x y ,且'PP 的坐标为(,)h k ); ②函数()x f y =按向量()k h a ,=平移后的解析式为()h x f k y -=-. 53.“按向量平移”的几个结论(1)点(,)P x y 按向量a =(,)h k 平移后得到点'(,)P x h y k ++.(2) 函数()y f x =的图象C 按向量a =(,)h k 平移后得到图象'C ,则'C 的函数解析式为()y f x h k =-+. (3) 图象'C 按向量a =(,)h k 平移后得到图象C ,若C 的解析式()y f x =,则'C 的函数解析式为()y f x h k =+-.(4)曲线C :(,)0f x y =按向量a =(,)h k 平移后得到图象'C ,则'C 的方程为(,)0f x h y k --=.(5) 向量m =(,)x y 按向量a =(,)h k 平移后得到的向量仍然为m =(,)x y .54. 三角形五“心”向量形式的充要条件设O 为ABC ∆所在平面上一点,角,,A B C 所对边长分别为,,a b c ,则(1)O 为ABC ∆的外心222OA OB OC ⇔==. (2)O 为ABC ∆的重心0OA OB OC ⇔++=.(3)O 为ABC ∆的垂心OA OB OB OC OC OA ⇔⋅=⋅=⋅. (4)O 为ABC ∆的内心0aOA bOB cOC ⇔++=. (5)O 为ABC ∆的A ∠的旁心aOA bOB cOC ⇔=+. 55.常用不等式:(1),a b R ∈⇒222a b ab +≥222b a ab +≤⇔(当且仅当a =b 时取“=”号).(2),a b R +∈⇒2a b +≥22⎪⎭⎫⎝⎛+≤⇔b a ab (当且仅当a =b 时取“=”号). (3) abc c b a 3333≥++⇔33abc c b a ≥++(当且仅当c b a ==时取“=”号).(4)b a b a b a +≤±≤-,(注意等号成立的条件).(5)10,0)112a b a b a b+≤≤≤>>+.(6)柯西不等式:22222()()(),,,,.a b c d ac bd a b c d R ++≥+∈56.极值定理:已知y x ,都是正数,则有(1)如果积xy 是定值p ,那么当y x =时和y x +有最小值p 2; (2)如果和y x +是定值s ,那么当y x =时积xy 有最大值241s . 57.解一元二次不等式20(0)ax bx c ++><或:若0>a ,则对于解集不是全集或空集时,对应的解集为“大两边,小中间”.如:当21x x <,()()21210x x x x x x x <<⇔<--;()()12210x x x x x x x x <>⇔>--或.58.含有绝对值的不等式:当0>a 时,有①a x a a x a x <<-⇔<⇔<22;②22x a x a x a >⇔>⇔>或x a <-.59.分式不等式: (1)()()()()00>⋅⇔>x g x f x g x f ; (2)()()()()00<⋅⇔<x g x f x g x f ; (3)()()()()()⎩⎨⎧≠≥⋅⇔≥000x g x g x f x g x f ; (4)()()()()()⎩⎨⎧≠≤⋅⇔≤000x g x g x f x g x f . 60.指数不等式与对数不等式 (1)当1a >时,()()()()f x g x aa f x g x >⇔>;()0log ()log ()()0()()a a f x f x g x g x f x g x >⎧⎪>⇔>⎨⎪>⎩.(2)当01a <<时,()()()()f x g x aa f x g x >⇔<;()0log ()log ()()0()()a a f x f x g x g x f x g x >⎧⎪>⇔>⎨⎪<⎩.61.斜率公式:2121y y k x x -=-,其中111(,)P x y 、222(,)P x y .直线的方向向量()b a v ,=,则直线的斜率为k =(0)ba a≠. 62.直线方程的五种形式(1)点斜式:11()y y k x x -=- (直线l 过点111(,)P x y ,且斜率为k ). (2)斜截式:y kx b =+(b 为直线l 在y 轴上的截距). (3)两点式:112121y y x x y y x x --=--(111(,)P x y 、222(,)P x y 12x x ≠,12y y ≠).(4)截距式:1=+bya x (其中a 、b 分别为直线在x 轴、y 轴上的截距,且0,0≠≠b a ). (5)一般式:0Ax By C ++=(其中A 、B 不同时为0).63.两条直线的平行和垂直(1)若111:l y k x b =+,222:l y k x b =+,则① 1l ∥2l 21k k =⇔,21b b ≠; ②12121l l k k ⊥⇔=-. (2)若1111:0l A x B y C ++=,2222:0l A x B y C ++=,则① 0//122121=-⇔B A B A l l 且01221≠-C A C A ;②1212120l l A A B B ⊥⇔+=. 64.①夹角公式:2121tan ||1k k k k α-=+.(111:l y k x b =+,222:l y k x b =+,121k k ≠-);(注意以下两种特殊情形下的夹角:①12l l ⊥,②1l 或2l 的斜率不存在). ②到角公式:直线l 1到l 2的角是2121tan 1k k k k α-=+(111:l y k x b =+,222:l y k x b =+,121k k ≠-). 65.点到直线的距离d =(点00(,)P x y ,直线l :0Ax By C ++=).66.两条平行线间的距离:若直线0:11=++C By Ax l ;0:22=++C By Ax l ,则d =.67. 0Ax By C ++>或0<所表示的平面区域设直线:0l Ax By C ++=,则0Ax By C ++>或0<所表示的平面区域是:若0B ≠,当B 与Ax By C ++同号时,表示直线l 的上方的区域;当B 与Ax By C ++异号时,表示直线l 的下方的区域.简言之,同号在上,异号在下.若0B =,当A 与Ax By C ++同号时,表示直线l 的右方的区域;当A 与Ax By C ++异号时,表示直线l 的左方的区域. 简言之,同号在右,异号在左. 68. 111222()()0A x B y C A x B y C ++++>或0<所表示的平面区域设曲线111222:()()0C A x B y C A x B y C ++++=(12120A A B B ≠),则111222()()0A x B y C A x B y C ++++>或0<所表示的平面区域是: 111222()()0A x B y C A x B y C ++++>所表示的平面区域上下两部分; 111222()()0A x B y C A x B y C ++++<所表示的平面区域上下两部分.69.圆的方程的四种形式(1)圆的标准方程:222()()x a y b r -+-=.(2)圆的一般方程:220x y Dx Ey F ++++=(224D E F +->0).(3)圆的参数方程:cos sin x a r y b r θθ=+⎧⎨=+⎩.(4)圆的直径式方程:1212()()()()0x x x x y y y y --+--=(圆的直径的端点是11(,)A x y 、22(,)B x y ).70.圆中有关重要结论:(1)若P(0x ,0y )是圆222x y r +=上的点,则过点P(0x ,0y )的切线方程为200xx yy r +=.(2)若P(0x ,0y )是圆222()()x a y b r -+-=上的点,则过点P(0x ,0y )的切线方程为200()()()()x a x a y b y b r --+--=.(3)若P(0x ,0y )是圆222x y r +=外一点,由P(0x ,0y )向圆引两条切线, 切点分别为A 、B则直线AB 的方程为200xx yy r +=.(4)若P(0x ,0y )是圆222()()x a y b r -+-=外一点, 由P(0x ,0y )向圆引两条切线, 切点分别为A 、B ,则直线AB 的方程为200()()()()x a x a y b y b r --+--=.71.圆的切线方程(1)已知圆220x y Dx Ey F ++++=.①若已知切点00(,)x y 在圆上,则切线只有一条,其方程是0000()()022D x xE y y x x y yF ++++++=. 当00(,)x y 圆外时, 0000()()022D x xE y y x x y yF ++++++=表示过两个切点的切点弦方程.②过圆外一点的切线方程可设为00()y y k x x -=-,再利用相切条件求k ,这时必有两条切线,注意不要漏掉平行于y 轴的切线.③斜率为k 的切线方程可设为y kx b =+,再利用相切条件求b ,必有两条切线.(2)已知圆222x y r +=.①过圆上的000(,)P x y 点的切线方程为200x x y y r +=;②斜率为k 的圆的切线方程为y kx =±72.椭圆22221(0)x y a b a b +=>>的参数方程是cos sin x a y b θθ=⎧⎨=⎩.73.(1)椭圆22221(0)x y a b a b +=>>的准线方程为2a x c =±,焦半径公式p ex a PF ±=;(2)椭圆22221(0)x y a b b a +=>>的准线方程为2a y c =±,焦半径公式p ey a PF ±=.74.(1)椭圆22221(0)x y a b a b +=>>的通径(过焦点且垂直于对称轴的弦)长为22b a ;(2) 双曲线22221(0,0)x y a b a b -=>>的通径(过焦点且垂直于对称轴的弦)长为22b a.75. 椭圆的切线方程(1)椭圆22221(0)x y a b a b +=>>上一点00(,)P x y 处的切线方程是00221x x y ya b +=.(2)过椭圆22221(0)x y a b a b+=>>外一点00(,)P x y 所引两条切线的切点弦方程是00221x x y ya b+=. (3)椭圆22221(0)x y a b a b +=>>与直线0Ax By C ++=相切的条件是22222A aB b c +=.76.(1)双曲线22221(0,0)x y a b a b -=>>的准线方程为2a x c =±,焦半径公式p ex a PF -=;(2)双曲线22221(0,0)x y a b b a -=>>的准线方程为2a y c =±,焦半径公式p ey a PF -=.77.(1)双曲线22221(0,0)x y a b a b -=>>的渐近线方程为by x a =±;(2)双曲线22221(0,0)x y a b b a -=>>的渐近线方程为ay x b=±.78. 双曲线的切线方程(1)双曲线22221(0,0)x y a b a b -=>>上一点00(,)P x y 处的切线方程是00221x x y ya b-=.(2)过双曲线22221(0,0)x y a b a b-=>>外一点00(,)P x y 所引两条切线的切点弦方程是00221x x y ya b-=. (3)双曲线22221(0,0)x y a b a b-=>>与直线0Ax By C ++=相切的条件是22222A a B b c -=.79.(1)P 是椭圆22221(0)x y a b a b+=>>上一点,F 1、F 2是它的两个焦点,∠F 1P F 2=θ,则△P F 1 F 2的面积=2tan2b θ.(2)P 是双曲线22221(0,0)x y a b a b-=>>上一点,F 1、F 2是它的两个焦点,∠F 1P F 2=θ,则△P F 1 F 2的面积=2cot2b θ.80.抛物线px y 22=上的动点()00,y x P 可设为P ),2(020y py 或)2,2(2pt pt P .81.(1)P(0x ,0y )是抛物线px y 22=上的一点,F 是它的焦点,则20p x PF +=;(2)抛物线px y 22=的焦点弦长22sin p l θ=,其中θ是焦点弦与x 轴的夹角; (3) 抛物线px y 22=的通径长为p 2.82. 抛物线的切线方程(1)抛物线px y 22=上一点00(,)P x y 处的切线方程是00()y y p x x =+.(2)过抛物线px y 22=外一点00(,)P x y 所引两条切线的切点弦方程是00()y y p x x =+.(3)抛物线22(0)y px p =>与直线0Ax By C ++=相切的条件是22pB AC =. 83.直线与圆锥曲线相交的弦长公式:若弦端点为A ),(),,(2211y x B y x ,则AB =或2211k x x AB +-=, 或22111ky y AB +-=. 84.圆锥曲线(,)0F x y =关于点00(,)P x y 成中心对称的曲线是00(2-,2)0F x x y y -=. 85.圆锥曲线的两类对称问题(1)曲线(,)0F x y =关于点00(,)P x y 成中心对称的曲线是00(2-,2)0F x x y y -=. (2)曲线(,)0F x y =关于直线0Ax By C ++=成轴对称的曲线是:22222()2()(,)0A Ax By C B Ax By C F x y A B A B ++++--=++.86.“四线”一方程对于一般的二次曲线220Ax Bxy Cy Dx Ey F +++++=,用0x x 代2x ,用0y y 代2y ,用002x y xy +代xy ,用02x x +代x ,用02y y+代y 即得方程 0000000222x y xy x x y yAx x B Cy y D E F ++++⋅++⋅+⋅+=,曲线的切线,切点弦,中点弦,弦中点方程均是此方程得到.87.共线向量定理:对空间任意两个向量a 、b (b ≠0),有a ∥b ⇔存在实数λ使a =λb . 88.对空间任一点O 和不共线的三点A 、B 、C ,满足OP xOA yOB zOC =++, 则四点P 、A 、B 、C 共面⇔1x y z ++=. 89.空间两个向量的夹角公式:232221232221332211b b b a a a b a b a b a ++⋅++++=,其中度()321,,a a a a =,()321,,b b b b =.90.直线AB 与平面α所成的角:==sin β,故=β,其中m 为平面α的法向量.91.锐二面角βα--l 的平面角:cos =θ,故=θ或-=πθ,其中m 、n 为平面α、β的法向量.92.空间两点间的距离公式:若()()222111,,x B ,,z y z y x A ,则()()()212212212,z z y y x x d B A -+-+-=.*93.点Q 到直线l 的距离:h =,点P 在直线l 上,直线l 的方向向量PA a =,向量PQ b =.94.点B 到平面α的距离:d =,n 为平面α的法向量,AB 是面α的一条斜线,α∈A .95. (1)设直线OA 为平面α的斜线,其在平面内的射影为OB ,OA 与OB 所成的角为1θ,OC 在平面α内,且与OB 所成的角为2θ,与OA 所成的角为θ,则12cos cos cos θθθ=. (2)若经过BOC ∠的顶点的直线OA 与BOC ∠的两边OB 、OC 所在的角相等,则OA 在BOC ∠所在平面上的射影为BOC ∠的角平分线;反之也成立.96. 面积射影定理:'cos S S θ=(平面多边形及其射影的面积分别是S 、'S ,它们所在平面所成锐二面角的为θ). 97.体积公式:Sh V 31=锥;Sh V =柱. 98.棱锥的平行截面的性质如果棱锥被平行于底面的平面所截,那么所得的截面与底面相似,截面面积与底面面积的比等于顶点到截面距离与棱锥高的平方比(对应角相等,对应边对应成比例的多边形是相似多边形,相似多边形面积的比等于对应边的比的平方);相应小棱锥与小棱锥的侧面积的比等于顶点到截面距离与棱锥高的平方比. 99. 球的半径是R ,则其体积是343V R π=,其表面积是24S R π=. 100.球的组合体(1)球与长方体的组合体:长方体的外接球的直径是长方体的体对角线长. (2)球与正方体的组合体:正方体的内切球的直径是正方体的棱长, 正方体的棱切球的直径是正方体的面对角线长, 正方体的外接球的直径是正方体的体对角线长. (3) 球与正四面体的组合体:棱长为a,. 101.分类计数原理:12n N m m m =+++.分步计数原理:12n N m m m =⨯⨯⨯.102.排列数公式:mn A =)1()1(+--m n n n =!!)(m n n -(n ,m ∈N *,且m n ≤).103.排列恒等式:①1(1)m m n n A n m A -=-+; ②1m mn n n A A n m-=-; ③11m m n n A nA --=;④11n n n n n n nA A A ++=-; ⑤11m m m n n n A A mA -+=+.104.组合数公式:m nC =m n m mA A =m m n n n ⨯⨯⨯+-- 21)1()1(=!!!)(m n m n -⋅(n ,m ∈N *,且m n ≤).105.组合数的性质:①mn C =mn n C - ;②m n C +1-m nC =m n C 1+;③11k k n n kC nC --=.106.组合恒等式:(1)11mm n n n m C C m --+=;(2)1m m n n n C C n m -=-;(3)11mm nn n C C m--=; (4)∑=nr r nC=n2;(5)1121++++=++++r n r n r r r r r r C C C C C .(6)nn n r n n n n C C C C C 2210=++++++ . (7)14205312-+++=+++n n n n n n n C C C C C C . (8)1321232-=++++n n n n n n n nC C C C . (9)rn m r n r m n r m n r m C C C C C C C +-=+++0110 . (10)nn n n n n n C C C C C 22222120)()()()(=++++ . 107.排列数与组合数的关系是:m mn n A m C =⋅!.108.单条件排列以下各条的大前提是从n 个元素中取m 个元素的排列. (1)“在位”与“不在位”①某(特)元必在某位有11--m n A 种;②某(特)元不在某位有11---m n m n A A (补集思想)1111---=m n n A A (着眼位置)11111----+=m n m m n A A A (着眼元素)种.(2)紧贴与插空(即相邻与不相邻)①定位紧贴:)(n m k k ≤≤个元在固定位的排列有km k n kk A A --种.②浮动紧贴:n 个元素的全排列把k 个元排在一起的排法有kk k n k n A A 11+-+-种.注:此类问题常用捆绑法;③插空:两组元素分别有k 、h 个(1+≤h k ),把它们合在一起来作全排列,k 个的一组互不能挨近的所有排列数有kh hh A A 1+种.(3)两组元素各相同的插空m 个大球n 个小球排成一列,小球必分开,问有多少种排法?当1+>m n 时,无解;当1+≤m n 时,有n m n nn m C A A 11++=种排法.(4)两组相同元素的排列:两组元素有m 个和n 个,各组元素分别相同的排列数为nn m C +. 109.分配问题(1)(平均分组有归属问题)将相异的m 、n 个物件等分给m 个人,各得n 件,其分配方法数共有mnn nn nn mn nn mn nmn n mn C C C C C N )!()!(22=⋅⋅⋅⋅⋅=-- . (2)(平均分组无归属问题)将相异的m ·n 个物体等分为无记号或无顺序的m 堆,其分配方法数共有mn nn n n n mn n n mn n mn n m mn m C C C C C N )!(!)!(!...22=⋅⋅⋅⋅=--. (3)(非平均分组有归属问题)将相异的)12m P(P=n +n ++n 个物体分给m 个人,物件必须被分完,分别得到1n ,2n ,…,m n 件,且1n ,2n ,…,m n 这m 个数彼此不相等,则其分配方法数共有!!...!!!! (212)11m n n n n p n p n n n m p m C C C N m m =⋅⋅=-.(4)(非完全平均分组有归属问题)将相异的)12m P(P=n +n ++n 个物体分给m 个人,物件必须被分完,分别得到1n ,2n ,…,m n 件,且1n ,2n ,…,m n 这m 个数中分别有a 、b 、c 、…个相等,则其分配方法数有!...!!!...211c b a m C C C N m m n n n n p n p ⋅⋅=- 12!!!!...!(!!!...)m p m n n n a b c =.(5)(非平均分组无归属问题)将相异的)12m P(P=n +n ++n 个物体分为任意的1n ,2n ,…,m n 件无记号的m 堆,且1n ,2n ,…,m n 这m 个数彼此不相等,则其分配方法数有!!...!!21m n n n p N =.(6)(非完全平均分组无归属问题)将相异的)12m P(P=n +n ++n 个物体分为任意的1n ,2n ,…,m n 件无记号的m 堆,且1n ,2n ,…,m n 这m 个数中分别有a 、b 、c 、…个相等,则其分配方法数有!...)!!(!!...!!21c b a n n n p N m =.(7)(限定分组有归属问题)将相异的p (2m p n n n =1+++)个物体分给甲、乙、丙,……等m 个人,物体必须被分完,如果指定甲得1n 件,乙得2n 件,丙得3n 件,…时,则无论1n ,2n ,…,m n 等m 个数是否全相异或不全相异其分配方法数恒有!!...!! (212)11m n n n n p n p n n n p C C C N m m =⋅=-.110.“错位问题”及其推广贝努利装错笺问题:信n 封信与n 个信封全部错位的组合数为:1111()![(1)]2!3!4!!n f n n n =-+-+-. 推广: n 个元素与n 个位置,其中至少有m 个元素错位的不同组合总数为1234(,)!(1)!(2)!(3)!(4)!(1)()!(1)()!m m m m ppmm mmf n m n C n C n C n C n C n p C n m =--+---+--+--++--12341224![1(1)(1)]p m pmm m m mmmp m n n n n nnC C C C C C n A A A A A A =-+-+-+-++-.111.二项式定理:nn n r r n r n n n n n n n n b C b a C b a C b a C a C b a ++++++=+--- 222110)( ;二项展开式的通项公式:rr n r n r b a C T -+=1)210(n r ,,, =.112.等可能性事件的概率:()mP A n=.(一次试验共有n 个结果等可能的出现,事件A 包含其中m 个结果)113.①互斥事件A 、B 有一个发生的概率:()()()B P A P B A P +=+;n 个互斥事件中有一个发生的概率:()()()()n n A P A P A P A A A P +⋅⋅⋅++=+⋅⋅⋅++2121; ②A 、B 是两个任意事件,则()()()B A P B A P B A P ⋅-=+-=+11.114.相互独立事件A 、B 同时发生的概率:()()()B P A P B A P ⋅=⋅;n 个相互独立事件同时发生的概率:()()()()n n A P A P A P A A A P ⋅⋅⋅⋅⋅⋅=⋅⋅⋅⋅⋅⋅2121.115.独立重复试验中:①二项分布:()()()p n k b p p C k P kn kk n n ,;1=-=-;②几何分布:()()p p p k g k 11,--=,其中⋅⋅⋅=,3,2,1k*116.若离散型随机变量ξ的概率分布为其中121=⋅⋅⋅++⋅⋅⋅++n p p p ,则①⋅⋅⋅++⋅⋅⋅++=n n p x p x p x E 2211ξ为ξ的数学期望.②()()()⋅⋅⋅+⋅-+⋅⋅⋅+⋅-+⋅-=n n p E x p E x p E x D 2222121ξξξξ为随机变量ξ的方差.③数学期望与方差的性质:()b aE b a E +=+ξξ;()ξξD a b a D 2=+;()22ξξξE E D -=. ①若()p n B ,~ξ,则()p np D np E -==1,ξξ; ②若()p k g ,~ξ,则21,1ppD pE -==ξξ; ③若10~-ξ分布,则()p p D p E -==1,ξξ.*117.正态分布密度函数()()()2226,,x f x x μ--=∈-∞+∞,式中的实数μ,σ(σ>0)是参数,分别表示个体的平均数与标准差.*118.标准正态分布密度函数()()22,,x f x x -=∈-∞+∞.对于标准正态总体N (0,1),)(0x Φ是总体取值小于0x 的概率,即 )()(00x x P x <=Φ,其中00>x ,图中阴影部分的面积表示为概率0()P x x < 只要有标准正态分布表即可查表解决.从图中不难发现:当00<x 时,)(1)(00x x -Φ-=Φ;而当00=x 时,Φ(0)=0.5*119.对于2(,)N μσ,取值小于x 的概率:()x F x μσ-⎛⎫=Φ ⎪⎝⎭.()()()12201x x P x x P x x x P <-<=<<()()21F x F x =-21x x μμσσ--⎛⎫⎛⎫=Φ-Φ ⎪ ⎪⎝⎭⎝⎭.120.①简单随机抽样:设一个总体中有有限个个体,如果通过逐个抽取的方法从中抽取一个样本,且每次抽取时各个个体被抽到的概率相等,就称这样的抽样为简单随机抽样.②系统抽样:当总体中的个体数较多时,可将总体分成均衡的几个部分,然后按照预先定出的规则从每一部分抽取1个个体,得到所需要的样本,这种抽样叫做系统抽样.③分层抽样:当已知总体由差异明显的几部分组成时,常将总体分成几部分,然后按照各部分所占的比进行抽样,这种抽样叫做分层抽样.注:这三种抽样的共同特点是在抽样过程中每个个体被抽取的概率相等; *121. C C n =∞→lim (C 为常数);②如果1<a ,那么0lim =∞→nn a ;③无穷递缩等比数列所有项的和qa S -=11,其中1<q ,0≠q . *122. ()()()a x f x f a x f x x x x x x ==⇔=+-→→→0lim lim lim*123.特殊数列的极限(1)0||1lim 11||11nn q q q q q →∞<⎧⎪==⎨⎪<=-⎩不存在或.(2)1101100()lim ()()k k k k tt t n t t kk t a n a n a a k t b n b n b b k t ---→∞-⎧<⎪+++⎪==⎨+++⎪⎪>⎩不存在 .(3)()111lim11nn a q a S qq→∞-==--(S 无穷等比数列}{11n a q - (||1q <)的和). *124.函数的极限定理lim ()x x f x a →=⇔0lim ()lim ()x x x x f x f x a -+→→==.*125.函数的夹逼性定理如果函数f(x),g(x),h(x)在点x 0的附近满足: (1)()()()g x f x h x ≤≤;(2)0lim (),lim ()x x x x g x a h x a →→==(常数),则0lim ()x x f x a →=.本定理对于单侧极限和∞→x 的情况仍然成立. *126.几个常用极限(1)1lim 0n n→∞=,lim 0n n a →∞=(||1a <); (2)00lim x x x x →=,0011lim x x x x →=.两个重要的极限(1)0sin lim 1x xx →=;(1)(sin sin //lim lim ==→→xx x xx x ) (2)1lim 1xx e x →∞⎛⎫+= ⎪⎝⎭(e=2.718281845…).*127.极限的四则运算法则:①函数的极限:如果()()b x g a x f x x x x ==→→0lim ,lim ,那么()()[]b a x g x f x x ±=±→0lim ;()()[]b a x g x f x x ⋅=⋅→0lim ;()()()0lim≠=→b bax g x f x x . ()[]()x f C x Cf x x x x 0lim lim →→=(C 为常数);()[]()nx x nx x x f x f ⎥⎦⎤⎢⎣⎡=→→00lim lim ()*∈N n .②数列的极限:如果b b a a n n n n ==∞→∞→lim ,lim ,那么()b a b a n n n ±=±∞→0lim ;()b a b a n n n ⋅=⋅∞→lim ;()0lim≠=∞→b b ab a nn n .*128.(1)函数()x f 在点0x 处连续必须满足三个条件:①函数()x f 在点0x x =处有意义; ②()x f x x 0lim →存在;③()()00lim x f x f x x =→.(2)如果函数()x f 在点0x 处可导,那么()x f 在点0x 处连续;如果函数()x f 在点0x 处连续,()x f 在该点却不一定可导.*129.最大值最小值定理:如果()x f 是闭区间[]b a ,上的连续函数,那么()x f 在闭区间[]b a ,上有最大值和最小值.130.)(x f 在0x 处的导数(或变化率或微商)00000()()()limlimx x x x f x x f x yf x y x x=∆→∆→+∆-∆''===∆∆. *131.瞬时速度00()()()limlimt t s s t t s t s t t tυ∆→∆→∆+∆-'===∆∆. *132.瞬时加速度00()()()limlimt t v v t t v t a v t t t∆→∆→∆+∆-'===∆∆. *133.)(x f 在),(b a 的导数()dy df f x y dx dx ''===00()()lim limx x y f x x f x x x∆→∆→∆+∆-==∆∆. 134. 函数)(x f y =在点0x 处的导数的几何意义:函数)(x f y =在点0x 处的导数是曲线)(x f y =在))(,(00x f x P 处的切线的斜率)(0x f ',相应的切线方程是))((000x x x f y y -'=- 135.导数与函数的单调性的关系(1)0)(>'x f 与)(x f 为增函数的关系:0)(>'x f 能推出)(x f 为增函数,但反之不一定.如函数3)(x x f =在),(+∞-∞上单调递增,但0)(≥'x f ,∴0)(>'x f 是)(x f 为增函数的 充分不必要条件.(2)0)(≥'x f 与)(x f 为增函数的关系:)(x f 为增函数,一定可以推出0)(≥'x f ,但反之不一定,因为0)(≥'x f ,即为0)(>'x f 或0)(='x f .当函数在某个区间内恒有0)(='x f ,则)(x f 为常数,函数不具有单调性.∴0)(≥'x f 是)(x f 为增函数的必要不充分条件. 136.常见函数的导数:①0='C (C 为常数);②()1-='n nnx x ()Q n ∈;③()x x cos sin =';④()x x sin cos -=';⑤()xx 1ln =',()e xx aa log 1log =';⑥()xxe e =',()a a a xxln ='.*137.可导函数四则运算的求导法则:①()v u v u '±'='±;②()v u v u uv '+'=',()u C Cu '=';③()02≠'-'='⎪⎭⎫ ⎝⎛v v v u v u v u .*138.复合函数的求导法则设函数()u x ϕ=在点x 处有导数''()x u x ϕ=,函数)(u f y =在点x 处的对应点U 处有导数''()u y f u =,则复合函数(())y f x ϕ=在点x 处有导数,且'''x u x y y u =⋅,或写作'''(())()()x f x f u x ϕϕ=.*139.复数的相等,a bi c di a c b d +=+⇔==.(,,,a b c d R ∈) *140.复数z a bi =+的模(或绝对值)||z =||a bi +*141.复数的四则运算法则(1)()()()()a bi c di a c b d i +++=+++;(2)()()()()a bi c di a c b d i +-+=-+-; (3)()()()()a bi c di ac bd bc ad i ++=-++; (4)2222()()(0)ac bd bc ada bi c di i c di c d c d +-+÷+=++≠++.*142.复数的乘法的运算律对于任何123,,z z z C ∈,有交换律:1221z z z z ⋅=⋅.结合律:123123()()z z z z z z ⋅⋅=⋅⋅. 分配律:1231213()z z z z z z z ⋅+=⋅+⋅ . *143.复平面上的两点间的距离公式12||d z z =-=(111z x y i =+,222z x y i =+).*144.向量的垂直非零复数1z a bi =+,2z c di =+对应的向量分别是1OZ ,2OZ ,则 12OZ OZ ⊥⇔12z z ⋅的实部为零⇔21z z 为纯虚数⇔2221212||||||z z z z +=+ ⇔2221212||||||z z z z -=+⇔1212||||z z z z +=-⇔0ac bd +=⇔12z iz λ= (λ为非零实数).*145.对虚数单位i ,有1 , ,1,4342414=-=-==+++n n n n i i i i i i.*146.共轭复数:当两个复数的实部相等,虚部互为相反数时,这两个复数互为共轭复数.如bi a + 与bi a -()R b a ∈,互为共轭复数.*147.()()1011123=⇔=++-⇔=ωωωωω或i 2321±-=ω. 注:带*的仅理科生掌握!高中数学会考复习必背知识点第一章 集合与简易逻辑 1、含n 个元素的集合的所有子集有n 2个 第二章 函数 1、求)(x f y =的反函数:解出)(1y fx -=,y x ,互换,写出)(1x fy -=的定义域;2、对数:①:负数和零没有对数,②、1的对数等于0:01log =a ,③、底的对数等于1:1log =a a ,④、积的对数:N M MN a a a log log )(log +=, 商的对数:N M NMa a alog log log -=,幂的对数:M n M a n a log log =;b mnb a na m log log =, 第三章 数列1、数列的前n 项和:n n a a a a S ++++= 321; 数列前n 项和与通项的关系:⎩⎨⎧≥-===-)2()1(111n S S n S a a n nn2、等差数列 :(1)、定义:等差数列从第2项起,每一项与它的前一项的差等于同一个常数; (2)、通项公式:d n a a n )1(1-+= (其中首项是1a ,公差是d ;) (3)、前n 项和:1.2)(1n n a a n S +=d n n na 2)1(1-+=(整理后是关于n 的没有常数项的二次函数)(4)、等差中项: A 是a 与b 的等差中项:2ba A +=或b a A +=2,三个数成等差常设:a-d ,a ,a+d3、等比数列:(1)、定义:等比数列从第2项起,每一项与它的前一项的比等于同一个常数,(0≠q )。
2020高考数学100个必考知识点详解17 函数的极值

第17 函数的极值一、基础知识: 1、函数极值的概念:(1)极大值:一般地,设函数()f x 在点0x 及其附近有定义,如果对0x 附近的所有的点都有()()0f x f x <,就说()0f x 是函数()f x 的一个极大值,记作()0y f x =极大值,其中0x 是极大值点(2)极小值:一般地,设函数()f x 在点0x 及其附近有定义,如果对0x 附近的所有的点都有()()0f x f x >,就说()0f x 是函数()f x 的一个极小值,记作()0y f x =极小值,其中0x 是极小值点 极大值与极小值统称为极值2、在定义中,取得极值的点称为极值点,极值点是自变量的值,极值指的是函数值。
请注意以下几点:(1)极值是一个局部概念:由定义,极值只是某个点的函数值与它附近点的函数值比较是最大或最小并不意味着它在函数的整个的定义域内最大或最小(2)函数的极值不是唯一的即一个函数在某区间上或定义域内极大值或极小值可以不止一个(3)极大值与极小值之间无确定的大小关系即一个函数的极大值未必大于极小值(4)函数的极值点一定出现在区间的内部,区间的端点不能成为极值点3、极值点的作用:(1)极值点为单调区间的分界点 (2)极值点是函数最值点的候选点4、费马引理:()f x 在0x x =处可导,那么0x x =为()f x 的一个极值点⇒()0'0f x = 说明:①前提条件:()f x 在0x x =处可导②单向箭头:在可导的前提下,极值点⇒导数0=,但是导数0=不能推出0x x =为()f x 的一个极值点,例如:3y x =在()0,0处导数值为0,但0x =不是极值点③费马引理告诉我们,判断极值点可以通过导数来进行,但是极值点的定义与导数无关(例如:y x =在()0,0处不可导,但是0x =为函数的极小值点) 5、求极值点的步骤: (1)筛选: 令()'0fx =求出()'f x 的零点(此时求出的点有可能是极值点)(2)精选:判断函数通过()'fx 的零点时,其单调性是否发生变化,若发生变化,则该点为极值点,否则不是极值点(3)定性: 通过函数单调性判断出是极大值点还是极小值点:先增后减→极大值点,先减后增→极小值点6、在综合题分析一个函数时,可致力于求出函数的单调区间,当求出单调区间时,极值点作为单调区间的分界点也自然体现出来,并且可根据单调性判断是极大值点还是极小指点,换言之,求极值的过程实质就是求函数单调区间的过程。
高考数学重要技巧定理100个【打印版】

■[定理 27]:等比数列爆强公式:S(n+m)=S(m)+(q^m) S(n) [作用:可以迅速求 q.记忆 方法:中间三个都是 m,头尾保持为 n]
■[定理 32]:关于三次函数:[三次函数曲线是中心对称图形],它有一个对称中心,求法 为二阶导后导数为 0,根 x 即为中心横坐标,纵坐标可以用 x 带入原函数界定。另外,图 像中必有唯一一条过该中心的直线与两旁相切。
■[定理 33]:关于复合函数:1、复合函数奇偶性:内偶则偶,内奇同外 2,复合函数单 调性:同增异减。[说明:对于复合函数,不要畏惧它有几重复合,关键理解在于每个函 数总是基函数得来的]
■[定理 20]:直观图的面积是原图面积的√2/4 倍.[斜二测画法是一个冷门,但不要忘记 掌握它的画法]
■[定理 21]正四面体的棱长为 a,则必有以下结论:它的高为 h=(√6)a/3,它的外接球的 半径 R=3h/4,它的内切球的半径 r=h/4,它的体积 V=[(√2)a^3]/12,它的任意两对棱间的 距离 d=(√2)a/2。[同学们有兴趣的可以自己推导:外接构造直角三角形,内切利用等体 积。公式写在笔记本上会整洁哦,这里为了不引起歧义以及编辑工具的问题所以有点繁琐, 敬请谅解]
■[定理 13]:射影公式:向量 a 在向量 b 上的射影=(向量 a×向量 b)[即数量积]/(向量 b 的模)。[记忆方法:在哪里射影除哪个的模,分子都是数量积] 说明:射影有正负。
■[定理 14]:椭圆焦点在 x 轴的表达形式:x^2/a^2+y^2/b^2=1(a>b>0)(a^2=b^2+c^2), 焦点在 y 轴,y^2/a^2+x^2/b^2=1(a>b>0)(a^2=b^2+c)^2;◆◆双曲线焦点在 x 轴: x^2/a^2-y^2/b^2=1(a>0,b>0)(c^2=a^2+b^2),焦点在 y 轴:y^2/a^2-x^2/b^2=1(a>0, b>0)(c^2=a^2+b^2)。[别看这个很基础,有些人只要一把焦点转到 y 轴就开始糊涂了, 等式和方程无法对应起来,现在整理出来,请务必搞懂]
高三数学知识点归纳

高三数学知识点归纳第一:高考数学中有函数、数列、三角函数、平面向量、不等式、立体几何等九大章节。
主要是考函数和导数,这是我们整个高中阶段里最核心的板块,在这个板块里,重点考察两个方面:第一个函数的性质,包括函数的单调性、奇偶性;第二是函数的解答题,重点考察的是二次函数和高次函数,分函数和它的一些分布问题,但是这个分布重点还包含两个分析就是二次方程的分布的问题,这是第一个板块。
第二:平面向量和三角函数。
重点考察三个方面:一个是划减与求值,第一,重点掌握公式,重点掌握五组基本公式。
第二,是三角函数的图像和性质,这里重点掌握正弦函数和余弦函数的性质,第三,正弦定理和余弦定理来解三角形。
难度比较小。
第三:数列。
数列这个板块,重点考两个方面:一个通项;一个是求和。
第四:空间向量和立体几何。
在里面重点考察两个方面:一个是证明;一个是计算。
第五:概率和统计。
这一板块主要是属于数学应用问题的范畴,当然应该掌握下面几个方面,第一等可能的概率,第二事件,第三是独立事件,还有独立重复事件发生的概率。
第六:解析几何。
这是我们比较头疼的问题,是整个试卷里难度比较大,计算量最高的题,当然这一类题,我总结下面五类常考的题型,包括第一类所讲的直线和曲线的位置关系,这是考试最多的内容。
考生应该掌握它的通法,第二类我们所讲的动点问题,第三类是弦长问题,第四类是对称问题,这也是20__年高考已经考过的一点,第五类重点问题,这类题时往往觉得有思路,但是没有答案,当然这里我相等的是,这道题尽管计算量很大,但是造成计算量大的原因,往往有这个原因,我们所选方法不是很恰当,因此,在这一章里我们要掌握比较好的算法,来提高我们做题的准确度,这是我们所讲的第六大板块。
第七:押轴题。
考生在备考复习时,应该重点不等式计算的方法,虽然说难度比较大,我建议考生,采取分部得分整个试卷不要留空白。
这是高考所考的七大板块核心的考点。
高考数学备考策略1、你究竟练熟了吗?年年都有一大票人栽在高考数学上,究其原因,不是其不会做,而是其做题做不精,做题做不熟。
千锤百炼-高考数学100个热点问题——第88炼 含有条件概率的随机变量问题

第88炼 含有条件概率的随机变量问题一、基础知识:1、条件概率:事件B 在事件A 已经发生的情况下,发生的概率称为B 在A 条件下的条件概率,记为|B A2、条件概率的计算方法:(1)按照条件概率的计算公式:()()()|P AB P B A P A =(2)考虑事件A 发生后,题目产生了如何的变化,并写出事件B 在这种情况下的概率 例如:5张奖券中有一张有奖,甲,乙,丙三人先后抽取,且抽完后不放回,已知甲没有中奖,则乙中奖的概率:按照(1)的方法:设事件A 为“甲没中奖”,事件B 为“乙中奖”,则所求事件为|B A ,按照公式,分别计算()(),P AB P A ,利用古典概型可得:()25415P AB A ==,()45P A =,所以()()()1|4P AB P B A P A ==按照(2)的方法:考虑甲已经抽完了,且没有中奖,此时还有4张奖券,1张有奖。
那么轮到乙抽时,乙抽中的概率即为143、含条件概率的乘法公式:设事件,A B ,则,A B 同时发生的概率()()()|P AB P A P B A =⋅ ,此时()|P B A 通常用方案(2)进行计算4、处理此类问题要注意以下几点:(1)要分析好几个事件间的先后顺序,以及先发生的事件对后面事件的概率产生如何的影响(即后面的事件算的是条件概率)(2)根据随机变量的不同取值,事件发生的过程会有所不同,要注意区别(3)若随机变量取到某个值时,情况较为复杂,不利于正面分析,则可以考虑先求出其它取值时的概率,然后用间接法解决。
二、典型例题:例1:袋中有大小相同的三个球,编号分别为1,2,3,从袋中每次取出一个球,若取到的球的编号为2,则把该球编号记下再把编号数改为1后放回袋中继续取球;若取到的球的编号为奇数,则取球停止,取球停止后用X 表示“所有被取球的编号之和” (1)求X 的分布列 (2)求X 的数学期望及方差思路:(1)依题意可知如果取球取出的是1,3,则取球停止,此时X 的值为1或3;当取球取出的是2号球时,按照规则要改为1号球放进去重取,再取时只能取到1或3,所有编号之和X 的值为3,5,所以可知X 可取的值为1,3,5,当1X =时,意味着直接取到了1号球(概率为13);当3X =时,分为两种情况,一种为直接取到3(概率为13),另一种为取到了2(概率为13),改完数字后再取到1(概率为23);当5X =时,为取到了2(概率为13),改完数字后再取到3(概率为13),从而可计算出概率。
高中数学知识点全总结(3篇)

高中数学知识点全总结一、直线与方程高考考试内容及考试要求:考试内容:1.直线的倾斜角和斜率;直线方程的点斜式和两点式;直线方程的一般式;2.两条直线平行与垂直的条件;两条直线的交角;点到直线的距离;考试要求:1.理解直线的倾斜角和斜率的概念,掌握过两点的直线的斜率公式,掌握直线方程的点斜式、两点式、一般式,并能根据条件熟练地求出直线方程;2.掌握两条直线平行与垂直的条件,两条直线所成的角和点到直线的距离公式能够根据直线的方程判断两条直线的位置关系;二、直线与方程课标要求:1.在平面直角坐标系中,结合具体图形,探索确定直线位置的几何要素;3.根据确定直线位置的几何要素,探索并掌握直线方程的几种形式(点斜式、两点式及一般式),体会斜截式与一次函数的关系;4.会用代数的方法解决直线的有关问题,包括求两直线的交点,判断两条直线的位置关系,求两点间的距离、点到直线的距离以及两条平行线之间的距离等。
要点精讲:1.直线的倾斜角:当直线l与x轴相交时,取x轴作为基准,x 轴正向与直线l向上方向之间所成的角α叫做直线l的倾斜角。
特别地,当直线l与x轴平行或重合时,规定α=0°.倾斜角α的取值范围:0°≤α<180°.当直线l与x轴垂直时,α=90°.2.直线的斜率:一条直线的倾斜角α(α≠90°)的正切值叫做这条直线的斜率,斜率常用小写字母k表示,也就是k=tanα(1)当直线l与x轴平行或重合时,α=0°,k=tan0°=0;(2)当直线l与x轴垂直时,α=90°,k不存在。
由此可知,一条直线l的倾斜角α一定存在,但是斜率k不一定存在。
3.过两点p1(x1,y1),p2(x2,y2)(x1≠x2)的直线的斜率公式:(若x1=x2,则直线p1p2的斜率不存在,此时直线的倾斜角为90°)。
4.两条直线的平行与垂直的判定(1)若l1,l2均存在斜率且不重合:注:上面的等价是在两条直线不重合且斜率存在的前提下才成立的,缺少这个前提,结论并不成立。
高考数学中的指数与对数知识点总结

高考数学中的指数与对数知识点总结数学是一门考验学生思维、逻辑和分析能力的学科。
其中,指数和对数是中学数学中的一对重要概念,涉及许多重要的定理和运算法则,在高考中也是必考的知识点。
本文将对这两个知识点进行总结,并以实例进行解析,帮助读者更好地理解和掌握这些重要概念。
一、指数指数这个概念相信大家都很熟悉,它是数学中的一种表示乘方的方法。
在指数的定义中,我们会发现一个重要的规律:指数是自然数。
例如,2的3次方就可以表示为2^3,其中3是指数,2是底数。
指数告诉我们底数要连乘几次,才能得到指数所表示的数值。
因此,指数也是幂运算的一种表现形式。
在高中数学中,我们需要掌握指数的基本定义和运算规则,以及指数函数。
1.指数的四种运算规则在指数的运算法则中,最基本的有四条,它们分别是:⑴基础规则:a^m * a^n = a^(m+n)这个规则告诉我们,在同一个底数下,指数相加等于底数的乘积的指数。
例如,2^3 * 2^4 = 2^(3+4) = 2^7 = 128⑵乘方规则:(a^m)^n = a^(m*n)这个规则告诉我们,若一个数的指数已经有了一个指定的次数,那么还可以对这个结果进行指数幂次的运算。
例如,(2^3)^2 = 2^(3*2) = 2^6 = 64⑶倒数规则:a^(-n) = 1 / a^n这个规则告诉我们,指数为负数时,底数等于1除以底数为正数的幂值。
例如,2^(-3) = 1/ 2^3 = 1/8⑷指数规则:a^m / a^n = a^(m-n)这个规则告诉我们,在同一个底数下,指数相减等于底数的商的指数。
例如,2^5 / 2^3 = 2^(5-3) = 2^2 = 42.指数函数指数函数是数学中的一个重要函数,它的定义形式如下:y=a^x(a>0 && a≠1)。
其中,a为底数,x为自变量,y为因变量。
指数函数的图像呈现出“鼓型”形状,它与直线y=0 相交于y轴,随着自变量x的增大而迅速增长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考数学常考的100个基础知识点广州市育才中学 邓军民 整理1.德摩根公式C U (A ∩B )= C u A ∪C u B ;B C A C )B A (C U U U =。
2.A ∩B =A ⇔A ∪B =B ⇔A ⊆B ⇔C U B ⊆C U A ⇔A ∩C U B =φ⇔C U A ∪B =R 3.card (A ∪B )=cardA +cardB -card (A ∩B ) 4.二次函数的解析式的三种形式 ①一般式f (x )=ax 2+bx +c (a ≠0); ②顶点式f (x )=a (x -h )2+k (a ≠0); ③零点式f (x )=a (x -x 1)(x -x 2)(a ≠0)。
5.设x 1,x 2∈[a ,b ],x 1≠x 2 那么⇔>--⇔>--0)()(0)]()()[(21212121x x x f x f x f x f x x f (x )在[a ,b ]上是增函数;⇔<--⇔<--0)()(0)]()()[(21212121x x x f x f x f x f x x f (x )在[a ,b ]上是减函数。
设函数y = f (x )在某个区间内可导,如果f ′(x ) > 0 ,则f (x ) 为增函数;如果f ′(x ) <0 ,则f (x ) 为减函数。
6.函数y = f (x ) 的图象的对称性: ① 函数y = f (x ) 的图象关于直线x = a 对称⇔ f (a +x )= f (a -x )⇔f (2a -x )= f (x )。
7.两个函数图象的对称性:(1)函数y = f (x )与函数y = f (-x )的图象关于直线x = 0(即y 轴)对称。
(2)函数y = f (x ) 和y = f-1(x ) 的图象关于直线y =x 对称。
8.分数指数幂nmnm aa 1=-(a >0,m ,n ∈N*,且n >1)。
分数指数幂nm nm a1a=-(a >0,m ,n ∈N*,且n >1)。
9.log a N=b ⇔a b =N (a >0,a ≠1,N>0)10.对数的换底公式a N N m m a log log log =,推论b mn b a na m log log =11.⎩⎨⎧≥-==-2111n s s n s a n nn ,,− ≥( 数列{ a n } 的前n 项的和为S n =a 1+a 2 +…+a n )。
(注意此公式第2 行顺推与逆推的应用,这是递推数列的常用公式,可以达到不同的目的) 12.等差数列的通项公式a n =a 1+(n -1)d =dn +a 1-d (n ∈N *)* 其前n 项和公式n d a n d d n n na a a n S n n )21(22)1(2)(1211-+=-+=+=13.等比数列的通项公式)(·1*11N n q qa q a a nnn ∈=-=; 其前n 项的和公式⎪⎩⎪⎨⎧=≠--=1,1,1)1(11q na q q q a S n n 或⎪⎩⎪⎨⎧=≠--=1,1,1)11q na q q q a a S n n n(小心:解答题利用错位相减法时要特别注意讨论q=1的情况) 14.同角三角函数的基本关系式 s i n 2θ+ cos 2θ=1,tan θ=1cot ·tan ,cos sin =θ⋅θθθ15.和角与差角公式s i n (α±β)=s i n αcos β±cos αs i n β; cos (α±β)=cos αcos β s i n αs i n β; tan (α±β)βαβ±α=tan tan 1tan tan 。
α-α=β-αβ+α22sin sin )sin()sin((平方正弦公式);cos (α+β)cos (α−β)=cos2α−s i n2β(平方余弦公式);)sin(cos sin 22ϕ+α+=α+αb a b a (辅助角ϕ所在象限由点(a ,b )的象限决定,abtan =ϕ)。
(建议利用ϕ的正弦和余弦来确定其位于哪个象限,这样比较好理解) 16.二倍角公式s i n 2α = 2s i n α·cos α。
α-α=α⋅α-=-α=α-α=α22222tan 1tan 22tan sin 211cos 2sin cos 2cos 。
17.三角函数的周期公式 函数y =s i n (ωx +ϕ),x ∈R 及函数y = cos (ωx +ϕ),x ∈R (A ,ω,ϕ为常数,且A ≠0,ω>0)的周期ωπ=2T ;函数)x tan(y ϕ+ω=,Z k 2k x ∈π+π≠,(A ,ω,ϕ为常数,且A ≠0,0>ω)的周期ωπ=T 。
(注意ω小于0的函数周期的求法)18.正弦定理R 2Csin cB sin b A sin a ===。
(学会利用后面的2R ) 19.余弦定理a 2=b 2+c 2−2bc cosA ;b 2=c 2+a 2−2ca cosB ;c 2=a 2+b 2−2ab cosC 。
(注意其变形公式) 20.面积定理 (1)c b a ch 21bh 21ah 21S ===(c b a h h h 、、分别表示a 、b 、c 边上的高)。
(2)B sin ca 21A sin bc 21C sin ab 21S ===。
21.三角形内角和定理 在△ABC 中,有)B A (22C 22BA 22C )B A (C C B A +-π=⇔+-π=⇔+-π=⇔π=++。
(很多与三角形有关的恒等变形或者纯粹解三角形的题目中会用到这些关系) 22.平面两点间的距离公式212212)()(||y y x x AB AB AB d BA -+-=→⋅→=→=,(A (11y x ,),B (22y x ,))。
23.向量的平行与垂直 设)()(2211y x b y x a ,,,==,且b ≠0,则0)0(0//21211221=+⇔=⋅⇔≠⊥=-⇔λ=⇔y y x x b a a b a y x y x a b b a24.线段的定比分公式 设)()()(222111y x P y x P y x P ,,,,,是线段P 1P 2的分点,λ是实数,且→→λ=21PP P P ,则⎪⎪⎩⎪⎪⎨⎧λ+λ+=λ+λ+=112121y y y x x x (这个公式很重要,不要记错!)25.三角形的重心坐标公式△ABC 三个顶点的坐标分别为)()(2211y x B y x A ,、,、)(33y x C ,,则△ABC 的重心的坐标是)33(321321y y y x x x G ++++,。
26.点的平移公式→+→=→⇔⎩⎨⎧-=-=⇔⎩⎨⎧+=+=''''''PP OP OP k y y hx x k y y h x x (图形F 上的任意一点P (x ,y )在平移后图形'F 上的对应点为)''('y x P ,,且→'PP 的坐标为(h ,k ))。
(要注意区别新坐标、旧坐标,区别新方程和旧方程,不要混淆,解答题务必要体现以上公式的使用过程,关键步骤不要省) 27.常用不等式:(1)a ,b ∈R ⇒a 2+b 2≥2ab (当且仅当a =b 时取“=”号)。
(2)a ,b ∈R +ab 2ba ≥+⇒(当且仅当a =b 时取“=”号)。
(3)a 3+b 3+c 3≥3abc (a >0,b >0,c >0)。
(4)柯西不等式R d c b a bd ac d c b a ∈+≥++,,,,22222)())((。
(建议:了解一下,尝试用向量数量积的方法证明之) (5)||||||||||b a b a b a +≤+≤- 28.极值定理 已知x ,y 都是正数,则有(1)如果积xy 是定值p ,那么当x =y 时和x +y 有最小值p 2;(2)如果和x +y 是定值s ,那么当x =y 时积xy 有最大值2s 41。
29.一元二次不等式ax 2 +bx +c >0(或<0)(a ≠0,Δ=b 2−4ac >0),如果a 与ax 2 +bx +c 同号,则其解集在两根之外;如果a 与ax 2 + bx + c 异号,则其解集在两根之间。
简言之:同号两根之外,异号两根之间。
)(0)(21121x x x x x x x <<-⇔<<;1x x <,或)(0))((21212x x x x x x x x <>--⇔>(这类问题一般可以借助于韦达定理或者结合图象特点寻找约束条件就可以解决问题) 30.含有绝对值的不等式当a > 0时,有a x a a x a x <<-⇔<⇔<22|| a x a x a x >⇔>⇔>22||或a x -<。
31.无理不等式(1)⎪⎩⎪⎨⎧>≥≥⇔>)()(0)(0)()()(x g x f x g x f x g x f(2)⎩⎨⎧<≥⎪⎩⎪⎨⎧>≥≥⇔>0)(0)()]([)(0)(0)()()(2x g x f x g x f x g x f x g x f 或 (3)⎪⎩⎪⎨⎧<>≥⇔<2)]([)(0)(0)()()(x g x f x g x f x g x f 32.指数不等式与对数不等式 (1)当a >1时,)()()()(x g x f a a x g x f >⇔>;⎪⎩⎪⎨⎧>>>⇔>)()(0)(0)()(log )(log x g x f x g x f x g x f a a(2)当0<a <1时,)()()()(x g x f a a x g x f <⇔>;⎪⎩⎪⎨⎧<>>⇔>)()(0)(0)()(log )(log x g x f x g x f x g x f a a33.斜率公式 ))()((2221111212y x P y x P x x y y k ,、,--=(很多代数问题可以利用这个公式转化为几何问题,简化解题过程,这是数型结合思想的重要体现)34.直线的四种方程(1)点斜式 )(11x x k y y -=-(直线l 过点)y x (P 111,,且斜率为k )。
