椭圆的画法
数学中常用几何画板绘制椭圆

数学中常⽤⼏何画板绘制椭圆圆锥曲线是⾼中数学的重点和难点,也是历来⾼考的必考内容,所以对于⾼中⽣来说,弄懂圆锥曲线这块难啃的⾻头,是很有必要的。
其中要熟练掌握的圆锥曲线之⼀就是椭圆,它是圆锥与平⾯的截线,其实要想画出椭圆,其⽅法不⽌⼀种,下⾯就⼀起来通过学学椭圆的五种画法。
⽅法⼀、利⽤椭圆第⼀定义构造椭圆椭圆第⼀定义:平⾯内到两个定点的距离之和等于定长2a(a>0)的点的轨迹就是椭圆,按照此定义可画出椭圆,具体步骤如下:1.单击“圆⼯具”,在画板的适当位置任意画⼀个圆,将圆⼼的标签改为F1。
单击“点⼯具”,在圆上任意画⼀点C,同时选中点F1和点C,执⾏“构造”-“线段”命令,构造出线段F1C。
单击“点⼯具”,在线段F1C任意画⼀点F2。
2.在圆上任意画⼀点E,并构造线段EF1和线段EF2。
选中线段EF2,执⾏“构造”-“中点”命令,构造线段EF2的中点F。
3.选中线段EF2和点F,执⾏“构造”-“垂线”命令,构造出线段EF2的垂直平分线j。
同时选中线段EF1和直线j,选择“构造”-“交点”命令,构造线段EF1和直线j的交点G。
4.选中点G和点E(把点E称做是点G的相关点,改变G点的位置,点E的位置也跟着改变),选择“构造”-“轨迹”命令,可画出椭圆。
拖动点B 和点F2可改变椭圆的形状。
⽅法⼆、利⽤椭圆第⼆定义画椭圆椭圆的第⼆定义:设动点M(x, y)与定点F(c, 0)的距离和它到定直线l: x=a2/c的距离的⽐是常数(a>c>0),则点M的轨迹是椭圆。
点F 是椭圆的⼀个焦点,直线l是椭圆中对应于焦点F的准线,常数e=c/a(0<e<1)。
具体的操作步骤如下:步骤⼀打开⼏何画板,使⽤“点⼯具”画任意⼀点F,使⽤“线⼯具”画直线L(点F不在L上)。
过点F作⼀条直线,在直线上取⼀点P;步骤⼆选中点F、P执⾏“度量”--“距离”命令,度量FP的长度;选中点F和度量的FP的长度,执⾏“构造”--“以圆⼼和半径绘圆”构造以点F为圆⼼,FP为半径的圆。
机械制图椭圆的画法2021推选

第六节 斜度和锥度
二、锥度
斜度=tan α=CA/AB=H/L
在图2-15b中,斜度=〔H-h〕/L
图2-14 用四心法画椭圆
椭圆长轴AB和短轴CD,用四心圆法作椭圆的步骤如下:
图2-16 斜度的画法
(1) 画出相互垂直且平分的长轴AB与短轴CD;
图2-15 斜度
第六节 斜度和锥度
一、斜度
2 斜度的画法
图2-16a所示斜度为1∶6,其作图方法如图2-16b所示。
图2-16 斜度的画法
第六节 斜度和锥度
一、斜度
3 斜度的标注
斜度的符号如图2-17a所示。符号的方向应与斜度的方向一致。 标注斜度时,可按图2-17b、c、d所示的方法标注。
图2-17 斜度的标注
2. 斜度的画法和标注
15 1:4
1个单位 7 17
椭锥圆度长 在轴图A样B图上和也短2以轴-11C∶9Dna,的所用简同化示心形物圆式法表体作示椭。的圆的右步部骤如是下:一个锥度为1∶3的圆锥台,其作图方 如果是圆锥法台,如那么图为2上-、1下9b底所圆直示径之。差与圆锥台高度之比,如图2-18所示。
图2-16 斜度的画法
第六节 斜度和锥度
一、斜度
图2-14 用四心法画椭圆
四心圆弧法作近似椭圆
M O4 C
M1
A O1
O
O3
B
D O2
E
H
F
G
第六节 斜度和锥度
一、斜度
1 斜度的概念
椭圆长轴AB和短斜轴C度D,用是同心指圆法一作椭直圆的线步骤(或如下平: 面)相对于另一直线(或平面)的
第 二六、节锥度斜度倾和锥斜度 程度,其大小用该两直线(或两平面)间夹角的正
机械制图-椭圆画法作图步骤

机械制图:椭圆画法作图步骤文章目录[隐藏]∙1已知长、短轴,作椭圆∙2已知共轭轴,作椭圆∙3确定椭圆长、短轴的方向和大小∙4作椭圆曲线上的切线及法线.∙5作椭圆的展开长度(近似作图)(图10)1已知长、短轴,作椭圆例1:己知椭圆的长轴AB、短轴CD,作椭圆(图1)。
图1已知椭圆长、短轴AB及CD找出椭圆的焦点F1、F2后,再作椭圆作图步骤:(1)以长、短轴为直径作两个同心的辅助圆;(2)在两辅助圆上作出对应的等分点,如1、2、3、...及1'、2'、3'、..... (等分数量随精确度要求而定);(3)依次自等分点1'、2'、...作铅垂线,同时自对应的等分点1、2、...作水平线;(4)各铅垂线与其对应的水平线的交点P1、P2、P3、......椭圆曲线上的点,从而可以作出椭圆。
例2:已知椭圆长、短轴AB及CD,找出椭圆的焦点F1、F2后,再作椭圆(图2)。
图2已知椭圆长、短轴AB及CD找出椭圆的焦点F1、F2后,再作椭圆作图步骤:(1)以短轴端点D为圆心,R=1/2AB为半径作辅助圆与AB交于F、F。
(即焦点);(2)将OF1、OF2分为相应的若干分段,如F11、12、23、...及F21'、1'2'、2'3'、....(靠近F1、F2处分段宜较密);(3)以F1为圆心,依次以A1、A2.....为半径作弧;以F2为圆心,依次以B1、B2、....为半径作弧;(4)两对应弧的交点P1、P2、P3、...即为椭圆曲线上的点,从而可以作出椭圆。
例3:己知椭圆的长、短轴AB、CD,用四心扁圆的方法作椭圆(近似作图)(图3)。
图3己知椭圆的长、短轴AB、CD,用四心扁圆的方法作椭圆近似作图作图步骤:(1)在短轴CD线上取0K=0A,得点K;(2)连接A、C,在AC线上取CK'=CK,得点K';(3)作AK'的中乘线,交OA于0),交O)D于02;(4)作O3、0。
椭圆画法

你用鸡蛋比着画应该可以吧。
有同心圆法,四心点法和相似菱形法,同心圆法比较简单。就是按照长短轴画两个圆,无数条直线通过圆心,其实就是若干条,然后大圆交点作垂线和小圆交电作平行线相交,就像个比较宽的直角三角形,交点直角的顶点就是椭圆上的点,然后用曲线板顺次连接,要是画多点就可以找到准确的用圆规画的半径 。
椭圆画法
一、四心近似法
已知相互垂直且平分的椭圆长轴和短轴,则椭圆的近似画法(四心近似法)步骤如下所示:
第一步:
画出长轴AB和短轴CD,连接AC;
第二步:
在AC上截取CF,使其等于AO与CO之差CE;
第三步:
作AF的垂直平分线,使其分别交AO和OD(或其延长线)于O1和O2点。以O为对称中心,找出O1的对称点O3及O2的对称点O4,此O1、O2、O3、O4各点即为所求的四圆心。通过O2和O1、O2和O3、O4和O3各点,分别作连线;
很简单。
现在桌面固定好两个点。在把一根细绳的两端系在两个点上,用铅笔把绳等紧,移动铅笔,其走过的痕迹就是一个椭圆。
高中课讲过用一根毛线,长度要求线的两端在十字的水平两端,将线的中间用笔撑直正好在十字的上端点。将两端固定,之后用笔撑着线画就好了。
一、四心近似法
已知相互垂直且平分的椭圆长轴和短轴,则椭圆的近似画法(四心近似法)步骤如下所示:
第四步:(双击恢复)
分别以O2和O4为圆心,O2C(或O4D)为半径画两弧。再分别以O1和O3为圆心,O1A(或O3B)为半径画两弧,使所画四弧的接点分别位于O2O1、O2O3、O4O1和O4O3的延长线上,即得所求的椭圆。
有同心圆法,四心点法和相似菱形法,同心圆法比较简单。就是按照长短轴画两个圆,无数条直线通过圆心,其实就是若干条,然后大圆交点作垂线和小圆交电作平行线相交,就像个比较宽的直角三角形,交点直角的顶点就是椭圆上的点,然后用曲线板顺次连接,要是画多点就可以找到准确的用圆规画的半径 。
(完整word版)椭圆的画法(word文档良心出品)
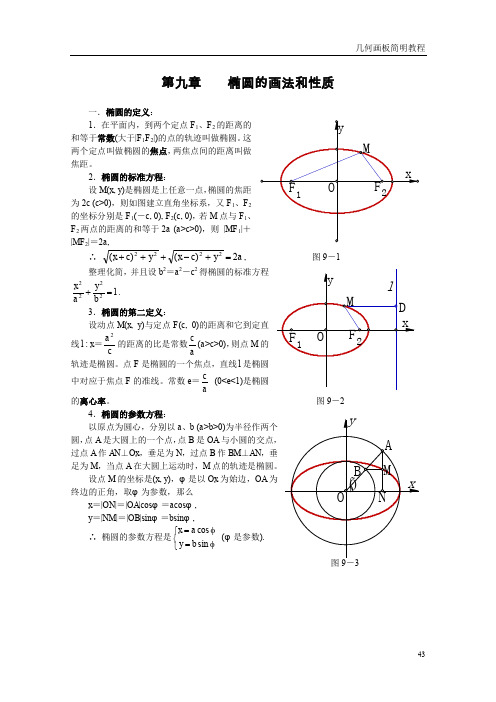
第九章 椭圆的画法和性质一.椭圆的定义:1.在平面内,到两个定点F 1、F 2的距离的和等于常数(大于|F 1F 2|)的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,两焦点间的距离叫做焦距。
2.椭圆的标准方程:设M (x , y )是椭圆是上任意一点,椭圆的焦距为2c (c >0),则如图建立直角坐标系,又F 1、F 2的坐标分别是F 1(-c , 0), F 2(c , 0),若M 点与F 1、F 2两点的距离的和等于2a (a >c >0),则 |MF 1|+|MF 2|=2a ,∴a y c x y c x 2)()(2222=+-+++, 图9-1整理化简,并且设b 2=a 2-c 2得椭圆的标准方程12222=+b y a x . 3.椭圆的第二定义:设动点M (x , y )与定点F (c , 0)的距离和它到定直线l : x =c a 2的距离的比是常数ac (a >c >0),则点M 的轨迹是椭圆。
点F 是椭圆的一个焦点,直线l 是椭圆中对应于焦点F 的准线。
常数e =ac(0<e <1)是椭圆的离心率。
图9-24.椭圆的参数方程:以原点为圆心,分别以a 、b (a >b >0)为半径作两个圆,点A 是大圆上的一个点,点B 是OA 与小圆的交点,过点A 作AN ⊥Ox ,垂足为N ,过点B 作BM ⊥AN ,垂足为M ,当点A 在大圆上运动时,M 点的轨迹是椭圆。
设点M 的坐标是(x , y ),φ是以Ox 为始边,OA 为终边的正角,取φ为参数,那么x =|ON |=|OA |cos φ=a cos φ, y =|NM |=|OB |sin φ=b sin φ,∴ 椭圆的参数方程是⎩⎨⎧φ=φ=sin cos b y a x (φ是参数).二.椭圆的画法:画法1:图9-41.在x 轴上取两点F 1、F 2,使|OF 1|=|OF 2|,用它们作为两个焦点; 2.在图形外作一条线段CD ,使|CD |=2a ,(|CD |>|F 1F 2|); 3.以O 为中心,在x 轴上取两点A 1、A 2,使|A 1A 2|=|CD |;4.在CD 上分别取C '、D ',使|CC '|=|A 1F 1|=|DD '|;作线段C 'D ',并用“作图”菜单中的“对象上的点”功能在C 'D '上作点M ;5.分别以F 1、F 2为圆心,用|CM |、|MD |为半径作圆,两圆相交于P 1、P 2两点;同样方法分别以F 1、F 2为圆心,用|DM |、|CD |为半径作圆,两圆相交于P 3、P 4两点;并将这四个点定义为“追踪点”;6.依次选中点M 、点P 1 (或点M 、点P 2),用“作图”菜单中的“轨迹”功能,作出椭圆。
机械制图:椭圆的画法

四心圆弧法作近似椭圆
M O4 C
M1
A O1
O
O3
B
D O2
E
H
F
G
第六节 斜度和锥度
一、斜度
1 斜度的概念 斜度是指一直线(或平面)相对于另一直线(或平面)的
倾斜程度,其大小用该两直线(或两平面)间夹角的正 切值来表示(图2-15a),即
斜度=tan α=CA/AB=H/L 在图2-15b中,斜度=(H-h)/L 通常在图样中把比值化成1∶n的形式。
图2-15 斜度
第六节 斜度和锥度
一、斜度
2 斜度的画法
图2-16a所示斜度为1∶6,其作图方法如图2-16b所示。
图2-16 斜度的画法
第六节 斜度和锥度
一、斜度
3 斜度的标注
斜度的符号如图2-17a所示。符号的方向应与斜度的方向一致。 标注斜度时,可按图2-17b、c、d所示的方法标注。
图2-17 斜度的标注
• 第一节 绘图工具及其使用 • 第二节 线段等分法 • 第三节 圆的等分法 • 第四节 圆弧连接 • 第五节 椭圆的画法 • 第六节 斜度和锥度 • 第七节 徒手画图
第五节 椭圆的画法
一、理论画法
已知椭圆长轴AB和短轴CD,用同心圆法作椭圆的步骤如下: (1) 以长轴AB和短轴CD为直径画两同心圆,然后过圆心作一 系列直线与两圆相交,如图2-13a所示; (2) 自大圆交点作垂线,小圆交点作水平线,得到的交点就是 椭圆上的点,如图2-13b所示; (3) 用曲线板光滑连接各点,即得所求椭圆(图2-13b)。
第一节绘图工具及其使用第二节线段等分法第三节圆的等分法第四节圆弧连接第五节椭圆的画法第六节斜度和锥度第七节徒手画图第五节椭圆的画法一理论画法图213用同心圆法画椭圆以长轴ab和短轴cd为直径画两同心圆然后过圆心作一系列直线与两圆相交如图213a所示
初三椭圆图像特征与画法

初三椭圆图像特征与画法椭圆是数学中一种重要的曲线形状,具有独特的特征和美观的图像。
在初三学习中,了解椭圆的特征以及正确的画法对于深入理解几何知识和提高绘图技能非常重要。
本文将介绍初三阶段学生可以掌握的椭圆图像特征和正确的画法。
一、椭圆的特征椭圆是平面上到两个定点F1和F2的距离之和等于常数2a的点的集合。
其中,F1和F2称为椭圆的焦点,2a为椭圆的长轴长度。
椭圆还具有以下特征:1. 椭圆的中点为中心点O,中心点到焦点的距离为c。
2. 椭圆的长轴长度2a与焦点之间的距离满足关系:2ae=2ac=2a。
3. 椭圆的短轴长度为2b,其中b的计算公式为b=sqrt(a^2-c^2)。
二、椭圆的画法在画椭圆时,需要掌握正确的步骤和方法。
下面将介绍一种常用的画椭圆的方法,即通过划定矩形框架和关键点的位置。
步骤一:确定椭圆的中心点和长轴长度首先,在纸上选择一个点作为椭圆的中心点O,然后确定椭圆的长轴长度2a。
可以使用尺子测量出适当的长度,或者取两个点F1和F2,使得两点与中心点的距离等于2a。
步骤二:画一个矩形边框以中心点O为中心,以长轴长度2a和短轴长度2b为边长,画一个矩形边框。
此时,矩形的两个侧边分别与椭圆相切。
步骤三:在边框上确定关键点的位置通过计算得到椭圆的焦点F1和F2,将这两个点分别标记在矩形边框的上下两侧。
这两个焦点与中心点O共同构成椭圆的关键点。
步骤四:连接关键点在矩形边框的左右两侧,分别与焦点F1和F2相连,形成一个椭圆形状的闭合曲线。
此时,可以用光滑的曲线连接焦点和关键点,使得椭圆的图像更加美观。
步骤五:擦除边框根据画好的椭圆,可以将矩形边框部分擦除,只保留椭圆的图像。
在保持椭圆形状的基础上,去掉多余的线条,使得椭圆更加清晰。
通过以上的画法步骤,初三学生可以较好地掌握椭圆的画法,练习时可以注意以下几点:1. 画椭圆时要保持手稳,尽量减少抖动,使得图像的线条更加流畅。
2. 可以使用铅笔轻轻地描绘关键点和轮廓线,之后再加深线条,以保持图像的正确性。
机械制图:椭圆的画法说课讲解

第六节 斜度和锥度
二、锥度
2 锥度的画法
图2-19a所示物体的右部是一个锥度为1∶3的圆锥台,其作图方 法如图2-19b所示。
图2-19 锥度的画法
锥度的画法和标注
1个单位 3个单位
14 18
1:3
2
25
55
第六节 斜度和锥度
二、锥度
3 锥度的标注
在图样上应采用图2-20a所示的 图形符号表示圆锥,该符号应配 置在基准线上(图2-20b)。表示圆 锥的图形符号和锥度应靠近圆锥 轮廓标注,基准线应通过指引线 与圆锥的轮廓素线相连。基准线 应与圆锥的轴线平行,图形符号 的方向应与圆锥方向相一致。
图2-13 用同心圆法画椭圆
同心圆法作椭圆CAOBD
四心圆弧法作近似椭圆
M O4 C
M1
A O1
O
O3
B
D O2
E
H
F
G
第六节 斜度和锥度
一、斜度
1 斜度的概念 斜度是指一直线(或平面)相对于另一直线(或平面)的
倾斜程度,其大小用该两直线(或两平面)间夹角的正 切值来表示(图2-15a),即
图2-17 斜度的标注
2. 斜度的画法和标注
15 1:4
1个单位 7 17
4个单位
33
第六节 斜度和锥度
二、锥度
1 锥度的概念 锥度是指正圆锥体底圆直径与锥高之比。如果是圆
锥台,则为上、下底圆直径之差与圆锥台高度之比,
如图2-18所示。锥度=2tan α=D/L=(D-d)/l 锥度在图样上也以1∶n的简化形式表示。
第五节 椭圆的画法
一、理论画法
已知椭圆长轴AB和短轴CD,用同心圆法作椭圆的步骤如下: (1) 以长轴AB和短轴CD为直径画两同心圆,然后过圆心作一 系列直线与两圆相交,如图2-13a所示; (2) 自大圆交点作垂线,小圆交点作水平线,得到的交点就是 椭圆上的点,如图2-13b所示; (3) 用曲线板光滑连接各点,即得所求椭圆(图2-13b)。
椭圆的定义及画法

第15页/共16页
谢谢您的观看!
第16页/共16页
问题1:当常数等于|F1F2|时,点的轨迹 是什么? 线段F1F2
问题2:当常数小于|F1F2|时,点的轨迹 是什么? 轨迹不存在
第8页/共16页
椭圆的简单几何性质
在如图所示的椭圆中,
线段A1A2, B1B2分别
A1
称为椭圆的长轴和短轴。
F1
y B1 M
A2
O
F2 x
它们的长分别等于2a和2b。
B2
a和b分别称为椭圆的长半轴 长和短半轴长。
焦距F1F 2=2c,
a,b,c之间的 关系为:
半焦距OF1 = OF2 =c。
b2+c2=a2
第9页/共16页
a,b,c的几何意义
(-a,0) A1
B1 (0,b)
b
aቤተ መጻሕፍቲ ባይዱc
(a,0)
F1 O
F2 A2 x
B2(0,-b)
a2 b2 c2
B1F1 B1F2 B2F1 B2F2 a
教学 重点
椭圆的画法,及对相应 概念的理解
教学 难点
椭圆面积的求解
第2页/共16页
在我们实际生活中, 同学们见过椭圆吗? 能举出一些实例吗?
第3页/共16页
生 活 中 的 椭 圆
同学们知道如何精确地设计、制作、建造 出现实生活中这些椭圆形的物件吗?
第4页/共16页
圆
椭圆
第5页/共16页
画圆时,要先确定圆心位置和半径大小。
第12页/共16页
由题意可知
a 1.2 0.6 b 0.8 0.4
2
2
故 S=abπ=0.6×0.4×π =0.24π
机械制图:椭圆的画法

同心圆法作椭圆
C
A
O
B
D
第五节 椭圆的画法
二、近似画法
已知椭圆长轴AB和短轴CD,用四心圆法作椭圆的步骤如下: (1) 画出相互垂直且平分的长轴AB与短轴CD; (2) 连接AC,并在AC上取CE=OA-OC,如图2-14a所示; (3) 作AE的中垂线,与长、短轴分别交于O1、O2,再作对称点O3、 O4,如图2-14b所示; (4) 以O1、O2、O3、O4各点为圆心,O1A、O2C、O3B、O4D为 半径,分别画弧,即得近似椭圆,如图2-14c所示。
锥度在图样上的标注如图2-20c、 d、e所示(图中的C为锥度)。
当所标注的锥度是标准圆锥系 列之一(尤其是莫氏锥度或米制锥 度)时,可用标准系列号和相应的 标记表示(图2-20f)。
图2-17 斜度的标注
图2-14 用四心法画椭圆
四心圆弧法作近似椭圆
M O4 C
M1
A O1
O
O3
B
D O2
E
H
F
G
第六节 斜度和锥度
一、斜度
1 斜度的概念 斜度是指一直线(或平面)相对于另一直线(或平面)的
倾斜程度,其大小用该两直线(或两平面)间夹角的正 切值来表示(图2-15a),即
斜度=tan α=CA/AB=H/L 在图2-15b中,斜度=(H-h)/L 通常在图样中把比值化成1∶n的形式。
图2-18 锥度
第六节 斜度和锥度
二、锥度
2 锥度的画法
图2-19a所示物体的右部是一个锥度为1∶3的圆锥台,其作图方 法如图2-19b所示。
图2-19 锥度的画法
锥度的画法和标注
1个单位 3个单位
椭圆的画法
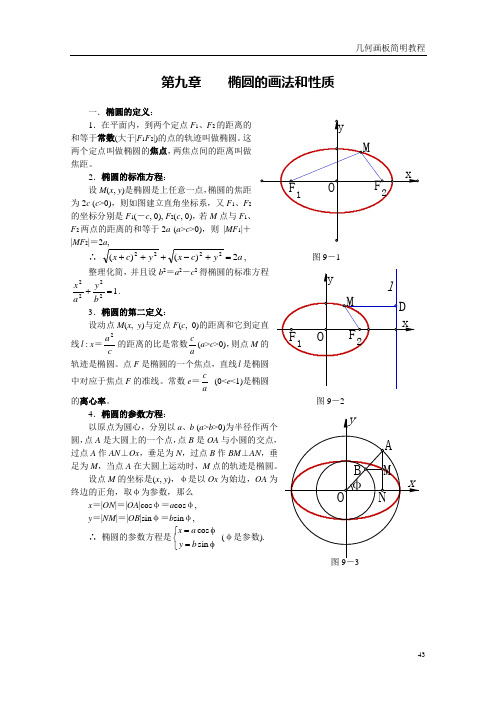
第九章 椭圆的画法和性质一.椭圆的定义:1.在平面内,到两个定点F 1、F 2的距离的和等于常数(大于|F 1F 2|)的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,两焦点间的距离叫做焦距。
2.椭圆的标准方程:设M (x , y )是椭圆是上任意一点,椭圆的焦距为2c (c >0),则如图建立直角坐标系,又F 1、F 2的坐标分别是F 1(-c , 0), F 2(c , 0),若M 点与F 1、F 2两点的距离的和等于2a (a >c >0),则 |MF 1|+|MF 2|=2a ,∴a y c x y c x 2)()(2222=+-+++, 图9-1整理化简,并且设b 2=a 2-c 2得椭圆的标准方程12222=+b y a x . 3.椭圆的第二定义:设动点M (x , y )与定点F (c , 0)的距离和它到定直线l : x =c a 2的距离的比是常数ac (a >c >0),则点M 的轨迹是椭圆。
点F 是椭圆的一个焦点,直线l 是椭圆中对应于焦点F 的准线。
常数e =ac(0<e <1)是椭圆的离心率。
图9-24.椭圆的参数方程:以原点为圆心,分别以a 、b (a >b >0)为半径作两个圆,点A 是大圆上的一个点,点B 是OA 与小圆的交点,过点A 作AN ⊥Ox ,垂足为N ,过点B 作BM ⊥AN ,垂足为M ,当点A 在大圆上运动时,M 点的轨迹是椭圆。
设点M 的坐标是(x , y ),φ是以Ox 为始边,OA 为终边的正角,取φ为参数,那么x =|ON |=|OA |cos φ=a cos φ, y =|NM |=|OB |sin φ=b sin φ,∴ 椭圆的参数方程是⎩⎨⎧φ=φ=sin cos b y a x (φ是参数).二.椭圆的画法:画法1:图9-41.在x 轴上取两点F 1、F 2,使|OF 1|=|OF 2|,用它们作为两个焦点; 2.在图形外作一条线段CD ,使|CD |=2a ,(|CD |>|F 1F 2|); 3.以O 为中心,在x 轴上取两点A 1、A 2,使|A 1A 2|=|CD |;4.在CD 上分别取C '、D ',使|CC '|=|A 1F 1|=|DD '|;作线段C 'D ',并用“作图”菜单中的“对象上的点”功能在C 'D '上作点M ;5.分别以F 1、F 2为圆心,用|CM |、|MD |为半径作圆,两圆相交于P 1、P 2两点;同样方法分别以F 1、F 2为圆心,用|DM |、|CD |为半径作圆,两圆相交于P 3、P 4两点;并将这四个点定义为“追踪点”;6.依次选中点M 、点P 1 (或点M 、点P 2),用“作图”菜单中的“轨迹”功能,作出椭圆。
几何画板画椭圆的几种方法介绍.

<<几何画板>>画椭圆的几种方法介绍随着课改的发展,数学问题“视觉化”显得越来越重要(“视觉化”直观,学生更容易接受,课程改革也是朝这个发展方向),《几何画板》以其学习入门容易和操作简单的优点及其强大的图形和图象功能、方便的动画功能被许多数学教师看好,并已成为制作中学数学课件的主要创作平台之一。
下面介绍几种椭圆画法:一、到两定点的距离和等于定长具,在绘图板中作一线段AB(线段AB的长度为椭圆的长轴长2a)。
用“点”工具在线段上任取一点C,先后选中A,C点,选择“变换”->“标记向量"A->C"”(下图)。
再用“线段”工具作线段DE(线段DE的长为2c),选中点D,选择“变换”->“平移”,显示按标记的向量“从A到C”,点击“平移”,会得到点D'。
先后选中点D和D',选择“作图”->“以圆心和圆周上的点画圆”,选中点D',先后选中B,C点,选择“变换”->“标记向量"B->C"”。
同样的把点E,按向量BC平移,得到点E'。
以E为圆心过E'作圆选中两个圆的圆周,选择“作图”->“交点”,作出交点F和G。
让点C在线段AB上移动(选中点C,点击“编辑”下的“操作类按钮”中的“动画”可以生成动画),交点F、G的轨迹就是我们要作的椭圆(最后可以把无用的点、线隐藏)。
二、同心圆法(教材例5)选择“图表”->“定义坐标系”,用“圆”工具作两圆心为原点的同心圆(外圆半径长就是最终椭圆的长半轴长a,内圆半径长就是最终椭圆的短半轴长b),光标放原点处,击左键拖动光标,松开左键就得到所需圆。
在外圆圆周上任取一点E(可以选中圆,点击“作图”下的“对象上的点”;或者选取“点”工具,然后把光(选中点A(原点)和点E,点击“作图”下的“线段、射线或直线”),再作AE与小圆的交点(选中线段AE和内圆圆周,可用快捷键Ctrl+I作出交点)F。
椭圆的五种画法及各种弦的制作(很不错的几何画板教程).
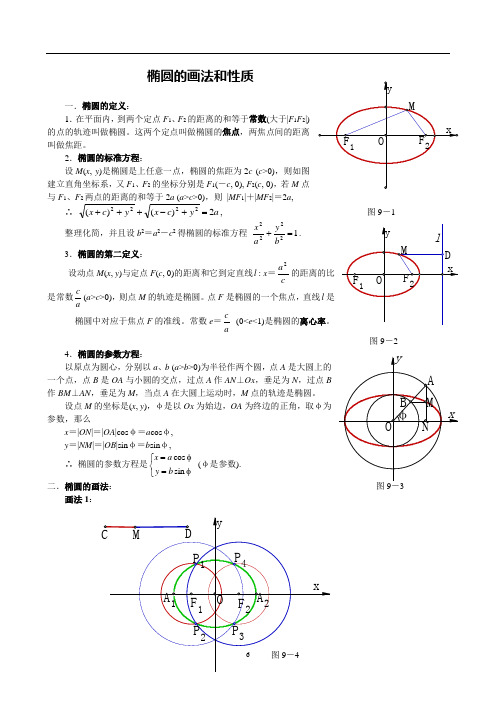
椭圆的画法和性质一.椭圆的定义: 1.在平面内,到两个定点F 1、F 2的距离的和等于常数(大于|F 1F 2|)的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,两焦点间的距离叫做焦距。
2.椭圆的标准方程:设M (x , y )是椭圆是上任意一点,椭圆的焦距为2c (c >0),则如图建立直角坐标系,又F 1、F 2的坐标分别是F 1(-c , 0), F 2(c , 0),若M 点与F 1、F 2两点的距离的和等于2a (a >c >0),则 |MF 1|+|MF 2|=2a ,∴a y c x y c x 2)()(2222=+-+++, 图9-1整理化简,并且设b 2=a 2-c 2得椭圆的标准方程12222=+b y a x . 3.椭圆的第二定义:设动点M (x , y )与定点F (c , 0)的距离和它到定直线l : x =ca2的距离的比是常数ac(a >c >0),则点M 的轨迹是椭圆。
点F 是椭圆的一个焦点,直线l 是椭圆中对应于焦点F 的准线。
常数e =ac(0<e <1)是椭圆的离心率。
图9-24.椭圆的参数方程:以原点为圆心,分别以a 、b (a >b >0)为半径作两个圆,点A 是大圆上的一个点,点B 是OA 与小圆的交点,过点A 作AN ⊥Ox ,垂足为N ,过点B 作BM ⊥AN ,垂足为M ,当点A 在大圆上运动时,M 点的轨迹是椭圆。
设点M 的坐标是(x , y ),φ是以Ox 为始边,OA 为终边的正角,取φ为参数,那么x =|ON |=|OA |cos φ=a cos φ,y =|NM |=|OB |sin φ=b sin φ,∴ 椭圆的参数方程是⎩⎨⎧φ=φ=sin cos b y a x (φ是参数).二.椭圆的画法:画法1:1.在x 轴上取两点F 1、F 2,使|OF 1|=|OF 2|,用它们作为两个焦点; 2.在图形外作一条线段CD ,使|CD |=2a ,(|CD |>|F 1F 2|); 3.以O 为中心,在x 轴上取两点A 1、A 2,使|A 1A 2|=|CD |;4.在CD 上分别取C '、D ',使|CC '|=|A 1F 1|=|DD '|;作线段C 'D ',并用“作图”菜单中的“对象上的点”功能在C 'D '上作点M ;5.分别以F 1、F 2为圆心,用|CM |、|MD |为半径作圆,两圆相交于P 1、P 2两点;同样方法分别以F 1、F 2为圆心,用|DM |、|CD |为半径作圆,两圆相交于P 3、P 4两点;并将这四个点定义为“追踪点”;6.依次选中点M 、点P 1 (或点M 、点P 2),用“作图”菜单中的“轨迹”功能,作出椭圆。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课题:椭圆的画法
刘本华
【教学目的】通过教学使学生了解本椭圆及椭圆物体的画法等。
【教学重点】椭圆的透视规律。
【教学难点】椭圆的画法。
【教学方法】讲授法、图片展示法。
【教学课时】3课时
【教学过程】
第一课时:椭圆的画法
一、教学导入
展示圆的变化,用一个水桶在视平线上下展示,引出圆的变化规律:离视平线越近越椭,离视平线越远越圆。
二、椭圆的画法,教师黑板上示范。
三、总结:
1、椭圆的边是连续弯曲的,绝对不会有直边和角出现比较两个不正确的图形,它们一个有角,一个有直边。
而正确的一个边缘是圆顷的弧形。
2、用横竖轴线将椭圆分害4成四等分.将椭圆四分之一部分涂上阴影。
如果分割后的四部分形状不一样,你就画得不对,虽然每块阴影的形状应该是同样的,但它从垂直、水平和对角方向上看是一模一样的。
3、我们看到的这组椭圆是圆在不同的水平线上的形状.当眼睛和圆在同一水平线时。
我们看到的是线;随着眼睛与圆之间的视角发生变化。
椭圆的长度增加了.而宽度不变;当眼睛垂直于水平面时.我们看到的是完整的圆。
四、学生练习
1、学生练习,教师巡回指导
2、及时表扬好的同学和纠正错误的画法。
五、课堂小结
1、总结本节课所学内容。
2、布置下节课内容及工具材料准备。
板书设计
第二课时:椭圆——单个物体画法
一、如何观察实物
注意它的整体形状;注意它的高度,比较它的宽度;注意光照的方向,它的颜色,它的质地。
它有反射光吗?它是被光线环绕着,还是光线从一个方向照射形成一定的角度?当你用这样的方法去观察一个物体时,真实的物体与你画的物体就非常接近了。
当你把这个物体视为形状、颜色或光照的形状时,你也就初具了用画家的眼光观察物体的能力,虽然你没有问上述这些问题,但实际上你想得越少,反而看得越多。
作为初学者,就是要经常想这些问题,才能使你所看见的水罐或杯子,能像画家眼中的形状、颜色、质地和构成一样,就好比照相机拍摄到的图像,它也被接收到我们的视网膜上。
二、教师示范实物画法
1黑板上示范画法。
2、绘画方法总结:变画边改
当你描绘完实物的轮廓时,把画举起,要不必移动你的头就能看到画和实物。
比较一下哪部分画得对,重要的是哪部分画得不对。
然后再仔细重画正确的线条,之后擦掉不正确的线条,不断地改正标记和线条,直到看上去像被画的物体为止。
当你画正确的线时,是在没有擦掉不正确的线之前,这样你比较容易画好。
因为你可以在参照和比较不正确的线的同时,找到正确的位置。
如果你先擦掉不正确的线,可能你又将画上不正确的线。
如果你对眼睛看到的部分感到迷茫或感觉杂乱,不要紧,因为眼睛会趋向于正确的部分,而忽略不正确的部分。
如果两个物体的形状不相似,眼睛能做出比较,并能非常迅速地告诉你哪个物体的形状是正确的,哪个物体的形状是不正确
的。
相信你的眼睛!相信它能非常准确地分辨物体的形状、颜色和质地。
三、学生练习,教师巡回指导。
四、课堂总结
画处于不同位置的同一个物体,你可能会发现有些位置很难画,这并不重要。
当你觉得你画得一团糟时,不要放弃。
只要坚持反复练习,你就能越来越准确地画好物体的轮廓。
你练习得越多,就会画得越好。
如果形状画得不准,只需找到原因即可。
原因可能有一种或多种:比如线条是要上移还是下移,左移还是右移?线条之间需要靠近一点,还是离远一点?线条是长一点,还是短一点?直一点,或者弯一点?角是不是画得对,钝角、锐角有没有画得过分了?画素描要有恒心,当看到错误时,要毫不犹豫地改正。
你一开始就本着这种态度,养成习惯,会很快进步。
当你感到累了、烦了,停下来,不要强迫自己,不要违背自己的意愿。
当你真的想画时,你会发现,你能不顾一切,什么疲倦和烦恼都没有了。
五、布置下节课内容及工具材料准备。
板书设计
课题:椭圆的画法
一、如何观察实物三、学生作品展示
二、实物画法
第三课时:椭圆——组合物体画法
一、复习上节课“单个物体画法”。
1、学生练习:
2、总结:把物体形状画好,应该测量物体的高、宽、中心线,中心线就像镜于一样,能检验物体的两边是否对称。
二、组合物体画法
1、教师黑板上示范:
示范(一)
绘画要点:实物之间的空间,当画一组实物时,不要只想实物的形状,还要注意它们之间的空间。
这些空间取决于实物的轮廓,也有确定的形状。
知道这些,把它们也当作你素描的一部分,你就能很容易改正错误。
你能把物体之间的空间画好,实物也就画好了。
在画家的视觉世界里,没有真正的空间,每个空间都有要表现的内容。
懂得这点会增强你观察物体时的兴趣。
绘画要点:将二三个物体放到一起,不要管示范(二)它们的形状是否相似,注意它们的大小、外形,
以及它们之间的距离和相互关系,会感觉更
有意思,也更有难度。
可以将一纽物体分开放,那样就可以看到
每个物体的全貌。
也可以把物体重叠放,当物
体的有些部分被遮住时,要推测物体形状变化
的样子。
3、学生练习,教师巡回指导。
三、课堂小结,及时表扬和鼓励。
四、布置下节课内容。
板书设计。
