大学物理学(课后答案解析)第1章
大学物理课后习题详解(第一章)中国石油大学

习 题 一1-1 一质点在平面xOy 内运动,运动方程为t x 2=,2219t y -= (SI ).(1)求质点的运动轨道;(2)求s 1=t 和s 2=t 时刻质点的位置矢量;(3)求s 1=t 和s 2=t 时刻质点的瞬时速度和瞬时加速度;(4)在什么时刻,质点的位置矢量和速度矢量垂直?这时x 、y 分量各为多少?(5)在什么时刻,质点离原点最近?最近距离为多大?[解] 质点的运动方程t x 2=,2219t y -= (1)消去参数t ,得轨道方程为:22119x y -= ()0≥x(2)把s 1=t 代入运动方程,得j i j i r 172+=+=y x把s 2=t 代入运动方程,得()j i j i r 1142219222+=⨯-+⨯=(3)由速度、加速度定义式,有4/d d ,0/d d 4/d d ,2/d d y y x x y x -====-====t v a t v a t t y v t x v所以,t 时刻质点的速度和加速度分别为=v j i j i t v v 42y x -=+j j i a 4y x -=+=a a所以,s 1=t 时,j i v 42-=,j a 4-=s 2=t 时,j i v 82-=,j a 4-= (4)当质点的位置矢量和速度矢量垂直时,有0=⋅v r即 ()[][]04221922=-⋅-+j i j i t t t 整理,得 093=-t t解得 01=t ; 32=t ;33-=t (舍去)m 19,0,s 011===y x t 时 m 1,m 6,s 322===y x t 时(5)任一时刻t 质点离原点的距离()()()222222192tt yx t r -+=+=令0d d =tr 可得 3=t所以,s 3=t 时,质点离原点最近 () 6.08m 3=r1-2 一粒子按规律59323+--=t t t x 沿x 轴运动,试分别求出该粒子沿x 轴正向运动;沿x 轴负向运动;加速运动;减速运动的时间间隔.[解] 由运动方程59323+--=t t t x 可得 质点的速度 ()()133963d d 2+-=--==t t t t tx v (1)粒子的加速度 ()16d d -==t tv a(2) 由式(1)可看出 当3s >t 时,0>v ,粒子沿x 轴正向运动;当3s <t 时,0<v ,粒子沿x 轴负向运动.由式(2)可看出 当1s >t 时,0>a ,粒子的加速度沿x 轴正方向;当1s <t 时,0<a ,粒子的加速度沿x 轴负方向. 因为粒子的加速度与速度同方向时,粒子加速运动,反向时,减速运动,所以,当s 3>t 或1s 0<<t 间隔内粒子加速运动,在3s 1s <<t 间隔内里粒子减速运动.1-3 一质点的运动学方程为2t x =,()21-=t y (S1).试求: (1)质点的轨迹方程;(2)在2=t s 时,质点的速度和加速度.[解] (1) 由质点的运动方程 2t x = (1)()21-=t y (2)消去参数t ,可得质点的轨迹方程 ()21-=x y(2) 由(1)、(2)对时间t 求一阶导数和二阶导数可得任一时刻质点的速度和加速度 t tx v 2d d x ==()12d d y -==t ty v所以 ()j i j i v 122y x -+=+=t t v v (3)2d d 22x ==tx a 2d d22y ==tya所以 j i a 22+= (4) 把2s =t 代入式(3)、(4),可得该时刻质点的速度和加速度.j i v 24+= j i a 22+=1-4 质点的运动学方程为t A x ωsin =,t B y ωcos =,其中 A 、B 、ω为正常数,质点的轨道为一椭圆.试证明质点的加速度矢量恒指向椭圆的中心.[证明] 由质点的运动方程 t A x ωs i n= (1) t B y ωc o s = (2)对时间t 求二阶导数,得质点的加速度 t A t x a ωωs i n d d 222x -==t B tya ωωcos d d222y -==所以加速度矢量为 ()r j i a 22c o s s i n ωωωω-=+-=t B t A可得加速度矢量恒指向原点——椭圆中心.1-5 质点的运动学方程为()j i r 222t t -+= (SI ),试求:(1)质点的轨道方程;(2)2s =t 时质点的速度和加速度.[解] (1) 由质点的运动方程,可得tx 2= 22t y -=消去参数t ,可得轨道方程2412x y -=(2) 由速度、加速度定义式,有j i r v t t 22d /d -==j r a 2d /d 22-==t将2s =t 代入上两式,得j i v 42-= j a 2-=1-6 已知质点的运动学方程为t r x ωcos =,t r y ωsin =,ct z =,其中r 、ω、c 均为常量.试求:(1)质点作什么运动?(2)其速度和加速度? (3)运动学方程的矢量式.[解] (1) 质点的运动方程 t r x ωc o s= (1) t r y ωsin = (2)ct z = (3)由(1)、(2)消去参数t 得 222r y x =+此方程表示以原点为圆心以r 为半径的圆,即质点的轨迹在xoy 平面上的投影为圆. 由式(2)可以看出,质点以速率c 沿z 轴匀速运动.综上可知,质点绕z 轴作螺旋线运动.(2) 由式(1)、(2)、(3)两边对时间t 求导数可得质点的速度tr tx v ωωsin d d x -==t r ty v ωωcos d d y ==c tz v ==d d z所以 k j i k j i v c t r t r v v v ++-=++=ωωωωc o s s i nz y x 由式(1)、(2)、(3)两边对时间求二阶导数,可得质点的加速度t r tx a x ωωcos d d 222-==t r ty a y ωωsin d d 222-==0z =a所以 j i k j i a t r t r a a a ωωωωs i n c o s22z y x --=++= (3) 由式(1)、(2)、(3)得运动方程的矢量式k j i k j i r ct t r t r z y x ++=++=ωωsin cos1-7 湖中一小船,岸边的人用跨过高处的定滑轮的绳子拉船靠岸(如图所示).当收绳速度为0v 时,试问:(1)船的运动速度u 比v 大还是小?(2)若常量=v .船能否作匀速运动?如果不能,其加速度为何值?[解] (1) 由图知222h s L +=两边对t 求导数,并注意到h 为常数,得 ts stL Ld d 2d d 2=又 ts u t L v d d ,d d -=-=所以 su Lv = (1) 即1>=s L vu因此船的速率u 大于收绳速率v .(2) 将(1)式两边对t 求导,并考虑到v 是常量tu sts utL vd d d d d d +=所以 sa v u =-22 即 ()32222sv h sv ua =-=1-8 质点沿x 轴运动,已知228t v +=,当8=t s 时,质点在原点左边52m 处(向右为x 轴正向).试求:(1)质点的加速度和运动学方程;(2)初速度和初位置;(3)分析质点的运动性质.[解] (1) 质点的加速度 t t v a 4/d d ==又 t x v /d d = 所以 t v x d d =对上式两边积分,并考虑到初始条件得()⎰⎰⎰+==-ttxt t t v x 82852d 28d d所以 3.4573283-+=t t x因而质点的运动学方程为 33283.457t t x ++-=(2) 将0=t 代入速度表达式和运动学方程,得m/s 802820=⨯+=vm 3.457032083.45730-=⨯+⨯+-=x(3) 质点沿x 轴正方向作变加速直线运动,初速度为8m/s ,初位置为3.457-m.1-9 一物体沿x 轴运动,其加速度与位置的关系为x a 62+=.物体在0=x 处的速度为s m 10,求物体的速度与位置的关系.[解] 根据链式法则 xv vtx x v tv a d d d d d d d d ===()x x x a v v d 62d d +==对上式两边积分并考虑到初始条件,得 ()⎰⎰+=xvx x v v 010d 62d故物体的速度与位置的关系为100462++=x x v s m1-10 一质点在平面内运动,其加速度j i a y x a a +=,且x a ,y a 为常量.(1)求t -v 和t -r 的表达式;(2)证明质点的轨迹为一抛物线.0=t 时,0r r =,0v v =.[解] 由 td d v a =得 t d a v =两边积分得⎰⎰=tvt 0d 0a v v因x a ,y a 为常量,所以a 是常矢量,上式变为t a v v =-0 即 t a v v +=0由 td d r v =得 ()t t t d d d 0a v v r +==两边积分,并考虑到0v 和a 是常矢量,()⎰⎰+=tr t t 00d d 0a v r r即 20021t t a v r r ++=(2) 为了证明过程简单起见,按如下方式选取坐标系,使一个坐标轴(如y 轴)与a平行,并使质点在0=t 时刻位于0r .这样 00x t v x x += (1)00221y t v at y y ++=(2)联立 (1)~(2)式,消去参数t 得()()00x0y 0202x021y x x v v x x v a y +-+-=此即为轨道方程,它为一条抛物线.1-11 在重力和空气阻力的作用下,某物体下落的加速度为Bv g a -=,g 为重力加速度,B 为与物体的质量、形状及介质有关的常数.设0=t 时物体的初速度为零.(1)试求物体的速度随时间变化的关系式;(2)当加速度为零时的速度(称为收尾速度)值为多大?[解] (1) 由tv a d d =得t Bvg v d d =-两边分别积分,得⎰⎰=-t v t Bvg v 0d d所以,物体的速率随时间变化的关系为:()Bte Bg v --=1(2) 当0=a 时 有 0=-=Bv g a (或以∞=t 代入)由此得收尾速率 Bg v =1-12 一质点由静止开始作直线运动,初始加速度为a ,此后随t 均匀增加,经时间τ后,加速度变为2a ,经τ2后,加速度变为3a ,…….求经时间τn 后,该质点的加速度和所走过的距离.[解] 由题意可设质点的加速度与时间t 的关系为kt a a +=t (k 为常数)由 a k a a 2τ=+=τ得τak =所以 a t t aa a ⎪⎭⎫ ⎝⎛+=+=ττ1t 故当τn t =时,质点的加速度 ()a n a 1n τ+=由tv a d d =得t a v d d =对上式两边积分得⎰⎰⎪⎭⎫ ⎝⎛+=tvt a t v 00d 1d τ 所以 22t aat v τ+=又 tx v d d = t v x d d =对上式两边积分⎰⎰⎪⎭⎫ ⎝⎛+=ττn st t a at x 020d 2d 经过时间τn 后,质点所走过的距离()2232361621τττa n nt a at s n +=⎪⎭⎫ ⎝⎛+=1-13 一物体悬挂于弹簧上沿竖直方向作谐振动,其加速ky a -=,k 为常数,y 是离开平衡位置的坐标值.设0y 处物体的速度为0v ,试求速度v 与y 的函数关系.[解] 根据链式法则 yv vty y v tv a d d d d d d d d ===y a v v d d =对上式两边积分⎰⎰⎰-==y y yy v y ky y a v v 000d d d v即 ()()2022022121y y k v v--=-故速度v 与y 的函数关系为()220202yy k v v -+=1-14 一艘正以速率0v 匀速行驶的舰艇,在发动机关闭之后匀减速行驶.其加速度的大小与速度的平方成正比,即2kv a -=, k 为正常数.试求舰艇在关闭发动机后行驶了x 距离时速度的大小.[解] 根据链式法则 xv vtx x v tv a d d d d d d d d ===v av x d d =对上式两边积分⎰⎰⎰-==vvvvxkvv v av x 0d d d 0化简得ln1v vkx -=所以kxev v -=0l-15 一粒子沿抛物线轨道2x y =运动,且知s m 3x =v .试求粒子在m 32=x 处的速度和加速度.[解] 由粒子的轨道方程 2x y = 对时间t 求导数 x y 2d d 2d d xv tx xty v ===(1)再对时间t 求导数,并考虑到x v 是恒量2x y 2d d v tv a ==(2)把m 32=x 代入式(1)得m 43322y =⨯⨯=v 所以,粒子在m 32=x 处的速度为s m 543222x 2x =+=+=v v v与x 轴正方向之间的夹角85334arctanarctanxy '===v v θ由式(2)得粒子在m 32=x 处的加速度为22s m 1832=⨯=a加速度方向沿y 轴的正方向.1-16 一质点沿半径为0.10m 的圆周运动,其角位置342t +=θ.(1)在2s =t 时,它的法向加速度和切向加速度各是多少?(2)切向加速度的大小恰是总加速度大小的一半时,θ值为多少?(3)何时切向加速度与法向加速度大小相等?[解] 质点的角速度 212d d t t==θω质点的线速度 222.11210.0t t R v =⨯==ω 质点的法向加速度n a ,切向加速度t a 为()4222n 4.1410.012t tR a =⨯==ω (1)t tv a 4.2d d t ==(2)(1)把2s =t 代入(1)式和(2)式,得此时2t 224n m/s8.424.2m/s 103.224.14=⨯=⨯=⨯=a a(2)质点的总加速度1364.262t 2n +=+=t t a a a由 a a 21t =得 1364.25.04.26+⨯=t t t解得 0.66s =t 所以 r a d 15.3423=+=t θ (3)当t n a a =即t t 4.24.144=时有 0.55s =t1-17 火车在曲率半径R =400m 的圆弧轨道上行驶.已知火车的切向加速度2.0t =a 2s m ,求火车的瞬时速率为s m 10时的法向加速度和加速度.[解] 火车的法向加速度 222n sm 25.040010===Rva方向指向曲率中心 火车的总加速度 2222t 2n s m 32.02.025.0=+=+=a a a设加速度a 与速度v 之间的夹角为θ,则025134.512.025.0arctanarctantn '====a a θ1-18 为了转播电视而发射的地球同步卫星在赤道上空的圆轨道上运动,周期等于地球的自转周期24h =T .求卫星离开地面的高度和卫星的速率(距地球中心r 处的重力加速度2e ⎪⎭⎫⎝⎛=r R g a ,e R 是地球的半径.)[解] 设同步卫星距地球的中心为r ,速率为v ,则Tr v π2=(1)2e 2⎪⎭⎫⎝⎛==r R g a r v(2) 解(2)式可得()()m 1022.443600241063788.947322233222e ⨯=⨯⨯⨯⨯==ππT gR r代入(1)式可得s m 1007.33600241022.42237⨯=⨯⨯==ππTr v所以,卫星距地面的高度m 1058.31063781022.4737e ⨯=⨯-⨯=-=R r h1-19 若登月舱在登上月球之前绕月球以半径e 31R r = (e R 为地球半径)作圆周运动,并且已知这时月球对登月舱的引力加速度g a 121=.试计算登月舱的速率和飞行一周所需要的时间.[解] 设登月舱的速率为v ,周期为T ,则a rv=2即g R v1213e2=(1)v Tr =π2 即v TR =32e π (2)解(1)式可得s m 1032.1106378368.93633e ⨯=⨯⨯==R g v代入(2)式可得s 1001.1368.931063782363243e⨯=⨯==ππg R T1-20 如图所示,一卷扬机自静止开始作匀加速运动,绞索上一点起初在A 处经3s 到达鼓轮的B 处,然后作圆周运动.已知0.45m =AB ,鼓轮半径0.5m =R ,求该点经过点C 时,其速度和加速度的大小和方向.[解] 设A 点的切向加速度为t a ,经过B 点时的速率为B v ,法向加速度为n a由A 到B 过程:2t 21t a AB =(1)t a v t B = (2)在B 点: R a R v //t B B ==βω, (3)由B 到C 过程:πβωω22B 2C =- (4)在C 点: R v C C ω= (5) 联立以上五式,得m 64.05.035.045.0435.045.02422222C C =⨯⨯⨯+⎪⎭⎫⎝⎛⨯⨯=+⎪⎭⎫⎝⎛==ππωR Rt AB Rt AB R v 方向沿切向Rv a 2C n =2t 2tAB a =22222n2ts m 83.05.064.0345.02=⎪⎪⎭⎫⎝⎛+⎪⎭⎫⎝⎛⨯=+=a a a 28330.4520.50.64arctanarctan22nt '=⨯==a a θ1-21 在一个转动的齿轮上,一个齿尖P 沿半径为R 的圆周运动,其路程随时间的变化规律为2021bt t v s +=,其中0v 和b 都是正常量.求t 时刻齿尖P 的速度及加速度的大小.[解] 设时刻t 齿尖P 的速率为v ,切向加速度t a ,法向加速度n a ,则Rbt v Rva b t va bt v t s v 202n t 0)(d d d d +====+==所以,t 时刻齿尖P 的加速度为24022n 2t )(Rbt v b a a a ++=+=1-22 一物体作斜抛运动,抛射角为α,初速度为0v ,轨迹为一抛物线(如图所示).试分别求抛物线顶点A 及下落点B 处的曲率半径.[解] 物体在A 点的速度设为A v ,法向加速度为nA a ,曲率半径为A ρ,由题图显然有αcos 0A v v = (1) nA a =g (2) A n A2Aa v =ρ (3)联立上述三式得 gv αρ220A c o s =物体在B 点的速度设为B v ,法向加速度为nB a ,曲率半径为B ρ,由题图显然有0B v v = (4) αcos nB g a = (5) nB B2Ba v =ρ (6)联立上述三式得 αρc o s 2B g v =1-23 一物体作如图所示的抛体运动,测得轨道的点A 处,速度的大小为v ,其方向与水平线的夹角为030,求点A 的切向加速度和该处的曲率半径.[解] 设A 点处物体的切向加速度为t a ,法向加速度为n a ,曲率半径为ρ,则 n t a a g +=由图知 g g a 5.030sin 0t -=-=2/330cos 0n g g a ==又 n 2a v=ρ所以 gv g va v3322/322n2===ρ1-24 一门火炮在原点处以仰角0130=θ、初速10v m 100=发射一枚炮弹.另有一门位于600=x m 处的火炮同时以初速8020=v s m 发射另一枚炮弹,其仰角2θ为何值时,可望能与第一枚炮弹在空中相碰? 相碰时间和位置如何(忽略空气阻力的影响)?[解] 设经过时间t 后,炮弹1、炮弹2的坐标分别为()11,y x 、()22,y x ,则 对炮弹1 t v x 1101cos θ= 2110121sin gt t v y -=θ对炮弹2 t v x x 22002cos θ+= 2220221sin gt t v y -=θ当炮弹1、炮弹2相碰时 21x x = 21y y =即 t v x t v 2200110cos cos θθ+= (1)2220211021sin 21sin gt t v gt t v -=-θθ (2)解(2)式可得 625.030sin 80100sin sin 0120102=⨯==θθv v (3)所以 02682.38625.0arcsin ==θ 由(1)式可得 s 48.2682.38cos 8030cos 10060cos cos 02201100=⨯-⨯=-=θθv v x t相遇时的坐标设为(x ,y ),则m 77.21448.230cos 100cos 011021=⨯⨯====t v x x x θm 86.9348.28.92148.230sin 10021sin 2211021=⨯⨯-⨯⨯=-===gtt v y y y θ1-25 河宽为d ,靠河岸处水流速度变为零,从岸边到中流,河水的流速与离开岸的距离成正比地增大,到中流处为0v .某人以相对水流不变的速率v 垂直水流方向驶船渡河,求船在达到中流之前的轨迹方程.[解] 取图示坐标系ky v =x已知 2d y =时,0x v v =代入上式得 d v k 02=所以 y dv v 0x 2=(1)又 v v =y积分得 vt y = (2) 代入(1)式得 vt d v v 0x 2=积分得 20vt d v x = (3)由(2)、(3)消去t 得 20y vdv x =1-26 如图所示,一航空母舰正以s m 17的速度向东行驶,一架直升飞机准备降落在舰的甲板上.海上有s m 12的北风吹着.若舰上的海员看到直升飞机以s m 5的速度垂直下降,求直升飞机相对海水及相对空气的速度?[解] 已知 k v 5-=机对舰 j v 17=舰对海 i v 12=气对海 故 ()s m 175j k v v v +-=+=舰对海机对舰机对海()m 51712k j i v v v -+-=+=海对气机对海机对气习题 1-26 图。
大学物理课后习题答案解析详解

第一章质点运动学1、(习题1.1):一质点在xOy 平面内运动,运动函数为2x =2t,y =4t 8-。
(1)求质点的轨道方程;(2)求t =1 s t =2 s 和时质点的位置、速度和加速度。
解:(1)由x=2t 得,y=4t 2-8 可得: y=x 2-8 即轨道曲线(2)质点的位置 : 22(48)r ti t j =+-r r r由d /d v r t =r r 则速度: 28v i tj =+r r r由d /d a v t =r r 则加速度: 8a j =r r则当t=1s 时,有 24,28,8r i j v i j a j =-=+=r r r r r rr r当t=2s 时,有 48,216,8r i j v i j a j =+=+=r r r r r rr r 2、(习题1.2): 质点沿x 在轴正向运动,加速度kv a -=,k 为常数.设从原点出发时速度为0v ,求运动方程)(t x x =.解:kv dtdv -= ⎰⎰-=t v v kdt dv v 001 tk e v v -=0t k e v dtdx-=0 dt e v dx t k t x -⎰⎰=000 )1(0t k e k v x --=3、一质点沿x 轴运动,其加速度为a 4t (SI),已知t 0时,质点位于x10 m处,初速度v 0.试求其位置和时间的关系式. 解: =a d v /d t 4=t d v 4=t d t ⎰⎰=vv 0d 4d tt t v 2=t 2v d =x /d t 2=t 2t t x txx d 2d 020⎰⎰= x 2= t 3 /3+10 (SI)4、一质量为m 的小球在高度h 处以初速度0v 水平抛出,求:(1)小球的运动方程;(2)小球在落地之前的轨迹方程;(3)落地前瞬时小球的d d r t v ,d d v t v,tvd d .解:(1) t v x 0= 式(1)2gt 21h y -= 式(2) 201()(h -)2r t v t i gt j =+v v v(2)联立式(1)、式(2)得 22v 2gx h y -=(3)0d -gt d rv i j t=v v v 而落地所用时间 gh2t =所以 0d 2gh d r v i j t =v vd d v g j t=-v v 2202y 2x )gt (v v v v -+=+= 2120212202)2(2])([gh v gh g gt v t g dt dv +=+=5、 已知质点位矢随时间变化的函数形式为22r t i tj =+vv v ,式中r 的单位为m ,t 的单位为s .求:(1)任一时刻的速度和加速度;(2)任一时刻的切向加速度和法向加速度。
大学物理课后习题1第一章答案

习题11.1选择题(1)一运动质点在某瞬时位于矢径),(y x r的端点处,其速度大小为()(A)dtdr (B)dtr d (C)dtr d || (D)22)()(dtdy dt dx +答案:(D)。
(2)一质点作直线运动,某时刻的瞬时速度s m v /2=,瞬时加速度2/2s m a -=,则一秒钟后质点的速度()(A)等于零(B)等于-2m/s (C)等于2m/s (D)不能确定。
答案:(D)。
(3)一质点沿半径为R 的圆周作匀速率运动,每t 秒转一圈,在2t 时间间隔中,其平均速度大小和平均速率大小分别为()(A)t R t R ππ2,2(B)tRπ2,0(C)0,0(D)0,2tRπ答案:(B)。
(4)质点作曲线运动,r表示位置矢量,v 表示速度,a 表示加速度,S 表示路程,τa 表示切向加速度,下列表达式中,()①a t = d /d v ,②v =t r d /d ,③v =t S d /d ,④τa t =d /d v.(A)只有①、④是对的.(B)只有②、④是对的.(C)只有②是对的.(D)只有③是对的.答案:(D)。
(5)一质点在平面上作一般曲线运动,其瞬时速度为v,瞬时速率为υ,某一时间内的平均速度为v,平均速率为v ,它们之间的关系必定有:()(A)vv v,v == (B)v v v,v =≠ (C)vv v,v ≠≠ (D)vv v,v ≠= 答案:(D)。
1.2填空题(1)一质点,以1-⋅s m π的匀速率作半径为5m 的圆周运动,则该质点在5s 内,位移的大小是;经过的路程是。
答案:10m;5πm。
(2)一质点沿x 方向运动,其加速度随时间的变化关系为a=3+2t (SI),如果初始时刻质点的速度v 0为5m ·s -1,则当t 为3s 时,质点的速度v=。
答案:23m·s -1.(3)一质点从静止出发沿半径R=1m 的圆周运动,其角加速度随时间t 的变化规律是α=12t 2-6t (SI),则质点的角速度ω=__________________;切向加速度τa =_________________.答案:4t 3-3t 2(rad/s),12t 2-6t (m/s 2)(4)一质点作直线运动,其坐标x 与时间t 的关系曲线如题1.2(4)图所示.则该质点在第___秒瞬时速度为零;在第秒至第秒间速度与加速度同方向.题1.2(4)图答案:3,36;(5)一质点其速率表示式为v s =+12,则在任一位置处其切向加速度a τ为。
《大学物理》各章练习题及答案解析

《大学物理》各章练习题及答案解析第1章 质点运动学一、选择题:1.以下五种运动中,加速度a保持不变的运动是 ( D ) (A) 单摆的运动。
(B) 匀速率圆周运动。
(C) 行星的椭圆轨道运动。
(D) 抛体运动。
(E) 圆锥摆运动。
2.下面表述正确的是( B )(A)质点作圆周运动,加速度一定与速度垂直; (B) 物体作直线运动,法向加速度必为零; (C)轨道最弯处法向加速度最大; (D)某时刻的速率为零,切向加速度必为零。
3.某质点做匀速率圆周运动,则下列说法正确的是( C )(A)质点的速度不变; (B)质点的加速度不变 (C)质点的角速度不变; (D)质点的法向加速度不变4.一运动质点在某瞬时位于矢径()y x r , 的端点处,其速度大小为( D )()()(()22⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛dt dy dt dx D C dtrd B dt drA5. 一质点在平面上运动,运动方程为:j t i t r222+=,则该质点作( B )(A)匀速直线运动 (B)匀加速直线运动(C)抛物线运动 (D)一般曲线运动6.一质点做曲线运动,r 表示位置矢量,v 表示速度,a表示加速度,s 表示路程,a t 表示切向加速度,对下列表达式,正确的是( B )(A)dt dr v = (B) dt ds v = (C) dtdv a = (D) dt vd a t=7. 某质点的运动方程为 3723+-=t t X (SI ),则该质点作 [ D ](A)匀加速直线运动,加速度沿 x 轴正方向; (B)匀加速直线运动,加速度沿 x 轴负方向; (C)变加速直线运动.加速度沿 x 轴正方向; (D)变加速直线运动,加速度沿 x 轴负方向8.一质点沿x 轴运动,其运动方程为()SI t t x 3235-=,当t=2s 时,该质点正在( A )(A)加速 (B)减速 (C)匀速 (D)静止1.D2. B3. C4.D5.B ,6B ,7A 8 A二 、填空题1. 一质点的运动方程为x =2t ,y =4t 2-6t ,写出质点的运动方程(位置矢量)j t t i t r)64(22-+=,t =1s 时的速度j i v22+=,加速度j a 8=,轨迹方程为x x y 32-=。
大学物理习题答案解析第一章

第一章 质点运动学1 -1 质点作曲线运动,在时刻t 质点的位矢为r ,速度为v ,速率为v ,t 至(t +Δt )时间内的位移为Δr , 路程为Δs , 位矢大小的变化量为Δr ( 或称Δ|r |),平均速度为v ,平均速率为v .(1) 根据上述情况,则必有( ) (A) |Δr |= Δs = Δr(B) |Δr |≠ Δs ≠ Δr ,当Δt →0 时有|d r |= d s ≠ d r (C) |Δr |≠ Δr ≠ Δs ,当Δt →0 时有|d r |= d r ≠ d s (D) |Δr |≠ Δs ≠ Δr ,当Δt →0 时有|d r |= d r = d s (2) 根据上述情况,则必有( )(A) |v |= v ,|v |= v (B) |v |≠v ,|v |≠ v (C) |v |= v ,|v |≠ v (D) |v |≠v ,|v |= v分析与解 (1) 质点在t 至(t +Δt )时间内沿曲线从P 点运动到P′点,各量关系如图所示, 其中路程Δs =PP′, 位移大小|Δr |=PP ′,而Δr =|r |-|r |表示质点位矢大小的变化量,三个量的物理含义不同,在曲线运动中大小也不相等(注:在直线运动中有相等的可能).但当Δt →0 时,点P ′无限趋近P 点,则有|d r |=d s ,但却不等于d r .故选(B).(2) 由于|Δr |≠Δs ,故tst ΔΔΔΔ≠r ,即|v |≠v . 但由于|d r |=d s ,故tst d d d d =r ,即|v |=v .由此可见,应选(C). 1 -2 一运动质点在某瞬时位于位矢r (x,y )的端点处,对其速度的大小有四种意见,即(1)t r d d ; (2)t d d r ; (3)t s d d ; (4)22d d d d ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛t y t x .下述判断正确的是( )(A) 只有(1)(2)正确 (B) 只有(2)正确 (C) 只有(2)(3)正确 (D) 只有(3)(4)正确分析与解trd d 表示质点到坐标原点的距离随时间的变化率,在极坐标系中叫径向速率.通常用符号v r 表示,这是速度矢量在位矢方向上的一个分量;td d r表示速度矢量;在自然坐标系中速度大小可用公式t s d d =v 计算,在直角坐标系中则可由公式22d d d d ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛=t y t x v 求解.故选(D).1 -3 质点作曲线运动,r 表示位置矢量, v 表示速度,a 表示加速度,s 表示路程, a t表示切向加速度.对下列表达式,即(1)d v /d t =a ;(2)d r /d t =v ;(3)d s /d t =v ;(4)d v /d t |=a t. 下述判断正确的是( )(A) 只有(1)、(4)是对的 (B) 只有(2)、(4)是对的 (C) 只有(2)是对的 (D) 只有(3)是对的分析与解td d v表示切向加速度a t,它表示速度大小随时间的变化率,是加速度矢量沿速度方向的一个分量,起改变速度大小的作用;t r d d 在极坐标系中表示径向速率v r (如题1 -2 所述);tsd d 在自然坐标系中表示质点的速率v ;而td d v表示加速度的大小而不是切向加速度a t.因此只有(3) 式表达是正确的.故选(D).1 -4 一个质点在做圆周运动时,则有( ) (A) 切向加速度一定改变,法向加速度也改变 (B) 切向加速度可能不变,法向加速度一定改变 (C) 切向加速度可能不变,法向加速度不变 (D) 切向加速度一定改变,法向加速度不变分析与解 加速度的切向分量a t起改变速度大小的作用,而法向分量a n 起改变速度方向的作用.质点作圆周运动时,由于速度方向不断改变,相应法向加速度的方向也在不断改变,因而法向加速度是一定改变的.至于a t是否改变,则要视质点的速率情况而定.质点作匀速率圆周运动时, a t恒为零;质点作匀变速率圆周运动时, a t为一不为零的恒量,当a t改变时,质点则作一般的变速率圆周运动.由此可见,应选(B).*1 -5 如图所示,湖中有一小船,有人用绳绕过岸上一定高度处的定滑轮拉湖中的船向岸边运动.设该人以匀速率v 0 收绳,绳不伸长且湖水静止,小船的速率为v ,则小船作( )(A) 匀加速运动,θcos 0v v =(B) 匀减速运动,θcos 0v v = (C) 变加速运动,θcos 0v v =(D) 变减速运动,θcos 0v v = (E) 匀速直线运动,0v v =分析与解 本题关键是先求得小船速度表达式,进而判断运动性质.为此建立如图所示坐标系,设定滑轮距水面高度为h,t 时刻定滑轮距小船的绳长为l ,则小船的运动方程为22h l x -=,其中绳长l随时间t 而变化.小船速度22d d d d h l t llt x -==v ,式中t l d d 表示绳长l 随时间的变化率,其大小即为v 0,代入整理后为θlh l cos /0220v v v =-=,方向沿x 轴负向.由速度表达式,可判断小船作变加速运动.故选(C).讨论 有人会将绳子速率v 0按x 、y 两个方向分解,则小船速度θcos 0v v =,这样做对吗? 1 -6 已知质点沿x 轴作直线运动,其运动方程为32262t t x -+=,式中x 的单位为m,t 的单位为 s .求:(1) 质点在运动开始后4.0 s 内的位移的大小; (2) 质点在该时间内所通过的路程;(3) t =4 s 时质点的速度和加速度.分析 位移和路程是两个完全不同的概念.只有当质点作直线运动且运动方向不改变时,位移的大小才会与路程相等.质点在t 时间内的位移Δx 的大小可直接由运动方程得到:0Δx x x t -=,而在求路程时,就必须注意到质点在运动过程中可能改变运动方向,此时,位移的大小和路程就不同了.为此,需根据0d d =tx来确定其运动方向改变的时刻t p ,求出0~t p 和t p ~t 内的位移大小Δx 1 、Δx 2 ,则t 时间内的路程21x x s ∆+∆=,如图所示,至于t =4.0 s 时质点速度和加速度可用tx d d 和22d d t x两式计算.解 (1) 质点在4.0 s 内位移的大小m 32Δ04-=-=x x x(2) 由 0d d =tx得知质点的换向时刻为s 2=p t (t =0不合题意)则m 0.8Δ021=-=x x xm 40Δ242-=-=x x x所以,质点在4.0 s 时间间隔内的路程为m 48ΔΔ21=+=x x s(3) t =4.0 s 时1s0.4s m 48d d -=⋅-==t t xv2s0.422m.s 36d d -=-==t t x a1 -7 一质点沿x 轴方向作直线运动,其速度与时间的关系如图(a)所示.设t =0 时,x =0.试根据已知的v -t 图,画出a -t 图以及x -t 图.分析 根据加速度的定义可知,在直线运动中v -t 曲线的斜率为加速度的大小(图中AB 、CD 段斜率为定值,即匀变速直线运动;而线段BC 的斜率为0,加速度为零,即匀速直线运动).加速度为恒量,在a -t 图上是平行于t 轴的直线,由v -t 图中求出各段的斜率,即可作出a -t 图线.又由速度的定义可知,x -t 曲线的斜率为速度的大小.因此,匀速直线运动所对应的x -t 图应是一直线,而匀变速直线运动所对应的x –t 图为t 的二次曲线.根据各段时间内的运动方程x =x (t ),求出不同时刻t 的位置x ,采用描数据点的方法,可作出x -t 图.解 将曲线分为AB 、BC 、CD 三个过程,它们对应的加速度值分别为2s m 20-⋅=--=AB AB AB t t a v v (匀加速直线运动)0=BC a (匀速直线运动)2s m 10-⋅-=--=CD CD CD t t a v v (匀减速直线运动)根据上述结果即可作出质点的a -t 图[图(B)].在匀变速直线运动中,有2021t t x x ++=v由此,可计算在0~2s和4~6s时间间隔内各时刻的位置分别为用描数据点的作图方法,由表中数据可作0~2s和4~6s时间内的x -t 图.在2~4s时间内, 质点是作1s m 20-⋅=v 的匀速直线运动, 其x -t 图是斜率k =20的一段直线[图(c)].1 -8 已知质点的运动方程为j i r )2(22t t -+=,式中r 的单位为m,t 的单位为s.求: (1) 质点的运动轨迹;(2) t =0 及t =2s时,质点的位矢;(3) 由t =0 到t =2s内质点的位移Δr 和径向增量Δr ;*(4) 2 s 内质点所走过的路程s .分析 质点的轨迹方程为y =f (x ),可由运动方程的两个分量式x (t )和y (t )中消去t 即可得到.对于r 、Δr 、Δr 、Δs 来说,物理含义不同,可根据其定义计算.其中对s 的求解用到积分方法,先在轨迹上任取一段微元d s ,则22)d ()d (d y x s +=,最后用⎰=s s d 积分求s.解 (1) 由x (t )和y (t )中消去t 后得质点轨迹方程为2412x y -= 这是一个抛物线方程,轨迹如图(a)所示.(2) 将t =0s和t =2s分别代入运动方程,可得相应位矢分别为j r 20= , j i r 242-=图(a)中的P 、Q 两点,即为t =0s和t =2s时质点所在位置. (3) 由位移表达式,得j i j i r r r 24)()(Δ020212-=-+-=-=y y x x其中位移大小m 66.5)(Δ)(ΔΔ22=+=y x r而径向增量m 47.2ΔΔ2020222202=+-+=-==y x y x r r r r*(4) 如图(B)所示,所求Δs 即为图中PQ 段长度,先在其间任意处取AB 微元d s ,则22)d ()d (d y x s +=,由轨道方程可得x x y d 21d -=,代入d s ,则2s内路程为m 91.5d 4d 42=+==⎰⎰x x s s Q P1 -9 质点的运动方程为23010t t x +-= 22015t t y -=式中x ,y 的单位为m,t 的单位为s.试求:(1) 初速度的大小和方向;(2) 加速度的大小和方向.分析 由运动方程的分量式可分别求出速度、加速度的分量,再由运动合成算出速度和加速度的大小和方向.解 (1) 速度的分量式为t t xx 6010d d +-==v t ty y 4015d d -==v当t =0 时, v o x =-10 m·s-1 , v o y =15 m·s-1 ,则初速度大小为120200s m 0.18-⋅=+=y x v v v设v o 与x 轴的夹角为α,则23tan 00-==xy αv vα=123°41′(2) 加速度的分量式为2s m 60d d -⋅==ta xx v , 2s m 40d d -⋅-==t a y y v则加速度的大小为222s m 1.72-⋅=+=y x a a a设a 与x 轴的夹角为β,则32tan -==x ya a β β=-33°41′(或326°19′)1 -10 一升降机以加速度1.22 m·s-2上升,当上升速度为2.44 m·s-1时,有一螺丝自升降机的天花板上松脱,天花板与升降机的底面相距2.74 m .计算:(1)螺丝从天花板落到底面所需要的时间;(2)螺丝相对升降机外固定柱子的下降距离.分析 在升降机与螺丝之间有相对运动的情况下,一种处理方法是取地面为参考系,分别讨论升降机竖直向上的匀加速度运动和初速不为零的螺丝的自由落体运动,列出这两种运动在同一坐标系中的运动方程y 1 =y 1(t )和y 2 =y 2(t ),并考虑它们相遇,即位矢相同这一条件,问题即可解;另一种方法是取升降机(或螺丝)为参考系,这时,螺丝(或升降机)相对它作匀加速运动,但是,此加速度应该是相对加速度.升降机厢的高度就是螺丝(或升降机)运动的路程.解1 (1) 以地面为参考系,取如图所示的坐标系,升降机与螺丝的运动方程分别为20121at t y +=v20221gt t h y -+=v当螺丝落至底面时,有y 1 =y 2 ,即20202121gt t h at t -+=+v vs 705.02=+=ag ht (2) 螺丝相对升降机外固定柱子下降的距离为m 716.021202=+-=-=gt t y h d v解2 (1)以升降机为参考系,此时,螺丝相对它的加速度大小a ′=g +a ,螺丝落至底面时,有2)(210t a g h +-=s 705.02=+=ag ht (2) 由于升降机在t 时间内上升的高度为2021at t h +='v则 m 716.0='-=h h d1 -11 一质点P 沿半径R =3.0 m 的圆周作匀速率运动,运动一周所需时间为20.0s,设t =0 时,质点位于O 点.按(a )图中所示Oxy 坐标系,求(1) 质点P 在任意时刻的位矢;(2)5s时的速度和加速度.分析 该题属于运动学的第一类问题,即已知运动方程r =r (t )求质点运动的一切信息(如位置矢量、位移、速度、加速度).在确定运动方程时,若取以点(0,3)为原点的O′x′y′坐标系,并采用参数方程x′=x′(t )和y′=y′(t )来表示圆周运动是比较方便的.然后,运用坐标变换x =x 0 +x ′和y =y 0 +y ′,将所得参数方程转换至Oxy 坐标系中,即得Oxy 坐标系中质点P 在任意时刻的位矢.采用对运动方程求导的方法可得速度和加速度.解 (1) 如图(B)所示,在O′x′y′坐标系中,因t Tθπ2=,则质点P 的参数方程为t T R x π2sin=', t T R y π2cos -='坐标变换后,在O x y 坐标系中有t TR x x π2sin='=, R t TR y y y +-=+'=π2cos0 则质点P 的位矢方程为j i r ⎪⎭⎫ ⎝⎛+-+=R t T R t T R π2cos π2sinj i )]π1.0(cos 1[3)π1.0(sin 3t t -+=(2) 5s时的速度和加速度分别为j j i r )s m π3.0(π2sin π2π2cos π2d d 1-⋅=+==t TT R t T T R t vi j i r a )s m π03.0(π2cos )π2(π2sin )π2(d d 222222-⋅-=+-==t TT R t T T R t 1 -12 地面上垂直竖立一高20.0 m 的旗杆,已知正午时分太阳在旗杆的正上方,求在下午2∶00 时,杆顶在地面上的影子的速度的大小.在何时刻杆影伸展至20.0 m ?分析 为求杆顶在地面上影子速度的大小,必须建立影长与时间的函数关系,即影子端点的位矢方程.根据几何关系,影长可通过太阳光线对地转动的角速度求得.由于运动的相对性,太阳光线对地转动的角速度也就是地球自转的角速度.这样,影子端点的位矢方程和速度均可求得.解 设太阳光线对地转动的角速度为ω,从正午时分开始计时,则杆的影长为s =h tg ωt ,下午2∶00 时,杆顶在地面上影子的速度大小为132s m 1094.1cos d d --⋅⨯===tωωh t s v 当杆长等于影长时,即s =h ,则s 606034πarctan 1⨯⨯===ωh s ωt 即为下午3∶00 时.1 -13 质点沿直线运动,加速度a =4 -t2 ,式中a 的单位为m·s-2 ,t 的单位为s.如果当t =3s时,x =9 m,v =2 m·s-1 ,求质点的运动方程.分析 本题属于运动学第二类问题,即已知加速度求速度和运动方程,必须在给定条件下用积分方法解决.由t a d d v =和tx d d =v 可得t a d d =v 和t x d d v =.如a =a (t )或v =v (t ),则可两边直接积分.如果a 或v 不是时间t 的显函数,则应经过诸如分离变量或变量代换等数学操作后再做积分.解 由分析知,应有⎰⎰=tt a 0d d 0vv v得 03314v v +-=t t (1)由⎰⎰=txx t x 0d d 0v得 00421212x t t t x ++-=v (2) 将t =3s时,x =9 m,v =2 m·s-1代入(1) (2)得v 0=-1 m·s-1,x 0=0.75 m .于是可得质点运动方程为75.0121242+-=t t x 1 -14 一石子从空中由静止下落,由于空气阻力,石子并非作自由落体运动,现测得其加速度a =A -B v ,式中A 、B 为正恒量,求石子下落的速度和运动方程.分析 本题亦属于运动学第二类问题,与上题不同之处在于加速度是速度v 的函数,因此,需将式d v =a (v )d t 分离变量为t a d )(d =v v后再两边积分. 解 选取石子下落方向为y 轴正向,下落起点为坐标原点.(1) 由题意知 v vB A ta -==d d (1) 用分离变量法把式(1)改写为t B A d d =-vv(2)将式(2)两边积分并考虑初始条件,有⎰⎰=-t t B A 0d d d 0v vvvv得石子速度 )1(Bt e BA--=v 由此可知当,t →∞时,BA→v 为一常量,通常称为极限速度或收尾速度. (2) 再由)1(d d Bt e BAt y --==v 并考虑初始条件有 t e BA y t Bt y d )1(d 00⎰⎰--= 得石子运动方程)1(2-+=-Bt e BAt B A y 1 -15 一质点具有恒定加速度a =6i +4j ,式中a 的单位为m·s-2 .在t =0时,其速度为零,位置矢量r 0 =10 m i .求:(1) 在任意时刻的速度和位置矢量;(2) 质点在Oxy 平面上的轨迹方程,并画出轨迹的示意图.分析 与上两题不同处在于质点作平面曲线运动,根据叠加原理,求解时需根据加速度的两个分量a x 和a y 分别积分,从而得到运动方程r 的两个分量式x (t )和y (t ).由于本题中质点加速度为恒矢量,故两次积分后所得运动方程为固定形式,即20021t a t x x x x ++=v 和20021t a t y y y y ++=v ,两个分运动均为匀变速直线运动.读者不妨自己验证一下.解 由加速度定义式,根据初始条件t 0 =0时v 0 =0,积分可得⎰⎰⎰+==ttt t 0)d 46(d d j i a vvj i t t 46+=v又由td d r=v 及初始条件t =0 时,r 0=(10 m)i ,积分可得 ⎰⎰⎰+==tt r r t t t t 0)d 46(d d 0j i r vj i r 222)310(t t ++=由上述结果可得质点运动方程的分量式,即x =10+3t 2y =2t 2消去参数t ,可得运动的轨迹方程3y =2x -20 m 这是一个直线方程.直线斜率32tan d d ===αx y k ,α=33°41′.轨迹如图所示. 1 -16 一质点在半径为R 的圆周上以恒定的速率运动,质点由位置A 运动到位置B,OA 和OB 所对的圆心角为Δθ.(1) 试证位置A 和B 之间的平均加速度为)Δ(/)Δcos 1(22θR θa v -=;(2) 当Δθ分别等于90°、30°、10°和1°时,平均加速度各为多少? 并对结果加以讨论.分析 瞬时加速度和平均加速度的物理含义不同,它们分别表示为t d d v =a 和tΔΔv =a .在匀速率圆周运动中,它们的大小分别为Ra n 2v =,t a ΔΔv = ,式中|Δv |可由图(B)中的几何关系得到,而Δt 可由转过的角度Δθ 求出.由计算结果能清楚地看到两者之间的关系,即瞬时加速度是平均加速度在Δt →0 时的极限值. 解 (1) 由图(b)可看到Δv =v 2 -v 1 ,故θΔcos 2Δ212221v v v v -+=v)Δcos 1(2θ-=v而vv θR s t ΔΔΔ==所以θR θt a Δ)cos Δ1(2ΔΔ2v -==v (2) 将Δθ=90°,30°,10°,1°分别代入上式,得R a 219003.0v ≈,Ra 229886.0v ≈ R a 239987.0v ≈,Ra 24000.1v ≈ 以上结果表明,当Δθ→0 时,匀速率圆周运动的平均加速度趋近于一极限值,该值即为法向加速度R2v . 1 -17 质点在Oxy 平面内运动,其运动方程为r =2.0t i +(19.0 -2.0t 2 )j ,式中r 的单位为m,t 的单位为s .求:(1)质点的轨迹方程;(2) 在t 1=1.0s 到t 2 =2.0s 时间内的平均速度;(3) t 1 =1.0s时的速度及切向和法向加速度;(4) t =1.0s 时质点所在处轨道的曲率半径ρ.分析 根据运动方程可直接写出其分量式x =x (t )和y =y (t ),从中消去参数t ,即得质点的轨迹方程.平均速度是反映质点在一段时间内位置的变化率,即t ΔΔr =v ,它与时间间隔Δt 的大小有关,当Δt →0 时,平均速度的极限即瞬时速度td d r =v .切向和法向加速度是指在自然坐标下的分矢量a t 和a n ,前者只反映质点在切线方向速度大小的变化率,即t t te a d d v =,后者只反映质点速度方向的变化,它可由总加速度a 和a t 得到.在求得t 1 时刻质点的速度和法向加速度的大小后,可由公式ρa n 2v =求ρ.解 (1) 由参数方程x =2.0t , y =19.0-2.0t 2消去t 得质点的轨迹方程:y =19.0 -0.50x 2(2) 在t 1 =1.00s 到t 2 =2.0s时间内的平均速度j i r r 0.60.2ΔΔ1212-=--==t t t r v (3) 质点在任意时刻的速度和加速度分别为j i j i j i t ty t x t y x 0.40.2d d d d )(-=+=+=v v v j j i a 222220.4d d d d )(-⋅-=+=s m ty t x t 则t 1 =1.00s时的速度v (t )|t =1s=2.0i -4.0j切向和法向加速度分别为t t y x t t t tt e e e a 222s 1s m 58.3)(d d d d -=⋅=+==v v v n n t n a a e e a 222s m 79.1-⋅=-=(4) t =1.0s质点的速度大小为122s m 47.4-⋅=+=y x v v v 则m 17.112==na ρv 1 -18 飞机以100 m·s-1 的速度沿水平直线飞行,在离地面高为100 m 时,驾驶员要把物品空投到前方某一地面目标处,问:(1) 此时目标在飞机正下方位置的前面多远? (2) 投放物品时,驾驶员看目标的视线和水平线成何角度?(3) 物品投出2.0s后,它的法向加速度和切向加速度各为多少?分析 物品空投后作平抛运动.忽略空气阻力的条件下,由运动独立性原理知,物品在空中沿水平方向作匀速直线运动,在竖直方向作自由落体运动.到达地面目标时,两方向上运动时间是相同的.因此,分别列出其运动方程,运用时间相等的条件,即可求解.此外,平抛物体在运动过程中只存在竖直向下的重力加速度.为求特定时刻t 时物体的切向加速度和法向加速度,只需求出该时刻它们与重力加速度之间的夹角α或β.由图可知,在特定时刻t ,物体的切向加速度和水平线之间的夹角α,可由此时刻的两速度分量v x 、v y 求出,这样,也就可将重力加速度g 的切向和法向分量求得.解 (1) 取如图所示的坐标,物品下落时在水平和竖直方向的运动方程分别为x =v t , y =1/2 gt 2飞机水平飞行速度v =100 m·s -1 ,飞机离地面的高度y =100 m,由上述两式可得目标在飞机正下方前的距离m 4522==gy x v(2) 视线和水平线的夹角为 o 5.12arctan==x y θ (3) 在任意时刻物品的速度与水平轴的夹角为vv v gt αx yarctan arctan == 取自然坐标,物品在抛出2s 时,重力加速度的切向分量与法向分量分别为2s m 88.1arctan sin sin -⋅=⎪⎭⎫ ⎝⎛==v gt g αg a t 2s m 62.9arctan cos cos -⋅=⎪⎭⎫ ⎝⎛==v gt g αg a n 1 -19 如图(a)所示,一小型迫击炮架设在一斜坡的底端O 处,已知斜坡倾角为α,炮身与斜坡的夹角为β,炮弹的出口速度为v 0,忽略空气阻力.求:(1)炮弹落地点P 与点O 的距离OP ;(2) 欲使炮弹能垂直击中坡面.证明α和β必须满足αβtan 21tan =并与v 0 无关. 分析 这是一个斜上抛运动,看似简单,但针对题目所问,如不能灵活运用叠加原理,建立一个恰当的坐标系,将运动分解的话,求解起来并不容易.现建立如图(a)所示坐标系,则炮弹在x 和y 两个方向的分运动均为匀减速直线运动,其初速度分别为v 0cos β和v 0sin β,其加速度分别为g sin α和gcos α.在此坐标系中炮弹落地时,应有y =0,则x =OP .如欲使炮弹垂直击中坡面,则应满足v x =0,直接列出有关运动方程和速度方程,即可求解.由于本题中加速度g 为恒矢量.故第一问也可由运动方程的矢量式计算,即20g 21t t +=v r ,做出炮弹落地时的矢量图[如图(B)所示],由图中所示几何关系也可求得OP (即图中的r 矢量).(1)解1 由分析知,炮弹在图(a)所示坐标系中两个分运动方程为αgt βt x sin 21cos 20-=v (1) αgt βt y cos 21sin 20-=v (2) 令y =0 求得时间t 后再代入式(1)得)cos(cos sin 2)sin sin cos (cos cos sin 2220220βααg ββαβααg βx OP +=-==v v 解2 做出炮弹的运动矢量图,如图(b)所示,并利用正弦定理,有βgt αt βαsin 212πsin 2πsin 20=⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛--v r 从中消去t 后也可得到同样结果.(2) 由分析知,如炮弹垂直击中坡面应满足y =0 和v x =0,则0sin cos 0=-=αgt βx v v (3)由(2)(3)两式消去t 后得αβsin 21tan = 由此可知.只要角α和β满足上式,炮弹就能垂直击中坡面,而与v 0 的大小无关.讨论 如将炮弹的运动按水平和竖直两个方向分解,求解本题将会比较困难,有兴趣读者不妨自己体验一下.1 -20 一直立的雨伞,张开后其边缘圆周的半径为R ,离地面的高度为h ,(1) 当伞绕伞柄以匀角速ω旋转时,求证水滴沿边缘飞出后落在地面上半径为g ωh R r /212+=的圆周上;(2) 读者能否由此定性构想一种草坪上或农田灌溉用的旋转式洒水器的方案?分析 选定伞边缘O 处的雨滴为研究对象,当伞以角速度ω旋转时,雨滴将以速度v 沿切线方向飞出,并作平抛运动.建立如图(a)所示坐标系,列出雨滴的运动方程并考虑图中所示几何关系,即可求证.由此可以想像如果让水从一个旋转的有很多小孔的喷头中飞出,从不同小孔中飞出的水滴将会落在半径不同的圆周上,为保证均匀喷洒对喷头上小孔的分布还要给予精心的考虑.解 (1) 如图(a)所示坐标系中,雨滴落地的运动方程为t ωR t x ==v (1)h gt y ==221 (2) 由式(1)(2)可得 g h ωR x 2222= 由图(a)所示几何关系得雨滴落地处圆周的半径为22221ωgh R R x r +=+= (2) 常用草坪喷水器采用如图(b)所示的球面喷头(θ0 =45°)其上有大量小孔.喷头旋转时,水滴以初速度v 0 从各个小孔中喷出,并作斜上抛运动,通常喷头表面基本上与草坪处在同一水平面上.则以φ角喷射的水柱射程为gR 2sin 0v = 为使喷头周围的草坪能被均匀喷洒,喷头上的小孔数不但很多,而且还不能均匀分布,这是喷头设计中的一个关键问题.1 -21 一足球运动员在正对球门前25.0 m 处以20.0 m·s-1 的初速率罚任意球,已知球门高为3.44 m .若要在垂直于球门的竖直平面内将足球直接踢进球门,问他应在与地面成什么角度的范围内踢出足球? (足球可视为质点)分析 被踢出后的足球,在空中作斜抛运动,其轨迹方程可由质点在竖直平面内的运动方程得到.由于水平距离x 已知,球门高度又限定了在y 方向的范围,故只需将x 、y 值代入即可求出.解 取图示坐标系Oxy ,由运动方程θt x cos v =, 221sin gt θt y -=v 消去t 得轨迹方程 222)tan 1(2tan x θg θx y +-=v以x =25.0 m,v =20.0 m·s-1 及3.44 m≥y ≥0 代入后,可解得71.11°≥θ1 ≥69.92°27.92°≥θ2 ≥18.89°如何理解上述角度的范围?在初速一定的条件下,球击中球门底线或球门上缘都将对应有两个不同的投射倾角(如图所示).如果以θ>71.11°或θ <18.89°踢出足球,都将因射程不足而不能直接射入球门;由于球门高度的限制,θ 角也并非能取71.11°与18.89°之间的任何值.当倾角取值为27.92°<θ <69.92°时,踢出的足球将越过门缘而离去,这时球也不能射入球门.因此可取的角度范围只能是解中的结果.1 -22 一质点沿半径为R 的圆周按规律2021bt t s -=v 运动,v 0 、b 都是常量.(1) 求t 时刻质点的总加速度;(2) t 为何值时总加速度在数值上等于b ?(3) 当加速度达到b 时,质点已沿圆周运行了多少圈?分析 在自然坐标中,s 表示圆周上从某一点开始的曲线坐标.由给定的运动方程s =s (t ),对时间t 求一阶、二阶导数,即是沿曲线运动的速度v 和加速度的切向分量a t,而加速度的法向分量为a n =v 2 /R .这样,总加速度为a =a te t+a n e n .至于质点在t 时间内通过的路程,即为曲线坐标的改变量Δs =s t -s 0.因圆周长为2πR,质点所转过的圈数自然可求得.解 (1) 质点作圆周运动的速率为bt ts -==0d d v v其加速度的切向分量和法向分量分别为b t s a t -==22d d , Rbt R a n 202)(-==v v 故加速度的大小为R )(402222bt b a a a a t tn -+=+=v 其方向与切线之间的夹角为⎥⎦⎤⎢⎣⎡--==Rb bt a a θt n 20)(arctan arctan v (2) 要使|a |=b ,由b bt b R R=-+4022)(1v 可得 bt 0v = (3) 从t =0 开始到t =v 0 /b 时,质点经过的路程为b s s s t 2200v =-= 因此质点运行的圈数为bRR s n π4π220v == 1 -23 一半径为0.50 m 的飞轮在启动时的短时间内,其角速度与时间的平方成正比.在t =2.0s 时测得轮缘一点的速度值为4.0 m·s-1.求:(1) 该轮在t′=0.5s的角速度,轮缘一点的切向加速度和总加速度;(2)该点在2.0s内所转过的角度.分析 首先应该确定角速度的函数关系ω=kt 2.依据角量与线量的关系由特定时刻的速度值可得相应的角速度,从而求出式中的比例系数k ,ω=ω(t )确定后,注意到运动的角量描述与线量描述的相应关系,由运动学中两类问题求解的方法(微分法和积分法),即可得到特定时刻的角加速度、切向加速度和角位移.解 因ωR =v ,由题意ω∝t 2 得比例系数322s rad 2-⋅===Rtt ωk v 所以 22)(t t ωω== 则t ′=0.5s 时的角速度、角加速度和切向加速度分别为12s rad 5.02-⋅='=t ω2s rad 0.24d d -⋅='==t tωα 2s m 0.1-⋅==R αa t总加速度n t t n R ωR αe e a a a 2+=+= ()()2222s m 01.1-⋅=+=R ωR αa在2.0s内该点所转过的角度rad 33.532d 2d 203202200====-⎰⎰t t t t ωθθ 1 -24 一质点在半径为0.10 m 的圆周上运动,其角位置为342t θ+=,式中θ 的单位为rad,t 的单位为s.(1) 求在t =2.0s时质点的法向加速度和切向加速度.(2) 当切向加速度的大小恰等于总加速度大小的一半时,θ 值为多少?(3) t 为多少时,法向加速度和切向加速度的值相等?分析 掌握角量与线量、角位移方程与位矢方程的对应关系,应用运动学求解的方法即可得到. 解 (1) 由于342t θ+=,则角速度212d d t tθω==.在t =2 s 时,法向加速度和切向加速度的数值分别为 22s 2s m 30.2-=⋅==ωr a t n 2s 2s m 80.4d d -=⋅==t ωr a t t(2) 当22212/t n t a a a a +==时,有223n t a a =,即 ()()422212243t r rt = 得 3213=t此时刻的角位置为 rad 15.3423=+=t θ(3) 要使t n a a =,则有()()422212243t r rt = t =0.55s1 -25 一无风的下雨天,一列火车以v 1=20.0 m·s-1 的速度匀速前进,在车内的旅客看见玻璃窗外的雨滴和垂线成75°角下降.求雨滴下落的速度v2 .(设下降的雨滴作匀速运动)分析 这是一个相对运动的问题.设雨滴为研究对象,地面为静止参考系S,火车为动参考系S′.v 1 为S′相对S 的速度,v 2 为雨滴相对S的速度,利用相对运动速度的关系即可解.解 以地面为参考系,火车相对地面运动的速度为v 1 ,雨滴相对地面竖直下落的速度为v 2 ,旅客看到雨滴下落的速度v 2′为相对速度,它们之间的关系为1'22v v v += (如图所示),于是可得 1o 12s m 36.575tan -⋅==v v 1 -26 如图(a)所示,一汽车在雨中沿直线行驶,其速率为v 1 ,下落雨滴的速度方向偏于竖直方向之前θ 角,速率为v 2′,若车后有一长方形物体,问车速v 1为多大时,此物体正好不会被雨水淋湿?分析 这也是一个相对运动的问题.可视雨点为研究对象,地面为静参考系S,汽车为动参考系S′.如图(a)所示,要使物体不被淋湿,在车上观察雨点下落的方向(即雨点相对于汽车的运动速度v 2′的方向)应满足hlαarctan ≥.再由相对速度的矢量关系122v v v -=',即可求出所需车速v 1.解 由122v v v -='[图(b)],有θθαcos sin arctan221v v v -= 而要使hlαarctan ≥,则 hl θθ≥-cos sin 221v v v ⎪⎭⎫ ⎝⎛+≥θh θl sin cos 21v v 1 -27 一人能在静水中以1.10 m·s-1 的速度划船前进.今欲横渡一宽为1.00 ×103 m 、水流速度为0.55 m·s-1 的大河.(1) 他若要从出发点横渡该河而到达正对岸的一点,那么应如何确定划行方向? 到达正对岸需多少时间? (2)如果希望用最短的时间过河,应如何确定划行方向? 船到达对岸的位置在什么地方?分析 船到达对岸所需时间是由船相对于岸的速度v 决定的.由于水流速度u 的存在, v 与船在静水中划行的速度v ′之间有v =u +v ′(如图所示).若要使船到达正对岸,则必须使v 沿正对岸方向;在划速一定的条件下,若要用最短时间过河,则必须使v 有极大值.解 (1) 由v =u +v ′可知v '=u αarcsin ,则船到达正对岸所需时间为。
大学物理课后习题及答案(1-4章)含步骤解

,根据流量守恒
,
(2)当
(3)当
时,
时,
−
,整理可得:
可得
,即
,
图1-34所示为输液的装置。设吊瓶的截面积为1 ,针孔的截面积为2 ,且1 ≫ 2 ,开始时( = 0),吊瓶内上下
液面距针孔的高度分别为ℎ1 和ℎ2 ,求吊瓶内药液全部输完时需要的时间。
,则针孔的流量为
液体总体积为
Ԧ =
= 2Ԧ − 2 Ԧ = −2Ԧ
1s末和2s末质点的速度为: 1 = 2Ԧ − 2Ԧ(m ∙ s−1 ),2 = 2Ԧ − 4Ԧ(m ∙ s −1 );
1s末和2s末质点的加速度相等:Ԧ = −2Ԧ (m ∙ s−2 )
已知一质点做直线运动,其加速度Ԧ = 4 + 3 m ∙ s−2 , 开始运动时,0 = 5 m,
= 0.06(m)
(2)设弹簧最大压缩量为∆′ , 与碰撞粘在一起的速度为 ′,0 = ( +
) ′,代入已知条件可得 ′ = 4Τ11, + 压缩弹簧的过程中,机械能守恒,则
1
(
2
1
+ ) 2 = 2 ∆′2 ,得∆′ =
+
≈ 0.04(m)
(1)角加速度 =
由 =
∆
∆
=
0−2×1500÷60
50
由 =
=
2×1500
60
= 50 (rad ∙ s −1 )
= − (rad ∙ s−2 )
= −,得 = −,两边进行积分
得到 − 50 = − − 0,
大学物理(上)课后习题答案解析

第1章质点运动学 P211.8一质点在xOy 平面上运动,运动方程为:x =3t +5, y =21t 2+3t -4. 式中t 以 s 计,x ,y 以m 计。
⑴以时间t 为变量,写出质点位置矢量的表示式;⑵求出t =1 s 时刻和t =2s 时刻的位置矢量,计算这1秒内质点的位移;⑶计算t=0 s 时刻到t =4s 时刻内的平均速度;⑷求出质点速度矢量表示式,计算t =4 s 时质点的速度;<5>计算t =0s 到t =4s 内质点的平均加速度;<6>求出质点加速度矢量的表示式,计算t =4s 时质点的加速度<请把位置矢量、位移、平均速度、瞬时速度、平均加速度、瞬时加速度都表示成直角坐标系中的矢量式>。
解:〔1j t t i t r)4321()53(2-+++=m⑵1=t s,2=t s 时,j i r5.081-=m ;2114r i j =+m∴213 4.5r r r i j ∆=-=+m⑶0t =s 时,054r i j =-;4t =s 时,41716r i j =+∴140122035m s 404r r r i j i j t --∆+====+⋅∆-v ⑷1d 3(3)m s d ri t j t-==++⋅v ,则:437i j =+v 1s m -⋅ <5> 0t =s 时,033i j =+v ;4t =s 时,437i j =+v<6> 2d 1 m s d a j t-==⋅v这说明该点只有y 方向的加速度,且为恒量。
1.9质点沿x 轴运动,其加速度和位置的关系为226a x =+,a 的单位为m/s 2,x 的单位为m 。
质点在x =0处,速度为10m/s,试求质点在任何坐标处的速度值。
解:由d d d d d d d d x a t x t x===v v v v得:2d d (26)d a x x x ==+v v 两边积分210d (26)d xx x =+⎰⎰vv v 得:2322250x x =++v∴ 31225 m s x x -=++⋅v1.11一质点沿半径为1 m 的圆周运动,运动方程为θ=2+33t ,式中θ以弧度计,t 以秒计,求:⑴t =2 s 时,质点的切向和法向加速度;⑵当加速度的方向和半径成45°角时,其角位移是多少?解: t tt t 18d d ,9d d 2====ωβθω ⑴s 2=t 时,2s m 362181-⋅=⨯⨯==βτR a⑵当加速度方向与半径成ο45角时,有:tan 451n a a τ︒== 即:βωR R =2,亦即t t 18)9(22=,解得:923=t 则角位移为:322323 2.67rad 9t θ=+=+⨯= 1.13 一质点在半径为0.4m 的圆形轨道上自静止开始作匀角加速度转动,其角加速度为α=0.2 rad/s 2,求t =2s 时边缘上各点的速度、法向加速度、切向加速度和合加速度。
大学物理第一章习题解析

3. 推广至一般平面曲线运动
r v2 r dv r a = n+ t ρ dt
2011学年秋季学期
ρ:曲率半径。
大学物理(1)
15
2. 掌握质点圆周运动的角量描述。 角位移: Δθ Δ θ dθ 角速度: ω = lim = Δt → 0 Δ t dt Δω dω d 2θ = = 2 α 角加速度: = lim
r r r r = r ′ + r0 r r r rPS = rP S ′ + rS ′S r r r v PS = v P S ′ + v S ′S r r r a PS = a P S ′ + a S ′S
2011学年秋季学期
参考系S′
r r r P ( r ′, v ′, a ′, t )
选择参考系,确定变换关系
解:
建立如图所示坐标系, 由题意可知
r v船水
r v风地
大学物理(1)
30o
r v水地
x 东
24
O
2011学年秋季学期
r v 船水
北 y
30 o
r v 风地
r v 水地
x 东
O
r r r r 根据相对速度公式,v PS = v P S ′ + v S ′S ′′ + v S ′′S r r r r r v烟船 = v风船 = v风地 + v地水 + v水船 r r r ( ) = v风地 − v船水 + v水地 r r r r o o = (−10)i − (−20 sin 30 i + 20 cos 30 j ) − 10i r r −1 = −10i − 17.3 j (km ⋅ h )
大学物理学第一章习题答案

习题11、1选择题(1) 一运动质点在某瞬时位于矢径的端点处,其速度大小为(A)(B)(C)(D)[答案:D](2) 一质点作直线运动,某时刻的瞬时速度,瞬时加速度,则一秒钟后质点的速度(A)等于零(B)等于-2m/s(C)等于2m/s (D)不能确定。
[答案:D](3) 一质点沿半径为R的圆周作匀速率运动,每t秒转一圈,在2t时间间隔中,其平均速度大小与平均速率大小分别为(A)(B)(C) (D)[答案:B]1、2填空题(1) 一质点,以的匀速率作半径为5m的圆周运动,则该质点在5s内,位移的大小就是;经过的路程就是。
[答案: 10m;5πm](2) 一质点沿x方向运动,其加速度随时间的变化关系为a=3+2t (SI),如果初始时刻质点的速度v0为5m·s-1,则当t为3s时,质点的速度v=。
[答案: 23m·s-1 ](3) 轮船在水上以相对于水的速度航行,水流速度为,一人相对于甲板以速度行走。
如人相对于岸静止,则、与的关系就是。
[答案:]1、3一个物体能否被瞧作质点,您认为主要由以下三个因素中哪个因素决定:(1) 物体的大小与形状;(2) 物体的内部结构;(3) 所研究问题的性质。
解:只有当物体的尺寸远小于其运动范围时才可忽略其大小的影响,因此主要由所研究问题的性质决定。
1、4下面几个质点运动学方程,哪个就是匀变速直线运动?(1)x=4t-3;(2)x=-4t3+3t2+6;(3)x=-2t2+8t+4;(4)x=2/t2-4/t。
给出这个匀变速直线运动在t=3s时的速度与加速度,并说明该时刻运动就是加速的还就是减速的。
(x单位为m,t单位为s)解:匀变速直线运动即加速度为不等于零的常数时的运动。
加速度又就是位移对时间的两阶导数。
于就是可得(3)为匀变速直线运动。
其速度与加速度表达式分别为t=3s时的速度与加速度分别为v=20m/s,a=4m/s2。
因加速度为正所以就是加速的。
大学物理课后习题答案第一章

第一章 质点运动学1.1 一质点沿直线运动,运动方程为x (t ) = 6t 2 - 2t 3.试求: (1)第2s 的位移和平均速度;(2)1s 末及2s 末的瞬时速度,第2s 的路程; (3)1s 末的瞬时加速度和第2s 的平均加速度.[解答](1)质点在第1s 末的位置为:x (1) = 6×12 - 2×13 = 4(m).在第2s 末的位置为:x (2) = 6×22 - 2×23 = 8(m). 在第2s 的位移大小为:Δx = x (2) – x (1) = 4(m),经过的时间为Δt = 1s ,所以平均速度大小为:=Δx /Δt = 4(m·s -1). (2)质点的瞬时速度大小为:v (t ) = d x /d t = 12t - 6t 2,因此v (1) = 12×1 - 6×12 = 6(m·s -1),v (2) = 12×2 - 6×22 = 0质点在第2s 的路程等于其位移的大小,即Δs = Δx = 4m . (3)质点的瞬时加速度大小为:a (t ) = d v /d t = 12 - 12t ,因此1s 末的瞬时加速度为:a (1) = 12 - 12×1 = 0,第2s 的平均加速度为:= [v (2) - v (1)]/Δt = [0 – 6]/1 = -6(m·s -2).[注意] 第几秒的平均速度和平均加速度的时间间隔都是1秒.1.2 一质点作匀加速直线运动,在t = 10s 走过路程s = 30m ,而其速度增为n = 5倍.试证加速度为,并由上述数据求出量值.[证明]依题意得v t = nv o ,根据速度公式v t = v o + at ,得a = (n – 1)v o /t , (1)根据速度与位移的关系式v t 2 = v o 2 + 2as ,得 a = (n 2 – 1)v o 2/2s ,(2) (1)平方之后除以(2)式证得:.计算得加速度为:= 0.4(m·s -2).1.3 一人乘摩托车跳越一个大矿坑,他以与水平成22.5°的夹角的初速度65m·s -1从西边起跳,准确地落在坑的东边.已知东边比西边低70m ,忽略空气阻力,且取g = 10m·s -2.问:(1)矿坑有多宽?他飞越的时间多长?(2)他在东边落地时的速度?速度与水平面的夹角? [解答]方法一:分步法.(1)夹角用θ表示,人和车(人)在竖直方向首先做竖直上抛运动,初速度的大小为v y 0 = v 0sin θ = 24.87(m·s -1).取向上的方向为正,根据匀变速直线运动的速度公式v t - v 0 = at ,这里的v 0就是v y 0,a = -g ;当人达到最高点时,v t = 0,所以上升到最高点的时间为t 1 = v y 0/g = 2.49(s).再根据匀变速直线运动的速度和位移的关系式:v t 2 - v 02 = 2a s , 可得上升的最大高度为:h 1 = v y 02/2g = 30.94(m).人从最高点开始再做自由落体运动,下落的高度为;h 2 = h 1 + h = 100.94(m). 根据自由落体运动公式s = gt 2/2,得下落的时间为:= 4.49(s). 因此人飞越的时间为:t = t 1 + t 2 = 6.98(s).人飞越的水平速度为;v x 0 = v 0cos θ = 60.05(m·s -1),v a 22(1)(1)n sa n t -=+22(1)(1)n sa n t -=+22(51)30(51)10a -=+222h t g=70m22.5º 图1.3所以矿坑的宽度为:x = v x 0t = 419.19(m).(2)根据自由落体速度公式可得人落地的竖直速度大小为:v y = gt = 69.8(m·s -1), 落地速度为:v = (v x 2 + v y 2)1/2 = 92.08(m·s -1),与水平方向的夹角为:φ = arctan(v y /v x ) = 49.30º,方向斜向下.方法二:一步法.取向上为正,人在竖直方向的位移为y = v y 0t - gt 2/2,移项得时间的一元二次方程, 解得:.这里y = -70m ,根号项就是人落地时在竖直方向的速度大小,由于时间应该取正值,所以公式取正根,计算时间为:t = 6.98(s).由此可以求解其他问题.1.4 一个正在沿直线行驶的汽船,关闭发动机后,由于阻力得到一个与速度反向、大小与船速平方成正比例的加速度,即d v /d t = -kv 2,k 为常数.(1)试证在关闭发动机后,船在t 时刻的速度大小为; (2)试证在时间t ,船行驶的距离为. [证明](1)分离变量得, 故 ,可得:. (2)公式可化为,由于v = d x/d t ,所以: 积分.因此 . 证毕.[讨论]当力是速度的函数时,即f = f (v ),根据牛顿第二定律得f = ma . 由于a = d 2x /d t 2, 而 d x /d t = v , a = d v /d t , 分离变量得方程:, 解方程即可求解.在本题中,k 已经包括了质点的质量.如果阻力与速度反向、大小与船速的n 次方成正比,则d v /d t = -kv n .(1)如果n = 1,则得, 积分得ln v = -kt + C .当t = 0时,v = v 0,所以C = ln v 0, 因此ln v/v 0 = -kt ,得速度为 :v = v 0e -kt .201sin 02gt v t y θ-+=0(sin t v g θ=011kt v v =+01ln(1)x v kt k=+2d d vk t v =-020d d v t v v k t v =-⎰⎰011kt v v =+001v v v kt=+00001d d d(1)1(1)v x t v kt v kt k v kt ==+++00001d d(1)(1)x tx v kt k v kt =++⎰⎰01ln(1)x v kt k=+d d ()m vt f v =d d vk t v=-而d v = v 0e -kt d t ,积分得:. 当t = 0时,x = 0,所以C` = v 0/k ,因此.(2)如果n ≠1,则得,积分得. 当t = 0时,v = v 0,所以,因此. 如果n = 2,就是本题的结果.如果n ≠2,可得,读者不妨自证.1.5 一质点沿半径为0.10m 的圆周运动,其角位置(以弧度表示)可用公式表示:θ = 2 + 4t 3.求:(1)t = 2s 时,它的法向加速度和切向加速度;(2)当切向加速度恰为总加速度大小的一半时,θ为何值? (3)在哪一时刻,切向加速度和法向加速度恰有相等的值? [解答](1)角速度为ω = d θ/d t = 12t 2 = 48(rad·s -1),法向加速度为 a n = rω2 = 230.4(m·s -2);角加速度为 β = d ω/d t = 24t = 48(rad·s -2), 切向加速度为 a t = rβ = 4.8(m·s -2). (2)总加速度为a = (a t 2 + a n 2)1/2,当a t = a /2时,有4a t 2 = a t 2 + a n 2,即.由此得,即 ,解得 .所以 =3.154(rad).(3)当a t = a n 时,可得rβ = rω2, 即: 24t = (12t 2)2,解得 : t = (1/6)1/3 = 0.55(s).1.6 一飞机在铅直面飞行,某时刻飞机的速度为v = 300m·s -1,方向与水平线夹角为30°而斜向下,此后飞机的加速度为a = 20m·s -2,方向与水平前进方向夹角为30°而斜向上,问多长时间后,飞机又回到原来的高度?在此期间飞机在水平方向飞行的距离为多少?[解答]建立水平和垂直坐标系,飞机的初速度的大小为 v 0x = v 0cos θ, v 0y = v 0sin θ.加速度的大小为a x = a cos α, a y = a sin α. 运动方程为, . 即 ,.令y = 0,解得飞机回到原来高度时的时间为:t = 0(舍去);(s).将t 代入x 的方程求得x = 9000m .0e `ktv x C k-=+-0(1-e )kt vx k -=d d n vk t v=-11n v kt C n -=-+-101n v C n-=-11011(1)n n n kt v v --=+-1(2)/(1)020{[1(1)]1}(2)n n n n n v kt x n v k----+--=-3n t a a =23r r ωβ=22(12)243t t =33/6t =3242(13/3)t θ=+=+32012x x x v t a t =+2012y y y v t a t =-+201cos cos 2x v t a t θα=⋅+⋅201sin sin 2y v t a t θα=-⋅+⋅02sin 103sin v t a θα== y xO α v 0θ a a xa yv 0x v 0y[注意]选择不同的坐标系,如x 方向沿着a 的方向或者沿着v 0的方向,也能求出相同的结果.1.7 一个半径为R = 1.0m 的轻圆盘,可以绕一水平轴自由转动.一根轻绳绕在盘子的边缘,其自由端拴一物体A .在重力作用下,物体A 从静止开始匀加速地下降,在Δt = 2.0s 下降的距离h = 0.4m .求物体开始下降后3s 末,圆盘边缘上任一点的切向加速度与法向加速度.[解答]圆盘边缘的切向加速度大小等于物体A 下落加速度.由于, 所以a t = 2h /Δt 2 = 0.2(m·s -2).物体下降3s 末的速度为v = a t t = 0.6(m·s -1),这也是边缘的线速度,因此法向加速度为= 0.36(m·s -2).1.8 一升降机以加速度1.22m·s -2上升,当上升速度为2.44m·s -1时,有一螺帽自升降机的天花板上松落,天花板与升降机的底面相距 2.74m .计算:(1)螺帽从天花板落到底面所需的时间;(2)螺帽相对于升降机外固定柱子的下降距离.[解答]在螺帽从天花板落到底面时,升降机上升的高度为;螺帽做竖直上抛运动,位移为. 由题意得h = h 1 - h 2,所以, 解得时间为= 0.705(s).算得h 2 = -0.716m ,即螺帽相对于升降机外固定柱子的下降距离为0.716m .[注意]以升降机为参考系,钉子下落时相对加速度为a + g ,而初速度为零,可列方程h = (a + g )t 2/2,由此可计算钉子落下的时间,进而计算下降距离.1.9 有一架飞机从A 处向东飞到B 处,然后又向西飞回到A 处.已知气流相对于地面的速度为u ,AB 之间的距离为l ,飞机相对于空气的速率v 保持不变.(1)如果u = 0(空气静止),试证来回飞行的时间为; (2)如果气流的速度向东,证明来回飞行的总时间为;(3)如果气流的速度向北,证明来回飞行的总时间为.[证明](1)飞机飞行来回的速率为v ,路程为2l ,所以飞行时间为t 0 = 2l /v . (2)飞机向东飞行顺风的速率为v + u ,向西飞行逆风的速率为v - u , 所以飞行时间为 . (3)飞机相对地的速度等于相对风的速度加风相对地的速度.为了使飞机沿着AB 之间的直线飞行,就要使其相对地的速度偏向北方,可作矢量三角形,其中沿AB 方向的速度大小为,所以飞行时间为212t h a t =∆2n v a R=21012h v t at =+22012h v t gt =-21()2h a g t =+2/()t h a g =+02l t v =1221/t t u v =-02221/t t u v=-1222l l vl t v u v u v u =+=+--022222/1/1/t l v u v u v==--22V v u =-RA图1.7AB AB vv + uv - uABvuuvv. 证毕.1.10 如图所示,一汽车在雨中沿直线行驶,其速度为v 1,下落雨的速度方向与铅直方向的夹角为θ,偏向于汽车前进方向,速度为v 2.今在车后放一长方形物体,问车速v 1为多大时此物体刚好不会被雨水淋湿?[解答]雨对地的速度等于雨对车的速度加车对地的速度,由此可作矢量三角形.根据题意得tan α = l/h .方法一:利用直角三角形.根据直角三角形得v 1 = v 2sin θ + v 3sin α,其中v 3 = v ⊥/cos α,而v ⊥ = v 2cos θ, 因此v 1 = v 2sin θ + v 2cos θsin α/cos α, 即 . 证毕. 方法二:利用正弦定理.根据正弦定理可得,所以:,即 . 方法三:利用位移关系.将雨滴的速度分解为竖直和水平两个分量,在t 时间,雨滴的位移为l = (v 1 – v 2sin θ)t , h = v 2cos θ∙t .两式消去时间t 即得所求. 证毕.22222222/1/l l l v t V v u u v ===--0221/t u v=-2v 3v 1v 12(sin cos )lv v hθθ=+12sin()sin(90)v v θαα=+︒-12sin()cos v v θαα+=2sin cos cos sin cos v θαθαα+=2(sin cos tan )v θθα=+12(sin cos )lv v hθθ=+v 1hl v 2θ图1.10v 1h lv 2θ v 3 α α v ⊥。
大学物理学第1章

第1章 质点运动学习 题一 选择题1-1 对质点的运动,有以下几种表述,正确的是[ ] (A)在直线运动中,质点的加速度和速度的方向相同(B)在某一过程中平均加速度不为零,则平均速度也不可能为零 (C)若某质点加速度的大小和方向不变,其速度的大小和方向可不断变化 (D)在直线运动中,加速度不断减小,则速度也不断减小解析:速度是描述质点运动的方向和快慢的物理量,加速度是描述质点运动速度变化的物理量,两者没有确定的对应关系,故答案选C 。
1-2 某质点的运动方程为)(12323m t t x +-=,则该质点作[ ] (A)匀加速直线运动,加速度沿ox 轴正向 (B)匀加速直线运动,加速度沿ox 轴负向 (C)变加速直线运动,加速度沿ox 轴正向 (D)变加速直线运动,加速度沿ox 轴负向 解析:229dx v t dt ==-,18dva tdt==-,故答案选D 。
1-3 一质点在平面上作一般曲线运动,其瞬时速度为v ,瞬时速率为v ,某一段时间内的平均速率为v ,平均速度为v ,他们之间的关系必定有[ ](A)v =v ,v =v (B)v ≠v ,v =v (C)v ≠v ,v ≠v (D)v =v ,v ≠v解析:瞬时速度的大小即瞬时速率,故v =v ;平均速率sv t∆=∆,而平均速度t∆∆rv =,故v ≠v 。
答案选D 。
1-4 质点作圆周运动时,下列表述中正确的是[ ](A)速度方向一定指向切向,所以法向加速度也一定为零 (B)法向分速度为零,所以法向加速度也一定为零 (C)必有加速度,但法向加速度可以为零 (D)法向加速度一定不为零解析:质点作圆周运动时,2n t v dva a dtρ=+=+n t n t a e e e e ,所以法向加速度一定不为零,答案选D 。
1-5 某物体的运动规律为2dvkv t dt=-,式中,k 为大于零的常量。
当0t =时,初速为0v ,则速率v 与时间t 的函数关系为[ ](A)2012v kt v =+ (B)20112kt v v =+(C)2012v kt v =-+ (D)20112kt v v =-+解析:由于2dvkv t dt=-,所以020()vtv dv kv t dt =-⎰⎰,得到20112kt v v =+,故答案选B 。
大学物理第一章课后习题答案

1.1 一质点在Oxy 平面内运动,运动方程为)SI (53+=t x ,)SI (432/2-+=t t y 。
(1)以时间t 为变量,写出质点位矢的表达式;(2)求出质点速度分量的表达式,并计算s 4=t 时,质点速度的大小和方向;(3)求出质点加速度分量的表达式,并计算出s 4=t 时,质点加速度的大小和方向。
解:(1))SI (53+=t x ,)SI (432/2-+=t t y 质点位矢的表达式为:j t t i t j y i x r )432/()53(2-+++=+=; (2)m/s 3)53(=+==t dt d dt dx v x ,m/s )3()432/(2+=-+==t t t dt d dt dy v ys 4=t ,m/s 3=x v ,m/s 7=y v ,m/s 6.7m/s 5822==+=y x v v v设θ是v 和x v 的夹角,则37tan ==x y v v θ,8.66=θ°; (3)2m/s 0)3(===dt d dt dv a x x ,2m/s 1)3(=+==t dt ddt dv a y ys 4=t ,2m/s 0=x a ,2m/s 1=y a ,222m/s 1=+=y x a a a方向沿y 轴方向。
1.2 质点在Oxy 平面内运动,运动方程为)SI (3t x =,)SI (22t y -=。
(1)写出质点运动的轨道方程;(2)s 2=t 时,质点的位矢、速度和加速度。
解:(1)质点运动方程)SI (3t x =,)SI (22t y -=,质点运动的轨道方程为:9/2)3(222x xy -=-=或2189x y -=;(2)j t i t j y i x r )2()3(2-+=+=,s 2=t 时: j i r 26-=j t i v 23-=,s 2=t 时:j i v43-=j a 2-=,s 2=t 时:j a2-=1.3质点沿直线运动,其坐标x 与时间t 有如下关系:)SI (cos t Ae x tωβ-=(A 和β皆为常量)。
大学物理答案第一章
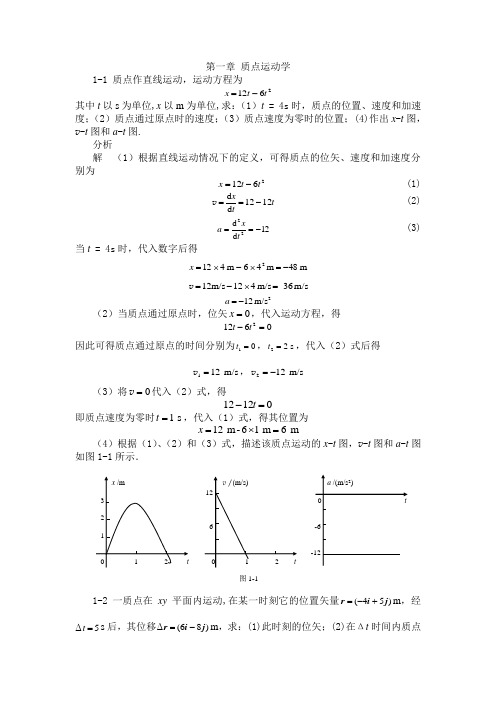
第一章 质点运动学1-1 质点作直线运动,运动方程为2612t t x -=其中t 以s 为单位,x 以m 为单位,求:(1)t = 4s 时,质点的位置、速度和加速度;(2)质点通过原点时的速度;(3)质点速度为零时的位置;(4)作出x -t 图,v -t 图和a -t 图.分析解 (1)根据直线运动情况下的定义,可得质点的位矢、速度和加速度分别为2612t t x -= (1)t tx 1212d d -==v (2) 12d d 22-==tx a (3) 当t = 4s 时,代入数字后得m 48m 46m 4122-=⨯-⨯=xm/s -36m/s 412m/s 12=⨯-=v2m/s 12-=a(2)当质点通过原点时,位矢0=x ,代入运动方程,得06122=-t t因此可得质点通过原点的时间分别为01=t ,s 22=t ,代入(2)式后得m/s 121=v ,m/s 122-=v(3)将0=v 代入(2)式,得01212=-t即质点速度为零时s 1=t ,代入(1)式,得其位置为m 6m 16-m 12=⨯=x(4)根据(1)、(2)和(3)式,描述该质点运动的x -t 图,v -t 图和a -t 图如图1-1所示.1-2 一质点在xy 平面内运动,在某一时刻它的位置矢量)54(j i r +-=m ,经5Δ=t s 后,其位移)86(Δj i r -=m ,求:(1)此时刻的位矢;(2)在Δt 时间内质点图1-1的平均速度.(i 、j 分别为x 、y 方向的单位矢.)分析解 (1)据题意,在t t ∆+时刻,该质点的位矢为m 32m )8-(6m )54(1)(j i j i j i r r r -=++-=∆+=(2)在Δt 时间内质点的平均速度为m/s )1.6-(1.2m/s 586j i j i r v =-=∆∆=t 1-3 质点在xy 平面上运动,运动方程为t y t x 4sin ,4cos 3ππ== 其中t 以s 为单位,x ,y 以m 为单位.(1)求质点运动轨道的正交坐标方程并在xy 平面上绘出质点的轨道;(2)求出质点的速度和加速度表示式,由此求出质点在轨道上运动的方向并证明质点的加速度指向坐标原点;(3)求t = 1 s 时质点的位置和速度与加速度的大小和方向.分析解 (1)质点的运动方程为 t x 43πcos = (1) t y 4πsin = (2) (1)式两边同乘以3并平方后与(2)式的平方相加,得正交坐标方程为 1322=+y x 上式表明质点的运动轨道是一个椭圆,如图1-2所示.(2)由(1)和(2)式可得质点速度和加速度的x ,y 方向分量分别为t t x 443d d ππsin -==x v (3) t t y 44d d ππcos ==y v (4) t t a x 4163d d 2ππcos -==x v (5) t t a y 416d d 2ππsin -==yv (6)则质点速度为 j i v t t 44443ππππcos sin +-= 当t =0时,由运动方程(1)和(2)式,得知质点位于横坐标上3的位置,图1-2由(3)和(4)式,知040>==πy x v v ,,即表明质点在椭圆上沿反时针方向运动. 质点加速度为 j i a 2t t 41641632ππππsin cos --= 由(1)和(2)式得t 时刻质点的位矢为j i r t t 44ππsin cos += (7) 位矢r 与x 轴的夹角ϕ由下式确定:t x y 433πϕtan tan == 而加速度a 与x 轴的夹角α则由下式确定:t a a x y433παtan tan == 即有ϕαtan tan =,注意到在曲线运动中加速度始终指向曲线凹的一侧,则得πϕα+=,表明a 与r 方向相反,指向原点,如图1-2所示.(3)当t = 1 s 时,由(1)--(2)式得m 26=x m 22=y m/s 86π-=x v m/s 82π=y v 22m/s 326π-=x a 22m/s 322π-=y a 速度的大小 m/s 42π=+=2y 2xv v v 速度v 与x 轴的夹角θ则由下式确定:33-==x yv v θtan 注意到此时v x <0,v y >0,则 πθ6533=-=)a r c t a n (. 加速度的大小 22m/s 162π=+=2y 2x a a a对于夹角α有 33==x ya a αtan 又因a x <0,a y <0,则 πα6733==)a r c t a n (. 1-4 质点沿直线运动,其速度2323++=t t v ,如果t = 2时,x = 4,求t = 3时质点的位置、速度和加速度.(其中v 以m/s 为单位,t 以s 为单位,x 以m 为单位)分析解 速度表示式对t 积分,得034241d x t t t t x +++==⎰v 将t = 2 s 时,x = 4 m 代入上式,得积分常数120-=x m ,则1224134-++=t t t x 速度表示式对t 求导数,得t t ta 63d d 2+==v 因此t = 3 s 时质点的位置、速度和加速度分别为m 2541m 12m 32m 3m 34134.=-⨯++⨯=x m/s 56m/s 2m/s 33m/s 323=+⨯+=v2222m/s 45m/s 36m/s 33=⨯+⨯=a1-5 质点沿直线运动,加速度24t a -=,如果当t = 3时,x = 9,v = 2,求质点的运动方程.(其中a 以m/s 2为单位,t 以s 为单位,x 以m 为单位,v 以m/s 为单位)分析解 加速度表示式对t 积分,得03431d v v ++-==⎰t t t a 0242121d x t t t t x +++-==⎰0v v 将t =3 s 时,x = 9 m ,v = 2 m/s 代入以上二式,得积分常数m/s 10-=v ,7500.=x m ,则14313-+-=t t v 750212124.+-+-=t t t x 1-6 质点以不变的速率5m/s 运动,速度的方向与x 轴间夹角等于t 弧度(t为时间的数值),当t = 0时,x = 0,y = 5m ,求质点的运动方程及轨道的正交坐标方程,并在xy 平面上描画出它的轨道.分析解 设质点的速率为v ,与x 轴间夹角为t 弧度,则速度的分量为t t x x cos v v ==d d t ty y s i n v v ==d d 以上两式分别积分,得1C t x +=sin v 2C t y +-=c o s v初始条件为t = 0时,x = 0,y = 5m ,代入以上两式后,得01=C m 102=C因此运动方程为t x sin 5= 105+-=t y cos从中消去t ,得质点运动轨道的正交坐标方程为251022=-+)(y x这是圆心在y 轴上10m 处的圆,半径为5m ,如图1-3所示.1-7 在离水面高度为h 的岸上,有人用绳子拉船靠岸,人以0v 的速率收绳,求当船离岸边的距离为s 时,船的速度和加速度.分析解 选如图1-4所示的直角坐标系,设t 时刻绳长为l ,船的速度为v ,则此时船的x ,y 方向坐标分别为22h l x -= h y =由速度定义得0d d d d ===th t y y v t l hl l t x d d d d 22-===x v v图1-3 图1-4因绳长l 随时间减小的速率等于人的收绳速率,即0d d v =-tl ,则当s x =时,船的速度为022022v v v s h s h l l+-=--= 其中负号表明船的速度方向沿x 轴的负向.又由加速度的定义得0d d ==t a yy v2023222022d d d d v v v x )(h l h h l l t t a a x --=⎪⎪⎭⎫ ⎝⎛--=== 当s x =时,加速度为 2032v sh a -= 其中负号表明船的加速度方向也沿x 轴的负向,且船作变加速直线运动.1-8 当物体以非常高的速度穿过空气时,由空气阻力产生的反向加速度大小与物体速度的平方成正比,即2v k a -=,其中k 为常量.若物体不受其它力作用沿x 方向运动,通过原点时的速度为0v ,试证明在此后的任意位置x 处其速度为x k -=e 0v v分析证 根据加速度的定义,得2v v k a t-==d d 因 tt x x t a d d d d d d d d v v v v ===,代入上式,整理后得 x d d 1-k v v= 应用初始条件0=x 时,0v v =,上式两边分别对v 和x 积分⎰⎰-=x x 0d d 10k v v vv 得 kx -=0v v ln 即有 x k -=e 0v v1-9 一支气枪竖直向上发射,发射速度为29.4m /s ,若发射两粒子弹的间隔时间为4s ,求二子弹将在距发射点多高的地方彼此相遇?分析解 以发射点为原点,竖直向上为y 坐标正向,第一粒子弹发射后的t 时刻,其位置为20121gt t y -=v (1) 其中0v 为发射速度,第二粒子弹此时(设4>t s )的位置为2024214)()(---=t g t y v (2) 当二子弹相遇时,21y y =,由(1)和(2)式得s 5s 2s 8942920=+=+=..g t v 将上式代入(1)式,得m 524m 58921m 5429212201...=⨯⨯-⨯=-=gt t y v 1-10 A 车通过某加油站后其行驶路程x 与时间t 的关系可以表示为24.02t t x +=(其中t 以s 为单位,x 以m 为单位)在A 车离开10 s 后B 车通过该加油站时速度为12 m/s ,且具有与A 车相同的加速度.求:(1)B 车离开加油站后追上A 车所需时间;(2)两车相遇时各自的速度.分析解 (1)令B 车通过该加油站时0=t ,则A 车的运动方程为2A 1040102)(.)(+++=t t xB 车的运动方程为2B 4012t t x .+=两车相遇时有B A x x =,由以上两式得2240121040102t t t t .)(.)(+=+++解得 s 30=t(2)根据速度的定义,相遇时两车速度分别为m/s 3410802d d A A =+⨯+==)(.t tx v m/s 368012d d B B =+==t tx .v 1-11 一升降机以加速度1.22m /s 2上升,当上升速度为2.44m /s 时,有一螺帽自升降机的天花板松落,天花板与升降机底面相距2.74m ,计算:(1)螺帽从天花板落到底面所需的时间;(2)螺帽相对于升降机外固定柱子的下降距离. 分析解 (1)以升降机外固定柱子为参考系,竖直向上为y 坐标正向,螺帽松落时升降机底面位置为原点.螺帽松落后从m 7420.=y 处以初速度m /s4420.=v 作竖直上抛运动,升降机底面则从原点以同样的初速度作向上的加速运动,加速度2m/s 221.=a ,它们的运动方程分别为螺帽: 200121gt t y y -+=v 底面: 20221at t y +=v 螺帽落到底面上时,21y y =,由以上两式可得s 0.705s 22189742220=+⨯=+=...a g y t (2)螺帽相对于升降机外固定柱子的下降距离为m 7150m 70508921m 7050442 2122010.....=⨯⨯+⨯-=+-=-=gt t y y s v 1-12 一小球自h = 4.9m 处落到一倾角θ= 45°的斜面上,设小球与斜面碰撞后速率不变,方向如图所示.求小球第二次与斜面碰撞时,离第一次碰撞处的距离L 为若干? 分析 解 以小球与斜面第一次相撞点为原点取直角坐标系如图1-5所示.第一次相撞后小球作平抛运动,初速度为0v .此前,小球为自由落体,因此有 gh 20=v小球作平抛运动的运动方程为t x 0v = 221gt y = 由于斜面倾角θ= 45°,当小球第二次碰到斜面时,应有y x =,则由以上二式解得 gt 02v =两次碰撞点之间的距离为m 27.7m 459444200=︒⨯=====sin .sin sin sin sin θθθθh g t x L 2v v 1-13 消防队员用水龙头喷射10 m 外的着火竖墙,水龙头每分钟喷水量为图1-5280 kg ,水喷出时速度为26 m/s ,与地面交角为45º。
大学物理第一章习题解答

习题一1.2. 一质点沿x 轴运动,坐标与时间的变化关系为224t t x -=,式中t x ,分别以m 、s 为单位,试计算(1)在最初s 2内的平均速度和s 2末的瞬时速度;(2)s 1末到s 3末的位移、平均速度;(3)s 1末到s 3末的平均加速度;此加速度是否可以 用式221a a a ave +=计算? (4)s 3末的瞬时加速度。
解:(1) 最初s 2内的平均速度为:)/(0200202s m x x t x v t t =-=-=∆∆=== (2) s 2末的瞬时速度为: s m t dt dxv t t /44422-=-==== s 1末到s 3末的位移、平均速度分别为:m x xx t t 82613-=--=-=∆== s m t x v /428-=-=∆∆= (3) s 1末到s 3末的平均加速度为213==-=∆∆=t t v v t v a 而 s m dtdxv t t /833-==== s m dtdx v t t /011==== 所以 2/4208s m a -=--= 而该质点的瞬时加速度为222222/4)24(s m dtt t d dt x d dt dv a -=-=== 保持不变,因此,加速度是否可以用式 221a a a ave +=计算, 事实上,该质点做匀加速直线运动。
1.3. 路灯距地面的高度为h ,一个身高为l 的人在路上匀速运动,速度为0v ,如图T1.3。
求(1)人影中头顶的移动速度;(2)影子长度增长的速率。
解:(1)人影中头顶位置应该在地面上做一维直线运动,设路灯的正下方为坐标原点O ,人影中头顶位置坐标为P ,根据三角形相似的原理,人影中头顶的移动速度为:0v lh h dt dOP v -== (2) 由于影子长度等于人影中头顶位置和人位置的水平距离,所以影子长度增长的速率为:00v l h l v v v -=-=' 1.4. 一质点的运动方程为k t j t i t r ++=24)(,式中r ,t 分别以m 、s 为单位。
大学物理第1章习题解答(全)

a
at
an
dv dt
et
v2 R
en
1-6 已知质点沿x轴作直线运动,其运动方程为
x 2 6t 2 2t3
求(1)质点在运动开始后4.0s内的位移大小;
(2)质点在该时间内所通过的路程;
(3)t=4 s 时质点的速度和加速度。
解:(1)质点在4.0s内的位移大小
arctan[ (v0
bt)2 ]
at
Rb
(2)要使 a a b ,即
1 R
R2b2 (v0 bt)4 b
可得 t v0 b
v v0 bt
此时速率为零(即运动方向反向)
t 0 开始到 t v0 b
质点经过的路程 L
L
st
s0
st
0
小的一半时, 值为多少?
(3)t为多少时,法向加速度和切向加速度 相等?
解 (1)由 2 4t3 得: d 12t2
dt
d 12t 2
dt
法向:an 2r (12t 2 )2 r an t2s 2.30102 m s2
切向:
at
r d
x x4 x0 32 m
(2)由
dx 0 dt
(2)由
dx 12t 6t 2 0 dt
得知质点换向的时刻为t 2 s(t=0不合题意)
-30
02
x(m)
10
t=4
t=0
t=2
则 x1 x2 x0 8m x2 x4 x2 40m
t 4s的路程:s1 x1 x2 48m
大学物理课后答案第1章质点运动学习题解答

,解得
(2) , ,
1-13质点M作平面曲线运动,自O点出发经图示轨迹运动到C点。图中,OA段为直线,AB、BC段分别为不同半径的两个1/4圆周。设 时,M在 点,已知运动方程为 (SI),求 s时刻,质点M的切向加速度和法向加速度的大小。
解: 时 此时质点在大圆上
…
时
1-14一质点沿半径为 的圆周按 的规律运动,其中 和 都是常数。求:(1)质点在 时刻的加速度;(2) 为何值时,加速度在数值上等于 ;(3)当加速度大小为 时质点已沿圆周运行了几圈
解:
,
&
1-8一艘正在沿直线行驶的快艇,在发动机关闭后,其加速度方向与速度方向相反,大小与速度平方成正比,即 ,式中 为正常数。试证明快艇在关闭发动机后又行驶 距离时的速度为 ,式中 是发动机关闭瞬时的速度。
解:
,
1-9一飞轮的转速在5s内由900rev/min均匀地减到800rev/min。求:(1)飞轮的角加速度;(2)在此5s内飞轮的总转数;(3)再经几秒飞轮将停止转动。
解: ,即
~
1-5一质点在 平面内运动,运动方程为 (SI)。(1)求质点运动的轨道方程并画出运动轨道;(2)计算1s末和2s末质点的瞬时速度和瞬时加速度;(3)在什么时刻质点的位置矢量与其速度矢量恰好垂直这时,它们的 、 分量各为多少(4)在什么时刻质点离原点最近算出这一距离。
解: , ,
(1) ,
消t,得轨道方程: ,
其曲线为开口向下的抛物线,如右图。
(2) ,
,
(3) ,
*
解得: ,
时, , , ,
时, , , ,
以上物理量均为国际单位。
(4)
令 ,解得
1-6一物体沿 轴运动,其加速度和位置的关系满足 (SI)。物体在 处的速度为10 m/s,求物体的速度和位置的关系。
大学物理第1章习题解答(全)ppt课件

23 23 t t 0 3 3
1-24 一质点在半径为0.10m 的圆周上运动, 3 2 4 t 其角位置为 ,式中 的单位为 rad , t的单位为s。求: (1)在 t=2.0s时质点的法向加速度和切向 加速度。 (2)当切向加速度的大小恰等于总加速度大 小的一半时, 值为多少? (3)t为多少时,法向加速度和切向加速度 相等? d 2 3 得: 12 t 2 4 t 解 (1)由 dt
(2)加速度的大小和方向。 解:(1)速度的分量式为 dx dy v 10 60 t v 15 40 t x y dt dt
v ( t ) v v 10 60 t 15 40 t
2 2 x y 2 2
v ( t ) v v 10 60 t 15 40 t
解 (1)由参数方程
x 2 . 0 t , y 19 . 0 2 . 0 t
2
消去t得质点的轨迹方程:
y 19 . 0 0 . 50 x
(2)
2
t1 1 .0 s
t2 2 .0 s
r r r 2 1 v 2 . 0 i 6 . 0 j t t t 2 1
dv d 2 2 2 a (v v ) 3 . 58 m s tt 1 x y dt dt
a a a 1 . 79 m s n
2 2 t
2
(4)
t 1 . 0 s时质点的速度大小为
2 2 1 v v v 4 . 47 m s x y
2
a a a 72 . 1 m s
设 a与 x 轴正向的夹角为
大学物理第一章课后习题答案

第一章质点运动学1.1一质点沿y 方向运动,它在任意时刻t 的位置由式1052+=t y 给出,式中t 以s 计,y 以m 计算下列各段时间内质点的平均速度大小:(1)2s 到3s (2)2s 到2.1s (3)2s 到2.001s (4)2s 到2.0001s 解:(1)令质点的始末时刻为s t 21=,s t 32=,则质点的平均速度大小为:{}sm sm t t y y /25)23(]10)2(5[10)3(5221212=−+−+=−−=υ(2)令质点的始末时刻为s t 21=,s t 1.22=,则质点的平均速度大小为:{}sm sm t t y y /5.20)21.2(]10)2(5[10)1.2(5221211=−+−+=−−=υ(3)令质点的始末时刻为s t 21=,s t 001.22=,则质点的平均速度大小为:{}sm smt t y y /005.20)2001.2(]10)2(5[10)001.2(5221212=−+−+=−−=υ(4)令质点的始末时刻为s t 21=,s t 0001.22=,则质点的平均速度大小为:sm smt t y y /0005.20)20001.2(]10)2(510)0001.2(5[221212=−−−+=−−=υ1.2一质点沿Ox 轴运动,其运动方程为2653t t x +−=;式中t 以s 计,x 以m 计,试求:(1)质点的初始位置和初始速度;(2)质点在任一时刻的速度和加速度;(3)质点做什么运动;(4)做出t x −图和t −υ图;(5)质点做匀加速直线运动吗?解:(1)设质点初始时刻00=t ,则质点的初始位置为:mm x 3]06053[20=×+×−=即质点的初始位置在Ox 轴正方向3m 处。
因为质点的速度为:tdt dx125+−==υ所以质点的初始速度为:220/5/)0125(s m s m dt dxt −=×+−===υ质点的初始速度大小为2/5s m ,方向沿Ox 轴负方向。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1章 质点运动学习 题一 选择题1-1 对质点的运动,有以下几种表述,正确的是[ ] (A)在直线运动中,质点的加速度和速度的方向相同(B)在某一过程中平均加速度不为零,则平均速度也不可能为零(C)若某质点加速度的大小和方向不变,其速度的大小和方向可不断变化 (D)在直线运动中,加速度不断减小,则速度也不断减小解析:速度是描述质点运动的方向和快慢的物理量,加速度是描述质点运动速度变化的物理量,两者没有确定的对应关系,故答案选C 。
1-2 某质点的运动方程为)(12323m t t x +-=,则该质点作[ ] (A)匀加速直线运动,加速度沿ox 轴正向 (B)匀加速直线运动,加速度沿ox 轴负向 (C)变加速直线运动,加速度沿ox 轴正向 (D)变加速直线运动,加速度沿ox 轴负向 解析:229dx v t dt ==-,18dva tdt==-,故答案选D 。
1-3 一质点在平面上作一般曲线运动,其瞬时速度为v ,瞬时速率为v ,某一段时间内的平均速率为v ,平均速度为v ,他们之间的关系必定有[ ](A)v =v ,v =v (B)v ≠v ,v =v (C)v ≠v ,v ≠v (D)v =v ,v ≠v解析:瞬时速度的大小即瞬时速率,故v =v ;平均速率sv t∆=∆,而平均速度t∆∆rv =,故v ≠v 。
答案选D 。
1-4 质点作圆周运动时,下列表述中正确的是[ ] (A)速度方向一定指向切向,所以法向加速度也一定为零 (B)法向分速度为零,所以法向加速度也一定为零 (C)必有加速度,但法向加速度可以为零 (D)法向加速度一定不为零解析:质点作圆周运动时,2n t v dva a dtρ=+=+n t n t a e e e e ,所以法向加速度一定不为零,答案选D 。
1-5 某物体的运动规律为2dvkv t dt=-,式中,k 为大于零的常量。
当0t =时,初速为0v ,则速率v 与时间t 的函数关系为[ ](A)2012v kt v =+ (B)20112kt v v =+(C)2012v kt v =-+ (D)20112kt v v =-+解析:由于2dvkv t dt=-,所以020()vtv dv kv t dt =-⎰⎰,得到20112kt v v =+,故答案选B 。
二 填空题1-6 已知质点位置矢量随时间变化的函数关系为2=4t +(2t+3)r i j ,则从0t =到1t s =时的位移为 ,1t s =时的加速度为 。
解析:45342=-=+-=+1010r r r i j j i j ,228d d dt dt ===111v ra i1-7 一质点以初速0v 和抛射角0θ作斜抛运动,则到达最高处的速度大小为 ,切向加速度大小为 ,法向加速度大小为 ,合加速度大小为 。
解析:以初速0v 、抛射角0θ作斜抛的运动方程:200001cos (sin )2v t v t gt θθ=+-r i j ,则0000cos (sin )d v v gt dt θθ==+-r v i j ,d g dt==-v a j 。
到达最高处时,竖直方向上的速度大小00sin 0j v v gt θ=-=,此时速度大小即为水平方向上的速度值00cos i v v v θ==。
切向加速度大小0t dva dt==,法向加速度大小n a g ==。
1-8 一飞轮做匀减速转动,在5s 内角速度由40rad s π减到10rad s π,则飞轮在这5s 内总共转过了 圈,飞轮再经过 的时间停止转动。
解析:角加速度22104065d d dt dt ωθππαπ-====-,所以角速度0406t t ωωαππ=+=-,角度22014032t t t t θωαππ=+=-。
因此,飞轮在这5s 内总共转过了5012562.5222N θθθππππ-∆====圈,再经过010 1.676t ωπαπ∆-∆==-秒后停止转动。
1-9 一质点从静止出发沿半径为3m 的圆周运动,切向加速度为23m s 并保持不变,则经过 s 后它的总加速度恰好与半径成45角。
在此时间内质点经过的路程为 m ,角位移为 rad ,在1s 末总加速度大小为 2m s 。
解析:由00v =、3R m =、23/t dv a m s dt==可得,03t v v a t t =+=,223n v a t R ==。
总加速度恰好与半径成45角意味着n t a a =,可得1t s =。
在此时间内经过的角位移22201111113()0.5222t a t t t t rad R R θωα=+===,路程1 1.5s R m θ==,在1s末总加速度大小为21 4.2/a m s ==。
1-10 半径为30cm 的飞轮,从静止开始以0.5rad s π的匀角速度转动,则飞轮边缘上一点在飞轮转过240时的切向加速度t a = ,法向加速度n a = 。
解析:匀速转动的线速度大小0.15/v R m s ωπ==,所以0t dva dt==,2220.075/n v a m s Rπ==。
三 计算题1-11 一电子的位置由23.00 4.00 2.00t t =-+r i j k 描述,式中t 单位为s , r 的单位为m 。
(1)求电子任意时刻的速度v ,(2)在 2.00t s =时,电子速度的大小。
解析:(1)38d t dt==-rv i j (2)由于2316=-v i j ,所以可以求出在2t s =时,电子速度的大小16.3(/)v m s ==。
1-12 质点作直线运动,其运动方程为2126x t t =-(式中x 以m 计,t 以s计),求:(1)4t s =时,质点的位置,速度和加速度;(2)质点通过原点时的速度;(3)质点速度为零时的位置;(4)作x t -图,v t -图,a t -图。
解析:(1)由运动方程2126x t t =-可得,1212dx v t dt ==-,12dva dt==-。
4t s =时,448x m =-,436/v m s =-,2412/v m s =-。
(2)质点通过原点时, 0x =,所以02t s s =或,得到12/12/v m s m s =-或。
(3)质点速度为零时,1t s =,此时6x m =。
(4)略。
1-13 一质点沿x 轴运动,加速度2,0a t t =-=时003,1x m v m s ==。
求:(1)t 时刻质点的速度和位置;(2)速度为零时质点的位置和加速度;(3)从开始(0t =)到速度为零这段时间内质点的位移大小。
解析:(1)2dva t dt ==-,01v m s =,所以200(2)121ttt v v t dt tdt t =+-=-=-⎰⎰。
又因为21dxv t dt==-,03x m =,所以23001(1)33tt x x t dt t t =+-=+-⎰。
(2)0v =时,1t s =,此时11113133x m =+-=,212/a m s =-。
(3)10112333x x x m ∆=-=-=。
1-14 质点沿直线运动,速度3232v t t =++(式中v 以/m s 计,t 以s 计),如果当2t s =时,质点位于4x m =处,求3t s =是时质点的位置、速度和加速度。
解析:由3232dx v t t dt==++得: 32434322211(32)4(2)21244ttx x t t dt t t t t t t =+++=+++=++-⎰,236dva t t dt==+, 所以,341.25x m =,356/v m s =,2345/x m s =。
1-15 质点沿直线运动,加速度24a t =- (式中a 以2/m s 计,t 以s 计),如果当3t s =时,质点位于9x m =处,2/v m s =,求质点的运动方程。
解析:由24dv a t dt==-得,23333311(4)2(4)4133ttv v t dt t t t t =+-=+-=-+-⎰。
又因为dxv dt=,所以34233113(41)23124tx x t t dt t t t =+-+-=-+-+⎰。
1-16 一个质点自原点开始沿抛物线22y x =运动,它在x 轴上的分速度为一常量,其值为4.0/m s ,求质点在2x m =处的速度和加速度。
解析:x 轴:00444x t x dx v dx dt x t dt ==⇒=⇒=⎰⎰,y 轴:22182y x t ==。
质点在2x m =处,0.5t s =。
因为16y dyv t dt==,216/y y dv a m s dt ==,0x a =,所以28/y x v m s ==。
故48(/)m s =2v i +j ,216(/)m s =2a j 。
1-17 (1)若已知一质点的位置由24123x t t =-+ (式中t 的单位为s , x 的单位为m )给出,它在1t s =末的速度为何值?(2)该时刻质点正在向x 的正方向还是负方向运动?(3)该时刻质点速率为何值?(4) 3t s =后,质点是否在某一时刻向x 轴负方向运动?解析:(1)126dxv t dt==-+,所以11266/v m s =-+=-,即6(/)m s =-v i 。
(2)负方向。
(3)66/m s =-=v i 。
(4)因为126v t =-+,若负向运动则0v <,2t <,所以3t s =后,质点不会在某一时刻向x 轴负方向运动。
1-18 已知质点的运动方程为:22,2x t y t ==- (x ,y 以m 为单位,t 以s 为单位)。
(1)求质点运动运动的轨道方程;(2)写出1t s =和2t s =时质点的位置矢量,并计算1s 到2s 的平均速度;(3)计算1s 末和2s 末的瞬时速度;(4)计算1s 末和2s 末的瞬时加速度。
解析:(1)22,2x t y t ==-,所以2124y x =-。
(2)22(),42(),23(/)m m m s t∆==-==-∆1rr i +j r i j v i j 。
(3)2,2x y dx dy v v t dt dt====-,所以22(/),24(/)m s m s =-=-12v i j v i j 。
(4)0,2y xx y dv dv a a dt dt====-,所以222(/),2(/)m s m s =-=-12a j a j 。
1-19 一小轿车作直线运动,刹车时速度为0v ,刹车后其加速度与速度成正比而反向,即kv a -=,k 为已知的大于零的常量。
