2019年高职单招对口招生数学试题
2019年浙江省高职考单招单考数学试卷(附答案)

2019年浙江省高职考单招单考数学试卷(附答案)2019浙江省高职单独考试数学试卷一、单项选择题(本大题共20小题,1―10小题每小题2分,11―20每小题3分,共50分.)1.已知集合A={-1,1},集合B={-3,-1,1,3},则A∩B=()A。
{-1,1}B。
{-1}C。
{1}D。
∅2.不等式x2-4x≤的解集为()A。
[0,4]B。
(0,4)C。
[-4,0)∪(0,4]D。
(-∞,0]∪[4,+∞)3.函数f(f)=ln(f−2)+1/(f−3)的定义域为()A。
(2,+∞)B。
[2,+∞)C。
(-∞,2]∪[3,+∞)D。
(2,3)∪(3,+∞)4.已知平行四边形ABCD,则向量AB→+BC→=()A。
DC→B。
BD→C。
AC→D。
CA→5.下列函数以π为周期的是()A。
y=sin(x−π/8)B。
y=2cos(x)C。
y=sin(x)D。
y=sin(2x)6.本学期学校共开设了20门不同的选修课,学生从中任选2门,则不同选法的总数是()A。
400B。
380C。
190D。
3807.已知直线的倾斜角为60°,则此直线的斜率为()A.−√3/3B.−√3C.√3D.√3/38.若sinα>0且tanα<0,则角α终边所在象限是()A.第一象限B.第二象限C.第三象限D.第四象限9.椭圆标准方程为x^2/2t+ y^2/4-t=1,一个焦点为(-3,0),则t的值为()A。
-1B。
0C。
1D。
210.已知两直线l1、l2分别平行于平面β,则两直线l1、l2的位置关系为()A.平行B.相交C.异面D.以上情况都有可能11.圆的一般方程为x^2+y^2-8x+2y+13=0,则其圆心和半径分别为()A。
(4,-1),4B。
(4,-1),2C。
(-4,1),4D。
(-4,1),212.已知100张奖券中共有2张一等奖、5张二等奖、10张三等奖,现从中任取一张,中奖概率为()A。
1/17B。
2019江苏高职单招院校单独招生联合测试真题卷(数学)

2019江苏高职单招院校单独招生联合测试真题卷数学注意事项考生在答题前请认真阅读本注意事项及各题答题要求1.本试卷包含选择题(第1题~第10题,共10题40分)、填空题(第11题~第15题,共5题20分)和解答题(第16题~第20题,共5题40分),满分100分。
考生答题全部答在答题卡上,答在本试卷上无效。
本次考试时间为75分钟。
考试结束后,请将本试卷和答题卡一并放在桌面,等待监考员收回。
2.答题前,请您务必将自己的姓名、准考证号用书写黑色字迹的0.5毫米签字笔填写在本试卷及答题卡上。
3.请认真核对监考员在答题卡右上角所粘贴条形码上的姓名、准考证号是否与本人的相符合。
4.答选择题必须用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,请用橡皮擦干净后,再选涂其他答案。
答非选择题必须用书写黑色字迹的0.5毫米签字笔写在答题卡上的指定位置,在其他位置答题一律无效。
参考公式:椎体的体积公式1=3V Sh ,其中S 是椎体的底面积,h 是椎体的高.一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.已知集合{}1,3A =,{}3log ,3B m =,若{}1,2,3A B =U ,则实数m = ( )A .2B .3C .6D .92.盒中装有大小、形状都相同的6个小球,分别标以号码1,2,3,4,5,6,从中随机取出一个小球,其号码为奇数的概率是 ( )A .12 B .13 C .14 D .163.已知函数()cos()(0)6f x x πωω=->的最小正周期为π,则ω的值为 ( )A .1B .2C .πD .2π4.如图,在ABC ∆中,AB a =u u u r r ,AC b =u u u r r .若点D 满足2BD DC =u u u r u u u r , 则AD =u u u r( )(第4题)A .2133a b +r rB .2133a b -r rC .1233a b +r rD .1233a b -r r5.如图是一个算法流程图,若输出x 的值为3,则输出s 的值为 ( )(第5题)A .2B .4C .8D .166.若变量x y ,满足22x y x x y ≤⎧⎪≤⎨⎪+≥⎩,则2z y x =-的最大值为 ( )A .-1B .0C .1D .2 7.在平面直角坐标系中,已知第一象限的点(),a b 在直线210x y +-=上,则12a b+的最小值为( ) A .11 B .9 C .8 D . 6 8.已知1(1)212f x x -=-,且()6f m =,则实数m 的值为 ( )A .12-B .14-C .1-D .34- 9.已知等差数列{}n a 的前n 项和为n S ,若151,15,a S ==则10S = ( ) A .55B .45C .35D .2510.已知圆C 与圆22(1)1x y ++=关于直线0x y +=对称,则圆C 的标准方程为 ( )A .22(11x y +-=) B .221x y += C .22(11x y -+=) D .22(11x y ++=)二、填空题(本大题共5小题,每小题4分,共20分) 11.若复数z 满足1i 42i z +=-() (i 为虚数单位),则z = .12.设平面向量(2),(1,2)a y b ==v v ,,若//a b v v ,则2a b +=vv .13.如图,已知三棱锥P ABC -中, PA ⊥底面,3ABC PA =,底面ABC 是边长为2的正三角形,三棱锥P ABC -的体积为 .(第13题)的频率为 . 分组 [10,20) [20,30) [30,40) [40,50) [50,60) [60,70]频数54321215.已知函数[]()211,1,3f x x a x x =-++∈图象上任意两点连线都与x 轴不平行,则实数a 的取值范围是 .三、解答题(本大题共5小题,共40分.解答时应写出文字说明、证明过程或演算步骤)16.(本题满分6分) 已知5cos α=,(0,)2πα∈. (1)求sin α和sin()4πα+的值; (2) 求tan2α的值.17.(本题满分6分)如图,在三棱锥S ABC -中,点D ,E ,F 分别为棱AC , SA , SC 的中点. (1)求证://EF 平面ABC ;(2)若SA SC =,BA BC =,求证:AC ⊥SB .(第17题)18.(本题满分8分)已知椭圆C 的中心在原点,焦点在x 轴上,短轴长为2,且点3在椭圆C 上. (1)求椭圆C 的方程;(2)若点P 在第二象限,2160F PF ∠=︒,求三角形12PF F 的面积. 19.(本题满分10分)已知正项数列{}n a 的前n 项和为n S ,且n S 是1与n a 的等差中项. (1)求数列{}n a 的通项公式;(2)求数列12n n a a +⎧⎫⎨⎬⎩⎭的前n 项和n T . 20.(本题满分10分)已知函数x a x x x f ln 2)(2+-= )(R a ∈.(1)当1=a 时,求函数)(x f 在))1(,1(f 处的切线方程; (2)当0>a 时,求函数)(x f 的单调区间.2019江苏高职单招院校单独招生联合测试真题卷数学答案一、1.D 解析:由题意知,3log 2,9m m =∴=.故选D .2.A 解析:从6个球中随机取出一个小球共有6种方法,其中号码为偶数的为1,3,5,共三种,由古典概型的概率公式可得,其号码为偶数的概率是3162P ==.故选A . 3.B 解析:由2||T πω=得,22πωπ==.故选B. 4.C 解析:∵2BD DC =u u u r u u u r ,∴2()AD AB AC AD -=-u u u r u u u r u u u r u u u r ,∴322AD AB AC a b =+=+u u u r u u u r u u u r r r ,∴1233AD a b =+u u u r r r.故选C .5.C 解析:1,13,2,234,338,4s k s k s k s k ==≤→==≤→==≤→==,不满足43k =≤,输出s =8.故选C .6.A 解析:作出可行域如图所示,由2z y x =-,得2yx z =+,由图可知,当直线2y x z =+过可行域内的点(11)C ,时,直线在y 轴上的截距最大,即121z =-=-.故选A .7.B 解析:∵第一象限的点()a b ,在直线210x y +-=上,∴210a b +-=,即21a b +=,且00a b >,>,∴()12122222()25529b a b aa b a b a b a b a b+=++=++≥+⋅=.故选B . 8.D 解析:由题意可得,7173216112244x x m x -=⇒==-=-=-,.故选D .9.A 解析:设等差数列{}n a 的公差为d ,则51545+152S a d ⨯==,1010,1d d ∴==,则101109101045552S a d ⨯=+=+=.故选A. 10.C 解析:由题意,圆22(1)1x y ++=的圆心为(0,1)-,半径为1r =,圆心(0,1)-关于直线0x y +=的对称点为(1,0),则圆C 的圆心为(1,0),半径为1,圆C 的标准方程为22(11x y -+=).故选C.二、11解析:由题意得,42i (42i)(1i)13i 1i (1i)(1i)z ---===-++-,故z =12.解析:由题意得2210y ⨯-⨯=,解得4y =,则()24,8a b +=v v ,故2a b +==v v13解析:因为该三棱锥是一个底面是等边三角形的直棱锥,所以该三棱锥的体积为1112233322ABC V S PA ∆=⋅=⨯⨯⨯⨯=14.0.3 解析:在区间[30,60)的频数为3+2+1=6,所以频率为630.32010P ===. 15.已知函数()[]2()211,1,3f x x a x x =-++∈图象上任意两点连线都与x 轴不平行,则实数a 的取值范围是 .15.1522∞∞U (-,][,+) 解析:由题意知函数()f x 在[]1,3上是单调函数,所以对称轴2112a +≤或2132a +≥,解得12a ≤或52a ≥,即实数a 的取值范围是1522∞∞U (-,][,+). 三、16.解析:(1)cos 5α=Q ,(0,)2πα∈,sin 5α∴==.(2分)sin()sin cos cos sin (44425510πππαααα+=+=+=.(4分)(2)由(1)得,sin tan 2cos ααα==,则22tan 44tan21tan 143ααα===---.(6分) 17.证明:(1)∵EF 是SAC ∆的中位线, ∴EF ∥AC .又∵EF ⊄平面ABC ,AC ⊂平面ABC , ∴EF ∥平面ABC .(3分)(2)∵SA SC =, AD DC =,∴SD ⊥AC . ∵BA BC =, AD DC =,∴BD ⊥AC .又∵SD ⊂平面SBD ,BD ⊂平面SBD ,SD DB D =I , ∴AC ⊥平面SBD ,(5分) 又∵SB ⊂平面SBD , ∴AC ⊥SB .(6分)18.解析:(1) 因为C 的焦点在x 轴上且短轴为2,故可设椭圆C 的方程为1222=+y ax (1>a ),因为点在椭圆C 上,所以14312=+a, (2分) 解得42=a , 所以,椭圆C 的方程为1422=+y x .(4分) (2) 设12,PF x PF y ==,由椭圆的定义得,4x y +=,由余弦定理得,2222cos 60412x y xy c +-︒==,即2212x y xy +-=,则2[()2]12x y xy xy +--=,解得,43xy =,(6分)从而得12114sin 6022323PF F S xy ∆=︒=⨯⨯=1sin 602S xy =︒=33.(8分) 19.解析:(1)由等差中项可得1n a =+,即24(1)n n S a =+,当1n =时,11a =;当2n ≥时,2114(1)n n S a --=+,又24(1)n n S a =+,由1n n n a S S -=-得,2211444(1)(1)n n n n n a S S a a --=-=+-+,(2分)化简得,221142121n n n n n a a a a a --=++---,221121210n n n n a a a a ---+---=,221121)(21)0n n n n a a a a ---+-++=(,即2211)(1)0n n a a ---+=(,则11()(2)0n n n n a a a a --+--=,又10,2n n n a a a ->∴-=Q ,(4分)故{}n a 是以1为首项,2为公差的等差数列,即21na n =-.当1n =时,11a =满足上式.综上,数列{}n a 的通项公式是21n a n =-.(6分) (2)12211(21)(21)2121n n a a n n n n -==--+-+Q,(8分) 111111(1)()()1335212121n T n n n ∴=-+-++-=--++L .(10分) 20.解析:(1)当1=a 时,,122)('xx x f +-=则,1)1(',1)1(=-=f f所以切线方程为11-=+x y .即2-=x y .(3分))0(2222)('22>+-=+-=x xax x x a x x f )(,令0)('=x f ,0 222=+-a x x , ①当,084≤-=∆a 即21≥a 时,,0)('≥x f ,函数)(x f 在),(∞+0上单调递增;(5分) ②当,084>-=∆a 且0>a ,即210≤<a 时,由,0 222=+-a x x ,得22112,1ax -±=, 由,0)('>x f ,得22110a x --<<或2211ax -+>;(7分) 由,0)('<x f ,得x a<--22112211a -+<.(9分) 综上,当21≥a 时,)(x f 的单调递增区间是),(∞+0; 当210<<a 时,)(x f 的单调递增区间是)2211,0(a --,),2211(+∞-+a ; 单调递减区间是)2211,2211(aa -+--.(10分)2019江苏高职单招院校单独招生联合测试真题卷数学注意事项考生在答题前请认真阅读本注意事项及各题答题要求1.本试卷包含选择题(第1题~第10题,共10题40分)、填空题(第11题~第15题,共5题20分)和解答题(第16题~第20题,共5题40分),满分100分。
四川省2019年普通高校职教师资和高职对口招生统一考试数学试题

四川省2019年普通高校职教师资和高职对口招生统一考试数学试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页,第Ⅱ卷3至4页,共4页。
满分150分,考试时间120分钟.考生作答时,须将答案答在答题卡上,在本试卷、草稿纸上答题无效。
考试结束后,将本试题卷和答题卡分别收回。
第Ⅰ卷(选择题 共60分)注意事项:1、选择题必须使用2B 铅笔在答题卡上将所选答案对应的标号涂黑.2、第Ⅰ卷共1大题,15小题,每小题材4分,共用60分。
一、选择题(本大题共15小题,每小题4分,共60分.每小题给出A ,B,C ,D 四个选项,其中只有一项是符合题目要求的. 1. 设集合{}{}2,2,1,2A B =-=-,则A B ={}{}{}{}.2.2,1.2,2.2,1,2A B C D -----2. sin 26ππ⎛⎫+= ⎪⎝⎭函数()211f x x =-的定义域()()()().1,1.1,.,1.1,A B C D --+∞-∞+∞3。
已知角α的终边经过点()1,1-,则cos α=2211....2222A B C D --4。
已知平面向量()()()5,43,2,7,6===a ,b c ,则a +b -c =()()()().0,0.1,0.0,1.1,1A B C D5. 绝对值不等式34x -<的解集为 ()()()()().,1.7,.1,7.,17,A B C D -∞-+∞--∞-+∞6。
函数()sin 23f x x π⎛⎫=+ ⎪⎝⎭在区间[],ππ-上的图像大致为7. 与直线3270x y --=垂直的直线的斜率是 2233....3322A B C D --8。
椭圆22143x y +=的焦点坐标是()()())()()()().1,0,1,0.3,0,3,0.2,0,2,0.7,0,7,0A B C D ----9。
已知球的半径为6cm ,则它的体积为 3333.36.144.288.864A cm B cm C cm D cm ππππ10. 计算:141lg5lg 2016-⎛⎫++= ⎪⎝⎭.1.2.3.4A B C D11。
河南省2019年对口升学数学真题答案及解析

)
. 3
【考点】
:等差数列的前 n 项和公式
【解析】选择 C.
2
2
3
2 = 21 + , 3 = 31 + 3,由 3 −
化简得1 + − (1 + ) = 1,
2
2
31 +3
= 1,得
= 1,
3
−
21 +
= 2,
2
= 1,
故选 C.
⃗⃗⃗⃗⃗ •
⃗⃗⃗⃗⃗ = ( )
因为2 − = ( − ) > 0,所以2 > ,
因为 > 2 = ( − ) > 0,所以 > 2 ,
根据不等式性质的传递性得2 > > 2 .故选择 D.
3.已知函数( + 1)的定义域为[-2,4],则函数(2 + 1)的定义域为( )
3 3
B.如果2 +2 ≠0,则 ≠ 0或 ≠ 0
C.如果 ≠ 0或 ≠ 0,则2 +2 >0
D.如果2 +2 ≠0,则 ≠ 0且 ≠ 0
【考点】
:命题
【解析】选择 A.
命题:已知2 + 2 = 0则 = 0, = 0
逆命题:如果 = 0, = 0,则2 + 2 = 0
显然 A 选项不成立,
1
−2
1
1
2
−1
=− >
= −1,
−1
B 选项不成立,
−2
1
−2
2
−1
= <
= 2,
C 选项不成立,(−2)2 = 4, (−2) × (−1) = 2,(−1)2 = 1, 4 > 2 > 1,故选择 D.
河南省2019年对口高考数学卷

河南省2019年普通高等学校对口招收中等职业学校毕业生考试数学试卷一、选择题(每小题3分, 共30分. 每小题只有一个选项是正确的,请将正确选项涂在答题卡上)1.已知2200,0a b a b 则+===.下列哪一个是前述命题的逆否命题( ) A .如果0a ¹或0b ¹,则220a b +?;B .如果220a b +?,则0a ¹或0b ¹;C .如果0a ¹,0b ¹,则220a b +>;D .如果220a b +?,则0a ¹且0b ¹. 2.已知,,,a b c R ab c 且?<,则下列式子中,正确的是( )A .22ac bc >B .11a b <C .b aa b> D .22a ab b >>3.已知函数(1)f x +的定义域为[24],-,则函数(21)f x +的定义域为( )A .33[]22,- B .[33],- C .[39],- D .[12],-4.下列各组函数中,表示同一函数的是( )①()()f x g x ==②()()f x x g x 和==③2()()f x x g x 和==④22()21()21f x x x g t t t 和=-+=-+A .①②B .①③C .③④D .①④ 5.已知等差数列{}n a 的前n 项和为n S ,若32132S S -=,数列{}n a 的公差d 的值为( )A .12B .1-C .2D .3 6.已知点(2,1),(1,3),(3,4)A B C -.则AB BC u u u r u u u rg =( )A .4-B .4C .3-D .37.抛物线28x y =的焦点到准线的距离为( ) A .1 B .2 C .4 D .88.三棱柱ABC-A 1B 1C 1的侧棱长和两个底面的边长都为2,侧棱垂直于底面,E ,F 分别为AB ,A 1C 1的中点,直线EF 与C 1C 所成角的余弦值为( ) A.2 B.5 C.5 D.29.一次掷甲乙两枚骰子的基本事件个数为( ) A .12 B .36 C .6 D .6610.从10个人中选出2人分别为正副班长,选法种数为( ) A .45 B .90 C .30 D .180 二、填空题(每小题3分, 共24分)11.已知集合{}{}{}21,3,,3,,3,A a B a A B a I 且===,则a = . 12.不等式2230x x --<的解集为 .13.已知22sin 1tan 3sin 2,则q q q+== . 14.若向量(12)(31)a b r r,,,==-,则()()a b a b r r r r g -= . 15.直线:2360l x y ++=在y 轴上的截距为 .16.已知正三棱锥的侧棱和底面连长都为1,则它的体积为 . 17.把4个不同的球分别放入不同的3个盒子里,一共有 种放法. 18.已知事件A 的对立事件为()0.4()A P A P A ,且,则== . 三、计算题(每小题8分, 共24分)19.在ABC D 中,1,cos , 4.43A B AC p ?== (1)求sin ;C ; (2)求ABC D 的面积.20.已知双曲线经过点()32,-,且与椭圆224936x y +=有相同的焦点,求双曲线的标准方程.21.已知()92390123921.x a a x a x a x a x L +=+++++ 求02468a a a a a ++++的值.四、证明题(每小题6分, 共11分)22.若函数()f x 是R 上的增函数,对任意实数a ,b ,若0a b +>, 求证:()()()()f a f b f a f b +>-+-.23.如图,已知矩形ABCD ,点E 为平面ABCD 外一点,EAD ABCD 平面平面^,且AE DE ^.求证EAB ECD 平面平面^.五、综合题(10分)24.等比数列{}n a 中,公比1q ¹,它的前n 项和为n S 。
2019单招数学试卷 (1)
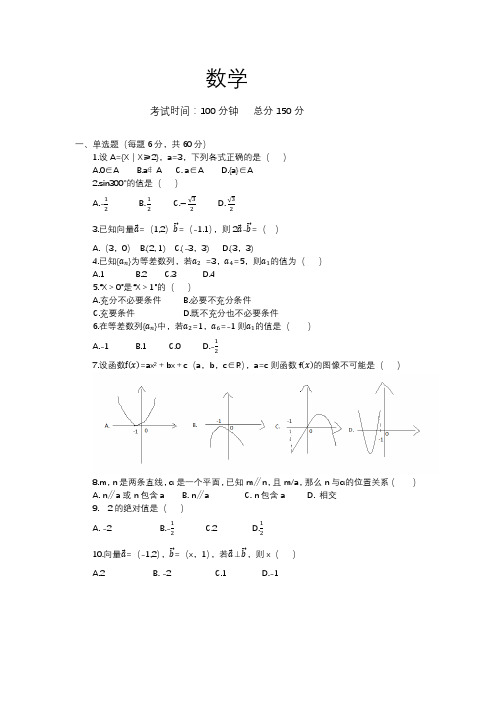
数学考试时间:100分钟总分150分一、单选题(每题6分,共60分)1.设A={X|X≥2},a=3,下列各式正确的是()A.0∈AB.a∉AC. a∈AD.{a}∈A2.sin300°的值是()A.-12B.12C.−√32D.√323.已知向量a⃗=(1,2)b⃗⃗=(-1.1),则2a⃗-b⃗⃗=()A.(3,0)B.(2, 1)C.(-3,3)D.(3,3)4.已知{a n}为等差数列,若a2=3,a4=5,则a1的值为()A.1B.2C.3D.45.“X>0”是“X>1”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6.在等差数列{a n}中,若a2=1,a6=-1则a1的值是()A.-1B.1C.0D.-127.设函数f(x)=ax²+bx+c(a,b,c∈R),a=c则函数f(x)的图像不可能是()8.m,n是两条直线,α是一个平面,已知m∥n,且m/a,那么n与α的位置关系()A. n∥a或n包含aB. n∥aC. n包含aD. 相交9. 2的绝对值是()A. -2B.-12C.2 D.1210.向量a⃗=(-1,2),b⃗⃗=(x,1),若a⃗⊥b⃗⃗,则x()A.2B. -2C.1D.-1二、填空题(每题10分,共30分)11.根据程序图输出的的S值为()12.已知复数Z=3+4i(i为虚数单位),则|Z|=()13.sin60°=()三、解答题(每题20分,共60分)14.已知函数f(x)=x²-4x,x∈【1,5】,则f(x)的最大值和最小值是多少。
15.已知全集U={1,2,3,4,5},其子集A={1,3},B={2,5}求:(1)∁uA;(2)A∪B;( 3 ) A∩B;( 4 ) (∁uA)∪(∁uB);16.画三视图。
江苏高职单招数学真题试卷.doc

2019 年江苏高职单招数学真题卷参考公式:锥体的体积公式V= h,其中 S 是锥体的底面积,h 是锥体的高一、选择题 (本大题共 10 小题,每小题 4 分共 40 分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合 A={1,3} ,B={l,3},若 AUB={1,2,3} ,则实数 m=A.2B.3C. 6D.92.盒中装有大小、形状都相同的 6 个小球,分别标以号码1,2,3,4,5,6,从中随机取出一个小球,其号码为奇数的概率是A.B C D.3.已知函数 f(x)=)(a>0) 的最小正周期为,则的值为_____A.1 B .2 C .D⋯24。
如图,在△ ABC 中,=a ,=b 。
若点 D 满足=2,则= A. a+ b B.. a- b C. . a+ b D. . a- b5。
如图是一个算法流程图,若输入x 的值为 3,则输出s 的值为A.2B.4C.8D.166。
若变量x, y 满足,则=y-2x 的最大值为A.-1B. 0 C .1 D.27.在平面直角坐标系中,已知第一象限的点(a,b)在直线 x+2y-1=0上,则+ 的最小值为_______A.11B.9C.8D.68.已知f(1-x)=2x-1 ,且f(m)=6则实数m的值为_______A. B. - C. -1 D. -9。
已知等差数列{an}的前 n 项和为 Sn,若=1 ,=15 ,则=___ A.55 B.45 C.35 D.2510。
已知圆 C 与圆+=1 关于直线x+y=0 对称,则圆 C 的标准方程为A +=1 B. +=1C. + =1D. + =1二、填空题 (本大题共 5 小题,每小题 4 分,共 20 分)11.若复数 z 满足 z(1+i)=4-2i(i为虚数单位),则=______________12.设平面向量a=(2 ,y),b=(1,2) ,若 a∥b,则=________________13.如图,已知三棱锥 P-ABC 中, PA⊥底面 ABC,PA=3 ,底面 ABC 是边长为 2 的正三角形,三棱锥 P-ABC 的体积为 _______________14.容量为 20 的样本数据,分组后的频数如下表,则样本数据落在区间[30,60) 的频率为 ____________分组[10,20] [20,30 )[30,40 )[40,50 )[50,60 ) [60,70]频数 5 4 3 2 1 215。
四川省2019年对口高考文化真题及答案(数学)

四川省2019年普通高校职教师资班和高职班对口招生统一考试数 学本试题卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)㊂第Ⅰ卷1 3页,第Ⅱ卷3 4页,共4页㊂考生作答时,须将答案答在答题卡上,在本试题卷㊁草稿纸上答题无效㊂满分150分㊂考试时间120分钟㊂考试结束后,将本试题卷和答题卡一并交回㊂第Ⅰ卷(共60分)注意事项:1.必须使用2B 铅笔在答题卡上将所选答案对应的标号涂黑㊂2.第Ⅰ卷共1大题,15小题,每小题4分,共60分㊂一㊁选择题(本大题共15小题,每小题4分,共60分㊂在每小题列出的四个选项中,只有一个是符合题目要求的)1.设集合A ={-2,2},B ={-1,2},则A ɣB =( )A.{2}B .{-2,-1}C .{-2,2} D.{-2,-1,2}2.函数f (x )=11-x 2的定义域是( )A.(-1,1)B .(-1,+ɕ)C .(-ɕ,1) D.(1,+ɕ)3.已知角α的终边经过点(-1,1),则c o s α=( )A.-22B .22C .-12 D.124.已知平面向量a =(5,4),b =(3,2),c =(7,6),则a +b -c =( )A.(0,0)B .(1,0)C .(0,1) D.(1,1)5.绝对值不等式|x -3|<4的解集为( )A.(-ɕ,-1)B .(7,+ɕ)C .(-1,7) D.(-ɕ,-1)ɣ(7,+ɕ)6.函数f (x )=s i n 2x +π3æèçöø÷在区间[-π,π]上的图象大致为( )7.与直线3x -2y -7=0垂直的直线的斜率是( )A.-23B .23C .-32 D.328.椭圆x 24+y 23=1的焦点坐标是( )A.(-1,0),(1,0)B .(-3,0),(3,0)C .(-2,0),(2,0) D.(-7,0),(7,0)9.已知球的半径为6c m ,则它的体积为( )A.36πc m 3B .144πc m 3C .288πc m 3D.864πc m 310.计算:116æèçöø÷-14+l g 5+l g 20=( )A.1B .2C .3 D.411. x >0 是 x >1的( )A.充分且不必要条件B .必要且不充分条件C .充要条件 D.既不充分又不必要条件12.某科技公司从银行贷款500万元,贷款期限为6年,年利率为5.76%,利息按 复利计息法 (把当年的本金与利息的和作为次年的本金来计算利息的方法)计算.如果6年后一次性还款,那么这家科技公司应偿还银行的钱是( )A.500ˑ0.94245万元B .500ˑ0.94246万元C .500ˑ1.05765万元 D.500ˑ1.05766万元13.已知a =l n12,b =2-3,c =l o g 1213,则a ,b ,c 的大小关系为( )A.b >c >a B .b >a >c C .c >b >a D.c >a >b14.已知甲㊁乙两个城市相距120千米,小王开汽车以100千米/时匀速从甲城市驶往乙城市,到达乙城市后停留1小时,再以80千米/时匀速返回甲城市.汽车从甲城市出发时,时间x (小时)记为0.在这辆汽车从甲城市出发至返回到甲城市的这段时间内,该汽车离甲城市的距离y (千米)表示成时间x (小时)的函数为( )A.y =100x ,0ɤx ɤ1.2,80x ,x >1.2.{B .y =100x ,0ɤx ɤ1.2,120-80x ,x >1.2.{C .y =100x ,0ɤx ɤ1.2,120,1.2<x ɤ2.2,120-80x ,2.2<x ɤ3.7.ìîíïïïï D.y =100x ,0ɤx ɤ1.2,120,1.2<x ɤ2.2,296-80x ,2.2<x ɤ3.7.ìîíïïïï15.函数f (a )=(a -1)2+(a -2)2+(a -3)2+ +(a -10)2的单调递增区间为( )A.[5,+ɕ)B .[5.5,+ɕ)C .[6,+ɕ) D.[6.5,+ɕ)第Ⅱ卷(共90分)注意事项:1.必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所指示的答题区域内作答㊂作图题可先用铅笔绘出,确认后再用0.5毫米黑色墨迹签字笔描清楚㊂答在试题卷㊁草稿纸上无效㊂2.第Ⅱ卷共2大题,11小题,共90分㊂二㊁填空题(本大题共5小题,每小题4分,共20分)16.已知平面向量a =(2,-1),b =(-3,-2),则a ㊃b =.17.双曲线x 2-y 23=1的离心率为.18.二项式x 2+1x æèçöø÷6展开式中的常数项为.(用数字作答)19.为落实精准扶贫工作,某单位计划从7名优秀干部中任选3名到贫困村驻村工作,不同的选派方案有种.20.计算:t a n 20ʎ+t a n 40ʎ+3t a n 20ʎt a n 40ʎ=.(用数字作答)三㊁解答题(本大题共6小题,共70分,解答应写出文字说明㊁证明过程或演算步骤)21.(本小题满分10分)设等差数列{a n }的前n 项和为S n ,a 5=2a 4,S 9=108,求数列{a n }的通项公式.22.(本小题满分12分)为弘扬勤俭节约的中华传统美德,某校开展了节约用水教育与问卷调查.调查得知某地区300名居民某月的用水量(单位:吨),将这些数据按照[0,1),[1,2),[2,3),[3,4),[4,5),[5,6]分成6组,制成了如图所示的频率直方图.(Ⅰ)求频率直方图中a 的值;(Ⅱ)若每组中各居民的用水量用该组的中间值来估计(如[0,1)的中间值为0.5),试估计该地区居民这个月的人均用水量(单位:吨).23.(本小题满分12分)在әA B C 中,内角A ,B ,C 的对边分别为a ,b ,c ,且a =2,t a n C =-2,әA B C 的面积为2.(Ⅰ)求边b 的长;(Ⅱ)求c o s B 的值.24.(本小题满分12分)如图,已知在长方体A B C D A1B1C1D1中,A B=1,B C=2,A A1= 3,E为A A1的中点.(Ⅰ)证明:A1Cʊ平面B D E;(Ⅱ)求A1C与平面A B C D所成的角的大小.第24题图25.(本小题满分12分)设圆O的方程是x2+y2=1,三点A(2,2),B(b,b2-2),C(c,c2-2)互不重合,直线A B与圆O相切.(Ⅰ)证明:3b2+4b-1=0;(Ⅱ)若直线A C与圆O相切,证明:直线B C与圆O也相切.26.(本小题满分12分)已知函数f(x)的定义域为R,并且对一切实数x都有f(-x)+f(x) =0,f(-x-2)=-f(x)成立,当xɪ(0,1)时f(x)=s i nπx+1.(Ⅰ)求f(0),f(1)的值;(Ⅱ)当xɪ(11,13)时,求f(x)的解析式.2019年普通高校职教师资班和高职班对口招生统一考试数学一、选择题1.D2.A3.A4.B5.C6.B7.A8.A9.C 10.D 11.B 12.D 13.C 14.D 15.B二、填空题16.-417.218.1519.3520.√3三、解答题21.【解】 解法一:设等差数列(a。
