第九章电磁感应电磁场理论
第九章电磁感应电磁场理论
返回 退出
结论 当穿过闭合回路的磁通量发生变化时,不管
这种变化是由什么原因的,回路中有电流产生。 称为电磁感应现象。
电磁感应现象中产生的电流称为感应电流, 相应的电动势称为感应电动势。
返回 退出
二、楞次定律 楞次定律: 感应电动势产生的感应电流方向,总 是使感应电流的磁场通过回路的磁通量阻碍原磁通 量的变化。
求:感应电动势和感应电流以及最大感应电动势和
最大感应电流。
解: 2 n 120 s-1
60
Φ B S BS cos
B r2 cos t
2
a
r
b
i
dΦ dt
B r2
2
sin t
返回 退出
i
dΦ dt
B r2
2
sin t
i max
1 2
B
r2
2.96(V)
Ii
i
R
B r2
2R
sin t
L 0
d
i
0I 2 cos
L
a
cos
ln
a
L cos
a
返回 退出
二、在磁场中转动的线圈内的感应电动势 矩形线圈为N 匝,面积
S,在匀强磁场中绕固定 的轴线OO' 转动,磁感应 强度与轴垂直。
当 t = 0 时, = 0。
任一位置时:
Φ BScos
i
N
dΦ dt
NBS sin
d
dt
返回 退出
(2)非闭合回路
∂B
a.
Ei dl
L
cS
∂t
dS
εi Ei dl
大学物理第九章

动生电动势
由于导体运动而产生的感应电动势。
dΦ B dS Bldx
i
dΦ dt
Bl
dx dt
Bl
d a
B
l
c b
dx
负号表示电动势的方向。
在磁场中运动的导线内的感应电动势
导线内每个自由电子受到的
洛仑F兹力e
B
非静E电k 场 强Fe
B
a
电场。
解:由场的对称性,变化磁场所激发的感生电场
线在管内、外都是与螺线管同轴的同心圆。
取任一电场线(半径为r)作
为闭合回 路, 则
L L
E E
E
ddll21LrESdSlBtBt2ddSrSE
ER
r
B
感生电场
1)
当r
S
<RB时 dS t
S
B t
dS
r 2 dB
dt
E
1
2r
S
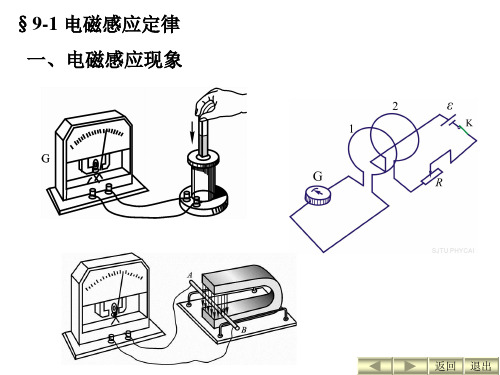
§9-1 电磁感应定律
法拉第(1791-1867英国)
1831年,发现电磁感应现象。 1833年,发现电解定律。 1837年,发现电解质对电容的影响, 引入电容率概念。 1845年,发现磁光效应,顺磁质、抗 磁质等。
§9-1 电磁感应定律
1. 电磁感应现象
N
S
现象1
条形磁铁N极(或S极)插入线圈时,线圈中就有电 流通过,这种电流称为感应电流。 实验表明:磁铁与线圈有相对运动时,线圈中就有感 应电流,相对速度越大,感应电流也越大。
(a)Φ 0, dΦ
B
dt en
0, i
0
i
(b)Φ 0, dΦ
B
dt en
第九章电磁感应电磁场理论b
解:由安培环路定理可得磁场分布:
B0
B 0I 2 r
r R2, r R1 R1 r R2
在筒内距轴心 r 处的磁能密度为:
r dr
I
R1
R2
l
I
1 B2
wm 2 0
0I 2 8 2r 2
取图示体积元,则: dV 2rl dr
此体积元的磁能为: dWm wmdV
例如:汽车和煤气炉的点火器、电警棍等都是感应圈的应用。
9—5 磁场的能量
R
L
一、载流自感线圈的磁能:
i
。。k
在开关合上后的一段时间内,电路中的电流 i 增长:0→I ,
在线圈上产生自感电动势:
L
L
di dt
由全电路欧姆定律有: L i R
iRL
iR Ld i dt
(电源的元功)
线圈的磁能元 (dt时间消耗在负载R上的焦耳热)
0t i dt 0t i2Rdt 0ILi di
(电源的电能) (负载上的焦耳热) (线圈的磁能)
即:线圈提供的电能一部分转化为负载的焦耳热, 另一部分作为磁能储存于线圈。
载流线圈的磁能为:
Wm 0ILi di
原因
L
H
dl
I 0
( S2面) ( S1面)
矛盾
电流的连续性在两极板间遭到破坏,即: j ds 0 s
2. 麦氏位移电流假设:
I
q0
S +++++++++
D
第九章电磁场理论的基本概念(电磁感应部分)精品PPT课件

设单位正电荷所受到的非
静电力为
Ek
I
则电源的电动势为:
i Ekdl
对如图的情况为: i Ek dl
+ + + + + + + Ek f非
+
-
E f静
---------
§ 9-1 法拉第电磁感应定律 一、电磁感应现象
1、 G
A
K
磁场发 生变化
K闭合和打开瞬间,电流计指针偏转。
a
2、
G
v
B
b
ab左右滑动时,电流计指针偏转。
切割磁 感应线
几个典型实验:
(1)
A (2)
B
v
i
B
x
(4) B
(3)
SN
(5)
A
当穿过一个闭合导体回路所包围的面积内的
第 九 章
电 磁 场 理 论 的 基 本 概 念
第九章 电磁场理论的基本概念
(电磁感应部分)
§ 9-1 法拉第电磁感应定律 § 9-2 动生电动势和感生电动势 § 9-3 自感现象和互感现象 § 9-4 磁场的能量
教学要求:
1. 掌握用法拉第定律和楞次定律计算感生电动 势及方向;
2. 理解感生电动势和动生电动势的产生原因; 3. 了解自感与互感,能计算简单回路的L,M; 4. 能计算简单磁场的Wm。
解:通过abcda的磁通量为
Φ=BS=BLx
b
aA
感应电动势为
i
dΦBd LxBv L=
dt
dt
-0.01
c
εi 的方向如图。
i
v
B
dB x
第九章 电磁感应 电磁场理论(完全版)要点

按楞次定律,要想维持回 路中电流,必须有外力不断作 功。这符合能量守恒定律。
如果把楞次定律中的“阻碍”改为“助长”, 则不需 外力作功,导线便会自动运动下去,从而不断获得电 能。这显然违背能量守恒定律。
6
对闭合导体回路而言, 感应电动势的方向和感 应电流的方向是相同的。
I
i
因而回路中感应电动势的方向 ,也用楞次定律来 判断。 应当指出,只要一个回路中的磁通量发生变化, 这个回路中便一定有感应电动势存在,这和回路由 什么材料组成无关。是否有感应电流,那就要看回 路是否闭合。 7
dm i N =Bab sin( t + ) 2 dt
=Bab cos t
m=Babcos ( t + ) 2
a b
图9-4
B
15
(2)一导线弯成角形(bcd=60º , bc=cd=a),在匀强 磁场B中绕oo´轴转动,转速每分钟n转, t=0时如图135所示,求导线bcd中的i。 c 我们连接bd组成一个三 B 角形回路bcd。由于bd段不 产生电动势,所以回路( o b d o´ bcd)中的电动势就是导线 bcd中电动势的。 图9-5 m=BScos ( t+o)
d m i dt
(9-1)
m Bds cos
s
d m (ii)求导: i dt
9
d m i dt
可用如下符号法则判定感应电动势的方向:
若i >0, 则i 的方向与原磁场的正方向组成右手螺 旋关系; 若i <0, 则i 的方向与原磁场的负方向组成右手螺 旋关系。
1
t2
2
1
1 dm R
(9-4)
大学物理-第九章 电磁感应 电磁场理论

2.电场强度沿任意闭合曲线的线积分等于以该曲线
为边界的任意曲面的磁通量的变化率的负值。 3.通过任意闭合曲面的磁通量恒等于零。
4.磁场强度沿任意闭合曲线的线积分等于穿过以该 曲线为边界的曲面的全电流。
第第九十章一电章磁真感空应中的电恒磁定场磁理场论
麦克斯韦方程组(物理含义)
(1) SDdSq (2)
例1 有一圆形平板电容器 R , 现对其充电,使电路上
的传导电流为 I ,若略去边缘效应, 求两极板间离开轴
线的距离为 r(r R) 的区域的(1)位移电流;
(2)磁感应强度 .
解 如图作一半径
Q Q
为 r平行于极板的圆形
回路,通过此圆面积的
电位移通量为
I
R P*r
I
ห้องสมุดไป่ตู้
D D(πr2)
D
Edl BdS
L
s t
(3) SBdS0
(4) LHdl IsD t dS
1.电荷是产生电场的源。
2.变化的磁场也是产生电场的源。
3.自然界没有单一的“磁荷”存在。
4.电流是产生磁场的源,变化的电场也是产生磁场的源。
第第九十章一电章磁真感空应中的电恒磁定场磁理场论
解:∵
B只分布在R 1
r
R 2
区
域内且
wm
B2 2
8
I2 2r 2
B I 2 r
第第九十章一电章磁真感空应中的电恒磁定场磁理场论
RR11 RR22
⊙⊙BB II
rr ⊕⊕BB
r dr
所以取体积元为 dVl2rdr
W m VwmdVR R1 28μπ2Ir22l2πrdr
第9 章 《电磁感应 电磁场理论》复习思考题

第9章 《电磁感应 电磁场理论》复习思考题一、填空题:1.飞机以1s m 200-⋅=v 的速度水平飞行,机翼两端相距离m 30=l ,两端这间可当作连续导体。
已知飞机所在处地磁场的磁感应强度B 在竖直方向上的分量T 1025-⨯。
机翼两端电势差U 为0.12V 。
2.当穿过一个闭合导体回路所包围的面积内的 磁通量 发生变化时,在导体回路中就会产生电流,这种现象称为电磁感应现象。
3.用导线制造成一半径为m 10.0=r 的闭合圆形线圈,其电阻Ω=10R ,均匀磁场B 垂直于线圈平面。
欲使电路有一稳定的感应电流A 01.0=I ,B 的变化率应为__3.18T/s_____________。
4.楞次定律:感生电流的磁场所产生的磁通量总是 阻碍引起感应电流的磁通量的变化。
5.如果导体不是闭合的,即使导体在磁场里做切割磁力线运动也不会产生感应电流,但在导体的两端产生_感应电动势____。
6.楞次定律是 能量守恒和转换 _定律在电磁现象领域中的表现。
二、单选题1.感生电场是 。
(A )由电荷激发,是无源场; (B )由电荷激发,是有源场;(C )由变化的磁场激发,是无源场; (D )由变化的磁场激发,是有源场。
2.关于感应电动势的正确说法是: 。
(A )导体回路中的感应电动势的大小与穿过回路的磁感应通量成正比;(B )当导体回路所构成的平面与磁场垂直时,平移导体回路不会产生感应电动势;(C )只要导体回路所在处的磁场发生变化,回路中一定产生感应电动势;(D )将导体回路改为绝缘体环,通过环的磁通量发生变化时,环中有可能产生感应电动势。
3.交流发电机是根据 原理制成的。
(A )电磁感应; B )通电线圈在磁场中受力转动;(C )奥斯特实验; (D )磁极之间的相互作用。
4.将形状完全相同的铜环和木环静止放置,并使通过两环面的磁通量随时间的变化率相等,则不计自感时, 。
(A )铜环中有感应电动势,木环中无感应电动势(B )铜环中感应电动势大,木环中感应电动势小(C )铜环中感应电动势小,木环中感应电动势大(D )两环中感应电动势相等。
第九章-电磁感应-电磁场理论PPT

在长直导线旁平行放置一矩形线圈,线圈平面与直导线
在同一平面内。已知线圈长为 ,宽为l ,线圈b近长直
导线的一边离直导线距离为 。求任a 一 处的
a
b
磁感应强度为 B 0I
I
2πx
l
选顺时针方向为矩形线圈的绕行
电动势 I
Ek
+-
Ek : 非静电力场强.
E Ek dl
闭合电路的总电动势
E l Ek dl
动生电动势的本质: 当MN速度v向右运动时,导线内每 个自由电子受的洛伦兹力为:
Fm ev B
+ B
+
+ +
Fe++M++++
+ +
++
+ +
v + + + - + + + +
+
+Fm+
vB
v
en
a
O
(2)当 sin 2ntπ, 1
即当 90、 等 2位70置 时电动势 最大 i
i NBl 2 2πn 1.32V
(3)当t=1s时,
i NBl 2 2πn sin 2πn 0
本题也可以将线圈看作由四段长为l的导线在磁场
中运动产生动生电动势之和。显然只有ab和cd两边
O轴转动,角速率ω=100 rπad/s, 求铜棒中的动生电
动势大小及方向。如果是半径为50cm的铜盘以上述 角速度转动,求盘中心和边缘之间的电势差。
解:在铜棒上距O点为 l处取
物理必修三第九章知识点梳理

物理必修三第九章知识点梳理物理必修三的第九章是重要的一章,涉及到从电磁原理到光学原理的许多内容。
本章的主要讨论的重点是电磁场的物理和物理原理。
本章小结涉及到以下几个知识点:首先要搞清楚电磁场的定义及其属性。
电磁场是一个场,其中的能量由局部的电场和磁场组成。
电场是一种由电流或静电场产生的变量量,磁场是由磁通量产生的变量量。
电磁场可以产生推力作用,是一种有趣的能量场,能影响到电荷的运动方式。
其次是电磁场的产生机理,对于电磁场的产生机理有以下理论:一是电荷的移动,通电的导体中的电荷的移动会产生电磁场,既能影响到电荷运动,又能影响到周围物体。
二是电磁感应现象,电磁感应现象是指电磁场产生时,可以改变电偶极子的磁场强度,产生电磁感应电动势。
三是高频电磁波,高频电磁波是指超过一定频率的电磁波,它具有较强的透射能力,可以用来传播信息。
第三要掌握电磁场的定律,电磁场的定律可以描述电磁场的基本特征。
其中最为重要的是电动势定律、磁动势定律、电磁感应定律、牛顿-曼定律等。
电动势定律是指电场中电子的受力关系,磁动势定律是指电磁场中磁通量的受力关系,电磁感应定律是指电磁场的变化对其他物体的影响,而牛顿-曼定律是指电荷受到电磁场的作用下,会有一个力,该力可以把电子从一个区域向另一个区域转移。
同时要了解电磁场的用途,电磁场是能量传递的重要方式,已经广泛应用于日常生活中,如电辐射、磁性材料及电磁共振等。
电辐射是一种电磁波,它可以传播信息、同步电路,用来接收讯号或数据,并进行交流。
磁性材料也可以用来磁性传输,比如吸铁石的磁性将电流转换为磁通量,同时用来实现电磁铁的动力拉力。
电磁共振是指电荷受到电磁场的作用,可以产生共振现象,比如电磁阀可以由电磁场控制,进行开关控制。
最后要搞清楚光学原理,光学原理是由隐士纳兹等人在19世纪提出的,认为光是一种由电场和磁场产生的波,其实质是电磁场的振动,可以把热能转换为电场和磁场能量,也可以把电场和磁场能量转化为可见光。
电磁感应与电磁场理论

电磁感应与电磁场理论电磁感应是电磁学中的一个重要概念,它描述了导体中自由电子受到磁场作用而产生电流的现象。
与此同时,电磁场理论探讨了电荷和电流产生的电磁场如何相互作用,相互影响。
本文将深入探讨电磁感应与电磁场理论相关的原理和应用。
一、电磁感应电磁感应是指当导体在磁场中运动,或磁场发生变化时,导体中的自由电子会受到力的作用而产生电流。
这一现象遵循法拉第电磁感应定律,即磁通量的变化率与感应电动势成正比。
这个定律可以用以下公式表示:ε = -dΦ/dt其中,ε代表感应电动势,Φ代表磁通量,t代表时间。
负号表示感应电动势的方向与磁通量变化的方向相反。
电磁感应广泛应用于发电机、变压器等电器设备中。
发电机通过旋转导体在磁场中切割磁力线,产生感应电动势和电流,进而转化为电能。
而变压器则利用电磁感应原理来改变交流电的电压大小。
二、电磁场理论电磁场理论是电磁学的基础理论之一。
根据麦克斯韦方程组,电磁场由电场和磁场组成,并且它们彼此相互依存、相互作用。
电场由带电粒子产生,而磁场则由电流产生。
电磁场理论的核心方程为麦克斯韦方程组,其中包括:1. 麦克斯韦第一和第二方程组成的电场方程:∇·E = ρ/ε0∇×E = -∂B/∂t其中,∇表示梯度运算符,E表示电场强度,ρ表示电荷密度,ε0表示真空介电常数,B表示磁感应强度,t表示时间。
2. 麦克斯韦第三和第四方程组成的磁场方程:∇·B = 0∇×B = μ0J + μ0ε0∂E/∂t其中,∇表示梯度运算符,B表示磁感应强度,J表示电流密度,μ0表示真空磁导率。
通过运用麦克斯韦方程组,我们可以推导出电磁波的性质,进一步探索电磁场的行为规律。
电磁场理论的应用非常广泛。
例如,电磁场理论在通信领域中的应用,我们利用电磁波传输信号,实现了无线通信。
此外,电磁场理论在电子技术、雷达、微波炉等方面也有许多重要的应用。
三、电磁感应与电磁场理论的联系电磁感应与电磁场理论密切相关。
大学物理 第九章 电磁感应 电磁场理论的基本概念

选择绕行方向如右图所示:
b v
o 0 I x bdr 2r 0 Ib x a dr 0 Ib x a x r 2 ln x 2
x
0 Ivab d m d m dx 方向 动 dt dx dt 2x( x a )
v
19
V a I d a d ω b c b cV
三、法拉第电磁感应定律的使用方法 1、规定任一绕行方向为回路的正方向。由右手螺旋 法则确定回路的正法线方向 en 。 d 正法线方向 2、计算 SB dS 及 dt en 3、由 d 之值确定 i 的方向 dt S d L
i
d dt 0, i 0, i的方向与绕行方向相同 d 0, 0, 的方向与绕行方向相反 i i dt
L
解二: 构成扇形闭合回路
AOCA
B
L
A
1 2 m B dS BS AOCA B L 2
o
C
d m 1 1 2 d BL BL2 dt 2 dt 2
沿OACO
由楞次定律:
A
o
17
例2. 如图所示,一矩形导线框在无限长载流导线I 的场中向右运 动,t时刻如图所示,求其动生电动势。
E涡 dl 0
法拉第电磁感应定律推广为
d E涡 dl L 22 dt
静电荷激发电场 E dl 0 保守力场(无旋场) 电场 d 变化磁场激发电场 E涡 dl dt
d 产生的原因不同。 E涡 dl 涡旋电场 dt 静电场 的区别 电力线不同。 E dl 0 环流不同
程守洙《普通物理学》(第5版)(上册)课后习题-电磁感应 电磁场理论(圣才出品)

第9章电磁感应电磁场理论9-1如图9-1所示,通过回路的磁感应线与线圈平面垂直,且指向图面,设磁通量依如下关系变化:φ=6t2+7t+1式中φ的单位为mWb,t的单位为s.求t=2时,回路中的感生电动势的量值和方向.图9-1解:由题意可知,回路中的感生电动势为:当时,电动势为:,方向为逆时针方向(即与设定的回路绕行t s2方向相反).9-2在两平行导线的平面内,有一矩形线圈,如图9-2所示.如导线中电流,随时间变化,试计算线圈中的感生电动势.图9-2解:根据题意建立坐标系,取坐标轴Ox,如图9-3所示.图9-3两电流在x处的磁感应强度大小为:,方向垂直纸面向里.取顺时针为回路的绕行方向,通过面元dS=l1dx的磁通量为:通过矩形线圈的磁通量为:矩形线圈中的感生电动势为:.9-3如图9-4所示,具有相同轴线的两个导线回路,小的回路在大的回路上面距离y 处,y远大于回路的半径R,因此当大回路中有电流,按图示方向流过时,小回路所围面积πr2之内的磁场几乎是均匀的.现假定y以匀速v=dy/dt而变化.(1)试确定穿过小回路的磁通量φ和y之间的关系;(2)当y=NR时(N为整数),小回路内产生的感生电动势;(3)若v>0,确定小回路内感应电流的方向.图9-4解:(1)根据导电线圈轴线上的磁感应强度分布,可得大回路在小回路处产生的磁感应强度:.由题意知,因此在距离大线圈平面y处的磁场可近似为均匀磁场,其次感应强度,则穿过小回路中的磁通量和y之间的关系为:.(2)小回路内产生的感生电动势为:.(3)由榜次定律可判定,当从上向下看时小回路的感应电流为逆时针方向.9-4PM和MN两段导线,其长均为10cm,在M处相接成30°角,若使导线在均匀磁场中以速度v=15m/s运动,方向如图9-5所示,磁场方向垂直纸面向内,磁感应强度为B=25×10-2T,问P、N两端之间的电势差为多少?哪一端电势高?图9-5解:由题意可知,P、N两端之间产生的动生电动势为:即运动导线上P端的电势高,N端电势低.9-5一均匀磁场与矩形导体回路面法线单位矢量e n间的夹角为θ=π/3(如图9-6),已知磁感应强度B随时间线性增加,即B=kt(k>0),回路的MN边长为l,以速度V向右运动,设t=0时,MN边在x=0处.求任意时刻回路中感应电动势的大小和方向.图9-6解:如图9-6所示,回路的面法线e n表明,回路的绕行方向为逆时针,则回路中感应电动势为:.又由题意知:则回路中感应电动势:方向由M指向N,即沿顺时针方向.9-6如图9-7所示,一长直导线通有电流,I=0.5A,在与其相距d=5.0cm处放有一矩形线圈,共1000匝.线圈以速度v=3.0m/s沿垂直于长导线的方向向右运动时,线圈中的动生电动势是多少?(设线圈长l=4.0cm,宽b=2.0cm.)图9-7解:由题意可知,线圈中的动生电动势为:.9-7如图9-8所示,导线MN在导线架上以速度V向右滑动.已知导线MN的长为50cm,V=4.0m/s,R=0.20Ω,磁感应强度B=0.50T,方向垂直于回路平面.试求:(1)MN运动时所产生的动生电动势;(2)电阻R上所消耗的功率;(3)磁场作用在MN上的力.图9-8解:(1)导线上产生的电动势为:.(2)电阻R上所消耗的功率为:.(3)由安培定理,可得回路中电流:导线MN上的安培力:,方向向左.9-8如图9-9所示,PQ和MN为两根金属棒,各长1m,电阻都是R=4Ω,放置在均匀磁场中,已知B=2T,方向垂直纸面向里.当两根金属棒在导轨上分别以v1=4m/s 和v2=2m/s的速度向左运动时,忽略导轨的电阻,试求:(1)两棒中动生电动势的大小和方向,并在图上标出;(2)金属棒两端的电势差;(3)两金属棒中点O1和O2之间的电势差.。
大学物理第九章练习参考答案

第九章 电磁感应 电磁场理论练 习 一一.选择题1. 在一线圈回路中,规定满足如图1所示的旋转方向时,电动势 ,磁通量为正值。
若磁铁沿箭头方向进入线圈,则有( B ) (A) d /dt 0, 0 ; (B) d /dt 0, 0 ; (C) d /dt 0,0 ; (D) d /dt 0,0。
2. 一磁铁朝线圈运动,如图2所示,则线圈内的感应电流的方向(以螺线管内流向为准)以及电表两端电势U A 和U B 的高低为( C )(A) I 由A 到B ,U A U B ; (B) I 由B 到A ,U A U B ; (C) I 由B 到A ,U A U B ; (D) I 由A 到B ,U A U B 。
3. 一长直螺线管,单位长度匝数为n ,电流为I ,其中部放一面积为A ,总匝数为N ,电阻为R 的测量线圈,如图3所示,开始时螺线管与测量线圈的轴线平行,若将测量线圈翻转180°,则通过测量线圈某导线截面上的电量q 为( A ) (A) 2nINA /R ; (B)nINA /R ; (C)NIA /R ; (D)nIA /R 。
4. 尺寸相同的铁环和铜环所包围的面积中,磁通量的变化率相同,则环中( A ) (A )感应电动势相同,感应电流不同; (B )感应电动势不同,感应电流相同; (C )感应电动势相同,感应电流相同; (D )感应电动势不同,感应电流不同。
S N v图1· ·GA B NS 图2IIA图3二.填空题1.真空中一长度为0l 的长直密绕螺线管,单位长度的匝数为n ,半径为R ,其自感系数L可表示为0220l R n L πμ=。
2. 如图4所示,一光滑的金属导轨置于均匀磁场B v中,导线ab 长为l ,可在导轨上平行移动,速度为v ,则回路中的感应电动势ε=θsin Blv ,a 、b 两点的电势a U < b U (填<、=、>),回路中的电流I=R Blv /sin θ,电阻R 上消耗的功率P=R Blv /)sin (2θ。
第九章 电磁感应 电磁场理论

一. 动生电动势产生的原因 任意时刻
Bl x
d ( Blx ) dt
d dt
l
Bl dx Blv dt
x
负号意思?
方向: ba
产生动生电动势的 原因,是洛仑兹力
f m ev B
例1 已知: l、 S、 n、.. 求:长直螺线管的自感L. [解] 设电流i B = ni =N=NBS =NniS (l / l) = n2iV L= /i=n2V (与电流i无关)
二、 互感应
什么叫互感 线圈1、2固定不动。 假设线圈1 中的电流 i1 随 时间 t 变化,在线圈2中 产生了感应电动势为( 21) 若周围无铁磁质, 则由毕萨定律: 电流i1的磁场正比于i1, 电流i1在线圈2中的磁通链数21也正比于i1 , 有
S
§9-1电磁感应定律
一、实验
实验一:
N
实验二:
上两实验都有相对运动.是不是无相对运动 就不会有电流?
电流变化也能引起磁通变化
结论:不论由于什么原因,当一个闭合电路的 磁通发生变化时,电路中都出现感应电流。 磁通发生变化产生的电动势叫感应电动势
二、法拉第电磁感应定律
d i K dt
国际单位制中 K=1
I
d
v
A
L
dl B
X
AB
d l d
d
vu0 I dx 2 x
vu0 I dl ln 2 d
AB 0
方向由 B A
A正 B负
d
A
dx
l
l
B X
大学物理-电子教案第9章 变化的电磁场

间内,通过电路的电量
t
t 1 d
1
1
q I dt
0
0R
dt
dt
0
R
d
R
(
0)
可见, q 与 ( 0 ) 成正比,而与磁通量改变快慢无关。设 t 0 时 0 0 ,只要测 出 R 和 q 、即可得到 ;如果已知回路面积、就可以算出磁感应强度 B。
二、楞次定律
闭合回路中感应电流的方向,总是使感应电流的磁场通过闭合回路的磁通量去补偿 或反抗引起感应电流的磁通量的变化。注意:“补偿或反抗”的是磁通量的变化,而不 是磁通量。
2.法拉第电磁感应定律
不论任何原因使通过回路面积的磁通量发生变化时,回路中产生的感应电动势与磁
通量对时间的变化率成正比.即
d dt
式中负号表明电动势的方向,
若线圈密绕 N 匝,则 N d d 其中 N 叫磁通链 dt dt
回路为纯电阻 R 的电路,电流 I 与电动势同相位 I 1 d ,在从 t 0 到 t 时 R dt
S
t
S1
t
S2
t
在非稳恒条件下,尽管传导电流密度 j 不一定连续,但 j + D 这个量是连续的。
t
由 D
D DS S q
所以 dD d dt dt
充电时, dD 与 D 同方向,也与充电电流 I 同方向; dt
放电—— dD 与 D 反方向, 也与放电电流 I 同方向, dt
dD dq dt dt
S
E dl =-
B
dS
l
S t
(法拉第电磁感应定律);
B dS =0
(磁场的“高斯定理”);
S
H dl =
张达宋《大学物理教程(第三版)》第九章 电磁感应 电磁场理论的基本概念

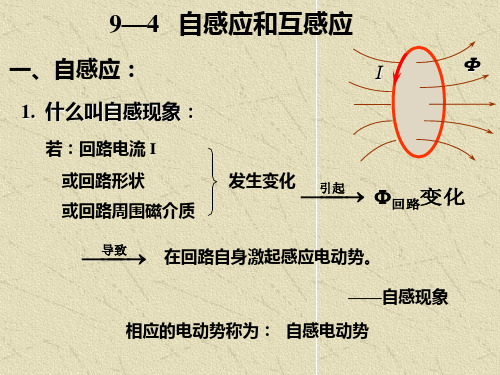
第九章 电磁感应 电磁场理论的基本概念自从1820年奥斯特发现电流的磁现象以后,1821年英国科学家法拉第就向自己提出任务,要研究这一现象的逆现象,也就是要利用磁场产生电流,经过10年的实验研究,终于在1831年发现电磁感应现象.在这一年和以后的几年中法拉第详细地研究了电磁感应现象,给出电磁感应现象的基本规律,这个发现无论在理论上或实际应用上均有重要意义.此后,麦克斯韦又指出变化的电场也会激发磁场,变化的电场和变化的磁场不是彼此孤立的,而总是互相联系、互相激发,形成一个统一的电磁场.麦克斯韦把前人从大量实验和理论中得出的规律加以概括、总结和推广,得出了描写电磁场的体系完整的方程组,称为麦克斯韦方程组(1862年).麦克斯韦方程组的一个重要成果是预言了电磁波的存在,揭示了电磁波的传播速度恰恰等于光速.麦克斯韦由此断言光波就是一种电磁波,光的现象就是一种电磁现象,把表面看来互不相关的两种现象统一起来,使我们对光的本性和物质世界的普遍联系的认识大大深入了一步.麦克斯韦电磁场理论又导致无线电波的发现,使今天的无线电广播、电视、微波通讯和雷达等等的出现成为可能,显示了理论对实践的指导意义.§9-1 法拉第电磁感应定律下面首先介绍电磁感应现象及其产生的条件,在此基础上介绍法拉第电磁感应定律.一、电磁感应现象电磁感应现象可通过两类演示实验来说明:一类是磁场不变线圈运动.如图9-1,线圈与电流计连成闭合回路,线圈放在蹄形磁铁的磁场中,把线圈很快地向右或向左拉动,电流计发生偏转,这表明线圈中有电流产生,当线圈静止不动时便没有电流产生.在此过程中,磁铁产生的磁场是不变的,当线圈向右或向左拉动时,通过线圈的磁通量发生变化.所以这个实验表明,当通过线圈的磁通量变化时,线圈中便有电流产生;当线圈静止不动时,通过线圈的磁通量无变化,便没有电流产生.这种由于通过线圈的磁通量发生变化而在线圈中产生电流的现象称为电磁感应,所产生的电流称为感应电流.另一类实验是线圈固定磁场变化.如图9-2,线圈A 与电源E 连成一闭合回路,线圈B 与电流计连成另一闭合回路.当开关K 接通或断开时,线圈A 中图9-1图9-2的电流及其在圆环形铁芯中所产生的磁场发生变化,并导致通过线圈B 的磁通量变化,这时线圈B 中亦有电流产生.当开关K 保持接通或断开状态时,线圈A 中电流不变或无电流通过,通过线圈B 的磁通量无变化,线圈B 中便没有电流产生.图9-3(a)所示的电吉他应用了类似的原理.在靠近可以被磁化的金属弦线的不同位置上设置了一些拾波线圈,线圈内中的磁铁使紧邻的弦线磁化.当吉他弦振动时,弦线上的磁化段使拾波线圈内的磁通量随振动频率变化,从而在线圈中产生感应电流,感应电流经放大器转换为声信号输出,如图9-3(b)所示. 以上的电磁感应现象表明:引起通过回路的磁通量变化的原因或是由于磁场不变线圈运动,或是由于线圈固定磁场变化,也可以是由于在磁场变化的同时线圈也在运动.不论引起磁通量变化的原因如何,线圈中都有感应电流产生.我们知道,要在闭合回路中产生电流必须有电动势,电磁感应产生的电动势称为感应电动势.二、法拉第电磁感应定律从以上实验可以看出:感应电流的大小与通过回路所围面积的磁通量变化的快慢有关,例如在图9-1中,当线圈向右或向左运动得越快,感应电流就越大,反之就越小.感应电动势的大小的变化也是这样.感应电动势的方向即感应电流的方向与通过回路的磁通量是增加还是减少有关.例如在图9-2中当开关K 接通时,通过线圈B 的磁通量增加,感应电流沿一个方向,当开关K 断开时,通过线圈B 的磁通量减少,感应电流沿相反的方向.法拉第定量地分析和总结了大量电磁感应实验的结果得出如下定律,称为法拉第电磁感应定律:在一闭合回路上产生的感应电动势E i 与通过回路所围面积的磁通量对时间的变化率t d d Φ成正比,即 t k d d i Φ-=E 其中k 为比例常数.如果采用国际单位制,E i 以伏特为单位,Φ以韦伯为单位,t 以秒为单位,则k = 1,而上式化为 td d i Φ-=E (9-1) 上式中引入“-”号是为了使该式不仅能用来确定感应电动势的大小而且能用来确定感应电动势的方向.应用上式步骤如下:首先在回路上取定一个绕行方(a) (b)图9-3图9-4向,并规定回路的绕行方向和回路所包围面积的正法线e n 的方向成一右手系统,即如果右手螺旋沿回路的绕行方向转动,则螺旋前进的方向为正法线e n 的方向,如图9-4所示.这样,任意取定了回路的绕行方向以后.便可确定这回路所包围面积的正法线方向,法线e n 即有了确定的方向,通过这回路的磁通量⎰⋅=S S d n e B Φ以及t d d Φ也就有了确定的正负号.如果td d Φ< 0,则由(9-1)式E i > 0,感应电动势的方向和绕行方向相同;如果td d Φ> 0,则E i < 0,感应电动势的方向和绕行方向相反.例如有回路如图9-5(a),磁场方向向上(图中实线),并且随时间减弱,取绕行方向如图,则Φ为正并随时间减少,因而td d Φ为负E i 为正,此时感应电动势的方向和取定的绕行方向相同.在图9-5(b)情形,磁场方向仍然是向上.但不是随时间减弱而是增强,取绕行方向如图,则Φ为正并随时间增加,td d Φ为正,E i 为负,此时感应电动势的方向和取定的绕行方向相反. 感应电流或感应电动势的方向亦可直接用楞次定律来确定,这条定律是1834年俄国物理学家楞次在法拉第的资料的基础上通过实验总结出来的,表述如下:闭合回路中感应电流的磁场总是要反抗引起感应电流的磁通量的变化(增加或减少).应用楞决定律得出的感应电流或感应电动势的方向与用法拉第定律得出的相同.例如在9-5 (a)中的情形,通过回路的磁通量是减少的,按照楞次定律感应电流的磁场要反抗原来磁通量减少,原来的磁感线的方向是通过回路向上,所以感应电流所产生的磁感线的方向也是通过回路向上,如图9-5(a)中虚线所示.由右手螺旋法则得知感应电流的方向与图中E i 的方向相同.在图9-5(b)中的情形,通过回路的磁通量是增加的,按照楞次定律感应电流的磁场要反抗原来磁通量增加,原来的磁感线的方向是通过回路向上,所以感应电流所产生的磁感线的方向是通过回路向下,如图9-5(b)中虚线所示.由右手螺旋法则得知感应电流的方向与图中E i 的方向相同. 例题9-1 设有长方形回路ABCD 放置在恒定磁场中如图9-6,其中AB 边可以左右滑动,磁场方向与回路平面垂直、向里.设导体(a ) (b )图9-5图9-6AB 以速度v 向右运动,求回路上感应电动势的大小及方向.解 取ADCB 方向为回路的绕行方向,又设AB 边长为l ,AD 边长为x (变量),则Φ = +Blx其中B 为磁场的磁感强度.根据法拉第定律(9-1)式得v Bl tx Bl t -=-=-=d d d d i ΦE (9-2) “-”号表示感应电动势的方向与取定的绕行方向相反,即沿ABCD 方向.必须指出,(9-1)式中的Φ中是通过回路的总磁通量,亦称磁通链数.如果回路由N 匝导线组成,且通过各匝的磁通量都相等,通过一匝的磁通量是φ,则总磁通量为Φ = N φ.如果闭合回路的电阻为R ,则由(9-1)式及闭合电路欧姆定律,得回路中的感应电流为tR R I d d 1i i Φ-==E (9-3) 利用(9-3)式及tq I d d =,可以计算在一段时间内通过回路中任一截面的感应电荷量.设在t 1及t 2时刻通过回路的磁通量分别为Φ1及Φ2,则在这一时间内通过回路中任一截面的感应电荷量为)(1d 1d 12i 2121ΦΦΦΦΦ-=-==⎰⎰RR t I q t t (9-4) 由上式看出,感应电荷量与通过回路面积的磁通量的改变成正比,而与磁通量改变的快慢无关.如果电路的电阻为已知,则通过对感应电荷量q 的测量可以得出通过回路的磁通量.常用的磁通计就是根据这个原理来设计的.§9-2 动生电动势和感生电动势按照磁通量变化的原因不相同,感应电动势可分为两类:(1) 磁场不变,由于导体在磁场中运动而产生的感应电动势称为动生电动势;(2) 导体回路固定,由于磁场变化而产生的感应电动势称为感生电动势.图9-1的实验中产生的感应电动势属于前一类,图9-2的实验中产生的感应电动势属于后一类.产生这两种电动势的非静电力不相同,分别讨论如下.一、动生电动势动生电动势是由洛伦兹力产生的,以图9-6中导体AB 在磁场中运动为例,当导体AB 以速度v 向右运动时,导体内的自由电子也以速度v 跟随着导体向右运动,按照洛伦兹力公式,自由电子受到的洛伦兹力为F = (-e ) v × B其中(-e )为自由电子的电荷,力F 的方向为沿导体从B 到A 的方向.自由电子在此力作用下沿BA 方向运动,因而形成ABCD 方向的电流.依定义动生电动势和其他电动势一样等于单位正电荷沿闭合回路移动一周时非静电力所作的功,在这种情形非静电力是洛伦兹力.作用于单位正电荷的洛伦兹力,即非静电性电场的电场强度为B F E ⨯=-=v e所以动生电动势为l B l E d )(d i ⋅⨯=⋅=⎰⎰v E容易看出动生电动势只存在于运动导体上,不运动的导体没有动生电动势,因此E i 可写为⎰⋅⨯=BA lB d )i (v E (9-5) 右式积分为由A 点沿着导线至B 点的线积分.在图9-6情形,由于v ⊥B ,且v × B 与d l 同向,故上式可写为v v Bl l B BA ==⎰d i E (9-6) 其中l 为导线AB 的长,此结果与上节从法拉第定律td d i Φ-=E 得出的结果相同.动生电动势的方向为矢量v × B 沿导线AB 的分量的方向.这样决定的动生电动势方向与用楞次定律得出的相同.(9-6)式只适用于图9-6的特殊情况(直导线、均匀磁场,而且导线、磁场及运动速度三者互相垂直),但(9-5)式适用于一般情况,即任意形状的一段导线(甚至闭合线圈),在任意恒定磁场中作任意运动,由此产生的动生电动势都可以用该式计算.如果运动导体是闭合的或与其他固定导体组成闭合回路,则亦可用法拉第定律计算,由此得出的结果与用(9-5)式算出的结果相同.如果运动导体AB 与其他固定导线无连接,如图9-7,洛伦兹力将使导体内的自由电子向A 端移动,结果A 端积聚负电荷,B 端积聚正电荷.这些正负电荷在导体内产生静电场E ,其方向为从B 到A 的方向.导体内的自由电子受到方向相反的两个力作用,即静电力-e E 及洛伦兹力-e (v × B ).开始时静电力小于洛伦兹力,因此自由电子继续向A 端移动,使两端的电荷逐渐增加,静电力逐渐增大,直至静电力与洛伦兹力成平衡为止.这时导体AB 可看作开路时的电源,A 端是负极,B 端是正极.由一段含源电路的欧姆定律,并考虑到开路时电流为零,则导体两端的电势差为 ⎰⋅⨯==-BA AB V V l B d )i (v E V B - V A 与E i 虽然数值相等但物理意义不同,V B - V A 是单位正电荷从B 端移至A 端时静电力所作的功,E i 是单位正电荷从A 端移至B 端时非静电力(此处即洛伦兹力)所作的功.例题9-2 在如图9-8所示的均匀磁场中,磁感强度为B .一根长为L 的导体棒OA 在垂直于磁感线的平面上以角速度ω绕固定轴O 旋转,求导体棒上的动生电动势和两端的电势差.解 在棒上取距O 点为l 的一小段d l ,在这小段上的动生电动势为图9-7 图9-8lB d )d i ⋅⨯=(v E 由图看出v × B 与d l 同向,故llB d d i ω=E 所以整个棒上的动生电动势为20i 21d d d )L B l l B l lB L A O A O ωωω===⋅⨯=⎰⎰⎰l B (v E 例题9-3 图9-9(a)为交流发电机的发电原理示意图,由N 匝导线组成的平面线圈面积为S ,在永久磁铁产生的磁感强度为B 的均匀磁场中绕轴线OO ’作匀速转动,角速度为ω.轴线OO ’与磁场方向垂直,线圈中产生的感应电流经汇流环和电刷传输到输出电路中.设t = 0时,线圈平面法线e n 与B 平行同向,求线圈中的感应电动势E i .解 设α为t 时刻线圈平面法线e n 与B 所成的角度.t 时刻通过线圈的总磁通量为Φ = NBS cos α.根据题设,t = 0时,α = 0,所以t 时刻α = ωt ,即Φ = NBS cos ωt由法拉第电磁感应定律,线圈中的感应电动势为t NBS tωωΦsin d d i =-=E 亦可写为tωsin i0i E E = 其中E i0 = NBS ω为线圈中感应电动势的最大值.上式表示,平面线圈在均匀磁场中转动时,线圈中产生的感应电动势随时间作周期性变化,周期为ωπ2,如图9-9(b)所示,即可输出角频率为ω的交变电流.二、感生电动势 涡旋电场动生电动势是洛伦兹力产生的,因为导体运动时,其内部的电子也跟随着运动,因而受到磁场的洛伦兹力作用.但在感生电动势情形,导体回路是固定的,其内部的电子并不受洛伦兹力作用,那么感生电动势是怎样产生的呢?即产生感生电动势的非静电力是什么呢?从实验结果知道,感生电动势与导体的性质,导体的温度以及其他物理状态无关,仅仅决定于磁场的变化情况.麦克斯韦分析了这种情况以后提出如下假说:变化的磁场在它的周围产生了电场,这种电场与导体无关,即使没有导体存在,只要磁场发生变化,就有这种电场存在.这种电场称为涡旋电场,它与静止电荷产生的静电场不同.静电场的电场线有始点和终点,不是闭合曲线,它的始点和终点就是产生电场的电荷所在处.涡旋电场是变化磁场产生的,不是电荷产生的,所以它的电场线没有始点和终点,是闭合曲线.例如有一磁铁处于平面ABCD 的上方(图9-10),其轴与平面垂直,N 极正对平面(a) (b)图9-9上O 点.今使磁铁向平面运动,则在磁铁的周围,由于磁场发生变化而产生涡旋电场.在平面ABCD 上涡旋电场的电场线是一系列以O 为心的同心圆,其回转方向如图中箭头所示.如果磁铁向相反方向运动,则电场线的回转方向改为沿相反方向.涡旋电场与静电场一样都对静止的电荷有作用力.正是涡旋电场力的作用导致导体回路上产生了感生电动势.涡旋电场力就是产生感生电动势的非静电力.设E 涡表示涡旋电场的电场强度.依定义,沿闭合回路L 的感生电动势E i 等于涡旋电场力使单位正电荷沿L 绕行一周所作的功.由此定义及法拉第定律得 t L d d d i Φ-=⋅=⎰l E 涡E (9-7) 必须指出,法拉第建立的电磁感应定律的原始形式,即(9-1)式只适用于由导体构成的闭合回路.但按照麦克斯韦假说,变化磁场产生的电场E 涡与导体无关,故不论闭合回路是否由导体构成,也不论闭合回路是在真空中或介质中,(9-7)式都正确.不同的是:如果闭合回路由导体构成,便有感应电流产生,否则就没有感应电流产生,但感应电动势在这两种情形下是相同的.对涡旋电场的性质还要说明一下.我们知道,静电场的电场强度E 静沿任何闭合曲线的环流0d =⋅⎰l E 静,所以静电场是保守力场,可以引入电势概念.但按照(9-7)式,在一般情况下涡旋电场的环流不等于零,所以涡旋电场不是保守力场,不能引入电势概念.涡旋电场的存在已为许多实验所证实,下面将要介绍的电子感应加速器就是最好的例证.例题9-4 如图9-11,均匀磁场B 被局限在半径为R 的圆柱体内(如长直螺线管的情况就是这样),磁场随时间的变化率为tB d d ,求圆柱体内外涡旋电场的场强E 涡. 解 根据磁场分布的对称性可知变化磁场激发的涡旋电场的电场线是一系列圆,圆心都在磁场的对称轴上.取半径为r 的电场线L 来考虑.E 涡必沿L 的切线方向,设Φ为通过圆周L 所围面积的磁通量,由(9-7)式有tL d d d Φ-=⋅⎰l E 涡 取圆周L 上的顺时针方向为线积分的积分方向,E 涡为E 涡沿积分方向切向的投影,因为圆周上各点的E 涡值相等,所以涡涡涡涡rE l E l E L L L π2d d d ===⋅⎰⎰⎰l E代入(9-7)式有 t rE d d π2Φ-=涡图9-10tr E d d π21Φ-=涡 (1) 在圆柱体内,r < R ,Φ = πr 2B ,则 t B r t d d πd d 2=Φ t B r E d d 2-=涡 (9-8) (2) 在圆柱体外,r > R ,Φ = πR 2B ,则 t B R t d d πd d 2=Φ 所以 tB r R E d d 22-=涡 (9-9) 如果|B |在减小,则tB d d < 0,由(9-8)或(9-9)式得知E 涡 > 0,这表示E 涡与沿L 的积分方向的切向同向,即沿顺时针方向;如果|B |在增大,则tB d d > 0,E 涡 < 0,这表示E 涡与沿L 的积分方向的切向反向,即沿逆时针方向.如果用楞次定律来判断E 涡的方向,可以得到与此相同的结论.计算感应电动势的方法 我们曾经通过例题9-2介绍过求动生电动势的方法,当导体或闭合回路在固定的磁场中运动时都可以用这种方法求动生电动势.从以上讨论我们又看到,当导体或闭合回路上各点的E 涡为已知时,我们可以应用感生电动势定义式⎰⋅=l E d i 涡E 求感生电动势,在一般情况下,即导体是运动的或磁场是变化的或两者兼有的情况下,都可以应用法拉第电磁感应定律求闭合回路上的感应电动势.应用法拉第电磁感应定律也可以求一段导体ab 上的感应电动势,但须作一辅助线与导体ab 合成一闭合回路,如果辅助线上的感应电动势为已知,则由td d Φ及辅助线上已知的感应电动势即可算出导体ab 上的感应电动势.三、电子感应加速器电子感应加速器是利用变化磁场产生的涡旋电场把电子加速以获得高能量的电子束的装置,因此它是变化磁场产生电场的最好例证.图9-12(a)表示电子感应加速器中央部分的铅直横截面,其中N 、S 为电磁铁的两极,D 为环形真空管道.图9-12(b)是环形真空管道的俯视图.电磁铁是用每秒几十周的交变电流来励磁的,在交变电流激发下两极之间出现交变磁场,其磁感线是对称分布的,某一瞬间的D 线如图中实线所示.这交变磁场又产生涡旋电场,在水平面上其电场线为许多同心圆,如图中虚线所示.当电子从电子枪射入环形真空管道时,电子便受到两个力作用,即涡旋电场的作用力和电子所在处的磁场的洛伦兹力.为了使电子在感应器中不断地被加速,第一,必须使电子作加速圆周运动;第二,必须使电子在给定的圆轨道上运动.为简单起见,下面着重讨论第一个问题.图9-11假设电子从电子枪沿如图方向射入真空管道,为了使电子作加速圆周运动,(1) 必须使洛伦兹力指向圆心;(2) 涡旋电场必须沿顺时针方向.现在来看怎样才能满足这个要求.交变磁场随时间作正弦变化,图9-13表示在一个周期内磁场变化的情况(B为正表示B 向上,B 为负表示B 向下),在第一个41周期中B 向上,|B |增加,由(9-8)式得知E 涡是沿顺时针方向,在第四个41周期中B 向下,|B |减少,由(9-8)式得知E 涡也是沿顺时针方向,而在第二、第三个41周期中E 涡则是沿反时针方向(图9-13),又在第一个41周期中间由于B 是向上的,洛伦兹力(-e )v × B 指向圆心[图9-12(b)],在第四个41周期中B 是向下的,洛伦兹力(-e )v × B 指向圆外不是指向圆心,所以在整个周期中只有第一个41周期能使电子作加速圆周运动.好在电子在不到41周期的时间内已经转了几十万圈,只要在该41周期之末将电子引离轨道进入靶室,就已能使其能量达到足够的数值.例如一个100MeV 的电子感应加速器能使电子加速到0.999 986c ,其中c 是光在真空中的速度. 电子在真空管道内运动不断被加速,要维持在给定的圆轨道上运动,其向心力(洛伦兹力)必须随速度作相应增加,这就需要对真空管道内的磁感强度值提出一定要求,讨论从略.§9-3 自感现象与互感现象一、自感现象当一回路中有电流通过时,电流所产生的磁通量必然要通过该回路本身.当回路中的电流变化时,通过回路的磁通量就要发生变化,根据法拉第定律,在回路中就要产生感应电动势.这种由于回路中的电流发生变化而在它本身引起感应电动势的现象称为自感现象.所产生的感应电动势称为自感电动势. 自感现象可用如下实验进行观察.如图9-14,B 1、B 2为两个相同的小灯泡,L 为有铁芯的线圈,R 为可变电阻器,调节可变电阻器R ,使两支路的电阻相等.当开关K 按下时,两支路上的图9-12 图9-13灯泡亮的快慢不一样.B 2瞬时就达到正常亮度,但B 1却是逐渐变亮,经过一段时间后,才和B 2一样亮.这表示这两个支路电流增加的快慢不一样.当二支路的电流达到稳定后,断开电源,两个灯泡并不立刻熄灭,而是亮度逐渐减弱至熄灭.这表明切断电源后,电流并不立刻消失.这种现象的产生可解释如下:当K 按下时,电流由零增加,在L 支路中通过线圈的磁通量随电流的增加而增加,因而在线圈中引起自感电动势.根据楞次定律这自感电动势要反抗通过线圈的磁通量增加,也就是反抗线圈中的电流增加,所以L 支路的灯泡亮得慢.在没有线圈的支路上由于没有这样的自感电动势,所以这支路中的电流很快就达到稳定值.当K 断开时,电流减少,通过线圈L 的磁通量减少,这样又在线圈中引起自感电动势.根据楞次定律这个自感电动势是反抗电流减少的,因而L B 1B 2RL 回路中的电流并不立刻消失,电灯并不立刻熄灭.自感系数 设通过回路的电流强度为I ,根据毕奥—萨伐尔定律,此电流在空间中任一点产生的磁感强度都与I 成正比,所以该回路的电流所产生的通过它本身的磁通量亦与I 成正比,即Φ = LI (9-10)其中L 为比例系数,它与回路的几何形状及回路周围的磁介质的磁导率有关.当回路周围不存在铁磁质时,L 与回路中的电流I 无关,L 称为回路的自感系数,简称为自感.当I = 1单位时,Φ与L 数值相等,所以回路的自感系数在数值上等于回路中电流为l 单位时通过回路的磁通量.根据法拉第定律,当Φ变化时,回路中就产生自感电动势⎪⎭⎫ ⎝⎛+-=-=t L I t I L t L d d d d d d ΦE 当开关K 按下时,如果回路的形状和周围的磁介质不随时间而变化,则L 亦不随时间而变化,即0d d =tL ,而上式化为 tI L L d d -=E (9-11) 在国际单位制中L 的单位为亨利,符号为H ,由(9-10)式,得Wb/A 1A11Wb H 1== 例题9-5 求长直螺线管的自感系数,设长直螺线管长度为l ,横截面积为S ,导线总匝数为N ,管中充满磁导率为μ的均匀介质(图9-15).解 当螺线管中有电流I 通过时,通过一匝线圈的磁通量IS lN BS μϕ==,通过N 匝线圈的磁通链数为IS lN N μϕΦ2== 图9-14由自感系数定义: V n Sl l N S l N I L 2222μμμΦ==== 其中V 为长直螺线管的体积,n 为单位长度的匝数. 由于计算中忽略了边缘效应,所以得出的结果只是近似的,实际测得的L 值比上述结果要小些.而对于细螺绕环,由于没有边缘效应,结果要精确得多.例题9-6 有一同轴电缆,由半径为R a 和R b 的同轴长圆筒组成,电流I 由内筒一端流入,经外筒的另一端流回.两圆筒间充满磁导率为μ的均匀介质,求单位长度同轴电缆的自感系数.解 应用安培环路定理可以证明,在内筒之内,外筒之外磁场强度均为零,在两圆筒之间距离轴线为r 处的磁场强度为r I H π2= 由此得r I H B π2μμ== 取长为h 的一段电缆来考虑,穿过长为h ,宽为(R b - R a )的矩形截面S 的磁通量为a b b a S R R Ih r r Ih ln π2d π2d μμΦ==⋅=⎰⎰S B 由自感系数的定义,长为h 的电缆的自感系数为ab R R h I L ln π2μΦ== 所以单位长度电缆的自感系数为ab R R h L L ln π21μ== 二、互感现象假设有两个邻近的线圈1和2,如图9-17,其中各有电流I 1及I 2通过,实线表示电流I 1产生的磁感线,虚线表示电流I 2产生的磁感线,电流I 1所产生的磁感线有一部分通过线圈2,用Φ21表示电流I 1产生的磁场通过线圈2的磁通量.当I 1变化时,Φ21亦发生变化,因而在线圈2上产生感生电动势.同理,电流I 2亦产生通过线圈1的磁通量,这磁通量用Φ12表示,当I 2变化时,Φ12亦发生变化,因而在线圈1上产生感生电动势,这一现象称为互感现象.由于一个线圈上的电流发生变化而在其邻近线圈上引起的感生电动势称为互感电动势.根据毕奥—萨伐尔定律.电流I 1在空间中任一点产生的磁感强度与I 1成正比,所以电流I 1产生的磁场通过线圈2的磁通量Φ21亦与I 1成正比,即Φ21 = M 21 I 1同理,Φ12 = M 12 I 2图9-15图9-16。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
N
N
N
i M Ek dl
N
M (v B ) d l Blv
——动生电动势实质是运动电荷受洛伦兹力的结果。
动生电动势的微分公式:
di
r Ek
r dl
(vr
rr B) dl
动生电动势的积分公式:
i
(vr
r B)
r dl
L
例题9-2 如图已知铜棒OA长L=50m,处在方向垂直 纸面向内的均匀磁场(B =0.01T)中,沿逆时针方向
++
+ + + N+ + + +
Fm方向从M指向N,电子在这个力的作用下克服静电 力Fe 将由M移向N。
Fm ——非静电力 Ek ——非静电力场强
平衡时 Fm Fe eEk
eEk ev B
Ek v B
M
M
l
按照电动势的定义,感应电
v
动势是这段导线内非静电力
作功的结果,所以
en
B
i
L
N
v
S
en
i L
B
S
v
N
Φ>0 dΦ >0 dt i <0
Φ<0 dΦ < 0 dt i >0
en
B
i
L
N v S
en
i L
B
S
v
N
Φ>0 dΦ <0 dt i >0
Φ<0 dΦ >0 dt i <0
3.若线圈回路有N匝:
总电动势为各匝中电动势的总和,即
i
N
解:金属棒上取长度元dx,每一 dx处磁场可看作均匀的
B 0I
2πx
因此,dx小段上的动生电动势为
I
v M
N
x dx
a
l
di
Bvdx
0 I
2πx
vdx
总的动生电动势为
i
di
al a
0I
2πx
vdx
0I
2π
v
ln
al a
4.4106 V
二、在磁场中转动的线圈内的动化快慢无关。
5.非静电力场强:Er k
感应电动势等于移动单位正电荷沿闭合回路一周
非静电力所作的功。用
r Ek
表示等效的非静电性场强,
则感应电动势可以表示为
i E k d l
rr
因为 Φ s B dS
i
r
Ñ Ek
r dl
dΦ dt
d dt
S
r Bd
r S
例题9-1 一长直导线中通有交变电流 I I0 sin t ,式
§9-3 感生电动势 感生电场
一、感生电场
➢感生电动势:导体回路不动,由于磁场变化而产 生的感应电动势。
➢感生电场:变化的磁场在其周围激发的电场。
➢以 E表i 示感生电场的场强,根据电源电动势的定义
及电磁感应定律,则有
L Ei d l
dΦ dt
d dt
S
B
d
S
B t
d
S
S
注意:(1)场的存在与空间中有无导体回路无关。
匀强磁场中绕固定轴OO’
转动,磁感应强度 B与 轴垂直。当 t 0时,en与
时B间之间t的, 夹en角与为B零之,间经的过夹
角为 。
c
v
v
B
d
O b
v
B
v
en
a
O
Φ BS cos
i
N
dΦ dt
NBS
sin
d
dt
因 t 故 i NBS sin t
令NBS 0
——瞬时最大电动势
i 0 sin t
I I0 sin( t )
在匀强磁场内转动的线圈 中所产生的电动势是随时间 作周期性变化的,这种电动 势称为交变电动势。线圈中 的电流也是交变的,称为交 变电流或交流。
c
v
v
B
d
i I
O b
v
B
v
en
a
O
0 o
t
例题9-4 正方形线圈l=5cm,在B=0.84T的磁场中绕轴 转动,线圈的电阻率为 1.7 108 m 截面积S=0.5m2
S
v N
(4)用右手螺旋法则 由感应电流磁场的方向 来确定感应电流的方向。
楞次定律的实质:能量守恒定律的 具体体现。
S
v
N
右图:线圈中感应电流激发的磁 场阻碍条形磁铁的运动。
——阻碍运动!
楞次定律的应用:磁悬浮列车制动。
钢轨内侧的 电磁线圈
斥力
N
N S
S
S
N
S
N
S
S
N
S
N
N
S
N
S
N
S
N
S
N
三、法拉第电磁感应定律
c
v
v
B
d
O b
v
B
v
en
a
O
圈磁通量为
Φ BS cos Bl2 cos
设线圈转动角速度为
2πn 2πnt
i
N
dΦ dt
N
d dt
Bl2 cos 2nt
NBl2 2πn sin 2πnt
(1)当 30
i NBl2 2πn sin 30o
0.66V
c
v
v
B
d
O b
场)。
感生电场与静电场的比较
场源 环流 电势
静电场
r Es
正负电荷
L E i d l 0
势场
感生电场
r Ei
变化的磁场
L
Ei
d
l
B t
d
S
S
非势场
场线 通量
不闭合
r
Òs E
r dS
1
0 i qi
闭合
rr
ÒS E dS 0
例题9-5 在半径为 R 的无限长螺线管内部的磁场 B
楞次(俄)
注意: (1)感应电流所激发的磁场要阻碍的是磁通量的 变化,而不一定减小磁通量。
(2)阻碍并不意味完全抵消。如果磁通量的变化完 全被抵消了,则感应电流也就不存在了。
S
v
N
判断感应电流的方向:
(1)判断原磁场的方向;
(2)判断磁通量的增减;
(3)确定感应电流磁 场的方向。
m B感与 B 反 向 m B感与 B 同 向
v
B
v
en
a
O
(2)当 sin 2ntπ 1,
即当 90、 270 等位置时电动势 i最大
i NBl 2 2πn 1.32V
(3)当t=1s时,
i NBl 2 2πn sin 2πn 0
本题也可以将线圈看作由四段长为l的导线在磁场
中运动产生动生电动势之和。显然只有ab和cd两边
实验总结:回路中的磁通量发生改变。
结论:当穿过一个闭合导体回路所包围的面积内的磁 通量发生变化时,不论这种变化是由什么原因引起的, 在导体回路中就会产生感应电流。这种现象称为电磁 感应现象。
二、楞次定律
闭合回路中感应电流的方向,总是使得
它激发的磁场阻碍引起感应电流的磁通量的
变化(增加或减少)———楞次(1833)
中 I 表示瞬时电流,I 0 电流振幅, 角频率,I 0和 是
常量。在长直导线旁平行放置一矩形线圈,线圈平面与
直导线在同一平面内。已知线圈长为 l ,宽为b,线圈
近长直导线的一边离直导线距离为 a 。求任一瞬时线圈
中的感应电动势。
解:某一瞬间,距离直导线 x 处
a
b
的磁感应强度为
B
0I
I
2πx
l
选顺时针方向为矩形线圈的绕行
电动势 I
Ek
+-
Ek : 非静电力场强.
E Ek dl
闭合电路的总电动势
E l Ek dl
动生电动势的本质:
当MN速度v向右运动时,导线内每
个自由电子受的洛伦兹力为:
r Fm
evr
r B
+ B+
++
Fe++M++++
+ + + -+
+
+ Fm+
-
+ -
+ + + +
++
++v++
1.基本表述:通过回路所包围面积的磁通 量发生变化时,回路中产生的感应电动势 与磁通量对时间的变化率成正比。
————法拉第(1831)
dΦ i dt
法拉第(英)
式中负号反映电动势的方向。
2.电动势方向的确定:
(1)规定回路的绕行方向,并由右手螺旋法则确定回 路面积的法向正方向;
迈克尔·法拉第(Michael Faraday,1791~1867)英国物 理学家、化学家。1791年9月22日出生于纽因顿一个贫 苦铁匠家庭。 1805-1812 图书装订学徒 1813-1829 任戴维助手并在戴维指导下工作 1824年 他被选为皇家学会院士 1825年 发现“苯” 1831年 发现电磁感应现象,引入“力场”的概念 1845年 发现了现在称为法拉第效应(磁致旋光)的现象 ——两次谢绝皇家学院的院长职务,谢绝英王室准备授 予他的爵士称号
切割磁感应线产生电动势
