最新八下平行四边形解答题难题训练(一)(有答案)

合集下载

八年级初二数学平行四边形练习题附解析

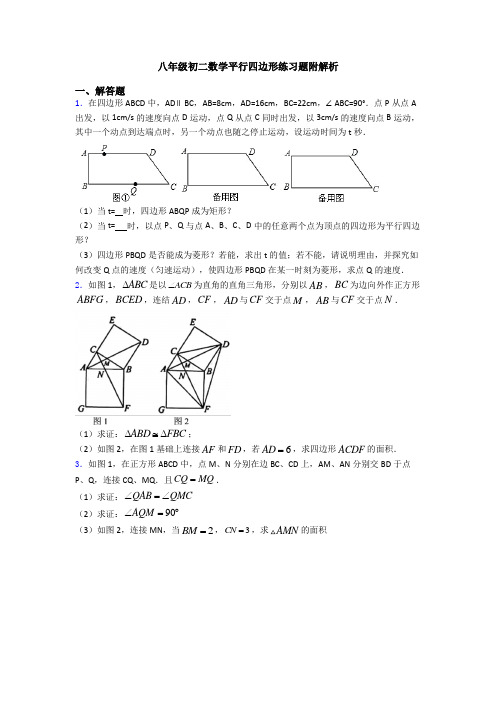
八年级初二数学平行四边形练习题附解析一、解答题1．在四边形ABCD 中，AD ∥BC ，AB=8cm ，AD=16cm ，BC=22cm ，∠ABC=90°．点P 从点A 出发，以1cm/s 的速度向点D 运动，点Q 从点C 同时出发，以3cm/s 的速度向点B 运动，其中一个动点到达端点时，另一个动点也随之停止运动，设运动时间为t 秒．（1）当t= 时，四边形ABQP 成为矩形？（2）当t= 时，以点P 、Q 与点A 、B 、C 、D 中的任意两个点为顶点的四边形为平行四边形？（3）四边形PBQD 是否能成为菱形？若能，求出t 的值；若不能，请说明理由，并探究如何改变Q 点的速度（匀速运动），使四边形PBQD 在某一时刻为菱形，求点Q 的速度．2．如图1，ABC ∆是以ACB ∠为直角的直角三角形，分别以AB ，BC 为边向外作正方形ABFG ，BCED ，连结AD ，CF ，AD 与CF 交于点M ，AB 与CF 交于点N ．（1）求证：ABD FBC ∆≅∆；（2）如图2，在图1基础上连接AF 和FD ，若6AD =，求四边形ACDF 的面积．3．如图1，在正方形ABCD 中，点M 、N 分别在边BC 、CD 上，AM 、AN 分别交BD 于点P 、Q ，连接CQ 、MQ ．且CQ MQ =．（1）求证：QAB QMC ∠=∠（2）求证：90AQM ∠=︒（3）如图2，连接MN ，当2BM =，3CN =，求AMN 的面积图1 图24．如图平行四边形ABCD ，E ，F 分别是AD ，BC 上的点，且AE ＝CF ，EF 与AC 交于点O ．（1）如图①．求证：OE ＝OF ；（2）如图②，将平行四边形ABCD （纸片沿直线EF 折叠，点A 落在A 1处，点B 落在点B 1处，设FB 交CD 于点G ．A 1B 分别交CD ，DE 于点H ，P ．请在折叠后的图形中找一条线段，使它与EP 相等，并加以证明；（3）如图③，若△ABO 是等边三角形，AB ＝4，点F 在BC 边上，且BF ＝4．则CF OF＝（直接填结果）．5．已知四边形ABCD 是正方形，将线段CD 绕点C 逆时针旋转α（090α︒<<︒），得到线段CE ，联结BE 、CE 、DE . 过点B 作BF ⊥DE 交线段DE 的延长线于F ．（1）如图，当BE =CE 时，求旋转角α的度数；（2）当旋转角α的大小发生变化时，BEF ∠的度数是否发生变化?如果变化，请用含α的代数式表示；如果不变，请求出BEF ∠的度数；（3）联结AF ，求证：2DE AF =．6．如图，锐角ABC ∆，AB AC =，点D 是边BC 上的一点，以AD 为边作ADE ∆，使AE AD =，EAD BAC ∠=∠．（1）过点E 作//EF DC 交AB 于点F ，连接CF （如图①）①请直接写出EAB ∠与DAC ∠的数量关系；②试判断四边形CDEF 的形状，并证明；（2）若60BAC ∠=，过点C 作//CF DE 交AB 于点F ，连接EF （如图②），那么（1）②中的结论是否任然成立？若成立，请给出证明，若不成立，请说明理由．7．如图，四边形ABCD 是边长为3的正方形，点E 在边AD 所在的直线上，连接CE ，以CE 为边，作正方形CEFG （点C 、E 、F 、G 按逆时针排列），连接BF.（1）如图1,当点E 与点D 重合时，BF 的长为；（2）如图2，当点E 在线段AD 上时，若AE=1，求BF 的长；（提示：过点F 作BC 的垂线，交BC 的延长线于点M ，交AD 的延长线于点N.）（3）当点E 在直线AD 上时，若AE=4，请直接写出BF 的长.8．已知：在矩形ABCD 中，点F 为AD 中点,点E 为AB 边上一点，连接CE 、EF 、CF ，EF 平分∠AEC ．(1)如图1，求证：CF ⊥EF;(2)如图2，延长CE 、DA 交于点K, 过点F 作FG ∥AB 交CE 于点G 若，点H 为FG 上一点，连接CH,若∠CHG=∠BCE, 求证：CH=FK;(3)如图3, 过点H 作HN ⊥CH 交AB 于点N,若EN=11,FH-GH=1,求GK 长.9．如图，在矩形 ABCD中， AB=16 ， BC=18 ，点 E在边 AB 上，点 F 是边 BC 上不与点 B、C 重合的一个动点，把△EBF沿 EF 折叠，点B落在点 B' 处.(I)若 AE=0 时，且点 B' 恰好落在 AD 边上，请直接写出 DB' 的长；(II)若 AE=3 时，且△CDB' 是以 DB' 为腰的等腰三角形，试求 DB' 的长；(III)若AE=8时，且点 B' 落在矩形内部（不含边长），试直接写出 DB' 的取值范围.10．如图，在平行四边形 ABCD中，AD=30 ，CD=10，F是BC 的中点，P 以每秒1 个单位长度的速度从 A向 D运动，到D点后停止运动；Q沿着A B C D→→→路径以每秒3个单位长度的速度运动，到D点后停止运动．已知动点 P，Q 同时出发，当其中一点停止后，另一点也停止运动．设运动时间为 t秒，问：（1）经过几秒，以 A，Q ，F ，P 为顶点的四边形是平行四边形（2）经过几秒，以A ，Q ，F ， P为顶点的四边形的面积是平行四边形 ABCD面积的一半？【参考答案】***试卷处理标记，请不要删除一、解答题1．（1）112；（2）112或4；（3）四边形PBQD不能成为菱形【分析】（1）由∠B=90°，AP ∥BQ ，由矩形的判定可知当AP=BQ 时，四边形ABQP 成为矩形；（2）由（1）可求得点P 、Q 与点A 、B 为顶点的四边形为平行四边形；然后由当PD=CQ时，CDPQ 是平行四边形，求得t 的值；（3）由PD ∥BQ ，当PD=BQ=BP 时，四边形PBQD 能成为菱形，先由PD=BQ 求出运动时间t 的值，再代入求BP ，发现BP≠PD ，判断此时四边形PBQD 不能成为菱形；设Q 点的速度改变为vcm/s 时，四边形PBQD 在时刻t 为菱形，根据PD=BQ=BP 列出关于v 、t 的方程组，解方程组即可求出点Q 的速度．【详解】（1）如图1，∵∠B=90°，AP ∥BQ ，∴当AP=BQ 时，四边形ABQP 成为矩形，此时有t=22﹣3t ，解得t=112． ∴当t=112时，四边形ABQP 成为矩形；故答案为112；（2）如图1，当t=112时，四边形ABQP 成为矩形，如图2，当PD=CQ 时，四边形CDPQ 是平行四边形，则16﹣t=3t ，解得：t=4， ∴当t=112或4时，以点P 、Q 与点A 、B 、C 、D 中的任意两个点为顶点的四边形为平行四边形；故答案为112或4；（3）四边形PBQD 不能成为菱形．理由如下：∵PD ∥BQ ，∴当PD=BQ=BP 时，四边形PBQD 能成为菱形．由PD=BQ ，得16﹣t=22﹣3t ，解得：t=3，当t=3时，PD=BQ=13，，∴四边形PBQD 不能成为菱形；如果Q 点的速度改变为vcm/s 时，能够使四边形PBQD 在时刻ts 为菱形，由题意，得162216t vtt -=-⎧⎪⎨-=⎪⎩62t v =⎧⎨=⎩．故点Q 的速度为2cm/s 时，能够使四边形PBQD 在某一时刻为菱形．【点睛】此题属于四边形的综合题．考查了矩形的判定、菱形的判定以及勾股定理等知识．注意掌握分类讨论思想与方程思想的应用是解此题的关键．2．（1）详见解析；（2）18【分析】（1）根据正方形的性质得出BC=BD ，AB=BF ，∠CBD=∠ABF=90°，求出∠ABD=∠CBF ，根据全等三角形的判定得出即可；（2）根据全等三角形的性质得出∠BAD=∠BFC ，AD=FC=6，求出AD ⊥CF ，根据三角形的面积求出即可．【详解】解：（1）四边形ABFG 、BCED 是正方形，AB FB ∴=，CB DB =，90ABF CBD ∠=∠=︒，ABF ABC CBD ABC ∴∠+∠=∠+∠，即ABD CBF ∠=∠在ABD ∆和FBC ∆中，AB FB ABD CBF DB CB =⎧⎪∠=∠⎨⎪=⎩()ABD FBC SAS ∴∆≅∆；图1 图2（2）ABD FBC ∆≅∆，BAD BFC ∴∠=∠，6AD FC ==，180AMF BAD CNA ∴∠=︒-∠-∠ 180()BFC BNF =︒-∠+∠1809090=︒-︒=︒AD CF ∴⊥-ACD ACF DFM ACM ACDF S S S S S ∆∆∆∆∴=++四边形11112222AD CM CF AM DM FM AM CM =⋅+⋅+⋅-⋅ 1133(6)(6)1822CM AM AM CM AM CM =++---⋅= 【点睛】本题考查了正方形的性质，全等三角形的性质和判定，三角形的面积等知识点，能求出△ABD ≌△FBC 是解此题的关键．3．（1）见解析（2）见解析（3）15【分析】（1）根据四边形ABCD 是正方形，得到∠QBA ＝∠QBC ，进而可得△QBA ≌ △QBC ，∠QAB ＝∠QCB ，再根据CQ ＝MQ ，得到∠QCB ＝∠QMC ，即可求证；（2）根据∠QAB ＝∠QMC ，∠QMC ＋∠QMB ＝180°，得到∠QAB ＋∠QMB ＝180°，在四边形QABM 中，∠QAB ＋∠QMB ＋∠ABM ＋∠AQM ＝360°可得∠ABM ＋∠AQM ＝180°，再根据∠ABM ＝90°即可求解；（3）设正方形ABCD 的边长为a ，延长ND 至点H ，使DH ＝BM ＝2，证得△ADH ≌△ABM ，得到∠DAH ＝∠BAM ，且AH ＝AM ，由（2）知，△QAM 是等腰直角三角形，易得∠NAM ＝∠NAH ，进而得到△NAM ≌ △NAH ，在Rt △MNC 中，利用勾股定理得到6a =，即可求解．【详解】解：（1）∵四边形ABCD 是正方形∴∠QBA ＝∠QBC在△QBA 和△QBC 中BA BC QBA QBC QB QB =⎧⎪∠=∠⎨⎪=⎩∴△QBA ≌ △QBC （SAS ）∴∠QAB ＝∠QCB又∵CQ ＝MQ∴∠QCB ＝∠QMC∴∠QAB ＝∠QMC （2）∵∠QAB ＝∠QMC又∵∠QMC ＋∠QMB ＝180°∴∠QAB ＋∠QMB ＝180°在四边形QABM 中∠QAB ＋∠QMB ＋∠ABM ＋∠AQM ＝360°∴∠ABM ＋∠AQM ＝180°而∠ABM ＝90°∴∠AQM ＝90°（3）设正方形ABCD 的边长为a ，则2MC a =-，3ND a =-延长ND 至点H ，使DH ＝BM ＝2易证△ADH ≌ △ABM∴∠DAH ＝∠BAM ，且AH ＝AM由（2）知，△QAM 是等腰直角三角形∴∠QAM ＝45°∴∠DAN ＋∠BAM ＝45°∴∠DAN ＋∠DAH ＝45°即∠NAH ＝45°∴∠NAM ＝∠NAH∴△NAM ≌ △NAH （SAS ）∴NM ＝NH ＝()321a a -+=-在Rt △MNC 中，222MN MC NC =+∴()()222123a a -=-+∴6a = ∴11651522AMN AHN S S AD NH ==⋅=⨯⨯=【点睛】此题主要考查正方形的性质、全等三角形的判断和性质、四边形的内角和、等腰直角三角形的性质及勾股定理，灵活运用性质是解题关键．4．（1）见解析；（2）FG=EP ，理由见解析；（32【分析】（1）证△ODE ≌△OFB （ASA ），即可得出OE=OF ；（2）连AC ，由（1）可知OE=OF ，OB=OD ，证△AOE ≌△COF （SAS ），得AE=CF ，由折叠性质得AE=A 1E=CF ，∠A 1=∠BAD=∠BCD ，∠B=∠B 1，则∠D=∠B 1，证△A 1PE ≌△CGF （AAS ），即可得出FG=EP ；（3）作OH ⊥BC 于H ，证四边形ABCD 是矩形，则∠ABC=90°，得∠OBC=30°，求出AC=8，由勾股定理得BC=43CF=3，由等腰三角形的性质得BH=CH=12BC=3HF=423-，OH=12OB=2，由勾股定理得OF=2622，进而得出答案．【详解】解：（1）证明：∵四边形ABCD 是平行四边形，∴AD ∥BC ，AD=BC ，∴∠ODE=∠OBF ，∠OED=∠OFB ，∵AE=CF ，∴AD-AE=BC-CF ，即DE=BF ，在△ODE 和△OFB 中， ODE OBF DE BFOED OFB ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△ODE ≌△OFB （ASA ），∴OE=OF ；（2）FG=EP ，理由如下：连AC ，如图②所示：由（1）可知：OE=OF ，OB=OD ，∵四边形ABCD 是平行四边形，∴AC 过点O ，OA=OC ，∠BAD=∠BCD ，∠D=∠B ，在△AOE 和△COF 中，OA OC AOE COF OE OF =⎧⎪∠=∠⎨⎪=⎩，∴△AOE ≌△COF （SAS ），∴AE=CF ，由折叠性质得：AE=A 1E=CF ，∠A 1=∠BAD=∠BCD ，∠B=∠B 1， ∴∠D=∠B 1，∵∠A 1PE=∠DPH ，∠PHD=∠B 1HG ，∴∠DPH=∠B 1GH ，∵∠B 1GH=∠CGF ，∴∠A 1PE=∠CGF ，在△A 1PE 和△CGF 中，111A PE CGF A FCG A E CF ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△A 1PE ≌△CGF （AAS ），∴FG=EP ；（3）作OH ⊥BC 于H ，如图③所示：∵△AOB 是等边三角形，∴∠ABO=∠AOB=∠BAO=60°，OA=OB=AB=4， ∵四边形ABCD 是平行四边形，∴OA=OC ，OB=OD ，∴AC=BD ，∴四边形ABCD 是矩形，∴∠ABC=90°，∴∠OBC=∠OCB=30°，∵AB=OB=BF=4，∴AC=BD=2OB=8，由勾股定理得：BC=2222=84AC AB --=43，∴CF=43-4， ∵OB=OC ，OH ⊥BC ，∴BH=CH=12BC=23， ∴HF=4-23，OH=12OB=2，在Rt △OHF 中，由勾股定理得：OF=22OH HF +=()222423+-=2622-，∴434226222CF OF -===-，故答案为：2．【点睛】本题是四边形综合题，考查了平行四边形的性质、矩形的判定与性质、翻折变换的性质、全等三角形的判定与性质、等腰三角形的性质、含30°角的直角三角形的性质、等边三角形的性质、勾股定理等知识；本题综合性强，解题的关键是准确寻找全等三角形解决问题，学会添加常用辅助线，属于中考压轴题．5．（1）30°；（2）不变；45°；（3）见解析【分析】（1）利用图形的旋转与正方形的性质得到△BEC 是等边三角形，从而求得α=∠DCE =30°．（2）因为△CED 是等腰三角形，再利用三角形的内角和即可求∠BEF =18045CED CEB ︒-∠-∠=︒.（3）过A 点与C 点添加平行线与垂线，作得四边形AGFH 是平行四边形，求得△ABG ≌△ADH .从而求得矩形AGFH 是正方形，根据正方形的性质证得△AHD ≌△DIC ，从而得出结论．【详解】（1）证明：在正方形ABCD 中, BC =CD .由旋转知，CE =CD ,又∵BE =CE ,∴BE =CE =BC ,∴△BEC 是等边三角形，∴∠BCE =60°.又∵∠BCD =90°,∴α=∠DCE =30°.（2）∠BEF 的度数不发生变化.在△CED 中，CE =CD ,∴∠CED =∠CDE =1809022︒-αα︒-，在△CEB 中,CE =CB ,∠BCE =90α︒-,∴∠CEB =∠CBE =1804522BCE α︒-∠=︒+, ∴∠BEF =18045CED CEB ︒-∠-∠=︒.（3）过点A 作AG ∥DF 与BF 的延长线交于点G ，过点A 作AH ∥GF 与DF 交于点H ，过点C 作CI ⊥DF 于点I易知四边形AGFH 是平行四边形，又∵BF ⊥DF ，∴平行四边形AGFH 是矩形.∵∠BAD =∠BGF =90°，∠BPF =∠APD ，∴∠ABG =∠ADH .又∵∠AGB =∠AHD =90°，AB =AD ，∴△ABG ≌△ADH .∴AG =AH ，∴矩形AGFH 是正方形.∴∠AFH =∠FAH =45°，∴AH =AF∵∠DAH +∠ADH =∠CDI +∠ADH =90°∴∠DAH =∠CDI又∵∠AHD =∠DIC =90°，AD =DC ，∴△AHD ≌△DIC∴AH =DI ，∵DE =2DI ，∴DE =2AH AF【点晴】本题考查正方形的性质和判定、图形的旋转、等腰三角形的性质、全等三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．6．（1）①EAB DAC ∠=∠； ② 平行四边形，证明见解析；（2）成立，证明见解析．【分析】（1）①根据EAD BAC ∠=∠，两角有公共角BAD ∠，可证EAB DAC ∠=∠；②连接EB ，证明△EAB ≌△DAC ，可得,ABE ACD EB CD ∠=∠=,再结合平行线的性质和等腰三角形的判定定理可得EF=DC ，由此可根据一组对边平行且相等的四边形是平行四边形证明四边形CDEF 为平行四边形．（2）根据60BAC ∠=︒，可证明△AED 和△ABC 为等边三角形，再根据ED ∥FC 结合等边三角形的性质，得出∠AFC=∠BDA ，求证△ABD ≌△CAF ，得出ED=CF ，进而求证四边形EDCF 是平行四边形．【详解】解：（1）①EAB DAC ∠=∠，理由如下：∵EAD BAC ∠=∠，EAD EAB BAD ∠=∠+∠，BAC BAD DAC ∠=∠+∠, ∴EAB BAD BAD DAC ∠+∠=∠+∠，∴EAB DAC ∠=∠；②证明：如下图，连接EB,在△EAB 和△DAC 中∵AE AD EAB DAC AB AC =⎧⎪∠=∠⎨⎪=⎩∴△EAB ≌△DAC （SAS ）∴,ABE ACD EB CD ∠=∠=,∵AB AC =，∴ABC ACD ∠=∠,∴ABE ABC ∠=∠，∵//EF DC ，∴EFB ABC ∠=∠,∴ABE EFB ∠=∠,∴EB EF =,∴DC EF =∴四边形CDEF 为平行四边形；（2）成立；理由如下：理由如下：∵60BAC ∠=︒，∴=60EAD BAC ∠=∠︒，∵AE=AD ，AB=AC ，∴△AED 和△ABC 为等边三角形，∴∠B=60°，∠ADE=60°，AD=ED,∵ED ∥FC ，∴∠EDB=∠FCB ，∵∠AFC=∠B+∠BCF=60°+∠BCF ，∠BDA=∠ADE+∠EDB=60°+∠EDB ，∴∠AFC=∠BDA ，在△ABD 和△CAF 中，60BDA AFC B BAC AB CA ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩∴△ABD ≌△CAF （AAS ），∴AD=FC ，∵AD=ED ，∴ED=CF ，又∵ED ∥CF ，∴四边形EDCF 是平行四边形．【点睛】本题考查全等三角形的性质和判定，等腰三角形的性质和判定，等边三角形的性质和判定，平行四边形的判定定理，平行线的性质．在做本题时可先以平行四边形的判定定理进行分析，在后两问中已知一组对边平行，所以只需证明这一组对边相等即可，一般证明线段相等就是证明相应的三角形全等．本题中是间接证明全等，在证明线段相等的过程中还应用到等腰三角形的判定定理（第（1）小题的第②问）和等边三角形的性质（第（2）小题），难度较大．7．（1）35；（2）41；（3）53101或【分析】（1）利用勾股定理即可求出.（2）过点F 作FH ⊥AD 交AD 于的延长线于点H ，作FM ⊥AB 于点M ，证出ECD FEH ∆∆≌，进而求得MF ，BM 的长，再利用勾股定理，即可求得.（3）分两种情况讨论，同（2）证得三角形全等，再利用勾股定理即可求得.【详解】（1）由勾股定理得：22223635BF AB AF =+=+=（2）过点F 作FH ⊥AD 交AD 于的延长线于点H ，作FM ⊥AB 于点M ，如图2所示：则FM=AH ，AM=FH∵四边形CEFG 是正方形 ∴EC=EF,∠FEC=90° ∴∠DEC+∠FEH=90°，又∵四边形ABCD 是正方形 ∴∠ADC=90° ∴∠DEC+∠ECD=90°，∴∠ECD=∠FEH 又∵∠EDC=∠FHE=90°，∴ECD FEH ∆∆≌ ∴FH=ED EH=CD=3∵AD=3,AE=1,ED=AD-AE=3-1=2,∴FH=ED=2∴MF=AH=1+3=4，MB=FH+CD=2+3=5在Rt △BFM 中，BF=22225441BM MF +=+=（3）分两种情况：①当点E 在边AD 的左侧时，过点F 作FM ⊥BC 交BC 的反向延长线于点M ，交DE 于点N.如图3所示：∆≅∆同（2）得：ENF DEC∴EN=CD=3，FN=ED=7∵AE=4∴AN=AE-EN=4-3=1∴MB=AN=1 FM=FN+NM=7+3=10∆中在Rt FMB由勾股定理得：2222=+=+=FB FM MB101101②当点E在边AD的右侧时，过点F作FN⊥AD交AD的延长线于点N，交BC延长线于M，如图4所示：∆≅∆同理得：CDE EFN∴NF=DE=1，EN=CD=3∴FM=3-1=2，CM=DN=DE+EN=1+3=4∴BM=CB+CM=3+4=7∆中在Rt FMB由勾股定理得：2222FB FM MB=+=+=2753或故BF53101【点睛】本题为考查三角形全等和勾股定理的综合题，难点在于根据E点位置的变化，画出图形，注意（3）分情况讨论，难度较大，属压轴题，熟练掌握三角形全等的性质和判定以及勾股定理的运用是解题关键.8．(1)证明见解析；(2)证明见解析；(3)CN=25.【解析】【分析】(1)如图，延长EF交CD延长线于点Q，先证明CQ=CE，再证明△FQD≌△FEA，根据全等三角形的对应边相等可得EF=FQ，再根据等腰三角形的性质即可得CF⊥EF；(2)分别过点F、H作FM⊥CE ，HP⊥CD，垂足分别为M、P，证明四边形DFHP是矩形，继而证明△HPC≌△FMK，根据全等三角形的性质即可得CH=FK；(3)连接CN，延长HG交CN于点T，设∠DCF=α，则∠GCF=α，先证明得到FG=CG=GE，∠CGT=2α，再由FG是BC的中垂线，可得BG = CG，∠CGT=∠FGK=∠BGT=2α，再证明HN∥BG，得到四边形HGBN是平行四边形，继而证明△HNC≌△KGF，推导可得出HT=CT=TN ，由FH-HG=1，所以设GH=m，则BN=m，FH=m+1，CE=2FG=4m+2，继而根据22222=-=-，可得关于m的方程，解方程求得m的值即可求得答案. BC CN BN CE BE【详解】(1)如图，延长EF交CD延长线于点Q，∵矩形ABCD，AB∥CD，∴∠AEF=∠CQE，∠A=∠QDF，又∵EF 平分∠AEC ，∴∠AEF=∠CEF，∴∠CEF=∠CQE，∴CQ=CE，∵点F是AD中点，∴AF=DF，∴△FQD≌△FEA，∴EF=FQ，又∵CE=CQ，∴CF⊥EF；(2)分别过点F、H作FM⊥CE ，HP⊥CD，垂足分别为M、P，∵CQ=CE ，CF⊥EF，∴∠DCF=∠FCE，又∵FD⊥CD，∴FM=DF，∵FG//AB，∴∠DFH=∠DAC=90°，∴∠DFH=∠FDP=∠DPH=90°，∴四边形DFHP 是矩形，∴DF=HP ，∴FM= DF=HP ，∵∠CHG=∠BCE ，AD ∥BC ，FG ∥CD ，∴∠K=∠BCE=∠CHG=∠DCH ，又∵∠FMK=∠HPC=90°，∴△HPC ≌△FMK ，∴CH=FK ；(3)连接CN ，延长HG 交CN 于点T ，设∠DCF=α，则∠GC F=α，∵FG ∥CD ，∴∠DCF=∠CFG ，∴∠FCG=∠CFG ，∴FG=CG ，∵CF ⊥EF ，∴∠FEG+∠FCG=90°，∠CFG+∠GFE=90°，∴∠GFE=∠FEG ，∴GF=FE ，∴FG=CG=GE ，∠CGT=2α，∵FG 是BC 的中垂线，∴BG = CG ， ∠CGT=∠FGK=∠BGT=2α，∵∠CHG=∠BCE=90°-2α，∠CHN=90°，∴∠GHN=∠FGK=∠BGT=2α，∴HN ∥BG ，∴四边形HGBN 是平行四边形，∴HG=BN ，HN=BG = CG =FG ，∴△HNC ≌△KGF ，∴GK=CN ，∠HNC=∠FGK=∠NHT=2α，∴HT=CT=TN ，∵FH-HG=1，∴设GH=m ，则BN=m ，FH=m+1，CE=2FG=4m+2，∵GT=1122EN =，∴CN=2HT=11+2m ， ∵22222BC CN BN CE BE =-=-，∴2222(112)(42)(11)m m m m +-=+-+∴1176m =-(舍去)，27m =， ∴CN=GK=2HT=25.【点睛】本题考查的是四边形综合题，涉及了等腰三角形的判定与性质，全等三角形的判定与性质，平行四边形的判定与性质，矩形的性质与判定，三角形外角的性质等，综合性较强，难度较大，正确添加辅助线，熟练掌握和灵活运用相关知识是解题的关键.9．(I) ；(II) 16或10；(III) .【解析】【分析】(I)根据已知条件直接写出答案即可.(II)分两种情况：或讨论即可.(III)根据已知条件直接写出答案即可.【详解】(I) ；(II)∵四边形是矩形，∴，.分两种情况讨论：（i）如图1，当时，即是以为腰的等腰三角形.（ii）如图2，当时，过点作∥，分别交与于点、.∵四边形是矩形,∴∥,.又∥，∴四边形是平行四边形，又，'⊥，∴□是矩形，∴，，即B H CD又，∴，，∵，∴，∴，在RtΔEGB'中，由勾股定理得：，∴，在中，由勾股定理得：，综上，的长为16或10.(III) . （或）.【点睛】本题主要考查了四边形的动点问题.10．（1）254秒或252秒；（2）15秒【分析】(1)Q点必须在BC上时，A，Q ，F ，P 为顶点的四边形才能是平行四边形，分Q点在BF和Q点在CF上时分类讨论，利用平行四边形对边相等的性质即可求解；(2)分Q点在AB、BC、CD之间时逐个讨论即可求解．【详解】解：(1)∵以A、Q、F、P为顶点的四边形是平行四边形，且AP在AD上，∴Q点必须在BC上才能满足以A、Q、F、P为顶点的四边形是平行四边形∵四边形ABCD是平行四边形，∴AD=BC=30，AB=CD=10，∵点F是BC的中点，∴BF=CF=12BC=15，AB+BF=25，情况一：当Q点在BF上时，AP=FQ，且AP=t，FQ=35-3t，故t=25-3t，解得254t ；情况二：当Q点在CF上时，AP=FQ，且AP=t，FQ=3t-35，故t=3t-25，解得t=25 2；故经过254或252秒，以A、Q、B、P为顶点的四边形是平行四边形；(2)情况一：当Q点在AB上时，0<t<103，此时P点还未运动到AD的中点位置，故四边形AQFP面积小于平行四边形ABCD面积的一半，情况二：当Q点在BC上且位于BF之间时，1025 33t，此时AP+FQ=t+35-3t=35-2t，∵102533t，∴35-2t ＜30，四边形AQFP面积小于平行四边形ABCD面积的一半，情况三：当Q点在BC上且位于FC之间时，2540 33t此时AP+FQ=t+3t-35=4t-35∵254033t，∴4t-35＜30，四边形AQFP面积小于平行四边形ABCD面积的一半，情况四：当Q点在CD上时，4050 33t<<当AP=BF=15时，t=15，1122 APF ABFP PFQ DCFP S S S S且∴1+2APF PFQ AFPQ ABCDS S S S，∴当t=15秒时，以A、Q、F、P为顶点的四边形面积是平行四边形ABCD面积的一半，故答案为：15秒．【点睛】本题考查了平行四边形的判定和性质，根据动点的位置不同需要分多种情况分类讨论，熟练掌握平行四边形的性质是解决本题的关键．。

北师大版八年级数学下册第一章特殊的平行四边形专项测试题-附答案解析(一)

正方形应是N的一部分，也是的一部分，
矩形形、正方形、菱形都属于平行四边形，
它们之间的关系是：．
二、填空题（本大题共有5小题，每小题5分，共25分）
16、已知矩形的一条对角线长，则另一条对角线的一半是 .
【答案】4
【解析】解：
根据矩形的对角线相等，另一条对角线长，则另一条对角线的一半是 .
故正确答案是 .
14、将四根长度相等的细木条首尾相接，用钉子钉成四边形，转动这个四边形，使它形状改变，当时，如图，测得，当时，如图，（）
A.
B.
C.
D.
15、如图所示，设表示平行四边形，表示矩形，表示菱形，表示正方形，则下列四个图形中，能表示它们之间关系的是（）
A.
B.
C.
D.
二、填空题（本大题共有5小题，每小题5分，共25分）
四条边相等的四边形是菱形，不一定是正方形，该说法错误，符合题意；
对角线相等的菱形是正方形，该说法正确，不符合题意；
对角线垂直的矩形是正方形，该说法正确，不符合题意．
故正确答案选：四条边相等的四边形是正方形.
3、矩形、菱形、正方形都具有的性质是（）.
A. 对角线互相垂直
B. 对角线平分每一组对角
C. 对角线互相平分
6、在中，，是边上一点，交于点，交于点，若要使四边形是菱形，只需添加条件( ).
A.
B.
C.
D.
【答案】C
【解析】解：只需添加
，
四边形是平行四边形
四边形是菱形
故正确答案是：
7、过矩形的四个顶点作对角线、的平行线分別交于、、、四点，则四边形是（).

新人教版八年级数学下册平行四边形解答题综合综合(共2份30题)

八年级数学人教版下册平行四边形解答题综合练习（一）1．在正方形ABCD中，点E、F分别在BC边和CD上，且满足△AEF是等边三角形，连接AC交EF于点G．（1）求证：CE＝CF；（2）若等边△AEF边长为2，求AC的长．2．如图，在▱ABCD中，∠ABC，∠BCD的平分线交于点F，E是边BC的中点，连接EF，AF，AF的延长线交边CD于点G，BF的延长线交CD的延长线于点H．（1）∠BFC＝°；（2）求证：BC＝CH；（3）若EF＝5，AB＝6，求CG的长．3．如图，四边形ABCD为正方形，点E、F分别是AB、CD的中点，DG⊥CF于点G．（1）求证：AE∥CF；（2）求证：∠AGE＝90°；（3）若正方形的边长为2，则线段CG的长度为．4．如图，在正方形中ABCD，E是AB上一点，F是AD延长线上一点，且DF＝BE．（1）求证：CE＝CF；（2）若点G在AD上，且∠GCE＝45°，判断线段GE、BE、GD之间的数量关系，并说明理由．5．如图，正方形ABCD中，点E在边AB上，连接ED，过点D作FD⊥DE与BC的延长线相交于点F，连接EF与边CD相交于点G、与对角线BD相交于点H．（1）若AB＝6，且BD＝BF，求BE的长；（2）若∠2＝2∠1，求证：HF＝HE+HD．6．如图，在正方形ABCD中，E为BC边上任意点，AF平分∠EAD，交CD于点F．（1）如图1，当AB＝2时，若点F恰好为CD中点，求CE的长；（2）如图2，延长AF交BC的延长线于点G，延长AE交DC的延长线于点H，连接HG，当CG＝DF时，求证：HG⊥AG．7．正方形ABCD，点E为射线DC上一点，连接BE，过点A作AF⊥BE，交直线BC于点F，交直线BE于点K．（1）如图，点E在边CD上，求证AF＝BE；（2）过点E作AF的平行线，交直线AD于点M，交直线BC于点N，请你用等式表示线段CE，DM，CN之间的数量关系：．8．如图，在平行四边形ABCD中，对角线AC与BD相交于点O，点E，F分别为OB，OD的中点．（1）求证：△ABE≌△CDF；（2）延长AE至G，使EG＝AE，连接CG，延长CF，交AD于点P．①当AB与AC满足什么数量关系时，四边形EGCF是矩形？请说明理由；②若AP＝2DP＝8，CP＝，CD＝5，求四边形EGCF的面积．9．如图，在边长为1的正方形ABCD中，E是边CD的中点，点P是边AD上一点（与点A，D不重合），射线PE与BC的延长线交于点Q．（1）求证：△PDE≌△QCE；（2）若点F是PB的中点，连接AF，当PB＝PQ时．①求证：四边形AFEP是平行四边形；②已知四边形AFEP是菱形，求的值．10．如图，在平行四边形ABCD中，对角线AC，BD相交于点O，点M为AD的中点，过点M作MN∥BD交CD延长线于点N．（1）求证：四边形MNDO是平行四边形；（2）请直接写出当四边形ABCD的边AB与BD满足什么关系时，四边形MNDO分别是菱形、矩形、正方形．11．如图，E，F分别是菱形ABCD的边AD，CD的中点，且AB＝5，BD＝6．（1）求线段EF的长；（2）探究四边形DEOF是什么特殊四边形？并对结论给予证明．12．如图，在正方形ABCD中，P是对角线BD上的一点，点E在边AD的延长线上，且PA＝PE，PE交CD于点F．（1）求证：PA＝PC；（2）求证：PC⊥PE．13．如图，菱形ABCD的对角线AC、BD相交于点O，E是AD的中点，点F、G在CD 边上，EF⊥CD，OG∥EF．（1）求证：四边形OEFG是矩形；（2）若FG＝5，EF＝4，求CG的长．14．如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD，等边△ABE，已知∠BAC＝30°，EF⊥AB，垂足为F，连接DF．（1）求证：△AEF≌△BAC；（2）四边形ADFE是平行四边形吗？请说明理由．15．如图，在正方形ABCD中，AB＝，E为正方形ABCD内一点，DE＝AB，∠EDC＝α（0°＜α＜90°），连结CE，AE，过点D作DF⊥AE，垂足为点F，交CE的延长线于点G，连结AG．（1）当α＝20°时，求∠DAE的度数；（2）判断△AEG的形状，并说明理由；（3）当GF＝1时，求CE的长．参考答案1．证明：（1）∵四边形ABCD是正方形，∴AB＝AD，∠B＝∠D＝90°，BC＝CD，∵△AEF是等边三角形，∴AE＝AF，在Rt△ABE和Rt△ADF中，∴Rt△ABE≌Rt△ADF（HL），∴BE＝DF，∴CE＝CF．（2）∵AE＝AF，CE＝CF，∴AC垂直平分EF，∴EG＝FG＝1．∴，，∴．2．解：（1）∵四边形ABCD是平行四边形，∴AB＝CD，AB∥CD，∴∠ABC+∠BCD＝180°，∵BF平分∠ABC，CF平分∠BCD，∴∠FBC＝∠ABC，∠DCF＝∠BCF＝∠BCD，∴∠FBC+∠BCF＝90°，∴∠BFC＝90°，故答案为90；（2）在△BCF和△HCF中，，∴△BCF≌△HCF（ASA），∴BC＝CH；（3）∵△BCF≌△HCF，∴BF＝FH，又∵E是边BC的中点，∴CH＝2EF＝10，∵AB∥CD，∴∠H＝∠ABF，在△ABF和△GHF中，，∴△ABF≌△HGF（ASA），∴AB＝HG＝6，∴CG＝CH﹣GH＝4．3．解：（1）∵AF＝CE，AF＝CE，∴四边形AFCE是平行四边形，∴AE∥CF；（2）如图，取AE和DG交于H，∵CF∥AE，DG⊥CF，∴DG⊥AE于H，∵E是CD的中点，∴EG＝ED，∴△DGE是等腰三角形，∴H是DG的中点，∴AG＝AD，在△ADE和△AGE中，，∴△ADE≌△AGE（SSS），∴∠AGE＝∠ADE＝90°；（3）∵AG＝AD＝2，DE＝1，∴AE＝，又∵GH⊥AE，∴，解得HG＝，∴DG＝，∴，故答案为．4．（1）证明：在正方形ABCD中，∵BC＝CD，∠B＝∠CDF，BE＝DF，在△CBE与△CDF中，，∴△CBE≌△CDF（SAS），∴CE＝CF；（2）解：GE＝BE+GD，理由：由（1）得△CBE≌△CDF，∴∠BCE＝∠DCF，CE＝CF．∵∠GCE＝45°，∴∠BCE+DCG＝45°，∴∠GCF＝∠DCF+∠DCG＝45°，在△ECG与△FCG中，，∴△ECG≌△FCG（SAS），∴GE＝GF，∴GE＝DF+GD＝BE+GD．5．（1）解：∵四边形ABCD是正方形，且FD⊥DE，∴AD＝CD，∠A＝∠DCB＝∠ADC＝90°，∵DE⊥DF，∴∠EDF＝90°，∴∠2＝90°﹣∠EDC＝∠CDF，∠A＝∠DCF＝90°，在△DAE和△DCF中，，∴Rt△DAE≌Rt△DCF（ASA），∴AE＝CF，∵CF＝BF﹣BC＝BD﹣BC＝6﹣6，∴AE＝6﹣6，∴BE＝AB﹣AE＝6﹣（6﹣6）＝12﹣6；（2）在HF上取一点P，使FP＝EH，连接DP，由（1）Rt△DAE≌Rt△DCF得△EDF是等腰直角三角形，∴DE＝DF，∠DEF＝∠DFE＝45°，在△DEH和△DPE中，，∴△DEH≌△DFP（SAS），∴DH＝DP，∠EDH＝∠FDP，在△DHE和△FHB中，∵∠DEF＝∠HBF＝45°，∠EHD＝∠BHF（对顶角相等），∴∠EDH＝∠1＝∠2＝（45°﹣∠EDH），∴∠EDH＝15°，∠FDP＝15°，∴∠HDP＝90°﹣15°﹣15°＝60°，∴△DHP是等边三角形，∴HD＝HP，∵HF＝HP+PF，∴HF＝HE+HD．6．解：（1）延长BC交AF的延长线于点G，∵AD∥CG，∴∠DAF＝∠FGC，又∵AF平分∠DAE，∴∠DAF＝∠EAF，∴∠G＝∠EAF，∴EA＝EG，∵点F为CD的中点，∴CF＝DF，在△ADF和△GCF中，，∴△ADF≌△GCF（AAS），∴AD＝CG＝2，设CE＝a，则BE＝2﹣a，∴AE＝EG＝EC+CG＝2+a，在Rt△ABE中，由勾股定理得，AB2+BE2＝AE2，即22+（2﹣a）2＝（2+a）2，解得a＝，∴CE＝；（2）连接DG，在△ADF和△DCG中，，∴△ADF≌△DCG（SAS），∴∠CDG＝∠DAF，∴∠HAF＝∠FDG，又∵∠AFH＝∠DFG，∴△AFH∽△DFG，∴＝，又∵∠AFD＝∠HFG，∴△ADF∽△HGF，∴∠ADF＝∠FGH，∵∠ADF＝90°，∴∠FGH＝90°，∴AG⊥GH．7．（1）证明∵四边形ABCD是正方形，∴AB＝BC，∠ABC＝∠C＝90°，∵AF⊥BE，∠BKF＝90°，∴∠ABK+∠BAK＝90°，又∵∠ABK+∠FBK＝90°，∴∠BAK＝∠FBK，在△ABF和△BCE中，，∴△ABF≌△BCE（ASA），∴AF＝BE；（2）解：①当E在边CD上时，如图：由（1）知△ABF≌△BCE，∴BF＝CE，∴CF＝DE，∵MN//AF，AM//FN，∴四边形AMNF是平行四边形，∴AM＝FN，而AM+DM＝AD＝CD，∴FN+DM＝CD，∴CN+CF+DM＝DE+CE，∴CE＝DM+CN；②当E在边DC的延长线上时，如图：∵∠FAB＝90°﹣∠F＝∠FBK＝∠EBC，AB＝BC，∠ABF＝∠BCE＝90°，∴△ABF≌△BCE（ASA），∴BF＝CE，∵MN∥AF，AM∥FN，∴四边形AFNM是平行四边形，∴AM＝FN，即AD+DM＝BF+BC+CN，而AD＝BC，∴DM＝CE+CN，∴CE＝DM﹣CN，故答案为：CE＝DM+CN或CE＝DM﹣CN．8．（1）证明：∵四边形ABCD是平行四边形，∴AB＝CD，AB∥CD，OB＝OD，∴∠ABE＝∠CDF，∵点E，F分别为OB，OD的中点，∴BE＝OB，DF＝OD，∴BE＝DF，在△ABE和△CDF中，，∴△ABE≌△CDF（SAS）；（2）解：①当AC＝2AB时，四边形EGCF是矩形；理由如下：∵AC＝2OA，AC＝2AB，∴AB＝OA，∵E是OB的中点，∴AG⊥OB，∴∠OEG＝90°，同理：CF⊥OD，∴AG∥CF，∴EG∥CF，∵EG＝AE，OA＝OC，∴OE是△ACG的中位线，∴OE∥CG，∴EF∥CG，∴四边形EGCF是平行四边形，∵∠OEG＝90°，∴四边形EGCF是矩形；②如图，过点C作CH⊥AD于H，连接CE，则CH2＝CD2﹣DH2＝CP2﹣PH2，∵AP＝2PD＝8，∴PD＝4，设DH＝x，则PH＝4﹣x，∴52﹣x2＝（）2﹣（4﹣x）2，∴x＝3，∴DH＝3，PH＝1，∴CH＝＝＝4，∵四边形ABCD是平行四边形，∴S△BCD＝S▱ABCD＝×（8+4）×4＝24，∵点E，F分别为OB，OD的中点，OB＝OD，∴EF＝BD，∴S△EFC＝S△BCD＝12，由①知：四边形EGCF是平行四边形，S四边形EGCF＝2S△EFC＝24．9．（1）证明：∵四边形ABCD是正方形，∴∠D＝∠BCD＝90°，∴∠ECQ＝90°＝∠D，∵E是CD的中点，∴DE＝CE，又∵∠DEP＝∠CEQ，∴△PDE≌△QCE；（2）①证明：①∵PB＝PQ，∴∠PBQ＝∠Q，∵AD∥BC，∴∠APB＝∠PBQ＝∠Q＝∠EPD，∵△PDE≌△QCE，∴PE＝QE，∵PF＝BF，∴EF是△PBQ的中位线，∴EF∥BQ，∴在Rt△PAB中，AF＝PF＝BF，∴∠APF＝∠PAF，∴∠PAF＝∠EPD，∴PE∥AF，∵EF∥BQ∥AD，∴四边形AFEP是平行四边形；②∵四边形AFEP是菱形，∴AP＝PE，设AP为x，则有，解得x＝，∴．10．（1）证明：∵四边形ABCD是平行四边形，∴OA＝OC，∵点M为AD的中点，∴OM是△ACD的中位线，∴OM//CD，即OM//DN，∵MN∥BD，∴四边形MNDO是平行四边形；（2）由（1）知四边形MNDO是平行四边形，若四边形MNDO是菱形，只需OM＝OD，而OM＝CD＝AB，OD＝BD，∴AB＝BD时，四边形MNDO是菱形；若四边形MNDO是矩形，只需∠MOD＝90°，而∠MOD＝∠ABD，∴∠ABD＝90°时，四边形MNDO是矩形，即AB⊥BD；若四边形MNDO是正方形，需OM＝OD，∠MOD＝90°，∴AB＝BD，AB⊥BD时，四边形MNDO是正方形．11．（1）证明：∵四边形ABCD是菱形，∴OA＝AC，OB＝OD＝BD＝3，AC⊥BD，∴∠AOB＝90°，∴OA＝＝＝4，∴AC＝2OA＝8，∵E、F分别是AB、AD的中点，∴EF是△ABD的中位线，∴EF＝BD＝4，（2）四边形DEOF是菱形．理由如下：∵四边形ABCD是菱形，∴DA＝DC，OA＝OC，OB＝OD，∴O是AC，BD的中点，∵E，F分别是菱形ABCD的边AD，CD的中点，∴DE＝DA，DF＝DC，OE，OF分别是△ACD和△CDA的中位线，∴DE＝DF，OE∥FD，OF∥DE，∴四边形DEOF平行四边形，∵DE＝DF，∴四边形DEOF是菱形．∴AD＝CD，∠ADP＝∠CDP，在△ADP和△CDP中，，∴△ADP≌△CDP（SAS），∴PA＝PC，∵PA＝PE，∴PC＝PE．（2）作PM⊥AE于M，PN⊥CD于N，∵PD平分∠ADC，∴PM＝PN，∵∠ADC＝90°，∴PNDM是矩形，∠MPN＝90°，在Rt△PME和Rt△PMC中，PC＝PE，PM＝PN，∴Rt△PME≌Rt△PNC（HL），∴∠MPE＝∠NPC，∴∠MPN＝∠MPE+∠NPE＝∠NPC+∠NPE＝∠EPC＝90°．∴PC⊥PE．∴OA＝OC，∵E是AD的中点，∴OE是△ACD的中位线，∴OE∥CD，∵OG∥EF，∴四边形OEFG是平行四边形，∵EF⊥CD，∴∠EFG＝90°，∴平行四边形OEFG是矩形；（2）解：由（1）得：四边形OEFG是矩形，∴OE＝FG＝5，∵四边形ABCD是菱形，∴AD＝CD，AC⊥BD，∴∠AOD＝90°，∵E是AD的中点，∴OE＝AD＝DE＝5，CD＝AD＝2OE＝10，在Rt△DEF中，DF＝＝＝3，∴CG＝CD﹣FG﹣DF＝10﹣5﹣3＝2．14．（1）证明：∵Rt△ABC中，∠BAC＝30°，∴AB＝2BC，∵△ABE是等边三角形，EF⊥AB，∴AB＝AE，AB＝2AF，∴AF＝BC，在Rt△AFE和Rt△BCA中，，∴Rt△AEF≌Rt△BAC（HL）；（2）解：四边形ADFE是平行四边形，理由如下：∵△ACD是等边三角形，∴∠DAC＝60°，AC＝AD，∴∠DAB＝∠DAC+∠BAC＝90°，∴AD⊥AB，又∵EF⊥AB，∴EF∥AD，由（1）得：△AEF≌△BAC，∴EF＝AC，∴EF＝AD，∴四边形ADFE是平行四边形．15．解：（1）∵四边形ABCD是正方形，∴∠ADC＝90°，AB＝AD，∵∠CDE＝20°，∴∠ADE＝70°，∵DE＝AB，∴DA＝DE，∴∠DAE＝∠DEA＝×（180°﹣70°）＝55°．（2）结论：△AEG是等腰直角三角形．理由：∵AD＝DE，DF⊥AE，∴DG是AE的垂直平分线，∴AG＝GE，∴∠GAE＝∠GEA，∵DE＝DC＝AD，∴∠DAE＝∠DEA，∠DEC＝∠DCE，∵∠DAE+∠DEA+∠DEC+∠DCE+∠ADC＝360°，∴∠DEA+∠DEC＝135°，∴∠GEA＝45°，∴∠GAE＝∠GEA＝45°，∴∠AGE＝90°，∴△AEG为等腰直角三角形．（3）如图，连接AC，∵四边形ABCD是正方形，∴AC＝AB＝，∵△AEG为等腰直角三角形，GF⊥AE，∴GF＝AF＝EF＝1，∴AG＝GE＝，∵AC2＝AG2+GC2，∴10＝2+（EC+）2，∴EC＝（负根已经舍弃）．八年级数学人教版下册平行四边形解答题综合练习（二）1．如图1，在正方形ABCD中，点E在AD的延长线上，P是对角线BD上的一点，且点P位于AE的垂直平分线上，PE交CD于点F．（1）猜测PC和PE有什么大小及位置关系，并给出证明．（2）如图2，把正方形ABCD改为菱形ABCD，其他条件不变，当∠ABC＝120°时，连接CE，试探究线段AP与线段CE的数量关系．并说明理由．2．如图，四边形ABCD为平行四边形，∠BAD的角平分线AE交CD于点F，交BC的延长线于点E．（1）求证：BE＝CD；（2）连接BF，若BF⊥AE，∠BEA＝60°，AB＝2，求平行四边形ABCD的面积．3．如图，在正方形ABCD中，AC，BD相交于点O，E，F分别在OA，OD上，∠ABE＝∠DCF．（1）求证：△ABE≌△DCF．（2）若BC＝4，AE＝3，求BE的长．4．正方形ABCD的边长为3，E、F分别是AB、BC边上的点，且∠EDF＝45°．（1）求证：EF＝AE+CF；（2）当AE＝1时，求EF的长．5．如图，若在正方形ABCD中，点E为CD边上一点，点F为AD延长线上一点，且DE ＝DF，则AE与CF之间有怎样的数量关系和位置关系？请说明理由．6．如图，正方形ABCD中，点P是对角线AC上一点，连接PB，边作PE⊥PB交AD边于于点E，且点E不与点A，D重合，作PM⊥AD，PN⊥AB，垂足分别为点M和N．（1）求证：PM＝PN；（2）求证：EM＝BN．7．（1）已知四边形ABCD是边长为6cm的正方形，P，Q是正方形边上的两个动点，点P从点A出发，以2cm/s的速度沿A→B→C方向运动，点Q同时从点D出发以1cm/s 速度沿D→C方向运动．设点P运动的时间为t（0＜t＜6）．①如图1，点P在AB边上，PQ，AC相交于点O，当PQ，AC互相平分时，求t的值；②如图2，点P在BC边上，AP，BQ相交于点H，当AP⊥BQ时，求t的值．8．如图，在▱ABCD中，过点D作DE⊥AB于点E，点F在边CD上，CF＝AE，连接AF，BF．（1）求证：四边形BFDE是矩形；（2）已知∠DAB＝60°，AF是∠DAB的平分线，若AD＝4，求▱ABCD的面积．9．如图，在▱ABCD中，对角线AC，BD交于点O，E是AD上任意一点，连接EO并延长，交BC于点F，连接AF，CE．（1）求证：四边形AFCE是平行四边形；（2）若∠DAC＝60°，∠ADB＝15°，AC＝4．①直接写出▱ABCD的边BC上的高h的值；②当点E从点D向点A运动的过程中，下面关于四边形AFCE的形状的变化的说法中，正确的是A．平行四边形→矩形→平行四边形→菱形→平行四边形B．平行四边形→矩形→平行四边形→正方形→平行四边形C．平行四边形→菱形→平行四边形→菱形→平行四边形D．平行四边形→菱形→平行四边形→矩形→平行四边形10．如图，在▱BCFD中，点E是DF的中点，连接CE并延长，与BD的延长线相交于点A，连接CD，AF．（1）求证：四边形ADCF是平行四边形；（2）若CA＝CB，则▱ADCF为（填矩形、菱形、正方形中的一个）．11．如图，E和F分别是菱形ABCD的边AB和AD的中点，且AB＝10，AC＝12．（1）判断△OEF的形状，并说明理由．（2）求线段EF的长．12．如图，已知四边形ABCD是正方形，对角线AC、BD相交于O．（1）如图1，设E、F分别是AD、AB上的点，且∠EOF＝90°，线段AF、BF和EF之间存在一定的数量关系．请你用等式直接写出这个数量关系；（2）如图2，设E、F分别是AB上不同的两个点，且∠EOF＝45°，请你用等式表示线段AE、BF和EF之间的数量关系，并证明．13．如图，菱形ABCD的对角线AC，BD相交于点O，E是AD的中点，点F，G在AB 上，EF⊥AB，OG∥EF．（1）OE AE（填＜、＝、＞）；（2）求证：四边形OEFG是矩形；（3）若AD＝10，EF＝4，求OE和BG的长．14．如图，以△ABC的三边为边，分别作等边△ACD，△ABE，△BCF，连接DF，EF．（1）求证：△EBF≌△ABC；（2）求证：四边形ADFE是平行四边形．15．如图，已知正方形ABCD中，E为CB延长线上一点，且BE＝AB，M、N分别为AE、BC的中点，连DE交AB于O，MN交，ED于H点．（1）求证：AO＝BO；（2）求证：∠HEB＝∠HNB；（3）过A作AP⊥ED于P点，连BP，则的值．参考答案1．解：（1）PC＝PE，PC⊥PE证明∵点P位于AE的垂直平分线上，∴PA＝PE，∵四边形ABCD是正方形，∴AB＝AC，∠ADB＝∠CDB，∵PD＝PD，∴△ABP≌△CBP（SAS）∴PA＝PC，∴PC＝PE，∵四边形ABCD是正方形，∴AD＝CD，∠ADP＝∠CBP，∵PB＝PB，∴△ADP≌△CDP（SAS），∴∠PAD＝∠PCD，∵PA＝PE，∴∠PAD＝∠E，∴∠PCD＝∠E，∵∠PFC＝∠DFE，∴△CPF∽△EDF，∴∠CPF＝∠FDE，∵四边形ABCD是正方形，，∴∠ADC＝90°，∴∠FDE＝90°，∴∠CPF＝90°，∴PC⊥PE．（2）PA＝CE．理由如下：证明：∵点P位于AE的垂直平分线上，∴PA＝PE，∵四边形ABCD是菱形，∴AB＝AC，∠ADB＝∠CDB，∵PD＝PD，∴△ABP≌△CBP，∴PA＝PC∴PC＝PE，∵四边形ABCD是菱形，∴AD＝CD，∠ADP＝∠CBP，∵PB＝PB，∴△ADP≌△CDP，∴∠PAD＝∠PCD，∵PA＝PE，∴∠PAD＝∠PED，∴∠PCD＝∠PED，∵∠PFC＝∠DFE，∴△CPF∽△EDF，∴∠CPF＝∠EDF，∵四边形ABCD是菱形，∠ABC＝120°∴∠ADC＝∠ABC＝120°∴∠EDF＝180°﹣∠ADC＝60°∴∠CPF＝60°∵PE＝PC∴△PCE是等边三角形∴CE＝PE∴AP＝CE．2．（1）证明：∵四边形ABCD是平行四边形，∴AD∥BC，AB∥CD，AB＝CD，∴∠AEB＝∠DAE，∵AE是∠BAD的平分线，∴∠BAE＝∠DAE，∴∠BAE＝∠AEB，∴AB＝BE，∴BE＝CD；（2）解：∵AB＝BE，∠BEA＝60°，∴△ABE是等边三角形，∵BF⊥AE，∴AF＝EF＝1，∴BF＝＝＝，∵AD∥BC，∴∠D＝∠ECF，∠DAF＝∠E，在△ADF和△ECF中，，∴△ADF≌△ECF（AAS），∴△ADF的面积＝△ECF的面积，∴平行四边形ABCD的面积＝△ABE的面积＝AE•BF＝×2×＝．3．证明：（1）∵四边形ABCD是正方形，∴AB＝CD，∠BAE＝∠CDF＝45°，∵∠ABE＝∠DCF，在△ABE与△DCF中，，∴△ABE≌△DCF（ASA）；（2）∵四边形ABCD是正方形，∴AB＝BC，OA＝OB＝OC＝OD，∠ABC＝∠AOB＝90°，∵BC＝4，∴AB＝4，∴AC＝，∵AE＝3，∴OE＝OA﹣AE＝4﹣3＝1，在Rt△BOE中，BE＝．4．解：（1）证明：延长BC至H，使CH＝AE，连接DH，如图，∵四边形ABCD是正方形，∴AD＝CD，∠A＝∠DCE＝90°．∴△DAE≌△DCH（SAS）．∴DE＝DH，∠ADE＝∠CDH．∵∠ADC＝90°，∠EDF＝45°，∴∠ADE+∠FDC＝45°．∴∠FDC+∠CDH＝45°．即∠FDH＝45°．∴∠EDF＝∠FDH＝45°．在△EDF和△HDF中，．∴△EDF≌△HDF（SAS）．∴EF＝FH．∵FH＝FC+CH＝FC+AE，（2）设EF＝x，则FH＝x．∵正方形ABCD的边长为3，∴AB＝BC＝3．∵AE＝1，∴BE＝2，CH＝1．∴FC＝x﹣1．∴BF＝BC﹣CF＝3﹣（x﹣1）＝4﹣x．在Rt△BEF中，∵BE2+BF2＝EF2，∴22+（4﹣x）2＝x2．解得：x＝．∴EF＝．5．解：AE＝CF，AE⊥CF，理由如下：如图，延长AE交CF于点G，∵四边形ABCD是正方形，∴AD＝CD，∠ADC＝∠CDE＝90°，在△ADE和△CDF中，，∴△ADE≌△CDF（SAS），∴AE＝CF，∠DAE＝∠DCF，∵∠DCF+∠F＝90°，∴∠DAE+∠F＝90°，∴AG⊥CF，即AE⊥CF．∴AE＝CF，AE⊥CF．6．证明：（1）∵四边形ABCD为正方形，∴AC平分∠BAD，又∵PM⊥AD，PN⊥AB，∴PM＝PN．（2）∵PM⊥AD，PN⊥AB，∠MAN＝90°，PM＝PN，∴四边形PMAN为正方形，∴∠MPN＝90°，即∠MPE+∠EPN＝90°．∵PE⊥PB，∴∠EPN+∠NPB＝90°，∴∠MPE＝∠NPB．∵PM⊥AD，PN⊥AB，∴∠PME＝∠PNB＝90°．在△PME和△PNB中，，∴△PME≌△PNB（ASA），∴EM＝BN．7．解：（1）由题意得DQ＝t，AP＝2t，∵四边形ABCD是边长为6cm的正方形，∴CQ＝6﹣t，当PQ，AC互相平分时，则四边形APCQ为平行四边形，∴AP＝CQ，∴2t＝6﹣t，解得，t＝2，（2）∵四边形ABCD是正方形，∴AB＝BC，∠ABP＝∠BCQ＝90°，∵AP⊥BQ，∴∠BAP+∠ABH＝∠ABH+∠CBQ＝90°，∴∠BAP＝∠CBQ，∴△ABP≌△BCQ（ASA），∴BP＝CQ，∵BP＝2t﹣AB＝2t﹣6，CQ＝6﹣t，∴2t﹣6＝6﹣t，解得，t＝4．8．（1）证明：∵四边形ABCD是平行四边形，∴DC∥AB，DC＝AB，∵CF＝AE，∴CD﹣CF＝AB﹣AE，∴DF＝BE且DC∥AB，∴四边形BFDE是平行四边形，又∵DE⊥AB，∴∠DEB＝90°，∴平行四边形BFDE是矩形；（2）解：∵∠DAB＝60°，AD＝4，DE⊥AB，∴∠ADE＝30°，∴AE＝AD＝2，DE＝AE＝2，由（1）得：四边形DFBE是矩形，∴BF＝DE＝2，∠ABF＝90°，∵AF平分∠DAB，∴∠FAB＝∠DAB＝30°，∴AB＝BF＝×2＝6，∴▱ABCD的面积＝AB×DE＝6×2＝12．9．证明：（1）∵四边形ABCD是平行四边形∴AD∥BC，AO＝CO∴∠AEF＝∠CFE，∠EAC＝∠FCA，且AO＝CO∴△AOE≌△COF（AAS）∴OF＝OE，且AO＝CO∴四边形AFCE是平行四边形；（2）①∵∠DAC＝60°∴sin∠DAC＝∴h＝×AC＝2②∵∠DAC＝60°，∠ADB＝15°，根据三角形得内角和定理得，∠AOD＝105°，∴点E从D点向A点移动过程中，当∠AOE＝90°时，EF⊥AC，∵OA＝OC，∴AE＝CE，∴平行四边形AECF是菱形；当∠BCE＝90°时，平行四边形AECF是矩形，∴OE＝OC，∠ACE＝30°，∴∠OEC＝30°，∴∠AOE＝2∠ACE＝60°，即：∠AOE＝60°时，平行四边形AECF是矩形；综上述，当点E从D点向A点移动过程中（点E与点D，A不重合），则四边形AFCE 的变化是：平行四边形→菱形→平行四边形→矩形→平行四边形．故选：D10．解：（1）在平行四边形BCFD中，DE∥BC，∵E是DF的中点，∴DE＝BC，∴DE是△ABC的中位线，∴E是AC的中点，∴四边形ADCF是平行四边形．（2）∵CA＝CB，DE是△ABC的中位线，∴AD＝AE，∵E是AC的中点，∴AE＝CE，∴AD＝AC，∴∠ADC＝90°，∠ACD＝30°，∴▱ADCF是矩形．故答案为：矩形11．解：（1）△OEF是等腰三角形，理由如下：∵四边形ABCD是菱形，∴BC＝CD，∵E、F分别是AB、AD的中点，∴OE是△ABC的中位线，OF是△ACD的中位线，∴OE＝BC，OF＝CD，∴OE＝OF，∴△OEF是等腰三角形；（2）∵四边形ABCD是菱形，∴OA＝OC＝AC＝6，OB＝OD，AC⊥BD，∴∠AOB＝90°，∴OB＝，∴BD＝2OB＝16，∵E、F分别是AB、AD的中点，∴EF是△ABD的中位线，∴EF＝BD＝8．12．解：（1）EF2＝AF2+BF2．理由：如图1，∵四边形ABCD是正方形，∴OA＝OB，∠OAE＝∠OBF＝45°，AC⊥BD，∴∠EOF＝∠AOB＝90°，∴∠EOA＝∠FOB，在△EOA和△FOB中，，∴△EOA≌△FOB（ASA），∴AE＝BF，在Rt△EAF中，EF2＝AE2+AF2＝AF2+BF2；（2）在BC上取一点H，使得BH＝AE．∵四边形ABCD是正方形，∴OA＝OB，∠OAE＝∠OBH，∠AOB＝90°，在△OAE和△OBH中，∴△OAE≌△OBH（SAS），∴AE＝BH，∠AOE＝∠BOH，OE＝OH，∵∠EOF＝45°，∴∠AOE+∠BOF＝45°，∴∠BOF+∠BOH＝45°，∴∠FOE＝∠FOH＝45°，在△FOE和△FOH中•，，∴△FOE≌△FOH（SAS），∴EF＝FH，∵∠FBH＝90°，∴FH2＝BF2+BH2，∴EF2＝BF2+AE2，13．（1）解：∵四边形ABCD是菱形，∴AC⊥BD，∵E是AD的中点，∴OE＝AD＝AE，故答案为：＝；（2）证明：∵四边形ABCD是菱形，∴OB＝OD，∵E是AD的中点，∴OE是△ABD的中位线，∴OE∥FG，∵OG∥EF，∴四边形OEFG是平行四边形，∵EF⊥AB，∴∠EFG＝90°，∴平行四边形OEFG是矩形；（3）解：∵四边形ABCD是菱形，∴BD⊥AC，AB＝AD＝10，∴∠AOD＝90°，∵E是AD的中点，∴OE＝AE＝AD＝5；由（1）知，四边形OEFG是矩形，∴FG＝OE＝5，∵AE＝5，EF＝4，∴AF＝＝＝3，∴BG＝AB﹣AF﹣FG＝10﹣3﹣5＝2．14．证明：（1）∵△ABE，△BCF是等边三角形，∴EB＝AB，BF＝BC，∠EBA＝∠FBC＝60°，∴∠EBA﹣∠FBA＝∠FBC﹣∠FBA，∴∠EBF＝∠ABC，在△EBF和△ABC中，，∴△EBF≌△ABC（SAS），（2）证明：由（1）知△EBF≌△ABC，∴EF＝AC，又∵△ACD是等边三角形，∴AC＝AD，∴EF＝AD，同（1）得：△DFC≌△ABC（SAS），∴DF＝AB＝AE，∴四边形ADFE是平行四边形．15．（1）证明：∵四边形ABCD是正方形，∴AD＝AB，AD∥BC，∴∠DAB＝∠ABE，∠ADO＝∠BCO，∵AB＝BE，∴AD＝BE，∴△ADO≌△BEO（ASA），∴AO＝BO；（2）证明：延长BC至F，且使CF＝BE，连接AF、DF，如图1所示：则BF＝CE，∵四边形ABCD是矩形，∴AB＝DC，AD∥BC，∠BAD＝∠ABC＝∠DCB＝90°，在△ABF和△DCE中，，∴△ABF≌△DCE（SAS），∴∠DEC＝∠AFB，∵EB＝CF，BN＝CN，∴N为EF的中点，∴MN为△AEF的中位线，∴MN∥AF，∴∠HNB＝∠AFB＝∠HEB；（3）解：过点B作BQ⊥BP交DE于Q，如图2所示：则∠PBQ＝90°，∵∠ABE＝180°﹣∠ABC＝90°，∴∠EBQ＝∠ABP，∵AD∥BC，∴∠ADP＝∠BEQ，∵AP⊥DE，∠BAD＝90°，由角的互余关系得：∠BAP＝∠ADP，∴∠BEQ＝∠BAP，在△BEQ和△BAP中，，∴△BEQ≌△BAP（ASA），∴PA＝QE，QB＝PB，∴△PBQ是等腰直角三角形，∴PQ＝PB，∴＝＝．。

人教版八年级下册数学平行四边形证明题专题训(带答案)

人教版八年级下册数学平行四边形证明题专题训练1．ABCD 中，点E 、F 是AC 上的两点，并且AE CF =．求证：四边形BFDE 是平行四边形．2．如图，矩形ABCD 的对角线AC ，BD 相交于点O ，且//,//DE AC CE BD ．求证：四边形OCED 是菱形．3．如图，在ABC 中，90CAB ∠=︒，DE ，DF 是ABC 的中位线，连接EF ，AD ．求证：EF AD =．4．如图，将▱AECF 的对角线EF 向两端延长，分别至点B 和点D ，且使EB ＝FD ．求证：四边形ABCD 为平行四边形．5．如图，在四边形ABCD 中，AB CD =，BE DF =；AE BD ⊥，CF BD ⊥，垂足分别为E ，F ．（1）求证：ABE △≌CDF ；（2）若AC 与BD 交于点O ，求证：AO CO =．6．如图，在ABCD中，点E，F分别在AD、BC上，且AE CF=，连接EF，AC交于点O．求证：OE OF=．7．已知：如图，矩形ABCD中，O是AC与BD的交点，过O点的直线EF与AB、CD的延长线分别相交于点E、F．（1）求证：△BOE≌△DOF；（2）当EF与AC满足什么关系时，以A、E、C、F为顶点的四边形是菱形？并给出证明．8．如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于F，且AF ＝BD，连接BF．（1）求证：D是BC的中点（2）如果AB＝AC，试判断四边形AFBD的形状，并证明你的结论．AC，连接CE、OE，连接AE交9．如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DE∥AC且DE＝12OD于点F．（1）求证：OE＝CD；（2）若菱形ABCD的边长为2，∠ABC＝60°，求AE的长．10．如图，在矩形ABCD中，AB＝6，BC＝10，点E在边CD上，连接AE，将四边形ABCE沿直线AE折叠，得''，且B C''恰好经过点D．到多边形AB C E（1）线段DC′的长度；（2）求ADE的面积．11．如图，在四边形ABCD中，AB＝CD，BF＝DE，AE⊥BD，CF⊥BD，垂足分别为E、F．（1）求证：△ABE≌△CDF；（2）若AC与BD交于点O，求证：AO＝CO．12．如图将矩形ABCD沿对角线AC对折,使△ABC落在△ACE的位置,且CE与AD相交于点F,求证:EF=DF.13．如图，在四边形ABCD中，AB＝AD，CB＝CD，E是CD上一点，BE交AC于点F，连接DF.(1)求证：∠BAC＝∠DAC，∠AFD＝∠CFE；(2)若AB∥CD，试证明四边形ABCD是菱形；(3)在(2)的条件下，试确定E点的位置，使∠EFD＝∠BCD，并说明理由．14．如图，在四边形ABCD中，AB=AD，CB=CD，E是CD上一点，BE交AC于F，连接DF，（1）证明：∠BAC=∠DAC．（2）若∠BEC=∠ABE，试证明四边形ABCD是菱形．15．如图，在ABCD中，过点D作DE AB=，连接AF，BF．⊥于点E，点F在边CD上，CF AE（1）求证：四边形BFDE是矩形；AD=，求DC的长度．（2）已知60∠=︒，AF是DABDAB∠的平分线，若316．如图，在▱ABCD中，对角线AC、BD交于点O，E是BD延长线上的点，且△ACE是等边三角形．（1）求证：四边形ABCD是菱形．（2）若∠AED＝2∠EAD，求证：四边形ABCD是正方形．17．如图，DE是△ABC的中位线，延长DE至F，使EF＝DE，连接BF．（1）求证：四边形ABFD是平行四边形；（2）求证：BF＝DC．18．如图，在□ABCD中，分别以AD、BC为边向内作等边△ADE和等边△BCF，连接BE、DF．求证：四边形BEDF 是平行四边形．19．如图，在△ABC中，点D为边BC的中点，点E在△ABC内，AE平分∠BAC，CE⊥AE点F在AB上，且BF=DE（1）求证：四边形BDEF 是平行四边形（2）线段AB ，BF ，AC 之间具有怎样的数量关系？证明你所得到的结论20．如图，在矩形ABCD 中，8AB cm =，16BC cm =，点P 从点D 出发向点A 运动，运动到点A 停止，同时，点Q 从点B 出发向点C 运动，运动到点C 即停止，点P 、Q 的速度都是1/cm s ．连接PQ 、AQ 、CP ．设点P 、Q 运动的时间为ts ．（1）当t 为何值时，四边形ABQP 是矩形；（2）当t 为何值时，四边形AQCP 是菱形；（3）分别求出（2）中菱形AQCP 的周长和面积．参考答案：1．证明：如图，连接,BD 交AC 于,OABCD ,,,OA OC OB OD ∴==,AE CF =,OA AE OC CF ∴-=-,OE OF ∴=∴四边形BFDE 是平行四边形．2．∵////DE AC CE BD ，，∴四边形OCED 是平行四边形．∵矩形ABCD 的对角线AC ，BD 相交于点O ，∴OC=OD ，∴四边形OCED 是菱形．3．证明：∵DE 、DF 是△ABC 的中位线，∴DE ∥AB ，DF ∥AC ，∴四边形DEAF 是平行四边形，∵∠CAB ＝90°，∴四边形DEAF 是矩形，∴EF ＝AD ．4．解：连接AC 交EF 于点O∵四边形AECF 为平行四边形∴OF OE =，OA OC =∵EB FD =∴OF FD OE EB +=+∴OD OB =∴四边形ABCD 为平行四边形5．【详解】（1）证明：∵AE BD ⊥，CF BD ⊥，∴90AEB CFD ∠=∠=︒，∵AB CD =，BE DF =，∴ABE △≌CDF ．（2）由（1）ABE △≌CDF ，∴AE CF =，∵AE BD ⊥，CF BD ⊥，∴90AEO CFO ∠=∠=︒，∵AOE COF ∠=∠，∴()AEO CFO AAS ≌∴AO CO =．6．证明：四边形ABCD 是平行四边形，//AD BC ∴，AEO CFO在AOE △和COF 中AOE COF AEO CFO AE CF ∠=∠⎧⎪∴∠=∠⎨⎪=⎩AOE COF ∴≅OE OF ∴=．7．（1）证明：∵四边形ABCD 是矩形，∴OB =OD ，∵AE //CF ，∴∠E =∠F ，∠OBE =∠ODF ，在△BOE 与△DOF 中，E F OBE ODF OB OD ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△BOE ≌△DOF （AAS ）；（2）当EF ⊥AC 时，四边形AECF 是菱形．证明：∵△BOE ≌△DOF ，∴OE =OF ，∵四边形ABCD 是矩形，∴OA =OC ，∴四边形AECF 是平行四边形，∵EF ⊥AC ，∴四边形AECF 是菱形．8．证明：（1）∵AF ∥BC ，∴∠AFE =∠DCE ，∵E 是AD 的中点，∴AE =DE ，∵∠AFE ＝∠DCE ， ∠AEF ＝∠DEC ，AE ＝DE ，∴△AEF≌△DEC（AAS），∴AF=DC，∵AF=BD，∴BD=CD，∴D是BC的中点；（2）四边形AFBD是矩形．理由：∵AB=AC，D是BC的中点，∴AD⊥BC，∴∠ADB=90°，∵AF=BD，过A点作BC的平行线交CE的延长线于点F，即AF∥BC，∴四边形AFBD是平行四边形，又∵∠ADB=90°，∴四边形AFBD是矩形．9．（1）∵四边形ABCD是菱形，∴OC＝1AC，AC⊥BD，2AC，∵DE＝12∴DE＝OC，∵DE∥AC，∴四边形OCED是平行四边形．∵AC⊥BD，∴平行四边形OCED是矩形．∴OE＝CD．（2）∵在菱形ABCD中，∠ABC＝60°，∴△ABC是等边三角形，∴AC＝AB＝2，AC=1，AC⊥BD，AD=2，∵OA=12∴OD=∴在矩形OCED 中，CE ＝OD∴在Rt △ACE 中，AE10．解：（1）∵四边形ABCD 是矩形∴AD=BC=10，AB=CD=6，∠B=∠C=90°∵将四边形ABCE 沿直线AE 折叠，得到多边形AB′C′E ， ∴AB=AB'=6，CE=C'E ，B'C'=BC=10，∠B'=∠B=90°，∠C=∠C'=90°∵8∴C'D=B'C'-B'D=2，（2）设DE=x ，则EC′=6-x ，由（1）可知∠C'=90°，C'D=2∴在Rt △C′DE 中，222(6)2x x -+=，解得：103x =∴ADE 的面积为111050102233AD DE ⋅=⨯⨯= 11．证明：（1）∵BF=DE ，∴BF EF DE EF -=-，即BE=DF ，∵AE ⊥BD ，CF ⊥BD ，∴∠AEB=∠CFD=90°，在Rt △ABE 与Rt △CDF 中，AB CD BE DF=⎧⎨=⎩, ∴Rt ABE Rt CDF ∆∆≌（HL ）；（2）如图，连接AC 交BD 于O ，∵Rt ABE Rt CDF ∆∆≌，∴ABE CDF ∠=∠，∴//D AB C ，∵=D AB C ，∴四边形ABCD 是平行四边形，∴AO CO =．12．∵四边形ABCD 是矩形，∴∠D =∠E ，AE =CD ，又∵∠AFE =∠CFD ，在△AEF 和△CDF 中，E D AFE CFD AE CD ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△AEF ≌△CDF (AAS )，∴EF =DF .13．(1)证明：在△ABC 和△ADC 中，AB AD CB CD AC AC =⎧⎪=⎨⎪=⎩∴△ABC ≌△ADC(SSS)，∴∠BAC=∠DAC ，在△ABF 和△ADF 中,AB AD BAF DAF AF AF =⎧⎪∠=∠⎨⎪=⎩∴△ABF ≌△ADF(SAS)，∴∠AFB=∠AFD ，∵∠CFE=∠AFB ，∴∠AFD=∠CFE ，∴∠BAC=∠DAC，∠AFD=∠CFE；(2)证明：∵AB∥CD，∴∠BAC=∠ACD，∵∠BAC=∠DAC，∴∠BAC=∠ACD，∴∠DAC=∠ACD，∴AD=CD，∵AB=AD，CB=CD，∴AB=CB=CD=AD，∴四边形ABCD是菱形；(3)BE⊥CD时，∠BCD=∠EFD；理由如下：∵四边形ABCD是菱形，∴BC=CD，∠BCF=∠DCF，∵CF=CF，∴△BCF≌△DCF，∴∠CBF=∠CDF，∵BE⊥CD，∴∠BEC=∠DEF=90°，∴∠BCD=∠EFD.14．（1）在△ABC和△ADC中，∵AB=AD，CB=CD，AC=AC，∴△ABC≌△ADC，∴∠BAC=∠DAC，在△ABF和△ADF中，∵AB=AD，∠BAC=∠DAC，AF=AF，∴△ABF≌△ADF，∴∠AFB=∠AFD．（2）证明：∵AB∥CD，∴∠BAC=∠ACD，∵∠BAC=∠DAC ，∴∠ACD=∠CAD ，∴AD=CD ，∵AB=AD ，CB=CD ，∴AB=CB=CD=AD ，∴四边形ABCD 是菱形．15．解：（1）证明：四边形ABCD 是平行四边形， //DC AB ∴，DC AB =，CF AE =，DF BE ∴=且//DC AB ，∴四边形DFBE 是平行四边形，又DE AB ⊥，∴四边形DFBE 是矩形；（2）60DAB ∠=︒，3AD =，DE AB ⊥，32AE ∴=，DE =四边形DFBE 是矩形，BF DE ∴==AF 平分DAB ∠，1302FAB DAB ∴∠=∠=︒，且BF AB ⊥， 92AB ∴==， 92CD ∴=． 16．证明：（1）∵▱ABCD ，∴AO ＝OC ，∵△ACE 是等边三角形，∴EO ⊥AC （三线合一）即 BD ⊥AC ，∴▱ABCD是菱形；（2）∵△ACE是等边三角形，∠EAC＝60°由（1）知，EO⊥AC，AO＝OC∴∠AEO＝∠OEC＝30°，△AOE是直角三角形∴∠EAO＝60°，∵∠AED＝2∠EAD，∴∠EAD＝15°，∴∠DAO＝∠EAO﹣∠EAD＝45°，∵▱ABCD是菱形，∴∠BAD＝2∠DAO＝90°，∴菱形ABCD是正方形．17．（1）∵DE是△ABC的中位线，∴DE∥AB，AB=2DE，AD=CD，∵EF=DE，∴DF=2DE，∴AB=DF，且AB∥DF，∴四边形ABFD是平行四边形；（2）∵四边形ABFD是平行四边形，∴AD=BF，且AD=CD，∴BF=DC．18．证明：∵四边形ABCD是平行四边形，∴CD=AB，AD=CB，∠DAB=∠BCD，又∵△ADE和△CBF都是等边三角形，∴DE=BF，AE=CF，∠DAE=∠BCF=60°，∴∠BCD-∠BCF=∠DAB-∠DAE，即∠DCF=∠BAE，∴△DCF≌△BAE（SAS），∴DF=BE，∴四边形BEDF是平行四边形.19．（1）证明：延长CE 交AB 于点G∵AE ⊥CE∴90AEG AEC ︒∠=∠=在AEG ∆和AEC ∆GAE CAE AE AEAEG AEC ∠=∠⎧⎪=⎨⎪∠=∠⎩∴AEG ∆≅AEC ∆∴GE=EC∵BD=CD∴DE 为CGB ∆的中位线∴DE //AB∵DE=BF∴四边形BDEF 是平行四边形（2）1()2BF AB AC =- 理由如下：∵四边形BDEF 是平行四边形∴BF=DE∵D ，E 分别是BC ，GC 的中点∴BF=DE=12BG∵AEG ∆≅AEC ∆∴AG=AC BF=12（AB-AG ）=12（AB-AC ）．20．解：（1）在矩形ABCD 中，8AB cm =，16BC cm =， 16BC AD cm ∴==，8AB CD cm ==，由已知可得，BQ DP tcm ==，(16)AP CQ t cm ==-，在矩形ABCD 中，90B ∠=︒，//AD BC ，当BQ AP =时，四边形ABQP 为矩形，16t t ∴=-，得8t =，故当8t s =时，四边形ABQP 为矩形；（2）AP CQ =，//AP CQ ，∴四边形AQCP 为平行四边形，∴当AQ CQ =时，四边形AQCP 为菱形16t -时，四边形AQCP 为菱形，解得6t =，故当6t s =时，四边形AQCP 为菱形；（3）当6t s =时，16610AQ CQ CP AP cm ====-=，则周长为41040cm cm ⨯=；面积为210880cm cm cm ⨯=．。

人教版数学八年级下册：第十八章平行四边形专题练习(附答案)

第十八章平行四边形专题练习专题1平行四边形的证明思路类型1若已知(已证)四边形中边的关系(1)已知一组对边平行，可以证这一组对边相等或另一组对边平行；(2)已知一组对边相等，可以证这一组对边平行或另一组对边相等1．如图，在△ABC中，AB＝AC，点D在AB上，过点D作BC的平行线，与AC相交于点E，点F在BC上，EF＝EC.求证：四边形DBFE是平行四边形．2．如图，在▱ABCD中，点O是对角线AC，BD的交点，点E是边CD的中点，点F在BC的延长线上，且CF＝12BC，求证：四边形OCFE是平行四边形．3．如图，点B，E，C，F在一条直线上，已知AB∥DE，AC∥DF，BE＝CF，连接AD.求证：四边形ABED是平行四边形．4．如图，在▱ABCD中，分别以AD，BC为边向内作等边△ADE和等边△BCF，连接BE，DF.求证：四边形BEDF是平行四边形．5．如图，已知点D，E，F分别在△ABC的边BC，AB，AC上，且DE∥AF，DE＝AF，将FD延长到点G，使FG＝2DF，连接AG，则ED与AG互相平分吗？请说明理由．6．如图，在▱ABCD中，E，F分别是AD，BC的中点，AF与BE交于点G，CE与DF交于点H，求证：四边形EGFH是平行四边形．类型2若已知条件(已证结论)与对角线有关，则可以通过证明对角线互相平分得到平行四边形7．如图，▱ABCD的对角线相交于点O，直线EF经过点O，分别与AB，CD的延长线交于点E，F.求证：四边形AECF是平行四边形．8．如图，在▱ABCD 中，点O 是对角线AC 的中点，EF 过点O，与AD，BC 分别相交于点E，F，GH 过点O，与AB，CD 分别相交于点G，H，连接EG，FG，FH，EH.求证：四边形EGFH 是平行四边形．专题2与正方形有关的四个常考模型模型1正方形中相交垂线段问题——教材P68复习题T8的变式与应用1．如图，ABCD是一个正方形花园，E，F是它的两个门，且DE＝CF.要修建两条路BE和AF，这两条路等长吗？它们有什么位置关系？为什么？【探究】若去掉“DE＝CF”这一条件，将两个结论中的一个作为条件能推出另一个结论成立吗？(1)若已知BE＝AF，则BE⊥AF成立吗？正方形内，分别连接两组对边上任意两点，得到的两条线段(如：图1中的线段AF与BE，图2中的线段AF与EG，图3中的线段HF与EG)满足：若垂直，则相等．模型2正方形中过对角线交点的直角问题2．如图，正方形ABCD的对角线AC和BD相交于点O，O又是正方形A1B1C1O的一个顶点，OA1交AB于点E，OC1交BC于点F.(1)求证：△AOE≌△BOF；(2)如果两个正方形的边长都为a，那么这两个正方形重叠部分的面积等于多少？为什么？【变式1】如图，正方形ABCD的边长为4，点O在对角线DB上运动(不与点B，D重合)，连接OA，作OP⊥OA，交直线BC于点P.判断线段OA，OP的数量关系，并说明理由．【变式2】如图，将n个边长都为2的正方形按如图所示摆放，点A1，A2，…，A n分别是正方形的中心，则这n个正方形重叠部分的面积之和是( )A．n B．n－1 C．4(n－1) D．4n正方形ABCD中，O为两条对角线的交点，点E，F分别在AB，BC上．若∠EOF为直角，OE，OF分别与DA，AB的延长线交于点G，H，则△AOE≌△BOF，△AOG≌△BOH，△OGH是等腰直角三角形，且S四边形OEBF＝14S正方形ABCD.模型3正方形中三垂直全等模型——教材P69复习题T14的变式与应用3．正方形ABCD的边长为6，点P在对角线BD上，点E是线段AD上或AD的延长线上的一点，且PE⊥PC.(1)如图1，点E在线段AD上，求证：PE＝PC；(2)如图2，点E在线段AD的延长线上，请补全图形，并判断(1)中的结论是否仍然成立？请说明理由．模型4正方形中的半角模型4．如图，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF＝BE.(1)求证：CE＝CF；(2)若点G在AD上，且∠GCE＝45°，则GE＝BE＋GD成立吗？为什么？(1)如图，正方形ABCD中，若∠EAF＝45°，则：①EF＝BE＋DF；②△CEF的周长为正方形ABCD边长的2倍；③FA平分∠DFE，EA平分∠BEF.(2)如图，正方形ABCD中，若∠EAF＝45°，FA平分∠DFE，则EF＝DF－BE.专题3特殊平行四边形的性质与判定1．如图，在菱形ABCD中，点P是BC边上一点，连接AP，点E，F是AP上的两点，连接DE，BF，使得∠AED＝∠ABC，∠ABF＝∠BPF.求证：(1)△ABF≌△DAE；(2)DE＝BF＋EF.2．如图，四边形ABCD，BEFG均为正方形，连接AG，CE.求证：(1)AG＝CE；(2)AG⊥CE.3．如图，在菱形ABCD中，AB＝2，∠DAB＝60°，点E是AD边的中点，点M是AB 边上一点(不与点A重合)，延长ME交射线CD于点N，连接MD，AN.(1)求证：四边形AMDN是平行四边形；(2)请求出AM的长为何值时，四边形AMDN是矩形，并说明理由．4.已知：如图，四边形ABCD四条边上的中点分别为E，F，G，H，顺次连接EF，FG，GH，HE，得到四边形EFGH(即四边形ABCD的中点四边形)．(1)四边形EFGH的形状是，证明你的结论；(2)当四边形ABCD的对角线满足条件时，四边形EFGH是矩形；(3)你学过的哪种特殊四边形的中点四边形是矩形？．5．如图，在矩形ABCD中，点E在边CD上，将△BCE沿BE折叠，点C落在AD边上的点F处，过点F作FG∥CD交BE于点G，连接CG.(1)求证：四边形CEFG是菱形；(2)若AB＝6，AD＝10，求四边形CEFG的面积．6．如图所示，在▱ABCD中，E，F分别是AB，CD的中点，AF与DE相交于点G，CE与BF相交于点H.(1)你能说明四边形EHFG是平行四边形吗？(2)当四边形ABCD满足什么条件时，四边形EHFG是一个菱形？(3)四边形EHFG会成为一个正方形吗？专题4四边形中的动点问题——教材P68复习题T13的变式与应用【例】如图，在四边形ABCD中，AD∥BC，∠B＝90°，AB＝8 cm，AD＝12 cm，BC ＝18 cm，点P从点A出发，以1 cm/s的速度向点D运动；点Q从点C同时出发，以2 cm/s 的速度向点B运动．规定其中一个动点到达端点时，另一个动点也随之停止运动．设点P，Q运动的时间为t s.(1)CD边的长度为cm，t的取值范围为；(2)从运动开始，当t取何值时，PQ∥CD?(3)从运动开始，当t取何值时，PQ＝CD?【拓展变式1】在整个运动过程中是否存在t值，使得四边形PQCD是菱形？若存在，请求出t值；若不存在，请说明理由．【拓展变式2】从运动开始，当t取何值时，四边形PQBA是矩形？【拓展变式3】在整个运动过程中是否存在t值，使得四边形PQBA是正方形？若存在，请求出t值；若不存在，请说明理由．【拓展变式4】是否存在t，使得△DQC是等腰三角形？若存在，请求出t值；若不存在，请说明理由．专题5特殊平行四边形中的折叠问题——教材P64“数学活动”的变式与应用【例】如图1，对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展平；再次折叠纸片，使点A落在EF上，并使折痕经过点B，得到折痕BM，同时得到线段BN，MN.请你观察图1，猜想∠MBN的度数是多少，并证明你的结论．图1【拓展延伸】再沿MN所在的直线折叠，点B落在AD上的点B′处，得到折痕MG，同时得到线段B′G，展开如图2.探究四边形MBGB′的形状，并证明你的结论．图2在折叠问题中，原图形与折叠后图形中所隐含的相等线段与相等角常常是解决问题的关键，注意翻折变换的性质的灵活运用，折叠前后，重叠部分是全等形，另外注意勾股定理等知识在求折叠图形的线段中的适当运用．1．如图，将矩形ABCD 折叠，使点C 和点A 重合，折痕为EF ，EF 与AC 交于点O.若AE ＝5，BF ＝3，则AO 的长为( )A . 5B .32 5 C ．2 5 D ．452．如图，将边长为6 cm 的正方形纸片ABCD 折叠，使点D 落在AB 边中点E 处，点C 落在点Q 处，折痕为FH ，则线段AF 的长是 cm .3．如图，将一张菱形纸片ABCD 的四个角向内折起，恰好拼成一个无缝隙无重叠的四边形EFGH.若EF ＝4，EH ＝3，则AB ＝．4．如图，在矩形ABCD 中，AB>AD ，把矩形沿对角线AC 所在直线折叠，使点B 落在点E 处，AE 交CD 于点F ，连接DE.求证： (1)△ADE ≌△CED ； (2)△DEF 是等腰三角形．专题6特殊平行四边形中的最值问题【例】如图，正方形ABCD的边长为4，E为BC上的一点，BE＝1，F为AB的中点，P 为AC上一个动点，求PF＋PE的最小值．【思路点拨】(1)先确定点P的位置：作点E关于AC的对称点E′，连接FE′，交AC于点P，则点P即为所求；(2)求E′F的长度：将E′F放到一个直角三角形中，利用勾股定理求出E′F的长，即求出了PF＋PE的最小值．求线段和最小时，若已知的两点在动点所在直线的同侧，将动点所在直线当作对称轴，作出其中一点的对称点，再将另一点与这个对称点连接，则其与直线的交点即为所求动点所在位置，再求出所连接的线段长即为所求．1．如图，菱形ABCD的边长为2，∠DAB＝60°，点E为BC边的中点，点P为对角线AC上一动点，则PB＋PE的最小值为．2．如图，在矩形ABCD 的边AD 上找一点P ，使得点P 到B ，C 两点的距离之和最短，则点P 的位置应该在．3．如图，四边形ABCD 是菱形，AB ＝8，且∠ABC ＝60°，M 为对角线BD(不含B 点)上任意一点，则AM ＋12BM 的最小值为．4．如图，以边长为2的正方形的对角线的交点O 为端点，引两条相互垂直的射线，分别与正方形的边交于A ，B 两点，求线段AB 的最小值．参考答案：专题1 平行四边形的证明思路1．证明：∵AB ＝AC ，∴∠B ＝∠C. ∵EF ＝EC ，∴∠EFC ＝∠C. ∴∠B ＝∠EFC. ∴AB ∥EF. 又∵DE ∥BC ，∴四边形DBFE 是平行四边形．2．证明：∵四边形ABCD 是平行四边形， ∴点O 是BD 的中点．又∵点E 是边CD 的中点， ∴OE 是△BCD 的中位线． ∴OE ∥BC ，且OE ＝12BC.又∵CF ＝12BC ，∴OE ＝CF.又∵点F 在BC 的延长线上， ∴OE ∥CF.∴四边形OCFE 是平行四边形． 3．证明：∵AB ∥DE ，∴∠B ＝∠DEF. ∵AC ∥DF ，∴∠ACB ＝∠F.∵BE ＝CF ，∴BE ＋CE ＝CF ＋CE ，即BC ＝EF. 在△ABC 和△DEF 中，⎩⎨⎧∠B ＝∠DEF ，BC ＝EF ，∠ACB ＝∠F ，∴△ABC ≌△DEF(ASA )．∴AB ＝DE. ∵AB ∥DE ，∴四边形ABED 是平行四边形．4．证明：∵四边形ABCD 是平行四边形， ∴CD ＝AB ，AD ＝CB ，∠DAB ＝∠BCD. 又∵△ADE 和△BCF 都是等边三角形，∴DE ＝AD ＝AE ，CF ＝BF ＝BC ，∠DAE ＝∠BCF ＝60°. ∴BF ＝DE ，CF ＝AE.∵∠DCF ＝∠BCD －∠BCF ，∠BAE ＝∠DAB －∠DAE ， ∴∠DCF ＝∠BAE. 在△DCF 和△BAE 中，⎩⎨⎧CD ＝AB ，∠DCF ＝∠BAE ，CF ＝AE ，∴△DCF ≌△BAE(SAS )． ∴DF ＝BE. 又∵BF ＝DE ，∴四边形BEDF 是平行四边形． 5．解：ED 与AG 互相平分．理由：连接EG ，AD. ∵DE ∥AF ，DE ＝AF ， ∴四边形AEDF 是平行四边形． ∴AE ∥DF ，AE ＝DF. 又∵FG ＝2DF ， ∴DG ＝DF. ∴AE ＝DG. 又∵AE ∥DG ，∴四边形AEGD 是平行四边形． ∴ED 与AG 互相平分．6．证明：∵四边形ABCD 是平行四边形， ∴AD ∥BC ，AD ＝BC.∵E ，F 分别是AD ，BC 的中点， ∴AE ＝12AD ，FC ＝12BC.∴AE ∥FC ，AE ＝FC.∴四边形AECF 是平行四边形． ∴GF ∥EH.同理可证：ED ∥BF 且ED ＝BF. ∴四边形BFDE 是平行四边形． ∴GE ∥FH.∴四边形EGFH 是平行四边形．7．证明：∵四边形ABCD 是平行四边形， ∴OD ＝OB ，OA ＝OC ，AB ∥CD. ∴∠DFO ＝∠BEO ，∠FDO ＝∠EBO. 在△FDO 和△EBO 中，⎩⎨⎧∠DFO ＝∠BEO ，∠FDO ＝∠EBO ，OD ＝OB ，∴△FDO ≌△EBO(AAS)． ∴OF ＝OE . 又∵OA ＝OC ，∴四边形AECF 是平行四边形．8．证明：∵四边形ABCD 是平行四边形， ∴AD ∥BC. ∴∠EAO ＝∠FCO. ∵O 为AC 的中点， ∴OA ＝OC.在△OAE 和△OCF 中，⎩⎨⎧∠EAO ＝∠FCO ，OA ＝OC ，∠AOE ＝∠COF ，∴△OAE ≌△OCF(ASA )． ∴OE ＝OF.同理可证：OG ＝OH.∴四边形EGFH 是平行四边形．专题2 与正方形有关的四个常考模型1．解：BE ＝AF 且BE ⊥AF ，理由： ∵四边形ABCD 是正方形，∴AB ＝AD ＝CD ，∠BAD ＝∠D ＝90°. 又∵DE ＝CF ，∴AE ＝DF. ∴△ABE ≌△DAF(SAS )． ∴BE ＝AF ，∠ABE ＝∠DAF.∵∠DAF ＋∠BAF ＝90°，∴∠ABE ＋∠BAF ＝90°. ∴∠AGB ＝90°，即BE ⊥AF.【探究】解：成立．理由：∵四边形ABCD 是正方形， ∴∠BAD ＝∠D ＝90°，AB ＝AD. 在Rt △ABE 和Rt △DAF 中，⎩⎨⎧AB ＝DA ，BE ＝AF ，∴Rt △ABE ≌Rt △DAF(HL )． ∴∠ABE ＝∠DAF.∵∠DAF ＋∠BAF ＝90°，∴∠ABE ＋∠BAF ＝90°.∴∠AGB ＝90°，即BE ⊥AF. (2)若已知BE ⊥AF ，则BE ＝AF 成立吗？解：成立．理由：∵四边形ABCD 是正方形， ∴AB ＝AD ，∠BAD ＝∠D ＝90°. 又∵BE ⊥AF ，∴∠AGB ＝90°. ∴∠ABE ＋∠BAF ＝90°.∵∠DAF ＋∠BAF ＝90°，∴∠ABE ＝∠DAF. ∴△ABE ≌△DAF(ASA )． ∴BE ＝AF.2．解：(1)证明：在正方形ABCD 中，AO ＝BO ，∠AOB ＝∠A 1OC 1＝90°，∠OAB ＝∠OBC ＝45°. ∴∠AOE ＋∠EOB ＝90°，∠BOF ＋∠EOB ＝90°. ∴∠AOE ＝∠BOF. 在△AOE 和△BOF 中，⎩⎨⎧∠OAE ＝∠OBF ，OA ＝OB ，∠AOE ＝∠BOF ，∴△AOE ≌△BOF(ASA )．(2)两个正方形重叠部分的面积等于14a 2.理由如下：∵△AOE ≌△BOF ，∴S 四边形OEBF ＝S △EOB ＋S △BOF ＝S △EOB ＋S △AOE ＝S △AOB ＝14S 正方形ABCD ＝14a 2.【变式1】解：OA ＝OP ，理由：过点O 作OG ⊥AB 于点G ，过点O 作OH ⊥BC 于点H ，∵四边形ABCD 是正方形， ∴∠ABO ＝∠CBO ，AB ＝BC. ∴OG ＝OH.∵∠OGB ＝∠GBH ＝∠BHO ＝90°， ∴四边形OGBH 是正方形． ∴∠GOH ＝90°.∵∠AOP ＝∠GOH ＝90°，∴∠AOG ＝∠POH. ∴△AGO ≌△PHO(ASA )． ∴OA ＝OP. 【变式2】 B3．解：(1)证明：过点P 作FG ∥DC 分别交AD ，BC 于点F ，G. 易得∠PFD ＝∠CGP ＝90°. ∵BD 为正方形ABCD 的对角线， ∴∠BDF ＝∠FPD ＝45°. ∴PF ＝FD.又∵FG ∥DC ，FD ∥GC ，∠ADC ＝90°， ∴四边形FGCD 为矩形． ∴DF ＝CG. ∴PF ＝CG. ∵PE ⊥PC ，∴∠FPE ＋∠GPC ＝90°. ∵∠FEP ＋∠FPE ＝90°， ∴∠FEP ＝∠GPC. ∴在△PFE 和△CGP 中，⎩⎨⎧∠PFE ＝∠CGP ，∠FEP ＝∠GPC ，PF ＝CG ，∴△PFE ≌△CGP(AAS )． ∴PE ＝CP.(2)成立．理由：过点P 作FG ∥DC 分别交AD ，BC 于点F ，G. 同理可证△PFE ≌△CGP(AAS )． ∴PE ＝PC.4．解：(1)证明：∵四边形ABCD 是正方形， ∴BC ＝CD ，∠B ＝∠CDF.又∵BE ＝DF ，∴△CBE ≌△CDF(SAS )．∴CE ＝CF.(2)GE ＝BE ＋GD 成立．理由：由(1)得，△CBE ≌△CDF ，∴∠BCE ＝∠DCF.∴∠BCE ＋∠ECD ＝∠DCF ＋∠ECD ，即∠BCD ＝∠ECF ＝90°.又∵∠GCE ＝45°，∴∠GCF ＝∠GCE ＝45°.∵CE ＝CF ，∠GCE ＝∠GCF ，GC ＝GC ，∴△ECG ≌△FCG(SAS )．∴GE ＝GF.∴GE ＝DF ＋GD ＝BE ＋GD.专题3 特殊平行四边形的性质与判定1．证明：(1)∵四边形ABCD 是菱形，∴AB ＝AD ，AD ∥BC.∴∠BPF ＝∠DAE.∵∠ABC ＝∠AED ，∴∠BAF ＝∠ADE.∵∠ABF ＝∠BPF ，∴∠ABF ＝∠DAE.∵AB ＝DA ，∴△ABF ≌△DAE(ASA )．(2)∵△ABF ≌△DAE ，∴AE ＝BF ，DE ＝AF.∵AF ＝AE ＋EF ＝BF ＋EF ，∴DE ＝BF ＋EF.2．证明：(1)∵四边形ABCD ，BEFG 均为正方形，∴AB ＝CB ，∠ABC ＝∠GBE ＝90°，BG ＝BE.∴∠ABG ＝∠CBE.在△ABG 和△CBE 中，⎩⎨⎧AB ＝CB ，∠ABG ＝∠CBE ，BG ＝BE ，∴△ABG ≌△CBE(SAS )．∴AG ＝CE.(2)设AG 交BC 于点M ，交CE 于点N.∵△ABG ≌△CBE ，∴∠BAG ＝∠BCE.∵∠ABC ＝90°，∴∠BAG ＋∠AMB ＝90°.∵∠AMB ＝∠CMN ，∴∠BCE ＋∠CMN ＝90°.∴∠CNM ＝90°.∴AG ⊥CE.3．解：(1)证明：∵四边形ABCD 是菱形，∴ND ∥AM.∴∠NDE ＝∠MAE ，∠DNE ＝∠AME.又∵点E 是AD 边的中点，∴DE ＝AE.∴△NDE ≌△MAE(AAS )．∴ND ＝MA.∴四边形AMDN 是平行四边形．(2)当AM 的长为1时，四边形AMDN 是矩形．理由如下：∵AM ＝1＝12AD ＝AE ，∠DAB ＝60°， ∴△AEM 是等边三角形．∴∠AME ＝∠AEM ＝60°，EM ＝AE ＝ED.∴∠EMD ＝∠EDM ＝30°.∴∠AMD ＝∠AME ＋∠EMD ＝90°.∴四边形AMDN 是矩形．4.(1)四边形EFGH 的形状是平行四边形，证明你的结论；(2)当四边形ABCD 的对角线满足互相垂直条件时，四边形EFGH 是矩形；(3)你学过的哪种特殊四边形的中点四边形是矩形？菱形．证明：连接BD.∵E ，H 分别是AB ，AD 中点，∴EH ∥BD ，EH ＝12BD. 同理FG ∥BD ，FG ＝12BD ， ∴EH ∥FG ，EH ＝FG.∴四边形EFGH 是平行四边形．5．解：(1)证明：由题意得△BCE ≌△BFE ，∴∠BEC ＝∠BEF ，FE ＝CE.∵FG ∥CE ，∴∠FGE ＝∠BEC.∴∠FGE ＝∠BEF.∴FG ＝FE.∴FG ＝EC.∴四边形CEFG 是平行四边形．又∵CE ＝FE ，∴四边形CEFG 是菱形．(2)∵矩形ABCD 中，AB ＝6，AD ＝10，BC ＝BF ，∴∠BAF ＝90°，AD ＝BC ＝BF ＝10.∴AF ＝BF 2－AB 2＝8.∴DF ＝2.设EF ＝x ，则CE ＝x ，DE ＝6－x.∵∠FDE ＝90°，∴22＋(6－x)2＝x 2.解得x ＝103.∴CE ＝103. ∴S 四边形CEFG ＝CE·DF ＝103×2＝203. 6．解：(1)能说明四边形EHFG 是平行四边形．∵四边形ABCD 是平行四边形，∴AB 綊CD.而AE ＝12AB ，CF ＝12CD ， ∴AE 綊CF.∴四边形AECF 是平行四边形．∴GF ∥EH.同理可得GE ∥HF.∴四边形EHFG 是平行四边形．(2)当四边形ABCD 是矩形时，四边形EHFG 是菱形．由(1)知，四边形EHFG 是平行四边形．连接EF.当四边形ABCD 是矩形时，四边形EBCF 也是矩形，∴EH ＝FH ，∴四边形EHFG 是菱形．(3)当四边形ABCD 是矩形且AB ＝2AD 时，四边形EHFG 是正方形．由(2)知，当四边形ABCD 是矩形时，四边形EHFG 是菱形．又由AB ＝2AD 可知，四边形EBCF 是正方形．根据正方形的性质知，EC⊥BF，即∠EHF＝90°，∴四边形EHFG是正方形．专题4四边形中的动点问题【例】(1)CD边的长度为10cm，t的取值范围为0≤t≤9；解：(2)设经过t s时，PQ∥CD，此时四边形PQCD为平行四边形，则PD＝CQ.∵PD＝(12－t)cm，CQ＝2t cm，∴12－t＝2t.∴t＝4.∴当t＝4时，PQ∥CD.(3)设经过t s时，PQ＝CD，分别过点P，D作BC边的垂线PE，DF，垂足分别为E，F.当CF＝EQ时，四边形PQCD为梯形(腰相等)或者平行四边形．∵∠B＝∠A＝∠DFB＝90°，∴四边形ABFD是矩形．∴AD＝BF.∵AD＝12 cm，BC＝18 cm，∴CF＝BC－BF＝6 cm.①当四边形PQCD为梯形(腰相等)时，PD＋2(BC－AD)＝CQ，∴(12－t)＋12＝2t.∴t＝8.∴当t＝8时，PQ＝CD；②当四边形PQCD为平行四边形时，由(2)知当t＝4 s时，PQ＝CD.综上，当t＝4或t＝8时，PQ＝CD.【拓展变式1】解：不存在．理由：要使四边形PQCD是菱形，则四边形PQCD一定是平行四边形．由例知当t＝4 s时，四边形PQCD是平行四边形．此时DP＝12－t＝8≠10，即DP≠DC，所以按已知速度运动，四边形PQCD只能是平行四边形，不可能是菱形．【拓展变式2】解：如图，由题意，得AP ＝t ，DP ＝12－t ，CQ ＝2t ，BQ ＝18－2t.要使四边形PQBA 是矩形，已有∠B ＝90°，AD ∥BC ，即AP ∥BQ ，只需满足AP ＝BQ ，即t ＝18－2t ，解得t ＝6.所以当t ＝6时，四边形PQBA 是矩形．【拓展变式3】解：不存在．理由：要使四边形PQBA 是正方形，则四边形PQBA 一定是矩形．由变式2知，当t ＝6时，四边形PQBA 是矩形．此时AP ＝t ＝6≠8，即AP ≠AB ，所以按已知速度运动，四边形PQBA 只能是矩形，不可能是正方形．【拓展变式4】解：△DQC 是等腰三角形时，分三种情况讨论：图1 图2 图3①如图1，当QC ＝DC 时，即2t ＝10，∴t ＝5.②如图2，当DQ ＝DC 时，过点D 作DH ⊥CQ ，则QH ＝CH ＝12CQ ＝t. 在矩形ABHD 中，BH ＝AD ＝12，∴CH ＝BC －BH ＝6，∴t ＝6.③如图3，当QD ＝QC 时，过点D 作DH ⊥CQ ，DH ＝8，CH ＝6，DC ＝10，CQ ＝QD ＝2t ，QH ＝|2t －6|.在Rt △DQH 中，DH 2＋QH 2＝DQ 2.∴82＋|2t －6|2＝(2t)2.解得t ＝256. 综上，当t ＝5或6或256时，△DQC 是等腰三角形专题5 特殊平行四边形中的折叠问题【例】解：∠MBN ＝30°.证明：连接AN .∵直线EF 是AB 的垂直平分线，点N 在EF 上，∴AN ＝BN .由折叠可知，BN ＝AB ，∴△ABN 是等边三角形．∴∠ABN ＝60°.∴∠MBN ＝∠ABM ＝12∠ABN ＝30°. 【拓展延伸】解：四边形MBGB′是菱形．证明：∵∠ABM ＝30°，∠A ＝∠ABC ＝90°，∴∠MBG ＝∠AMB ＝60°.根据折叠的性质，得BM ＝MB′，BG ＝B′G ，∠BMN ＝∠AMB.∴∠BMN ＝∠MBG ＝60°.∴△MBG 是等边三角形．∴BM ＝BG.∴BM ＝MB′＝BG ＝B′G.∴四边形MBGB′是菱形．1．C2． 94cm . 3．5．4．证明：(1)由折叠相关性质可知，AE ＝AB ，CE ＝CB.∵四边形ABCD 是矩形，∴AE ＝AB ＝DC ，CE ＝CB ＝AD.在△ADE 和△CED 中，⎩⎨⎧AD ＝CE ，AE ＝CD ，DE ＝ED ，∴△ADE ≌△CED(SSS )．(2)由(1)知，△ADE ≌△CED ，∴∠AED ＝∠CDE.∴△DEF 是等腰三角形．小专题(十) 特殊平行四边形中的最值问题【例】解：作点E 关于直线AC 的对称点E′(易知点E′在CD 上)，连接E′F ，交AC 于点P.则PE ＝PE′，CE ′＝CE.∴PE ＋PF ＝PE′＋PF ＝E′F.∴P 即为所求的使PF ＋PE 最短的点．∵正方形ABCD 的边长为4，BE ＝1，F 为AB 的中点， ∴BF ＝2，CE ＝CB －BE ＝3.∴CE ′＝CE ＝3.过点F 作FG ⊥CD 于点G ，则∠FGE′＝∠FGC ＝90°. ∵四边形ABCD 是正方形，∴∠B ＝∠BCD ＝∠FGC ＝90°.∴四边形FBCG 是矩形．∴CG ＝BF ＝2，FG ＝BC ＝4.∴E ′G ＝E′C －CG ＝1.∴在Rt △E ′FG 中，E ′F ＝FG 2＋E′G 2＝42＋12＝17. ∴PF ＋PE 的最小值为17.12．AD 的中点．34．解：∵四边形CDEF 是正方形，∴∠OCA ＝∠ODB ＝45°，∠COD ＝90°，OC ＝OD. ∵AO ⊥OB ，∴∠AOB ＝90°.∴∠COA ＋∠AOD ＝90°，∠AOD ＋∠DOB ＝90°. ∴∠COA ＝∠DOB.在△COA 和△DOB 中，⎩⎨⎧∠OCA ＝∠ODB ，OC ＝OD ，∠COA ＝∠DOB ，∴△COA ≌△DOB(ASA )．∴OA ＝OB.∵∠AOB ＝90°，∴△AOB 是等腰直角三角形．由勾股定理，得AB ＝OA 2＋OB 2＝2OA ，要使AB 最小，只要OA 取最小值即可，根据垂线段最短，得OA ⊥CD 时，OA 最小，∵四边形CDEF 是正方形，∴OD ＝OC.又∵OA ⊥CD ，∴CA ＝DA.∴OA ＝12CF ＝1.∴AB ＝ 2.∴AB的最小值为 2.。

2020-2021学年人教版八年级数学下册第18章平行四边形解答题典型必练(一)

人教版八年级数学下册第18章《平行四边形》解答题典型必练（一）1．如图，点E在▱ABCD内部，AF∥BE，DF∥CE．（1）求证：△BCE≌△ADF；（2）设▱ABCD的面积为6，求四边形AEDF面积．2．如图，点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA（不包括端点）上运动，且满足AE＝CG，AH＝CF．（1）求证：四边形EFGH是平行四边形；（2）请探究四边形EFGH的周长一半与矩形ABCD一条对角线长的大小关系，并说明理由．3．如图，在正方形ABCD中，AC，BD相交于点O，E，F分别在OA，OD上，∠ABE ＝∠DCF．（1）求证：△ABE≌△DCF．（2）若BC＝4，AE＝3，求BE的长．4．如图，在正方形ABCD中，E是边AB上的一动点（不与点A，B重合），连接DE，点A关于直线DE的对称点为F，连接EF并延长交BC于点G，连接DG，过点E作EH⊥DE交DG的延长线于点H，连接BH．（1）直接写出GF与GC的数量关系：；（2）用等式表示线段BH与AE的数量关系，并证明．5．四边形ABCD是矩形，点P在边CD上，∠PAD＝30°，点G与点D关于直线AP对称，连接BG．（1）如图，若四边形ABCD是正方形，求∠GBC的度数；（2）连接CG，设AB＝a，AD＝b，探究当∠CGB＝120°时，a与b的数量关系．6．如图，在正方形ABCD中，点E为AB上的点（不与A，B重合），△ADE与△FDE 关于DE对称，作射线CF，与DE的延长线相交于点G，连接AG，（1）当∠ADE＝15°时，求∠DGC的度数；（2）若点E在AB上移动，请你判断∠DGC的度数是否发生变化，若不变化，请证明你的结论；若会发生变化，请说明理由；（3）如图2，当点F落在对角线BD上时，点M为DE的中点，连接AM，FM，请你判断四边形AGFM的形状，并证明你的结论．7．如图，在正方形ABCD中，点E为线段BC上一动点（点E不与点B、C重合），点B关于直线AE的对称点为F，作射线EF交CD于H，连接AF．（1）求证：AF⊥EH；（2）连接AH，小王通过观察、实验，提出猜想：点E在运动过程中，∠EAH的度数始终保持不变．你帮助小王求出∠EAH的度数．8．如图，正方形ABCD中，点E是BC延长线上一点，连接DE，过点B作BF⊥DE于点F，连接FC．（1）求证：∠FBC＝∠CDF；（2）作点C关于直线DE的对称点G，连接CG，FG，猜想线段DF，BF，CG之间的数量关系，并证明你的结论．9．已知AP为正方形ABCD外的一条射线，B′为点B关于直线AP的对称点，连接B′D．如图1所示．（1）如果∠BAP＝20°，求∠ADB′的度数的大小．（2）如图2所示，M为射线B′B上一点，且∠BMC＝135°．①求证：BB′＝CM．②求证：CM∥B′D．10．在正方形ABCD外侧作直线AP，点B关于直线AP的对称点为E，连接BE，DE，其中DE交直线AP于点F．（1）依题意补全图1；图2；（2）若∠PAB＝25°，求∠ADF的度数；（3）如图2，若45°＜∠PAB＜90°，用等式表示线段AB，FE，FD之间数量关系，并证明．11．如图，已知正方形ABCD边长为1，点P是射线AD的上的一个动点，点A关于直线BP的对称点是点Q，设AP＝x．（1）求当D，Q，B三点在同一直线上时对应的x的值．（2）当△CDQ为等腰三角形时，求x的值．12．在正方形ABCD中，点P是射线CB上一个动点．连接PA，PD，点M，N分别为BC，AP的中点，连接MN交PD于点Q．（1）如图1，当点P在线段CB的延长线上时，请判断△QPM的形状，并说明理由．（2）如图2，正方形的边长为4，点P'与点P关于直线AB对称，且点P'在线段BC上．连接AP'，若点Q恰好在直线AP'上，求P'M的长．13．如图，在边长为6的正方形ABCD中，G是边BC的中点，点C关于直线DG的对称点为F，连接GF并延长交AB于点E，过点E作EH⊥DE交DG的延长线于点H，连接BH．（1）求证：△ADE≌△FDE；（2）求AE的长；（3）求BH的长；14．如图，经过正方形ABCD的顶点A在其外侧作直线AP，点B关于直线AP的对称点为E，连接BE、DE，其中DE交直线AP于点F．（1）依题意补全图1．（2）若∠PAB＝30°，求∠ADF的度数．（3）如图，若45°＜∠PAB＜90°，用等式表示线段AB，FE，FD之间的数量关系，并证明．15．在小学，我们已经初步了解到，正方形的每个角都是90°，每个边都是相等．如图，在正方形ABCD外侧作直线AQ，点D关于直线AQ的对称点为E，连接DE、BE，BE交AD于点F，若∠QAD＝15°．（1）求∠ABE的度数；（2）若AB＝6，求AF的长．参考答案1．（1）证明：∵四边形ABCD是平行四边形，∴AD＝BC，AD∥BC，∴∠ABC+∠BAD＝180°，∵AF∥BE，∴∠EBA+∠BAF＝180°，∴∠CBE＝∠DAF，同理得∠BCE＝∠ADF，在△BCE和△ADF中，，∴△BCE≌△ADF（ASA）；（2）解：∵点E在▱ABCD内部，，∴S△BEC+S△AED＝S▱ABCD由（1）知：△BCE≌△ADF，∴S△BCE＝S△ADF，∴S四边形AEDF＝S△ADF+S△AED＝S△BEC+S△AED＝S，▱ABCD ∵▱ABCD的面积为6，∴四边形AEDF的面积为3．2．（1）证明：∵四边形ABCD是矩形，∴∠A＝∠C．∴在△AEH与△CGF中，，∴△AEH≌△CGF（SAS），∴EH＝GF，同理证得△EBF≌△GDH，则EF＝GH，∴四边形EFGH是平行四边形；（2）解：四边形EFGH的周长一半大于或等于矩形ABCD一条对角线长度．理由如下：作G关于BC的对称点G′，连接EG′，可得EG′的长度就是EF+FG的最小值．连接AC，∵CG′＝CG＝AE，AB∥CG′，∴四边形AEG′C为平行四边形，∴EG′＝AC．在△EFG′中，∵EF+FG′＞EG′＝AC，∴四边形EFGH的周长一半大于或等于矩形ABCD一条对角线长度．3．证明：（1）∵四边形ABCD是正方形，∴AB＝CD，∠BAE＝∠CDF＝45°，∵∠ABE＝∠DCF，在△ABE与△DCF中，，∴△ABE≌△DCF（ASA）；（2）∵四边形ABCD是正方形，∴AB＝BC，OA＝OB＝OC＝OD，∠ABC＝∠AOB＝90°，∵BC＝4，∴AB＝4，∴AC＝，∴OA＝OB＝4，∵AE＝3，∴OE＝OA﹣AE＝4﹣3＝1，在Rt△BOE中，BE＝．4．证明：（1）如图1，连接DF，∵四边形ABCD是正方形，∴DA＝DC，∠A＝∠C＝90°，∵点A关于直线DE的对称点为F，∴△ADE≌△FDE，∴DA＝DF＝DC，∠DFE＝∠A＝90°，∴∠DFG＝90°，在Rt△DFG和Rt△DCG中，，∴Rt△DFG≌Rt△DCG（HL），∴GF＝GC；（2）BH＝AE，理由是：证法一：如图，在线段AD上截取AM，使AM＝AE，∵AD＝AB，∴DM＝BE，由（1）知：∠ADE＝∠EDF，∠FDG＝∠GDC，∵∠ADC＝90°，∴∠ADE+∠EDF+∠FDG+∠GDC＝90°，∴2∠EDF+2∠FDG＝90°，∴∠EDF+∠FDG＝45°，即∠EDG＝45°，∵EH⊥DE，∴∠DEH＝90°，∴△DEH是等腰直角三角形，∴∠AED+∠BEH＝∠AED+∠ADE＝90°，DE＝EH，∴∠ADE＝∠BEH，在△DME和△EBH中，，∴△DME≌△EBH（SAS），∴EM＝BH，Rt△AEM中，∠A＝90°，AM＝AE，∴EM＝AE，∴BH＝AE；证法二：如图，过点H作HN⊥AB于N，∴∠ENH＝90°，由方法一可知：DE＝EH，∠1＝∠NEH，在△DAE和△ENH中，，∴△DAE≌△ENH（AAS），∴AE＝HN，AD＝EN，∵AD＝AB，∴AB＝EN＝AE+BE＝BE+BN，∴AE＝BN＝HN，∴△BNH是等腰直角三角形，∴BH＝HN＝AE．5．解：（1）连接DG，交AP于点E，连接AG，如图1，∵点G与点D关于直线AP对称，∴AP垂直平分DG，∴AD＝AG．∵在△ADG中，AD＝AG，AE⊥DG，∴∠PAG＝∠PAD＝30°，又∵在正方形ABCD中，AD＝AB，∠DAB＝∠ABC＝90°，∴AG＝AB，∠GAB＝∠DAB﹣∠PAD﹣∠PAG＝30°，∴在△GAB中，∠ABG＝∠AGB＝＝75°，∴∠GBC＝∠ABC﹣∠ABG＝15°；（2）连接DG，AG．由（1）可知，在△ADG中，AD＝AG，∠DAG＝∠PAD+∠PAG＝60°，∴△ADG是等边三角形，∴DG＝AG＝AD，∠DAG＝∠ADG＝∠DGA＝60°，又∵在矩形ABCD中，AB＝DC，∠DAB＝∠ADC＝∠ABC＝90°，∴∠DAB﹣∠DAG＝∠ADC﹣∠ADG，即∠GAB＝∠GDC＝30°，∴△GAB≌△GDC（SAS），∴GB＝GC．当∠CGB＝120°时，点G可能在矩形ABCD的内部或外部．若点G在矩形ABCD的内部，∵在△BGC中，GB＝GC，∠CGB＝120°，∴∠GBC＝＝30°，∴∠GBA＝∠ABC﹣∠GBC＝90°﹣30°＝60°，在△ABG中，∠AGB＝180°﹣∠GAB﹣∠GBA＝90°，∴a＝b，若点G在矩形ABCD的外部，在△BGC中，∠GBC＝30°，∴∠ABG＝120°，又∵∠GAB＝30°，∴∠AGB＝180°﹣30°﹣120°＝30°．∴BA＝BG，过点B作BH⊥AG，垂足为H，∴AH＝AG＝b．在Rt△ABH中，∠AHB＝90°，∠HAB＝30°，∴cos∠HAB＝＝，∴a＝b，在Rt△ADP中，∠ADP＝90°，∠PAD＝30°，∴tan∠PAD＝＝，∴DP＝b．所以无论点G在矩形ABCD内部还是点G在矩形ABCD外部，都有DP≤DC，均符合题意．综上，当∠CGB＝120°时a与b的数量关系为a＝b或a＝b．6．解：（1）∵∠ADE＝15°，∴∠FDE＝15°，∠CDF＝60°．∵DC＝AD＝DF，∴∠CFD＝60°．又∠CFD＝∠DGC+∠FDE＝15°+∠DGC，∴∠DGC＝45°；（2）不变，理由如下：∵△ADE与△FDE关于DE对称，∴∠AGD＝∠DGF．设∠ADE＝x，可得∠FDE＝x，∠CDF＝90°﹣2x，∵DC＝AD＝DF，∴∠CFD＝45°+x．又∠CFD＝∠DGC+∠FDE＝x+∠DGC，∴∠DGC＝45°；（3）四边形AGFM是正方形；理由：∵∠DAE＝∠DFE＝90°，点M为DE的中点，∴AM＝FM＝DM＝DE，∴∠ADM＝∠DAM，∠MDF＝∠DFM，∴∠AME＝∠EMF＝2∠ADM＝2∠MDF＝45°，∴∠AMF＝90°，∵∠MGF＝45°，∴FM＝FG，在△ADG与△FDG中，，∴△ADG≌△FDG（SAS），∴AG＝FG，∴AM＝MF＝FG＝AG，∵∠AMF＝90°，∴四边形AGFM是正方形．7．解：（1）证明：∵点B关于直线AE的对称点为F，∴AB＝AF，BE＝EF，又∵AE＝AE，∴△ABE≌△AFE（SSS），∴∠AFE＝∠B＝90°，∴AF⊥EH；（2）连接AH，如图：由（1）得AB＝AF，AF⊥EH，∴AF＝AD，∠D＝∠AFH＝90°，AH＝AH，∴△AFH≌△ADH（HL），∴∠FAH＝∠DAH，又∵∠BAE＝∠FAE，在正方形ABCD中，∠BAD＝90°，∴∠EAH＝45°．8．解：（1）∵ABCD为正方形，∴∠DCE＝90°．∴∠CDF+∠E＝90°，又∵BF⊥DE，∴∠FBC+∠E＝90°，∴∠FBC＝∠CDF（2）如图所示：在线段FB上截取FM，使得FM＝FD．∵∠BDC＝∠MDF＝45°，∴∠BDM＝∠CDF，∴∠CFE＝∠FCD+∠CDF＝∠DBM+∠BDM＝∠DMF＝45°，∴∠EFG＝∠EFC＝45°，∴∠CFG＝90°，∵CF＝FG，∴CG＝CF，∴BM＝CG，∴BF＝BM+FM＝CG+DF．补充方法：连接GM，证明四边形BMGC是平行四边形即可．9．（1）解：连接AB'，如图1，∵B′为点B关于直线AP的对称点，∴AB＝AB'，∴∠BAP＝∠B'AP＝20°，∵四边形ABCD是正方形，∴AB＝AD，∴AB'＝AD，∴∠AB'D＝∠ADB'，∵∠B'AD＝∠B'AB+∠BAD＝90°+40°＝130°，∴∠ADB'＝25°．（2）证明：①设B'D与AP的交点为N，连接AB'，BN．由（1）得：∠1＝∠2，∠3＝∠4，∵∠1+∠2+∠3+∠4＝90°，∴∠1+∠3＝45°，∴∠B'NP＝45°，∵∠B'NP＝∠BNP，∴∠BNP＝45°，则△BNB'为等腰直角三角形．∴BB'＝BN，∠ANB＝135°，∴∠BMC＝∠ANB＝135°，∵∠5+∠6＝45°，∠4+∠5＝45°，∴∠4＝∠6．在△ANB和△BMC中，，∴△ANB≌△BNC（AAS），∴BN＝CM，∴BB'＝CM；②∵△BB'N为等腰直角三角形，∴∠NB'B＝45°，∴∠NB'B＝∠7＝45°，∴B'D∥MC．10．解：（1）如图1、图2所示：（2）连接AE，如图3所示：则∠PAB＝∠PAE＝25°，AE＝AB＝AD，∴∠AED＝∠ADF，∵四边形ABCD是正方形，∴∠BAD＝90°，∴∠EAD＝90°+25°+25°＝140°，∴∠ADF＝（180°﹣∠EAD）＝20°；（3）连接AE、BF、BD，如图4所示：则EF＝BF，AE＝AB＝AD，∴∠ABF＝∠AEF＝∠ADF，∴∠BFD＝∠BAD＝90°，∴BF2+FD2＝BD2，∴EF2+FD2＝AB2+AD2＝2AB2，即EF2+FD2＝2AB2．11．解：（1）连接DB，若Q点落在BD上，由AP＝x，则PD＝1﹣x，PQ＝x．∵∠PDQ＝45°，∴PD＝PQ，即1﹣x＝x．∴x＝﹣1．（2）①如图2，连接BQ1、CQ1，作PQ1⊥BQ1交AD于P，过点Q1，作EF⊥AD于E，交BC于F．∵△BCQ1为等边三角形，正方形ABCD边长为1，∴Q1F＝Q1E＝．在四边形ABPQ1中，∵∠ABQ1＝30°，∴∠APQ1＝150°，∴△PEQ1为含30°的直角三角形，∴PE＝Q1E＝，∵AE＝，∴x＝AP＝AE﹣PE＝2﹣．②如图3，连接BQ2，AQ2，过点Q2作PG⊥BQ2，交AD于P，连接BP，过点Q2作EF⊥CD于E，交AB于F．∵EF垂直平分CD，∴EF垂直平分AB，∴AQ2＝BQ2．∵AB＝BQ2，∴△ABQ2为等边三角形．在四边形ABQP中，∵∠BAD＝∠BQP＝90°，∠ABQ2＝60°，∴∠ABP＝30°，∴x＝AP＝．③如图4，连接BQ1，CQ1，BQ3，CQ3，过点Q3作BQ3⊥PQ3，交AD的延长线于P，连接BP，过点Q1，作EF⊥AD于E，此时Q3在EF上，不妨记Q3与F重合．∵△BCQ1为等边三角形，△BCQ3为等边三角形，BC＝1，∴Q1Q2＝，Q1E＝，∴EF＝．在四边形ABQ3P中，∵∠ABF＝∠ABC+∠CBQ3＝150°，∴∠EPF＝30°，∴EP＝EF＝．∵AE＝，∴x＝AP＝AE+PE＝+2．综上所述，△CDQ为等腰三角形时x的值为2﹣，，2+．12．解：（1）△QPM是等腰三角形，理由如下：延长BC至E，使CE＝BP，连接AE，∵PB＝CE，∴PB+BC＝CE+BC，∴CP＝BE，∵四边形ABCD是正方形，∴AB＝CD，∠ABC＝∠DCB＝90°，在△DCP和△ABE中，∴△DCP≌△ABE（SAS）∴∠DPC＝∠AEB，∵M是BC的中点，∴MB＝MC，∴MB+BP＝MC+CE，∴MP＝ME，∴M是PE的中点，又∵N是AP的中点，∴MN∥AE，∴∠PMN＝∠AEB，∴∠PMN＝∠DPC，∴QP＝QM，∴△QPM是等腰三角形；（2）延长BC至E，使CE＝BP，连接AE，∵M是BC的中点，BC＝4，∴BM＝CM＝2，又∵BP＝CE，∴BM+BP＝CM+CE，即PM＝ME，∴M是PE的中点，且点N是AP中点，13．证明：（1）如图1，连接DF，∵四边形ABCD是正方形，∴DA＝DC，∠A＝∠C＝90°，∵点C关于直线DG的对称点为F，∴△DCG≌△DFG，∴DC＝DF＝DA，∠DFG＝∠C＝90°，∴∠DFE＝90°，在Rt△ADE和Rt△FDE中，∵，∴Rt△ADE≌Rt△FDE（HL）；（2）∵G是边BC的中点，BC＝6，∴CG＝BG＝FG＝3，∵△ADE≌△FDE，∴AE＝EF，设AE＝x，则BE＝6﹣x，EG＝EF+FG＝x+3，∵在Rt△EBG中，BE2+BG2＝EG2，∴（6﹣x）2+32＝（x+3）2，解得x＝2，∴AE＝2；（3）如图2，过点H作HN⊥AB于点N，∴∠ENH＝90°，由（1）知∠ADE＝∠EDF，∠FDG＝∠CDG，∵∠ADC＝90°，∴2∠EDF+2∠FDG＝90°，∴∠EDF+∠FDG＝45°，即∠EDG＝45°，∵EH⊥DE，∴∠DEH＝90°，△DEH是等腰直角三角形，∴DE＝EH，∠ADE＝∠NEH，在△DAE和△ENH中，∵，∴△DAE≌△ENH（AAS），∴AE＝HN，AD＝EN，∵AD＝AB，∴AB＝EN＝AE+BE＝BE+BN，∴AE＝BN＝HN，∴△BNH是等腰直角三角形，∴BH＝．14．解：（1）如图1、图2所示：（2）连接AE，如图3所示：则∠PAB＝∠PAE＝30°，AE＝AB＝AD，∴∠AED＝∠ADF，∵四边形ABCD是正方形，∴∠BAD＝90°，∴∠EAD＝90°+30°+30°＝150°，∴∠ADF＝（180°﹣∠EAD）＝15°；（3）连接AE、BF、BD，如图4所示：则EF＝BF，AE＝AB＝AD，∴∠ABF＝∠AEF＝∠ADF，∴∠BFD＝∠BAD＝90°，∴BF2+FD2＝BD2，∴EF2+FD2＝AB2+AD2＝2AB2，即EF2+FD2＝2AB2．15．解：（1）连接AE，如图1所示：∵点D关于直线AQ的对称点为E，∴AE＝AD，AQ垂直平分DE，∴∠EAQ＝∠QAD＝15°，∵四边形ABCD是正方形，∴∠BAD＝90°，AB＝AD，∴∠BAE＝15°+15°+90°＝120°，AE＝AB，∴∠ABE＝（180°﹣120°）＝30°；（2）作A⊥BE于M，如图2所示：则∠AMB＝∠AMF＝90°，∴AM＝AB＝3，∵∠1＝90°﹣30°＝60°，∴∠2＝90°﹣60°＝30°，∴∠FAM＝15°+30°＝45°，∴△AMF是等腰直角三角形，∴AF＝AM＝3．。

八年级平行四边形专题练习(含答案)

中考专题复习平行四边形知识考点：理解并掌握平行四边形的判定和性质精典例题：【例1】已知如图：在四边形ABCD 中，AB ＝CD ，AD ＝BC ，点E 、F 分别在BC 和AD 边上，AF ＝CE ，EF 和对角线BD 相交于点O ，求证：点O 是BD 的中点。

分析：构造全等三角形或利用平行四边形的性质来证明BO ＝DO 略证：连结BF 、DE在四边形ABCD 中，AB ＝CD ，AD ＝BC ∴四边形ABCD 是平行四边形 ∴AD ∥BC ，AD ＝BC 又∵AF ＝CE∴FD ∥BE ，FD ＝BE ∴四边形BEDF 是平行四边形∴BO ＝DO ，即点O 是BD 的中点。

【例2】已知如图：在四边形ABCD 中，E 、F 、G 、H 分别是AB 、BC 、CD 、DA 边上的中点，求证：四边形EFGH 是平行四边形。

分析：欲证四边形EFGH 是平行四边形，根据条件需从边上着手分析，由E 、F 、G 、H 分别是各边上的中点，可联想到三角形的中位线定理，连结AC 后，EF 和GH 的关系就明确了，此题也便得证。

（证明略）变式1：顺次连结矩形四边中点所得的四边形是菱形。

变式2：顺次连结菱形四边中点所得的四边形是矩形。

变式3：顺次连结正方形四边中点所得的四边形是正方形。

变式4：顺次连结等腰梯形四边中点所得的四边形是菱形。

变式5：若AC ＝BD ，AC ⊥BD ，则四边形EFGH 是正方形。

变式6：在四边形ABCD 中，若AB ＝CD ，E 、F 、G 、H 分别为AD 、BC 、BD 、AC 的中点，求证：EFGH 是菱形。

娈式6图娈式7图变式7：如图：在四边形ABCD 中，E 为边AB 上的一点，△ADE 和△BCE 都是等边三角形，P 、Q 、M 、N 分别是AB 、BC 、CD 、DA 边上的中点，求证：四边形PQMN 是菱形。

例1图 O F E D CB A 例2图探索与创新：【问题】已知如图，在△ABC 中，∠C ＝900，点M 在BC 上，且BM ＝AC ，点N 在AC 上，且AN ＝MC ，AM 和BN 相交于P ，求∠BPM 的度数。

北师大版八年级下册数学第六章平行四边形含答案(各地真题)

北师大版八年级下册数学第六章平行四边形含答案一、单选题(共15题，共计45分)1、如果一个多边形的内角和等于它的外角和的2倍，则这个多边形是（）A.三角形B.四边形C.五边形D.六边形2、已知一个多边形的内角和等于这个多边形外角和的2倍，则这个多边形的边数是（）A.4B.5C.6D.83、若一个正多边形的一个外角是36°，则这个正多边形的边数是（）A.7B.8C.9D.104、若一个多边形的内角和是外角和的5倍，则这个多边形的边数是（）A.12B.10C.8D.115、正多边形的一个内角是150°，则这个正多边形的边数为（）A.10B.11C.12D.136、若一个多边形的内角和为1080°，则这个多边形的边数为（）A.6B.7C.8D.97、如图，七边形ABCDEFG中，AB、ED的延长线交于点O，着∠1、∠2、∠3、∠4对应的邻补角和等于215°，则∠BOD的度数为（）A.30°B.35°C.40°D.45°8、正六边形的每个内角都是（）A.60°B.80°C.100°D.120°9、下列结论：①一个三角形的3个外角的度数之比为2：3：4，则与之相应的3个内角度数之比为5：3：1；②在△ABC中，若∠A=2∠B=3∠C，则△ABC为直角三角形；③一个多边形的边数每增加一条，这个多边形的内角和就增加180°；④一个五边形最多有3个内角是直角；⑤两条直线被第三条直线所截，同位角的角平分线互相平行．其中正确结论有（）A.2个B.3个C.4个D.5个10、一个正多边形的内角和是1440°，那么这个正多边形的每个外角是（）A.30°B.36°C.40°D.45°11、正六边形的每个内角度数为（）A.60°B.120°C.135°D.140°12、内角和等于外角和多边形是( )A.三角形B.四边形C.五边形D.六边形13、小磊利用所学的数学知识，给同伴出了这样一道题：如图，某人从点A出发，沿直线走米后，向左转，接着沿左转后的方向前进米后，再向左转，再沿左转后的方向前进米如此下去，当他第一次回到A点时，发现自己走了米，则的度数为（）A. B. C. D.14、若一个正多边形的一个外角是45°，则这个正多边形的边数是（）A.5B.6C.7D.815、一个n边形的内角和为360°，则n等于（）A.3B.4C.5D.6二、填空题(共10题，共计30分)16、如图所示，在矩形中，，，两条对角线相交于点，、为邻边作第1个平行四边形，对角线相交于点，以为、邻边作第2个平行四边形，对角线相交于；再以、为邻边作第3个平行四边形……此类推，第2020个平行四边形的面积________．17、如果一个正多边形的中心角为45°，那么这个正多边形的边数是________.18、在平行四边形ABCD中，∠BAD的平分线AE交BC于点E，且BE=3，若平行四边形ABCD的周长是16，则EC等于________．19、如图，将平行四边形ABCD的一边BC延长至E，若∠A=110°，则∠1=________．20、如图，五边形ABCDE是一块草地．小明从点S出发，沿着这个五边形的边步行一周，最后仍回到起点S处，小明在各拐弯处转过的角度之和是________21、如图，，，是多边形的三个外角，边CD，AE的延长线交于点F，如果，那么的度数是________.22、如图，在直角坐标系中，四边形OABC的顶点O、A、C的坐标分别是（0，0）、（5，0）、（2，3），当点B的坐标为________时，四边形OABC是平行四边形．23、如图，在中，D、E、F分别在、、上，，，，，则的长为________.24、如图，在四边形中，, 是的中点点以每秒1个单位长度的速度从点出发，沿向点运动;点同时以每秒3个单位长度的速度从点出发，沿向点运动.点停止运动时，点也随之停止运动.当运动时间秒时，以点为顶点的四边形是平行四边形.则的值为________.25、如图，小漩从A点出发前进10m后，向右转15°，再前进10m，向右转15°，…，这样一直走下去，她第一次回到出发点A时，一共走了________ m．三、解答题(共5题，共计25分)26、如图，点M、N在▱ABCD的对角线AC上，且AM=CN，求证：四边形BMDN是平行四边形．27、如图，正方形ABCO的边OA、OC在坐标轴上，点B坐标为（6，6），将正方形ABCO绕点C逆时针旋转角度α（0°＜α＜90°），得到正方形CDEF，ED 交线段AB于点G，ED的延长线交线段OA于点H，连CH、CG．（1）求证：△CBG≌△CD G；（2）求∠HCG的度数；并判断线段HG、OH、BG之间的数量关系，说明理由；（3）连结BD、DA、AE、EB得到四边形AEBD，在旋转过程中，四边形AEBD能否为矩形？如果能，请求出点H的坐标；如果不能，请说明理由．28、如图所示，已知平行四边形ABCD的对角线交于O，过O作直线交AB、CD 的反向延长线于E、F，求证：OE＝OF.29、已知：如图，平行四边形ABCD中，BE平分∠ABC交AD于E，CF平分∠BCD 交AD于F，求证：AF=DE30、如图，平行四边形ABCD的对角线相交于点O，过点O的任意一条直线与边AD相交于点E，与边BC相交于点F，求证：OE=OF．参考答案一、单选题(共15题，共计45分)1、D2、C3、D4、A5、C6、C8、D9、B10、B11、B12、B13、B14、D15、B二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题，共计25分)27、29、30、。

初二数学平行四边形解答题大全100题 (1)

初二数学平行四边形解答题大全100题一、解答题1．如图，在▱ABCD中，AE⊥BC，AF⊥CD，垂足分别为E，F，且BE=DF．（1）求证：▱ABCD是菱形；（2）若AB=5，AC=6，求▱ABCD的面积．∆中，AD是BC边上的中线，E是AD的中点，过点A作BC的平2．如图，在ABC行线交BE的延长线于点F，连接CF.=；（1）求证：AF DC⊥，试判断四边形ADCF的形状，并证明你的结论.（2）若AB AC3．如图，在▱ABCD 中，对角线AC，BD 相交于点O，过点O 的一条直线分别交AD，BC 于点E，F．求证：AE=CF．4．如图，ABCD是平行四边形，P是CD上一点，且AP和BP分别平分∠DAB和∠CBA．(1)求∠APB的度数；(2)如果AD＝5cm，AP＝8cm，求△APB的周长．5．如图，在矩形ABCD中，AB＝8cm，BC＝16cm，点P从点D出发向点A运动，运动到点A停止，同时，点Q从点B出发向点C运动，运动到点C即停止，点P、Q的速度都是1cm/s．连接PQ、AQ、CP．设点P、Q运动的时间为ts．(1)当t为何值时，四边形ABQP是矩形；(2)当t为何值时，四边形AQCP是菱形；(3)分别求出(2)中菱形AQCP的周长和面积．6．如图，△ABC中，D是BC边上一点，E是AD的中点，过点A作BC的平行线交BE的延长线于F，且AF=CD，连接CF．（1）求证：△AEF≌△DEB；（2）若AB=AC，试判断四边形ADCF的形状，并证明你的结论．7．如图，将矩形ABCD沿对角线AC翻折，点B落在点F处，FC交AD于E．（1）求证：△AFE≌△CDF；（2）若AB=4，BC=8，求图中阴影部分的面积．8．如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD，等边△ABE．已知∠BAC=30°，EF⊥AB，垂足为F，连接DF．（1）试说明AC=EF；（2）求证：四边形ADFE是平行四边形．9．如图：在平行四边形ABCD的边AB，CD上截取AF，CE，使得AF=CE，连接EF，点M，N是线段EF上两点，且EM=FN，连接AN，CM．（1）求证：△AFN≌△CEM；（2）若∠CMF=107°，∠CEM=72°，求∠NAF的度数．10．如图，正方形ABCD的边长为6，E，F分别是AB，BC边上的点，且，将△绕点D逆时针旋转，得到△．求证：．当时，求EF的长．11．如图，在矩形ABCD中，BD的垂直平分线分别交AB、CD、BD于E、F、O，连接DE、BF．（1）求证：四边形BEDF是菱形；（2）若AB＝8cm，BC＝4cm，求四边形DEBF的面积．12．如图，将矩形ABCD（纸片）折叠，使点B与AD边上的点K重合，EG为折痕；点C与AD边上的点K重合，FH为折痕．已知∠1=67.5°，∠2=75°，+1，求BC的长．13．如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DE∥AC且DE=12 AC，连接CE、OE，连接AE交OD于点F．（1）求证：OE=CD；（2）若菱形ABCD的边长为2，∠ABC=60°，求AE的长．14．如图，Rt△ABC中，∠ABC＝90°，点D，F分别是AC，AB的中点，CE∥DB，BE∥DC．(1)求证：四边形DBEC是菱形；(2)若AD＝3，DF＝1，求四边形DBEC面积．15．已知：如图，在△ABC中，AD是BC边上的高线，CE是AB边上的中线，DG⊥CE 于G，且CD=AE.（1）求证：CG=EG.（2）求证：∠B=2∠ECB．16．如图，在▱ABCD中，E为BC边上一点，且AB＝AE．（1）求证：△ABC≌△EAD；（2）若∠B＝65°，∠EAC＝25°，求∠AED的度数．17．如图，点A在∠MON的边ON上，AB⊥OM于B，AE=OB，DE⊥ON于E，AD=AO，DC⊥OM于C．（1）求证：四边形ABCD是矩形；（2）若DE=3，OE=9，求AB、AD的长.18．如图，在△ABC中，∠ACB=90°，点D，E分别是边BC，AB上的中点，连接DE 并延长至点F，使EF=2DF，连接CE、AF．（1）证明：AF=CE；（2）当∠B=30°时，试判断四边形ACEF的形状并说明理由．19．在正方形ABCD中，对角线BD所在的直线上有两点E、F满足BE=DF，连接AE、AF、CE、CF，如图所示．（1）求证：△ABE≌△ADF；（2）试判断四边形AECF的形状，并说明理由．20．如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BD 相交于点O，与BC相交于点N，连接BM、DN．()1求证：四边形BMDN是菱形；()2若4AB=，8AD=，求菱形BMDN的面积和对角线MN的长．21．如图，在▱ABCD中，点O是对角线AC、BD的交点，点E是边CD的中点，点F在BC的延长线上，且CF＝12BC，求证：四边形OCFE是平行四边形．22．如图，□ABCD的对角线AC，BD相交于点O，点E、F在BD上，且BE＝DF.求证：四边形AECF是平行四边形.23．如图，矩形ABCD中，AB＝6，BC＝10，将矩形沿AC折叠，使点B与点E重合，AD与EC相交于点F．（1）求证：AF＝CF；（2）求△AEF的面积．24．已知：如图，在平行四边形ABCD中，M、N分别是AD和BC的中点．（1）求证：四边形AMCN是平行四边形；（2）若AC＝CD，求证四边形AMCN是矩形；（3）若∠ACD＝90°，求证四边形AMCN是菱形；（4）若AC＝CD，∠ACD＝90°，求证四边形AMCN是正方形．25．如图，平行四边形ABCD中，BD⊥AD，∠A＝45°，E，F分别是AB，CD上的点，且BE＝DF，连接EF交BD于点O．（1）求证：BO=DO；（2）若EF⊥AB，延长EF交AD的延长线于G，当FG=1时，求AE的长．26．已知：如图，四边形ABCD中，AD∥BC，AD=CD，E是对角线BD上一点，且EA=EC．（1）求证：四边形ABCD是菱形；（2）如果BE=BC，且∠CBE：∠BCE=2：3，求证：四边形ABCD是正方形．27．如图，四边形ABCD是矩形，△PBC和△QCD都是等边三角形，且点P在矩形上方，点Q在矩形内．证明：（1）∠PBA＝∠PCQ＝30°．（2）PA＝PQ．28．如图，已知四边形ABCD是平行四边形，点E，F分别是AB，BC上的点，AE=CF，并且∠AED=∠CF D．求证：（1）△AED≌△CFD；（2）四边形ABCD是菱形．29．如图，将▱ABCD的边AB延长到点E，使BE=AB，连接DE，交边BC于点F．（1）求证：△BEF≌△CDF；（2）连接BD、CE，若∠BFD=2∠A，求证：四边形BECD是矩形．30．如图，在平行四边形ABCD中，点M为边AD的中点，过点C作AB的垂线交AB 于点E，连接ME，已知AM=2AE=4，∠BCE=30°.(1)求平行四边形ABCD的面积；(2)求证：∠EMC=2∠AEM .31．如图，在△ABC中，AD是高，CE是中线，DG垂直平分CE，连接DE．（1）求证：DC＝BE；（2）若∠AEC＝72°，求∠BCE的度数．32．如图，平行四边形ABCD中，CG⊥AB于点G，∠ABF=45°，F在CD上，BF交CD于点E，连接AE，AE⊥AD．(1)若BG=1，，求EF的长度；(2)求证：．33．如图，在矩形ABCD中，沿EF将矩形折叠，使A、C重合，AC与EF交于点H.(1)求证：△ABE≌△AGF；(2)若AB=6，BC=8，求△ABE的面积．34．如图，在Rt△ABC中，∠ACB＝90°，过点C的直线MN∥AB，D为AB边上一点，过点D作DE⊥BC，交直线MN于E，垂足为F，连接CD、BE．（1）求证：CE＝AD；（2）当D在AB中点时，四边形BECD是什么特殊四边形？说明你的理由．，垂足为E 35．如图，在Rt ABC中，CD是斜边AB上的中线，DE AC()1如果BC5cm=，那么AB=______cm，CD=______cm：=，AC12cm()2求证：AE CE=．36．如图，点E是正方形ABCD外一点，点F是线段AE上一点，△EBF是等腰直角三角形，其中∠EBF=90°，连接CE、CF．（1）求证：△ABF≌△CBE；（2）判断△CEF的形状，并说明理由．37．如图1，在矩形纸片ABCD中，AB＝3cm，AD＝5cm，折叠纸片使B点落在边AD 上的E处，折痕为PQ，过点E作EF∥AB交PQ于F，连接BF．(1)求证：四边形BFEP为菱形；(2)当点E在AD边上移动时，折痕的端点P、Q也随之移动；①当点Q与点C重合时(如图2)，求菱形BFEP的边长；②若限定P、Q分别在边BA、BC上移动，求出点E在边AD上移动的最大距离．38．如图，在长方形ABCD中，AB=CD=6cm，BC=10cm，点P从点B出发，以2cm/秒的速度沿BC向点C运动，设点P的运动时间为t秒：（1）PC=______cm．（用t的代数式表示）（2）当t为何值时，△ABP≌△DCP？（3）当点P从点B开始运动，同时，点Q从点C出发，以v cm/秒的速度沿CD向点D运动，是否存在这样v的值，使得△ABP与△PQC全等？若存在，请求出v的值；若不存在，请说明理由．39．如图，已知A、F、C、D四点在同一条直线上，AF=CD，AB∥DE，且AB=DE．（1）求证：△ABC≌△DEF；（2）若EF=3，DE=4，∠DEF=90°，请直接写出使四边形EFBC为菱形时AF的长度．40．如图，四边形ABCD是平行四边形，E，F是对角线BD上的点，∠1=∠2.求证：（1）BE=DF；（2）AF∥CE.41．如图正方形ABCD的边长为4，E、F分别为DC、BC中点．（1）求证：△ADE≌△ABF．（2）求△AEF的面积．42．在Rt△ABC中，∠BAC=,D是BC的中点，E是AD的中点．过点A作AF∥BC 交BE的延长线于点F．（1）求证：△AEF≌△DEB；（2）证明四边形ADCF是菱形；（3）若AC=4，AB=5，求菱形ADCFD 的面积．43．如图，在▱ABCD中，作对角线BD的垂直平分线EF，垂足为O，分别交AD，BC 于E，F，连接BE，DF．求证：四边形BFDE是菱形．44．已知：如图，在△ABC中，AB=AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM 的平分线，CE⊥AN，垂足为点E，(1)求证：四边形ADCE为矩形；(2)当△ABC满足什么条件时，四边形ADCE是一个正方形？并给出证明．45．已知正方形ABCD与正方形CEFG，M是AF的中点，连接DM，EM．（1）如图1，点E在CD上，点G在BC的延长线上，请判断DM，EM的数量关系与位置关系，并直接写出结论；（2）如图2，点E在DC的延长线上，点G在BC上，（1）中结论是否仍然成立？请证明你的结论；（3）将图1中的正方形CEFG绕点C旋转，使D，E，F三点在一条直线上，若AB=13，CE=5，请画出图形，并直接写出MF的长．46．在□ABCD，过点D作DE⊥AB于点E，点F在边CD上，DF＝BE，连接AF，BF.（1）求证：四边形BFDE是矩形；（2）若CF＝3，BF＝4，DF＝5，求证：AF平分∠DAB．47．如图，▱ABCD的对角线AC，BD相交于点O．E，F是AC上的两点，并且AE=CF，连接DE，BF．（1）求证：△DOE≌△BOF；（2）若BD=EF，连接DE，BF．判断四边形EBFD的形状，并说明理由．48．如图，在正方形ABCD中，E、F分别为边AD和CD上的点，且AE=CF，连接AF、CE交于点G．求证：AG=CG．49．已知：如图，E、F是四边形ABCD的对角线AC上的两点，AF=CE，DF=BE，DF∥BE．ＤＣＥＦＡＢ求证：（1）△AFD≌△CEB．（2）四边形ABCD是平行四边形．50．如图，已知，矩形ABCD中，AB=4cm，BC=8cm，AC的垂直平分线EF分别交AD、BC于点E、F，垂足为O，连接AF、CE．（1）求证：△AOE≌△COF；（2）求证：四边形AFCE为菱形；（3）求菱形AFCE的周长．51．如图所示，四边形ABCD是边长为10cm的菱形，其中对角线BD的长为16cm，求（1）对角线AC的长度；（2）菱形ABCD的面积．52．如图所示，O是矩形ABCD的对角线的交点，DE∥AC，CE∥BD．（1）求证：OE⊥DC．（2）若∠AOD＝120°，DE＝2，求矩形ABCD的面积．53．已知，在平行四边形ABCD中，E为AD上一点，且AB＝AE，连接BE交AC于点H，过点A作AF⊥BC于F，交BE于点G．（1）若∠D＝50°，求∠EBC的度数；（2）若AC⊥CD，过点G作GM∥BC交AC于点M，求证：AH＝MC．54．如图，已知△ABC中，AB＝BC，D为AC中点，过点D作DE∥BC，交AB于点E．（1）求证：AE＝DE；（2）若∠C＝65°，求∠BDE的度数．55．如图，在矩形ABCD 中，E 是AB 的中点，连接DE 、CE ．（1）求证：△ADE ≌△BCE ；（2）若AB=6，AD=4，求△CDE 的周长．56．如图，在四边形ABCD 中，∠ABC=90°，AC=AD ，M ，N 分别为AC ，CD 的中点，连接BM ，MN ，BN ．（1）求证：BM=MN ；（2）∠BAD=60°，AC 平分∠BAD ，AC=2，求BN 的长．57．综合与实践问题情境：在数学活动课上，老师出示了这样一个问题：如图1，在矩形ABCD 中，AD=2AB ，E 是AB 延长线上一点，且BE=AB ，连接DE ，交BC 于点M ，以DE 为一边在DE 的左下方作正方形DEFG ，连接AM ．试判断线段AM 与DE 的位置关系．探究展示：勤奋小组发现，AM 垂直平分DE ，并展示了如下的证明方法：证明：∵BE=AB ，∴AE=2AB ．∵AD=2AB ，∴AD=AE ．∵四边形ABCD 是矩形，∴AD ∥BC ． ∴EM EB DM AB=．（依据1） ∵BE=AB ，∴1EM DM =．∴EM=DM ．即AM 是△ADE 的DE 边上的中线，又∵AD=AE ，∴AM ⊥DE ．（依据2）∴AM 垂直平分DE ．反思交流：（1）①上述证明过程中的“依据1”“依据2”分别是指什么？②试判断图1中的点A是否在线段GF的垂直平分线上，请直接回答，不必证明；（2）创新小组受到勤奋小组的启发，继续进行探究，如图2，连接CE，以CE为一边在CE的左下方作正方形CEFG，发现点G在线段BC的垂直平分线上，请你给出证明；探索发现：（3）如图3，连接CE，以CE为一边在CE的右上方作正方形CEFG，可以发现点C，点B都在线段AE的垂直平分线上，除此之外，请观察矩形ABCD和正方形CEFG的顶点与边，你还能发现哪个顶点在哪条边的垂直平分线上，请写出一个你发现的结论，并加以证明．58．如图，△ABC中，AB＝AC＝1，∠BAC＝45°，△AEF是由△ABC绕点A按顺时针方向旋转得到的，连接BE，CF相交于点D．（1）求证：BE＝CF ；（2）当四边形ACDE为菱形时，求BD的长．59．如图，在四边形ABCD中，AB＝CD，BF＝DE，AE⊥BD，CF⊥BD，垂足分别为E、F．（1）求证：△ABE≌△CDF；（2）若AC与BD交于点O，求证：AO＝CO．60．如图，▱ABCD的对角线AC、BD交于点O，E、F分别是AO、CO的中点，连接BE、DE、DF、BF，（1）求证：四边形EBFD是平行四边形．（2）求证：当AC=2BD时，四边形EBFD是矩形．61．如图，在▱ABCD中，AC是对角线，BE⊥AC，DF⊥AC，垂足分别为点E，F，求证：AE=CF．62．如图，在平行四边形ABCD中，P是对角线BD上的一点，过点C作CQ∥DB，且CQ＝DP，连接AP、BQ、PQ．(1)求证：△APD≌△BQC；(2)若∠ABP+∠BQC＝180°，求证：四边形ABQP为菱形．63．已知：如图，平行四边形ABCD，对角线AC与BD相交于点E，点G为AD的中点，连接CG，CG的延长线交BA的延长线于点F，连接FD．（1）求证：AB=AF；（2）若AG=AB，∠BCD=120°，判断四边形ACDF的形状，并证明你的结论．64．如图，矩形ABCD的对角线AC，BD相交于点O，点E，F在BD上，BE=DF．（1）求证：AE=CF；（2）若AB=6，∠COD=60°，求矩形ABCD的面积．65．如图，DB∥AC，且DB=12AC，E是AC的中点，（1）求证：BC=DE；（2）连接AD、BE，若要使四边形DBEA是矩形，则给△ABC添加什么条件，为什么？66．如图，平行四边形ABCD中，E、F分别是边BC、AD的中点，求证：∠ABF=∠CDE．67．如图，在△ABC中，∠ACB＝90°，CD为AB边上的中线，过点C作CE//AB，过点B作BE//CD，CE、BE相交于点E．求证：四边形BECD为菱形．68．如图，在△ABC中，AD是△ABC的高线，CE是△ABC的角平分线，它们相交于点P．（1）若∠B＝40°，∠AEC＝75°，求证：AB＝BC；（2）若∠BAC＝90°，AP为△AEC边EC上中线，求∠B的度数．69．已知：如图，在平行四边形ABCD中，AE⊥BD，CF⊥BD，垂足分别为E，F．求证：△ADE≌△CBF .70．如图，在□ABCD中，点E、F分别在边CB、AD的延长线上，且BE＝DF，EF分别与AB、CD交于点G、H，求证：AG＝CH.71．如图，在平行四边形ABCD中，边AB的垂直平分线交AD于点E，交CB的延长线于点F，连接AF，BE.(1)求证：△AGE≌△BGF；(2)试判断四边形AFBE的形状，并说明理由．72．如图，点B、E、C、F在一条直线上，AB=DF，AC=DE，BE=FC．（1）求证：△ABC≌△DFE；（2）连接AF、BD，求证：四边形ABDF是平行四边形．73．如图,菱形ABCD的对角线AC和BD交于点O,分别过点C．D作CE∥BD,DE∥AC，CE和DE交于点E.（1）求证：四边形ODEC是矩形；（2）当∠ADB=60°EA的长。

初二下册平行四边形练习题加答案

初二下册平行四边形练习题加答案一、选择题1. 若一平行四边形的一个内角是140°，则其对顶角的度数是：A. 40°B. 140°C. 180°D. 220°答案：A. 40°2. 若两个平行四边形的对应内角相等，那么这两个四边形一定是：A. 相似B. 全等C. 同一个形状D. 同一个大小答案：B. 全等3. 已知平行四边形ABCD的边长为5cm，对角线AC长为8cm，则平行四边形的面积为：A. 20cm²B. 25cm²C. 30cm²D. 40cm²答案：B. 25cm²4. 若一平行四边形的两个内角分别是60°和120°，则其对边的夹角的度数是：A. 30°B. 60°C. 80°D. 150°答案：B. 60°二、填空题1. 若一个平行四边形的底边长为6cm，高为3cm，则该平行四边形的面积为______cm²。

答案：18cm²2. 若一个平行四边形的底边长为8cm，高为4cm，则该平行四边形的面积为______cm²。

答案：32cm²3. 若一个平行四边形的两个相邻边长分别为7cm和10cm，夹角为120°，该平行四边形的面积为______cm²。

答案：35cm²4. 若一个平行四边形的对边互相垂直，其中一边的长度为5cm，另一边的长度为12cm，则该平行四边形的面积为______cm²。

答案：60cm²三、解答题1. 在平行四边形ABCD中，已知AB = 6cm，BC = 8cm，AC延长线与CD的交点为E，连接DE。

求证：∠DCE = ∠ABE。

解答：首先，由平行四边形的性质可知∠ADE = ∠DCB（对应角相等）。

又因为平行线AC延长线与CD相交于点E，所以∠CAE = ∠CDA （同位角相等）。

八年级数学下册《平行四边形》练习题与答案(人教版)

八年级数学下册《平行四边形》练习题与答案(人教版)一、选择题1.如图，▱ABCD的对角线AC，BD相交于点O，且AC＋BD＝16，CD＝6，则△ABO周长是( )A.10B.14C.20D.222.如图，在▱ABCD中，BC＝BD，∠C＝74°，则∠ADB的度数是( )A.16°B.22°C.32°D.68°3.下列条件中，不能判定四边形是平行四边形的是( )A.两组对边分别平行B.一组对边平行，另一组对边相等C.两组对边分别相等D.一组对边平行且相等4.如图，已知点E是菱形ABCD的边BC上一点，且∠DAE＝∠B＝80°，那么∠CDE度数为( )A.20°B.25°C.30°D.35°5.如图，已知菱形ABCD中，对角线AC与BD相交于点O，OE∥AB交BC于点E，AD＝6cm，则OE的长为( )A.6cmB.4cmC.3cmD.2cm6.如图，将矩形纸片ABCD沿BD折叠，得到△BC′D，C′D与AB交于点E.若∠1＝35°，则∠2的度数为( )A.20°B.30°C.35°D.55°7.如图，将边长为3a的正方形沿虚线剪成两块正方形和两块长方形.若拿掉边长2b的小正方形后，再将剩下的三块拼成一块矩形，则这块矩形较长的边长为( )A.3a＋2bB.3a＋4bC.6a＋2bD.6a＋4b8.在四边形ABCD中，AC与BD相交于点O，且OA＝OC，OB＝OD.如果再增加条件AC＝BD，此四边形一定是( )A.正方形B.矩形C.菱形D.都有可能9.如图，把正方形纸片ABCD沿对边中点所在的直线对折后展开，折痕为MN，再过点B折叠纸片，使点A落在MN上的点F处，折痕为BE.若AB的长为2，则FM的长为( )A.2B. 3C. 2D.110.如图，正方形ABCD的边长为3，点E、F分别在边BC、CD上，将AB、AD分别沿AE、AF折叠，点B、D 恰好都落在点G处，已知BE＝1，则EF的长为( )A.1.5B.2.5C.2.25D.311.如图，顺次连接四边形ABCD各边中点得四边形EFGH，要使四边形EFGH为矩形，应添加的条件是( )A.AB∥DCB.AC＝BDC.AC⊥BDD.AB＝DC12.如图,在四边形ABCD中,AC＝a,BD＝b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2,…,如此进行下去,得到四边形A n B n C n D n.下列结论正确的是( )①四边形A 4B 4C 4D 4是菱形;②四边形A 3B 3C 3D 3是矩形;③四边形A 7B 7C 7D 7的周长为a ＋b 8; ④四边形A n B n C n D n 的面积为ab 2n . A.①②③ B.②③④ C.①③④ D.①②③④二、填空题13.如图，在四边形ABCD 中，AD//BC ，在不添加任何辅助线的情况下，请你添加一个条件，使四边形ABCD 是平行四边形(填一个即可).14.如图所示，已知▱ABCD ，下列条件：①AC ＝BD ，②AB ＝AD ，③∠1＝∠2，④AB ⊥BC 中，能说明▱ABCD 是矩形的有(填写序号) ．15.如图，如果要使平行四边形ABCD 成为一个菱形，需要添加一个条件，那么你添加的条件是_________.16.如图，把矩形ABCD 绕着点A 逆时针旋转90°可以得到矩形AEFG ，则图中△AFC 是三角形.17.如图，四边形ABCD 是正方形，延长AB 到点E ，使AE ＝AC ，则∠BCE 的度数是 .18.如图，在矩形纸片ABCD中，AB＝6，BC＝10，BC边上有一点E，BE＝4，将纸片折叠，使A点与E点重合，折痕MN交AD于M点，则线段AM的长是.三、解答题19.如图，平行四边形ABCD，E、F两点在对角线BD上，且BE＝DF，连接AE，EC，CF，FA.(1)求证：四边形AECF是平行四边形.(2)若AF＝EF，∠BAF＝108°，∠CDF＝36°，直接写出图中所有的等腰三角形.20.如图，已知在△ABC中，AB＝AC，AD是BC边上的中线，AE∥BC，CE⊥AE，垂足为E.(1)求证：△ABD≌△CAE.(2)连结DE，线段DE与AB之间有怎样的位置关系和数量关系？请证明你的结论．21.如图，在△ABC中，∠A CB＝90°，O，D分别是边AC，AB的中点，过点C作CE∥AB交DO的延长线于点E，连接AE.(1)求证：四边形AECD 是菱形；(2)若四边形AECD 的面积为24，BC ：AC ＝34，求BC 的长.22.如图，已知点E 是正方形ABCD 的边CD 上一点，点F 是CB 的延长线上一点，且EA ⊥AF.求证：DE ＝BF.23.已知：如图1，四边形ABCD 四条边上的中点分别为E 、F 、G 、H ，顺次连接EF 、FG 、GH 、HE ，得到四边形EFGH(即四边形ABCD 的中点四边形)．(1)四边形EFGH 的形状是，证明你的结论．(2)如图2，请连接四边形ABCD 的对角线AC 与BD ，当AC 与BD 满足条件时，四边形EFGH 是矩形；证明你的结论．(3)你学过的哪种特殊四边形的中点四边形是矩形？说明理由．24.已知四边形ABCD为正方形，E是BC的中点，连接AE，过点A作∠AFD，使∠AFD＝2∠EAB，AF交CD于点F，如图①，易证：AF＝CD＋CF．(1)如图②，当四边形ABCD为矩形时，其他条件不变，线段AF，CD，CF之间有怎样的数量关系？请写出你的猜想，并给予证明；(2)如图③，当四边形ABCD为平行四边形时，其他条件不变，线段AF，CD，CF之间又有怎样的数量关系？请直接写出你的猜想．参考答案1.B.2.C3.B4.C.5.C6.A.7.A.8.B.9.B10.B11.C12.B.13.答案为：AD＝BC(答案不唯一).14.答案为：①④.15.答案为：AB＝AD或AC⊥BD；16.答案为：等腰直角.17.答案为：22.5°.18.答案为13 2.19.证明：(1)如图，连接AC交BD于点O，在▱ABCD中，OA＝OC，OB＝OD∵BE＝DF∴OB﹣BE＝OD﹣DF，即OE＝OF∴四边形AECF是平行四边形(对角线互相平分的四边形是平行四边形)；(2)解：∵AB∥CD∴∠ABF＝∠CDF＝36°∴∠AFB＝180°﹣108°﹣36°＝36°∴AB＝AF∵AF＝EF∴△ABF 和△AFE 是等腰三角形同理△EFC 与△CDE 是等腰三角形.20.证明：(1)∵AB ＝AC∴∠B ＝∠ACB又∵AD 是BC 边上的中线∴AD ⊥BC ，即∠ADB ＝90°.∵AE ∥BC∴∠EAC ＝∠ACB∴∠B ＝∠EAC.∵CE ⊥AE ，所以∠CEA ＝90°∴∠ADB ＝∠CEA.又∵AB ＝CA∴△ABD ≌△CAE(AAS)．(2)解：AB ∥DE 且AB ＝DE.证明：由△ABD ≌△CAE 可得AE ＝BD又∵AE ∥BD∴四边形ABDE 是平行四边形∴AB ∥DE 且AB ＝DE.21.(1)证明：∵点O 是AC 的中点∴OA ＝OC.∵CE ∥AB∴∠DAO ＝∠ECO.又∵∠AOD ＝∠COE∴△AOD ≌△COE(ASA)∴AD ＝CE∴四边形AECD 是平行四边形.又∵CD 是Rt △ABC 斜边AB 上的中线∴CD ＝AD ＝12AB∴四边形AECD 是菱形；(2)由(1)知，四边形AECD 是菱形∴AC ⊥ED.在Rt △AOD 中 OD OA 34可设OD ＝3x ，OA ＝4x则ED ＝2OD ＝6x ，AC ＝2OA ＝8x.由题意可得12·6x ·8x ＝24 ∴x ＝1∴OD ＝3.∵O ，D 分别是AC ，AB 的中点∴OD 是△ABC 的中位线∴BC ＝2OD ＝6.22.证明：∵∠FAB ＋∠BAE ＝90°，∠DAE ＋∠BAE ＝90°∴∠FAB ＝∠DAE∵∠AB ＝AD ，∠ABF ＝∠ADE∴△AFB ≌△ADE∴DE ＝BF.23.解：(1)四边形EFGH 的形状是平行四边形．理由如下：如图1，连结BD ． ∵E 、H 分别是AB 、AD 中点∴EH ∥BD ，EH ＝12BD同理FG ∥BD ，FG ＝12BD∴EH ∥FG ，EH ＝FG∴四边形EFGH 是平行四边形；(2)当四边形ABCD 的对角线满足互相垂直的条件时，四边形EFGH 是矩形．理由如下：如图2，连结AC 、BD ．∵E 、F 、G 、H 分别为四边形ABCD 四条边上的中点∴EH ∥BD ，HG ∥AC∵AC ⊥BD∴EH ⊥HG又∵四边形EFGH 是平行四边形∴平行四边形EFGH 是矩形；(3)菱形的中点四边形是矩形．理由如下：如图3，连结AC 、BD ．∵E 、F 、G 、H 分别为四边形ABCD 四条边上的中点∴EH ∥BD ，HG ∥AC ，FG ∥BD ，EH ＝12BD ，FG ＝12BD∴EH ∥FG ，EH ＝FG∴四边形EFGH是平行四边形．∵四边形ABCD是菱形∴AC⊥BD∵EH∥BD，HG∥AC∴EH⊥HG∴平行四边形EFGH是矩形．故答案为：平行四边形；互相垂直．24.解：(1)AF=CD+CF；(2)AF=CD+CF.。

平行四边形专题训练(含答案)

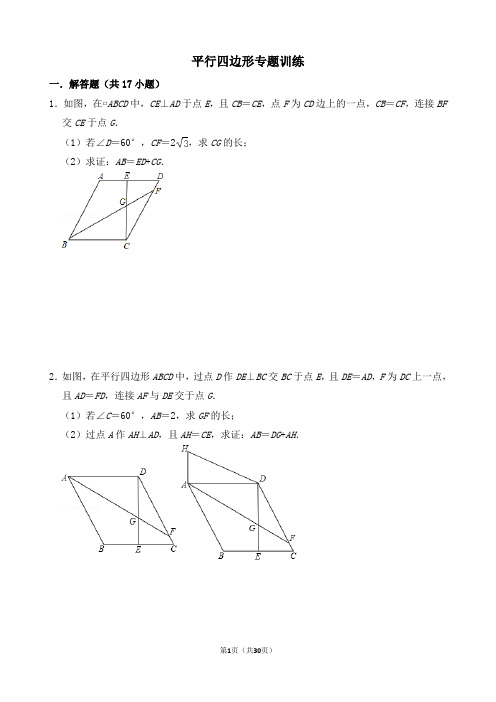
平行四边形专题训练一．解答题（共17小题）1．如图，在▱ABCD中，CE⊥AD于点E，且CB＝CE，点F为CD边上的一点，CB＝CF，连接BF 交CE于点G．（1）若∠D＝60°，CF＝2，求CG的长；（2）求证：AB＝ED+CG．2．如图，在平行四边形ABCD中，过点D作DE⊥BC交BC于点E，且DE＝AD，F为DC上一点，且AD＝FD，连接AF与DE交于点G．（1）若∠C＝60°，AB＝2，求GF的长；（2）过点A作AH⊥AD，且AH＝CE，求证：AB＝DG+AH．3．如图，已知▱ABCD中，DE⊥BC于点E，DH⊥AB于点H，AF平分∠BAD，分别交DC、DE、DH 于点F、G、M，且DE＝AD．（1）求证：△ADG≌△FDM．（2）猜想AB与DG+CE之间有何数量关系，并证明你的猜想．4．如图，已知▱ABCD中，AE平分∠BAD交DC于E，DF⊥BC于F，交AE于G，且AD＝DF．过点D作DC的垂线，分别交AE、AB于点M、N．（1）若M为AG中点，且DM＝2，求DE的长；（2）求证：AB＝CF+DM．5．在平行四边形ABCD中，BE⊥AD，F为CD边上一点，满足BF＝BC＝BE．（1）如图1，若BC＝12，CD＝13，求DE的长；（2）如图2，过点G作DG∥BE交BF于点G．求证：BG＝AE+DG．6．如图，在平行四边形ABCD中，∠ACB＝45°，点E在对角线AC上，BE的延长线交CD于点F，交AD的延长线于点G．（1）若BE＝，EC＝，求△BCE的面积；（2）若∠ABE＝2∠EBC，且AB＝BE，求证：EC＝DG．7．如图1，在平行四边形ABCD中，AE⊥BC于点E，E恰为BC的中点，tan B＝2．（1）求证：AD＝AE；（2）如图2，点P在线段BE上，作EF⊥DP于点F，连接AF，求证：；（3）请你在图3中画图探究：当P为射线EC上任意一点（P不与点E重合）时，作EF 垂直直线DP，垂足为点F，连接AF，线段DF、EF与AF之间有怎样的数量关系？直接写出你的结论．8．如图①，在平行四边形ABCD中，对角线AC、BD交于点O，AB＝AC，AB⊥AC，过点A作AE⊥BD于点E．（1）若BC＝6，求AE的长度；（2）如图②，点F是BD上一点，连接AF，过点A作AG⊥AF，且AG＝AF，连接GC交AE 于点H，证明：GH＝CH．9．在▱ABCD中，点E是BC的中点，过点A作AF⊥CD交直线CD于点F，连接AE、DE（1）如图1，当点F与点C重合时，AB＝AC＝2，求线段DE的长；（2）如图2，若∠EAF＝30°，AE＝CF，求证：BE＝AF．10．已知，在▱ABCD中，AB⊥AC，点E是AC上一点，连换BE，延长BE交AD于点F，BE＝CE．（1）如图1，当∠AEB＝60°，BF＝2时，求▱ABCD的面积；（2）如图2，点G是过点E且与BF垂直的直线上一点，连接GF，GC，FC，当GF＝GC时，求证：AB＝2EG．ABCD BD AD E CD AE BD F G为AF的中点，连接DG．（1）如图1，若DG＝DF＝1，BF＝3，求CD的长；（2）如图2，连接BE，且BE＝AD，∠AEB＝90°，M、N分别为DG，BD上的点，且DM＝BN，H为AB的中点，连接HM、HN，求证：∠MHN＝∠AFB．12．在△BCF中，点D是边CF上的一点，过点D作AD∥BC，过点B作BA∥CD交AD于点A，点G是BC的中点，点E是线段AD上一点，且∠CDG＝∠ABE＝∠EBF．（1）若∠F＝60°，∠C＝45°，BC＝2，请求出AB的长；（2）求证：CD＝BF+DF．13．已知在平行四边形ABCD中，过点D作DE⊥BC于点E，且AD＝DE．连接AC交DE于点F，作DG⊥AC于点G．（1）如图1，若，AF＝，求DG的长；（2）如图2，作EM⊥AC于点M，连接DM，求证：AM﹣EM＝2DG．14．已知，在平行四边形ABCD中，点E是AD边上一点，且DE＝DC．（1）若点E与点A重合（如图1），点B沿MN翻折后的点B1恰好落在AC上，且∠MNB1＝45°，AB1＝1，AM＝2，BM＝．求：①∠AMN的度数；②BN的长；（2）如图2，若CE交对角线BD于F，∠ABD＝2∠DBC，求证：BC＝DF+AB．15．在平行四边形ABCD中，点E是AD边上的点，连接BE．（1）如图1，若BE平分∠ABC，BC＝8，ED＝3，求平行四边形ABCD的周长；（2）如图2，点F是平行四边形外一点，FB＝CD．连接BF、CF，CF与BE相交于点G，若∠FBE+∠ABC＝180°，点G是CF的中点，求证：2BG+ED＝BC．16．如图，在平行四边形ABCD中，点O是对角线AC的中点，点E是BC上一点，且AB＝AE，连接EO并延长交AD于点F．过点B作AE的垂线，垂足为H，交AC于点G．（1）若AH＝3，HE＝1，求△ABE的面积；（2）若∠ACB＝45°，求证：DF＝CG．17．如图，在▱ABCD中，∠ACB＝45°，点E在对角线AC上，BE＝BA，BF⊥AC于点F，BF的延长线交AD于点G．点H在BC的延长线上，且CH＝AG，连接EH．（1）若BC＝12，AB＝13，求AF的长；（2）求证：EB＝EH．18．如图，平行四边形ABCD中，过点C作CE⊥AB于点E，点F是AD上一点，连结BF、CF，交CE于点G。

八下第九章平行四边形解答题难题训练(一)(有答案)

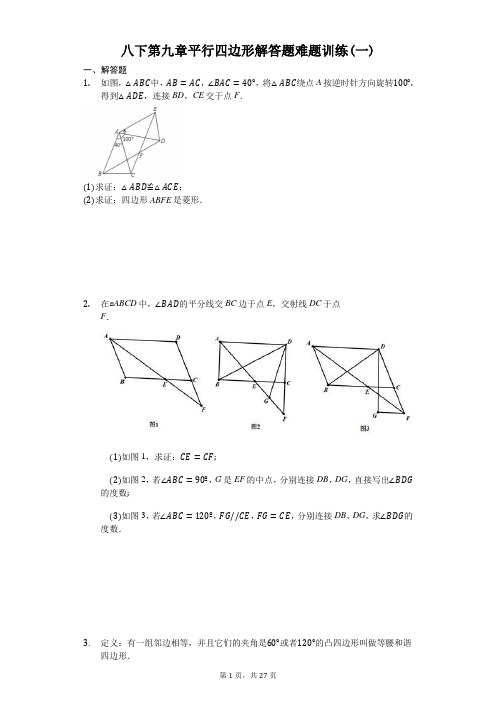
八下第九章平行四边形解答题难题训练(一)一、解答题1.如图，△ABC中，AB=AC，∠BAC=40°，将△ABC绕点A按逆时针方向旋转100°.得到△ADE，连接BD，CE交于点F．(1)求证：△ABD≌△ACE；(2)求证：四边形ABFE是菱形．2.在▱ABCD中，∠BAD的平分线交BC边于点E，交射线DC于点F．(1)如图1，求证：CE=CF;(2)如图2，若∠ABC=90º，G是EF的中点，分别连接DB，DG，直接写出∠BDG的度数;(3)如图3，若∠ABC=120º，FG//CE，FG=CE，分别连接DB，DG，求∠BDG的度数．3.定义：有一组邻边相等，并且它们的夹角是60°或者120°的凸四边形叫做等腰和谐四边形．(1)如图①，在等腰和谐四边形ABCD中，AB=BC，∠ABC=60°．①若AB=CD=2，AB//CD，求对角线BD的长；②若BD平分AC，求证：AD=CD；(2)如图②，在平行四边形ABCD中，∠ABC<90°，AB=6，BC=10，点P是对角线BD上的中点，过点P作直线分别交边AD，BC于点E，F，且∠BFE<90°，若四边形ABFE是等腰和谐四边形，求BF的长．4.如图，矩形OABC的边OA在x轴正半轴上，边OC在y轴正半轴上，B点的坐标为(1,3).矩形O′A′BC′是矩形OABC绕B点逆时针旋转得到的．O′点恰好在x轴的正半轴上，O′C′交AB于点D．(1)求点O′的坐标，并判断△O′DB的形状(要说明理由)(2)求边C′O′所在直线的解析式．(3)延长BA到M使AM=1，在(2)中求得的直线上是否存在点P，使得△POM是以线段OM为直角边的直角三角形？若存在，请直接写出P点的坐标；若不存在，请说明理由．5.如图，在△ABC中，∠BAC=90°，∠ACB=30°，BC=8，以BC为边，在△ABC外作等边△BCD，点E为BC中点，连接AE并延长交CD于点F．(1)求证：四边形ABDF是平行四边形；(2)如图2，将图1中的ABCD折叠，使点D和点A重合，折痕为GH，求CG的长．6.如图1，平行四边形ABCD，点E为AD的中点，连接BE，将△ABE沿BE翻折，得到△FBE，EF交BC于点G．(1)求证：BG=EG；(2)如图2，连接DF，交BC于点P，求证：四边形BEDP是平行四边形；(3)在(2)的条件下，若AD=10，∠AEB=30°，求DF的长．7.看图，回答下列小题(1)提出问题：如图1，将三角板放在正方形ABCD上，使三角板的直角顶点P在对角线AC上，一条直角边经过点B，另一条直角边交边DC与点E，求证：PB=PE(2)分析问题：请你选择下述一种方法给予证明．学生甲：如图1，过点P作PM⊥BC，PN⊥CD，垂足分别为M，N通过证明两三角形全等，进而证明两条线段相等．学生乙：连接DP，如图2，很容易证明PD=PB，然后再通过“等角对等边”证明PE=PD，就可以证明PB=PE了．(3)问题延伸：如图3，移动三角板，使三角板的直角顶点P在对角线AC上，一条直角边经过点B，另一条直角边交DC的延长线于点E，PB=PE还成立吗？若成立，请证明；若不成立，请说明理由．8.如图1，在正方形ABCD中，点E，F分别是边BC，AB上的点，且BE=AF.连接DE，过点E作EG⊥DE，使EG=DE，连接FG，FC．(1)请判断：FG与CE的关系是(直接填写答案)；(2)如图2，若点E，F分别是边CB，BA延长线上的点，其它条件不变，(1)中结论是否仍然成立？请作出判断并给予证明；(3)若点E，F分别是边BC，AB延长线上的点，其它条件不变，请在已给的正方形ABCD上画出符合条件的图形(3)，并判断对于该图形(3)，(1)中结论是否仍然成立？请直接写出你的判断．9.如图所示，AF、BE是△ABC的中线，AF⊥BE于点P，设BC=a，AC=b，AB=c．［特例探究］(1)如图1，当∠PBA=45°，c=2√2时，则EF=________，a=________，b=________；(2)如图2，当∠PBA=60°，c=4时，则EF=________，a=________，b=________；［归纳证明］(3)请你观察(1)(2)中的计算结果，当∠PBA=30°时，猜想a2、b2、c2三者之间的关系，用等式表示出来，并利用图3证明你的结论．10.如图，在矩形ABCD中，AB=1cm，AD=3cm，点Q从A点出发，以1cm/s的速度沿AD向终点D运动，点P从点C出发，以1cm/s的速度沿CB向终点B运动，当这两点中有一点到达自己的终点时，另一点也停止运动，两点同时出发，运动了t秒.(1)当0<t<3，判断四边形BQDP的形状，并说明理由；(2)求四边形BQDP的面积S与运动时间t的函数关系式；(3)求当t为何值时，四边形BQDP为菱形．11.如图1，在△OAB中，∠OAB=90°，∠AOB=30°，OB=8.以OB为边，在△OAB外作等边△OBC，D是OB的中点，连接AD并延长交OC于E．(1)求证：四边形ABCE是平行四边形；(2)如图2，将图1中的四边形ABCO折叠，使点C与点A重合，折痕为FG，求OG的长．12.如图，在平面直角坐标系的第一象限找一点A，第二象限找一点B，使OA=√5，OB=2√5，AB=5，且A，B都是格点，连接OA，OB，AB.(画出一个△OAB即可)(1)判断△OAB的形状，并说明理由；(2)是否存在点C，使得O，A，B，C四点构成的四边形为平行四边形⋅如果存在，请直接写出点C的坐标；如果不存在，请说明理由．13.如图，O为坐标原点，四边形OABC为矩形，A(10,0)，C(0,4)，点D是OA的中点，点P在BC上以每秒1个单位的速度由C向B运动，运动时间为t秒．(1)求四边形ODPC的面积S与时间t的函数关系式．(2)t为何值时，四边形PODB是平行四边形？(3)在线段PB上是否存在一点Q，使得ODQP为菱形．若存在求t值，若不存在，说明理由．(4)当△OPD为等腰三角形时，求点P的坐标．14.(1)如下图，在Rt△ABC中，∠B=90°，AB=6，∠C=30°，点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动，同时点E从点A出发沿AB方向以每秒1个单位长度的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动，设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F，连接DE、EF．求证：四边形AEFD是平行四边形；(2)在Rt△ABC中，∠B=90°，AB=6，∠C=30°，点D从点C出发沿射线CA方向以每秒2个单位长的速度匀速运动，同时点E从点A出发沿射线AB方向以每秒1个单位长度的速度匀速运动，，设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F，连接DE、EF.当t为何值时，△ADE为等腰三角形？请说明理由，并求此时线段DE的长度．15.类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”．(1)如图1，在四边形ABCD中，添加一个条件使得四边形ABCD是“等邻边四边形”.请写出你添加的一个条件．(2)小红猜想：对角线互相平分的“等邻边四边形”是菱形．她的猜想正确吗？请说明理由．(3)如图2，小红作了一个Rt△ABC，其中∠ABC=90°，AB=2，BC=1，并将Rt△ABC沿∠ABC的平分线BB′方向平移得到△A′B′C′，连结AA′，BC′.小红要使得平移后的四边形ABC′A′是“等邻边四边形”，应平移多少距离(即线段B′B的长)？16.在四边形ABCD中，AD//BC，BC⊥CD，AD=6cm，BC=10cm，点E从A出发以1cm/s的速度向D运动，点F从点B出发，以2cm/s的速度向点C运动，当其中一点到达终点，而另一点也随之停止，设运动时间为t(1)t取何值时，四边形EFCD为矩形⋅(2)M是BC上一点，且BM=4cm，t取何值时，以A、M、E、F为顶点的四边形是平行四边形⋅答案和解析1.(1)证明：∵ABC绕点A按逆时针方向旋转100°，∴∠BAC=∠DAE=40°，∴∠BAD=∠CAE=100°，又∵AB=AC，∴AB=AC=AD=AE，在△ABD与△ACE中，{AB=AC∠BAD=∠CAE AD=AE，∴△ABD≌△ACE(SAS)．(2)证明：∵∠BAD=∠CAE=100°，AB=AC=AD=AE，∴∠ABD=∠ADB=∠ACE=∠AEC=40°．∵∠BAE=∠BAD+∠DAE=140°，∴∠BFE=360°−∠BAE−∠ABD−∠AEC=140°，∴∠BAE=∠BFE，∴四边形ABFE是平行四边形，∵AB=AE，∴平行四边形ABFE是菱形．2.(1)证明：∵四边形ABCD是平行四边形，∴AB//CD，AD//BC，∴∠DAE=∠AEB，∠F=∠BAE，∵AF平分∠BAD，∴∠DAE=∠BAE，∴∠F=∠AEB，∵∠AEB=∠CEF，∴∠F=∠CEF，∴CE=CF；(2)45°；(3)解：延长AB，FG交H，连接HD，∵AD//GF，AB//DF，∴四边形AHFD为平行四边形，∵∠ABC=120°，AF平分∠BAD，∴∠DAF=30°，∠ADC=120°，∠DFA=30°，∴△DAF为等腰三角形，∴AD=DF，∴平行四边形AHFD为菱形，∴△ADH，△DHF为全等的等边三角形，∴DH=DF，∠BHD=∠GFD=60°，∵FG=CE，CE=CF，CF=BH，∴BH=GF，在△BHD和△GFD中，{BH=GF∠BHD=∠GFD DH=DF，∴△BHD≅△GFD，∴∠BDH=∠GDF，∴∠BDG=∠BDH+∠HDG=∠GDF+∠HDG=60°．解：(2)连接BG，CG，如图2，∵四边形ABCD是平行四边形，∠ABC=90°，∴四边形ABCD是矩形，∴∠ABE=∠BCD=∠BAD=90°，AB=CD，∵∠BAE=∠AEB，∴∠AEB=45°，AB=BE=DC，∴∠BEG=135°，∵∠ECF=∠BCD=90°，G为EF中点，CE=CF，∴CG=EG=FG，CG⊥EF，∠GCE=∠GCF=45°，∴∠DCG=∠BEG，在△BEG和△DCG中，{BE=DC∠BEG=∠DCG EG=CG，∴△BEG≅△DCG，∴BG=DG，∠BGE=∠DGC，∵CG⊥EF，∴∠CGE=90°=∠CGD+∠DGE=∠BGE+∠DGE=∠BGD，∴∠GDB=∠DBG=45°．故答案为45°；3.解：(1)①如图①中，设AC交BD于O．∵AB=BC，∠ABC=60°，∴△ABC是等边三角形，∵AB=CD，AB//CD，∴四边形ABCD是平行四边形，∵AB=BC，∴四边形ABCD菱形，∴AC⊥BD，∵OB=AB⋅sin60°=√3，∴BD=2√3．②如图①中，∵AB=BC，∠DBA=∠DBC，BD=BD，∴△DBA≌△DBC，∴DA=DC．(2)①如图②中，当AB=BF，∠ABC=60°时，四边形ABFE是等腰和谐四边形．由题意BD=14，BP=7，BF=6，此时∠BFE>90°，不合题意；②如图②−1中，当EF=BF，∠BFE=60°时，四边形ABFE是等腰和谐四边形．作AH⊥BD于H.连接BE，DF.易证四边形BEDF是菱形，△BEF，△DEF都是等边三角形．∴∠ADH=30°，AD=5，DH=5√3，BH=√AB2−AH2=√11，∴AH=12∴BD=√11+5√3，(√11+5√3)，∴PB=PD=12∴BF=PB÷cos30°=15+√33；3．综上所述，满足条件的BF的值为15+√3334.解：(1)如图，连接OB，O′B，则OB=O′B，∵四边形OABC是矩形，∴BA⊥OA，∴AO=AO′，∵B点的坐标为(1,3)，∴OA=1，∴AO′=1，∴点O′的坐标是(2,0)，△O′DB为等腰三角形，理由如下：在△BC′D与△O′AD中，{∠C′=∠DAO′=90°∠BDC′=∠O′DA BC′=AO′=1，∴△BC′D≌△O′AD(AAS)，∴BD =O′D ，∴△O′DB 是等腰三角形；(2)设点D 的坐标为(1,a)，则AD =a ，∵点B 的坐标是(1,3)，∴O′D =3−a ，在Rt △ADO′中，AD 2+AO′2=O′D 2，∴a 2+12=(3−a)2，解得a =43，∴点D 的坐标为(1,43)，设直线C′O′的解析式为y =kx +b ，则{2k +b =0k +b =43，解得{k =−43b =83， ∴边C′O′所在直线的解析式：y =−43x +83；(3)∵AM =1，AO =1，且AM ⊥AO ，∴△AOM 是等腰直角三角形，①PM 是另一直角边时，∠PMA =45°，∴PA =AM =1，点P 与点O′重合，∴点P 的坐标是(2,0)，②PO 是另一直角边，∠POA =45°，则PO 所在的直线为y =x ， ∴{y =−43x +83y =x，解得{x =87y =87， ∴点P 的坐标为P(2,0)或(87,87).5.(1)证明：∵∠BAC =90°，点E 为BC 中点，∴AE =12BC =BE ，∵∠ACB =30°，∴∠ABC =60°，∴△ABE 是等边三角形，∴∠AEB =60°，∵△BCD 是等边三角形，∴∠DBC =∠BCD =60°，∴∠ACD =∠ACB +∠BCD =30°+60°=90°，∵∠DBC=∠AEB=60°，∠BAC=∠ACD=90°，∴AB//CD，BD//AF，∴四边形ABDF是平行四边形；(2)解：∵∠BAC=90°，∠ACB=30°，BC=8，∴AB=4，AC=√BC2−AB2=√82−42=4√3，∵△BCD是等边三角形，∴CD=BC=8，设CG=x，则DG=8−x，在Rt△ACG中，AG2=AC2+CG2，即：(8−x)2=x2+(4√3)2，解得：x=1，∴CG=1．6.解：(1)在平行四边形ABCD中，AD//BC，∴∠AEB=∠EBG，∵△ABE沿BE折叠后得到△FBE，∴∠AEB=∠BEF，故∠BEF=∠EBG，∴BG=EG；(2)∵点E为AD的中点，∴AE=DE，将△ABE沿BE翻折，得到△FBE，∴AE=EF，∴EF=ED，∴∠4=∠EFD，∵AD//BC，∴∠4=∠5=∠GPF，∴∠EFD=∠GPF，故GF=GP，∵BG=EG，∴BP=EF=ED，∵BP//ED，∴四边形BEDP是平行四边形；(3)连接AF，由(2)知，AE=EF=ED，∴△AFD是直角三角形，∠AFD=90°，又因为在平行四边形BEDP中，BE//DP，所以∠4=∠1=30°，AD=5在直角三角形AFD中，AF=12DF=√AD2−AF2=√102−52=5√3．7.证明：(1)如图1，∵四边形ABCD为正方形，∴∠BCD=90°，AC平分∠BCD，∵PM⊥BC，PN⊥CD，∴四边PMCN为矩形，PM=PN，∵∠BPE=90°，∠BCD=90°，∴∠PBC+∠CEP=180°，而∠CEP+∠PEN=180°，∴∠PBM=∠PEN，在△PBM和△PEN中{∠PMB=∠PNE ∠PBM=∠PEN PM=PN∴△PBM≌△PEN(AAS)，∴PB=PE；(2)如图2，连结PD，∵四边形ABCD为正方形，∴CB=CD，CA平分∠BCD，∴∠BCP=∠DCP，在△CBP和△CDP中{CB=CD∠BCP=∠DCP CP=CP，∴△CBP≌△CDP(SAS)，∴PB=PD，∠CBP=∠CDP，∵∠BPE=90°，∠BCD=90°，∴∠PBC+∠CEP=180°，而∠CEP+∠PEN=180°，∴∠PBC=∠PED，∴∠PED=∠PDE，∴PD=PE，∴PB=PD；(3)如图3，PB=PE还成立．理由如下：过点P作PM⊥BC，PN⊥CD，垂足分别为M，N，∵四边形ABCD为正方形，∴∠BCD=90°，AC平分∠BCD，∵PM⊥BC，PN⊥CD，∴四边PMCN为矩形，PM=PN，∴∠MPN=90°，∵∠BPE=90°，∠BCD=90°，∴∠BPM+∠MPE=90°，而∠MEP+∠EPN=90°，∴∠BPM=∠EPN，在△PBM和△PEN中{∠PMB=∠PNE ∠BPM=∠EPN PM=PN，∴△PBM≌△PEN(AAS)，∴PB=PE．8.解：(1)FG=CE，FG//CE．(2)结论仍然成立．理由：如图2中，设DE与CF交于点M.∵四边形ABCD是正方形，∴BC=CD，∠ABC=∠DCE=90°，在△CBF和△DCE中，BF=CE，∠CBF=∠ECD，BC=CD，∴△CBF≌△DCE，∴∠BCF=∠CDE，CF=DE，∵∠BCF+∠DCM=90°，∴∠CDE+∠DCM=90°，∴∠CMD=90°，∴CF⊥DE，∵GE⊥DE，∴EG//CF，∵EG=DE，CF=DE，∴EG=CF，∴四边形EGFC是平行四边形．∴GF=EC，∴GF=EC，GF//EC.(3)如图所示，结论仍然成立．解：(1)理由：如图1中，设DE与CF交于点M.∵四边形ABCD是正方形，BE=AF∴BC=CD，∠ABC=∠DCE=90°，BF=CE，在△CBF和△DCE中，BF=CE，∠CBF=∠ECD，BC=CD，∴△CBF≌△DCE，∴∠BCF=∠CDE，CF=DE，∵∠BCF+∠DCM=90°，∴∠CDE+∠DCM=90°，∴∠CMD=90°，∴CF⊥DE，∵GE⊥DE，∴EG//CF，∵EG=DE，CF=DE，∴EG=CF，∴四边形EGFC是平行四边形．∴GF=EC，∴GF=EC，GF//EC；故答案为FG=CE，FG//CE．(2)见答案；(3)见答题图，理由：如图3中，设DE与FC的延长线交于点M.∵四边形ABCD是正方形，∴BC=CD，∠ABC=∠DCE=90°，∴∠CBF=∠DCE=90°在△CBF和△DCE中，BF=CE，∠CBF=∠DCE，BC=CD，，∴△CBF≌△DCE，∴∠BCF=∠CDE，CF=DE∵∠BCF+∠DCM=90°，∴∠CDE+∠DCM=90°，∴∠CMD=90°，∴CF⊥DE，∵GE⊥DE，∴EG//CF，∵EG=DE，CF=DE，∴EG=CF，∴四边形EGFC是平行四边形．∴GF=EC，∴GF=EC，GF//EC．9.解：(1)√2，2√5，2√5(2)2，2√7，2√13(3)结论：a2+b2=5c2，证明：如题图3，因为AF、BE是△ABC的中线，所以E、F分别为AC、BC的中点，则EF//AB，EF=12AB=12c．因为∠PBA=30°，则PA=12c，PB=√AB2−PA2=√32c，在直角三角形EFP中，因为EF//AB，所以∠FEP=∠PBA=30°，则PF=14c，PE=√EF2−PF2=√34c，则AE=√PA2+PE2=√74c，BF=√PB2+PF2=√134c，所以a=BC=2BF=√132c，b=AC=2AE=√72c，则a2+b2=5c2．解：(1)连接EF，则EF是三角形ABC的中位线，所以EF=12AB=√2，因为∠PBA=45°，BE⊥AF，所以三角形APB是等腰直角三角形，因为EF//AB，所以三角形EPF也是等腰直角三角形，则AP=BP=2，EP=FP=1，所以AE=BF=√5，则a=b=2√5；(2)连接EF，则EF是三角形ABC的中位线，因为∠PBA=60°，BE⊥AF，c=4，所以BP=2，AP=2√3，因为EF//AB，AB=2，∠PEF=60°，则EF=12所以PF=√3，PE=1，所以BF=√7，AE=√13，则a=2√7，b=2√13；10.解：(1)∵四边形ABCD是矩形，∴AD//BC，AD=BC=3∵点Q从点A出发，以1cm/s的速度沿AD向终点D运动，同时，点Q从点C出发，以1cm/s的速度沿CB向终点B运动，∴PC=AQ=t，∴QD=BP=3−t∴四边形BQDP是平行四边形；(2)∵DQ=3−t，=DQ⋅AB=(3−t)×1=3−t；∴S四边形BQDP(3)四边形BQDP可能为菱形．∵一组邻边相等的平行四边形是菱形，∴BQ=QD，∵AQ=t，AB=1，∴BQ=√AQ2+AB2=√t2+12，QD=3−t，∴t2+1=(3−t)2，解得t=4．3∴当t=4时，四边形BQDP为菱形．311.(1)证明：∵Rt△OAB中，D为OB的中点，∴AD=12OB，OD=BD=12OB∴DO=DA，∴∠DAO=∠DOA=30°，∠EOA=90°，∴∠AEO=60°，又∵△OBC为等边三角形，∴∠BCO=∠AEO=60°，∴BC//AE，∵∠BAO=∠COA=90°，∴CO//AB，∴四边形ABCE是平行四边形；(2)解：设OG=x，由折叠可得：AG=GC=8−x，在Rt△ABO中，∵∠OAB=90°，∠AOB=30°，BO=8，∴AO=BO⋅cos30°=8×√32=4√3，在Rt△OAG中，OG2+OA2=AG2，x2+(4√3)2=(8−x)2，解得：x=1，∴OG=1．12.解：(1)△OAB是直角三角形，理由如下：∵AB2=25，OA2+OB2=5+20=25，∴AB2=OA2+OB2，∴△OAB是直角三角形；(2)存在，如图(1)(2)(1)(2)由图可得点C坐标为(−5,0)，(5,0)，(−3,4)或(0,5)，(−4,3)，(4,−3)．13.解：(1)由题意，根据梯形的面积公式，得S=(t+5)×4=2t+10；2(2)∵四边形PODB是平行四边形，∴PB=OD=5，∴PC=5，∴t=5；(3)∵ODQP为菱形，∴OD=OP=PQ=5，∴在Rt△OPC中，由勾股定理得：PC=3∴t=3；(4)当P1O=OD=5时，由勾股定理可以求得P1C=3，∴P1(3,4)；P2O=P2D时，作P2E⊥OA，∴OE=ED=2.5，∴P2(2.5,4)；当P3D=OD=5时，作DF⊥BC，由勾股定理，得P3F=3，∴P3C=2，∴P3(2,4)；当P4D=OD=5时，作P4G⊥OA，由勾股定理，得DG=3，∴OG=8，∴P4(8,4)；∴P的坐标为：(2,4)，(2.5,4)，(3,4)，(8,4)．14.解：(1)在△DFC中，∠DFC=90°，∠C=30°，DC=2t，∴DF=t，又∵AE=t，∴AE=DF;m又∵AE//DF，∴四边形AEFD是平行四边形．(2)①当点E、D分别在线段AB和AC上，当AE=AD时，∵∠A=60°，∴△AED是等边三角形，∴DE=AE，∴t=12−2t，∴t=4，∴DE=AE=4;②当点E、D分别在线段AB和AC的延长线上，∵∠A=60°，∴∠EAD=120°，∴当△ADE为等腰三角形，只有AD=AE时，∴2t−12=t，∴t=12，过点A作AG⊥DE于点G，在RtADG中，AG=6，DG=6√3，∵AE=AD，AG⊥ED，∴ED=2DG=12√3，综上：当t=4时，△ADE是等腰三角形，此时DE=4，当t=12时，△ADE是等腰三角形，此时DE=12√3．15.(1)解：AB=BC或BC=CD或CD=AD或AD=AB(2)解：小红的结论正确．理由如下：∵四边形的对角线互相平分，∴这个四边形是平行四边形，∵四边形是“等邻边四边形”，∴这个四边形有一组邻边相等，∴这个“等邻边四边形”是菱形，(3)解：由∠ABC=90°，AB=2，BC=1，得：AC=√5，∵将Rt△ABC平移得到Rt△A′B′C′，∴BA′=AA′，A′B′//AB，A′B′=AB=2，B′C′=BC=1，A′C′=AC=√5，(I)如图1，当AA′=AB时，BB′=AA′=AB=2，(II)如图2，当AA′=A′C′时，BB′=AA′=AC′=√5，(III)当AC′=BC′=√5时，如图3，延长C′B′交AB 于点D ，则C′B′⊥AB ∵BB′平分∠ABC ，∴∠ABB′=12∠ABC =45° ∴∠BB′D =∠ABB′=45°，∴B′D =BD ，设B′D =BD =x ，则C′D =x +1，BB′=√2x ∵根据在Rt △BC′D 中，BC′2=C′D 2+BD 2即x 2+(x +1)2=5 解得：x =1或x =−2(不合题意，舍去) ∴BB′=√2x =√2，(IV)当BC′=AB =2时，如图4，与(III)方法同理可得：x =−1+√72或x =−1−√72， x =−1+√72或x =−1−√72(舍去)∴BB′=√2x =−√2+√142．故应平移2或√5或√2或−√2+√142．16.解：(1)当DE =CF 时，四边形EFCD 为矩形，则有6−t =10−2t ，解得t =4，答：t =4s 时，四边形EFCD 为矩形．(2)①当点F 在线段BM 上，AE =FM 时，以A 、M 、E 、F 为顶点的四边形是平行四边形，则有t =4−2t ，解得t =43，②当F 在线段CM 上，AE =FM 时，以A 、M 、E 、F 为顶点的四边形是平行四边形，则有t =2t −4，解得t =4，s时，以A、M、E、F为顶点的四边形是平行四边形．综上所述，t=4s或43。

八下第九章平行四边形难题训练(一)(有答案)

八下第九章平行四边形难题训练（一）姓名：___________班级：___________考号：___________一、选择题1.如图，平行四边形ABCD中，P是CD上一点，且AP和BP分别平分∠DAB和∠CBA，若AD=5，AP=8，则BP的长为()A. 3B. 4C. 5D. 62.如图，在正方形ABCD对角线BD上截取BE=BC，连接CE并延长交AD于点F，连接AE，过B作BG⊥AE于点G，交AD于点H，则下列结论错误的是()A. AH=DFB. S四边形EFHG=S△DCF+S△AGHC. ∠AEF=45°D. △ABH≌△DCF3.如图，在矩形ABCD中，点E，F分别在BC，CD上，将△ABE沿AE折叠，使点B落在AC上的点B′处，又将△CEF沿EF折叠，使点C落在EB′与AD的交点C′处．则下列说法正确的是()①∠BAC=60°;②AB=2BE;③CC′//AE;④四边形AEC C′是菱形．A. ①②③B. ②③④C. ①②④D. ①③④4.如图，四边形ABCD为矩形纸片，把纸片ABCD折叠，使点B恰好落在CD边的中点E处，折痕为AF，若CD=6，则AF等于()A. 4√3B. 3√3C. 4√2D. 85.如图，在矩形ABCD中，AC、BD相交于点O，AE平分∠BAD交BC于E，若∠EAO=15°，则∠BOE的度数为()．A. 85°B. 80°C. 75°D. 70°6.如图．在矩形ABCD中，AB=8，BC=4，将矩形沿AC折叠，点D落在点E处，且CE与AB交于F，那么S△ACF为()A. 12B. 15C. 6D. 107.如图，正方形ABCB1中，AB=1，AB与直线l的夹角为30°，延长CB1交直线l于点A1，作正方形A1B1C1B2，延长C1B2交直线l于点A2，作正方形A2B2C2B3，延长C2B3交直线l于点A3，作正方形A3B3C3B4…依此规律，则A2017A2018=()A. (√3)2017B. (√3)2018C. 2(√3)2017D. 2(√3)2018二、填空题8.如图，在边长为6√2的正方形ABCD中，E是边CD的中点，F在BC边上，且，连接EF，则BF的长为___________．9.在平行四边形ABCD中，AE平分∠BAD交边BC于E，DF平分∠ADC交边BC于F，若AD=11，EF=5，则AB=____．10.已知平行四边形ABCD的周长为40，ΔBOC的周长比ΔAOB的周长大10，则边长AB的长为_____．11.已知平行四边形ABCD中，AB=6，BC=4，BC边上的高AE=3，AF⊥DC于F，则DF的长是____．12.如图，在平行四边形ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E∠BCD，(2)EF=CF；在线段AB上，连接EF、CF，则下列结论：(1)∠DCF=12(3)S△BEC=2S△CEF；(4)∠DFE=3∠AEF，其中正确的结论是____________．13.如图，在正方形ABCD中，AB=12，点E在边CD上，CD=3DE.将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG，CF.有下列结论：①△ABG≌△AFG；②BG=GC；③AG//CF；④S△FGC=6.其中正确的结论是________．14.如图，把RtΔABC放在直角坐标系内，其中∠CAB=90∘，BC=5，点A，B的坐标分别为(1,0)，(4,0)，将ΔABC沿x轴向右平移，当点C落在直线y=2x−6上时，线段BC扫过的面积为______cm2。

浙教版初中数学八年级下册第四单元《平行四边形》(标准困难)(含答案解析)

浙教版初中数学八年级下册第四单元《平行四边形》（标准困难）（含答案解析）考试范围：第四单元；   考试时间：120分钟；总分：120分，第I卷（选择题）一、选择题（本大题共12小题，共36.0分。

在每小题列出的选项中，选出符合题目的一项）1. 一个多边形截去一个角后，形成一个六边形，那么原多边形边数为( )A. 5B. 5或6C. 5或7D. 5或6或72. 如图，已知O是四边形ABCD内一点，OA=OB=OC，∠ABC=∠ADC=70°，则∠DAO+∠DCO的大小是( )A. 70°B. 110°C. 140°D. 150°3. 如图，在▱ABCD中，对角线AC的垂直平分线分别交AD、BC于点E、F，连接CE，若△CED的周长为6，则▱ABCD的周长为( )A. 6B. 12C. 18D. 244. 在▱ABCD中，∠A∶∠B∶∠C=3∶6∶3，则∠D的度数为( )A. 90°B. 67.5°C. 112.5°D. 120°5. 利用圆内接正多边形，可以设计出非常有趣的图形．下列图形中，是中心对称图形，但不是轴对称图形的是．( )A. B. C. D.6. 若两个图形关于某点成中心对称，则以下说法中正确的是．( )①这两个图形一定全等；②对称点的连线一定经过对称中心；③一定存在某条直线，沿该直线折叠后的两个图形能互相重合．A. ①②B. ①③C. ②③D. ①②③7. 如图，在四边形ABCD中，对角线AC，BD相交于点O，不能判定四边形ABCD是平行四边形的是( )A. AB//CD，AD//BCB. AB=CD，AD=BCC. AD//BC，∠ABC=∠ADCD. AB=CD，AD//BC8. 如图，在四边形ABCD中，AC、BD相交于点O，下列条件不能判定四边形ABCD为平行四边形的是( )A. AD//BC，OA=OCB. OB=OD，∠ABD=∠CDBC. AB//CD，∠ABC=∠ADCD. AD//BC，AB=CD9. 如图，已知四边形ABCD中，R，P分别是BC，CD上的点，E，F分别是AP，RP的中点，当点P在CD上从点C向点D移动而点R不动时，下列结论成立的是( )A. 线段EF的长度逐渐增大B. 线段EF的长度逐渐减小C. 线段EF的长度不变D. 线段EF的长度与点P的位置有关10. 如图，在四边形ABCD中，∠ABC=90°，点E、F分别是AC、AD的中点，且BE=EF，若AB=8，BC=4，则CD的长为( )A. 4√5B. 4√3C. 2√5D. 811. 下列说法：①伸缩门的制作运用了四边形的不稳定性；②夹在两条平行线间的垂线段相等；③用反证法证明命题“已知△ABC中，AB=AC，求证：∠B<90°”时，应先假设∠B> 90°；④在直角坐标系中，点P(2,a−1)与点Q(b+2,3)关于原点对称，则a+b=−6.其中正确的个数为( )A. 1个B. 2个C. 3个D. 4个12. 用反证法证明：三角形三内角至少有一个不小于60°时，应假设( )A. 三个角都大于60°B. 三个角都小于60°C. 三个角都不大于60°D. 三个角都不小于60°第II卷（非选择题）二、填空题（本大题共4小题，共12.0分）13. 如图，小明在操场上从A点出发，沿直线前进10m后向左转40∘，再沿直线前进10m后，又向左转40∘，照这样走下去，他第一次回到出发地A点时，一共走了______m.14. 如图是4×4正方形网格，把其中一个标有数字的白色小正方形涂成蓝色，就可以使图中的蓝色部分构成一个中心对称图形，则这个白色小正方形内的数字是．15. 如图，在▱ABCD中，E、F分别是边AD、BC的中点，连接BE、DF，则BE、DF之间的数量和位置关系分别是．16. 如图，D，E，F分别是△ABC各边的中点，AH是BC边上的高，若HF=3，则ED的长为．三、解答题（本大题共9小题，共72.0分。

人教版八年级初二数学下学期平行四边形单元易错题难题提优专项训练

人教版八年级初二数学下学期平行四边形单元易错题难题提优专项训练一、解答题1．如图，在正方形ABCD 中，点G 在对角线BD 上（不与点B ，D 重合），GE ⊥DC 于点E ，GF ⊥BC 于点F ，连结AG ．（1）写出线段AG ，GE ，GF 长度之间的数量关系，并说明理由；（2）若正方形ABCD 的边长为1，∠AGF=105°，求线段BG 的长．2．如图，在矩形ABCD 中，点E 是AD 上的一点（不与点A ，D 重合），ABE ∆沿BE 折叠，得BEF ，点A 的对称点为点F ．（1）当AB AD =时，点F 会落在CE 上吗？请说明理由．（2）设()01AB m m AD=<<，且点F 恰好落在CE 上． ①求证：CF DE =．②若AE n AD=，用等式表示m n ，的关系． 3．如图，在ABC ∆中，BD 平分ABC ∠交AC 于点D ，EF 垂直平分BD ，分别交AB ，BC ，BD 于点E ，F ，G ，连接DE ，DF ．（1）求证：四边形BEDF 是菱形；（2）若15BDE ∠=︒，45C ∠=︒，2DE =，求CF 的长；（3）在（2）的条件下，求四边形BEDF 的面积．4．如图，正方形ABCO 的边OA 、OC 在坐标轴上，点B 坐标为（6，6），将正方形ABCO 绕点C 逆时针旋转角度α（0°＜α＜90°），得到正方形CDEF ，ED 交线段AB 于点G ，ED的延长线交线段OA 于点H ，连结CH 、CG ．（1）求证：CG 平分∠DCB ；（2）在正方形ABCO 绕点C 逆时针旋转的过程中，求线段HG 、OH 、BG 之间的数量关系；（3）连结BD 、DA 、AE 、EB ，在旋转的过程中，四边形AEBD 是否能在点G 满足一定的条件下成为矩形？若能，试求出直线DE 的解析式；若不能，请说明理由．5．如图①，已知正方形ABCD 的边长为3，点Q 是AD 边上的一个动点，点A 关于直线BQ 的对称点是点P ，连接QP 、DP 、CP 、BP ，设AQ =x ．（1）BP ＋DP 的最小值是_______，此时x 的值是_______；（2）如图②，若QP 的延长线交CD 边于点M ，并且∠CPD =90°．①求证：点M 是CD 的中点；②求x 的值．（3）若点Q 是射线AD 上的一个动点，请直接写出当△CDP 为等腰三角形时x 的值．6．如图，菱形纸片ABCD 的边长为2,60,BAC ∠=︒翻折,,B D ∠∠使点,B D 两点重合在对角线BD 上一点,,P EF GH 分别是折痕．设()02AE x x =<<．（1）证明：AG BE =；（2）当02x <<时，六边形AEFCHG 周长的值是否会发生改变，请说明理由；（3）当02x <<时，六边形AEFCHG 的面积可能等于53吗?如果能，求此时x 的值；如果不能，请说明理由．7．如图1，在正方形ABCD （正方形四边相等，四个角均为直角）中，AB ＝8，P 为线段BC 上一点，连接AP ，过点B 作BQ ⊥AP ，交CD 于点Q ，将△BQC 沿BQ 所在的直线对折得到△BQC ′，延长QC ′交AD 于点N ．（1）求证：BP ＝CQ ；（2）若BP ＝13PC ，求AN 的长；（3）如图2，延长QN 交BA 的延长线于点M ，若BP ＝x （0＜x ＜8），△BMC '的面积为S ，求S 与x 之间的函数关系式．8．如图，在四边形OABC 是边长为4的正方形点P 为OA 边上任意一点（与点O A 、不重合），连接CP ，过点P 作PM CP ⊥，且PM CP =，过点M 作MN AO ∥，交BO 于点,N 联结BM CN 、，设OP x =.（1）当1x =时，点M 的坐标为（，）（2）设CNMB S y =四形边，求出y 与x 的函数关系式，写出函数的自变量的取值范围.（3）在x 轴正半轴上存在点Q ，使得QMN 是等腰三角形，请直接写出不少于4个符合条件的点Q 的坐标（用x 的式子表示）9．阅读下列材料，并解决问题：如图1，在Rt ABC ∆中，90C ∠=︒，8AC =，6BC =，点D 为AC 边上的动点（不与A 、C 重合），以AD ，BD 为边构造ADBE ，求对角线DE 的最小值及此时AD AC的值是多少．在解决这个问题时，小红画出了一个以AD ，BD 为边的ADBE （如图2），设平行四边形对角线的交点为O ，则有AO BO =．于是得出当OD AC ⊥时，OD 最短，此时DE 取最小值，得出DE 的最小值为6．参考小红的做法，解决以下问题：（1）继续完成阅读材料中的问题：当DE的长度最小时，ADAC=_______；（2）如图3，延长DA到点F，使AF DA=．以DF，DB为边作FDBE，求对角线DE的最小值及此时ADAC的值．10．已知：正方形ABCD和等腰直角三角形AEF，AE=AF（AE＜AD），连接DE、BF，P是DE的中点，连接AP．将△AEF绕点A逆时针旋转．（1）如图①，当△AEF的顶点E、F恰好分别落在边AB、AD时，则线段AP与线段BF的位置关系为，数量关系为．（2）当△AEF绕点A逆时针旋转到如图②所示位置时，证明：第（1）问中的结论仍然成立．（3）若AB=3,AE=1，则线段AP的取值范围为．【参考答案】***试卷处理标记，请不要删除一、解答题1．（1）AG2=GE2+GF2，理由见解析；（2326+【分析】（1）结论：AG2=GE2+GF2．只要证明GA=GC，四边形EGFC是矩形，推出GE=CF，在Rt △GFC 中，利用勾股定理即可证明；（2）作BN ⊥AG 于N ，在BN 上截取一点M ，使得AM=BM ．设AN=x ．易证AM=BM=2x ，MN=3x ，在Rt △ABN 中，根据AB 2=AN 2+BN 2，可得1=x 2+（2x+3x ）2，解得x=624-，推出BN=624+，再根据BG=BN÷cos30°即可解决问题. 【详解】解：（1）结论：AG 2=GE 2+GF 2．理由：连接CG ．∵四边形ABCD 是正方形，∴A 、C 关于对角线BD 对称，∵点G 在BD 上，∴GA=GC ，∵GE ⊥DC 于点E ，GF ⊥BC 于点F ，∴∠GEC=∠ECF=∠CFG=90°，∴四边形EGFC 是矩形，∴CF=GE ，在Rt △GFC 中，∵CG 2=GF 2+CF 2，∴AG 2=GF 2+GE 2．（2）作BN ⊥AG 于N ，在BN 上截取一点M ，使得AM=BM ．设AN=x ．∵∠AGF=105°，∠FBG=∠FGB=∠ABG=45°，∴∠AGB=60°，∠GBN=30°，∠ABM=∠MAB=15°，∴∠AMN=30°，∴AM=BM=2x ，MN=3x ，在Rt △ABN 中，∵AB 2=AN 2+BN 2，∴1=x 2+（2x+3x ）2，解得x=624-， ∴BN=624+， ∴BG=BN÷cos30°=326+．【点睛】本题考查正方形的性质，矩形的判定和性质，勾股定理，直角三角形30度的性质．2．（1）不会，理由见解析；（2）①见解析；②²²20m n n =+-【分析】（1）根据BEF BEA ≅得到BF BA =，根据三角形的三边关系得到BC BF BA >=，与已知矛盾；（2）①根据90BFC BFE ∠=∠=︒、DEC FCB ∠=∠和BF=CD ，利用AAS 证得BCF CED ≅，根据全等三角形的性质即可证明；②设1AD =，则可表示出AE 和AB ，然后根据等角对等边证得CE=CB ，然后在Rt CDE ∆中应用勾股定理即可求解．【详解】（1）由折叠知BEF BEA ≅ ，所以90BF BA BFE A =∠=∠=︒，．若点F 在CE 上，则90BFC ∠=︒，BC BF BA >=，与AB AD =矛盾，所以点F 不会落在CE 上．（2）①因为()01AB m m AD=<<，则AB AD < ，因为点F 落在CE 上，所以90BFC BFE ∠=∠=︒ ，所以BF BA CD == ．因为//AD BC ，所以DEC FCB ∠=∠ ，所以BCF CED ≅ ，所以CF DE =．②若AE n AD=，则AE nAD =．设1AD =，则AE n AB m ==，．因为//AD BC ，所以BEA EBC ∠=∠ ．因为BEF BEA ∠=∠ ，所以EBC BEC ∠=∠ ，所以1CE CB AD === ．在Rt CDE ∆中，11DE n CE CD m ===一，，，所以22211()n m -+= ，所以²²20m n n =+-．故答案为（1）不会，理由见解析；（2）①见解析；②²²20m n n =+-．【点睛】本题考查了三角形全等的性质和判定，和等边对等角，此题属于矩形的折叠问题类综合题，熟练掌握三角形全等的性质，和做出示意图是本题的关键．3．（1）见解析；（2）3+1；（3）2【分析】（1）由线段垂直平分线的性质可得BE=DE ，BF=DF ，可得∠EBD=∠EDB ，∠FBD=∠FDB ，由角平分线的性质可得∠EBD=∠BDF=∠EDB=∠DBF ，可证BE ∥DF ，DE ∥BF ，可得四边形DEBF 是平行四边形，即可得结论；（2）由菱形的性质和外角性质可得∠DFC=30°，由直角三角形的性质可求CF 的长；（3）过点D 作BC 的垂线，垂足为H ，根据菱形的性质得出∠DFH=∠ABC=30°，从而得到DH 的长度，再利用底乘高得出结果．【详解】解：证明：（1）∵BD 平分∠ABC ，∴∠ABD=∠DBC ，∵EF 垂直平分BD ，∴BE=DE ，BF=DF ，∵∠EBD=∠EDB ，∠FBD=∠FDB ，∴∠EBD=∠BDF ，∠EDB=∠DBF ，∴BE ∥DF ，DE ∥BF ，∴四边形DEBF 是平行四边形，且BE=DE ，∴四边形BEDF 是菱形；（2）过点D 作DH ⊥BC 于点H ，∵四边形BEDF 是菱形，∴BF=DF=DE=2，∴∠FBD=∠FDB=∠BDE=15°，∴∠DFH=30°，且DH ⊥BC ，∴DH=12DF=1，33， ∵∠C=45°，DH ⊥BC ，∴∠C=∠CDH=45°，∴DH=CH=1，∴FC=FH+CH=3+1；（3）过点D作BC的垂线，垂足为H，∵四边形BEDF是菱形，∠BDE=15°，∴∠DBF=∠BDF=∠ABD=15°，∴∠DFH=∠ABC=30°，∵DE=DF=2，∴DH=1，∴菱形BEDF的面积=BF×DH=2×1=2．【点睛】本题考查了菱形的判定和性质，线段垂直平分线的性质，直角三角形的性质等知识，掌握菱形的判定方法是本题的关键．4．（1）见解析；（2）HG＝OH+BG；（3）能成矩形，y33 42x=-．【分析】（1）根据旋转和正方形的性质可得出CD＝CB，∠CDG＝∠CBG＝90，根据全等直角三角形的判定定理（HL）即可证出Rt△CDG≌Rt△CBG，即∠DCG＝∠BCG，由此即可得出CG平分∠DCB；（2）由（1）的Rt△CDG≌Rt△CBG可得出BG＝DG，根据全等直角三角形的判定定理（HL）即可证出Rt△CHO≌Rt△CHD，即OH＝HD，再根据线段间的关系即可得出HG＝HD+DG＝OH+BG；（3）根据（2）的结论即可找出当G点为AB中点时，四边形AEBD为矩形，再根据正方形的性质以及点B的坐标可得出点G的坐标，设H点的坐标为（x，0），由此可得出HO＝x，根据勾股定理即可求出x的值，即可得出点H的坐标，结合点H、G的坐标利用待定系数法即可求出直线DE的解析式．【详解】（1）∵正方形ABCO绕点C旋转得到正方形CDEF，∴CD＝CB，∠CDG＝∠CBG＝90°．在Rt△CDG和Rt△CBG中，∵CG CGCD CB=⎧⎨=⎩，∴Rt△CDG≌Rt△CBG（HL），∴∠DCG＝∠BCG，即CG平分∠DCB．（2）由（1）证得：Rt△CDG≌Rt△CBG，∴BG＝DG．在Rt△CHO和Rt△CHD中，∵CH CH CO CD =⎧⎨=⎩，∴Rt △CHO ≌Rt △CHD （HL ），∴OH ＝HD ，∴HG ＝HD +DG ＝OH +BG ．（3）假设四边形AEBD 可为矩形．当G 点为AB 中点时，四边形AEBD 为矩形，如图所示．∵G 点为AB 中点，∴BG ＝GA 12=AB ，由（2）证得：BG ＝DG ，则BG ＝GA ＝DG 12=AB 12=DE ＝GE ，又AB ＝DE ，∴四边形AEBD 为矩形，∴AG ＝EG ＝BG ＝DG ．∵AG 12=AB ＝3，∴G 点的坐标为（6，3）．设H 点的坐标为（x ，0），则HO ＝x ，∴HD ＝x ，DG ＝3．在Rt △HGA 中，HG ＝x +3，GA ＝3，HA ＝6﹣x ，由勾股定理得：（x +3）2＝32+（6﹣x ）2，解得：x ＝2，∴H 点的坐标为（2，0）．设直线DE 的解析式为：y ＝kx +b （k ≠0），将点H （2，0）、G （6，3）代入y ＝kx +b 中，得：2063k b k b +=⎧⎨+=⎩，解得：3432k b ⎧=⎪⎪⎨⎪=-⎪⎩，∴直线DE 的解析式为：y 3342x =-．故四边形AEBD 能为矩形，此时直线DE 的解析式为：y 3342x =-．【点睛】本题考查了矩形的性质、旋转的性质、全等三角形的判定及性质、待定系数法求函数解析式以及勾股定理．解题的关键是：（1）证出Rt △CDG ≌Rt △CBG ；（2）找出BG ＝DG 、OH ＝HD ；（3）求出点H 、G 的坐标．本题属于中档题，难度不大，解决该题型题目时，根据全等三角形的性质找出相等的边和角是关键．5．（1）32323；（2）①见详解；②x=1；（3）△CDP 为等腰三角形时x 的值为：633-或3633+．【分析】（1）BP+DP 为点B 到D 两段折线的和．由两点间线段最短可知，连接DB ，若P 点落在BD上，此时和最短，且为32．考虑动点运动，这种情形是存在的，由AQ=x ，则QD=3-x ，PQ=x ．又PDQ=45°，所以QD ＝2PQ ，即3-x=2x ．求解可得答案；（2）由已知条件对称分析，AB=BP=BC ，则∠BCP=∠BPC ，由∠BPM=∠BCM=90°，可得∠MPC=∠MCP ．那么若有MP=MD ，则结论可证．再分析新条件∠CPD=90°，易得①结论．②求x 的值，通常都是考虑勾股定理，选择直角三角形QDM ，发现QM ，DM ，QD 都可用x 来表示，进而易得方程，求解即可．（3）若△CDP 为等腰三角形，则边CD 比为改等腰三角形的一腰或者底边．又P 点为A 点关于QB 的对称点，则AB=PB ，以点B 为圆心，以AB 的长为半径画弧，则P 点只能在弧AB 上．若CD 为腰，以点C 为圆心，以CD 的长为半径画弧，两弧交点即为使得△CDP 为等腰三角形（CD 为腰）的P 点．若CD 为底边，则作CD 的垂直平分线，其与弧AC 的交点即为使得△CDP 为等腰三角形（CD 为底）的P 点．则如图所示共有三个P 点，那么也共有3个Q 点．作辅助线，利用直角三角形性质求之即可．【详解】解：（1）连接DB ，若P 点落在BD 上，此时BP+DP 最短，如图：由题意，∵正方形ABCD 的边长为3，∴223332BD =+=∴BP ＋DP 的最小值是32由折叠的性质，PQ AQ x ==，则3QD x =-，∵∠PDQ=45°，∠QPD=90°，∴△QPD 是等腰直角三角形，∴22QD QP x ==，∴32x x -=，解得：323x =；故答案为：32323；（2）如图所示：①证明：在正方形ABCD中，有AB=BC，∠A=∠BCD=90°．∵P点为A点关于BQ的对称点，∴AB=PB，∠A=∠QPB=90°，∴PB=BC，∠BPM=∠BCM，∴∠BPC=∠BCP，∴∠MPC=∠MPB-∠CPB=∠MCB-∠PCB=∠MCP，∴MP=MC．在Rt△PDC中，∵∠PDM=90°-∠PCM，∠DPM=90°-∠MPC，∴∠PDM=∠DPM，∴MP=MD，∴CM=MP=MD，即M为CD的中点．②解：∵AQ=x，AD=3，∴QD=3-x，PQ=x，CD=3．在Rt△DPC中，∵M为CD的中点，∴DM=QM=CM=32，∴QM=PQ+PM=x+32，∴(x+32)2＝(3−x)2+(32)2，解得：x=1．（3）如图，以点B为圆心，以AB的长为半径画弧，以点C为圆心，以CD的长为半径画弧，两弧分别交于P1，P3．此时△CDP1，△CDP3都为以CD为腰的等腰三角形．作CD的垂直平分线交弧AC于点P2，此时△CDP2以CD为底的等腰三角形．；①讨论P1，如图作辅助线，连接BP1、CP1，作QP1⊥BP1交AD于Q，过点P1，作EF⊥AD 于E，交BC于F．∵△BCP1为等边三角形，正方形ABCD边长为3，∴P1F＝332，P1E＝333．在四边形ABP1Q中，∵∠ABP1=30°，∴∠AQP1=150°，∴△QEP1为含30°的直角三角形，∴31＝9 332．∵AE=32，∴x=AQ=AE-QE=39(33)633 22-=-②讨论P2，如图作辅助线，连接BP2，AP2，过点P2作QG⊥BP2，交AD于Q，连接BQ，过点P2作EF⊥CD于E，交AB于F．∵EF垂直平分CD，∴EF垂直平分AB，∴AP2=BP2．∵AB=BP2，∴△ABP2为等边三角形．在四边形ABP2Q中，∵∠BAD=∠BP2Q=90°，∠ABP2=60°，∴∠AQG=120°∴∠EP2G=∠DQG=180°-120°=60°，∴P2E＝33 3∴EG=9 332，∴DG=DE+GE=3933333 22+=，∴QD=33，∴3③对P3，如图作辅助线，连接BP1，CP1，BP3，CP3，过点P3作BP3⊥QP3，交AD的延长线于Q，连接BQ，过点P1，作EF⊥AD于E，此时P3在EF上，不妨记P3与F重合．∵△BCP 1为等边三角形，△BCP 3为等边三角形，BC=3，∴P 1P 3＝33P 1E ＝3332-， ∴EF ＝333+．在四边形ABP 3Q 中∵∠ABF=∠ABC+∠CBP 3=150°，∴∠EQF=30°，∴39332． ∵AE=32， ∴x=AQ=AE+QE=32+9333362=．综合上述，△CDP 为等腰三角形时x 的值为：633-3633+．【点睛】本题第一问非常基础，难度较低．第二问因为动点的原因，思路不易找到，这里就需要做题时充分分析已知条件，尤其是新给出的条件．其中求边长是勾股定理的重要应用，是很重要的考点．第三问是一个难度非常高的题目，可以利用尺规作图的思想将满足要求的点P 找全．另外求解各个Q 点也是考察三角函数及勾股定理的综合应用，有着极高的难度．6．（1）见解析；（2）不变，见解析；（3）能，21x =-21+ 【分析】（1）由折叠的性质得到BE=EP ，BF=PF ，得到BE=BF ，根据菱形的性质得到AB ∥CD ∥FG ，BC ∥EH ∥AD ，于是得到结论；（2）由菱形的性质得到BE=BF ，AE=FC ，推出△ABC 是等边三角形，求得∠B=∠D=60°，得到∠B=∠D=60°，于是得到结论；（3）记AC 与BD 交于点O ，得到∠ABD=30°，解直角三角形得到AO=1，BO=3，求得S 四边形ABCD =23，当六边形AEFCHG 的面积等于534时，得到S △BEF +S △DGH =334，设GH 与BD 交于点M ，求得GM=12x ，根据三角形的面积列方程即可得到结论．【详解】解:()1折叠后B 落在BD 上， ,BE EP ∴=BF PF =BD 平分,ABC ∠BE BF ∴=，∴四边形BEPF 为菱形，同理四边形GDHP 为菱形，////,// //,AB CD FG BC EH AD ∴∴四边形AEPG 为平行四边形，AG EP BE ∴==.()2不变.理由如下:由()1得.AG BE =四边形BEPF 为菱形，,.BE BF AE FC ∴==60,BAC ABC ∠=︒为等边三角60B D ∴∠=∠=︒，,,EF BE GH DG ∴==36AEFCHG C AE EF FC CH GH AG AB ∴=+++++==六边形为定值.()3记AC 与BD 交于点O .2,60,AB BAC =∠=30,ABD ∴∠=1,AO ∴=3,BO =12332ABC S ∴=⨯⨯= 23ABCD S ∴=四边形当六边形AEFCHG 的面积为534时， 53233344DEF DGH S S +=-= 由()1得BE AG =AE DG ∴=DG x =2BE x ∴=-记GH 与BD 交于点,M12GM x ∴=，3DM x = 23DHG S x ∴= 同理)2233233BEF Sx x x =-= 223333334x x x +=化简得22410,x x -+= 解得1212x =-，2212x =+ ∴当21x =-或21+时，六边形AEPCHG 的面积为534. 【点睛】此题是四边形的综合题，主要考查了菱形的性质，等边三角形的判定和性质，三角形的面积公式，菱形的面积公式，解本题的关键是用x 表示出相关的线段，是一道基础题目．7．（1）见解析；（2）4.8；（3）1282x x- 【分析】（1）证明△ABP ≌△BCQ 即可得到结论；（2）证明Rt △ABN ≌△Rt △C 'BN 求出DQ ，设AN ＝NC '＝a ，则DN ＝8﹣a ，利用勾股定理即可求出a ；（3）过Q 点作QG ⊥BM 于G ，设MQ ＝BM ＝y ，则MG ＝y ﹣x ，利用勾股定理求出MQ ，再根据面积相减得到答案.【详解】解：（1）证明：∵∠ABC ＝90°∴∠BAP +∠APB ＝90°∵BQ ⊥AP∴∠APB +∠QBC ＝90°，∴∠QBC ＝∠BAP ，在△ABP 于△BCQ 中， ABP BCQ AB BCBAP QBC ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△ABP ≌△BCQ （ASA ），∴BP ＝CQ ，（2）由翻折可知，AB ＝BC '，连接BN ，在Rt △ABN 和Rt △C 'BN 中，AB ＝BC '，BN ＝BN ，∴Rt △ABN ≌△Rt △C 'BN （HL ），∴AN ＝NC '，∵BP ＝13PC ，AB ＝8， ∴BP ＝2＝CQ ，CP ＝DQ ＝6，设AN ＝NC '＝a ，则DN ＝8﹣a ，∴在Rt △NDQ 中，（8﹣a ）2+62＝（a +2）2解得：a ＝4．8，即AN ＝4．8．（3）解：过Q 点作QG ⊥BM 于G ，由（1）知BP ＝CQ ＝BG ＝x ，BM ＝MQ ．设MQ ＝BM ＝y ，则MG ＝y ﹣x ，∴在Rt △MQG 中，y 2＝82+（y ﹣x ）2，∴322x y x =+． ∴S △BMC ′＝S △BMQ ﹣S △BC 'Q ＝1122BM QG BC QC ''⋅-⋅, ＝1321()88222x x x +⨯-⨯，＝1282x x-．【点睛】此题考查正方形的性质，三角形全等的判定及性质，勾股定理，正确理解题意画出图形辅助做题是解题的关键.8．（1）点M 的坐标为(51)，；（2）()44y x =-()04x <<；（3）()224160Q x x +-， ()234160Q x x +- ，()24160Q x x -，()25160(224)Q x x x -<< 【分析】（1）过点M 作ME OA ⊥，由“AAS ”可证COP PEM ∆≅∆，可得4CO PE ==，1OP ME ==，即可求点M 坐标；（2）由（1）可知COP PEM ∆≅∆,设OP=x ，则可得M 点坐标为（4+x ，x ），由直线OB 解析式可得N （x ，x ），即可知MN=4，由一组对边平行而且相等的四边形是平行四边形即可证明四边形BCNM 是平行四边形，进而可求y 与x 的函数关系式；（3）首先画出符合要求的点Q 的图形，共分三种情况，第一种情况：当MN 为底边时，第二种情况：当M 为顶点MN 为腰时，第三种情况：当N 为顶点MN 为腰时，然后根据图形特征结合勾股定理求出各种情况点的坐标即可解答．【详解】解：（1）如图，过点M 作ME OA ⊥，CP PM ⊥90CPO MPE ∴∠+∠=︒，且90CPO PCO ∠+∠=︒PCO MPE ∴∠=∠，且CP PM =，90COP PEM ∠=∠=︒()COP PEM AAS ∴∆≅∆4CO PE ∴==，1OP ME ==5OE ∴=∴点M 坐标为(5,1)故答案为(5,1)（2）由（1）可知COP PEM ∆≅∆4CO PE ∴==，OP ME x ==∴点M 坐标为(4,)x x +四边形OABC 是边长为4的正方形，∴点(4,4)B∴直线BO 的解析式为：y x =//MN AO ，交BO 于点N ，∴点N 坐标为(,)x x4MN BC ∴==，且//BC MN∴四边形BCNM 是平行四边形4(4)y x ∴=- (04)x <<（3）在x 轴正半轴上存在点Q ，使得QMN ∆是等腰三角形，此时点Q 的坐标为：1(2,0)Q x +，22(416Q x x +-，0)，23(416Q x x ++-，240)(16Q x x +-，250)(16Q x x --，0)其中(04)x <<，理由：当（2）可知，(04)OP x x =<<，4MN PE ==，//MN x 轴，所以共分为以下几种请：第一种情况：当MN 为底边时，作MN 的垂直平分线，与x 轴的交点为1Q ，如图2所示111222PQ PE MN ===， 12OQ x ∴=+，1(2,0)Q x ∴+第二种情况：如图3所示，当M 为顶点MN 为腰时，以M 为圆心，MN 的长为半径画弧交x 轴于点2Q 、3Q ，连接2MQ 、3MQ ，则234MQ MQ ==，2222Q E MQ ME ∴=-222416OQ OE Q E x x ∴=-=+-，22(416Q x x ∴+-0)，32Q E Q E =，233416OQ OE Q E x x =+=+-23(416Q x x ∴++-0)；第三种情况，当以N 为顶点、MN 为腰时，以N 为圆心，MN 长为半径画圆弧交x 轴正半轴于点4Q ，当022x <<时，如图4所示，则2224416PQ NQ NP x =-=-，24416OQ OP PQ x x ∴=+=+-，即24(16Q x x +-，0)．当22x =时，则4ON =，此时Q 点与O 点重合，舍去；当224x <<时，如图5，以N 为圆心，MN 为半径画弧，与x 轴的交点为4Q ，5Q ．4Q 的坐标为：24(16Q x x -0)．2516OQ x x =-25(16Q x x ∴-0)所以，综上所述，1(2,0)Q x +，22(416Q x x +-，0)，23(416Q x x ++-，240)(16Q x x +-250)(16Q x x -，0)使QMN ∆是等腰三角形．【点睛】本题考查四边形综合题，解题的关键是明确题意，画出相应的图象，找出所求问题需要的条件，利用数形结合的思想解答问题．9．（1）12；（2）13AD AC =．【分析】（1）易证四边形CDEB 是矩形，由条件“四边形ADBE 是平行四边形可得AD ＝EB ＝DC ，从而得到AD AC 的值．（2）由题可知当DE AC ⊥时，DE 最短，可以证到四边形DCBE 是矩形．从而可以得到各边关系从而求出AD AC 的值．【详解】解：（1）∵四边形ADBE 是平行四边形，∴AD ∥BE ，AD ＝BE ．∵DE ⊥AC ，∠ACB ＝90°，∴∠ADE ＝∠C ＝90°．∴DE ∥BC ．∵DC ∥BE ，DE ∥BC ，∠C ＝90°，∴四边形DCBE 是矩形．∴EB ＝DC ．∴AD ＝DC ．∴AD AC=＝12．故答案为：12．（2）如图，由题可知当DE AC ⊥时，DE 最短．最小值是6．∵四边形FDBE 是平行四边形，∴//DF BE ，DF BE =．∵DE AC ⊥，90C ∠=︒，∴90ADE C ∠=∠=︒．∴//DE BC ．∴四边形CDEB 是平行四边形，又∵90C ∠=︒，∴四边形CDEB 是矩形．∴BE CD =，6DE BC ==．∴DF CD =．∵AF AD =，∴2DC DF AD ==．∴3AC AD DC AD =+=． ∴13AD AC =．【点睛】本题考查了平行线之间的距离、平行线的判定、矩形的判定与性质、平行四边形的性质等知识，具有一定的综合性；本题还考查了阅读能力，体现了自主探究与合作交流相结合的新课程理念，是一道好题．10．（1）AP⊥BF，12AP BF =（2）见解析；（3）1≤AP ≤2 【分析】（1）根据直角三角形斜边中线定理可得12AP ED PD == ，即△APD 为等腰三角形推出∠DAP=∠EDA，可证△AED≌△ABF 可得∠ABF=∠EDA=∠DAP 且 BF=ED 由三角形内角和可得∠AOF=90°即AP ⊥BF 由全等可得1122AP ED BF == 即12AP BF = （2）延长AP 至Q 点使得DQ ∥AE，PA 延长线交于G 点，利用P 是DE 中点，构造△AEP≌△PDQ 可得∠EAP=∠PQD，DQ=AE=FA 可得∠QDA=∠FAB 可证△FAB≌△QDA 得到∠AFB=∠PQD=∠EAP，AQ=FB 由三角形内角和可得∠FAG=90°得出AG⊥FB 即AP⊥BF 由全等可得1122AP AQ FB == （3）由于12AP BF =即求BF 的取值范围，当BF 最小时，即F 在AB 上，此时BF=2，AP=1当BF 最大时，即F 在BA 延长线上，此时BF=4，AP=2可得1≤AP ≤2【详解】（1）根据直角三角形斜边中线定理有AP是△AED中线可得12AP ED PD==，即△APD为等腰三角形．∴∠DAP=∠EDA又AE=AF，∠BAF=∠DAE=90°，AB=AD ∴△AED≌△ABF∴∠ABF=∠EDA=∠DAP 且 BF=ED设AP与BF相交于点O∴∠ABF+∠AFB=90°=∠DAP+∠AFB∴∠AOF=90°即AP⊥BF∴1122AP ED BF==即12AP BF=故答案为AP⊥BF，12 AP BF=（2）延长AP至Q点使得DQ∥AE，PA延长线交于G点∴∠EAP=∠PQD，∠AEP=∠QDP∵P是DE中点，∴EP=DP∴△AEP≌△PDQ则∠EAP=∠PQD，DQ=AE=FA∠QDA=180°-（∠PAD+∠PQD）=180°-∠EAD而∠FAB=180°-∠EAD，则∠QDA=∠FAB ∵AF=DQ，∠QDA=∠FAB ，AB=AD∴△FAB≌△QDA∴∠AFB=∠PQD=∠EAP，AQ=FB而∠EAP+∠FAG=90°∴∠AFB+∠FAG=90°∴∠FAG=90°∴AG⊥FB即AP⊥BF又1122 AP AQ FB ==∴1 AP2BF=（3）∵12 AP BF=∴即求BF的取值范围BF最小时，即F在AB上，此时BF=2，AP=1BF最大时，即F在BA延长线上，此时BF=4，AP=2∴ 1≤AP≤2【点睛】掌握三角形全等以及直角三角形斜边上的中线，灵活运用各种角关系是解题的关键．。