信息论与编码课程大作业信道容量的迭代算法
信息论与编码课程大作业信道容量的迭代算法

信息论与编码课程大作业题目:信道容量的迭代算法学生姓名:____________________学号:2010020200 __________________专业班级:10电子信息工程2013年5 月 18日信道容量的迭代算法1信道容量的迭代算法的步骤、用了 matlab 实现DMC 容量迭代的算法如下: 第一步:首先要初始化信源分布:P(k)0,1, ,r,置k 0,选1 deta 0r第三步:exp[ P ji logt kj ]j计算P k 1exp[ P ji logtU]ij第四步:第五步:执行下面的程序2. Matlab 实现clear;deta=i nput('输入信道容量的精度:'); (k)一个精度,本次中我选 deta=0.000001 。
(k)第二步: 根据式子tij ()piP ji ,得到反向转移概率矩阵{t ij (k)}。
(k) P i ( )p jii由式C k 1I P k1,t krlog expi 0P ji log t j k 计算 c k 1。
j 0C (k1) —C(k 1)C (k) deta , 则执行k=k+1,然后转第二步。
直至转移条件不成立,接着第六步:输出迭代次数 k 和C k 1和P k 1,程序终止。
r=input('输入信源个数: '); s=input('输入信宿个数:');Q=ran d(r,s);%形成r 行s 列随机矩阵Q可编辑A=sum(Q,2); %把Q矩阵每一行相加和作为一个列矩阵AB=repmat(A,1,s); %把矩阵A的那一列复制为S列的新矩阵%判断信道转移概率矩阵输入是否正确P=input('输入信道转移矩阵P: ')%从这句话开始将用下面两句代替可自动生成信道转移矩阵[r,s]=size(P);for i=1:rif(sum(P(i,:))~=1) %检测概率转移矩阵是否行和为 1.error( '概率转移矩阵输入有误!!')return ;endfor j=1:sif(P(i,j)<0||P(i,j)>1) %检测概率转移矩阵是否负值或大于 1error( '概率转移矩阵输入有误!!')return ;endendend%将上面的用下面两句代替可自动生成信道转移矩阵%disp(' 信道转移概率矩阵 :')%P=Q./B 信道转移概率矩阵(每一个原矩阵的新数除以所在行的数总和)i=1:1:r; %设置循环首项为1,公差为1,末项为r (Q的行数)的循环p(i)=1/r; %原始信源分布r个信源,等概率分布disp( ' 原始信源分布: ')p(i)E=repmat(p',1,s); %把r个等概率元素组成一列,复制为s列for k=1:1:1/detam=E.*P; % m=p.*E; %后验概率的分子部分a=sum(m); %把得到的矩阵m每列相加之和构成一行su仁repmat(a,r,1); %把得到的行矩阵a复制r行,成一新矩阵sul,后验概率的分母部分t=m./su1; %后验概率矩阵n=exp(sum(P .*log(t),2)); %信源分布的分子部分su2=sum(n); %信源分布的分母部分p=n/su2; %信源分布E=repmat(p,1,s);C(k+1)=log(sum(exp(sum(P .*log(t),2))))/log(2);kk=abs(C(k+1)-C(k))/C(k+1);if(kk<=deta)break ;enddisp( '迭代次数: k=' ),disp(k)enddisp( '最大信道容量时的信源分布: p=' ),disp(p')可编辑disp('最大信道容量:C=' ),disp(C(k+1))3•运行结果及分析(宋体四号,加粗)结果分析:这两组数据都是我随机选的,都是选的信源个数为足,然后输出k 和C k 1和P k 1。
信息论与编码C 第三章 信道容量

3.2单符号离散信道的信道容量
信息传输率R: 信道中平均每个符号所能传送的信息量。由于 平均互信息I(X;Y)的含义是接收到符号Y后,平均每个符号获 得的关于X的信息量,因此信道信息传输率就是平均互信息。
噪声熵 H(Y/X) = 0 I(X;Y)=H(X)-H(X|Y)=H(Y)-H(Y|X)=H(Y) H(X) > H(Y)
思考:p(x)应该 怎样取值?
C max I ( X ; Y ) max H (Y ) log 2 m
p ( xi ) p ( xi )
3.2单符号离散信道的信道容量
例:对于二元对称信道
0( p)
q
I(X;Y)
X
1( p)
q q
q
0
Y
1
0
1-H(q) 0.5 1 p
如果信源分布X={p,1-p},则
I ( X ; Y ) H ( pq pq) H (q)
信道容量为:
C max I ( X ; Y ) 1 H (q),
p ( xi )
3.2单符号离散信道的信道容量
二进制对称信道(n=2)
p C log 2 n p log 2 p p log 2 n 1 1 p log 2 p p log 2 p 1 H ( p)
H ( p) p log2 p p log2 p
C 1
0
0.5
1
p
3.2单符号离散信道的信道容量
(2)输出符号的概率 n P(b j ) p(ai ) p(b j / ai )
信息论中的信道容量与编码速率

信息论中的信道容量与编码速率信息论是数学与通信工程学科的交叉领域,它研究了信息传输的基本原理与极限。
在信息传输过程中,我们需要考虑信道容量和编码速率这两个重要的概念。
本文将详细介绍信息论中的信道容量和编码速率,并探讨它们对于信息传输的影响。
一、信道容量信道容量是指在特定的通信信道中传输信息的最大速率。
它是指在不引入任何差错的情况下,信道所能够传输的最高信息率。
信道容量取决于信道的带宽、噪声水平和信噪比等因素。
在信息论中,香农公式被广泛应用于计算信道容量。
根据香农公式,信道容量C可以通过以下公式计算得出:C = B * log2(1 + S/N)其中,B为信道的带宽,S为信道的信号功率,N为信道的噪声功率。
通过这个公式,我们可以看出,信道容量与带宽成正比,与信噪比也成正比。
在实际应用中,我们可以通过增加带宽或提高信噪比的方式来增加信道容量。
但是,无论如何提高这些因素,信道容量都有一定的极限,这是由信道本身的特性所决定的。
二、编码速率编码速率是指信息在信道中传输时的速率,也被称为传输速率。
它决定了我们可以多快地将信息输入到信道中,并对应着信号的频率。
编码速率一般用比特每秒(bps)来衡量。
在设计通信系统时,我们需要根据信道容量和所需的传输质量来确定编码速率。
一般来说,我们希望编码速率尽可能接近信道容量,以实现高效的信息传输。
但是,如果编码速率超过信道容量,就会发生信息传输的错误,这是由信道的限制所决定的。
为了实现高效的信息传输,我们需要选择合适的编码方案。
常见的编码技术有冗余编码、差错纠正编码等。
这些编码技术可以在保证传输质量的同时,提高编码速率。
三、信道容量与编码速率的关系信道容量与编码速率之间存在着紧密的关系。
通常情况下,编码速率不能超过信道容量,否则会导致传输错误。
因此,为了实现高效的信息传输,我们需要控制编码速率与信道容量的关系。
在信道容量小于编码速率的情况下,我们需要对输入信号进行压缩处理,以降低编码速率,来适应信道的限制。
实验二:信道容量的迭代算法

实验二信道容量迭代算法一、实验目的:了解信道容量的计算方法二、实验内容与原理:内容:1.令pe1=pe2=0.1和pe1=pe2=0.01,分别计算该对称信道的信道容量和最佳分布;2.令pe1=0.15,pe2=0.1和pe1=0.075pe2=0.01,分别计算该信道的信道容量和最佳分布;信道容量是信息传输率的极限,当信息传输率小于信道容量时,通过信道编码,能够实现几乎无失真的数据传输;当数据分布满足最佳分布时,实现信源与信道的匹配,使得信息传输率能够达到信道容量。
本实验利用信道容量的迭代算法,使用计算机完成信道容量的计算。
三、程序代码#include<stdio.h>#include<math.h>int main(){double Pe1,Pe2,Pa1_=0,Pa2_=0; double b1a1,b2a1,b1a2,b2a2;double Pa1=0,Pa2=0;double I=0,max=0;//平均互信息量,最大平均互信息量int count=0;printf("输入信道容量参数Pe1:");scanf("%lf",&Pe1);printf("输入信道容量参数Pe2:");scanf("%lf",&Pe2);printf("信道容量参数:Pe1=%lf Pe2=%f\n",Pe1,Pe2);b1a1=1-Pe1;b2a1=Pe1;b1a2=Pe2;b2a2=1-Pe2;for(Pa1=0.01;Pa1<=1;Pa1=Pa1+0.01){ Pa2=1-Pa1;count=count+1;I=Pa1*b1a1*( log( b1a1/(Pa1*b1a1+Pa2*b1a2) )/log(2) )+Pa1*b2a1*( log(b2a1/(Pa1*b2a1+Pa2*b2a2) )/log(2) )+Pa2*b1a2*( log(b1a2/(Pa1*b1a1+Pa2*b1a2) )/log(2) )+Pa2*b2a2*( log(b2a2/(Pa1*b2a1+Pa2*b2a2) )/log(2) );printf("%10lf",I);if (I>max){max=I;Pa1_=Pa1,Pa2_=Pa2;}elsecontinue;}printf("\n");printf(" 一共计算机了:%d\n",count);printf(" 最大互信息量为:%lf\n",max);printf(" 最大互信息量的P(a1)=%lf;P(a2)=%lf\n",Pa1_,Pa2_); }四、运行结果。
实验二---一般信道容量迭代算法.doc

实验二---一般信道容量迭代算法.doc实验二一般信道容量迭代算法1.实验目的掌握一般离散信道的迭代运算方法。
2.实验要求1)理解和掌握信道容量的概念和物理意义2)理解一般离散信道容量的迭代算法3)采用Matlab 编程实现迭代算法4)认真填写试验报告3.算法步骤①初始化信源分布),,,,,(21)0(p p p p P ri =(一般初始化为均匀分布) ,置迭代计数器k=0 ,设信道容量相对误差门限为δ ,δ>0 ,可设-∞=C )0(;②∑=i k i ij k i ij k ji p p p p )()()(? s j r i ,??=??=,1;,,1 ③∑∑∑??=+i k ji j ij k ji j ij k i p p p ??)()()1(ln exp ln exp r i ,,1??= ④??=∑∑+ik ji j ij k p C ?)()1(ln exp ln ⑤如果δ≤-++C C Ck k k )1()()1( ,转向⑦;⑥置迭代序号k k →+1,转向②;⑦输出p k i )1(+和C k )(1+的结果;⑧停止。
4.代码P=input('转移概率矩阵P=')e=input('迭代精度e=')[r,s]=size(P);n=0;C=0;C_k=0;C_k1=0;X=ones(1,r)/r;A=zeros(1,r);B=zeros(r,s);%初始化各变量while(1)n=n+1;for i=1:rfor j=1:sB(i,j)=log(P(i,j)/(X*P(:,j))+eps); if P(i,j)==0B(i,j)=0;elseendendA(1,i)=exp(P(i,:)*B(i,:)');endC_k=log2(X*A');C_k1=log2(max(A));if (abs(C_0-C_1)。
信道容量实验报告

湖南大学信息科学与工程学院实验报告实验名称信道容量的迭代算法课程名称信息论与编码第1页共9页1.实验目的(1)进一步熟悉信道容量的迭代算法; (2)学习如何将复杂的公式转化为程序;(3)掌握C 语言数值计算程序的设计和调试技术。
2、实验方法硬件:pc 机开发平台:visual c++软件 编程语言:c 语言3、实验要求(1)已知:信源符号个数r 、信宿符号个数s 、信道转移概率矩阵P 。
(2)输入:任意的一个信道转移概率矩阵。
信源符号个数、信宿符号个数和每个具体的转移概率在运行时从键盘输入。
(3)输出:最佳信源分布P*,信道容量C 。
4.算法分析1:procedure CHANNEL CAPACITY(r,s,(jip ))2:initialize:信源分布ip =1/r ,相对误差门限σ,C=—∞3:repeat 4:5:6:C2211log [exp(log )]rsji ij r j p φ==∑∑7:until C Cσ∆≤8:output P*=()i rp ,C9:end procedure21211exp(log )exp(log )sji ij j r sjiij r j p pφφ===∑∑∑ip 1i jiri jii p p p p=∑ijφ5.程序调试1、头文件引入出错f:\visualc++\channel\cpp1.cpp(4) : fatal error C1083: Cannot open include file: 'unistd.h': No such file or directory————#include<unistd.h>纠错://#include<unistd.h>f:\visualc++\channel\cpp1.cpp(5) : fatal error C1083: Cannot open include file: 'values.h': No such file or directory————#include<values.h>纠错://#include<values.h>2、变量赋值错误f:\visualc++\channel\cpp1.cpp(17) : error C2065: 'ij' : undeclared identifierf:\visualc++\channel\cpp1.cpp(17) : error C2440: 'initializing' : cannot convert from 'int' to 'float ** ' Conversion from integral type to pointer type requires reinterpret_cast, C-style cast or function-style cast————float **phi_ij=ij=NULL;纠错:float **phi_ij=NULL;3、常量定义错误f:\visualc++\channel\cpp1.cpp(40) : error C2143: syntax error : missing ';' before 'for' ————for(i=0;i<r;i++)phi_ij[i]=(float *)calloc(s,sizeof(float));f:\visualc++\channel\cpp1.cpp(52) : error C2021: expected exponent value, not ' '————if(fabs(validate -1.0)>DELTA)f:\visualc++\channel\Cpp1.cpp(84) : error C2021: expected exponent value, not ' '————if(fabs(p_j)>=DELTA)f:\visualc++\channel\Cpp1.cpp(100) : error C2021: expected exponent value, not ' '————if(fabs(phi_ij[i][j])>=DELTA)f:\visualc++\channel\Cpp1.cpp(116) : error C2021: expected exponent value, not ' ' ————while(fabs(C-C_pre)/C>DELTA);纠错:#define DELTA 0.000001;F:\visualc++\channel\Cpp1.cpp(68) : error C2065: 'MAXFLOAT' : undeclared identifierF:\visualc++\channel\Cpp1.cpp(68) : warning C4244: '=' : conversion from 'int' to 'float', possible loss of data————C=-MAXFLOAT;纠错:#define MAXFLOAT 1000000;3、引用中文逗号f:\visualc++\channel\cpp1.cpp(60) : error C2018: unknown character '0xa1'f:\visualc++\channel\cpp1.cpp(60) : error C2018: unknown character '0xb1'f:\visualc++\channel\cpp1.cpp(60) : error C2065: 'Starting' : undeclared identifierf:\visualc++\channel\cpp1.cpp(60) : error C2059: syntax error : '.'f:\visualc++\channel\cpp1.cpp(60) : error C2017: illegal escape sequencef:\visualc++\channel\cpp1.cpp(60) : error C2018: unknown character '0xa1'f:\visualc++\channel\cpp1.cpp(60) : error C2018: unknown character '0xb1'————fprintf(stdout,”Starting..\n”);纠错:fprintf(stdout,"Starting..\n");4、没有进行强制转换F:\visualc++\channel\Cpp1.cpp(65) : warning C4244: '=' : conversion from 'double' to 'float', possible loss of data————p_i[i]=1.0/(float)r;纠错:p_i[i]=(float)(1.0/(float)r);F:\visualc++\channel\Cpp1.cpp(101) : warning C4244: '+=' : conversion from 'double' to 'float', possible loss of data————sum[i]+=p_ji[i][j]*log( phi_ij[i][j])/ log(2.0);纠错:sum[i]+=(float)(p_ji[i][j]*log( phi_ij[i][j])/ log(2.0));F:\visualc++\channel\Cpp1.cpp(103) : warning C4244: '=' : conversion from 'double' to 'float', possible loss of data————sum[i]=pow(2.0,sum[i]);纠错:sum[i]=(float)(pow(2.0,sum[i]));F:\visualc++\channel\Cpp1.cpp(114) : warning C4244: '=' : conversion from 'double' to 'float', possible loss of data————C= log(p_j)/ log(2.0);纠错:C= (float)(log(p_j)/ log(2.0));4、表达式错误F:\visualc++\channel\Cpp1.cpp(86) : error C2065: 'phi_ji' : undeclared identifierF:\visualc++\channel\Cpp1.cpp(86) : error C2109: subscript requires array or pointer typeF:\visualc++\channel\Cpp1.cpp(86) : error C2109: subscript requires array or pointer type ————phi_ij[i][j]=p_i[i]* phi_ji[i][j]/p_j;纠错:phi_ij[i][j]=p_i[i]* p_ji[i][j]/p_j;F:\visualc++\channel\Cpp1.cpp(122) : error C2065: 'fprint' : undeclared identifierF:\visualc++\channel\Cpp1.cpp(122) : error C2018: unknown character '0xa1'F:\visualc++\channel\Cpp1.cpp(122) : error C2018: unknown character '0xb1'F:\visualc++\channel\Cpp1.cpp(122) : error C2065: 'The' : undeclared identifierF:\visualc++\channel\Cpp1.cpp(122) : error C2146: syntax error : missing ')' before identifier 'iteration'F:\visualc++\channel\Cpp1.cpp(122) : error C2017: illegal escape sequenceF:\visualc++\channel\Cpp1.cpp(122) : error C2017: illegal escape sequenceF:\visualc++\channel\Cpp1.cpp(122) : error C2018: unknown character '0xa1'F:\visualc++\channel\Cpp1.cpp(122) : error C2018: unknown character '0xb1'————fprint(stdout,”The iteration number is %d.\n\n”,k);纠错:fprintf(stdout,"The iteration number is %d.\n\n",k);F:\visualc++\channel\Cpp1.cpp(145) : error C2143: syntax error : missing ')' before ';' ————free((p_i);纠错:free(p_i);5、没有返回值F:\visualc++\channel\Cpp1.cpp(149) : warning C4508: 'main' : function should return a value; 'void' return type assumed、纠错:return 0;6.改进程序/*引入头文件*/#include<stdio.h>#include<math.h>#include<stdlib.h>/*定义常量*/#define DELTA 0.0000001//DELTA为相对误差门限#define MAXFLOAT 1000000;//MAXFLOAT为初始化信道容量值int main( void){/*定义全局变量*//*register允许直接从寄存器中读取变量,提高速率*/register int i,j;//i、j为整型变量register int k;//信道容量迭代计算次数int r,s;//r为信源符号个数,s为新宿符号个数float *p_i=NULL;//r个信源符号发生的概率float **p_ji=NULL;//信源到新宿的信道转移概率矩阵Pfloat **phi_ij=NULL;float C,C_pre,validate;//C为信道容量,C_pre为信道最大容量,validate为判定输入转移概率矩阵是否合法float * sum=NULL;//信源符号所带的全部信息量float p_j;//条件概率/*输入信源符号和新宿符号个数*/printf("请输入信源符号个数r、信宿符号个数s...\n");printf("+++++注意!!!r必须大于等于s!!+++++\n");fscanf(stdin,"%d",&r);fscanf(stdin,"%d",&s);/*为 p_i,p_ji 和 phi_ij 分配内存空间*/p_i=(float *)calloc(r,sizeof(float));p_ji=(float **)calloc(r,sizeof(float));/*为每个p_ji分配大小为s的内存空间*/for(i=0;i<r;i++)p_ji[i]=(float *)calloc(s,sizeof(float));phi_ij=(float **)calloc(r,sizeof(float*));/*输入转移概率矩阵*/for(i=0;i<r;i++)/*为每个phi_ij分配大小为s的内存空间*/phi_ij[i]=(float *)calloc(s,sizeof(float));printf("信道转移概率矩阵P...\n");for(i=0;i<r;i++)for(j=0;j<s;j++)fscanf(stdin,"%f",&p_ji[i][j]);/*判定输入的转移概率矩阵是否正确*/for(i=0;i<r;i++){validate=0.0;for(j=0;j<s;j++){validate +=p_ji[i][j];}if((validate-1.0)>=0)//如果转移概率矩阵的概率和大于1,输入数据不合法{fprintf(stdout,"invalid input data.\n");exit(-1);}}/*显示开始计算..*/fprintf(stdout,"Starting..\n");/*初始化 p_i 和 phi_ij*/for(i=0;i<r;i++){/* p_i为等概率,即概率为1/r*/p_i[i]=(float)(1.0/(float)r);}/*初始化信道容量c,迭代次数k和临时变量variable*/C=-MAXFLOAT;k=0;/* 为sum分配大小为r的内存空间*/sum=(float *)calloc(r,sizeof(float));/*开始迭代计算*/do{k++;//每进行一次迭代,迭代次数k加1/* 计算phi_ij(k)*/for(j=0;j<s;j++){p_j=0.0;for(i=0;i<r;i++)p_j+=p_i[i]*p_ji[i][j];if(fabs(p_j)>=DELTA)for(i=0;i<r;i++)phi_ij[i][j]=p_i[i]* p_ji[i][j]/p_j;elsefor(i=0;i<r;i++)phi_ij[i][j]=0.0;}/*计算p_i(k+1)*/p_j=0.0;for(i=0;i<r;i++){sum[i]=0.0;for(j=0;j<s;j++){/*相对误差门限为0*/if(fabs(phi_ij[i][j])>=DELTA)sum[i]+=(float)(p_ji[i][j]*log( phi_ij[i][j])/ log(2.0)); }sum[i]=(float)(pow(2.0,sum[i]));p_j+=sum[i];}for(i=0;i<r;i++){p_i[i]=sum[i]/p_j;}C_pre=C;C= (float)(log(2.0)/log(p_j) );}while(fabs(C-C_pre)/C>DELTA);free(sum);sum=NULL;/*显示结果*/fprintf(stdout,"The iteration number is %d.\n\n",k);//迭代次数fprintf(stdout,"The capacity of the channel is %.6f bit/symbol:\n\n",C);//信道容量fprintf(stdout,"The best input probability distribution is :\n");//最佳信源分布 for(i=0;i<r;i++)fprintf(stdout,"%.6f\n",p_i[i]);fprintf(stdout,"\n");/* 释放指针空间*/for(i=s-1;i>=0;i--){free(phi_ij[i]);phi_ij[i]=NULL;}free(phi_ij);phi_ij=NULL;for(i=r-1;i>=0;i--){free(p_ji[i]);p_ji[i]=NULL;}free(p_ji);p_ji=NULL;free(p_i);p_i=NULL;exit(0);return 0;}7.实验结果八、实验结论信道容量是指信道能无错误传送的最大信息率。
迭代求解信道容量

谢谢~~
Page
15
j
H (Y / X ) p (ai ) p (b j / ai ) log p (b j / ai ) p (b j / ai ) log p (b j / ai ) H (Y / xi )
j i j
•输出对称
1 p (b j ) p (ai ) p (b j / ai ) p (b j / ai ) n i i
迭代算法计算信道容量
信道的基本概念
信道分类:
研究信道主要考虑信道中受干扰的影响,由于信道存在的干扰使输入信号和输出 信号之间没有固定的函数关系,只有统计依赖关系,因此可以通过分析输入和输出信 号之间的统计特性来研究信道。 实际通信系统中,信道的种类很多,包含的设备也不相同,因此可以按照不同的 角度对信道进行分类。 根据用用户数量:信道可以分为单用户信道和多用户信道。 单用户信道只有一个输入端和一个输出端,信息只朝一个方向单向传输; 多用户信道的信号输入和输出端至少有一端有两个以上用户,信息在两个方向都能传 输。 根据输入端和输出端关系:无反馈信道、有反馈信道 根据信道参数与时间的关系:固定参数信道(光纤、电缆)、时变参数信道(无线信 道)。 根据噪声种类: 随机差错信道(高斯白噪声为主题的信道)、突发差错信道(噪声干 扰的影响前后相关,如:衰落信道、码间干扰信道)。 根据输入输出信号的特点:离散信道、连续信道、半离散半连续信道以及波形信道。
0.3 0.1 0.6; 0.2 0.5 0.3;
C1=logm(PX*B') C2=logm(max(B)) while (1) if abs(C1-C2)<e break; end for i=1:1:S(1) PX(i)=PX(i)*B(i)/(PX*B'); end for k=1:1:S(1) I=0; PY=zeros(1,S(2)); for j=1:1:S(2) for i=1:1:S(1) PY(j)=PY(j)+PX(i)*PY_X(i,j); end I=I+PY_X(k,j)*log2(PY_X(k,j)/PY(j)); end B(k)=expm(I); end C1=logm(PX*B'); C2=logm(max(B)); end C=C1
信息论基础——信道容量的计算

p p1 p 1
将p=3/5代入(2),得到信道容为:C=0.32bit/sym.
20
信道容量的计算
2 达到信道容量输入分布的充要条件
令
I (xi ;Y )
s j 1
p( y j
|
xi ) log
p( y j | xi ) p( yj )
def
D(Q( y |
x) ||
p( y))
定理4.2.2 一般离散信道的互信息I(X;Y)达到极大值
1 信道容量的计算原理
C是选择不同的输入概率分布p(x),在满足
∑p(x)=1条件下,求互信息的极大值:
I(X ;Y )
r i 1
s j 1
p(xi ) p( y j | xi ) log
p( y j | xi ) p(yj )
Lagrange乘子
法
17
信道容量的计算
例1、设某二进制数字传输系统接收判决器
6
数据可靠传输和信道编码
4.1 离散无记忆信道和信道容量 4.2 信道容量的计算
4.3 信道编码理论 4.4 带反馈的信道模型 4.5 联合信源-信道编码定理 4.6 线性分组码 习题四
7
8
接入信道容量的分析与寻呼信道不一样,寻呼信道用于前 向链路,容量的分析主要在于对寻呼信道占用率的计算, 而接入信道用于反向链路,对 CDMA 系统来说,反向链 路容量主要用于干扰的分析。即使采用时隙化的随机接入 协议,接入信道也可能有较高的通过量,大量的接入业务 会在反向链路中产生无法接受的干扰。如前所述,第一个 接入试探失败后,下一个接入试探将增加一定量的功率, 最终的结果将导致小区接收功率的增加以及反向链路容量 的减少。
信息论与编码第3章 信道与信道容量

几点讨论: 1、对于给定信道最佳分布总是存在的。 如果信道输入满足最佳分布,信息传输率 最大,即达到信息容量C; 如果信道输入的先验分布不是最佳分布, 那么信息传输率不能够达到信息容量。 2、信道传输的信息量R必须小于信道容量C,否 则传输过程中会造成信息损失,出现错误; 如果R<C成立,可以通过信道编码方法保证 信息能够几乎无失真地传送到接收端。
p( y | x)
X
Y
信道
随机变量 随机变量
离散无记忆信道模型
输入符号集合X、输出符号集合Y内部不存在 关联性,集合X和集合Y之间有关联 。
条件转移概率
用来描述信道特性。 输入x=ai,输出y=bj对应的条件转移概率为
p( y | x) p( y bj | x ai ) p(bj | ai )
p( x)
上述的极值问题实际是有约束条件的,先验概率分布 p( x) 应当满足下列条件
p( x ai ) 0
p(a ) 1
i 1 i
r
对于给定信道,前向概率p(x)是一定的,所以信道容 量就是在信道前向概率一定的情况下,寻找某种先 验概率分布,从而使得平均互信息量最大,这种先 验分布概率称为最佳分布。
0 0 1 1
(3)有噪无损信道
信道输出符号Y集合的数量大于信道输入符号X集合 的数量,即r<s,形成一对多的映射关系,可得:
H (Y | X ) 0 H(X | Y) 0
p( x) p( x)
X
0.4 0.6 0.7 0.3
Y
信道容量 C max{I ( X ; Y )} max{H ( X )} lbr 输入符号分布等概时,即 p(ai ) 1/ r I(X;Y)最大,达到信道容量
大学信息论_信道容量的迭代算法

陕西科技大学实验报告 班级: XXXX 学号:XXXXXXXXX 姓名:XXX 实验组别: 实验日期: 报告日期: 成绩: 报告内容:(目的和要求、原理、步骤、数据、计算、小结等)实验名称:信道容量的迭代算法一、实验目的(1) 进一步熟悉信道容量的迭代算法。
(2) 学习如何将复杂的公式转化为程序。
(3) 掌握高级语言数值计算程序的设计和调试技术。
二、实验要求(1)已知:信源符号个数r 、信宿符号个数s 、信道转移概率矩阵P 。
(2)输入:任意的一个信道转移概率矩阵。
信源符号个数、信宿符号个数和每个具体的转移概率在运行时从键盘输入。
(3)输出:信道容量C 。
三、实验原理(流程图):1: procedure ChannelCapacity(r, s, (ji p ))2: initialize: 信源分布1i p r =,相对误差门限δ,C =-∞ 3: repeat4: 1i jiij r ijii p p p p φ=←∑ 5: 111exp log exp log s ji ij j i r s ji ij i j p p p φφ===⎛⎫ ⎪⎝⎭←⎛⎫ ⎪⎝⎭∑∑∑ 6: 11log exp log r s ji ij i j C p φ==⎡⎤⎛⎫←⎢⎥ ⎪⎢⎥⎝⎭⎣⎦∑∑ 7: until C Cδ∆≤ 8: output C9: end procedure四、实验数据(源代码):#include<stdio.h>#include<math.h>#define MAX 100double Calculate_a(int k,double pa[]); double Calculate_C1(double pa[],double a[]); double Calculate_C2(double a[]);int r,s;double pba[3][3];void main(){int i,j;double C1,C2,E;double a[MAX],pa[3];E=0.000001;r=3;s=3;pa[0]=0.2;pa[1]=0.3;pa[2]=0.5;pba[3][3]={0.5,0.33333333,0.16666666,0.16666666,0.5,0.333333333,0.333 33333,0.16666666,0.5};do{for(i=0;i<r;i++)a[i]=Calculate_a(i,pa);C1=Calculate_C1(pa,a);C2=Calculate_C2(a);if(C2-C1>=E){double sum=0;for(i=0;i<r;i++)sum+=pa[i]*a[i];for(i=0;i<r;i++)pa[i]=pa[i]*a[i]/sum;}else{printf("最佳信源概率:\n");for(i=0;i<r;i++)printf(" %lf \n",pa[i]);}}while(C2-C1>=E);printf("信道容量为:%lf\n",C1/log(2));}double Calculate_a(int k,double pa[]){int i,j;double temp,sum2=0;for(j=0;j<s;j++){double sum1=0;for(i=0;i<r;i++){sum1+=pa[i]*pba[i][j];}temp=pba[k][j]/sum1;temp=log(temp);sum2+=pba[k][j]*temp;}return exp(sum2);}double Calculate_C1(double pa[],double a[]){int i;double sum=0;for(i=0;i<r;i++)sum+=pa[i]*a[i];return log(sum);}double Calculate_C2(double a[]){int i;double max=a[0];for(i=0;i<r;i++)if(max<a[i]) max=a[i];return log(max);}五、程序运行结果:最佳信源概率:0.3333300.3333340.333337信道容量为:0.125815Press any key to continue六、实验小结:通过本次实验,我了解了信道容量的迭代算法,在理论的掌握基础上,更进一步的实现了程序的运行算法,同时又加深了编程语言上的一些不足和毛病.。
信息论与编码第3章 信道与信道容量

Rt 的单位:bit/符号÷s/符号=bit/s
定义3.1 设某信道的平均互信息量为I(X;Y),信道输
入符号的先验概率为p(x),该信道的信道容量C定义
为
C max{I ( X ;Y )} p(x)
上述的极值问题实际是有约束条件的,先验概率分布
p(x) 应当满足下列条件
p(x ai ) 0
第3章 信道与信道容量
吴晓青
目录
3.1信道分类 3.2 单符号离散信道及其容量
➢ 3.2.1 数学模型 ➢ 3.2.2信道容量 ➢ 3.2.3 离散信道容量的迭代算法
3.3 离散序列信道及其容量 3.4 信源与信道的匹配 3.5 连续信道及其容量
➢ 3.5.1 连续单符号加性信道 ➢ 3.5.2 多维无记忆加性连续信道 ➢ 3.5.3 加性高斯白噪声波形信道
定义3.3 如果信道转移概率矩阵中所有列矢量都是第 一列的某种置换,则称信道关于输出是对称的,这 种信道称为输出对称离散信道。
1 0 P 0.5 0.5
0 1
0.7 0.2 0.1 P 0.2 0.1 0.7
0.1 0.7 0.2
如果信道是输出对称的,那么当信道输入符号为等概 率分布时,信道输出也是等概率分布的。
前向概率、后验概率
由公式
p(ai ,bj ) p(ai ) p(bj | ai )
信道的条件转移概率p(bj|ai)通常称为前向概率,表 示在输入为ai时,通过信道后接收为bj的概率,描 述了信道噪声的特性。
由公式
p(ai , bj ) p(bj ) p(ai | bj )
p(ai|bj)称为后向概率,表示当接收符号为bj时,信 道输入为ai的概率,所以也称为后验概率。
信道容量迭代算法

附录:实验代码(C++)
#include<iostream> using namespace std; #include<math.h> #define MAX 50 double Calculate_C1(double p[],double a[]); double Calculate_C2(double a[]); int r,s; double P[MAX][MAX]; int main() { int i,j; double C1,C2,E; double a[MAX],p[MAX]; E=0.000001; cout<<"请输入信源符号个数 r:\n"; cin>>r; cout<<"请输入信宿符号个数 s:\n"; cin>>s; cout<<"请输入信道转移概率矩阵 P[bj][ai]:\n"; for(i=0;i<r;i++) for(j=0;j<s;j++) cin>>P[i][j]; for(i=0;i<r;i++) p[i]=1.0/r; do { for(i=0;i<r;i++) { int w,j; double temp,sum2=0; for(j=0;j<s;j++) { double qj=0; for(w=0;w<r;w++) { qj+=p[w]*P[w][j]; } temp=P[i][j]/qj;
算法原理
1. 2.
1 (0) 初始化信源分布:pi= ,循环变量 k=1,门限△,C =- r
实验一:信道容量的迭代算法
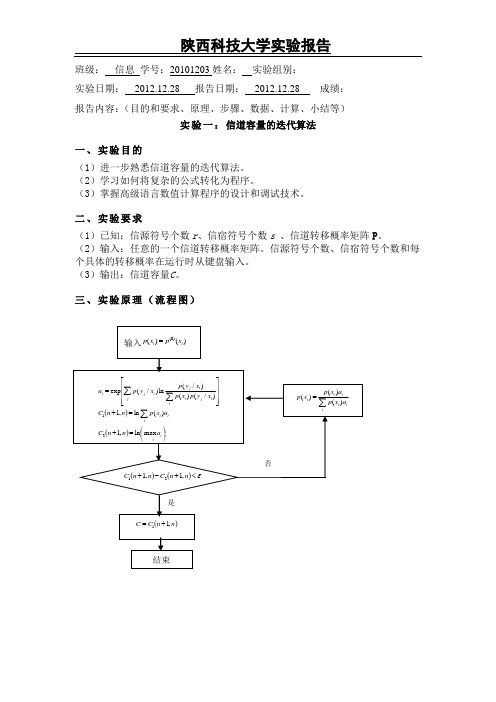
陕西科技大学实验报告 班级: 信息 学号:20101203姓名: 实验组别:实验日期: 2012.12.28 报告日期: 2012.12.28 成绩: 报告内容:(目的和要求、原理、步骤、数据、计算、小结等)实验一:信道容量的迭代算法一、实验目的(1)进一步熟悉信道容量的迭代算法。
(2)学习如何将复杂的公式转化为程序。
(3)掌握高级语言数值计算程序的设计和调试技术。
二、实验要求(1)已知:信源符号个数r 、信宿符号个数s 、信道转移概率矩阵P 。
(2)输入:任意的一个信道转移概率矩阵。
信源符号个数、信宿符号个数和每个具体的转移概率在运行时从键盘输入。
(3)输出:信道容量C 。
三、实验原理(流程图)是 否 ()()⎪⎭⎫ ⎝⎛=+=+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=∑∑∑i i i i i j i i j i i j i j i a n n C a x p n n C x y p x p x y p x y p a max ln ,1)(ln ,1)/()()/(ln )/(exp 21 输入)()()0(i i x p x p = ()()ε<+-+n n C n n C ,1,121 ()n n C C ,11+= ∑=i i i i i i a x p a x p x p )()()( 结束四、实验数据(源代码)#include <stdio.h>#include <math.h>//以2为底的对数为logx#include <stdlib.h>void main(){register int i,j;register int k;int N,M;//行,列float *p=0;float *q=0;float *d=0;float *a=0;float *sum=0; //sum数组为各行概率累加求和float **p_yx=0; //二维数组p_yx存放信道矩阵float C,b,u,max,IL,IU; //C为信道容量,b为迭代精度printf("请输入信源符号个数: "); //输入行列scanf("%d",&N);printf("请输出信宿符号个数: ");scanf("%d",&M);p=(float *)calloc(N,sizeof(float)); //初始化需要用到的数组q=(float *)calloc(M,sizeof(float));d=(float *)calloc(N,sizeof(float));a=(float *)calloc(N,sizeof(float));sum=(float *)calloc(N,sizeof(float));p_yx=(float **)calloc(N,sizeof(float));for(i=0;i<N;i++){p_yx[i]=(float *)calloc(M,sizeof(float));}printf("请输入信道转移概率矩阵:\n"); //输入信道矩阵for(i=0;i<N;i++){for(j=0;j<M;j++){printf("p_yx[%d][%d]=",i,j);scanf("%f",&p_yx[i][j]);}printf("\n");}for(i=0;i<N;i++) //判断输入的信道矩阵是否符合概率分布{sum[i]=0.0;for(j=0;j<M;j++)sum[i]=sum[i]+p_yx[i][j];}for(i=0;i<N;i++){if(sum[i]<=0.999999||sum[i]>=1.000001)printf("不符合概率分布");elseif(sum[N-1]>=0.999999&&sum[N-1]<1.000001) {printf("请输入迭代精度:");scanf("%f",&b);}break;}for(i=0;i<N;i++) //取初始概率为均匀分布p[i]=1.0/N;for(j=0;j<M;j++) //计算q[j]{q[j]=0;for (i=0;i<N;i++)q[j]=q[j]+p[i]*p_yx[i][j];}for(i=0;i<N;i++) //计算a[i]{d[i]=0;for(j=0;j<M;j++){if(p_yx[i][j]==0)d[i]=d[i]+0;elsed[i]=d[i]+p_yx[i][j]*log(p_yx[i][j]/q[j]); }a[i]=exp(d[i]);}u=0.0;for(i=0;i<N;i++) //计算uu=u+p[i]*a[i];IL=log(u)/log(2.0); //计算ILmax=a[0];for(i=0;i<N;i++){if(a[i]>=max)max=a[i];}IU=log(max)/log(2.0); //计算IUk=1;C=IL;while((IU-IL)>=b)//迭代计算{for(i=0;i<N;i++)p[i]=p[i]*a[i]/u;for(j=0;j<M;j++) //计算q[j]{q[j]=0;for (i=0;i<N;i++)q[j]=q[j]+p[i]*p_yx[i][j];}for(i=0;i<N;i++) //计算a[i]{d[i]=0;for(j=0;j<M;j++){if(p_yx[i][j]==0)d[i]=d[i]+0;elsed[i]=d[i]+p_yx[i][j]*log(p_yx[i][j]/q[j]); }a[i]=exp(d[i]);}u=0.0;for(i=0;i<N;i++) //计算uu=u+p[i]*a[i];IL=log(u)/log(2.0); //计算ILmax=a[0];for(i=0;i<N;i++){if(a[i]>=max)max=a[i];}IU=log(max)/log(2.0); //计算IUk=k+1;}C=IL;printf("信道矩阵为:\n"); //输出for(i=0;i<N;i++){for(j=0;j<M;j++){printf("%.2f ",p_yx[i][j]);}printf("\n");}printf("此次信道的迭代次数:k=%d\n",k);printf("信道容量C=%f比特/符号\n",C);}五、程序运行结果:六、实验小结:本次试验是建立在迭代的基础上,首先要深刻理解信道容量的迭代算法,其次是如何将复杂的公式转化为程序通过此次实验,我了解了信道容量的迭代算法的基本知识,学会了如何将复杂的公式如何用程序语言描述出来,掌握了高级语言数值计算过程程序的设计和调试的相关知识,对于将实际问题公式转化为程序的能力有提高。
信道容量的迭代算法

输入
s P(y j | x i ) ai(n) exp y j | x i ) ln q(y j ) j 1 (i=1,2...)
u (n) p(x i )ai (n)
i
I L log 2 (u (n) ), IU log 2 (max(a i(n) ))
I (X; Y) p(x i ) p(y j | x i ) ln
i j
p(x ) p(y
i i
p(y j | x i )
j
| xi )
(1)
要求信道容量 C 就是要在 p(x i ) 的约束下,求 I (X; Y) 的极大值。 首先引入后验概率,即:
q(x i | y j )
p(x ) p(y
表 1.1 ε的选取与信道容量关系 因此,使用该算法计算 C 的时候要选取适当的ε值,才能保证 值的准确性。
四 程序说明 1、程序采用的是C++语言,编译环境为visual studio 2010 2、信道矩阵放在“Channel_matrix.txt”中,其中初始信源为等概 1/R(R表示信源个数),并放在vector<float> pxi中。 3、本程序使用#define wucha ε 定义误差,因此通过改变 wucha 的值就可以控制迭代的次数 4、程序为:channel_code.cpp 信道矩阵为:Channel_matrix.txt
信道容量的迭代算—彭海军
研究信道的目的是要讨论信道中平均每个符号所能传送的信息 量,而将最大的信息传输率称为信道容量。由于对于普通的线性信 道(信道矩阵 r=s),直接可以采用 C ln e 求解信道容量。但当
信息论中的信道容量与编码速率

信息论中的信道容量与编码速率信息论是研究信息传输和处理的数学理论,其中信道容量和编码速率是信息论中的重要概念。
信道容量指的是一个通信信道所能传输的最大信息速率,而编码速率则是在给定信道容量下实现可靠通信所需要的编码速率。
本文将分别介绍信道容量和编码速率在信息论中的作用和重要性。
信道容量是一个通信系统的重要指标,它描述了在给定信道条件下最大的数据传输速率。
信道容量的计算取决于信道的物理特性以及噪声水平。
通常情况下,信道容量可以通过香农公式进行计算,该公式考虑了信道的带宽、信噪比等因素。
信道容量的大小直接影响到通信系统的传输效率,理论上,如果通信系统的编码速率大于信道容量,那么就可以实现无限接近于理论上的最大传输速率。
因此,信道容量是通信系统设计中一个重要的参考指标。
与信道容量相关的是编码速率,编码速率是指在信道容量限制下实现可靠通信所需要的编码速率。
编码速率的选择与信道编码技术密切相关,通信系统需要设计合适的编码方案来提高数据传输的可靠性和效率。
传统的编码技术包括奇偶校验码、循环冗余校验码等,而近年来,随着深度学习和人工智能的发展,基于神经网络的编码技术也得到了广泛的应用。
选择适当的编码速率可以提高数据传输的可靠性,减小误码率和延迟,提升通信系统的性能。
在实际通信系统中,信道容量和编码速率通常需要进行折中考虑。
信道容量较大时,可以选择更高的编码速率来提高传输速率,但也会增加误码率和复杂度;而信道容量较小时,则需要降低编码速率以保证数据传输的可靠性。
通信系统的设计者需要根据实际需求和信道条件来合理选择信道容量和编码速率,从而实现较好的通信性能。
综上所述,信息论中的信道容量和编码速率是通信系统设计中不可或缺的重要概念。
合理选择适当的信道容量和编码速率可以提高通信系统的传输效率和可靠性,为信息传输提供更好的保障。
在未来的通信技术发展中,信道容量和编码速率仍将是信息论研究的热点领域,不断推动通信技术的进步和创新。
信道容量迭代算法(信息与编码论)

实验四信道容量迭代算法一、实验目的让学生初步掌握信道容量的基础知识、计算方法及迭代算法计算方法,以及取得信道容量的判别算法,并学会使用c 语言完成迭代算法。
二、实验原理信息率失真函数迭代算法具体如下:(1)首先假设绝对值足够大的负数作为斜率S 的取值,并且选择试验信道的转移概率1(|)j k p b a 为等分布的,且令1n =。
(2)根据公式1()(|)()rn j n j k k k p b p b a p a ==∑计算出()n j p b 。
(2)将()n j p b 代入公式1()exp((,))(|)()exp[(,)]n j i j n j i n j i jj p b Sd a b p b a p b Sd a b +=∑计算出1(|)n j i p b a +。
(4)计算平均失真和信息率1111()(|)(,)s r n i n j i i j j i D p a p b a d a b ++===∑∑11(|)()(|)log()r s n j i n i n j i i j n j p b a R p a p b a p b ===∑∑(5)如果1||n n D D ε+-≤,则跳转到(6);否则,令1n n =+,跳转到(2)。
其中ε为事先确定的精度。
(6)令()n D S D =,()n R S R =;改变斜率值S ,选择初始条件概率为等概率分布,令1n =,然后跳转到(2),直至斜率足够接近0为止。
三、实验内容1)给定一个两输入的概率分布和失真矩阵测度分别如下12()1X a a p x p p ⎡⎤⎡⎤=⎢⎥⎢⎥-⎣⎦⎣⎦11122122(,)(,)01(,)(,)10d a b d a b d a b d a b ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦D 令p=0.5,初始斜率s=-20,斜率递增步长为0.05,利用迭代算法完成信息率失真函数的计算;将失真和信息率的值写入excel 文档,利用excel 的绘图工具画出信息率失真函数曲线;2)令p=0.3,0.1重复上述过程。
信息论与编码-第10、11讲-第3章信道容量

THANKS
感谢观看
信道容量决定了单位时间内传输 的信息量,容量越大,传输效率 越高。
02
编码技术对信息传 输效率的影响
采用高效的编码技术可以减小信 息的冗余度,提高信息传输效率 。
03
多路复用技术提高 信道利用率
多路复用技术允许多个信号在同 一信道上同时传输,提高了信道 的利用率。
信道容量与信号设计
1 2
信号设计对信道容量的影响
02
它反映了信道在噪声干扰下传输信息的能力,是衡量信道性 能的重要指标。
03
信道容量可以通过特定的编码方式和技术实现接近,但无法 达到。
信道容量的性质
确定性
对于确定的信道,其容量是确定的,与使用的信号和 编码方式无关。
可加性
对于并联的多个信道,其容量等于各个信道容量的总 和。
单调性
随着输入信号的平均功率增加,信道容量通常会增加 ,但增加的幅度逐渐减小。
通信系统设计中的关键问题
如何提高信号传输的可靠 性和速率?
如何平衡传输质量和系统 复杂度?
如何降低噪声和干扰对信 号的影响?
如何实现高效、低成本的 通信系统设计?
05
CATALOGUE
信道容量与实际应用
无线通信中的信道容量问题
无线信道的不确定性
无线通信中,由于信号传播的复杂性和多径效应,信道容量存在不 确定性。
信道容量的计算方法
离散无记忆信道容量
01
通过计算输入信号的熵和输出信号的熵,再根据互信息公式计
算得出。
连续无记忆信道容量
02
通过计算输入信号的功率谱密度和输出信号的功率谱密度,再
根据互信息公式计算得出。
有记忆信道容量
信息论中的信道容量与编码速率

信息论中的信道容量与编码速率信息论是研究数据传输与通信的一门学科,旨在量化信息的传输和处理过程。
在信息论中,信道容量和编码速率是两个重要的概念。
本文将介绍信道容量和编码速率的定义、关系以及它们在通信系统中的应用。
一、信道容量的定义与计算信道容量是指在给定通信信道条件下,能够传输的最高信息率。
它是通过信道的带宽、信噪比和信道的性质来决定的。
在信息论中,最为广泛应用的是香农信道容量公式,即:C = B * log2(1 + SNR)其中,C表示信道容量,B表示信道的带宽,SNR表示信道的信噪比。
这个公式告诉我们,在给定的信道带宽和信噪比条件下,信道最高能够传输的信息速率。
信道容量的计算可以帮助我们设计合理的通信系统。
当信道容量大于实际传输的信息速率时,我们可以使用更高效的编码方式,提高数据传输效率。
而当信道容量小于实际传输的信息速率时,我们需要采取其他策略,如增加信道带宽或提高信噪比,以提高数据的可靠性。
二、编码速率的定义与计算编码速率是指按照一定编码方式传输的信息率。
它是通过不同的编码技术和信道容量来决定的。
在通信系统中,我们常用的编码方式有固定长度编码、可变长度编码和差错编码等。
固定长度编码是指以固定长度的编码符号来表示一个信息符号。
它的编码速率为:R = log2(M)其中,R表示编码速率,M表示编码符号的个数。
固定长度编码常用于简单的通信系统,如二进制通信系统。
可变长度编码是指根据信息出现的概率来分配编码长度。
常见的可变长度编码方式有霍夫曼编码和算术编码等。
可变长度编码的速率决定于不同信息出现的概率分布。
差错编码是指通过增加冗余信息来提高传输的可靠性。
常见的差错编码方式有海明码和卷积码等。
差错编码的速率通常会比源信息的速率高,以保证传输的可靠性。
编码速率的选择要考虑信息传输的可靠性和效率。
高速率的编码可以提高信息传输速度,但可能会降低可靠性;而低速率的编码可以提高传输的可靠性,但效率较低。
因此,选择适合的编码速率是信息传输设计中的重要问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信息论与编码课程大作业
题目:信道容量的迭代算法
学生姓名:
学号:2010020200
专业班级:10电子信息工程
2013 年5 月18 日
信道容量的迭代算法
1信道容量的迭代算法的步骤
一、用了matlab 实现DMC 容量迭代的算法如下: 第一步:首先要初始化信源分布:.0deta 10,1,0,1
)
(>>=⋯==,选置,,k r i r
P k i
即选取一个精度,本次中我选deta=0.000001。
第二步:}{,)
()()()
(k ij i
ji
k i
ji
k i k ij t p p
p p t 得到反向转移概率矩阵根据式子∑=。
第三步:
()()()()(){}
111]
log exp[]
log exp[+++==
∑∑∑k i k i
j
ij k ji
j
ij k ji k i p P t p
t p p 计算由式。
第四步:
()
()()
()()()。
C t p t P
I C
k r i s j k ij ji k k k 10011log exp log ,+==++⎪⎭⎪⎬⎫
⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡==∑∑计算由式
第五步: 若
a C
C C k k k det )
1()
()1(>-++,则执行k=k+1,然后转第二步。
直至转移条件不成立,接着
执行下面的程序。
第六步:输出迭代次数k 和()1+k C 和1+k P ,程序终止。
2. Matlab 实现
clear;
r=input('输入信源个数:'); s=input('输入信宿个数:');
deta=input('输入信道容量的精度: '); Q=rand(r,s); %形成r 行s 列随机矩阵Q
A=sum(Q,2); %把Q矩阵每一行相加和作为一个列矩阵A
B=repmat(A,1,s); %把矩阵A的那一列复制为S列的新矩阵
%判断信道转移概率矩阵输入是否正确
P=input('输入信道转移矩阵P:')%从这句话开始将用下面两句代替可自动生成信道转移矩阵
[r,s]=size(P);
for i=1:r
if(sum(P(i,:))~=1) %检测概率转移矩阵是否行和为1.
error('概率转移矩阵输入有误!!')
return;
end
for j=1:s
if(P(i,j)<0||P(i,j)>1) %检测概率转移矩阵是否负值或大于1
error('概率转移矩阵输入有误!!')
return;
end
end
end
%将上面的用下面两句代替可自动生成信道转移矩阵
%disp('信道转移概率矩阵:')
%P=Q./B 信道转移概率矩阵(每一个原矩阵的新数除以所在行的数总和)
i=1:1:r; %设置循环首项为1,公差为1,末项为r(Q的行数)的循环
p(i)=1/r; %原始信源分布r个信源,等概率分布
disp('原始信源分布:')
p(i)
E=repmat(p',1,s);%把r个等概率元素组成一列,复制为s列
for k=1:1:1/deta
m=E.*P; % m=p.*E; %后验概率的分子部分
a=sum(m); %把得到的矩阵m每列相加之和构成一行
su1=repmat(a,r,1);%把得到的行矩阵a复制r行,成一新矩阵sul,后验概率的分母部分
t=m./su1; %后验概率矩阵
n=exp(sum(P.*log(t),2)); %信源分布的分子部分
su2=sum(n); %信源分布的分母部分
p=n/su2; %信源分布
E=repmat(p,1,s);
C(k+1)=log(sum(exp(sum(P.*log(t),2))))/log(2);
kk=abs(C(k+1)-C(k))/C(k+1);
if(kk<=deta)
break;
end
disp('迭代次数:k='),disp(k)
end
disp('最大信道容量时的信源分布:p='),disp(p')
disp('最大信道容量:C='),disp(C(k+1))
3.运行结果及分析(宋体四号,加粗)
结果分析:这两组数据都是我随机选的,都是选的信源个数为2,信宿的个数为3,选用的精度为
0.000001。
然后输入信道转移矩阵
P ,执行
}
{,)
()()()
(k ij i
ji
k i
ji
k i k ij
t p p
p p t 得到反向转移概率矩阵∑=
,
将
得
到
的
结
果
代
入
()()()()(){}
111]
log exp[]
log exp[+++==
∑∑∑k i k i
j
ij k ji
j
ij k ji k i p P t p
t p p 计算由式,
得
到
)
1(+k p 后
()
()()
()()()。
C t p t P
I C
k r i s j k ij ji k k k 10011log exp log ,+==++⎪⎭
⎪⎬⎫
⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡==∑∑计算由式,再进行
a C C C k k k det )
1()
()1(>-++的判断,这个条件满足时继续求
)
(k ij
t ,再依次往下计算,直至这个条件不
满足,然后输出k 和()
1+k C
和1+k P 。
总的来说这不过是将矩阵不断的代入公式,当最后的
精度不大于0.000001.输出k 和()1+k C 和1+k P 。
第二组数据:
4.心得体会
在此次matlab编程实现信道容量的迭代算法的过程中,开始我觉得这十分的困难,经过网上查阅资料和请教同学,最后才对本次设计有了一定的理解,详细理解了信道容量的迭代算法过程。
经过理解,发现这种编码其实挺简单的,最重要的是怎样用程序把它实现,这对我们的编程能力也是一次考验。
编程时逻辑要十分的严谨,严格的遵守编程的规则,一点的错误都会造成整个程序的无法运行。
调试过程会发现很多问题,这时不能烦躁,要耐心的去发现问题,不断掌握matlab软件的各种调试方法。
通过这次设计我深刻体会到细节决定成败,同时也发觉自己知识学的太浅薄,没有从本质上把握住要点,运用知识不灵活。
让我认识到在今后学习当中,要注意去深度思考,把所学知识有机联系起来,掌握本质,理解要领。
此次实验进一步加强了我的编程能力和严谨的逻辑思维能力,受益颇多。
很感谢老师给了我这么一次锻炼的机会,让我对自己有了新的认识,感谢同学在这次作业的完成对我的帮助,让我有了新的提高。
