滚动轴承点接触弹流油膜厚度及摩擦力矩的分析计算

合集下载

滚动轴承摩擦力矩的试验数据分析

Meng Fannian
Supervisor:
Xia Xintao
ABSTRACT
Friction torque is one key performance parameter of a rolling bearing. Some important functions of the rolling bearing, such as rotating stability and precision are affected by it. However, some special bearings, such as satellite bearing, rocket bearing, aircraft bearing and wind power bearing require higher quality of the friction torque. As we know, almost all the mechanical products need to use bearing. Therefore, the improvement of bearing’s quality has an important effect on the whole mechanical performance. In order to design bearings with higher quality, more research must be done on the friction torque.
摩擦力矩受一些非线性因素的影响，所以滚动轴承摩擦力矩呈现非线性，混沌理论能够很好的解决非线性问题，用混沌理论计算试验数据最大 Lyapunov 指数大于 0，这表明滚动轴承摩擦力矩是混沌的，在此基础上研究其非线性量化参数关联维数以及盒维数，以用来分析滚动轴承摩擦力矩的非线性动力学问题。研究表明：关联维数具有饱和现象，这同样也可以判别出其试验数据是混沌的。另外，关联维数和盒维数也随轴承转速的增大而增加。

轴承的摩擦系数及摩擦力矩计算

轴承的摩擦系数
为便于与滑动轴承比较，滚动轴承的摩擦力矩可按轴承内径由下式计算：M=uPd/2
这里,
M：摩擦力矩，mN.m
u：摩擦系数，表1
P：轴承负荷，N
d：轴承公称内径，mm
摩擦系数u受轴承型式、轴承负荷、转速、润滑方式等的影响较大，一般条件下稳定旋转时的摩擦系数参考值如表１所示。

对于滑动轴承，一般u=0.01-0.02，有时也达0.1-0.2。

各类轴承的摩擦系数u
轴承型式摩擦系数u
深沟球轴承 0.0010-0.0015
角接触球轴承 0.0012-0.0020
调心球轴承 0.0008-0.0012
圆柱滚子轴承0.0008-0.0012
满装型滚针轴承0.0025-0.0035
带保持架滚针轴承0.0020-0.0030
圆锥滚子轴承 0.0017-0.0025
调心滚子轴承 0.0020-0.0025
推力球轴承 0.0010-0.0015
推力调心滚子轴承0.0020-0.0025
由轴承摩擦引起的轴承功率损失可用以下计算公式得出
NR = 1,05 x 10-4 Mn
其中
NR = 功率损失，W
M = 轴承的总摩擦力矩，Nmm
n = 转速，r/min
电机扭矩公式：T=9550*P/n
T：电机转矩N.M
P：电机功率KW
n：转速r/min。

油润滑球轴承摩擦效应计算方法

油润滑球轴承摩擦效应计算方法摘要：油润滑轴承中的摩擦和发热主要是由于球滚道接触处的滑动以及球，保持架，轴承套圈空隙间润滑剂的搅动。

在一个良好润滑的轴承中，轴承的耐久度高度依赖于用来把滚动体和滚道分隔开的油膜厚度。

油膜厚度又取决于润滑剂的粘度性质。

摩擦产生的热量以及热耗散率之间的平衡决定轴承温度的函数。

在轴承的设计应用中，合理准确的预测轴承的摩擦热产生率是十分重要的。

例如飞机燃气涡轮机中高速转子和低速转子支撑轴承。

本文提供出一种方法去得到所需计算和考虑的轴承负荷和速度，润滑剂的真实流变性能，和比较简单的轴承套圈，滚动体，润滑剂之间的热传导系统。

分析的结果和实验数据相比也十分的接近。

关键词：滚动轴承，摩擦，热效应球道接触面上的弹流润滑大多数球轴承在球滚道接触上受到赫兹压力负荷，如图1所示：图1 在一个球滚道接触椭圆区域赫兹压力分布表现了在椭圆接触区域的压力分布，在大多数应用中，球道接触面基本上的弹流润滑和混合润滑，甚至是润滑脂，它是能够实现润滑油膜功能的固体的油。

在弹流润滑的影响下，在球滚接触面上的赫兹压力分布有所改变。

如图2所示，图2 在椭圆轨道接触面受较大负载的情况下，弹流润滑压力呈现一个峰值在原点弹流润滑压力分布呈现了峰值，在大多数应用中，球滚道的负载是相当重的，压力尖峰对轴承性能的影响仅仅是轻微的，尖峰对着的接触面积只有一小部分。

球滚道的摩擦和牵引一般的，稳定的负载和速度下运动的球轴承在流体润滑状态下摩擦是非常小的。

实际上滚珠和滚柱轴承通常被称为抗摩擦轴承。

然而，摩擦是轴承的一个非常重要的参数，在大多数情况下，它决定了轴承的温度，并且影响轴承的耐久度。

预测轴承温度的方法是由哈里斯1991年提出的，决定轴承疲劳耐力的球道轴承接触摩擦应力的总结方法也由哈里斯1998年提出。

为了有效的概括球轴承在实际应用中滚动，滑动摩擦的性能和算法，必须描述球道表面摩擦应力。

即，接触面上的剪切应力，相关于轴承的几何形状和材料，轴承和润滑剂的参数。

滚动轴承点接触弹流油膜厚度及摩擦力矩的分析计算

3 结束语
滚动轴承的摩擦力矩问题涉及到弹性力学、接触力学、摩擦、润滑等学科 , 且各种因素相互影响 ,相互作用 ,使摩擦力矩的精确分析计算不易进行。新的摩擦力矩计算公式可以定量地分析轴承弹流油膜厚度与摩擦力矩的关系 , 也可以应用于轴承的设计和工艺 ,提高轴承的性能 , 进而增强机械设备的可靠性 ,增加设备利用率。
(1
-
e ) - 0. 68k
(3)
材料参数 G′=αE′
(4)
E1′=
1 21 (-源自ν2 1E1+
1
-
ν2 2
)
E2
速度参数 U ′=ηE0′RUx
(5)
U
π =
(Dp2w
-
Dw2 co sβ)
120Dpw
| ne
-
ni
|
载荷参数W
′=
W
E ′R2x
(6)
W = Fa / Z sinβ
椭圆率 k = 1. 03 ( Ry ) 0. 64
(1. 河南科技大学机电工程学院 ,河南洛阳 471003; 2. 洛阳轴承研究所 ,河南洛阳 471039)
摘要 :点接触弹流润滑的实际计算较为复杂 ,对点接触弹流油膜厚度及摩擦力矩的计算进行了详细分析并给出了计算实例。同时对弹流油膜厚度与轴承摩擦力矩的关系进行了探讨 ,提出了新的摩擦力矩经验计算公式。关键词 :滚动轴承 ;点接触 ;弹流润滑 ;油膜厚度 ;摩擦力矩中图分类号 : TH133. 33; TH117 文献标志码 : B 文章编号 : 1000 - 3762 (2008) 04 - 0010 - 03
对试验所得的数据进行整理分析 , 提出了新的摩擦力矩经验计算公式为

轴承的摩擦系数及摩擦力矩计算04.03

轴承的摩擦系数
为便于与滑动轴承比较，滚动轴承的摩擦力矩可按轴承内径由下式计算：M=uPd/2
这里,
M：摩擦力矩，
u：摩擦系数，表1
P：轴承负荷，N
d：轴承公称内径，mm
摩擦系数u受轴承型式、轴承负荷、转速、润滑方式等的影响较大，一般条件下稳定旋转时的摩擦系数参考值如表１所示。

对于滑动轴承，一般u=，有时也达。

各类轴承的摩擦系数u
轴承型式摩擦系数u
深沟球轴承
角接触球轴承
调心球轴承
圆柱滚子轴承
满装型滚针轴承
带保持架滚针轴承
圆锥滚子轴承
调心滚子轴承
推力球轴承
推力调心滚子轴承由轴承摩擦引起的轴承功率损失可用以下计算公式得出
NR = 1,05 x 10-4 Mn
其中
NR = 功率损失，W
M = 轴承的总摩擦力矩，Nmm
n = 转速，r/min
电机扭矩公式：T=9550*P/n
T：电机转矩
P：电机功率KW
n：转速r/min。

滚动轴承热弹流润滑数值分析

关键词：多重网格法；滚动轴承；热弹流润滑中图分类号：Ｔ３．３Ｈ１３３文献标识码：Ａ
０引言
其中，Ｄ为内、外圈平均半径。则滚子与内圈滚道的
接触点的当量曲率半径为：
，
如果从设计和制造精度上严格控制，滚动轴承的滚动体与滚道之间可以保持一定厚度的弹流油膜。要进行滚动轴承的弹流润滑计算，必须事先确定滚动体与座圈之间的运动关系和力的作用。然而，滚动轴承的动力学分析十分复杂，而且轴承内部各元件的运动情况与所处的润滑状态密切相关。Ｄｗｓｎ等人对滚ｏｏ子轴承的分析表明：果采用弹流润滑理论进行分析，如则证明弹流油膜可以传递滚子与座圈之间的作用力而不产生明显的滑动［。所以弹流润滑下的滚子轴承其１】内部运动关系属于纯滚动。１滚动轴承运动参数计算前人研究结论已经表明：当弹性模量分别为Ｅ和Ｅ、松比分别为。：泊和：的两个弹性圆柱相接触时，
’
… … … … … …
・３・５一Fra bibliotek“一
… … …
（一ｃ八
… … … … …
一
…
’
… … … …
。 …
（）４
２滚动轴承弹流润滑数值计算本文采用６网格求解接触点处的油膜形状、压层
力分布和温度分布，计算所需的输入参数包括轴承结构参数、材料参数和润滑油的材料参数。当其它条件

SKF摩擦力矩计算公式

SKF摩擦力矩计算公式SKF（瑞典瑞典轴承制造公司）是全球领先的轴承和密封制造商，提供给各个行业的工程师和设计师广泛的技术知识和解决方案。

摩擦力矩是衡量轴承运转阻力的重要参数之一，它决定了轴承的运转效率和寿命，因此对于轴承性能的评估和选择非常重要。

1.滚动轴承的摩擦力矩计算公式：µm=µr×µv×µc×µk其中，µm为摩擦力矩（Nm）、µr为滚动摩擦系数、µv为粘滞摩擦系数、µc为轴承的摩擦力系数，µk为轴承的损失系数。

2.滑动轴承的摩擦力矩计算公式：µm=µv×µc×µk×F其中，µm为摩擦力矩（Nm）、µv为粘滞摩擦系数、µc为轴承的摩擦力系数，µk为轴承的损失系数，F为轴承的负载（N）。

3.混合轴承的摩擦力矩计算公式：µm=µr×µv×µc×µk×F其中，µm为摩擦力矩（Nm）、µr为滚动摩擦系数、µv为粘滞摩擦系数、µc为轴承的摩擦力系数，µk为轴承的损失系数，F为轴承的负载（N）。

不同类型的轴承使用不同的摩擦力矩计算公式，这些公式通常是通过试验和实验数据进行验证和确定的。

在实际应用中，轴承的运转状态、负载、润滑方式以及环境条件等因素都会对摩擦力矩产生影响，因此在计算摩擦力矩时需要考虑这些因素。

除了摩擦力矩的计算公式，SKF还提供了多种工具和软件来辅助工程师和设计师进行轴承选择和计算。

例如，SKF Bearing Calculator是一个在线工具，可以根据特定的应用条件和需求来选择和计算最佳的轴承类型和尺寸。

此外，SKF还提供了技术手册和培训课程，以帮助用户更好地理解和应用轴承摩擦力矩的相关知识。

轴承的摩擦系数及摩擦力矩计算04.03

对于滑动轴承，一般u=0.01-0.02，有时也达0.1-0.2。

球轴承点接触区油膜阻尼系数的计算与理论分析

ＣｈｅｎＢｉｎＬｉＳｏｎｇｓｈｅｎｇＣｈｅｎＪｉａｎＬｕＹｕｘｉｎ
（ＳｃｈｏｏｌｏｆＭｅｃｈａｔｒｏｎｉｃＥｎｇｉｎｅｅｉｒｎｇａｎｄＡｕｔｏｍａｔｉｏｎ，ＳｈａｎｇｈａｉＵｎｉｖｅｒｓｉｔｙ，Ｓｈａｎｇｈａｉ２０００７２，Ｃｈｉｎａ）Ａｂｓｔｒａｃｔ：Ｂａｓｅｄｏｎｐｏｉｎｔｃｏｎｔａｃｔｅｌａｓｔｏｈｙｄｒｏｄｙｎａｍｉｃｌｕｂｉｒｃａｔｉｏｎ（ＥＨＬ）ｅｑｕａｔｉｏｎ，ｔｈｅｃａｌｃｕｌａｔｉｏｎｍｏｄｅｌｏｆｏｉｌ — ｉｆｌｍ
ｃｕｌａｔｉｏｎｍｏｄｅｌｃｏｒｒｅｓｐｏｎｄｔｏｔｈｅｔｈｅｏｒｅｔｉｃａｌｐｒｅｄｉｃｔｒｅｓｕｌｔｓ，ｗｈｉｃｈｓｈｏｗｓｔｈｅｄｅｐｅｎｄａｂｉｌｉｔｙｏｆｔｈｉｓｍｏｄｅ１．Ｔｈｅｅｆｆｅｃｔｓｏｆｌｕ — ｂｉｃｒａｎｔｅｎｔｒａｉｎｍｅｎｔｖｅｌｏｃｉｔｙａｎｄｉｎｉｔｉａｌｖｉｓｃｏｓｉｔｙ，ａｎｄｔｈｅｃｏｎｔａｃｔｌｏａｄｏｎｏｉｌ — ｉｌｆｍｄａｍｐｉｎｇｗｅｒｅａｎａｌｙｚｅｄ．Ｔｈｅｒｅｓｕｌｔｓｓｈｏｗ

一种快速求解点接触弹流问题的直接迭代算法

上，同时具有更宽的载荷适用范围。
关键词：点接触；弹流动力润滑；快速算法中图分类号：ＴＩ３文献标识码：Ａ文章编号：２４— １０（００Ｈ１０５０５２１）８— ４０３—
ＡｓｒｃｔｒｔｖｇｒｔｍｏａｔｈｄｒｄｎａｉＦａｔＤｉｅｔＩｅａｉｅＡｌｏｉｈｆｒＥｌｓｏｙｏｙｍｃＬｕｒｃｔｏｆＰｏｎｎｔｃｂｉａｉｎｏｉｔＣｏａｔ
１
Ａ３
，Ａ４
式中：为有分布压力作用的整个域；Ｅ为当量（力综合）弹性模量。
（润滑剂黏度方程：４）
２２量纲一化Ｒｙｏｄ．ｅｎｌｓ方程的离散及系统迭代方程组的形成
采用目前弹流研究中广泛使用的Ｒｅｎｓｏｌｄ黏压ａ关系式：叼＝／ｘ｛１叼＋．７［１５１一）一１）７ｅｐ（“ ｏ９６）（＋．１］ｏＸ０Ｐ
ＸｉｑａＧｕｎｉＬｎａＢｏｉｎｏＸｉｗｅｉＹｉｇ
（ｅａｍｎｏｃａｉｌｎｉｅｎ，ｈｎｚｏｎｖｒｔ，ｈｎｚｏｅａ５０１ＣｉａＤｐｒｅｔｆｔＭｅｈｎｃｇｅｒｇＺｅｇｕＵｉｓｙＺｅｇｈｕＨｎｎ００，ｈｎ）ａＥｎｉｈｅｉ４
润滑剂为Ｎｗｏ流体的稳态等温点接触弹性流ｅｎｔ体动力润滑问题的基本方程组如下：
润滑与密封

滚动轴承的受力分析、载荷计算、失效和计算准则

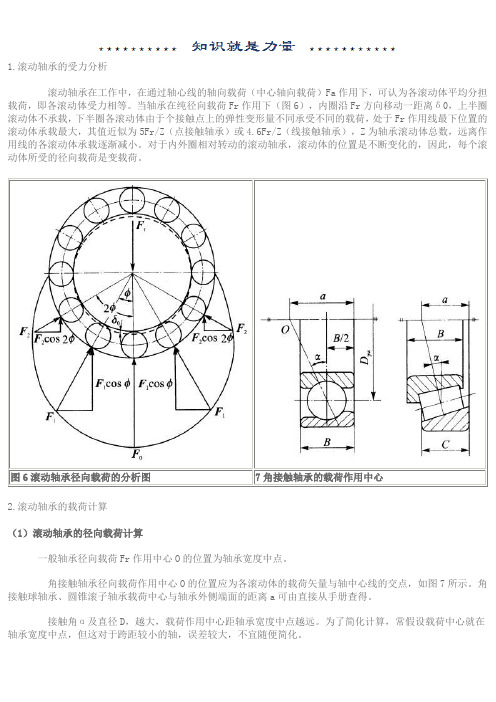
1.滚动轴承的受力分析滚动轴承在工作中，在通过轴心线的轴向载荷（中心轴向载荷）Fa作用下，可认为各滚动体平均分担载荷，即各滚动体受力相等。

当轴承在纯径向载荷Fr作用下（图6），内圈沿Fr方向移动一距离δ0，上半圈滚动体不承载，下半圈各滚动体由于个接触点上的弹性变形量不同承受不同的载荷，处于Fr作用线最下位置的滚动体承载最大，其值近似为5Fr/Z（点接触轴承）或4.6Fr/Z（线接触轴承），Z为轴承滚动体总数，远离作用线的各滚动体承载逐渐减小。

对于内外圈相对转动的滚动轴承，滚动体的位置是不断变化的，因此，每个滚动体所受的径向载荷是变载荷。

图6滚动轴承径向载荷的分析图7角接触轴承的载荷作用中心2.滚动轴承的载荷计算（1）滚动轴承的径向载荷计算一般轴承径向载荷Fr作用中心O的位置为轴承宽度中点。

角接触轴承径向载荷作用中心O的位置应为各滚动体的载荷矢量与轴中心线的交点，如图7所示。

角接触球轴承、圆锥滚子轴承载荷中心与轴承外侧端面的距离a可由直接从手册查得。

接触角α及直径D，越大，载荷作用中心距轴承宽度中点越远。

为了简化计算，常假设载荷中心就在轴承宽度中点，但这对于跨距较小的轴，误差较大，不宜随便简化。

图8角接触轴承受径向载荷产生附加轴向力1)滚动轴承的轴向载荷计算当作用于轴系上的轴向工作合力为FA，则轴系中受FA作用的轴承的轴向载荷Fa=FA，不受FA作用的轴承的轴向载荷Fa=0。

但角接触轴承的轴向载荷不能这样计算。

角接触轴承受径向载荷Fr时，会产生附加轴向力FS。

图8所示轴承下半圈第i个球受径向力Fri。

由于轴承外圈接触点法线与轴承中心平面有接触角α，通过接触点法线对轴承内圈和轴的法向反力Fi将产生径向分力Fri；和轴向分力FSi。

各球的轴向分力之和即为轴承的附加轴向力FS。

按一半滚动体受力进行分析，有FS ≈ 1.25 Frtan α(1)计算各种角接触轴承附加轴向力的公式可查表5。

表中Fr为轴承的径向载荷；e为判断系数，查表6；Y为圆锥滚子轴承的轴向动载荷系数，查表7。

滚动轴承接触问题数值计算及有限元分析

２０１１年第６期机械工程与自动化
· ５３ ·
参考文献：［１］庞振基，黄其圣．精密机械设计［Ｍ］．北京：机械工业出版
社，２０００．［２］李黎明．ＡＮＳＹＳ有限元分析实用教程［Ｍ］．北京：清华大
∑ ρⅡ２＝０．０５４８。将数值代入式（１）、式（２）得： ρ ＝
０．２７０９，Ｆ（ρ）＝０．９５５０。将相关参数代入式（３）、式（４）可求得ａ＝２．２１
ｍｍ，ｂ＝１．９９ｍｍ。最后由式（５）、式（６）可得最大接触应力σｍａｘ＝３７５ＭＰａ，平均接触应力σｍ＝σｍａｘ／１．５＝２５０ＭＰａ，钢球与内圈的弹性趋近量Ｓ＝０．０２９ｍｍ。
２滚动轴承的有限元计算本次计算选用深沟球轴承６２０６，接触面上使用中
节点单元，采用Ｃｏｗｔａ４８单元进行分析，有限元模型如图２所示。然后对轴承进行约束，在ｙ方向施加了－０．００５ｍｍ的位移约束，并且施加载荷进行求解。图３为模型的网格划分，图４为ｙ方向的应力图，图５为其等效应力图。
根据赫兹接触理论，接触区椭圆的长短轴ａ、ｂ分别为：
∑ ａ＝α［２３Ｑρ（１Ｅ－１μ２１＋１Ｅ－２μ２２）］１／３。 ……… （３）
收稿日期：２０１１－０６－３０；修回日期：２０１１－０７－０２作者简介：马文（１９８４－），男，山西大同人，助理工程师，本科，主要从事强度检测和应力测试及分析工作。

滚动轴承摩擦力矩的计算分析

●产品设计与应用◆
ｌ一３
滚动轴承摩擦力矩的计算分析
朱爱华１，朱成九１，张卫华２
（１．华东交通大学，南昌３３００１３；２．西南交通大学，成都６１００３１）
摘要：对ＳＫＦ最新推出的滚动轴承摩擦力矩计算模型及其影响因素进行了分析，并结合算例对ＳＫＦ推出的滚
动轴承摩擦力矩的计算模型和一般计算方法进行了对比，重点探讨了载荷和转速对滚动轴承摩擦力矩的影响。
２实例比较及影响因素分析
某钢厂的重型设备使用ＳＫＦ密封球面滚子轴承２４０２６—２ＣＳ２／、吓１４３，乃＝４００ｒ／ｍｉｎ，实际径向
一ｃ－ｕＩ旨．矗手＿０一×＼．＇＾嫡制※罩鲁单
万方数据
３Ｏ２５２Ｏｌ５ｌＯＯ５
０ —ｃ－ｇＥ面子＿０一×一＼．Ｉ＾瑙锨式罩昌单
图１拖曳损失变量与油位高度日和轴承平均直径屯之比曲线
ｉ．为球列数；砭为根据轴承类型而定的几何常数；鼠为根据滚子轴承类型而定的几何常数［５】。在油浴润滑中，轴承部分被浸没，或在某些特殊情况下，轴承被完全浸没，储油池的大小、几何结构和油位对轴承的摩擦力矩会有实质的影响。但对于储油池非常大的油浴润滑，可以不考虑储油池尺寸的相互作用，也不考虑在轴承附近工作的其他机械元件（油搅动器、齿轮或凸轮）的影响。
方向为轴承设计。Ｅ—ｍａｉｌ：ｚａｈｕａ２３７＠ｙａｈｏｏ．锄．ｅｎ。
擦力矩的因素，介绍了计算滚动轴承总摩擦力矩的方法，并结合算例进行了详细地分析。
１滚动轴承的总摩擦力矩Ｍ
１．１一般计算方法Ｈ１
Ｍ＝％＋Ｍ１Ｍ＝石Ｐ，以坻＝五（ｔ，ｎ）争以×１０‘７
式中：Ｍ０为与轴承载荷大小、润滑剂用量、粘度及转速有关的摩擦力矩分量；Ｍ。为与轴承载荷大小、滚动体和滚道间接触弹性变形量及滑动摩擦有关的摩擦力矩分量斩为载荷系数；Ｐ１为由摩擦力矩分量Ｍ。决定的轴承载荷；ｄ。为轴承平均直径，ｄ。＝Ｏ．５（ａ＋Ｄ）；ｄ为轴承的内径；Ｄ为轴承的外径以为考虑轴承结构和润滑方法的系数；ｎ为轴承转速；ｕ为润滑剂的运动粘度，对于润滑脂，则为基油的粘度。

轴承的摩擦系数及摩擦力矩计算04.03

对于滑动轴承，一般u=0.01-0.02，有时也达0.1-0.2。

skf轴承摩擦力矩的计算公式

摩擦是导致滚动轴承发热的主要原因，因此也是决定轴承工作温度的关键因素。

摩擦的大小取决于负荷和几个其它因素，其中最重要的是轴承的类型和尺寸、转速、润滑剂的特性和润滑剂的用量。

轴承转动时的总阻力，是由部件之间的滚动和滑动摩擦所构成，包括滚动体和保持架之间的接触、引导面与滚动体或保持架的接触，还有闰滑剂内的摩擦和接触式密封的滑动摩擦。

摩擦力矩的估算在一定的条件下：．轴承负荷P约等于0，1 C．润滑良好●一般的工作条件运用以下的公式，使用固定的摩擦系数U·可以足够准确地计算出摩擦力矩：M=0，5，uPd式中M=摩擦力矩，NmmU=轴承的固定摩擦系数P=当量动负荷，Nd =轴承内任，mm摩擦力矩的准确计算计算滚动轴承摩擦力矩的其中一种方法是将摩擦力矩分成独立的部分，包括不受负荷影响的力矩Mo和与取决于负荷的力矩M1然后把两者相加起来，得出：M=Mo+M1这种方法沿用至今。

但如果不仅考虑负荷的因素，而是根据导致摩擦的根本原因来详细分析。

则可给出更准确的计算方法。

实际上，Mo表示的是负荷以外的摩擦，如果加上滚动摩擦中“流体动力”的分量，也变成有与负荷相关的部分要更准确地计算滚动轴承的摩擦力矩，必须考虑四个不同导致摩擦的原因M = Mrr + Msl + Mseal + Mdrag式中M =总摩擦力矩，NmmMrr =滚动摩擦力矩，NmmMsl =滑动摩擦力矩，NmmMseal = 密封件的摩擦力矩，NmmMdrag = 由于拖曳损失、涡流和飞溅等导致的摩擦力矩，Nmm这种新方法确定发生在轴承中每种导致摩擦的原因并可将这些因素结合起来。

此外，还可根据需要，加入密封件和其它额外原因导致的摩擦来计算总摩擦力矩。

由于这个模型是把每一个接触部分(滚道和挡边)分别考虑，因此有便于改变设计和改进表面质量的工作，而且更能将SKF轴承设计中的改进体现出来。

这个模型也较容易更新。

在接下来的章节中，会由浅入深地介绍SKF新的摩擦力矩计算模型，从最简单的影响因素，如滚动，滑动和密封：至较为复杂的情况，如轴承的油位、高速下的贫油、润滑油的切入发热效应和混合润滑状态等。

滚动轴承摩擦力矩、发热量及油量计算

滚动轴承摩擦⼒矩、发热量及油量计算滚动轴承摩擦⼒矩、发热量及油润滑所需油量的计算1、摩擦⼒矩的估算公式Pd M µ5.0=式中M : 摩擦⼒矩，Nmmµ : 轴承的摩擦系数P : 当量动负荷，Nd : 轴承公称内径，mm2、摩擦⼒矩的精确计算公式：Mdrag Mseal Msl Mrr M +++=式中M : 总摩擦⼒矩， NmmMrr : 滚动摩擦⼒矩，NmmMsl : 滑动摩擦⼒矩，NmmMseal : 密封件的摩擦⼒矩，NmmMdrag: 由于拖曳损失、涡流和飞溅等导致的摩擦⼒矩，Nmm3、轴承的摩擦损失在轴承内部⼏乎全部变为热量，因⽽致使轴承温度升⾼，轴承的发热量可以⽤以下公式进⾏计算：Mn Q 41005.1-?=式中Q : 发热量，kWM : 摩擦⼒矩，Nmmn : 轴承转速，r/min4、循环油润滑及喷油润滑所需油量计算公式Tr c dnP G =-601088.14µ 式中G : 所需油量，L/minµ : 摩擦系数，d : 轴承公称内径，mmn : 轴承转速，r/minP : 轴承当量动负荷，Nc : 油的⽐热，kJ/kg ℃r : 油的密度，g/cm 3△T : 油的温升，℃上式计算得到的是发热量全部通过油带⾛时所需的油量，未考虑其余散热因素。

⼀般来说，实际油量约为以上计算油量的1/2-2/3。

但散热量随着使⽤机械及使⽤条件⽽有所不同，因此宜先以计算油量的2/3进⾏运转，通过测量轴承温度和进、排油温度逐渐减⼩油量，直⾄确定最佳油量。

附表：各类轴承的摩擦系数（参考）。

滚动轴承的工作情况分析及计算

第一讲一、教学目标（一）能力目标能判断常用滚动轴承的类型；理解其代号的含义；会选用滚动轴承（二）知识目标1.了解滚动轴承的类型、特点，掌握滚动轴承的代号2.掌握滚动轴承的选择二、教学内容滚动轴承的类型、代号及选用三、教学的重点与难点重点：滚动轴承的类型、特点及代号。

难点：滚动轴承类型的选择。

四、教学方法与手段采用多媒体教学（加动画演示），结合教具，提高学生的学习兴趣。

14.1 轴承的功用和类型轴承的功用：支承轴及轴上的旋转零件，使其回转并保证一定的旋转精度，减少相对摩擦和磨损。

轴承的分类：按摩擦的性质分，轴承可分为滑动轴承和滚动轴承。

滑动轴承滚动轴承14.2 滚动轴承的组成、类型及特点滚动轴承是标准件，由专业工厂生产。

设计时只需根据轴承工作条件选用合适的类型和尺寸的滚动轴承，进行寿命计算，并对轴承的安装、润滑、密封给予合理设计和安排。

滚动轴承的特点优点：1）f小起动力矩小，η高；2）运转精度高（可用预紧方法消除游隙）；3）轴向尺寸小；4）某些轴能同时承受Fr和Fa，使机器结构紧凑；5）润滑方便、简单、易于密封和维护；6）互换性好（标准零件）缺点：1）承受冲击载荷能力差；2）高速时噪音、振动较大；3）高速重载寿命较低；4）径向尺寸较大（相对于滑动轴承）应用：广泛应用于中速、中载和一般工作条件下运转的机械设备。

14.2.1 滚动轴承的组成滚动轴承一般由外圈、内圈、滚动体和保持架所组成。

滚动体的形状短圆柱形柱形长圆柱形螺旋滚子滚柱轴承圆锥滚子鼓形滚子滚针保持架是使滚动体等距分布，并减少滚动体间的摩擦和磨损。

滚动轴承的材料：内、外圈、滚动体—GCr15、GCr15-SiMn等轴承钢，热处理后硬度HRC60~65；保持架：低碳钢、铜合金或塑料、聚四氟乙烯。

14.2.2 滚动轴承的基本类型及特点接触角α：滚动体与外圈内滚道接触点的法线方向与轴承径向平面所夹的角。

滚动轴承按能承受的负荷方向或公称接触角不同，可分为向心轴承和推力轴承。

轴承的摩擦系数及摩擦力矩计算04.03

对于滑动轴承，一般u=0.01-0.02，有时也达0.1-0.2。

点接触弹流润滑的数值求解方法

点接触弹流润滑的数值求解方法摘要：本文以球轴承为研究对象，并简化钢球与滚道为球与平板，基于弹性流体动力润滑理论建立点接触弹流润滑数值模型。

编写Fortran程序并通过有限差分法实现点接触弹流润滑数值模型的快速求解，探究了不同卷吸速度下的弹流润滑性能演变规律。

结果表明：卷吸速度影响油膜厚度的分布，油膜厚度随卷吸速度的增大而增大，在一定范围内较大的卷吸速度有利于球轴承的润滑。

关键词：点接触；弹性变形；润滑；数值求解1.点接触弹流润滑模型球轴承具有承受载荷能力强、服役周期长等优点，被广泛应用于车辆、工程机械等领域。

为研究球轴承的弹流润滑性能，将球轴承滚动体与滚道简化为弹性钢球与平板的接触模型，并建立点接触弹流润滑的数值计算模型。

以下是点接触弹流润滑模型的控制方程。

（1）Reynolds 方程(1)式中，x（m）表示计算域横坐标，y（m）表示计算域纵坐标，p（Pa）表示油膜压力，h（m）表示油膜厚度，u s（m/s）表示卷吸速度，η（Pa·s）表示润滑油粘度，ρ（kg/m3）表示润滑油密度。

（2）油膜厚度方程弹流润滑中的油膜厚度方程由上下接触表面的间隙和弹性变形构成：(2)式中，h0是刚体中心膜厚，用于调节载荷平衡的待定常数；R x=R y（m）是当量主曲率半径，ν（m）是表面弹性变形。

（3）粘压、密压方程在球轴承的运行中，润滑油的粘度并不是稳定的，在高压时其粘度会增加，润滑油密度受到压力的影响。

(3)(4)式中，η0（Pa·s）是润滑油初始粘度，z是实验常数，本文取0.68；ρ0（kg/m3）是润滑油初始密度。

（4）载荷平衡方程弹流润滑问题是在已知外载荷的情况下求解的，所以Reynolds方程求解出的压力需要必须满足载荷平衡条件，即求解域内压力的积分应该等于外载荷，w （N）是外载荷，载荷平衡方程如下：(5)2.求解方法本文采用有限差分法求解点接触弹流润滑模型，首先根据罗剑等[1]的方法对控制方程进行无量纲处理，此举是为了提高数值的收敛性。

球轴承点接触区油膜阻尼系数的计算与理论分析

ＣｈｅｎＢｉｎＬｉＳｏｎｇｓｈｅｎｇＣｈｅｎＪｉａｎＬｕＹｕｘｉｎ
（ＳｃｈｏｏｌｏｆＭｅｃｈａｔｒｏｎｉｃＥｎｇｉｎｅｅｉｒｎｇａｎｄＡｕｔｏｍａｔｉｏｎ，ＳｈａｎｇｈａｉＵｎｉｖｅｒｓｉｔｙ，Ｓｈａｎｇｈａｉ２０００７２，Ｃｈｉｎａ）Ａｂｓｔｒａｃｔ：Ｂａｓｅｄｏｎｐｏｉｎｔｃｏｎｔａｃｔｅｌａｓｔｏｈｙｄｒｏｄｙｎａｍｉｃｌｕｂｉｒｃａｔｉｏｎ（ＥＨＬ）ｅｑｕａｔｉｏｎ，ｔｈｅｃａｌｃｕｌａｔｉｏｎｍｏｄｅｌｏｆｏｉｌ — ｉｆｌｍ
中图分类号：Ｔｉｌｌ１７．２；ＴＨ１３３．３文献标识码：Ａ文章编号：０２５４— ０１５０（２０１３）２— ０６２— ５
ＴｈｅｏｒｅｔｉｃａｌＡｎａｌｙｓｉｓａｎｄＣａｌｃｕｌａｔｉｏｎｏｆＢａｌｌＢｅａｒｉｎｇＯｉｌＦｉｌｍＤａｍｐｉｎｇ
ｐｕｒｅｓｑｕｅｅｚｅＥＨＬｅｑｕａｔｉｏｎ．ＡｃｃｏｒｄｉｎｇｔｏｔｈｅｒｅｌａｔｉｏｎｓｈｉｐｂｅｔｗｅｅｎｔｈｉｓｃａｌｃｕｌａｔｉｏｎｍｏｄｅｌｓｏｌｕｔｉｏｎａｎｄＥＨＬｅｑｕａｔｉｏｎｓｏｌｕ — ｔｉｏｎ，ａｎｅｗｍｅｔｈｏｄｆｏｒｓｏｌｖｉｎｇｔｈｉｓｍｏｄｅｌｗａｓｐｒｏｐｏｓｅｄ．Ａｒｅｖｉｓｅｅｑｕａｔｉｏｎｗａｓｄｅｄｕｃｅｄｃｏｎｓｉｄｅｒｉｎｇｂａｌｌｂｅａｉｒｎｇｃｏｎｔａｃｔ

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

m /s
收稿日期 : 2007 - 12 - 05;修回日期 : 2007 - 12 - 13
W ———钢球与内、外沟道接触点处的法向载荷,N
Fa ———轴向载荷 , N Z ———钢球数 Dpw ———球组节圆直径 , mm Dw ———钢球直径 , mm β———原始接触角 ne ———外圈转速 , r/m in ni ———内圈转速 , r/m in 轴承性能的主要评价因素之一是其摩擦力矩的大小 ,其直接影响轴承的能量损耗。过大的摩擦力矩不仅使轴承运转时温度升高、润滑剂劣化、磨损加剧 ,甚至导致表面损伤以致轴承失效 , 而能否形成一定厚度的弹流油膜直接关系到轴承摩擦力矩的大小。弹流油膜厚度与轴承摩擦力矩的大小有一定的关系 , 可以通过弹流油膜厚度来计算轴承摩擦力矩的大小。
r=
i =1
= 0. 892 2
n
n
∑ ∑ ( xi - x) 2
( yi - y) 2
i =1
i =1
( 14 )
n
∑ SSe =
( yi - y^) 2 = 0. 192 2
i =1
( 15 )
式中 : r为相关系数 ; SSe 为残差 ; xi , yi 为试验值 ; x,
《轴承》2008. №. 4
(1. 河南科技大学机电工程学院 ,河南洛阳 471003; 2. 洛阳轴承研究所 ,河南洛阳 471039)
摘要 :点接触弹流润滑的实际计算较为复杂 ,对点接触弹流油膜厚度及摩擦力矩的计算进行了详细分析并给出了计算实例。同时对弹流油膜厚度与轴承摩擦力矩的关系进行了探讨 ,提出了新的摩擦力矩经验计算公式。关键词 :滚动轴承 ;点接触 ;弹流润滑 ;油膜厚度 ;摩擦力矩中图分类号 : TH133. 33; TH117 文献标志码 : B 文章编号 : 1000 - 3762 (2008) 04 - 0010 - 03
由于影响滚动轴承摩擦力矩的因素较多 , 所
以 ( 8) 、( 9)式的计算值与实测值仍有较大差距。
为了从多方面研究轴承的动态特性 , 这里用轴承
弹流油膜厚度来评价轴承的摩擦力矩。进一步加
深对轴承摩擦力矩的研究。
2. 2 经验公式的建立
已知一角接触球轴承 , 钢球与内沟道接触点
处的数据如下 : Dpw = 31. 004 mm, Dw = 6. 35 mm,
(1
-
e ) - 0. 68k
(3)
材料参数 G′=αE′
(4)
E1′=
1 2
1 (
-
ν2 1
E1
+
1
-
ν2 2
)
E2
速度参数 U ′=ηE0′RUx
(5)
U
π =
(Dp2w
-
Dw2 co sβ)
120Dpw
| ne
-
ni
|
载荷参数W
′=
W
E ′R2x
(6)
W = Fa / Z sinβ
椭圆率 k = 1. 03 ( Ry ) 0. 64
机械设计手册 [3 ]给出的轴承摩擦力矩计算公式为
M = 12μdF
(8)
式中 :μ为轴承摩擦系数 ; d为轴承内径 , mm; F 为轴承载荷 , N。
Harris T A[4 ]给出的轴承摩擦力矩计算公式为
M =M 0 +M 1
M0
= 10 - 7 f0
(νn
)
2
/
3
D
3 pw
(νn ≥2
000)
η 0
= 0.
136
2
Pa · s,
Z
= 12, α = 2.
029
9
×10 - 8
m2 /N, E′= E1 = E2 = 2. 040 83 ×1011 N /m2 , Fa = 81
N,β= 15°, Rx = 1. 632 4 mm, Ry = 2. 524 4 mm, k =
1. 546 4; 在不同转速条件下测得的轴承摩擦力矩
3 结束语
滚动轴承的摩擦力矩问题涉及到弹性力学、接触力学、摩擦、润滑等学科 , 且各种因素相互影响 ,相互作用 ,使摩擦力矩的精确分析计算不易进行。新的摩擦力矩计算公式可以定量地分析轴承弹流油膜厚度与摩擦力矩的关系 , 也可以应用于轴承的设计和工艺 ,提高轴承的性能 , 进而增强机械设备的可靠性 ,增加设备利用率。
值和用 ( 2) ～ ( 7 ) 式计算所得的弹流油膜厚度值
见表 1。
表 1 不同转速条件下轴承摩擦力矩与弹流油膜厚度
转速 / ( r·m in - 1 ) 弹流膜厚 /μm 摩擦力矩 / ( ×10 - 3N ·m )
300 500 700 900 1 000 1 200 1 400 1 600 1 800 2 000 2 500 3 000 3 500 4 000 4 500 5 000 5 500 6 000
y为算术平均值 ; y^为回归值。经验公式采用简单的二次多项式函数 , 计算
方便 , ( 13) 式计算值曲线与试验曲线基本吻合。由于两条曲线的前半部分不是很吻合 ,可以用 ( 9) 式计算非全膜弹流润滑轴承的摩擦力矩 , 用 ( 13) 式计算全膜弹流润滑轴承的摩擦力矩 , 以更好地反映油膜厚度与轴承摩擦力矩之间的关系。同时 , 经验公式的提出 , 是建立在某型号角接触球轴承的试验数据的基础上 , 是否适用于其他型号的轴承而具有普遍的指导意义 ,尚有待于进一步检验。
触表面综合粗糙度 , μm, σ =
σ2 1
+σ22
;
σ 1
和
σ 2
是两接触表面轮廓的均方根偏差 ,μm。
当 λ < 1时 , 属于边界润滑 ; 1 <λ < 3时 , 属于
部分弹流润滑 ;λ > 3 时 , 属于全膜弹流润滑。若
轴承在弹流润滑状态下工作 , 摩擦力矩小 , 寿命就
会大大提高。设计和选择轴承时 , 为了了解轴承
(1. Electromechanical Engineering College, Henan University of Science and Technology, Luoyang 471003, China; 2. Luoyang Bearing Research Institute, Luoyang 471039, China)
(7)
Rx
1=1 +1 Ry Ry1 Ry2
1=1 +1 Rx Rx1 Rx2
2 轴承摩擦力矩的计算
摩擦力矩是衡量轴承动态特性的综合性指标 ,也是选定轴承优化运转参数的依据性指标。为了确保轴承的高性能和高可靠性 , 研究轴承的摩擦力矩特性十分必要。 2. 1 常用计算公式
M 0 = 160 ×10 - 7 f0 Dp3w (νn < 2 000)
(9) ( 10 ) ( 11 )
M 1 = f1 PDpw
( 12 )
式中 : f0 , f1 为经验系数 ; ν为润滑油运动粘度 ,
m2 / s; n为轴承转速 , r/m in; P 为当量载荷 , N。
参考文献 :
[ 1 ] 吉继贤. 滚动轴承的弹性流体动压润滑设计 [ J ]. 河南机电高等专科学校校报 , 2004, 12 (1) : 41 - 42.
[ 2 ] 温诗铸 ,黄平. 摩擦学原理 [M ]. 2 版. 北京 : 清华大学出版社 , 2002: 77 - 78.
[ 3 ] 成大先. 机械设计手册 [M ]. 4版. 北京 :化学工业出版社 , 2001: 206.
符号说明
α ———润滑剂粘压系数 , m2 /N
η 0
———润滑剂的动力粘度
,
Pa·s
E′———两接触表面材料的当量弹性模量 , N /m2
E1 , E2 ———两接触表面材料的弹性模量 , N /m2
ν 1
,ν2
———两接触表面材料的泊松比
Rx ———钢球与内、外沟道接触点在运动方向
的当量曲率半径 , mm
对试验所得的数据进行整理分析 , 提出了新的摩擦力矩经验计算公式为
·12·
M = A hm2 in + B hm in + C
( 13 )
式中 :M 为平均摩擦力矩 , N ·m; hm in为最小油膜厚度 ,μm; A 为与载荷有关的系数 ; B 为与转速有
关的系数 ; C为修正系数。
Rx1 , Rx2 ———钢球与内、外沟道接触点在运动方向的曲率半径 , mm
Ry ———钢球与内、外沟道接触点在垂直于运动方向的当量点在垂直于运
动方向的曲率半径 , mm
U ———钢球与内、外圈接触处的平均速度 ,
根据最小二乘法原理计算所得的系数值为 : A
= 16. 01, B = - 10. 25, C = 3. 542。将 ( 13)式的预
测值与试验值进行对比 ,如图 1所示。
图 1 弹流膜厚 - 摩擦力矩曲线
2. 3 经验公式的精度分析 ( 13)式的相关系数和残差为
n
∑( xi - x) ( yi - y)
Abstract: The p ractical calculation of EHL in ellip tical contact zone is relatively comp lex. The detailed calculation of oil film thickness in EHL ellip tical contact zone and an examp le are given. A t the same time, relations between oil film thickness in EHL ellip tical contact zone and bearing friction torque are discussed. A new bearing emp irical friction torque exp ression is built. Key words: rolling bearing; ellip tical contact zone; EHL; oil film thickness; friction torque