江西省2015年中考数学试题及答案(word版)
2015年江西省南昌市中考数学试卷

数学试卷 第1页(共6页) 数学试卷 第2页(共6页)绝密★启用前江西省南昌市2015年初中毕业暨中等学校招生考试数 学本试卷满分120分,考试时间120分钟.第Ⅰ卷(选择题 共18分)一、选择题(本大题共6小题,每小题3分,共18分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.计算0(1)的结果为 ( )A .1B .1-C .0D .无意义 2.2015年初,一列CRH5型高速车组进行了“300000千米正线运营考核”,标志着中国高铁车从“中国制造”到“中国创新”的飞跃.将数300000用科学记数法表示为( ) A .6310⨯ B .5310⨯ C .60.310⨯ D .43010⨯3.下列运算正确的是 ( ) A .236(2)6a a =B .2232533a b ab a b -=-C .21111a a a -=-+D .1b a a b b a +=--- 4.如图是将正方体切去一个角后形成的几何体,则该几何体的左视图为( )5.如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD ,B 与D 两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化.下列判断错误的是 ( ) A .四边形ABCD 由矩形变为平行四边形 B .BD 的长度增大C .四边形ABCD 的面积不变 D .四边形ABCD 的周长不变6.已知抛物线2(0)y ax bx c a =++>过(2,0),(2,3)-两点,那么抛物线的对称轴 ( ) A .只能是1x =- B .可能是y 轴C .在y 轴右侧且在直线2x =的左侧D .在y 轴左侧且在直线2x =-的右侧第Ⅱ卷(非选择题 共102分)二、填空题(本大题共8小题,每小题3分,共24分.把答案填写在题中的横线上) 7.一个角的度数是20,则它的补角的度数为 .8.不等式组11023x x ⎧-⎪⎨⎪-⎩≤<9的解集是 .9.如图,OP 平分MON ∠,PE OM ⊥于点E ,PE ON ⊥于点F ,OA OB =,则图中 有 对全等三角形.10.如图,点,,A B C 在O 上,CO 的延长线交AB 于点D ,50,30A B ∠=∠=则ADC ∠的度数为 .11.已知一元二次方程2430x x --=的两根为,m n ,则22m mn n -+= .12.如图1是小志同学书桌上的一个电子相框,将其侧面抽象为如图2所示的几何图形,已知15cm AB AC ==,40BAC ∠=,则点A 到BC 的距离为 cm (参考数据:sin200.342,cos200.940,sin400.643,cos400.766.≈≈≈≈结果精确到0.1cm ,可用科学计算器).13.两组数据:3,,2,5a b 与,6,a b 的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的中位数为 .14.如图,在ABC △中,4AB BC ==,AO BO =,P 是射线CO 上的一个动点,60AOC ∠=,则当PAB △为直角三角形时,AP的长为.AB C D 毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第3页(共6页) 数学试卷 第4页(共6页)三、解答题(本大题共10小题,共78分.解答应写出文字说明、证明过程或演算步骤) 15.(本小题满分6分)先化简,再求值:22(2)(2)a a b a b +-+,其中1,a b =-=16.(本小题满分6分)如图,正方形ABCD 与正方形1111A B C D 关于某点中心对称.已知1,,A D D 三点的坐标分别是(0,4),(0,3),(0,2). (1)求对称中心的坐标;(2)写出顶点11,,,B C B C 的坐标.17.(本小题满分6分)O 为ABC △的外接圆,请仅用无刻度的直尺,根据下列条件分别在图1,图2中画出一条弦,使这条弦将ABC △分成面积相等的两部分(保留作图痕迹,不写作法).(1)如图1,AC BC =;(2)如图2,直线l 与O 相切于点P ,且l BC ∥.18.(本小题满分6分)在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个. (1)先从袋子中取出() 1m m >个红球,再从袋子中随机摸出1个球.将“摸出黑球”记为事件(2)先从袋子中取出m 个红球,再放入m 个一样的黑球并摇匀,随机摸出1个球是黑球的概率等于45,求m 的值.19.(本小题满分8分)某校为了了解学生家长对孩子使用手机的态度情况,随机抽取部分学生家长进行问卷调查,发出问卷140份,每位学生的家长1份,每份问卷仅表明一种态度.将回收的问卷进行整理(假设回收的问卷都有效),并绘制了如下两幅不完整的统计图.学生家长对孩子使用手机的态度情况统计图根据以上信息解答下列问题: (1)回收的问卷数为 份,“严加干涉”部分对应扇形的圆心角度数为 ; (2)把条形统计图补充完整;(3)若将“稍加询问”和“从来不管”视为“管理不严”,已知学校共1500名学生,请估计该校对孩子使用手机“管理不严”的家长大约有多少人?20.(本小题满分8分)(1)如图1,纸片□ABCD 中,5AD =,15ABCDS=.过点A 作AE BC ⊥,垂足为E ,沿AE 剪下ABE △,将它平移至DCE '△的位置,拼成四边形AEE D ',则四边形AEE D '的形状为 ( ) A .平行四边形 B .菱形 C .矩形 D .正方形(2)如图2,在(1)中的四边形纸片AEE D '中,在EE '上取一点F ,使4EF =,剪下AEF △,将它平移至DE F ''△的位置,拼成四边形AFF D '. ①求证:四边形AFF D '是菱形;②求四边形AFF D '的两条对角线的长.l图2图1AA类别严加干涉稍加询问从来不管从来不管 25%严加干涉稍加询问图2图1数学试卷 第5页(共6页) 数学试卷 第6页(共6页)21.(本小题满分8分)如图,已知直线y ax b =+与双曲线(0)ky x x=>交于1122(,)(,)A x y B x y ,两点(A 与 B 不重合),直线AB 与x 轴交于点0(,0)P x ,与y 轴交于点C . (1)若,A B 两点坐标分别为2(1,3),(3,)y ,求点P 的坐标; (2)若11b y =+,点P 的坐标为6,0(),且AB BP =,求,A B 两点的坐标; (3)结合(1)(2)中的结果,猜想并用等式表示120,,x x x 之间的关系(不要求证明).22.(本小题满分9分)甲、乙两人在100米直道AB 上练习匀速往返跑,若甲、乙分别在,A B 两端同时出发,分别到另一端点处掉头,掉头时间不计,速度分别5m /s 和4m /s . (1)在坐标系中,虚线表示乙离A 端的距离s (单位:m )与运动时间t (单位:s )之间的函数图象(0200)t ≤≤,请在同一坐标系中用实线画出甲离A 端的距离s 与运动时间t 之间的函数图象(0200)t ≤≤;t 的取值范围;②当390s t =时,他们此时相遇吗?若相遇,应是第几次?若不相遇,请通过计算说理由,并求此时甲离A 端的距离.23.(本小题满分9分)如图,已知二次函数21:23(0)L y ax ax a a =-++>和二次函数22:(1)1L y a x =-++(0)a >图象的顶点分别为M ,N ,与y 轴分别交于点E ,F .(1)函数223(0)y ax ax a a =-++>的最小值为 ;当二次函数12L L ,的y 值同时随着x 的增大而减小时,x 的取值范围是 ;(2)当EF MN =时,求a 的值,并判断四边形ENFM 的形状(直接写出,不必证明); (3)若二次函数2L的图象与x 轴的右交点为(,0)A m ,当AMN △为等腰三角形时,求方程2(1)10a x -++=的解.24.(本小题满分12分)我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,,AF BE 是ABC △的中线,AF BE ⊥,垂足为P ,像ABC △这样的三角形均为“中垂三角形”.设BC a =,AC b =,AB c =.特例探索(1)如图1,当45ABE ∠=,c =,a = ,b = ;如图2,当30ABE ∠=,4c =时,a =,b =;归纳证明(2)请你观察(1)中的计算结果,猜想222,,a b c 三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式;拓展应用(3)如图4,在□ABCD 中,点,,E F G 分别是,,AD BC CD 的中点,BE EG ⊥,AD =,3AB =.求AF 的长.毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------。
2015年江西省南昌市中考数学试题及解析

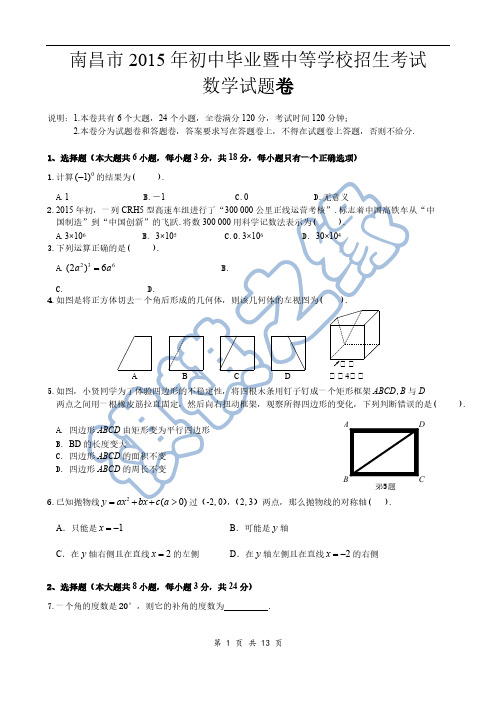
2015年江西省南昌市中考数学试题及解析2015年江西省南昌市中考数学试卷一、选择题(本大题共6小题,每小题3分,共18分,每小题只有一个正确选项)1.(3分)(2015•南昌)计算(﹣1)0的结果为()A.1B.﹣1 C.0D.无意义2.(3分)(2015•南昌)2015年初,一列CRH5型高速车组进行了“300000公里正线运营考核”标志着中国高速快车从“中国制造”到“中国创造”的飞跃,将300000用科学记数法表示为()A.3×106B.3×105C.0.3×106D.30×1043.(3分)(2015•南昌)下列运算正确的是()A.(2a2)3=6a6B.﹣a2b2•3ab3=﹣3a2b5 C.•=﹣1 D.+=﹣16.(3分)(2015•南昌)已知抛物线y=ax2+bx+c (a>0)过(﹣2,0),(2,3)两点,那么抛物线的对称轴()A.只能是x=﹣1B.可能是y轴C.在y轴右侧且在直线x=2的左侧D.在y轴左侧且在直线x=﹣2的右侧二、填空题(本大题共8小题,每小题3分,共24分)7.(3分)(2015•南昌)一个角的度数为20°,则它的补角的度数为.8.(3分)(2015•南昌)不等式组的解集是.9.(3分)(2015•南昌)如图,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB,则图中有对全等三角形.10.(3分)(2015•南昌)如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC的度数为.11.(3分)(2015•南昌)已知一元二次方程x2﹣4x﹣3=0的两根为m,n,则m2﹣mn+n2=.12.(3分)(2015•南昌)如图1是小志同学书桌上的一个电子相框,将其侧面抽象为如图2所示的几何图形,已知BC=BD=15cm,∠CBD=40°,则点B到CD的距离为cm(参考数据sin20°≈0.342,cos20°≈0.940,sin40°≈0.643,cos40°≈0.766,结果精确到0.1cm,可用科学计算器).13.(3分)(2015•南昌)两组数据:3,a,2b,5与a,6,b的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的中位数为.14.(3分)(2015•南昌)如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为.三、解答题(本大题共4小题,每小题6分,共24分)15.(6分)(2015•南昌)先化简,再求值:2a (a+2b)﹣(a+2b)2,其中a=﹣1,b=.16.(6分)(2015•南昌)如图,正方形ABCD 于正方形A1B1C1D1关于某点中心对称,已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).(1)求对称中心的坐标.(2)写出顶点B,C,B1,C1的坐标.17.(6分)(2015•南昌)⊙O为△ABC的外接圆,请仅用无刻度的直尺,根据下列条件分别在图1,图2中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法).(1)如图1,AC=BC;(2)如图2,直线l与⊙O相切于点P,且l∥BC.18.(6分)(2015•南昌)在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格:事件A 必然事件随机事件m的值(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于,求m的值.四、解答题(本大题共3小题,每小题8分,共24分)19.(8分)(2015•南昌)某校为了了解学生家长对孩子使用手机的态度情况,随机抽取部分学生家长进行问卷调查,发出问卷140份,每位学生家长1份,每份问卷仅表明一种态度,将回收的问卷进行整理(假设回收的问卷都有效),并绘制了如图两幅不完整的统计图.根据以上信息解答下列问题:(1)回收的问卷数为份,“严加干涉”部分对应扇形的圆心角度数为.(2)把条形统计图补充完整(3)若将“稍加询问”和“从来不管”视为“管理不严”,已知全校共1500名学生,请估计该校对孩子使用手机“管理不严”的家长大约有多少人?20.(8分)(2015•南昌)(1)如图1,纸片▱ABCD 中,AD=5,S▱ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE′的位置,拼成四边形AEE′D,则四边形AEE′D的形状为A.平行四边形B.菱形C.矩形D.正方形(2)如图2,在(1)中的四边形纸片AEE′D 中,在EE′上取一点F,使EF=4,剪下△AEF,将它平移至△DE′F′的位置,拼成四边形AFF′D.①求证:四边形AFF′D是菱形.②求四边形AFF′D的两条对角线的长.21.(8分)(2015•南昌)如图,已知直线y=ax+b 与双曲线y=(x>0)交于A(x 1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的坐标.(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.(3)结合(1),(2)中的结果,猜想并用等式表示x1,x2,x0之间的关系(不要求证明).五、解答题(本大题共2小题,每小题9分,共18分)22.(9分)(2015•南昌)甲、乙两人在100米直道AB上练习匀速往返跑,若甲、乙分别中A,B两端同时出发,分别到另一端点处掉头,掉头时间不计,速度分别为5m/s和4m/s.(1)在坐标系中,虚线表示乙离A端的距离s (单位:m)与运动时间t(单位:s)之间的函数图象(0≤t≤200),请在同一坐标系中用实线画出甲离A端的距离s与运动时间t之间的函数图象(0≤t≤200);(2)根据(1)中所画图象,完成下列表格:两人相遇次数1 2 3 4 …n (单位:次)100 300 …两人所跑路程之和(单位:m)(3)①直接写出甲、乙两人分别在第一个100m 内,s与t的函数解析式,并指出自变量t的取值范围;②当t=390s时,他们此时相遇吗?若相遇,应是第几次?若不相遇,请通过计算说明理由,并求出此时甲离A端的距离.23.(9分)(2015•南昌)如图,已知二次函数L1:y=ax2﹣2ax+a+3(a>0)和二次函数L2:y=﹣a(x+1)2+1(a>0)图象的顶点分别为M,N,与y轴分别交于点E,F.(1)函数y=ax2﹣2ax+a+3(a>0)的最小值为,当二次函数L1,L2的y值同时随着x的增大而减小时,x的取值范围是.(2)当EF=MN时,求a的值,并判断四边形ENFM的形状(直接写出,不必证明).(3)若二次函数L2的图象与x轴的右交点为A (m,0),当△AMN为等腰三角形时,求方程﹣a(x+1)2+1=0的解.六、解答题(本大题共12分)24.(12分)(2015•南昌)我们把两条中线互相垂直的三角形称为“称为中垂三角形”,例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均称为“中垂三角形”,设BC=a,AC=b,AB=c.特例探索(1)如图1,当∠ABE=45°,c=2时,a=,b=.如图2,当∠ABE=30°,c=4时,a=,b=.归纳证明(2)请你观察(1)中的计算结果,猜想a2,b2,c2三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.拓展应用(3)如图4,在▱ABCD中,点E、F、G分别是AD,BC,CD的中点,BE⊥EG,AD=2,AB=3,求AF的长.2015年江西省南昌市中考数学试卷参考答案与试题解析一、选择题(本大题共6小题,每小题3分,共18分,每小题只有一个正确选项)1.(3分)(2015•南昌)计算(﹣1)0的结果为( )A . 1B . ﹣1C . 0D . 无意义考点: 零指数幂. 分析: 根据零指数幂的运算方法:a 0=1(a ≠0),求出(﹣1)0的结果为多少即可. 解答: 解:∵(﹣1)0=1,∴(﹣1)0的结果为1.故选:A .点评: 此题主要考查了零指数幂的运算,要熟练掌握,解答此题的关键是要明确:(1)a 0=1(a ≠0);(2)00≠1.2.(3分)(2015•南昌)2015年初,一列CRH5型高速车组进行了“300000公里正线运营考核”标志着中国高速快车从“中国制造”到“中国创造”的飞跃,将300000用科学记数法表示为( )A . 3×106B . 3×105C . 0.3×106D . 30×104考点: 科学记数法—表示较大的数. 分析: 科学记数法的表示形式为a ×10n 的形式,其中1≤|a|<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n 是负数.解答: 解:将300000用科学记数法表示为:3×105. 故选:B . 点评: 此题考查科学记数法的表示方法.科学记数法的表示形式为a ×10n 的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a的值以及n 的值.3.(3分)(2015•南昌)下列运算正确的是( )A . (2a 2)3=6a 6B . ﹣a 2b 2•3ab 3=﹣3a 2b 5C . •=﹣1D . +=﹣1考点: 分式的乘除法;幂的乘方与积的乘方;单项式乘单项式;分式的加减法. 专题: 计算题. 分析: A 、原式利用幂的乘方与积的乘方运算法则计算得到结果,即可做出判断; B 、原式利用单项式乘以单项式法则计算得到结果,即可做出判断;C 、原式约分得到结果,即可做出判断;D 、原式变形后,利用同分母分式的减法法则计算,约分即可得到结果.解答: 解:A 、原式=8a 4,错误;B 、原式=﹣3a 3b 5,错误;C 、原式=a ﹣1,错误;D 、原式===﹣1,正确; 故选D .点此题考查了分式的乘除法,幂的乘方与积的评: 乘方,单项式乘单项式,以及分式的加减法,熟练掌握运算法则是解本题的关键.4.(3分)(2015•南昌)如图是将正方体切去一个角后形成的几何体,则该几何体的左视图为( )A .B .C .D .考点: 简单组合体的三视图. 分析: 找到从左面看所得到的图形即可,注意所有的看到的棱都应表现在视图中. 解答: 解:从左面看所得到的图形是正方形,切去部分的棱能看到,用实线表示, 故选:C .点评: 本题考查了三视图的知识,掌握主视图是从物体的正面看得到的视图,左视图是从物体的左面看得到的视图,俯视图是从物体的上面看得到的视图是解题的关键.5.(3分)(2015•南昌)如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD ,B 与D 两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化,下列判断错误的是( )A . 四边形ABCD 由矩形变为平行四边形B . B D 的长度增大C . 四边形ABCD 的面积不变D . 四边形ABCD 的周长不变考点: 矩形的性质;平行四边形的性质. 分析: 由将四根木条用钉子钉成一个矩形框架ABCD ,B 与D 两点之间用一根橡皮筋拉直固定,然后向右扭动框架,由平行四边形的判定定理知四边形变成平行四边形,由于四边形的每条边的长度没变,所以周长没变;拉成平行四边形后,高变小了,但底边没变,所以面积变小了,BD 的长度增加了.解答: 解:∵矩形框架ABCD ,B 与D 两点之间用一根橡皮筋拉直固定,然后向右扭动框架,∴AD=BC ,AB=DC ,∴四边形变成平行四边形,故A 正确;BD 的长度增加,故B 正确;∵拉成平行四边形后,高变小了,但底边没变,∴面积变小了,故C 错误;∵四边形的每条边的长度没变,∴周长没变,故D 正确,故选C .点评: 本题主要考查了矩形的性质和平行四边形的性质,弄清图形变化后的变量和不变量是解答此题的关键.6.(3分)(2015•南昌)已知抛物线y=ax 2+bx+c (a >0)过(﹣2,0),(2,3)两点,那么抛物线的对称轴( )A . 只能是x=﹣1B . 可能是y 轴C . 在y 轴右侧且在直线x=2的左侧D . 在y 轴左侧且在直线x=﹣2的右侧考点: 二次函数的性质. 分析: 根据题意判定点(﹣2,0)关于对称轴的对称点横坐标x 2满足:﹣2<x 2<2,从而得出﹣2<<0,即可判定抛物线对称轴的位置.解答: 解:∵抛物线y=ax 2+bx+c (a >0)过(﹣2,0),(2,3)两点, ∴点(﹣2,0)关于对称轴的对称点横坐标x 2满足:﹣2<x 2<2,∴﹣2<<0, ∴抛物线的对称轴在y 轴左侧且在直线x=﹣2的右侧.故选D .点评: 本题考查了二次函数的性质,根据点坐标判断出另一个点的位置是解题的关键.二、填空题(本大题共8小题,每小题3分,共24分)7.(3分)(2015•南昌)一个角的度数为20°,则它的补角的度数为 160° .考点: 余角和补角. 分析: 根据互为补角的两个角的和等于180°列式进行计算即可得解. 解答: 解:180°﹣20°=160°. 故答案为:160°. 点评: 本题考查了余角和补角,解决本题的关键是熟记互为补角的和等于180°.8.(3分)(2015•南昌)不等式组的解集是 ﹣3<x ≤2 .考点: 解一元一次不等式组. 专题: 计算题. 分析: 分别求出不等式组中两不等式的解集,找出解集的公共部分即可. 解答: 解:,由①得:x ≤2,由②得:x >﹣3,则不等式组的解集为﹣3<x ≤2.故答案为:﹣3<x ≤2点评: 此题考查了解一元一次不等式组,熟练掌握运算法则是解本题的关键.9.(3分)(2015•南昌)如图,OP 平分∠MON ,PE ⊥OM 于E ,PF ⊥ON 于F ,OA=OB ,则图中有3 对全等三角形.考点: 全等三角形的判定;角平分线的性质. 分析: 由OP 平分∠MON ,PE ⊥OM 于E ,PF ⊥ON于F ,得到PE=PF ,∠1=∠2,证得△AOP ≌△BOP ,再根据△AOP ≌△BOP ,得出AP=BP ,于是证得△AOP ≌△BOP ,和R t △AOP ≌R t △BOP .解答: 解:OP 平分∠MON ,PE ⊥OM 于E ,PF ⊥ON 于F ,∴PE=PF ,∠1=∠2,在△AOP 与△BOP 中,,∴△AOP ≌△BOP ,∴AP=BP ,在△EOP 与△FOP 中,,∴△AOP ≌△BOP ,在R t △AOP 与R t △BOP 中,,∴R t △AOP ≌R t △BOP ,∴图中有3对全等三角形,故答案为:3.点评: 本题考查了角平分线的性质,全等三角形的判定和性质,熟练掌握全等三角形的判定定理是解题的关键.10.(3分)(2015•南昌)如图,点A ,B ,C 在⊙O 上,CO 的延长线交AB 于点D ,∠A=50°,∠B=30°,则∠ADC的度数为 110° .考点: 圆周角定理. 分析:根据圆周角定理求得∠BOC=100°,进而根据三角形的外角的性质求得∠BDC=70°,然后根据邻补角求得∠ADC的度数.解答: 解:∵∠A=50°,∴∠BOC=2∠A=100°, ∵∠B=30°,∠BOC=∠B+⊂BDC ,∴∠BDC=∠BOC ﹣∠B=100°﹣30°=70°,∴∠ADC=180°﹣∠BDC=110°,故答案为110°.点评: 本题考查了圆心角和圆周角的关系及三角形外角的性质,圆心角和圆周角的关系是解题的关键.11.(3分)(2015•南昌)已知一元二次方程x 2﹣4x ﹣3=0的两根为m ,n ,则m 2﹣mn+n 2= 25 .考点: 根与系数的关系. 分析: 由m 与n 为已知方程的解,利用根与系数的关系求出m+n 与mn 的值,将所求式子利用完全平方公式变形后,代入计算即可求出值.解答: 解:∵m ,n 是一元二次方程x 2﹣4x ﹣3=0的两个根,∴m+n=4,mn=﹣3,则m 2﹣mn+n 2=(m+n )2﹣3mn=16+9=25.故答案为:25. 点评:此题考查了一元二次方程根与系数的关系,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.12.(3分)(2015•南昌)如图1是小志同学书桌上的一个电子相框,将其侧面抽象为如图2所示的几何图形,已知BC=BD=15cm ,∠CBD=40°,则点B 到CD的距离为 14.1cm (参考数据sin20°≈0.342,cos20°≈0.940,sin40°≈0.643,cos40°≈0.766,结果精确到0.1cm ,可用科学计算器).考解直角三角形的应用.点:分析: 作BE ⊥CD 于E ,根据等腰三角形的性质和∠CBD=40°,求出∠CBE 的度数,根据余弦的定义求出BE 的长.解答: 解:如图2,作BE ⊥CD 于E ,∵BC=BD ,∠CBD=40°, ∴∠CBE=20°,在Rt △CBE 中,cos ∠CBE=,∴BE=BC •cos ∠CBE=15×0.940=14.1cm .故答案为:14.1.点评: 本题考查的是解直角三角形的应用,掌握锐角三角函数的概念是解题的关键,作出合适的辅助线构造直角三角形是解题的重要环节.13.(3分)(2015•南昌)两组数据:3,a ,2b ,5与a ,6,b 的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的中位数为 6 .考点: 中位数;算术平均数. 分析: 首先根据平均数的定义列出关于a 、b 的二元一次方程组,再解方程组求得a 、b 的值,然后求中位数即可.解答: 解:∵两组数据:3,a ,2b ,5与a ,6,b的平均数都是6, ∴, 解得, 若将这两组数据合并为一组数据,按从小到大的顺序排列为3,4,5,6,8,8,8,一共7个数,第四个数是6,所以这组数据的中位数是6.故答案为6.点评:本题考查平均数和中位数.平均数是指在一组数据中所有数据之和再除以数据的个数.一组数据的中位数与这组数据的排序及数据个数有关,因此求一组数据的中位数时,先将该组数据按从小到大(或按从大到小)的顺序排列,然后根据数据的个数确定中位数:当数据个数为奇数时,则中间的一个数即为这组数据的中位数;当数据个数为偶数时,则最中间的两个数的算术平均数即为这组数据的中位数.14.(3分)(2015•南昌)如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP 的长为2或2或2.考点:勾股定理;含30度角的直角三角形;直角三角形斜边上的中线.专题:分类讨论.分析: 利用分类讨论,当∠APB=90°时,易得∠PAB=30°,利用锐角三角函数得AP 的长;当∠ABP=90°时,分两种情况讨论,情况一:如图2易得BP ,利用勾股定理可得AP 的长;情况二:如图3,利用直角三角形斜边的中线等于斜边的一半得出结论. 解答: 解:当∠APB=90°时(如图1),∵AO=BO ,∴PO=BO ,∵∠AOC=60°,∴∠BOP=60°,∴△BOP 为等边三角形,∵AB=BC=4,∴AP=AB •sin60°=4×=2;当∠ABP=90°时,情况一:(如图2),∵∠AOC=∠BOP=60°,∴∠BPO=30°,∴BP===2,在直角三角形ABP 中, AP==2,情况二:如图3,∵AO=BO ,∠APB=90°,∴PO=AO ,∵∠AOC=60°,∴△AOP 为等边三角形,∴AP=AO=2,故答案为:2或2或2.点评: 本题主要考查了勾股定理,含30°直角三角形的性质和直角三角形斜边的中线,分类讨论,数形结合是解答此题的关键.三、解答题(本大题共4小题,每小题6分,共24分)15.(6分)(2015•南昌)先化简,再求值:2a (a+2b )﹣(a+2b )2,其中a=﹣1,b=.考点: 整式的混合运算—化简求值. 专题: 计算题. 分析: 原式第一项利用单项式乘以多项式法则计算,第二项利用完全平方公式化简,去括号合并得到最简结果,把a 与b 的值代入计算即可求出值.解答: 解:原式=2a 2+4ab ﹣a 2﹣4ab ﹣4b 2=a 2﹣4b 2, 当a=﹣1,b=时,原式=1﹣12=﹣11. 点评: 此题考查了整式的混合运算﹣化简求值,熟练掌握运算法则是解本题的关键.16.(6分)(2015•南昌)如图,正方形ABCD 于正方形A 1B 1C 1D 1关于某点中心对称,已知A ,D 1,D 三点的坐标分别是(0,4),(0,3),(0,2).(1)求对称中心的坐标.(2)写出顶点B ,C ,B 1,C 1的坐标.考点: 中心对称;坐标与图形性质. 分析: (1)根据对称中心的性质,可得对称中心的坐标是D 1D 的中点,据此解答即可. (2)首先根据A ,D 的坐标分别是(0,4),(0,2),求出正方形ABCD 与正方形A 1B 1C 1D 1的边长是多少,然后根据A ,D 1,D 三点的坐标分别是(0,4),(0,3),(0,2),判断出顶点B ,C ,B 1,C 1的坐标各是多少即可.解答: 解:(1)根据对称中心的性质,可得对称中心的坐标是D 1D 的中点, ∵D 1,D 的坐标分别是(0,3),(0,2),∴对称中心的坐标是(0,2.5).(2)∵A ,D 的坐标分别是(0,4),(0,2),∴正方形ABCD 与正方形A 1B 1C 1D 1的边长都是:4﹣2=2,∴B ,C 的坐标分别是(﹣2,4),(﹣2,2),∵A 1D 1=2,D 1的坐标是(0,3),∴A 1的坐标是(0,1),∴B 1,C 1的坐标分别是(2,1),(2,3),综上,可得顶点B ,C ,B 1,C 1的坐标分别是(﹣2,4),(﹣2,2),(2,1),(2,3).点评: (1)此题主要考查了中心对称的性质和应用,要熟练掌握,解答此题的关键是要明确中心对称的性质:①关于中心对称的两个图形能够完全重合;②关于中心对称的两个图形,对应点的连线都经过对称中心,并且被对称中心平分.(2)此题还考查了坐标与图形的性质的应用,要熟练掌握,解答此题的关键是要明确点到坐标轴的距离与这个点的坐标是有区别的,表现在两个方面:①到x 轴的距离与纵坐标有关,到y 轴的距离与横坐标有关;②距离都是非负数,而坐标可以是负数,在由距离求坐标时,需要加上恰当的符号.17.(6分)(2015•南昌)⊙O 为△ABC 的外接圆,请仅用无刻度的直尺,根据下列条件分别在图1,图2中画出一条弦,使这条弦将△ABC 分成面积相等的两部分(保留作图痕迹,不写作法).(1)如图1,AC=BC ;(2)如图2,直线l 与⊙O 相切于点P ,且l ∥BC .考点: 作图—复杂作图;三角形的外接圆与外心;切线的性质. 专题: 作图题. 分析: (1)过点C 作直径CD ,由于AC=BC ,=,根据垂径定理的推理得CD 垂直平分AB ,所以AD 将△ABC 分成面积相等的两部分;(2)连结PO 并延长交BC 于E ,过点A 、E 作弦AD ,由于直线l 与⊙O 相切于点P ,根据切线的性质得OP ⊥l ,而l ∥BC ,则PE ⊥BC ,根据垂径定理得BE=CE ,所以弦AE 将△ABC 分成面积相等的两部分.解答: 解:(1)如图1,直径CD 为所求;(2)如图2,弦AD 为所求.点评: 本题考查了复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了切线的性质.18.(6分)(2015•南昌)在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.(1)先从袋子中取出m (m >1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A ,请完成下列表格:事件A 必然事件 随机事件m 的值 4 2,3(2)先从袋子中取出m 个红球,再放入m 个一样的黑球并摇匀,随机摸出1个黑球的概率等于,求m 的值.考点: 概率公式;随机事件. 分析: (1)当袋子中全部为黑球时,摸出黑球才是必然事件,否则就是随机事件; (2)利用概率公式列出方程,求得m 的值即可.解答: 解:(1)当袋子中全为黑球,即摸出4个红球时,摸到黑球是必然事件;当摸出2个或3个时,摸到黑球为随机事件, 故答案为:4;2,3.(2)根据题意得:=,解得:m=2,所以m 的值为2.点评: 本题考查的是概率的求法.如果一个事件有n 种可能,而且这些事件的可能性相同,其中事件A 出现m 种结果,那么事件A 的概率P (A )=.四、解答题(本大题共3小题,每小题8分,共24分)19.(8分)(2015•南昌)某校为了了解学生家长对孩子使用手机的态度情况,随机抽取部分学生家长进行问卷调查,发出问卷140份,每位学生家长1份,每份问卷仅表明一种态度,将回收的问卷进行整理(假设回收的问卷都有效),并绘制了如图两幅不完整的统计图.根据以上信息解答下列问题:(1)回收的问卷数为 120 份,“严加干涉”部分对应扇形的圆心角度数为 30° .(2)把条形统计图补充完整(3)若将“稍加询问”和“从来不管”视为“管理不严”,已知全校共1500名学生,请估计该校对孩子使用手机“管理不严”的家长大约有多少人?考点: 条形统计图;用样本估计总体;扇形统计图. 分析:(1)用“从来不管”的问卷数除以其所占百分比求出回收的问卷总数;用“严加干涉”部分的问卷数除以问卷总数得出百分比,再乘以360°即可;(2)用问卷总数减去其他两个部分的问卷数,得到“稍加询问”的问卷数,进而补全条形统计图;(3)用“稍加询问”和“从来不管”两部分所占的百分比的和乘以1500即可得到结果. 解答: 解:(1)回收的问卷数为:30÷25%=120(份),“严加干涉”部分对应扇形的圆心角度数为:×360°=30°.故答案为:120,30°;(2)“稍加询问”的问卷数为:120﹣(30+10)=80(份),补全条形统计图,如图所示:(3)根据题意得:1500×=1375(人), 则估计该校对孩子使用手机“管理不严”的家长大约有1375人.点评: 本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.也考查了利用样本估计总体.20.(8分)(2015•南昌)(1)如图1,纸片▱ABCD 中,AD=5,S ▱ABCD =15,过点A 作AE ⊥BC ,垂足为E ,沿AE 剪下△ABE ,将它平移至△DCE ′的位置,拼成四边形AEE ′D ,则四边形AEE ′D的形状为 CA .平行四边形B .菱形C .矩形D .正方形(2)如图2,在(1)中的四边形纸片AEE ′D 中,在EE ′上取一点F ,使EF=4,剪下△AEF ,将它平移至△DE ′F ′的位置,拼成四边形AFF ′D .①求证:四边形AFF ′D 是菱形.②求四边形AFF ′D 的两条对角线的长.考点: 图形的剪拼;平行四边形的性质;菱形的判定与性质;矩形的判定;平移的性质. 分析: (1)根据矩形的判定,可得答案;(2)①根据菱形的判定,可得答案; ②根据勾股定理,可得答案.解答: 解:(1)如图1,纸片▱ABCD 中,AD=5,S ▱ABCD =15,过点A 作AE ⊥BC ,垂足为E ,沿AE 剪下△ABE ,将它平移至△DCE ′的位置,拼成四边形AEE ′D ,则四边形AEE ′D 的形状为矩形,故选:C ;(2)①证明:∵纸片▱ABCD 中,AD=5,S ▱ABCD =15,过点A 作AE ⊥BC ,垂足为E , ∴AE=3.如图2:,∵△AEF ,将它平移至△DE ′F ′,∴AF ∥DF ′,AF=DF ′,∴四边形AFF ′D 是平行四边形.在Rt △AEF 中,由勾股定理,得 AF===5,∴AF=AD=5,∴四边形AFF ′D 是菱形;②连接AF ′,DF ,如图3:在Rt △DE ′F 中E ′F=FF ′﹣E ′F ′=5﹣4=1,DE ′=3,∴DF===, 在Rt △AEF ′中EF ′=EF+FF ′=4+5=9,AE=3,∴AF ′===3. 点评: 本题考查了图形的剪拼,利用了矩形的判定,菱形的判定,勾股定理.21.(8分)(2015•南昌)如图,已知直线y=ax+b 与双曲线y=(x >0)交于A (x 1,y 1),B (x 2,y 2)两点(A 与B 不重合),直线AB 与x 轴交于P (x 0,0),与y 轴交于点C .(1)若A ,B 两点坐标分别为(1,3),(3,y 2),求点P 的坐标.(2)若b=y 1+1,点P 的坐标为(6,0),且AB=BP ,求A ,B 两点的坐标.(3)结合(1),(2)中的结果,猜想并用等式表示x 1,x 2,x 0之间的关系(不要求证明).考点:反比例函数与一次函数的交点问题.分析: (1)先把A (1,3)),B (3,y 2)代入y=求得反比例函数的解析式,进而求得B 的坐标,然后把A 、B 代入y=ax+b 利用待定系数法即可求得直线的解析式,继而即可求得P 的坐标;(2)作AD ⊥y 轴于D ,AE ⊥x 轴于E ,BF ⊥x轴于F ,BG ⊥y 轴于G ,AE 、BG 交于H ,则AD ∥BG ∥x 轴,AE ∥BF ∥y 轴,得出=,==,根据题意得出=,==,从而求得B (,y 1),然后根据k=xy 得出x 1•y 1=•y 1,求得y 1=2,代入=,解得x 1=2,即可求得A 、B 的坐标;(3)合(1),(2)中的结果,猜想x 1+x 2=x 0.解答: 解:(1)∵直线y=ax+b 与双曲线y=(x >0)交于A (1,3),∴k=1×3=3,∴y=,∵B (3,y 2)在反比例函数的图象上,∴y 2==1,∴B (3,1),∵直线y=ax+b 经过A 、B 两点, ∴解得, ∴直线为y=﹣x+4,令y=0,则x=4,∴P (4,O );(2)如图,作AD ⊥y 轴于D ,AE ⊥x 轴于E ,BF ⊥x 轴于F ,BG ⊥y 轴于G ,AE 、BG 交于H ,则AD ∥BG ∥x 轴,AE ∥BF ∥y 轴, ∴=,==,∵b=y 1+1,AB=BP , ∴=, ==,∴B (,y 1)∵A ,B 两点都是反比例函数图象上的点,∴x 1•y 1=•y 1,解得y 1=2, 代入=,解得x 1=2,∴A (2,2),B (4,1).(3)根据(1),(2)中的结果,猜想:x 1,x 2,x 0之间的关系为x 1+x 2=x 0.点评: 本题考查了待定系数法求解析式以及反比例函数和一次函数的交点问题,数形结合思想的运用是解题的关键.五、解答题(本大题共2小题,每小题9分,共18分)22.(9分)(2015•南昌)甲、乙两人在100米直道AB 上练习匀速往返跑,若甲、乙分别中A ,B 两端同时出发,分别到另一端点处掉头,掉头时间不计,速度分别为5m/s 和4m/s .(1)在坐标系中,虚线表示乙离A 端的距离s (单位:m )与运动时间t (单位:s )之间的函数图象(0≤t ≤200),请在同一坐标系中用实线画出甲离A 端的距离s 与运动时间t 之间的函数图象(0≤t ≤200);(2)根据(1)中所画图象,完成下列表格: 两人相遇次数(单位:次)12 3 4 … n两人所跑路程之和(单位:m )100 300500 700 … 200n ﹣100 (3)①直接写出甲、乙两人分别在第一个100m 内,s 与t 的函数解析式,并指出自变量t 的取值范围;②当t=390s 时,他们此时相遇吗?若相遇,应是第几次?若不相遇,请通过计算说明理由,并求出此时甲离A 端的距离.考点: 一次函数的应用. 分析: (1)根据甲跑100米所用的时间为100÷5=20(秒),画出图象即可; (2)根据甲和乙第一次相遇时,两人所跑路程之和为100米,甲和乙第二次相遇时,两人所跑路程之和为100×2+100=300(米),甲和乙第三次相遇时,两人所跑路程之和为200×2+100=500(米),甲和乙第四次相遇时,两人所跑路程之和为300×2+100=700(米),找到规律即可解答;(3)①根据路程、速度、时间之间的关系即可解答;②由200n ﹣100=9×390,解得:n=18.05,根据n 不是整数,所以此时不相遇,当t=400s 时,甲回到A ,所以当t=390s 时,甲离A 端距离为(400﹣390)×5=50m .解解:(1)如图:。
2015年江西省中考数学试卷(解析版)

2015年江西省中考数学试卷一、选择题(本大题共6小题,每小题3分,共18分,每小题只有一个正确选项)1.(3分)计算(﹣1)0的结果为()A.1 B.﹣1 C.0 D.无意义2.(3分)2015年初,一列CRH5型高速车组进行了“300000公里正线运营考核”标志着中国高速快车从“中国制造”到“中国创造”的飞跃,将300000用科学记数法表示为()A.3×106B.3×105C.0.3×106D.30×1043.(3分)如图所示的几何体的左视图为()A.B.C.D.4.(3分)下列运算正确的是()A.(2a2)3=6a6B.﹣a2b2•3ab3=﹣3a2b5C.+=﹣1 D.•=﹣15.(3分)如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD,B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化,下列判断错误的是()A.四边形ABCD由矩形变为平行四边形B.BD的长度增大C.四边形ABCD的面积不变D.四边形ABCD的周长不变6.(3分)已知抛物线y=ax2+bx+c(a>0)过(﹣2,0),(2,3)两点,那么抛物线的对称轴()A.只能是x=﹣1B.可能是y轴C.可能在y轴右侧且在直线x=2的左侧D.可能在y轴左侧且在直线x=﹣2的右侧二、填空题(本大题共8小题,每小题3分,共24分)7.(3分)一个角的度数为20°,则它的补角的度数为.8.(3分)不等式组的解集是.9.(3分)如图,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB,则图中有对全等三角形.10.(3分)如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC的度数为.11.(3分)已知一元二次方程x2﹣4x﹣3=0的两根为m,n,则m2﹣mn+n2=.12.(3分)两组数据:3,a,2b,5与a,6,b的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的中位数为.13.(3分)如图1是小志同学书桌上的一个电子相框,将其侧面抽象为如图2所示的几何图形,已知BC=BD=15cm,∠CBD=40°,则点B到CD的距离为cm (参考数据sin20°≈0.342,cos20°≈0.940,sin40°≈0.643,cos40°≈0.766,结果精确到0.1cm,可用科学计算器).14.(3分)如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为.三、(本大题共4小题,每小题6分,共24分)15.(6分)先化简,再求值:2a(a+2b)﹣(a+2b)2,其中a=﹣1,b=.16.(6分)如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).(1)求对称中心的坐标.(2)写出顶点B,C,B1,C1的坐标.17.(6分)⊙O为△ABC的外接圆,请仅用无刻度的直尺,根据下列条件分别在图1,图2中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法).(1)如图1,AC=BC;(2)如图2,直线l与⊙O相切于点P,且l∥BC.18.(6分)在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格:(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于,求m的值.四、(本大题共4小题,每小题8分,共32分)19.(8分)某校为了了解学生家长对孩子使用手机的态度情况,随机抽取部分学生家长进行问卷调查,发出问卷140份,每位学生家长1份,每份问卷仅表明一种态度,将回收的问卷进行整理(假设回收的问卷都有效),并绘制了如图两幅不完整的统计图.根据以上信息解答下列问题:(1)回收的问卷数为份,“严加干涉”部分对应扇形的圆心角度数为.(2)把条形统计图补充完整(3)若将“稍加询问”和“从来不管”视为“管理不严”,已知全校共1500名学生,请估计该校对孩子使用手机“管理不严”的家长大约有多少人?20.(8分)(1)如图1,纸片▱ABCD中,AD=5,S▱ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE′的位置,拼成四边形AEE′D,则四边形AEE′D的形状为A.平行四边形B.菱形C.矩形D.正方形(2)如图2,在(1)中的四边形纸片AEE′D中,在EE′上取一点F,使EF=4,剪下△AEF,将它平移至△DE′F′的位置,拼成四边形AFF′D.①求证:四边形AFF′D是菱形.②求四边形AFF′D的两条对角线的长.21.(8分)如图,已知直线y=ax+b与双曲线y=(x>0)交于A(x1,y1),B (x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的坐标.(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.(3)结合(1),(2)中的结果,猜想并用等式表示x1,x2,x0之间的关系(不要求证明).22.(8分)甲、乙两人在100米直道AB上练习匀速往返跑,若甲、乙分别在A,B两端同时出发,分别到另一端点处掉头,掉头时间不计,速度分别为5m/s和4m/s.(1)在坐标系中,虚线表示乙离A端的距离s(单位:m)与运动时间t(单位:s)之间的函数图象(0≤t≤200),请在同一坐标系中用实线画出甲离A端的距离s与运动时间t之间的函数图象(0≤t≤200).(2)根据(1)中所画图象,完成下列表格:(3)①直接写出甲、乙两人分别在第一个100m内,t与s的函数解析式,并指出自变量t的取值范围.②求甲、乙第6次相遇时t的值.五、(本大题共10分)23.(10分)如图,已知二次函数L1:y=ax2﹣2ax+a+3(a>0)和二次函数L2:y=﹣a(x+1)2+1(a>0)图象的顶点分别为M,N,与y轴分别交于点E,F.(1)函数y=ax2﹣2ax+a+3(a>0)的最小值为,当二次函数L1,L2的y值同时随着x的增大而减小时,x的取值范围是.(2)当EF=MN时,求a的值,并判断四边形ENFM的形状(直接写出,不必证明).(3)若二次函数L2的图象与x轴的右交点为A(m,0),当△AMN为等腰三角形时,求方程﹣a(x+1)2+1=0的解.六、(本大题共12分)24.(12分)我们把两条中线互相垂直的三角形称为“称为中垂三角形”,例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均称为“中垂三角形”,设BC=a,AC=b,AB=c.特例探索(1)如图1,当∠ABE=45°,c=2时,a=,b=.如图2,当∠ABE=30°,c=4时,a=,b=.归纳证明(2)请你观察(1)中的计算结果,猜想a2,b2,c2三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.拓展应用(3)如图4,在▱ABCD中,点E、F、G分别是AD,BC,CD的中点,BE⊥EG,AD=2,AB=3,求AF的长.2015年江西省中考数学试卷参考答案与试题解析一、选择题(本大题共6小题,每小题3分,共18分,每小题只有一个正确选项)1.(3分)计算(﹣1)0的结果为()A.1 B.﹣1 C.0 D.无意义【分析】根据零指数幂的运算方法:a0=1(a≠0),求出(﹣1)0的结果为多少即可.【解答】解:∵(﹣1)0=1,∴(﹣1)0的结果为1.故选:A.2.(3分)2015年初,一列CRH5型高速车组进行了“300000公里正线运营考核”标志着中国高速快车从“中国制造”到“中国创造”的飞跃,将300000用科学记数法表示为()A.3×106B.3×105C.0.3×106D.30×104【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n 是负数.【解答】解:将300000用科学记数法表示为:3×105.故选:B.3.(3分)如图所示的几何体的左视图为()A.B.C.D.【分析】找到从左面看所得到的图形即可,注意所有的看到的棱都应表现在左视图中.【解答】解:从左面看易得左视图为:.故选:D.4.(3分)下列运算正确的是()A.(2a2)3=6a6B.﹣a2b2•3ab3=﹣3a2b5C.+=﹣1 D.•=﹣1【分析】A、原式利用幂的乘方及积的乘方运算法则计算得到结果,即可做出判断;B、原式利用单项式乘以单项式法则计算得到结果,即可做出判断;C、原式变形后,利用同分母分式的减法法则计算得到结果,即可做出判断;D、原式约分得到结果,即可做出判断.【解答】解:A、原式=8a6,错误;B、原式=﹣3a3b5,错误;C、原式===﹣1,正确;D、原式=•=,错误,故选:C.5.(3分)如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD,B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化,下列判断错误的是()A.四边形ABCD由矩形变为平行四边形B.BD的长度增大C.四边形ABCD的面积不变D.四边形ABCD的周长不变【分析】由将四根木条用钉子钉成一个矩形框架ABCD,B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,由平行四边形的判定定理知四边形变成平行四边形,由于四边形的每条边的长度没变,所以周长没变;拉成平行四边形后,高变小了,但底边没变,所以面积变小了,BD的长度增加了.【解答】解:∵矩形框架ABCD,B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,∴AD=BC,AB=DC,∴四边形变成平行四边形,故A正确;BD的长度增加,故B正确;∵拉成平行四边形后,高变小了,但底边没变,∴面积变小了,故C错误;∵四边形的每条边的长度没变,∴周长没变,故D正确,故选:C.6.(3分)已知抛物线y=ax2+bx+c(a>0)过(﹣2,0),(2,3)两点,那么抛物线的对称轴()A.只能是x=﹣1B.可能是y轴C.可能在y轴右侧且在直线x=2的左侧D.可能在y轴左侧且在直线x=﹣2的右侧【分析】根据题意判定点(﹣2,0)关于对称轴的对称点横坐标x2满足:x2<2,从而得出<0,即可判定抛物线对称轴的位置.【解答】解:∵抛物线y=ax2+bx+c(a>0)过(﹣2,0),(2,3)两点,∴点(﹣2,0)关于对称轴的对称点横坐标x2满足:x2<2,∴<0,∴抛物线的对称轴可能在y轴左侧且在直线x=﹣2的右侧.故选:D.二、填空题(本大题共8小题,每小题3分,共24分)7.(3分)一个角的度数为20°,则它的补角的度数为160°.【分析】根据互为补角的两个角的和等于180°列式进行计算即可得解.【解答】解:180°﹣20°=160°.故答案为:160°.8.(3分)不等式组的解集是﹣3<x≤2.【分析】分别求出不等式组中两不等式的解集,找出解集的公共部分即可.【解答】解:,由①得:x≤2,由②得:x>﹣3,则不等式组的解集为﹣3<x≤2.故答案为:﹣3<x≤29.(3分)如图,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB,则图中有3对全等三角形.【分析】由OP平分∠MON,PE⊥OM于E,PF⊥ON于F,得到PE=PF,∠1=∠2,证得△AOP≌△BOP,再根据△AOP≌△BOP,得出AP=BP,于是证得△AOP≌△BOP,和R t△AOP≌R t△BOP.【解答】解:OP平分∠MON,PE⊥OM于E,PF⊥ON于F,∴PE=PF,∠1=∠2,在△AOP与△BOP中,,∴△AOP≌△BOP,∴AP=BP,在△EOP与△FOP中,,∴△EOP≌△FOP,在R t△AEP与R t△BFP中,,∴R t△AEP≌R t△BFP,∴图中有3对全等三角形,故答案为:3.10.(3分)如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC的度数为110°.【分析】根据圆周角定理求得∠BOC=100°,进而根据三角形的外角的性质求得∠BDC=70°,然后根据邻补角求得∠ADC的度数.【解答】解:∵∠A=50°,∴∠BOC=2∠A=100°,∵∠B=30°,∠BOC=∠B+∠BDC,∴∠BDC=∠BOC﹣∠B=100°﹣30°=70°,∴∠ADC=180°﹣∠BDC=110°,故答案为110°.11.(3分)已知一元二次方程x2﹣4x﹣3=0的两根为m,n,则m2﹣mn+n2=25.【分析】由m与n为已知方程的解,利用根与系数的关系求出m+n与mn的值,将所求式子利用完全平方公式变形后,代入计算即可求出值.【解答】解:∵m,n是一元二次方程x2﹣4x﹣3=0的两个根,∴m+n=4,mn=﹣3,则m2﹣mn+n2=(m+n)2﹣3mn=16+9=25.故答案为:25.12.(3分)两组数据:3,a,2b,5与a,6,b的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的中位数为6.【分析】首先根据平均数的定义列出关于a、b的二元一次方程组,再解方程组求得a、b的值,然后求中位数即可.【解答】解:∵两组数据:3,a,2b,5与a,6,b的平均数都是6,∴,解得,若将这两组数据合并为一组数据,按从小到大的顺序排列为3,4,5,6,8,8,8,一共7个数,第四个数是6,所以这组数据的中位数是6.故答案为6.13.(3分)如图1是小志同学书桌上的一个电子相框,将其侧面抽象为如图2所示的几何图形,已知BC=BD=15cm,∠CBD=40°,则点B到CD的距离为14.1 cm(参考数据sin20°≈0.342,cos20°≈0.940,sin40°≈0.643,cos40°≈0.766,结果精确到0.1cm,可用科学计算器).【分析】作BE⊥CD于E,根据等腰三角形的性质和∠CBD=40°,求出∠CBE的度数,根据余弦的定义求出BE的长.【解答】解:如图2,作BE⊥CD于E,∵BC=BD,∠CBD=40°,∴∠CBE=20°,在Rt△CBE中,cos∠CBE=,∴BE=BC•cos∠CBE=15×0.940=14.1cm.故答案为:14.1.14.(3分)如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为2或2或2.【分析】利用分类讨论,当∠ABP=90°时,如图2,由对顶角的性质可得∠AOC=∠BOP=60°,易得∠BPO=30°,易得BP的长,利用勾股定理可得AP的长;当∠APB=90°时,分两种情况讨论,情况一:如图1,利用直角三角形斜边的中线等于斜边的一半得出PO=BO,易得△BOP为等边三角形,利用锐角三角函数可得AP的长;易得BP,利用勾股定理可得AP的长;情况二:如图3,利用直角三角形斜边的中线等于斜边的一半可得结论.【解答】解:当∠APB=90°时(如图1),∵AO=BO,∴PO=BO,∵∠AOC=60°,∴∠BOP=60°,∴△BOP为等边三角形,∵AB=BC=4,∴AP=AB•sin60°=4×=2;当∠ABP=90°时(如图2),∵∠AOC=∠BOP=60°,∴∠BPO=30°,∴BP===2,在直角三角形ABP中,AP==2,情况二:如图3,∵AO=BO,∠APB=90°,∴PO=AO,∵∠AOC=60°,∴△AOP为等边三角形,∴AP=AO=2,故答案为:2或2或2.三、(本大题共4小题,每小题6分,共24分)15.(6分)先化简,再求值:2a(a+2b)﹣(a+2b)2,其中a=﹣1,b=.【分析】原式第一项利用单项式乘以多项式法则计算,第二项利用完全平方公式化简,去括号合并得到最简结果,把a与b的值代入计算即可求出值.【解答】解:原式=2a2+4ab﹣a2﹣4ab﹣4b2=a2﹣4b2,当a=﹣1,b=时,原式=1﹣12=﹣11.16.(6分)如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).(1)求对称中心的坐标.(2)写出顶点B,C,B1,C1的坐标.【分析】(1)根据对称中心的性质,可得对称中心的坐标是D1D的中点,据此解答即可.(2)首先根据A,D的坐标分别是(0,4),(0,2),求出正方形ABCD与正方形A1B1C1D1的边长是多少,然后根据A,D1,D三点的坐标分别是(0,4),(0,3),(0,2),判断出顶点B,C,B1,C1的坐标各是多少即可.【解答】解:(1)根据对称中心的性质,可得对称中心的坐标是D1D的中点,∵D1,D的坐标分别是(0,3),(0,2),∴对称中心的坐标是(0,2.5).(2)∵A,D的坐标分别是(0,4),(0,2),∴正方形ABCD与正方形A1B1C1D1的边长都是:4﹣2=2,∴B,C的坐标分别是(﹣2,4),(﹣2,2),∵A1D1=2,D1的坐标是(0,3),∴A1的坐标是(0,1),∴B1,C1的坐标分别是(2,1),(2,3),综上,可得顶点B,C,B1,C1的坐标分别是(﹣2,4),(﹣2,2),(2,1),(2,3).17.(6分)⊙O为△ABC的外接圆,请仅用无刻度的直尺,根据下列条件分别在图1,图2中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法).(1)如图1,AC=BC;(2)如图2,直线l与⊙O相切于点P,且l∥BC.【分析】(1)过点C作直径CD,由于AC=BC,=,根据垂径定理的推理得CD垂直平分AB,所以CD将△ABC分成面积相等的两部分;(2)连结PO并延长交BC于E,过点A、E作弦AD,由于直线l与⊙O相切于点P,根据切线的性质得OP⊥l,而l∥BC,则PE⊥BC,根据垂径定理得BE=CE,所以弦AE将△ABC分成面积相等的两部分.【解答】解:(1)如图1,直径CD为所求;(2)如图2,弦AD为所求.18.(6分)在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格:(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于,求m的值.【分析】(1)当袋子中全部为黑球时,摸出黑球才是必然事件,否则就是随机事件;(2)利用概率公式列出方程,求得m的值即可.【解答】解:(1)当袋子中全为黑球,即摸出4个红球时,摸到黑球是必然事件;当摸出2个或3个时,摸到黑球为随机事件,故答案为:4;2,3.(2)根据题意得:=,解得:m=2,所以m的值为2.四、(本大题共4小题,每小题8分,共32分)19.(8分)某校为了了解学生家长对孩子使用手机的态度情况,随机抽取部分学生家长进行问卷调查,发出问卷140份,每位学生家长1份,每份问卷仅表明一种态度,将回收的问卷进行整理(假设回收的问卷都有效),并绘制了如图两幅不完整的统计图.根据以上信息解答下列问题:(1)回收的问卷数为120份,“严加干涉”部分对应扇形的圆心角度数为30°.(2)把条形统计图补充完整(3)若将“稍加询问”和“从来不管”视为“管理不严”,已知全校共1500名学生,请估计该校对孩子使用手机“管理不严”的家长大约有多少人?【分析】(1)用“从来不管”的问卷数除以其所占百分比求出回收的问卷总数;用“严加干涉”部分的问卷数除以问卷总数得出百分比,再乘以360°即可;(2)用问卷总数减去其他两个部分的问卷数,得到“稍加询问”的问卷数,进而补全条形统计图;(3)用“稍加询问”和“从来不管”两部分所占的百分比的和乘以1500即可得到结果.【解答】解:(1)回收的问卷数为:30÷25%=120(份),“严加干涉”部分对应扇形的圆心角度数为:×360°=30°.故答案为:120,30°;(2)“稍加询问”的问卷数为:120﹣(30+10)=80(份),补全条形统计图,如图所示:(3)根据题意得:1500×=1375(人),则估计该校对孩子使用手机“管理不严”的家长大约有1375人.20.(8分)(1)如图1,纸片▱ABCD中,AD=5,S▱ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE′的位置,拼成四边形AEE′D,则四边形AEE′D的形状为CA.平行四边形B.菱形C.矩形D.正方形(2)如图2,在(1)中的四边形纸片AEE′D中,在EE′上取一点F,使EF=4,剪下△AEF,将它平移至△DE′F′的位置,拼成四边形AFF′D.①求证:四边形AFF′D是菱形.②求四边形AFF′D的两条对角线的长.【分析】(1)根据矩形的判定,可得答案;(2)①根据菱形的判定,可得答案;②根据勾股定理,可得答案.【解答】解:(1)如图1,纸片▱ABCD中,AD=5,S▱ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE′的位置,拼成四边形AEE′D,则四边形AEE′D的形状为矩形,故选:C;(2)①证明:∵纸片▱ABCD中,AD=5,S▱ABCD=15,过点A作AE⊥BC,垂足为E,∴AE=3.如图2:,∵△AEF,将它平移至△DE′F′,∴AF∥DF′,AF=DF′,∴四边形AFF′D是平行四边形.在Rt△AEF中,由勾股定理,得AF===5,∴AF=AD=5,∴四边形AFF′D是菱形;②连接AF′,DF,如图3:在Rt△DE′F中E′F=FF′﹣E′F′=5﹣4=1,DE′=3,∴DF===,在Rt△AEF′中EF′=EF+FF′=4+5=9,AE=3,∴AF′===3.21.(8分)如图,已知直线y=ax+b与双曲线y=(x>0)交于A(x1,y1),B (x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的坐标.(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.(3)结合(1),(2)中的结果,猜想并用等式表示x1,x2,x0之间的关系(不要求证明).【分析】(1)先把A(1,3)),B(3,y2)代入y=求得反比例函数的解析式,进而求得B的坐标,然后把A、B代入y=ax+b利用待定系数法即可求得直线的解析式,继而即可求得P的坐标;(2)作AD⊥y轴于D,AE⊥x轴于E,BF⊥x轴于F,BG⊥y轴于G,AE、BG交于H,则AD∥BG∥x轴,AE∥BF∥y轴,得出=,==,根据题意得出=,==,从而求得B(,y1),然后根据k=xy得出x1•y1=•y1,求得x1=2,代入=,解得y1=2,即可求得A、B的坐标;(3)合(1),(2)中的结果,猜想x1+x2=x0.【解答】解:(1)∵直线y=ax+b与双曲线y=(x>0)交于A(1,3),∴k=1×3=3,∴y=,∵B(3,y2)在反比例函数的图象上,∴y2==1,∴B(3,1),∵直线y=ax+b经过A、B两点,∴解得,∴直线为y=﹣x+4,令y=0,则x=4,∴P(4,O);(2)如图,作AD⊥y轴于D,AE⊥x轴于E,BF⊥x轴于F,BG⊥y轴于G,AE、BG交于H,则AD∥BG∥x轴,AE∥BF∥y轴,∴=,==,∵b=y1+1,AB=BP,∴=,==,∴B(,y1)∵A,B两点都是反比例函数图象上的点,∴x1•y1=•y1,解得x1=2,代入=,解得y1=2,∴A(2,2),B(4,1).(3)根据(1),(2)中的结果,猜想:x1,x2,x0之间的关系为x1+x2=x0.22.(8分)甲、乙两人在100米直道AB上练习匀速往返跑,若甲、乙分别在A,B两端同时出发,分别到另一端点处掉头,掉头时间不计,速度分别为5m/s和4m/s.(1)在坐标系中,虚线表示乙离A端的距离s(单位:m)与运动时间t(单位:s)之间的函数图象(0≤t≤200),请在同一坐标系中用实线画出甲离A端的距离s与运动时间t之间的函数图象(0≤t≤200).(2)根据(1)中所画图象,完成下列表格:(3)①直接写出甲、乙两人分别在第一个100m内,t与s的函数解析式,并指出自变量t的取值范围.②求甲、乙第6次相遇时t的值.【分析】(1)根据甲跑100米所用的时间为100÷5=20(秒),画出图象即可;(2)根据甲和乙第一次相遇时,两人所跑路程之和为100米,甲和乙第二次相遇时,两人所跑路程之和为100×2+100=300(米),甲和乙第三次相遇时,两人所跑路程之和为200×2+100=500(米),甲和乙第四次相遇时,两人所跑路程之和为300×2+100=700(米),找到规律即可解答;(3)根据路程、速度、时间之间的关系即可解答;(4)根据当甲和乙第6次相遇时,两人所跑路程之和为500×2+100=1100(米),根据题意得:5t+4t=1100,即可解答.【解答】解:(1)如图:(2)甲和乙第一次相遇时,两人所跑路程之和为100米,甲和乙第二次相遇时,两人所跑路程之和为100×2+100=300(米),甲和乙第三次相遇时,两人所跑路程之和为200×2+100=500(米),甲和乙第四次相遇时,两人所跑路程之和为300×2+100=700(米),…甲和乙第n次相遇时,两人所跑路程之和为(n﹣1)×100×2+100=200n﹣100(米),故答案为:500,700,200n﹣100;(3)①s甲=5t(0≤t≤20),s乙=100﹣4t(0≤t≤25).②当甲和乙第6次相遇时,两人所跑路程之和为500×2+100=1100(米),根据题意得:5t+4t=1100,解得:t=.五、(本大题共10分)23.(10分)如图,已知二次函数L1:y=ax2﹣2ax+a+3(a>0)和二次函数L2:y=﹣a(x+1)2+1(a>0)图象的顶点分别为M,N,与y轴分别交于点E,F.(1)函数y=ax2﹣2ax+a+3(a>0)的最小值为3,当二次函数L1,L2的y值同时随着x的增大而减小时,x的取值范围是﹣1≤x≤1.(2)当EF=MN时,求a的值,并判断四边形ENFM的形状(直接写出,不必证明).(3)若二次函数L2的图象与x轴的右交点为A(m,0),当△AMN为等腰三角形时,求方程﹣a(x+1)2+1=0的解.【分析】(1)把二次函数L1:y=ax2﹣2ax+a+3化成顶点式,即可求得最小值,分别求得二次函数L1,L2的y值随着x的增大而减小的x的取值,从而求得二次函数L1,L2的y值同时随着x的增大而减小时,x的取值范围;(2)先求得E、F点的坐标,作MG⊥y轴于G,则MG=1,作NH⊥y轴于H,则NH=1,从而求得MG=NH=1,然后证得△EMG≌△FNH,∠MEF=∠NFE,EM=NF,进而证得EM∥NF,从而得出四边形ENFM是平行四边形;(3)作MN的垂直平分线,交MN于D,交x轴于A,先求得D的坐标,继而求得MN的解析式,进而就可求得直线AD的解析式,令y=0,求得A的坐标,根据对称轴从而求得另一个交点的坐标,就可求得方程﹣a(x+1)2+1=0的解.【解答】解:(1)∵二次函数L1:y=ax2﹣2ax+a+3=a(x﹣1)2+3,∴顶点M坐标为(1,3),∵a>0,∴函数y=ax2﹣2ax+a+3(a>0)的最小值为3,∵二次函数L1的对称轴为x=1,当x<1时,y随x的增大而减小;二次函数L2:y=﹣a(x+1)2+1的对称轴为x=﹣1,当x>﹣1时,y随x的增大而减小;∴当二次函数L1,L2的y值同时随着x的增大而减小时,x的取值范围是﹣1≤x ≤1;故答案为:3,﹣1≤x≤1.(2)由二次函数L1:y=ax2﹣2ax+a+3可知E(0,a+3),由二次函数L2:y=﹣a(x+1)2+1=﹣a2x﹣2ax﹣a+1可知F(0,﹣a+1),∵M(1,3),N(﹣1,1),∴EF=MN==2,∴a+3﹣(﹣a+1)=2,∴a=﹣1,作MG⊥y轴于G,则MG=1,作NH⊥y轴于H,则NH=1,∴MG=NH=1,∵EG=a+3﹣3=a,FH=1﹣(﹣a+1)=a,∴EG=FH,在△EMG和△FNH中,,∴△EMG≌△FNH(SAS),∴∠MEF=∠NFE,EM=NF,∴EM∥NF,∴四边形ENFM是平行四边形;∵EF=MN,∴四边形ENFM是矩形;(3)由△AMN为等腰三角形,可分为如下三种情况:①如图2,当MN=NA=2时,过点N作ND⊥x轴,垂足为点D,则有ND=1,DA=m﹣(﹣1)=m+1,在Rt△NDA中,NA2=DA2+ND2,即(2)2=(m+1)2+12,∴m1=﹣1,m2=﹣﹣1(不合题意,舍去),∴A(﹣1,0).由抛物线y=﹣a(x+1)2+1(a>0)的对称轴为x=﹣1,∴它与x轴的另一个交点坐标为(﹣1﹣,0).∴方程﹣a(x+1)2+1=0的解为x1=﹣1,x2=﹣1﹣.②如图3,当MA=NA时,过点M作MG⊥x轴,垂足为G,则有OG=1,MG=3,GA=|m﹣1|,∴在Rt△MGA中,MA2=MG2+GA2,即MA2=32+(m﹣1)2,又∵NA2=(m+1)2+12,∴(m+1)2+12=32+(m﹣1)2,m=2,∴A(2,0),则抛物线y=﹣a(x+1)2+1(a>0)的左交点坐标为(﹣4,0),∴方程﹣a(x+1)2+1=0的解为x1=2,x2=﹣4.③当MN=MA时,32+(m﹣1)2=(2)2,∴m无实数解,舍去.综上所述,当△AMN为等腰三角形时,方程﹣a(x+1)2=0的解为x1=﹣1,x2=﹣1﹣或x1=2,x2=﹣4.六、(本大题共12分)24.(12分)我们把两条中线互相垂直的三角形称为“称为中垂三角形”,例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均称为“中垂三角形”,设BC=a,AC=b,AB=c.特例探索(1)如图1,当∠ABE=45°,c=2时,a=2,b=2.如图2,当∠ABE=30°,c=4时,a=2,b=2.归纳证明(2)请你观察(1)中的计算结果,猜想a2,b2,c2三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.拓展应用(3)如图4,在▱ABCD中,点E、F、G分别是AD,BC,CD的中点,BE⊥EG,AD=2,AB=3,求AF的长.【分析】(1)由等腰直角三角形的性质得到AP=BP=AB=2,根据三角形中位线的性质,得到EF∥AB,EF=AB=,再由勾股定理得到结果;(2)连接EF,设∠ABP=α,类比着(1)即可证得结论.(3)连接AC交EF于H,设BE与AF的交点为P,由点E、G分别是AD,CD的中点,得到EG是△ACD的中位线于是证出BE⊥AC,由四边形ABCD是平行四边形,得到AD∥BC,AD=BC=2,∠EAH=∠FCH根据E,F分别是AD,BC的中点,得到AE=BF=CF=AD=,证出四边形ABFE是平行四边形,证得EH=FH,推出EH,AH分别是△AFE的中线,由(2)的结论得即可得到结果.或构造出“中垂三角形”,利用(2)结论计算即可.【解答】解:(1)∵AF⊥BE,∠ABE=45°,∴AP=BP=AB=2,∵AF,BE是△ABC的中线,∴EF∥AB,EF=AB=,∴∠PFE=∠PEF=45°,∴PE=PF=1,在Rt△FPB和Rt△PEA中,AE=BF==,∴AC=BC=2,∴a=b=2,如图2,连接EF,同理可得:EF=×4=2,∵EF∥AB,∴△PEF~△ABP,∴,在Rt△ABP中,AB=4,∠ABP=30°,∴AP=2,PB=2,∴PF=1,PE=,在Rt△APE和Rt△BPF中,AE=,BF=,∴a=2,b=2,故答案为:2,2,2,2;(2)猜想:a2+b2=5c2,如图3,连接EF,设∠ABP=α,∴AP=csinα,PB=ccosα,由(1)同理可得,PF=PA=,PE==,AE2=AP2+PE2=c2sin2α+,BF2=PB2+PF2=+c2cos2α,∴=c2sin2α+,=+c2cos2α,∴+=+c2cos2α+c2sin2α+,∴a2+b2=5c2;(3)如图4,连接AC,EF交于H,AC与BE交于点Q,设BE与AF的交点为P,∵点E、G分别是AD,CD的中点,∴EG∥AC,∵BE⊥EG,∴BE⊥AC,∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC=2,∴∠EAH=∠FCH,∵E,F分别是AD,BC的中点,∴AE=AD,BF=BC,∴AE=BF=CF=AD=,∵AE∥BF,∴四边形ABFE是平行四边形,∴EF=AB=3,AP=PF,在△AEH和△CFH中,,∴△AEH≌△CFH,∴EH=FH,∴EP,AH分别是△AFE的中线,由(2)的结论得:AF2+EF2=5AE2,∴AF2=5﹣EF2=16,∴AF=4.或连接F与AB的中点M,证MF垂直BP,构造出“中垂三角形”,因为AB=3,BC=1/2AD=根号5,根据上一问的结论,直接可求AF.。
江西省2015年中考数学试题(word版,含答案)

准考证号姓名(在此卷上答题无效)机密★2015年6月19日江西省2015年中等学校招生考试数学试题卷 说明:1.本卷共有六个大题,24个小题,全卷满分120分,考试时间120分钟.2.本卷分为试题卷和答题卷,答案要求写在答题卷上,不得在试题卷上作答,否则不给分.一、选择题(本大题共6小题,每小题3分,共18分.每小题只有一个正确选项)1.计算(-1)°的结果为()A .1B .-1C .0D .无意义2.2015年初,一列CRH5型高速车组进行了“300 000公里正线运营考核”,标志着中国高铁车从“中国制造”到“中国创新”的飞跃.将数300 000用科学计数法表示为()A .6310⨯B .5310⨯C .60.310⨯D .43010⨯ 3.如图所示的几何体的左视图为()4.下列运算正确的是()A .236(2)6a a =B .2232533a b ab a b -•=-C .1b a a b b a +=---D .21111a a a -•=-+ 5.如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD ,B 与D 两点之间用一根橡皮筋...拉直固定,然后向右扭动框架,观察所得四边形的变化.下面判断错误..的是() A .四边形ABCD 由矩形变为平行四边形B .BD 的长度增大C .四边形ABCD 的面积不变D .四边形ABCD 的周长不变6.已知抛物线y =ax 2+bx +c (a >0)过(-2,0),(2,3)两点,那么抛物线的对称轴( )A .只能是x =-1B .可能是y 轴C .在y 轴右侧且在直线x =2的左侧D .在y 轴左侧且在直线x =-2的右侧二、填空题(本大题共8小题,每小题3分,共24分)7.一个角的度数为20°,则它的补角的度数为.8.不等式组110239x x ⎧-⎪⎨⎪-<⎩≤,的解集是.9.如图,OP 平分∠MON ,PE ⊥OM 于E ,PF ⊥ON 于F ,OA =OB .则图中有对全等三角形.10.如图,点A ,B ,C 在⊙O 上,CO 的延长线交AB 于点D ,∠A =50°,∠B =30°,则∠ADC 的度数为.11.已知一元二次方程x 2-4x -3=0的两根为m ,n ,则m 2-mn +n 2=.12.两组数据:3,a ,2b ,5与a ,6,b 的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的中位数为.13.如图1是小志同学书桌上的一个电子相框,将其侧面抽象为如图2所示的几何图形,已知BC =BD =15cm ,∠CBD =40°,则点B 到CD 的距离为cm(参考数据:sin 20°≈0.342,cos20°≈0.940,sin40°≈0.643,cos40°≈014.如图,在△ABC 中,AB =BC =4,AO =BO ,P 是射线CO 上的一个动点,∠AOC =60°,则当△P AB 为直角三角形时,AP 的长为.三、(本大题共4小题,每小题6分,共24分)15.先化简,再求值:22(2)(2)a a b a b +-+,其中1a =-,3b =.16.如图,正方形A BCD 与正方形A 1B 1C 1D 1关于某点中心对称.已知A ,D 1,D 三点的坐标分别是(0,4),(0,3),(0,2).(1)求对称中心的坐标;(2)写出顶点B ,C ,B 1,C 1的坐标.17.⊙O 为△ABC 的外接圆,请仅用无刻度的直尺........,根据下列条件分别在图1,图2中画出一条弦.,使这条弦将△ABC 分成面积相等的两部分(保留作图痕迹,不写作法).(1)如图1,AC =BC ;(2)如图2,直线l 与⊙O 相切与点P ,且l ∥B C .18.在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.(1)先从袋子中取出m (m >1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A .请完成下列表格: 事件A必然事件 随机事件m 的值 (2)先从袋子中取出m 个红球,再放入m 个一样的黑球并摇匀,随机摸出1个球是黑球的概率等于45,求m 的值. 四、(本大题共4小题,每小题8分,共32分)19.某校为了了解学生家长对孩子使用手机的态度情况,随机抽取部分学生家长进行问卷调查,发出问卷140份,每位学生的家长1份,每份问卷仅表明一种态度.将回收的问卷进行整理(假设回收的问卷都有效),并绘制了如下两幅不完整的统计图.学生家长对孩子使用手机的态度情况统计图根据以上信息回答下列问题:(1)回收的问卷数为份,“严加干涉”部分对应扇形的圆心角度数为;(2)把条形统计图补充完整;(3)若将“稍加询问”和“从来不管”视为“管理不严”,已知全校共1500名学生,请估计该校对孩子使用手机“管理不严”的家长大约有多少人?20.(1)如图1,纸片□ABCD 中,AD =5,S □ABCD =15.过点A 作AE ⊥BC ,垂足为E ,沿AE 剪下△ABE ,将它平移至△DCE'的位置,拼成四边形AEE'D ,则四边形AEE'D 的形状为()A .平行四边形B .菱形C .矩形D .正方形(2)如图2,在(1)中的四边形纸片AEE'D 中,在EE'上取一点F ,使EF =4,剪下△AEF ,将它平移至△DE'F'的位置,拼成四边形AFF'D .①求证:四边形AFF'D 是菱形;②求四边形AFF'D 的两条对角线的长.21.如图,已知直线y =ax +b 与双曲线(0)k y x x=>交于A (x 1,y 1),B (x 2,y 2)两点(A 与B 不重合),直线AB 与x 轴交于点P (x 0,0),与y 轴交于点C .(1)若A ,B 两点坐标分别为(1,3),(3,y 2).求点P 的坐标;(2)若b =y 1+1,点P 的坐标为(6,0),且AB =BP ,求A ,B 两点的坐标;(3)结合(1),(2)中的结果,猜想并用等式表示x1,x2,x0之间的关系(不要求证明).22.甲、乙两人在100米直道AB上练习匀速往返跑,若甲、乙分别在A,B两端同时出发,分别到另一端点掉头,掉头时间不计,速度分别为5m/s和4m/s.(1)在坐标系中,虚线表示乙离..A.端.的距离s(单位:m)与运动时间t(单位:s)之间的函数图象(0≤t≤200),请在同一坐标系中用实线画出甲离A端的距离s与运动时间t之间的函数图象(0≤t≤200);(2)根据(1)中所画图象,完成下列表格:两人相遇次数1 2 3 4 …n(单位:次)两人所跑路程之和100 300 …(单位:m)(3)①直接写出甲、乙两人分别在第一个100m内,s与t的函数解析式,并指出自变量t的取值范围;②求甲、乙第6此相遇时t的值.五、(本大题共10分)23.如图,已知二次函数L1:y=ax2-2ax+a+3(a>0)和二次函数L2:y=-a(x+1)2+1(a>0)图像的顶点分别为M,N,与y轴分别交于点E,F.(1)函数y=ax2-2ax+a+3(a>0)的最小值为;当二次函数L1,L2的y值同时随着x的增大而减小时,x的取值范围是;(2)当EF=MN时,求a的值,并判断四边形ENFM的形状(直接写出,不必证明);(3)若二次函数L2的图象与x轴的右交点为A(m,0),当△AMN为等腰三角形时,求方程-a(x+1)2+1=0的解.六、(本大题共12分)24.我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.特例探索(1)如图1,当∠ABE=45°,c=22时,a=,b=;如图2,当∠ABE=30°,c=4时,a=,b=;归纳证明(2)请你观察(1)中的计算结果,猜想a2,b2,c2三者之间的关系,用等式表示出来,请利用图3证明你发现的关系式;拓展应用(3)如图4,在□ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=25 AB=3.求AF的长.。
2015年江西南昌中考真题数学

2015年江西省南昌市中考真题数学一、选择题(本大题共6小题,每小题3分,共18分,每小题只有一个正确选项)1.计算(﹣1)0的结果为()A.1B.﹣1C.0D.无意义解析:∵(﹣1)0=1,∴(﹣1)0的结果为1.答案:A.2. 2015年初,一列CRH5型高速车组进行了“300000公里正线运营考核”标志着中国高速快车从“中国制造”到“中国创造”的飞跃,将300000用科学记数法表示为()A.3×106B.3×105C.0.3×106D.30×104解析:将300000用科学记数法表示为:3×105.答案:B.3.下列运算正确的是()A.(2a2)3=6a6B.﹣a2b2·3ab3=﹣3a2b5C.D.解析:A、原式=8a6,错误;B、原式=﹣3a3b5,错误;C、原式=,错误;D、原式=,正确;答案:D.4.如图是将正方体切去一个角后形成的几何体,则该几何体的左视图为()A.B.C.D.解析:从左面看所得到的图形是正方形,切去部分的棱能看到,用实线表示,答案:C.5.如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD,B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化,下列判断错误的是()A.四边形ABCD由矩形变为平行四边形B.BD的长度增大C.四边形ABCD的面积不变D.四边形ABCD的周长不变解析:∵矩形框架ABCD,B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,∴AD=BC,AB=DC,∴四边形变成平行四边形,故A正确;BD的长度增加,故B正确;∵拉成平行四边形后,高变小了,但底边没变,∴面积变小了,故C错误;∵四边形的每条边的长度没变,∴周长没变,故D正确,答案:C.6.已知抛物线y=ax2+bx+c(a>0)过(﹣2,0),(2,3)两点,那么抛物线的对称轴()A.只能是x=﹣1B.可能是y轴C.在y轴右侧且在直线x=2的左侧D.在y轴左侧且在直线x=﹣2的右侧解析:∵抛物线y=ax2+bx+c(a>0)过(﹣2,0),(2,3)两点,∴点(﹣2,0)关于对称轴的对称点横坐标x2满足:﹣2<x2<2,∴﹣2<<0,∴抛物线的对称轴在y轴左侧且在直线x=﹣2的右侧.答案:D.二、填空题(本大题共8小题,每小题3分,共24分)7.一个角的度数为20°,则它的补角的度数为.解析:180°﹣20°=160°.答案:160°.8.不等式组的解集是.解析:,由①得:x≤2,由②得:x>﹣3,则不等式组的解集为﹣3<x≤2.答案:﹣3<x≤29.如图,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB,则图中有对全等三角形.解析:OP平分∠MON,PE⊥OM于E,PF⊥ON于F,∴PE=PF,∠1=∠2,在△AOP与△BOP中,,∴△AOP≌△BOP,∴AP=BP,在△EOP与△FOP中,,∴△AOP≌△BOP,在R t△AOP与R t△BOP中,,∴R t△AOP≌R t△BOP,∴图中有3对全等三角形,答案:3.10.如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC 的度数为.解析:∵∠A=50°,∴∠BOC=2∠A=100°,∵∠B=30°,∠BOC=∠B+⊂BDC,∴∠BDC=∠BOC﹣∠B=100°﹣30°=70°,∴∠ADC=180°﹣∠BDC=110°,答案:110°.11.已知一元二次方程x2﹣4x﹣3=0的两根为m,n,则m2﹣mn+n2= .解析:∵m,n是一元二次方程x2﹣4x﹣3=0的两个根,∴m+n=4,mn=﹣3,则m2﹣mn+n2=(m+n)2﹣3mn=16+9=25.答案:25.12.如图1是小志同学书桌上的一个电子相框,将其侧面抽象为如图2所示的几何图形,已知BC=BD=15cm,∠CBD=40°,则点B到CD的距离为cm(参考数据sin20°≈0.342,cos20°≈0.940,sin40°≈0.643,cos40°≈0.766,结果精确到0.1cm,可用科学计算器).解析:如图2,作BE⊥CD于E,∵BC=BD,∠CBD=40°,∴∠CBE=20°,在Rt△CBE中,cos∠CBE=,∴BE=BC·cos∠CBE=15×0.940=14.1cm.答案:14.1.13.两组数据:3,a,2b,5与a,6,b的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的中位数为.解析:∵两组数据:3,a,2b,5与a,6,b的平均数都是6,∴,解得,若将这两组数据合并为一组数据,按从小到大的顺序排列为3,4,5,6,8,8,8,一共7个数,第四个数是6,所以这组数据的中位数是6.答案:6.14.如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB 为直角三角形时,AP的长为.解析:当∠APB=90°时(如图1),∵AO=BO,∴PO=BO,∵∠AOC=60°,∴∠BOP=60°,∴△BOP为等边三角形,∵AB=BC=4,∴AP=AB·sin60°=4×=2;当∠ABP=90°时,情况一:(如图2),∵∠AOC=∠BOP=60°,∴∠BPO=30°,∴BP===2,在直角三角形ABP中,AP==2,情况二:如图3,∵AO=BO,∠APB=90°,∴PO=AO,∵∠AOC=60°,∴△AOP为等边三角形,∴AP=AO=2,答案:2或2或2.三、解答题(本大题共4小题,每小题6分,共24分)15.先化简,再求值:2a(a+2b)﹣(a+2b)2,其中a=﹣1,b=.解析:原式第一项利用单项式乘以多项式法则计算,第二项利用完全平方公式化简,去括号合并得到最简结果,把a与b的值代入计算即可求出值.答案:原式=2a2+4ab﹣a2﹣4ab﹣4b2=a2﹣4b2,当a=﹣1,b=时,原式=1﹣12=﹣11.16.如图,正方形ABCD于正方形A1B1C1D1关于某点中心对称,已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).(1)求对称中心的坐标.(2)写出顶点B,C,B1,C1的坐标.解析:(1)根据对称中心的性质,可得对称中心的坐标是D1D的中点,据此解答即可. (2)首先根据A,D的坐标分别是(0,4),(0,2),求出正方形ABCD与正方形A1B1C1D1的边长是多少,然后根据A,D1,D三点的坐标分别是(0,4),(0,3),(0,2),判断出顶点B,C,B1,C1的坐标各是多少即可.答案:(1)根据对称中心的性质,可得对称中心的坐标是D1D的中点,∵D1,D的坐标分别是(0,3),(0,2),∴对称中心的坐标是(0,2.5).(2)∵A,D的坐标分别是(0,4),(0,2),∴正方形ABCD与正方形A1B1C1D1的边长都是:4﹣2=2,∴B,C的坐标分别是(﹣2,4),(﹣2,2),∵A1D1=2,D1的坐标是(0,3),∴A1的坐标是(0,1),∴B1,C1的坐标分别是(2,1),(2,3),综上,可得顶点B,C,B1,C1的坐标分别是(﹣2,4),(﹣2,2),(2,1),(2,3).17.⊙O为△ABC的外接圆,请仅用无刻度的直尺,根据下列条件分别在图1,图2中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法).(1)如图1,AC=BC;(2)如图2,直线l与⊙O相切于点P,且l∥BC.解析:(1)过点C作直径CD,由于AC=BC,=,根据垂径定理的推理得CD垂直平分AB,所以CD将△ABC分成面积相等的两部分;(2)连结PO并延长交BC于E,过点A、E作弦AD,由于直线l与⊙O相切于点P,根据切线的性质得OP⊥l,而l∥BC,则PE⊥BC,根据垂径定理得BE=CE,所以弦AE将△ABC分成面积相等的两部分.答案:(1)如图1,直径CD为所求;(2)如图2,弦AD为所求.18.在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格:(2个黑球的概率等于,求m的值.解析:(1)当袋子中全部为黑球时,摸出黑球才是必然事件,否则就是随机事件;(2)利用概率公式列出方程,求得m的值即可.答案:(1)当袋子中全为黑球,即摸出4个红球时,摸到黑球是必然事件;当摸出2个或3个时,摸到黑球为随机事件,答案:4;2,3.(2)根据题意得:=,解得:m=2,所以m的值为2.四、解答题(本大题共3小题,每小题8分,共24分)19.某校为了了解学生家长对孩子使用手机的态度情况,随机抽取部分学生家长进行问卷调查,发出问卷140份,每位学生家长1份,每份问卷仅表明一种态度,将回收的问卷进行整理(假设回收的问卷都有效),并绘制了如图两幅不完整的统计图.根据以上信息解答下列问题:(1)回收的问卷数为份,“严加干涉”部分对应扇形的圆心角度数为.(2)把条形统计图补充完整(3)若将“稍加询问”和“从来不管”视为“管理不严”,已知全校共1500名学生,请估计该校对孩子使用手机“管理不严”的家长大约有多少人?解析:(1)用“从来不管”的问卷数除以其所占百分比求出回收的问卷总数;用“严加干涉”部分的问卷数除以问卷总数得出百分比,再乘以360°即可;(2)用问卷总数减去其他两个部分的问卷数,得到“稍加询问”的问卷数,进而补全条形统计图;(3)用“稍加询问”和“从来不管”两部分所占的百分比的和乘以1500即可得到结果. 答案:(1)回收的问卷数为:30÷25%=120(份),“严加干涉”部分对应扇形的圆心角度数为:×360°=30°.故答案为:120,30°;(2)“稍加询问”的问卷数为:120﹣(30+10)=80(份),补全条形统计图,如图所示:(3)根据题意得:1500×=1375(人),则估计该校对孩子使用手机“管理不严”的家长大约有1375人.=15,过点A作AE⊥BC,垂足为E,沿AE剪下20.(1)如图1,纸片▱ABCD中,AD=5,S▱ABCD△ABE,将它平移至△DCE′的位置,拼成四边形AEE′D,则四边形AEE′D的形状为 C A.平行四边形 B.菱形 C.矩形 D.正方形(2)如图2,在(1)中的四边形纸片AEE′D中,在EE′上取一点F,使EF=4,剪下△AEF,将它平移至△DE′F′的位置,拼成四边形AFF′D.①求证:四边形AFF′D是菱形.②求四边形AFF′D的两条对角线的长.解析:(1)根据矩形的判定,可得答案;(2)①根据菱形的判定,可得答案;②根据勾股定理,可得答案.=15,过点A作AE⊥BC,垂足为E,沿AE剪答案:(1)如图1,纸片▱ABCD中,AD=5,S▱ABCD下△ABE,将它平移至△DCE′的位置,拼成四边形AEE′D,则四边形AE E′D的形状为矩形,故选:C;(2)①证明:∵纸片▱ABCD中,AD=5,S=15,过点A作AE⊥BC,垂足为E,▱ABCD∴AE=3.如图2:,∵△AEF,将它平移至△DE′F′,∴AF∥DF′,AF=DF′,∴四边形AFF′D是平行四边形.在Rt△AEF中,由勾股定理,得∴AF=AD=5,∴四边形AFF′D是菱形;②连接AF′,DF,如图3:在Rt△DE′F中E′F=FF′﹣E′F′=5﹣4=1,DE′=3,在Rt△AEF′中EF′=EF+FF′=4+5=9,AE=3,21.如图,已知直线y=ax+b与双曲线y=(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的坐标.(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.(3)结合(1),(2)中的结果,猜想并用等式表示x1,x2,x0之间的关系(不要求证明).解析:(1)先把A(1,3)),B(3,y2)代入y=求得反比例函数的解析式,进而求得B的坐标,然后把A、B代入y=ax+b利用待定系数法即可求得直线的解析式,继而即可求得P的坐标;(2)作AD⊥y轴于D,AE⊥x轴于E,BF⊥x轴于F,BG⊥y轴于G,AE、BG交于H,则AD∥BG∥x 轴,AE∥BF∥y轴,得出=,==,根据题意得出,==,从而求得,然后根据k=xy得出x1·y1=·y1,求得y1=2,代入=,解得x1=2,即可求得A、B的坐标;(3)合(1),(2)中的结果,猜想x1+x2=x0.答案:(1)∵直线y=ax+b与双曲线y=(x>0)交于A(1,3),∴k=1×3=3,∴y=,∵B(3,y2)在反比例函数的图象上,∴y2==1,∴B(3,1),∵直线y=ax+b经过A、B两点,∴解得,∴直线为y=﹣x+4,令y=0,则x=4,∴P(4,O);(2)如图,作AD⊥y轴于D,AE⊥x轴于E,BF⊥x轴于F,BG⊥y轴于G,AE、BG交于H,则AD∥BG∥x轴,AE∥BF∥y轴,∴=,==,∵b=y1+1,AB=BP,∴=,==,∴B(,y1)∵A,B两点都是反比例函数图象上的点,∴x1·y1=·y1,解得y1=2,代入=,解得x1=2,∴A(2,2),B(4,1).(3)根据(1),(2)中的结果,猜想:x1,x2,x0之间的关系为x1+x2=x0.五、解答题(本大题共2小题,每小题9分,共18分)22.甲、乙两人在100米直道AB上练习匀速往返跑,若甲、乙分别中A,B两端同时出发,分别到另一端点处掉头,掉头时间不计,速度分别为5m/s和4m/s.(1)在坐标系中,虚线表示乙离A端的距离s(单位:m)与运动时间t(单位:s)之间的函数图象(0≤t≤200),请在同一坐标系中用实线画出甲离A端的距离s与运动时间t之间的函数图象(0≤t≤200);(3)①直接写出甲、乙两人分别在第一个100m内,s与t的函数解析式,并指出自变量t 的取值范围;②当t=390s时,他们此时相遇吗?若相遇,应是第几次?若不相遇,请通过计算说明理由,并求出此时甲离A端的距离.解析:(1)根据甲跑100米所用的时间为100÷5=20(秒),画出图象即可;(2)根据甲和乙第一次相遇时,两人所跑路程之和为100米,甲和乙第二次相遇时,两人所跑路程之和为100×2+100=300(米),甲和乙第三次相遇时,两人所跑路程之和为200×2+100=500(米),甲和乙第四次相遇时,两人所跑路程之和为300×2+100=700(米),找到规律即可解答;(3)①根据路程、速度、时间之间的关系即可解答;②由200n﹣100=9×390,解得:n=18.05,根据n不是整数,所以此时不相遇,当t=400s 时,甲回到A,所以当t=390s时,甲离A端距离为(400﹣390)×5=50m.答案:(1)如图:(2)甲和乙第一次相遇时,两人所跑路程之和为100米,甲和乙第二次相遇时,两人所跑路程之和为100×2+100=300(米),甲和乙第三次相遇时,两人所跑路程之和为200×2+100=500(米),甲和乙第四次相遇时,两人所跑路程之和为300×2+100=700(米),…甲和乙第n次相遇时,两人所跑路程之和为(n﹣1)×100×2+100=200n﹣100(米),故答案为:500,700,200n﹣100;(3)①s甲=5t(0≤t<20),s乙=4t(0≤t≤25).②由200n﹣100=9×390,解得:n=18.05,∵n不是整数,∴此时不相遇,当t=400s时,甲回到A,当t=390s时,甲离A端距离为(400﹣390)×5=50m.23.如图,已知二次函数L1:y=ax2﹣2ax+a+3(a>0)和二次函数L2:y=﹣a(x+1)2+1(a >0)图象的顶点分别为M,N,与y轴分别交于点E,F.(1)函数y=ax2﹣2ax+a+3(a>0)的最小值为,当二次函数L1,L2的y值同时随着x 的增大而减小时,x的取值范围是.(2)当EF=MN时,求a的值,并判断四边形ENFM的形状(直接写出,不必证明). (3)若二次函数L2的图象与x轴的右交点为A(m,0),当△AMN为等腰三角形时,求方程﹣a(x+1)2+1=0的解.解析:(1)把二次函数L1:y=ax2﹣2ax+a+3化成顶点式,即可求得最小值,分别求得二次函数L1,L2的y值随着x的增大而减小的x的取值,从而求得二次函数L1,L2的y值同时随着x的增大而减小时,x的取值范围;(2)先求得E、F点的坐标,作MG⊥y轴于G,则MG=1,作NH⊥y轴于H,则NH=1,从而求得MG=NH=1,然后证得△EMG≌△FNH,∠MEF=∠NFE,EM=NF,进而证得EM∥NF,从而得出四边形ENFM是平行四边形;(3)作MN的垂直平分线,交MN于D,交x轴于A,先求得D的坐标,继而求得MN的解析式,进而就可求得直线AD的解析式,令y=0,求得A的坐标,根据对称轴从而求得另一个交点的坐标,就可求得方程﹣a(x+1)2+1=0的解.答案:(1)∵二次函数L1:y=ax2﹣2ax+a+3=a(x﹣1)2+3,∴顶点M坐标为(1,3),∵a>0,∴函数y=ax2﹣2ax+a+3(a>0)的最小值为3,∵二次函数L1的对称轴为x=1,当x<1时,y随x的增大而减小;二次函数L2:y=﹣a(x+1)2+1的对称轴为x=﹣1,当x>﹣1时,y随x的增大而减小;∴当二次函数L1,L2的y值同时随着x的增大而减小时,x的取值范围是﹣1≤x≤1;故答案为:3,﹣1≤x≤1.(2)由二次函数L1:y=ax2﹣2ax+a+3可知E(0,a+3),由二次函数L2:y=﹣a(x+1)2+1=﹣a2x﹣2ax﹣a+1可知F(0,﹣a+1),∵M(1,3),N(﹣1,1),∴EF=MN=,∴a+3﹣(﹣a+1)=2,∴a=﹣1,作MG⊥y轴于G,则MG=1,作NH⊥y轴于H,则NH=1,∴MG=NH=1,∵EG=a+3﹣3=a,FH=1﹣(﹣a+1)=a,∴EG=FH,在△EMG和△FNH中,∴△EMG≌△FNH(SAS),∴∠MEF=∠NFE,EM=NF,∴EM∥NF,∴四边形ENFM是平行四边形;∵EF=MN,∴四边形ENFM是矩形;(3)由△AMN为等腰三角形,可分为如下三种情况:①如图2,当MN=NA=2时,过点N作ND⊥x周,垂足为点D,则有ND=1,DA=m﹣(﹣1)=m+1,在Rt△NDA中,NA2=DA2+ND2,即(2)2=(m+1)2+12,∴m1=﹣1,m2=﹣﹣1(不合题意,舍去),∴A(﹣1,0).由抛物线y=﹣a(x+1)2+1(a>0)的对称轴为x=﹣1,∴它与x轴的另一个交点坐标为(﹣1﹣,0).∴方程﹣a(x+1)2+1=0的解为x1=﹣1,x2=﹣1﹣.②如图3,当MA=NA时,过点M作MG⊥x轴,垂足为G,则有OG=1,MG=3,GA=|m﹣1|,∴在Rt△MGA中,MA2=MG2+GA2,即MA2=32+(m﹣1)2,又∵NA2=(m+1)2+12,∴(m+1)2+12=32+(m﹣1)2,m=2,∴A(2,0),则抛物线y=﹣a(x+1)2+1(a>0)的左交点坐标为(﹣4,0),∴方程﹣a(x+1)2+1=0的解为x1=2,x2=﹣4.③当MN=MA时,32+(m﹣1)2=(2)2,∴m无实数解,舍去.综上所述,当△AMN为等腰三角形时,方程﹣a(x+1)2=0的解为x1=﹣1,x2=1﹣或x1=2,x2=﹣4.六、解答题(本大题共12分)24.我们把两条中线互相垂直的三角形称为“称为中垂三角形”,例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均称为“中垂三角形”,设BC=a,AC=b,AB=c.特例探索(1)如图1,当∠ABE=45°,c=2时,a= ,b= .如图2,当∠ABE=30°,c=4时,a= ,b= .归纳证明(2)请你观察(1)中的计算结果,猜想a2,b2,c2三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.拓展应用(3)如图4,在▱ABCD中,点E、F、G分别是AD,BC,CD的中点,BE⊥EG,AD=2,AB=3,求AF的长.解析:(1)由等腰直角三角形的性质得到AP=BP=AB=2,根据三角形中位线的性质,得到EF∥AB,EF=AB=,再由勾股定理得到结果;(2)连接EF,设∠ABP=α,类比着(1)即可证得结论.(3)连接AC交EF于H,设BE与AF的交点为P,由点E、G分别是AD,CD的中点,得到EG是△ACD的中位线于是证出BE⊥AC,由四边形ABCD是平行四边形,得到AD∥BC,AD=BC=2,∠EAH=∠FCH根据E,F分别是AD,BC的中点,得到AE=BF=CF=AD=,证出四边形ABFE是平行四边形,证得EH=FH,推出EH,AH分别是△AFE的中线,由(2)的结论得即可得到结果.答案:(1)∵AH⊥BE,∠ABE=45°,∴AP=BP=AB=2,∵AF,BE是△ABC的中线,∴EF∥AB,EF=AB=,∴∠PFE=∠PEF=45°,∴PE=PF=1,在Rt△FPB和Rt△PEA中,AE=BF==,∴AC=BC=2,∴a=b=2,如图2,连接EF,同理可得:EF=×4=2,∵EF∥AB,∴△PEF~△ABP,∴,在Rt△ABP中,AB=4,∠ABP=30°,∴AP=2,PB=2,∴PF=1,PE=,在Rt△APE和Rt△BPF中,AE=,BF=,∴a=2,b=2,故答案为:2,2,2,2;(2)猜想:a2+b2=5c2,如图3,连接EF,设∠ABP=α,∴AP=csinα,PB=ccosα,由(1)同理可得,PF=PA=,PE==,AE2=AP2+PE2=c2sin2α+,BF2=PB2+PF2=+c2cos2α,∴=c2sin2α+,=+c2cos2α,∴+=+c2cos2α+c2sin2α+,∴a2+b2=5c2;(3)如图4,连接AC,EF交于H,AC与BE交于点Q,设BE与AF的交点为P,∵点E、G分别是AD,CD的中点,∴EF∥AC,∵BE⊥EG,∴BE⊥AC,∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC=2,∴∠EAH=∠FCH,∵E,F分别是AD,BC的中点,∴AE=AD,BF=BC,∴AE=BF=CF=AD=,∵AE∥BF,∴四边形ABFE是平行四边形,∴EF=AB=3,AP=PF,在△AEH和△CFH中,,∴△AEH≌△CFH,∴EH=FH,∴EH,AH分别是△AFE的中线,由(2)的结论得:AF2+EF2=5AE2,∴AF2=5﹣EF2=16,∴AF=4.。
中考试卷数学(江西省卷)

准考证号姓名(在此卷上答题无效)机密★2015年 6月 19 日江西省 2015 年中等学校招生考试数学试题卷说明: 1.本卷共有六个大题, 24 个小题,全卷满分120 分,考试时间 120 分钟.2.本卷分为试题卷和答题卷,答案要求写在答题卷上,不得在试题卷上作答,否则不给分.一、选择题 (本大题共 6 小题,每题 3 分,共 18 分.每题只有一个正确选项) 1.计算 (-1) °的结果为 ()A.1B.- 1C.0D.没心义2.2015 年初,一列 CRH5 型高速车组进行了“ 300000 公里正线运营核查”,标志着中国高铁车从“中国制造”到“中国创新”的飞驰.将数300000 用科学计数法表示为 ()A.3 106B.3 105C.0.3 106D.30 1043.以下列图的几何体的左视图为()4.以下运算正确的选项是 ()A.(2 a2)36a6B.a2b2?3ab33a2b5C.ba1D. a2 1 ? 11 a b b a a a15.如图,小贤为了体验四边形的不牢固性,将四根木条用钉子钉成一个矩形框架ABCD,B 与D 两点之间用一根橡皮筋拉直固...定,尔后向右扭动框架,观察所得四边形的变化.下面判断错误的选项是..()A.四边形ABCD由矩形变为平行四边形B.BD 的长度增大C.四边形 ABCD 的面积不变D.四边形 ABCD 的周长不变6 .已知抛物线 y=ax2+bx+c(a>0) 过(-2,0),(2,3)两点,那么抛物线的对称轴() A.只能是 x=- 1B.可能是 y 轴C.在 y 轴右侧且在直线x=2的左侧D.在 y 轴左侧且在直线x=- 2 的右侧二、填空题 ( 本大题共 8 小题,每题 3 分,共 24 分)7.一个角的度数为20°,则它的补角的度数为.1 x ≤ ,8.不等式组2 1 0的解集是.3x99.如图, OP 均分∠ MON,PE⊥OM 于 E,PF⊥ON 于 F,OA=OB.则图中有对全等三角形.10.如图,点 A,B,C 在⊙ O 上,CO 的延长线交 AB 于点 D,∠A=50°,∠B=30°,则∠ ADC 的度数为.11.已知一元二次方程x2-4x-3=0 的两根为 m,n,则 m2-mn+n2=.12.两组数据: 3,a,2b,5 与 a,6,b 的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的中位数为.13.如图 1 是小志同学书桌上的一个电子相框,将其侧面抽象为如图 2 所示的几何图形,已知 BC=BD=15cm,∠ CBD=40°,则点 B 到 CD 的距离为 cm(参照数据:sin20°≈0.342,cos20°≈0.940,sin40°≈0.643,cos40°≈0.766.计算结果精确到,可用科学计算器 ).14.如图,在△ ABC 中,AB=BC=4,AO=BO,P 是射线 CO 上的一个动点,∠AOC=60°,则当△PAB 为直角三角形时, AP 的长为.三、 ( 本大题共 4 小题,每题 6 分,共 24 分)15.先化简,再求值:2a(a 2b)(a 2b)2,其中a 1 ,b 3 .16.如图,正方形 ABCD 与正方形 A1B1C1D1关于某点中心对称.已知 A,D1,D 三点的坐标分别是 (0,4),(0,3),(0,2).(1)求对称中心的坐标;(2)写出极点 B,C,B1,C1的坐标.17.⊙ O 为△ ABC 的外接圆,请仅用无刻度的直尺,依照以下条件分别在图1,图2........中画出一条弦,使这条弦将△ ABC 分成面积相等的两部分 (保留作图印迹,不写作法 )..(1)如图 1,AC=BC;(2)如图 2,直线 l 与⊙ O 相切与点 P,且 l∥BC.18.在一个不透明的袋子中装有仅颜色不相同的10个小球,其中红球 4 个,黑球 6 个.(1)先从袋子中取出 m(m>1)个红球,再从袋子中随机摸出 1 个球,将“摸出黑球”记为事件 A.请完成以下表格:事件 A必然事件随机事件m的值(2)先从袋子中取出m 个红球,再放入 m 个相同的黑球并摇匀,随机摸出 1 个球是黑球的概率等于4,求 m 的值.5四、 ( 本大题共 4 小题,每题 8 分,共 32 分)19.某校为了认识学生家长对孩子使用手机的态度情况,随机抽取部分学生家进步行问卷检查,发出问卷 140 份,每位学生的家长 1 份,每份问卷仅表示一种态度.将回收的问卷进行整理 (假设回收的问卷都有效),并绘制了以下两幅不完满的统计图.学生家长对孩子使用手机的态度情况统计图依照以上信息回答以下问题:(1)回收的问卷数为份,“严加干涉”部分对应扇形的圆心角度数为;(2)把条形统计图补充完满;(3)若将“略加咨询”和“向来无论”视为“管理不严”,已知全校共1500 名学生,请估计该校订孩子使用手机“管理不严”的家长大体有多少人?20.(1)如图 1,纸片□ABCD 中,AD=5,S□ABCD=15.过点 A 作 AE⊥BC,垂足为 E,沿 AE 剪下△ ABE,将它平移至△DCE'的地址,拼成四边形 AEE'D,则四边形 AEE'D的形状为 ()A.平行四边形B.菱形C.矩形D.正方形(2)如图 2,在(1)中的四边形纸片AEE'D 中,在 EE'上取一点 F,使 EF=4,剪下△AEF,将它平移至△DE'F' 的地址,拼成四边形AFF'D .①求证:四边形AFF'D 是菱形;②求四边形 AFF'D 的两条对角线的长..如图,已知直线y =+与双曲线 yk( x 0) 交于A(x1,y,,y两点(A21ax b x1)B(x2 2)与 B 不重合 ),直线 AB 与 x 轴交于点 P(x0,0),与 y 轴交于点 C.(1)若 A,B 两点坐标分别为 (1,3),(3, y2).求点 P 的坐标;(2)若b= 1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标;y(3)结合 (1),(2)中的结果,猜想并用等式表示x 1,x2,x0之间的关系 (不要求证明 ).22.甲、乙两人在 100 米直道 AB 上练习匀速往返跑,若甲、乙分别在A,B 两端同时出发,分别到另一端点掉头,掉头时间不计,速度分别为5m/s 和 4m/s.(1)在坐标系中,虚线表示乙离 A 端的距离 s(单位:m)与运动时间 t(单位:s)之间的函....数图象 (0≤t≤200),请在同一坐标系中用实线画出甲离 A 端的距离s 与运动时间t 之间的函数图象(0≤t≤200);(2)依照 (1)中所画图象,完成以下表格:两人相遇次数1234⋯n(位:次 )两人所跑行程之和100300⋯( 位: m)(3)①直接写出甲、乙两人分别在第一个100m 内, s 与 t 的函数剖析式,并指出自变量 t 的取值范围;②求甲、乙第 6 此相遇时 t 的值.五、 ( 本大题共 10 分)23.如图,已知二次函数L1:y=ax2-2ax+a+3(a>0) 和二次函数 L2:y=- a(x+1)2+1(a>0)图像的极点分别为M ,N,与 y 轴分别交于点 E, F.(1)函数y=ax2-2ax+a+3(a>0)的最小值为;当二次函数L1,L2的y 值同时随着x 的增大而减小时,x 的取值范围是;(2)当 EF=MN 时,求 a 的值,并判断四边形ENFM 的形状 (直接写出,不用证明 );(3)若二次函数 L2的图象与 x 轴的右交点为 A(m,0),当△ AMN 为等腰三角形时,求方程-a(x+1)2+1=0 的解.六、 ( 本大题共 12分)24.我们把两条中线互相垂直的三角形称为“中垂三角形”.比方图1,图 2,图 3中,AF,BE 是△ ABC 的中线, AF⊥BE,垂足为 P,像△ ABC 这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.特例研究(1)如图 1,当∠ ABE=45°,c=2 2时, a=, b=;如图 2,当∠ ABE=30°,c=4 时, a=,b=;归纳证明(2)请你观察 (1)中的计算结果,猜想a2,b2,c2三者之间的关系,用等式表示出来,请利用图 3 证明你发现的关系式;拓展应用(3)如图 4,在□ABCD 中,点 E,F,G 分别是 AD,BC,CD 的中点, BE⊥EG,AD = 2 5 ,AB=3.求AF的长.。
江西省南昌市2015年中考数学真题试题(含解析)

中考衣食住用行衣:中考前这段时间,提醒同学们出门一定要看天气,否则淋雨感冒,就会影响考场发挥。
穿着自己习惯的衣服,可以让人在紧张时产生亲切感和安全感,并能有效防止不良情绪产生。
食:清淡的饮食最适合考试,切忌吃太油腻或者刺激性强的食物。
如果可能的话,每天吃一两个水果,补充维生素。
另外,进考场前一定要少喝水!住:考前休息很重要。
好好休息并不意味着很早就要上床睡觉,根据以往考生的经验,太早上床反而容易失眠。
考前按照你平时习惯的时间上床休息就可以了,但最迟不要超过十点半。
用:出门考试之前,一定要检查文具包。
看看答题的工具是否准备齐全,应该带的证件是否都在,不要到了考场才想起来有什么工具没带,或者什么工具用着不顺手。
行:看考场的时候同学们要多留心,要仔细了解自己住的地方到考场可以坐哪些路线的公交车?有几种方式可以到达?大概要花多长时间?去考场的路上有没有修路堵车的情况?考试当天,应该保证至少提前20分钟到达考场。
江西省南昌市2015年中考数学真题试题说明:1.本卷共有6个大题,24个小题,全卷满分120分,考试时间120分钟;2.本卷分为试题卷和答题卷,答案要求写在答题卷上,不得在试题卷上答题,否则不给分.一、选择题(本大题共6小题,每小题3分,共18分,每小题只有一个正确选项) 1.计算0(1)-的结果为( ).A.1B.-1C.0D.无意义 2.2015年初,一列CRH5型高速车组进行了“300 000公里正线运营考核”.标志着中国高铁车从“中国制造”到“中国创新”的飞跃.将数300 000用科学记数法表示为( ).A.3×106B. 3×105C.0.3×106D. 30×1043.下列运算正确的是( ).A.236(2)6a a = B.C. D.4.如图是将正方体切去一个角后形成的几何体,则该几何体的左视图为( ).(第4题)正面D C B A5.如图,小贤同学为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD ,B 与D 两点之间用一根橡皮筋...拉直固定,然后向右扭动框架,观察所得四边形的变化,下列判断错误..的是( ). A. 四边形ABCD 由矩形变为平行四边形 B. BD 的长度变大C. 四边形ABCD 的面积不变D. 四边形ABCD 的周长不变6.已知抛物线2(0)y ax bx c a =++>过(-2,0),(2,3)两点,那么抛物线的对称轴( ). A .只能是1x =- B .可能是y 轴C .在y 轴右侧且在直线2x =的左侧D .在y 轴左侧且在直线2x =-的右侧二、选择题(本大题共8小题,每小题3分,共24分) 7.一个角的度数是20°,则它的补角的度数为 .8.不等式组x x ì-?ïíï-<9î11023的解集是 .9.如图,OP 平分∠MON , PE ⊥OM 于E , PF ⊥ON 于F ,OA =OB , 则图中有 对全等三角形.第10题第9题MDBFE OOP A BA C第5题B10.如图,点A , B , C 在⊙O 上,CO 的延长线交AB 于点D ,∠A =50°,∠B =30°则∠ADC 的度数为.11.已知一元二次方程2430x x --=的两根为m ,n ,则22m mn n -+= .12.两组数据:3,a ,2b , 5与a ,6 ,b 的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的中位数为 .13.如图1是小志同学书桌上的一个电子相框,将其侧面抽象为如图2所示的几何图形,已知BC =BD =15cm, ∠CBD =40°,则点B 到CD 的距离为 cm (参考数据:sin20°≈ 0.342, com20°≈0.940, sin40°≈ 0.643, com40°≈ 0.766.精确到0.1cm,可用科学计算器).(第14题)(第13题)图2图1O DCABA BCP14.如图,在△ABC 中,AB =BC =4,AO=BO ,P 是射线CO 上的一个动点,∠AOC =60°,则当△PAB 为直角三角形时,AP 的长为 . 三、(本大题共4小题,每小题6分,共24分)15.先化简,再求值:()()2222a a b a b +-+,其中,1a =- 3b =.16.如图,正方形ABCD 与正方形A 1B 1C 1D 1关于某点中心对称,已知A, D 1 ,D 三点的坐标分别是(0,4),(0,3),(0,2). (1)对称中心的坐标; (2)写出顶点B, C, B 1 , C 1 的坐标.17.⊙O 为△ABC 的外接圆,请仅用无刻度的直尺........,根据下列条件分别在图1,图2中画出一条弦,使这条弦将△ABC 分成面积相等的两部分(保留作图痕迹,不写作法). (1) 如图1,AC=BC ;(2) 如图2,直线l 与⊙O 相切于点P ,且l ∥BC .l图2图1PAO OCBBCAxyB 1CC 1BAD 1DO A 118.在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个. (1) 先从袋子中取出m (m>1)个红球,再从袋子中随机摸出一个球,将“摸出黑球”记为事件A. 请完成下列表格:(2) 先从袋子中取出m 个红球,再放入m 个一样的黑球并摇匀,随机摸出一个球是黑球的概率等于45,求m 的值. 四、(本大题共4小题,每小题8分,共32分)19.某校为了了解学生家长对孩子使用手机的态度情况,随机抽取部分学生家长进行问卷调查,发出问卷140份 ,每位学生家长1份,每份问卷仅表明一种态度,将回收的问卷进行整理(假设回收的问卷都有效),并绘制了如下两幅不完整的统计图.学生家长对孩子使用手机的态度情况统计图类别问卷数严加干涉稍加询问从来不管从来不管 25%严加干涉稍加询问1090705030100806040020根据以上信息解答下列问题:(1)回收的问卷数为 份,“严加干涉”部分对应扇形的圆心角的度数为 ; (2)把条形统计图补充完整;(3)若将:“稍加询问”和“从来不管”视为“管理不严”,已知学校共1500名学生,请估计该校对孩子使用手机“管理不严”的家长大约有多少人?20.(1)如图1,纸片□ABCD 中,AD =5,S □ABCD =15,过点A 作AE ⊥BC ,垂足为E ,沿AE 剪下△ABE ,将它平移至△DCE ′ 的位置,拼成四边形AEE′D ,则四边形AEE′D 的形状为( ) A.平行四边形 B.菱形 C.矩形 D.正方形(2)如图2,在(1)中的四边形纸片AEE′D 中,在EE′上取一点F ,使EF =4,剪下△AEF ,将它平移至△DE′F′ 的位置,拼成四边形AFF′D . ① 求证四边形AFF′D 是菱形;② 求四边形AFF′D 两条对角线的长.事件A 必然事件 随机事件 m 的值图2图1E'ADDA21.如图,已知直线y ax b =+与双曲线()0ky x x=>交于A (,11x y ),B (,22x y )两点(A 与B 不重合), 直线AB 与x 轴交于P (,00x ),与y 轴交于点C .(1) 若A ,B 两点的坐标分别为(1,3),(3,y 2).求点P 的坐标;(2)若11b y =+,点P 的坐标为(6,0),且AB BP =.求,A B 两点的坐标; (3)结合(1),(2)中的结果,猜想并用等式表示,,120x x x 之间的关系(不要求证明).xy CPBAO22.甲、乙两人在100米直道AB 上练习匀速往返跑,若甲、乙分别在A,B 两端同时出发,分别到另一端点处掉头,掉头时间不计,速度分别5 m/s 和4 m/s .(1)在坐标系中,虚线表示乙离A 端的距离S (单位:m )与运动时间t (单位:s )之间的函数图象(0≤t ≤200),请在同一坐标系中用实线画出甲离A 端的距离S 与运动时间t 之间的函数图象(0≤t ≤200);xy E F NMOt /sS /m甲———乙------20018016014012010080604010080604020O 20(2)根据(1)中所画图象,完成下列表格:两人相遇次数 (单位:次) 1 2 34…n两人所跑路程之和(单位:m)100300…(3)①直接写出甲、乙两人分别在第一个100m 内,s 与t 的函数解析式,并指出自变量的取值范围;②求甲、乙第六次相遇时t 的值.五、(本大题共10分)23.如图,已知二次函数L 1:()2230y ax ax a a =-++>和二次函数L 2:()211y a x =-++(0a >)图象的顶点分别为M ,N , 与y 轴分别交于点E, F.(1) 函数()2230y ax ax a a =-++>的最小值为 ;当二次函数L 1 ,L 2 的y 值同时随着x 的增大而减小时,x 的取值范围是 ;(2)当EF MN =时,求a 的值,并判断四边形ENFM 的形状(直接写出,不必证明); (3)若二次函数L 2 的图象与x 轴的右交点为(,)0A m ,当△AMN 为等腰三角形时,求方程()2110a x -++=的解.六、 (本大题共12分)24.我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,AF ,BE 是△ABC 的中线, AF ⊥BE , 垂足为P .像△ABC 这样的三角形均为“中垂三角形”.设BC =a ,AC b =,AB c =. 特例探索(1)如图1,当∠ABE =45°,c =22时,a = ,b = ; 如图2,当∠ABE =30°,c =4时, a = ,b = ;45°30°图3图2图1EFBEFPCEF PAPA归纳证明(2)请你观察(1)中的计算结果,猜想,,a b c 222三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式;拓展应用(3)如图4,在□ABCD 中,点E ,F ,G 分别是AD ,BC ,CD 的中点,BE ⊥EG , AD = 25,AB =3.求AF 的长.BEGD A2015年江西省南昌中考数学解析一、选择题(本大题共6小题,每小题3分,共18分,每小题只有一个正确选项) 1.解析:选A. ∵除0外,任何数的0次方等于1. ∴选A.2.解析:选B. ∵科学记数法是:把一个数写成“10´n a ,其中1≤a <10”. ∴选B.3.解析:选D. ∵()1b a b a b a a b a b b a a b a b a b a b---+=-===------- . ∴选D. 4.解析:选C. ∵根据光的正投影可知,几何体的左视图是图C. ∴选C.5.解析:选C. ∵向右扭动框架, 矩形变为平行四边形 ,底长不变,高变小,所以面积变小. ∴选C.6.解析:选D. ∵抛物线2(0)y ax bx c a =++>过(-2,0),(2,3)两点,∴420423a b c a b c ì-+=ïí++=ïî ,解得34b =,∴对称轴3028b x a a=-=-<,又对称轴在(-2,2)之间, ∴选D.二、填空题(本大题共8小题,每小题3分,共24分)7.解析:∵两角互补,和为180°,∴它的补角=180°-20°=160°. 8.解析: 由112x -≤0得x ≤2 ,由-3x <9得x >-3,∴不等式组的解集是-3<x ≤2. 9.解析:∵∠POE=∠POF, ∠PEO=∠PFO=90°OP=OP,∴△POE≌△POF(AAS), 又OA=OB,∠POA=∠POB,OP=OP,∴△POA≌△POB(AAS), ∴PA=PB,∵PE=PF,∴Rt△PAE≌Rt△PBF(HL). ∴图中共有3对全的三角形.10.解析:∵∠A=50°, ∴∠BOC=100°, ∴∠BOD=80°, ∴∠ADC=∠B+∠BOD=30°+ 80°=110° 11.解析:由一元二次方程根与系数关系得m +n =4,mn =﹣3,又()2223m mn n m n mn -+=+- ∴原式=()243325-?=.12.解析:由题意得32564663a b a b ì+++=ïïí++ï=ïî ,解得84a b ì=ïí=ïî,∴这组新数据是3,4,5,6,8,8,8,其中位数是6.13.解析:如右图,作BE⊥CD 于点E.∵BC=BD, BE⊥CD, ∴∠CBE=∠DBE=20°, 在Rt△BCD 中,cos ,BEDBE=BDÐ ∴cos BE 2015?, ∴BE≈15×0.940=14.1AB14.解析:如图,分三种情况讨论:图(1)中,∠APB=90°,∵AO=BO, ∠APB=90°,∴PO=AO=BO=2, 又∠AOC=60°, ∴△APO 是等边三角形,∴AP=2; 图(2)中,∠APB=90°,∵AO=BO, ∠APB=90°,∴PO=AO=BO=2,又∠AOC=60°, ∴∠BAP=30°,在Rt△ABP 中,AP=cos30°×4=23 .图(3)中,∠ABP=90°, ∵BO=AO=2 , ∠BOP=∠AOC=60°, ∴PB=23()2242327+= ∴AP 的长为2,23或27三、(本大题共4小题,每小题6分,共24分)15.解析:原式 ()[()]()()22222224a b a a b a b a b a b =+-+=+-=-把,1a =-3b ==()(2214311--?-16.解析:(1) ∵正方形ABCD 与正方形A 1B 1C 1D 1关于某点中心对称, ∴A,A 1 是对应点,∴AA 1 的中点是对称中心, ∵A(0,4),D(2,0),∴AD=2, ∴A 1D 1 = AD=2, 又∵D 1(0,3) ,∴A 1(0,1),∴对称中心的坐标为(0, 2.5);(2)∵正方形的边长为2, 点A,D 1 ,D ,A 1在y 轴上,∴B(-2,4), C(-2,2), B 1(2,1), C 1(2,3) .17.解析:如右图所示.图1,∵AC=BC,∴))AC BC =,∴点C 是)AB 的中点,连接CO ,交AB 于点E ,由垂径定理知, 点E 是AB 的中点, 延长CE 交⊙O 于点D , 则CD 为所求作的弦;(1)POBA (2)POBA(3)POBAxyB 1CC 1BAD 1DO A 1l图2图1E FDE DPAO OCBBCA图2,∵l 切⊙O 于点P, 作射线PO ,交BC 于点E ,则PO⊥l , ∵l ∥BC , ∴PO⊥BC, 由垂径定理知,点E 是BC 的中点,连接AE 交⊙O 于F ,则AF 为所求作的弦. 18. 解析:(1)若事件A 为必然事件,则袋中应全为黑球,∴m=4, 若事件A 为随机事件,则袋中有红球,∵m>1 ,∴m=2或3.(2)64105m +=, ∴m=2 .四、(本大题共4小题,每小题8分,共32分)19.解析:(1) 30÷25%=120 10÷120×360°=30° ∴回收的问卷数为120份,圆心角的度数为30°(2) 如下图:(3) (30+80)÷120×1500=1375 ∴对孩子使用手机“管理不严”的家长大约有1375人.问卷数严加干涉稍加询问从来不管109070503010080604002020.解析:(1) 由平移知:AE //DE′, ∴四边形AEE′D 是平行四边形,又AE⊥BC, ∴∠AEE′=90°, ∴四边形AEE′D 是矩形,∴C 选项正确.(2) ① ∵AF //DF′, ∴四边形AFF′D 是平行四边形,∵AE=3, EF=4 ,∠E=90°, ∴AF=5, ∵S □ABCD =AD·AE=15, ∴AD=5 , ∴AD=AF , ∴四边形AFF′D 是菱形. ② 如下图, 连接AF′, DF ,在Rt△AEF′中, AE=3, EF′=9, ∴AF′=310 在Rt△DFE′中, FE′=1, DE′=AE=3, ∴10 ∴四边形AFF′D 两条对角线的长分别是31010 .事件A必然事件随机事件 m 的值42、3DA21.解析:(1) 把A(1,3)代入k y x =得:3k =, 把B (,)23y 代入3y x=得:21y =,∴B(3,1). 把A(1,3),B(3,1)分别代入y ax b =+得:331a b a b ì+=ïí+=ïî,解得:14a b ì=-ïí=ïî,∴4AB y x =-+ ,令0AB y =,得4x =, ∴(,)40P (2) ∵AB PB =, ∴B 是AP 的中点,由中点坐标公式知:,1122622x yx y +==, ∵,A B 两点都在双曲线上,∴1111622x y x y +=?,解得12x =, ∴24x = . 作AD⊥x 于点D (如右图), 则△PAD ∽△PDO , ∴AD PD CO PO =,即146y b =, 又11b y =+, ∴12y = ,∴21y =. ∴(,),(,)2241A B(3) 结论:120x x x +=.理由如下:∵A (,11x y ),B (,22x y ),∴1122ax b y ax b y ì+=ïí+=ïî, ∴2112212121y y x y x y y x x x x x --=---令0y =,得122121x y x y x y y -=- ,∵1122x y x y =, ∴()()122121122121x y x y y y x x x y y y y --+==--=12x x + , 即120x x x +=22.解析:(1)如下图:xyCPBAODt /ss /m(2)填表如下:两人相遇次数(单位:次) 1234…n两人所跑路程之和(单位:m)100 300 500 700…100(2n -1)(3) ① =5S t 甲 (0≤t≤20) ,=-4100S t +乙 (0≤t ≤25). ② ()54100621t t +=创- , ∴ 11009t = , ∴第六次相遇t 的值是11009. 五、(本大题共10分)23.解析:(1)∵()222313y ax ax a a x =-++=-+, ∴min =3y ;∵(,),(,)M N -1311 ,∴当x <1时,L 1的y 值随着x 的增大而减小,当x >-1时, L 2 的y 值随着x 的增大而减小,∴x 的取值范围是x -<<11(2)∵(,),(,)M N -1311, ∴MN =∵(,),(,)Ea F a +-+0301,∴()EF aa a =+--=+3122, ∴a +=22,a =1如图,∵MN y x =+2, ∴(,)A 02,∴AM AN =AM AN = ∵a =1,∴(,(,E F -0202∴AE AF == ∴AE AF = ∴四边形ENFM 是平行四边形, 已知EF MN =,∴四边形ENFM是矩形(对角线相等且互相平分的四边形是矩形) (3)∵(,),(,)M N -1311,(,)A m 0,∴MN AM =① 当AM MN ==()m -=-211,等式不成立; ② 当AM AN =∴m =2;③ 当MN AN =,∴,(m m =1211舍去)x∴(,)A20或,)A10,∵()y a x=-++211的对称轴为x=-1,∴左交点坐标分别是(-4,0)或(-1,0),∴方程()a x-++=2110的解为,,,x x x x==-=-12342411.x七、(本大题共12分)24.解析:(1)如图1,连接EF,则EF是△ABC的中位线,∴EF=AB12=,∵∠ABE=45°,AE⊥EF ∴△ABP是等腰直角三角形,∵EF∥AB ,∴△EFP也是等腰直角三角形,∴a b==如图2,连接EF,则EF是△ABC的中位线.∵∠ABE=30°,AE⊥BF,AB=4,∴AP=2, BP=∵EF//AB12∴a=b=(2) a b c+=2225如图3,连接EF,设AP=m ,BP=n.,则c AB m n==+2222图1CA图2CB∵EF //AB 12, ∴PE=12BP=12n , PF=12AP=12m,∴AE m n =+22214 , BF n m =+22214,∴b AC AE m n ===+2222244, a BC BF n m ===+2222244 ∴()a b m n c +=+=2222255 (3)O M NPQBEG CD A如上图,延长EG,BC 交于点Q, 延长QD,BA 交于点P,延长QE,BE 分别交PB ,PQ 于点M,N,连接EF. ∵四边形ABCD 是平行四边形,∴AD //BC, AB //CD,∵E,G 是分别是AD,CD 的中点,∴△EDG≌△QCG≌△EAM, ∴CQ=DE=5, DG=AM=1.5,∴BM=4.5.∵CD CQ BP BQ =,∴BP =3535,∴BP=9, ∴M 是BP 的中点; ∵AD //FQ, ∴四边形ADQF 是平行四边形,∴AF∥P Q,∵E,F 分别是AD ,BC 的中点,∴AE //BF, ∴四边形ABFE 是平行四边形,∴OA=O F, 由AF∥PQ 得:,OF BF QN BQ ==51335OA BA PN BP ===3193, ∴OA OF PN QN =, ∴PN=QN, ∴N 是PQ 的中点; ∴△BQP 是“中垂三角形”, ∴()PQ BQ BP =-=?=2222255359144,∴PQ =12, ∴AF PQ ==143。
2015年江西省南昌市初三中考真题数学试卷(有答案)

■■■■(AA«.X«A<)■ ■♦20僅半•■ ■,円江西省南昌市2015年初中毕业登中,学校招生,试数学试题卷in^.f turn ixe#AJ B--I GO D.Xft£1 »U *W,-HCRH3 ■■■■姑建■了・300 000 公9tiE,fl|・・,・.•力■中Olll・t:• CMW"**(<><» 过(・2.0)J,.3]L•■么■院■的対■■'■只・是,1♦■■■右《|,在,健,2的左■AJ M I0»C03M MJ»DJO N IO11 下胃■■!£・,■(). • ■ 9■ m^vX・SL小11角了,・日以偌的不■定性.料网,,娥用个—・A ■ % D ■jfiLZ,,度日[圖■.所at»nA( x ' ♦E边部』乂为,冇覇边形职?的■度繽点■网8拿,&印的•風不■DU边静4皿的胃长不,i'®*' ■火.■ •小・■・小■,■.*.”)15, —,.严5..;.",■)<9 10«>:• EC,.■,,tt0O±. CO,・*H■“,点D w Z4«5(r. Z./»■»•< WX^DC 銷1,e*-元二_____________________________________________________,lto® I *小丰同孝•.上的一个•于力18IB 2富示的几何田用,已,"U】5gK/MCTr・・Q,HBC的屈||为_____________ anO^KBaiaJir-0.342.,0・・OMhSr・Q64Ls40・・0・7。
.场e■.珥用籽<ttt算■).」,.■JBSh 3. , .如5与•. ♦. ♦的弔除■再, 6.覇含髭为一■岐ttLKit 組》・的中•■为.■ ■■ •• A4此中ttffl 8上,_■題.・△用■方■角三4,的长为________________ .■分.,24 分)耽,化M.M»a:2<i(at26)-(at2A)\ JC, ■・〕. A«v<T .】■ W®.王方雁AMD如正方* A咼GP,,,事点中C期,■■■,Q.♦三■的•■分剧■(♦.♦). (0.3). C04).• )■>!*中心的熒辱:Q)■,U■丄C."•Cy.[•■<9:* 12使用文档IB. ■一♦不,明的K 子中眼,01,色不胃的《>,,■.■中UMt •个.■■ 6 t.子中■出从鯉子■■■■出 I ♦仲• .■出4. 3 I ■■”(2)能从铢孑中It 出■个■,,再故入-个一■的■勺,題机・出1个・是11*估■,・,,.史5的,nd*大■矣3小11.<1小■•分,编24分)盼.菱包为■,■■生!《£”,,使JH ♦机鎗*!!■■. ■,・・■》■生故,■料10,・ ■ .■出际,M0但.■位羊生的衣长I 份.■伊阿♦,善身一Mi 度,■岐约,•表行, ,(■设,收的何♦,可败).JHHI 了凶下肴,不■■的■卄,*1 •:•■以上,4専等下刑简')■•的问卷散为 __________ e/Fia 干,・■分■統■•角■■为 ______________ I. •一 " • .•(■苦尊・《|加询柯,■•从落不1T ■力■■黑不,•.巳,名■生.请•计■■ 对•于♦用手仇■■■■■.的■-大,•■:少人,tt*BUI«B3K (#6 1)精品文档使用文档=稣U 易聽库第一时间费供)易题座Worcfi中考苴冊答笑及解析wwwvnwucN 使用文档■」•大■■ 2•小.•分•■■■•)2X ♦.乙■ A<E 1<** ■■■通作■■•万専,分創.., ■,即■之胃的■200)t0 ■,■⑴,JW ■用■.瓷■下”康絡,exD,■■出,.乙隋人分,&* 一个loo,内“与并■出a M ・n ■•■790»时.,们11时相污,?若10,・食屋的几,,看不1111・,,速计,幔-,由・3 ID劉.巳■二■■數 原.・W ・2ar,z3 (见)■二■■敏(^>0>■ a^9点分明为,• M 与,常,别交于点£/・ ,)■,■ ■“・:《■,,SX ))fi9,小■力I lattyfllW 时■書■■■大■■小,. 1的,,陌・姫 __________ »(2)肖•的,.并例新,,是功H (的搜間出•♦•通,"⑴■二次MfcG 的图”対■■的右交点,,《叫,)・*,45为,・■♦,(,■>!)■西省年中等竿,招生考试数学试题参考答案及评分意见, 本■,的■■■也♦■■■♦♦,1・・的併四.■■■纳・霎,■■・■■,,:(,■,,■・分.ti不■厨■分•♦册的■鲁有•,,的・误,|1♦•分1 ■,覇■厝■分贼••承■,正・・刑at-,■!«的・■,■-一.艰■■(■,■■•小!■.■小■ 3分•興"分■,・■,一,■・,◎)IJI IB 3.D 4.C 3£ 6D二8 ,■■.・,■ 3 分.共24 分1,.皿A ・39. 3 10. 1!<FIL2S 11 14.1 13.6 K 2 A 2 VJ ・?VT ■ I 个■ I ■.■■■一个IP 1分•扣畫为出豆・。
2015年江西省南昌市中考数学试卷-答案

江西省南昌市2015年初中毕业暨中等学校招生考试数学答案解析第Ⅰ卷一、选择题 1.【答案】A【解析】∵()011-=,∴()01-的结果为1,故选:A 。
【考点】非零实数的零次幂 2.【答案】B【解析】科学记数法的表示形式为10n a ⨯的形式,其中110a ≤<,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n 是负数,将300 000用科学记数法表示为:5310⨯,故选:B 。
【考点】科学计数法表示较大的数 3.【答案】D【解析】A 中原式=48a ,错误;B 中原式=353a b ﹣,错误;C 中原式=1a ﹣,错误;D 中原式=()1ab b a a b a b---==---,正确;故选D 。
【考点】整式及分式的计算 4.【答案】C【解析】从左面看所得到的图形是正方形,切去部分的棱能看到,用实线表示,故选:C 。
【考点】几何体的三视图 5.【答案】C【解析】∵矩形框架ABCD ,B 与D 两点之间用一根橡皮筋拉直固定,然后向右扭动框架,∴AD BC =,AB DC =,∴四边形变成平行四边形,故A 正确;BD 的长度增加,故B 正确;∵拉成平行四边形后,高变小了,但底边没变,∴面积变小了,故C 错误;∵四边形的每条边的长度没变,∴周长没变,故D 正确,故选C 。
【考点】平行四边形的性质 6.【答案】D【解析】∵抛物线20y ax bx c a =++(>)过20(﹣,),23(,)两点,∴点20(﹣,)关于对称轴的对称点横坐标x 2满足:222x ﹣<<,∴12202x x +-<<,∴抛物线的对称轴在y 轴左侧且在直线2x =﹣的右侧,故选D 。
【考点】二次函数的性质第Ⅱ卷二、填空题 7.【答案】160°【解析】以为互为补角的两个角的和诗180°,所以有18020160︒︒=︒-,故答案为:160°。
江西省南昌市2015年中考数学试题(Word解析版)-推荐下载
1.计算 (1)0 的结果为(
A.1
B.-1
).
C.0
2.2015 年初,一列 CRH5 型高速车组进行了“300 000 公里正线运营考核”.标志着中国高铁车从“中
国制造”到“中国创新”的飞跃.将数 300 000 用科学记数法表示为( ).
A.3×106
3.下列运算正确的是( ).
A. (2a2 )3 6a6
.
别别
别 别 4别 别
A
B
第5题
D
C
8.不等式组 2
1
x
3x
1
0
的解集是
9.如图,OP 平分∠MON , PE⊥OM 于 E, PF⊥ON 于 F,OA=OB, 则图中有
O
M
E A
B
第9题
F N
P
.
10.如图,点 A, B, C 在⊙O 上,CO 的延长线交 AB 于点 D,∠A=50°,∠B=30°则∠ADC 的度数为
A. 四边形 ABCD 由矩形变为平行四边形
B. BD 的长度变大
C. 四边形 ABCD 的面积不变
D. 四边形 ABCD 的周长不变
6.已知抛物线 y ax2 bx c(a 0) 过(-2,0),(2,3)两点,那么抛物线的对称轴( ).
A.只能是 x 1
C.在 y 轴右侧且在直线 x 2 的左侧
(2)写出顶点 B, C, B1 , C1 的坐标.
.
17.⊙O 为△ABC 的外接圆,请仅用无刻度的直尺,根据下列条件分别在图 1,图 2 中画出一条弦,使这
第 2 页 共 13 页
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电通,力1根保过据护管生高线产中0不工资仅艺料可高试以中卷解资配决料置吊试技顶卷术层要是配求指置,机不对组规电在范气进高设行中备继资进电料行保试空护卷载高问与中题带资2负料2,荷试而下卷且高总可中体保资配障料置2试时32卷,3各调需类控要管试在路验最习;大题对限到设度位备内。进来在行确管调保路整机敷使组设其高过在中程正资1常料中工试,况卷要下安加与全强过,看度并25工且52作尽22下可护都能1关可地于以缩管正小路常故高工障中作高资;中料对资试于料卷继试连电卷接保破管护坏口进范处行围理整,高核或中对者资定对料值某试,些卷审异弯核常扁与高度校中固对资定图料盒纸试位,卷置编工.写况保复进护杂行层设自防备动腐与处跨装理接置,地高尤线中其弯资要曲料避半试免径卷错标调误高试高等方中,案资要,料求编试技5写、卷术重电保交要气护底设设装。备备置管4高调、动线中试电作敷资高气,设料中课并技3试资件且、术卷料中拒管试试调绝路包验卷试动敷含方技作设线案术,技槽以来术、及避管系免架统不等启必多动要项方高方案中式;资,对料为整试解套卷决启突高动然中过停语程机文中。电高因气中此课资,件料电中试力管卷高壁电中薄气资、设料接备试口进卷不行保严调护等试装问工置题作调,并试合且技理进术利行,用过要管关求线运电敷行力设高保技中护术资装。料置线试做缆卷到敷技准设术确原指灵则导活:。。在对对分于于线调差盒试动处过保,程护当中装不高置同中高电资中压料资回试料路卷试交技卷叉术调时问试,题技应,术采作是用为指金调发属试电隔人机板员一进,变行需压隔要器开在组处事在理前发;掌生同握内一图部线纸故槽资障内料时,、,强设需电备要回制进路造行须厂外同家部时出电切具源断高高习中中题资资电料料源试试,卷卷线试切缆验除敷报从设告而完与采毕相用,关高要技中进术资行资料检料试查,卷和并主检且要测了保处解护理现装。场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
2015年江西省南昌市中考数学试题及解析讲解

2015年江西省南昌市中考数学试卷一、选择题(本大题共 6小题,每小题3分,共18分,每小题只有一个正确选项)1.( 3分)(2015?南昌)计算(-1) 0的结果为() A . 1 B . - 1 C . 0 D .无意义2. (3分)(2015?南昌)2015年初,一列 CRH5型高速车组进行了 300000公里正线运营考 核”标志着中国高速快车从 中国制造”到中国创造”的飞跃,将300000用科学记数法表示为 ( )A . 3 XI06B . 5 3X 0C . 6 0.3X 0D . 4 30X 03. ( 3分)(2015?南昌)下列运算正确的是( )A (2a 2) 3 6 --------------------------------------------------- =6aB . ----- 2 2 3 -a b ?3ab = ------- 2 5 -3a bC .D . '+ = a a 2-l 3? = - 1 a+1 =-14. (3分)(2015?南昌)如图是将正方体切去一个角后形成的几何体,则该几何体的左视图 为( )jfl - 1■ * 1 * i 『* *1『/ .........11 L -------------- 1 IZ 佥面5. (3分)(2015?南昌)如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一 个矩形框架ABCD , B 与D 两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化,下列判断错误的是( )A .四边形ABCD 由矩形变为平行四边形B . BD 的长度增大C .四边形ABCD 的面积不变D .四边形ABCD 的周长不变26. ( 3分)(2015?南昌)已知抛物线 y=ax +bx+c (a >0)过(-2, 0), (2, 3)两点,那么 抛物线的对称轴() A .只能是x= - 1B .可能是y 轴C .在y 轴右侧且在直线 x=2的左侧D .在y 轴左侧且在直线 x= - 2的右侧9. ( 3 分)(2015?南昌)如图, OP 平分/ MON , PE 丄 OM 于 E , PF 丄 ON 于 F , OA=OB , 则图中有 _____________ 对全等三角形.10. (3分)(2015?南昌)如图,点A , B , C 在O O 上,CO 的延长线交 AB 于点D ,/ A=50 ° / B=30 °则/ ADC 的度数为 _________________ .2 211.(3分)(2015?南昌)已知一元二次方程 x - 4x - 3=0的两根为m , n ,则m -2 mn+n = ____________ .12.二、填空题(本大题共 (2015?南昌) 7. (3 分)8小题,每小题一个角的度数为 3分,共24分)20°则它的补角的度数为 (3分)(2015?南昌) 1<0的解集是-3x<9 集是(3分)(2015?南昌)如图1是小志同学书桌上的一个电子相框,将其侧面抽象为如图2所示的几何图形,已知BC=BD=15cm , / CBD=40 °则点B到CD的距离为 ________________ cm (参考数据sin20 ° 0.342, cos20° 0.940, sin40° 0.643 , cos40° 出766,结果精确到0.1cm , 可用科学计算器).13. (3分)(2015?南昌)两组数据:3, a, 2b, 5与a, 6, b的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的中位数为______________________ .14. (3分)(2015?南昌)如图,在△ ABC中,AB=BC=4 , AO=BO , P是射线CO上的一个动点,/ AOC=60 °则当△ PAB为直角三角形时,AP的长为_________________ .三、解答题(本大题共4小题,每小题6分,共24分)_15. (6 分)(2015?南昌)先化简,再求值:2a(a+2b)-(a+2b)2,其中a=- 1, b=;.16. (6分)(2015?南昌)如图,正方形ABCD于正方形A1B1C1D1关于某点中心对称,已知A , D1, D三点的坐标分别是(0, 4), (0, 3) , (0, 2).(1)求对称中心的坐标.(2)写出顶点B , C, B1, C1的坐标.17. (6分)(2015?南昌)0 O ABC的外接圆,请仅用无刻度的直尺,根据下列条件分别在图1,图2中画出一条弦,使这条弦将△ ABC分成面积相等的两部分(保留作图痕迹, 不写作法).(1)如图1, AC=BC ;(2)如图2,直线I与O O相切于点P,且I// BC .18. (6分)(2015?南昌)在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.(1 )先从袋子中取出m (m> 1)个红球,再从袋子中随机摸出1个球,将摸出黑球”记为事件A,请完成下列表格:事件A必然事件随机事件m的值(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于〉求m的值.四、解答题(本大题共3小题,每小题8分,共24分)19. (8分)(2015?南昌)某校为了了解学生家长对孩子使用手机的态度情况,随机抽取部分学生家长进行问卷调查,发出问卷140份,每位学生家长1份,每份问卷仅表明一种态度,将回收的问卷进行整理(假设回收的问卷都有效),并绘制了如图两幅不完整的统计图.学生赢长对孩子使用手机的态度情况统计图问卷数根据以上信息解答下列问题:(1 )回收的问卷数为___________ 份,严加干涉”部分对应扇形的圆心角度数为____________ .(2 )把条形统计图补充完整(3)若将稍加询问”和从来不管”视为管理不严”已知全校共1500名学生,请估计该校对孩子使用手机管理不严”的家长大约有多少人?20. (8 分)(2015?南昌)(1)如图1 ,纸片?ABCD 中,AD=5 , S?ABCD=15,过点A 作AE 丄BC,垂足为E,沿AE剪下△ ABE,将它平移至△ DCE 的位置,拼成四边形AEE 'D,则四边形AEE D的形状为______________________A •平行四边形B •菱形C.矩形D.正方形(2)如图2,在(1)中的四边形纸片AEE 'D中,在EE 上取一点F,使EF=4,剪下△ AEF , 将它平移至△ DE 'F的位置,拼成四边形AFF D •① 求证:四边形AFF D是菱形.21. (8分)(2015?南昌)如图,已知直线y=ax+b与双曲线沪二(x > 0)交于A (x i, y i),XB (X2, y2)两点(A与B不重合),直线AB与x轴交于P (X0, 0),与y轴交于点C.(1 )若A, B两点坐标分别为(1, 3) , (3, y2),求点P的坐标.(2)若b=y1+1,点P的坐标为(6, 0),且AB=BP,求A , B两点的坐标.(3)结合(1), (2)中的结果,猜想并用等式表示X1, X2, X0之间的关系(不要求证明).y八五、解答题(本大题共2小题,每小题9分,共18分)22. (9分)(2015?南昌)甲、乙两人在100米直道AB上练习匀速往返跑,若甲、乙分别中A , B两端同时出发,分别到另一端点处掉头,掉头时间不计,速度分别为5m/s和4m/s. (1)在坐标系中,虚线表示乙离A端的距离s (单位:m)与运动时间t (单位:s)之间的函数图象(0电€00),请在同一坐标系中用实线画出甲离A端的距离s与运动时间t之间的函数图象(0W€00);(2)根据(1)中所画图象,完成下列表格:两人相遇次数(单位:次)1 2 3 4n 两人所跑路程之 100 300②当t=390s 时,他们此时相遇吗?若相遇,应是第几次?若不相遇, 请通过计算说明理由, 并求出此时甲离A 端的距离. 2 23. (9分)(2015?南昌)如图,已知二次函数 L 1: y=ax - 2ax+a+3 ( a >0)和二次函数L 2: 2 y= - a (x+1) +1 (a > 0)图象的顶点分别为 M , N ,与y 轴分别交于点 E , F . (1) ________________________________________________ 函数y=ax 2 - 2ax+a+3 ( a > 0)的最小值为 _________________________________________________ ,当二次函数L 1, L 2的y 值同 时随着x 的增大而减小时,x 的取值范围是 ________________ .(2) 当EF=MN 时,求a 的值,并判断四边形 ENFM 的形状(直接写出,不必证明).(3) 若二次函数L 2的图象与x 轴的右交点为 A ( m , 0),当厶AMN 为等腰三角形时,求 2 方程-a (x+1) +1=0的解.六、解答题(本大题共 12分)24. (12分)(2015?南昌)我们把两条中线互相垂直的三角形称为称为中垂三角形”,例如 图1,图2,图3中,AF , BE 是厶ABC 的中线,AF 丄BE ,垂足为 卩,像厶ABC 这样的三 角形均称为 中垂三角形”,设BC=a , AC=b , AB=c .特例探索(1) 如图 1,当/ ABE=45 ° c=2时, a= _______________ , b= ____________ .如图 2,当/ ABE=30 °, c=4 时,a= ____________ , b= ____________ .归纳证明(2) 请你观察(1)中的计算结果,猜想 a 2, b 2, c 2三者之间的关系,用等式表示出来,并 利用图3证明你发现的关系式.拓展应用 _(3) 如图 4,在?ABCD 中,点 E 、F 、G 分别是 AD , BC , CD 的中点,BE 丄 EG , AD=2 ■., AB=3,和(单位:m )(3)① 直接写出甲、乙两人分别在第一个100m 内,s 与t 的函数解析式,并指出自变量 t的取值范围;求AF的长.2015年江西省南昌市中考数学试卷参考答案与试题解析一、选择题(本大题共 6小题,每小题3分,共18分,每小题只有一个正确选项)2. (3分)(2015?南昌)2015年初,一列 CRH5型高速车组进行了 300000公里正线运营考 核”标志着中国高速快车从 中国制造”到中国创造”的飞跃,将300000用科学记数法表示为 ( )6564A . 3XI0B . 3X 0C . 0.3X 0D . 30X 0考点:科学记数法 表示较大的数.分析::丿 科学记数法的表示形式为 a X 0n 的形式,其中1弓a|v 10, n 为整数.确定n 的值时, 要看把原数变成 a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.解答:丿 解:将300000用科学记数法表示为:3 X 05. 故选:B . 点评:J此题考查科学记数法的表示方法.科学记数法的表示形式为 a X 0n 的形式,其中1<|a| v 10, n 为整数,表示时关键要正确确定 a 的值以及n 的值.3. ( 3分)(2015?南昌)下列运算正确的是( A .a 2 -1考点:分式的乘除法;幕的乘方与积的乘方;单项式乘单项式;分式的加减法. 专题:计算题. 分析:A 、原式利用幕的乘方与积的乘方运算法则计算得到结果,即可做出判断;B 、 原式利用单项式乘以单项式法则计算得到结果,即可做出判断;C 、 原式约分得到结果,即可做出判断;D 、 原式变形后,利用同分母分式的减法法则计算,约分即可得到结果. 解答:解:A 、原式=8a 4,错误;2、36 (2a ) =6-a 2b 2?3ab 3分析:由将四根木条用钉子钉成一个矩形框架 ABCD , B 与D 两点之间用一根橡皮筋拉直固定,然后向右扭动框架,由平行四边形的判定定理知四边形变成平行四边形,由于四B 、 原式=-3a 3b 5,错误;-1C 、 原式=a ,错误;h 亠 b _ a - (a _ b ) 十/ D 、 原式= = ------------ : ------ =—1,正确;a ~b a b 故选D .点评:此题考查了分式的乘除法,幕的乘方与积的乘方,单项式乘单项式,以及分式的加减 法,熟练掌握运算法则是解本题的关键.4. (3分)(2015?南昌)如图是将正方体切去一个角后形成的几何体,则该几何体的左视图佥面考点:简单组合体的三视图.分析:找到从左面看所得到的图形即可,注意所有的看到的棱都应表现在视图中.解答:丿解:从左面看所得到的图形是正方形,切去部分的棱能看到,用实线表示, 故选:C . 点评::本题考查了三视图的知识,掌握主视图是从物体的正面看得到的视图, 左视图是从物 体的左面看得到的视图,俯视图是从物体的上面看得到的视图是解题的关键.5. (3分)(2015?南昌)如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一 个矩形框架ABCD , B 与D 两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所 得四边形的变化,下列判断错误的是(A •四边形ABCD 由矩形变为平行四边形B . BD 的长度增大C .四边形ABCD 的面积不变D .四边形ABCD 的周长不变 考点:矩形的性质;平行四边形的性质.边形的每条边的长度没变,所以周长没变;拉成平行四边形后,高变小了,但底边没变,所以面积变小了,BD的长度增加了.解答:丿解 : :•矩形框架ABCD , B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,••• AD=BC , AB=DC ,•••四边形变成平行四边形,故A正确;BD的长度增加,故B正确;•••拉成平行四边形后,高变小了,但底边没变,•面积变小了,故C错误;•••四边形的每条边的长度没变,•周长没变,故D正确,故选C.点评::| j 本题主要考查了矩形的性质和平行四边形的性质,弄清图形变化后的变量和不变量是解答此题的关键.26. (3分)(2015?南昌)已知抛物线y=ax +bx+c (a>0)过(-2, 0), (2, 3)两点,那么抛物线的对称轴()A .只能是x= - 1B .可能是y轴C .在y轴右侧且在直线x=2的左侧D .在y轴左侧且在直线x= - 2的右侧考点:「二次函数的性质.分析::1根据题意判疋点(2, 0)关于对称轴的对称点横坐标X2满足:2< X2< 2,从而得出- 2< ' < 0,即可判定抛物线对称轴的位置.2解答:丿2解:•••抛物线y=ax+bx+c (a>0)过(-2, 0), (2, 3)两点,••点(2, 0)关于对称轴的对称点横坐标X2满足:2<X2< 2,X 1 + X 9•- 2< ' < 0,2•抛物线的对称轴在y轴左侧且在直线x= - 2的右侧.点评:本题考查了二次函数的性质,根据点坐标判断出另一个点的位置是解题的关键.二、填空题(本大题共8小题,每小题3分,共24分)7. (3分)(2015?南昌)一个角的度数为20°则它的补角的度数为160°考点:余角和补角.分析:根据互为补角的两个角的和等于180冽式进行计算即可得解.解答:丿解: 180°- 20°=160°故答案为:160 °点本题考查了余角和补角,解决本题的关键是熟记互为补角的和等于180 °1<0& ( 3分)(2015?南昌)不等式组* 2的解集是 -3v x Q-3x<9考点:解一兀一次不等式组. 专题: 计算题.分析:: 分别求出不等式组中两不等式的解集,找出解集的公共部分即可. 解答: 解: ’由① 由② - i<oO, -3K <9@得: x<2, 得:x >- 3,右式组的解集为-3 v x 电.{为:-3 v x 电点评:J比题考查了解一兀一次不等式组,熟练掌握运算法则是解本题的关键. 9. ( 3 分)(2015?南昌)如图, OP 平分/ MON , PE 丄 OM 于 E , PF 丄 ON 于 F , OA=OB , 则图中有 3对全等三角形.考点:全等三角形的判定;角平分线的性质.分析: 由OP 平分/ MON , PE 丄OM 于E , PF 丄ON 于F ,得到PE=PF ,Z 1 = / 2,证得△ AOPBOP ,再根据△ AOPBOP ,得出 AP=BP ,于是证得△ AOPBOP ,A 解答:丿 解 : OP 平分/ MON , PE 丄 OM 于 E , PF 丄 ON 于 F , •• PE=PF ,Z 1 = / 2,&△ AOP 与厶BOP 中,r0A=0BZ>Z2, QP 二 OPAOP 也厶 BOP , •• AP=BP ,&△ EOP 与厶FOP 中,rzi=Z2ZOEP=ZOFP=90* , t OP=OPAOP BA BOP ,在R t A AOP 与R t△ BOP 中,/PA=PB1PE=P?••• R t△ AOP也R t△ BOP ,•••图中有3对全等三角形,故答案为:3.点评:本题考查了角平分线的性质,全等三角形的判定和性质,熟练掌握全等三角形的判定定理是解题的关键.10. (3分)(2015?南昌)如图,点A , B, C在O O上,CO的延长线交AB于点D,/ A=50 ° / B=30 °则/ ADC的度数为110°.考点:圆周角定理.分析:根据圆周角定理求得/ BOC=100 °进而根据三角形的外角的性质求得/ BDC=70 °然后根据邻补角求得/ ADC的度数.解答:丿解 : A=50 °•••/ BOC=2 / A=100 °•••/ B=30 ° ° / BOC= / B+?BDC ,•••/ BDC= / BOC -Z B=100。
2015年江西省南昌市中考数学试卷(含详细答案)

数学试卷 第1页(共34页) 数学试卷 第2页(共34页)绝密★启用前江西省南昌市2015年初中毕业暨中等学校招生考试数 学本试卷满分120分,考试时间120分钟.第Ⅰ卷(选择题 共18分)一、选择题(本大题共6小题,每小题3分,共18分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.计算0(1)的结果为 ( )A .1B .1-C .0D .无意义 2.2015年初,一列CRH5型高速车组进行了“300000千米正线运营考核”,标志着中国高铁车从“中国制造”到“中国创新”的飞跃.将数300000用科学记数法表示为( ) A .6310⨯ B .5310⨯ C .60.310⨯ D .43010⨯3.下列运算正确的是 ( ) A .236(2)6a a =B .2232533a b ab a b -=-C .21111a a a -=-+D .1b a a b b a+=--- 4.如图是将正方体切去一个角后形成的几何体,则该几何体的左视图为( )5.如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD ,B 与D 两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化.下列判断错误的是 ( ) A .四边形ABCD 由矩形变为平行四边形 B .BD 的长度增大C .四边形ABCD 的面积不变 D .四边形ABCD 的周长不变6.已知抛物线2(0)y ax bx c a =++>过(2,0),(2,3)-两点,那么抛物线的对称轴 ( ) A .只能是1x =- B .可能是y 轴C .在y 轴右侧且在直线2x =的左侧D .在y 轴左侧且在直线2x =-的右侧第Ⅱ卷(非选择题 共102分)二、填空题(本大题共8小题,每小题3分,共24分.把答案填写在题中的横线上) 7.一个角的度数是20,则它的补角的度数为 .8.不等式组11023x x ⎧-⎪⎨⎪-⎩≤<9的解集是 .9.如图,OP 平分MON ∠,PE OM ⊥于点E ,PE ON ⊥于点F ,OA OB =,则图中 有 对全等三角形.10.如图,点,,A B C 在O 上,CO 的延长线交AB 于点D ,50,30A B ∠=∠=则ADC ∠的度数为 .11.已知一元二次方程2430x x --=的两根为,m n ,则22m mn n -+= .12.如图1是小志同学书桌上的一个电子相框,将其侧面抽象为如图2所示的几何图形,已知15cm AB AC ==,40BAC ∠=,则点A 到BC 的距离为 cm (参考数据:sin200.342,cos200.940,sin400.643,cos400.766.≈≈≈≈结果精确到0.1cm ,可用科学计算器).13.两组数据:3,,2,5a b 与,6,a b 的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的中位数为 .14.如图,在ABC △中,4AB BC ==,AO BO =,P 是射线CO 上的一个动点,60AOC ∠=,则当PAB △为直角三角形时,AP 的长为.AB C D 毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第3页(共34页) 数学试卷 第4页(共34页)三、解答题(本大题共10小题,共78分.解答应写出文字说明、证明过程或演算步骤) 15.(本小题满分6分)先化简,再求值:22(2)(2)a a b a b +-+,其中1,3a b =-=.16.(本小题满分6分)如图,正方形ABCD 与正方形1111A B C D 关于某点中心对称.已知1,,A D D 三点的坐标分别是(0,4),(0,3),(0,2). (1)求对称中心的坐标;(2)写出顶点11,,,B C B C 的坐标.17.(本小题满分6分)O 为ABC △的外接圆,请仅用无刻度的直尺,根据下列条件分别在图1,图2中画出一条弦,使这条弦将ABC △分成面积相等的两部分(保留作图痕迹,不写作法).(1)如图1,AC BC =;(2)如图2,直线l 与O 相切于点P ,且l BC ∥.18.(本小题满分6分)在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个. (1)先从袋子中取出() 1m m >个红球,再从袋子中随机摸出1个球.将“摸出黑球”记为事件事件A 必然事件随机事件m 的值(2)先从袋子中取出m 个红球,再放入m 个一样的黑球并摇匀,随机摸出1个球是黑球的概率等于45,求m 的值.19.(本小题满分8分)某校为了了解学生家长对孩子使用手机的态度情况,随机抽取部分学生家长进行问卷调查,发出问卷140份,每位学生的家长1份,每份问卷仅表明一种态度.将回收的问卷进行整理(假设回收的问卷都有效),并绘制了如下两幅不完整的统计图.学生家长对孩子使用手机的态度情况统计图根据以上信息解答下列问题: (1)回收的问卷数为 份,“严加干涉”部分对应扇形的圆心角度数为 ; (2)把条形统计图补充完整;(3)若将“稍加询问”和“从来不管”视为“管理不严”,已知学校共1500名学生,请估计该校对孩子使用手机“管理不严”的家长大约有多少人?20.(本小题满分8分)(1)如图1,纸片□ABCD 中,5AD =,15ABCDS =.过点A 作AE BC ⊥,垂足为E ,沿AE 剪下ABE △,将它平移至DCE '△的位置,拼成四边形AEE D ',则四边形AEE D'的形状为 ( )A .平行四边形B .菱形C .矩形D .正方形(2)如图2,在(1)中的四边形纸片AEE D '中,在EE '上取一点F ,使4EF =,剪下AEF △,将它平移至DE F ''△的位置,拼成四边形AFF D '. ①求证:四边形AFF D '是菱形;②求四边形AFF D '的两条对角线的长.l图2图1AO OCBBCA类别问卷数严加干涉稍加询问从来不管从来不管 25%严加干涉稍加询问1090705030100806040020图2图1ADDA数学试卷 第5页(共34页) 数学试卷 第6页(共34页)21.(本小题满分8分)如图,已知直线y ax b =+与双曲线(0)ky x x=>交于1122(,)(,)A x y B x y ,两点(A 与 B 不重合),直线AB 与x 轴交于点0(,0)P x ,与y 轴交于点C . (1)若,A B 两点坐标分别为2(1,3),(3,)y ,求点P 的坐标; (2)若11b y =+,点P 的坐标为6,0(),且AB BP =,求,A B 两点的坐标; (3)结合(1)(2)中的结果,猜想并用等式表示120,,x x x 之间的关系(不要求证明).22.(本小题满分9分)甲、乙两人在100米直道AB 上练习匀速往返跑,若甲、乙分别在,A B 两端同时出发,分别到另一端点处掉头,掉头时间不计,速度分别5m /s 和4m /s . (1)在坐标系中,虚线表示乙离A 端的距离s (单位:m )与运动时间t (单位:s )之间的函数图象(0200)t ≤≤,请在同一坐标系中用实线画出甲离A 端的距离s 与运动时间t 之间的函数图象(0200)t ≤≤;两人相遇次数(单位:次)1234…n两人所跑路程之和(单位:m )100 300… t 的取值范围;②当390s t =时,他们此时相遇吗?若相遇,应是第几次?若不相遇,请通过计算说理由,并求此时甲离A 端的距离.23.(本小题满分9分)如图,已知二次函数21:23(0)L y ax ax a a =-++>和二次函数22:(1)1L y a x =-++(0)a >图象的顶点分别为M ,N ,与y 轴分别交于点E ,F .(1)函数223(0)y ax ax a a =-++>的最小值为 ;当二次函数12L L ,的y 值同时随着x 的增大而减小时,x 的取值范围是 ;(2)当EF MN =时,求a 的值,并判断四边形ENFM 的形状(直接写出,不必证明); (3)若二次函数2L 的图象与x 轴的右交点为(,0)A m ,当AMN △为等腰三角形时,求方程2(1)10a x -++=的解.24.(本小题满分12分)我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,,AF BE 是ABC △的中线,AF BE ⊥,垂足为P ,像ABC △这样的三角形均为“中垂三角形”.设BC a =,AC b =,AB c =.特例探索(1)如图1,当45ABE ∠=,22c =,a = ,b = ; 如图2,当30ABE ∠=,4c =时,a = ,b = ;归纳证明(2)请你观察(1)中的计算结果,猜想222,,a b c 三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式;毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第7页(共34页) 数学试卷 第8页(共34页)拓展应用(3)如图4,在□ABCD 中,点,,E F G 分别是,,AD BC CD 的中点,BE EG ⊥,25AD =,3AB =.求AF 的长.5 / 17江西省南昌市2015年初中毕业暨中等学校招生考试数学答案解析第Ⅰ卷一、选择题 1.【答案】A【解析】∵()011-=,∴()01-的结果为1,故选:A 。
最新江西省中考数学试题及答案解析(Word版)

准考证号 姓名(在此卷上答题无效)机密★2015年6月19日江西省2015年中等学校招生考试数学试题卷说明:1.本卷共有六个大题,24个小题,全卷满分120分,考试时间120分钟.2.本卷分为试题卷和答题卷,答案要求写在答题卷上,不得在试题卷上作答,否则不给分.一、选择题(本大题共6小题,每小题3分,共18分.每小题只有一个正确选项) 1.计算(-1)°的结果为( ) A .1B .-1C .0D .无意义2.2015年初,一列CRH5型高速车组进行了“300 000公里正线运营考核”,标志着中国高铁车从“中国制造”到“中国创新”的飞跃.将数300 000用科学计数法表示为( ) A .6310⨯B .5310⨯C .60.310⨯D .43010⨯3.如图所示的几何体的左视图为( )4.下列运算正确的是( )A .236(2)6a a =B .2232533a b ab a b -•=-C .1b a a b b a+=---D .21111a a a -•=-+ 5.如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD ,B 与D 两点之间用一根橡皮筋...拉直固定,然后向右扭动框架,观察所得四边形的变化.下面判断错误..的是( ) A .四边形ABCD 由矩形变为平行四边形B .BD 的长度增大C .四边形ABCD 的面积不变D .四边形ABCD 的周长不变6.已知抛物线y =ax 2+bx +c (a >0)过(-2,0),(2,3)两点,那么抛物线的对称轴( ) A .只能是x =-1B .可能是y 轴C .在y 轴右侧且在直线x =2的左侧D .在y 轴左侧且在直线x =-2的右侧二、填空题(本大题共8小题,每小题3分,共24分) 7.一个角的度数为20°,则它的补角的度数为 .8.不等式组110239x x ⎧-⎪⎨⎪-<⎩≤,的解集是 .9.如图,OP 平分∠MON ,PE ⊥OM 于E ,PF ⊥ON 于F ,OA =OB .则图中有 对全等三角形.10.如图,点A ,B ,C 在⊙O 上,CO 的延长线交AB 于点D ,∠A =50°,∠B =30°,则∠ADC 的度数为 .11.已知一元二次方程x 2-4x -3=0的两根为m ,n ,则m 2-mn +n 2= . 12.两组数据:3,a ,2b ,5与a ,6,b 的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的中位数为 .13.如图1是小志同学书桌上的一个电子相框,将其侧面抽象为如图2所示的几何图形,已知BC =BD =15cm ,∠CBD =40°,则点B 到CD 的距离为 cm(参考数据:sin20°≈0.342,cos20°≈0.940,sin40°≈0.643,cos40°≈0.766.计算结果精确到0.1cm ,可用科学计算器).14.如图,在△ABC 中,AB =BC =4,AO =BO ,P 是射线CO 上的一个动点,∠AOC =60°,则当△P AB 为直角三角形时,AP 的长为 . 第10题第9题O三、(本大题共4小题,每小题6分,共24分)15.先化简,再求值:22(2)(2)a a b a b +-+,其中1a =-,b =16.如图,正方形ABCD 与正方形A 1B 1C 1D 1关于某点中心对称.已知A ,D 1,D 三点的坐标分别是(0,4),(0,3),(0,2). (1)求对称中心的坐标;(2)写出顶点B ,C ,B 1,C 1的坐标.17.⊙O 为△ABC 的外接圆,请仅用无刻度的直尺........,根据下列条件分别在图1,图2中画出一条弦.,使这条弦将△ABC 分成面积相等的两部分(保留作图痕迹,不写作法). (1)如图1,AC =BC ; (2)如图2,直线l 与⊙O相切与点P ,且l ∥B C .(第14题)(第13题)图2图1ABxlPAA18.在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个. (1)先从袋子中取出m (m >1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A .请完成下列表格:(2)先从袋子中取出m 个红球,再放入m 个一样的黑球并摇匀,随机摸出1个球是黑球的概率等于45,求m 的值.四、(本大题共4小题,每小题8分,共32分)19.某校为了了解学生家长对孩子使用手机的态度情况,随机抽取部分学生家长进行问卷调查,发出问卷140份,每位学生的家长1份,每份问卷仅表明一种态度.将回收的问卷进行整理(假设回收的问卷都有效),并绘制了如下两幅不完整的统计图. 学生家长对孩子使用手机的态度情况统计图类别严加干涉稍加询问从来不管从来不管 25%严加干涉稍加询问根据以上信息回答下列问题:(1)回收的问卷数为 份,“严加干涉”部分对应扇形的圆心角度数为 ; (2)把条形统计图补充完整;(3)若将“稍加询问”和“从来不管”视为“管理不严”,已知全校共1500名学生,请估计该校对孩子使用手机“管理不严”的家长大约有多少人?20.(1)如图1,纸片□ABCD 中,AD =5,S □ABCD =15.过点A 作AE ⊥BC ,垂足为E ,沿AE 剪下△ABE ,将它平移至△DCE'的位置,拼成四边形AEE'D ,则四边形AEE'D 的形状为( )A .平行四边形B .菱形C .矩形D .正方形(2)如图2,在(1)中的四边形纸片AEE'D 中,在EE'上取一点F ,使EF =4,剪下△AEF ,将它平移至△DE'F'的位置,拼成四边形AFF'D . ①求证:四边形AFF'D 是菱形; ②求四边形AFF'D 的两条对角线的长.图2图121.如图,已知直线y =ax +b 与双曲线(0)ky x x=>交于A (x 1,y 1),B (x 2,y 2)两点(A 与B 不重合),直线AB 与x 轴交于点P (x 0,0),与y 轴交于点C . (1)若A ,B 两点坐标分别为(1,3),(3,y 2).求点P 的坐标;(2)若b =y 1+1,点P 的坐标为(6,0),且AB =BP ,求A ,B 两点的坐标; (3)结合(1),(2)中的结果,猜想并用等式表示x 1,x 2,x 0之间的关系(不要求证明).x22.甲、乙两人在100米直道AB 上练习匀速往返跑,若甲、乙分别在A ,B 两端同时出发,分别到另一端点掉头,掉头时间不计,速度分别为5m/s 和4m/s .(1)在坐标系中,虚线表示乙离..A .端.的距离s (单位:m)与运动时间t (单位:s)之间的函数图象(0≤t ≤200),请在同一坐标系中用实线画出甲离A 端的距离s 与运动时间t 之间的函数图象(0≤t ≤200);(2)根据(1)中所画图象,完成下列表格:(3)①直接写出甲、乙两人分别在第一个100m 内,s 与t 的函数解析式,并指出自变量t 的取值范围;②求甲、乙第6此相遇时t 的值.五、(本大题共10分)23.如图,已知二次函数L 1:y =ax 2-2ax +a +3(a >0)和二次函数L 2:y =-a (x +1)2+1(a >0)图像的顶点分别为M ,N ,与y 轴分别交于点E ,F .(1)函数y =ax 2-2ax +a +3(a >0)的最小值为 ;当二次函数L 1,L 2的y 值同时随着x 的增大而减小时,x 的取值范围是 ;(2)当EF =MN 时,求a 的值,并判断四边形ENFM 的形状(直接写出,不必证明); (3)若二次函数L 2的图象与x 轴的右交点为A (m ,0),当△AMN 为等腰三角形时,求方程-a (x +1)2+1=0的解.sS /m------O六、(本大题共12分)24.我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.特例探索(1)如图1,当∠ABE=45°,c=a=,b=;如图2,当∠ABE=30°,c=4时,a=,b=;图3图2图1A B A归纳证明(2)请你观察(1)中的计算结果,猜想a2,b2,c2三者之间的关系,用等式表示出来,请利用图3证明你发现的关系式;拓展应用(3)如图4,在□ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=AB=3.求AF的长.EA2015年江西省中考数学解析一、选择题(本大题共6小题,每小题3分,共18分,每小题只有一个正确选项) 1.解析:选A. ∵除0外,任何数的0次方等于1. ∴选A.2.解析:选B. ∵科学记数法是:把一个数写成“10´n a ,其中1≤a <10”. ∴选B.3.解析:选D. ∵()1b a b a b a a b a b b a a b a b a b a b---+=-===------- . ∴选D. 4.解析:选C. ∵根据光的正投影可知,几何体的左视图是图C. ∴选C.5.解析:选C. ∵向右扭动框架, 矩形变为平行四边形 ,底长不变,高变小,所以面积变小. ∴选C.6.解析:选D. ∵抛物线2(0)y ax bx c a =++>过(-2,0),(2,3)两点,∴420423a b c a b c ì-+=ïí++=ïî,解得34b =,∴对称轴3028b x a a=-=-<,又对称轴在(-2,2)之间, ∴选D.二、填空题(本大题共8小题,每小题3分,共24分) 7.解析:∵两角互补,和为180°,∴它的补角=180°-20°=160°. 8.解析: 由112x -≤0得x ≤2 ,由-3x <9得x >-3,∴不等式组的解集是-3<x ≤2. 9.解析:∵∠POE=∠POF, ∠PEO=∠PFO=90°OP=OP ,∴△POE ≌△POF(AAS), 又OA=OB,∠POA=∠POB,OP=OP ,∴△POA ≌△POB(AAS), ∴PA=PB,∵PE=PF, ∴Rt △PAE ≌Rt △PBF(HL). ∴图中共有3对全的三角形.10.解析:∵∠A=50°, ∴∠BOC=100°, ∴∠BOD=80°, ∴∠ADC=∠B+∠BOD=30°+ 80°=110° 11.解析:由一元二次方程根与系数关系得m +n =4,mn =﹣3,又()2223m mn n m n mn -+=+- ∴原式=()243325-?=.12.解析:由题意得32564663a b a b ì+++=ïïí++ï=ïî ,解得84a b ì=ïí=ïî,∴这组新数据是3,4,5,6,8,8,8,其中位数是6.13.解析:如右图,作BE ⊥CD 于点E.∵BC=BD, BE ⊥CD, ∴∠CBE=∠DBE=20°, 在Rt △BCD 中,cos ,BEDBE=BDÐ ∴cos BE 2015?, ∴BE≈15×0.940=14.114.解析:如图,分三种情况讨论:图(1)中,∠APB=90°,∵AO=BO, ∠APB=90°,∴PO=AO=BO=2, 又∠AOC=60°, ∴△APO 是等边三角形,∴AP=2;图(2)中,∠APB=90°,∵AO=BO, ∠APB=90°,∴PO=AO=BO=2,又∠AOC=60°, ∴∠BAP=30°,在Rt △ABP 中,AP=cos30°×4= .图(3)中,∠ABP=90°, ∵BO=AO=2 , ∠BOP=∠AOC=60°, ∴PB=∴= ∴AP 的长为2,或三、(本大题共4小题,每小题6分,共24分)15.解析:原式 ()[()]()()22222224a b a a b a b a b a b =+-+=+-=-把,1a =-b ==()221411--?-16.解析:(1) ∵正方形ABCD 与正方形A 1B 1C 1D 1关于某点中心对称, ∴A,A 1 是对应点,∴AA 1 的中点是对称中心, ∵A(0,4),D(2,0),∴AD=2, ∴A 1D 1 = AD=2, 又∵D 1(0,3) ,∴A 1(0,1), ∴对称中心的坐标为(0, 2.5);(2)∵正方形的边长为2, 点A,D 1 ,D ,A 1在y 轴上,∴B(-2,4), C(-2,2), B 1(2,1), C 1(2,3) .17.解析:如右图所示.(1)BA(2)BA(3)Ax图1,∵AC=BC,∴))AC BC =,∴点C 是)AB 的中点,连接CO ,交AB 于点E ,由垂径定理知, 点E 是AB 的中点, 延长CE 交⊙O 于点D , 则CD 为所求作的弦;图2,∵l 切⊙O 于点P , 作射线PO ,交BC 于点E ,则PO ⊥l , ∵l ∥BC , ∴PO ⊥BC, 由垂径定理知,点E 是BC 的中点,连接AE 交⊙O 于F ,则AF 为所求作的弦. 18. 解析:(1)若事件A 为必然事件,则袋中应全为黑球,∴m=4, 若事件A 为随机事件,则袋中有红球,∵m>1 ,∴m=2或3.(2)64105m +=, ∴m=2 .四、(本大题共4小题,每小题8分,共32分)19.解析:(1) 30÷25%=120 10÷120×360°=30° ∴回收的问卷数为120份,圆心角的度数为30°(2) 如下图:(3) (30+80)÷120×1500=1375 ∴对孩子使用手机“管理不严”的家长大约有1375人.严加干涉稍加询问从来不管20.解析:(1) 由平移知:AE //DE ′, ∴四边形AEE ′D 是平行四边形,又AE ⊥BC, ∴∠AEE ′=90°,∴四边形AEE ′D 是矩形,∴C 选项正确.(2) ① ∵AF //DF ′, ∴四边形AFF ′D 是平行四边形,∵AE=3, EF=4 ,∠E=90°, ∴AF=5,l图2图1AA∵S □ABCD =AD·AE=15, ∴AD=5 , ∴AD=AF , ∴四边形AFF ′D 是菱形. ② 如下图, 连接AF ′, DF ,在Rt △AEF ′中, AE=3, EF ′=9, ∴AF ′= 在Rt △DFE ′中, FE ′=1, DE ′=AE=3, ∴∴四边形AFF ′D两条对角线的长分别是.21.解析:(1) 把A(1,3)代入k y x =得:3k =, 把B (,)23y 代入3y x=得:21y =,∴B(3,1). 把A(1,3),B(3,1)分别代入y ax b =+得:331a b a b ì+=ïí+=ïî,解得:14a b ì=-ïí=ïî,∴4AB y x =-+ ,令0AB y =,得4x =, ∴(,)40P (2) ∵AB PB =, ∴B 是AP 的中点,由中点坐标公式知:,1122622x yx y +==, ∵,A B 两点都在双曲线上,∴1111622x y x y +=?,解得12x =, ∴24x = . 作AD ⊥x 于点D (如右图), 则△PAD ∽△PDO , ∴AD PD CO PO =,即146y b =, 又11b y =+, ∴12y = ,∴21y =. ∴(,),(,)2241A B(3) 结论:120x x x +=.理由如下:∵A (,11x y ),B (,22x y ),∴1122ax b y ax b y ì+=ïí+=ïî, ∴2112212121y y x y x y y x x x x x --=---x令0y =,得122121x y x y x y y -=- ,∵1122x y x y =, ∴()()122121122121x y x y y y x x x y y y y --+==-- =12x x + , 即120x x x +=22.解析:(1)如下图:t /ss /m(2(3) ① =5S t 甲 (0≤t≤20) ,=-4100S t +乙 (0≤t ≤25). ② ()54100621t t +=创- , ∴ 11009t = , ∴第六次相遇t 的值是11009.五、(本大题共10分)23.解析:(1)∵()222313y ax ax a a x =-++=-+, ∴min =3y ;∵(,),(,)M N -1311 ,∴当x <1时,L 1的y 值随着x 的增大而减小,当x >-1时,L 2 的y 值随着x 的增大而减小, ∴x 的取值范围是x -<<11(2)∵(,),(,)M N -1311, ∴MN =∵(,),(,)E aF a +-+0301,∴()EF a a a =+--=+3122, ∴a +=22,a =1如图,∵MN y x =+2, ∴(,)A 02,∴AM AN =AM AN = ∵a 1,∴(,(,E F -0202∴AE AF = ∴AE AF =∴四边形ENFM 是平行四边形, 已知EF MN =,∴四边形ENFM 是矩形(对角线相等且互相平分的四边形是矩形)(3)∵(,),(,)M N -1311,(,)A m 0,∴MN AM =① 当AM MN ==()m -=-211,等式不成立; ② 当AM AN =∴m =2; ③ 当MN AN =,∴,(m m =-1211舍去)∴(,)A 20或,)A 10, ∵()y a x =-++211的对称轴为x =-1, ∴左交点坐标分别是(-4,0)或(-1,0),∴方程()a x -++=2110的解为 ,,,x x x x ==-=12342411.x六、(本大题共12分) 24. 解析:(1)如图1,连接EF,则EF 是△ABC 的中位线, ∴EF=AB 12∵∠ABE=45°,AE ⊥EF ∴△ABP 是等腰直角三角形,∵EF ∥AB ,∴△EFP 也是等腰直角三角形, ∴AP=BP=2 ,EP=FP=1,∴, ∴a b ==如图2,连接EF,则EF 是△ABC 的中位线. ∵∠ABE=30°,AE ⊥BF,AB=4, 图1CA∴AP=2, BP= ∵EF //AB 12, ∴,PF=1, ∴∴a =, b = (2) a b c +=2225如图3,连接EF , 设AP=m ,BP=n.,则c AB m n ==+2222∵EF //AB 12, ∴PE=12BP=12n , PF=12AP=12m, ∴AE m n =+22214 , BF n m =+22214,∴b AC AE m n ===+2222244, a BC BF n m ===+2222244 ∴()a b m n c +=+=2222255 (3)如上图,延长EG,BC 交于点Q, 延长QD,BA 交于点P ,延长QE,BE 分别交PB ,PQ 于点M,N,连接EF. ∵四边形ABCD 是平行四边形,∴AD //BC, AB //CD,∵E,G 是分别是AD,CD 的中点,∴△EDG ≌△QCG ≌△EAM, ∴,∴BM=4.5.∵CD CQ BP BQ =,∴BP 3,∴BP=9, ∴M 是BP 的中点;图3A∵AD //FQ, ∴四边形ADQF 是平行四边形,∴AF ∥PQ,∵E,F 分别是AD ,BC 的中点,∴AE //BF, ∴四边形ABFE 是平行四边形,∴OA=OF, 由AF ∥PQ 得:,OF BF QN BQ ==13OA BA PN BP ===3193, ∴OA OF PN QN =, ∴PN=QN, ∴N 是PQ 的中点;∴△BQP 是“中垂三角形”, ∴(PQ BQ BP =-=?=22222559144,∴PQ =12, ∴AF PQ ==143。
2015年江西省南昌市中考数学试题及解析

2015年江西省南昌市中考数学试卷一、选择题(本大题共6小题,每小题3分,共18分,每小题只有一个正确选项)2.(3分)(2015•南昌)2015年初,一列CRH5型高速车组进行了“300000公里正线运营考核”标志着中国高速快. (2a )=6a B . ﹣a b •3ab =﹣3a b •=﹣1+=﹣14.(3分)(2015•南昌)如图是将正方体切去一个角后形成的几何体,则该几何体的左视图为( )CD5.(3分)(2015•南昌)如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD ,B 与D 两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化,下列判断错误的是( )2)二、填空题(本大题共8小题,每小题3分,共24分)7.(3分)(2015•南昌)一个角的度数为20°,则它的补角的度数为.8.(3分)(2015•南昌)不等式组的解集是.9.(3分)(2015•南昌)如图,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB,则图中有对全等三角形.10.(3分)(2015•南昌)如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC 的度数为.11.(3分)(2015•南昌)已知一元二次方程x2﹣4x﹣3=0的两根为m,n,则m2﹣mn+n2=.12.(3分)(2015•南昌)如图1是小志同学书桌上的一个电子相框,将其侧面抽象为如图2所示的几何图形,已知BC=BD=15cm,∠CBD=40°,则点B到CD的距离为cm(参考数据sin20°≈0.342,cos20°≈0.940,sin40°≈0.643,cos40°≈0.766,结果精确到0.1cm,可用科学计算器).13.(3分)(2015•南昌)两组数据:3,a,2b,5与a,6,b的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的中位数为.14.(3分)(2015•南昌)如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为.三、解答题(本大题共4小题,每小题6分,共24分)15.(6分)(2015•南昌)先化简,再求值:2a(a+2b)﹣(a+2b)2,其中a=﹣1,b=.16.(6分)(2015•南昌)如图,正方形ABCD于正方形A1B1C1D1关于某点中心对称,已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).(1)求对称中心的坐标.(2)写出顶点B,C,B1,C1的坐标.17.(6分)(2015•南昌)⊙O为△ABC的外接圆,请仅用无刻度的直尺,根据下列条件分别在图1,图2中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法).(1)如图1,AC=BC;(2)如图2,直线l与⊙O相切于点P,且l∥BC.18.(6分)(2015•南昌)在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格:(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于,求m的值.四、解答题(本大题共3小题,每小题8分,共24分)19.(8分)(2015•南昌)某校为了了解学生家长对孩子使用手机的态度情况,随机抽取部分学生家长进行问卷调查,发出问卷140份,每位学生家长1份,每份问卷仅表明一种态度,将回收的问卷进行整理(假设回收的问卷都有效),并绘制了如图两幅不完整的统计图.根据以上信息解答下列问题:(1)回收的问卷数为份,“严加干涉”部分对应扇形的圆心角度数为.(2)把条形统计图补充完整(3)若将“稍加询问”和“从来不管”视为“管理不严”,已知全校共1500名学生,请估计该校对孩子使用手机“管理不严”的家长大约有多少人?20.(8分)(2015•南昌)(1)如图1,纸片▱ABCD中,AD=5,S▱ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE′的位置,拼成四边形AEE′D,则四边形AEE′D的形状为A.平行四边形B.菱形C.矩形D.正方形(2)如图2,在(1)中的四边形纸片AEE′D中,在EE′上取一点F,使EF=4,剪下△AEF,将它平移至△DE′F′的位置,拼成四边形AFF′D.①求证:四边形AFF′D是菱形.②求四边形AFF′D的两条对角线的长.21.(8分)(2015•南昌)如图,已知直线y=ax+b与双曲线y=(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的坐标.(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.(3)结合(1),(2)中的结果,猜想并用等式表示x1,x2,x0之间的关系(不要求证明).五、解答题(本大题共2小题,每小题9分,共18分) 22.(9分)(2015•南昌)甲、乙两人在100米直道AB 上练习匀速往返跑,若甲、乙分别中A ,B 两端同时出发,分别到另一端点处掉头,掉头时间不计,速度分别为5m/s 和4m/s .(1)在坐标系中,虚线表示乙离A 端的距离s (单位:m )与运动时间t (单位:s )之间的函数图象(0≤t ≤200),请在同一坐标系中用实线画出甲离A 端的距离s 与运动时间t 之间的函数图象(0≤t ≤200);的取值范围;②当t=390s 时,他们此时相遇吗?若相遇,应是第几次?若不相遇,请通过计算说明理由,并求出此时甲离A 端的距离.23.(9分)(2015•南昌)如图,已知二次函数L 1:y=ax 2﹣2ax+a+3(a >0)和二次函数L 2:y=﹣a (x+1)2+1(a >0)图象的顶点分别为M ,N ,与y 轴分别交于点E ,F .(1)函数y=ax 2﹣2ax+a+3(a >0)的最小值为 ,当二次函数L 1,L 2的y 值同时随着x 的增大而减小时,x 的取值范围是 .(2)当EF=MN 时,求a 的值,并判断四边形ENFM 的形状(直接写出,不必证明).(3)若二次函数L 2的图象与x 轴的右交点为A (m ,0),当△AMN 为等腰三角形时,求方程﹣a (x+1)2+1=0的解.六、解答题(本大题共12分)24.(12分)(2015•南昌)我们把两条中线互相垂直的三角形称为“称为中垂三角形”,例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均称为“中垂三角形”,设BC=a,AC=b,AB=c.特例探索(1)如图1,当∠ABE=45°,c=2时,a=,b=.如图2,当∠ABE=30°,c=4时,a=,b=.归纳证明(2)请你观察(1)中的计算结果,猜想a2,b2,c2三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.拓展应用(3)如图4,在▱ABCD中,点E、F、G分别是AD,BC,CD的中点,BE⊥EG,AD=2,AB=3,求AF的长.2015年江西省南昌市中考数学试卷参考答案与试题解析一、选择题(本大题共6小题,每小题3分,共18分,每小题只有一个正确选项)2.(3分)(2015•南昌)2015年初,一列CRH5型高速车组进行了“300000公里正线运营考核”标志着中国高速快.(2a)=6a B.﹣a b•3ab=﹣3a b+=﹣1•=﹣1==4.(3分)(2015•南昌)如图是将正方体切去一个角后形成的几何体,则该几何体的左视图为( )CD5.(3分)(2015•南昌)如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD ,B 与D 两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化,下列判断错误的是( )2)<<二、填空题(本大题共8小题,每小题3分,共24分)7.(3分)(2015•南昌)一个角的度数为20°,则它的补角的度数为160°.8.(3分)(2015•南昌)不等式组的解集是﹣3<x≤2.,9.(3分)(2015•南昌)如图,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB,则图中有3对全等三角形.10.(3分)(2015•南昌)如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC 的度数为110°.11.(3分)(2015•南昌)已知一元二次方程x2﹣4x﹣3=0的两根为m,n,则m2﹣mn+n2=25.12.(3分)(2015•南昌)如图1是小志同学书桌上的一个电子相框,将其侧面抽象为如图2所示的几何图形,已知BC=BD=15cm,∠CBD=40°,则点B到CD的距离为14.1cm(参考数据sin20°≈0.342,cos20°≈0.940,sin40°≈0.643,cos40°≈0.766,结果精确到0.1cm,可用科学计算器).,13.(3分)(2015•南昌)两组数据:3,a,2b,5与a,6,b的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的中位数为6.,,14.(3分)(2015•南昌)如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为2或2或2.×=2BP===2AP=,或或三、解答题(本大题共4小题,每小题6分,共24分)15.(6分)(2015•南昌)先化简,再求值:2a(a+2b)﹣(a+2b)2,其中a=﹣1,b=.时,原式16.(6分)(2015•南昌)如图,正方形ABCD于正方形A1B1C1D1关于某点中心对称,已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).(1)求对称中心的坐标.(2)写出顶点B,C,B1,C1的坐标.17.(6分)(2015•南昌)⊙O为△ABC的外接圆,请仅用无刻度的直尺,根据下列条件分别在图1,图2中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法).(1)如图1,AC=BC;(2)如图2,直线l与⊙O相切于点P,且l∥BC.,,根据垂径定理的推理得18.(6分)(2015•南昌)在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于,求m的值.)根据题意得:=.四、解答题(本大题共3小题,每小题8分,共24分)19.(8分)(2015•南昌)某校为了了解学生家长对孩子使用手机的态度情况,随机抽取部分学生家长进行问卷调查,发出问卷140份,每位学生家长1份,每份问卷仅表明一种态度,将回收的问卷进行整理(假设回收的问卷都有效),并绘制了如图两幅不完整的统计图.根据以上信息解答下列问题:(1)回收的问卷数为120份,“严加干涉”部分对应扇形的圆心角度数为30°.(2)把条形统计图补充完整(3)若将“稍加询问”和“从来不管”视为“管理不严”,已知全校共1500名学生,请估计该校对孩子使用手机“管理不严”的家长大约有多少人?××20.(8分)(2015•南昌)(1)如图1,纸片▱ABCD中,AD=5,S▱ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE′的位置,拼成四边形AEE′D,则四边形AEE′D的形状为CA.平行四边形B.菱形C.矩形D.正方形(2)如图2,在(1)中的四边形纸片AEE′D中,在EE′上取一点F,使EF=4,剪下△AEF,将它平移至△DE′F′的位置,拼成四边形AFF′D.①求证:四边形AFF′D是菱形.②求四边形AFF′D的两条对角线的长.====321.(8分)(2015•南昌)如图,已知直线y=ax+b与双曲线y=(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的坐标.(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.(3)结合(1),(2)中的结果,猜想并用等式表示x1,x2,x0之间的关系(不要求证明).求得反比例函数的解析式,进而求得=,=,根据题意得出===(y•y=,解得y=,=1解得=,=,==,,y=,解得五、解答题(本大题共2小题,每小题9分,共18分)22.(9分)(2015•南昌)甲、乙两人在100米直道AB 上练习匀速往返跑,若甲、乙分别中A ,B 两端同时出发,分别到另一端点处掉头,掉头时间不计,速度分别为5m/s 和4m/s .(1)在坐标系中,虚线表示乙离A 端的距离s (单位:m )与运动时间t (单位:s )之间的函数图象(0≤t ≤200),请在同一坐标系中用实线画出甲离A 端的距离s 与运动时间t 之间的函数图象(0≤t ≤200);的取值范围;②当t=390s 时,他们此时相遇吗?若相遇,应是第几次?若不相遇,请通过计算说明理由,并求出此时甲离A 端的距离.23.(9分)(2015•南昌)如图,已知二次函数L1:y=ax2﹣2ax+a+3(a>0)和二次函数L2:y=﹣a(x+1)2+1(a >0)图象的顶点分别为M,N,与y轴分别交于点E,F.(1)函数y=ax2﹣2ax+a+3(a>0)的最小值为3,当二次函数L1,L2的y值同时随着x的增大而减小时,x 的取值范围是﹣1<x<1.(2)当EF=MN时,求a的值,并判断四边形ENFM的形状(直接写出,不必证明).(3)若二次函数L2的图象与x轴的右交点为A(m,0),当△AMN为等腰三角形时,求方程﹣a(x+1)2+1=0的解.EF=MN==2﹣,六、解答题(本大题共12分)24.(12分)(2015•南昌)我们把两条中线互相垂直的三角形称为“称为中垂三角形”,例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均称为“中垂三角形”,设BC=a,AC=b,AB=c.特例探索(1)如图1,当∠ABE=45°,c=2时,a=2,b=2.如图2,当∠ABE=30°,c=4时,a=2,b=2.归纳证明(2)请你观察(1)中的计算结果,猜想a2,b2,c2三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.拓展应用(3)如图4,在▱ABCD中,点E、F、G分别是AD,BC,CD的中点,BE⊥EG,AD=2,AB=3,求AF的长.AP=BP=EF=AB=,再由勾股定理得到结果;,∠AD=AP=BP=EF=AB=AC=BC=2a=b=2EF=×PB=2PE=,,,,PF=PA=,PE=,+=+=AD=BC=2AD BCAD=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
准考证号 姓名
(在此卷上答题无效)
机密★2015年6月19日
江西省2015年中等学校招生考试
数学试题卷
说明:1.本卷共有六个大题,24个小题,全卷满分120分,考试时间120分钟.
2.本卷分为试题卷和答题卷,答案要求写在答题卷上,不得在试题卷上作答,否则不给分.
一、选择题(本大题共6小题,每小题3分,共18分.每小题只有一个正确选项) 1.计算(-1)°的结果为( ) A .1
B .-1
C .0
D .无意义
2.2015年初,一列CRH5型高速车组进行了“300 000公里正线运营考核”,标志着中国高铁车从“中国制造”到“中国创新”的飞跃.将数300 000用科学计数法表示为( ) A .6
310⨯
B .5
310⨯
C .6
0.310⨯
D .4
3010⨯
3.如图所示的几何体的左视图为( )
4.下列运算正确的是( ) A .23
6
(2)6a a =
B .22325
33a b ab a b -•=-
C .1b a
a b b a
+=---
D .211
11
a a a -•=-+ 5.如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD ,B 与D 两点之间用一根橡皮..筋.
拉直固定,然后向右扭动框架,观察所得四边形的变化.下面判断错误..
的是( ) A .四边形ABCD 由矩形变为平行四边形
B .BD 的长度增大
C.四边形ABCD的面积不变
D.四边形ABCD的周长不变
6.已知抛物线y=ax2+bx+c(a>0)过(-2,0),(2,3)两点,那么抛物线的对称轴( ) A.只能是x=-1
B.可能是y轴
C.在y轴右侧且在直线x=2的左侧
D.在y轴左侧且在直线x=-2的右侧
二、填空题(本大题共8小题,每小题3分,共24分)
7.一个角的度数为20°,则它的补角的度数为.
8.不等式组
1
10
2
39
x
x
⎧
-
⎪
⎨
⎪-<
⎩
≤,
的解集是.
9.如图,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB.则图中有对全等三角形.
10.如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC 的度数为.
11.已知一元二次方程x2-4x-3=0的两根为m,n,则m2-mn+n2=.
12.两组数据:3,a,2b,5与a,6,b的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的中位数为.
13.如图1是小志同学书桌上的一个电子相框,将其侧面抽象为如图2所示的几何图形,已知BC=BD=15cm,∠CBD=40°,则点B到CD的距离为cm(参考数据:sin20°≈0.342,cos20°≈0.940,sin40°≈0.643,cos40°≈0.766.计算结果精确到0.1cm,可用科学计算器).
14.如图,在△ABC 中,AB =BC =4,AO =BO ,P 是射线CO 上的一个动点,∠AOC =60°,则当△PAB 为直角三角形时,AP 的长为 . 三、(本大题共4小题,每小题6分,共24分)
15.先化简,再求值:2
2(2)(2)a a b a b +-+,其中1a =-,3b =.
16.如图,正方形ABCD 与正方形A 1B 1C 1D 1关于某点中心对称.已知A ,D 1,D 三点的坐标分别是(0,4),(0,3),(0,2). (1)求对称中心的坐标;
(2)写出顶点B ,C ,B 1,C 1的坐标.
17.⊙O 为△ABC 的外接圆,请仅用无...刻度的直尺.....,根据下列条件分别在图1,图2中画出一条弦.,使这条弦将△ABC 分成面积相等的两部分(保留作图痕迹,不写作法). (1)如图1,AC =BC ;
(2)如图2,直线l 与⊙O 相切与点P ,且l ∥B C .
18.在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A.请完成下列表格:
事件A必然事件随机事件
m的值
(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个球是黑球的概
率等于4
5
,求m的值.
四、(本大题共4小题,每小题8分,共32分)
19.某校为了了解学生家长对孩子使用手机的态度情况,随机抽取部分学生家长进行问卷调查,发出问卷140份,每位学生的家长1份,每份问卷仅表明一种态度.将回收的问卷进行整理(假设回收的问卷都有效),并绘制了如下两幅不完整的统计图.
学生家长对孩子使用手机的态度情况统计图
根据以上信息回答下列问题:
(1)回收的问卷数为份,“严加干涉”部分对应扇形的圆心角度数为;
(2)把条形统计图补充完整;
(3)若将“稍加询问”和“从来不管”视为“管理不严”,已知全校共1500名学生,请估计该校对孩子使用手机“管理不严”的家长大约有多少人?
20.(1)如图1,纸片□ABCD中,AD=5,S□ABCD=15.过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE'的位置,拼成四边形AEE'D,则四边形AEE'D的形状为( )
A .平行四边形
B .菱形
C .矩形
D .正方形
(2)如图2,在(1)中的四边形纸片AEE'D 中,在EE'上取一点F ,使EF =4,剪下△AEF ,将它平移至△DE'F'的位置,拼成四边形AFF'D . ①求证:四边形AFF'D 是菱形; ②求四边形AFF'D 的两条对角线的长.
21.如图,已知直线y =ax +b 与双曲线(0)k
y x x
=
>交于A (x 1,y 1),B (x 2,y 2)两点(A 与B 不重合),直线AB 与x 轴交于点P (x 0,0),与y 轴交于点C . (1)若A ,B 两点坐标分别为(1,3),(3,y 2).求点P 的坐标;
(2)若b =y 1+1,点P 的坐标为(6,0),且AB =BP ,求A ,B 两点的坐标; (3)结合(1),(2)中的结果,猜想并用等式表示x 1,x 2,x 0之间的关系(不要求证明).
22.甲、乙两人在100米直道AB 上练习匀速往返跑,若甲、乙分别在A ,B 两端同时出发,分别到另一端点掉头,掉头时间不计,速度分别为5m/s 和4m/s .
(1)在坐标系中,虚线表示乙离..A .端.的距离s (单位:m)与运动时间t (单位:s)之间的函数图象(0≤t ≤200),请在同一坐标系中用实线画出甲离A 端的距离s 与运动时间t 之间的函数图象(0≤t ≤200);
(2)根据(1)中所画图象,完成下列表格:
两人相遇次数
1 2 3 4 …n
(单位:次)
两人所跑路程之和
100 300 …
(单位:m)
(3)①直接写出甲、乙两人分别在第一个100m内,s与t的函数解析式,并指出自变量t的取值范围;
②求甲、乙第6此相遇时t的值.
五、(本大题共10分)
23.如图,已知二次函数L1:y=ax2-2ax+a+3(a>0)和二次函数L2:y=-a(x+1)2+1(a>0)图像的顶点分别为M,N,与y轴分别交于点E,F.
(1)函数y=ax2-2ax+a+3(a>0)的最小值为;当二次函数L1,L2的y值同时随着x 的增大而减小时,x的取值范围是;
(2)当EF=MN时,求a的值,并判断四边形ENFM的形状(直接写出,不必证明);
(3)若二次函数L2的图象与x轴的右交点为A(m,0),当△AMN为等腰三角形时,求方程-a(x+1)2+1=0的解.
六、(本大题共12分)
24.我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
特例探索
(1)如图1,当∠ABE=45°,c=22时,a=,b=;
如图2,当∠ABE=30°,c=4时,a=,b=;
归纳证明
(2)请你观察(1)中的计算结果,猜想a2,b2,c2三者之间的关系,用等式表示出来,请利用图3证明你发现的关系式;
拓展应用
(3)如图4,在□ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=25,AB=3.求AF的长.。
