大学物理第八章习题及答案
大学物理习题解答 第八章

8-1.已知波源在原点(x=0)的平面简谐波的方程为)cos(Cx Bt A y -=式中A,B,C 为正值恒量.试求:(1)波的振幅,波速,频率,周期与波长;(2)写出传播放向上距离波源l 处一点的振动方程;(3)试求任何时刻,在波传播放向上相距为D 的两点的位相差;解:(1) ∵A 、B 、C 为正值恒量,所以该波沿X 轴正方向传播,与平面简谐波的波动方程)(cos cxt A y -=ω比较系数,可得波的振幅为A ,B =ω, π2B f =, B T π2=, C c=ω,C B C c ==ω ,因为f c λ=,所以C B C B CT ππλ22=⋅==. 所以该波的振幅为A,波速为CB,频率为π2B ,周期为B π2,波长为C π2.(2)传播方向上距波源l 处一点的振动方程为:)cos(Cl Bt A y -=.(3)设t 时刻,传播方向上相距为D 的两点分别为x 1,x 2. 那么这两点所对应的波动方程分别为: )cos(11Cx Bt A y -= )cos(22Cx Bt A y -= 所以这两点的相位差Δφ为CD x x C =-=-=∆1221φφφ.8-2. 一列横波沿绳子传播时的波动方程为)410cos(05.0x t y ππ-=,式中x,y 以m 计,t 以s 计.(1)求此波的振幅、波速、频率、和波长;(2)求绳子上各质点振动时的最大速度和最大加速度;(3)求x=0.2m 处的质点在t=1s 时的相位,它是原点处质点在哪一时刻的位相. 这一位相所代表的运动状态在t=1.25s 时刻到达哪一点?在t=1.5s 时刻到达哪一点?(4)分别图示t=1s,1.1s,1.25s,1.5s 各时刻的波形.解:(1)通过与平面简谐波的波动方程比较系数,可得 此波的振幅为:A=0.05m, 波速为:ππ410=c =2.5(m/s). 频率为:ππ210=f =5(HZ). 波长为:f c =λ=0.5(m).答:该波的振幅为0.05m, 波速为2.5m/s, 频率为5HZ,波长为0.5m.(2) ∵平面简谐波的波动方程为:)(cos cxt A y -=ω.∴绳子上各质点的振动速度为: )(sin cxt A t y v --=∂∂=ωω.绳子上各质点的振动加速度为: )(cos 222c xt A ty a --=∂∂=ωω.∴绳子上各质点振动时的最大速度为 ωA v =max =0.5π=1.57(m/s). 绳子上各质点振动时的最大加速度为 2m ax ωA a = =52π=49.35(m/s 2). 答:绳子上各质点振动时的最大速度为1.57m/s ,最大加速度为49.35m/s 2. (3)X=0.2m 处的质点在t=1s 时的位相: φ=9.2π 设该位相是原点处质点在t 时刻的位相,可得 φ=9.2π=10πt t=0.92(s) 这一位相代表的运动状态在t=1.25s 时距离原点的位置为: )(825.0)125.1(2.02.0m c t c x =-+=∆+=同理,在t=1.5s 时,该位相所代表的运动状态,距离原点的位置为: t c x '∆+=2.0=1.45 (m). (4)t=1s 时,x y π4cos 05.0=. t=1.1s 时,x y π4cos 05.0-=. t=1.25s 时,x y π4sin 05.0=. t=1.5s 时,x y π4cos 05.0-=.8-3. 已知平面余弦波波源的振动周期T=21s,所激起的波的波长λ=10m,振幅为0.1m,当t=0时,波源处振动的位移恰为正方向的最大值,取波源处为原点并设波沿+X 方向传播,求: (1)此波的方程;(2)沿波传播方向距离波源为2λ处的振动方程; (3)当4T t =时,波源和距离波源为 4λ,2λ,43λ及λ的各点各自离开平衡位置的位移;(4)当4T t =时,波源和距离波源为 4λ,2λ,43λ及λ的各点自离开平衡位置的位移;并根据(3)(4)计算结果画出波形(y-x)曲线; (5)当4T t =和2T 时,距离波源4λ处质点的振动速度. 解:(1)根据题意可知,该平面余弦波的振幅 A=0.1m, 频率f =2(HZ),波速f c λ==20(m/s),初相位φ0=0. 当取波源为原点并沿该波沿+X 方向传播时,波动方程为 )54cos(1.0x t y ππ-=.(2)沿波传播方向距离波源为λ/2处的振动方程为: )254cos(1.0λππ⋅-=t y =-0.1cos4πt.(3)距离波源分别为4λ,2λ,43λ和λ的各点的振动方程为 t y π4sin 1.0=, t y π4cos 1.0-= t y π4sin 1.0-=, t y π4cos 1.0=当4Tt =时,它们各自离开平衡位置的位移为 44sin 1.01Ty ⋅=π=0.1(m), 2y =0(m),3y =-0.1(m), 4y =0(m)(4)与(3)的方法类似,易求得 4λ=x 时, y=0(m). 2λ=x 时, y=0.1(m).43λ=x 时,y=0(m). λ=x 时,y=-0.1(m).(5)各质点的振动速度,)54sin(4.0x t t y v πππ--=∂∂= 当4Tt =时,距离波源4λ处质点的振动速度为: )4544sin(4.0λπππ⨯-⨯-=T v =0(m/s)同理,当2T t =时,距离波源4λ处质点的振动速度为:v =-0.4π(m/s)答:当4Tt =和2T 时,距离波源4λ处质点的振动速度分别为0m/s 和-0.4πm/s. 8-4. 一波源做简谐振动,周期为1001s,经平衡位置向正方向运动时,作为计时起点.设此振动以c=400m/s 的速度沿直线传播,求: (1)这波沿某一波线的方程;(2)距波源为16m 处和20m 处质点振动方程和初位相; (3)距波源为15m 和16 m 的两质点的位相差是多少?解:(1)根据题意可知,该简谐波的频率为ƒ=100(HZ), 波速c=400m/s, 初相位20πφ-=, 设该平面简谐波的波动方程为 )22cos(0φλπλπ+-=x ct A y 将上面的结果代入可得,)222cos(πλππ--=x t T A y =)22200cos(πππ--x t A(2)距波源为16m 和20m 处质点振动方程为:将x=16m 代入上式,得 )2200()2216200cos(1πππππ-=-⨯-=t Aos t A y同理,)2200cos()2220200cos(2πππππ-=-⨯-=t A t A y 初相位分别为:t=0时,210πφ-=,220πφ-=.(3)距波源为15m 和16m 的两质点的位相差: λπφ2⨯∆=∆x =2π. 8-5. 已知某平面简谐波的波源振动方程为)2sin(06.0πt y =,式中y 以m 计,t 以s计.设波速为2m/s,试求离波源5m 处质点的振动方程.这点的位相所表示的运动状态相当波源在哪一时刻的运动状态?解:离波源5m 处质点的振动方程为:将X=5m 代入波动方程得 )5(2sin06.0c t y -=π=)452sin(06.0ππ-t 设该点的位相所代表的运动状态相当波源在t ′时刻的运动状态,所以 t t '=-2452πππ可得 t ′=(t-2.5)(s).8-6.如图所示,A 和B 是两个同位相的波源,相距d=0.10m,同时以30Hz 的频率发出波动,波速为0.50m/s.P 点位于AB 上方,AP 与AB 夹角为30o ,且PA=4m ,求两波通过P 点位相差.解:依题意可知,PA=4m,AB=0.1m, 利用余弦定理,可得 PB=3.91(m),两波通过P 点相位差: λπφ2)(⨯-=∆PB PA又∵fc=λ ∴Δφ=10.8π. 8-7. S 1和S 2是两个相干波源,相距41波长,S 1比S 2的位相超前2π.设两列波在 S 1,S 2连线方向的强度相同且不随距离变化,问S 1,S 2连线上在S 1外侧各点处的合成波的强度如何?又在S 2外侧各点的强度如何?解:两列相干波在空间任意点P 所形成的振动的振幅为 α∆=cos A 2A +A +A 212221A其中Δα为两列相干波在空间任一点所引起的两个振动的位相差 λπααα2)(1212⨯---=∆r r当P 点在S 1外侧时,根据题中所给的条件,可得 πλλππλπααα-=⨯--=⨯---=∆4222)(1212r r∴0)cos(-2A 2A 2020=+=πA 又∵波的强度与振幅的平方成正比 ∴I=0. 同理,当P 点在S 2外侧时, 02)4(22)(1212=⨯---=⨯---=∆λπλπλπαααr r ⇒A=2A 0 ∴04I I =答:S 1,S 2连线上在S 1外侧各点处的合成波的强度为0,而在S 2外侧合成波的强度为4I 0.8-8.图所示,设平面横波1沿BP 方向传播,它在B 点的振动方程为t y πcos 102.021-⨯=,平面横波2沿AP 方向传播,A 点的振动方程为)2cos(102.022ππ+⨯=-t y ,两式中y 以m计,t以s计,P处与B相距0.40m ,与A 相距0.05m,波速为0.20m/s.求: (1)两波传到P 处的为相差; (2)在P 处合振动的振幅;(3)如果在P 处相遇的两横波,振动方向是互相垂直的,则合振动的振幅又如何?解:(1)两波传到P 处的位相差Δα: λπααα2)(1212⨯---=∆r r由题中给出A,B 两点的振动方程可知,A 比B 的位相超前π ∴ππωππλππα5.22)(22)(-=⨯-⨯-=--=∆CPB PA PB PA (2)在P 处合振动的振幅为:α∆++=cos A 2A A A 2010220210A 21083.2-⨯= (m). (3)由于两列横波振幅相同,频率相同,相位差Δα=25π, 所以,当振动方向相互垂直时,合成的结果是圆周运动. ∴A=A 10=0.2×10-2(m).8-9. 一列正弦式空气波,沿直径为0.14m 的圆柱形管行进,波的平均强度为18*10-3J/s ·m 2,频率为300Hz,波速为300m/s,问: (1)波中的平均能量密度和最大能量密度是多少?(2)每两个相邻的,相位差为2π的同相面(亦即相距1波长的两同相面)之间的波段中有多少能量?解:(1)根据题中所给的条件,由C I ω= 则cI=ω=300/10183-⨯=5106-⨯(J ·m -3). 由)(sin 222c rt A -=ωωρω 可得ωωρω222max ==A =4102.1-⨯(J ·m -3)(2)V W ∆⋅=ωd r 2πω==9.23×710-(J)8-10. 为了保持波源的振动不变,需要消耗4W 的功率,如果波源发出的是球面波,且认为媒质不吸收波的 能量,求距离波源1m 和2m 处的能流密度. 解:因为IS P =,所以距离波源1m 处的能流密度为ππ1442111===r S P I =0.318(w ·m -2)距离波源2m 处的能流密度为222244r S P I π===0.08(w ·m -2). 8-11. 两个波在一根很长的细绳上传播,它们的方程设为 )4(cos 06.01t x y -=π,)4(cos 06.02t x y +=π,式中x,y 以m 计,t 以s 计;(1) 求各波的频率,波长,波速和传播方向;(2) 试求这细绳上是做驻波式振动,求节点的位置和腹点的位置; (3)波腹处的振幅多大?在x=1.2m 处振幅多大?解:(1)与波动方程形式)cos(crt A y -=ω作比较,可得)4(4cos 06.01x t y -=π, )4(4cos 06.02xt y +=ππω41= ⇒πω211=f =2(Hz), s m c /41= 111T c =λ=2(m) 传播方向沿x 轴正方向 πω42=, ƒ2=2(Hz), C 2=-4m/s.222T c =λ =2(m). 传播方向沿x 轴负方向(2)由于两列波同频率,同振幅,同振动方向,并且传播速率相同方向相反,故满足驻波条件,所以做的是驻波式振动t x y y y ππ4cos cos 12.021⋅=+= 节点的位置: 2)12(ππ+=k x (k=0,±1, ±2,………) ⇒2)12(+=k x . 腹点的位置: ππk x = (k=0,±1, ±2, ……) ⇒k x =. (3)波腹处的振幅为0.12m.x=1.2m 处的振幅: )2.1cos(12.0π=0.097(m). 8-12. 设入射波的波动方程为)(2cos 1λπxT t A y +=,在x=0处发生反射,反射点为一自由端.求: (1)反射波的波动方程;(2)合成波(驻波)的方程,并由合成波方程说明哪些点是波腹,哪些点是波节.解:(1)反射波的波动方程为: )(2cos 2λπxT t A y -=(2) )2cos()2cos(221T tx A y y πλπ⋅=+波腹点:πλπk x =2 (k=0,±1, ±2,………) ⇒2λk x =.波节点位置:2)12(2πλπ+=k x (k=0,±1, ±2,………) ⇒4)12(λ+=k x8-13. 在实验室中做驻波试验时,将一根长3米的弦线的一端系于电动音叉的一个臂上,这音叉在 垂直于眩线长度的方向撒谎那个以60Hz 的频率做振动,眩线的质量为60*0.001kg.如果使这根弦线产生有四个波腹的振动,必须给这根弦线施多大的力.解:由8.14题的结论可知 μυTl n n 2=(n=1, 2,3,………) 根据题中所给的已知条件,可得 l =3m,n=44υ=60HZ, μ=60·10-3/3=kg 2102-⨯. 代入上式,解得24)2(nlT υμ==162(N).8-14. 把两端固定的一根弦线波动一下,就有横向振动弦线的两固定端传去,并被反射回来形成驻波图样, 一根长度为l 的弦线,它的驻波图样是一定的,所以它可按呈现一个波腹,二个波腹,三个波腹,……的形式做振动或这种基本振动叠加.试证明:一根长度为l 的弦线只能发出下列一些固有频率.μυTl n n 2=n=1,2,3,….. 式中μ是弦线单位的质量,T 是绳中的张力.证明:假设长度为l 的弦线,它的驻波图样可以产生n 个波腹,则n 2λ=l ① 又因波在弦线中传播的速率为 μTc =其中T 是绳中的张力,μ是弦线单位长度的质量μυυλTc nn == ②联立①②,解得 μυTl n n 2=. 故结论得证. 8-15. (1)有一支频率未知的音叉和一支频率已知为384Hz 的标准音叉一起振动时每秒产生三个拍,当这音叉上涂上少量石蜡时,拍频减少,沃尔玛这支音叉频率是多少?(2)某一波形可以用下式表示:11sin sin 3sin 535Y A x A x A x =+++试分别作出该级数前三项的图形,并作出叠加之后的图形. 解:(1)由拍频的定义,可知 123υυυ-==∴ 312±=υυ 即2υ=387或381(Hz). (2)图如下:11。
大学物理第8章试卷答案

第8章电磁感应作业题答案一、选择题1、圆铜盘水平放置在均匀磁场中,B得方向垂直盘面向上,当铜盘绕通过中心垂直于盘面得轴沿图示方向转动时,(A) 铜盘上有感应电流产生,沿着铜盘转动得相反方向流动。
(B) 铜盘上有感应电流产生,沿着铜盘转动得方向流动。
(C) 铜盘上有感应电流产生,铜盘中心处电势最高。
(D)铜盘上有感应电流产生,铜盘边缘处电势最高。
答案(D)2.在尺寸相同得铁环与铜环所包围得面积中穿过相同变化率得磁通量,则两环中A.感应电动势相同,感应电流相同;B.感应电动势不同,感应电流不同;ﻫC.感应电动势相同,感应电流不同;ﻫD.感应电动势不同,感应电流相同。
答案(C)ﻫ3. 两根无限长得平行直导线有相等得电流,2.但电流得流向相反如右图,而电流得变化率均大于零,有一矩形线圈与两导线共面,则ﻫ A.线圈中无感应电流;B.线圈中感应电流为逆时针方向;C.线圈中感应电流为顺时针方向;D.线圈中感应电流不确定。
答案: B(解:两直导线在矩形线圈处产生得磁场方向均垂直向里,且随时间增强,由楞次定律可知线圈中感应电流为逆时针方向。
)4.如图所示,在长直载流导线下方有导体细棒,棒与直导线垂直且共面。
(a)、(b)、(c)处有三个光滑细金属框。
今使以速度向右滑动。
设(a)、(b)、(c)、(d)四种情况下在细棒中得感应电动势分别为ℇa、ℇb、ℇc、ℇd,则ﻫﻫA.ℇa=ℇb =ℇc <ℇdB.ℇa =ℇb=ℇc>ℇdC.ℇa=ℇb=ℇc =ℇd D.ℇa>ℇb <ℇc<ℇd答案:C5.一矩形线圈,它得一半置于稳定均匀磁场中,另一半位于磁场外,如右图所示,磁感应强度得方向与纸面垂直向里。
欲使线圈中感应电流为顺时针方向则ﻫA.线圈应沿轴正向平动;ﻫB.线圈应沿轴正向平动;C.线圈应沿轴负向平动;D.线圈应沿轴负向平动答案(A).*6.两个圆线圈、相互垂直放置,如图所示。
当通过两线圈中得电流、均发生变化时,那么ﻫ A.线圈中产生自感电流,线圈中产生互感电流;B.线圈中产生自感电流,ﻫ线圈中产生互感电流;ﻫC.两线圈中同时产生自感电流与互感电流;D.两线圈中只有自感电流,不产生互感电流。
《大学物理》 第二版 第八章课后习题答案

习题精解8-1 一根无限长直导线有交变电流0sin i I t ω=,它旁边有一与它共面的矩形线圈ABCD ,如图8.3所示,长为l 的AB 和CD 两边与直导向平行,它们到直导线的距离分别为a 和b ,试求矩形线圈所围面积的磁通量,以及线圈中的感应电动势。
解 建立如图8.3所示的坐标系,在矩形平面上取一矩形面元dS ldx =,载流长直导线的磁场穿过该面元的磁通量为02m id B dS ldx xμφπ=⋅= 通过矩形面积CDEF 的总磁通量为 00ln 22bm ai il bldx x aμμφππ==⎰由法拉第电磁感应定律有0ln cos 2m d il bt dt aφμωεωπ=-=- 8-2 有一无限长直螺线管,单位长度上线圈的匝数为n ,在管的中心放置一绕了N 圈,半径为r 的圆形小线圈,其轴线与螺线管的轴线平行,设螺线管内电流变化率为dI dt ,球小线圈中感应的电动势。
解 无限长直螺线管内部的磁场为0B nI μ= 通过N 匝圆形小线圈的磁通量为20m NBS N nI r φμπ== 由法拉第电磁感应定律有20m d dIN n r dt dtφεμπ=-=- 8-3 一面积为S 的小线圈在一单位长度线圈匝数为n ,通过电流为i 的长螺线管内,并与螺线管共轴,若0sin i i t ω=,求小线圈中感生电动势的表达式。
解 通过小线圈的磁通量为0m BS niS φμ==由法拉第电磁感应定律有000cos m d dinS nSi t dt dtφεμμωω=-=-=- 8-4 如图8.4所示,矩形线圈ABCD 放在16.010B T -=⨯的均匀磁场中,磁场方向与线圈平面的法线方向之间的夹角为60α=︒,长为0.20m 的AB 边可左右滑动。
若令AB 边以速率15.0v m s -=∙向右运动,试求线圈中感应电动势的大小及感应电流的方向。
解 利用动生电动势公式0.20()50.6sin(60)0.30()2BAv B dl dl V πε=⨯∙=⨯⨯-︒=⎰⎰感应电流的方向从A B →.8-5 如图8.5所示,两段导体AB 和CD 的长度均为10cm ,它们在B 处相接成角30︒;磁场方向垂直于纸面向里,其大小为22.510B T -=⨯。
大学物理第八章课后习题答案

大学物理第八章课后习题答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第八章电磁感应电磁场8 -1一根无限长平行直导线载有电流I,一矩形线圈位于导线平面内沿垂直于载流导线方向以恒定速率运动(如图所示),则()(A)线圈中无感应电流(B)线圈中感应电流为顺时针方向(C)线圈中感应电流为逆时针方向(D)线圈中感应电流方向无法确定分析与解由右手定则可以判断,在矩形线圈附近磁场垂直纸面朝里,磁场是非均匀场,距离长直载流导线越远,磁场越弱.因而当矩形线圈朝下运动时,在线圈中产生感应电流,感应电流方向由法拉第电磁感应定律可以判定.因而正确答案为(B).8 -2将形状完全相同的铜环和木环静止放置在交变磁场中,并假设通过两环面的磁通量随时间的变化率相等,不计自感时则()(A)铜环中有感应电流,木环中无感应电流(B)铜环中有感应电流,木环中有感应电流(C)铜环中感应电动势大,木环中感应电动势小(D)铜环中感应电动势小,木环中感应电动势大23分析与解 根据法拉第电磁感应定律,铜环、木环中的感应电场大小相等,但在木环中不会形成电流.因而正确答案为(A ).8 -3 有两个线圈,线圈1 对线圈2 的互感系数为M 21 ,而线圈2 对线圈1的互感系数为M 12 .若它们分别流过i 1 和i 2 的变化电流且ti t i d d d d 21<,并设由i 2变化在线圈1 中产生的互感电动势为ε12 ,由i 1 变化在线圈2 中产生的互感电动势为ε21 ,下述论断正确的是( ).(A )2112M M = ,1221εε=(B )2112M M ≠ ,1221εε≠(C )2112M M =, 1221εε<(D )2112M M = ,1221εε<分析与解 教材中已经证明M21 =M12 ,电磁感应定律t i M εd d 12121=;ti M εd d 21212=.因而正确答案为(D ). 8 -4 对位移电流,下述四种说法中哪一种说法是正确的是( )(A ) 位移电流的实质是变化的电场(B ) 位移电流和传导电流一样是定向运动的电荷(C ) 位移电流服从传导电流遵循的所有定律(D ) 位移电流的磁效应不服从安培环路定理分析与解 位移电流的实质是变化的电场.变化的电场激发磁场,在这一点位移电流等效于传导电流,但是位移电流不是走向运动的电荷,也就不服从焦耳热效应、安培力等定律.因而正确答案为(A ).48 -5 下列概念正确的是( )(A ) 感应电场是保守场(B ) 感应电场的电场线是一组闭合曲线(C ) LI Φm =,因而线圈的自感系数与回路的电流成反比(D ) LI Φm =,回路的磁通量越大,回路的自感系数也一定大 分析与解 对照感应电场的性质,感应电场的电场线是一组闭合曲线.因而正确答案为(B ).8 -6 一铁心上绕有线圈100匝,已知铁心中磁通量与时间的关系为()Wb π100sin 100.85t Φ⨯=,求在s 100.12-⨯=t 时,线圈中的感应电动势.分析 由于线圈有N 匝相同回路,线圈中的感应电动势等于各匝回路的感应电动势的代数和,在此情况下,法拉第电磁感应定律通常写成tψt ΦN ξd d d d -=-=,其中ΦN ψ=称为磁链. 解 线圈中总的感应电动势()()t tΦNξπ100cos 51.2d d =-= 当s 100.12-⨯=t 时,V 51.2=ξ. 8 -7 有两根相距为d 的无限长平行直导线,它们通以大小相等流向相反的电流,且电流均以tI d d 的变化率增长.若有一边长为d 的正方形线圈与两导线处于同一平面内,如图所示.求线圈中的感应电动势.5分析 本题仍可用法拉第电磁感应定律tΦξd d -=来求解.由于回路处在非均匀磁场中,磁通量就需用⎰⋅=SΦS B d 来计算(其中B 为两无限长直电流单独存在时产生的磁感强度B 1 与B 2 之和). 为了积分的需要,建立如图所示的坐标系.由于B 仅与x 有关,即()B B x =,故取一个平行于长直导线的宽为dx 、长为d 的面元dS ,如图中阴影部分所示,则x d S d d =,所以,总磁通量可通过线积分求得(若取面元y x S d d d =,则上述积分实际上为二重积分).本题在工程技术中又称为互感现象,也可用公式tl M E M d d -=求解. 解1 穿过面元dS 的磁通量为()x d xI μx d d x I μΦd π2d π2d d d d 0021-+=⋅+⋅=⋅=S B S B S B 因此穿过线圈的磁通量为()43ln π2d π2d π2d 02020Id μx x Id μx d x Id μΦΦd d dd =-+==⎰⎰⎰ 再由法拉第电磁感应定律,有6tI d μt ΦE d d 43ln π2d d 0⎪⎭⎫ ⎝⎛=-= 解2 当两长直导线有电流I 通过时,穿过线圈的磁通量为 43ln π20dI μΦ=线圈与两长直导线间的互感为 43ln π20d μI ΦM == 当电流以tl d d 变化时,线圈中的互感电动势为 tI d μt I M E d d 43ln π2d d 0⎪⎭⎫ ⎝⎛=-= 试想:如线圈又以速率v 沿水平向右运动,如何用法拉第电磁感应定律求图示位置的电动势呢此时线圈中既有动生电动势,又有感生电动势.设时刻t ,线圈左端距右侧直导线的距离为ξ,则穿过回路的磁通量()ξf ΦS,1d =⋅=⎰S B ,它表现为变量I 和ξ的二元函数,将Φ代入t ΦE d d -= 即可求解,求解时应按复合函数求导,注意,其中v =tξd d ,再令ξ=d 即可求得图示位置处回路中的总电动势.最终结果为两项,其中一项为动生电动势,另一项为感生电动势.8 -8 有一测量磁感强度的线圈,其截面积S =4.0 cm 2 、匝数N =160 匝、电阻R =50Ω.线圈与一内阻R i =30Ω的冲击电流计相连.若开始时,线圈的平面与均匀磁场的磁感强度B 相垂直,然后线圈的平面很快地转到与B 的方向平行.此时从冲击电流计中测得电荷值54.010C q -=⨯.问此均匀磁场的磁感强度B 的值为多少7分析 在电磁感应现象中,闭合回路中的感应电动势和感应电流与磁通量变化的快慢有关,而在一段时间内,通过导体截面的感应电量只与磁通量变化的大小有关,与磁通量变化的快慢无关.工程中常通过感应电量的测定来确定磁场的强弱. 解 在线圈转过90°角时,通过线圈平面磁通量的变化量为NBS NBS ΦΦΦ=-=-=0Δ12 因此,流过导体截面的电量为ii R RNBS R R Φq +=+=Δ 则 ()T 050.0=+=NSR R q B i 8 -9 如图所示,一长直导线中通有I =5.0 A 的电流,在距导线9.0 cm 处,放一面积为0.10 cm 2 ,10 匝的小圆线圈,线圈中的磁场可看作是均匀的.今在1.0 ×10-2 s 内把此线圈移至距长直导线10.0 cm 处.求:(1) 线圈中平均感应电动势;(2) 设线圈的电阻为1.0×10-2Ω,求通过线圈横截面的感应电荷.8分析 虽然线圈处于非均匀磁场中,但由于线圈的面积很小,可近似认为穿过线圈平面的磁场是均匀的,因而可近似用NBS ψ=来计算线圈在始、末两个位置的磁链.解 (1) 在始、末状态,通过线圈的磁链分别为1011π2r ISμN S NB ψ==,2022π2r IS μN S NB ψ== 则线圈中的平均感应电动势为 V 1011.111πΔ2ΔΔ8210-⨯=⎪⎪⎭⎫ ⎝⎛-==r r t IS μN t ΦE 电动势的指向为顺时针方向.(2) 通过线圈导线横截面的感应电荷为tΦE d d -= 8 -10 如图(a)所示,把一半径为R 的半圆形导线OP 置于磁感强度为B 的均匀磁场中,当导线以速率v 水平向右平动时,求导线中感应电动势E 的大小,哪一端电势较高9分析 本题及后面几题中的电动势均为动生电动势,除仍可由tΦE d d -=求解外(必须设法构造一个闭合回路),还可直接用公式()l B d ⋅⨯=⎰l E v 求解.在用后一种方法求解时,应注意导体上任一导线元dl 上的动生电动势()l B d d ⋅⨯=v E .在一般情况下,上述各量可能是dl 所在位置的函数.矢量(v ×B )的方向就是导线中电势升高的方向. 解1 如图(b)所示,假想半圆形导线O P 在宽为2R 的静止形导轨上滑动,两者之间形成一个闭合回路.设顺时针方向为回路正向,任一时刻端点O 或端点P 距 形导轨左侧距离为x ,则B R Rx Φ⎪⎭⎫ ⎝⎛+=2π212 即B R tx RB t ΦE v 2d d 2d d -=-=-= 由于静止的 形导轨上的电动势为零,则E =-2R v B .式中负号表示电动势的方向为逆时针,对OP 段来说端点P 的电势较高. 解2 建立如图(c )所示的坐标系,在导体上任意处取导体元dl ,则()θR θB l θB E o d cos d cos 90sin d d v v ==⋅⨯=l B vB R θθBR E v v 2d cos d E π/2π/2===⎰⎰- 由矢量(v ×B )的指向可知,端点P 的电势较高.10 解3 连接OP 使导线构成一个闭合回路.由于磁场是均匀的,在任意时刻,穿过回路的磁通量==BS Φ常数.由法拉第电磁感应定律tΦE d d -=可知,E =0 又因 E =E OP +E PO即 E OP =-E PO =2R v B由上述结果可知,在均匀磁场中,任意闭合导体回路平动所产生的动生电动势为零;而任意曲线形导体上的动生电动势就等于其两端所连直线形导体上的动生电动势.上述求解方法是叠加思想的逆运用,即补偿的方法.8 -11 长为L 的铜棒,以距端点r 处为支点,以角速率ω绕通过支点且垂直于铜棒的轴转动.设磁感强度为B 的均匀磁场与轴平行,求棒两端的电势差.分析 应该注意棒两端的电势差与棒上的动生电动势是两个不同的概念,如同电源的端电压与电源电动势的不同.在开路时,两者大小相等,方向相反(电动势的方向是电势升高的方向,而电势差的正方向是电势降落的方向).本题可直接用积分法求解棒上的电动势,亦可以将整个棒的电动势看作是O A 棒与O B 棒上电动势的代数和,如图(b)所示.而E O A 和E O B 则可以直接利用第8 -2 节例1 给出的结果.解1 如图(a)所示,在棒上距点O 为l 处取导体元dl ,则()()r L lB ωl lB ωE L-r r AB AB 221d d --=-=⋅⨯=⎰⎰-l B v 因此棒两端的电势差为()r L lB ωE U AB AB 221--== 当L >2r 时,端点A 处的电势较高解2 将AB 棒上的电动势看作是O A 棒和O B 棒上电动势的代数和,如图(b)所示.其中221r ωB E OA =,()221r L B ωE OB -= 则()r L BL ωE E E OB OA AB 221--=-= 8 -12 如图所示,长为L 的导体棒OP ,处于均匀磁场中,并绕OO ′轴以角速度ω旋转,棒与转轴间夹角恒为θ,磁感强度B 与转轴平行.求OP 棒在图示位置处的电动势.分析 如前所述,本题既可以用法拉第电磁感应定律t ΦE d d -= 计算(此时必须构造一个包含OP 导体在内的闭合回路, 如直角三角形导体回路OPQO ),也可用()l B d ⋅⨯=⎰lE v 来计算.由于对称性,导体OP 旋转至任何位置时产生的电动势与图示位置是相同的.解1 由上分析,得()l B d ⋅⨯=⎰OP OP E v l αB l o d cos 90sin ⎰=v()()l θB θωl o d 90cos sin ⎰-=l()⎰==L θL B ωl l θB ω022sin 21d sin 由矢量B ⨯v 的方向可知端点P 的电势较高.解2 设想导体OP 为直角三角形导体回路OPQO 中的一部分,任一时刻穿过回路的磁通量Φ为零,则回路的总电动势QO PQ OP E E E t ΦE ++==-=0d d 显然,E QO =0,所以()221PQ B ωE E E QO PQ OP ==-= 由上可知,导体棒OP 旋转时,在单位时间内切割的磁感线数与导体棒QP 等效.后者是垂直切割的情况.8 -13 如图(a)所示,金属杆AB 以匀速12.0m s -=⋅v 平行于一长直导线移动,此导线通有电流I =40A .求杆中的感应电动势,杆的哪一端电势较高分析 本题可用两种方法求解.(1) 用公式()l B d ⋅⨯=⎰lE v 求解,建立图(a )所示的坐标系,所取导体元x l d d =,该处的磁感强度xI μB π20=.(2) 用法拉第电磁感应定律求解,需构造一个包含杆AB 在内的闭合回路.为此可设想杆AB 在一个静止的形导轨上滑动,如图(b)所示.设时刻t ,杆AB 距导轨下端CD 的距离为y ,先用公式⎰⋅=SΦS B d 求得穿过该回路的磁通量,再代入公式tΦE d d -=,即可求得回路的电动势,亦即本题杆中的电动势. 解1 根据分析,杆中的感应电动势为()V 1084.311ln 2πd 2πd d 50m 1.1m 1.00-⨯-=-=-==⋅⨯=⎰⎰v v v I μx x μxl E AB AB l B 式中负号表示电动势方向由B 指向A ,故点A 电势较高. 解2 设顺时针方向为回路AB CD 的正向,根据分析,在距直导线x 处,取宽为dx 、长为y 的面元dS ,则穿过面元的磁通量为x y xI μΦd 2πd d 0=⋅=S B 穿过回路的磁通量为11ln 2πd 2πd 0m1.1m 1.00⎰⎰-===S Iy μx y x I μΦΦ 回路的电动势为V 1084.32πd d 11ln 2πd d 500-⨯-=-=-=-=Iy μt y x I μt ΦE 由于静止的形导轨上电动势为零,所以 V 1084.35-⨯-==E E AB式中负号说明回路电动势方向为逆时针,对AB 导体来说,电动势方向应由B 指向A ,故点A 电势较高.8 -14 如图(a)所示,在“无限长”直载流导线的近旁,放置一个矩形导体线框,该线框在垂直于导线方向上以匀速率v 向右移动,求在图示位置处,线框中感应电动势的大小和方向.分析 本题亦可用两种方法求解.其中应注意下列两点:1.当闭合导体线框在磁场中运动时,线框中的总电动势就等于框上各段导体中的动生电动势的代数和.如图(a)所示,导体eh 段和fg 段上的电动势为零[此两段导体上处处满足()0l B =⋅⨯d v ],因而线框中的总电动势为()()()()hg ef hgef gh ef E E E -=⋅⨯-⋅⨯=⋅⨯+⋅⨯=⎰⎰⎰⎰l B l B l B l B d d d d v v v v 其等效电路如图(b)所示.2.用公式tΦE d d -=求解,式中Φ是线框运动至任意位置处时,穿过线框的磁通量.为此设时刻t 时,线框左边距导线的距离为ξ,如图(c )所示,显然ξ是时间t 的函数,且有v =tξd d .在求得线框在任意位置处的电动势E (ξ)后,再令ξ=d ,即可得线框在题目所给位置处的电动势.解1 根据分析,线框中的电动势为hg ef E E E -=()()⎰⎰⋅⨯-⋅⨯=hgef l B l B d d v v ()⎰⎰+-=2201000d 2πd 2πl l l l d I μl d I μv v ()1202πl d I I μ+=1vI 由E ef >E hg 可知,线框中的电动势方向为efgh .解2 设顺时针方向为线框回路的正向.根据分析,在任意位置处,穿过线框的磁通量为()()ξl ξξx Il μdx ξx Il μΦl 120020ln π2π21++=+=⎰ 相应电动势为()()1120π2d d l ξξl l I μt ΦξE +=-=v 令ξ=d ,得线框在图示位置处的电动势为 ()1120π2l d d l l I μE +=v 由E >0 可知,线框中电动势方向为顺时针方向.*8 -15 有一长为l ,宽为b 的矩形导线框架,其质量为m ,电阻为R .在t =0时,框架从距水平面y =0 的上方h 处由静止自由下落,如图所示.磁场的分布为:在y =0 的水平面上方没有磁场;在y =0 的水平面下方有磁感强度为B 的均匀磁场,B 的方向垂直纸面向里.已知框架在时刻t 1 和t 2 的位置如图中所示.求在下述时间内,框架的速度与时间的关系:(1) t 1 ≥t >0,即框架进入磁场前;(2) t 2 ≥t ≥t 1 ,即框架进入磁场, 但尚未全部进入磁场;(3)t >t 2 ,即框架全部进入磁场后.分析 设线框刚进入磁场(t 1 时刻)和全部进入磁场(t 2 时刻)的瞬间,其速度分别为v 10 和v 20 .在情况(1)和(3)中,线框中无感应电流,线框仅在重力作用下作落体运动,其速度与时间的关系分别为v =gt (t <t 1)和v =v 20 +g (t -t 2 )(t >t 2 ).而在t 1<t <t 2这段时间内,线框运动较为复杂,由于穿过线框回路的磁通量变化,使得回路中有感应电流存在,从而使线框除受重力外,还受到一个向上的安培力F A ,其大小与速度有关,即()A A F F =v .根据牛顿运动定律,此时线框的运动微分方程为()tv v d d m F mg A =-,解此微分方程可得t 1<t <t 2 时间内线框的速度与时间的关系式.解 (1) 根据分析,在1t t ≤时间内,线框为自由落体运动,于是()11t t gt ≤=v 其中1t t =时,gh 2101==v v(2) 线框进入磁场后,受到向上的安培力为v Rl B IlB F A 22== 根据牛顿运动定律,可得线框运动的微分方程tv m v d d 22=-R l B mg 令mRl B K 22=,整理上式并分离变量积分,有 ⎰⎰=-t t t g 110d d vv Kv v 积分后将gh 210=v 代入,可得()()[]1212t t K e gh K g g K----=v (3) 线框全部进入磁场后(t >t 2),作初速为v 20 的落体运动,故有()()()[]()222031221t t g e gh K g g Kt t g t t K -+--=-+=--v v 8 -16 有一磁感强度为B 的均匀磁场,以恒定的变化率t d d B 在变化.把一块质量为m 的铜,拉成截面半径为r 的导线,并用它做成一个半径为R 的圆形回路.圆形回路的平面与磁感强度B 垂直.试证:这回路中的感应电流为td d π4B d ρm I =式中ρ 为铜的电阻率,d 为铜的密度. 解 圆形回路导线长为πR 2,导线截面积为2πr ,其电阻R ′为22rR ρS l ρR ==' 在均匀磁场中,穿过该回路的磁通量为BS Φ=,由法拉第电磁感应定律可得回路中的感应电流为t t t d d 2πd d π1d d 122B ρRr B R R ΦR R E I ='='='= 而2ππ2r R d m =,即dm Rr π2π2=,代入上式可得 td d π4B d ρm I = 8 -17 半径为R =2.0 cm 的无限长直载流密绕螺线管,管内磁场可视为均匀磁场,管外磁场可近似看作零.若通电电流均匀变化,使得磁感强度B 随时间的变化率td d B 为常量,且为正值,试求:(1) 管内外由磁场变化激发的感生电场分布;(2) 如1s T 010.0d d -⋅=tB ,求距螺线管中心轴r =5.0 cm 处感生电场的大小和方向.分析 变化磁场可以在空间激发感生电场,感生电场的空间分布与场源———变化的磁场(包括磁场的空间分布以及磁场的变化率td d B 等)密切相关,即S B l E d d ⋅∂∂-=⎰⎰S S k t .在一般情况下,求解感生电场的分布是困难的.但对于本题这种特殊情况,则可以利用场的对称性进行求解.可以设想,无限长直螺线管内磁场具有柱对称性,其横截面的磁场分布如图所示.由其激发的感生电场也一定有相应的对称性,考虑到感生电场的电场线为闭合曲线,因而本题中感生电场的电场线一定是一系列以螺线管中心轴为圆心的同心圆.同一圆周上各点的电场强度E k 的大小相等,方向沿圆周的切线方向.图中虚线表示r <R 和r >R 两个区域的电场线.电场线绕向取决于磁场的变化情况,由楞次定律可知,当0d d <t B 时,电场线绕向与B 方向满足右螺旋关系;当0d d >t B 时,电场线绕向与前者相反.解 如图所示,分别在r <R 和r >R 的两个区域内任取一电场线为闭合回路l (半径为r 的圆),依照右手定则,不妨设顺时针方向为回路正向.(1) r <R , tB r t r E E k l k d d πd d d π2d 2-=⋅-=⋅=⋅=⎰⎰S B l E tB r E k d d 2-= r >R , t B R t r E E k lk d d πd d d π2d 2-=⋅-=⋅=⋅=⎰⎰S B l E tB r R E k d d 22-= 由于0d d >tB ,故电场线的绕向为逆时针. (2) 由于r >R ,所求点在螺线管外,因此tB r R E k d d 22-= 将r 、R 、tB d d 的数值代入,可得15m V 100.4--⋅⨯-=k E ,式中负号表示E k 的方向是逆时针的.8 -18 在半径为R 的圆柱形空间中存在着均匀磁场,B 的方向与柱的轴线平行.如图(a)所示,有一长为l 的金属棒放在磁场中,设B 随时间的变化率tB d d 为常量.试证:棒上感应电动势的大小为分析 变化磁场在其周围激发感生电场,把导体置于感生电场中,导体中的自由电子就会在电场力的作用下移动,在棒内两端形成正负电荷的积累,从而产生感生电动势.由于本题的感生电场分布与上题所述情况完全相同,故可利用上题结果,由⎰⋅=lk E l E d 计算棒上感生电动势.此外,还可连接OP 、OQ ,设想PQOP 构成一个闭合导体回路,用法拉第电磁感应定律求解,由于OP 、OQ 沿半径方向,与通过该处的感生电场强度E k 处处垂直,故0d =⋅l E k ,OP 、OQ 两段均无电动势,这样,由法拉第电磁感应定律求出的闭合回路的总电动势,就是导体棒PQ 上的电动势.证1 由法拉第电磁感应定律,有 22Δ22d d d d d d ⎪⎭⎫ ⎝⎛-==-==l R l t B t B S t ΦE E PQ 证2 由题8 -17可知,在r <R 区域,感生电场强度的大小tB r E k d d 2= 设PQ 上线元dx 处,E k 的方向如图(b )所示,则金属杆PQ 上的电动势为()()222202/2d d d 2/d d 2d cos d l R l t B x r l R t B r x θE E l k k PQ -=-==⋅=⎰⎰x E 讨论 假如金属棒PQ 有一段在圆外,则圆外一段导体上有无电动势 该如何求解8 -19 截面积为长方形的环形均匀密绕螺绕环,其尺寸如图(a)所示,共有N 匝(图中仅画出少量几匝),求该螺绕环的自感L .分析 如同电容一样,自感和互感都是与回路系统自身性质(如形状、匝数、介质等)有关的量.求自感L 的方法有两种:1.设有电流I 通过线圈,计算磁场穿过自身回路的总磁通量,再用公式IΦL =计算L .2.让回路中通以变化率已知的电流,测出回路中的感应电动势E L ,由公式t I E L L d /d =计算L .式中E L 和tI d d 都较容易通过实验测定,所以此方法一般适合于工程中.此外,还可通过计算能量的方法求解.解 用方法1 求解,设有电流I 通过线圈,线圈回路呈长方形,如图(b)所示,由安培环路定理可求得在R 1 <r <R 2 范围内的磁场分布为xNI μB π20=由于线圈由N 匝相同的回路构成,所以穿过自身回路的磁链为 12200ln π2d π2d 21R R hI N μx h x NI μN N ψS R R ==⋅=⎰⎰S B 则1220ln π2R R h N μI ψL = 若管中充满均匀同种磁介质,其相对磁导率为μr ,则自感将增大μr 倍.8 -20 如图所示,螺线管的管心是两个套在一起的同轴圆柱体,其截面积分别为S 1 和S 2 ,磁导率分别为μ1 和μ2 ,管长为l ,匝数为N ,求螺线管的自感.(设管的截面很小)分析 本题求解时应注意磁介质的存在对磁场的影响.在无介质时,通电螺线管内的磁场是均匀的,磁感强度为B 0 ,由于磁介质的存在,在不同磁介质中磁感强度分别为μ1 B 0 和μ2 B 0 .通过线圈横截面的总磁通量是截面积分别为S 1 和S 2 的两部分磁通量之和.由自感的定义可解得结果.解 设有电流I 通过螺线管,则管中两介质中磁感强度分别为I L N μnl μB 111==,I LN μnl μB 222== 通过N 匝回路的磁链为221121S NB S NB ΨΨΨ+=+=则自感2211221S μS μlN I ψL L L +==+= 8 -21 有两根半径均为a 的平行长直导线,它们中心距离为d .试求长为l的一对导线的自感(导线内部的磁通量可略去不计).分析 两平行长直导线可以看成无限长但宽为d 的矩形回路的一部分.设在矩形回路中通有逆时针方向电流I ,然后计算图中阴影部分(宽为d 、长为l )的磁通量.该区域内磁场可以看成两无限长直载流导线分别在该区域产生的磁场的叠加.解 在如图所示的坐标中,当两导线中通有图示的电流I 时,两平行导线间的磁感强度为()r d I μr I μB -+=π2π200 穿过图中阴影部分的磁通量为 aa d l μr Bl ΦS a d a -==⋅=⎰⎰-ln πd d 0S B 则长为l 的一对导线的自感为aa d l μI ΦL -==ln π0 如导线内部磁通量不能忽略,则一对导线的自感为212L L L +=.L 1 称为外自感,即本题已求出的L ,L 2 称为一根导线的内自感.长为l 的导线的内自感8π02l μL =,有兴趣的读者可自行求解. 8 -22 如图所示,在一柱形纸筒上绕有两组相同线圈AB 和A ′B ′,每个线圈的自感均为L ,求:(1) A 和A ′相接时,B 和B ′间的自感L 1 ;(2) A ′和B 相接时,A 和B ′间的自感L 2 .分析 无论线圈AB 和A ′B ′作哪种方式连接,均可看成一个大线圈回路的两个部分,故仍可从自感系数的定义出发求解.求解过程中可利用磁通量叠加的方法,如每一组载流线圈单独存在时穿过自身回路的磁通量为Φ,则穿过两线圈回路的磁通量为2Φ;而当两组线圈按(1)或(2)方式连接后,则穿过大线圈回路的总磁通量为2Φ±2Φ,“ ±”取决于电流在两组线圈中的流向是相同或是相反.解 (1) 当A 和A ′连接时,AB 和A ′B ′线圈中电流流向相反,通过回路的磁通量亦相反,故总通量为0221=-=ΦΦΦ,故L 1 =0.(2) 当A ′和B 连接时,AB 和A ′B ′线圈中电流流向相同,通过回路的磁通量亦相同,故总通量为ΦΦΦΦ4222=+=, 故L I ΦI ΦL 4422===. 本题结果在工程实际中有实用意义,如按题(1)方式连接,则可构造出一个无自感的线圈.8 -23 如图所示,一面积为4.0 cm 2 共50 匝的小圆形线圈A ,放在半径为20 cm 共100 匝的大圆形线圈B 的正中央,此两线圈同心且同平面.设线圈A 内各点的磁感强度可看作是相同的.求:(1) 两线圈的互感;(2) 当线圈B 中电流的变化率为-50 A·s-1 时,线圈A 中感应电动势的大小和方向.分析 设回路Ⅰ中通有电流I 1 ,穿过回路Ⅱ的磁通量为Φ21 ,则互感M =M 21 =Φ21I 1 ;也可设回路Ⅱ通有电流I 2 ,穿过回路Ⅰ的磁通量为Φ12 ,则21212I ΦM M == . 虽然两种途径所得结果相同,但在很多情况下,不同途径所涉及的计算难易程度会有很大的不同.以本题为例,如设线圈B 中有电流I 通过,则在线圈A 中心处的磁感强度很易求得,由于线圈A 很小,其所在处的磁场可视为均匀的,因而穿过线圈A 的磁通量Φ≈BS .反之,如设线圈A 通有电流I ,其周围的磁场分布是变化的,且难以计算,因而穿过线圈B 的磁通量也就很难求得,由此可见,计算互感一定要善于选择方便的途径.解 (1) 设线圈B 有电流I 通过,它在圆心处产生的磁感强度R I μN B B 200=穿过小线圈A 的磁链近似为 A B A A A A S RI μN N S B N ψ200== 则两线圈的互感为H 1028.6260-⨯===RS μN N I ψM A B A A (2)V 1014.3d d 4-⨯=-=tI M E A 互感电动势的方向和线圈B 中的电流方向相同.8 -24 如图所示,两同轴单匝线圈A 、C 的半径分别为R 和r ,两线圈相距为d .若r 很小,可认为线圈A 在线圈C 处所产生的磁场是均匀的.求两线圈的互感.若线圈C 的匝数为N 匝,则互感又为多少解 设线圈A 中有电流I 通过,它在线圈C 所包围的平面内各点产生的磁感强度近似为()2/322202d R IR μB +=穿过线圈C 的磁通为 ()22/32220π2r d R IR μBS ψC +==则两线圈的互感为 ()2/3222202πdR R r μI ψM +== 若线圈C 的匝数为N 匝,则互感为上述值的N 倍. 8 -25 如图所示,螺绕环A 中充满了铁磁质,管的截面积S 为2.0 cm 2 ,沿环每厘米绕有100 匝线圈,通有电流I 1 =4.0 ×10 -2 A ,在环上再绕一线圈C ,共10 匝,其电阻为0.10 Ω,今将开关S 突然开启,测得线圈C 中的感应电荷为2.0 ×10 -3C .求:当螺绕环中通有电流I 1 时,铁磁质中的B 和铁磁质的相对磁导率μr .分析 本题与题8 -8 相似,均是利用冲击电流计测量电磁感应现象中通过回路的电荷的方法来计算磁场的磁感强度.线圈C 的磁通变化是与环形螺线管中的电流变化相联系的. 解 当螺绕环中通以电流I 1 时,在环内产生的磁感强度110I n μμB r =则通过线圈C 的磁链为S I n μμN BS N ψr c 11022==设断开电源过程中,通过C 的感应电荷为q C ,则有()RS I n μμN ψR ψR qc r c c 110201Δ1=--=-= 由此得 T 10.02110===S N Rqc I n μμB r 相对磁导率1991102==I n μS N Rqc μr8 -26 一个直径为0.01 m ,长为0.10 m 的长直密绕螺线管,共1 000 匝线圈,总电阻为7.76 Ω.求:(1) 如把线圈接到电动势E =2.0 V 的电池上,电流稳定后,线圈中所储存的磁能有多少 磁能密度是多少*(2) 从接通电路时算起,要使线圈储存磁能为最大储存磁能的一半,需经过多少时间分析 单一载流回路所具有的磁能,通常可用两种方法计算:(1) 如回路自感为L (已知或很容易求得),则该回路通有电流I 时所储存的磁能221LI W m =,通常称为自感磁能.(2) 由于载流回路可在空间激发磁场,磁能实际是储存于磁场之中,因而载流回路所具有的能量又可看作磁场能量,即V w W V m m d ⎰=,式中m w 为磁场能量密度,积分遍及磁场存在的空间.由于μB w m 22=,因而采用这种方法时应首先求载流回路在空间产生的磁感强度B 的分布.上述两种方法还为我们提供了计算自感的另一种途径,即运用V w LI V m d 212⎰=求解L . 解 (1) 密绕长直螺线管在忽略端部效应时,其自感l S N L 2=,电流稳定后,线圈中电流RE I =,则线圈中所储存的磁能为J 1028.3221522202-⨯===lRSE N μLI W m 在忽略端部效应时,该电流回路所产生的磁场可近似认为仅存在于螺线管。
大学物理第8章答案

第8章 磁场8-10一均匀密绕直螺线管的半径为 ,单位长度上有 匝线圈,每匝线圈中的电流为 ,用毕奥—萨伐尔定律求此螺线管轴线上的磁场。
分析:由于线圈密绕,因此可以近似地把螺线管看成一系列圆电流的紧密排列,且每一匝圆电流在轴线上任一点的磁场均沿轴向。
解: 取通过螺线管的轴线并与电流形成右旋的方向(即磁场的方向)为x 轴正向,如习题8-10图解(a )所示。
在螺线管上任取一段微元dx ,则通过它的电流为dI nIdx =,把它看成一个圆线圈,它在轴线上O 点产生的磁感应强度dB 为2022322()R nIdxdB R x μ=+由叠加原理可得,整个螺线管在O 点产生的磁感应强度B 的大小为212022322()x Lx R nIdxB dB R x μ==+⎰⎰0212212221221[]2()()nIx x R x R x μ=-++ 由图可知12122212221212cos os ()()x x R x R x ββ==++ c ,代入上式并整理可得 021(cos cos )2nIB μββ=-式中12ββ和分别为x 轴正向与从O 点引向螺线管两端的矢径r 之间的夹角。
讨论:(1)若螺线管的长度远远大于其直径,即螺线管可视为无限长时,20β=,1βπ=,则有nI B 0μ=上式说明,无限长密绕长直螺线管内部轴线上各点磁感应强度为常矢量。
理论和实验均证明:在整个无限长螺线管内部空间里,上述结论也适用。
即无限长螺线管内部空间里的磁场为均匀磁场,其磁感应强度B 的大小为0nI μ,方向与轴线平行;(2)若点O位于半无限长载流螺线管一端,即12πβ=,20β=或12πβ=,2βπ=时,无论哪一种情况均有nI B 021μ=------(8-19) 可见半无限长螺线管端面中心轴线上磁感应强度的大小为管内的一半;综上所述,密绕长直螺线管轴线上各处磁感应强度分布见习题8-10图解(b )所示,从图中也可看出,长直螺线管内中部的磁场可以看成是均匀的。
大学物理第八章习题及答案

V 第八章 热力学基础8-1如图所示,bca 为理想气体绝热过程,b1a 和b2a 是任意过程,则上述两过程中气体做功与吸收热量的情况是:(B ) (A) b1a 过程放热,作负功;b2a 过程放热,作负功(B) b1a 过程吸热,作负功;b2a 过程放热,作负功(C) b1a 过程吸热,作正功;b2a 过程吸热,作负功 (D) b1a 过程放热,作正功;b2a 过程吸热,作正功8-2 如图,一定量的理想气体由平衡态A 变到平衡态B ,且它们的压强相等,则在状态A 和状态B 之间,气体无论经过的是什么过程,气体必然( B ) (A)对外作正功 (B)内能增加 (C)从外界吸热 (D)向外界放热8-3 两个相同的刚性容器,一个盛有氢气,一个盛氦气(均视为刚性分子理想气体),开始时它们的压强温度都相同,现将3J 热量传给氦气,使之升高到一定温度,若使氢气也升高同样温度,则应向氢气传递热量为( C ) (A) 6 J (B) 3 J (C) 5J (D) 10 J 8-4 有人想象了如题图四个理想气体的循环过程,则在理论上可以实现的为( )(A) (B)(C) (D)8-5一台工作于温度分别为327o C和27o C的高温热源和低温源之间的卡诺热机,每经历一个循环吸热2 000 J,则对外作功( B )(A) 2 000 J (B) 1 000 J(C) 4 000 J (D) 500 J8-6 根据热力学第二定律( A )(A) 自然界中的一切自发过程都是不可逆的(B) 不可逆过程就是不能向相反方向进行的过程(C) 热量可以从高温物体传到低温物体,但不能从低温物体传到高温物体(D)任何过程总是沿着熵增加的方向进行8-7 一定质量的气体,在被压缩的过程中外界对气体做功300J,但这一过程中气体的内能减少了300J,问气体在此过程中是吸热还是放热?吸收或放出的热量是多少?解:由于外界对气体做功,所以:300J=W-由于气体的内能减少,所以:J∆E=300-根据热力学第一定律,得:J∆+=W=EQ300-600300=--又由公式WQ e 2=得:J 421005.1⨯==eW Q 8-12理想卡诺热机在温度为27C 0和127C 0的两个热源之间工作,若在正循环中,该机从高温热源吸收1200J 的热量,则将向低温热源放出多少热量?对外做了多少功?解:由1121Q W T T =-=η得:J 3001200400300400)1(121=⨯-=-=T T Q WJ 90012=-=W Q Q8-13一卡诺热机在1000K 和270C 的两热源之间工作。
大学物理题库-第8章-电磁感应习题(含答案解析)

第八章 电磁感应一 选择题1、 (130101104)一圆形线圈的一半放在分布于方形区域内的匀强磁场B中,另一半位于磁场之外,如图13-2所示。
欲使圆线圈中产生逆时针方向的感应电流,应使[ ](A )线圈向右平移 (B )线圈向上平移 (C )线圈向左平移 (D )磁场强度减弱2、(130201202) 如图所示,直角三角形金属框架abc 放在均匀磁场中,磁场B平行于ab 边,bc 的长度为l .当金属框架绕ab 边以匀角速度ω转动时,abc回路中的感应电动势ε和a 、c 两点间的电势差U a – U c 为 (A)ε=0,U a – U c =221l B ω.(B) ε=0,U a – U c =221l B ω-.(C) ε=2l B ω,U a – U c =221l B ω.(D) ε=2l B ω,U a – U c =221l B ω-. [ ]3、(130201204)如图13-4所示,在圆柱形空间内有一磁感应强度为B的均匀磁场,其变化率为dt dB 。
若在图中a 、b 两点间放置一直导线ab 和弯曲导线ab ,下列说法中正确的是[ ] (A )电动势只在ab 中产生 (B )电动势只在ab 中产生(C )ab 和ab 中都产生电动势,且大小相等(D )ab 中的电动势小于ab 中的电动势.4、(130201205)均匀磁场被局限在圆柱形空间内,且随时间变化。
图13-22所示为圆柱形截面,M 、N 分别为圆柱形空间内、外两点,M E 、N E 分别表示这两点的有旋电场强度大小,则 [ ](A )0=M E , 0=N E (B )0=M E ,0≠N E (C )0≠M E ,0≠N E (D ) 0≠M E ,0=N E5、 (130301203)已知圆环式螺线管的自感系数为L ,若将该螺线管锯成两个半环式的螺线管,则两个半环螺线管的自感系数[ ](A )都等于2/L (B )一个大于2/L ,另一个小于2/L (C )都大于2/L (D )都小于2/LB⨯⨯⨯⨯⨯⨯⨯⨯⨯图13-2⨯⨯⨯Bb ⨯⨯⨯⨯a 图13-4 N⨯⨯B⨯⨯M 图13-22Ba bclω6、 (130401101)用线圈的自感系数L 来表示载流线圈磁场能量的公式221LI W m =(A) 只适用于无限长密绕螺线管. (B) 只适用于单匝圆线圈. (C) 只适用于一个匝数很多,且密绕的螺绕环.(D) 适用于自感系数L一定的任意线圈. [ ]7、(130401102)真空中一根无限长直导线上通有电流强度为I 的电流,则距导线垂直距离为a 的空间某点处的磁能密度为[ ] (A )200)2(21a I πμμ (B )200)2(21a I πμμ (C )20)2(21a I πμ (D )200)2(21aI μμ 8、(130401201) 有两个长直密绕螺线管,长度及线圈匝数均相同,半径分别为r 1和r 2.管内充满均匀介质,其磁导率分别为μ1和μ2.设r 1∶r 2=1∶2,μ1∶μ2=2∶1,当将两只螺线管串联在电路中通电稳定后,其自感系数之比L 1∶L 2与磁能之比W m 1∶W m 2分别为: (A) L 1∶L 2=1∶1,W m 1∶W m 2 =1∶1. (B) L 1∶L 2=1∶2,W m 1∶W m 2 =1∶1. (C) L 1∶L 2=1∶2,W m 1∶W m 2 =1∶2.(D) L 1∶L 2=2∶1,W m 1∶W m 2 =2∶1. [ ] 9、(130401301)两根无限长的平行导线,其间距离为d ,与电源组成回路如图13-21所示,已知导线上的电流为I ,两根导线横截面半径均为0r ,设用L 表示两导线回路单位长度的自感系数,则沿导线单位长度的空间总磁能0W 为[ ](A )221LI (B )rdr r d I r I LI ππμπμ2])(22[2120002+-+⎰∞(C )∞ (D )rdI LI ln 22102πμ+10、(130501101)对位移电流,有下述四种说法,请指出哪一种说法正确.(A) 位移电流是指变化电场. (B) 位移电流是由线性变化磁场产生的. (C) 位移电流的热效应服从焦耳─楞次定律.(D) 位移电流的磁效应不服从安培环路定理. [ ]11、 如图,平板电容器(忽略边缘效应)充电时,沿环路L 1的磁场强度H 的环流与沿环路L 2的磁场强度H的环流两者,必有:(A) >'⎰⋅1d L l H ⎰⋅'2d L l H . (B) ='⎰⋅1d L l H ⎰⋅'2d L l H.(C) <'⎰⋅1d L l H⎰⋅'2d L l H. (D)0d 1='⎰⋅L l H. [ ]二 填空题1、如图所示,在一长直导线L 中通有电流I ,ABCD 为一矩形线圈,它与L 皆在纸面内,且AB 边与L 平行. (1) 矩形线圈在纸面内向右移动时,线圈中感应电动势方 向为________________________________.2r d图13-21I LADC BHL 1L 2(2) 矩形线圈绕AD 边旋转,当BC 边已离开纸面正向外运 动时,线圈中感应动势的方向为_________________________.2、(130102201)半径为r 的小绝缘圆环,置于半径为R 的大导线圆环中心,二者在同一平面内,且r <<R .在大导线环中通有正弦电流(取逆时针方向为正)I =I 0sin ωt ,其中ω、I 0为常数,t 为时间,则任一时刻小线环中感应电动势(取逆时针方向为正)为_________________________________.3、(130202201)长为l 的金属直导线在垂直于均匀磁场的平面内以角速度ω转动.如果转轴在导线上的位置是在____________,整个导线上的电动势为最大,其值为____________;如果转轴位置是在____________,整个导线上的电动势为最小,其值为____________.4、(130202203)如图13-23所示,半径为R 的圆弧abc 在磁感应强度为B的均匀磁场中沿x轴向右移动,已知︒=∠=∠150cox aox ,若移动速度为v,则在圆弧abc 中的感应电动势为 。
大学物理课后习题8第八章答案

4 0me
(5)一正方形线圈,由细导线做成,边长为 a ,共有 N 匝,可以绕
通过其相对两边中点的一个竖直 轴自由转动.现在线圈中通有电流 I ,并
把线圈放在均匀 的水平外磁场 B 中,线圈对其转轴的转动惯量为 J .求线
圈磁矩与磁场 B 的夹角为 时,线圈受到的转动力矩为
[答案:(1) 6.67 106 T , 7.20 1021 A.m2 ]
(4)氢原子中,电子绕原子核沿半径为 r 的圆周运动,它等效于一 个圆形电流.如果外加一个磁感强度为 B 的磁场,其磁感线与轨道平面平 行,那么这个圆电流所受的磁力矩的大小 M =____________________.(设 电子质量为 me,电子电荷的绝对值为 e)
(3) b r c
B2r
0 I
r2 c2
b2 b2
பைடு நூலகம்
0I
B
0 I (c2 2r(c 2
r2) b2 )
(4) r c B2r 0
B0
题 8.11 图
无题图(应删掉)
题 8.12 图
8.12 在磁感应强度为 B 的均匀磁场中,垂直于磁场方向的平面内有
一段载流弯曲导线,电流为
I
解:在曲线上取 dl ,则
Pm // B
M 0.
8.14 一铜片厚为 d=1.0mm,放在 B=1.5T 的均匀磁场中,磁场方向与 铜片表面垂直。一直铜片内每立方厘米中有 8.4 1022 个自由电子,每个电 子的电荷为 e 1.6 1019C ,当铜片中垂直于磁场方向通有 I=200A 的电流 时,求铜片两侧的霍尔电势差。
题8.7 图 解:如题 8.7 图所示, BA 方向垂直纸面向里
(完整版)大学物理学(课后答案)第8章

第八章课后习题解答一、选择题8-1如图8-1所示,一定量的理想气体,由平衡态A 变到平衡态B ,且它们的压强相等,即=A B p p 。
则在状态A 和状态B 之间,气体无论经过的是什么过程,气体必然[ ](A) 对外作正功 (B) 内能增加 (C) 从外界吸热 (D) 向外界放热分析:由p V -图可知,A A B B p V p V =,即知A B T T <,则对一定量理想气体必有B A E E >,即气体由状态A 变化到状态B ,内能必增加。
而作功、热传递均是过程量,与具体的热力学过程相关,所以(A )、(C )、(D )不是必然结果,只有(B )正确。
8-2 两个相同的刚性容器,一个盛有氢气,一个盛有氦气(均视为刚性分子理想气体)。
开始时它们的压强和温度都相同。
现将3 J 热量传给氦气,使之升高到一定的温度。
若使氢气也升高同样的温度,则应向氢气传递热量为[ ](A) 6 J (B) 3 J (C) 5 J (D) 10 J分析:由热力学第一定律Q E W =∆+知在等体过程中Q E =∆。
故可知欲使氢气和氦气升高相同的温度,由理想气体的内能公式2m i E R T M '∆=∆,知需传递的热量之比22222:():():5:3HHe H He H He H He H Hem m Q Q i i i i M M ''===。
故正确的是(C )。
8-3 一定量理想气体分别经过等压、等温和绝热过程从体积1V 膨胀到体积2V ,如图8-3所示,则下述正确的是[ ]习题8-1图(A) A C →吸热最多,内能增加(B) A D →内能增加,作功最少(C) A B →吸热最多,内能不变(D) A C →对外作功,内能不变分析:根据p V -图可知图中A B →为等压过程,A C →为等温过程,A D →为绝热过程。
又由理想气体的物态方程pV vRT =可知,p V -图上的pV 积越大,则该点温度越高,因此图中D A B C T T T T <==,又因对于一定量的气体而言其内能公式2i E vRT =,由此知0AB E ∆>,0AC E ∆=,0AD E ∆<。
大学物理课后习题答案 真空中的静电场

第八章 真空中的静电场 1、[D] 2、[C]要使p 点的电场强度为零,有两种可能:1、在p 点的右侧放正电荷;2、在p 点的左侧放负电荷。
根据题意为负电荷,根据点电荷强度的公式:204rQ E πε=。
其中r=1,负电荷产生的电场:2442120210=⇒=r rQ r Q πεπε,该点在原点的左边。
3、[D]1、粒子作曲线运动的条件必须存在向心力。
2、粒子从A 点出发经C 点运动到B 点是速率递增,存在和运动方向一致的切向力。
3、依据粒子带正电荷,作出作用在质点上的静电力后,符合上诉1、2条件的是[D]。
4、[C]5、[B]6、[D]1、点电荷的电场强度:r e rq E204πε=;2、无限长均匀带电直导线:r rq e rq E r20022πεπε==;3、无限大均匀带电平面:r e E2εσ=4、半径为R 的均匀带电球面外的电场强度:r r R r R r e rq E r302230204414εσσππεπε=⋅==7、[C]对高斯定理的理解。
E是高斯面上各处的电场强度,它是由曲面内外所有静止点和产生的。
∑=0q 并不能说明E有任何特定的性质。
8、[A]应用高斯定理有:⎰=⋅sS d E 0,即:⎰⎰⎰⎰=∆Φ+⋅=⋅+⋅=⋅∆ses s s S d E S d E S d E S d E 0⎰∆Φ-=⋅seS d E9、[B]10、[C]依据公式:R r rQ E ≥=,420πε已知:,4,22σπR Q R r ==代入上式可得:2024444εσπεσπ==RR E11、[D]先构建成一个边长为a 的立方体,表面为高斯面,应用高斯定理,一个侧面的磁通量为: 0661εq S d E S d E ss=⋅=⋅⎰⎰12、[D]13、[D]半径为R 的均匀带电球面:R r R Q U <=,40πεR r r Q U >=,40πε半径为R 的均匀带电球体: R r r Q U >=,40πεR r RQ r R RQ U <+-=,4)(802230πεπε正点电荷: ,40rQ U πε=负点电荷: ,40rQ U πε-=14、[C]分析:先求以无限远处为电势的零点.则半径为R 电量为Q 的球面的电势: 0)(,4)(0=∞=U RQ R U πε,4)()(0RQ R U U U R πε-=-∞=∞对15、[B]利用电势的叠加来解。
大学物理习题答案第八章

大学物理习题答案第八章-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN[习题解答]8-2 在一个容器内盛有理想气体,而容器的两侧分别与沸水和冰相接触(热接触)。
显然,当沸水和冰的温度都保持不变时,容器内理想气体的状态也不随时间变化。
问这时容器内理想气体的状态是否是平衡态为什么解不是平衡态,因为平衡态的条件有二:一是系统的宏观性质不随时间变化,二是没有外界的影响和作用。
题目所说的情况不满足第二条。
8-3 氧气瓶的容积是32 dm3 ,压强为130 atm,规定瓶内氧气的压强降至10 atm时,应停止使用并必须充气,以免混入其他气体。
今有一病房每天需用1.0 atm的氧气400 dm3 ,问一瓶氧气可用几天?解当压强为、体积为时,瓶内氧气的质量M1为.当压强降至、体积仍为时,瓶内氧气的质量M2为.病房每天用压强为、体积为的氧气质量m为.以瓶氧气可用n天:.8-4在一个容积为10 dm3 的容器中贮有氢气,当温度为7℃时,压强为50 atm。
由于容器漏气,当温度升至17℃时,压强仍为50 atm,求漏掉氢气的质量。
解漏气前氢气的质量为M1 , 压强为, 体积为, 温度为,于是M1可以表示为.漏气后氢气的质量为M2, 压强为, 体积为, 温度为, 于是M2可以表示为.所以漏掉氢气的质量为.计算中用到了氢气的摩尔质量。
8-5 气缸中盛有可视为理想气体的某种气体,当温度为T1 = 200 K时,压强和摩尔体积分别为p1 和V m1 。
如果将气缸加热,使系统中气体的压强和体积同时增大,在此过程中,气体的压强p 和摩尔体积V m满足关系p = αV m,其中α为常量。
(1)求常量α;(2)当摩尔体积增大到2V m1 时,求系统的温度。
解(1) 1 mol理想气体的物态方程可以表示为,当温度为T1 (= 200 K)、压强为p1 和摩尔体积为V m1时,上式应写为. (1)升温过程满足,在温度为T1 时,上式应写为, (2)将式(2)代入式(1),得. (3)由上式可以解得或 .(2)根据式(3)可以得到,取,代入上式,得, (4)将式(4)与式(3)联立,可以求得. 8-8 证明式(8-9)。
大学物理第八章部分答案

大学物理习题及解答熵增加习题八8-1 电量都是q 的三个点电荷,分别放在正三角形的三个顶点.试问:(1)在这三角形的中心放一个什么样的电荷,就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)?(2)这种平衡与三角形的边长有无关系? 解: 如题8-1图示(1) 以A 处点电荷为研究对象,由力平衡知:q '为负电荷20220)33(π4130cos π412a q q a q '=︒εε解得q q 33-='(2)与三角形边长无关.题8-1图 题8-2图8-2 两小球的质量都是m ,都用长为l 的细绳挂在同一点,它们带有相同电量,静止时两线夹角为2θ,如题8-2图所示.设小球的半径和线的质量都可以忽略不计,求每个小球所带的电量.解: 如题8-2图示⎪⎩⎪⎨⎧===220)sin 2(π41sin cos θεθθl q F T mg T e解得θπεθtan 4sin 20mg l q =8-3 根据点电荷场强公式204r qE πε=,当被考察的场点距源点电荷很近(r →0)时,则场强→∞,这是没有物理意义的,对此应如何理解?解:20π4r r q E ϖϖε=仅对点电荷成立,当0→r 时,带电体不能再视为点电荷,再用上式求场强是错误的,实际带电体有一定形状大小,考虑电荷在带电体上的分布求出的场强不会是无限大.8-4 在真空中有A ,B 两平行板,相对距离为d ,板面积为S ,其带电量分别为+q 和-q .则这两板之间有相互作用力f ,有人说f =2024d q πε,又有人说,因为f =qE ,S qE 0ε=,所以f =S q 02ε.试问这两种说法对吗?为什么? f 到底应等于多少?解: 题中的两种说法均不对.第一种说法中把两带电板视为点电荷是不对的,第二种说法把合场强S qE 0ε=看成是一个带电板在另一带电板处的场强也是不对的.正确解答应为一个板的电场为S q E 02ε=,另一板受它的作用力S q S q q f 02022εε==,这是两板间相互作用的电场力. 8-6 长l =15.0cm的直导线AB 上均匀地分布着线密度λ=5.0x10-9C ·m-1的正电荷.试求:(1)在导线的延长线上与导线B 端相距1a =5.0cm 处P 点的场强;(2)在导线的垂直平分线上与导线中点相距2d =5.0cm 处Q 点的场强.解: 如题8-6图所示(1)在带电直线上取线元x d ,其上电量q d 在P 点产生场强为20)(d π41d x a x E P -=λε2220)(d π4d x a xE E llP P -==⎰⎰-ελ ]2121[π40l a l a +--=ελ)4(π220l a l-=ελ用15=l cm ,9100.5-⨯=λ1m C -⋅, 5.12=a cm 代入得21074.6⨯=P E 1C N -⋅ 方向水平向右(2)同理2220d d π41d +=x xE Q λε 方向如题8-6图所示 由于对称性⎰=l QxE 0d ,即Q E ϖ只有y 分量,∵22222220d d d d π41d ++=x x xE Qyλε22π4d d ελ⎰==lQy Qy E E ⎰-+2223222)d (d ll x x2220d 4π2+=l lελ以9100.5-⨯=λ1cm C -⋅, 15=l cm ,5d 2=cm 代入得21096.14⨯==Qy Q E E 1C N -⋅,方向沿y 轴正向8-7 一个半径为R 的均匀带电半圆环,电荷线密度为λ,求环心处O 点的场强. 解: 如8-7图在圆上取ϕRd dl =题8-7图ϕλλd d d R l q ==,它在O 点产生场强大小为20π4d d R R E εϕλ=方向沿半径向外则 ϕϕελϕd sin π4sin d d 0R E E x ==ϕϕελϕπd cos π4)cos(d d 0R E E y -=-=积分R R E x 000π2d sin π4ελϕϕελπ==⎰0d cos π400=-=⎰ϕϕελπR E y∴R E E x 0π2ελ==,方向沿x 轴正向.8-9 (1)点电荷q 位于一边长为a 的立方体中心,试求在该点电荷电场中穿过立方体的一个面的电通量;(2)如果该场源点电荷移动到该立方体的一个顶点上,这时穿过立方体各面的电通量是多少?*(3)如题8-9(3)图所示,在点电荷q 的电场中取半径为R 的圆平面.q 在该平面轴线上的A 点处,求:通过圆平面的电通量.(x Rarctan=α)解: (1)由高斯定理0d εq S E s⎰=⋅ϖϖ 立方体六个面,当q 在立方体中心时,每个面上电通量相等∴ 各面电通量06εqe =Φ.(2)电荷在顶点时,将立方体延伸为边长a 2的立方体,使q 处于边长a 2的立方体中心,则边长a 2的正方形上电通量06εq e =Φ对于边长a 的正方形,如果它不包含q 所在的顶点,则024εqe =Φ,如果它包含q 所在顶点则0=Φe .如题8-9(a)图所示.题8-9(3)图题8-9(a)图 题8-9(b)图 题8-9(c)图(3)∵通过半径为R 的圆平面的电通量等于通过半径为22x R +的球冠面的电通量,球冠面积*]1)[(π22222xR x x R S +-+=∴)(π42200x R Sq +=Φε02εq=[221x R x +-]*关于球冠面积的计算:见题8-9(c)图ααα⎰⋅=0d sin π2r r S ααα⎰⋅=02d sin π2r)cos 1(π22α-=r8-10 均匀带电球壳内半径6cm ,外半径10cm ,电荷体密度为2×510-C ·m -3求距球心5cm ,8cm ,12cm 各点的场强.解: 高斯定理0d ε∑⎰=⋅qS E sϖϖ,02π4ε∑=qr E当5=r cm 时,0=∑q ,=E ϖ8=r cm 时,∑q 3π4p=3(r )3内r - ∴()2023π43π4r r r E ερ内-=41048.3⨯≈1C N -⋅, 方向沿半径向外. 12=r cm 时,3π4∑=ρq -3(外r )内3r∴ ()420331010.4π43π4⨯≈-=r r r E ερ内外 1C N -⋅ 沿半径向外.8-11 半径为1R 和2R (2R >1R )的两无限长同轴圆柱面,单位长度上分别带有电量λ和-λ,试求:(1)r <1R ;(2) 1R <r <2R ;(3) r >2R 处各点的场强.解: 高斯定理0dε∑⎰=⋅qSE sϖϖ取同轴圆柱形高斯面,侧面积rl S π2=则rlE S E Sπ2d =⋅⎰ϖϖ对(1) 1R r < 0,0==∑E q(2) 21R r R <<λl q =∑∴r E 0π2ελ=沿径向向外(3) 2R r > 0=∑q ∴ 0=E题8-12图8-14 一电偶极子由q =1.0×10-6C 的两个异号点电荷组成,两电荷距离d=0.2cm ,把这电偶极子放在1.0×105N ·C -1的外电场中,求外电场作用于电偶极子上的最大力矩.解: ∵ 电偶极子p ϖ在外场E ϖ中受力矩E p M ϖϖϖ⨯= ∴ qlE pE M ==max代入数字 4536max 100.2100.1102100.1---⨯=⨯⨯⨯⨯⨯=M m N ⋅8-15 两点电荷1q =1.5×10-8C ,2q =3.0×10-8C ,相距1r =42cm ,要把它们之间的距离变为2r =25cm ,需作多少功?解:⎰⎰==⋅=22210212021π4π4d d r r r r q q r r q q r F A εεϖϖ)11(21r r - 61055.6-⨯-=J外力需作的功 61055.6-⨯-=-='A A J题8-16图8-16 如题8-16图所示,在A ,B 两点处放有电量分别为+q ,-q 的点电荷,AB 间距离为2R ,现将另一正试验点电荷0q 从O 点经过半圆弧移到C 点,求移动过程中电场力作的功.解: 如题8-16图示0π41ε=O U 0)(=-R qR q0π41ε=O U )3(R q R q -R q0π6ε-=∴R qq U U q A oC O 00π6)(ε=-=8-17 如题8-17图所示的绝缘细线上均匀分布着线密度为λ的正电荷,两直导线的长度和半圆环的半径都等于R .试求环中心O 点处的场强和电势.解: (1)由于电荷均匀分布与对称性,AB 和CD 段电荷在O 点产生的场强互相抵消,取θd d R l =则θλd d R q =产生O 点E ϖd 如图,由于对称性,O 点场强沿y 轴负方向题8-17图θεθλππcos π4d d 2220⎰⎰-==R R E E y R 0π4ελ=[)2sin(π-2sinπ-] R 0π2ελ-=(2) AB 电荷在O 点产生电势,以0=∞U⎰⎰===AB 200012ln π4π4d π4d R R x x x x U ελελελ同理CD 产生 2ln π402ελ=U半圆环产生0034π4πελελ==R R U∴0032142ln π2ελελ+=++=U U U U O8-18 一电子绕一带均匀电荷的长直导线以2×104m ·s -1的匀速率作圆周运动.求带电直线上的线电荷密度.(电子质量0m =9.1×10-31kg ,电子电量e =1.60×10-19C)解: 设均匀带电直线电荷密度为λ,在电子轨道处场强r E 0π2ελ=电子受力大小r e eE F e 0π2ελ==∴ r v mre 20π2=ελ得1320105.12π2-⨯==e mv ελ1m C -⋅ 8-21 证明:对于两个无限大的平行平面带电导体板(题8-21图)来说,(1)相向的两面上,电荷的面密度总是大小相等而符号相反;(2)相背的两面上,电荷的面密度总是大小相等而符号相同.证: 如题8-21图所示,设两导体A 、B 的四个平面均匀带电的电荷面密度依次为1σ,2σ,3σ,4σ题8-21图(1)则取与平面垂直且底面分别在A 、B 内部的闭合柱面为高斯面时,有)(d 32=∆+=⋅⎰S S E sσσϖϖ∴ +2σ03=σ 说明相向两面上电荷面密度大小相等、符号相反;(2)在A 内部任取一点P ,则其场强为零,并且它是由四个均匀带电平面产生的场强叠加而成的,即0222204030201=---εσεσεσεσ又∵ +2σ03=σ∴ 1σ4σ=说明相背两面上电荷面密度总是大小相等,符号相同.8-22 三个平行金属板A ,B 和C 的面积都是200cm 2,A 和B 相距4.0mm ,A 与C 相距2.0mm .B ,C 都接地,如题8-22图所示.如果使A 板带正电3.0×10-7C ,略去边缘效应,问B 板和C 板上的感应电荷各是多少?以地的电势为零,则A 板的电势是多少?解: 如题8-22图示,令A 板左侧面电荷面密度为1σ,右侧面电荷面密度为2σ题8-22图(1)∵ AB AC U U =,即∴AB AB AC AC E E d d =∴ 2d d 21===AC ABAB AC E E σσ且 1σ+2σS q A=得,32S q A =σ S q A 321=σ 而7110232-⨯-=-=-=A C q S q σC C10172-⨯-=-=S q B σ(2)301103.2d d ⨯===AC AC AC A E U εσV 8-23 两个半径分别为1R 和2R (1R <2R )的同心薄金属球壳,现给内球壳带电+q ,试计算:(1)外球壳上的电荷分布及电势大小;(2)先把外球壳接地,然后断开接地线重新绝缘,此时外球壳的电荷分布及电势; *(3)再使内球壳接地,此时内球壳上的电荷以及外球壳上的电势的改变量.解: (1)内球带电q +;球壳内表面带电则为q -,外表面带电为q +,且均匀分布,其电势题8-23图⎰⎰∞∞==⋅=22020π4π4d d R R R qr r q r E U εεϖϖ(2)外壳接地时,外表面电荷q +入地,外表面不带电,内表面电荷仍为q -.所以球壳电势由内球q +与内表面q -产生:π4π42020=-=R qR qU εε(3)设此时内球壳带电量为q ';则外壳内表面带电量为q '-,外壳外表面带电量为+-q q '(电荷守恒),此时内球壳电势为零,且π4'π4'π4'202010=+-+-=R q q R q R q U A εεε得 q R R q 21='外球壳上电势()22021202020π4π4'π4'π4'R qR R R q q R q R q U B εεεε-=+-+-=8-24 半径为R 的金属球离地面很远,并用导线与地相联,在与球心相距为R d 3=处有一点电荷+q ,试求:金属球上的感应电荷的电量.解: 如题8-24图所示,设金属球感应电荷为q ',则球接地时电势0=O U8-24图由电势叠加原理有:=O U 03π4π4'00=+R qR q εε得 -='q 3q8-25 有三个大小相同的金属小球,小球1,2带有等量同号电荷,相距甚远,其间的库仑力为0F.试求:(1)用带绝缘柄的不带电小球3先后分别接触1,2后移去,小球1,2之间的库仑力; (2)小球3依次交替接触小球1,2很多次后移去,小球1,2之间的库仑力.解: 由题意知2020π4r q F ε=(1)小球3接触小球1后,小球3和小球1均带电2q q =',小球3再与小球2接触后,小球2与小球3均带电qq 43=''∴ 此时小球1与小球2间相互作用力0220183π483π4"'2F rqr q q F =-=εε (2)小球3依次交替接触小球1、2很多次后,每个小球带电量均为32q.∴ 小球1、2间的作用力0294π432322F r qq F ==ε *8-26 如题8-26图所示,一平行板电容器两极板面积都是S ,相距为d ,分别维持电势A U =U ,B U =0不变.现把一块带有电量q 的导体薄片平行地放在两极板正中间,片的面积也是S ,片的厚度略去不计.求导体薄片的电势.解: 依次设A ,C ,B 从上到下的6个表面的面电荷密度分别为1σ,2σ,3σ,4σ,5σ,6σ如图所示.由静电平衡条件,电荷守恒定律及维持U U AB =可得以下6个方程题8-26图⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧++++==+=+-==+=+===+6543215432065430021001σσσσσσσσσσεσσσσεσσd US q S qdU U C S S q B A解得S q261==σσ S qd U 2032-=-=εσσ S qd U 2054+=-=εσσ所以CB 间电场S q d U E 00422εεσ+== )2d (212d 02S q U E U U CB C ε+===注意:因为C 片带电,所以2U U C ≠,若C 片不带电,显然2UU C =8-27 在半径为1R 的金属球之外包有一层外半径为2R 的均匀电介质球壳,介质相对介电常数为r ε,金属球带电Q .试求: (1)电介质内、外的场强; (2)电介质层内、外的电势; (3)金属球的电势. 解: 利用有介质时的高斯定理∑⎰=⋅qS D Sϖϖd(1)介质内)(21R r R <<场强303π4,π4r rQ E r r Q D r εεϖϖϖϖ==内; 介质外)(2R r <场强303π4,π4r r Q E r Qr D εϖϖϖ==外 (2)介质外)(2R r >电势r Q E U 0rπ4r d ε=⋅=⎰∞ϖϖ外介质内)(21R r R <<电势rd r d ϖϖϖϖ⋅+⋅=⎰⎰∞∞rrE E U 外内2020π4)11(π4R Q R r qr εεε+-=)11(π420R r Q r r -+=εεε(3)金属球的电势rd r d 221ϖϖϖϖ⋅+⋅=⎰⎰∞R R R E E U 外内⎰⎰∞+=222020π44πdrR R R r r Qdrr Q εεε )11(π4210R R Q r r -+=εεε8-28 如题8-28图所示,在平行板电容器的一半容积内充入相对介电常数为r ε的电介质.试求:在有电介质部分和无电介质部分极板上自由电荷面密度的比值.解: 如题8-28图所示,充满电介质部分场强为2E ϖ,真空部分场强为1E ϖ,自由电荷面密度分别为2σ与1σ 由∑⎰=⋅0d q S D ϖϖ得11σ=D ,22σ=D而101E D ε=,202E D r εε=d 21UE E ==∴ r D D εσσ==1212题8-28图 题8-29图8-29 两个同轴的圆柱面,长度均为l ,半径分别为1R 和2R (2R >1R ),且l >>2R -1R ,两柱面之间充有介电常数ε的均匀电介质.当两圆柱面分别带等量异号电荷Q 和-Q 时,求: (1)在半径r 处(1R <r <2R =,厚度为dr ,长为l 的圆柱薄壳中任一点的电场能量密度和整个薄壳中的电场能量; (2)电介质中的总电场能量; (3)圆柱形电容器的电容. 解: 取半径为r 的同轴圆柱面)(S 则 rlDS D S π2d )(=⋅⎰ϖϖ当)(21R r R <<时,Q q =∑∴rl Q D π2=(1)电场能量密度22222π82l r Q D w εε== 薄壳中rl rQ rl r l r Q w W εευπ4d d π2π8d d 22222=== (2)电介质中总电场能量⎰⎰===211222ln π4π4d d R R V R R l Q rl r Q W W εε(3)电容:∵C Q W 22=∴)/ln(π22122R R lW Q C ε== *8-30 金属球壳A 和B 的中心相距为r ,A 和B 原来都不带电.现在A 的中心放一点电荷1q ,在B 的中心放一点电荷2q ,如题8-30图所示.试求:(1) 1q 对2q 作用的库仑力,2q 有无加速度;(2)去掉金属壳B ,求1q 作用在2q 上的库仑力,此时2q 有无加速度. 解: (1)1q 作用在2q 的库仑力仍满足库仑定律,即2210π41r q q F ε=但2q 处于金属球壳中心,它受合力为零,没有加速度.(2)去掉金属壳B ,1q 作用在2q 上的库仑力仍是2210π41r q q F ε=,但此时2q 受合力不为零,有加速度.题8-30图 题8-31图8-31 如题8-31图所示,1C =0.25μF ,2C =0.15μF ,3C =0.20μF .1C 上电压为50V .求:AB U .解: 电容1C 上电量111U C Q =电容2C 与3C 并联3223C C C +=其上电荷123Q Q =∴355025231123232⨯===C U C C Q U86)35251(5021=+=+=U U U AB V8-32 1C 和2C 两电容器分别标明“200 pF 、500 V ”和“300 pF 、900 V ”,把它们串联起来后等值电容是多少?如果两端加上1000 V 的电压,是否会击穿? 解: (1) 1C 与2C 串联后电容1203002003002002121=+⨯=+='C C C C C pF(2)串联后电压比231221==C C U U ,而100021=+U U∴ 6001=U V ,4002=U V即电容1C 电压超过耐压值会击穿,然后2C 也击穿.8-33 将两个电容器1C 和2C 充电到相等的电压U 以后切断电源,再将每一电容器的正极板与另一电容器的负极板相联.试求: (1)每个电容器的最终电荷; (2)电场能量的损失.解: 如题8-33图所示,设联接后两电容器带电分别为1q ,2q题8-33图则⎪⎪⎩⎪⎪⎨⎧==-=-=+2122112121201021U U U C U C q q U C U C q q q q解得 (1) =1q UC C C C C q U C C C C C 21212221211)(,)(+-=+-(2)电场能量损失W W W -=∆0)22()2121(2221212221C q C q U C U C +-+= 221212U C C C C +=8-34 半径为1R =2.0cm 的导体球,外套有一同心的导体球壳,壳的内、外半径分别为2R =4.0cm 和3R =5.0cm ,当内球带电荷Q =3.0×10-8C时,求:(1)整个电场储存的能量;(2)如果将导体壳接地,计算储存的能量; (3)此电容器的电容值.解: 如图,内球带电Q ,外球壳内表面带电Q -,外表面带电Q题8-34图(1)在1R r <和32R r R <<区域0=E ϖ在21R r R <<时 301π4r rQ E εϖϖ=3R r >时 302π4r rQ E εϖϖ=∴在21R r R <<区域⎰=21d π4)π4(21222001R R r r r QW εε⎰-==21)11(π8π8d 2102202R R R R Q rr Q εε 在3R r >区域⎰∞==32302220021π8d π4)π4(21R R Q r r rQ W εεε ∴ 总能量)111(π83210221R R R Q W W W +-=+=ε 41082.1-⨯=J(2)导体壳接地时,只有21R r R <<时30π4r rQ E εϖϖ=,02=W∴ 4210211001.1)11(π8-⨯=-==R R Q W W ε J(3)电容器电容)11/(π422102R R Q W C -==ε 121049.4-⨯=F。
大学物理第8章习题答案
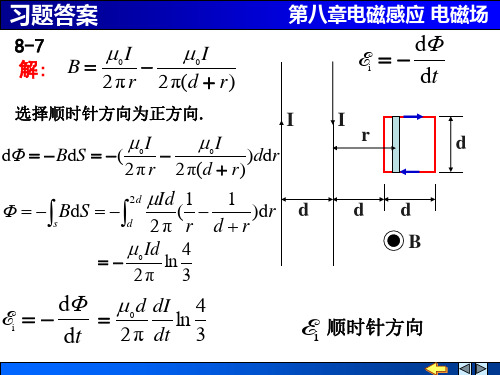
µId 1
d
d
d B
dΦ µ d dI 4 Ei = − ln = 2 π dt 3 dt
0
Ei
顺时针方向
习题答案
8-12 解:
第八章电磁感应 电磁场 第八章电磁感应
r v v dEi = ( v × B ) ⋅ dl
O′
= vBdlsinθ
= ωrBsinθdl
= Bωl sin θdl
2
v B
O
a
l
L
b
Ei 方向
a
b
习题答案
第八章电磁感应 电磁场 第八章电磁感应
v v b 解:Eab = ∫a E k ⋅ d l
b
r dB r < R Ek = 2 dt
× × × × × × × × × × × × × × × ×
× × × × r dB dl cos θ = ∫a B × × × × × 2 dt × × × × × L h dB = ∫0 dl O × × × × × 2 dt EK h = r cosθ h θ hL dB × = a b 2 dt dl
L = µn V
2
N 2 πd 2 N 2 πd 2 L = µ 0 n 2V = µ0 ( ) l = µ0 l 4 l 4
2 2 2 2 2
1 2 1 N πd ε 2 µ 0 N πd ε Wm = LI = µ 0 ( ) = = 3.28 × 10 −5 J 2 2 l 4 R 8R 2l
2
习题答案
8-18
+
第八章电磁感应 电磁场 第八章电磁感应 连接oa和 与 构成回路 构成回路oab. 解:连接 和ob与ab构成回路
大学物理第八章课后习题答案

第八章电磁感应电磁场8 -1一根无限长平行直导线载有电流I,一矩形线圈位于导线平面内沿垂直于载流导线方向以恒定速率运动(如图所示),则()(A)线圈中无感应电流(B)线圈中感应电流为顺时针方向(C)线圈中感应电流为逆时针方向(D)线圈中感应电流方向无法确定分析与解由右手定则可以判断,在矩形线圈附近磁场垂直纸面朝里,磁场是非均匀场,距离长直载流导线越远,磁场越弱.因而当矩形线圈朝下运动时,在线圈中产生感应电流,感应电流方向由法拉第电磁感应定律可以判定.因而正确答案为(B).8 -2将形状完全相同的铜环和木环静止放置在交变磁场中,并假设通过两环面的磁通量随时间的变化率相等,不计自感时则()(A)铜环中有感应电流,木环中无感应电流(B)铜环中有感应电流,木环中有感应电流(C)铜环中感应电动势大,木环中感应电动势小(D)铜环中感应电动势小,木环中感应电动势大分析与解根据法拉第电磁感应定律,铜环、木环中的感应电场大小相等,但在木环中不会形成电流.因而正确答案为(A).8 -3 有两个线圈,线圈1 对线圈2 的互感系数为M 21 ,而线圈2 对线圈1的互感系数为M 12 .若它们分别流过i 1 和i 2 的变化电流且t i t i d d d d 21<,并设由i 2变化在线圈1 中产生的互感电动势为ε12 ,由i 1 变化在线圈2 中产生的互感电动势为ε21 ,下述论断正确的是( ).(A )2112M M = ,1221εε=(B )2112M M ≠ ,1221εε≠(C )2112M M =, 1221εε<(D )2112M M = ,1221εε<分析与解 教材中已经证明M21 =M12 ,电磁感应定律t i M εd d 12121=;ti M εd d 21212=.因而正确答案为(D ). 8 -4 对位移电流,下述四种说法中哪一种说法是正确的是( )(A ) 位移电流的实质是变化的电场(B ) 位移电流和传导电流一样是定向运动的电荷(C ) 位移电流服从传导电流遵循的所有定律(D ) 位移电流的磁效应不服从安培环路定理分析与解 位移电流的实质是变化的电场.变化的电场激发磁场,在这一点位移电流等效于传导电流,但是位移电流不是走向运动的电荷,也就不服从焦耳热效应、安培力等定律.因而正确答案为(A ).8 -5 下列概念正确的是( )(A ) 感应电场是保守场(B ) 感应电场的电场线是一组闭合曲线(C ) LI Φm =,因而线圈的自感系数与回路的电流成反比(D ) LI Φm =,回路的磁通量越大,回路的自感系数也一定大分析与解 对照感应电场的性质,感应电场的电场线是一组闭合曲线.因而 正确答案为(B ).8 -6 一铁心上绕有线圈100匝,已知铁心中磁通量与时间的关系为()Wb π100sin 100.85t Φ⨯=,求在s 100.12-⨯=t 时,线圈中的感应电动势.分析 由于线圈有N 匝相同回路,线圈中的感应电动势等于各匝回路的感应电动势的代数和,在此情况下,法拉第电磁感应定律通常写成t ψt ΦN ξd d d d -=-=,其中ΦN ψ=称为磁链. 解 线圈中总的感应电动势()()t tΦNξπ100cos 51.2d d =-= 当s 100.12-⨯=t 时,V 51.2=ξ. 8 -7 有两根相距为d 的无限长平行直导线,它们通以大小相等流向相反的电流,且电流均以tI d d 的变化率增长.若有一边长为d 的正方形线圈与两导线处于同一平面内,如图所示.求线圈中的感应电动势.分析 本题仍可用法拉第电磁感应定律tΦξd d -=来求解.由于回路处在非均匀磁场中,磁通量就需用⎰⋅=S ΦS B d 来计算(其中B 为两无限长直电流单独存在时产生的磁感强度B 1 与B 2 之和).为了积分的需要,建立如图所示的坐标系.由于B 仅与x 有关,即()B B x =,故取一个平行于长直导线的宽为dx 、长为d 的面元dS ,如图中阴影部分所示,则x d S d d =,所以,总磁通量可通过线积分求得(若取面元y x S d d d =,则上述积分实际上为二重积分).本题在工程技术中又称为互感现象,也可用公式tl ME M d d -=求解. 解1 穿过面元dS 的磁通量为 ()x d xI μx d d x I μΦd π2d π2d d d d 0021-+=⋅+⋅=⋅=S B S B S B 因此穿过线圈的磁通量为 ()43ln π2d π2d π2d 02020Id μx x Id μx d x Id μΦΦd d dd =-+==⎰⎰⎰ 再由法拉第电磁感应定律,有tI d μt ΦE d d 43ln π2d d 0⎪⎭⎫ ⎝⎛=-= 解2 当两长直导线有电流I 通过时,穿过线圈的磁通量为43ln π20dI μΦ=线圈与两长直导线间的互感为 43ln π20d μI ΦM ==当电流以tl d d 变化时,线圈中的互感电动势为 tI d μt I M E d d 43ln π2d d 0⎪⎭⎫ ⎝⎛=-= 试想:如线圈又以速率v 沿水平向右运动,如何用法拉第电磁感应定律求图示位置的电动势呢?此时线圈中既有动生电动势,又有感生电动势.设时刻t ,线圈左端距右侧直导线的距离为ξ,则穿过回路的磁通量()ξf ΦS ,1d =⋅=⎰S B ,它表现为变量I 和ξ的二元函数,将Φ代入tΦE d d -= 即可求解,求解时应按复合函数求导,注意,其中v =tξd d ,再令ξ=d 即可求得图示位置处回路中的总电动势.最终结果为两项,其中一项为动生电动势,另一项为感生电动势.8 -8 有一测量磁感强度的线圈,其截面积S =4.0 cm 2 、匝数N =160 匝、电阻R =50Ω.线圈与一内阻R i =30Ω的冲击电流计相连.若开始时,线圈的平面与均匀磁场的磁感强度B 相垂直,然后线圈的平面很快地转到与B 的方向平行.此时从冲击电流计中测得电荷值54.010C q -=⨯.问此均匀磁场的磁感强度B 的值为多少?分析 在电磁感应现象中,闭合回路中的感应电动势和感应电流与磁通量变化的快慢有关,而在一段时间内,通过导体截面的感应电量只与磁通量变化的大小有关,与磁通量变化的快慢无关.工程中常通过感应电量的测定来确定磁场的强弱.解 在线圈转过90°角时,通过线圈平面磁通量的变化量为 NBS NBS ΦΦΦ=-=-=0Δ12 因此,流过导体截面的电量为ii R R NBS R R Φq +=+=Δ 则 ()T 050.0=+=NSR R q B i 8 -9 如图所示,一长直导线中通有I =5.0 A 的电流,在距导线9.0 cm 处,放一面积为0.10 cm 2 ,10 匝的小圆线圈,线圈中的磁场可看作是均匀的.今在1.0 ×10-2 s 内把此线圈移至距长直导线10.0 cm 处.求:(1) 线圈中平均感应电动势;(2) 设线圈的电阻为1.0×10-2Ω,求通过线圈横截面的感应电荷.分析 虽然线圈处于非均匀磁场中,但由于线圈的面积很小,可近似认为穿过线圈平面的磁场是均匀的,因而可近似用NBS ψ=来计算线圈在始、末两个位置的磁链.解 (1) 在始、末状态,通过线圈的磁链分别为1011π2r IS μN S NB ψ==,2022π2r IS μN S NB ψ== 则线圈中的平均感应电动势为V 1011.111πΔ2ΔΔ8210-⨯=⎪⎪⎭⎫ ⎝⎛-==r r t IS μN t ΦE 电动势的指向为顺时针方向.(2) 通过线圈导线横截面的感应电荷为tΦE d d -= 8 -10 如图(a)所示,把一半径为R 的半圆形导线OP 置于磁感强度为B 的均匀磁场中,当导线以速率v 水平向右平动时,求导线中感应电动势E 的大小,哪一端电势较高?分析 本题及后面几题中的电动势均为动生电动势,除仍可由t ΦE d d -=求解外(必须设法构造一个闭合回路),还可直接用公式()l B d ⋅⨯=⎰l E v 求解.在用后一种方法求解时,应注意导体上任一导线元dl 上的动生电动势()l B d d ⋅⨯=v E .在一般情况下,上述各量可能是dl 所在位置的函数.矢量(v ×B )的方向就是导线中电势升高的方向.解1 如图(b)所示,假想半圆形导线OP 在宽为2R 的静止形导轨上滑动,两者之间形成一个闭合回路.设顺时针方向为回路正向,任一时刻端点O 或端点P 距 形导轨左侧距离为x ,则B R Rx Φ⎪⎭⎫ ⎝⎛+=2π212 即B R tx RB t ΦE v 2d d 2d d -=-=-= 由于静止的 形导轨上的电动势为零,则E =-2RvB .式中负号表示电动势的方向为逆时针,对OP 段来说端点P 的电势较高.解2 建立如图(c )所示的坐标系,在导体上任意处取导体元dl ,则()θR θB l θB E o d cos d cos 90sin d d v v ==⋅⨯=l B vB R θθBR E v v 2d cos d E π/2π/2===⎰⎰- 由矢量(v ×B )的指向可知,端点P 的电势较高.解3 连接OP 使导线构成一个闭合回路.由于磁场是均匀的,在任意时刻,穿过回路的磁通量==BS Φ常数.由法拉第电磁感应定律t ΦE d d -=可知,E =0又因 E =E OP +E PO即 E OP =-E PO =2RvB由上述结果可知,在均匀磁场中,任意闭合导体回路平动所产生的动生电动势为零;而任意曲线形导体上的动生电动势就等于其两端所连直线形导体上的动生电动势.上述求解方法是叠加思想的逆运用,即补偿的方法.8 -11 长为L 的铜棒,以距端点r 处为支点,以角速率ω绕通过支点且垂直于铜棒的轴转动.设磁感强度为B 的均匀磁场与轴平行,求棒两端的电势差.分析 应该注意棒两端的电势差与棒上的动生电动势是两个不同的概念,如同电源的端电压与电源电动势的不同.在开路时,两者大小相等,方向相反(电动势的方向是电势升高的方向,而电势差的正方向是电势降落的方向).本题可直接用积分法求解棒上的电动势,亦可以将整个棒的电动势看作是O A 棒与O B 棒上电动势的代数和,如图(b)所示.而E O A 和E O B 则可以直接利用第8 -2 节例1 给出的结果.解1 如图(a)所示,在棒上距点O 为l 处取导体元dl ,则()()r L lB ωl lB ωE L-r r AB AB 221d d --=-=⋅⨯=⎰⎰-l B v 因此棒两端的电势差为()r L lB ωE U AB AB 221--== 当L >2r 时,端点A 处的电势较高解2 将AB 棒上的电动势看作是O A 棒和O B 棒上电动势的代数和,如图(b)所示.其中221r ωB E OA =,()221r L B ωE OB -= 则 ()r L BL ωE E E OB OA AB 221--=-= 8 -12 如图所示,长为L 的导体棒OP ,处于均匀磁场中,并绕OO ′轴以角速度ω旋转,棒与转轴间夹角恒为θ,磁感强度B 与转轴平行.求OP 棒在图示位置处的电动势.分析 如前所述,本题既可以用法拉第电磁感应定律tΦE d d -= 计算(此时必须构造一个包含OP 导体在内的闭合回路, 如直角三角形导体回路OPQO ),也可用()l B d ⋅⨯=⎰lE v 来计算.由于对称性,导体OP 旋转至任何位置时产生的电动势与图示位置是相同的.解1 由上分析,得()l B d ⋅⨯=⎰OP OP E v l αB l o d cos 90sin ⎰=v()()l θB θωl o d 90cos sin ⎰-=l()⎰==L θL B ωl l θB ω022sin 21d sin 由矢量B ⨯v 的方向可知端点P 的电势较高.解2 设想导体OP 为直角三角形导体回路OPQO 中的一部分,任一时刻穿 过回路的磁通量Φ为零,则回路的总电动势QO PQ OP E E E t ΦE ++==-=0d d 显然,E QO =0,所以 ()221PQ B ωE E E QO PQ OP ==-= 由上可知,导体棒OP 旋转时,在单位时间内切割的磁感线数与导体棒QP 等效.后者是垂直切割的情况.8 -13 如图(a)所示,金属杆AB 以匀速12.0m s -=⋅v 平行于一长直导线移动,此导线通有电流I =40A .求杆中的感应电动势,杆的哪一端电势较高?分析 本题可用两种方法求解.(1) 用公式()l B d ⋅⨯=⎰lE v 求解,建立图(a )所示的坐标系,所取导体元x l d d =,该处的磁感强度xI μB π20=.(2) 用法拉第电磁感应定律求解,需构造一个包含杆AB 在内的闭合回路.为此可设想杆AB 在一个静止的形导轨上滑动,如图(b)所示.设时刻t ,杆AB距导轨下端CD 的距离为y ,先用公式⎰⋅=S ΦS B d 求得穿过该回路的磁通量,再代入公式tΦE d d -=,即可求得回路的电动势,亦即本题杆中的电动势. 解1 根据分析,杆中的感应电动势为()V 1084.311ln 2πd 2πd d 50m 1.1m 1.00-⨯-=-=-==⋅⨯=⎰⎰v v v I μx x μxl E AB AB l B 式中负号表示电动势方向由B 指向A ,故点A 电势较高.解2 设顺时针方向为回路ABCD 的正向,根据分析,在距直导线x 处,取宽为dx 、长为y 的面元dS ,则穿过面元的磁通量为x y xI μΦd 2πd d 0=⋅=S B 穿过回路的磁通量为 11ln 2πd 2πd 0m1.1m 1.00⎰⎰-===S Iy μx y x I μΦΦ 回路的电动势为V 1084.32πd d 11ln 2πd d 500-⨯-=-=-=-=Iy μt y x I μt ΦE 由于静止的形导轨上电动势为零,所以V 1084.35-⨯-==E E AB 式中负号说明回路电动势方向为逆时针,对AB 导体来说,电动势方向应由B 指向A ,故点A 电势较高.8 -14 如图(a)所示,在“无限长”直载流导线的近旁,放置一个矩形导体线框,该线框在垂直于导线方向上以匀速率v 向右移动,求在图示位置处,线框中感应电动势的大小和方向.分析 本题亦可用两种方法求解.其中应注意下列两点:1.当闭合导体线框在磁场中运动时,线框中的总电动势就等于框上各段导体中的动生电动势的代数和.如图(a)所示,导体eh 段和fg 段上的电动势为零[此两段导体上处处满足()0l B =⋅⨯d v ],因而线框中的总电动势为()()()()hg ef hgef gh ef E E E -=⋅⨯-⋅⨯=⋅⨯+⋅⨯=⎰⎰⎰⎰l B l B l B l B d d d d v v v v 其等效电路如图(b)所示.2.用公式tΦE d d -=求解,式中Φ是线框运动至任意位置处时,穿过线框的磁通量.为此设时刻t 时,线框左边距导线的距离为ξ,如图(c )所示,显然ξ是时间t 的函数,且有v =tξd d .在求得线框在任意位置处的电动势E (ξ)后,再令ξ=d ,即可得线框在题目所给位置处的电动势.解1 根据分析,线框中的电动势为hg ef E E E -=()()⎰⎰⋅⨯-⋅⨯=hgef l B l B d d v v ()⎰⎰+-=2201000d 2πd 2πl l l l d I μl d I μv v ()1202πl d I I μ+=1vI 由E ef >E hg 可知,线框中的电动势方向为efgh .解2 设顺时针方向为线框回路的正向.根据分析,在任意位置处,穿过线框的磁通量为()()ξl ξξx Il μdx ξx Il μΦl 120020ln π2π21++=+=⎰相应电动势为 ()()1120π2d d l ξξl l I μt ΦξE +=-=v 令ξ=d ,得线框在图示位置处的电动势为 ()1120π2l d d l l I μE +=v 由E >0 可知,线框中电动势方向为顺时针方向.*8 -15 有一长为l ,宽为b 的矩形导线框架,其质量为m ,电阻为R .在t =0时,框架从距水平面y =0 的上方h 处由静止自由下落,如图所示.磁场的分布为:在y =0 的水平面上方没有磁场;在y =0 的水平面下方有磁感强度为B 的均匀磁场,B 的方向垂直纸面向里.已知框架在时刻t 1 和t 2 的位置如图中所示.求在下述时间内,框架的速度与时间的关系:(1) t 1 ≥t >0,即框架进入磁场前;(2) t 2 ≥t ≥t 1 ,即框架进入磁场, 但尚未全部进入磁场;(3)t >t 2 ,即框架全部进入磁场后.分析 设线框刚进入磁场(t 1 时刻)和全部进入磁场(t 2 时刻)的瞬间,其速度分别为v 10 和v 20 .在情况(1)和(3)中,线框中无感应电流,线框仅在重力作用下作落体运动,其速度与时间的关系分别为v =gt (t <t 1)和v =v 20 +g (t -t 2 )(t >t 2 ).而在t 1<t <t 2这段时间内,线框运动较为复杂,由于穿过线框回路的磁通量变化,使得回路中有感应电流存在,从而使线框除受重力外,还受到一个向上的安培力F A ,其大小与速度有关,即()A A F F =v .根据牛顿运动定律,此时线框的运动微分方程为()tv v d d mF mg A =-,解此微分方程可得t 1<t <t 2 时间内线框的速度与时间的关系式. 解 (1) 根据分析,在1t t ≤时间内,线框为自由落体运动,于是()11t t gt ≤=v 其中1t t =时,gh 2101==v v(2) 线框进入磁场后,受到向上的安培力为v Rl B IlB F A 22==根据牛顿运动定律,可得线框运动的微分方程tv m v d d 22=-R l B mg 令mRl B K 22=,整理上式并分离变量积分,有 ⎰⎰=-t t t g 110d d v v Kv v 积分后将gh 210=v 代入,可得 ()()[]1212t t K e gh K g g K ----=v (3) 线框全部进入磁场后(t >t 2),作初速为v 20 的落体运动,故有()()()[]()222031221t t g e gh K g g Kt t g t t K -+--=-+=--v v 8 -16 有一磁感强度为B 的均匀磁场,以恒定的变化率t d d B 在变化.把一块质量为m 的铜,拉成截面半径为r 的导线,并用它做成一个半径为R 的圆形回路.圆形回路的平面与磁感强度B 垂直.试证:这回路中的感应电流为 td d π4B d ρm I = 式中ρ 为铜的电阻率,d 为铜的密度. 解 圆形回路导线长为πR 2,导线截面积为2πr ,其电阻R ′为22rR ρS l ρR ==' 在均匀磁场中,穿过该回路的磁通量为BS Φ=,由法拉第电磁感应定律可得回路中的感应电流为tt t d d 2πd d π1d d 122B ρRr B R R ΦR R E I ='='='= 而2ππ2r R d m =,即dm Rr π2π2=,代入上式可得t d d π4B d ρm I = 8 -17 半径为R =2.0 cm 的无限长直载流密绕螺线管,管内磁场可视为均匀磁场,管外磁场可近似看作零.若通电电流均匀变化,使得磁感强度B 随时间的变化率td d B 为常量,且为正值,试求:(1) 管内外由磁场变化激发的感生电场分布;(2) 如1s T 010.0d d -⋅=tB ,求距螺线管中心轴r =5.0 cm 处感生电场的大小和方向.分析 变化磁场可以在空间激发感生电场,感生电场的空间分布与场源———变化的磁场(包括磁场的空间分布以及磁场的变化率t d d B 等)密切相关,即S B l E d d ⋅∂∂-=⎰⎰S S k t.在一般情况下,求解感生电场的分布是困难的.但对于本题这种特殊情况,则可以利用场的对称性进行求解.可以设想,无限长直螺线管内磁场具有柱对称性,其横截面的磁场分布如图所示.由其激发的感生电场也一定有相应的对称性,考虑到感生电场的电场线为闭合曲线,因而本题中感生电场的电场线一定是一系列以螺线管中心轴为圆心的同心圆.同一圆周上各点的电场强度E k 的大小相等,方向沿圆周的切线方向.图中虚线表示r <R 和r >R 两个区域的电场线.电场线绕向取决于磁场的变化情况,由楞次定律可知,当0d d <t B 时,电场线绕向与B 方向满足右螺旋关系;当0d d >tB 时,电场线绕向与前者相反. 解 如图所示,分别在r <R 和r >R 的两个区域内任取一电场线为闭合回路l (半径为r 的圆),依照右手定则,不妨设顺时针方向为回路正向.(1) r <R , tB r t r E E k l k d d πd d d π2d 2-=⋅-=⋅=⋅=⎰⎰S B l E tB r E k d d 2-= r >R , tB R t r E E k l k d d πd d d π2d 2-=⋅-=⋅=⋅=⎰⎰S B l E tB r R E k d d 22-= 由于0d d >tB ,故电场线的绕向为逆时针. (2) 由于r >R ,所求点在螺线管外,因此tB r R E k d d 22-= 将r 、R 、tB d d 的数值代入,可得15m V 100.4--⋅⨯-=k E ,式中负号表示E k 的方向是逆时针的.8 -18 在半径为R 的圆柱形空间中存在着均匀磁场,B 的方向与柱的轴线平行.如图(a)所示,有一长为l 的金属棒放在磁场中,设B 随时间的变化率tB d d 为常量.试证:棒上感应电动势的大小为分析 变化磁场在其周围激发感生电场,把导体置于感生电场中,导体中的自由电子就会在电场力的作用下移动,在棒内两端形成正负电荷的积累,从而产生感生电动势.由于本题的感生电场分布与上题所述情况完全相同,故可利用上题结果,由⎰⋅=l k E l E d 计算棒上感生电动势.此外,还可连接OP 、OQ ,设想PQOP 构成一个闭合导体回路,用法拉第电磁感应定律求解,由于OP 、OQ 沿半径方向,与通过该处的感生电场强度E k 处处垂直,故0d =⋅l E k ,OP 、OQ 两段均无电动势,这样,由法拉第电磁感应定律求出的闭合回路的总电动势,就是导体棒PQ 上的电动势.证1 由法拉第电磁感应定律,有22Δ22d d d d d d ⎪⎭⎫ ⎝⎛-==-==l R l t B t B S t ΦE E PQ 证2 由题8 -17可知,在r <R 区域,感生电场强度的大小t B r E k d d 2= 设PQ 上线元dx 处,E k 的方向如图(b )所示,则金属杆PQ 上的电动势为()()222202/2d d d 2/d d 2d cos d l R l t B x r l R t B r x θE E l k k PQ -=-==⋅=⎰⎰x E 讨论 假如金属棒PQ 有一段在圆外,则圆外一段导体上有无电动势? 该如何求解?8 -19 截面积为长方形的环形均匀密绕螺绕环,其尺寸如图(a)所示,共有N 匝(图中仅画出少量几匝),求该螺绕环的自感L .分析 如同电容一样,自感和互感都是与回路系统自身性质(如形状、匝数、介质等)有关的量.求自感L 的方法有两种:1.设有电流I 通过线圈,计算磁场穿过自身回路的总磁通量,再用公式IΦL =计算L .2.让回路中通以变化率已知的电流,测出回路中的感应电动势E L ,由公式t I E L L d /d =计算L .式中E L 和tI d d 都较容易通过实验测定,所以此方法一般适合于工程中.此外,还可通过计算能量的方法求解.解 用方法1 求解,设有电流I 通过线圈,线圈回路呈长方形,如图(b)所示,由安培环路定理可求得在R 1 <r <R 2 范围内的磁场分布为 x NI μB π20= 由于线圈由N 匝相同的回路构成,所以穿过自身回路的磁链为12200ln π2d π2d 21R R hI N μx h x NI μN N ψS R R ==⋅=⎰⎰S B 则1220ln π2R R h N μI ψL = 若管中充满均匀同种磁介质,其相对磁导率为μr ,则自感将增大μr 倍. 8 -20 如图所示,螺线管的管心是两个套在一起的同轴圆柱体,其截面积分别为S 1 和S 2 ,磁导率分别为μ1 和μ2 ,管长为l ,匝数为N ,求螺线管的自感.(设管的截面很小)分析 本题求解时应注意磁介质的存在对磁场的影响.在无介质时,通电螺线管内的磁场是均匀的,磁感强度为B 0 ,由于磁介质的存在,在不同磁介质中磁感强度分别为μ1 B 0 和μ2 B 0 .通过线圈横截面的总磁通量是截面积分别为S 1 和S 2 的两部分磁通量之和.由自感的定义可解得结果.解 设有电流I 通过螺线管,则管中两介质中磁感强度分别为I L N μnl μB 111==,I LN μnl μB 222== 通过N 匝回路的磁链为 221121S NB S NB ΨΨΨ+=+=则自感2211221S μS μlN I ψL L L +==+= 8 -21 有两根半径均为a 的平行长直导线,它们中心距离为d .试求长为l的一对导线的自感(导线内部的磁通量可略去不计).分析 两平行长直导线可以看成无限长但宽为d 的矩形回路的一部分.设在矩形回路中通有逆时针方向电流I ,然后计算图中阴影部分(宽为d 、长为l )的磁通量.该区域内磁场可以看成两无限长直载流导线分别在该区域产生的磁场的叠加.解 在如图所示的坐标中,当两导线中通有图示的电流I 时,两平行导线间的磁感强度为()r d I μr I μB -+=π2π200 穿过图中阴影部分的磁通量为a a d l μr Bl ΦS a d a -==⋅=⎰⎰-ln πd d 0S B 则长为l 的一对导线的自感为aa d l μI ΦL -==ln π0 如导线内部磁通量不能忽略,则一对导线的自感为212L L L +=.L 1 称为外自感,即本题已求出的L ,L 2 称为一根导线的内自感.长为l 的导线的内自感8π02l μL =,有兴趣的读者可自行求解. 8 -22 如图所示,在一柱形纸筒上绕有两组相同线圈AB 和A ′B ′,每个线圈的自感均为L ,求:(1) A 和A ′相接时,B 和B ′间的自感L 1 ;(2) A ′和B 相接时,A 和B ′间的自感L 2 .分析 无论线圈AB 和A ′B ′作哪种方式连接,均可看成一个大线圈回路的两个部分,故仍可从自感系数的定义出发求解.求解过程中可利用磁通量叠加的方法,如每一组载流线圈单独存在时穿过自身回路的磁通量为Φ,则穿过两线圈回路的磁通量为2Φ;而当两组线圈按(1)或(2)方式连接后,则穿过大线圈回路的总磁通量为2Φ±2Φ,“ ±”取决于电流在两组线圈中的流向是相同或是相反.解 (1) 当A 和A ′连接时,AB 和A ′B ′线圈中电流流向相反,通过回路的磁通量亦相反,故总通量为0221=-=ΦΦΦ,故L 1 =0.(2) 当A ′和B 连接时,AB 和A ′B ′线圈中电流流向相同,通过回路的磁通量亦相同,故总通量为ΦΦΦΦ4222=+=, 故L I ΦI ΦL 4422===. 本题结果在工程实际中有实用意义,如按题(1)方式连接,则可构造出一个无自感的线圈.8 -23 如图所示,一面积为4.0 cm 2 共50 匝的小圆形线圈A ,放在半径为20 cm 共100 匝的大圆形线圈B 的正中央,此两线圈同心且同平面.设线圈A 内各点的磁感强度可看作是相同的.求:(1) 两线圈的互感;(2) 当线圈B 中电流的变化率为-50 A ·s-1 时,线圈A 中感应电动势的大小和方向.分析 设回路Ⅰ中通有电流I 1 ,穿过回路Ⅱ的磁通量为Φ21 ,则互感M =M 21 =Φ21I 1 ;也可设回路Ⅱ通有电流I 2 ,穿过回路Ⅰ的磁通量为Φ12 ,则21212I ΦM M == . 虽然两种途径所得结果相同,但在很多情况下,不同途径所涉及的计算难易程度会有很大的不同.以本题为例,如设线圈B 中有电流I 通过,则在线圈A 中心处的磁感强度很易求得,由于线圈A 很小,其所在处的磁场可视为均匀的,因而穿过线圈A 的磁通量Φ≈BS .反之,如设线圈A 通有电流I ,其周围的磁场分布是变化的,且难以计算,因而穿过线圈B 的磁通量也就很难求得,由此可见,计算互感一定要善于选择方便的途径.解 (1) 设线圈B 有电流I 通过,它在圆心处产生的磁感强度R I μN B B 200=穿过小线圈A 的磁链近似为 A B A A A A S RI μN N S B N ψ200== 则两线圈的互感为H 1028.6260-⨯===R S μN N I ψM A B A A (2)V 1014.3d d 4-⨯=-=tI M E A 互感电动势的方向和线圈B 中的电流方向相同.8 -24 如图所示,两同轴单匝线圈A 、C 的半径分别为R 和r ,两线圈相距为d .若r 很小,可认为线圈A 在线圈C 处所产生的磁场是均匀的.求两线圈的互感.若线圈C 的匝数为N 匝,则互感又为多少?解 设线圈A 中有电流I 通过,它在线圈C 所包围的平面内各点产生的磁 感强度近似为()2/322202d R IR μB +=穿过线圈C 的磁通为 ()22/32220π2r d R IR μBS ψC +==则两线圈的互感为 ()2/3222202πd R R r μI ψM +== 若线圈C 的匝数为N 匝,则互感为上述值的N 倍.8 -25 如图所示,螺绕环A 中充满了铁磁质,管的截面积S 为2.0 cm 2 ,沿环每厘米绕有100 匝线圈,通有电流I 1 =4.0 ×10 -2 A ,在环上再绕一线圈C ,共10 匝,其电阻为0.10 Ω,今将开关S 突然开启,测得线圈C 中的感应电荷为2.0 ×10 -3 C .求:当螺绕环中通有电流I 1 时,铁磁质中的B 和铁磁质的相对磁导率μr .分析 本题与题8 -8 相似,均是利用冲击电流计测量电磁感应现象中通过回路的电荷的方法来计算磁场的磁感强度.线圈C 的磁通变化是与环形螺线管中的电流变化相联系的.解 当螺绕环中通以电流I 1 时,在环内产生的磁感强度110I n μμB r =则通过线圈C 的磁链为S I n μμN BS N ψr c 11022==设断开电源过程中,通过C 的感应电荷为q C ,则有()RS I n μμN ψR ψR qc r c c 110201Δ1=--=-= 由此得 T 10.02110===S N Rqc I n μμB r 相对磁导率1991102==I n μS N Rqc μr 8 -26 一个直径为0.01 m ,长为0.10 m 的长直密绕螺线管,共1 000 匝线圈,总电阻为7.76 Ω.求:(1) 如把线圈接到电动势E =2.0 V 的电池上,电流稳定后,线圈中所储存的磁能有多少? 磁能密度是多少?*(2) 从接通电路时算起,要使线圈储存磁能为最大储存磁能的一半,需经过多少时间?分析 单一载流回路所具有的磁能,通常可用两种方法计算:(1) 如回路自感为L (已知或很容易求得),则该回路通有电流I 时所储存的磁能221LI W m =,通常称为自感磁能.(2) 由于载流回路可在空间激发磁场,磁能实际是储存于磁场之中,因而载流回路所具有的能量又可看作磁场能量,即V w W V m m d ⎰=,式中m w 为磁场能量密度,积分遍及磁场存在的空间.由于μB w m 22=,因而采用这种方法时应首先求载流回路在空间产生的磁感强度B 的分布.上述两种方法还为我们提供了计算自感的另一种途径,。
大学物理第八章电磁感应部分的习题及答案

第八章 电磁感应一、简答题1、简述电磁感应定律答:当穿过闭合回路所围面积的磁通量发生变化时,不论这种变化是什么原因引起的,回路中都会建立起感应电动势,且此感应电动势等于磁通量对时间变化率的负值,即dtd i φε-=。
2、简述动生电动势和感生电动势答:由于回路所围面积的变化或面积取向变化而引起的感应电动势称为动生电动势。
由于磁感强度变化而引起的感应电动势称为感生电动势。
3、简述自感和互感答:某回路的自感在数值上等于回路中的电流为一个单位时,穿过此回路所围成面积的磁通量,即LI LI =Φ=Φ。
两个线圈的互感M M 值在数值上等于其中一个线圈中的电流为一单位时,穿过另一个线圈所围成面积的磁通量,即212121MI MI ==φφ或。
4、简述感应电场与静电场的区别? 答:感生电场和静电场的区别5、写出麦克斯韦电磁场方程的积分形式。
答:⎰⎰==⋅svqdv ds D ρdS tB l E sL⋅∂∂-=⋅⎰⎰d0d =⋅⎰S S B dS t D j l H s l ⋅⎪⎭⎫ ⎝⎛∂∂+=⋅⎰⎰d6、简述产生动生电动势物理本质答:在磁场中导体作切割磁力线运动时,其自由电子受洛仑滋力的作用,从而在导体两端产生电势差7、 简述何谓楞次定律答:闭合的导线回路中所出现的感应电流,总是使它自己所激发的磁场反抗任何引发电磁感应的原因(反抗相对运动、磁场变化或线圈变形等).这个规律就叫做楞次定律。
二、选择题1、有一圆形线圈在均匀磁场中做下列几种运动,那种情况在线圈中会产生感应电流 ( D )A 、线圈平面法线沿磁场方向平移B 、线圈平面法线沿垂直于磁场方向平移C 、线圈以自身的直径为轴转动,轴与磁场方向平行D 、线圈以自身的直径为轴转动,轴与磁场方向垂直2、对于位移电流,下列四种说法中哪一种说法是正确的 ( A ) A 、位移电流的实质是变化的电场 B 、位移电流和传导电流一样是定向运动的电荷 C 、位移电流服从传导电流遵循的所有规律 D 、位移电流的磁效应不服从安培环路定理3、下列概念正确的是 ( B )。
(完整版)大学物理学(课后答案)第8章

第八章课后习题解答一、选择题8-1如图8-1所示,一定量的理想气体,由平衡态A 变到平衡态B ,且它们的压强相等,即=A B p p 。
则在状态A 和状态B 之间,气体无论经过的是什么过程,气体必然[ ](A) 对外作正功 (B) 内能增加 (C) 从外界吸热 (D) 向外界放热分析:由p V -图可知,A A B B p V p V =,即知A B T T <,则对一定量理想气体必有B A E E >,即气体由状态A 变化到状态B ,内能必增加。
而作功、热传递均是过程量,与具体的热力学过程相关,所以(A )、(C )、(D )不是必然结果,只有(B )正确。
8-2 两个相同的刚性容器,一个盛有氢气,一个盛有氦气(均视为刚性分子理想气体)。
开始时它们的压强和温度都相同。
现将3 J 热量传给氦气,使之升高到一定的温度。
若使氢气也升高同样的温度,则应向氢气传递热量为[ ](A) 6 J (B) 3 J (C) 5 J (D) 10 J分析:由热力学第一定律Q E W =∆+知在等体过程中Q E =∆。
故可知欲使氢气和氦气升高相同的温度,由理想气体的内能公式2m i E R T M '∆=∆,知需传递的热量之比22222:():():5:3HHe H He H He H He H Hem m Q Q i i i i M M ''===。
故正确的是(C )。
8-3 一定量理想气体分别经过等压、等温和绝热过程从体积1V 膨胀到体积2V ,如图8-3所示,则下述正确的是[ ]习题8-1图(A) A C →吸热最多,内能增加(B) A D →内能增加,作功最少(C) A B →吸热最多,内能不变(D) A C →对外作功,内能不变分析:根据p V -图可知图中A B →为等压过程,A C →为等温过程,A D →为绝热过程。
又由理想气体的物态方程pV vRT =可知,p V -图上的pV 积越大,则该点温度越高,因此图中D A B C T T T T <==,又因对于一定量的气体而言其内能公式2i E vRT =,由此知0AB E ∆>,0AC E ∆=,0AD E ∆<。
大学物理课后习题答案第八章

大学物理课后习题答案第八章第八章光的偏振8.1两偏振片组装成起偏和检偏器,当两偏振片的偏振化方向夹角成30o时观察一普通光源,夹角成60o时观察另一普通光源,两次观察所得的光强相等,求两光源光强之比.[解答]第一个普通光源的光强用I1表示,通过第一个偏振片之后,光强为I0 = I1/2.22当偏振光通过第二个偏振片后,根据马吕斯定律,光强为I = I0cosθ1= I1cosθ1/2.2同理,对于第二个普通光源可得光强为I = I2cosθ2/2.2222因此光源的光强之比I2/I1 = cosθ1/cosθ2 = cos30o/cos60o = 1/3.8.2一束线偏振光和自然光的混合光,当它通过一偏振片后,发现随偏振片的取向不同,透射光的强度可变化四倍,求入射光束中两种光的强度各占入射光强度的百分之几?[解答]设自然光强为I1,线偏振光强为I2,则总光强为I0 = I1 + I2.当光线通过偏振片时,最小光强为自然光强的一半,即Imin = I1/2;最大光强是线偏振光强与自然光强的一半之和,即Imax = I2 + I1/2.由题意得Imax/Imin = 4,因此2I2/I1 + 1 = 4,解得I2 = 3I1/2.此式代入总光强公式得I0 = I1 + 3I1/2.因此入射光中自然光强的比例为I1/I0 = 2/5 = 40%.由此可得线偏振光的光强的比例为I2/I0 = 3/5 = 60%.[讨论]如果Imax/Imin = n,根据上面的步骤可得I1/I0 = 2/(n + 1),I2/I0 = (n - 1)/(n + 1),可见:n的值越大,入射光中自然光强的比例越小,线偏振光的光强的比例越大.8.3水的折射率为1.33,玻璃的折射率为1.50,当光由水射向玻璃时,起偏角为多少?若光由玻璃射向水时,起偏角又是多少?这两个角度数值上的关系如何?[解答]当光由水射向玻璃时,水的折射率为n1,玻璃的折射率为n2,根据布儒斯特定律tani0 = n2/n1 = 1.1278,得起偏角为i0 = 48.44o.当光由玻璃射向水时,玻璃的折射率为n1,水的折射率为n2,根据布儒斯特定律tani0 = n2/n1 = 0.8867,得起偏角为i0 = 41.56o.可见:两个角度互为余角.8.4根据布儒斯特定律可测量不透明介质的折射率,今测得某釉质的起偏角为58o,则该釉质的折射率为多少?[解答]空气的折射率取为1,根据布儒斯特定律可得釉质的折射率为n = tan i0 = 1.6003.8.5三个偏振片堆叠在一起,第一块与第三块偏振化方向互相垂直,第二块与第一块的偏振化方向互相平行,现令第ωθ二块偏振片以恒定的角速度ω0绕光传播方向旋转,如图所示.设入射自然光的光强为I0,试证明:此自然光通过这一系统后出射光强度为I = I0(1 �C cos4ωt)/16.[证明]自然光通过偏振片P1之后,形成偏振光,光强为 P1 P2 P3I1= I0/2.图8.5经过时间t,P3的偏振化方向转过的角度为θ = ωt,2根据马吕斯定律,通过P3的光强为I3= I1cosθ.由于P1与P2的偏振化方向垂直,所以P2与P3的偏振化方向的夹角为φ = π/2 �C θ,再根据马吕斯定律,通过P2的光强为I = I3cos2φ = I3sin2θ= I0(cos2θsin2θ)/2 = I0(sin22θ)/8= I0(1 �Ccos4θ)/16,即I = I0(1 �C cos4ωt)/16.证毕.8.6如图所示,自然光以起偏角i0从空气射向水面,水中有一块玻璃板,若以玻璃反射之光亦为线偏振光,求水面和玻璃平面的夹角(n玻 = 1.50,n水 = 1.33).[解答]根据布儒斯特定律:i0 tani0 = n水,可得空气的起偏角为i0 = arctann水= 53.06°.θ θ 水折射角为γ = 90° - i0 = 36.94°.再根据布儒斯特定律:tani = n玻/n水 = 1.128,i γ 玻璃可得玻璃的起偏角为i = 48.44°.水面和玻璃平面的夹角为θ = i �C γ= 11.5°.图8.6[讨论]为了简便起见,设n1 = n水,n2 = n玻,那么tani0 = n1,tani = n2/n1,水面与玻璃平面的夹角为θ = i �C γ = (i + i0) - 90°,因此tan???cot(i?i0)??1tan(i?i0)??1?tanitani0tani?tani0?n2?1n2/n1?n1?n1(n2?1)n2?n12.这是最终公式,代入数值得tanθ = 0.2034,夹角为θ= 11.5°.8.7一方解石晶体置于两平行的且偏振化方向相同的偏振片之间,晶体的主截面与偏振片的偏振化方向成30o,入射光在晶体的主截面内,求以下两种情况下的o光和e光强度之比.(1)从晶体出射时;(2)从检偏器出射时.[解答](1)从偏振片入射到晶体的光分成o光和e光,o光垂直于主截面,e光平行于主截面.设入射偏振光的振幅为A,则Ao = Asinθ,Ae = Acosθ,当光从晶体出射时,o光和e光强度之比为IoIe?AoAe22?tan??tan30??2213.(2)从晶体出射的o光和e光入射到第二块偏振片时,只有沿偏振化方向的光能够通过,o光和e光的振幅为A`o = Aosinθ,A`e = Aecosθ,当光从偏振片出射时,o光和e光强度之比为IoI`e`?AoA`2`2e?AoA22etan??tan??tan430??2419.8.8某晶体对波长为632.8nm的光的主折射率为no = 1.66,ne = 1.49.用其制成适应于该波长光的1/4玻片,晶片至少要多厚?该波片的光轴方向如何? A [解答]对于1/4玻片,o光和e光的位相差为o θ θ 2??o e e ???(no?ne)l?(2k?1),?02当k = 0时晶片厚度最小l = λ0/4(n o - ne) = 930.6(nm).要形成圆偏振光,波片的光轴方向要与光的偏振化方向成45度角.P1 P P2感谢您的阅读,祝您生活愉快。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
V 第八章 热力学基础8-1如图所示,bca 为理想气体绝热过程,b1a 和b2a 是任意过程,则上述两过程中气体做功与吸收热量的情况是:(B ) (A) b1a 过程放热,作负功;b2a 过程放热,作负功(B) b1a 过程吸热,作负功;b2a 过程放热,作负功(C) b1a 过程吸热,作正功;b2a 过程吸热,作负功 (D) b1a 过程放热,作正功;b2a 过程吸热,作正功8-2 如图,一定量的理想气体由平衡态A 变到平衡态B ,且它们的压强相等,则在状态A 和状态B 之间,气体无论经过的是什么过程,气体必然( B ) (A)对外作正功 (B)内能增加 (C)从外界吸热 (D)向外界放热8-3 两个相同的刚性容器,一个盛有氢气,一个盛氦气(均视为刚性分子理想气体),开始时它们的压强温度都相同,现将3J 热量传给氦气,使之升高到一定温度,若使氢气也升高同样温度,则应向氢气传递热量为( C ) (A) 6 J (B) 3 J (C) 5J (D) 10 J 8-4 有人想象了如题图四个理想气体的循环过程,则在理论上可以实现的为( )(A) (B)(C) (D)8-5一台工作于温度分别为327o C和27o C的高温热源和低温源之间的卡诺热机,每经历一个循环吸热2 000 J,则对外作功( B )(A) 2 000 J (B) 1 000 J(C) 4 000 J (D) 500 J8-6 根据热力学第二定律( A )(A) 自然界中的一切自发过程都是不可逆的(B) 不可逆过程就是不能向相反方向进行的过程(C) 热量可以从高温物体传到低温物体,但不能从低温物体传到高温物体(D)任何过程总是沿着熵增加的方向进行8-7 一定质量的气体,在被压缩的过程中外界对气体做功300J,但这一过程中气体的内能减少了300J,问气体在此过程中是吸热还是放热?吸收或放出的热量是多少?解:由于外界对气体做功,所以:300J=W-由于气体的内能减少,所以:J∆E=300-根据热力学第一定律,得:J∆+=W=EQ300-600300=--又由公式WQ e 2=得:J 421005.1⨯==eW Q 8-12理想卡诺热机在温度为27C 0和127C 0的两个热源之间工作,若在正循环中,该机从高温热源吸收1200J 的热量,则将向低温热源放出多少热量?对外做了多少功?解:由1121Q W T T =-=η得:J 3001200400300400)1(121=⨯-=-=T T Q WJ 90012=-=W Q Q8-13一卡诺热机在1000K 和270C 的两热源之间工作。
若(1)高温热源温度提高到1100K ,(2)低温热源降到200K ,求理论上的热机效率各增加多少? 解:本题为卡诺循环问题%70100030011120=-=-=T T η (1)%7.72110030011121=-=-=T T η ,%7.201=-=∆ηηη (2)%802001122=-=-=T η , %1002=-=∆ηηη 经历J 506501010013.1135-=⨯⨯⨯⨯-J 5.12662-=∆E ,J 5.93702-+∆=W E Q 8-15摩尔质量为mol M 自由度为i 的分子组成的理想气体总质量为m ',开始时处于压强为1P 温度为1T 的平衡态,后经过一个绝热过程,压强变为2P ,求在此过程中气体对外作的功。
解:由于绝热过程存在公式=--v v T P 1恒量,所以有:11122T P P T vv -⎪⎪⎭⎫⎝⎛=所以,]1[2)(2112121vv P P T iRM m T T iR M m E W -⎪⎪⎭⎫ ⎝⎛-⨯'=-⨯'=∆-=mol mol8-16汽缸内贮有36g 水蒸汽(水蒸汽分子视为刚性分子理想气体分子), 如图所示经ABCDA 循环过程。
其中AB 、CD 为等体过程,BC 为等温过程,DA 为等压 过程。
试求:(1)DA 过程对外做功; (2)AB 过程内能增量;(3)循环过程 水蒸汽做的净功;(4)循环效率。
解:(1)DA 过程对外做功J D A A D A 5066)(-=-=V V P W (2)()()J 3039732=-=-⨯⨯'=∆A B A A B AB P P V T T iRM m E (3)J BC B B B C BC 10543ln ln ==⨯⨯'=V V V P V V RT M m W ,J DA BC 5477=+=W W W (4)J BC A B BC A B 409401=+∆=+=W E Q Q Q ,%4.131==Q Wη。
8-17物质的量为1mol 理想气体从状态),(11V P A 变化至状态),(22V P B ,已知其定体摩尔热容为R 25,其变化的V P -图线如图所示。
求:(1) 气体内能增量;(2)气体对外做功;(3)气体 吸收的热量。
解:(1))(25)(25)(11221212V P V P T T R M m T T C M m E mol vm mol -=-'=-'=∆ (2)用图形面积求: ()112221V P V P W -=(3)由W E Q +∆=得:)(31122V P V P Q -=8-18下图所示的循环是由两个等体过程和 两个绝热过程组成的正循环。
已知B,C 两状态的温度分别是B T 和C T ,试求此循 环的热机效率是多少?解:A 到B 过程,放热的多少为)(2B A vm T T C M m Q -'=C 到D 过程,吸热的多少为)(1C D vm T T C Mm Q -'= CD B A T T T T Q Q Q W ---=-==11121η 由于DA 过程:11--=γγD D A A V T V T ,BC 过程:11--=γγCC B B V T V T 所以,C D B A T T T T =,C C D B B A T T T T T T -=-,CBC D B A T T T T T T =-- 故:CB C D B A T TT T T T -=---=11η8-19一定量的理想气体经历如图所示的循环过程。
其中BC ,DA 为绝热过程,已知K 300=C T ,K 400=B T ,求循环效率。
解:A 到B 过程,吸热的多少为)(1A B pm T T C M m Q -'=C 到D 过程,放热的多少为)(2D C pm T T C Mm Q -'= AB D CT T T T Q Q Q W---=-==11121η由于DA 过程:v D v D v A v A T P T P ----=11 ,BC 过程:vC v C v B v B T P T P ----=11所以,D C A B T T T T =,D DC A A B T T T T T T -=-,BC AD A B D C T T T T T T T T ==-- 故:BC A BD C T T T T T T Q Q Q W-=---=-==111121η , %254003001=-=η8-20 如图为某种理想气体,已知该气体 的定压摩尔热容与定体摩尔热容之比为v ,图中1V ,2V ,1P ,2P 也均为已知量,BC为绝热过程,试用以上五个已知量表示出热机循环效率。
解:A 到B 过程,吸热的多少为)(1A B vm T T C Mm Q -'=, 等体过程12P P T T A B =C 到A 过程,放热的多少为)(2A C pm T T C Mm Q -'= 等压过程12V V T T A C =所以,111111)()(11121212---=---=-'-'-=-=P P VV v T T T T v T T C M m T T C M m Q Q A B A C A B vm A C pm η8-21 如下图为某单原子理想气体循环过 程的V P -图,AC 为等温线,且A c V V 2=。
求:(1)该气体的定体摩尔热容和定压摩 尔热容;(2)循环效率。
解:(1)J/mol.K 47.1223==R C v ,J/mol.K 76.2025==R C P (2)设),,(A A A T V P A ,则)2,2,(A A A T V P B ,),2,2(A A AT V P C , 计算得:A P A B P AB T Cm T T C m Q ⋅'=-'=)( 2ln 21ln ln A A C A A CA CA RT Mm RT M m V V RT M m W Q '-='='== AB Q Q =1, BC BC Q Q Q +=2热机效率为:3.12)2ln (1112=⋅+⋅-=-=A P A A V T C Mm RT T C M mQ Q η﹪。
