转动惯量计算
转动惯量计算

转动惯量计算
转动惯量是物理中一个重要的参量,它用来描述绕物体轴心转动一周时物体所受的转动力大小,判断力学系统的转动状态。
转动惯量及其计算方法非常重要,因此本文将简要介绍转动惯量的概念和相关计算方法。
转动惯量是物理学中一个重要的参量,它描述物体转动一周时受到的转动力大小。
物体转动时,单位角动量是恒定的,转动惯量定义为绕转动轴的力矩的商。
这意味着,当惯量不变时,物体的转动角动量也不变,也就是说,当物体转动时,转速不会发生显著变化。
转动惯量的计算方法主要分为三类:
1.于规则的几何体,例如球体或柱面,可以采用几何体特性计算转动惯量。
2.于不规则的几何体,可以采用称量和转动杆计算转动惯量。
3.可以采用动力学方程或变形分析计算转动惯量。
上述计算方法均可用于计算几何体的转动惯量,但是需要注意的是,不同的计算方法会有不同的适用情况和精度,因此,在计算转动惯量时,应根据实际情况选择合适的计算方法。
此外,由于转动惯量与物体质量、形状、尺寸和转动形式等有关,因此转动惯量的计算还包括估算质量、计算形状和尺寸参数以及确定转动形式等步骤,这些步骤也需要相应的物理计算方法。
综上所述,转动惯量是物理中一个重要的参量,它用来描述绕物体轴心转动一周时物体所受的转动力大小。
计算转动惯量的方法主要
有几何体特性计算、称量法和动力学方程法三类;并且,计算转动惯量还需要计算物体质量,形状参数,以及转动形式等。
因此,在计算转动惯量时,应根据实际情况选择适当的计算方法,同时考虑实际情况下的物理参数。
转动惯量计算公式是什么

转动惯量计算公式是什么 转动惯量是⼤学物理中⼀个⼗分重要的知识点。
下⾯是由店铺编辑为⼤家整理的“转动惯量的定义以及计算公式”,仅供参考,欢迎⼤家阅读本⽂。
转动惯量 转动惯量(Moment of Inertia),⼜称质量惯性矩,简称惯距,是经典⼒学中物体绕轴转动时惯性的量度,常⽤⽤字⺟I或J表⽰。
转动惯量的SI单位为kg·m²。
对于⼀个质点,I=mr²,其中,m是其质量,r是质点和转轴的垂直距离。
和线性动⼒学中的质量相类似,在旋转动⼒学中,转动惯量的⾓⾊相当于物体旋转运动的惯性,可⽤于建⽴⾓动量、⾓速度、⼒矩和⾓加速度等数个量之间的关系。
对于规则物体,其转动惯量可以按照相应公式直接计算;对于外形复杂和质量分布不均的物体,转动惯量可通过实验⽅法来测定。
实验室中最常⻅的转动惯量测试⽅法为三线摆法。
转动惯量计算公式 1、对于细杆: 当回转轴过杆的中点(质⼼)并垂直于杆时I=mL²/I²;其中m是杆的质量,L是杆的⻓度。
当回转轴过杆的端点并垂直于杆时I=mL²/3;其中m是杆的质量,L是杆的⻓度。
2、对于圆柱体: 当回转轴是圆柱体轴线时I=mr²/2;其中m是圆柱体的质量,r是圆柱体的半径。
3、对于细圆环: 当回转轴通过环⼼且与环⾯垂直时,I=mR²;当回转轴通过环边缘且与环⾯垂直时,I=2mR²;I=mR²/2沿环的某⼀直径;R为其半径。
4、对于⽴⽅体: 当回转轴为其中⼼轴时,I=mL²/6;当回转轴为其棱边时I=2mL²/3;当回转轴为其体对⾓线时,I=3mL²/16;L为⽴⽅体边⻓。
5、对于实⼼球体: 当回转轴为球体的中⼼轴时,I=2mR²/5;当回转轴为球体的切线时,I=7mR²/5;R为球体半径。
转动惯量公式

转动惯量公式转动惯量是物体对于绕指定轴旋转的惯性特性的度量。
它与物体的质量、形状以及旋转轴的位置有关。
在这篇文章中,我们将介绍转动惯量的概念以及相关的公式。
1. 转动惯量的定义转动惯量是描述物体绕某个轴旋转时对其惯性的度量。
物体的质量分布越集中,转动惯量越小,物体的形状越分散,转动惯量越大。
对于一个质量分布均匀的物体来说,转动惯量可以通过以下公式计算:转动惯量公式转动惯量公式其中,I 是转动惯量,r 是与旋转轴的距离,dm 是物体的微小质量元素。
转动惯量的单位是千克·米²。
2. 转动惯量的计算方法对于一些常见的几何形状,我们可以通过特定的公式计算它们的转动惯量。
下面是一些常见形状的转动惯量计算公式:•线状物体(绕与物体平行的轴旋转):线状物体转动惯量公式线状物体转动惯量公式其中,m 是线状物体的质量,l 是线状物体长度。
•圆盘状物体(绕与盘面平行的轴旋转):圆盘状物体转动惯量公式圆盘状物体转动惯量公式其中,m 是圆盘状物体的质量,r 是圆盘状物体半径。
•球体(绕球的直径轴旋转):球体转动惯量公式球体转动惯量公式其中,m 是球体的质量,r 是球体的半径。
这些公式可以帮助我们计算常见几何形状物体的转动惯量。
对于复杂的物体形状,可以使用积分计算转动惯量。
3. 转动惯量的应用转动惯量在物理学中有广泛的应用。
它是理解刚体转动运动的重要参数,可以帮助我们研究物体在旋转过程中的角动量、角加速度等性质。
转动惯量的大小决定了物体在给定轴上旋转的难易程度。
当转动惯量较大时,物体旋转需要更大的力矩才能实现,导致旋转速度较慢。
相反,转动惯量较小的物体则更容易加速旋转。
此外,转动惯量还与物体的稳定性有关。
当物体的质量分布越接近旋转轴时,转动惯量越小,物体越稳定。
4. 结论转动惯量是描述物体绕某个轴旋转时对其惯性的度量。
它与物体的质量、形状以及旋转轴的位置有关。
我们可以根据物体的几何形状和分布情况,使用特定的公式来计算转动惯量。
5.4 转动惯量的计算

dm
mr
转轴
分散系统
J
mi
ri
2
连续体
J r2 d m m
J 由质量对轴的分布决定,与转动状态无关。
一. 常见刚体的转动惯量的计算
1、细圆环
z
R C
m
dm
JC mR2
J r2dm m
2、均匀圆盘
z
JC
1 2
mR2
dm
C Rm
r dr
JC
R
R
r 2dm 2rdr
m
0
0
R 2
r2
1 mR2 2
3、均匀细杆 m l
zA
dr
对A轴的转动惯量
A
r dm
JA
1 3
m l2
J A
l 0
r 2dm
l 0
r2
m l
dr
1 ml2 3
AC
m 对过质心C轴的转动惯量l Nhomakorabeal
2
2
zC
JC
1 ml2 12
二、计算转动惯量的几条规律
J Jc md 2
平行轴定理应用
z
zc
求相对于求外任 一轴的转动惯量
JC
2 mR2 5
3、对薄平板刚体的正交轴定理
z
薄板刚体
xi O x
ri
yi
Oxyz 在刚体平面内
y
mi (xi, yi, zi )
J z miri2 mi xi2 mi yi2
Jx mi zi2 mi yi2 J y mi zi2 mi xi2
转动惯量 计算公式

转动惯量计算公式嘿,咱今天来好好聊聊转动惯量的计算公式!你知道吗,转动惯量这玩意儿在物理学中可是相当重要的。
先来说说转动惯量到底是啥。
想象一下,一个圆盘在旋转,不同大小、不同质量分布的圆盘,转起来的“费劲”程度可不一样,而转动惯量就是用来衡量这种“费劲”程度的物理量。
那转动惯量的计算公式是啥呢?一般来说,对于一个质点,转动惯量 I = mr²,这里的 m 是质点的质量,r 是质点到转轴的距离。
但实际情况中,物体可不是简单的质点,往往是各种形状复杂的家伙。
比如说一个均匀的细圆环,它的转动惯量 I = mR²,其中 m 是圆环的质量,R 是圆环的半径。
要是一个均匀的圆盘,那转动惯量 I = 1/2 mR²。
再复杂点,像一个长方体,计算转动惯量就得分别考虑沿着不同轴的情况。
给你讲讲我曾经在课堂上的一件事儿。
有一次上课,我给学生们讲转动惯量的计算,有个调皮的小家伙一直嚷着说:“这有啥用啊,又不能当饭吃!”我笑了笑,拿起一个小陀螺,问大家:“你们觉得这个陀螺转起来容易不?”大家七嘴八舌地讨论起来。
然后我就用转动惯量的知识给他们解释,为啥有的陀螺转得稳,转得久,有的就不行。
那个调皮的孩子一下子就来了兴趣,眼睛瞪得大大的,认真听起来。
咱们继续说转动惯量的计算公式。
在实际应用中,很多时候要通过积分来计算不规则物体的转动惯量。
这可能听起来有点头疼,但其实只要掌握了基本原理,也没那么可怕。
比如说一个质量分布不均匀的物体,我们就得把它分成无数个小的部分,每个部分都当成质点来计算转动惯量,然后再把所有部分加起来。
这就像是拼拼图,一块一块地拼,最后就能得到整个物体的转动惯量。
转动惯量的计算公式在很多领域都有大用处。
比如在机械设计中,要设计一个高效的旋转部件,就得考虑转动惯量,不然机器运转起来可能就不顺畅。
在体育运动中,运动员的动作和器械的转动也和转动惯量有关。
总之,转动惯量的计算公式虽然看起来有点复杂,但只要咱们用心去理解,多做些题目,多联系实际,就能掌握它,让它为我们所用。
转动惯量与功率计算公式

转动惯量与功率计算公式转动惯量和功率是研究物体旋转运动的重要物理量之一、本文将介绍转动惯量和功率的计算公式,并探讨它们的应用和意义。
一、转动惯量1.定义转动惯量是描述物体对转动运动的惯性大小的物理量。
对于质量分布连续的物体而言,转动惯量的计算公式可以写为:I = ∫r^2 dm其中,I表示物体的转动惯量,r表示离转轴的距离,dm是物体所包含的质量微元。
2.旋转轴为直线的物体对于旋转轴为直线的物体,其转动惯量的计算公式可以根据不同的几何形状进行推导。
以下列举几种常见几何形状的转动惯量计算公式:(1)细长直杆绕一个端点转动:I = (1/3)ml^2(2)细长直杆绕中心点转动:I = (1/12)ml^2(3)以一个端点为轴,自由转动的细杆:I = (1/3)ml^2(4)球体的转动惯量:I = (2/5)mr^2(5)圆盘的转动惯量:I = (1/2)mr^2(6)圆环的转动惯量:I = mr^2(7)圆柱体绕轴心转动:I = (1/2)mr^2以上公式中,m表示物体的质量,l表示物体的长度,r表示物体的半径。
3.平行轴定理若物体的转轴不在质心上,而是平行于通过质心的转轴,我们可以利用平行轴定理来计算转动惯量。
平行轴定理的公式如下:I = Ic + md^2其中,Ic表示物体绕通过质心的转轴的转动惯量,m表示物体的质量,d表示质心到平行轴的距离。
二、功率1.定义功率是描述物体在单位时间内转动做功的大小。
对于旋转物体而言,其功率的计算公式可以写为:P=τω其中,P表示物体的功率,τ表示作用在物体上的力矩,ω表示物体的角速度。
对于不同情况下的物体,其功率计算公式有所不同。
(1)恒力矩的功率:P=τω其中,τ为恒定的力矩大小。
(2)变力矩的功率:P=∫τdω其中,τ为力矩的函数。
3.转动惯量和功率的关系转动惯量和功率之间存在一定的关系。
对于转动惯量为常量的物体,其功率可以表示为:P=(1/2)Iω^2其中,I表示物体的转动惯量,ω表示物体的角速度。
电机转动惯量计算公式

电机转动惯量计算公式
电机转动惯量是指电机在相同转速下所需的力矩大小,它是电机的一项重要参数。
电机转动惯量的大小取决于电机的物理结构,它可以通过一个特定的公式来计算。
电机转动惯量的计算公式如下:
J = (1/2)mvr2
其中,J是电机转动惯量,单位是千克·米2/秒2;m是转子的质量,单位是千克;v是转子的半径,单位是米;r是转速,单位是转/秒。
电机转动惯量的大小与转子的质量、半径和转速有关,当转子的质量、半径和转速增大时,电机转动惯量也会增大;当转子的质量、半径和转速减小时,电机转动惯量也会减小。
此外,电机转动惯量还受到电机物理结构的影响,比如电机的转子形状、磁芯材料以及绕组的结构都会影响电机转动惯量的大小。
电机转动惯量的计算公式可以帮助设计人员更好地了解电机的特性,帮助他们设计出更加合适的电机。
电机转动惯量的计算公式也可以帮助维修人员预测电机的表现,诊断电机的故障。
总的来说,电机转动惯量的计算公式是一个重要的工具,可以帮助设计人员更好地了解电机的特性,也可以帮助维修人员预测电机的
表现,诊断电机的故障。
转动惯量计算公式-转动惯量公式

1.圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)之欧侯瑞魂创作82MD J =对于钢材:341032-⨯⨯=gLrD J π)(1078.0264s cm kgf L D ⋅⋅⨯-M-圆柱体质量(kg);D-圆柱体直径(cm); L-圆柱体长度或厚度(cm); r-资料比重(gf /cm 3)。
2.丝杠折算到马达轴上的转动惯量:2iJsJ =(kgf·cm·s 2)J s –丝杠转动惯量(kgf·cm·s 2); i-降速比,12z z i =3. 工作台折算到丝杠上的转动惯量g w22⎪⎭⎫ ⎝⎛⋅=n v J π g w2s 2⎪⎭⎫ ⎝⎛=π(kgf·cm·s 2) v -工作台移动速度(cm/min); n-丝杠转速(r/min); w-工作台重量(kgf); g-重力加速度,g=980cm/s 2; s-丝杠螺距(cm)2. 丝杠传动时传动系统折算到驱轴上的总转动惯量:())s cm (kgf 2g w 122221⋅⋅⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+++=πs J J iJ J S tJ 1-齿轮z 1及其轴的转动惯量; J 2-齿轮z 2的转动惯量(kgf·cm·s 2); J s -丝杠转动惯量(kgf·cm·s 2); s-丝杠螺距,(cm); w-工件及工作台重量(kfg).5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量2gw R J =(kgf·cm·s 2)R-齿轮分度圆半径(cm); w-工件及工作台重量(kgf)6. 齿轮齿条传动时传动系统折算到马达轴上的总转动惯量⎪⎪⎭⎫⎝⎛++=2221g w 1R J i J J tJ 1,J 2-分别为Ⅰ轴,Ⅱ轴上齿轮的转动惯量(kgf·cm·s 2);R-齿轮z 分度圆半径(cm);w-工件及工作台重量(kgf)。
转动惯量计算公式-转动惯量公式

1.圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)之樊仲川亿创作82MD J =对于钢材:341032-⨯⨯=gLrD J π)(1078.0264s cm kgf L D ⋅⋅⨯-M-圆柱体质量(kg);D-圆柱体直径(cm); L-圆柱体长度或厚度(cm); r-资料比重(gf /cm 3)。
2.丝杠折算到马达轴上的转动惯量:2iJsJ =(kgf·cm·s 2)J s –丝杠转动惯量(kgf·cm·s 2); i-降速比,12z z i =3. 工作台折算到丝杠上的转动惯量g w22⎪⎭⎫ ⎝⎛⋅=n v J π g w2s 2⎪⎭⎫ ⎝⎛=π(kgf·cm·s 2) v -工作台移动速度(cm/min); n-丝杠转速(r/min); w-工作台重量(kgf); g-重力加速度,g=980cm/s 2; s-丝杠螺距(cm)2. 丝杠传动时传动系统折算到驱轴上的总转动惯量:())s cm (kgf 2g w 122221⋅⋅⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+++=πs J J iJ J S tJ 1-齿轮z 1及其轴的转动惯量; J 2-齿轮z 2的转动惯量(kgf·cm·s 2); J s -丝杠转动惯量(kgf·cm·s 2); s-丝杠螺距,(cm); w-工件及工作台重量(kfg).5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量2gw R J =(kgf·cm·s 2)R-齿轮分度圆半径(cm); w-工件及工作台重量(kgf)6. 齿轮齿条传动时传动系统折算到马达轴上的总转动惯量⎪⎪⎭⎫⎝⎛++=2221g w 1R J i J J tJ 1,J 2-分别为Ⅰ轴,Ⅱ轴上齿轮的转动惯量(kgf·cm·s 2);R-齿轮z 分度圆半径(cm);w-工件及工作台重量(kgf)。
转动惯量计算公式

转动惯量计算公式转动惯量(也称为惯性矩或转动惯性)是物体抵抗转动的能力的度量,是物体转动时的一项重要物理性质。
在机械工程、物理学、航空航天等领域中,转动惯量的计算是解决相关问题的关键。
转动惯量可以通过各种形状的物体的质量分布来计算,例如直线、薄片、圆筒、球体等。
不同形状的物体转动惯量的计算公式也有所不同。
在本文中,我们将介绍几种常见形状的物体的转动惯量计算公式。
1. 直线的转动惯量计算公式当物体是一个直线时,其转动惯量可以用关于质量和长度的公式来计算。
以下是直线转动惯量的计算公式:•绕质心轴的转动惯量:$I = \\frac{1}{3} m l^2$•绕端点轴的转动惯量:$I = \\frac{1}{12} m l^2$其中,I是转动惯量,I是物体的质量,I是直线的长度。
2. 圆筒的转动惯量计算公式圆筒是一种常见的物体形状,例如水桶、轮胎等。
对于圆筒的转动惯量计算,有以下公式:•绕质心轴的转动惯量:$I = \\frac{1}{2} m r^2$•绕圆轴的转动惯量:I=II2其中,I是转动惯量,I是圆筒的质量,I是圆筒的半径。
3. 薄片的转动惯量计算公式薄片是一个平面形状的物体,例如纸片、金属片等。
对于薄片的转动惯量计算,有以下公式:•绕质心轴的转动惯量:$I = \\frac{1}{4} m a^2$•绕边缘轴的转动惯量:$I = \\frac{1}{3} m a^2$其中,I是转动惯量,I是薄片的质量,I是薄片的边长。
4. 球体的转动惯量计算公式球体是一个球形物体,例如篮球、乒乓球等。
对于球体的转动惯量计算,有以下公式:•绕质心轴的转动惯量:$I = \\frac{2}{5} m r^2$•绕直径轴的转动惯量:$I = \\frac{2}{3} m r^2$其中,I是转动惯量,I是球体的质量,I是球体的半径。
5. 其他形状的转动惯量计算公式除了上述常见形状的物体,其他形状的转动惯量计算公式也可以通过积分或者几何关系得到。
电机转动惯量计算公式

电机转动惯量计算公式
电机转动惯量是电机的一个重要参数,它代表电机的转动惯量大小,影响着电机的转速、加速度和动力,因此,电机转动惯量的计算是电机设计和制造过程中必不可少的一步。
电机转动惯量的计算公式如下:
惯量J = m*r^2
其中,m为电机的质量,r为电机的转动半径。
电机转动惯量的计算公式比较简单,但实际计算过程中仍需要注意以下几点:
1. 计算电机转动惯量时,必须使用正确的电机质量m和转动半径r,以确保计算结果的准确性。
2. 电机质量m包括电机本身的质量和附件的质量,因此,在计算电机转动惯量时,一定不要忽略附件的质量。
3. 电机转动半径r是电机外缘到转轴的距离,因此,在计算电机转动惯量时,需要准确测量电机外缘到转轴的距离。
4. 电机转动惯量的计算结果受到电机本身的结构和工艺条件的影响,因此,在计算电机转动惯量时,需要根据电机的实际结构和工艺条
件进行修正。
总之,电机转动惯量的计算是电机设计和制造过程中不可或缺的一部分,正确使用电机转动惯量计算公式,是电机质量和性能的重要保证。
转动惯量计算公式-转动惯量公式
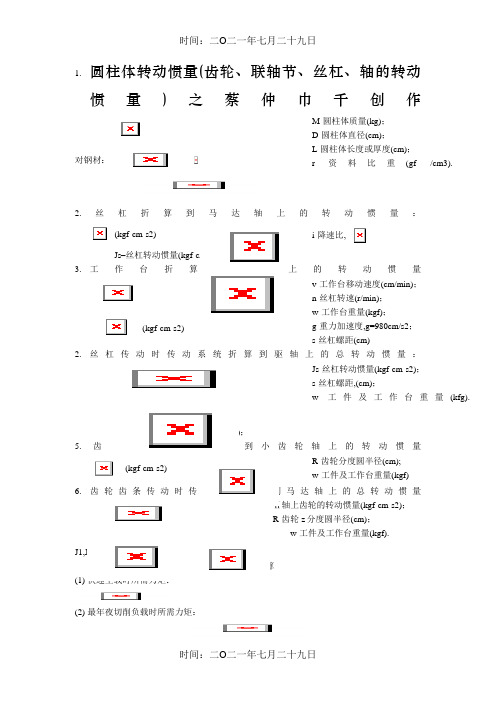
1.圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)之蔡仲巾千创作对钢材:M-圆柱体质量(kg);D-圆柱体直径(cm);L-圆柱体长度或厚度(cm);r-资料比重(gf /cm3).2.丝杠折算到马达轴上的转动惯量:(kgf·cm·s2)Js–丝杠转动惯量(kgf·cm·s2);i-降速比,3.工作台折算到丝杠上的转动惯量(kgf·cm·s2)v-工作台移动速度(cm/min);n-丝杠转速(r/min);w-工作台重量(kgf);g-重力加速度,g=980cm/s2;s-丝杠螺距(cm)2.丝杠传动时传动系统折算到驱轴上的总转动惯量:J1-齿轮z1及其轴的转动惯量;J2-齿轮z2的转动惯量(kgf·cm·s2);Js-丝杠转动惯量(kgf·cm·s2);s-丝杠螺距,(cm);w-工件及工作台重量(kfg).5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量(kgf·cm·s2)R-齿轮分度圆半径(cm); w-工件及工作台重量(kgf)6. 齿轮齿条传动时传动系统折算到马达轴上的总转动惯量J1,J2-分别为Ⅰ轴,Ⅱ轴上齿轮的转动惯量(kgf·cm·s2);R-齿轮z分度圆半径(cm);w-工件及工作台重量(kgf).马达力矩计算(1) 快速空载时所需力矩:(2) 最年夜切削负载时所需力矩:(3) 快速进给时所需力矩:式中Mamax—空载启动时折算到马达轴上的加速力矩(kgf·m);Mf—折算到马达轴上的摩擦力矩(kgf·m);M0—由于丝杠预紧引起的折算到马达轴上的附加摩擦力矩(kgf·m);Mat—切削时折算到马达轴上的加速力矩(kgf·m);Mt—折算到马达轴上的切削负载力矩(kgf·m).在采纳滚动丝杠螺母传动时,Ma、Mf、M0、Mt的计算公式如下:(4) 加速力矩:(kgf·m)Jr—折算到马达轴上的总惯量;T—系统时间常数(s);n—马达转速(r/min);当n=nmax时,计算Mamaxn=nt时,计算Matnt—切削时的转速(r/min)(5) 摩擦力矩:(kgf·m)F0—导轨摩擦力(kgf);s—丝杠螺距(cm);i—齿轮降速比;η—传动链总效率;一般η=0.7~0.85.(6) 附加摩擦力矩:(kgf·m)P0—滚珠丝杠预加载荷(kg·f);s—丝杠螺距(cm);η—传动链总效率;i —齿轮降速比;η0—滚珠丝杠未预紧式的效率,计算公式见本手册第2测第425页,一般η0≥0.9.(7)切削力矩:(kgf·m)Pt—进给方向的最年夜切削力(kg·f);s—丝杠螺距(cm);η—传动链总效率;i—齿轮降速比.。
转动惯量计算

转动惯量计算
惯量是物体对转动的惯性的度量,可以通过以下公式计算:
1. 对于质点的转动惯量:
I = m * r^2
其中,I代表转动惯量,m代表质量,r代表离转轴的距离。
2. 对于刚体的转动惯量:
I = Σ(m * r^2)
其中,I代表转动惯量,Σ表示对所有质点求和,m代表质量,r代表质点离转轴的距离。
3. 对于一些常见几何形状的转动惯量,可以使用以下公式
计算:
- 球体的转动惯量:
I = (2/5) * m * r^2
- 圆柱体绕轴线的转动惯量:
I = (1/2) * m * r^2
- 薄圆环绕直径轴线的转动惯量:
I = (1/2) * m * r^2
- 均匀长方体绕轴线的转动惯量:
I = (1/12) * m * (a^2 + b^2)
其中,I代表转动惯量,m代表质量,r代表半径,a和b 代表长方体的边长。
需要注意的是,以上公式仅适用于一些简单的几何形状,对于其他复杂的形状,转动惯量的计算可能需要使用积分或其他数值方法进行近似求解。
转动惯量的计算

转动惯量的计算
一、转动惯量的概念
1、转动惯量的定义:转动惯量是测量一个物体围绕它的转轴转动时所
需要的动能的定义。
它可以用来衡量物体的运动情况和它们之间的相
互作用。
2、转动惯量的单位:在国际单位制中,转动惯量的单位被称为千克米
2(kg·m2)。
二、转动惯量的重要作用
1、用于物体调整速度的作用:转动惯量可以用来调整物体的转动速度,特别是在多个物体之间的相互作用中,这些物体的转动惯量之和不变。
2、用于物体的转动稳定性:由于转动惯量可以表示物体的转动稳定性,因此它可以用来表示物体的转动稳定性,这样可以保证物体的转动稳定,从而降低事故发生的可能性。
三、计算转动内惯量的公式
1、转动内惯量的体积公式:I=2/5 mr2,其中m是物体的质量,r是物
体的半径。
2、转动内惯量的面积公式:I=1/2 M2,其中M是物体的质量或轴距。
3、转动内惯量的位置公式:I=mr2,其中r是质心到轴距的距离。
四、转动惯量的计算方法
1、运用数学公式计算:可以利用上述的转动内惯量的公式来计算。
2、采用实验方法计算:可以采用实验测量的方法来计算转动惯量,如采用双摆的实验、腰椎的实验等。
3、利用计算机软件计算:还可以利用计算机软件来模拟物体的运动状态,并计算物体的转动惯量。
转动惯量计算公式-转动惯量公式

1.圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)之马矢奏春创作82MD J =对于钢材:341032-⨯⨯=gLrD J π)(1078.0264s cm kgf L D ⋅⋅⨯-M-圆柱体质量(kg);D-圆柱体直径(cm); L-圆柱体长度或厚度(cm); r-资料比重(gf /cm 3)。
2.丝杠折算到马达轴上的转动惯量:2iJsJ =(kgf·cm·s 2)J s –丝杠转动惯量(kgf·cm·s 2); i-降速比,12z z i =3. 工作台折算到丝杠上的转动惯量g w22⎪⎭⎫ ⎝⎛⋅=n v J π g w2s 2⎪⎭⎫ ⎝⎛=π(kgf·cm·s 2)v -工作台移动速度(cm/min);n-丝杠转速(r/min); w-工作台重量(kgf);g-重力加速度,g=980cm/s 2; s-丝杠螺距(cm)2. 丝杠传动时传动系统折算到驱轴上的总转动惯量:())s cm (kgf 2g w 122221⋅⋅⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+++=πs J J i J J S tJ 1-齿轮z 1及其轴的转动惯量; J 2-齿轮z 2的转动惯量(kgf·cm·s 2); J s -丝杠转动惯量(kgf·cm·s 2); s-丝杠螺距,(cm);w-工件及工作台重量(kfg).5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量2g wR J =(kgf·cm·s 2)R-齿轮分度圆半径(cm); w-工件及工作台重量(kgf)6. 齿轮齿条传动时传动系统折算到马达轴上的总转动惯量⎪⎪⎭⎫⎝⎛++=2221g w 1R J i J J tJ 1,J 2-分别为Ⅰ轴, Ⅱ轴上齿轮的转动惯量(kgf·cm·s 2); R-齿轮z 分度圆半径(cm); w-工件及工作台重量(kgf)。
机械设计转动惯量计算公式

1. 圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)82MD J =对于钢材:341032-⨯⨯=gLrD J π)(1078.0264s cm kgf L D ⋅⋅⨯- M-圆柱体质量(kg); D-圆柱体直径(cm); L-圆柱体长度或厚度(cm); r-材料比重(gf /cm 3)。
2. 丝杠折算到马达轴上的转动惯量:2i Js J =(kgf·c m·s 2) J s –丝杠转动惯量(kgf·c m·s 2); i-降速比,12z z i =3. 工作台折算到丝杠上的转动惯量gw22⎪⎭⎫ ⎝⎛⋅=n v J π g w2s 2⎪⎭⎫ ⎝⎛=π (kgf·c m·s 2)v -工作台移动速度(cm/min);n-丝杠转速(r/min); w-工作台重量(kgf);g-重力加速度,g = 980cm/s 2; s-丝杠螺距(cm)2. 丝杠传动时传动系统折算到驱轴上的总转动惯量:())s cm (kgf 2g w 122221⋅⋅⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+++=πs J J iJ J S tJ 1-齿轮z 1及其轴的转动惯量; J 2-齿轮z 2的转动惯量(kgf ·cm ·s 2); J s -丝杠转动惯量(kgf ·cm ·s 2); s-丝杠螺距,(cm); w-工件及工作台重量(kfg).5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量2gw R J(kgf ·c m·s 2)R-齿轮分度圆半径(cm);w-工件及工作台重量(kgf)6. 齿轮齿条传动时传动系统折算到马达轴上的总转动惯量⎪⎪⎭⎫⎝⎛++=2221g w 1R J i J J tJ 1,J 2-分别为Ⅰ轴,Ⅱ轴上齿轮的转动惯量(kgf ·c m·s 2);R-齿轮z 分度圆半径(cm);w-工件及工作台重量(kgf)。
转动惯量的计算方法与应用

转动惯量的计算方法与应用转动惯量是描述物体对转动运动的惯性特性的物理量,它在理论与实际应用中有着广泛的研究与应用。
本文将介绍转动惯量的计算方法及其在不同领域中的应用。
一、转动惯量的定义与计算方法转动惯量是描述物体绕某一轴旋转时所表现出的惯性力矩的物理量。
对于具有质量分布的物体,其转动惯量(I)可以通过积分的方法计算。
对于质量均匀分布的物体,可以根据几何形状的特点直接计算。
以下是常见几何形状物体的转动惯量计算公式:1. 线状物体:对于长度为L,质量均匀分布在其上的线状物体,其绕与线垂直的轴的转动惯量计算公式为:I = (1/3) * m * L^22. 薄圆盘:对于半径为R,质量均匀分布在其上的薄圆盘,其绕与垂直于平面的轴的转动惯量计算公式为:I = (1/4) * m * R^23. 球体:对于半径为R,质量均匀分布的球体,其绕通过球心的轴的转动惯量计算公式为:I = (2/5) * m * R^2二、转动惯量的应用转动惯量在不同领域中有着广泛的应用,下面分别介绍其在物理学、工程学和体育运动中的应用。
1. 物理学中的应用转动惯量在物理学中有着重要的应用,特别是在刚体力学和旋转动力学中。
例如在角动量定理的推导中,转动惯量是一个关键的物理量。
此外,在旋转力矩计算、质点旋转、刚体平衡等问题中,转动惯量也起到了重要的作用。
2. 工程学中的应用转动惯量在工程学中有着广泛的应用。
例如在机械工程中,转动惯量的计算可以用于设计旋转系统的传动装置。
在自动化控制系统中,转动惯量的测量和调整可以影响系统的稳定性和响应速度。
另外,在机械结构设计和振动控制中,转动惯量也具有重要的意义。
3. 体育运动中的应用在体育运动中,转动惯量的计算对于评估运动员在进行旋转动作时的稳定性和敏捷性非常重要。
例如在体操运动中,转体和翻转动作的转动惯量计算可以帮助教练和运动员设计合适的训练方案,提高技术水平和竞技成绩。
此外,转动惯量也在其他体育项目如滑雪、滑板和自行车等中有着应用。
转动惯量计算

转动惯量计算
转动惯量计算是引入到物理学中的一种重要概念,用于理解物体在某个轴向上的旋转行为。
它可以被定义为物体在转动时所需要的力的绝对值。
它可以帮助我们在解决物理问题时,更加准确地了解物体旋转时所发生的各种力。
转动惯量的重要性在于它表示物体在进行旋转时所需要的力的
绝对值。
举个例子,当把一个质量为m的物体放在空间的中心,它会在旋转时受到偏心力的影响,这会影响到它的转动惯量。
如果偏心力太大,物体就会倾斜,而物体转动惯量则会减小,因此物体会绕着更细的轨道围绕中心旋转,这就是轨道减小的原因。
转动惯量的计算公式可以用一般的力学方程表示:
I = mr^2
其中I为物体的转动惯量,m为物体的质量,r为物体与旋转中
心的距离。
从这个公式可以看出,转动惯量的大小取决于物体的质量和物体与旋转中心的距离,而这两个变量又受到物体本身的重力影响,因此我们可以推出:重力对转动惯量是有重大影响的。
转动惯量计算也与局部力有关,了解局部力的大小可以更好地理解物体在旋转时所发生的各种力,从而更加准确地计算出物体转动惯量。
转动惯量计算不仅在基础物理学上有重要意义,而且在工程上也有广泛应用。
它主要用于工程中对物体转动的分析,比如飞行器的设计和控制系统的分析,它们的转动都需要计算惯性力。
此外,转动惯
量也被用于机器人系统设计、电机驱动系统分析等领域。
总之,转动惯量计算是一种重要的概念,主要用于理解物体在某个轴向上的旋转行为,它可以帮助我们准确地推理和分析物体在转动时所产生的各种力。
此外,转动惯量在工程上也有广泛应用,为工程设计提供了重要的参考依据。
转动惯量的计算

说明:本文《转动惯量的计算》特地收集贡献出来供各位工程技术人员在参阅本人劣作《风机动平衡调试方法》时参考。
深圳华晶玻璃瓶有限公司工程部(动力车间)李宜斌编辑2010-10-21转动惯量的计算转动惯量应用于刚体各种运动的动力学计算中。
单个质点的转动惯量:I = m× r2.质点系的转动惯量:I = Σ m i×r i2.质量连续分布的刚体的转动惯量:I = ∫m r2dm。
以上各式中的r理解为质点到转轴的距离。
刚体绕轴转动惯性的度量。
其数值为J=∑ mi*ri^2,式中mi表示刚体的某个质点的质量,ri表示该质点到转轴的垂直距离。
求和号(或积分号)遍及整个刚体。
转动惯量只决定于刚体的形状、质量分布和转轴的位置,而同刚体绕轴的转动状态(如角速度的大小)无关。
规则形状的均质刚体,其转动惯量可直接计得。
不规则刚体或非均质刚体的转动惯量,一般用实验法测定。
描述刚体绕互相平行诸转轴的转动惯量之间的关系,有如下的平行轴定理:刚体对一轴的转动惯量,等于该刚体对同此轴平行并通过质心之轴的转动惯量加上该刚体的质量同两轴间距离平方的乘积。
由于和式的第二项恒大于零,因此刚体绕过质量中心之轴的转动惯量是绕该束平行轴诸转动惯量中的最小者。
垂直轴定理:一个平面刚体薄板对于垂直它的平面轴的转动惯量,等于绕平面内与垂直轴相交的任意两正交轴的转动惯量之和。
表达式:Iz=Ix+Iy刚体对一轴的转动惯量,可折算成质量等于刚体质量的单个质点对该轴所形成的转动惯量。
由此折算所得的质点到转轴的距离,称为刚体绕该轴的回转半径κ,转动惯量的量纲为L^2M,在SI单位制中,它的单位是kg·m^2。
刚体绕某一点转动的惯性由更普遍的惯量张量描述。
惯量张量是二阶对称张量,它完整地刻画出刚体绕通过该点任一轴的转动惯量的大小。
补充对转动惯量的详细解释及其物理意义:先说转动惯量的由来,先从动能说起大家都知道动能E=(1/2)mv^2,而且动能的实际物理意义是:物体相对某个系统(选定一个参考系)运动的实际能量,(P势能实际意义则是物体相对某个系统运动的可能转化为运动的实际能量的大小)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5
0.1598×10-2
12
0.2509×10-1
6
0.1515×10-2
90
10
0.4122×10-1
8
0.1489×10-2
12
0.3852×10-1
45
6
0.2562×10-2
100
12
0.06370
8
0.2407×10-2
16
0.06033
10
0.2219×10-2
20
0.05516
50
n=nt时计算Mat
nt—切削时的转速,r/min
摩擦力矩Mf
F0—导轨摩擦力,N
P —丝杠螺距,mm
i —齿轮传动比
η—传动链总效率
一般η=0.70~0.85
附加摩擦力矩M0
P0—滚珠丝杠预加载荷,N
P—丝杠螺距,mm
r1—传动链总效率
i —齿轮传动比
η0—滚珠丝杠未预紧时的效率,
一般η0≥0.9
切削力矩Mt
Pt—进给方向的最大切削力,N
P—丝杠螺距,mm
η—传动链总效率
i —齿轮传动比
表22-2-8马达转矩计算[6]
计算内容
计算公式
说明
快速空载起动时所需转矩
Mamax—空载起பைடு நூலகம்时折算到马达轴上的加速转矩,N·m
Mf—折算到马达轴上的摩擦转矩,N·m
M0—由于丝杠预紧引起的折算到马达轴上的附加摩擦转矩,N·m
Mat—切削时折算到马达轴上的加速转矩,N·m
Mt—折算到马达轴上的切削载荷转矩,N·m
6
0.3898×10-2
120
20
0.12101
8
0.3691×10-2
24
0.11225
注:1.应用示例:求名义直径60mm、螺距12mm、长度1530mm的滚珠丝杠的转动惯量,表中查出0.7351×10-2则转动惯量为0.7351×10-2×1.53=0.01125kg·m2。
2.粗略计算时可按光轴从图22-2-2中查出J(略)。
丝杠螺距,mm
4
5
6
8
10
12
16
20
24
32
1000kg工作台的折算转动惯量,kg·m2
0.00041
0.00063
0.00091
0.00162
0.00253
0.00365
0.00648
0.01013
0.01459
0.02594
注:应用示例:求丝杠螺距12mm,工作台质量2800kg的折算转动惯量,由表中查出0.00365,则此时折算转动惯量为0.00365×2.8=0.01022kg·m2。
工作台折算到丝杠上的转动惯量
v —工作台移动速度,mm/min
n —丝杠转速,r/min
m —工作台质量,kg
P —丝杠螺距,mm
丝杠传动时传动系统折算到马达轴上的总转动惯量
J1—齿轮Z1及其轴的转动惯量,kg·m2
J2—齿轮Z2的转动惯量,kg·m2
JS—丝杠转动惯量, kg·m2
P —丝杠螺距,mm
采用滚珠丝杠螺母传动时,Ma、Mf、M0、Mt的计算公式见表22-2-9
最大切削载荷时所需力矩
快速进给时所需转矩
表22-2-9丝杠传动时Ma、Mf、M0、Mt计算公式
力矩名称
计算公式
符号代表的意义
加速力矩Ma
Jr—折算到马达轴上总转动惯量,kg·m2
T —系统时间常数,s
n —马达转速,r/min
当n=nmax时计算Mamax
m —工件及工作台质量,kg
齿轮齿条传动时工作台折算到小齿轮轴上的转动惯量
R —齿轮分度圆半径,mm
m —工件及工作台质量,kg
齿轮齿条传动时传动系统折算到马达轴上的总转动惯量
J1,J2—分别为I轴、Ⅱ轴上齿轮的转动惯量,kg·m2
R —齿轮Z分度圆半径,mm
m —工件及工作台质量,kg
表22-2-6工作台折算到丝杠轴上的转动惯量
表22-2-7滚珠丝杠的转动惯量[6]
丝杠名义直径mm
螺距mm
1m长丝杠的转动惯量kg·m2
丝杠名义直径mm
螺距mm
1m长丝杠的转动惯量kg·m2
20
4
0.0921×10-3
50
10
0.3507×10-2
5
0.0823×10-3
12
0.3136×10-2
25
5
0.2196×10-3
60
8
0.8000×10-2
表22-2-5传动惯量计算公式(摘自《机床设计手册》)
种类
计算公式
简图及符号的意义
圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)
对于钢材:
m—圆柱体质量,kg
D —圆柱体直径,mm
L —圆柱体长度或厚度,㎜
ρ—材料刻度,g/cm3
丝杠折算到马达轴上的转动惯量
Js —丝杠转动惯量,kg·m2
i —传动比,
6
0.1961×10-3
10
0.7651×10-2
30
5
0.4815×10-3
12
0.7351×10-2
6
0.4383×10-3
70
8
0.1543×10-1
35
5
0.9080×10-3
10
0.1476×10-1
6
0.8551×10-3
12
0.1423×10-1
8
0.8139×10-3
80
10
0.2584×10-1
