信息安全数学基础期末考试试卷及答案(A卷)
信息安全数学基础期末考试试卷及答案(A卷)

信息安全数学基础期末考试试卷及答案(A卷)装订线装订线三、解同余方程(本大题共2小题,每小题10分,共20分)1.求解一次同余方程1714(mod21)x 。
2.解同余方程组2(mod3)3(mod5)2(mod7) xxx≡≡≡⎧⎪⎨⎪⎩四、证明题(本大题共3小题,每小题7分,共21分)2.f是群G到G'的一个同态,{}=∈=,其f a a G f a e'ker|,()中e'是G'的单位元。
证明:ker f是G的正规子群。
3. 证明:如果p 和q 是不同的素数,则111(mod )q p p q pq --+=。
五、应用题(共11分)RSA 公钥加密算法的密钥生成步骤如下:选择 两个大的素数p 和q ,计算n =pq 。
选择两个正整数e 和d ,满足:ed =1(mod ()n )。
Bob 的公钥是(n ,e ),对外公布。
Bob 的私钥是d ,自己私藏。
如果攻击者分解n 得到p =47,q =23,并且已知e =257,试求出Bob 的私钥d 。
答案 一、填空题(每空2分,共24分) 1. 两个整数a ,b ,其最大公因数和最小公倍数的关系为[,](,)ab a b a b =。
2. 给定一个正整数m ,两个整数a ,b 叫做模m 同余,如果|m a b -,记作(mod )a b m ≡;否则,叫做模m 不同余,记作a ≡(mod )b m 。
3. 设m ,n 是互素的两个正整数,则()mn ϕ=()()m n ϕϕ。
4. 设1m >是整数,a 是与m 互素的正整数。
则使得1(mod )e a m ≡成立的最小正整数e 叫做a 对模m 的指数,记做()m ord a 。
如果a 对模m 的指数是()m ϕ,则a 叫做模m 的 原根 。
5. 设n 是一个奇合数,设整数b 与n 互素,如果整数n 和b 满足条件11(mod )n b n -≡,则n 叫做对于基b 的拟素数。
信息安全数学基础参考试卷

《信息安全数学基础》参考试卷一.选择题(在每小题的备选答案中只有一个正确答案,将正确答案序号填入下列叙述中的括号内,多选不给分):(每题2分,共20分)1.576的欧拉函数值ϕ(576) =()。
(1) 96,(2) 192,(3) 64,(4) 288。
2.整数kn和k(n+2)的最大公因数(kn , k(n+2))=()。
(1) 1或2,(2) | kn|,(3) | n|或| kn|,(4) | k|或2| k|。
3.模10的一个简化剩余系是( )。
(1) 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,(2) 11, 17, 19 , 27(3) 11, 13, 17, 19,(4) 0, 1, 2, 3, 4, 5, 6, 7, 8, 9。
4.29模23的逆元是( )。
(1) 2,(2) 4,(3) 6,(4) 11。
5.设m1,m2是两个正整数,x1遍历模m1的完全剩余系,x2遍历模m2的完全剩余系,若( )遍历m1m2的完全剩余系。
(1) (m1,m2)=1,则m1x1+m2x2(2) m1和m2是素数,则m1x1+m2x2(3) (m1,m2)=1,则m2x1+m1x2(4)m1和m2是素数,则m2x1+m1x26.下面的集合和运算构成群的是( ) 。
(1) <N,+> (N是自然数集,“+”是加法运算)(2) <R,×> (R是实数集,“×”是乘法运算)(3) <Z,+> (Z是整数集,“+”是加法运算)(4) <P(A),∩> (P(A)={U | U是A的子集}是集合A的幂集,“∩”是集合的交运算)7.下列各组数对任意整数n均互素的是( ) 。
(1) 3n+2与2n,(2) n-1与n2+n+1,(3) 6n+2与7n,(4) 2n+1与4n+1。
8.一次同余式234x ≡ 30(mod 198)的解数是( )。
信息安全数学基础习题答案 2

信息安全数学基础习题答案第一章整数的可除性1.证明:因为2|n 所以n=2k , k∈Z5|n 所以5|2k ,又(5,2)=1,所以5|k 即k=5 k1,k1∈Z7|n 所以7|2*5 k1 ,又(7,10)=1,所以7| k1即k1=7 k2,k2∈Z 所以n=2*5*7 k2即n=70 k2, k2∈Z因此70|n2.证明:因为a3-a=(a-1)a(a+1)当a=3k,k∈Z 3|a 则3|a3-a当a=3k-1,k∈Z 3|a+1 则3|a3-a当a=3k+1,k∈Z 3|a-1 则3|a3-a所以a3-a能被3整除。
3.证明:任意奇整数可表示为2 k0+1,k0∈Z(2 k0+1)2=4 k02+4 k0+1=4 k0 (k0+1)+1由于k0与k0+1为两连续整数,必有一个为偶数,所以k0 (k0+1)=2k所以(2 k0+1)2=8k+1 得证。
4.证明:设三个连续整数为a-1,a,a+1 则(a-1)a(a+1)= a3-a由第二题结论3|(a3-a)即3|(a-1)a(a+1)又三个连续整数中必有至少一个为偶数,则2|(a-1)a(a+1)又(3,2)=1 所以6|(a-1)a(a+1) 得证。
5.证明:构造下列k个连续正整数列:(k+1)!+2, (k+1)!+3, (k+1)!+4,……, (k+1)!+(k+1), k∈Z对数列中任一数 (k+1)!+i=i[(k+1)k…(i+1)(i-1)…2*1+1], i=2,3,4,…(k+1)所以i|(k+1)!+i 即(k+1)!+i为合数所以此k个连续正整数都是合数。
6.证明:因为1911/2<14 ,小于14的素数有2,3,5,7,11,13经验算都不能整除191 所以191为素数。
因为5471/2<24 ,小于24的素数有2,3,5,7,11,13,17,19,23经验算都不能整除547 所以547为素数。
由737=11*67 ,747=3*249 知737与747都为合数。
(完整word版)2014-2015第一学期信息安全基础期末考试试卷(A卷)答案

山东科技大学2014—2015学年第一学期《信息安全基础》期末考试试卷(A卷)答案一、填空1、认证业务不可否认业务2、反馈函数3、1284、数论5、有限域上离散对数问题6、行移位(ShiftRow)、列混合(MixColumn)7、248、王小云二、名词解释1、离散对数:设p是素数,a是p的本原根。
即a1,a2,…,a p-1在 mod p下产生1到p-1的所有值,所以对b∈{1,…,p-1},有惟一的i∈{1,…,p-1}使得b≡a i mod p。
称i为模p下以a为底b的离散对数,记为b(mod p)。
i≡loga2、陷门单向函数:t是与f有关的一个参数。
已知x, 计算y使得y=f(x)容易;如果不知道t,已知y, 计算x使得y=f(x)是难的,但知道t时,已知y, 计算x使得y=f(x)是容易的。
参数t称为陷门(Trapdoor)。
3、寻找函数H的具有相同输出的两个任意输入的攻击方式,称为第II类生日攻击。
4、在交互证明系统中,设P知道某一秘密,并向V证明自己掌握这一秘密,但又不向V泄露这一秘密,这就是最小泄露证明。
进一步,如果V除了知道P能证明某一事实外,不能得到其他任何信息,则称P实现了零知识证明,相应的协议称为零知识证明协议。
三、问答题1、答:应考虑以下几个方面:1)加密算法。
(3分)2)用于加密算法的秘密信息。
(3分)3)秘密信息的分布和共享。
(8分)4)使用加密算法和秘密信息以获得安全服务所需的协议。
(10分)2、设计一个性能良好的序列密码最基本的设计原则是什么?它又可分为哪些基本原则?答:最基本的设计原则是“密钥流生成器的不可预测性”,它可分解为下述基本原则:答:①长周期。
②高线性复杂度。
③统计性能良好。
④足够的“混乱”。
⑤足够的“扩散”。
⑥抵抗不同形式的攻击。
(少一个扣2分)3、在具有仲裁方式的数字签字中,如果仲裁方和发送方共谋否认曾发过的消息,也可和接收方共谋以伪造发送方的签字,如何解决这个问题,请给出实例。
信息安全数学基础答案

信息安全数学基础答案【篇一:信息安全数学基础习题答案】xt>第一章整数的可除性1.证明:因为2|n 所以n=2k , k?z5|n 所以5|2k ,又(5,2)=1,所以5|k 即k=5 k1 ,k1?z 7|n 所以7|2*5 k1 ,又(7,10)=1,所以7| k1 即k1=7 k2,k2?z 所以n=2*5*7 k2 即n=70 k2, k2?z因此70|n32.证明:因为a-a=(a-1)a(a+1)3当a=3k,k?z 3|a 则3|a-a3当a=3k-1,k?z 3|a+1 则3|a-a3当a=3k+1,k?z 3|a-1 则3|a-a3所以a-a能被3整除。
3.证明:任意奇整数可表示为2 k0+1, k0?z22(2 k0+1)=4 k0+4 k0+1=4 k0 (k0+1)+1由于k0与k0+1为两连续整数,必有一个为偶数,所以k0(k0+1)=2k2所以(2 k0+1)=8k+1 得证。
34.证明:设三个连续整数为a-1,a,a+1 则(a-1)a(a+1)= a-a3由第二题结论3|(a-a)即3|(a-1)a(a+1)又三个连续整数中必有至少一个为偶数,则2|(a-1)a(a+1)又(3,2)=1所以6|(a-1)a(a+1) 得证。
5.证明:构造下列k个连续正整数列:(k+1)!+2, (k+1)!+3, (k+1)!+4,……, (k+1)!+(k+1), k?z对数列中任一数 (k+1)!+i=i[(k+1)k…(i+1)(i-1)…2*1+1],i=2,3,4,…(k+1) 所以i|(k+1)!+i即(k+1)!+i为合数所以此k个连续正整数都是合数。
1/26.证明:因为191<14 ,小于14的素数有2,3,5,7,11,13经验算都不能整除191所以191为素数。
1/2因为547<24 ,小于24的素数有2,3,5,7,11,13,17,19,23经验算都不能整除547所以547为素数。
信息安全数学基础考试题

信息安全数学基础2005年考题1、已知a=66,b=75,求正整数x,y,使ax-by=(a,b)成立 .2、证明:对于任意整数a、b、c,如果(a,c)=1,c|ab,则必有c|b .3、集合{0,1,······9998}中有多少个元素与9999互素?4、已知a=5,b=42,n=265, 求a b mod n .5、求如下同余式组的解x≡1(mod 5)x≡3(mod 7)x≡2(mod 9)6、求同余式x5-x4+x2+6≡(mod 73)的所有解。
7、求J(29,97)的值。
8、求x2≡13(mod 113)的解。
9、已知59582=2×313,求模59582的一个原根。
1.2008-05-04课堂补充求F2[x]中f(x)=x8+x4+x3+x+1的周期,并求y∈F2[x]/(f(x)),使得y、y2、y4、y8为F2[x]/(f(x))的基底2.2008-05-04课堂补充求F2[x]中f(x)=x8+x4+x3+x2+1的周期,并求y∈F2[x]/(f(x)),使得y、y2、y4、y8为F2[x]/(f(x))的基底3.2008-05-04课堂补充设a(x)=x3+x+1,b(x)=x2+x+1,计算a(x)+b(x)、a(x).b(x)、a(x)/b(x)4.第11章课件2证明:如果α≠0和β都是有理数域Q上的代数数,则α+β和α-1也是有理数域Q上的代数数5.第11章课件3α叫做代数整数,如果存在一个首一正系数多项式f(x),使得f(α)=0。
证明:如果α≠0和β是代数整数,则α+β和α-1也是代数整数6.第12章课件3证明x8+x4+x3+x+1是F2[x]中的不可约多项式,从而F2[x]/(x8+x4+x3+x+1)是一个F28域7.第12章课件4求F28=F2[x]/(x8+x4+x3+x+1)中的生成元g(x),并计算g(x)t,t=1,2,…,255和所有生成元8.第12章课件3证明x8+x4+x3+x2+1是F2[x]中的不可约多项式,从而F2[x]/(x8+x4+x3+x2+1)是一个F28域2008-05-04交,共3题1.2008-04-18课堂补充求F2上的所有8次不可约多项式注:x8+x4+x3+x+1是不可约非本原多项式,用于AES;x8+x4+x3+x2+1是不可约本原多项式,用于欧洲通信标准提示:非零多项式有28-1=255个,次数为偶数时一定可约,奇数次系数为0时可约2.2008-04-30课堂补充求Q(√2,3√3)的基底3.2008-04-30课堂补充求u使Q(√2,√3)=Q(u)2008-04-18交,共9题1.对3DES对称密码算法的S盒进行轮换分解补充:DES算法标准FIPS 46-2 - (DES), Data Encryption Standard页面中搜索“PRIMITIVE FUNCTIONS FOR THE DATA ENCRYPTION ALGORITHM”就可找到标准建议的S盒函数还有一个C语言的3DES实现FPGA芯片上的3DES实现思路2.第十章课件14证明:置换群S4的一组生成元为(1,2),(1,3),(1,4)进一步,用该组生成元来给出S4的所有子群3.第十章课件154.2008-04-11课堂补充假设K是有限域,p是K的特征。
信息安全数学基础期末试卷及答案
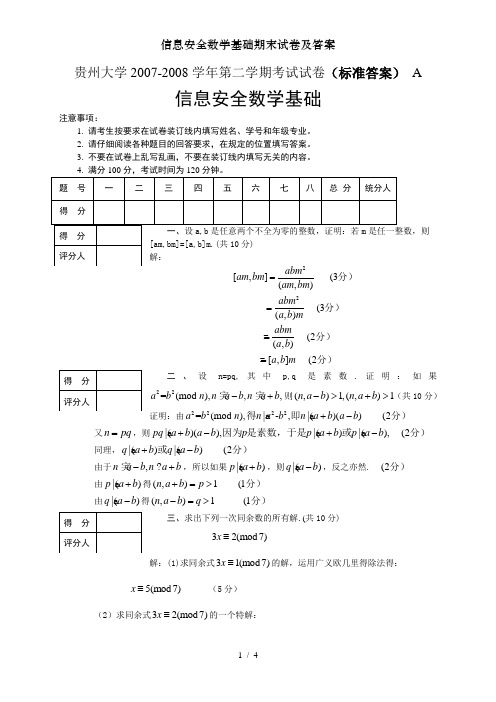
贵州大学2007-2008学年第二学期考试试卷(标准答案) A信息安全数学基础注意事项:1. 请考生按要求在试卷装订线内填写姓名、学号和年级专业。
2. 请仔细阅读各种题目的回答要求,在规定的位置填写答案。
3. 不要在试卷上乱写乱画,不要在装订线内填写无关的内容。
2[,](3(,)(3(,)(2(,)[,](2am bmam bmabma b mabma ba b m====分)分)分)分)==二、设n=pq,其中p,q是素数.证明:如果22=(mod),,,a b n n a b n a b-+宎宎则(,)1,(,)1n a b n a b->+>(共10分)证明:由2222=(mod),|-,|()()a b n n a b n a b a b+-得即a a(2分)又n pq=,则|()(),|()|(),pq a b a b p p a b p a b+-+-因为是素数,于是或a a a(2分)同理,|()|()q a b q a b+-或a a(2分)由于,n a b n a b-+宎?,所以如果|()p a b+a,则|()q a b-a,反之亦然. (2分)由|()p a b+a得(,)1n a b p+=>(1分)由|()q a b-a得(,)1n a b q-=>(1分)三、求出下列一次同余数的所有解.(共10分)32(mod7)x≡解:(1)求同余式31(mod7)x≡的解,运用广义欧几里得除法得:5(mod7)x≡(5分)(2)求同余式32(mod7)x≡的一个特解:10(mod 7)x ≡ (4分)(3)写出同余式32(mod 7)x ≡的全部解:102(mod7),0x t t ≡+= (1分)四、求解同余式组:(共15分)1234(mod5)(mod 6)(mod 7)(mod11)x b x b x b x b =⎧⎪=⎪⎨=⎪⎪=⎩解:令m=5.6.7.11=23101234 6.7.11462(15.7.11385(15.6.11330(15.6.7210(1M M M M ========分)分)分)分)分别求解同余式'M 1(mod ),1,2,3,4i i i M m i ≡=得到:''''12343,1,1,1(4M M M M ====分)故同余式的解为:12343462385330210(mod 2310)(2x b b b b ≡⋅⋅+⋅+⋅+⋅分)五、求满足方程23:51(mod 7)E y x x =++的所有点. (共10分) 解:对x=0,1,2,3,4,5,6,分别求出y.22222220,1(mod 7),1,6(mod 7)(21,0(mod 7),(22,5(mod 7),(13(mod 7),(11(mod 7),1,6(mod 7)(25,4(mod 7),2,5(mod 7)(16,2(mod 7),3,4(mod 7)(1x y y x y x y y y y x y y x y y =≡≡=≡≡=≡≡≡≡=≡≡=≡≡分)y 0(mod7)分)无解分)x=3,无解分)x=4,分)分)分)六、判断同余式2137(mod 227)x ≡是否有解.(共15分) 解:因为227是素数,2137901235253227227227227227227⎛⎫⋅⋅⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭--===- (分)又222712262288821(1)=13227⋅⎛⎫ ⎪⎝⎭-=(-)=-- (分) 又251512271822522721==11322755⋅⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭---=(-)(-)=- (分)因此,13713227⎛⎫⎪⎝⎭=- (分)同余式2137(mod 227)x ≡无解. (3分)七、设1m >是整数,a 是与m 互素的整数,假如()m ord a st =,那么()s m ord a t =.(共10分)解: 由()m ord a st =得:()1(mod )5st s ta a m =≡(分)由()m ord a st =知,t 是同余式()1(mod )s ta m ≡成立的最小正整数, 故,()sm ord a t =. (5分)八、证明整数环Z 是主理想环. (共10分)证:设I 是Z 中的一个非零理想.当a I ∈时,有00(1)a I a a I =∈=-∈及-.(2分) 因此,I 中有正整数存在. (1分)设d 是I 中的最小正整数,则()I d = (1分)事实上,对任意a I ∈,存在整数q,r 使得 (1分),0a dq r r d =+≤< (1分)这样,由a I ∈及dq I ∈,得到r a dq I =-∈. (1分)但r d <以及d 是I 中的最小正整数.因此,r=0,()a dq d =∈.(1分) 从而()I d ⊂,(1分)又显然()d I ⊂.故()I d =,故Z 是主理想. (1分)九、设p 是素数,则()P p =是整数环Z 的素理想. (共10分) 证:对任意整数a,b ,若(),|ab P p p ab ∈=则. (3分) 于是||.p a p b 或 (3分)因此得到,a P b P ∈∈或. (3分)因此,()P p =是整数环Z 的素理想. (1分)。
信息安全数学基础习题答案.pdf

“信息安全数学基础”习题答案第一章1、证明: (1)|()|()()|a b b ma m Z c d d nc n Z bd acmn mn Z ac bd ⇒=∈⇒=∈∴=∈∵,,,即。
(2)12111112|,|,,|11(3)|(),,k k k k a b a b a b a b c b c b c c c c ∴−+++∵ ,根据整除的性质及递归法,可证得:,其中为任意整数。
2、证明:1-2(2)(3,5)13|5|15|,(15,7)17|105|a a a a a =∴=∴∵∵∵根据例题的证明结论知:,又且,又,且,。
3、证明:1n p n p n >>因为,且是的最小素因数,若假设n/p 不是素数,则有121223131312,2,,,,2,,k k n p p p p k p p p p k n p p p p n p p n n p n n p =×××≥≥==×≥∴≥≤>> (其中为素数且均)若,则即,与题设矛盾,所以假设不成立,即为素数得证。
7、证明:首先证明形如6k -1的正整数n 必含有6k -1形式的素因子,这显然是成立的。
因为如果其所有素因数均为6k +1形式,则12,(61,1,2,,)j i i n p p p p k i j =×××=+= ,从而得到n 是形如6k +1形式的正整数,这与题设矛盾。
其次,假设形如6k -1的素数为有限个,依次为1212,,6s s q q q n q q q = ,考虑整数-1, 则n 是形如6k -1的正整数,所以n 必有相同形式的素因数q ,使得使得q = q j (1≤j ≤s )。
由整数的基本性质(3)有:12|(6)1s q q q q n −= ,这是不可能的。
故假设错误,即存在无穷多个形如4k -1的素数得证。
2n3n最小非负余数最小正余数绝对值最小余数最小非负余数最小正余数绝对值最小余数3 0、1 1、3 0、1 0、1、2 1、2、3 -1、0、14 0、1 1、4 0、1 0、1、3 1、3、4 -1、0、1 8 0、1、4 1、4、8 1,0 0、1、3、5、7 1、3、5、7、8 3、1、-3、-1、0 10 0、1、4、5、6、9 1、4、5、6、9、10 -4、-1、0、1、4、5 0,1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,10-5,-4,-3,-2,-1,0,1,2,3,413、解: (1)259222137222376(222,259)37372592221,1,1s t =×+=×⇒==−×∴==−(2)139571316827136821316823122(1395,713)31317136821713(13957131)2713(1)1395,1,2s t =×+=×+=×⇒==−×=−−×=×+−×∴=−=16、解: (1)(112,56)5611256[112,56]112(112,56)=×== (2)(67,335)6767335[67,335]335(67,335)=×== (3)(1124,1368)411241368[1124,1368]384408(1124,1368)=×==(7,4)1,0,7(1)4211,24410,1,2,771||1000142||100040,1,1427c s t k x k k k y k x k y x kk y k ==∴×−+×=∴=−=⎧=−=−⎪⎪=±±⎨⎪==⎪⎩≤⎧∴≤⎨≤⎩=−⎧∴=±±⎨=⎩∵ 而不定方程的一切解为: 其中,又方程的全部解为 ,其中 ,第二章1、解:(1) 错误。
信息安全数学基础参考试卷

,考试作弊将带来严重后果!华南理工大学期末考试XXXX 级《信息安全数学基础》试卷A1. 考前请将密封线内填写清楚;2. 所有答案请直接答在试卷上;3.考试形式:闭卷;不许使用计算器;选择题(在每小题的备选答案中只有一个正确答案,将正确答案序号填入下): (每题2分,共10分)1.设 m 是大于 1 的整数, a 是满足(a , m )=1 的整数,则 ( )。
(1) a m ≡a (mod ϕ (m )), (2) a ϕ (m )≡a (mod m ), (3) a m ≡1 (mod ϕ (m )), (4) a ϕ (m )≡1 (mod m )。
2.设m 是一个正整数,a , b 是整数,下面正确的是( )。
(1) 若ad ≡bd (mod m ),则 a ≡b (mod m ); (2) 若a ≡b (mod m ) , 则 ak ≡bk (mod mk );(3) 若a ≡ b (mod m ),正整数 d | (a , b , m ),则mod()a b m d d d≡; (4) a ≡b (mod m ), 如果m | d ,则 a ≡b (mod d )。
3.整数kn 和k (n +2)的最大公因数(kn , k (n +2))=( )。
(1) 1或2, (2) | kn |, (3) | n | 或 | kn |, (4) | k | 或2| k | 。
4.设 a =23×32×54×116 ,b =22×36×74×113,使得a' | a ,b' | b ,a' ×b'=[a ,b ],a',b' )=1 的a',b' 分别为( )。
(1) 54 ×116 ,22×36×74, (2) 23×54 ,36×74×113, (3) 23×54 ×116 ,36×74, (4) 23×54 ×116 ,36×74×1135.集合F 上定义了“+”和“ · ”两种运算。
最新。信息安全数学基础习题答案

最新。
信息安全数学基础习题答案信息安全数学基础习题答案第⼀章整数的可除性1.证明1:因为2|n 所以n=2k , k1Z5|n 所以5|2k ,⼜(5,2)=1,所以5|k 即k=5 k1,k11Z7|n 所以7|2*5 k1 ,⼜(7,10)=1,所以7| k1即k1=7 k2,k21Z所以n=2*5*7 k2即n=70 k2, k21Z因此70|n证明2:n是2、5、7的公倍数,所以[2,5,7]|n,⼜知2、5、7互素,所以[2,5,7]=2*5*7=70,即70|n。
2.证明:因为a3-a=(a-1)a(a+1)当a=3k,k22(mod)a b p≡Z 3|a 则3|a3-a当a=3k-1,k p a b-Z 3|a+1 则3|a3-a当a=3k+1,k p a b+Z 3|a-1 则3|a3-a所以a3-a能被3整除。
3.证明:任意奇整数可表⽰为2 k0+1, k022(mod)≡Za b p(2 k0+1)2=4 k02+4 k0+1=4 k0 (k0+1)+1由于k0与k0+1为两连续整数,必有⼀个为偶数,所以k0 (k0+1)=2k所以(2 k0+1)2=8k+1 得证。
4.证明:设三个连续整数为a-1,a,a+1 则(a-1)a(a+1)= a3-a由第⼆题结论3|(a3-a)即3|(a-1)a(a+1)⼜三个连续整数中必有⾄少⼀个为偶数,则2|(a-1)a(a+1)⼜(3,2)=1 所以6|(a-1)a(a+1) 得证。
5.证明:构造下列k个连续正整数列:(k+1)!+2, (k+1)!+3, (k+1)!+4,……, (k+1)!+(k+1), k p a b-Z对数列中任⼀数 (k+1)!+i=i[(k+1)k…(i+1)(i-1)…2*1+1], i=2,3,4,…(k+1)所以i|(k+1)!+i 即(k+1)!+i为合数所以此k个连续正整数都是合数。
6.证明:因为1911/2<14 ,⼩于14的素数有2,3,5,7,11,13经验算都不能整除191 所以191为素数。
信安数学期末习题

判断题:1、整环就是含有单位元的交换环。
2、),(+Z 到),(+m Z 的映射__:x x f →是单同态映射。
3、若今天是星期二,那么 天后仍是星期二。
4、模11的二次非剩余一共有5个。
5、6阶群中一定存在4阶子群。
6、均不为零,且b a Z b a ,,,∈若(,)a b d =,则(,)1a b d d =。
计算题与证明题:1、 使用扩展的Euclid 算法求解(a,b)及整数s ,t,使得sa+tb=(a,b),其中a=666,b=1516。
2、写出模7的同余类集合,并列出其加法运算表和乘法运算表。
3、 求解下列同余方程或同余方程组(1) )27(mod 1215≡x(2)4、已知3是模17的一个原根,(1)由原根3推导出模17的其他原根。
(2)以原根3为底,构造模17的指数表。
(3)求解同余方程)17(mod 253≡x 。
⎪⎩⎪⎨⎧≡=≡)5(mod 213)9(mod 57)2(mod 3x x x 201025、在整数集合中定义运算:2-+=b a b a ,Z b a ∈,,证明),( Z 是群。
6、令⎭⎬⎫⎩⎨⎧⎪⎪⎭⎫⎝⎛=为实数b a b a R ,00,求证:R 关于矩阵加法和矩阵乘法构成环。
7、求解 、 8、判断下列方程是否有解:)3599(mod 2)365(mod 122≡-≡x x9、求所有以3为其二次剩余的奇素数。
10、写出 的所有非平凡子群和关于这些非平凡子群的陪集。
11、写出对称群 的所有非平凡子群及关于这些非平凡子群的陪集。
12、关于多项式环][2x F ,(1)证明1)(2++=x x x f 是][2x F 的不可约多项式;(2)列出有限域)/(][2f x F 中的所有元素。
13、设图G 的邻接矩阵A=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛0100101111011000,计算2A ,3A 和4A ,并求出G 的可达性矩阵P 。
14、设一棵树有2n 个结点度数为2,3n 个结点度数为3,4n 个结点度数为4,请求出它有几个度数为1的结点? ⎪⎭⎫ ⎝⎛227137)137(m od 12-=x )227(mod 22=x 3391979⎛⎫ ⎪⎝⎭()+,6Z 3S。
2007级信息安全数学基础试卷-A-答案

, ),8.(中国剩余定理) 设m 1, …, m k 是k 个两两互素的正整数,则对任意的整数b 1, …, b k 同余式组x ≡ b 1 (mod m 1)… … … …x ≡ b k (mod m k )有唯一解。
令m =m 1…m k ,m =m i M i ,i =1,…,k ,则同余式组的解为: x ≡ M 1' M 1b 1+…+ M k ' M k b k (mod m ) ,其中 M i ' M i ≡1 (mo d m i ) , i =1 , 2 ,…, k 。
9.正整数n 有标准因数分解式为 kk p p n αα 11=,则n 的欧拉函数10.设 m 是一个正整数, ad ≡bd (mod m )。
如果 (d , m ) =1 ,则a ≡b (mod m )。
三.证明题 (写出详细证明过程):(共30分)1.证明:如果m 和n 是互素的大于1的整数,则m ϕ(n )+n ϕ(m ) ≡1 (mod mn )。
(7分)证明 根据欧拉定理 m ϕ (n ) ≡1 (mod n ), 又 n ϕ (m ) ≡0 (mod n ),根据2.1节定理4 m ϕ(n )+n ϕ(m ) ≡1 (mod n ) (1) 类似的,根据欧拉定理 n ϕ (m ) ≡1 (mod m ), 又m ϕ(n ) ≡0 (mod m ),根据2.1节定理4 m ϕ(n )+n ϕ(m ) ≡1 (mod m ) (2)由(1)和(2), m 和 n 是互素, 以及根据2.1节定理12得: m ϕ(n )+n ϕ(m ) ≡1 (mod [n , m ]),即m ϕ(n )+n ϕ(m ) ≡1 (mod nm )。
2.证明:如果a k ≡ b k (mod m ),a k +1 ≡ b k +1 (mod m ) ,a ,b ,k ,m 是整数,k >11110,并且(a,m) =1,那么a ≡ b (mod m)。
最新信息安全数学基础期末试卷及答案

贵州大学2007-2008学年第二学期考试试卷(标准答案) A信息安全数学基础注意事项:1. 请考生按要求在试卷装订线内填写姓名、学号和年级专业。
2. 请仔细阅读各种题目的回答要求,在规定的位置填写答案。
3. 不要在试卷上乱写乱画,不要在装订线内填写无关的内容。
4. 满分100分,考试时间为120分钟。
一、设a,b 是任意两个不全为零的整数,证明:若m 是任一整数,则 [am,bm]=[a,b]m.(共10分) 解:22[,](3(,)(3(,)(2(,)[,](2abm am bm am bm abm a b mabma b a b m ====分)分)分)分)==二、设n=pq,其中p,q是素数.证明:如果22=(mod ),,,a b n n a b n a b -+宎宎 则(,)1,(,)1n a b n a b ->+>(共10分)证明:由2222=(mod ),|-,|()()a b n n a b n a b a b +-得即a a (2分)又n pq =,则|()(),|()|(),pq a b a b p p a b p a b +-+-因为是素数,于是或a a a (2分) 同理,|()|()q a b q a b +-或a a (2分)由于,n a b n a b -+宎?,所以如果|()p a b +a ,则|()q a b -a ,反之亦然. (2分) 由|()p a b +a 得(,)1n a b p +=> (1分) 由|()q a b -a 得(,)1n a b q -=> (1分)三、求出下列一次同余数的所有解.(共10分)32(mod 7)x ≡解:(1)求同余式31(mod 7)x ≡的解,运用广义欧几里得除法得:5(mod7)x ≡ (5分)(2)求同余式32(mod 7)x ≡的一个特解: 10(mod 7)x ≡ (4分) (3)写出同余式32(mod 7)x ≡的全部解: 102(mod7),0x t t ≡+= (1分)四、求解同余式组:(共15分)1234(m o d 5)(m o d 6)(m o d 7)(m o d 11)x b x b x b x b =⎧⎪=⎪⎨=⎪⎪=⎩解:令m=5.6.7.11=23101234 6.7.11462(15.7.11385(15.6.11330(15.6.7210(1M M M M ========分)分)分)分)分别求解同余式'M 1(mod ),1,2,3,4i i i M m i ≡=得到:''''12343,1,1,1(4M M M M ====分)故同余式的解为:12343462385330210(mod 2310)(2x b b b b ≡⋅⋅+⋅+⋅+⋅分)五、求满足方程23:51(mod 7)E y x x =++的所有点. (共10分)解:对x=0,1,2,3,4,5,6,分别求出y.22222220,1(mod 7),1,6(mod 7)(21,0(mod 7),(22,5(mod 7),(13(mod 7),(11(mod 7),1,6(mod 7)(25,4(mod 7),2,5(mod 7)(16,2(mod 7),3,4(mod 7)(1x y y x y x y y y y x y y x y y =≡≡=≡≡=≡≡≡≡=≡≡=≡≡分)y 0(mod7)分)无解分)x=3,无解分)x=4,分)分)分)六、判断同余式2137(mod 227)x ≡是否有解.(共15分)解:因为227是素数,2137901235253227227227227227227⎛⎫⋅⋅⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭--===- (分)又222712262288821(1)=13227⋅⎛⎫ ⎪⎝⎭-=(-)=-- (分) 又251512271822522721==11322755⋅⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭---=(-)(-)=- (分) 因此,13713227⎛⎫⎪⎝⎭=- (分)同余式2137(mod 227)x ≡无解. (3分)七、设1m >是整数,a 是与m 互素的整数,假如()m ord a st =,那么()s m ord a t =.(共10分)解: 由()m ord a st =得:()1(mod )5st s ta a m =≡(分)由()m ord a st =知,t 是同余式()1(mod )s ta m ≡成立的最小正整数,故,()sm ord a t =. (5分)八、证明整数环Z 是主理想环. (共10分)证:设I 是Z 中的一个非零理想.当a I ∈时,有00(1)a I a a I =∈=-∈及-.(2分) 因此,I 中有正整数存在. (1分)设d 是I 中的最小正整数,则()I d = (1分) 事实上,对任意a I ∈,存在整数q,r 使得 (1分) ,0a dq r r d =+≤< (1分)这样,由a I ∈及dq I ∈,得到r a dq I =-∈. (1分)但r d <以及d 是I 中的最小正整数.因此,r=0,()a dq d =∈.(1分) 从而()I d ⊂,(1分)又显然()d I ⊂.故()I d =,故Z 是主理想. (1分)九、设p 是素数,则()P p =是整数环Z 的素理想. (共10分)证:对任意整数a,b ,若(),|ab P p p ab ∈=则. (3分) 于是||.p a p b 或 (3分)因此得到,a P b P ∈∈或. (3分)因此,()P p =是整数环Z 的素理想. (1分)。
信息安全数学基础习题答案

4
21.解: (1)因为 875961*2753≡[(36mod9)(17mod9)]mod9 ≡0(mod9) 2410520633≡26(mod9) ≡8(mod9) 所以等式 875961*2753=2410520633 不成立 (2)因为 14789*23567≡[(29mod9)(23mod9)]mod9 ≡1(mod9) 348532367≡41(mod9) ≡5(mod9) 所以等式 14789*23567=348532367 不成立 (3)因为 24789*43717≡[(30mod9)(22mod9)]mod9 ≡3(mod9) 1092700713≡30(mod9) ≡3(mod9) 所以等式 24789*43717=1092700713 可能成立 (4)这种判断对于判断等式不成立时简单明了,但对于判断等式成立时,可能会较 复杂。 22.解:因为 7 为素数,由 Wilso 定理知:(7-1)! ≡-1(mod7) 即 6!≡-1(mod7) 所以 8*9*10*11*12*13≡1*2*3*4*5*6(mod7) ≡6!(mod7) ≡-1(mod7) 31.证明:因为 c1,c2,…,c ϕ (m)是模 m 的简化剩余系 对于任一 ci,有 m-ci 也属于模 m 的简化剩余系 所以 ci+(m-ci)≡0(modm) 因此 c1+c2+…+c ϕ (m)≡0(modm) 32.证明:因为 a ϕ (m)≡1(modm) 所以 a ϕ (m)-1≡0(modm) a ϕ (m)-1=(a-1)(1+a+ a2+…+ a ϕ (m)-1) ≡0(modm) 又(a-1,m)=1 所以 1+a+ a2+…+ a ϕ (m)-1 ≡0(modm) 33.证明:因为 7 为素数,由 Fermat 定理知 a7 ≡a(mod7) 又( a ,3 ) =1 所以 (a,9)=1 由 Euler 定理 知 a ϕ (9) ≡ a6 ≡ 1(mod9) a(mod9) 又(7,9)=1, 所以 a7≡a(mod7*9) 即 a7≡a(mod63) 34.证明:因为 32760=23*32*5*7*13 又(a,32760)=1 所以(a,2)=(a,3)=(a,5)=(a,7)=(a,13)=1 有:a ϕ (13)≡1(mod13) 即 a12≡1(mod13) a ϕ (8)≡a4≡1(mod8) 即 a12≡1(mod8) a ϕ (5)≡a4≡1(mod5) 即 a12≡1(mod5) a ϕ (7)≡a6≡1(mod7) 即 a12≡1(mod7) a ϕ (9)≡a6≡1(mod9) 即 a12≡1(mod9) 又因为[5,7,8,9,13]=32760 所以 a12≡1(mod32760) 35.证明:因为(p,q)=1 p,q 都为素数 所以 ϕ (p)=p-1, ϕ (q)=q-1 由 Euler 定理知:p ϕ (q)≡1(modq) q ϕ (p)≡1(modp) 即 pq-1≡1(modq) qp-1≡1(modp) 又 qp-1≡0(modq) pq-1≡0(modp) 所以 pq-1+qp-1≡1(modq) qp-1+pq-1≡1(modp) 又[p,q]=pq 所以 pq-1+qp-1≡1(modpq) 36.证明:因为(m,n)=1 由 Euler 定理知:m ϕ (n)≡1(modn) n ϕ (m)≡1(modm) 所以 m ϕ (n)+n ϕ (m)≡(m ϕ (n)modn)+ (n ϕ (m)modn)≡1+0≡1(modn)
2006级信息安全数学基础试卷-A

,考试作弊将带来严重后果!华南理工大学期末考试《信息安全数学基础》试卷A1. 考前请将密封线内填写清楚;所有答案请直接答在试卷上;.考试形式:闭卷;选择题:(每题2分,共20分)1.如果a≡b(mod m),c是任意整数,则下列结论错误的是()。
(1) ac≡bc (mod mc),(2) m|a-b,(3) (a, m)=(b, m) ,(4) a=b+mt, t∈Z。
2.设a, b, c≠0是三个整数,c|a,c|b,如果存在整数s, t,使得sa+tb=1,则( ) 。
(1) (a, b)= c,(2) c=1,(3) c=sa+tb,(4) c=± 1 。
3.模30的简化剩余系是( )。
(1) -1, 2, 5, 7, 9, 19, 20, 29,(2) -1, -7, 10, 13, 17, 25, 23, 29,(3) 1, 7, 11, 13, 17, 19, 23, 29,(4) 3, 7, 11, 13, 17, 19, 23, 29 。
4.设a, b, c是三个不全为零的整数。
如果a = bq + c, 其中q是整数,则有( )。
(1) (a, b) = (q, c),(2) (a, b) = (b, c),(3) (a, b) = c,(4) (a, b) = (a, c)。
5.设n是正整数,则|()d nd ϕ=∑( ) 。
(1) d,(2) n,(3) nd,(4) ϕ(n)。
6.下面的集合和运算是群的是( ) 。
(1) <N,+> (运算“+”是自然数集N上的普通加法)(2) <R,×> (R是实数集,“×”是普通乘法)(3) <Z,+> (运算“+”是整数集Z上的普通加法)(4) <P (S ),∩> (P (S )是集合S 的幂集,“∩”为集合的交)7.下面各组数中,均为模7的平方剩余的是 ( )。
信息安全数学基础习题答案

信息安全数学基础习题答案第一章整数的可除性1.证明:因为2|n 所以n=2k , k∈Z5|n 所以5|2k ,又(5,2)=1,所以5|k 即k=5 k1,k1∈Z7|n 所以7|2*5 k1 ,又(7,10)=1,所以7| k1即k1=7 k2,k2∈Z 所以n=2*5*7 k2即n=70 k2, k2∈Z因此70|n2.证明:因为a3-a=(a-1)a(a+1)当a=3k,k∈Z 3|a 则3|a3-a当a=3k-1,k∈Z 3|a+1 则3|a3-a当a=3k+1,k∈Z 3|a-1 则3|a3-a所以a3-a能被3整除。
3.证明:任意奇整数可表示为2 k0+1,k0∈Z(2 k0+1)2=4 k02+4 k0+1=4 k0 (k0+1)+1由于k0与k0+1为两连续整数,必有一个为偶数,所以k0 (k0+1)=2k所以(2 k0+1)2=8k+1 得证。
4.证明:设三个连续整数为a-1,a,a+1 则(a-1)a(a+1)= a3-a由第二题结论3|(a3-a)即3|(a-1)a(a+1)又三个连续整数中必有至少一个为偶数,则2|(a-1)a(a+1)又(3,2)=1 所以6|(a-1)a(a+1) 得证。
5.证明:构造下列k个连续正整数列:(k+1)!+2, (k+1)!+3, (k+1)!+4,……, (k+1)!+(k+1), k∈Z对数列中任一数 (k+1)!+i=i[(k+1)k…(i+1)(i-1)…2*1+1], i=2,3,4,…(k+1)所以i|(k+1)!+i 即(k+1)!+i为合数所以此k个连续正整数都是合数。
6.证明:因为1911/2<14 ,小于14的素数有2,3,5,7,11,13经验算都不能整除191 所以191为素数。
因为5471/2<24 ,小于24的素数有2,3,5,7,11,13,17,19,23经验算都不能整除547 所以547为素数。
由737=11*67 ,747=3*249 知737与747都为合数。
信息安全数学基础期末试卷

B) (a, b, c)
C) (a, c )(b, c) D) (a, b)(b, c)
5. 2017 年 1 月 9 日是星期一(为第 0 天),之后的第 220170109 天是( )。
A) 星期二
B) 星期三
C) 星期四
D) 星期五
6. 11 的原根有( )个。
A) 1 B) 2
C) 3 D) 4
7. a,b 为互素的整数,则存在唯一的整数 s,t,使得 sa tb 1 。( )
8. 设 m 是正整数,如果 ad { bd(mod m),则 a { b(mod m)。( )
9. 设 a 是整数,若 x 遍历正整数模 m 的完全剩余系,则 ax 也遍历模 m 的完全剩余系。( )
Hale Waihona Puke 10. 设 p,q 是不同的素数,则M( pq) ( p 1)(q 1) 。(
)
11. n 是整数,如果 a2 { b2 (mod n) ,而 n 不整除 (a b) 和 (a b) ,则 n 为合数。( )
§ a2 · ¨ ¸1 12. 设 (a, p) 1,则 © p ¹ 。( )
13. 设整数 m>1, (a, m) 1,则整数 d 满足 ad { 1 (mod m) 的必要条件是 ordm(a) d 。( )
5. 求解 x2≡ 2 (mod 17)。
四、 证明题(25 分,5 分/小题,需写出证明过程)
1. 证明:形如 4k+1 和 4k-1 的素数都有无限个。
2. 证明:对素数 P, P 都是无理数。 3. 证明:设 P1 d P2 d P3 是素数,n 是正整数,若 P1P2P3|n ,则 P1 d n1/3 , P2 d(n/2)1/2 。
信息安全数学基础期末考试试卷及答案(A卷)

信息安全数学基础期末考试试卷及答案(A卷)信息安全数学基础期末考试试卷及答案(A卷)⼀、填空题(本⼤题共8⼩题,每空2分,共24分)1.两个整数a,b,其最⼤公因数和最⼩公倍数的关系为。
2.给定⼀个正整数m,两个整数a,b叫做模m同余,如果 ____________________________ ,记作a三b(modm);否则,叫做模m不同余,记作 ________________________ 。
3.设m,n是互素的两个正整数,则 ?(m n)= ______________________________ 。
e ..4.设m 1是整数,a是与m互素的正整数。
则使得a三1(modm)成⽴的最⼩正整数e叫做a对模m的指数,记做 ________________ 如果a对模m的指数是? (m),贝U a叫做模m的________________ 。
5.设n是⼀个奇合数,设整数b与n互素,如果整数n和b满⾜条件______________________ ,贝U n叫做对于基b的拟素数。
6.设G,G是两个群,f是G到G的⼀个映射。
如果对任意的a,b G,都有__________________ ,那么f叫做G到G'的⼀个同态。
7.加群Z的每个⼦群H都是 _______________________________ 群,并且有H M O A或H = _____________________ 。
8.我们称交换环R为⼀个域,如果R对于加法构成⼀个 ____________ ,戌=R\{0}对于乘法构成⼀个 ____________ 。
⼆、计算题(本⼤题共3⼩题,每⼩题8分,共24分)1.令a =1613, b =3589。
⽤⼴义欧⼏⾥德算法求整数s,t,使得sa tb ⼆(a,b)。
2.求同余⽅程x2三2(mod67)的解数。
3.计算3模19的指数。
叫⑶。
三、解同余⽅程(本⼤题共2⼩题,每⼩题10分,共20分)1.求解⼀次同余⽅程17x =14(mod 21)。
信息安全数学基础习题答案

因此70|n
2.证明:因为a3-a=(a-1)a(a+1)
当a=3k,k Z 3|a 则3|a3-a
当a=3k-1,k Z 3|a+1 则3|a3-a
当a=3k+1,k Z 3|a-1 则3|a3-a
所以a3-a能被3整除。
3.证明:任意奇整数可表示为2 k0+1, k0 Z
(2 k0+1)2=4 k02+4 k0+1=4 k0 (k0+1)+1
由于k0与k0+1为两连续整数,必有一个为偶数,所以k0 (k0+1)=2k
所以(a+b,4)=4
37.证明:反证法
假设n为素数,则n| a2- b2=(a+b)(a-b)
由1.4定理2知n|a+b或n|a-b,与已知条件矛盾
所以假设不成立,原结论正确,n为合数。
40.证明:(1)假设是21/2有理数,则存在正整数p,q,使得21/2=p/q,且(p, q)=1
=13*41-14*(161-3*41)
=-14*161+55*(363-2*161)
=55*363+(-124)*(1613-4*363)
=(-124)*1613+551*(3589-2*1613)
所以(2t+1,2t-1)=1
(2)解:2(n+1)=1*2n+2
2n=n*2
所以(2n,2(n+1))=2
32.(1)解:1=3-1*2
=3-1*(38-12*3)
=-38+13*(41-1*38)
信息安全数学基础参考试卷.doc

《信息安全数学基础》参考试卷一.选择题(在每小题的备选答案中只有一个正确答案,将正确答案序号填入下列叙述中的括号内,多选不给分):(每题2分,共20分)1.576的欧拉函数值(576) =()。
(1) 96,(2) 192,(3) 64,(4) 288。
2.整数kn和k(n+2)的最大公因数(kn , k(n+2))=()。
(1) 1或2,(2) kn ,(3) n 或kn ,(4) k 或2 k。
3.模10的一个简化剩余系是( )。
(1) 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,(2) 11, 17, 19 , 27(3) 11, 13, 17, 19,(4) 0, 1, 2, 3, 4, 5, 6, 7, 8, 9。
4.29模23的逆元是( )。
(1) 2,(2) 4,(3) 6,(4) 11。
5.设m1,m2是两个正整数,x1遍历模m1的完全剩余系,x2遍历模m2的完全剩余系,若( )遍历m1m2的完全剩余系。
(1) (m1,m2)=1,则m1x1+m2x2(2) m1和m2是素数,则m1x1+m2x2(3) (m1,m2)=1,则m2x1+m1x2(4) m1和m2是素数,则m2x1+m1x2 6.下面的集合和运算构成群的是( ) 。
(1) <N,+> (N是自然数集,“+”是加法运算)(2) <R,×> (R是实数集,“×”是乘法运算)(3) <Z,+> (Z是整数集,“+”是加法运算)(4) <P(A),∩> (P(A)={U | U是A的子集}是集合A的幂集,“∩”是集合的交运算)7.下列各组数对任意整数n均互素的是( ) 。
(1) 3n+2与2n,(2) n-1与n2+n+1,(3) 6n+2与7n,(4) 2n+1与4n+1。
8.一次同余式234x ≡30(mod 198)的解数是( )。
(1) 0,(2) 6,(3) 9,(4) 18。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信息安全数学基础期末考试试卷及答案(A 卷)
一、 填空题(本大题共8小题,每空2分,共24分)
1. 两个整数a ,b ,其最大公因数和最小公倍数的关系为 ________________。
2. 给定一个正整数m ,两个整数a ,b 叫做模m 同余,如果______________,记作(mod )a b m ≡;否则,叫做模m 不同余,记作_____________。
3. 设m ,n 是互素的两个正整数,则()mn ϕ=________________。
4. 设1m >是整数,a 是与m 互素的正整数。
则使得1(mod )e
a m ≡成立的最小正
整数e 叫做a 对模m 的指数,记做__________。
如果a 对模m 的指数是()m ϕ,则a 叫做模m 的____________。
5. 设n 是一个奇合数,设整数b 与n 互素,如果整数n 和b 满足条件
________________,则n 叫做对于基b 的拟素数。
6. 设,G G '是两个群,f 是G 到G '的一个映射。
如果对任意的,a b G ∈,都有
_______________,那么f 叫做G 到G '的一个同态。
7. 加群Z 的每个子群H 都是________群,并且有0H =<>或
H =______________。
8. 我们称交换环R 为一个域,如果R 对于加法构成一个______群,*
\{0}R R =对
于乘法构成一个_______群。
二、计算题(本大题共 3小题,每小题8分,共24分)
1. 令1613,a = 3589b =。
用广义欧几里德算法求整数,s t ,使得
(,)sa tb a b +=。
2. 求同余方程2
2(mod 67)x ≡-的解数。
3. 计算3模19的指数19ord (3)。
三、解同余方程(本大题共2小题,每小题10分,共20分)
1. 求解一次同余方程1714(mod 21)x ≡。
2. 解同余方程组2(mod 3)3(mod 5)2(mod 7)x x x ≡≡≡⎧⎪
⎨⎪⎩
四、证明题(本大题共3小题,每小题7分,共21分)
1. 证明:如果a 是整数,则3
a a -能够被6整除。
2. f 是群G 到G '的一个同态,{}ker |,()f a a G f a e '=∈=,其中e '是G '的单位元。
证明:ker f 是G 的正规子群。
3. 证明:如果p 和q 是不同的素数,则1
11(mod )q p p q pq --+=。
五、应用题(共11分)RSA公钥加密算法的密钥生成步骤如下:选择
两个大的素数p和q,计算n=pq。
选择两个正整数e和d,满足:
)。
Bob的公钥是(n,e),对外公布。
Bob的私钥是d,自己私藏。
如果攻ed=1(mod()n
击者分解n得到p=47,q=23,并且已知e=257,试求出Bob的私钥d。
答案
一、填空题(每空2分,共24分)
1. 两个整数a ,b ,其最大公因数和最小公倍数的关系为[,](,)ab a b a b =。
2. 给定一个正整数m ,两个整数a ,b 叫做模m 同余,如果|m a b -,记作
(mod )a b m ≡;否则,叫做模m 不同余,记作a ≡(mod )b m 。
3. 设m ,n 是互素的两个正整数,则()mn ϕ=()()m n ϕϕ。
4. 设1m >是整数,a 是与m 互素的正整数。
则使得1(mod )e
a m ≡成立的最小正整数e 叫
做a 对模m 的指数,记做()m ord a 。
如果a 对模m 的指数是()m ϕ,则a 叫做模
m 的 原根 。
5. 设n 是一个奇合数,设整数b 与n 互素,如果整数n 和b 满足条件1
1(mod )n b n -≡,则
n 叫做对于基b 的拟素数。
6. 设,G G '是两个群,f 是G 到G '的一个映射。
如果对任意的,a b G ∈,都有
()()()f ab f a f b =,那么f 叫做G 到G '的一个同态。
7. 加群Z 的每个子群H 都是 循环 群,并且有0H =<>或H =()m mZ <>=或。
8. 我们称交换环R 为一个域,如果R 对于加法构成一个 交换 群,*
\{0}R R =对于乘法
构成一个 交换 群。
二、计算题(每题8分,共24分)
1. 解: 3589=2*1613+363
1613=4*363+161 363=2*161+41 161=3*41+38 41=1*38+3 38=12*3+2 3=1*2+1 2=2*1 (a,b)=1,从而 1=3-1*2
=3-1*(38-12*3) =-38+13*(41-1*38) =13*41-14*(161-3*41)
=-14*161+55*(363-2*161) =55*363+(-124)*(1613-4*363) =(-124)*1613+551*(3589-2*1613) =551*3589+(-1226)*1613 所以s=-1226 t=551
2. 解:因为(-2/67)=(65/67) =(13/67)(5/67)
=(-1)12*66/4(-1)4*66/4
(2/13)(2/5)
=1*1*(-1)(13*13-1)/8(-1)(5*5-1)/8
=-1*(-1)=1 所以-2是67的平方剩余
所以x 2
≡-2(mod67)有2个解。
3. 解:因为ϕ(19)=18,所以只需对18的因数d=1,2,3,6,9,18计算a d
(mod19) 因为31
≡3, 32
≡9, 33
≡8, 36
≡7, 39
≡-1, 218
≡1(mod19) 所以3模19的指数为18;
三、解同余方程(每题10分,共20分)
1. 解:因为(17,21)=1 | 14 故原同余式有解。
又17x ≡1(mod21,所以 特解x 0'≡5(mod21)。
同余式17x ≡14(mod21)的一个特解为x 0≡14*x 0'=14*5≡7(mod21) 所有解为:x ≡7(mod21)
2. 解:令1233,5,7m m m ===, 3*5*7105m ==,
1235*735,3*721,3*515M M M ======。
分别求解同余式1(mod )i i i M M m '≡(i =1,2,3)
得到12M '=,2
1M '=,31M '=。
故同余式的解为 112
233*2*3*2(mod105)2*35*21*21*31*15*2(mod105)23(mod105)
x M M M M M M '''≡++≡++≡
四、证明题(每题7分,共21分)
1. 证明:因为a 3
-a =(a-1)a(a+1)
当a=3k ,k ∈Z 3|a 则3|a 3
-a
当a=3k-1,k ∈Z 3|a+1 则3|a 3
-a
当a=3k+1,k ∈Z 3|a-1 则3|a 3
-a
所以a 3
-a 能被3整除。
又因为(a-1),a ,(a+1)是3个连续的整数,所以至少有一个是偶数,
从而 2|a 3-a 。
因此,a 3
-a 能够被6整除。
2. 证明:因为(p,q)=1 p,q 都为素数 所以ϕ(p)=p-1, ϕ(q)=q-1
由Euler 定理知:p
ϕ(q)≡1(modq) q ϕ(p)≡1(modp)
即p q-1
≡1(modq) q p-1
≡1(modp)
又 q p-1≡0(modq) p q-1
≡0(modp)
所以p q-1+q p-1≡1(modq) q p-1+p q-1
≡1(modp)
又[p,q]=pq 所以p q-1+q p-1
≡1(modpq)
3. 证明:对任意,ker a b f ∈,有(),()f a e f b e ''==,从而,
1111()()()()()()()f ab f a f b f a f b f a f a e ----'====。
因此,ker
b f
∈,ker f 是群G 的子群。
对任意a G ∈,ker b f ∈,我们有
1111()()()()()()()()f aba f a f b f a f a ef a f a f a e ----'====。
这说明1
ker aba f -∈。
从而,ker f 是群G 的正规子群。
五 (11分) 解:
p=47,q=23,n=pq=1081.所以,
()(4723)(47)(23)46221012n ϕϕϕϕ=⨯==⨯=。
要求Bob 的私钥d ,即解同余式257d=1(mod 1012). 利用欧几里得算法解得该同余式的解为949。
故Bob 的私钥是d=949.。
