多项式的加减全章知识点总结

合集下载

初中数学人教七年级上册第二章整式的加减-多项式

个足球需要z元，买3个篮球、5个排球、2个足球共
需要 (3x+5y+2z)元.
探究新知
3.如图三角尺的面积
为
( 1 ab πr2 ) 2
.
a
r
b
4.如图是一所住宅区的建筑平面图，这所住宅的建筑面积是(x2+2x+18) m2.
x米 2米 x米
x米
4米 3米
3米 2米
探究新知
探究下列各式是单项式吗？这些式子有什么共同特点？：与单项式有什么关系？
2.多项式
是关于a、b的四次三项
式，且最高次项的系数为－2，则x =__-_5_，
y =__3__.
探究新知
素养考点 1 多项式有关概念的识别
例1 下列整式中哪些是多项式？是多项式的指出其项和次
数：
－ 1 a2b, m4n2 , x2 y2 1, x, 32t 3 , ,
2
7
3
3x2－y＋3xy3 x4 1, 2x y.
4. 多项式里次数最高项的次数就是多项式的次数.
次数
项常数项
例如 3x3 5x 8
：
叫做三次三项式
5. 单项式与多项式统称为整式.
巩固练习
连接中考
1. 当x=﹣1时，代数式3x+1的值是( B )
A．﹣1
B．﹣2
C．4Biblioteka D．﹣4解析：把x=﹣1代入代数式中，得 3x+1=﹣3+1=﹣2．
课堂检测
（3）-x-y-z是三次三项式．（ × ）是一次三项式
课堂检测
基础巩固题
3. 一个关于字母x的二次三项式的二次项系数为4 ，一次项系数为1，常数项为7，则这个二次三项式为＿4x＿2+x＿+＿7 ＿．

2024年秋新人教版七年级上册数学课件第四章整式的加减 4.1整式(第2课时)多项式

第2课时多项式
重点
1.理解多项式、整式的概念；难点
2.会确定一个多项式的项数和次数.
1.什么叫单项式？
3ab2c
2.-
的系数、次数分别是多少？
7
观察下面的式子有什么特点？ v+2.5，v-2.5，3x+5y+2z，x2 +2x+18.
v-2.5可以看作单项式v与-2.5的和
上述几个式子都是两个或者多个单项式相加的形式.
（4）一个多项式的最高次项可以不唯一.
知识点2 整式
1.定义：单项式与多项式统称整式． 2.特别解读 (1)单项式是整式； (2)多项式是整式； (3)如果一个式子既不是单项式又不是多项式，那么它
一定不是整式．
例
用多项式填空，并指出它们的项和次数.
（1）一个长方形相邻两条边的长分别为a,b，则这个长方形的周长
பைடு நூலகம்
单项式整式
多项式
系数：数字因数
次数：所有字母的指数的和项：多项式中的每个单项式.
（其中不含字母的项叫作常数项）次数：多项式中次数最高的项的次数.
同学们，通过这节课的学习，你有什么收获呢？
谢谢大家
爱心.诚心.细心.耐心，让家长放心.孩子安心。
A．3，2，1
B．－3，2，0
C．－3，2，1
D．3，2，0
2.如果多项式xn－2－5x＋2是关于x的三次三项式，那么n等于( C ) A．3 B．4 C．5 D．6
小结
（1）多项式的各项应包括它前面的符号；（2）多项式没有系数的概念，但其每一项均有系数，每一项的系数也包括前面的符号；
（3）要确定一个多项式的次数，先要确定此多项式中各项(单项式)的次数，然后找次数最高的；

辅导作业知识点总结

一、数学知识点总结1. 数学基础知识- 整数运算- 分数运算- 小数运算- 百分数运算- 正数、负数的性质和运算规律2. 代数知识- 一次函数及其应用- 二次函数及其应用- 多项式的加减乘除- 平方根与实数- 方程与不等式3. 几何知识- 几何图形的基本属性- 直线、角度的性质- 圆的基本性质- 四边形、三角形的性质- 相似三角形和全等三角形4. 概率与统计- 事件发生的概率- 概率统计- 中心倾向和离散度- 随机事件的分布规律1. 词语辨析- 近义词、反义词的区分- 成语、俗语的运用- 诗歌、文章中的比喻、拟人、夸张等修辞手法2. 作文写作- 议论文、说明文、记叙文的写作技巧- 写作结构、段落的衔接- 表达思想观点的方法3. 阅读理解- 阅读文章的主旨、要点- 文章的中心思想- 文学作品的分析与理解4. 古诗文词- 古文阅读与欣赏- 古诗词的鉴赏与吟诵- 古代文学作品的传统与现代意义三、英语知识点总结1. 语法知识- 时态、语态的使用- 名词、代词、形容词的用法- 动词的时态和语态- 副词、介词、连词的用法2. 句型转换- 否定句、疑问句的转换- 虚拟语气、感叹句的运用3. 阅读理解- 阅读文章的主旨、要点- 阅读文章的语境理解- 阅读文章的信息获取和推断4. 写作技巧- 书面表达的结构和语言- 表达思想观点的方法- 文章主题思想的扩展和丰富四、物理知识点总结1. 机械知识- 运动的描述和分析- 力和压力的概念- 力的合成和分解- 运动、力和功的关系2. 热学知识- 温度与热量的概念- 物态变化与热力学- 热传递与热工作3. 光学知识- 光的传播和成像- 光的反射和折射- 光的波动性和粒子性4. 电学知识- 电流、电阻与电压的关系- 电路的基本原理与应用五、化学知识点总结1. 化学元素- 元素的基本性质- 元素的分类与周期律- 元素的化合规律2. 化学反应- 化学反应的基本特征- 化学方程式的写法和平衡- 化学反应的速率与平衡3. 物质状态- 物质的固态、液态、气态- 溶液、浓度和溶解度- 混合物的分离4. 化学能- 化学能的储存和转化- 火焰、发酵等化学能的应用- 化学能与生活、环境的关系六、生物知识点总结1. 生物基本概念- 细胞的结构和功能- 组织器官的结构和功能- 生物体、生物群落的组成和结构2.- 遗传物质的结构和作用- 遗传规律的探究和应用- 基因重组技术和生物工程应用3. 生物进化- 进化论的基本观点- 生物多样性的维护和利用- 生物进化与环境适应4. 生物生态- 生物与环境的相互关系- 生态系统的组成和特点- 生态平衡、生态环境保护以上是辅导作业常见的知识点总结，通过掌握这些知识点，可以更好地完成各科目的作业和考试。

代数运算知识点总结

代数运算知识点总结一、基本运算1.加法在代数中，加法是指将两个数或多个数相加得到一个和的运算。

在代数中，通常用符号“+”表示加法，例如：a + b。

当多个数相加时，可以用括号将它们括起来，例如：(a + b) + c。

加法的性质：（1）交换律：a + b = b + a（2）结合律：(a + b) + c = a + (b + c)（3）加法恒元：a + 0 = a（4）加法逆元：a + (-a) = 02.减法在代数中，减法是指将一个数减去另一个数得到一个差的运算。

在代数中，通常用符号“-”表示减法，例如：a - b。

减法的性质：减法没有交换律和结合律。

例如：a - b ≠ b - a（a - b）- c ≠ a - （b - c）3.乘法在代数中，乘法是指将两个数或多个数相乘得到一个积的运算。

在代数中，通常用符号“*”表示乘法，例如：a * b。

当多个数相乘时，可以用括号将它们括起来，例如：(a * b) * c。

乘法的性质：（1）交换律：a * b = b * a（2）结合律：(a * b) * c = a * (b * c)（3）分配律：a * (b + c) = a * b + a * c（4）乘法恒元：a * 1 = a（5）乘法逆元：a * （1/a) = 14.除法在代数中，除法是指将一个数除以另一个数得到一个商的运算。

在代数中，通常用符号“/”表示除法，例如：a / b。

除法的性质：除法没有交换律和结合律。

例如：a / b ≠ b / a（a / b）/ c ≠ a / （b / c）5.指数运算在代数中，指数运算是指将一个数称为底数，另一个数称为指数，得到一个乘积的运算。

在代数中，通常用符号“^”表示指数运算，例如：a^b。

指数运算的性质：（1）指数相加：a^m * a^n = a^(m+n)（2）指数相减：a^m / a^n = a^(m-n)（3）指数相乘：(a^m)^n = a^(m*n)二、多项式运算1.多项式的加减法多项式是由一系列项组合而成的代数表达式。

七年级下数学(重要知识点总结)

七年级数学（下）重要知识点总结第一章：整式的运算一、概念1、代数式：2、单项式:由数字与字母的乘积的代数式叫做单项式。

单项式不含加减运算，分母中不含字母。

3、多项式:几个单项式的和叫做多项式。

多项式含加减运算。

4、整式:单项式和多项式统称为整式。

二、公式、法则：（1）同底数幂的乘法：a m ﹒a n =a m+n （同底，幂乘，指加）逆用： a m+n =a m ﹒a n （指加，幂乘，同底）（2）同底数幂的除法：a m ÷a n =a m-n （a ≠0）。

（同底，幂除，指减）逆用：a m-n = a m ÷a n （a ≠0）（指减，幂除，同底）（3）幂的乘方：（a m ）n =a mn （底数不变，指数相乘）逆用：a mn =（a m ）n（4）积的乘方：（ab ）n =a n b n 推广：逆用， a n b n =（ab ）n （当ab=1或-1时常逆用）（5）零指数幂：a 0=1（注意考底数范围a ≠0）。

（6）负指数幂：11()(0)p p p a a a a -==≠(底倒，指反)（7）单项式与多项式相乘：m(a+b+c)=ma+mb+mc 。

（8）多项式与多项式相乘：(m+n)(a+b)=ma+mb+na+nb 。

（9）平方差公式：（a+b ）(a-b)=a 2-b 2 公式特点：（有一项完全相同，另一项只有符号不同，结果=22()-相同）（不同推广（项数变化）：连用变化：（10）完全平方公式： 222222()2,()2,a b a ab b a b a ab b +=++-=-+逆用：2222222(),2().a ab b a b a ab b a b ++=+-+=-完全平方公式变形（知二求一）：完全平方和公式中间项=完全平方差公式中间项=完全平方公式中间项=例如：229x +mxy+4y 是一个完全平方和公式，则m = ；是一个完全平方差公式，则m = ；是一个完全平方公式，则m = ；（11）多项式除以单项式的法则:().a b c m a m b m c m ++÷=÷+÷+÷（12）常用变形：221((n n x y x y +--2n 2n+1）=(y-x), ）=-(y-x)第二章平行线与相交线一、余角与补角1、如果两个角的和是直角，那么称这两个角互为余角，简称为互余，称其中一个角是另一个角的余角。

多项式的加减乘除四则运算

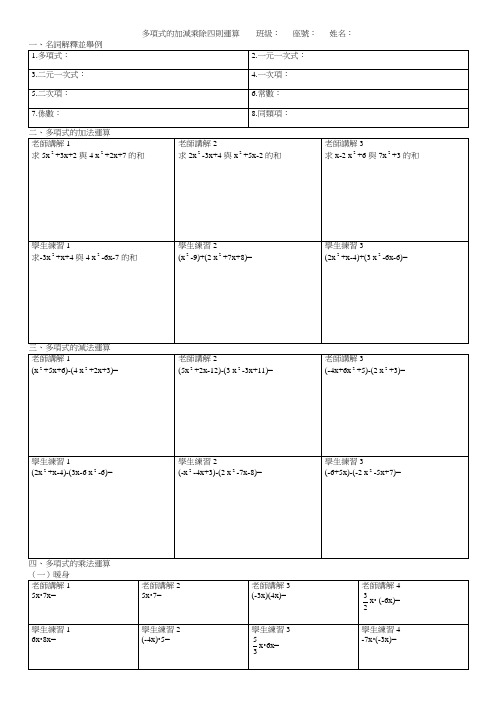
多項式的加減乘除四則運算班級：座號：姓名：
五、多項式的除法運算
四、十字交乘法(三項式) 班級：座號：姓名：
2
2. x2項的係數「不是1」的十字交乘法
二、完全平方數：背1~20的平方
三、平方根的定義
四、利用方格紙畫圖，作出面積是2 平方單位、5 平方單位、18平方單位的正方形-----介紹無理數
五、非完全平方數的平方根：根號引入的必須
六、利用方格紙畫圖，作出1、2、3、4、5、……. 、n
七、正數、零、負數的平方根
（一）正數：
（二）零：
（三）負數：
八、利用標準分解式計算平方根
九、十分逼近法：求無理數的近似值
十、電算器求平方根
一元二次方程式班級：座號：姓名：
5. a x2+bx+c=0，a和b 和c是常數（、十字交乘法）
6. 綜合題
7. 應用問題。

七年级上册数学多项式知识点总结

七年级上册数学多项式知识点总结一、什么是多项式？多项式指的是一种形式为幂次函数之和的函数，即由单项式相加或相减而成的代数式。

例如：$ax^2 + bx + c$就是一个二次多项式。

二、多项式的基本操作1.加减法将同类项合并，即系数相加减外，变量的指数要保持不变。

例如：$2x^2+3x+1+(3x^2-2x)+4x^2-3x=x^2+4x+1$2.乘法将多项式的各项按照升幂排列，分别乘以另一个多项式的各项，生成新的多项式。

最后再将各项合并，即同类项系数相加减。

例如：$(2x+1)(3x+4)=6x^2+14x+4$3.除法求多项式的商和余数，方法是用除数的首项除被除数的首项，得到商的首项，再将商的首项乘以除数，与被除数的前几项相减，得到余数的前几项。

例如：$5x^3+3x^2+2x+1 \div x + 2=5x^2+x-2 \cdots{1}$3x^2+x-2________________x+2 |5x^3+3x^2+2x+1-x^3-2x^2_______________3x^2+2x-3x^2-6x___________8x+1-8x-16________17所以，原式$=5x^2+x-2+\dfrac{17}{x+2}$三、多项式的值及根1. 多项式的值多项式的值是指将指定的数值代入多项式中求得的结果。

例如，$f(x)=2x^2+3x+1$，当$x=2$时，$f(2)=2\times2^2+3\times2+1=15$。

2. 多项式的根多项式的根指的是将多项式中的变量$x$换成某个数值后，使得原来的多项式的值等于0的数值，称为多项式的根或零点。

例如，$f(x)=2x^2+3x+1$，当$x=-1$ 或 $-0.5$ 时，$f(x)=0$。

四、多项式的因式分解多项式的因式分解是一种将多项式分解成多个单项式相乘的运算。

例如：$6x^2+3x=3x(2x+1)$$2x^3-4x^2+4x-8=2(x-2)(x^2+x+2)$$2x^2-2xy-4y^2=2(x-\sqrt{2}y)(x+\sqrt{2}y)$五、多项式的最高公因式和最低公倍数1.最高公因式多项式的最高公因式是指多个多项式拥有的公共因式中，次数最大的因式。

整式的加减全章(经典例题)

整式的加减【要点梳理】要点一、整式的相关概念1．单项式：由数或字母的积组成的代数式叫做单项式，单独的一个数或一个字母也是单项式．要点诠释：（1）单项式的系数是指单项式中的数字因数．（2）单项式的次数是指单项式中所有字母的指数和．2．多项式：几个单项式的和叫做多项式．在多项式中，每个单项式叫做多项式的项．要点诠释：（1）在多项式中，不含字母的项叫做常数项．（2）多项式中次数最高的项的次数，就是这个多项式的次数．。

（3）多项式的次数是n次，有m个单项式，我们就把这个多项式称为n次m项式．3. 多项式的降幂与升幂排列：把一个多项式按某一个字母的指数从大到小的顺序排列起来，叫做把这个多项式按这个字母降幂排列．另外，把一个多项式按某一个字母的指数从小到大的顺序排列起来，叫做把这个多项式按这个字母升幂排列．要点诠释：（1）利用加法交换律重新排列时，各项应连同它的符号一起移动位置；（2）含有多个字母时，只按给定的字母进行降幂或升幂排列．4．整式：单项式和多项式统称为整式．要点二、整式的加减1．同类项：所含字母相同，并且相同字母的指数也相同的项叫做同类项．所有的常数项都是同类项．要点诠释：辨别同类项要把准“两相同，两无关”：（1）“两相同”是指：①所含字母相同；②相同字母的指数相同；'（2）“两无关”是指：①与系数无关；②与字母的排列顺序无关．2．合并同类项：把多项式中的同类项合并成一项，叫做合并同类项．要点诠释：合并同类项时，只是系数相加减，所得结果作为系数，字母及字母的指数保持不变．3．去括号法则：括号前面是“+”，把括号和它前面的“+”去掉后，原括号里各项的符号都不改变；括号前面是“-”，把括号和它前面的“-”号去掉后，原括号里各项的符号都要改变．4．添括号法则：添括号后，括号前面是“+”，括号内各项的符号都不改变；添括号后，括号前面是“-”，括号内各项的符号都要改变．5．整式的加减运算法则：几个整式相加减，通常用括号把每一个整式括起来，再用加、减号连接，然后去括号，合并同类项．【典型例题】类型一、整式的相关概念>1．指出下列各式中哪些是单项式哪些是多项式哪些是整式，，，10，，，，，，（举一反三：【变式】指出下列代数式中的单项式，并写出各单项式的系数和次数．，，，，，a-3，，，2．（2016春•新泰市期中）下列说法正确的是（）22x y +x -3a b +61xy +1x 217m n 225x x --22x x +7a 234a b -a -442x a mn 223a y π5-382-310tm ⨯2x yA ．1﹣xy 是单项式B ．ab 没有系数#C ．﹣5是一次一项式D ．﹣a 2b+ab ﹣abc 2是四次三项式举一反三：【变式1】（2014•佛山）多项式2a 2b ﹣ab 2﹣ab 的项数及次数分别是（）A ．3，3B ．3，2C ．2，3D ．2，2【变式2】若多项式31(4)5(2)n m x x x n m -++---+是关于x 的二次三项式，则________m =，________n =，这个二次三项式为 ."3. 已知多项式． (1)求多项式各项的系数和次数．(2)如果多项式是七次五项式，求m 的值．32312246753m x xy x y y x y ---+--举一反三：:【变式】多项式是关于的二次三项式，求a 与b 的差的相反数．类型二、同类项及合并同类项4.判别下列各题中的两个项是不是同类项：(1)-4a 2b 3与5b 3a 2；(2)与；(3)-8和0；(4)-6a 2b 3c 与8ca 2． ·()34b a x x x b --+-x 2213x y z -2213xy z -5．（2016•邯山区一模）如果单项式5mx a y 与﹣5nx 2a ﹣3y 是关于x 、y 的单项式，且它们是同类项．求（1）（7a ﹣22）2013的值；（2）若5mx a y ﹣5nx 2a ﹣3y=0，且xy ≠0，求（5m ﹣5n ）2014的值．《举一反三：【变式1】（2015•石城县模拟）如果单项式﹣x a+1y 3与x 2y b 是同类项，那么a 、b 的值分别为（）A. a=2，b=3B. a=1，b=2C. a=1，b=3D. a=2，b=2;【变式2】若315212135m n m n x y x y --+-与是同类项，求出m, n 的值，并把这两个单项式相加.6．合并同类项：}；；;【()221324325x x x x -++--()2222265256a b ab b a -++-()2223542625yx xy xy x y xy -+-+++举一反三：【变式1】化简：（1）（2） (a-2b)2+(2b-a)-2(2b-a)2+4(a-2b)？．类型三、去（添）括号7.（2015•模拟）化简m ﹣n ﹣（m+n ）化简2211()22x x x x ⎡⎤--+⎢⎥⎣⎦．?举一反三：【变式1】下列去括号正确的是( )． 32313125433xy x y xy x ---+A．2222--+=--+(2)2a ab b a a b bB．2222(2)()2-+--+=-++-x y x y x y x yC．22x x x x--=-+23(5)235D．3232---+-=-++-[4(13)]431a a a a a a#【变式2】(1) (x＋y)2－10x－10y＋25＝(x＋y)2－10(______)＋25;(2) (a－b＋c－d)(a＋b－c－d)＝[(a－d)＋(______)][(a－d)－(______)]．类型五、化简求值8.（2016春•盐城校级月考）先化简，再求值：3x2y﹣[2x2﹣（xy2﹣3x2y）﹣4xy2]，其中|x|=2，y=，且xy＜0．】举一反三：【变式1】当时，求多项式的值．）【变式2】若，求多项式的值．;1,2a b ==-3232399111552424ab a b ab a b ab a b --+---243(32)0a b b +++=222(23)3(23)8(23)7(23)a b a b a b a b +-+++-+【变式3】.】类型六、综合应用9. 对于任意有理数x ，比较多项式2452x x -+与2352x x --的值的大小．#举一反三：3422323323622已知与是同类项，求代数式的值a b x y xy b a b b a b +----+）【变式】设22232A x xy y x y =-+-+, 224623B x xy y x y =-++-. 若22(3)0x a y -++=且2B A a -=，求a .、【巩固练习】一、选择题1．A 、B 、C 、D 均为单项式，则A+B+C+D 为( )．A ．单项式B ．多项式C ．单项式或多项式D ．以上都不对2．下列计算正确的个数（）① ab b a 523=+；② 32522=-y y ； ③ y x x y y x 22254=-；④ 532523x x x =+； ⑤ xy xy xy =+-33]A ．2B ．1C ．4D ．03．现规定一种运算：a * b ＝ ab + a - b ，其中a ，b 为有理数，则3 * 5的值为( )．A ．11B ．12C ．13D ．144．（2016春•钦州期末）﹣[x ﹣（y ﹣z ）]去括号后应得（）A ．﹣x+y ﹣zB ．﹣x ﹣y+zC ．﹣x ﹣y ﹣zD ．﹣x+y+z5．已知a-b ＝-3，c+d ＝2，则(b+c)-(a-d)为( )．A ．-1B ．-5C ．5D ．16. 有理数a ，b ，c 在数轴上的位置如右图所示，则a c c b b a ++--+= （）A ．－2bB ．0C ．2cD ．2c －2b{7．（2015•临沂）观察下列关于x 的单项式，探究其规律：x ，3x 2，5x 3，7x 4，9x 5，11x 6，…按照上述规律，第2015个单项式是（）A ．2015x 2015B ．4029x 2014C ．4029x 2015D ． 4031x 20158．如果32(1)n m a a --++是关于a 的二次三项式，那么m ，n 应满足的条件是( )．A ．m ＝1，n ＝5B ．m ≠1，n ＞3C ．m ≠-1，n 为大于3的整数D ．m ≠-1，n ＝5二、填空题9．（2015•大丰市一模）若﹣2a m b 4与5a 2b n+7是同类项，则m+n= ．10．（1）-=+-222x y xy x （___________）；（2）2a －3（b －c ）＝___________．（3）2561x x -+-(________)＝7x+8．11．当b ＝________时，式子2a+ab-5的值与a 无关．12．若45a b c -+=，则30()b a c --=________．三、解答题14.已知关于x 的整式（k 2－9）x 3＋（k-3）x 2－k①若是二次式，求k 2＋2k ＋1的值 ②若是二项式，求k 的值15.（2015•宝应县校级模拟）先化简，再求值：（﹣4x2+2x﹣8y）﹣（﹣x﹣2y），其中x=，y=2012．)。

知识点整式的加减

知识点整式的加减（一）单项式1、单项式：像mn，a2b，10%a这样的代数式，它们都是由数与字母（或字母与字母）相乘组成的代数式，我们把这样的代数式叫做单项式。

注：单独一个数或一个字母也叫单项式。

如：5和a也叫单项式。

2、单项式中的数字因数叫做这个单项式的系数，所有字母的指数的和叫做这个单项式的次数。

如：单项式mn的系数是1，次数是2；a2b的系数是1，次数是3；10%a的系数是10%，次数是1。

注：单项式的系数是1或-1时，“1”通常省略不写；常数的次数为0。

如：-a的系数为-1；5的系数为5，次数为0。

（二）多项式b这样的代数式，它们都是由单项式相加组成的代数1、多项式：像10y+10x，10y+x，a2−14式，我们把这样的代数式叫做多项式。

2、多项式是由若干个单项式的和组成的。

我们把多项式中的每一个单项式都叫做这个多项式的项，把不含字母的项叫做常数项。

3、多项式含有几项，这个多项式就叫做几项式。

4、在多项式里，最高次项的次数，叫做这个多项式的次数。

多项式的次数式几，这个多项式就叫做几次式。

b是二次二项式，最高次项为a2。

如：多项式10y+10x和10y+x是一次二项式，a2−14注：写多项式的各项时要注意不要忘带负号。

如：−2x+x3−3的次数是三次，项数是三项，是三次三项式，各项分别为−2x、x3、−3，其中最高次项是x3，常数项是−3。

5、单项式和多项式统称为整式。

（三）合并同类项1、同类项：在多项式中，我们把那些所含的字母相同，并且相同字母的指数也相同的项，叫做同类项。

注：几个常数项也叫同类项。

2、在多项式中，几个同类项可以合并成一项，这个合并的过程，叫做合并同类项。

3、在合并同类项时，把同类项的系数相加，字母和字母的指数保持不变。

注：当同类项的系数互为相反数时，合并后的结果为0。

（四）去括号法则1、括号前是“+”时，把括号和它前面的“+”去掉，原括号里的各项都不改变符号。

2、括号前是“-”时，把括号和它前面的“-”去掉，原括号里的各项都改变符号。

第二章整式的加减全章知识点总结精选全文

可编辑修改精选全文完整版第二章整式的加减知识点1、单项式的概念式子x 3,m t xy a ---,6.2,,32它们都是数或字母的积，象这样的式子叫做单项式，单独的一个数或一个字母也是单项式。

注意：单项式是一种特殊的式子，它包含一种运算、三种类型。

一种运算是指数与字母、字母与字母之间只能是乘法的一种运算，不能有加、减、除等运算符号；三种类型是指：一是数字与字母相乘组成的式子，如ab 2;二是字母与字母组成的式子，如3xy ;三是单独的一个数或字母，如m a ,2-，。

知识点2、单项式的系数单项式中的数字因数叫做这个单项式的系数。

注意：（1）单项式的系数可以是整数，也可能是分数或小数。

如42x 的系数是2；3ab 的系数是31，2.7m 的系数是2.7。

（2）单项式的系数有正有负，确定一个单项式的系数，要注意包含在它前面的符号，如－()xy 2的系数是－2. （3）对于只含有字母因素的单项式，其系数是1或－1，不能认为是0，如－2xy 的系数是－1；2xy 的系数是1。

（4）表示圆周率的π，在数学中是一个固定的常数，当它出现在单项式中时，应将其作为系数的一部分，而不能当成字母。

如2πxy 的系数就是2π. 知识点3、单项式的次数一个单项式中，所有字母的指数和叫做这个单项式的次数。

注意：（1）计算单项式的次数时，应注意是所有字母的指数和，不要漏掉字母指数是1的情况。

如单项式z y x 342的次数是字母z y x ,,的指数和，即4＋3＋1=8，而不是7次，应注意字母Z 的指数是1而不是0.。

（2）单项式是一个单独字母时，它的指数是1，如单项式m 的指数是1，单项式是单独的一个常数时，一般不讨论它的次数。

（3）单项式的指数只和字母的指数有关，与系数的指数无关。

如单项式－43242z y x 的次数是字母z y x ,,的指数和，即2＋3＋4=9而不是13次（4）单项式通常根据字母的次数进行命名。

数学公式知识：多项式的加减乘除及其因式分解

数学公式知识：多項式的加减乘除及其因式分解多项式是数学上重要的一类函数形式，由多项式的系数和次数组成。

其中，系数可以是实数、复数或其他某些域中的元素，而次数通常是自然数。

在代数学中，多项式的加减乘除以及因式分解都是非常重要的知识点。

一、多项式的加减多项式的加减是指将两个或多个多项式相加或相减的过程。

同样次数的项可以直接相加和相减，而不同次数的项需要进行配对后再进行运算。

例如，将多项式f(x) = 3x^2 + 5x + 2和g(x) = 2x^2 +3x +1相加，则有：f(x) + g(x) = (3x^2 + 5x + 2) + (2x^2 + 3x + 1)= 5x^2 + 8x + 3将这两个多项式相加后，得到的结果多项式的最高次数为2，其系数为5。

因此，图中的结果多项式可以简化为5x^2 + 8x + 3。

同样的，两个多项式进行减法的步骤也类似，例如，将多项式f(x) = 4x^3 + 2x^2 + 3x - 1和g(x) = 2x^3 - x^2 - 4x + 2相减，则有：f(x) - g(x) = (4x^3 + 2x^2 + 3x - 1) - (2x^3 - x^2 - 4x + 2)= 2x^3 + 3x^2 + 7x - 3通过以上的计算表明，多项式的加减法不难掌握，只需要注意相同次数项的加减运算与不同次数的项配对就可以。

二、多项式的乘法多项式的乘法是指将两个或多个多项式进行相乘的运算。

怎么相乘？这里我给出一个例子：将多项式f(x) = 3x^2 + 2x + 1和g(x) = x + 2相乘，则有：f(x) × g(x) = （3x^2 + 2x + 1)×(x + 2)= 3x^3 + 8x^2 + 7x + 2通过以上计算表明，多项式的乘法是将两个多项式的单项式逐一进行相乘，并将值相加得到的新多项式。

在这个过程中，需要注意每一个项中的系数和指数和进行相乘。

多项式的加减运算

多项式的加减运算多项式是学习数学中的重要概念之一，它在代数学和数值分析等领域中应用广泛。

在这篇文章中，我们将重点讨论多项式的加减运算，探究其规则和方法。

一、多项式的定义和表示形式在开始讨论多项式的加减运算之前，我们先来回顾一下多项式的定义和表示形式。

一个多项式包含若干项的代数和，每一项都由系数与指数的乘积组成。

一般表示为：P(x) = anxn + an-1xn-1 + ... + a2x2 + a1x + a0其中，P(x)表示多项式，ai表示系数，xi表示未知数，n表示多项式的次数。

二、多项式的加法运算多项式的加法运算是指将两个多项式相加，合并相同次数的项，对应系数相加的过程。

具体步骤如下：1. 对应次数的项进行系数相加。

2. 如果某个多项式中没有与另一个多项式对应次数的项，则保留原有的项。

3. 最后化简得到新的多项式。

例如，考虑以下两个多项式的加法运算：P(x) = 2x3 - 5x2 + 3x + 1Q(x) = -3x3 + 4x - 2按照上述步骤进行计算，我们可以得到它们的相加结果为：P(x) + Q(x) = -1x3 - 5x2 + 7x - 1三、多项式的减法运算多项式的减法运算是指将一个多项式减去另一个多项式，合并相同次数的项，对应系数相减的过程。

具体步骤如下：1. 对应次数的项进行系数相减。

2. 如果某个多项式中没有与另一个多项式对应次数的项，则保留原有的项。

3. 最后化简得到新的多项式。

举个例子，考虑以下两个多项式的减法运算：P(x) = 2x3 - 5x2 + 3x + 1Q(x) = -3x3 + 4x - 2按照上述步骤进行计算，我们可以得到它们的相减结果为：P(x) - Q(x) = 5x3 - 5x2 - 1x + 3四、多项式的加减混合运算在实际问题中，我们常常会遇到多项式的加减混合运算。

这时，我们需要按照以下步骤进行计算：1. 先进行多项式的加法运算。

2. 再进行多项式的减法运算。

《高等代数》第一章多项式

§1 数域关于数的加、减、乘、除等运算的性质通常称为数的代数性质.代数所研究的问题主要涉及数的代数性质，这方面的大部分性质是有理数、实数、复数的全体所共有的.定义1 设P 是由一些复数组成的集合，其中包括0与1.如果P 中任意两个数的和、差、积、商（除数不为零）仍然是中的数，那么P 就称为一个数域.显然全体有理数组成的集合、全体实数组成的集合、全体复数组成的集合都是数域.这三个数域分别用字母Q 、R 、C 来代表.全体整数组成的集合就不是数域.如果数的集合P 中任意两个数作某一种运算的结果都仍在P 中，就说数集P 对这个运算是封闭的.因此数域的定义也可以说成，如果一个包含0，1在内的数集P 对于加法、减法、乘法与除法（除数不为零）是封闭的，那么P 就称为一个数域.例1 所有具有形式2b a +的数（其中b a ,是任何有理数），构成一个数域.通常用)2(Q 来表示这个数域.例2 所有可以表成形式m m nn b b b a a a ππππ++++++ 1010 的数组成一数域，其中m n ,为任意非负整数，),,1,0;,,1,0(,m j n i b a j i ==是整数.例 3 所有奇数组成的数集，对于乘法是封闭的，但对于加、减法不是封闭的.性质：所有的数域都包含有理数域作为它的一部分.一、一元多项式定义2 设n 是一非负整数，形式表达式111a x a x a x a n n n n ++++-- ,(1) 其中n a a a ,,,10 全属于数域P ，称为系数在数域P 中的一元多项式，或者简称为数域P 上的一元多项式.在多项式（1）以后用 ),(),(x g x f 或 ,,g f 等来表示多项式.注意：这里定义的多项式是符号或文字的形式表达式.定义3 如果在多项式)(x f 与)(x g 中，除去系数为零的项外，同次项的系数全相等)()(x g x f =.系数全为零的多项式称为零多项式，记为0.在（1）中，如果0≠n a n a 称为首项系数，n 称为多项式（1）的次数.零多项式是唯一不定义次数的多项式.多项式)(x f二、多项式的运算设0111)(a x a x a x a x f n n n n ++++=--0111)(b x b x b x b x g m m m m ++++=--是数域P 上两个多项式，那么可以写成∑==ni i i x a x f 0)(∑==mj j j x b x g 0)(在表示多项式)(x f 与)(x g 的和时，如m n ≥，为了方便起见，在)(x g 中令011====+-m n n b b b ，那么)(x f 与)(x g 的和为∑=---+=++++++++=+n i i i i n n n n n n xb a b a x b a x b a x b a x g x f 00011111)()()()()()()(而)(x f 与)(x g 的乘积为其中s 次项的系数是∑=+--=++++s j i j i s s s sb a b a b a b a b a 011110所以)(x f )(x g 可表成显然，数域P 上的两个多项式经过加、减、乘运算后，所得结果仍然是数域P 上的多项式.对于多项式的加减法，不难看出对于多项式的乘法，可以证明，若0)(,0)(≠≠x g x f ，则0)()(≠x g x f ，并且由以上证明看出，多项式乘积的首项系数就等于因子首项系数的乘积.显然上面的结果都可以推广到多个多项式的情形.多项式的运算满足以下的一些规律：1. 加法交换律：)()()()(x f x g x g x f +=+.2. 加法结合律：))()(()()())()((x h x g x f x h x g x f ++=++3. 乘法交换律：. )()()()(x f x g x g x f =4. 乘法结合律：))()()(()())()((x h x g x f x h x g x f =5. 乘法对加法的分配律：)()()()())()()((x h x f x g x f x h x g x f +=+6. 乘法消去律：若)()()()(x h x f x g x f =且0)(≠x f ，则)()(x h x g =.定义4 所有系数在数域P 中的一元多项式的全体，称为数域P 上的一元多项式环，记为][x P ，P 称为][x P 的系数域.§3 整除的概念在一元多项式环中，可以作加、减、乘三种运算，但是乘法的逆运算—除法—并不是普遍可以做的.因之整除就成了两个多项式之间的一种特殊的关系.一、整除的概念带余除法对于][x P 中任意两个多项式)(x f 与)(x g ，其中0)(≠x g ，一定有][x P 中的多项式)(),(x r x q 存在，使(1))(),(x r x q 是唯一决定的.带余除法中所得的)(x q 通常称为)(x g 除)(x f 的商，)(x r 称为)(x g 除)(x f 的余式.定义5 数域P 上的多项式)(x g 称为整除)(x f ，如果有数域P 上的多项式)(x h 使等式成立.用表示)(x g 整除)(x f ，用“)(|)(x f x g /”表示)(x g 不能整除)(x f .当)(|)(x f x g 时，)(x g 就称为)(x f 的因式，)(x f 称为)(x g 的倍式.当0)(≠x g 时，带余除法给出了整除性的一个判别条件.定理1 对于数域P 上的任意两个多项式)(x f ，)(x g ，其中0)(≠x g ，)(|)(x f x g 的充要条件是)(x g 除)(x f 的余式为零.带余除法中)(x g 必须不为零.但)(|)(x f x g 中，)(x g 可以为零.这时0)(0)()()(=⋅=⋅=x h x h x g x f .当)(|)(x f x g 时，如0)(≠x g ，)(x g 除)(x f 的商)(x q 有时也用)()(x g x f 来表示.二、整除的性质1. 任一多项式)(x f 一定整除它自身.2. 任一多项式)(x f 都能整除零多项式.3. 零次多项式，即非零常数，能整除任一个多项式.4. 若)(|)(),(|)(x f x g x g x f ，则)()(x cg x f =,其中c 为非零常数.5. 若)(|)(),(|)(x h x g x g x f ，则)(|)(x h x f （整除的传递性）.6. 若r i x g x f i ,,2,1),(|)( =，则))()()()()()((|)(2211x g x u x g x u x g x u x f r r +++ ,其中)(x u i 是数域P 上任意的多项式.通常，)()()()()()(2211x g x u x g x u x g x u r r +++ 称为)(,),(),(21x g x g x g r 的最后，两个多项式之间的整除关系不因系数域的扩大而改变.即若)(x f ，)(x g 是][x P 中两个多项式，P 是包含P 的一个较大的数域.当然，)(x f ，)(x g 也可以看成是][x P 中的多项式.从带余除法可以看出，不论把)(x f ，)(x g 看成是][x P 中或者是][x P 中的多项式，用)(x g 去除)(x f 所得的商式及余式都是一样的.因此，若在][x P 中)(x g 不能整除)(x f ，则在][x P 中，)(x g 也不能整除)(x f .例1 证明若)()(|)(),()(|)(2121x f x f x g x f x f x g -+，则)(|)(),(|)(21x f x g x f x g例2 求l k ,，使1|32++++kx x l x x .例3 若)(|)(),(|)(x h x g x f x g /，则)()(|)(x h x f x g +/.§4 多项式的最大公因式一、多项式的最大公因式如果多项式)(x ϕ既是)(x f 的因式，又是)(x g 的因式，那么)(x ϕ就称为)(x f 与)(x g 的一个公因式.定义 6 设)(x f 与)(x g 是][x P 中两个多项式. ][x P 中多项式)(x d 称为)(x f ，)(x g 的一个公因式,如果它满足下面两个条件：1）)(x d 是)(x f 与)(x g 的公因式；2）)(x f ，)(x g 的公因式全是)(x d 的因式.例如，对于任意多项式)(x f ，)(x f 就是)(x f 与0的一个最大公因式.特别地，根据定义，两个零多项式的最大公因式就是0.引理如果有等式)()()()(x r x g x q x f += (1)成立，那么)(x f ，)(x g 和)(x g ，)(x r 有相同的公因式.定理2 对于][x P 的任意两个多项式)(x f ，)(x g ，在][x P 中存在一个最大公因式)(x d ，且)(x d 可以表成)(x f ，)(x g 的一个组合，即有][x P 中多项式)(),(x v x u 使由最大公因式的定义不难看出，如果)(),(21x d x d 是)(x f ，)(x g 的两个最大公因式，那么一定有)(|)(21x d x d 与)(|)(12x d x d ，也就是说0),()(21≠=c x cd x d .这就是说，两个多项式的最大公因式在可以相差一个非零常数倍的意义下是唯一确定的.两个不全为零的多项式的最大公因式总是一个非零多项式.在这个情形，我们约定，用来表示首项系数是1的那个最大公因式.定理证明中用来求最大公因式的方法通常称为辗转相除法(division algorithm).例设343)(234---+=x x x x x f32103)(23-++=x x x x g求（)(x f ，)(x g ），并求)(),(x v x u 使)()()()()(x g x v x f x u x d +=.注：定理2的逆不成立.例如令1)(,)(+==x x g x x f ,则122)1)(1()2(2-+=-+++x x x x x x .但1222-+x x 显然不是)(x f 与)(x g 的最大公因式.但是当(2)式成立，而)(x d 是)(x f 与)(x g 的一个公因式，则)(x d 一定是)(x f 与)(x g 的一个最大公因式.二、多项式互素定义7 ][x P 中两个多项式)(x f ，)(x g 称为互素（也称为互质）的，如果显然,两个多项式互素,那么它们除去零次多项式外没有其他的公因式，反之亦然.定理3 ][x P 中两个多项式)(x f ，)(x g 互素的充要条件是有][x P 中多项式)(),(x v x u 使推论2 如果1))(),((1=x g x f ,1))(),((2=x g x f ,那么1))(),()((21=x g x f x f 推广：对于任意多个多项式)2)((,),(),(21≥s x f x f x f s ，)(x d 称为)2)((,),(),(21≥s x f x f x f s 的一个最大公因式，如果)(x d 具有下面的性质：1）s i x f x d i ,,2,1),(|)( =;2）如果s i x f x i ,,2,1),(|)( =ϕ，那么)(|)(x d x ϕ.我们仍用))(,),(),((21x f x f x f s 符号来表示首项系数为1的最大公因式.不难证明)(,),(),(21x f x f x f s 的最大公因式存在，而且当)(,),(),(21x f x f x f s 全不为零时，))()),(,),(),(((121x f x f x f x f s s -就是)(,),(),(21x f x f x f s 的最大公因式，即))(,),(),((21x f x f x f s =))()),(,),(),(((121x f x f x f x f s s -同样，利用以上这个关系可以证明，存在多项式s i x u i ,,2,1),( =,使))(,),(),(()()()()()()(212211x f x f x f x f x u x f x u x f x u s s s =+++如果1))(,),(),((21=x f x f x f s ，那么)(,),(),(21x f x f x f s 就称为互素的.同样有类似定理3的结论.注意 1)当一个多项式整除两个多项式之积时,若没有互素的条件,这个多项式一般不能整除积的因式之一.例如222)1()1(|1-+-x x x ,但22)1(|1+/-x x ,且22)1(|1-/-x x .2) 推论1中没有互素的条件,则不成立.如1)(2-=x x g ,1)(1+=x x f , )1)(1()(2-+=x x x f ,则)(|)(),(|)(21x g x f x g x f ,但)(|)()(21x g x f x f .注意:s )2(≥s 个多项式)(,),(),(21x f x f x f s 互素时,它们并不一定两两互素.例如,多项式34)(,65)(,23)(232221+-=+-=+-=x x x f x x x f x x x f是互素的,但2))(),((21-=x x f x f . 令P 是含P 的一个数域, )(x d 是][x P 的多项式)(x f 与)(x g 在][x P 中的首项系数为1的最大公因式,而)(x d 是)(x f 与)(x g 在][X P 中首项系数为1的最大公因式,那么)()(x d x d =.即从数域P 过渡到数域P 时, )(x f 与)(x g 的最大公因式本质上没有改变. 互素多项式的性质可以推广到多个多项式的情形：1)若多项式),()()(|)(21x f x f x f x h s )(x h 与)(,),(),(,),(111x f x f x f x f s i i +- 互素，则)1)((|)(s i x f x h i ≤≤.2) 若多项式)(,),(),(21x f x f x f s 都整除)(x h ，且)(,),(),(21x f x f x f s 两两互素，则)(|)()()(21x h x f x f x f s .3) 若多项式)(,),(),(21x f x f x f s 都与)(x h 互素，则1))(),()()((21=x h x f x f x f s .§5 因式分解定理一、不可约多项式Con i x i x x x R on x x x Q on x x x )2)(2)(2)(2()2)(2)(2()2)(2(42224+-+-=++-=+-=-. 定义8 数域P 上次数1≥的多项式)(x p 称为域P 上的不可约多项式(irreducible polynomical)，如果它不能表成数域P 上的两个次数比)(x p 的次数低的多项式的乘积.根据定义，一次多项式总是不可约多项式.一个多项式是否可约是依赖于系数域的.显然，不可约多项式)(x p 的因式只有非零常数与它自身的非零常数倍)0)((≠c x cp 这两种，此外就没有了.反过来，具有这个性质的次数1≥的多项式一定是不可约的.推广：如果不可约多项式)(x p 整除一些多项式)(,),(),(21x f x f x f s 的乘积)()()(21x f x f x f s ，那么)(x p 一定整除这些多项式之中的一个.二、因式分解定理因式分解及唯一性定理数域P 上次数1≥的多项式)(x f 都可以唯一地分解成数域P 上一些不可约多项式的乘积.所谓唯一性是说，如果有两个分解式)()()()()()()(2121x q x q x q x p x p x p x f t s ==,那么必有t s =，并且适当排列因式的次序后有s i x q c x p i i i ,,2,1,)()( ==.其中),,2,1(s i c i =是一些非零常数.应该指出，因式分解定理虽然在理论上有其基本重要性，但是它并没有给出一个具体的分解多项式的方法.实际上，对于一般的情形，普遍可行的分解多项式的方法是不存在的.在多项式)(x f 的分解式中，可以把每一个不可约因式的首项系数提出来，使它们成为首项系数为1的多项式，再把相同的不可约因式合并.于是)(x f 的分解式成为)()()()(2121x p x p x cp x f s r s r r =,其中c 是)(x f 的首项系数，)(,),(),(21x p x p x p s 是不同的首项系数为1的不可约多项式，而s r r r ,,,21 是正整数.这种分解式称为标准分解式.如果已经有了两个多项式的标准分解，就可以直接写出两个多项式的最大公因式.多项式)(x f 与)(x g 的最大公因式)(x d 就是那些同时在)(x f 与)(x g 的标准分解式中出现的不可约多项式方幂的乘积，所带的方幂的指数等于它在)(x f 与)(x g 中所带的方幂中较小的一个.由以上讨论可以看出，带余除法是一元多项式因式分解理论的基础.若)(x f 与)(x g 的标准分解式中没有共同的不可约多项式，则)(x f 与)(x g 互素.注意：上述求最大公因式的方法不能代替辗转相除法，因为在一般情况下，没有实际分解多项式为不可约多项式的乘积的方法，即使要判断数域P 上一个多项式是否可约一般都是很困难的.例在有理数域上分解多项式22)(23--+=x x x x f 为不可约多项式的乘积.§6 重因式一、重因式的定义定义9 不可约多项式)(x p 称为多项式)(x f 的k 重因式,如果)(|)(x f x p k ,但)(|)(1x f x p k /+.如果0=k ，那么)(x p 根本不是)(x f 的因式；如果1=k ，那么)(x p 称为)(x f 的单因式；如果1>k ，那么)(x p 称为)(x f 的重因式.注意. k 重因式和重因式是两个不同的概念,不要混淆.显然，如果)(x f 的标准分解式为)()()()(2121x p x p x cp x f s r s r r =,那么)(,),(),(21x p x p x p s 分别是)(x f 的1r 重，2r 重，… ,s r 重因式.指数1=i r 的那些不可约因式是单因式；指数1>i r 的那些不可约因式是重因式.使得)()()(x g x p x f k =,且)(|)(x g x p /.二、重因式的判别设有多项式0111)(a x a x a x a x f n n n n ++++=-- ,规定它的微商（也称导数或一阶导数）是1211)1()(a x n a nx a x f n n n n ++-+='--- .通过直接验证,可以得出关于多项式微商的基本公式:).()()()()()(()())((),()())()((x g x f x g x f x g x f x f c x cf x g x f x g x f '+'=''=''+'='+）))()(())((1x f x f m x f m m '='-同样可以定义高阶微商的概念.微商)(x f '称为)(x f 的一阶微商；)(x f '的微商)(x f ''称为)(x f 的二阶微商；等等. )(x f 的k 阶微商记为)()(x f k .一个)1(≥n n 次多项式的微商是一个1-n 次多项式；它的n 阶微商是一个常数；它的1+n 阶微商等于0.定理6 如果不可约多项式)(x p 是多项式)(x f 的一个)1(≥k k 重因式,那么)(x p 是微商)(x f '的1-k 重因式.分析: 要证)(x p 是微商)(x f '的1-k 重因式,须证)(|)(1x f x p k '-,但)(|)(x f x p k '/.注意:定理6的逆定理不成立.如333)(23++-=x x x x f , 22)1(3363)(-=+-='x x x x f ,1-x 是)(x f '的2重因式,但根本不是)(x f 是因式.当然更不是三重因式.推论 1 如果不可约多项式)(x p 是多项式)(x f 的一个)1(≥k k 重因式,那么)(x p 是)(x f ，)(x f ',…,)()1(x f k -的因式,但不是)()(x f k 的因式.)(x f 与)(x f '的公因式.推论3 多项式)(x f 没有重因式1))(),((='⇔x f x f这个推论表明，判别一个多项式有无重因式可以通过代数运算——辗转相除法来解决，这个方法甚至是机械的.由于多项式的导数以及两个多项式互素与否的事实在由数域P 过渡到含P 的数域P 时都无改变,所以由定理6有以下结论:若多项式)(x f 在][x P 中没有重因式,那么把)(x f 看成含P 的某一数域P 上的多项式时, )(x f 也没有重因式.例1 判断多项式2795)(234+-+-=x x x x x f有无重因式三、去掉重因式的方法设)(x f 有重因式,其标准分解式为s r s r r x p x p x cp x f )()()()(2121 =.那么由定理5),()()()()(1121121x g x p x p x p x f s r s r r ---='此处)(x g 不能被任何),,2,1)((s i x p i =整除.于是11211)()()()())(),((21---=='s r s r r x p x p x p x d x f x f用)(x d 去除)(x f 所得的商为)()()()(21x p x p x cp x h s =这样得到一个没有重因式的多项式)(x h .且若不计重数, )(x h 与)(x f 含有完全相同的不可约因式.把由)(x f 找)(x h 的方法叫做去掉重因式方法.例2 求多项式16566520104)(23456++++--=x x x x x x x f的标准分解式.§7 多项式函数到目前为止，我们始终是纯形式地讨论多项式，也就是把多项式看作形式表达式.在这一节，将从另一个观点，即函数的观点来考察多项式.一、多项式函数设0111)(a x a x a x a x f n n n n ++++=-- (1)是][x P 中的多项式，α是P 中的数，在(1)中用α代x 所得的数0111a a a a n n n n ++++--ααα称为)(x f 当α=x 时的值,记为)(αf .这样，多项式)(x f 就定义了一个数域上的函数.可以由一个多项式来定义的函数就称为数域上的多项式函数.因为x 在与数域P 中的数进行运算时适合与数的运算相同的运算规律，所以不难看出，如果,)()()(,)()()(21x g x f x h x g x f x h =+=那么.)()()(,)()()(21ααααααg f h g f h =+=定理7(余数定理)用一次多项式去除多项式)(x f ，所得的余式是一个常数，这个常数等于函数值)(αf .如果)(x f 在α=x 时函数值0)(=αf ，那么α就称为)(x f 的一个根或零点. 由余数定理得到根与一次因式的关系.推论 α是)(x f 的根的充要条件是)(|)(x f x α-.由这个关系，可以定义重根的概念. α称为)(x f 的k 重根，如果)(α-x 是)(x f 的k 重因式.当1=k 时，α称为单根；当1>k 时，α称为重根.定理8 ][x P 中n 次多项式)0(≥n 在数域P 中的根不可能多于n 个，重根按重数计算.二、多项式相等与多项式函数相等的关系在上面看到，每个多项式函数都可以由一个多项式来定义.不同的多项式会不会定义出相同的函数呢？这就是问，是否可能有)()(x g x f ≠,而对于P 中所有的数α都有)()(ααg f =?由定理8不难对这个问题给出一个否定的回答.定理9 如果多项式)(x f ,)(x g 的次数都不超过n ,而它们对n+1个不同的数有相同的值即)()(i i g f αα=,1,,2,1+=n i ,那么)(x f =)(x g .因为数域中有无穷多个数，所以定理9说明了，不同的多项式定义的函数也不相同.如果两个多项式定义相同的函数，就称为恒等，上面结论表明，多项式的恒等与多项式相等实际上是一致的.换句话说，数域P 上的多项式既可以作为形式表达式来处理，也可以作为函数来处理.但是应该指出，考虑到今后的应用与推广，多项式看成形式表达式要方便些.三、综合除法根据余数定理,要求)(x f 当c x =时的值,只需用带余除法求出用c x -除)(x f 所得的余式.但是还有一个更简便的方法,叫做综合除法.设n n n n n a x a x a x a x a x f +++++=---122110)(并且设r x q c x x f +-=)()()(. (2)其中.)(12322110-----+++++=n n n n n b x b x b x b x b x q比较等式(2)中两端同次项的系数.得到.,,,,121112201100-----=-=-=-==n n n n n cb r a cb b a cb b a cb b a b a⇒ .,,,,112121210100n n n n n a cb r a cb b a cb b a cb b a b +=+=+=+==---- 这样,欲求系数k b ,只要把前一系数1-k b 乘以c 再加上对应系数k a ,而余式r 也可以按照类似的规律求出.因此按照下表所指出的算法就可以很快地陆续求出商式的系数和余式:rb b b b cb cb cb cb a a a a ac n n n n n |)|12101210121---------------------------------+ 表中的加号通常略去不写.例1 用3+x 除94)(24-++=x x x x f .例2 求k 使355)(234+++-=kx x x x x f 能被3-x 整除注意 :若)(x f 缺少某一项,在作综合除法时该项系数的位置要补上零.四、拉格朗日插值公式已知次数n ≤的多项式)(x f 在)1,,2,1(+==n i c x i 的值)1,,,2,1()(+==n i b c f i i .设∑+=++-----=111111)())(()()(n i n i i i c x c x c x c x k x f依次令c x =代入)(x f ,得)())(()(1111++-----=n i i i i i i i i c c c c c c c c b k ∑+=++-++---------=1111111111)())(()()())(()()(n i n i i i i i i n i i i c c c c c c c c c x c x c x c x b x f 这个公式叫做拉格朗日(Lagrange)插值公式.例3 求次数小于3的多项式)(x f ,使3)2(,3)1(,1)1(==-=f f f .下面介绍将一个多项式表成一次多项式α-x 的方幂和的方法.所谓n 次多项式)(x f 表成α-x 的方幂和，就是把)(x f 表示成0111)()()()(b x b x b x b x f n n n n +-++-+-=--ααα的形式.如何求系数011,,,,b b b b n n -，把上式改写成01211)]()()([)(b x b x b x b x f n n n n +-++-+-=---ααα ,就可看出0b 就是)(x f 被α-x 除所得的余数，而12111)()()(b x b x b x q n n n n ++-+-=--- αα就是)(x f 被α-x 除所得的商式.又因为123121)]()()([)(b x b x b x b x q n n n n +-++-+-=---ααα .又可看出1b 是商式)(1x q 被α-x 除所得的余式，而233122)()()()(b x b x b x b x q n n n n +-++-+-=---ααα .就是)(1x q 被α-x 除所得商式.这样逐次用α-x 除所得的商式，那么所得的余数就是n n b b b b ,,,,110- .例4 将5)2()2(3)2(2)2()(234+-+---+-=x x x x x f 展开成x 的多项式. 解令2-=x y ，则2+=y x .于是532)2(234++-+=+y y y y y f .问题变为把多项式532234++-+y y y y 表成2+y （即x ）的方幂和,-2 | 1 2 -3 1 5+) -2 0 6 -14--------------------------------------------------------2 | 1 0 -3 7 | -9+) -2 4 -2-------------------------------------------------------2 | 1 -2 1 | 5+) -2 8------------------------------------------------2 | 1 -4 | 9+) -2----------------------------------1 | -6所以9596)(234-++-=x x x x x f .注意：将)(x f 表成α-x 的方幂和，把α写在综合除法的左边，将α-x 的方幂和展开成x 的多项式，那么相当于将)(x f 表成c c x +-)(的方幂和，要把c -写在综合除法的左边.§8 复系数和实系数多项式的因式分解一、复系数多项式因式分解定理代数基本定理每个次数1≥的复系数多项式在复数域中有一个根.利用根与一次因式的关系，代数基本定理可以等价地叙述为：每个次数1≥的复系数多项式在复数域上一定有一个一次因式.由此可知，在复数域上所有次数大于1的多项式都是可约的.换句话说，不可约多项式只有一次多项式.于是，因式分解定理在复数域上可以叙述成：复系数多项式因式分解定理每个次数1≥的复系数多项式在复数域上都可以唯一地分解成一次因式的乘积.因此，复系数多项式具有标准分解式s l s l l n x x x a x f )()()()(2121ααα---=其中s ααα,,,21 是不同的复数，s l l l ,,,21 是正整数.标准分解式说明了每个n 次复系数多项式恰有n 个复根（重根按重数计算）.二、实系数多项式因式分解定理对于实系数多项式，以下事实是基本的：如果α是实系数多项式)(x f 的复根，那么α的共轭数α也是)(x f 的根,并且α与α有同一重数.即实系数多项式的非实的复数根两两成对.实系数多项式因式分解定理每个次数1≥的实系数多项式在实数域上都可以唯一地分解成一次因式与含一对非实共轭复数根的二次因式的乘积.实数域上不可约多项式,除一次多项式外,只有含非实共轭复数根的二次多项式.因此，实系数多项式具有标准分解式r s k r r k l s l l n q x p x q x p x c x c x c x a x f )()()()()()(211221121++++---= 其中r r s q q p p c c ,,,,,,,,111 全是实数，s l l l ,,,21 ,r k k ,,1 是正整数，并且),,2,1(2r i q x p x i i =++是不可约的，也就是适合条件r i q p i i ,,2,1,042 =<-..代数基本定理虽然肯定了n 次方程有n 个复根，但是并没有给出根的一个具体的求法.高次方程求根的问题还远远没有解决.特别是应用方面，方程求根是一个重要的问题，这个问题是相当复杂的，它构成了计算数学的一个分支.三、n 次多项式的根与系数的关系.令.)(11n n n a x a x x f +++=- (1)是一个n (>0)次多项式,那么在复数域C 中)(x f 有n 个根,,,,21n ααα 因而在][x C 中)(x f 完全分解为一次因式的乘积:).())(()(21n x x x x f ααα---=展开这一等式右端的括号,合并同次项,然后比较所得出的系数与(1)式右端的系数,得到根与系数的关系.,)1(),()1(),(),),(21323112111124213213131212211n n n n n n n n n n n n n n a a a a a αααααααααααααααααααααααααααααα-=+++-=+++-=+++=+++-=------（其中第),,2,1(n k k =个等式的右端是一切可能的k 个根的乘积之和,乘以k )1(-.若多项式 n n n a x a x a x f +++=- 110)(的首项系数,10≠a 那么应用根与系数的关系时须先用0a 除所有的系数,这样做多项式的根并无改变.这时根与系数的关系取以下形式:.)1(,),(21013121022101n n n n n n a a a a a a αααααααααααα-=+++=+++-=-利用根与系数的关系容易求出有已知根的多项式.例1 求出有单根5与-2,有二重根3的四次多项式.例2. 分别在复数域和实数域上分解1-n x 为标准分解式.§9 有理系数多项式作为因式分解定理的一个特殊情形，有每个次数≥1的有理系数多项式都能分解成不可约的有理系数多项式的乘积.但是对于任何一个给定的多项式，要具体地作出它的分解式却是一个很复杂的问题，即使要判别一个有理系数多项式是否可约也不是一个容易解决的问题，这一点是有理数域与复数域、实数域不同的.在这一节主要是指出有理系数多项式的两个重要事实：第一，有理系数多项式的因式分解的问题，可以归结为整（数）系数多项式的因式分解问题，并进而解决求有理系数多项式的有理根的问题.第二，在有理系数多项式环中有任意次数的不可约多项式.一、有理系数多项式的有理根设011)(a x a x a x f n n n n +++=--是一个有理系数多项式.选取适当的整数c 乘)(x f ，总可以使)(x cf 是一个整系数多项式.如果)(x cf 的各项系数有公因子，就可以提出来，得到)()(x dg x cf =,也就是)()(x g cd x f = 其中)(x g 是整系数多项式，且各项系数没有异于±1的公因子.如果一个非零的整系数多项式011)(b x b x b x g n n n n +++=-- 的系数01,,,b b b n n -没有异于±1的公因子,也就是说它们是互素的,它就称为一个本原多项式.上面的分析表明，任何一个非零的有理系数多项式)(x f 都可以表示成一个有理数r 与一个本原多项式)(x g 的乘积，即)()(x rg x f =.可以证明，这种表示法除了差一个正负号是唯一的.亦即，如果)()()(11x g r x rg x f ==,其中)(),(1x g x g 都是本原多项式，那么必有)()(,11x g x g r r ±=±=因为)(x f 与)(x g 只差一个常数倍，所以)(x f 的因式分解问题，可以归结为本原多项式)(x g 的因式分解问题.下面进一步指出，一个本原多项式能否分解成两个次数较低的有理系数多项式的乘积与它能否分解成两个次数较低的整系数多项式的乘积的问题是一致的.定理10(Gauss 引理) 两个本原多项式的乘积还是本原多项式.定理11 如果一非零的整系数多项式能够分解成两个次数较低的有理系数多项式的乘积，那么它一定可以分解两个次数较低的整系数多项式的乘积.以上定理把有理系数多项式在有理数域上是否可约的问题归结到整系数多项式能否分解成次数较低的整系数多项式的乘积的问题.推论设)(x f ，)(x g 是整系数多项式，且)(x g 是本原多项式，如果)()()(x h x g x f =，其中)(x h 是有理系数多项式，那么)(x h 一定是整系数多项式.这个推论提供了一个求整系数多项式的全部有理根的方法. 定理12 设011)(a x a x a x f n n n n +++=--是一个整系数多项式.而sr是它的一个有理根,其中s r ,互素,那么(1) 0|,|a r a s n ;特别如果)(x f 的首项系数1=n a ，那么)(x f 的有理根都是整根，而且是0a 的因子.(2) ),()()(x q srx x f -= 其中)(x q 是一个整系数多项式.给了一个整系数多项式)(x f ,设它的最高次项系数的因数是k v v v ,,,21 ,常数项的因数是.,,,21l u u u 那么根据定理12,欲求)(x f 的有理根,只需对有限个有理数ji v u 用综合除法来进行试验.当有理数jiv u 的个数很多时,对它们逐个进行试验还是比较麻烦的.下面的讨论能够简化计算.首先,1和-1永远在有理数jiv u 中出现,而计算)1(f 与)1(-f 并不困难.另一方面,若有理数)1(±≠a 是)(x f 的根,那么由定理12,)()()(x q x x f α-=而)(x q 也是一个整系数多项式.因此商)1(1)1(),1(1)1(--=+-=-q af q af 都应该是整数.这样只需对那些使商a f a f +--1)1(1)1(与都是整数的ji v u来进行试验.(我们可以假定)1(f 与)1(-f 都不等于零.否则可以用1-x 或1+x 除)(x f 而考虑所得的商.)例1 求多项式2553)(234-+++=x x x x x f的有理根.例2 证明15)(3+-=x x x f在有理数域上不可约.二、有理数域上多项式的可约性定理13 (艾森斯坦(Eisenstein)判别法) 设011)(a x a x a x f n n n n +++=--是一个整系数多项式.若有一个素数p ,使得1. n a p |/;2. 021,,,|a a a p n n --;3. 02|a p /.则多项式)(x f 在有理数域上不可约.由艾森斯坦判断法得到:有理数域上存在任意次的不可约多项式.例如2)(+=n x x f .,其中n 是任意正整数.艾森斯坦判别法的条件只是一个充分条件.有时对于某一个多项式)(x f ,艾森斯坦判断法不能直接应用,但把)(x f 适当变形后,就可以应用这个判断法.例3 设p 是一个素数,多项式1)(21++++=--x x x x f p p叫做一个分圆多项式,证明)(x f 在][x Q 中不可约.证明：令1+=y x ，则由于1)()1(-=-p x x f x ,yCyC y y y yf p pp ppp 1111)1()1(--+++=-+=+ ,令)1()(+=y f y g ，于是1211)(---+++=p p p p p C yC y y g ,由艾森斯坦判断法，)(y g 在有理数域上不可约，)(x f 也在有理数域上不可约.第一章多项式(小结)一元多项式理论,主要讨论了三个问题:整除性理论(整除,最大公因式,互素);因式分解理论(不可约多项式,典型分解式,重因式);根的理论(多项式函数,根的个数).其中整除性是基础,因式分解是核心.一、基本概念.1.一元多项式(零多项式),多项式的次数.多项式的相等,多项式的运算,一元多项式环.2．基本结论:(1) 多项式的加法,减法和乘法满足一些运算规律.(3) 多项式乘积的常数项(最高次项系数)等于因子的常数项(最高次项系数)的乘积.二、整除性理论1.整除的概念及其基本性质.2.带余除法. (1) 带余除法定理.(2) 设1)()()()(|)(,0)(][)(),(=⇔≠∈x r x f x g x f x g x g x F x g x f 的余式除，. 因此多项式的整除性不因数域的扩大而改变.3. 最大公因式和互素. (1) 最大公因式,互素的概念.(2) 最大公因式的存在性和求法------辗转相除法.(3) 设)(x d 是)(x f 与)(x g 的最大公因式,反之不然.三、因式分解理论 1.不可约多项式(1) 不可约多项式的概念.(2) 不可约多项式p(x)有下列性质:(4) 艾森斯坦判断法. 2.因式分解的有关结果: (1) 因式分解及唯一性定理.(2) 次数大于零的复系数多项式都可以分解成一次因式的乘积.(3) 次数大于零的实系数多项式都可以分解成一次因式和二次不可约因式的乘积.3.重因式(1) 重因式的概念.(2) 若不可约多项式)(x p 是)(x f 的k 重因式)1(≥k ,则)(x p 是)(x f 的1-k 重因式.(4) 消去重因式的方法:))(),(()(x f x f x f '是一个没有重因式的多项式,它与)(x f 具有完全相同的不可约因式.四、多项式根的理论1.多项式函数,根和重根的概念.2.余数定理.c x -去除)(x f 所得的余式为)(x f ,则.0)()(|=⇔-c f x f c x3.有理系数多项式的有理根的求法.4.实系数多项式虚根成对定理.5.代数基本定理.每个)1(≥n n 次复系数多项式在复数域中至少有一个根.因而n 次复系数多项式恰有n 个复根(重根按重数计算).6.韦达定理.。

第三章整式及其加减

第三章整式及其加减【要点梳理】要点一、字母表示数用字母表示数之后，有些数量之间的关系用含有字母的式子表示，看上去更加简明，更具有普遍意义了．举例：如果用a 、b 表示任意两个有理数，那么加法交换律可以用字母表示为：a ＋b ＝b ＋a ．乘法交换律可以用字母表示为：ab ＝ba要点二、代数式1.代数式的定义：诸如：16n ，2a+3b ，34，2n ，2)(b a +等式子，它们都是用运算符号把数和字母连接而成的，像这样的式子叫做代数式，单独的一个数或一个字母也是代数式.要点诠释：带等号或不等号的式子不是代数式，如33x =，33x >，33x ≠等都不是代数式.2.列代数式：在解决实际问题时，常常先把问题中与数量有关的词语用代数式表示出来，即列出代数式，使问题变得简洁，更具一般性．要点诠释：代数式的书写规范：（1）字母与数字或字母与字母相乘时，通常把乘号写成“·”或省略不写；（2）除法运算一般以分数的形式表示；（3）字母与数字相乘时，通常把数字写在字母的前面；（4）字母前面的数字是分数的，如果既能写成带分数又能写成假分数，一般写成假分数的形式；（5）如果字母前面的数字是1，通常省略不写.3.代数式的值：一般地，用具体数值代替代数式中的字母，按照代数式中的运算关系计算得出的结果，叫做代数式的值.要点三、整式1.单项式（1）单项式的定义：如22xy ，13mn ，-1，它们都是数与字母的积，像这样的式子叫单项式，单独的一个数或一个字母也是单项式．要点诠释：单项式一定是代数式，但若分母中含有字母的代数式，如5m 就不是单项式，因为它无法写成数字与字母的乘积．（2）单项式的系数：单项式中的数字因数叫做这个单项式的系数．要点诠释：①确定单项式的系数时，最好先将单项式写成数与字母的乘积的形式，再确定其系数．②圆周率π是常数，单项式中出现π时，应看作系数．③当一个单项式的系数是1或-1时，“1”通常省略不写． ④单项式的系数是带分数时，通常写成假分数，如：2114x y 写成254x y ．（3）单项式的次数：一个单项式中，所有字母的指数和叫做这个单项式的次数．要点诠释：没有写指数的字母，实际上其指数是1，计算时不能将其遗漏．2．多项式(1)多项式的定义：几个单项式的和叫做多项式．要点诠释：“几个”是指两个或两个以上．(2)多项式的项：在多项式中，每个单项式叫做多项式的项，不含字母的项叫做常数项．要点诠释：①多项式的每一项包括它前面的符号．②一个多项式含有几项，就叫几项式，如：2x x--是一个三项式．627(3)多项式的次数：一个多项式中，次数最高的项的次数，叫做这个多项式的次数．要点诠释：①多项式的次数不是所有项的次数之和，而是多项式中次数最高的单项式的次数．②一个多项式中的最高次项有时不止一个，在确定最高次项时，都应写出．（4）升幂排列与降幂排列：把一个多项式按某一个字母的指数从大到小的顺序排列起来,叫做把多项式按这个字母降幂排列；若按某一个字母的指数从小到大的顺序排列起来，叫做把多项式按这个字母升幂排列．1x2y4-5x4-6是六次五项式,按x的降幂排列为如:多项式2x3y2-xy3+2-5x4+2x3y2+1x2y4-xy3-6,在这里只考虑x的指数,而不考虑其它字母;按y的升幂排2列为-6-5x4+2x3y2-xy3+1x2y4．2要点诠释：①重新排列多项式时,每一项一定要连同它的正负号一起移动；②含有两个或两个以上字母的多项式,常常按照其中某一个字母的升幂排列或降幂排列．3.整式：单项式与多项式统称为整式．要点诠释：（1）单项式、多项式、整式与代数式这四者之间的关系：单项式、多项式必是整式，整式必是代数式，但反过来就不一定成立．（2）分母中含有字母的式子一定不是整式，但是代数式．【典型例题】类型一、字母表示数1．填空：(1)某商场将一种商品A按标价的9折出售(即优惠10%)仍可获利10%，若商场商品A的标价为a元，那么该商品的进价为________元(列出式子即可，不用化简)．(2)有a 名男生和b 名女生在社区做义工，他们为建花坛搬砖．男生每人搬了40块，女生每人搬了30块．这a 名男生和b 名女生一共搬了块砖（用含a ．b 的代数式表示）．【思路点拨】和、差形式的代数式要在单位前把代数式括起来.【答案】(1)90%10%1a +；(2)（40a +30b ）【解析】本例属于实际生活问题，应分清“进价”、“标价”、“利润”、“利润率”、“打折”等问题，打几折就是标价的十分之几．【总结升华】解答本例需弄清以下两个数量关系：(1)利润＝售价－进价;(2)利润率＝-售价进价进价．举一反三：【变式】为庆祝战胜利70周年，我市某楼盘让利于民，决定将原价为a 元/米2的商品房价降价10%销售，降价后的销售价为（）A ．a ﹣10%B ． a ?10%C ． a （1﹣10%）D ．a （1+10%）【答案】C ．类型二、代数式2．为了节约能源，某单位按以下规定收取每月电费：用电不超过140度，按每度0.43元收费；如果超过140度，超过部分按每度0.57元收费．（1）若某用户10月份用去a 度电，则他应缴多少电费？（2）若该用户11月份用了150度电，则该缴多少电费？【思路点拨】当a ﹥140，应付费用分为两部分，一部分为0.43×140元，另一部分为0.57×（a-140）元.【答案与解析】解：（1）当a≤140时，电费为0.43a 元；当a ＞140时，电费为：0.431400.57(140)(0.5719.6)a a ⨯+⨯-=-元.（2）因为用电量为150度，大于140度，因此把a ＝150代入代数式0.5719.6a -，得0.5715019.665.9⨯-=（元）.因此，该缴电费65.9元.【总结升华】根据a 的不同取值，分别对应不同的代数式．举一反三：【变式1】一个堤坝的截面是等腰梯形，最上面一层铺石块a 块，往下每层多铺一块，最下面一层铺了b 块，共铺了n 层，共铺石块块？当a ＝20，b ＝40，n ＝17时，堤坝的这个截面铺石块块？【答案】12（a ＋b ）n ，510块.【变式2】代数式12（a ＋b ）n 的意义.【答案】答案不唯一，举一例：设某两数为a b 、，则()a b n +12表示“这两个数平均数的n 倍.类型三、整式3．整式中是单项式的个数有（） A ．2个 B ． 3个 C ． 4个D ．5个【答案】C ．【解析】解：整式中，单项式有：﹣0.3x 2y ，0，，﹣2a 2b 3c ，共4个．【总结升华】根据单项式的定义：数或字母的积组成的式子叫做单项式，单独的一个数或字母也是单项式，即可得出答案．举一反三：【变式】下列代数式：322332111;;;;2;-232a x y ab x x y x y y x+--++π①②③④⑤⑥，其中单项式是_______________，多项式是_______________.【答案】①②③，④⑥4．已知多项式32312246753m x xy x y y x y ---+--． (1)求多项式各项的系数和次数．(2)如果多项式是七次五项式，求m 的值．【答案与解析】(1)依题意知此多项式是五项式，第一项26xy -的系数是-6，次数是3；第二项3127m x y --的系数是-7，次数是3m+1；第三项343x y 的系数是43，次数是4；第四项2x y -系数是-l ，次数3；第五项-5系数是-5，次数是0．(2)由多项式是七次五项式，可得3127m x y --的次数是7，即3m-1+2＝7，解得m ＝2．【总结升华】对于单项式3127m x y --的次数为3m+1，可能不太习惯，通过适量的练习，会对用字母表示多项式的次数或系数有较深地认识．举一反三：【变式】多项式()34b a x x x b --+-是关于x 的二次三项式，求a 与b 的差的相反数．【答案】5．已知：x 2﹣5x=6，请你求出代数式10x ﹣2x 2+5的值．【思路点拨】先把10x ﹣2x 2+5变形为﹣2（x 2﹣5x ）+5，然后把x 2﹣5x=6整体代入进行计算即可．【答案与解析】解：10x ﹣2x 2+5=﹣2（x 2﹣5x ）+5，∵x 2﹣5x=6，∴原式=﹣2×6+5=﹣12+5=﹣7．【总结升华】本题考查了代数式求值：先根据已知条件把代数式进行变形，然后利用整体代入进行求值．【巩固练习】1.判断正误：对的画“√”，错的画“×”.（1）5y 是单项式；（）（2）5y ＋1是单项式；（）（3）13是单项式；（）（4）单项式ab 的系数是0；（）（5）单项式2ab的系数是2；（）3（6）单项式xy2次数是2；（）（7）单项式4xy2是三次单项式.（）2.填空：青藏铁路线上，在格尔木到拉萨之间有一段很长的冻土地段.列车在冻土地段行驶速度是每小时100千米，它2小时行驶的路程是千米，3小时行驶的路程是千米，t小时行驶的路程是千米.3.用单项式填空：（1）底边长为a，高为h的三角形的面积是；（2）一辆汽车从拉萨出发，3小时后到达相距s千米的尼木县城，这辆长途汽车的平均速度是；（3）一台电视机原价a元，现按原价的9折（9折就是90%）出售，这台电视机现在的售价为元.4.填空：（1）多项式x2＋3x＋4是单项式______，_______，_______的和，它的项是______，______，______，常数项是________；（2）多项式－x2－3＋x是单项式______，_______，_______的和，它的项是______，______，______，常数项是________；（3）多项式m2－1是单项式______，_______，_______的和，它的项是______，______，______，常数项是________；（4）多项式2x＋3y2－3xy2是单项式______，_______，_______的和，它的项是______，______，______.5.填空：（1）多项式3＋2x 2－4x 次数最高项是____，次数最高项的次数是______，这个多项式的次数是______；（2）多项式m 3－1次数最高项是____，次数最高项的次数是______，这个多项式的次数是______；（3）多项式2x －3xy 2＋1次数最高项是____，次数最高项的次数是______，这个多项式的次数是______；（4）多项式3x 4－2x 2y 2次数最高项是____，次数最高项的次数是______，这个多项式的次数是______.1.填空（1）单项式3x 的系数是_______，次数是______，是_______次单项式；（2）单项式πr 2的系数是_______，次数是______，是_______次单项式；（3）单项式－x 2y 的系数是_______，次数是______，是_______次单项式；（4）单项式22a b 2的系数是_______，次数是______，是_______次单项式.2.填空：（1）多项式―x 2―3x ＋4的项是________________，最高次项是______，常数项是______，次数是________；（2）多项式3－m 2的项是___________，最高次项是＿＿＿＿，常数项是＿＿＿，次数是＿＿＿；（3）多项式a 3＋a 2b ＋ab 2的项是__________________，最高次项是＿＿＿＿＿＿，次数是＿＿＿.3.判断正误：对的画"√"，错的画"×".（1）多项式3a －5的项是3a ，5；（）（2）多项式x 3＋x 2y 2的次数3次；（）（3）几个多项式的和仍是多项式；（）（4）单项式和多项式统称整式.（）4.用多项式填空：（1）温度由－3度下降t 度后是＿＿＿度；（2）温度由－3度上升t 度后是＿＿＿度；（3）一个数比x 的2倍小3，则这个数为＿＿＿＿＿＿；（4）a 与b 两数平方的和为＿＿＿＿＿＿；（5）如图，三角尺的面积为＿＿＿＿＿＿.5.用整式填空：（1）体重由x 千克增加2千克后是_____千克；（2）1千克大米售价1.2元，x 千克大米售价＿＿＿＿＿元；（3）a ，b 分别表示长方形的长与宽，则长方形的周长为＿＿＿＿＿；（4）a ，b 分别表示梯形的上底和下底，h 表示梯形的高，则梯形的面积为＿＿＿＿＿＿＿＿＿；（5）买一个篮球需要x 元，买一个排球需要y 元，买一个足球需要z 元，买3个篮球、5个排球、2个足球共需＿＿＿＿＿＿＿＿＿＿元.（6）如图，是一所住宅的建筑平面图，这所住宅的建筑面积是＿＿＿＿＿＿＿平方米.6.思考题：如图，搭1个正方形需要4根小棒，搭2个正方形需要＿＿＿根小棒，搭3个正方形需要＿＿＿根小棒，搭x个正方形需要＿＿＿＿根小棒，搭2008个正方形需要＿＿＿＿根小棒.【课后作业】一、选择题1．在代数式222515,1,32,,,1x x x x x x π+--+++中，整式有（）A.3个B.4个C.5个D.6个2．下面计算正确的是（）A 、2233x x -=B 、235325a a a +=C 、33x x +=D 、10.2504ab ab -+= 3．多项式2112xx ---的各项分别是（） A.21,,12x x - B.21,,12x x --- C.21,,12x x D.21,,12x x -- 4．下列去括号正确的是（）A.()5252+-=+-x xB.()222421+-=--x xC.()n m n m +=-323231D.x m x m 232232+-=⎪⎭⎫ ⎝⎛-- 5.下列各组中的两个单项式能合并的是（）A ．4和4xB ．32323x y y x -和C ．c ab ab 221002和D ．2m m 和6.单项式233xy z π-的系数和次数分别是（）A.－π，5B.－1，6C.－3π，6D.－3，7 7一个多项式与2x －2x ＋1的和是3x －2，则这个多项式为（） A ：2x －5x ＋3B ：－2x ＋x －1C ：－2x ＋5x －3D ：2x －5x －138、原产量n 吨，增产30%之后的产量应为（）A 、（1-30%）n 吨B 、（1+30%）n 吨C 、n+30%吨D 、30%n 吨二、填空题1．单项式522xy -的系数是____________，次数是_______________。

(完整word版)初一整式的加减所有知识点总结和常考题提高难题压轴题练习(含答案解析)

第1页（共17页）初一整式的加减所有知识点总结和常考题知识点：1单项式：表示数字或字母乘积的式子，单独的一个数字或字母也叫单项式。

2 •单项式系数：单项式中不为零的数字因数，叫单项式数字系数，简称单项式的系数；3. 单项式的次数：单项式中所有字母的指数的和，叫单项式的次数4. 多项式：几个单项式的和叫做多项式。

5•多项式的项与项数：多项式中每个单项式叫多项式的项；不含字母的项叫做常数项。

多项式里所含单项式的个数就是多项式的项数；6•多项式的次数：多项式里，次数最高项的次数叫多项式的次数；常数项的次数为0注意：（若a、b、c、p、q是常数）ax2+bx+c和x2+px+q是常见的两个二次三项式.7.多项式的升幕排列：把一个多项式的各项按某个字母的指数从小到大排列起来，叫做按这个字母的升幕排列。

多项式的降幕排列：把一个多项式的各项按某个字母的指数从大到小排列起来，叫做按这个字母的降幂排列。

（注意：多项式计算的最后结果一般应该进行升幕（或降幕）排列8•整式：单项式和多项式统称为整式，即凡不含有除法运算，或虽含有除法运算但除式中不含字母的代数式叫整式.9•整式分类：整式/单项式. （注意：分母上含有字母的不是整式。

）i多项式10.同类项：所含字母相同，并且相同字母的指数也相同的单项式是同类项11.合并同类项法：各同类项系数相加，所得结果作为系数，字母和字母指数不变。

12•去括号的法则：（原理：乘法分配侓）（1）括号前面是“ +”号，把括号和它前面的“ +”号去掉，括号里各项的符号都不变；（2）括号前面是“一”号，把括号和它前面的“一”号去掉，括号里各项的符号都要改变。

13.添括号的法则：（1）若括号前边是“ +”号，括号里的各项都不变号；（2）若括号前边是“-”号，括号里的各项都要变号.14.整式的加减：进行整式的加减运算时，如果有括号先去括号，再合并同类项；整式的加减，实际上是在去括号的基础上，把多项式的同类项合并整式加减的步骤：（1）列出代数式；（2）去括号；（3）添括号（4）合并同类项。

整式及其加减知识点知识点

整式及其加减知识点知识点整式是指由数字和字母按照加法、减法和乘法运算规则组成的多项式。

整式是代数中的基本概念，其理解和运算是学习代数的基础。

一、整式的定义和形式整式是由数字和字母按照加法、减法和乘法运算规则组成的多项式。

整式的形式可以是常项、单项或多项式。

常项是指只由数字组成的整式，单项是指只有字母与一定次数的乘方的整式，而多项式是由字母与各种次数的乘方的连乘积的和。

二、整式的加法和减法运算整式的加法和减法是整式运算的基本方法，其组合规则如下：1.同类项的加减法：同类项指的是指数部分相同的项。

对于同类项，只需将系数相加或相减，指数不变。

例如：3x^2+2x^2=5x^22.同类项之外的项相加减：对于不同类项，不能直接相加减。

只能合并同类项后再进行运算。

例如：3x+2x^2-4x^2+5x=2x^2-x+5x。

3.括号展开运算：对于整式中有括号的情况，可以通过分配律将括号内的整式与外部整式相乘。

例如：(3x+2)(x+1)=3x^2+3x+2x+2=3x^2+5x+2三、整式的乘法运算整式的乘法是通过对各项的系数和指数进行相乘得到的。

乘法运算的规则如下：1. 系数相乘：将整式中各项的系数进行相乘。

例如：2x * 3y = 6xy。

2.指数相加：对于同一个字母，如果有两个或多个指数，则将这些指数相加。

例如：x^2*x^3=x^(2+3)=x^53.同类项相乘：将系数和指数分别相乘，得到同类项的乘积。

不能合并同类项之外的项。

例如：2x*3x=6x^24.括号的乘法：将括号内的整式与外部整式分别进行乘法运算。

结果通过分配律得出。

例如：3x*(2x+1)=6x^2+3x。

四、整式的综合运算整式的综合运算是指整式的加减法和乘法在一起进行的运算。

综合运算需要根据题目给出的式子和要求进行相应的计算步骤。

在进行整式运算时，可以利用运算法则和分配律进行合理的转换和化简。

整式的加减法和乘法都需要注意合并同类项和保持字母指数的正确运算。

多元多项式的加减全章知识点总结

多元多项式的加减全章知识点总结本文档将总结多元多项式的加减法的全章知识点，包括定义、规则和示例。

定义多元多项式是指含有多个变量和多个项的代数式。

每个项由一个系数和各个变量的幂次组成。

多元多项式通常用字母表示变量，如x、y和z。

规则1. 同类项相加减：只有当多项式的各项的变量和次数完全相同时，才可以进行加减法运算。

具体做法是将同类项的系数相加减，并保留变量和次数不变。

2. 非同类项相加减：对于不同变量或次数的项，无法直接相加减。

需要将多个多项式化简为相同形式，再进行运算。

3. 加减法的交换律和结合律：多元多项式的加减法满足交换律和结合律。

换言之，可以改变多项式项的顺序，也可以改变加减法运算的顺序，结果不受影响。

4. 零多项式的加减：零多项式是所有系数都为0的多项式。

无论与任何多项式相加减，结果都等于原多项式。

示例1. 加法示例：f(x, y) = 2x^2y + 3xy^2g(x, y) = 4x^2y + 2xy^2f(x, y) + g(x, y) = (2x^2y + 3xy^2) + (4x^2y + 2xy^2)= 6x^2y + 5xy^22. 减法示例：f(x, y) = 2x^2y + 3xy^2g(x, y) = 4x^2y + 2xy^2f(x, y) - g(x, y) = (2x^2y + 3xy^2) - (4x^2y + 2xy^2)= -2x^2y + xy^2以上是关于多元多项式的加减法的全章知识点总结。

通过掌握定义、规则和示例，能够正确理解和运用多元多项式的加减法。

整式加减的知识点总结

整式加减的知识点总结
整式由多项式和单项式组成，所以整式加减的运算规则就是多项式加减和单项式加减的运算规则。

一、多项式加减的基本步骤：
1. 把同类项合并：将同一变量的幂相同的项合并成一项，并将它们的系数相加或相减。

例如，将3x^2y-5xy+2x^2y+4xy进行整理，先合并同类项3x^2y和2x^2y，然后合并同类项-5xy和4xy，整理得：5x^2y-x.
2. 按照指数的大小顺序排列。

例如, 将2x^2-4x^3+3x^2+x^3整理为：-4x^3+x^3+2x^2+3x^2, 排列整齐后为-3x^3+5x^2.
二、单项式加减的基本步骤：
1. 对于同类项，把它们的系数相加或相减，字母部分保持不变。

例如，将3xy-5xy+2xy进行整理，合并同类项得：xy.
2. 对于不同类项，直接相加或相减。

例如，将3x-5y+2z+4t进行整理，合并得：3x-5y+2z+4t.
在进行整式加减的过程中，需要注意以下几点：
1. 观察是否为同类项。

2. 看清各项之间的加减关系。

3. 注意每一步运算的准确性和细致性。

综上所述，整式加减是代数学中基础的运算内容，通过多项式加减和单项式加减的基本规则，能够解决代数问题中的各种加减计算过程。

能够熟练地掌握整式加减的运算方法，对于提高解决代数问题的能力至关重要。

希望以上内容能够对你有所帮助，如果还有其他问题需要解答，可以随时向我提问。

整式的加减测试题多项式加减的技巧总结

整式的加减测试题多项式加减的技巧总结在代数学中，整式的加减是我们需要掌握的基本技巧之一。

掌握整式的加减运算方法，不仅能够帮助我们解决复杂的代数表达式，还能够为我们在数学问题中提供更多的解题思路。

本文将从多项式的加减入手，总结出一些技巧和方法，以便更好地应对整式的加减测试题。

一、加法运算的基本方法在多项式的加法运算中，我们需要注意以下几个基本方法：1. 将同类项相加：当两个多项式相加时，我们需要将其中所有同类项的系数相加。

同类项是指具有相同字母的幂次的项。

例如，对于多项式3x² + 4x + 5和2x² + 3x - 2，我们可以将同类项相加，得到总和为(3x² + 2x²) + (4x + 3x) + (5 - 2) = 5x² + 7x + 3。

2. 注意符号的运算：在多项式的加法中，我们需要注意正负号的运算。

当两个项的系数具有相同的符号时，我们可以将它们相加，并保持符号不变。

例如，对于多项式2x + 3和4x + 5，我们可以将同类项相加，得到(2x + 4x) + (3 + 5) = 6x + 8。

当两个项的系数具有相反的符号时，我们需要注意符号的运算。

例如，对于多项式2x + 3和(-4x) - 5，我们可以将同类项相加，得到(2x - 4x) + (3 - 5) = -2x - 2。

3. 去掉相同项的规则：当两个多项式相加时，如果我们发现它们具有相同的项，我们可以将它们合并成一个项，并保持该项的系数不变。

例如，对于多项式3x² + 4x + 5和2x² + 3x - 5，我们可以将同类项相加，并合并相同项，得到(3x² + 2x²) + (4x + 3x) + (5 - 5) = 5x² + 7x。

二、减法运算的基本方法在多项式的减法运算中，我们同样需要注意以下几个基本方法：1. 将减数取相反数：当两个多项式相减时，我们需要先将减数取相反数，然后按照加法运算的方法进行计算。