矩阵的特征值分解和奇异值分解
奇异值分解与特征值分解的比较分析(六)

奇异值分解与特征值分解是线性代数中非常重要的两个概念,它们在数据分析、图像处理、信号处理等领域都有着广泛的应用。
在本文中,我们将对这两种分解方法进行比较分析,探讨它们的优势和局限性。
奇异值分解(Singular Value Decomposition,简称SVD)是一种将一个矩阵分解成三个矩阵的操作,通常用于降维和矩阵逆的计算。
给定一个矩阵A,它的奇异值分解可以写成A=UΣV^T,其中U和V是正交矩阵,Σ是对角矩阵,对角线上的元素称为奇异值。
特征值分解(Eigenvalue Decomposition)则是将一个方阵分解成特征向量和特征值的操作。
给定一个方阵A,它的特征值分解可以写成A=QΛQ^T,其中Q是特征向量矩阵,Λ是特征值对角矩阵。
首先,我们来比较两种分解方法的适用范围。
特征值分解只适用于方阵,而奇异值分解则可适用于任意形状的矩阵。
这使得SVD在实际应用中更加灵活,能够处理各种形状的数据。
另一方面,特征值分解在对称矩阵上有更好的性能,因为对称矩阵的特征向量是正交的,从而使得特征值分解更加简洁和高效。
其次,我们来比较两种分解方法的稳定性和数值计算的复杂度。
在数值计算中,特征值分解的计算复杂度通常高于奇异值分解,特别是在矩阵规模较大时。
此外,特征值分解对矩阵的条件数非常敏感,如果矩阵的条件数较大,计算结果可能会出现较大误差。
相比之下,奇异值分解对矩阵的条件数不太敏感,因此更加稳定。
另外,我们还可以从几何的角度来比较奇异值分解和特征值分解。
特征值分解实质上是将一个线性变换表示成一组基向量的缩放变换,而奇异值分解则是将一个线性变换表示成两个正交变换的叠加。
因此,奇异值分解能够提供更加直观的几何解释,对于理解数据的结构和特征更加有帮助。
最后,我们来谈谈两种分解方法在数据降维和信息提取方面的应用。
奇异值分解在图像压缩、信号处理等领域有着广泛的应用,能够帮助我们去除数据中的噪音和冗余信息,从而实现数据的降维和信息的提取。
特征值分解与奇异值分解

特征值:一矩阵A作用与一向量a,结果只相当与该向量乘以一常数λ。
即A*a=λa,则a 为该矩阵A的特征向量,λ为该矩阵A的特征值。
奇异值:设A为m*n阶矩阵,A H A的n个特征值的非负平方根叫作A的奇异值。
记(A)为σi上一次写了关于PCA与LDA的文章,PCA的实现一般有两种,一种是用特征值分解去实现的,一种是用奇异值分解去实现的。
在上篇文章中便是基于特征值分解的一种解释。
特征值和奇异值在大部分人的印象中,往往是停留在纯粹的数学计算中。
而且线性代数或者矩阵论里面,也很少讲任何跟特征值与奇异值有关的应用背景。
奇异值分解是一个有着很明显的物理意义的一种方法,它可以将一个比较复杂的矩阵用更小更简单的几个子矩阵的相乘来表示,这些小矩阵描述的是矩阵的重要的特性。
就像是描述一个人一样,给别人描述说这个人长得浓眉大眼,方脸,络腮胡,而且带个黑框的眼镜,这样寥寥的几个特征,就让别人脑海里面就有一个较为清楚的认识,实际上,人脸上的特征是有着无数种的,之所以能这么描述,是因为人天生就有着非常好的抽取重要特征的能力,让机器学会抽取重要的特征,SVD是一个重要的方法。
在机器学习领域,有相当多的应用与奇异值都可以扯上关系,比如做feature reduction的PCA,做数据压缩(以图像压缩为代表)的算法,还有做搜索引擎语义层次检索的LSI(Latent Semantic Indexing)另外在这里抱怨一下,之前在百度里面搜索过SVD,出来的结果都是俄罗斯的一种狙击枪(AK47同时代的),是因为穿越火线这个游戏里面有一把狙击枪叫做 SVD,而在Google上面搜索的时候,出来的都是奇异值分解(英文资料为主)。
想玩玩战争游戏,玩玩COD不是非常好吗,玩山寨的CS有神马意思啊。
国内的网页中的话语权也被这些没有太多营养的帖子所占据。
真心希望国内的气氛能够更浓一点,搞游戏的人真正是喜欢制作游戏,搞Data Mining的人是真正喜欢挖数据的,都不是仅仅为了混口饭吃,这样谈超越别人才有意义,中文文章中,能踏踏实实谈谈技术的太少了,改变这个状况,从我自己做起吧。
矩阵的特征分解和奇异值分解

矩阵的特征分解和奇异值分解在线性代数中,矩阵的特征分解和奇异值分解是两种重要的分解方法。
特征分解可以将一个方阵分解为特征向量和对应的特征值,而奇异值分解则适用于非方阵,将矩阵分解为奇异向量和对应的奇异值。
本文将详细介绍这两种分解方法的原理和应用。
一、特征分解特征分解是将一个方阵分解为特征向量和对应的特征值的过程。
对于一个n阶方阵A,存在特征向量x和对应的特征值λ,使得满足下式:Ax = λx其中λ是一个标量,x是非零向量。
特征分解的步骤如下:1. 求方阵A的特征多项式:先计算A减去λ乘以单位矩阵I的行列式,得到特征多项式。
2. 求特征多项式的根:解特征多项式的方程,得到所有特征值λ。
3. 求特征向量:对每个特征值λ,带入原方程组(A-λI)x = 0,求解齐次线性方程组,得到特征向量x。
4. 归一化特征向量:对每个特征值对应的特征向量进行归一化处理。
特征分解是一种重要的矩阵分解方式,可以用于求解线性方程组、矩阵运算和特征值问题等。
特征分解的结果可以提供矩阵的基本性质和结构信息。
二、奇异值分解奇异值分解是将一个m×n矩阵分解为奇异向量和对应的奇异值的过程。
对于一个m×n矩阵A,存在奇异向量u和v以及对应的奇异值σ,使得满足下式:Av = σu其中σ是一个非负标量,u和v是非零向量。
奇异值分解的步骤如下:1. 求矩阵A的转置矩阵A'的乘积AA'的特征值和对应的特征向量。
2. 求矩阵A的乘积A'A的特征值和对应的特征向量。
3. 计算奇异值:将特征值开根号得到矩阵A的奇异值。
4. 求解奇异向量:将特征向量与奇异值对应,得到矩阵A的奇异向量。
奇异值分解是一种常用的矩阵分解方法,它能够提取矩阵的结构信息和重要特征。
奇异值分解在信号处理、图像压缩、数据降维和推荐系统等领域得到广泛应用。
三、特征分解与奇异值分解的比较特征分解和奇异值分解都是将矩阵分解为向量和标量的过程,但它们的目的和应用场景有所不同。
线性代数基本定理

线性代数基本定理线性代数是数学中的一个重要分支,研究向量空间、线性变换、矩阵和线性方程组等概念和性质。
线性代数基本定理是线性代数中的核心定理,它揭示了矩阵的奇异值分解(SVD)和特征值分解(EVD)的重要性质。
本文将介绍线性代数基本定理及其应用。
一、奇异值分解奇异值分解是矩阵分析中最基本的分解之一,它将任意矩阵分解为三个矩阵的乘积:A=UΣV^T。
其中,U和V是正交矩阵,Σ是一个对角矩阵,对角线上的元素称为奇异值。
线性代数基本定理指出,对于任意的矩阵A,它的奇异值分解一定存在,并且是唯一的。
这意味着任何矩阵都可以通过奇异值分解进行表示,奇异值的大小和特征决定了矩阵的性质和重要特征。
奇异值分解在数据降维、图像处理、推荐系统等领域具有广泛的应用。
通过保留矩阵的主要奇异值,可以将高维数据映射到低维空间,从而减少数据的维度和冗余信息,提高计算效率和数据处理速度。
二、特征值分解特征值分解是线性代数中另一个重要的矩阵分解方法,它将一个矩阵分解为两个矩阵的乘积:A=QΛQ^(-1)。
其中,Q是正交矩阵,Λ是一个对角矩阵,对角线上的元素称为特征值。
线性代数基本定理指出,对于任意的方阵A,它的特征值分解一定存在,并且是唯一的。
特征值分解可以帮助我们理解线性变换对向量空间的作用,特征值和特征向量决定了矩阵变换的主要性质。
特征值分解在物理学、工程学、计算机科学等领域有广泛的应用。
通过求解特征值和特征向量,可以得到矩阵的主要特征和重要特性,如稳定性、动力学行为等。
特征值分解还可以用于对称矩阵的对角化和正定矩阵的判定。
三、线性代数基本定理的应用1. 数据降维奇异值分解可以将高维数据映射到低维空间,从而实现数据降维。
通过保留最重要的奇异值和对应的奇异向量,可以大大减少数据的维度,并且保留数据的主要分布和性质。
数据降维在机器学习、数据挖掘等领域具有重要意义,可以提高算法的效率和准确性。
2. 图像压缩奇异值分解可以对图像进行压缩和恢复。
矩阵的“特征值分解”和“奇异值分解”区别

矩阵的“特征值分解”和“奇异值分解”区别在信号处理中经常碰到观测值的⾃相关矩阵,从物理意义上说,如果该观测值是由⼏个(如 K 个)相互统计独⽴的源信号线性混合⽽
成,则该相关矩阵的秩或称维数就为 K,由这 K 个统计独⽴信号构成 K 维的线性空间,可由⾃相关矩阵最⼤ K 个特征值所对应的特征向量或观测值矩阵最⼤ K 个奇异值所对应的左奇异向量展成的⼦空间表⽰,通常称信号⼦空间,它的补空间称噪声⼦空间,两类⼦空间相互正交。
理论上,由于噪声的存在,⾃相关矩阵是正定的,但实际应⽤时,由于样本数量有限,可能发⽣奇异,矩阵条件数⽆穷⼤,造成数值不稳定,并且⾃相关矩阵特征值是观测值矩阵奇异值的平⽅,数值动态范围⼤,因⽽⼦空间分析时常采⽤观测值矩阵奇异值分解,当然奇异值分解也可对奇异的⾃相关矩阵进⾏。
在⾃相关矩阵正定时,特征值分解是奇异值分解的特例,且实现时相对简单些,实际中,常采⽤对⾓加载法保证⾃相关矩阵正定,对各特征⼦空间没有影响。
在信号处理领域,两者都⽤于信号的特征分析,但两者的主要区别在于:奇异植分解主要⽤于数据矩阵,⽽特征植分解主要⽤于⽅型的相关矩阵。
矩阵特征分解计算矩阵的特征值分解和奇异值分解

矩阵特征分解计算矩阵的特征值分解和奇异值分解矩阵特征分解是一种常见的矩阵分解方法,用于计算矩阵的特征值和特征向量。
而奇异值分解也是一种重要的矩阵分解技术,可以将一个矩阵分解为三个矩阵的乘积。
本文将详细介绍矩阵特征分解和奇异值分解的原理以及其在计算机科学和工程领域中的应用。
一、矩阵特征分解矩阵特征分解是一种将一个方阵分解为特征向量和特征值的方法。
对于一个n × n的方阵A,如果存在一个非零向量x和标量λ,使得Ax = λx,那么x称为A的特征向量,λ称为A的特征值。
特征向量和特征值是成对出现的,每个特征值对应一个特征向量。
特征分解的过程可以表述为:A = QΛQ^(-1),其中Q是一个由特征向量构成的矩阵,Λ是一个对角阵,对角线上的元素是A的特征值。
矩阵特征分解在很多领域都有广泛的应用,比如在物理学中用于描述振动模式,化学中用于描述分子的电子云运动,图像处理中用于特征提取和图像压缩等。
二、奇异值分解奇异值分解是一种将一个矩阵分解为三个矩阵的乘积的方法。
对于一个m × n的矩阵A,它的奇异值分解可以表述为:A = UΣV^T,其中U是m × m的正交矩阵,Σ是一个对角阵,对角线上的元素是矩阵A的奇异值,V^T是n × n的正交矩阵的转置。
奇异值分解广泛应用于数据降维、图像压缩和推荐系统等领域。
在数据降维中,通过保留较大的奇异值可以有效地提取出重要的特征,减少数据的维度;在图像压缩中,利用奇异值分解可以将图像矩阵分解为若干个部分,其中一部分的奇异值较大,可以用于恢复图像的大部分信息。
三、特征分解与奇异值分解的联系和区别虽然特征分解和奇异值分解都为矩阵分解的方法,但两者在应用场景和结果解释上有所不同。
特征分解更适用于方阵,可以得到矩阵的特征向量和特征值,用于描述矩阵的振动模式、电子云运动等。
而奇异值分解适用于任意矩阵,可以得到矩阵的奇异值和正交矩阵,常用于数据降维和图像压缩。
矩阵分解法

矩阵分解法
矩阵分解法是一种被广泛应用于矩阵和数据分析领域的数学方法,它能够对复杂的数据集进行简单而有效的分解,为更深入的分析提供基础。
本文将详细介绍矩阵分解法的基本原理及各种应用,以及它能够解决的相关问题。
矩阵分解法的基本概念是使用矩阵的特定分解技术,将一个大的复杂的矩阵分解成若干较小的更简单的矩阵,这些矩阵之间可能存在一定的关系。
最常用的矩阵分解方法是奇异值分解(Singular Value Decomposition,SVD),它能够有效地将一个矩阵分解成三个矩阵,这三个矩阵可以用来描述矩阵的行、列和特征。
其中,最重要的矩阵是特征值矩阵,它能够描述矩阵中特征之间的关系,这些特征信息可以作为进一步分析的依据。
同时,这些特征也能够影响到矩阵的值,从而有助于解决机器学习和数据挖掘中的关系推断问题,从而获得新的结论。
此外,矩阵分解还可以用于对数据进行统计和预测,这是因为矩阵分解能够提取出高维数据中隐藏的模式,从而将复杂的数据集简化为易于理解的表示形式。
因此,矩阵分解法在实际的数据分析中有着重要的应用,如文本分类、推荐系统和图像识别等。
另外,矩阵分解法还能够帮助数据科学家们解决压缩和特征选择的问题。
首先,矩阵分解能够帮助我们压缩数据集,从而节省存储空间;其次,这种方法也可以帮助我们提取出有用的特征,从而达到减少计算负担的目的。
(尾)总之,矩阵分解法是一种极其重要的数学方法,它可以帮助我们对复杂的数据集进行分解,提取有用信息,从而为进一步分析提供基础,同时还可以用于压缩和特征选择等目的。
因此,矩阵分解法可以说是数据科学领域的一个重要的数学工具,值得进一步关注和研究。
毕业论文矩阵的特征值与特征向量的求法及其关系

毕业论文矩阵的特征值与特征向量的求法及其关系矩阵的特征值和特征向量是矩阵理论中的重要概念,广泛应用于数学、物理、工程等领域。
在毕业论文中,研究矩阵的特征值和特征向量是非常具有意义的。
一、特征值与特征向量的定义给定一个n阶方阵A,如果存在数值λ和非零向量x,使得下式成立:Ax=λx其中,λ称为矩阵A的特征值,x称为矩阵A的特征向量。
二、求解特征值与特征向量的方法1.特征值的求解:要求解矩阵A的特征值,可以通过以下步骤进行:(1) 解特征方程 det(A-λI) = 0,其中I为单位矩阵。
(2)求解得到的特征方程所对应的λ的值,即为矩阵A的特征值。
2.特征向量的求解:已知矩阵A的特征值λ后,可以通过以下步骤求解矩阵A的特征向量:(1)将特征值λ代入到方程(A-λI)x=0中,并求解该齐次线性方程组。
(2)求得的非零解即为矩阵A的特征向量。
三、特征值与特征向量的关系1.特征向量之间的关系:若x1和x2分别是矩阵A相应于特征值λ1和λ2的特征向量,则对于任意实数k1和k2,k1x1+k2x2也是矩阵A相应于特征值λ1和λ2的特征向量。
2.特征值的性质:(1)矩阵A与其转置矩阵AT具有相同的特征值。
(2)对于方阵A和B,若AB=BA,则矩阵A和B具有相同的特征值。
3.特征向量的性质:(1)对于方阵A的任意特征值λ,与其对应的特征向量构成的集合形成一个向量子空间,称为A的特征子空间。
(2)若特征值λ的重数为m,则与λ相关联的特征向量的个数至少为m个。
四、应用举例特征值和特征向量在实际问题中具有广泛的应用,包括:(1)矩阵的对角化:通过矩阵的特征值和特征向量,可以将矩阵对角化,简化问题的求解。
(2)矩阵的谱分解:将矩阵表示为特征值和特征向量的线性组合形式,用于求解矩阵的高次幂和逆。
(3)矩阵的奇异值分解:奇异值分解是特征值分解的推广,能够对非方阵进行分解,用于降维和数据压缩等问题。
总结:矩阵的特征值和特征向量是矩阵理论中的重要概念。
奇异值分解与特征值分解的比较分析(Ⅰ)

奇异值分解与特征值分解是线性代数中两个重要的矩阵分解方法。
它们在数据分析、信号处理、图像压缩等领域都有着广泛的应用。
本文将对这两种分解方法进行比较分析,探讨它们的优缺点及适用范围。
一、奇异值分解(SVD)奇异值分解是一种将一个矩阵分解成三个矩阵的方法,即将一个m×n的矩阵A分解为U、Σ和V三个矩阵的乘积,其中U是一个m×m的酉矩阵,Σ是一个m×n的对角矩阵,V是一个n×n的酉矩阵。
奇异值分解有着许多优点,比如对于任意的矩阵A,都存在奇异值分解。
并且,对于奇异值分解的性质有许多重要的应用,比如在矩阵压缩和降维、矩阵逆的计算等方面。
二、特征值分解(EVD)特征值分解是一种将一个方阵分解成三个矩阵的方法,即将一个n×n的方阵A分解为P、Λ和P-1三个矩阵的乘积,其中P是一个n×n的可逆矩阵,Λ是一个n×n的对角矩阵,P-1是P的逆矩阵。
特征值分解也有着诸多优点,比如对于对称矩阵来说,特征值分解是唯一的,而且特征值分解在对称矩阵的对角化、矩阵对称化等方面有着重要的应用。
三、奇异值分解与特征值分解的比较分析1. 计算复杂度在计算复杂度方面,特征值分解的计算复杂度通常比奇异值分解高。
特征值分解需要解特征值问题,而奇异值分解只需要进行奇异值分解,因此在计算复杂度上,奇异值分解更加高效。
2. 适用范围特征值分解对于对称矩阵有着很好的适用性,而奇异值分解对于任意矩阵都有着适用性。
因此,在实际应用中,奇异值分解的适用范围更广。
3. 稳定性在矩阵的微小扰动下,特征值分解的结果可能会有较大的变化,而奇异值分解对于矩阵的微小扰动具有更好的稳定性。
因此在数值计算中,奇异值分解更加稳定可靠。
四、结论奇异值分解与特征值分解是两种重要的矩阵分解方法,它们在不同的领域有着不同的应用。
在计算复杂度、适用范围和稳定性等方面,奇异值分解相对于特征值分解具有更多的优势。
讲一下numpy的矩阵特征值分解与奇异值分解

讲⼀下numpy的矩阵特征值分解与奇异值分解1、特征值分解主要还是调包:from numpy.linalg import eig特征值分解: A = P*B*P T当然也可以写成 A = Q T*B*Q 其中B为对⾓元为A的特征值的对⾓矩阵,P=Q T,⾸先A得对称正定,然后才能在实数域上分解,>>> A = np.random.randint(-10,10,(4,4))>>> Aarray([[ 6, 9, -10, -1],[ 5, 9, 5, -5],[ -8, 7, -4, 4],[ -1, -9, 0, 6]])>>> C = np.dot(A.T, A)>>> Carray([[126, 52, -3, -69],[ 52, 292, -73, -80],[ -3, -73, 141, -31],[-69, -80, -31, 78]])>>> vals, vecs = eig(C)>>> valsarray([357.33597086, 174.10172008, 8.84429957, 96.71800949])>>> vecsarray([[-0.28738314, -0.51589436, -0.38221983, -0.71075449],[-0.87487263, 0.12873861, -0.24968051, 0.39456798],[ 0.2572149 , -0.69304313, -0.33950158, 0.58161018],[ 0.29300052, 0.48679627, -0.82237845, -0.02955945]])故使⽤时应先将特征值转换为矩阵:>>> Lambda = np.diag(vals)>>> Lambdaarray([[357.33597086, 0. , 0. , 0. ],[ 0. , 174.10172008, 0. , 0. ],[ 0. , 0. , 8.84429957, 0. ],[ 0. , 0. , 0. , 96.71800949]])>>> np.dot(np.dot(vecs, Lambda), vecs.T) # 与C=A.T*A相等array([[126., 52., -3., -69.],[ 52., 292., -73., -80.],[ -3., -73., 141., -31.],[-69., -80., -31., 78.]])>>> np.dot(np.dot(vecs.T, Lambda), vecs)array([[171.65817919, 45.58778569, 53.20435074, 13.37512137],[ 45.58778569, 125.15670964, 28.22684299, 134.91290105],[ 53.20435074, 28.22684299, 129.48789571, 80.5284382 ],[ 13.37512137, 134.91290105, 80.5284382 , 210.69721545]])故验证了使⽤np中的eig分解为A=P*B*P T⽽不是A=Q T*B*Q,其中P=vecs,即 C = vecs * np.diag(vals) * vecs.T # 这⾥简写*为矩阵乘法然后再来看使⽤np中的eig分解出来的vec中⾏向量是特征向量还是列向量是特征向量,只需验证:A*vecs[0] = vals[0]*vecs[0] >>> np.dot(C, vecs[0])array([-12.84806258, -80.82266859, 6.66283128, 17.51094927])>>> vals[0]*vecs[0]array([-102.69233303, -184.34761071, -136.58089252, -253.97814676])>>> np.dot(C, vecs[:,0])array([-102.69233303, -312.62346098, 91.91213634, 104.69962583])>>> vals[0]*vecs[:, 0]array([-102.69233303, -312.62346098, 91.91213634, 104.69962583])后者两个是相等的,故使⽤np中的eig分解出的vecs的列向量是特征向量。
矩阵分析与计算--05-矩阵分解-02-Schur、SVD

1
酉矩阵: U U
H
1
U 为酉矩阵 U的列(行)向量为C n的标准正交基
任意复方阵都可以酉相 似于一个上三角矩阵
U AU R=+N
H
定理证明:对n作数学归纳法
当n =1,结论显然成立。 假设结论对n-1的矩阵成立,下面考虑A为n方阵 取矩阵A的一个特征值为 1 ,设其对应的单位特 征向量为 1 ,则有
2.概念:酉相抵
1. 酉相抵:
酉
F 上的m n矩阵A与B称为酉相抵,如果有m阶 和n阶酉方阵U 和V , 使UAV B, 记为A B
酉相抵关系是一种等价关系!也称为“酉等价”
酉相抵标准型定理:
酉相抵标准型定理
定理3
设A F mn ,rankA = r ,记
2 specAH A 12 , 2 ,
i Ai
T i
Ai 为A的 投影阵
单纯矩阵的 谱分解
三、矩阵的奇异值分解
Singular value decomposition
(SVD)
1.概述
前面介绍的Jordan分解、Schur分解、谱分解 只适用于方阵。 对角矩阵比上三角矩阵更容易计算 奇异值分解把矩阵分解称为酉矩阵与对角矩阵 的乘积 奇异值分解基本适用于内积空间中与矩阵秩相 关的问题 A的奇异值分解依赖于正规矩阵A HA的酉相似 分解的。
Matrix Analysis and Computations
矩 阵 分 析 与 计 算 ——矩阵分解(二)
Matrix Decomposition 理学院 2011年10月
本讲主要内容 Schur分解、谱分解与奇异值分解
矩阵因式分解公式

矩阵因式分解公式是将一个矩阵分解成几个矩阵的乘积的公式。
常见的矩阵因式分解公式包括以下几种:
1. 特征值分解:对于一个$n\times n$的方阵$A$,可以将其分解为特征值和特征向量的乘积,即$A=PDP^{-1}$,其中$P$是特征向量组成的矩阵,$D$是对角矩阵,其对角线上的元素是$A$的特征值。
2. 奇异值分解:对于一个$m\times n$的矩阵$A$(其中$m\geq n$),可以将其分解为奇异值和奇异向量的乘积,即$A=UΣV^T$,其中$U$是$m\times m$的酉矩阵,$Σ$是$m\times n$的对角矩阵,其对角线上的元素是$A$的奇异值,$V$是$n\times n$的酉矩阵。
3. Cholesky 分解:对于一个正定对称矩阵$A$,可以将其分解为下三角矩阵$L$的平方,即$A=L^TL$。
4. QR 分解:对于一个$m\times n$的矩阵$A$(其中$m\geq n$),可以将其分解为一个正交矩阵$Q$和一个上三角矩阵$R$的乘积,即$A=QR$。
以上是常见的矩阵因式分解公式,不同的分解公式适用于不同的矩阵类型和问题。
矩阵奇异值的几何意义

矩阵奇异值的几何意义【原创实用版6篇】篇1 目录一、矩阵奇异值的概念二、矩阵奇异值的几何意义三、矩阵奇异值分解的应用四、结论篇1正文一、矩阵奇异值的概念矩阵奇异值(Singular Value)是指矩阵在进行奇异值分解(Singular Value Decomposition,简称 SVD)时,得到的奇异向量对应的标量值。
奇异值分解是将一个矩阵分解为三个矩阵的乘积,这三个矩阵分别是由奇异向量构成的矩阵 U、奇异值构成的对角矩阵Σ和奇异向量构成的矩阵V*(V 的共轭转置矩阵)。
二、矩阵奇异值的几何意义矩阵奇异值分解的几何意义可以从线性变换的角度来理解。
矩阵可以看作是一种线性变换,它将一个向量映射到另一个向量。
奇异值分解表示的就是这种线性变换的效果。
具体来说,奇异值分解将原始矩阵映射到一个由奇异向量构成的空间,然后在这个空间中进行缩放(通过奇异值)和旋转(通过奇异向量),最后再将结果映射回原始空间。
这样,我们就可以通过观察奇异值和奇异向量来了解原始矩阵对数据的变换效果。
三、矩阵奇异值分解的应用矩阵奇异值分解在很多领域都有广泛应用,比如机器学习、图像处理、信号处理等。
以下是一些常见的应用场景:1.矩阵降维:通过奇异值分解,我们可以找到矩阵中的主要特征方向,从而将高维数据降到低维数据,减少计算复杂度。
2.矩阵分解:奇异值分解可以将一个复杂的矩阵分解为几个简单的矩阵的乘积,从而方便我们对矩阵进行分析和处理。
3.矩阵谱聚类:奇异值分解可以用于矩阵谱聚类,即将一组矩阵按照其奇异值进行聚类。
4.推荐系统:在推荐系统中,奇异值分解可以用于对用户和物品的兴趣进行建模,从而提高推荐的准确性。
篇2 目录一、矩阵奇异值的概念与定义二、矩阵奇异值的几何意义三、矩阵奇异值分解的应用四、结论篇2正文矩阵奇异值是线性代数中一个重要的概念,它广泛应用于矩阵分解、信号处理、图像处理等领域。
矩阵奇异值的几何意义可以从矩阵的特征值分解和奇异值分解中得到。
特征分解和奇异值分解的真正意义
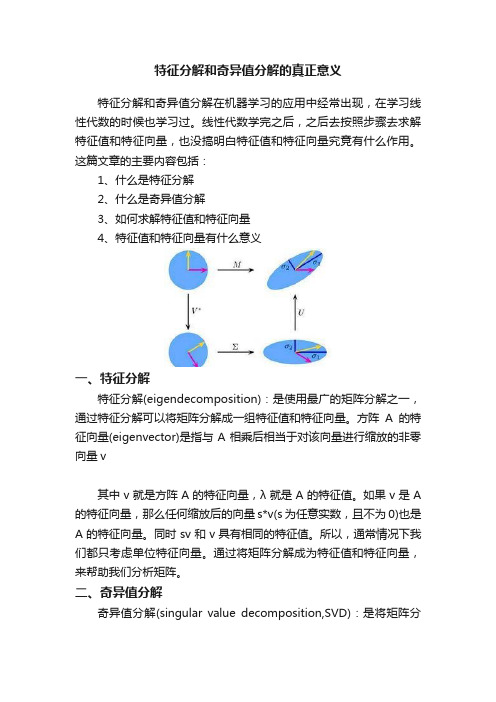
特征分解和奇异值分解的真正意义特征分解和奇异值分解在机器学习的应用中经常出现,在学习线性代数的时候也学习过。
线性代数学完之后,之后去按照步骤去求解特征值和特征向量,也没搞明白特征值和特征向量究竟有什么作用。
这篇文章的主要内容包括:1、什么是特征分解2、什么是奇异值分解3、如何求解特征值和特征向量4、特征值和特征向量有什么意义一、特征分解特征分解(eigendecomposition):是使用最广的矩阵分解之一,通过特征分解可以将矩阵分解成一组特征值和特征向量。
方阵A的特征向量(eigenvector)是指与A相乘后相当于对该向量进行缩放的非零向量v其中v就是方阵A的特征向量,λ就是A的特征值。
如果v是A 的特征向量,那么任何缩放后的向量s*v(s为任意实数,且不为0)也是A的特征向量。
同时sv和v具有相同的特征值。
所以,通常情况下我们都只考虑单位特征向量。
通过将矩阵分解成为特征值和特征向量,来帮助我们分析矩阵。
二、奇异值分解奇异值分解(singular value decomposition,SVD):是将矩阵分解成为特征值和特征向量的另一种方法,通过奇异值分解,可以将矩阵分解为奇异向量(singular vector)和奇异值(singular value)。
通过奇异值分解,我们可以得到一些与特征分解相同类型的信息。
而且,奇异值分解的应用非常广泛,如推荐系统、图片压缩等。
每一个实数矩阵都有一个奇异值分解,但不一定有特征分解。
非方阵的矩阵没有特征分解,此时我们只能使用奇异值分解。
奇异值分解,可以将矩阵A分成三个矩阵的乘积:假设A是一个m×n的矩阵,那么U是一个m×m的矩阵,D是一个m×n的矩阵,V是一个n×n的矩阵。
其中,矩阵U和V都是正交矩阵,而矩阵D是对角矩阵。
矩阵D不一定是方阵。
对角矩阵D对角线上的元素就是矩阵A的奇异值(singular value)。
矩阵的特征分解与奇异值分解

矩阵的特征分解与奇异值分解矩阵是线性代数中重要的概念之一,广泛应用于各个领域。
在矩阵的研究中,特征分解与奇异值分解是两个常用的方法。
本文将对矩阵的特征分解和奇异值分解进行详细介绍,并探讨它们在实际应用中的意义。
一、特征分解特征分解是一种将矩阵分解为特征向量和特征值的方法。
对于一个n阶方阵A,如果存在非零向量x和标量λ,使得Ax=λx成立,那么向量x称为矩阵A的特征向量,标量λ称为矩阵A的特征值。
特征分解的目的就是将矩阵A表示为特征向量和特征值的线性组合。
特征分解的步骤如下:1. 求出矩阵A的特征方程det(A-λI)=0,其中I是单位矩阵。
2. 解特征方程得到矩阵A的特征值λ。
3. 对于每一个特征值λ,求出对应的特征向量x。
4. 将特征向量和特征值组合,得到矩阵A的特征分解。
特征分解在实际应用中有广泛的用途,例如在图像处理中,可以利用特征分解对图像进行降维处理,提取图像的主要特征;在物理学中,特征分解可以用于求解量子力学中的定态问题等。
二、奇异值分解奇异值分解是一种将矩阵分解为奇异值和特征向量的方法。
对于一个m×n的矩阵A,假设它的秩为r,那么奇异值分解的结果可以表示为A=UΣV^T,其中U是一个m×r的正交矩阵,Σ是一个r×r的对角矩阵,V^T是一个r×n的正交矩阵。
奇异值分解的步骤如下:1. 求出矩阵A的转置矩阵A^T与矩阵A的乘积AA^T的特征值和特征向量。
2. 对特征值进行排序,得到矩阵A的奇异值。
3. 根据奇异值计算矩阵A的奇异向量。
4. 将奇异向量和奇异值组合,得到矩阵A的奇异值分解。
奇异值分解在数据压缩、图像处理、语音识别等领域有广泛的应用。
例如在图像处理中,可以利用奇异值分解对图像进行压缩,减少存储空间的占用;在语音识别中,奇异值分解可以用于提取语音信号的主要特征。
总结:特征分解和奇异值分解是矩阵分解的两种常用方法。
特征分解将矩阵分解为特征向量和特征值的线性组合,而奇异值分解将矩阵分解为奇异值和特征向量的线性组合。
矩阵svd分解算法

矩阵svd分解算法矩阵SVD分解算法是一种常用的矩阵分解方法。
SVD代表奇异值分解,在现代数学和计算机科学中具有广泛的应用。
矩阵SVD分解算法是一种将矩阵分解成若干个特征向量和特征值的方法,可以用于矩阵压缩、信号处理、图像处理、语音处理等领域。
下面将具体介绍矩阵SVD分解算法的实现过程。
1.矩阵的奇异值分解假设有一个矩阵A,形式如下:A=U∑V*其中,U是一个m×m的酉矩阵,Σ是一个m×n的矩阵,对角线上的元素称为奇异值,用σ1,σ2,...,σr表示,U的列向量称为左奇异向量,V的列向量称为右奇异向量。
*代表矩阵的共轭转置,也称为伴随矩阵。
2.矩阵的分解接下来我们将具体介绍矩阵SVD分解算法的实现过程。
(1)创建矩阵A,假设A是一个m×n的矩阵。
(2)求出矩阵A*A的特征向量和特征值,得到特征向量矩阵U 和特征值矩阵Σ。
(3)求出矩阵AA*的特征向量和特征值,得到特征向量矩阵V和特征值矩阵Σ。
(4)对Σ矩阵进行对角化处理,即将对角线上的元素按照降序排列。
(5)将U矩阵的各列按照Σ的降序排列,得到左奇异向量矩阵U1。
(6)将V矩阵的各列按照Σ的降序排列,得到右奇异向量矩阵V1。
(7)根据A=U1ΣV1*的形式,得到分解后的矩阵A。
3.矩阵的压缩矩阵SVD分解算法可以用于矩阵压缩。
假设A是一个m×n的矩阵,我们可以将其分解成A=U1Σ1V1*的形式,然后只保留其中的前k 个奇异值和对应的左奇异向量和右奇异向量,得到一个压缩后的矩阵Ak=UkΣkVk*,其中Uk、Σk、Vk*分别是U1、Σ1、V1*的前k列。
由于大部分的信息都被包含在前面的奇异值中,所以只保留前面的奇异值和对应的奇异向量,就能够实现对矩阵的有效压缩。
总之,矩阵SVD分解算法是一种重要的矩阵分解方法,可用于矩阵压缩、信号处理、图像处理、语音处理等领域。
SVD的分解过程包括特征向量和特征值的求解及对角化,求解过程较为复杂,但实现后可以大幅度提高矩阵计算的效率和精度。
矩阵分解公式

矩阵分解公式摘要:一、矩阵分解公式简介1.矩阵分解的定义2.矩阵分解的意义二、矩阵分解的几种方法1.奇异值分解(SVD)2.谱分解(eigenvalue decomposition)3.非负矩阵分解(NMF)三、矩阵分解在实际应用中的案例1.图像处理2.信号处理3.数据降维四、矩阵分解的发展趋势和挑战1.高维数据的处理2.矩阵分解算法的优化3.新型矩阵分解方法的研究正文:矩阵分解公式是线性代数中一个重要的概念,它涉及到矩阵的诸多操作,如矩阵的乘法、求逆、迹等。
矩阵分解的意义在于将一个复杂的矩阵简化为易于处理的形式,从而便于进行矩阵运算和数据分析。
本文将介绍几种常见的矩阵分解方法,并探讨它们在实际应用中的案例和发展趋势。
首先,我们来了解一下矩阵分解的定义。
设A是一个m×n的矩阵,矩阵分解就是将A表示为若干个矩阵的乘积,即A = UΣV*,其中U是m×m的酉矩阵(满足UU* = I),Σ是m×n的非负实对角矩阵,对角线上的元素称为奇异值,V是n×n的酉矩阵(满足VV* = I),V*是V的共轭转置。
通过矩阵分解,我们可以得到矩阵A的秩、奇异值、特征值等信息。
矩阵分解有多种方法,其中较为常见的有奇异值分解(SVD)、谱分解(eigenvalue decomposition)和非负矩阵分解(NMF)。
奇异值分解是将矩阵A分解为三个矩阵的乘积:UΣV*,其中U和V是酉矩阵,Σ是对角矩阵。
谱分解是将矩阵A分解为两个矩阵的乘积:A = UΣV*,其中U和V是酉矩阵,Σ是对角矩阵,对角线上的元素是矩阵A的特征值。
非负矩阵分解是将矩阵A分解为两个非负矩阵的乘积:A = WH,其中W和H都是非负矩阵。
矩阵分解在实际应用中有着广泛的应用,尤其在图像处理、信号处理和数据降维等领域。
在图像处理中,矩阵分解可以用于图像压缩、去噪和特征提取等任务。
在信号处理中,矩阵分解可以用于信号降噪、特征提取和频谱分析等任务。
矩阵的奇异值与特征值有什么相似之处与区别之处?-1

(当然,类比并不能代替严谨的证明;类比来自双线性代数。) 实际上,奇异值就是 的特征值。由于 是正算子,其特征值都是非负 的规范正交基(正算子是自伴的),所以
的,所以奇异值自然都是非负的。 而谱定理表明,正算子的本征向量可以组成 我们可以把 对角化,代入极分解中就得到了奇异值分解。
也就是说,极分解与谱定理共同保证了奇异值分解的可行性。 嗯,我知道后半部分写得很不清楚……但教材写得清楚呀=w= 想具体了解还是好好看教 材。 再次推荐《Linear Algebra Done Right》(中文版《线性代数应该这样学》),这本书 也是此回答的参考资料。 那么就这样=w=
由于奇异值关于不同的基,所以可以扩展到任意;但如果找不到由特征向量组成的基,就没有办法 把线性变换表示为漂亮的对角矩阵了。 此外,奇异值都是非负的,而特征值可能是负的,但这个区别光看图是看不出来的。 后者很好理解,特征值是负的就意味着有些特征向量被线性变换反向了。 而要理解前者,则需要更深入地理解奇异值分解,我这里非常简要地说一下。 先给一些定义: 有一些线性算子不改变向量的长度(范数),也就是说,对于所有的 ,这样的线性算子 被称为等距同构。 ,都有
实内积空间上的等距同构就是正交算子,复内积空间的等距同构就是酉算子。 如果线性算子 如果线性算子 等于其伴随 ,那么就称 为自伴的(self-adjoint)。 ,都有 ,那么称
是自伴的,并且对于所有的
为正的(positive)或者半正定的(positive semidefinite)。 正算子的所有特征值都是非负的。 我们可以做一个类比:每一个非零复数 都可以写成
赞同
@赵文和的答案=w= 奇异值分解把线性变换清晰地分解为旋转、缩放、投影这三 种基本线性变换。
矩阵特征值分解与奇异值分解

矩阵特征值分解与奇异值分解1.原理矩阵特征值分解是一种将一个矩阵分解为特征向量和特征值的方法。
对于一个n×n的方阵A,如果存在非零向量v和数λ,使得Av=λv,其中v为特征向量,λ为特征值,那么矩阵A的特征值分解可以表示为A=VΛV^(-1),其中V为由矩阵A的n个特征向量组成的矩阵,Λ为由特征值组成的对角矩阵。
2.性质(1)特征值的个数等于矩阵的秩;(2)特征向量组成的矩阵V是可逆矩阵;(3)特征向量组成的矩阵V的列向量是线性无关的。
3.应用(1)矩阵相似变换:特征值分解可以将一个矩阵通过相似变换转化为对角矩阵,方便矩阵的计算和分析。
(2)数据降维:特征值分解可以将高维数据降为低维,保留主要特征,有助于数据的可视化和分析。
(3)图像压缩:特征值分解可以对图像进行压缩,减少存储空间和传输带宽的占用。
1.原理奇异值分解是一种将一个m×n的矩阵分解为三个矩阵的乘积的方法。
对于一个m×n的矩阵A,其奇异值分解可以表示为A=UΣV^T,其中U为m×m的酉矩阵,Σ为m×n的对角矩阵(对角线上的元素为奇异值),V 为n×n的酉矩阵。
2.性质奇异值分解有以下几个重要的性质:(1)奇异值最大的那些对应的左奇异向量和右奇异向量是矩阵A的主要特征分量;(2)奇异值分解是矩阵的一种最优逼近,在最小二乘意义下,将一个矩阵分解为三个矩阵的乘积时,奇异值最大的那些对应的分量可以得到最小的近似误差。
3.应用奇异值分解在很多领域都有广泛的应用,例如:(1)图像处理:奇异值分解可以用于图像去噪、图像压缩和图像恢复等方面。
(2)推荐系统:奇异值分解可以用于推荐系统中的协同过滤算法,通过分解用户-物品评分矩阵,得到用户和物品的特征向量,从而进行推荐。
(3)主题模型:奇异值分解可以用于主题模型中的矩阵分解算法,通过分解文档-词项矩阵,得到文档和词项的潜在语义表示。
总结:矩阵特征值分解和奇异值分解是两种常用的矩阵分解方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
矩阵的特征值分解和奇异值分解矩阵的特征值分解和奇异值分解是线性代数中非常重要的理论和方法。
它们在很多领域都有着广泛的应用,如机器学习、图像处理、信号处理等。
本文将详细介绍矩阵的特征值分解和奇异值分解的概念、计算方法以及应用。
一、特征值分解(Eigenvalue Decomposition)
特征值分解是将一个矩阵分解为可对角化的形式,其中对角线上的元素为特征值,对应的非零特征值所对应的特征向量构成的集合构成了矩阵的特征向量矩阵。
特征值分解可以表示为以下形式:
A = PDP^{-1}
其中,A是一个n×n的矩阵,P是一个由特征向量构成的矩阵,D 是一个对角阵,对角线上的元素是矩阵A的特征值。
特征值分解可以用于解决线性方程组、矩阵对角化、矩阵幂的计算等问题。
它在降维、特征提取、谱聚类等领域也有广泛的应用。
二、奇异值分解(Singular Value Decomposition)
奇异值分解是将一个矩阵分解为三个矩阵的乘积,形式如下:
A = UΣV^T
其中,A是一个m×n的矩阵,U是一个m×m的酉矩阵,Σ是一个m×n的矩阵,对角线上的元素称为奇异值,V是一个n×n的酉矩阵的转置。
奇异值分解是一种对矩阵进行降维和压缩的方法。
它可以用于最小
二乘问题的求解、图像压缩、特征提取等领域。
在机器学习中,奇异
值分解也常用于主成分分析(PCA)方法。
三、特征值分解与奇异值分解的计算
特征值分解的计算比较复杂,需要求解矩阵的特征多项式,然后通
过求解特征多项式的根来得到特征值和特征向量。
对于大规模矩阵,
特征值分解计算的时间复杂度较高。
奇异值分解的计算相对简单,可以通过多种算法来实现,如Jacobi
迭代法、分裂法等。
在实际应用中,大部分计算都是基于奇异值分解
来进行的。
四、特征值分解与奇异值分解的应用
特征值分解和奇异值分解在科学研究和工程实践中有着广泛的应用。
以下列举几个常见的应用场景:
1. 图像处理和压缩:奇异值分解可以用于图像压缩,通过取前k个
奇异值实现图像的降维和压缩。
2. 数据降维和特征提取:奇异值分解和特征值分解可以用于降维和
特征提取,有助于减少冗余信息、提高计算效率和提取数据的主要特征。
3. 推荐系统:奇异值分解可以用于协同过滤算法,通过分解评分矩阵,找到用户和物品之间的隐含关系,从而实现个性化推荐。
4. 信号处理:特征值分解可以用于频域分析,提取信号的频谱特性。
奇异值分解可以用于音频降噪、滤波等方面。
总结:
矩阵的特征值分解和奇异值分解是线性代数中重要的理论和方法,
它们在众多领域都有着广泛的应用。
特征值分解将矩阵分解为对角阵
和特征向量矩阵,奇异值分解将矩阵分解为三个矩阵的乘积。
特征值
分解和奇异值分解在数据分析、图像处理、推荐系统等方面发挥着重
要作用。
