电力系统分析基础(第七章)n
电力系统分析第七章 同步发电机的基本方程

maD 0 0
0 maQ 0
3 2maf LRS P 1 3 2maD 0
0 0 3 2maQ
0 0 0
16
郑州航空工业管理学院
• Park方程:磁链方程
L0 m0 3 l2 2 d 0 q 0 0 f 3 maf 2 D 3 m 2 aD Q 0
2017/4/16 郑州航空工业管理学院 12
一. 派克变换 4. 物理意义: 将观察者的立场由静止的定子转移 至旋转的转子,原来定子三个静绕组 abc由两个与转子同步旋转的dq绕组代 替,实现交直流变换。 结论:经派克变换后的同步发电机的原 始方程就是一组常系数微分方程。
二. dq0坐标下的同步发电机的 等效结构 d轴方向: d(定子)、f(励磁)、D q轴方向: q(定子)、Q d轴方向相当于一个三卷变; q轴方向相当于一个双卷变; 0轴方向相当于一个单匝线圈;
7
郑州航空工业管理学院
磁链方程可记为:
abc LSS fDQ RS
LSR iabc LRR i fDQ
LSS :定子绕组间自感、互感系数矩阵
LRR :转子绕组间自感、互感系数矩阵
LRS , LSR :定转子绕组间互感系数矩阵
18
郑州航空工业管理学院
四. 电压方程的坐标变换
• Park方程:电压方程
vabc abc Rs v fDQ fDQ 0
vabc abc Rsiabc vdq 0 Pvabc P abc PRsiabc P abc Rsidq 0 dq 0 P P 1 dq 0 Rsidq 0
电力系统分析 第七章(三相短路)ppt课件

S XX 1 *
2 * x d ''* N
B 0 .1 2 5 1 0 0 0 .8 3 1 5
S G N
X 3 * X 1 0 R 0 % U 3 I N N U S B 2 B 1 0 4 03 6 0 .4 6 1 . 0 3 0 2 0 .8 7 2
U S
k 2 %B7 .5 1 0 0 1
B 2x5
B 2
4
3
第三节 恒定电势源电路的三相短路
• 恒定电势源(又称无限大功率电源),是指端电压幅值 和频率都保持恒定的电源,其内阻抗为零。
一、三相短路的暂态过程
图1-2 简单三相电路短路
•短路前电路处于稳态:
eEmsin(t ) i Im0 sin(t )
Im0
Em
(RR)22(LL)2
②恶劣天气:雷击造成的闪络放电或避雷器动作,架 空线路由于大风或导线覆冰引起电杆倒塌等。
③人为误操作,如运行人员带负荷拉刀闸,线路或设 备检修后未拆除地线就加上电压引起短路。
④挖沟损伤电缆,鸟兽跨接在裸露的载流部分等。
三、短路的危害
(1)电流剧增:设备发热增加,若短路持续时间较长,可 能使设备过热甚至损坏;由于短路电流的电动力效应, 导体间还将产生很大的机械应力,致使导体变形甚至 损坏。
B
4
T 1 N
%
%
US US T 2 x 4 * j1 0 k 2 0
B T 3 x 6 * j1 0 k 3 0
B
S S T 2 N
T 3 N
3、输电线
2
UU S S x 3 *j x 3 3
4
B 2x 3
B 2
UUU U 2 3 4
电力系统分析第七章(1)

& jX dΣ I d & jX qΣ I d
Pe ( E ′) = PU ( E ′) =
q
& Eq
& EQ
需要指出,式中δ’不是发电机的 功角,但它的变化仍能近似反映 发电机转子的相对运行,在电力 系统稳定性分析中也经常使用。 尽管E’恒定时,Pe与δ’存在正弦 关系,但与功角δ却存在较为复杂 的关系,经推导可得:
机械角加速度, 静加速转矩
J : ( kg ⋅ m 2 )
转动惯量,
A : ( rad / s 2 )
dΩ d 2 Θ Α= = 2 dt dt
如发电机的极对数为p,则实际发电机 转子的机械几何角Θ、角速度 、角加 速度A与电气角θ、电气角速度ω加速度 a。之间有如下关系
θ = pΘ ω = pΩ α = pA
′ EqU
& jX qΣ I d
& jX dΣ I d
&& Pe = PU = Re(UI * ) = U d I d + U q I q
&′ Eq
& E′
& U Gq
& Uq & Iq
& jX qΣ I q
& UG
& U
& I
δ
δ′
ϕ
& Ud
& Id
当发电机为隐极机时xd=xq
′ ′ Pe ( Eq ) = PU ( Eq ) =
X TL = X T1 + X L1 // X L2 + X T2
U d = U sin δ
& Eq
电力系统分析习题集(第七章)
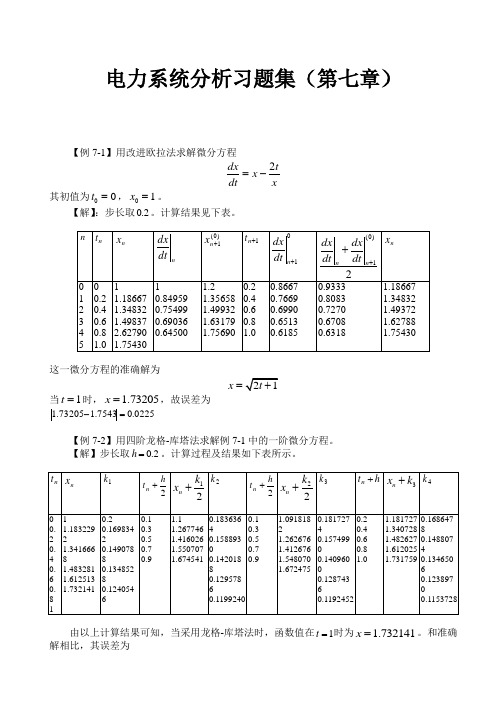
电力系统分析习题集(第七章)【例7-1】用改进欧拉法求解微分方程2dx t x dt x=- 其初值为00t =,01x =。
【解】:步长取2.0。
计算结果见下表。
这一微分方程的准确解为x =当1t =时, 1.73205x =,故误差为 0225.07543.173205.1=-【例7-2】用四阶龙格-库塔法求解例7-1中的一阶微分方程。
【解】步长取2.0=h 。
计算过程及结果如下表所示。
由以上计算结果可知,当采用龙格-库塔法时,函数值在1=t 时为 1.732141x =。
和准确解相比,其误差为.1=-0000973205.1.0732141和例7-1相比精确度提高很显著。
【例7-3】考虑图7-12所示的9节点电力系统[5]。
该系统有3台发电机、3个负荷以及9条支路。
支路数据和发电机参数分别列于表7-5和表7-6,正常运行情况下的系统潮流如表7-7所示,系统频率为60Hz。
图7-12 9节点系统单线结构图【解】下面针对该系统进行简单模型下的暂态稳定性分析。
干扰是在零秒线路5-7靠近母线7处发生三相接地短路,故障在5个周波(约0.08333秒)由断开线路5-7而被消除。
E'保持恒定来模拟,各负荷用恒定阻抗模拟,电力网络用导纳矩阵各发电机用暂态电势q描述,微分方程用改进欧拉法求解,网络方程用直接法求解。
根据图6-8中暂态稳定性分析的基本过程和上节所介绍的方法及计算公式,暂态稳定性分析可归纳如下:1) 初值计算根据式错误!未找到引用源。
计算各负荷的等值并联导纳,结果如下:负荷(节点5):50440.026099.1j - 负荷(节点6):29255.087765.0j - 负荷(节点8):33914.096898.0j -根据式错误!未找到引用源。
错误!未找到引用源。
计算各发电机的暂态电势qE '、初始功角)0(δ及其输入机械功率)0(m P ,结果如表7-8所示。
另外各发电机角速度的初值为1)0(3)0(2)0(1===ωωω。
【范文】国网考试之电力系统分析:第七章复习题---3页

第七章复习题一、选择题1、发生概率最多的短路是( )A. 三相短路B. 两相短路接地C. 两相短路D. 单相接地短路2、无限大功率电源供电的三相对称系统,发生三相短路,短路电流的非周期分量的衰减速度()A.A、B、C三相相同B.只有B、C两相相同C.只有A、B两相相同D.只有A、C两相相同3、无限大容量电源供电的简单系统三相短路暂态过程中( )A. 短路电流无限大B. 短路功率无限大C. 短路电流有周期和非周期分量D. 短路电流有2倍频分量4、由无限大容量电源供电的短路电流中,大小不变的分量是( )。
A. 直流分量B. 倍频分量C. 自由分量D. 周期分量6、短路冲击电流是指()。
短路冲击电流在()时刻出现。
(1) a. 短路电流瞬时值;b. 短路电流有效值;c. 短路电流最大瞬时值;d. 短路电流最大有效值;(2) a. 0秒;b. 半个周期; c. 一个周期7、短路冲击电流是指短路电流的()。
A.有效值B.平均值C.均方根值D.最大可能瞬时值8、冲击系数k ch的数值变化范围是( )A.0≤k ch≤1 B.1≤k ch≤2 C.0≤k ch≤2 D.1≤k ch≤39、不属于无穷大电源特点的是()A.电压恒定B.电流恒定C.功率无限大D.频率恒定10、将三个不对称相量分解为三组对称相量的方法是()A.小干扰法B.对称分量法C.牛顿—拉夫逊法D.龙格—库塔法11、输电线路的正序阻抗与负序阻抗相比,其值要()A.大B.小C.相等D.都不是12、在输电线路上各序阻抗间关系为()A.Z1>Z2B.Z2>Z1C.Z0<Z1D.Z1=Z213、单回输电线零序阻抗Z(0)和有架空地线的单回输电线零序阻抗Z(0)(w)的关系为()。
a. Z(0)大于Z(0)(w);b. Z(0)小于Z(0)(w);c. Z(0)等于Z(0)(w)14、当电力系统发生不对称短路时,变压器中性线上通过的电流为()。
电力系统稳态分析7 电力系统故障的基本知识

其中:
Im
Um
(RR)22(LL)2
tg1(LL)
RR
整理课件
(2)三相短路过程中电流分析
uaU msi nt ()
ia=? f ( 3 )
ubU msi nt (12 )0
ib=?
ucU msi nt (24 )0 ic=?
特征:对于无限大容量电源系统,发生短路过程中,由
于电源端口的电压和频率保持不变,因此,可忽略电源内
最大有效值即为短路整后理课第件一个周期内的电流有效值
将I短t公 路式T 1 冲代tt 击入T T//2 2 电,i2 d 流得tT 1tt T T//2 2(i交 + i直 )2d t=I m / 22 i直 2 I i m 短p 路电I 流m / 最2 大2 i 直 2 ( t 0 .0 1 s )I m /2 2 i i m p I m 2
也是,冲击电流产生 的条件!
短路前空载
由于X>>R,故 k 900 , 得: 00或 1800
意味着:此时电压过零。
整理课件
③ 短路冲击电流发生的时间点:
ia
短路前空载
全电流
t
电压过零点
短路后半个周
整理课件
期:T/2
④ 短路冲击电流的数学描述:
全电流表达式:
iaImsi nt (k)
t
[Imsi n ()Imsi n (k)e ]Ta ( t0)
1)发电机低压母线短路 Kimp 1.9 2)发电厂高压母线后短路 Kimp1.85 3)其他地点短路: Kimp1.80
短路冲击电流的作用:检验设备动稳定性 整理课件
IV 短路电流的最大有效值
ia
短路前空载
现代电力系统分析理论与方法 第7章 电力系统最优潮流

最优潮流计算
在系统的结构参数及负荷情况给定情况下,通过控制变量的优选, 找到能够满足所有给定的约束条件,并使系统的某一技术指标达到 最优(如网损、煤耗)时的潮流分布。
注:u为待选变量 约束条件分为等式约束条件和不等式约束条件。 采用的方法为:非线性规划
4
第一节
概述
随着电力系统规模扩大,对计算速度和系统安全性提出了更高要求,这 些经典调度理论已不能满足要求。将电力系统的潮流计算和优化理论结合, 并且计及系统的各种约束条件和电能质量,即形成了经典的优化理论—— 最优潮流(OPF)。OPF已在电力市场很多经济理论中广泛应用。
11
第二节
最优潮流的数学模型
考虑电力系统的经济因素,20世纪60年代末出现了一些经济调度理论, 例如最优分配有功负荷分布的等耗量微增率和无功电源最优分布的等网损 微增率。等耗量微增率准则是指系统所有发电机组具有同样的耗量微增率 时,系统运行所需要的费用最小,等网损微增率是指系统所有无功电源配 置具有相同的网损微增率时,系统网损最小。
最优潮 流的目 标函数
全系统火电机组燃料总费用,即 f Ki (PGi ) inG
式中:nG 为全系统所有发电机的集合,Ki (PGi ) 为第i台发 电机的耗量特性,一般用二次多项式表示,PGi 为第i台发电
机的有功出力。
有功网损,即 f (Pij Pji ) (i, j )nl 式中,nl 表示所有支路的集合。 9
可以证明最优潮流包含了等耗量微增率和等网损微增率,是这2个准则 在电力系统中的进一步发展运用(通过对目标函数的比较、约束条件的比 较、物理含义的分析等等)。
12
第三节
最优潮流的简化梯度算法
13
第三节
电力系统分析第7章习题答案

第七章 思考题及习题答案7-1 电力系统短路的分类、危害及短路计算的目的是什么?答:短路的类型有三相短路、两相短路、单相接地短路和两相接地短路。
短路对电力系统的危害有:短路电流很大,并会电气设备使发热急剧增加,导致设备因过热而损坏;导体产生很大的电动力,有可能引起设备机械变形、扭曲甚至损坏;短路时系统电压大幅度下降,会影响电气设备的正常工作;发生不对称短路时,不平衡电流所产生的不平衡磁通会对邻近的通信系统造成干扰;短路情况严重时,会导致并列运行的发电厂失去同步,破坏系统的稳定性。
短路计算目的有:设计和选择合理的发电厂、变电所及电力系统的电气主接线;选择有足够动稳定度和热稳定度的电气设备及载流导体;合理配置各种继电保护和自动装置并正确地整定其参数;分析和计算在短路情况下电力系统的稳定问题。
7-2 无限大功率电源的含义是什么?由无限大电源供电的系统三相短路时,短路电流包括几种分量?有什么特点?答:无限大功率电源是指其容量为无限大、内阻抗为零的电源。
由无限大功率电源供电的系统三相短路时,短路电流包括周期分量和非周期分量。
其特点是在外电路发生短路时,电源电压基本上保持恒定,因此周期分量不随时间而变化。
7-3 什么叫短路冲击电流?它出现在短路后的哪一时刻?冲击系数的大小与什么有关? 答:短路冲击电流是指在最严重短路情况下三相短路电流的最大瞬时值。
它出现在短路发生半个周期(0.01s )时。
冲击系数与短路回路中电抗与电阻的相对大小有关。
7-4 什么是短路功率?在三相短路计算中,对某一短路点,短路功率的标幺值与短路电流的标幺值有何关系?答:短路功率等于短路电流有效值乘以短路处的正常工作电压(一般用平均额定电压)。
短路功率的标幺值与短路电流的标幺值相等。
7-5 什么是短路电流的最大有效值?与冲击系数有什么关系?答:短路电流的最大有效值是指短路后第一周的电流有效值。
它与冲击系数的关系为2)1(21−+=imp p imp K I I7-6 什么是电力系统三相短路的实用计算?分为几个方面的内容?答:电力系统三相短路的实用计算,主要是计算系统中含多台发电机、电源并非无限大功率电源供电时,三相短路电流周期分量的有效值。
电力系统分析基础(第七章)(2)

// x0 // x0 x0 xd xq 2 2 2
2
不同状态,值不同 不同形式的值差别不大,随外电路电抗的值增大而减少 实用计算中取
x
// d
// / 2 xq
3、同步发电机的零序电抗 定子绕组的零序电流只产生定子绕组的漏磁通 // 零序电抗的变化范围为: x 0 0.15~ 0.6xd 发电机中性点通常不接地, x 0
结束
四、短路点在线路上任意处的计算公式
j f lzjk (1-l)zjk k
增加一节点,矩阵增加一阶
Zfi(=Zif)
由Zfi的定义:i点注入单位电流,其余节点注入均 为零时,f点对地电压即为Zfi
Z ji Z ki lz jk (1 l ) Z ji l Z ki Z fi U F U j I jk lz jk Z ji z jk
Z (2)
负序等值电路:
Ia ( 2)
a ( 2) U
Z (0)
Ia ( 0)
零序等值电路:
a (0) U
a ( 0) a ( 0 ) U Z (0) I
三、如何计算不对称故障序分量
a 0 U b 0 I 六个序分量,三个等值电路,还需三个式子(边界条件) c 0 I
各序分量是独立的,分序计算
各序分量是对称的,分析一相
二、各序等值电路
对如图所示的简单系统单相接地故障:
K
(1)
Z (1)
正序等值电路:
a E
Ia (1)
a (1) U
a (1) a Z (1) I a (1) U E a ( 2) a ( 2 ) U Z ( 2) I
电力系统分析第7章电力系统的潮流计算

Sa 1 Sb 2
( Z12 Z b 2 )S1 Z b 2 S2 Za 2 Z12 Z b 2 Za1 S1 ( Za1 Z12 )S2 Za 2 Z12 Z b 2
* * * * * * * * *
*
*
*
(U a U b )U N Z a 2 Z12 Z b 2
4.运算功率 发电厂的等值电源功率减去发电厂输出母线上所有相连线路的充电功率 的一半称为发电厂的运算电源功率,简称运算功率。
电力系统分析 7.3.2开式网络的潮流计算方法
第7章 电力系统的潮流计算
计算步骤:
1、计算电力网各元件参数,作电力网等值电路。 2、计算变电所的运算负荷和发电厂的运算功率,并将它们接在相应的节点上, 从而组成了只包括运算负荷和运算功率及网络参数的等值网络。 3、如果已知电源电压和末端负荷,由末端向首端逐段计算功率损耗,这种情况 由于各点电压未知,可用电网额定电压代替实际电压,求取电力网的功率分布。 求得电源功率后,再运用已知电源电压和求得的首端功率向末端逐段求电压降 落,计算出各点电压。此过程不必重新计算功率损耗,在110kv的高压电网中也 可忽略电压降落的横分量。 4如果已知末端电压和负荷,从末端开始逐段交替计算电压降落和功率损耗。向 电源端推算功率分布和各节点电压。如果有变压器,还应进行电压归算。
P2 X U 2 ( U 2 U 2 )
电力系统分析 结论
第7章 电力系统的潮流计算
电压降落的纵分量取决于所输送的无功功率的大小; 电压降落的横分量主要取决于所输送的有功功率的大小。 纵分量主要影响电压的大小, 横分量主要影响电压的相角。 (2)电压损耗:电力线路首末端或电力网任意两节点间电压的代数差。 电压损耗近似等于电压的纵分量大小
第七章 电力系统的静态稳定性分析

b
° a a’’° a’
b'' ( ),PEqb '' PEq (0) Pb '' P T P Eqb '' 0 a 如图7-2(b)中虚线所示 减速 M 0
b
a
t
b'
a
b'' °
t=0 t
b°
t=0
(a)
(a) 在a点运行; (b) 在b点运行
(b)
dp E 图7-3 d 的变化特征
0
90
180 (º)
三、静态稳定的储备
PMP M P 0 0P K % 100% % 100% 静态稳定储备系数 K p p P 0 0P PM:最大功率 P0:某一运行情况下的输送功率
正常运行时, K p 不小于15%~20%;事故后 K p 不应小于10%。
图7-2 受小干扰后功率角的变化过程
二、电力系统静态稳定的实用判据
对简单系统,静态稳定的判据为: S Eq
S Eq :称整步功率系数
dp E 0 d
dpE EqU cos 由(1)式知 d Xd
PE S Eq
δ <90º ,整步功率系数为正,稳态运行
PE
δ =90º ,整步功率系数分界点,静态稳定极限 静态稳定极限所对应的攻角与最大功率或功率极 限的功角一致。
Eq
.
jXL jXd jXT1 jXL jXT2
U 定值
.
其功-角特性关系为
Xd
PE UI cos
EqU Xd
sin
(1)
1 X d XT1 X L 2
电力系统分析考点7电力系统复杂故障分析的计算方法

网络导纳型参数方程
I1(1) I2(1)
Y11(1) Y21(1)
Y12(1) Y22(1)
U U
1(1) 2(1)
IIyy12
II12((22))
Y11(2) Y21(2)
Y12(2) Y22(2)
UU 12((22))
II12((00))
Y11(0) Y21(0)
式(4-36),并计及式(4-37),可得
Z 11 Z 21
Z12 Z 22
II12((11))
nn21((11))UU
z1 z2
0 0
(4-38)
求职俱乐部吉老师整理提供:精准可依赖
其中
Z11 Z11(1) Z11(2) Z11(0)
Z12 Z 21
n1(1) n2(1)
n2(1) n1(1)
nn21((11))
I y1 I y 2
求职俱乐部吉老师整理提供:精准可依赖
II12((22))
Y11(2)
n2(2) n1(2)
Y21(2)
n1(2) n2(2)
Y12(2)
Y22(2)
U U
1(2) 2 (2)
I1(0) I2 (0)
Y11(0) Y21(0)
Z11(1)
n2(1) n1(1)
Z 21(1)
(4-31) n1(1)
n2(1)
Z12(1)
Z 22(1)
I1(1) I2 (1)
nn21((11))UU
z1 z2
再列出负序网络的两端口网络阻抗型参数
方程
U U
1(2) 2(2)
Z 11( 2) Z 21(2)
Z12(2) Z 22(2)
电力系统分析-第七章复习题3页

第七章复习题一、选择题1、发生概率最多的短路是( )A. 三相短路B. 两相短路接地C. 两相短路D. 单相接地短路2、无限大功率电源供电的三相对称系统,发生三相短路,短路电流的非周期分量的衰减速度()A.A、B、C三相相同B.只有B、C两相相同C.只有A、B两相相同D.只有A、C两相相同3、无限大容量电源供电的简单系统三相短路暂态过程中( )A. 短路电流无限大B. 短路功率无限大C. 短路电流有周期和非周期分量D. 短路电流有2倍频分量4、由无限大容量电源供电的短路电流中,大小不变的分量是( )。
A. 直流分量B. 倍频分量C. 自由分量D. 周期分量6、短路冲击电流是指()。
短路冲击电流在()时刻出现。
(1) a. 短路电流瞬时值;b. 短路电流有效值;c. 短路电流最大瞬时值;d. 短路电流最大有效值;(2) a. 0秒;b. 半个周期; c. 一个周期7、短路冲击电流是指短路电流的()。
A.有效值B.平均值C.均方根值D.最大可能瞬时值8、冲击系数k ch的数值变化范围是( )A.0≤k ch≤1 B.1≤k ch≤2 C.0≤k ch≤2 D.1≤k ch≤39、不属于无穷大电源特点的是()A.电压恒定B.电流恒定C.功率无限大D.频率恒定10、将三个不对称相量分解为三组对称相量的方法是()A.小干扰法B.对称分量法C.牛顿—拉夫逊法D.龙格—库塔法11、输电线路的正序阻抗与负序阻抗相比,其值要()A.大B.小C.相等D.都不是12、在输电线路上各序阻抗间关系为()A.Z1>Z2B.Z2>Z1C.Z0<Z1D.Z1=Z213、单回输电线零序阻抗Z(0)和有架空地线的单回输电线零序阻抗Z(0)(w)的关系为()。
a. Z(0)大于Z(0)(w);b. Z(0)小于Z(0)(w);c. Z(0)等于Z(0)(w)14、当电力系统发生不对称短路时,变压器中性线上通过的电流为()。
电力系统分析第7章

0 rD 0
0 i f 0 i D iQ rQ
(7.2)
为交链到转子绕组的磁链。
阻尼绕组为短路回路,电压为零,u D 0 , uQ 0
•
发电机各绕组的磁链是由本绕组的自感磁链和 其他绕组与本绕组间的互感磁链组成,各绕组 的磁链方程:
•磁链方程的派克变换形式
d Ld 0 q 0 0 3 f 2 maf D 3 2 maD Q 0 0 Lq 0 0 0 3 2 maQ 0 0 L0 0 0 0 maf 0 0 Lf mr 0 maD 0 0 mr LD 0 0 id i maQ q 0 i0 0 if 0 iD LQ iQ
定子绕组与直轴阻尼绕组间的互感系数
M aD maD cos M bD maD cos( 120 ) M cD maD cos( 120 )
定子绕组与交轴阻尼绕组间的互感系数
M aQ maQ cos( 90 ) M bQ mbQ cos( 30 ) M cQ mcQ cos( 150 )
ZB UB IB
(7.23)
•
转子侧基准值
转子侧基准值有多种选择方法。可将同步发电机看 做等效变压器,设n和nf分别为定子一相绕组和励磁 绕组的有效匝数。匝数比k=n/nf。 励磁绕组的基准值为: u fB uB
k
fB
B
k
3 i f B iB k 2 u fB B fB z fB i
因为a、b绕组在空间相差120度,a相绕组的负值 电流所产生的磁链为正值时,交链到b相绕组为负 磁ቤተ መጻሕፍቲ ባይዱ,故Mab恒为负值,且Mab=Mba。
第7章电力系统短路分析

在某些情况下,高额定电压的电抗器可以装在低额 定电压的系统上,在计算电抗器电抗的标幺值时, 当电抗器的额定电压与所装系统的额定电压不同级 时,仍 2021/7/30 采用电抗器本身的额定电压值;同级时,也
(4)鸟兽跨接在裸露的载流部分以及风、雪、雹等自 然灾害也会造成短路。
2021/7/30
➢ 短路对电力系统正常运行和电气设备有很大的 危害。 在发生短路时,由于供电回路的阻抗减小以 及突然短路时的暂态过程,使短路点及其附近 设备流过的短路电流值大大增加,可能超过该 回路额定电流许多倍。短路点距发电机的电气 距离愈近(即阻抗愈小),短路电流愈大。
2021/7/30
2.短路电流造成的后果
(1)短路电流的热效应会使设备发热急剧增加 ,可能导致设备过热而损坏甚至烧毁;
(2)短路电流将在电气设备的导体间产生很大 的电动力,可引起设备机械变形、扭曲甚至损 坏;
(3)短路电流基本上是电感性电流,它将产生 较强的去磁性电枢反应,从而使发电机的端电 压下降,同时短路电流流过线路使其电压损失 增加。
I d Sd 3U d
Z d U d
3I d
U
2 d
Sd
(7-4)
2021/7/30
它们的标幺值分别为
S * U *I *
U
*
Z *I *
I
*
I
Id
3U d I Sd
Z * R*
jX * Sd R
U
2 d
j Sd X
U
2 d
(7-5)
在标幺制中,三相电路计算公式与单相计算公式完 全相同。因此,有名单位制中单相电路的基本公式 ,可直接应用于三相电路中标幺值的运算。
电力系统故障分析第七章电力系统振荡分析课件

当 M N 11 EM EN E 时:
EM EN Ee jMt Ee jNt E(e j(M -N )t 1)e jNt E(e jσ 1)e jNt
(M N )t st
振荡电流幅值为:
I E ejσ 1= 2E sin s t 2E sin
Z11
Z11
2
Z11
2
振荡电流作周期性平滑变化:
③振荡中电压与电流的相位差是变化的,而短路故障中电压与电流之间的 相位差基本保持不变。
④振荡中心的电压在 180 时为0,相当于在振荡中心发生三相短路, 但是与三相短路故障还是有区别的。如是振荡,即使振荡中心在线路上, 两侧流过相同的振荡电流;如在振荡中心发生三相短路,尽管振荡中心电 压为0,但是线路两侧电流均流向故障点。
教学目的:
➢建立电力系统振荡的概念 ➢掌握电力系统振荡时电气量的变化特点 ➢掌握识别振荡和故障的方法
第一节 振荡时电气量变化分析
振荡产生的原因:
系统短路故障切除较慢;系统联系薄弱,线路输送功率超过静稳定极限;系 统无功不足,引起电压降低;线路非同期重合闸;同步发电机励磁降低或消 失等。
稳定振荡或同步振荡:
压最大达E;当 180 时,为最小值0,从电压角度看相当于在Z点发 生了三相短路,此时必然会甩掉负荷。
UZ UP cos 90
如果P点是母线M,则U P 就是保护安装处电压,振荡电流 I 和振荡电压 UP
均可以从保护安装处测得,意味着振荡中心电压也可以在保护安装处测 得。
四、系统母线电压与振荡电流的相位关系
两部分等值电动势的夹角摆动范围没有超过,并经过若干摆动后又恢复同步 运行的情况.
非稳定振荡或非同步振荡:
两部分等值电动势的夹角摆动范围超过,并经过若干摆动后不能恢复同步运 行的情况 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
级
•采用平均电压后简化计算,无需考虑变压器变比归算
•1、发电 机
•2、变压 器
•3、输电 线
•四、短路回路总电抗标幺值XdΣ计算
•1、绘制计算电路图 ✓用单相节线图表示—计算电路图 ✓标明各元件额定参数 ✓各元件均按顺序编号
•0.4Ω/km
•6
•15km
•27.5MVA •4
•Uk%=7.5
•6K V•400A •XR%=4
•b •a
•第四节 计算机计算复杂系统短路电流交流分量初值的原理
•数学模型—网络的线性代数方程(网络节点方程) •一、等值网 络
•二、用节点阻抗矩阵的计算方法
•特征:
•满阵存储量 •大形成计算量 大•修改麻烦
•在故障分量网络中,只有故障点f有注入电流- ,故有:
•三、用节点导纳矩阵的计算方法
•三、短路冲击电流ich和冲击系数kch •id的最大瞬时值——短路冲击电流ich • 出现在t=T/2时
• kch与R,X的大小有关:R=0时, kch=2; L=0时, kch=1
•1≤ kch ≤ 2
•发电机母线时kch=1.9, ich =2.7 Idz •高压电网时kch=1.8, ich =2.55 Idz
Idf非周期分量出现的物理原因是:电感中电流不能突 变
•二、产生最大短路全电流的条件 •稳态分量—取决于短路后的电路
•短路全电流 •暂态分量—和短路时刻、短路前运行状态及回 路阻抗有关
•要使短路全电流最大——使暂态分量最大(无载,一相过零) •短路前电路为空载:Im=0
•电压“合闸相角”α=0 •Φd=π/2,纯电感电 路
•2、高压电网只计及电抗,当RdΣ< XdΣ/3时,忽略RdΣ
•二、各元件统一基准值电抗标幺值计算
•在第二章中,将额定值下的标幺值归算到统一基准值下的标幺值
•在短路计算中,一般采用近似计算法,认为 •额定电压UN =平均电压Upj ,基准电压Uj =Upj •1、同步发电 机 •2、变压器
•3、线路 •4、电抗器
例题P72例3-2
习题
1
•第二节 应用运算曲线求任意时刻短路点的短路电 流
• 由于计算任意时刻的短路电流,涉及到不同时段的时间常 数和电抗值及指数运算,因此工程上一般采用运算曲线来计 算。
•一、运算曲线的制定
•发电机计算电抗 :
•(注意:发电机额定值下的标么值)
➢ 改变XL的值,得到不同的I*(t),对于不同的时刻t,以计算 电抗Xjs为横坐标,I*为纵坐标,所得的点连成运算曲线。
➢ 不同的发电机参数不同,运算曲线是不同的(见附录C,P247)
•二、应用运算曲线计算短路电流的方法 •1、计算步骤 1) 网络化简,得到各电源对短路点得转移阻抗Xif。
2) 将各电源对短路点得转移阻抗Xif归算到各发电机额 定参数下得计算电抗Xjsi。 Xjsi= Xif×SNi/SB
3) 查曲线,得到以发电机额定功率为基准值得各电源 送至短路点电流得标么值
•d(3)
•L
•R’ •L’
•三相短路是对称 故障,可用一相分 析
•Ub •R •L •Uc •R •L
•R’ •L’ •R’ •L’
➢短路前
•Z
•Z
’
•U
➢短路后
一阶常系数线性微分方 程
•R •L •id
•U
•R •L ’’
idz周期分量(强制分量) Idf非周期分量(自由分量)
➢如何确定A(楞次定律)
•Idf经0.2s衰减完毕,
•在无限大容量,
•二、有名制法
•适用于: 1KV以下的低压系统和电压等级少、接线简单的高压系统 ➢ 短路点所在电压级作为基本级
➢ 各元件的阻抗用变压器的近似变比归算到基本级,求出
电源至短路点的总阻抗ZΣ ➢ 计及电阻时
不计电 阻
➢ 计算冲击电流、最大有效值、断路器的短路容量 •kch=1.8时, ich =2.55 Idz
•S=∞
•2
•10.5K V
•d(3)
•X=0
•1
•3
•115KV
•100k m•0.4Ω/km
•220MVA
•Uk%=10.
解:①有名制法:取10.5KV电压5级为基本级
•d(3)
•等值电路
•Upj=10.5KV
➢回路总阻抗 ➢周期分量有效值 ➢冲击电流 ➢全电流最大有效值 ➢短路容量
②标幺制法:取 Sj=100MVA,Uj=Upj
4) 求得各电流得有名值之和,即为短路点得短路电流。
•2、计算的简化 • 把短路电流变化规律大体相同的发电机合并成等值机。 一般将接在同一母线(非短路点)上的发电机合并。
例题P80例3-4
•第三节 转移阻抗及其求法
•转移阻抗Zif的定义:任一复杂网络,经网络化简消去了除 电源电势和短路点以外的所有中间节点,最后得到的各电源 与短路点之间的直接联系阻抗为转移阻抗。
•转移阻抗Zif的物理意义:除Ei外,其余电动势均为零(短 路接地),则Ei与此时f点电流之比值即为电源i与短路点f之 间的转移阻抗。
•1、网络化简法 • 消去了除电源电势和短路点以外的所有中间节点,最后 得到的各电源与短路点之间的直接联系阻抗为转移阻抗
•2、单位电流法 •对辐射形网络,用该方法最好
电力系统分析基础(第七 章)n
2020年7月21日星期二
•电力系统故障分析的主要内容
•在电专业课中——电力系统故障分析
•三相短路电流分析与计算 •同步发电机突然三相短路分析 •电力系统三相短路的实用计算 •对称分量法及电力系统元件的各序参数和等值电路 •不对称故障的分析与计算 •复故障的分析与计算
短路电流的计算主要是求短路电流周期分量的起始值
,即次暂态电流
等值法
计算方法主要 有
叠加原理法 运算曲线法 转移阻抗法
•第一节 交流电流初始值计算
•一、简单系统 计算—等值法 1) 计算故障前正常运行时的潮流分布。首先求得各发 电机(包括短路点附近得大型电动机)的端电压和定子 电流,然后计算它们的次暂态电动势。
短路类型
示意图
符号 发生的机率
•对称
三相短路 二相短路
d(3)
5%
d(2)
10%
•不对 称
二相接地短路
d(1,1)
20%
单相接地短路
d(1)
65%
•二、产生的原因 •绝缘被破坏
•过电压、雷击 •风、雪、鸟、兽等
•绝缘老化、污染
•设计、安装、维护不当,人为因素
•三、产生的危害
•引起发热:10~20倍额定电流,达几万甚至几十万安 •引起电动力效应:传导体变形甚至损坏—机械稳定性 •引起网络中电压降落 •使稳定性遭到破坏 •短路可能干扰通信系统
•
注意:没让UN=Uj
是因为电抗器有时不按额
定电压使用
•三、具有变压器的多电压级网络标幺值等值电路的建立(近似法)
•G •Ⅰ •T1
•Ⅱ
•T2
•Ⅲ
•T3 •Ⅳ
•x1
•x2
•x3
• x4
•x5 • x6
•U1
•U2
•U3
•U4
•x1*j •x2*j •x3*j •x4*j •x5*j •x6*j
•取U4为基本
➢三角分解法求解节点导纳方程 •节点导纳方程:I=YU •Y为非奇异的对称阵,按三角分解法:Y=LDLT= R•DTD为R对角阵;L为单位下三角阵;R为单位上三角阵;且L= RT
•式中d、l和r为D、L、和R的相应元素
•节点导纳方程:YU=I
RTDRU=I
•分解为三个方程: RTW=I
•kch=1.8时, Ich =1.52 Idz
•三、标幺值法 •适用于: 多电压等级、接线复杂的高压系统 ➢取基准值Sj,Upj ➢ 计算短路电流周期分量标幺值
➢ 计算三相短路容量的标幺值
➢ 计算有名值
•四、例题
• 如图所示电路发生三相短路,试分别用有名制法和标幺
制法计算Idz、ich、Ich和Sd(Kch=1.8)
(d),分别求解可得最终结果。
•(a)
•j0.
•k
1
•M
•j0. 2
•j0.
•k
1
•j0. 2
•(b
)
•j0.
•j0.
•k
1
2
•j0.
•j0.
2
2
•(d
•(c
)
)
•利用叠加原理的解题步骤: 1) 由正常运行等值电路(c) ,求出网络中各节点的正常 电压和各支路的正常电流,如: 2) 由故障分量等值电路(d) ,求出网络中各节点电压变 化量和各支路电流的变化量,如: 3) 将正常和故障分量相叠加,可得故障后各节点电压和 各支路电流,如:
•三、措施
•限制短路电流(加电抗器) •继电保护快切 •结线方式 •设备选择
•第二节 无限大容量电源供电系统三相短路过渡过程分析
•无限大电源——恒压源(内阻=0) ➢短路不影响电源的U,f(Z=0,U=C,S=∞) ➢实际内阻<短路回路总阻抗10%,即无限个有限源组成
•一、暂态过程分析
•Ua •R
• ich用于校验电气设备和载流导体的电动力稳定性
•四、短路全电流最大有效值Ich
• 假设idf的数值在第一个周波内是恒定不变的,t=T/2时值
•1≤ kch ≤ 2
•发电机母线时kch=1.9, Ich =1.62 Idz •高压电网时kch=1.8, Ich =1.52 Idz
• 不管求ich还是求Ich,只须求得Idz,而求Idz的关键是求由电 源开始到短路点的总阻抗ZdΣ
•特征:
•稀疏阵 •形成容 易•修改方 便
