100测评网高中数学复习文化练习

合集下载

100测评网高二数学练习卷高中排列、组合与二项式定理练习题.doc

株洲市十七中高二排列、组合与二项式定理测试卷一、选择题：（本人题共10小题，每小题5分，共50分）1.若从集合P到集合Q={a,b,c}所冇不同的映射共冇81个，则从集合Q到集合P可作的不同的映射共冇（）A. 32 个B. 27 个C. 81 个D. 64 个2.某班举行联欢会，原定的五个节目已排出节目单，演出前乂增加了两个节目，若将这两个节目插入原节目单中，则不同的插法总数为（）A. 42B. 36C. 30D. 123.全班48名学生坐成6排，每排8人，排法总数为P,排成前后两排，每排24人，排法总数为Q,则冇（）A. P>QB. P=QC. P<QD.不能确定4.从正方体的六个面小选取3个面，其小有2个面不相邻的选法共有（）种A. 8B. 12C. 16D. 205.12名同学分别到三个不同的路口进行车流量的调查，若每个路口4人，则不同的分配A. B. D.方案共冇（）6.某单位准备用不同花色的装饰石材分别装饰办公楼中的办公室、走廊.大厅的地而及楼的外墙，现有编号为1〜6的六种不同花色的装饰石材可选择，具屮1号石材有微量的放射性, 不可用于办公室内，则不同的装饰效果有（）种A. 350B. 300C. 65D. 507.有8人已站成一排，现在要求其中4人不动，其余4人重新站位，则有（）种重新站位的方法A. 1680B. 256C. 360D. 2808.一排九个坐位有六个人坐，若每个空位两边都坐有人，共有（）种不同的坐法A. 7200B. 3600C. 2400D. 12009.在（Jg + J舌）"的展开式中，所有奇数项一项式系数Z和等J - 1024,则中间项的二A.462B. 33()C.682D.792项式系数是（）10.在（1 + d x）7的展开式屮，x'项的系数是/项系数与xh页系数的等比中项，则d的值为（）5二、填空题（本大题共5小题，每小题4分，共20分）11.某公园现有A、B、C三只小船，A船可乘3人，B船可乘2人，C船可乘1人，今有三个成人和2个儿童分乘这些船只（每船必须坐人），为安全起见，儿童必须由人人陪同方可乘船，他们分乘这些船只的方法有__________________ 种。

100测评网东海高级中学高二文科数学模拟试题三

高二文科数学期末模拟试题（三）命题人：李顺之审核人：李美玲一、填空题：1．4张卡片上分别写有数字1，2，3，4，从这4张卡片中随机抽取2张，则取出的2张卡片上的数字之和为奇数的概率为______________________。

2．从某项综合能力测试中抽取100人的成绩，统计如表，则这100人成绩的标准差为______________________。

3．若方程2212516x y m m+=-+表示焦点在y 轴上的椭圆，则实数m 的取值范围是____________. 4．抛物线的顶点在原点，对称轴为坐标轴，焦点在直线01243=--y x 上，则抛物线的方程为______________________。

5．双曲线12222=-by a x （a ＞0，b ＞0）左右焦点分别是F 1、F 2，过F 2与x 轴垂直的弦PQ ，且∠PF 1Q=60°则双曲线的离心率等于______________________。

6．已知二次函数()x f 的图象如图1所示 , 则其导函数()x f'的图象大致形状是（）7．“双曲线的方程为221916x y -=”是“双曲线的准线方程为“95x =±”的______________条件。

（填充分不必要、必要不充分、充分必要）8．如图2所示，函数)(x f y =的图象在点P 处的切线方程是8+-=x y ，则()5f = ，()5f '= ．9．已知各个命题A 、B 、C 、D ，若A 是B 的充分不必要条件，C 是B 的必要不充分条件，D 是C 的充分必要条件，则D 是A 的条件.10．阅读图4的程序框图，若输入4m =，3n =，则输出a =，i = ． 11．函数x x x f ln 2)(2-=在定义域的一个子区间()1,1+-k k 上不是单调函数，则实数k 的取值范围是 .12．在曲线106323-++=x x x y 的切线中斜率最小的切线方程是___________________.13．函数x x x f ln 2)(2-=在定义域的一个子区间()1,1+-k k 上不是单调函数，则实数k 的取值范围是___________________.14．若偶函数)(x f ，当+∈Rx 时，满足,0)1(,)()(=>'f x x f x f 且则的解0)(≥xx f 集是___________________.二、解答题15．某初级中学共有学生2000名，各年级男、女生人数如下表：已知在全校学生中随机抽取1名，抽到初二年级女生的概率是0.19. （1）求x 的值；（2）现用分层抽样的方法在全校抽取48名学生，问应在初三年级抽取多少名？已知y ≥245,z ≥245,求初三年级中女生比男生多的概率.图416．已知曲线32:x x y S -=.（1）利用导数的定义来求函数)(x f y =的导数；（2）求曲线S 在点)1,1(A 处的切线方程；（3）求过点)0,2(B 并与曲线S 相切的直线方程.17．一炮弹在A 处的东偏北60°的某处爆炸，在A 处测到爆炸信号的时间比在B 处早4秒，已知A 在B 的正东方、相距6千米， P 为爆炸地点，（该信号的传播速度为每秒1千米）求A 、P 两地的距离．18．已知命题：“}11|{<<-∈∃x x x ，使等式02=--m x x 成立”是真命题，（1）求实数m 的取值集合M ；（2）设不等式()(2)0x a x a -+-<的解集为N ，若x ∈N 是x ∈M 的必要条件，求a 的取值范围．19．已知()()()f x x x a x b =--．（Ⅰ）若1a b ==，求函数()f x 的单调递增区间；（Ⅱ）若函数()f x 的导函数()f x '满足：当1x ≤时，有()f x '≤23恒成立，求函数()f x 的解析式．20．已知函数2()ln f x x b x =-在(1,2]是增函数，()g x x =-在(0,1)为减函数．（1）求b 的值；（2）求函数)(x g 的极值；（3）设函数21()2h x ax x =-是区间(0,1]上的增函数，且对于]1,0(内的任意两个变量 s 、t ，()()f s h t ≥恒成立，求实数a 的取值范围．11、[)[)∞+-，10,1 15.（1）380……4分（2）12……5分（3）115………5分17．解：以直线AB 为x 轴，线段AB 的垂直平分线为y 轴，建立直角坐标系，则A （3，0）、B （－3，0）614||||<⨯=-PA PB 3,5,2===∴c b a15422=-∴y x P 是双曲线右支上的一点 …………6分∵P 在A 的东偏北60°方向，∴360tan == AP k ． ∴线段AP 所在的直线方程为)3(3-=x y …8分解方程组⎪⎪⎪⎩⎪⎪⎪⎨⎧>>-==-0)3(315422y x x y y x⎩⎨⎧==358y x 得，即P 点的坐标为（8，35） ………10分∴A 、P 两地的距离为22)350()83(-+-=AP =10（千米）．………12分18、解：（1）已知命题：“∃x ∈{x |–1< x <1}，使等式x 2–x –m = 0成立”是真命题，得f (x )= x 2–x –m = 0在（-1，1）有解， …………2分由对称轴x =12，则140(1)110m f m ∆=+≥⎧⎨-=+->⎩， (4)分得m ∈1,24⎡⎫-⎪⎢⎣⎭. ……………7分（或由02=--m x x 得x x m +=2求得结论也给分）（2）不等式()(2)0x a x a -+-<1、当a a ->2，即1>a 时解集N 为（a -2,a ），若x ∈N 是x ∈M 的必要条件，则M ⊆N, ∴a 的取值范围29,1424a a a ≥⎧⎪∴>⎨-<-⎪⎩. ……………10分2、当a a >-2，即1<a 时解集N 为（a ,a -2），若x ∈N 是x ∈M 的必要条件，则M ⊆N,∴a的取值范围221,144a a a -≥⎧⎪∴<-⎨<-⎪⎩. 13分19a (,)(,)44∈-∞-+∞综上． …15分19、解：(Ⅰ) x x x x f +-=232)(, 143)('2+-=x x x f 2分令'()0f x ≥得01432≥+-x x ，解得113x x ≤≥或故()f x 的增区间1(,]3-∞和[1,)+∞ 6分（注：区间写成开区间也可以，但写成1(,]3-∞或．[1,)+∞及1(,]3-∞⋃[1,)+∞者扣2分）（Ⅱ）f '(x)=ab x b a x ++-)(232 当x ∈[-1，1]时，恒有|f '(x)|≤23. 故有23-≤f '(1)≤23，23-≤f '(-1)≤23，及23-≤f '(0)≤23, 9分即33 32() ,2233 32() ,2233 .22a b ab a b ab ab ⎧-≤-++≤⎪⎪⎪-≤+++≤⎨⎪⎪-≤≤⎪⎩………………………………… …12分①+②，得29-≤ab ≤23-，又由③，得ab =23-， 14分将上式代回①和②，得0=+b a ，故x x x f 23)(3-=. 15分20、解：（1）()2b f x x x'=-，由题意0)(≥'x f 在(1,2]x ∈恒成立，即22b x ≤恒成立，∴2b ≤ (2)分；()1g x '=-又，由题意()0g x '≤在(0,1)x ∈恒成立，即b ≥2b ≥.……2分 ∴2b =.…………………………5分（2）由（1）得x x x g 2)(-=，∴xx xx g 111)('-=-=……………………7分∴ 当1)0(，∈x 时，0)('<x g ；当)1(∞+∈，x 时，0)('>x g ………………9分∴ 函数)(x g 有极小值1)1(-=g ；无极大值。

100测评网江苏省东海高级中学高二数学期末复习考前训练2

ˆ 3.5 0.7 4.5 0.35 ˆ Y bX a
x 100 ,
y 100 0.7 0.35 70.35 吨,
f ( x)
所求的回归方程为
y 0.7 x 0.35 (3)

0
-
0

预测生产 100 吨甲产品的生产能耗比技改前降低 90 70.35 19.65 (吨) 18．解（1） e
16 5 7 20 5 .、 .、 1 . 36 9 36 36 9
100
16（理）． 45． 16.（文）解：（I）当 x 40 时，汽车从甲地到乙地行驶了 40
1 3 ( 403 40 8) 2.5 17.5 128000 80 （升）。
2.5
3．下列流程图运行输出的结果为
2 2 4. 已知定点 A(2, 3) ， F 是椭圆 x y 1 的右焦点， M 是椭圆上
15、箱子中装有 6 张卡片，分别写有 1 到 6 这 6 个整数. 从箱子中任意取出一张卡片，记下它的读数 x ，然后放回箱子，第二次再从箱子中取出一张卡片，记下它的读数 y ，试求： (Ⅰ) 率； (Ⅱ)
3 2
10．设等边 ABC 的边长为 a ， P 是 ABC 内的任意一点，且 P 到三边 AB, BC, CA 的距离分别为
d1 , d 2 , d 3 ，则有 d1 d 2 d 3 为定值
3 ；由以上平面图形的特性类比空间图形：设正四面体 a 2
ABCD 的棱
欢迎登录《100 测评网》进行学习检测，有效提高学习成绩.
6、若实数 a、b 满足函数 f ( x) 是 .

1
1
f ( x)dx =

100测评网高二数学练习卷两平面的平行的判定和性质

典型例题一例1：已知正方体1111-D C B A ABCD ．求证：平面//11D AB 平面BD C 1．证明：∵1111-D C B A ABCD 为正方体，∴B C A D 11//，又 ⊂B C 1平面BD C 1，故 //1A D 平面BD C 1．同理 //11B D 平面BD C 1．又 1111D B D A D = ， ∴ 平面//11D AB 平面BD C 1．说明：上述证明是根据判定定理1实现的．本题也可根据判定定理2证明，只需连接C A 1即可，此法还可以求出这两个平行平面的距离．典型例题二例2：如图，已知βα//，a A ∈，α∈A β//a ．求证：α⊂a ．证明：过直线a 作一平面γ，设1a =αγ ，b =γβ ．∵βα// ∴b a //1又β//a∴b a //在同一个平面γ内过同一点A 有两条直线1,a a 与直线b 平行∴a 与1a 重合，即α⊂a ．说明：本题也可以用反证法进行证明．典型例题三例3：如果一条直线与两个平行平面中的一个相交，那么它和另一个也相交．已知：如图，βα//，A l =α ．求证：l 与β相交．证明：在β上取一点B ，过l 和B 作平面γ，由于γ与α有公共点A ，γ与β有公共点B ．∴γ与α、β都相交．设a =αγ ，b =γβ ． ∵βα// ∴b a //又l 、a 、b 都在平面γ内，且l 和a 交于A ． ∵l 与b 相交．所以l 与β相交．典型例题四例4：已知平面βα//，AB ，CD 为夹在a ，β间的异面线段，E 、F 分别为AB 、CD 的中点．求证： α//EF ，β//EF ．证明：连接AF 并延长交β于G ． ∵F CD AG =∴ AG ，CD 确定平面γ，且AC =αγ ，DG =βγ ．∵βα//，所以 DG AC //， ∴ GDF ACF ∠=∠，又 DFG AFC ∠=∠，DF CF =， ∴ △ACF ≌△DFG ． ∴ FG AF =．又 BE AE =，∴ BG EF //，β⊂BG ．故 β//EF ．同理α//EF说明：本题还有其它证法，要点是对异面直线的处理．典型例题六例6 如图，已知矩形ABCD 的四个顶点在平面上的射影分别为1A 、1B 、1C 、1D ，且1A 、1B 、1C 、1D 互不重合，也无三点共线．求证：四边形1111D C B A 是平行四边形．证明：∵α⊥1AA ， α⊥1DD∴11//DD AA不妨设1AA 和1DD 确定平面β．同理1BB 和1CC 确定平面γ．又11//BB AA ，且γ⊂1BB ∴γ//1AA 同理γ//AD 又A AD AA = 1∴γβ//又11D A =βα ，11C B =γα∴1111//C B D A ．同理1111//D C B A ．∴四边形1111D C B A 是平行四边形．典型例题七例7 设直线l 、m ，平面α、β，下列条件能得出βα//的是（）． A ．α⊂l ，α⊂m ，且β//l ，β//m B ．α⊂l ，β⊂m ，且m l // C ．α⊥l ，β⊥m ，且m l // D ．α//l ，β//m ，且m l //分析：选项A 是错误的，因为当m l //时，α与β可能相交．选项B 是错误的，理由同A ．选项C 是正确的，因为α⊥l ，l m //，所以α⊥m ，又∵β⊥m ，∴βα//．选项D 也是错误的，满足条件的α可能与β相交．答案：C说明：此题极易选A ，原因是对平面平行的判定定理掌握不准确所致．本例这样的选择题是常见题目，要正确得出选择，需要有较好的作图能力和对定理、公理的准确掌握、深刻理解，同时要考虑到各种情况．典型例题八例8 设平面α⊥平面γ，平面β⊥平面γ，且α、β分别与γ相交于a 、b ，b a //．求证：平面α//平面β．分析：要证明两平面平行，只要设法在平面α上找到两条相交直线，或作出相交直线，它们分别与β平行（如图）．证明：在平面α内作直线PQ ⊥直线a ，在平面β内作直线MN ⊥直线b ． ∵平面α⊥平面γ，∴PQ ⊥平面γ，MN ⊥平面γ， ∴MN PQ //．又∵p a //，Q a PQ = ，N b MN = ， ∴平面α//平面β．说明：如果在α、β内分别作γ⊥PQ ，γ⊥MN ，这样就走了弯路，还需证明PQ 、MN 在α、β内，如果直接在α、β内作a 、b 的垂线，就可推出MN PQ //．由面面垂直的性质推出“线面垂直”，进而推出“线线平行”、“线面平行”，最后得到“面面平行”，最后得到“面面平行”．其核心是要形成应用性质定理的意识，在立体几何证明中非常重要．典型例题九例9 如图所示，平面α//平面β，点A 、C α∈，点β∈D B 、，a AB =是α、β的公垂线，CD 是斜线．若b BD AC ==，c CD =，M 、N 分别是AB 和CD 的中点，(1)求证：β//MN ； (2)求MN 的长．分析：（1）要证β//MN ，取AD 的中点P ，只要证明MN 所在的平面β//PMN ．为此证明β//PM ，β//PN 即可．(2)要求MN 之长，在CMA ∆中，CM 、CN 的长度易知，关键在于证明CD MN ⊥，从而由勾股定理可以求解．证明：(1)连结AD ，设P 是AD 的中点，分别连结PM 、PN ． ∵M 是AB 的中点，∴BD PM //．又β⊂BD ，∴β//PM ．同理∵N 是CD 的中点，∴AC PN //． ∵α⊂AC ，∴α//PN ．∵βα//，P PM PN = ，∴平面β//PMN ． ∵MN ⊂平面PMN ，∴β//MN ． (2)分别连结MC 、MD ． ∵b BD AC ==，a BM AM 21==，又∵AB 是α、β的公垂线，∴︒=∠=∠90DBM CAM ， ∴ACM Rt ∆≌BDM Rt ∆，∴DM CM =， ∴DMC ∆是等腰三角形．又N 是CD 的中点，∴CD MN ⊥．在CMN Rt ∆中，22222421c a b CN CM MN -+=-=．说明：(1)证“线面平行”也可以先证“面面平行”，然后利用面面平行的性质，推证“线面平行”，这是一种以退为进的解题策略．(2)空间线段的长度，一般通过构造三角形、然后利用余弦定理或勾股定理来求解． (3)面面平行的性质：①面面平行，则线面平行；②面面平行，则被第三个平面所截得的交线平行．典型例题十例10 如果平面α内的两条相交直线与平面β所成的角相等，那么这两个平面的位置关系是__________．分析：按直线和平面的三种位置关系分类予以研究．解：设a 、b 是平面α内两条相交直线．(1)若a 、b 都在平面β内，a 、b 与平面β所成的角都为︒0，这时α与β重合，根据教材中规定，此种情况不予考虑．(2)若a 、b 都与平面β相交成等角，且所成角在)90,0(︒︒内； ∵a 、b 与β有公共点，这时α与β相交．若a 、b 都与平面β成︒90角，则b a //，与已知矛盾．此种情况不可能．(3)若a 、b 都与平面β平行，则a 、b 与平面β所成的角都为︒0，α内有两条直线与平面β平行，这时βα//．综上，平面α、β的位置关系是相交或平行．典型例题十一例11 试证经过平面外一点有且只有一个平面和已知平面平行．已知：α平面∉A ，求证：过A 有且只有一个平面αβ//．分析：“有且只有”要准确理解，要先证这样的平面是存在的，再证它是惟一的，缺一不可．证明：在平面α内任作两条相交直线a 和b ，则由α∉A 知，a A ∉，b A ∉．点A 和直线a 可确定一个平面M ，点A 和直线b 可确定一个平面N ．在平面M 、N 内过A 分别作直线a a //'、b b //'，故'a 、'b 是两条相交直线，可确定一个平面β． ∵α⊄'a ，α⊂a ，a a //'，∴α//'a ．同理α//'b ．又β⊂'a ，β⊂'b ，A b a =''，∴αβ//．所以过点A 有一个平面αβ//．假设过A 点还有一个平面αγ//，则在平面α内取一直线c ，c A ∉，点A 、直线c 确定一个平面ρ，由公理2知：m =ρβ ，n =ργ ，∴c m //，c n //，又m A ∈，n A ∈，这与过一点有且只有一条直线与已知直线平行相矛盾，因此假设不成立，所以平面β只有一个．所以过平面外一点有且只有一个平面与已知平面平行．典型例题十二例12 已知点S 是正三角形ABC 所在平面外的一点，且SC SB SA ==，SG 为SAB ∆上的高，D 、E 、F 分别是AC 、BC 、SC 的中点，试判断SG 与平面DEF 内的位置关系，并给予证明分析1：如图，观察图形，即可判定//SG 平面DEF ，要证明结论成立，只需证明SG 与平面DEF 内的一条直线平行．观察图形可以看出：连结CG 与DE 相交于H ，连结FH ，FH 就是适合题意的直线．怎样证明FH SG //？只需证明H 是CG 的中点．证法1：连结CG 交DE 于点H ， ∵DE 是ABC ∆的中位线， ∴AB DE //．在ACG ∆中，D 是AC 的中点，且AG DH //， ∴H 为CG 的中点．∵FH 是SCG ∆的中位线，∴SG FH //．又SG ⊄平面DEF ，FH ⊂平面DEF ， ∴//SG 平面DEF ．分析2：要证明//SG 平面DEF ，只需证明平面SAB //平面DEF ，要证明平面DEF //平面SAB ，只需证明DF SA //，EF SB //而DF SA //，EF SB //可由题设直接推出．证法2：∵EF 为SBC ∆的中位线， ∴SB EF //．∵⊄EF 平面SAB ，⊂SB 平面SAB ， ∴//EF 平面SAB ．同理：//DF 平面SAB ，F DF EF = ，∴平面SAB //平面DEF ，又∵⊂SG 平面SAB ， ∴//SG 平面DEF ．典型例题十三例13 如图，线段PQ 分别交两个平行平面α、β于A 、B 两点，线段PD 分别交α、β于C 、D 两点，线段QF 分别交α、β于F 、E 两点，若9=PA ，12=AB ，12=BQ ，ACF ∆的面积为72，求BDE ∆的面积．分析：求BDE ∆的面积，看起来似乎与本节内容无关，事实上，已知ACF ∆的面积，若BDE ∆与ACF ∆的对应边有联系的话，可以利用ACF ∆的面积求出BDE ∆的面积．解：∵平面AF QAF =α ，平面BE QAF =β ，又∵βα//，∴BE AF //．同理可证：BD AC //，∴FAC ∠与EBD ∠相等或互补，即EBD FAC ∠=∠sin sin ．由BE FA //，得212412∶∶∶∶===QA QB AF BE， ∴AF BE 21=由AC BD //，得：73219∶∶∶∶===PB PA BD AC ，∴AC BD 37=．又∵ACF ∆的面积为72，即72sin 21=∠⋅⋅FAC AC AF ． ∴EBD BD BE S DBE ∠⋅⋅=∆sin 21FAC AC AF ∠⋅⋅⋅=sin 372121 FAC AC AF ∠⋅⋅⋅=sin 2167 847267=⨯=． ∴BDE ∆的面积为84平方单位．说明：应用两个平行的性质一是可以证明直线与直线的平行，二是可以解决线面平行的问题．注意使用性质定理证明线线平行时，一定第三个平面与两个平行平面相交，其交线互相平行．典型例题十四例14 在棱长为a 的正方体中，求异面直线BD 和C B 1之间的距离．分析：通过前面的学习，我们解决了如下的问题：若a 和b 是两条异面直线，则过a 且平行于b 的平面必平行于过b 且平行于a 的平面．我们知道，空间两条异面直线，总分别存在于两个平行平面内．因此，求两条异面直线的距离，有时可以通过求这两个平行平面之间的距离来解决．具体解法可按如下几步来求：①分别经过BD 和C B 1找到两个互相平等的平面；②作出两个平行平面的公垂线；③计算公垂线夹在两个平等平面间的长度．解：如图，根据正方体的性质，易证：1111111//////D CB BD A C D B A D B BD 平面平面⇒⎭⎬⎫连结1AC ，分别交平面BD A 1和平面11D CB 于M 和N因为1CC 和1AC 分别是平面ABCD 的垂线和斜线，AC 在平面ABCD 内，BD AC ⊥ 由三垂线定理：BD AC ⊥1，同理：D A AC 11⊥ ∴⊥1AC 平面BD A 1，同理可证：⊥1AC 平面11D CB ∴平面BD A 1和平面11D CB 间的距离为线段MN 长度．如图所示：在对角面1AC 中，1O 为11C A 的中点，O 为AC 的中点 ∴a AC NC MN AM 333111====． ∴BD 和C B 1的距离等于两平行平面BD A 1和11D CB 的距离为a 33．说明：关于异面直线之间的距离的计算，有两种基本的转移方法：①转化为线面距．设a 、b 是两条异面直线，作出经过b 而和a 平行的平面α，通过计算a 和α的距离，得出a 和b 距离，这样又回到点面距离的计算；②转化为面面距，设a 、b 是两条异面直线，作出经过b 而和a 平行的平面α，再作出经过a 和b 平行的平面β，通过计算α、β之间的距离得出a 和b 之间的距离．典型例题十五例15 正方体1111D C B A ABCD -棱长为a ，求异面直线AC 与1BC 的距离．解法1：（直接法）如图：取BC 的中点P ，连结PD 、1PB 分别交AC 、1BC 于M 、N 两点，易证：MN DB //1，AC DB ⊥1，11BC DB ⊥． ∴MN 为异面直线AC 与1BC 的公垂线段，易证：a DB MN 33311==．小结：此法也称定义法，这种解法是作出异面直线的公垂线段来解．但通常寻找公垂线段时，难度较大．解法2：（转化法）如图：∵//AC 平面B C A 11，∴AC 与1BC 的距离等于AC 与平面B C A 11的距离，在1OBO Rt ∆中，作斜边上的高OE ，则OE 长为所求距离， ∵a OB 22=，a OO =1， ∴a B O 231=，∴a B O OB OO OE 3311=⋅=．小结：这种解法是将线线距离转化为线面距离．解法3：（转化法）如图：∵平面1ACD //平面B C A 11，∴AC 与1BC 的距离等于平面1ACD 与平面B C A 11的距离． ∵⊥1DB 平面1ACD ，且被平面1ACD 和平面B C A 11三等分；∴所求距离为a D B 33311=．小结：这种解法是线线距离转化为面面距离．解法4：（构造函数法）如图：任取点1BC Q ∈，作BC QR ⊥于R 点，作AC PK ⊥于K 点，设x RC =，则x a QR BR -==，KR CK =，且222CR CK KR =+∴2222121x CR KR ==．则222)(21x a x QK -+=2223131)32(23a a a x ≥+-=，故QK 的最小值，即AC 与1BC 的距离等于a 33．小结：这种解法是恰当的选择未知量，构造一个目标函数，通过求这个函数的最小值来得到二异面直线之间的距离．解法5：（体积桥法）如图：当求AC 与1BC 的距离转化为求AC 与平面B C A 11的距离后，设C 点到平面B C A 11的距离为h ，则1111BCC A B C A C V V --=． ∵222131)2(4331a a a h ⋅⋅=⋅， ∴a h33．即AC 与1BC 的距离等于a 33．小结：本解法是将线线距离转化为线面距离，再将线面距离转化为锥体化为锥体的高，然后用体积公式求之．这种方法在后面将要学到．说明：求异面直线距离的方法有：(1)（直接法）当公垂线段能直接作出时，直接求．此时，作出并证明异面直线的公垂线段，是求异面直线距离的关键．(2)（转化法）把线线距离转化为线面距离，如求异面直线a 、b 距离，先作出过a 且平行于b 的平面α，则b 与α距离就是a 、b 距离．（线面转化法）．也可以转化为过a 平行b 的平面和过b 平行于a 的平面，两平行平面的距离就是两条异面直线距离．（面面转化法）．(3)（体积桥法）利用线面距再转化为锥体的高用何种公式来求．(4)（构造函数法）常常利用距离最短原理构造二次函数，利用求二次函数最值来解．两条异面直线间距离问题，教科书要求不高（要求会计算已给出公垂线时的距离），这方面的问题的其他解法，要适度接触，以开阔思路，供学有余力的同学探求．典型例题十六例16 如果βα//，AB 和AC 是夹在平面α与β之间的两条线段，AC AB ⊥，且2=AB ，直线AB 与平面α所成的角为︒30，求线段AC 长的取值范围．解法1：如图所示：作β⊥AD 于D ，连结BD 、CD 、BC∵BD AB >，DC AC >，222BC AC AB =+，∴在BDC ∆中，由余弦定理，得：022cos 222222=⋅-+<⋅-+=∠CDBD BC AC AB CD BD BC CD BD BDC ．∵β⊥AD ，∴ABD ∠是AB 与β所在的角．又∵βα//，∴ABD ∠也就等于AB 与α所成的角，即︒=∠30ABD ．∵2=AB ，∴1=AD ，3=BD ，12-=AC DC ，24AC BC +=，∴01324131222<-⋅---+≤-AC AC AC ，即：31102≤-<AC ．∴332≥AC ，即AC 长的取值范围为⎪⎪⎭⎫⎢⎣⎡∞+,332．解法2：如图：∵AC AB ⊥∴AC 必在过点A 且与直线AB 垂直的平面γ内设l =βγ ，则在γ内，当l AC ⊥时，AC 的长最短，且此时ABC AB AC ∠⋅=tan33230tan =︒⋅AB 而在γ内，C 点在l 上移动，远离垂足时，AC 的长将变大，从而332≥AC ，即AC 长的取值范围是⎪⎪⎭⎫⎢⎣⎡∞+,332．说明：(1)本题考查直线和直线、直线和平面、平面和平面的位置关系，对于运算能力和空间想象能力有较高的要求，供学有余力的同学学习．(2)解法1利用余弦定理，采用放缩的方法构造出关于AC 长的不等式，再通过解不等式得到AC 长的范围，此方法以运算为主．(3)解法2从几何性质角度加以解释说明，避免了繁杂的运算推导，但对空间想象能力要求很高，根据此解法可知线段AC 是连结异面直线AB 和l 上两点间的线段，所以AC 是AB 与l 的公垂线段时，其长最短．典型例题十七例17 如果两个平面分别平行于第三个平面，那么这两个平面互相平行．已知：γα//，γβ//，求证：βα//．分析：本题考查面面平行的判定和性质定理以及逻辑推理能力．由于两个平面没有公共点称两平面平行，带有否定性结论的命题常用反证法来证明，因此本题可用反证法证明．另外也可以利用平行平面的性质定理分别在三个平面内构造平行且相交的两条直线，利用线线平行来推理证明面面平行，或者也可以证明这两个平面同时垂直于某一直线．证明一：如图，假设α、β不平行，则α和β相交．∴α和β至少有一个公共点A ，即α∈A ，β∈A ． ∵γα//，γβ//， ∴γ∉A ．于是，过平面γ外一点A 有两个平面α、β都和平面γ平行，这和“经过平面外一点有且只有一个平面与已知平面平行”相矛盾，假设不成立。

100测评网随堂步步高高三数学单元测试卷(共18套)试题

⑵若对于任何实数b，函数恒有两相异的不动点，求实数a的取值范围；
⑶在⑵的条件下，若的图象上A、B两点的横坐标是函数的不动点，且直线是线段AB的垂直平分线，求实数b的取值范围．
高三数学·单元测试卷(二)
第二单元函数
(时量:120分钟150分)
一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．
7．设数列{an}是公比为a(a≠1)，首项为b的等比数列，Sn是前n项和，对任意的n∈N＋，点(Sn，Sn+1)在
A．直线y＝ax－b上B．直线y＝bx＋a上
C．直线y＝bx－a上D．直线y＝ax＋b上
8．数列{an}中，a1＝1，Sn是前n项和，当n≥2时，an＝3Sn，则的值是
A．－2B．－ C．－ D．1
⑵若|x1|<2且|x1－x2|＝2，求b的取值范围．
高三数学·单元测试卷(三)
第三单元数列
(时量:120分钟150分)
一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，
只有一项是符合题目要求的．
1．数列－1，，－，，…的一个通项公式是
A．an＝(－1)n B．an＝(－1)n
16．（本小题满分12分）
二次函数f(x)满足f(x＋1)－f(x)＝2x且f(0)＝1．
⑴求f(x)的解析式；
⑵在区间[－1，1]上，y＝f(x)的图象恒在y＝2x＋m的图象上方，试确定实数m的范围．
17．（本小题满分12分）
已知集合A＝，B＝．
⑴当a＝2时，求A B；
⑵求使B A的实数a的取值范围．
A．线段AB和线段ADB．线段AB和线段CD

100测评网高二(文科)数学试题参考答案

官桥中学2006~2007学年度第一学期期末考试高二（文科）数学试题参考答案一、选择题(5’×10=50’)CABDD DBCBC 二、填空题（5’×4=20’）11、－3 12、12 13、k 10≤ 14、（甲）1 （乙）109三、解答题：15. 解：（1）()2cos 22sin(2)6f x x x x π=+=+…………4分22T ππ== …………6分（2）由3222()262k x k k Z πππππ+≤+≤+∈得263k x k ππππ+≤≤+，…………10分所以，减区间为2[,]()63k k k Z ππππ++∈ …………12分 16、解：⑴∵{a n }为公比为q 的等比数列，a n+2＝12n na a ++（n ∈N *）∴a n ·q 2＝2n na q a + …………2分即2q 2―q ―1＝0 解得q ＝－12或 q ＝1 …………4分 ∴a n ＝112n -⎛⎫- ⎪⎝⎭或a n ＝1 …………6分⑵当a n ＝1时，b n ＝n ， S n ＝1＋2＋3＋…＋n ＝()12n n + …………8分当a n ＝112n -⎛⎫- ⎪⎝⎭时b n ＝n ·112n -⎛⎫- ⎪⎝⎭S n ＝1＋2·（－12）＋3·212⎛⎫- ⎪⎝⎭＋…＋（n －1）·212n -⎛⎫- ⎪⎝⎭＋n ·112n -⎛⎫- ⎪⎝⎭①－12 S n ＝（－12）＋2·212⎛⎫- ⎪⎝⎭＋…＋（n －1）·112n -⎛⎫- ⎪⎝⎭＋n 12n⎛⎫- ⎪⎝⎭②…………10分①—②得32 S n ＝1＋12⎛⎫- ⎪⎝⎭＋212⎛⎫- ⎪⎝⎭＋…＋112n -⎛⎫- ⎪⎝⎭－n 12n⎛⎫- ⎪⎝⎭＝112112n⎛⎫-- ⎪⎝⎭+－n ·12n⎛⎫- ⎪⎝⎭ ＝ ⎪⎭⎫⎝⎛-⋅-⎪⎭⎫ ⎝⎛--21213232n n…………13分⎪⎭⎫⎝⎛-⋅-⎪⎭⎫ ⎝⎛--=2132219494n S nn …………14分17．(Ⅰ)证明: ∵O 是AC 的中点，D 是AB 的中点∴OD//BC,又BC ⊆平面SCD,OD ⊄平面SCD∴ OD//平面SBC; …………………………………7分(Ⅱ) 证明:SAC ∆是正三角形, O 是AC 的中点，∴SO AC ⊥.又∵平面SAC ⊥平面ABC ，∴SO ACB ⊥平面，∴SO AB ⊥. …………………………………14分18、解：设分别采用甲、乙两种原料各y x ,千克，可生产产品z 千克，…………………1分依题意，约束条件为⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+0024.05.065.1y x y x y x …………………6分目标函数为=z y x 10090+把目标函数化为100109z x y +-=，当直线100109z x y +-=的纵截距取最大值时，z 也取最大值。

100测评网东海高级中学高二文科数学模拟试题五

___．
2 7．已知命题 p : “ x [1, 2], x2 a 0 ” ，命题 q ： “ x Rx , a x2 a 2
0
”若命
题“ p 且 q ”是真命题，则实数的取值范围为
.
x2 y2 8.椭圆＋＝1上一点 M 到右准线的距离是 6，则点 M 到该椭圆左焦点的距离是 16 12
2 1 ,n 3 3

1 3 , ] 4 4
18.（1）
（2） OM ON 4 （2）最小的正整数 k 为 2008

19.（1） m
20.（1） W 2000 t st ，当 t （2） y 1000 (
2
10002 时，乙方获得最大利润。 s2
2
欢迎登录《100 测评网》进行学习检测，有效提高学习成绩.
参考答案: 一、填空题 1. S1 S 2.充分不必要 8.5 3. y 2 x 1 9. x2 8 y 14.③④ 4. a 1 10. 34 1 5. [1, 2) 6. (
y2 x2 1 表示双曲线的_____________的条件. k 3 k 3 x 3.已知曲线 C： f ( x) sin x e ，则在 x=0 处切线方程为 .
4．已知条件 p :| x 1| 2, 条件 q : x a , 且 p 是 q 的充分不必要条件，则 a 的取值范围可以是 _____________. 5．若是假命题，则 x 的取值范围是 “x 2,5 或 x x x 1或x 4 ” 6．函数 y x 2sin x 在（0，2 ）内的单调增区间为 ______．
欢迎登录《100 测评网》进行学习检测，有效提高学习成绩.

100测评网东海高级中学高二文科数学期末模拟四

东海高级中学高二文科数学期末模拟四命题人：张允倩审核人：刘艳洁一、填空题：（本大题共14小题，每小题5分，共70分．）1．已知条件:|1|2,p x +>条件:,q x a >且p ⌝是q ⌝的充分不必要条件，则a 的取值范围是．2．已知双曲线22221(0,0)x y a b a b -=>>的两条渐近线方程为y x =，若顶点到渐近线的距离为1，则双曲线方程为． 3．曲线sin ln x y e x x =-+在2x π=处的切线的斜率为．4．已知，y 的取值如下表所示：从散点图分析，y 与x 线性相关，且ˆ0.95yx a =+，则a 的值为． 5．为了了解高三学生的身体状况．抽取了部分男生的体重，将所得的数据整理后，画出了频率分布直方图(如图)，已知图中从左到右的前3个小组的频率之比为1︰2︰3，第2小组的频数为12，则抽取的男生人数是． 6．离心率为21，长轴长为8的焦点在x 轴上的椭圆标准方程为． 7．向面积为S 的ABC ∆内任投一点P ,则PBC ∆的面积小于2S的概率为． 8．某篮球学校的甲、乙两名运动员练习罚球，每人练习10次，每次罚球40个.命中个数的茎叶图如右图．则罚球命中率较高的运动员是． 9．如果双曲线的两个焦点分别为12(3,0),(3,0)F F -，一条渐近线方程为x y 2=，则该双曲线的方程为．10．直线b x y +=2是曲线x x y ln =的一条切线，则实数b ＝ __________0．0．11．若抛物线px y 22=的焦点与椭圆12622=+y x的右焦点重合，则p 的值为． 12．根据如图所示的伪代码，输出结果为．I←1While I ＜8 S←2I+3 I←I+2 End While Print S 13．右图给出的是计算201614121+⋅⋅⋅+++的值的一个程序框图,其中判断框内应填入对i14．如图:已知P 为抛物线24y x =上的动点，过P 作y 轴与直线40x y -+=的垂线，垂足分别为A 则PA +PB 的最小值为．二、解答题：（本大题共6小题,共90分.解答应写出文字说明,证明过程或演算步骤．） 15．设函数32()33f x x ax bx =-+的图像与直线1210x y +-=相切于点(1,11)-．（1）求,a b 的值；（2）讨论函数()f x 的单调性16．设p ：方程221122x y m m +=-+表示双曲线；q ：函数324()()63g x x mx m x =++++在R 上有极大值点和极小值点各一个．求使“p 且q ”为真命题的实数m 的取值范围．17．设12,F F 分别是椭圆2222:1x y C a b+=(0)a b >>的左、右焦点（1）若椭圆C 上的点3(1,)2A 到12,F F 两点的距离之和等于4，写出椭圆C 的方程和焦点坐标；（2）设点P 是（1）中所得椭圆上的动点，1(0,)2Q ，求PQ 的最大值；18．如图所示，F 1、F 2分别为椭圆C ：)0(12222>>=+b a by a x 的左、右两个焦点，A 、B为两个顶点，已知椭圆C 上的点)23,1(到F 1、F 2两点的距离之和为4.（1）求椭圆C 的方程和焦点坐标；（2）过椭圆C 的焦点F 2作AB 的平行线交椭圆于P 、Q 两点，求△F 1PQ 的面积.19．(本题满分14分)如图，已知矩形ABCD 的一边AB 在x 轴上，另两个顶点C ，D 落在抛物线弧y = -x 2+2x (0＜x ＜2) 上．设点C（1）将矩形ABCD 的面积S (x )表示为x 的函数；（2）求S (x )的最大值．20．（本小题满分18分）设常数0a ≥，函数2()ln 2ln 1f x x x a x =-+-((0,))x ∈+∞. （1）令()()g x xf x '=(0)x >，求()g x 的最小值，并比较()g x 的最小值与零的大小；（2）求证：()f x 在(0,)+∞上是增函数；（3）求证：当1x >时，恒有2ln 2ln 1x x a x >-+．模拟练习参考答案：1．2,10x R x ∀∈+≥；2．(1,0)；3．22e ππ+；4．2.6；5．48；6．1121622=+yx ；7．43；8．甲； 9．17；10.4 11 10i >(或填11i =)；12．22136x y -=；13.l 1225-;14．D 15．解：（1）求导得2()363f x x ax b '=-+,由于()f x 的图像与直线1210x y +-=相切于点(1,11)-,所以(1)11(1)12f f =-⎧⎨'=-⎩即1331136312a b a b -+=-⎧⎨-+=-⎩, 解得1,3a b ==-（2）由1,3a b ==-得：22()3633(23)3(1)(3)f x x ax b x x x x '=-+=--=+- 令()0f x '>，解得1x <-或3x >；由()0f x '<，解得13x -<<．故函数()f x 在区间(,1),(3,)-∞-+∞上单调递增，在区间(1,3)-上单调递减.16．解：∵方程221122x y m m +=-+表示双曲线，∴(12)(2)0m m -+<，即2m <-或12m >∵函数324()()63g x x mx m x =++++在R 上有极大值点和极小值点各一个， ∴24()3203g x x mx m '=+++=有两个不同的解1212,()x x x x <，即△＞0，由△＞0，得m ＜－1或m ＞4．又当1(,)x x ∈-∞时，()0g x '>，()g x 在1(,)x -∞上单调递增；当12(,)x x x ∈时，()0g x '<，()g x 在12(,)x x 上单调递减；当2(,)x x ∈+∞时，()0g x '>，()g x 在2(,)x +∞上单调递增，∴12,x x 分别是函324()()63g x x mx m x =++++的极大值点和极小值点．要使“p 且q ”为真命题，则p ，q都是真命题，∴ 12,24214m m m m m m ⎧<->⎪<->⎨⎪<->⎩或解得或或m ∴的取值范围是(,2)(4,)-∞-+∞.17．解：（1）椭圆C 的焦点在x 轴上，由椭圆上的点A 到12,F F 两点的距离之和是4，得24a =即2a =，又3(1,)2A 在椭圆上，223()1212b∴+=，解得23b =，于是21c =所以椭圆C 的方程是22143x y +=，焦点12(1,0),(1,0)F F -设(,)P x y ，则22143x y +=，22443x y ∴=-222222214111713()4()52343432PQ x y y y y y y y =+-=-+-+=--+=-++又3y -≤≤∴当32y =-时，max PQ 18．解：（1）由题设知：2a = 4，即a = 2；将点)23,1(代入椭圆方程得2223()1212b+=，解得b 2 = 3；∴c 2 = a 2－b 2 = 4－3 = 1，故椭圆方程为22143x y +=，焦点F 1、F 2的坐标分别为（-1，0）和（1，0），（2）由（1）知)3,0(),0,2(B A -，23==∴AB PQ k k ， ∴PQ 所在直线方程为)1(23-=x y，由221)143y x x y ⎧=-⎪⎪⎨⎪+=⎪⎩得 2890y +-=，设P (x 1，y 1)，Q (x 2，y 2)，则121298y y y y +=⋅=-，12y y ∴-1121211222F PQ S F F y y ∆=⋅-=⨯19．解：因点C 的横坐标为x ，故C 的纵坐标为y = -x 2+2x ，B 的坐标(x ，0)，A (2-x ，0)．矩形ABCD 的面积为()(22)S x x y =-2(22)(2)x x x =--+32264x x x =-+-（1＜x ＜2）．令 2()61240S x x x '=-+-= ，得 1x =．由于11x =-，故舍去，于是1x =+．当x ∈(1，2)时，()S x '的符号如下：此时，S = 322(16(14(1-++-+ ． 20．解：（1）∵()(ln )(ln )2ln 1f x x x x a x =-+-，(0,)x ∈+∞ ∴112()1[ln (ln )]a f x x x x x x '=-⨯+⨯+， 2ln 21x ax x=-+，∴()()2ln 2g x xf x x x a '==-+，(0,)x ∈+∞ ∴22()1x g x x x-'=-=，令()0g x '=，得2x =，列表如下：∴()g x 在2x =处取得极小值(2)22ln 22g a =-+，即()g x 的最小值为(2)22ln 22g a =-+,(2)2(1ln 2)2g a =-+，∵ln 21<，∴1ln 20->，又0a ≥，∴(2)0g >．证明：（2）由（1）知，()g x 的最小值是正数，∴对一切(0,)x ∈+∞，恒有()()0g x xf x '=>，从而当0x >时，恒有()0f x '>，故()f x 在(0)+，∞上是增函数．证明：（3）由（2）知：()f x 在(0)+，∞上是增函数，∴当1x >时，()(1)f x f >，又2(1)1ln 12ln110f a =-+-=，∴()0f x >，即21ln 2ln 0x x a x --+>， ∴2ln 2ln 1x x a x >-+故当1x >时，恒有2ln 2ln 1x x a x >-+．=====================================================================适用版本：人教版,苏教版, 鲁教版,北京版,语文A 版,语文S 版,冀教版,沪教版,北大师大版,人教版新版,外研版,新起点,牛津译林,华师大版,湘教版,新目标,苏科版,粤沪版,北京版,岳麓版适用学科：语文,数学,英语,科学,物理,化学,生物,政治,历史,地理适用年级：一年级,二年级,三年级,四年级,五年级,六年级,七年级,八年级,九年级,小一,小二,小三,小四,小五,小六,初一,初二,初三,高一,高二,高三,中考,高考,小升初适用领域及关键字：100ceping,51ceping,52ceping,ceping,xuexi,zxxx,zxjy,zk,gk,xiti,教学,教学研究,在线教学,在线学习,学习,测评,测评网,学业测评, 学业测评网,在线测评, 在线测评网,测试,在线测试,教育,在线教育,中考,高考,中小学,中小学学习,中小学在线学习,试题,在线试题,练习,在线练习,在线练习,小学教育,初中教育,高中教育,小升初复习,中考复习,高考复习,教案,学习资料,辅导资料,课外辅导资料,在线辅导资料,作文,作文辅导,文档,教学文档,真题,试卷,在线试卷,答案,解析,课题,复习资料,复习专题,专项练习,学习网,在线学习网,学科网,在线学科网,在线题库,试题库,测评卷,小学学习资料，中考学习资料,单元测试,单元复习,单元试卷,考点,模拟试题,模拟试卷,期末考试,期末试卷,期中考试,期中试卷=====================================================================本卷由《100测评网》整理上传,专注于中小学生学业检测,练习与提升.=========================================================== 适用版本：人教版,苏教版, 鲁教版,北京版,语文A 版,语文S 版,冀教版,沪教版,北大师大版,人教版新版,外研版,新起点,牛津译林,华师大版,湘教版,新目标,苏科版,粤沪版,北京版,岳麓版适用学科：语文,数学,英语,科学,物理,化学,生物,政治,历史,地理适用年级：一年级,二年级,三年级,四年级,五年级,六年级,七年级,八年级,九年级,小一,小二,小三,小四,小五,小六,初一,初二,初三,高一,高二,高三,中考,高考,小升初适用领域及关键字：100ceping,51ceping,52ceping,ceping,xuexi,zxxx,zxjy,zk,gk,xiti,教学,教学研究,在线教学,在线学习,学习,测评,测评网,学业测评, 学业测评网,在线测评, 在线测评网,测试,在线测试,教育,在线教育,中考,高考,中小学,中小学学习,中小学在线学习,试题,在线试题,练习,在线练习,在线练习,小学教育,初中教育,高中教育,小升初复习,中考复习,高考复习,教案,学习资料,辅导资料,课外辅导资料,在线辅导资料,作文,作文辅导,文档,教学文档,真题,试卷,在线试卷,答案,解析,课题,复习资料,复习专题,专项练习,学习网,在线学习网,学科网,在线学科网,在线题库,试题库,测评卷,小学学习资料，中考学习资料,单元测试,单元复习,单元试卷,考点,模拟试题,模拟试卷,期末考试,期末试卷,期中考试,期中试卷===========================================================本卷由《100测评网》整理上传,专注于中小学生学业检测,练习与提升.。

100测评网高二数学练习卷直线的方程

典型例题一例1 直线l 过点P （－1，3），倾斜角的正弦是54，求直线l 的方程．分析：根据倾斜角的正弦求出倾斜角的正切，注意有两解．解：因为倾斜角α的范围是：πα<≤0 又由题意：54sin =α，所以：34tan ±=α，直线过点P （－1，3），由直线的点斜式方程得到：()1343+±=-x y 即：01334=+-y x 或0534=-+y x ．说明：此题是直接考查直线的点斜式方程，在计算中，要注意当不能判断倾斜角α的正切时，要保留斜率的两个值，从而满足条件的解有两个．典型例题二例2 求经过两点A （2，m ）和B （n ，3）的直线方程．分析：本题有两种解法，一是利用直线的两点式；二是利用直线的点斜式．在解答中如果选用点斜式，只涉及到n 与2的分类；如果选用两点式，还要涉及m 与3的分类．解：法一：利用直线的两点式方程∵直线过两点A （2，m ）和B （n ，3）（1）当3=m 时，点A 的坐标是A （2，3），与点B （n ，3）的纵坐标相等，则直线AB 的方程是3=y ；（2）当2=n 时，点B 的坐标是B （2，3）,与点A （2，m ）的横坐标相等，则直线AB 的方程是2=x ；（3）当3≠m ，2≠n 时，由直线的两点式方程121121x x x x y y y y --=--得： 223--=--n x m m y 法二：利用直线的点斜式方程（1）当2=n 时，点B A ,的横坐标相同，直线AB 垂直与x 轴，则直线AB 的2=x ；（2）当2≠n 时，过点B A ,的直线的斜率是23--=n mk ，又∵过点A （2，m ）∴由直线的点斜式方程()11x x k y y -=-得过点B A ,的直线的方程是：()223---=-x n mm y 说明：本题的目的在于使学生理解点斜式和两点式的限制条件，并体会分类讨论的思想方法．典型例题三例3 把直线方程()00≠=++ABC c By Ax 化成斜截式______，化成截距式______．分析：因为0≠ABC ，即0≠A ，0≠B ，0≠C ，按斜截式、截距式的形式要求变形即可．解：斜截式为BC x B A y --=，截距式为A C x -+BC Y -＝1说明：此题考查的是直线方程的两种特殊形式：斜截式和截距式．典型例题四例4 直线023cos =++y x θ的倾斜角的取值范围是_____________．分析：将直线的方程化为斜截式，得出直线的斜率，再由斜率和倾斜角的关系，得出关于θ的一个三角不等式即可．解：已知直线的方程为323cos --=x y θ，其斜率3cos θ-=k ．由313cos ≤=θk ，得31tan ≤α，即33tan 33≤≤-α．由[)πα,0∈，得),65[6,0πππα ⎥⎦⎤⎢⎣⎡∈．说明：解题易得出错误的结果⎥⎦⎤⎢⎣⎡-∈6,6ππα，其原因是没有注意到倾斜角的取值范围．典型例题五例5 直线l 经过点)2,3(，且在两坐标轴上的截距相等，求直线l 的方程．分析：借助点斜式求解，或利用截距式求解．解法一：由于直线l 在两轴上有截距，因此直线不与x 、y 轴垂直，斜率存在，且0≠k ．设直线方程为)3(2-=-x k y ，令0=x ，则23+-=k y ，令0=y ，则kx 23-=．由题设可得k k 2323-=+-，解得1-=k 或32=k ．所以，l 的方程为)3(2--=-x y 或)3(322-=-x y ．故直线l 的方程为05=-+y x 或032=-y x ．解法二：由题设，设直线l 在x 、y 轴的截距均为a ．若0=a ，则l 过点)0,0(，又过点)2,3(，∴l 的方程为x y 32=，即l ：032=-y x ．若0≠a ，则设l 为1=+a ya x ．由l 过点)2,3(，知123=+aa ，故5=a ．∴l 的方程05=-+y x ．综上可知，直线l 的方程为032=-y x 或05=-+y x ．说明：对本例，常见有以下两种误解：误解一：如下图，由于直线l 的截距相等，故直线l 的斜率的值为1±．若1=k ，则直线方程为32-=-x y ；若1-=k ，则直线方程为)3(2--=-x y ．故直线方程为01=-+y x 或05=-+y x ．误解二：由题意，直线在两轴上的截距相等，则可设直线方程为1=+aya x ．由直线过点)2,3(，得123=+aa ，即5=a ，也即方程为05=-+y x ．在上述两种误解中，误解一忽视了截距的意义，截距不是距离，它可正可负，也可以为0．显见，当1=k 时，直线01=--y x 的两轴上的截距分别为1和－1，它们不相等．另外，这种解法还漏掉了直线在两轴上的截距均为0的这种特殊情形．误解二中，没有注意到截距式方程的适用范围，同样也产生了漏解．典型例题六例6 已知在第一象限的ABC ∆中，)1,1(A 、)1,5(B ，3π=∠A ，4π=∠B ，求：(1)AB 边的方程；(2)AC 和BC 所在直线的方程．分析：(1)当直线与x 轴平行时或垂直时，不能用两点式求直线的方程．(2)由图可知AC 、BC 的斜率，根据点斜式方程即可得出结果．解：(1)如图，AB 的方程为1=y )51(≤≤x ．(2)由AB ∥x 轴，且ABC ∆在第一象限知AC 的斜率33tan==πAC k ，BC 的斜率1)4tan(-=-=ππBC k ．所以，AC 边所在直线的方程为)1(31-=-x y ，即0313=-+-y x ． BC 边所在直线的方程为)5(11--=-x y ，即06=-+y x ．说明：(1)AB 边是一条线段，要注意变量x 的取值范围．(2)解题中，要注意画出图形，便于直观地得到所求直线所具备的条件．典型例题七例7 若ABC ∆的顶点)4,3(A ，)0,6(B ，)2,5(--C ，求A ∠的平分线AT 所在的直线的方程．分析：两个条件确定一条直线．要求AT 的方程，已知点A 的坐标，只要再找出AT 的斜率或点T 的坐标就可以了．在三角形中，A ∠的平分线有下列性质：(1)TAB CAT ∠=∠；(2)AT 上任一点到两边AB 、AC 的距离相等；(3)ABCA TBCT =．用其中任何一个性质，都可以确定第二个条件．解法一：∵10)24()53(22=+++=AC ，54)63(22=+-=AB ，∴T 分BC 所成的比为2===ABACTB CT λ．设T 的坐标为),(y x ，则：3721625=+⨯+-=x ，3221022-=+⨯+-=y ，即)32,37(-T ．由两点式得AT 的方程为3733732432--=++x y ，即0177=--y x ．解法二：直线AC 到AT 的角等于AT 到AB 的角，43)5(3)2(4=----=AC k ，346304-=--=AB k ．设AT 的斜率为k (34-<k 或34>k )，则有 k k k k )43(14343143-+--=+-．解得7=k 或71-=k （舍去）．∴直线AT 的方程为)3(74-=-x y ，即0177=--y x ．解法三：设直线AT 上动点),(y x P ，则P 点到AC 、AB 的距离相等，即：574352434+-=-+y x y x ，∴037=-+y x 或0177=--y x结合图形分析，知037=-+y x 是ABC ∆的角A 的外角平分线，舍去．所以所求的方程为0177=--y x ．说明：(1)确定不同条件下的直线方程是高考的重要内容，其方法主要是待定系数法（如解法一、解法二）和轨迹法（如解法三）．要熟练掌握直线方程各种形式间的相互转化．点斜式是直线方程最重要的一种形式，要加强这方面的训练．(2)解法三涉及到后面将要学到的知识．这里先把它列出来，作为方法积累．典型例题八例8 求过点)4,5(--P 且分别满足下列条件的直线方程： (1)与两坐标轴围成的三角形面积为5；(2)与x 轴和y 轴分别交于A 、B 两点，且53∶∶=BP AP ．分析：对于(1)，既可借助于截距式求解，也可以利用点斜式来求解；对于(2)，利用截距式求解较为简便．解法一：设所求的直线方程为1=+b ya x ．由直线过点)4,5(--P ，得145=-+-ba ，即ab b a -=+54．又521=⋅b a ，故10=ab ．联立方程组⎩⎨⎧=-=+,10,54ab ab b a 解得⎪⎩⎪⎨⎧=-=425b a 或⎩⎨⎧-==25b a ．故所求直线方程为1425=+-y x 和125=-+yx ，即： 02058=+-y x 和01052=--y x ．解法二：设所求直线方程为)5(4+=+x k y ，它与两坐轴的交点为)0,54(kk-，)45,0(-k ．由已知，得5544521=-⋅-kk k ，即k k 10)45(2=-．当0>k 时，上述方程可变成01650252=+-k k ，解得58=k ，或52=k ．由此便得欲求方程为02058=+-y x 和01052=--y x ．(2)解：由P 是AB 的分点，得53±==PB AP λ．设点A 、B 的坐标分别为)0,(a ，),0(b ．当P 是AB 的内分点时，53=λ．由定比分点公式得8-=a ，332-=b ．再由截距式可得所求直线方程为03234=++y x ．当点P 是AB 的外分点时，53-=λ．由定比分点公式求得2-=a ，38=b ．仿上可得欲求直线方程为0834=+-y x ．故所求的直线方程为03234=++y x ，或0834=+-y x ．说明：对于(1)，应注意对题意的理解，否则，就较易得到ab b a -=+54，且10=ab ，从而遗漏了10-=ab 的情形；对于(2)，应当区分内分点与外分点两种不同的情形．必要时，可画出草图直观地加以分析，防止漏解．求直线的方程时，除应注意恰当地选择方程的形式外，还应注意到不同形式的方程的限制条件．如点斜式的限定条件是直线必须存在斜率；截距式的限定条件为两轴上的截距都存在且不为0；两点式的限定条件是直线不与x 轴垂直，也不与y 轴垂直．除此以外，还应注意直线方程形式之间的相互转化．典型例题九例9 已知两直线0111=++y b x a 和0122=++y b x a 的交点为)3,2(P ，求过两点),(11b a Q 、),(22b a Q 的直线方程．分析：利用点斜式或直线与方程的概念进行解答．解法一：∵)3,2(P 在已知直线上，∴⎩⎨⎧=++=++0132********b a b a ∴0)(3)(22121=-+-b b a a ，即322121-=--a a b b ．故所求直线方程为)(3211a x b y --=-． ∴0)32(3211=+-+b a y x ，即0132=++y x ．解法二：∵点P 在已知直线上，∴⎩⎨⎧=++=++0132********b a b a 可见),(111b a Q 、),(222b a Q 都满足方程0132=++y x ， ∴过1Q 、2Q 两点的直线方程为0132=++y x ．说明：解法二充分体现了“点在直线上，则点的坐标满足直线方程；反之，若点的坐标满足方程，则直线一定过这个点”．此解法独特，简化了计算量，能培养学生的思维能力．典型例题十例10 过点)4,1(P 引一条直线，使它在两条坐标轴上的截距为正值，且它们的和最小，求这条直线方程．分析：利用直线方程的点斜式，通过两截距之和最小求出直线的斜率，从而求出直线方程．或借助直线方程的截距式，通过两截距之和最小，求出直线在两轴上的截距，从而求出直线的方程．解法一：设所求的直线方程为)1(4-=-x k y ．显见，上述直线在x 轴、y 轴上的截距分别为k41-、k -4．由于041>-k，且04>-k 可得0<k ．直线在两坐标轴上的截距之和为：945)4()(5)4()41(=+≥-+-+=-+-=k k k k S ，当且仅当kk 4-=-，即2-=k 时，S最小值为9．故所求直线方程为)1(24--=-x y ，即062=-+y x ．解法二：设欲求的直线方程为1=+bya x (0>a ，0>b )．据题设有141=+ba ， ① 令b a S +=． ②①×②，有94545)41)((=+≥++=++=ba ab bab a S ．当且仅当b a a b 4=时，即b a =2，且141=+ba ，也即3=a ，6=b 时，取等号．故所求的直线方程为163=+yx ，即062=-+y x ．说明：在解法一中，应注意到0<k 这个隐含条件．否则，由)4(5kk S +-=，将很有可能得出错误的结果．如145)4(5=-≥+-=k k S ，145)4(5=-≤+-=kk S 等等．在解法二中，应注意运算过程中的合理性，即讲究算理，不然，将会使运算过程不胜其繁．如采取下述方法：由①，用a 来表示b ，再代入②中，把S 化归成a 的函数．从解题思维方法上说无可厚非，但这种方法将使运算难度陡然增加．不如保持本质、顺其自然好．典型例题十一例11 已知523=+b a ，其中a 、b 是实常数，求证：直线010=-+by ax 必过一定点．分析与解：观察条件与直线方程的相似之处，可把条件变形为01046=-+b a ，可知6=x ，4=y 即为方程010=-+by ax 的一组解，所以直线010=-+by ax 过定点（6，4）．说明：此问题属于直线系过定点问题，此类问题的彻底解决宜待学完两直线位置之后较好，当然现在也可以研究，并且也有一般方法．典型例题十二例12 直线l 过点M （2，1），且分别交x 轴、y 轴的正半轴于点A 、B ．点O 是坐标原点，（1）求当ABO ∆面积最小时直线l 的方程；（2）当MA MB 最小时，求直线l 的方程．解：（1）如图，设OA a =，OB b =，ABO ∆的面积为S ，则ab S 21=并且直线l 的截距式方程是a x ＋by＝1 由直线通过点（2，1），得a 2＋b1＝1 所以:2a ＝b111-＝1-b b因为A 点和B 点在x 轴、y 轴的正半轴上，所以上式右端的分母01>-b ．由此得:b b b b a S ⨯-=⨯=121111112-++=-+-=b b b b2111+-+-=b b 422=+≥ 当且仅当=-1b 11-b ，即2=b 时，面积S 取最小值4，这时4=a ，直线的方程是:4x ＋2y＝1即:042=-+y x（2）设θ=∠BAO ，则MA ＝θsin 1，MB ＝θcos 2，如图，所以 MA MB ＝θsin 1θcos 2＝θ2sin 4当θ＝45°时MA MB 有最小值4，此时1=k ，直线l 的方程为03=-+y x ．说明：此题与不等式、三角联系紧密，解法很多，有利于培养学生发散思维，综合能力和灵活处理问题能力．动画素材中有关于此题的几何画板演示．典型例题十三例13 一根铁棒在20°时，长10.4025米，在40°时，长10.4050米，已知长度l 和温度t 的关系可以用直线方程来表示，试求出这个方程，并且根据这个方程，求这跟铁棒在25°时的长度．解：这条直线经过两点（20，10.4025）和（20，10.4050），根据直线的两点式方程，得：4025.104050.104025.10--l ＝204020--t即 l ＝0.002520t⨯＋10.4000当t ＝25°时 l ＝0.00252025⨯＋10.4000＝0.0031＋10.4000＝10.4031即当t ＝25°时，铁棒长为10.4031米．说明：直线方程在实际中应用非常广泛．典型例题十三例13 一根铁棒在20°时，长10.4025米，在40°时，长10.4050米，已知长度l 和温度t 的关系可以用直线方程来表示，试求出这个方程，并且根据这个方程，求这跟铁棒在25°时的长度．解：这条直线经过两点（20，10.4025）和（20，10.4050），根据直线的两点式方程，得：4025.104050.104025.10--l ＝204020--t即 l ＝0.002520t⨯＋10.4000当t ＝25°时 l ＝0.00252025＋10.4000＝0.0031＋10.4000＝10.4031 即当t ＝25°时，铁棒长为10.4031米．说明：直线方程在实际中应用非常广泛．本卷由《100测评网》整理上传，专注于中小学生学业检测、练习与提升.。

100测评网高二数学期末复习练习题(文科)

高二数学期末复习练习题（文科）班级姓名学号一、选择题（共10小题，每题5分，共50分）1.在等差数列}{n a 中，已知前15项和为9015=S ，那么8a =（）A.3B.4C.6D.122.满足条件︒===45,23,4A b a 的△ABC 的个数是（）A.一个B.两个C.无数个D.不存在 3.“0≠k ”是“方程b kx y +=表示直线”的（）条件A.必要不充分B.充分不必要C.充要D.既不充分也不必要4.动圆的圆心在抛物线x y 82=上，且动圆恒与直线02=+x 相切，则动圆必过点（） A.)0,4( B.)0,2( C.)2,0( D.)2,0(-5.若2)(0='x f ，则kx f k x f k 2)()(lim000--→等于（）A.-1B.-2C.1D.21 6.数列}{n a 的前n 项和为n S ，满足1322+-=n n S n ，则1054a a a +++ 等于（）A.171B.21C.10D.161 7.已知12=+y x ，则yx42+的最小值为（）A.8B.6C.22D.238.在△ABC 中，三个角A 、B 、C 的对边分别为a 、b 、c ，且有C b a cos 2=，则△ABC 的形状一定是（）A.等腰三角形B.直角三角形C.等腰直角三角形D.等腰或直角三角形 9.函数)1()(2x x x f -=在]1,0[上的最大值为（） A.932 B.922 C.923 D.8310.若椭圆)1(1222>=+m y m x 和双曲线)0(1222>=-n y nx 有相同的焦点1F 、P F ,2是两条曲线的一个交点，则△PF 1F 2的面积是（） A.4 B.2 C.1210- D.1 二、填空题（共4小题，每题5分，共20分）11.命题“相似三角形的面积相等”的否命题是，它的否定是；12.若△ABC 面积)(341222a c b S -+=，则A= ；13.不等式11<-x ax的解集为}2,1|{><x x x 或，则a 的值为；14.给出平面区域如图，若使目标函数)0(>+=a y ax z 取得最大值的最优解有无穷多个，则a 的值为 .三、解答题（共6题，共80分）15.(12分)已知函数3)1(4)54(22+-+-+=x k x k k y 的图像都在x 轴上方，求实数k 的取值范围.16.(14分)命题甲：关于x 的不等式0)1(22≤+-+a x a x 的解集为∅；命题乙：函数x a a y )2(2-= 为增函数. 分别求符合下列条件的实数a 的取值范围.(1)甲、乙至少有一个是真命题； (2)甲、乙中有且只有一个是真命题.17.(12分)已知△ABC 中，.552cos ,10,45==︒=∠C AC B (1)求BC 边的长；(2)记AB 的中点为D ，求中线CD 的长.18.(14分)已知函数d cx bx x x f +++=23)(的图像过点)2,0(P ，且在点))1(,1(--f M 处的切线方程为.076=+-y x(1)求函数)(x f y =的解析式； (2)求函数)(x f y =的单调区间.19.(14分)从社会效益和经济效益出发，某地投入资金进行生态环境建设，并以此发展旅游产业. 根据规划，本年度投入800万元，以后每年投入将比上年减少15. 本年度当地旅游业收入估计为400万元，由于该项建设对旅游业的促进作用，预计今后的旅游业收入每年会比上年增加14.(1)设n 年内（本年度为第一年）总投入为n a 万元，旅游业总收入为n b 万元 .写出n a ，n b 的表达式； (2)至少经过几年旅游业的总收入才能超过总投入？20.(14分)椭圆)0(12222>>=+b a b y a x 与直线01=-+y x 相交于P 、Q 两点，且OQ OP ⊥（O 为原点）. (1)求证2211ba +等于定值； (2)当椭圆离心率]22,33[∈e 时，求椭圆长轴长的取值范围.【答案】（供参考）1～10 CBBBA DCAAD11 .若两个三角形不相似，则它们的面积不相等；相似三角形的面积不相等； 12.6π ; 13. 21 ; 14.53 ;15. k 的取值范围是)19,1[.16.(1)),31()21,(+∞--∞ ; (2))21,1[]1,31(-- . 17.(1)23=BC ; (2)13=CD .18.(1)233)(23+--=x x x x f ; (2)在)21,(--∞及),21(+∞+上递增；在)21,21(+-上递减.19.(1)454000[1()],1600[()1]54n nn n a b =-=- ；(2) 5n ≥20.(1)21122=+b a ；(2)]6,5[.增城中学沈金荣2006-10-16 =========================================================== 适用版本：人教版,苏教版, 鲁教版,北京版,语文A 版,语文S 版,冀教版,沪教版,北大师大版,人教版新版,外研版,新起点,牛津译林,华师大版,湘教版,新目标,苏科版,粤沪版,北京版,岳麓版适用学科：语文,数学,英语,科学,物理,化学,生物,政治,历史,地理适用年级：一年级,二年级,三年级,四年级,五年级,六年级,七年级,八年级,九年级,小一,小二,小三,小四,小五,小六,初一,初二,初三,高一,高二,高三,中考,高考,小升初适用领域及关键字：100ceping,51ceping,52ceping,ceping,xuexi,zxxx,zxjy,zk,gk,xiti,教学,教学研究,在线教学,在线学习,学习,测评,测评网,学业测评, 学业测评网,在线测评, 在线测评网,测试,在线测试,教育,在线教育,中考,高考,中小学,中小学学习,中小学在线学习,试题,在线试题,练习,在线练习,在线练习,小学教育,初中教育,高中教育,小升初复习,中考复习,高考复习,教案,学习资料,辅导资料,课外辅导资料,在线辅导资料,作文,作文辅导,文档,教学文档,真题,试卷,在线试卷,答案,解析,课题,复习资料,复习专题,专项练习,学习网,在线学习网,学科网,在线学科网,在线题库,试题库,测评卷,小学学习资料，中考学习资料,单元测试,单元复习,单元试卷,考点,本卷由《100测评网》整理上传,专注于中小学生学业检测,练习与提升.。

100测评网(新)高三数学期末检测试卷(文)

2008学年第一学期高三数学期终抽测试卷（文）考生注意：1、答卷前，考生务必将学校、姓名、班级、学号等填写清楚。

2、本试卷共有21道试题，满分150分，考试时间120分钟。

请考生用钢笔或圆一、填空题（本大题满分60分，本大题共有12题，只要求直接填写结果，每个空格填对得5分，否则一律得零分）1、不等式0231>--x 的解集为 ___________________．2、函数xx x f -++=211)(的定义域为________________ 3、函数x x x f cos 3sin )(-=的单调递增区间为________________ 4、根据框图，写出所打印数列{}n a 的递推公式 5、若指数函数)()(R x a x f x ∈=的部分对应值如右表：则不等式0|)1(|1<--x f的解集为________________6、已知函数]4,32[,3)3()(2a a x xb ax x f --∈+-+=是偶函数,则._____=+b a 7、等比数列｛a n ｝的公比为21-，前n 项和为n S 满足∞→n lim n S =11a ，那么a 1的值为.______8、如图，三行三列的方阵中有9个数(123123)ij a i j ==，，；，，，从中任取三个数，111213212223313233a a a a a a a a a ⎛⎫⎪⎪ ⎪⎝⎭ 则至少有两个数位于同行或同列的概率是. (结果用分数表示) 9、若)3,(2)2(23≥∈+++++=+n N n cx bx ax x x nnn且2:3:=b a ，则._____=n 10、一个圆锥形的空杯子上面放着一个球形的冰淇淋，圆锥底的直径与球的直径相同均为10，如果冰淇淋融化后全部流在空杯子中，并且不会溢出杯子，则杯子的高度最小为.______第4题11、已知命题0)1)(3(:>+-x x p ，命题)0(012:22>>-+-m m x x q ，若命题p 是命题q 的充分不必要条件，则实数m 的范围是.______12、设函数⎪⎩⎪⎨⎧>≤-=1|||,|lg 1||,1)(2x x x x x f ，若关于x 方程|2|)(-=a x f 有两个不同的实数解，则a 的取值范围是.______二、选择题（每小题4分，计16分）13、如图，P 为正方体1111D C B A ABCD -的中心，则PAC ∆在该正方体各个面上的射影可能是（）① ② ③ ④A ．①②③④B ．①③C ．①④D．②④14、设C x ∈，方程0||||2=-x x 的解集为（）A.{}1,0B.{}1,1,0-C.{}i i --,,1,1,0D.以上都不对15、下列四个命题中错误．．的个数是（） ①经过球面上任意两点，可以作且只可以作球的一个大圆； ②球面积是它大圆面积的四倍；③球面上两点的球面距离，是这两点所在截面圆上以这两点为端点的劣弧的长。

100测评网新课标高二数学文同步测试(2)(1-1第二章圆锥曲线方程与几何性质)

普通高中课程标准实验教科书——数学 [人教版]（选修1-1、1-2）高中学生学科素质训练新课标高二数学文同步测试（2）（1-1第二章圆锥曲线方程与几何性质）说明：本试卷分第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷50分，第Ⅱ卷100分，共150分；答题时间120分钟。

第Ⅰ卷（选择题共50分）一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内（每小题5分，共50分）。

1．在同一坐标系中，方程a 2x 2+b 2y 2=1与ax +by 2=0（a ＞b ＞0）的曲线大致是（）2．已知椭圆222253n y m x +和双曲线222232n y m x -＝1有公共的焦点，那么双曲线的渐近线方程是（）A ．x ＝±y 215B ．y ＝±x 215 C ．x ＝±y 43 D ．y ＝±x 433．过抛物线y =ax 2（a ＞0）的焦点F 用一直线交抛物线于P 、Q 两点，若线段PF 与FQ 的长分别是p 、q ，则qp11+等于（）A ．2aB ．a21C ．4aD ．a44．若椭圆)0(12222〉〉=+b a by a x 的左、右焦点分别为F 1、F 2，线段F 1F 2被抛物线y 2=2bx 的焦点分成5:3两段，则此椭圆的离心率为（）A ．1716B ．17174C ．54D ．5525．椭圆31222y x +=1的一个焦点为F 1，点P 在椭圆上.如果线段PF 1的中点M 在y 轴上，那么点M 的纵坐标是（） A ．±43B ．±23C ．±22D ．±43 6．设F 1和F 2为双曲线1422=-y x 的两个焦点，点P 在双曲线上，且满足∠F 1PF 2＝90°，则△F 1PF 2的面积是（） A ．1B ．25C ．2D ．57．已知F 1、F 2是两个定点，点P 是以F 1和F 2为公共焦点的椭圆和双曲线的一个交点，并且 PF 1⊥PF 2，e 1和e 2分别是椭圆和双曲线的离心率，则有（）A ．221≥e eB ．42221≥+e eC ．2221≥+e eD ．2112221=+e e 8．已知方程1||2-m x +my -22=1表示焦点在y 轴上的椭圆，则m 的取值范围是（）A ．m<2B ．1<m<2C ．m<－1或1<m<2D ．m<－1或1<m<23 9．已知双曲线22a x －22b y =1和椭圆22m x +22by =1(a >0,m>b >0)的离心率互为倒数，那么以a 、b 、m 为边长的三角形是（） A ．锐角三角形 B ．直角三角形C ．钝角三角形D ．锐角或钝角三角形10．椭圆13422=+y x 上有n 个不同的点: P 1, P 2, …, P n , 椭圆的右焦点为F. 数列｛|P n F |｝是公差大于1001的等差数列, 则n 的最大值是（）A ．198B ．199C ．200D ．201第Ⅱ卷（非选择题共100分）二、填空题：请把答案填在题中横线上（每小题6分，共24分）。

100测评网高三数学复习综合试卷3

100测评网高三数学复习综合试卷3高三数学试卷命题人、责任人：盛兆兵分值：160分考试时间：120分钟1、已知集合A={某|1某4}，B={某|2某6}，则A∩B=▲2、(1i)(12i)=▲.3、已知两条直线ya某2和y(a2)某1互相垂直，则a等于▲4、设直线某m分别交函数yin某、yin(某的距离的最大值为▲5、已知向量a(3,4)，向量b满足b∥a，且|b|1，则b=▲6、在△OAB中,OA(2co,2in),OB(5co,5in),若OAOB5,则2)的图像于M、N两点，则M、NSOAB=▲.7、一个几何体的三视图如图，则它的体积V=▲233某≥1主视图228、如果实数某,y满足不等式组某y1≤0则某y的最小值为▲2某y2≤09、在复平面内，复数z左视图43i对应的点位于第▲象限。

俯视图2i10、在正三棱锥P－ABC中，D，E分别是AB，BC的中点，有下列三个结论：①AC⊥PB；②AC∥平面PDE；③AB⊥平面PDE。

则所有正确结论的序号是▲11、已知曲线ye上一点P（1,e）处的切线分别交某轴、y轴于A，B两点，O为坐标某某原点，则△OAB的面积为▲12、设Sn表示等比数列{an}（nN）的前n项和，已知S10S3，则15S5S5▲13、观察下列算式，猜测由此表提供的一般法则，用适当的数学式子表示它。

1=13+5=87+9+11=2713+15+17+19=6421+23+25+27+29=125……则这个式子为▲14、已知：圆M：某y2y0，直线l的倾斜角为120，与圆M交于P、Q两点，若OPOQ0(O为原点)，则l在某轴上的截距为▲.高三数学试卷一、填空题：1．8．2．9．3．10.4．11..5.12.6．13.7．14二、解答题（本大题共6小题，每小题15分，满分90分）15、已知向量a(in,3),b(1,co),((Ⅰ)若ab,求；(7分),).22(Ⅱ)求|ab|的最大值.(7分)16、在△ABC中，已知a、b、c分别是角A、B、C的对边，不等式某2coC4某inC60对一切实数某恒成立。

100测评网高二数学典型例题四

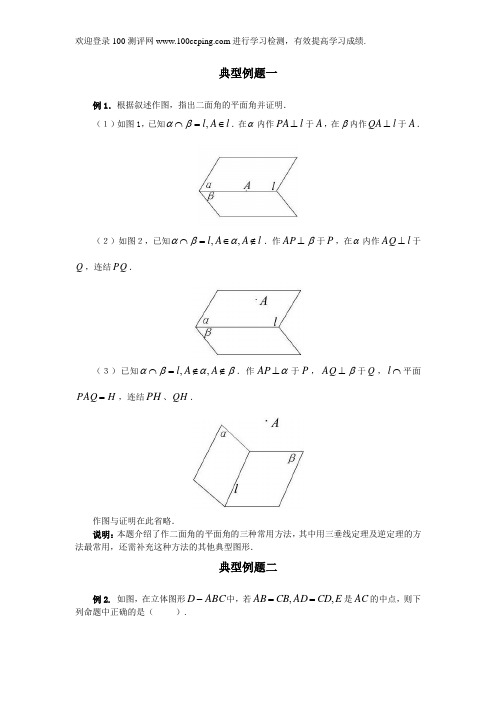
典型例题一例1．根据叙述作图，指出二面角的平面角并证明．（１）如图1，已知l A l ∈=⋂,βα．在α内作l PA ⊥于A ，在β内作l QA ⊥于A ．（２）如图２，已知l A A l ∉∈=⋂,,αβα．作β⊥AP 于P ，在α内作l AQ ⊥于Q ，连结PQ ．（３）已知βαβα∉∉=⋂A A l ,,．作α⊥AP 于P ，β⊥AQ 于Q ，⋂l 平面H PAQ =，连结PH 、QH ．作图与证明在此省略．说明：本题介绍了作二面角的平面角的三种常用方法，其中用三垂线定理及逆定理的方法最常用，还需补充这种方法的其他典型图形．典型例题二例2. 如图，在立体图形ABC D -中，若E CD AD CB AB ,,==是AC 的中点，则下列命题中正确的是（）.（A ）平面ABC ⊥平面ABD（B ）平面ABD ⊥平面BDC（C ）平面ABC ⊥平面BDE ，且平面ADC ⊥平面BDE（D ）平面ABC ⊥平面ADC ，且平面ADC ⊥平面BDE分析：要判断两个平面的垂直关系，就需固定其中一个平面，找另一个平面内的一条直线与第一个平面垂直.解：因为,CB AB =且E 是AC 的中点，所以,AC BE ⊥同理有AC DE ⊥，于是⊥AC 平面BDE .因为⊂A C 平面ABC ，所以平面ABC ⊥平面BDE .又由于⊂AC 平面ACD ,所以平面ACD ⊥平面BDE .所以选C.说明：本题意图是训练学生观察图形，发现低级位置关系以便得到高级位置关系.在某一个平面内,得到线线垂直的重要途径是出现等腰三角形底边的中线,由线线垂直得到线面垂直,由线面垂直可得到面面垂直.典型例题三例３．如图，P 是ABC ∆所在平面外的一点，且⊥PA 平面ABC ，平面⊥PAC 平面PBC ．求证AC BC ⊥．分析：已知条件是线面垂直和面面垂直，要证明两条直线垂直，应将两条直线中的一条纳入一个平面中，使另一条直线与该平面垂直，即从线面垂直得到线线垂直．．证明：在平面PAC 内作PC AD ⊥，交PC 于D ．因为平面⊥PAC 平面PBC 于PC ，⊂AD 平面PAC ，且PC AD ⊥，所以PBC AD 平面⊥．又因为⊂BC 平面PBC ，于是有BC AD ⊥①．另外⊥PA 平面ABC ，⊂BC 平面ABC ，所以BC PA ⊥．由①②及A PA AD = ，可知⊥BC 平面PAC ．因为⊂AC 平面PAC ，所以AC BC ⊥．说明：在空间图形中，高一级的垂直关系中蕴含着低一级的垂直关系，通过本题可以看到，面面垂直⇒线面垂直⇒线线垂直．典型例题四例４．如图，AB 是⊙O 的直径，PA 垂直于⊙O 所在的平面，C 是圆周上异于A 、B 的任意一点，求证：平面PAC ⊥平面PBC ．分析：证明面面垂直的有两个依据，一是证明二面角的平面角为直角，二是利用两个平面垂直的判定定理．由于C 点的任意性，用方法一的可能性不大，所以要寻求线面垂直．证明：因为AB 是⊙O 的直径，C 是圆周上的点，所以有AC BC ⊥①．因为⊥PA 平面ABC ，⊂BC 平面ABC ，则BC PA ⊥②．由①②及A PA AC = ，得⊥BC 平面PAC ．因为⊂BC 平面PBC ，有平面PAC ⊥平面PBC ．说明：低一级的垂直关系是判定高一级垂直关系的依据，根据条件，由线线垂直⇒线面垂直⇒面面垂直．通过这个例题展示了空间直线与平面的位置关系的内在联系，垂直关系的判定和性质共同构成了一个完整的知识体系．典型例题五例５．如图，点A 在锐二面角βα--MN 的棱MN 上，在面α内引射线AP ，使AP 与MN 所成的角PAM ∠为 45，与面β所成的角大小为30，求二面角βα--MN 的大小．分析：首先根据条件作出二面角的平面角，然后将平面角放入一个可解的三角形中（最好是直角三角形），通过解三角形使问题得解．解：在射线AP 上取一点B ，作β⊥BH 于H ，连结AH ，则BAH ∠为射线AP 与平面β所成的角，30=∠∴BAH ．再作MN BQ ⊥，交MN 于Q ，连结HQ ，则HQ 为BQ 在平面β内的射影．由三垂线定理的逆定理，MN HQ ⊥，BQH ∠∴为二面角βα--MN 的平面角．设a BQ =，在B A Q Rt ∆中，a AB BAM BQA 2,45,90=∴=∠=∠ ,在Rt △BHQ 中，,22,,90a BH a BQ BHQ ===∠ 2222sin ===∠a a BQ BH BQH , BQH ∠ 是锐角， 45=∠∴BQH ,即二面角βα--MN 等于 45．说明：本题综合性较强，在一个图形中出现了两条直线所称的角，斜线与平面所称的角，二面角等空间角，这些空间角都要转化为平面角，而且还要彼此联系相互依存，要根据各个平面角的定义添加适当的辅助线．典型例题六例６．如图，将边长为a 的正三角形ABC 以它的高AD 为折痕折成一个二面角C AD C --'．（１）指出这个二面角的面、棱、平面角；（２）若二面角C AD C --'是直二面角，求C C '的长；（３）求C A '与平面CD C '所成的角；（４）若二面角C AD C --'的平面角为 120，求二面角D C C A -'-的平面角的正切值．分析：根据问题及图形依次解决．解：（１）∴'⊥⊥∴⊥,,,C D AD DC AD BC AD 二面角C AD C --'的面为ADC 和面C AD '，棱为AD ，二面角的平面角为C CD '∠．（２）若 90='∠C CD ，a C C a C D DC a AC 22,21,='∴='=∴= ．（３）⊥∴⊥'⊥AD DC AD C D AD ,, 平面C C D '，D C A '∠∴为C A '与平面CD C '所成的角．在直角三角形C AD '中， 30,21='∠∴='=C DA AC C D DC ，于是 60='∠D C A ．（４）取C C '的中点E ，连结AE 、DE ，C C DE C C AE AC C A DC CD '⊥'⊥∴='=',,, ，AED ∠∴为二面角D C C A -'-的平面角．,41,21,120a DE a CD D C DC C =∴=='='∠ 在直角三角形AED 中，,23a AD =DE AD AED =∠∴tan 324123==a a ．说明：这是一个折叠问题，要不断地将折叠前后的图形加以比较，抓住折叠前后的变与不变量．典型例题七例7 正方体1111D C B A ABCD -的棱长为1，P 是AD 的中点．求二面角P BD A --1的大小．分析：求二面角关键是确定它的平面角，按定义在二面角的棱上任取了点，在二个半平面上分别作棱的垂线，方法虽简便，但因与其他条件没有联系，要求这个平面角一般是很不容易的，所以在解题中不大应用．在解题中应用得较多的是“三垂线定理”的方法，如图考虑到AB 垂直于平面1AD ，1BD 在平面1AD 上的射影就是1AD ．再过P 作1AD 的垂线PF ，则PF ⊥面1ABD ，过F 作B D 1的垂线FE ，PEF ∠即为所求二面角的平面角了．解：过P 作1BD 及1AD 的垂线，垂足分别是E 、F ，连结EF ．∵AB ⊥面1AD ，PF ⊂面1AD ，∴PF AB ⊥，又1AD PF ⊥，∴PF ⊥面1ABD ．又∵1BD PE ⊥，∴1BD EF ⊥，∴PEF ∠为所求二面角的平面角．∵D AD Rt 1∆∽PFA ∆，∴11AD AP DD PF =．而21=AP ，11=DD ，21=AD ，∴42=PF ．在1PBD ∆中，251==PB PD ． ∵1BD PE ⊥，∴2321==BD BE ．在PEB Rt ∆中，2222=-=BE PB PE ，在PEF Rt ∆中，21sin ==∠PE PF PEF ， ∴︒=∠30PEF ．典型例题八例8 在ABC ∆所在平面外有一点S ，已知AB SC ⊥，SC 与底面ABC 所成角为θ，二面角C AB S --的大小为ϕ，且︒=+90ϕθ．求二面角A SB C --的大小．分析：由题设易证SD SC ⊥，由已知得SC ⊥平面SAB ，显然所求的二面角是直二面角，此时只需证明二面有的两个面垂直即可．在解这种类型题时，如果去作二面角A SB C --的平面角，那么可能会走弯路．解：如图所示，作SO ⊥平面ABC 于O ，连结CO 并延长交AB 于D ，连结SD ． ∵SO ⊥平面ABC ，∴SCO ∠是SC 与平面ABC 所成角，θ=∠SCO ．∵SO ⊥平面ABC ，AB SC ⊥，∴CD AB ⊥，SD AB ⊥．∴SDO ∠是二面角C AB S --的平面角，ϕ=∠SDO ．∵︒=+90ϕθ，∴SD SC ⊥．又∵AB SC ⊥，∴SC ⊥平面SAB ，∴平面SBC ⊥平面SAB ，∴二面角A SB C --的大小为︒90．说明：二面角的平面角满足三个条件：(1)顶点在棱上，(2)两边在面内，(3)两边与棱垂直．应注意CSB ∠不满足第(3)条，不是二面角A SB C --的平面角．在求二面角大小时，若其平面角不易作出时，则可考虑判定两平面是否垂直，如果两平面垂直，则其二面角为︒90，反之亦然．典型例题九例9 如果αβ⊥，αγ⊥，a =γβ ，那么α⊥a ．分析：(1)本题是一道高考题，考查线面垂直和面面垂直的性质和逻辑推理能力．要证α⊥a ，只要证明直线a 与平面α内的两条相交直线垂直就可以了，从而借助平面与平面垂直的性质达到证明α⊥a 的目的；(2)要证α⊥a ，只要证明a 平行于平面α的一条垂线就可以了，这也可以借助面面垂直的性质加以考虑；(3)可以用“同一法”来证明．证法一：如图所示，设b =βα ，c =γα ，过平面α内一点P 作b PA ⊥于A ，作c PB ⊥于B ．∵αβ⊥，∴β⊥PA ．又a =γβ ，∴a PA ⊥，同理可证a PB ⊥．∵P PB PA = 且α⊂PB PA 、，∴α⊥a ．证法二：如图所示，设b =βα ，在平面β内作直线b l ⊥1．∵βα⊥，∴α⊥1l ．设c =γα ，在平面γ内作直线c l ⊥2．同理可证a l ⊥2，因此21//l l ．由于β⊂1l ，β⊄2l ，∴β//2l ．而γ⊂2l ，γβ =a ，∴a l //2．故由a l //2知，α⊥a ．证法三：如图所示过直线a 上一点P 作直线α⊥'a ．∵γβ =a ，a P ∈，∴β∈P ，根据课本第37页例2（如果两个平面互相垂直，那么经过第一个平面内的一点垂直于第二个平面的直线在第一个平面内），∴β⊂'a ．同理可证γ⊂'a ，故γβ ='a ．椐公理2可知，直线'a 与直线a 重合．∴α⊥a说明：(1)本例实际上可作为两个平面垂直的性质定理，主要用于判断直线和平面的垂直，在很多习题中都可以用到本例的结论．(2)本例的三种证明方法其思维角度不同，但都是围绕“面面垂直”、“线面面垂直”的判定与性质定理来进行思考的，希望同学们今后在解题中多进行这方面的训练，这对提高数学思维能力是大有裨益的．典型例题十例10 设由一点S 发出三条射线SA 、SB 、SC ，α=∠ASB ，β=∠BSC ，θ=∠ASC ，α、β、θ均为锐角，且θβαcos cos cos =⋅．求证：平面ASB ⊥平面BSC ．分析：欲证两平面垂直，只需证明其中一平面内有一直线垂直于另一平面即可，此题设法通过线段关系过渡．证明：如图，任取点A ，作SB AB ⊥于B ，过B 作SC BC ⊥于C ，连结AC ． ∵αcos ⋅=AS SB ，βcos ⋅=SB SC ，故βαcos cos ⋅⋅=AS SC ．又由θβαcos cos cos =⋅，则θcos ⋅=AS SC ，从而可得︒=∠90ACS ，即SC AC ⊥，已作SC BC ⊥，故SC ⊥平面ACB ，即有SC AB ⊥，已作SB AB ⊥，从而AB ⊥平面BSC ，故平面ASB ⊥平面BSC ．说明：本题易犯错误是：作SB AB ⊥于B ，作SC BC ⊥于C ，连结AC ，由三垂线定理得AC SC ⊥，∴SC ⊥平面ACB ，∴SC AB ⊥，∴AB ⊥平面SBC ．其错误原因是作SB AB ⊥后，将AB 误认为是平面SBC 的垂线．此题的证明也可以作SB AB ⊥于B ，SC AC ⊥于C ，连结BC ．在SBC ∆中，由余弦定理及条件θβαcos cos cos =⋅，证明222SC BC SB +=，从而BC SC ⊥，∴SC ⊥面ABC ，∴SC AB ⊥．由此进一步证明，平面ASB ⊥平面BSC ．典型例题十一例11 如果二面角βα--l 的平面角是锐角，点P 到α、β和棱l 的距离分别为22、4、24，求二面角的大小．分析：如果二面角βα--l 内部，也可能在外部，应区别处理．解：如图甲是点P 在二面角βα--l 的内部时，乙是点P 在二面角βα--l 的外部时．∵α⊥PA ，∴l PA ⊥．∵l AC ⊥，∴面l PAC ⊥．同理，面l PBC ⊥，而面PAC 面PBC PC =∴面PAC 与面PBC 应重合，即A 、C 、B 、P 在同一平面内，ACB ∠是二面角的平面角．在APC Rt ∆中，212422sin ===∠PB PA ACP ， ∴︒=∠30ACP ．在BPC Rt ∆中，22244sin ===∠PC PB BCP ， ∴︒=∠45BCP ，故︒=︒+︒=∠754530ACB （图甲）或︒=︒-︒=∠153045ACB （图乙）．说明：作一个垂直于棱的平面，此平面与两个半平面的交线所成的角就是二面角的平面角．这是本题得到二面平面角的方法，即所谓垂面法．典型例题十二例12 P 为︒120的二面角βα--a 内一点，P 到α和β的距离均为10，求点P 到棱a 的距离．分析：本题已知二面角的大小而求点到直线的距离，须做出二面角的平面角，然后将条件揉和在一起，便可解决问题．解：如图，过点P 作α⊥PA 于A ，β⊥PB 于B ，设相交直线PA 、PB 确定的平面为γ，O a =γ ，则OA =αγ ，OB =βγ 连结PO ，则10==BP AP∵α⊥PA ，β⊥PB ，∴γ⊥a ，而⊂PO 平面γ，∴PO a ⊥，∴PO 的长即为点P 到直线a 的距离．又∵γ⊥a ，γ⊂OA ，γ⊂OB∴AOB ∠是二面角βα--a 的平面角，即︒=∠120AOB ．而四边形AOBP 为一圆内接四边形，且PO 为该四边形的外接圆直径．∵四边形AOBP 的外接圆半径等于由A 、B 、O 、P 中任意三点确定的三角形的外接圆半径，因此求PO 的长可利用APB ∆．在APB ∆中，10==BP AP ，︒=∠60APB ，∴10=AB ．由正弦定理：332060sin 2=︒==AB R PO ．说明：(1)该题寻找︒120的二面角的平面角，所采取的方法即为垂面法，由此可见，若题目可找到与棱垂直的平面，用“垂面法”确定二面角的平面角也是一种可取的方法．(2)充分借助于四边形PAOB 为一圆内接四边形，∵OA PA ⊥，OB PB ⊥，∵PO 即为其外接圆直径，然后借助于四边有的外接圆直径等于其中任一三角形的外接圆直径进行转移，由正弦定理帮助解决了问题．典型例题十三例13 如图，正方体的棱长为1，O BC C B =11 ，求：(1)AO 与11C A 所成的角；(2)AO 与平面AC 所成角的正切值；(3)平面AOB 与平面AOC 所成的角．解：(1)∵AC C A //11，∴AO 与11C A 所成的角就是OAC ∠．∵OB OC ⊥，⊥AB 平面1BC ，∴OA OC ⊥（三垂线定理）．在AOC Rt ∆中，22=OC ，2=AC ，∴︒=∠30OAC ．(2)作BC OE ⊥，平面1BC ⊥平面AC ．∴OE ⊥平面AC ，OAE ∠为OA 与平面AC 所成的角．在OAE Rt ∆中，21=OE ，25)21(122=+=AE ． ∴55tan ==∠AE OE OAE ． (3)∵OA OC ⊥，OB OC ⊥，∴⊥OC 平面AOB ．又∵⊂OC 平面AOC ，∴平面AOB ⊥平面AOC ．说明：本题包含了线线角、线面角和面面角三类问题．求角度问题主要是求两条异面直线所成角⎥⎦⎤ ⎝⎛2,0π，直线和平面所成角⎥⎦⎤⎢⎣⎡2,0π，二面角(]π,0三种．典型例题十四例14 如图，矩形ABCD ，PD ⊥平面ABCD ，若2=PB ，PB 与平面PCD 所成的角为︒45，PB 与平面ABD 成︒30角，求：(1)CD 的长；(2)求PB 与CD 所在的角；(3)求二面角D PB C --的余弦值．分析：从图中可以看出，四面体BCD P -是一个基础四面体，前面已推导出平面PBC 与平面BCD 所成的二面角的余弦值为333221=⨯⨯=⋅⋅BD PC BC PD ，可见，基础四面体作为一部分，经常出现在某些几何体中．解：(1)∵⊥PD 平面ABCD ，∴BC PD ⊥．又⊥BC 平面PDC ，∴BPC ∠为PB 与平面PCD 所在的角，即︒=∠45BPC ．同理：PBD ∠即为PB 与平面ABD 所成的角，∴︒=∠30PBD ，在PBC Rt ∆中，∵2=PB ，∴2==PC BC ．在PBD Rt ∆中，︒=∠30PBD ，∴1=PD ，3=BD ．在BCD Rt ∆中，2=BC ，3=BD ，∴1=CD ．(2)∵CD AB //，∴PB 与CD 所成的角，即为PB 与AB 所成的角，PBA ∠即为PB 与AB 所成的角∵⊥PD 平面ABCD ，AB AD ⊥，∴AB PA ⊥（三垂线定理）．在PAB Rt ∆中，1==CD AB ，2=PB ，∴︒=∠60PBA ．(3)由点C 向BD 作垂线，垂足为E ，由点E 向PB 作垂线，垂足为F ，连结CF ． ∵⊥PD 平面ABCD ，∴CE PD ⊥．又BD CE ⊥，∴⊥CE 平面PBD ，CF 为平面PBD 的斜线，由于PB EF ⊥，∴由三垂线定理：CF PB ⊥．∴CEF ∠为二面角D PB C --的平面角在BCD Rt ∆中，2=BC ，1=DC ，3=BD ， ∴36=⋅=BD CD BC CE ．在PCB Rt ∆中，2=BC ，2=PC ，2=PB ， ∴1=⋅=PBCP BC CF ， ∴36sin ==∠CF CB CFE ． ∴33cos =∠CFE ， ∴二面角D PB C --的余弦值为33．说明：解空间几何计算问题，一般要做两件事：一件是根据问题的需要作必要证明，如本题中的线线所成的角、面面所成的角从理认上都必须说清楚究竟是谁；另一件事才是计算，这两件事是根据问题解答逻辑上的需要有机的结合在一起的．典型例题十五例15 过点S 引三条不共面的直线SA 、SB 、SC ，如图，︒=∠90BSC ，︒=∠=∠60ASB ASC ，若截取a SC SB SA ===(1)求证：平面ABC ⊥平面BSC ；(2)求S 到平面ABC 的距离．分析：要证明平面ABC ⊥平面BSC ，根据面面垂直的判定定理，须在平面ABC 或平面BSC 内找到一条与另一个平面垂直的直线．(1)证明：∵a SC SB SA ===，又︒=∠=∠60ASB ASC ，∴ASB ∆和ASC ∆都是等边三角形，∴a AC AB ==，取BC 的中点H ，连结AH ，∴BC AH ⊥．在BSC Rt ∆中，a CS BS ==，∴BC SH ⊥，a BC 2=， ∴2)22(222222a a a CH AC AH =-=-=，∴222a SH =．在SHA ∆中，∴222a AH =，222a SH =，22a SA =， ∴222HA SH SA +=，∴SH AH ⊥，∴⊥AH 平面SBC ．∵⊂AH 平面ABC ，∴平面ABC ⊥平面BSC ．或：∵AB AC SA ==，∴顶点A 在平面BSC 内的射影H 为BSC ∆的外心，又BSC ∆为∆Rt ，∴H 在斜边BC 上，又BSC ∆为等腰直角三角形，∴H 为BC 的中点，∴⊥AH 平面BSC ．∵⊂AH 平面ABC ，∴平面ABC ⊥平面BSC ．(2)解：由前所证：AH SH ⊥，BC SH ⊥，∴⊥SH 平面ABC ，∴SH 的长即为点S 到平面ABC 的距离，a BC SH 222==， ∴点S 到平面ABC 的距离为a 22．典型例题十六例16 判断下列命题的真假(1)两个平面垂直，过其中一个平面内一点作与它们交线垂直的直线，必垂直于另一个平面．(2)两个平面垂直，分别在两个平面内且互相垂直的两直线，一定分别与另一平面垂直；(3)两平面垂直，分别在这两个平面内的两直线互相垂直．分析：(1)若该点在两个平面的交线上，则命题是错误的，如图，正方体C A 1中，平面AC ⊥平面1AD ，平面 AC 平面1AD AD =，在AD 上取点A ，连结1AB ，则AD AB ⊥1，即过棱上一点A 的直线1AB 与棱垂直，但1AB 与平面ABCD 不垂直，其错误的原因是1AB 没有保证在平面11A ADD 内．可以看出：线在面内这一条件的重要性；(2)该命题注意了直线在平面内，但不能保证这两条直线都与棱垂直，如图，在正方体C A 1中，平面1AD ⊥平面AC ，1AD ⊂平面11A ADD ，AB ⊂平面ABCD ，且1AD AB ⊥，即AB 与1AD 相互垂直，但1AD 与平面ABCD 不垂直；(3)如上图，正方体C A 1中，平面11A ADD ⊥平面ABCD ，1AD ⊂平面11A ADD ，⊂AC 平面ABCD ，1AD 与AC 所成的角为︒60，即1AD 与AC 不垂直．说明：必须注意两个平面垂直的性质定理成立的条件：(1)线在面内，(2)线垂直于交线，从而可得出线面垂直．典型例题十七例17 如图，在︒60二面角βα--a 内有一点P ，P 到α、β的距离分别为3和5，求P 到交线a 的距离．解：作α⊥PA 于A ，β⊥PB 于B ，设PA ，PB 所确定的平面为γ，Q a = γ，连AQ ，BQ ，∵α⊥PA ，∴a PA ⊥．同理a PB ⊥，∴⊥a 平面γ，∴PQ a ⊥，则PQ 是P 到a 的距离．在四边形PAQB 中，︒=∠=∠90B A ，∴PAQB 是圆的内接四边形，且R PQ 2=．又∵︒=∠60BQA ，︒=∠120BPA ， ∴7120cos 53253=︒⋅⋅-+=AB ，331432760sin 2=⨯=︒==AB R PQ ．说明：本例作二面角的平面角用作垂面法，避免了再证明P 、B 、A 、Q 四点共面，同时用到正弦定理和余弦定理．典型例题十八例18 如图，四面体SABC 中，A B C ∆是等腰三角形，a BC AB 2==，︒=∠120ABC ，且⊥SA 平面ABC ，a SA 3=．求点A 到平面SBC 的距离．分析：考虑利用两个平面垂直的性质定理作出点A 到SBC 的垂线，先确定一个过点A 和平面SBC 垂直的平面，∵⊥SA 平面ABC ，故作BC AD ⊥于D ，连结SD ，则平面SAD ⊥平面SBC ，平面SAD 实际上就是二面角A BC S --的平面角SDA 所在的平面，因此，它的作图过程和用三垂线法作二面角A BC S --的平面角的作图过程完全相同．解：作BC AD ⊥交BC 于D ，连结SD ，∵⊥SA 平面ABC ，根据三垂线定理有BC SD ⊥，又D AD SD = ，∴BC ⊥平面SAD ，又BC ⊂平面SBC ，∴平面SBC ⊥平面ADS ，且平面SBC 平面ADS SD =，∴过点A 作SD AH ⊥于H ，由平面与平面垂直的性质定理可知：⊥AH 平面SBC ．在SAD Rt ∆中，a SA 3=，a AB AD 360sin =︒⋅=， ∴23)3()3(332222a a a a a AD SA ADSA AH =+⋅=+⋅=，即点A 到平面SBC 的距离为23a ．说明：二面角的平面角所在的平面垂直于二面角的棱，同时垂直于二面角的两个两．从本例可以看出：要求点到平面的距离，只要过该点找到与已知平面垂直的平面，则点面距即可根据面面垂直的性质作出．本卷由《100测评网》整理上传，专注于中小学生学业检测、练习与提升.。

100测评网_高考复习专题三函数地基本性质下学期6_必修5数学下学期

欢迎登录? 100 测评网?100ceping 进展学习检测，有效提高学习成绩.一、单项选择题〔每题5 分，共 80 分〕1、以下函数中，既是偶函数，又是在区间(0,) 上单调递减的函数为A 、yln1B 、yx 3C 、y2xD、yc os x x答案A解析选项B ， yx 3不是偶函数；y2 x 在区间(0,) 上单调递增；y cos x 在区间 (0, ) 上既不单调递减也不单调递增，所以答案选A 。

2、设奇函数 f ( x)在(0,) 上为增函数，且f (1)0 ，那么不等式f( x)f ( x) 0 的x解集为A 、( 1,0)(1, )B 、 (, 1) (0,1)C 、( , 1) (1,)D、 ( 1,0) (0,1)答案 D解析因为函数 f (x) 是奇函数，所以 f (x)f ( x), f ( x)f ( x) 2 f ( x) 0 ，xx又f (1) 0，所以f ( 1) f (1) 0，当 x ＞ 0，f ( x) 0 ；当 x ＜0，0 f ( 1) 。

f ( x)又 f ( x)在(0, ) 上为增函数，那么奇函数 f ( x)在( ,0) 上为增函数，故0＜ x ＜ 1或 -1 ＜x ＜0，f ( x)f ( x)，答案选。

0 Dx3、设函数f ( x)是定义在 R 上的奇函数，当 x 0时， f ( x) 2x 2 x, 那么f (1)等于A 、-3B、-1C 、 1D 、 3答案 A 解析欢迎登录? 100 测评网?100ceping进展学习检测，有效提高学习成绩.当 x 0时， f (x)2x2x, 所以 f ( 1)2 (1)3，又函数f ( x)是定义在R 上的奇函数，所以f (1) f ( 1)3，答案选A。

4、设函数f ( x)是定义在 R上的奇函数，当x 0时， f (x) 2x 2x b(b为常数 ), 那么f ( 1) =A、3B、1C、-1D、 -3答案D解析因为函数 f (x) 是定义在R上的奇函数，所以f (0)0,200 b0,b 1,即当 x 0时， f(x)2x2x 1, 那么f ( 1)f (1)(2121) 3 ，答案选 D。

100测评网高中数学复习10-5月19_20日课本基础知识回归

通州中学5月19日课本基础知识回归（必修4）命题者：徐建良姓名得分一、填空题（每题8分）1．=-00020cos 20sin 10cos 2 ．2．已知tan α＝11cos()14αβ＋＝－，α、β都是锐角，则=βcos ．3．已知向量a ＝(cos sin )αα，，b ＝(cos sin )ββ，，且≠±a b ，那么+a b 与-a b 的夹角的大小是． 4．函数)2sin(x y -=π的单调递减区间是．=α 时，扇形面积S 最大的条②横坐标变为原来的21,再④向左平移8π,再将横坐标)42π+x 的图像的是．）0,),0(a 其中常数0>a ，点P 在线段AB 上，且=t (0≤t ≤1)，则⋅的最大值为．9．已知定义在R 上的奇函数)(x f 在区间),0(+∞上单调递增，若0)1(=f ，△ABC 的内角A 满足0)(cos <A f ，则A 范围是．10．已知△ABC 所在平面内一点P ，满足：AP 中点为Q ，BQ 的中点为R ，CR 的中点为P b a==,，如图，向量= ．二、解答题（每题20分）11．设两个非零向量1e 和2e 不共线．（1）如果21e e AB +=，2182e e BC +=，21CD =D 三点共线；（2）若2||1=e ，3||2=e ，1e 与2e 的夹角为60，是否存在实数m ，使得21e e m +与21e e -垂直？并说明理由．5月19日答案：1．3 2．21 3．π24．Z k k k ∈+-],125,12[ππππ5．2，L 2166．必要不充分 7．①和② 8．2a 9．),32()2,3(ππππ 10．b a7472+=11．解： AD =++=（1e +2e ）+（128e +2e ）+（133e -2e ）=6（1e +2e ）=6∴ //AD AB 且AD 与AB 有共同起点 ∴ A 、B 、D 三点共线m e 2与1e -2e 垂直，则（m 1e 2e +）⋅（1e -2e ）=0222(1)0me m e e e +-⋅-=|=3，1e 与2e 的夹角为60224e e ==22229e e ==，cos cos603e e e e θ⋅==90-= ∴ m故存在实数6m =，使得4．125．±27．①和③ 8．79- 9．(11)-，（只要满足0a b +=的一组数字即可）10．311．解：a x x f +++=1)62sin(2)(，a =1通州中学5月20日课本基础知识回归（必修4）命题者：徐建良姓名得分一、填空题（每题8分） 1．已知34παβ+=，则(1tan )(1tan )αβ--的值是________． 2．=+)10tan 31(50sin 00________．3．△ABC 中=，=，=，a c c b ⋅=⋅=⋅，则△ABC 的形状为．4．定义一种新运算：θsin ||||b a b a =⊗，其中θ为a 与b 的夹角．已知(3,1)a =-(,0)2b =，则5．在△ABC ，则⋅的值2-，的有向线84 ④将函数)32cos(π-=x y 的图象向左平移3π单位，得到函数x y 2cos =的图象；其中正确的命题的序号是．8．若31)6sin(=-απ，则=+)232cos(απ ．9．若ππ()sin()sin()(0)44f x a x b x ab =++-≠是偶函数，则有序实数对()a b ，可以是．10．已知1||=,3||=,0=⋅，点C 在AOB ∠内，且30AOC ∠=︒，设()OC mOA nOB m n =+∈R ，二、解答题（每题20分）11．已知)2sin 3,1(),1,2cos 1(a x N x M ++x (y ⋅=（O 为坐标原点）．； 4，求a 的值；x y sin =的图象如何。

100测评网2022届高三数学第一轮复习资料——平面向量

100测评网2022届高三数学第一轮复习资料——平面向量由100测评网上传提供,一线特高级教师整理编辑,非常有助于中小学生的学业提升平面向量第2章平面向量§2.1向量的概念及其表示考纲要求：①了解向量的实际背景．②理解平面向量的概念及向量相等的含义．③理解向量的几何表示．经典例题：下列命题正确的是（）A.ａ与ｂ共线，ｂ与ｃ共线，则ａ与c也共线B.任意两个相等的非零向量的始点与终点是一平行四边形的四顶点C.向量ａ与ｂ不共线，则ａ与ｂ都是非零向量D.有相同起点的两个非零向量不平行当堂练习：1.下列各量中是向量的是()A.密度B.体积C.重力D.质量2下列说法中正确的是（）A.平行向量就是向量所在的直线平行的向量B.长度相等的向量叫相等向量C.零向量的长度为零D.共线向量是在一条直线上的向量3．设O是正方形ABCD的中心，则向量AO、OB、CO、OD是（）A．平行向量B．有相同终点的向量C．相等的向量D．模都相同的向量4.下列结论中,正确的是()A.零向量只有大小没有方向B.对任一向量a,|a|>0总是成立的C.||=||D.||与线段BA的长度不相等5.若四边形ABCD是矩形,则下列命题中不正确的是()A.AB与CD共线B.AC与BD相等C.AD与CB是相反向量D.AB与CD模相等6．已知O是正方形ABCD对角线的交点，在以O，A，B，C，D这5点中任意一点为起点，另一点为终点的所有向量中，（1）与BC相等的向量有；（2）与OB长度相等的向量有；（3）与DA共线的向量有．7．在①平行向量一定相等；②不相等的向量一定不平行；③共线向量一定相等；④相等向量一定共线；⑤长度相等的向量是相等向量；⑥平行于同一个向量的两个向量是共线向量中，不正确的命题是．并对你的判断举例说明由100测评网上传提供,一线特高级教师整理编辑,非常有助于中小学生的学业提升．8．如图，O是正方形ABCD对角线的交点，四边形OAED，OCFB都是正方形，在图中所示的向量中：（1）与AO相等的向量有；（2）写出与AO共线的向有；（3）写出与AO的模相等的有；（4）向量AO与CO是否相等？答．9．O是正六边形ABCDE的中心，且OAa，OBb，ABc，在以A，B，C，D，E，O为端点的向量中：（1）与a相等的向量有；（2）与b相等的向量有；（3）与c相等的向量有10．在如图所示的向量a，b，c，d，e中（小正方形的边长为1），是否存在：（1）是共线向量的有；（2）是相反向量的为；（3）相等向量的的；（4）模相等的向量．11．如图，△ABC中，D，E，F分别是边BC，AB，CA的中点，在以A、B、C、D、E、F为端点的有向线段中所表示的向量中，（1）与向量FE共线的有．（2）与向量DF的模相等的有．（3）与向量ED相等的有．FC12．如图，中国象棋的半个棋盘上有一只“马”，开始下棋时，它位于A点，这只“马”第一步有几种可能的走法？试在图中画出来．若它位于图中的P点，这只“马”第一步有几种可能的走法？它能否从点A走到与它相邻的B？它能否从一交叉点出发，走到棋盘上的其它任何一个交叉点？第2章平面向量§2.2向量的线性运算重难点：灵活运用向量加法的三角形法则和平行四边形法则解决向量加法的问题，利用交换律和结合律进行向量运算；灵活运用三角形法则和平行四边形法则作两个向量的差，以及求两个向量的差的问题；理解实数与向量的积的定义掌握实数与向量的积的运算律体会两向量共线的充要条件．考纲要求：①掌握向量加法，减法的运算，并理解其几何意义．②掌握向量数乘的运算及其意义。