固体物理答案
固体物理习题解答

《固体物理学》部分习题解答1.3 证明:体心立方晶格的倒格子是面心立方;面心立方晶格的倒格子是体心立方 。
解 由倒格子定义2311232a a b a a a π⨯=⋅⨯ 3121232a a b a a a π⨯=⋅⨯ 1231232a a b a a a π⨯=⋅⨯体心立方格子原胞基矢123(),(),()222a a aa i j k a i j k a i j k =-++=-+=-+ 倒格子基矢231123022()()22a a a ab i j k i j k a a a v ππ⨯==⋅-+⨯+-⋅⨯202()()4a i j k i j k v π=⋅-+⨯+-2()j k a π=+ 同理31212322()a ab i k a a a aππ⨯==+⋅⨯ 32()b i j a π=+ 可见由123,,b b b 为基矢构成的格子为面心立方格子 面心立方格子原胞基矢123()/2()/2()/2a a j k a a k i a a i j =+=+=+ 倒格子基矢2311232a a b a a a π⨯=⋅⨯ 12()b i j k a π=-++ 同理22()b i j k a π=-+ 32()b i j k aπ=-+ 可见由123,,b b b 为基矢构成的格子为体心立方格子1.4 证明倒格子原胞的体积为03(2)v π,其中0v 为正格子原胞体积证 倒格子基矢2311232a a b a a a π⨯=⋅⨯3121232a a b a a a π⨯=⋅⨯1231232a a b a a a π⨯=⋅⨯倒格子体积*0123()v b b b =⋅⨯3*23311230(2)()()()v a a a a a a v π=⨯⋅⨯⨯⨯ 3*00(2)v v π=1.5 证明:倒格子矢量112233G hb h b h b =++垂直于密勒指数为123()hh h 的晶面系。
固体物理答案

3.1 已知一维单原子链,其中第j 个格波,在第n 个格点引起的位移nj μ为:sin()nj j j j j a t naq μωδ=++j δ为任意相位因子。
并已知在较高温度下每个格波的平均能量为B k T 。
具体计算每个原子的平方平均位移。
解:(1)根据2011sin ()2T j j j t naq dt T ωδ⎰++= 其中2jT πω=为振动周期,所以22221sin ()2nj j j j j j a t naq a μωδ=++=(2) 第j 个格波的平均动能 (3) 经典的简谐运动有:每个格波的平均动能=平均势能=12格波平均能量=12B k T 振幅222B j j k T a Nm ω=, 所以 22212B nj j jk T a Nm μω==。
而每个原子的平方平均位移为:222221()2B n nj nj j jjjjjk Ta Nm μμμω====∑∑∑∑。
3.2讨论N 个原胞的一维双原子链(相邻原子间距为a ),其2N 个格波的解。
当m M =时与一维单原子链一一对应。
解:(1)一维双原子链: 22q a aππ-≤<声学波:12222411sin ()m M mM aq mM m M ωβ-⎧⎫⎡⎤+⎪⎪=--⎨⎬⎢⎥+⎣⎦⎪⎪⎩⎭当m M =时,有2224(1cos )sin 2aqaq m m ββω-=-= 。
光学波:12222411sin ()m M mM aq mM m M ωβ+⎧⎫⎡⎤+⎪⎪=+-⎨⎬⎢⎥+⎣⎦⎪⎪⎩⎭当m M =时,有2224(1cos )cos 2aqaq m m ββω+=+= 。
(2)一维双原子链在m M =时的解 22224sin 2422cos 2aq m q aq aam βωππβω-+⎧=⎪⎪-≤<⎨⎪=⎪⎩与一维单原子链的解 224sin 2aqq m aaβππω=-≤<是一一对应的。
固体物理简答题(附答案)

简答题1、原子结合成晶体时,原子的价电子产生重新分布,从而产生不同的结合力,分析离子性、共价性、金属性和范德瓦耳斯性结合力的特点。
答案:离子性结合:正、负离子之间靠库仑吸引力作用而相互靠近,当靠近到一定程度时,由于泡利不相容原理,两个离子的闭合壳层的电子云的交迭会产生强大的排斥力。
当排斥力和吸引力相互平衡时,形成稳定的离子晶体;共价性结合:靠两个原子各贡献一个电子,形成所谓的共价键;金属性结合:组成晶体时每个原子的最外层电子为所有原子所共有,因此在结合成金属晶体时,失去了最外层(价)电子的原子实“沉浸”在由价电子组成的“电子云”中。
在这种情况下,电子云和原子实之间存在库仑作用,体积越小电子云密度越高,库仑相互作用的库仑能愈低,表现为原子聚合起来的作用。
范德瓦耳斯性结合:惰性元素最外层的电子为8个,具有球对称的稳定封闭结构。
但在某一瞬时由于正、负电中心不重合而使原子呈现出瞬时偶极矩,这就会使其它原子产生感应极矩。
非极性分子晶体就是依靠这瞬时偶极矩的互作用而结合的。
2. 什么叫简正振动模式?简正振动数目、格波数目或格波振动模式数目是否是一回事?答案:为了使问题既简化又能抓住主要矛盾,在分析讨论晶格振动时,将原子间互作用力的泰勒级数中的非线形项忽略掉的近似称为简谐近似. 在简谐近似下, 由N个原子构成的晶体的晶格振动, 可等效成3N个独立的谐振子的振动. 每个谐振子的振动模式称为简正振动模式, 它对应着所有的原子都以该模式的频率做振动, 它是晶格振动模式中最简单最基本的振动方式. 原子的振动, 或者说格波振动通常是这3N个简正振动模式的线形迭加.简正振动数目、格波数目或格波振动模式数目是一回事, 这个数目等于晶体中所有原子的自由度数之和, 即等于3N.3. 长光学支格波与长声学支格波本质上有何差别?答案:长光学支格波的特征是每个原胞内的不同原子做相对振动, 振动频率较高, 它包含了晶格振动频率最高的振动模式. 长声学支格波的特征是原胞内的不同原子没有相对位移, 原胞做整体运动, 振动频率较低, 它包含了晶格振动频率最低的振动模式, 波速是一常数. 任何晶体都存在声学支格波, 但简单晶格(非复式格子)晶体不存在光学支格波.4. 长声学格波能否导致离子晶体的宏观极化?答案:长光学格波所以能导致离子晶体的宏观极化, 其根源是长光学格波使得原胞内不同的原子(正负离子)产生了相对位移. 长声学格波的特点是, 原胞内所有的原子没有相对位移. 因此, 长声学格波不能导致离子晶体的宏观极化.5. 何谓极化声子? 何谓电磁声子?答案:长光学纵波引起离子晶体中正负离子的相对位移, 离子的相对位移产生出宏观极化电场, 称长光学纵波声子为极化声子.由本教科书的(3.103)式可知, 长光学横波与电磁场相耦合, 使得它具有电磁性质, 人们称长光学横波声子为电磁声子.6、什么是声子?答案:晶格振动的能量量子。
固体物理简答题及答案

固体物理简答题及答案简答题1、原子结合成晶体时,原子的价电子产生重新分布,从而产生不同的结合力,分析离子性、共价性、金属性与范德瓦耳斯性结合力的特点。
答案: 离子性结合:正、负离子之间靠库仑吸引力作用而相互靠近,当靠近到一定程度时,由于泡利不相容原理,两个离子的闭合壳层的电子云的交迭会产生强大的排斥力。
当排斥力与吸引力相互平衡时,形成稳定的离子晶体;共价性结合:靠两个原子各贡献一个电子,形成所谓的共价键;金属性结合:组成晶体时每个原子的最外层电子为所有原子所共有,因此在结合成金属晶体时,失去了最外层(价)电子的原子实“沉浸”在由价电子组成的“电子云”中。
在这种情况下,电子云与原子实之间存在库仑作用,体积越小电子云密度越高,库仑相互作用的库仑能愈低,表现为原子聚合起来的作用。
范德瓦耳斯性结合:惰性元素最外层的电子为8个,具有球对称的稳定封闭结构。
但在某一瞬时由于正、负电中心不重合而使原子呈现出瞬时偶极矩,这就会使其它原子产生感应极矩。
非极性分子晶体就就是依靠这瞬时偶极矩的互作用而结合的。
2、什么叫简正振动模式?简正振动数目、格波数目或格波振动模式数目就是否就是一回事?答案:为了使问题既简化又能抓住主要矛盾,在分析讨论晶格振动时,将原子间互作用力的泰勒级数中的非线形项忽略掉的近似称为简谐近似、在简谐近似下, 由N个原子构成的晶体的晶格振动, 可等效成3N 个独立的谐振子的振动、每个谐振子的振动模式称为简正振动模式, 它对应着所有的原子都以该模式的频率做振动, 它就是晶格振动模式中最简单最基本的振动方式、原子的振动, 或者说格波振动通常就是这3N 个简正振动模式的线形迭加、简正振动数目、格波数目或格波振动模式数目就是一回事, 这个数目等于晶体中所有原子的自由度数之与, 即等于3N、3、长光学支格波与长声学支格波本质上有何差别?答案:长光学支格波的特征就是每个原胞内的不同原子做相对振动, 振动频率较高, 它包含了晶格振动频率最高的振动模式、长声学支格波的特征就是原胞内的不同原子没有相对位移, 原胞做整体运动, 振动频率较低, 它包含了晶格振动频率最低的振动模式, 波速就是一常数、任何晶体都存在声学支格波, 但简单晶格(非复式格子)晶体不存在光学支格波、4、长声学格波能否导致离子晶体的宏观极化?答案:长光学格波所以能导致离子晶体的宏观极化, 其根源就是长光学格波使得原胞内不同的原子(正负离子)产生了相对位移、长声学格波的特点就是, 原胞内所有的原子没有相对位移、因此, 长声学格波不能导致离子晶体的宏观极化、5、何谓极化声子? 何谓电磁声子?答案:长光学纵波引起离子晶体中正负离子的相对位移, 离子的相对位移产生出宏观极化电场, 称长光学纵波声子为极化声子、由本教科书的(3、103)式可知, 长光学横波与电磁场相耦合, 使得它具有电磁性质, 人们称长光学横波声子为电磁声子、6、什么就是声子?答案: 晶格振动的能量量子。
《固体物理》课后习题答案

1.1 如果将等体积球分别排列成下列结构,设x 表示钢球所占体积与总体积之比,证明结构x简单立方π/ 6 ≈0.52 体心立方3π/ 8 ≈0.68 面心立方2π/ 6 ≈0.74六方密排2π/ 6 ≈0.74 金刚石3π/16 ≈0.34解:设钢球半径为r ,根据不同晶体结构原子球的排列,晶格常数a 与r 的关系不同,分别为:简单立方:a = 2r金刚石:根据金刚石结构的特点,因为体对角线四分之一处的原子与角上的原子紧贴,因此有1.3 证明:体心立方晶格的倒格子是面心立方;面心立方晶格的倒格子是体心立方。
证明:体心立方格子的基矢可以写为面心立方格子的基矢可以写为根据定义,体心立方晶格的倒格子基矢为同理与面心立方晶格基矢对比,正是晶格常数为4π/ a的面心立方的基矢,说明体心立方晶格的倒格子确实是面心立方。
注意,倒格子不是真实空间的几何分布,因此该面心立方只是形式上的,或者说是倒格子空间中的布拉菲格子。
根据定义,面心立方的倒格子基矢为同理而把以上结果与体心立方基矢比较,这正是晶格常数为4πa的体心立方晶格的基矢。
证明:根据定义,密勒指数为的晶面系中距离原点最近的平面ABC 交于基矢的截距分别为即为平面的法线根据定义,倒格子基矢为则倒格子原胞的体积为1.6 对于简单立方晶格,证明密勒指数为(h, k,l)的晶面系,面间距d 满足其中a 为立方边长。
解:根据倒格子的特点,倒格子与晶面族(h, k,l)的面间距有如下关系因此只要先求出倒格,求出其大小即可。
因为倒格子基矢互相正交,因此其大小为则带入前边的关系式,即得晶面族的面间距。
1.7 写出体心立方和面心立方晶格结构的金属中,最近邻和次近邻的原子数。
若立方边长为a ,写出最近邻和次近邻的原子间距。
答:体心立方晶格的最近邻原子数(配位数)为8,最近邻原子间距等于次近邻原子数为6,次近邻原子间距为a ;面心立方晶格的最近邻原子数(配位数)为12,最近邻原子间距等于次近邻原子数为6,次近邻原子间距为a 。
固体物理习题答案PPT课件

5 解: A2 b c,B 2 c a,C 2 a b
V c
V c
V c
V A (B C ) (2)3( b c )[ c ( a ) ( a b )] V c
A (B C )(A C )B (A B )C
6解:当 KCl 取 ZnS 结构时,晶体总相互作用
能为 utotN(zeRR q2)
已知:N=6.023*1023/mol, ρ=0.326埃,αZnS=1.6381,(见P103) 为NaCl结构时,Zλ=2.05*10-8erg, Z=6 当为ZnS 结构时,Z=4, Zλ=(4/6)*2.05*10-8erg
设ZnS 结构时,其晶格常数与NaCl结构相同, (为原子最近邻距离)
即 a=6.294埃(见P20,图20配位数为6,参见表10,表11, a=2*1.33+1.81=6.2埃),31/2a/4=2.72埃(为原子最近邻距
离)
u to 6 . 0 t 1 2 2 [ 3 0 6 4 2 2 . 0 1 5 8 e 0 0 2 . 3 . 7 2 2 1 . 6 6 2 . ( 3 7 4 . 8 1 8 2 1 8 0 1 0 e 1 5 0 0 ) 3 ] s 1 u . 8 K 5/ m 3 C
第二章 习题答案
3解:
(c)衍射先只出现在同时满足以下二个方程的方
向上:(1)acosθ1=nλ,(2) bcosθ2=mλ
(
a,b
为二个方向矢量)
所以在二个锥面的交线上出现衍射极大。当底板
//原子面时,衍射花样为二个锥面的交线与底板
的交点。
(d)反射式低能电子衍射(LEED)中,只有表面 层原子参与衍射,故为二维衍射,衍射点的周期 大小与晶体表面原子排列方向上周期大小成反比。
固体物理答案

(1)共价键结合的特点?共价结合为什么有“饱和性”和“方向性”?之答禄夫天创作饱和性和方向性饱和性:由于共价键只能由为配对的电子形成,故一个原子能与其他原子形成共价键的数目是有限制的。
N<4,有n个共价键;n>=4,有(8-n)个共价键。
其中n为电子数目。
方向性:一个院子与其他原子形成的各个共价键之间有确定的相对取向。
(2)如何理解电负性可用电离能加亲和能来表征?电离能:使原子失去一个电子所必须的能量其中A为第一电离能,电离能可表征原子对价电子束缚的强弱;亲和势能:中性原子获得电子成为-1价离子时放出的能量,其中B为释放的能量,也可以标明原子束缚价电子的能力,而电负性是用来暗示原子得失电子能力的物理量。
故电负性可用电离能加亲和势能来表征。
(3)引入玻恩-卡门条件的理由是什么?在求解原子运动方程是,将一维单原子晶格看做无限长来处理的。
这样所有的原子的位置都是等价的,每个原子的振动形式都是一样的。
而实际的晶体都是有限的,形成的键不是无穷长的,这样的链两头原子就不克不及用中间的原子的运动方程来描述。
波恩—卡门条件解决上述困难。
(4)温度一定,一个光学波的声子数目多呢,还是一个声学波的声子数目多?对同一振动模式,温度高时的声子数目多呢,还是温度低的声子数目多?温度一定,一个声学波的声子数目多。
对于同一个振动模式,温度高的声子数目多。
(5)长声学格波能否导致离子晶体的宏观极化?不克不及。
长声学波代表的是原胞的运动,正负离子相对位移为零。
(6)晶格比热理论中德拜(Debye)模型在低温下与实验符合的很好,物理原因是什么?爱因斯坦模型在低温下与实验存在偏差的根源是什么?在甚低温下,不但光学波得不到激发,而且声子能量较大的短声学波也未被激发,得到激发的只是声子能量较小的长声学格波。
长声学格波即弹性波。
德拜模型只考虑弹性波对热容德贡献。
因此,在甚低温下,德拜模型与事实相符,自然与实验相符。
爱因斯坦模型过于简单,假设晶体中各原子都以相同的频率做振动,忽略了各格波对热容贡献的差别,依照爱因斯坦温度的定义可估计出爱因斯坦频率为光学支格波。
(参考资料)固体物理习题带答案

D E ( ) ,其中 , 表示沿 x , y , z 轴的分量,我们选取 x , y , z
沿立方晶体的三个立方轴的方向。
显然,一般地讲,如果把电场 E 和晶体同时转动, D 也将做相同转动,我们将以 D' 表示转
动后的矢量。
设 E 沿 y 轴,这时,上面一般表达式将归结为:Dx xyE, Dy yyE, Dz zy E 。现在
偏转一个角度 tg 。(2)当晶体发生体膨胀时,反射线将偏转角度
tg , 为体胀系数
3
解:(1)、布拉格衍射公式为 2d sin ,既然波长改变,则两边同时求导,有
2d cos ,将两式组合,则可得 tg 。
(2)、当晶体发生膨胀时,则为 d 改变,将布拉格衍射公式 2d sin 左右两边同时对 d
考虑把晶体和电场同时绕 y 轴转动 / 2 ,使 z 轴转到 x 轴, x 轴转到 z 轴, D 将做相同
转动,因此
D'x Dz zy E
D'y Dy yyE
D'z Dx xy E 但是,转动是以 E 方向为轴的,所以,实际上电场并未改变,同时,上述转动时立方晶体
的一个对称操作,所以转动前后晶体应没有任何差别,所以电位移矢量实际上应当不变,即
第一章:晶体结构 1. 证明:立方晶体中,晶向[hkl]垂直于晶面(hkl)。
证 明 : 晶 向 [hkl] 为 h1 k2 l3 , 其 倒 格 子 为
b1
2
a1
a2
a3
(a2 a3 )
b2
2
a1
a3 a1 (a2 a3)
b3
2
a1
a1
a2
(a2 a3)
。可以知道其倒格子矢量
固体物理课后习题答案

(
)
⎞ 2π k⎟= −i + j + k 同理 ⎠ a
(
)
(
)
(
)
2π ⎧ ⎪b1 = a −i + j + k ⎪ 2π ⎪ i− j+k ⎨b 2 = a ⎪ 2π ⎪ ⎪b3 = a i + j − k ⎩
(
)
(
)
(
)
由此可得出面心立方格子的倒格子为一体心立方格子; 所以体心立方格子和面心立方格子互为正倒格子。 2.2 在六角晶系中,晶面常用四个指数(hkil)来表示,如图 所示,前三个指数表示晶面族中最靠近原点的晶面在互成 1200的 共面轴 a1 , a2 , a3 上的截距为
设两法线之间的夹角满足
K 1 i K 2 = K1 i K 2 cos γ
K 1iK 2 cos γ = = K1 i K 2 2π 2π (h1 i + k1 j + l1 k )i (h2 i + k2 j + l2 k ) a a 2π 2π 2π 2π (h1 i + k1 j + l1 k )i (h1 i + k1 j + l1 k ) i (h2 i + k2 j + l2 k )i (h2 i + k2 j + l2 k ) a a a a
a1 a2 a3 , , ,第四个指数表示该晶面 h k i
在六重轴c上的截距为
c 。证明: l
i = −(h + k )
并将下列用(hkl)表示的晶面改用(hkil)表示:
2
第一章 晶体的结构
( 001) , (133) , (110 ) , ( 323) , (100 ) , ( 010 ) , ( 213) .
固体物理答案

第一章 晶体结构1.1、(1)对于简立方结构:(见教材P2图1-1)a=2r , V=3r 34π,Vc=a 3,n=1 ∴52.06r8r34a r 34x 3333=π=π=π= (2)对于体心立方:晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯= (3)对于面心立方:晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4,Vc=a 374.062)r 22(r 344a r 344x 3333≈π=π⨯=π⨯= (4)对于六角密排:a=2r 晶胞面积:S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积:V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个 74.062r224r 346x 33≈π=π⨯= (5)对于金刚石结构,晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 334.063r 338r 348a r 348x 33333≈π=π⨯=π⨯=1.3证明:(1)面心立方的正格子基矢(固体物理学原胞基矢):123()2()2()2a a j k a a i k a a i j ⎧=+⎪⎪⎪=+⎨⎪⎪=+⎪⎩r r r r r rr r r由倒格子基矢的定义:1232()b a a π=⨯Ωr r r31230,,22(),0,224,,022a a a a a a a a a a Ω=⋅⨯==r r rQ ,223,,,0,()224,,022i j ka a a a a i j k a a ⨯==-++r rr r r r r r213422()()4a b i j k i j k a aππ∴=⨯⨯-++=-++r r rr r r r同理可得:232()2()b i j k ab i j k aππ=-+=+-r r r r r r r r 即面心立方的倒格子基矢与体心立方的正格基矢相同。
固体物理学答案-王矜奉

第一章、晶体的结构习题1.以刚性原子球堆积模型,计算以下各结构的致密度分别为:(1)简立方,;(2)体心立方,6π;83(3)面心立方,(4)六角密积,;62;62π(5)金刚石结构,;163[解答]设想晶体是由刚性原子球堆积而成,一个晶胞中刚性原子球占据的体积与晶胞体积的比值称为结构的致密度,设n 为一个晶胞中的刚性原子球数,r 表示刚性原子球半径,V 表示晶胞体积,则致密度=ρVr n 334π(1)对简立方晶体,任一个原子有6个最近邻,若原子以刚性球堆积,如图1.2所示,中心在1,2,3,4处的原子球将依次相切,因为,,433a V r a ==面1.2简立方晶胞晶胞内包含1个原子,所以=ρ6)(33234π=a a (2)对体心立方晶体,任一个原子有8个最近邻,若原子刚性球堆积,如图1.3所示,体心位置O 的原子8个角顶位置的原子球相切,因为晶胞空间对角线的长度为晶胞内包含2个原子,所以,,433a V r a ===ρππ83(*2334334=aa图1.3体心立方晶胞(3)对面心立方晶体,任一个原子有12个最近邻,若原子以刚性球堆积,如图1.4所示,中心位于角顶的原子与相邻的3个面心原子球相切,因为,1个晶胞内包含4个原子,所以3,42a V r a ===.ρ62(*4334234ππ=a a图1.4面心立方晶胞(4)对六角密积结构,任一个原子有12个最近邻,若原子以刚性球堆积,如图1。
5所示,中心在1的原子与中心在2,3,4的原子相切,中心在5的原子与中心在6,7,8的原子相切,图 1.5六角晶胞图 1.6正四面体晶胞内的原子O 与中心在1,3,4,5,7,8处的原子相切,即O 点与中心在5,7,8处的原子分布在正四面体的四个顶上,因为四面体的高h =223232c r a ==晶胞体积V =,222360sin ca ca =�一个晶胞内包含两个原子,所以ρ=.ππ62)(*22233234=ca a(5)对金刚石结构,任一个原子有4个最近邻,若原子以刚性球堆积,如图1.7所示,中心在空间对角线四分之一处的O 原子与中心在1,2,3,4处的原子相切,因为,83r a =晶胞体积,3a V=图1.7金刚石结构一个晶胞内包含8个原子,所以ρ=.163)83(*83334ππ=aa 2.在立方晶胞中,画出(102),(021),(1),和(2)晶面。
固体物理简答题及答案

简答题1、原子结合成晶体时,原子的价电子产生重新分布,从而产生不同的结合力,分析离子性、共价性、金属性和范德瓦耳斯性结合力的特点。
答案:离子性结合:正、负离子之间靠库仑吸引力作用而相互靠近,当靠近到一定程度时,由于泡利不相容原理,两个离子的闭合壳层的电子云的交迭会产生强大的排斥力。
当排斥力和吸引力相互平衡时,形成稳定的离子晶体;共价性结合:靠两个原子各贡献一个电子,形成所谓的共价键;金属性结合:组成晶体时每个原子的最外层电子为所有原子所共有,因此在结合成金属晶体时,失去了最外层(价)电子的原子实“沉浸”在由价电子组成的“电子云”中。
在这种情况下,电子云和原子实之间存在库仑作用,体积越小电子云密度越高,库仑相互作用的库仑能愈低,表现为原子聚合起来的作用。
范德瓦耳斯性结合:惰性元素最外层的电子为8个,具有球对称的稳定封闭结构。
但在某一瞬时由于正、负电中心不重合而使原子呈现出瞬时偶极矩,这就会使其它原子产生感应极矩。
非极性分子晶体就是依靠这瞬时偶极矩的互作用而结合的。
2. 什么叫简正振动模式?简正振动数目、格波数目或格波振动模式数目是否是一回事?答案:为了使问题既简化又能抓住主要矛盾,在分析讨论晶格振动时,将原子间互作用力的泰勒级数中的非线形项忽略掉的近似称为简谐近似. 在简谐近似下, 由N个原子构成的晶体的晶格振动, 可等效成3N个独立的谐振子的振动. 每个谐振子的振动模式称为简正振动模式, 它对应着所有的原子都以该模式的频率做振动, 它是晶格振动模式中最简单最基本的振动方式. 原子的振动, 或者说格波振动通常是这3N个简正振动模式的线形迭加.简正振动数目、格波数目或格波振动模式数目是一回事, 这个数目等于晶体中所有原子的自由度数之和, 即等于3N.3. 长光学支格波与长声学支格波本质上有何差别?答案:长光学支格波的特征是每个原胞内的不同原子做相对振动, 振动频率较高, 它包含了晶格振动频率最高的振动模式. 长声学支格波的特征是原胞内的不同原子没有相对位移, 原胞做整体运动, 振动频率较低, 它包含了晶格振动频率最低的振动模式, 波速是一常数. 任何晶体都存在声学支格波, 但简单晶格(非复式格子)晶体不存在光学支格波.4. 长声学格波能否导致离子晶体的宏观极化?答案:长光学格波所以能导致离子晶体的宏观极化, 其根源是长光学格波使得原胞内不同的原子(正负离子)产生了相对位移. 长声学格波的特点是, 原胞内所有的原子没有相对位移. 因此, 长声学格波不能导致离子晶体的宏观极化. 5. 何谓极化声子? 何谓电磁声子?答案:长光学纵波引起离子晶体中正负离子的相对位移, 离子的相对位移产生出宏观极化电场, 称长光学纵波声子为极化声子.由本教科书的(3.103)式可知, 长光学横波与电磁场相耦合, 使得它具有电磁性质, 人们称长光学横波声子为电磁声子.6、什么是声子?答案:晶格振动的能量量子。
固体物理习题解答-完整版
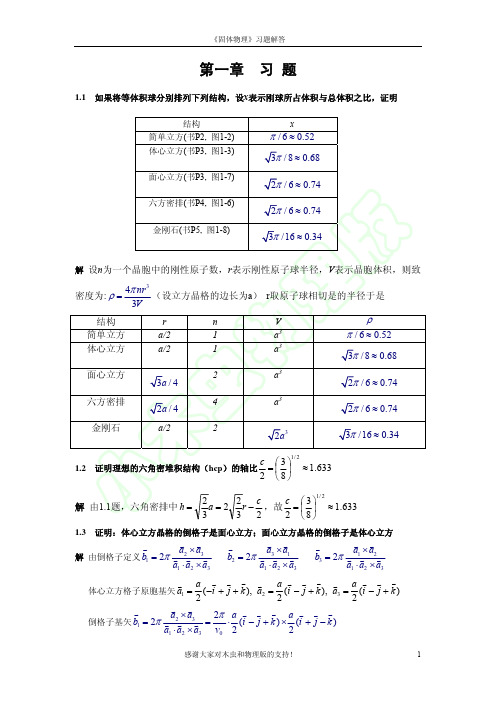
ρ
π / 6 ≈ 0.52
3π / 8 ≈ 0.68 2π / 6 ≈ 0.74 2π / 6 ≈ 0.74 3π /16 ≈ 0.34
1/ 2
3a / 4
2a / 4
a/2
2a 3
c ⎛3⎞ 1.2 证明理想的六角密堆积结构(hcp)的轴比 = ⎜ ⎟ 2 ⎝8⎠
ε A ,对六角晶系,绕 x 轴
(即 a 轴)旋转 180 度和绕 z 轴(即 c 轴)旋转 120 度都是对称操作,坐标变换矩阵分别为
⎛1 0 0⎞ ⎜ ⎟ Ax = ⎜ 0 − 1 0 ⎟ ⎜0 0 1⎟ ⎝ ⎠
⎛ −1/ 2 ⎜ Az = ⎜ − 3 / 2 ⎜ ⎜ 0 ⎝
3 / 2 0⎞ ⎟ −1/ 2 0⎟ ⎟ 0 1⎟ ⎠
6 a
3a / 2
6 a
2a
1.7
画体心立方和面心立方晶格结构的金属在 (100) , (110) , (111) 面上 解:
原子排列.
感谢大家对木虫和物理版的支持!
3
《固体物理》习题解答
体心立方
面心立方
1.9 指出立方晶格(111)面与(100)面,(111)面与(110)面的交线的晶向 解 (111)面与(100)面的交线的 AB-AB 平移, A 与 O 重合。B 点位矢 RB = −aj + ak (111) 与 (100) 面的交线的晶向 AB = − aj + ak —— 晶 向指数 ⎡011⎤
面指数越简单的晶面,其晶面的间距越大 晶面上格点的密度越大,这样的晶面越容易解理 1.7 写出体心立方和面心立方晶格结构中,最近邻和次近邻的原子数,若立方边长为a,写 出最近邻和次近邻原子间距 解 简立方 最近邻数 最近邻间距 次近邻数 次近邻间距 6 a 12 面心立方 12 体心立方 8
固体物理简答题及答案

固体物理简答题及答案简答题1、原子结合成晶体时,原子的价电子产生重新分布,从而产生不同的结合力,分析离子性、共价性、金属性和范德瓦耳斯性结合力的特点。
答案:离子性结合:正、负离子之间靠库仑吸引力作用而相互靠近,当靠近到一定程度时,由于泡利不相容原理,两个离子的闭合壳层的电子云的交迭会产生强大的排斥力。
当排斥力和吸引力相互平衡时,形成稳定的离子晶体;共价性结合:靠两个原子各贡献一个电子,形成所谓的共价键;金属性结合:组成晶体时每个原子的最外层电子为所有原子所共有,因此在结合成金属晶体时,失去了最外层(价)电子的原子实“沉浸”在由价电子组成的“电子云”中。
在这种情况下,电子云和原子实之间存在库仑作用,体积越小电子云密度越高,库仑相互作用的库仑能愈低,表现为原子聚合起来的作用。
XXX耳斯性结合:惰性元素最外层的电子为8个,具有球对称的稳定封闭结构。
但在某一瞬时由于正、负电中心不重合而使原子呈现出瞬时偶极矩,这就会使其它原子产生感应极矩。
非极性分子晶体就是依靠这瞬时偶极矩的互作用而结合的。
2.什么叫简正振动形式?简正振动数量、格波数量或格波振动形式数量是不是是一回事?答案:为了使问题既简化又能抓住主要矛盾,在分析讨论晶格振动时,将原子间互作用力的泰勒级数中的非线形项忽略掉的近似称为简谐近似.在简谐近似下,由N个原子构成的晶体的晶格振动,可等效成3N个独立的谐振子的振动.每个谐振子的振动模式称为简正振动模式,它对应着所有的原子都以该模式的频率做振动,它是晶格振动模式中最简单最基本的振动方式.原子的振动,或者说格波振动通常是这3N个简正振动模式的线形迭加.简正振动数目、格波数目或格波振动模式数目是一回事,这个数目等于晶体中所有原子的自由度数之和,即等于3N.3.长光学支格波与长声学支格波本质上有何差别?答案:长光学支格波的特征是每个原胞内的不同原子做相对振动,振动频率较高,它包含了晶格振动频率最高的振动模式.长声学支格波的特征是原胞内的不同原子没有相对位移,原胞做整体运动,振动频率较低,它包含了晶格振动频率最低的振动模式,波速是一常数.任何晶体都存在声学支格波,但简单晶格(非复式格子)晶体不存在光学支格波.4.长声学格波能否导致离子晶体的宏观极化?答案:长光学格波所以能导致离子晶体的宏观极化,其根源是长光学格波使得原胞内不同的原子(正负离子)产生了相对位移.长声学格波的特点是,原胞内所有的原子没有相对位移.因此,长声学格波不能导致离子晶体的宏观极化.5.何谓极化声子?何谓电磁声子?答案:长光学纵波引起离子晶体中正负离子的相对位移,离子的相对位移产生出宏观极化电场,称长光学纵波声子为极化声子.由本教科书的(3.103)式可知,长光学横波与电磁场相耦合,使得它具有电磁性质,人们称长光学横波声子为电磁声子.6、什么是声子?答案:晶格振动的能量量子。
固体物理作业答案

ω2 ω02
= dω
dq =
= dω
a ω02 − ω 2 dq 2
代入 ρ (ω )d ω= 2 ×
N Na dq = 2 × π 2π
ω02 − ω 2
2N
dω 1
一维单原子链的频率分布函数 ρ (ω ) =
π
ω −ω2
2 0
3.7.设三维晶格的光学振动在 q=0 附近的长波极限有 ω (q = ) ω0 − Aq 2
N α β (− m + n ) r 2 r N mα nβ 1 ( m +1 − n +1 ) = 2 r r 3 NAr 2
∂ 2U N ∂r ∂ mα nβ 1 = [( m +1 − n +1 ) ] 2 ∂V 2 ∂V ∂r r r 3 NAr 2 体弹性模量 = K ( ∂ 2U )V ⋅ V0 ∂V 2 0
1.3 证明:体心立方晶格的倒格子是面心立方;面心立方晶格的倒格子是体心立 方 。 a2 × a3 a3 × a1 a1 × a2 解 由倒格子定义 b1 = 2π b2 = 2π b3 = 2π a1 ⋅ a2 × a3 a1 ⋅ a2 × a3 a1 ⋅ a2 × a3
5
求证:频率分布函数为 f ( = ω)
V 1 1/ 2 ω − ω ) , ω < ω0 ; 2 3/ 2 ( 0 4π A
f (ω ) = 0 .
解
2
, ω > ω0
2
1 2 1 2
= 0, ω < 0 ⇒ ω0 − ω = Aq ⇒ q = A ( ω0 − ω ) ω > ω0时,ω − ω0= Aq > 0 f (ω )
固体物理学答案(朱建国版)

固体物理学·习题指导配合《固体物理学(朱建国等编著)》使用2020年6月21日第1章晶体结构 0第2章晶体的结合 (13)第3章晶格振动和晶体的热学性质 (22)第4章晶体缺陷 (35)第5章金属电子论 (39)第1章晶体结构有许多金属即可形成体心立方结构,也可以形成面心立方结构。
从一种结构转变为另一种结构时体积变化很小.设体积的变化可以忽略,并以R f和R b代表面心立方和体心立方结构中最近邻原子间的距离,试问R f/R b等于多少答:由题意已知,面心、体心立方结构同一棱边相邻原子的距离相等,都设为a:对于面心立方,处于面心的原子与顶角原子的距离为:R f=2a对于体心立方,处于体心的原子与顶角原子的距离为:R b=2a那么,Rf Rb晶面指数为(123)的晶面ABC是离原点O最近的晶面,OA、OB和OC分别与基失a1,a2和a3重合,除O点外,OA,OB和OC上是否有格点若ABC面的指数为(234),情况又如何答:晶面族(123)截a1,a2,a3分别为1,2,3等份,ABC面是离原点O最近的晶面,OA的长度等于a1的长度,OB的长度等于a2长度的1/2,OC的长度等于a3长度的1/3,所以只有A 点是格点。
若ABC面的指数为(234)的晶面族,则A、B和C都不是格点。
二维布拉维点阵只有5种,试列举并画图表示之。
答:二维布拉维点阵只有五种类型,两晶轴ba、,夹角ϕ,如下表所示。
4长方2,πϕ=≠ba简单长方(图中4所示)有心长方(图中5所示)1mm,2mm1 简单斜方2 简单正方3 简单六角4 简单长方5 有心长方二维布拉维点阵在六方晶系中,晶面常用4个指数(hkil)来表示,如图所示,前3个指数表示晶面族中最靠近原点的晶面在互成120°的共平面轴a1,a2,a3上的截距a1/h,a2/k,a3/i,第四个指数表示该晶面的六重轴c上的截距c/l.证明:i=-(h+k)并将下列用(hkl)表示的晶面改用(hkil)表示:(001)(133)(110)(323)(100)(010)(213)答:证明设晶面族(hkil)的晶面间距为d,晶面法线方向的单位矢量为n°。
固体物理学课后题答案

第一章 晶体结构1.1、 如果将等体积球分别排成下列结构,设x 表示钢球所占体积与总体积之比,证明:结构 X简单立方52.06=π体心立方68.083≈π 面心立方74.062≈π 六角密排74.062≈π 金刚石34.063≈π解:实验表明,很多元素的原子或离子都具有或接近于球形对称结构。
因此,可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。
这样,一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。
它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比,即:晶体原胞的空间利用率, VcnVx = (1)对于简立方结构:(见教材P2图1-1) a=2r , V=3r 34π,Vc=a 3,n=1 ∴52.06834343333====πππrra r x (2)对于体心立方:晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)334(3423423333≈=⨯=⨯=πππr r a r x (3)对于面心立方:晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4,Vc=a 374.062)22(3443443333≈=⨯=⨯=πππr r a r x (4)对于六角密排:a=2r 晶胞面积:S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233晶胞的体积:V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个 74.062)22(3443443333≈=⨯=⨯=πππr r a r x (5)对于金刚石结构,晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 334.06333834834833333≈=⨯=⨯=πππr r a r x 1.3、证明:面心立方的倒格子是体心立方;体心立方的倒格子是面心立方。
固体物理学答案详细版

《固体物理学》部分习题参考解答第一章1.1 有许多金属即可形成体心立方结构,也可以形成面心立方结构。
从一种结构转变为另一种结构时体积变化很小.设体积的变化可以忽略,并以R f 和R b 代表面心立方和体心立方结构中最近邻原子间的距离,试问R f /R b 等于多少?答:由题意已知,面心、体心立方结构同一棱边相邻原子的距离相等,都设为a :对于面心立方,处于面心的原子与顶角原子的距离为:R f=2 a 对于体心立方,处于体心的原子与顶角原子的距离为:R b=2a 那么,Rf Rb1.2 晶面指数为(123)的晶面ABC 是离原点O 最近的晶面,OA 、OB 和OC 分别与基失a 1,a 2和a 3重合,除O 点外,OA ,OB 和OC 上是否有格点?若ABC 面的指数为(234),情况又如何?答:根据题意,由于OA 、OB 和OC 分别与基失a 1,a 2和a 3重合,那么 1.3 二维布拉维点阵只有5种,试列举并画图表示之。
答:二维布拉维点阵只有五种类型:正方、矩形、六角、有心矩形和斜方。
分别如图所示:1.4 在六方晶系中,晶面常用4个指数(hkil )来表示,如图所示,前3个指数表示晶面族中最靠近原点的晶面在互成120°的共平面轴a 1,a 2,a 3上的截距a 1/h ,a 2/k ,a 3/i ,第四个指数表示该晶面的六重轴c 上的截距c/l.证明:i=-(h+k ) 并将下列用(hkl )表示的晶面改用(hkil )表示:(001)(133)(110)(323)(100)(010)(213)答:证明设晶面族(hkil )的晶面间距为d ,晶面法线方向的单位矢量为n °。
因为晶面族(hkil )中最靠近原点的晶面ABC 在a 1、a 2、a 3轴上的截距分别为a 1/h ,a 2/k ,a 3/i ,因此123o o o a n hda n kd a n id=== ……… (1) 正方 a=b a ^b=90° 六方 a=b a ^b=120° 矩形 a ≠b a ^b=90° 带心矩形 a=b a ^b=90° 平行四边形 a ≠b a ^b ≠90°由于a 3=–(a 1+ a 2)313()o o a n a a n =-+把(1)式的关系代入,即得()id hd kd =-+ ()i h k =-+根据上面的证明,可以转换晶面族为(001)→(0001),(133)→(1323),(110)→(1100),(323)→(3213),(100)→(1010),(010)→(0110),(213)→(2133)1.5 如将等体积的硬球堆成下列结构,求证球可能占据的最大面积与总体积之比为(1)简立方:6π(2(3)面心立方:6(4)六方密堆积:6(5)金刚石:。
固体物理.pdf

单选题1.在倒格子空间中以某一倒格点为原点,作所有倒格矢的中垂面,围成的一个个封闭多面体称为A.原胞B.晶胞C.布拉伐格子D.布里渊区答案:D2.晶体学中考虑到晶体对称性,将晶体结构划分为()个晶系,()种布拉伐格子.A.7,7B.7,14C.14,7D.14,14答案:B3.在长波极限情况,()晶体的长光学波可以与电磁波发生共振,引起远红外光在共振频率附近的强烈吸收.A.离子B.分子C.共价D.金属答案:A4.结构介于晶体和非晶体之间,具有准周期结构的称为().A.晶体B.非晶体C.准晶体D.固体答案:C5.长波近似情况下,一维双原子链的相邻原子的振动振幅比为1,表明A.长声学波的相邻原子相对振动;B.长声学波描述原胞质心的振动;C.长光学波描述原胞中原子的相对振动;D.长光学波的原子做相对振动,且质心不动;答案:B6.晶体中体积最小的周期性结构单元常称()A.原胞B.晶胞C.布拉伐格子D.晶格答案:A7.晶体中的原子、离子实际上不是静止在晶格平衡位置上的,而是围绕平衡位置作微振动,称为A.简谐振动B.晶格振动C.原子振动D.分子振动答案:B8.冰和固态氟化氢是典型的()结合类型晶体.A.离子B.金属C.氢键D.范德瓦尔斯答案:C9.()代表正格子空间中的一族晶面.A.一个格点B.一个倒格点C.一个原子D.一个原子团答案:B10.布里渊区的特征之一是所有布里渊区都是()对称的.A.轴B.线C.面D.中心答案:D11.简立方结构的配位数是A.12B.8C.6D.4答案:C12.晶体的对称性A.分为宏观对称性和微观对称性;B.是指晶体宏观对称性,由晶体的点对称操作来描述;C.是指晶体微观对称性;D.是指布喇菲原胞的对称性;答案:A13.()是典型的混合键类型的晶体,具有范德瓦尔斯键,金属键和共价键.A.金刚石B.石墨C.冰D.固态氟化氢答案:B14.离子晶体的长光学波可以与电磁波发生共振,可以引起远红外光在()附近的强烈吸收.A.光波频率B.共振频率C.电磁波频率D.晶格振动频率答案:B15.原子的动能加原子间的相互作用势能之和称为晶体的A.相互作用势能B.晶体结合能C.动能D.内能答案:D16.早在两世纪前,人们就开始了对晶体结构的研究。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1) 共价键结合的特点?共价结合为什么有“饱和性”和“方向性”?饱和性和方向性饱和性:由于共价键只能由为配对的电子形成,故一个原子能与其他原子形成共价键的数目是有限制的。
N<4,有n 个共价键;n>=4,有(8-n )个共价键。
其中n 为电子数目。
方向性:一个院子与其他原子形成的各个共价键之间有确定的相对取向。
(2) 如何理解电负性可用电离能加亲和能来表征?电离能:使原子失去一个电子所必须的能量其中A 为第一电离能,电离能可表征原子对价电子束缚的强弱;亲和势能:中性原子获得电子成为-1价离子时放出的能量,其中B 为释放的能量,也可以表明原子束缚价电子的能力,而电负性是用来表示原子得失电子能力的物理量。
故电负性可用电离能加亲和势能来表征。
(3) 引入玻恩-卡门条件的理由是什么?在求解原子运动方程是,将一维单原子晶格看做无限长来处理的。
这样所有的原子的位置都是等价的,每个原子的振动形式都是一样的。
而实际的晶体都是有限的,形成的键不是无穷长的,这样的链两头原子就不能用中间的原子的运动方程来描述。
波恩—卡门条件解决上述困难。
(4) 温度一定,一个光学波的声子数目多呢,还是一个声学波的声子数目多? 对同一振动模式,温度高时的声子数目多呢,还是温度低的声子数目多?温度一定,一个声学波的声子数目多。
对于同一个振动模式,温度高的声子数目多。
(5) 长声学格波能否导致离子晶体的宏观极化?不能。
长声学波代表的是原胞的运动,正负离子相对位移为零。
(6)晶格比热理论中德拜(Debye )模型在低温下与实验符合的很好,物理原因是什么?爱因斯坦模型在低温下与实验存在偏差的根源是什么?在甚低温下,不仅光学波得不到激发,而且声子能量较大的短声学波也未被激发,得到激发的只是声子能量较小的长声学格波。
长声学格波即弹性波。
德拜模型只考虑弹性波对热容德贡献。
因此,在甚低温下,德拜模型与事实相符,自然与实验相符。
爱因斯坦模型过于简单,假设晶体中各原子都以相同的频率做振动,忽略了各格波对热容贡献的差异,按照爱因斯坦温度的定义可估计出爱因斯坦频率为光学支格波。
在低温主要对热容贡献的是长声学支格波。
(7)试解释在晶体中的电子等效为经典粒子时,它的有效质量为什么有正、有负、无穷大值?带顶和带底的电子与晶格的作用各有什么特点?m F m m l +=* m F m v F mv F l ⋅+⋅=⋅⇒*])()[(1])()[(1电子给予晶格德外力给予电子德晶格给予电子德外力给予电子德-=+p p m p p m mp ∆∆∆∆=∆*当电子从外场获得的动量大于电子传递给晶格的动量时,有效质量为正;当电子从外场获得的动量小于电子传递给晶格的动量时,有效质量为负; 当电子从外场获得的动量等于电子传递给晶格的动量时,有效质量为无穷。
(8)为什么温度升高,费米能级反而降低?体积膨胀时,费米能级的变化? 在温度升高时,费米面以内能量离约范围的能级上的电子被激发到之上约范围的能级。
故费米球体积V 增大,又电子总数N 不变,则电子浓度减小,又,则费米半径变小,费米能级也减小。
当体积膨胀时,V 增大,同理费米能级减小。
(9)什么是p 型、N 型半导体?试用能带结构解释。
P型半导体:在四价元素(硅或锗)半导体中参入微量的三价元素(硼或铝),主要依赖空穴导电;N型半导体:在四价元素(硅或锗)半导体中参入少量五价元素(磷或砷)杂质,主要依赖电子导电。
(10)德拜模型的三点假设?(1)晶体视为连续介质,格波视为弹性波(2)有一支纵波两支横波(3)晶格震动频率在0~之间(为德拜频率)(11)布洛赫定理的内容?(12)金刚石结构有几支格波?几支声学波?几支光学波?设晶体有N个原胞,晶体振动模式数为多少?金刚石为复式格子,每个原胞中有两个原子。
则m=3,n=2.(m表示晶体的维数,n是原胞中原子的数目)所以,有6支格波,3支声学波,3支光学波。
振动模式数为6N(13)近自由电子模型与紧束缚模型各有何特点?近自由电子:(1)在k=nπ/a时(在布里渊区边界上),电子的能量出现禁带,禁带宽度为(2)在k=nπ/a附近,能带底部电子能量与波矢的关系是向上弯曲的抛物线,能带顶部是向下弯曲的抛物线(3)在k远离nπ/a处,电子的能量与自由电子的能量相近。
紧束缚:, 表示相剧为的两个格点上的波函数的重叠积分,它依赖于与的重叠程度,重叠最完全,即最大,其次是最邻近格点的波函数的重叠积分,涉及较远的格点的积分甚小,通常可以忽略不计。
近邻原子的波函数重叠越多,的值越大,能带宽度越宽。
由此可见,与原子内层原子所对应的能带较窄,而不同的原子态所对应的和是不同的。
(14)紧束缚模型下,内层电子的能带与外层电子的能带相比较,哪一个宽?为什么?外层电子的能带较宽,因为近邻原子的波函数重叠越多,的值越大,能带将越宽。
(15)在晶格常数为a的一维简单晶格中,波长=4a和=4a/5的两个格波所对应的原子振动有无不同?画图说明之。
没有不同(16)在什么情况下必须可以忽略电子对固体热容量的贡献,并说明原因。
在什么情况下必须考虑电子对固体热容量的贡献,并说明原因。
在常温下晶格振动对摩尔热容量的贡献的量级为,而电子比热容的量级为,晶格热容量比电子热容量大得多,可以忽略。
这是因为尽管金属中有大量的自由电子,但只有费米面附近范围的电子才能受热激发而跃迁至较高的能级,所以电子热容量很小。
在低温范围,晶格热容量迅速下降,在低温的极限趋于0,电子热容量和T 成正比,随温度下降比较缓慢。
(17)请简述满带、空带、价带、导带和带隙。
满带:能带中所有电子状态结构被电子所填满 空带:能带中所有电子状态均未被电子占据 价带:最外层电子所处的能带导带:能带中只有部分电子状态被电子占据,其余为空态 带隙:量能带之间的间隔近满态:能带中大部分电子状态被电子占据,只有少数空态 (18)请解释晶向指数、晶面指数和密勒指数。
任意两格点连线称为晶列,晶列的取向称为晶向,描写晶向的一组数据称为晶向指数。
如果取某一原子为原点,沿晶向到最近邻的原子的位矢为 ,, , 为固体物理学原胞基矢。
为该晶列的晶列指数。
在晶格中,通过任意三个在同一直线上的格点,作一平面,称为晶面,描写晶面方位的一组数称为晶面指数(密勒指数)。
1试证明倒格矢332211b h b h b h G h++=与正格子晶面族(h 1,h 2,h 3)正交;并证明晶面族(h 1,h 2,h 3)面间距为3213212h h h h h h G d π=,其中321h h h G 为倒格矢332211b h b h b h G h++=的长度。
2.证明对于基矢量321,,a a a 互相正交的晶格,证明密勒指数为(h ,k ,ι)的晶面系,面间距d 满足: ])()()/[(12322212a a k a h d ι++=。
解:k a b j a b i a b 3322112,2,2πππ=== 倒格矢321b l b k b h G kl h++=与正格子晶面族(h,k,ι)正交。
])()()[(1)(23222122a l a k a h G d hkl++==3. 某单价金属,为平面正六方形晶格如图所示,六角形两个对边的间距是a, 基矢j a i a a j a i a a232,23221+-=+=, 1)求出正格子原胞的体积;求出倒格子基矢,并画出倒格子点阵原胞,和画出此晶体的第一布里渊区;2)若价电子可以看成是自由电子,原胞数为N ,求能态密度N (E ); 3)求T =0k 时的费米能级E F 0。
若晶格为平面正三角形,相邻原子间距为a ?(1)i a a =1, j a i a a 2322+=, k a =3 正格子原胞体积:232a V = ()()⎪⎪⎭⎫⎝⎛-=+=+=⨯⎪⎪⎭⎫ ⎝⎛+-=⨯Ω=j i a j i a i j a k j a i a a a a b33233233223223222321πππππ j aa a b342132ππ=⨯Ω=(2)选定一倒格点为原点,原点的最近邻倒格矢有6个,它们是 )(,,2121b b b b +±±±,a 2a 122222232)2(232)( πππmNa mkk aN E N =⨯=⎰=00)(FE dE E N NN E m Na F =02223π mNa N E F 22032 π=4. 已知由N 个原子组成的惰性元素晶体总势能可写为:⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=6612122)(r A r A N r U σσε,其中454.14,132.12612==A A ,求:(1)原子平衡时距离; (2)晶体结合能。
(1)平衡时 ()00==r r drr dU 有 0612270661301212=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛-r A r A N σσε σσ09.12616120=⎪⎪⎭⎫ ⎝⎛=A A r (2)结合能:()εεN A N A r U E b 6.8212260==-= 5.若晶体中两相邻原子的相互作用能nmrr r U βα+-=)(,求(1)平衡时原子间距;(2)单个原子结合能。
6.试从k 的取值范围和E(k)~k 的关系两方面,画出一维晶格能带扩展 能区图或简约能区图。
7.考虑一个双原子链的晶格振动,链上最近邻原子间的力常数交错地等于C 和10C 。
令两种原子的质量m 相等,近邻原子间距为a/2,(1)求色散关系ω(k),要求写出推导过程并粗略地画出简约区的色散关系图。
运动方程:)(10)()(10)(122122n n n n nn n n n n v c v c dtv d m v c v c dtd m μμμμμ----=----=+- (1)设试探解:][][nka wt i n nka wt i nBe v Ae ----==μ (2)代入(1)式,cBB ec B mw cAB e c A mw ikaika 11)10(11)10(22-+=--+=-- (3)有解的条件:011)10()10(1122=-++--cmw e c e c cmw ikaika (4)0)cos 1(20222242=-+-ka c mcw w m ])cos 1(2012111[2ka mc w --±=±当k =0,0,2222==-+w mc w 当k =π/a ,mc w m c w 2,2022==-+ 8.考虑一维双原子链的晶格振动,平衡时相邻原子间距为a ,质量为m 和M (m<M ),恢复系数为β,(1)求色散关系ω(k)要求写出推导过程。
