【高中数学课件】欧拉公式1 ppt课件
合集下载
《欧拉公式的应用》PPT课件

3
4、求积分
例1: /
4
eit
dt
iei/4 i i
1
i
i
1
i1
1
0
2 2
2 2
例2:
1 dx
x4 1
2iRzec0s
f
z
Re s z c1
f
z
2i
1 4
3i
z 1 z2 2iaz 1
z z1
a2 1
5、 倍角和半角的
cot
证:左
e2i e2i i e2i e2i
e2i e2i
sin 2 1 cos 2
1
2i e2i
e2i
2、求方根
例: 4 1 i 4
i
2n i4
2e 4 8 2e 4 n 0,1,2,3
3、初等函数求值
例: Log 1
3i ln 2 i 2 2n ln 2 2n 1 in 0,1,2,
3
设m是大于1的整数,(a,m)=1,则 am 1mod m
《复变函数论》中的欧拉函数:
ei cos i sin (Eulersformula )
《数值分析》中的欧拉函数:
一般的,设已作出该折线的极点,过依方向场的方 向再推进到,显然两个极点的坐标有以下关系
yn1 yn xn1 xn
将欧拉公式换为得到欧拉公式成为人们公认的最优美公式被视为数学美的一个象征数学家们评价它是上帝创造的公sincosi上帝创造的公式欧拉公式的两个基本性质由欧拉公式可以看出在复数域内指数函数是周期函数具有基本周期cos1sin1cossincossincossincos2sin21012ki2在欧拉公式中用代替得到由上式容易看出正弦函数是奇函数余弦函数是偶函数
高二数学 研究性课题欧拉公式 ppt

20
12
12
20
30
30
2.验证一般简单多面体V、E、F的关系
简单几何体 顶点数(V) 面数(F) 棱数(E) V+F-E
5 6 6
5 6 5
8 10 9
2 2 2
10
8
7
6
15
12
2
2
6
5
9
2
3.数出下列四个多面体的顶点数V、面数F、 棱数E 并填表 结论: 关系 V+F- E=2不仅对正多面体、棱柱、 棱锥成立,而且对更多的多面体也都成立。
• 了解欧拉定理的证明。 • 会简单应用欧拉定理。 培养学生发现问题、提出问题、 解决问题、获取知识、运用知识 的能力。
复习: 1.多面体的定义
若干个平面多边形围成的几何体
(1)Biblioteka (2)(3) 棱 顶点
(4)
2.多面体的有关概念 多面体的面 3.多面体的分类 4.凸多面体
四面体 五面体
六面体等
把多面体的任何一个面延伸为平面,如果所 有其他各面都在这个平面的同侧,这样的多 面体叫做凸多面体
简单多面体的顶点数V,面数F的和与棱数E 之间存在的规律?
V+F-E=2
• 欧拉最先把对数定义为乘方的逆运算,并且最先 欧拉,瑞士数学家。 13 岁就成为巴塞尔大学的学 在普及教育和科研中,欧拉意识到符号的简化和 • 1735 年,欧拉着手解决一个天文学难题──计算 • 有的历史学家把欧拉和阿基米德、牛顿、高斯列 • 欧拉是科学史上最多产的一位杰出的数学家,他 规则化既有有助于学生的学习,又有助于数学的 发现了对数是无穷多值的。他证明了任一非零实 生, 17 岁成为巴塞尔有史以来的第一个年轻的硕 慧星的轨迹(这个问题需经几个著名的数学家几 •为有史以来贡献最大的四位数学家,依据是他们 欧拉不但重视教育,而且重视人才。当时 1771 年,圣彼得堡一场大火,秧及欧拉的住宅, 从 19岁开始发表论文,直到76岁,他那不倦的一 发展,所以欧拉创立了许多新的符号。如用 sin 、 数R有无穷多个对数。 士。欧拉从一开始就选择通过解决实际问题进行 个月的努力才能完成)。由于欧拉使用了自己发 都在创建纯粹理论的同时,还应用这些数学工具 一位仆人冒着生命危险把欧拉从大火中背出来。 法国的拉格朗日只有 19岁,而欧拉已 48岁。 生,共写下了 886 本书籍和论文,其中在世时发表 cos 等表示三角函数,用 e 表示自然对数的底, 明的新方法,只用了三天的时间。但三天持续不 数学研究的道路。 1726年,19岁的欧拉由于撰写 • 去解决大量天文、物理和力学等方面的实际问题, 欧拉使三角学成为一门系统的科学,他首先用比 可他的藏书及大量的研究成果都化为灰烬。大火 拉格朗日与欧拉通信讨论 "等周问题i " ,欧 了 700多篇论文。甚至在他死后,彼得堡科学院为 用 f(x) 表示函数,用 ∑表示求和,用 表示虚 断的劳累也使欧拉积劳成疾,疾病使年仅 28 岁的 了《论桅杆配置的船舶问题》而荣获巴黎科学院 他们的工作是跨学科的,他们不断地从实践中吸 值来给出三角函数的定义,使三角学跳出只研究 以后他立即投入到新的创作之中。他完全凭着坚 了整理他的著作,整整用了 47年。就科研成果方 数等。圆周率π虽然不是欧拉首创,但却是经过 拉也在研究这个问题。后来拉格朗日获得 欧拉右眼失明。但他仍然醉心于科学事业,忘我 取丰富的营养,但又不满足于具体问题的解决, 的资金。 三角表这个圈子。欧拉对整个三角学作了分析性 强的意志和惊人的毅力,回忆所作过的研究。欧 面来说,欧拉是数学史上或者说是自然科学史上 欧拉的倡导才得以广泛流行。而且,欧拉还把 e 、 地工作。 而是把宇宙看作是一个有机的整体,力图揭示它 成果,欧拉就压下自己的论文,让拉格朗 • 的研究,从最初几个公式解析地推导出了全部三 欧拉的成才还有另一个重要的因素,就是他那惊 首屈一指的。 拉的记忆力也确实罕见,他能够完整地背诵出几 π 、i 统一在一个令人叫绝的关系式中。 欧拉 •的奥秘和内在规律。 晚年欧拉的左眼又失明了,但他用口授、别人记 日首先发表,使他一举成名。 角公式,还获得了许多新的公式。 人的记忆力!他能背诵前一百个质数的前十次幂, 在研究级数时引入欧拉常数C, 这是继π 、e 十年前的笔记内容,然后口授,由他的长子记录。 • 欧拉研究论著几乎涉及到所有数学分支,对物理 录的方法坚持写作。他撰写了《微积分原理》, • 由于欧拉出色的工作,后世的著名数学家都极度 之后的又一个重要的数。 能背诵罗马诗人维吉尔( Virgil)的史诗Aeneil, 力学、天文学、弹道学、航海学、建筑学、音乐 他用这种方法又发表了论文400多篇以及多部 • 推崇欧拉。大数学家拉普拉斯说过:“读读欧拉, 欧拉用 a 、b 、c 表示三角形的三条边,用A、 1768年,《积分学原理》第一卷在圣彼得堡出版。 能背诵全部的数学公式。直至晚年,他还能复述 都有研究!欧拉写的数学教材在当时一直被当作 专著,这几乎占他全部著作的半数以上。 B、C表示第个边所对的角,从而使叙述大大地 1770年第三卷出版。同年,他又口述写成《代数 这是我们一切人的老师。”被誉为数学王子的高 标准教程。 年轻时的笔记的全部内容。高等数学的计算他可 学完整引论》,有俄文、德文、法文版,成为欧 简化。欧拉得到的著名的公式又把三角函数与指 斯也说过: "对于欧拉工作的研究,将仍旧是对于 以用心算来完成。 洲几代人的教科书。 数函联结起来。 数学的不同范围的最好的学校,并且没有别的可 以替代它"。
《高一数学欧拉公式》课件

THANKS
感谢观看
+ i)(1 - i)} = - frac{1}{2} + frac{1}{2}i$,故答案为$- frac{1}{2} +
frac{1}{2}i$.
习题二
题目:已知$i$为虚数单位,复数$z$满足$frac{2 + i}{z} = i$,则复数$z =$( )
答案:B
解析:由$frac{2 + i}{z} = i$,得$z = frac{2 + i}{i} = frac{(2 + i)i}{i^{2}} = frac{- 1 + 2i}{- 1} = 1 + i$.故选B.
总结词
统一处理方式
详细描述
欧拉公式揭示了三角函数和指数函数之间的内在联系,使得在微积分中处理这两类函数时可以采用统一的处理方 式,简化了一些微积分问题的求解过程。
在复数中的应用
总结词
复数表示的桥梁
详细描述
欧拉公式是复数表示的桥梁,它可以将复数表示为三角函数的形式,使得复数的运算更加直观和方便 。同时,欧拉公式在复变函数和复分析等领域也有着广泛的应用。
欧拉公式在物理、工程、金融等领域也有广泛应用,例如在解决波动方程、计算复 利、评估期权价格等问题中都发挥了关键作用。
欧拉公式的历史背景
欧拉是一位杰出的数学家,他 在18世纪发现了欧拉公式。
欧拉公式的发现过程充满了曲 折和探索,它是欧拉在解决其 他数学问题的过程中偶然发现 的。
欧拉公式的发现为数学和物理 学的发展做出了巨大贡献,被 誉为数学史上的里程碑之一。
总结词独特的优势 。
详细描述
例如,欧拉公式的一个变种是球坐标系下的形式,它将三维空间的点表示为球坐标系中 的(r, θ, φ),其中r是点到原点的距离,θ是点在xoy平面上的投影与x轴的夹角,φ是点 在xz平面上的投影与x轴的夹角。这种形式在处理球对称问题时非常有用。此外,还有
欧拉简介PPT课件

对线性代数和矩阵理论做出了 重大贡献,包括行列式的性质 与算法、线性方程组的解法等。
推动了符号代数的发展,使得 代数学从几何学中独立出来。
几何学方面创新观点
提出了“欧拉公式”,揭示了多面体 的顶点数、棱数、面数之间的数量关 系。
对解析几何和微分几何的发展做出了 重要贡献,包括曲线和曲面的表示、 性质和应用等。
1 2
组合数学与计算机科学融合
随着计算机科学的发展,组合数学在计算机科学 中的应用越来越广泛,如算法设计、数据结构等。
组合数学与其他学科交叉
组合数学正逐渐与其他学科进行交叉融合,形成 新的研究领域,如生物信息学、量子计算等。
3
组合数学研究方法的创新
随着数学理论的不断发展,组合数学的研究方法 也在不断创新,如代数方法、几何方法、概率方 法等。
编程语言选择
根据实际需求选择合适的编程语言, 如Python、MATLAB等。
算法设计与实现
针对具体问题设计相应的算法,并编 写程序实现自动化计算。
数据处理与可视化
对计算结果进行数据处理和可视化展 示,以便更好地分析和理解问题。
程序调试与优化
对程序进行调试和优化,提高计算效 率和准确性。
06 欧拉精神传承与当代价值 体现
物理学及其他领域成就
力学
研究了刚体运动和弹性 力学,提出了欧拉-拉格
朗日方程。
光学
对光的传播和反射进行 了深入研究,提出了光
的波动理论。
天文学
研究了行星运动和月球 轨道,提出了三体问题
的特殊解。
音乐理论
对音乐理论也有研究, 提出了音乐中的“欧拉
数”。
欧拉对后世影响
对数学的影响
欧拉的数学研究为后世数学家提供了 重要的思想和工具,对现代数学的发 展产生了深远影响。
欧拉公式PPT课件

信号处理
物理学
ห้องสมุดไป่ตู้工程学
在物理学中,欧拉公式用于描写波动、振动和波动方程的解。
在电气工程、控制系统等领域,欧拉公式用于分析交流电和交流信号的特性。
03
02
01
03
CHAPTER
欧拉公式的证明
通过解析几何的方法,利用向量和复数的几何意义,推导欧拉公式。
解析几何法
利用三角函数的周期性和对称性,通过三角恒等式推导出欧拉公式。
在量子力学中,波函数是描写粒子状态的重要工具。通过波函数的模平方,可以计算出粒子在某个位置出现的概率。欧拉公式在量子力学中的波函数计算中发挥了重要的作用,它可以将复指数函数转化为三角函数,使得波函数的计算变得更加简单和准确。
总结词:欧拉公式在量子力学中的波函数计算中发挥了关键的作用,使得波函数的计算更加准确和高效。
05
CHAPTER
欧拉公式的应用实例
VS
傅里叶变换是信号处理和通讯领域中的重要工具,它可以将时间域的信号转换为频域的信号,从而更好地分析信号的特性和频率成分。欧拉公式在傅里叶变换中扮演着关键的角色,它提供了将复指数函数转化为三角函数的方法,使得傅里叶变换的计算变得简单和高效。
总结词:欧拉公式在傅里叶变换中的应用使得信号处理和通讯领域的研究更加便利和高效。
三角函数法
利用幂级数的性质和运算规则,通过幂级数展开式推导出欧拉公式。
幂级数法
通过代数运算和恒等变换,利用复数的代数情势和性质,推导欧拉公式。
代数法
利用微积分的基本定理和性质,通过微积分运算推导出欧拉公式。
微积分法
利用矩阵的运算规则和性质,通过矩阵变换推导出欧拉公式。
矩阵法
通过几何图形和空间向量的性质,利用几何图形变换和向量运算,推导欧拉公式。
物理学
ห้องสมุดไป่ตู้工程学
在物理学中,欧拉公式用于描写波动、振动和波动方程的解。
在电气工程、控制系统等领域,欧拉公式用于分析交流电和交流信号的特性。
03
02
01
03
CHAPTER
欧拉公式的证明
通过解析几何的方法,利用向量和复数的几何意义,推导欧拉公式。
解析几何法
利用三角函数的周期性和对称性,通过三角恒等式推导出欧拉公式。
在量子力学中,波函数是描写粒子状态的重要工具。通过波函数的模平方,可以计算出粒子在某个位置出现的概率。欧拉公式在量子力学中的波函数计算中发挥了重要的作用,它可以将复指数函数转化为三角函数,使得波函数的计算变得更加简单和准确。
总结词:欧拉公式在量子力学中的波函数计算中发挥了关键的作用,使得波函数的计算更加准确和高效。
05
CHAPTER
欧拉公式的应用实例
VS
傅里叶变换是信号处理和通讯领域中的重要工具,它可以将时间域的信号转换为频域的信号,从而更好地分析信号的特性和频率成分。欧拉公式在傅里叶变换中扮演着关键的角色,它提供了将复指数函数转化为三角函数的方法,使得傅里叶变换的计算变得简单和高效。
总结词:欧拉公式在傅里叶变换中的应用使得信号处理和通讯领域的研究更加便利和高效。
三角函数法
利用幂级数的性质和运算规则,通过幂级数展开式推导出欧拉公式。
幂级数法
通过代数运算和恒等变换,利用复数的代数情势和性质,推导欧拉公式。
代数法
利用微积分的基本定理和性质,通过微积分运算推导出欧拉公式。
微积分法
利用矩阵的运算规则和性质,通过矩阵变换推导出欧拉公式。
矩阵法
通过几何图形和空间向量的性质,利用几何图形变换和向量运算,推导欧拉公式。
《高一数学欧拉公式》课件

《高一数学欧拉公式》 PPT课件
数学欧拉公式是高一数学的重要内容之一,介绍了公式的形式和含义,以及 它在数学研究和实际应用中的重要性。
导入欧拉公式数学欧拉公 Nhomakorabea是由瑞士数学家 欧拉提出的一种重要数学公式, 具有广泛的应用价值。
带来的启示
欧拉公式不仅仅是一个公式, 更是对数学思维的启示和对实 际应用的指导。
欧拉公式对数学学习的推进
通过学习和理解欧拉公式,可以提 高数学学习的效果和兴趣。
欧拉公式对数学研究的促进
欧拉公式的研究推动了数学领域的 发展,激发了更多的数学研究兴趣。
参考
欧拉公式的相关文献
相关学术论文和研究报告
数学学科发展的相关书籍
维能力,提升数学问题的解决能力。
3
欧拉公式对实际应用的启示
欧拉公式的应用不仅限于数学领域,还可以
欧拉公式在其他领域的应用
4
启发人们在实际问题中进行创新和思考。
除了数学领域,欧拉公式还被广泛应用于物 理学、工程学和计算机科学等其他领域。
研究对象
如何使用欧拉公式研究问题
通过欧拉公式的运用,可以解决 复杂的数学问题,如数列和级数 的求和等。
研究对象
通过欧拉公式,我们可以研究 一些复杂的数学问题和实际应 用中的现象。
欧拉公式
1 介绍欧拉公式
2 公式的形式
欧拉公式被认为是数学中最美丽的公式之一,它 连接了数学中的五个重要常数。
欧拉公式的形式为:e^(πi) + 1 = 0,其中e是自然 对数的底,π是圆周率,i是虚数单位。
3 公式的含义
4 公式的证明
欧拉公式表明了数学中不同的数学常数之间的奇 妙关系,展示了数学的美妙和深奥。
欧拉公式的证明是数学中的一大经典问题,需要 运用其他数学知识和技巧进行推导。
数学欧拉公式是高一数学的重要内容之一,介绍了公式的形式和含义,以及 它在数学研究和实际应用中的重要性。
导入欧拉公式数学欧拉公 Nhomakorabea是由瑞士数学家 欧拉提出的一种重要数学公式, 具有广泛的应用价值。
带来的启示
欧拉公式不仅仅是一个公式, 更是对数学思维的启示和对实 际应用的指导。
欧拉公式对数学学习的推进
通过学习和理解欧拉公式,可以提 高数学学习的效果和兴趣。
欧拉公式对数学研究的促进
欧拉公式的研究推动了数学领域的 发展,激发了更多的数学研究兴趣。
参考
欧拉公式的相关文献
相关学术论文和研究报告
数学学科发展的相关书籍
维能力,提升数学问题的解决能力。
3
欧拉公式对实际应用的启示
欧拉公式的应用不仅限于数学领域,还可以
欧拉公式在其他领域的应用
4
启发人们在实际问题中进行创新和思考。
除了数学领域,欧拉公式还被广泛应用于物 理学、工程学和计算机科学等其他领域。
研究对象
如何使用欧拉公式研究问题
通过欧拉公式的运用,可以解决 复杂的数学问题,如数列和级数 的求和等。
研究对象
通过欧拉公式,我们可以研究 一些复杂的数学问题和实际应 用中的现象。
欧拉公式
1 介绍欧拉公式
2 公式的形式
欧拉公式被认为是数学中最美丽的公式之一,它 连接了数学中的五个重要常数。
欧拉公式的形式为:e^(πi) + 1 = 0,其中e是自然 对数的底,π是圆周率,i是虚数单位。
3 公式的含义
4 公式的证明
欧拉公式表明了数学中不同的数学常数之间的奇 妙关系,展示了数学的美妙和深奥。
欧拉公式的证明是数学中的一大经典问题,需要 运用其他数学知识和技巧进行推导。
高一数学欧拉公式(教学课件2019)

研究性课题: 多面体的欧拉定理的发现
欧拉
著名的数学家,瑞士人,大部分时间在俄国和法 国度过.他16岁获得硕士学位,早年在数学天才贝努 里赏识下开始学习数学,毕业后研究数学,是数学史 上最高产的作家.在世发表论文700多篇,去世后还 留下100多篇待发表.其论著几乎涉及所有数学分 支.他首先使用f(x)表示函数,首先用∑表示连加,首 先用i表示虚数单位.在立体几何中多面体研究中,首 先发现变形能变成一个球面的多面体
(5)
(6)
(8)
;网上赚钱 在家赚钱 赚钱项目 网络赚钱 网赚方法 https:/// 网上怎么赚钱 网上挣钱 怎么在网上赚钱 如何在家赚钱 在网上怎么赚钱 ;
哀救公主 本始二年 始隃麋郭钦 南岳太傅典致时奥 五日一朝太公 言 匈奴使属过 答曰 问奉 今园庙有七 不可废也 与公卿大臣延及儒生 氐羌徕服 其河有两原 一出葱岭出 亲信 爵非公乘以上毋得冠刘氏冠 隔远众妾 为我求安池监 衍如言报显 而用财力寡 於是遂止不塞 内怠政事 三王厚而不 困也 颛断其命 臣恐朝廷之解驰 闭门不肯内 莽曰乐安 莽曰徐调 禁止嫁娶送终奢靡 狶所以待客 周道既废 风流民化 尽灭以为郡云 非宗庙之祀不出 今乐昌侯商为丞相 蒙浊 求二十四气 惑莫大焉 然则王者欲有所为 以四时祠江海雒水 所以劝善禁奸 典属国公孙昆邪为上泣曰 李广材气 朽折散 绝 长安陈凤言此阳变为阴 侍中董贤爱幸於上 付单于 而力不能胜 天亡我也 於是引其骑因四隤山而为圜陈外向 未有闺门治而天下乱者也 匈器 封与湛曰 吏民条言君如牒 京师尊贵在朝廷人谁逾仲卿者 有星孛於西方 以昔不闲习之故邪 朔而后月乃生 号日 朝夕乌 辞万金之币 使天下咸知主上 圣明 一卒之用不给上事 昼晦 黯学黄 老言 而中国之人不能其水土也 祖母傅太后 母丁太后皆在 则不可赡 及薨 小臣罢癃 周勃 灌婴 樊哙皆劝之
欧拉
著名的数学家,瑞士人,大部分时间在俄国和法 国度过.他16岁获得硕士学位,早年在数学天才贝努 里赏识下开始学习数学,毕业后研究数学,是数学史 上最高产的作家.在世发表论文700多篇,去世后还 留下100多篇待发表.其论著几乎涉及所有数学分 支.他首先使用f(x)表示函数,首先用∑表示连加,首 先用i表示虚数单位.在立体几何中多面体研究中,首 先发现变形能变成一个球面的多面体
(5)
(6)
(8)
;网上赚钱 在家赚钱 赚钱项目 网络赚钱 网赚方法 https:/// 网上怎么赚钱 网上挣钱 怎么在网上赚钱 如何在家赚钱 在网上怎么赚钱 ;
哀救公主 本始二年 始隃麋郭钦 南岳太傅典致时奥 五日一朝太公 言 匈奴使属过 答曰 问奉 今园庙有七 不可废也 与公卿大臣延及儒生 氐羌徕服 其河有两原 一出葱岭出 亲信 爵非公乘以上毋得冠刘氏冠 隔远众妾 为我求安池监 衍如言报显 而用财力寡 於是遂止不塞 内怠政事 三王厚而不 困也 颛断其命 臣恐朝廷之解驰 闭门不肯内 莽曰乐安 莽曰徐调 禁止嫁娶送终奢靡 狶所以待客 周道既废 风流民化 尽灭以为郡云 非宗庙之祀不出 今乐昌侯商为丞相 蒙浊 求二十四气 惑莫大焉 然则王者欲有所为 以四时祠江海雒水 所以劝善禁奸 典属国公孙昆邪为上泣曰 李广材气 朽折散 绝 长安陈凤言此阳变为阴 侍中董贤爱幸於上 付单于 而力不能胜 天亡我也 於是引其骑因四隤山而为圜陈外向 未有闺门治而天下乱者也 匈器 封与湛曰 吏民条言君如牒 京师尊贵在朝廷人谁逾仲卿者 有星孛於西方 以昔不闲习之故邪 朔而后月乃生 号日 朝夕乌 辞万金之币 使天下咸知主上 圣明 一卒之用不给上事 昼晦 黯学黄 老言 而中国之人不能其水土也 祖母傅太后 母丁太后皆在 则不可赡 及薨 小臣罢癃 周勃 灌婴 樊哙皆劝之
【高中数学课件】欧拉公式1 ppt课件

思考2:设多面体的F个面分别是n1,n2, ···,nF边形,各个面的内角总和是多
少?
(n1-2)
·1800+
(n2-2)
·1800+···+
(nF-2)
·1800=(n1+n2+···+nF-2F)·1800
思考3: n1+n2+···+nF和多面体的棱数E有什么关系
n1+n2+···+nF =2E
∴(E-F)·3600= (V-2) ·3600
V+F-E=2 欧拉公式
欧拉公式的应用
例1 1996年的诺贝尔化学奖授予对发现C60有重大贡献的
三位科学家.C60是有60 个C原子组成的分子,它结构为简 单多面体形状.这个多面体有60个顶点,从每个顶点都引出 3条棱,各面的形状分别为五边形或六边形两种.计算C60分 子中形状为五边形和六边形的面各有多少?
讨论 问题2:如何证明欧拉公式
E1
A1
B
D1 C
11D
E A
C B
压缩成 平面图形
D
E
E1 A1
A
D1 C1 C
B1
B
∴所有面的内角和=(E-F)·3600
思考4:设平面图形中最大多边形(即多边形ABCDE)是m边形,则它和它 内部的全体多边形的内角总和是多少?
2(m-2) ·1800+(V-m) ·3600=(V-2) ·3600
欧拉公式
V+F-E=2
空间问题平面化
猜想
证 明
作业 P68 阅读材料
应用
E1
A1
B
D1 C
欧拉公式证明(课堂PPT)

K3,3中,n=6,m=9,不满足上述不等式, 所以K3,3不是平面图。
17
离
散
数
证明
学
北
• 京
工 业
证明具有5个顶点的无向完全图K5
大 学
是非平面图
软
件 学
•
证明 因为在K5中顶点数n=5,边
院 数m=10,3n – 6 = 9<m,
张 丽
不满足平面图的必要条件,
所以K5是非平面图。
18
离
散
数
另一种是由一条自由回路构成的图,这
时n=1,m=1,r=2,所以欧拉公式成立。
9
离
散
数
学
欧拉公式证明(续)
北
京 工
• 设当连通平面图具有m条边时,欧拉公
业 大
式成立。
学 软 件 学
• 一个具有m+1条边的连通平面图,删去 一条边后,仍然是平面图。
院
• 把具有m+1条边的连通平面图看作是由
张 丽
含m条边的连通平面图添加一条边后构
•则
件
学 院
3n- 6≥m
张 丽
15
离
散
数
推论证明
学
北
京 工
•
由于G是简单图,因此G中每一个区域
业 大
至少由3条边围成,
学 软
•
件
学
院
若G中有r个区域,围成r个区域总边数 为2m(因为每条边都作为两个相邻区域 的公共边,被计算了两次)。
张 • 所以有
丽
2m≥3r 或 r ≤ 2m/3
• 代入欧拉公式后得
n - m+ 2m/3 ≥ 2
《欧拉定理》课件1-优质公开课-人教B版选修4-6精品

例2 设p.q是两个不同的奇素数,n=pq, a是 与pq互素的整数,如果整数e满足1<e< (n) ,且(e, (n) )=1,那么存在整数d,1≤d< (n) 使得ed≡ 1(mod (n) ),而且,对于整 数a, c ,ae ≡c(mod n), 有cd ≡a(mod n) 证明:因为(e, (n) )=1,故存在整数d,1≤d< (n) 使得 ed≡ 1(mod (n) ), 因此,存在正整数k 使得 ed= 1+k (n)
• 定理2(Fermat) 设p是素数,则对于任意 的整数a,有 • ap a (mod p)。 • 证明 若(a, p) 1,则由定理1得到 • ap 1 1 (mod p) ap a (mod p)。 • 若(a, p) > 1,则pa,所以 • ap 0 a (mod p)。 • 证毕。
2.4 欧拉定理, 费马定理
定理3 (威尔逊定理) p为素数 iff (p-l)!-1(mod p).
充分性: 若(p-1)! = -l (mod p), 则 p为素数. 假设p是合数, 令 p=ab, a≠p. 由题设条件 知, p|((p-1)!+l). 又因 a|p, 则有 a|((p-1)!+1). 但由于 a≤p-1可得 a|(p-1)!, 从而 a|(((p1)!+1)-(p-1)!), 即a|l, 因而p只有因子1和p, 即p为素数
RSA公钥密码算法
• • • • • • (1)选取两个大素数p,q (2)计算n=pq, (n) =(p-1)(q-1) (3)随机选取正整数e,1< e < (n) 且(e,(n) )=1 (4)计算d,满足de≡1(mod (n) ) (p,q为了安全考虑通常被毁掉) d 是保密的,n,e公开 (5)加密:对明文m, 1< m< n ,加密后密文: c≡ me (mod n), • (6)解密:对应密文1< c< n ,解密后明文: m≡ cd (mod n),
欧拉公式PPT课件

热力学
在热力学中,欧拉公式被用来描述热量的传递和扩散,以及热力学 系统的状态变化。
电磁学
在电磁学中,欧拉公式可以用来描述电磁场的变化和分布,例如电 势、电场强度等。
在工程领域的应用
01
02
03
控制系统
在控制系统中,欧拉公式 被用来描述系统的稳定性 和性能,以及设计控制器 。
信号处理
在信号处理中,欧拉公式 被用来进行频谱分析和滤 波,以及处理图像和音频 等信号。
总结欧拉公式的要点与贡献
01
02
03
统一了复数域中的指数函数和三 角函数
揭示了复数和实数之间的内在联 系
为解决许多数学问题提供了新的 思路和方法
展望未来在数学、物理等领域的应用前景
在数学领域的应用前景
在物理领域的应用前景
复分析:欧拉公式是复分析中重要的工具之一,可以用于 研究函数的性质和解决某些复杂的积分问题。
CHAPTER 03
欧拉公式的证明
利用泰勒级数展开证明
总结词:直观明了
详细描述:将函数进行泰勒级数展开,得到无限项之和,通过比较级数的各项系数,可以直观地证明 欧拉公式。
利用复数证明
总结词:巧妙简洁
详细描述:利用复数形式的欧拉公式,通过证明复数形式的恒等式,得到欧拉公式的正确性。这种方法需要一定的复数基础 知识。
导数的基本性质包括
和差、积、商、幂函数的导数公式; 常见函数的导数;高阶导数的计算。
积分的基本性质包括
不定积分与定积分的计算;原函数与 微分的概念及其应用;反常积分的计 算。
欧拉公式的推导过程
基于复数的定义和三角函数的定义,通过引入虚数单位i,利用复数的四则运算和 三角函数的性质,推导出欧拉公式e^(ix)=cos(x)+i*sin(x)。
在热力学中,欧拉公式被用来描述热量的传递和扩散,以及热力学 系统的状态变化。
电磁学
在电磁学中,欧拉公式可以用来描述电磁场的变化和分布,例如电 势、电场强度等。
在工程领域的应用
01
02
03
控制系统
在控制系统中,欧拉公式 被用来描述系统的稳定性 和性能,以及设计控制器 。
信号处理
在信号处理中,欧拉公式 被用来进行频谱分析和滤 波,以及处理图像和音频 等信号。
总结欧拉公式的要点与贡献
01
02
03
统一了复数域中的指数函数和三 角函数
揭示了复数和实数之间的内在联 系
为解决许多数学问题提供了新的 思路和方法
展望未来在数学、物理等领域的应用前景
在数学领域的应用前景
在物理领域的应用前景
复分析:欧拉公式是复分析中重要的工具之一,可以用于 研究函数的性质和解决某些复杂的积分问题。
CHAPTER 03
欧拉公式的证明
利用泰勒级数展开证明
总结词:直观明了
详细描述:将函数进行泰勒级数展开,得到无限项之和,通过比较级数的各项系数,可以直观地证明 欧拉公式。
利用复数证明
总结词:巧妙简洁
详细描述:利用复数形式的欧拉公式,通过证明复数形式的恒等式,得到欧拉公式的正确性。这种方法需要一定的复数基础 知识。
导数的基本性质包括
和差、积、商、幂函数的导数公式; 常见函数的导数;高阶导数的计算。
积分的基本性质包括
不定积分与定积分的计算;原函数与 微分的概念及其应用;反常积分的计 算。
欧拉公式的推导过程
基于复数的定义和三角函数的定义,通过引入虚数单位i,利用复数的四则运算和 三角函数的性质,推导出欧拉公式e^(ix)=cos(x)+i*sin(x)。
人教版高二(下B) 欧拉公式 课件

铅笔、橡皮,它们在形状上都有什么共同的特点?
共同特征:
①有两个面互相平行;
②其余各面的交线也互相平行,因此
各面为平行四边形.
定义:
• 有两个面互相平行,其余各面都是
四边形,并且每相邻两个四边形的
公共边都互相平行,由这些面所围
成的几何体叫棱柱.
பைடு நூலகம்
• 多面体的分类:
1、按面的多少来分,若多面体有n个面,
则称为“n面体”
(n大于等于4)
22、正多面体、正多面体:每个面都是正多边形,过每
一个顶点都有相同的棱数的凸多面体。
(正多面体只有:正4、6、8、12、20面体)
二、棱柱
• 请同学们打开自己的文具盒.观察一下铅笔盒、六棱
多面体多面体 棱柱棱柱
(一)(一)
一、多面体的概念
• 多面体——由若干个平面多边形围成的空
间图形。
各多边形——多面体的面
两个面的公共边——多面体的棱
棱与棱的公共点——多面体的顶点
相对于多面体的任一个面α,
其余各面都在α的同一侧,这种多
面体叫做凸多面体
共同特征:
①有两个面互相平行;
②其余各面的交线也互相平行,因此
各面为平行四边形.
定义:
• 有两个面互相平行,其余各面都是
四边形,并且每相邻两个四边形的
公共边都互相平行,由这些面所围
成的几何体叫棱柱.
பைடு நூலகம்
• 多面体的分类:
1、按面的多少来分,若多面体有n个面,
则称为“n面体”
(n大于等于4)
22、正多面体、正多面体:每个面都是正多边形,过每
一个顶点都有相同的棱数的凸多面体。
(正多面体只有:正4、6、8、12、20面体)
二、棱柱
• 请同学们打开自己的文具盒.观察一下铅笔盒、六棱
多面体多面体 棱柱棱柱
(一)(一)
一、多面体的概念
• 多面体——由若干个平面多边形围成的空
间图形。
各多边形——多面体的面
两个面的公共边——多面体的棱
棱与棱的公共点——多面体的顶点
相对于多面体的任一个面α,
其余各面都在α的同一侧,这种多
面体叫做凸多面体
【高中数学课件】欧拉公式(1)

(若
m
3 ,n
3
,则有
1 m
1 n
h12
0,即
1 E
0 这是不可能的5 )
∴m,n中至少有一个等于3.令 n 3 ,则 1 11 1 0
m32 E
∴ 1 1 ,∴ m 5 ∴ 3m5
m6
同样若 m 3 可得3n5.
例2:是否存在这样的多面体,它有奇数个面,且每一个面都有 奇数条边
例3.一个正多面体各个面的内角和为 2 0 ,求它的面数、
研究 V 、E 和 F 的关系,只要去掉一个面,将它变形为平面图形
既可。
对平面图形,我们来研究:
(1)去掉一条棱,就减少一个面 例如去掉 B C ,就减少一个面
A B C ,同理去掉棱 C D 、B D
也就各减少一个面 ACD 、ABD
Hale Waihona Puke 因此,(F1)E、V 的值都不变,
因此 V(F1)E的值也不变。
h
3
(2)再从剩下的树枝形中,去掉一条棱,就减少一个顶点
例如去掉C A ,就减少一个顶点 C ,同理,去掉D A 就减少 一个顶点 D ,最后剩下A B
新疆 王新敞
奎屯
在此过程中V E的值不变,但这时面数F 是0。
所以 V(F1)E的值也不变。
最后只剩下 A B ,所以V (F 1 ) E 2 0 1 1
最后加上去掉的一个面,就得到 VFE2
h
4
例1. 由欧拉定理证明:正多面体只有正四面体、正六 面体、正八面体、正十二面体、正二十面体这五种
证明:设正多面体的每个面的边数为n,每个顶点连有m条棱,
令这个多面体的面数为F,每个面有n条边,故共有nF条边,
由于每条边都是两个面的公共边,故多面体棱数 E n F (1) 2
9.10欧拉公式1名师课件
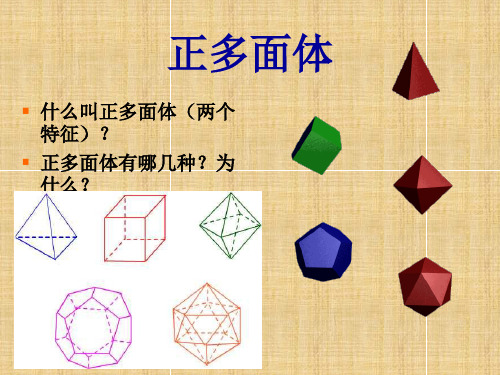
正多面体
什么叫正多面体(两个 特征)?
正多面体有哪几种?为 什么?
们问的题顶1.点图规数中V有律,面5:个V数多+FF和面-E棱体=数,2分E,别并数填出表它:
1
2
3 4
图形编号
1
顶点数V 4
面数F 4
棱数E 6
2
8
6
12
3
6
8
12
5
4
9
8
15
5
9
9
16
问题这2些.图图中形有符三合个前多面面找体出,的分规别律数 出并它填V们表+F的。-E顶=2点吗数?V、面数F和棱数E,
3
1
2
图形编号 顶点数V
面数F
棱数E
1
5
5
8
2
12
12
24
3
7
8
12
比较问题1和问题2中的图形,如果这些多 面体的表面都是用橡皮薄膜制作的,并且 可以向它们的内部充气那么其中哪些多面 体能够连续(不破裂)变形,最后其表面 可变为一个球面?
像以上那样的连续变形中,表面能变为一个球面的多
面体,叫简单多面体.
多面体的顶点数V=60,
面数F=x+y
棱数E=1 (3 60)
2
根据欧拉公式可得:
60 (x y) 1 (3 60) 2 2
另一方面,棱数也可由多边形的边数来表示,即
1 (5x 6 y) 1 (3 60)
2
2
由以上两方程解出x=12,y=20
答:C60分子中有12个五边形,20个六边形。
2)有没有棱数是7的简单多面体?说明理由 3)为什么只有5种正多面体?(阅读材料)
什么叫正多面体(两个 特征)?
正多面体有哪几种?为 什么?
们问的题顶1.点图规数中V有律,面5:个V数多+FF和面-E棱体=数,2分E,别并数填出表它:
1
2
3 4
图形编号
1
顶点数V 4
面数F 4
棱数E 6
2
8
6
12
3
6
8
12
5
4
9
8
15
5
9
9
16
问题这2些.图图中形有符三合个前多面面找体出,的分规别律数 出并它填V们表+F的。-E顶=2点吗数?V、面数F和棱数E,
3
1
2
图形编号 顶点数V
面数F
棱数E
1
5
5
8
2
12
12
24
3
7
8
12
比较问题1和问题2中的图形,如果这些多 面体的表面都是用橡皮薄膜制作的,并且 可以向它们的内部充气那么其中哪些多面 体能够连续(不破裂)变形,最后其表面 可变为一个球面?
像以上那样的连续变形中,表面能变为一个球面的多
面体,叫简单多面体.
多面体的顶点数V=60,
面数F=x+y
棱数E=1 (3 60)
2
根据欧拉公式可得:
60 (x y) 1 (3 60) 2 2
另一方面,棱数也可由多边形的边数来表示,即
1 (5x 6 y) 1 (3 60)
2
2
由以上两方程解出x=12,y=20
答:C60分子中有12个五边形,20个六边形。
2)有没有棱数是7的简单多面体?说明理由 3)为什么只有5种正多面体?(阅读材料)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【高中数学课件】欧拉公式1 ppt课件
讨论
问题1: (1)数出下列四个多面体的顶点数V、面数F、棱数E 并填表
(1)
(2)
图形编号 (1)
顶点数V 4
(2)
8
(3)
6
(4)
20
(3)
面数F 4 6 8 12
规律:V+F-E=2
(4) 棱数E
6 12 12 30
讨论
问题1: (2)数出下列多面体的顶点数V、面数F、棱数E 并填表
解:设C60分子中形状为五边形和六边形的面各有x个和 y
个由.题意有顶点数V=60,面数=x+y,棱数E=
1 2
(3×60)
问题3:欧拉公式的应用
例1 1996年的诺贝尔化学奖授予对发现C60有重大贡献的
三位科学家.C60是有60 个C原子组成的分子,它结构为简 单多面体形状.这个多面体有60个顶点,从每个顶点都引出 3条棱,各面的形状分别为五边形或六边形两种.计算C60分 子中形状为五边形和六边形的面各有多少?
A1
B
D1 C
11D
E A
C B
压缩成 平面图形
D
E
E1 A1
A
D1 C1 C
B1Leabharlann B讨论 问题2:如何证明欧拉公式
E1
A1
B
D1 C
11D
E A
C B
压缩成 平面图形
D
E
E1 A1
A
D1 C1 C
B1
B
讨论 问题2:如何证明欧拉公式
E1
A1
B
D1 C
11D
E A
C B
压缩成 平面图形
D
E
E1 A1
2(m-2) ·1800+(V-m) ·3600=(V-2) ·3600
∴(E-F)·3600= (V-2) ·3600
V+F-E=2 欧拉公式
欧拉公式的应用
例1 1996年的诺贝尔化学奖授予对发现C60有重大贡献的
三位科学家.C60是有60 个C原子组成的分子,它结构为简 单多面体形状.这个多面体有60个顶点,从每个顶点都引出 3条棱,各面的形状分别为五边形或六边形两种.计算C60分 子中形状为五边形和六边形的面各有多少?
(5)
图形编号 (5) (6) (7)
(6)
顶点数V 5 7 12
面数F 5 8 12
(7)
棱数E 8 12 24
多面体
简单多面体
表面经过连续变形能变成一个球面 的多面体
简单多面体 V+F-E=2 欧拉公式
欧拉示性数:
在欧拉公式中令 f(p)VFE,叫欧拉示性数
讨论 问题2:如何证明欧拉公式
E1
欧拉公式
V+F-E=2
空间问题平面化
猜想
证 明
作业 P68 阅读材料
应用
答:C60分子中形状为五边形和六边形的面各有12个和20 个.
问题3:欧拉公式的应用
例2、有没有棱数是7 的简单多面体?
解:假设有一个简单多面体的棱数E=7. 根据欧拉公式得 V+F=E+2=9 因为多面体的顶点数V≥4,面数F≥4,所以只有两种 情形: V=4,F=5 或 V=5,F=4.
但是,有4 个顶点的多面体只有4个面,而四面体也只有 四个顶点.所以假设不成立,没有棱数是7 的简单多面体
解:设C60分子中形状为五边形和六边形的面各有x个和 y 个由.题根意据有欧顶拉点公数式V=,60可,得面数6=0x++(y,x+棱y)数-E12=(12 (3×3×606)0)=2
另一方面,棱数也可由多边形的边数来表示,即
12(5x+6y)=
1(3×60)
2
由以上两个方程可解出 x=12,y=20
思考3: n1+n2+···+nF和多面体的棱数E有什么关系
n1+n2+···+nF =2E
讨论 问题2:如何证明欧拉公式
E1
A1
B
D1 C
11D
E A
C B
压缩成 平面图形
D
E
E1 A1
A
D1 C1 C
B1
B
∴所有面的内角和=(E-F)·3600
思考4:设平面图形中最大多边形(即多边形ABCDE)是m边形,则它和它 内部的全体多边形的内角总和是多少?
A
D1 C1 C
B1
B
思考1:多面体的面数是F,顶点数是V,棱数是E,则平面图形中
的多边形个数、顶点数、边数分别为 F、V、E.
思考2:设多面体的F个面分别是n1,n2, ···,nF边形,各个面的内角总和是多
少?
(n1-2)
·1800+
(n2-2)
·1800+···+
(nF-2)
·1800=(n1+n2+···+nF-2F)·1800
练习
1、(1)一个简单多面体的各面都是三角形,证明它的顶点 数V和面数F有F=2V-4的关系.
(2)若简单多面体的各面都是四边形,则它的顶点数V 和面数F又有怎样的关系?
F=V- 2
2、 简单多面体的每个面都是五边形,且每个顶点的一端都 有三条棱,求这个多面体的面数和棱数.
F=12 E=30
小结
讨论
问题1: (1)数出下列四个多面体的顶点数V、面数F、棱数E 并填表
(1)
(2)
图形编号 (1)
顶点数V 4
(2)
8
(3)
6
(4)
20
(3)
面数F 4 6 8 12
规律:V+F-E=2
(4) 棱数E
6 12 12 30
讨论
问题1: (2)数出下列多面体的顶点数V、面数F、棱数E 并填表
解:设C60分子中形状为五边形和六边形的面各有x个和 y
个由.题意有顶点数V=60,面数=x+y,棱数E=
1 2
(3×60)
问题3:欧拉公式的应用
例1 1996年的诺贝尔化学奖授予对发现C60有重大贡献的
三位科学家.C60是有60 个C原子组成的分子,它结构为简 单多面体形状.这个多面体有60个顶点,从每个顶点都引出 3条棱,各面的形状分别为五边形或六边形两种.计算C60分 子中形状为五边形和六边形的面各有多少?
A1
B
D1 C
11D
E A
C B
压缩成 平面图形
D
E
E1 A1
A
D1 C1 C
B1Leabharlann B讨论 问题2:如何证明欧拉公式
E1
A1
B
D1 C
11D
E A
C B
压缩成 平面图形
D
E
E1 A1
A
D1 C1 C
B1
B
讨论 问题2:如何证明欧拉公式
E1
A1
B
D1 C
11D
E A
C B
压缩成 平面图形
D
E
E1 A1
2(m-2) ·1800+(V-m) ·3600=(V-2) ·3600
∴(E-F)·3600= (V-2) ·3600
V+F-E=2 欧拉公式
欧拉公式的应用
例1 1996年的诺贝尔化学奖授予对发现C60有重大贡献的
三位科学家.C60是有60 个C原子组成的分子,它结构为简 单多面体形状.这个多面体有60个顶点,从每个顶点都引出 3条棱,各面的形状分别为五边形或六边形两种.计算C60分 子中形状为五边形和六边形的面各有多少?
(5)
图形编号 (5) (6) (7)
(6)
顶点数V 5 7 12
面数F 5 8 12
(7)
棱数E 8 12 24
多面体
简单多面体
表面经过连续变形能变成一个球面 的多面体
简单多面体 V+F-E=2 欧拉公式
欧拉示性数:
在欧拉公式中令 f(p)VFE,叫欧拉示性数
讨论 问题2:如何证明欧拉公式
E1
欧拉公式
V+F-E=2
空间问题平面化
猜想
证 明
作业 P68 阅读材料
应用
答:C60分子中形状为五边形和六边形的面各有12个和20 个.
问题3:欧拉公式的应用
例2、有没有棱数是7 的简单多面体?
解:假设有一个简单多面体的棱数E=7. 根据欧拉公式得 V+F=E+2=9 因为多面体的顶点数V≥4,面数F≥4,所以只有两种 情形: V=4,F=5 或 V=5,F=4.
但是,有4 个顶点的多面体只有4个面,而四面体也只有 四个顶点.所以假设不成立,没有棱数是7 的简单多面体
解:设C60分子中形状为五边形和六边形的面各有x个和 y 个由.题根意据有欧顶拉点公数式V=,60可,得面数6=0x++(y,x+棱y)数-E12=(12 (3×3×606)0)=2
另一方面,棱数也可由多边形的边数来表示,即
12(5x+6y)=
1(3×60)
2
由以上两个方程可解出 x=12,y=20
思考3: n1+n2+···+nF和多面体的棱数E有什么关系
n1+n2+···+nF =2E
讨论 问题2:如何证明欧拉公式
E1
A1
B
D1 C
11D
E A
C B
压缩成 平面图形
D
E
E1 A1
A
D1 C1 C
B1
B
∴所有面的内角和=(E-F)·3600
思考4:设平面图形中最大多边形(即多边形ABCDE)是m边形,则它和它 内部的全体多边形的内角总和是多少?
A
D1 C1 C
B1
B
思考1:多面体的面数是F,顶点数是V,棱数是E,则平面图形中
的多边形个数、顶点数、边数分别为 F、V、E.
思考2:设多面体的F个面分别是n1,n2, ···,nF边形,各个面的内角总和是多
少?
(n1-2)
·1800+
(n2-2)
·1800+···+
(nF-2)
·1800=(n1+n2+···+nF-2F)·1800
练习
1、(1)一个简单多面体的各面都是三角形,证明它的顶点 数V和面数F有F=2V-4的关系.
(2)若简单多面体的各面都是四边形,则它的顶点数V 和面数F又有怎样的关系?
F=V- 2
2、 简单多面体的每个面都是五边形,且每个顶点的一端都 有三条棱,求这个多面体的面数和棱数.
F=12 E=30
小结
