2020年陕西省中考数学试题及答案
2020年陕西省中考数学试卷(有详细解析)

2020年陕西省中考数学试卷班级:___________姓名:___________得分:___________一、选择题(本大题共10小题,共30.0分)1.−18的相反数是()A. 18B. −18C. 118D. −1182.若∠A=23°,则∠A余角的大小是()A. 57°B. 67°C. 77°D. 157°3.2019年,我国国内生产总值约为990870亿元,将数字990870用科学记数法表示为()A. 9.9087×105B. 9.9087×104C. 99.087×104D. 99.087×1034.如图,是A市某一天的气温随时间变化的情况,则这天的日温差(最高气温与最低气温的差)是()A. 4℃B. 8℃C. 12℃D. 16℃5.计算:(−23x2y)3=()A. −2x6y3B. 827x6y3 C. −827x6y3 D. −827x5y46.如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为()A. 1013√13B. 913√13C. 813√13D. 713√137.在平面直角坐标系中,O为坐标原点.若直线y=x+3分别与x轴、直线y=−2x交于点A、B,则△AOB的面积为()A. 2B. 3C. 4D. 68.如图,在▱ABCD中,AB=5,BC=8.E是边BC的中点,F是▱ABCD内一点,且∠BFC=90°.连接AF并延长,交CD于点G.若EF//AB,则DG的长为()A. 52B. 32C. 3D. 29.如图,△ABC内接于⊙O,∠A=50°.E是边BC的中点,连接OE并延长,交⊙O于点D,连接BD,则∠D的大小为()A. 55°B. 65°C. 60°D. 75°10. 在平面直角坐标系中,将抛物线y =x 2−(m −1)x +m(m >1)沿y 轴向下平移3个单位.则平移后得到的抛物线的顶点一定在( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限 二、填空题(本大题共4小题,共12.0分) 11. 化简:(2+√3)(2−√3)=______.12. 如图,在正五边形ABCDE 中,DM 是边CD 的延长线,连接BD ,则∠BDM 的度数是______.13. 在平面直角坐标系中,点A(−2,1),B(3,2),C(−6,m)分别在三个不同的象限.若反比例函数y =k x (k ≠0)的图象经过其中两点,则m 的值为______.14. 如图,在菱形ABCD 中,AB =6,∠B =60°,点E 在边AD 上,且AE =2.若直线l 经过点E ,将该菱形的面积平分,并与菱形的另一边交于点F ,则线段EF 的长为______.三、计算题(本大题共1小题,共7.0分)15. 如图所示,小明家与小华家住在同一栋楼的同一单元,他俩想测算所住楼对面商业大厦的高MN.他俩在小明家的窗台B 处,测得商业大厦顶部N 的仰角∠1的度数,由于楼下植物的遮挡,不能在B 处测得商业大厦底部M 的俯角的度数.于是,他俩上楼来到小华家,在窗台C 处测得大厦底部M 的俯角∠2的度数,竟然发现∠1与∠2恰好相等.已知A ,B ,C 三点共线,CA ⊥AM ,NM ⊥AM ,AB =31m ,BC =18m ,试求商业大厦的高MN .四、解答题(本大题共10小题,共71.0分)16. 解不等式组:{3x >6,2(5−x)>4.17. 解分式方程:x−2x −3x−2=1.18.如图,已知△ABC,AC>AB,∠C=45°.请用尺规作图法,在AC边上求作一点P,使∠PBC=45°.(保留作图痕迹.不写作法)19.如图,在四边形ABCD中,AD//BC,∠B=∠C.E是边BC上一点,且DE=DC.求证:AD=BE.20.王大伯承包了一个鱼塘,投放了2000条某种鱼苗,经过一段时间的精心喂养,存活率大致达到了90%.他近期想出售鱼塘里的这种鱼.为了估计鱼塘里这种鱼的总质量,王大伯随机捕捞了20条鱼,分别称得其质量后放回鱼塘.现将这20条鱼的质量作为样本,统计结果如图所示:(1)这20条鱼质量的中位数是______,众数是______.(2)求这20条鱼质量的平均数;(3)经了解,近期市场上这种鱼的售价为每千克18元,请利用这个样本的平均数.估计王大伯近期售完鱼塘里的这种鱼可收入多少元?21.某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗早期在农科所的温室中生长,长到大约20cm时,移至该村的大棚内,沿插杆继续向上生长.研究表明,60天内,这种瓜苗生长的高度y(cm)与生长时间x(天)之间的关系大致如图所示.(1)求y与x之间的函数关系式;(2)当这种瓜苗长到大约80cm时,开始开花结果,试求这种瓜苗移至大棚后.继续生长大约多少天,开始开花结果?22.小亮和小丽进行摸球试验.他们在一个不透明的空布袋内,放入两个红球,一个白球和一个黄球,共四个小球.这些小球除颜色外其它都相同.试验规则:先将布袋内的小球摇匀,再从中随机摸出一个小球,记下颜色后放回,称为摸球一次.(1)小亮随机摸球10次,其中6次摸出的是红球,求这10次中摸出红球的频率;(2)若小丽随机摸球两次,请利用画树状图或列表的方法,求这两次摸出的球中一个是白球、一个是黄球的概率.23.如图,△ABC是⊙O的内接三角形,∠BAC=75°,∠ABC=45°.连接AO并延长,交⊙O于点D,连接BD.过点C作⊙O的切线,与BA的延长线相交于点E.(1)求证:AD//EC;(2)若AB=12,求线段EC的长.24.如图,抛物线y=x2+bx+c经过点(3,12)和(−2,−3),与两坐标轴的交点分别为A,B,C,它的对称轴为直线l.(1)求该抛物线的表达式;(2)P是该抛物线上的点,过点P作l的垂线,垂足为D,E是l上的点.要使以P、D、E为顶点的三角形与△AOC全等,求满足条件的点P,点E的坐标.25.问题提出(1)如图1,在Rt△ABC中,∠ACB=90°,AC>BC,∠ACB的平分线交AB于点D.过点D分别作DE⊥AC,DF⊥BC.垂足分别为E,F,则图1中与线段CE相等的线段是______.问题探究(2)如图2,AB是半圆O的直径,AB=8.P是AB⏜上一点,且PB⏜=2PA⏜,连接AP,BP.∠APB的平分线交AB于点C,过点C分别作CE⊥AP,CF⊥BP,垂足分别为E,F,求线段CF的长.问题解决(3)如图3,是某公园内“少儿活动中心”的设计示意图.已知⊙O的直径AB=70m,点C在⊙O上,且CA=CB.P为AB上一点,连接CP并延长,交⊙O于点D.连接AD,BD.过点P分别作PE⊥AD,PF⊥BD,重足分别为E,F.按设计要求,四边形PEDF内部为室内活动区,阴影部分是户外活动区,圆内其余部分为绿化区.设AP的长为x(m),阴影部分的面积为y(m2).①求y与x之间的函数关系式;②按照“少儿活动中心”的设计要求,发现当AP的长度为30m时,整体布局比较合理.试求当AP=30m时.室内活动区(四边形PEDF)的面积.答案和解析1. A解:−18的相反数是:18.2. B解:∵∠A =23°,∴∠A 的余角是90°−23°=67°.3. A解:990870=9.9087×105,4. C解:从折线统计图中可以看出,这一天中最高气温8℃,最低气温是−4℃,这一天中最高气温与最低气温的差为12℃,5. C解:(−23x 2y)3=(−23)3⋅(x 2)3⋅y 3=−827x 6y 3.6. D解:由勾股定理得:AC =√22+32=√13,∵S △ABC =3×3−12×1×2−12×1×3−12×2×3=3.5,∴12AC ⋅BD =72, ∴√13⋅BD =7,∴BD =7√1313, 7. B解:在y =x +3中,令y =0,得x =−3,解{y =x +3y =−2x得,{x =−1y =2, ∴A(−3,0),B(−1,2),∴△AOB 的面积=12×3×2=3,8. D解:∵E 是边BC 的中点,且∠BFC =90°,∴Rt △BCF 中,EF =12BC =4, ∵EF//AB ,AB//CG ,E 是边BC 的中点,∴F 是AG 的中点,∴EF 是梯形ABCG 的中位线,∴CG =2EF −AB =3,又∵CD =AB =5,∴DG =5−3=2,9. B解:连接CD ,∵∠A =50°,∴∠CDB =180°−∠A =130°,∵E 是边BC 的中点,∴OD ⊥BC ,∴BD =CD ,∴∠ODB =∠ODC =12∠BDC =65°,10. D解:∵y =x 2−(m −1)x +m =(x −m−12)2+m −(m−1)24, ∴该抛物线顶点坐标是(m−12,m −(m−1)24),∴将其沿y 轴向下平移3个单位后得到的抛物线的顶点坐标是(m−12,m −(m−1)24−3), ∵m >1,∴m −1>0,∴m−12>0,∵m −(m−1)24−3=4m−(m 2−2m+1)−124=−(m−3)2−44=−(m−3)24−1<0, ∴点(m−12,m −(m−1)24−3)在第四象限;11. 1解:原式=22−(√3)2=4−3=1.12. 144°解:因为五边形ABCDE是正五边形,=108°,BC=DC,所以∠C=(5−2)⋅180°5=36°,所以∠BDC=180°−108°2所以∠BDM=180°−36°=144°,13.−1解:∵点A(−2,1),B(3,2),C(−6,m)分别在三个不同的象限,点A(−2,1)在第二象限,∴点C(−6,m)一定在第三象限,(k≠0)的图象经过其中两点,∵B(3,2)在第一象限,反比例函数y=kx(k≠0)的图象经过B(3,2),C(−6,m),∴反比例函数y=kx∴3×2=−6m,∴m=−1,14.2√7解:如图,过点A和点E作AG⊥BC,EH⊥BC于点G和H,得矩形AGHE,∴GH=AE=2,∵在菱形ABCD中,AB=6,∠B=60°,∴BG=3,AG=3√3=EH,∴HC=BC−BG−GH=6−3−2=1,∵EF平分菱形面积,∴FC=AE=2,∴FH=FC−HC=2−1=1,在Rt△EFH中,根据勾股定理,得EF=√EH2+FH2=√27+1=2√7.15.解:如图,过点C作CE⊥MN于点E,过点B作BF⊥MN于点F,∴∠CEF=∠BFE=90°,∵CA ⊥AM ,NM ⊥AM ,∴四边形AMEC 和四边形AMFB 均为矩形,∴CE =BF ,ME =AC ,∠1=∠2,∴△BFN≌△CEM(ASA),∴NF =EM =31+18=49,由矩形性质可知:EF =CB =18,∴MN =NF +EM −EF =49+49−18=80(m).答:商业大厦的高MN 为80m .16. 解:{3x >6 ①2(5−x)>4 ②, 由①得:x >2,由②得:x <3,则不等式组的解集为2<x <3.17. 解:方程x−2x −3x−2=1,去分母得:x 2−4x +4−3x =x 2−2x ,解得:x =45,经检验x =45是分式方程的解.18. 解:如图,点P 即为所求.19. 证明:∵DE =DC ,∴∠DEC =∠C .∵∠B =∠C ,∴∠B =∠DEC ,∴AB//DE ,∵AD//BC ,∴四边形ABED 是平行四边形.∴AD =BE .20. 1.45kg 1.5kg解:(1)∵这20条鱼质量的中位数是第10、11个数据的平均数,且第10、11个数据分别为1.4、1.5,∴这20条鱼质量的中位数是1.4+1.52=1.45(kg),众数是1.5kg , 故答案为:1.45kg ,1.5kg .(2)x −=1.2×1+1.3×4+1.4×5+1.5×6+1.6×2+1.7×220=1.45(kg),∴这20条鱼质量的平均数为1.45kg ;(3)18×1.45×2000×90%=46980(元),答:估计王大伯近期售完鱼塘里的这种鱼可收入46980元.21. 解:(1)当0≤x ≤15时,设y =kx(k ≠0),则:20=15k ,解得k =43,∴y =43x ; 当15<x ≤60时,设y =k′x +b(k ≠0),则:{20=15k′+b 170=60k′+b, 解得{k′=103b =−30, ∴y =103x −30,∴y ={43x(0≤x ≤15)103x −30(15<x ≤60); (2)当y =80时,80=103x −30,解得x =33,33−15=18(天),∴这种瓜苗移至大棚后.继续生长大约18天,开始开花结果.22. 解:(1)小亮随机摸球10次,其中6次摸出的是红球,这10次中摸出红球的频率=610=35; (2)画树状图得:∵共有16种等可能的结果,两次摸出的球中一个是白球、一个是黄球的有2种情况, ∴两次摸出的球中一个是白球、一个是黄球的概率=216=18.23.证明:(1)连接OC,∵CE与⊙O相切于点C,∴∠OCE=90°,∵∠ABC=45°,∴∠AOC=90°,∵∠AOC+∠OCE=180°,∴∴AD//EC(2)如图,过点A作AF⊥EC交EC于F,∵∠BAC=75°,∠ABC=45°,∴∠ACB=60°,∴∠D=∠ACB=60°,∴sin∠ADB=ABAD =√32,∴AD=√3=8√3,∴OA=OC=4√3,∵AF⊥EC,∠OCE=90°,∠AOC=90°,∴四边形OAFC是矩形,又∵OA=OC,∴四边形OAFC是正方形,∴CF=AF=4√3,∵∠BAD=90°−∠D=30°,∴∠EAF=180°−90°−30°=60°,∵tan∠EAF=EFAF=√3,∴EF=√3AF=12,∴CE=CF+EF=12+4√3.24.解:(1)将点(3,12)和(−2,−3)代入抛物线表达式得{12=9+3b+c−3=4−2b+c,解得{b=2c=−3,故抛物线的表达式为:y=x2+2x−3;(2)抛物线的对称轴为x=−1,令y=0,则x=−3或1,令x=0,则y=−3,故点A、B的坐标分别为(−3,0)、(1,0);点C(0,−3),故OA=OC=3,∵∠PDE=∠AOC=90°,∴当PD=DE=3时,以P、D、E为顶点的三角形与△AOC全等,设点P(m,n),当点P在抛物线对称轴右侧时,m−(−1)=3,解得:m=2,故n=22+2×2−5=5,故点P(2,5),故点E(−1,2)或(−1,8);当点P在抛物线对称轴的左侧时,由抛物线的对称性可得,点P(−4,5),此时点E坐标同上,综上,点P的坐标为(2,5)或(−4,5);点E的坐标为(−1,2)或(−1,8).25.CF、DE、DF解:(1)∵∠ACB=90°,DE⊥AC,DF⊥BC,∴四边形CEDF是矩形,∵CD平分∠ACB,DE⊥AC,DF⊥BC,∴DE=DF,∴四边形CEDF是正方形,∴CE=CF=DE=DF,故答案为:CF、DE、DF;(2)连接OP,如图2所示:∵AB是半圆O的直径,PB⏜=2PA⏜,∴∠APB=90°,∠AOP=13×180°=60°,∴∠ABP=30°,同(1)得:四边形PECF是正方形,∴PF=CF,在Rt△APB中,PB=AB⋅cos∠ABP=8×cos30°=8×√32=4√3,在Rt△CFB中,BF=CFtan∠ABC=CFtan30∘=√33=√3CF,∵PB=PF+BF,∴PB=CF+BF,即:4√3=CF+√3CF,解得:CF=6−2√3;(3)①∵AB为⊙O的直径,∴∠ACB=∠ADB=90°,∵CA=CB,∴∠ADC=∠BDC,同(1)得:四边形DEPF是正方形,∴PE=PF,∠APE+∠BPF=90°,∠PEA=∠PFB=90°,∴将△APE绕点P逆时针旋转90°,得到△A′PF,PA′=PA,如图3所示:则A′、F、B三点共线,∠APE=∠A′PF,∴∠A′PF+∠BPF=90°,即∠A′PB=90°,∴S△PAE+S△PBF=S△PA′B=12PA′⋅PB=12x(70−x),在Rt△ACB中,AC=BC=√22AB=√22×70=35√2,∴S△ACB=12AC2=12×(35√2)2=1225,∴y=S△PA′B+S△ACB=12x(70−x)+1225=−12x2+35x+1225;②当AP=30时,A′P=30,PB=AB−AP=70−30=40,在Rt△A′PB中,由勾股定理得:A′B=2+PB2=√302+402=50,∵S△A′PB=12A′B⋅PF=12PB⋅A′P,∴12×50×PF=12×40×30,解得:PF=24,∴S四边形PEDF=PF2=242=576(m2),∴当AP=30m时.室内活动区(四边形PEDF)的面积为576m2.。
2020年陕西省中考数学试题(含答案解析)

2020年陕西省中考数学试卷(共25题,满分120)一、选择题(共10小题,每小题3分,计30分.每小题只有一个选项是符合题意的) 1.・18的相反数是( ) A. 18B. - 18C.1 1 Q1D.——1 C 2.若ZA = 23° , 则Z4余角的大小是( )A. 57°B. 67°C. 77°D. 157°3・2019年,我国国内生产总值约为990870亿元,将数字990870用科学记数法表示 为()A. 9.9087XKFB. 9.9087X 104C. 99.087X 104D. 99.087X1034.如图,是4市某一天的气温随时间变化的情况,则这天的日温差(最高气温与最 6. 如图,在3X3的网格中,每个小正方形的边长均为1, 若是△ABC 的高,则的长为()C. 12°C D ・ 16°C8 C • -------点A, B, C 都在格点上,低气温的差)是(D.AA. -V13B. -V13 c. -V13 D. -V1312 12 1Q 127.在平面直角坐标系中,O为坐标原点.若直线y=x+3分别与x轴、直线y=・2r交于点A、B,则ZLAOB的面积为()A. 2B. 3C. 4D. 68.如图,在「ABCD中,AB=5, BC=S. E是边BC的中点,F是Q ABCD内一点,且ZBFC=90°•连接AF并延长,交CD于点G.若EF//AB,则DG的长为()9•如图,AABC内接于OO, ZA = 50° • E是边BC的中点,连接OE并延长,交OO于点D,连接BD,则ZD的大小为()A. 55°B. 65°C. 60°D・ 75°10.在平面直角坐标系中,将抛物线『=齐・(〃厂l)x+加(加>1)沿),轴向下平移3个单位.则平移后得到的抛物线的顶点一定在()A.第一象限B.第二象限C.第三象限D・第四象限二、填空题(共4小题,每小题3分,计12分)11.________________________________ 计算:(2+V^)(2—— .12.如图,在正五边形ABCDE中,DW是边CD的延长线,连接BD,则ZBDM的度数是_______.13.在平面直角坐标系中,点A (・2, 1), B(3, 2), C ( - 6, m)分别在三个不同的象限.若反比例函数y=-(^0)的图象经过其中两点,则加的值为_____________ .14.如图,在菱形ABCD中,AB = 6, ZB = 60°,点E在边AD上,且AE=2.若直线/经过点E.将该菱形的面积平分,并与菱形的另一边交于点F,则线段EF三、解答题(共11小题,计78分.解答应写出过程)(3 兀>6,15・(5分)解不等式组:\Y—9 216・(5分)解分式方程:—=1--V* v—017. (5分)如图,已知ZVIBC, AC>AB, ZC=45° .请用尺规作图法,在AC边上求作一点P使ZPBC=45°•(保留作图痕迹.不写作法)A18. (5分)如图,在四边形ABCD中,AD//BC, ZB=ZC. E是边BC上一点,且19.(7分)王大伯承包了一个鱼塘,投放了2000条某种鱼苗,经过一段时间的精心喂养,存活率大致达到了90%.他近期想出售鱼塘里的这种鱼.为了估计鱼塘里这种鱼的总质量,王大伯随机捕捞了20条鱼,分别称得其质量后放回鱼塘.现将这20条鱼的质量作为样本,统计结果如图所示:(1)______________________________ 这20条鱼质量的中位数是,众数是.(2)求这20条鱼质量的平均数;(3)经了解,近期市场上这种鱼的售价为每千克18元,请利用这个样本的平均数.佔讣王大伯近期售完鱼塘里的这种鱼可收入多少元?所捕捞鱼的质量统计图20.(7分)如图所示,小明家与小华家住在同一栋楼的同一单元,他俩想测算所住楼对面商业大厦的I S J MN.他俩在小明家的窗台B处,测得商业大厦顶部W的仰角Z1的度数,山于楼下植物的遮挡,不能在B处测得商业大厦底部M的俯角的度数.于是,他俩上楼来到小华家,在窗台C处测得大厦底部M的俯角Z2的度数,竟然发现Z1与Z2恰好相等.已知A, B, C三点共线,CA丄AM, NM丄AM, AB=3\m, BC=18〃7,试求商业大厦的高MN.21.(7分)某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗早期在农科所的温室中生长,长到大约20c枷时,移至该村的大棚内,沿插杆继续向上生长.研究表明,60天内,这种瓜苗生长的高度),(c/n)与生长时间x (天)之间的关系大致如图所示.(1)求y与x之间的函数关系式;(2)当这种瓜苗长到大约80c加时,开始开花结果,试求这种瓜苗移至大棚后.继续生长大约多少天,开始开花结果?22.(7分)小亮和小丽进行摸球试验.他们在一个不透明的空布袋内,放入两个红球, 一个口球和一个黃球,共四个小球.这些小球除颜色外其它都相同.试验规则:先将布袋内的小球摇匀,再从中随机摸出一个小球,记下颜色后放回,称为摸球一次.(1)小亮随机摸球10次,其中6次摸出的是红球,求这10次中摸出红球的频率;(2)若小丽随机摸球两次,请利用画树状图或列表的方法,求这两次摸出的球中一个是白球、一个是黃球的概率.23.(8分)如图,△4BC是OO的内接三角形,ZBAC=75。
2020年陕西省中考数学试卷及答案

2020年陕西省中考数学试卷一、选择题(共10小题,每小题3分,计30分.每小题只有一个选项是符合题意的)1.(3分)﹣18的相反数是( )A .18B .﹣18C .118D .−1182.(3分)若∠A =23°,则∠A 余角的大小是( )A .57°B .67°C .77°D .157°3.(3分)2019年,我国国内生产总值约为990870亿元,将数字990870用科学记数法表示为( )A .9.9087×105B .9.9087×104C .99.087×104D .99.087×1034.(3分)如图,是A 市某一天的气温随时间变化的情况,则这天的日温差(最高气温与最低气温的差)是( )A .4℃B .8℃C .12℃D .16℃ 5.(3分)计算:(−23x 2y )3=( )A .﹣2x 6y 3B .827x 6y 3C .−827x 6y 3D .−827x 5y 4 6.(3分)如图,在3×3的网格中,每个小正方形的边长均为1,点A ,B ,C 都在格点上,若BD 是△ABC 的高,则BD 的长为( )A .1013√13B .913√13C .813√13D .713√137.(3分)在平面直角坐标系中,O 为坐标原点.若直线y =x +3分别与x 轴、直线y =﹣2x交于点A 、B ,则△AOB 的面积为( )A .2B .3C .4D .68.(3分)如图,在▱ABCD 中,AB =5,BC =8.E 是边BC 的中点,F 是▱ABCD 内一点,且∠BFC =90°.连接AF 并延长,交CD 于点G .若EF ∥AB ,则DG 的长为( )A .52B .32C .3D .29.(3分)如图,△ABC 内接于⊙O ,∠A =50°.E 是边BC 的中点,连接OE 并延长,交⊙O 于点D ,连接BD ,则∠D 的大小为( )A .55°B .65°C .60°D .75°10.(3分)在平面直角坐标系中,将抛物线y =x 2﹣(m ﹣1)x +m (m >1)沿y 轴向下平移3个单位.则平移后得到的抛物线的顶点一定在( )A .第一象限B .第二象限C .第三象限D .第四象限二、填空题(共4小题,每小题3分,计12分)11.(3分)计算:(2+√3)(2−√3)= .12.(3分)如图,在正五边形ABCDE 中,DM 是边CD 的延长线,连接BD ,则∠BDM 的度数是 .13.(3分)在平面直角坐标系中,点A (﹣2,1),B (3,2),C (﹣6,m )分别在三个不同的象限.若反比例函数y =k x (k ≠0)的图象经过其中两点,则m 的值为 .14.(3分)如图,在菱形ABCD 中,AB =6,∠B =60°,点E 在边AD 上,且AE =2.若直线l 经过点E ,将该菱形的面积平分,并与菱形的另一边交于点F ,则线段EF 的长为 .三、解答题(共11小题,计78分.解答应写出过程)15.(5分)解不等式组:{3x >6,2(5−x)>4.16.(5分)解分式方程:x−2x −3x−2=1.17.(5分)如图,已知△ABC ,AC >AB ,∠C =45°.请用尺规作图法,在AC 边上求作一点P ,使∠PBC =45°.(保留作图痕迹.不写作法)18.(5分)如图,在四边形ABCD 中,AD ∥BC ,∠B =∠C .E 是边BC 上一点,且DE =DC .求证:AD =BE .19.(7分)王大伯承包了一个鱼塘,投放了2000条某种鱼苗,经过一段时间的精心喂养,存活率大致达到了90%.他近期想出售鱼塘里的这种鱼.为了估计鱼塘里这种鱼的总质量,王大伯随机捕捞了20条鱼,分别称得其质量后放回鱼塘.现将这20条鱼的质量作为样本,统计结果如图所示:(1)这20条鱼质量的中位数是 ,众数是 .(2)求这20条鱼质量的平均数;(3)经了解,近期市场上这种鱼的售价为每千克18元,请利用这个样本的平均数.估计王大伯近期售完鱼塘里的这种鱼可收入多少元?20.(7分)如图所示,小明家与小华家住在同一栋楼的同一单元,他俩想测算所住楼对面商业大厦的高MN.他俩在小明家的窗台B处,测得商业大厦顶部N的仰角∠1的度数,由于楼下植物的遮挡,不能在B处测得商业大厦底部M的俯角的度数.于是,他俩上楼来到小华家,在窗台C处测得大厦底部M的俯角∠2的度数,竟然发现∠1与∠2恰好相等.已知A,B,C三点共线,CA⊥AM,NM⊥AM,AB=31m,BC=18m,试求商业大厦的高MN.21.(7分)某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗早期在农科所的温室中生长,长到大约20cm时,移至该村的大棚内,沿插杆继续向上生长.研究表明,60天内,这种瓜苗生长的高度y(cm)与生长时间x(天)之间的关系大致如图所示.(1)求y与x之间的函数关系式;(2)当这种瓜苗长到大约80cm时,开始开花结果,试求这种瓜苗移至大棚后.继续生长大约多少天,开始开花结果?22.(7分)小亮和小丽进行摸球试验.他们在一个不透明的空布袋内,放入两个红球,一个白球和一个黄球,共四个小球.这些小球除颜色外其它都相同.试验规则:先将布袋内的小球摇匀,再从中随机摸出一个小球,记下颜色后放回,称为摸球一次.(1)小亮随机摸球10次,其中6次摸出的是红球,求这10次中摸出红球的频率;(2)若小丽随机摸球两次,请利用画树状图或列表的方法,求这两次摸出的球中一个是白球、一个是黄球的概率.23.(8分)如图,△ABC是⊙O的内接三角形,∠BAC=75°,∠ABC=45°.连接AO并延长,交⊙O于点D,连接BD.过点C作⊙O的切线,与BA的延长线相交于点E.(1)求证:AD∥EC;(2)若AB=12,求线段EC的长.24.(10分)如图,抛物线y=x2+bx+c经过点(3,12)和(﹣2,﹣3),与两坐标轴的交点分别为A,B,C,它的对称轴为直线l.(1)求该抛物线的表达式;(2)P是该抛物线上的点,过点P作l的垂线,垂足为D,E是l上的点.要使以P、D、E为顶点的三角形与△AOC全等,求满足条件的点P,点E的坐标.25.(12分)问题提出(1)如图1,在Rt△ABC中,∠ACB=90°,AC>BC,∠ACB的平分线交AB于点D.过点D分别作DE⊥AC,DF⊥BC.垂足分别为E,F,则图1中与线段CE相等的线段是.问题探究̂上一点,且PB̂=2PÂ,连接AP,BP.∠(2)如图2,AB是半圆O的直径,AB=8.P是ABAPB的平分线交AB于点C,过点C分别作CE⊥AP,CF⊥BP,垂足分别为E,F,求线段CF的长.问题解决(3)如图3,是某公园内“少儿活动中心”的设计示意图.已知⊙O的直径AB=70m,点C在⊙O上,且CA=CB.P为AB上一点,连接CP并延长,交⊙O于点D.连接AD,BD.过点P分别作PE⊥AD,PF⊥BD,重足分别为E,F.按设计要求,四边形PEDF内部为室内活动区,阴影部分是户外活动区,圆内其余部分为绿化区.设AP的长为x(m),阴影部分的面积为y(m2).①求y与x之间的函数关系式;②按照“少儿活动中心”的设计要求,发现当AP的长度为30m时,整体布局比较合理.试求当AP=30m时.室内活动区(四边形PEDF)的面积.2020年陕西省中考数学试卷订单一、选择题(共10小题,每小题3分,计30分.每小题只有一个选项是符合题意的)1.(3分)﹣18的相反数是()A.18B.﹣18C.118D.−118【解答】解:﹣18的相反数是:18.故选:A.2.(3分)若∠A=23°,则∠A余角的大小是()A.57°B.67°C.77°D.157°【解答】解:∵∠A=23°,∴∠A的余角是90°﹣23°=67°.故选:B.3.(3分)2019年,我国国内生产总值约为990870亿元,将数字990870用科学记数法表示为()A.9.9087×105B.9.9087×104C.99.087×104D.99.087×103【解答】解:990870=9.9087×105,故选:A.4.(3分)如图,是A市某一天的气温随时间变化的情况,则这天的日温差(最高气温与最低气温的差)是()A.4℃B.8℃C.12℃D.16℃【解答】解:从折线统计图中可以看出,这一天中最高气温8℃,最低气温是﹣4℃,这一天中最高气温与最低气温的差为12℃,故选:C.5.(3分)计算:(−23x2y)3=()A .﹣2x 6y 3B .827x 6y 3C .−827x 6y 3D .−827x 5y 4 【解答】解:(−23x 2y )3=(−23)3⋅(x 2)3⋅y 3=−827x 6y 3. 故选:C . 6.(3分)如图,在3×3的网格中,每个小正方形的边长均为1,点A ,B ,C 都在格点上,若BD 是△ABC 的高,则BD 的长为( )A .1013√13 B .913√13 C .813√13 D .713√13 【解答】解:由勾股定理得:AC =√22+32=√13, ∵S △ABC =3×3−12×1×2−12×1×3−12×2×3=3.5,∴12AC ⋅BD =72, ∴√13⋅BD =7,∴BD =7√1313, 故选:D .7.(3分)在平面直角坐标系中,O 为坐标原点.若直线y =x +3分别与x 轴、直线y =﹣2x交于点A 、B ,则△AOB 的面积为( )A .2B .3C .4D .6【解答】解:在y =x +3中,令y =0,得x =﹣3,解{y =x +3y =−2x得,{x =−1y =2, ∴A (﹣3,0),B (﹣1,2),∴△AOB 的面积=12×3×2=3,故选:B .8.(3分)如图,在▱ABCD 中,AB =5,BC =8.E 是边BC 的中点,F 是▱ABCD 内一点,且∠BFC =90°.连接AF 并延长,交CD 于点G .若EF ∥AB ,则DG 的长为( )A .52B .32C .3D .2【解答】解:∵E 是边BC 的中点,且∠BFC =90°,∴Rt △BCF 中,EF =12BC =4,∵EF ∥AB ,AB ∥CG ,E 是边BC 的中点,∴F 是AG 的中点,∴EF 是梯形ABCG 的中位线,∴CG =2EF ﹣AB =3,又∵CD =AB =5,∴DG =5﹣3=2,故选:D .9.(3分)如图,△ABC 内接于⊙O ,∠A =50°.E 是边BC 的中点,连接OE 并延长,交⊙O 于点D ,连接BD ,则∠D 的大小为( )A .55°B .65°C .60°D .75°【解答】解:连接CD ,∵∠A =50°,∴∠CDB =180°﹣∠A =130°,∵E 是边BC 的中点,∴OD ⊥BC ,∴BD =CD ,∴∠ODB =∠ODC =12∠BDC =65°,故选:B .10.(3分)在平面直角坐标系中,将抛物线y =x 2﹣(m ﹣1)x +m (m >1)沿y 轴向下平移3个单位.则平移后得到的抛物线的顶点一定在( )A .第一象限B .第二象限C .第三象限D .第四象限 【解答】解:∵y =x 2﹣(m ﹣1)x +m =(x −m−12)2+m −(m−1)24, ∴该抛物线顶点坐标是(m−12,m −(m−1)24), ∴将其沿y 轴向下平移3个单位后得到的抛物线的顶点坐标是(m−12,m −(m−1)24−3), ∵m >1,∴m ﹣1>0,∴m−12>0,∵m −(m−1)24−3=4m−(m 2−2m+1)−124=−(m−3)2−44=−(m−3)24−1<0, ∴点(m−12,m −(m−1)24−3)在第四象限; 故选:D .二、填空题(共4小题,每小题3分,计12分)11.(3分)计算:(2+√3)(2−√3)= 1 .【解答】解:原式=22﹣(√3)2=4﹣3=1.12.(3分)如图,在正五边形ABCDE 中,DM 是边CD 的延长线,连接BD ,则∠BDM 的度数是 144° .【解答】解:因为五边形ABCDE 是正五边形,所以∠C=(5−2)⋅180°5=108°,BC=DC,所以∠BDC=180°−108°2=36°,所以∠BDM=180°﹣36°=144°,故答案为:144°.13.(3分)在平面直角坐标系中,点A(﹣2,1),B(3,2),C(﹣6,m)分别在三个不同的象限.若反比例函数y=kx(k≠0)的图象经过其中两点,则m的值为﹣1.【解答】解:∵点A(﹣2,1),B(3,2),C(﹣6,m)分别在三个不同的象限,点A (﹣2,1)在第二象限,∴点C(﹣6,m)一定在第三象限,∵B(3,2)在第一象限,反比例函数y=kx(k≠0)的图象经过其中两点,∴反比例函数y=kx(k≠0)的图象经过B(3,2),C(﹣6,m),∴3×2=﹣6m,∴m=﹣1,故答案为:﹣1.14.(3分)如图,在菱形ABCD中,AB=6,∠B=60°,点E在边AD上,且AE=2.若直线l经过点E,将该菱形的面积平分,并与菱形的另一边交于点F,则线段EF的长为2√7.【解答】解:如图,过点A和点E作AG⊥BC,EH⊥BC于点G和H,得矩形AGHE,∴GH=AE=2,∵在菱形ABCD中,AB=6,∠B=60°,∴BG =3,AG =3√3=EH ,∴HC =BC ﹣BG ﹣GH =6﹣3﹣2=1,∵EF 平分菱形面积,∴FC =AE =2,∴FH =FC ﹣HC =2﹣1=1,在Rt △EFH 中,根据勾股定理,得EF =√EH 2+FH 2=√27+1=2√7.故答案为:2√7.三、解答题(共11小题,计78分.解答应写出过程)15.(5分)解不等式组:{3x >6,2(5−x)>4.【解答】解:{3x >6①2(5−x)>4②, 由①得:x >2,由②得:x <3,则不等式组的解集为2<x <3.16.(5分)解分式方程:x−2x −3x−2=1. 【解答】解:方程x−2x −3x−2=1,去分母得:x 2﹣4x +4﹣3x =x 2﹣2x ,解得:x =45,经检验x =45是分式方程的解.17.(5分)如图,已知△ABC ,AC >AB ,∠C =45°.请用尺规作图法,在AC 边上求作一点P ,使∠PBC =45°.(保留作图痕迹.不写作法)【解答】解:如图,点P即为所求.18.(5分)如图,在四边形ABCD中,AD∥BC,∠B=∠C.E是边BC上一点,且DE=DC.求证:AD=BE.【解答】证明:∵DE=DC,∴∠DEC=∠C.∵∠B=∠C,∴∠B=∠DEC,∴AB∥DE,∵AD∥BC,∴四边形ABED是平行四边形.∴AD=BE.19.(7分)王大伯承包了一个鱼塘,投放了2000条某种鱼苗,经过一段时间的精心喂养,存活率大致达到了90%.他近期想出售鱼塘里的这种鱼.为了估计鱼塘里这种鱼的总质量,王大伯随机捕捞了20条鱼,分别称得其质量后放回鱼塘.现将这20条鱼的质量作为样本,统计结果如图所示:(1)这20条鱼质量的中位数是 1.45kg,众数是 1.5kg.(2)求这20条鱼质量的平均数;(3)经了解,近期市场上这种鱼的售价为每千克18元,请利用这个样本的平均数.估计王大伯近期售完鱼塘里的这种鱼可收入多少元?【解答】解:(1)∵这20条鱼质量的中位数是第10、11个数据的平均数,且第10、11个数据分别为1.4、1.5,∴这20条鱼质量的中位数是1.4+1.52=1.45(kg),众数是1.5kg,故答案为:1.45kg,1.5kg.(2)x=1.2×1+1.3×4+1.4×5+1.5×6+1.6×2+1.7×220=1.45(kg),∴这20条鱼质量的平均数为1.45kg;(3)18×1.45×2000×90%=46980(元),答:估计王大伯近期售完鱼塘里的这种鱼可收入46980元.20.(7分)如图所示,小明家与小华家住在同一栋楼的同一单元,他俩想测算所住楼对面商业大厦的高MN.他俩在小明家的窗台B处,测得商业大厦顶部N的仰角∠1的度数,由于楼下植物的遮挡,不能在B处测得商业大厦底部M的俯角的度数.于是,他俩上楼来到小华家,在窗台C处测得大厦底部M的俯角∠2的度数,竟然发现∠1与∠2恰好相等.已知A,B,C三点共线,CA⊥AM,NM⊥AM,AB=31m,BC=18m,试求商业大厦的高MN.【解答】解:如图,过点C作CE⊥MN于点E,过点B作BF⊥MN于点F,∴∠CEF=∠BFE=90°,∵CA⊥AM,NM⊥AM,∴四边形AMEC和四边形AMFB均为矩形,∴CE=BF,ME=AC,∠1=∠2,∴△BFN≌△CEM(ASA),∴NF=EM=31+18=49,由矩形性质可知:EF=CB=18,∴MN=NF+EM﹣EF=49+49﹣18=80(m).答:商业大厦的高MN为80m.21.(7分)某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗早期在农科所的温室中生长,长到大约20cm时,移至该村的大棚内,沿插杆继续向上生长.研究表明,60天内,这种瓜苗生长的高度y(cm)与生长时间x(天)之间的关系大致如图所示.(1)求y与x之间的函数关系式;(2)当这种瓜苗长到大约80cm时,开始开花结果,试求这种瓜苗移至大棚后.继续生长大约多少天,开始开花结果?【解答】解:(1)当0≤x≤15时,设y=kx(k≠0),则:20=15k ,解得k =43,∴y =43x ;当15<x ≤60时,设y =k ′x +b (k ≠0),则:{20=15k ′+b 170=60k′+b, 解得{k ′=103b =−30, ∴y =103x −30, ∴y ={43x(0≤x ≤15)103x −30(15<x ≤60);(2)当y =80时,80=103x −30,解得x =33,33﹣15=18(天),∴这种瓜苗移至大棚后.继续生长大约18天,开始开花结果.22.(7分)小亮和小丽进行摸球试验.他们在一个不透明的空布袋内,放入两个红球,一个白球和一个黄球,共四个小球.这些小球除颜色外其它都相同.试验规则:先将布袋内的小球摇匀,再从中随机摸出一个小球,记下颜色后放回,称为摸球一次.(1)小亮随机摸球10次,其中6次摸出的是红球,求这10次中摸出红球的频率;(2)若小丽随机摸球两次,请利用画树状图或列表的方法,求这两次摸出的球中一个是白球、一个是黄球的概率.【解答】解:(1)小亮随机摸球10次,其中6次摸出的是红球,这10次中摸出红球的频率=610=35; (2)画树状图得:∵共有16种等可能的结果,两次摸出的球中一个是白球、一个是黄球的有2种情况,∴两次摸出的球中一个是白球、一个是黄球的概率=216=18.23.(8分)如图,△ABC是⊙O的内接三角形,∠BAC=75°,∠ABC=45°.连接AO并延长,交⊙O于点D,连接BD.过点C作⊙O的切线,与BA的延长线相交于点E.(1)求证:AD∥EC;(2)若AB=12,求线段EC的长.【解答】证明:(1)连接OC,∵CE与⊙O相切于点C,∴∠OCE=90°,∵∠ABC=45°,∴∠AOC=90°,∵∠AOC+∠OCE=180°,∴∴AD∥EC(2)如图,过点A作AF⊥EC交EC于F,∵∠BAC=75°,∠ABC=45°,∴∠ACB=60°,∴∠D=∠ACB=60°,∴sin∠ADB=ABAD=√32,∴AD=3=8√3,∴OA=OC=4√3,∵AF⊥EC,∠OCE=90°,∠AOC=90°,∴四边形OAFC是矩形,又∵OA=OC,∴四边形OAFC是正方形,∴CF=AF=4√3,∵∠BAD=90°﹣∠D=30°,∴∠EAF=180°﹣90°﹣30°=60°,∵tan∠EAF=EFAF=√3,∴EF=√3AF=12,∴CE=CF+EF=12+4√3.24.(10分)如图,抛物线y=x2+bx+c经过点(3,12)和(﹣2,﹣3),与两坐标轴的交点分别为A,B,C,它的对称轴为直线l.(1)求该抛物线的表达式;(2)P是该抛物线上的点,过点P作l的垂线,垂足为D,E是l上的点.要使以P、D、E为顶点的三角形与△AOC全等,求满足条件的点P,点E的坐标.【解答】解:(1)将点(3,12)和(﹣2,﹣3)代入抛物线表达式得{12=9+3b +c −3=4−2b +c ,解得{b =2c =−3, 故抛物线的表达式为:y =x 2+2x ﹣3;(2)抛物线的对称轴为x =﹣1,令y =0,则x =﹣3或1,令x =0,则y =﹣3, 故点A 、B 的坐标分别为(﹣3,0)、(1,0);点C (0,﹣3),故OA =OC =3,∵∠PDE =∠AOC =90°,∴当PD =DE =3时,以P 、D 、E 为顶点的三角形与△AOC 全等,设点P (m ,n ),当点P 在抛物线对称轴右侧时,m ﹣(﹣1)=3,解得:m =2, 故n =22+2×2﹣5=5,故点P (2,5),故点E (﹣1,2)或(﹣1,8);当点P 在抛物线对称轴的左侧时,由抛物线的对称性可得,点P (﹣4,5),此时点E 坐标同上,综上,点P 的坐标为(2,5)或(﹣4,5);点E 的坐标为(﹣1,2)或(﹣1,8).25.(12分)问题提出(1)如图1,在Rt △ABC 中,∠ACB =90°,AC >BC ,∠ACB 的平分线交AB 于点D .过点D 分别作DE ⊥AC ,DF ⊥BC .垂足分别为E ,F ,则图1中与线段CE 相等的线段是 CF 、DE 、DF .问题探究(2)如图2,AB 是半圆O 的直径,AB =8.P 是AB ̂上一点,且PB ̂=2PA ̂,连接AP ,BP .∠APB 的平分线交AB 于点C ,过点C 分别作CE ⊥AP ,CF ⊥BP ,垂足分别为E ,F ,求线段CF的长.问题解决(3)如图3,是某公园内“少儿活动中心”的设计示意图.已知⊙O的直径AB=70m,点C在⊙O上,且CA=CB.P为AB上一点,连接CP并延长,交⊙O于点D.连接AD,BD.过点P分别作PE⊥AD,PF⊥BD,重足分别为E,F.按设计要求,四边形PEDF 内部为室内活动区,阴影部分是户外活动区,圆内其余部分为绿化区.设AP的长为x(m),阴影部分的面积为y(m2).①求y与x之间的函数关系式;②按照“少儿活动中心”的设计要求,发现当AP的长度为30m时,整体布局比较合理.试求当AP=30m时.室内活动区(四边形PEDF)的面积.【解答】解:(1)∵∠ACB=90°,DE⊥AC,DF⊥BC,∴四边形CEDF是矩形,∵CD平分∠ACB,DE⊥AC,DF⊥BC,∴DE=DF,∴四边形CEDF是正方形,∴CE=CF=DE=DF,故答案为:CF、DE、DF;(2)连接OP,如图2所示:∵AB是半圆O的直径,PB̂=2PÂ,∴∠APB=90°,∠AOP=13×180°=60°,∴∠ABP=30°,同(1)得:四边形PECF是正方形,∴PF=CF,在Rt △APB 中,PB =AB •cos ∠ABP =8×cos30°=8×√32=4√3, 在Rt △CFB 中,BF =CF tan∠ABC =CF tan30°=CF 33=√3CF , ∵PB =PF +BF ,∴PB =CF +BF ,即:4√3=CF +√3CF ,解得:CF =6﹣2√3;(3)①∵AB 为⊙O 的直径,∴∠ACB =∠ADB =90°,∵CA =CB ,∴∠ADC =∠BDC ,同(1)得:四边形DEPF 是正方形, ∴PE =PF ,∠APE +∠BPF =90°,∠PEA =∠PFB =90°,∴将△APE 绕点P 逆时针旋转90°,得到△A ′PF ,P A ′=P A ,如图3所示: 则A ′、F 、B 三点共线,∠APE =∠A ′PF ,∴∠A ′PF +∠BPF =90°,即∠A ′PB =90°,∴S △P AE +S △PBF =S △P A ′B =12P A ′•PB =12x (70﹣x ),在Rt △ACB 中,AC =BC =√22AB =√22×70=35√2,∴S △ACB =12AC 2=12×(35√2)2=1225,∴y =S △P A ′B +S △ACB =12x (70﹣x )+1225=−12x 2+35x +1225;②当AP =30时,A ′P =30,PB =AB ﹣AP =70﹣30=40,在Rt △A ′PB 中,由勾股定理得:A ′B =√A′P 2+PB 2=√302+402=50, ∵S △A ′PB =12A ′B •PF =12PB •A ′P ,∴12×50×PF =12×40×30, 解得:PF =24,∴S 四边形PEDF =PF 2=242=576(m 2),∴当AP =30m 时.室内活动区(四边形PEDF )的面积为576m 2.。
(中考数学)陕西省中考数学试题(解析版)

2020年陕西省中考数学试卷一.选择题(共10小题)1.﹣18的相反数是( )A.18B.﹣18C.D.﹣2.若∠A=23°,则∠A余角的大小是( )A.57°B.67°C.77°D.157°3.2019年,我国国内生产总值约为990870亿元,将数字990870用科学记数法表示为( )A.9.9087×105B.9.9087×104C.99.087×104D.99.087×103 4.如图,是A市某一天的气温随时间变化的情况,则这天的日温差(最高气温与最低气温的差)是( )A.4℃B.8℃C.12℃D.16℃5.计算:(﹣x2y)3=( )A.﹣2x6y3B.x6y3C.﹣x6y3D.﹣x5y46.如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD 是△ABC的高,则BD的长为( )A.B.C.D.7.在平面直角坐标系中,O为坐标原点.若直线y=x+3分别与x轴、直线y=﹣2x交于点A、B,则△AOB的面积为( )A.2B.3C.4D.68.如图,在▱ABCD中,AB=5,BC=8.E是边BC的中点,F是▱ABCD内一点,且∠BFC =90°.连接AF并延长,交CD于点G.若EF∥AB,则DG的长为( )A.B.C.3D.29.如图,△ABC内接于⊙O,∠A=50°.E是边BC的中点,连接OE并延长,交⊙O于点D,连接BD,则∠D的大小为( )A.55°B.65°C.60°D.75°10.在平面直角坐标系中,将抛物线y=x2﹣(m﹣1)x+m(m>1)沿y轴向下平移3个单位.则平移后得到的抛物线的顶点一定在( )A.第一象限B.第二象限C.第三象限D.第四象限二.填空题(共4小题)11.计算:(2+)(2﹣)= .12.如图,在正五边形ABCDE中,DM是边CD的延长线,连接BD,则∠BDM的度数是 .13.在平面直角坐标系中,点A(﹣2,1),B(3,2),C(﹣6,m)分别在三个不同的象限.若反比例函数y=(k≠0)的图象经过其中两点,则m的值为 .14.如图,在菱形ABCD中,AB=6,∠B=60°,点E在边AD上,且AE=2.若直线l 经过点E,将该菱形的面积平分,并与菱形的另一边交于点F,则线段EF的长为 .三.解答题(共11小题)15.解不等式组:16.解分式方程:﹣=1.17.如图,已知△ABC,AC>AB,∠C=45°.请用尺规作图法,在AC边上求作一点P,使∠PBC=45°.(保留作图痕迹.不写作法)18.如图,在四边形ABCD中,AD∥BC,∠B=∠C.E是边BC上一点,且DE=DC.求证:AD=BE.19.王大伯承包了一个鱼塘,投放了2000条某种鱼苗,经过一段时间的精心喂养,存活率大致达到了90%.他近期想出售鱼塘里的这种鱼.为了估计鱼塘里这种鱼的总质量,王大伯随机捕捞了20条鱼,分别称得其质量后放回鱼塘.现将这20条鱼的质量作为样本,统计结果如图所示:(1)这20条鱼质量的中位数是 ,众数是 .(2)求这20条鱼质量的平均数;(3)经了解,近期市场上这种鱼的售价为每千克18元,请利用这个样本的平均数.估计王大伯近期售完鱼塘里的这种鱼可收入多少元?20.如图所示,小明家与小华家住在同一栋楼的同一单元,他俩想测算所住楼对面商业大厦的高MN.他俩在小明家的窗台B处,测得商业大厦顶部N的仰角∠1的度数,由于楼下植物的遮挡,不能在B处测得商业大厦底部M的俯角的度数.于是,他俩上楼来到小华家,在窗台C处测得大厦底部M的俯角∠2的度数,竟然发现∠1与∠2恰好相等.已知A,B,C三点共线,CA⊥AM,NM⊥AM,AB=31m,BC=18m,试求商业大厦的高MN.21.某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗早期在农科所的温室中生长,长到大约20cm时,移至该村的大棚内,沿插杆继续向上生长.研究表明,60天内,这种瓜苗生长的高度y(cm)与生长时间x(天)之间的关系大致如图所示.(1)求y与x之间的函数关系式;(2)当这种瓜苗长到大约80cm时,开始开花结果,试求这种瓜苗移至大棚后.继续生长大约多少天,开始开花结果?22.小亮和小丽进行摸球试验.他们在一个不透明的空布袋内,放入两个红球,一个白球和一个黄球,共四个小球.这些小球除颜色外其它都相同.试验规则:先将布袋内的小球摇匀,再从中随机摸出一个小球,记下颜色后放回,称为摸球一次.(1)小亮随机摸球10次,其中6次摸出的是红球,求这10次中摸出红球的频率;(2)若小丽随机摸球两次,请利用画树状图或列表的方法,求这两次摸出的球中一个是白球、一个是黄球的概率.23.如图,△ABC是⊙O的内接三角形,∠BAC=75°,∠ABC=45°.连接AO并延长,交⊙O于点D,连接BD.过点C作⊙O的切线,与BA的延长线相交于点E.(1)求证:AD∥EC;(2)若AB=12,求线段EC的长.24.如图,抛物线y=x2+bx+c经过点(3,12)和(﹣2,﹣3),与两坐标轴的交点分别为A,B,C,它的对称轴为直线l.(1)求该抛物线的表达式;(2)P是该抛物线上的点,过点P作l的垂线,垂足为D,E是l上的点.要使以P、D、E为顶点的三角形与△AOC全等,求满足条件的点P,点E的坐标.25.问题提出(1)如图1,在Rt△ABC中,∠ACB=90°,AC>BC,∠ACB的平分线交AB于点D.过点D分别作DE⊥AC,DF⊥BC.垂足分别为E,F,则图1中与线段CE相等的线段是 .问题探究(2)如图2,AB是半圆O的直径,AB=8.P是上一点,且=2,连接AP,BP.∠APB的平分线交AB于点C,过点C分别作CE⊥AP,CF⊥BP,垂足分别为E,F,求线段CF的长.问题解决(3)如图3,是某公园内“少儿活动中心”的设计示意图.已知⊙O的直径AB=70m,点C在⊙O上,且CA=CB.P为AB上一点,连接CP并延长,交⊙O于点D.连接AD,BD.过点P分别作PE⊥AD,PF⊥BD,重足分别为E,F.按设计要求,四边形PEDF 内部为室内活动区,阴影部分是户外活动区,圆内其余部分为绿化区.设AP的长为x (m),阴影部分的面积为y(m2).①求y与x之间的函数关系式;②按照“少儿活动中心”的设计要求,发现当AP的长度为30m时,整体布局比较合理.试求当AP=30m时.室内活动区(四边形PEDF)的面积.2020年陕西省中考数学试卷参考答案与试题解析一.选择题(共10小题)1.﹣18的相反数是( )A.18B.﹣18C.D.﹣【分析】直接利用相反数的定义得出答案.【解答】解:﹣18的相反数是:18.故选:A.2.若∠A=23°,则∠A余角的大小是( )A.57°B.67°C.77°D.157°【分析】根据∠A的余角是90°﹣∠A,代入求出即可.【解答】解:∵∠A=23°,∴∠A的余角是90°﹣23°=67°.故选:B.3.2019年,我国国内生产总值约为990870亿元,将数字990870用科学记数法表示为( )A.9.9087×105B.9.9087×104C.99.087×104D.99.087×103【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.【解答】解:990870=9.9087×105,故选:A.4.如图,是A市某一天的气温随时间变化的情况,则这天的日温差(最高气温与最低气温的差)是( )A.4℃B.8℃C.12℃D.16℃【分析】根据A市某一天内的气温变化图,分析变化趋势和具体数值,即可求出答案.【解答】解:从折线统计图中可以看出,这一天中最高气温8℃,最低气温是﹣4℃,这一天中最高气温与最低气温的差为12℃,故选:C.5.计算:(﹣x2y)3=( )A.﹣2x6y3B.x6y3C.﹣x6y3D.﹣x5y4【分析】根据积的乘方运算法则计算即可,积的乘方,等于每个因式乘方的积.【解答】解:(﹣x2y)3==.故选:C.6.如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD 是△ABC的高,则BD的长为( )A.B.C.D.【分析】根据勾股定理计算AC的长,利用面积差可得三角形ABC的面积,由三角形的面积公式即可得到结论.【解答】解:由勾股定理得:AC==,∵S△ABC=3×3﹣=3.5,∴,∴,∴BD=,故选:D.7.在平面直角坐标系中,O为坐标原点.若直线y=x+3分别与x轴、直线y=﹣2x交于点A、B,则△AOB的面积为( )A.2B.3C.4D.6【分析】根据方程或方程组得到A(﹣3,0),B(﹣1,2),根据三角形的面积公式即可得到结论.【解答】解:在y=x+3中,令y=0,得x=﹣3,解得,,∴A(﹣3,0),B(﹣1,2),∴△AOB的面积=3×2=3,故选:B.8.如图,在▱ABCD中,AB=5,BC=8.E是边BC的中点,F是▱ABCD内一点,且∠BFC =90°.连接AF并延长,交CD于点G.若EF∥AB,则DG的长为( )A.B.C.3D.2【分析】依据直角三角形斜边上中线的性质,即可得到EF的长,再根据梯形中位线定理,即可得到CG的长,进而得出DG的长.【解答】解:∵E是边BC的中点,且∠BFC=90°,∴Rt△BCF中,EF=BC=4,∵EF∥AB,AB∥CG,E是边BC的中点,∴F是AG的中点,∴EF是梯形ABCG的中位线,∴CG=2EF﹣AB=3,又∵CD=AB=5,∴DG=5﹣3=2,故选:D.9.如图,△ABC内接于⊙O,∠A=50°.E是边BC的中点,连接OE并延长,交⊙O于点D,连接BD,则∠D的大小为( )A.55°B.65°C.60°D.75°【分析】连接CD,根据圆内接四边形的性质得到∠CDB=180°﹣∠A=130°,根据垂径定理得到OD⊥BC,求得BD=CD,根据等腰三角形的性质即可得到结论.【解答】解:连接CD,∵∠A=50°,∴∠CDB=180°﹣∠A=130°,∵E是边BC的中点,∴OD⊥BC,∴BD=CD,∴∠ODB=∠ODC=BDC=65°,故选:B.10.在平面直角坐标系中,将抛物线y=x2﹣(m﹣1)x+m(m>1)沿y轴向下平移3个单位.则平移后得到的抛物线的顶点一定在( )A.第一象限B.第二象限C.第三象限D.第四象限【分析】根据平移规律得到平移后抛物线的顶点坐标,然后结合m的取值范围判断新抛物线的顶点所在的象限即可.【解答】解:∵y=x2﹣(m﹣1)x+m=(x﹣)2+m﹣,∴该抛物线顶点坐标是(,m﹣),∴将其沿y轴向下平移3个单位后得到的抛物线的顶点坐标是(,m﹣﹣3),∵m>1,∴m﹣1>0,∴>0,∵m﹣﹣3===﹣﹣1<0,∴点(,m﹣﹣3)在第四象限;故选:D.二.填空题(共4小题)11.计算:(2+)(2﹣)= 1 .【分析】先利用平方差公式展开得到原式=22﹣()2,再利用二次根式的性质化简,然后进行减法运算.【解答】解:原式=22﹣()2=4﹣3=1.12.如图,在正五边形ABCDE中,DM是边CD的延长线,连接BD,则∠BDM的度数是 144° .【分析】根据正五边形的性质和内角和为540°,求得每个内角的度数为108°,再结合等腰三角形和邻补角的定义即可解答.【解答】解:因为五边形ABCDE是正五边形,所以∠C==108°,BC=DC,所以∠BDC==36°,所以∠BDM=180°﹣36°=144°,故答案为:144°.13.在平面直角坐标系中,点A(﹣2,1),B(3,2),C(﹣6,m)分别在三个不同的象限.若反比例函数y=(k≠0)的图象经过其中两点,则m的值为 ﹣1 .【分析】根据已知条件得到点A(﹣2,1)在第三象限,求得点C(﹣6,m)一定在第三象限,由于反比例函数y=(k≠0)的图象经过其中两点,于是得到反比例函数y=(k≠0)的图象经过B(3,2),C(﹣6,m),于是得到结论.【解答】解:∵点A(﹣2,1),B(3,2),C(﹣6,m)分别在三个不同的象限,点A (﹣2,1)在第二象限,∴点C(﹣6,m)一定在第三象限,∵B(3,2)在第一象限,反比例函数y=(k≠0)的图象经过其中两点,∴反比例函数y=(k≠0)的图象经过B(3,2),C(﹣6,m),∴3×2=﹣6m,∴m=﹣1,故答案为:﹣1.14.如图,在菱形ABCD中,AB=6,∠B=60°,点E在边AD上,且AE=2.若直线l 经过点E,将该菱形的面积平分,并与菱形的另一边交于点F,则线段EF的长为 2 .【分析】过点A和点E作AG⊥BC,EH⊥BC于点G和H,可得矩形AGHE,再根据菱形ABCD中,AB=6,∠B=60°,可得BG=3,AG=3=EH,由题意可得,FH=FC ﹣HC=2﹣1=1,进而根据勾股定理可得EF的长.【解答】解:如图,过点A和点E作AG⊥BC,EH⊥BC于点G和H,得矩形AGHE,∴GH=AE=2,∵在菱形ABCD中,AB=6,∠B=60°,∴BG=3,AG=3=EH,∴HC=BC﹣BG﹣GH=6﹣3﹣2=1,∵EF平分菱形面积,∴FC=AE=2,∴FH=FC﹣HC=2﹣1=1,在Rt△EFH中,根据勾股定理,得EF===2.故答案为:2.三.解答题(共11小题)15.解不等式组:【分析】分别求出不等式组中两不等式的解集,找出两解集的方法部分即可.【解答】解:,由①得:x>2,由②得:x<3,则不等式组的解集为2<x<3.16.解分式方程:﹣=1.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:方程﹣=1,去分母得:x2﹣4x+4﹣3x=x2﹣2x,解得:x=,经检验x=是分式方程的解.17.如图,已知△ABC,AC>AB,∠C=45°.请用尺规作图法,在AC边上求作一点P,使∠PBC=45°.(保留作图痕迹.不写作法)【分析】根据尺规作图法,作一个角等于已知角,在AC边上求作一点P,使∠PBC=45°即可.【解答】解:如图,点P即为所求.18.如图,在四边形ABCD中,AD∥BC,∠B=∠C.E是边BC上一点,且DE=DC.求证:AD=BE.【分析】根据等边对等角的性质求出∠DEC=∠C,在由∠B=∠C得∠DEC=∠B,所以AB∥DE,得出四边形ABCD是平行四边形,进而得出结论.【解答】证明:∵DE=DC,∴∠DEC=∠C.∵∠B=∠C,∴∠B=∠DEC,∴AB∥DE,∵AD∥BC,∴四边形ABED是平行四边形.∴AD=BE.19.王大伯承包了一个鱼塘,投放了2000条某种鱼苗,经过一段时间的精心喂养,存活率大致达到了90%.他近期想出售鱼塘里的这种鱼.为了估计鱼塘里这种鱼的总质量,王大伯随机捕捞了20条鱼,分别称得其质量后放回鱼塘.现将这20条鱼的质量作为样本,统计结果如图所示:(1)这20条鱼质量的中位数是 1.45kg ,众数是 1.5kg .(2)求这20条鱼质量的平均数;(3)经了解,近期市场上这种鱼的售价为每千克18元,请利用这个样本的平均数.估计王大伯近期售完鱼塘里的这种鱼可收入多少元?【分析】(1)根据中位数和众数的定义求解可得;(2)利用加权平均数的定义求解可得;(3)用单价乘以(2)中所得平均数,再乘以存活的数量,从而得出答案.【解答】解:(1)∵这20条鱼质量的中位数是第10、11个数据的平均数,且第10、11个数据分别为1.4、1.5,∴这20条鱼质量的中位数是=1.45(kg),众数是1.5kg,故答案为:1.45kg,1.5kg.(2)==1.45(kg),∴这20条鱼质量的平均数为1.45kg;(3)18×1.45×2000×90%=46980(元),答:估计王大伯近期售完鱼塘里的这种鱼可收入46980元.20.如图所示,小明家与小华家住在同一栋楼的同一单元,他俩想测算所住楼对面商业大厦的高MN.他俩在小明家的窗台B处,测得商业大厦顶部N的仰角∠1的度数,由于楼下植物的遮挡,不能在B处测得商业大厦底部M的俯角的度数.于是,他俩上楼来到小华家,在窗台C处测得大厦底部M的俯角∠2的度数,竟然发现∠1与∠2恰好相等.已知A,B,C三点共线,CA⊥AM,NM⊥AM,AB=31m,BC=18m,试求商业大厦的高MN.【分析】过点C作CE⊥MN于点E,过点B作BF⊥MN于点F,可得四边形AMEC和四边形AMFB均为矩形,可以证明△BFN≌△CEM,得NF=EM=49,进而可得商业大厦的高MN.【解答】解:如图,过点C作CE⊥MN于点E,过点B作BF⊥MN于点F,∴∠CEF=∠BFE=90°,∵CA⊥AM,NM⊥AM,∴四边形AMEC和四边形AMFB均为矩形,∴CE=BF,ME=AC,∠1=∠2,∴△BFN≌△CEM(ASA),∴NF=EM=31+18=49,由矩形性质可知:EF=CB=18,∴MN=NF+EM﹣EF=49+49﹣18=80(m).答:商业大厦的高MN为80m.21.某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗早期在农科所的温室中生长,长到大约20cm时,移至该村的大棚内,沿插杆继续向上生长.研究表明,60天内,这种瓜苗生长的高度y(cm)与生长时间x(天)之间的关系大致如图所示.(1)求y与x之间的函数关系式;(2)当这种瓜苗长到大约80cm时,开始开花结果,试求这种瓜苗移至大棚后.继续生长大约多少天,开始开花结果?【分析】(1)分段函数,利用待定系数法解答即可;(2)利用(1)的结论,把y=80代入求出x的值即可解答.【解答】解:(1)当0≤x≤15时,设y=kx(k≠0),则:20=15k,解得k=,∴y=;当15<x≤60时,设y=k′x+b(k≠0),则:,解得,∴y=,∴;(2)当y=80时,80=,解得x=33,33﹣15=18(天),∴这种瓜苗移至大棚后.继续生长大约18天,开始开花结果.22.小亮和小丽进行摸球试验.他们在一个不透明的空布袋内,放入两个红球,一个白球和一个黄球,共四个小球.这些小球除颜色外其它都相同.试验规则:先将布袋内的小球摇匀,再从中随机摸出一个小球,记下颜色后放回,称为摸球一次.(1)小亮随机摸球10次,其中6次摸出的是红球,求这10次中摸出红球的频率;(2)若小丽随机摸球两次,请利用画树状图或列表的方法,求这两次摸出的球中一个是白球、一个是黄球的概率.【分析】(1)由频率定义即可得出答案;(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次摸出的球中一个是白球、一个是黄球的情况,利用概率公式求解即可求得答案.【解答】解:(1)小亮随机摸球10次,其中6次摸出的是红球,这10次中摸出红球的频率==;(2)画树状图得:∵共有16种等可能的结果,两次摸出的球中一个是白球、一个是黄球的有2种情况,∴两次摸出的球中一个是白球、一个是黄球的概率==.23.如图,△ABC是⊙O的内接三角形,∠BAC=75°,∠ABC=45°.连接AO并延长,交⊙O于点D,连接BD.过点C作⊙O的切线,与BA的延长线相交于点E.(1)求证:AD∥EC;(2)若AB=12,求线段EC的长.【分析】(1)连接OC,由切线的性质可得∠OCE=90°,由圆周角定理可得∠AOC=90°,可得结论;(2)过点A作AF⊥EC交EC于F,由锐角三角函数可求AD=8,可证四边形OAFC 是正方形,可得CF=AF=4,由锐角三角函数可求EF=12,即可求解.【解答】证明:(1)连接OC,∵CE与⊙O相切于点C,∴∠OCE=90°,∵∠ABC=45°,∴∠AOC=90°,∵∠AOC+∠OCE=180°,∴∴AD∥EC(2)如图,过点A作AF⊥EC交EC于F,∵∠BAC=75°,∠ABC=45°,∴∠ACB=60°,∴∠D=∠ACB=60°,∴sin∠ADB=,∴AD==8,∴OA=OC=4,∵AF⊥EC,∠OCE=90°,∠AOC=90°,∴四边形OAFC是矩形,又∵OA=OC,∴四边形OAFC是正方形,∴CF=AF=4,∵∠BAD=90°﹣∠D=30°,∴∠EAF=180°﹣90°﹣30°=60°,∵tan∠EAF=,∴EF=AF=12,∴CE=CF+EF=12+4.24.如图,抛物线y=x2+bx+c经过点(3,12)和(﹣2,﹣3),与两坐标轴的交点分别为A,B,C,它的对称轴为直线l.(1)求该抛物线的表达式;(2)P是该抛物线上的点,过点P作l的垂线,垂足为D,E是l上的点.要使以P、D、E为顶点的三角形与△AOC全等,求满足条件的点P,点E的坐标.【分析】(1)将点(3,12)和(﹣2,﹣3)代入抛物线表达式,即可求解;(2)由题意得:PD=DE=3时,以P、D、E为顶点的三角形与△AOC全等,分点P在抛物线对称轴右侧、点P在抛物线对称轴的左侧两种情况,分别求解即可.【解答】解:(1)将点(3,12)和(﹣2,﹣3)代入抛物线表达式得,解得,故抛物线的表达式为:y=x2+2x﹣3;(2)抛物线的对称轴为x=﹣1,令y=0,则x=﹣3或1,令x=0,则y=﹣3,故点A、B的坐标分别为(﹣3,0)、(1,0);点C(0,﹣3),故OA=OC=3,∵∠PDE=∠AOC=90°,∴当PD=DE=3时,以P、D、E为顶点的三角形与△AOC全等,设点P(m,n),当点P在抛物线对称轴右侧时,m﹣(﹣1)=3,解得:m=2,故n=22+2×2﹣5=5,故点P(2,5),故点E(﹣1,2)或(﹣1,8);当点P在抛物线对称轴的左侧时,由抛物线的对称性可得,点P(﹣4,5),此时点E坐标同上,综上,点P的坐标为(2,5)或(﹣4,5);点E的坐标为(﹣1,2)或(﹣1,8).25.问题提出(1)如图1,在Rt△ABC中,∠ACB=90°,AC>BC,∠ACB的平分线交AB于点D.过点D分别作DE⊥AC,DF⊥BC.垂足分别为E,F,则图1中与线段CE相等的线段是 CF、DE、DF .问题探究(2)如图2,AB是半圆O的直径,AB=8.P是上一点,且=2,连接AP,BP.∠APB的平分线交AB于点C,过点C分别作CE⊥AP,CF⊥BP,垂足分别为E,F,求线段CF的长.问题解决(3)如图3,是某公园内“少儿活动中心”的设计示意图.已知⊙O的直径AB=70m,点C在⊙O上,且CA=CB.P为AB上一点,连接CP并延长,交⊙O于点D.连接AD,BD.过点P分别作PE⊥AD,PF⊥BD,重足分别为E,F.按设计要求,四边形PEDF 内部为室内活动区,阴影部分是户外活动区,圆内其余部分为绿化区.设AP的长为x (m),阴影部分的面积为y(m2).①求y与x之间的函数关系式;②按照“少儿活动中心”的设计要求,发现当AP的长度为30m时,整体布局比较合理.试求当AP=30m时.室内活动区(四边形PEDF)的面积.【分析】(1)证明四边形CEDF是正方形,即可得出结果;(2)连接OP,由AB是半圆O的直径,=2,得出∠APB=90°,∠AOP=60°,则∠ABP=30°,同(1)得四边形PECF是正方形,得PF=CF,在Rt△APB中,PB=AB•cos∠ABP=4,在Rt△CFB中,BF==CF,推出PB=CF+BF,即可得出结果;(3)①同(1)得四边形DEPF是正方形,得出PE=PF,∠APE+∠BPF=90°,∠PEA =∠PFB=90°,将△APE绕点P逆时针旋转90°,得到△A′PF,PA′=PA,则A ′、F、B三点共线,∠APE=∠A′PF,证∠A′PB=90°,得出S△PAE+S△PBF=S△PA2=′B=PA′•PB=x(70﹣x),在Rt△ACB中,AC=BC=35,S△ACB=AC1225,由y=S△PA′B+S△ACB,即可得出结果;②当AP=30时,A′P=30,PB=40,在Rt△A′PB中,由勾股定理得A′B==50,由S△A′PB=A′B•PF=PB•A′P,求PF,即可得出结果.【解答】解:(1)∵∠ACB=90°,DE⊥AC,DF⊥BC,∴四边形CEDF是矩形,∵CD平分∠ACB,DE⊥AC,DF⊥BC,∴DE=DF,∴四边形CEDF是正方形,∴CE=CF=DE=DF,故答案为:CF、DE、DF;(2)连接OP,如图2所示:∵AB是半圆O的直径,=2,∴∠APB=90°,∠AOP=×180°=60°,∴∠ABP=30°,同(1)得:四边形PECF是正方形,∴PF=CF,在Rt△APB中,PB=AB•cos∠ABP=8×cos30°=8×=4,在Rt△CFB中,BF====CF,∵PB=PF+BF,∴PB=CF+BF,即:4=CF+CF,解得:CF=6﹣2;(3)①∵AB为⊙O的直径,∴∠ACB=∠ADB=90°,∵CA=CB,∴∠ADC=∠BDC,同(1)得:四边形DEPF是正方形,∴PE=PF,∠APE+∠BPF=90°,∠PEA=∠PFB=90°,∴将△APE绕点P逆时针旋转90°,得到△A′PF,PA′=PA,如图3所示:则A′、F、B三点共线,∠APE=∠A′PF,∴∠A′PF+∠BPF=90°,即∠A′PB=90°,∴S△PAE+S△PBF=S△PA′B=PA′•PB=x(70﹣x),在Rt△ACB中,AC=BC=AB=×70=35,∴S△ACB=AC2=×(35)2=1225,∴y=S△PA′B+S△ACB=x(70﹣x)+1225=﹣x2+35x+1225;②当AP=30时,A′P=30,PB=AB﹣AP=70﹣30=40,在Rt△A′PB中,由勾股定理得:A′B===50,∵S△A′PB=A′B•PF=PB•A′P,∴×50×PF=×40×30,解得:PF=24,∴S四边形PEDF=PF2=242=576(m2),∴当AP=30m时.室内活动区(四边形PEDF)的面积为576m2.。
2020年陕西中考数学试卷(解析版)

2020年陕西中考数学试卷(解析版)一、选择题(本大题共10小题,每小题3分,共30分)1.的相反数是( ).A. B. C. D.2.若,则余角的大小是( ).A. B. C. D.3.年,我国国内生产总值约为亿元,将数字用科学记数法表示( ).A.B.C.D.4.如图,是市某一天的气温随时间变化的情况,则这天的日温差(最高气温与最低气温的差)是( ).A.B.C.D.5.计算:( ).A.D.6.如图,在的网格中,每个小正方形的边长均为,点,,都在格点上,若是的高,则的长为( ).A.B.C.D.7.在平面直角坐标系中,为坐标原点.若直线分别与轴,直线交于点、,则的面积为( ).A.B.C.D.8.如图,在平行四边形中,,.是边的中点,是平行四边形内一点,且.连接并延长,交于点.若,则的长为( ).A.B.9.如图,内接于⊙,.是边的中点,连接并延长,交⊙于点,连接,则的大小为( ).A.B.C.D.10.在平面直角坐标系中,将抛物线沿轴向下平移个单位,则平移后得到的抛物线的顶点一定在( ).A.第一象限B.第二象限C.第三象限D.第四象限二、填空题(本大题共4小题,每小题3分,共12分)11.化简: .12.如图,在正五边形中,是边的延长线,连接,则的度数是 .13.在平面直角坐标系中,点,,分别在三个不同的象限.若反比例函数的图象经过其中两点,则的值为 .14.如图,在菱形中,,,点在边上,且.若直线经过点,将该菱形的面积平分,并与菱形的另一边交于点.则线段的长为 .三、解答题(本大题共11小题,共78分)15.解不等式组:.16.解分式方程:.17.如图,已知,,,请用尺规作图法,在边上求作一点,.(保留作图痕迹,不写作法)18.如图,在四边形中,,,是边上一点,且.求证:.19.(1)(2)(3)王大伯承包了一个鱼塘,投放了条某种鱼苗,经过一段时间的精心喂养,存活率大致达到了,他近期想出售鱼塘里的这种鱼,为了估计鱼塘里这种鱼的总质量,王大伯随机捕捞了条鱼,分别称得其质量后放回鱼塘.现将这条鱼的质量作为样本,统计结果如图所示:质量条数所捕捞鱼的质量统计图这条鱼质量的中位数是 ,众数是 .求这条鱼质量的平均数.经了解,近期市场上这种鱼的售价为每千克元,请利用这个样本的平均数,估计王大伯近期售完鱼塘里的这种鱼可收入多少元?20.如图所示,小明家与小华家住在同一栋楼的同一单元.他俩想测算所住楼对面商业大厦的高.他俩在小明家的窗台处.测得商业大厦顶部的仰角的度数,由于楼下植物的遮挡,不能在处测得商业大厦底部的俯角的度数.于是,他俩上楼来到小华家,在窗台处测得商业大厦底部的俯角的度数,竟然发现与恰好相等.已知、、三点共线,,,,,试求商业大厦的高.21.某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗早期在农科所的温室中生长,长到大约时,移至该村的大棚内.沿插杆继续向上生长.研究表明,天内,这种瓜苗生长的高度()与生长时间(天)之间的关系大致如图所示.(1)(2)天求与之间的函数关系式.当这种瓜苗长到大约时,开始开花结果,试求这种瓜苗移至大棚后,继续生长大约多少天,开始开花结果?(1)(2)22.小亮和小丽进行摸球试验.他们在一个不透明的空布袋内,放入两个红球,一个白球和一个黄球,共四个小球.这些小球除颜色外其它都相同.试验规则:先将布袋内的小球摇匀,再从中随机摸出一个小球,记下颜色后放回,称为摸球一次.小亮随机摸球次,其中次摸出的是红球,求这次中摸出红球的.若小丽随机摸球两次,请利用画树状图或列表的方法,求这两次摸出的球中一个是白球、一个是黄球的概率.频.率.(1)(2)23.如图,是⊙的内接三角形,,.连接并延长,交⊙于点,连接.过点作⊙的切线,与的延长线相交于点.求证:.若,求线段的长.24.如图,抛物线经过点和,与两坐标轴的交点分别为、、,它的对称轴为直线.(1)(2)求该抛物线的表达式.是该抛物线上的点,过点作的垂线,垂足为,是上的点,要使以、、为顶点的三角形与全等,求满足条件的点、点的坐标.(1)(2)(3)25.解答下列各题.问题提出如图,在,,,的平分线交于点,过点分别作,,垂足分别为、,则图中与线段相等的线段是 .图问题探究如图,是半圆的直径,,是上一点,且,连接,,的平分线交于,过点分别作,,垂足分别为、,求线段的长.图问题解决如图,是某公园内“少儿活动中心”的设计示意图,已知⊙的直径,点在⊙上,且,为上一点,连接并延长,交⊙于点,连接、,过点分别作,,垂足分别为、,按设计要求,四边形内部为室内活动区,阴影部分是户外活动区,圆内其余部分为绿化区,设的长为,阴影部分的面积为.【答案】解析:.故选.解析:的余角.故选.解析:.故选.12图求与之间的函数关系式.按照“少儿活动中心”的设计要求,发现当的长度为时,整体布局比较合理,试求当时,室内活动区(四边形)的面积.A 1.B 2.A 3.解析:考察正负数的计算,最高温度:,最低温度:,∴温差即为:.故选.解析:考察整式乘除中幂的运算,.解析:考查等积法求三角形的高,,,∴,即,∴.故选.解析:在直线中,令,解得,C 4.C 5.D 6.B 7.∴,联立,∴,∴,∴.故选.解析:∵点为中点,,∴为四边形中位线,∵,,∴,又,即,∴,∴,∴.故选.解析:连接、,∵,∴,∵为中点,D 8.B 9.∴,,在中,,,∴.解析:向下平移个单位,得,,,故平移后抛物线顶点坐标为.当时,,∴,,∴顶点在第四象限.故选.解析:原式.解析:∵为正五边形,内角和为,∴,∴,∴.故答案为:.D 10.11.12.13.解析:∵,在不同象限,∴为负数,∵反比例函数过一、三象限或二、四象限,∴反比例函数过,两点,∴,将点坐标代入,∴,∴.解析:如图,连接,交于点,作于点,作于,∵,,∴,∵平分面积,∴,关于对角线交点对称,∴,∴,又∵,∴.解析:由①得:,14..15.由②得:,,,所以原不等式组的解集为.解析:经检验:为原方程的解.解析:以大于的长度为半径,点、点为圆心画弧,连接交点得的垂直平分线,交于点,连接,得.解析:∵,∴,∵,.16.,画图见解析.17.证明见解析.18.(1)(2)(3)∴,∴.∵,∴四边形为平行四边形.∴.解析:将条鱼的质量从小到大重新排列后得到:,,,,,,,,,,,,,,,,,,,,观察数据可知:最中间的两个数分别是,,所以中位数为:;出现次数最多,故众数是.(),∴这条鱼质量的平均数是.(元).∴估计王大伯近期售完鱼塘里的这种鱼可收入元.解析:如图,过点作,垂足为,过点作,垂足为,∴,(1) ; (2).(3)元.19..20.(1)(2)(1)(2)∵,,∴四边形和四边形是均为矩形,∴,,又知,∴≌,∴,由矩形性质,易得,∴,∴商业大厦的高为.解析:当时,设,则,∴,∴;当时,设,则,解之,得,∴;∴.当时,,解之,得.(天),∴这种瓜苗移至大棚后,继续生长大约天,开始开花结果.解析:摸出红球的频率为.列表如下:(1).(2)天.21.,,(1).(2).22.(1)(2)第二次第一次红红白黄红(红,红)(红,红)(红,白)(红,黄)红(红,红)(红,红)(红,白)(红,黄)白(白,红)(白,红)(白,白)(白,黄)黄(黄,红)(黄,红)(黄,白)(黄,黄)由上表可知,共有种等可能的结果,其中摸出一白一黄的结果有种,∴.解析:如图,连接,∵与⊙相切于点,∴,又∵,,∴.如图,过点作,垂足为.(摸出一白一黄)(1)证明见解析.(2).23.(1)(2)∵,∴四边形为正方形,∵,,∴,∴,∵是直径,∴,∴,在中,.∴.∵,∴,在中,.∴.解析:将,代入得,,解得,∴抛物线解析式为:.由()知,(1).(2),,,.24.(1)令得,即,令得,,即,,∴,,∴是等腰直角三角形,∵以点、、为顶点的三角形与全等,且,∴,由知,,如图:∴,或,∴或,∴,∴或.解析:连接,(1)、、(2).12(3)..25.(2)1(3)图∵为平分线,,,∴,又,∴四边形为正方形,∴与相等的线段有、、.∵,∴,,∴,又,∴设,则,,∴,∴,即.如图,图∵为直径,∴,∵,∴,∴,2∴四边形为正方形,∴,,∴将绕点逆时针旋转,得到,,则、,三点共线,为直角三角形,,∴,在中,,∴,∴.当时,,,在中,,∵,∴,∴,∴,∴当时,室内活动区(四边形)的面积为.四边形。
2020学年陕西省中考数学试题(含答案)
陕西省2020年中考数学试题第Ⅰ卷(选择题 共30分)A 卷一、选择题(共10小题,每小题3分,计30分.每小题只有一个选项是符合题意的) 1.下列四个数中最小的数是( ) A .-2B.0C.31-D.5 2.如图,下面的几何体是由一个圆柱和一个长方体组成的,则它的俯视图是( )3.如图,AB ∥CD ,∠CED=90°,∠AEC=35°,则∠D 的大小为( ) A.65° B.55° C.45° D.35°4.不等式组⎪⎩⎪⎨⎧--321021 x x 的解集为( ) A. > B.<-1 C. -<< D. >- 5.我省某市五月份第二周连续七天的空气质量指数分别为:111,96,47,68,70,77,105.则这七天空气质量指数的平均数是( ) A.71.8 B.77 C.82 D.95.7 6.如果一个正比例函数的图象经过不同..象限的两点A (2,m )、B (n ,3),那么一定有( ) A. m >0,n >0 B. m >0,n <0 C. m <0,n >0 D. m <0,n <07.如图,在四边形ABCD 中,AB=AD ,CD=CB.若连接AC 、BD 相交于点O ,则图中全等三角形共有( ) A.1对 B.2对 C.3对 D.4对8.P 的值为( )A.1 B .-1 C.3 D.-39.如图,在矩形ABCD 中,AD=2AB ,点M 、N 分别在边AD 、BC 上,连接BM 、DN.若四边形MBND 是菱形,则MDAM等于( ) A. B. C. D.10.已知两点A (-5,1y )、B (3,2y )均在抛物线()02≠++=a c bx ax y 上,点C (0x ,0y )是EDB CA (第2题图) (第3题图)A B C D O DBCA(第7题图) NMDBCA(第9题图)该抛物线的顶点,若1y >2y ≥0y ,则0x 的取值范围是( ) A. 0x >-5 B. 0x >-1 C .-5<0x <-1 D .-2<0x <3 B 卷第Ⅱ卷(非选择题 共90分)二、填空题(共6小题,每小题3分,共18分) 11.计算:()()03132-+-= .12.一元二次方程032=-x x 的根是 .13.请从经以下两个小题中任选一个....作答,若多选,则按所选的第一题计分. A.在平面直角坐标系中,线段AB 的两个端点的坐标分别为A (-2,1)、B (1,3,)将线段AB 经过平移后得到线段A ′B ′.若点A 的对应点为A ′(3,2),则点B 的对应点B ′的坐标是 . B.比较8cos31(填“>”、“=”若“<”)14.如图,四边形ABCD 的对角线AC 、BD 相交于点O ,且BD 平分AC.若BD=8,AC=6,∠BOC=120°,则四边形ABCD 的面积为 .(结果保留根号) 15.如果一个正比例函数的图象与反比例函数xy 6=的图象交于A (1x ,1y )、B (2x ,2y )两点,那么(2x -1x )(2y -1y )的值为 .16.如图,AB 是⊙O 的一条弦,点C 是⊙O 上一动点,且∠ACB=30°,点E 、F 分别是AC 、BC 的中点,直线EF 与⊙O 交于G 、H 两点.若⊙O 的半径为7,则GE+FH 的最大值为 .三、解答题(共9小题,计72分.解答应写出过程) 17.(本题满分5分) 解分式方程:12422=-+-x xx .18.(本题满分6分)如图,∠AOB=90°,OA=OB ,直线L 经过点O ,分别过A 、B 两点作AC ⊥L 交L 于点C ,BD ⊥L 交L 于点D.OD B CAC(第14题图) (第16题图)求证:AC=OD19.(本题满分7分)我省教育厅下发了《在全省中小学幼儿园广泛深入开展节约教育的通知》通知中要求各学校全面持续开展“光盘行动”.某市教育局督导检查组为了调查学生对“节约教育”内容的了解程度(程度分为:“A —了解很多”,B —“了解较多”,“C —了解较少”,“D —不了解”),对本市一所中学的学生进行了抽样调查.我们将这次调查的结果绘制了以下两幅统计图.根据以上信息,解答下列问题:(1) 本次抽样调查了多少名学生? (2) 补全两幅统计图;(3) 若该中学共有1800名学生,请你估计这所中学的所有学生中,对“节约教育”内容“了解较多”的有多少名?20.(本题满分8分)一天晚上,李明和张龙利用灯光下的影子长来测量一路灯D 的高度.如图,当李明走到点A 处时,张龙测得李明直立向高AM 与其影子长AE 正好相等;接着李明沿AC 方向继续向前走,走到点B 处时,李明直立时身高BN 的影子恰好是线段AB ,并测得AB=1.25m.已知李明直立时的身高为1.75m ,求路灯的高度CD 的长.(精确到0.1m )lO D B C A(第18题图) 了解程度人数624060504030201036D B C A (第19题图) 被调查学生对“节约教育”内容了解程度的统计图 NMED B C21.(本题满分8分)“五一节”期间,申老师一家自架游去了离家170千米的某地.下面是他们离家的距离(千米)与汽车行驶时间(小时)之间的函数图象.(1) 求他们出发半小时时,离家多少千米? (2) 求出AB 段图象的函数表达式;(3) 他们出发2小时时,离目的地还有多少千米?22.(本题满分8分)甲、乙两人用手指玩游戏,规则如下:ⅰ)每次游戏时,两人同时随机地各伸出一根手指:ⅱ)两人伸出的手指中,大拇指只胜食指、食指只胜中指、中指只胜无名指、无名指只胜小拇指,小拇指只胜大拇指,否则不分胜负.依据上述规则,当甲、乙两人同时随机地各伸出一根手指时. (1)求甲伸出小拇指取胜的概率; (2)求乙取胜的概率.23.(本题满分8分)x/小时y/千米2.51.517090O B A (第20题图) (第21题图)如图,直线L 与⊙O 相切于点D.过圆心O 作EF ∥L 交⊙O 于E 、F 两点,点A 是⊙O 上一点,连接AE 、AF.并分别延长交直线L 于 B 、C 两点. (1) 求证:∠ABC+∠ACB=90°;(2) 当⊙O 的半径R=5,BD=12时,求tan ∠ABC 的值.24.(本题满分10分)在平面直角坐标系中,一个二次函数的图象经过A (1,0)、B (3,0)两点. (1) 写出这个二次函数图象的对称轴;(2) 设这个二次函数图象的顶点为D ,与轴交于点C ,它的对称轴与轴交于点E ,连接AC 、DE 和DB.当⊿AOC 与⊿DEB 相似时,求这个函数的表达式.25.(本题满分12分) 问题探究(1) 请在图①中作出两条直线,使它们将圆面四等分;(2) 如图②,M 是正方形ABCD 内一定点,请在图②中作出两条直线(要求其中一条直线必须过点M ),使它们将正方形ABCD 的面积四等分,并说明理由.问题解决(3)如图③,在四边形ABCD 中,AB ∥CD ,AB+CD=BC ,点P 是AD 的中点.如果AB=,CD=,且>,那么在边BC 上是否存在一点Q ,使PQ 所在直线将四边形ABCD 的面积分成相等的两部分?若存在,求出BQ 的长;若不存在,说明理由.l FOE DB C A(第23题图) xy–1–2–3–41234–1–2–3–41234O (第24题图) M D BCA P DBCA①②③(第25题图)参考答案1.A;2.D;3.B;4.A;5.C;6.D;7.C;8.A;9.C;10.B11.-7;12.0,3;13.A:(6,4)B:>;14.123;15.24;16.10.5;。
2020年陕西省中考数学试卷及解答分析

2020年陕西省中考数学试卷第一部分〔选择题 共30分〕一、选择题 (共10小题,每小题3分,计30分,每小题只有一个选项是符合题意的) 1. -18的和反数是( )A . 18B .-18C .181 D .-181 2. 若∠A =23°,∠A 余角的大小是( )A . 57°B .67°C .77°D .157°3. 2019年,我国国内产总值约为990 870亿元,将数字990 870用科学记数法表示( )A .9.9087×105B .9.9087×104C .99.087×104D .99.087×103 4. 如图,是A 市某一天的气温随时间变化的情况,则这天的日温差(最高气温与最低气温的差)是( ) A .4°C B .8°C C .12°C D .16°C5. 计算:(-32x 2y ) 3 =( )A .-2 x 6y 3B .278 x 6y 3 C . -278 x 6y 3 D .-278 x 5y 46. 如图,在3×3的网将中,每个小正方形的边长为为1,点A 、B 、C 都在格点上,若BD 是△ABC 的高,则BD 的长为( ) A .131310 B . 13139 C . 13138 D . 131377. 在平面直角坐标系中,O 为坐标原点.若直找y =x +3分别与x 轴,直线y =-2x 交于点A 、B ,则△AOB 的面积为( )A .2B .3C .4D .6 8. 如图,在□ABCD 中AB =5,BC =8.E 是边BC 的中点F 是□ABCD 内一点,且∠BFC =90°,连接AF 并延长,交CD于点G ,若 EF ∥AB ,则DG 的长为( ) A .25 B . 23C .2D .3 9. 如图,△ABC 内接于⊙O ,∠A =50°,E 是边BC 的中点,连接OE 并延长,交⊙O 于点D ,连接BD ,则∠D 的大小为( ) A . 55° B .65° C .60° D .75°/hDCBA 第6题F EDCBA第8题第9题10.在平面直角坐标系中,将抛物线y=x 2-( m -1)x +m (m >1)沿y 轴向下平移3个单位,则平移后得到的抛物线的项点一定在A . 第一象限B . 第二象限C . 第三象限D . 第四象限第二部分(非选择题 共90分)二,填空题(共4小题,每小题3分,计12分) 11.计算:(2+3)(2-3)=12.如图,在正五边形 ABCDE 中,DM 是边CD 的延长线.连接BD , 则∠BDM 的度数是_______.13.在平面直角坐标系中,A (-2,1),B (3,2),C (-6,)分别在三个不同的象限,若反比例函数y =xk(k ≠0)的图象经过其中两点,则m 的值为_______. 14.如图,在菱形ABCD 中,AB =6,∠B =60°,点E 在边AD 上, 且AE =2,若直线l 经过点E ,将菱用的面积平分,并与菱形 的另一边交于点F ,则线段EF 的长为_______. 三、解答题(共11小题,计78分,解答应写出过程) 15.(本题满分5分)解不等式组:>>4)5(263x x16. (本题满分5分)解分式方程:1232=x xx17. (本题满分5分)如图,已知△ABC ,AC >AB ,∠C =45°. 请用尺规作图法,在AC 边上求一点P ,∠PBC =45°. (保留作电迹,不写作法)MECB A第12题D第14题CBA如图,在四边形ABCD 中,AD ∥BC ,∠B =∠C ,E 是边BC 上一点,且DE =DC . 求证:AD =BE .19. (本题满分7分)王大伯承包了一个鱼塘,投入了2000条某种鱼苗,经过一段时间的精心喂养,存活率大致达到了90%,他近期想出售鱼塘里的这种鱼.为了估计鱼塘里这种鱼的总质量,王大伯随机捕捞了20条鱼,分别称得其质量后放回鱼塘.现将这20条鱼的质量作为样本,统计结果如图所示:(1)这20条鱼质量的中位娄得________,众数是________; (2)求这20条鱼的平均数;(3)经了解,近期市场上这种鱼的售价为每千克18元,请利用这个样本的平均数,估计王大伯近期售完鱼塘里的这种鱼可收入多少元?20. (本题满分7分)如图所示,小明家与小华家住在同一栋楼的同一单元.他俩想测算所住楼对面商业大厦的高MN .他俩在小明家的窗台B 处,测得商业大厦顶部N 的仰角∠1的度数.由于楼下植物的遮档,不能在B 处测得商业大厦底部M 的角的度数,于是他俩上楼来到小华家,在窗台C 处测得商业大厦底都M 的的俯角∠2的度数,竟然发现∠1与∠2恰好相等,已知A 、B 、C 三点共线,CA ⊥AM ,NM ⊥AM ,若AB =31m ,BC =18m ,试求商业大厦的高MN .NM21ABC EDCBA质量/kg某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗早期在农科所的温室中生长,长到大约20cm时,移至该村的大棚内,沿插杆继续向上生长.研究表明,60天内这种瓜苗生长的高度y(cm)与生长时阿x(天)之间的关系大致如图所示.(1)求y与x之间的函数关系式;(2)当这种瓜苗长到大约80cm时,开始开花结,试求这种瓜苗移至大棚后,继续生长大约多少天,开始开花结果?22.(本题满分7分)小亮和小丽进行摸球试验,他们在一个不透明的空布袋内,放入两个红球,一个白球和一个黄球,共四个小球,这些小球除颜色外其它都相同.试验规则:先将布袋内的小球摇匀,再从中随机摸出一个小球,记下颜色后放回,称为摸球一次.(1)小亮随机球10次,其中6次摸出的是红球,求这10次中摸出红球的概率;(2)若小丽随机摆球两次,请利用画树状图或列表的方法,求这两次摸出的球中一个是白球、一个是黄球的概率.23. (本题满分8分)如图,△ABC是⊙O的内接三角形,∠BAC=75°,∠ABC=45°,连接AO并延长,交⊙O于点D,连接BD,过点C作⊙O的切线,与BA的延长线相交于点E.(1)求证:AD∥EC;(2)若AB=12,求线段EC的长.C如图,抛物线y=x 2+bx+c 经过点(3,12)和(-2,-3),与两坐标轴的交点分别为A 、B 、C ,它的对称轴为直线l .(1)求该抛物线的表达式;(2)P 是该抛物线上的点,过点P 作l 的垂线,垂足为D 点,E 是l 上的点,要使以P 、D 、E 为顶点的三角形与△AOC 全等,求满足条件的点P 、点E25. (本题满分12分) 【问题提出】(1)如图1,在Rt △ABC ,∠ACB =90°,AC >BC ,∠ACB 的平分线交AB 于点D ,过点D 分别作DE ⊥AC ,DF ⊥BC ,垂足分别为E 、F ,则图1中与线段CE 相等的线段是_____. 【问题探究】(2)如图2,AB 是半圆O 的直径,AB =8,P 是⌒AB 上一点,且⌒PB =2⌒PA ,连接AP 、BP ,∠APB 的平分线交AB 于C ,过点C 分别作CE ⊥AP ,CF ⊥BP ,垂足分别为E 、F ,求线段CF 的长. 【问题解决】(3)如图3,是某公园内“少儿活动中心”的设计示意图,已知⊙O 的直径AB =70m ,点C 在⊙O 上,且CA=CB ,P 为AB 上一点,连接CP 并延长,交⊙O 于点D ,连接AD 、BD ,过点P 分别作PE ⊥AD ,PF ⊥BD ,垂足分别为E 、F ,按设计要求,四边形PEDF 内部为室内活动区,阴影部分是户外活动区,园内其余部分为绿化区,设AP 的长为x (m ),阴影部分的面积为y (m 2) . ①求y 与x 之间的函数关系式;②按照“少儿活动中心”的设计要求,发现当AP 的长度为30m 时,整体布局比较合理,试求当AP =30m 时,室内活动区(四边形PEDF )的面积.图3B图2B图1FEDCBA参考答案一、ABACC DBDBD二、11.1;12.144°;13.-1;14.27。
2020年陕西省中考数学试题及答案
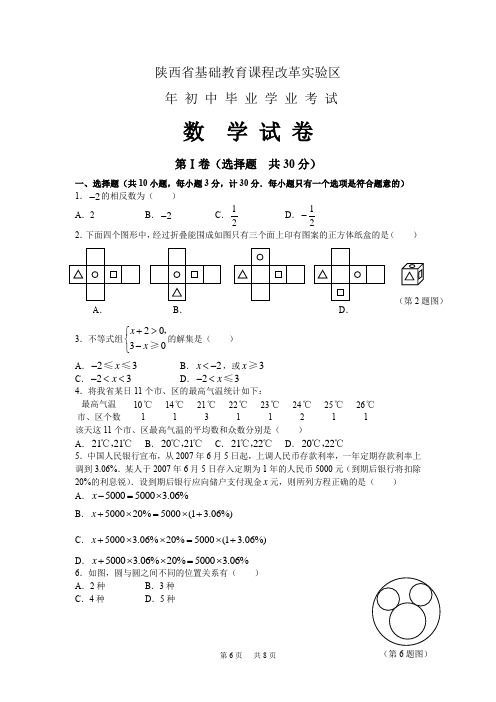
tan 52 1.2799 )
15.小说《达 芬奇密码》中的一个故事里出现了一串神密排列的数,将这串令人费解的数
按从小到大的顺序排列为:1,1,2,3,5,8,…,则这列数的第 8 个数是
.
16.如图,要使输出值 y 大于 100,则输入的最小正整数 x 是
.
输入正整数 x
奇数
偶数
?
输出 y (第 16 题图)
C
(1)求证: BED C ;
(2)若 OA 5,AD 8 ,求 AC 的长.
E
D
A
24.(本题满分 10 分)
y
如图,在直角梯形 OBCD中, OB 8,BC 1,CD 10. D
(1)求 C,D 两点的坐标;
(2)若线段 OB 上存在点 P ,使 PD⊥PC ,求过 D,P,C
三点的抛物线的表达式.
x(x 1) 3 (x 1)(x 1) . ············································································2 分
x2 x 3 x2 1.
x 2 .········································································································3 分
y k (k 0) 的图象上的点是
.
x
A
13.如图, ABC 50 ,AD 垂直平分线段 BC 于点 D,ABC 的
平分线 BE 交 AD 于点 E ,连结 EC ,则 AEC 的度数是
.
E
B
D
C
(第 13 题图)
2020年陕西省中考数学试题及参考答案(word解析版)

2020年陕西省初中毕业学业考试数学试卷(满分120分,考试时间120分钟)第一部分(选择题共30分)一、选择题(共10小题,每小题3分,计30分.每小题只有一个选项是符合题意的)1.﹣18的相反数是()A.18 B.﹣18 C.D.﹣2.若∠A=23°,则∠A余角的大小是()A.57°B.67°C.77°D.157°3.2019年,我国国内生产总值约为990870亿元,将数字990870用科学记数法表示为()A.9.9087×105B.9.9087×104C.99.087×104D.99.087×1034.如图,是A市某一天的气温随时间变化的情况,则这天的日温差(最高气温与最低气温的差)是()A.4℃B.8℃C.12℃D.16℃5.计算:(﹣x2y)3=()A.﹣2x6y3B.x6y3C.﹣x6y3D.﹣x5y46.如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为()A.B.C.D.7.在平面直角坐标系中,O为坐标原点.若直线y=x+3分别与x轴、直线y=﹣2x交于点A、B,则△AOB的面积为()A.2 B.3 C.4 D.68.如图,在▱ABCD中,AB=5,BC=8.E是边BC的中点,F是▱ABCD内一点,且∠BFC=90°.连接AF并延长,交CD于点G.若EF∥AB,则DG的长为()A.B.C.3 D.29.如图,△ABC内接于⊙O,∠A=50°.E是边BC的中点,连接OE并延长,交⊙O于点D,连接BD,则∠D的大小为()A.55°B.65°C.60°D.75°10.在平面直角坐标系中,将抛物线y=x2﹣(m﹣1)x+m(m>1)沿y轴向下平移3个单位.则平移后得到的抛物线的顶点一定在()A.第一象限B.第二象限C.第三象限D.第四象限第二部分(非选择题共90分)二、填空题(共4小题,每小题3分,计12分)11.计算:(2+)(2﹣)=.12.如图,在正五边形ABCDE中,DM是边CD的延长线,连接BD,则∠BDM的度数是.13.在平面直角坐标系中,点A(﹣2,1),B(3,2),C(﹣6,m)分别在三个不同的象限.若反比例函数y=(k≠0)的图象经过其中两点,则m的值为.14.如图,在菱形ABCD中,AB=6,∠B=60°,点E在边AD上,且AE=2.若直线l经过点E,将该菱形的面积平分,并与菱形的另一边交于点F,则线段EF的长为.三、解答题(共11小题,计78分.解答应写出过程)15.(5分)解不等式组:16.(5分)解分式方程:﹣=1.17.(5分)如图,已知△ABC,AC>AB,∠C=45°.请用尺规作图法,在AC边上求作一点P,使∠PBC=45°.(保留作图痕迹.不写作法)18.(5分)如图,在四边形ABCD中,AD∥BC,∠B=∠C.E是边BC上一点,且DE=DC.求证:AD=BE.19.(7分)王大伯承包了一个鱼塘,投放了2000条某种鱼苗,经过一段时间的精心喂养,存活率大致达到了90%.他近期想出售鱼塘里的这种鱼.为了估计鱼塘里这种鱼的总质量,王大伯随机捕捞了20条鱼,分别称得其质量后放回鱼塘.现将这20条鱼的质量作为样本,统计结果如图所示:(1)这20条鱼质量的中位数是,众数是.(2)求这20条鱼质量的平均数;(3)经了解,近期市场上这种鱼的售价为每千克18元,请利用这个样本的平均数.估计王大伯近期售完鱼塘里的这种鱼可收入多少元?20.(7分)如图所示,小明家与小华家住在同一栋楼的同一单元,他俩想测算所住楼对面商业大厦的高MN.他俩在小明家的窗台B处,测得商业大厦顶部N的仰角∠1的度数,由于楼下植物的遮挡,不能在B处测得商业大厦底部M的俯角的度数.于是,他俩上楼来到小华家,在窗台C处测得大厦底部M的俯角∠2的度数,竟然发现∠1与∠2恰好相等.已知A,B,C三点共线,CA⊥AM,NM⊥AM,AB=31m,BC=18m,试求商业大厦的高MN.21.(7分)某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗早期在农科所的温室中生长,长到大约20cm时,移至该村的大棚内,沿插杆继续向上生长.研究表明,60天内,这种瓜苗生长的高度y(cm)与生长时间x(天)之间的关系大致如图所示.(1)求y与x之间的函数关系式;(2)当这种瓜苗长到大约80cm时,开始开花结果,试求这种瓜苗移至大棚后.继续生长大约多少天,开始开花结果?22.(7分)小亮和小丽进行摸球试验.他们在一个不透明的空布袋内,放入两个红球,一个白球和一个黄球,共四个小球.这些小球除颜色外其它都相同.试验规则:先将布袋内的小球摇匀,再从中随机摸出一个小球,记下颜色后放回,称为摸球一次.(1)小亮随机摸球10次,其中6次摸出的是红球,求这10次中摸出红球的频率;(2)若小丽随机摸球两次,请利用画树状图或列表的方法,求这两次摸出的球中一个是白球、一个是黄球的概率.23.(8分)如图,△ABC是⊙O的内接三角形,∠BAC=75°,∠ABC=45°.连接AO并延长,交⊙O于点D,连接BD.过点C作⊙O的切线,与BA的延长线相交于点E.(1)求证:AD∥EC;(2)若AB=12,求线段EC的长.24.(10分)如图,抛物线y=x2+bx+c经过点(3,12)和(﹣2,﹣3),与两坐标轴的交点分别为A,B,C,它的对称轴为直线l.(1)求该抛物线的表达式;(2)P是该抛物线上的点,过点P作l的垂线,垂足为D,E是l上的点.要使以P、D、E为顶点的三角形与△AOC全等,求满足条件的点P,点E的坐标.25.(12分)问题提出(1)如图1,在Rt△ABC中,∠ACB=90°,AC>BC,∠ACB的平分线交AB于点D.过点D分别作DE⊥AC,DF⊥BC.垂足分别为E,F,则图1中与线段CE相等的线段是.问题探究(2)如图2,AB是半圆O的直径,AB=8.P是上一点,且=2,连接AP,BP.∠APB的平分线交AB于点C,过点C分别作CE⊥AP,CF⊥BP,垂足分别为E,F,求线段CF 的长.问题解决(3)如图3,是某公园内“少儿活动中心”的设计示意图.已知⊙O的直径AB=70m,点C在⊙O上,且CA=CB.P为AB上一点,连接CP并延长,交⊙O于点D.连接AD,BD.过点P 分别作PE⊥AD,PF⊥BD,垂足分别为E,F.按设计要求,四边形PEDF内部为室内活动区,阴影部分是户外活动区,圆内其余部分为绿化区.设AP的长为x(m),阴影部分的面积为y(m2).①求y与x之间的函数关系式;②按照“少儿活动中心”的设计要求,发现当AP的长度为30m时,整体布局比较合理.试求当AP=30m时.室内活动区(四边形PEDF)的面积.参考答案与解析第一部分(选择题共30分)一、选择题(共10小题,每小题3分,计30分.每小题只有一个选项是符合题意的)1.﹣18的相反数是()A.18 B.﹣18 C.D.﹣【知识考点】相反数.【思路分析】直接利用相反数的定义得出答案.【解题过程】解:﹣18的相反数是:18.故选:A.【总结归纳】此题主要考查了相反数,正确把握相反数的定义是解题关键.2.若∠A=23°,则∠A余角的大小是()A.57°B.67°C.77°D.157°【知识考点】余角和补角.【思路分析】根据∠A的余角是90°﹣∠A,代入求出即可.【解题过程】解:∵∠A=23°,∴∠A的余角是90°﹣23°=67°.故选:B.【总结归纳】本题考查了互余的应用,注意:如果∠A和∠B互为余角,那么∠A=90°﹣∠B.3.2019年,我国国内生产总值约为990870亿元,将数字990870用科学记数法表示为()A.9.9087×105B.9.9087×104C.99.087×104D.99.087×103【知识考点】科学记数法—表示较大的数.【思路分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.【解题过程】解:990870=9.9087×105,故选:A.【总结归纳】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.4.如图,是A市某一天的气温随时间变化的情况,则这天的日温差(最高气温与最低气温的差)是()A.4℃B.8℃C.12℃D.16℃【知识考点】函数的图象.【思路分析】根据A市某一天内的气温变化图,分析变化趋势和具体数值,即可求出答案.【解题过程】解:从折线统计图中可以看出,这一天中最高气温8℃,最低气温是﹣4℃,这一天中最高气温与最低气温的差为12℃,故选:C.【总结归纳】本题考查了函数图象,认真观察函数图象图,从图中得到必要的信息是解决问题的关键.5.计算:(﹣x2y)3=()A.﹣2x6y3B.x6y3C.﹣x6y3D.﹣x5y4【知识考点】幂的乘方与积的乘方.【思路分析】根据积的乘方运算法则计算即可,积的乘方,等于每个因式乘方的积.【解题过程】解:(﹣x2y)3==.故选:C.【总结归纳】本题主要考查了幂的乘方与积的乘方,熟记幂的运算法则是解答本题的关键.6.如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC 的高,则BD的长为()A.B.C.D.【知识考点】勾股定理.【思路分析】根据勾股定理计算AC的长,利用面积差可得三角形ABC的面积,由三角形的面积公式即可得到结论.【解题过程】解:由勾股定理得:AC==,∵S△ABC=3×3﹣=3.5,∴,∴,∴BD=,故选:D.【总结归纳】本题考查了勾股定理,三角形的面积的计算,掌握勾股定理是解题的关键.7.在平面直角坐标系中,O为坐标原点.若直线y=x+3分别与x轴、直线y=﹣2x交于点A、B,则△AOB的面积为()A.2 B.3 C.4 D.6【知识考点】一次函数的性质;两条直线相交或平行问题.【思路分析】根据方程或方程组得到A(﹣3,0),B(﹣1,2),根据三角形的面积公式即可得到结论.【解题过程】解:在y=x+3中,令y=0,得x=﹣3,解得,,∴A(﹣3,0),B(﹣1,2),∴△AOB的面积=3×2=3,故选:B.【总结归纳】本题考查了直线围成图形面积问题,其中涉及了一次函数的性质,三角形的面积的计算,正确的理解题意是解题的关键.8.如图,在▱ABCD中,AB=5,BC=8.E是边BC的中点,F是▱ABCD内一点,且∠BFC=90°.连接AF并延长,交CD于点G.若EF∥AB,则DG的长为()A.B.C.3 D.2【知识考点】直角三角形斜边上的中线;平行四边形的性质;梯形中位线定理.【思路分析】依据直角三角形斜边上中线的性质,即可得到EF的长,再根据梯形中位线定理,即可得到CG的长,进而得出DG的长.【解题过程】解:∵E是边BC的中点,且∠BFC=90°,∴Rt△BCF中,EF=BC=4,∵EF∥AB,AB∥CG,E是边BC的中点,∴F是AG的中点,∴EF是梯形ABCG的中位线,∴CG=2EF﹣AB=3,又∵CD=AB=5,∴DG=5﹣3=2,故选:D.【总结归纳】本题主要考查了平行四边形的性质以及梯形中位线定理,梯形的中位线平行于两底,并且等于两底和的一半.9.如图,△ABC内接于⊙O,∠A=50°.E是边BC的中点,连接OE并延长,交⊙O于点D,连接BD,则∠D的大小为()A.55°B.65°C.60°D.75°【知识考点】圆周角定理;三角形的外接圆与外心.【思路分析】连接CD,根据圆内接四边形的性质得到∠CDB=180°﹣∠A=130°,根据垂径定理得到OD⊥BC,求得BD=CD,根据等腰三角形的性质即可得到结论.【解题过程】解:连接CD,∵∠A=50°,∴∠CDB=180°﹣∠A=130°,∵E是边BC的中点,∴OD⊥BC,∴BD=CD,∴∠ODB=∠ODC=BDC=65°,故选:B.【总结归纳】本题考查了三角形的外接圆与外心,圆内接四边形的性质,垂径定理,等腰三角形的性质,正确的理解题意是解题的关键.10.在平面直角坐标系中,将抛物线y=x2﹣(m﹣1)x+m(m>1)沿y轴向下平移3个单位.则平移后得到的抛物线的顶点一定在()A.第一象限B.第二象限C.第三象限D.第四象限【知识考点】二次函数的性质;二次函数图象与几何变换.【思路分析】根据平移规律得到平移后抛物线的顶点坐标,然后结合m的取值范围判断新抛物线的顶点所在的象限即可.【解题过程】解:∵y=x2﹣(m﹣1)x+m=(x﹣)2+m﹣,∴该抛物线顶点坐标是(,m﹣),∴将其沿y轴向下平移3个单位后得到的抛物线的顶点坐标是(,m﹣﹣3),∵m>1,∴m﹣1>0,∴>0,∵m﹣﹣3===﹣﹣1<0,∴点(,m﹣﹣3)在第四象限;故选:D.【总结归纳】本题考查了二次函数的图象与性质、平移的性质、抛物线的顶点坐标等知识;熟练掌握二次函数的图象和性质,求出抛物线的顶点坐标是解题的关键.第二部分(非选择题共90分)二、填空题(共4小题,每小题3分,计12分)11.计算:(2+)(2﹣)=.【知识考点】二次根式的混合运算.【思路分析】先利用平方差公式展开得到原式=22﹣()2,再利用二次根式的性质化简,然后进行减法运算.【解题过程】解:原式=22﹣()2=4﹣3=1.【总结归纳】本题考查了二次根式的混合运算:在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.12.如图,在正五边形ABCDE中,DM是边CD的延长线,连接BD,则∠BDM的度数是.【知识考点】多边形内角与外角.【思路分析】根据正五边形的性质和内角和为540°,求得每个内角的度数为108°,再结合等腰三角形和邻补角的定义即可解答.【解题过程】解:因为五边形ABCDE是正五边形,所以∠C==108°,BC=DC,所以∠BDC==36°,所以∠BDM=180°﹣36°=144°,故答案为:144°.【总结归纳】本题考查了正五边形.解题的关键是掌握正五边形的性质:各边相等,各角相等,内角和为540°.熟记定义是解题的关键.13.在平面直角坐标系中,点A(﹣2,1),B(3,2),C(﹣6,m)分别在三个不同的象限.若反比例函数y=(k≠0)的图象经过其中两点,则m的值为.【知识考点】反比例函数图象上点的坐标特征.【思路分析】根据已知条件得到点A(﹣2,1)在第二象限,求得点C(﹣6,m)一定在第三象限,由于反比例函数y=(k≠0)的图象经过其中两点,于是得到反比例函数y=(k≠0)的图象经过B(3,2),C(﹣6,m),于是得到结论.【解题过程】解:∵点A(﹣2,1),B(3,2),C(﹣6,m)分别在三个不同的象限,点A(﹣2,1)在第二象限,∴点C(﹣6,m)一定在第三象限,∵B(3,2)在第一象限,反比例函数y=(k≠0)的图象经过其中两点,∴反比例函数y=(k≠0)的图象经过B(3,2),C(﹣6,m),∴3×2=﹣6m,∴m=﹣1,故答案为:﹣1.【总结归纳】本题考查了反比例函数图象上点的坐标特征,正确的理解题意是解题的关键.14.如图,在菱形ABCD中,AB=6,∠B=60°,点E在边AD上,且AE=2.若直线l经过点E,将该菱形的面积平分,并与菱形的另一边交于点F,则线段EF的长为.【知识考点】菱形的性质.【思路分析】过点A和点E作AG⊥BC,EH⊥BC于点G和H,可得矩形AGHE,再根据菱形ABCD中,AB=6,∠B=60°,可得BG=3,AG=3=EH,由题意可得,FH=FC﹣HC=2﹣1=1,进而根据勾股定理可得EF的长.【解题过程】解:如图,过点A和点E作AG⊥BC,EH⊥BC于点G和H,得矩形AGHE,∴GH=AE=2,∵在菱形ABCD中,AB=6,∠B=60°,∴BG=3,AG=3=EH,∴HC=BC﹣BG﹣GH=6﹣3﹣2=1,∵EF平分菱形面积,∴FC=AE=2,∴FH=FC﹣HC=2﹣1=1,在Rt△EFH中,根据勾股定理,得EF===2.故答案为:2.【总结归纳】本题考查了菱形的性质,解决本题的关键是掌握菱形的性质.三、解答题(共11小题,计78分.解答应写出过程)15.(5分)解不等式组:【知识考点】解一元一次不等式组.【思路分析】分别求出不等式组中两不等式的解集,找出两解集的公共部分即可.【解题过程】解:,由①得:x>2,由②得:x<3,则不等式组的解集为2<x<3.【总结归纳】此题考查了解一元一次不等式组,熟练掌握不等式组的解法是解本题的关键.16.(5分)解分式方程:﹣=1.【知识考点】解分式方程.【思路分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解题过程】解:方程﹣=1,去分母得:x2﹣4x+4﹣3x=x2﹣2x,解得:x=,经检验x=是分式方程的解.【总结归纳】此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.17.(5分)如图,已知△ABC,AC>AB,∠C=45°.请用尺规作图法,在AC边上求作一点P,使∠PBC=45°.(保留作图痕迹.不写作法)【知识考点】作图—基本作图.【思路分析】根据尺规作图法,作一个角等于已知角,在AC边上求作一点P,使∠PBC=45°即可.【解题过程】解:如图,点P即为所求.【总结归纳】本题考查了作图﹣基本作图,解决本题的关键是掌握基本作图方法.18.(5分)如图,在四边形ABCD中,AD∥BC,∠B=∠C.E是边BC上一点,且DE=DC.求证:AD=BE.【知识考点】平行四边形的判定与性质.【思路分析】根据等边对等角的性质求出∠DEC=∠C,再由∠B=∠C得∠DEC=∠B,所以AB ∥DE,得出四边形ABED是平行四边形,进而得出结论.【解题过程】证明:∵DE=DC,∴∠DEC=∠C.∵∠B=∠C,∴∠B=∠DEC,∴AB∥DE,∵AD∥BC,∴四边形ABED是平行四边形.∴AD=BE.【总结归纳】本题主要考查了平行四边形的判定和性质.解题的关键是熟练掌握平行四边形的判定定理和性质定理的运用.19.(7分)王大伯承包了一个鱼塘,投放了2000条某种鱼苗,经过一段时间的精心喂养,存活率大致达到了90%.他近期想出售鱼塘里的这种鱼.为了估计鱼塘里这种鱼的总质量,王大伯随机捕捞了20条鱼,分别称得其质量后放回鱼塘.现将这20条鱼的质量作为样本,统计结果如图所示:(1)这20条鱼质量的中位数是,众数是.(2)求这20条鱼质量的平均数;(3)经了解,近期市场上这种鱼的售价为每千克18元,请利用这个样本的平均数.估计王大伯近期售完鱼塘里的这种鱼可收入多少元?【知识考点】V5:用样本估计总体;W1:算术平均数;W4:中位数;W5:众数.【思路分析】(1)根据中位数和众数的定义求解可得;(2)利用加权平均数的定义求解可得;(3)用单价乘以(2)中所得平均数,再乘以存活的数量,从而得出答案.【解题过程】解:(1)∵这20条鱼质量的中位数是第10、11个数据的平均数,且第10、11个数据分别为1.4、1.5,∴这20条鱼质量的中位数是=1.45(kg),众数是1.5kg,故答案为:1.45kg,1.5kg.(2)==1.45(kg),∴这20条鱼质量的平均数为1.45kg;(3)18×1.45×2000×90%=46980(元),答:估计王大伯近期售完鱼塘里的这种鱼可收入46980元.【总结归纳】本题考查了用样本估计总体、加权平均数、众数及中位数的知识,解题的关键是正确的用公式求得加权平均数,难度不大.20.(7分)如图所示,小明家与小华家住在同一栋楼的同一单元,他俩想测算所住楼对面商业大厦的高MN.他俩在小明家的窗台B处,测得商业大厦顶部N的仰角∠1的度数,由于楼下植物的遮挡,不能在B处测得商业大厦底部M的俯角的度数.于是,他俩上楼来到小华家,在窗台C 处测得大厦底部M的俯角∠2的度数,竟然发现∠1与∠2恰好相等.已知A,B,C三点共线,CA⊥AM,NM⊥AM,AB=31m,BC=18m,试求商业大厦的高MN.【知识考点】全等三角形的判定与性质.【思路分析】过点C作CE⊥MN于点E,过点B作BF⊥MN于点F,可得四边形AMEC和四边形AMFB均为矩形,可以证明△BFN≌△CEM,得NF=EM=49,进而可得商业大厦的高MN.【解题过程】解:如图,过点C作CE⊥MN于点E,过点B作BF⊥MN于点F,∴∠CEF=∠BFE=90°,∵CA⊥AM,NM⊥AM,∴四边形AMEC和四边形AMFB均为矩形,∴CE=BF,ME=AC,∠1=∠2,∴△BFN≌△CEM(ASA),∴NF=EM=31+18=49,由矩形性质可知:EF=CB=18,∴MN=NF+EM﹣EF=49+49﹣18=80(m).答:商业大厦的高MN为80m.【总结归纳】本题考查了全等三角形的判定与性质,解决本题的关键是掌握仰角俯角定义,构造全等三角形解决问题.21.(7分)某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗早期在农科所的温室中生长,长到大约20cm时,移至该村的大棚内,沿插杆继续向上生长.研究表明,60天内,这种瓜苗生长的高度y(cm)与生长时间x(天)之间的关系大致如图所示.(1)求y与x之间的函数关系式;(2)当这种瓜苗长到大约80cm时,开始开花结果,试求这种瓜苗移至大棚后.继续生长大约多少天,开始开花结果?【知识考点】一次函数的应用.【思路分析】(1)分段函数,利用待定系数法解答即可;(2)利用(1)的结论,把y=80代入求出x的值即可解答.【解题过程】解:(1)当0≤x≤15时,设y=kx(k≠0),则:20=15k,解得k=,∴y=;当15<x≤60时,设y=k′x+b(k≠0),则:,解得,∴y=,∴;(2)当y=80时,80=,解得x=33,33﹣15=18(天),∴这种瓜苗移至大棚后.继续生长大约18天,开始开花结果.【总结归纳】本题考查了一次函数的应用,主要利用了待定系数法求一次函数解析式,已知函数值求自变量的值,仔细观察图象,准确获取信息是解题的关键.22.(7分)小亮和小丽进行摸球试验.他们在一个不透明的空布袋内,放入两个红球,一个白球和一个黄球,共四个小球.这些小球除颜色外其它都相同.试验规则:先将布袋内的小球摇匀,再从中随机摸出一个小球,记下颜色后放回,称为摸球一次.(1)小亮随机摸球10次,其中6次摸出的是红球,求这10次中摸出红球的频率;(2)若小丽随机摸球两次,请利用画树状图或列表的方法,求这两次摸出的球中一个是白球、一个是黄球的概率.【知识考点】列表法与树状图法.【思路分析】(1)由频率定义即可得出答案;(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次摸出的球中一个是白球、一个是黄球的情况,利用概率公式求解即可求得答案.【解题过程】解:(1)小亮随机摸球10次,其中6次摸出的是红球,这10次中摸出红球的频率==;(2)画树状图得:∵共有16种等可能的结果,两次摸出的球中一个是白球、一个是黄球的有2种情况,∴两次摸出的球中一个是白球、一个是黄球的概率==.【总结归纳】本题考查的是用列表法或画树状图法求概率.注意列表法或树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.注意概率=所求情况数与总情况数之比.23.(8分)如图,△ABC是⊙O的内接三角形,∠BAC=75°,∠ABC=45°.连接AO并延长,交⊙O于点D,连接BD.过点C作⊙O的切线,与BA的延长线相交于点E.(1)求证:AD∥EC;(2)若AB=12,求线段EC的长.【知识考点】三角形的外接圆与外心;切线的性质.【思路分析】(1)连接OC,由切线的性质可得∠OCE=90°,由圆周角定理可得∠AOC=90°,可得结论;(2)过点A作AF⊥EC交EC于F,由锐角三角函数可求AD=8,可证四边形OAFC是正方形,可得CF=AF=4,由锐角三角函数可求EF=12,即可求解.【解题过程】证明:(1)连接OC,∵CE与⊙O相切于点C,∴∠OCE=90°,∵∠ABC=45°,∴∠AOC=90°,∵∠AOC+∠OCE=180°,∴∴AD∥EC(2)如图,过点A作AF⊥EC交EC于F,∵∠BAC=75°,∠ABC=45°,∴∠ACB=60°,∴∠D=∠ACB=60°,∴sin∠ADB=,∴AD==8,∴OA=OC=4,∵AF⊥EC,∠OCE=90°,∠AOC=90°,∴四边形OAFC是矩形,又∵OA=OC,∴四边形OAFC是正方形,∴CF=AF=4,∵∠BAD=90°﹣∠D=30°,∴∠EAF=180°﹣90°﹣30°=60°,∵tan∠EAF=,∴EF=AF=12,∴CE=CF+EF=12+4.【总结归纳】本题考查了切线的性质,圆周角定理,锐角三角函数,正方形的判定和性质,熟练运用这些性质进行推理是本题的关键.24.(10分)如图,抛物线y=x2+bx+c经过点(3,12)和(﹣2,﹣3),与两坐标轴的交点分别为A,B,C,它的对称轴为直线l.(1)求该抛物线的表达式;(2)P是该抛物线上的点,过点P作l的垂线,垂足为D,E是l上的点.要使以P、D、E为顶点的三角形与△AOC全等,求满足条件的点P,点E的坐标.【知识考点】二次函数综合题.【思路分析】(1)将点(3,12)和(﹣2,﹣3)代入抛物线表达式,即可求解;(2)由题意得:PD=DE=3时,以P、D、E为顶点的三角形与△AOC全等,分点P在抛物线对称轴右侧、点P在抛物线对称轴的左侧两种情况,分别求解即可.【解题过程】解:(1)将点(3,12)和(﹣2,﹣3)代入抛物线表达式得,解得,故抛物线的表达式为:y=x2+2x﹣3;(2)抛物线的对称轴为x=﹣1,令y=0,则x=﹣3或1,令x=0,则y=﹣3,故点A、B的坐标分别为(﹣3,0)、(1,0);点C(0,﹣3),故OA=OC=3,∵∠PDE=∠AOC=90°,∴当PD=DE=3时,以P、D、E为顶点的三角形与△AOC全等,设点P(m,n),当点P在抛物线对称轴右侧时,m﹣(﹣1)=3,解得:m=2,故n=22+2×2﹣3=5,故点P(2,5),故点E(﹣1,2)或(﹣1,8);当点P在抛物线对称轴的左侧时,由抛物线的对称性可得,点P(﹣4,5),此时点E坐标同上,综上,点P的坐标为(2,5)或(﹣4,5);点E的坐标为(﹣1,2)或(﹣1,8).【总结归纳】本题考查的是二次函数综合运用,涉及到三角形全等等,有一定的综合性,难度适中,其中(2)需要分类求解,避免遗漏.25.(12分)问题提出(1)如图1,在Rt△ABC中,∠ACB=90°,AC>BC,∠ACB的平分线交AB于点D.过点D分别作DE⊥AC,DF⊥BC.垂足分别为E,F,则图1中与线段CE相等的线段是.问题探究(2)如图2,AB是半圆O的直径,AB=8.P是上一点,且=2,连接AP,BP.∠APB的平分线交AB于点C,过点C分别作CE⊥AP,CF⊥BP,垂足分别为E,F,求线段CF 的长.问题解决(3)如图3,是某公园内“少儿活动中心”的设计示意图.已知⊙O的直径AB=70m,点C在⊙O上,且CA=CB.P为AB上一点,连接CP并延长,交⊙O于点D.连接AD,BD.过点P 分别作PE⊥AD,PF⊥BD,垂足分别为E,F.按设计要求,四边形PEDF内部为室内活动区,阴影部分是户外活动区,圆内其余部分为绿化区.设AP的长为x(m),阴影部分的面积为y(m2).①求y与x之间的函数关系式;②按照“少儿活动中心”的设计要求,发现当AP的长度为30m时,整体布局比较合理.试求当AP=30m时.室内活动区(四边形PEDF)的面积.【知识考点】圆的综合题.【思路分析】(1)证明四边形CEDF是正方形,即可得出结果;(2)连接OP,由AB是半圆O的直径,=2,得出∠APB=90°,∠AOP=60°,则∠ABP=30°,同(1)得四边形PECF是正方形,得PF=CF,在Rt△APB中,PB=AB•cos∠ABP =4,在Rt△CFB中,BF==CF,推出PB=CF+BF,即可得出结果;(3)①同(1)得四边形DEPF是正方形,得出PE=PF,∠APE+∠BPF=90°,∠PEA=∠PFB =90°,将△APE绕点P逆时针旋转90°,得到△A′PF,PA′=PA,则A′、F、B三点共线,∠APE=∠A′PF,证∠A′PB=90°,得出S△PAE+S△PBF=S△PA′B=PA′•PB=x(70﹣x),在Rt△ACB中,AC=BC=35,S△ACB=AC2=1225,由y=S△PA′B+S△ACB,即可得出结果;②当AP=30时,A′P=30,PB=40,在Rt△A′PB中,由勾股定理得A′B==50,由S△A′PB=A′B•PF=PB•A′P,求PF,即可得出结果.【解题过程】解:(1)∵∠ACB=90°,DE⊥AC,DF⊥BC,∴四边形CEDF是矩形,∵CD平分∠ACB,DE⊥AC,DF⊥BC,∴DE=DF,∴四边形CEDF是正方形,∴CE=CF=DE=DF,故答案为:CF、DE、DF;(2)连接OP,如图2所示:∵AB是半圆O的直径,=2,∴∠APB=90°,∠AOP=×180°=60°,∴∠ABP=30°,同(1)得:四边形PECF是正方形,∴PF=CF,在Rt△APB中,PB=AB•cos∠ABP=8×cos30°=8×=4,在Rt△CFB中,BF====CF,∵PB=PF+BF,∴PB=CF+BF,即:4=CF+CF,解得:CF=6﹣2;(3)①∵AB为⊙O的直径,∴∠ACB=∠ADB=90°,∵CA=CB,∴∠ADC=∠BDC,同(1)得:四边形DEPF是正方形,∴PE=PF,∠APE+∠BPF=90°,∠PEA=∠PFB=90°,∴将△APE绕点P逆时针旋转90°,得到△A′PF,PA′=PA,如图3所示:则A′、F、B三点共线,∠APE=∠A′PF,∴∠A′PF+∠BPF=90°,即∠A′PB=90°,21∴S △PAE +S △PBF =S △PA ′B =PA ′•PB =x (70﹣x ), 在Rt △ACB 中,AC =BC =AB =×70=35, ∴S △ACB =AC 2=×(35)2=1225,∴y =S △PA ′B +S △ACB =x (70﹣x )+1225=﹣x 2+35x+1225; ②当AP =30时,A ′P =30,PB =AB ﹣AP =70﹣30=40,在Rt △A ′PB 中,由勾股定理得:A ′B ===50, ∵S △A ′PB =A ′B •PF =PB •A ′P , ∴×50×PF =×40×30,解得:PF =24,∴S 四边形PEDF =PF 2=242=576(m 2),∴当AP =30m 时.室内活动区(四边形PEDF )的面积为576m 2.【总结归纳】本题是圆综合题,主要考查了圆周角定理、勾股定理、矩形的判定、正方形的判定与性质、角平分线的性质、旋转的性质、三角函数定义、三角形面积与正方形面积的计算等知识;熟练掌握圆周角定理和正方形的判定与性质是解题的关键.。
2020年陕西省中考数学试卷及答案解析

2020年陕西省中考数学试卷一、选择题(共10小题,每小题3分,计30分.每小题只有一个选项是符合题意的)1.(3分)﹣18的相反数是( )A .18B .﹣18C .118D .−1182.(3分)若∠A =23°,则∠A 余角的大小是( )A .57°B .67°C .77°D .157°3.(3分)2019年,我国国内生产总值约为990870亿元,将数字990870用科学记数法表示为( )A .9.9087×105B .9.9087×104C .99.087×104D .99.087×1034.(3分)如图,是A 市某一天的气温随时间变化的情况,则这天的日温差(最高气温与最低气温的差)是( )A .4℃B .8℃C .12℃D .16℃ 5.(3分)计算:(−23x 2y )3=( )A .﹣2x 6y 3B .827x 6y 3C .−827x 6y 3D .−827x 5y 4 6.(3分)如图,在3×3的网格中,每个小正方形的边长均为1,点A ,B ,C 都在格点上,若BD 是△ABC 的高,则BD 的长为( )A .1013√13B .913√13C .813√13D .713√137.(3分)在平面直角坐标系中,O 为坐标原点.若直线y =x +3分别与x 轴、直线y =﹣2x交于点A 、B ,则△AOB 的面积为( )A .2B .3C .4D .68.(3分)如图,在▱ABCD 中,AB =5,BC =8.E 是边BC 的中点,F 是▱ABCD 内一点,且∠BFC =90°.连接AF 并延长,交CD 于点G .若EF ∥AB ,则DG 的长为( )A .52B .32C .3D .29.(3分)如图,△ABC 内接于⊙O ,∠A =50°.E 是边BC 的中点,连接OE 并延长,交⊙O 于点D ,连接BD ,则∠D 的大小为( )A .55°B .65°C .60°D .75°10.(3分)在平面直角坐标系中,将抛物线y =x 2﹣(m ﹣1)x +m (m >1)沿y 轴向下平移3个单位.则平移后得到的抛物线的顶点一定在( )A .第一象限B .第二象限C .第三象限D .第四象限二、填空题(共4小题,每小题3分,计12分)11.(3分)计算:(2+√3)(2−√3)= .12.(3分)如图,在正五边形ABCDE 中,DM 是边CD 的延长线,连接BD ,则∠BDM 的度数是 .13.(3分)在平面直角坐标系中,点A (﹣2,1),B (3,2),C (﹣6,m )分别在三个不同的象限.若反比例函数y =k x (k ≠0)的图象经过其中两点,则m 的值为 .14.(3分)如图,在菱形ABCD 中,AB =6,∠B =60°,点E 在边AD 上,且AE =2.若直线l 经过点E ,将该菱形的面积平分,并与菱形的另一边交于点F ,则线段EF 的长为 .三、解答题(共11小题,计78分.解答应写出过程)15.(5分)解不等式组:{3x >6,2(5−x)>4.16.(5分)解分式方程:x−2x −3x−2=1.17.(5分)如图,已知△ABC ,AC >AB ,∠C =45°.请用尺规作图法,在AC 边上求作一点P ,使∠PBC =45°.(保留作图痕迹.不写作法)18.(5分)如图,在四边形ABCD 中,AD ∥BC ,∠B =∠C .E 是边BC 上一点,且DE =DC .求证:AD =BE .19.(7分)王大伯承包了一个鱼塘,投放了2000条某种鱼苗,经过一段时间的精心喂养,存活率大致达到了90%.他近期想出售鱼塘里的这种鱼.为了估计鱼塘里这种鱼的总质量,王大伯随机捕捞了20条鱼,分别称得其质量后放回鱼塘.现将这20条鱼的质量作为样本,统计结果如图所示:(1)这20条鱼质量的中位数是 ,众数是 .(2)求这20条鱼质量的平均数;(3)经了解,近期市场上这种鱼的售价为每千克18元,请利用这个样本的平均数.估计王大伯近期售完鱼塘里的这种鱼可收入多少元?20.(7分)如图所示,小明家与小华家住在同一栋楼的同一单元,他俩想测算所住楼对面商业大厦的高MN.他俩在小明家的窗台B处,测得商业大厦顶部N的仰角∠1的度数,由于楼下植物的遮挡,不能在B处测得商业大厦底部M的俯角的度数.于是,他俩上楼来到小华家,在窗台C处测得大厦底部M的俯角∠2的度数,竟然发现∠1与∠2恰好相等.已知A,B,C三点共线,CA⊥AM,NM⊥AM,AB=31m,BC=18m,试求商业大厦的高MN.21.(7分)某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗早期在农科所的温室中生长,长到大约20cm时,移至该村的大棚内,沿插杆继续向上生长.研究表明,60天内,这种瓜苗生长的高度y(cm)与生长时间x(天)之间的关系大致如图所示.(1)求y与x之间的函数关系式;(2)当这种瓜苗长到大约80cm时,开始开花结果,试求这种瓜苗移至大棚后.继续生长大约多少天,开始开花结果?22.(7分)小亮和小丽进行摸球试验.他们在一个不透明的空布袋内,放入两个红球,一个白球和一个黄球,共四个小球.这些小球除颜色外其它都相同.试验规则:先将布袋内的小球摇匀,再从中随机摸出一个小球,记下颜色后放回,称为摸球一次.(1)小亮随机摸球10次,其中6次摸出的是红球,求这10次中摸出红球的频率;(2)若小丽随机摸球两次,请利用画树状图或列表的方法,求这两次摸出的球中一个是白球、一个是黄球的概率.23.(8分)如图,△ABC是⊙O的内接三角形,∠BAC=75°,∠ABC=45°.连接AO并延长,交⊙O于点D,连接BD.过点C作⊙O的切线,与BA的延长线相交于点E.(1)求证:AD∥EC;(2)若AB=12,求线段EC的长.24.(10分)如图,抛物线y=x2+bx+c经过点(3,12)和(﹣2,﹣3),与两坐标轴的交点分别为A,B,C,它的对称轴为直线l.(1)求该抛物线的表达式;(2)P是该抛物线上的点,过点P作l的垂线,垂足为D,E是l上的点.要使以P、D、E为顶点的三角形与△AOC全等,求满足条件的点P,点E的坐标.25.(12分)问题提出(1)如图1,在Rt△ABC中,∠ACB=90°,AC>BC,∠ACB的平分线交AB于点D.过点D分别作DE⊥AC,DF⊥BC.垂足分别为E,F,则图1中与线段CE相等的线段是.问题探究̂上一点,且PB̂=2PÂ,连接AP,BP.∠(2)如图2,AB是半圆O的直径,AB=8.P是ABAPB的平分线交AB于点C,过点C分别作CE⊥AP,CF⊥BP,垂足分别为E,F,求线段CF的长.问题解决(3)如图3,是某公园内“少儿活动中心”的设计示意图.已知⊙O的直径AB=70m,点C在⊙O上,且CA=CB.P为AB上一点,连接CP并延长,交⊙O于点D.连接AD,BD.过点P分别作PE⊥AD,PF⊥BD,重足分别为E,F.按设计要求,四边形PEDF内部为室内活动区,阴影部分是户外活动区,圆内其余部分为绿化区.设AP的长为x(m),阴影部分的面积为y(m2).①求y与x之间的函数关系式;②按照“少儿活动中心”的设计要求,发现当AP的长度为30m时,整体布局比较合理.试求当AP=30m时.室内活动区(四边形PEDF)的面积.2020年陕西省中考数学试卷参考答案与试题解析一、选择题(共10小题,每小题3分,计30分.每小题只有一个选项是符合题意的)1.(3分)﹣18的相反数是()A.18B.﹣18C.118D.−118【解答】解:﹣18的相反数是:18.故选:A.2.(3分)若∠A=23°,则∠A余角的大小是()A.57°B.67°C.77°D.157°【解答】解:∵∠A=23°,∴∠A的余角是90°﹣23°=67°.故选:B.3.(3分)2019年,我国国内生产总值约为990870亿元,将数字990870用科学记数法表示为()A.9.9087×105B.9.9087×104C.99.087×104D.99.087×103【解答】解:990870=9.9087×105,故选:A.4.(3分)如图,是A市某一天的气温随时间变化的情况,则这天的日温差(最高气温与最低气温的差)是()A.4℃B.8℃C.12℃D.16℃【解答】解:从折线统计图中可以看出,这一天中最高气温8℃,最低气温是﹣4℃,这一天中最高气温与最低气温的差为12℃,故选:C.5.(3分)计算:(−23x2y)3=()A .﹣2x 6y 3B .827x 6y 3C .−827x 6y 3D .−827x 5y 4 【解答】解:(−23x 2y )3=(−23)3⋅(x 2)3⋅y 3=−827x 6y 3. 故选:C . 6.(3分)如图,在3×3的网格中,每个小正方形的边长均为1,点A ,B ,C 都在格点上,若BD 是△ABC 的高,则BD 的长为( )A .1013√13 B .913√13 C .813√13 D .713√13 【解答】解:由勾股定理得:AC =√22+32=√13, ∵S △ABC =3×3−12×1×2−12×1×3−12×2×3=3.5,∴12AC ⋅BD =72, ∴√13⋅BD =7,∴BD =7√1313, 故选:D .7.(3分)在平面直角坐标系中,O 为坐标原点.若直线y =x +3分别与x 轴、直线y =﹣2x交于点A 、B ,则△AOB 的面积为( )A .2B .3C .4D .6【解答】解:在y =x +3中,令y =0,得x =﹣3,解{y =x +3y =−2x得,{x =−1y =2, ∴A (﹣3,0),B (﹣1,2),∴△AOB 的面积=12×3×2=3,故选:B .8.(3分)如图,在▱ABCD 中,AB =5,BC =8.E 是边BC 的中点,F 是▱ABCD 内一点,且∠BFC =90°.连接AF 并延长,交CD 于点G .若EF ∥AB ,则DG 的长为( )A .52B .32C .3D .2【解答】解:∵E 是边BC 的中点,且∠BFC =90°,∴Rt △BCF 中,EF =12BC =4,∵EF ∥AB ,AB ∥CG ,E 是边BC 的中点,∴F 是AG 的中点,∴EF 是梯形ABCG 的中位线,∴CG =2EF ﹣AB =3,又∵CD =AB =5,∴DG =5﹣3=2,故选:D .9.(3分)如图,△ABC 内接于⊙O ,∠A =50°.E 是边BC 的中点,连接OE 并延长,交⊙O 于点D ,连接BD ,则∠D 的大小为( )A .55°B .65°C .60°D .75°【解答】解:连接CD ,∵∠A =50°,∴∠CDB =180°﹣∠A =130°,∵E 是边BC 的中点,∴OD ⊥BC ,∴BD =CD ,∴∠ODB =∠ODC =12∠BDC =65°,故选:B .10.(3分)在平面直角坐标系中,将抛物线y =x 2﹣(m ﹣1)x +m (m >1)沿y 轴向下平移3个单位.则平移后得到的抛物线的顶点一定在( )A .第一象限B .第二象限C .第三象限D .第四象限 【解答】解:∵y =x 2﹣(m ﹣1)x +m =(x −m−12)2+m −(m−1)24, ∴该抛物线顶点坐标是(m−12,m −(m−1)24), ∴将其沿y 轴向下平移3个单位后得到的抛物线的顶点坐标是(m−12,m −(m−1)24−3), ∵m >1,∴m ﹣1>0,∴m−12>0,∵m −(m−1)24−3=4m−(m 2−2m+1)−124=−(m−3)2−44=−(m−3)24−1<0, ∴点(m−12,m −(m−1)24−3)在第四象限; 故选:D .二、填空题(共4小题,每小题3分,计12分)11.(3分)计算:(2+√3)(2−√3)= 1 .【解答】解:原式=22﹣(√3)2=4﹣3=1.12.(3分)如图,在正五边形ABCDE 中,DM 是边CD 的延长线,连接BD ,则∠BDM 的度数是 144° .【解答】解:因为五边形ABCDE 是正五边形,所以∠C=(5−2)⋅180°5=108°,BC=DC,所以∠BDC=180°−108°2=36°,所以∠BDM=180°﹣36°=144°,故答案为:144°.13.(3分)在平面直角坐标系中,点A(﹣2,1),B(3,2),C(﹣6,m)分别在三个不同的象限.若反比例函数y=kx(k≠0)的图象经过其中两点,则m的值为﹣1.【解答】解:∵点A(﹣2,1),B(3,2),C(﹣6,m)分别在三个不同的象限,点A (﹣2,1)在第二象限,∴点C(﹣6,m)一定在第三象限,∵B(3,2)在第一象限,反比例函数y=kx(k≠0)的图象经过其中两点,∴反比例函数y=kx(k≠0)的图象经过B(3,2),C(﹣6,m),∴3×2=﹣6m,∴m=﹣1,故答案为:﹣1.14.(3分)如图,在菱形ABCD中,AB=6,∠B=60°,点E在边AD上,且AE=2.若直线l经过点E,将该菱形的面积平分,并与菱形的另一边交于点F,则线段EF的长为2√7.【解答】解:如图,过点A和点E作AG⊥BC,EH⊥BC于点G和H,得矩形AGHE,∴GH=AE=2,∵在菱形ABCD中,AB=6,∠B=60°,∴BG =3,AG =3√3=EH ,∴HC =BC ﹣BG ﹣GH =6﹣3﹣2=1,∵EF 平分菱形面积,∴FC =AE =2,∴FH =FC ﹣HC =2﹣1=1,在Rt △EFH 中,根据勾股定理,得EF =√EH 2+FH 2=√27+1=2√7.故答案为:2√7.三、解答题(共11小题,计78分.解答应写出过程)15.(5分)解不等式组:{3x >6,2(5−x)>4.【解答】解:{3x >6①2(5−x)>4②, 由①得:x >2,由②得:x <3,则不等式组的解集为2<x <3.16.(5分)解分式方程:x−2x −3x−2=1. 【解答】解:方程x−2x −3x−2=1,去分母得:x 2﹣4x +4﹣3x =x 2﹣2x ,解得:x =45,经检验x =45是分式方程的解.17.(5分)如图,已知△ABC ,AC >AB ,∠C =45°.请用尺规作图法,在AC 边上求作一点P ,使∠PBC =45°.(保留作图痕迹.不写作法)【解答】解:如图,点P即为所求.18.(5分)如图,在四边形ABCD中,AD∥BC,∠B=∠C.E是边BC上一点,且DE=DC.求证:AD=BE.【解答】证明:∵DE=DC,∴∠DEC=∠C.∵∠B=∠C,∴∠B=∠DEC,∴AB∥DE,∵AD∥BC,∴四边形ABED是平行四边形.∴AD=BE.19.(7分)王大伯承包了一个鱼塘,投放了2000条某种鱼苗,经过一段时间的精心喂养,存活率大致达到了90%.他近期想出售鱼塘里的这种鱼.为了估计鱼塘里这种鱼的总质量,王大伯随机捕捞了20条鱼,分别称得其质量后放回鱼塘.现将这20条鱼的质量作为样本,统计结果如图所示:(1)这20条鱼质量的中位数是 1.45kg,众数是 1.5kg.(2)求这20条鱼质量的平均数;(3)经了解,近期市场上这种鱼的售价为每千克18元,请利用这个样本的平均数.估计王大伯近期售完鱼塘里的这种鱼可收入多少元?【解答】解:(1)∵这20条鱼质量的中位数是第10、11个数据的平均数,且第10、11个数据分别为1.4、1.5,∴这20条鱼质量的中位数是1.4+1.52=1.45(kg),众数是1.5kg,故答案为:1.45kg,1.5kg.(2)x=1.2×1+1.3×4+1.4×5+1.5×6+1.6×2+1.7×220=1.45(kg),∴这20条鱼质量的平均数为1.45kg;(3)18×1.45×2000×90%=46980(元),答:估计王大伯近期售完鱼塘里的这种鱼可收入46980元.20.(7分)如图所示,小明家与小华家住在同一栋楼的同一单元,他俩想测算所住楼对面商业大厦的高MN.他俩在小明家的窗台B处,测得商业大厦顶部N的仰角∠1的度数,由于楼下植物的遮挡,不能在B处测得商业大厦底部M的俯角的度数.于是,他俩上楼来到小华家,在窗台C处测得大厦底部M的俯角∠2的度数,竟然发现∠1与∠2恰好相等.已知A,B,C三点共线,CA⊥AM,NM⊥AM,AB=31m,BC=18m,试求商业大厦的高MN.【解答】解:如图,过点C作CE⊥MN于点E,过点B作BF⊥MN于点F,∴∠CEF=∠BFE=90°,∵CA⊥AM,NM⊥AM,∴四边形AMEC和四边形AMFB均为矩形,∴CE=BF,ME=AC,∠1=∠2,∴△BFN≌△CEM(ASA),∴NF=EM=31+18=49,由矩形性质可知:EF=CB=18,∴MN=NF+EM﹣EF=49+49﹣18=80(m).答:商业大厦的高MN为80m.21.(7分)某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗早期在农科所的温室中生长,长到大约20cm时,移至该村的大棚内,沿插杆继续向上生长.研究表明,60天内,这种瓜苗生长的高度y(cm)与生长时间x(天)之间的关系大致如图所示.(1)求y与x之间的函数关系式;(2)当这种瓜苗长到大约80cm时,开始开花结果,试求这种瓜苗移至大棚后.继续生长大约多少天,开始开花结果?【解答】解:(1)当0≤x≤15时,设y=kx(k≠0),则:20=15k ,解得k =43,∴y =43x ;当15<x ≤60时,设y =k ′x +b (k ≠0),则:{20=15k ′+b 170=60k′+b, 解得{k ′=103b =−30, ∴y =103x −30, ∴y ={43x(0≤x ≤15)103x −30(15<x ≤60);(2)当y =80时,80=103x −30,解得x =33,33﹣15=18(天),∴这种瓜苗移至大棚后.继续生长大约18天,开始开花结果.22.(7分)小亮和小丽进行摸球试验.他们在一个不透明的空布袋内,放入两个红球,一个白球和一个黄球,共四个小球.这些小球除颜色外其它都相同.试验规则:先将布袋内的小球摇匀,再从中随机摸出一个小球,记下颜色后放回,称为摸球一次.(1)小亮随机摸球10次,其中6次摸出的是红球,求这10次中摸出红球的频率;(2)若小丽随机摸球两次,请利用画树状图或列表的方法,求这两次摸出的球中一个是白球、一个是黄球的概率.【解答】解:(1)小亮随机摸球10次,其中6次摸出的是红球,这10次中摸出红球的频率=610=35; (2)画树状图得:∵共有16种等可能的结果,两次摸出的球中一个是白球、一个是黄球的有2种情况,∴两次摸出的球中一个是白球、一个是黄球的概率=216=18.23.(8分)如图,△ABC是⊙O的内接三角形,∠BAC=75°,∠ABC=45°.连接AO并延长,交⊙O于点D,连接BD.过点C作⊙O的切线,与BA的延长线相交于点E.(1)求证:AD∥EC;(2)若AB=12,求线段EC的长.【解答】证明:(1)连接OC,∵CE与⊙O相切于点C,∴∠OCE=90°,∵∠ABC=45°,∴∠AOC=90°,∵∠AOC+∠OCE=180°,∴∴AD∥EC(2)如图,过点A作AF⊥EC交EC于F,∵∠BAC=75°,∠ABC=45°,∴∠ACB=60°,∴∠D=∠ACB=60°,∴sin∠ADB=ABAD=√32,∴AD=√3=8√3,∴OA=OC=4√3,∵AF⊥EC,∠OCE=90°,∠AOC=90°,∴四边形OAFC是矩形,又∵OA=OC,∴四边形OAFC是正方形,∴CF=AF=4√3,∵∠BAD=90°﹣∠D=30°,∴∠EAF=180°﹣90°﹣30°=60°,∵tan∠EAF=EFAF=√3,∴EF=√3AF=12,∴CE=CF+EF=12+4√3.24.(10分)如图,抛物线y=x2+bx+c经过点(3,12)和(﹣2,﹣3),与两坐标轴的交点分别为A,B,C,它的对称轴为直线l.(1)求该抛物线的表达式;(2)P是该抛物线上的点,过点P作l的垂线,垂足为D,E是l上的点.要使以P、D、E为顶点的三角形与△AOC全等,求满足条件的点P,点E的坐标.【解答】解:(1)将点(3,12)和(﹣2,﹣3)代入抛物线表达式得{12=9+3b +c −3=4−2b +c ,解得{b =2c =−3, 故抛物线的表达式为:y =x 2+2x ﹣3;(2)抛物线的对称轴为x =﹣1,令y =0,则x =﹣3或1,令x =0,则y =﹣3, 故点A 、B 的坐标分别为(﹣3,0)、(1,0);点C (0,﹣3),故OA =OC =3,∵∠PDE =∠AOC =90°,∴当PD =DE =3时,以P 、D 、E 为顶点的三角形与△AOC 全等,设点P (m ,n ),当点P 在抛物线对称轴右侧时,m ﹣(﹣1)=3,解得:m =2, 故n =22+2×2﹣5=5,故点P (2,5),故点E (﹣1,2)或(﹣1,8);当点P 在抛物线对称轴的左侧时,由抛物线的对称性可得,点P (﹣4,5),此时点E 坐标同上,综上,点P 的坐标为(2,5)或(﹣4,5);点E 的坐标为(﹣1,2)或(﹣1,8).25.(12分)问题提出(1)如图1,在Rt △ABC 中,∠ACB =90°,AC >BC ,∠ACB 的平分线交AB 于点D .过点D 分别作DE ⊥AC ,DF ⊥BC .垂足分别为E ,F ,则图1中与线段CE 相等的线段是 CF 、DE 、DF .问题探究(2)如图2,AB 是半圆O 的直径,AB =8.P 是AB ̂上一点,且PB ̂=2PA ̂,连接AP ,BP .∠APB 的平分线交AB 于点C ,过点C 分别作CE ⊥AP ,CF ⊥BP ,垂足分别为E ,F ,求线段CF的长.问题解决(3)如图3,是某公园内“少儿活动中心”的设计示意图.已知⊙O的直径AB=70m,点C在⊙O上,且CA=CB.P为AB上一点,连接CP并延长,交⊙O于点D.连接AD,BD.过点P分别作PE⊥AD,PF⊥BD,重足分别为E,F.按设计要求,四边形PEDF 内部为室内活动区,阴影部分是户外活动区,圆内其余部分为绿化区.设AP的长为x(m),阴影部分的面积为y(m2).①求y与x之间的函数关系式;②按照“少儿活动中心”的设计要求,发现当AP的长度为30m时,整体布局比较合理.试求当AP=30m时.室内活动区(四边形PEDF)的面积.【解答】解:(1)∵∠ACB=90°,DE⊥AC,DF⊥BC,∴四边形CEDF是矩形,∵CD平分∠ACB,DE⊥AC,DF⊥BC,∴DE=DF,∴四边形CEDF是正方形,∴CE=CF=DE=DF,故答案为:CF、DE、DF;(2)连接OP,如图2所示:∵AB是半圆O的直径,PB̂=2PÂ,∴∠APB=90°,∠AOP=13×180°=60°,∴∠ABP=30°,同(1)得:四边形PECF是正方形,∴PF=CF,在Rt △APB 中,PB =AB •cos ∠ABP =8×cos30°=8×√32=4√3, 在Rt △CFB 中,BF =CF tan∠ABC =CF tan30°=CF √33=√3CF , ∵PB =PF +BF ,∴PB =CF +BF ,即:4√3=CF +√3CF ,解得:CF =6﹣2√3;(3)①∵AB 为⊙O 的直径,∴∠ACB =∠ADB =90°,∵CA =CB ,∴∠ADC =∠BDC ,同(1)得:四边形DEPF 是正方形, ∴PE =PF ,∠APE +∠BPF =90°,∠PEA =∠PFB =90°,∴将△APE 绕点P 逆时针旋转90°,得到△A ′PF ,P A ′=P A ,如图3所示: 则A ′、F 、B 三点共线,∠APE =∠A ′PF ,∴∠A ′PF +∠BPF =90°,即∠A ′PB =90°,∴S △P AE +S △PBF =S △P A ′B =12P A ′•PB =12x (70﹣x ),在Rt △ACB 中,AC =BC =√22AB =√22×70=35√2,∴S △ACB =12AC 2=12×(35√2)2=1225,∴y =S △P A ′B +S △ACB =12x (70﹣x )+1225=−12x 2+35x +1225;②当AP =30时,A ′P =30,PB =AB ﹣AP =70﹣30=40,在Rt △A ′PB 中,由勾股定理得:A ′B =√A′P 2+PB 2=√302+402=50, ∵S △A ′PB =12A ′B •PF =12PB •A ′P ,∴12×50×PF =12×40×30, 解得:PF =24,∴S 四边形PEDF =PF 2=242=576(m 2),∴当AP =30m 时.室内活动区(四边形PEDF )的面积为576m 2.。
2020年陕西省中考数学试题(WORD版含答案)

2020年陕西省中考数学试卷一.选择题(共10小题,每小题3分,计30分)1.﹣18的相反数是()A.18B.﹣18C.D.﹣2.若∠A=23°,则∠A余角的大小是()A.57°B.67°C.77°D.157°3.2019年,我国国内生产总值约为990870亿元,将数字990870用科学记数法表示为()A.9.9087×105B.9.9087×104C.99.087×104D.99.087×103 4.如图,是A市某一天的气温随时间变化的情况,则这天的日温差(最高气温与最低气温的差)是()A.4℃B.8℃C.12℃D.16℃5.计算:(﹣x2y)3=()A.﹣2x6y3B.x6y3C.﹣x6y3D.﹣x5y46.如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD 是△ABC的高,则BD的长为()A.B.C.D.7.在平面直角坐标系中,O为坐标原点.若直线y=x+3分别与x轴、直线y=﹣2x交于点A、B,则△AOB的面积为()A.2B.3C.4D.68.如图,在▱ABCD中,AB=5,BC=8.E是边BC的中点,F是▱ABCD内一点,且∠BFC =90°.连接AF并延长,交CD于点G.若EF∥AB,则DG的长为()A.B.C.3D.29.如图,△ABC内接于⊙O,∠A=50°.E是边BC的中点,连接OE并延长,交⊙O于点D,连接BD,则∠D的大小为()A.55°B.65°C.60°D.75°10.在平面直角坐标系中,将抛物线y=x2﹣(m﹣1)x+m(m>1)沿y轴向下平移3个单位.则平移后得到的抛物线的顶点一定在()A.第一象限B.第二象限C.第三象限D.第四象限二.填空题(共4小题,每小题3分,计12分)11.计算:(2+)(2﹣)=.12.如图,在正五边形ABCDE中,DM是边CD的延长线,连接BD,则∠BDM的度数是.13.在平面直角坐标系中,点A(﹣2,1),B(3,2),C(﹣6,m)分别在三个不同的象限.若反比例函数y=(k≠0)的图象经过其中两点,则m的值为.14.如图,在菱形ABCD中,AB=6,∠B=60°,点E在边AD上,且AE=2.若直线l 经过点E,将该菱形的面积平分,并与菱形的另一边交于点F,则线段EF的长为.三.解答题(共11小题,,计78分)15.(5分)解不等式组:16.(5分)解分式方程:﹣=1.17.(5分)如图,已知△ABC,AC>AB,∠C=45°.请用尺规作图法,在AC边上求作一点P,使∠PBC=45°.(保留作图痕迹.不写作法)18.(5分)如图,在四边形ABCD中,AD∥BC,∠B=∠C.E是边BC上一点,且DE=DC.求证:AD=BE.19.(7分)王大伯承包了一个鱼塘,投放了2000条某种鱼苗,经过一段时间的精心喂养,存活率大致达到了90%.他近期想出售鱼塘里的这种鱼.为了估计鱼塘里这种鱼的总质量,王大伯随机捕捞了20条鱼,分别称得其质量后放回鱼塘.现将这20条鱼的质量作为样本,统计结果如图所示:(1)这20条鱼质量的中位数是,众数是.(2)求这20条鱼质量的平均数;(3)经了解,近期市场上这种鱼的售价为每千克18元,请利用这个样本的平均数.估计王大伯近期售完鱼塘里的这种鱼可收入多少元?20.(7分)如图所示,小明家与小华家住在同一栋楼的同一单元,他俩想测算所住楼对面商业大厦的高MN.他俩在小明家的窗台B处,测得商业大厦顶部N的仰角∠1的度数,由于楼下植物的遮挡,不能在B处测得商业大厦底部M的俯角的度数.于是,他俩上楼来到小华家,在窗台C处测得大厦底部M的俯角∠2的度数,竟然发现∠1与∠2恰好相等.已知A,B,C三点共线,CA⊥AM,NM⊥AM,AB=31m,BC=18m,试求商业大厦的高MN.21.(7分)某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗早期在农科所的温室中生长,长到大约20cm时,移至该村的大棚内,沿插杆继续向上生长.研究表明,60天内,这种瓜苗生长的高度y(cm)与生长时间x(天)之间的关系大致如图所示.(1)求y与x之间的函数关系式;(2)当这种瓜苗长到大约80cm时,开始开花结果,试求这种瓜苗移至大棚后.继续生长大约多少天,开始开花结果?22.小亮和小丽进行摸球试验.他们在一个不透明的空布袋内,放入两个红球,一个白球和一个黄球,共四个小球.这些小球除颜色外其它都相同.试验规则:先将布袋内的小球摇匀,再从中随机摸出一个小球,记下颜色后放回,称为摸球一次.(1)小亮随机摸球10次,其中6次摸出的是红球,求这10次中摸出红球的频率;(2)若小丽随机摸球两次,请利用画树状图或列表的方法,求这两次摸出的球中一个是白球、一个是黄球的概率.23.如图,△ABC是⊙O的内接三角形,∠BAC=75°,∠ABC=45°.连接AO并延长,交⊙O于点D,连接BD.过点C作⊙O的切线,与BA的延长线相交于点E.(1)求证:AD∥EC;(2)若AB=12,求线段EC的长.24.如图,抛物线y=x2+bx+c经过点(3,12)和(﹣2,﹣3),与两坐标轴的交点分别为A,B,C,它的对称轴为直线l.(1)求该抛物线的表达式;(2)P是该抛物线上的点,过点P作l的垂线,垂足为D,E是l上的点.要使以P、D、E为顶点的三角形与△AOC全等,求满足条件的点P,点E的坐标.25.问题提出(1)如图1,在Rt△ABC中,∠ACB=90°,AC>BC,∠ACB的平分线交AB于点D.过点D分别作DE⊥AC,DF⊥BC.垂足分别为E,F,则图1中与线段CE相等的线段是.问题探究(2)如图2,AB是半圆O的直径,AB=8.P是上一点,且=2,连接AP,BP.∠APB的平分线交AB于点C,过点C分别作CE⊥AP,CF⊥BP,垂足分别为E,F,求线段CF的长.问题解决(3)如图3,是某公园内“少儿活动中心”的设计示意图.已知⊙O的直径AB=70m,点C在⊙O上,且CA=CB.P为AB上一点,连接CP并延长,交⊙O于点D.连接AD,BD.过点P分别作PE⊥AD,PF⊥BD,重足分别为E,F.按设计要求,四边形PEDF 内部为室内活动区,阴影部分是户外活动区,圆内其余部分为绿化区.设AP的长为x(m),阴影部分的面积为y(m2).①求y与x之间的函数关系式;②按照“少儿活动中心”的设计要求,发现当AP的长度为30m时,整体布局比较合理.试求当AP=30m时.室内活动区(四边形PEDF)的面积.参考答案一.ABACC DBDBD二.11.112.144°.13.﹣1.14.2.三.15.解:,由①得:x>2,由②得:x<3,则不等式组的解集为2<x<3.16.解:方程﹣=1,去分母得:x2﹣4x+4﹣3x=x2﹣2x,解得:x=,经检验x=是分式方程的解.17.解:如图,点P即为所求.18.证明:∵DE=DC,∴∠DEC=∠C.∵∠B=∠C,∴∠B=∠DEC,∴AB∥DE,∵AD∥BC,∴四边形ABED是平行四边形.∴AD=BE.19.解:(1)∵这20条鱼质量的中位数是第10、11个数据的平均数,且第10、11个数据分别为1.4、1.5,∴这20条鱼质量的中位数是=1.45(kg),众数是1.5kg,(2)==1.45(kg),∴这20条鱼质量的平均数为1.45kg;(3)18×1.45×2000×90%=46980(元),答:估计王大伯近期售完鱼塘里的这种鱼可收入46980元.20.解:如图,过点C作CE⊥MN于点E,过点B作BF⊥MN于点F,∴∠CEF=∠BFE=90°,∵CA⊥AM,NM⊥AM,∴四边形AMEC和四边形AMFB均为矩形,∴CE=BF,ME=AC,∠1=∠2,∴△BFN≌△CEM(ASA),∴NF=EM=31+18=49,由矩形性质可知:EF=CB=18,∴MN=NF+EM﹣EF=49+49﹣18=80(m).答:商业大厦的高MN为80m.21.解:(1)当0≤x≤15时,设y=kx(k≠0),则:20=15k,解得k=,∴y=;当15<x≤60时,设y=k′x+b(k≠0),则:,解得,∴y=,∴;(2)当y=80时,80=,解得x=33,33﹣15=18(天),∴这种瓜苗移至大棚后.继续生长大约18天,开始开花结果.22.解:(1)小亮随机摸球10次,其中6次摸出的是红球,这10次中摸出红球的频率==;(2)画树状图得:∵共有16种等可能的结果,两次摸出的球中一个是白球、一个是黄球的有2种情况,∴两次摸出的球中一个是白球、一个是黄球的概率==.23.证明:(1)连接OC,∵CE与⊙O相切于点C,∴∠OCE=90°,∵∠ABC=45°,∴∠AOC=90°,∵∠AOC+∠OCE=180°,∴∴AD∥EC(2)如图,过点A作AF⊥EC交EC于F,∵∠BAC=75°,∠ABC=45°,∴∠ACB=60°,∴∠D=∠ACB=60°,∴sin∠ADB=,∴AD==8,∴OA=OC=4,∵AF⊥EC,∠OCE=90°,∠AOC=90°,∴四边形OAFC是矩形,又∵OA=OC,∴四边形OAFC是正方形,∴CF=AF=4,∵∠BAD=90°﹣∠D=30°,∴∠EAF=180°﹣90°﹣30°=60°,∵tan∠EAF=,∴EF=AF=12,∴CE=CF+EF=12+4.24.解:(1)将点(3,12)和(﹣2,﹣3)代入抛物线表达式得,解得,故抛物线的表达式为:y=x2+2x﹣3;(2)抛物线的对称轴为x=﹣1,令y=0,则x=﹣3或1,令x=0,则y=﹣3,故点A、B的坐标分别为(﹣3,0)、(1,0);点C(0,﹣3),故OA=OC=3,∵∠PDE=∠AOC=90°,∴当PD=DE=3时,以P、D、E为顶点的三角形与△AOC全等,设点P(m,n),当点P在抛物线对称轴右侧时,m﹣(﹣1)=3,解得:m=2,故n=22+2×2﹣5=5,故点P(2,5),故点E(﹣1,2)或(﹣1,8);当点P在抛物线对称轴的左侧时,由抛物线的对称性可得,点P(﹣4,5),此时点E坐标同上,综上,点P的坐标为(2,5)或(﹣4,5);点E的坐标为(﹣1,2)或(﹣1,8).25.解:(1)∵∠ACB=90°,DE⊥AC,DF⊥BC,∴四边形CEDF是矩形,∵CD平分∠ACB,DE⊥AC,DF⊥BC,∴DE=DF,∴四边形CEDF是正方形,∴CE=CF=DE=DF,(2)连接OP,如图2所示:∵AB是半圆O的直径,=2,∴∠APB=90°,∠AOP=×180°=60°,∴∠ABP=30°,同(1)得:四边形PECF是正方形,∴PF=CF,在Rt△APB中,PB=AB•cos∠ABP=8×cos30°=8×=4,在Rt△CFB中,BF====CF,∵PB=PF+BF,∴PB=CF+BF,即:4=CF+CF,解得:CF=6﹣2;(3)①∵AB为⊙O的直径,∴∠ACB=∠ADB=90°,∵CA=CB,∴∠ADC=∠BDC,同(1)得:四边形DEPF是正方形,∴PE=PF,∠APE+∠BPF=90°,∠PEA=∠PFB=90°,∴将△APE绕点P逆时针旋转90°,得到△A′PF,P A′=P A,如图3所示:则A′、F、B三点共线,∠APE=∠A′PF,∴∠A′PF+∠BPF=90°,即∠A′PB=90°,∴S△P AE+S△PBF=S△P A′B=P A′•PB=x(70﹣x),在Rt△ACB中,AC=BC=AB=×70=35,∴S△ACB=AC2=×(35)2=1225,∴y=S△P A′B+S△ACB=x(70﹣x)+1225=﹣x2+35x+1225;②当AP=30时,A′P=30,PB=AB﹣AP=70﹣30=40,在Rt△A′PB中,由勾股定理得:A′B===50,∵S△A′PB=A′B•PF=PB•A′P,∴×50×PF=×40×30,解得:PF=24,∴S四边形PEDF=PF2=242=576(m2),∴当AP=30m时.室内活动区(四边形PEDF)的面积为576m2.。
陕西省2020年中考数学试卷

陕西省2020年中考数学试卷一、选择题(共10题;共20分)1. ( 2分) (2020·陕西)﹣18的相反数是()A. 18B. ﹣18C.D. ﹣2. ( 2分) (2020·陕西)若∠A=23°,则∠A余角的大小是()A. 57°B. 67°C. 77°D. 157°3. ( 2分) (2020·陕西)2019年,我国国内生产总值约为990870亿元,将数字990870用科学记数法表示为()A. 9.9087×105B. 9.9087×104C. 99.087×104D. 99.087×1034. ( 2分) (2020·陕西)如图,是A市某一天的气温随时间变化的情况,则这天的日温差(最高气温与最低气温的差)是()A. 4℃B. 8℃C. 12℃D. 16℃5. ( 2分) (2020·陕西)计算:(﹣x2y)3=()A. ﹣2x6y3B. x6y3C. ﹣x6y3D. ﹣x5y46. ( 2分) (2020·陕西)如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为()A. B. C. D.7. ( 2分) (2020·陕西)在平面直角坐标系中,O为坐标原点.若直线y=x+3分别与x轴、直线y=﹣2x交于点A、B,则△AOB的面积为()A. 2B. 3C. 4D. 68. ( 2分) (2020·陕西)如图,在▱ABCD中,AB=5,BC=8.E是边BC的中点,F是▱ABCD内一点,且∠BFC =90°.连接AF并延长,交CD于点G.若EF∥AB,则DG的长为()A. B. C. 3 D. 29. ( 2分) (2020·陕西)如图,△ABC内接于⊙O,∠A=50°.E是边BC的中点,连接OE并延长,交⊙O 于点D,连接BD,则∠D的大小为()A. 55°B. 65°C. 60°D. 75°10. ( 2分) (2020·陕西)在平面直角坐标系中,将抛物线y=x2﹣(m﹣1)x+m(m>1)沿y轴向下平移3个单位.则平移后得到的抛物线的顶点一定在()A. 第一象限B. 第二象限C. 第三象限D. 第四象限二、填空题(共4题;共4分)11. ( 1分) (2020·陕西)计算:(2+ )(2﹣)=________.12. ( 1分) (2020·陕西)如图,在正五边形ABCDE中,DM是边CD的延长线,连接BD,则∠BDM的度数是________.13. ( 1分) (2020·陕西)在平面直角坐标系中,点A(﹣2,1),B(3,2),C(﹣6,m)分别在三个不同的象限.若反比例函数y=(k≠0)的图象经过其中两点,则m的值为________.14. ( 1分) (2020·陕西)如图,在菱形ABCD中,AB=6,∠B=60°,点E在边AD上,且AE=2.若直线l 经过点E,将该菱形的面积平分,并与菱形的另一边交于点F,则线段EF的长为________.三、解答题(共11题;共87分)15. ( 5分) (2020·陕西)解不等式组:16. ( 5分) (2020·陕西)解分式方程:.17. ( 5分) (2020·陕西)如图,已知△ABC,AC>AB,∠C=45°.请用尺规作图法,在AC边上求作一点P,使∠PBC=45°.(保留作图痕迹.不写作法)18. ( 5分) (2020·陕西)如图,在四边形ABCD中,AD∥BC,∠B=∠C.E是边BC上一点,且DE=DC.求证:AD=BE.19. ( 11分) (2020·陕西)王大伯承包了一个鱼塘,投放了2000条某种鱼苗,经过一段时间的精心喂养,存活率大致达到了90%.他近期想出售鱼塘里的这种鱼.为了估计鱼塘里这种鱼的总质量,王大伯随机捕捞了20条鱼,分别称得其质量后放回鱼塘.现将这20条鱼的质量作为样本,统计结果如图所示:(1)这20条鱼质量的中位数是________,众数是________.(2)求这20条鱼质量的平均数;(3)经了解,近期市场上这种鱼的售价为每千克18元,请利用这个样本的平均数.估计王大伯近期售完鱼塘里的这种鱼可收入多少元?20. ( 5分) (2020·陕西)如图所示,小明家与小华家住在同一栋楼的同一单元,他俩想测算所住楼对面商业大厦的高MN.他俩在小明家的窗台B处,测得商业大厦顶部N的仰角∠1的度数,由于楼下植物的遮挡,不能在B处测得商业大厦底部M的俯角的度数.于是,他俩上楼来到小华家,在窗台C处测得大厦底部M的俯角∠2的度数,竟然发现∠1与∠2恰好相等.已知A,B,C三点共线,CA⊥AM,NM⊥AM,AB =31m,BC=18m,试求商业大厦的高MN.21. ( 10分) (2020·陕西)某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗早期在农科所的温室中生长,长到大约20cm时,移至该村的大棚内,沿插杆继续向上生长.研究表明,60天内,这种瓜苗生长的高度y(cm)与生长时间x(天)之间的关系大致如图所示.(1)求y与x之间的函数关系式;(2)当这种瓜苗长到大约80cm时,开始开花结果,试求这种瓜苗移至大棚后.继续生长大约多少天,开始开花结果?22. ( 10分) (2020·陕西)小亮和小丽进行摸球试验.他们在一个不透明的空布袋内,放入两个红球,一个白球和一个黄球,共四个小球.这些小球除颜色外其它都相同.试验规则:先将布袋内的小球摇匀,再从中随机摸出一个小球,记下颜色后放回,称为摸球一次.(1)小亮随机摸球10次,其中6次摸出的是红球,求这10次中摸出红球的频率;(2)若小丽随机摸球两次,请利用画树状图或列表的方法,求这两次摸出的球中一个是白球、一个是黄球的概率.23. ( 10分) (2020·陕西)如图,△ABC是⊙O的内接三角形,∠BAC=75°,∠ABC=45°.连接AO并延长,交⊙O于点D,连接BD.过点C作⊙O的切线,与BA的延长线相交于点E.(1)求证:AD∥EC;(2)若AB=12,求线段EC的长.24. ( 10分) (2020·陕西)如图,抛物线y=x2+bx+c经过点(3,12)和(﹣2,﹣3),与两坐标轴的交点分别为A,B,C,它的对称轴为直线l.(1)求该抛物线的表达式;(2)P是该抛物线上的点,过点P作l的垂线,垂足为D,E是l上的点.要使以P、D、E为顶点的三角形与△AOC全等,求满足条件的点P,点E的坐标.25. ( 11分) (2020·陕西)如图(1)问题提出如图1,在Rt△ABC中,∠ACB=90°,AC>BC,∠ACB的平分线交AB于点D.过点D分别作DE⊥AC,DF⊥BC.垂足分别为E,F,则图1中与线段CE相等的线段是________.(2)问题探究如图2,AB是半圆O的直径,AB=8.P是上一点,且,连接AP,BP.∠APB的平分线交AB 于点C,过点C分别作CE⊥AP,CF⊥BP,垂足分别为E,F,求线段CF的长.(3)问题解决如图3,是某公园内“少儿活动中心”的设计示意图.已知⊙O的直径AB=70m,点C在⊙O上,且CA=CB.P 为AB上一点,连接CP并延长,交⊙O于点D.连接AD,BD.过点P分别作PE⊥AD,PF⊥BD,重足分别为E,F.按设计要求,四边形PEDF内部为室内活动区,阴影部分是户外活动区,圆内其余部分为绿化区.设AP的长为x(m),阴影部分的面积为y(m2).①求y与x之间的函数关系式;②按照“少儿活动中心”的设计要求,发现当AP的长度为30m时,整体布局比较合理.试求当AP=30m时.室内活动区(四边形PEDF)的面积.答案解析部分一、选择题1.【答案】A【考点】相反数及有理数的相反数【解析】【解答】解:﹣18的相反数是18.故答案为:A.【分析】在数轴上,分别位于原点的两侧,且到原点距离相等的两点所表示的数是互为相反数,根据相反数的定义可以判断答案.2.【答案】B【考点】余角、补角及其性质【解析】【解答】解:∵∠A=23°,∴∠A的余角是90°﹣23°=67°.故答案为:B.【分析】根据∠A的余角是90°﹣∠A,代入求出即可.3.【答案】A【考点】科学记数法—表示绝对值较大的数【解析】【解答】解:990870=9.9087×105.故答案为:A.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.4.【答案】C【考点】函数的图象,有理数的减法【解析】【解答】解:从折线统计图中可以看出,这一天中最高气温8℃,最低气温是﹣4℃,这一天中最高气温与最低气温的差为12℃,故答案为:C.【分析】根据A市某一天内的气温变化图,分析变化趋势和具体数值,即可求出答案.5.【答案】C【考点】积的乘方【解析】【解答】解:(﹣x2y)3==.故答案为:C.【分析】先根据积的乘方运算法则计算,再根据幂的乘方运算法则进行计算即可,积的乘方,等于每个因式乘方的积.6.【答案】D【考点】三角形的面积,勾股定理【解析】【解答】解:由勾股定理得:AC==,∵S△ABC=3×3﹣=,∴,∴,∴BD=,故答案为:D.【分析】根据勾股定理计算AC的长,利用面积和差关系可求的面积,由三角形的面积法求高即可.7.【答案】B【考点】两一次函数图象相交或平行问题【解析】【解答】解:在y=x+3中,令y=0,得x=﹣3,解得,,∴A(﹣3,0),B(﹣1,2),∴△AOB的面积=3×2=3,故答案为:B.【分析】根据方程或方程组得到A(﹣3,0),B(﹣1,2),根据三角形的面积公式即可得到结论.8.【答案】D【考点】平行四边形的性质,三角形的中位线定理,直角三角形斜边上的中线【解析】【解答】解:连接AC,交EF于点H,如图,∵E是边BC的中点,且∠BFC=90°,∴Rt△BCF中,EF=BC=4,∵EF∥AB,AB∥CG,E是边BC的中点,∴H是AC的中点,F是AG的中点,∴EH是△ABC的中位线,FH是△ACG的中位线,∴,,而FH=EF-FH=4- ,∴CG=3FH=3,又∵CD=AB=5,∴DG=5﹣3=2,故答案为:D.【分析】连接AC,依据直角三角形斜边上中线的性质,即可得到EF的长,再根据三角形中位线定理,即可得到CG的长,进而得出DG的长.9.【答案】B【考点】垂径定理,圆内接四边形的性质【解析】【解答】解:连接CD,∵∠A=50°,∴∠CDB=180°﹣∠A=130°,∵E是边BC的中点,∴OD⊥BC,∴BD=CD,∴∠ODB=∠ODC=∠BDC=65°,故答案为:B.【分析】连接CD,根据圆内接四边形的性质得到∠CDB=180°﹣∠A=130°,根据垂径定理得到OD⊥BC,求得BD=CD,根据等腰三角形的性质即可得到结论.10.【答案】D【考点】二次函数图象的几何变换【解析】【解答】解:,该抛物线顶点坐标是,,将其沿轴向下平移3个单位后得到的抛物线的顶点坐标是,,,,,,点,在第四象限;故答案为:.【分析】根据平移规律得到平移后抛物线的顶点坐标,然后结合的取值范围判断新抛物线的顶点所在的象限即可.二、填空题11.【答案】1【考点】平方差公式及应用,二次根式的性质与化简【解析】【解答】解:原式=22﹣=4﹣3=1.故答案为:1.【分析】先利用平方差公式展开得到原式=22﹣,再利用二次根式的性质化简,然后进行减法运算.12.【答案】144°【考点】多边形内角与外角,正多边形的性质【解析】【解答】解:∵五边形ABCDE是正五边形,∴∠C==108°,BC=DC,∴∠BDC==36°,∴∠BDM=180°﹣36°=144°,故答案为:144°.【分析】根据正五边形的性质和内角和为540°,求得每个内角的度数为108°,再结合等腰三角形和邻补角的定义即可解答.13.【答案】-1【考点】反比例函数的性质,反比例函数图象上点的坐标特征【解析】【解答】解:点,,分别在三个不同的象限,点在第二象限,点一定在第三象限,在第一象限,反比例函数的图象经过其中两点,反比例函数的图象经过,,,,故答案为:-1.【分析】根据已知条件得到点在第二象限,求得点一定在第三象限,由于反比例函数的图象经过其中两点,于是得到反比例函数的图象经过,,于是得到结论.14.【答案】【考点】勾股定理,菱形的性质,矩形的判定与性质【解析】【解答】解:如图,过点A和点E作AG⊥BC,EH⊥BC于点G和H,得矩形AGHE,∴GH=AE=2,∵在菱形ABCD中,AB=6,∠B=60°,∴BG=3,AG=3 =EH,∴HC=BC﹣BG﹣GH=6﹣3﹣2=1,∵EF平分菱形面积,∴FC=AE=2,∴FH=FC﹣HC=2﹣1=1,在Rt△EFH中,根据勾股定理,得EF===2 .故答案为:2 .【分析】过点A和点E作AG⊥BC,EH⊥BC于点G和H,可得矩形AGHE,再根据菱形ABCD中,AB=6,∠B=60°,可得BG=3,AG=3 =EH,由题意可得,FH=FC﹣HC=2﹣1=1,进而根据勾股定理可得EF的长.三、解答题15.【答案】解:,由①得:,由②得:,则不等式组的解集为.【考点】解一元一次不等式组【解析】【分析】分别求出不等式组中两不等式的解集,然后根据“大小小大取中间”找出两解集的公共部分即可.16.【答案】解:方程,去分母得:x2﹣4x+4﹣3x=x2﹣2x,移项得:-5x=-4,系数化为1得:x=,经检验x=是分式方程的解.【考点】解分式方程【解析】【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.17.【答案】解:如图,点P即为所求.【考点】作图—基本作图【解析】【解答】解:作法:(1)以点C为圆心,以任意长为半径画弧交AC于D,交BC于E,( 2 )以点B为圆心,以CD长为半径画弧,交BC于F,( 3 )以点F为圆心,以DE长为半径画弧,交前弧于点M,( 3 )连接BM,并延长BM与AC交于点P,则点P即为所求.【分析】根据尺规作图法,作一个角等于已知角,在AC边上求作一点P,使∠PBC=45°即可.18.【答案】证明:∵DE=DC,∴∠DEC=∠C.∵∠B=∠C,∴∠B=∠DEC,∴AB∥DE,∵AD∥BC,∴四边形ABED是平行四边形.∴AD=BE.【考点】平行四边形的判定与性质【解析】【分析】利用已知先证明AB∥DE,进而根据平行四边形的定义:两组对边平行的四边形是平行四边形,即可得出结论.19.【答案】(1)1.45kg;1.5kg(2)解:==1.45(kg),∴这20条鱼质量的平均数为1.45kg;(3)解:18×1.45×2000×90%=46980(元),答:估计王大伯近期售完鱼塘里的这种鱼可收入46980元.【考点】用样本估计总体,条形统计图,加权平均数及其计算,中位数,众数【解析】【解答】解:(1)∵这20条鱼质量的中位数是第10、11个数据的平均数,且第10、11个数据分别为1.4、1.5,∴这20条鱼质量的中位数是=1.45(kg),众数是1.5kg,故答案为:1.45kg,1.5kg.【分析】(1)根据中位数和众数的定义求解可得;(2)利用加权平均数的定义求解可得;(3)用单价乘以(2)中所得平均数,再乘以存活的数量,从而得出答案.20.【答案】解:如图,过点C作CE⊥MN于点E,过点B作BF⊥MN于点F,∴∠CEF=∠BFE=90°,∵CA⊥AM,NM⊥AM,∴四边形AMEC和四边形AMFB均为矩形,∴CE=BF,ME=AC,∠1=∠2,∴△BFN≌△CEM(ASA),∴NF=EM=31+18=49,由矩形性质可知:EF=CB=18,∴MN=NF+EM﹣EF=49+49﹣18=80(m).答:商业大厦的高MN为80m.【考点】解直角三角形的应用﹣仰角俯角问题【解析】【分析】过点C作CE⊥MN于点E,过点B作BF⊥MN于点F,可得四边形AMEC和四边形AMFB 均为矩形,可以证明△BFN≌△CEM,得NF=EM=49,进而可得商业大厦的高MN.21.【答案】(1)解:当0≤x≤15时,设y=kx(k≠0),∵y=kx(k≠0)的图象过(15,20),则:20=15k,解得k=,∴y=;当15<x≤60时,设y=k′x+b(k≠0),∵y=k′x+b(k≠0)的图象过(15,20),(60,170),则:,解得,∴y=,∴;(2)解:当y=80时,80=,解得x=33,33﹣15=18(天),∴这种瓜苗移至大棚后.继续生长大约18天,开始开花结果.【考点】一次函数的实际应用【解析】【分析】(1)分段函数,利用待定系数法解答即可;(2)利用(1)的结论,把y=80代入求出x的值即可解答.22.【答案】(1)解:小亮随机摸球10次,其中6次摸出的是红球,这10次中摸出红球的频率==;(2)解:画树状图得:∵共有16种等可能的结果,两次摸出的球中一个是白球、一个是黄球的有2种情况,∴两次摸出的球中一个是白球、一个是黄球的概率==.【考点】列表法与树状图法【解析】【分析】(1)由频率定义即可得出答案;(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次摸出的球中一个是白球、一个是黄球的情况,利用概率公式求解即可求得答案.23.【答案】(1)证明:连接OC,∵CE与⊙O相切于点C,∴∠OCE=90°,∵∠ABC=45°,∴∠AOC=90°,∵∠AOC+∠OCE=180°,∴∴AD∥EC;(2)解:如图,过点A作AF⊥EC交EC于F,∵∠BAC=75°,∠ABC=45°,∴∠ACB=60°,∴∠D=∠ACB=60°,∴sin∠ADB=,∴AD==8 ,∴OA=OC=4 ,∵AF⊥EC,∠OCE=90°,∠AOC=90°,∴四边形OAFC是矩形,又∵OA=OC,∴四边形OAFC是正方形,∴CF=AF=4 ,∵∠BAD=90°﹣∠D=30°,∴∠EAF=180°﹣90°﹣30°=60°,∵tan∠EAF=,∴EF=AF=12,∴CE=CF+EF=12+4 .【考点】圆的综合题【解析】【分析】(1)连接OC,由切线的性质可得∠OCE=90°,由圆周角定理可得∠AOC=90°,可得结论;(2)过点A作AF⊥EC交EC于F,由锐角三角函数可求AD=8 ,可证四边形OAFC是正方形,可得CF=AF=4 ,由锐角三角函数可求EF=12,即可求解.24.【答案】(1)解:将点(3,12)和(﹣2,﹣3)代入抛物线表达式得,解得,故抛物线的表达式为:y=x2+2x﹣3;(2)解:抛物线的对称轴为x=﹣1,令y=0,则x=﹣3或1,令x=0,则y=﹣3,故点A、B的坐标分别为(﹣3,0)、(1,0);点C(0,﹣3),故OA=OC=3,∵∠PDE=∠AOC=90°,∴当PD=DE=3时,以P、D、E为顶点的三角形与△AOC全等,设点P(m,n),当点P在抛物线对称轴右侧时,m﹣(﹣1)=3,解得:m=2,故n=22+2×2﹣5=5,故点P(2,5),故点E(﹣1,2)或(﹣1,8);当点P在抛物线对称轴的左侧时,由抛物线的对称性可得,点P(﹣4,5),此时点E坐标同上,综上,点P的坐标为(2,5)或(﹣4,5);点E的坐标为(﹣1,2)或(﹣1,8).【考点】二次函数的实际应用-几何问题【解析】【分析】(1)根据待定系数法,将点(3,12)和(﹣2,﹣3)代入抛物线表达式,即可求解;(2)在△AOC中,OA=OC=3,由题意:以P、D、E为顶点的三角形与△AOC全等可知PD=DE=3,再分点P在抛物线对称轴右侧、点P在抛物线对称轴的左侧两种情况,求解即可.25.【答案】(1)CF、DE、DF(2)解:连接OP,如图2所示:∵AB是半圆O的直径,,∴∠APB=90°,∠AOP=×180°=60°,∴∠ABP=30°,同(1)得:四边形PECF是正方形,∴PF=CF,在Rt△APB中,PB=AB•cos∠ABP=8×cos30°=8× =4 ,在Rt△CFB中BF====CF,∵PB=PF+BF,∴PB=CF+BF,即:4 =CF+ CF,解得:CF=6﹣2 ;(3)解:①∵AB为⊙O的直径,∴∠ACB=∠ADB=90°,∵CA=CB,∴∠ADC=∠BDC,同(1)得:四边形DEPF是正方形,∴PE=PF,∠APE+∠BPF=90°,∠PEA=∠PFB=90°,∴将△APE绕点P逆时针旋转90°,得到△A′PF,PA′=PA,如图3所示:则A′、F、B三点共线,∠APE=∠A′PF,∴∠A′PF+∠BPF=90°,即∠A′PB=90°,∴S△PAE+S△PBF=S△PA′B=PA′•PB=x(70﹣x),在Rt△ACB中,AC=BC=AB=×70=35 ,∴S△ACB=AC2=×(35 )2=1225,∴y=S△PA′B+S△ACB=x(70﹣x)+1225=﹣x2+35x+1225;②当AP=30时,A′P=30,PB=AB﹣AP=70﹣30=40,在Rt△A′PB中,由勾股定理得:A′B===50,∵S△A′PB=A′B•PF=PB•A′P,∴×50×PF=×40×30,解得:PF=24,∴S四边形PEDF=PF2=242=576(m2),∴当AP=30m时.室内活动区(四边形PEDF)的面积为576m2.【考点】圆的综合题【解析】【解答】解:(1)∵∠ACB=90°,DE⊥AC,DF⊥BC,∴四边形CEDF是矩形,∵CD平分∠ACB,DE⊥AC,DF⊥BC,∴DE=DF,∴四边形CEDF是正方形,∴CE=CF=DE=DF,故答案为:CF、DE、DF;【分析】(1)证明四边形CEDF是正方形,即可得出结果;(2)连接OP,由AB是半圆O的直径,,得出∠APB=90°,∠AOP=60°,则∠ABP=30°,同(1)得四边形PECF是正方形,得PF=CF,在Rt△APB中,PB=AB•cos∠ABP=4 ,在Rt△CFB中,BF==CF,推出PB=CF+BF,即可得出结果;(3)① 同(1)得四边形DEPF是正方形,得出PE=PF,∠APE+∠BPF=90°,∠PEA=∠PFB=90°,将△APE绕点P逆时针旋转90°,得到△A′PF,PA′=PA,则A′、F、B三点共线,∠APE=∠A′PF,证∠A′PB=90°,得出S△PAE+S△PBF=S△PA′B=PA′•PB=x(70﹣x),在Rt△ACB中,AC=BC=35 ,S△ACB=AC2=1225,由y=S△PA′B+S△ACB,即可得出结果;② 当AP=30时,A′P=30,PB=40,在Rt△A′PB 中,由勾股定理得A′B===50,由S△A′PB=A′B•PF=PB•A′P,求PF,即可得出结果.试卷分析部分1. 试卷总体分布分析2. 试卷题量分布分析3. 试卷难度结构分析4. 试卷知识点分析。
2020陕西中考数学试卷及答案

中考模拟试题一、选择题(数学老师,中学一级数学教师)1. −12的绝对值等于( )A. −2B. 2C. −12D. 122. 如图所示的几何体的俯视图是( )A. B.C. D.3. 下列计算正确的是( )A. a2⋅a3=a6B. a6÷a3=a2C. (−2a2)3=−8a6D. 4a3−3a2=14. 将一副三角板如图放置,使点a在aa上,aa∥aa,∠a=45∘,∠a=30∘,则∠aaa的度数为( )A. 10∘B. 15∘C. 20∘D. 25∘5. 正比例函数a=(2a+1)a,若a的值随a值增大而增大,则a的取值围是( )A. a>−12B. a<−12C. a=−12D. a=06. 如图,aa是△aaa的中位线,点a在aa上,且∠aaa=90∘,若aa=10,aa=16,则aa的长为( )A. 5B. 3C. 8D. 107. 一次函数 a =43a +a (a >0) 与 a =43a −1 图象之间的距离等于 3,则 a 的值为 ( ) A. 2B. 3C. 4D. 68. 如图,正方形 aaaa 的对角线 aa ,aa 相交于点 a ,aa 平分 ∠aaa 交 aa 于点 a ,若 aa =4,则线段 aa 的长为 ( )A. 43√2B. 4−2√2C. √2D. √2−29. 如图,⊙a 的半径 aa ⊥弦aa 于点 a ,连接 aa 并延长交 ⊙a 于点 a ,连接 aa ,若 aa =4,aa =1,则 aa 的长为 ( )A. √13B. 4C. √10D. √1510、已知抛物线y =x 2+(m +1)x +m ,当x =1时,y >0,且当x <-2时,y 的值随x 的增大而减小,则m的取值围是( )A. 1->mB. 3<mC. 31≤<-mD. 43≤<m二、填空题(共4小题;共12分)11. 分解因式:a 2a +2aa 2+a 3= . 12. 若正多边形的一个外角是 45∘,则该正多边形的边数是 .13. 如图,在 Rt △aaa 中,∠aaa =90∘,点 a 在 a 轴上,且 a (−12,0),a 点的横坐标是 1,aa =3aa ,双曲线 a =4aa(a >0) 经过 a 点,双曲线 a =−2aa经过 a 点,则 a 的值为 .14. 如图,△aaa中,aa=2√2,∠aaa=90∘,在aa的同侧作正△aaa、正△aaa和正△aaa,则四边形aaaa面积的最大值是.三、解答题(共11小题;共72分)15. 计算:√12+(π−2015)0+(12)−1−6tan30∘.16. 解方程a+1a−1+41−a2=1 .17. 如图,点a是⊙a上一点,请用尺规过点a作⊙a的切线(不写画法,保留作图痕迹).18. 某中学组织全体学生参加了“服务社会献爱心”的活动,为了了解九年级学生参加活动情况,从九年级学生中随机抽取部分学生进行调查,统计了该天他们打扫街道,去敬老院服务和到社区文艺演出的人数,并绘制了如下不完整的条形统计图和扇形统计图,其中到社区文艺演出的人数占所调查的九年级学生人数的310,请根据两幅统计图中的信息,回答下列问题:(1)本次调查共抽取了多少名九年级学生?(2)补全条形统计图.(3)若该中学九年级共有1400名学生,请你估计该中学九年级去敬老院的学生有多少名?19. 如图,已知:在矩形aaaa中,点a在边aa上,点a在边aa上,且aa=aa,aa⊥aa,求证:aa=aa.20. 如图,在航线a的两侧分别有观测点a和a,点a到航线a的距离aa为4km,点a位于点a北偏西60∘方向且与a相距20km处.现有一艘轮船从位于点a南偏东74∘方向的a处,沿该航线自东向西航行至观测点a的正南方向a处.求这艘轮船的航行路程aa的长度.(结果精确到0.1km)(参考数据:√3≈1.73,sin74∘≈0.96,cos74∘≈0.28,tan74∘≈3.49)21. 小是某服装厂的一名工人,负责加工A,B两种型号服装,他每月的工作时间为22天,月收入由底薪和计件工资两部分组成,其中底薪900元,加工A型服装1件可得20元,加工B 型服装1件可得12元.已知小每天可加工A型服装4件或B型服装8件,设他每月加工A 型服装的时间为a天,月收入为a元.(1)求a与a的函数关系式;(2)根据服装厂要求,小每月加工A型服装数量应不少于B型服装数量的3,那么他的月收入5最高能达到多少元?22. 某化妆品专卖店,为了吸引顾客,在“母亲节”当天举办了某种品牌化妆品有奖酬宾活动,凡购物满188元者,有两种奖励方案供选择,一是直接获得18元的礼金券,二是得到一次摇奖的机会.已知在摇奖机装有2个红球和2个白球,除颜色外其它都相同,摇奖者必须从摇奖机一次连续摇出两个球,根据球的颜色决定送礼金券的多少(如表).(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率.(2)如果一名顾客当天在本店购物满188元,若只考虑获得最多的礼金券,请你帮助分析选择哪种方案较为实惠.23. 如图,aa为⊙a的切线,a为切点,过a作aa的垂线aa,垂足为a,交⊙a于点a,连接aa,aa,并延长aa交⊙a于点a,与aa的延长线交于点a.(1)求证:aa是⊙a的切线;,aa=16,求aa的长.(2)若tan a=51224. 如图,抛物线a=−a2+a+6与a轴交于a,a两点,点a在点a的左侧,抛物线与a轴交于点a,抛物线的顶点为a,直线a过点a交a轴于a(6,0).(1)写出顶点a的坐标和直线a的解析式;(2)点a在a轴的正半轴上运动,过a作a轴的平行线,交直线a于点a,交抛物线于点a,连接aa,将△aaa沿aa翻转,a的对应点为aa.探究:是否存在点a,使得aa恰好落在a轴上?若存在,请求出a的坐标;若不存在,请说明理由.25. (1)如图①,点a、点a在直线a的同侧,请你在直线a上找一点a,使得aa+aa的值最小(不需要说明理由);(2)如图②,菱形aaaa的边长为6,对角线aa=6√3,点a,a在aa上,且aa=2,求aa+aa的最小值;(3)如图③,四边形aaaa中,aa=aa=6,∠aaa=60∘,∠aaa=120∘,四边形aaaa的周长是否存在最大值,若存在,请求出最大值;若不存在,请说明理由.答案第二部分13. 316【解析】过点a作aa⊥a轴于点a,过点a作aa⊥a轴于点a,∵a点的横坐标是1,且在双曲线a=4aa上,∴a(1,4a),∵∠aaa=90∘,∴∠aaa+∠aaa=∠aaa+∠aaa=90∘,∠aaa=∠aaa,∴△aaa∽△aaa,∴aaaa =aaaa=aaaa=13,∴aa=12,aa=4a3,∴a(−12−4a3,12),∵双曲线a=−2aa经过a点,∴12(−12−4a3)=−2a,∴a=316.14. 2【解析】如图,延长aa交aa于点a,∵∠aaa=90∘,∠aaa=∠aaa=60∘,∴∠aaa=150∘,∴∠aaa=180∘−150∘=30∘,∴aa平分∠aaa,又∵aa=aa,∴aa⊥aa,设Rt△aaa中,aa=a,aa=a,则aa=12aa=12a,a2+a2=8,∵△aaa和△aaa都是等边三角形,∴aa=aa,aa=aa,∠aaa=∠aaa=60∘,∴∠aaa=∠aaa,在△aaa和△aaa中,{aa=aa,∠aaa=∠aaa, aa=aa,∴△aaa≌△aaa(SAS),∴aa=aa=aa,同理可得:△aaa≌△aaa(SAS),∴aa=aa=aa,∴四边形aaaa是平行四边形,∴a四边形aaaa =aa×aa=a×12a=12aa,又∵(a−a)2=a2−2aa+a2≥0,∴2aa≤a2+a2=8,∴12aa≤2,即四边形aaaa面积的最大值为2.14. a(a+a)2第三部分15. 原式=2√3+1+2−6×√3 3=3. 16. 原方程可变为:a+1 a−1−4(a+1)(a−1)=1.两边同时乘以(a+1)(a−1),得:(a+1)2−4=(a+1)(a−1).解得:a=1.检验:把a=1代入(a+1)(a−1)得:(a+1)(a−1)=0.所以a=1不是方程的解,即原方程无解17. 连接aa并延长,过a作aa的垂线,即为⊙a的切线,如图所示:18. (1)根据题意得:15÷310=50(名),则本次共抽取了50名九年级学生.(2)去敬老院服务的学生有50−(25+15)=10(名).(3)根据题意得:1400×1050=280(名),则该中学九年级去敬老院的学生约有280名.19. 因为四边形aaaa为矩形,所以∠a=∠a=90∘,因为aa⊥aa,所以∠aaa=90∘,所以∠aaa+∠aaa=∠aaa+∠aaa=90∘,所以∠aaa=∠aaa,在△aaa和△aaa中,{∠aaa=∠aaa,∠a=∠a,aa=aa.所以△aaa≌△aaa,所以aa=aa.20. 如图,在Rt△aaa中,∵∠aaa=60∘,aa=4km,∴aa=aacos60∘=8km,∵aa=20km,∴aa=12km,∵∠aaa=∠aaa,∠aaa=∠aaa,∴△aaa∽△aaa,∴aaaa =aaaa,∴aa=6km,在Rt△aaa中,aa=aa⋅tan74∘≈20.9km.故这艘轮船的航行路程aa的长度是20.9km..21. (1)依题意得a=20×4a+12×8(22−a)+900,即a与a的函数关系式为a=−16a+3012.(2)依题意得4a≥35×8(22−a),∴a≥12.在a=−16a+3012中,−16<0,∴a随a的增大而减小,∴当a=12时,a取得最大值,此时a=−16×12+3012=2820.答:他月收入最高能达到2820元.22. (1)树状图为:∴一共有6种等可能的情况,摇出一红一白的情况共有4种,摇出一红一白的概率=23.(2)∵两红的概率a=16,两白的概率a=16,一红一白的概率a=23,∴摇奖的平均收益是:16×12+23×24+16×12=20(元).∵20>18,∴顾客应该选择摇奖.23. (1)连接aa,则aa=aa,∵aa⊥aa,∴aa=aa,∴aa是aa的垂直平分线,∴aa=aa,在△aaa和△aaa中,∵{aa=aa, aa=aa, aa=aa,∴△aaa≌△aaa,∴∠aaa =∠aaa ,aa =aa ,∵aa 为 ⊙a 的切线,a 为切点,∴∠aaa =90∘,∴∠aaa =90∘,即 aa ⊥aa ,∴aa 是 ⊙a 的切线.(2) ∵tan a =512,∴ 设 aa =5a ,aa =12a ,则 aa =13a ,∴aa =8a ,由切割线定理得,aa 2=aa ⋅aa ,即 (8a )2=16×(12a ),∴a =3,∴aa =39.24. (1) 当 a =0 时,a =−a 2+a +6=6,则 a (0,6),a =−a 2+a +6=−(a −12)2+234, 则 a 点坐标为 (12,234), 设直线 a 的解析式为 a =aa +a ,把 a (0,6),a (6,0) 代入得 {6a +a =0,a =6, 解得 {a =−1,a =6,∴ 直线 a 的解析式为 a =−a +6. (2) 存在.直线 aa 交 a 轴于点 a ,作 aa ⊥a 于点 a ,如图,利用折叠的性质得 aa 平分 ∠aaaa ,则根据角平分线的性质得 aa =aa ,设 aa =a ,则 aa =a ,aa =6−a ,∵aa =aa ,∴△aaa 为等腰直角三角形,∴∠aaa =45∘,∴△aaa 为等腰直角三角形,∴aa =√2aa ,即 6−a =√2a ,解得 a =6(√2−1),∴a (6(√2−1),0),设直线 aa 的解析式为 a =aa +a ,a (0,6),a (6(√2−1),0) 代入得 {a =6,6(√2−1)a +a =0, 解得 {a =−(√2+1),a =6,∴ 直线 aa 的解析式为 a =−(√2+1)a +6,解方程组 {a =−a 2+a +6,a =−(√2+1)a +6, 得 {a =0,a =6 或 {a =2+√2,a =2−3√2,∴a (2+√2,2−3√2),∵aa ⊥a 轴,∴a (2+√2,0).25. (1) 如图 ① 中,作点 a 关于直线 a 的对称点 aa ,连接 aaa 交直线 a 于点 a ,连接 aa ,则点 a 即为所求的点.(2) 如图 ② 中,作 aa ∥aa ,使得 aa =aa =2,连接 aa 交 aa 于点 a ,∵aa =aa ,aa ∥aa ,∴ 四边形 aaaa 是平行四边形,∴aa =aa ,∴aa +aa =aa +aa =aa ,根据两点之间线段最短可知,此时 aa +aa 最短,∵ 四边形 aaaa 是菱形,∴aa ⊥aa ,aa =aa =3√3,在 Rt △aaa 中,aa =√aa 2−aa 2=3,∴aa =6,∵aa ∥aa ,∴∠aaa =∠aaa =90∘,∴aa =√aa 2+aa 2=√62+22=2√10.∴aa +aa 的最小值为 2√10.(3)四边形aaaa的周长存在最大值.如图③中,连接aa,aa,在aa上取一点,使得aa=aa.∵∠aaa=60∘,∠aaa=120∘,∴∠aaa+∠aaa=180∘,∴a,a,a,a四点共圆,∵aa=aa,∠aaa=60∘,∴△aaa是等边三角形,∴∠aaa=∠aaa=60∘,∵aa=aa,∴△aaa是等边三角形,∴∠aaa=∠aaa=60∘,aa=aa,∴∠aaa=∠aaa,在△aaa和△aaa中,{aa=aa,∠aaa=∠aaa, aa=aa,∴△aaa≌△aaa,∴aa=aa,∴aa=aa+aa=aa+aa,∵四边形aaaa的周长=aa+aa+aa+aa=aa+aa+aa,∵aa=aa=6,∴当aa最大时,四边形aaaa的周长最大,∴当aa为△aaa的外接圆的直径时,四边形aaaa的周长最大,易知aa的最大值= 4√3,∴四边形aaaa的周长最大值为12+4√3.。
2020陕西中考数学试题(含答案)

7.在平面直角坐标系中,0为坐标原点.若直线j =x+3分别与x轴.直线y = -2x交于点4、B. 则△408的面积为()S.如图.在O48CD中・.48:5./?C=8. £是边2。
的中点,F是口4BCD内一点,且HT=90。
,连接4尸并延长,交CD于点G.若EF 〃 AB .则。
G的长为()A I)(第8题图)9.如图,ZUBC内接于。
,4=5(T,£是边£C的中点,连接。
£并延长,交。
于点Q,连接BD, WJN0的大小为()D(第9题图)A. 55°B. 65°C. 60°D. 75°10.在于而直角坐标系中,将抛物线工十皿〃>1)沿y轴向下平移3个单位,则平移后得到的抛物线的顶点一定在()A.第一象限B.第二象限C.第三象限D.第四象限第二部分(非选择题共90分)二、填空题(共4小题,每小题3分,计12分)11.ii算:|2 +石“2-6)=.12.如图,在正五边形/J8C0E中,D.〃是边C0的延长殁.连接80,则45DW的度数是(第12题图)13 .在平面直角坐标系中•点.4(-2. 1), 8(3.2),分别在三个不同的象限,若反比例的数,=%人工0)的图您经过其中两点,则,〃的值为.14 .如图,在菱形/8CD 中,48 = 6, 4=60。
,点E 在边4。
上,且/£ = 2,若直线/经过点£,将 该菱形的面积平分,并与菱形的另一边交千点F,则地段EF 的长为.D三、解答题(共11小题,计加分,解答应写出过程) 15 .(本题满分5分) 16 .(本麴满分5分)V-? 3解分式方程:——^-=1.X A-2解不等式组:3x)62(5-x)>4 (第14题17.(本题本分5分)如图,已知△,4孔,.4c>4B, NC=45。
,请用尺规作图法,在抚边上求作一点尸,“BC =45,(保留作图痕迹,不写作法)24.(本题满分10分)如图,抛物线尸f ♦以经过点(3. 12)和(-2, -3).与两坐标轴的交点分别为,4、八C它的对称轴为直线/.(I)求该抛物线的表达式:(2)P是该抛物线上的点,过点尸作/的垂线,垂足为0, E是I卜.的点,要使以0、D、E为项点的三角形与全等,求满足条件的点八点E的坐标.5(1225 .(本题满分12分)问题提出(1)如图1.在RiAHBC, ZJCff=90°. AC>BC. 4CB 的平分线交于点O ,过点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
陕西省2020年中考数学试卷一.选择题(共10小题)1.﹣18的相反数是()A.18B.﹣18C.D.﹣2.若∠A=23°,则∠A余角的大小是()A.57°B.67°C.77°D.157°3.2019年,我国国内生产总值约为990870亿元,将数字990870用科学记数法表示为() A.9.9087×105B.9.9087×104C.99.087×104D.99.087×103 4.如图,是A市某一天的气温随时间变化的情况,则这天的日温差(最高气温与最低气温的差)是()A.4℃B.8℃C.12℃D.16℃5.计算:(﹣x2y)3=()A.﹣2x6y3B.x6y3C.﹣x6y3D.﹣x5y46.如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD 是△ABC的高,则BD的长为()A.B.C.D.7.在平面直角坐标系中,O为坐标原点.若直线y=x+3分别与x轴、直线y=﹣2x交于点A、B,则△AOB的面积为()A.2B.3C.4D.68.如图,在▱ABCD中,AB=5,BC=8.E是边BC的中点,F是▱ABCD内一点,且∠BFC =90°.连接AF并延长,交CD于点G.若EF∥AB,则DG的长为()A.B.C.3D.29.如图,△ABC内接于⊙O,∠A=50°.E是边BC的中点,连接OE并延长,交⊙O于点D,连接BD,则∠D的大小为()A.55°B.65°C.60°D.75°10.在平面直角坐标系中,将抛物线y=x2﹣(m﹣1)x+m(m>1)沿y轴向下平移3个单位.则平移后得到的抛物线的顶点一定在()A.第一象限B.第二象限C.第三象限D.第四象限二.填空题(共4小题)11.计算:(2+)(2﹣)=.12.如图,在正五边形ABCDE中,DM是边CD的延长线,连接BD,则∠BDM的度数是.13.在平面直角坐标系中,点A(﹣2,1),B(3,2),C(﹣6,m)分别在三个不同的象限.若反比例函数y=(k≠0)的图象经过其中两点,则m的值为.14.如图,在菱形ABCD中,AB=6,∠B=60°,点E在边AD上,且AE=2.若直线l 经过点E,将该菱形的面积平分,并与菱形的另一边交于点F,则线段EF的长为.三.解答题(共11小题)15.解不等式组:16.解分式方程:﹣=1.17.如图,已知△ABC,AC>AB,∠C=45°.请用尺规作图法,在AC边上求作一点P,使∠PBC=45°.(保留作图痕迹.不写作法)18.如图,在四边形ABCD中,AD∥BC,∠B=∠C.E是边BC上一点,且DE=DC.求证:AD=BE.19.王大伯承包了一个鱼塘,投放了2000条某种鱼苗,经过一段时间的精心喂养,存活率大致达到了90%.他近期想出售鱼塘里的这种鱼.为了估计鱼塘里这种鱼的总质量,王大伯随机捕捞了20条鱼,分别称得其质量后放回鱼塘.现将这20条鱼的质量作为样本,统计结果如图所示:(1)这20条鱼质量的中位数是,众数是.(2)求这20条鱼质量的平均数;(3)经了解,近期市场上这种鱼的售价为每千克18元,请利用这个样本的平均数.估计王大伯近期售完鱼塘里的这种鱼可收入多少元?20.如图所示,小明家与小华家住在同一栋楼的同一单元,他俩想测算所住楼对面商业大厦的高MN.他俩在小明家的窗台B处,测得商业大厦顶部N的仰角∠1的度数,由于楼下植物的遮挡,不能在B处测得商业大厦底部M的俯角的度数.于是,他俩上楼来到小华家,在窗台C处测得大厦底部M的俯角∠2的度数,竟然发现∠1与∠2恰好相等.已知A,B,C三点共线,CA⊥AM,NM⊥AM,AB=31m,BC=18m,试求商业大厦的高MN.21.某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗早期在农科所的温室中生长,长到大约20cm时,移至该村的大棚内,沿插杆继续向上生长.研究表明,60天内,这种瓜苗生长的高度y(cm)与生长时间x(天)之间的关系大致如图所示.(1)求y与x之间的函数关系式;(2)当这种瓜苗长到大约80cm时,开始开花结果,试求这种瓜苗移至大棚后.继续生长大约多少天,开始开花结果?22.小亮和小丽进行摸球试验.他们在一个不透明的空布袋内,放入两个红球,一个白球和一个黄球,共四个小球.这些小球除颜色外其它都相同.试验规则:先将布袋内的小球摇匀,再从中随机摸出一个小球,记下颜色后放回,称为摸球一次.(1)小亮随机摸球10次,其中6次摸出的是红球,求这10次中摸出红球的频率;(2)若小丽随机摸球两次,请利用画树状图或列表的方法,求这两次摸出的球中一个是白球、一个是黄球的概率.23.如图,△ABC是⊙O的内接三角形,∠BAC=75°,∠ABC=45°.连接AO并延长,交⊙O于点D,连接BD.过点C作⊙O的切线,与BA的延长线相交于点E.(1)求证:AD∥EC;(2)若AB=12,求线段EC的长.24.如图,抛物线y=x2+bx+c经过点(3,12)和(﹣2,﹣3),与两坐标轴的交点分别为A,B,C,它的对称轴为直线l.(1)求该抛物线的表达式;(2)P是该抛物线上的点,过点P作l的垂线,垂足为D,E是l上的点.要使以P、D、E为顶点的三角形与△AOC全等,求满足条件的点P,点E的坐标.25.问题提出(1)如图1,在Rt△ABC中,∠ACB=90°,AC>BC,∠ACB的平分线交AB于点D.过点D分别作DE⊥AC,DF⊥BC.垂足分别为E,F,则图1中与线段CE相等的线段是.问题探究(2)如图2,AB是半圆O的直径,AB=8.P是上一点,且=2,连接AP,BP.∠APB的平分线交AB于点C,过点C分别作CE⊥AP,CF⊥BP,垂足分别为E,F,求线段CF的长.问题解决(3)如图3,是某公园内“少儿活动中心”的设计示意图.已知⊙O的直径AB=70m,点C在⊙O上,且CA=CB.P为AB上一点,连接CP并延长,交⊙O于点D.连接AD,BD.过点P分别作PE⊥AD,PF⊥BD,重足分别为E,F.按设计要求,四边形PEDF 内部为室内活动区,阴影部分是户外活动区,圆内其余部分为绿化区.设AP的长为x(m),阴影部分的面积为y(m2).①求y与x之间的函数关系式;②按照“少儿活动中心”的设计要求,发现当AP的长度为30m时,整体布局比较合理.试求当AP=30m时.室内活动区(四边形PEDF)的面积.2020年陕西省中考数学试卷参考答案与试题解析一.选择题(共10小题)1.﹣18的相反数是()A.18B.﹣18C.D.﹣【分析】直接利用相反数的定义得出答案.【解答】解:﹣18的相反数是:18.故选:A.2.若∠A=23°,则∠A余角的大小是()A.57°B.67°C.77°D.157°【分析】根据∠A的余角是90°﹣∠A,代入求出即可.【解答】解:∵∠A=23°,∴∠A的余角是90°﹣23°=67°.故选:B.3.2019年,我国国内生产总值约为990870亿元,将数字990870用科学记数法表示为() A.9.9087×105B.9.9087×104C.99.087×104D.99.087×103【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n 的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.【解答】解:990870=9.9087×105,故选:A.4.如图,是A市某一天的气温随时间变化的情况,则这天的日温差(最高气温与最低气温的差)是()A.4℃B.8℃C.12℃D.16℃【分析】根据A市某一天内的气温变化图,分析变化趋势和具体数值,即可求出答案.【解答】解:从折线统计图中可以看出,这一天中最高气温8℃,最低气温是﹣4℃,这一天中最高气温与最低气温的差为12℃,故选:C.5.计算:(﹣x2y)3=()A.﹣2x6y3B.x6y3C.﹣x6y3D.﹣x5y4【分析】根据积的乘方运算法则计算即可,积的乘方,等于每个因式乘方的积.【解答】解:(﹣x2y)3==.故选:C.6.如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD 是△ABC的高,则BD的长为()A.B.C.D.【分析】根据勾股定理计算AC的长,利用面积差可得三角形ABC的面积,由三角形的面积公式即可得到结论.【解答】解:由勾股定理得:AC==,∵S△ABC=3×3﹣=3.5,∴,∴,∴BD=,故选:D.7.在平面直角坐标系中,O为坐标原点.若直线y=x+3分别与x轴、直线y=﹣2x交于点A、B,则△AOB的面积为()A.2B.3C.4D.6【分析】根据方程或方程组得到A(﹣3,0),B(﹣1,2),根据三角形的面积公式即可得到结论.【解答】解:在y=x+3中,令y=0,得x=﹣3,解得,,∴A(﹣3,0),B(﹣1,2),∴△AOB的面积=3×2=3,故选:B.8.如图,在▱ABCD中,AB=5,BC=8.E是边BC的中点,F是▱ABCD内一点,且∠BFC =90°.连接AF并延长,交CD于点G.若EF∥AB,则DG的长为()A.B.C.3D.2【分析】依据直角三角形斜边上中线的性质,即可得到EF的长,再根据梯形中位线定理,即可得到CG的长,进而得出DG的长.【解答】解:∵E是边BC的中点,且∠BFC=90°,∴Rt△BCF中,EF=BC=4,∵EF∥AB,AB∥CG,E是边BC的中点,∴F是AG的中点,∴EF是梯形ABCG的中位线,∴CG=2EF﹣AB=3,又∵CD=AB=5,∴DG=5﹣3=2,故选:D.9.如图,△ABC内接于⊙O,∠A=50°.E是边BC的中点,连接OE并延长,交⊙O于点D,连接BD,则∠D的大小为()A.55°B.65°C.60°D.75°【分析】连接CD,根据圆内接四边形的性质得到∠CDB=180°﹣∠A=130°,根据垂径定理得到OD⊥BC,求得BD=CD,根据等腰三角形的性质即可得到结论.【解答】解:连接CD,∵∠A=50°,∴∠CDB=180°﹣∠A=130°,∵E是边BC的中点,∴OD⊥BC,∴BD=CD,∴∠ODB=∠ODC=BDC=65°,故选:B.10.在平面直角坐标系中,将抛物线y=x2﹣(m﹣1)x+m(m>1)沿y轴向下平移3个单位.则平移后得到的抛物线的顶点一定在()A.第一象限B.第二象限C.第三象限D.第四象限【分析】根据平移规律得到平移后抛物线的顶点坐标,然后结合m的取值范围判断新抛物线的顶点所在的象限即可.【解答】解:∵y=x2﹣(m﹣1)x+m=(x﹣)2+m﹣,∴该抛物线顶点坐标是(,m﹣),∴将其沿y轴向下平移3个单位后得到的抛物线的顶点坐标是(,m﹣﹣3),∵m>1,∴m﹣1>0,∴>0,∵m﹣﹣3===﹣﹣1<0,∴点(,m﹣﹣3)在第四象限;故选:D.二.填空题(共4小题)11.计算:(2+)(2﹣)=1.【分析】先利用平方差公式展开得到原式=22﹣()2,再利用二次根式的性质化简,然后进行减法运算.【解答】解:原式=22﹣()2=4﹣3=1.12.如图,在正五边形ABCDE中,DM是边CD的延长线,连接BD,则∠BDM的度数是144°.【分析】根据正五边形的性质和内角和为540°,求得每个内角的度数为108°,再结合等腰三角形和邻补角的定义即可解答.【解答】解:因为五边形ABCDE是正五边形,所以∠C==108°,BC=DC,所以∠BDC==36°,所以∠BDM=180°﹣36°=144°,故答案为:144°.13.在平面直角坐标系中,点A(﹣2,1),B(3,2),C(﹣6,m)分别在三个不同的象限.若反比例函数y=(k≠0)的图象经过其中两点,则m的值为﹣1.【分析】根据已知条件得到点A(﹣2,1)在第三象限,求得点C(﹣6,m)一定在第三象限,由于反比例函数y=(k≠0)的图象经过其中两点,于是得到反比例函数y=(k≠0)的图象经过B(3,2),C(﹣6,m),于是得到结论.【解答】解:∵点A(﹣2,1),B(3,2),C(﹣6,m)分别在三个不同的象限,点A(﹣2,1)在第二象限,∴点C(﹣6,m)一定在第三象限,∵B(3,2)在第一象限,反比例函数y=(k≠0)的图象经过其中两点,∴反比例函数y=(k≠0)的图象经过B(3,2),C(﹣6,m),∴3×2=﹣6m,∴m=﹣1,故答案为:﹣1.14.如图,在菱形ABCD中,AB=6,∠B=60°,点E在边AD上,且AE=2.若直线l 经过点E,将该菱形的面积平分,并与菱形的另一边交于点F,则线段EF的长为2.【分析】过点A和点E作AG⊥BC,EH⊥BC于点G和H,可得矩形AGHE,再根据菱形ABCD中,AB=6,∠B=60°,可得BG=3,AG=3=EH,由题意可得,FH=FC ﹣HC=2﹣1=1,进而根据勾股定理可得EF的长.【解答】解:如图,过点A和点E作AG⊥BC,EH⊥BC于点G和H,得矩形AGHE,∴GH=AE=2,∵在菱形ABCD中,AB=6,∠B=60°,∴BG=3,AG=3=EH,∴HC=BC﹣BG﹣GH=6﹣3﹣2=1,∵EF平分菱形面积,∴FC=AE=2,∴FH=FC﹣HC=2﹣1=1,在Rt△EFH中,根据勾股定理,得EF===2.故答案为:2.三.解答题(共11小题)15.解不等式组:【分析】分别求出不等式组中两不等式的解集,找出两解集的方法部分即可.【解答】解:,由①得:x>2,由②得:x<3,则不等式组的解集为2<x<3.16.解分式方程:﹣=1.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:方程﹣=1,去分母得:x2﹣4x+4﹣3x=x2﹣2x,解得:x=,经检验x=是分式方程的解.17.如图,已知△ABC,AC>AB,∠C=45°.请用尺规作图法,在AC边上求作一点P,使∠PBC=45°.(保留作图痕迹.不写作法)【分析】根据尺规作图法,作一个角等于已知角,在AC边上求作一点P,使∠PBC=45°即可.【解答】解:如图,点P即为所求.18.如图,在四边形ABCD中,AD∥BC,∠B=∠C.E是边BC上一点,且DE=DC.求证:AD=BE.【分析】根据等边对等角的性质求出∠DEC=∠C,在由∠B=∠C得∠DEC=∠B,所以AB∥DE,得出四边形ABCD是平行四边形,进而得出结论.【解答】证明:∵DE=DC,∴∠DEC=∠C.∵∠B=∠C,∴∠B=∠DEC,∴AB∥DE,∵AD∥BC,∴四边形ABED是平行四边形.∴AD=BE.19.王大伯承包了一个鱼塘,投放了2000条某种鱼苗,经过一段时间的精心喂养,存活率大致达到了90%.他近期想出售鱼塘里的这种鱼.为了估计鱼塘里这种鱼的总质量,王大伯随机捕捞了20条鱼,分别称得其质量后放回鱼塘.现将这20条鱼的质量作为样本,统计结果如图所示:(1)这20条鱼质量的中位数是 1.45kg,众数是 1.5kg.(2)求这20条鱼质量的平均数;(3)经了解,近期市场上这种鱼的售价为每千克18元,请利用这个样本的平均数.估计王大伯近期售完鱼塘里的这种鱼可收入多少元?【分析】(1)根据中位数和众数的定义求解可得;(2)利用加权平均数的定义求解可得;(3)用单价乘以(2)中所得平均数,再乘以存活的数量,从而得出答案.【解答】解:(1)∵这20条鱼质量的中位数是第10、11个数据的平均数,且第10、11个数据分别为1.4、1.5,∴这20条鱼质量的中位数是=1.45(kg),众数是1.5kg,故答案为:1.45kg,1.5kg.(2)==1.45(kg),∴这20条鱼质量的平均数为1.45kg;(3)18×1.45×2000×90%=46980(元),答:估计王大伯近期售完鱼塘里的这种鱼可收入46980元.20.如图所示,小明家与小华家住在同一栋楼的同一单元,他俩想测算所住楼对面商业大厦的高MN.他俩在小明家的窗台B处,测得商业大厦顶部N的仰角∠1的度数,由于楼下植物的遮挡,不能在B处测得商业大厦底部M的俯角的度数.于是,他俩上楼来到小华家,在窗台C处测得大厦底部M的俯角∠2的度数,竟然发现∠1与∠2恰好相等.已知A,B,C三点共线,CA⊥AM,NM⊥AM,AB=31m,BC=18m,试求商业大厦的高MN.【分析】过点C作CE⊥MN于点E,过点B作BF⊥MN于点F,可得四边形AMEC和四边形AMFB均为矩形,可以证明△BFN≌△CEM,得NF=EM=49,进而可得商业大厦的高MN.【解答】解:如图,过点C作CE⊥MN于点E,过点B作BF⊥MN于点F,∴∠CEF=∠BFE=90°,∵CA⊥AM,NM⊥AM,∴四边形AMEC和四边形AMFB均为矩形,∴CE=BF,ME=AC,∠1=∠2,∴△BFN≌△CEM(ASA),∴NF=EM=31+18=49,由矩形性质可知:EF=CB=18,∴MN=NF+EM﹣EF=49+49﹣18=80(m).答:商业大厦的高MN为80m.21.某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗早期在农科所的温室中生长,长到大约20cm时,移至该村的大棚内,沿插杆继续向上生长.研究表明,60天内,这种瓜苗生长的高度y(cm)与生长时间x(天)之间的关系大致如图所示.(1)求y与x之间的函数关系式;(2)当这种瓜苗长到大约80cm时,开始开花结果,试求这种瓜苗移至大棚后.继续生长大约多少天,开始开花结果?【分析】(1)分段函数,利用待定系数法解答即可;(2)利用(1)的结论,把y=80代入求出x的值即可解答.【解答】解:(1)当0≤x≤15时,设y=kx(k≠0),则:20=15k,解得k=,∴y=;当15<x≤60时,设y=k′x+b(k≠0),则:,解得,∴y=,∴;(2)当y=80时,80=,解得x=33,33﹣15=18(天),∴这种瓜苗移至大棚后.继续生长大约18天,开始开花结果.22.小亮和小丽进行摸球试验.他们在一个不透明的空布袋内,放入两个红球,一个白球和一个黄球,共四个小球.这些小球除颜色外其它都相同.试验规则:先将布袋内的小球摇匀,再从中随机摸出一个小球,记下颜色后放回,称为摸球一次.(1)小亮随机摸球10次,其中6次摸出的是红球,求这10次中摸出红球的频率;(2)若小丽随机摸球两次,请利用画树状图或列表的方法,求这两次摸出的球中一个是白球、一个是黄球的概率.【分析】(1)由频率定义即可得出答案;(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次摸出的球中一个是白球、一个是黄球的情况,利用概率公式求解即可求得答案.【解答】解:(1)小亮随机摸球10次,其中6次摸出的是红球,这10次中摸出红球的频率==;(2)画树状图得:∵共有16种等可能的结果,两次摸出的球中一个是白球、一个是黄球的有2种情况,∴两次摸出的球中一个是白球、一个是黄球的概率==.23.如图,△ABC是⊙O的内接三角形,∠BAC=75°,∠ABC=45°.连接AO并延长,交⊙O于点D,连接BD.过点C作⊙O的切线,与BA的延长线相交于点E.(1)求证:AD∥EC;(2)若AB=12,求线段EC的长.【分析】(1)连接OC,由切线的性质可得∠OCE=90°,由圆周角定理可得∠AOC=90°,可得结论;(2)过点A作AF⊥EC交EC于F,由锐角三角函数可求AD=8,可证四边形OAFC是正方形,可得CF=AF=4,由锐角三角函数可求EF=12,即可求解.【解答】证明:(1)连接OC,∵CE与⊙O相切于点C,∴∠OCE=90°,∵∠ABC=45°,∴∠AOC=90°,∵∠AOC+∠OCE=180°,∴∴AD∥EC(2)如图,过点A作AF⊥EC交EC于F,∵∠BAC=75°,∠ABC=45°,∴∠ACB=60°,∴∠D=∠ACB=60°,∴sin∠ADB=,∴AD==8,∴OA=OC=4,∵AF⊥EC,∠OCE=90°,∠AOC=90°,∴四边形OAFC是矩形,又∵OA=OC,∴四边形OAFC是正方形,∴CF=AF=4,∵∠BAD=90°﹣∠D=30°,∴∠EAF=180°﹣90°﹣30°=60°,∵tan∠EAF=,∴EF=AF=12,∴CE=CF+EF=12+4.24.如图,抛物线y=x2+bx+c经过点(3,12)和(﹣2,﹣3),与两坐标轴的交点分别为A,B,C,它的对称轴为直线l.(1)求该抛物线的表达式;(2)P是该抛物线上的点,过点P作l的垂线,垂足为D,E是l上的点.要使以P、D、E为顶点的三角形与△AOC全等,求满足条件的点P,点E的坐标.【分析】(1)将点(3,12)和(﹣2,﹣3)代入抛物线表达式,即可求解;(2)由题意得:PD=DE=3时,以P、D、E为顶点的三角形与△AOC全等,分点P在抛物线对称轴右侧、点P在抛物线对称轴的左侧两种情况,分别求解即可.【解答】解:(1)将点(3,12)和(﹣2,﹣3)代入抛物线表达式得,解得,故抛物线的表达式为:y=x2+2x﹣3;(2)抛物线的对称轴为x=﹣1,令y=0,则x=﹣3或1,令x=0,则y=﹣3,故点A、B的坐标分别为(﹣3,0)、(1,0);点C(0,﹣3),故OA=OC=3,∵∠PDE=∠AOC=90°,∴当PD=DE=3时,以P、D、E为顶点的三角形与△AOC全等,设点P(m,n),当点P在抛物线对称轴右侧时,m﹣(﹣1)=3,解得:m=2,故n=22+2×2﹣5=5,故点P(2,5),故点E(﹣1,2)或(﹣1,8);当点P在抛物线对称轴的左侧时,由抛物线的对称性可得,点P(﹣4,5),此时点E坐标同上,综上,点P的坐标为(2,5)或(﹣4,5);点E的坐标为(﹣1,2)或(﹣1,8).25.问题提出(1)如图1,在Rt△ABC中,∠ACB=90°,AC>BC,∠ACB的平分线交AB于点D.过点D分别作DE⊥AC,DF⊥BC.垂足分别为E,F,则图1中与线段CE相等的线段是CF、DE、DF.问题探究(2)如图2,AB是半圆O的直径,AB=8.P是上一点,且=2,连接AP,BP.∠APB的平分线交AB于点C,过点C分别作CE⊥AP,CF⊥BP,垂足分别为E,F,求线段CF的长.问题解决(3)如图3,是某公园内“少儿活动中心”的设计示意图.已知⊙O的直径AB=70m,点C在⊙O上,且CA=CB.P为AB上一点,连接CP并延长,交⊙O于点D.连接AD,BD.过点P分别作PE⊥AD,PF⊥BD,重足分别为E,F.按设计要求,四边形PEDF 内部为室内活动区,阴影部分是户外活动区,圆内其余部分为绿化区.设AP的长为x(m),阴影部分的面积为y(m2).①求y与x之间的函数关系式;②按照“少儿活动中心”的设计要求,发现当AP的长度为30m时,整体布局比较合理.试求当AP=30m时.室内活动区(四边形PEDF)的面积.【分析】(1)证明四边形CEDF是正方形,即可得出结果;(2)连接OP,由AB是半圆O的直径,=2,得出∠APB=90°,∠AOP=60°,则∠ABP=30°,同(1)得四边形PECF是正方形,得PF=CF,在Rt△APB中,PB=AB•cos ∠ABP=4,在Rt△CFB中,BF==CF,推出PB=CF+BF,即可得出结果;(3)①同(1)得四边形DEPF是正方形,得出PE=PF,∠APE+∠BPF=90°,∠PEA=∠PFB=90°,将△APE绕点P逆时针旋转90°,得到△A′PF,P A′=P A,则A′、F、B三点共线,∠APE=∠A′PF,证∠A′PB=90°,得出S△P AE+S△PBF=S△P A′B=P A′•PB=x(70﹣x),在Rt△ACB中,AC=BC=35,S△ACB=AC2=1225,由y=S△P A′B+S△ACB,即可得出结果;②当AP=30时,A′P=30,PB=40,在Rt△A′PB中,由勾股定理得A′B==50,由S△A′PB=A′B•PF=PB•A′P,求PF,即可得出结果.【解答】解:(1)∵∠ACB=90°,DE⊥AC,DF⊥BC,∴四边形CEDF是矩形,∵CD平分∠ACB,DE⊥AC,DF⊥BC,∴DE=DF,∴四边形CEDF是正方形,∴CE=CF=DE=DF,故答案为:CF、DE、DF;(2)连接OP,如图2所示:∵AB是半圆O的直径,=2,∴∠APB=90°,∠AOP=×180°=60°,∴∠ABP=30°,同(1)得:四边形PECF是正方形,∴PF=CF,在Rt△APB中,PB=AB•cos∠ABP=8×cos30°=8×=4,在Rt△CFB中,BF====CF,∵PB=PF+BF,∴PB=CF+BF,即:4=CF+CF,解得:CF=6﹣2;(3)①∵AB为⊙O的直径,∴∠ACB=∠ADB=90°,∵CA=CB,∴∠ADC=∠BDC,同(1)得:四边形DEPF是正方形,∴PE=PF,∠APE+∠BPF=90°,∠PEA=∠PFB=90°,∴将△APE绕点P逆时针旋转90°,得到△A′PF,P A′=P A,如图3所示:则A′、F、B三点共线,∠APE=∠A′PF,∴∠A′PF+∠BPF=90°,即∠A′PB=90°,∴S△P AE+S△PBF=S△P A′B=P A′•PB=x(70﹣x),在Rt△ACB中,AC=BC=AB=×70=35,∴S△ACB=AC2=×(35)2=1225,∴y=S△P A′B+S△ACB=x(70﹣x)+1225=﹣x2+35x+1225;②当AP=30时,A′P=30,PB=AB﹣AP=70﹣30=40,在Rt△A′PB中,由勾股定理得:A′B===50,∵S△A′PB=A′B•PF=PB•A′P,∴×50×PF=×40×30,解得:PF=24,∴S四边形PEDF=PF2=242=576(m2),∴当AP=30m时.室内活动区(四边形PEDF)的面积为576m2.。
