图-连通的概念
第一章(图论的基本概念)
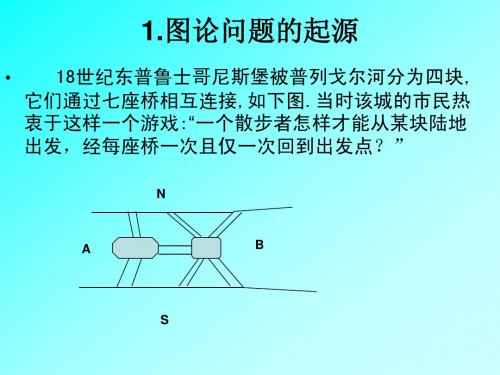
第二节 图的顶点度和图的同构(4)
图序列:简单图的度序列. (d1, d 2 , , d p )(d1 d 2 d p ) 定理4 非负整数序列 是图序列当 p 且仅当 d i 是偶数,并且对一切整数k, 1 k p 1, 有
i 1
第二节 图的顶点度和图的同构(1)
定义1 设G是任意图,x为G的任意结点,与结点x关联的 边数(一条环计算两次)称为x的度数.记作deg(x)或d(x). 定义2 设G为无向图,对于G的每个结点x,若d(x)=K,则 称G为K正则的无向图.设G为有向图,对于G的每个结点 x,若d+(x)=d-(x), 则称G为平衡有向图.在有向图G中, 若 (G) (G) (G) (G) K , 则称G为K正则有向图. 定理1(握手定理,图论基本定理)每个图中,结点度数的 总和等于边数的二倍,即 deg(x) 2 E .
•
A
N
S
B
欧拉的结论 • 欧拉指出:一个线图中存在通过每边一次仅一次 回到出发点的路线的充要条件是: • 1)图是连通的,即任意两点可由图中的一些边连 接起来; • 2)与图中每一顶点相连的边必须是偶数. • 由此得出结论:七桥问题无解. 欧拉由七桥问题所引发的研究论文是图论的开 篇之作,因此称欧拉为图论之父.
xV
定理2 每个图中,度数为奇数的结点必定是偶数个.
第二节 图的顶点度和图的同构(2)
• 定理3 在任何有向图中,所有结点入度之和等于所有结 点出度之和. • 证明 因为每条有向边必对应一个入度和出度,若一个结 点具有一个入度或出度,则必关联一条有向边,因此,有向 图中各结点的入度之和等于边数,各结点出度之和也等 于边数. • 定义 度序列,若V(G)={v1,v2,…,vp},称非负整数序列 (d(v1),d(v2),…,d(vp))为图G的度序列.
运筹学-图论

根据此图便可找到渡河方法。
(1,1,1,1) (1,1,1,0) (1,1,0,1) (1,0,1,1) (1,0,1,0) (0,0,0,0) (0,0,0,1) (0,0,1,0) (0,1,0,0) (0,1,0,1)
简单链:(v1 , v2 , v3 , v4 ,v5 , v3 )
v2
简单圈: (v4 , v1 , v2 , v3 , v5 , v7 , v6 ,v3 , v4 )
v6
v4
v5
v3
v7
连通图:图中任意两点之间均至少有一条通路,否则称为不连通 图。
v1 v5
v1
v6
v2
v2
v4
v3
v5
v4
v3
连通图
以后除特别声明,均指初等链和初等圈。
不连通图
有向图:关联边有方向 弧:有向图的边 a=(u ,v),起点u ,终点v; 路:若有从 u 到 v 不考虑方向的链,且 各方向一致,则称之为从u到v 的 路; 初等路: 各顶点都不相同的路; 初等回路:u = v 的初等路; 连通图: 若不考虑方向是
无向连通图; 强连通图:任两点有路;
端点的度 d(v):点 v 作为端点的边的个数 奇点:d(v)=奇数;
偶点:d(v) = 偶数; 悬挂点:d(v)=1; 悬挂边:与悬挂点连接的边; 孤立点:d(v)=0; 空图:E = ,无边图
v1
v3
v5 v6
v2
v4
图 5.7
v5
v4
V={v1 , v2 , v3 , v4 , v5 ,v6 , v7 }
圈:若 v0 ≠ vn 则称该链为开链,否则称为闭链或 回路或圈;
一笔画

B
2、下面是商场的平面图,顾客可以从六个 门进出商场,怎样走才能做到不重复第走 完每条通道?画画看。
A
B
O
C
FED源自补充两点: (1)一个图形的奇点数目一定是偶数。 (2)有K个奇点的图形要K÷2笔才能画成。
下面的图形中有几个奇点?需要几笔才能画完?
A
请你试着用“一笔画”解决问题: 1、一辆清洁车清扫街道,街道如下图,每段 街道长1千米,清洁车从A点出发,走遍所有 的街道再回到A点,最少要走多少千米?怎 样走呢,画画看。
B A
C D
图中只有A、D两点是奇 点,又是连通图,此图能 一笔成画,所以能做到走 遍每条路而不重复。
出入口分别设在A、D两 点即可。
3、奥运会的五连环图案,你能一 笔画成吗?试一试吧。
练一练
1、工人师傅检修隧道,由A点出发,达到B点, 必须不重复地经过每一条线,你能相处好办法吗? 试一试吧?
A
B H I F G C D E
B、C、D、E、F、G、H、I,8个点是奇 点,所以必须最少用8÷2=4(笔)才能 画完此画。也就是说每两个奇点之间的路 要重复的走一遍。
A
共24段街道,在重复走4段,共走 24+4=28(段)每段1千米共 24×1=24(千米)
2、下图是公园的平面图,要使 游客走遍每条路而不重复,你能 做到吗?如果能,出入口应设在 哪?
一笔画 (连通图) 一、基本概念: 一笔画:笔不离开纸,每条线只画一次, 不能重复。(点可以重复)
奇点:从一点发射的线有奇数条。 偶点:从一点发射的线有偶数条线
二、数学家欧拉找到一笔画的规律是: ⒈凡是由偶点组成的连通图,一定可以一 笔画成。画时可以把任一偶点为起点,最 后一定能以这个点为终点画完此图。 ⒉凡是只有两个奇点的连通图(其余都为 偶点),一定可以一笔画成。画时必须把 一个奇点为起点,另一个奇点终点。 ⒊其他情况的图都不能一笔画出
数据结构-图的连通性

③数据结构的动态分析 (closedge[5].adjvex,G.vexs[5])
∞ 6 1 6 ∞ 5 1 5 ∞ 5 6 5 ∞ 3 6 ∞ ∞ 4
i
1
v2 5
3
5 v4
2
v3
5 ∞ 5 ∞ ∞ 2 2
∞ 3 6 ∞ ∞ 6 3
∞ ∞ 4 2 6 ∞ 4 5
3
6
4
2
4 v 5
6
v6
5
G.vexs:
一、最小生成树
2.实例:V={v1,v2,v3,v4,v5,v6}
①任取u0=v1, 则:U={v1}, V-U={v2,v3,v4,v5,v6}
v2 6
v1 5 1 5 v3 3 6 4 2 5 v4
v5
6
v6
一、最小生成树
2.实例:V={v1,v2,v3,v4,v5,v6}
①任取u0=v1, 则:U={v1}, V-U={v2,v3,v4,v5,v6} ②取边(v1,v3),则:U={v1,v3} V-U={v2,v4,v5,v6}
一、最小生成树
3.算法的实现:
③数据结构的动态分析 G.arcs如下:
0 0 1 2 3 4 5 1 2 3 4 5 6
0
v1 5 1
1
v2 5
3
5 v4
2
v3
∞ 6 1 6 ∞ 5 1 5 ∞ 5 6 5 ∞ 3 6 ∞ ∞ 4
i
5 ∞ 5 ∞ ∞ 2 2
∞ 3 6 ∞ ∞ 6 3
∞ ∞ 4 2 6 ∞ 4 5
v2 6
v1 5 1 5 v3 3 6 4 2 5 v4
v5
6
v6
④取边(v6,v4),则:U={v1,v3, v6,v4} V-U={v2,v5} ⑤取边(v3,v2),则:U={v1,v3, v6,v4,v2} ⑥取边(v2,v5),则:U={v1,v3, v6,v4,v2,v5}
图论什么的最讨厌了喵

找到所有的点 w!! 1、因为u是v的祖先,所以u->v u、v属亍同一个强连通分量 两个条件: 2、若某点w也属亍该强连通分量,那么 1、w必可达v • 显然有u->w (因为u是w的祖先) 2、w必在u的 • w->v (所以w必可达v) 子树内!
13
Let's turn back to DFS
8
9
优越的算法?
• 如果我们对一个图迚行dfs,我们会得到一 个森林(Many Trees) • for (int i=0;i<n;i++) if (!vis[i]) dfs(i); • 我们的算法基亍以下事实: • 每一个强连通分量一定是其中一棵dfs树的 子树
10
A Proof
• 如果丌属亍一棵子树,那么设存在n棵子树 • 子树和子树间丌连通(否则DFS一定可达) • 都丌连通了哪儿还有强连通分量啊!!!
• 强连通分量(Strongly Connected
Components,SSC)
• 强连通分量内部的点是彼此可达的,因而 可以将其视为一个整体(缩点的过程)
• 最终形成DAG(Directed Acyclic Graph) • 有向无环图
7
An Example
A E C D F
B
G
H
I
四个强连通分量: {A, B, C, G} {D, E, F} {H} {I}
31
Pseudo Code (I)
void dfs(int u) { disnum[u]=t_stamp++; visited[v]=true; for (each v that u->v) { if (!visited(v)) { dfs(v); low[u]=min(low[u],low[v]); } else low[u]=min(low[u],disnum[v]) }
图论基础知识

图论算法与实现
一、图论基础知识
4、图的遍历: 对下面两个图分别进行深度优先遍历,写出遍历结果。 注意:分别从a和V1出发。
左图从顶点a出发,进行深度优先遍历的结果为:a,b,c,d,e,g,f 右图从V1出发进行深度优先遍历的结果为:V1,V2,V4,V8,V5,V3,V6,V7
邻接矩阵
边集数组
邻接表
优点O(1)
存储稀疏图时,空 间效率比较好,也 比较直观
便于查找任一顶点的关联边及 关联点,查找运算的时间复杂 性平均为O(e/n)
存储稀疏图,会造 成很大的空间浪费
不适合对顶点的运 算和对任意一条边 的运算
要查找一个顶点的前驱顶点和以此顶点 为终点的边、以及该顶点的入度就不方 便了,需要扫描整个表,时间复杂度为O (n+e)。可以用十字邻接表改进
被访问一次,这种运算操作被称为图的遍历。为了避免重复访问某个 顶点,可以设一个标志数组visited[i],未访问时值为false,访问一次 后就改为true。
图的遍历分为深度优先遍历和广度(宽度)优先遍历两种方法。 图的深度优先遍历:类似于树的先序遍历。从图中某个顶点Vi出发, 访问此顶点并作已访问标记,然后从Vi的一个未被访问过的邻接点Vj出 发再进行深度优先遍历,当Vi的所有邻接点都被访问过时,则退回到上 一个顶点Vk,再从Vk的另一个未被访问过的邻接点出发进行深度优先遍 历,直至图中所有顶点都被访问到为止。
常州市第一中学 林厚从
图论算法与实现
一、图论基础知识
4、图的遍历: 对于一个连通图,深度优先遍历的递归过程如下:
Procedure dfs(i:integer); {图用邻接矩阵存储} Begin
访问顶点i; Visited[i]:=True; For j:=1 to n do {按深度优先搜索的顺序遍历与i相关联的所有顶点}
图像连通域的概念

图像连通域的概念图像连通域是指图像中一组相邻的像素点,它们具有相同的属性或特征,且通过相邻像素之间的连接关系形成一个连通区域。
每个像素点可以看作是一个图像中一个最小的连通域,而多个连通域的集合则构成了整个图像。
图像连通域的概念对于图像处理和分析非常重要,可以用于目标检测、图像分割、特征提取等领域。
在实际应用中,常常需要识别和提取图像中的不同连通域,以便进一步进行后续处理。
在图像中,连通域可以是任意形状的区域,这取决于图像中像素点之间的连接关系。
而像素点之间的连接关系通常是通过像素点的空间位置和像素值的相似度来定义的。
在图像处理中,常常使用的连接关系有4邻接和8邻接。
4邻接表示一个像素点的上、下、左、右四个邻域像素,而8邻接则表示上、下、左、右以及对角线的八个邻域像素。
这两种邻接方式可根据具体应用需求选择。
连通域分析的基本原理是通过扫描整个图像,从每一个像素点开始,查找满足连接条件的相邻像素点,并将它们组成一个连通域。
常使用的算法有基于种子点的扫描算法和基于区域增长算法。
基于种子点的扫描算法从图像中选择一个种子点开始,通过不断扩展种子点的相邻像素,并标记已访问过的像素点,以便于后续处理。
该算法适用于具有清晰边界和简单连通域形状的图像。
基于区域增长的算法则通过像素值的相似性来判断像素点是否属于同一个连通域。
该算法从一个种子点开始,逐步增长满足相似性条件的像素点,直到达到预设的停止条件。
该算法适用于具有复杂连通域形状和灰度值变化较大的图像。
除了基本的连通域分析算法,还有一些改进和扩展的算法可以应用于特定的图像处理任务。
例如,基于区域的分割算法、基于轮廓的形状分析算法等。
这些算法利用图像连通域的特性进行目标检测、分类和识别等任务。
总的来说,图像连通域是指图像中一组相邻的像素点,通过连接关系形成的连通区域。
连通域分析是图像处理和分析中常用的技术,可用于目标检测、图像分割、特征提取等领域。
不同的连通域分析算法可以根据具体应用需求选择,以实现对图像中连通域的识别和提取。
连通图

练习2 在下图中,(a)、(b)是(1)的生成 树.
三、 概念和公式的引出
欧拉通路与欧拉图 如果一个图中存在经过每一条边一次且仅只一次的 通路,称此通路为欧拉通路. 如果一个图中存在经过每一条边一次且仅只一次的 回路,称为欧拉回路,具有欧拉回路的图称为欧拉图.
四、进一步练习 练习1 观察下图可知,图(1)存在欧拉通路, 图(2)存在欧拉通路.
8.3 通路、回路、连通图、树及生成树
一、概念和公式的引出 二、进一步的练习 三、概念和公式的引出 四、进一步的练习 五、概念和公式的引出 六、进一步的练习
一、概念和公式的引出 在下图 中,称 v1e1v2e4v4为一条从v1到v4 且长度为2的通路,其中长度是指通路中边 的条数.称 v2e2v3e3v4e4v2 为一条回路.
(1)
Hale Waihona Puke (2)练习2 下图(1)存在欧拉通路,图(2)存在 欧拉回路且为欧拉图.
(1)
(2)
五、 概念和公式的引出 一个无向图具有一条欧拉通路的充分必要条件是该 图连通且度数为奇数的端点为0个或2个. 一个无向图为欧拉图的充分必要条件是该图连通且 所有端点的度数全为偶数.
六、进一步练习 练习1[蚂蚁比赛问题] 甲、乙两只蚂蚁分别位于 下图中的a、b两处,并设abcde为一正5边形的顶 点.甲、乙进行比赛:从它们所在的点出发, 走过图中的所有边,最后到达点c处.如果它们 c 速度相同,问谁先到达目的地?
连通图 任意两点之间都有通路的图为连通图. 树 如果一个图是一个连通的,且不包含回路,这样 的图称为树 。 生成树 如果一个连通图的某个子图是一棵树,则称该树 为此图的生成树 。
二、进一步练习
v 练习1 在下图中,1e1v2e2v3e5v4 为一条从
图论+第3章+图的连通性

直观上看,右边的比左边的图连通“程度”
要好。
(点)连通度
图的(点)连通度我们常常省略“点”字称连
通度。 树是具有最小连通度的图。 若κ (G ) ≥ k ,则称G是k-连通的。 若G是平凡图或非连通图,则κ (G ) = 0 。 所有非平凡连通图都是1连通的。
边连通度
边连通度λ (G )=min{ S | S是G的边割集} 完全图的边连通度定义为 λ ( K v ) = v − 1。 空图的边连通度定义为0。 边连通度λ (G ) 有时又记作 κ ′(G ) 。
2-连通图的性质
定理 3.2.4:若G是 p ≥ 3的2-连通图,则G的
任意两条边都在同一个圈上。
证明:(板书)
2-连通图的性质
对于一个无环且无孤立点的图G,下面的条
件是等价的:
(1)图是不可分的; (2)图是2-连通的; (3)过任意两个顶点总有一个圈; (4)过任意两条边总有一个圈。
不可分图
没有割点的非平凡的连通图称为不可分图 (non separable graph)。
定理3.1.5 不可分图的任一边至少在一个圈中。 证明:设e是不可分图G的任意边,e=(x,y),x和y都 不是割点,所以图G-e是连通的,故G-e必有一条(x,y) 道路P。于是P+e就是构成G中的一个圈。
e相连接。于是u和v在G-e中成为连通的。故矛盾。
(2)假设e=(x,y)不是割边,那么G-e和G的分支数
相同。由于G中存在一条(x,y)道路,所以x和y均 在G的同一分支。于是x和y在G-e的同一分支中, 故在G-e中存在一条(x,y)道路P,这样边e就在G的 圈P+e中。
割点定理(1)
定理3.1.2 当且仅当在G中存在与顶点v 不同
运筹学-图论

圈:若 v0 ≠ vn 则称该链为开链,否则称为闭链或 回路或圈;
简单圈:如果在一个圈中所含的边均不相同 初等圈:除起点和终点外链中所含的点均不相
同的圈;
初等链: (v1 , v2 , v3 , v6 , v7 , v5 )
v1
初等圈: (v1 , v2 , v3 , v5 , v4 , v1 )
图的基本概念
图论中的图是由点、点与点之间的线所组成的。通常, 我们把点与点之间不带箭头的线叫做边,带箭头的线叫 做弧。
如果一个图是由点和边所构成的,那么称为无向图,
记作G=(V,E),其中V表示图G 的点集合,E表示图G的
边集合。连接点vi , vj V 的边记作[vi , vj],或者[vj , vi]。 如果一个图是由点和弧所构成的,那么称为它为有向
v2 (3) v3 (3)
(2)
v5
(4)
v1
v4(6)
多重图
以点v为端点的边的个数称为点v的度(次),记 作 d(v), 如 图 5.4 中 d(v1)=3 , d(v2 )=4 , d(v3 )=4 , d(v4 )=3。
度为零的点称为弧立点,度为1的点称为悬挂点。 悬挂点的边称为悬挂边。度为奇数的点称为奇点, 度为偶数的点称为偶点。
郑州
济南 徐州
青岛 连云港
重庆
武汉 南京
上海
图5.3
例5.2 有六支球队进行足球比赛,我们分别用
点v1 ,…,v6表示这六支球队,它们之间的比赛情 况,也可以用图反映出来,已知v1队战胜v2 队,v2 队战胜v3 队,v3 队战胜v5队,如此等等。这个胜负
情况,可以用图5.3所示的有向图反映出来
图论第三章

是G 的顶点割。
-3-
图论及其应用第三章 (2)k 顶点割:含有k 个元素的顶点割。 注:1)1 顶点割与割点是两个不同的概念。
u
{u} 是1 顶点割,但 u 不是割点
v
v 是割点,但 {v} 不是1 顶点割
2)G 连通且无环,则 v 是割点
(G v ) (G )
{v} 是1顶点割
-10-
图论及其应用第三章 (2)k 边割 {e}为1 边割 {e}为割边。
(3)G 的连通度 (G ) 定义如下:
min{ k | G 有 k 边割 }, G 是非平凡图 (G ) 0, G 是平凡图
注: 1) (G ) 0
G 平凡或不连通
2)G 是含有割边的连通图
( n ≥l )
(G ) 1 (G xy ) (G )
(G ) 1 (G x )
-14-
图论及其应用第三章 三. 连通度的基本结果
。 证明:(1)先证 。 若G 平凡或不连通,则
定理3.1
0
-17-
图论及其应用第三章
例5
G
(G ) ( 2 ), (G ) ( 3 ), (G ) ( 4 )
-18-
图论及其应用第三章 例6
A 4-edge-connected graph G such that G-{x1, x2, x3, x4} is connected
-19-
(G ) 1
-11-
图论及其应用第三章 3) (G ) k 0 G 的k 边割均为键
(4)k 连通图:若 (G ) k ,则称G 为k 边连通图 的。 注第三章 例4 1、分别找G1和G2两个边割; 2、给出它们的边连通度。 v2 v1 v5 v6 v9 v 7 v8 v4 G1 v3 v1 v3 G 2 v8 v2 v4 v5 v6 v7
CH7 图的基本概念 2 3 通路、回路、图的连通性

有向图的连通性
定义 设D=<V,E>为一个有向图。vi,vj∈V,若从 vi到vj存在通路,则称vi可达vj,记作vi→vj, 规定vi总是可达自身的,即vi→vi。 若vi→vj且vj→vi,则称vi与vj是相互可达的,记 作vi vj。 规定vivi。
设无向图G=<V,E>,V={v1,v2,· ,vn},E={e1,e2,· ,em}, · · · ·
令mij为顶点vi与边ej的关联次数,则称(mij)n×m为G的 关联矩阵,记为M(G)。
性质:P163
2.有向图的关联矩阵
设简单有向图
G=<V,E>,V={v1,v2,·· n},E={e1,e2,·· m}, 则称 ·,v ·,e (mij)n×m为G的关联矩阵,记为M(G)。其中,
性质:P164
3. 图的邻接矩阵
设图
G=<V,E>,V={v1,v2,·· n},E={e1,e2,·· m}, ·,v ·,e 则称(aij)n×m为G的邻接矩阵,记为A(G)。 其中, aij为vi邻接(到)vj的边的条数.
0 2 2 0 1 1 0 0
1 1 0 0
0 0 0 0
1 0 0 0
7.3 图的矩阵表示
图的表示:
数学定义 图形表示 矩阵表示 便于用代数知识来研究图的性质 便于用计算机处理 矩阵的行列有固定的顺序,因此在用矩阵表示图之 前,必须将图的顶点和边(如果需要)编号。 本节学习: • 图的关联矩阵 • 图的邻接矩阵 • 有向图的可达矩阵
图论课件第三章 图的连通性

(Gv)(G)
证明:“必要性” 设v是G的割点。则E(G)可划分为两个非空边子集E1与 E2,使G[E1],G[E2]恰好以v为公共点。由于G没有环,所
17
第17页,本讲稿共29页
以,G[E1],G[E2]分别至少包含异于v的G的点,这样,Gv的分支数比G的分支数至少多1,所以:
(Gv)(G)
“充分性” 由割点定义结论显然。 定理7 v是树T的顶点,则v是割点,当且仅当v是树的 分支点。
定理1 边 e 是图G的割边当且仅当 e 不在G的任何圈中。
证明:可以假设G连通。 “必要性” 若不然。设 e 在图G的某圈 C 中,且令e = u v.
考虑P = C- e,则P是一条u v路。下面证明G-e连通。
对任意 x, y V(G-e) 由于G连通,所以存在x ---y路
Q.若Q不含e,则x与y在G-e里连通;若Q含有e,则可选 择路:x ---u P v --- y,说明x与y在G-e里也连通。所以,若 边e在G的某圈中,则G-e连通。
定义6 设G是连通图,T是G的一棵生成树。如果G的 一个割集S恰好包含T的一条树枝,称S是G的对于T的一 个基本割集。
14
第14页,本讲稿共29页
例如:在图G中
f a
bc
e
d
图G
G的相对于T的基本割集为: {a , e}, {f , c}, {f, b , e}, {d}.
关于基本割集,有如下重要结论:
证明:(必要性)设G是块。因G没有割点,所以,它 不能有环。对任意u, v ∈V(G),下面证明u, v位于某一圈上 。
对d (u, v) 作数学归纳法证明。 当d (u, v) =1时,由于G是至少3个点的块,所以,边 uv不能为割边,否则,u或v为割点,矛盾。由割边性质 ,uv必然在某圈中。 设当d (u, v) <k时结论成立。
图的基本概念(连通性)汇总共63页文档

•
29、在一切能够接受法律支配的人类 的状态 中,哪 里没有 法律, 那里就 没有自 由。— —洛克
•
30、风俗可以造就法律,也可以废除 法律。 ——塞·约翰逊
6、最大的骄傲于最大的自卑都表示心灵的最软弱无力。——斯宾诺莎 7、自知之明是最难得的知识。——西班牙 8、勇气通往天堂,怯懦通往地狱。——塞内加 9、有时候读书是一种巧妙地避开思考的方法。——赫尔普斯 10、阅读一切好书如同和过去最杰出的人谈话。——笛卡儿
图的基本概念(连通性)汇总
•
26、我们像鹰一样,生来就是自由的 ,但是 为了生 存,我 们不得 不为自 己编织 一个笼 子,然 后把自 己关在 里面。 ——博时 间再长 ,也还 是没有 制约力 的。— —爱·科 克
•
28、好法律是由坏风俗创造出来的。 ——马 克罗维 乌斯
西交《运筹学》重要知识点解析和例题分析第六部分

《运筹学》重要知识点解析和例题分析第六部分一.图的基本概念 定义一个图G 是指一个二元组(V(G),E(G)).即图是由点及点之间的联线所组成。
其中: 1)图中的点称为图的顶点(vertex).记为:v2)图中的连线称为图的边(edge).记为:,i j e v v ⎡⎤=⎣⎦.,i j v v 是边 e 的端点。
3)图中带箭头的连线称为图的弧(arc).记为:(),i j a v v =.,i j v v 是弧 a 的端点。
—— 要研究某些对象间的二元关系时.就可以借助于图进行研究 分类▪ 无向图:点集V 和边集E 构成的图称为无向图(undirected graph).记为: G(V.E)—— 若这种二元关系是对称的.则可以用无向图进行研究▪ 有向图:点集V 和弧集A 构成的图称为有向图(directed graph) .记为:D(V.A)—— 若这种二元关系是非对称的.则可以用有向图进行研究▪ 有限图: 若一个图的顶点集和边集都是有限集.则称为有限图.只有一个顶点的图称为平凡图.其他的所有图都称为非平凡图.图的特点:1 图反映对象之间关系的一种工具.与几何图形不同。
2 图中任何两条边只可能在顶点交叉.在别的地方是立体交叉.不是图的顶点。
3 图的连线不用按比例画.线段不代表真正的长度.点和线的位置有任意性。
4 图的表示不唯一。
如:以下两个图都可以描述“七桥问题”。
点(vertex)的概念1 端点:若e =[u.v] ∈E.则称u.v 是 e 的端点。
2 点的次:以点 v 为端点的边的个数称为点 v 的次.记为:()d v 。
在无向图G 中.与顶点v 关联的边的数目(环算两次),称为顶点v 的度或次数.记为()d v 或 dG(v).在有向图中.从顶点v 引出的边的数目称为顶点v 的出度.记为d+(v).从顶点v 引入的边的数目称为v 的入度.记为d -(v). 称()d v = d+(v)+d -(v)为顶点v 的度或次数. 3 奇点:次为奇数的点。
图论 图的基本概念

闭的迹称为回(circuit);闭的道路称作圈(cycle)
道路:v1v2v3v6
道路 (path)
若链 µ的边 e1e2...ek 均不相同,则称该链为 迹(trail)。
若所有顶点v0v1v2...vk均不相同(所有边必然不 相同),则称该途径为道路(path) 。
子图
若V (H ) ⊆ V (G), E(H ) ⊆ E(G),且H中边的重 数不超过G,则H称为G的子图,记作 H ⊆ G
若以下条件有一项成立,则H称为G的真子图。 (1) V (H ) ⊂ V (G); (2)E(H ) ⊂ E(G);
(3)H中至少有一条边的重数小于G中对应边重数
子图
生成子图(Spanning graph),又称支撑子图。
哥尼斯堡七桥问题
图论起源于著名的哥尼斯堡七桥问题:
哥尼斯堡市跨越河的两岸,河中心有两个小岛。 小岛与河的两岸有七条桥连接。在所有桥都只 走一遍的前提下,如何才能把这个地方所有的 桥都走遍?
哥尼斯堡七桥问题
在任何顶点出发,必须从一条边进,从另一条边出 一进一出,每个顶点相关联的边必须为偶数。
莱昂哈德·欧拉 在1735年圆满地解决了这个问题, 证明七桥问题无解,同时,欧拉还给出了任意一种 河-桥图能否全部走一次的判定法则,以及怎样快速 找到所要求的路线。这些解析,最后发展成为了数 学中的图论。
d (v1) = 2, d (v2 ) = 4, d (v3) = 3, d (v4 ) = 3, d (v5 ) = 4
∑ d (vi ) = (2 + 4 + 3 + 3 + 4) = 16 v E =8
并查集-判断图的连通

并查集-判断图的连通来看⼀个实例,⾸先在地图上给你若⼲个城镇,这些城镇都可以看作点,然后告诉你哪些对城镇之间是有道路直接相连的。
最后要解决的是整幅图的连通性问题。
⽐如随意给你两个点,让你判断它们是否连通,或者问你整幅图⼀共有⼏个连通分⽀,也就是被分成了⼏个互相独⽴的块。
像畅通⼯程这题,问还需要修⼏条路,实质就是求有⼏个连通分⽀。
如果是1个连通分⽀,说明整幅图上的点都连起来了,不⽤再修路了;如果是2个连通分⽀,则只要再修1条路,从两个分⽀中各选⼀个点,把它们连起来,那么所有的点都是连起来的了;如果是3个连通分⽀,则只要再修两条路……以下⾯这组数据输⼊数据来说明4 2 1 3 4 3第⼀⾏告诉你,⼀共有4个点,2条路。
下⾯两⾏告诉你,1、3之间有条路,4、3之间有条路。
那么整幅图就被分成了1-3-4和2两部分。
只要再加⼀条路,把2和其他任意⼀个点连起来,畅通⼯程就实现了,那么这个这组数据的输出结果就是1。
好了,现在编程实现这个功能吧,城镇有⼏百个,路有不知道多少条,⽽且可能有回路。
这可如何是好?我以前也不会呀,⾃从⽤了并查集之后,嗨,效果还真好!我们全家都⽤它!并查集由⼀个整数型的数组和两个函数构成。
数组pre[]记录了每个点的前导点是什么,函数find是查找,join是合并。
int pre[1010]; //存放第i个元素的⽗节点int find(int x) //查找根结点{int r=x;while(r != pre[r]) //寻找根结点r = pre[r];int i=x,j;while(pre[i]!=r) //路径压缩{j = pre[i];pre[i] = r;i = j;}return r;}void join(int root1, int root2) //判断是否连通,不连通就合并{int x, y;x = find(root1);y = find(root2);if(x != y) //如果不连通,就把它们所在的连通分⽀合并pre[x] = y;}为了解释并查集的原理,我将举⼀个更有爱的例⼦。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、连通性3.1 连通性和Whitmey定理定义V真包含于V(G), G[V(G)-V'不连通,而G是连通图,则称V是G的顶剖分集。
最小顶剖分集中顶的个数,记成K (G)叫做G的连通度;规定K (Kv)=-U; K不连通图)=平凡图)=0。
由一个顶组成的顶剖分集叫割顶。
没有割顶的图叫做块,G中的成块的极大子图叫做G的块。
定义E包含于E(G),G为连通图,而G-E'从G中删除E'中的边)不连通,则称E'为G的边剖分集,若G中已无边剖分集E〃,使得|E 〃|v|E则称|E '为G的边连通度,记成K' (G归’|=时,E'中的边叫做桥。
规定K不连通图)=0,K' (Kv)= u1。
定义K (G)>=k时,G叫做k连通图;K' (G)>=k,G称为k边连通图。
k连通图,当k>1时,也是k-1连通图。
k边连通图,当k>1时,也是k-1边连通图。
上面就是顶连通与边连通的概念,好象不指明的就是指顶连通了。
定理1 K (G)=< K' 2)=可以复习一下第一章的1.2:S =min{d(v)})证:设d(v)=,则删除与v边关联的S条边后,G变不连通图,所以这S 条边形成一个边剖分集,故最小边剖分集边数不超过即K' (G)=<T证K =<K'分情形讨论之。
若G中无桥,则有K' >条边,移去它们之后,G变成不连通图。
于是删除这K条中的K'条后,G变成有桥的图。
设此桥为e=uv,我们对于上述K'条删去的每条边上,选取一个端点,删除这些(不超过K'个)端点,若G变得不边能,则K =<K-1;若仍连通,则再删去u或v,即可使G变得不连通,于是K =<K'证毕。
这个定理很好理解,图论中的一些定理常以这种友好”的面目出现。
F面就是Whitmey定理定理2(Whitney,1932) u >的图是2连通图的充要条件是任二顶共圈(在一个圈上)。
证:若任二顶共圈,任删除一个顶w后,得图G-w。
任取两顶u,v € V(G-w), u,v在G中共存于圈C 上,若w不在C上,则G-w中仍有圈C,即u与v在G-w 中仍连通;若w 在G 中时在 C 上,在G-w 中u 与v 在轨C-w 上,故u 与v 仍连通。
由u与v之任意性,G-w是连通图,故K (G)>=2即G是2连通图。
反之,若G是2连通图,u >=3任取u,v€ V(G),用对d(u,v)的归纳法证明u 与v 之间有两条无公共内顶的轨当d(u,v)=1是时,因K =<K',故K' >=2uv边不是桥,G-uv仍连通,于是G-uv 中存在从u到v的轨P1(u,v),这样从u到v有两条无公共内顶的轨P1(u,v) 与边uv。
假设d(u,v)<k时(k>=2),结论已成立,考虑d(u,v)=k的情形。
令PO(u,v)之长为k,w是PO(u,v)上与v相邻的顶,贝U d(u,w)=k-1,由归纳法假设,在u,w之间有两条无公共内顶P与Q,因G是2连通较长,故G-w仍连通。
在G-w中存在轨P' (u,v)<>PO(u,v)令x是P U Q上P'的最后一个顶。
因u€ P U Q,故x存在(可能x=u)。
不妨设x € V(P),则G有两个u,v之间无公共内顶的轨:一个是P上从u到x段并在P'上从x到v段;一个是Q+wv。
证毕。
图论的定理证明,没有其他数学的那么多推导,那么多的公式,符号也是有限的几个,看多了就明白了。
概念清晰还是很重要,很多东西是概念性的。
还有就是构造了,照题能构造出的相应的图有时就迎而解了。
就是打字时中英文切换麻烦。
3.2 割顶、桥、块割顶、桥、块都是一个图的关键部位了。
本节给出三个定理来阐述这三个概念,好象少了点,不过这本书的东西有些地方很语焉不详的,而且有些东西到处穿插,并且有很强的理论性,很少涉及实践中的问题。
看起来比较的累人。
定理 3 v 是连通图的一个顶点,则下可述命题等价:(1) v 是割顶(2) 存在与v不同的两个顶u,w,使得v在每一条由u到w的轨上(3) 存在V-{v}的一个划分V-{v}=U U W,U A W环,使得对任意的u € U,w € W,v在每一条由u到w的轨上。
定理4 x是G的一边,G是连通图,则下述命题等价:(1) x 是G 的桥。
(2) x 不在G 的任一圈上。
(3) 存在顶u,v € V(G),使得x在每一个从u到v的轨上。
(4) 存在V(G)的划分U与W,使得任二顶u,w,u€ U,w€ W 时,x 在每条从u 到v 的轨上。
上面的都没什么可证的,就是轨、连通片、割顶、桥等概念翻来覆去的用就是了定理5 G连通,u >=3则下列命题等价:(1) G 是块。
(2) G 的任二顶共圈。
(3) G 的任一顶与任一边共圈(4) G 的任二边共圈(5) 任给G 的二顶及一边,存在连接此二顶含此边之轨(6) 对G 的三个不同的顶,存在一轨,连接其中两个顶,含第三个顶(7) 对G 的三个不同的顶,存在一轨,连接其中两个顶,不含第三个顶。
(本也没什么可证的了,但就这样结束了也太快了,这个证一下)证: (1)>>(2),(2)>>(1) 见定理 2(2) >>(3)只考虑u为G的任给一个顶,vu是G中任给定的一条边,且u<>v,u<>w的情形。
设C是含u与v的圈,若w在C上,则C上含u的轨P(v,w) 与边vw形成一个圈,它含u及边vw。
若w不在C上,因v不是割顶,由定理3,存在不含v的轨P(w,u)。
令u'是P(w,u)与C从w沿P(w,u)看来的第一个公共顶,贝U由边vw,P(w,u)上w到u'段,以及C上含u的轨P' (u '并成一个圈,此圈满足(3)的要求。
(3) >>(4)与(2)>>(3)类似证明。
(4) >>(5)已知任二边共圈,设u,v是G上任给定的两个顶,x是任给定的一条边,只考虑x与u,v皆不相关联的情形。
由任二边共圈显然有任二顶共圈,于是由于(2)>>(3)知u与x共圈,设此圈C1;同理v与x共圈,设此圈是C2;若v € C1 或u€ C2,则⑸成立;若u不属于C2,且v不属于C1,则如下构作含x之轨P(u,v): 从u出发沿C1到达C1与C2上第一个公共顶w,再从w出发沿C2含x的部分到达v。
(5) >>(6)设u,v,w是G的三个顶,且与w相关联的一条边是x,由⑸存在轨P(u,v),x 在P(u,v)上,于是w 在P(u,v)上。
(6) >>(7) u,v,w € V(G),由(6),存在轨P(u,w), P(u,w)含顶v,则P(u,w)的从u 到v的一段不含w。
(7) >>(1)由(7),对任给定的二顶u与v,不存在这样的顶,它在从u到v的每一轨上,由定理3, G 无割顶,故G 是块。
证毕。
讲了这么多,下节才涉及到实践中的问题。
下节讲可靠通讯网的构作。
不过下节又是本章的最后一节了。
3.3 可靠通讯网的构作我们要构作一个有线通讯网, 使得敌人炸坏我几通讯站后, 其余的通讯站仍然可彼此通话。
显然, 有两个要求是必要的:一是不怕被敌人炸坏站的数目要多, 一是整个造价要小。
这个实际问题的数学艺术模型如下:G是加权连通图,k是给定的自然数,求G的有最小权的k连通生成子图。
当k=1 时,它就是用Kruskal 算法求得的生成树;当k>1 时,是尚未解决的难解问题之一。
哦,原来k>1 时是没解决的难题,自己以前也想过这方面的东西,只是想了半天也想不出个所以然,原来是个大难题呀。
当G=K u每边权皆为1时,Harary于1962年解决了这一问题。
下面介绍Harary的工作。
令f(m,n)表示n个顶的m连通图当中边数的最小值,m<n。
由工d(v)=2eK =< K' =< Sf(m,n)>={mn/2}Harary 实际上构作出一个n 顶的m 连通图,它的边数恰为{mn/2} 条,且f(m,n)={mn/2} 。
此图记成H(m,n) 。
⑴m是偶数,m=2r。
H(2r,n)以{0,1,2,…询为顶集合。
当i-r=vj=<i+r 时,在顶点i 与j 之间连一边,这里的加法在mod n意义下进行。
(2) m 是奇数,m=2r+1,n 是奇数。
先构作H(2r,n),然后对1=<i=<n/2 的i,在i 与i+n/2 间加上一条边得H(2r+1,n)。
(3) m 是奇数,m=2r+1,n 是奇数。
先构作H(2r,n),然后在顶点0与(n-1)/2,0与(n+1)/2之间加上边,在顶i与i+(n+1)/2间加上边,其中仁<i=<(n-1)/2,则得到H(2r+1,n)。
无法把图画上来,H(6,8)、H(5,8)、H(5,9)看一下图就明白这个构作的方法了。
下面证上面的构作出来的东西是符合要求的。
定理6 H(m,n)是m连通图,且边数最少证:m=2r时,我们来证明H(2r,n),设有少于2r个顶组成的顶剖分集。
若V'是一个顶剖分集,且|V'|<2r,又设i与j两个顶分别属于H(2r,n)-V'的不同连通片,令S={i,i+1,...,j-1,j},T={j,j+1,...,i-1,i},其中加法在mod n下执行。
因为|V'|<2r,不失一般性,设|V' n S|<r则显然存在S-V'中的序列,从i如至j终,使得序列中连续二顶之差的绝对值最大是丫。
但这样的序列中相邻顶之间由(1)知存在边,即在H(2r,n)-V'中有轨P(i,j),与i,j分居于H(2r,n)-V'的两年连通片中相矛盾,故H(2r,n)是2r连通的。
相似地可以证明m=2叶1时,H(2叶1,n)是2r+1连通的。
由于f(m,n)>={mn/2}, £ (H(m,n))={mn/2},而H(m,n)是n顶m连通图,故有f(m,n)=<{mn/2},从而得£ (H(m,n))=f(m,n)={mn/2}。
证毕由于K =<K,故 H(m,n)也是m连通图,若用g(m,n)表示n个顶m边连通图中最少边数,则对1<m<n,g(m,n)={mn/2}。
就这样第三章也结束了,理论讲了一大堆一、通论1. 1图论的内容与历史回顾一上来总要先回顾一下历史,让人了解一下这个学科的来龙去脉,见怪不怪了。
