关于三维坐标转换参数的讨论

合集下载

基于改进SQPM算法的三维直角坐标转换

实验表明该方法能在大范围内实现收敛且结果稳定、精度较高，适合于大旋转角的三维直角坐标转换。［关键词］三维直角坐标转换；ＳＰ；七参数ＱＭ［中图分类号］Ｐ２２６［文献标识码］Ａ［文章编号］１７ — ０９（０１５００— ３６４５１２１）０ — ２８０
３ｒｃａｇｌｒｃｏｄｎｔａｓｏａｉｎＤｅｔｎｕａｏｒｉａｅｔｎｆｒｔ．ｒｍｏ
Ｋｅｒｓ３ｏｒｉａｅｒｎｆｒａｏ；ＱＰＳｖｎｐｒｍｅｅｓｙｗｏｄ：ＤｃｏｄｎｔｔｓｍｔｎＳＭ；ｅｅａａｔｒａｏｉ
３ＲｅｔｎｕａｏｄｎｔａｆｒａｉｎＢａｅｎＤｃａｇｌｒＣｏｒｉａｅＴｒｎｓｏｍｔｏｓｄｏ
ＩｒｖｄＳＰＡｌｏｉｍｍｐｏｅＱＭｇｒｈｔ
ＬＡＮｕ—ｉＧＵＯＸｉｏ—ａＹｌｎｌａｌｎ（．ｅｇｕｔｏｇｉｇＰｓｅｇｒｉｙＣｏＬｄ，ｅｇｕ６０，ｉａ２Ｉｓｉｔｆｕｖｙｎｎ１ＣｈｎｄＣｈｎｑｎａｓｎｅｌ，．ｔ．Ｃｈｎｄ３Ｃｈｎ；．ｎｔｕｅｏｒｅｉｇａｄｏＲａｗａ１１０ｔＳ
Ｍａｐｎ，ｕＣｕｔ，ｈｎｏｇＰｏｉｃ，ｉｈｏ２６０，ｈｎ）ｐｉｇＪｏｎｒＳａｄｎｒｖｎｅＲｚａ７５０Ｃｉａｙ
Ａｂｔａｔｈｉｏｏｓｆｒｌｆ３ｒｃａｇｌｒｃｏｄｎｔｒｎｆｒａｉｎｗｉａａｔｒｒｒｓｎｅ．ｈｓｒｃ：ＴｅｒｇｒｕｏｍｕａｏＤｅｔｎｕａｏｒｉａｅｔａｓｏｍｔｏｔ７ｐｒｍｅｅｓａｅｐｅｅｔｄＴｅｈ

坐标系转换方法和技巧

坐标系转换方法和技巧1.二维坐标系转换：二维坐标系转换是将平面上的点从一个坐标系转换到另一个坐标系中。

常用的方法有旋转、平移和缩放。

-旋转：通过改变坐标系的旋转角度，可以将点从一个坐标系转换到另一个坐标系。

-平移：通过改变坐标系的平移量，可以将点从一个坐标系平移到另一个坐标系。

-缩放：通过改变坐标系的比例尺，可以将点从一个坐标系缩放到另一个坐标系。

2.三维坐标系转换：三维坐标系转换是将空间中的点从一个坐标系转换到另一个坐标系中。

常用的方法有旋转、平移和缩放。

-旋转：通过改变坐标系的旋转角度，可以将点从一个坐标系转换到另一个坐标系。

-平移：通过改变坐标系的平移量，可以将点从一个坐标系平移到另一个坐标系。

-缩放：通过改变坐标系的比例尺，可以将点从一个坐标系缩放到另一个坐标系。

3.地理坐标系转换：地理坐标系转换是将地球表面点的经纬度坐标转换为平面坐标系（如UTM坐标系）或其他地理坐标系中的点。

常用的方法有投影转换和大地坐标转换。

-投影转换：根据不同的地理投影模型，将地理坐标系中的点投影到平面上。

常用的地理投影包括墨卡托投影、兰伯特投影等。

-大地坐标转换：根据椭球模型和大地测量的理论，将地理坐标系中的点转换为具有X、Y、Z三维坐标的点。

常见的大地坐标系包括WGS84和GCJ-02等。

4.坐标系转换的技巧：-精度控制：在坐标系转换过程中，需要注意精度的控制，以确保转换后的坐标满足要求。

-参考点选择：在坐标系转换过程中，选取合适的参考点可以提高转换的准确性和稳定性。

-坐标系转换参数的确定：在进行坐标系转换时，需要确定旋转角度、平移量和比例尺等参数，可以通过多点共面条件、最小二乘法等方法进行确定。

-转换效率优化：针对大规模的坐标系转换，可以采用分块处理、并行计算等技术来提高转换效率。

在进行坐标系转换时，需要根据具体的需求选择适当的方法和技巧，并结合具体的软件工具进行实现。

同时，还需要注意坐标系转换的精度和准确性，确保转换结果符合要求。

三维多段线转二维多段的方法

三维多段线转二维多段的方法-概述说明以及解释1.引言1.1 概述概述是文章引言部分的一部分，旨在简要介绍本文所要讨论的主题以及解决问题的目的。

对于本篇文章《三维多段线转二维多段的方法》，我们将探讨如何将三维多段线转换为二维多段线的方法。

在计算机辅助设计中，多段线是一种常用的图形元素，它由一组节点和与节点相连接的线段组成。

我们常见的三维多段线指的是在三维空间中定义的多段线，它可以用来描述复杂的三维图形。

然而，在某些情况下，我们可能需要将三维多段线转换为二维多段线，以满足某些特定需求，例如在平面图绘制、建筑规划和展示等方面。

这个过程需要定义一种方法，能够有效地将三维多段线的信息投影到二维平面上，从而得到二维多段线的表示。

为了实现这个目标，本文将介绍两种常见的方法：投影法和剖面法。

这两种方法各有其特点和适用场景，读者可以根据具体需求选择合适的方法来进行三维多段线转二维多段的操作。

通过本文的研究，我们将为读者提供清晰的方案和技术参考，帮助他们理解并掌握将三维多段线转换为二维多段线的方法。

同时，通过对这些方法的比较和分析，我们也可以深入了解不同方法的局限性和优缺点，为今后的相关研究和应用提供参考依据。

综上所述，本篇文章旨在介绍三维多段线转二维多段的方法，通过对两种常用方法的描述和分析，帮助读者理解并应用这些方法，以满足实际需求。

在接下来的章节中，我们将详细介绍三维多段线和二维多段线的定义和特点，并说明两种转换方法的实现原理和应用场景。

1.2 文章结构文章结构部分的内容可以是：文章结构部分旨在为读者提供关于本文的组织和内容概述。

本文将按照以下结构展开：引言部分将首先对本文的主题进行概述，介绍三维多段线转二维多段线的方法。

接着，文章将介绍文章的整体结构，包括各个章节的内容和主要观点。

最后，我们将强调本文的目的，即为读者提供了解这一方法的全面指导。

正文部分将首先介绍三维多段线的定义和特点，包括它在三维坐标系中表示空间曲线的方法和特征。

三维_极坐标与直角坐标的互化_解释说明

三维极坐标与直角坐标的互化解释说明1. 引言1.1 概述在数学和物理学中，坐标系统是一种用于描述物体位置的工具。

我们常用的直角坐标系是由三个相互垂直的坐标轴构成，可以描述点在平面上的位置。

然而，在某些情况下，直角坐标系并不能很好地描述物体的位置信息，特别是当涉及到球对称结构或者极向性场景时。

为了解决这个问题，人们引入了三维极坐标系。

极坐标系使用两个参数来描述点的位置：径向距离与方位角。

它将空间划分为一组同心圆和一组以原点为顶点的旋转平面锥（还包括了一个垂直于这些平面锥的半径轴），从而提供了另一种描述三维空间中点位置的方式。

本文将深入探讨三维极坐标与直角坐标之间的互化关系，包括它们各自的定义与表示方法以及彼此之间的转换方法。

1.2 文章结构本文共分为四个部分：引言、三维极坐标与直角坐标的互化、应用场景和优劣势比较以及结论。

在引言部分，我们将对本文的主题进行概述，并介绍直角坐标系与三维极坐标系的基本概念。

在第二部分，我们将详细介绍三维极坐标与直角坐标的定义与表示方法，包括如何确定点在两种坐标系下的位置。

第三部分将探讨应用场景和优劣势比较。

我们将分析在不同领域中使用三维极坐标和直角坐标的情况，并比较它们各自的优势和劣势。

此外，我们还会通过实际应用案例来说明其具体应用。

最后，在结论部分，我们将总结主要观点和发现结果，并对未来发展趋势提出展望和建议。

1.3 目的本文的目的是深入探究三维极坐标与直角坐标之间的互化关系。

通过详细介绍它们两者的定义、表示方法以及转换方法，希望读者能够更好地理解它们之间的联系和差异，并能够根据具体问题选择适合的坐标系统进行描述。

同时，通过对应用场景和优劣势比较的探讨，进一步增进对这两种坐标系统特点及其适用性的认识，并为未来的研究和应用提供一定的参考和启示。

2. 三维极坐标与直角坐标的互化:2.1 三维极坐标的定义与表示方法:三维极坐标是一种在空间中描述点位置的方式。

它使用一个距离、一个仰角和一个方位角来表示点的坐标。

极坐标方程和直角坐标方程怎么互化三维

极坐标方程和直角坐标方程怎么互化三维在三维几何学中，我们常用的坐标系统是直角坐标系，也称为笛卡尔坐标系。

这种坐标系使用三个坐标轴（x、y、z轴）来表示空间中任意一点的位置。

然而，在某些情况下，使用极坐标系来描述三维空间中的点更加方便和直观。

极坐标系使用极径（r）、极角（θ）和高度（h）来表示一个点的位置。

互换的必要性在一些领域，如天体物理学、工程设计和计算机图形学中，常常需要在直角坐标系和极坐标系之间进行互换。

通过这种互换，我们可以更方便地描述和处理某些特定几何形状和问题。

极坐标方程转直角坐标方程下面我们来介绍如何将给定的极坐标方程转换为直角坐标方程。

假设我们有一个极坐标方程，形如：r = f(θ)其中f(θ)是一个关于极角θ的函数。

要将其转换为直角坐标方程，我们可以使用以下关系：x = r * cos(θ)y = r * sin(θ)通过这些关系，我们可以将极坐标方程中的r和θ转换为直角坐标系中的x和y。

这样，我们就得到了一个用直角坐标表示的方程。

这个方程描述了一个曲线、平面或曲面，并可以在直角坐标系中方便地进行分析和计算。

直角坐标方程转极坐标方程与极坐标方程转换为直角坐标方程相反，我们也可以将给定的直角坐标方程转换为极坐标方程。

假设我们有一个直角坐标方程，形如：F(x, y) = 0其中F(x, y)是一个关于x和y的函数。

要将其转换为极坐标方程，我们可以使用以下关系：x = r * cos(θ)y = r * sin(θ)将上述方程代入直角坐标方程，我们可以得到：F(r * cos(θ), r * sin(θ)) = 0这样，我们就得到了一个用极坐标表示的方程。

这个方程描述了一个极坐标系中的曲线、极面或极体，并可以在极坐标系中方便地进行分析和计算。

示例让我们来看一个具体的例子。

假设我们有一个极坐标方程：r = 2sin(θ)。

根据之前的转换关系，我们可以将其转换为直角坐标方程：x = r * cos(θ)y = r * sin(θ)代入r = 2sin(θ)：x = 2sin(θ) * cos(θ)y = 2sin(θ) * sin(θ)化简得：x = 2sin(θ) * cos(θ) = sin(2θ)y = 2sin^2(θ) = 1 - cos(2θ)通过这个转换，我们将极坐标方程r = 2sin(θ)转换为了直角坐标方程x = sin(2θ)和y = 1 - cos(2θ)。

相控阵雷达波束调度中的三维坐标转换方法

或ｆ
— —
ＩＲｃＯｎＸｐｓｓ￣ｐｉＰｏ
转换矩阵记为Ｈ，则从雷达直角坐标系旋转到天线阵面直角坐标系的转换公式为（３）
ｒ１●
，●
Ｉ，，』ｘ，ＹＺＨＹｐｐ，ｚＪ
（１１）
｛ａ（ｒｃｘｔ￣ａｎ
作者简介：温丹昊（９０）男，，１８一，汉工程师，硕士，主要从事雷达资源调度、数据处理方面研究。
・
２・６
科技论坛
ｃ０ｌ『ｓ０一ｉｌ１ｏｓｏｘ￣［ｖｌ１０ ’ Ｉ０
０ｃｓ。
（）１０
关系为
Ｉ＝ＲｃｓｎＡＸｏＥｓｉ
１ｎｌＲＥ肌ＡＺｓｉ一
或
：
（Ｉ）
（）２
任何两坐标系的旋转变换关系可由以上式（）８一式（０中的３１）个基本旋转矩阵的合成得到。由２１２３节的描述能够看出天线阵面直角坐标系可以由雷．和．达直角坐标系经过两步旋转得到，一步，第雷达直角坐标系绕天线方位轴ｚ轴顺时针旋转Ａｐ的角度（即逆时针旋转一ｐ的角度）第Ａ，二步，天线俯仰轴ｘ轴逆时针旋转Ｅ绕ｐ的角度，这样就形成了天线阵面直角坐标系，中Ａ其ｐ为阵面方位角，ｐ为阵面俯仰角，Ｅ都可以事先由专用设备测量得到。由此，以得知从雷达直角坐标系旋可转得到天线阵面直角坐标系的转换矩阵为
ｌ云）
（４）
３．４波束指向信息坐标转换过程波束调度模块从跟踪模块等得到的跟踪波束指向信息（即雷达的目标测量值）是基于雷达球坐标系的，记为（，，，ＲＡＥ）波束的方位角Ａ和仰角Ｅ是相对与正北向和水平面的．综合上述坐标转换公式，相控阵雷达波束调度模块进行波束指向信息的三维坐标转换过

三维坐标转换模型的原理

．
１ＯＯ
０
）与（、五、五）两者之间的关系为三维转换
，
．．
模型。
『＿
一］
ＩＩ－，ｎ１／７／，ｌ
１布尔莎模型
布尔莎模型即七参数模型，如图１所示。（Ｘ、Ｙ、Ｚ）与（Ｘ、ｙ１、Ｚ）采用最小二乘法求得。上
以讨论。
关键词：三级转换模型；布尔荷模型；莫洛金斯基接型；武测模型；原理
中图分类号：Ｐ２２８．４文献标识码Ｂ
与０一
— ．．．．．．。．
假设有两个空间直角坐标系一
，
１●●●
＿．．．．。．．
这两个坐标系具有不同的原点以及不相互平
图１两个空间直角坐标系间的关系
图中显示有两个定向的直角坐标系，即０一ＸＹＺ与Ｑ一ｙｌｚ， △ｙ △ｚ；两个坐标系的坐标轴
以此写成如下误差方程式的形式：
２０１５年第３期（第４３卷）
黑
龙
江
水
利科
技
Ｎｏ．３．２０１５
ＨｅｉｌｏｎｇｊｉａｎｇＳｃｉｅｎｃｅａｎｄＴｅｅｈｎｏｌｏｇｙｏｆＷａｔｅｒＣｏｎｓｅｒｖａｎｃｙ
摘要：大地坐标系按其原点对地球质心的位置可分为两部分，即局部坐标系与地心坐标系。
局部坐标系通常是以经典测绘技术为基础而研究建立的。地心坐标系则是以卫星大地测量为

3维坐标转换参数直接计算的严密公式

3维坐标转换参数直接计算的严密公式在三维空间中，坐标转换参数用于将一个坐标系中的点的坐标转换到另一个坐标系中。

在这个过程中，我们需要确定相对位置和方向的参数。

假设我们有两个坐标系，分别为坐标系A和坐标系B。

坐标系A的原点为O_A，坐标系B的原点为O_B。

我们需要将一个在坐标系A中点的坐标(x_A,y_A,z_A)转换到坐标系B中的坐标(x_B,y_B,z_B)。

要完成这个转换，我们需要确定两个参数：平移向量和旋转矩阵。

平移向量确定了两个坐标系原点之间的相对位置。

我们可以通过测量两个原点之间的直线距离来获得平移向量的长度，然后通过向量运算获得平移向量的方向。

平移向量可以表示为(Tx,Ty,Tz)。

旋转矩阵确定了两个坐标系之间的旋转方向和角度。

旋转矩阵是一个3x3的矩阵，可以表示为：R=[r11r12r13][r21r22r23][r31r32r33]其中r11、r12、r13等元素是旋转矩阵的元素。

为了确定旋转矩阵，我们可以使用欧拉角、四元数或旋转矩阵之间的转换关系。

这些方法可以将旋转矩阵表示为方便计算的形式。

在坐标转换中，我们首先将点的坐标向量表示为[x_A,y_A,z_A]，然后将其平移到新的坐标系中：[x_B',y_B',z_B']=[x_A,y_A,z_A]-[Tx,Ty,Tz]其中[x_B',y_B',z_B']是相对于坐标系B中原点的新坐标。

接下来，我们将新坐标通过旋转矩阵进行旋转：[x_B,y_B,z_B]=R*[x_B',y_B',z_B']这样，我们就得到了点在坐标系B中的新坐标。

综上所述，坐标系的转换可以通过确定平移向量和旋转矩阵来实现。

通过测量两个坐标系原点之间的距离，并计算旋转矩阵的元素，我们可以直接通过计算得到坐标系的转换参数。

这些参数可以用于将一个坐标系中的点的坐标转换到另一个坐标系中。

尽管这个过程可能比较复杂，但是通过严密的数学推导和计算，我们可以得到准确的坐标转换结果。

三维四参数空间直角坐标转换计算方法

一、引言在地图制图、航空航天、导航定位等领域，经常需要进行三维空间直角坐标的转换计算。

在进行这类计算时，常常会涉及到三维四参数空间直角坐标的转换。

本文将介绍三维四参数空间直角坐标转换的计算方法及其应用。

二、三维四参数空间直角坐标的定义三维空间中，直角坐标系通常用(x, y, z)表示。

在进行坐标转换时，需要考虑到可能存在的平移、旋转、缩放等变换。

三维四参数空间直角坐标则包括了平移在x、y、z三个方向上的位移和绕某个轴的旋转角度。

三、三维四参数空间直角坐标转换的计算方法1. 平移变换的计算方法平移变换是指在x、y、z三个方向上的位移。

假设平移量分别为tx、ty、tz，那么进行平移变换后的坐标可以表示为：x' = x + txy' = y + tyz' = z + tz2. 旋转变换的计算方法绕某个轴的旋转变换通常用旋转矩阵来表示。

以绕z轴的旋转为例，旋转角度为θ，那么进行旋转变换后的坐标可以表示为：x' = x*cosθ - y*sinθy' = x*sinθ + y*cosθz' = z3. 综合变换的计算方法综合平移和旋转变换后，坐标的变换可以表示为：x' = (x - xs)*cosθ - (y - ys)*sinθ + xty' = (x - xs)*sinθ + (y - ys)*cosθ + ytz' = z + zt四、三维四参数空间直角坐标转换的应用在实际应用中，三维四参数空间直角坐标转换通常用于地图制图、航空航天、导航定位等领域。

在地图制图中，需要将世界坐标系中的地理坐标转换为局部坐标系中的平面坐标，就需要进行三维四参数空间直角坐标的转换。

在航空航天领域，导航定位系统也需要进行三维坐标的转换计算，以确定飞行器的位置和姿态。

五、结论三维四参数空间直角坐标转换是现代科学技术中常见的数学计算方法，具有广泛的应用价值。

三维坐标系的建立与转换方法

三维坐标系的建立与转换方法引言：三维坐标系作为一种常用的数学工具，广泛应用于几何学、物理学、计算机图形学等领域。

本文将介绍三维坐标系的建立方法以及常用的转换方法，并阐述其在实际问题中的应用。

一、三维坐标系的建立三维坐标系是由三个相互垂直的轴线组成的。

在建立三维坐标系时，我们首先需要确定一个参考点，称为原点，通常用O表示。

然后，确定三个相互垂直的轴线，分别为x轴、y轴和z轴。

x轴通常表示水平方向，y轴表示竖直方向，z轴表示垂直于水平和竖直方向的第三个轴线。

二、三维坐标的表示方法在三维坐标系中，我们可以用有序三元组(x, y, z)来表示一个点。

其中，x表示点在x轴上的投影长度，y表示点在y轴上的投影长度，z表示点在z轴上的投影长度。

这种表示方法被称为直角坐标系。

三、直角坐标系与极坐标系的转换除了直角坐标系外，我们还可以使用极坐标系来表示点的位置。

极坐标系由极径和极角两个参数组成。

在平面坐标系中，极径表示点到原点的距离，极角表示点和x轴正半轴的夹角。

当我们知道一个点在直角坐标系中的坐标(x, y, z)时，可以通过以下方法将其转换为极坐标系中的坐标(r, θ, φ)：- 计算点到原点的距离r，即r=sqrt(x^2+y^2+z^2)；- 计算点在x-y平面上的极角θ，即θ=atan2(y, x)；- 计算点在x-z平面上的极角φ，即φ=atan2(sqrt(x^2+y^2), z)。

反过来，如果我们已知一个点在极坐标系中的坐标(r, θ, φ)，可以通过以下方法将其转换为直角坐标系中的坐标(x, y, z)：- 计算点在x-y平面上的投影长度x，即x=r*cos(θ)；- 计算点在x-y平面上的投影长度y，即y=r*sin(θ)；- 计算点在z轴上的投影长度z，即z=r*cos(φ)。

四、坐标系的旋转与平移在实际问题中，我们常常需要对三维模型进行旋转和平移。

这就要借助坐标系的变换方法。

1. 坐标系的平移：假设有一个坐标系A，其原点为Oa，与另一个坐标系B的原点Ob之间的向量为v = (dx, dy, dz)。

高程转换模型参数

高程转换模型参数高程转换模型参数是地理信息系统中常用的一种技术，用于将地球表面上的三维坐标转换为大地高程。

本文将介绍高程转换模型参数的含义、作用以及常用的转换方法。

一、高程转换模型参数的含义高程转换模型参数是指在进行高程转换时所需的一组参数，用于将地球表面上的坐标转换为相应的高程值。

这些参数包括大地椭球参数、投影参数、高程基准参数等。

其中，大地椭球参数用于描述地球的形状，投影参数用于描述地球表面上的坐标系统，高程基准参数用于描述地球表面上的高程系统。

高程转换模型参数在地理信息系统中起着至关重要的作用。

首先，它们可以帮助我们准确地将地球表面上的三维坐标转换为相应的高程值，从而实现地球表面上各个位置的精确测量和分析。

其次，它们可以帮助我们进行地球表面上的坐标转换，使得不同地区的地理数据能够进行有效的集成和分析。

三、常用的高程转换方法在地理信息系统中，常用的高程转换方法有大地水准面转换、大地高程转换和大地高程模型转换等。

1. 大地水准面转换大地水准面转换是将地球表面上的三维坐标转换为相应的高程值的一种常用方法。

它基于大地水准面的概念，通过测量地球表面上的水准线来确定各个位置的高程值。

在进行大地水准面转换时，需要使用到高程基准参数，以确保所得到的高程值具有一定的准确性。

2. 大地高程转换大地高程转换是将地球表面上的三维坐标转换为相应的高程值的另一种常用方法。

它基于大地高程的概念，通过测量地球表面上的高程点来确定各个位置的高程值。

在进行大地高程转换时，需要使用到大地椭球参数和投影参数，以确保所得到的高程值与实际情况相符。

3. 大地高程模型转换大地高程模型转换是将地球表面上的三维坐标转换为相应的高程值的一种高级方法。

它基于大地高程模型的概念，通过建立地球表面上的高程模型来确定各个位置的高程值。

在进行大地高程模型转换时，需要使用到大地椭球参数、投影参数和高程基准参数，以确保所得到的高程值具有更高的精度和准确性。

坐标系转换问题及转换参数的计算方法

坐标系转换问题及转换参数的计算方法对于坐标系的转换，给很多GPS的使用者造成一些迷惑，尤其是对于刚刚接触的人，搞不明白到底是怎么一回事。

我对坐标系的转换问题，也是一知半解，对于没学过测量专业的人来说，各种参数的搞来搞去实在让人迷糊。

在我有限的理解范围内，我想在这里简单介绍一下，主要是抛砖引玉，希望能引出更多的高手来指点迷津。

我们常见的坐标转换问题，多数为WGS84转换成北京54或西安80坐标系。

其中WGS84坐标系属于大地坐标，就是我们常说的经纬度坐标，而北京54或者西安80属于平面直角坐标。

对于什么是大地坐标，什么是平面直角坐标，以及他们如何建立，我们可以另外讨论。

这里不多罗嗦。

那么，为什么要做这样的坐标转换呢？因为GPS卫星星历是以WGS84坐标系为根据而建立的，我国目前应用的地形图却属于1954年北京坐标系或1980年国家大地坐标系；因为不同坐标系之间存在着平移和旋转关系（WGS84坐标系与我国应用的坐标系之间的误差约为80），所以在我国应用GPS进行绝对定位必须进行坐标转换，转换后的绝对定位精度可由80提高到5-10米。

简单的来说，就一句话，减小误差，提高精度。

下面要说到的，才是我们要讨论的根本问题：如何在WGS84坐标系和北京54坐标系之间进行转换。

说到坐标系转换，还要罗嗦两句，就是上面提到过的椭球模型。

我们都知道，地球是一个近似的椭球体。

因此为了研究方便，科学家们根据各自的理论建立了不同的椭球模型来模拟地球的形状。

而且我们刚才讨论了半天的各种坐标系也是建立在这些椭球基准之上的。

比如北京54坐标系采用的就是克拉索夫斯基椭球模型。

而对应于WGS84坐标系有一个WGS84椭球，其常数采用IUGG第17届大会大地测量常数的推荐值。

WGS84椭球两个最常用的几何常数：长半轴：6378137±2(m)；扁率：1：298.257223563之所以说到半长轴和扁率倒数是因为要在不同的坐标系之间转换，就需要转换不同的椭球基准。

浅谈坐标转换的步骤和方法的选择

工，选择合适的土方量测量计算方法尤为重要。
玎一
在目前的工程施工中，比较常用的土方量测量方法有：方格
ａ０ — ，
４ｎ
！
。
网法、断面法和等高线法等，下面就这三种基本方法进行分析。
其中，，， ∑ ∑ ∑ ，中别为点、、 ∑Ｈ分角边点拐
收稿Ｅ期：０１０ —９ｌ２１－７１
作者简介：丁
峰（９７，助理工程师，阳市国土资源调查规划与测绘院，１７．）男，安河南安阳
４５０５００
王
静（９９，，理工程师，阳市国土资源调查规划与测绘院，１７一）女助安河南安阳４５０５００
科沃大地坐标系相联结后建立的我国过渡性大地坐标系。属于换点的坐标转换到目标坐标系。
参心大地坐标系，采用了前苏联的克拉索夫斯基椭球体。其长半
轴口＝６３８２５ｎ，率，＝１２８３７４ｌ扁／９．。
２转换模型
坐标转换模型有以下几种。
１２西安８．０坐标系１７９８年，国决定建立新的国家大地坐标系统，我并且在新的
大地坐标系统中进行全国天文大地网的整体平差，这个坐标系统
２１四参数坐标转换方法．
对于点的附近区域是有效的。
１４２０国家大地坐标系．００

三维坐标变换

三维坐标变换第⼆章三维观察1.三维观察坐标系1.1观察坐标系为了在不同的距离和⾓度上观察物体，需要在⽤户坐标系下建⽴观察坐标系x v,y v,z v(通常是右⼿坐标系)也称(View Reference Coordinate)。

如下图所⽰，其中，点p0(x o, y o, z0)为观察参考点（View Reference Point），它是观察坐标系的原点。

图1.1 ⽤户坐标系与观察坐标系依据该坐标系定义垂直于观察坐标系z v轴的观察平⾯(view palne)，有时也称投影平⾯(projection plane)。

图1.2 沿z v轴的观察平⾯1.2观察坐标系的建⽴观察坐标系的建⽴如下图所⽰：图1.3 法⽮量的定义观察平⾯的⽅向及z v轴可以定义为观察平⾯(view plane)N法⽮量N: 在⽤户坐标系中指定⼀个点为观察参考点，然后在此点指定法⽮量N，即z v轴的正向。

法⽮量V：确定了⽮量N后，再定义观察正向⽮量V，该⽮量⽤来建⽴y v轴的正向。

通常的⽅法是先选择任⼀不平⾏于N的⽮量V'，然后由图形系统使该⽮量V'投影到垂直于法⽮量N的平⾯上，定义投影后的⽮量为⽮量V。

法⽮量U：利⽤⽮量N和V，可以计算第三个⽮量U，对应于x z轴的正向。

的指定视图投影到显⽰设备表⾯上的过程来处理对象的描述。

2.世界坐标系在现实世界中，所有的物体都具有三维特征，但是计算机本⾝只能处理数字，显⽰⼆维的图形，将三维物体和⼆维数据联系到⼀起的唯⼀纽带就是坐标。

为了使被显⽰的物体数字化，要在被显⽰的物体所在的空间中定义⼀个坐标系。

该坐标系的长度单位和坐标轴的⽅向要适合被显⽰物体的描述。

该坐标系被称为世界坐标系，世界坐标系是固定不变的。

OpenGL 中世界坐标⽤来描述场景的坐标，Z+轴垂直屏幕向外，X+从左到右，Y+轴从下到上。

世界坐标系是右⼿笛卡尔坐标系统。

我们⽤这个坐标系来描述物体及光源的位置。

世界坐标系以屏幕中⼼为原点(0,0,0)，长度单位这样来定：窗⼝范围按此单位恰好是(-1,-1)到(1,1)。

计算机图形学2010_06三维图形变换

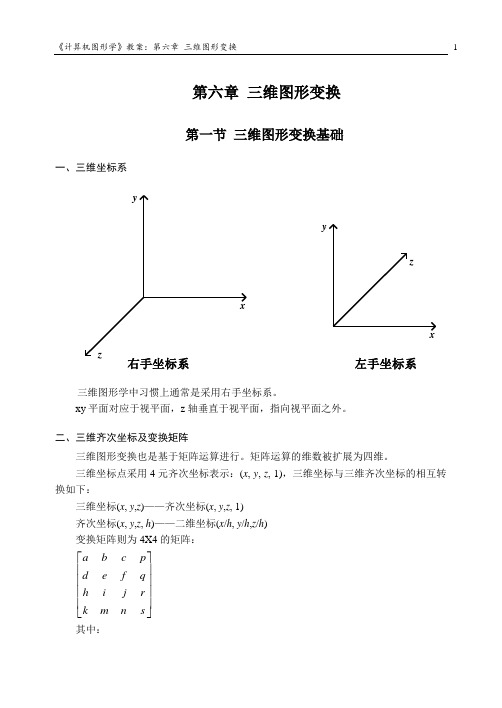
第六章三维图形变换第一节三维图形变换基础一、三维坐标系xyzxyz右手坐标系左手坐标系三维图形学中习惯上通常是采用右手坐标系。

xy 平面对应于视平面，z 轴垂直于视平面，指向视平面之外。

二、三维齐次坐标及变换矩阵三维图形变换也是基于矩阵运算进行。

矩阵运算的维数被扩展为四维。

三维坐标点采用4元齐次坐标表示：(x , y , z , 1)，三维坐标与三维齐次坐标的相互转换如下：三维坐标(x , y ,z )——齐次坐标(x , y ,z , 1) 齐次坐标(x , y ,z , h )——二维坐标(x /h , y /h ,z /h ) 变换矩阵则为4X4的矩阵：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡s nm kr j i h q f e d p c b a 其中：平移变换第二节三维几何变换一、三维基本变换 1. 平移变换⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1010000100001nmk T )1,,,()1,,,(n z m y k x T z y x +++=⋅2. 比例变换)1,,,()1,,,(1000000000000jz ey ax T z y x j e a T =⋅⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡= 3. 旋转变换三维的基本旋转变换分为三种，即绕三个坐标轴的旋转变换。

(1)绕z 轴旋转γ角旋转后z 值不变，x,y 值将发生改变，x,y 值的计算公式与平面旋转相同，即：zz y x y y x x ='+='-='γγγγcos sin sin cos 则变换矩阵为：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=1000010000cos sin 00sin cos γγγγT 有：)1,1,cos sin ,sin cos ()1,,,(γγγγy x y x z y x +-=T(2)绕x 轴旋转α角则旋转后x 的坐标值不变，y 和z 的坐标值将改变，相当于在yz 平面上绕平面原点进行旋转变换。

平面转转变换的公式为：ααααcos sin sin cos y x y y x x +='-='对应而来，这里y 对应于x ，z 对应y ，有：ααααcos sin sin cos z y z z y y +='-='则变换矩阵为：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=10000cos sin 00sin cos 00001ααααT )1,cos sin ,sin cos ,()1,,,(ααααz y z y x z y x +-=T(3)绕y 轴旋转β角这时，z 对应于x ，x 对应于y 。

三维坐标转换中高程误差对转换精度的影响

三维坐标转换中高程误差对转换精度的影响作者：吴清波,向为,刘文祥,孙广富来源：《现代电子技术》2011年第09期摘要：以Bursa-Wolf坐标转换模型和参数求解方法为基础，根据误差传播理论，推导出测区内任意待转换点三维坐标转换精度数学公式。

通过对该数学模型的分析可得：公共点所在测区内待测点的转换精度随高程变化呈抛物线分布。

当高程在(-100 m,1 000 m)区间变化时，转换精度在-2量级浮动,对坐标转换的影响很小。

最后通过算例验证了结论的正确性。

关键词：七参数转换；坐标转换；高程误差；转换精度；坐标系中图分类号：TN911-34文献标识码：A文章编号：1004-373X(2011)09-0186-04Effect of Elevation Error on Accuracy in 3-D Coordinate TransformationWU Qing-bo,XIANG Wei,LIU Wen-xiang,SUN Guang-(Electronic Science & Engineering College,National University of DefenseTechnology,Changsha 410073,China)Abstract： Based on Bursa-Wolf coordinate transformation model and parameter solving methods,a mathematical model for the 3-D accuracy of coordinate conversion for arbitrary measured point in the surveying area is derive with the theory of error propagation. According to the analysis of the mathematical model,it can be concluded that the variation of conversion accuracy of measured point presents a parabola distribution with the change of altitude. Meanwhile,when the variation of altitude is in the scope of --2 m,which has a trivial effect on the coordinate transformation. The theoretical validity of the conclusions was proved by experiment.Keywords： seven-parameter transformation; coordinate transformation; vertical error; transformation accuracy; geodetic coordinate system0 引言目前，全球定位系统GPS在我国的应用日益广泛，GPS采用的是以ITRF标准为框架的地心坐标系WGS84，是一种以地球整体拟合最佳为标准得到的椭球。

三维坐标系的转换原理

三维坐标系的转换原理
三维坐标系的转换原理主要涉及到旋转、平移和尺度参数的确定。

在大地测量、工程测量、摄影测量等领域中，这种转换是必不可少的。

坐标转换过程通常分两步：首先，通过公共点的坐标解算转换参数；然后，利用这些参数转换非公共点。

其中，旋转参数的确定是坐标转换的核心。

传统的三维坐标转换模型通常使用三个旋转角作为旋转参数，建立的模型是非线性的，常需要用泰勒级数展开的方法将模型线性化，计算比较繁杂。

在小角度旋转情况下，可以对旋转矩阵作近似处理，得到线性模型，如常用的布尔莎模型。

针对大旋角的坐标转换问题，多采用罗德里格矩阵表示旋转矩阵的坐标转换方法，这种方法仅有三个旋转参数，计算过程无需线性化，且能适用大旋角转换。

除了旋转，平移是将一个坐标系的原点移动到另一个坐标系的原点，尺度参数则是用来调整坐标系之间尺度差异。

此外，还需要注意的是，坐标转换可能会涉及到不同的坐标系统，如笛卡尔坐标系、极坐标系等，以及不同的转换方法，如仿射变换、刚体变换等。

在进行坐标转换时，需要根据具体的应用场景和需求选择合适的坐标系统和转换方法。

总的来说，三维坐标系的转换原理是通过确定旋转、平移和
尺度参数，将一个坐标系下的点或物体转换到另一个坐标系下，从而实现坐标系的统一和数据的整合。

三维坐标转换的高斯-赫尔默特模型及其抗差解法

三维坐标转换的高斯-赫尔默特模型及其抗差解法高斯-赫尔默特模型（Gauss-Helmert model）是一种用于三维坐标转换的数学模型，常用于大地测量和地理空间数据处理中。

该模型通过最小二乘法估计一组参数，以将一个坐标系中的点数据转换到另一个坐标系中。

高斯-赫尔默特模型的基本形式为：[X'] = [P] [X] + [a]其中，[X']和[X]分别表示转换后和转换前的三维点坐标向量，[P]是一个3×3的转换矩阵，[a]是一个3×1的平移向量。

为了解决数据中存在的异常值和系统性偏差等问题，可以使用抗差解法对高斯-赫尔默特模型进行优化。

常用的抗差解法包括最小二乘法中的加权最小二乘法（WLS）和鲁棒估计方法，如最小绝对值估计（L1）和最小二乘中位数估计（L2）等。

在加权最小二乘法中，给每个观测值赋予一个权重，根据观测值的精度和可靠性来确定权重值。

较高权重的观测值对参数估计的影响更大，较低权重的观测值对参数估计的影响更小。

通过优化加权最小二乘目标函数，可以得到更稳健的参数估计结果。

鲁棒估计方法则不依赖于精确的权重分配，通过引入鲁棒损失函数来抑制异常值的影响。

常用的鲁棒损失函数包括Huber损失和Tukey's双曲线损失等。

这些损失函数在保证了对于小残差值的平方损失近似于最小二乘估计的同时，对于大残差值具有更强的抗干扰能力。

抗差解法可以有效减少异常值对参数估计的影响，提高三维坐标转换的鲁棒性和可靠性。

然而，在使用抗差解法时需要进行参数的迭代估计，计算复杂度较高。

同时，对于一些拟合精度较高的数据集，传统的最小二乘法已经能够取得较好的拟合效果，抗差解法的优势不一定显著。

因此，在选择是否使用抗差解法时，需要根据具体问题和数据特点来进行判断。

54年椭球的偏移量+cgcs2000三维七参数坐标系转换常数

54年椭球的偏移量+cgcs2000三维七参数坐标系转换常数1. 引言1.1 概述在地理信息系统（GIS）领域中，椭球的偏移量和坐标系转换常数是非常重要的参数，它们对于准确测量和精确定位至关重要。

本文将详细讨论54年椭球的偏移量以及CGCS2000三维七参数坐标系转换常数，并分析其应用与意义。

1.2 文章结构本文共分为五个主要部分。

首先是引言部分，介绍了文章的背景和目的。

接下来将详细探讨54年椭球的偏移量，包括椭球定义与参数、偏移量计算方法以及应用与意义。

然后，我们会仔细研究CGCS2000三维七参数坐标系转换常数，首先介绍CGCS2000的基本情况，然后探讨七参数坐标系转换原理，并详细解释常数计算与应用。

接着，在实验与结果分析章节中，我们将描述数据来源和实验设计，并阐述分析过程和方法使用，最后进行结果解读和讨论。

最后，在结论与展望部分，我们将总结主要研究结论并展望未来工作方向。

1.3 目的本文的目的是探究和分析54年椭球的偏移量以及CGCS2000三维七参数坐标系转换常数的计算方法和应用。

通过实验与结果分析，我们希望能够得出相关结论，并为今后类似研究提供参考。

同时，本文也将讨论当前研究的局限性，并对未来工作方向进行展望。

通过这些内容，读者将能够更好地理解椭球偏移量和坐标系转换常数在GIS领域中的重要性和应用价值。

2. 54年椭球的偏移量:2.1 椭球定义与参数:在地理信息系统和大地测量中，椭球是描述地球形状的一个数学模型。

54年椭球是一种常用的椭球模型，其参数可以用来近似地描述中国大陆地区的地形。

该椭球的定义包括长半轴、扁率以及其他公式中使用到的相关参数。

2.2 偏移量计算方法:54年椭球的偏移量是指利用该椭球模型进行经纬度转换时所引入的误差。

通过数学计算方法，可以将基于WGS84等其他椭球体系确定的经纬度坐标转换为基于54年椭球体系确定的经纬度坐标，从而实现不同坐标系之间的互相转换。

偏移量计算方法通常涉及到参考坐标点的选择、数据处理和合适的数学公式应用。