《圆周角定理》练习题(A)
中考数学专项练习圆周角定理(含解析)

0° 0 中考数学专项练习圆周角定理(含解析)是⊙O 的直径,弦 CD ⊥ AB ,∠ CAB=40 D+ ∠ABD 的度数为〔 〕A. 100°B. 110°C. 120°D. 1502.A 、C 、B 是⊙O 上三点,假设∠ AOC=40°,那么∠ ABC 的度数是 ()A. 1 0°B.C.80°C 的外接圆,∠ OCB=40 °,那么∠ A 的度数等于A. 6B. 5C. 4,连接 BD , O D. 3.如图,⊙ O 是△ A一】单项选择题 图,那么DD. 304.如图,EF是⊙ O的直径,把∠ A为60°的直角三角板ABC的一条直角边BC放在直线EF上,斜边AB 与⊙ O交于点P,点B与点O 重合.将三角板ABC 沿OE方向平移,使得点B与点E重合为止.设∠ POF=x°,那么x 的取值范围是( )A. 30≤x≤60B. 30≤x≤90C.30≤x≤120D.60≤x≤1205.如图,圆心角∠ BOC=100°,那么圆周角∠ BAC 的大小是A. 50°B.100°C.130°D.200°6.以下各命题正确的选项是:〔〕A. 假设两弧相等,那么两弧所对圆周角相等B. 有一组对边平行的四边形是梯形.C. 垂直于弦的直线必过圆心 D. 有一边上的中线等于这边一半的三角形是直角三角形.7.某数学研究性学习小组制作了如下的三角函数计算图尺:在半径为 1 的半圆形量角器中,画一个直径为 10的圆,把刻度尺 CA 的 0刻度固定在 刻度尺可以绕点 O 旋转.从图中所示的图尺可读出 sin 〕B.C.D. 【二】填空题 8.如图, P 是⊙ 0 直径那么∠ A 的度数为10.如图,在以 AB 为直径的半圆中,有一个边长为 1 的内接正方形 CF ,那么以 AC 和 BC 的长为两根的一元二次方程是 ___ ..如图, AB 是⊙的直径,点 C 是半径 OA 的中点,过点 C 作DE ⊥AB ,交 O 于点 D ,E 两点,过点 D 作直径 DF ,连结 AF ,那么∠ DEA= AB 延长线上的点, PC 切⊙0于 C 、假设∠ P=40是半圆 的直径, ,那么 的大小是假设∠ BO ∠BCD ,那么弧 BD 的长为11 A. 半圆的圆 AOB 的o12. 如图,⊙ O的半径为6,四边形ABCD 内接于⊙ O,连接OB,OD,13. __________________________ 如图,AB 是⊙O的直径,C、D、E都是⊙ O上的点,∠ A=55°,∠B=70°,那么∠ E的度数是.14. _____________________________________ 如图,AD 和AC 分别是⊙ O的直径和弦,且∠ CAD=30°,OB⊥A D交AC于点B,假设OB=5,那么BC等于__________________________ .O 的内接四边形ABCD 中,∠ A=105°,那么∠ BOD 等于【三】解答题16. 如图,在⊙ O 中,AC 与BD 是圆的直径,BE⊥ AC,CF⊥BD,垂足分别为E、F形ABCD 是什么特殊的四边形?请判断并说明理由;2〕求证:BE=CF.17. 如图,AB 是? O的直径,点C在? O上,过点C的直线与AB 的延长线交于点P,AC=PC,∠ COB=2∠PCB.〔1〕求证:PC是? O 的切线;〔2〕求证:BC= AB ;〔3〕点M 是弧AB 的中点,CM 交AB 于点N,假设AB=4 ,求MN ·M C 的值.【四】综合题18. 如图,⊙ O 是△ABC 的外接圆,AB=AC ,P是⊙O 上一点.〔1〕操作:请你只用无刻度的直尺,分别画出图①和图②中∠ P 的平分线;2〕说理:结合图②,说明你这样画的理由.〔1〕⊙D 的半径;〔2〕CE 的长. 【一】单项选择题【考点】垂径定理,圆周角定理 【考点】圆周角定理 【解析】【解答】根据圆周角和圆心角的关系解决问题,由〝一条弧所 对的圆周角等于它所对的圆心角的一半〞解答 . 【分析】此题考查了原周角和圆心角的联系 .【考点】圆周角定理【解析】【解答】解:在△ OCB 中, OB=OC 〔⊙ O 的半径〕,∴∠O BC=∠0CB 〔等边对等角〕;∵∠ OCB=40°,∠ C0B=180°﹣∠ OBC ﹣∠ 0CB , ∴∠COB=100°; 又∵∠ A= ∠C0B 〔同弧所对的圆周角是所对的圆心角的一半〕 , ∴∠ A=50 °, 应选 B 、【分析】在等腰三角形 OCB 中,求得两个底角∠ OBC 、∠0CB 的度数,然 后根据三角形的内角和求得∠ COB=100°;最后由圆周角定理求得∠ A 的 度数并作出选择.【考点】圆周角定理【考点】圆周角定理【解析】【分析】∠ BOC ,∠ BAC 是同弧所对的圆周角和圆心角,∠ B OC=2∠ BAC ,因为圆心角∠ BOC=100°,所以圆周角∠ BAC=50°.【点评】此题考查圆周角和圆心角,解此题的关键是掌握同弧所对的圆周 角和圆心角关系,然后根据题意来解答。
圆周角定理及圆的内接四边形-练习题 含答案解析

解: , , , ,
在 中, , , ,
在 中, , , .
【解析】 由AB为直径, ,易得 ,然后由垂径定理证得, ,继而证得结论; 由 , ,可求得OE的长,继而求得DE,AE的长,则可求得 ,然后由圆周角定理,证得 ,则可求得答案.
此题考查了圆周角定理、垂径定理以及勾股定理 此题难度适中,注意掌握数形结合思想的应用.
【解答】
解: 是 的直径, , , , .
故答案为 .
9. 如图,已知圆周角 ,则圆心角 ______.
【答案】
【解析】解: , .
故答案为 .
根据圆周角定理即可得出结论.
本题考查了圆周角定理 在同圆或等圆中,同弧和等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.
10. 如图,在圆内接四边形ABCD中,O为圆心, ,则 的度数为______.
解得: , , ,
故选:C.
设 的度数 , 的度数 ,由题意可得 ,求出 即可解决问题.
该题主要考查了圆周角定理及其应用问题;应牢固掌握该定理并能灵活运用.
4. 如图,已知AC是 的直径,点B在圆周上 不与A、C重合 ,点D在AC的延长线上,连接BD交 于点E,若 ,则
A. B. C. D.
【答案】D
又AD平分 ,所以,即劣弧AE是劣弧DE的2倍, 正确. , , , ,故 错误. , ,
又 ,
故 错误.
故答案为: .
先利用等腰三角形的性质求出 、 的度数,即可求 的度数,再运用弧、弦、圆心角的关系即可求出 、 .
本题利用了: 等腰三角形的性质; 圆周角定理; 三角形内角和定理.
7. 如图,AB为 直径,点C、D在 上,已知 , ,则 ______度
圆周角定理 专题练习

圆周角定理专题练习1.在圆周角定理中,已知∠CBO=45°,∠CAO=15°,求∠AOB的度数。
答案:B.60°。
2.在平面直角坐标系中,已知⊙A经过原点O,并且分别与x轴、y轴交于B、C两点,已知B(8,),C(,6),求⊙A的半径。
答案:C.5.3.在圆周角定理中,已知点A,B,C在⊙O上,且∠A=50°,求∠BOC的度数。
答案:A.130°。
4.已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,求∠BCD的度数。
答案:A.116°。
5.已知圆心角∠BOC=78°,求圆周角∠BAC的度数。
答案:A.156°。
6.在圆周角定理中,已知OA,OB是⊙O的两条半径,且OA⊥OB,点C在⊙O上,求∠XXX的度数。
答案:D.20°。
7.在圆周角定理中,已知AB是半圆的直径,点D是AC 的中点,∠ABC=50°,求∠DAB的度数。
答案:XXX°。
8.在圆周角定理中,已知A、B、C三点在⊙O上,且∠AOB=80°,求∠XXX的度数。
答案:D.40°。
9.已知AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BAC=12∠BOD,求⊙O的半径。
答案:B.5.10.在圆周角定理中,已知DC是⊙O直径,XXX⊥CD于F,连接BC,DB,判断下列结论错误的是:答案:B.AF=XXX。
11.在圆周角定理中,已知点A,B,C,D为⊙O上的四个点,AC平分∠BAD,AC交BD于点E,CE=4,CD=6,求AE的长。
答案:B.5.12.在圆周角定理中,已知点A、B、C在⊙O上,且∠C=30°,求∠AOB的度数。
答案:XXX°。
13.在圆周角定理中,已知⊙O中∠BAC=∠CDA=20°,求∠ABO的度数。
答案:B.70°。
圆周角定理练习题

圆周角定理练习题一、选择题1. 圆周角定理指出,圆周角的度数是它所对弧的中心角的度数的多少?A. 1/2B. 1/3C. 2倍D. 3倍2. 在圆中,如果一个圆周角的度数是30°,那么它所对的弧的中心角的度数是多少?A. 60°B. 90°C. 120°D. 180°3. 已知圆的半径为5,圆周角为40°,求该圆周角所对的弦长。
A. 4B. 5C. 8D. 10二、填空题4. 若圆周角α的度数为60°,则它所对的弧的中心角的度数为______。
5. 在圆中,如果圆周角的度数是中心角度数的一半,那么该圆周角所对的弧长是半径的______倍。
6. 已知圆的半径为r,圆周角为θ,根据圆周角定理,该圆周角所对的弦长为______。
三、判断题7. 圆周角定理只适用于圆的内部角。
(对/错)8. 如果一个圆周角的度数是90°,那么它所对的弧的中心角的度数是180°。
(对/错)9. 圆周角定理同样适用于圆的外部角。
(对/错)四、简答题10. 解释圆周角定理的含义,并给出一个实际应用的例子。
11. 如何利用圆周角定理计算圆内接四边形的对角线长度?五、计算题12. 在半径为10的圆中,有一个圆周角为60°,求该圆周角所对的弧长。
13. 已知圆的半径为8,圆周角为120°,求该圆周角所对的弦长。
14. 一个圆周角的度数是45°,求它所对的弧的中心角的度数,并计算该圆周角所对的弦长,如果圆的半径为15。
六、证明题15. 证明:如果两个圆周角所对的弧相等,那么这两个圆周角的度数也相等。
16. 证明:在同一个圆中,相等的圆周角所对的弧长也相等。
七、应用题17. 在一个半径为7的圆中,有一个圆周角为80°,求该圆周角所对的弦长,并计算该弦所对的圆心角的度数。
18. 如果在一个圆中,有一个圆周角的度数是圆心角度数的1/3,求这个圆周角的度数,如果圆心角的度数是120°。
圆周角的专项练习30题(有答案)ok

圆周角定理专项练习30题(有答案)1.如图AB是⊙O的直径,C是⊙O上的一点,若AC=8cm,AB=10cm,OD⊥BC于点D,求BD的长.2.如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=65°.(1)求∠B的大小;(2)已知AD=6,求圆心O到BD的距离.3.已知AB是⊙O的直径,半径OC⊥AB,D为上任意一点,E为弦BD上一点,且BE=AD,求证:△CDE为等腰直角三角形.4.如图,AB是圆O的直径,AD=DC,∠CAB=30°,AC=2.求AD的长.5.如图,AB,CD是⊙O的两条弦,它们相交于点P,连接AD,BD.已知AD=BD=4,PC=6,求CD的长.6.如图,已知点C、D在以O为圆心,AB为直径的半圆上,且OC⊥BD于点M,CF⊥AB于点F交BD于点E,BD=8,CM=2.(1)求⊙O的半径;(2)求证:CE=BE.7.如图,A是以EF为直径的半圆上的一点,作AG⊥EF交EF于G,又B为AG上一点,EB的延长线交半圆于K,求证:(1)△AEB∽△KEA;(2)AE2=EB•EK.8.如图,BC是⊙O的直径,P为⊙O上一点,点A是的中点,AD⊥BC,垂足为D,PB分别与AD、AC相交于点E、F.(1)若∠BAD=36°,求∠ACB,∠ABP;(2)如果AE=3,求BE.9.如图,△ABC内接于⊙O,AB=AC,弦AD交BC于点E,AE=4,ED=5,(1)求证:AD平分∠BDC;(2)求AC的长;(3)若∠BCD的平分线CI与AD相交于点I,求证:AI=AC.10.如图,AB是⊙O的直径,点C在⊙O上,AB=6,AC=5,求tanA的值.11.如图,AB是⊙O的直径,弦CD与AB相交于点E,∠ACD=60°,∠CEB=100°.求∠ADC的度数.12.已知如图,在⊙O中,弦BC平行于半径OA,AC交BO于M,∠C=25°.求∠AMB的度数.13.如图,⊙O是△ABC的外接圆,∠A=45°,BD是直径,且BD=2,连接CD,求BC的长.14.已知:如图,AD平分∠BAC,DE∥AC,且AB=5cm,求DE的长.15.已知如图,在△ABC中,∠BAC=90°,AB=AC=,D是BC中点,作半径是的圆经过点A和D且交AB于F,交AC于E.求∠ADF的正弦值.16.如图,在△ABC中,AB是⊙O的直径,⊙O与AC交于点D,AB=,∠B=60°,∠C=75°,求∠BOD的度数.17.如图:在⊙O中,AB是直径,∠ACB的平分线交⊙O于点D,AD=5cm.求:BD与⊙O半径的长.18.如图,AB是⊙O的直径,P是弦AC延长线上的一点,且AC=PC,直线PB交⊙O于点D,若∠BDC=30°,求∠P的度数.19.如图,△ABC中,∠B=45°,∠C=60°,AB=cm,以AB为直径的⊙O交BC于点D,求CD的长?20.如图,已知AD是△ABC的高,AE是△ABC的外接圆的直径.(1)求证:AC•AB=AD•AE;(2)若AB=6,AC=5,AD=3,求⊙O的面积.21.如图,⊙0为四边形ABCD的外接圆,AC为⊙0的直径,CD∥AB,点E、F分别在BC和AD上,且EF经过圆心0.求证:OE=OF.22.如图,等腰三角形ABC中,以腰AB为直径的⊙O交底边BC于点D,交AC于点E,连接DE.(1)求证:BD=DE;(2)若⊙O的半径为3,BC=4,求CE的长.23.如图,已知⊙0的半径为5,AB是⊙0的直径,点C、D都在⊙0上,若∠D=30°,求AC的长.24.如下图,已知△ABC内接于⊙O,若∠C=45°,AB=4,求⊙O的面积.25.如图,⊙O的直径AB为4cm,弦AC为3cm,∠ACB的平分线交⊙O于D,求:①BC的长;②AD与BD的长.26.如图,⊙O为四边形ABCD的外接圆,圆心O在AD上,OC∥AB.(1)求证:AC平分∠DAB;(2)若AC=8,AC:CD=2:1,试求⊙O的半径.27.如图,点A、B、C、D在圆上,AB=8,BC=6,AC=10,CD=4,求AD的长.28.如图,AB是⊙O的直径,弦CD与AB相交于点E,∠ACD=50°,∠ADC=45°,求∠CDB及∠CEB的度数.29.如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.(1)若∠AOD=54°,求∠DEB的度数;(2)若DC=2,AB=8,求⊙O的直径.30.如图,已知△ABC内接于⊙O,AE平分∠BAC,且AD⊥BC于点D,连接OA.求证:∠OAE=∠EAD.参考答案:1.∵AB是⊙O的直径,∴∠ACB=90°;∵OD⊥BC,∴OD∥AC,又∵AO=OB,∴OD是△ABC的中位线,即BD=BC;Rt△ABC中,AB=10cm,AC=8cm;由勾股定理,得:BC==6cm;故BD=BC=3cm2.(1)∵∠APD=∠C+∠CAB,∴∠C=65°﹣40°=25°,∴∠B=∠C=25°;(2)作OE⊥BD于E,则DE=BE,又∵AO=BO,∴,圆心O到BD的距离为3.3.连接AC、BC,由圆周角定理得∠CBE=∠CAD,∵CO⊥AB,∴点C是弧ABC的中点,∴AC=BC,又∵BE=AD∴△ACD≌△BCE,∴CD=CE.∠ADC=∠BEC,∵AB是直径,∴∠ADB=90°,∵∠BEC=∠DCE+∠CDB,∠ADC=∠ADB+∠CDB,∴∠DCE=∠ADB=90°,即△DCE是等腰直角三角形.4.连接OD;∵D 是的中点,∴OD垂直平分AC;∴∠AOD=90°﹣∠CAB=60°;又∵OA=OD,∴△OAD是等边三角形;∴OA=AD;Rt△ABC中,∠CAB=30°,AC=2;∴AB==4,OA=2;即:AD=OA=2.故AD的长为2.5.连接AC,∵AD=BD,∴=.∵∠C=∠BAD,又∵∠ADP=∠CDA,∴△ADP∽△CDA.∴=,即AD2=CD•DP.∵AD=4,PC=6,设CD=x,则42=x(x﹣6),解得:x1=8,x2=﹣2(不合题意,舍去)∴CD=8.6.1)解:∵OC为⊙O的半径,OC⊥BD,∴;∵DB=8,∴MB=4(1分)设⊙O的半径为r,∵CM=2,∴OM=r﹣2,在Rt△OMB中,根据勾股定理得(r﹣2)2+42=r2,解得r=5;(2)证明:方法一:连接AC、CB,∵AB是直径,∴∠ACB=90°.∴∠ACF+∠FCB=90°.又∵CF⊥AB,∴∠CAF+∠ACF=90°∴∠FCB=∠CAF∵OC为⊙O的半径,OC⊥BD,∴C 是的中点,∴∠CAF=∠CBD.∴∠FCB=∠DBC.∴CE=BE;方法二:如图,连接BC,补全⊙O,延长CF交⊙O于点G;又∵CF⊥AB,AB为直径,∴=.∴OC为⊙O的半径,OC⊥BD.∴C 是的中点,∴=.∴=.∴∠FCB=∠DBC.∴CE=BE.7.(1)连接AK、AF,∴∠K=∠F=90°﹣∠AEF=90°﹣∠AEG.∠EAG=90°﹣∠AEG.∴∠K=∠EAG∠KEA=∠AEB.∴△AEB∽△KEA.(2)由①得△AEB∽△KEA,∴.∴AE2=EB•EK.8.(1)因为BC是⊙O的直径所以∠CAB=90°所以∠ABD+∠ACB=90°因为AD⊥BC所以∠ABD+∠BAD=90°所以∠ACB=∠BAD=36°因为A 是的中点,则所以∠ABP=∠ACB=36°.(2)因为∠ABP=∠ACB,∠BAD=∠ACB所以∠ABP=∠BAD因为AE=3所以BE=3.9.(1)∵AB=AC,∴;∴AD平分∠BDC;解:(2)∵∠ACB=∠ADB,∠CDA=∠ADB,∴∠CDA=∠ACB;∵∠CAE=∠DAC,∴△ACE∽△ADC;∴,即;∴AC=6;证明:(3)∠AIC=∠ADC+∠DCI,∠ACI=∠BCI+∠ACB;∴∠AIC=∠ACI;∴AI=AC.10.∵AB是⊙O的直径,∴∠ACB=90°.在Rt△ABC中,∠ACB=90°,AB=6,AC=5,∴BC===.∴tanA==.11.连接BC.∵AB是⊙O的直径,∴∠ACB=90°,∵∠ACD=60°,∴∠BCE=30°,∵∠CEB=100°,∴∠B=50°,∴∠ADC=∠B=50°.12.∵BC∥OA,∠C=25°,∴∠A=∠C=25°,在⊙O中,∵∠O=2∠C,∴∠O=50°,又∵∠AMB=∠A+∠O,∴∠AMB=75°13.在⊙O中,∵∠A=45°,∠D=45°,∵BD为⊙O的直径,∴∠BCD=90°,∴△BCD是等腰直角三角形,∴BC=BD•sin45°,∵BD=2,∴14.连接AE,BD,∵AD平分∠BAC,∴∠BAD=∠CAD,∵DE∥AC,∴∠ADE=∠CAD,∴∠ADE=∠BAD,∴AE=BD,∴AB=DE,∵AB=5cm,∴DE=5cm15.连接EF,ED(1分)在△ABC中∵AB=AC,∠BAC=90°,BD=CD,∴AD=,∠DAF=∠DCE=45°,∠ADC=90°,∴∠ADE+∠EDC=90°,在⊙O中,∵∠BAC=90°,∴EF是⊙O的直径,(3分)∴∠FDE=90°,∴∠FDA+∠ADE=90°,∴∠EDC=∠FDA,∴△EDC≌△FDA,∴AF=CE,(4分)设AF=x,则CE=x,AE=AC﹣CE=﹣x,∵⊙O 的半径是,∴EF=,在Rt△AEF 中,,解得,∠ADF=∠AEF,(5分)∴当x=1时,sin∠ADF=sin∠AEF==,当x=时,sin∠ADF=sin∠AEF==,∴∠ADF 的正弦值为或.16.在△ABC中,∵∠B=60°,∠C=75°,∴∠A=45°.∵AB是⊙O的直径,⊙O与AC交于点D,∴∠DOB=2∠A=90°.故答案为:90°17.∵∠ACB的平分线交⊙O于点D,∴∠ACD=∠BCD,∴AD=BD,∵AB是直径,∴∠ADB=90°,∵AD=5cm,∴BD=5cm;在Rt△ABD中,2AD2=AB2,∴AB=5cm,∴圆的半径为cm.18.连接BC,∵AB是直径,∴BC⊥AC,(2分)∵AC=CP,∴AB=BP,(3分)∴∠P=∠A,(4分)∵∠A=∠D=30°,(5分)∴∠P=30°.19.连接AD.(1分)∵AB是⊙O的直径.∴∠ADB=90°.(3分)在Rt△ADB中,AD=AB•sinB=2sin45°=2×=2(6分)在Rt△ADC中,CD=,即CD 的长为m.20.(1)证明:连接BE,∵AD是△ABC的高,AE是△ABC的外接圆的直径,∴∠ADC=∠ABE=90°,∵∠C=∠E,∴△ADC∽△ABE.∴AC:AE=AD:AB,∴AC•AB=AD•AE;(2)解:∵AB=6,AC=5,AD=3,∴AE===10,∴OA=5,∴⊙O的面积为:π×52=25π21.∵AC为⊙0的直径,∴∠B=∠D=90°,∵CD∥AB,∴∠B+∠BCD=180°,∴∠BCD=90°,∴∠BCD+∠D=90°,∴AD∥BC,∴∠FAO=∠ECO,在△AOF和△COE中,,∴△AFO≌△CEO(ASA),∴OE=OF22.(1)证明:连接AD,∵AB为圆O的直径,∴AD⊥BC,∵AB=AC,∴D为BC的中点,即BD=CD,∵∠DEC为圆内接四边形ABDE的外角,∴∠DEC=∠B,∵AB=AC,∴∠B=∠C,∴∠DEC=∠C,∴DE=DC,∴BD=DE;(2)解:∵∠DEC=∠B,∠C=∠C,∴△DEC∽△ABC,∴=,即=,则EC=.23.连接BC.∵AB是⊙0的直径,∴∠ACB=90°,在直角△ABC中,∠A=∠D=30°,AB=2×5=10.∴AC=AB•cosA=10×=5.24.连接OA,OB;则OA=OB,∠AOB=2∠C;(2分)∵∠C=45°,∴∠AOB=90°,∴OA2+OB2=AB2;(4分)又∵AB=4,∴2OA2=42,OA2=8;(6分)∴S⊙O=π•OA2=8π.25.①∵AB为直径,∴∠ACB=90°,∵AB=4,AC=3,∴BC===;②∵AB为直径,∴∠ADB=90°,∵CD平分∠ACB,∴∠ACD=∠BCD=45°,∵∠ABD=∠ACD,∠BCD=∠BAD,∴∠DAB=∠DBA=45°,∴AD=DB,∵AD2+BD2=AB2,∴AD=DB=2,26.(1)证明:∵OC∥AB,∴∠OCA=∠CAB,∵OA=OC,∴∠OAC=∠OCA,∴∠OAC=∠CAB,即AC平分∠DAB;(2)解∵AD是⊙O的直径,∴∠ACD=90°,∵AC=8,AC:CD=2:1,∴CD=4,在Rt△ACD中,AD==4,∴OA=AD=2,∴⊙O的半径为2.27.△ABC中,AB=8,BC=6,AC=10,∴AC2=AB2+BC2,∴∠B=90°,∴AC为直径,∴∠D=90°,Rt△ADC中,AD====2.∴AD的长为2.28.连接BC,则∠ACB=90°(圆周角定理),∵∠CBA=∠ADC=45°,∴∠CAB=90°﹣∠CBA=45°(直角三角形的两个锐角互余);∴∠CEB=∠CAB+∠ACD=45°+50°=95°(外角定理).∠CDB=∠CAB=45°.综上可得:∠CDB=45°,∠CEB=95°29.(1)∵OD⊥AB∴弧AD=弧BD∴∠DEB=∠AOD=×54°=27°…3分(2)∵OD⊥AB∴AC=AB=×8=4设⊙O的半径为R,则OC=R﹣2在Rt△AOC中,由勾股定理得:42+(R﹣2)2=R2解得:R=5∴⊙O的直径为1030.连接OE,∵AE平分∠BAC,∴∠BAE=∠CAE,∴=,∴OE⊥BC,∵AD⊥BC,∴OE∥AD,∴∠OEA=∠EAD,∵OA=OE,∴∠OEA=∠OAE,∴∠OAE=∠EAD.11。
圆周角定理经典训练卷(含答案)

圆周角定理经典训练卷一.选择题1.如图,AB、CD都是⊙O的弦,且AB⊥CD.若∠CDB=62°,则∠ACD的大小为()(1)(2)(3)A.28°B.31°C.38°D.62°2.如图,⊙O是△ABC的外接圆,已知∠ABO=40°,则∠ACB的大小为()A.40°B.30°C.45°D.50°3.如图,AB是⊙O的弦,点C在圆上,已知∠OBA=40°,则∠C=()A.40°B.50°C.60°D.80°4.如图,已知AB、AD是⊙O的弦,∠B=30°,点C在弦AB上,连接CO并延长CO交于⊙O于点D,∠D=20°,则∠BAD的度数是()(4)(5)(6)(7)A.30°B.40°C.50°D.60°5.如图,已知圆心角∠BOC=100°,则圆周角∠BAC的大小是()A.50°B.55°C.60°D.65°6.如图,A,B,P是半径为2的⊙O上的三点,∠APB=45°,则弦AB的长为()A.2B.4C.D.27.如图,OA、OB是⊙O的半径,C是⊙O上一点,∠ACB=20°,则∠OAB的度数为()A.80°B.75°C.70°D.65°8.如图,在⊙O中,AB平分∠CAO,∠BAO=25°,则∠BOC的大小为()A.25°B.50°C.65°D.80°(8)(9)(10)9.如图,⊙O中,劣弧AB所对的圆心角∠AOB=120°,点C在劣弧AB上,则圆周角∠ACB=()A.60°B.120°C.135°D.150°10.如图,⊙O的半径是2,AB是⊙O的弦,点P是弦AB上的动点,且1≤OP≤2,则弦AB所对的圆周角的度数是()A.60°B.120°C.60°或120°D.30°或150°11.如图,P是⊙O外一点,PA、PB分别交⊙O于C、D两点,已知和所对的圆心角分别为90°和50°,则∠P=()A.45°B.40°C.25°D.20°12.已知△ABC中,AB=AC,∠A=50°,⊙O是△ABC的外接圆,D是优弧BC上任一点(不与A、B、C重合),则∠ADB的度数是()A.50°B.65°C.65°或50°D.115°或65°13.如图,AB是⊙O的直径,BC是⊙O的弦.若∠OBC=60°,则∠BAC的度数是()(13)(14)(15)A.75°B.60°C.45°D.30°14.如图,BD是⊙O的直径,∠CBD=30°,则∠A的度数为()A.30°B.45°C.60°D.75°15.如图,已知CD是⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数是()A.25°B.30°C.40°D.50°16.如图,AB是⊙O的直径,CD是⊙O的弦.若∠BAC=23°,则∠ADC的大小为()A.23°B.57°C.67°D.77°17.如图,AB为⊙O的直径,CD为⊙O的弦,∠ABD=53°,则∠BCD为()(16)A.37°B.47°C.45°D.53°(17)(18)(19)18.如图,若AB为⊙O的直径,CD是⊙O的弦,∠ABD=65°,则∠BCD的度数为()A.25°B.45°C.55°D.75°19.如图,AB是⊙O的直径,C、D是⊙O上的两点,分别连接AC、BC、CD、OD.若∠DOB=140°,则∠ACD=()A.20°B.30°C.40°D.70°20.在⊙O中,点A、B在⊙O上,且∠AOB=84°,则弦AB所对的圆周角是()A.42°B.84°C.42°或138°D.84°或96°二.填空题21.如图,在⊙O中,弦AC=2,点B是圆上一点,且∠ABC=45°,则⊙O的半径R=.(21)(22)(23)22.如图,在⊙O中,弦AB∥CD,若∠ABC=40°,则∠BOD=.23.如图,⊙O的直径CD经过弦EF的中点G,∠DCF=20°,则∠EOD等于.24.如图,在⊙O中,∠CBO=45°,∠CAO=15°,则∠AOB的度数是°.25.如图,CD是⊙O的直径,A、B是⊙O上的两点,若∠B=20°,则∠ADC的度数为.26.如图,BD是⊙O的直径,∠CBD=30°,则∠A的度数为.27.如图,在平面直角坐标系中,⊙A经过原点O,并且分别与x轴、y轴交于B、C两点,已知B(8,0),C(0,6),则⊙A的半径为.(25)(26)(27)28.如图,在⊙O中,AB为直径,C、D为⊙O上两点,若∠C=25°,则∠ABD=.29.如图,△ABC内接于⊙O,AB是⊙O的直径,∠BAC=60°,弦AD平分∠BAC,若AD=6,那么AC=.(28)(29)(30)30.如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于D,若AC:BC=4:3,AB=10cm,则OD的长为cm.三.解答题31.如图,AB是⊙O的直径,C是⊙O上的点,AC=6cm,BC=8cm,∠ACB的平分线交⊙O于点D,求AB和BD的长.32、如图,△ABC的高AD、BE相交于点H,延长AD交ABC的外接圆于点G,连接BG.求证:HD=GD.33.已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E.∠BAC=40°(1)求∠EBC的度数;(2)求证:BD=CD.34.如图,△ABC是⊙O的内接三角形,∠A=30°,BC=3cm.求⊙O的半径.35.如图,AB是⊙O的直径,过圆上一点C作CD⊥AB于点D,点C是弧AF的中点,连接AF交CD于点E,连接BC交AF于点G.(1)求证:AE=CE;.36.如图,△ABC中,AB>AC,∠BAC的平分线交外接圆于D,DE⊥AB于E,DM⊥AC 于M.(1)求证:BE=CM.(2)求证:AB﹣AC=2BE.37.如图,△ABC的三个顶点都在⊙O上,CD是高,D是垂足,CE是直径,求证:∠ACD=∠BCE.8.如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,作CE⊥AD,垂足为E,CE的延长线与AB交于F.试分析AC、AF、AB的关系,并说明理由.39.如图,△ABC内接于⊙O,AD为△ABC的外角平分线,交⊙O于点D,连接BD,CD,(1)判断△DBC的形状,并说明理由.(2)若∠BAC=60°,判断AD、AB、AC有怎样的关系?并说明理由.40.如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,G是上的任意一点,AG、DC 的延长线相交于点F,∠FGC与∠AGD的大小有什么关系?为什么?一.选择题(共20小题)1.D;2.C;3.A;4.C;5.A;6.D;7.A;8.B;9.C;10.A;11.D;12.C;13.C;14.B;15.B;16.A;17.C;18.D;19.A;20.D;二.填空题(共10小题)21.;22.80°;23.70°;24.60°;25.5;26.40°;27.60;28.65°;29.;30.4;三解答题28.如图,AB是⊙O的直径,C是⊙O上的点,AC=6cm,BC=8cm,∠ACB的平分线交⊙O于点D,求AB和BD的长.【解答】解:如图,∵AB是⊙O的直径,∴∠ACB=90°,∠ADB=90°.∴AB===10(cm).∵AC=6cm,BC=8cm,∵CD是∠ACB的平分线,∴∠ACD=∠BCD,则=,∴AD=BD,∴BD=AB=5cm.综上所述,AB和BD的长分别是10cm,5cm.29.如图,△ABC是⊙O的内接三角形,∠A=30°,BC=3cm.求⊙O的半径.【解答】解:作直径CD,连结BD,如图,∵CD为直径,∴∠CBD=90°,∵∠D=∠A=30°,∴CD=2BC=2×3=6,∴⊙O的半径为3cm.30.如图,AB是⊙O的直径,过圆上一点C作CD⊥AB于点D,点C是弧AF的中点,连接AF交CD于点E,连接BC交AF于点G.(1)求证:AE=CE;(2)已知AG=10,ED:AD=3:4,求AC的长.【解答】(1)证明:∵点C是弧AF的中点,∴∠B=∠CAE,∵AB是⊙O的直径,∴∠ACB=90°,即∠ACE+∠BCD=90°,∵CD⊥AB,∴∠B+∠BCD=90°,∴∠B=∠CAE=∠ACE,∴AE=CE …(6分)(2)解:∵∠ACB=90°,∴∠CAE+∠CGA=90°,又∵∠ACE+∠BCD=90°,∴∠CGA=∠BCD,∵AG=10,∴CE=EG=AE=5,∵ED:AD=3:4,∴AD=4,DE=3,∴AC=…(10分).31.(2015秋•扬中市期中)如图,△ABC中,AB>AC,∠BAC的平分线交外接圆于D,DE⊥AB于E,DM⊥AC于M.(1)求证:BE=CM.(2)求证:AB﹣AC=2BE.【解答】证明:(1)连接BD,DC,∵AD平分∠BAC,∴∠BAD=∠CAD,∴弧BD=弧CD,∴BD=CD,∵∠BAD=∠CAD,DE⊥AB,DM⊥AC,∵∠M=∠DEB=90°,DE=DM,在Rt△DEB和Rt△DMC中,,∴Rt△DEB≌Rt△DMC(HL),∴BE=CM.(2)∵DE⊥AB,DM⊥AC,∵∠M=∠DEA=90°,在Rt△DEA和Rt△DMA中∴Rt△DEA≌Rt△DMA(HL),∴AE=AM,∴AB﹣AC,=AE+BE﹣AC,=AM+BE﹣AC,=AC+CM+BE﹣AC,=BE+CM,=2BE.34.(2009秋•哈尔滨校级期中)如图,△ABC的三个顶点都在⊙O上,CD是高,D是垂足,CE是直径,求证:∠ACD=∠BCE.【解答】解:连接AE,∵CE为直径,∴∠EAC=90°,∴∠ACE=90°﹣∠AEC,∵CD是高,D是垂足,∴∠BCD=90°﹣∠B,∵∠B=∠AEC(同弧所对的圆周角相等),∴∠ACE=∠BCD,∴∠ACE+∠ECD=∠BCD+∠ECD,∴∠ACD=∠BCE.39.如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,作CE⊥AD,垂足为E,CE 的延长线与AB交于F.试分析∠ACF与∠ABC是否相等,并说明理由.【解答】解:延长CE交⊙O于M,∵AD是⊙O的直径,作CE⊥AD,∴弧AC=弧AM,∴∠ACF=∠ABC(在同圆中,等弧所对的圆周角相等).40.如图,△ABC内接于⊙O,AD为△ABC的外角平分线,交⊙O于点D,连接BD,CD,判断△DBC的形状,并说明理由.【解答】解:△DBC为等腰三角形.理由如下:∵AD为△ABC的外角平分线,∴∠EAD=∠DAC,∵∠EAD=∠DCB,∠DBC=∠DAC,∴∠DBC=∠DCB,∴△DBC为等腰三角形.1.如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,G是上的任意一点,AG、DC 的延长线相交于点F,∠FGC与∠AGD的大小有什么关系?为什么?【解答】解:∠FGC与∠AGD相等.理由如下:连接AD,如图,∵CD⊥AB,∴=,∴∠AGD=∠ADC,∵∠FGC=∠ADC,∴∠FGC=∠AGD11。
中考数学专题复习:圆周角定理

36.已知:在△ABC 中,以 AC 边为直径的⊙O 交 BC 于点 D,在劣弧 上取一 点 E 使∠EBC=∠DEC,延长 BE 依次交 AC 于点 G,交⊙O 于 H.
A.32°
B.38°
C.52°
D.66°
12.如图,⊙O 中,弦 BC 与半径 OA 相交于点 D,连接 AB,OC.若∠A=60°,
∠ADC=85°,则∠C 的度数是( )
A.25°
B.27.5°
C.30°
D.35°
第 12 题
第 13 题
13.如图,点 D 在半圆 O 上,半径 OB= ,AD=10,点 C 在弧 BD 上移动,
8.解:连接 OA, ∵OA=OC, ∴∠OAC=∠C=28°, ∴∠OAB=64°, ∵OA=OB, ∴∠B=∠OAB=64°, 故选:C.
9.解:连接 OC, ∵AO∥DC,
∴∠ODC=∠AOD=70°, ∵OD=OC, ∴∠ODC=∠OCD=70°, ∴∠COD=40°, ∴∠AOC=110°, ∴∠B= ∠AOC=55°. 故选:D. 10.解:圆上取一点 A,连接 AB,AD,如图所示,
∵DH⊥AC,
∴∠AHD=90°,
∴点 H 在以 M 为圆心,MD 为半径的⊙M 上,
∴当 M、H、B 共线时,BH 的值最小,
∵AB 是直径,
∴∠ADB=90°,
∴BD=
=12,
BM=
=
=13,
∴BH 的最小值为 BM﹣MH=13﹣5=8. 故选:D. 14.解:∵PA 是圆的切线. ∴∠OAP=90°, 同理∠OBP=90°, 根据四边形内角和定理可得: ∠AOB=360°﹣∠OAP﹣∠OBP﹣∠P=360°﹣90°﹣90°﹣40°=140°,
九年级数学圆周角定理(基础)(含答案)

圆周角定理(基础)一、单选题(共11道,每道8分)1.如图,点A,B,C都在⊙O上,若∠ACB=48°,则∠AOB的度数为( )A.96°B.48°C.42°D.24°答案:A解题思路:圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半∵∠ACB与∠AOB对着同一条弧AB,∠ACB=48°∴∠AOB=2∠ACB=96°试题难度:三颗星知识点:略2.如图,A,B,C,D是⊙O上的点,则图中与∠A相等的角是( )A.∠BB.∠CC.∠DEBD.∠D答案:D解题思路:同弧或等弧所对的圆周角相等∵∠A与∠D都是弧BC所对的圆周角∴∠D=∠A试题难度:三颗星知识点:略3.如图,⊙O中,弦BC与半径OA相交于点D,连接AB,OC.若∠A=60°,∠ADC=85°,则∠C的度数是( )A.25°B.27.5°C.30°D.35°答案:D解题思路:∵∠A=60°,∠ADC=85°∴∠B=∠ADC-∠A=25°∵∠B与∠AOC对着同一条弧AC∴∠AOC=2∠B=50°∴∠C=∠ADC-∠AOC=35°试题难度:三颗星知识点:略4.如图,AB是⊙O的直径,C,D为圆上两点,若∠AOC=130°,则∠D等于( )A.20°B.25°C.35°D.50°答案:B解题思路:∵AB是⊙O的直径,∠AOC=130°∴∠BOC=180°-∠AOC=50°∵∠D与∠BOC对着同一条弧BC∴∠D=∠BOC=25°试题难度:三颗星知识点:略5.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的度数分别为88°,30°,则∠ACB的大小为( )A.15°B.28°C.29°D.34°答案:C解题思路:如图,点A,B的度数分别为88°,30°∴∠AOB=88°-30°=58°∵∠ACB与∠AOB对着同一条弧AB∴∠ACB=∠AOB=29°试题难度:三颗星知识点:略6.如图,已知圆心角∠AOB=110°,则圆周角∠ACB=( )A.55°B.110°C.120°D.125°答案:D解题思路:如图,设点E是优弧AB上的一点,连接EA,EB∵∠E与∠AOB对着同一条弧AB,∠AOB=110°∴∠E=∠AOB=55°又∠ACB+∠E=180°∴∠ACB=180°-55°=125°试题难度:三颗星知识点:略7.如图,在⊙O中,AD是直径,∠ABC=40°,则∠CAD等于( )A.40°B.50°C.60°D.70°答案:B解题思路:∵∠ADC与∠ABC对着同一条弧AC,∠ABC=40°∴∠ADC=∠ABC=40°∵AD是⊙O的直径∴∠DCA=90°∴∠CAD=90°-∠ADC=50°试题难度:三颗星知识点:略8.如图,AB是⊙O的弦,OC⊥AB交⊙O于点C,点D是⊙O上一点,∠ADC=30°,则∠BOC 的度数为( )A.30°B.40°C.50°D.60°答案:D解题思路:∵∠AOC与∠ADC对着同一条弧AC,∠ADC=30°∴∠AOC=2∠ADC=60°∵AB是⊙O的弦,OC⊥AB交⊙O于点C∴弧AC=弧BC∴∠BOC=∠AOC=60°试题难度:三颗星知识点:略9.如图,四边形ABCD内接于⊙O,若∠A=40°,则∠C=( )A.110°B.120°C.135°D.140°答案:D解题思路:∵四边形ABCD内接于⊙O∴∠A+∠C=180°又∠A=40°∴∠C=180°-40°=140°试题难度:三颗星知识点:略10.如图,圆内接四边形ABCD中,边BA的延长线上有一点E,且∠EAD=50°,则∠C的度数为( )A.50°B.40°C.130°D.140°答案:A解题思路:∵点E在BA的延长线上,∠EAD=50°∴∠BAD=180°-∠EAD=130°∵四边形ABCD内接于圆∴∠C+∠BAD=180°∴∠C=180°-∠BAD=50°试题难度:三颗星知识点:略11.如图,四边形ABCD是半圆的内接四边形,AB是直径,弧CB=弧CD.若∠C=110°,则∠ABC 的度数等于( )A.55°B.60°C.65°D.70°答案:A解题思路:如图,连接AC∵四边形ABCD是半圆的内接四边形,∠C=110°∴∠DAB=180°-∠C=70°又弧CB=弧CD∴∠BAC=∠DAC=∠DAB=35°∵AB是直径∴∠ACB=90°∴∠ABC=90°-∠BAC=55°试题难度:三颗星知识点:略。
圆周角定理练习题(A)
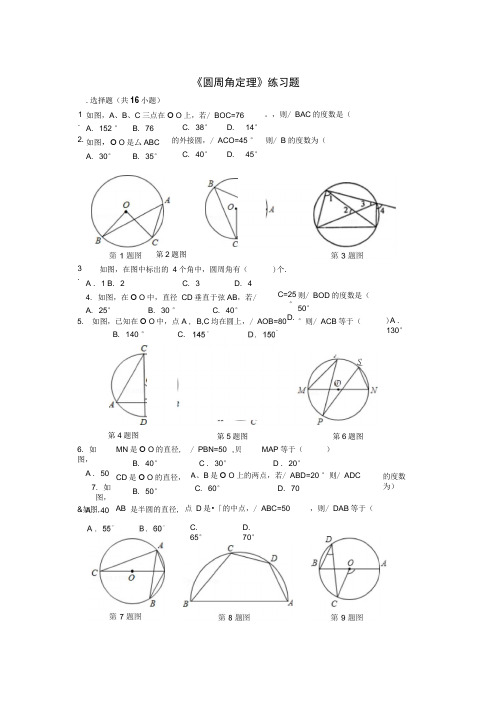
1. 2. 《圆周角定理》练习题.选择题(共16小题) 如图,A 、B 、C 三点在O O 上,若/ BOC=76A . 152 °B . 76 如图,O O 是厶ABC A . 30° B . 35° C . 38°D . 14° 的外接圆,/ ACO=45 ° C . 40° D . 45° 。
,则/ BAC 的度数是( 则/ B 的度数为( 第2题图 如图,在图中标出的 4个角中,圆周角有( A . 1 B . 2C . 3D . 4 4. 如图,在O O 中,直径 CD 垂直于弦AB ,若/ A . 25°B . 30 °C . 40° 3.)个. C=25 °D . 5. 如图,已知在O O 中,点A , B,C 均在圆上,/ AOB=80 B . 140 ° C .则/ BOD 的度数是( 50° °则/ ACB 等于( )A . 130°OS 06.如图,A . 507. 如图, A . 40 第4题图 MN 是O O 的直径, B . 40°CD 是O O 的直径, B . 50° &如图, 是半圆的直径, AB 第5题图/ PBN=50 °,贝 C . 30°第6题图 MAP 等于( )D . 20°A 、B 是O O 上的两点,若/ ABD=20 °则/ ADC C . 60°D . 70 点 D 是•「的中点,/ ABC=50C .65°D . 70° ,则/ DAB 等于( 的度数为)9. 如图,AB 是O O 的直径,C , D 为圆上两点,/ AOC=130 °则/ D 等于( A . 25°B . 30°C . 3510. 如图,/ 1、/ 2、/ 3、/ 4的大小关系是A . / 4</ 1 </ 2</ 3 C ./4</ 1 </3/211 .如图,AB 是半圆O 的直径, A . 30° B . 45°12 . 如图,在O O 中, OA 丄 BC , / AOC=50 ° 贝9/ ADB 的度数为( )A . 15°B . 20°C . 25 °D . 50° 13 . 在O O 中, 点A 、 B 在O O 上,且/ AOB=84 ° 则弦 AB 所对的圆周角是( )A . 42°B . 84°C . 42°或 138°D . 84 °或 96°14 .如图所示, 在O O 中,AB 是O O 的直径,/ ACB 的角平分线 CD 交O O 于 D ,则/ ABD的度数等于( )A . 90°B .60°C . 45°D .30°15 . 已知如图, AB 是O O 的直径, CD 是O O 的弦, / CDB=40 °, 则/ CBA 的度数为(4<Z 1 = / 3<Z 2 4<Z 1<Z 3= /2)B . / D . / / BAC=60 ° D 是半圆上任意一点,那么/ D 的度数是()16.如图,AB A . 30°是圆的直径, B .AB 丄 CD ,/ BAD=30C . 60°贝AEC D . B第12题图的度数等于( 70°8小题)二.填空题(共 17.如图,O O 的直径CD 经过弦EF 的中点G ,/DCF=20 °,则/ EOD 等于DBo第11题图第12题图DB50°C. 40°D. 30 °A . 60° B.21. 如图,等腰△ ABC 的底边BC 的长为4cm ,以腰AB 为直径的O O 交BC 于点D ,交 AC 于点E ,贝U DE 的长为 _____ cm . 22.如图,在 世界杯”足球比赛中,甲带球向对方球门PQ 进攻,当他带球冲到 A 点时,同 样乙已经助攻冲到 B 点,丙助攻到C 点•有三种射门方式:第一种是甲直接射门;第二 种是甲将球传给乙,由乙射门•第三种是甲将球传给丙,由丙射门•仅从射门角度考虑, 应选择 ____ 种射门方式. 三•解答题(共16小题)25. 28.如图,AB 是O O 的直径,C 是O O 上的点,AC=6cm , BC=8cm ,/ ACB 的平分 线交O O 于点D ,求AB 和BD 的长.26. 如图,已知 CD 是O O 的直径,弦 AB 丄CD ,垂足为点 M ,点P 是八上一点,且/ BPC=60 °试判断△ ABC 的形状,并说明你的理由.第19题图18. 占 八、第17题图 第18题图如图,点 A 、B 在O O 上,/ AOB=100 °点C 是劣弧 AB 上不与A 、B 重合的任意 则/ C=在O O 中,弦AB=2cm ,/ ACB=30 °则O O 的直径为_ 如图,O O 中弦AB 等于半径R ,则这条弦所对的圆心角是cm .—,圆周角是C第21题图Q3第20题图pB第22题图BB27、如图,△ ABC的高AD、BE相交于点H,延长AD交ABC的外接圆于点G,连接BG . 求证:HD=GD .28. 已知:如图,AB为O O的直径,AB=AC , BC交O O于点D , AC交O O于点E./BAC=40 °(1) 求/ EBC的度数;(2) 求证:BD=CD .29. 如图,△ ABC是O O的内接三角形,/ A=30 °, BC=3cm .求O O的半径.B 30. 如图,AB是O O的直径,过圆上一点C作CD丄AB于点D,点C是弧AF的中点,连接AF交CD于点E,连接BC交AF于点G.(1)求证:AE=CE ;.31. 如图,△ ABC中,AB > AC,/ BAC的平分线交外接圆于于M .(1)求证:BE=CM .(2)求证:AB - AC=2BE .32. 如图,0A是O 0的半径,以OA为直径的O C与O 0的弦AB相交于点 D .求证:AD=BD .33. 如图,已知: AB 是O O 的弦,D 为O O 上一点, 证:M 是弧AB 的中点.35.已知:如图, AE 是O O 的直径,AF 丄BC 于D ,证明:BE=CF .34.如图,△ ABC 的三个顶点都在O O 上,CD 是高, D 是垂足,CE 是直径,求证:/ ACD=BDC 丄AB 于C , DM 平分/ CDO .求BCD5三ODBE36.已知AB 为O O 的直径,弦 BE=DE , AD , BE 的延长线交于点 C ,求证:AC=ABC37.如图,AB 是圆O 的直径,OC 丄AB ,交O O 于点C , D 是弧AC 上一点,E 是AB 上 一点,EC 丄CD ,交BD 于点F .问:AD 与BF 相等吗?为什么?38. 如图,AB是O O的直径,AC、DE是O O的两条弦,且于点DE丄AB,延长AC、DE相交F,求证:/ FCD= / ACE .39. 如图,已知O O是厶ABC的外接圆,AD是O O的直径,作CE丄AD,垂足为E,CE 的延长线与AB交于F.试分析/ ACF与/ ABC是否相等,并说明理由.40. 如图,△ ABC内接于O O, AD ABC的外角平分线,交O O于点D,连接BD , CD , 判断△ DBC的形状,并说明理由.EDB<?41.如图,AB是O O的直径,弦CD丄AB,垂足为点E, G是「'上的任意一点,AG、DC 的延长线相交于点F,/ FGC与/ AGD的大小有什么关系?为什么?42.如图,AB是圆0的直径,C是圆0上一点,D是弧AC中点,DE丄AB垂足为E, AC 分别与DE、DB相交于点F、G,则AF与FG是否相等?为什么?43. 如图,0A是O 0的半径,以0A为直径的O C与O 0的弦AB交于点D,求证:D是AB的中点.44. 如图,在△ ABC中,/ ACB=90 ° D是AB的中点,以边于DC为直径的O O交厶ABC的G , F, E点.求证:(1) F是BC的中点;(2)/ A= / GEF.45. 如图,圆内接四边形ABCD的外角/ DCH= / DCA , DP I AC垂足为P, DH丄BH垂足为H,求证:CH=CP, AP=BH .《圆周角定理》2222222222参考答案与试题解析一•选择题(共16小题)1. (2012?呼伦贝尔)如图,A、B、C三点在O O上,若/ BOC=76 °则/ BAC的度数是()A. 152°B. 76°C. 38°D. 14°【解答】解:•••;'所对的圆心角是/ BOC,圆周角是/ BAC ,又•••/ BOC=76 °•••/ A=76 °X—=38 ° 故选C.2. (2015?眉山)如图,O O是厶ABC的外接圆,/ ACO=45 °则/ B的度数为()CA. 30°B. 35°C. 40 °D. 45°【解答】解:I OA=OC,/ ACO=45 °•••/ OAC=45 °•••/ AOC=180 °- 45 °- 45°90 °•••/ B= - / AOC=45 °故选D .3. (2010秋?海淀区校级期末)如图,在图中标出的4个角中,圆周角有()个.D . 4【解答】解: /1和/3符合圆周角的定义,/ 2顶点不在圆周上,/ 4的一边不和圆相交,故图中圆周角有/ 1和/ 3两个.故选B .4. ( 2015?珠海)如图,在O O 中,直径CD 垂直于弦 AB ,若/ C=25 °则/ BOD 的度数是 ( )40 ° D . 50°【解答】解:•••在O O 中,直径CD 垂直于弦AB , •••二匸 11,•••/ DOB=2 / C=50 ° 故选:D .5. ( 1997?陕西)如图,已知在O O 中,点 A , B , C 均在圆上,/ AOB=80 °则/ ACB 等•••/ AOB=80 ° •••/ E= 1 / AOB=40 ° 2•••/ ACB=180 °-Z E=140°故选:B .C . 145D . 150 °【解答】解:设点E 是优弧AB 上的一点,连接EA , EBA . 130°B . 140A . 40°B . 50°C . 60°D . 70【解答】解:vZ ABD=20 °• Z C=Z ABD=20 °v CD 是O O 的直径• Z CAD=90 ° 6.如图,MN 是O O 的直径,/ PBN=50 °则/ MAP 等于() 可得/ MAP= 1 / MOP ,/ NBP=— / NOP ,2 2 •/ MN 为直径,•••/ MOP + Z NBP=180 °•••/ MAP+Z NBP=90 °vZ PBN=50 °• Z MAP=90 °-Z PBN=40 ° 故选B .7. (2007?太原)如图,CD 是O O 的直径,A 、B 是O O 上的两点, 若Z ABD=20 ° 贝UZ ADCA . 50°B . 40°C . 30°D . 20°【解答】解:连接OP ,•••/ ADC=90 ° - 20 °70 ° 故选D .& ( 2013?苏州)如图,AB 是半圆的直径,点 D 是AC 的中点,/ ABC=50 °则/ DAB 等于•••点D 是;的中点,即弧 CD=弧AD , •••/ ABD= / CBD , 而/ ABC=50 °•••/ ABD= X 50°25 ° 2•/ AB 是半圆的直径,•••/ ADB=90 °•••/ DAB=90 ° - 25 °65 ° 故选C .【解答】 解:•••/ AOC=130° •••/ BOC=50 ° •••/。
专题03 圆周角定理(原卷版)

15.如图,在⊙O中, 所对的∠AOB的度数为m,C是 上一点,D、E是 上不同的两点(不与A、B两点重合),则∠D+∠E的度数为.
16.如右图,四个边长为1的小正方形拼成一个大正方形,A、B、O是小正方形顶点,⊙O的半径为1,P是⊙O上的点,且位于右上方的小正方形内,则sin∠APB等于.
17.如图,在Rt△ABC中,∠BAC=90°,且AB=2AC,以AB为直径作⊙O,交于BC点D,点E为⊙O上的另外一点,那么tan∠AED=.
三.解答题
18.如图,AB是⊙O的直径, = ,∠COD=60°.
(1)△AOC是等边三角形吗?请说明理由;
(2)求证:OC∥BD.
19.已知:如图.△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连接AD.
A.1个B.2个C.3个D.4个
8.如图,在△ABC中,AB=5,AC=4,BC=3,经过点C且与边AB相切的动圆与CB、CA分别相交于点E、F,则线段EF长度的最小值是( )
A.2.4B.2C.2.5D.
9.如图所示,AB是⊙O的直径,AD=DE,AE与BD交于点C,则图中与∠DEA相等的角有( )
A.12.5°B.25°C.37.5°D.50°
4.如图,△ABC内接于圆,AD是高,AE为圆的直径,AB=4,AC=3,AD=2,则直径AE的长为( )
A.5B.6C.7D.8
5.如图所示,已知四边形ABCD的四个顶点都在⊙O上,∠BCD=120°,则∠B0D=( )
A.100°B.120°C.130°D.150°
(1)求证:∠DAC=∠DBA;
《圆周角定理》练习题(A)

《圆周角定理》练习题一.选择题(共16小题)1.如图,A、B、C三点在⊙O上,若∠BOC=76°,则∠BAC的度数是()A.152° B.76°C.38°D.14°2.如图,⊙O是△ABC的外接圆,∠ACO=45°,则∠B的度数为()A.30°B.35°C.40°D.45°第1题图第2题图第3题图3.如图,在图中标出的4个角中,圆周角有()个.A.1 B.2 C.3 D.44.如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠BOD的度数是()A.25°B.30°C.40°D.50°5.如图,已知在⊙O中,点A,B,C均在圆上,∠AOB=80°,则∠ACB等于()A.130°B.140° C.145° D.150°第4题图第5题图第6题图6.如图,MN是⊙O的直径,∠PBN=50°,则∠MAP等于()A.50°B.40°C.30°D.20°7.如图,CD是⊙O的直径,A、B是⊙O上的两点,若∠ABD=20°,则∠ADC的度数为)A.40°B.50°C.60°D.70°8.如图,AB是半圆的直径,点D是的中点,∠ABC=50°,则∠DAB 等于()A.55°B.60°C.65°D.70°第7题图第8题图第9题图9.如图,AB是⊙O的直径,C,D为圆上两点,∠AOC=130°,则∠D 等于()A.25°B.30°C.35°D.50°10.如图,∠1、∠2、∠3、∠4的大小关系是()A.∠4<∠1<∠2<∠3 B.∠4<∠1=∠3<∠2C.∠4<∠1<∠3∠2 D.∠4<∠1<∠3=∠211.如图,AB是半圆O的直径,∠BAC=60°,D是半圆上任意一点,那么∠D的度数是()A.30°B.45°C.60°D.90°第10题图第11题图第12题图12.如图,在⊙O中,OA⊥BC,∠AOC=50°,则∠ADB的度数为()A.15°B.20° C.25°D.50°13.在⊙O中,点A、B在⊙O上,且∠AOB=84°,则弦AB所对的圆周角是()A.42°B.84°C.42°或138°D.84°或96°14.如图所示,在⊙O中,AB是⊙O的直径,∠ACB的角平分线CD交⊙O于D,则∠ABD的度数等于()A.90°B.60°C.45°D.30°15.已知如图,AB是⊙O的直径,CD是⊙O的弦,∠CDB=40°,则∠CBA的度数为()A.60°B.50°C.40°D.30°第10题图第11题图第12题图16.如图,AB是圆的直径,AB⊥CD,∠BAD=30°,则∠AEC的度数等于()A.30°B.50°C.60°D.70°二.填空题(共8小题)17.如图,⊙O的直径CD经过弦EF的中点G,∠DCF=20°,则∠EOD 等于.第17题图第18题图第19题图18.如图,点A、B在⊙O上,∠AOB=100°,点C是劣弧AB上不与A、B重合的任意一点,则∠C=°.19.在⊙O中,弦AB=2cm,∠ACB=30°,则⊙O的直径为cm.20.如图,⊙O中弦AB等于半径R,则这条弦所对的圆心角是,圆周角是.第20题图第21题图第22题图21.如图,等腰△ABC的底边BC的长为4cm,以腰AB为直径的⊙O交BC于点D,交AC于点E,则DE的长为cm.22.如图,在“世界杯”足球比赛中,甲带球向对方球门PQ进攻,当他带球冲到A点时,同样乙已经助攻冲到B点,丙助攻到C点.有三种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门.第三种是甲将球传给丙,由丙射门.仅从射门角度考虑,应选择种射门方式.三.解答题(共16小题)25.28.如图,AB是⊙O的直径,C是⊙O上的点,AC=6cm,BC=8cm,∠ACB的平分线交⊙O于点D,求AB和BD的长.26.如图,已知CD是⊙O的直径,弦AB⊥CD,垂足为点M,点P是上一点,且∠BPC=60°.试判断△ABC的形状,并说明你的理由.27、如图,△ABC的高AD、BE相交于点H,延长AD交ABC的外接圆于点G,连接BG.求证:HD=GD.28.已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E.∠BAC=40°(1)求∠EBC的度数;(2)求证:BD=CD.29.如图,△ABC是⊙O的内接三角形,∠A=30°,BC=3cm.求⊙O 的半径.30.如图,AB是⊙O的直径,过圆上一点C作CD⊥AB于点D,点C是弧AF的中点,连接AF交CD于点E,连接BC交AF于点G.(1)求证:AE=CE;.31.如图,△ABC中,AB>AC,∠BAC的平分线交外接圆于D,DE⊥AB于E,DM⊥AC于M.(1)求证:BE=CM.(2)求证:AB﹣AC=2BE.32.如图,OA是⊙0的半径,以OA为直径的⊙C与⊙0的弦AB相交于点D.求证:AD=BD.33.如图,已知:AB是⊙O的弦,D为⊙O上一点,DC⊥AB于C,DM 平分∠CDO.求证:M是弧AB的中点.34.如图,△ABC的三个顶点都在⊙O上,CD是高,D是垂足,CE是直径,求证:∠ACD=∠BCE.35.已知:如图,AE是⊙O的直径,AF⊥BC于D,证明:BE=CF.36.已知AB为⊙O的直径,弦BE=DE,AD,BE的延长线交于点C,求证:AC=AB.37.如图,AB是圆O的直径,OC⊥AB,交⊙O于点C,D是弧AC上一点,E是AB上一点,EC⊥CD,交BD于点F.问:AD与BF相等吗?为什么?38.如图,AB是⊙O的直径,AC、DE是⊙O的两条弦,且DE⊥AB,延长AC、DE相交于点F,求证:∠FCD=∠ACE.39.如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,作CE⊥AD,垂足为E,CE的延长线与AB交于F.试分析∠ACF与∠ABC是否相等,并说明理由.40.如图,△ABC内接于⊙O,AD为△ABC的外角平分线,交⊙O于点D,连接BD,CD,判断△DBC的形状,并说明理由.41.如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,G是上的任意一点,AG、DC的延长线相交于点F,∠FGC与∠AGD的大小有什么关系?为什么?42.如图,AB是圆O的直径,C是圆O上一点,D是弧AC中点,DE ⊥AB垂足为E,AC分别与DE、DB相交于点F、G,则AF与FG是否相等?为什么?43.如图,OA是⊙O的半径,以OA为直径的⊙C与⊙O的弦AB交于点D,求证:D是AB的中点.44.如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的边于G,F,E点.求证:(1)F是BC的中点;(2)∠A=∠GEF.45.如图,圆内接四边形ABCD的外角∠DCH=∠DCA,DP⊥AC垂足为P,DH⊥BH垂足为H,求证:CH=CP,AP=BH.《圆周角定理》2222222222参考答案与试题解析一.选择题(共16小题)1.(2012•呼伦贝尔)如图,A、B、C三点在⊙O上,若∠BOC=76°,则∠BAC的度数是()A.152° B.76°C.38°D.14°【解答】解:∵所对的圆心角是∠BOC,圆周角是∠BAC,又∵∠BOC=76°,∴∠A=76°×=38°.故选C.2.(2015•眉山)如图,⊙O是△ABC的外接圆,∠ACO=45°,则∠B 的度数为()A.30°B.35°C.40°D.45°【解答】解:∵OA=OC,∠ACO=45°,∴∠OAC=45°,∴∠AOC=180°﹣45°﹣45°=90°,∴∠B=∠AOC=45°.故选D.3.(2010秋•海淀区校级期末)如图,在图中标出的4个角中,圆周角有()个.A.1 B.2 C.3 D.4【解答】解:∠1和∠3符合圆周角的定义,∠2顶点不在圆周上,∠4的一边不和圆相交,故图中圆周角有∠1和∠3两个.4.(2015•珠海)如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠BOD的度数是()A.25°B.30°C.40°D.50°【解答】解:∵在⊙O中,直径CD垂直于弦AB,∴=,∴∠DOB=2∠C=50°.故选:D.5.(1997•陕西)如图,已知在⊙O中,点A,B,C均在圆上,∠AOB=80°,则∠ACB等于()A.130° B.140° C.145° D.150°【解答】解:设点E是优弧AB上的一点,连接EA,EB∵∠AOB=80°∴∠E=∠AOB=40°∴∠ACB=180°﹣∠E=140°.6.如图,MN是⊙O的直径,∠PBN=50°,则∠MAP等于()A.50°B.40°C.30°D.20°【解答】解:连接OP,可得∠MAP=∠MOP,∠NBP=∠NOP,∵MN为直径,∴∠MOP+∠NBP=180°,∴∠MAP+∠NBP=90°,∵∠PBN=50°,∴∠MAP=90°﹣∠PBN=40°.故选B.7.(2007•太原)如图,CD是⊙O的直径,A、B是⊙O上的两点,若∠ABD=20°,则∠ADC的度数为()A.40°B.50°C.60°D.70°【解答】解:∵∠ABD=20°∴∠C=∠ABD=20°∵CD是⊙O的直径∴∠CAD=90°∴∠ADC=90°﹣20°=70°.故选D.8.(2013•苏州)如图,AB是半圆的直径,点D是的中点,∠ABC=50°,则∠DAB等于()A.55°B.60°C.65°D.70°【解答】解:连结BD,如图,∵点D是的中点,即弧CD=弧AD,∴∠ABD=∠CBD,而∠ABC=50°,∴∠ABD=×50°=25°,∵AB是半圆的直径,∴∠ADB=90°,∴∠DAB=90°﹣25°=65°.故选C.9.(2009•枣庄)如图,AB是⊙O的直径,C,D为圆上两点,∠AOC=130°,则∠D等于()A.25°B.30°C.35°D.50°【解答】解:∵∠AOC=130°,∴∠BOC=50°,∴∠D=∠BOC=25°.故选A.10.(2013秋•沙洋县校级月考)如图,∠1、∠2、∠3、∠4的大小关系是()A.∠4<∠1<∠2<∠3 B.∠4<∠1=∠3<∠2 C.∠4<∠1<∠3∠2 D.∠4<∠1<∠3=∠2【解答】解:如图,利用圆周角定理可得:∠1=∠3=∠5=∠6,根据三角形的外角的性质得:∠5>∠4,∠2>∠6,∴∠4<∠1=∠3<∠2,故选B.11.(2012秋•天津期末)如图,AB是半圆O的直径,∠BAC=60°,D 是半圆上任意一点,那么∠D的度数是()A.30°B.45°C.60°D.90°【解答】解:连接BC,∵AB是半圆的直径∴∠ACB=90°∵∠BAC=60°,∴∠ABC=90°﹣∠BAC=30°,∴∠D=∠ABC=30°.故选A.12.(2009•塘沽区二模)如图,在⊙O中,OA⊥BC,∠AOC=50°,则∠ADB的度数为()A.15°B.20°C.25°D.50°【解答】解:∵OA⊥BC,∠AOC=50°,∴,∴∠ADB=∠AOC=25°.故选C.13.(2012秋•宜兴市校级期中)在⊙O中,点A、B在⊙O上,且∠AOB=84°,则弦AB所对的圆周角是()A.42°B.84°C.42°或138°D.84°或96°【解答】解:如图,∵∠AOB=84°,∴∠ACB=∠AOB=×84°=42°,∴∠ADB=180°﹣∠ACB=138°.∴弦AB所对的圆周角是:42°或138°.故选C.14.(2011•南岸区一模)如图所示,在⊙O中,AB是⊙O的直径,∠ACB的角平分线CD交⊙O于D,则∠ABD的度数等于()A.90°B.60°C.45°D.30°【解答】解:连接AD,∵在⊙O中,AB是⊙O的直径,∴∠ADB=90°,∵CD是∠ACB的角平分线,∴=,∴AD=BD,∴△ABD是等腰直角三角形,∴∠ABD=45°.故选C.15.(2015秋•合肥校级期末)已知如图,AB是⊙O的直径,CD是⊙O 的弦,∠CDB=40°,则∠CBA的度数为()A.60°B.50°C.40°D.30°【解答】解:连接AC,∵AB是⊙O的直径,∴∠ACB=90°,∵∠A=∠CDB=40°,∴∠CBA=90°﹣∠A=50°.故选B.16.(2013•万州区校级模拟)如图,AB是圆的直径,AB⊥CD,∠BAD=30°,则∠AEC的度数等于()A.30°B.50°C.60°D.70°【解答】解:∵∠BAD=30°,∴=60°,∵AB是圆的直径,AB⊥CD,∴==60°,∴=180°﹣60°=120°,∴∠AEC==×120°=60°.故选C.二.填空题(共8小题)17.(2016•大冶市模拟)如图,⊙O的直径CD经过弦EF的中点G,∠DCF=20°,则∠EOD等于40°.【解答】解:∵⊙O的直径CD过弦EF的中点G,∠DCF=20°,∴弧DF=弧DE,且弧的度数是40°,∴∠DOE=40°,答案为40°.18.(2015•历城区二模)如图,AB是半圆的直径,点D是弧AC的中点,∠ABC=50°,则∠DAB的度数是65°.【解答】解:连结BD,如图,∵点D是的中点,即弧CD=弧AD,∴∠ABD=∠CBD,而∠ABC=50°,∴∠ABD=×50°=25°,∵AB是半圆的直径,∴∠ADB=90°,∴∠DAB=90°﹣25°=65°.故答案为65°.19.(2013秋•滨湖区校级期末)如图,点A、B在⊙O上,∠AOB=100°,点C是劣弧AB上不与A、B重合的任意一点,则∠C= 130 °.【解答】解:在优弧AB上取点D,连结AD、BD,如图,∴∠D=∠AOB=×100°=50°,∵∠D+∠C=180°,∴∠C=180°﹣50°=130°.故答案为130.20.(2008秋•苏州校级期中)球员甲带球冲到A点时,同伴乙已经助攻冲到B点.有两种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门.仅从射门角度考虑,应选择第二种种射门方式较为合理.【解答】解:连接OC.根据圆周角定理,得∠PCQ=∠B,根据三角形的外角的性质,得∠PCQ>∠A,则∠B>∠A.故答案为第二种.21.(2015•黄岛区校级模拟)在⊙O中,弦AB=2cm,∠ACB=30°,则⊙O的直径为 4 cm.【解答】解:连接OA,OB,∵∠ACB=30°,∴∠AOB=60°,∴△AOB是等边三角形,∴OA=OB=AB=2cm,∴⊙O的直径=4cm.故答案为:4.22.(2014春•海盐县校级期末)如图,⊙O中弦AB等于半径R,则这条弦所对的圆心角是60°,圆周角是30°或150°.【解答】解:连结OA、OB,∠APB和∠AP′B为弦AB所对的圆周角,如图,∵弦AB等于半径R,∴△OAB为等边三角形,∴∠AOB=60°,∴∠APB=∠AOB=30°,∴∠AP′B=180°﹣∠APB=150°,即这条弦所对的圆心角是60°,圆周角是30°或150°.故答案为60°;是30°或150°.23.(2012•义乌市模拟)如图,等腰△ABC的底边BC的长为4cm,以腰AB为直径的⊙O交BC于点D,交AC于点E,则DE的长为 2 cm.【解答】解:连接AD,∵∠DEC为圆内接四边形ABDE的外角,∴∠DEC=∠B,又等腰△ABC,BC为底边,∴AB=AC,∴∠B=∠C,∴∠DEC=∠C,∴DE=DC,∵AB为圆O的直径,∴∠ADB=90°,即AD⊥BC,∴BD=CD=BC,又BC=4cm,∴DE=2cm.故答案为:224.(2012秋•哈密地区校级月考)如图,在“世界杯”足球比赛中,甲带球向对方球门PQ进攻,当他带球冲到A点时,同样乙已经助攻冲到B点,丙助攻到C点.有三种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门.第三种是甲将球传给丙,由丙射门.仅从射门角度考虑,应选择第二种射门方式.【解答】解:设AP与圆的交点是C,连接CQ;则∠PCQ>∠A;由圆周角定理知:∠PCQ=∠B;所以∠B>∠A;因此选择第二种射门方式更好.故答案为:第二.三.解答题(共16小题)25.(2009•沈阳模拟)如图,△ABC的高AD、BE相交于点H,延长AD交ABC的外接圆于点G,连接BG.求证:HD=GD.【解答】证明:∵∠C=∠G,△ABC的高AD、BE,∴∠C+∠DAC=90°,∠AHE+∠DAC=90°,∴∠C=∠AHE,∵∠AHE=∠BHG=∠C,∴∠G=∠BHG,∴BH=BG,又∵AD⊥BC,∴HD=DG.26.(2013秋•虞城县校级期末)如图,已知CD是⊙O的直径,弦AB ⊥CD,垂足为点M,点P是上一点,且∠BPC=60°.试判断△ABC 的形状,并说明你的理由.【解答】解:△ABC为等边三角形.理由如下:∵AB⊥CD,CD为⊙O的直径,∴弧AC=弧BC,∴AC=BC,又∵∠BPC=∠A=60°,∴△ABC为等边三角形.27.(2013秋•耒阳市校级期末)已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E.∠BAC=40°(1)求∠EBC的度数;(2)求证:BD=CD.【解答】(1)解:∵AB=AC,∴∠ABC=∠C,∵∠BAC=40°,∴∠C=(180°﹣40°)=70°,∵AB为⊙O的直径,∴∠AEB=90°,∴∠EBC=90°﹣∠C=20°;证明:连结AD,如图,∵AB为⊙O的直径,∴∠ADB=90°,∴AD⊥BC,而AB=AC,∴BD=DC.28.(2014秋•高密市期中)如图,AB是⊙O的直径,C是⊙O上的点,AC=6cm,BC=8cm,∠ACB的平分线交⊙O于点D,求AB和BD的长.【解答】解:如图,∵AB是⊙O的直径,∴∠ACB=90°,∠ADB=90°.∴AB===10(cm).∵AC=6cm,BC=8cm,∵CD是∠ACB的平分线,∴∠ACD=∠BCD,则=,∴AD=BD,∴BD=AB=5cm.综上所述,AB和BD的长分别是10cm,5cm.29.(2013秋•宜兴市校级期中)如图,△ABC是⊙O的内接三角形,∠A=30°,BC=3cm.求⊙O的半径.【解答】解:作直径CD,连结BD,如图,∵CD为直径,∴∠CBD=90°,∵∠D=∠A=30°,∴CD=2BC=2×3=6,∴⊙O的半径为3cm.30.(2010秋•瑞安市校级月考)如图,AB是⊙O的直径,过圆上一点C作CD⊥AB于点D,点C是弧AF的中点,连接AF交CD于点E,连接BC交AF于点G.(1)求证:AE=CE;(2)已知AG=10,ED:AD=3:4,求AC的长.【解答】(1)证明:∵点C是弧AF的中点,∴∠B=∠CAE,∵AB是⊙O的直径,∴∠ACB=90°,即∠ACE+∠BCD=90°,∵CD⊥AB,∴∠B+∠BCD=90°,∴∠B=∠CAE=∠ACE,∴AE=CE …(6分)(2)解:∵∠ACB=90°,∴∠CAE+∠CGA=90°,又∵∠ACE+∠BCD=90°,∴∠CGA=∠BCD,∵AG=10,∴CE=EG=AE=5,∵ED:AD=3:4,∴AD=4,DE=3,∴AC=…(10分).31.(2015秋•扬中市期中)如图,△ABC中,AB>AC,∠BAC的平分线交外接圆于D,DE⊥AB于E,DM⊥AC于M.(1)求证:BE=CM.(2)求证:AB﹣AC=2BE.【解答】证明:(1)连接BD,DC,∵AD平分∠BAC,∴∠BAD=∠CAD,∴弧BD=弧CD,∴BD=CD,∵∠BAD=∠CAD,DE⊥AB,DM⊥AC,∵∠M=∠DEB=90°,DE=DM,在Rt△DEB和Rt△DMC中,,∴Rt△DEB≌Rt△DMC(HL),∴BE=CM.(2)∵DE⊥AB,DM⊥AC,∵∠M=∠DEA=90°,在Rt△DEA和Rt△DMA中∴Rt△DEA≌Rt△DMA(HL),∴AE=AM,∴AB﹣AC,=AE+BE﹣AC,=AM+BE﹣AC,=AC+CM+BE﹣AC,=BE+CM,=2BE.32.(2013•宁夏模拟)如图,OA是⊙0的半径,以OA为直径的⊙C 与⊙0的弦AB相交于点D.求证:AD=BD.【解答】证明:连结OD,如图,∵OA为⊙C的直径,∴∠ADO=90°,∴OD⊥AB,∴AD=BD.33.(2011秋•宁波期中)如图,已知:AB是⊙O的弦,D为⊙O上一点,DC⊥AB于C,DM平分∠CDO.求证:M是弧AB的中点.【解答】解:连接OM∵OD=OM,∴∠ODM=∠OMD,∵DM平分∠ODC,∴∠ODM=∠CDM,∴∠CDM=∠OMD,∴CD∥OM,∵CD⊥AB,∴OM⊥AB,∴弧AM=弧BM,即点M为劣弧AB的中点.34.(2009秋•哈尔滨校级期中)如图,△ABC的三个顶点都在⊙O上,CD是高,D是垂足,CE是直径,求证:∠ACD=∠BCE.【解答】解:连接AE,∵CE为直径,∴∠EAC=90°,∴∠ACE=90°﹣∠AEC,∵CD是高,D是垂足,∴∠BCD=90°﹣∠B,∵∠B=∠AEC(同弧所对的圆周角相等),∴∠ACE=∠BCD,∴∠ACE+∠ECD=∠BCD+∠ECD,∴∠ACD=∠BCE.35.已知:如图,AE是⊙O的直径,AF⊥BC于D,证明:BE=CF.【解答】证明:∵AE是⊙O的直径,∴∠ABE=90°,∴∠E+∠BAE=90°,∵AF⊥BC于D,∴∠FAC+∠ACB=90°,∵∠E=∠ACB,∴∠BAE=∠FAC,∴弧BE=弧CF,∴BE=CF.36.(2015秋•哈尔滨校级期中)已知AB为⊙O的直径,弦BE=DE,AD,BE的延长线交于点C,求证:AC=AB.【解答】证明:连接AE,∵AB为⊙O的直径,∴∠AEB=90°,∴∠AEB=∠AEC=90°,∵弦BE=DE,∴=,∴∠DAE=∠BAE,∵∠C=90°﹣∠DAE,∠B=90°﹣∠BAE,∴∠B=∠C,∴AC=AB.37.如图,AB是圆O的直径,OC⊥AB,交⊙O于点C,D是弧AC上一点,E是AB上一点,EC⊥CD,交BD于点F.问:AD与BF相等吗?为什么?【解答】解:AD和BF相等.理由:如图,连接AC、BC,∵OC⊥AB,∴∠BOC=90°∴∠BDC=∠BAC=45°∵EC⊥CD,∴∠DCE=∠ACB=90°,∴△DCF和△ACB都是等腰直角三角形,∴DC=FC,AC=BC,∵∠DCA+∠ACF=∠BCF+∠ACF=90°,∴∠DCA=∠FCB在△ACD和△BCF中,{,∴△ACD≌△BCF∴DA=BF.38.如图,AB是⊙O的直径,AC、DE是⊙O的两条弦,且DE⊥AB,延长AC、DE相交于点F,求证:∠FCD=∠ACE.【解答】证明:连接AD,AE,∵AB是直径.AB⊥DE,∴AB平分DE,弧ACE=弧AD,∴∠ACD=∠ADE,∵A、C、E、D四点共圆,∴∠FCE=∠ADE,∴∠FCE=∠ACD,∴∠FCE+∠DCE=∠DAC+∠ECD,∴∠FCD=∠ACE.39.如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,作CE⊥AD,垂足为E,CE的延长线与AB交于F.试分析∠ACF与∠ABC是否相等,并说明理由.【解答】解:延长CE交⊙O于M,∵AD是⊙O的直径,作CE⊥AD,∴弧AC=弧AM,∴∠ACF=∠ABC(在同圆中,等弧所对的圆周角相等).40.如图,△ABC内接于⊙O,AD为△ABC的外角平分线,交⊙O于点D,连接BD,CD,判断△DBC的形状,并说明理由.【解答】解:△DBC为等腰三角形.理由如下:∵AD为△ABC的外角平分线,∴∠EAD=∠DAC,∵∠EAD=∠DCB,∠DBC=∠DAC,∴∠DBC=∠DCB,∴△DBC为等腰三角形.一.解答题(共6小题)1.如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,G是上的任意一点,AG、DC的延长线相交于点F,∠FGC与∠AGD的大小有什么关系?为什么?【解答】解:∠FGC与∠AGD相等.理由如下:连接AD,如图,∵CD⊥AB,∴=,∴∠AGD=∠ADC,∵∠FGC=∠ADC,∴∠FGC=∠AGD2.如图,AB是圆O的直径,C是圆O上一点,D是弧AC中点,DE⊥AB垂足为E,AC分别与DE、DB相交于点F、G,则AF与FG是否相等?为什么?【解答】解:AF=FG,理由是:连接AD,∵AB是直径,DE⊥AB,∴∠ADB=∠DEB=90°,∴∠ADE=∠ABD,∵D为弧AC中点,∴∠DAC=∠ABD,∴∠ADE=∠DAC,∴AF=DF,∠FAE=∠DAC,∴DF=FG,∴AF=FG.3.如图,AB为⊙O的直径,以OA为直径作⊙C,AD为⊙O的弦,交⊙C于E,试问,当D点在⊙O上运动时(不与A重合),AE与ED的长度有何关系?证明你的结论.【解答】解:AE=ED.理由:连接OE,∵AO是⊙C的直径,∴∠OEA=90°,∴OE⊥AD,∵OE过圆O的圆心O,∴AE=ED.4.如图,OA是⊙O的半径,以OA为直径的⊙C与⊙O的弦AB交于点D,求证:D是AB的中点.【解答】证明:连接OD,∵OA为⊙C的直径,∴∠ODA=90°,即OD⊥AB,∴D是AB的中点.5.(2007•鄂尔多斯)如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的边于G,F,E点.求证:(1)F是BC的中点;(2)∠A=∠GEF.【解答】证明一:(1)连接DF,∵∠ACB=90°,D是AB的中点,∴BD=DC=AB,(2分)∵DC是⊙O的直径,∴DF⊥BC,(4分)∴BF=FC,即F是BC的中点;(5分)(2)∵D,F分别是AB,BC的中点,∴DF∥AC,(6分)∴∠A=∠BDF,(7分)∵∠BDF=∠GEF(圆周角定理),(8分)∴∠A=∠GEF.(9分)证明二:(1)连接DF,DE,∵DC是⊙O直径,∴∠DEC=∠DFC=90°.(1分)∵∠ECF=90°,∴四边形DECF是矩形.∴EF=CD,DF=EC.(2分)∵D是AB的中点,∠ACB=90°,∴EF=CD=BD=AB.(3分)∴△DBF≌△EFC.(4分)∴BF=FC,即F是BC的中点.(5分)(2)∵△DBF≌△EFC,∴∠BDF=∠FEC,∠B=∠EFC.(6分)∵∠ACB=90°(也可证AB∥EF,得∠A=∠FEC),∴∠A=∠FEC.(7分)∵∠FEG=∠BDF(同弧所对的圆周角相等),(8分)∴∠A=∠GEF.(9分)(此题证法较多,大纲卷参考答案中,又给出了两种不同的证法,可供参考.)6.(2000•兰州)如图,圆内接四边形ABCD的外角∠DCH=∠DCA,DP ⊥AC垂足为P,DH⊥BH垂足为H,求证:CH=CP,AP=BH.【解答】证明:(1)在△DHC与△DPC中,∵∠DCH=∠DCA,DP⊥AC,DH⊥BH,DC为公共边,∴△DHC≌△DPC,∴CH=CP.(2)连接DB,由圆周角定理得,∠DAC=∠DBH,∵△DHC≌△DPC,∴DH=DP,∵DP⊥AC,DH⊥BH,∴∠DHB=∠DPC=90°,∴△DAP≌△DBH,∴AP=BH.。
九年级圆周角练习题

九年级圆周角练习题一、选择题(每题3分,共15分)1. 圆周角定理指出,圆周角的度数是它所对弧的圆心角的度数的一半。
以下哪个选项正确描述了圆周角定理?A. 圆周角的度数是它所对弧的圆心角的度数的两倍B. 圆周角的度数等于它所对弧的圆心角的度数C. 圆周角的度数是它所对弧的圆心角的度数的一半D. 圆周角的度数与它所对弧的圆心角的度数无关2. 在圆中,有一条弦AB,弦AB上的圆周角是40°,那么弦AB所对的圆心角的度数是多少?A. 20°B. 40°C. 80°D. 120°3. 如果一个圆的半径为r,圆周角的度数为θ,那么这个圆周角所对的弧长是多少?A. rθB. 2rθB. rθ/180D. 2πrθ/3604. 已知圆O的半径为5,圆周角∠AOB=60°,求弦AB的长度。
A. 5B. 10C. 2.5D. 2√155. 在圆中,如果两个圆周角的度数之和为180°,这两个角所对的弧是:A. 同弧B. 半圆C. 等弧D. 不能确定二、填空题(每题2分,共20分)6. 圆的直径所对的圆周角是______度。
7. 如果圆周角的度数为90°,那么它所对的圆心角的度数是______度。
8. 圆的半径为3,圆周角的度数为120°,那么这个圆周角所对的弧长是______。
9. 已知圆的半径为7,圆周角∠AOB=70°,求弦AB的长度,答案是______。
10. 如果圆周角的度数为120°,那么它所对的圆心角的度数是______度。
11. 两个圆周角的度数之和为360°,这两个角所对的弧是______。
12. 圆周角定理告诉我们,圆周角的度数等于它所对弧的圆心角的度数的______。
13. 在圆中,如果一条弦所对的圆周角是30°,那么这条弦所对的圆心角的度数是______度。
14. 圆的半径为8,圆周角的度数为150°,那么这个圆周角所对的弧长是______。
圆周角定理及其推论随堂练习考试卷
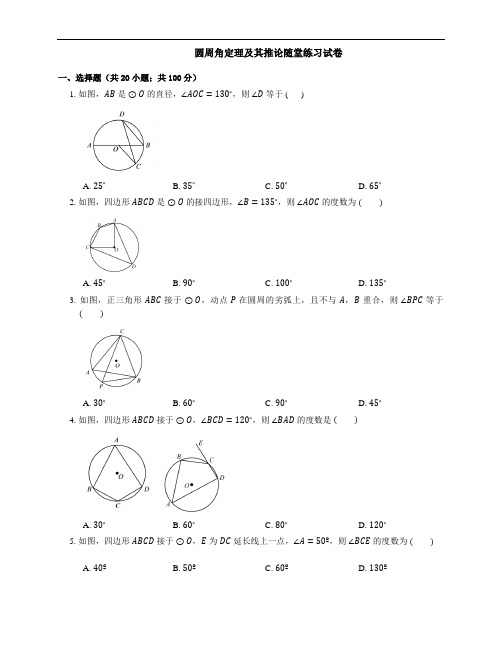
圆周角定理及其推论随堂练习试卷一、选择题(共20小题;共100分)1. 如图,AB是⊙O的直径,∠AOC=130∘,则∠D等于 ( )A. 25∘B. 35∘C. 50∘D. 65∘2. 如图,四边形ABCD是⊙O的接四边形,∠B=135∘,则∠AOC的度数为( )A. 45∘B. 90∘C. 100∘D. 135∘3. 如图,正三角形ABC接于⊙O,动点P在圆周的劣弧上,且不与A,B重合,则∠BPC等于( )A. 30∘B. 60∘C. 90∘D. 45∘4. 如图,四边形ABCD接于⊙O,∠BCD=120∘,则∠BAD的度数是( )A. 30∘B. 60∘C. 80∘D. 120∘5. 如图,四边形ABCD接于⊙O,E为DC延长线上一点,∠A=50º,则∠BCE的度数为( )A. 40ºB. 50ºC. 60ºD. 130º6. 小宏用直角三角板检查某些工件的弧形凹面是否是半圆,下列工件的弧形凹面一定是半圆的是( )A. B.C. D.7. 如图,AB是⊙O的直径,C、D是⊙O上两点,CD⊥AB,如果∠DAB=65∘,那么∠AOC等于( )A. 25∘B. 30∘C. 50∘D. 65∘8. 如图.四边形ABCD接于⊙O,E为CD延长线上一点,如果∠ADE=120∘,那么∠B等于 ( )A. 130∘B. 120∘C. 80∘D. 60∘9. 如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,cosD=23,则AB的长为( )A. 8√133B. 163C. 24√55D. 1210. 在数学实践活动课中,小辉利用自己制作的一把“直角角尺”测量、计算一些圆的直径.如图,直角角尺中,∠AOB=90∘,将点O放在圆周上,分别确定OA,OB与圆的交点C,D,读得数据OC=8,OD=9,则此圆的直径约为( )A. 17B. 14C. 12D. 1011. 如图,△ABC接于⊙O,若∠AOB=100∘,则∠ACB的度数是( )A. 40∘B. 50∘C. 60∘D. 80∘12. 如图1,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发沿图中某一个扇形顺时针匀速运动,设∠APB=y(单位:度),如果y与点P运动的时间x(单位:秒)的函数关系的图象大致如图 2所示,那么点P的运动路线可能为( )A. O→B→A→OB. O→A→C→OC. O→C→D→OD. O→B→D→O13. 如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20∘,那么∠AOD等于( )A. 160∘B. 150∘C. 140∘D. 120∘14. 如图,A,B,C三点在已知的圆上,在△ABC中,∠ABC=70∘,∠ACB=30∘,D是BAC的中点,连接DB,DC,则∠DBC的度数为( )A. 30∘B. 45∘C. 50∘D. 70∘15. 如图,四边形ABCD接于⊙O,∠A=110∘,则∠BOD的度数是( )A. 70∘B. 110∘C. 120∘D. 140∘16. 如图,△ABC为等边三角形,点O在过点A且平行于BC的直线上运动,以△ABC的高为半径的⊙O分别交线段AB,AC于点E,F,则EF所对的圆周角的度数( )A. 从0∘到30∘变化B. 从30∘到60∘变化C. 总等于30∘D. 总等于60∘17. 如图,四边形ABCD接于⊙O,F是CD上一点,且DF=BC,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105∘,∠BAC=25∘,则∠E的度数为( )A. 45∘B. 50∘C. 55∘D. 60∘18. 如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=58∘,则∠BCD的度数为( )A. 32∘B. 58∘C. 64∘D. 116∘19. 如图所示,△ABC为⊙O的接三角形,AB=1,∠C=30∘,则⊙O的接正方形的面积为( )A. 2B. 4C. 8D. 1620. 如图,AB是⊙O的直径,C,D两点在⊙O上,如果∠C=40∘,那么∠ABD的度数为( )A. 40∘B. 90∘C. 80∘D. 50∘二、填空题(共10小题;共50分)21. 已知⊙O,如图所示.(1)求作⊙O的接正方形(要求尺规作图,保留作图痕迹,不写作法);(2)若⊙O的半径为4,则它的接正方形的边长为.22. 如图,在⊙O中,∠BOC=100º,则∠A的度数是.23. 如右图,四边形ABCD接于⊙O,E是BC延长线上一点,若BAD=105∘,则∠DCE的度数是.24. 阅读下面材料:在数学课上,老师提出如下问题:小芸的作法如下:①取AB=c,作AB的垂直平分线交AB于点O;②以点O为圆心,OB长为半径画圆;③以点B为圆心,a长为半径画弧,与⊙O交于点C;④连接BC,AC.则Rt△ABC即为所求.老师说:"小芸的作确."请回答:小芸的作法中判断∠ACB是直角的依据是.25. 数学课上,老师让学生用尺规作图画Rt△ABC,使其斜边AB=c,一条直角边BC=a.小明的做法如图所示,你认为小明这种做法中判断∠ACB是直角的依据是.26. 阅读下面材料:在学习《圆》这一章时,老师给同学们布置了一道尺规作图题:小敏的作法如下:老师认为小敏的作确.请回答:连接OA,OB后,可证∠OAP=∠OBP=90∘,其依据是;由此可证明直线PA,PB都是⊙O的切线,其依据是.27. 如图,⊙O是△ABC的外接圆,点A在优弧BC上,∠BOC=100∘,则∠A的度数为.28. 如图,弦AB的长等于⊙O的半径,那么弦AB所对的圆周角的度数是.29. 如图,已知四边形ABCD接于⊙O,点O在∠D的部,∠OAD+∠OCD=50∘,则∠B=.30. 如图是由两个长方形组成的工件平面图(单位,mm),直线l是它的对称轴,能完全覆盖这个平面图形的圆面的最小半径是( )mm.三、解答题(共5小题;共65分)31. 如图,AB是直径,弦CD⊥AB,E是AC上一点,AE,DC的延长线交于点F.求证:∠AED=∠CEF.32. 已知:如图,A、B、C为⊙O上的三个点,⊙O的直径为4cm,∠ACB=45∘,求AB的长.33. 如图,在△ABC中,AB是⊙O的直径,AC与⊙O交于点D.点E在BD上,连接DE,AE,连接CE并延长交AB于点F,∠AED=∠ACF.Ⅰ求证:CF⊥AB;Ⅱ若CD=4,CB=4√5,cos∠ACF=4,求EF的长.534. 已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.Ⅰ求证:AB=AC;Ⅱ若AB=4,BC=2√3,求CD的长.35. 已知:⊙O是△ABC的外接圆,点M为⊙O上一点.Ⅰ如图,若△ABC为等边三角形,BM=1,CM=2,求AM的长;小明在解决这个问题时采用的方法是:延长MC到E,使ME=AM,从而可证△AME为等边三角形,并且△ABM≌△ACE,进而就可求出线段AM的长.请你借鉴小明的方法写出AM的长,并写出推理过程.Ⅱ若△ABC为等腰直角三角形,∠BAC=90∘,BM=a,CM=b(其中b>a),直接写出AM的长(用含有a,b的代数式表示).圆周角定理及其推论随堂练习试卷答案第一部分1. A2. B3. B4. B5. B6. A7. C8. B9. D 10. C11. B 12. C 13. C 14. C 15. D16. C 17. B 18. A 19. A 20. D第二部分21. (1)如图:(2)4√223. 105∘24. 直径所对的圆周角是直角.25. 直径所对的圆周角是直角26. 直径所对的圆周角是直角;经过半径外端并且垂直于这条半径的直线是圆的切线27. 50∘28. 30∘或150∘29. 130∘30. 50第三部分31. 连接AD.因为AD=AC,所以∠AED=∠ADC,因为∠CEF+∠AEC=∠ADC+∠AEC=180∘,所以∠ADC=∠CEF.所以∠AED=∠CEF.32. 连接OA、OB.∵∠ACB=45∘,∴∠AOB=2∠ACB=90∘ .又OA=OB .∴△AOB是等腰直角三角形.∴AB2=OA2+OB2=22+22=8 .∴AB=2√2 .答:AB的长为2√2cm.33. (1)连接BD,如图 1.∵AB是⊙O的直径,∴∠ADB=90∘.∴∠DAB+∠1=90∘.∵∠1=∠2,∠2=∠3,∴∠1=∠3.∴∠DAB+∠3=90∘.∴∠CFA=180∘−(∠DAB+∠3)=90∘.∴CF⊥AB.(2)连接OE,如图 2.∵∠ADB=90∘,∴∠CDB=180∘−∠ADB=90∘.∵在Rt△CDB中,CD=4,CB=4√5,∴DB=√CB2−CD2=8.∵∠1=∠3,∴cos∠1=cos∠3=45.∵在Rt△ABD中,cos∠1=DBAB =45,∴AB=10.∴OA=OE=5,AD=√AB2−DB2=6.∵CD=4,∴AC=AD+CD=10.∴在Rt△ACF中,CF=AC⋅cos∠3=8.∴AF=√AC2−CF2=6.∴OF=AF−OA=1.∴在Rt△OEF中,EF=√OE2−OF2=2√6.34. (1)因为ED=EC,所以∠EDC=∠C,因为∠EDC=∠B,所以∠B=∠C,所以AB=AC.(2)连接AE,因为AB为直径,所以AE⊥BC,由(1)知AB=AC,BC=√3,所以BE=CE=12因为CE⋅CB=CD⋅CA,AC=AB=4,所以√3⋅2√3=4CD,所以CD=3.235. (1)AM=3.延长MC到E,使ME=AM.∵△ABC为等边三角形,∴∠ABC=60∘.∴∠AME=60∘.∴△AME为等边三角形.∴AM=AE,∠BAM=∠CAE.又AB=AC,∴△ABM≌△ACE.∴AM=ME=3.(2)AM=√22(a+b)或√22(b−a).。
中考数学复习----《圆周角定理》知识点总结与专项练习题(含答案)

中考数学复习----《圆周角定理》知识点总结与专项练习题(含答案)知识点总结1.圆心角、弦以及弧之间的关系:①定理:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
②推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。
说明:同一条弦对应两条弧,其中一条是优弧,一条是劣弧,而在本定理和推论中的“弧”是指同为优弧或劣弧。
2.圆周角的定义:顶点在圆上,并且两边都与圆相交的角叫做圆周角。
3.圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半。
4.圆周角定理的推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径。
5.圆的内接四边形:①定义:四个顶点都在圆上的四边形叫做圆的内接四边形。
②性质:I:圆内接四边形的对角互补。
II:圆内接四边形的任意一个外角等于它的内对角。
练习题1、(2022•襄阳)已知⊙O的直径AB长为2,弦AC长为2,那么弦AC所对的圆周角的度数等于.【分析】首先利用勾股定理逆定理得∠AOC=90°,再根据一条弦对着两种圆周角可得答案.【解答】解:如图,∵OA=OC=1,AC=,∴OA2+OC2=AC2,∴∠AOC=90°,∴∠ADC=45°,∴∠AD'C=135°,故答案为:45°或135°.2、(2022•日照)一圆形玻璃镜面损坏了一部分,为得到同样大小的镜面,工人师傅用直角尺作如图所示的测量,测得AB=12cm,BC=5cm,则圆形镜面的半径为.【分析】连接AC,根据∠ABC=90°得出AC是圆形镜面的直径,再根据勾股定理求出AC 即可.【解答】解:连接AC,∵∠ABC=90°,且∠ABC是圆周角,∴AC是圆形镜面的直径,由勾股定理得:AC===13(cm),所以圆形镜面的半径为cm,故答案为:cm.3、(2022•永州)如图,AB是⊙O的直径,点C、D在⊙O上,∠ADC=30°,则∠BOC=度.【分析】根据在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半求出∠AOC的度数,根据平角的定义即可得到∠BOC=180°﹣∠AOC的度数.【解答】解:∵∠ADC是所对的圆周角,∴∠AOC=2∠ADC=2×30°=60°,∴∠BOC=180°﹣∠AOC=180°﹣60°=120°.故答案为:120.4、(2022•苏州)如图,AB是⊙O的直径,弦CD交AB于点E,连接AC,AD.若∠BAC=28°,则∠D=°.【分析】如图,连接BC,证明∠ACB=90°,求出∠ABC,可得结论.【解答】解:如图,连接BC.∵AB是直径,∴∠ACB=90°,∴∠ABC=90°﹣∠CAB=62°,∴∠D=∠ABC=62°,故答案为:62.5、(2022•湖州)如图,已知AB 是⊙O 的弦,∠AOB =120°,OC ⊥AB ,垂足为C ,OC 的延长线交⊙O 于点D .若∠APD 是AB ⌒所对的圆周角,则∠APD 的度数是 .【分析】由垂径定理得出,由圆心角、弧、弦的关系定理得出∠AOD =∠BOD ,进而得出∠AOD =60°,由圆周角定理得出∠APD =∠AOD =30°,得出答案.【解答】解:∵OC ⊥AB ,∴,∴∠AOD =∠BOD ,∵∠AOB =120°,∴∠AOD =∠BOD =∠AOB =60°,∴∠APD =∠AOD =×60°=30°,故答案为:30°.6、(2022•徐州)如图,A 、B 、C 点在圆O 上,若∠ACB =36°,则∠AOB = .【分析】利用一条弧所对的圆周角等于它所对的圆心角的一半即可得出结论.【解答】解:∵∠ACB =∠AOB ,∠ACB =36°,∴∠AOB =2×∠ACB =72°.故答案为:72°.7、(2022•锦州)如图,四边形ABCD内接于⊙O,AB为⊙O的直径,∠ADC=130°,连接AC,则∠BAC的度数为.【分析】利用圆内接四边形的性质和∠ADC的度数求得∠B的度数,利用直径所对的圆周角是直角得到∠ACB=90°,然后利用直角三角形的两个锐角互余计算即可.【解答】解:∵四边形ABCD内接于⊙O,∠ADC=130°,∴∠B=180°﹣∠ADC=180°﹣130°=50°,∵AB为⊙O的直径,∴∠ACB=90°,∴∠CAB=90°﹣∠B=90°﹣50°=40°,故答案为:40°.8、(2022•雅安)如图,∠DCE是⊙O内接四边形ABCD的一个外角,若∠DCE=72°,那么∠BOD的度数为.【分析】根据邻补角的概念求出∠BCD,根据圆内接四边形的性质求出∠A,根据圆周角定理解答即可.【解答】解:∵∠DCE=72°,∴∠BCD=180°﹣∠DCE=108°,∵四边形ABCD内接于⊙O,∴∠A=180°﹣∠BCD=72°,由圆周角定理,得∠BOD=2∠A=144°,故答案为:144°.9、(2022•甘肃)如图,⊙O是四边形ABCD的外接圆,若∠ABC=110°,则∠ADC=°.【分析】根据圆内接四边形的对角互补即可得到结论.【解答】解:∵四边形ABCD内接于⊙O,∠ABC=110°,∴∠ADC=180°﹣∠ABC=180°﹣110°=70°,故答案为:70.。
圆周角规范练习题A

圆周角规范练习题A1. 在标准坐标系中,点A坐标为(2, 0),点B坐标为(6, 0)。
计算角AOB的度数。
解答:点O为原点,根据点的坐标可以得知A、B都位于x轴上,因此角AOB是一个圆周角,度数为360°。
2. 在平面直角坐标系中,点C(4, 1)是圆O的圆心,点A(5, 3)在圆O上。
求角AOC的度数。
解答:首先,计算O到A的向量OA为(5-4, 3-1) = (1, 2)。
然后,计算OA的模长|OA|,使用勾股定理,可以得知|OA| = √(1^2 +2^2) = √5。
因此,根据OA和OC的坐标可以求出它们之间的夹角,即角AOC。
使用向量的内积公式:OA·OC = |OA|·|OC|·cos(AOC)。
将已知数据代入公式,得到1·(5-4) + 2·(3-1) = √5·|OC|·cos(AOC)。
根据解方程可以得到cos(AOC) = (3√5)/5。
进一步,可以求得AOC的度数为arccos((3√5)/5)。
3. 圆O的圆心为A,点B在圆上,且弧AB的度数为135°。
求角AOB的度数。
解答:根据题目中的描述,弧AB的度数为135°,因此角AOB的度数也为135°。
4. 在平面直角坐标系中,点C(7, 3)是圆O的圆心,点D(6, 4)在圆上。
求角COD的度数。
解答:首先,计算O到D的向量OD为(6-7, 4-3) = (-1, 1)。
然后,计算OD的模长|OD|,使用勾股定理,可以得知|OD| = √((-1)^2 + 1^2) = √2。
因此,在已知OD和OC的坐标的前提下,可以求出它们之间的夹角,即角COD。
使用向量的内积公式:OD·OC =|OD|·|OC|·cos(COD)。
将已知数据代入公式,得到-1·(7-6) + 1·(3-4) = √2·|OC|·cos(COD)。
圆周角圆心角练习题

圆周角圆心角练习题一、选择题1. 圆周角定理指出,圆周角的度数是同弧所对圆心角的度数的______。
A. 1/2B. 2倍C. 3倍D. 4倍2. 若圆心角为40°,则同弧所对的圆周角为______。
A. 20°B. 40°C. 80°D. 120°3. 在圆中,若一条弦所对的圆心角为60°,则这条弦所对的圆周角是______。
A. 30°B. 45°C. 60°D. 90°4. 圆内接四边形ABCD中,若∠A=60°,则∠B的度数为______。
A. 60°B. 120°C. 180°D. 240°5. 已知圆的半径为5,圆心角为120°,那么这个圆心角所对的弧长为______。
A. 5πB. 10πC. 15πD. 20π二、填空题6. 若圆周角为45°,则同弧所对的圆心角为______。
7. 在圆中,若弦AB所对的圆心角为100°,则弦AB所对的圆周角为______。
8. 已知圆的半径为10,圆心角为150°,则这个圆心角所对的弧长为______。
9. 圆内接四边形ABCD中,若∠A=90°,则∠B的度数为______。
10. 若圆的半径为8,圆心角为90°,则这个圆心角所对的弧长为______。
三、简答题11. 解释什么是圆周角,并说明它与圆心角的关系。
12. 给出一个圆内接四边形的例子,并说明其对角互补的性质。
13. 解释如何计算一个圆心角所对的弧长。
14. 在圆中,如果知道圆周角的度数,如何计算同弧所对的圆心角的度数?15. 圆内接四边形的对角互补性质在实际问题中有哪些应用?四、解答题16. 已知圆的半径为6,圆心角为60°,求这个圆心角所对的弧长。
17. 在圆中,若弦AB所对的圆心角为120°,求弦AB所对的圆周角的度数。
圆周角定理练习题

圆周角定理练习题圆周角定理练习题圆周角定理是几何学中的一个重要定理,它描述了圆周上的角度与圆心角的关系。
在这篇文章中,我们将通过一些练习题来加深对圆周角定理的理解。
练习题1:在一个半径为5厘米的圆上,有一个圆心角的度数为60°。
求这个圆心角所对的弧长。
解析:根据圆周角定理,圆心角所对的弧长等于半径乘以圆心角的弧度数。
首先,我们需要将60°转换为弧度数。
由于一个圆周上的角度为360°,而一周的弧度数为2π,所以60°对应的弧度数为60/360乘以2π。
计算得到的结果约为1.047弧度。
然后,将半径5厘米乘以1.047弧度,得到的弧长约为5.236厘米。
练习题2:在一个半径为8厘米的圆上,有一个弧长为12厘米的弧。
求这个弧所对的圆心角的度数。
解析:根据圆周角定理,圆心角所对的弧长等于半径乘以圆心角的弧度数。
首先,我们需要将弧长12厘米转换为弧度数。
由于圆周长等于2π乘以半径,所以弧长12厘米对应的弧度数为12/(2π乘以8)。
计算得到的结果约为0.238弧度。
然后,将半径8厘米乘以0.238弧度,得到的圆心角的弧长约为1.904厘米。
最后,我们将这个圆心角的弧长转换为度数。
由于一周的弧度数为2π,所以1.904弧度对应的度数为(1.904/2π)乘以360。
计算得到的结果约为64.3°。
练习题3:在一个圆的内切四边形中,两个相对的内角分别为120°和150°。
求这个四边形内切圆的半径。
解析:首先,我们需要知道内切四边形的两个对角线相互垂直且交于圆心。
根据圆周角定理,圆心角所对的弧长相等。
所以,我们可以得知内切四边形的两个对角线所对的圆心角的度数分别为120°和150°。
由于对角线相互垂直,所以这两个圆心角的度数之和为90°。
根据这个关系,我们可以得到一个方程:120° + 150° + x + y = 360°,其中x和y分别表示另外两个圆心角的度数。
圆周角练习题

圆周角练习题一、选择题1. 一个圆的半径为5,圆周角的度数为60°,那么这个圆周角所对的弦长是多少?A. 5B. 10C. 15D. 202. 在圆中,圆周角的度数是圆心角的度数的几倍?A. 1/2B. 1C. 2D. 43. 已知一个圆的直径为12,圆周角为45°,求这个圆周角所对的弧长。
A. 6πB. 3πC. 2πD. π二、填空题4. 圆周角定理指出,圆周角的度数等于它所对圆心角的______倍。
5. 如果一个圆的半径为r,圆周角为θ,那么这个圆周角所对的弧长为______。
6. 在一个半径为10的圆中,如果圆周角为120°,那么这个圆周角所对的弦长是______。
三、简答题7. 解释什么是圆周角,并说明它与圆心角的关系。
8. 给出一个例子,说明如何计算一个圆周角所对的弦长。
四、计算题9. 已知一个圆的半径为7,圆周角为30°,求这个圆周角所对的弧长。
10. 在一个半径为8的圆中,如果圆周角为150°,求这个圆周角所对的弦长。
五、证明题11. 证明:在一个圆中,同弧所对的圆周角相等。
12. 证明:在一个圆中,如果两个圆周角所对的圆心角相等,那么这两个圆周角也相等。
六、应用题13. 一个自行车轮的直径为60厘米,当自行车行驶了100米,求车轮转过的圈数。
14. 一个圆的半径为15,圆周角为120°,求这个圆周角所对的扇形面积。
七、探索题15. 探索圆周角定理在实际生活中的应用,并给出至少两个例子。
八、综合题16. 一个圆的半径为20,圆周角为90°,求这个圆周角所对的弧长、弦长以及扇形面积。
九、开放性问题17. 如果你有一个圆,半径为r,圆周角为θ,你将如何设计一个实验来测量这个圆周角所对的弧长和弦长?十、拓展题18. 假设你有一个圆,半径为r,圆周角为θ,圆心角为α,讨论并证明圆周角与圆心角之间的关系。
请注意,本试卷中的题目需要根据圆周角定理和相关公式进行解答。
圆周角定理练习题(A)

《圆周角定理》练习题一.选择题(共16小题)1.如图,A、B、C三点在⊙O上,若∠BOC=76°,则∠BAC的度数是()A.152°B.76°C.38°D.14°2.如图,⊙O是△ABC的外接圆,∠ACO=45°,则∠B的度数为()A.30°B.35°C.40°D.45°第1题图第2题图第3题图3.如图,在图中标出的4个角中,圆周角有()个.A.1 B.2 C.3 D.44.如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠BOD的度数是()A.25°B.30°C.40°D.50°5.如图,已知在⊙O中,点A,B,C均在圆上,∠AOB=80°,则∠ACB等于()A.130°B.140°C.145°D.150°第4题图第5题图第6题图6.如图,MN是⊙O的直径,∠PBN=50°,则∠MAP等于()A.50°B.40°C.30°D.20°7.如图,CD是⊙O的直径,A、B是⊙O上的两点,若∠ABD=20°,则∠ADC的度数为)A.40°B.50°C.60°D.70°8.如图,AB是半圆的直径,点D是的中点,∠ABC=50°,则∠DAB等于()A.55°B.60°C.65°D.70°第7题图第8题图第9题图9.如图,AB是⊙O的直径,C,D为圆上两点,∠AOC=130°,则∠D等于()A.25°B.30°C.35°D.50°10.如图,∠1、∠2、∠3、∠4的大小关系是()A.∠4<∠1<∠2<∠3 B.∠4<∠1=∠3<∠2C.∠4<∠1<∠3∠2 D.∠4<∠1<∠3=∠211.如图,AB是半圆O的直径,∠BAC=60°,D是半圆上任意一点,那么∠D的度数是()A.30°B.45°C.60°D.90°第10题图第11题图第12题图12.如图,在⊙O中,OA⊥BC,∠AOC=50°,则∠ADB的度数为()A.15°B.20°C.25°D.50°13.在⊙O中,点A、B在⊙O上,且∠AOB=84°,则弦AB所对的圆周角是()A.42°B.84°C.42°或138°D.84°或96°14.如图所示,在⊙O中,AB是⊙O的直径,∠ACB的角平分线CD交⊙O于D,则∠ABD 的度数等于()A.90°B.60°C.45°D.30°15.已知如图,AB是⊙O的直径,CD是⊙O的弦,∠CDB=40°,则∠CBA的度数为()A.60°B.50°C.40°D.30°第10题图第11题图第12题图16.如图,AB是圆的直径,AB⊥CD,∠BAD=30°,则∠AEC的度数等于()A.30°B.50°C.60°D.70°二.填空题(共8小题)17.如图,⊙O的直径CD经过弦EF的中点G,∠DCF=20°,则∠EOD等于.第17题图第18题图第19题图18.如图,点A、B在⊙O上,∠AOB=100°,点C是劣弧AB上不与A、B重合的任意一点,则∠C=°.19.在⊙O中,弦AB=2cm,∠ACB=30°,则⊙O的直径为cm.20.如图,⊙O中弦AB等于半径R,则这条弦所对的圆心角是,圆周角是.第20题图第21题图第22题图21.如图,等腰△ABC的底边BC的长为4cm,以腰AB为直径的⊙O交BC于点D,交AC于点E,则DE的长为cm.22.如图,在“世界杯”足球比赛中,甲带球向对方球门PQ进攻,当他带球冲到A点时,同样乙已经助攻冲到B点,丙助攻到C点.有三种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门.第三种是甲将球传给丙,由丙射门.仅从射门角度考虑,应选择种射门方式.三.解答题(共16小题)25.28.如图,AB是⊙O的直径,C是⊙O上的点,AC=6cm,BC=8cm,∠ACB的平分线交⊙O于点D,求AB和BD的长.26.如图,已知CD是⊙O的直径,弦AB⊥CD,垂足为点M,点P是上一点,且∠BPC=60°.试判断△ABC的形状,并说明你的理由.27、如图,△ABC的高AD、BE相交于点H,延长AD交ABC的外接圆于点G,连接BG.求证:HD=GD.28.已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E.∠BAC=40°(1)求∠EBC的度数;(2)求证:BD=CD.29.如图,△ABC是⊙O的内接三角形,∠A=30°,BC=3cm.求⊙O的半径.30.如图,AB是⊙O的直径,过圆上一点C作CD⊥AB于点D,点C是弧AF的中点,连接AF交CD于点E,连接BC交AF于点G.(1)求证:AE=CE;.31.如图,△ABC中,AB>AC,∠BAC的平分线交外接圆于D,DE⊥AB于E,DM⊥AC 于M.(1)求证:BE=CM.(2)求证:AB﹣AC=2BE.32.如图,OA是⊙0的半径,以OA为直径的⊙C与⊙0的弦AB相交于点D.求证:AD=BD.33.如图,已知:AB是⊙O的弦,D为⊙O上一点,DC⊥AB于C,DM平分∠CDO.求证:M是弧AB的中点.34.如图,△ABC的三个顶点都在⊙O上,CD是高,D是垂足,CE是直径,求证:∠ACD=∠BCE.35.已知:如图,AE是⊙O的直径,AF⊥BC于D,证明:BE=CF.36.已知AB为⊙O的直径,弦BE=DE,AD,BE的延长线交于点C,求证:AC=AB.37.如图,AB是圆O的直径,OC⊥AB,交⊙O于点C,D是弧AC上一点,E是AB上一点,EC⊥CD,交BD于点F.问:AD与BF相等吗?为什么?38.如图,AB是⊙O的直径,AC、DE是⊙O的两条弦,且DE⊥AB,延长AC、DE相交于点F,求证:∠FCD=∠ACE.39.如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,作CE⊥AD,垂足为E,CE 的延长线与AB交于F.试分析∠ACF与∠ABC是否相等,并说明理由.40.如图,△ABC内接于⊙O,AD为△ABC的外角平分线,交⊙O于点D,连接BD,CD,判断△DBC的形状,并说明理由.41.如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,G是上的任意一点,AG、DC 的延长线相交于点F,∠FGC与∠AGD的大小有什么关系?为什么?42.如图,AB是圆O的直径,C是圆O上一点,D是弧AC中点,DE⊥AB垂足为E,AC 分别与DE、DB相交于点F、G,则AF与FG是否相等?为什么?43.如图,OA是⊙O的半径,以OA为直径的⊙C与⊙O的弦AB交于点D,求证:D是AB的中点.44.如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的边于G,F,E点.求证:(1)F是BC的中点;(2)∠A=∠GEF.45.如图,圆内接四边形ABCD的外角∠DCH=∠DCA,DP⊥AC垂足为P,DH⊥BH垂足为H,求证:CH=CP,AP=BH.《圆周角定理》2222222222参考答案与试题解析一.选择题(共16小题)1.(2012•呼伦贝尔)如图,A、B、C三点在⊙O上,若∠BOC=76°,则∠BAC的度数是()A.152°B.76°C.38°D.14°【解答】解:∵所对的圆心角是∠BOC,圆周角是∠BAC,又∵∠BOC=76°,∴∠A=76°×=38°.故选C.2.(2015•眉山)如图,⊙O是△ABC的外接圆,∠ACO=45°,则∠B的度数为()A.30°B.35°C.40°D.45°【解答】解:∵OA=OC,∠ACO=45°,∴∠OAC=45°,∴∠AOC=180°﹣45°﹣45°=90°,∴∠B=∠AOC=45°.故选D.3.(2010秋•海淀区校级期末)如图,在图中标出的4个角中,圆周角有()个.A.1 B.2 C.3 D.4【解答】解:∠1和∠3符合圆周角的定义,∠2顶点不在圆周上,∠4的一边不和圆相交,故图中圆周角有∠1和∠3两个.故选B.4.(2015•珠海)如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠BOD的度数是()A.25°B.30°C.40°D.50°【解答】解:∵在⊙O中,直径CD垂直于弦AB,∴=,∴∠DOB=2∠C=50°.故选:D.5.(1997•陕西)如图,已知在⊙O中,点A,B,C均在圆上,∠AOB=80°,则∠ACB等于()A.130°B.140°C.145°D.150°【解答】解:设点E是优弧AB上的一点,连接EA,EB∵∠AOB=80°∴∠E=∠AOB=40°∴∠ACB=180°﹣∠E=140°.故选:B.6.如图,MN是⊙O的直径,∠PBN=50°,则∠MAP等于()A.50°B.40°C.30°D.20°【解答】解:连接OP,可得∠MAP=∠MOP,∠NBP=∠NOP,∵MN为直径,∴∠MOP+∠NBP=180°,∴∠MAP+∠NBP=90°,∵∠PBN=50°,∴∠MAP=90°﹣∠PBN=40°.故选B.7.(2007•太原)如图,CD是⊙O的直径,A、B是⊙O上的两点,若∠ABD=20°,则∠ADC 的度数为()A.40°B.50°C.60°D.70°【解答】解:∵∠ABD=20°∴∠C=∠ABD=20°∵CD是⊙O的直径∴∠CAD=90°∴∠ADC=90°﹣20°=70°.故选D.8.(2013•苏州)如图,AB是半圆的直径,点D是的中点,∠ABC=50°,则∠DAB等于()A.55°B.60°C.65°D.70°【解答】解:连结BD,如图,∵点D是的中点,即弧CD=弧AD,∴∠ABD=∠CBD,而∠ABC=50°,∴∠ABD=×50°=25°,∵AB是半圆的直径,∴∠ADB=90°,∴∠DAB=90°﹣25°=65°.故选C.9.(2009•枣庄)如图,AB是⊙O的直径,C,D为圆上两点,∠AOC=130°,则∠D等于()A.25°B.30°C.35°D.50°【解答】解:∵∠AOC=130°,∴∠BOC=50°,∴∠D=∠BOC=25°.故选A.10.(2013秋•沙洋县校级月考)如图,∠1、∠2、∠3、∠4的大小关系是()A.∠4<∠1<∠2<∠3 B.∠4<∠1=∠3<∠2 C.∠4<∠1<∠3∠2 D.∠4<∠1<∠3=∠2【解答】解:如图,利用圆周角定理可得:∠1=∠3=∠5=∠6,根据三角形的外角的性质得:∠5>∠4,∠2>∠6,∴∠4<∠1=∠3<∠2,故选B.11.(2012秋•天津期末)如图,AB是半圆O的直径,∠BAC=60°,D是半圆上任意一点,那么∠D的度数是()A.30°B.45°C.60°D.90°【解答】解:连接BC,∵AB是半圆的直径∴∠ACB=90°∵∠BAC=60°,∴∠ABC=90°﹣∠BAC=30°,∴∠D=∠ABC=30°.故选A.12.(2009•塘沽区二模)如图,在⊙O中,OA⊥BC,∠AOC=50°,则∠ADB的度数为()A.15°B.20°C.25°D.50°【解答】解:∵OA⊥BC,∠AOC=50°,∴,∴∠ADB=∠AOC=25°.故选C.13.(2012秋•宜兴市校级期中)在⊙O中,点A、B在⊙O上,且∠AOB=84°,则弦AB所对的圆周角是()A.42°B.84°C.42°或138°D.84°或96°【解答】解:如图,∵∠AOB=84°,∴∠ACB=∠AOB=×84°=42°,∴∠ADB=180°﹣∠ACB=138°.∴弦AB所对的圆周角是:42°或138°.故选C.14.(2011•南岸区一模)如图所示,在⊙O中,AB是⊙O的直径,∠ACB的角平分线CD 交⊙O于D,则∠ABD的度数等于()A.90°B.60°C.45°D.30°【解答】解:连接AD,∵在⊙O中,AB是⊙O的直径,∴∠ADB=90°,∵CD是∠ACB的角平分线,∴=,∴AD=BD,∴△ABD是等腰直角三角形,∴∠ABD=45°.故选C.15.(2015秋•合肥校级期末)已知如图,AB是⊙O的直径,CD是⊙O的弦,∠CDB=40°,则∠CBA的度数为()A.60°B.50°C.40°D.30°【解答】解:连接AC,∵AB是⊙O的直径,∴∠ACB=90°,∵∠A=∠CDB=40°,∴∠CBA=90°﹣∠A=50°.故选B.16.(2013•万州区校级模拟)如图,AB是圆的直径,AB⊥CD,∠BAD=30°,则∠AEC的度数等于()A.30°B.50°C.60°D.70°【解答】解:∵∠BAD=30°,∴=60°,∵AB是圆的直径,AB⊥CD,∴==60°,∴=180°﹣60°=120°,∴∠AEC==×120°=60°.故选C.二.填空题(共8小题)17.(2016•大冶市模拟)如图,⊙O的直径CD经过弦EF的中点G,∠DCF=20°,则∠EOD 等于40°.【解答】解:∵⊙O的直径CD过弦EF的中点G,∠DCF=20°,∴弧DF=弧DE,且弧的度数是40°,∴∠DOE=40°,答案为40°.18.(2015•历城区二模)如图,AB是半圆的直径,点D是弧AC的中点,∠ABC=50°,则∠DAB的度数是65°.【解答】解:连结BD,如图,∵点D是的中点,即弧CD=弧AD,∴∠ABD=∠CBD,而∠ABC=50°,∴∠ABD=×50°=25°,∵AB是半圆的直径,∴∠ADB=90°,∴∠DAB=90°﹣25°=65°.故答案为65°.19.(2013秋•滨湖区校级期末)如图,点A、B在⊙O上,∠AOB=100°,点C是劣弧AB 上不与A、B重合的任意一点,则∠C=130°.【解答】解:在优弧AB上取点D,连结AD、BD,如图,∴∠D=∠AOB=×100°=50°,∵∠D+∠C=180°,∴∠C=180°﹣50°=130°.故答案为130.20.(2008秋•苏州校级期中)球员甲带球冲到A点时,同伴乙已经助攻冲到B点.有两种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门.仅从射门角度考虑,应选择第二种种射门方式较为合理.【解答】解:连接OC.根据圆周角定理,得∠PCQ=∠B,根据三角形的外角的性质,得∠PCQ>∠A,则∠B>∠A.故答案为第二种.21.(2015•黄岛区校级模拟)在⊙O中,弦AB=2cm,∠ACB=30°,则⊙O的直径为4cm.【解答】解:连接OA,OB,∵∠ACB=30°,∴∠AOB=60°,∴△AOB是等边三角形,∴OA=OB=AB=2cm,∴⊙O的直径=4cm.故答案为:4.22.(2014春•海盐县校级期末)如图,⊙O中弦AB等于半径R,则这条弦所对的圆心角是60°,圆周角是30°或150°.【解答】解:连结OA、OB,∠APB和∠AP′B为弦AB所对的圆周角,如图,∵弦AB等于半径R,∴△OAB为等边三角形,∴∠AOB=60°,∴∠APB=∠AOB=30°,∴∠AP′B=180°﹣∠APB=150°,即这条弦所对的圆心角是60°,圆周角是30°或150°.故答案为60°;是30°或150°.23.(2012•义乌市模拟)如图,等腰△ABC的底边BC的长为4cm,以腰AB为直径的⊙O 交BC于点D,交AC于点E,则DE的长为2cm.【解答】解:连接AD,∵∠DEC为圆内接四边形ABDE的外角,∴∠DEC=∠B,又等腰△ABC,BC为底边,∴AB=AC,∴∠B=∠C,∴∠DEC=∠C,∴DE=DC,∵AB为圆O的直径,∴∠ADB=90°,即AD⊥BC,∴BD=CD=BC,又BC=4cm,∴DE=2cm.故答案为:224.(2012秋•哈密地区校级月考)如图,在“世界杯”足球比赛中,甲带球向对方球门PQ进攻,当他带球冲到A点时,同样乙已经助攻冲到B点,丙助攻到C点.有三种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门.第三种是甲将球传给丙,由丙射门.仅从射门角度考虑,应选择第二种射门方式.【解答】解:设AP与圆的交点是C,连接CQ;则∠PCQ>∠A;由圆周角定理知:∠PCQ=∠B;所以∠B>∠A;因此选择第二种射门方式更好.故答案为:第二.三.解答题(共16小题)25.(2009•沈阳模拟)如图,△ABC的高AD、BE相交于点H,延长AD交ABC的外接圆于点G,连接BG.求证:HD=GD.【解答】证明:∵∠C=∠G,△ABC的高AD、BE,∴∠C+∠DAC=90°,∠AHE+∠DAC=90°,∴∠C=∠AHE,∵∠AHE=∠BHG=∠C,∴∠G=∠BHG,∴BH=BG,又∵AD⊥BC,∴HD=DG.26.(2013秋•虞城县校级期末)如图,已知CD是⊙O的直径,弦AB⊥CD,垂足为点M,点P是上一点,且∠BPC=60°.试判断△ABC的形状,并说明你的理由.【解答】解:△ABC为等边三角形.理由如下:∵AB⊥CD,CD为⊙O的直径,∴弧AC=弧BC,∴AC=BC,又∵∠BPC=∠A=60°,∴△ABC为等边三角形.27.(2013秋•耒阳市校级期末)已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E.∠BAC=40°(1)求∠EBC的度数;(2)求证:BD=CD.【解答】(1)解:∵AB=AC,∴∠ABC=∠C,∵∠BAC=40°,∴∠C=(180°﹣40°)=70°,∵AB为⊙O的直径,∴∠AEB=90°,∴∠EBC=90°﹣∠C=20°;证明:连结AD,如图,∵AB为⊙O的直径,∴∠ADB=90°,∴AD⊥BC,而AB=AC,∴BD=DC.28.(2014秋•高密市期中)如图,AB是⊙O的直径,C是⊙O上的点,AC=6cm,BC=8cm,∠ACB的平分线交⊙O于点D,求AB和BD的长.【解答】解:如图,∵AB是⊙O的直径,∴∠ACB=90°,∠ADB=90°.∴AB===10(cm).∵AC=6cm,BC=8cm,∵CD是∠ACB的平分线,∴∠ACD=∠BCD,则=,∴AD=BD,∴BD=AB=5cm.综上所述,AB和BD的长分别是10cm,5cm.29.(2013秋•宜兴市校级期中)如图,△ABC是⊙O的内接三角形,∠A=30°,BC=3cm.求⊙O的半径.【解答】解:作直径CD,连结BD,如图,∵CD为直径,∴∠CBD=90°,∵∠D=∠A=30°,∴CD=2BC=2×3=6,∴⊙O的半径为3cm.30.(2010秋•瑞安市校级月考)如图,AB是⊙O的直径,过圆上一点C作CD⊥AB于点D,点C是弧AF的中点,连接AF交CD于点E,连接BC交AF于点G.(1)求证:AE=CE;(2)已知AG=10,ED:AD=3:4,求AC的长.【解答】(1)证明:∵点C是弧AF的中点,∴∠B=∠CAE,∵AB是⊙O的直径,∴∠ACB=90°,即∠ACE+∠BCD=90°,∵CD⊥AB,∴∠B+∠BCD=90°,∴∠B=∠CAE=∠ACE,∴AE=CE …(6分)(2)解:∵∠ACB=90°,∴∠CAE+∠CGA=90°,又∵∠ACE+∠BCD=90°,∴∠CGA=∠BCD,∵AG=10,∴CE=EG=AE=5,∵ED:AD=3:4,∴AD=4,DE=3,∴AC=…(10分).31.(2015秋•扬中市期中)如图,△ABC中,AB>AC,∠BAC的平分线交外接圆于D,DE⊥AB于E,DM⊥AC于M.(1)求证:BE=CM.(2)求证:AB﹣AC=2BE.【解答】证明:(1)连接BD,DC,∵AD平分∠BAC,∴∠BAD=∠CAD,∴弧BD=弧CD,∴BD=CD,∵∠BAD=∠CAD,DE⊥AB,DM⊥AC,∵∠M=∠DEB=90°,DE=DM,在Rt△DEB和Rt△DMC中,,∴Rt△DEB≌Rt△DMC(HL),∴BE=CM.(2)∵DE⊥AB,DM⊥AC,∵∠M=∠DEA=90°,在Rt△DEA和Rt△DMA中∴Rt△DEA≌Rt△DMA(HL),∴AE=AM,∴AB﹣AC,=AE+BE﹣AC,=AM+BE﹣AC,=AC+CM+BE﹣AC,=BE+CM,=2BE.32.(2013•宁夏模拟)如图,OA是⊙0的半径,以OA为直径的⊙C与⊙0的弦AB相交于点D.求证:AD=BD.【解答】证明:连结OD,如图,∵OA为⊙C的直径,∴∠ADO=90°,∴OD⊥AB,∴AD=BD.33.(2011秋•宁波期中)如图,已知:AB是⊙O的弦,D为⊙O上一点,DC⊥AB于C,DM平分∠CDO.求证:M是弧AB的中点.【解答】解:连接OM∵OD=OM,∴∠ODM=∠OMD,∵DM平分∠ODC,∴∠ODM=∠CDM,∴∠CDM=∠OMD,∴CD∥OM,∵CD⊥AB,∴OM⊥AB,∴弧AM=弧BM,即点M为劣弧AB的中点.34.(2009秋•哈尔滨校级期中)如图,△ABC的三个顶点都在⊙O上,CD是高,D是垂足,CE是直径,求证:∠ACD=∠BCE.【解答】解:连接AE,∵CE为直径,∴∠EAC=90°,∴∠ACE=90°﹣∠AEC,∵CD是高,D是垂足,∴∠BCD=90°﹣∠B,∵∠B=∠AEC(同弧所对的圆周角相等),∴∠ACE=∠BCD,∴∠ACE+∠ECD=∠BCD+∠ECD,∴∠ACD=∠BCE.35.已知:如图,AE是⊙O的直径,AF⊥BC于D,证明:BE=CF.【解答】证明:∵AE是⊙O的直径,∴∠ABE=90°,∴∠E+∠BAE=90°,∵AF⊥BC于D,∴∠FAC+∠ACB=90°,∵∠E=∠ACB,∴∠BAE=∠FAC,∴弧BE=弧CF,∴BE=CF.36.(2015秋•哈尔滨校级期中)已知AB为⊙O的直径,弦BE=DE,AD,BE的延长线交于点C,求证:AC=AB.【解答】证明:连接AE,∵AB为⊙O的直径,∴∠AEB=90°,∴∠AEB=∠AEC=90°,∵弦BE=DE,∴=,∴∠DAE=∠BAE,∵∠C=90°﹣∠DAE,∠B=90°﹣∠BAE,∴∠B=∠C,∴AC=AB.37.如图,AB是圆O的直径,OC⊥AB,交⊙O于点C,D是弧AC上一点,E是AB上一点,EC⊥CD,交BD于点F.问:AD与BF相等吗?为什么?【解答】解:AD和BF相等.理由:如图,连接AC、BC,∵OC⊥AB,∴∠BOC=90°∴∠BDC=∠BAC=45°∵EC⊥CD,∴∠DCE=∠ACB=90°,∴△DCF和△ACB都是等腰直角三角形,∴DC=FC,AC=BC,∵∠DCA+∠ACF=∠BCF+∠ACF=90°,∴∠DCA=∠FCB在△ACD和△BCF中,{,∴△ACD≌△BCF∴DA=BF.38.如图,AB是⊙O的直径,AC、DE是⊙O的两条弦,且DE⊥AB,延长AC、DE相交于点F,求证:∠FCD=∠ACE.【解答】证明:连接AD,AE,∵AB是直径.AB⊥DE,∴AB平分DE,弧ACE=弧AD,∴∠ACD=∠ADE,∵A、C、E、D四点共圆,∴∠FCE=∠ADE,∴∠FCE=∠ACD,∴∠FCE+∠DCE=∠DAC+∠ECD,∴∠FCD=∠ACE.39.如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,作CE⊥AD,垂足为E,CE 的延长线与AB交于F.试分析∠ACF与∠ABC是否相等,并说明理由.【解答】解:延长CE交⊙O于M,∵AD是⊙O的直径,作CE⊥AD,∴弧AC=弧AM,∴∠ACF=∠ABC(在同圆中,等弧所对的圆周角相等).40.如图,△ABC内接于⊙O,AD为△ABC的外角平分线,交⊙O于点D,连接BD,CD,判断△DBC的形状,并说明理由.【解答】解:△DBC为等腰三角形.理由如下:∵AD为△ABC的外角平分线,∴∠EAD=∠DAC,∵∠EAD=∠DCB,∠DBC=∠DAC,∴∠DBC=∠DCB,∴△DBC为等腰三角形.一.解答题(共6小题)1.如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,G是上的任意一点,AG、DC 的延长线相交于点F,∠FGC与∠AGD的大小有什么关系?为什么?【解答】解:∠FGC与∠AGD相等.理由如下:连接AD,如图,∵CD⊥AB,∴=,∴∠AGD=∠ADC,∵∠FGC=∠ADC,∴∠FGC=∠AGD2.如图,AB是圆O的直径,C是圆O上一点,D是弧AC中点,DE⊥AB垂足为E,AC 分别与DE、DB相交于点F、G,则AF与FG是否相等?为什么?【解答】解:AF=FG,理由是:连接AD,∵AB是直径,DE⊥AB,∴∠ADB=∠DEB=90°,∴∠ADE=∠ABD,∵D为弧AC中点,∴∠DAC=∠ABD,∴∠ADE=∠DAC,∴AF=DF,∠FAE=∠DAC,∴DF=FG,∴AF=FG.3.如图,AB为⊙O的直径,以OA为直径作⊙C,AD为⊙O的弦,交⊙C于E,试问,当D点在⊙O上运动时(不与A重合),AE与ED的长度有何关系?证明你的结论.【解答】解:AE=ED.理由:连接OE,∵AO是⊙C的直径,∴∠OEA=90°,∴OE⊥AD,∵OE过圆O的圆心O,∴AE=ED.4.如图,OA是⊙O的半径,以OA为直径的⊙C与⊙O的弦AB交于点D,求证:D是AB的中点.【解答】证明:连接OD,∵OA为⊙C的直径,∴∠ODA=90°,即OD⊥AB,∴D是AB的中点.5.(2007•鄂尔多斯)如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的边于G,F,E点.求证:(1)F是BC的中点;(2)∠A=∠GEF.【解答】证明一:(1)连接DF,∵∠ACB=90°,D是AB的中点,∴BD=DC=AB,(2分)∵DC是⊙O的直径,∴DF⊥BC,(4分)∴BF=FC,即F是BC的中点;(5分)(2)∵D,F分别是AB,BC的中点,∴DF∥AC,(6分)∴∠A=∠BDF,(7分)∵∠BDF=∠GEF(圆周角定理),(8分)∴∠A=∠GEF.(9分)证明二:(1)连接DF,DE,∵DC是⊙O直径,∴∠DEC=∠DFC=90°.(1分)∵∠ECF=90°,∴四边形DECF是矩形.∴EF=CD,DF=EC.(2分)∵D是AB的中点,∠ACB=90°,∴EF=CD=BD=AB.(3分)∴△DBF≌△EFC.(4分)∴BF=FC,即F是BC的中点.(5分)(2)∵△DBF≌△EFC,∴∠BDF=∠FEC,∠B=∠EFC.(6分)∵∠ACB=90°(也可证AB∥EF,得∠A=∠FEC),∴∠A=∠FEC.(7分)∵∠FEG=∠BDF(同弧所对的圆周角相等),(8分)∴∠A=∠GEF.(9分)(此题证法较多,大纲卷参考答案中,又给出了两种不同的证法,可供参考.)6.(2000•兰州)如图,圆内接四边形ABCD的外角∠DCH=∠DCA,DP⊥AC垂足为P,DH⊥BH垂足为H,求证:CH=CP,AP=BH.【解答】证明:(1)在△DHC与△DPC中,∵∠DCH=∠DCA,DP⊥AC,DH⊥BH,DC为公共边,∴△DHC≌△DPC,∴CH=CP.(2)连接DB,由圆周角定理得,∠DAC=∠DBH,∵△DHC≌△DPC,∴DH=DP,∵DP⊥AC,DH⊥BH,∴∠DHB=∠DPC=90°,∴△DAP≌△DBH,∴AP=BH.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《圆周角定理》练习题一.选择题(共16小题)1.如图,A、B、C三点在⊙O上,若∠BOC=76°,则∠BAC的度数是()A.152° B.76°C.38° D.14°2.如图,⊙O是△ABC的外接圆,∠ACO=45°,则∠B的度数为()A.30° B.35°C.40° D.45°第1题图第2题图第3题图3.如图,在图中标出的4个角中,圆周角有()个.A.1 B.2 C.3 D.44.如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠BOD的度数是()A.25° B.30° C.40° D.50°5.如图,已知在⊙O中,点A,B,C均在圆上,∠AOB=80°,则∠ACB等于()A.130° B.140° C.145° D.150°第4题图第5题图第6题图6.如图,MN是⊙O的直径,∠PBN=50°,则∠MAP等于()A.50° B.40° C.30° D.20°7.如图,CD是⊙O的直径,A、B是⊙O上的两点,若∠ABD=20°,则∠ADC的度数为) A.40° B.50° C.60° D.70°8.如图,AB是半圆的直径,点D是的中点,∠ABC=50°,则∠DAB等于()A.55° B.60° C.65° D.70°第7题图第8题图第9题图9.如图,AB是⊙O的直径,C,D为圆上两点,∠AOC=130°,则∠D等于()A.25° B.30° C.35° D.50°10.如图,∠1、∠2、∠3、∠4的大小关系是()A.∠4<∠1<∠2<∠3 B.∠4<∠1=∠3<∠2C.∠4<∠1<∠3∠2 D.∠4<∠1<∠3=∠211.如图,AB是半圆O的直径,∠BAC=60°,D是半圆上任意一点,那么∠D的度数是() A.30° B.45° C.60° D.90°第10题图第11题图第12题图12.如图,在⊙O中,OA⊥BC,∠AOC=50°,则∠ADB的度数为()A.15° B.20° C.25° D.50°13.在⊙O中,点A、B在⊙O上,且∠AOB=84°,则弦AB所对的圆周角是()A.42° B.84° C.42°或138° D.84°或96°14.如图所示,在⊙O中,AB是⊙O的直径,∠ACB的角平分线CD交⊙O于D,则∠ABD的度数等于()A.90° B.60° C.45° D.30°15.已知如图,AB是⊙O的直径,CD是⊙O的弦,∠CDB=40°,则∠CBA的度数为()A.60° B.50° C.40° D.30°第10题图第11题图第12题图16.如图,AB是圆的直径,AB⊥CD,∠BAD=30°,则∠AEC的度数等于()A.30°B.50° C.60° D.70°二.填空题(共8小题)17.如图,⊙O的直径CD经过弦EF的中点G,∠DCF=20°,则∠EOD等于.第17题图第18题图第19题图18.如图,点A、B在⊙O上,∠AOB=100°,点C是劣弧AB上不与A、B重合的任意一点,则∠C= °.19.在⊙O中,弦AB=2cm,∠ACB=30°,则⊙O的直径为cm.20.如图,⊙O中弦AB等于半径R,则这条弦所对的圆心角是,圆周角是.第20题图第21题图第22题图21.如图,等腰△ABC的底边BC的长为4cm,以腰AB为直径的⊙O交BC于点D,交AC于点E,则DE的长为cm.22.如图,在“世界杯”足球比赛中,甲带球向对方球门PQ进攻,当他带球冲到A点时,同样乙已经助攻冲到B点,丙助攻到C点.有三种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门.第三种是甲将球传给丙,由丙射门.仅从射门角度考虑,应选择种射门方式.三.解答题(共16小题)25.28.如图,AB是⊙O的直径,C是⊙O上的点,AC=6cm,BC=8cm,∠ACB的平分线交⊙O 于点D,求AB和BD的长.26.如图,已知CD是⊙O的直径,弦AB⊥CD,垂足为点M,点P是上一点,且∠BPC=60°.试判断△ABC的形状,并说明你的理由.27、如图,△ABC的高AD、BE相交于点H,延长AD交ABC的外接圆于点G,连接BG.求证:HD=GD.28.已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E.∠BAC=40°(1)求∠EBC的度数;(2)求证:BD=CD.29.如图,△ABC是⊙O的内接三角形,∠A=30°,BC=3cm.求⊙O的半径.30.如图,AB是⊙O的直径,过圆上一点C作CD⊥AB于点D,点C是弧AF的中点,连接AF 交CD于点E,连接BC交AF于点G.(1)求证:AE=CE;.31.如图,△ABC中,AB>AC,∠BAC的平分线交外接圆于D,DE⊥AB于E,DM⊥AC于M.(1)求证:BE=CM.(2)求证:AB﹣AC=2BE.32.如图,OA是⊙0的半径,以OA为直径的⊙C与⊙0的弦AB相交于点D.求证:AD=BD.33.如图,已知:AB是⊙O的弦,D为⊙O上一点,DC⊥AB于C,DM平分∠CDO.求证:M 是弧AB的中点.34.如图,△ABC的三个顶点都在⊙O上,CD是高,D是垂足,CE是直径,求证:∠ACD=∠BCE.35.已知:如图,AE是⊙O的直径,AF⊥BC于D,证明:BE=CF.36.已知AB为⊙O的直径,弦BE=DE,AD,BE的延长线交于点C,求证:AC=AB.37.如图,AB是圆O的直径,OC⊥AB,交⊙O于点C,D是弧AC上一点,E是AB上一点,EC⊥CD,交BD于点F.问:AD与BF相等吗为什么38.如图,AB是⊙O的直径,AC、DE是⊙O的两条弦,且DE⊥AB,延长AC、DE相交于点F,求证:∠FCD=∠ACE.39.如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,作CE⊥AD,垂足为E,CE的延长线与AB交于F.试分析∠ACF与∠ABC是否相等,并说明理由.40.如图,△ABC内接于⊙O,AD为△ABC的外角平分线,交⊙O于点D,连接BD,CD,判断△DBC的形状,并说明理由.41.如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,G是上的任意一点,AG、DC的延长线相交于点F,∠FGC与∠AGD的大小有什么关系为什么42.如图,AB是圆O的直径,C是圆O上一点,D是弧AC中点,DE⊥AB垂足为E,AC分别与DE、DB相交于点F、G,则AF与FG是否相等为什么43.如图,OA是⊙O的半径,以OA为直径的⊙C与⊙O的弦AB交于点D,求证:D是AB的中点.44.如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的边于G,F,E点.求证:(1)F是BC的中点;(2)∠A=∠GEF.45.如图,圆内接四边形ABCD的外角∠DCH=∠DCA,DP⊥AC垂足为P,DH⊥BH垂足为H,求证:CH=CP,AP=BH.《圆周角定理》22参考答案与试题解析一.选择题(共16小题)1.(2012•呼伦贝尔)如图,A、B、C三点在⊙O上,若∠BOC=76°,则∠BAC的度数是()A.152°B.76° C.38° D.14°【解答】解:∵所对的圆心角是∠BOC,圆周角是∠BAC,又∵∠BOC=76°,∴∠A=76°×=38°.故选C.2.(2015•眉山)如图,⊙O是△ABC的外接圆,∠ACO=45°,则∠B的度数为()A.30° B.35° C.40° D.45°【解答】解:∵OA=OC,∠ACO=45°,∴∠OAC=45°,∴∠AOC=180°﹣45°﹣45°=90°,∴∠B=∠AOC=45°.故选D.3.(2010秋•海淀区校级期末)如图,在图中标出的4个角中,圆周角有()个.A.1 B.2 C.3 D.4【解答】解:∠1和∠3符合圆周角的定义,∠2顶点不在圆周上,∠4的一边不和圆相交,故图中圆周角有∠1和∠3两个.故选B.4.(2015•珠海)如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠BOD的度数是()A.25° B.30° C.40° D.50°【解答】解:∵在⊙O中,直径CD垂直于弦AB,∴=,∴∠DOB=2∠C=50°.故选:D.5.(1997•陕西)如图,已知在⊙O中,点A,B,C均在圆上,∠AOB=80°,则∠ACB等于()A.130°B.140°C.145°D.150°【解答】解:设点E是优弧AB上的一点,连接EA,EB∵∠AOB=80°∴∠E=∠AOB=40°∴∠ACB=180°﹣∠E=140°.故选:B.6.如图,MN是⊙O的直径,∠PBN=50°,则∠MAP等于()A.50° B.40° C.30° D.20°【解答】解:连接OP,可得∠MAP=∠MOP,∠NBP=∠NOP,∵MN为直径,∴∠MOP+∠NBP=180°,∴∠MAP+∠NBP=90°,∵∠PBN=50°,∴∠MAP=90°﹣∠PBN=40°.故选B.7.(2007•太原)如图,CD是⊙O的直径,A、B是⊙O上的两点,若∠ABD=20°,则∠ADC 的度数为()A.40° B.50° C.60° D.70°【解答】解:∵∠ABD=20°∴∠C=∠ABD=20°∵CD是⊙O的直径∴∠CAD=90°∴∠ADC=90°﹣20°=70°.故选D.8.(2013•苏州)如图,AB是半圆的直径,点D是的中点,∠ABC=50°,则∠DAB等于()A.55° B.60° C.65° D.70°【解答】解:连结BD,如图,∵点D是的中点,即弧CD=弧AD,∴∠ABD=∠CBD,而∠ABC=50°,∴∠ABD=×50°=25°,∵AB是半圆的直径,∴∠ADB=90°,∴∠DAB=90°﹣25°=65°.故选C.9.(2009•枣庄)如图,AB是⊙O的直径,C,D为圆上两点,∠AOC=130°,则∠D等于()A.25° B.30° C.35° D.50°【解答】解:∵∠AOC=130°,∴∠BOC=50°,∴∠D=∠BOC=25°.故选A.10.(2013秋•沙洋县校级月考)如图,∠1、∠2、∠3、∠4的大小关系是()A.∠4<∠1<∠2<∠3 B.∠4<∠1=∠3<∠2 C.∠4<∠1<∠3∠2 D.∠4<∠1<∠3=∠2【解答】解:如图,利用圆周角定理可得:∠1=∠3=∠5=∠6,根据三角形的外角的性质得:∠5>∠4,∠2>∠6,∴∠4<∠1=∠3<∠2,故选B.11.(2012秋•天津期末)如图,AB是半圆O的直径,∠BAC=60°,D是半圆上任意一点,那么∠D的度数是()A.30° B.45° C.60° D.90°【解答】解:连接BC,∵AB是半圆的直径∴∠ACB=90°∵∠BAC=60°,∴∠ABC=90°﹣∠BAC=30°,∴∠D=∠ABC=30°.故选A.12.(2009•塘沽区二模)如图,在⊙O中,OA⊥BC,∠AOC=50°,则∠ADB的度数为()A.15° B.20° C.25° D.50°【解答】解:∵OA⊥BC,∠AOC=50°,∴,∴∠ADB=∠AOC=25°.故选C.13.(2012秋•宜兴市校级期中)在⊙O中,点A、B在⊙O上,且∠AOB=84°,则弦AB所对的圆周角是()A.42° B.84° C.42°或138°D.84°或96°【解答】解:如图,∵∠AOB=84°,∴∠ACB=∠AOB=×84°=42°,∴∠ADB=180°﹣∠ACB=138°.∴弦AB所对的圆周角是:42°或138°.故选C.14.(2011•南岸区一模)如图所示,在⊙O中,AB是⊙O的直径,∠ACB的角平分线CD交⊙O于D,则∠ABD的度数等于()A.90° B.60° C.45° D.30°【解答】解:连接AD,∵在⊙O中,AB是⊙O的直径,∴∠ADB=90°,∵CD是∠ACB的角平分线,∴=,∴AD=BD,∴△ABD是等腰直角三角形,∴∠ABD=45°.故选C.15.(2015秋•合肥校级期末)已知如图,AB是⊙O的直径,CD是⊙O的弦,∠CDB=40°,则∠CBA的度数为()A.60° B.50° C.40° D.30°【解答】解:连接AC,∵AB是⊙O的直径,∴∠ACB=90°,∵∠A=∠CDB=40°,∴∠CBA=90°﹣∠A=50°.故选B.16.(2013•万州区校级模拟)如图,AB是圆的直径,AB⊥CD,∠BAD=30°,则∠AEC的度数等于()A.30° B.50° C.60° D.70°【解答】解:∵∠BAD=30°,∴=60°,∵AB是圆的直径,AB⊥CD,∴==60°,∴=180°﹣60°=120°,∴∠AEC==×120°=60°.故选C.二.填空题(共8小题)17.(2016•大冶市模拟)如图,⊙O的直径CD经过弦EF的中点G,∠DCF=20°,则∠EOD 等于40°.【解答】解:∵⊙O的直径CD过弦EF的中点G,∠DCF=20°,∴弧DF=弧DE,且弧的度数是40°,∴∠DOE=40°,答案为40°.18.(2015•历城区二模)如图,AB是半圆的直径,点D是弧AC的中点,∠ABC=50°,则∠DAB的度数是65°.【解答】解:连结BD,如图,∵点D是的中点,即弧CD=弧AD,∴∠ABD=∠CBD,而∠ABC=50°,∴∠ABD=×50°=25°,∵AB是半圆的直径,∴∠ADB=90°,∴∠DAB=90°﹣25°=65°.故答案为65°.19.(2013秋•滨湖区校级期末)如图,点A、B在⊙O上,∠AOB=100°,点C是劣弧AB上不与A、B重合的任意一点,则∠C= 130 °.【解答】解:在优弧AB上取点D,连结AD、BD,如图,∴∠D=∠AOB=×100°=50°,∵∠D+∠C=180°,∴∠C=180°﹣50°=130°.故答案为130.20.(2008秋•苏州校级期中)球员甲带球冲到A点时,同伴乙已经助攻冲到B点.有两种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门.仅从射门角度考虑,应选择第二种种射门方式较为合理.【解答】解:连接OC.根据圆周角定理,得∠PCQ=∠B,根据三角形的外角的性质,得∠PCQ>∠A,则∠B>∠A.故答案为第二种.21.(2015•黄岛区校级模拟)在⊙O中,弦AB=2cm,∠ACB=30°,则⊙O的直径为 4 cm.【解答】解:连接OA,OB,∵∠ACB=30°,∴∠AOB=60°,∴△AOB是等边三角形,∴OA=OB=AB=2cm,∴⊙O的直径=4cm.故答案为:4.22.(2014春•海盐县校级期末)如图,⊙O中弦AB等于半径R,则这条弦所对的圆心角是60°,圆周角是30°或150°.【解答】解:连结OA、OB,∠APB和∠AP′B为弦AB所对的圆周角,如图,∵弦AB等于半径R,∴△OAB为等边三角形,∴∠AOB=60°,∴∠APB=∠AOB=30°,∴∠AP′B=180°﹣∠APB=150°,即这条弦所对的圆心角是60°,圆周角是30°或150°.故答案为60°;是30°或150°.23.(2012•义乌市模拟)如图,等腰△ABC的底边BC的长为4cm,以腰AB为直径的⊙O交BC于点D,交AC于点E,则DE的长为 2 cm.【解答】解:连接AD,∵∠DEC为圆内接四边形ABDE的外角,∴∠DEC=∠B,又等腰△ABC,BC为底边,∴AB=AC,∴∠B=∠C,∴∠DEC=∠C,∴DE=DC,∵AB为圆O的直径,∴∠ADB=90°,即AD⊥BC,∴BD=CD=BC,又BC=4cm,∴DE=2cm.故答案为:224.(2012秋•哈密地区校级月考)如图,在“世界杯”足球比赛中,甲带球向对方球门PQ 进攻,当他带球冲到A点时,同样乙已经助攻冲到B点,丙助攻到C点.有三种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门.第三种是甲将球传给丙,由丙射门.仅从射门角度考虑,应选择第二种射门方式.【解答】解:设AP与圆的交点是C,连接CQ;则∠PCQ>∠A;由圆周角定理知:∠PCQ=∠B;所以∠B>∠A;因此选择第二种射门方式更好.故答案为:第二.三.解答题(共16小题)25.(2009•沈阳模拟)如图,△ABC的高AD、BE相交于点H,延长AD交ABC的外接圆于点G,连接BG.求证:HD=GD.【解答】证明:∵∠C=∠G,△ABC的高AD、BE,∴∠C+∠DAC=90°,∠AHE+∠DAC=90°,∴∠C=∠AHE,∵∠AHE=∠BHG=∠C,∴∠G=∠BHG,∴BH=BG,又∵AD⊥BC,∴HD=DG.26.(2013秋•虞城县校级期末)如图,已知CD是⊙O的直径,弦AB⊥CD,垂足为点M,点P是上一点,且∠BPC=60°.试判断△ABC的形状,并说明你的理由.【解答】解:△ABC为等边三角形.理由如下:∵AB⊥CD,CD为⊙O的直径,∴弧AC=弧BC,∴AC=BC,又∵∠BPC=∠A=60°,∴△ABC为等边三角形.27.(2013秋•耒阳市校级期末)已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E.∠BAC=40°(1)求∠EBC的度数;(2)求证:BD=CD.【解答】(1)解:∵AB=AC,∴∠ABC=∠C,∵∠BAC=40°,∴∠C=(180°﹣40°)=70°,∵AB为⊙O的直径,∴∠AEB=90°,∴∠EBC=90°﹣∠C=20°;证明:连结AD,如图,∵AB为⊙O的直径,∴∠ADB=90°,∴AD⊥BC,而AB=AC,∴BD=DC.28.(2014秋•高密市期中)如图,AB是⊙O的直径,C是⊙O上的点,AC=6cm,BC=8cm,∠ACB的平分线交⊙O于点D,求AB和BD的长.【解答】解:如图,∵AB是⊙O的直径,∴∠ACB=90°,∠ADB=90°.∴AB===10(cm).∵AC=6cm,BC=8cm,∵CD是∠ACB的平分线,∴∠ACD=∠BCD,则=,∴AD=BD,∴BD=AB=5cm.综上所述,AB和BD的长分别是10cm,5cm.29.(2013秋•宜兴市校级期中)如图,△ABC是⊙O的内接三角形,∠A=30°,BC=3cm.求⊙O的半径.【解答】解:作直径CD,连结BD,如图,∵CD为直径,∴∠CBD=90°,∵∠D=∠A=30°,∴CD=2BC=2×3=6,∴⊙O的半径为3cm.30.(2010秋•瑞安市校级月考)如图,AB是⊙O的直径,过圆上一点C作CD⊥AB于点D,点C是弧AF的中点,连接AF交CD于点E,连接BC交AF于点G.(1)求证:AE=CE;(2)已知AG=10,ED:AD=3:4,求AC的长.【解答】(1)证明:∵点C是弧AF的中点,∴∠B=∠CAE,∵AB是⊙O的直径,∴∠ACB=90°,即∠ACE+∠BCD=90°,∵CD⊥AB,∴∠B+∠BCD=90°,∴∠B=∠CAE=∠ACE,∴AE=CE …(6分)(2)解:∵∠ACB=90°,∴∠CAE+∠CGA=90°,又∵∠ACE+∠BCD=90°,∴∠CGA=∠BCD,∵AG=10,∴CE=EG=AE=5,∵ED:AD=3:4,∴AD=4,DE=3,∴AC=…(10分).31.(2015秋•扬中市期中)如图,△ABC中,AB>AC,∠BAC的平分线交外接圆于D,DE⊥AB于E,DM⊥AC于M.(1)求证:BE=CM.(2)求证:AB﹣AC=2BE.【解答】证明:(1)连接BD,DC,∵AD平分∠BAC,∴∠BAD=∠CAD,∴弧BD=弧CD,∴BD=CD,∵∠BAD=∠CAD,DE⊥AB,DM⊥AC,∵∠M=∠DEB=90°,DE=DM,在Rt△DEB和Rt△DMC中,,∴Rt△DEB≌Rt△DMC(HL),∴BE=CM.(2)∵DE⊥AB,DM⊥AC,∵∠M=∠DEA=90°,在Rt△DEA和Rt△DMA中∴Rt△DEA≌Rt△DMA(HL),∴AE=AM,∴AB﹣AC,=AE+BE﹣AC,=AM+BE﹣AC,=AC+CM+BE﹣AC,=BE+CM,=2BE.32.(2013•宁夏模拟)如图,OA是⊙0的半径,以OA为直径的⊙C与⊙0的弦AB相交于点D.求证:AD=BD.【解答】证明:连结OD,如图,∵OA为⊙C的直径,∴∠ADO=90°,∴OD⊥AB,∴AD=BD.33.(2011秋•宁波期中)如图,已知:AB是⊙O的弦,D为⊙O上一点,DC⊥AB于C,DM 平分∠CDO.求证:M是弧AB的中点.【解答】解:连接OM∵OD=OM,∴∠ODM=∠OMD,∵DM平分∠ODC,∴∠ODM=∠CDM,∴∠CDM=∠OMD,∴CD∥OM,∵CD⊥AB,∴OM⊥AB,∴弧AM=弧BM,即点M为劣弧AB的中点.34.(2009秋•哈尔滨校级期中)如图,△ABC的三个顶点都在⊙O上,CD是高,D是垂足,CE是直径,求证:∠ACD=∠BCE.【解答】解:连接AE,∵CE为直径,∴∠EAC=90°,∴∠ACE=90°﹣∠AEC,∵CD是高,D是垂足,∴∠BCD=90°﹣∠B,∵∠B=∠AEC(同弧所对的圆周角相等),∴∠ACE=∠BCD,∴∠ACE+∠ECD=∠BCD+∠ECD,∴∠ACD=∠BCE.35.已知:如图,AE是⊙O的直径,AF⊥BC于D,证明:BE=CF.【解答】证明:∵AE是⊙O的直径,∴∠ABE=90°,∴∠E+∠BAE=90°,∵AF⊥BC于D,∴∠FAC+∠ACB=90°,∵∠E=∠ACB,∴∠BAE=∠FAC,∴弧BE=弧CF,∴BE=CF.36.(2015秋•哈尔滨校级期中)已知AB为⊙O的直径,弦BE=DE,AD,BE的延长线交于点C,求证:AC=AB.【解答】证明:连接AE,∵AB为⊙O的直径,∴∠AEB=90°,∴∠AEB=∠AEC=90°,∵弦BE=DE,∴=,∴∠DAE=∠BAE,∵∠C=90°﹣∠DAE,∠B=90°﹣∠BAE,∴∠B=∠C,∴AC=AB.37.如图,AB是圆O的直径,OC⊥AB,交⊙O于点C,D是弧AC上一点,E是AB上一点,EC⊥CD,交BD于点F.问:AD与BF相等吗为什么【解答】解:AD和BF相等.理由:如图,连接AC、BC,∵OC⊥AB,∴∠BOC=90°∴∠BDC=∠BAC=45°∵EC⊥CD,∴∠DCE=∠ACB=90°,∴△DCF和△ACB都是等腰直角三角形,∴DC=FC,AC=BC,∵∠DCA+∠ACF=∠BCF+∠ACF=90°,∴∠DCA=∠FCB在△ACD和△BCF中,{,∴△ACD≌△BCF∴DA=BF.38.如图,AB是⊙O的直径,AC、DE是⊙O的两条弦,且DE⊥AB,延长AC、DE相交于点F,求证:∠FCD=∠ACE.【解答】证明:连接AD,AE,∵AB是直径.AB⊥DE,∴AB平分DE,弧ACE=弧AD,∴∠ACD=∠ADE,∵A、C、E、D四点共圆,∴∠FCE=∠ADE,∴∠FCE=∠ACD,∴∠FCE+∠DCE=∠DAC+∠ECD,∴∠FCD=∠ACE.39.如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,作CE⊥AD,垂足为E,CE的延长线与AB交于F.试分析∠ACF与∠ABC是否相等,并说明理由.【解答】解:延长CE交⊙O于M,∵AD是⊙O的直径,作CE⊥AD,∴弧AC=弧AM,∴∠ACF=∠ABC(在同圆中,等弧所对的圆周角相等).40.如图,△ABC内接于⊙O,AD为△ABC的外角平分线,交⊙O于点D,连接BD,CD,判断△DBC的形状,并说明理由.【解答】解:△DBC为等腰三角形.理由如下:∵AD为△ABC的外角平分线,∴∠EAD=∠DAC,∵∠EAD=∠DCB,∠DBC=∠DAC,∴∠DBC=∠DCB,∴△DBC为等腰三角形.一.解答题(共6小题)1.如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,G是上的任意一点,AG、DC的延长线相交于点F,∠FGC与∠AGD的大小有什么关系为什么【解答】解:∠FGC与∠AGD相等.理由如下:连接AD,如图,∵CD⊥AB,∴=,∴∠AGD=∠ADC,∵∠FGC=∠ADC,∴∠FGC=∠AGD2.如图,AB是圆O的直径,C是圆O上一点,D是弧AC中点,DE⊥AB垂足为E,AC分别与DE、DB相交于点F、G,则AF与FG是否相等为什么【解答】解:AF=FG,理由是:连接AD,∵AB是直径,DE⊥AB,∴∠ADB=∠DEB=90°,∴∠ADE=∠ABD,∵D为弧AC中点,∴∠DAC=∠ABD,∴∠ADE=∠DAC,∴AF=DF,∠FAE=∠DAC,∴DF=FG,∴AF=FG.3.如图,AB为⊙O的直径,以OA为直径作⊙C,AD为⊙O的弦,交⊙C于E,试问,当D 点在⊙O上运动时(不与A重合),AE与ED的长度有何关系证明你的结论.【解答】解:AE=ED.理由:连接OE,∵AO是⊙C的直径,∴∠OEA=90°,∴OE⊥AD,∵OE过圆O的圆心O,∴AE=ED.4.如图,OA是⊙O的半径,以OA为直径的⊙C与⊙O的弦AB交于点D,求证:D是AB的中点.【解答】证明:连接OD,∵OA为⊙C的直径,∴∠ODA=90°,即OD⊥AB,∴D是AB的中点.5.(2007•鄂尔多斯)如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O 交△ABC的边于G,F,E点.求证:(1)F是BC的中点;(2)∠A=∠GEF.【解答】证明一:(1)连接DF,∵∠ACB=90°,D是AB的中点,∴BD=DC=AB,(2分)∵DC是⊙O的直径,∴DF⊥BC,(4分)∴BF=FC,即F是BC的中点;(5分)(2)∵D,F分别是AB,BC的中点,∴DF∥AC,(6分)∴∠A=∠BDF,(7分)∵∠BDF=∠GEF(圆周角定理),(8分)∴∠A=∠GEF.(9分)证明二:(1)连接DF,DE,∵DC是⊙O直径,∴∠DEC=∠DFC=90°.(1分)∵∠ECF=90°,∴四边形DECF是矩形.∴EF=CD,DF=EC.(2分)∵D是AB的中点,∠ACB=90°,∴EF=CD=BD=AB.(3分)∴△DBF≌△EFC.(4分)∴BF=FC,即F是BC的中点.(5分)(2)∵△DBF≌△EFC,∴∠BDF=∠FEC,∠B=∠EFC.(6分)∵∠ACB=90°(也可证AB∥EF,得∠A=∠FEC),∴∠A=∠FEC.(7分)∵∠FEG=∠BDF(同弧所对的圆周角相等),(8分)∴∠A=∠GEF.(9分)(此题证法较多,大纲卷参考答案中,又给出了两种不同的证法,可供参考.)6.(2000•兰州)如图,圆内接四边形ABCD的外角∠DCH=∠DCA,DP⊥AC垂足为P,DH⊥BH 垂足为H,求证:CH=CP,AP=BH.【解答】证明:(1)在△DHC与△DPC中,∵∠DCH=∠DCA,DP⊥AC,DH⊥BH,DC为公共边,∴△DHC≌△DPC,∴CH=CP.(2)连接DB,由圆周角定理得,∠DAC=∠DBH,∵△DHC≌△DPC,∴DH=DP,∵DP⊥AC,DH⊥BH,∴∠DHB=∠DPC=90°,∴△DAP≌△DBH,∴AP=BH.。
