BP程序
用matlab编BP神经网络预测程序
求用matlab编BP神经网络预测程序求一用matlab编的程序P=[。
];输入T=[。
];输出% 创建一个新的前向神经网络net_1=newff(minmax(P),[10,1],{'tansig','purelin'},'traingdm')% 当前输入层权值和阈值inputWeights=net_1.IW{1,1}inputbias=net_1.b{1}% 当前网络层权值和阈值layerWeights=net_1.LW{2,1}layerbias=net_1.b{2}% 设置训练参数net_1.trainParam.show = 50;net_1.trainParam.lr = 0.05;net_1.trainParam.mc = 0.9;net_1.trainParam.epochs = 10000;net_1.trainParam.goal = 1e-3;% 调用TRAINGDM 算法训练BP 网络[net_1,tr]=train(net_1,P,T);% 对BP 网络进行仿真A = sim(net_1,P);% 计算仿真误差E = T - A;MSE=mse(E)x=[。
]';%测试sim(net_1,x) %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%不可能啊我200928对初学神经网络者的小提示第二步：掌握如下算法:2.最小均方误差,这个原理是下面提到的神经网络学习算法的理论核心,入门者要先看《高等数学》（高等教育出版社，同济大学版）第8章的第十节：“最小二乘法”。
3.在第2步的基础上看Hebb学习算法、SOM和K-近邻算法，上述算法都是在最小均方误差基础上的改进算法，参考书籍是《神经网络原理》（机械工业出版社，Simon Haykin著，中英文都有）、《人工神经网络与模拟进化计算》（清华大学出版社，阎平凡，张长水著）、《模式分类》（机械工业出版社，Richard O. Duda等著，中英文都有）、《神经网络设计》（机械工业出版社，Martin T. Hargan等著，中英文都有）。
BP算法过程
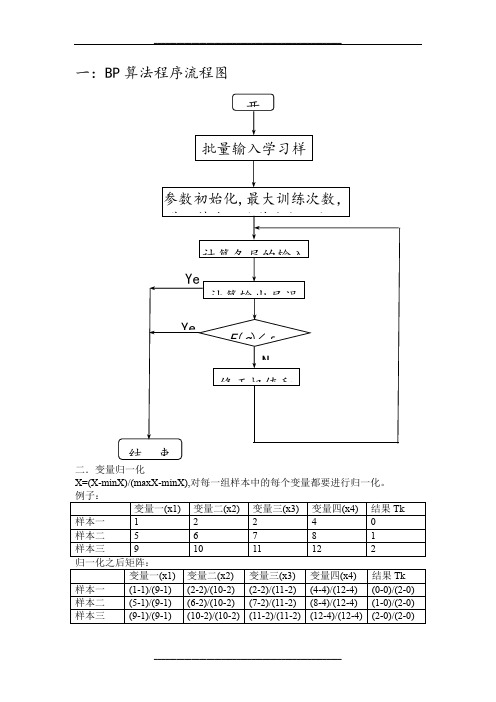
一：BP 算法程序流程图二．变量归一化X=(X -minX)/(maxX -minX),对每一组样本中的每个变量都要进行归一化。
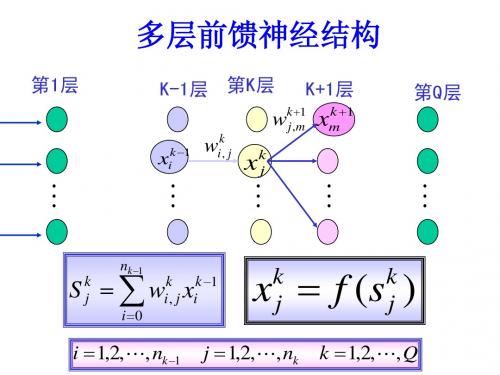
例子： 变量一(x1) 变量二(x2) 变量三(x3) 变量四(x4) 结果Tk 样本一 1 2 2 4 0 样本二 5 6 7 8 1 样本三 9 10 11 12 2 归一化之后矩阵： 变量一(x1) 变量二(x2) 变量三(x3) 变量四(x4) 结果Tk 样本一 (1-1)/(9-1) (2-2)/(10-2) (2-2)/(11-2) (4-4)/(12-4) (0-0)/(2-0) 样本二 (5-1)/(9-1) (6-2)/(10-2) (7-2)/(11-2) (8-4)/(12-4) (1-0)/(2-0) 样本三 (9-1)/(9-1) (10-2)/(10-2) (11-2)/(11-2) (12-4)/(12-4) (2-0)/(2-0)结 束参数初始化,最大训练次数，学习精度，隐节点数，初始批量输入学习样计算各层的输入计算输出层误E (q )<ε修正权值和YeNYe开三．数学过程输出层中M=14，隐含层中q=9，学习率ƞ=0.01，L=1，ε=1e-10，最大训练次数为5000次.这个神经网络就只有一个输出神经元，所以每组样本值输出一个值一般取初始权值在（-1，1）之间的随机数，初始阈值取（0,1）之间的随机数表示隐含层第i个节点到输入层第j个节点之间的权值；表示隐含层第i个节点的阈值；表示隐含层的激励函数；=1/(1+e-x)表示输出层第个节点到隐含层第i个节点之间的权值，i=1,…,q；表示输出层第k个节点的阈值,k=1,…,L；表示输出层的激励函数，=x；表示输出层第个节点的输出，k=1。
（1）信号的前向传播过程隐含层第i个节点的输入net i：（3-1）隐含层第i个节点的输出y i：（3-2）输出层第k个节点的输入net k，k=1：ijwiθ()xφ()xφkiw kka()xψ()xψko k1Mi ij j ijnet w xθ==+∑1()()Mi i ij j ijy net w xφφθ===+∑………………输出变量输入变量输入层隐含层输出层（3-3）输出层第k 个节点的输出o k ，k=1：（3-4）（2）误差的反向传播过程误差的反向传播，即首先由输出层开始逐层计算各层神经元的输出误差，然后根据误差梯度下降法来调节各层的权值和阈值，使修改后的网络的最终输出能接近期望值。
标准的BP神经网络算法程序MATLAB
count=1;
while (count<=maxcount) %结束条件1迭代1000次
c=1;
while (c<=samplenum)
for k=1:outputNums
d(k)=expectlist(c,k); %获得期望输出的向量,d(1:3)表示一个期望向量内 的值
end
break;
end
count=count+1;%训练次数加1
end%第一个while结束
error(maxcount+1)=error(maxcount);
p=1:count;
pp=p/50;
plot(pp,error(p),"-"); %显示误差
deltv(i,j)=alpha*yitay(j)*x(i); %同上deltw
v(i,j)=v(i,j)+deltv(i,j)+a*dv(i,j);
dv(i,j)=deltv(i,j);
end
end
c=c+1;
end%第二个while结束；表示一次BP训练结束
double tmp;
for i=1:inputNums
x(i)=samplelist(c,i); %获得输入的向量（数据）,x(1:3)表一个训练向量
字串4
end
%Forward();
for j=1:hideNums
net=0.0;
for i=1:inputNums
net=net+x(i)*v(i,j);
dw=zeros(hideNums,outputNums); %10*3
BP预报程序(外推预测)示例
A(4) A(5) A(6) A(7);
A(5) A(6) A(7) A(8);
A(6) A(7) A(8) A(9);
A(7) A(8) A(9) A(10);
A(8) A(9) A(10) A(11)]'; %预报值测试样本
可以对神经网络在MATLAB平台上的具体操作有较快的入门。
说明：此程序数据序列较短，仅为示意。
BP 程序在外推预测方面不大如意，希望能结合灰色理论或时间序列方面的相关知识以进行优化。
out=sim(net,P_test);
for i=1:8 %数据反归一化
predict(i)=out(i)*(max(x0)-min(x0))+min(x0)
end
仔细阅读，飞思科技产品研发中心.
神经网络理论与MATLAB7实现[M]. 北京: 电子工业出版社, 2005 一书，
end
P=[A(1) A(2) A(3) A(4);
A(2) A(3) A(4) A(5);
A(3) A(4) A(5) A(6);
A(4) A(5) A(6) A(7);
A(5) A(6) A(7) A(8);
A(6) A(7) A(8) A(9);
A(7) A(8) A(9) A(10)]';
net.trainParam.goal=0.00001;
LP.lr=0.1;
net.trainParam.epochs=1000;
net=train(net,P,T); %网络训练 பைடு நூலகம்
P_test=[A(1) A(2) A(3) A(4);
基于C语言的BP神经网络预测程序开发-任务书
毕业设计（论文）任务书
学生姓名 指导教师姓名
题目名称 一、设计（论文）目的、意义
系部
汽车工程系
专业、班级
职称
实验师
从事 专业
汽车工程 是否外聘 □是√否
基于 C 语言的 BP 神经网络预测程序开发
应用 C 语言解决实际问题，开发 BP 神经网络预测程序。
BP算法程序实现
BP算法程序实现BP（Back Propagation）神经网络是一种常见的人工神经网络模型，是一种监督学习算法。
在BP算法中，神经网络的参数通过反向传播的方式得到更新，以最小化损失函数。
BP神经网络的实现主要分为前向传播和反向传播两个步骤。
首先，我们需要定义BP神经网络的结构。
一个典型的BP神经网络包括输入层、隐藏层和输出层。
输入层接收原始数据，隐藏层进行特征提取和转换，输出层进行最终的预测。
在实现BP神经网络时，我们首先需要进行初始化。
初始化可以为神经网络的权重和偏置添加一些随机的初始值。
这里我们使用numpy库来处理矩阵运算。
前向传播的过程实际上就是将输入数据通过神经网络的每一层，直到输出层。
在每一层中，我们将对应权重和输入数据进行点乘运算，并加上偏置项，然后通过一个激活函数进行非线性转换。
这里我们可以选择sigmoid函数作为激活函数。
在反向传播中，我们根据损失函数对权重和偏置进行调整。
首先，我们计算输出误差，即预测值与真实值之间的差异。
然后，我们根据链式法则来计算每一层的误差，并将误差传递回前一层。
根据误差和激活函数的导数，我们可以计算每个权重和偏置的更新量，然后使用梯度下降法对权重和偏置进行更新。
实现BP算法的程序如下：```pythonimport numpy as npclass NeuralNetwork:def __init__(self, layers):yers = layersself.weights = [np.random.randn(y, x) for x, y inzip(layers[:-1], layers[1:])]self.biases = [np.random.randn(y, 1) for y in layers[1:]] def forward(self, x):a = np.array(x).reshape(-1, 1)for w, b in zip(self.weights, self.biases):z = np.dot(w, a) + ba = self.sigmoid(z)return adef backward(self, x, y, lr=0.01):a = np.array(x).reshape(-1, 1)targets = np.array(y).reshape(-1, 1)# forward passactivations = [a]zs = []for w, b in zip(self.weights, self.biases):z = np.dot(w, a) + bzs.append(z)a = self.sigmoid(z)activations.append(a)# backward passdeltas = [self.loss_derivative(activations[-1], targets) * self.sigmoid_derivative(zs[-1])]for l in range(2, len(yers)):z = zs[-l]sp = self.sigmoid_derivative(z)deltas.append(np.dot(self.weights[-l + 1].T, deltas[-1]) * sp)deltas.reverse# update weights and biasesfor l in range(len(yers) - 1):self.weights[l] += -lr * np.dot(deltas[l], activations[l].T) self.biases[l] += -lr * deltas[l]def sigmoid(x):return 1 / (1 + np.exp(-x))def sigmoid_derivative(x):return NeuralNetwork.sigmoid(x) * (1 -NeuralNetwork.sigmoid(x))def loss_derivative(y_pred, y_true):return y_pred - y_true```上述代码中，首先我们定义一个NeuralNetwork类，包含两个主要方法：forward(和backward(。
bp是什么意思
BP是什么意思1. 介绍在计算机科学和信息技术领域，BP通常指的是“背景处理器”（Background Processor）或“基准点”（Base Point）。
BP还可以代表“血压”（Blood Pressure）或“企业计划”（Business Plan）等其他含义。
在本文中，我们将重点介绍BP在计算机领域中的常见含义。
2. 背景处理器在计算机系统中，背景处理器（BP）是一种独立运行的程序，负责在后台处理一些重要的任务。
这些任务通常是与用户交互无关的，但对系统整体性能和功能起着重要作用。
背景处理器可以运行在计算机的操作系统内核中，也可以作为一个独立的进程或线程运行。
背景处理器通常用于处理以下类型的任务：•系统维护和监控•数据库和文件系统管理•定时任务调度•网络通信和数据传输•安全性和权限控制通过将这些任务交给背景处理器处理，可以提高系统的并发性和响应速度，避免阻塞用户界面。
3. 基准点在某些情况下，BP还可以指代基准点（Base Point）。
在计算机图形学和计算机视觉领域，基准点是表示物体位置或坐标系原点的参考点。
基准点可以是屏幕上的特定像素，或者是物体模型的原点。
基准点的选择和定义在图形处理和检测中起着重要的作用，因为它们可以影响到图形和图像处理的精度和准确性。
4. 血压除了计算机领域，BP也可以指代血压（Blood Pressure）。
血压是衡量血液对血管壁施加的压力的指标。
血压通常用两个数字表示，分别表示收缩压和舒张压。
收缩压指血液被心脏推出时对血管壁的最大压力，舒张压指心脏舒张期间对血管壁的最小压力。
血压是健康监测中一个重要的指标，高血压或低血压可能与各种健康问题相关。
5. 企业计划此外，在商业和管理领域，BP也可以指代企业计划（Business Plan）。
企业计划是一个详细描述企业发展目标、战略和操作计划的文档。
它通常包括企业的使命和愿景、市场分析、产品和服务策略、营销计划、财务预测等内容。
基于BP神经网络的非线性函数拟合——程序设计说明
基于BP神经网络的非线性函数拟合——程序设计说明程序设计说明：1.确定网络结构首先，需要确定BP神经网络的结构，包括输入层、隐藏层和输出层的节点数。
输入层的节点数由样本的特征数确定，隐藏层的节点数可以通过试验确定，输出层的节点数则由问题的要求确定。
2.初始化网络参数初始化网络的权值和偏置，可以使用随机数生成，初始值不能太大或太小。
权值和偏置的初始值会对模型的训练效果产生影响，一般可以根据问题的复杂程度来选择。
3.前向传播通过前向传播，将样本数据输入到神经网络中，并计算每个神经元的激活值。
激活函数可以选择Sigmoid函数或者ReLU函数等非线性函数。
4.计算误差5.反向传播通过反向传播，将误差从输出层向输入层传播，更新网络的权值和偏置。
反向传播的过程可以使用梯度下降法来更新网络参数。
6.训练网络7.测试网络使用未参与训练的样本数据测试网络的泛化能力，计算测试误差。
如果测试误差较小，说明网络能够较好地拟合非线性函数。
8.参数调优根据训练误差和测试误差结果，可以调整网络的参数，如学习率、隐藏层节点数等，以提高网络的训练效果和泛化能力。
9.反复训练和测试网络根据需要，反复进行训练和测试的过程，直至网络的训练误差和测试误差均满足要求。
这是一个基于BP神经网络的非线性函数拟合的程序设计说明，通过实现以上步骤，可以有效地进行非线性函数的拟合和预测。
在具体实现中，可以使用Python等编程语言和相应的神经网络框架，如TensorFlow、PyTorch等，来简化程序的编写和调试过程。
同时，为了提高程序的性能和效率，可以使用并行计算和GPU加速等技术。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
例1 采用动量梯度下降算法训练BP 网络。
训练样本定义如下：输入矢量为p =[-1 -2 3 1-1 1 5 -3]目标矢量为t = [-1 -1 1 1]解：% P 为输入矢量P=[-1, -2, 3, 1; -1, 1, 5, -3];% T 为目标矢量T=[-1, -1, 1, 1];% 创建一个新的前向神经网络net=newff(minmax(P),[3,1],{'tansig','purelin'},'traingdm') % 当前输入层权值和阈值inputWeights=net.IW{1,1}inputbias=net.b{1}% 当前网络层权值和阈值layerWeights=net.LW{2,1}layerbias=net.b{2}% 设置训练参数net.trainParam.show = 50;net.trainParam.lr = 0.05;net.trainParam.mc = 0.9;net.trainParam.epochs = 1000;net.trainParam.goal = 1e-3;% 调用TRAINGDM 算法训练BP 网络[net,tr]=train(net,P,T);% 对BP 网络进行仿真A = sim(net,P)% 计算仿真误差E = T - AMSE=mse(E)例2 采用贝叶斯正则化算法提高BP 网络的推广能力。
在本例中，我们采用两种训练方法，即L-M 优化算法（trainlm）和贝叶斯正则化算法（trainbr），用以训练BP 网络，使其能够拟合某一附加有白噪声的正弦样本数据。
其中，样本数据可以采用如下MATLAB 语句生成：输入矢量：P = [-1:0.05:1]；目标矢量：randn(’seed’,78341223)；T = sin(2*pi*P)+0.1*randn(size(P))；解：本例的MATLAB 程序如下：% P 为输入矢量P = [-1:0.05:1];% T 为目标矢量randn('seed',78341223); T = sin(2*pi*P)+0.1*randn(size(P));% 绘制样本数据点plot(P,T,'+');hold on;plot(P,sin(2*pi*P),':');% 绘制不含噪声的正弦曲线% 创建一个新的前向神经网络net=newff(minmax(P),[20,1],{'tansig','purelin'});disp('1. L-M 优化算法TRAINLM'); disp('2. 贝叶斯正则化算法TRAINBR');choice=input('请选择训练算法(1,2):');figure(gcf);if(choice==1)% 采用L-M 优化算法TRAINLMnet.trainFcn='trainlm';% 设置训练参数net.trainParam.epochs = 500;net.trainParam.goal = 1e-6;net=init(net);% 重新初始化elseif(choice==2)% 采用贝叶斯正则化算法TRAINBRnet.trainFcn='trainbr';% 设置训练参数net.trainParam.epochs = 500;randn('seed',192736547);net = init(net);% 重新初始化end% 调用相应算法训练BP 网络[net,tr]=train(net,P,T);% 对BP 网络进行仿真A = sim(net,P);% 计算仿真误差E = T - A;MSE=mse(E)% 绘制匹配结果曲线close all;plot(P,A,P,T,'+',P,sin(2*pi*P),':');echo off通过采用两种不同的训练算法，我们可以得到如图1和图2所示的两种拟合结果。
图中的实线表示拟合曲线，虚线代表不含白噪声的正弦曲线，“＋”点为含有白噪声的正弦样本数据点。
显然，经trainlm 函数训练后的神经网络对样本数据点实现了“过度匹配”，而经trainbr 函数训练的神经网络对噪声不敏感，具有较好的推广能力。
值得指出的是，在利用trainbr 函数训练BP 网络时，若训练结果收敛，通常会给出提示信息“Maximum MU reached”。
此外，用户还可以根据SSE 和SSW 的大小变化情况来判断训练是否收敛：当SSE 和SSW 的值在经过若干步迭代后处于恒值时，则通常说明网络训练收敛，此时可以停止训练。
观察trainbr 函数训练BP 网络的误差变化曲线,可见，当训练迭代至320 步时，网络训练收敛，此时SSE 和SSW 均为恒值，当前有效网络的参数（有效权值和阈值）个数为11.7973。
例3 采用“提前停止”方法提高BP 网络的推广能力。
对于和例2相同的问题，在本例中我们将采用训练函数traingdx 和“提前停止”相结合的方法来训练BP 网络，以提高BP 网络的推广能力。
解：在利用“提前停止”方法时，首先应分别定义训练样本、验证样本或测试样本，其中，验证样本是必不可少的。
在本例中，我们只定义并使用验证样本，即有验证样本输入矢量：val.P = [-0.975:.05:0.975]验证样本目标矢量：val.T = sin(2*pi*val.P)+0.1*randn(size(val.P))值得注意的是，尽管“提前停止”方法可以和任何一种BP 网络训练函数一起使用，但是不适合同训练速度过快的算法联合使用，比如trainlm 函数，所以本例中我们采用训练速度相对较慢的变学习速率算法traingdx 函数作为训练函数。
本例的MATLAB 程序如下：close allclearecho onclc% NEWFF——生成一个新的前向神经网络% TRAIN——对BP 神经网络进行训练% SIM——对BP 神经网络进行仿真pause% 敲任意键开始clc% 定义训练样本矢量% P 为输入矢量P = [-1:0.05:1];% T 为目标矢量randn('seed',78341223);T = sin(2*pi*P)+0.1*randn(size(P));% 绘制训练样本数据点plot(P,T,'+');echo offhold on;plot(P,sin(2*pi*P),':'); % 绘制不含噪声的正弦曲线echo onclcpauseclc% 定义验证样本val.P = [-0.975:0.05:0.975]; % 验证样本的输入矢量val.T = sin(2*pi*val.P)+0.1*randn(size(val.P)); % 验证样本的目标矢量pauseclc% 创建一个新的前向神经网络net=newff(minmax(P),[5,1],{'tansig','purelin'},'traingdx');pauseclc% 设置训练参数net.trainParam.epochs = 500;net = init(net);pauseclc% 训练BP 网络[net,tr]=train(net,P,T,[],[],val);pauseclc% 对BP 网络进行仿真A = sim(net,P);% 计算仿真误差E = T - A;MSE=mse(E)pauseclc% 绘制仿真拟合结果曲线close all;plot(P,A,P,T,'+',P,sin(2*pi*P),':');pause;clcecho off下面给出了网络的某次训练结果，可见，当训练至第136 步时，训练提前停止，此时的网络误差为0.0102565。
给出了训练后的仿真数据拟合曲线，效果是相当满意的。
[net,tr]=train(net,P,T,[],[],val);TRAINGDX, Epoch 0/500, MSE 0.504647/0, Gradient 2.1201/1e-006TRAINGDX, Epoch 25/500, MSE 0.163593/0, Gradient 0.384793/1e-006TRAINGDX, Epoch 50/500, MSE 0.130259/0, Gradient 0.158209/1e-006TRAINGDX, Epoch 75/500, MSE 0.086869/0, Gradient 0.0883479/1e-006TRAINGDX, Epoch 100/500, MSE 0.0492511/0, Gradient 0.0387894/1e-006TRAINGDX, Epoch 125/500, MSE 0.0110016/0, Gradient 0.017242/1e-006TRAINGDX, Epoch 136/500, MSE 0.0102565/0, Gradient 0.01203/1e-006TRAINGDX, Validation stop.例3 用BP网络估计胆固醇含量这是一个将神经网络用于医疗应用的例子。
我们设计一个器械，用于从血样的光谱组成的测量中得到血清的胆固醇含量级别，我们有261个病人的血样值，包括21种波长的谱线的数据，对于这些病人，我们得到了基于光谱分类的胆固醇含量级别hdl,ldl,vldl。
(1) 样本数据的定义与预处理。
choles_all.mat 文件中存储了网络训练所需要的全部样本数据。
利用load 函数可以在工作空间中自动载入网络训练所需的输入数据p 和目标数据t，即load choles_allsizeofp = size (p)sizeofp = 21 264sizeoft = size (t)sizeoft = 3 264可见，样本集的大小为264。
为了提高神经网络的训练效率，通常要对样本数据作适当的预处理。
首先，利用prestd 函数对样本数据作归一化处理，使得归一化后的输入和目标数据均服从正态分布，即[pn,meanp,stdp,tn,meant,stdt] = prestd(p,t);然后，利用prepca 函数对归一化后的样本数据进行主元分析，从而消除样本数据中的冗余成份，起到数据降维的目的。
[ptrans,transMat] = prepca(pn,0.001);[R,Q] = size(ptrans)R = 4 Q = 264可见，主元分析之后的样本数据维数被大大降低，输入数据的维数由21 变为4。