胶体稳定性
合集下载
胶体化学第5章胶体的稳定性
体的移动速度来计算电渗和电动现象，从而判断胶体的稳定性。
02 03
沉降法
沉降法是通过测量胶体在重力场中的沉降速度来判断其稳定性。如果沉 降速度很快，说明胶体的稳定性较差；如果沉降速度很慢，说明胶体的 稳定性较好。
光学法
光学法是通过观察胶体在光学显微镜下的形态来判断其稳定性。如果观 察到明显的聚沉现象，说明胶体的稳定性较差；如果没有观察到明显的 聚沉现象，说明胶体的稳定性较好。
反絮凝
是指通过某些措施使已经 絮凝的胶体重新分散成小 聚集体的过程。
04 胶体的应用
胶体在化学工业中的应用
胶体在化学工业中有着广泛的应用， 如涂料、颜料、粘合剂、印染等。胶 体作为分散相，能够提高产品的性能 和稳定性，改善产品的外观和手感。
胶体在化学工业中还可以用于制备功 能性材料，如光敏材料、电绝缘材料 ห้องสมุดไป่ตู้磁性材料等，以满足不同领域的需 求。
A
B
C
D
电子信息领域
利用胶体化学制备高性能的电子材料和器 件，推动电子信息技术的进步和发展。
能源与催化领域
利用胶体化学制备高效催化剂和燃料添加 剂，提高能源利用效率和减少环境污染。
感谢您的观看
THANKS
分散剂的作用
分散剂可以降低胶体粒子 之间的相互作用力，使胶 体粒子在介质中均匀分散。
分散剂的种类
常用的分散剂包括表面活 性剂、高分子物质等。
胶体的絮凝与反絮凝
胶体的絮凝
是指在某些条件下，胶体 粒子通过相互作用形成较 大聚集体的现象。
絮凝的条件
电解质、高分子物质、温 度变化等都可能引起胶体 的絮凝。
根据分散相粒子的大小，胶体可 分为粗分散体系、溶胶、高分子 溶液和缔合胶体等。
第五章胶体的稳定性
R 其中：
64 n KT 2 0 2 k) d 0exp( k
式5-10
exp( Ze KT ) 1 0/2 0 exp( Ze KT ) 1 0/2
R 表示两平板质点的双电层在单位面积上的相互排斥能（斥力位能）。
当 0 很高时，Ze 0 >>1，则 0 →1， R 与 0 无关
§5-1 电解质的聚沉作用
一、聚沉与老化
聚沉：胶粒聚集变大而沉淀的过程，与沉淀反应不同， 因聚沉电解质的量远少于沉淀量，其间不存在当量关系。
老化：由于小颗粒具有大的溶解度，静止时，溶液中的 小颗粒溶解，大颗粒长大，直到形成分散度较单一的大颗粒 ，这一过程称为老化。
二、聚沉值及其测定方法
聚沉值：在指定条件下，使溶胶聚沉所需电解质的最 低浓度，以mol/L表示。
一、胶粒间的范德华吸引能
a、永久偶极之间 1、分子间的范德华吸引能
对于同种分子
b、色散吸引能 c、诱导偶极与永久偶极之间
6 x 分
式5-1 （六次律）
式中： 分 ：分子间总的范德华引力
2 2 3 2 2 hv 3 KT 4
式5-2
x：分子间距离 α ：分子的极化度
对斥能峰的高低有较大影响。 ② s 的影响 ， A与 0无关，而 0 随 A 上升而增加，所以 R 2 0 与A相同时，势垒能 s 增加而上升。 泥浆不抗盐是因为电解质对双电层的压缩，使 s下降 ，势垒下降。
R 2 ，所以A与 不变时， ③ 的影响 A与 无关， 0 越小，双电层越厚，势垒越高。
1 1 1 ∶ ∶ 1 2 3
6
6
6
聚沉值与离子价数的6次方成反比，即schulze-hardy 规则。除了反离子外，同号离子的性质、大小均对聚沉值 有影响。
64 n KT 2 0 2 k) d 0exp( k
式5-10
exp( Ze KT ) 1 0/2 0 exp( Ze KT ) 1 0/2
R 表示两平板质点的双电层在单位面积上的相互排斥能（斥力位能）。
当 0 很高时，Ze 0 >>1，则 0 →1， R 与 0 无关
§5-1 电解质的聚沉作用
一、聚沉与老化
聚沉：胶粒聚集变大而沉淀的过程，与沉淀反应不同， 因聚沉电解质的量远少于沉淀量，其间不存在当量关系。
老化：由于小颗粒具有大的溶解度，静止时，溶液中的 小颗粒溶解，大颗粒长大，直到形成分散度较单一的大颗粒 ，这一过程称为老化。
二、聚沉值及其测定方法
聚沉值：在指定条件下，使溶胶聚沉所需电解质的最 低浓度，以mol/L表示。
一、胶粒间的范德华吸引能
a、永久偶极之间 1、分子间的范德华吸引能
对于同种分子
b、色散吸引能 c、诱导偶极与永久偶极之间
6 x 分
式5-1 （六次律）
式中： 分 ：分子间总的范德华引力
2 2 3 2 2 hv 3 KT 4
式5-2
x：分子间距离 α ：分子的极化度
对斥能峰的高低有较大影响。 ② s 的影响 ， A与 0无关，而 0 随 A 上升而增加，所以 R 2 0 与A相同时，势垒能 s 增加而上升。 泥浆不抗盐是因为电解质对双电层的压缩，使 s下降 ，势垒下降。
R 2 ，所以A与 不变时， ③ 的影响 A与 无关， 0 越小，双电层越厚，势垒越高。
1 1 1 ∶ ∶ 1 2 3
6
6
6
聚沉值与离子价数的6次方成反比，即schulze-hardy 规则。除了反离子外，同号离子的性质、大小均对聚沉值 有影响。
胶体的稳定性和聚沉作用
2021/11/3
溶胶的稳定性
抗聚结稳定性 胶粒之间有相互吸引的能量Va和相互排斥的能量Vr，总作用能 为 Va+Vr。如图所示：
当粒子相距较大时，主要为 吸力，总势能为负值；当靠近 到一定距离，双电层重叠，排 斥力起主要作用， 势能升高。要使粒子聚结必须 克服这个势垒。
2021/11/3
影响溶胶稳定性的因素
高分子化合物在低浓度时，大量胶粒会吸附在同一个高分子线型分子上，整个系 统质量增大，发生聚沉。这种现象称为敏化作用。在敏化作用中，高分子化合物起到 了一个桥梁的作用，通过吸附架桥，从而破坏胶体，使其发生聚沉。
2021/11/3
高分子化合物的作用
但是，高分子化合物浓度较高时，能大大提高溶胶的稳定性，这就是高分子化合物 对溶胶的保护作用。
1、电解质的聚沉作用 2、高分子化合物的聚沉作用 3、带相反电荷的溶胶的聚沉作用
2021/11/3
电解质的聚沉作用
当向溶胶中加入电解质后，电解质中与溶胶带相反 电性的离子会进入吸附层，中和了电位离子，减少或者中 和胶粒的带电量，从而使胶粒在碰撞后易于聚结而沉降。 因此，电解质的聚沉作用主要是减少胶粒带电，使ξ电位 下降，促使胶粒聚结。水处理中常用明矾或聚合氯化铝来 使水中黏土等负电性胶体聚沉。再如豆腐的制作、河流入 海口三角洲的形成等，都是这个原理。
例如，对于给定的溶胶，异电性离子分别为一、 二、三价，则聚沉值的比例为：
2021/11/3
1 1
6
:
1 2
6
:
1 3
6
电解质的聚沉作用
当起聚沉作用的离子电荷数相同时，其聚沉能力也会因离子的活泼性不同而有 所差别。
例如，对带负电的溶胶，一价阳离子硝酸盐的聚沉能力次序为： H+>Cs+>Rb+>NH4+>K+>Na+>Li+ 而碱土金属离子的聚沉能力大小为
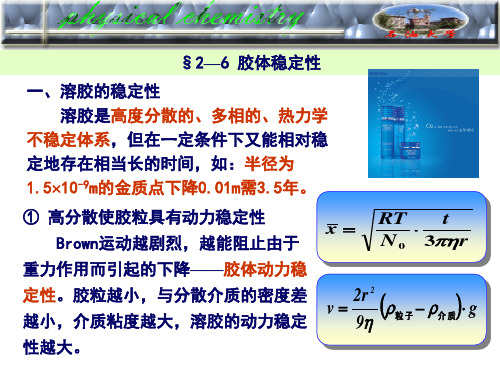
溶胶的稳定性
抗聚结稳定性 胶粒之间有相互吸引的能量Va和相互排斥的能量Vr，总作用能 为 Va+Vr。如图所示：
当粒子相距较大时，主要为 吸力，总势能为负值；当靠近 到一定距离，双电层重叠，排 斥力起主要作用， 势能升高。要使粒子聚结必须 克服这个势垒。
2021/11/3
影响溶胶稳定性的因素
高分子化合物在低浓度时，大量胶粒会吸附在同一个高分子线型分子上，整个系 统质量增大，发生聚沉。这种现象称为敏化作用。在敏化作用中，高分子化合物起到 了一个桥梁的作用，通过吸附架桥，从而破坏胶体，使其发生聚沉。
2021/11/3
高分子化合物的作用
但是，高分子化合物浓度较高时，能大大提高溶胶的稳定性，这就是高分子化合物 对溶胶的保护作用。
1、电解质的聚沉作用 2、高分子化合物的聚沉作用 3、带相反电荷的溶胶的聚沉作用
2021/11/3
电解质的聚沉作用
当向溶胶中加入电解质后，电解质中与溶胶带相反 电性的离子会进入吸附层，中和了电位离子，减少或者中 和胶粒的带电量，从而使胶粒在碰撞后易于聚结而沉降。 因此，电解质的聚沉作用主要是减少胶粒带电，使ξ电位 下降，促使胶粒聚结。水处理中常用明矾或聚合氯化铝来 使水中黏土等负电性胶体聚沉。再如豆腐的制作、河流入 海口三角洲的形成等，都是这个原理。
例如，对于给定的溶胶，异电性离子分别为一、 二、三价，则聚沉值的比例为：
2021/11/3
1 1
6
:
1 2
6
:
1 3
6
电解质的聚沉作用
当起聚沉作用的离子电荷数相同时，其聚沉能力也会因离子的活泼性不同而有 所差别。
例如，对带负电的溶胶，一价阳离子硝酸盐的聚沉能力次序为： H+>Cs+>Rb+>NH4+>K+>Na+>Li+ 而碱土金属离子的聚沉能力大小为
讲-第章-胶体的稳定性
(iii)若H >0，S <0，均可使G >0，此时焓变及 熵变均使系统稳定，为复合稳定。（温度对稳定的影 响不明显）
(ii) 脱水效应—高聚物分子由于亲水，其水化作用较胶粒 水化作用强(憎水)，从而高聚物的加入夺去胶粒的水化外壳 的保护作用。
(iii) 电中和效应—离子型高聚物的加入吸附在带电的胶 粒上而中和胶粒表面电荷。
2. 空间稳定理论（ steric stabilization）
向溶胶中加入高聚物或非离子表面活性剂，虽降低了电势， 但却显著地提高了溶胶系统的稳定性，这是用DLVO理论所解 释不了的。这种结果可用空间稳定理论加以解释。空间稳定理 论认为这是由于溶胶粒子表面吸附了高聚物，吸附的高聚物层 引起系统的G >0.
可见，聚沉能力是聚沉值的倒数，即聚沉值愈小，该电解 质的聚沉能力就愈大；反之，聚沉值越小的电解质，其聚沉能 力越强。
（1）电解质中与胶粒所带电荷相反的离子是其主要聚沉作用 的离子，并且离子价数越高，电解质的聚沉能力越大。
对某一给定溶胶，一、二、三价反离子聚沉值的比例大约是：
100 :1.6 : 0.14
当x缩小，先出现一 极小值F，则发生粒子的
Born排斥 {U}
聚集称为絮凝（可逆的）。
UR ∝exp{-x} —德拜参量
Umax
当x再缩小，则出现 极大值Umax。只有两胶 粒通过热运动积聚的动 能超过15kT时才有可能
超过此能量值，进而出 现极小值C，在此处发
生粒子间的聚沉（不可 逆）。
势垒
exp( Ze0 ) 1
2kT
exp( Ze0 ) 1
2kT
B：常数； ：介电常数；Z：分散离子价数 ； ：复合比 (complex ration) ; kB :波尔滋曼常数
(ii) 脱水效应—高聚物分子由于亲水，其水化作用较胶粒 水化作用强(憎水)，从而高聚物的加入夺去胶粒的水化外壳 的保护作用。
(iii) 电中和效应—离子型高聚物的加入吸附在带电的胶 粒上而中和胶粒表面电荷。
2. 空间稳定理论（ steric stabilization）
向溶胶中加入高聚物或非离子表面活性剂，虽降低了电势， 但却显著地提高了溶胶系统的稳定性，这是用DLVO理论所解 释不了的。这种结果可用空间稳定理论加以解释。空间稳定理 论认为这是由于溶胶粒子表面吸附了高聚物，吸附的高聚物层 引起系统的G >0.
可见，聚沉能力是聚沉值的倒数，即聚沉值愈小，该电解 质的聚沉能力就愈大；反之，聚沉值越小的电解质，其聚沉能 力越强。
（1）电解质中与胶粒所带电荷相反的离子是其主要聚沉作用 的离子，并且离子价数越高，电解质的聚沉能力越大。
对某一给定溶胶，一、二、三价反离子聚沉值的比例大约是：
100 :1.6 : 0.14
当x缩小，先出现一 极小值F，则发生粒子的
Born排斥 {U}
聚集称为絮凝（可逆的）。
UR ∝exp{-x} —德拜参量
Umax
当x再缩小，则出现 极大值Umax。只有两胶 粒通过热运动积聚的动 能超过15kT时才有可能
超过此能量值，进而出 现极小值C，在此处发
生粒子间的聚沉（不可 逆）。
势垒
exp( Ze0 ) 1
2kT
exp( Ze0 ) 1
2kT
B：常数； ：介电常数；Z：分散离子价数 ； ：复合比 (complex ration) ; kB :波尔滋曼常数
胶体化学第5章 胶体的稳定性
12 H
式中，VA为范德华引力势能（为负值）；a是球半径；H是两球最短 距离；A是Hamaker常数 。 两平行的等同平板粒子：
VA A 12 D
2
式中，D是两板间距。
上两式表明，VA随距离的增大而下降。 Hamaker常数A是一个重要的参数，它与粒子性质有关，是物质的 特性常数，具有能量的单位，在10－19~10－20J之间。下表是一些物质的 Hamaker常数。
影响絮凝作用的主要因素有： ①絮凝剂的分子结构 絮凝效果好的高分子应有直链结 构，交联和支链结构的效果差。应有水化基团和架桥 功能，电离度越大，荷电越多，分子越伸展，利于架 桥；但若高分子与胶粒荷相同电性时，带电多，产生 静电斥力不利于絮凝。 ②絮凝剂的分子量 分子量越大越好，但过大时，不容 性和远距离则不利絮凝，一般分子量在106左右。 ③絮凝剂的浓度 研究表明存在一个最佳浓度，为胶 粒表面饱和吸附量一般是最好，可见上图示。 ④搅拌 要均匀，不可带激烈。 ⑤酸性和盐 它们对絮凝影响很大。 下面给出了一些代表性的高分子絮凝剂：
4．临界聚沉浓度 电解质是影响V的重要因素之一。见下图示。电解质浓度大（κ亦大）， 势垒越低。把势垒值为零时的电解质浓度称为临界聚沉浓度，用Cccc表 示。根据DLVO理论的势能公式，可得到
C ccc 常数
（ kT )
3 5
4 0
A z
2
6
这表明，Cccc 与离子价数的六次 方成反比，这与Schulze-Hardy经 验规则相符，也证明了DLVO理 论的合理性。
4.3 高分子的稳定性和絮凝作用
1.空间稳定作用 人们很早就发现高分子物质对溶胶具有稳定作用。稳定机理有如下几 个原因。 ①带电高分子吸附後会增加胶粒间的静电斥力势能。 ②高分子吸附层通常能减小Hamaker常数，从而降低粒子间的范德华 引力势能。 ③带有高分子吸附层的胶粒相互接近时，吸附层的重叠会产生新的斥 力势能阻止粒子聚集。这种稳定作用称为空间稳定作用，产生的斥力势 能称为空间斥力势能，用VS表示。这样粒子间总的相互作用势能为 V = VA + VR + VS
式中，VA为范德华引力势能（为负值）；a是球半径；H是两球最短 距离；A是Hamaker常数 。 两平行的等同平板粒子：
VA A 12 D
2
式中，D是两板间距。
上两式表明，VA随距离的增大而下降。 Hamaker常数A是一个重要的参数，它与粒子性质有关，是物质的 特性常数，具有能量的单位，在10－19~10－20J之间。下表是一些物质的 Hamaker常数。
影响絮凝作用的主要因素有： ①絮凝剂的分子结构 絮凝效果好的高分子应有直链结 构，交联和支链结构的效果差。应有水化基团和架桥 功能，电离度越大，荷电越多，分子越伸展，利于架 桥；但若高分子与胶粒荷相同电性时，带电多，产生 静电斥力不利于絮凝。 ②絮凝剂的分子量 分子量越大越好，但过大时，不容 性和远距离则不利絮凝，一般分子量在106左右。 ③絮凝剂的浓度 研究表明存在一个最佳浓度，为胶 粒表面饱和吸附量一般是最好，可见上图示。 ④搅拌 要均匀，不可带激烈。 ⑤酸性和盐 它们对絮凝影响很大。 下面给出了一些代表性的高分子絮凝剂：
4．临界聚沉浓度 电解质是影响V的重要因素之一。见下图示。电解质浓度大（κ亦大）， 势垒越低。把势垒值为零时的电解质浓度称为临界聚沉浓度，用Cccc表 示。根据DLVO理论的势能公式，可得到
C ccc 常数
（ kT )
3 5
4 0
A z
2
6
这表明，Cccc 与离子价数的六次 方成反比，这与Schulze-Hardy经 验规则相符，也证明了DLVO理 论的合理性。
4.3 高分子的稳定性和絮凝作用
1.空间稳定作用 人们很早就发现高分子物质对溶胶具有稳定作用。稳定机理有如下几 个原因。 ①带电高分子吸附後会增加胶粒间的静电斥力势能。 ②高分子吸附层通常能减小Hamaker常数，从而降低粒子间的范德华 引力势能。 ③带有高分子吸附层的胶粒相互接近时，吸附层的重叠会产生新的斥 力势能阻止粒子聚集。这种稳定作用称为空间稳定作用，产生的斥力势 能称为空间斥力势能，用VS表示。这样粒子间总的相互作用势能为 V = VA + VR + VS
胶体的稳定性
聚沉值
使溶胶发生明显聚沉时外加电解质的最小 浓度称为该电解质对该溶胶的聚沉值 浓度称为该电解质对该溶胶的聚沉值
聚沉能力
聚沉能力＝1/聚沉值 聚沉能力＝1/聚沉值
解释： 解释：
ci ↑ I ↑
κ↑
VR ↓↓ V ↓↓
斥力不足以克服引力——聚沉 聚沉 斥力不足以克服引力 聚沉值： 聚沉值：
∂V
V = V A + VR = 0
（3）法扬斯（Fajans)规则 法扬斯（Fajans)规则 能与晶体的组成离子形成不溶物或难电离化合物的 异电离子优先被吸附，具有强的聚沉能力。 异电离子优先被吸附，具有强的聚沉能力。
（4）不规则聚沉 有时，少量电解质使溶胶聚沉，电解质浓度高时， 有时，少量电解质使溶胶聚沉，电解质浓度高时， 又重新分散，浓度再高又聚沉，此为不规则聚沉， 又重新分散，浓度再高又聚沉，此为不规则聚沉，多发 不规则聚沉 生在以大离子或高价离子为聚沉剂的情况——大离子或 生在以大离子或高价离子为聚沉剂的情况 大离子或 高价离子引起电动电势反号。 高价离子引起电动电势反号。 （5）有机离子一般具有较强聚沉能力——特殊吸附力 有机离子一般具有较强聚沉能力 特殊吸附力 （6）同号离子的影响 大的同号有机离子因与质点强烈的van 大的同号有机离子因与质点强烈的van der Waals 引力而被吸附，从而改变质点的表面性质。一般说来， 引力而被吸附，从而改变质点的表面性质。一般说来， 大的或高价的负离子对于负溶胶有一定稳定作用， 大的或高价的负离子对于负溶胶有一定稳定作用，大的 或高价正离子对于正溶胶有一定稳定作用。 或高价正离子对于正溶胶有一定稳定作用。
-
- + + ++ + + + ++
食品中的胶体稳定性研究
食品中的胶体稳定性研究胶体稳定性是指液体中分散相颗粒的稳定状态，是食品行业研究的一个重要课题。
胶体稳定性影响着食品的质量和口感，因此对其进行深入研究具有重要意义。
胶体稳定性与胶体颗粒之间的相互作用密切相关。
在食品中，常见的胶体颗粒有胶状体、脂质体、乳液等。
这些胶体颗粒存在于各种食品中，例如酱料、乳制品、饮料等。
胶体颗粒的稳定性受到多种因素的影响，包括表面电荷、溶液中的离子浓度、温度等。
首先，胶体稳定性与胶体颗粒的表面电荷有关。
在水溶液中，胶体颗粒的表面带有电荷，这种表面电荷使胶体颗粒之间形成静电斥力，防止其聚集。
这种静电斥力是维持胶体颗粒分散状态的重要力量。
然而，当溶液中的离子浓度增加时，胶体颗粒的表面电荷可能被中和，导致静电斥力减弱，使得胶体颗粒易于聚集。
其次，胶体稳定性还受到离子浓度和pH值的影响。
溶液中存在的离子可以干扰胶体颗粒的电荷平衡，从而影响胶体的稳定性。
离子浓度较高时，离子与胶体颗粒表面电荷之间发生相互作用，导致胶体的稳定性降低。
此外，溶液的pH值也会影响胶体稳定性。
适当的pH值可以保持胶体颗粒表面电荷的平衡，从而维持胶体的稳定性。
温度是另一个影响胶体稳定性的重要因素。
随着温度的升高，分子的活动性增加，这可能导致胶体颗粒的聚集。
此外，一些食品中的成分在高温下可能发生变化，从而影响胶体稳定性，例如乳制品中的蛋白质在高温下会发生变性，导致乳液的稳定性降低。
针对食品中的胶体稳定性问题，研究人员提出了一些解决方案。
一种常用的方法是添加稳定剂或乳化剂。
稳定剂可以增加胶体颗粒表面的电荷密度，从而增强胶体分散的稳定性。
乳化剂则可以在液体中形成薄膜或界面活性剂层，减少胶体颗粒之间的相互作用。
这些添加剂的选择和使用方法需要进行深入研究，以确保其对食品质量和安全性的影响。
此外，利用纳米技术也是研究胶体稳定性的新方法。
纳米颗粒具有较大的比表面积和特殊的物理化学性质，可以在食品中起到纳米稳定剂的作用。
通过纳米技术可以制备具有独特结构和性质的纳米胶体颗粒，从而提高胶体的稳定性。
胶体的稳定性
稳定的溶胶必须同时兼备聚结稳定性和动力稳定性，其中聚结稳 定性更为重要，一旦失去聚结稳定性，粒子相互聚结变大，最终将导 致失去动力学稳定性。
无机电解质和高分子都能对溶胶的稳定性产生重大影响，但其机 理不同。为加以区别，通常：
把无机电解质使溶胶沉淀的作用称为聚沉作用 把高分子使溶胶沉淀的作用称为絮凝作用
引力位能皆 规定为负值
三、DLVO理论
（2）两平行的等同平板粒子：
A EA 12πH2
H——两板间最短距离。
从以上两式可以看出，EA随距离增大而下降。
Hamaker常数A是一个重要参数，与粒子性质有 关，是物质的特性参数，具有能量单位，一般在 10－19～10－20J之间。
三、DLVO理论
2．双电层的斥力势能
稳定区
聚沉区
+30mv 0
－30mv
稳定区
不规则聚沉示意图
当ζ电势绝对值低于临界值（一般为30mv）时，溶胶就聚 沉，高于此值，体系稳定。
二、聚沉作用（coagulation）
（4）溶胶相互聚沉
两种电性相反的溶胶混合时可胶发粒生所相带 互聚沉作用，聚沉 的程度与两胶体的比例有关，比例电相荷差为很零 大时，聚沉不完全 或不发生聚沉，在等电点附近沉淀最完全。
第四讲 胶体的稳定性
胶体的稳定性
胶体溶液的稳定性实指其某种性质（如分散相浓度、颗粒 大小、体系黏度和密度等）在一定程度的不变性。
虽然胶体本质上是热力学不稳定体系，但是 实际上它总能稳定一定的时间，有时长达数年， 甚至数十年之久。
稳定性只具有动力学意义，故而是相对的。
一、胶体的三种稳定性
1．热力学稳定性
很早以前，人们就发现高分子物质对溶胶具有稳定作用。如我国 古代制造的墨汁就掺进树胶，以保护炭粉不致聚结。现代工业上制造 的油溶性油漆、涂料、油墨等均利用了高分子的稳定作用。
无机电解质和高分子都能对溶胶的稳定性产生重大影响，但其机 理不同。为加以区别，通常：
把无机电解质使溶胶沉淀的作用称为聚沉作用 把高分子使溶胶沉淀的作用称为絮凝作用
引力位能皆 规定为负值
三、DLVO理论
（2）两平行的等同平板粒子：
A EA 12πH2
H——两板间最短距离。
从以上两式可以看出，EA随距离增大而下降。
Hamaker常数A是一个重要参数，与粒子性质有 关，是物质的特性参数，具有能量单位，一般在 10－19～10－20J之间。
三、DLVO理论
2．双电层的斥力势能
稳定区
聚沉区
+30mv 0
－30mv
稳定区
不规则聚沉示意图
当ζ电势绝对值低于临界值（一般为30mv）时，溶胶就聚 沉，高于此值，体系稳定。
二、聚沉作用（coagulation）
（4）溶胶相互聚沉
两种电性相反的溶胶混合时可胶发粒生所相带 互聚沉作用，聚沉 的程度与两胶体的比例有关，比例电相荷差为很零 大时，聚沉不完全 或不发生聚沉，在等电点附近沉淀最完全。
第四讲 胶体的稳定性
胶体的稳定性
胶体溶液的稳定性实指其某种性质（如分散相浓度、颗粒 大小、体系黏度和密度等）在一定程度的不变性。
虽然胶体本质上是热力学不稳定体系，但是 实际上它总能稳定一定的时间，有时长达数年， 甚至数十年之久。
稳定性只具有动力学意义，故而是相对的。
一、胶体的三种稳定性
1．热力学稳定性
很早以前，人们就发现高分子物质对溶胶具有稳定作用。如我国 古代制造的墨汁就掺进树胶，以保护炭粉不致聚结。现代工业上制造 的油溶性油漆、涂料、油墨等均利用了高分子的稳定作用。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
二、DLVO理论 理论
20世纪 年代，苏联物理化学家 世纪40年代 苏联物理化学家Derjaguin和Landau， 世纪 年代， 和 ， 荷兰物理化学家Verwey和Overbeek分别独立提出疏液胶体稳 和 荷兰物理化学家 分别独立提出疏液胶体稳 理论。 定性理论，统称为 理论 定性理论，统称为DLVO理论。 DLVO理论认为，溶胶在一定条件下是稳定存在还是聚 理论认为， 理论认为 沉，取决于粒子间的相互吸引力和静电斥力。若斥力大于吸 取决于粒子间的相互吸引力和静电斥力。 引力则溶胶稳定，反之则不稳定。 引力则溶胶稳定，反之则不稳定。
三、溶胶的聚沉
溶胶的“稳定”是有条件的， 溶胶的“稳定”是有条件的，一旦稳定被破 溶胶中的粒子就会聚集，长大， 坏，溶胶中的粒子就会聚集，长大，最后从介质 中沉淀出来，这种现象就称为聚沉。 中沉淀出来，这种现象就称为聚沉。 影响溶胶稳定性的因素
A、外加电解质的影响 这影响最大，主要影响胶粒的带电情况， 这影响最大，主要影响胶粒的带电情况，使ζ电位下 降，促使胶粒聚结。 促使胶粒聚结。 B、浓度的影响 浓度增加，粒子碰撞机会增多。 浓度增加，粒子碰撞机会增多。 C、温度的影响 温度升高，粒子碰撞机会增多，碰撞强度增加。 温度升高，粒子碰撞机会增多，碰撞强度增加。 胶体体系的相互作用。 D、胶体体系的相互作用。 带不同电荷的胶粒互吸而聚沉。 带不同电荷的胶粒互吸而聚沉。
Hamaker 假设（远程相互作用） 假设（远程相互作用）
Hamaker (1937)假设：一个颗粒所包含 假设： 假设 的分子之间的相互作用具有加和性， 的分子之间的相互作用具有加和性，由此可 得颗粒间的引力位 引力位能 得颗粒间的引力位能EA。
对于大小相同的两个球形粒子 Hamaker常数 常数
Aa EA = − 12 H
球半径 两球间的最短距离
Hamaker常数 是物质的特性参数，具有能 常数A是物质的特性参数 常数 是物质的特性参数， 量单位，其值常在10 左右 左右。 量单位，其值常在 -20J左右。
对于两个彼此平行的平板粒子
A EA = − 2 12πD
两极间的距离
对于分散在介质中的粒子， 必须用有效的 对于分散在介质中的粒子，A必须用有效的 常数代替
(a) 反离子所带的电荷数越高，聚沉能力越强。 反离子所带的电荷数越高，聚沉能力越强。 (b) 价数相同的反离子的水合半径越小，聚沉 价数相同的反离子的水合半径越小， 能力越强。 能力越强。 例如，对一价阳离子 按聚沉能力排列 按聚沉能力排列： 例如，对一价阳离子,按聚沉能力排列： H+ > Cs+ > Rb+ > NH4+ > K+ > Na+ > Li+
影响电解质聚沉能力的因素
电解质的聚沉能力主要与电解质中与胶粒带相反电荷的 电解质的聚沉能力主要与电解质中与胶粒带相反电荷的 主要与电解质中与胶粒带 离子价数、离子半径、同电性离子价数等有关 等有关。 离子价数、离子半径、同电性离子价数等有关。其中外加电 解质的反号离子的价数影响最大。 反号离子的价数影响最大 解质的反号离子的价数影响最大。
2. 溶胶的相互聚沉 当两种带相反电荷的溶胶所带电量相等 相互混合也会发生聚沉。 时，相互混合也会发生聚沉。
明矾净水原理:水中含有泥沙等污物的负溶胶， 明矾净水原理 水中含有泥沙等污物的负溶胶， 水中含有泥沙等污物的负溶胶 加入KAl(SO4)2在水中水解生成 在水中水解生成Al(OH)3正溶胶。 正溶胶。 加入 在适当量下，发生相互聚沉。 在适当量下，发生相互聚沉。 与加入电解质情况不同的是， 与加入电解质情况不同的是，当两种溶胶的用 量恰能使其所带电荷的量相等时，才会完全聚沉， 量恰能使其所带电荷的量相等时，才会完全聚沉， 否则会不完全聚沉，甚至不聚沉。 否则会不完全聚沉，甚至不聚沉。
1、空间稳定理论 、
（1）ER ） S Fisher认为：良溶剂有利于增大 认为： 认为 空间斥力位能，使胶体稳定， 空间斥力位能，使胶体稳定，吸附 力越强、吸附层越厚，胶体越稳定。 力越强、吸附层越厚，胶体越稳定。
（2）EA 具有高聚物吸附层的粒子之间的引 ） 力位能取决于高聚物-溶剂 溶剂-胶粒三者之间相互 力位能取决于高聚物 溶剂 胶粒三者之间相互 作用的强弱。若吸附层使E 增加， 作用的强弱。若吸附层使 A增加，胶体的稳定 性下降，反之，稳定性增加。 性下降，反之，稳定性增加。 （3）影响空间稳定性的因素有高聚物的分子 ） 结构、高聚物的分子量、吸附层的厚度、 结构、高聚物的分子量、吸附层的厚度、分散 介质。 介质。
两球间的最短距离
对于两个平行的等同板状粒子
2 64n0 kTν 0 exp(− KD ) ER = K
两板间的距离
C、胶粒间的总相互作用能 、
胶粒间存在的斥力位能和引力位能的相对大小决定了系统的总位能， 胶粒间存在的斥力位能和引力位能的相对大小决定了系统的总位能，亦决定了胶 图1-2 胶粒间作用能和距离的关系 体的稳定性。 体的稳定性。 当斥力位能>引力位能，可以阻止胶粒由于布朗运动碰撞而粘结，胶体稳定， 当斥力位能 引力位能，可以阻止胶粒由于布朗运动碰撞而粘结，胶体稳定， 引力位能 当引力位能>斥力位能时，胶粒靠拢而聚沉。 当引力位能 斥力位能时，胶粒靠拢而聚沉。 斥力位能时 调整其相对大小，可改变胶体的稳定性。 调整其相对大小，可改变胶体的稳定性。
胶体稳定性
主讲人： 主讲人：雷开臣 纺织化学与染整工程 1015043004
一、胶体稳定性理论
胶体化学是在讨论胶体稳定性的过程中发展起来的 －－P. －－ Hiemenz 在讨论稳定性时，强调胶体是化学稳定的， 在讨论稳定性时，强调胶体是化学稳定的，即其中不涉及 化学反应。 化学反应。 胶体稳定性的实指其某种性质（如分散相浓度、密度、体 胶体稳定性的实指其某种性质（如分散相浓度、密度、 系黏度和颗粒大小等）有一定程度的不变形。 系黏度和颗粒大小等）有一定程度的不变形。 胶体稳定性的表征： 胶体稳定性的表征： 热力学稳定性 动力学稳定性 聚集稳定性 聚沉作用： 聚沉作用：无机电解质使胶体沉淀的作用 絮凝作用： 絮凝作用：高分子化合物使胶体沉淀的作用 聚集作用：不知何种药剂， 聚集作用：不知何种药剂，使胶体沉淀时的笼统称
带电胶粒靠拢时扩散层重叠时产生的静电排斥 力就称为胶粒的斥力位能ER。
对于大小相同的球形粒子
球半径
2 0
64πan0 kTν ER = exp(− KH ) 2 K
Zeψ s exp −1 2kT ν0 = Zeψ s exp +1 2kT
为电导率， 为电导率， 其倒数为双电 层的厚度
A121 = A
10-21J
(
1/ 2 11
−A
1/ 2 2 22
)
粒子
Байду номын сангаас
介质
介质的存在使粒子间吸引力减弱 介质的性质与质点越接近， 介质的性质与质点越接近，粒子间的吸引力越弱
B、胶粒间的相互排斥 、
如图所示， 如图所示，当胶粒相 互接近到离子氛发生重叠 时，处于重叠区中的离子 浓度显然较大，破坏了原 浓度显然较大， 来电荷分布的对称性， 来电荷分布的对称性，引 起了离子氛中电荷的重新 分布， 分布，即离子从浓度较大 的重叠区间向未重叠区扩 散，使带正电的胶粒受到 斥力而相互脱离。 斥力而相互脱离。 图1-1 离子氛重叠
1. 电解质的聚沉作用
聚沉值和聚沉率
聚沉值：使溶胶以明显速率聚沉所需的电解质的最小浓度。 聚沉值：使溶胶以明显速率聚沉所需的电解质的最小浓度。 聚沉能力：是聚沉值的倒数。 聚沉能力：是聚沉值的倒数。聚沉值越大的电解质其聚沉能力 越小；反之，聚沉值越小的电解质，其聚沉能力越强。 越小；反之，聚沉值越小的电解质，其聚沉能力越强。
电解质聚沉值rc与反离子价 之间的关系 之间的关系: 电解质聚沉值 与反离子价Z之间的关系
D (KT ) rc = C 2 6 6 AeZ
3
5
1 rc ∝ 6 Z
上式中：C为与电解质阴阳离子性质有关的常数； 上式中： 为与电解质阴阳离子性质有关的常数； 为与电解质阴阳离子性质有关的常数 D为介质的介电常数；K为Boltzmann常数；T为绝对 为介质的介电常数； 为 常数； 为绝对 为介质的介电常数 常数 温度； 为范德华引力常数 为单位电荷 为范德华引力常数； 为单位电荷； 为反离 温度；A为范德华引力常数；e为单位电荷；Z为反离 子价数。 子价数。
2、空位稳定理论 、
若胶粒表面层内的高聚物浓度低于体相中的 浓度，则胶粒表面生成空位层。 浓度，则胶粒表面生成空位层。 以平行板胶粒浸入高聚物溶液中为例， 以平行板胶粒浸入高聚物溶液中为例，当两 胶粒互相靠近时，存在引力与斥力。 胶粒互相靠近时，存在引力与斥力。高聚物的 浓度决定了这两种力的大小。 浓度决定了这两种力的大小。 若高聚物浓度较大，胶体呈稳定状态， 若高聚物浓度较大，胶体呈稳定状态，称之 空位稳定作用。 为空位稳定作用。 若高聚物浓度较小，胶体出现絮凝， 若高聚物浓度较小，胶体出现絮凝，称之为 空位絮凝作用。 空位絮凝作用。
A、胶粒间的相互吸引 、
胶粒间存在相互吸引的作用力， 胶粒间存在相互吸引的作用力，其本质为 范德华力。 范德华力。 由于胶粒是许多分子的聚集体， 由于胶粒是许多分子的聚集体，故胶粒间 的吸力是胶粒中所有分子引力的总和。 的吸力是胶粒中所有分子引力的总和。 胶粒间的吸引力与胶粒间的距离的3次方成 胶粒间的吸引力与胶粒间的距离的 次方成 反比， 反比，说明胶粒在比较远的距离时胶粒间仍 有一定的吸引力，即有长程范德华力。 有一定的吸引力，即有长程范德华力。
对一价阴离子，按聚沉能力排列： 对一价阴离子，按聚沉能力排列： F- > Cl- > Br- > NO3- > I这种将同符号、 这种将同符号、同价的离子按聚沉能力 排成的顺序，通常称为感胶离子序 感胶离子序。 排成的顺序，通常称为感胶离子序。 (c) 与胶粒电性相同的离子，一般说来，价数 与胶粒电性相同的离子，一般说来， 越高，水合半径越小，聚沉能力越弱。 越高，水合半径越小，聚沉能力越弱。