等积法
2021年中考数学必考点培优系列 14 等面积法的应用(有答案)

等面积法的应用在解决几何问题时,通常可采用等积法来解决一些问题,即同一个图形采用不同的面积表示方法来建立等式.等积法也常在证明某些定理时被用到.【例题讲解】例题1 已知:如图,在Rt △ABC 中,∠BAC =90°,AB =4,AC =3,AD ⊥BC ,求AD 的长为 .D CB A答案: AD =2.4.例题2、如图,E 是边长为1的正方形ABCD 的对角线上一点,且BE =BC ,P 为CE 上任意一点,PQ ⊥BC 于点Q ,PR ⊥BE 于点R ,则PQ +PR 的值为 .RQPEDCBA. 【解析】连接BP ,易知BEC S △=BEP S △+BCP S △,所以12·BE ·CM =12·BE ·PR +12·BC ·PQ ,由BC =BE ,等号两边同时约掉,剩下CM =PR +PQ ,所以CMBC. 连接BP ,过C 作CM ⊥BD , ∵BEC S △=BEP S △+BCP S △ =BC ×PQ ×12+BE ×PR ×12=BC ×(PQ +PR )×12=BE ×CM ×12, BC =BE , ∴PQ +PR =CM ,∵BE =BC =1,且正方形对角线BD又∵BC =CD ,CM =BD ,∴M 为BD 中点,又△BDC 为直角三角形, ∴CM =12BD,即PQ +PR. MR QPEDCBA【对于填空选择题,可用特殊值法!】例题3 如图,正方形ABCD 的边长为1,点P 为边BC 上任意一点(可与B 点或C 点重合),分别过B 、C 、D 作射线AP 的垂线,垂足分别是B '、C '、D ',则B B '+C C '+D D '的最大值为 ,最小值为 .PB'C 'D 'DCBA答案:2【解析】连接AC 、DP , ABCD S 正方形=1×1×1,由勾股定理得:AC∵AB =1, ∴1≤APDPC S ∆=APC S ∆=12AP ×C C ', 1=ABCD S 正方形=ABP S ∆+ADP S ∆+DPC S ∆=12AP (B B '+C C '+D D '), B B '+C C '+D D '=2AP, ∵1≤APB B '+C C '+D D '≤2,PB'C'D'D CBA【巩固练习】1、如图,点P为等边△ABC内任意一点,AB=2,则点P到△ABC三边的距离之和为 .2、如图,在矩形ABCD中,已知AD=12,AB=5,P是AD边上任意一点,PE⊥BD,PE⊥AC,E、F分别是垂足,则PE+PF的长为.3、如图,D是Rt△ABC斜边AB上一点,且BD=BC=AC=1,P为CD上任意一点,PF⊥BC于点F,PE ⊥AB于点E,则PE+PF的值是 .4.如图,已知直线y=2x-2上有一动点Q,点P坐标为(-1,0),则PQ的最小值为 .【请用等积法】5.如图,在Rt △ABC 中,∠ABC =90°,点D 是斜边上的中点,点P 在AB 上,PE ⊥BD 于E ,PF ⊥AC 于F ,若AB =6,BC =3.,则PE +PF = .PFE D CBA6.将两个全等的直角三角形按图1所示摆放,其中∠DAB =90°,求证:a ²+b ²=c ².7.如图,在△ABC 中,∠ A =90°,D 是AC 上的一点,BD =DC ,P 是BC 上的任一点,PE ⊥BD ,PF ⊥AC ,E 、F 为垂足.求证:PE +PF =AB .PFE D CBA8.如图,平行四边形ABCD 中,AB : BC =3:2,∠DAB =60°,E 在AB 上,且AE : EB =1:2,F 是BC 的中点,过D 分别作DP ⊥AF 于P ,DQ ⊥CE 于Q ,求证:DP CEDQ AFQP FEDCBA图4 图59.在△ABC 中,AB =13,BC =14.(1)如图1,AD ⊥BC 于点D ,且BD =5,则△ABC 的面积为 ;(2)在(1)的条件下,如图2,点H 是线段AC 上任意一点,分别过点A ,C 作直线BH 的垂线,垂足为E ,F ,设BH =x ,AE =m ,CF =n ,请用含x 的代数式表示m +n ,并求m +n 的最大值和最小值.CBA HFEDCB A10.【问题情境】张老师给爱好学习的小军和小俊提出这样一个问题:如图1,在△ABC 中,AB =AC ,点P 为边BC 上的任一点,过点P 作PD ⊥AB ,PE ⊥AC ,垂足分别为D 、E ,过点C 作CF ⊥AB ,垂足为F .求证:PD +PE =CF .FE PD CBA FGE PD CBAEFABC DP小军的证明思路是:如图2,连接AP ,由△ABP 与△ACP 面积之和等于△ABC 的面积可以证得:PD +PE =CF .小俊的证明思路是:如图2,过点P 作PG ⊥CF ,垂足为G ,可以证得:PD =GF ,PE =CG ,则PD +PE =CF .【变式探究】如图3,当点P 在BC 延长线上时,其余条件不变,求证:PD -PE =CF ; 请运用上述解答中所积累的经验和方法完成下列两题:【结论运用】如图4,将矩形ABCD 沿EF 折叠,使点D 落在点B 上,点C 落在点C 处,点P P 为折痕EF 上的任一点,过点P 作PG ⊥BE 、PH ⊥BC ,垂足分别为G 、H ,若AD =8,CF =3,求PG +PH 的值;C'PH GFEDCBA【迁移拓展】图5是一个航模的截面示意图.在四边形ABCD 中,E 为AB 边上的一点,ED ⊥AD ,EC ⊥CB ,垂足分别为D 、C ,且AD ·CE =DE ·BC ,AB =,AD =3dm ,BD .M 、N 分别为AE 、BE 的中点,连接DM 、CN ,求△DEM 与△CEN 的周长之和.NM E DCBA参考答案1..2.答案:60 13.3.答案:2.【解析】如图所示,过C作CH AB⊥于H,D是Rt ABC∆斜边AB上一点,且1BD BC AC===,CH∴=∴111222BDCS BD CH∆==⨯=,又1111112222BCD BPC BPDS S S BD PE BC PF PE PF∆∆∆=+=+=⨯⨯+⨯⨯,PE PF∴+=.HPFDCBA4..【解析】如图,过点P作PQ⊥AB于点Q,过点Q作QC+QB,则∵y=2x-2∴A(0,-2),B(1,0)∵△PQB∽△AOB∴BQOB=PBAB∵AB,PB=2,OB=1∴1BQ∴BQ∴PQ.5.65如图作BM ⊥AC 于M ,连接PD .MPFE D CBA∵∠ABC =90°,AD =DC ,AB =6,BC =3, ∴BD =AD =DC ,AC 22AB BC +35 ∵12·AB ·BC =12·AC ·BM , ∴BM 65∴ABD S ∆=ADP S ∆+BDP S ∆, ∴12·AD ·BM =12·AD ·PF =12·BD ·PE , ∴PE +PF =BM 65MPFE D CBA6.答案:连接DB ,过点D 作BC 边上的高DF ,则DF =EC =b -a . ∵ADCB S 四边形=ACD S ∆+ABC S ∆=12b ²+12ab . 又∵ADCB S 四边形=ADB S ∆+DCB S ∆=12c ²+12a (b -a ) ∴12b ²+12ab =12c ²+12a (b -a ) ∴a ²+b ²=c ².FDBFb EA请参照上述证法,利用图2证明:a ²+b ²=c ².【解析】连结BD ,过点B 作DE 边上的高BF ,可得BF =b -a , ∵ACBED S 五边形=ACB S ∆+ABE S ∆+ADE S ∆=12ab +12b ²+12ab , 又ACBED S 五边形=ACB S ∆+ABD S ∆+BDE S ∆=12ab +12c ²+12a (b -a ), ∴12ab +12b ²+12ab =12ab +12c ²+12a (b -a ), ∴a ²+b ²=c ².Fb A7.【解析】过P 作PG ⊥AB 于G ,交BD 于O , ∵PF ⊥AC ,∠A =90°, ∴∠A =∠AGP =∠PF A =90°, ∴四边形AGPF 是矩形, ∴AG =PF ,PG ∥AC , ∵BD =DC ,∴∠C =∠GPB =∠DBP , ∴OB =OP ,∵PG ⊥AB ,PE ⊥BD , ∴∠BGO =∠PEO =90°, 在△BGO 和△PEO 中 BGO PEO GOB EOP OB OP ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△BGO ≌△PEO , ∴PE =BG , ∵AB =BG +AG , ∴PE +PF =AB .G O P FED CBA8.【解析】连接DE 、DF ,∵根据三角形的面积和平行四边形的面积得:12DEC DFA ABCD S S S ∆∆==平行四边形,即12AF ×DF =12CE ×DQ ,∴AF ×DP =CE ×DQ , ∴DP CE DQ AF=. Q PFE DCB A9.【解析】(1)在Rt △ABD 中,AB =13,BD =5, ∴AD12.∵BC =14,∴ABC S △=12BC ·AD =12×14×12=84. 故答案为:84.(2)∵ABC S △=ABH S △+BHC S △, ∴12BH ·AE +12BH ·CF =84. ∴xm +xn =168.∴m +n =168x∵AD =12,DC =14-5=9,∴AC=15,∵m +n 与x 成反比,∴当BH ⊥AC 时,m +n 有最大值.∴(m +n )BH =AC ·BH .∴m +n =AC =15.∵m +n 与x 成反比,∴当BH 值最大时,m +n 有最小值.∴当点H 与点C 重合时m +n 有最小值.∴m +n =16814, ∴m +n 等于12.∴m +n 的最大值为15,最小值为12.10.【解析】【问题情境】证明:(小军的方法)连接AP ,如图②∵PD ⊥AB ,PE ⊥AC ,CF ⊥AB ,且ABC S △=ABP S △+ACP S △, ∴12AB ·CF =12AB ·PD +12AC ·PE . ∵AB =AC ,∴CF =PD +PE .(小俊的方法)过点P 作PG ⊥CF ,垂足为G ,如图②. ∵PD ⊥AB ,CF ⊥AB ,PG ⊥FC ,∴∠CFD =∠FDP =∠FGP =90°∴四边形PDFG 是矩形.∴DP =FG ,∠DPG =90°.∴∠CGP =90°∵PE ⊥AC ,∴∠CEP =90°,∴∠PGC =∠CEP .∵∠BDP =∠DPG =90°,∴PG ∥AB .∴∠GPC =∠B .∵AB =AC ,∴∠B =∠ACB .∴∠GPC =∠ECP .在△PGC 和△CEP 中,PGC CEP GPC ECP PC CP ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△PGC ≌△CEP .∴CG =PE .CF =CG +FG=PE +PDG E P FDC BA【变式探究】证明:连接AP ,如图③.∵PD ⊥AB ,PE ⊥AC ,CF =AB ,且ABC S △=ABP S △-ACP S △, ∴12AB ·CF =12AB ·PD -12AC ·PE . ∵AB =AC ,∴CF =PD -PE .GE FABC DP【结论运用】过点E 作EQ ⊥BC ,垂足为Q ,如图④,∵四边形ABCD 是矩形,∴AD =BC ,∠C =∠ADC =90°.∵AD =8,CF =3,∴BF =BC -CF =AD -CF =5.由折叠可得:DF =BF ,∠BEF =∠DEF .∴DF =5.∵∠C =90°,∴DC=4.∵EQ ⊥BC ,∠C =∠ADC =90°,∴∠EQC =90°=∠C =∠ADC .∴四边形EQCD 是矩形.∴EQ =DC =4.∵AD ∥BC ,∴∠DEF =∠EFB .∵∠BEF =∠DEF ,∴∠BEF =∠EFB .∴BE =BF .由问题情境中的结论可得:PG +PH =EQ .∴PG +PH =4.∴PG +PH 的值为4.Q C 'P H G FEDCB A【迁移拓展】延长AD 、BC 交于点F ,作BH ⊥AF ,垂足为H ,如图⑤. ∵AD ·CE =DE ·BC , ∴AD DE =BC EC . ∵ED ⊥AD ,EC ⊥CB ,∴∠ADE =∠BCE =90°.∴△ADE ∽△BCE .∴∠A =∠CBE .∴F A =FB .由问题情境中的结论可得:ED +EC =BH .设DH =x dm ,则AH =AD +DH =(3+x )dm .∵BH ⊥AF ,∴∠BHA =90°.∴BH ²=BD ²-DH ²=AB ²-AH ².∵AB=AD =3,BDx²=()²-(3+x )².解得:x =1.∴BH ²=BD ²-DH ²=37-1=36.∴BH =6dm.∴ED +EC =6.∵∠ADE =∠BCE =90°,且M 、N 分别为AE 、BE 的中点,∴DM =AM =EM =12AE ,CN =BN =EN =12BE . ∴△DEM 与△CEN 的周长之和=DE +DM +EM +CN +EN +EC=DE +AE +BE +EC=DE +AB +EC=DE +EC +AB=6+∴△DEM 与△CEN 的周长之和为(6+dm . FHNM E DC BA。
等积法的公式

等积法的公式等积法是一种常用的数学方法,用于解决一些与面积、体积相关的问题。
在等积法中,我们通过保持一个物体的面积或体积不变,来推导出其他相关的数学关系。
下面我们来详细介绍一些常见的等积法公式及其应用。
一、长方形的等积法公式在等积法中,长方形是最常见的几何形状之一。
我们可以通过等积法来推导出长方形的一些重要公式。
假设一个长方形的长为a,宽为b,面积为S。
根据等积法,我们可以得到以下公式:1. 面积公式:S = a * b;2. 周长公式:P = 2 * (a + b)。
利用这些公式,我们可以解决一些与长方形相关的问题。
例如,已知一个长方形的面积为20平方米,我们可以通过面积公式计算出长和宽之间的关系。
如果长方形的长为4米,那么根据面积公式,可以得到宽为5米。
同样地,我们可以通过周长公式计算出周长为18米。
二、平行四边形的等积法公式平行四边形也是常见的几何形状之一。
通过等积法,我们可以推导出平行四边形的面积公式和周长公式。
假设平行四边形的底为a,高为h,面积为S。
根据等积法,我们可以得到以下公式:1. 面积公式:S = a * h;2. 周长公式:P = 2 * (a + b)。
利用这些公式,我们可以解决一些与平行四边形相关的问题。
例如,已知一个平行四边形的面积为24平方米,我们可以通过面积公式计算出底和高之间的关系。
如果底为6米,那么根据面积公式,可以得到高为4米。
同样地,我们可以通过周长公式计算出周长为20米。
三、圆的等积法公式圆是另一个常见的几何形状,通过等积法,我们可以推导出圆的面积公式和周长公式。
假设圆的半径为r,面积为S,周长为C。
根据等积法,我们可以得到以下公式:1. 面积公式:S = π * r^2,其中π是一个常数,约等于3.14159;2. 周长公式:C = 2 * π * r。
利用这些公式,我们可以解决一些与圆相关的问题。
例如,已知一个圆的半径为5厘米,我们可以通过面积公式计算出面积为78.53975平方厘米。
"等积法"在高考解题中的应用

S AA A1 曰 . ・ . 6 脚 h = a A 口 = A c = × s “ ‘ A Al 即三
J
2 、 /6
棱锥c . 一 A B B 的体积 为 。
6
二 求 点 到 平 面 的 距 离
总之 , 用等积法 的关键是找准问题 的角度 , 注意 观察 , 从不 同角度思考 , 充分利用 同一几何体体积不 B
,
B
…
. ・ .
1 x d x  ̄ 2
3
- 三 棱锥C , 肋 的体 积。
-- 2
图 3
分析: 利用 等体积代换求 出三棱锥的体积。
解 : 在 三 棱 柱 C — 1 日 C中 , 。 . ’ S△AB B =
2k F 6
.
=
,
故 异 面 直 线4 E 和G , 间 的距 离 为
知:
3 ×d×s = 1
× ×s
三 、 求体 积
如图3 , 正 三 棱 柱 A 曰 c —A B C 的 底 面 边 长
A I B j  ̄ B I B = ÷x 2 x 2 = 2 。
由 A I - B I F C  ̄ -
为3 , 侧锨 A =
三 求 B
A I B} Cl D{ 中, AA 1 = AB= 2, AD=
1 , 点 E、 F 、 G 分 别是D D. 、 A B、
C C 的 中点 , 求 异面 直线A E
和G F 的距 离 。
分析 :把 异而直线 问的距离转化为直线与平 面
问的距离 , 再转 化 为 点 1 BF . BD . s i n Z_ F BD : 1
.
— 一
等面积法求线段相等

等积法求相等的线段说题稿杨得封原题 :如图,AD 垂直平分BC ,D 为垂足,DM ⊥AC ,DN ⊥AB ,M ,N 分别为垂足,求证:DM=DNA一、说背景与价值此题选自人教版八年级上第十二章《12.3角平分线的性质》习题第二题。
解决此题涉及的知识有垂直的定义,垂直平分线的定义及性质,三角形全等的判定,角平分线的性质,三角形的面积等。
本习题是在学生学习三角形全等的判定定理“AAS 〞,及角平分线的性质的根底上给出的。
课本设置此练习的目的旨在稳固三角形全等的判定及角平分线的性质。
大局部学生想到利用三角形全等,然而解题的方法较多,需要学生发散思维,充分联系与求证,综合运用已学的知识来解决,在众多的方法中进行选优,从而获得一定的解题经验。
二、说教学与改良学生已经学会了三角形全等的判定定理“SSS 〞,“SAS 〞,“ASA 〞,“AAS 〞,对于证明相等的线段,根本上具备了解决此题的知识储藏和技能。
而学生往往会思维定势,联想到证明三角形全等,而无视了此时证明的是垂线段这个重要信息,缺乏相应的想象。
学生可能的做法:1、先证明△ADC ≅△ADB 得∠B=∠C ,再证明△DCM △DBN ,得到DM=DN ;2、先证明△ADC ≅△ADB 得∠CAD=∠BAD ,再证明△DAM ≅△DAN ,得到DM=DN ;3、先证明△ADC ≅△ADB 得AD 是角平分线,再利用角平分线的性质,得到DM=DN ;4、先由中垂线的性质证明AB=AC ,再由三角形的中线将三角形的面积二等分,得ADB ADC S S ∆∆=,由DM ⊥AC ,DN ⊥AB ,得到DM=DN 。
在原先的教学中,让学生思考后答复,发现大局部学生是第1,2种解法,很少出现第3,4的解法,然后再追问,还有其他的方法吗?能利用今天学过的知识来解决吗?能利用角平分线的性质吗?终于有了第3种方法,可是学生缺乏想象,这样的教学效果不好。
针对很少学生想出方法3,方法4,以及充分发挥这道题目的价值,在教学中进行如下的改良。
三角形等面积法的计算

三角形等面积法的计算
三角形等面积法是一种计算三角形面积的方法,它将三角形分成两个或多个子三角形,使得每个子三角形的面积容易计算,然后将它们的面积加起来得到完整三角形的面积。
这种方法特别适用于不规则三角形和无法使用海龙公式等简单公式计算面积的三角形。
具体的计算步骤如下:
1.将三角形分成两个或多个子三角形,使得每个子三角形的面积容易计算。
2.计算每个子三角形的面积。
可以使用海龙公式、高度乘以底边一半等方法计算。
3.将每个子三角形的面积加起来得到完整三角形的面积。
S(AOD)=1/2×AD×OD。
S(BOC)=1/2×BC×OC。
然后将两个子三角形的面积加起来得到完整三角形的面积:
S(ABC)=S(AOD)+S(BOC)=1/2×AD×OD+1/2×BC×OC。
其中,AD和BC是三角形ABC的两个底边,OD和OC是对应的高。
在计算过程中,需要注意底边和高的正确对应关系。
中考:等面积法
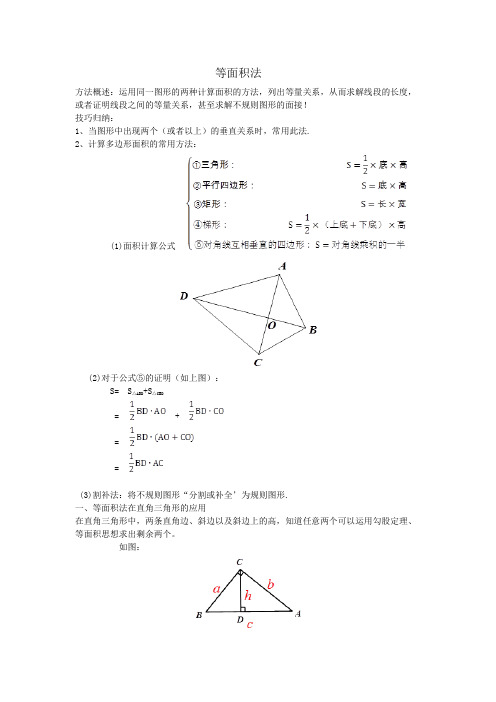
等面积法方法概述:运用同一图形的两种计算面积的方法,列出等量关系,从而求解线段的长度,或者证明线段之间的等量关系,甚至求解不规则图形的面接!技巧归纳:1、当图形中出现两个(或者以上)的垂直关系时,常用此法.2、计算多边形面积的常用方法:(1)面积计算公式(2)对于公式⑤的证明(如上图):S= S△ABD+S△CBD= +==(3)割补法:将不规则图形“分割或补全’为规则图形.一、等面积法在直角三角形的应用在直角三角形中,两条直角边、斜边以及斜边上的高,知道任意两个可以运用勾股定理、等面积思想求出剩余两个。
如图:基本公式: ①勾股定理:②等面积法:证明②:即:,例题1:如图,在Rt ABC ,∠C=90°,当直角边AC =4,斜边AB =5时,求该直角三角形斜边AB上的高CD ?例题2:如图,在Rt ABC (BC AC ) ,∠C=90°,当斜边AB =10cm,斜边AB上的高CD =4.8cm 时,求该直角三角形直角边AC和BC的长度?巩固练习:1、如图,在Rt ABC,∠C=90°,且AC=24, BC=7,作ABC 的三个内角的角平分线交于点P,再过点P 依次作PD⊥AB于D,作PE⊥BC于E, 作PF⊥AC于F .(1)求证:PD = PE = PF ;(2)求出:PD的值.2、如图,△ABC的顶点A,B,C在边长为1的正方形网格的格点上,则BC边长的高为()A.22二、等面积法在等腰三角形的应用在等腰三角形中,可以运用“割补法”的等面积思想,先建立有关“腰以及腰上的高”的等式,再通过等式两边约分来探索出线段之间的数量关系!例题1:如图,在△ABC 中, AB=AC, AC 边上的高BD=10cm.(1)如图1,求AB 边上高CE 的长;(2)如图2,若点P 为BC 边上任意一点, PM⊥AB 于点M, PN⊥AC 于点N,求PM+PN 的值;(3)如图3,若点P 为BC 延长线上任意一点,PM⊥AB 于M,PN⊥AC 于点N,在①PM+PN ;②PM PN 中有一个是定值,判断出来并求值.例题2:已知等边△ABC和内部一点P,设点P 到△ABC三边的AB、BC 、AC 的距离分别是h1,h2,h3,△ABC的高为h,问h1、h2、h3 与h 之间有怎样的数量关系?请说明理由。
【例题讲解】“等积法”求面积例 完整版课件
A M B
O
C ND
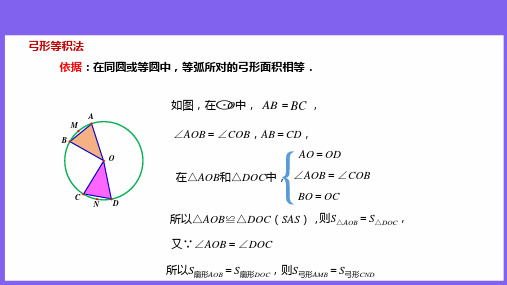
如图,在 O中, AB =BC ,
∠AOB=ห้องสมุดไป่ตู้COB,AB=CD, AO=OD
在△AOB和△DOC中, ∠AOB=∠COB BO=OC
所以△AOB≌△DOC(SAS),则S△AOB=S△DOC, 又∵∠AOB=∠DOC
所以S扇形AOB=S扇形DOC,则S弓形AMB=S弓形CND
∴∠AOE= ∠COD, ∴AE=CD=4, S弓形AME=S弓形CND,
在Rt△ABE中,根据勾股定理可得:BE2=AE2+AB2,∴BE= 82 42=4 5 .
∴S阴影=S半圆-SRt△ABE
=1 2
π
4
5 2
2
1 2
8
4=10
π-16.
主要利用了等弧所对的弓形面积相等,将阴影面积进行等积变换,起到简化的作用.
再见
例 点A、B、C、D是圆周上四点,AB CD AC BD ,弦AB=8,CD=4,求两个阴影部分的
面积之和.
A
B
分析
连接AE
弦AE等于弦CD
S弓形AME = S弓形CND
M
O
D
E
N
C
解答 作圆O的直径BE,连接AE,OA,OC,OD 则∠BAE=90°
∵ AB CD AC BD ∴∠AOB+∠COD= ∠AOC+∠BOD=180°, ,∵ ∠AOB+∠AOE=180°,
初二数学等面积法压轴题

初二数学等面积法压轴题
等面积法是解决几何问题的一种重要方法,特别是在求解压轴题时。
以下是一道典型的初二数学等面积法压轴题:
题目:
已知矩形ABCD,AB = 3,AD = 2,以A为圆心作图,设⊙A的半径为r,用等面积法求证:r > 2 - √7。
证明:
第一步,由于题目没有明确说明哪些图形与圆相切,我们首先考虑与圆相切的特殊情况。
假设⊙A与线段CD相切于点E,则AE为半径,即r = AE。
第二步,根据矩形的性质和勾股定理,我们有AE² + DE² = AD²。
代入已知的AB、AD和AE的值,我们可以得到一个关于DE的二次方程。
第三步,解这个二次方程,我们得到DE = √7 - 1。
由于DE < CD(因为CD = AB = 3),我们知道这种情况是不可能的。
第四步,为了证明r > 2 - √7,我们需要找到一个与⊙A相切且使得r满足这个不等式的切线。
考虑到线段CD与⊙A相切的情况,我们可以使用等面积法来找到这条切线。
第五步,根据等面积法,我们知道矩形的面积等于圆的面积加上四分之一圆的面积。
即3 × 2 = πr² - (1/4)πr²。
解这个方程,我们得到r = 2 + √7。
第六步,根据第五步的结果,我们得到r > 2 - √7。
综上,我们证明了r > 2 - √7。
完整word版面积——等面积法

面积法在中学数学解题中的巧用利用同一图形的面积相等,可以列方程计算线段的值,或证明线段间的数量关系;利用图形面积的和、差关系列方程,将相等的高或底约去,可以计算或证明线段间的数量关系。
利用等积变形,可以排除图形的干扰,实现“从形到数”的转化,从而从数量方面巧妙地解决问题。
用面积法解题就是根据题目给出的条件,利用等积变换原理和有关面积计算的公式、定理或图形的面积关系进行解题的方法。
运用面积法,巧设未知元,可获“柳暗花明”的效果。
有关面积的公式1(1)矩形的面积公式:S=长?宽(2)三角形的面积公式:ahS?2(3)平行四边形面积公式: S=底?高1(4)梯形面积公式: S=?(上底+下底)?高2(5)对角线互相垂直的四边形:S=对角线乘积的一半(如正方形、菱形等)有关面积的公理和定理1、面积公理(1)全等形的面积相等;(2)一个图形的面积等它各部分面积之和;2、相关定理(1)等底等高的两个三角形面积相等;夹在平行线间的两个共底的三角形面积相等;如下图;S=S△△BCDACDCD AB平行于反之,如果,则可知直线SS?BCD△△ACD(2)等底等高的平行四边形、梯形(梯形等底应理解为两底的和相等)的面积相等;(3)等底的三角形、平行四边形面积之比等于其高之比;等高的三角形、平行四边形面积之比等于其底之比;(4)相似三角形的面积的比等于相似比的平方;(5)在两个三角形中,若两边对应相等,其夹角互补,则这两个三角形面积相等;(6)等底等高的平行四边形面积是三角形面积的2倍。
一个长方形分成4个不同的三角形,绿色三角形面积是长方形面积的15%,平方厘米。
__________平方厘米。
问:长方形的面积是21黄色三角形的面积是等面积法的应用一:利用平行线间两个共底的三角形面积相等解题。
如图,矩形ABCD中,AB=3cm,AD=6cm,点E为AB边上的任意一点,四边形2,则 9 EFGB也是矩形,且EF=2BE Scm AFC△如图,在四边形ABCD中,动点P从点A开始沿A→B→C→D的路径匀速前进到D 为止。
2024年浙教版八年级上册数学期末培优复习第7招三角形中的等面积法

由【问题情境】中的结论可得 PG + PH = EQ .
∴ PG + PH =4.∴ PG + PH 的值为4.
返回
1
2
3
4
⊥ BE , PH ⊥ BC ,垂足分别为 G , H ,若 AD =8, CF =
3,求 PG + PH 的值.
返回
1
2
3
4
分类训练
【解】如图②,过点 E 作 EQ ⊥ BC ,垂足为 Q .
∵四边形 ABCD 是长方形,
∴ AD = BC ,∠ C =90°, AD ∥ BC .
∵ AD =8, CF =3,
又∵ AD ⊥ BC ,
∴3×4÷2=5× AD ÷2,
∴ AD =2.4.
返回
1
2
3
4
分类训练
2. 如图,正方形网格的每个小方格边长均为1,△ ABC 的顶
点在格点上.请求出 AC 边上的高线的长度 h .
返回
1
2
3
4
分类训练
【解】根据题意可得 AC = + =5,
S△ ABC = ×4×3-1- ×1×3- ×1×2= .利用等面
积法得 ×5× h = ,解得 h =1.
返回
1
2
3
4
分类训练
3. 如图,有一块直角三角形纸片,两直角边 AC =6 cm,
BC =8 cm,现将直角边 AC 沿直线 AD 折叠,使它落在斜
边 AB 上,且与 AE 重合,求 CD 的长.
【解】在Rt△ ABC 中, AC =6 cm, BC =8 cm,
平行线的等面积法

平行线的等面积法
平行线的等面积法是一种在几何学中常用的解题方法。
当两条平行线被一组横截线所截时,它们与横截线所围成的各个小图形的面积相等。
这个性质在解题中非常有用,特别是当我们需要证明某些几何关系或者求解某些几何量时。
使用平行线的等面积法,我们可以先确定一组平行线和一组横截线,然后观察它们所围成的各个小图形。
由于这些小图形的面积相等,我们可以利用这个性质来建立等式或者不等式,从而求解问题。
需要注意的是,平行线的等面积法只适用于平行线和横截线所围成的图形。
如果图形不满足这个条件,那么这个方法就不适用。
因此,在使用平行线的等面积法时,我们需要先仔细分析题目中的条件,确定是否可以使用这个方法。
梯形中的等面积法

梯形中的等面积法概述:梯形是一个具有四边的四边形,其中两条边是平行的。
在数学中,我们经常需要求解梯形的面积。
本文介绍一种名为“等面积法”的方法来解决求解梯形面积的问题。
方法:等面积法是一种简单而有效的方法,通过将梯形分割为两个三角形和一个矩形来求解梯形的面积。
具体步骤如下:1. 首先,绘制一条平行于梯形的基线,将梯形分成上下两个小梯形。
2. 通过绘制两条连接梯形顶点和基线的垂线,将梯形分割为两个三角形和一个矩形。
3. 分别计算两个三角形和一个矩形的面积。
4. 将两个三角形的面积相加,并减去矩形的面积,得到梯形的总面积。
范例:假设我们要计算一个梯形的面积,其中上底长为3厘米,下底长为7厘米,高为4厘米。
按照等面积法,我们可以如下计算:1. 将梯形分割为两个三角形和一个矩形,如图所示。
2. 计算上三角形的面积:(3 * 4) / 2 = 6平方厘米。
3. 计算下三角形的面积:(7 * 4) / 2 = 14平方厘米。
4. 计算矩形的面积:7 * 4 = 28平方厘米。
5. 计算梯形的面积:6 + 14 - 28 = -8平方厘米。
结论:通过等面积法,我们得出梯形的面积为-8平方厘米。
这个结果可能看起来不合理,因为一个几何图形的面积不应该是负数。
可能是在计算过程中出现了错误。
我们需要仔细检查每个步骤,确保计算正确。
总结:等面积法是求解梯形面积的一种简单方法。
分割梯形为三个几何图形并计算各个图形的面积,然后相加减去矩形的面积,可以得到梯形的总面积。
然而,在实际应用中,我们需要确保每个步骤的计算都正确,避免出现错误的结果。
等积转换法

等积转换法
等积法包括等面积法和等体积法.等积法的前提是几何图形(或几何体)的面积(或体积)通过已知条件可以得到,利用等积法可以用来求解几何图形的高或几何体的高,特别是在求三角形的高和三棱锥的高,这一方法回避了具体通过作图得到三角形(或三棱锥)的高,而通过直接计算得到高的数值.
“等积转换法”是针对当所给几何体的体积不能直接套用公式或涉及的某一量(底面积或高)不易求解时,可以转换一下几何体中有关元素的相对位置进行计算,该方法尤其适用于求三棱锥的体积.
【例解】 在边长为a 的正方体ABCD —A 1B 1C 1D 1中,M 、N 、P 分别是棱A 1B 1、A 1D 1、A 1A 上的点,且满足11112A M A B =
,112A N ND =,1134
A P A A =,如图,试求三棱锥A 1—MNP 的体积.
分析 若用公式13V sh =直接计算三棱锥A 1
—MNP 的体积,则需要求出△MNP 的面积和该三棱锥的高,两者显然都不易求出,但若将三棱锥A 1—MNP 的顶点和
底面转换一下,变为求三棱锥P —A 1MN 的体积,显然就容易解答了.
解析
点评 转换顶点和底面是求三棱锥体积的一种常用的方法,也是求后面要学习到的求点到平面距离的一个理论依据,相应的方法叫等积法.
MN A P MNP A V V 11--=.24
1433221213121313111a a a a P A N A M A =⋅⋅⨯⨯=⋅⋅⋅⨯=。
三角形等面积法在初中教学中的应用

三角形等面积法在初中教学中的应用摘要:关于三角形等面积法是近些年初中数学的一种常规解题思路,它的优势在于可以更加快速的找到解题关键,将一些晦涩难懂的知识点变得简单化。
本文将结合现有的一些典型例题,利用三角形等面积法解决相关问题,以此来培养学生的数学思维,提高学生的解题能力。
关键词:三角形等面积法;初中数学;具体应用前言:在现有的初中数学教学中,采用三角形等面积法是一个比较快捷实用的方法,结合几年的教学经验可以发现,即便部分几何题目的问题并没有涉及到三角形的面积计算,但是我们却可以按照图形进行数形结合,将其与实际问题相联系,进而解决这类问题一、分析三角形之间的相关联系,提升学生简单几何的能力在解决三角形的面积时,通常会利用到三角形的边长以及角度之间的关系。
尤其是在一些几何题目当中可能会让你求解一些与已知条件看似毫无关系的边长和角度,此时,很多同学就会将问题复杂化,但实际上如果你仔细观察就会发现,这道题很可能就是利用了三角形的等面积公式,将一个复杂的几何问题转变为一个解方程的题目,而这类题型的实际目的就是让学生发现图形中图形之间的关系,培养学生的数学几何能力,采用“以数解形”的思想,了解几何题背后的实际含义。
例题1如图,直角三角形ABC中,∠ACB=90°BC=4,AC=4,求CD的长度图1解:∵根据勾股定理可知,AB²=AC²+BC²∴AB=4又∵S△ABC=AB*CD/2=AC*BC/2即4*CD/2=4*4/2∴CD=4二、熟悉三角形的基本属性,培养学生的空间想象能力在一些复杂的几何题目中,通常会将圆、平行四边形等图形与三角形结合起来,此时学生不仅要熟知三角形的一些基本定理,尤其是等腰三角形、等边三角形等特殊图形,要充分利用45°、60°等角度。
同时也要熟悉相关图形的定理,做到活学活用,最后看能否利用等面积法将几何问题转换为简单方程,进而更快速的求解题目。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
“等积法”在勾股定理中的应用
一、“等积法”
用不同的方法.....
表示同一个图形的面积,结果相等。
[分析]1、当所表示的图形是“规则”的图形时,(如三角形、平行四边形、矩形、正方形、梯形等可以用面积公式计算),“不同的方法”指的是①直接用面积公式表示②其他图形面积的和或差表示。
2、当所表示的图形是“不规则”的图形时,“不同的方法”指的是:“割”或“补”。
二、勾股定理的证明
证法一:如图,用四个全等的直角三角形拼成下图,运用“等积法”证明勾股定理
证法二:如图,用四个全等的直角三角形拼成下图,运用“等积法”证明勾股定
理
D G C F A H
E B a b c
a b c a b c a b c b a c G D A C B
F E H
证法三:如图,用两个全等的直角三角形拼成下图,运用“等积法”证明勾股定理
三、“等积法”的练习
1、利用“等积法”证明:“等腰三角形底边上任意一点到两腰的距离和等于一腰上的高”
2、如图,矩形ABCD中,AC、BD交于O点,B E⊥AC于E,C F⊥BD于F,
求证:BE=CF
四、“等积法”的拓展应用
1、“同底等高”
2、“等底同高”
3、两个三角形高相等,底成倍数关系,面积也成同样的倍数关系;同理,两个三角形底相等、高成倍数关系,面积也成同样的倍数关系。
例:梯形ABCD 中,AD ∥BC ,对角线AC 、BD 交
于O 点,AO:CO=1:2,
求:AOD S ∆:COD S ∆=?
【补充】
勾股定理--证法四:
如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D .
利用相似三角形的性质说明:222c b a =+
证法五:“青朱出入图”
(自己动手完成)
A B
D C
a
c b
你还收集了哪些证明勾股定理的方法?。
