【数学】培优易错试卷相似辅导专题训练含详细答案

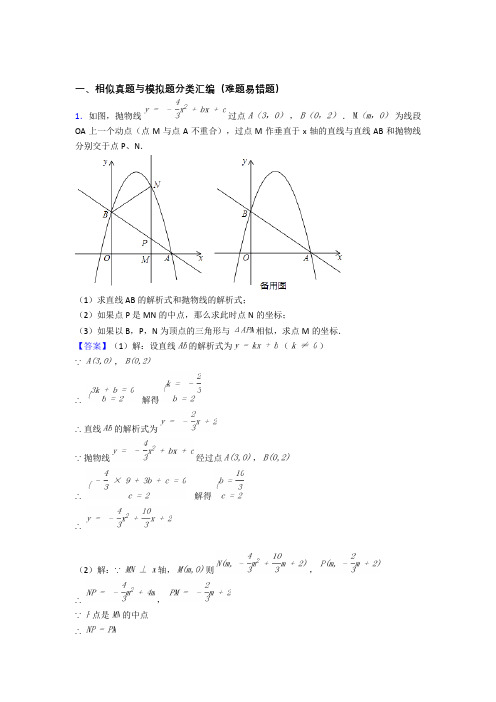
一、相似真题与模拟题分类汇编（难题易错题）1．如图，在△ABC中，∠C＝90°，AC＝8，BC＝6。

P是AB边上的一个动点（异于A、B两点），过点P分别作AC、BC边的垂线，垂足为M、N设AP=x.（1）在△ABC中，AB＝ ________；（2）当x＝________时，矩形PMCN的周长是14；（3）是否存在x的值，使得△PAM的面积、△PBN的面积与矩形PMCN的面积同时相等？请说出你的判断，并加以说明。

【答案】（1）10（2）5（3）解：∵PM⊥AC，PN⊥BC，∴∠AMP=∠PNB=∠C=90º.∴AC∥PN，∠A=∠NPB.∴△AMP∽△PNB∽△ABC.当P为AB中点时，可得△AMP≌△PNB此时S△AMP=S△PNB= ×4×3=6而S矩形PMCN=PM·MC=3×4=12.所以不存在x的值，能使△AMP的面积、△PNB的面积与矩形PMCN面积同时相等.【解析】【解答】（1）∵△ABC为直角三角形，且AC=8，BC=6，（ 2 ）∵PM⊥AC PN⊥BC∴MP∥BC，AC∥PN（垂直于同一条直线的两条直线平行），∴，∵AP=x，AB=10，BC=6，AC=8，BP=10-x，∴矩形PMCN周长=2（PM+PN）=2（ x+8- x）=14，解得x=5；【分析】在△ABC中，∠C=90°，AC=8，BC=6根据勾股定理，可求出AB的长；AP=x，可以得到矩形PMCN的周长的表达式，构造方程，解方程得到x值.可以证明△AMP∽△PNB∽△ABC，只有当P为AB中点时，可得△AMP≌△PNB，此时S△AMP=S△PNB，分别求出当P为AB中点时△PAM的面积、△PBN的面积与矩形PMCN的面积比较即可.2．如图,在一间黑屋子里用一盏白炽灯照一个球.（1）球在地面上的影子是什么形状?（2）当把白炽灯向上平移时,影子的大小会怎样变化?（3）若白炽灯到球心的距离是1 m,到地面的距离是3 m,球的半径是0.2 m,则球在地面上影子的面积是多少?【答案】（1）解：球在地面上的影子的形状是圆.（2）解：当把白炽灯向上平移时,影子会变小.（3）解：由已知可作轴截面，如图所示：依题可得：OE=1 m，AE=0.2 m，OF=3 m，AB⊥OF于H，在Rt△OAE中，∴OA= = = (m)，∵∠AOH=∠EOA，∠AHO=∠EAO=90°，∴△OAH∽△OEA，∴，∴OH= == (m)，又∵∠OAE=∠AHE=90°，∠AEO=∠HEA，∴△OAE∽△AHE，∴ = ，∴AH= ==2625 (m).依题可得：△AHO∽△CFO，∴ AHCF=OHOF ，∴CF= AH⋅OFOH = 2625×32425=64 (m)，∴S影子=π·CF2=π· (64)2 = 38 π=0.375π(m2).答：球在地面上影子的面积是0.375π m2.【解析】【分析】（1）球在灯光的正下方，根据中心投影的特点可得影子是圆.（2）根据中心投影的特点：在灯光下，离点光源近的物体它的影子短，离点光源远的物体它的影子长；所以白炽灯向上移时，阴影会逐渐变小.（3）作轴截面（如图）由相似三角形的判定得三组三角形相似，再根据相似三角形的性质对应边成比例，可求得阴影的半径，再根据面积公式即可求出面积.3．已知直线m∥n，点C是直线m上一点，点D是直线n上一点，CD与直线m、n不垂直，点P为线段CD的中点．（1）操作发现：直线l⊥m，l⊥n，垂足分别为A、B，当点A与点C重合时（如图①所示），连接PB，请直接写出线段PA与PB的数量关系：________．（2）猜想证明：在图①的情况下，把直线l向上平移到如图②的位置，试问（1）中的PA与PB的关系式是否仍然成立？若成立，请证明；若不成立，请说明理由．（3）延伸探究：在图②的情况下，把直线l绕点A旋转，使得∠APB=90°（如图③所示），若两平行线m、n之间的距离为2k．求证：PA•PB=k•AB．【答案】（1）PA=PB（2）解：把直线l向上平移到如图②的位置，PA=PB仍然成立，理由如下：如图②，过C作CE⊥n于点E，连接PE，，∵三角形CED是直角三角形，点P为线段CD的中点，∴PD=PE，∴PC=PE；∵PD=PE，∴∠CDE=∠PEB，∵直线m∥n，∴∠CDE=∠PCA，∴∠PCA=∠PEB，又∵直线l⊥m，l⊥n，CE⊥m，CE⊥n，∴l∥CE，∴AC=BE，在△PAC和△PBE中，∴△PAC∽△PBE，∴PA=PB（3）解：如图③，延长AP交直线n于点F，作AE⊥BD于点E，，∵直线m∥n，∴，∴AP=PF，∵∠APB=90°，∴BP⊥AF，又∵AP=PF，∴BF=AB；在△AEF和△BPF中，∴△AEF∽△BPF，∴，∴AF•BP=AE•BF，∵AF=2PA，AE=2k，BF=AB，∴2PA•PB=2k．AB，∴PA•PB=k•AB．【解析】【解答】解：（1）∵l⊥n，∴BC⊥BD，∴三角形CBD是直角三角形，又∵点P 为线段CD的中点，∴PA=PB．【分析】（1）根据直角三角形斜边上的中线等于斜边上的一半；（2）把直线l向上平移到如图②的位置，PA=PB仍然成立，理由如下：如图②，过C作CE⊥n于点E，连接PE，根据直角三角形斜边上的中线等于斜边上的一半得出PD=PE=PC，根据等边对等角得出∠CDE=∠PEB，根据二直线平行，内错角相等得出∠CDE=∠PCA，故∠PCA=∠PEB，根据夹在两平行线间的平行线相等得出AC=BE，然后利用SAS判断出△PAC∽△PBE，根据全等三角形的对应边相等得出PA=PB；（3）如图③，延长AP交直线n于点F，作AE⊥BD于点E，根据平行线分线段成比例定理得出AP=PF，根据线段垂直平分线上的点到线段两个端点的距离相等得出BF=AB；然后判断出△AEF∽△BPF，根据相似三角形的对应边成比例即可得出AF•BP=AE•BF，根据等量代换得出2PA•PB=2k．AB，即PA•PB=k•AB．4．如图，已知AB是⊙O的直径，点C在⊙O上，过点C的直线与AB的延长线交于点P，AC=PC，∠COB=2∠PCB.（1）求证：PC是⊙O的切线；（2）求证：BC= AB；（3）点M是弧AB的中点，CM交AB于点N，若AB=4，求MN MC的值.【答案】（1）证明：∵OA=OC，∴∠A=∠ACO，又∵∠COB=2∠A，∠COB=2∠PCB，∴∠A=∠ACO=∠PCB，又∵AB是⊙O的直径，∴∠ACO+∠OCB=90°，∴∠PCB+∠OCB=90°，即OC⊥CP，∵OC是⊙O的半径，∴PC是⊙O的切线（2）证明：∵AC=PC，∴∠A=∠P，∴∠A=∠ACO=∠PCB=∠P．又∵∠COB=∠A+∠ACO，∠CBO=∠P+∠PCB，∴∠COB=∠CBO，∴BC=OC，∴（3）解：连接MA，MB，∵点M是弧AB的中点，∴弧AM=弧BM，∴∠ACM=∠BCM，∵∠ACM=∠ABM，∴∠BCM=∠ABM，∵∠BMN=∠BMC，∴△MBN∽△MCB，∴，∴ BM2=MN⋅MC ，又∵AB是⊙O的直径，弧AM=弧BM，∴∠AMB=90°，AM=BM，∵AB=4，∴，∴ MN⋅MC=BM2=8 ．【解析】【分析】(1)根据等边对等角得出∠A=∠ACO，运用外角的性质和已知条件得出∠A=∠ACO=∠PCB，再根据直径所对的圆周角是直角得出∠PCB+∠OCB=90°，进而求解.（2）根据等边对等角得出∠A=∠P，再根据第一问中的结论求解即可，（3）连接MA，MB，根据同弧或等弧所对的圆周角相等得出∠ACM=∠ABM，∴∠BCM=∠ABM，证出△MBN∽△MCB，得出比例式进而求解即可.5．如图1，在矩形ABCD中，AB=6cm，BC=8cm，E、F分别是AB、BD的中点，连接EF，点P从点E出发，沿EF方向匀速运动，速度为1cm/s，同时，点Q从点D出发，沿DB方向匀速运动，速度为2cm/s，当点P停止运动时，点Q也停止运动．连接PQ，设运动时间为t（0＜t＜4）s，解答下列问题：（1）求证：△BEF∽△DCB；（2）当点Q在线段DF上运动时，若△PQF的面积为0.6cm2，求t的值；（3）如图2过点Q作QG⊥AB，垂足为G，当t为何值时，四边形EPQG为矩形，请说明理由；（4）当t为何值时，△PQF为等腰三角形？试说明理由．【答案】（1）解：∵四边形是矩形，在中，分别是的中点，（2）解：如图1，过点作于，（舍）或秒（3）解：四边形为矩形时,如图所示：解得：（4）解：当点在上时，如图2，当点在上时，如图3，时，如图4，时，如图5，综上所述，或或或秒时，是等腰三角形【解析】【分析】（1）要证△BEF∽△DCB，根据有两对角对应相等的两个三角形相似可得证。

根据三角形中位线定理可得EF∥AD∥BC，可得一组内错角相等，由矩形的性质可得∠C=∠A=∠BEF=，所以△BEF∽△DCB；（2）过点Q 作QM⊥EF于M，结合已知易得QM∥BE，根据相似三角形的判定可得△QMF∽△BEF，则得比例式,QM可用含t的代数式表示，PF=4-t，所以三角形PQF的面积=QM PF=06，解方程可得t的值；（3）因为QG⊥AB，结合题意可得PQ AB，根据相似三角形的判定可得QPF BEF，于是可得比例式求解；（4）因为Q在对角线BD上运动，情况不唯一。

当点Q在DF上运动时，PF=QF；当点Q在BF上运动时，分三种情况：第一种情况;PF =QF ;第二种情况：PQ=PF；第三种情况：PQ=FQ。

6．已知菱形的一个角与三角形的一个角重合，然后它的对角顶点在这个重合角的对边上，这个菱形称为这个三角形的亲密菱形，如图，在△CFE中，CF=6,CE=12,∠FCE=45°,以点C为圆心，以任意长为半径作AD，再分别以点A和点D为圆心，大于 AD长为半径做弧，交于点B,AB∥CD.（1）求证：四边形ACDB为△CFE的亲密菱形；（2）求四边形ACDB的面积.【答案】（1）证明：由已知得：AC=CD,AB=DB,由已知尺规作图痕迹得：BC是∠FCE的角平分线,∴∠ACB=∠DCB，又∵AB∥CD,∴∠ABC=∠DCB，∴∠ACB=∠ABC，∴AC=AB，又∵AC=CD,AB=DB,∴AC=CD=DB=BA，四边形ACDB是菱形，又∵∠ACD与△FCE中的∠FCE重合，它的对角∠ABD顶点在EF上，∴四边形ACDB为△FEC的亲密菱形.（2）解：设菱形ACDB的边长为x，∵CF=6,CE=12,∴FA=6-x，又∵AB∥CE,∴△FAB∽△FCE,∴ ,即，解得：x=4，过点A作AH⊥CD于点H,在Rt△ACH中，∠ACH=45°,∴sin∠ACH= ,∴AH=4× =2 ,∴四边形ACDB的面积为： .【解析】【分析】（1）依题可得：AC=CD,AB=DB,BC是∠FCE的角平分线,根据角平分线的定义和平行线的性质得∠ACB=∠ABC，根据等角对等边得AC=AB，从而得AC=CD=DB=BA，根据四边相等得四边形是菱形即可得四边形ACDB是菱形；再根据题中的新定义即可得证.（2）设菱形ACDB的边长为x，根据已知可得CF=6,CE=12,FA=6-x，根据相似三角形的判定和性质可得，解得：x=4,过点A作AH⊥CD于点H,在Rt△ACH中，根据锐角三角形函数正弦的定义即可求得AH ,再由四边形的面积公式即可得答案.7．如图，抛物线y=ax2+bx+c过原点O、点A （2，﹣4）、点B （3，﹣3），与x轴交于点C，直线AB交x轴于点D，交y轴于点E．（1）求抛物线的函数表达式和顶点坐标；（2）直线AF⊥x轴，垂足为点F，AF上取一点G，使△GBA∽△AOD，求此时点G的坐标；（3）过直线AF左侧的抛物线上点M作直线AB的垂线，垂足为点N，若∠BMN=∠OAF，求直线BM的函数表达式．【答案】（1）解：将原点O（0,0）、点 A （2，﹣4）、点 B （3，﹣3），分别代入y=ax2+bx+c，得，解得，∴y=x2-4x= ，∴顶点为（2，-4）.（2）解：设直线AB为y=kx+b，由点A（2，-4），B（3，-3），得解得，∴直线AB为y=x-6.当y=0时，x=6，∴点D（6，0）.∵点A（2，-4），D（6,0），B（3，-3），∴OA= ，OD=6，AD= ，AF=4，OF=2，DF=4，AB= ，∴DF=AF，又∵AF⊥x轴，∴∠AD0=∠DAF=45°，∵△GBA∽△AOD，∴，∴，解得，∴FG=AF-AG=4- ，∴点G（2，）.（3）解：如图1，∵∠BMN=∠OAF，，∴∠MBN=∠AOF，设直线BM与AF交于点H，∵∠ABH=∠AOD，∠HAB=∠ADO，∴∴，则，解得AH= ，∴H（2，）.设直线BM为y=kx+b，∵将点B、G的坐标代入得，解得．∴直线BM的解析式为y= ；如图2，BD=AD-AB= ．∵∠BMN=∠OAF，∠GDB=∠ODA，∴△HBD∽△AOD．∴，即，解得DH=4．∴点H的坐标为（2，0）．设直线BM的解析式为y=kx+b．∵将点B和点G的坐标代入得：，解得k=-3，b=6．∴直线BM的解析式为y=-3x+6．综上所述，直线MB的解析式为y= 或y=-3x+6．【解析】【分析】（1）将原点O（0,0）、点A （2，﹣4）、点B （3，﹣3），分别代入y=ax2+bx+c，联立方程组解答即可a,b,c的值，得到二次函数解析式；将解析式配成顶点式，可得顶点；（2）由△GBA∽△AOD，可得，分别求出AD，AB，OD的长即可求出AG，由点A的坐标，即可求出点G；（3）点M在直线AF的左侧，可发出垂足N可以在线段AB上，也可以在AB的延长线上，故有如图1和如图2两种可能；设直线BM与直线AF的交点为H，由（2）可知，参加（2）的方法可求出点H的坐标，从而求出直线BM的解析式.8．如图，正方形、等腰的顶点在对角线上(点与、不重合)，与交于，延长线与交于点，连接 .（1）求证： .（2）求证：（3）若，求的值.【答案】（1）解：∵是正方形，∴，，∵是等腰三角形，∴，，∴，∴，∴（2）解：∵是正方形，∴，，∵是等腰三角形，∴，∵，∵，∴，∴，∴，∴，∴，（3）解：由(1)得，，，∴，由(2) ，∴，∵，∴，在中，，∴【解析】【分析】（1）证出∠ABP=∠CBQ，由SAS证明△ABP≌△CBQ可得结论；（2）根据正方形的性质和全等三角形的性质得到，∠APF=∠ABP，可证明△APF∽△ABP，再根据相似三角形的性质即可求解；（3）根据全等三角形的性质得到∠BCQ=∠BAC=45°，可得∠PCQ=90°，根据三角函数和已知条件得到，由（2）可得，等量代换可得∠CBQ=∠CPQ即可求解．9．已知二次函数y=ax2+bx+3的图象分别与x轴交于点A（3，0），C（-1，0），与y轴交于点B．点D为二次函数图象的顶点．（1）如图①所示，求此二次函数的关系式：（2）如图②所示，在x轴上取一动点P（m， 0），且1＜m＜3，过点P作x轴的垂线分别交二次函数图象、线段AD，AB于点Q、F，E，求证：EF=EP；（3）在图①中，若R为y轴上的一个动点，连接AR，则BR+AR的最小值________（直接写出结果）．【答案】（1）解：将A（3，0），C（-1，0）代入y=ax2+bx+3，得：，解得：，∴此二次函数的关系式为y=-x2+2x+3（2）证明：∵y=-x2+2x+3=-（x-1）2+4，∴点D的坐标为（1，4）．设线段AB所在直线的函数关系式为y=kx+c（k≠0），将A（3，0），C（0，3）代入y=kx+c，得：，解得：，∴线段AB所在直线的函数关系式为y=-x+3．同理，可得出：线段AD所在直线的函数关系式为y=-2x+6．∵点P的坐标为（m，0），∴点E的坐标为（m，-m+3），点F的坐标为（m，-2m+6），∴EP=-m+3，EF=-m+3，∴EF=EP．（3）【解析】【解答】解（3）如图③，连接BC，过点R作RQ⊥BC，垂足为Q．∵OC=1，OB=3，∴BC= ．(勾股定理)∵∠CBO=∠CBO，∠BOC=∠BQR=90°，∴△BQR∽△AOB，∴ ,即 ,∴RQ= BR，∴AR+ BR=AR+RQ，∴当A，R，Q共线且垂直AB时，即AR+ BR=AQ时，其值最小．∵∠ACQ=∠BCO，∠BOC=∠AQC，∴△CQA∽△COB，∴ ,即∴AQ= ，∴ BR+CR的最小值为．故答案为：．【分析】（1）根据A，C点的坐标，利用待定系数法可求出二次函数的关系式；（2）利用待定系数法求出线段AB，AD所在直线的函数关系式，用m表示EF，EP的长，可证得结论；（3）连接BC，过点R作RQ⊥BC，垂足为Q，则△BQR∽△AOB，利用相似三角形的性质可得出RQ= BR，结合点到直线之间垂直线段最短可得出当A，R，Q共线且垂直AB时，即AR+ BR=AQ时，其值最小，由∠ACQ=∠BCO，∠BOC=∠AQC可得出△CQA∽△COB，利用相似三角形的性质可求出AQ的值，此题得解．10．如图，在平面直角坐标系中，平行四边形ABOC如图放置，将此平行四边形绕点O顺时针旋转90°得到平行四边形A′B′OC′．抛物线y＝﹣x2+2x+3经过点A、C、A′三点．（1）求A、A′、C三点的坐标；（2）求平行四边形ABOC和平行四边形A′B′OC′重叠部分△C′OD的面积；（3）点M是第一象限内抛物线上的一动点，问点M在何处时，△AMA′的面积最大？最大面积是多少？并写出此时M的坐标．【答案】（1）解：当y＝0时，﹣x2+2x+3＝0，解得x1＝3，x2＝﹣1，则C（﹣1，0），A′（3，0），当x＝0时，y＝3，则A（0，3）（2）解：∵四边形ABOC为平行四边形，∴AB OC，AB＝OC，而C（﹣1，0），A（0，3），∴B（1，3），∴OB＝＝，S△AOB＝ ×3×1＝，又∵平行四边形ABOC旋转90°得平行四边形A′B′OC′，∴∠ACO＝∠OC′D，OC′＝OC＝1，又∵∠ACO＝∠ABO，∴∠ABO＝∠OC′D．又∵∠C′OD＝∠AOB，∴△C′OD∽△BOA，∴＝( )2＝（）2＝，∴S△C′OD＝ × ＝（3）解：设M点的坐标为（m，﹣m2+2m+3），0＜m＜3，作MN y轴交直线AA′于N，易得直线AA′的解析式为y＝﹣x+3，则N（m，﹣m+3），∵MN＝﹣m2+2m+3﹣（﹣m+3）＝﹣m2+3m，∴S△AMA′＝S△ANM+S△MNA′＝MN•3＝（﹣m2+3m）＝﹣m2+ m＝﹣（m﹣）2+ ，∴当m＝时，S△AMA'的值最大，最大值为，此时M点坐标为（，）．【解析】【分析】（1）利用抛物线与x轴的交点问题可求出C（﹣1，0），A′（3，0）；计算自变量为0时的函数值可得到A（0，3）；（2）先由平行四边形的性质得AB∥OC，AB＝OC，易得B（1，3），根据勾股定理和三角形面积公式得到OB＝，S△AOB＝，再根据旋转的性质得∠ACO＝∠OC′D，OC′＝OC＝1，接着证明△C′OD∽△BOA，利用相似三角形的性质得＝( )2，则可计算出S△C′OD；（3）根据二次函数图象上点的坐标特征，设M点的坐标为（m，﹣m2+2m+3），0＜m＜3，作MN y轴交直线AA′于N，求出直线AA′的解析式为y＝﹣x+3，则N（m，﹣m+3），于是可计算出MN＝﹣m2+3m，再利用S△AMA′＝S△ANM+S△MNA′和三角形面积公式得到S△AMA′＝﹣m2+ m，然后根据二次函数的最值问题求出△AMA′的面积最大值，同时即可确定此时M点的坐标．11．如图，半径为4且以坐标原点为圆心的圆O交x轴，y轴于点B、D、A、C，过圆上的动点不与A重合作，且在AP右侧．（1）当P与C重合时，求出E点坐标；（2）连接PC，当时，求点P的坐标；（3）连接OE，直接写出线段OE的取值范围．【答案】（1）解：当P与C重合时，，的半径为4，且在AP右侧，，点坐标为；（2）解：如图，作于点F，为的直径，，，∽，，，，，，点P的坐标为或；（3）解：如图，连结OP，OE，AB，BE，AE，，都为等腰直角三角形，，，，∽，，，，【解析】【分析】当P与C重合时，因为，的半径为4，且在AP右侧，所以，所以E点坐标为；作于点F，证明∽，可求得CF长，在中求得PF的长，进而得出点P的坐标；连结OP，OE，AB，BE，AE，证明∽，可得，根据，即可得出OE的取值范围．12．抛物线y=ax2+bx+3（a≠0）经过点A（﹣1，0），B（，0），且与y轴相交于点C．（1）求这条抛物线的表达式；（2）求∠ACB的度数；（3）设点D是所求抛物线第一象限上一点，且在对称轴的右侧，点E在线段AC上，且DE⊥AC，当△DCE与△AOC相似时，求点D的坐标．【答案】（1）解：当x=0，y=3，∴C（0,3）设抛物线的解析式为y=a(x+1)(x- ).将c（0，3）代入得：- a=3，解得a=2，∴抛物线的解析式为y=-2x2+x+3（2）解：过点B作BM⊥AC，垂足为M，过点M作MN⊥OA，垂足为N。