距离保护的振荡闭锁
距离保护断线闭锁及振荡闭锁
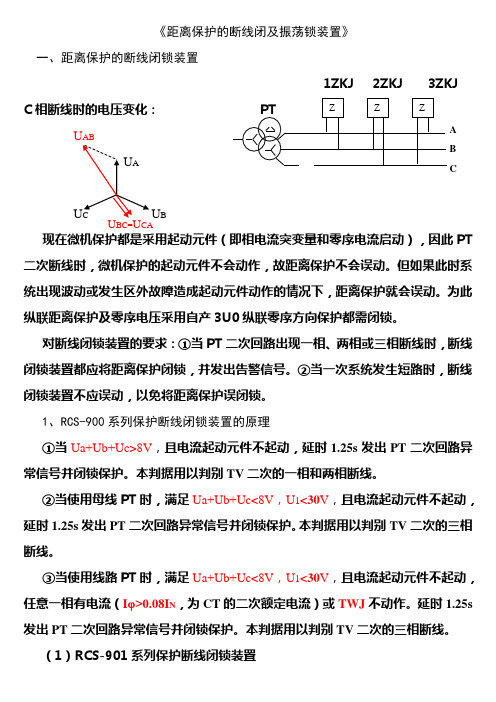
《距离保护的断线闭及振荡锁装置》一、距离保护的断线闭锁装置1ZKJ 2ZKJ 3ZKJC 相断线时的电压变化:ABU B 现在微机保护都是采用起动元件(即相电流突变量和零序电流启动),因此PT 二次断线时,微机保护的起动元件不会动作,故距离保护不会误动。
但如果此时系统出现波动或发生区外故障造成起动元件动作的情况下,距离保护就会误动。
为此纵联距离保护及零序电压采用自产3U0纵联零序方向保护都需闭锁。
对断线闭锁装置的要求:①当PT 二次回路出现一相、两相或三相断线时,断线闭锁装置都应将距离保护闭锁,并发出告警信号。
②当一次系统发生短路时,断线闭锁装置不应误动,以免将距离保护误闭锁。
1、RCS-900系列保护断线闭锁装置的原理①当Ua+Ub+Uc >8V ,且电流起动元件不起动,延时1.25s 发出PT 二次回路异常信号并闭锁保护。
本判据用以判别TV 二次的一相和两相断线。
②当使用母线PT 时,满足Ua+Ub+Uc <8V ,U 1<30V ,且电流起动元件不起动,延时1.25s 发出PT 二次回路异常信号并闭锁保护。
本判据用以判别TV 二次的三相断线。
③当使用线路PT 时,满足Ua+Ub+Uc <8V ,U 1<30V ,且电流起动元件不起动,任意一相有电流(I φ>0.08I N ,为CT 的二次额定电流)或TWJ 不动作。
延时1.25s 发出PT 二次回路异常信号并闭锁保护。
本判据用以判别TV 二次的三相断线。
(1)RCS-901系列保护断线闭锁装置A B CBC=CATV断线信号动作的同时,将纵联变化量方向和纵联零序退出,保留工频变化量阻抗元件,退出距离保护,自动投入TV断线相过流和TV断线相零序过流保护,TV断线相过流保护由距离保护压板投退,TV断线相零序过流保护由零序保护压板投退。
对于零序过电流保护,RCS-901A将零序II段退出,III段不经方向元件控制;RCS-901B将零序I、II段退出,IV段不经方向元件控制,若“零序III段经方向”,则退出III段零序方向过流。
电力系统继电保护原理-距离保护的振荡闭锁

M侧:
Zm
U
M
IM
EM IM
IM
ZM
EM
IM
ZM
1
Z e
j
ZM
∵
1- e jδ
= 1-
2 jctgδ
2
∴
Z
=
m
Z∑ (12
jctgδ2
)
-
ZM
=
(
Z∑ 2
- ZM)-
j
Z∑ 2
ctgδ2
7
Z
=
m
Z∑ (12
jctgδ2
)
-ZMΒιβλιοθήκη =(Z∑ 2
- ZM)-
j
Z∑ 2
ctgδ2
jX O’
Zm
N
Z∑ 2
17
3.5.4 振荡过程中再故障的判断
振荡过程中又发生不对称短路,判据:
I2 I0 m I1
振荡过程中又发生三相短路,判据:
U cos:近似为电弧电压,其值一般不会超过6%额
定电压,且与故障距离无关,基本不随时间 变化,振荡时,短时满足;短路时,一直满 足。
0.03p.u. U cos 0.08p.u.
响,但Ⅱ、 Ⅲ段定值较大,振荡时的测量阻抗比较
容易进入其动作区。
10
系统振荡时,阻抗继电器是 否误动、误动的时间长短与:
•
保护安装位置
•
保护动作范围
•
动作特性的形状
•
振荡周期长短等有关
11
4. 振荡与短路的区别:
①从电流和各点电压的幅值的变化上看:
振荡:作周期性变化 短路: di du 大
dt dt
3.5 距离保护的振荡闭锁
继电保护47振荡闭锁闭锁

s
2
180 时,阻抗变化率最小,即
dZ m dt
m in
Z 1 4
s
4.7 距离保护振荡闭锁
因
s
2
Tswi
,据统计,振荡周
期最大值为3s,于是
s
m in
2
3
测量阻抗变化率为
≥ dZ m dt
Z 1
6
只要适当选择保护 开放条件,可保证 保护不误动。
arg Z1
4.7 距离保护振荡闭锁
设两侧电源不相等,设 EM Ke EN e j
保护安装处电压、电流表示为:
UM K e EN e j Iswi Z M1
设电势相等,则
Iswi
EN Z 1
(Kee
j
1)
相角差为:
ctg
arctg
图中 ___
OZ E cos
2
___
PQ 2E sin
2
___
PZ E sin
2
、令
m Z M1 / Z1
则 ___ ___
m PM/ PQ
,所以
___
PM
2mE sin
2
___ ____
MZ PZ PM ( 1 2m )E sin
2
于是
UM
(E cos )2 [(1 2m)E sin ]2
2
2
E 1 4m(1 m) sin 2
2
4.7 距离保护振荡闭锁
0 有UM E ,M母线电压最高。
电力系统继电保护 ——距离保护振荡闭锁、故障类型判别和故障选相、距离保护特殊问题的分析、工频故障分量

[0] [0] [0] ICA ( IC I A ) ( IC I [0] ) ( I I ) ( I I C A A C A ) I C I A
U M EM I M Z M EM 1 Zm ZM Z ZM j IM IM IM 1 e
1 e
j
1 cos j sin
2 1 jctg 2
一、距离保护的振荡闭锁
EM
M 1
I
2
N
EN
1 Z m Z Z M 2
过渡电阻对接地距离元件的影响要大于对相间距离元件的影 响。
三、距离保护特殊问题的分析
线路串联补偿电容对距离保护的影响:
串联补偿电容的存在会对距离保护产生十分严重的影响。
(1)采用直线型动作特性克服反方向误动
(2)用负序功率方向元件闭锁误动的距离保护 (3)选取故障前的记忆电压为参考电压来克服串联补偿电 容的影响 (4)通过整定计算来减小串联补偿电容的影响 补偿度可调的可控串补TCSC -电力系统电力电子化
振荡时,若阻抗测量元件误动作,则在一个振荡周期内动作 和返回各一次;短路时,可能动作,可能不动作。
利用系统短路时的负序、零序分量或电流突然变化,短路开 放保护,实现振荡闭锁 利用测量阻抗变化率不同构成振荡闭锁 利用动作的延时实现振荡闭锁
距离保护的振荡闭锁措施
二、故障类型判别和故障选相
四、工频故障分量距离保护
1. 称呼:故障分量、故障变化量、突变量 2. 组成:工频故障分量、故障暂态分量 3. 不存在由于对侧电源助增引起的稳态超越问题 特点: (1)基本上不受非故障状态影响,无需加振荡闭锁 (2)不,动作速度较快
3.5 距离保护的闭锁振荡

根据对振荡闭锁的要求,利用短路与振荡时电气量变化的特征,一般 可采取以下三种闭锁措施。
1.利用负序、零序分量或突变量,实现振荡闭锁 基本原理:在系统没有故障时,距离保护一直处于闭 锁状态,当系统发生故障时,短时开放距离保护允许保护 出口跳闸。
若开放时间内保护动作,说明故障在保护范围内,将 故障线路跳开;若在开放时间内保护未动作,说明故障不 在保护区内,重新将保护闭锁。
阻抗缓慢变为保护安装处到振荡 中心点的线路阻抗; 根据阻抗变化的速度不同 就可以构成振荡闭锁,俗称 “大圆套小圆”原理。
Z1 Z2
Zk
ZM ZL
3.5.3 距离保护的振荡闭锁措施
利用测量阻抗的变化率不同构成振荡闭锁实现原理图:
KZ2
Z
KZ1
D2 & D1 & DT
开放保护
Z
t
0
3.5.3 距离保护的振荡闭锁措施
3.5.1 振荡闭锁的概念
并联运行的电力系统或发电厂之间出现功率角大范围周期性 变化的情况,称为电力系统的振荡。 电力系统振荡时,系统两侧的等效电动势间的夹角δ可能在 0°~360°范围内作周期变化,系统中个点的电压、线路电流、 功率大小和方向以及保护的测量阻抗也都呈周期性变化。 电力系统的振荡属于严重的不正常工作状态,但可以通过控 制手段恢复正常。但由于测量阻抗的周期性变化保护可能误动 作而造成事故的扩大。
35距离保护的闭锁振荡振荡闭锁的概念振荡对测量元件的影响距离保护的振荡闭锁措施振荡过程中再故障的判断351振荡闭锁的概念并联运行的电力系统或发电厂之间出现功率角大范围周期性变化的情况称为电力系统的振荡
3.5 距离保护的闭锁振荡
——振荡闭锁的概念 ——振荡对测量元件的影响 ——距离保护的振荡闭锁措施 ——振荡过程中再故障的判断
第五节 距离保护的振荡闭锁

− A相 地 接
− B相 地 接
有 零 序 分 量 无
ɺ ɺ ɺ ɺ m∆I AB ≤ ∆ICA ∩m∆I AB ≤ ∆IBC ɺ ɺ ɺ K(1,1) ∆I AB 、∆IBC 、∆ICA
− C相 地 接
最 者 故 相 大 为 障
− AB −B C − CA
ɺ ɺ ɺ ɺ m∆IC < ∆I A ∩m∆IC < ∆IB
第六节 故障类型判别及故障选相
ɺ EM
M1 ɺ I
2N
ɺ EN
ɺ U
判断故障距离 单相重合闸
(故障类型,故障相) 找出故障环路 故障类型,故障相)
电流突变量的概念: 电流突变量的概念:
ɺ ɺ ɺ ɺ ɺ[ ɺ ɺ ∆I AB = (I A − IB ) −(I [0] − IB0] ) = ∆I A − ∆IB A ɺ ɺ ɺ ɺ[ ɺ[ ɺ ɺ ∆IBC = (IB − IC ) − (IB0] − IC0] ) = ∆IB − ∆IC ɺ ɺ ɺ ɺ ɺ ɺ ɺ ∆I = (I − I ) − (I [0] − I [0] ) = ∆I − ∆I
二、振荡对距离保护测量元件的影响 1.振荡时电压电流的变化规律 1.振荡时电压电流的变化规律
ɺ EM
M1 ɺ I
2N
ɺ EN
三相系统-→单相系统
对称
ɺ U
振荡原因:(1)输电线输送功率过大,超过静稳极限;
ɺ ɺ ɺ EM − EN EM (1− e− jδ ) ɺ I= = ZΣ ZΣ
ɺ ɺ ɺ UM = EM − I ZM
3.振荡对距离保护的影响 3.振荡对距离保护的影响
ɺ EM
M1 ɺ I
2N
ɺ EN
距离保护第4讲:振荡闭锁

3.8.3 距离保护振荡闭锁措施
(二)措施1:故障启动时保护的短时开放
利用短路故障电气量突变的特点,实现振荡闭锁。 具体实现方案: ➢ 启动元件动作,距离保护短时开放保护150ms ➢ 对于距离Ⅱ段若在上述开放时间内动作,则保持其动
作状态
3.8.3 距离保护振荡闭锁措施
(二)措施1:故障启动时保护的短时开放
启动判据:
3.8.3 距离保护振荡闭锁措施
(三)措施2:利用测量阻抗变化率(大圆套小圆式)
短路故障时, 测量阻抗因负荷阻抗突变为短路阻抗而 发生瞬间变化
系统振荡时, 测量阻抗 则按振荡过程较为缓慢地变化 为保护安装处到振荡中心点的线路阻抗
3.8.3 距离保护振荡闭锁措施
(四)措施3:利用动作延时
➢ 距离保护的延时大于测量阻抗穿越动作区的时间(一般 为1.0~1.5s), 就可避免系统振荡引起的误动作;
➢ 适用于距离Ⅲ段; ➢ 因为不退出III段,为振荡中线路再故障保留了一个简单
可靠的后备距离Ⅲ 段。 ➢ 与距离Ⅰ 、 Ⅱ 段的振荡闭锁措施相结合, 可构成距离
保护振荡闭锁的完整方案
3.8.4 振荡过程中再故障的判断
1. 电力系统振荡
振荡表现形式: 1)衰减振荡,机组间功角变化幅度逐渐减小,最后振荡 平息 2)系统失去同步,机组间功角在0-360度之间作周期性 变化
两者的不同表现在振荡时功角的变化范围和变化周期 不同。
两者的共同点在于功角均近似作周期性变化
3.8.1振荡闭锁的概念
2. 电力系统振荡对保护的影响 电力系统振荡会引起系统各个点的电流、电压、测量阻
3.8.3 距离保护振荡闭锁措施
(一)对振荡闭锁元件的基本要求
1. 系统发生全相或非全相振荡时,保护装置不应误动 作,即单纯振荡要可靠闭锁保护
距离保护的振荡闭锁方法综述

而 使距 离保 护 跳 闸 , 因此 , 分 析 振荡产 生 的原 因并 找 出 合 理 的方 法避 免保 护跳 闸显 得 极其 重要 。距 离保 护振 荡 闭锁 措施 应 满足 如下 要求 :
处于对称状态 , 电压 和电流不包括负序分量或零序分 量; 而当发生单相接地 、 两相短路和两相接地短路等三 相不对称短路时 , 电压 和电流 中都会有较大的负序分
Ke y wo r d s: s wi n g b l o c k i n g ; u n s y mme t r i c l a f a u l t : i mp e d a n c e c h a n g e r a t e
2 目前距 离保 护的判 断依 据
1 引 言
电流突变量的判断元件两种 。电力网络在正常运行时
或者 因静 态稳 定遭 到 破 坏 而 引起 振 荡 , 电力 系 统 三相
或变电站发生故障时 , 可能引起系统振荡 , 在振荡的过 程 中, 电压和电流值可能达到很高 , 容易引起距离保护 误 动跳 闸 , 造成 系统 大 面积停 电 。另 外 , 目前 大量 使用 的非线性负载会产生高次谐 波, 也容易引起 系统振荡
<电气开 关> ( 2 0 1 3 . N o . 3 )
距离保护断线闭锁及振荡闭锁

《距离保护的断线闭及振荡锁装置》一、距离保护的断线闭锁装置1ZKJ 2ZKJ 3ZKJC 相断线时的电压变化:ABU B 现在微机保护都是采用起动元件(即相电流突变量和零序电流启动),因此PT 二次断线时,微机保护的起动元件不会动作,故距离保护不会误动。
但如果此时系统出现波动或发生区外故障造成起动元件动作的情况下,距离保护就会误动。
为此纵联距离保护及零序电压采用自产3U0纵联零序方向保护都需闭锁。
对断线闭锁装置的要求:①当PT 二次回路出现一相、两相或三相断线时,断线闭锁装置都应将距离保护闭锁,并发出告警信号。
②当一次系统发生短路时,断线闭锁装置不应误动,以免将距离保护误闭锁。
1、RCS-900系列保护断线闭锁装置的原理①当Ua+Ub+Uc >8V ,且电流起动元件不起动,延时1.25s 发出PT 二次回路异常信号并闭锁保护。
本判据用以判别TV 二次的一相和两相断线。
②当使用母线PT 时,满足Ua+Ub+Uc <8V ,U 1<30V ,且电流起动元件不起动,延时1.25s 发出PT 二次回路异常信号并闭锁保护。
本判据用以判别TV 二次的三相断线。
③当使用线路PT 时,满足Ua+Ub+Uc <8V ,U 1<30V ,且电流起动元件不起动,任意一相有电流(I φ>0.08I N ,为CT 的二次额定电流)或TWJ 不动作。
延时1.25s 发出PT 二次回路异常信号并闭锁保护。
本判据用以判别TV 二次的三相断线。
(1)RCS-901系列保护断线闭锁装置A B CBC=CATV断线信号动作的同时,将纵联变化量方向和纵联零序退出,保留工频变化量阻抗元件,退出距离保护,自动投入TV断线相过流和TV断线相零序过流保护,TV断线相过流保护由距离保护压板投退,TV断线相零序过流保护由零序保护压板投退。
对于零序过电流保护,RCS-901A将零序II段退出,III段不经方向元件控制;RCS-901B将零序I、II段退出,IV段不经方向元件控制,若“零序III段经方向”,则退出III段零序方向过流。
3.5距离保护的振荡闭锁

3.5.2 电力系统振荡对距离保护测量元件的影响
2、电力系统振荡时测量阻抗的变化规律
1 1 1 1 Z m ( Z Z M ) j Z ctg ( M ) Z j Z ctg 2 2 2 2 2 2
N侧电源
360
O
N
1 ( M )Z 2
N
O
阻抗比较容易落入动作区,但是否误作时限分析
jX
1
Z m1
O
M
R
M侧电源
M
R
3.5.2 电力系统振荡对距离保护测量元件的影响
4、电力系统振荡与短路时电气量的差异
对称性差异:
振荡时系统三相对称,无负序和零序分量。不对称短路则有负序和零序
分量出现。对称短路往往是由不对称短路发展而来,因而故障初期, 一般也会出现短时的负序和零序分量; 电气量变化速率的差异: 振荡时,电气量呈现周期性变化,其变化过程是渐变的,变化范围大。 而故障时电流电压的变化是突变的,且故障后测量电流电压、阻抗 的测量值基本不变;
距离保护特殊问题的分析
• 振荡闭锁的概念
• 电力系统振荡对距离保护测量元件的影响
• 距离保护的振荡闭锁措施
3.5.1 振荡闭锁的概念
电力系统振荡:并联运行的电力系统或发电厂之间出现功率 角大范围周期性变化的现象
M
1
EM
I
N
EN
产生振荡的原因:
U
1、电网建设规划不合理,电气联系弱
2、无功功率不足,电压下降 3、大型发电机励磁异常 正常运行 4、切除故障慢,限制有功传输 系统振荡
O
UN
E
距离保护的振荡闭锁

距离保护的振荡闭锁1电力系统振荡1.1简介在电力系统正常运行时,所有发电机都以同步转速旋转,这时并列运行的各发电机之间相位没有相对变化,系统各发电机之间的电势差为常数,系统中各点电压和各回路的电流均不变。
当电力系统由于某种原因受到干扰时(如短路、故障切除、电源的投入或切除等),这时并列运行的各同步发电机间电势差相角差将随时间变化,系统中各点电压和各回路电流也随时间变化,这种现象称为振荡。
电力系统的振荡有同步振荡和异步振荡两种情况,能够保持同步而稳定运行的振荡称为同步振荡,导致失去同步而不能正常运行的振荡称为异步振荡。
电力系统中的电磁参量(电流、电压、功率、磁链等)的振幅和机械参量(功角、转速等)的大小随时间发生等幅、衰减或发散的周期性变化的现象。
(当电力系统由于某种原因受到干扰时(如短路、故障切除、电源的投入或切除等),这时并列运行的各同步发电机间电势差相角差将随时间变化,系统中各点电压和各回路电流也随时间变化,这种现象称为振荡。
)1.2系统振荡的五大原因1、输电线路输送功率超过极限值造成静态稳定破坏;2、电网发生短路故障,切除大容量的发电、输电或变电设备,负荷瞬间发生较大突变等造成电力系统暂态稳定破坏;3、环状系统(或并列双回线)突然开环,使两部分系统联系阻抗突然增大,引启动稳定破坏而失去同步;4、大容量机组跳闸或失磁,使系统联络线负荷增大或使系统电压严重下降,造成联络线稳定极限降低,易引起稳定破坏;5、电源间非同步合闸未能拖入同步。
1.3系统发生振荡时的主要现象1)发电机和电源联络线上的功率、电流及某些节点上的电压将会产生不同程度的周期性变化。
2)连接失去同步的发电厂或系统联络线上的电流表和功率表的表针摆动得最大;电压振荡最激烈的地方是系统振荡中心,振荡电压每周期降低至零值一次;随着偏离振荡中心距离的增加,电压的波动幅度逐渐减小。
3)对于失步发电机,定子电流表指针的摆动最为激烈;有功功率表和无功功率表的摆动也很厉害;定子电压也有摆动,但不会到零值;转子电流和电压都在正常值左右摆动。
电力系统继电保护技术 4.7振荡闭锁闭锁新

整理课件
11
4.7 距离保护振荡闭锁
0 有UME ,M母线电压最高。
当 180 时,UM(2m1)E
当m=0.5时,M母线电压为零。
M越趋近0.5。变化幅度越大。
U M(E co 2)s 2[1 (2 m )E si2 n ]2 E 14m(1m)sin2
2
16.08.2021
整理课件
12
4.7 距离保护振荡闭锁
U MK eE N ejIsw Z M i1
设电势相等,则
IswiZEN1 (Keej 1)
相角差为:
ctg
a
rc
t(g 2 ) 12m
aU I r s M w g a i Z r K e 1 e K g j e e j( 1 Z M 1 ) a1 r e g 1 j/ ( K e m )
设系统总阻抗角与被保护线路阻抗角相等,则可
在保护安装处测得振荡中心电压。
U Z U M co s9(0 )
arU gM/Iswi
P
EM U M
Iswi
ZN Q
U N
E N
arZ g1
16.08.2021
整理课件
13
4.7 距离保护振荡闭锁
设两侧电源不相等,设 EMKeENej
保护安装处电压、电流表示为:
因
s
2
T swi
,据统计,振荡周
期最大值为3s,于是
s
min
2
3
测量阻抗变化率为
≥ dZ m dt
Z 1 6
只要适当选择保护 开放条件,可保证 保护不误动。
16.08.2021
整理课件
22
4.7 距离保护振荡闭锁
距离保护的振荡闭锁

§3.5距离保护得振荡闭锁(Power SwingBlocking ofDistanceProtection)§3。
5。
1振荡闭锁得概念(Concept of PowerS wing Blocking)并联运行得电力系统或发电厂失去同步得现象,称为电力系统得振荡(Power Swing)、电力系统振荡时,系统两侧等效电动势间得夹角在范围内作周期性变化,从而使系统中各点得电压、线路电流、功率方向以及距离保护得测量阻抗也都呈现周期性变化、这样,以上述这些量为测量对象得各种保护得测量元件,就有可能因系统振荡而动作。
电力系统得振荡就是属于严重得不正常运行状态,而不就是故障状态,大多数情况下能够通过自动装置得调节自行恢复同步、如果在振荡过程中继电保护动作,切除了重要得联络线,或断开了电源与负荷,不仅不利于振荡得自动恢复,而且还有可能使事故扩大,造成更为严重后果。
所以在系统振荡时,要采取必要得措施,防止保护因测量元件动作而误动、这种用来防止系统振荡时保护误动得措施,就称为振荡闭锁。
因电流保护、电压保护与功率方向保护等一般都只应用在电压等级较低得中低压配电系统,这些系统出现振荡得可能性很小,振荡时保护误动产生得后果也不会太严重,所以一般不需要采取振荡闭锁措施。
距离保护一般用在较高电压等级得电力系统,系统出现振荡得可能性大,保护误动造成得损失严重,所以必须考虑振荡闭锁问题、在无特殊说明得情况下,本书所提及得振荡闭锁,都就是指距离保护得振荡闭锁。
§3。
5。
2电力系统振荡对距离保护测量元件得影响(Effect of Power Swing to MeasuringUnitof DistanceProtection)1.电力系统振荡时电流、电压得变化规律现以图3—31所示得双侧电源得电力系统为例,分析系统振荡时电流、电压得变化规律。
(即功角)为,等效电源之间得阻抗为,为N侧系统得等值阻抗,为联络线路得阻抗,则线路中得电流与母线M、N上得电压分别为:(3—144)(3-145)(3-146)它们之间得相位关系如图3—32(a)所示、以为参考相量,当δ在0o~360o范围内变化时,相当于相量在0o~360o范围内旋转。
3 电网距离保护第5讲New

2
δ
o
Zm
1
2Z
M
Ke 1 o
oR
(
1 2
M
)
Z
2
Ke 1
图 3-31 测量阻抗的变化轨迹
其中
Ke
EM EN
3.5.2 振荡时电气量的变化规律及特点
(三)电力系统振荡对距离 保护的影响
当振荡中心落入保护范围内,
功角在 1 2 范围内保护的
测量阻抗落入动作区,保护误 动。随功角周期变化,阻抗继 电器反复动作。
(1)不对称故障开放元件(振荡过程中再故障的处理) 如果在振荡中又发生故障,需要开放保护切除故障。
• 利用不对称短路时,系统中出现零序或负序分量原理实现 振荡中开放保护。可以实现瞬时开放。
• 开放判据:
I0 I2 m I1
m:比例系数,一般取0.5~0.7
3.5.3 距离保护振荡闭锁原理
(2)对称故障开放元件(振荡过程中再故障的处理) U cos :电压相量在电流相量方向上的投影,是一个标量
其次要保证在区外故障引起振荡时,测量阻抗不会在 故障后的开放时间内进入动作区。
开放时间一般取150ms左右。
3.5.3 距离保护振荡闭锁原理
(二)振荡闭锁方法
启动元件(又称故障判别元件) 作用:完成系统是否发生短路的判断 要求:灵敏度高,动作速度快,系统振荡时不误动作
稳态量启动元件:采用零序电流或负序电流 突变量启动元件:反映电流突变量
(一)电力系统振荡时电流、电压的变化规律
振荡中心的概念:
振荡时,沿线路不同点电压幅值的变化范围不同,沿线路
电压最低的一点称为振荡中心。所有阻抗角均相同时,振
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§3.5距离保护的振荡闭锁(Power Swing Blocking of DistanceProtection)§3.5.1 振荡闭锁的概念 ( Concept of Power Swing Blocking)并联运行的电力系统或发电厂失去同步的现象,称为电力系统的振荡(Power Swing)。
电力系统振荡时,系统两侧等效电动势间的夹角在0o~360o范围内作周期性变化,从而使系统中各点的电压、线路电流、功率方向以及距离保护的测量阻抗也都呈现周期性变化。
这样,以上述这些量为测量对象的各种保护的测量元件,就有可能因系统振荡而动作。
电力系统的振荡是属于严重的不正常运行状态,而不是故障状态,大多数情况下能够通过自动装置的调节自行恢复同步。
如果在振荡过程中继电保护动作,切除了重要的联络线,或断开了电源和负荷,不仅不利于振荡的自动恢复,而且还有可能使事故扩大,造成更为严重后果。
所以在系统振荡时,要采取必要的措施,防止保护因测量元件动作而误动。
这种用来防止系统振荡时保护误动的措施,就称为振荡闭锁。
因电流保护、电压保护和功率方向保护等一般都只应用在电压等级较低的中低压配电系统,这些系统出现振荡的可能性很小,振荡时保护误动产生的后果也不会太严重,所以一般不需要采取振荡闭锁措施。
距离保护一般用在较高电压等级的电力系统,系统出现振荡的可能性大,保护误动造成的损失严重,所以必须考虑振荡闭锁问题。
在无特殊说明的情况下,本书所提及的振荡闭锁,都是指距离保护的振荡闭锁。
§3.5.2电力系统振荡对距离保护测量元件的影响(Effect of Power Swing to Measuring Unit of DistaneeProtectio n)1电力系统振荡时电流、电压的变化规律现以图3-31所示的双侧电源的电力系统为例,分析系统振荡时电流、电压的变化规律。
E M M KZ I N E NE之——------------------1U图3-31双侧电源的电力系统设系统两侧等效电动势E M和E N的幅值相等,相角差(即功角)为,等效电源之间的阻抗为Z Z M乙Z N,其中Z M为M侧系统的等值阻抗,Z N为N侧系统的等值阻抗,乙为联络线路的阻抗,则线路中的电流和母线M、N上的电压分别为:E M E N_E E M (1 e」) (3-144)U M E M 1 Z M (3-145)U N E N I Z N (3-146)它们之间的相位关系如图3-32(a)所示。
以E M 为参考相量,当S 在0。
〜3600范围内变化时,相当于E N相量在0。
〜360。
范围内旋转。
图3-32系统振荡时的电流和电压(a)相量图;(b)电流有效值变化曲线;(c )电压有效值变化曲线(c)由图可以看出电势差的有效值为所以线路电流的有效值为电流有效值随S 变化的曲线如图(b)所示。
电流的相位 滞后于E E M E N 的角度为d ,其相量末端的随S 变化的轨 迹如图(a)中的虚线圆周所示。
假设系统中各部分的阻抗角都相等,则线路上任意一 点的电压相量的末端,都必然落在由E M 和E N 的末端连接而 成的直线上(即E 上)。
M 、N 两母线处的电压相量U M 和U N 标在图(a)中。
其有效值随&变化的曲线,如图(c)所示。
在图(a)中,由o 点向相量 E 作一垂线,并将该垂线代 表的电压相量记为U os ,显然,在 为0以外的任意值时,电 压U os 都是全系统最低的,特别是当 180o 时,该电压的有 效值变为0。
电力系统振荡时,电压最低的这一点称为振荡 中心,在系统各部分的阻抗角都相等的情况下,振荡中心的1位置就位于阻抗中心-Z 处。
由图(a)可见,振荡中心电压的 有效值可以表示为U os E M cos 2 2 •电力系统振荡时测量阻抗的变化规律E 2EM Sin 2 (3-147)2E M sin — (3-148)(3-149)1 1 1 Z M ) j-Z ctg- (- M )Z j-Z ctg^(3-151)M式中 M 2"为M 侧系统阻抗占总串联阻抗的比例。
可见,系统振荡时,M 处的测量阻抗由两大部分组成, 1 第一部分为 (-M )z ,它对应于线路上从母线 M 到振荡 中心z 一段线路的阻抗,是不随 变化的。
第二部分为 1j 2Z ct g^,它垂直于Z ,随着的变化而变化。
当由°。
变 化到3600时,测量阻抗Z m 的末端沿着一条经过阻抗中心点 2Z ,且垂直于Z 的直线00自右向左移动,如图3-33所示。
当0。
()时,测量阻抗Z m 位于复平面的右侧,其值为无穷大; 当180。
时,第二部分阻抗等于°,总测量阻抗变成(? M )Z ; 当360。
()时,测量阻抗的值也为无穷大,但位于复平面的 左侧。
系统振荡时,安装在M点处的测量元件的测量阻抗为 Z UM Zm 1 E M 1 M Z M E1 M(3-150) 因为cos jsin 1 jctg?图3-33测量阻抗的变化轨迹如果E M 和E N 的幅值不相等,则分析表明,系统振荡时 测量阻抗末端的轨迹将不再是一条直线,而是一个圆弧。
设 K e EM E N ,当K e 1及K e 1时,测量阻抗末端的轨迹如图 中的虚线圆弧1和2所示。
由图可见,保护安装处 M 到振荡中心z 一段线路的阻1 1 抗为(-M )Z ,它与比值M 的大小密切相关。
当 M -时, 它与Z 同方向,振荡中心Z 点位于阻抗平面的第一象限,振 荡时测量阻抗末端轨迹的直线00在第一象限内与Z 相交;1当M 2时,该阻抗等于0,振荡中心z 正好位于M 点,测 量阻抗末端轨迹的直线 00在坐标原点处与 Z 相交;当1 -M 2时,它与Z 方向相反,振荡中心z 点位于阻抗平面的第三象限,振荡时测量阻抗末端轨迹的直线00在第三象限 jXN0 1 Z m 22K e 1M )Z K e 1M(1 K e 1内与Z相交Z N亠若令N ~Z~,则当M和N都小于1时,振荡中心就落在线路MN 上,其它情况下,振荡中心将落在线路MN之外。
3•电力系统振荡对距离保护测量元件的影响在图3-31所示的双侧电源系统中,假设M、N两处均装有距离保护,其测量元件均采用圆特性的方向阻抗元件,距离I段的整定阻抗为线路阻抗的80%,则两侧测量元件的动作特性如图3-34所示,实线圆为M侧I段的动作特性,虚线圆为N侧I段的动作特性。
根据前面的分析,若M和N都小于1,振荡中心就落在2母线M、N之间的线路上。
当S变化时,M、N两处的测量阻抗的末端,都将沿图3-34中的直线oo移动。
由图可见,当8 在8〜8范围内时,N侧测量阻抗落入动作范围图3-34振荡对测量元件的影响之内,其测量元件动作;当8在8〜8范围内时,M侧测量阻抗也落入动作范围之内,其测量元件也动作。
即在振荡中心落在本线路上的情况下,当6变至1800 左右时,线路两侧保护I段的测量元件都可能动作。
当M和N任意一个不小于1时,振荡中心都将落在本线路之外,这时两侧保护的测量阻抗都不会进入I段的动作区,本线路的距离I段将不受振荡的影响。
但由于II段及III段的整定阻抗一般较大,振荡时的测量阻抗比较容易进入其动作区,所以II段及III段的测量元件可能会动作。
总之,电力系统振荡时,阻抗继电器有可能因测量阻抗进入其动作区而动作,并且整定值越大的阻抗继电器越容易受振荡的影响。
在整定值相同的情况下,动作特性曲线在与整定阻抗垂直方向的动作区越大时,越容易受振荡的影响。
比如,与方向圆阻抗特性相比,全阻抗特性在与整定阻抗垂直方向的动作区较大,所以它受振荡的影响就较大;而方向阻抗特性在整定阻抗垂直方向的动作区较橄榄形特性大,所以它受振荡的影响要比橄榄特性大。
4•引发电力系统振荡的原因引起电力系统振荡的原因主要有两种,一种则是因为联络线中传输的功率过大而导致静稳定破坏,另一种是因电力系统受到大的扰动(如短路、大机组或重要联络线的误切除等)而导致暂态稳定破坏。
电力系统正常运行时,系统中各点的电压均接近额定电压,线路中的电流为负荷电流,传输的功率为负荷功率,此时两侧电源之间的功角 &小于900。
当线路中传输的功率逐渐增加时,功角A将逐渐增大,一旦6超过900,系统就有可能发生振荡。
由于负荷变化的过程并不是突发的,所以系统从正常状态变到振荡状态的过程中,电气量不会发生突然的变化。
进入振荡状态后,电压、电流、功率和测量阻抗等电气量都将随着6的变化而不断的变化,阻抗继电器可能因测量阻抗进入其动作范围而误动作。
此外,在静稳定破坏引发振荡的情况下,系统的三相仍然是完全对称的,不会出现负序量和零序量。
电力系统发生短路、断线等较大冲击的情况下,功率可能会出现严重的不平衡,若处置不当,很容易引发系统振荡。
这种振荡是由于电气量的突然剧变引起的,所以系统从正常状态变为振荡状态的过程中,电气量会发生突变,系统也可能出现三相不对称。
进入振荡状态后,电气量将随着6的变化而不断的变化,阻抗继电器也可能因测量阻抗进入其动作范围而误动作。
由此可见,虽然由静稳定破坏引发的系统振荡和由暂态稳定破坏引发的系统振荡的电气量变化过程有所不同,但在进入振荡状态后,阻抗继电器都有可能误动作,为防止距离保护误动作,在两种情况下,都应将保护闭锁。
§3.5.3距离保护振荡闭锁的措施(Measures of Power Swing Blocking)距离保护的振荡闭锁,应能够准确地区分振荡与短路,并应满足以下的基本要求:(1)系统发生振荡而没有故障时,应可靠地将保护闭锁,且振荡不平息,闭锁不解除。
(2)系统发生各种类型的故障时,保护不应被闭锁,以保证保护正确动作。
(3)振荡过程中再发生故障时,保护应能够正确地动作(即保护区内故障可靠动作,区外故障可靠不动)。
(4)若振荡的中心不在本保护的保护区内,则阻抗继电器就不可能因振荡而误动,这种情况下保护可不采用振荡闭锁。
如上所述,电力系统正常运行时,阻抗继电器感受到的测量阻抗为阻抗值基本不变的负荷阻抗,其阻抗值较大、阻抗角较小,一般均落在阻抗继电器的动作区域之外,阻抗继电器不会动作;电力系统因静稳定破坏而引发振荡时,电压、电流和测量阻抗等电气量将随着功角3的变化而不断的缓慢变化,经一定时间后,阻抗继电器可能因测量阻抗进入其动作区而动作;电力系统因暂态稳定破坏而引发振荡时,在大扰动发生的瞬间,电压、电流和测量阻抗等电气量有一个突变的过程,扰动过后的振荡过程中,电气量也将随着功角A的变化而不断的缓慢变化,一定时间后阻抗继电器也可能误动作;保护区内发生短路故障时,故障电压、电流都会发生突变,测量阻抗也将从负荷阻抗突变为短路阻抗,并基本维持短路阻抗不变,测量元件立即动作,并在故障切除前一直处于动作状态。
