圆的垂径定理试题(卷)(附答案解析)
部编数学九年级上册专题08垂径定理、圆心角、圆周角之六大题型(解析版)含答案

专题08垂径定理、圆心角、圆周角之六大题型利用垂径定理求值【答案】2【分析】根据垂径定理和勾股定理列方程求解即可.【详解】解:设OC=△中,由勾股定理得,在Rt COE【变式训练】【答案】45cm/4【分析】连接BO,延长22=,即可求解.BC OB OC-【详解】解:如图,连接=,由折叠得:CD CEQ D是OC的中点,\=,CD OD\==,CE CD OD2\==,4OC OE【答案】310【分析】由题意易得【详解】解:连接OD∵AB 是O e 的直径,AB ∴152OD OB AB ===,∵CD AB ^,6CD =,∴13,2DE CD DEO ==Ð∴22OE OD DE =-=垂径定理的实际应用【点睛】本题考查了勾股定理和垂径定理,灵活运用所学知识,掌握垂直于弦的直径平分弦,且平分弦所对的弧,是解决本题的关键.【变式训练】1.(2023上·福建龙岩·九年级统考期末)筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧.如图1,点M 表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O (O 在水面上方)为圆心的圆,且圆O 被水面截得的弦AB 长为8米.若筒车工作时,盛水桶在水面以下的最大深度为2米,则这个圆的半径为( )A .2米B .3米C .4米D .5米【答案】D 【分析】过圆O 作OD AB ^于E ,如图所示,由垂径定理可知4AE BE ==,设圆的半径为r ,再利用勾股定理列方程求解即可得到答案.【详解】解:过圆O 作OD AB ^于E ,如图所示:Q 弦AB 长为8米,\4AE BE ==,Q 盛水桶在水面以下的最大深度为2米,设圆的半径为r ,在Rt AOE △中,90AEO Ð=°,OA r =,4AE =,2OE OD ED r =-=-,则由勾【答案】26【分析】连接AO ,依题意,得出222AO AC CO =+,解方程即可求解.【详解】解:如图所示,连接∵1CD =,10AB =,AB ∴5AC =,设半径为r ,则AO r =在Rt AOC V 中,2AO =利用弧、弦、圆心角的关系求解A.AB OC=C.12ABC BOC Ð+Ð=【答案】D 【变式训练】【答案】80°/80度【分析】利用等腰三角形的性质和三角形内角和计算出即可求出答案.Ð【详解】解:∵OBC半圆(直径)所对的圆周角是直角A.43【答案】B【分析】如图:连接AQ QB=,最后根据勾股定理即可解答.【点睛】本题主要考查了圆周角定理、等腰三角形的判定与性质、勾股定理等知识点,灵活运用勾股定理成为解答本题的关键.【变式训练】【答案】13【分析】连接BD ,先由三角形内角和定理求出求出30ABD Ð=°,即有【详解】解:连接BD∵在ABC V 中,55B Ð=∴60A Ð=°,∵AB 为O e 的直径,∴90ADB CDB Ð=Ð=°Ð的度数;(1)求BAC(2)若点E为OB中点,CE 【答案】(1)45°(2)3590°的圆周角所对的弦是直径例题:(2023上·广东汕头DA DC =,2AB BC ==【答案】32【分析】连接AC ,过点角三角形,勾股定理求得∵90ADC Ð=°,∴AC 是直径,∴90ABC Ð=°【变式训练】1.(2023上·山东济南·九年级统考期末)如图,正方形ABCD 中,4AB =,E 点沿线段AD 由A 向D【答案】2p【分析】连接BD 交EF 于点1222OB OD BD ===,再由∵四边形ABCD 是正方形,∴4BC AB AD ===,EDO Ð∴242BD AB ==,【答案】90°Ð【分析】(1)由ABP (2)首先证明点P理求出OC即可得到则OP OA OB ==,\点P 在以AB 为直径的O e 在Rt BCO V 中,90OBC Ð=225OC BO BC \=+=,532PC OC OP =-=-=,已知圆内接四边形求角度【答案】102°【分析】根据圆内接四边形的性质得出【详解】解:∵四边形∴180A DCB Ð+Ð=°,又180DCE DCB Ð+Ð=°,∴102DCE A ÐÐ==°,故答案为102°.【点睛】本题主要考查了圆内接四边形的性质,熟知圆内接四边形的对角互补是解决此题的关键.【变式训练】【答案】40【分析】根据已知可得»»BCBD =56DAC BAC BAD Ð=Ð+Ð=°,再利用圆内接四边形对角互补以及平角的定义可得56DBE DAC Ð=Ð=°,继而利用角平分线定义及三角形内角和定理即可求解.(1)求证:A AEBÐ=Ð(2)若90Ð=°,点CEDC【答案】(1)见解析e的半径为25 (2)O一、单选题1.(2023上·河北张家口·九年级统考期末)O e 中的一段劣弧»AB 的度数为80o ,则AOB Ð=( )A .10oB .80oC .170oD .180o【答案】B 【分析】根据圆心角、弧、弦之间的关系得出答案即可.【详解】解:Q O e 中的一段劣弧»AB 的度数为80°,80AOB \Ð=°,故选:B .A .32°B .42【答案】A 【分析】先根据同弧所对的圆周角相等得到小即可.【详解】解:∵50A Ð=°,∴50D A Ð=Ð=°,A .10【答案】D∴12AH BH AB===在Rt BOHV中,OH∴线段OP长的最小值为A.105°B.110【答案】D【分析】先根据圆内接四边形的性质和平角的定义求出求解.A .1米B .()35+米C .3米【答案】D 【分析】连接OC 交AB 于D ,根据圆的性质和垂径定理可知理求得OD 的长,由CD OC OD =-即可求解.则OC AB ^,12AD BD AB ==在Rt OAD △中,3OA =,AD ∴225OD AO AD =-=,【点睛】本题考查圆的性质、垂径定理、勾股定理,熟练掌握垂径定理是解答的关键.【答案】120【分析】过O 点作OD AC ^AD CD =,根据三角形中位线定理可得由折叠可得:12OD OE ==∵AB 是直径,∴90ACB Ð=°,12OD BC =【答案】64°/64度【分析】根据在同圆中,Ð=Ð可推出AOC BOD【详解】解:Q»AE=【答案】3【分析】由圆的性质可得OA后根据中位线的性质即可解答.【答案】45【分析】连接AC ,如图所示,由直径所对的圆周角为直角可知及勾股定理求出AC 【详解】解:连接Q OC AB ^,AB =12AD BD AB \==在Rt AOD V 中,OA 420r \=,解得r【答案】4【分析】如图,连接CD直角三角形斜边上的中线等于斜边的一半可得【点睛】本题考查直径所对的圆周角为直角,直角三角形斜边上的中线等于斜边的一半,勾股定理.掌握直径所对的圆周角为直角是解题的关键.三、解答题e的直径AB垂直于弦CD,垂足为E,11.(2023上·安徽合肥·九年级统考期末)如图,O,.==28AE CD(1)求O e 的半径长;(2)连接 BC ,作OF BC ^【答案】(1)5(2)5在Rt OCE V 中,2OE ∴()22224R R -+=,解得5R =,∴O e 的半径长为5;(1)若这个输水管道有水部分的水面宽半径;OE AB ^Q ,11168cm 22BD AB \==´=(1)连接AD,求证:(2)若52,==CD AB 【答案】(1)详见解析;(2)6Ð相等吗?为什么?(1)BAFÐ和CAD^,垂足为(2)过圆心O作OH AB【答案】(1)相等,理由见解析(2)10【详解】(1)解:连接BF ,Q AF 是O e 的直径,90F BAF \Ð+Ð=°Q AC BD ^,\90CAD BDA Ð+Ð=°,Q F BDA Ð=Ð,\BAF CAD Ð=Ð.(2)解:OH AB ^Q ,AH BH \=,OA OF =Q ,210BF OH \==,BAF CAD Ð=ÐQ ,10CD BF \==.【点睛】本题考查的是圆周角定理,等角的余角相等,圆心角、弦的关系,三角形的中位线性质,垂径定理,掌握圆心角、弦的关系,三角形的中位线性质以及垂径定理是解题的关键.15.(2023上·山东威海·九年级统考期末)【初识模型】如图1,在ABC V 中,,90AB AC BAC =Ð=°.点D 为BC 边上一点,以AD 为边作ADE V ,使=90DAE а,AE AD =,连接CE ,则CE 与BD 的数量关系是__________;【构建模型】如图2,ABC V 内接于,O BC e 为O e 的直径,AB AC =,点E 为弧AC 上一点,连接,,AE BE CE .若3,9CE BE ==,求AE 的长;【运用模型】如图3,等边ABC V 内接于O e ,点E 为弧AC 上一点,连接,,AE BE CE .若6,10CE BE ==,求AE 的长.【答案】(1)BD CE =;(2)32;(3)4【分析】(1)只需要利用SAS 证明BAD CAE V V ≌,即可证明BD CE =(2)如图所示,过点A 作AD AE ^交BE 于D ,由BC 是直径,得到明BAD CAE Ð=Ð,再证明45ADE AED Ð=Ð=°,得到AD AE =,即可证明2(3)如图所示,在BE 上取一点∵ABC V 是等边三角形,∴60AB AC ACB ==°,∠,∴60AEB ACB Ð=Ð=°,∴ADE V 是等边三角形,∴60AE DE DAE ==°=,∠∠∴BAC CAD DAE Ð-Ð=Ð-Ð【点睛】本题主要考查了全等三角形的性质与判定,等边三角形的性质与判定,圆周角定理,勾股定理等等,正确作出辅助线构造全等三角形是解题的关键.。
2020--2021学年中考数学一轮复习专项练习圆的三大定理:垂径定理(含答案)

一轮复习专项练习圆的三大定理:垂径定理一.选择题1.如图所示,在半径为10cm的⊙O中,弦AB=16cm,OC⊥AB于点C,则OC等于()A.3cm B.4cm C.5cm D.6cm2.如图,△ABC中,AB=5,AC=4,BC=2,以A为圆心AB为半径作圆A,延长BC交圆A 于点D,则CD长为()A.5 B.4 C.D.23.如图,在半径为3的⊙O中,AB是直径,AC是弦,D是的中点,AC与BD交于点E.若E是BD的中点,则AC的长是()A.B.3C.3D.44.如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BAC=∠BOD,则⊙O的半径为()A.4B.5 C.4 D.35.如图,AB是⊙O的直径,弦CD⊥AB,垂足为P.若CD=8,OP=3,则⊙O的半径为()A.10 B.8 C.5 D.36.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为()A.2B.8 C.2D.27.如图,将⊙O沿着弦AB翻折,劣弧恰好经过圆心O.如果半径为4,那么⊙O的弦AB长度为()A.2 B.4 C.2D.48.如图,点C是半圆O的中点,AB是直径,CF⊥弦AD于点E,交AB于点F,若CE=1,EF =,则BF的长为()A.B.1 C.D.9.如图,AB是⊙O的直径,弦CD⊥AB,DE∥CB.若AB=10,CD=6,则DE的长为()A.B.C.6 D.10.如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为边向外作正方形ACDE,BCFG,DE,FG,AC,BC的中点分别是M,N,PQ若MP+NQ=12,AC+BC=18,则AB的长为()A.9B.C.11 D.15二.填空题11.若过⊙O内一点M的最长弦为10,最短弦为6,则OM的长为.12.已知⊙O的半径为13,弦AB=24,CD=10,且AB∥CD,则弦AB与CD之间的距离为.13.如图AB是⊙O的直径,弦CD⊥OB于点E,交⊙O于点D,已知OC=5cm,CD=8cm,则AE=cm.14.已知AB是⊙O的直径,弦CD⊥AB于点E,弦PQ∥AB交弦CD于点M,BE=18,CD=PQ =24,则OM的长为.15.在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为,则a的值是.三.解答题16.如图,AB为⊙O的直径,C,D是半圆上两点,且AC=CD=DB,AB=10cm (1)求AC的长度;(2)证明CD∥AB.17.如图,已知BC是⊙O的直径,弦AD⊥BC于点H,与弦BF交于点E,AD=8,BH=2.(1)求⊙O的半径;(2)若∠EAB=∠EBA,求证:BF=2AH.18.如图①,已知点O是∠EPF的平分线上的一点,以点O为圆心的圆与角两边分别交于A,B和C,D四点.(1)求证:AB=CD;(2)若角的顶点P在圆上,如图②,其他条件不变,结论成立吗?(3)若角的顶点P在圆内,如图③,其他条件不变,结论成立吗?19.如图,直线l:y=x,点A1坐标为(1,0),过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1为半径画弧交x轴于点A2;再过点A2作x的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去.求:(1)点B1的坐标和∠A1OB1的度数;(2)弦A4B3的弦心距的长度.20.如图,A,B,C,D在⊙O上,AB∥CD经过圆心O的线段EF⊥AB于点F,与CD交于点E.(1)如图1,当⊙O半径为5,CD=4,若EF=BF,求弦AB的长;(2)如图2,当⊙O半径为,CD=2,若OB⊥OC,求弦AC的长.参考答案一.选择题1.解:连接OA,如图:∵AB=16cm,OC⊥AB,∴AC=AB=8cm,在Rt△OAC中,OC===6(cm),故选:D.2.解:如图,过点A作AE⊥BD于点E,连接AD,∴AD=AB=5,根据垂径定理,得DE=BE,∴CE=BE﹣BC=DE﹣2,根据勾股定理,得AD2﹣DE2=AC2﹣CE2,∴52﹣DE2=42﹣(DE﹣2)2,解得DE=,∴CD=DE+CE=2DE﹣2=.故选:C.3.解:连接OD,交AC于F,∵D是的中点,∴OD⊥AC,AF=CF,∴∠DFE=90°,∵OA=OB,AF=CF,∴OF=BC,∵AB是直径,∴∠ACB=90°,在△EFD和△ECB中∴△EFD≌△ECB(AAS),∴DF=BC,∴OF=DF,∵OD=3,∴OF=1,∴BC=2,在Rt△ABC中,AC2=AB2﹣BC2,∴AC===4,故选:D.4.解:∵∠BAC=∠BOD,∴=,∴AB⊥CD,∵AE=CD=8,∴DE=CD=4,设OD=r,则OE=AE﹣r=8﹣r,在Rt△ODE中,OD=r,DE=4,OE=8﹣r,∵OD2=DE2+OE2,即r2=42+(8﹣r)2,解得r=5.故选:B.5.解:连接OC,∵CD⊥AB,CD=8,∴PC=CD=×8=4,在Rt△OCP中,∵PC=4,OP=3,∴OC===5.故选:C.6.解:∵⊙O的半径OD⊥弦AB于点C,AB=8,∴AC=AB=4,设⊙O的半径为r,则OC=r﹣2,在Rt△AOC中,∵AC=4,OC=r﹣2,∴OA2=AC2+OC2,即r2=42+(r﹣2)2,解得r=5,∴AE=2r=10,连接BE,∵AE是⊙O的直径,∴∠ABE=90°,在Rt△ABE中,∵AE=10,AB=8,∴BE===6,在Rt△BCE中,∵BE=6,BC=4,∴CE===2.故选:D.7.解:如图;过O作OC⊥AB于D,交⊙O于C,连接OA;则AD=BD,由折叠的性质得:OD=CD,在Rt△OAD中,OD=CD=OC=2,OA=4;根据勾股定理得:AD===2,∴AB=2AD=4;故选:D.8.解:如图,连接AC,BC,OC,过点B作BH⊥CF交CF的延长线于H,设OC交AD于J.∵=,∴AC=BC,OC⊥AB,∵AB是直径,∴ACB=90°,∴∠ACJ=∠CBF=45°,∵CF⊥AD,∴∠ACF+∠CAJ=90°,∠ACF+∠BCF=90°,∴∠CAJ=∠BCF,∴△CAJ≌△BCF(ASA),∴CJ=BF,AJ=CF=1+=,∵OC=OB,∴OJ=OF,设BF=CJ=x.OJ=OF=y,∵∠AEC=∠H=90°,∠CAE=∠BCH,CA=CB,∴△ACE≌△CBH(AAS),∴EC=BH=1,∵∠ECJ=∠FCO,∠CEJ=∠COF=90°,∴△CEJ∽△COF,∴==,∴==,∴EJ=,∵BF=CJ,∠H=∠CEJ,∠CJE=∠BFH,∴△BHF≌△CEJ(AAS),∴FH=EJ=,∵AE∥BH,∴=,∴=,整理得,10x2+7xy﹣6y2=0,解得x=y或x=﹣y(舍弃),∴y=2x,∴=,解得x=或﹣(舍弃).∴BF=,故选:A.9.解:设AB与CD交于H,连接OD,作OM⊥DE,交BC于N,作DG⊥BC,∵DE∥BC,∴MN⊥BC,DG⊥DE,∴DG=MN,∵OM⊥DE,ON⊥BC,∴DM=EM=DE,BN=CN,∵AB是⊙O的直径,弦CD⊥AB,弦DE∥CB.∴CH=DH=CD=3,∴OH===4,∴BH=9,∴BC==3,∴BN=BC=,∴ON==,∵sin∠BCH==,即=,∴DG=,∴MN=DG=,∴OM=MN﹣ON=,∴DM==,∴DE=2DM=.故选:A.10.解:连接OP,OQ,∵DE,FG,,的中点分别是M,N,P,Q,∴OP⊥AC,OQ⊥BC,∴H、I是AC、BD的中点,∴OH+OI=(AC+BC)=9,∵MH+NI=AC+BC=18,MP+NQ=12,∴PH+QI=18﹣12=6,∴AB=OP+OQ=OH+OI+PH+QI=9+6=15,故选:D.二.填空题(共5小题)11.解:由已知可知,最长的弦是过M的直径AB,最短的是垂直平分直径的弦CD,已知AB=10,CD=6,则OD=5,MD=3,由勾股定理得OM=4.故答案为:4.12.解:①当弦AB和CD在圆心同侧时,如图1,∵AB=24,CD=10,∴AE=12,CF=5,∵OA=OC=13,∴EO=5,OF=12,∴EF=12﹣5=7;②当弦AB和CD在圆心异侧时,如图2,∵AB=24,CD=10,∴AE=12,CF=5,∵OA=OC=13,∴EO=5,OF=12,∴EF=OF+OE=17.∴AB与CD之间的距离为7或17.故答案为7或17.13.解:∵CD⊥OB,∴CE=DE=CD=4,在Rt△OCE中,OE==3,∴AE=AO+OE=5+3=8(cm).故答案为8.14.解:作OF⊥PQ于F,连接OP,∴PF=PQ=12,∵CD⊥AB,PQ∥AB,∴CD⊥PQ,∴四边形MEOF为矩形,∵CD=PQ,OF⊥PQ,CD⊥AB,∴OE=OF,∴四边形MEOF为正方形,设半径为x,则OF=OE=18﹣x,在直角△OPF中,x2=122+(18﹣x)2,解得x=13,则MF=OF=OE=5,∴OM=5.故答案为:5.15.解:过P点作PE⊥AB于E,过P点作PC⊥x轴于C,交AB于D,连接PA.∵AB=2,∴AE=,PA=2,∴PE=1.∵点D在直线y=x上,∴∠AOC=45°,∵∠DCO=90°,∴∠ODC=45°,∴∠PDE=∠ODC=45°,∴∠DPE=∠PDE=45°,∴DE=PE=1,∵⊙P的圆心是(2,a),∴点D的横坐标为2,∴OC=2,∴DC=OC=2,∴a=PD+DC=2+.故答案为:2+.三.解答题(共5小题)16.解:(1)连接OC,OD,∵AB为⊙O的直径,AB=10cm,∴OA=OB=5cm.∵AC=CD=DB,∴∠AOC=∠COD=∠BOD=60°,∴△AOC是等边三角形,∴OA=AC=5cm;(2)∵由(1)知∠AOC=∠COD=∠BOD=60°,∴△AOC、△COD与△BOD均是等边三角形,∴∠A+∠ACD=180°,∴CD∥AB.17.(1)解:连结OA交BF于G,如图,⊙O的半径为r,∵AD⊥OB,在Rt△OHA中,OH=r﹣2,OA=r,∴r2=42+(r﹣2)2,解得r=5,即⊙O的半径为5;(2)证明:连结CF,如图,∵AD⊥OB,∴弧AB=弧DB,∵∠EAB=∠EBA,∴弧BD=弧AF,∴弧AB=弧AF,∴OA⊥BG,∴BG=FG,∴∠OAH=∠OBG,在△OAH和△OBG中,,∴△OAH≌△OBG(AAS),∴AH=BG,∴BF=2AH.18.解:(1)相等.如图:作OG⊥AB于G,OH⊥CD于H,连接OA,OC,OB,OD.AG=BG,CH=DH,∵∠EPO=∠FPO,∴OG=OH.在Rt△OBG和Rt△ODH中,由HL定理得:△OBG≌△ODH,∴GB=HD,∴AB=CD;(2)点P在圆上,结论成立:顶点P在圆上,此时点P,A,C重合于点A,作OG⊥AB于G,OH⊥AD于H,∴AG=GB,AH=HD,∵∠EAO=∠DAO,∴OG=OH.在Rt△OAG和Rt△OAH中,由HL定理得:△OAG≌△OAH,∴AG=AH,∴AB=AD.即点P在圆上,结论成立.(3)顶点P在圆内,作OG⊥AB于G,OH⊥CD于H,则AG=GB,CH=HD,∵∠EPO=∠FPO,∴OG=OH,∴GB=HD,∴AB=CD.即点P在圆内,结论成立.19.解:(1)∵直线的解析式y=x,∴tan∠A1OB1==,∴∠A1OB1=60°,OA1=1,∴A1B1=,OA2=OB1=2,∴B1(1,).(2)连接A 4B 3,作OH ⊥A 4B 3于H .由题意OA 1=1,OA 2=2,OA 3=4,OA 4=8,∵OA 4=OB 3,OH ⊥A 4B 3,∴∠A 4OH =∠A 4OB 3=30°,∴OH =OA 4•cos30°=8×=4.20.解:(1)如图1中,连接OB ,OC .设BF =EF =x ,OF =y .∵AB ∥CD ,EF ⊥AB ,∴EF ⊥CD ,∴∠CEF =∠BFO =90°∴AF =BF =x ,DE =EC =2, 根据勾股定理可得:, 解得(舍弃)或,∴BF =4,AB =2BF =8.(2)如图2中,作CH ⊥AB 于H .∵OB⊥OC,∴∠A=∠BOC=45°,∵AH⊥CH,∴△ACH是等腰直角三角形,∵AC=CH,∵AB∥CD,EF⊥AB,∴EF⊥CD,∠CEF=∠EFH=∠CHF=90°,∴四边形EFHC是矩形,∴CH=EF,在Rt△OEC中,∵EC=,OC=,OE===2,∵∠EOC+∠OCE=90°,∠EOC+∠FOB=90°,∴∠FOB=∠ECO,∵OB=OC,∴△OFB≌△CEO(AAS),∴OF=EC=,∴CH=EF=3,∴AC=EF=6.。
部编数学九年级上册专题24.2垂径定理的应用(重点题专项讲练)(人教版)(解析版)含答案

专题24.2 垂径定理的应用【典例1】如图,有一座圆弧形拱桥,桥下水面宽度AB为12m,拱高CD为4m.(1)求拱桥的半径;(2)有一艘宽为5m的货船,船舱顶部为长方形,并高出水面3.4m,则此货船是否能顺利通过此圆弧形拱桥,并说明理由.(1)根据垂径定理和勾股定理求解;(2)连接ON,OB,根据勾股定理即可得到结论.解:(1)如图,连接ON,OB.∵OC⊥AB,∴D为AB中点,∵AB=12m,∴BD=12AB=6m.又∵CD=4m,设OB=OC=ON=r,则OD=(r﹣4)m.在Rt△BOD中,根据勾股定理得:r2=(r﹣4)2+62,解得r=6.5.∴拱桥的半径为6.5m.(2)∵CD=4m,船舱顶部为长方形并高出水面3.4m,∴CE=4﹣3.4=0.6(m),∴OE=r﹣CE=6.5﹣0.6=5.9(m),在Rt△OEN中,EN2=ON2﹣OE2=6.52﹣5.92=7.44,∴EN m).∴MN=2EN=2×≈5.4m>5m.∴此货船能顺利通过这座拱桥.1.(2022•南海区校级一模)如图,武汉晴川桥可以近似地看作半径为250m的圆弧,桥拱和路面之间用数根钢索垂直相连,其正下方的路面AB长度为300m,那么这些钢索中最长的一根为( )A.50m B.45m C.40m D.60m【思路点拨】设圆弧的圆心为O,过O作OC⊥AB于C,交AB于D,连接OA,先由垂径定理得AC=BC=12AB=150,再由勾股定理求出OC=200,然后求出CD的长即可.【解题过程】解:设圆弧的圆心为O,过O作OC⊥AB于C,交AB于D,连接OA,如图所示:则OA=OD=250,AC=BC=12AB=150,∴OC=200,∴CD=OD﹣OC=250﹣200=50(m),即这些钢索中最长的一根为50m ,故选:A .2.(2022•旌阳区二模)筒车是我国古代发明的一种水利灌溉工具,如图1,筒车盛水桶的运行轨道是以轴心O 为圆心的圆,如图2,已知圆心O 在水面上方,且⊙O 被水面截得弦AB 长为4米,⊙O 半径长为3米.若点C 为运行轨道的最低点,则点C 到弦AB 所在直线的距离是( )A .1米B .2米C .米D .(3+米【思路点拨】连接OC ,OC 交AB 于D ,由垂径定理得AD =BD =12AB =2(米),再由勾股定理得OD 后求出CD 的长即可.【解题过程】解:连接OC ,OC 交AB 于D ,由题意得:OA =OC =3米,OC ⊥AB ,∴AD =BD =12AB =2(米),∠ADO =90°,∴OD ==∴CD=OC﹣OD=(3即点C到弦AB所在直线的距离是(3故选:C.3.(2022•宣州区二模)如图所示的是一圆弧形拱门,其中路面AB=2m,拱高CD=3m,则该拱门的半径为( )A.53m B.2m C.83m D.3m【思路点拨】取圆心为O,连接OA,由垂径定理设⊙O的半径为rm,则OC=OA=rm,由拱高CD=3m,OD=(3﹣r)m,OD⊥AB,由垂径定理得出AD=1m,由勾股定理得出方程r2=12+(3﹣r)2,解得:r=53,得出该拱门的半径为53m,即可得出答案.【解题过程】解:如图,取圆心为O,连接OA,设⊙O的半径为rm,则OC=OA=rm,∵拱高CD=3m,∴OD=(3﹣r)m,OD⊥AB,∵AB=2m,∴AD=BD=12AB=1m,∵OA2=AD2+OD2,∴r2=12+(3﹣r)2,解得:r=5 3,∴该拱门的半径为53 m,故选:A.4.(2021秋•海淀区校级期中)数学活动课上,同学们想测出一个残损轮子的半径,小的解决方案如下:如图,在轮子圆弧上任取两点A,B,连接AB,再作出AB的垂直平分线,交AB于点C,交AB于点D,测出AB,CD的长度,即可计算得出轮子的半径.现测出AB=40cm,CD=10cm,则轮子的半径为( )A.50cm B.35cm C.25cm D.20cm【思路点拨】由垂径定理,可得出BC的长;连接OB,在Rt△OBC中,可用半径OB表示出OC的长,进而可根据勾股定理求出得出轮子的半径,即可得出轮子的直径长.【解题过程】解:设圆心为O,连接OB.Rt△OBC中,BC=12AB=20cm,根据勾股定理得:OC2+BC2=OB2,即:(OB﹣10)2+202=OB2,解得:OB=25;故轮子的半径为25cm.故选:C.5.(2021秋•曾都区期中)在圆柱形油槽内装有一些油,油槽直径MN为10分米.截面如图,油面宽AB 为6分米,如果再注入一些油后,当油面宽变为8分米,油面AB上升( )A.1分米B.4分米C.3分米D.1分米或7分米【思路点拨】实质是求两条平行弦之间的距离.根据勾股定理求弦心距,作和或差分别求解.【解题过程】解:连接OA.作OG⊥AB于G,则在直角△OAG中,AG=3分米,因为OA=5cm,根据勾股定理得到:OG=4分米,即弦AB的弦心距是4分米,同理当油面宽AB为8分米时,弦心距是3分米,当油面没超过圆心O时,油上升了1分米;当油面超过圆心O时,油上升了7分米.因而油上升了1分米或7分米.故选:D.6.(2021秋•宁波期末)把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=6cm,则球的半径为( )A.3cm B.134cm C.154cm D.174cm【思路点拨】设球的平面投影圆心为O,过点O作ON⊥AD于点N,延长NO交BC于点M,连接OF,由垂径定理得:NF=EN=12EF=3(cm),设OF=xcm,则OM=(4﹣x)cm,再在Rt△MOF中由勾股定理求得OF的长即可.【解题过程】解:设球的平面投影圆心为O,过点O作ON⊥AD于点N,延长NO交BC于点M,连接OF,如图所示:则NF=EN=12EF=3(cm),∵四边形ABCD是矩形,∴∠C=∠D=90°,∴四边形CDNM是矩形,∴MN=CD=6cm,设OF=xcm,则OM=OF,∴ON=MN﹣OM=(6﹣x)cm,在Rt△ONF中,由勾股定理得:ON2+NF2=OF2,即:(6﹣x)2+32=x2,解得:x=15 4,即球的半径长是154cm,故选:C.7.(2022•鄂州)工人师傅为检测该厂生产的一种铁球的大小是否符合要求,设计了一个如图(1)所示的工件槽,其两个底角均为90°,将形状规则的铁球放入槽内时,若同时具有图(1)所示的A、B、E三个接触点,该球的大小就符合要求.图(2)是过球心及A、B、E三点的截面示意图,已知⊙O的直径就是铁球的直径,AB是⊙O的弦,CD切⊙O于点E,AC⊥CD、BD⊥CD,若CD=16cm,AC=BD=4cm,则这种铁球的直径为( )A .10cmB .15cmC .20cmD .24cm【思路点拨】连接OE ,交AB 于点F ,连接OA ,∵AC ⊥CD 、BD ⊥CD ,由矩形的判断方法得出四边形ACDB 是矩形,得出AB ∥CD ,AB =CD =16cm ,由切线的性质得出OE ⊥CD ,得出OE ⊥AB ,得出四边形EFBD 是矩形,AF =12AB =12×16=8(cm ),进而得出EF =BD =4cm ,设⊙O 的半径为rcm ,则OA =rcm ,OF =OE ﹣EF =(r ﹣4)cm ,由勾股定理得出方程r 2=82+(r ﹣4)2,解方程即可求出半径,继而求出这种铁球的直径.【解题过程】解:如图,连接OE ,交AB 于点F ,连接OA ,∵AC ⊥CD 、BD ⊥CD ,∴AC ∥BD ,∵AC =BD =4cm ,∴四边形ACDB 是平行四边形,∴四边形ACDB 是矩形,∴AB ∥CD ,AB =CD =16cm ,∵CD 切⊙O 于点E ,∴OE ⊥CD ,∴OE ⊥AB ,∴四边形EFBD 是矩形,AF =12AB =12×16=8(cm ),∴EF =BD =4cm ,设⊙O 的半径为rcm ,则OA =rcm ,OF =OE ﹣EF =(r ﹣4)cm ,在Rt△AOF中,OA2=AF2+OF2,∴r2=82+(r﹣4)2,解得:r=10,∴这种铁球的直径为20cm,故选:C.8.(2022•上海)如图所示,小区内有个圆形花坛O,点C在弦AB上,AC=11,BC=21,OC=13,则这个花坛的面积为 400π .(结果保留π)【思路点拨】根据垂径定理,勾股定理求出OB2,再根据圆面积的计算方法进行计算即可.【解题过程】解:如图,连接OB,过点O作OD⊥AB于D,∵OD⊥AB,OD过圆心,AB是弦,∴AD=BD=12AB=12(AC+BC)=12×(11+21)=16,∴CD=BC﹣BD=21﹣16=5,在Rt△COD中,OD2=OC2﹣CD2=132﹣52=144,在Rt△BOD中,OB2=OD2+BD2=144+256=400,∴S⊙O=π×OB2=400π,故答案为:400π.9.(2021秋•溧水区期末)在一个残缺的圆形工件上量得弦BC=8cm,BC的中点D到弦BC的距离DE=2cm,则这个圆形工件的半径是 5 cm.【思路点拨】由垂径定理的推论得圆心在直线DE上,设圆心为0,连接OB,半径为R,再由垂径定理得BE=CE=12 BC=4(cm),然后由勾股定理得出方程,解方程即可.【解题过程】解:∵DE⊥BC,DE平分弧BC,∴圆心在直线DE上,设圆心为O,半径为Rcm,如图,连接OB,则OD⊥BC,OE=R﹣DE=(R﹣2)cm,∴BE=CE=12BC=4(cm),在Rt△OEB中,OB2=BE2+OE2,即R2=42+(R﹣2)2,解得:R=5,即这个圆形工件的半径是5cm,故答案为:5.10.(2022•柯桥区一模)《九章算术》是中国传统数学重要的著作之一,奠定了中国传统数学的基本框架.其中卷九中记载了一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”其意思是:如图,AB为⊙O的直径,弦CD⊥AB于点E,BE=1寸,CD=1尺,那么直径AB的长为多少寸?(注:1尺=10寸)根据题意,该圆的直径为 26 寸.【思路点拨】连接OC,由直径AB与弦CD垂直,根据垂径定理得到E为CD的中点,由CD的长求出DE的长,设OC =OA=x寸,则AB=2x寸,OE=(x﹣1)寸,由勾股定理得出方程,解方程求出半径,即可得出直径AB 的长.【解题过程】解:连接OC,∵弦CD⊥AB,AB为圆O的直径,∴E为CD的中点,又∵CD=10寸,∴CE=DE=12CD=5寸,设OC=OA=x寸,则AB=2x寸,OE=(x﹣1)寸,由勾股定理得:OE2+CE2=OC2,即(x﹣1)2+52=x2,解得x=13,∴AB=26寸,即直径AB的长为26寸,故答案为:26.11.(2021秋•瑞安市期末)某公路上有一隧道,顶部是圆弧形拱顶,圆心为O,隧道的水平宽AB为24m,AB离地面的高度AE=10 m,拱顶最高处C离地面的高度CD为18m,在拱顶的M,N处安装照明灯,且M,N离地面的高度相等都等于17m,则MN= 10 m.【思路点拨】根据题意和垂径定理得到CG=8m,AG=12m,CH=1m,根据勾股定理求得半径,进而利用勾股定理求得MH,即可求得MN.【解题过程】解:设CD于AB交于G,与MN交于H,∵CD=18m,AE=10m,AB=24m,HD=17m,∴CG=8m,AG=12m,CH=1m,设圆拱的半径为r,在Rt△AOG中,OA2=OG2+AG2,∴r2=(r﹣8)2+122,解得r=13,∴OC=13m,∴OH=13﹣1=12m,在Rt△MOH中,OM2=OH2+MH2,∴132=122+MH2,解得MH2=25,∴MH=5m,∴MN=10m,故答案为10.12.(2022•荆州)如图,将一个球放置在圆柱形玻璃瓶上,测得瓶高AB=20cm,底面直径BC=12cm,球的最高点到瓶底面的距离为32cm,则球的半径为 7.5 cm(玻璃瓶厚度忽略不计).【思路点拨】设球心为O,过O作OM⊥AD于M,连接OA,设球的半径为rcm,由垂径定理得AM=DM=12AD=6(cm)然后在Rt△OAM中,由勾股定理得出方程,解方程即可.【解题过程】解:如图,设球心为O,过O作OM⊥AD于M,连接OA,设球的半径为rcm,由题意得:AD=12cm,OM=32﹣20﹣r=(12﹣r)(cm),由垂径定理得:AM=DM=12AD=6(cm),在Rt△OAM中,由勾股定理得:AM2+OM2=OA2,即62+(12﹣r)2=r2,解得:r=7.5,即球的半径为7.5cm,故答案为:7.5.13.(2021秋•温州校级月考)如图是郑州圆形“戒指桥”,其数学模型为如图所示.已知桥面跨径AB=20米,D为圆上一点,DC⊥AB于点C,且CD=BC=14米,则该圆的半径长为 26 米.【思路点拨】过O作ON⊥AB于N,过D作DM⊥ON于M,由垂径定理得AN=BN=12AB=10(米),再证四边形DCNM是矩形,则MN=CD=14米,DM=CN=BC+BN=24(米),设该圆的半径长为r米,然后由题意列出方程组,解方程组即可.【解题过程】解:过O作ON⊥AB于N,过D作DM⊥ON于M,如图所示:则AN=BN=12AB=10(米),∠ONC=∠DMN=90°,∵DC⊥AB,∴∠DCN=90°,∴四边形DCNM是矩形,∴MN=CD=14米,DM=CN=BC+BN=24(米),设该圆的半径长为r米,由题意得:ON2=r2−102 OM2=r2−242 OM=ON−14,解得:r=26ON=24 OM=10,即该圆的半径长为26米,故答案为:26.14.(2021秋•金安区校级期末)往直径为680mm的圆柱形油槽内装入一些油以后,截面如图所示,若油面宽AB=600mm,求油的最大深度.【思路点拨】连接OB,过点O作OC⊥AB于点D,交⊙O于点C,先由垂径定理求出BD的长,再根据勾股定理求出OD 的长,进而可得出CD的长.【解题过程】解:过点O作OC⊥AB于点D,交弧AB于点C.∵OC⊥AB于点D∴BD=12AB=12×600=300mm,∵⊙O的直径为680mm∴OB=340mm…(5分)∵在Rt△ODB中,OD=160(mm),∴DC=OC﹣OD=340﹣160=180(mm);答:油的最大深度为180mm.15.(2021秋•惠城区校级期中)如图,⊙O为水管横截面,水面宽AB=24cm,水的最大深度为18cm,求⊙O的半径.【思路点拨】由垂径定理可知AD=12cm,设⊙O的半径为rcm,则OD=(18﹣r)cm,在Rt△AOd中,再利用勾股定理即可求出r的值.【解题过程】解:作OD⊥AB于D,交⊙O于E,连接OA,∴AD=12AB=12×24=12cm,设⊙O的半径为rcm,则OD=ED﹣OE=(18﹣r)cm,在Rt△AOD中,由勾股定理得:OA2=OD2+AD2,即r2=(18﹣r)2+122,解得:r=13,即⊙O的半径为13cm.16.(2021秋•奈曼旗期中)如图所示,测得AB是8mm,测得钢珠顶端离零件表面的距离为8mm,求这个圆的直径.【思路点拨】过O作OC⊥AB于C,交优弧AB于D,连接AO,由垂径定理得AC=BC=12AB=4(mm),设⊙O的半径为rmm,则OC=CD﹣OD=(8﹣r)mm,然后在Rt△AOC中,由勾股定理得出方程,解方程即可.【解题过程】解:如图,过O作OC⊥AB于C,交优弧AB于D,连接AO,则AC=BC=12AB=4(mm),CD=8mm,设⊙O的半径为rmm,则OC=CD﹣OD=(8﹣r)mm,在Rt△AOC中,由勾股定理得:42+(8﹣r)2=r2,解得:r=5,即⊙O的半径为5mm,∴⊙O的直径为10mm.17.(2021秋•阜阳月考)《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就,它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸).问这块圆形木材的直径(AC)是多少?”如图所示,请根据所学的知识解答上述问题.【思路点拨】设⊙O的半径为x寸.在Rt△ADO中,AD=5寸,OD=(x﹣1)寸,OA=x寸,则有x2=(x﹣1)2+52,解方程即可.【解题过程】解:设⊙O的半径为x寸,∵OE⊥AB,AB=10寸,∴AD=BD=12AB=5寸,在Rt△AOD中,OA=x,OD=x﹣1,由勾股定理得x2=(x﹣1)2+52,解得x=13,∴⊙O的直径AC=2x=26(寸),答:这块圆形木材的直径(AC)是26寸.18.(2021秋•高新区期中)某居民小区的一处圆柱形的输水管道破裂,维修人员为更换管道,需要确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.(1)请你补全这个输水管道的圆形截面图;(要求尺规作图,保留作图痕迹,不写作法)(2)若这个输水管道有水部分的水面宽AB=32cm,水最深处的地方高度为8cm,求这个圆形截面的半径.【思路点拨】(1)根据尺规作图的步骤和方法做出图即可;(2)先过圆心O作半径OD⊥AB,交AB于点D,设半径为r,得出AD、OD的长,在Rt△AOD中,根据勾股定理求出这个圆形截面的半径.【解题过程】解:(1)如图所示;(2)作OD⊥AB于D,并延长交⊙O于C,则D为AB的中点,∵AB=32cm,∴AD=12AB=16.设这个圆形截面的半径为xcm,又∵CD=8cm,∴OC=x﹣8,在Rt△OAD中,∵OD2+AD2=OA2,即(x﹣8)2+162=x2,解得,x=20.∴圆形截面的半径为20cm.19.(2021秋•黔西南州期末)如图,在一座圆弧形拱桥,它的跨度AB为60m,拱高PM为18m,当洪水泛滥到跨度只有30m时,就要采取紧急措施,若某次洪水中,拱顶离水面只有4m,即PN=4m时,试通过计算说明是否需要采取紧急措施.【思路点拨】由垂径定理可知AM=BM、A′N=B′N,利用AB=60,PM=18,可先求得圆弧所在圆的半径,再计算当PN =4时A′B′的长度,与30米进行比较大小即可.【解题过程】解:设圆弧所在圆的圆心为O,连接OA、OA′,设半径为x米,则OA=OA′=OP,由垂径定理可知AM=BM,A′N=B′N,∵AB=60米,∴AM=30米,且OM=OP﹣PM=(x﹣18)米,在Rt△AOM中,由勾股定理可得AO2=OM2+AM2,即x2=(x﹣18)2+302,解得x=34,∴ON=OP﹣PN=34﹣4=30(米),在Rt△A′ON中,由勾股定理可得A′N=16(米),∴A′B′=32米>30米,∴不需要采取紧急措施.20.(2021秋•余干县期中)如图是某蔬菜基地搭建一座圆弧型蔬菜棚,跨度AB=3.2米,拱高CD=0.8米(C为AB的中点,D为弧AB的中点).(1)求该圆弧所在圆的半径;(2)在距蔬菜棚的一端0.4米处竖立支撑杆EF,求支撑杆EF的高度.【思路点拨】(1)设弧AB所在的圆心为O,D为弧AB的中点,CD⊥AB于C,延长DC至O点,设⊙O的半径为R,利用勾股定理求出即可;(2)利用垂径定理以及勾股定理得出HF的长,再求出EF的长即可.【解题过程】解:(1)设弧AB所在的圆心为O,D为弧AB的中点,CD⊥AB于C,延长DC经过O点,则BC=12AB=1.6(米),设⊙O的半径为R,在Rt△OBC中,OB2=OC2+CB2,∴R2=(R﹣0.8)2+1.62,解得R=2,即该圆弧所在圆的半径为2米;(2)过O作OH⊥FE于H,则OH=CE=1.6﹣0.4=1.2=65(米),OF=2米,在Rt△OHF中,HF== 1.6(米),∵HE=OC=OD﹣CD=2﹣0.8=1.2(米),∴EF=HF﹣HE=1.6﹣1.2=0.4(米),即支撑杆EF的高度为0.4米.21.如图①,圆形拱门屏风是中国古代家庭中常见的装饰隔断,既美观又实用,彰显出中国元素的韵味.图②是一款拱门的示意图,其中C为AB中点,D为拱门最高点,线段CD经过圆心,已知拱门的半径为1.5m,拱门最下端AB=1.8m.(1)求拱门最高点D到地面的距离;(2)现需要给房间内搬进一个长和宽为2m,高为1.2m的桌子,已知搬桌子的两名工人在搬运时所抬高度相同,且高度为0.5m 2.236)【思路点拨】(1)如图②中,连接AO.利用勾股定理求出OC即可;(2)如图②﹣1,弦EF=2m,且EF⊥CD,连接OE.求出CJ即可.【解题过程】解:(1)如图②中,连接AO.∵CD⊥AB,CD经过圆心O,∴AC=CB=0.9m,∴OC= 1.2(m),∴CD=OD+PC=1.5+1.2=2.7(m),∴拱门最高点D到地面的距离为2.7m;(2)如图②﹣1,弦EF=2m,且EF⊥CD,连接OE.∵CD⊥EF,CD经过圆心,∴EJ=JF=1m,≈1.118,∴OJ=2∴CJ=1.2﹣1.118=0.082(m),∵0.5>0.082,∴搬运该桌子时能够通过拱门.22.(2021秋•姑苏区校级月考)诗句“君到姑苏见,人家尽枕河”所描绘的就是有东方威尼斯之称的水城苏州.小勇要帮忙船夫计算一艘货船是否能够安全通过一座圆弧形的拱桥,现测得桥下水面AB宽度16m时,拱顶高出水平面4m,货船宽12m,船舱顶部为矩形并高出水面3m.(1)请你帮助小勇求此圆弧形拱桥的半径;(2)小勇在解决这个问题时遇到困难,请你判断一下,此货船能顺利通过这座拱桥吗?说说你的理由.【思路点拨】(1)根据垂径定理和勾股定理求解;(2)连接ON,利用勾股定理求出EN,得出MN的长,即可得到结论.【解题过程】解:(1)如图,连接OB.∵OC⊥AB,∴D为AB中点,∵AB=16m,∴BD=12AB=8(m),又∵CD=4m,设OB=OC=r,则OD=(r﹣4)m.在Rt△BOD中,根据勾股定理得:r2=(r﹣4)2+82,解得r=10.答:此圆弧形拱桥的半径为10m.(2)此货船不能顺利通过这座拱桥,理由如下:连接ON,∵CD=4m,船舱顶部为长方形并高出水面3m,∴CE=4﹣3=1(m),∴OE=r﹣CE=10﹣1=9(m),在Rt△OEN中,由勾股定理得:EN∴MN=2EN=<12m.∴此货船B不能顺利通过这座拱桥.。
(名师整理)最新人教版数学中考《垂径定理 圆心角 圆周角定理》专题精练(含答案解析)

垂径定理圆心角圆周角定理一选择题:1、如图,⊙O是△ABC的外接圆,∠OBC=42°,则∠A的度数是()A.42°B.48°C.52°D.58°2.如图,A、B、C、D四个点均在⊙O上,∠AOD=50°,AO∥DC,则∠B的度数为( )A.50° B.55° C.60° D.65°3.如图,点B、D、C是⊙O上的点,∠BDC=130°,则∠BOC是()A.100° B.110° C.120°D.130°4.如图,⊙O的半径为5,弦AB的长为8,点M在线段AB(包括端点A,B)上移动,则OM取值范围是()A.3≤OM≤5B.3≤OM<5C.4≤OM≤5 D.4≤OM<55、如图所示,AB是⊙O的直径,AD=DE,AE与BD交于点C,则图中与∠BCE相等的角有()A.2个 B.3个 C.4个 D.5个6.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B 的读数分别为86°、30°,则∠ACB的大小为( )A.15°B.28° C.29°D.34°7.如图,C为⊙O直径AB上一动点,过点C的直线交⊙O于D、E两点,且∠ACD=45°,DF⊥AB于点F,EG⊥AB于点G,当点C在AB上运动时,设AF=x,DE=y,下列中图象中,能表示y与x的函数关系式的图象大致是( )8.如图.⊙O 中,AB、AC是弦,O在∠ABO的内部,,,,则下列关系中,正确的是()A. B. C. D.9.如图,四边形ABCD内接于⊙O,BC是直径,AD=DC,∠ADB=20º,则∠ACB,∠DBC分别为()A.15º与30º B.20º与35º C.20º与40º D.30º与35º10.图中∠BOD的度数是()A.55° B.110° C.125° D.150°11.如图,点I为△ABC的内心,点O为△ABC的外心,∠O=140°,则∠I为()(A)140°(B)125°(C)130°(D)110°12.如图,弦AB∥CD,E为上一点,AE平分,则图中与相等(不包括)的角共有()A.3个 B.4个 C.5个 D.6个13、如图,已知的半径为1,锐角内接于,于点,于点,则的值等于()A.的长 B.的长 C.的长 D.的长14.如图,在直角∠O的内部有一滑动杆AB,当端点A沿直线AO向下滑动时,端点B会随之自动地沿直线OB向左滑动,如果滑动杆从图中AB处滑动到A′B′处,那么滑动杆的中点C所经过的路径是()A.直线的一部分B.圆的一部分C.双曲线的一部分 D.抛物线的一部分15.如图,AB是⊙O的直径,弦BC=2cm,∠ABC=60°.若动点P以2cm/s的速度从B点出发沿着B→A的方向运动,点Q从A点出发沿着A→C的方向运动,当点P到达点A时,点Q也随之停止运动.设运动时间为t(s),当△APQ是直角三角形时,t的值为()A. B. C.或 D.或或16.如图,,在以为直径的半圆上,,在上,为正方形,若正方形边长为1,,,则下列式子中,不正确的是()A. B. C. D.17.如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点.若MN=1,则△PMN周长的最小值为()A.4 B.5 C.6 D.718.如图,在△ABC中,AD是高,AE是直径,AE交BC于G,有下列四个结论:•①AD2=BD·CD;②BE2=EG·AE;③AE·AD=AB·AC;④AG·EG=BG·CG.其中正确结论的有()A.1个 B.2个 C.3个 D.4个19.如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为边向外作正方形ACDE,BCFG,DE,FG,,的中点分别是M,N,P,Q。
2020年九年级中考数学专题复习:圆的垂径定理的应用(含解析)

中考数学专题复习:圆的垂径定理的应用(含解析)班级:姓名:一、单选题1.如图,把一个宽度为2cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:cm),那么光盘的直径是( )A. 5cmB. 8cmC. 10cmD. 12cm2.下列命题:①三点确定一个圆,②弦的平分线过圆心,③弦所对的两条弧的中点的连线是圆的直径,④平分弦的直线平分弦所对的弧,其中正确的命题有()A. 3个B. 2个C. 1个D. 0个3.如图,⊙O的半径为5,AB为弦,半径OC⊥AB,垂足为点E,若CE=2,则AB的长是( )A. 4B. 6C. 8D. 104.一根水平放置的圆柱形输水管道横截面如图所示,其中有水部分水面宽0.8米,最深处水深0.2米,则此输水管道的直径是( )A. 0.5B. 1C. 2D. 45.如图,⊙O的弦AB=8,C是AB的中点,且OC=3,则⊙O的半径等于( )A. 8B. 5C. 10D. 46.如图表示一圆柱形输水管的横截面,阴影部分为有水部分,如果输水管的半径为5cm,水面宽AB为8cm,则水的最大深度CD为()A. 4cmB. 3cmC. 2cmD. 1cm7.如图,以O为圆心的两个同心圆中,半径分别为3和5,若大圆的弦AB与小圆相交,则弦AB的长的取值范围是()A. 8≤AB≤10B. 8<AB<10C. 8<AB≤10D. 6≤AB≤108.如图,△ABC内接于⊙O,D为线段AB的中点,延长OD交⊙O于点E,连接AE,BE,则下列五个结论①AB⊥DE,②AE=BE,③OD=DE,④∠AEO=∠C,⑤弧AE=弧AEB,正确结论的个数是( )A. 2B. 3C. 4D. 59.如图,⊙O的直径AB的长为10,弦AC长为6,∠ACB的平分线交⊙O于D,则AD长为()A. 8B. 5C. D.二、填空题10.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=16厘米,则球的半径为________厘米.11.如图,已知⊙O的半径为5,点P是弦AB上的一动点,且弦AB的长为8.则OP的取值范围为________.12.“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何”此问题的实质就是解决下面的问题:“如图,CD为⊙O的直径,弦AB⊥CD于点E,CE=1,AB=10,求CD的长”.根据题意可得CD的长为________.三、解答题13.如图①是某校存放学生自行车的车棚的示意图(尺寸如图所示,单位:m),车棚顶部是圆柱侧面的一部分,其展开图是矩形;如图②是车棚顶部截面的示意图, 所在圆的圆心为点O,车棚顶部是用一种帆布覆盖的,求覆盖棚顶的帆布的面积.(不考虑接缝等因素,计算结果保留π)14.如图,在破残的圆形残片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D,已知AB=8 cm,CD=2 cm.求破残的圆形残片的半径.15.如图,某公司的一座石拱桥是圆弧形(劣弧),其跨度AB为24m,拱高CD为8m,求石拱桥拱的半径.四、综合题16.如图,C、D两点在以AB为直径的半圆O上,AD平分∠BAC,AB=20,AD=4 ,DE⊥AB于E.(1)求DE的长.(2)求证:AC=2OE.17.如图,在平面直角坐标系中,四边形OABC四个顶点的坐标分别为O(0,0),A(﹣3,0),B(﹣4,2),C(﹣1,2).将四边形OABC绕点O顺时针旋转90°后,点A,B,C分别落在点A′,B′,C′处.(1)请你在所给的直角坐标系中画出旋转后的四边形OA′B′C′;(2)点C旋转到点C′所经过的弧的半径是________,点C经过的路线长是________.答案解析部分一、单选题1.【答案】C【考点】垂径定理的应用【解析】【解答】解:设光盘的圆心为O,如图所示:过点O作OA垂直直尺于点A,连接OB,设OB=r,∵一边与光盘边缘两个交点处的读数恰好是“2”和“10”,∴AB=×(10﹣2)=4,∵刻度尺宽2cm,∴OA=r﹣2,在Rt△OAB中,OA2+AB2=OB2 ,即(r﹣2)2+42=r2 ,解得:r=5.∴该光盘的直径是10cm.故选:C.【分析】设光盘的圆心为O,过点O作OA垂直直尺于点A,连接OB,再设OB=r,利用勾股定理求出r的值即可.2.【答案】C【考点】垂径定理的应用,三角形的外接圆与外心,命题与定理【解析】【解答】解:①不在同一直线上的3个点确定一个圆,故错误;②弦的垂直平分线经过圆心,故错误;③根据圆的轴对称性可得,正确;④平分弦(非直径)的直径平分弦所对的弧,故错误;正确的有1个,故选C.【分析】根据垂径定理的知识及过3点圆的知识可得正确选项.3.【答案】C【考点】垂径定理的应用【解析】【分析】由于半径OC⊥AB,利用垂径定理可知AB=2AE,又CE=2,OC=5,易求OE,在Rt△AOE中利用勾股定理易求AE,进而可求AB.【解答】如右图,连接OA,∵半径OC⊥AB,∴AE=BE=AB,∵OC=5,CE=2,∴OE=3,在Rt△AOE中,∴AB=2AE=8,故选C.【点评】本题考查了垂径定理、勾股定理,解题的关键是利用勾股定理先求出AE4.【答案】B【考点】垂径定理的应用【解析】【解答】解:设半径为r,过O作OE⊥AB交AB于点D,连接OA、OB,则AD=AB=×0.8=0.4米,设OA=r,则OD=r﹣DE=r﹣0.2,在Rt△OAD中,OA2=AD2+OD2 ,即r2=0.42+(r﹣0.2)2 ,解得r=0.5米,故此输水管道的直径=2r=2×0.5=1米.故选B.【分析】根据题意知,已知弦长和弓形高,求半径(直径).根据垂径定理和勾股定理求解.5.【答案】B【考点】垂径定理的应用【解析】【分析】连接OA,即可证得△OAM是直角三角形,根据垂径定理即可求得AM,根据勾股定理即可求得OA的长.【解答】连接OA,∵M是AB的中点,∴OM⊥AB,且AM=4在直角△OAM中,OA==5故选B.【点评】本题主要考查了垂径定理,以及勾股定理,根据垂径定理求得AM的长,证明△OAM是直角三角形是解题的关键.6.【答案】C【考点】勾股定理,垂径定理的应用【解析】【解答】解:如图所示:∵输水管的半径为5cm,水面宽AB为8cm,水的最大深度为CD,∴DO⊥AB,∴AO=5cm,AC=4cm,∴CO= =3(cm),∴水的最大深度CD为:2cm.故选:C.【分析】根据题意可得出AO=5cm,AC=4cm,进而得出CO的长,即可得出答案.7.【答案】C【考点】勾股定理,垂径定理的应用【解析】【分析】此题可以首先计算出当AB与小圆相切的时候的弦长.连接过切点的半径和大圆的一条半径,根据勾股定理和垂径定理,得AB=8.若大圆的弦AB与小圆有两个公共点,即相交,此时AB>8;又因为大圆最长的弦是直径10,则8<AB≤10.【解答】当AB与小圆相切,∵大圆半径为5,小圆的半径为3,∵大圆的弦AB与小圆有两个公共点,即相交,∴8<AB≤10.故选C.【点评】本题综合运用了切线的性质、勾股定理和垂径定理.此题可以首先计算出和小圆相切时的弦长,再进一步分析相交时的弦长.8.【答案】B【考点】垂径定理的应用,圆周角定理【解析】【分析】已知OE是⊙O的半径,D是弦AB的中点,可根据垂径定理的推论来判断所给出的结论是否正确.【解答】∵OE是⊙O的半径,且D是AB的中点,∴OE⊥AB,弧AE=弧BE=弧AEB;(故①⑤正确)∴AE=BE;(故②正确)由于没有条件能够证明③④一定成立,所以一定正确的结论是①②⑤;故选B.9.【答案】D【考点】垂径定理的应用,圆周角定理【解析】【分析】首先连接BD,易得△ABD是等腰直角三角形,然后由特殊角的三角函数值,求得AD的长.【解答】连接BD,∵AB是⊙O的直径,∴∠ACB=∠ADB=90°,∵CD是∠ACB的平分线,∴∠ACD=∠ACB=45°,∴∠ABD=∠ACD=45°,∴AD=BD,∵AB=10,∴AD=AB•sin45°=.故选D.【点评】此题考查了圆周角定理、等腰直角三角形的性质.此题难度不大,注意掌握辅助线的作法,注意数形结合思想的应用二、填空题10.【答案】10【考点】勾股定理,垂径定理的应用【解析】【解答】解:EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,设OF=x,则OM=16﹣x,MF=8,在直角三角形OMF中,OM2+MF2=OF2即:(16﹣x)2+82=x2解得:x=10故答案为:10.【分析】首先找到EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,设OF=x,则OM是16﹣x,MF=8,然后在直角三角形MOF中利用勾股定理求得OF的长即可.11.【答案】3≤OP≤5【考点】垂径定理的应用【解析】【解答】解:过点O作OE⊥AB,垂足为E,连结OA.则可得当点P与点E重合时,线段OP为最短距离.∵点O为圆心,OE⊥AB,AB为圆的一条弦,∴AE=BE.∵AB=8,∴AE=BE=4.∵OE⊥AB,AE=4,OA=5,∴OE=3.当点P落在点A或点B处时,OP的长度最长,等于圆的半径,即为5.故OP的取值范围是3≤OP≤5.12.【答案】26【考点】垂径定理的应用【解析】【解答】解:连接OA,AB⊥CD,由垂径定理知,点E是AB的中点,AE= AB=5,OE=OC﹣CE=OA﹣CE,设半径为r,由勾股定理得,OA2=AE2+OE2=AE2+(OA﹣CE)2 ,即r2=52+(r﹣1)2 ,解得:r=13,所以CD=2r=26,即圆的直径为26.【分析】根据垂径定理和勾股定理求解.三、解答题13.【答案】解:如图,连结OB,过点O作OE⊥AB,垂足为E,交于F,由垂径定理知,E是AB的中点,F是的中点,从而EF是弓形的高.∵AB=4,∴AE= AB=2 m,EF=2 m.设半径为Rm,则OE=(R-2)m.在Rt△AOE中,∴R2=(R-2)2+(2 )2.∴R=4.在Rt△AEO中,∵AO=2OE,∴∠OAE=30°,∠AOE=60°,∴∠AOB=120°.∴的长为=(m).∴覆盖棚顶的帆布的面积为×60=160π(m2).【考点】含30度角的直角三角形,勾股定理,垂径定理的应用,弧长的计算【解析】【分析】如图,连结OB,过点O作OE⊥AB,垂足为E,交于F,由垂径定理知:E是AB的中点,F是AB⌢的中点,从而EF是弓形的高;设半径为Rm,则OE=(R-2)m.在Rt△AOE中,根据勾股定理计算出半径R,再由在直角三角形中,30度所对的直角边等于斜边的一半,从而得出∠AOB的度数,根据弧长公式即可求出弧AB的长度,最后得出覆盖棚顶的帆布的面积.14.【答案】解:在直线CD上取圆心O ,连接OA ,设半径为r cm.∵弦AB的垂直平分线交弧AB于点C ,交弦AB于点D .在Rt△ADO中,OA2=AD2+OD2 ,∴r2=42+(r-2)2 ,∴r=5答:破残的圆形残片的半径为5 cm.【考点】勾股定理,垂径定理的应用【解析】【分析】设圆的半径为r cm,根据AB CD和已知条件求出AD=AB,在Rt △ADO中,利用勾股定理为等量关系列方程,求出半径即可.15.【答案】解:延长CD到O,使得OC=OA,则O为圆心,∵拱桥的跨度AB=24cm,拱高CD=8cm,∴AD=12cm,∴AD2=OA2﹣(OC﹣CD)2 ,即122=AO2﹣(AO﹣8)2 ,解得AO=13cm.即圆弧半径为13米.答:石拱桥拱的半径为13m.【考点】勾股定理,垂径定理的应用【解析】【分析】将拱形图进行补充,构造直角三角形,利用勾股定理和垂径定理解答四、综合题16.【答案】(1)解:连接BD.∵AB为直径,∴∠ADB=90°,在Rt△ADB中,BD= ==4 ,∵S△ADB= AD•BD= AB•DE∴AD•BD=AB•DE,∴DE= = =4 ,即DE=4 ;(2)解:证明:连接OD,作OF⊥AC于点F.∵OF⊥AC,∴AC=2AF,∵AD平分∠BAC,∴∠BAC=2∠BAD.又∵∠BOD=2∠BAD,∴∠BAC=∠BOD,Rt△OED和Rt△AFO中,∵∴△AFO≌△OED(AAS),∴AF=OE,∵AC=2AF,∴AC=2OE.【考点】全等三角形的判定与性质,垂径定理的应用【解析】【分析】(1)出现直径时,连接直径的端点和圆周上的一点,构成90度圆周角,利用勾股定理和面积法可以解决;(2)过圆心向弦引垂线,由垂径定理,得平分,构造出AC的一半,再证△AFO≌△OED,可证出结论.17.【答案】(1)解:如图所示,四边形OA′B′C′即为所求作的图形(2);π【考点】垂径定理的应用,弧长的计算,旋转的性质,作图-旋转变换【解析】【解答】解:(2)根据勾股定理,OC= = ,C经过的路线长= = π.【分析】(1)根据网格结构找出点A、B、C的对应点A′、B′、C′的位置,然后顺次连接即可;(2)先利用勾股定理求出OC的长度,再根据弧长的计算公式列式进行计算即可得解.。
2022-2023学年北师大版九年级数学下册《3-3垂径定理》同步练习题(附答案)

2022-2023学年北师大版九年级数学下册《3.3垂径定理》同步练习题(附答案)一.选择题1.如图,在半径为的⊙O中,弦AB与CD交于点E,∠DEB=75°,AB=6,AE=1,则CD的长是()A.2B.2C.2D.42.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD =8cm,AE=2cm,则OF的长度是()A.3cm B.cm C.2.5cm D.cm3.如图,C是以AB为直径的半圆O上一点,连接AC,BC,分别以AC、BC为直径作半圆,其中M,N分别是AC、BC为直径作半圆弧的中点,,的中点分别是P,Q.若MP+NQ=7,AC+BC=26,则AB的长是()A.17B.18C.19D.204.如图,MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=30°,B为的中点,P 是直径MN上一动点,则P A+PB的最小值为()A.B.C.1D.25.如图,⊙P内含于⊙O,⊙O的弦AB切⊙P于点C,且AB∥OP,若阴影部分的面积为9π,则弦AB的长为()A.3B.4C.6D.96.如图,弦CD垂直于⊙O的直径AB,垂足为H,且CD=,BD=,则AB的长为()A.2B.3C.4D.57.如图,在平面直角坐标系中,⊙P与x轴相切于原点O,平行于y轴的直线交⊙P于M,N两点.若点M的坐标是(2,﹣1),则点N的坐标是()A.(2,﹣4)B.(2,﹣4.5)C.(2,﹣5)D.(2,﹣5.5)8.小明想知道一块扇形铁片OAB中的的拱高(弧的中点到弦的距离)是多少?但他没有任何测量工具,聪明的小明观察发现身旁的墙壁是由10cm的正方形瓷砖密铺而成(接缝忽略不计).他将扇形OAB按如图方式摆放,点O,A,B恰好与正方形瓷砖的顶点重合,根据以上操作,的拱高约是()A.10cm B.20cm C.D.9.小王不慎把一面圆形镜子打碎了,其中三块如图所示,三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是()A.①B.②C.③D.都不能二.填空题10.如图,⊙O是Rt△ABC的外接圆,OE⊥AB交⊙O于点E,垂足为点D,AE,CB的延长线交于点F.如果OD=3,AB=8,那么FC的长是.11.《九章算术》是中国传统数学重要的著作之一,奠定了中国传统数学的基本框架.其中卷九中记载了一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”其意思是:如图,AB为⊙O的直径,弦CD⊥AB于点E,BE=1寸,CD=1尺,那么直径AB的长为多少寸?(注:1尺=10寸)根据题意,该圆的直径为寸.12.如图,在梯形ABCD中,AB∥DC,AB⊥BC,AB=2cm,CD=4cm.以BC上一点O 为圆心的圆经过A、D两点,且∠AOD=90°,则圆心O到弦AD的距离是cm.13.如图,点A,B是⊙O上两点,AB=10,点P是⊙O上的动点(P与A,B不重合),连接AP,PB,过点O分别作OE⊥AP于E,OF⊥PB于F,则EF=.14.已知,⊙O的直径CD=10,弦AB=8,AB⊥CD,垂足为M,则DM的长为.15.在半径为10cm的⊙O中,弦AB的长为16cm,则点O到弦AB的距离是cm.16.如图,⊙O是△ABC的外接圆,∠BAC=45°,AD⊥BC于点D,延长AD交⊙O于点E,若BD=4,CD=1,则AD的长是.三.解答题17.如图,在⊙O中,AB,AC为弦,CD为直径,AB⊥CD于E,BF⊥AC于F,BF与CD 相交于G.(1)求证:ED=EG;(2)若AB=8,OG=1,求⊙O的半径.18.如图,△ABC内接于⊙O,高AD经过圆心O.(1)求证:AB=AC;(2)若BC=8,⊙O的半径为5,求△ABC的面积.19.如图所示,某地欲搭建一座圆弧型拱桥,跨度AB=32米,拱高CD=8米(C为AB的中点,D为弧AB的中点).(1)求该圆弧所在圆的半径;(2)在距离桥的一端4米处欲立一桥墩EF支撑,求桥墩的高度.20.如图1是小明制作的一副弓箭,点A、D分别是弓臂BAC与弓弦BC的中点,弓弦BC =60cm.沿AD方向拉弓的过程中,假设弓臂BAC始终保持圆弧形,弓弦不伸长.如图2,当弓箭从自然状态的点D拉到点D1时,有AD1=30cm,∠B1D1C1=120°.(1)图2中,弓臂两端B1,C1的距离为cm.在自然状态下,弓臂BAC的长为cm;(2)如图3,将弓箭继续拉到点D2,使弓箭B2AC2为半圆,求D1D2的长.21.如图,将一个两边带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆交于点D、E,量出半径OC=5cm,弦DE=8cm,求直尺的宽.22.一座桥如图,桥下水面宽度AB是20米,高CD是4米.要使高为3米的船通过,则其宽度须不超过多少米.(1)如图1,若把桥看作是抛物线的一部分,建立如图坐标系.要使高为3米的船通过,则其宽度须不超过多少米?(2)如图2,若把桥看作是圆的一部分.要使高为3米的船通过,则其宽度须不超过多少米?23.车辆转弯时,能否顺利通过直角弯道的标准是:车辆是否可以行驶到和路的边界夹角是45°的位置(如图1中②的位置),例如,图2是某巷子的俯视图,巷子路面宽4m,转弯处为直角,车辆的车身为矩形ABCD,CD与DE、CE的夹角都是45°时,连接EF,交CD于点G,若GF的长度至少能达到车身宽度,则车辆就能通过.(1)试说明长8m,宽3m的消防车不能通过该直角转弯;(2)为了能使长8m,宽3m的消防车通过该弯道,可以将转弯处改为圆弧(分别是以O 为圆心,以OM和ON为半径的弧),具体方案如图3,其中OM⊥OM′,请你求出ON 的最小值.24.李明到某影剧城游玩,看见一圆弧形门如图所示,李明想知道这扇门的相关数据.于是她从景点管理人员处打听到:这个圆弧形门所在的圆与水平地面是相切的,AB=CD=40cm,BD=320cm,且AB,CD与水平地面都是垂直的.根据以上数据,请你帮助李明计算出这个圆弧形门的最高点离地面的高度是多少?25.某施工工地安放了一个圆柱形饮水桶的木制支架(如图1),若不计木条的厚度,其俯视图如图2所示,已知AD垂直平分BC,AD=BC=48cm,求圆柱形饮水桶的底面半径的最大值.参考答案一.选择题1.解:过点O作OF⊥CD于点F,OG⊥AB于G,连接OB、OD、OE,如图所示:则DF=CF,AG=BG=AB=3,∴EG=AG﹣AE=2,在Rt△BOG中,OG===2,∴EG=OG,∴△EOG是等腰直角三角形,∴∠OEG=45°,OE=OG=2,∵∠DEB=75°,∴∠OEF=30°,∴OF=OE=,在Rt△ODF中,DF===,∴CD=2DF=2;故选:C.2.解:连接AB,OB,∵AC是⊙O的直径,弦BD⊥AO于E,BD=8cm,AE=2cm,在Rt△ABE中,AE2+BE2=AB2,即AB=,∵OA=OC,OB=OC,OF⊥BC,∴BF=FC,∴OF=.故选:D.3.解:连接OP,OQ,分别交AC,BC于H,I,∵M,N分别是AC、BC为直径作半圆弧的中点,,的中点分别是P,Q,∴OP⊥AC,OQ⊥BC,由对称性可知:H,P,M三点共线,I,Q,N三点共线,∴H、I是AC、BC的中点,∴OH+OI=(AC+BC)=13,∵MH+NI=AC+BC=13,MP+NQ=7,∴PH+QI=13﹣7=6,∴AB=OP+OQ=OH+OI+PH+QI=13+6=19,故选:C.4.解:作A关于MN的对称点Q,连接MQ,BQ,BQ交MN于P,此时AP+PB=QP+PB =QB,根据两点之间线段最短,P A+PB的最小值为QB的长度,连接AO,OB,OQ,∵B为中点,∴∠BON=∠AMN=30°,∴∠QON=2∠QMN=2×30°=60°,∴∠BOQ=30°+60°=90°.∵直径MN=2,∴OB=1,∴BQ==.则P A+PB的最小值为.故选:B.5.解:设PC=r,AO=R,连接PC,⊙O的弦AB切⊙P于点C,故AB⊥PC,作OD⊥AB,则OD∥PC.又∵AB∥OP,∴OD=PC=r,∵阴影部分的面积为9π,∴πR2﹣πr2=9π,即R2﹣r2=9,于是AD==3.∵OD⊥AB,∴AB=3×2=6.故选:C.6.解:连接OD.由垂径定理得HD=,由勾股定理得HB=1,设圆O的半径为R,在Rt△ODH中,OH=R﹣1,DH=则R2=()2+(R﹣1)2,由此得2R=3,或由相交弦定理得()2=1×(2R﹣1),由此得2R=3,所以AB=3故选:B.7.解:过点M作MA⊥OP,垂足为A设PM=x,P A=x﹣1,MA=2则x2=(x﹣1)2+4,解得x=,∵OP=PM=,P A=﹣1=,∴OP+P A=4,所以点N的坐标是(2,﹣4)故选:A.8.解:连接AB,过O作OC⊥AB于C,交于D,则AC=BC=AB=20(cm),OC=30cm,由勾股定理得:OD=OA===10(cm),∴CD=OD﹣OC=(10﹣30)(cm),即的拱高约是(10﹣30)cm,故选:D.9.解:第②块出现两条完整的弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.故选:B.二.填空题10.解:∵OE⊥AB,∴∠ADO=90°,∵∠ABC=90°,∴∠ABC=∠ADO=90°,∴OD∥BC,∵OA=OC,∴AD=DB=AB=4,AE=EF,∴OE是△AFC的中位线,∴CF=2OE,在Rt△ADO中,AO===5,∴CF=2OE=10,故答案为:10.11.解:连接OC,∵弦CD⊥AB,AB为圆O的直径,∴E为CD的中点,又∵CD=10寸,∴CE=DE=CD=5寸,设OC=OA=x寸,则AB=2x寸,OE=(x﹣1)寸,由勾股定理得:OE2+CE2=OC2,即(x﹣1)2+52=x2,解得x=13,∴AB=26寸,即直径AB的长为26寸,故答案为:26.12.解:如图,作AE⊥CD,垂足为E,OF⊥AD,垂足为F,则四边形AECB是矩形,CE=AB=2cm,DE=CD﹣CE=4﹣2=2cm,∵∠AOD=90°,AO=OD,所以△AOD是等腰直角三角形,AO=OD,∠OAD=∠ADO=45°,BO=CD,∵AB∥CD,∴∠BAD+∠ADC=180°∴∠ODC+∠OAB=90°,∵∠ODC+∠DOC=90°,∴∠DOC=∠BAO,∵∠B=∠C=90°∴△ABO≌△OCD,∴OC=AB=2cm,OB=CD=4cm,BC=BO+OC=AE=6cm,由勾股定理知,AD2=AE2+DE2,得AD=2cm,∴AO=OD=2cm,S△AOD=AO•DO=AD•OF,∴OF=cm.13.解:点P是⊙O上的动点(P与A,B不重合),但不管点P如何动,因为OE⊥AP于E,OF⊥PB于F,根据垂径定理,E为AP中点,F为PB中点,EF为△APB中位线.根据三角形中位线定理,EF=AB=×10=5.14.解:①连接OA,如图所示:∵⊙O的直径CD=10,∴OA=5,∵弦AB=8,AB⊥CD,∴AM=AB=×8=4,在Rt△AOM中,由勾股定理得:OM===3,∴DM=OD+OM=5+3=8;②连接OA,如图所示:同①得:OM=3,∴DM=OD﹣OM=5﹣3=2;综上所述,DM的长为8或2,故答案为:8或2.15.解:连接OA,作OC⊥AB于C,如图,∵OC⊥AB,∴AC=BC=AB=8,在Rt△AOC中,OC===6,即点O到弦AB的距离为6cm.故答案为6.16.解:如图,连接OA,过O点作OF⊥BC于F,作OG⊥AE于G,∵⊙O是△ABC的外接圆,∠BAC=45°,∴∠BOC=90°,∵BD=4,CD=1,∴BC=4+1=5,∴OB=OC=,∴OA=,OF=BF=,∴DF=BD﹣BF=,∴OG=,GD=,在Rt△AGO中,AG==,∴AD=AG+GD=.故答案为:.三.解答题17.(1)证明:如图:连接BD,∵AB⊥CD于E,BF⊥AC于F,∴∠CFG=∠GEB,∵∠CGF=∠BGE,∴∠C=∠GBE,∵∠C=∠DBE,∴∠GBE=∠DBE,∵AB⊥CD于E,∴∠GEB=∠DEB,在△GBE和△DBE中,,∴△BGE≌△BDE(ASA),∴ED=EG.(2)解:如图:连接OA,设OA=r,则DG=r+1,由(1)可知ED=EG,∴OE=,∵AB⊥CD于E,AB=8,∴AE=BE=4,∴在Rt△OAE中,根据勾股定理得:OE2+AE2=OA2,即()2+42=r2,解得:r=,即⊙O的半径为.18.(1)证明:∵OD⊥BC,∴=,∴AB=AC;(2)解:连接OB,∵OD⊥BC,BC=8,∴BD=DC=BC=×8=4,在Rt△ODB中,OD===3,∴AD=5+3=8,∴S△ABC=×8×8=32.19.解:(1)设弧AB所在的圆心为O,D为弧AB的中点,CD⊥AB于C,延长DC经过O 点,设⊙O的半径为R,在Rt△OBC中,OB2=OC2+CB2,∴R2=(R﹣8)2+162,解得R=20;(2)OH⊥FE于H,则OH=CE=16﹣4=12,OF′=R=20,在Rt△OHF中,HF==16,∵HE=OC=OD﹣CD=20﹣8=12,EF=HF﹣HE=16﹣12=4(米),∴在离桥的一端4米处,桥墩高4米.20.解:(1)如图2中,连接B1C1交DD1于H.∵D1A=D1B1=30∴D1是的圆心,∵AD1⊥B1C1,∴B1H=C1H=30×sin60°=15,∴B1C1=30∴弓臂两端B1,C1的距离为30,∴弓臂BAC的长为L扇形B1D1C1==20πcm;(2)如图3中,连接B1C1交DD1于H,连接B2C2交DD2于G.设半圆的半径为r,则πr=,∴r=20,∴AG=GB2=20,GD1=30﹣20=10,在Rt△GB2D2中,GD2==10∴D1D2=10﹣10.故答案为30,20π.21.解:过点O作OM⊥DE于点M,连接OD.∴DM=DE.∵DE=8(cm)∴DM=4(cm)在Rt△ODM中,∵OD=OC=5(cm),∴OM===3(cm)∴直尺的宽度为3cm.22.解:(1)设抛物线解析式为:y=ax2+c,∵桥下水面宽度AB是20米,高CD是4米,∴A(﹣10,0),B(10,0),D(0,4),∴,解得:∴抛物线解析式为:y=﹣x2+4,∵要使高为3米的船通过,∴y=3,则3=﹣x2+4,解得:x=±5,∴EF=10米;(2)设圆半径r米,圆心为W,∵BW2=BC2+CW2,∴r2=(r﹣4)2+102,解得:r=14.5;在Rt△WGF中,由题可知,WF=14.5,WG=14.5﹣1=13.5,根据勾股定理知:GF2=WF2﹣WG2,即GF2=14.52﹣13.52=28,所以GF=2,此时宽度EF=4米.23.解:(1)消防车不能通过该直角转弯.理由如下:如图,作FH⊥EC,垂足为H,∵FH=EH=4,∴EF=4,且∠GEC=45°,∵GC=4,∴GE=GC=4,∴GF=4﹣4<3,即GF的长度未达到车身宽度,∴消防车不能通过该直角转弯;(2)若C、D分别与M′、M重合,则△OGM为等腰直角三角形,∴OG=4,OM=4,∴OF=ON=OM﹣MN=4﹣4,∴FG=OG﹣OF=×8﹣(4﹣4)=8﹣4<3,∴C、D在上,设ON=x,连接OC,在Rt△OCG中,OG=x+3,OC=x+4,CG=4,由勾股定理得,OG2+CG2=OC2,即(x+3)2+42=(x+4)2,解得x=4.5.答:ON至少为4.5米.24.解:如图,连接AC,作AC的中垂线交AC于G,交BD于N,交圆的另一点为M.则MN为直径.取MN的中点O,则O为圆心,连接OA、OC.∵AB⊥BD,CD⊥BD,∴AB∥CD∵AB=CD∴ABCD为矩形∴AC=BD=320cm,GN=AB=CD=40cm∴AG=GC=160cm,设⊙O的半径为R,得R2=(R﹣40)2+1602,解得R=340cm,340×2=680(cm).答:这个圆弧形门的最高点离地面的高度为680cm.25.解:过A、B、C三点作⊙O,连接OB.∵AD垂直平分BC∴点O必在AD上,BD=CD=24设⊙O的半径为r,则OD=48﹣r∵OD2+BD2=OB2∴(48﹣r)2+242=r2解得,r=30∴圆柱形饮水桶的底面半径的最大值30cm.。
垂径定理同步培优题典(解析版)

专题4.2垂径定理姓名:__________________ 班级:______________ 得分:_________________注意事项:本试卷满分100分,试题共24题.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.(2019秋•涪城区校级月考)下列语句,错误的是()A.直径是弦B.弦的垂直平分线一定经过圆心C.相等的圆心角所对的弧相等D.平分弧的半径垂直于弧所对的弦【分析】根据直径、弦的定义对A进行判断;根据垂径定理的推论对B、D进行判断;根据圆心角、弧、弦的关系对C进行判断.【解析】A、直径为弦,所以A选项的说法正确;B、弦的垂直平分线一定经过圆心,所以B选项的说法正确;C、在同圆或等圆中,相等的圆心角所对的弧相等,所以C选项的说法错误;D、平分弧的半径垂直于弧所对的弦,所以D选项的说法正确.故选:C.2.(2020•龙泉驿区模拟)如图,AB是⊙O的直径,弦CD⊥AB于点E,BE=1cm,CD=6cm,则AE为()cm.A.4B.9C.5D.8【分析】设OC=OB=xcm,在Rt△OEC中,利用勾股定理求解即可.【解析】设OC=OB=xcm,∵AB⊥CD,AB是直径,∴EC=DE=3cm,在Rt△OEC中,∵OC2=CE2+OE2,∴x2=32+(x﹣1)2,∴x=5,∴OE=4cm,∴AE=OA+OE=5+4=9cm,故选:B.3.(2019秋•蔡甸区期中)P为⊙O内一点,且OP=2,若⊙O的半径为3,则过点P的最短的弦是()A.1B.2C.√5D.2√5【分析】先作出最短弦AB,过P作弦AB⊥OP,连接OB,构造直角三角形,由勾股定理求出BP,根据垂径定理求出AB即可.【解析】过P作弦AB⊥OP,则AB是过P点的最短弦,连接OB,由勾股定理得:BP=√OB2−OP2=√32−22=√5,∵OP⊥AB,OP过圆心O,∴AB=2BP=2√5,故选:D.4.(2019秋•通州区期末)如图,将⊙O沿着弦AB翻折,劣弧恰好经过圆心O.如果弦AB=4√3,那么⊙O 的半径长度为()A.2B.4C.2√3D.4√3【分析】作OD⊥AB于D,连接OA,先根据勾股定理列方程可解答.【解析】作OD⊥AB于D,连接OA.∵OD⊥AB,AB=4√3,∴AD=12AB=2√3,由折叠得:OD=12AO,设OD=x,则AO=2x,在Rt△OAD中,AD2+OD2=OA2,(2√3)2+x2=(2x)2,x=2,∴OA=2x=4,即⊙O的半径长度为4;故选:B.5.(2018秋•鞍山期末)如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,则下列说法中正确的是()A.AD=2OB B.点B是劣弧CD的中点C.OE=EB D.点D是AB弧中点【分析】根据垂径定理逐一判断即可得.【解析】A.AB=2OB,而AB>AD,故此选项错误;B.由AB⊥CD知点B是劣弧CD的中点,故此选项正确;C.OE与EB不一定相等,故此选项错误;D.当CD过圆心且AB⊥CD时,点D是AB弧中点,故此选项错误;故选:B.6.(2019秋•玄武区期末)如图,AB是⊙O的直径,弦CD⊥AB于点M,若CD=8cm,MB=2cm,则直径AB的长为()A.9 cm B.10 cm C.11 cm D.12 cm【分析】如图,连接OC.设OA=OB=OC=r.在Rt△OCM中,利用勾股定理构建方程即可解决问题.【解析】如图,连接OC.设OA=OB=OC=r.∵AB⊥CD,∴CN=MD=12CD=4cm,在Rt△OCM中,∵OC2=CM2+OM2,∴r2=42+(r﹣2)2,解得r=5,∴AB=2OA=10,故选:B.7.(2019秋•仪征市期末)如图,在⊙O中,分别将AB̂、CD̂沿两条互相平行的弦AB、CD折叠,折叠后的弧均过圆心,若⊙O的半径为4,则四边形ABCD的面积是()A.8B.16 √3C.32D.32√3【分析】过O作OH⊥AB交⊙O于E,反向延长EO交CD于G,交⊙O于F,连接OA,OB,OD,根据平行线的性质得到EF⊥CD,根据折叠的性质得到OH=12OA,推出△AOD是等边三角形,得到D,O,B三点共线,且BD为⊙O的直径,求得∠DAB=90°,同理,∠ABC=∠ADC=90°,得到四边形ABCD 是矩形,于是得到结论.【解析】过O作OH⊥AB交⊙O于E,反向延长EO交CD于G,交⊙O于F,连接OA,OB,OD,∵AB∥CD,∴EF⊥CD,∵分别将AB̂、CD̂沿两条互相平行的弦AB、CD折叠,折叠后的弧均过圆心,∴OH=12OA,∴∠HAO=30°,∴∠AOH=60°,同理∠DOG=60°,∴∠AOD=60°,∴△AOD是等边三角形,∵OA=OB,∴∠ABO=∠BAO=30°,∴∠AOB=120°,∴∠AOD+∠AOB=180°,∴D,O,B三点共线,且BD为⊙O的直径,∴∠DAB=90°,同理,∠ABC=∠ADC=90°,∴四边形ABCD是矩形,∴AD=AO=4,AB=√3AD=4√3,∴四边形ABCD的面积是16√3,故选:B.8.(2019秋•泗阳县期末)如图,⊙O的直径为10,弦AB的长为8,点P是弦AB上的一个动点,使线段OP的长度为整数的点P有()A.3个B.4个C.5个D.6个【分析】当P为AB的中点时OP最短,利用垂径定理得到OP垂直于AB,在直角三角形AOP中,由OA与AP的长,利用勾股定理求出OP的长;当P与A或B重合时,OP最长,求出OP的范围,由OP 为整数,即可得到OP所有可能的长.【解析】当P为AB的中点时,利用垂径定理得到OP⊥AB,此时OP最短,∵AB=8,∴AP=BP=4,在直角三角形AOP中,OA=5,AP=4,根据勾股定理得:OP=√OA2−AP2=3,即OP的最小值为3;当P与A或B重合时,OP最长,此时OP=5,∴3≤OP≤5,则使线段OP的长度为整数的点P有3,4,5,共5个.故选:C.9.(2019秋•连云港期中)如图,四边形ABCD内接于⊙O,AB=AD,BC=3.劣弧BC沿弦BC翻折,刚好经过圆心O.当对角线BD最大时,则弦AB的长是()A .√6B .2√3C .32D .2√2 【分析】作OH ⊥BC 于H ,连接OB ,如图,利用垂径定理得到BH =12BC =32,再根据折叠的性质得到OH =12OB ,则∠OBH =30°,于是可计算出OH =√32,OB =√3,接着利用BD 为直径时,即BD =2√3时,对角线BD 最大,根据圆周角得到此时∠BAD =90°,再判断△ABD 为等腰直角三角形,然后根据等腰直角三角形的性质计算出AB 的长.【解析】作OH ⊥BC 于H ,连接OB ,如图,则BH =CH =12BC =32,∵劣弧BC 沿弦BC 翻折,刚好经过圆心O ,∴OH =12OB ,∴∠OBH =30°,∴OH =√33BH =√32,∴OB =2OH =√3,当BD 为直径时,即BD =2√3时,对角线BD 最大,则此时∠BAD =90°,∵AB =AD ,∴此时△ABD 为等腰直角三角形,∴AB =√22BD =√22×2√3=√6.故选:A .10.(2019秋•松滋市期中)如图,AB、AC、BC都是⊙O的弦,OM⊥AB,ON⊥AC,垂足分别为M、N,若MN=2,则BC的值为()A.3.5B.2C.3D.4【分析】先根据垂径定理得出M、N分别是AB与AC的中点,故MN是△ABC的中位线,由三角形的中位线定理即可得出结论.【解析】∵OM⊥AB,ON⊥AC垂足分别为M、N,∴M、N分别是AB与AC的中点,∴MN是△ABC的中位线,∴BC=2MN=4,故选:D.二.填空题(共8小题)11.(2019秋•铁西区期末)如图,在半径为10cm的圆形铁片上切下一块高为4cm的弓形铁片,则弓形弦AB的长为16cm.【分析】首先构造直角三角形,再利用勾股定理得出BC的长,进而根据垂径定理得出答案.【解析】如图,过O作OD⊥AB于C,交⊙O于D∵CD=4cm,OD=10cm,∴OC=6cm,又∵OB=10cm,∴Rt△BCO中,BC=√OB2−OC2=8(cm),∴AB=2BC=16cm.故答案为:16cm.12.(2020•新抚区二模)如图所示,⊙O的半径为5,AB为弦,半径OC⊥AB,垂足为D,如果CD=2,那么AB的长是8.【分析】连接OA,由于半径OC⊥AB,利用垂径定理可知AB=2AD,又CD=2,OC=5,易求OD,在Rt△AOD中利用勾股定理易求AD,进而可求AB.【解析】连接OA,∵半径OC⊥AB,∴AD=BD=12AB,∵OC=5,CD=2,∴OE=3,在Rt△AOD中,AD=√OA2−OD2=√52−32=4,∴AB=2AD=8,故答案为8.13.(2019秋•瑞安市期末)某公路上有一隧道,顶部是圆弧形拱顶,圆心为O,隧道的水平宽AB为24m,AB离地面的高度AE=10 m,拱顶最高处C离地面的高度CD为18m,在拱顶的M,N处安装照明灯,且M,N离地面的高度相等都等于17m,则MN=10m.【分析】根据题意和垂径定理得到CG=8m,AG=12m,CH=1m,根据勾股定理求得半径,进而利用勾股定理求得MH,即可求得MN.【解析】设CD于AB交于G,与MN交于H,∵CD=18m,AE=10m,AB=24m,HD=17m,∴CG=8m,AG=12m,CH=1m,设圆拱的半径为r,在Rt△AOG中,OA2=OG2+AG2,∴r2=(r﹣8)2+122,解得r=13,∴OC=13m,∴OH=13﹣1=12m,在Rt△MOH中,OM2=OH2+MH2,∴132=122+MH2,解得MH2=25,∴MH=5m,∴MN=10m,故答案为10.14.(2020•常州模拟)石拱桥是中国传统桥梁四大基本形式之一,如图,已知一石拱桥的桥顶到水面的距离CD为8m,桥拱半径OC为5m,求水面宽AB=8m.【分析】连接OA,根据垂径定理可知AD=BD=12AB,在Rt△ADO中,利用勾股定理即可求出AD的长,进而可得出AB的长,此题得解.【解析】连接OA,如图所示.∵CD⊥AB,∴AD=BD=12AB.在Rt△ADO中,OA=OC=5m,OD=CD﹣OC=3m,∠ADO=90°,∴AD=√OA2−OD2=√52−32=4(m),∴AB=2AD=8m.故答案为:8.15.(2019秋•海陵区校级期末)如图,⊙O与矩形ABCD的边AB、CD分别相交于点E、F、G、H,若AE+CH =6,则BG+DF为6.【分析】作OM⊥GH于M,OM交EF于N,如图,先证明OM⊥EF,利用垂径定理得到EN=FN,GM =HM,利用四边形ABMN和四边形MNDC为矩形得到AN=BM,DN=CM,然后根据等线段代换得到BG+DF=AE+CH.【解析】作OM⊥GH于M,OM交EF于N,如图,∵EF∥GH,∴OM⊥EF,∴EN=FN,GM=HM,易得四边形ABMN和四边形MNDC为矩形,∴AN=BM,DN=CM,∴BG+DF=BM﹣GM+DN﹣NF=AN﹣HM+CM﹣EN=AN﹣EN+CM﹣HM=AE+CH=6.故答案为6.16.(2019秋•秦淮区期末)如图,⊙O是一个油罐的截面图.已知⊙O的直径为5m,油的最大深度CD=4m(CD⊥AB),则油面宽度AB为4m.【分析】根据垂径定理和勾股定理进行解答即可.【解析】连接OA,由题意得,OA=2.5m,OD=1.5m,∵CD⊥AB,∴AD=√OA2−OD2=2m,∴AB=2AD=4m,故答案为:4.17.(2019秋•泗阳县期末)如图,AB是⊙O的直径,点C在⊙O上,且CD⊥AB,垂足为D,CD=4,OD =3,则DB=2.【分析】连接OC,利用勾股定理求出OC即可解决问题.【解析】连接OC.∵CD⊥AB,∴∠ODC=90°,∴OC=OB=√OD2+CD2=√32+42=5,∴BD=OB﹣OD=5﹣3=2,故答案为2.18.(2019秋•宿豫区期中)如图,⊙O的半径为5,OP=3,过点P画弦AB,则AB的取值范围是8≤AB ≤10.【分析】过点P作CD⊥OP,⊙O于C,D.连接OC.利用勾股定理求出CD,可得点P的最短的弦,过点P的最长的弦即可解决问题.【解析】过点P作CD⊥OP,交⊙O于C,D.连接OC.∵OC=5,OP=3,∠OPC=90°,∴PC=√OC2−OP2=√52−32=4,∵OP⊥CD,∴PC=PD=4,∴CD=8,∴过点P的最短的弦长为8,最长的弦长为10,即AB的取值范围是8≤AB≤10,故答案为:8≤AB≤10.三.解答题(共6小题)19.(2019秋•苍南县期中)把一个球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知CD =EF=24cm,求这个球的直径.【分析】过O作OG⊥AD于G交⊙O于H,求得GF=12EF=12,设半径为r,则OG=24﹣r,根据勾股定理即可得到结论.【解析】过O作OG⊥AD于G交⊙O于H,则GF=12EF=12cm,设半径为rcm,则OG=24﹣r,根据勾股定理得,(24﹣r)2+122=r2,解得:r=15,答:这个球的直径为30cm.̂=2AD̂,请说明AB 20.(2019秋•新北区期中)如图,A、B、C、D为⊙O上四点,若AC⊥OD于E,且AB =2AE.̂=2AD̂,AC=2AE,再由,AB̂=2AD̂,可得∴AB̂=AĈ,即可得AB=AC,【分析】由垂径定理可得,AC所以AB=2AE.【解析】∵AC⊥OD,̂=2AD̂,AC=2AE,∴AĈ=2AD̂,∵AB̂=AĈ,∴AB∴AB=AC,∴AB=2AE.21.(2019秋•沛县期中)“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何”.这是《九章算术》中的问题,用数学语言可表述为:如图,CD为⊙O的直径,弦AB⊥CD于点E,CE=1寸,AB=10寸,求直径CD的长.【分析】根据垂径定理和勾股定理求解.【解析】连接OA,如图所示,设直径CD的长为2x,则半径OC=x,∵CD为⊙O的直径,弦AB⊥CD于E,AB=10寸,∴AE=BE=12AB=12×10=5寸,连接OA,则OA=x寸,根据勾股定理得x2=52+(x﹣1)2,解得x=13,直径CD的长为2x=2×13=26(寸).22.(2019秋•海淀区期中)如图,一条公路的转弯处是一段圆弧(AB̂),点O是这段弧所在圆的圆心.AB =100m,C是AB̂上一点,OC⊥AB,垂足为D,CD=10m,求这段弯路的半径.【分析】根据题意,可以推出AD=BD=50,若设半径为r,则OD=r﹣10,OB=r,结合勾股定理可推出半径r的值.【解析】设这段弯路的半径为r m,∵OC⊥AB于D,AB=100(m),∴BD=DA=12AB=50(m)∴CD=10(m),得OD=r﹣10(m).∵Rt△BOD中,根据勾股定理有BO2=BD2+DO2即r2=502+(r﹣10)2解得r=130(m).答:这段弯路的半径为130 m.23.(2019秋•秦淮区期中)如图,在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C、D.(1)求证AC =BD ;(2)若AC =3,大圆和小圆的半径分别为6和4,则CD 的长度是 113 .【分析】(1)作CH ⊥CD 于H ,如图,根据垂径定理得到CH =DH ,AH =BH ,利用等量减等量差相等可得到结论;(2)连接OC ,如图,设CH =x ,利用勾股定理得到OH 2=OC 2﹣CH 2=42﹣x 2,OH 2=OA 2﹣AH 2=62﹣(3+x )2,则42﹣x 2=62﹣(3+x )2,然后解方程求出x 即可得到CD 的长.【解答】(1)证明:作CH ⊥CD 于H ,如图,∵OH ⊥CD ,∴CH =DH ,AH =BH ,∴AH ﹣CH =BH ﹣DH ,∴AC =BD ;(2)解:连接OC ,如图,设CH =x ,在Rt △OCH 中,OH 2=OC 2﹣CH 2=42﹣x 2,在Rt △OAH 中,OH 2=OA 2﹣AH 2=62﹣(3+x )2,∴42﹣x 2=62﹣(3+x )2,解得x =116,∴CD =2CH =113. 故答案为:113.24.(2019秋•东台市期中)如图,在⊙O 中,直径为MN ,正方形ABCD 的四个顶点分别在半径OM 、OP 以及⊙O 上,并且∠POM =45°,若AB =1.(1)求OD 的长;(2)求⊙O 的半径.【分析】(1)由四边形ABCD为正方形,得DC=BC=AB=1,则∠DCO=∠ABC=90°,又∠DCO=45°,CO=DC=1,求出OD;(2)连接OA,构造直角三角形,求出AB和BO的长,然后利用勾股定理即可求出圆的半径.【解析】(1)如图,∵四边形ABCD为正方形,∴DC=BC=AB=1,∠DCO=∠ABC=90°,∵∠DCO=45°,∴CO=DC=1,∴OD=√2CO=√2×1=√2;(2)BO=BC+CO=BC+CD1+1=2,.连接AO,则△ABO为直角三角形,于是AO=√AB2+BO2=√12+22=√5.即⊙O的半径为√5.。
中考数学复习:垂径定理(圆)(综合提升训练必备)(含解析)

2019年中考数学复习:垂径定理(圆)一、选择题(共15小题)1、如图,A点是半圆上一个三等分点,B点是弧AN的中点,P点是直径MN上一动点,⊙O的半径为1,则AP+BP的最小值为( )A。
1ﻩB、ﻩC、D、2、如图,梯形ABCD中,AB∥DC,AB⊥BC,AB=2cm,CD=4cm、以BC上一点O 为圆心的圆经过A、D两点,且∠AOD=90°,则圆心O到弦AD的距离是( )A、cmﻩB、cm C、cmﻩD、cm3。
如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被⊙P截得的弦AB的长为,则a的值是( )A、4ﻩB、ﻩC、D、4、已知⊙O的半径为10,P为⊙O内一点,且OP=6,则过P点,且长度为整数的弦有( )A。
5条ﻩB。
6条ﻩC、8条D。
10条5、已知⊙O的半径OA=2,弦AB,AC的长分别是2,2,则∠BAC的度数为()A、15°B、75°C、15°或75°ﻩD、15°或45°6、如图,四边形PAOB是扇形OMN的内接矩形,顶点P在上,且不与M,N重合,当P点在上移动时,矩形PAOB的形状、大小随之变化,则AB的长度()A、变大B、变小C、不变D。
不能确定7、给出下列四个命题:(1)假如某圆锥的侧面展开图是半圆,则其轴截面一定是等边三角形;(2)若点A在直线y=2x﹣3上,且点A到两坐标轴的距离相等,则点A在第一或第四象限;(3)半径为5的圆中,弦AB=8,则圆周上到直线AB的距离为2的点共有四个; (4)若A(a,m)、B(a﹣1,n)(a〉0)在反比例函y=的图象上,则m〈n、其中,正确命题的个数是( )A、1个ﻩB。
2个C、3个ﻩD、4个8、已知⊙O的半径为10cm,弦AB∥CD,AB=12cm,CD=16cm,则AB和CD 的距离为( )A、2cmﻩB。
14cmﻩC、2cm或14cmﻩD、10cm或20cm9、已知⊙O的半径为3,△ABC内接于⊙O,AB=3,AC=3,D是⊙O上一点,且AD =3,则CD的长应是( )A。
专题22 圆锥曲线中的垂径定理(解析版)
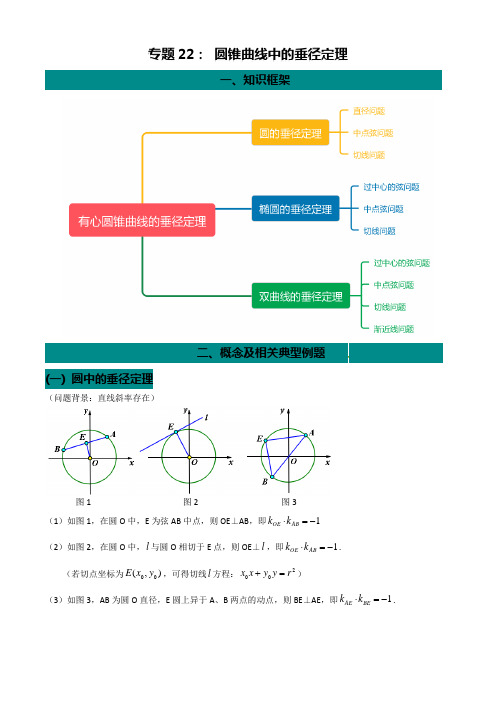
专题22: 圆锥曲线中的垂径定理一、知识框架二、概念及相关典型例题 (一) 圆中的垂径定理(问题背景:直线斜率存在)图1 图2 图3 (1)如图1,在圆O 中,E 为弦AB 中点,则OE ⊥AB ,即1-=⋅AB OE k k (2)如图2,在圆O 中,l 与圆O 相切于E 点,则OE ⊥l ,即1-=⋅AB OE k k .(若切点坐标为),(00y x E ,可得切线l 方程:200r y y x x =+)(3)如图3,AB 为圆O 直径,E 圆上异于A 、B 两点的动点,则BE ⊥AE ,即1-=⋅BE AE k k .(二)圆锥曲线中的垂径定理(问题情景假设:假设下列问题讨论所涉及的直线斜率都存在情况下)1.椭圆中的垂径定理(以焦点在x 轴的椭圆方程)0(12222>>=+b a b y a x 为例)图1 图2 图3 (1)如图1,在椭圆C 中,E 为弦AB 的中点,则22ab k k ABOE -=⋅;(证明:用点差法)(2)如图2,在椭圆C 中,l 与椭圆相切于E 点,则22ab k k l OE -=⋅;(证明:法一:极限思想,当A 无穷接近B 点;法二:换元法变换为122='+'y x 证明即可;法三:导数)(3)如图3,l 过中心O,交椭圆于A,B 两点,E 是椭圆上异于A 、B 点的动点则22ab k k AEBE -=⋅.(证明:取AE 重点M ,连接OM ,即可用(1)证明)2.双曲线中的垂径定理(以焦点在x 轴的双曲线方程)00(12222>>=-b a by a x ,为例)图1 图2 图3 图4 图5(1)如图1或图2,E 为弦AB 的中点,则22ab k k ABOE =⋅; (2)如图3,l 与双曲线相切于E 点,则22ab k k l OE =⋅;(3)如图4,过O 点的l 交双曲线于A,B 两点,E 是双曲线上异于A 、B 点的动点,则22abk k AEBE =⋅. (4)如图5,l 交上双曲线两渐近线于A,B 两点,E 为线段AB 的中点,则22ab k k ABOE =⋅. 【注意:若焦点在y 轴上的双曲线方程)00(12222>>=-b a b x a y ,,则上面斜率乘积结论变为:22ba ,即=⋅AB OE k k =⋅l OE k k 22ba k k AEBE =⋅】(三)例题点评1.例题初探【例1】过点M(1,1)作斜率为21-的直线与椭圆)0(12222>>=+b a b y a x C :相交于A,B 两点,若M 是线段AB的中点,则该椭圆的离心率为 .【解析】方法一:点差法 方法二:由垂径定理,22)21(11a b k k ABOM -=-⨯=⋅,2122222=-=a c a a b ,即2112=-e ,因为0<e<1,所以圆、椭圆与双曲线中的垂径定理可以归结为(统称为有心圆锥曲线):(1)若方程,且00(122>>=+n m ny m x 或0<mn )存在以上关系,则上述结论可表述为:m n -, 即=⋅AB OE k k =⋅l OE k k mn k k AE BE -=⋅,其中n m ,分别是22,y x 系数的倒数. (2)若方程)0,00(122<>>=+AB B A By Ax 或且存在以上关系,则上述结论可表述为:BA -, 即=⋅AB OE k k =⋅l OE k k BA k k AE BE -=⋅,其中B A ,分别是22,y x 系数.解的22=e 【例2】已知A 、B 为椭圆)0(12222>>=+b a by a x 的左右顶点,P 为椭圆上异于A 、B 的点,PA 、PB 的斜率分别为21,k k ,且4321-=k k ,则该椭圆的离心率为 【解析】答案为21=e【例3】设双曲线C :)0,0(12222>>=-b a by a x 的顶点为21,A A ,P 为双曲线上一点,直线1PA 交双曲线C 的一条渐近线于M 点,直线M A 2和P A 2的斜率分别为21,k k ,若12PA M A ⊥且0421=+k k ,则双曲线C 离心率为( ) A 、2 B 、25C 、5D 、4【解析】利用双曲线过中心弦结论2221a b k k PA PA =,即22114141ab k k ==⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛- 答案:B 【例4】已知A 、B 是双曲线)0,0(12222>>=-b a bx a y 的两个顶点,P 是双曲线上异于A 、B 的另一点,P 关于y 轴的对称点为Q ,记直线AP 、BQ 的斜率分别为21,k k ,且5421-=k k ,则双曲线的离心率为【解析】1k k AQ -=,由垂径定理得235411221=⇒=-=-e e k k 答案:23【例5】过双曲线)0(12222>>=-b a by a x 的左焦点F 且斜率为1的直线与双曲线的两条渐近线交于A 、B 两点,记线段AB 的中点为M ,且FM 等于半焦距,则双曲线的离心率=e【解析】 0>>b a ,∴双曲线的开口较小,渐近线斜率的绝对值比1小,故直线与双曲线的交点都位于y 轴左侧,当直线竖起来时中点即F ,而直线斜率为1,故中点M 位于第三象限,由 135=∠MFO ,FO FM =(O 为坐标原点),∴125.22tan -== OM k由垂径定理得21122=⇒-=⋅e e k OM 答案:42【例6】已知直线l 的斜率为1,且与双曲线2212x y -=相切于第一象限于点A ,则点A 的坐标为______.来源学科网ZXXK]【解析】法一:因为直线l 的斜率为1,所以设:l y x m =+代入双曲线2212x y -=得224220x mx m +++=因为直线与双曲线相切,所以0∆=,即()22164220m m -+=,解得1m =±当1m =时,22112y x x y =+⎧⎪⎨-=⎪⎩,解得21x y =-⎧⎨=-⎩,当1m =-时,22112y x x y =-⎧⎪⎨-=⎪⎩,解得21x y =⎧⎨=⎩ 因为切点A 在第一象限,所以点()2,1A .故答案为:()2,1. 法二:设切点坐标为()00,y x A ,由垂径定理得:212200===⋅a b x y K K l OA ,又因为点()00,y x A 在双曲线上,可得:122020=-y x ,解得10=y ,所以20=x , 所以点()2,1A .故答案为:()2,1.2.提高与巩固例题【例1】已知直线l 交椭圆805422=+y x 于M 、N 两点,B 是椭圆与y 轴正半轴的交点,若△BMN 的重心恰好为椭圆的右焦点,则直线l 的方程为【解析】设),(11y x M ,),(22y x N ,)4,0(B ,由重心公式得6021=++x x ,0421=++y y【三角形ABC 重心的坐标公式为)3,3(321321y y y x x x ++++,其中),(),,(),,(332211y x C y x B y x A 】 ∴线段MN 的中点为)2,3(-D ,由垂径定理得5412-=-=⋅e k k MN OD (O 为坐标原点)∴56=MN k ,∴直线l 的方程为02856=--y x【例2】已知椭圆1422=+y x ,P 是椭圆的上顶点,过P 作斜率为)0(≠k k 的直线l 交椭圆于另一点A ,设点A 关于原点的对称点为B , (1)求△PAB 面积的最大值(2)设线段PB 的中垂线与y 轴交于点N ,若点N 在椭圆内部,求斜率k 的取值范围【解析】(1)B PAB x x x S =-=∆2121,∴面积最大为2 (2)方法一(与椭圆联立):4122-=-=a b k k BP AP ,∴k k kk BP 441=⇒-=中垂线,N 刚到下顶点)1,0(-时,中垂线14-=kx y ,PB :141+-=x k y 与椭圆联立可求得⎪⎪⎭⎫ ⎝⎛+-+1414,148222k k k k B ∴PB 中点为⎪⎪⎭⎫⎝⎛++144,144222k k k k M 在中垂线上,代入得42±=k 方法二(与直线联立):由垂径定理得4112-=-=e kk BP ,∴PB :141+-=x ky 与边AP 平行的中位线kx y =联立得PB 中点为⎪⎪⎭⎫ ⎝⎛++144,144222k k k k M ,由M 与)1,0(-构成的中垂线斜率k k k k k 41441144222=+++,解得42±=k 【例3】设直线)0(03≠=+-m m y x 与双曲线)0,0(12222>>=-b a by a x 两条渐近线分别交于A ,B ,若点)0,(m P 满足PB PA =,则该双曲线的离心率是【解析】方法一(垂径定理):记M 为PM 的中点,则PM :033=-+m y x 与直线AB 联立,容易得)53,54(m m M由垂径定理得141122-=⇒-=e e k k PM AB 答案:25方法二(暴力计算)直线分别与两条渐近线联立得)3,3(a b bm a b am A --,)3,3(ba bmb a am B ++-∴AB 的中点为)93,9(222222a b m b a b m a --,所以线段AB 的中垂线斜率为3923222-=-=ba b k 方法三(渐近线点差法):设AB 中点为),(00y x ,则由点差法知310202==y a x b k又中点在直线上,故0300=+-m y x ①,由PB PA =得300-=-mx y ②由①②得34333000000=⇒+=-=x y x y x y m ,∴4122=a b 【例4】已知某椭圆的焦点是)0,4(),0,4(21F F -,过点2F 并垂直于x 轴的直线与椭圆的一个交点为B ,且三、自我素养养成练习与思考1.如图,已知椭圆)0(12222>>=+b a by a x ,过原点的直线交椭圆于点P 、A 两点(其中点P 在第一象限),过点P 作x 轴的垂线,垂线为C ,连AC 并延长交椭圆于B ,若PB PA ⊥,则椭圆的离心率为【解析】记1k k PB =,2k k AB =,延长PC 交椭圆于D ,连AD ,由初中几何知识得22k k AP =,由PBPA ⊥得1221-=k k ,由垂径定理得1221-=e k k 答案:222.已知双曲线)0,0(12222>>=-b a by a x 的左右焦点为21,F F ,右顶点为A ,P 为双曲线右支上一点,1PF 交双曲线的左支于点Q ,与渐近线x aby =交于点R ,线段PQ 的中点为M ,若12PF RF ⊥,1PF AM ⊥,则双曲线的离心率为【解析】由直角三角形斜边的中线等于斜边的一半得c OR =,故),(b a R ∴ca b k PQ += 由垂径定理得2222)(1a c a b k a b e k k OM PQOM +=⇒=-=⋅联立直线PQ :)(c x c a b y ++=与直线OM :x ac a b y 2)(+=得)2)(,2(2c a c a b c a a M +++,)0,(a A 由2)(ac a b b c a k AM +=+-=得0202222=--⇒=+-e e ac c a ,解得2=e 答案:23.如图,已知椭圆)0(12222>>=+b a by a x 的左右顶点分别为A 、B ,P 为第一象限内一点,且AB PB ⊥,连接PA 交椭圆于点C ,连BC 、OP ,若BC OP ⊥,则椭圆的离心率为【解析】1k k PA =,2k k BC =,由初中几何知识得12k k OP =, 1221-=k k ,∴由垂径定理得211221-=-=e k k22=⇒e 答案:22 4.如图,1F ,2F 分别是双曲线C :)0,0(12222>>=-b a by a x 的左右焦点,B 是虚轴的端点,直线B F 1与C的两条渐近线分别交于P ,Q 两点,线段PQ 的垂直平分线MN 与x 轴交于点M ,若212F F MF =,则C 的离心率是 。
圆及垂径定理(讲练10题型)(原卷版)

24.1.1&24.1.2 圆及垂径定理圆的定义(1)动态:如图,在一个平面内,线段OA 绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫做圆,固定的端点O 叫做圆心,线段OA 叫做半径. 以点O 为圆心的圆,记作“⊙O ”,读作“圆O”.(2)静态:圆心为O,半径为r的圆是平面内到定点O的距离等于定长r的点的集合.注意:①圆心确定圆的位置,半径确定圆的大小;确定一个圆应先确定圆心,再确定半径,二者缺一不可;②圆是一条封闭曲线.题型1:圆的概念1.到圆心的距离不大于半径的点的集合是()A.圆的外部B.圆的内部C.圆D.圆的内部和圆【变式11】下列条件中,能确定一个圆的是()A.以点O为圆心B.以10m长为半径C.以点A为圆心,4cm长为半径D.经过已知点M与圆有关的概念1.弦弦:连结圆上任意两点的线段叫做弦.直径:经过圆心的弦叫做直径.弦心距:圆心到弦的距离叫做弦心距.2. 弧弧:圆上任意两点间的部分叫做圆弧,简称弧.以A、B 为端点的弧记作,读作“圆弧AB”或“弧AB”.半圆:圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆;优弧:大于半圆的弧叫做优弧;劣弧:小于半圆的弧叫做劣弧.圆心相同,半径不等的两个圆叫做同心圆.圆心不同,半径相等的两个圆叫做等圆.同圆或等圆的半径相等.在同圆或等圆中,能够完全重合的弧叫做等弧.题型2:与圆有关的概念2.判断题(对的打√,错的打×,并说明理由)①半圆是弧,但弧不一定是半圆;()②弦是直径;()③长度相等的两段弧是等弧;()④直径是圆中最长的弦. ()【变式21】下列说法:(1)长度相等的弧是等弧,(2)相等的圆心角所对的弧相等,(3)劣弧一定比优弧短,(4)直径是圆中最长的弦.其中正确的有()A.1个B.2个C.3个D.4个【变式22】下列说法:①直径是弦;②弦是直径;③半径相等的两个半圆是等弧;④长度相等的两条弧是等弧;⑤半圆是弧,但弧不一定是半圆.正确的说法有()A.1个B.2个C.3个D.4个题型3:确定圆心和圆3.将图中的破轮子复原,已知弧上三点A,B,C.画出该轮的圆心;【变式31】如图所示,BD,CE是△ABC的高,求证:E,B,C,D四点在同一个圆上.圆的性质①旋转不变性:圆是旋转对称图形,绕圆心旋转任一角度都和原来图形重合;圆是中心对称图形,对称中心是圆心;②圆是轴对称图形:任何一条直径所在直线都是它的对称轴.或者说,经过圆心的任何一条直线都是圆的对称轴.题型4:圆的对称性4.已知:如图,两个以O为圆心的同心圆中,大圆的弦AB交小圆于C,D.求证:AC=BD.【变式41】如图,两个圆都以点O为圆心,大圆的弦AB交小圆于C,D两点,求证:AD=BC.【变式42】如图,在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C、D.(1)求证AC=BD;(2)若AC=3,大圆和小圆的半径分别为6和4,则CD的长度是.垂径定理及推论垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.常见辅助线做法:1)过圆心,作垂线,连半径,造,用勾股,求长度;2)有弧中点,连中点和圆心,得垂直平分.题型5:垂径定理与计算5.如图,AB是⊙O的直径,弦CD⊙AB于点E.若AB=10,BE=2,求弦CD的长.【变式51】如图,AB是⊙O的弦,C为AB的中点,OC的延长线与⊙O交于点D,若CD=2,AB=12,求⊙O的半径.【变式52】如图,AB是⊙O的直径,弦CD⊙AB于点E,OC=10cm,CD=16cm,求AE的长.题型6:垂径定理与证明6.如图,AB是⊙O的弦,C、D为直线AB上两点,OC=OD,求证:AC=BD.【变式61】如图,AB和CD分别是⊙O上的两条弦,过点O分别作ON⊥CD于点N,OM⊥AB于点M,若ON=AB,证明:OM=CD.⌢=BD⌢【变式62】如图,AB、CD都是⊙O的弦,且AB⊙CD,求证:AC题型7:垂径定理分类讨论问题7.在圆柱形油槽内装有一些油,截面如图所示,已知截面⊙O半径为5cm,油面宽AB为6cm,如果再注入一些油后,油面宽变为8cm,则油面AB上升了()cmA.1B.3C.3或4D.1或7题型8:垂径定理翻折问题8.如图,⊙O的半径为4,将⊙O的一部分沿着弦AB翻折,劣弧恰好经过圆心O,则折痕AB的长为.【变式81】如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,求折痕AB的长.【变式82】如图, AB是以点O为圆心的圆形纸片的直径,弦CD⊥AB于点E, AB=10,BE= 3.将阴影部分沿着弦AC翻折压平,翻折后,弧AC对应的弧为G,则点O与弧G所在圆的位置关系为.题型9:垂径定理的应用拱桥问题9.如图所示,某地新建一座石拱桥,桥拱是圆弧形,它的跨度(弧所对的弦的长)为40m,拱高(弧的中点到弦的距离)为8m,求桥拱得半径R.【变式91】如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.(1)求圆弧所在的圆的半径r的长;(2)当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?【变式92】如图,有一拱形公路桥,圆弧形桥拱的水面跨度AB=80m,拱高(弧的中点到弦的距离CD)为20m,求桥拱所在圆的半径.题型10:垂径定理的应用油管问题10.储油罐的截面如图所示,内径1000mm装入一些油后,若油面宽AB=600mm,求油的最大深度.【变式101】在半径为17dm的圆柱形油罐内装进一些油后,横截面如图.(1)若油面宽AB=16dm,求油的最大深度.(2)在(1)的条件下,若油面宽变为CD=30dm,求油的最大深度上升了多少dm?【变式102】在直径为1000毫米的圆柱形油罐内装进一些油.其横截面如图.油面宽AB=600毫米.(1)求油的最大深度;(2)如果再注入一些油后,油面宽变为800毫米,此时油面上升了多少毫米?一、单选题1.已知⊙O中,最长的弦长为16cm,则⊙O的半径是()A.4cm B.8cm C.16cm D.32cm2.如图在⊙O中,弦AB=8,OC⊙AB,垂足为C,且OC=3,则⊙O的半径()A.5B.10C.8D.63.如图,已知⊙O的直径CD=8,AB是⊙O的弦,AB⊥CD,垂足为M,OM=2,则AB的长为()A.2B.2√3C.4D.4√34.下列说法正确的是()A.长度相等的两条弧是等弧B.平分弦的直径垂直于弦C.直径是同一个圆中最长的弦D.过三点能确定一个圆5.如图,AB是⊙O的直径,CD是弦,AB⊙CD,垂足为点E,连接OD、CB、AC,⊙DOB=60°,EB=2,那么CD的长为()A.√3B.2 √3C.3 √3D.4 √36.如图,AB是⊙O的直径,弦CD⊙AB,垂足为E,如果AB=20,CD=16,那么线段OE的长为()A.10B.8C.6D.4二、填空题7.在半径为10的圆中有一条长为16的弦,那么这条弦的弦心距等于.8.如图,在半径为6的⊙O中,劣弧AB⌢的度数是120°,则弦AB的长是.9.如图,平面直角坐标系xOy中,M点的坐标为(3,0),⊙M的半径为2,过M点的直线与⊙M的交点分别为A,B,则⊙AOB的面积的最大值为,此时A,B两点所在直线与x轴的夹角等于°.10.已知⊙O的直径CD=10,AB是⊙O的弦,AB⊙CD,垂足为M,且AB=8,则AC的长为.三、计算题11.如图是一名考古学家发现的一块古代车轮碎片.(1)请你帮他找到这个车轮的圆心(保留作图痕迹);(2)若这个圆的半径为10cm,请求出弦心距为5cm的弦长.四、解答题12.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).求证:AC=BD.13.如图为桥洞的形状,其正视图是由CD⌢和矩形ABCD构成.O点为CD⌢所在⊙O的圆心,点O⌢所又恰好在AB为水面处.若桥洞跨度CD为8米,拱高(OE⊙弦CD于点F )EF为2米.求CD在⊙O的半径DO.14.已知:如图,在⊙O中,弦CD垂直于直径AB,垂足为点E,如果⊙BAD=30°,且BE=2,求弦CD的长.五、综合题15.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图所示).(1)求证:AC=BD;(2)若大圆的半径R=10,小圆的半径r=8,且圆心O到直线AB的距离为6,求AC的长16.《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架.《九章算术》中记载:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,间径几何?”(如图①)阅读完这段文字后,小智画出了一个圆柱截面示意图(如图②),其中BO⊙CD于点A,求间径就是要求⊙O的直径.(1)再次阅读后,发现AB=寸,CD=寸(一尺等于十寸),通过运用有关知识即可解决这个问题.请你补全题目条件.(2)帮助小智求出⊙O的直径.。
九年级圆的垂径定理与圆心角圆周角的大题精选(含答案)
圆的性质大题一.解答题(共25小题)1.如图,⊙O中,弦CD与直径AB交于点H.(1)当∠B+∠D=90°时,求证:H是CD的中点;(2)若H为CD的中点,且CD=2,BD=,求AB的长.2.如图,∠BAC=60°,AD平分∠BAC交⊙O于点D,连接OB、OC、BD、CD.(1)求证:四边形OBDC是菱形;(2)当∠BAC为多少度时,四边形OBDC是正方形?3.如图,CD是⊙O的直径,∠EOD=84°,AE交⊙O于点B,且AB=OB,求∠A 的度数.4.如图,在⊙O中,DE是⊙O的直径,AB是⊙O的弦,AB的中点C在直径DE 上.已知AB=8cm,CD=2cm(1)求⊙O的面积;(2)连接AE,过圆心O向AE作垂线,垂足为F,求OF的长.5.如图,点A、B、C、D、E都在⊙O上,AC平分∠BAD,且AB∥CE,求证:AD=CE.6.如图,在⊙O中,=2,AD⊥OC于D.求证:AB=2AD.7.已知在△ABC中,AB=AC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED.(1)求证:ED=EC;(2)若CD=3,EC=2,求AB的长.8.如图,在⊙O中,弦AD、BC相交于点E,连接OE,已知AD=BC,AD⊥CB.(1)求证:AB=CD;(2)如果⊙O的半径为5,DE=1,求AE的长.9.如图,⊙O的半径为5,弦AB⊥CD于E,AB=CD=8.(1)求证:AC=BD;(2)若OF⊥CD于F,OG⊥AB于G,试说明四边形OFEG是正方形.10.如图,已知AB是圆O的直径,弦CD⊥AB,垂足H在半径OB上,AH=5,CD=,点E在弧AD上,射线AE与CD的延长线交于点F.(1)求圆O的半径;(2)如果AE=6,求EF的长.11.在⊙O中,AB是⊙O直径,AC是弦,∠BAC=50°.(Ⅰ)如图(1),D是AB上一点,AD=AC,延长CD交⊙O于点E,求∠CEO的大小;(Ⅱ)如图(2),D是AC延长线上一点,AD=AB,连接BD交⊙O于点E,求∠CEO的大小.12.如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.(1)求证:四边形ABFC是菱形;(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.13.如图,在⊙O中,AB是⊙O的弦,CD是⊙O的直径,且AB⊥CD,垂足为G,点E在劣弧上,连接CE.(1)求证:CE平分∠AEB;(2)连接BC,若BC ∥AE,且CG=4,AB=6,求BE的长.14.如图,已知AD是⊙O的直径,BC切⊙O于点E,交AD延长线于点B,过点A作AC⊥BC交⊙O于点G,交DE于点F.(1)求证:AD=AF;(2)若DE=2CF,试说明四边形OEFG为菱形.15.如图,点A、B、C是圆O上的三点,AB∥OC(1)求证:AC平分∠OAB;(2)过点O作OE⊥AB于E,交AC于点P,若AB=2,∠AOE=30°,求圆O的半径OC及PE的长.16.如图,在△ABC中,CA=CB,E是边BC上一点,以AE为直径的⊙O经过点C,并交AB于点D,连结ED.(1)判断△BDE的形状并证明.(2)连结CO并延长交AB于点F,若BE=CE=3,求AF的长.17.一条排水管的截面如图所示,已知排水管的半径OA=1m,水面宽AB=1.2m,某天下雨后,水管水面上升了0.2m,求此时排水管水面的宽CD.18.如图,点B,C为⊙O上两定点,点A为⊙O上一动点,过点B作BE∥AC,交⊙O于点E,点D为射线BC上一动点,且AC平分∠BAD,连接CE.(1)求证:AD∥EC;(2)连接EA,若BC=CD,试判断四边形EBCA的形状,并说明理由.19.如图,在⊙O的内接四边形ABCD中,∠BCD=120°,CA平分∠BCD.(1)求证:△ABD是等边三角形;(2)若BD=3,求⊙O的半径.20.如图,点B,C为⊙O上一动点,过点B作BE∥AC,交⊙O于点E,点D为射线BC上一动点,且AC平分∠BAD,连接CE.(1)求证:AD∥EC;(2)连接EA,若BC=6,则当CD=时,四边形EBCA是矩形.21.如图所示,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E,连接AC、OC、BC.(1)求证:∠ACO=∠BCD;(2)若EB=8,CD=24,求⊙O的直径.22.如图,AB是⊙O的直径,弦CD⊥AB于E,∠A=15°,AB=4.求弦CD的长.23.已知:如图,⊙O的直径AB的长为5cm,C为⊙O上的一个点,∠ACB的平分线交⊙O于点D,求BD的长.24.如图,在⊙O中,半径OA与弦BD垂直,点C在⊙O上,∠AOB=80°(1)若点C在优弧BD上,求∠ACD的大小;(2)若点C在劣弧BD上,直接写出∠ACD的大小.25.如图,AB是⊙O的直径,C、D两点在⊙O上,若∠C=45°,(1)求∠ABD的度数;(2)若∠CDB=30°,BC=3,求⊙O的半径.圆的性质大题参考答案与试题解析一.解答题(共25小题)1.【解答】(1)证明:∵∠B+∠D=90°,∴∠BHD=180°﹣90°=90°,即AB⊥CD,∵AB过O,∴CH=DH,即H是CD的中点;(2)解:连接OD,∵H为CD的中点,CD=2,AB过O,∴DH=CH=CD=,AB⊥CD,∴∠BHD=90°,由勾股定理得:BH===1,设⊙O的半径为R,则AB=2R,OB=OD=R,在Rt△OHD中,由勾股定理得:OH2+DH2=OD2,即(R﹣1)2+()2=R2,解得:R=,∴AB=2×=3.2.【解答】证明:(1)连接OD,∵∠BAC=60°,∴∠BOC=120°,∵AD平分∠BAC交⊙O于点D,∴∠BAD=∠CAD,∴,∴∠BOD=∠COD=60°,∵OB=OD=OC,∴△BOD和△COD都是等边三角形,∴OB=BD=DC=OC,∴四边形OBDC是菱形;(2)当∠BAC为45度时,四边形OBDC是正方形,理由是:∵∠BAC=45°,∴∠BOC=90°,∴四边形OBDC是正方形.3.【解答】解:∵AB=BO,∴∠BOC=∠A,∴∠EBO=∠BOC+∠A=2∠A,而OB=OE,得∠E=∠EBO=2∠A,∴∠EOD=∠E+∠A=3∠A,而∠EOD=84°,∴3∠A=84°,∴∠A=28°.4.【解答】解:(1)连接OA,如图1所示∵C为AB的中点,AB=8cm,∴AC=4cm又∵CD=2cm设⊙O的半径为r,则(r﹣2)2+42=r2解得:r=5∴S=πr2=π×25=25π(2)OC=OD﹣CD=5﹣2=3EC=EO+OC=5+3=8∴EA===4∴EF===2∴OF===5.【解答】证明:如图,∵AB∥CE,∴∠ACE=∠BAC.又∵AC平分∠BAD,∴∠BAC=∠DAC,∴∠C=∠CAD,∴=,∴+=+,∴=,∴AD=CE.6.【解答】证明:延长AD交⊙O于E,∵OC⊥AD,∴,AE=2AD,∵,∴,∴AB=AE,∴AB=2AD.7.【解答】解:(1)∵∠EDC+∠EDA=180°、∠B+∠EDA=180°,∴∠B=∠EDC,又∵AB=AC,∴∠B=∠C,∴∠EDC=∠C,∴ED=EC;(2)连接AE,∵AB是直径,∴AE⊥BC,又∵AB=AC,∴BC=2EC=4,∵∠B=∠EDC、∠C=∠C,∴△ABC∽△EDC,∴AB:EC=BC:CD,又∵EC=2、BC=4、CD=3,∴AB=8.8.【解答】(1)证明:如图,∵AD=BC,∴=,∴﹣=﹣,即=,∴AB=CD;(2)如图,过O作OF⊥AD于点F,作OG⊥BC于点G,连接OA、OC.则AF=FD,BG=CG.∵AD=BC,∴AF=CG.在Rt△AOF与Rt △COG中,,∴Rt△AOF≌Rt△COG(HL),∴OF=OG,∴四边形OFEG是正方形,∴OF=EF.设OF=EF=x,则AF=FD=x+1,在直角△OAF中.由勾股定理得到:x2+(x+1)2=52,解得x=3.则AF=3+1=4,即AE=AF+3=7.9.【解答】(1)证明:∵AB=CD,∴=,∴﹣=﹣,即=,∴AC=BD(2)四边形OFEG是正方形理由如下:如图,连接OA、OD.∵AB⊥CD,OF⊥CD,OG⊥AB,∴四边形OFEG是矩形,,.∵AB=CD,∴DF=AG.∵OD=OA,∴OD=OA,∴△OFD≌△OGA,∴OF=OG.∴矩形OFEG是正方形10.【解答】解:(1)连接OD,∵直径AB⊥弦CD,CD=4,∴DH=CH=CD=2,在Rt△ODH中,AH=5,设圆O的半径为r,根据勾股定理得:OD2=(AH﹣OA)2+DH2,即r2=(5﹣r)2+20,解得:r=4.5,则圆的半径为4.5;(2)过O作OG⊥AE于G,∴AG=AE=×6=3,∵∠A=∠A,∠AGO=∠AHF,∴△AGO∽△AHF,∴,∴,∴AF=,∴EF=AF﹣AE=﹣6=.11.【解答】解:(Ⅰ)∵AD=AC,∠A=50°,∴∠C=∠ADC=65°,∴∠ADE=180°﹣∠ADC=180°﹣65°=115°∵∠AOE=2∠C=130°,∴∠CEO=∠AOE﹣∠ADE=130°﹣115°=15°(Ⅱ)∵AD=AB,∠A=50°∴∠D=∠B=65°,∵OB=OE,∴∠OEB=∠B=65°,∵四边形ABEC是圆内接四边形,∴∠BEC=180°﹣∠A=130°∴∠CEO=∠CEB﹣∠OEB=130°﹣65°=65°12.【解答】(1)证明:∵AB是直径,∴∠AEB=90°,∴AE⊥BC,∵AB=AC,∴BE=CE,∵AE=EF,∴四边形ABFC 是平行四边形,∵AC=AB,∴四边形ABFC是菱形.(2)设CD=x.连接BD.∵AB是直径,∴∠ADB=∠BDC=90°,∴AB2﹣AD2=CB2﹣CD2,∴(7+x)2﹣72=42﹣x2,解得x=1或﹣8(舍弃)∴AC=8,BD==,∴S菱形ABFC=8.∴S=•π•42=8π.13.【解答】(1)证明:∵CD⊥半圆AB,CD是直径,∴=.∴∠AEC=∠BEC;∴CE平分∠AEB;(2)解:∵CD ⊥AB,∴BG=AG=3.∠BGC=90°,在Rt△BGC中,∵CG=4,BG=3,∴BC=5,∵BC∥AE,∴∠AEC=∠BCE.又∠AEC=∠BEC,∴∠BCE=∠BEC∴BE=BC=5.14.【解答】证明:(1)如图,连接OE,∵BC是⊙O的切线,OE是半径,∴OE⊥BC,∴∠BEO=90°,∵∠ACB=90°,∴OE∥AC,∴∠OED=∠F,∵OD=OE,∴∠OED=∠ODE,∴∠ODE=∠F,∴AD=AF;(2)连接OG,∵OE∥AF,OD=OA,∴DE=EF,∵DE=2CF,∴EF=2CF,∵∠ACB=90°,∴∠F=60°,∵AD=AF,∴△ADF是等边三角形,∵∠A=60°,∵OA=OG,∴∠OGA=60°,∴∠OGA=∠F,∴OG∥EF,∵OE∥AF,∴四边形OEFG 是平行四边形,∵OE=OG,∴平行四边形OEFG是菱形.15.【解答】(1)证明:∵AB∥OC,∴∠C=∠BAC.∵OA=OC,∴∠C=∠OAC.∴∠BAC=∠OAC.即AC平分∠OAB.(2)∵OE⊥AB,∴AE=BE=AB=1.又∵∠AOE=30°,∠PEA=90°,∴∠OAE=60°.OA=2,∴∠EAP=∠OAE=30°,∴PE=AE×tan30°=1×=,即PE的长是.16.【解答】(1)证明:△BDE是等腰直角三角形.∵AE是⊙O 的直径∴∠ACB=∠ADE=90°,∴∠BDE=180°﹣90°=90°.∵CA=CB,∴∠B=45°,∴△BDE是等腰直角三角形.(2)过点F作FG⊥AC于点G,则△AFG是等腰直角三角形,且AG=FG.∵OA=OC,∴∠EAC=∠FCG.∵BE=CE=3,∴AC=BC=2CE=6,∴tan∠FCG=tan∠EAC=.∴CG=2FG=2AG.∴FG=AG=2,∴AF=2.17.【解答】解:如图:作OE⊥AB于E,交CD于F,∵AB=1.2m,OE⊥AB,OA=1m,∴OE=0.8m,∵水管水面上升了0.2m,∴OF=0.8﹣0.2=0.6m,∴CF==0.8m,∴CD=1.6m.18.【解答】(1)证明:∵AC平分∠BAD,∴∠BAC=∠DAC∵∠E=∠BAC∴∠E=∠DAC,∵BE∥AC∴∠E=∠ECA∴∠ECA=∠DAC∴EC‖AD;(2)四边形EBCA是矩形.理由如下,∵AC平分∠BAD,∴∠BAC=∠DAC又∵BC=CD∴∠ACB=∠ACD=90°∴AB为⊙O的直径.∴∠AEB=90°,又∵BE∥AC∴∠EBC=∠ACD=90°∴四边形EBCA是矩形.19.【解答】解:(1)∵∠BCD=120°,CA平分∠BCD,∴∠ACD=∠ACB=60°,由圆周角定理得,∠ADB=∠ACB=60°,∠ABD=∠ACD=60°,∴△ABD是等边三角形;(2)连接OB、OD,作OH⊥BD于H,则DH=BD=,∠BOD=2∠BAD=120°,∴∠DOH=60°,在Rt△ODH中,OD==,∴⊙O的半径为.20.【解答】(1)证明:∵AC平分∠BAD,∴∠BAC=∠DAC,∵∠E=∠BAC,∴∠E=∠DACM∵BE∥AC,∴∠E=∠ACE,∴∠ACE=∠DAC,∴AD∥EC.(2)解:当四边形ACBE是矩形时,∠ACB=90°,∴∠ACB=∠ACD=90°,∵∠BAC=∠DAC,∴∠ABD=∠D,∴AB=AD,∴BC=CD=6,故答案为6.21.【解答】(1)证明:∵AB⊥CD,∴,∴∠A=∠BCD,∵OA=OC,∴∠A=∠ACO,∴∠ACO=∠BCD;(2)解:设⊙O的半径为r,则OC=r,OE=OA﹣BE=r﹣8,∵AB ⊥CD,∴CE=DE=CD=×24=12,在Rt△OCE中,122+(r﹣8)2=r2,解得r=13,∴⊙O的直径=2r=26.22.【解答】解:∵∠A=15°,∴∠COB=30°.∵AB=4,∴OC=2.∵弦CD⊥AB于E,∴CE=CD.在Rt△OCE中,∠CEO=90°,∠COB=30°,OC=2,∴CE=1.∴CD=2.23.【解答】解:∵AB为直径,∴∠ADB=90°,∵CD 平分∠ACB,∴∠ACD=∠BCD,∴=.∴AD=BD,在等腰直角三角形ADB中,BD=ABsin45°=5×=,∴BD=.24.【解答】解:(1)∵AO⊥BD,∴=,∴∠AOB=2∠ACD,∵∠AOB=80°,∴∠ACD=40°;(2)①当点C1在上时,∠AC1D=∠ACD=40°;②当点C2在上时,∵∠AC2D+∠ACD=180°,∴∠AC2D=140°综上所述,∠ACD=140°或40°.25.【解答】解:(1)∵∠C=45°,∴∠A=∠C=45°,∵AB是⊙O的直径,∴∠ADB=90°,∴∠ABD=45°;(2)连接AC,∵AB是⊙O的直径,∴∠ACB=90°,∵∠CAB=∠CDB=30°,BC=3,∴AB=6,∴⊙O的半径为3.。
垂径定理应用练习1

垂径定理应用练习1一.选择题(共40小题)1.如图,有一圆弧形门拱,拱高AB=1m,跨度CD=4m,那么这个门拱的半径为()A.2m B.2.5m C.3m D.5m2.如图,OA,OB,OC都是⊙O的半径,若∠AOB是锐角,且∠AOB=2∠BOC.则下列结论正确的是()A.AB=2BC B.AB<2BC C.∠AOB=2∠CAB D.∠ACB=4∠CAB3.如图,AB是⊙O的直径,弦CD⊥AB于点E,则下列结论正确的是()A.OE=BE B.=C.△BOC是等边三角形D.四边形ODBC是菱形4.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连接CO,AD,∠BAD=20°,则下列说法中正确的是()A.AD=2OB B.CE=EO C.∠OCE=40°D.∠BOC=2∠BAD5.如图,圆柱形水管内原有积水的水平面宽CD=20cm,水深GF=2cm,若水面上升2cm(即EG=2cm),则此时水面宽AB为()A.8cm B.16cm C.8cm D.16cm6.如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为()A. B.2 C.2D.87.一条排水管的截面如图所示,已知排水管的截面圆半径OB=5,截面圆圆心O 到水面的距离OC是3,则水面宽AB是()A.8 B.5 C.4 D.38.如图,圆弧形石拱桥的桥顶到水面的距离CD为6m,桥拱半径OC为4m,则水面宽AB为()A .mB .2mC .4mD .6m9.如图,⊙O 的半径为5,AB 为弦,半径OC ⊥AB ,垂足为点E ,若OE=3,则AB 的长是( )A .4B .6C .8D .1010.如图,点P 是半径为5的⊙O 内一点,且OP=3.过点P 任作一条弦AB ,则弦AB 的长不可能为( )A .7.9B .8.5C .9D .1011.如图,AB 是⊙O 的直径,弦CD ⊥AB 于点E .若AB=8,AE=1,则弦CD 的长是( )A .B .2C .6D .812.如图,⊙O 中,OA ⊥BC ,AD ∥OC ,∠AOC=40°,则∠B 的度数为( )A.100°B.110°C.115° D.120°13.如图,CD为⊙O的直径,弦AB⊥CD,垂足为M,若AB=12,OM:MD=5:8,则⊙O的周长为()A.26πB.13πC.D.14.下列判断中正确的是()A.平分弦的直线垂直于弦B.平分弦的直线也必平分弦所对的两条弧C.弦的垂直平分线必平分弦所对的两条弧D.平分一条弧的直线必平分这条弧所对的弦15.如图,在三个等圆上各自有一条劣弧、、,如果+=,那么AB+CD 与EF的大小关系是()A.AB+CD=EF B.AB+CD>EF C.AB+CD<EF D.不能确定16.如图,⊙O的直径CD⊥弦AB于点P,且点P为OD的中点,已知AB=2,则CD的值为()A.2 B.4 C.D.17.上体育课时,老师在运动场上教同学们学习掷铅球,训练时,李力同学掷出的铅球在场地上砸出了一个坑口直径约为10cm、深约为2cm的小坑,则该铅球的直径约为()cm.A.20 B.19.5 C.14.5 D.1018.如图,⊙O的直径AB=12,CD是⊙O的弦,CD⊥AB,垂足为P,且BP:AP=1:5,则CD的长为()A.4 B.8 C.2 D.419.某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则中间柱CD的高度为()米?A.6 B.4 C.8 D.520.如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是()A.AB=AD B.BC=CD C.D.∠BCA=∠DCA21.如图.⊙O的直径AB垂直弦CD于E点,∠A=22.5°,OC=4,CD的长为()A.4 B.8 C.2 D.422.一条排水管的截面如图所示,已知该排水管的半径OA=10,水面宽AB=16,则排水管内水的最大深度CD的长为()A.8 B.6 C.5 D.423.如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,若AC=12,则OF的长为()A.8 B.7 C.6 D.424.在半径为1的圆中,长度等于的弦所对的弧的度数为()A.90°B.145°C.270° D.90°或270°25.如图,AB是圆O的直径,BC、CD、DA是圆O的弦,且BC=CD=DA,则∠BCD 等于()A.100°B.110°C.120° D.135°26.如图,已知⊙O的半径为5,点A到圆心O的距离为3,则过点A的所有弦中,最短弦的长为()A.4 B.6 C.8 D.1027.如图,在半径为13cm的圆形铁片上切下一块高为8cm的弓形铁片,则弓形弦AB的长为()A.10cm B.16cm C.24cm D.26cm28.如图,在Rt△ABC中,∠ACB=90°,∠A=56°.以BC为直径的⊙O交AB于点D.E是⊙O上一点,且=,连接OE.过点E作EF⊥OE,交AC的延长线于点F,则∠F的度数为()A.92°B.108°C.112° D.124°29.在半径为10的⊙O内有一点P,OP=6,在过点P的弦中,长度为整数的弦的条数为()A.5条 B.6条 C.7条 D.8条30.在⊙O中,弦CD与直径AB相交于点P,夹角为30°,且分直径为1:5两部分,AB=6厘米,则弦CD的长为多少厘米()A.B.C.D.31.已知半径为5的⊙O中,弦AB=5,弦AC=5,则∠BAC的度数是()A.15°B.210°C.105°或15°D.210°或30°32.如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB 的长为()A.2cm B.cm C.D.33.如图所示,小范从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走.按照这种方式,小范第五次走到场地边缘时处于弧AB上,此时∠AOE=48°,则α的度数是()A.60°B.51°C.48°D.76°34.如图,在等边△ABC中,AB、AC都是圆O的弦,OM⊥AB,ON⊥AC,垂足分别为M、N,如果MN=1,那么BC的值为()A.1 B.2 C.3 D.435.如图,AD为圆O的直径.甲、乙两人想在圆上找B,C两点,作一个正三角形ABC,其作法如下:甲:1.作OD中垂线,交圆于B,C两点,2.连AB,AC,△ABC即为所求.乙:1.以D为圆心,OD长为半径画弧,交圆于B,C两点,2.连AB,BC,CA,△ABC即为所求.对于甲、乙两人的作法,下列判断何者正确()A.甲、乙皆正确B.甲、乙皆错误C.甲正确、乙错误 D.甲错误、乙正确36.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为()A.2B.2C.2D.837.如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,若DE=6,∠BAC+∠EAD=180°,则弦BC的长等于()A.8 B.10 C.11 D.1238.如图,AB为⊙O的直径,弦DC垂直AB于点E,∠DCB=30°,EB=3,则弦AC的长度为()A.3 B.C.D.39.如图,弧BE是半径为6的圆D的圆周,C点是上的任意一点,△ABD是等边三角形,则四边形ABCD的周长P的取值范围是()A.12<P≤18 B.18<P≤24 C.18<P≤18+6D.12<P≤12+640.如图,点C是⊙O上一点,⊙O的半径为,D、E分别是弦AC、BC上一动点,且OD=OE=,则AB的最大值为()A.B.C.D.垂径定理应用练习1参考答案与试题解析一.选择题(共40小题)1.如图,有一圆弧形门拱,拱高AB=1m,跨度CD=4m,那么这个门拱的半径为()A.2m B.2.5m C.3m D.5m【分析】设这个门拱的半径为r,则OB=r﹣1,根据垂径定理求出BC的长,再根据勾股定理求出r的值即可.【解答】解:设这个门拱的半径为r,则OB=r﹣1,∵CD=4m,AB⊥CD,∴BC=CD=2m,在Rt△BOC中,∵BC2+OB2=OC2,即22+(r﹣1)2=r2,解得r=2.5m.故选B.【点评】本题考查的是垂径定理的应用,此类问题应用垂径定理和勾股定理相结合,构造直角三角形,可解决计算弦长、半径、弦心距等问题.2.如图,OA,OB,OC都是⊙O的半径,若∠AOB是锐角,且∠AOB=2∠BOC.则下列结论正确的是()A.AB=2BC B.AB<2BC C.∠AOB=2∠CAB D.∠ACB=4∠CAB【分析】首先取的中点D,连接AD,BD,由∠AOB=2∠BOC,易得AD=BD=BC,继而证得AB<2BC,又由圆周角定理,可得∠AOB=4∠CAB,∠ACB=∠BOC=2∠CAB.【解答】解:取的中点D,连接AD,BD,∵∠AOB=2∠BOC,∴=2,∴==,∴AD=BD=BC,∵AB<AD+BD,∴AB<2BC.故A错误,B正确;∵∠AOB=2∠BOC,∠BOC=2∠CAB,∴∠AOB=4∠CAB;故C错误;∵∠AOB=2∠ACB,∴∠ACB=∠BOC=2∠CAB,故D错误.故选B.【点评】此题考查了弧、弦与圆心角的关系以及圆周角定理.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.3.如图,AB是⊙O的直径,弦CD⊥AB于点E,则下列结论正确的是()A.OE=BE B.=C.△BOC是等边三角形D.四边形ODBC是菱形【分析】根据垂径定理判断即可.【解答】解:∵AB⊥CD,AB过O,∴DE=CE,=,根据已知不能推出OE=BE,△BOC是等边三角形,四边形ODBC是菱形.故选:B.【点评】本题考查了垂径定理的应用,主要考查学生的推理能力和辨析能力.4.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连接CO,AD,∠BAD=20°,则下列说法中正确的是()A.AD=2OB B.CE=EO C.∠OCE=40°D.∠BOC=2∠BAD【分析】先根据垂径定理得到=,CE=DE,再利用圆周角定理得到∠BOC=40°,则根据互余可计算出∠OCE的度数,于是可对各选项进行判断.【解答】解:∵AB⊥CD,∴=,CE=DE,∴∠BOC=2∠BAD=40°,∴∠OCE=90°﹣40°=50°.故选D.【点评】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了圆周角定理.5.如图,圆柱形水管内原有积水的水平面宽CD=20cm,水深GF=2cm,若水面上升2cm(即EG=2cm),则此时水面宽AB为()A.8cm B.16cm C.8cm D.16cm【分析】连接OA、OC.设⊙O的半径是R,则OG=R﹣2,OE=R﹣4.根据垂径定理,得CG=10.在直角三角形OCG中,根据勾股定理求得R的值,再进一步在直角三角形OAE中,根据勾股定理求得AE的长,从而再根据垂径定理即可求得AB的长.【解答】解:如图所示,连接OA、OC.设⊙O的半径是R,则OG=R﹣2,OE=R﹣4.∵OF⊥CD,∴CG=CD=10cm.在直角三角形COG中,根据勾股定理,得R2=102+(R﹣2)2,解,得R=26.在直角三角形AOE中,根据勾股定理,得AE==8cm.根据垂径定理,得AB=16(cm),故选B.【点评】本题考查了勾股定理,垂径定理的应用,能构造直角三角形是解此题的关键,注意:垂直于弦的直径平分弦.6.如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为()A. B.2 C.2D.8【分析】作OH⊥CD于H,连结OC,如图,根据垂径定理由OH⊥CD得到HC=HD,再利用AP=2,BP=6可计算出半径OA=4,则OP=OA﹣AP=2,接着在Rt△OPH中根据含30度的直角三角形的性质计算出OH=OP=1,然后在Rt△OHC中利用勾股定理计算出CH=,所以CD=2CH=2.【解答】解:作OH⊥CD于H,连结OC,如图,∵OH⊥CD,∴HC=HD,∵AP=2,BP=6,∴AB=8,∴OA=4,∴OP=OA﹣AP=2,在Rt△OPH中,∵∠OPH=30°,∴∠POH=30°,∴OH=OP=1,在Rt△OHC中,∵OC=4,OH=1,∴CH==,∴CD=2CH=2.故选C.【点评】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理以及含30度的直角三角形的性质.7.一条排水管的截面如图所示,已知排水管的截面圆半径OB=5,截面圆圆心O 到水面的距离OC是3,则水面宽AB是()A.8 B.5 C.4 D.3【分析】先根据勾股定理求出BC的长,再由垂径定理得出AB=2BC,进而可得出结论.【解答】解:∵OB=5,OC=3,∴BC===4,∵OC⊥AB,∴AB=2BC=2×4=8.故选A.【点评】本题考查的是垂径定理在实际生活中的应用,有利于培养学生理论联系实际的能力.8.如图,圆弧形石拱桥的桥顶到水面的距离CD为6m,桥拱半径OC为4m,则水面宽AB为()A.m B.2m C.4m D.6m【分析】连接OA,根据桥拱半径OC为4m,求出OA=4m,根据CD=6m,求出OD=2m,根据AD=求出AD,最后根据AB=2AD即可得出答案.【解答】解:连接OA,∵桥拱半径OC为4m,∴OA=4m,∵CD=6m,∴OD=6﹣4=2m,∴AD===2m,∴AB=2AD=2×2=4(m);故选C.【点评】此题考查了垂径定理的应用,关键是根据题意做出辅助线,用到的知识点是垂径定理、勾股定理.9.如图,⊙O的半径为5,AB为弦,半径OC⊥AB,垂足为点E,若OE=3,则AB的长是()A.4 B.6 C.8 D.10【分析】连接OA,根据勾股定理求出AE的长,进而可得出结论.【解答】解:连接OA,∵OC⊥AB,OA=5,OE=3,∴AE===4,∴AB=2AE=8.故选C.【点评】本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.10.如图,点P是半径为5的⊙O内一点,且OP=3.过点P任作一条弦AB,则弦AB的长不可能为()A.7.9 B.8.5 C.9 D.10【分析】先作辅助线,再根据垂径定理和勾股定理即可求出.【解答】解:过点P的最短的弦是作AB⊥OP,连接OA,根据垂径定理和勾股定理,得AB=8过点P最长的弦长是10,显然下列答案中,只有A不符合.故选A.【点评】注意能够正确分析出过圆内一点P的最长的弦即是直径,最短的弦即是垂直于OP的弦.综合运用勾股定理以及垂径定理.11.如图,AB是⊙O的直径,弦CD⊥AB于点E.若AB=8,AE=1,则弦CD的长是()A.B.2 C.6 D.8【分析】根据垂径定理,可得答案.【解答】解:连接OC,由题意,得OE=OB﹣AE=4﹣1=3,CE=ED==,CD=2CE=2,故选:B.【点评】本题考查了垂径定理,利用勾股定理,垂径定理是解题关键.12.如图,⊙O中,OA⊥BC,AD∥OC,∠AOC=40°,则∠B的度数为()A.100°B.110°C.115° D.120°【分析】由平行线的性质得出∠A=∠AOC=40°,由对顶角相等得出∠2=∠1=50°,由垂径定理得出,得出∠AOB=∠AOC=40°,由圆周角定理求出∠D,再由三角形内角和定理即可得出结果.【解答】解:连接OB,如图所示:∵AD∥OC,∴∠A=∠AOC=40°,∵OA⊥BC,∴∠1=∠2=90°﹣∠A=90°﹣40°=50°,,∴∠AOB=∠AOC=40°,∴∠D=∠AOB=20°,∴∠B=180°﹣50°﹣20°=110°;故选:B.【点评】本题考查了垂径定理、圆周角定理、平行线的性质等知识;熟练掌握垂径定理是解决问题的关键.13.如图,CD为⊙O的直径,弦AB⊥CD,垂足为M,若AB=12,OM:MD=5:8,则⊙O的周长为()A.26πB.13πC.D.【分析】连接OA,根据垂径定理得到AM=AB=6,设OM=5x,DM=8x,得到OA=OD=13x,根据勾股定理得到OA=×13,于是得到结论.【解答】解:连接OA,∵CD为⊙O的直径,弦AB⊥CD,∴AM=AB=6,∵OM:MD=5:8,∴设OM=5x,DM=8x,∴OA=OD=13x,∴AM=12x=6,∴x=,∴OA=×13,∴⊙O的周长=2OA•π=13π,故选B.【点评】本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.14.下列判断中正确的是()A.平分弦的直线垂直于弦B.平分弦的直线也必平分弦所对的两条弧C.弦的垂直平分线必平分弦所对的两条弧D.平分一条弧的直线必平分这条弧所对的弦【分析】根据垂径定理对各选项进行逐一判断即可.【解答】解:A、平分弦(非直径)的直径垂直于弦,故本选项错误;B、平分弦的直径也必平分弦所对的两条弧,故本选项错误;C、弦的垂直平分线必平分弦所对的两条弧,符合垂径定理,故本选项正确;D、平分一条弧的直径必平分这条弧所对的弦,故本选项错误.故选:C.【点评】本题考查的是垂径定理,熟知弦的垂直平分线平分弦、垂直于弦,平分弦所对的两条弧是解答此题的关键.15.如图,在三个等圆上各自有一条劣弧、、,如果+=,那么AB+CD 与EF的大小关系是()A.AB+CD=EF B.AB+CD>EF C.AB+CD<EF D.不能确定【分析】在弧EF上取一点M使弧EM=弧CD,推出弧FM=弧AB,根据圆心角、弧、弦的关系得到AB=FM,CD=EM,根据三角形的三边关系定理求出FM+EM>FE即可.【解答】解:如图,在弧EF上取一点M使弧EM=弧CD,则弧FM=弧AB,∴AB=FM,CD=EM,在△MEF中,FM+EM>EF,∴AB+CD>EF.故选B.【点评】本题主要考查对三角形的三边关系定理,圆心角、弧、弦的关系等知识点的理解和掌握,能正确作辅助线是解此题的关键.16.如图,⊙O的直径CD⊥弦AB于点P,且点P为OD的中点,已知AB=2,则CD的值为()A.2 B.4 C.D.【分析】连接OA,由CD垂直于AB,利用垂径定理得到P为AB的中点,求出AP的长,设OA=OD=x,由P为OD中点,得到OP为x,在直角三角形AOP中,利用勾股定理列出关于x的方程,求出方程的解即可得到x的值,即为圆的半径,进而求出CD的长.【解答】解:连接OA,∵CD⊥AB,∴P为AB的中点,∴AP=AB=,∵P为AB的中点,∴OP=PD=OD,在Rt△AOP中,OA=x,OP=x,根据勾股定理得:OA2=OP2+AP2,即x2=x2+3,即x2=4,解得:x=2,则CD=4.故选B【点评】此题考查了垂径定理,勾股定理,利用了方程的思想,熟练掌握垂径定理是解本题的关键.17.上体育课时,老师在运动场上教同学们学习掷铅球,训练时,李力同学掷出的铅球在场地上砸出了一个坑口直径约为10cm、深约为2cm的小坑,则该铅球的直径约为()cm.A.20 B.19.5 C.14.5 D.10【分析】根据垂径定理,构造直角三角形,小坑的直径就是圆中的弦长,小坑的深就是拱高,利用勾股定理,设出未知数,列出方程,即可求出铅球的直径.【解答】解:根据题意,画出图形如图所示,由题意知,AB=10,CD=2,OD是半径,且OC⊥AB,∴AC=CB=5,设铅球的半径为r,则OC=r﹣2,在Rt△AOC中,根据勾股定理,OC2+AC2=OA2,即(r﹣2)2+52=r2,解得:r=7.25,所以铅球的直径为:2×7.25=14.5 cm故选:C.【点评】本题考查的是垂径定理和勾股定理的应用,解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形,若设圆的半径为r,弦长为a,这条弦的弦心距为d,则r2=d2+()2成立,知道这三个量中的任意两个,就可以求出另外一个.18.如图,⊙O的直径AB=12,CD是⊙O的弦,CD⊥AB,垂足为P,且BP:AP=1:5,则CD的长为()A.4 B.8 C.2 D.4【分析】先根据⊙O的直径AB=12求出OB的长,再由BP:AP=1:5求出BP的长,故可得出OP的长,连接OC,在Rt△OPC中利用勾股定理可求出PC的长,再根据垂径定理即可得出结论.【解答】解:∵⊙O的直径AB=12,∴OB=AB=6,∵BP:AP=1:5,∴BP=AB=×12=2,∴OP=OB﹣BP=6﹣2=4,∵CD⊥AB,∴CD=2PC.如图,连接OC,在Rt△OPC中,∵OC=6,OP=4,∴PC===2,∴CD=2PC=2×2=4.故选D.【点评】本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.19.某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则中间柱CD的高度为()米?A.6 B.4 C.8 D.5【分析】由垂径定理,可得AD=AB,然后由勾股定理求得OD的长,继而求得中间柱CD的高度.【解答】解:∵CD是中间柱,即=,∴OC⊥AB,∴AD=BD=AB=×16=8(m),∵半径OA=10m,在Rt△AOD中,OD==6(m),∴CD=OC﹣OD=10﹣6=4(m).故选B.【点评】此题考查了垂径定理的应用与勾股定理.此题比较简单,注意数形结合思想的应用.20.如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是()A.AB=AD B.BC=CD C.D.∠BCA=∠DCA【分析】根据圆心角、弧、弦的关系对各选项进行逐一判断即可.【解答】解:A、∵∠ACB与∠ACD的大小关系不确定,∴AB与AD不一定相等,故本选项错误;B、∵AC平分∠BAD,∴∠BAC=∠DAC,∴BC=CD,故本选项正确;C、∵∠ACB与∠ACD的大小关系不确定,∴与不一定相等,故本选项错误;D、∠BCA与∠DCA的大小关系不确定,故本选项错误.故选B.【点评】本题考查的是圆心角、弧、弦的关系,在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.21.如图.⊙O的直径AB垂直弦CD于E点,∠A=22.5°,OC=4,CD的长为()A.4 B.8 C.2 D.4【分析】根据等边对等角可得∠OAC=∠OCA=22.5°,再根据三角形外角的性质可得∠COE=45°,然后利用三角函数可得CE的长,再根据垂径定理可得答案.【解答】解:∵CO=AO,∴∠OAC=∠OCA=22.5°,∴∠COE=45°,∵CD⊥AB,∴∠CEO=90°,CD=2CE,∴CE=EO,∴CE=CO•sin45°=4×=2,∴CD=4,故选:D.【点评】此题主要考查了垂径定理,关键是掌握垂直弦的直径平分这条弦,并且平分弦所对的两条弧.22.一条排水管的截面如图所示,已知该排水管的半径OA=10,水面宽AB=16,则排水管内水的最大深度CD的长为()A.8 B.6 C.5 D.4【分析】先根据垂径定理求出AC的长,再根据勾股定理求出OC的长,由CD=OD ﹣OC即可得出结论.【解答】解:∵AB=16,OD⊥AB,OA=10,∴AC=AB=8,∴OC==6,∴CD=OD﹣OC=10﹣6=4.故选D.【点评】本题考查的是垂径定理的应用,熟知平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧是解答此题的关键.23.如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,若AC=12,则OF的长为()A.8 B.7 C.6 D.4【分析】先根据平行线的性质得∠A=∠FOE,再利用垂径定理得到AD=CD=AC=6,然后证明△ODA≌△EFO,则利用全等三角形的性质易得OF=AD=6.【解答】解:∵OE∥AC,∴∠A=∠FOE,∵OD⊥AC,∴AD=CD=AC=6,∠ADO=90°,∵EF⊥OB,∴∠OFE=90°,在△ODA和△EFO中,∴△ODA≌△EFO,∴AD=OF=6.故选C.【点评】本题考查了垂径定理:垂直弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了全等三角形的判定与性质.24.在半径为1的圆中,长度等于的弦所对的弧的度数为()A.90°B.145°C.270° D.90°或270°【分析】利用AB=,OA=OB=1,则AB2=OA2+OB2,根据勾股定理的逆定理得到△AOB为直角三角形,且∠AOB=90°进而得出长度等于的弦所对的弧长有两段,分别求出即可.【解答】解:如图,连接OA、OB;∵在⊙O中,AB=,OA=OB=1,∴AB2=OA2+OB2,∴△AOB为直角三角形,且∠AOB=90°,即长度等于的弦所对的弧长有两段:一段所对圆心角为90°,另一段所对圆心角为270°,∴长度等于的弦所对的弧的度数为90°或270°.故选:D.【点评】本题考查了勾股定理的逆定理以及圆心角、弧、弦的关系,利用已知得出长度等于的弦所对的弧长有两段,注意不要漏解.25.如图,AB是圆O的直径,BC、CD、DA是圆O的弦,且BC=CD=DA,则∠BCD 等于()A.100°B.110°C.120° D.135°【分析】由已知可得,弦BC、CD、DA三等分半圆,从而不难求得∠BCD的度数.【解答】解:连接OC、OD,∵BC=CD=DA,∴∠COB=∠COD=∠DOA,∵∠COB+∠COD+∠DOA=180°,∴∠COB=∠COD=∠DOA=60°,∴∠BCD=×2(180°﹣60°)=120°.故选C.【点评】本题考查了弧、弦与圆心角的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.注意半圆对的圆心角为180°.26.如图,已知⊙O的半径为5,点A到圆心O的距离为3,则过点A的所有弦中,最短弦的长为()A.4 B.6 C.8 D.10【分析】最短弦是过A点垂直于OA的弦.根据垂径定理和勾股定理求解.【解答】解:由垂径定理得,该弦应该是以OA为中垂线的弦BC.连接OB.已知OB=5,OA=3,由勾股定理得AB=4.所以弦BC=8.故选C.【点评】此题主要考查了学生对垂径定理及勾股定理的理解运用.27.如图,在半径为13cm的圆形铁片上切下一块高为8cm的弓形铁片,则弓形弦AB的长为()A.10cm B.16cm C.24cm D.26cm【分析】首先构造直角三角形,再利用勾股定理得出BC的长,进而根据垂径定理得出答案.【解答】解:如图,过O作OD⊥AB于C,交⊙O于D,∵CD=8,OD=13,∴OC=5,又∵OB=13,∴Rt△BCO中,BC==12,∴AB=2BC=24.故选:C.【点评】此题主要考查了垂径定理以及勾股定理,得出AC的长是解题关键.28.如图,在Rt△ABC中,∠ACB=90°,∠A=56°.以BC为直径的⊙O交AB于点D.E是⊙O上一点,且=,连接OE.过点E作EF⊥OE,交AC的延长线于点F,则∠F的度数为()A.92°B.108°C.112° D.124°【分析】直接利用互余的性质再结合圆周角定理得出∠COE的度数,再利用四边形内角和定理得出答案.【解答】解:∵∠ACB=90°,∠A=56°,∴∠ABC=34°,∵=,∴2∠ABC=∠COE=68°,又∵∠OCF=∠OEF=90°,∴∠F=360°﹣90°﹣90°﹣68°=112°.故选:C.【点评】此题主要考查了圆周角定理以及四边形内角和定理,正确得出∠OCE的度数是解题关键.29.在半径为10的⊙O内有一点P,OP=6,在过点P的弦中,长度为整数的弦的条数为()A.5条 B.6条 C.7条 D.8条【分析】过点P的弦有无数条,求出最长的和最短的弦,再判断长度为整数的条数.【解答】解:最长的弦是直径为20,最短的弦为16,∴长度为整数的弦还有19,18,17各2条,∴经过P点的所有弦中长度为整数的有8条,故选D.【点评】本题考查了勾股定理和垂径定理,解此类题目要注意将圆的问题转化成三角形的问题再进行计算.注:最长的弦是直径,最短的弦是与直径垂直的弦.30.在⊙O中,弦CD与直径AB相交于点P,夹角为30°,且分直径为1:5两部分,AB=6厘米,则弦CD的长为多少厘米()A.B.C.D.【分析】先作图,然后连接OC.再求OE(在直角三角形中,30°角所对的直角边等于斜边的一半),再求CE,从而求出CD.【解答】解:如图,过点O作OE⊥CD于E,连接OC在Rt△OPE中,OP=3﹣1=2又∠EPO=30°∴OE=1在Rt△COE中,OC=3,OE=1∴CE=∴CD=2CE=故选B.【点评】此题主要考查垂径定理及在圆中的计算问题,还有勾股定理的使用.31.已知半径为5的⊙O中,弦AB=5,弦AC=5,则∠BAC的度数是()A.15°B.210°C.105°或15°D.210°或30°【分析】连接OC,OA,OB,根据已知可得到△OAC是等边三角形,△OAB是等腰直角三角形,从而分两种情况进行分析,不难求得∠BAC的度数.【解答】解:连接OC,OA,OB∵OC=OA=AC=5∴△OAC是等边三角形∴∠CAO=60°∵OA=OB=5,AB=5∴OA2+OB2=50=AB2∴△OAB是等腰直角三角形.∴∠OAB=45°点C的位置有两种情况:如图,C不在弧AB上时:∠BAC=∠CAO+∠OAB=60°+45°=105°如图,C在弧AB上时:∠BAC=∠CAO﹣∠OAB=60°﹣45°=15°.故选C.【点评】本题利用了等边三角形的判定和性质,勾股定理的逆定理求解.32.如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB 的长为()A.2cm B.cm C.D.【分析】在图中构建直角三角形,先根据勾股定理得AD的长,再根据垂径定理得AB的长.【解答】解:作OD⊥AB于D,连接OA.根据题意得:OD=OA=1cm,再根据勾股定理得:AD=cm,根据垂径定理得:AB=2cm.故选:C.【点评】注意由题目中的折叠即可发现OD=OA=1.考查了勾股定理以及垂径定理.33.如图所示,小范从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走.按照这种方式,小范第五次走到场地边缘时处于弧AB上,此时∠AOE=48°,则α的度数是()A.60°B.51°C.48°D.76°【分析】连接OD,要求α的度数,只需求出∠AOB的度数,根据已知条件,易证∠AOB=∠BOC=∠COD=∠DOE,所以可以求出α的度数.【解答】解:连接OD,∵∠BAO=∠CBO=α,∴∠AOB=∠BOC=∠COD=∠DOE,∵∠AOE=48°,∴∠AOB==78°,∴α==51°.故选B.【点评】本题考查的是圆心角、弧、弦的关系,熟知,在圆中,半径处处相等,由半径和弦组成的三角形是等腰三角形等知识是解答此题的关键.34.如图,在等边△ABC中,AB、AC都是圆O的弦,OM⊥AB,ON⊥AC,垂足分别为M、N,如果MN=1,那么BC的值为()A.1 B.2 C.3 D.4【分析】先根据垂径定理得出M、N分别是AB与AC的中点,故MN是△ABC 的中位线,由三角形的中位线定理即可得出结论.【解答】解:∵OM⊥AB,ON⊥AC垂足分别为M、N,∴M、N分别是AB与AC的中点,∴MN是△ABC的中位线,∴BC=2MN=2,故选:B.【点评】本题考查的是垂径定理,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.35.如图,AD为圆O的直径.甲、乙两人想在圆上找B,C两点,作一个正三角形ABC,其作法如下:甲:1.作OD中垂线,交圆于B,C两点,2.连AB,AC,△ABC即为所求.乙:1.以D为圆心,OD长为半径画弧,交圆于B,C两点,2.连AB,BC,CA,△ABC即为所求.对于甲、乙两人的作法,下列判断何者正确()A.甲、乙皆正确B.甲、乙皆错误C.甲正确、乙错误 D.甲错误、乙正确【分析】根据垂径定理和等边三角形的判定求解.【解答】解:甲的作图:BC是OD的中垂线,则在直角△OBE中,OE=OB,则∠OBE=30°,∠BOE=60°,∠BOC=120°,∴∠BAC=60°.根据条件易证AB=AC,则△ABC是等边三角形.乙的作图:连接BD,则△OBD是等边三角形.因而∠BAD=30°,∠BAC=60°.根据条件易证AB=AC,则△ABC是等边三角形.所以甲乙皆正确,【点评】AD经过圆心,则AD所在的直线是本题图形的对称轴.36.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为()A.2B.2C.2D.8【分析】设⊙O半径为r,根据勾股定理列方程求出半径r,由勾股定理依次求BE和EC的长.【解答】解:连接BE,设⊙O半径为r,则OA=OD=r,OC=r﹣2,∵OD⊥AB,∴∠ACO=90°,AC=BC=AB=4,在Rt△ACO中,由勾股定理得:r2=42+(r﹣2)2,r=5,∴AE=2r=10,∵AE为⊙O的直径,∴∠ABE=90°,由勾股定理得:BE=6,在Rt△ECB中,EC===2.【点评】本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.37.如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,若DE=6,∠BAC+∠EAD=180°,则弦BC的长等于()A.8 B.10 C.11 D.12【分析】作AH⊥BC于H,作直径CF,连结BF,先利用等角的补角相等得到∠DAE=∠BAF,然后再根据同圆中,相等的圆心角所对的弦相等得到DE=BF=6,由AH⊥BC,根据垂径定理得CH=BH,易得AH为△CBF的中位线,然后根据三角形中位线性质得到AH=BF=3,再利用勾股定理,可求得BH的长,继而求得答案.【解答】解:作AH⊥BC于H,作直径CF,连结BF,如图,∵∠BAC+∠EAD=180°,而∠BAC+∠BAF=180°,∴∠DAE=∠BAF,∴=,∴DE=BF=6,∵AH⊥BC,∴CH=BH,∵CA=AF,∴AH为△CBF的中位线,∴AH=BF=3.∴BH===4,∴BC=2BH=8.【点评】此题考查了圆周角定理、垂径定理、三角形中位线的性质以及勾股定理.注意掌握辅助线的作法.38.如图,AB为⊙O的直径,弦DC垂直AB于点E,∠DCB=30°,EB=3,则弦AC的长度为()A.3 B.C.D.【分析】连结OC,AC,先根据直角的性质得到∠ABC的度数,再圆周角定理得到∠AOC的度数,根据等边三角形的性质和垂径定理得到⊙O的半径和直径,再解直角三角形即可求解.【解答】解:连结OC,AC,∵弦DC垂直AB于点E,∠DCB=30°,∴∠ABC=60°,∴△BOC是等边三角形,∵EB=3,∴OB=6,∴AB=12,AB为⊙O的直径,∴∠ACB=90°,在Rt△ACB,AC=12×=6.。
九年级数学下册圆27.1.3垂径定理同步练习含答案解析华师版课时作业

垂径定理27.1.3一.选择题(共5小题)1.如图,⊙O的半径为5,弦心距OC=3,则弦AB的长是()A.4B.6C.8D.52.如图,AB为⊙O直径,弦CD⊥AB于E,则下面结论中错误的是()A.CE=DE B.=C.∠BAC=∠BAD D.OE=BE 3.如图,⊙O的半径为10cm,弦AB的弦心距OC为6cm,则AB的长是()A.16cm B.10cm C.8cm D.6cm 4.在⊙O中,弦AB垂直且平分一条半径,则劣弧的度数等于()A.30°B.120°C.150°D.60°5.如图,⊙O中,OD⊥AB于点C,OB=13,AB=24,则OC的长为()A.3B.4C.5D.6二.填空题(共10小题)6.如图,⊙O的直径为10,弦AB=8,P是弦AB上一动点,那么OP长的取值范围是.7.如图,AB是⊙O的直径,OD⊥AC于点D,BC=6cm,则OD=cm.8.如图,在⊙O中,OC⊥弦AB于点C,AB=4,OC=1,则OB的长是.9.如图,⊙O是△ABC的外接圆,且AB=AC=5,BC=8,则⊙O的半径为.10.如图,⊙O的直径CD与弦AB(非直径)交于点M,添加一个条件:,使得=.11.AB是⊙O的弦,半径OA=20cm,∠AOB=120°,则△AOB的面积是cm2.12.如图,∠P AC=30°,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F两点,则线段EF的长是cm.13.如图,⊙O的直径AB与弦CD交于点E,AE=5,BE=1,CD=4,则∠AED=.14.如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为10,AB=16,则CD的长是.15.半径等于16的圆中,垂直平分半径的弦长为.三.解答题(共6小题)16.在圆O中,直径CD⊥弦AB于E,AB=6,=,求DE的长.17.如图,△ABC中,∠ACB=90°,CA=15cm,CB=20cm,以CA为半径的⊙C交AB 于D,求AD的长.18.如图,AB是⊙O的弦,半径OC⊥AB于点D,且AB=8cm,OC=5cm,求DC的长.19.如图,AB是半圆O的直径,点C在半圆O上,CD⊥AB于D,AB=12,DB=4,求CD的长.20.如图,⊙O的半径OA=5cm,AB是弦,C是AB上一点,且OC⊥OA,OC=BC (1)求∠A的度数.(2)求AB的长.21.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,CD=6,求BE的长.垂径定理27.1.3参考答案与试题解析一.选择题(共5小题)1.如图,⊙O的半径为5,弦心距OC=3,则弦AB的长是()A.4B.6C.8D.5解:连接OA,如图所示:∵OC⊥AB,OC=3,OA=5,∴AB=2AC,∵AC===4,∴AB=2AC=8.故选:C.2.如图,AB为⊙O直径,弦CD⊥AB于E,则下面结论中错误的是()A.CE=DE B.=C.∠BAC=∠BAD D.OE=BE 解:根据垂径定理和等弧对等弦,得A、B、C正确,只有D错误.故选:2.D.3.如图,⊙O的半径为10cm,弦AB的弦心距OC为6cm,则AB的长是()A.16cm B.10cm C.8cm D.6cm 解:连接OA,∵弦AB垂直OC,⊙O的半径为10cm,∴OA=10cm,OC=6cm,由勾股定理得:AC==8cm,∴AB=2AC=16cm,故选:A.4.在⊙O中,弦AB垂直且平分一条半径,则劣弧的度数等于()A.30°B.120°C.150°D.60°解:如图所示:连接OA,OB,∵AB垂直且平分OD,∴AB=2AE,OA=2EO,∴∠OAE=30°,∴∠AOE=60°,同理,∠BOE=60°,∴∠AOB=∠AOE+∠BOE=120°.故选:4.B.5.如图,⊙O中,OD⊥AB于点C,OB=13,AB=24,则OC的长为()A.3B.4C.5D.6解:∵OD⊥AB,∴AC=BC=AB=×24=12,在Rt△OBC中,OC==5.故选:C.二.填空题(共10小题)6.如图,⊙O的直径为10,弦AB=8,P是弦AB上一动点,那么OP长的取值范围是3≤OP≤5.解:如图:连接OA,作OM⊥AB与M,∵⊙O的直径为10,∴半径为5,∴OP的最大值为5,∵OM⊥AB与M,∴AM=BM,∵AB=8,∴AM=4,在Rt△AOM中,OM=,OM的长即为OP的最小值,∴6.3≤OP≤5.7.如图,AB是⊙O的直径,OD⊥AC于点D,BC=6cm,则OD=3cm.解:∵OD⊥AC于点D,∴AD=CD,又∵OA=OB,∴OD为△ABC的中位线,∴OD=BC,∵BC=6cm,∴OD=3cm.故答案为3.8.如图,在⊙O中,OC⊥弦AB于点C,AB=4,OC=1,则OB的长是.解:∵OC⊥弦AB于点C,∴BC=AC=AB=×4=2,在Rt△OBC中,OC=1,BC=2,∴OB==.故答案为9.如图,⊙O是△ABC的外接圆,且AB=AC=5,BC=8,则⊙O的半径为.解:过A作AD⊥BC于D,连接BO,△ABC中,AB=AC,AD⊥BC,则AD必过圆心O,Rt△ABD中,AB=5,BD=3∴AD=3设⊙O的半径为x,Rt△OBD中,OB=x,OD=x﹣3根据勾股定理,得:OB2=OD2+BD2,即x2=(x﹣3)2+42,解得:x=.故答案是:.10.如图,⊙O的直径CD与弦AB(非直径)交于点M,添加一个条件:AB⊥CD,使得=.解:∵CD为⊙O的直径,AB为弦(非直径),∴可添加AB⊥CD,或AB平分CD即可,故答案为AB⊥CD,或AB平分CD(答案不唯一).11.AB是⊙O的弦,半径OA=20cm,∠AOB=120°,则△AOB的面积是100cm2.解:过O作OC⊥AB,交AB于点C,如图所示,则C为AB的中点,即AC=BC,∵OA=OB,∠AOB=120°,∴∠A=∠B=30°,在Rt△AOC中,OA=20cm,∠A=30°,∴OC=OA=10cm,根据勾股定理得:AC==10cm,∴AB=2AC=20cm,则S△AOB=AB•OC=×20×10=100cm2.故答案为:10012.如图,∠P AC=30°,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F两点,则线段EF的长是6cm.解:过O点作OH⊥EF于H,连OF,如图则EH=FH,在Rt△AOH中,AO=AD+OD=3+5=8,∠A=30°,则OH=OA=4,在Rt△OHF中,OH=4,OF=5,则HF==3,则EF=2HF=6cm.故答案为6.13.如图,⊙O的直径AB与弦CD交于点E,AE=5,BE=1,CD=4,则∠AED=30°.解:连接OD,过圆心O作OH⊥CD于点H.∴DH=CH=CD(垂径定理);∵CD=4,∴DH=2;又∵AE=5,BE=1,∴AB=6,∴OA=OD=3(⊙O的半径);∴OE=2;∴在Rt△ODH中,OH==1(勾股定理);在Rt△OEH中,OH=OE,∴∠OEH=30°,即∠AED=30°.故答案为:30°.14.如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为10,AB=16,则CD的长是4.解:连接OA,如图,∵OC⊥AB,∴AD=BD=AB=×16=8,在Rt△OAD中,OD==6,∴CD=OC﹣OD=10﹣6=4.故答案为4.15.半径等于16的圆中,垂直平分半径的弦长为16.解:如图,OA=16,则OC=8,根据勾股定理得,AC==8,∴弦AB=16.故答案为:16.三.解答题(共6小题)16.在圆O中,直径CD⊥弦AB于E,AB=6,=,求DE的长.16.解:∵=,∴CE=3DE,∴CD=CE+DE=4DE,∴OD=CD=2DE,∴OE=OD﹣DE=DE,∴OA=OD=2DE,∴OA=2OE.∵CD垂直平分AB,∴AE=AB=×6=3,∠AEO=90°,∴∠OAE=30°,∴OA===2,∴DE=OA=×2=.17.如图,△ABC中,∠ACB=90°,CA=15cm,CB=20cm,以CA为半径的⊙C交AB 于D,求AD的长.解:∵在Rt△ABC中,∠ACB=90°,AC=8,BC=15,∴AB===25.过C作CM⊥AB,交AB于点M,如图所示,∵CM⊥AB,∴M为AD的中点,∵S△ABC=AC•BC=AB•CM,且AC=15,BC=20,AB=25,∴CM==12,在Rt△ACM中,根据勾股定理得:AC2=AM2+CM2,即225=AM2+144,解得:AM=9,∴AD=2AM=18.18.如图,AB是⊙O的弦,半径OC⊥AB于点D,且AB=8cm,OC=5cm,求DC的长.18.解:连接OA,∵OC⊥AB,∴AD=AB=4,由勾股定理得,OD==3,∴DC=OC﹣OD=2cm.19.如图,AB是半圆O的直径,点C在半圆O上,CD⊥AB于D,AB=12,DB=4,求CD的长.19.解:连接OC.∵AB是半圆O的直径,∴OC=OB=AB=×12=6.∴OD=OB﹣DB=6﹣4=2,∴在直角△OCD中,CD===4.20.如图,⊙O的半径OA=5cm,AB是弦,C是AB上一点,且OC⊥OA,OC=BC (1)求∠A的度数.(2)求AB的长.解:(1)连接OB,∵AO=OB,OC=BC,∴∠A=∠B=∠BOC.∵OA⊥OC,∴∠AOC=90°.∵∠A+∠B+∠BOC+∠AOC=180°,∴3∠A+90°=180°,∴∠A=30°;(2)∵∠A=30°,OA=5cm,∴AC===cm,BC=OC=AC=cm,∴AB=AC+BC=+=5(cm).21.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,CD=6,求BE的长.解:如图,连接OC.∵弦CD⊥AB于点E,CD=6,∴CE=ED=CD=3.∵在Rt△OEC中,∠OEC=90°,CE=3,OC=4,∴OE==,∴BE=OB﹣OE=4﹣.。
垂径定理-中考数学专项训练(含解析)

垂径定理一、单选题A.82.如图,圆弧形桥拱的跨度A.2米B.43.如图,一个圆柱形的玻璃水杯,将其水平放置,截面是个圆,是弧AB的中点,2CD=cm,杯内水面宽A.6cm4.如图,CD是圆O长为()A.33A .45︒6.如图,O 的半径是A .27.如图是一段圆弧 AB 点.若63,AB CD =A .6πB .4π8.如图,在O 中,半径23r =,AB 过点C 作CD OC ⊥交O 于点D ,则A .4B的直径,11.如图,AB是O==,则CD5,3AB BC的弦,半径12.如图,AB是O中,直径13.如图,在O一点,连AE,过点C作14.如图,在圆O中,弦的直径15.如图.O为.的外接圆,16.如图,⊙O是ABC∠的度数为于点D,连接BD,则D三、解答题17.如图,AB为半圆O点D,若4,==AB AC(1)DE的长.(2)阴影部分的面积.18.如图,AB 为O 的直径,CD 为弦,CD AB ⊥于点E ,连接DO 并延长交O 于点F ,连接AF 交CD 于点G ,CG AG =,连接AC .(1)求证:AC DF ∥;(2)若12AB =,求AC 和GD 的长.19.如图,在以O 为圆心的两个同心圆中,大圆的弦AB 交小圆于C D 、两点,若16cm 6cm AB CD ==,.(1)求AC 的长;(2)若大圆半径为10cm ,求小圆的半径.∠;(1)连接AD,求OAD(2)点F在 BC上,CDF∠=参考答案:∵OA OB =,C 为弦AB 中点,∴OC AB ⊥,4AC =,∴OE 平分 AB ,∵D 为 AB 的中点,∴点,D E 重合,∴,,O C D 三点共线,设圆的半径为r ,则:2OC OD CD r =-=-,由勾股定理,得:222OA AC OC =+,∴()22242r r =+-,解得:=5r ;故选B .4.C【分析】本题考查了勾股定理的应用,垂径定理,熟练掌握和运用垂径定理是解决本题的关键.连接OC ,首先根据题意可求得63OC OE ==,,根据勾股定理即可求得CE 的长,再根据垂径定理即可求得CD 的长.【详解】解:如图,连接OC ,∵123AB BE ==,,∴63OB OC OE ===,,∵AB CD ⊥,∵50BOC ∠=︒,OC ∴OCB OBC ∠=∠=∵OC AB ⊥,∴AD BD =,故选:B.7.B【分析】本题考查的是垂径定理,勾股定理及弧长的计算公式,先根据垂径定理求出=长,由题意得OD OAOE AB ⊥ ,132AE BE AB ∴===,22OE OA AE ∴=-=在Rt COE △中,∵AB 是O 的直径,∴152OD OB AB ===∵,6CD AB CD ⊥=,∴13,2DE CD DEO ==∠∴22OE OD DE =-=∵5AB =,∴25OE =,∵DE 切O 于点E ,∴OE DE ⊥,∴90OED ∠=︒,∵1OA =,120AOB ∠=︒,∴30A B ==︒∠∠,AC BC =∴1122OC OA ==,AC =∵直径CD 长为4,∴1422OD =⨯=,∵1OG =,∴1DG OD OG =-=,∴AB 垂直平分OD ,OH 经过圆心O ,12AH BH AB ∴===∴2AO AH OH =+故答案为:5.在Rt AOD 中,12OD OA ==,,1cos 2AOD \Ð=,60AOD ∴=︒∠,OE AC ⊥ ,由垂径定理知,点E是CD的中点,也是AB是 的直径,CD⊥AB∴垂直平分CD,M是OA的中点,∴1122OM OA OD==,OA CD于点M,⊥∴点M是CD的中点,∴垂直平分CD,ABNC ND∴=,Q,∠=︒45CDFNCD NDC∴∠=∠=︒,45∴∠=︒,90CND。
垂径定理练习试题和答案解析

垂径定理一.选择题★1.如图1,⊙O 的直径为10,圆心O 到弦AB 的距离OM 的长为3,那么弦AB 的长是( )A .4B .6C .7D .8答案:D★★2.如图,⊙O 的半径为5,弦AB 的长为8,M 是弦AB 上的一个动点,则线段OM 长的最小值为( )A .2B .3C .4D .5答案:B★★3.过⊙O 内一点M 的最长弦为10 cm ,最短弦长为8cm ,则OM 的长为( )A .9cmB .6cmC .3cmD .cm 41答案:C★★4.如图,小明同学设计了一个测量圆直径的工具,标有刻度的尺子OA 、OB 在O 点钉在一起,并使它们保持垂直,在测直径时,把O 点靠在圆周上,读得刻度OE=8个单位,OF=6个单位,则圆的直径为( )A .12个单位B .10个单位C .1个单位D .15个单位答案:B★★5.如图,O ⊙的直径AB 垂直弦CD 于P ,且P 是半径OB 的中点,6cm CD ,则直径AB 的长是( )A .B .C .D .答案:D★★6.下列命题中,正确的是()A.平分一条直径的弦必垂直于这条直径B.平分一条弧的直线垂直于这条弧所对的弦C.弦的垂线必经过这条弦所在圆的圆心D.在一个圆内平分一条弧和它所对的弦的直线必经过这个圆的圆心答案:D★★★7.如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高为( )A.5米 B.8米 C.7米 D.53米答案:B★★★8.⊙O的半径为5cm,弦AB//CD,且AB=8cm,CD=6cm,则AB与CD之间的距离为( ) A. 1 cm B. 7cm C. 3 cm或4 cm D. 1cm 或7cm答案:D★★★9.已知等腰△ABC的三个顶点都在半径为5的⊙O上,如果底边BC的长为8,那么BC边上的高为( )A.2 B.8 C.2或8 D.3答案:C二.填空题★1.已知AB是⊙O的弦,AB=8cm,OC⊥AB与C,OC=3cm,则⊙O的半径为 cm答案:5 cm★2.在直径为10cm的圆中,弦AB的长为8cm,则它的弦心距为 cm答案:3 cm★3.在半径为10的圆中有一条长为16的弦,那么这条弦的弦心距等于答案:6★★4.已知AB是⊙O的弦,AB=8cm,OC⊥AB与C,OC=3cm,则⊙O的半径为 cm 答案:5 cm★★5.如图,⊙O的直径AB垂直于弦CD,垂足为E,若∠COD=120°,OE=3厘米,则CD =厘米图 4答案:★★6.半径为6cm 的圆中,垂直平分半径OA 的弦长为 cm.答案:★★7.过⊙O 内一点M 的最长的弦长为6cm ,最短的弦长为4cm,则OM 的长等于 cm ★★8.已知AB 是⊙O 的直径,弦CD ⊥AB ,E 为垂足,CD=8,OE=1,则AB=____________ 答案:★★9.如图,AB 为⊙O 的弦,⊙O 的半径为5,OC ⊥AB 于点D ,交⊙O 于点C , 且CD =l ,则弦AB 的长是答案:6★★10.某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示,已知AB =16m,半径OA =10m ,则中间柱CD 的高度为 m答案:4★★11.如图,在直角坐标系中,以点P 为圆心的圆弧与轴交于A 、B 两点,已知P(4,2) 和A(2,0),则点B 的坐标是答案:(6,0)★★12.如图,AB 是⊙O 的直径,OD ⊥AC 于点D ,BC=6cm ,则OD= cm答案:3★★13.如图,矩形ABCD 与圆心在AB 上的圆O 交于点G 、B 、F 、E ,GB=10,EF=8,那么AD=答案:3★★14.如图,⊙O 的半径是5cm ,P 是⊙O 外一点,PO=8cm ,∠P=30º,则AB= cmPBAO答案:6★★★15.⊙O 的半径为13 cm ,弦AB ∥CD ,AB =24cm ,CD =10cm ,那么AB 和CD 的距离是 Cm答案:7cm 或17cm★★★16.已知AB 是圆O 的弦,半径OC 垂直AB ,交AB 于D ,若AB=8,CD=2,则圆的半径为答案:5★★★17.一个圆弧形门拱的拱高为1米,跨度为4米,那么这个门拱的半径为 米 答案:52★★★18.在直径为10厘米的圆中,两条分别为6厘米和8厘米的平行弦之间的距离是 厘米答案:7或1★★★19.如图,是一个隧道的截面,如果路面AB 宽为8米,净高CD 为8米,那么这个 隧道所在圆的半径OA 是___________米答案:5★★★20.如图,AB 为半圆直径,O 为圆心,C 为半圆上一点,E 是弧AC 的中点,OE 交弦AC 于点D 。
(完整版)圆的垂径定理习题及答案

圆的垂径定理习题一.选择题1.如图1,⊙O的直径为10,圆心O到弦AB的距离OM的长为3,那么弦AB的长是()A.4 B.6 C.7 D.8 2.如图,⊙O的半径为5,弦AB的长为8,M是弦AB上的一个动点,则线段OM长的最小值为()A.2 B.3 C.4 D.53.过⊙0内一点M的最长弦为10cm,最短弦长为8cm,则OM的长为()4.如图,小明同学设计了一个测量圆直径的工具,标有刻度的尺子OA、OB在O点钉在一起,并使它们保持垂直,在测直径时,把O点靠在圆周上,读得刻度OE=8个单位,OF=6个单位,则圆的直径为()A.12个单位B.10个单位C.1个单位D.15个单位5.如图,O⊙的直径AB垂直弦CD于P,且P是半径OB的中点,6cmCD,则直径AB的长是()6.下列命题中,正确的是()A.平分一条直径的弦必垂直于这条直径B.平分一条弧的直线垂直于这条弧所对的弦C.弦的垂线必经过这条弦所在圆的圆心D.在一个圆内平分一条弧和它所对的弦的直线必经过这个圆的圆心7.如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高为( )8.⊙O的半径为5cm,弦AB//CD,且AB=8cm,CD=6cm,则AB与CD之间的距离为( )A. 1 cm B.7cm C. 3 cm或4 cm D.1cm 或7cm 9.已知等腰△ABC的三个顶点都在半径为5的⊙O上,如果底边BC的长为8,那么BC边上的高为( ) A.2 B.8 C.2或8 D.3二、填空题1.已知AB是⊙O的弦,AB=8cm,OC⊥AB与C,OC=3cm,则⊙O的半径为cm 2.在直径为10cm的圆中,弦AB的长为8cm,则它的弦心距为cm3.在半径为10的圆中有一条长为16的弦,那么这条弦的弦心距等于4. 已知AB是⊙O的弦,AB=8cm,OC⊥AB与C,OC=3cm,则⊙O的半径为cm 5.如图,⊙O的直径AB垂直于弦CD,垂足为E,若∠COD=120°,OE=3厘米,则CD=厘米6.半径为6cm的圆中,垂直平分半径OA的弦长为cm7.过⊙O内一点M的最长的弦长为6cm,最短的弦长为4cm,则OM的长等于 cm8.已知AB是⊙O的直径,弦CD⊥AB,E为垂足,CD=8,OE=1,则AB=9.如图,AB为⊙O的弦,⊙O的半径为5,OC⊥AB于点D,交⊙O于点C,且CD=l,则弦AB的长是10.某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则中间柱CD 的高度为m11. 如图,在直角坐标系中,以点P为圆心的圆弧与轴交于A、B两点,已知P(4,2) 和A(2,0),则点B的坐标是12.如图,AB是⊙O的直径,OD⊥AC于点D,BC=6cm,则OD= cm13.如图,矩形ABCD与圆心在AB上的圆O交于点G、B、F、E,GB=10,EF=8,那么AD=14.如图,⊙O的半径是5cm,P是⊙O外一点,PO=8cm,∠P=30º,则AB= cm15.⊙O的半径为13 cm,弦AB∥CD,AB=24cm,CD=10cm,那么AB和CD的距离是Cm16.已知AB是圆O的弦,半径OC垂直AB,交AB于D,若AB=8,CD=2,则圆的半径为17.一个圆弧形门拱的拱高为1米,跨度为4米,那么这个门拱的半径为米18.在直径为10厘米的圆中,两条分别为6厘米和8厘米的平行弦之间的距离是厘米19. 如图,是一个隧道的截面,如果路面AB宽为8米,净高CD为8米,那么这个隧道所在圆的半径OA是___________米20.如图,AB为半圆直径,O 为圆心,C为半圆上一点,E是弧AC的中点,OE交弦AC于点D。
2022-2023学年浙教版九年级数学上册《垂径定理》同步练习题(含答案)

2022-2023学年浙教版九年级数学上册《3.3垂径定理》同步练习题(附答案)一.选择题1.如图,AB是⊙O的直径,OD垂直于弦AC于点D,DO的延长线交⊙O于点E.若AC =4,DE=4,则BC的长是()A.1B.C.2D.42.过⊙O内一点M的最长弦为20cm,最短弦为16cm,那么OM的长为()A.3cm B.6cm C.8cm D.9cm3.如图,CD是圆O的弦,直径AB⊥CD,垂足为E,若AB=12,BE=3,则四边形ACBD 的面积为()A.36B.24C.18D.724.工人师傅为检测该厂生产的一种铁球的大小是否符合要求,设计了一个如图(1)所示的工件槽,其两个底角均为90°,将形状规则的铁球放入槽内时,若同时具有图(1)所示的A、B、E三个接触点,该球的大小就符合要求.图(2)是过球心及A、B、E三点的截面示意图,已知⊙O的直径就是铁球的直径,AB是⊙O的弦,CD切⊙O于点E,AC ⊥CD、BD⊥CD,若CD=16cm,AC=BD=4cm,则这种铁球的直径为()A.10cm B.15cm C.20cm D.24cm5.如图,在⊙O中,直径AB=8,弦DE⊥AB于点C,若AD=DE,则BC的长为()A.B.C.1D.26.如图,在⊙O中,直径CD垂直弦AB于点E,且OE=DE.点P为上一点(点P不与点B,C重合),连接AP,BP,CP,AC,BC.过点C作CF⊥BP于点F.给出下列结论:①△ABC是等边三角形;②在点P从B→C的运动过程中,的值始终等于.则下列说法正确的是()A.①,②都对B.①对,②错C.①错,②对D.①,②都错二.填空题7.如图,AB是半圆O的直径,四边形CDMN和DEFG都是正方形,其中C,D,E在AB 上,F、N在半圆上.若则正方形CDMN的面积与正方形DEFG的面积之和是16,则AB 的长为.8.如图,以AB为直径的⨀O中,点C为⨀O上一点,且AC=BC=,过点O作OD⊥AC,垂足为D,点P为直线OD上一个动点,则弧BC,PB,PC构成的封闭图形周长最小值为.9.如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分,如果C是⊙O中弦AB的中点,CD经过圆心O交⊙O于点D,并且AB=4m,CD=6m,则⊙O的半径长为m.10.如图,在⊙O中,AD⊥BC,连接AB、CD,当AB=2,CD=6时,则⊙O半径长为.11.平面直角坐标系xOy如图所示,以原点O为圆心,以2为半径的⊙O中,弦AB=,点C是弦AB中点,P(+1,﹣1),连接PC,当弦AB在⊙O上滑动,线段PC扫过的面积为.12.如图,AB是⊙O的直径,弦CD交AB于点P,AP=4,BP=12,∠APC=30°,则CD的长为.13.如图,圆O的半径为4,点P是直径AB上定点,AP=1,过P的直线与圆O交于C,D两点,则△COD面积的最大值为;作弦DE∥AB,CH⊥DE于H,则CH的最大值为.三.解答题14.如图,在⊙O中,AB,AC为弦,CD为直径,AB⊥CD于E,BF⊥AC于F,BF与CD 相交于G.(1)求证:ED=EG;(2)若AB=8,OG=1,求⊙O的半径.15.石拱桥是我国古代入民勤劳和智慧的结晶(如图1),隋代建造的赵州桥距今约有1400年历史,是我国古代石拱桥的代表.如图2是根据某石拱桥的实物图画出的几何图形,桥的主桥拱是圆弧形,表示为.桥的跨度(弧所对的弦长)AB=26m,设所在圆的圆心为O,半径OC⊥AB,垂足为D.拱高(弧的中点到弦的距离)CD=5m.连接OB.(1)直接判断AD与BD的数量关系;(2)求这座石拱桥主桥拱的半径(精确到1m).16.如图,⊙O中两条互相垂直的弦AB,CD交于点E.(1)OM⊥CD于点M,CD=24,⊙O的半径长为4,求OM的长.(2)点G在BD上,且AG⊥BD交CD于点F,求证:CE=EF.17.如图,在⊙O中,AB、AC是互相垂直且相等的两条弦,OD⊥AB,OE⊥AC,垂足分别为D、E.(1)求证:四边形ADOE是正方形;(2)若AC=2cm,求⊙O的半径.18.如图,线段AB=10,AC=8,点D,E在以AB为直径的半圆O上,且四边形ACDE 是平行四边形,过点O作OF⊥DE于点F,求AE的长.19.如图,圆柱形水管内原有积水的水平面宽CD=20cm,水深GF=2cm.若水面上升2cm (EG=2cm),则此时水面宽AB为多少?20.某隧道的截面是由如图所示的图形构成,图形下面是长方形ABCD,上面是半圆形,其中AB=10米,BC=2.5米,隧道设双向通车道,中间有宽度为2米的隔离墩,一辆满载家具的卡车,宽度为3米,高度为4.9米,请计算说明这辆卡车是否能安全通过这个隧道?参考答案一.选择题1.解:∵AB是⊙O的直径,∴∠C=90°,∵OD⊥AC,∴点D是AC的中点,∴OD是△ABC的中位线,∴OD∥BC,且OD=BC,设OD=x,则BC=2x,∵DE=4,∴OE=4﹣x,∴AB=2OE=8﹣2x,在Rt△ABC中,由勾股定理可得,AB2=AC2+BC2,∴(8﹣2x)2=(4)2+(2x)2,解得x=1.∴BC=2x=2.故选:C.2.解:由题意知,最长的弦为直径,最短的弦为垂直于直径的弦,如图所示.直径ED⊥AB于点M,则ED=20cm,AB=16cm,由垂径定理知:点M为AB中点,∴AM=8cm,∵半径OA=10cm,∴OM2=OA2﹣AM2=100﹣64=36,∴OM=6cm.故选:B.3.解:如图,连接OC,∵AB=12,BE=3,∴OB=OC=6,OE=3,∵AB⊥CD,在Rt△COE中,EC=,∴CD=2CE=6,∴四边形ACBD的面积=.故选:A.4.解:如图,连接OE,交AB于点F,连接OA,∵AC⊥CD、BD⊥CD,∴AC∥BD,∵AC=BD=4cm,∴四边形ACDB是平行四边形,∴四边形ACDB是矩形,∴AB∥CD,AB=CD=16cm,∵CD切⊙O于点E,∴OE⊥CD,∴OE⊥AB,∴四边形EFBD是矩形,AF=AB=×16=8(cm),∴EF=BD=4cm,设⊙O的半径为rcm,则OA=rcm,OF=OE﹣EF=(r﹣4)cm,在Rt△AOF中,OA2=AF2+OF2,∴r2=82+(r﹣4)2,解得:r=10,∴这种铁球的直径为20cm,故选:C.5.解:∵DE⊥AB,AB过圆心O,∴DC=CE=DE,∠ACD=∠BCD=90°,∵AD=DE,∴DC=AD,∴∠DAC=30°,∵AB是⊙O的直径,∴∠ADB=90°,∴BD=AB==4,∵∠ADB=90°,∠DAB=30°,∴∠ABD=60°,∵∠DCB=90°,∴∠CDB=30°,∴BC=BD=,故选:D.6.解:如图,作CM⊥AP于M,连接AD.∵AE⊥OD,OE=DE,∴AO=AD,∵OA=OD,∴AO=AD=OD,∴△AOD是等边三角形,∴∠D=∠ABC=60°,∵CD⊥AB,∴AE=EB,∴CA=CB,∴△ABC是等边三角形,故①正确,∵∠CP A=∠ABC=60°,∠APB=∠ACB=60°,∴∠CPF=180°﹣60°﹣60°=60°,∵∠CPM=∠CPF=60°,CF⊥PF,CM⊥P A,∴CF=CM,∵PC=PC,∠CFP=∠CMP,∴Rt△CPF≌Rt△CPM(HL),∴PF=PM,∵AC=BC,CM=CF,∠AMC=∠CFB=90°,∴Rt△AMC≌Rt△BFC(HL),∴AM=BF,∴AP﹣PB=PM+AM﹣(BF﹣PF)=2PM=2PF,∴=,在Rt△CPF中,∵∠CPF=60°,∠CFP=90°,∴CF=PF,∴PF=CF,∴=,故②正确,故选:A.二.填空题7.解:连接ON,OF,设正方形CDMN的边长为a,正方形DEFG边长为b,OD=c,则CN=CD=a,DE=EF=b,∵四边形CDMN和DEFG都是正方形,∴∠NCD=90°,∠FED=90°,设OA=ON=OF=OB=r,由勾股定理得:NC2+CO2=ON2,OE2+EF2=OF2,∴a2+(a+c)2=r2①,b2+(b﹣c)2=r2②,①﹣②,得a2+(a+c)2﹣b2﹣(b﹣c)2=0,(a2﹣b2)+[(a+c)2﹣(b﹣c)2)]=0,(a+b)(a﹣b)+(a+c+b﹣c)(a+c﹣b+c)=0,(a+b)(a﹣b)+(a+b)(a﹣b+2c)=0,(a+b)(a﹣b+a﹣b+2c)=0,2(a+b)(a﹣b+c)=0,∵a+b≠0,∴a﹣b+c=0,即b=a+c,把b=a+c代入①,得a2+b2=r2,∵正方形CDMN的面积与正方形DEFG的面积之和是16,∴a2+b2=16,∴r2=16,解得r=4(负值舍去),∴AB=2r=8.故答案为:8.8.解:要使得弧BC,PB,PC构成的封闭图形周长最小,弧BC的值不变,则BP+PC最小即可,∵OD⊥AC,∴点C关于PD的对称点为点A,即当P点与O点重合时,BP+PC最小,即弧BC,PB,PC构成的封闭图形周长最小,连接OC,∵AC=BC=,∴∠BOC=90°,OB=OC=BC==1,∴弧BC的长为=,∴弧BC,PB,PC构成的封闭图形周长最小为:2+.故答案为:2.9.解:连接OA,如图,设⊙O的半径为rm,∵C是⊙O中弦AB的中点,CD过圆心,∴CD⊥AB,AC=BC=AB=2m,在Rt△AOC中,∵OA=rcm,OC=(6﹣r)m,∴22+(6﹣r)2=r2,解得r=,即⊙O的半径长为m.故答案为:.10.解:如图,连接CO,延长CO交⊙O于H,连接BH,DH,BD.∵CH是直径,∴∠CBH=∠CDH=90°,∴CB⊥BH,∵CB⊥AD,∴AD∥BH,∴∠CDB=∠DBH,∴=,∴DH=BA=2,而CD=6,根据勾股定理CH==2,故答案为2.11.解:连接OC,OA,如图,∵点C是弦AB中点,∴OC⊥AB,AC=BC=AB=,∴OC==.∵弦AB在⊙O上滑动,∴点C的轨迹为以点O为圆心,以为半径的圆,如图中的虚线⊙O,过点P作该圆的切线PD,PE,连接OD,OE,PO,如上图,则OD=OE=.利用勾股定理可求得PO=,∵PD,PE是虚线⊙O的切线,∴OD⊥PD,OE⊥PE,PD=PE,∠DPO=∠EPO.∴∠OPD=30°,∴∠OPE=30°,∴∠DOP=60°,∠EOP=60°,∴∠DOE=120°.∵线段PC扫过的面积为四边形DOEP的面积+大扇形ODE的面积,∴线段PC扫过的面积为2×PD•OD+=+π.故答案为:+π.12.解:过O作OI⊥CD于I,连接OD,则∠OID=∠OIP=90°,∵AP=4,BP=12,∴直径AB=4+12=16,即半径OD=OA=8,∴OP=OA﹣AP=8﹣4=4,∵∠IPO=∠APC=30°,∴OI=OP==2,由勾股定理得:DI===2,∵OI⊥CD,OI过圆心O,∴DI=CI=2,即CD=DI+CI=4,故答案为:4.13.解:如图1,∵OC•OD•sin∠COD,∴当∠COD=90°时,△COD面积有最大值,且最大值=×4×4×1=8;设△APO的PO边上的高为h1,△DPO的边PO上的高为h2,如图,∵S△CDO=S△PCO+S△DPO,∴当△COD面积有最大值时,PO×h1+PO×h2=8.∴×3×(h1+h2)=8,∴h1+h2=.∴CH的最大值为.故答案为:8;.三.解答题14.(1)证明:如图:连接BD,∵AB⊥CD于E,BF⊥AC于F,∴∠CFG=∠GEB,∵∠CGF=∠BGE,∴∠C=∠GBE,∵∠C=∠DBE,∴∠GBE=∠DBE,∵AB⊥CD于E,∴∠GEB=∠DEB,在△GBE和△DBE中,,∴△BGE≌△BDE(ASA),∴ED=EG.(2)解:如图:连接OA,设OA=r,则DG=r+1,由(1)可知ED=EG,∴OE=,∵AB⊥CD于E,AB=8,∴AE=BE=4,∴在Rt△OAE中,根据勾股定理得:OE2+AE2=OA2,即()2+42=r2,解得:r=,即⊙O的半径为.15.解:(1)∵OC⊥AB,∴AD=BD;(2)设主桥拱半径为R,由题意可知AB=26,CD=5,∴BD=AB=13,OD=OC﹣CD=R﹣5,∵∠ODB=90°,∴OD2+BD2=OB2,∴(R﹣5)2+132=R2,解得R=19.4≈19,答:这座石拱桥主桥拱的半径约为19m.16.(1)解:如图,连接OD,∵OM⊥CD,OM过圆心,CD=24,∴DM=CM=CD=12,∠OMD=90°,由勾股定理得,OM===4,即OM的长为4;(2)证明:如图,连接AC,∵AG⊥BD,∴∠DGF=90°,∴∠DFG+∠D=90°,∵AB⊥CD,∴∠CEA=90°,∴∠C+∠EAC=90°,∵∠EAC=∠D,∠DFG=∠AFC,∴∠C=∠AFC,∴AF=AC,∵AB⊥CD,∴CE=EF.17.(1)证明:∵OD⊥AB,OE⊥AC,∴AD=AB,AE=AC,∵AB=AC,∴AD=AE,∵∠ADO=∠A=∠AEO=90°,∴四边形ADOE是正方形;(2)解:连接OA,∵AC=2cm,∴AE=1cm,在Rt△AOE中,OA==(cm),答:⊙O的半径是cm.18.解:过点E作EG⊥AB于点G,连接OE,则OE=OA=,∠EGO=90°,∵四边形ACDE是平行四边形,∴DE=AC=8,DE∥AB,∵OF⊥DE,即∠OFE=90°,∴EF==4,∠FOG=∠OFE=90°,∴四边形OFEG是矩形,∴OG=EF=4,∴AG=5﹣4=1,在Rt△OEG中,EG=,在Rt△AGE中,AE=.19.解:连接OA、OC,∵由题意知:AB∥CD,OE⊥AB,OF⊥CD,CD=20cm,∴CG=CD=10cm,在Rt△OGC中,由勾股定理得:OC2=CG2+OG2,OC2=102+(OC﹣2)2,解得:OC=26(cm),则OE=26cm﹣2cm﹣2cm=22cm,∵在Rt△OEA中,由勾股定理得:OA2=OE2+AE2,∴262=222+AE2,∴AE=8,∵OE⊥AB,OE过圆心O,∴AB=2AE=16cm.20.解:如图,作OM⊥AB于M,交AB于M,图中KN=3,作KF⊥CD于H,交⊙O于F,连接OF.易知四边形OHKM是矩形,四边形ABCD是矩形,OH=KM=4,AB=CD=10,OF=OD=5,在Rt△OHF中,FH===3,∵HK=BC=2.5,∴FK=2.5+3=5.5,∵5.5>4.9,∴这辆卡车能安全通过这个隧道.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013 中考全国 100 份试卷分类汇编圆的垂径定理1、( 2013 年潍坊市)如图,⊙ O 的直径 AB=12 ,CD 是⊙O 的弦, CD ⊥AB ,垂足为 P ,且 BP : AP=1:5, 则 CD 的长为( )半径的圆与 AB 交于点 D ,则 AD 的长为( )3、(2013 河南省)如图,CD 是 O 的直径,弦 AB CD 于点 G ,直线 EF 与 O 相切与点 D ,则下列结论中不一定正确的是( )则圆 O 的半径为4、(2013 ?泸州)已知⊙O 的直径 CD=10cm ,AB 是⊙O 的弦,AB ⊥CD ,垂足为 M ,且 AB=8cm ,则 AC 的长为()A. cmB. cmC. cm 或 cmD. cm 或 cm5、( 2013 ?广安)如图,已知半径OD 与弦 AB 互相垂直,垂足为点 C ,若 AB=8cm ,CD=3cm ,A.4 2B.8 2C.2 5D.4 52、(2013 年黄石 )如右图,在 Rt ABC 中, ACB 90 ,AC 3 , BC 4 ,以点 C 为圆心,CA 为A.9B.24C. 18D. 5A. AG =BGB. AB ∥BFC.AD ∥BCD. ∠ABC =ADCA. cmB. 5cmC. 4cmD. cm6、(2013 ?绍兴)绍兴市著名的桥乡,如图,石拱桥的桥顶到水面的距离CD 为8m ,桥拱半径OC为5m ,则水面宽AB 为()A. 4mB. 5mC. 6mD. 8m7、(2013 ?温州)如图,在⊙O 中,OC⊥弦AB 于点C,AB=4,OC=1 ,则OB 的长是()A.B. C. D.8、(2013?嘉兴)如图,⊙O 的半径OD⊥弦AB 于点C,连结AO 并延长交⊙O 于点E,连结EC.若则EC 的长为(A. 2B.C.D.9、(2013 ?莱芜)将半径为3cm 的圆形纸片沿AB 折叠后,圆弧恰好能经过圆心O,用图中阴影部分的扇形围成一个圆锥的侧面,则这个圆锥的高为(A. B. C. D. 3210、(2013?徐州)如图,AB 是⊙O 的直径,弦CD⊥AB,垂足为P.若CD=8 ,OP=3,则⊙OA. 10B. 8C. 5D. 311 、(2013 浙江丽水)一条排水管的截面如图所示,已知排水管的半径OB=10 ,水面宽AB=16 ,则截面圆心O 到水面的距离OC 是A. 4B. 5C.6D.812、(2013?宜昌)如图,DC 是⊙O 直径,弦AB ⊥CD 于F,连接BC,DB,则下列结论错误的是()A. B. AF=BF C. OF=CF D. ∠DBC=9013、(2013?毕节地区)如图在⊙O 中,弦AB=8 ,OC⊥AB,垂足为C,且OC=3,则⊙O 的半径A. 5B. 10C. 8D. 614 、(2013 ?南宁)如图,AB 是⊙O 的直径,弦CD 交AB 于点E,且AE=CD=8 ,∠BAC= ∠BOD,则⊙ O 的半径为()A. 4B. 5C. 4D. 315 、( 2013 年佛山)半径为 3 的圆中,一条弦长为 4,则圆心到这条弦的距离是()A.3B.4C. 5D. 716 、(2013 甘肃兰州 4 分、12)如图是一圆柱形输水管的横截面,阴影部分为有水部分,如果水3k+4 与⊙O 交于 B 、C 两点,则弦 BC 的长的最小值为18 、(13 年安徽省 4 分、10 )如图,点 P 是等边三角形 ABC 外接圆⊙O 上的点,在以下判断中,不.正.确.的是( )AE 是半圆 O 的直径,弦 AB=BC=4 ,弦 CD=DE=4 ,连结OB ,OD ,则该输水管的半径为C .5cmD .6cmxOy 中,以原点 O 为圆心的圆过点A (13,0),直线 y=kx ﹣2cm , 4cm17、(2013?内江)在平面直角坐标系19、(2013?宁波)如图,图 20 图 21 图 2220 、(2013?宁夏)如图,将半径为 2cm 的圆形纸片折叠后,圆弧恰好经过圆心 O ,则折痕 AB 的长为cm .21、(2013?包头)如图,点A 、B 、C 、D 在⊙O 上,OB ⊥AC ,若∠BOC=56°,则∠ADB= 度.22、(2013?株洲)如图 AB 是⊙O 的直径, ∠BAC=42 °,点 D 是弦 AC 的中点,则 ∠DOC 的度 数是度.23 、(2013 ?黄冈)如图,M 是 CD 的中点,EM ⊥CD ,若CD=4 ,EM=8 ,则 所在圆的半径为24、(2013?绥化)如图,在 ⊙O 中,弦 AB 垂直平分半径 OC ,垂足为 D ,若⊙O 的半径为 2,则 弦 AB的长为 .25 、( 2013 哈尔滨)如图,直线 AB 与⊙O 相切于点 A ,AC 、CD 是⊙O 的两条弦,且 CD ∥AB ,5若⊙O 的半径为 5 ,CD=4 ,则弦 AC 的长为 .226、(2013?张家界)如图,⊙O 的直径 AB 与弦 CD 垂直,且∠BAC=40 °,则∠BOD=27 、(2013 ?遵义)如图,OC 是⊙O 的半径,AB 是弦,且 OC ⊥AB ,点 P 在⊙O 上,∠APC=26 则∠ BOC=度.图 26 图 27 图 2828 、(2013 陕西)如图,AB 是⊙O的一条弦,点C 是⊙O 上一动点,且∠ACB=30°,点E、F 分别是AC、BC 的中点,直线EF 与⊙O交于G、H 两点,若⊙O 的半径为7,则GE+FH 的最大值为.29 、(2013 年广州市)如图7,在平面直角坐标系中,点O 为坐标原点,点P在第一象限,P 与x轴交于O,A 两点,点A 的坐标为(6,0 ),P的半径为13,则点P 的坐标为_____________________________30 、(2013 年深圳市)如图5 所示,该小组发现8 米高旗杆DE 的影子EF 落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在图的半径的活动。
小刚身高1.6 米,测得其影长为2.4 米,同时测得EG 的长为3 米,HF 的长为1 米,测得拱高(弧GH 的中点到弦GH 的距离,即MN 的长)为2 米,求小桥所在圆的半径。
31、(2013?白银)如图,在⊙O中,半径OC 垂直于弦AB,垂足为点E.(1)若OC=5 ,AB=8,求tan ∠BAC ;2)若∠DAC=∠BAC,且点D在⊙O 的外部,判断直线AD 与⊙O的位置关系,并加以证明.1)求证: CB ∥PD ;32)若 BC=3,sin ∠P= ,求⊙O 的直径.533、(2013?恩施州)如图所示,AB 是⊙O 的直径,AE 是弦,C 是劣弧 AE 的中点,过C 作CD ⊥AB 于点 D ,CD 交 AE 于点 F ,过 C 作 CG ∥AE 交 BA 的延长线于点 G . 2)求证: AF=CF .(3)若∠EAB=30 °,CF=2,求 GA 的长.34 、( 2013 ?资阳)在⊙ O 中, AB 为直径,点 C 为圆上一点,将劣弧沿弦 AC 翻折交 AB 于点 D , 连结 CD .(1)如图 1,若点 D 与圆心 O 重合, AC=2 ,求⊙O 的半径 r ;(2)如图 2,若点 D 与圆心 O 不重合, ∠BAC=25 °,请直接写出 ∠DCA的度数.32、(2013?黔西南州)如图, AB 是⊙O 的直径,弦 CD ⊥AB 与点 E ,点 P 在⊙O 上,∠1=∠C ,参考答案1、【答案】D.【考点】垂径定理与勾股定理.【点评】连接圆的半径,构造直角三角形,再利用勾股定理与垂径定理解决.2、【答案】C4【解析】由勾股定理得AB=5,则sinA=,作CE⊥AD 于E,则AE =DE,在Rt△AEC 中,5CE 4 CE 12 9 18sinA =,即,所以,CE =,AE =,所以,AD=AC 5 3 5 5 53、【答案】C【解析】由垂径定理可知:A一定正确。
由题可知:EF ⊥CD,又因为AB⊥CD,所以AB∥EF, 即B 一定正确。
因为∠ ABC 和∠ADC 所对的弧是劣弧,AC 根据同弧所对的圆周角相等可知D 一定正确。
4、【答案】C【考点】垂径定理;勾股定理.【专题】分类讨论【分析】先根据题意画出图形,由于点C 的位置不能确定,故应分两种情况进行讨论【解答】解:连接AC ,AO,∵⊙O 的直径CD=10cm ,AB⊥ CD ,AB=8cm ,∴AM=AB= ×8=4cm ,OD=OC=5cm ,当C点位置如图1 所示时,∵OA=5cm ,AM=4cm ,CD⊥AB,∴OM= = =3cm , ∴CM=OC+OM=5+3=8cm ,∴AC== =4 cm ;当 C 点位置如图 2 所示时,同理可得 OM=3cm ,∵OC=5cm ,∴ MC=5 ﹣3=2cm , 在 Rt △ AMC 中, AC== =2 cm .【点评】本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键5、【答案】 A【考点】垂径定理;勾股定理.【分析】连接 AO ,根据垂径定理可知 AC= AB=4cm ,设半径为 x ,则 OC=x ﹣3,根据勾股定理 即可求得 x 的值【解答】解:连接 AO ,∵半径 OD 与弦 AB 互相垂直, ∴AC= AB=4cm ,设半径为 x ,则OC=x ﹣3,在Rt △ACO 中,AO 2=AC 2+OC 2,【点评】 本题考查了垂径定理及勾股定理的知识, 解答本题的关键是熟练掌握垂径定理、 勾股定 理的内容,难度一般6、【答案】 D【考点】垂径定理的应用;勾股定理.【分析】连接 OA ,根据桥拱半径 OC 为 5m ,求出 OA=5m ,根据 CD=8m ,求出 OD=3m ,根 据AD= 求出 AD ,最后根据 AB=2AD 即可得出答案.即 x 2=42+(x ﹣3)解答】【点评】此题考查了垂径定理的应用,关键是根据题意做出辅助线,用到的知识点是垂径定理、勾股定理.7、【答案】B【考点】垂径定理;勾股定理.【分析】根据垂径定理可得AC=BC= AB ,在Rt△OBC 中可求出OB.【解答】解:∵ OC ⊥弦AB 于点C,∴AC=BC= AB ,在Rt△OBC 中,OB= = .【点评】本题考查了垂径定理及勾股定理的知识,解答本题的关键是熟练掌握垂径定理的内容8、【答案】D【考点】垂径定理;勾股定理;圆周角定理【分析】先根据垂径定理求出AC 的长,设⊙O 的半径为r,则OC=r﹣2,由勾股定理即可得出r 的值,故可得出AE 的长,连接BE,由圆周角定理可知∠ABE=90 °,在Rt △BCE 中,根据勾股定理即可求出CE 的长.解答】【点评】本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键9、【答案】A【考点】圆锥的计算.【分析】过O 点作OC ⊥AB,垂足为D,交⊙O 于点C,由折叠的性质可知OD 为半径的一半,而OA 为半径,可求∠A=30 °,同理可得∠B=30°,在△AOB 中,由内角和定理求∠AOB ,然后求得弧AB 的长,利用弧长公式求得围成的圆锥的底面半径,最后利用勾股定理求得其高即可.解答】10、【答案】C【考点】垂径定理;勾股定理.【分析】连接OC ,先根据垂径定理求出PC 的长,再根据勾股定理即可得出OC 的长解答】【点评】本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键11、【答案】C【考点】垂径定理;勾股定理.【分析】根据垂径定理得出AB =2BC ,再根据勾股定理求出OC 的长【解答】解:∵OC⊥AB,AB=16,∴BC 等于AB=8。
