2015年南京市中考数学试题及答案
2015年江苏省南京市中考数学试卷

精品文档,名师推荐! 来源网络,造福学生
———————欢迎下载,祝您学习进步,成绩提升——————— 在
绝密★启用前
江苏省南京市 2015 年初中毕业生学业考试
数学
此
A. 2.3105 辆 5.估计 5 1 介于
2 ()
A. 0.4 与 0.5 之间
B. 3.2 105 辆 B. 0.5 与 0.6 之间
.
9.计算 5 15 的结果是
.
3
10.分解因式 (a b)(a 4b) ab 的结果是
.
2x 1>-1,
11.不等式组 2x 1<3 的解集是
.
12. 已 知 方 程 x2 mx 3 0 的 一 个 根 是 1, 则 它 的 另 一 个 根 是
, m 的值
是
.
13.在平面直角坐标系中,点 A 的坐标是 (2, 3) ,作点 A 关于 x 轴的对称点,得到点 A ,再
该工程队员工月工资的方差
(填“变小”“不变”或“变大”).
15. 如 图 , 在 O 的 内 接 五 边 形 ABCDE 中 , CAD 35 , 则 B E
效
数学试卷 第 1页(共 18页)
数学试卷 第 2页(共 18页)
o.
16.如图,过原点 O 的直线与反比例函数 y1 , y2 的图像在第一象限内分别交于点 A, B ,且
作点 A 关于 y 轴的对称点,得到点 A ,则点 A 的坐标是(
,
).
14.某工程队有 14 名员工,他们的工种及相应每人每月工资如下表所示.
工种 电工 木工 瓦工
人数
5 4 5
每人每月工资/元 7000 6000 5000
现该工程队进行了人员调整:减少木工 2 名,增加电工、瓦工各 1 名.与调整前相比,
2015年江苏南京中考数学

介于 B. 0.5 与 0.6 之间 D. 0.7 与 0.8 之间
A. 0.4 与 0.5 之间 C. 0.6 与 0.7 之间
6. 如图,在矩形 ������������������������ 中,������������ = 4,������������ = 5,������������ ,������������,������������ 分别与 ⊙ ������ 相切于 ������ ,������ ,������ 三点, 过点 ������ 作 ⊙ ������ 的切线交 ������������ 于点 ������,切点为 ������,则 ������������ 的长为 ( )
Ⅰ 求证:四边形 ������������������������ 是矩形. Ⅱ 小明在完成(1)的证明后继续进行了探索.过 ������ 作 ������������∥������������ ,分别交 ������������,������������ 于点 ������ ,������ , 过 ������ 作 ������������∥������������ ,分别交 ������������ ,������������ 于点 ������ , ������ ,得到四边形 ������������������������ .此时,他猜想四边形 ������������������������ 是菱形,请在下列框图中补全他的证明思路.
24. 如图,������������∥������������,点 ������ ,������ 分别在 ������������ 、 ������������ 上,连接 ������������ ,∠������������������ ,∠������������������ 的平分线交于点 ������ , ∠������������������,∠������������������ 的平分线交于点 ������.
★2015江苏南京中考数学试题及答案_南京中考数学试题及答案

以下是南京2015年全部科目的试题发布入口:
ቤተ መጻሕፍቲ ባይዱ南京
数学 数学 英语 化学 物理 历史 政治
数学 数学 英语 化学 物理 历史 政治
出国留学网中考频道的小编会及时为广大考生提供2015年南京中考数学试题及答案有需要的考生可以在考题公布后刷新本页面按ctrlf5希望对大家有所帮助
★2015江苏南京中考数学试题及答案_南京中考数学试题及答案
家中父母吃苦受累盼的是捷报频传,灯下学子沤心沥血想的是金榜题名。中考频道的小编会及时为广大考生提供2015年南京中考数学试题及答案,有需要的考生可以在考题公布后刷新本页面(按ctrl+F5),希望对大家有所帮助。
2015南京市中考数学试卷

南京市2015年初中毕业生学业考试数学试题选择题(本大题共6小题,每小题2分,共12分) 1 •计算丨—5 + 3丨的结果是()A. - 2B. 2C. — 82 .计算(—xy32的结果是()A. x2y 6B. — x2y 6C. x2y 93.如图,在△ ABC 中,DE AE 1 A.EC 2-△ ADE 的周长 1C.△ ABC 的周长=3 4 .某市2013年底机动车的数量是 2014年底机动车的数量是( ) A. 2.3 氷05 辆 B. 3.2 X 05 辆 C. 2.3 氷06 辆 D. 3.2 X 06 辆5 .估计一5”介于()A.0.4与0.5之间B. 0.5与0.6之间C. 0.6与0.7之间D. 0.7与0.8之间ABCD 中,AB=4 , AD=5 , AD 、AB 、 BC 分别与O O 相切于E 、F 、G 三点,过点D 作O O 的切线交BC 于点M ,切点为N ,贝U DM 的长为( ) A.号B. 2C. 4 .帀D.2 .5二.填空题(本大题共10小题,每小题2分,共20分) 7. 4的平方根是;4的算术平方根是.&若式子.x+1在实数范围内有意义,则 x 的取值范围是10. ____________________________________________ 分解因式(a — b )(a — 4b ) + ab 的结果是 _____________________________________________ .2x+1 111. 不等式组2x+1 V 3的解集是 __________ .12. _________________________________________________________ 已知方程 x2+ mx +3=0的一个根是1,则它的另一个根是 _________________________________ , m 的值是 ______ . 13.在平面直角坐标系中, 点A 的坐标是(2, — 3),作点A 关于x 轴的对称点,得到点A ,再作点A 关于y 轴的对称点,得到点 A”,则点A”的坐标是( _________ , _). 14 .某工程队有14名员工,他们的工种及相应每人每月工资如下表所示.DE 1 B.BC =2A△ ADE 的面积 1/ \D. △ ABC 的面积=3B CB第3题图C9. 5X 15计算「3的结果是D. 8D. — x 步96.如图,在矩形AD 1 // BC , AD =石,则下列结论中正确的是 (2 X106辆,2014年新增3X105辆.用科学记数法表示该市16•如图,过原点 0的直线与反比例函数1 小A 为0B 的中点.若函数 y 1= -,则y 2与x 的函数表达式是x三.解答题(本大题共11小题,共88分)J _______ J _____ I ______ I ______ I ______ I JpT 2 -0123第17题图(1)求证:△ ACD s △ CBD ; ⑵求/ ACB 的大小.工种 人数 每人每月工资 元电工 5 7000 木工4 6000 瓦丄55000现该工程队进行了人员调整:减少木工 2名,增加电工、瓦工各 程队员工月工资的方差 ________ (填“变小”,“不变”或“变1名.与调整前相比,该工 ). 15.如图,在O O 的内接五边形 ABCDE中,/ CAD=35°,则/1yy1=xB +/ E=y 1、y 2的图像在第一象限内分别交于点 A 、B ,且17. (6分) 解不等式2(x + 1) — 1 > 3x +2,并把它的解集在数轴上表示出来. 18. (7 分)解方程x —h19. (7分)、A _2 计算 a2 — b2 a2 —ab亠 a a+b20. (8分)如图,△ ABC 中,CD 是边AB 上的高,且AD CD CD BD .E21. (8分)为了了解2014年某地区10万名大、中、小学生 50米跑成绩情况,教育部门从 这三类学生群体中各抽取了10%的学生进行检测,整理样本数据,并结合2010年抽样结果,得到下列统计图.(1) 本次检测抽取了大、中、小学生共名,其中小学生名;(2) 根据抽样的结果,估计 2014年该地区10万名大、中、小学生中,50米跑成绩合格的中 学生人数为名;(3) 比较2010年与2014年抽样学生50米跑成绩合格率情况,写出一条正确的结论. 22. ( 8分)某人的钱包内有 10元、20元和50元的纸币各1张.从中随机取出 2张纸币. (1) 求取出纸币的总额是 30元的概率;(2) 求取出纸币的总额可购买一件 51元的商品的概率.23. (8分)如图,轮船甲位于码头 O 的正西方向 A 处,轮船乙位于码头 O 的正北方向C 处,测得/ CAO=45 .轮船甲自西向东匀速行驶, 同时轮船乙沿正北方向匀速行驶, 它们的 速度分别为45km/h 和36km/h .经过0.1h ,轮船甲行驶至 B 处,轮船乙行驶至 D 位,测得/24. (8 分)如图,AB // CD ,点 E 、F 分别在 AB 、CD 上,连接 EF ,/ AEF 、/ CFE 的 平分线交于点 G ,/ BEF 、/ DFE 的平分线交于点 H . (1)求证:四边形 EGFH 是矩形.DBO=58°,此时B 处距离码头 O 有多远?(参考数据:sin58 ° 〜0.85, cos58 ° 〜0.53, tan58 ° 〜 1.60)D CO北东⑵小明在完成⑴的证明后继续进行了探索. 过G作MN // EF,分别交AB、CD于点M、N,过H作PQ // EF,分别交AB、CD于点P、Q,得到四边形MNQP .此时,他猜想四边形MNQP是菱形,请在下列框图中补全他的证明思路.小明的证明思路由AB // CD , MN // EF, PQ // EF,易证四边形MNQP是平行四边形.要证?MNQP是菱形,只要证NM=NQ .由已知条件,MN // EF,可证NG = NF,故只要证GM = FQ,即证△ MGE QFH .易证_______________ , __________ ,故只要证Z MGE = Z QFH,工QFH = Z GEF ,Z QFH= Z EFH , ,即可得证.一刃25. (10分)如图,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形. (要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)26. (8分)如图,四边形ABCD是O O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.⑴求证:Z A= Z AEB .⑵连接0E,交CD于点F, 0E丄CD •求证:△ ABE是等边三角形.E27. 某企业生产并销售某种产品,假设销售量与产量相等.下图中的折线ABD、线段CD分别表示该产品每千克生产成本y1(单位:元)、销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.(1)请解释图中点D的横坐标、纵坐标的实际意义.(2)求线段AB所表示的y i与x之间的函数表达式.⑶当该产品产量为多少时,获得的利润最大?最大利润是多少?•15-南京市2015年初中毕业生学业考试 数学试卷参考答案及评分标准说明:本许分标准毎JS 给出了一种或几种I?法供参考 如果考生的解法与本鱗答不同.希照本评分标准的精神给分.-、选择JH «*大越共6小每小題2分.共12分丿题号1 2 3 4 56 袴案B ACCCA二.《本大Hi 共10小Uh 毎小88 2分.并20分〉• 7. ±2: 2 8. *二一1 9. 5 10. (a-2bf 11. -l<x<l 12. 3: -4B. -2: 314.变大15. 21516.力斗三、 解答M (本大18共II 小越.共対分)17.(本題6分〉解,去括号.冯2x+2— 1工3°+2・移项.褂2r-3rP2-2+l ・ 仑井冋类项. 系数化为1.得JC W-I.这个不等式的觴儀亦敬轴卜•丧术如*图所示.18.(本题7分〉M :方程两边集心一3).得2r=30r —3).M 得 x=9.检验^当*=9对.xU-3)H0・所以•原方丹的解为才=9・ 19・(本越7分)Ms(-^7—侖24/—(CJ + Q) a+b u(a+b)(a —b) nu — b aa(a+6Ra —6) a数学试堆審垮拎*及评分杯准魁丨炎(其5贝〉2(o 厶以卩一0) u(a-b). 2aa(a+Z>)(Q —b) a+b・16 •20・(本程8分)(l> iff 明,•: CD 足辿上的高.••• Z"C=ZCD 〃=90°・ © AD CD只时而(2) M : v ZUCDsZSCBD.;• W” 二厶 SCO ・ 在ZUG 中./*DC=*r ・•••" + ZACD ・2 ・10 0001 4 S00» •••*•••••••«•・・・«••••••••• --•••・•・•••・•》••・・・・・• x ・・・・・・・・・・・/*・・.・・・・・・•••・・■・••••••・•••• 2夕>16000・.. .... .. ......................... .. ................... .. ....... .... ......... ...... .. ... .. (5)木IB 答案不惟 ・卜列解法供參考.例釦・9 2010年相比・2014^^市大学牛50米跑成绩合格卓下降了 5% ............................ .................... ...................... .. ・・・・・•・・“8分C^H K 分)H>果人从钱包内随机取出2张烁币•可腌出现的结果有3种.W (!0> 20〉. <10. 50). <20. 50><并且它们出现的可能性相等.仃)取出城币的总飯足30元(记为弔件4)的箱果冇丨种■即(10. 20).所以P (Q=7 ......................... .... ••••・••— ................................................................................. 4 分(2)取出瓯币的总帧刊购头r 51元的丽品(记为耶fM )怖給眾有21 ap (io. 50).23.(本888 分) 解:设〃处血离码头0xkm ・在 IUAC4O 中.ZC4O=45°・COV tan/C4O 二而.A CO«/lO*UinZC4O (45X0.1 fx)・ tan45° 4.5^4.左Ri △加O 中・ZDBO 5^.V UmZDBO^ 器./. DO RO • tm/DUO—x • tan58c ・ 7 DC^DO-CO. :.36XO.|=x« tan58°-(4 5+x).••• ZBCD4 "CD 90%HP Z.ACB 3。
2015年江苏省南京市中考数学试题(解析版)

2015年江苏省南京市中考数学试题一、选择题1.计算:|﹣5+3|的结果是()A.﹣2 B.2 C.﹣8 D.8【答案】B.考点:1.有理数的加法;2.绝对值.2.的计算结果是()A. B. A. D.【答案】A.【解析】试题分析:原式=.故选A.考点:幂的乘方与积的乘方.3.如图所示,△ABC中,DE∥BC,若,则下列结论中正确的是()A.B.C.D.【答案】C.【解析】试题分析:∵DE∥BC,∴△ADE∽△ABC,∵AD:DB=1:2,∴AD:AB=1:3,∴两相似三角形的相似比为1:3,∵周长的比等于相似比,面积的比等于相似比的平方,∴C正确.故选C.考点:相似三角形的判定与性质.4.某市2013年底机动车的数量是2×106辆,2014年新增3×105辆,用科学记数法表示该市2014年底机动车的数量是()A.2.3×105辆B.3.2×105辆C.2.3×106辆D.3.2×106辆【答案】C.考点:科学记数法—表示较大的数.5.估计介于()A.0.4与0.5之间B.0.5与0.6之间C.0.6与0.7之间D.0.7与0.8之间【答案】C.【解析】试题分析:∵≈2.235,∴≈1.235,∴≈0.617,∴介于0.6与0.7之间,故选C.考点:估算无理数的大小.6.如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线BC于点M,切点为N,则DM的长为()A.B.C.D.【答案】A.【解析】试题分析:连接OE,OF,ON,OG,在矩形ABCD中,∵∠A=∠B=90°,CD=AB=4,∵AD,AB,BC分别与⊙O 相切于E,F,G三点,∴∠AEO=∠AFO=∠OFB=∠BGO=90°,∴四边形AFOE,FBGO是正方形,∴AF=BF=AE=BG=2,∴DE=3,∵DM是⊙O的切线,∴DN=DE=3,MN=MG,∴CM=5﹣2﹣MN=3﹣MN,在R t△DMC中,,∴,∴NM=,∴DM==,故选A.考点:1.切线的性质;2.矩形的性质.二.填空题7.4的平方根是,算术平方根是.【答案】±2;2.考点:1.算术平方根;2.平方根.8.若式子在实数范围内有意义,则x的取值范围是.【答案】.【解析】试题分析:根据题意得:x+1≥0,解得,故答案为:.考点:二次根式有意义的条件.9.计算的结果是.【答案】5.考点:二次根式的乘除法.10.分解因式的结果是.【答案】.【解析】试题分析:===.故答案为:.考点:因式分解-运用公式法.11.不等式组的解集是.【答案】﹣1<x<1.考点:解一元一次不等式组.12.已知方程的一个根是1,则它的另一个根是,m的值是.【答案】3,﹣4.【解析】试题分析:设方程的另一个解是a,则1+a=﹣m,1×a=3,解得:m=﹣4,a=3.故答案为:3,﹣4.考点:1.根与系数的关系;2.一元二次方程的解.13.在平面直角坐标系中,点A的坐标是(2,﹣3),作点A关于x轴的对称点,得到点A′,再作点A′关于y轴的对称点,得到点A″,则点A″的坐标是(,).【答案】﹣2;3.【解析】试题分析:∵点A的坐标是(2,﹣3),作点A关于x轴的对称点,得到点A′,∴A′的坐标为:(2,3),∵点A′关于y轴的对称点,得到点A″,∴点A″的坐标是:(﹣2,3).故答案为:﹣2;3.考点:关于x轴、y轴对称的点的坐标.14.某工程队有14名员工,他们的工种及相应每人每月工资如下表所示:现该工程队进行了人员调整:减少木工2名,增加电工、瓦工各1名,与调整前相比,该工程队员工月工资的方差(填“变小”、“不变”或“变大”).【答案】变大.【解析】试题分析:∵减少木工2名,增加电工、瓦工各1名,∴这组数据的平均数不变,但是每个数据减去平均数后平方和增大,则该工程队员工月工资的方差变大.故答案为:变大.考点:方差.15.如图,在⊙O的内接五边形ABCDE中,∠CAD=35°,则∠B+∠E= °.【答案】215.考点:圆内接四边形的性质.16.如图,过原点O的直线与反比例函数,的图象在第一象限内分别交于点A,B,且A为OB的中点,若函数,则与x的函数表达式是.【答案】.【解析】试题分析:过A作AC⊥x轴于C,过B作BD⊥x轴于D,∵点A在反比例函数上,∴设A(a,),∴OC=a,AC=,∵AC⊥x轴,BD⊥x轴,∴AC∥BD,∴△OAC∽△OBD,∴,∵A为OB的中点,∴,∴BD=2AC=,OD=2OC=2a,∴B(2a,),设,∴k=,∴与x的函数表达式是:.故答案为:.考点:反比例函数与一次函数的交点问题.三.解答题17.解不等式,并把它的解集在数轴上表示出来.【答案】.考点:1.解一元一次不等式;2.在数轴上表示不等式的解集.18.解方程:.【答案】.【解析】试题分析:观察可得最简公分母是,方程两边乘最简公分母,可以把分式方程转化为整式方程求解.试题解析:方程两边同乘以,得.解这个方程,得.检验:将代入知,.所以是原方程的根.考点:解分式方程.19.计算:.【答案】.【解析】试题分析:首先将括号里面通分运算,进而利用分式的性质化简求出即可.试题解析:原式====.考点:分式的混合运算.20.如图,△ABC中,CD是边AB上的高,且.(1)求证:△ACD∽△CBD;(2)求∠ACB的大小.【答案】(1)证明见试题解析;(2)90°.【解析】试题分析:(1)根据两边对应成比例且夹角相等的两个三角形相似,即可证明△ACD∽△CBD;(2)由(1)可知△ACD∽△CBD,然后根据相似三角形的对应角相等可得:∠A=∠BCD,再由∠A+∠ACD=90°,可得:∠BCD+∠ACD=90°,即∠ACB=90°.试题解析:(1)∵CD是边AB上的高,∴∠ADC=∠CDB=90°,∵,∴△ACD∽△CBD;(2)∵△ACD∽△CBD,∴∠A=∠BCD,在△ACD中,∠ADC=90°,∴∠A+∠ACD=90°,∴∠BCD+∠ACD=90°,即∠ACB=90°.考点:相似三角形的判定与性质.21.为了了解2014年某地区10万名大、中、小学生50米跑成绩情况,教育部门从这三类学生群体中各抽取了10%的学生进行检测,整理样本数据,并结合2010年抽样结果,得到下列统计图:(1)本次检测抽取了大、中、小学生共名,其中小学生名;(2)根据抽样的结果,估计2014年该地区10万名大、中、小学生中,50米跑成绩合格的中学生人数为名;(3)比较2010年与2014年抽样学生50米跑成绩合格率情况,写出一条正确的结论.【答案】(1)10000,4500;(2)3600;(3)例如:与2010年相比,2014年该市大学生50米跑成绩合格率下降了5%(答案不唯一).(3)根据条形图,写出一条即可,答案不唯一.试题解析:(1)100000×10%=10000(人),10000×45%═4500(人).故答案为:10000,4500;(2)100000×40%×90%=3600(人).故答案为:3600;(3)例如:与2010年相比,2014年该市大学生50米跑成绩合格率下降了5%(答案不唯一).考点:1.条形统计图;2.用样本估计总体;3.扇形统计图.22.某人的钱包内有10元、20元和50元的纸币各1张,从中随机取出2张纸币.(1)求取出纸币的总额是30元的概率;(2)求取出纸币的总额可购买一件51元的商品的概率.【答案】(1);(2).【解析】试题分析:(1)先列表得到所有3种等可能的结果数,再找出总额是30元所占结果数,然后根据概率公式计算;(2)找出总额超过51元的结果数,然后根据概率公式计算.试题解析:(1)列表:共有3种等可能的结果数,其中总额是30元占1种,所以取出纸币的总额是30元的概率=;(2)共有3种等可能的结果数,其中总额超过51元的有2种,所以取出纸币的总额可购买一件51元的商品的概率为.考点:列表法与树状图法.23.如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向C处,测得∠CAO=45°,轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km/h和36km/h,经过0.1h,轮船甲行驶至B处,轮船乙行驶至D处,测得∠DBO=58°,此时B处距离码头O多远?(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1,60)【答案】13.5km.【解析】试题分析:设B处距离码头Oxkm,分别在Rt△CAO和Rt△DBO中,根据三角函数求得CO和DO,再利用DC=DO ﹣CO,得出x的值即可.试题解析:设B处距离码头Oxkm,在Rt△CAO中,∠CAO=45°,∵tan∠CAO=,∴CO=AO•tan∠CAO=(45×0.1+x)•tan45°=4.5+x,在Rt△DBO中,∠DBO=58°,∵tan∠DBO=,∴DO=BO•tan∠DBO=x•tan58°,∵DC=DO﹣CO,∴36×0.1=x•tan58°﹣(4.5+x),∴x=.因此,B处距离码头O大约13.5km.考点:解直角三角形的应用.24.如图,AB∥CD,点E,F分别在AB,CD上,连接EF,∠AEF、∠CFE的平分线交于点G,∠BEF、∠DFE 的平分线交于点H.(1)求证:四边形EGFH是矩形;(2)小明在完成(1)的证明后继续进行了探索,过G作MN∥EF,分别交AB,CD于点M,N,过H作PQ∥EF,分别交AB,CD于点P,Q,得到四边形MNQP,此时,他猜想四边形MNQP是菱形,请在下列框中补全他的证明思路.【答案】(1)证明见试题解析;(2)答案不唯一,例如:FG平分∠CFE;GE=FH;∠GME=∠FQH;∠GEF=∠EFH.【解析】试题分析:(1)利用角平分线的定义结合平行线的性质得出∠FEH+∠EFH=90°,进而得出∠GEH=90°,进而求出四边形EGFH是矩形;(2)利用菱形的判定方法首先得出要证▱MNQP是菱形,只要证MN=NQ,再证∠MGE=∠QFH得出即可.试题解析:(1)∵EH平分∠BEF,∴∠FEH=∠BEF,∵FH平分∠DFE,∴∠EFH=∠DFE,∵AB∥CD,∴∠BEF+∠DFE=180°,∴∠FEH+∠EFH=(∠BEF+∠DFE)=×180°=90°,∵∠FEH+∠EFH+∠EHF=180°,∴∠EHF=180°﹣(∠FEH+∠EFH)=180°﹣90°=90°,同理可得:∠EGF=90°,∵EG平分∠AEF,∴∠EFG=∠AEF,∵EH平分∠BEF,∴∠FEH=∠BEF,∵点A、E、B在同一条直线上,∴∠AEB=180°,即∠AEF+∠BEF=180°,∴∠FEG+∠FEH=(∠AEF+∠BEF)=×180°=90°,即∠GEH=90°,∴四边形EGFH是矩形;考点:1.菱形的判定;2.全等三角形的判定与性质;3.矩形的判定.25.如图,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)【答案】答案见试题解析.【解析】试题分析:①以A为圆心,以3为半径作弧,交AD、AB两点,连接即可;②连接AC,在AC上,以A为端点,截取1.5个单位,过这个点作AC的垂线,交AD、AB两点,连接即可;③以A为端点在AB上截取3个单位,以截取的点为圆心,以3个单位为半径画弧,交BC一个点,连接即可;④连接AC,在AC上,以C为端点,截取1.5个单位,过这个点作AC的垂线,交BC、DC两点,然后连接A与这两个点即可;⑤以A为端点在AB上截取3个单位,再作着个线段的垂直平分线交CD一点,连接即可.试题解析:满足条件的所有图形如图所示:考点:1.作图—应用与设计作图;2.等腰三角形的判定;3.勾股定理;4.正方形的性质.26.如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.(1)求证:∠A=∠AEB;(2)连接OE,交CD于点F,OE⊥CD,求证:△ABE是等边三角形.【答案】(1)证明见试题解析;(2)证明见试题解析.试题解析:(1)∵四边形ABCD是⊙O的内接四边形,∴∠A+∠BCD=180°,∵∠DCE+∠BCD=180°,∴∠A=∠DCE,∵DC=DE,∴∠DCE=∠AEB,∴∠A=∠AEB;(2)∵∠A=∠AEB,∴△ABE是等腰三角形,∵EO⊥CD,∴CF=DF,∴EO是CD的垂直平分线,∴ED=EC,∵DC=DE,∴DC=DE=EC,∴△DCE是等边三角形,∴∠AEB=60°,∴△ABE是等边三角形.考点:1.圆内接四边形的性质;2.等边三角形的判定与性质;3.圆周角定理.27.某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD、线段CD分别表示该产品每千克生产成本(单位:元)、销售价(单位:元)与产量x(单位:kg)之间的函数关系.(1)请解释图中点D的横坐标、纵坐标的实际意义;(2)求线段AB所表示的与x之间的函数表达式;(3)当该产品产量为多少时,获得的利润最大?最大利润是多少?【答案】(1)点D的横坐标、纵坐标的实际意义:当产量为130kg时,该产品每千克生产成本与销售价相等,都为42元;(2)y=﹣0.2x+60(0≤x≤90);(3)当该产品产量为75kg时,获得的利润最大,最大值为2250.(3)利用总利润=单位利润×产量列出有关x的二次函数,求得最值即可.试题解析:(1)点D的横坐标、纵坐标的实际意义:当产量为130kg时,该产品每千克生产成本与销售价相等,都为42元;(2)设线段AB所表示的与x之间的函数关系式为,∵的图象过点(0,60)与(90,42),∴,∴解得:,∴这个一次函数的表达式为:y=﹣0.2x+60(0≤x≤90);(3)设与x之间的函数关系式为,∵经过点(0,120)与(130,42),∴,解得:,∴这个一次函数的表达式为(0≤x≤130),设产量为xkg时,获得的利润为W元,当0≤x≤90时,W==,∴当x=75时,W的值最大,最大值为2250;当90≤x130时,W==,∴当x=90时,W=,由﹣0.6<0知,当x>65时,W随x的增大而减小,∴90≤x≤130时,W≤2160,因此当该产品产量为75kg时,获得的利润最大,最大值为2250.考点:二次函数的应用.。
2015年 江苏省南京市中考数学试卷
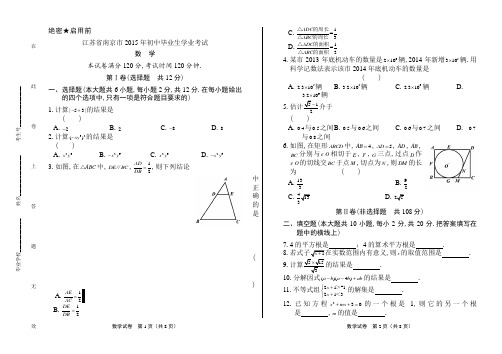
数学试卷 第1页(共8页) 数学试卷 第2页(共8页)绝密★启用前江苏省南京市2015年初中毕业生学业考试数 学本试卷满分120分,考试时间120分钟.第Ⅰ卷(选择题 共12分)一、选择题(本大题共6小题,每小题2分,共12分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.计算|53|-+的结果是( )A .2-B .2C .8-D .8 2.计算32()xy -的结果是( )A .26x yB .26x y -C .29x yD .29x y -3.如图,在ABC △中,DE BC ∥,12AD DB=,则下列结论中正确的是( )A.AE AC B .2DE DB = C .1=3ADC ABC △的周长△的周长D .1=3ADC ABC △的面积△的面积 4.某市2013年底机动车的数量是6210⨯辆,2014年新增5310⨯辆.用科学记数法表示该市2014年底机动车的数量是 ( )A .52.310⨯辆B .53.210⨯辆C .62.310⨯辆D .63.210⨯辆 5.( )A .0.4与0.5之间B .0.5与0.6之间C .0.6与0.7之间D .0.7与0.8之间6.如图,在矩形ABCD 中,4AB =,5AD =,AD ,AB ,BC 分别与O 相切于E ,F ,G 三点,过点D 作O 的切线交BC 于点M ,切点为N ,则DM 的长为 ( ) A .133B .92CD.第Ⅱ卷(非选择题 共108分)二、填空题(本大题共10小题,每小2分,共20分.把答案填写在题中的横线上)7.4的平方根是 ;4的算术平方根是 .8.,则x 的取值范围是 . 9.的结果是 .10.分解因式()(4)a b a b ab --+的结果是 . 11.不等式组211,213x x +⎧⎨+⎩>-<的解集是.12.已知方程230x mx ++=的一个根是1,则它的另一个根是 ,m 的值是 .毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------13.在平面直角坐标系中,点A的坐标是(2,3)-,作点A关于x轴的对称点,得到点A',再作点A'关于y轴的对称点,得到点A'',则点A''的坐标是( , ).14.某工程队有14名员工,他们的工种及相应每人每月工资如下表所示.现该工程队进行了人员调整:减少木工2名,增加电工、瓦工各1名.与调整前相比,该工程队员工月工资的方差(填“变小”“不变”或“变大”).15.如图,在O的内接五边形A B C D E中,35CAD∠=,则B E∠+∠=o.16.如图,过原点O的直线与反比例函数1y,2y的图像在第一象限内分别交于点,A B,且A为OB的中点.若函数11yx=,则2y与x的函数表达式是.三、解答题(本大题共11小题,88分.解答应写出文字说明、证明过程或演算步骤)17.(本小题满分6分)解不等式2(1)132x x+-+≥,并把它的解集在数轴上表示出来. 18.(本小题满分7分)解方程233x x=-.19.(本小题满分7分)计算:22221()aa b a ab a b-÷--+.20.(本小题满分8分)如图,ABC△中,CD是边AB上的高,且AD CDCD BD=.(1)求证:ACD CBD△∽△;(2)求ACB∠的大小.21.(本小题满分8分)为了了解2014年某地区10万名大、中、小学生50米跑成绩情况,教育部门从这三类学生群体中各抽取了10%的学生进行检测.整理样本数据,并结合2010年抽样结果,得到下列统计图. 2014年某地区抽样学生人数分布扇形统计图2010年、2014年某地区抽样学生50米跑成绩合格率条形统计图数学试卷第3页(共8页)数学试卷第4页(共8页)数学试卷 第5页(共8页) 数学试卷 第6页(共8页)(1)本次检测抽取了大、中、小学生共 名,其中小学生 名;(2)根据抽样的结果,估计2014年该地区10万名大、中、小学生中,50米跑成绩合格的中学生人数为 名;(3)比较2010年与2014年抽样学生50米跑成绩合格率情况,写出一条正确的结论. 22.(本小题满分8分) 某人的钱包内有10元、20元和50元的纸币各1张.从中随机取出2张纸币.(1)求取出纸币的总额是30元的概率; (2)求取出纸币的总额可购买一件51元的商品的概率.23.(本小题满分8分)如图,轮船甲位于码头O 的正西方向A 处,轮船乙位于码头O 的正北方向C 处,测得45CAO ∠=.轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km/h 和36km/h .经过0.1h ,轮船甲行驶至B 处,轮船乙行驶至D 位,测得58DBO ∠=,此时B 处距离码头O 有多远?(参考数据:sin580.85,cos580.53,tan58 1.60≈≈≈)24.(本小题满分8分)如图,AB CD ∥,点,E F 分别在,AB CD 上,连接EF .,AEF CFE ∠∠的平分线交于点G ,,BEF DFE ∠∠的平分线交于点H . (1)求证:四边形EGFH 是矩形.(2)小明在完成(1)的证明后继续进行了探索.过G 作MN EF ∥,分别交,AB CD 于点,M N ,过H 作PQ EF ∥,分别交,AB CD 于点,P Q ,得到四边形MNQP .此时,他猜想四边形MNQP 是菱形,请在下列框图中补全他的证明思路.25.(本小题满分10分)如图,在边长为4的正方形ABCD 中,请画出以A 为一个顶点,另外两个顶点在正方形ABCD 的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3).小明的证明思路毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第7页(共8页) 数学试卷 第8页(共8页)26.(本小题满分8分)如图,四边形ABCD 是O 的内接四边形,BC 的延长线与AD 的延长线交于点E ,且DC DE =. (1)求证:A AEB ∠=∠.(2)连接OE ,交CD 于点F ,OE CD ⊥.求证:ABE △是等边三角形.27.(本小题满分10分)某企业生产并销售某种产品,假设销售量与产量相等.下图中的折线ABD 、线段CD 分别表示该产品每千克生产成本1y (单位:元)、销售价2y (单位:元)与产量x (单位:kg )之间的函数关系. (1)请解释图中点D 的横坐标、纵坐标的实际意义; (2)求线段AB 所表示的1y 与x 之间的函数表达式;(3)当该产品产量为多少时,获得的利润最大?最大利润是多少?。
2015南京中考数学试题及答案

第6题图F B 江苏省南京市2015年初中毕业生学业考试数学试题一. 选择题(本大题共6小题,每小题2分,共12分) 1.计算︱- 5+3︱的结果是( )A. - 2B. 2C. - 8D. 8 2.计算(-xy ³)²的结果是( ) A. x ²y 6 B. -x ²y 6C. x ²y 9D. -x ²y 93.如图,在△ABC 中,DE ∥ BC ,AD DB = 12,则下列结论中正确的是(A.AE EC = 12B .DE BC = 12C .△ADE 的周长△ABC 的周长 = 13D.△ADE 的面积△ABC 的面积= 134.某市2013年底机动车的数量是2×106辆,2014年新增3×105辆.用科学记数法表示该市2014年底机动车的数量是( ) A. 2.3×105辆 B. 3.2×105辆 C. 2.3×106辆 D. 3.2×106辆 5.估计5 -12介于()A.0.4与0.5之间B. 0.5与0.6之间C. 0.6与0.7之间D. 0.7与0.8之间6.如图,在矩形ABCD 中,AB =4,AD =5,AD 、AB 、BC 分别与⊙O 相切于E 、F 、G 三点,过点D 作⊙O 的切线交BC 于点M ,切点为N ,则DM 的长为( )A. 133B. 92C. 4313 D.2 5二. 填空题(本大题共10小题,每小题2分,共20分) 7.4的平方根是 ;4的算术平方根是 .8.若式子x +1在实数范围内有意义,则x 的取值范围是 . 9.计算5×153的结果是 . 10.分解因式(a - b )(a - 4b )+ab 的结果是 .11.不等式组⎩⎨⎧2x +1>-12x +1 < 3的解集是 .12.已知方程x ²+mx +3=0的一个根是1,则它的另一个根是 ,m 的值是 .第3题图13.在平面直角坐标系中,点A 的坐标是(2,- 3),作点A 关于x 轴的对称点,得到点A',再作点A '关于y 轴的对称点,得到点A '',则点A''的坐标是( , ). 14.某工程队有14名员工,他们的工种及相应每人每月工资如下表所示.现该工程队进行了人员调整:减少木工2名,增加电工、瓦工各1名.与调整前相比,该工程队员工月工资的方差 (填“变小”,“不变”或“变大”). 15.如图,在⊙O 的内接五边形ABCDE 中,∠CAD =35°,则∠B +∠E = °.16.如图,过原点O 的直线与反比例函数y 1、y 2的图像在第一象限内分别交于点A 、B ,且A 为OB 的中点.若函数y 1= 1x ,则y 2与x 的函数表达式是 .三. 解答题(本大题共11小题,共88分)17.(6分)解不等式2(x +1)-1≥ 3x +2,并把它的解集在数轴上表示出来.18.(7分)解方程2x -3 = 3xy 第15题图y 1=1B E第17题图–1–2–312319.(7分)计算⎝⎛⎭⎫2a 2-b 2 - 1a ² - ab ÷ aa +b20.(8分)如图,△ABC 中,CD 是边AB 上的高,且AD CD = CDBD.(1) 求证:△ACD ∽ △CBD ;(2) 求∠ACB 的大小. 21.(8分)为了了解2014年某地区10万名大、中、小学生50米跑成绩情况,教育部门从这三类学生群体中各抽取了10%的学生进行检测,整理样本数据,并结合2010年抽样结果,得到下列统计图.(1) 本次检测抽取了大、中、小学生共名,其中小学生名;(2) 根据抽样的结果,估计2014年该地区10万名大、中、小学生中,50米跑成绩合格的中学生人数为名;(3) 比较2010年与2014年抽样学生50米跑成绩合格率情况,写出一条正确的结论.第20题图A22.(8分)某人的钱包内有10元、20元和50元的纸币各1张.从中随机取出2张纸币.(1)求取出纸币的总额是30元的概率;(2)求取出纸币的总额可购买一件51元的商品的概率.23.(8分)如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向C 处,测得∠CAO=45°.轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km/h和36km/h.经过0.1h,轮船甲行驶至B处,轮船乙行驶至D位,测得∠DBO=58°,此时B处距离码头O有多远?(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)C24.(8分)如图,AB ∥ CD ,点E 、F 分别在AB 、CD 上,连接EF ,∠AEF 、∠CFE 的平分线交于点G ,∠BEF 、∠DFE 的平分线交于点H . (1) 求证:四边形EGFH 是矩形.(2) 小明在完成(1)的证明后继续进行了探索.过G 作MN ∥ EF ,分别交AB 、CD 于点M 、N ,过H 作PQ ∥ EF ,分别交AB 、CD 于点P 、Q ,得到四边形MNQP .此时,他猜想四边形MNQP 是菱形,请在下列框图中补全他的证明思路.25.(10分)如图,在边长为4的正方形ABCD 中,请画出以A 为一个顶点,另外两个顶点在正方形ABCD 的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)小明的证明思路第24题图B C 第25题图AB26.(8分)如图,四边形ABCD 是⊙O 的内接四边形,BC 的延长线与AD 的延长线交于点E ,且DC =DE .(1) 求证:∠A =∠AEB .(2) 连接OE ,交CD 于点F ,OE ⊥ CD .求证:△ABE 是等边三角形.27.某企业生产并销售某种产品,假设销售量与产量相等.下图中的折线ABD 、线段CD 分别表示该产品每千克生产成本y 1(单位:元)、销售价y 2(单位:元)与产量x (单位:kg)之间的函数关系.(1)请解释图中点D 的横坐标、纵坐标的实际意义. (2)求线段AB 所表示的y 1与x 之间的函数表达式.(3)当该产品产量为多少时,获得的利润最大?最大利润是多少?(第26题)/kg y /(第27题)2015南京中考答案1.B 2A 3C 4C 5C 6A 7. ±2;2.8.x≥﹣1 9. 5 10.(a﹣2b)2.11.﹣1<x<1 12. 3,﹣4 13. ﹣2;3 14.增大15. 215 16. y=17.解:去括号,得2x+2﹣1≥3x+2,移项,得2x﹣3x≥2﹣2+1,合并同类项,得﹣x≥1,系数化为1,得x≤﹣1,这个不等式的解集在数轴上表示为:18.解:方程两边同乘以x(x﹣3),得2x=3(x﹣3).解这个方程,得x=9.检验:将x=9代入x(x﹣3)知,x(x﹣3)≠0.所以x=9是原方程的根.19.解:(﹣)÷=[﹣]×=[﹣]×=×=.20.(1)证明:∵CD是边AB上的高,∴∠ADC=∠CDB=90°,∵=.∴△ACD∽△CBD;(2)解:∵△ACD∽△CBD,∴∠A=∠BCD,在△ACD中,∠ADC=90°,∴∠A+∠ACD=90°,∴∠BCD+∠ACD=90°,即∠ACB=90°.21.解:(1)100000×10%=10000(人),10000×45%═4500(人).故答案为:10000,4500;(2)100000×40%×90%=3600(人).故答案为:3600;(3)例如:与2010年相比,2014年该市大学生50米跑成绩合格率下降了5%(答案不唯一).22.解:(1)列表:共有3种等可能的结果数,其中总额是30元占1种,所以取出纸币的总额是30元的概率=;(2)共有3种等可能的结果数,其中总额超过51元的有2种,所以取出纸币的总额可购买一件51元的商品的概率为.23.解:设B处距离码头Oxkm,在Rt△CAO中,∠CAO=45°,∵tan∠CAO=,∴CO=AO•tan∠CAO=(45×0.1+x)•tan45°=4.5+x,在Rt△DBO中,∠DBO=58°,∵tan∠DBO=,∴DO=BO•tan∠DBO=x•tan58°,∵DC=DO﹣CO,∴36×0.1=x•tan58°﹣(4.5+x),∴x=≈=13.5.因此,B处距离码头O大约13.5km.24.(1)证明:∵EH平分∠BEF,∴∠FEH=∠BEF,∵FH平分∠DFE,∴∠EFH=∠DFE,∵AB∥CD,∴∠BEF+∠DFE=180°,∴∠FEH+∠EFH=(∠BEF+∠DFE)=×180°=90°,∵∠FEH+∠EFH+∠EHF=180°,∴∠EHF=180°﹣(∠FEH+∠EFH)=180°﹣90°=90°,同理可得:∠EGF=90°,∵EG平分∠AEF,∴∠EFG=∠AEF,∵EH平分∠BEF,∴∠FEH=∠BEF,∵点A、E、B在同一条直线上,∴∠AEB=180°,即∠AEF+∠BEF=180°,∴∠FEG+∠FEH=(∠AEF+∠BEF)=×180°=90°,即∠GEH=90°,∴四边形EGFH是矩形;(2)解:答案不唯一:由AB∥CD,MN∥EF,PQ∥EF,易证四边形MNQP是平行四边形,要证▱MNQP是菱形,只要证MN=NQ,由已知条件:FG平分∠CFE,MN∥EF,故只要证GM=FQ,即证△MGE≌△QFH,易证GE=FH、∠GME=∠FGH.故只要证∠MGE=∠QFH,易证∠MGE=∠GEF,∠QFH=∠EFH,∠GEF=∠EFH,即可得证.25.解:满足条件的所有图形如图所示:26.证明:(1)∵四边形ABCD是⊙O的内接四边形,∴∠A+∠BCD=180°,∵∠DCE+∠BCD=180°,∴∠A=∠DCE,∵DC=DE,∴∠DCE=∠AEB,∴∠A=∠AEB;(2)∵∠A=∠AEB,∴△ABE是等腰三角形,∵EO⊥CD,∴CF=DF,∴EO是CD的垂直平分线,∴ED=EC,∵DC=DE,∴DC=DE=EC,∴△DCE是等边三角形,∴∠AEB=60°,∴△ABE是等边三角形.27.解:(1)点D的横坐标、纵坐标的实际意义:当产量为130kg时,该产品每千克生产成本与销售价相等,都为42元;(2)设线段AB所表示的y1与x之间的函数关系式为y=k1x+b1,∵y=k1x+b1的图象过点(0,60)与(90,42),∴∴,∴这个一次函数的表达式为;y=﹣0.2x+60(0≤x≤90);(3)设y2与x之间的函数关系式为y=k2x+b2,∵经过点(0,120)与(130,42),∴,解得:,∴这个一次函数的表达式为y2=﹣0.6x+120(0≤x≤130),设产量为xkg时,获得的利润为W元,当0≤x≤90时,W=x[(﹣0.6x+120)﹣(﹣0.2x+60)]=﹣0.4(x﹣75)2+2250,∴当x=75时,W的值最大,最大值为2250;当90≤x130时,W=x[(﹣0.6x+120)﹣42]=﹣0.6(x﹣65)2+2535,∴当x90时,W=﹣0.6(90﹣65)2+2535=2160,由﹣0.6<0知,当x>65时,W随x的增大而减小,∴90≤x≤130时,W≤2160,因此当该产品产量为75kg时,获得的利润最大,最大值为2250.。
2015年江苏省南京市中考数学试卷-答案

江苏省南京市2015年初中毕业生学业考试数学答案解析第Ⅰ卷一、选择题 1.【答案】B【解析】负数的绝对值等于它的相反数,原式=5322-+=-=。
【考点】有理数的加法,绝对值的求法 2.【答案】A【解析】()()()2223326xyx y x y -=-=。
【考点】幂的乘方和积的乘方 3.【答案】C【解析】此题的关键是:熟记相似三角形的对应边之比等于相似比;相似三角形的周长之比等于相似比;相似三角形的面积之比等于相似比的平方。
DE BC ∥,ADE ABC ∴△∽△,AD AE DEAB AC BC∴==,12AD DB =,13AD AE DE AB AC BC ===,故A 、B 选项均错误;ADE ABC △∽△,1==3ADE AD ABC AB ∴△的周长△的周长,21==9ADE AD ABC AB ⎛⎫∴ ⎪⎝⎭△的面积△的面积,故C 选项正确,D 错误。
【考点】比例的性质,相似三角形的判定与性质 4.【答案】C【解析】通过单项式的加法进行加减之后,用科学记数法的表示形式为10n a ⨯的形式,其中110a ≤<,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值1>时,n 是正数;当原数的绝对值1<时,n 是负数。
2014年底机动车的数量为:566310210 2.310⨯+⨯=⨯。
【考点】单项式的加法,科学记数法 5.【答案】C2.235≈1 1.235≈,10.6172≈。
【考点】估算有理数的大小 6.【答案】A【解析】本题正确的作出辅助线是解题的关键,连接OE ,OF ,ON ,OG ,在矩形ABCD 中,90A B ∠=∠=︒,4CD AB ==,AD ,AB ,BC 分别与O 相切于E ,F ,G 三点,90AEO AFO OFB BGO ∴∠=∠=∠=∠=︒,∴四边形AFOE ,FBGO 是正方形,∴2AF BF AE BG ====,3DE ∴=,∵DM 是O 的切线,3DN DE ∴==,MN MG =,523CM MN MN ∴=--=-,在Rt DMC△中,222DM CD CM =+,∴()()222334NM NM +=-+,∴43NM =,∴413333DM =+=,故选A 。
南京市2015年中考数学试卷

南京市2015年中考数学试卷 (满分:120分 时间:120分钟)一、 选择题(本大题共6小题,每小题2分,共12分) 1. 计算|-5+3|的结果是( ) A. -2 B. 2 C. -8 D. 8 2. 计算(-xy 3)2的结果是( )A. x 2y 6B. -x 2y 6C. x 2y 9D. -x 2y 93. 如图,在△ABC 中,DE ∥BC ,AD DB =12,则下列结论中正确的是( )A.AE AC =12 B. DE BC =12C. △ADE 的周长△ABC 的周长=13D. △ADE 的面积△ABC 的面积=13第3题 第6题4. 某市2013年底机动车的数量是2×106辆,2014年新增3×105辆.用科学记数法表示该市2014年底机动车的数量是( )A. 2.3×105辆B. 3.2×105辆C. 2.3×106辆D. 3.2×106辆 5. 估计5-12介于( )A. 0.4与0.5之间B. 0.5与0.6之间C. 0.6与0.7之间D. 0.7与0.8之间6. 如图,在矩形ABCD 中,AB =4,AD =5,AD 、AB 、BC 分别与⊙O 相切于E 、F 、G 三点,过点D 作⊙O 的切线交BC 于点M ,切点为N ,则DM 的长为( )A.133 B. 92 C. 4313 D. 25 二、 填空题(本大题共10小题,每小题2分,共20分) 7. 4的平方根是________;4的算术平方根是________.8. 若式子x +1在实数范围内有意义,则x 的取值范围是________.9. 计算5×153的结果是________. 10. 分解因式(a -b)(a -4b)+ab 的结果是________.11. 不等式组⎩⎪⎨⎪⎧2x +1>-1,2x +1<3的解集是________.12. 已知方程x 2+mx +3=0的一个根是1,则它的另一个根是________,m 的值是________.13. 在平面直角坐标系中,点A 的坐标是(2,-3),作点A 关于x 轴的对称点,得到点A′,再作点A′关于y 轴的对称点,得到点A″,则点A″的坐标是(________,________).14. 某工程队有.现该工程队进行了人员调整:减少木工2名,增加电工、瓦工各1名.与调整前相比,该工程队员工月工资的方差________(填“变小”,“不变”或“变大”).15. 如图,在⊙O 的内接五边形ABCDE 中,∠CAD =35°,则∠B +∠E =________°.第15题 第16题16. 如图,过原点O 的直线与反比例函数y 1、y 2的图像在第一象限内分别交于点A 、B ,且A 为OB 的中点.若函数y 1=1x,则y 2与x 的函数表达式是________.三、 解答题(本大题共11小题,共88分)17. (本小题满分6分)解不等式2(x +1)-1≥3x +2,并把它的解集在数轴上表示出来.第17题18. (本小题满分7分)解方程2x -3=3x .19. (本小题满分7分)计算⎝ ⎛⎭⎪⎫2a 2-b 2-1a 2-ab ÷aa +b.20. (本小题满分8分)如图,△ABC 中,CD 是边AB 上的高,且AD CD =CDBD .(1) 求证:△ACD ∽△CBD ; (2) 求∠ACB 的大小.第20题21. (本小题满分8分)为了了解2014年某地区10万名大、中、小学生50米跑成绩情况,教育部门从这三类学生群体中各抽取了10%的学生进行检测.整理样本数据,并结合2010年抽样结果,得到下列统计图.第21题(1) 本次检测抽取了大、中、小学生共________名,其中小学生________名;(2) 根据抽样的结果,估计2014年该地区10万名大、中、小学生中,50米跑成绩合格的中学生人数为________名;(3) 比较2010年与2014年抽样学生50米跑成绩合格率情况,写出一条正确的结论.22. (本小题满分8分)某人的钱包内有10元、20元和50元的纸币各1张.从中随机取出2张纸币.(1) 求取出纸币的总额是30元的概率;(2) 求取出纸币的总额可购买一件51元的商品的概率.23. (本小题满分8分)如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向C处,测得∠CAO=45°.轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45 km/h和36 km/h.经过0.1 h,轮船甲行驶至B处,轮船乙行驶至D 处,测得∠DBO=58°.此时B处距离码头O有多远?(参考数据:sin 58°≈0.85,cos 58°≈0.53,tan 58°≈1.60)第23题24. (本小题满分8分)如图,AB∥CD,点E、F分别在AB、CD上,连接EF.∠AEF、∠CFE的平分线交于点G,∠BEF、∠DFE的平分线交于点H.(1) 求证:四边形EGFH是矩形;(2) 小明在完成(1)的证明后继续进行了探索.过G作MN∥EF,分别交AB、CD于点M、N,过H作PQ∥EF,分别交AB、CD于点P、Q,得到四边形MNQP.此时,他猜想四边形MNQP是菱形.请在下列框图中补全他的证明思路.25. (本小题满分10分)如图,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)第25题26. (本小题满分8分)如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.(1) 求证:∠A=∠AEB;(2) 连接OE,交CD于点F,OE⊥CD.求证:△ABE是等边三角形.第26题27. (本小题满分10分)某企业生产并销售某种产品,假设销售量与产量相等.下图中的折线ABD、线段CD分别表示该产品每千克生产成本y1(单位:元)、销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.(1) 请解释图中点D的横坐标、纵坐标的实际意义;(2) 求线段AB所表示的y1与x之间的函数表达式;(3) 当该产品产量为多少时,获得的利润最大?最大利润是多少?第27题南京市2015年中考数学试卷1. B [解析]先计算-5+3,再求绝对值即可.∵ -5+3=-2,∴ |-5+3|=|-2|=2.2. A [解析](-xy 3)2=(-x)2(y 3)2=x 2y 6,即计算(-xy 3)2的结果是x 2y 6.3. C [解析]由DE ∥BC ,可得△ADE ∽△ABC ,然后由相似三角形的对应边成比例可得AD AB =AE AC =DE BC ,再由AD DB =12,得出相似比为13,即可判断选项A 、B 错误,然后根据相似三角形的周长之比等于相似比,面积之比等于相似比的平方即可判断选项C 正确,选项D 错误.4. C [解析]2014年底机动车的数量为2×106+3×105=2.3×106(辆).5. C [解析]方法一:用计算器计算,然后选择答案;方法二:先估算5的范围,再进一步估算5-12,即可解答. 6. A [解析]如图,连接OE 、OF 、ON 、OG.在矩形ABCD 中,∠A =∠B =90°,CD =AB =4,由于AD 、AB 、BC 分别与⊙O 相切于E 、F 、G 三点,得到∠AEO =∠AFO =∠OFB =∠BGO =90°,再根据OF =OE ,OF =OG ,可推出四边形AFOE 、FBGO 是正方形,从而得到AF =OF =BF =AE =BG =2.由切线长定理可得DE =DN ,MG =MN.由AE =2,AD =5,可得DE =AD -AE =3,从而DN =3,设MG =MN =x ,可得DM =MN +ND =x +3,CM =BC -BG -GM =3-x ,从而在Rt △CDM 中利用勾股定理得到关于x 的方程,解出x 的值即MN 的长,再求出DM 的长.第6题7. ±2 2 [解析]如果一个非负数x 的平方等于a ,那么x 是a 的算术平方根,由此即可求出结果.8. x ≥-1 [解析]根据二次根式的定义可知被开方数必须为非负数,列不等式即可求解. 9. 5 [解析]5×153=5×153=753=753=25=5.10. (a -2b)2 [解析]首先去括号,进而合并同类项,然后利用完全平方公式分解因式得出结果.11. -1<x<1 [解析]分别解每一个不等式,再求解集的公共部分. 12. 3 -4 [解析]方法一:∵ x =1是方程的一个根,∴ 代入方程中肯定是成立的.此时方程转化为关于m 的一元一次方程,即可求出m 的值,进而求出另一个根.方法二:可以根据根与系数的关系,求出另一个解和m 的值.13. -2 3 [解析]分别利用x 轴、y 轴对称点的性质,得出点A′、A″的坐标进而得出答案.14. 变大 [解析]∵ 减少木工2名,增加电工、瓦工各1名,∴ 这组数据的平均数不变,但是每个数据减去平均数后的平方和增大.∴ 该工程队员工月工资的方差变大.15. 215 [解析]在圆内接四边形ABCD 中,∠B +∠ADC =180°,可得∠B =180°-∠ADC ;在圆内接四边形ACDE 中,∠E +∠ACD =180°,可得∠E =180°-∠ACD ,∴ ∠B +∠E =180°-∠ADC +180°-∠ACD =180°+(180°-∠ADC -∠ACD)=180°+∠CAD =180°+35°=215°.16. y 2=4x [解析]如图,过点A 作AC ⊥x 轴于点C ,过点B 作BD ⊥x 轴于点D.由于点A 在反比例函数y 1=1x 上,设A ⎝⎛⎭⎫a ,1a ,则根据A 为OB 的中点,求得点B 的坐标为⎝⎛⎭⎫2a ,2a .设y 2=k x ,将点B 的坐标代入反比例函数的表达式,得k =2a·2a =4.∴ y 2与x 的函数表达式是y 2=4x.第16题17. [解析]将不等式去括号、移项、合并同类项、系数化为1,即可求出不等式的解集,再在数轴上表示出该不等式的解集即可.解:去括号,得2x +2-1≥3x +2.移项,得2x -3x ≥2-2+1.合并同类项,得-x ≥1.系数化为1,得x ≤-1.这个不等式的解集在数轴上表示如下:第17题18. [解析]观察可得最简公分母是x(x -3),方程两边同乘最简公分母,可以把分式方程转化为整式方程求解,但需注意检验.解:方程两边同乘x(x -3),得2x =3(x -3).解这个方程,得x =9.经检验,x =9是原方程的根.∴ 原方程的根是x =9.19. [解析]先确定分式的运算顺序:先算小括号内的,再将除法运算转化为乘法运算,在计算时要把分子或分母中的多项式进行因式分解,最后约分化简即可.解:⎝ ⎛⎭⎪⎫2a 2-b 2-1a 2-ab ÷a a +b=⎣⎢⎡⎦⎥⎤2(a +b )(a -b )-1a (a -b )×a +ba=⎣⎢⎡⎦⎥⎤2aa (a +b )(a -b )-a +b a (a +b )(a -b )×a +b a =2a -(a +b )a (a +b )(a -b )×a +b a =1a 2. 20. [解析](1) 由两边对应成比例且夹角相等的两个三角形相似,即可证明△ACD ∽△CBD ;(2) 由(1)知△ACD ∽△CBD ,根据相似三角形的对应角相等可得∠A =∠BCD ,然后由∠A +∠ACD =90°,可得∠BCD +∠ACD =90°,即∠ACB =90°.解:(1) ∵ CD 是边AB 上的高,∴ ∠ADC =∠CDB =90°.又∵AD CD =CDBD,∴ △ACD ∽△CBD ; (2) ∵ △ACD ∽△CBD ,∴ ∠A =∠BCD.在△ACD 中,∠ADC =90°,∴ ∠A +∠ACD =180°-∠ADC =90°.∴ ∠BCD +∠ACD =90°,即∠ACB =90°.21. [解析](1) 根据“教育部门从这三类学生群体中各抽取了10%的学生进行检测”,而学生总人数为10万,即可得到本次检测抽取了大、中、小学生共多少名,再根据扇形图可知小学生占45%,即可解答;(2) 先计算出样本中50米跑成绩合格的中学生所占的百分比,再乘以10万,即可解答;(3) 根据条形图,写出一条即可,答案不唯一.解:(1) 10 000 4 500;(2) 36 000;(3) 答案不唯一,如与2010年相比,2014年该地区大学生50米跑成绩合格率下降了5%.22. [解析](1) 先列举出所有等可能的结果,再找出总额是30元的结果数,然后根据概率公式计算;(2) 找出总额等于或超过51元的结果数,然后根据概率公式计算.解:(1) 某人的钱包内有10元、20元和50元的纸币各1张,从中随机取出2张纸币,所有可能出现的结果有:(10元,20元)、(10元,50元)、(20元,50元),共3种,它们出现的可能性相同,其中总额是30元的结果有1种,∴ P(取出纸币的总额是30元)=13;(2) 3种等可能的结果中,总额等于或超过51元的结果有2种,∴ P(取出纸币的总额可购买一件51元的商品)=23.23. [解析]设B 处距离码头O x km ,分别在Rt △CAO 和Rt △DBO 中,根据三角函数求得CO 和DO ,再利用DC =DO -CO 列方程,求出x 的值即可.解:设B 处距离码头O x km.在Rt △CAO 中,∠CAO =45°,∵ tan ∠CAO =COAO,∴ CO =AO·tan ∠CAO =(45×0.1+x)·tan 45°=(4.5+x) km.在Rt △DBO 中,∠DBO =58°,∵ tan ∠DBO =DOBO ,∴ DO=BO·tan ∠DBO =x·tan 58° km.∵ DC =DO -CO ,∴ 36×0.1=x·tan 58°-(4.5+x).∴ x =36×0.1+4.5tan 58°-1≈36×0.1+4.51.60-1=13.5.∴ B 处距离码头O 约13.5 km. 24. [解析](1) 利用角平分线的定义结合平行线的性质得出∠FEH +∠EFH =90°,从而得出∠EHF =90°,同理可得∠EGF =90°,再利用A 、E 、B 三点共线得出∠GEH =90°,进而求出四边形EGFH 是矩形;(2) 利用菱形的判定方法.要证▱MNQP 是菱形,只要证MN =NQ ,即证NG =NF ,GM =FQ.而证明GM =FQ ,只要证出△MGE ≌△QFH 即可.解:(1) ∵ EH 平分∠BEF ,∴ ∠FEH =12∠BEF.∵ FH 平分∠DFE ,∴ ∠EFH =12∠DFE.∵ AB ∥CD ,∴ ∠BEF +∠DFE =180°.∴ ∠FEH +∠EFH =12(∠BEF +∠DFE)=12×180°=90°.∵∠FEH +∠EFH +∠EHF =180°,∴ ∠EHF =180°-(∠FEH +∠EFH)=180°-90°=90°.同理可得∠EGF =90°.∵ EG 平分∠AEF ,∴ ∠FEG =12∠AEF.∵ 点A 、E 、B 在同一条直线上,∴ ∠AEB =180°,即∠AEF +∠BEF =180°.∴ ∠FEG +∠FEH =12(∠AEF +∠BEF)=12×180°=90°,即∠GEH =90°.∴ 四边形EGFH 是矩形;(2) FG 平分∠NFE GE =FH∠GME =∠FQH ∠GEF =∠EFH.25. [解析]本题应分类讨论,按3为底边长或腰长进行分类:若3为底边长,还应考虑A 点为顶角顶点还是底角顶点;若3为腰长,也应考虑A 点为顶角顶点还是底角顶点,画出图形.解:满足条件的所有等腰三角形如图所示.第25题26. [解析](1) 根据圆内接四边形的性质可得∠A +∠BCD =180°,根据邻补角互补可得∠DCE +∠BCD =180°,进而得到∠A =∠DCE ,然后利用等边对等角可得∠DCE =∠AEB ,进而可得∠A =∠AEB ;(2) 首先根据∠A =∠AEB ,可得△ABE 是等腰三角形,再证明△DCE 是等边三角形,进而可得∠AEB =60°,进而可得△ABE 是等边三角形.证明:(1) ∵ 四边形ABCD 是⊙O 的内接四边形,∴ ∠A +∠BCD =180°.∵ ∠DCE +∠BCD =180°,∴ ∠A =∠DCE.∵ DC =DE ,∴ ∠DCE =∠AEB.∴ ∠A =∠AEB ;(2) ∵ ∠A =∠AEB ,∴ △ABE 是等腰三角形.∵ OE ⊥CD ,∴ CF =DF.∴ EO 是CD 的垂直平分线.∴ ED =EC.∵ DC =DE ,∴ DC =DE =EC.∴ △DCE 是等边三角形.∴ ∠AEB =60°.∴ △ABE 是等边三角形.27. [解析](1) 点D 的横坐标、纵坐标的实际意义:当产量为130 kg 时,该产品每千克生产成本与销售价相等,都为42元;(2) 根据线段AB 经过的两点的坐标,利用待定系数法确定一次函数的表达式即可;(3) 利用“总利润=每千克的利润×产量”列出有关x 的二次函数,求得最值即可.解:(1) 点D 的横坐标、纵坐标的实际意义:当产量为130 kg 时,该产品每千克生产成本与销售价相等,都为42元;(2) 设线段AB 所表示的y 1与x 之间的函数表达式为y 1=k 1x +b 1.∵ y 1=k 1x +b 1的图象过点(0,60)与(90,42),∴ ⎩⎪⎨⎪⎧b 1=60,90k 1+b 1=42,解得⎩⎪⎨⎪⎧b 1=60,k 1=-0.2.∴ y 1与x 之间的函数表达式为y 1=-0.2x +60(0≤x ≤90);(3) 设y 2与x 之间的函数表达式为y 2=k 2x +b 2.∵ y 2=k 2x +b 2的图象过点(0,120)与(130,42),∴ ⎩⎪⎨⎪⎧b 2=120,130k 2+b 2=42,解得⎩⎪⎨⎪⎧b 2=120,k 2=-0.6.∴ y 2与x 之间的函数表达式为y 2=-0.6x +120(0≤x ≤130);设该产品产量为x kg 时,获得的利润为W 元,则当0≤x ≤90时,W =x[(-0.6x +120)-(-0.2x +60)]=-0.4(x -75)2+2 250,∴ 当x =75时,W 的值最大,最大值为2 250;当90≤x ≤130时,W =x[(-0.6x +120)-42]=-0.6(x -65)2+2 535,由-0.6<0知,当x>65时,W 随x 的增大而减小,∴ 当x =90时,W 的取值最大,且W =-0.6×(90-65)2+2 535=2 160.∴ 当该产品产量为75 kg 时,获得的利润最大,最大利润是2 250元.。
南京市2015年中考数学试卷

A BDE第3题第6题南京市2015年初中毕业生学业考试数 学一、选择题(本大题共6小题,每小题2分,共12分,在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填在括号中) 1.计算||-+53的结果是( )A .-2B .2C .-8D .82.计算()xy -32的结果是( )A .x y 26B .x y -26C .x y 29D .x y -293.如图,在△ABC 中,DE ∥BC ,AD DB =12,则下列结论中正确的是( )A .AE AC =12B .DE BC =12C . ADE ABC ∆=∆的周长1的周长3D . ADE ABC ∆=∆的面积1的面积34.某市2013年底机动车的数量是⨯6210辆,2014年新增⨯5310辆,用科学记数法表示该市2014年底机动车的数量是( ) A ..⨯52310 B ..⨯53210C ..⨯62310D ..⨯632105介于( ) A .0.4与0.5之间B .0.5与0.6之间C .0.6与0.7之间D .0.7与0.8之间6.如图,在矩形ABCD 中,AB =4,AD =5,AD 、AB 、BC 分别与⊙O 相切于E 、F 、G 三点,过点D 作⊙O 的切线交BC 于点M ,切点为N ,则DM 的长为( )A .133B .92CD.二、填空题(本大题共10小题,每小题2分,共20分) 7.4的平方根是 ;4的算术平方根是 .8在实数范围内有意义,则x 的取值范围是 . 9的结果是 .10.分解因式()()a b a b ab --+4的结果是 .11.不等式x x +>-⎧⎨+<⎩211213的解集是 .12.已知方程x mx ++=230的一个根是1,则它的另一个根是 ,m 的值是 .13.在平面直角坐标系中,点A 的坐标是(2,-3),作点A 关于x 轴的对称点,得到点A ′,再作点A ′关于y 轴的对称点,得到点A ′′,则点A ′′的坐标是( , ).14.某工程队有14名员工,他们的工种及相应每人每月工资如下表所示.现该工程队进行了人员调整:减少木工2名,增加电工,瓦工各1名.与调整前相比,该工程队员工月工资的方差(填“变小”,“不变”或“变大”).15.如图,在⊙O的内接五边形ABCDE中,∠CAD=35°,则∠B+∠E=°.第15题第16题16.如图,过原点O的直线与反比例函数y1,y2的图像在第一象限内分别交于点A、B,且A为OB的中点.若函数yx=11,则y2与x的函数表达式是.三、解答题(本大题共11小题,共88分,解答时应写出必要的文字说明、证明过程或演算步骤)17.(6分)解不等式()x x+-≥+21132,并把它的解集在数轴上表示出来.18.(7分)解方程x x=-233.19.(7分)计算aa b a ab a b⎛⎫-÷⎪--+⎝⎭22221.CA BD5060708090年 年2010年、2014年某地区抽样学生50米跑成绩合格率条形统计图大学生 15%小学生45%中学生 40% 2014年某地区抽样学生 人数分布扇形统计图20.(8分)如图,在△ABC 中,CD 是边AB 上的高,且AD CDCD BD. (1)求证:△ACD ∽△CBD ; (2)求∠ACB 的大小.21.(8分)为了了解2014年某地区10万名大、中、小学生50米跑成绩情况,教育部门从这三类学生群体中各抽取了10%的学生进行检测.整理样本数据,并结合2010年抽样结果,得到下列统计图. (1)本次检测抽取了大、中、小学生共 名,其中小学生 名;(2)根据抽样的结果,估计2014年该地区10万名大、中、小学生中,50米跑成绩合格的中学生人数为 名;(3)比较2010年与2014年抽样学生50米跑成绩合格率情况,写出一条正确的结论.22.(8分)某人的钱包内有10元、20元和50元的纸币各1张,从中随机取出2张纸币. (1)求取出纸币的总额是30元的概率;(2)求取出纸币的总额可购买一件51元的商品的概率.ABCDA BCD O 北东A BC DEFGHM NP Q 23.(8分)如图,轮船甲位于码头O 的正西方向A 处,轮船乙位于码头O 的正北方向C 处,测得∠CAO =45°.轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km/h 和36km/h .经过0.1h ,轮船甲行驶至B 处,轮船乙行驶至D 处,测得∠DBO =58°,此时B 处距离码头O 有多远?(参考数据:sin 58°≈0.85,cos 58°≈0.53,tan 58°≈1.60)24.(8分)如图,AB ∥CD ,点E 、F 分别在AB 、CD 上,连接EF ,∠AEF 、∠CFE 的平分线交于点G ,∠BEF 、∠DFE 的平分线交于点H . (1)求证:四边形EGFH 是矩形;(2)小明在完成(1)的证明后继续进行了探索,过G 作MN ∥EF ,分别交AB 、CD 于点M 、N ,过H 作PQ ∥EF ,分别交AB 、CD 交于点P 、Q ,得到四边形MNQP .此时,他猜想四边形MNQP 是菱形.请在下列框图中补全他的证明思路.25.(10分)如图,在边长为4的正方形ABCD 中,请画出以A 为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3) 小明的证明思路26.(8分)如图,四边形ABCD 是⊙O 的内接四边形,BC 的延长线与AD 的延长线交于点E ,DC =DE . (1)求证:∠A =∠AEB ;(2)连接OE ,交CD 于点F ,OE ⊥CD .求证:△ABE 是等边三角形.27.(10分)某企业生产并销售某种产品,假设销售量与产量相等.下图中的折线ABD 、线段CD 分别表示该产品每千克生产成本y 1(单位:元)、销售价y 2(单位:元)与产量x (单位:kg )之间的函数关系.(1)请解释图中点D 的横坐标、纵坐标的实际意义; (2)求线段AB 所表示的y 1与x 之间的函数表达式;(3)当该产品产量为多少时,获得的利润最大?最大利润是多少?南京市2015年初中毕业生学业考试数学参考答案一、选择题(本大题共6小题,每小题2分,共12分,在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填在括号中)二、填空题(本大题共10小题,每小题2分,共20分)7.±2,2; 8.x ≥-1; 9.5; 10.()a b -22;11.x -<<11;12.3,-4; 13.-2,3; 14.变大; 15.215; 16.y x=24. 三、解答题(本大题共11小题,共88分,解答时应写出必要的文字说明、证明过程或演算步骤) 17.(6分)解:去括号,得x x +-≥+22132,移项,得x x -≥-+23221, 合并同类项,得x -≥1, 系数化为1,得x ≤-1,这个不等式的解集在数轴上表示如下图所示.18.(7分)解:方程两边乘()x x -3,得()x x =-233,解得x =9.检验:当x =9时,()x x -≠30.所以,原方程的解为x =9. 19.(7分)解:a a ba ab a b ⎛⎫-÷ ⎪--+⎝⎭22221 ()()()a ba b a b a a b a ⎡⎤+=-⋅⎢⎥+--⎣⎦21 ()()()()a a b a b a a b a b a a b a b a ⎡⎤++=-⋅⎢⎥+-+-⎣⎦2 ()()()a a b a ba ab a b a -++=⋅+-2()()a b a ba ab a b a-+=⋅+-a=21.(1)证明:∵CD 是边AB 上的高,∴∠ADC =∠CDB =90°,又AD CDCD BD=,∴△ACD ∽△CBD ;(4分) (2)解:∵△ACD ∽△CBD ,∴∠A =∠BCD ,在△ACD 中,∠ADC =90°,∴∠A +∠ACD =90°, ∴∠BCD +∠ACD =90°,即∠ACB =90°.(8分)21.(8分)解:(1)10000,4500;(2分) (2)36000;(5分)(3)本题答案不唯一,下列解法供参考.例如,与2010年相比,2014年该市大学生50米跑成绩合格率下降了5%.(8分)22.(8分)解:某人从钱包内随机取出2张纸币,可能出现的结果有3种,即(10,20)、(10、50)、(20,50),并且它们出现的可能性相等.(1)取出纸币的总数是30元(记为事件A )的结果有1种,即(10,20),所以()P A =13;(4分)(2)取出纸币的总额可购买一件51元的商品(记为事件B )的结果有2种,即(10,50)、(20,50),所以()P B =23.(8分)23.(8分) 解:设B 处距离码头O x km .在Rt △CAO 中,∠CAO =45°,∵tan COCAO AO∠=,∴tan (.)tan .CO AO CAO x x =⋅∠=⨯+⋅︒=+45014545.在Rt △DBO 中,∠DBO =58°,∵tan DODBO BO∠=,∴tan tan DO BO DBO x =⋅∠=⋅︒58.∵DC =DO -CO ,∴.tan (.)x x ⨯=⋅︒-+36015845,∴......tan .x ⨯+⨯+=≈=︒--3601453601451355811601.因此,B 处距离码头O 大约13.5km . 24.(8分)(1)证明:∵EH 平分∠BEF ,∴FEH BEF ∠=∠12.∵FH 平分∠DFE ,∴EFH DFE ∠=∠12.∵AB ∥CD ,∴BEF D FE ∠+∠=︒180,∴()FEH EFH BEF DFE ∠+∠=∠+∠=⨯︒=︒111809022.又 ∵FEH EFH EH F ∠+∠+∠=︒180,∴()EHF FEH EFH ∠=︒-∠+∠=︒-︒=︒1801809090.同理可证,EGF ∠=︒90.∵EG 平分∠AEF ,∴FEG AEF ∠=∠12.∵EH 平分∠BEF ,∴FEH BEF ∠=∠12.∵点A 、E 、B 在同一条直线上,∴AEB ∠=︒180,即AEF BEF ∠+∠=︒180,∴()FEG FEH AEF BEF ∠+∠=∠+∠=⨯︒=︒111809022,即 GEH ∠=︒90,∴四边形EGFH 是矩形;(4分) (2)本题答案不惟一,下列解法供参考.例如,FG 平分∠CFE ;GE =FH ;∠GME =∠FQH ;∠GEF =∠EFH .(8分)A B D 3 3A BD 3A BD 33A B D 3A B D3解:满足条件的所有等腰三角形如下图所示.26.(8分)证明:(1)∵四边形ABCD 是⊙O 的内接四边形,∴∠A+∠BCD =180°.又∵∠DCE +∠BCD =180°,∴∠A =∠DCE .∵DC =DE ,∴∠DCE =∠AEB ,∴∠A =∠AEB ;(4分)(2)∵∠A =∠AEB ,∴△ABE 是等腰三角形.∵OE ⊥CD ,∴CF =DF ,∴OE 是CD 的垂直平分线,∴ED =EC ,又∵DC =DE ,∴DC =DE =EC ,∴△DCE 是等边三角形,∴∠AEB =60°,∴△AEB 是等边三角形.(8分)27.(10分)解:(1)点D 的横坐标、纵坐标的实际意义:当产量为为130kg 时,该产品每千克生产成本与销售价相等,都为42元;(2分)(2)设线段AB 所表示的y 1与x 之间的函数关系式为y k x b =+111,因为y k x b =+111的图像过(0,60)与(90,42),所以b k b =⎧⎨+=⎩111609042,解方程组得.k b =-⎧⎨=⎩110260,这个一次函数的表达式为.y x =-+10260(x ≤≤090);(5分) (3)设y 2与x 之间的函数表达式为y k x b =+222,因为y k x b =+222的图像过(0,120)与(130,42),所以b k b =⎧⎨+=⎩22212013042,解方程组得.k b =-⎧⎨=⎩2206120,这个一次函数的表达式为.y x =-+206120(x ≤≤0130).设产量为x kg 时,获得的利润为W 元,当x ≤≤090时,[(.)(.)].()W x x x x =-+--+=--+206120026004752250,所以当x =75时,W 的值最大,最大值为2250;当x ≤≤90130时,[(.)].()W x x x =-+-=--+2061204206652535,当x =90时,.()W =--+=206906525352160,由.-<060知,当x >65时,W 随x 的增大而减小,所以当x ≤≤90130时,W ≤2160.因此,当该产品产量为75kg 时获得的利润最大,最大利润是2250元.(10分)。
2015年江苏省南京市中考数学试卷附详细答案(原版+解析版)

2015年江苏省南京市中考数学试卷一.选择题(本大题共6小题,每小题2分,共12分) 1.计算︱- 5+3︱的结果是( )A. - 2B. 2C. - 8D. 82.计算(-xy ³)²的结果是() A. x ²y 6B. -x ²y 6C. x ²y 9D. -x ²y 93.如图,在△ABC 中,DE ∥ BC ,AD DB = 12,则下列结论中正确的是()第3题图A. AE EC = 12B.DE BC = 12C.△ADE 的周长△ABC 的周长 = 13D. △ADE 的面积△ABC 的面积 = 134.某市2013年底机动车的数量是2×106辆,2014年新增3×105辆.用科学记数法表示该市2014年底机动车的数量是( )A. 2.3×105辆B. 3.2×105辆C. 2.3×106辆D. 3.2×106辆5.估计5 -12介于() A.0.4与0.5之间 B. 0.5与0.6之间C. 0.6与0.7之间D. 0.7与0.8之间6.如图,在矩形ABCD 中,AB=4,AD=5,AD 、AB 、BC 分别与⊙O 相切于E 、F 、G 三点,过点D 作⊙O 的切线交BC 于点M ,切点为N ,则DM 的长为()第6题图F A. 133B. 92C. 4313D.2 5二.填空题(本大题共10小题,每小题2分,共20分) 7.4的平方根是;4的算术平方根是.8.若式子x +1在实数范围内有意义,则x 的取值范围是 . 9.计算5×153的结果是 . 10.分解因式(a - b )(a - 4b )+ab 的结果是 .11.不等式组⎩⎪⎨⎪⎧2x +1>-12x +1 < 3 的解集是 .12.已知方程x ²+mx +3=0的一个根是1,则它的另一个根是 ,m 的值是 .13.在平面直角坐标系中,点A 的坐标是(2,- 3),作点A 关于x 轴的对称点,得到点A',再作点A'关于y 轴的对称点,得到点A'',则点A''的坐标是( , ). 14.某工程队有14名员工,他们的工种及相应每人每月工资如下表所示.现该工程队进行了人员调整:减少木工2名,增加电工、瓦工各1名.与调整前相比,该工程队员工月工资的方差 (填“变小”,“不变”或“变大”). 15.如图,在⊙O 的内接五边形ABCDE 中,∠CAD=35°,则∠B +∠E= °.y 第第15题图y 2y 1=xBOBA16.如图,过原点O 的直线与反比例函数y 1、y 2的图像在第一象限内分别交于点A 、B ,且A 为OB 的中点.若函数y 1= 1x ,则y 2与x 的函数表达式是 .y 1=1三.解答题(本大题共11小题,共88分)17.(6分)解不等式2(x +1) - 1 ≥ 3x +2,并把它的解集在数轴上表示出来.第17题图–1–2–312318.(7分)解方程2x -3= 3x19.(7分)计算⎝ ⎛⎭⎪⎫2a ²-b ² - 1a ² - ab ÷ a a +b20.(8分)如图,△ABC 中,CD 是边AB 上的高,且AD CD = CDBD .(1) 求证:△ACD ∽ △CBD ; (2) 求∠ACB 的大小.第20题图A21.(8分)为了了解2014年某地区10万名大、中、小学生50米跑成绩情况,教育部门从这三类学生群体中各抽取了10%的学生进行检测,整理样本数据,并结合2010年抽样结果,得到下列统计图.(1)本次检测抽取了大、中、小学生共名,其中小学生名;(2)根据抽样的结果,估计2014年该地区10万名大、中、小学生中,50米跑成绩合格的中学生人数为名;(3)比较2010年与2014年抽样学生50米跑成绩合格率情况,写出一条正确的结论.22.(8分)某人的钱包内有10元、20元和50元的纸币各1张.从中随机取出2张纸币.(1)求取出纸币的总额是30元的概率;(2)求取出纸币的总额可购买一件51元的商品的概率.23.(8分)如图,轮船甲位于码头O 的正西方向A 处,轮船乙位于码头O 的正北方向C 处,测得∠CAO=45°.轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km /h 和36km /h .经过0.1h ,轮船甲行驶至B 处,轮船乙行驶至D 位,测得∠DBO=58°,此时B 处距离码头O 有多远? (参考数据:sin 58° ≈ 0.85,cos 58° ≈ 0.53,tan 58° ≈ 1.60)24.(8分)如图,AB ∥ CD ,点E 、F 分别在AB 、CD 上,连接EF ,∠AEF 、∠CFE 的平分线交于点G ,∠BEF 、∠DFE 的平分线交于点H . (1) 求证:四边形EGFH 是矩形.(2) 小明在完成(1)的证明后继续进行了探索.过G 作MN ∥ EF ,分别交AB 、CD 于点M 、N ,过H 作PQ ∥ EF ,分别交AB 、CD 于点P 、Q ,得到四边形MNQP .此时,他猜想四边形MNQP 是菱形,请在下列框图中补全他的证明思路.第24题图BC小明的证明思路25.(10分)如图,在边长为4的正方形ABCD 中,请画出以A 为一个顶点,另外两个顶点在正方形ABCD 的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)第25题图A26.(8分)如图,四边形ABCD 是⊙O 的内接四边形,BC 的延长线与AD 的延长线交于点E ,且DC=DE . (1) 求证:∠A=∠AEB .(2) 连接OE ,交CD 于点F ,OE ⊥ CD .求证:△ABE 是等边三角形.(第26题)27.某企业生产并销售某种产品,假设销售量与产量相等.下图中的折线ABD 、线段CD 分别表示该产品每千克生产成本y 1(单位:元)、销售价y 2(单位:元)与产量x (单位:kg )之间的函数关系.(1)请解释图中点D 的横坐标、纵坐标的实际意义. (2)求线段AB 所表示的y 1与x 之间的函数表达式.(3)当该产品产量为多少时,获得的利润最大?最大利润是多少?/kgy /(第27题)2015年江苏省南京市中考数学试卷参考答案与试题解析一、选择题(本大题共6小题,每小题2分,共12分)1.计算︱-5+3︱的结果是( )A. -2B. 2C. -8D. 8【考点】有理数的加法;绝对值..【分析】先计算﹣5+3,再求绝对值即可.【解答】解:原式=|﹣2|=2.故选B.【点评】本题考查了有理数的加法,以及绝对值的求法,负数的绝对值等于它的相反数.2.计算(-xy³)²的结果是( )A. x²y6B. -x²y6C. x²y9D. -x²y9【考点】幂的乘方与积的乘方..【分析】根据幂的乘方和积的乘方的运算方法:①(a m)n=a mn(m,n是正整数);②(ab)n=a n b n(n是正整数);求出计算(﹣xy3)2的结果是多少即可.【解答】解:(﹣xy3)2=(﹣x)2•(y3)2=x2y6,即计算(﹣xy3)2的结果是x2y6.故选:A.【点评】此题主要考查了幂的乘方和积的乘方,要熟练掌握,解答此题的关键是要明确:①(a m)n=a mn(m,n是正整数);②(ab)n=a n b n(n是正整数).3.如图,在△ABC中,DE ∥BC,ADDB=12,则下列结论中正确的是( )第3题图A. AEEC=12B.DEBC=12C.△ADE的周长△ABC的周长=13D.△ADE的面积△ABC的面积=13【考点】相似三角形的判定与性质..【分析】由DE∥BC,可得△ADE∽△ABC ,然后由相似三角形的对应边成比例可得,然后由=,即可判断A、B的正误,然后根据相似三角形的周长之比等于相似比,面积之比等于相似比的平方即可判断C、D的正误.【解答】解:∵DE∥BC,∴△ADE∽△ABC ,∴,∵=,∵=,故A、B选项均错误;∵△ADE ∽△ABC ,∴==,=()2=,故C选项正确,D选项错误.故选C.【点评】此题考查了相似三角形的判定与性质,解题的关键是:熟记相似三角形的对应边之比等于相似比;相似三角形的周长之比等于相似比;相似三角形的面积之比等于相似比的平方.4.某市2013年底机动车的数量是2×106辆,2014年新增3×105辆.用科学记数法表示该市2014年底机动车的数量是( )A. 2.3×105辆B. 3.2×105辆C. 2.3×106辆D. 3.2×106辆【考点】科学记数法—表示较大的数..【分析】科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n 是负数.【解答】解:2014年底机动车的数量为:3×105+2×106=2.3×106. 故选C .【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a 的值以及n 的值.5.估计 5 -12介于( ) A.0.4与0.5之间 B. 0.5与0.6之间C. 0.6与0.7之间D. 0.7与0.8之间【考点】估算无理数的大小.. 【分析】先估算的范围,再进一步估算,即可解答.【解答】解:∵ 2.235,∴﹣1≈1.235,∴≈0.617,∴介于0.6与0.7之间,故选:C .【点评】本题考查了估算有理数的大小,解决本题的关键是估算的大小.6.如图,在矩形ABCD 中,AB=4,AD=5,AD 、AB 、BC 分别与⊙O 相切于E 、F 、G 三点,过点D 作⊙O 的切线交BC 于点M ,切点为N ,则DM 的长为()第6题图F A. 133B. 92C. 4313D.2 5【考点】切线的性质;矩形的性质..【分析】连接OE,OF,ON,OG,在矩形ABCD中,得到∠A=∠B=90°,CD=AB=4,由于AD,AB,BC分别与⊙O相切于E,F,G三点得到∠AEO=∠AFO=∠OFB=∠BGO=90°,推出四边形AFOE,FBGO是正方形,得到AF=BF=AE=BG=2,由勾股定理列方程即可求出结果.【解答】解:连接OE,OF,ON,OG,在矩形ABCD中,∵∠A=∠B=90°,CD=AB=4,∵AD,AB,BC分别与⊙O相切于E,F,G三点,∴∠AEO=∠AFO=∠OFB=∠BGO=90°,∴四边形AFOE,FBGO是正方形,∴AF=BF=AE=BG=2,∴DE=3,∵DM是⊙O的切线,∴DN=DE=3,MN=MG,∴CM=5﹣2﹣MN=3﹣MN,在R t△DMC中,DM2=CD2+CM2,∴(3+NM)2=(3﹣NM)2+42,∴NM=,∴DM=3=,故选A.【点评】本题考查了切线的性质,勾股定理,正方形的性质,正确的作出辅助线是解题的关键.二、填空题(本大题共10小题,每小题2分,共20分)7.4的平方根是;4的算术平方根是.【考点】算术平方根;平方根..【分析】如果一个非负数x的平方等于a,那么x是a的算术平方根,由此即可求出结果.【解答】解:4的平方根是±2;4的算术平方根是2.故答案为:±2;2.【点评】此题主要考查了平方根和算术平方根的概念,算术平方根易与平方根的概念混淆而导致错误.8.若式子x+1在实数范围内有意义,则x的取值范围是.【考点】二次根式有意义的条件..【分析】根据二次根式的定义可知被开方数必须为非负数,列不等式求解.【解答】解:根据题意得:x+1≥0,解得x≥﹣1,故答案为:x≥﹣1.【点评】主要考查了二次根式的意义和性质.概念:式子(a≥0)叫二次根式.性质:二次根式中的被开方数必须是非负数,否则二次根式无意义.9.计算5×153的结果是.【考点】二次根式的乘除法..【分析】直接利用二次根式的性质化简求出即可.【解答】解:=×=5.故答案为:5.【点评】此题主要考查了二次根式的乘除运算,正确掌握二次根式的性质是解题关键.10.分解因式(a-b)(a-4b)+ab的结果是.【考点】因式分解-运用公式法..【分析】首先去括号,进而合并同类项,再利用完全平方公式分解因式得出即可.【解答】解:(a ﹣b )(a ﹣4b )+ab=a 2﹣5ab+4b 2+ab=a 2﹣4ab+4b 2=(a ﹣2b )2.故答案为:(a ﹣2b )2.【点评】此题主要考查了多项式乘法以及公式法分解因式,熟练应用完全平方公式是解题关键.11.不等式组⎩⎪⎨⎪⎧2x +1>-12x +1 < 3 的解集是 .【考点】解一元一次不等式组..【分析】分别解每一个不等式,再求解集的公共部分.【解答】解:,解不等式①得:x >﹣1,解不等式②得:x <1,所以不等式组的解集是﹣1<x <1.故答案为:﹣1<x <1.【点评】本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.还可以观察不等式的解,若x >较小的数、<较大的数,那么解集为x 介于两数之间.12.已知方程x ²+mx +3=0的一个根是1,则它的另一个根是 ,m 的值是 .【考点】根与系数的关系;一元二次方程的解..【分析】利用一元二次方程的根与系数的关系,两根的和是﹣m ,两个根的积是3,即可求解.【解答】解:设方程的另一个解是a ,则1+a=﹣m ,1×a=3,解得:m=﹣4,a=3.故答案是:3,﹣4.【点评】本题考查了一元二次方程的根与系数的关系,正确理解根与系数的关系是关键.13.在平面直角坐标系中,点A的坐标是(2,-3),作点A关于x轴的对称点,得到点A',再作点A'关于y轴的对称点,得到点A'',则点A''的坐标是( ,).【考点】关于x轴、y轴对称的点的坐标..【分析】分别利用x轴、y轴对称点的性质,得出A′,A″的坐标进而得出答案.【解答】解:∵点A的坐标是(2,﹣3),作点A关于x轴的对称点,得到点A′,∴A′的坐标为:(2,3),∵点A′关于y轴的对称点,得到点A″,∴点A″的坐标是:(﹣2,3).故答案为:﹣2;3.【点评】此题主要考查了关于x轴、y轴对称点的性质.(1)关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数.即点P(x,y)关于x轴的对称点P′的坐标是(x,﹣y).(2)关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变.即点P(x,y)关于y轴的对称点P′的坐标是(﹣x,y).14.某工程队有14名员工,他们的工种及相应每人每月工资如下表所示.现该工程队进行了人员调整:减少木工2名,增加电工、瓦工各1名.与调整前相比,该工程队员工月工资的方差(填“变小”,“不变”或“变大”).【考点】方差..【分析】利用已知方差的定义得出每个数据减去平均数后平方和增大,进而得出方差变大.【解答】解:∵减少木工2名,增加电工、瓦工各1名,∴这组数据的平均数不变,但是每个数据减去平均数后平方和增大,则该工程队员工月工资的方差变大.故答案为:增大.【点评】此题主要考查了方差的定义,正确把握方差中每个数据的意义是解题关键.15.如图,在⊙O的内接五边形ABCDE中,∠CAD=35°,则∠B+∠E= °.y第第15题图y2y1=1xBOB A【考点】圆内接四边形的性质..【分析】连接CE,根据圆内接四边形对角互补可得∠B+∠AEC=180°,再根据同弧所对的圆周角相等可得∠CED=∠CAD,然后求解即可.【解答】解:如图,连接CE,∵五边形ABCDE是圆内接五边形,∴四边形ABCE是圆内接四边形,∴∠B+∠AEC=180°,∵∠CED=∠CAD=35°,∴∠B+∠E=180°+35°=215°.故答案为:215.【点评】本题考查了圆内接四边形的性质,同弧所对的圆周角相等的性质,熟记性质并作辅助线构造出圆内接四边形是解题的关键.16.如图,过原点O 的直线与反比例函数y 1、y 2的图像在第一象限内分别交于点A 、B ,且A 为OB 的中点.若函数y 1= 1x ,则y 2与x 的函数表达式是 .y 1=1【考点】反比例函数与一次函数的交点问题..【分析】过A 作AC ⊥x 轴于C ,过B 作BD ⊥x 轴于D ,由于点A 在反比例函数y 1=上,设A (a ,),求得点B 的坐标代入反比例函数的解析式即可求出结果.【解答】解:过A 作AC ⊥x 轴于C ,过B 作BD ⊥x 轴于D ,∵点A 在反比例函数y 1=上,∴设A (a ,),∴OC=a ,AC=,∵AC ⊥x 轴,BD ⊥x 轴,∴AC ∥BD ,∴△OAC ∽△OBD ,∴,∵A 为OB 的中点,∴=,∴BD=2AC=,OD=2OC=2a ,∴B (2a ,),设y 2=,∴k=2a•=4,∴y 2与x 的函数表达式是:y=.故答案为:y=.【点评】本题主要考查了待定系数法求反比例函数,相似三角形的判定和性质,反比例函数中k 的几何意义要注意数形结合思想的运用.三、解答题(本大题共11小题,共88分)17.(6分)解不等式2(x +1) - 1 ≥ 3x +2,并把它的解集在数轴上表示出来. 第17题图–1–2–31230【考点】解一元一次不等式;在数轴上表示不等式的解集..【分析】不等式去括号、移项合并、系数化为1即可求出不等式的解集,再在数轴上表示出不等式的解集即可.【解答】解:去括号,得2x+2﹣1≥3x+2,移项,得2x ﹣3x≥2﹣2+1,合并同类项,得﹣x≥1,系数化为1,得x≤﹣1,这个不等式的解集在数轴上表示为:【点评】本题考查了一元一次不等式的解法,在数轴上表示不等式的解集,>,≥向右画;<,≤向左画,在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.18.(7分)解方程2x -3= 3x 【考点】解分式方程..【专题】计算题.【分析】观察可得最简公分母是x (x ﹣3),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.【解答】解:方程两边同乘以x (x ﹣3),得2x=3(x ﹣3).解这个方程,得x=9.检验:将x=9代入x (x ﹣3)知,x (x ﹣3)≠0.所以x=9是原方程的根.【点评】本题考查分式方程的解法,需要注意的是在解分式方程时需对得到的解进行检验.19.(7分)计算⎝ ⎛⎭⎪⎫2a ²-b ² - 1a ² - ab ÷ a a +b 【考点】分式的混合运算..【分析】首先将括号里面通分运算,进而利用分式的性质化简求出即可.【解答】解:(﹣)÷ =[﹣]× =[﹣]×=×=.【点评】此题主要考查了分式的混合运算,正确进行通分运算是解题关键.20.(8分)如图,△ABC 中,CD 是边AB 上的高,且AD CD = CD BD .(3) 求证:△ACD ∽ △CBD ;(4) 求∠ACB 的大小.第20题图A【考点】相似三角形的判定与性质..【分析】(1)由两边对应成比例且夹角相等的两个三角形相似,即可证明△ACD ∽△CBD ;(2)由(1)知△ACD ∽△CBD ,然后根据相似三角形的对应角相等可得:∠A=∠BCD ,然后由∠A+∠ACD=90°,可得:∠BCD+∠ACD=90°,即∠ACB=90°.【解答】(1)证明:∵CD 是边AB 上的高,∴∠ADC=∠CDB=90°,∵=. ∴△ACD ∽△CBD ;(2)解:∵△ACD ∽△CBD ,∴∠A=∠BCD ,在△ACD 中,∠ADC=90°,∴∠A+∠ACD=90°,∴∠BCD+∠ACD=90°,即∠ACB=90°.【点评】此题考查了相似三角形的判定与性质,解题的关键是:熟记相似三角形的判定定理与性质定理.21.(8分)为了了解2014年某地区10万名大、中、小学生50米跑成绩情况,教育部门从这三类学生群体中各抽取了10%的学生进行检测,整理样本数据,并结合2010年抽样结果,得到下列统计图.(4)本次检测抽取了大、中、小学生共名,其中小学生名;(5)根据抽样的结果,估计2014年该地区10万名大、中、小学生中,50米跑成绩合格的中学生人数为名;(6)比较2010年与2014年抽样学生50米跑成绩合格率情况,写出一条正确的结论.【考点】条形统计图;用样本估计总体;扇形统计图..【分析】(1)根据“教育部门从这三类学生群体中各抽取了10%的学生进行检测”,可得100000×10%,即可得到本次检测抽取了大、中、小学生共多少名,再根据扇形图可得小学生所占45%,即可解答;(2)先计算出样本中50米跑成绩合格的中学生所占的百分比,再乘以10万,即可解答;(3)根据条形图,写出一条即可,答案不唯一.【解答】解:(1)100000×10%=10000(人),10000×45%═4500(人).故答案为:10000,4500;(2)100000×40%×90%=3600(人).故答案为:3600;(3)例如:与2010年相比,2014年该市大学生50米跑成绩合格率下降了5%(答案不唯一).【点评】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.22.(8分)某人的钱包内有10元、20元和50元的纸币各1张.从中随机取出2张纸币.(3)求取出纸币的总额是30元的概率;(4)求取出纸币的总额可购买一件51元的商品的概率.【考点】列表法与树状图法..【专题】计算题.【分析】(1)先列表展示所有3种等可能的结果数,再找出总额是30元所占结果数,然后根据概率公式计算;(2)找出总额超过51元的结果数,然后根据概率公式计算.【解答】解:(1)列表:共有3种等可能的结果数,其中总额是30元占1种,所以取出纸币的总额是30元的概率=;(2)共有3种等可能的结果数,其中总额超过51元的有2种,所以取出纸币的总额可购买一件51元的商品的概率为.【点评】本题考查了列表法与树状图法:利用列表法和树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.23.(8分)如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向C处,测得∠CAO=45°.轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km/h和36km/h.经过0.1h,轮船甲行驶至B 处,轮船乙行驶至D位,测得∠DBO=58°,此时B处距离码头O有多远?(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)【考点】解直角三角形的应用..【分析】设B处距离码头Oxkm,分别在Rt△CAO和Rt△DBO中,根据三角函数求得CO和DO,再利用DC=DO﹣CO,得出x的值即可.【解答】解:设B处距离码头Oxkm,在Rt△CAO中,∠CAO=45°,∵tan∠CAO=,∴CO=AO•tan∠CAO=(45×0.1+x)•tan45°=4.5+x,在Rt△DBO中,∠DBO=58°,∵tan∠DBO=,∴DO=BO•tan∠DBO=x•tan58°,∵DC=DO ﹣CO,∴36×0.1=x•tan58°﹣(4.5+x),∴x=≈=13.5.因此,B处距离码头O大约13.5km.【点评】本题考查了解直角三角形的应用,熟练掌握三角形中的边角关系是解题的关键.24.(8分)如图,AB ∥CD,点E、F分别在AB、CD上,连接EF,∠AEF、∠CFE的平分线交于点G,∠BEF、∠DFE的平分线交于点H.(3)求证:四边形EGFH是矩形.(4)小明在完成(1)的证明后继续进行了探索.过G作MN ∥EF,分别交AB、CD于点M、N,过H作PQ ∥EF,分别交AB、CD于点P、Q,得到四边形MNQP.此时,他猜想四边形MNQP是菱形,请在下列框图中补全他的证明思路.第24题图B C【考点】菱形的判定;全等三角形的判定与性质;矩形的判定..【分析】(1)利用角平分线的定义结合平行线的性质得出∠FEH+∠EFH=90°,进而得出∠GEH=90°,进而求出四边形EGFH 是矩形;(2)利用菱形的判定方法首先得出要证▱MNQP 是菱形,只要证MN=NQ ,再证∠MGE=∠QFH 得出即可.【解答】(1)证明:∵EH 平分∠BEF ,∴∠FEH=∠BEF ,∵FH 平分∠DFE ,∴∠EFH=∠DFE ,∵AB ∥CD ,∴∠BEF+∠DFE=180°,∴∠FEH+∠EFH=(∠BEF+∠DFE )=×180°=90°,∵∠FEH+∠EFH+∠EHF=180°,∴∠EHF=180°﹣(∠FEH+∠EFH )=180°﹣90°=90°,同理可得:∠EGF=90°,∵EG 平分∠AEF ,∴∠EFG=∠AEF ,∵EH 平分∠BEF ,∴∠FEH=∠BEF ,小明的证明思路∵点A 、E 、B 在同一条直线上,∴∠AEB=180°,即∠AEF+∠BEF=180°,∴∠FEG+∠FEH=(∠AEF+∠BEF )=×180°=90°,即∠GEH=90°,∴四边形EGFH 是矩形;(2)解:答案不唯一:由AB ∥CD ,MN ∥EF ,PQ ∥EF ,易证四边形MNQP 是平行四边形,要证▱MNQP 是菱形,只要证MN=NQ ,由已知条件:FG 平分∠CFE ,MN ∥EF , 故只要证GM=FQ ,即证△MGE ≌△QFH ,易证 GE=FH 、∠GME=∠FGH .故只要证∠MGE=∠QFH ,易证∠MGE=∠GEF ,∠QFH=∠EFH ,∠GEF=∠EFH ,即可得证.【点评】此题主要考查了矩形的判定以及菱形的判定和角平分线的性质,根据题意得出证明菱形的方法是解题关键.25.(10分)如图,在边长为4的正方形ABCD 中,请画出以A 为一个顶点,另外两个顶点在正方形ABCD 的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3) 第25题图A【考点】作图—应用与设计作图;等腰三角形的判定;勾股定理;正方形的性质..【分析】①以A为圆心,以3为半径作弧,交AD、AB两点,连接即可;②连接AC,在AC上,以A为端点,截取1.5个单位,过这个点作AC的垂线,交AD、AB两点,连接即可;③以A为端点在AB上截取3个单位,以截取的点为圆心,以3个单位为半径画弧,交BC一个点,连接即可;④连接AC,在AC上,以C 为端点,截取1.5个单位,过这个点作AC的垂线,交BC、DC两点,然后连接A 与这两个点即可;⑤以A为端点在AB上截取3个单位,再作着个线段的垂直平分线交CD一点,连接即可.【解答】解:满足条件的所有图形如图所示:【点评】此题主要考查了作图﹣应用与设计作图,关键是掌握等腰三角形的判定方法.26.(8分)如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.(3)求证:∠A=∠AEB.(4)连接OE,交CD于点F,OE ⊥CD.求证:△ABE是等边三角形.(第26题)【考点】圆内接四边形的性质;等边三角形的判定与性质;圆周角定理..【分析】(1)根据圆内接四边形的性质可得∠A+∠BCD=180°,根据邻补角互补可得∠DCE+∠BCD=180°,进而得到∠A=∠DCE,然后利用等边对等角可得∠DCE=∠AEB,进而可得∠A=∠AEB;(2)首先证明△DCE是等边三角形,进而可得∠AEB=60°,再根据∠A=∠AEB,可得△ABE是等腰三角形,进而可得△ABE是等边三角形.【解答】证明:(1)∵四边形ABCD是⊙O的内接四边形,∴∠A+∠BCD=180°,∵∠DCE+∠BCD=180°,∴∠A=∠DCE,∵DC=DE,∴∠DCE=∠AEB,∴∠A=∠AEB;(2)∵∠A=∠AEB,∴△ABE是等腰三角形,∵EO⊥CD,∴CF=DF,∴EO是CD的垂直平分线,∴ED=EC,∵DC=DE,∴DC=DE=EC,∴△DCE是等边三角形,∴∠AEB=60°,∴△ABE是等边三角形.【点评】此题主要考查了等边三角形的判定和性质,以及圆内接四边形的性质,关键是掌握圆内接四边形对角互补.27.某企业生产并销售某种产品,假设销售量与产量相等.下图中的折线ABD、线段CD 分别表示该产品每千克生产成本y 1(单位:元)、销售价y 2(单位:元)与产量x (单位:kg )之间的函数关系.(1)请解释图中点D 的横坐标、纵坐标的实际意义.(2)求线段AB 所表示的y 1与x 之间的函数表达式.(3)当该产品产量为多少时,获得的利润最大?最大利润是多少?/kg y /(第27题)【考点】二次函数的应用..【分析】(1)点D 的横坐标、纵坐标的实际意义:当产量为130kg 时,该产品每千克生产成本与销售价相等,都为42元;(2)根据线段AB 经过的两点的坐标利用待定系数法确定一次函数的表达式即可;(3)利用总利润=单位利润×产量列出有关x 的二次函数,求得最值即可.【解答】解:(1)点D 的横坐标、纵坐标的实际意义:当产量为130kg 时,该产品每千克生产成本与销售价相等,都为42元;(2)设线段AB 所表示的y 1与x 之间的函数关系式为y=k 1x+b 1,∵y=k 1x+b 1的图象过点(0,60)与(90,42),∴∴,∴这个一次函数的表达式为;y=﹣0.2x+60(0≤x≤90);(3)设y 2与x 之间的函数关系式为y=k 2x+b 2,∵经过点(0,120)与(130,42),∴,解得:,∴这个一次函数的表达式为y2=﹣0.6x+120(0≤x≤130),设产量为xkg时,获得的利润为W元,当0≤x≤90时,W=x[(﹣0.6x+120)﹣(﹣0.2x+60)]=﹣0.4(x﹣75)2+2250,∴当x=75时,W的值最大,最大值为2250;当90≤x130时,W=x[(﹣0.6x+120)﹣42]=﹣0.6(x﹣65)2+2535,∴当x90时,W=﹣0.6(90﹣65)2+2535=2160,由﹣0.6<0知,当x>65时,W随x的增大而减小,∴90≤x≤130时,W≤2160,因此当该产品产量为75kg时,获得的利润最大,最大值为2250.【点评】本题考查了二次函数的应用,解题的关键是从实际问题中抽象出二次函数模型,难度不大.。
2015年江苏省南京市中考数学试卷(含解析)

2015年江苏省南京市中考数学试卷一、选择题(本大题共6小题,每小题2分,共12分,在每小题给出的四个选项中,恰有一项是符合题目要求的)1.(2分)(2015•南京)计算:|﹣5+3|的结果是( )A.﹣2B.2C.﹣8D.82.(2分)(2015•南京)计算(﹣xy3)2的结果是( )A.x2y6B.﹣x2y6C.x2y9D.﹣x2y93.(2分)(2015•南京)如图,在△ABC中,DE∥BC ,=,则下列结论中正确的是( )A.=B .=C .=D .=4.(2分)(2015•南京)某市2013年底机动车的数量是2×106辆,2014年新增3×105辆,用科学记数法表示该市2014年底机动车的数量是( )A.2.3×105辆B.3.2×105辆C.2.3×106辆D.3.2×106辆5.(2分)(2015•南京)估计介于( )A.0.4与0.5之间B.0.5与0.6之间C.0.6与0.7之间D.0.7与0.8之间6.(2分)(2015•南京)如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线BC于点M,切点为N,则DM的长为( )t i me di b A .B .C .D .2二、填空题(本大题共10小题,每小题2分,共20分)7.(2分)(2015•南京)4的平方根是 ;4的算术平方根是 . 8.(2分)(2015•南京)若式子在实数范围内有意义,则x 的取值范围是 . 9.(2分)(2015•南京)计算的结果是 .10.(2分)(2015•南京)分解因式(a ﹣b )(a ﹣4b )+ab 的结果是 . 11.(2分)(2015•南京)不等式组的解集是 .12.(2分)(2015•南京)已知方程x 2+mx+3=0的一个根是1,则它的另一个根是 ,m 的值是 . 13.(2分)(2015•南京)在平面直角坐标系中,点A 的坐标是(2,﹣3),作点A 关于x 轴的对称点,得到点A ′,再作点A ′关于y 轴的对称点,得到点A ″,则点A ″的坐标是( , ). 14.(2分)(2015•南京)某工程队有14名员工,他们的工种及相应每人每月工资如下表所示:工种人数每人每月工资/元电工57000木工46000瓦工55000现该工程队进行了人员调整:减少木工2名,增加电工、瓦工各1名,与调整前相比,该工程队员工月工资的方差 (填“变小”、“不变”或“变大”). o 15.(2分)(2015•南京)如图,在⊙O的内接五边形ABCDE中,∠CAD=35°,则∠B+∠E= .°16.(2分)(2015•南京)如图,过原点O的直线与反比例函数y1,y2的图象在第一象限内分别交于点A,B,且A为OB的中点,若函数y1=,则y2与x的函数表达式是 .三、解答题(本大题共11小题,共88分,解答时应写出文字说明、证明过程或演算步骤)17.(6分)(2015•南京)解不等式2(x+1)﹣1≥3x+2,并把它的解集在数轴上表示出来.18.(7分)(2015•南京)解方程:.19.(7分)(2015•南京)计算:(﹣)÷.20.(8分)(2015•南京)如图,△ABC中,CD是边AB 上的高,且=.(1)求证:△ACD∽△CBD;(2)求∠ACB的大小.h 21.(8分)(2015•南京)为了了解2014年某地区10万名大、中、小学生50米跑成绩情况,教育部门从这三类学生群体中各抽取了10%的学生进行检测,整理样本数据,并结合2010年抽样结果,得到下列统计图:(1)本次检测抽取了大、中、小学生共 名,其中小学生 名;(2)根据抽样的结果,估计2014年该地区10万名大、中、小学生中,50米跑成绩合格的中学生人数为 名;(3)比较2010年与2014年抽样学生50米跑成绩合格率情况,写出一条正确的结论. 22.(8分)(2015•南京)某人的钱包内有10元、20元和50元的纸币各1张,从中随机取出2张纸币.(1)求取出纸币的总额是30元的概率;(2)求取出纸币的总额可购买一件51元的商品的概率. 23.(8分)(2015•南京)如图,轮船甲位于码头O 的正西方向A 处,轮船乙位于码头O 的正北方向C 处,测得∠CAO=45°,轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km/h 和36km/h ,经过0.1h ,轮船甲行驶至B 处,轮船乙行驶至D 处,测得∠DBO=58°,此时B 处距离码头O 多远?(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)24.(8分)(2015•南京)如图,AB∥CD,点E,F分别在AB,CD上,连接EF,∠AEF、∠CFE的平分线交于点G,∠BEF、∠DFE的平分线交于点H.(1)求证:四边形EGFH是矩形;(2)小明在完成(1)的证明后继续进行了探索,过G作MN∥EF,分别交AB,CD于点M,N,过H作PQ∥EF,分别交AB,CD于点P,Q,得到四边形MNQP,此时,他猜想四边形MNQP是菱形,请在下列框中补全他的证明思路.25.(10分)(2015•南京)如图,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要)求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字326.(8分)(2015•南京)如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.(1)求证:∠A=∠AEB;是等边三角形.(2)连接OE,交CD于点F,OE⊥CD,求证:△ABE27.(10分)(2015•南京)某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD、线段CD分别表示该产品每千克生产成本y1(单位:元)、销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.(1)请解释图中点D的横坐标、纵坐标的实际意义;(2)求线段AB所表示的y1与x之间的函数表达式;(3)当该产品产量为多少时,获得的利润最大?最大利润是多少?2015年江苏省南京市中考数学试卷参考答案与试题解析一、选择题(本大题共6小题,每小题2分,共12分,在每小题给出的四个选项中,恰有一项是符合题目要求的)1.(2分)(2015•南京)计算:|﹣5+3|的结果是( )A.﹣2B.2C.﹣8D.8【考点】有理数的加法;绝对值.【分析】先计算﹣5+3,再求绝对值即可.【解答】解:原式=|﹣2|=2.故选B.【点评】本题考查了有理数的加法,以及绝对值的求法,负数的绝对值等于它的相反数.2.(2分)(2015•南京)计算(﹣xy3)2的结果是( )A.x2y6B.﹣x2y6C.x2y9D.﹣x2y9【考点】幂的乘方与积的乘方.【分析】根据幂的乘方和积的乘方的运算方法:①(a m)n=a mn(m,n是正整数);②(ab)n=a n b n(n是正整数);求出计算(﹣xy3)2的结果是多少即可.【解答】解:(﹣xy3)2=(﹣x)2•(y3)2=x2y6,即计算(﹣xy3)2的结果是x2y6.故选:A.【点评】此题主要考查了幂的乘方和积的乘方,要熟练掌握,解答此题的关键是要明确:①(a m)n=a mn(m,n是正整数);②(ab)n=a n b n(n是正整数).3.(2分)(2015•南京)如图,在△ABC中,DE∥BC ,=,则下列结论中正确的是( )A.=B .=C .=D .=【考点】相似三角形的判定与性质.【分析】由DE∥BC,可得△ADE∽△ABC ,然后由相似三角形的对应边成比例可得,然后由=,即可判断A、B的正误,然后根据相似三角形的周长之比等于相似比,面积之比等于相似比的平方即可判断C、D的正误.【解答】解:∵DE∥BC,∴△ADE∽△ABC,∴,∵=,∵=,故A、B选项均错误;∵△ADE∽△ABC,∴==,=()2=,故C选项正确,D选项错误.故选C.【点评】此题考查了相似三角形的判定与性质,解题的关键是:熟记相似三角形的对应边之比等于相似比;相似三角形的周长之比等于相似比;相似三角形的面积之比等于相似比的平方.4.(2分)(2015•南京)某市2013年底机动车的数量是2×106辆,2014年新增3×105辆,用科学记数法表示该市2014年底机动车的数量是( )A.2.3×105辆B.3.2×105辆C.2.3×106辆D.3.2×106辆【考点】科学记数法—表示较大的数.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:2014年底机动车的数量为:3×105+2×106=2.3×106.故选C.【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.5.(2分)(2015•南京)估计介于( )A.0.4与0.5之间B.0.5与0.6之间C.0.6与0.7之间D.0.7与0.8之间【考点】估算无理数的大小.【分析】先估算的范围,再进一步估算,即可解答.【解答】解:∵ 2.235,∴﹣1≈1.235,∴≈0.617,∴介于0.6与0.7之间,故选:C.【点评】本题考查了估算有理数的大小,解决本题的关键是估算的大小.6.(2分)(2015•南京)如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线BC于点M,切点为N,则DM的长为( )A.B.C.D.2【考点】切线的性质;矩形的性质.【专题】压轴题.【分析】连接OE,OF,ON,OG,在矩形ABCD中,得到∠A=∠B=90°,CD=AB=4,由于AD,AB,BC分别与⊙O相切于E,F,G三点得到∠AEO=∠AFO=∠OFB=∠BGO=90°,推出四边形AFOE,FBGO是正方形,得到AF=BF=AE=BG=2,由勾股定理列方程即可求出结果.【解答】解:连接OE,OF,ON,OG,在矩形ABCD中,∵∠A=∠B=90°,CD=AB=4,∵AD,AB,BC分别与⊙O相切于E,F,G三点,∴∠AEO=∠AFO=∠OFB=∠BGO=90°,∴四边形AFOE,FBGO是正方形,∴AF=BF=AE=BG=2,i ∴DE=3,∵DM 是⊙O 的切线,∴DN=DE=3,MN=MG ,∴CM=5﹣2﹣MN=3﹣MN ,在R t △DMC 中,DM 2=CD 2+CM 2,∴(3+NM )2=(3﹣NM )2+42,∴NM=,∴DM=3=,故选A.【点评】本题考查了切线的性质,勾股定理,正方形的性质,正确的作出辅助线是解题的关键. 二、填空题(本大题共10小题,每小题2分,共20分)7.(2分)(2015•南京)4的平方根是 ±2 ;4的算术平方根是 2 .【考点】算术平方根;平方根.【分析】如果一个非负数x 的平方等于a ,那么x 是a 的算术平方根,由此即可求出结果.【解答】解:4的平方根是±2;4的算术平方根是2.故答案为:±2;2.【点评】此题主要考查了平方根和算术平方根的概念,算术平方根易与平方根的概念混淆而导致错误. 8.(2分)(2015•南京)若式子在实数范围内有意义,则x 的取值范围是 x ≥﹣1 .【考点】二次根式有意义的条件.【分析】根据二次根式的定义可知被开方数必须为非负数,列不等式求解.【解答】解:根据题意得:x+1≥0,解得x ≥﹣1,故答案为:x ≥﹣1.【点评】主要考查了二次根式的意义和性质.概念:式子(a ≥0)叫二次根式.a 性质:二次根式中的被开方数必须是非负数,否则二次根式无意义. 9.(2分)(2015•南京)计算的结果是 5 .【考点】二次根式的乘除法.【分析】直接利用二次根式的性质化简求出即可.【解答】解:=×=5.故答案为:5.【点评】此题主要考查了二次根式的乘除运算,正确掌握二次根式的性质是解题关键. 10.(2分)(2015•南京)分解因式(a ﹣b )(a ﹣4b )+ab 的结果是 (a ﹣2b )2 .【考点】因式分解-运用公式法.【分析】首先去括号,进而合并同类项,再利用完全平方公式分解因式得出即可.【解答】解:(a ﹣b )(a ﹣4b )+ab=a 2﹣5ab+4b 2+ab=a 2﹣4ab+4b 2=(a ﹣2b )2.故答案为:(a ﹣2b )2.【点评】此题主要考查了多项式乘法以及公式法分解因式,熟练应用完全平方公式是解题关键. 11.(2分)(2015•南京)不等式组的解集是 ﹣1<x <1 .【考点】解一元一次不等式组.【分析】分别解每一个不等式,再求解集的公共部分.【解答】解:,解不等式①得:x >﹣1,解不等式②得:x <1,所以不等式组的解集是﹣1<x <1.故答案为:﹣1<x <1.o 【点评】本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.还可以观察不等式的解,若x >较小的数、<较大的数,那么解集为x 介于两数之间. 12.(2分)(2015•南京)已知方程x 2+mx+3=0的一个根是1,则它的另一个根是 3 ,m 的值是 ﹣4 .【考点】根与系数的关系;一元二次方程的解.【分析】利用一元二次方程的根与系数的关系,两根的和是﹣m ,两个根的积是3,即可求解.【解答】解:设方程的另一个解是a ,则1+a=﹣m ,1×a=3,解得:m=﹣4,a=3.故答案是:3,﹣4.【点评】本题考查了一元二次方程的根与系数的关系,正确理解根与系数的关系是关键. 13.(2分)(2015•南京)在平面直角坐标系中,点A 的坐标是(2,﹣3),作点A 关于x 轴的对称点,得到点A ′,再作点A ′关于y 轴的对称点,得到点A ″,则点A ″的坐标是( ﹣2 , 3 ).【考点】关于x 轴、y 轴对称的点的坐标.【分析】分别利用x 轴、y 轴对称点的性质,得出A ′,A ″的坐标进而得出答案.【解答】解:∵点A 的坐标是(2,﹣3),作点A 关于x 轴的对称点,得到点A ′,∴A ′的坐标为:(2,3),∵点A ′关于y 轴的对称点,得到点A ″,∴点A ″的坐标是:(﹣2,3).故答案为:﹣2;3.【点评】此题主要考查了关于x 轴、y 轴对称点的性质.(1)关于x 轴对称点的坐标特点:横坐标不变,纵坐标互为相反数.即点P (x ,y )关于x 轴的对称点P ′的坐标是(x ,﹣y ).(2)关于y 轴对称点的坐标特点:横坐标互为相反数,纵坐标不变.即点P (x ,y )关于y 轴的对称点P ′的坐标是(﹣x ,y ). 14.(2分)(2015•南京)某工程队有14名员工,他们的工种及相应每人每月工资如下表所示:工种人数每人每月工资/元电工57000木工46000瓦工55000现该工程队进行了人员调整:减少木工2名,增加电工、瓦工各1名,与调整前相比,该工程队员工月工资的方差 变大 (填“变小”、“不变”或“变大”).【考点】方差.【分析】利用已知方差的定义得出每个数据减去平均数后平方和增大,进而得出方差变大.【解答】解:∵减少木工2名,增加电工、瓦工各1名,∴这组数据的平均数不变,但是每个数据减去平均数后平方和增大,则该工程队员工月工资的方差变大.故答案为:变大.【点评】此题主要考查了方差的定义,正确把握方差中每个数据的意义是解题关键. 15.(2分)(2015•南京)如图,在⊙O 的内接五边形ABCDE 中,∠CAD=35°,则∠B+∠E= 215 °.【考点】圆内接四边形的性质.【分析】连接CE ,根据圆内接四边形对角互补可得∠B+∠AEC=180°,再根据同弧所对的圆周角相等可得∠CED=∠CAD ,然后求解即可.【解答】解:如图,连接CE ,∵五边形ABCDE是圆内接五边形,∴四边形ABCE 是圆内接四边形,∴∠B+∠AEC=180°,∵∠CED=∠CAD=35°,∴∠B+∠E=180°+35°=215°.故答案为:215.【点评】本题考查了圆内接四边形的性质,同弧所对的圆周角相等的性质,熟记性质并作辅助线构造出圆内接四边形是解题的关键.o r16.(2分)(2015•南京)如图,过原点O 的直线与反比例函数y 1,y 2的图象在第一象限内分别交于点A ,B ,且A 为OB 的中点,若函数y 1=,则y 2与x 的函数表达式是 y 2= .【考点】反比例函数与一次函数的交点问题.【专题】压轴题.【分析】过A 作AC ⊥x 轴于C ,过B 作BD ⊥x 轴于D ,由于点A 在反比例函数y 1=上,设A (a ,),求得点B 的坐标代入反比例函数的解析式即可求出结果.【解答】解:过A 作AC ⊥x 轴于C ,过B 作BD ⊥x 轴于D ,∵点A 在反比例函数y 1=上,∴设A (a ,),∴OC=a ,AC=,∵AC ⊥x 轴,BD ⊥x 轴,∴AC ∥BD ,∴△OAC ∽△OBD ,∴,∵A 为OB 的中点,∴=,∴BD=2AC=,OD=2OC=2a ,∴B (2a ,),设y 2=,∴k=2a •=4,∴y2与x的函数表达式是:y2=..故答案为:y2=【点评】本题主要考查了待定系数法求反比例函数,相似三角形的判定和性质,反比例函数中k的几何意义要注意数形结合思想的运用.三、解答题(本大题共11小题,共88分,解答时应写出文字说明、证明过程或演算步骤),并把它的解集在数轴上表示出来.17.(6分)(2015•南京)解不等式2(x+1)﹣1≥3x+2【考点】解一元一次不等式;在数轴上表示不等式的解集.【分析】不等式去括号、移项合并、系数化为1即可求出不等式的解集,再在数轴上表示出不等式的解集即可.【解答】解:去括号,得2x+2﹣1≥3x+2,移项,得2x﹣3x≥2﹣2+1,合并同类项,得﹣x≥1,系数化为1,得x≤﹣1,这个不等式的解集在数轴上表示为:【点评】本题考查了一元一次不等式的解法,在数轴上表示不等式的解集,>,≥向右画;<,≤向左画,在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.18.(7分)(2015•南京)解方程:.【考点】解分式方程.【专题】计算题.【分析】观察可得最简公分母是x(x﹣3),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.【解答】解:方程两边同乘以x(x﹣3),得2x=3(x﹣3).解这个方程,得x=9.检验:将x=9代入x(x﹣3)知,x(x﹣3)≠0.所以x=9是原方程的根.【点评】本题考查分式方程的解法,需要注意的是在解分式方程时需对得到的解进行检验.19.(7分)(2015•南京)计算:(﹣)÷.【考点】分式的混合运算.【分析】首先将括号里面通分运算,进而利用分式的性质化简求出即可.【解答】解:(﹣)÷=[﹣]×=[﹣]×=×=.【点评】此题主要考查了分式的混合运算,正确进行通分运算是解题关键.20.(8分)(2015•南京)如图,△ABC中,CD是边AB 上的高,且=.(1)求证:△ACD∽△CBD;(2)求∠ACB的大小.【考点】相似三角形的判定与性质.【分析】(1)由两边对应成比例且夹角相等的两个三角形相似,即可证明△ACD∽△CBD;d(2)由(1)知△ACD ∽△CBD ,然后根据相似三角形的对应角相等可得:∠A=∠BCD ,然后由∠A+∠ACD=90°,可得:∠BCD+∠ACD=90°,即∠ACB=90°.【解答】(1)证明:∵CD 是边AB 上的高,∴∠ADC=∠CDB=90°,∵=.∴△ACD ∽△CBD ;(2)解:∵△ACD ∽△CBD ,∴∠A=∠BCD ,在△ACD 中,∠ADC=90°,∴∠A+∠ACD=90°,∴∠BCD+∠ACD=90°,即∠ACB=90°.【点评】此题考查了相似三角形的判定与性质,解题的关键是:熟记相似三角形的判定定理与性质定理. 21.(8分)(2015•南京)为了了解2014年某地区10万名大、中、小学生50米跑成绩情况,教育部门从这三类学生群体中各抽取了10%的学生进行检测,整理样本数据,并结合2010年抽样结果,得到下列统计图:(1)本次检测抽取了大、中、小学生共 10000 名,其中小学生 4500 名;(2)根据抽样的结果,估计2014年该地区10万名大、中、小学生中,50米跑成绩合格的中学生人数为 36000 名;(3)比较2010年与2014年抽样学生50米跑成绩合格率情况,写出一条正确的结论.【考点】条形统计图;用样本估计总体;扇形统计图.【分析】(1)根据“教育部门从这三类学生群体中各抽取了10%的学生进行检测”,可得100000×10%,即可得到本次检测抽取了大、中、小学生共多少名,再根据扇形图可得小学生所占45%,即可解答;(2)先计算出样本中50米跑成绩合格的中学生所占的百分比,再乘以10万,即可解答;(3)根据条形图,写出一条即可,答案不唯一.【解答】解:(1)100000×10%=10000(名),10000×45%═4500(名).故答案为:10000,4500;(2)100000×40%×90%=36000(名).故答案为:36000;(3)例如:与2010年相比,2014年该地区大学生50米跑成绩合格率下降了5%(答案不唯一).【点评】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.22.(8分)(2015•南京)某人的钱包内有10元、20元和50元的纸币各1张,从中随机取出2张纸币.(1)求取出纸币的总额是30元的概率;(2)求取出纸币的总额可购买一件51元的商品的概率.【考点】列表法与树状图法.【专题】计算题.【分析】(1)先列表展示所有3种等可能的结果数,再找出总额是30元所占结果数,然后根据概率公式计算;(2)找出总额超过51元的结果数,然后根据概率公式计算.【解答】解:(1)列表:共有3种等可能的结果数,其中总额是30元占1种,所以取出纸币的总额是30元的概率=;(2)共有3种等可能的结果数,其中总额超过51元的有2种,所以取出纸币的总额可购买一件51元的商品的概率为.【点评】本题考查了列表法与树状图法:利用列表法和树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.23.(8分)(2015•南京)如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O 的正北方向C处,测得∠CAO=45°,轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km/h和36km/h,经过0.1h,轮船甲行驶至B处,轮船乙行驶至D处,测得∠DBO=58°,此时B处距离码头O多远?(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)【考点】解直角三角形的应用.【分析】设B处距离码头Oxkm,分别在Rt△CAO和Rt△DBO中,根据三角函数求得CO 和DO,再利用DC=DO﹣CO,得出x的值即可.【解答】解:设B处距离码头Oxkm,在Rt△CAO中,∠CAO=45°,∵tan∠CAO=,∴CO=AO•tan∠CAO=(45×0.1+x)•tan45°=4.5+x,在Rt△DBO中,∠DBO=58°,∵tan∠DBO=,∴DO=BO•tan∠DBO=x•tan58°,∵DC=DO﹣CO,∴36×0.1=x•tan58°﹣(4.5+x),∴x=≈=13.5.因此,B处距离码头O大约13.5km.【点评】本题考查了解直角三角形的应用,熟练掌握三角形中的边角关系是解题的关键. 24.(8分)(2015•南京)如图,AB∥CD,点E,F分别在AB,CD上,连接EF,∠AEF、∠CFE的平分线交于点G,∠BEF、∠DFE的平分线交于点H.(1)求证:四边形EGFH是矩形;(2)小明在完成(1)的证明后继续进行了探索,过G作MN∥EF,分别交AB,CD于点M,N,过H作PQ∥EF,分别交AB,CD于点P,Q,得到四边形MNQP,此时,他猜想四边形MNQP是菱形,请在下列框中补全他的证明思路.【考点】菱形的判定;全等三角形的判定与性质;矩形的判定.【专题】证明题.【分析】(1)利用角平分线的定义结合平行线的性质得出∠FEH+∠EFH=90°,进而得出∠GEH=90°,进而求出四边形EGFH是矩形;(2)利用菱形的判定方法首先得出要证▱MNQP是菱形,只要证MN=NQ,再证∠MGE=∠QFH得出即可.【解答】(1)证明:∵EH平分∠BEF,∴∠FEH=∠BEF,∵FH平分∠DFE,∴∠EFH=∠DFE,∵AB∥CD,∴∠BEF+∠DFE=180°,∴∠FEH+∠EFH=(∠BEF+∠DFE)=×180°=90°,∵∠FEH+∠EFH+∠EHF=180°,∴∠EHF=180°﹣(∠FEH+∠EFH)=180°﹣90°=90°,同理可得:∠EGF=90°,∵EG平分∠AEF,∴∠GEF=∠AEF,∵EH平分∠BEF,∴∠FEH=∠BEF,∵点A、E、B在同一条直线上,∴∠AEB=180°,即∠AEF+∠BEF=180°,∴∠FEG+∠FEH=(∠AEF+∠BEF)=×180°=90°,即∠GEH=90°,∴四边形EGFH是矩形;(2)解:答案不唯一:由AB∥CD,MN∥EF,PQ∥EF,易证四边形MNQP是平行四边形,要证▱MNQP是菱形,只要证MN=NQ,由已知条件:FG平分∠CFE,MN∥EF,故只要证GM=FQ,即证△MGE≌△QFH,易证GE=FH、∠GME=∠FQH.,即可得证.故只要证∠MGE=∠QFH,易证∠MGE=∠GEF,∠QFH=∠EFH,∠GEF=∠EFH【点评】此题主要考查了矩形的判定以及菱形的判定和角平分线的性质,根据题意得出证明菱形的方法是解题关键.25.(10分)(2015•南京)如图,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要)求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3【考点】作图—应用与设计作图;等腰三角形的判定;勾股定理;正方形的性质.【专题】作图题.【分析】①以A为圆心,以3为半径作弧,交AD、AB两点,连接即可;②连接AC,在AC上,以A为端点,截取1.5个单位,过这个点作AC的垂线,交AD、AB两点,连接即可;③以A为端点在AB上截取3个单位,以截取的点为圆心,以3个单位为半径画弧,交BC一个点,连接即可;④连接AC,在AC上,以C为端点,截取1.5个单位,过这个点作AC的垂线,交BC、DC两点,然后连接A与这两个点即可;⑤以A为端点在AB上截取3个单位,再作着个线段的垂直平分线交CD一点,连接即可.【解答】解:满足条件的所有图形如图所示:【点评】此题主要考查了作图﹣应用与设计作图,关键是掌握等腰三角形的判定方法.26.(8分)(2015•南京)如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD 的延长线交于点E,且DC=DE.(1)求证:∠A=∠AEB;(2)连接OE,交CD于点F,OE⊥CD,求证:△ABE是等边三角形.【考点】圆内接四边形的性质;等边三角形的判定与性质;圆周角定理.【专题】证明题.【分析】(1)根据圆内接四边形的性质可得∠A+∠BCD=180°,根据邻补角互补可得∠DCE+∠BCD=180°,进而得到∠A=∠DCE,然后利用等边对等角可得∠DCE=∠AEB,进而可得∠A=∠AEB;(2)首先证明△DCE是等边三角形,进而可得∠AEB=60°,再根据∠A=∠AEB,可得△ABE 是等腰三角形,进而可得△ABE是等边三角形.【解答】证明:(1)∵四边形ABCD是⊙O的内接四边形,∴∠A+∠BCD=180°,∵∠DCE+∠BCD=180°,∴∠A=∠DCE,∵DC=DE,∴∠DCE=∠AEB,∴∠A=∠AEB;(2)∵∠A=∠AEB,∴△ABE是等腰三角形,∵EO⊥CD,∴CF=DF,∴EO是CD的垂直平分线,∴ED=EC,∵DC=DE,∴DC=DE=EC,∴△DCE是等边三角形,∴∠AEB=60°,∴△ABE是等边三角形.【点评】此题主要考查了等边三角形的判定和性质,以及圆内接四边形的性质,关键是掌握圆内接四边形对角互补.27.(10分)(2015•南京)某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD、线段CD分别表示该产品每千克生产成本y1(单位:元)、销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.(1)请解释图中点D的横坐标、纵坐标的实际意义;(2)求线段AB所表示的y1与x之间的函数表达式;)当该产品产量为多少时,获得的利润最大?最大利润是多少?(3【考点】二次函数的应用.【专题】压轴题.【分析】(1)点D的横坐标、纵坐标的实际意义:当产量为130kg时,该产品每千克生产成本与销售价相等,都为42元;(2)根据线段AB经过的两点的坐标利用待定系数法确定一次函数的表达式即可;(3)利用总利润=单位利润×产量列出有关x的二次函数,求得最值即可.【解答】解:(1)点D的横坐标、纵坐标的实际意义:当产量为130kg时,该产品每千克生产成本与销售价相等,都为42元;(2)设线段AB所表示的y1与x之间的函数关系式为y=k1x+b1,∵y=k1x+b1的图象过点(0,60)与(90,42),∴∴,∴这个一次函数的表达式为;y=﹣0.2x+60(0≤x≤90);(3)设y2与x之间的函数关系式为y=k2x+b2,∵经过点(0,120)与(130,42),∴,解得:,∴这个一次函数的表达式为y2=﹣0.6x+120(0≤x≤130),设产量为xkg时,获得的利润为W元,当0≤x≤90时,W=x[(﹣0.6x+120)﹣(﹣0.2x+60)]=﹣0.4(x﹣75)2+2250,∴当x=75时,W的值最大,最大值为2250;当90≤x≤130时,W=x[(﹣0.6x+120)﹣42]=﹣0.6(x﹣65)2+2535,由﹣0.6<0知,当x>65时,W随x的增大而减小,∴90≤x≤130时,W≤2160,∴当x=90时,W=﹣0.6(90﹣65)2+2535=2160,因此当该产品产量为75kg时,获得的利润最大,最大值为2250.【点评】本题考查了二次函数的应用,解题的关键是从实际问题中抽象出二次函数模型,难度不大.参与本试卷答题和审题的老师有:张其铎;放飞梦想;zcl5287;caicl;sdwdmahongye;王学峰;1987483819;gbl210;sd2011;星期八;733599;zhangCF;CJX;gsls;守拙;sjzx(排名不分先后)菁优网2016年3月1日。
2015年南京市中考数学试题解析

22015年江苏省南京市中考数学试卷(满分1 2 0分,考试时间120分钟)、选择题(本大题共 6小题,每小题2分,满分12分,在每小题给出的四个选项中,只 有一项是符合题目要求的.)【答案】5. (2015江苏省南京市 5, 2分)估计【解析】2.236,则丄」0.6185 2.3 10 5B . 3.2 106 C . 2.3 10 6D . 3.2 101. (2015江苏省南京市, 1, 2分)计算5 3的结果是 A . - 2 【答案】BC . — 8【解析】2. (2015江苏省南京市, 2, 2分) 计算( xy3)2的结果是 【答案】【解A由积的乘方公式可得3. (2015江苏省南京市, 3, 2分) 如图,在△ ABC 中,DE // BCAD 1 DB 2,则下列结论中正确的是AE 1 A .AC 2DE 1 BC 2ADE 的周长 1C =—'ABC 的周长 3ADE 的面积_ 1 ABC 的面积=3【答案】C【解析】由周长比等于相似比4. (2015江苏省南京市,4, 2分)某市2013年底机动车的数量是106辆,2014年新增【解析】2 1063 1052.3 106A . 0.4与0.5之间 【答案】CB . 0.5与0.6之间C . 0.6与0.7之间D . 0.7与0.8之间6, 2 分)如图,在矩形 ABCD 中,AB=4, AD=5, AD 、AB 、BC分别与O O 相切于E 、F 、G 三点,过点D 作O O 的切线交139A .B .-3 2C . 4>/13D . 2/53【答案】A【解析】由勾股定理得:设GM=x , (3 x )242 (3 X )2413 解得,X ,所以DM = —.33二、填空题(本大题共10小题,每小题2分,共20分•不需写出解答过程,请把答案直接 填在答题卡相应位置上)7. (2015江苏省南京市, 乙2分)4的平方根是 ▲ ; 4的算术平方根是 ▲【答案】 2 ; 2【解析】 、忆 2,-、4 28. jscm (2015江苏省南京市,8, 2分)若式子在实数范围内有意义,则 x 的取值范围 是 ▲ .【答案】X 1 【解析】x 10,x 15 . 159. jscm ( 2015江苏省南京市,9, 2分)计算的结果是 _________ .V3【答案】5 【解析】二5—砧,5,5 510. jscm (2015江苏省南京市,10, 2分)分解因式(a b )(a 4b ) ab 的结果是 ▲ .【答案】(a 2b )2【解析】(a b )(a 4b ) ab a 2 4ab ab 4b 2 ab a 2 4ab 4b 2 (a 2b )22x 11“” … 11. (2015江苏省市,11, 2分)不等式 的解集是▲ .2x 1 3【答案】 1 x 16. (2015江苏省南京市, BC 于点M ,贝U DM 的长为【解析】2x 1 1,2x 2, x 12x 1 3,2x 2,x 11 x 1212. (2015省市,12,分)已知方程x mx 3 0的一个根是1,则它的另一个根是▲ __ , m的值是▲.【答案】3; -4【解析】1 m 3 0, m 4x24x 3 0(x 1)(x 3) 0x 1,x 313. (2015江苏省南京市,13,2分)在平面直角坐标系中,点A的坐标是(2,-3),作点A关于x轴的对称点得到点A'再作点A'关于y轴的对称点,得到点A ;则点A'' 的坐标是(▲,▲).【答案】-2; 3【解析】(2, -3)关于x轴对称(2, 3),关于y轴对称(-2, 3)14. (2015江苏省南京市,14, 2分)某工程队有14名员工,他们的工种及相应每人每月工资如下表所示.工种人数每人每月工资/元电工57000木工46000瓦丄56000现该工程队进行了人员调整:减少木工2名,增加电工,瓦工各1名.与调整前相比,该工程队员工月工资的方差▲(填变小” 不变”或变大”.【答案】变大【解析】电工的工资高于瓦工工资。
2015南京市中考试卷(权威数学原卷附标准答案)

A为 OB 的中点. 若函数Yi
=工 ,
则Yz与z的函数表达式是
•
12
三、解答题(本大题共11小题,共88分.请在答题卡指定区域内作答,解答时应写出文字说 明、证明过程或演算步骤) 17. (6分)解不等式2(x十1) 1二三 3x
+z,并把它的解集在数轴上表示出来.
题 。 口
吵,“ 哼/“
句3
第
现该工程队进行了人员调整: 减少木工 2名, 增加电工、 瓦工各1名. 与调整前相比, 该工程队员工月工资的方差 • 15. 如图, 在①0的内接五边形 ABCDE 中, ζ CAD = 35 , 则ζB十ζE= Yty, = � A
B
E
X
(第15题)
(第16题)
一 象限内分别交于点A、 B, 且 16. 如图, 过原点。的直线与反比例函数川、 川的图像在第
l-5 十 31 的结果是
2 B. 2 xy 3 ) 的结果是
2
C. -8
y
D. 8
9
2.计算(- A. x 2 y 6
B. -x 2
6
C. x 2
y
D. ·-x 2
y
9
3.如图,在
!::,.
ABC 中 , DE//BC,
AD → 1 一一= ,则下列结论中正确的是 DB
B. �
A
A. 主主_l AC 2 C.
一 一
19. (7分)计算
20. (8分)如图, liABC 中,CD是边 AB 上的高,且 (1)求证 liACD
U)
(2)求ζACB 的大小.
21. (8分)为了了解2014年某地区10万名大、中、小学生50米跑成绩情况,教育部门从这 三类学生群体中各抽取了10%的学生进行检测.整理样本数据,并结合2010年抽样结 果,得到下列统计图. 2014年某地区抽样学生 人数分布扇形统计图 2010年、2014年某地区抽样学生50米跑 成绩合格率条形统计圄
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学试卷
第 5 页 (共 11 页)
27. (10 分)某企业生产并销售某种产品,假设销售量与产量相等.下图中的折线 ABD、线段 CD 分别表示该产品每千克生产成本 y1(单位:元) 、销售价 y2(单位:元)与产量 x(单 位:kg)之间的函数关系. (1)请解释图中点 D 的横坐标、纵坐标的实际意义. (2)求线段 AB 所表示的 y1 与 x 之间的函数表达式. (3)当该产品产量为多少时,获得的利润最大?最大利润是多少?
由 AB∥CD,MN∥EF,PQ∥EF,易证四边 形 MNQP 是平行四边形.要证□MNQP 是菱形, 只要证 NM=NQ. 由已知条件 ≌△QFH.易证 ∠EFH, ▲ ▲ , ▲ ▲ , MN∥EF, ,故只要证∠ 可证 NG=NF,故只要证 GM=FQ,即证△MGE MGE=∠QFH.易证∠MGE=∠GEF,∠QFH= ,即可得证. C N G D A M E P B
二、填空题(本大题共 10 小题,每小题 2 分,共 20 分) 7.±2;2 12.3;-4 8.x≥-1 13.-2;3 9. 5 14.变大 10.(a-2b)2 15.215 11.-1<x<1 16.y2= 4 x
三、解答题(本大题共 11 小题,共 88 分) 17. (本题 6 分) 解:去括号,得 2x+2-1≥3x+2. 移项,得 2x-3x≥2-2+1. 合并同类项,得-x≥1. 系数化为 1,得 x≤-1. 这个不等式的解集在数轴上表示如下图所示.
H
F (第 24 题)
Q
数学试卷
第 4 页 (共 11 页)
25. (10 分)如图,在边长为 4 的正方形 ABCD 中,请画出以 A 为一个顶点,另外两个顶点在 正方形 ABCD 的边上,且含边长为 3 的所有大小不同的等腰三角形. (要求:只要画出示 意图,并在所画等腰三角形长为 3 的边上标注数字 3)
10.分解因式(a-b)(a-4b)+ab 的结果是 11.不等式组 的解集是 ▲
12.已知方程 x2+mx+3=0 的一个根是 1,则它的另一个根是 再作点 A′关于 y 轴的对称点,得到点 A′′,则点 A′′的坐标是( 工种 电工 木工 瓦工 人数 5 4 5
13.在平面直角坐标系中,点 A 的坐标是(2,-3) ,作点 A 关于 x 轴的对称点,得到点 A′, ▲ , ▲ ) . 14.某工程队有 14 名员工,他们的工种及相应每人每月工资如下表所示. 每人每月工资/元 7000 6000 5000
A D E
B.2
C.-8
D. 8
3.如图,在△ABC 中,DE∥BC, AE 1 A. = AC 2 C.
AD 1 = ,则下列结论中正确的是 DB 2 DE 1 B. = BC 2
△ADE 的周长 1 △ADE 的面积 1 B C = D. = 3 (第 3 题) △ABC 的周长 △ABC 的面积 3 4.某市 2013 年底机动车的数量是 2×106 辆,2014 年新增 3×105 辆.用科学记数法表示该市 2014 年底机动车的数量是 A.2.3×105 辆 5.估计 5-1 介于 2 B.0.5 与 0.6 之间 C.0.6 与 0.7 之间 D.0.7 与 0.8 之间 B.3.2×105 辆 C.2.3×106 辆 D.3.2×106 辆
AD CD = . CD BD
C
A
D (第 20 题)
B
21. (8 分)为了了解 2014 年某地区 10 万名大、中、小学生 50 米跑成绩情况,教育部门从这 三类学生群体中各抽取了 10%的学生进行检测.整理样本数据,并结合 2010 年抽样结果, 得到下列统计图.
2014 年某地区抽样学生 人数分布扇形统计图 合格率 90% 中学生 小学生 45% 40% 大学生 15% 80% 70% 60% 50% 0 大学生 中学生 小学生 学生群体 80% 75% 75% 90% 80% 70% 2010 年、2014 年某地区抽样学生 50 米跑 成绩合格率条形统计图 2010 年 2014 年
2
·······················7 分
2 1 a+b - · (a+b)(a-b) a(a-b) a a+b 2a a+ b - · a (a+b)(a-b) a a(a+b)(a-b)
2a-(a+b) a+ b = · a a(a+b)(a-b) a-b a+ b = · a a(a+b)(a-b)
数学试卷
第 7 页 (共 11 页)
1 = 2. a
·································································································7 分
20. (本题 8 分) (1)证明:∵ ∴ 又 ∴ (2)解:∵ ∴ ∴ ∴ 即 21. (本题 8 分) 解: (1)10 000;4 500. (2)36 000. ········································································ 2 分 ········································································5 分 ···················································· 8 分 CD 是边 AB 上的高, ∠ADC=∠CDB=90°. AD CD = , CD BD △ACD∽△CBD. △ACD∽△CBD, ∠A=∠BCD. ∠A+∠ACD=90°. ∠BCD+∠ACD=90°, ∠ACB=90°. ··································································· 8 分 ··························································· 4 分
22. (8 分)某人的钱包内有 10 元、20 元和 50 元的纸币各 1 张.从中随机取出 2 张纸币. (1)求取出纸币的总额是 30 元的概率; (2)求取出纸币的总额可购买一件 51 元的商品的概率.
23. (8 分)如图,轮船甲位于码头 O 的正西方向 A 处,轮船乙位于码头 O 的正北方向 C 处, 测得∠CAO=45°.轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速 度分别为 45 km/h 和 36 km/h.经过 0.1 h,轮船甲行驶至 B 处,轮船乙行驶至 D 处,测得 ∠DBO=58°.此时 B 处距离码头 O 有多远? (参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)
G M (第 6 题)
数学试卷
第 1 页 (共 11 页)
二、填空题(本大题共 10 小题,每小题 2 分,共 20 分.不需写出解答过程,请把答案直接 填写在答题卡相应位置 上) ....... 7.4 的平方根是 ▲ ;4 的算术平方根是 ▲ . ▲ . 8.若式子 x+1在实数范围内有意义,则 x 的取值范围是 9.计算 5× 15 的结果是 3 2x+1>-1, 2x+1<3 ▲ . ▲ . ▲ , m 的值是 ▲ . .
A.0.4 与 0.5 之间
6.如图,在矩形 ABCD 中,AB=4,AD=5,AD、AB、BC 分别与⊙O 相切于 E、F、G 三点, 过点 D 作⊙O 的切线交 BC 于点 M,切点为 N,则 DM 的长为 13 A. 3 C. 4 13 3 9 B. 2 D. 2 5
A F B E D
O
N C
2 3 18. (7 分)解方程 = . x-3 x
-3 -2
-1
0
1
2
3
(第 17 题)
19. (7 分)计算
2 1 a - 2 ÷ . 2 a -b a -ab a+b
2
20. (8 分)如图,△ABC 中,CD 是边 AB 上的高,且 (1)求证△ACD∽△CBD; (2)求∠ACB 的大小.
(第 21 题)
(1)本次检测抽取了大、中、小学生共
▲
名,其中小学生
▲
名;
(2)根据抽样的结果,估计 2014 年该地区 10 万名大、中、小学生中,50 米跑成绩合格 的中学生人数为 ▲ 名; (3)比较 2010 年与 2014 年抽样学生 50 米跑成绩合格率情况,写出一条正确的结论.
数学试卷 第 3 页 (共 11 页)
B
O
C
(第 15 题)
16.如图,过原点 O 的直线与反比例函数 y1、y2 的图像在第一象限内分别交于点 A、B,且 A 1 为 OB 的中点.若函数 y1= ,则 y2 与(共 11 页)
三、解答题(本大题共 11 小题,共 88 分.请在答题卡指定区域 内作答,解答时应写出文字说 ....... 明、证明过程或演算步骤) 17. (6 分)解不等式 2(x+1)-1≥3x+2,并把它的解集在数轴上表示出来.
A D
B (第 25 题)
C
26. (8 分)如图,四边形 ABCD 是⊙O 的内接四边形,BC 的延长线与 AD 的延长线交于点 E, 且 DC=DE. (1)求证∠A=∠AEB. (2)连接 OE,交 CD 于点 F,OE⊥CD.求证:△ABE 是等边三角形.
A
O B F C (第 26 题)
D E
南京市 2015 年初中毕业生学业考试
数
注意事项:
学
1.本试卷共 6 页.全卷满分 120 分.考试时间为 120 分钟.考生答题全部答在答题卡上,答 在本试卷上无效. 2.请认真核对监考教师在答题卡上所粘贴条形码的姓名、考试证号是否与本人相符合,再将 自己的姓名、考试证号用 0.5 毫米黑色墨水签字笔填写在答题卡及本试卷上. 3.答选择题必须用 2B 铅笔将答题卡上对应的答案标号涂黑.如需改动,请用橡皮擦干净后, 再选涂其他答案.答非选择题必须用 0.5 毫米黑色墨水签字笔写在答题卡上的指定位置, 在其他位置答题一律无效. 4.作图必须用 2B 铅笔作答,并请加黑加粗,描写清楚. 一、选择题(本大题共 6 小题,每小题 2 分,共 12 分.在每小题所给出的四个选项中,恰有 一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡 相应位置 上) ... .... 1.计算│-5+3│的结果是 A.-2 2.计算(-xy3)2 的结果是 A.x2y6 B.-x2y6 C.x2y9 D.-x2y9
