山西省太原市中考真题
初三太原试题及答案

初三太原试题及答案一、选择题(每题2分,共20分)1. 太原是中国哪个省份的省会?A. 山西省B. 河北省C. 河南省D. 陕西省答案:A2. 太原的别称是什么?A. 龙城B. 凤城C. 虎城D. 鹿城答案:A3. 太原的著名景点之一是?A. 五台山B. 云冈石窟C. 龙门石窟D. 峨眉山答案:B4. 太原的气候类型是什么?A. 温带季风气候B. 热带雨林气候C. 亚热带季风气候D. 温带大陆性气候答案:A5. 太原的市花是什么?A. 牡丹B. 玫瑰C. 菊花D. 月季答案:D6. 太原的市树是什么?A. 松树B. 柳树C. 槐树D. 柏树答案:C7. 太原的市歌是什么?A. 《太原之歌》B. 《龙城之歌》C. 《山西之歌》D. 《黄河大合唱》答案:B8. 太原的市鸟是什么?A. 燕子B. 麻雀C. 鸽子D. 鹰答案:C9. 太原的市石是什么?A. 玉石B. 玛瑙C. 翡翠D. 钻石答案:B10. 太原的市旗是什么颜色?A. 红色B. 蓝色C. 绿色D. 黄色答案:A二、填空题(每题1分,共10分)11. 太原是中国历史上著名的_________,有着悠久的历史文化。
答案:古都12. 太原的标志性建筑是_________。
答案:双塔寺13. 太原的市花月季花象征着_________。
答案:爱情14. 太原的市树槐树代表着_________。
答案:坚韧15. 太原的市歌《龙城之歌》表达了对太原的_________。
答案:热爱16. 太原的市鸟鸽子象征着_________。
答案:和平17. 太原的市石玛瑙以其_________而闻名。
答案:美丽18. 太原的市旗颜色红色代表着_________。
答案:热情19. 太原是中国_________省的省会。
答案:山西省20. 太原的气候类型是_________。
答案:温带季风气候三、简答题(每题5分,共30分)21. 请简述太原的地理位置。
答案:太原位于中国山西省中部,东临太行山,西靠吕梁山,南濒汾河,北依恒山,地理位置优越。
太原市中考数学试卷真题

太原市中考数学试卷真题一、选择题1. 设函数$f(x)=2x+3$,则$f(-2)$的值为多少?A. -1B. 1C. -4D. 72. 若$3x-2y=7$,则当$x=2$时,$y$的值为多少?A. 4B. 5C. 6D. 73. 已知等差数列的前三项分别为3,6,9,则这个等差数列的公差是多少?A. 2B. 3C. 4D. 54. 直角三角形的斜边长是5,其中一个直角边长是3,求另一个直角边长的值。
A. 4B. 15C. 2D. 65. 若$m:n=3:5$,且$m=15$,则$n$的值是多少?A. 9B. 19C. 25D. 35二、填空题1. 交换律是数学中的一条基本性质,其表达为$a+b=b+a$,当$a=3$,$b=5$时,按照交换律,$a+b$的值为______。
2. 若$\frac{3}{4}x=36$,则$x$的值为______。
3. 若$2x-5=7$,则$x$的值为______。
4. 一个等差数列的公差是2,第一项是3,若第五项等于13,则这个数列的第十项的值为______。
5. 一条直线上有A、B两个点,其中A点的坐标是(-2, 3),B点的坐标是(4, -5),则线段AB的长度为______。
三、解答题1. 解方程:$2x+7=15$。
2. 已知等差数列的前两项是3和8,前五项的和是40,求这个等差数列的公差。
3. 在直角三角形ABC中,已知$\sin A=\frac{1}{2}$,求$\cos A$的值。
4. 某商品原价100元,现在打八折出售,请计算打折后的价格。
5. 小明花了1.5小时从家里到学校,如果他的平均速度是12km/h,求他家到学校的距离。
文章到这里结束。
太原语文中考试题及答案

太原语文中考试题及答案####### 一、积累与运用(共20分)1. 下列词语中,加点字的读音完全正确的一项是()(2分)A. 倔强(jué)B. 矜持(jīn)C. 恣意(zì)D. 蹒跚(pán)2. 下列词语中,没有错别字的一项是()(2分)A. 锐不可挡B. 再接再励C. 黄粱美梦D. 甘败下风3. 下列句子中,加点成语使用正确的一项是()(2分)A. 他虽然年过花甲,但精神矍铄,真是老当益壮。
B. 他虽然年过花甲,但精神矍铄,真是老气横秋。
C. 他虽然年过花甲,但精神矍铄,真是风华正茂。
D. 他虽然年过花甲,但精神矍铄,真是意气风发。
4. 下列句子中,没有语病的一项是()(2分)A. 通过这次活动,使我们对环保有了更深的认识。
B. 这次活动,使我们对环保有了更深的认识。
C. 通过这次活动,我们对环保有了更深的认识。
D. 这次活动,对环保有了更深的认识。
5. 将下列句子组成语意连贯的一段话,排序正确的一项是()(2分)①他是一位著名的作家。
②他的作品深受读者喜爱。
③他的作品多次获奖。
④他的作品风格独特。
A. ①④②③B. ①②④③C. ①④③②D. ①③④②6. 根据题目要求,将下列句子改写成被动句。
(2分)原句:我们经常帮助他。
改写:他经常被我们帮助。
7. 根据题目要求,将下列句子改写成双重否定句。
(2分)原句:他一定会来。
改写:他不可能不来。
8. 根据题目要求,将下列句子改写成反问句。
(2分)原句:他是一个诚实的人。
改写:他难道不是一个诚实的人吗?9. 根据题目要求,将下列句子改写成设问句。
(2分)原句:我们应该保护环境。
改写:我们为什么要保护环境呢?因为保护环境是每个人的责任。
10. 根据题目要求,将下列句子改写成感叹句。
(2分)原句:春天真美丽。
改写:春天多么美丽啊!#### 二、阅读理解(共40分)(一)阅读下面的文章,完成11-15题。
(20分)《故乡的云》我的故乡在北方的一个小镇,那里的天空总是那么高远,那么湛蓝。
山西省太原市道德与法治中考测试试卷及答案解析

山西省太原市道德与法治中考测试试卷及答案解析一、单项选择题(本大题有12小题,每小题4分,共48分)1、以下关于公民权利与义务的说法,正确的是()A. 公民的权利和义务是相互依存、相互促进的B. 公民既是合法权利的享有者,又是法定义务的承担者C. 公民的权利与义务具有一致性D. 公民的权利可以放弃,法定义务必须履行答案:C解析:本题要求选出关于公民权利与义务关系说法正确的选项。
选项A,公民的权利和义务是相互依存、相互促进的,但这只是描述权利与义务之间关系的一个方面,没有全面概括两者的关系,故选项A可排除。
选项B,公民既是合法权利的享有者,又是法定义务的承担者,这是公民身份的双重性,但同样没有全面反映权利与义务的关系,故选项B可排除。
选项C,公民的权利与义务具有一致性,既相互依存也相互促进。
公民权利的实现需要义务的履行,义务的履行促进权利的实现,这是权利与义务关系的全面概括,故选项C正确。
选项D,公民的权利确实可以放弃,但法定义务必须履行,这虽然描述了权利与义务的不同性质,但并未直接反映两者的关系,故选项D可排除。
2、2023年1月1日起,《中华人民共和国家庭教育促进法》正式实施,该法规定:“未成年人的父母或者其他监护人负责实施家庭教育,国家和社会为家庭教育提供指导、支持和服务。
”这说明()A. 家庭教育和学校教育是相辅相成的B. 家庭教育在未成年人成长中起决定性作用C. 家庭教育要落实立德树人根本任务D. 未成年人应自觉接受家庭、学校等各方面的教育答案:C解析:本题要求分析《中华人民共和国家庭教育促进法》中关于家庭教育的规定所体现的道理。
选项A,虽然家庭教育和学校教育在未成年人的成长过程中都扮演着重要角色,但题干中并未提及学校教育,故选项A与题意不符。
选项B,家庭教育在未成年人成长中起着重要作用,但说它起“决定性作用”过于绝对,故选项B错误。
选项C,《中华人民共和国家庭教育促进法》明确规定父母或其他监护人负责实施家庭教育,且家庭教育需要落实立德树人的根本任务,这体现了家庭教育的重要性和其应承担的教育责任,故选项C正确。
太原中考数学试题及答案

太原中考数学试题及答案一、选择题(每题3分,共30分)1. 以下哪个数是无理数?A. 2B. √2C. 0.33333...D. π答案:B2. 已知函数y=2x+3,当x=1时,y的值为:A. 5B. 6C. 7D. 8答案:A3. 以下哪个图形是轴对称图形?A. 平行四边形B. 矩形C. 梯形D. 任意三角形答案:B4. 计算下列表达式的结果:(3x^2 - 2x + 1) - (x^2 - 4x + 3) =A. 2x^2 + 2x - 2B. 2x^2 + 2x + 2C. x^2 + 2x - 2D. x^2 + 2x + 2答案:C5. 一个圆的半径为5,求其周长:A. 10πB. 20πC. 25πD. 30π答案:B6. 如果一个角的补角是120°,那么这个角的度数为:A. 60°B. 30°C. 90°D. 120°答案:B7. 以下哪个选项是正确的因式分解?A. x^2 - 4 = (x - 2)(x + 2)B. x^2 - 4 = (x - 4)(x + 4)C. x^2 - 4 = (x + 2)(x - 2)D. x^2 - 4 = (x - 2)^2答案:A8. 已知等腰三角形的两边长分别为3和5,求其周长:A. 11B. 13C. 16D. 14答案:B9. 计算下列概率:一个袋子里有3个红球和2个蓝球,随机抽取一个球,抽到红球的概率为:A. 0.3B. 0.4C. 0.5D. 0.6答案:D10. 以下哪个选项是正确的几何定理?A. 内角和定理B. 外角和定理C. 对顶角相等定理D. 以上都是答案:D二、填空题(每题3分,共15分)11. 已知等差数列的首项为2,公差为3,求第5项的值:___答案:1712. 一个直角三角形的两条直角边长分别为6和8,求斜边长:___答案:1013. 已知函数y=x^2-6x+8,求顶点的横坐标:___答案:314. 一个扇形的圆心角为60°,半径为4,求扇形的面积:___答案:4π15. 计算下列表达式的值:(2x+3)(2x-3) = ___答案:4x^2 - 9三、解答题(每题10分,共40分)16. 已知一个二次函数y=ax^2+bx+c,其中a=1,b=-4,c=3,求该函数的顶点坐标。
山西省2024年中考考试数学真题试卷(含答案)
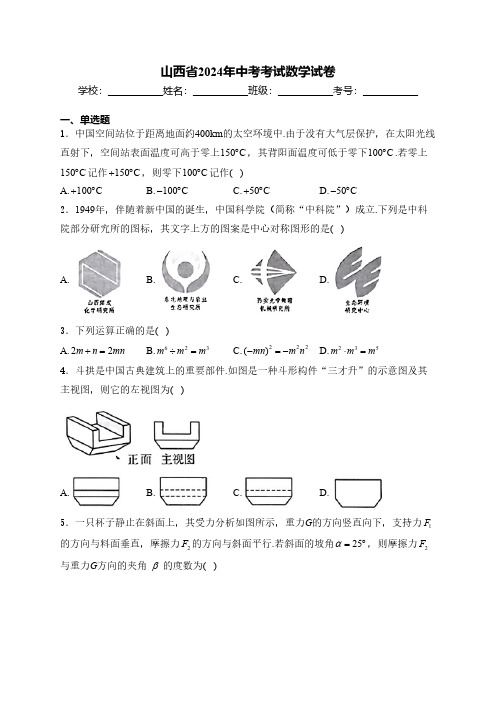
山西省2024年中考考试数学试卷学校:___________姓名:___________班级:___________考号:___________一、单选题1.中国空间站位于距离地面约400km 的太空环境中.由于没有大气层保护,在太阳光线直射下,空间站表面温度可高于零上150C ︒,其背阳面温度可低于零下100C ︒.若零上150C ︒记作150C +︒,则零下100C ︒记作( )A.100C +︒B.100C -︒C.50C +︒D.50C-︒2.1949年,伴随着新中国的诞生,中国科学院(简称“中科院”)成立.下列是中科院部分研究所的图标,其文字上方的图案是中心对称图形的是( )A. B. C. D.3.下列运算正确的是( )A.22m n mn += B.623m m m ÷= C.222()mn m n -=- D.235m m m ⋅=4.斗拱是中国古典建筑上的重要部件.如图是一种斗形构件“三才升”的示意图及其主视图,则它的左视图为( )A. B. C. D.5.一只杯子静止在斜面上,其受力分析如图所示,重力G 的方向竖直向下,支持力1F 的方向与料面垂直,摩擦力2F 的方向与斜面平行.若斜面的坡角25α=︒,则摩擦力2F 与重力G 方向的夹角β的度数为( )A.155︒B.125︒C.115︒D.65︒6.已知点()11,A x y ,()22,B x y 都在正比例函数3y x =的图象上,若12x x <,则1y 与2y 的大小关系是( )A.12y y >B.12y y <C.12y y =D.12y y ≥7.如图,已知ABC △,以AB 为直径的O 交BC 于点D ,与AC 相切于点A ,连接OD .若80AOD ∠=︒,则C ∠的度数为( )A.30︒B.40︒C.45︒D.50︒8.一个不透明的盒子里装有一个红球、一个白球和一个绿球,这些球除颜色外都相同.从中随机摸出一个球,记下颜色后不放回,再从中随机摸出一个球,则两次摸到的球恰好有一个红球的概率是( )A.13 B.23 C.49 D.599.生物学研究表明,某种蛇在一定生长阶段.其体长(cm)y 是尾长(cm)x 的一次函数,部分数据如下表所示,则y 与x 之间的关系式为( )尾长(cm)x 6810体长(cm)y 45.560.575.5A.7.5.0.5y x =+ B.7.5.0.5y x =- C.15y x = D.1545.5y x =+10.在四边形ABCD 中,点E ,F ,G ,H 分别是边AB ,BC ,CD ,DA 的中点,EG ,FH 交于点O .若四边形ABCD 的对角线相等,则线段EG 与FH 一定满足的关系为( )A.互相垂直平分B.互相平分且相等C.互相垂直且相等D.互相垂直平分且相等二、填空题________2(填“>”“<”或“=”).12.黄金分割是汉字结构最基本的规律.借助如图的正方形习字格书写的汉字“晋”端庄稳重、舒展美观.已知一条分制线的端点A ,B 分别在习字格的边MN ,PQ 上,且//AB NP ,“晋”字的笔画“、”的位置在AB 的黄金分割点C 处,且BC AB =若2cm NP =,则BC 的长为________cm (结果保留根号).13.机器狗是一种模拟真实犬只形态和部分行为的机器装置,其最快移动速度(m /s)v 是载重后总质量(kg)m 的反比例函数.已知一款机器狗载重后总质量60kg m =时,它的最快移动速度6m /s v =;当其载重后总质量90kg m =时,它的最快移动速度v =________m /s .14.如图1是小区围墙上的花窗,其形状是扇形的一部分,图2是其几何示意图(阴影部分为花窗).通过测量得到扇形AOB 的圆心角为90︒,1m OA =,点C ,D 分别为OA ,OB 的中点,则花窗的面积为________2m .15.如图,在ABCD 中,AC 为对角线,AE BC ⊥于点E ,点F 是AE 延长线上一点,且ACF CAF ∠=∠,线段AB ,CF 的延长线交于点G .若AB =4AD =,tan 2ABC ∠=,则BG 的长为________.三、解答题16.(1)计算:211(6)[(3)(1)]32-⎛⎫-⨯-+-+- ⎪⎝⎭;(2)化简:2112111x x x x +⎛⎫+÷ ⎪-+-⎝⎭.17.为加强校园消防安全,学校计划购买某种型号的水基灭火器和干粉灭火器共50个.其中水基灭火器的单价为540元/个,干粉灭火器的单价为380元/个.若学校购买这两种灭火器的总价不超过21000元则最多可购买这种型号的水基灭火器多少个?18.为激发青少年崇尚科学、探索木知的热情,学校开展“科学小博士”知识竞赛.各班以小组为单位组织初赛,规定满分为10分,9分及以上为优秀.数据整理:小夏将本班甲、乙两组同学(每组8人)初赛的成绩整理成如下的统计图,数据分析:小夏对这两个小组的成绩进行了如下分析:平均数(分)中位数(分)众数(分)方差优秀率甲组7.625a 7 4.4837.5%乙组7.6257b 0.73c请认真阅读上述信息,回答下列问题:(1)填空:a =________,b =________,c =________.(2)小祺认为甲、乙两组成绩的平均数相等,因此两个组成绩一样好.小夏认为小祺的观点比较片面,请结合上表中的信息帮小夏说明理由(写出两条即可).19.当下电子产品更新换代速度加快,废旧智能手机数量不断增加,科学处理废旧智能手机,既可减少环境污染,还可回收其中的可利用资源据研究,从每吨废旧智能手机中能提炼出的白银比黄金多760克.已知从2.5吨废旧智能手机中提炼出的黄金,与从0.6吨废旧智能手机中提炼出的白银克数相等.求从每吨废旧智能手机中能提炼出黄金与白银各多少克.20.研学实践:为重温解放军东渡黄河“红色记忆”,学校组织研学活动.同学们来到毛主席东渡黄河纪念碑所在地,在了解相关历史背景后,利用航模搭载的3D 扫描仪采集纪念碑的相关数据.数据采集:如下图,点A 是纪念碑顶部一点,AB 的长表示点A 到水平地面的距离.航模从纪念碑前水平地面的点M 处竖直上升,飞行至距离地面20米的点C 处时,测得点A 的仰角18.4ACD ∠=︒;然后沿CN 方向继续飞行,飞行方向与水平线的夹角37NCD ∠=︒,当到达点A 正上方的点E 处时,测得9AE =米;…数据应用:已知图中各点均在同一竖直平面内,E ,A ,B 三点在同一直线上.请根据上述数据,计䇡纪念碑顶部点A 到地面的距离AB 的长(结果精确到1米.参考数据:sin 370.60︒≈,cos370.80︒≈,tan 370.75︒≈,sin18.40.32︒≈,cos18.40.95︒≈,tan18.40.33︒≈).21.阅读与思考下面是博学小组研究性学习报告的部分内容,请认真阅读”并完成相应任务.(1)直接写出研究报告中“▲”处空缺的内容;_________.(2)如图3,六边形ABCDEF 是等边半正六边形.连接对角线AD ,猜想BAD ∠与FAD ∠的数量关系,并说明理由;(3)如图4,已知ACE △是正三角形、O 是它的外接圆.请在图4中作一个等边半正六边形ABCDEF (要求:尺规作图、保留作图痕迹,不写作法).22.综合与实践问题情境:如图1,矩形MNKL 是学校花园的示意图,其中一个花坛的轮廓可近似看成由抛物线的一部分与线段AB 组成的封闭图形,点A ,B 在矩形的边MN 上.现要对该花坛内种植区域进行划分,以种植不同花卉,学校而向全体同学征集设计方案,方案设计:如图2,6AB =米,AB 的垂直平分线与抛物线交于点P ,与AB 交于点O ,点P 是抛物线的顶点,且9PO =米,欣欣设计的方案如下:第一步:在线段OP 上确定点C ,使90ACB ∠=︒.用篱笆沿线段AC ,BC 分隔出ABC △区域,种植串串红;第二步:在线段CP 上取点F (不与C ,P 重合),过点F 作AB 的平行线,交抛物线于点D ,E .用篱笆沿DE ,CF 将线段AC ,BC 与抛物线围成的区域分隔成三部分,分别种植不同花色的月季.方案实施:学校采用了欣欣的方案、在完成第一步ABC △区域的分隔后,发现仅剩6米篱笆材料.若要在第二步分隔中恰好用完6米材料,需确定DE 与CF 的长.为此,欣欣在图2中以AB 所在直线为x 轴,OP 所在直线为y 轴建立平面直角坐标系.请按照她的方法解决问题:(1)在图2中画出坐标系,并求抛物线的函数表达式;(2)求6米材料恰好用完时DE 与CF 的长;(3)种植区域分隔完成后,欣欣又想用灯带对该花坛进行装饰,计划将灯带围成一个矩形.她尝试借助图2设计矩形四个顶点的位置,其中两个顶点在抛物线上,另外两个顶点分别在线段AC ,BC 上.直接写出符合设计要求的矩形周长的最大值.23.综合与探究问题情境:如图1,四边形ABCD 是菱形,过点A 作AE BC ⊥于点E ,过点C 作CF AD ⊥于点F .猜想证明:(1)判断四边形AECF 的形状,并说明理由;深入探究:(2)将图1中的ABE △绕点A 逆时针旋转,得到AHG △,点E ,B 的对应点分别为点G,H.①如图2,当线段AH经过点C时,GH所在直线分别与线段AD,CD交于点M,N.猜想线段CH与MD的数量关系,并说明理由;②当直线GH与直线CD垂直时,直线GH分别与直线AD,CD交于点M,N,直线AH与线段CD交于点Q.若5,4==,直接写出四边形AMNQ的面积.AB BE参考答案1.答案:B解析:2.答案:A解析:3.答案:D解析:4.答案:C解析:5.答案:C解析:6.答案:B解析:7.答案:D解析:8.答案:B解析:9.答案:A解析:10.答案:A解析:11.答案:>解析:12.答案:1)解析:13.答案:4解析:14.答案:π1 48⎛⎫-⎪⎝⎭解析:解析:16.答案:(1)-10(2)22xx +解析:(1)原式24(4)=--+-10=-(2)原式11(1)(1)(1)(1)2x x x x x x x ++-+-=⋅+-+2(1)(.1)2(1)(1)22x x x x x x x x +-=⋅=+-++.17.答案:最多可购买这种型号的水基灭火器12个解析:设可购买这种型号的水基灭火器x 个,根据题意,得5403805021000x x +-≤().得12.5x ≤.因为x 为整数,且x 取最大值,所以12x =.答:最多可购买这种型号的水基灭火器12个.18.答案:(1)7.5;7;25%(2)见解析解析:(1)7.5;7;25%.(2)答案不唯一,例如:①甲组成绩的优秀率为37.5%,高于乙组成绩的优秀率25%,所以从优秀率的角度看,甲组成绩比乙组好;②虽然甲、乙两组成绩的平均数相等,但甲组成绩的方差为4.48,高于乙组成绩的方差0.73,所以从方差的角度看,乙组成绩更整齐;③甲组成绩的中位数为7.5分,高于乙组成绩的中位数7分,所以从中位数的角度看,甲组成绩比乙组好,等.因此不能仅从平均数的角度说明两组成绩一样好,可见,小祺的观点比较片面.19.答案:从每吨废旧智能手机中能提炼出黄金210克,白银1000克解析:设从每吨废旧智能手机中能提炼出黄金x 克,白银y 克.根据题意,得7602.50.6y x x y=+⎧⎨=⎩.解得2401000x y =⎧⎨=⎩.答:从每吨废旧智能手机中能提炼出黄金210克,白银1000克.20.答案:27米解析:延长CD 交AB 于点H .由题意得,四边形CMBH 为矩形.20CM HB ∴==.在Rt ACH △中,90AHC ∠=︒,18.4ACH ∠=︒,tan AH ACH CH∴∠=,tan tan18.40.33AH AH AH CH ACH ∴==≈∠︒,在Rt ECH △中,90EHC ∠=︒,37ECH ∠=︒,tan EH ECH CH∴∠=,tan tan 370.75EH EH EH CH ECH ∴==≈∠︒.设AH x =.9AE = ,0~9EH ∴=,90.75x +∴.解得7.1x ≈.7.12027.127AB AH HB ∴=+≈+=≈(米)答:点A 到地面的距离AB 的长约为27米.21.答案:(1)240(2)见解析(3)见解析解析:(1)240.(2)BAD FAD ∠=∠.理由如下:连接BD ,FD .六边形ABCDEF 是等边半正六边形.AB BC CD DE EF FA ∴=====,C E ∠=∠.BCD FED ∴≌△△,BD FD ∴=.在ABD △与AFD △中,,,,AB AF BD FD AD AD =⎧⎪=⎨⎪=⎩BAD FAD ∴≌△△,BAD FAD ∴∠=∠.(3)答案不唯一,例如:如图,六边形ABCDEF 即为所求.22.答案:(1)29(33)y x x =-+-≤≤(2)DE 的长为4米,CF 的长为2米(3)332解析:(1)建立如图所示的平面直角坐标系.OP 所在直线是AB 的垂直平分线,且6AB =,116322OA OB AB ∴===⨯=.∴点B 的坐标为(3,0).9OP = ,∴点P 的坐标为(0,9). 点P 是抛物线的顶点,∴设抛物线的函数表达式为2.9y a x =+. 点(3,0)B 在抛物线29y ax =+上,990a ∴+=.解得1a =-.∴抛物线的函数表达式为29(33)y x x =-+-≤≤.(2) 点D ,E 在抛物线29y x =-+上,∴设点E 的坐标为()2,9m m -+.//DE AB ,交y 轴于点F ,DF EF m ∴==,29OF m =-+,2DE m ∴=. 在Rt ABC △中,90ACB ∠=︒,OA OB =,116322OC AB ∴==⨯=.22936CF OF OC m m ∴=-=-+-=-+.根据题意,得6DE CF +=,2626m m ∴-++=.解,得12m =,20m =(不符合题意,舍去),2m ∴=.24DE m ∴==,262CF m =-+=.答:DE 的长为4米,CF 的长为2米.(3)332.23.答案:(1)矩形(2)①CH MD =;②94或634解析:(1)四边形AECF 为矩形.理由如下:AE BC ⊥ ,CF AD ⊥,90AEC ∴∠=︒,90AFC ∠=︒. 四边形ABCD 为菱形,//AD BC ∴,180AFC ECF ∴∠+∠=︒.18090ECF AFC ∴∠=︒-∠=︒.∴四边形AECF 为矩形.(2)①CH MD =.理由如下:证法一: 四边形ABCD 为菱形,AB AD ∴=,B D ∠=∠.ABE △旋转得到AHG △,AB AH ∴=,B H ∠=∠.AH AD ∴=,H D ∠=∠.HAM DAC ∠=∠ ,HAM DAC ∴≌△△.AM AC ∴=,AH AC AD AM ∴-=-.CH MD ∴=.证法二:如图,连接HD .四边形ABCD 为菱形,AB AD ∴=,B ADC ∠=∠.ABE △旋转得到AHG △,AB AH ∴=,B AHM ∠=∠.AH AD ∴=,AHM ADC ∠=∠.AHD ADH ∴∠=∠.HD AHM ADH ADC ∠∠-∠=∠-∠ .MHD CDH ∴∠=∠.DH HD = ,CDH MHD ∴≌△△.CH MD ∴=.9 4或634.②。
太原中考英语试题及答案

太原中考英语试题及答案一、听力理解(共20分)1. 听下面对话,选择正确答案。
A. 去图书馆B. 去公园C. 去电影院正确答案:C2. 根据对话内容,回答下列问题。
A. 8:00B. 9:00C. 10:00正确答案:A二、阅读理解(共30分)阅读下列短文,回答3-5题。
短文内容:(略)3. 文章主要讨论了什么?A. 环保B. 教育C. 科技正确答案:A4. 作者对环保的态度是什么?A. 支持B. 反对C. 中立正确答案:A5. 文章中提到的具体措施有哪些?A. 减少塑料使用B. 增加公共交通C. 推广太阳能正确答案:A三、完形填空(共20分)阅读下面的短文,从6-10题的选项中选择一个最佳答案填空。
短文内容:(略)6. A. becauseB. soC. but正确答案:A7. A. decidedB. decided toC. decided on正确答案:B8. A. althoughB. asC. if正确答案:A9. A. interestedB. interestingC. interest正确答案:A10. A. to finishB. finishingC. finished正确答案:A四、语法填空(共15分)阅读下面的短文,用括号内单词的适当形式填空。
短文内容:(略)11. I ________ (be) to the Great Wall twice.正确答案:have been12. She ________ (not finish) her homework yet.正确答案:hasn't finished13. ________ (not speak) loudly in the library.正确答案:Don't speak14. The book is ________ (interest) than that one.正确答案:more interesting15. ________ (be) there any milk in the fridge?正确答案:Is there五、书面表达(共15分)根据提示写一篇不少于80词的短文。
初三太原考试题目及答案

初三太原考试题目及答案一、选择题(每题2分,共20分)1. 下列哪个选项是太原的著名历史人物?A. 李白B. 关羽C. 杜甫D. 王安石答案:B2. 太原的市花是什么?A. 牡丹B. 菊花C. 月季D. 玫瑰答案:C3. 太原位于中国的哪个省份?A. 山西省B. 河北省C. 陕西省D. 河南省答案:A4. 太原的著名景点晋祠始建于哪个朝代?A. 唐朝B. 宋朝C. 明朝D. 清朝5. 太原的气候类型属于?A. 温带季风气候B. 亚热带季风气候C. 热带季风气候D. 寒带气候答案:A6. 太原的标志性建筑是什么?A. 太原火车站B. 太原博物馆C. 太原电视塔D. 太原国际会议中心答案:C7. 太原的市树是什么?A. 松树B. 柳树C. 银杏D. 杨树答案:C8. 太原的市鸟是什么?A. 燕子B. 麻雀C. 喜鹊D. 鸽子答案:C9. 太原的著名小吃刀削面是哪个省份的特色?B. 河北省C. 陕西省D. 河南省答案:A10. 太原的著名历史事件是什么?A. 太原起义B. 武昌起义C. 南京条约D. 辛亥革命答案:A二、填空题(每题2分,共20分)1. 太原是中国历史文化名城,其历史可以追溯到_______时期。
答案:春秋2. 太原的市歌是_______。
答案:《太原之歌》3. 太原的著名景点双塔寺,其双塔建于_______朝。
答案:明朝4. 太原的著名特产之一是_______。
答案:老陈醋5. 太原的著名大学有_______大学。
答案:太原理工大学6. 太原的著名历史人物狄仁杰是_______朝的宰相。
答案:唐朝7. 太原的著名景点天龙山石窟始建于_______朝。
答案:北齐8. 太原的著名小吃头脑是_______省的传统名吃。
答案:山西省9. 太原的著名历史事件太原会战发生在_______年。
答案:193710. 太原的著名景点龙山石窟是_______朝的文化遗产。
答案:元朝三、简答题(每题10分,共20分)1. 简述太原在中国历史上的地位和作用。
太原市初三考试题及答案

太原市初三考试题及答案一、语文1. 阅读下面的文言文,完成下列各题。
(1)解释下列句子中加点词的含义。
A. 子墨子解带为城B. 公输盘踌躇C. 子墨子九距之D. 公输盘服答案:A. 子墨子解带为城:子墨子,指墨子;解带,解开衣带;为城,作为城墙。
B. 公输盘踌躇:公输盘,指公输班;踌躇,犹豫不决。
C. 子墨子九距之:九,多次;距,抵御。
D. 公输盘服:服,认输。
(2)翻译下列句子。
A. 子墨子曰:“吾知子之所以距我矣。
吾不言。
”B. 子墨子曰:“吾知子之所以攻宋矣。
吾不攻宋矣。
”答案:A. 墨子说:“我知道你用来抵抗我的原因,我不说。
”B. 墨子说:“我知道你用来攻打宋国的原因,我不攻打宋国了。
”2. 阅读下面的现代文,完成下列各题。
(1)文章中“他”指的是谁?答案:文章中的“他”指的是主人公的父亲。
(2)文章中“她”指的是谁?答案:文章中的“她”指的是主人公的母亲。
二、数学1. 计算下列表达式的值。
(1)(3x - 2)(2x + 3)答案:6x^2 + 7x - 6(2)(x + 4)^2答案:x^2 + 8x + 162. 解下列方程。
(1)2x - 3 = 7答案:x = 5(2)3x + 5 = 14答案:x = 3三、英语1. 单项选择。
(1)What _______ you do last weekend?A. didB. doC. doesD. are答案:A(2)She _______ to the park yesterday.A. wentB. goC. goesD. going答案:A2. 阅读理解。
阅读下面的短文,然后回答问题。
Passage:Last Sunday, Tom and his family went to the park. They played games and had a picnic. Tom's sister, Lily, flew a kite. In the afternoon, they went home.(1)What did Tom and his family do last Sunday?答案:They went to the park.(2)Who flew a kite?答案:Lily.四、物理1. 计算下列物理量。
山西省太原市中考语文试题及参考答案

山西省太原市中考语文试题及参考答案山西省太原市中考语文试题及参考答案太原市中考语文试题是每年都备受关注的一道试题,因为这道试题可以反映出当前中考语文命题的趋势和方向。
今年的太原市中考语文试题与往年相比,在题型、分值、难度等方面都有一些变化。
本文将详细介绍2024年太原市中考语文试题及参考答案,帮助大家更好地了解中考语文命题的最新动态。
一、总体评价2024年太原市中考语文试题总体上保持了稳定,试题注重基础知识的考察,同时强调能力的运用。
试题题型分为单项选择、多项选择、填空、简答、阅读理解、写作六大类,与往年相比没有太大变化。
难度方面,整体上保持了适当的难度,注重考察学生的语文综合素养。
二、具体分析1、单项选择题今年的单项选择题主要涉及汉字拼音、词语用法、病句修改、标点符号等内容,与往年相比没有太大变化。
题目难度适中,注重基础知识的考察,尤其是对拼音和词语用法的考察更加重视。
2、多项选择题今年的多项选择题主要涉及古诗词欣赏、现代文阅读、语言运用等内容,与往年相比也没有太大变化。
题目难度适中,注重考察学生的阅读理解和欣赏能力,尤其是对古诗词的欣赏能力要求更高。
3、填空题今年的填空题主要涉及古诗词名句填写、文学常识、语境填空等内容,与往年相比没有太大变化。
题目难度适中,注重考察学生的记忆和理解能力,尤其是对古诗词名句的理解和运用能力要求更高。
4、简答题今年的简答题主要涉及口语交际、语言运用、短文改错等内容,与往年相比没有太大变化。
题目难度适中,注重考察学生的语言运用和表达能力,尤其是对口语交际和短文改错的要求更高。
5、阅读理解题今年的阅读理解题主要涉及记叙文、说明文、议论文等不同文体的阅读,与往年相比没有太大变化。
题目难度适中,注重考察学生的阅读理解和分析能力,尤其是对文章主旨和作者意图的理解要求更高。
6、写作题今年的写作题主要涉及议论文和记叙文的写作,与往年相比没有太大变化。
题目难度适中,注重考察学生的写作能力和表达能力,尤其是对文章结构和语言表达的要求更高。
山西太原中考卷

山西太原中考卷一、选择题(每题4分,共40分)A. 大同B. 太原C. 晋中D. 长治A. 五台山B. 恒山C. 晋祠D. 应县木塔A. 王勃B. 白居易C. 罗贯中D. 关羽4. 山西省的简称是?()A. 鲁B. 冀C. 晋D. 豫A. 重阳节B. 元宵节C. 太原国际马拉松节D. 晋祠文化节6. 太原市的城市精神是?()A. 团结、拼搏、创新、发展B. 勤奋、务实、团结、创新C. 诚信、和谐、创新、发展D. 开放、包容、创新、共赢A. 北魏B. 前秦C. 北齐D. 北宋8. 太原市第一条地铁线路是?()A. 地铁1号线B. 地铁2号线C. 地铁3号线D. 地铁4号线A. 山西大学B. 太原理工大学C. 中北大学D. 都在太原10. 太原市的市花是什么?()A. 菊花B. 牡丹C. 月季D. 芍药二、填空题(每题4分,共40分)11. 太原市地处_________,是山西省的政治、经济、文化中心。
12. 太原市总面积约为_________平方公里。
13. 太原市下辖_________个市辖区、_________个县,代管_________个县级市。
14. 太原市的地标性建筑有_________、_________等。
15. 山西省的煤炭资源丰富,被誉为“_________”。
16. 太原市的历史名人有_________、_________等。
17. 太原市的主要旅游景点有_________、_________等。
18. 太原市的特色美食有_________、_________等。
19. 太原市的城市轨道交通系统于_________年开通运营。
20. 太原市的友好城市有_________、_________等。
三、简答题(每题10分,共30分)21. 请简要介绍太原市的历史沿革。
22. 请列举太原市的三条主要河流及其特点。
23. 请简述太原市在抗日战争中的历史地位。
四、论述题(20分)24. 结合实际,谈谈你对太原市未来发展的看法和建议。
2024年山西太原中考物理试题及答案

2024年山西太原中考物理试题及答案二、选择题(本大题共10个小题,每小题3分,共30分。
在每小题的四个选项中,只有一项符合题目要求,请选出并在答题卡上将该项涂黑)1. 如图是为了纪念老红军谢宝金而立的铜像。
在长征途中他背着一台68kg的发电机走完全程,创造了长征路上的奇迹。
以下与这台发电机质量最接近的是( )A. 一支铅笔B. 一本物理教科书C. 一个篮球D. 一名中学生2. 安全用电是每一位公民的必备素养。
在家庭电路中,下列做法符合安全用电的是( )A. 更换灯泡时不需要断开开关B. 电冰箱的金属外壳需接地线C. 电路着火可以立即用水扑灭D. 湿抹布可擦拭工作中的台灯3. 如图所示为科技小组制作的“火焰琴”。
展示时,试管中金属丝和空气被加热,堵住或松开塑料管上不同的孔能发出不同声音。
下列说法正确的是( )A. 琴声不是由物体振动产生的B. 琴声在真空中传播速度最大C. 琴声是通过空气传入人耳的D. 按压不同的孔可以改变音色4. 如图为运动员撑杆跳高的场景。
他通过助跑将撑杆压弯后起跳,越过横杆,松手后撑杆恢复原状。
下列说法正确的是( )A. 助跑时运动员相对于地面是静止的B. 压弯撑杆说明力能改变物体的形状C. 运动员鞋底的花纹是为了减小摩擦D. 松手后运动员仍然受撑杆的作用力5. 如图为青少年眼病患者眼球与正常眼球对比图。
关于该患者的晶状体及视力矫正,下列说法正确的是( )A. 对光的会聚能力太强,需佩戴近视眼镜B. 对光的会聚能力太强,需佩戴远视眼镜C. 对光的会聚能力太弱,需佩戴近视眼镜D. 对光的会聚能力太弱,需佩戴远视眼镜6. 如图所示,一辆公交车正在水平路面匀速向右行驶,遇到突发情况紧急刹车时,下列能正确表示车内拉环情形的是( )AB.C. D.7. 近年来风能和太阳能发电逐渐增多。
为增加供电稳定性,需要储能系统进行调节。
研究发现可利用“深井拉铁”技术储存电能,还能实现废旧矿井的再利用。
初三太原试题及答案

初三太原试题及答案一、选择题(每题3分,共30分)1. 下列关于太原的描述,哪一项是正确的?A. 太原是山西省的省会城市B. 太原位于中国的南部C. 太原是山西省最大的城市D. 太原是山西省的第二大城市答案:A2. 太原的著名景点之一是:A. 五台山B. 云冈石窟C. 晋祠D. 悬空寺答案:C3. 太原的气候类型属于:A. 温带季风气候B. 热带雨林气候C. 寒带气候D. 亚热带季风气候答案:A4. 太原的特产之一是:A. 汾酒B. 龙井茶C. 茅台酒D. 普洱茶5. 太原的历史文化中,以下哪一项是著名的历史事件?A. 太原起义B. 武昌起义C. 辛亥革命D. 五四运动答案:A6. 太原的著名建筑之一是:A. 太原古县城B. 太原博物馆C. 太原火车站D. 太原电视塔答案:A7. 太原的地理位置是:A. 位于山西省中部B. 位于山西省东部C. 位于山西省西部D. 位于山西省南部答案:A8. 太原的人口数量在2019年大约是:A. 400万B. 500万C. 600万D. 700万答案:B9. 太原的著名小吃之一是:B. 兰州拉面C. 重庆小面D. 武汉热干面答案:A10. 太原的著名企业之一是:A. 太重集团B. 长虹集团C. 海尔集团D. 格力集团答案:A二、填空题(每题2分,共20分)1. 太原的市花是______。
答案:菊花2. 太原的市树是______。
答案:国槐3. 太原的市歌是______。
答案:《太原之歌》4. 太原的市标是______。
答案:龙城5. 太原的著名历史人物之一是______。
答案:傅山6. 太原的著名现代建筑之一是______。
答案:山西大剧院7. 太原的著名公园之一是______。
答案:迎泽公园8. 太原的著名大学之一是______。
答案:太原理工大学9. 太原的著名桥梁之一是______。
答案:迎泽大桥10. 太原的著名历史事件之一是______。
答案:太原会战三、简答题(每题10分,共30分)1. 请简述太原的历史沿革。
2023年山西太原中考英语真题及答案

Length: around 1,100 km long Price: 487.5yuanfor a second class
The railway line has been in service since July 1970. From Chengdu, with an altitude of 400 meters or so, the train goes up to about 2,000 meters across mountains. This line is called Geological Museum(地质博物馆)because of the special geography along the railway line.
六、完形填空(每小题1分,共8分)
请阅读下面短文,理解其大意,然后从每小题所给的A、B、C三个选项中,选出一个能填入空白处的最佳选项,并在答题卡上将该项涂黑。
Joe got a bar of chocolate from his father for his cleaning work at home.___6___he was ready to eat it, his elder brother Jack returned home from school. He___7___the chocolate from Joe and put it in his mouth and ran away. Joe rushed to his room___8___and locked the room from the inside and fell on his bed, with tears on his face, worrying about his lost chocolate.
2023年山西太原中考语文真题及答案

2023年山西太原中考语文真题及答案一、读·书(12分)【书法笔墨浓淡里的博雅气韵】1. 三晋碑林院荟萃了数量众多的明清文化名家楹联,左侧的两个七言联碑便出自于此。
请从下面的选项中为甲、乙两碑分别选出最恰当的评价。
(2分)A.字体端正秀美,是传统文化中关于修身的劝勉之词。
B.字体龙飞凤舞,赞扬了不怕困难、努力拼搏的精神。
贪 C.字体灵动飘逸,以竹、兰比喻君子高尚纯粹的节操和品格。
D.字体蚕头雁尾,表达了读书证验古今,弹琴调和心性的人生乐事。
甲:(C) 乙:(A)甲:(▲)乙:(▲)【诗文盛世花香中的大美中国】2.源远流长的中国古典文化中,借花传情的诗文是其中重要的组成部分。
课堂上,九年级(1)班的同学围绕主题“花开盛世·大美中国”进行了佳句竞答活动。
请把下面空缺处的古诗文原句写在横线上。
(10分)主持人:盛世中国,我们都是幸福的看花人。
小宇:“乱花渐欲迷人眼,浅草才能没马蹄”,这是欣欣向荣的中国。
小文:“为篱下黄花开遍,秋容如拭”,这是明净如洗的中国。
小美:“岸芷汀兰,郁郁青青”,春天的中国花草相映,生机盎然。
小欣:“忽如一夜春风来,千树万树梨花开”(岑参《白雪歌送武判官归京》),冬日的中国似有春花满枝,壮美浪漫。
主持人:盛世中国,我们都是有爱的护花人。
小德:“予独爱莲之出淤泥而不染,濯清涟而不妖”,我们用挚爱守护高洁。
小智:“落红不是无情物,化作春泥更护花”(龚自珍《己亥杂诗》(其五)),我们用奉献守护初心。
小启:用爱守护“芳草鲜美,落英缤纷”的人间奇景。
小慧:用心体验“山重水复疑无路,柳暗花明又一村”的欣喜之情。
二、读·思(38分) (一)为弘扬优秀文化,厚植家国情怀,学校开展了主题为“从中国文化中汲取力量”的系列活动。
【活动一分享选文·缅怀革命先烈】1942年5月25日,左权在与日军的战斗中牺牲在太行山上,年仅37岁,是抗日战争中八路军牺牲的最高将领。
2024年山西太原中考英语试题及答案

2024年山西太原中考英语试题及答案听力部分(共20分)一、情景反应(每小题1分,共5分)本题共有五个小题,每小题你将听到一组对话。
请从每小题所给的A、B、C三幅图片中,选出与你所听到的信息相关联的一项,并在答题卡上将该项涂黑。
1.A.B.C.2.A.B.C.3.A.B.C.4.A.B.C.5.A.B.C.二、对话理解(每小题1分,共5分)本题共有五个小题,每小题你将听到一组对话和一个问题。
请从每小题所给的A、B、C三个选项中,选出一个最佳选项,并在答题卡上将该项涂黑。
6.A.Amy. B.Tom. C.Bill.7.A.Two. B.Three. C.Five.8.A.Sunny. B.Rainy. C.Windy.9.A.Classmates. B.Neighbors. C.Strangers.10.A.She encourages the boy to keep on. B.She can teach the boy to play the piano.C.She wants the boy to do something easier.三、语篇理解(每小题1分,共5分)本题你将听到一个语篇,请根据所听内容和所提出的五个问题,从每小题所给的A、B、C三个选项中,选出一个最佳选项,并在答题卡上将该项涂黑。
11.What was Sam like?A.He loved to win. B.He cared for his grandpa.C.He was good with people.12.How did Sam feel after the first two races?A.Nervous. B.Happy. C.Surprised.13.Who competed with Sam in the third race?A.Some young boys. B.Some strong men. C.An old lady and a blind man.14.How did Sam run the third race?A.He ran much faster than he was expected.B.He made special efforts and finished first again.C.He took the other runners to finish the race together.15.What can we learn from the story?A.Competing helps develop the sports spirit.B.Having a good habit makes a big difference.C.Showing love is more important than winning.四、听力填空(每小题1分,共5分)本题你将听到一个语篇,请根据所听内容,完成下面的句子,并将获取的信息写在答题卡相应的位置上。
太原中考试题

太原中考试题太原中考,作为山西省的中等教育选拔考试之一,对考生的知识掌握、思维能力和应对压力的能力都提出了较高的要求。
以下是一套太原中考的试题,请考生认真阅读并按要求完成。
第一部分:选择题1. 下面哪个选项的意思和“太原”最接近?A. 北京B. 上海C. 南京D. 山西2. 请你给下面的句子选择正确的标点符号:太原是山西省的省会A. 写小数点B. 写逗号C. 时间用点号D. 不加标点3. 太原位于山西的:A. 江南B. 东部C. 西部D. 中国中北部4. 请你在下列选项中找出正确的发音:太原A. [tàiyuán]B. [táiyuán]C. [tāiyuán]D. [taìyuán]5. 以下哪项是太原市的著名景点?A. 故宫B. 颐和园C. 迪士尼乐园D. 平遥古城第二部分:填空题根据问题,在横线上填入正确的答案。
6. 太原历史悠久,是中国的_________文明发祥地之一。
7. 太原的省会名号已经有_________多年的历史了。
8. 除了历史文化,太原还以丰富的_________资源而闻名。
9. 太原是中国重要的工业基地之一,其中_________工业发达。
10. 太原的_________环境十分优美,是游客休闲度假的好去处。
第三部分:阅读理解阅读下面的短文,然后根据短文内容回答问题。
太原是中国山西省省会,位于山西北部的中部偏东地区。
是中国历史文化名城,也是中国九大古都之一。
太原地区境内历史悠久,有3000多年的历史。
太原因其悠久的历史和独特的地理环境而成为了中国的重要旅游景点。
问答题:11. 太原位于山西省的哪个部分?12. 太原有多少年的历史?13. 太原是中国九大古都之一吗?14. 什么原因使得太原成为中国重要的旅游景点?第四部分:写作题请根据你对太原的认识,写一篇不少于200字的短文,介绍太原的特点和魅力。
______________________注意:以上是一套太原中考试题,供参考和练习使用。
太原中考理综卷子

太原中考理综卷子标题:太原中考理综卷子第一部分:物理一、选择题(共10小题,每小题2分,共20分)1. 下列叙述中,不正确的是()A. 音叉产生的声音是纯音横波B. 调弦器可以改变乐器的音高C. 长笛属于气鸣乐器D. 听音区的最低可听音频率为20Hz2. 我国某市新建了一座高耸的摩天大楼,为了减小楼体对强风的阻力,应在楼顶进行什么处理?A. 事先设定一个风档B. 在楼体两侧增加天线杆C. 在楼顶安装尖顶D. 加强楼体的牢固度3. 甲、乙两辆汽车在直线上以相等速率向同一方向行驶,若甲车速度小于乙车,则下列哪个说法正确?A. 甲车行驶距离小于乙车B. 甲车行驶时间大于乙车C. 甲车行驶的加速度小于乙车D. 甲车行驶的匀速度大于乙车4. 将物体在自由下落过程中的速度随时间变化的关系绘制成图形,该图形的特点是()A. 曲线始终呈负斜率B. 曲线始终呈正斜率C. 曲线逐渐变平缓D. 曲线逐渐向上转折5. 小明用手指放在眼前,闭上一个眼睛后,再闭上另一个眼睛,发现手指位移了,这是因为()A. 手指真的发生了位移B. 双眼之间的角度改变了C. 光线经过手指发生了折射D. 手指产生了光6. 为了不伤害地球,我们应该尽量减少使用()A. 化石燃料B. 化肥和农药C. 草原和森林资源D. 手机释放的电磁波7. 下列是关于卫星的说法,不正确的是()A. 卫星只能在地球正上方静止悬停B. 卫星是人工制造并送入轨道的C. 卫星靠地球引力做周期性运动D. 卫星通常用来传送电视信号和电话信号8. 高空弹跳表演使用的大型弹簧起高的原因是()A. 弹簧的弹性系数大B. 弹簧的刚度大C. 弹簧的长度长D. 弹簧的重力大9. 某学生实验室进行了用烧杯测量水的体积实验,下列步骤中有误的是()A. 烧杯放置在平台上B. 将盛有水的烧杯放到台秤上进行称重C. 读取以太阳能为电量的电子天平的重量D. 从毛细管处读取水的体积10. 下列说法中,哪个说法是正确的?()A. 动量守恒定律表明,只有外力做功的质点的动能才能改变B. 转动运动的物体具有动能,只有有关其转动状态的量改变,才能改变物体的动能C. 仅静止物体的动能可以改变D. 质点在势能方面具有优势的改变,其做功就有势能的减少二、填空题(共5小题,每小题4分,共20分)1. 将0.5cm的物体贴在20cm远处的凸透镜上,得到的像离透镜有0.4倍焦距,求该凸透镜的焦距大小为____cm。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
令 =0,则 3.分
解得 4分
∴函数图象与 轴的交点的坐标为 5分
23.解:设计划生产甲产品 件,则生产乙产品 件,1分
根据题意,得 3分
解得 .4分
为整数,∴ 此时, (件).5分
答:公司应安排生产甲产品11件,乙产品9件.6分
24.解:由已知,得
于点 .
2分
在 中,
成绩(分)
20
21
22
23
24
25
26
27
28
29
30
人数(人)
1
1
2
4
5
6
5
8
10
6
2
A.30分B.28分C.25分D.10人
4.已知一个多项式与 的和等于 ,则这个多项式是()
A. B. C. D.
5.用配方法解方程 时,原方程应变形为()
A. B.
C. D.
6.如图, , =30°,则 的度数为()
4分
在 中,
6分
(米).
答:建筑物 间的距离为 米.8分
25.解:(1) (瓶).
答:该天这5个班平均每班购买饮料10瓶.3分
(2) (瓶).
答:该校所有班每周购买饮料1500瓶.6分
(3) (元), (元).
答:该校所有班级学生一周用于购买瓶装饮料的费用为2250元至3750元.8分
26.解:(1)如图,射线 为所求作的图形.3分
由题设,得四边形 和四边形 关于直线 对称.
∴ 垂直平分 .∴ 1分
∵四边形 是正方形,∴
∵ 设 则
在 中, .
∴ 解得 ,即 3分
在 和在 中,
,
,
5分
设 则 ∴
解得 即 6分
∴ 7分
方法二:同方法一, 3分
如图(1-2),过点 做 交 于点 ,连接
∵ ∴四边形 是平行四边形.
∴
同理,四边形 也是平行四边形.∴
把答案填在题中的横线上或2.若反比例函数的图象经过点 ,则它的表达式是.
13.自2005年以来,太原市城市绿化走上了快车道.目前我市园林绿化总面积达到了7101.5万平方米.这个数据用科学记数法表示为万平方米.
14.方程 的解是.
15.如图是一种贝壳的俯视图,点 分线段 近似于黄金分割.已知 =10 ,则 的长约为 .(结果精确到0.1 )
28.(本小题满分9分)
、 两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往 城,乙车驶往 城,甲车在行驶过程中速度始终不变.甲车距 城高速公路入口处的距离 (千米)与行驶时间 (时)之间的关系如图.
(1)求 关于 的表达式;
(2)已知乙车以60千米/时的速度匀速行驶,设行驶过程中,两车相距的路程为 (千米).请直接写出 关于 的表达式;
图象经过点(0,300),(2,120),∴ 2分
解得 3分
∴ 即 关于 的表达式为 4分
方法二:由图知,当 时, ; 时,
所以,这条高速公路长为300千米.
甲车2小时的行程为300-120=180(千米).
∴甲车的行驶速度为180÷2=90(千米/时).3分
∴ 关于 的表达式为 ( ).4分
(2) 5分
三、解答题(本大题含9个小题,共70分)
解答应写出文字说明、证明过程或演算步骤
21.(每小题满分5分)
化简:
22.(本小题满分5分)
已知,二次函数的表达式为 .写出这个函数图象的对称轴和顶点坐标,并求图象与 轴的交点的坐标.
23.(本小题满分6分)
某公司计划生产甲、乙两种产品共20件,其总产值 (万元)满足:1150< <1200,相关数据如下表.为此,公司应怎样设计这两种产品的生产方案.
(1)求该天这5个班平均每班购买饮料的瓶数;
(2)估计该校所有班级每周(以5天计)购买饮料的瓶数;
(3)若每瓶饮料售价在1.5元至2.5元之间,估计该校所有学生一周用于购买瓶装饮料的费用范围.
26.(本小题满分9分)
如图, 是 边 上一点, .
(1)在图中作 的角平分线 ,交 于点 ;(要求:尺规作图,保留作图痕迹,不写作法和证明)
(2)方法一: 平分
5分
6分
在 和 中
7分
∴四边形 是平行四边形.8分
∴四边形 是菱形.9分
方法二:同方法一, 5分
于点 ,∴ 6分
在 和 中
∴ 7分
∴四边形 是平行四边形.8分
(或 ),∴四边形 是菱形.9分
27.解:这种方法不公平.一次摸球可能出现的结果列表如下:4分
1
2
3.
4
1
(1,1)
(1,2)
∵
在 与 中
∴ 5分
∵ 6分
∴ 7分
类比归纳
(或 ); ; 10分
联系拓广
12分
评分说明:1.如你的正确解法与上述提供的参考答案不同时,可参照评分说明进行估分.
2.如解答题由多个问题组成,前一问题解答有误或未答,对后面问题的解答没有影响,可依据参考答案及评分说明进行估分.
产品名称
每件产品的产值(万元)
甲
45
乙
75
24.(本小题满分8分)
如图,从热气球 上测得两建筑物 、 底部的俯角分别为30°和 .如果这时气球的高度 为90米.且点 、 、 在同一直线上,求建筑物 、 间的距离.
25.(本小题满分8分)
为了解某校学生每周购买瓶装饮料的情况,课外活动小组从全校30个班中采用科学的方法选了5个班.并随机对这5个班学生某一天购买瓶装饮料的瓶数进行了统计,结果如下图所示.
2009年山西省太原市初中毕业学业考试试卷
数学
一、选择题(本大题含10个小题,每小题3分,共30分)
在每小题给出的四个选项中,只有一项符合题目要求,请选出并在答题卡上将该项涂黑.
1.在数轴上表示 的点离开原点的距离等于()
A.2B. C. D.
2.下列计算中,结果正确的是()
A. B. C. D.
3.学业考试体育测试结束后,某班体育委员将本班50名学生的测试成绩制成如下的统计表.这个班学生体育测试成绩的众数是()
(3)在 中.当 时,
即甲乙两车经过2小时相遇.6分
在 中,当 .所以,相遇后乙车到达终点所用的时间为 (小时).
乙车与甲车相遇后的速度
(千米/时).
∴ (千米/时).7分
乙车离开 城高速公路入口处的距离 (千米)与行
驶时间 (时)之间的函数图象如图所示.9分
29.问题解决
解:方法一:如图(1-1),连接 .
18.如图 、 是 的两条弦, =30°,过点 的切
线与 的延长线交于点 ,则 的度数为.
19.有两把不同的锁和三把钥匙,其中两把钥匙分别能打开其中一把锁,第三把钥匙不能打开这两把锁,任意取出一把钥匙去开任意的一把锁,一次打开锁的概率为 .
20.如图,在等腰梯形 中, , =4 = , =45°.直角三角板含45°角的顶点 在边 上移动,一直角边始终经过点 ,斜边与 交于点 .若 为等腰三角形,则 的长等于.
10.在二行三列的方格棋盘上沿骰子的某条棱翻动骰子(相对面上分别标有1点和6点,2点和5点,3点和4点),在每一种翻动方式中,骰子不能后退.开始时骰子如图(1)那样摆放,朝上的点数是2;最后翻动到如图(2)所示的位置,此时骰子朝上的点数不可能是下列数中的()
A.5B.4C.3D.1
二、选择题(本大题含10个小题,每小题2分,共20分)
(1,3)
(1,4)
2
(2,1)
(2,2)
(2,3)
(2,4)
3.
(3.,1)
(3.,2)
(3,3)
(3.,4)
4
(4,1)
(4,2)
(4,3)
(4,4)
由上表可知,一次摸球出现的结果共有16种可能的情况,且每种情况出现的可能性相同.其中和为2的一种,和为3的两种,和为4的三种,和为5的四种,和为6的三种,和为7的两种,和为8的一种.6分
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
答案
A
C
B
A
B
B
A
D
C
D
二、填空题
11.2;12. ;13.7.1015× ;14. (或5);15.6.2;16.9
17.3200 (或 或 )
18.30°19. 20. ,2, .
三、解答题
21.解:原式= 2分
= 4分
=1.5分
22.解:在 中,
∴
∴这个函数图象的对称轴是 ,顶点坐标是: 2分
16.甲、乙两盏路灯底部间的距离是30米,一天晚上,当小华走到距路灯乙底部5米处时,发现自己的身影顶部正好接触路灯乙的底部.已知小华的身高为1.5米,那么路灯甲的高为米.
17.某种品牌的手机经过四、五月份连续两次降价,每部售价由
3200元降到了2500元.设平均每月降价的百分率为 ,根据题意列出的方程是.
(和为2)= (和为8)= , (和为3)= (和为7)= ,
(和为4)= (和为6)= , (和为5)= .
所以 7分
因为二班至八班各班被选中的概率不全相等,所以这种方法不公平.8分
评分说明:只要计算出二至八班中有两个班被选中的概率不相等,就可得分.
28.解:(1)方法一:由图知 是 的一次函数,设 1分
类比归纳
在图(1)中,若 则 的值等于;若 则 的值等于;若 ( 为整数),则 的值等于.(用含 的式子表示)
