边际图
农业投入产出的边际分析36页PPT

36、“不可能”这个字(法语是一个字 ),只 在愚人 的字典 中找得 到。--拿 破仑。 37、不要生气要争气,不要看破要突 破,不 要嫉妒 要欣赏 ,不要 托延要 积极, 不要心 动要行 动。 38、勤奋,机会,乐观是成功的三要 素。(注 意:传 统观念 认为勤 奋和机 会是成 功的要 素,但 是经过 统计学 和成功 人士的 分析得 出,乐 观是成 功的第 三要素 。
23、一切节省,归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰,决心到最后会全部推倒。——莎士比亚
25、学习是劳动,是充满思想的劳动。——乌申斯基
谢谢!
39、没有不老的誓言,没有不变的承 诺,踏 上旅途 ,义无 反顾。 40、对时间的价值没有没有深切认识 的人, 决不会 坚韧勤 勉。
21、要知道对好事的称颂过于夸2、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
财务管理边际贡献与盈亏临界点PPT课件

三、盈亏临界点(保本点)分析
(一)盈亏临界点及其分析
盈亏临界点,既销售收入和销售成本相等、 损益平衡、不盈不亏、利润为零
盈亏临界点分析,也称保本点分析, 就是研究当企业恰好处于保本状态时 本量利关系的一种定量分析方法。
第12页/共32页
(二)盈亏临界点(保本点)的计算
保本点是指能使企业达到保本状态 的业务量的总称。
销保售本额=安全边际量
单价
安全边际率
安全边际量 现有或预计销售量100%
安全边际额 现有或预计销售额10
பைடு நூலகம்0%
安全边际率+保本作业率=1
第20页/共32页
[例7-6] Open your book to
P147.
3、销售利润率
销售利润率是指销售利润与销售 收入的比率。
销售利润率 =(销售收入-变动成本-固定成本)/销售收入
第4页/共32页
(二)本量利分析的基本假 定
★成本性态分析的假定 ★相关范围及线性假定 ★产销平衡和品种结构稳定的假定 ★变动成本法的假定
教材P149
第5页/共32页
(三)本量利关系的基本方程 式
销售利润=销售收入-总成本 =销售收入-(变动成本+固定成本) =销售收入-变动成本-固定成本 =单价×销量-单位变动成本×销量-固定成本
各产品的销售比重 各产品的销售额/ 销售收入总额
第23页/共32页
某产品保本额
综合保 本额
该产品的 销售比重
某产品保本量=该产品保本额/单价
[例7-7] Open your book to
P143.
第24页/共32页
在其他条件不变的前提下,企业应积极采取 措施,努力提高边际贡献率水平较高的产品的 销售比重,降低边际贡献率水平较低的产品的 销售比重,从而提高企业的综合边际贡献率水 平,达到降低全厂保本额和保利额的目的。
Minitab15 培训教材

包含连接线和组,多组变量,每个点之间绘制连接线
为每个可能的组合创建一个图。
如果有很多变量,并且希望查看变量对之间的关系,则使用图的矩阵会很有效。
有时称为窗格图或窗扉显示,这种矩阵接受Y 和X 轴变量,然后为每个可能的
组合创建一个图。
如果您只关注特定变量对之间的关系,则这种类型的矩阵会很有效。
解释结果:
散点图显示,在放电恢复时间与放电后电压之间可能存在负相关;也就是说,放电恢复时间随电压的降低而增加。
包含拟合,图中显示一列数据的条形柱和拟合线包含拟合和组,图中显示多列数据的拟合线
解释结果:
一个
简单、含组和堆叠组三种图形。
多个
简单、堆叠
多个:在图形中同时显示多列数据的概率
总体中的第87 个百分位数介于3.84295 到4.58790 之间的可信度为95%。
一个Y:每个列单独显示一个图形。
多个Y:同一图形上显示多个数据列
一个Y:每个列单独显示一个图形。
多个Y:同一图形上显示多个数据列
一个Y:每个列单独显示一个图形。
多个Y:同一图形上显示多个数据列
唯一值计数:一列或多列类别数据
变量函数:一列或多列数量型数据
来自表格的值:一列或多列汇总数据简单聚类堆叠
解释结果:
在每个类别中,可以看到每个时段的瑕疵数。
在四个类别的三个中,多数瑕疵都出。
含组:显示含组的时间序列图
多个含组:同一图形中重叠多个含组的时间序列图
含组:图中显示多组变量的关系
线框:图中显示线框。
边际产量曲线的图形及边际产量递减规律

边际产量曲线的图形及边际产量递减规律
劳动的边际产量先递增,劳动投入达到一定程度L1后,MP最大,然后递减,继续增加劳动投入到L3,MP=0。
如果再增加劳动投入,边际产量为负。
边际产量递减规律也称为边际报酬递
减规律,其基本含义是:在技术水平和其他投入保持不变的条件下,连续追加一种生产要素的投入量,总是存在着一个临界点,在这一点之前,边际产量递增,超过这一点之后,边际产量将出现递减的趋势,直到出现负值。
【例题·单选题】边际产量递减规律的基本含义是()。
A.在技术水平和其他投入保持不变的条件下,连续追加一种生产要素的投入量,总是存在着一个临界点,在这一点之前,边际产量递增,超过这一点之后,边际产量将出现递
减的趋势,直到出现负值
B.在技术水平和其他投入变动的条件下,连续追加一种生产要素的投入量,总是存在着一个临界点,在这一点之前,边际产量递增,超过这一点之后,边际产量将出现递减的趋势,直到出现负值
C.在技术水平和其他投入保持不变的条件下,连续追加一种生产要素的投入量,边际产量总是递增的
D.在技术水平和其他投入保持不变的条件下,连续追加一种生产要素的投入量,边际产量总是递减的
【答案】A。
边际成本边际收益

• 举例:
• 边际利润在经济学的定义是每多(少)生成一 单位产品,生产者得到(损失)的理论。
• 比如说杂志印刷,如果成本是5元/本,定价15 元/本。
• 平时由于卖不完,所以多印一本只会损失5元 成本,得不到任何收益,边际利润就是-5元。
• 而如果是限量版,大家都抢着买,这时多印一 本除去成本费5元,还能得到10元的利润(155),边际利润就是10元。
谢谢
• 图示:
• 边际成本的变动规律:
• 最初在产量开始增加时由于各种生产要素的效率未得到充 分发挥,因此,产量很小。
• 随着生产的进行,生产要素利用率增大,产量的增长速度 大于成本的增长速度,所以边际成本随产量的增加而递减 。
• 当产量增加到一定程度时,由于边际收益递减规律的作用 ,边际成本又随产量的增加而增加。如果不考虑最初的短 暂情况,那么,它的变动规律主要表现就是:边际成本先 是随产量增加而减少,当产量增加到一定程度时,就随产 量增加而增加,因此,边际成本曲线也是一条先下降而后 上升的“U”形曲线。
• 南林某餐厅,餐馆每天人员工资与设施设备折旧是 500元,每天可以最多准备1000份饭菜,每份饭菜制 作成本为2元,卖4元一份。
• 假设有100个人来吃,有1000个人来吃,则每份饭总 成本:
• 100人来吃:(100*2+500)/100=7元
• 总结:
• 当实际产量未达到一定限度,边际成本 随产量的扩大而递减;
• 当产量超过一定限度(生产能力)时, 边际成本随产量的扩大而递增。
二、边际利润
• 概念:(marginal profit 或 margin of profit ),是指厂商每增加一单位的产出 所带来边际利润的纯利润的增量。
西方经济学常用曲线图集锦

、基本曲线与变动图需求曲线需求变动与需求量变动需求变动减少增加D2Q o Q i Q i需求量变动D。
供给曲线供给变动与供给量变动需求收入弹性UTUM总效用与边际效用、无差异曲线与无差异图X消费者均衡(一)收入-消费线与恩格尔曲线Y的恩格尔线■■XIIY的恩格尔线1 1收入-消费线_______ X的恩格尔线收入弹性高XPX收入变动与需求曲线移动(1)正常商品的两种效应X价格下降(补偿约束线)替代效应收入效应总效应价格弹性MP L短期产量曲线预算约束线替代的可行区域:脊线等产量曲线L宀兀衡全一竞 :争超厂额商利短润期均完全竞争厂商短期均衡三:亏损最小长期总成木与短期总成木「:平均成木CAcCTSh A V CQ* Q短期成本曲线一完全竞争厂商短期均完全竞争厂商短期均衡三:亏损最小完全竞争厂商均衡四:停止营业点完全竞争厂商短期均衡四:停止营业 STCQ *完全竞争厂商长期均衡 Q L *Q。
边际成本边际收益

• 总结:
• 当实际产量未达到一定限度,边际成本 随产量的扩大而递减;
• 当产量超过一定限度(生产能力)时, 边际成本随产量的扩大而递增。
ห้องสมุดไป่ตู้
二、边际利润
• 概念:(marginal profit 或 margin of profit ),是指厂商每增加一单位的产出 所带来边际利润的纯利润的增量。
• 南林某餐厅,餐馆每天人员工资与设施设备折旧是 500元,每天可以最多准备1000份饭菜,每份饭菜制 作成本为2元,卖4元一份。
• 假设有100个人来吃,有1000个人来吃,则每份饭总 成本:
• 100人来吃:(100*2+500)/100=7元
• 101人来吃:(101*2+500)/101=6.99元
谢谢观赏
• 举例1
• 【为什么麦当劳愿意以半 价出售第二杯饮料?】对 于麦当劳而言,一杯饮料 的成本包括了店租、水电、 人工和原材料,你在买第 一杯的时候已经把所有这 些费用都分担了,后面半 价的第二杯只需要原材料 的成本,即为边际成本, 而这个很低。所以也许第 二杯麦当劳从你身上赚的 钱更多。
• 举例2:
C.停止某一产品的生产必须要以其他产品增产所带来的边际 利润大于停产产品的边际利润为前提。边际利润的大小取 决于边际收入和边际成本的大小。它们之间的关系是:边 际利润=边际收入一边际成本。等式中的边际收入和边际 成本是指在原产销量基础上,每增加一个单位产销量所引 起的收入变动额和成本变动额。
• 举例:
• 边际利润在经济学的定义是每多(少)生成一 单位产品,生产者得到(损失)的理论。
• 比如说杂志印刷,如果成本是5元/本,定价15 元/本。
经济学知识-边际篇

边际成本(MC,marginal cost)【定义】边际成本是指厂商每增加一单位产量所增加的成本,也就是MC=△TC/△Q。
在经济学和金融学中,边际成本(marginal cost)指的是每一单位新增生产的产品(或者购买的产品)带来到总成本的增量。
这个概念表明每一单位的产品的成本与总产品量有关。
比如,仅生产一辆汽车的成本是极其巨大的,而生产第101辆汽车的成本就低得多,而生产第10000汽车的成本就更低了(这是因为规模经济)。
但是,考虑到机会成本,随着生产量的增加,边际成本可能会增加。
还是这个例子,生产新的一辆汽车时,所用的材料可能有更好的用处,所以要尽量用最少的材料生产出最多的车,这样才能提高边际收益。
边际成本和单位平均成本不一样,单位平均成本考虑了全部的产品,而边际成本忽略了最后一个产品之前的。
例如,每辆汽车的平均成本包括生产第一辆车的很大的固定成本(在每辆车上进行分配);而边际成本根本不考虑固定成本。
在数学上,边际成本(MC,marginal cost)用总成本(TC,total cost)和数量(Q,quantity)的偏导数来表示:边际成本定价是销售商品时使用的经营战略。
其思想就是边际成本是商品可以销售的最低价,这样才能使企业在经济困难时期维持下去。
因为固定成本几乎沉没,理论上边际成本可以使企业无损失的继续运转。
【拓展】其他的成本的定义固定成本指不随着产出变化的成本,长期来看,所有的成本都可以看成变量。
变动成本指营业成本、最初成本、间接成本和直接成本等。
这些都随着产出而直接变化,例如劳动力,燃料,能源和原材料成本。
平均成本指每一单位产出分担的总成本。
平均固定成本指每一单位产出分担的固定成本。
平均变动成本指每一单位产出分担的变动成本。
【应用】运用边际成本法取得信息,对企业管理者进行相关分析和决策具有重要的指导作用,以下几个方面阐述了其在企业实际工作中的应用:它克服了完全成本法的缺点,避免操纵短期利润,有利于短期产量决策。
各种图图表的作用和用法

8
上海华普汽车
9
上海华普汽车
10
上海华普汽车
11
上海华普汽车
解释:BMI 和脂肪数据的散点图显示了两 个变量之间的强度很大的正线性关系。体 重指数 (BMI) 可能是身体脂肪百分比的一 个好的预测变量。
2
上海华普汽车
使用散点图评估两个变量之间的关系的方向、强度和线性: · 同时趋向于上升的数据值指示正相关性。 · 如果随着一个数据值的降低而另一个数据值升高,则指示负的相关性。 · 关系强度越大,所生成的数据点聚类就越紧密。 · 异常值将落于远离主要点组处。 可以直观地确定关系是直线还是曲线。如果关系是曲线,则您可能需要包括高次项以准确地对弯曲程度建模(请参见多项 式回归 )。 当依赖时间变化的数据不是按时间顺序排列,或数据采集区间不规则时,应使用散点图而不是时间序列图。
4
上海华普汽车
边际图 使用边际图可以: · 图解两个变量之间的关系 · 评估两个变量的分布 · 检查有无异常值 边际图是在 x 和 y 轴的边际中带有直方图、箱线图或点图的散点图。通过将散点图 与这些其他图形之一合并,边际图可以提供比单个图形所能提供更多的信息。散点 图突出显示两个变量之间的关系,而边际中的图形突出显示每个变量的分布。 数据说明:由于目标客户在身高和体重方面的变化,一家服装制造商正在考虑更改对服装尺寸的测量方法以 及每种尺寸生产的比例。作为其初步研究的一部分,他们测量了 79 名十岁以下女孩(重要客户群)的身高 (米)和体重(千克)。 典型的边际图包含下列元素: · 一个散点图 · 在 x 和 y 轴边际中的直方图、箱线图或点图 通过将散点图与这些其他图形之一合并,边际图可以提供比单个 图形更多的信息。 观察散点图以检查两个变量之间关系的方向、强度和线性。边际 中的图形突出显示每个变量的分布 在身高和体重数 据中,散点图显 示两个变量之间 有略微弯曲的正 关系。身高直方 图显示此分布以 1.5 米为中心并且 对称。体重直方 图显示此分布的 众数在大约 45 千 克处,并且正向 偏斜。
边际贡献)和产品边际贡献(总营业边际贡献)

就单一产品企业来说,盈亏临界点的计算并不困难。
由于计算利润的公式为:
利润=单价×销量-单位变动成本×销量-固定成本
令利润等于0,此时的销量为盈亏临界点销售量:
0=单价× - × -
=
又由于:单价-单位变动成本=单位边际贡献
所以,上式又可写成: =
【例13—17】某企业生产一种产品,单价2元,单位变动成本1.20元,固定成本1600元/月,计算其盈亏临界点销售量。
表13—7加权平均边际贡献率单位:元、%
产品
单价
单位边际贡献
销量
边际贡献
销售收入
边际
贡献率
占总销售
比重
甲
10
2
100
200
1000
20.00
12.99
乙
9
3
300
900
2700
33.33
35.06
丙
8
4
500
2000
4000
50.00
51.95
合计
3100
7700
100.00
加权平均边际贡献率=20%×12.99%+33.33%×35.06%+50%×51.95%
边际贡献)和产品边际贡献(总营业边际贡献)。
销售收入-产品变动成本=制造边际贡献
制造边际贡献-销售和管理变动成本=产品边际贡献
通常,如果在“边际贡献”前未加任何定语,那么则是指“产品边际贡献”。
【例13—14】某企业只生产一种产品,单价6元,单位制造变动成本2元,单位销售、管理费变动成本1元,销量600件,则:
所以:利润=销售收入×边际贡献率-固定成本
Hilbert边际谱
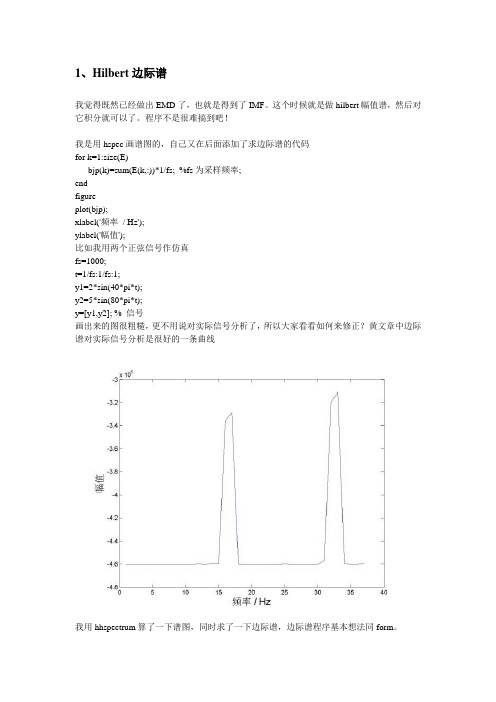
1、Hilbert边际谱我觉得既然已经做出EMD了,也就是得到了IMF。
这个时候就是做hilbert幅值谱,然后对它积分就可以了。
程序不是很难搞到吧!我是用hspec画谱图的,自己又在后面添加了求边际谱的代码for k=1:size(E)bjp(k)=sum(E(k,:))*1/fs; %fs为采样频率;endfigureplot(bjp);xlabel('频率/ Hz');ylabel('幅值');比如我用两个正弦信号作仿真fs=1000;t=1/fs:1/fs:1;y1=2*sin(40*pi*t);y2=5*sin(80*pi*t);y=[y1,y2]; % 信号画出来的图很粗糙,更不用说对实际信号分析了,所以大家看看如何来修正?黄文章中边际谱对实际信号分析是很好的一条曲线我用hhspectrum算了一下谱图,同时求了一下边际谱,边际谱程序基本想法同form。
结果也不太好,20HZ处还行,40HZ就有些问题了,见附图你自己再用这个试试我没有用rilling的hhspectrumnspab:function h1= nspab(data,nyy,minw,maxw,dt)% The function NSPAB generates a smoothed HHT spectrum of data(n,k)% in time-frequency space, where% n specifies the length of time series, and% k is the number of IMF components.% The frequency-axis range is prefixed.% Negative frequency sign is reversed.%% MATLAB Library function HILBERT is used to calculate the Hilbert transform. %% Example, [h,xs,w] = nspab(lod78_p',200,0,0.12,1,3224).%% Functions CONTOUR or IMG can be used to view the spectrum,% for example contour(xs,w,h) or img(xs,w,h).%% Calling sequence-% [h,xs,w] = nspab(data,nyy,minw,maxw,t0,t1)%% data - 2-D matrix data(n,k) of IMF components% nyy - the frequency resolution% minw - the minimum frequency% maxw - the maximum frequency% t0 - the start time% t1 - the end time% Output-% h - 2-D matrix of the HHT spectrum, where% the 1st dimension specifies the number of frequencies, % the 2nd dimension specifies the number of time values % xs - vector that specifies the time-axis values% w - vector that specifies the frequency-axis values% Z. Shen (JHU) July 2, 1995 Initial%----- Get dimensions (number of time points and components)[npt,knb] = size(data);%----- Get time interval%----- Apply Hilbert Transformdata=hilbert(data);a=abs(data);omg=abs(diff(unwrap(angle(data))))/(2*pi*dt);%----- Smooth amplitude and frequencyfiltr=fir1(8,.1);for i=1:knba(:,i)=filtfilt(filtr,1,a(:,i));omg(:,i)=filtfilt(filtr,1,omg(:,i));end%----- Limit frequency and amplitudefor i=1:knbfor i1=1:npt-1if omg(i1,i) >=maxw,omg(i1,i)=maxw;a(i1,i)=0;elseif omg(i1,i)<=minw,omg(i1,i)=minw;a(i1,i)=0;endendendclear filtr data%va=var(omg(200:1200))%----- Get local frequencydw=maxw - minw;wmx=maxw;wmn=minw;%----- Construct the ploting matrixclear p;h1=zeros(npt-1,nyy+1);p=round(nyy*(omg-wmn)/dw)+1;for j1=1:npt-1for i1=1:knbii1=p(j1,i1);h1(j1,ii1)=h1(j1,ii1)+a(j1,i1);endend%----- Do 3-point to 1-point averaging[nx,ny]=size(h1);%n1=fix(nx/3);%h=zeros(n1,ny);%for i1=1:n1%h(i1,:)=(h1(3*i1,:)+h1(3*i1-1,:)+h1(3*i1-2,:)); %end%clear h1;%----- Do 3-points smoothing in x-directionfltr=1./3*ones(3,1);for j1=1:nyh1(:,j1)=filtfilt(fltr,1,h1(:,j1));endclear fltr;%----- Define the results%w=linspace(wmn,wmx,ny-1)';%xs=linspace(t0,t1,nx)';h1=flipud(rot90(h1));h1=h1(1:ny-1,:);form求边际谱时所用程序是没有问题的,用的是矩形积分公式。
六西格玛中图形分析的Minitab实现解读

8六西格玛管理中DMAIC模型的第三个阶段是分析(A),在量测阶段识别了发生什么(Y)之后,接下来的工作就是通过分析寻找发生问题的原因。
即最终确定出一组按重要程度排列的影响Y的因素x1、x2、…、xn。
分析阶段所用的方法在很大程度上取决于所解决的问题和面对的业务流程,通常采取数据分析和流程分析相结合的方法。
数据分析主要是利用已经收集的数据或为分析而需要收集的数据来分辨问题模式、问题发展趋势或其他一些有关因素;流程分析主要是从整个流程运行的角度,辨别不一致的、不相关的或可能引起问题发生或导致问题发生的某些领域.将各种方法发现的结论放在一起,获得对影响因素的全面认识.从六西格玛管理的角度看,分析阶段实现的目标具体说有三个:找出影响项目Y的所有因素;辨别出关键少数的因素;评估预测改进效益。
分析阶段的工具根据工具的类型分为三大类,由头脑风暴法等组成的定性分析方法、由统计技术支撑的定量分析方法以及由统计技术和管理技术支撑的图形工具。
图形分析工具主要包括:比较两组数据差异的箱线图、描述因素变量间相关关系的散点图、显示影响因素的直方图、描述影响因素之间关系的多变量图、从客户要求、技术、产品要求的角度进行综合分析的质量功能展开、通过二维图表分析三个变量间关系的等高线图、通过流程寻找原因的流程图等。
下面结合Minitab软件重点介绍箱线图、散点图、边际图、矩阵图、等高线图、多变量图等。
一、箱线图(BoxPlots)箱形图是通过一个或几个箱形来描述数据分布特征的绘图工具。
在六西格玛质量管理中,它的主要作用表现在以下两个方面:比较不同样本间数据的分散程度与集中程度,找出差异为下一步的判断和决策提供依据.对于每个独立的箱形图,判断数据是否有异常点(outlier)的存在,对异常点应重点分析,总结原因。
要建立与分析箱形图,必须先了解Q值。
Q是quartile的缩写,代表数据的1/4,每一个样本共有4个Q值,当将样本数据按由小到大排序后,把这些数据均分为4部分,则每一部分的最大值即为六西格玛中图形分析的Minitab实现文/王作成方何样本相应的4个Q值,这4个Q值依次为:Q1、Q2、Q3、Q4,位于中间位置的数据或两个数据的算术平均数称为中位数。
