c语言构造树及树的三种遍历
文件目录结构的树形显示(数据结构课程设计,树、队列,C语言描述)

⽂件⽬录结构的树形显⽰(数据结构课程设计,树、队列,C语⾔描述)⼀、要解决的问题给出某⼀个操作系统下⽬录和⽂件信息,输⼊的数据第⼀⾏为根⽬录节点。
若是⽬录节点,那么它的孩⼦节点将在第⼆⾏中被列出,同时⽤⼀对圆括号“()”界定。
同样,如果这些孩⼦节点中某⼀个也是⽬录的话,那么这个⽬录所包含的内容将在随后的⼀⾏中列出,由⼀对圆括号“()”界定。
⽬录的输⼊输⼊格式为:*name size,⽂件的输⼊输⼊格式为:name size。
Name为⼀串不超过10个字符组成,并且字符串中不能有‘(’,‘)’,‘[‘,’]’和’*’。
Size是该⽂件/⽬录的⼤⼩,⽂件的size输⼊值为该⽂件的⼤⼩,⽬录的size输⼊值都为1。
树结构最多10层,每⼀层最多2个⽂件/⽬录。
要求编程实现将其排列成⼀棵有⼀定缩进的树,输出要求:第d层的⽂件/⽬录名前⾯需要缩进8*d个空格,兄弟节点要在同⼀列上。
并计算每⼀个⽬录⼤⼩,⽬录⼤⼩为所包含的所有⼦⽬录和⽂件⼤⼩以及⾃⾝⼤⼩的总和。
例如输⼊:*/usr 1(*mark 1 *alex 1)(hw.c 3 *course 1) (hw.c 5)(aa.txt 12)输出|_*/usr[24]|_*mark[17]| |_hw.c[3]| |_*course[13]| |_aa.txt[12]|_*alex[6]|_hw.c[3]⼆、算法基本思想描述:采⽤孩⼦兄弟双亲链表的数据存储结构建⽴⼆叉树,再先序遍历该⼆叉树输出所有节点。
输出时,通过parent节点的第⼀个孩⼦是否有兄弟节点控制缩进输出” | ”或” ”;⽬录的⼤⼩为该⽬录左⼦树(以其第⼀个孩⼦为根的树)所有节点的size和加上它本⾝⼤⼩。
三、设计1. 数据结构的设计和说明在⼀开始设计要采⽤的数据结构时,虽然课题只要求“树结构最多10层(树的深度),每⼀层最多2个⽂件/⽬录”,考虑到问题的实际意义,我决定把它优化消除这⼀限制,于是采⽤孩⼦兄弟的数据结构,后来由于缩进输出的需要⼜增加了parent域。
树结构遍历算法

树结构遍历算法
树结构遍历算法是指按照一定的规则对一棵树形数据结构中的所有结点进行遍历的过程。
常见的树结构遍历算法有三种:前序遍历、中序遍历和后序遍历。
1. 前序遍历:
从根节点开始,先输出当前结点,然后分别递归遍历当前结点的左子树和右子树。
因此,前序遍历的顺序为"根-左-右"。
2. 中序遍历:
从根节点开始,先递归遍历当前结点的左子树,然后输出当前结点,最后递归遍历右子树。
因此,中序遍历的顺序为"左-根-右"。
3. 后序遍历:
从根节点开始,先递归遍历当前结点的左子树和右子树,最后输出当前结点。
因此,后序遍历的顺序为"左-右-根"。
对于每个结点,以上三种遍历方式都要遍历到,只是输出的顺序不同。
同时,在实际应用中,还有深度优先遍历和广度优先遍历等更多遍历方法。
树的遍历(先序、中序、后序详解)

树的遍历(先序、中序、后序详解) 树的遍历主要有三种
1、先序遍历:先遍历根节点,再遍历左节点,最后遍历右节点;
2、中序遍历:先遍历左节点,再遍历根节点,最后遍历右节点;
3、后序遍历:先遍历左节点,再遍历右节点,最后遍历根节点;
总结:先、中、后就表⽰根节点的遍历处于哪个位置,⽰总是先左节点后右节点。
例如先序遍历,“先”表⽰根节点最先遍历,再左节点,
最后右节点。
依此类推中序遍历,后序遍历。
接下来看⽰个题⽰,看⽰下你们是怎么做的。
我们以中序遍历为例来讲(每次以三个节点为⽰个整体):
⽰先从树的根节点开始即C F E
我们再依次来看,先看C,则以C为根节点的三个节点(即A C D)按中序遍历则为A C D。
故A放在C之前,把D放在C之后。
故A C D F E
再看A,由于以A为根节点的三个节点中其他两个没有,故看下⽰个D 同理可得B D
故把B放在D之前,即A C B D F E
类似可得中序遍历为A C B D F H E M G
这样是不是再也不怕树的遍历了。
二叉树,树,森林遍历之间的对应关系

二叉树,树,森林遍历之间的对应关系一、引言在计算机科学中,数据结构是非常重要的知识点之一。
而树这一数据结构,作为基础的数据结构之一,在软件开发中有着广泛的应用。
本文将重点探讨二叉树、树和森林遍历之间的对应关系,帮助读者更加全面地理解这些概念。
二、二叉树1. 二叉树的定义二叉树是一种特殊的树结构,每个节点最多有两个子节点,分别称为左子节点和右子节点。
二叉树可以为空,也可以是一棵空树。
2. 二叉树的遍历在二叉树中,有三种常见的遍历方式,分别是前序遍历、中序遍历和后序遍历。
在前序遍历中,节点的访问顺序是根节点、左子树、右子树;在中序遍历中,节点的访问顺序是左子树、根节点、右子树;在后序遍历中,节点的访问顺序是左子树、右子树、根节点。
3. 二叉树的应用二叉树在计算机科学领域有着广泛的应用,例如用于构建文件系统、在数据库中存储有序数据、实现算法中的搜索和排序等。
掌握二叉树的遍历方式对于理解这些应用场景非常重要。
三、树1. 树的定义树是一种抽象数据类型,由n(n>0)个节点组成一个具有层次关系的集合。
树的特点是每个节点都有零个或多个子节点,而这些子节点又构成了一颗子树。
树中最顶层的节点称为根节点。
2. 树的遍历树的遍历方式有先根遍历、后根遍历和层次遍历。
在先根遍历中,节点的访问顺序是根节点、子树1、子树2...;在后根遍历中,节点的访问顺序是子树1、子树2...,根节点;在层次遍历中,节点的访问顺序是从上到下、从左到右依次访问每个节点。
3. 树的应用树广泛用于分层数据的表示和操作,例如在计算机网络中的路由算法、在操作系统中的文件系统、在程序设计中的树形结构等。
树的遍历方式对于处理这些应用来说至关重要。
四、森林1. 森林的定义森林是n(n>=0)棵互不相交的树的集合。
每棵树都是一颗独立的树,不存在交集。
2. 森林的遍历森林的遍历方式是树的遍历方式的超集,对森林进行遍历就是对每棵树进行遍历的集合。
3. 森林的应用森林在实际编程中经常用于解决多个独立树结构的问题,例如在数据库中对多个表进行操作、在图像处理中对多个图形进行处理等。
c语言哈夫曼树的构造及编码

c语言哈夫曼树的构造及编码一、哈夫曼树概述哈夫曼树是一种特殊的二叉树,它的构建基于贪心算法。
它的主要应用是在数据压缩和编码中,可以将频率高的字符用较短的编码表示,从而减小数据存储和传输时所需的空间和时间。
二、哈夫曼树的构造1. 哈夫曼树的定义哈夫曼树是一棵带权路径长度最短的二叉树。
带权路径长度是指所有叶子节点到根节点之间路径长度与其权值乘积之和。
2. 构造步骤(1) 将待编码字符按照出现频率从小到大排序。
(2) 取出两个权值最小的节点作为左右子节点,构建一棵新的二叉树。
(3) 将新构建的二叉树加入到原来排序后队列中。
(4) 重复上述步骤,直到队列只剩下一个节点,该节点即为哈夫曼树的根节点。
3. C语言代码实现以下代码实现了一个简单版哈夫曼树构造函数:```ctypedef struct TreeNode {int weight; // 权重值struct TreeNode *leftChild; // 左子节点指针struct TreeNode *rightChild; // 右子节点指针} TreeNode;// 构造哈夫曼树函数TreeNode* createHuffmanTree(int* weights, int n) {// 根据权值数组构建节点队列,每个节点都是一棵单独的二叉树TreeNode** nodes = (TreeNode**)malloc(sizeof(TreeNode*) * n);for (int i = 0; i < n; i++) {nodes[i] = (TreeNode*)malloc(sizeof(TreeNode));nodes[i]->weight = weights[i];nodes[i]->leftChild = NULL;nodes[i]->rightChild = NULL;}// 构建哈夫曼树while (n > 1) {int minIndex1 = -1, minIndex2 = -1;for (int i = 0; i < n; i++) {if (nodes[i] != NULL) {if (minIndex1 == -1 || nodes[i]->weight < nodes[minIndex1]->weight) {minIndex2 = minIndex1;minIndex1 = i;} else if (minIndex2 == -1 || nodes[i]->weight < nodes[minIndex2]->weight) {minIndex2 = i;}}}TreeNode* newNode =(TreeNode*)malloc(sizeof(TreeNode));newNode->weight = nodes[minIndex1]->weight + nodes[minIndex2]->weight;newNode->leftChild = nodes[minIndex1];newNode->rightChild = nodes[minIndex2];// 将新构建的二叉树加入到原来排序后队列中nodes[minIndex1] = newNode;nodes[minIndex2] = NULL;n--;}return nodes[minIndex1];}```三、哈夫曼编码1. 哈夫曼编码的定义哈夫曼编码是一种前缀编码方式,它将每个字符的编码表示为二进制串。
树的遍历的三种方法

树的遍历的三种方法树是一种非线性的数据结构,由节点和边组成的集合,节点代表实体,边代表节点之间的连接关系。
在树的操作中,遍历是一种重要的基本操作,它用于按照一定的顺序访问树中的所有节点。
树的遍历方法主要有三种:前序遍历、中序遍历和后序遍历。
下面将对这三种遍历方法进行详细的介绍。
一、前序遍历(Preorder Traversal)前序遍历是从根节点开始,按照根节点-左子树-右子树的顺序访问所有节点。
具体步骤如下:1.若树为空,则直接返回。
2.访问当前节点。
3.递归地前序遍历左子树。
4.递归地前序遍历右子树。
前序遍历的代码示例:```pythondef preorder(root):if root is None:returnprint(root.val)preorder(root.left)preorder(root.right)```二、中序遍历(Inorder Traversal)中序遍历是从左子树开始,按照左子树-根节点-右子树的顺序访问所有节点。
具体步骤如下:1.若树为空,则直接返回。
2.递归地中序遍历左子树。
3.访问当前节点。
4.递归地中序遍历右子树。
中序遍历的代码示例:```pythondef inorder(root):if root is None:returninorder(root.left)print(root.val)inorder(root.right)```三、后序遍历(Postorder Traversal)后序遍历是从左子树开始,按照左子树-右子树-根节点的顺序访问所有节点。
具体步骤如下:1.若树为空,则直接返回。
2.递归地后序遍历左子树。
3.递归地后序遍历右子树。
4.访问当前节点。
后序遍历的代码示例:```pythondef postorder(root):if root is None:returnpostorder(root.left)postorder(root.right)print(root.val)```以上是树的三种遍历方法的详细介绍及示例代码。
c语言二叉树的先序,中序,后序遍历
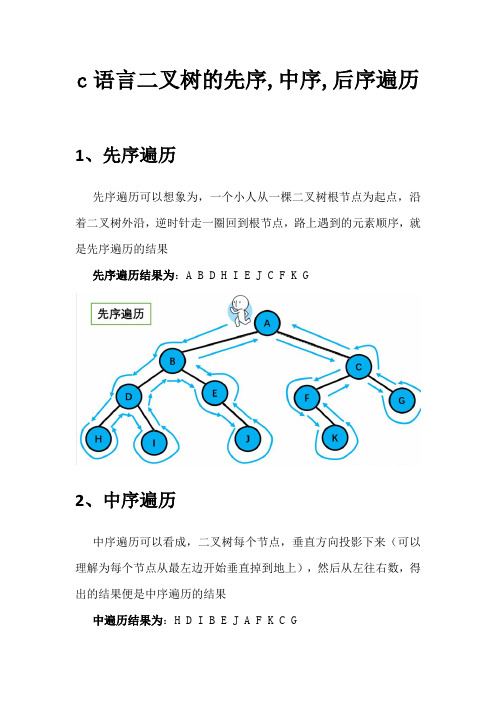
c语言二叉树的先序,中序,后序遍历1、先序遍历先序遍历可以想象为,一个小人从一棵二叉树根节点为起点,沿着二叉树外沿,逆时针走一圈回到根节点,路上遇到的元素顺序,就是先序遍历的结果先序遍历结果为:A B D H I E J C F K G2、中序遍历中序遍历可以看成,二叉树每个节点,垂直方向投影下来(可以理解为每个节点从最左边开始垂直掉到地上),然后从左往右数,得出的结果便是中序遍历的结果中遍历结果为:H D I B E J A F K C G3、后序遍历后序遍历就像是剪葡萄,我们要把一串葡萄剪成一颗一颗的。
还记得我上面提到先序遍历绕圈的路线么?(不记得翻上面理解)就是围着树的外围绕一圈,如果发现一剪刀就能剪下的葡萄(必须是一颗葡萄)(也就是葡萄要一个一个掉下来,不能一口气掉超过1个这样),就把它剪下来,组成的就是后序遍历了。
后序遍历中,根节点默认最后面后序遍历结果:H I D J E B K F G C A4、口诀先序遍历:先根再左再右中序遍历:先左再根再右后序遍历:先左再右再根这里的根,指的是每个分叉子树(左右子树的根节点)根节点,并不只是最开始头顶的根节点,需要灵活思考理解5、代码展示#include<stdio.h>#include<stdlib.h>typedef struct Tree{int data; // 存放数据域struct Tree *lchild; // 遍历左子树指针struct Tree *rchild; // 遍历右子树指针}Tree,*BitTree;BitTree CreateLink(){int data;int temp;BitTree T;scanf("%d",&data); // 输入数据temp=getchar(); // 吸收空格if(data == -1){ // 输入-1 代表此节点下子树不存数据,也就是不继续递归创建return NULL;}else{T = (BitTree)malloc(sizeof(Tree)); // 分配内存空间T->data = data; // 把当前输入的数据存入当前节点指针的数据域中printf("请输入%d的左子树: ",data);T->lchild = CreateLink(); // 开始递归创建左子树printf("请输入%d的右子树: ",data);T->rchild = CreateLink(); // 开始到上一级节点的右边递归创建左右子树return T; // 返回根节点}}// 先序遍历void ShowXianXu(BitTree T) // 先序遍历二叉树{if(T==NULL) //递归中遇到NULL,返回上一层节点{return;}printf("%d ",T->data);ShowXianXu(T->lchild); // 递归遍历左子树ShowXianXu(T->rchild); // 递归遍历右子树}// 中序遍历void ShowZhongXu(BitTree T) // 先序遍历二叉树{if(T==NULL) //递归中遇到NULL,返回上一层节点{return;}ShowZhongXu(T->lchild); // 递归遍历左子树printf("%d ",T->data);ShowZhongXu(T->rchild); // 递归遍历右子树}// 后序遍历void ShowHouXu(BitTree T) // 后序遍历二叉树{if(T==NULL) //递归中遇到NULL,返回上一层节点{return;}ShowHouXu(T->lchild); // 递归遍历左子树ShowHouXu(T->rchild); // 递归遍历右子树printf("%d ",T->data);}int main(){BitTree S;printf("请输入第一个节点的数据:\n");S = CreateLink(); // 接受创建二叉树完成的根节点printf("先序遍历结果: \n");ShowXianXu(S); // 先序遍历二叉树printf("\n中序遍历结果: \n");ShowZhongXu(S); // 中序遍历二叉树printf("\n后序遍历结果: \n");ShowHouXu(S); // 后序遍历二叉树return 0;}。
树和森林的遍历方式

树和森林的遍历方式
树和森林是常见的数据结构,它们是由节点和边组成的非线性结构。
遍历是对树和森林进行操作的重要方法之一。
树的遍历方式有三种:前序遍历、中序遍历和后序遍历。
前序遍历是先遍历根节点,再遍历左子树和右子树;中序遍历是先遍历左子树,再遍历根节点和右子树;后序遍历是先遍历左子树和右子树,再遍历根节点。
这三种遍历方式都能够遍历树中的所有节点,但遍历顺序不同。
森林是由多棵树组成的结构,因此其遍历方式可以看作是多棵树的遍历。
对于森林的遍历,可以采用先序遍历、中序遍历和后序遍历的方式,依次对每棵树进行遍历。
除了以上三种常见的遍历方式外,还有层次遍历。
层次遍历是从根节点开始,按照层次逐层遍历树中的节点。
具体做法是使用队列数据结构,将根节点入队列,然后依次出队列并将其子节点入队列,直到队列为空。
对于树和森林的遍历方式,需要根据具体的需求来选择合适的方式。
比如,前序遍历可以用于复制树的结构,中序遍历可以用于输出有序的节点序列,后序遍历可以用于释放树的空间。
层次遍历则可以用于求解树的深度、宽度等问题。
- 1 -。
《数据结构——C语言描述》第6章:树

先根遍历: -+a*b–cd/ef 中根遍历: a+b*c–d–e/f 后根遍历: abcd-*+ef/-
typedef struct Node { datatype data; struct Node *Lchild; struct Node *Rchild; } BTnode,*Btree;
满二叉树:一棵深度为k且有2k-1个结 点的二叉树称为满二叉树。 完全二叉树:深度为k,有n个结点的 二叉树当且仅当其每一个结点都与深度 为k的满二叉树中编号从1至n的结点一一 对应时,称为完全二叉树。
1 2 4 8 9 10 5 11 12 6 13 14 3 7 15 4 6 2
1 3 5 7
树的度:树中最大的结点的度数即为 树的度。图6.1中的树的度为3。 结点的层次(level):从根结点算起, 根为第一层,它的孩子为第二层……。 若某结点在第l层,则其孩子结点就在 第l+1层。图6.1中,结点A的层次为1, 结点M的层次为4。 树的高度(depth):树中结点的最大层 次数。图6.1中的树的高度为4。 森林(forest):m(m≥0)棵互不相交的 树的集合。
C语言 二叉树的建立,撤销与遍历

C语言二叉树的建立,撤销与遍历二叉树是一种特殊的树,每个节点只能有最多二个孩子节点,或者没有孩子节点。
建立,与撤销或遍历二叉树主要是靠递归的方法。
#include<stdio.h>#include<stdlib.h>typedef struct stud/*定义二叉树的结构,只有一个数据项,和两个孩子节点*/{char data;struct stud *left;struct stud *right;} bitree;void destroy(bitree **root)/*撤销二叉树,这里用的是递归和二级指针*/ {if(*root!=NULL&&(*root)->left!=NULL)/*当前结点与左子树不空,递归撤销左子树*/destroy(&(*root)->left);if(*root!=NULL&&(*root)->right!=NULL)/*当前结点与右子树不空,递归撤销右子树*/destroy(&(*root)->right);free(*root);/*左右子树都为空,撤销该节点,并递归撤销其上的所有节点*/ }void inititate(bitree **root)/*初始化二叉树的头结点,并分配空间*/ {*root=(bitree *)malloc(sizeof(bitree ));(*root)->left=NULL;(*root)->right=NULL;}bitree *insert_left(bitree *curr,char x)/*在左子树插入数据*/{bitree *s,*t;if(curr==NULL)return NULL;t=curr->left;/*保存当前左子树的数据*/s=(bitree *)malloc(sizeof(bitree));s->data=x;s->left=t;/*新结点指向原来的左子树*/s->right=NULL;curr->left=s;/*原来的节点指向新结点*/return curr->left;}bitree *insert_right(bitree *curr,char x)/*在这个节点的右子树插入数据*/{bitree *s,*t;if(curr==NULL)return NULL;t=curr->right;s=(bitree *)malloc(sizeof(bitree));s->data=x;s->left=NULL;s->right=t;curr->right=s;return curr->right;}bitree *delete_left(bitree *curr)/*删除当前结点的左子树*/{if(curr!=NULL&&curr->left!=NULL)destroy(&curr->left);/*删除左子树本身及其以后的所有节点*/curr->left=NULL;return curr;}bitree *delete_right(bitree *curr)/*删除右子树*/{if(curr!=NULL&&curr->right!=NULL)destroy(&curr->right);curr->right=NULL;return curr;}void preorder(bitree *root)/*递归先序遍历根节点*/ {if(root!=NULL){printf("%c ",root->data);preorder( root->left);preorder( root->right);}}void midorder(bitree *root)/*递归中序遍历根节点*/ {if(root!=NULL){midorder( root->left);printf("%c ",root->data);midorder(root->right);}}void postorder(bitree *root))/*递归后序遍历根节点*/ {if(root!=NULL){postorder(root->left);postorder( root->right);printf("%c ",root->data);}}bitree *search(bitree *root,char x))/*递归某一数值*/ {bitree *find=NULL;if(root!=NULL){if(root->data==x)find=root;else{find=search (root->left,x);)/*在左子树查找*/ if(find==NULL))/*左子树没有找到的话*/find=search (root->right,x);/*右子树找*/}}return find;}void main(){bitree *root,*s,*p,*find;int i,j,k;char c='E';inititate(&root);p=insert_left(root,'A');p=insert_left(p,'B');p=insert_left(p,'D');p=insert_right(p,'G');p=insert_right(root->left,'C');insert_left(p,'E');insert_right(p,'F');printf("前序遍历为\n");preorder(root->left);printf("\n中序遍历为\n");midorder(root->left);printf("\n后序遍历为\n");postorder(root->left);find=search(root->left,c);if(find)printf("这个元素%c在二叉树中\n",c);elseprintf("这个元素%c不在二叉树中\n",c);printf("撤销根节点的左子树为\n");delete_left(root->left);printf("\n前序遍历为\n");preorder(root->left);printf("\n中序遍历为\n");midorder(root->left);printf("\n后序遍历为\n");postorder(root->left);printf("\n撤销根节点的右子树为\n"); delete_right(root->left);printf("前序遍历为\n");preorder(root->left);printf("\n中序遍历为\n");midorder(root->left);printf("\n后序遍历为\n");postorder(root->left);destroy(&root);}。
c++实现树(二叉树)的建立和遍历算法(一)(前序,中序,后序)

c++实现树(⼆叉树)的建⽴和遍历算法(⼀)(前序,中序,后序)最近学习树的概念,有关⼆叉树的实现算法记录下来。
不过学习之前要了解的预备知识:树的概念;⼆叉树的存储结构;⼆叉树的遍历⽅法。
⼆叉树的存储结构主要了解⼆叉链表结构,也就是⼀个数据域,两个指针域,(分别为指向左右孩⼦的指针),从下⾯程序1,⼆叉树的存储结构可以看出。
⼆叉树的遍历⽅法:主要有前序遍历,中序遍历,后序遍历,层序遍历。
(层序遍历下⼀篇再讲,本篇主要讲的递归法)下篇主要是,之后会有c++模板实现和。
如这样⼀个⼆叉树:它的前序遍历顺序为:ABDGHCEIF(规则是先是根结点,再前序遍历左⼦树,再前序遍历右⼦树)它的中序遍历顺序为:GDHBAEICF(规则是先中序遍历左⼦树,再是根结点,再是中序遍历右⼦树)它的后序遍历顺序为:GHDBIEFCA(规则是先后序遍历左⼦树,再是后序遍历右⼦树,再是根结点)如果不懂的话,可以参看有关数据结构的书籍。
1,⼆叉树的存储结构(⼆叉链表)//⼆叉树的⼆叉链表结构,也就是⼆叉树的存储结构,1个数据域,2个指针域(分别指向左右孩⼦)typedef struct BiTNode{ElemType data;struct BiTNode *lchild, *rchild;}BiTNode, *BiTree;2,⾸先要建⽴⼀个⼆叉树,建⽴⼆叉树必须要了解⼆叉树的遍历⽅法。
//⼆叉树的建⽴,按前序遍历的⽅式建⽴⼆叉树,当然也可以以中序或后序的⽅式建⽴⼆叉树void CreateBiTree(BiTree *T){ElemType ch;cin >> ch;if (ch == '#')*T = NULL; //保证是叶结点else{*T = (BiTree)malloc(sizeof(BiTNode));//if (!*T)//exit(OVERFLOW); //内存分配失败则退出。
C语言实现二叉树的中序遍历(递归)

C语 言 实 现 二 叉 树 的 中 序 遍 历 ( 递 归 )
二叉树的前序遍历、中序遍历、后续遍历 (包括递归、非递归,共六种) 1、中序遍历(递归): #include #include struct BiTNode//定义结构体 { char data; struct BiTNode *lchild,*rchild; }; void later(struct BiTNode *&p) //前序创建树 { char ch; scanf("%c",&ch); if(ch==' ') p=NULL; else { p=(struct BiTNode *)malloc(sizeof(struct BiTNode)); p->data=ch; later(p->lchild); later(p->rchild); } } void print(struct BiTNode *p) //中序遍历(输出二叉树) { if(p!=NULL) { print(p->lchild); printf("%c",p->data); print(p->rchild); } else printf(" ");
树的三种遍历方式

树的三种遍历方式树是一种非常重要的数据结构,它在计算机科学中应用广泛。
树可以用于搜索、排序、数据表、文件系统等诸多领域。
而树的遍历方式,则是在树中搜索数据的一种方法。
树的遍历方式有三种,分别是前序遍历、中序遍历和后序遍历。
这三种遍历方式在树的数据结构中有着重要的作用,它们可以用来检索所有节点的信息。
下面我们将对它们一一进行介绍。
1.前序遍历前序遍历也称为先序遍历,它的顺序是根节点->左子树->右子树。
它的算法描述如下:前序遍历的递归算法实现:void PreOrderTraversal(TraversalNode T){ if (T) { visit(T); PreOrderTraversal(T->left); PreOrderTraversal(T->right); } }前序遍历的非递归算法实现:void PreOrderTraversal(TraversalNode T){ while (T || !StackIsEmpty(S)) { while (T) { visit(T); push(Stack,T); T = T->left; } if(!StackIsEmpty(S)) { T = pop(Stack);T = T->right; } } }2.中序遍历中序遍历的顺序是左子树->根节点->右子树。
它的算法描述如下:中序遍历的递归算法实现:void InOrderTraversal(TraversalNode T) { if(T) { InOrderTraversal(T->left);visit(T);InOrderTraversal(T->right); } }中序遍历的非递归算法实现:void InOrderTraversal(TraversalNode T){ while (T || !StackIsEmpty(S)) { while(T) { push(Stack, T); T =T->left; } if (!StackIsEmpty(S)){ T = pop(Stack); visit(T); T = T->right; } } }3.后序遍历后序遍历的顺序是左子树->右子树->根节点。
树的前序遍历、中序遍历、后序遍历详解

树的前序遍历、中序遍历、后序遍历详解1.前序遍历图1对于当前节点,先输出该节点,然后输出他的左孩⼦,最后输出他的右孩⼦。
以上图为例,递归的过程如下:(1):输出 1,接着左孩⼦;(2):输出 2,接着左孩⼦;(3):输出 4,左孩⼦为空,再接着右孩⼦;(4):输出 6,左孩⼦为空,再接着右孩⼦;(5):输出 7,左右孩⼦都为空,此时 2 的左⼦树全部输出,2 的右⼦树为空,此时 1 的左⼦树全部输出,接着 1 的右⼦树;(6):输出 3,接着左孩⼦;(7):输出 5,左右孩⼦为空,此时 3 的左⼦树全部输出,3 的右⼦树为空,⾄此 1 的右⼦树全部输出,结束。
2.中序遍历对于当前结点,先输出它的左孩⼦,然后输出该结点,最后输出它的右孩⼦。
以上图为例:(1):1-->2-->4,4 的左孩⼦为空,输出 4,接着右孩⼦;(2):6 的左孩⼦为空,输出 6,接着右孩⼦;(3):7 的左孩⼦为空,输出 7,右孩⼦也为空,此时 2 的左⼦树全部输出,输出 2,2 的右孩⼦为空,此时 1 的左⼦树全部输出,输出1,接着 1 的右孩⼦;(4):3-->5,5 左孩⼦为空,输出 5,右孩⼦也为空,此时 3 的左⼦树全部输出,⽽ 3 的右孩⼦为空,⾄此 1 的右⼦树全部输出,结束。
3.后序遍历对于当前结点,先输出它的左孩⼦,然后输出它的右孩⼦,最后输出该结点。
依旧以上图为例:(1):1->2->4->6->7,7 ⽆左孩⼦,也⽆右孩⼦,输出 7,此时 6 ⽆左孩⼦,⽽ 6 的右⼦树也全部输出,输出 6,此时 4 ⽆左⼦树,⽽ 4的右⼦树全部输出,输出 4,此时 2 的左⼦树全部输出,且 2 ⽆右⼦树,输出 2,此时 1 的左⼦树全部输出,接着转向右⼦树;(2):3->5,5 ⽆左孩⼦,也⽆右孩⼦,输出 5,此时 3 的左⼦树全部输出,且 3 ⽆右孩⼦,输出 3,此时 1 的右⼦树全部输出,输出 1,结束。
c语言实现构造哈夫曼树代码

c语言实现构造哈夫曼树代码一、哈夫曼树简介哈夫曼树是一种特殊的二叉树,其每个叶子节点都对应一个权值,而非叶子节点则没有权值。
哈夫曼树的构造过程中,将权值较小的节点放在左子树,权值较大的节点放在右子树,这使得哈夫曼树的带权路径最短。
哈夫曼编码就是利用这种特性实现对数据进行压缩。
二、C语言实现构造哈夫曼树1. 定义结构体首先需要定义一个结构体来表示哈夫曼树中的节点。
结构体中包含了该节点的权值以及指向左右子节点的指针。
```typedef struct TreeNode {int weight;struct TreeNode *left;struct TreeNode *right;} TreeNode;2. 构造哈夫曼树接下来需要实现构造哈夫曼树的函数。
该函数接收一个数组作为输入,数组中存储了每个叶子节点的权值。
首先需要将数组中所有元素转化为TreeNode类型,并将它们存储在一个链表中。
```TreeNode *createTreeNodes(int weights[], int size) {TreeNode *nodes[size];for (int i = 0; i < size; i++) {nodes[i] = (TreeNode *)malloc(sizeof(TreeNode));nodes[i]->weight = weights[i];nodes[i]->left = NULL;nodes[i]->right = NULL;}return nodes;}```接下来,需要实现一个函数来找到权值最小的两个节点。
该函数接收一个链表作为输入,并返回该链表中权值最小的两个节点。
```void findMinNodes(TreeNode **nodes, int size, TreeNode**minNode1, TreeNode **minNode2) {*minNode1 = *minNode2 = NULL;for (int i = 0; i < size; i++) {if (*minNode1 == NULL || (*nodes)[i].weight <(*minNode1)->weight) {*minNode2 = *minNode1;*minNode1 = &(*nodes)[i];} else if (*minNode2 == NULL || (*nodes)[i].weight < (*minNode2)->weight) {*minNode2 = &(*nodes)[i];}}}```接下来,需要实现一个函数来构造哈夫曼树。
前序遍历 中序遍历 后序遍历

前序遍历中序遍历后序遍历1.遍历思想前序遍历首先访问根节点,然后访问左子树,最后访问右子树。
中序遍历先访问左子树,然后访问根节点,最后访问右子树。
后续遍历先访问左子树,然后访问右子树,最后访问根节点。
层序遍历则是从上到下,从左到右的进行遍历。
遍历树结构如下所示:。
2.实际代码1.首先建立节点类public class Node {private String data;private Node leftNode;private Node rightNode;public Node(String data,Node leftNode,Node rightNode){ this.data = data;this.leftNode = leftNode;this.rightNode = rightNode;}public String getData({return this.data;}public Node getLeftNode({return this.leftNode;}public Node getRightNode({return this.rightNode;}}。
2.实现前序遍历,中序遍历,后序遍历,层序遍历的遍历工具类,前序遍历,中序遍历,后序遍历实现方法采用递归方法。
而层序遍历使用了队列容器对结点进行遍历。
import java.util.Queue;import java.util.concurrent.LinkedBlockingQueue;public class TraverseTool {//前序遍历public void preTraverse(Node node){System.out.print(node.getData();preTraverse(node.getLeftNode(); }if(node.getRightNode( != null){preTraverse(node.getRightNode(); }}//中序遍历public void midTraverse(Node node){if(node.getLeftNode( != null){midTraverse(node.getLeftNode(); }System.out.print(node.getData();if(node.getRightNode( != null){midTraverse(node.getRightNode(); }}//后续遍历public void postTraverse(Node node){postTraverse(node.getLeftNode();}if(node.getRightNode( != null){postTraverse(node.getRightNode();}System.out.print(node.getData();}//层序遍历public void seqTraverse(Node node){Queue<Node> queue = new LinkedBlockingQueue<>(; queue.add(node);Node nextNode;while (!queue.isEmpty(){nextNode = queue.remove(;if(nextNode.getLeftNode( !=null){queue.add(nextNode.getLeftNode();}if(nextNode.getRightNode( !=null){queue.add(nextNode.getRightNode();}System.out.print(nextNode.getData();}}}。
数据结构C语言版_二叉树的三叉链表存储表示

{
BiPTree a;
if(T) // 非空树
{
a=Point(T,e); // a是结点e的指针
// T中存在结点e且e存在右兄弟
if(a&&a!=T&&a->parent->rchild&&a->parent->rchild!=a)
int BiTreeEmpty(BiPTree T)
{
if(T)
return 0;
else
return 1;
}
// 返回T的深度
int BiTreeDepth(BiPTree T)
{
int i,j;
if(!T)
return 0;
if(T->lchild)
{
QElemType data; //数据域
struct QNode *next; //指针域
}QNode,*QueuePtr;
typedef struct
{
QueuePtr front,//队头指针,指针域指向队头元素
rear; //队尾指针,指向队尾元素
}LinkQueue;
int DeQueue(LinkQueue *Q,QElemType *e) f((*Q).front==(*Q).rear)
return 0;
p=(*Q).front->next; //队头元素
*e=p->data;
(*Q).front->next=p->next;
三种遍历方法

三种遍历方法一、前序遍历前序遍历是二叉树遍历的一种方法,也是最常见的遍历方式之一。
在前序遍历中,首先访问根节点,然后递归地遍历左子树,最后递归地遍历右子树。
前序遍历的应用非常广泛,例如在二叉树的构建和重建、树的深度优先搜索等问题中都会用到前序遍历。
在进行前序遍历时,可以采用递归或者非递归的方式。
1. 递归实现前序遍历:递归实现前序遍历非常简单,具体步骤如下:- 首先判断当前节点是否为空,若为空则返回;- 访问当前节点;- 递归遍历左子树;- 递归遍历右子树。
2. 非递归实现前序遍历:非递归实现前序遍历需要借助栈来实现,具体步骤如下:- 将根节点入栈;- 循环执行以下步骤,直到栈为空:- 弹出栈顶节点,并访问该节点;- 若该节点的右子节点不为空,则将右子节点入栈;- 若该节点的左子节点不为空,则将左子节点入栈。
二、中序遍历中序遍历是二叉树遍历的另一种方法,同样也是一种常用的遍历方式。
在中序遍历中,首先递归地遍历左子树,然后访问根节点,最后递归地遍历右子树。
中序遍历的应用也非常广泛,例如在二叉搜索树的操作中,中序遍历可以按照升序输出所有节点的值。
1. 递归实现中序遍历:递归实现中序遍历的步骤如下:- 首先判断当前节点是否为空,若为空则返回;- 递归遍历左子树;- 访问当前节点;- 递归遍历右子树。
2. 非递归实现中序遍历:非递归实现中序遍历同样需要借助栈来实现,具体步骤如下:- 将根节点入栈;- 循环执行以下步骤,直到栈为空:- 若当前节点不为空,则将当前节点入栈,并将当前节点指向其左子节点;- 若当前节点为空,则弹出栈顶节点,并访问该节点,然后将当前节点指向其右子节点。
三、后序遍历后序遍历是二叉树遍历的另一种方式,也是最后一种常见的遍历方式。
在后序遍历中,首先递归地遍历左子树,然后递归地遍历右子树,最后访问根节点。
后序遍历的应用也非常广泛,例如在二叉树的删除操作中,需要先删除子节点,再删除根节点。
用C语言编写二叉树的建立与遍历

用C语言编写二叉树的建立与遍历1.对题目要有需求分析在需求分析中,将题目中要求的功能进行叙述分析,并且设计解决此问题的数据存储结构,设计或叙述解决此问题的算法。
给出实现功能的一组或多组测试数据,程序调试后,将按照此测试数据进行测试的结果列出来。
如果程序不能正常运行,写出实现此算法中遇到的问题和改进方法;2.对题目要有相应的源程序源程序要按照写程序的规则来编写。
要结构清晰,重点函数的重点变量,重点功能部分要加上清晰的程序注释。
(注释量占总代码的四分之一)程序能够运行,要有基本的容错功能。
尽量避免出现操作错误时出现死循环;3.最后提供的主程序可以象一个应用系统一样有主窗口,通过主菜单和分级菜单调用课程设计中要求完成的各个功能模块,调用后可以返回到主菜单,继续选择其他功能进行其他功能的选择。
二叉树的建立与遍历[问题描述]建立一棵二叉树,并对其进行遍历(先序、中序、后序),打印输出遍历结果。
[基本要求]从键盘接受输入,以二叉链表作为存储结构,建立二叉树,并对其进行遍历(先序、中序、后序),将遍历结果打印输出。
以下是我的数据结构实验的作业:肯定好用,里面还包括了统计树的深度和叶子数!记住每次做完一个遍历还要重新输入你的树哦!#include "stdio.h"#include "string.h"#define NULL 0typedef struct BiTNode{char data;struct BiTNode *lchild,*rchild;}BiTNode,*BiTree;BiTree Create(BiTree T){char ch;ch=getchar();if(ch=='#')T=NULL;else{if(!(T=(BiTNode *)malloc(sizeof(BiTNode))))printf("Error!");T->data=ch;T->lchild=Create(T->lchild);T->rchild=Create(T->rchild); }return T;}void Preorder(BiTree T){if(T){printf("%c",T->data); Preorder(T->lchild); Preorder(T->rchild);}}int Sumleaf(BiTree T){int sum=0,m,n;if(T){if((!T->lchild)&&(!T->rchild)) sum++;m=Sumleaf(T->lchild);sum+=m;n=Sumleaf(T->rchild);sum+=n;}return sum;}void zhongxu(BiTree T){if(T){zhongxu(T->lchild);printf("%c",T->data); zhongxu(T->rchild);}}void houxu(BiTree T){if(T){houxu(T->lchild);houxu(T->rchild);printf("%c",T->data);}}int Depth(BiTree T){int dep=0,depl,depr;if(!T) dep=0;else{depl=Depth(T->lchild);depr=Depth(T->rchild);dep=1+(depl>depr?depl:depr);}return dep;}main(){BiTree T;int sum,dep;T=Create(T);Preorder(T);printf("\n");zhongxu(T);printf("\n");houxu(T);printf("\n");sum=Sumleaf(T);printf("%d",sum);dep=Depth(T);printf("\n%d",dep);}在Turbo C的环境下,先按Ctrl+F9运行程序,此时就是建立二叉树的过程,例如输入序列ABC##DE#G##F###(其中的“#”表示空,并且输入过程中不要加回车,因为回车也有对应的ASCII码,是要算字符的,但是输入完之后可以按回车退出),然后再按ALT+F5显示用户界面,这时候就能够看到结果了。
c语言实现二叉树各种基本运算的算法

c语言实现二叉树各种基本运算的算法二叉树是一种常见的数据结构,可以应用于许多算法和问题中。
在C语言中,我们可以使用指针和结构体来实现二叉树的各种基本运算。
本文将详细介绍二叉树的创建、插入、删除、查找以及遍历等基本操作的算法。
1.创建二叉树创建二叉树可以通过递归的方式来实现。
首先定义一个表示二叉树节点的结构体,包含一个值和左右子节点指针。
然后,通过递归地创建左右子树来构建整个二叉树。
```ctypedef struct TreeNode {int data;struct TreeNode* left;struct TreeNode* right;} TreeNode;//创建二叉树TreeNode* createBinaryTree() {int data;scanf("%d", &data);if (data == -1) { // -1表示空节点return NULL;}TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode)); node->data = data;node->left = createBinaryTree();node->right = createBinaryTree();return node;}```2.插入节点在二叉树中插入节点可以按照二叉搜索树的性质进行。
如果要插入的值小于当前节点的值,则将其插入到左子树中,否则插入到右子树中。
如果子树为空,则直接创建一个新节点作为子树。
```c//插入节点TreeNode* insertNode(TreeNode* root, int data) {if (root == NULL) {TreeNode* newNode = (TreeNode*)malloc(sizeof(TreeNode));newNode->data = data;newNode->left = NULL;newNode->right = NULL;return newNode;}if (data < root->data) {root->left = insertNode(root->left, data);} else {root->right = insertNode(root->right, data);}return root;}```3.删除节点删除二叉树中的节点可以分为三种情况:删除叶子节点、删除只有一个子节点的节点、删除有两个子节点的节点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
#include<>
#include<>
#include <>
#define error 0
#define ok 1
typedef struct BiTNode
{
char data;
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
int CreateBiTree(BiTree &T)
{
char ch;
scanf("%c",&ch);
if(ch=='#') T=NULL;
else
{
if(!(T=(BiTNode *)malloc(sizeof(BiTNode)))) exit(error);
T->data=ch;
CreateBiTree(T->lchild);
CreateBiTree(T->rchild);
}
return ok;
}
void PreOrderBiTree(BiTree T)
{
if(T)
{
printf("%c",T->data);
PreOrderBiTree(T->lchild);
PreOrderBiTree(T->rchild);
}
}
void InOrderBiTree(BiTree T)
{
if(T)
{
InOrderBiTree(T->lchild); //中序遍历左子树
printf("%c",T->data); //访问结点
InOrderBiTree(T->rchild); //中序遍历右子树}
}
void PostOrderBiTree(BiTree T)
{
if(T)
{
PostOrderBiTree(T->lchild);
PostOrderBiTree(T->rchild);
printf("%c",T->data);
}
}
main()
{
int i;
BiTree T;
printf("\t请输入树的各元素:\n\t");
CreateBiTree(T);
do
{
printf(" /*****************************/\n");
printf("\t1键:先序输出; \n\t2键:中序输出;\n\t3键:后序输出!\n\t0键:退出程序!\n");
printf("\t请输入你的选择:\n\t");
scanf("%d",&i);
switch(i)
{
case 1:printf("\n\t你选择的是先序输出!! \n");
printf("\n\t输出结果为:\n");
printf("\t");
PreOrderBiTree(T);break;
case 2:printf("\n\t你选择的是中序输出!! \n");
printf("\n\t输出结果为:\n");
printf("\t");
InOrderBiTree(T);break;
case 3:printf("\n\t你选择的是后序输出!! \n");
printf("\n\t输出结果为:\n");
printf("\t");
PostOrderBiTree(T);break;
}
printf("\n");
}while(i!=0);
}。
