PID算法简单实例
pid位置控制算法例题

假设有一个温度控制系统,需要将温度保持在设定值(例如50℃)附近。
使用PID位置控制算法来实现这个系统。
1. 确定系统的输入和输出:
输入:设定温度值(例如50℃)
输出:加热器功率(例如0-100%)
2. 确定控制器参数:
比例增益Kp、积分增益Ki、微分增益Kd
3. 实现PID控制器:
根据公式:u(t) = Kp*e(t) + Ki*∫e(t)dt + Kd*de(t)/dt,其中u(t)为控制器输出,e(t)为误差信号(设定温度与实际温度之差),计算得到加热器功率的控制信号。
4. 实现系统闭环控制:
将计算出的加热器功率控制信号施加到系统中,不断检测实际温度并反馈给控制器,通过调整加热器功率来使实际温度保持在设定温度附近。
c2000 pid编程实例

c2000 pid编程实例全文共四篇示例,供读者参考第一篇示例:C2000 PID编程实例PID控制器是一种经典的控制算法,广泛应用于各种工业系统中,以实现对被控对象的精准控制。
C2000系列是德州仪器公司推出的一款高性能数字信号处理器(DSP),具有高速、低功耗等特点,在工业控制领域得到广泛应用。
本文将介绍如何在C2000系列DSP上实现PID控制,通过一个简单的示例展示PID算法的具体应用。
1. 基本原理PID控制器是由比例(P)、积分(I)和微分(D)三个部分组成的控制算法,其输出值由这三个部分的加权和决定。
通过不断调整P、I、D的系数,可以实现对被控对象的精确控制,使其达到设定值。
具体的PID算法如下:\[ u(t) = K_p e(t) + K_i \int e(t) dt + K_d \frac{de(t)}{dt} \]\( u(t) \)为控制器输出,\( e(t) \)为误差信号(设定值与实际值之差),\( K_p \)、\( K_i \)、\( K_d \)为比例、积分、微分系数。
2. 实现步骤在C2000系列DSP上实现PID控制的步骤如下:1)初始化PID参数:设置比例系数\( K_p \)、积分系数\( K_i \)、微分系数\( K_d \);2)读取传感器数据:读取被控对象的实际值;3)计算误差信号:计算设定值与实际值之差,得到误差信号;4)根据PID算法计算输出值:根据PID算法计算出控制器输出值;5)将输出值送入执行器:将计算得到的控制器输出值送入执行器,控制被控对象。
3. 编程实例下面以控制一个直流电机的转速为例,演示如何在C2000系列DSP上实现PID控制。
步骤一:初始化PID参数```Cfloat Kp = 0.1;float Ki = 0.01;float Kd = 0.05;```步骤二:读取传感器数据```Cfloat read_sensor(){// 读取传感器数据return sensor_value;}```步骤三:计算误差信号```Cfloat compute_error(float set_point, float actual_value){ float error = set_point - actual_value;return error;}```步骤四:计算PID输出值```Cfloat compute_pid_output(float error){static float integral = 0;static float prev_error = 0;// 计算比例项float p = Kp * error;// 计算积分项integral += error;float i = Ki * integral;// 计算微分项float derivative = error - prev_error; float d = Kd * derivative;// 计算输出值float output = p + i + d;prev_error = error;return output;}```通过以上实例,我们可以看到如何在C2000系列DSP上实现PID 控制,并将其应用于直流电机的转速控制中。
PID控制原理和实例

PID控制原理和特点143401010529 二班李卓奇工程实际中,应用最为广泛调节器控制规律为比例、积分、微分控制,简称PID 控制,又称PID调节。
PID控制器问世至今已有近70年历史,它以其结构简单、稳定性好、工作可靠、调整方便而成为工业控制主要技术之一。
当被控对象结构和参数不能完全掌握,或不到精确数学模型时,控制理论其它技术难以采用时,系统控制器结构和参数必须依靠经验和现场调试来确定,这时应用PID控制技术最为方便。
即当我们不完全了解一个系统和被控对象﹐或不能有效测量手段来获系统参数时,最适合用PID控制技术。
PID控制,实际中也有PI和PD控制。
PID 控制器就是系统误差,利用比例、积分、微分计算出控制量进行控制。
1、比例控制(P):比例控制是最常用的控制手段之一,比方说我们控制一个加热器的恒温100度,当开始加热时,离目标温度相差比较远,这时我们通常会加大加热,使温度快速上升,当温度超过100度时,我们则关闭输出,通常我们会使用这样一个函数e(t) = SP – y(t)-u(t) = e(t)*PSP——设定值e(t)——误差值y(t)——反馈值u(t)——输出值P——比例系数滞后性不是很大的控制对象使用比例控制方式就可以满足控制要求,但很多被控对象中因为有滞后性。
也就是如果设定温度是200度,当采用比例方式控制时,如果P选择比较大,则会出现当温度达到200度输出为0后,温度仍然会止不住的向上爬升,比方说升至230度,当温度超过200度太多后又开始回落,尽管这时输出开始出力加热,但温度仍然会向下跌落一定的温度才会止跌回升,比方说降至170度,最后整个系统会稳定在一定的范围内进行振荡。
如果这个振荡的幅度是允许的比方说家用电器的控制,那则可以选用比例控制2、比例积分控制(PI):积分的存在是针对比例控制要不就是有差值要不就是振荡的这种特点提出的改进,它常与比例一块进行控制,也就是PI控制。
c语言pid算法

c语言pid算法PID(Proportional-Integral-Derivative)控制器是一种非常常见且有效的控制系统算法,主要用于调节一个过程或者系统的输出,使其尽可能接近期望的设定值。
PID控制器的名字来源于它的三个主要组成部分:比例(Proportional)、积分(Integral)和微分(Derivative)。
在C语言中,一个简单的PID控制器可以如下实现:c复制代码#include<stdio.h>typedef struct {double kp; // 比例系数double ki; // 积分系数double kd; // 微分系数double last_error; // 上一次的误差double integral; // 误差的积分} PIDController;double calculatePID(PIDController* pid, double setpoint, double actual_value, double dt) {double error = setpoint - actual_value;// Proportional termdouble pout = pid->kp * error;// Integral termpid->integral += error * dt;double iout = pid->ki * pid->integral;// Derivative termdouble derivative = (error - pid->last_error) / dt;double dout = pid->kd * derivative;// Save error for next timepid->last_error = error;// Return total outputreturn pout + iout + dout;}int main() {PIDController pid;pid.kp = 1.0;pid.ki = 0.1;pid.kd = 0.01;st_error = 0;pid.integral = 0;double setpoint = 100.0; // 目标值double actual_value = 0.0; // 实际值double dt = 0.1; // 时间间隔for (int i = 0; i < 100; i++) {double output = calculatePID(&pid, setpoint, actual_value, dt);actual_value += output * dt; // 更新实际值printf("Setpoint: %f, Actual Value: %f, Output: %f\n", setpoint, actual_value, output);}return0;}在这个示例中,我们定义了一个PIDController结构体,它包含了PID控制器的所有参数。
PID控制算法实例_电机_温度
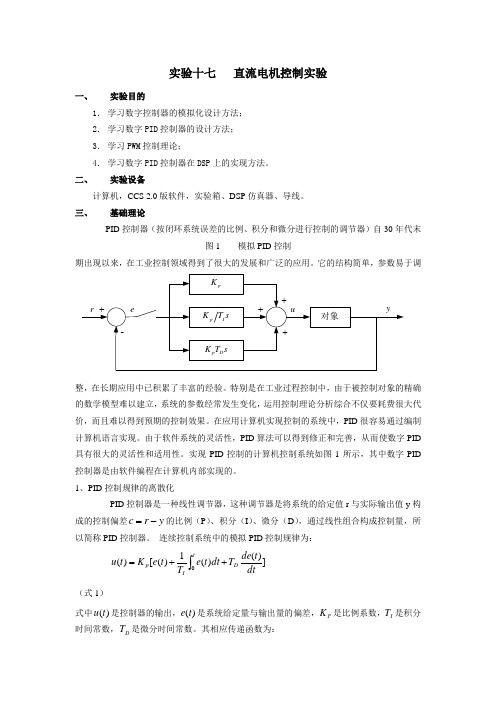
实验十七 直流电机控制实验一、 实验目的1. 学习数字控制器的模拟化设计方法;2. 学习数字PID 控制器的设计方法;3. 学习PWM 控制理论;4. 学习数字PID 控制器在DSP 上的实现方法。
二、实验设备 计算机,CCS 2.0版软件,实验箱、DSP 仿真器、导线。
三、基础理论 PID 控制器(按闭环系统误差的比例、积分和微分进行控制的调节器)自30年代末图1 模拟PID 控制期出现以来,在工业控制领域得到了很大的发展和广泛的应用。
它的结构简单,参数易于调整,在长期应用中已积累了丰富的经验。
特别是在工业过程控制中,由于被控制对象的精确的数学模型难以建立,系统的参数经常发生变化,运用控制理论分析综合不仅要耗费很大代价,而且难以得到预期的控制效果。
在应用计算机实现控制的系统中,PID 很容易通过编制计算机语言实现。
由于软件系统的灵活性,PID 算法可以得到修正和完善,从而使数字PID 具有很大的灵活性和适用性。
实现PID 控制的计算机控制系统如图1所示,其中数字PID 控制器是由软件编程在计算机内部实现的。
1、PID 控制规律的离散化PID 控制器是一种线性调节器,这种调节器是将系统的给定值r 与实际输出值y 构成的控制偏差y r c -=的比例(P )、积分(I )、微分(D ),通过线性组合构成控制量,所以简称PID 控制器。
连续控制系统中的模拟PID 控制规律为:])()(1)([)(0dtt de T dt t e T t e K t u D t I p ++=⎰ (式1)式中)(t u 是控制器的输出,)(t e 是系统给定量与输出量的偏差,P K 是比例系数,I T 是积分时间常数,D T 是微分时间常数。
其相应传递函数为:)11()(s T sT K s G D I p ++= (式2) 比例调节器、积分调节器和微分调节器的作用:(1)比例调节器:比例调节器对偏差是即时反应的,偏差一旦出现,调节器立即产生控制作用,使输出量朝着减小偏差的方向变化,控制作用的强弱取决于比例系数P K 。
超级经典的且通俗易懂的PID例子

超级经典的且通俗易懂的PID例子
超级经典的且通俗易懂的PID例子
作者:程序匠人
PID与其说是一种控制算法,不如说是一种控制思想。
这个思想的核心,就是P、I、D。
但是实际上,PID并不神秘。
在生活中的例子也是比比皆是。
比如你骑自行车,如何控制才能确保自行车不倒呢?
会骑车的都知道,当车的重心向一个方向倾斜时,笼头要向同方向打。
而且这个打的角度,与重心倾斜的角度是成正比的,倾斜度越大,笼头角度也要打得越多。
——这就是P(比例)控制。
打完笼头后,车是不会倒了,但是并不意味着你的车轮就能走直线,可能还会歪歪扭扭。
为什么呢?因为还存在静态误差,需要在骑的过程中,不断地“微调”修正,才能确保行车路径笔直。
——这就是I(积分)控制。
有时为了急转弯,我们会把笼头打过头,接下来就要赶紧回打,以抵消刚才的过调,求得平衡。
——这就是D(微分)控制。
骑车时,人的大脑就是控制器,眼睛是传感器,手足是执行器。
推而广之,在其它自动控制系统(温控、速度控制、转速、水位调节等等)中,也可以使用这套思想(或算法)。
PID例子

-0.008时,系统无振荡,过渡过程时间大约25.5s; ④Ki= -0.014时,系统出现振荡,过渡过程时间大约41s。 ⑤在Kp=-0.06时,参数Ki在-0.008附近的一个小区间(0.009~-0.006)内,系统的动、静态特性较好:没有静 态误差,不出现振荡和超调现象,过渡时间较短。 如果偏离这一个小区间,Ki过大时,使系统的超调量 增加,振荡次数增多,响应时间过长,动态特性变坏, 如果Ki过小,虽然系统没有超调,但响应迟缓。
北京交通大学 3
(五)PID算法的改进
1、微分项的改进 (1)微分项对高频干扰非常敏感,当输入e(kt)受到高频干扰,经微分后 会将干扰信号放大并传输到输出端。
(2)采用微分平滑方法,以t0=(KT-1.5T)为中心,取附加4个点的微分平 均值作微分项的输出。 TD u(kT ) [e(k ) 3e(k 1) 3e(k 2) e(k 3)] 6
(2)当 e(KT) >a 时,U(K)=Kp(k)+Kd[e(k)-e(k-1)]
当 e(KT) <a 时,U(K)= Kp(k)+Ki∑E(i)+Kd[e(k)-e(k-1)] (3)经实验,a取30。
3、数字滤波
该系统中,卤钨灯管会产生电磁辐射,对热电偶的信号产生干扰。除了 在硬件上采用抗干扰措施外,软件方面采用了数字滤波技术。
由于前方没有车辆,采用速度控制的方法进行控制, 使自车平稳地达到并保持巡航速度。仿真结果见图所示。
图13 仿真实验一:速度、时间响应曲线
北京交通大学 24
自车以 vc 18m / s 速度行驶,突然前方一速度为 v p 20m / s 的车拐入本车道,两车实际距离 d r 25m。
写一段pid算法例程

写一段pid算法例程以下是一个简单的PID控制算法的例程:```// 定义PID参数float Kp = 1; // 比例系数float Ki = 0.1; // 积分系数float Kd = 0.01; // 微分系数// 定义PID变量float error = 0; // 误差float last_error = 0; // 上一次的误差float integral = 0; // 积分项// 定义输入输出变量float setpoint = 50; // 目标值float input = 0; // 输入值float output = 0; // 输出值void PID_Control() {// 计算误差error = setpoint - input;// 计算积分项integral += error;// 避免积分饱和if (integral > 100) {integral = 100;}if (integral < -100) {integral = -100;}// 计算微分项float derivative = error - last_error;// 更新上次误差last_error = error;// 计算输出值output = Kp * error + Ki * integral + Kd * derivative;// 避免输出饱和if (output > 100) {output = 100;}if (output < -100) {output = -100;}// 输出控制信号digitalWrite(12, output);}```该例程中,通过设置比例系数Kp、积分系数Ki和微分系数Kd的大小来调节PID算法的效果。
在实际的项目中,这些系数需要根据具体的控制器性能和控制对象特性进行调整。
PID控制原理和实例

PID控制原理和特点143401010529 二班李卓奇工程实际中,应用最为广泛调节器控制规律为比例、积分、微分控制,简称PID 控制,又称PID调节。
PID控制器问世至今已有近70年历史,它以其结构简单、稳定性好、工作可靠、调整方便而成为工业控制主要技术之一。
当被控对象结构和参数不能完全掌握,或不到精确数学模型时,控制理论其它技术难以采用时,系统控制器结构和参数必须依靠经验和现场调试来确定,这时应用PID控制技术最为方便。
即当我们不完全了解一个系统和被控对象﹐或不能有效测量手段来获系统参数时,最适合用PID控制技术。
PID控制,实际中也有PI和PD控制。
PID 控制器就是系统误差,利用比例、积分、微分计算出控制量进行控制。
1、比例控制(P):比例控制是最常用的控制手段之一,比方说我们控制一个加热器的恒温100度,当开始加热时,离目标温度相差比较远,这时我们通常会加大加热,使温度快速上升,当温度超过100度时,我们则关闭输出,通常我们会使用这样一个函数e(t) = SP – y(t)-u(t) = e(t)*PSP——设定值e(t)——误差值y(t)——反馈值u(t)——输出值P——比例系数滞后性不是很大的控制对象使用比例控制方式就可以满足控制要求,但很多被控对象中因为有滞后性。
也就是如果设定温度是200度,当采用比例方式控制时,如果P选择比较大,则会出现当温度达到200度输出为0后,温度仍然会止不住的向上爬升,比方说升至230度,当温度超过200度太多后又开始回落,尽管这时输出开始出力加热,但温度仍然会向下跌落一定的温度才会止跌回升,比方说降至170度,最后整个系统会稳定在一定的范围内进行振荡。
如果这个振荡的幅度是允许的比方说家用电器的控制,那则可以选用比例控制2、比例积分控制(PI):积分的存在是针对比例控制要不就是有差值要不就是振荡的这种特点提出的改进,它常与比例一块进行控制,也就是PI控制。
简单有效的PID温控算法

宫 赂 宝 研 亩南 拓 庶
I { ESEAR( : H AND EXl , I OR^TJ ( ) N I N LAB ( )RAr r 《 )R、
第 3 6卷 筇 1 0期
Vo 1 . 3 6 No . 1 0
2 0 I 7年 1 0
一
控制 器 因为结 构简 单 、 技 术 成熟 、 鲁 棒 性 强 等优 点 ,
股 采用模 糊理论 或神 经 网络对 P 1 D 参 数 进 行 线 修
正, 形 成 自适应 P I D控 制器 来控 制温 度 … 。另外 , 门子 P L C中 的 P I D温 控 程 序 采 用 了 A s h ’ o n l和
1 P I D 温 控 的 加 热 过 程
当 以一定 加热 速度 进行 加热 的同时也 伴 随着 热流 失, 如果加 热 速度 大 于热 流 失速 度 , 那 么温 度 将 升 高 ,
( 2 )积 分过 量 。过快 的积 分速 度使 得 到达设 定 温
度时, 积 分分 量大 大超 过平 衡关 系公 式所 要求 的量 。 自适 应 P I D控 制 器通过 对 P I D的参 数进 行在 线修 正, 以避免 上 述情 况 。 本 文避 开 复 杂 的 参 数 自整 定方
c o n t r o l l e r a c h i e v e d g o o d e f f e c t i n t i r e l e mp m’ a t u r e e o n t l ’ o l s y s t e m o f a s pi n n i n g d r o p t e n s i o me t e r . Th e PI D C O l r l i ’ o i l e r
PID控制算法通俗讲解(转)
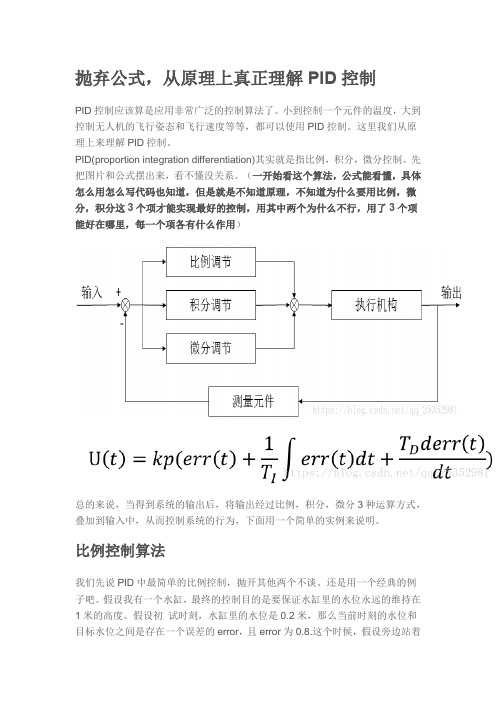
抛弃公式,从原理上真正理解PID控制PID控制应该算是应用非常广泛的控制算法了。
小到控制一个元件的温度,大到控制无人机的飞行姿态和飞行速度等等,都可以使用PID控制。
这里我们从原理上来理解PID控制。
PID(proportion integration differentiation)其实就是指比例,积分,微分控制。
先把图片和公式摆出来,看不懂没关系。
(一开始看这个算法,公式能看懂,具体怎么用怎么写代码也知道,但是就是不知道原理,不知道为什么要用比例,微分,积分这3个项才能实现最好的控制,用其中两个为什么不行,用了3个项能好在哪里,每一个项各有什么作用)总的来说,当得到系统的输出后,将输出经过比例,积分,微分3种运算方式,叠加到输入中,从而控制系统的行为,下面用一个简单的实例来说明。
比例控制算法我们先说PID中最简单的比例控制,抛开其他两个不谈。
还是用一个经典的例子吧。
假设我有一个水缸,最终的控制目的是要保证水缸里的水位永远的维持在1米的高度。
假设初试时刻,水缸里的水位是0.2米,那么当前时刻的水位和目标水位之间是存在一个误差的error,且error为0.8.这个时候,假设旁边站着一个人,这个人通过往缸里加水的方式来控制水位。
如果单纯的用比例控制算法,就是指加入的水量u和误差error是成正比的。
即u=kp*error假设kp取0.5,那么t=1时(表示第1次加水,也就是第一次对系统施加控制),那么u=0.5*0.8=0.4,所以这一次加入的水量会使水位在0.2的基础上上升0.4,达到0.6.接着,t=2时刻(第2次施加控制),当前水位是0.6,所以error是0.4。
u=0.5*0.4=0.2,会使水位再次上升0.2,达到0.8.如此这么循环下去,就是比例控制算法的运行方法。
可以看到,最终水位会达到我们需要的1米。
但是,单单的比例控制存在着一些不足,其中一点就是–稳态误差!(我也是看了很多,并且想了好久才想通什么是稳态误差以及为什么有稳态误差)。
plc自己编写pid案例

plc自己编写pid案例在工业自动化控制领域,PLC(可编程逻辑控制器)是一种常用的控制设备,而PID(比例-积分-微分)控制是一种常见的闭环控制算法。
在本文中,我们将介绍如何使用PLC自己编写PID控制的案例。
首先,我们需要了解PID控制的基本原理。
PID控制器根据当前偏差的大小,通过比例、积分和微分三个部分来调节控制输出,以使系统稳定在设定值附近。
在实际应用中,我们需要根据系统的特性来调节PID参数,以达到最佳的控制效果。
接下来,我们将以温度控制系统为例,介绍如何使用PLC自己编写PID控制。
假设我们需要控制一个加热器,使其保持在设定温度附近。
首先,我们需要安装温度传感器,并将其信号接入PLC的输入端口。
然后,我们需要将加热器的控制信号接入PLC的输出端口。
在PLC编程软件中,我们可以创建一个PID控制的函数块,并在其中设置比例、积分和微分参数。
然后,我们需要编写一个主程序,通过读取温度传感器的数值,并根据PID算法计算出控制输出,最终控制加热器的工作状态。
在实际编写PID控制程序时,我们需要注意以下几点,首先,根据系统的特性来调节PID参数,以使系统稳定在设定温度附近;其次,需要考虑系统的动态响应特性,避免出现过调和欠调现象;最后,需要对控制输出进行限幅处理,以避免对加热器的损坏。
通过以上步骤,我们就可以使用PLC自己编写PID控制的案例。
通过合理调节PID参数,我们可以实现对加热器的精确控制,使其保持在设定温度附近,从而提高生产效率并节约能源消耗。
总之,PLC自己编写PID案例是工业自动化控制中常见的应用之一。
通过合理调节PID参数,并结合PLC的控制功能,我们可以实现对各种控制系统的精确控制,从而提高生产效率并降低成本。
希望本文的介绍能够对大家有所帮助,谢谢阅读!。
PID应用实例

PID控制是一个二阶线性控制器定义:通过调整比例、积分和微分三项参数,使得大多数的工业控制系统获得良好的闭环控制性能。
优点a. 技术成熟b. 易被人们熟悉和掌握c. 不需要建立数学模型d. 控制效果好e. 鲁棒性通常依据控制器输出与执行机构的对应关系,将基本数字PID算法分为位置式PID 和增量式PID两种。
1 位置式PID控制算法基本PID控制器的理想算式为(1)式中u(t)——控制器(也称调节器)的输出;e(t)——控制器的输入(常常是设定值与被控量之差,即e(t)=r(t)-c(t));Kp——控制器的比例放大系数;Ti ——控制器的积分时间;Td——控制器的微分时间。
设u(k)为第k次采样时刻控制器的输出值,可得离散的PID算式(2)式中,。
由于计算机的输出u(k)直接控制执行机构(如阀门),u(k)的值与执行机构的位置(如阀门开度)一一对应,所以通常称式(2)为位置式PID控制算法。
位置式PID控制算法的缺点:当前采样时刻的输出与过去的各个状态有关,计算时要对e(k)进行累加,运算量大;而且控制器的输出u(k)对应的是执行机构的实际位置,如果计算机出现故障,u(k)的大幅度变化会引起执行机构位置的大幅度变化。
2 增量式PID控制算法增量式PID是指数字控制器的输出只是控制量的增量Δu(k)。
采用增量式算法时,计算机输出的控制量Δu(k)对应的是本次执行机构位置的增量,而不是对应执行机构的实际位置,因此要求执行机构必须具有对控制量增量的累积功能,才能完成对被控对象的控制操作。
执行机构的累积功能可以采用硬件的方法实现;也可以采用软件来实现,如利用算式u(k)=u(k-1)+Δu(k)程序化来完成。
由式(2)可得增量式PID控制算式(3)式中Δe(k)=e(k)-e(k-1)进一步可以改写成(4)式中、、一般计算机控制系统的采样周期T在选定后就不再改变,所以,一旦确定了Kp、Ti、Td,只要使用前后3次测量的偏差值即可由式(3)或式(4)求出控制增量。
PID算法举例

总所周知,PID算法是个很经典的东西。
而做自平衡小车,飞行器PID是一个必须翻过的坎。
因此本节我们来好好讲解一下PID,根据我在学习中的体会,力求通俗易懂。
并举出PID的形象例子来帮助理解PID。
一、首先介绍一下PID名字的由来:P:Proportion(比例),就是输入偏差乘以一个常数。
I :Integral(积分),就是对输入偏差进行积分运算。
D:Derivative(微分),对输入偏差进行微分运算。
注:输入偏差=读出的被控制对象的值-设定值。
比如说我要把温度控制在26度,但是现在我从温度传感器上读出温度为28度。
则这个26度就是”设定值“,28度就是“读出的被控制对象的值”。
然后来看一下,这三个元素对PID算法的作用,了解一下即可,不懂不用勉强。
P,打个比方,如果现在的输出是1,目标输出是100,那么P的作用是以最快的速度达到100,把P理解为一个系数即可;而I呢?大家学过高数的,0的积分才能是一个常数,I就是使误差为0而起调和作用;D呢?大家都知道微分是求导数,导数代表切线是吧,切线的方向就是最快到至高点的方向。
这样理解,最快获得最优解,那么微分就是加快调节过程的作用了。
二、然后要知道PID算法具体分两种:一种是位置式的,一种是增量式的。
在小车里一般用增量式,为什么呢?位置式PID的输出与过去的所有状态有关,计算时要对e(每一次的控制误差)进行累加,这个计算量非常大,而明显没有必要。
而且小车的PID控制器的输出并不是绝对数值,而是一个△,代表增多少,减多少。
换句话说,通过增量PID算法,每次输出是PWM要增加多少或者减小多少,而不是PWM的实际值。
所以明白增量式PID 就行了。
三、接着讲PID参数的整定,也就是PID公式中,那几个常数系数Kp,Ti,Td等是怎么被确定下来然后带入PID算法中的。
如果要运用PID,则PID参数是必须由自己调出来适合自己的项目的。
通常四旋翼,自平衡车的参数都是由自己一个调节出来的,这是一个繁琐的过程。
PID的调节实例
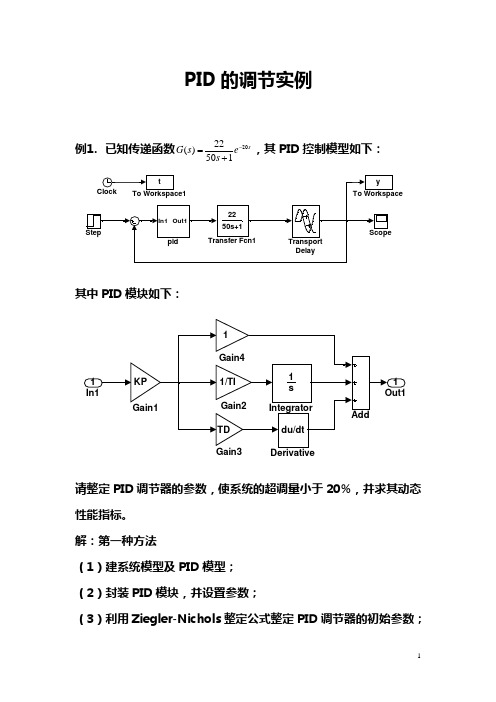
PID 的调节实例例1. 已知传递函数2022()501sG s e s -=+,其PID 控制模型如下:其中PID 模块如下:请整定PID 调节器的参数,使系统的超调量小于20%,并求其动态性能指标。
解:第一种方法(1)建系统模型及PID 模型; (2)封装PID 模块,并设置参数;(3)利用Ziegler-Nichols 整定公式整定PID 调节器的初始参数;表1. 调节器Ziegler-Nichols 整定公式根据题目已知,T=50,K=22, τ=20,可求得PID参数如下:利用此时的PID参数,得到的响应如下:(4)对PID参数进行微调,使性能指标满足系统要求。
利用此时的PID参数,得到的响应如下:性能指标求取程序如下:%性能指标求取程序xinnengzhibiao.mplot(t,y)[a,b]=size(y);wentai=y(a)caotiao=100*(max(y)-wentai)/wentaiINDEXtm=find(max(y)==y);Tm=t(INDEXtm) %峰值时间TT=t(find((abs(y-wentai)/wentai)>0.05));Ts=max(TT) %调节时间m=length(y); %求上升时间for i=1:mif y(i)>wentaitime=t(i);break;endendTr=time求取的性能指标如下:wentai = 1.0010caotiao = 6.4881Tm = 55.5694Ts = 61.5694Tr = 49.5694第二种方法:(1)利用稳定边界法整定PID参数。
表2. 稳定边界法PID整定公式取TI=inf,TD=O,求得此时的Km=0.213,Tu=72,带入上表,得:此时响应曲线为:(2)对PID参数进行微调,使性能指标满足系统要求。
性能指标:wentai = 1.0006caotiao = 7.7695Tm = 55.4754Ts = 115.4754(误差为2%)Tr = 49.4754例2.已知模型如下:其中PID模块如下:请用整定PID调节器的参数,使系统的超调量小于20%,并求其动态性能指标。
通俗易懂的PID控制算法讲解

最优控制旨在寻找一种最优的控制策 略,使得系统性能达到最优。与PID 控制相比,最优控制具有更高的性能 指标和更好的全局优化能力。然而, 最优控制的实现需要精确的数学模型 和大量的计算资源,且对系统参数变 化较为敏感。
05
PID控制算法的应用实例
工业自动化领域的应用
要点一
温度控制
在工业生产过程中,PID控制算法被 广泛应用于温度控制系统中,如熔炼 炉、热处理炉等设备的温度控制。通 过实时采集温度数据,与设定值进行 比较,PID控制器能够自动调节加热 元件的功率,使温度稳定在设定值附 近。
该传递函数描述了PID控制器在频域中的特性,可用于分析系统的稳定性、动态性能和 稳态精度等。
通过调整Kp、Ki和Kd三个参数,可以实现对系统性能的优化。在实际应用中,常采用 试凑法、经验法或优化算法等方法来确定PID参数。
03
PID控制算法的参数整定
参数整定的意义
提高系统性能
通过调整PID控制器的参数,可以优化系统 的动态响应和稳态精度,从而提高系统的整 体性能。
适应不同应用场景
不同的被控对象和不同的应用场景需要不同的PID 参数配置,参数整定可以使PID控制器适应各种应 用场景。
保证系统稳定性
合理的参数配置可以保证系统的稳定性,避 免系统出现振荡或失控等不稳定现象。
参数整定的方法
试凑法
根据经验或实验数据,逐步调整 PID控制器的参数,观察系统的响 应情况,直到满足性能指标要求 。
PID控制算法由比例(P)、积分(I) 和微分(D)三个部分组成,每个部 分都有不同的作用,通过调整三个部 分的参数可以实现对系统的精确控制 。
PID控制算法的应用领域
01
02
03
位置式pid算法c语言程序

位置式pid算法c语言程序下面是一个简单的位置式PID算法的C语言程序示例: c.#include <stdio.h>。
// 定义PID控制器的参数。
#define Kp 1.0。
#define Ki 0.1。
#define Kd 0.2。
// 定义全局变量。
double error_sum = 0; // 误差累积。
double last_error = 0; // 上一次的误差。
// PID控制器函数。
double pid_controller(double setpoint, double measured_value) {。
double error = setpoint measured_value; // 计算当前误差。
double p_term, i_term, d_term, output;// 比例控制器。
p_term = Kp error;// 积分控制器。
error_sum += error;i_term = Ki error_sum;// 微分控制器。
d_term = Kd (error last_error);last_error = error;// 计算PID输出。
output = p_term + i_term + d_term;return output;}。
int main() {。
double setpoint = 100; // 设定值。
double measured_value = 0; // 测量值。
double output;// 模拟PID控制过程。
for (int i = 0; i < 100; i++) {。
// 模拟测量值的变化。
measured_value += 1;// 计算PID输出。
output = pid_controller(setpoint, measured_value);// 输出PID控制器的输出。
printf("PID输出: %f\n", output);}。
PID算法优化(以平衡小车代码为例)

PID算法优化(以平衡小车代码为例)PID控制是一种常用的反馈控制方法,广泛应用于自动控制系统中。
在平衡小车的代码中,PID算法被用于控制小车的平衡。
本文将以平衡小车代码为例,探讨如何优化PID算法。
优化PID算法的第一步是确定合适的初始参数。
可以使用经验法确定初始参数,然后再进行调整。
例如,可以将初始参数都设置为1,然后观察系统的响应情况,根据实际效果逐步调整。
其次,可以使用自适应或自校正的方法来优化PID算法。
自适应PID算法可以根据系统的实时状态动态调整PID参数,从而提高系统的控制效果。
自校正PID算法可以通过系统的实时反馈信息来判断是否需要调整PID参数,从而提高系统的稳定性和鲁棒性。
此外,可以考虑在PID算法中引入限制项,以避免超出系统能够承受的范围。
例如,在平衡小车代码中,可以限制小车的加速度和角度的变化范围,以防止系统过载或翻倒。
在优化PID算法过程中,还需要考虑系统的实时响应速度和稳定性。
必要时,可以进行系统参数的调整,以提高系统的响应速度和稳定性。
例如,可以调整调节参数的时间常数,改变PID算法的响应速度。
另外,可以考虑使用非线性控制方法来优化PID算法。
非线性控制方法可以更好地适应复杂的控制系统,提高系统的性能。
在平衡小车代码中,可以尝试使用基于神经网络的非线性控制方法,从而提高平衡小车系统的控制精度和稳定性。
最后,需要进行系统的实时监测和调试。
通过对系统的实时监测和调试,可以及时发现和解决问题,进一步提高系统的控制效果。
例如,可以使用PID调试工具对系统的实时响应进行监测和调试,从而找到问题的根源,进行相应的调整和优化。
综上所述,通过确定合适的初始参数、使用自适应或自校正的方法、引入限制项、调整系统参数、使用非线性控制方法和进行实时监测和调试,可以对PID算法进行优化,提高系统的控制效果和稳定性。
在平衡小车代码中,这些优化方法可以帮助实现更精确和稳定的平衡控制。
PID控制原理分析(举例法)
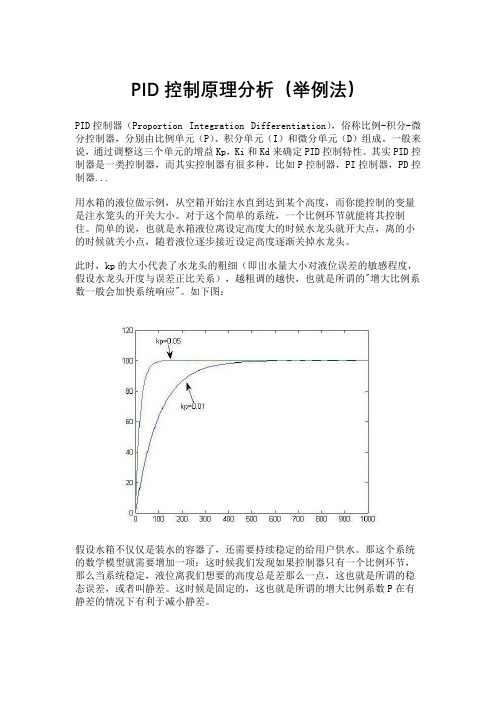
PID控制原理分析(举例法)PID控制器(Proportion Integration Differentiation),俗称比例-积分-微分控制器,分别由比例单元(P)、积分单元(I)和微分单元(D)组成。
一般来说,通过调整这三个单元的增益Kp,Ki和Kd来确定PID控制特性。
其实PID控制器是一类控制器,而其实控制器有很多种,比如P控制器,PI控制器,PD控制器...用水箱的液位做示例,从空箱开始注水直到达到某个高度,而你能控制的变量是注水笼头的开关大小。
对于这个简单的系统,一个比例环节就能将其控制住。
简单的说,也就是水箱液位离设定高度大的时候水龙头就开大点,离的小的时候就关小点,随着液位逐步接近设定高度逐渐关掉水龙头。
此时,kp的大小代表了水龙头的粗细(即出水量大小对液位误差的敏感程度,假设水龙头开度与误差正比关系),越粗调的越快,也就是所谓的"增大比例系数一般会加快系统响应"。
如下图:假设水箱不仅仅是装水的容器了,还需要持续稳定的给用户供水。
那这个系统的数学模型就需要增加一项:这时候我们发现如果控制器只有一个比例环节,那么当系统稳定,液位离我们想要的高度总是差那么一点,这也就是所谓的稳态误差,或者叫静差。
这时候是固定的,这也就是所谓的增大比例系数P在有静差的情况下有利于减小静差。
始终有个静差肯定是不行的,然后有人就想到,前后两者相比,不就是多了一个漏水的窟窿么。
它漏多少我给它补多少,那不就成了简单系统了,靠谁补呢?积分环节这时候就派上用场了。
我们把之前的控制器变成比例环节+积分环节。
积分环节的意义就相当于你增加了一个水龙头,这个水龙头的开关规则是水位比预定高度低就一直往大了拧,比预定高度高就往小了拧。
如果漏水速度不变,那么总有一天这个水龙头出水的速度恰好跟漏水的速度相等了,系统就和前面的那个一样了。
那时,静差就没有了。
这就是所谓的积分环节可以消除系统静差。
啥叫积分时间常数呢?一般PID控制里,表示积分环节敏感度的那个系数, 这个就是积分时间常数。
