人教版八年级复习资料
人教版八年级上册期中复习资料

塔里木盆地
塔里木盆地
青藏高原
二、气候多样 季风显著 ⒈南北气温的差异 ⑴冬季我国南北气温相差很大;夏季除青藏高原等地区外,全国大多数地 区普遍高温。夏季气温青藏高原最低。 ⒉我国降水的分布 ⑴我国降水量从东南沿海向西北内陆逐渐递减。 ⑵我国年降水量最多的是台湾的火烧寮,最少的是吐鲁番盆地的托克逊。 ⒊我国降水集中在夏秋季节,给我国带来大量降水的是夏季风。 ⒋我国气候的主要特征:季风气候显著、气候复杂多样。
围湖造田减弱了湖泊对河流水量的调蓄能力,为了实现长江流域的可持续发展, 政府实行了平垸行洪、退田还湖和移民建镇计划,教育人们退耕还林还草还湖。
长江综合治理的主要任务是防洪。 (4)长江水能集中在上游河段(原因:位于一、二阶梯交界处,落差大), 四、自然灾害 1.我国常见的自然灾害有气象灾害、地质灾害等。 气象灾害主要有干旱、洪涝、台风、寒潮等灾害。 地质灾害主要有地震、滑坡、泥石流。 2.当地震发生时,如果条件允许,应及时、有序撤到安全的空旷地带;如果不能 及时撤离,可以暂时躲在小空间的墙角。 3.当发生泥石流时,应向垂直于泥石流流动方向的山坡上跑。 4.四川汶川地处亚欧板块和印度洋板块交界处附近,地壳活跃,地震频繁。
会填图阶梯的分界线:
第一、二级阶梯分界线:昆仑山——祁连山——横断山
第二、三级阶梯分界线:大兴安岭——太行山——巫山——雪峰山
2.五种基本地形中,我国最大的地形区是山地,为 33%,
3.会填图
山脉
大兴安岭 太行山 山脉 天山 昆仑山
两侧的地形
西侧
东侧
内蒙古高原
东北平原
黄土高原
华北平原
北侧
南侧
准噶尔盆地
我国在各少数民族聚居的地区实行民族区域自治,设立自治机关、各民族不论 大小,一律平等。 12、民族风情:蒙古族——摔跤、那达慕大会;云南傣族——孔雀舞、泼水节; 藏族——藏袍、集体舞、开斋节、朝鲜族—长鼓舞,跳板、彝族—火把节。 (注意观察舞蹈姿势)
人教版八年级上册语文字词复习资料

人教版八年级上册语文字词复习资料第一部分【易错词】蹿(cuān) 消耗(hào 鄂(è)疟子(yào) 张皇失措管辖(xiá)竹篙(gāo) 仄歪(zè)提防(dī) 水淀(diàn) 飒飒(sà)寒噤(jìn) 转弯抹角(mò)泅(qiú)【词语解释】尖(jiān)利(lì):尖锐,锋利。
能(néng)耐(nài):本事;技能。
悠(yōu)闲(xián):从容闲适而无所牵挂,悠然闲静的意思。
寒(hán)噤(jìn):因寒冷而哆嗦。
阴(yīn)惨(cǎn):悲伤凄惨。
仄(zè)歪(wāi):倾斜,歪斜。
央(yāng)告(gào):央求,恳求。
转(zhuǎn)弯(wān)抹(mò)角(jiǎo):形容路弯弯曲曲或走弯弯曲曲的路。
月(yuè)明(míng)风(fēng)清(qīng):月光明亮,清风微动。
形容美好的夜晚。
只与清风、明月为伴。
张(zhāng)皇(huáng)失(shī)措(cuò):慌慌张张,不知道怎么办才好。
蹿(cuān)向上或向前跳。
疟子(yàozi):即疟疾,一种急性传染病。
症状是发愣发热,发热后大量出汗,头痛,口渴,全身无力。
阴森:阴沉可怕飒飒(sà):形容风雨声。
闷热:天气很热,气压低,湿度大,使人感到呼吸不畅快。
人教版八年级上册语文字词复习资料第二部分【易错词】箱箧(qiè) 琉璃(liú) 脂粉(zhī)地窖(jiào) 赃物(zāng) 珐琅(fà láng)颤巍巍(chàn)瞥见(piē) 朱鹭(lù)恍若(huǎng) 杀戮(lù) 盟誓(shì)劫掠(jié lüè)【词语解释】赃(zāng)物(wù):偷或者抢来的东西。
人教版地理八年级上册理论知识复习资料

人教版地理八年级上册理论知识复习资料
一、自然地理部分
1. 地球与地球的运动
- 地球的形状和结构
- 地球的运动包括自转和公转
- 自转和公转带来的影响:昼夜更替、季节变化
2. 地球的水资源
- 水资源的分布与利用
- 中国的主要水系
- 世界上的大洋和大洲
3. 地球的气候
- 气候要素:温度、降水、气压、风
- 气候类型及其分布规律
- 中国的主要气候类型
4. 中国的自然环境
- 自然景观:高原、平原、盆地、丘陵、山地- 土壤资源及其分布
- 植被类型及其分布
二、人文地理部分
1. 人口与城市
- 人口分布与人口迁移
- 人口增长与控制
- 中国的人口问题
- 城市的特点和分类
2. 交通与通信
- 交通方式及其发展
- 中国的交通网络
- 通信方式及其发展
- 中国的通信发展与现状
3. 旅游资源与旅游业
- 旅游资源的类型与分布
- 中国的主要旅游景点
- 旅游业的发展与影响
4. 区域经济发展
- 区域发展不平衡的原因
- 区域发展规划及政策
- 中国的主要经济区域
- “一带一路”倡议及其影响
以上是人教版地理八年级上册理论知识的复资料,希望对你有所帮助。
如需更详细的内容,请参考教材原文或相关参考资料。
人教版语文八年级上册作者作品复习资料

人教版八年级上册语文文学常识期末复习材料1、《新闻两则》选自《人民日报》作者毛泽东新闻又称消息,是报道国内外最新发生的重大事件或新气象,新成就的记叙文。
2、《芦花荡》作者孙犁,选自《孙犁文集》,孙犁,现代小说家,散文家,《荷花淀》派代表作家,著有《白洋淀纪事》。
本文是孙犁的“白洋淀纪事之二”,之一是他的另一篇小说《荷花淀》。
中篇小说《铁木前传》、散文《津门小集》、论文《文学短论》。
3、《蜡烛》选自《阅读与欣赏》。
作者西蒙诺夫,苏联作家。
本文是一篇战地通讯。
4、《就英法联军远征中国给巴特勒上尉的信》选自《雨果文集》。
雨果,法国浪漫主义作家。
代表作品有《悲惨世界》、《九三年》、《巴黎圣母院》等。
5、《亲爱的爸爸妈妈》选自《人民日报》。
作者聂华苓,美国华裔作家,代表作《台湾轶事》。
6、《阿长与<山海经>》选自《朝花夕拾》,作者鲁迅,文学家,思想家,革命家。
小说集《呐喊》、《彷徨》、《故事新编》,杂文集《二心集》、《而已集》,散文集《朝花夕拾》。
第一篇白话小说《狂人日记》,中篇小说《阿Q正传》。
7、《背影》选自《朱自清散文全集》,作者朱自清,字佩弦,散文家、诗人、学者、民主战士。
作品收在《朱自清全集》里。
代表作诗文集《踪迹》、《欧旅杂记》。
8、《台阶》选自小说集《台阶》,作者李森祥。
9、《老王》选自《杨绛散文》,作者杨绛。
10、《信客》选自《秋雨散文》作者余秋雨。
11、《中国石拱桥》选自《人民日报》作者茅以升,字唐臣,江苏镇江人。
中国桥梁学家,教育家。
著有《中国古桥与新桥》。
12、《桥之美》选自《吴冠中人生小品》,作者吴冠中,中国现代画家。
油画代表作:《长江三峡》、《鲁迅的故乡》,中国画代表作《春雪》、《狮子林》、《长城》。
13、《苏州园林》选自《百科知识》,作者叶圣陶,原名绍钧,自圣陶。
江苏苏州人。
作家,教育家,编辑家。
作品收在《叶圣陶集》里。
14、《故宫博物院》作者黄传惕,选自《地理知识》。
人教版八年级全册生物复习资料

人教版八年级全册生物复习资料第一单元生物和生物圈第一章认识生物一.生物的特征:1.生物的生活需要营养2.生物能进行呼吸3.生物能排出身体内产生的废物4.生物能对外界的刺激做出反应5.生物能生长和繁殖除病毒以外,生物都是由细胞构成的。
二,调查我们身边的生物调查是科学探究常用的方法之一第二章生物圈是所有生物的家一.生物圈是最大的生态系统1.生物圈的范围:大气圈的底部、水圈的大部、岩石圈的表面以海平面为准,上达10千米,下达10千米。
2.生物圈中的生物:a.大气圈中主要有能够飞翔的昆虫和鸟类,以及细菌等微小生物b.水圈中的生物大多数生活在水面150米以内c.岩石圈是一切陆生生物的“立足点”3.生物圈为生物生存提供基本的条件:营养物质、水、空气、阳光、适宜的温度、一定的生存空间4.生态系统的类型:森林生态系统是绿色水库、草原生态系统、海洋生态系统、淡水生态系统、湿地生态系统、农田生态系统、城市生态系统5.生物圈是最大的生态系统,是一个统一的整体。
6.保护生物圈,人人有责。
二.环境对生物的影响1. 非生物因素对生物的影响光、温度、水分、空气等等。
(1)植物和人体内各种物质的运输需要水(2)植物进行光合作用需要在光下进行,并需要水、二氧化碳作原料(3)动物、植物的呼吸作用都需要空气中的氧气,也需要在适宜的温度下进行当环境中的几个或者一个因素发生急剧变化时,就会影响生物的生活,甚至导致生物死亡。
(4)科学探究的一般过程:提出问题、做出假设、制定计划、实施计划、得出结论、表达和交流。
2.生物因素对生物的影响:自然界中的每一种生物都受到其他生物的影响。
生物之间的关系:捕食关系、竞争关系、合作关系三.生物对环境的适应和影响1.生物对环境的适应:每一种生物都具有与其生活的环境相适应的形态结构和生活方式、生物的适应性是普遍存在的。
2.生物对环境的影响:生物影响环境,蚯蚓使土壤更加疏松和肥沃。
第二单元生物和细胞第一章观察细胞的结构一.练习使用显微镜1. 显微镜的构造(P36)2. 显微镜的使用方法:(1) 取镜和安放;右握左托(右手握镜臂,左手托镜座)(2) 对光:升、转、看、调(3) 观察:放、压、降、看、升、看、调(4) 整理取镜和安放:右手握住镜臂,左手托住镜座。
人教版八年级语文上册复习资料

八年级(上)语文复习资料第一单元战争记忆第1课新闻两则一、重点字词1. 给下列加点字注音。
荻.dí溃.kuì退泄.xiè气阻遏.è绥.suí聿.yù2. 解释下列词语。
(1) 业已:已经。
(2) 锐不可当:锋利无比, 不可抵挡。
二、重点句子背记知识清单白崇禧经常说;“不怕共产党凶, 只怕共产党生根。
”他是怕对了。
我们在所有江淮河汉区域, 不仅是树木, 而且是森林了。
不仅生了根, 而且枝叶茂盛了。
三、文学(文体)常识背记知识清单1. 《人民解放军百万大军横渡长江》和《中原我军解放南阳》两则新闻的作者是毛泽东。
2. 新闻的特征是用事实说话。
3. 新闻的六要素是人物、时间、地点、事件发生的原因、经过、结果。
4. 新闻的结构包括五部分标题、导语、主体、背景、结语。
第2课芦花荡一、重点字词1. 给下列加点字注音。
提防..dī fang 疟.yào子寒噤.jìn吆喝..yāo he 蹿.cuān 仄.zè歪转弯抹.mò角(点拨: 注意“提”、“喝”、“抹”等是多音字。
)2.解释下列词语。
(1) 寒噤: 因寒冷而哆嗦。
(2) 张皇失措: 慌慌张张, 不知怎么办才好。
3. 用恰当词语填空。
(1) 可是假如是月明风清的夜晚, 人们的眼再尖利一些, 就可以看见有一只小船从苇塘里撑出来, 在淀里, 像一片苇叶, 奔着东南去了。
(2) 每天夜里, 在敌人紧紧封锁的水面上, 就像一个没事人, 他按照早出晚归捕鱼撒网那股悠闲的心情撑着船, 编算着使自己高兴也使别人高兴的事情。
二、文学(文体)常识背记知识清单《芦花荡》的作者是现代著名作家孙犁, 选自《孙犁文集》, 本文是作者的“白洋淀纪事之二”, “之一”是他的另一篇小说《荷花淀》。
第3课蜡烛一、重点字词1. 给下列加点字注音。
匍匐..pú fú揣.chuāi在怀里衰.shuāi老淹没mò (点拨: 注意多音宇“揣”“没”的读音。
人教版八年级上册地理单元知识点归纳复习资料

人教版八年级上册地理单元知识点归纳复习资料第一章中国的自然地理环境中国的自然地理环境概况- 中国是世界上土地面积第三大的国家- 中国分为东部沿海地区、中部内陆地区和西部边疆地区三大自然地理区- 中国的海岸线总长约1.8万千米,是个南北长的狭长地带中国的地形地貌- 中国地域辽阔,地形地貌多样,有高山、高原、平原、丘陵等景观- 景观类型:喀斯特地貌、黄土高原、丹霞地貌等中国的气候分布- 中国气候种类繁多、变化复杂- 影响气候的因素:地理位置、地形地貌、影响大气运动的地球自转等第二章人口与城市中国的人口分布- 中国人口数量众多,人口分布不均衡- 人口密集的地带:黄河中下游平原、长江中下游平原和东南沿海地区- 人口稀少或无人区:青藏高原、沙漠、盆地、山地等中国的城市发展- 中国城市化率逐年提高,城市规模逐渐扩大- 中国城市分为一线城市、二线城市、三线城市、四线城市和五线城市- 中国城市面临的问题:交通拥堵、污染严重、房价高等第三章人口与经济中国的经济发展- 中国是世界第二大经济体- 经济改革开放以来,中国经济处于高速增长阶段中国的产业分布- 中国的主要产业有第一产业、第二产业和第三产业- 产业布局方面,东部沿海地区产业发达,中西部地区相对欠发达中国的对外贸易- 中国是世界最大的出口国之一- 中国对外贸易的主要合作对象是美国、欧盟等发达国家第四章人口与农业中国的农业资源- 中国农业资源丰富,主要农作物有稻谷、小麦、玉米、大豆等- 不同气候和地貌区域的耕种方式也不相同中国的农业生产- 中国农业生产规模较大,粮食总产量居世界第一位- 中国的农业机械化水平逐步提高中国的农村改革- 中国的农村改革经历了不同的阶段,改革措施和政策也不同- 目前的农村改革方向为实施乡村振兴战略。
人教版八年级语文(上册)古诗文复习资料(整理)

人教版八年级语文(上册)古诗、词、文专题复习资料第一部分古诗、词、文背诵默写一、课内古诗、词、文背诵默写(一)填空式默写1、土地平旷,屋舍俨然,有良田美池桑竹之属。
——陶渊明《桃花源记》2、斯是陋室,唯吾德馨。
苔痕上阶绿,草色入帘青。
——刘禹锡《陋室铭》3、于独爱莲之出淤泥而不染,濯清涟而不妖,中通外直,不蔓不枝,香远益清,亭亭净直,可远观而不可亵玩焉。
——周敦颐《爱莲说》4、闭之,则右刻“山高月小,水落石出”,左刻“清风徐来,水波不兴”,石青糁之。
船头坐三人,中峨冠而多髯者为东坡,佛印居右,鲁直居左。
佛印绝类弥勒,袒胸露乳,矫首昂视,神情与苏、黄不属。
其人视端容寂,若听茶声然。
——《核舟记》5、是故谋闭而不兴,盗窃乱贼而不作,故外户而不闭,是谓大同。
——《大道之行也》6、造化钟神秀,阴阳割昏晓。
——杜甫《望岳》7、白头搔更短,浑欲不胜簪。
——杜甫《春望》8、存者且偷生,死者长已矣。
——杜甫《石壕吏》9、重岩叠嶂,隐天蔽日,自非亭午夜分,不见曦月。
故渔者歌曰:“巴东三峡巫峡长,猿鸣三声泪沾裳。
”——郦道元《三峡》10、晓雾将歇,猿鸟乱鸣;夕日欲颓,沉鳞竞跃。
——陶弘景《答谢中书书》11、庭下如积水空明,水中藻、荇交横,盖竹柏影也。
——苏轼《记承天寺夜游》12、雾凇沆砀,天与云与山与水,上下一白。
——张岱《湖心亭看雪》13、晨兴理荒秽,带月荷锄归。
——陶渊明《归园田居》14、征蓬出汉塞,归雁入胡天。
——王维《使至塞上》15、月下飞天镜,云生结海楼。
——李白《渡荆门送别》16、箫鼓追随春社近,衣冠简朴古风存。
——陆游《游山西村》17、万里来游还望远,三年多难更凭危。
白头吊古风霜里,老木沧波无恨悲。
——陈与义《登岳阳楼》(其一)(二)理解性默写《桃花源记》陶渊明1、描绘桃花林中草美花繁的句子是“芳草鲜美,落英缤纷。
”2、描写桃花源美好自然环境的句子是“土地平旷,屋舍俨然,有良田美池桑竹之属。
”3、描写桃花源社会环境安宁的句子是“阡陌交通,鸡犬相闻。
人教版八年级上册地理复习资料全

人教版八年级上册地理复习资料全第一单元中国地理1. 地理位置:中国位于东亚,东临大海,陆地面积居世界第三。
2. 地形地貌:中国地形复杂多样,包括山脉、高原、平原、丘陵、盆地等。
3. 气候分布:中国气候南北差异大,分为北方地区、东南沿海地区、西南地区和青藏高原地区四个气候区。
4. 人口分布:中国人口众多,主要集中在东部沿海地区和沿江沿海地区。
第二单元自然环境与人类活动1. 自然环境:包括自然资源、生态环境和气候状况等。
2. 自然资源:中国拥有丰富的自然资源,如煤炭、铁矿、石油、天然气、铜、铝等。
3. 生态环境:中国生态环境问题突出,包括水污染、空气污染、土地退化等。
4. 人类活动:农业、工业、交通运输等人类活动对自然环境造成影响。
第三单元人口与城市1. 人口问题:中国人口众多,人口老龄化、人口流动、人口控制等问题日益突出。
2. 城市发展:中国城市化水平不断提高,大城市人口集中,城市规模不断扩大。
3. 城市规划:城市规划是城市发展的重要组成部分,合理规划有助于解决城市问题,提高人民生活质量。
第四单元区域经济发展1. 经济发展:中国经济发展快速,东部地区经济发达,中西部地区经济欠发达。
2. 产业布局:东部地区以制造业和服务业为主,西部地区以农业和资源开发为主。
3. 区域发展:中国加强区域发展,推动中西部地区经济发展,缩小区域差距。
第五单元生活与消费1. 生活方式:中国人生活方式多样,城乡差异大,饮食、交通、娱乐等方面有差异。
2. 消费特点:中国消费者消费观念逐渐转变,消费水平提高,消费需求多样化。
3. 旅游消费:中国旅游业快速发展,旅游消费呈现增长趋势。
第六单元流域与水资源1. 流域特点:中国流域众多,包括长江、黄河、珠江等,水资源分布不均衡。
2. 水资源开发利用:中国加强水资源开发利用,建设水利工程,提高水资源利用率。
3. 水污染问题:水污染对水资源的破坏严重,加强水环境保护刻不容缓。
第七单元农业与农村1. 农业发展:中国农业发展快速,种植业和养殖业规模不断扩大,农产品产量稳步增加。
统编教材部编版人教版八年级生物知识点体系复习学习资料上下册
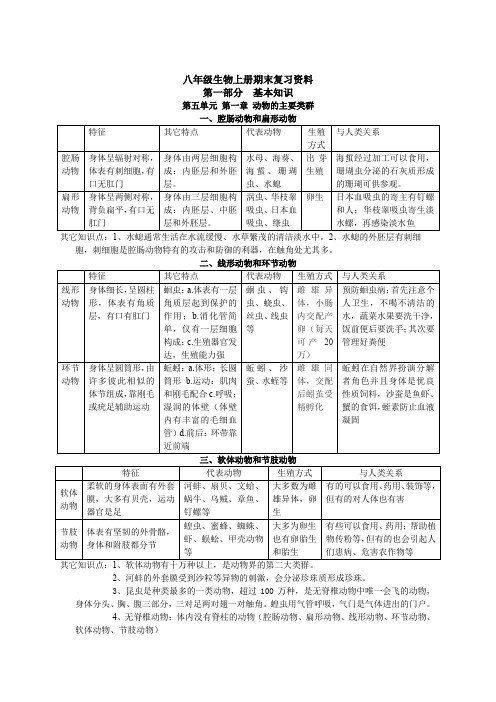
八年级生物上册期末复习资料第一部分基本知识第五单元第一章动物的主要类群其它知识点:1、水螅通常生活在水流缓慢、水草繁茂的清洁淡水中。
2、水螅的外胚层有刺细胞,刺细胞是腔肠动物特有的攻击和防御的利器,在触角处尤其多。
二、线形动物和环节动物其它知识点:1、软体动物有十万种以上,是动物界的第二大类群。
2、河蚌的外套膜受到沙粒等异物的刺激,会分泌珍珠质形成珍珠。
3、昆虫是种类最多的一类动物,超过100万种,是无脊椎动物中唯一会飞的动物,身体分头、胸、腹三部分,三对足两对翅一对触角。
蝗虫用气管呼吸,气门是气体进出的门户。
4、无脊椎动物:体内没有脊柱的动物(腔肠动物、扁形动物、线形动物、环节动物、软体动物、节肢动物)5、脊椎动物:体内有脊柱的动物(鱼类、两栖类、爬行类、鸟类、哺乳类)四、鱼类1、鱼类所以能生活在水中的特点:一是靠游泳来获取食物和防御敌害,二是能在水中呼吸。
2、结构特点:外形:体形梭形减小阻力;体色上深下浅有利于觅食避敌;体表有黏液减小阻力口和鳃盖后缘交替张合:水口鳃丝鳃盖后缘用鳃呼吸鳃是鲜红的是因为鳃丝内有丰富的毛细血管鳃丝既多又密,大大增加了与水接触的面积用鳍游泳:维持身体平衡:背鳍一个,臀鳍一个,腹鳍一对,胸鳍一对;尾鳍一个:控制身体运动的方向,尾部的摆动提供前进的动力3、鱼的体型:身体分为头、躯干和尾三部分,呈流线型,体表有鳞片和黏液。
4、鱼的运动:鱼靠尾部和躯干部的摆动和各种鳍的协调作用游泳。
5、鱼的呼吸:鱼用鳃呼吸,水从口进入,从鳃盖后缘流出,经过鳃,完成气体交换。
6、鱼的主要特征:生活在水中,体表常有鳞片覆盖,用鳃呼吸,通过尾部和躯干部的摆动以及鳍的协调作用游泳。
7、我国的四大家鱼:青鱼、草鱼、鲢鱼、鳙鱼。
8、常见的海洋鱼有:带鱼、鲨鱼、大黄鱼、小黄鱼等。
9、鱼与人类的关系:养殖业和捕捞业,可以食用,要合理利用和保护。
海马是鱼不是马,娃娃鱼是两栖动物,章、墨、鱿鱼都为软,美人鱼学名儒艮是哺乳动物。
八年级上册语文复习资料人教版

八年级上册语文复习资料人教版作为初中阶段的重点学科,语文在学生的学习生活中扮演着至关重要的角色。
而作为语文学习的一项重要任务,复习更是不可或缺的一环。
八年级上学期的语文课程是初中语文课程中的一个关键而又重要的环节,掌握好这个学期的内容对于中考语文成绩的提高具有非常关键的作用。
下面,本文将对八年级上册语文复习资料人教版进行介绍。
一、基础知识篇1.字词语法:包括词语的构成、词义、词性、词的变化和构词法等方面的知识。
2.句法:包括句子的成分、结构和作用等内容,以及句子的类型、语态和语气等方面的知识。
3.修辞运用:包括语言、形象、联想等修辞手法的应用,以及修辞手法对文章的作用等知识。
4.阅读理解:包括阅读技巧、阅读方法、阅读题型等知识,以及阅读文章后的推理和判断等能力。
二、课文篇1.散文经典:《鲁迅散文精选》《七里香》《狂人日记》等经典的散文作品,重点学生要着重阅读和理解。
2.文言文经典:《史记》、《论语》、《左传》等文言文作品,要求学生掌握古汉语的基本语法和词汇用法,以及文言文的基本阅读技巧。
3.现代文经典:《红楼梦》、《围城》、《茶馆》等现代文作品,要求学生理解现代文的语言技巧和文化内涵,并学会运用阅读技巧进行深入理解。
三、阅读篇1.新闻报道:要求学生学会分析新闻的条理和结构,理解新闻的背景、事件和人物,以及掌握新闻写作的基本技巧和语言表达能力。
2.科技报告:要求学生理解科技报告的技术术语和相关知识,了解科学技术发展的趋势和前沿,以及懂得科技报告的阅读方法和技巧。
3.文学作品:要求学生阅读具有文学价值的作品,如小说、散文、诗歌等,以提高学生的文学素养和阅读能力。
四、写作篇1.感受作文:教育学生如何表达自己的感受和思考,让学生学会运用语言表达情感,增强思维能力和语言表达能力。
2.议论文:要求学生能够掌握论点的选取和论据的列举,理解论证和反驳的技巧,以及掌握议论文的基本结构和写作方法。
3.叙事作文:教育学生如何运用语言、表情和情节来构建故事情节,通过叙事的方式表达思想和情感。
最新人教版八年级上册生物复习资料(全册)

最新人教版八年级上册生物复习资料(全册)第一章动物的主要类型1、现在生活在地球上的动物种类已知的大约有150万种,根据体内有没有脊柱可分为两大类:脊椎动物和无脊椎动物。
动物和植物的显著区别是:动物不像植物那样通过光合作用制造有机物,只能靠摄取食物来获取现存的食物,从而维持生存和繁衍。
2、腔肠动物大多数生活在海洋中,如水母、海葵等,它们的形态各异,但基本结构相似。
它们的主要特征是:身体呈辐射对称,体表有刺细胞;有口无肛门。
水螅的身体有内外两层细胞:内胚层和外胚层。
食物从口进入消化腔,食物残渣仍由口排出,腔肠动物特有的攻击和防御利器是刺细胞,在触手处尤其多。
3、扁形动物的特征是:身体呈两侧对称,背腹扁平;有口无肛门。
涡虫是一类扁形动物,形状像柳叶,有专门的感觉器官和运动器官。
4、线形动物的特征是:身体细长,呈圆柱形;体表有角质层;有口有肛门。
如蛔虫。
5、蚯蚓身体分节,可以使躯体运动灵活,体壁有发达的肌肉,可以和刚毛配合完成运动。
蚯蚓靠湿润的体壁完成呼吸。
环节动物的主要特征是:身体呈圆筒形,由许多彼此相似的体节组成;靠刚毛或疣足辅助运动。
6、软体动物的主要特征是:身体柔软,体表有外套膜,大多具有贝壳,运动器官是足。
7、节肢动物是最大的动物类群,目前已知的大约有120万种。
节肢动物的主要特征是:体表有外骨骼,身体和附肢都分节。
外骨骼不随身体的长大而长大,所以会出现蜕皮现象,外骨骼的作用是保护和支持内部结构,防止体内水分过度散失。
8、鱼类生活在水中的原因有两个:一是靠游泳来获取食物和防御敌害;二是能在水中呼吸。
鱼类有的生活在淡水中,其中四大家鱼包括青鱼、草鱼、鲢鱼、鳙鱼。
有的生活在海水中,如带鱼、大黄鱼等。
鱼类的主要特征是:生活在水中;体表常有鳞片覆盖;用鳃呼吸;通过躯干部和尾部的摆动以及鳍的协调作用游泳。
9、被称为田园卫士的青蛙,幼体蝌蚪和成体的形态结构和生活习性都发生很大的变化,特别是呼吸器官的变化依次是外鳃——内鳃——肺。
人教版八年级上册语文复习资料以及知识点

第一课:新闻两则1、新闻特点:观点鲜明,内容真实,报道及时,语言准确、简洁。
本文:语言准确简洁,感情色彩鲜明。
2、新闻的表达方式:记叙(主要)、描写、议论(最主要)。
3、新闻结构五部分:标题、导语、主体、背景、结语。
4、毛泽东:字润之,湖南韶山人,军事家、政治家、思想家。
5、标题:迅速了解全文内容。
电头:表明材料真实准确,报道及时,交代了通讯社的名称、地点和时间。
导语:比较详细地了解新闻的内容。
《人民解放军百万大军横渡长江》6、这篇新闻是按时间顺序来写的。
7、电头:表明材料真实准确,报道及时,交代了通讯社的名称、地点和时间。
《中原我军解放南阳》8、导语比标题多:背景、人物、时间。
第二课:芦花荡①人物:描写方法(外貌、语言、心理、动作)1、小说三要素人物形象(品质、精神、性格、心理)②情节:(序幕)、开端、发展、高潮、结局、(尾声)③环境:自然环境、社会环境衬托人物心理、渲染气氛、突出人物品质、为情节作铺垫。
2、芦花荡中体现的小说要素:第一要素:老头子的英雄性格(人物)(1)爱国抗日的热情,老当益壮的气概(第④小节,外貌描写;54—61小节)(2)爱憎分明的强烈感情(第10、17、18、47、53、60、61小节)(3)过于自信和自尊(第5小节,语言描写;32——45小节)(4)智勇双全的英雄行为(54—61小节)第三要素:环境描写星星第①小节水鸟宁静,渲染了阴森恐怖的气氛。
苇子拟人,生动形象地描写了芦苇的形象,表现白洋淀人民在残酷的环境中顽强抗争的意志。
侧面描写表现老头子的功劳很大。
第61小节:用优美的景物烘托了老英雄打鬼子时内心的轻松、愉快第三课:蜡烛1、文体:战地通讯;详细描写、真实2、主题:赞美反法西斯同盟各国战斗的友谊,讴歌南斯拉夫人民对苏联红军的深厚感情。
⑴炮火连天,环境危险——不怕生死、勇敢3、感人因素⑵年老体弱,行动吃力——“爬”对战士的崇敬、爱戴⑶视若亲人,沉痛哀悼——“跪”“画”“吻”不分国界、情同母子⑷结婚喜烛,意义特殊——对烈士的感情强烈、深沉、至高无上4、细节描写炮火:11次蜡烛:7次黑围巾:5次第四课:就英法联军远征中国给巴特勒上尉的信1、主题:赞美了瑰宝般的建筑——圆明园,谴责了英法联军的强盗行为。
人教版八年级数学上册知识点总结和复习要点

人教版八年级数学上册知识点总结和复习要点一、全等三角形1全等三角形的概念与性质概念:能够完全重合的两个三角形叫做全等三角形。
性质:全等三角形的对应边相等,对应角相等。
2全等三角形的判定条件SSS(边边边):三边对应相等的两个三角形全等。
SAS(边角边):两边及其夹角对应相等的两个三角形全等。
ASA(角边角):两角及其夹边对应相等的两个三角形全等。
AAS(角角边):两角及其一角的对边对应相等的两个三角形全等。
HL(直角、斜边):在一对直角三角形中,斜边及另一条直角边相等。
例子:若△ABC与△DEF中,AB = DE,AC = DF,∠A = ∠D,则根据SAS判定条件,△ABC ≌△DEF。
二、轴对称1轴对称的概念概念:如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴。
2轴对称的性质性质:轴对称图形上对应点到对称轴的距离相等;对应点的连线与对称轴垂直。
例子:等腰三角形是轴对称图形,其对称轴是底边上的高(中线或顶角平分线)。
三、实数1平方根与立方根的概念平方根:如果一个数的平方等于a,那么这个数就叫做a的平方根(或二次方根)。
立方根:如果一个数的立方等于a,那么这个数就叫做a的立方根(或三次方根)。
2实数的分类与性质实数可以分为有理数和无理数两大类。
有理数包括整数和分数,而无理数则是无限不循环小数。
实数具有封闭性、有序性和传递性等性质。
例子:√4 = 2,是4的平方根;∛8 = 2,是8的立方根。
四、一次函数1一次函数的概念概念:一般地,形如y = kx + b(k,b是常数,k ≠0)的函数,叫做一次函数。
2一次函数的性质性质:一次函数的图像是一条直线;当k > 0时,函数值y随x的增大而增大;当k < 0时,函数值y随x的增大而减小。
例子:函数y = 2x + 1是一次函数,其图像是一条斜率为2、截距为1的直线。
五、整式的乘法与因式分解1整式的乘法整式的乘法包括单项式乘单项式、单项式乘多项式、多项式乘多项式等。
人教版八年级生物上册复习资料

第五单元生物圈中的其他生物第一章各种环境中的动物一、水中生活的动物1、目前已知的动物约150 万种,按有无脊柱分为脊椎动物和无脊椎动物两大类。
按生活环境分为陆地生活的动物、水中生活的动物和空中飞行的动物。
2、水生动物最常见的是鱼类,此外,还有①腔肠动物,如海葵、珊瑚虫;②软体动物,如乌贼、章鱼;③甲壳动物,如虾、蟹;④哺乳动物,如蓝鲸、海豚等、爬行动物,如龟、鳖等其他水生动物。
3、鱼适应水中生活最重要的两个特点:①能靠游泳来获取食物和防御敌害。
② 能在水中呼吸。
4、四大家鱼是:青鱼、鲢鱼、草鱼和鳙鱼。
5、鱼是较低等的脊椎动物。
6、鱼体分三大部分:头部、躯干部和尾部。
其外形呈流线形,作用是:减少游泳时水的阻力。
8、鱼在游泳时主要靠身体 _躯干部 _和尾鳍 _的左右摆动产生前进的动力,其它鱼鳍起辅助作用。
鱼在运动时,背鳍、胸鳍和腹鳍都有维持身体平衡的作用,尾鳍有控制前进方向的作用。
9、鱼的感觉器官是侧线(感知水流和测定方向)。
10、鱼鳃为鲜红色,因为其内含丰富的毛细血管;鳃丝既多又细,其作用是大大增加了跟水的接触面积,促进血液与外界进行气体交换。
12、水由鱼口流入鳃,然后由鳃盖后缘(鳃孔)排出。
在水流经鳃丝时,水中溶解的氧气进入鳃丝的毛细血管中,而二氧化碳由鳃丝排放到水中;所以经鳃流出的水流与由口流入的水流相比,氧气的含量减少,二氧化碳的含量增高。
13、鱼类主要特征有:适于水中生活;体表被鳞片;用鳃呼吸;通过尾部的摆动和鳍的协调作用游泳。
14、海葵、海蜇、珊瑚虫等动物的结构简单,它们有口无肛门,食物从口进入消化腔,消化后的食物残渣仍由口排出体外。
这些动物统称为腔肠动物。
115、像河蚌、田螺等身体柔软靠贝壳来保护身体的动物称为软体动物。
乌贼(又叫墨鱼)、章鱼、鱿鱼、鲍鱼等贝壳退化为内壳,也都是软体动物。
16、虾类和蟹类等体表长有质地坚硬的甲,叫甲壳动物。
(属于节肢动物门)17、水中的各种生物都是水域生态系统的重要组成部分。
人教版八年级上册期末复习政治知识点归纳总结

人教版八年级上册期末复习政治知识点归纳总结一、政治制度1. 社会主义制度- 具有社会主义性质的中国特色社会主义制度是中国领导的、基于人民民主的社会主义制度。
- 主要特点包括:坚持党的领导、人民当家作主、依法治国、维护社会稳定等。
2. 人民代表大会制度- 中国特色的社会主义政治制度的核心是人民代表大会制度。
- 人民代表大会制度的特点包括:代表人民利益、多党合作和政治协商制度、民主集中制。
二、政治文化1. 马克思主义- 马克思主义是无产阶级的世界观和方法论,也是中国的指导思想。
- 主要内容包括:历史唯物主义、辩证唯物主义、共产主义理论等。
2. 社会主义核心价值观- 社会主义核心价值观是指社会主义核心价值体系中的核心内涵和主要内容。
- 包括:富强、民主、文明、和谐、自由、平等、公正、法治、爱国、敬业、诚信、友善等价值观。
3. 中国梦- 中国梦是实现中华民族伟大复兴的梦想,是全体中国人民的共同梦想。
- 包括:国家富强、民族振兴、人民幸福等内容。
三、思想道德与法律基础1.- 是指中国必须始终代表中国先进社会生产力的发展要求、始终代表中国先进文化的前进方向、始终代表中国最广大人民的根本利益。
- 的核心要义是党要始终代表中国先进社会生产力的发展要求,体现了党的先进性和人民性的统一。
2. 中华优秀传统文化- 中华优秀传统文化是中华民族的文化宝库,包含了中国传统的哲学、文学、历史、艺术、礼仪等丰富内容。
- 中华优秀传统文化具有传承性、创新性、开放性等特点。
3. 基本法律常识- 基本法律常识包括宪法、刑法、民法等法律法规的基本内容和原则。
- 具备基本法律常识可以更好地维护自己的权益和为社会稳定作出贡献。
四、国家安全与国防建设1. 国家安全观- 国家安全观是国家对自身安全状况的判断和对策的基本观点和原则。
- 基本原则包括:坚持总体安全观、坚持互利共赢的国际安全观、坚持共同、合作、综合、可持续的安全观。
2. 国防建设和军事战略- 国防建设是国家利益需要和人民利益需要的重要组成部分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教版八年级复习资料
人教版八年级复习资料一第一章勾股定理
1.勾股定理:直角三角形两直角边的平方和等于斜边的平方;即。
2.勾股定理的证明:用三个正方形的面积关系进行证明(两种方法)。
3.勾股定理逆定理:如果三角形的三边长,,满足,那么这个三角形是直角三角形。
满足的三个正整数称为勾股数。
第二章实数
1.平方根和算术平方根的概念及其性质:
(1)概念:如果,那么是的平方根,记作:;其中叫做的算术平方根。
(2)性质:①当≥0时,≥0;当0)。
人教版八年级复习资料二第三章图形的平移与旋转
1.平移:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移。
平移不改变图形大小和形状,改变了图形的位置;经过平移,对应点所连的线段平行且相等;对应线段平行且相等,对应角相等。
2.旋转:在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。
这点定点称为旋转中心,转动的角称为旋转角。
旋转不改变图形大小和形状,改变了图形
的位置;经过旋转,图形点的每一个点都绕旋转中心沿相同方向转动了相同和角度;任意一对对应点与旋转中心的连线所成的角都是旋转角;对应点到旋转中心的距离相等。
3.作平移图与旋转图。
第四章四边形性质的探索
1.多边形的分类:
2.平行四边形、菱形、矩形、正方形、等腰梯形的定义、性质、判别:
(1)平行四边形:两组对边分别平行的四边形叫做平行四边形。
平行四边形的对边平行且相等;对角相等,邻角互补;对角线互相平分。
两条对角线互相平分的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形。
(2)菱形:一组邻边相等的平行四边形叫做菱形。
菱形的四条边都相等;对角线互相垂直平分,每一条对角线平分一组对角。
四条边都相等的四边形是菱形;对角线互相垂直的平行四边形是菱形;一组邻边相等的平行四边形是菱形;对角线互相平分且垂直的四边形是菱形。
菱形的面积等于两条对角线乘积的一半(面积计算,即s菱形=l1*l2/2)。
(3)矩形:有一个内角是直角的平行四边形叫做矩形。
矩形的对角线相等;四个角都是直角。
对角线相等的平行四边形是矩形;有一个角是直角的平行四边形是矩形。
直角三角形斜边上的中线等于斜边长的一半;在直角三角形中30°所对的直角边是斜边的
一半。
(4)正方形:一组邻边相等的矩形叫做正方形。
正方形具有平行四边形、菱形、矩形的一切性质。
(5)等腰梯形同一底上的两个内角相等,对角线相等。
同一底上的两个内角相等的梯形是等腰梯形;对角线相等的梯形是等腰梯形;对角互补的梯形是等腰梯形。
(6)三角形中位线:连接三角形相连两边重点的线段。
性质:平行且等于第三边的一半
3.多边形的内角和公式:(n-2)*180°;多边形的外角和都等于。
4.中心对称图形:在平面内,一个图形绕某个点旋转,如果旋转前后的图形互相重合,那么这个图形叫做中心对称图形。
人教版八年级复习资料三第五章位置的确定
1.直角坐标系及坐标的相关知识。
2.点的坐标间的关系:如果点a、b横坐标相同,则∥轴;如果点a、b纵坐标相同,则∥轴。
3.将图形的纵坐标保持不变,横坐标变为原来的倍,所得到的图形与原图形关于轴对称;将图形的横坐标保持不变,纵坐标变为原来的倍,所得到的图形与原图形关于轴对称;将图形的横、纵坐标都变为原来的倍,所得到的图形与原图形关于原点成中心对称。
第六章一次函数
1.一次函数定义:若两个变量间的关系可以表示成(为常数,)的形式,则称是的一次函数。
当时称是的正比例函数。
正比例函
数是特殊的一次函数。
2.作一次函数的图象:列表取点、描点、连线,标出对应的函数关系式。
3.正比例函数图象性质:经过;>0时,经过一、三象限;0时,随的增大而增大,图象呈上升趋势;当0,>0时函数图象经过一、二、三象限;>0,0时函数图象经过一、二、四象限;<0,<0时函数图象经过二、三、四象限。
(4)在两个一次函数中,当它们的值相等时,其图象平行;当它们的值不等时,其图象相交;当它们的值乘积为时,其图象垂直。
4.已经任意两点求一次函数的表达式、根据图象求一次函数表达式。
5.运用一次函数的图象解决实际问题。
