2017高考数学真题导数专题

合集下载

2017年全国各地高考数学分类汇编8-导数

2017年全国各地高考数学分类汇编8-导数一、选择题（共3小题；共15分）1. 已知奇函数 f (x ) 在 R 上是增函数，g (x )=xf (x )．若 a =g (−log 25.1)，b =g (20.8)，c =g (3)，则 a ，b ，c 的大小关系为 ( ) A. a <b <c B. c <b <a C. b <a <c D. b <c <a2. 若 x =−2 是函数 f (x )=(x 2+ax −1)e x−1 的极值点，则 f (x ) 的极小值为 ( ) A. −1B. −2e −3C. 5e −3D. 13. 函数 y =f (x ) 的导函数 y =fʹ(x ) 的图象如图所示，则函数 y =f (x ) 的图象可能是 ( )A. B.C. D.二、填空题（共6小题；共30分）4. 设 f (x ) 是定义在 R 上且周期为 1 的函数，在区间 [0,1) 上，f (x )={x 2,x ∈Dx,x ∉D ，其中集合 D ={x∣ x =n−1n,n ∈N ∗}，则方程 f (x )−lgx =0 的解的个数是．5. 已知函数 f (x )=x 3−2x +e x −1ex ，其中 e 是自然对数的底数．若 f (a −1)+f (2a 2)≤0．则实数 a 的取值范围是．6. 已知 a ∈R ，设函数 f (x )=ax −lnx 的图象在点 (1,f (1)) 处的切线为 l ，则 l 在 y 轴上的截距为．7. 曲线 y =x 2+1x 在点 (1,2) 处的切线方程为．8. 如图，圆形纸片的圆心为 O ，半径为 5 cm ，该纸片上的等边三角形 ABC 的中心为 O ．D ，E ，F 为圆 O 上的点，△DBC ，△ECA ，△FAB 分别是以 BC ，CA ，AB 为底边的等腰三角形．沿虚线剪开后，分别以 BC ，CA ，AB 为折痕折起 △DBC ，△ECA ，△FAB ，使得 D ，E ，F 重合，得到三棱锥．当 △ABC 的边长变化时，所得三棱锥体积（单位：cm 3）的最大值为．9. 若函数 e x f (x )（e ≈2.71828⋯ 是自然对数的底数）在 f (x ) 的定义域上单调递增，则称函数 f (x ) 具有 M 性质．下列函数中所有具有 M 性质的函数的序号为． ① f (x )=2−x ② f (x )=3−x ③ f (x )=x 3 ④ f (x )=x 2+2．三、解答题（共15小题；共195分）10. 已知函数 f (x )=(x −√2x −1)e −x (x ≥12)．（1）求 f (x ) 的导函数；（2）求 f (x ) 在区间 [12,+∞) 上的取值范围．11. 设函数 f (x )=(1−x 2)e x ．（1）讨论 f (x ) 的单调性；（2）当 x ≥0 时，f (x )≤ax +1，求 a 的取值范围．12. 设 A ，B 为曲线 C ：y =x 24 上两点，A 与 B 的横坐标之和为 4．（1）求直线 AB 的斜率；（2）设 M 为曲线 C 上一点，C 在 M 处的切线与直线 AB 平行，且 AM ⊥BM ，求直线 AB 的方程．13. 已知函数 f (x )=x 3+ax 2+bx +1(a >0,b ∈R ) 有极值，且导函数 fʹ(x ) 的极值点是 f (x ) 的零点（极值点是指函数取极值时对应的自变量的值）．（1）求 b 关于 a 的函数关系式，并写出定义域；（2）证明：b 2>3a ；（3）若 f (x )，fʹ(x ) 这两个函数的所有极值之和不小于 −72，求 a 的取值范围．14. 设 a ∈Z ，已知定义在 R 上的函数 f (x )=2x 4+3x 3−3x 2−6x +a 在区间 (1,2) 内有一个零点x 0，g (x ) 为 f (x ) 的导函数．（1）求 g (x ) 的单调区间；（2）设 m ∈[1,x 0)∪(x 0,2]，函数 ℎ(x )=g (x )(m −x 0)−f (m )，求证：ℎ(m )ℎ(x 0)<0；（3）求证：存在大于 0 的常数 A ，使得对于任意的正整数 p ，q ，且 pq ∈[1,x 0)∪(x 0,2]，满足 ∣∣∣p q −x 0∣∣∣≥1Aq 4．15. 已知函数 f (x )=x −1−alnx ．（1）若 f (x )≥0，求 a 的值；（2）设 m 为整数，且对于任意正整数 n ，(1+12)(1+122)⋯(1+12n )<m ，求 m 的最小值．16. 设 a,b ∈R ，∣a ∣≤1．已知函数 f (x )=x 3−6x 2−3a (a −4)x +b ，g (x )=e x f (x )．（1）求f(x)的单调区间；（2）已知函数y=g(x)和y=e x的图象在公共点(x0,y0)处有相同的切线，（i）求证：f(x)在x=x0处的导数等于0；（ii）若关于x的不等式g(x)≤e x在区间[x0−1,x0+1]上恒成立，求b的取值范围．17. 已知函数f(x)=e x(e x−a)−a2x．（1）讨论f(x)的单调性；（2）若f(x)≥0，求a的取值范围．18. 已知函数f(x)=x2+2cosx，g(x)=e x(cosx−sinx+2x−2)，其中e≈2.17828⋯是自然对数的底数．（1）求曲线y=f(x)在点(π,f(π))处的切线方程；（2）令ℎ(x)=g(x)−af(x)(a∈R)，讨论ℎ(x)的单调性并判断有无极值，有极值时求出极值．19. 已知函数f(x)=lnx+ax2+(2a+1)x．（1）讨论f(x)的单调性；（2）当a<0时，证明f(x)≤−34a−2．20. 已知函数f(x)=13x3−12ax2，a∈R，（1）当a=2时，求曲线y=f(x)在点(3,f(3))处的切线方程；（2）设函数g(x)=f(x)+(x−a)cosx−sinx，讨论g(x)的单调性并判断有无极值，有极值时求出极值．21. 已知函数f(x)=ae2x+(a−2)e x−x．（1）讨论f(x)的单调性；（2）若f(x)有两个零点，求a的取值范围．22. 已知数列{x n}满足：x1=1，x n=x n+1+ln(1+x n+1)(n∈N∗)，证明：当n∈N∗时，（1）0<x n+1<x n；（2）2x n+1−x n≤x n x n+12；（3）12n−1≤x n≤12n−2．23. 在平面直角坐标系xOy中，已知椭圆C:x2a2+y2b2=1(a>b>0)的离心率为√22，椭圆C截直线y=1所得线段的长度为2√2．（1）求椭圆C的方程；（2）动直线l:y=kx+m(m≠0)交椭圆C于A，B两点，交y轴于点M%.．点N是M关于O的对称点，⊙N的半径为∣NO∣．设D为AB的中点，DE，DF与⊙N分别相切于点E，F%,，求∠EDF的最小值．24. 如图，已知抛物线x2=y，点A(−12,14)，B(32,94)，抛物线上的点P(x,y)(−12<x<32)，过点B作直线AP的垂线，垂足为Q．（1）求直线AP斜率的取值范围；（2）求∣PA∣⋅∣PQ∣的最大值．答案第一部分1. C 【解析】奇函数f(x)在R上是增函数，当x>0，f(x)>f(0)=0，且fʹ(x)>0，所以g(x)=xf(x)，则gʹ(x)=f(x)+xfʹ(x)>0，所以g(x)在(0,+∞)单调递增，且g(x)=xf(x)偶函数，所以a=g(−log25.1)=g(log25.1)，则2<−log25.1<3，1<20.8<2，由g(x)在(0,+∞)单调递增，则g(20.8)<g(log25.1)<g(3)，所以b<a<c．2. A 【解析】函数f(x)=(x2+ax−1)e x−1，可得fʹ(x)=(2x+a)e x−1+(x2+ax−1)e x−1，x=−2是函数f(x)=(x2+ax−1)e x−1的极值点，可得：−4+a+(3−2a)=0．解得a=−1．可得fʹ(x)=(2x−1)e x−1+(x2−x−1)e x−1=(x2+x−2)e x−1,函数的极值点为：x1=−2，x2=1．当x<−2或x>1时，fʹ(x)>0，函数是增函数；x∈(−2,1)时，fʹ(x)<0，函数是减函数，x=1时，函数取得极小值：f(1)=(12−1−1)e1−1=−1．3. D 【解析】由当fʹ(x)<0时，函数f(x)单调递减，当fʹ(x)>0时，函数f(x)单调递增，则由导函数y=fʹ(x)的图象可知：f(x)先单调递减，再单调递增，然后单调递减，最后单调递增，排除 A，C，且第二个拐点（即函数的极大值点）在x轴上的右侧，排除B．第二部分4. 8【解析】由于f(x)∈[0,1)，则需考虑1≤x<10的情况，在此范围内，x∈Q且x∈D时，设x=q p，p,q∈N∗，p≥2，且p，q互质，若lgx∈Q，则由lgx∈(0,1)，可设lgx=nm，m,n∈N∗，m≥2，且m，n互质，因此10n m=qp ，则10n=(qp)m，此时左边为整数，右边为非整数，矛盾，因此lgx∉Q，因此lgx不可能与每个周期内x∈D对应的部分相等，只需考虑lgx与每个周期x∉D的部分的交点，画出函数图象，图中交点除外 (1,0) 其他交点横坐标均为无理数，属于每个周期 x ∉D 的部分，且 x =1 处 yʹ∣x=1=(lgx )ʹ∣x=1=1xln10∣x=1=1ln10<1，则在 x =1 附近仅有一个交点，因此方程 f (x )−lgx =0 的解的个数为 8． 5. [−1,12]6. 17. x −y +1=0 8. 4√15 cm 3【解析】由题意，连接 OD ，交 BC 于点 G ，由题意得 OD ⊥BC ，OG =√36BC ，即 OG 的长度与 BC 的长度成正比，设 OG =x ，则 BC =2√3x ，DG =5−x ，三棱锥的高 ℎ=√DG 2−OG 2=√25−10x +x 2−x 2=√25−10x ， S △ABC =12×√32×(2√3x)2=3√3x 2，则 V =13S △ABC ×ℎ=√3x 2×√25−10x =√3⋅√25x 4−10x 5，令 f (x )=25x 4−10x 5，x ∈(0,52)，fʹ(x )=100x 3−50x 4，令 fʹ(x )≥0，即 x 4−2x 3≤0，解得 x ≤2，故 f (x ) 在 (0,2] 上单调递增，在 [2,52) 上单调递减，则 f (x )≤f (2)=80，所以 V ≤√3×√80=4√15 cm 3，所以体积最大值为 4√15 cm 3． 9. ①④【解析】对于①，f (x )=2−x ，则 g (x )=e x f (x )=e x ⋅2−x =(e2)x为实数集上的增函数；对于②，f (x )=3−x ，则 g (x )=e x f (x )=e x ⋅3−x =(e3)x为实数集上的减函数；对于③，f (x )=x 3，则 g (x )=e x f (x )=e x ⋅x 3，gʹ(x )=e x ⋅x 3+3e x ⋅x 2=e x (x 3+3x 2)=e x ⋅x 2(x +3)，当 x <−3 时，gʹ(x )<0，所以 g (x )=e x f (x ) 在定义域 R 上先减后增；对于④，f (x )=x 2+2，则 g (x )=e x f (x )=e x (x 2+2)，gʹ(x )=e x (x 2+2)+2xe x =e x (x 2+2x +2)>0 在实数集 R 上恒成立，所以 g (x )=e x f (x ) 在定义域 R 上是增函数．所以具有 M 性质的函数的序号为①④．第三部分10. （1）函数 f (x )=(x −√2x −1)e −x (x ≥12)，导数fʹ(x )=(1−12√2x−12)e −x −(x −√2x −1)e −x =(1−x +√2x−1e −x=(1−x )(1√2x−1)e −x ;（2）由 f (x ) 的导数 fʹ(x )=(1−x )(1√2x−1e −x ，可得 fʹ(x )=0 时，x =1或52，当 12<x <1 时，fʹ(x )<0，f (x ) 递减；当 1<x <52 时，fʹ(x )>0，f (x ) 递增；当 x >52 时，fʹ(x )<0，f (x ) 递减，且 x ≥√2x −1⇔x 2≥2x −1⇔(x −1)2≥0，则 f (x )≥0．由 f (12)=12e −12，f (1)=0，f (52)=12e −52，即有 f (x ) 的最大值为 12e −12，最小值为 f (1)=0．则 f (x ) 在区间 [12,+∞) 上的取值范围是 [0,12e −12]．11. （1）因为 f (x )=(1−x 2)e x ,x ∈R ，所以 fʹ(x )=(1−2x −x 2)e x ，令 fʹ(x )=0 可知 x =−1±√2，当 x <−1−√2 或 x >−1+√2 时 fʹ(x )<0，当 −1−√2<x <−1+√2 时 fʹ(x )>0，所以 f (x ) 在 (−∞,−1−√2)，(−1+√2,+∞) 上单调递减，在 (−1−√2,−1+√2) 上单调递增；（2）由题可知 f (x )=(1−x )(1+x )e x ．下面对 a 的范围进行讨论： ①当 a ≥1 时，设函数 ℎ(x )=(1−x )e x ，则 ℎʹ(x )=−xe x <0(x >0)，因此 ℎ(x ) 在 [0,+∞) 上单调递减，又因为 ℎ(0)=1，所以 ℎ(x )≤1，所以 f (x )=(1+x )ℎ(x )≤x +1≤ax +1；②当 0<a <1 时，设函数 g (x )=e x −x −1，则 gʹ(x )=e x −1>0(x >0)，所以 g (x ) 在 [0,+∞) 上单调递增，又 g (0)=1−0−1=0，所以 e x ≥x +1．因为当 0<x <1 时 f (x )>(1−x )(1+x )2，所以 (1−x )(1+x )2−ax −1=x (1−a −x −x 2)，取x0=√5−4a−12∈(0,1)，则(1−x0)(1+x0)2−ax0−1=0，所以f(x0)>ax0+1，矛盾；③当a≤0时，取x0=√5−12∈(0,1)，则f(x0)>(1−x0)(1+x0)2−1≥ax0+1，矛盾；综上所述，a的取值范围是[1,+∞)．12. （1）设A(x1,x124)，B(x2,x224)为曲线C：y=x24上两点，则直线AB的斜率为k=x124−x224x1−x2=14(x1+x2)=14×4=1；（2）设直线AB的方程为y=x+t，代入曲线C：y=x24，可得x2−4x−4t=0，即有Δ>0，x1+x2=4，x1x2=−4t，再由y=x24的导数为yʹ=12x，设M(m,m 24)，可得M处切线的斜率为12m，由C在M处的切线与直线AB平行，可得12m=1，解得m=2，即M(2,1)，由AM⊥BM可得，k AM⋅k BM=−1，即为x124−1x1−2⋅x224−1x2−2=−1，化为x1x2+2(x1+x2)+20=0，即为−4t+8+20=0，解得t=7，满足Δ>0，则直线AB的方程为y=x+7．13. （1）因为f(x)=x3+ax2+bx+1，所以g(x)=fʹ(x)=3x2+2ax+b，gʹ(x)=6x+2a，令gʹ(x)=0，解得x=−a3．由于当x>−a3时gʹ(x)>0，g(x)=fʹ(x)单调递增；当x<−a3时gʹ(x)<0，g(x)=fʹ(x)单调递减；所以fʹ(x)的极小值点为x=−a3，由于导函数fʹ(x)的极值点是原函数f(x)的零点，所以f(−a3)=0，即−a327+a39−ab3+1=0，所以b=2a29+3a(a>0)．因为f(x)=x3+ax2+bx+1(a>0,b∈R)有极值，所以fʹ(x)=3x2+2ax+b=0有两个不等的实根，所以4a2−12b>0，即a2−2a23+9a>0，解得a>3，所以b=2a29+3a(a>3)．（2）由（1）可知ℎ(a)=b2−3a=4a481−5a3+9a2=181a2(4a3−27)(a3−27)，由于a>3，所以ℎ(a)>0，即b2>3a．（3）由（1）可知fʹ(x)的极小值为fʹ(−a3)=b−a23，设x1，x2是y=f(x)的两个极值点，则x1+x2=−2a3，x1x2=b3，所以f(x1)+f(x2)=x13+x23+a(x12+x22)+b(x1+x2)+2=(x1+x2)[(x1+x2)2−3x1x2]+a[(x1+x2)2−2x1x2]+b(x1+x2)+2=4a327−2ab3+2.又因为f(x)，fʹ(x)这两个函数的所有极值之和不小于−72，所以b−a23+4a327−2ab3+2=3a−a29≥−72，因为a>3，所以2a3−63a−54≤0，所以2a(a2−36)+9(a−6)≤0，所以(a−6)(2a2+12a+9)≤0，由于a>3时2a2+12a+9>0，所以a−6≤0，解得a≤6，所以a的取值范围是(3,6]．14. （1）由f(x)=2x4+3x3−3x2−6x+a，可得g(x)=fʹ(x)=8x3+9x2−6x−6，进而可得gʹ(x)=24x2+18x−6．令gʹ(x)=0，解得x=−1，或x=14．当x变化时，gʹ(x)，g(x)的变化情况如下表：x(−∞,−1)(−1,14)(14,+∞)gʹ(x)+−+ g(x)↗↘↗所以，g(x)的单调递增区间是(−∞,−1)，(14,+∞)，单调递减区间是(−1,14)．（2）由ℎ(x)=g(x)(m−x0)−f(m)，得ℎ(m)=g(m)(m−x0)−f(m)，ℎ(x0)=g(x0)(m−x0)−f(m)．令函数H1(x)=g(x)(x−x0)−f(x)，则Hʹ1(x)=gʹ(x)(x−x0)．由（Ⅰ）知，当x∈[1,2]时，gʹ(x)>0，故当x∈[1,x0)时，Hʹ1(x)<0，H1(x)单调递减；当x∈(x0,2]时，Hʹ1(x)>0，H1(x)单调递增．因此，当x∈[1,x0)∪(x0,2]时，H1(x)>H1(x0)=−f(x0)=0，可得H1(m)>0即ℎ(m)>0，令函数H2(x)=g(x0)(x−x0)−f(x)，则H2ʹ(x)=gʹ(x0)−g(x)．由（Ⅰ）知，g(x)在[1,2]上单调递增，故当x∈[1,x0)时，H2ʹ(x)>0，H2(x)单调递增；当 x ∈(x 0,2] 时，H 2ʹ(x )<0，H 2(x ) 单调递减．因此，当 x ∈[1,x 0)∪(x 0,2] 时，H 2(x )>H 2(x 0)=0，可得 H 2(m )<0 即 ℎ(x 0)<0．所以，ℎ(m )ℎ(x 0)<0．（3）对于任意的正整数 p ，q ，且 pq ∈[1,x 0)∪(x 0,2]，令 m =pq ，函数 ℎ(x )=g (x )(m −x 0)−f (m )．由（Ⅱ）知，当 m ∈[1,x 0) 时，ℎ(x ) 在区间 (m,x 0) 内有零点；当 m ∈(x 0,2] 时，ℎ(x ) 在区间 (x 0,m ) 内有零点．所以 ℎ(x ) 在 (1,2) 内至少有一个零点，不妨设为 x 1，则 ℎ(x 1)=g (x 1)(p q −x 0)−f (pq )=0．由（Ⅰ）知 g (x ) 在 [1,2] 上单调递增，故 0<g (1)<g (x 1)<g (2)，于是 ∣∣∣p q −x 0∣∣∣=∣∣∣∣f(pq )g (x 1)∣∣∣∣≥∣∣∣f(pq )∣∣∣g (2)=∣2p 4+3p 3q−3p 2q 2−6pq 3+aq 4∣g (2)q 4．因为当 x ∈[1,2] 时，g (x )>0，故 f (x ) 在 [1,2] 上单调递增，所以 f (x ) 在区间 [1,2] 上除 x 0 外没有其他的零点，而 pq ≠x 0，故 f (pq )≠0．又因为 p ，q ，a 均为整数，所以 ∣2p 4+3p 3q −3p 2q 2−6pq 3+aq 4∣ 是正整数，从而 ∣2p 4+3p 3q −3p 2q 2−6pq 3+aq 4∣≥1．所以 ∣∣∣p q −x 0∣∣∣≥1g (2)q 4．所以，只要取 A =g (2)，就有 ∣∣∣p q −x 0∣∣∣≥1Aq 4． 15. （1）因为函数 f (x )=x −1−alnx ，x >0，所以 fʹ(x )=1−ax =x−a x，且 f (1)=0．所以当 a ≤0 时 fʹ(x )>0 恒成立，此时 y =f (x ) 在 (0,+∞) 上单调递增，这与 f (x )≥0 矛盾；当 a >0 时令 fʹ(x )=0，解得 x =a ，所以 y =f (x ) 在 (0,a ) 上单调递减，在 (a,+∞) 上单调递增，即 f (x )min =f (a )，又因为 f (x )min =f (a )≥0，所以 a =1；（2）由（1）可知当 a =1 时 f (x )=x −1−lnx ≥0，即 lnx ≤x −1，所以 ln (x +1)≤x 当且仅当 x =0 时取等号，所以 ln (1+12k )<12k ，k ∈N ∗．一方面，ln (1+12)+ln (1+122)+⋯+ln (1+12n )<12+122+⋯+12n=1−12n<1,即 (1+12)(1+122)⋯(1+12n )<e ；另一方面，n ≥3 时，(1+12)(1+122)⋯(1+12n )≥(1+12)(1+122)(1+123)=13564>2,所以当 n ≥3 时，(1+12)(1+122)⋯(1+12n )∈(2,e )．因为 m 为整数，且对于任意正整数 n ，(1+12)(1+122)⋯(1+12n )<m 成立，所以 m 的最小值为 3．16. （1）由 f (x )=x 3−6x 2−3a (a −4)x +b ，可得 fʹ(x )=3x 2−12x −3a (a −4)=3(x −a )(x −(4−a ))，令 fʹ(x )=0，解得 x =a ，或 x =4−a ．由 ∣a ∣≤1，得 a <4−a ．当 x 变化时，fʹ(x )，f (x ) 的变化情况如下表：x(−∞,a )(a,4−a )(4−a,+∞)fʹ(x )+−+f (x )↗↘↗所以 f (x ) 的单调递增区间为 (−∞,a )，(4−a,+∞)，单调递减区间为 (a,4−a )；（2）（i ）因为 gʹ(x )=e x(f (x )+fʹ(x ))，由题意知 {g (x 0)=e x 0,gʹ(x 0)=e x 0,所以 {f (x 0)e x 0=e x 0,e x 0(f (x 0)+fʹ(x 0))=e x 0,解得 {f (x 0)=1,fʹ(x 0)=0.所以 f (x ) 在 x =x 0 处的导数等于 0；（ii ）因为 g (x )≤e x ，x ∈[x 0−1,x 0+1]，由 e x >0，可得 f (x )≤1．又因为 f (x 0)=1，fʹ(x 0)=0，故 x 0 为 f (x ) 的极大值点，由（1）知 x 0=a ．另一方面，由于 ∣a ∣≤1，故 a +1<4−a ，由（1）知 f (x ) 在 (a −1,a ) 内单调递增，在 (a,a +1) 内单调递减，故当 x 0=a 时，f (x )≤f (a )=1 在 [a −1,a +1] 上恒成立，从而 g (x )≤e x 在 [x 0−1,x 0+1] 上恒成立．由 f (a )=a 3−6a 2−3a (a −4)a +b =1，得 b =2a 3−6a 2+1，−1≤a ≤1．令 t (x )=2x 3−6x 2+1，x ∈[−1,1]，所以 tʹ(x )=6x 2−12x ，令 tʹ(x )=0，解得 x =2（舍去），或 x =0．因为 t (−1)=−7，t (1)=−3，t (0)=1，故 t (x ) 的值域为 [−7,1]．所以 b 的取值范围是 [−7,1]． 17. （1） f (x )=e x (e x −a )−a 2x ，所以 fʹ(x )=2e 2x −ae x −a 2=(2e x +a )(e x −a )， ①当 a =0 时，fʹ(x )>0 恒成立，所以 f (x ) 在 R 上单调递增，②当a>0时，2e x+a>0，令fʹ(x)=0，解得x=lna，当x<lna时，fʹ(x)<0，函数f(x)单调递减，当x>lna时，fʹ(x)>0，函数f(x)单调递增，③当a<0时，e x−a>0，令fʹ(x)=0，解得x=ln(−a2)，当x<ln(−a2)时，fʹ(x)<0，函数f(x)单调递减，当x>ln(−a2)时，fʹ(x)>0，函数f(x)单调递增，综上所述，当a=0时，f(x)在R上单调递增，当a>0时，f(x)在(−∞,lna)上单调递减，在(lna,+∞)上单调递增，当a<0时，f(x)在(−∞,ln(−a2))上单调递减，在(ln(−a2),+∞)上单调递增．（2）①当a=0时，f(x)=e2x>0恒成立，②当a>0时，由（1）可得f(x)min=f(lna)=−a2lna≥0，所以lna≤0，所以0<a≤1，③当a<0是，由（1）可得f(x)min=f(ln(−a2))=3a24−a2ln(−a2)≥0，所以ln(−a2)≤34，所以−2e34≤a<0，综上所述a的取值范围为[−2e 34,1]．18. （1）f(π)=π2−2．fʹ(x)=2x−2sinx，所以fʹ(π)=2π，所以曲线y=f(x)在点(π,f(π))处的切线方程为：y−(π2−2)=2π(x−π)．化为：2πx−y−π2−2=0．（2）ℎ(x)=g(x)−af(x)=e x(cosx−sinx+2x−2)−a(x2+2cosx)，ℎʹ(x)=e x(cosx−sinx+2x−2)+e x(−sinx−cosx+2)−a(2x−2sinx) =2(x−sinx)(e x−a)=2(x−sinx)(e x−e lna)．令u(x)=x−sinx，则uʹ(x)=1−cosx≥0，所以函数u(x)在R上单调递增．因为u(0)=0，所以x>0时，u(x)>0；x<0时，u(x)<0．（1）a≤0时，e x−a>0，所以x>0时，ℎʹ(x)>0，函数ℎ(x)在(0,+∞)单调递增；x<0时，ℎʹ(x)<0，函数ℎ(x)在(−∞,0)单调递减，所以x=0时，函数ℎ(x)取得极小值，ℎ(0)=−1−2a．（2）a>0时，令ℎʹ(x)=2(x−sinx)(e x−e lna)=0．解得x1=lna，x2=0．①0<a<1时，x∈(−∞,lna)时，e x−e lna<0，ℎʹ(x)>0，函数ℎ(x)单调递增；x∈(lna,0)时，e x−e lna>0，ℎʹ(x)<0，函数ℎ(x)单调递减；x∈(0,+∞)时，e x−e lna>0，ℎʹ(x)>0，函数ℎ(x)单调递增．所以当x=0时，函数ℎ(x)取得极小值，ℎ(0)=−2a−1，当x=lna时，函数ℎ(x)取得极大值，ℎ(lna)=−a[ln2a−2lna+sin(lna)+cos(lna)+2]．②当a=1时，lna=0，x∈R时，ℎʹ(x)≥0，所以函数ℎ(x)在R上单调递增．③1<a时，lna>0，x∈(−∞,0)时，e x−e lna<0，ℎʹ(x)>0，函数ℎ(x)单调递增；x∈(0,lna)时，e x−e lna<0，ℎʹ(x)<0时，函数ℎ(x)单调递减；x∈(lna,+∞)时，e x−e lna>0，ℎʹ(x)>0，函数ℎ(x)单调递增．所以当x=0时，函数ℎ(x)取得极小值，ℎ(0)=−2a−1．当x=lna时，函数ℎ(x)取得极大值，ℎ(lna)=−a[ln2a−2lna+sin(lna)+cos(lna)+2]．综上所述，a≤0时，函数ℎ(x)在(0,+∞)单调递增；x<0时，函ℎ(x)在(−∞,0)单调递减．x=0时，函数ℎ(x)取得极小值，ℎ(0)=−1−2a．0<a<1时，函数ℎ(x)在x∈(−∞,lna)是单调递增；函数ℎ(x)在x∈(lna,0)上单调递减．当x=0时，函数ℎ(x)取得极小值，ℎ(0)=−2a−1．当x=lna时，函数ℎ(x)取得极大值，ℎ(lna)=−a[ln2a−2lna+sin(lna)+cos(lna)+2]．当a=1时，lna=0，函数ℎ(x)在R上单调递增．a>1时，函数ℎ(x)在(−∞,0)，(lna,+∞)上单调递增，函数ℎ(x)在(0,lna)上单调递减．当x=0时，函数ℎ(x)取得极大值，ℎ(0)=−2a−1．当x=lna时，函数ℎ(x)取得极小值，ℎ(lna)=−a[ln2a−2lna+sin(lna)+cos(lna)+2]．19. （1）因为f(x)=lnx+ax2+(2a+1)x，求导fʹ(x)=1x+2ax+(2a+1)=2ax2+(2a+1)x+1x=(2ax+1)(x+1)x(x>0),①当a=0时，fʹ(x)=1x+1>0恒成立，此时y=f(x)在(0,+∞)上单调递增；②当a>0，由于x>0，所以(2ax+1)(x+1)>0恒成立，此时y=f(x)在(0,+∞)上单调递增；③当a<0时，令fʹ(x)=0，解得：x=−12a．因为当x∈(0,−12a )，fʹ(x)>0，当x∈(−12a,+∞)，fʹ(x)<0，所以y=f(x)在(0,−12a )上单调递增，在(−12a,+∞)上单调递减．综上可知：当a≥0时f(x)在(0,+∞)上单调递增，当a<0时，f(x)在(0,−12a )上单调递增、在(−12a,+∞)上单调递减；（2）由（1）可知：当a<0时f(x)在(0,−12a )上单调递增，在(−12a,+∞)上单调递减，所以当x=−12a 时函数y=f(x)取最大值f(x)max=f(−12a)=−1−ln2−14a+ln(−1a)．从而要证f(x)≤−34a −2，即证f(−12a)≤−34a−2，即证−1−ln2−14a +ln(−1a)≤−34a−2，即证−12(−1a)+ln(−1a)≤−1+ln2．令t=−1a ，则t>0，问题转化为证明：−12t+lnt≤−1+ln2.(∗)令g(t)=−12t+lnt，则gʹ(t)=−12+1t，令gʹ(t)=0可知t=2，则当0<t<2时gʹ(t)>0，当t>2时gʹ(t)<0，所以y=g(t)在(0,2)上单调递增，在(2,+∞)上单调递减，即g(t)≤g(2)=−12×2+ln2=−1+ln2，即（∗）式成立，所以当a<0时，f(x)≤−34a−2成立．20. （1）当a=2时，f(x)=13x3−x2，所以fʹ(x)=x2−2x，所以k=fʹ(3)=9−6=3，f(3)=13×27−9=0，所以曲线y=f(x)在点(3,f(3))处的切线方程y=3(x−3)，即3x−y−9=0．（2）函数g(x)=f(x)+(x−a)cosx−sinx=13x3−12ax2+(x−a)cosx−sinx,所以gʹ(x)=x2−ax+cosx−(x−a)sinx−cosx=x2−ax+(x−a)sinx=(x−a)(x+sinx),令gʹ(x)=0，解得x=a，或x=0，当x<0时，x+sinx<0，当x≥0，x+sinx≥0，①若a>0时，当x<0时，gʹ(x)>0恒成立，故g(x)在(−∞,0)上单调递增，当x>a时，gʹ(x)>0恒成立，故g(x)在(a,+∞)上单调递增，当0<x<a时，gʹ(x)<0恒成立，故g(x)在(0,a)上单调递减，所以当x=a时，函数有极小值，极小值为g(a)=−16a3−sina，当x=0时，有极大值，极大值为g(0)=−a，②若a<0时，当x>0时，gʹ(x)>0恒成立，故g(x)在(−∞,0)上单调递增，当x<a时，gʹ(x)>0恒成立，故g(x)在(−∞,a)上单调递增，当a<x<0时，gʹ(x)<0恒成立，故g(x)在(a,0)上单调递减，所以当x=a时，函数有极大值，极大值为g(a)=−16a3−sina，当x=0时，有极小值，极小值为g(0)=−a，③当a=0时，gʹ(x)=x(x+sinx)，当x>0时，gʹ(x)>0恒成立，故g(x)在(0,+∞)上单调递增，当x<0时，gʹ(x)>0恒成立，故g(x)在(−∞,0)上单调递增，所以g(x)在R上单调递增，无极值．21. （1）由 f (x )=ae 2x +(a −2)e x −x ，求导 fʹ(x )=2ae 2x +(a −2)e x −1，当 a =0 时，fʹ(x )=−2e x −1<0，所以当 x ∈R ，f (x ) 单调递减，当 a >0 时，fʹ(x )=(2e x +1)(ae x −1)=2a (e x +12)(e x −1a )，令 fʹ(x )=0，解得：x =ln 1a ，当 fʹ(x )>0，解得：x >ln 1a ，当 fʹ(x )<0，解得：x <ln 1a ，所以 x ∈(−∞,ln 1a ) 时，f (x ) 单调递减，x ∈(ln 1a ,+∞) 时单调递增；当 a <0 时，fʹ(x )=2a (e x +12)(e x −1a )<0 恒成立，所以当 x ∈R ，f (x ) 单调递减，综上可知：当 a ≤0 时，f (x ) 在 R 上是单调减函数，当 a >0 时，f (x ) 在 (−∞,ln 1a ) 上是减函数，在 (ln 1a ,+∞) 上是增函数．方法二：由 f (x )=ae 2x +(a −2)e x −x ，求导 fʹ(x )=2ae 2x +(a −2)e x −1，当 a =0 时，fʹ(x )=2e x −1<0，所以当 x ∈R ，f (x ) 单调递减，当 a >0 时，fʹ(x )=(2e x +1)(ae x −1)=2a (e x +12)(e x −1a )，令 fʹ(x )=0，解得：x =−lna ，当 fʹ(x )>0，解得：x >−lna ，当 fʹ(x )<0，解得：x <−lna ，所以 x ∈(−∞,−lna ) 时，f (x ) 单调递减，x ∈(−lna,+∞) 时单调递增；当 a <0 时，fʹ(x )=2a (e x +12)(e x −1a )<0，恒成立，所以当 x ∈R ，f (x ) 单调递减，综上可知：当 a ≤0 时，f (x ) 在 R 上是单调减函数，当 a >0 时，f (x ) 在 (−∞,−lna ) 上是减函数，在 (−lna,+∞) 上是增函数．（2） ①若 a ≤0 时，由（1）可知：f (x ) 最多有一个零点，当 a >0 时，f (x )=ae 2x +(a −2)e x −x ，当 x →−∞ 时，e 2x →0，e x →0，所以当 x →−∞ 时，f (x )→+∞，当 x →+∞，e 2x →+∞，且远远大于 e x 和 x ，所以当 x →+∞，f (x )→+∞，所以函数有两个零点，f (x ) 的最小值小于 0 即可，由 f (x ) 在 (−∞,ln 1a ) 是减函数，在 (ln 1a ,+∞) 是增函数，所以 f (x )min =f (ln 1a )=a ×1a 2+(a −2)×1a −ln 1a <0，所以 1−1a −ln 1a <0，即 ln 1a +1a −1>0，设 t =1a ，则 g (t )=lnt +t −1(t >0)，因为gʹ(t)=1t+1>0，所以g(t)在(0,+∞)上单调递增，又因为g(1)=0，所以t=1a>1，解得：0<a<1，所以a的取值范围(0,1)．方法二：①若a≤0时，由（1）可知：f(x)最多有一个零点，②当a>0时，由（1）可知：当x=−lna时，f(x)取得最小值，f(x)min=f(−lna)=1−1a −ln1a，当a=1时，f(−lna)=0，故f(x)只有一个零点，当a∈(1,+∞)时，由1−1a −ln1a>0，即f(−lna)>0，故f(x)没有零点，当a∈(0,1)时，1−1a −ln1a<0，f(−lna)<0，由f(−2)=ae−4+(a−2)e−2+2>−2e−2+2>0，故f(x)在(−∞,−lna)有一个零点，假设存在正整数n0，满足n0>ln(3a−1)，则f(n0)=e n0(ae n0+a−2)−n0>e n0−n0>2n0−n0> 0，由ln(3a−1)>−lna，因此在(−lna,+∞)有一个零点．所以a的取值范围(0,1)．22. （1）用数学归纳法证明：x n>0，当n=1时，x1=1>0，成立，假设当n=k时成立，则x k>0，那么n=k+1时，若x k+1<0，则0<x k=x k+1+ln(1+x k+1)<0，矛盾，故x n+1>0，因此x n>0(n∈N∗)，所以x n=x n+1+ln(1+x n+1)>x n+1，因此0<x n+1<x n(n∈N∗)．（2）由x n=x n+1+ln(1+x n+1)得x n x n+1−4x n+1+2x n=x n+12−2x n+1+(x n+1+2)ln(1+x n+1)，记函数f(x)=x2−2x+(x+2)ln(1+x)，x≥0，所以fʹ(x)=2x2+xx+1+ln(1+x)>0，所以f(x)在(0,+∞)上单调递增，所以f(x)≥f(0)=0，因此x n+12−2x n+1+(x n+1+2)ln(1+x n+1)≥0，故2x n+1−x n≤x n x n+12．（3）因为x n=x n+1+ln(1+x n+1)≤x n+1+x n+1=2x n+1，所以x n≥12n−1，由x n x n+12≥2x n+1−x n得1x n+1−12≥2(1x n−12)>0，所以1x n −12≥2(1x n−1−12)≥⋯≥2n−1(1x1−12)=2n−2，所以x n≤12n−2，综上所述12n−1≤x n≤12n−2．23. （1）因为椭圆C的离心率为√22，所以a 2−b 2a 2=12，a 2=2b 2%,，因为椭圆 C 截直线 y =1 所得线段的长度为 2√2%,，所以椭圆 C 过点 (√2,1)%,，因为 2a 2+1b 2=1%,，所以 b 2=2，a 2=4%,，所以椭圆 C 的方程为x 24+y 22=1．（2）设 A ，B 的横坐标为 x 1，x 2，则 A (x 1,kx 1+m )，B (x 2,kx 2+m )，D (x 1+x 22,k 2(x 1+x 2)+m)，联立 {x 24+y 22=1,y =kx +m%sin α2=EN DN =ONDN =2m1+2k 2√k 4+3k 2+1=22√k 4+3k 2+1可得 (1+2k 2)x 2+4kmx +2m 2−4=0，所以 x 1+x 2=−4km1+2k 2，所以 D (−2km1+2k 2,m1+2k 2)%sinα2=EN DN=ON DN=2m1+2k 2√k 4+3k 2+1=22√k 4+3k 2+1，因为 M (0,m )，则 N (0,−m )，所以 ⊙N 的半径为 ∣m ∣，∣DN ∣=√(m 1+2k 2+m)2+(−2km 1+2k 2)2=∣2m∣1+2k 2√k 4+3k 2+1，设 ∠EDF =α，所以sin α2=EN DN =ONDN =2m1+2k 2√k 4+3k 2+1=22√k 4+3k 2+1令 y =22√k 4+3k 2+1，则 yʹ=22√k 4+3k 2+1(k 4+3k 2+1) 当 k =0 时，sin α2 取得最小值，最小值为 12，所以 ∠EDF 的最小值是 60∘．24. （1）由题可知 P (x,x 2)，−12<x <32，所以 k AP =x 2−14x+12=x −12∈(−1,1)，故直线 AP 斜率的取值范围是：(−1,1)．（2）由（1）知 P (x,x 2)，−12<x <32，所以 PA ⃗⃗⃗⃗⃗ =(−12−x,14−x 2)，设直线 AP 的斜率为 k ，则 AP:y =kx +12k +14，BP:y =−1k x +32k +94，联立直线 AP ，BP 方程可知 Q (3+4k−k 22k 2+2,9k 2+8k+14k 2+4)，故 PQ⃗⃗⃗⃗⃗ =(1+k−k 2−k 31+k 2,−k 4−k 3+k 2+k1+k 2)，又因为 PA ⃗⃗⃗⃗⃗ =(−1−k,−k 2−k )，故−∣PA ∣⋅∣PQ ∣=PA ⃗⃗⃗⃗⃗ ⋅PQ ⃗⃗⃗⃗⃗ =(1+k )3(k−1)1+k 2+k 2(1+k )3(k−1)1+k 2=(1+k )3(k −1),所以 ∣PA ∣⋅∣PQ ∣=(1+k )3(1−k )，令 f (x )=(1+x )3(1−x )，−1<x <1，则 fʹ(x )=(1+x )2(2−4x )=−2(1+x )2(2x −1)，由于当 −1<x <−12 时 fʹ(x )>0，当 12<x <1 时 fʹ(x )<0，故 f (x )max =f (12)=2716，即 ∣PA ∣⋅∣PQ ∣ 的最大值为 2716．。

2017年高考数学理试题分类汇编：导数及其应用

2017年高考数学理试题分类汇编：导数及其应用D故h (x )≤1，所以f (x )=（x +1）h (x )≤x +1≤ax +1当0＜a ＜1时，设函数g （x ）=e x -x -1，g ’（x ）=e x -1＞0（x ＞0），所以g （x ）在在[0，+∞)单调递增，而g (0)=0，故e x ≥x +1当0＜x ＜1，2()(1)(1)f x x x =-+，22(1)(1)1(1)x x ax x a x x -+--=---，取05412a x-=则2000(0,1),(1)(1)0,()1x x x ax f x ax ∈-+-=〉+故当00000510,()1-(1)2112a x f x x x ax ≤=〉+=〉+时，取（）综上，a 的取值范围[1，+∞）(2017年新课标Ⅰ文) 21．已知函数()f x =e x (e x ﹣a )﹣a 2x ．（1）讨论()f x 的单调性；（2）若()0f x ≥，求a 的取值范围． 21. （12分）（1）函数()f x 的定义域为(,)-∞+∞，22()2(2)()xxxxf x e ae a e a e a '=--=+-，①若0a =，则2()xf x e =，在(,)-∞+∞单调递增. ②若0a >，则由()0f x '=得ln x a =.当(,ln )x a ∈-∞时，()0f x '<；当(ln ,)x a ∈+∞时，()0f x '>，所以()f x 在(,ln )a -∞单调递减，在(ln ,)a +∞单调递增. ③若0a <，则由()0f x '=得ln()2a x =-. 当(,ln())2a x ∈-∞-时，()0f x '<；当(ln(),)2a x ∈-+∞时，()0f x '>，故()f x 在(,ln())2a -∞-单调递减，在(ln(),)2a -+∞单调递增.（2）①若0a =，则2()xf x e =，所以()0f x ≥.②若0a >，则由（1）得，当ln x a =时，()f x 取得最小值，最小值为2(ln )ln f a a a=-.从而当且仅当2ln 0aa -≥，即1a ≤时，()0f x ≥.③若0a <，则由（1）得，当ln()2a x =-时，()f x 取得最小值，最小值为23(ln())[ln()]242a af a -=--.从而当且仅当23[ln()]042aa --≥，即342e a ≥-时()0f x ≥.综上，a 的取值范围为34[2e ,1]-. 14．(2017年新课标Ⅰ文)曲线21y x x=+在点（1，2）处的切线方程为_y=x+1(2017年新课标Ⅰ) 21.已知函数2()(2)xx f x aea e x=+--.（1）讨论()f x 的单调性；（2）若()f x 有两个零点，求a 的取值范围.综上，a 的取值范围为(0,1).20．(2017年浙江卷)已知函数f (x )=（x–21x -）e x-（12x ≥）.（Ⅰ）求f (x )的导函数；（Ⅱ）求f (x )在区间1[+)2∞，上的取值范围. 【答案】（Ⅰ）f ＇（x ）=（1-x ）（1-221x -）xe -；（Ⅱ）[0,1212e -].（Ⅱ）由解得或.因为x（）1 （）（）- 0+ 0-f （x ）↓ 0 ↑ ↓又，所以f （x ）在区间[）上的取值范围是.(2017年北京卷理) （19）已知函数f （x ）=e x cos x −x .（Ⅰ）求曲线y = f （x ）在点（0，f （0））处的切线方程；（Ⅱ）求函数f （x ）在区间[0，π2]上的最大值和最小值. 【答案】（Ⅰ）f (x )=e x ·cos x －x ∴f (0)=1∴f ´(x )=e x （cos x －sin x ）－1 f ´(0)=0∴y =f (x )在（0，f (0)）处切线过点（0,1），k =0 ∴切线方程为y =1（Ⅱ）f ´(x )=e x （cos x -sin x ）－1，设f ´(x )=g (x ) ∴g ´(x )=－2sin x ·e x ≤0 ∴g (x )在［0，2π］上单调递减， ∴g (x )≤g (0)=0 ∴f ’（x ）≤0∴f (x )在［0，2π］上单调递减， f (x )max =f (0)=1 ∴f (x )min =f (2π)=－2π (2017年江苏卷) 11．已知函数31()2e e x xf x x x =-+-，其中e 是自然对数的底数．若2(1)(2)0f a f a -+≤，则实数a 的取值范围是 ▲ ．【解析】因为31()2e ()ex x f xx f x x -=-++-=-，所以函数()f x 是奇函数，因为22()32e e 322e e 0x x x x f 'xx x --=-++≥-+⋅≥，所以数()f x 在R 上单调递增，又21)02()(f f a a +-≤，即2())2(1a a f f ≤-，所以221aa≤-，即2120aa +-≤，解得112a -≤≤，故实数a 的取值范围为1[1,]2-. (2017年江苏卷) 20．已知函数32()1(0,)f x xax bx a b =+++>∈R 有极值，且导函数()f x '的极值点是()f x 的零点．（极值点是指函数取极值时对应的自变量的值）（1）求b 关于a 的函数关系式，并写出定义域；（2）证明：23b a>；（3）若()f x ，()f x '这两个函数的所有极值之和不小于72-，求a 的取值范围．20. 【解析】（1）因为2()32f x x ax b'=++，所以()620f x x a ''=+=，所以3a x =-，所以()03af -=，所以3239a b a=+，因为24120ab ∆=->，所以3a >.（2）26345-39813b a a a =-+，23459(27)813y t t t a =-+=>因为135278t =<，所以min(27)0yy >=，所以b ²>3a .7. ( 2017年全国Ⅲ卷文)函数2sin 1xy x x=++的部分图像大致为（）答案：D12. ( 2017年全国Ⅲ卷文)已知函数)(2)(112+--++-=x x e e a x x x f 有唯一零点，则=a （） A 21- B 31C 21 D 1【解析】 0)(22)(11'=-+-=+--x x e ea x x f得1=x即1=x 为函数的极值点，故0)1(=f 则0221=+-a ，21=a 21. ( 2017年全国Ⅲ卷文)设函数2()ln (21)f x x axa x=+++.（1）讨论()f x 的单调性；（2）当0a <时，证明3()24f x a ≤--. 解：（1）由2()ln (21),(0)f x x ax a x x =+++>有'1()221f x ax a x=+++ 22(21)1ax a x x+++= (2)①当0a =时，'()10,()f x f x =>单增 ① 当0a ≠时，令'()0f x =，即22(21)10axa x +++= 解得1211(,2x xa=-=-舍)…………2()2(21)1g x ax a x =+++ⅰ.当0a >时，()g x 开口向上，102a -<,()0g x >,即'()0f x >，()f x 单增 ⅱ.当0a <时，()g x 开口向上，102a ->，此时，在1(0,)2a -上，()0g x <，即'()0f x <，()f x 单减在1(,)2a-+∞上，()0g x >，即'()0f x >，()f x 单增 (6)（2）由（1）可得：max111()()ln()1224f x f a a a=-=---故要证3()24f x a ≤--即证113ln()12244a a a ---≤-- ……即证11ln()1022a a -++≤ 即证ln 10(0)t t t -+≤>…令()ln 1g t t t =-+ 则'1()1g t t=-令'()0g t ≥，得1t <max ()(1)0g t g ∴==()0g t ∴≤ (12)故原命题得证.（15）(2017年山东卷理)若函数()xe f x （ 2.71828e =是自然对数的底数）在()f x 的定义域上单调递增，则称函数()f x 具有M 性质.下列函数中所有具有M 性质的函数的序号为 . ①()2xf x -= ②()3xf x -= ③()3f x x = ④()22f x x=+【答案】①④ 【解析】①()22xx x x e e f x e -⎛⎫=⋅= ⎪⎝⎭在R 上单调递增，故()2xf x -=具有M 性质；②()33xxxxe ef x e -⎛⎫=⋅= ⎪⎝⎭在R 上单调递减，故()3xf x -=不具有M 性质；③()3xxe f x ex =⋅，令()3xg x ex =⋅，则()()32232xx x g x ex e x x e x '=⋅+⋅=+，∴当2x >-时，()0g x '>，当2x <-时，()0g x '<，∴()3xxe f x e x =⋅在(),2-∞-上单调递减，在()2,-+∞上单调递增，故()3f x x =不具有M 性质；④()()22xxe f x e x =+，令()()22xg x e x =+，则()()()2222110xx x g x e xe x e x ⎡⎤'=++⋅=++>⎣⎦，∴()()22x x e f x e x =+在R 上单调递增，故()22f x x =+具有M 性质．（10）(2017年天津卷文)已知a ∈R ，设函数()ln f x ax x =-的图象在点（1，(1)f ）处的切线为l ，则l 在y 轴上的截距为___________．【答案】1（20）(2017年山东卷理)已知函数()22cos f x x x=+，()()cos sin 22xg x e x x x =-+-，其中 2.71828e =是自然对数的底数.（Ⅰ）求曲线()y f x =在点()(),f x π处的切线方程；（Ⅱ）令()()()()h x g x af x a R =-∈，讨论()h x 的单调性并判断有无极值，有极值时求出极值. 【答案】（Ⅰ）222y x ππ=--.（Ⅱ）综上所述：当0a ≤时，()h x 在(),0-∞上单调递减，在()0,+∞上单调递增，函数()h x 有极小值，极小值是()021h a =--；当01a <<时，函数()h x 在(),ln a -∞和()0,ln a 和()0,+∞上单调递增，在()ln ,0a 上单调递减，函数()h x 有极大值，也有极小值，极大值是()()()2ln ln 2ln sin ln cos ln 2h a a a a a a ⎡⎤=--+++⎣⎦极小值是()021h a =--；当1a =时，函数()h x 在(),-∞+∞上单调递增，无极值；当1a >时，函数()h x 在(),0-∞和()ln ,a +∞上单调递增，在()0,ln a 上单调递减，函数()h x 有极大值，也有极小值，极大值是()021h a =--；极小值是()()()2ln ln 2ln sin ln cos ln 2h a a a a a a ⎡⎤=--+++⎣⎦.【解析】解：（Ⅰ）由题意()22f ππ=-又()22sin f x x x '=-，所以()2f ππ'=，因此曲线()y f x =在点()(),f ππ处的切线方程为()()222y x πππ--=-，即222y x ππ=--.（Ⅱ）由题意得()()()22cos sin 222cos h x e x x x a x x =-+--+，因为()()()()cos sin 22sin cos 222sin xxh x e x x x e x x a x x '=-+-+--+--()()2sin 2sin x e x x a x x =---()()2sin x e a x x =--，令()sin m x x x =-则()1cos 0m x x '=-≥所以()m x 在R 上单调递增. 所以当0x >时，()m x 单调递减，当0x >时，()0m x < 当a 0exa ≤->时，(2)当0a >时，()()()ln 2sin xa h x ee x x '=--由()0h x '=得1ln x a=，2=0x①当01a <<时，ln 0a <，当(),ln x a ∈-∞时，()ln 0,0xa e e h x '-<>，()h x 单调递增；当()ln ,0x a ∈时，()ln 0,0xa e e h x '-><，()h x 单调递减；当()0,x ∈+∞时，()ln 0,0xa ee h x '->>，()h x 单调递增.所以当ln x a =时()h x 取得极大值. 极大值为()()()2ln ln 2ln sin ln cos ln 2h a a a a a a ⎡⎤=--+++⎣⎦，当0x =时()h x 取到极小值，极小值是()021h a =--；②当1a =时，ln 0a =，所以当(),x ∈-∞+∞时，()0h x '≥，函数()h x 在(),-∞+∞上单调递增，无极值；极小值是()()()2ln ln 2ln sin ln cos ln 2h a a a a a a ⎡⎤=--+++⎣⎦.综上所述：当0a ≤时，()h x 在(),0-∞上单调递减，在()0,+∞上单调递增，函数()h x 有极小值，极小值是()021h a =--；当01a <<时，函数()h x 在(),ln a -∞和()0,ln a 和()0,+∞上单调递增，在()ln ,0a 上单调递减，函数()h x 有极大值，也有极小值，极大值是()()()2ln ln 2ln sin ln cos ln 2h a a a a a a ⎡⎤=--+++⎣⎦极小值是()021h a =--；当1a =时，函数()h x 在(),-∞+∞上单调递增，无极值；当1a >时，函数()h x 在(),0-∞和()ln ,a +∞上单调递增，在()0,ln a 上单调递减，函数()h x 有极大值，也有极小值，极大值是()021h a =--；极小值是()()()2ln ln 2ln sin ln cos ln 2h a a a a a a ⎡⎤=--+++⎣⎦.（10）(2017年山东卷文)若函数()e xf x (e=2.71828是自然对数的底数)在()f x 的定义域上单调递增,学@科网则称函数()f x 具有M 性质.下列函数中具有M 性质的是（A ）()2xf x -= （B ）()2f x x = （C ）()3xf x -= （D ）()cos f x x = 【答案】A【解析】对于A,令()e2xx g x -=⋅,11()e (22ln )e 2(1ln )022x x x x x g x ---'=+=+>,则()g x 在R上单调递增,故()f x 具有M 性质,故选A. （20）(2017年山东卷文)已知函数()3211,32f x xax a =-∈R .（Ⅰ）当a =2时,求曲线()y f x =在点()()3,3f 处的切线方程；（Ⅱ）设函数()()()cos sin g x f x x a x x =+--,讨论()g x 的单调性并判断有无极值,有极值时求出极值. 【答案】（Ⅰ）390x y --=,（Ⅱ）见解析.3x-y-9=0（20）(2017年天津卷理)设a ∈Z ，已知定义在R 上的函数432()2336f x x x x x a=+--+在区间(1,2)内有一个零点0x ，()g x 为()f x 的导函数.（Ⅰ）求()g x 的单调区间；（Ⅱ）设00[1,)(,2]m x x ∈，函数0()()()()h x g x m x f m =--，求证：0()()0h m h x <；（Ⅲ）求证：存在大于0的常数A ，使得对于任意的正整数,p q ，且00[1,)(,2],px x q∈ 满足041||px qAq -≥.【答案】（1）增区间是(,1)-∞-，1(,)4+∞，减区间是1(1,)4-.（2）（3）证明见解析【解析】（Ⅰ）由432()2336f x x x x x a=+--+，可得32()()8966g x f x xx x '==+--，进而可得2()24186g x xx '=+-.令()0g x '=，解得1x =-，或14x =. 当x 变化时，(),()g x g x '的变化情况如下表：x (,1)-∞- 1(1,)4- 1(,)4+∞()g x ' + - + ()g x↗↘↗所以，()g x 的单调递增区间是(,1)-∞-，1(,)4+∞，单调递减区间是1(1,)4-. （Ⅱ）证明：由0()()()()h x g x m x f m =--，得0()()()()h m g m m x f m =--，000()()()()h x g x m x f m =--.（III ）证明：对于任意的正整数 p ，q ，且00[1)(,],2px x q∈，令pm q =，函数0()()()()h g m x x x m f =--.由（II ）知，当0[1),m x ∈时，()h x 在区间0(,)m x 内有零点；当0(,2]m x ∈时，()h x 在区间0(),x m 内有零点.1110x ,)()()()0p pg x x f q q=--=不妨设为则 h(x所以041|2|()px qg q -≥.所以，只要取()2A g =，就有041||p x qAq -≥.（19）(2017年天津卷文)设,a b ∈R，||1a ≤．已知函数32()63(4)f x x x a a x b=---+，()e ()x g x f x =．（Ⅰ）求()f x 的单调区间；（Ⅱ）已知函数()y g x =和e xy =的图象在公共点（x 0，y 0）处有相同的切线，（i ）求证：()f x 在0x x =处的导数等于0；（ii ）若关于x 的不等式()e xg x ≤在区间00[1,1]x x -+上恒成立，求b 的取值范围．【解析】（Ⅰ）由324()63()f x x a x x a b=--+-，可得2()3123()3()((44))f 'x x a x a a x x a -=---=--，令()0f 'x =，解得x a =或4x a =-．由||1a ≤，得4a a <-．当x 变化时，()f 'x ，()f x 的变化情况如下表：x(,)a -∞(),4a a -(4,)a -+∞()f 'x +-+()f x所以，()f x 的单调递增区间为(,)a -∞，(4,)a -+∞，单调递减区间为(),4a a -．（Ⅱ）（i ）因为()e (()())xx x g'f f 'x =+，由题意知0000()e ()e xx x x g g'⎧=⎪⎨=⎪⎩，所以000000()e e e (()())ex x xx f f f x 'x x ⎧=⎪⎨+=⎪⎩，解得00()1()0f 'x x f =⎧⎨=⎩．所以，()f x 在0x x =处的导数等于0．（ii ）因为()e xg x ≤，00[11],x xx ∈-+，由ex>，可得()1f x ≤．又因为0()1f x =，0()0f 'x =，故0x 为()f x 的极大值点，由（Ⅰ）知0x a=．另一方面，由于||1a ≤，故14a a +<-，。

高考数学导数切线专题

类型一：在型切线方程1．(2017·高考全国卷Ⅰ)曲线y ＝x 2＋1x在点(1,2)处的切线方程为________．2．(2017·高考天津卷)已知a ∈R ，设函数f (x )＝ax －ln x 的图象在点(1，f (1))处的切线为l ，则l 在y 轴上的截距为________．3：2016考全国卷Ⅲ)已知f (x )为偶函数，当x ＜0时，f (x )＝ln(－x )＋3x ，则曲线y ＝f (x )在点(1，－3)处的切线方程是________．4．曲线y ＝a ln x (a ＞0)在x ＝1处的切线与两坐标轴围成的三角形的面积为4，则a ＝________.5．(2018·山师附中质检)已知直线y ＝kx ＋b 与曲线y ＝ax 2＋2＋ln x 相切于点P (1,4)，则b 的值为( )A ．3B ．1C ．－3D ．－16．(2018·福州质检)如图，y ＝f (x )是可导函数，直线l ：y ＝kx ＋2是曲线y ＝f (x )在x ＝3处的切线，令g (x )＝xf (x )，g ′(x )是g (x )的导函数，则g ′(3)＝( )A ．－1B ．0C ．2D ．47．(2018·赣中南五校联考)已知函数f n (x )＝x n ＋1，n ∈N 的图象与直线x ＝1交于点P ，若图象在点P 处的切线与x 轴交点的横坐标为x n ，则log 2 019x 1＋log 2 019x 2＋…＋log 2 019x 2 018的值为( )A ．－1B ．1－log 2 0192 018C ．－log 2 0192 018D ．18．(2018·兰州模拟)已知函数f (x )，g (x )满足f (5)＝5，f ′(5)＝3，g (5)＝4，g ′(x )＝1，则函数y ＝f (x )＋2g (x )的图象在x ＝5处的切线方程为________．9．设函数f (x )＝ax －bx ，曲线y ＝f (x )在点(2，f (2))处的切线方程为7x －4y －12＝0.则f (x )的解析式为________．类型二：过型切线方程1. 已知函数f (x )＝x ln x ，若直线l 过点(0，－1)，并且与曲线y ＝f (x )相切，则直线l 的方程为( )A ．x ＋y －1＝0B ．x －y －1＝0C ．x ＋y ＋1＝0D ．x －y ＋1＝02 若直线y ＝2x ＋m 是曲线y ＝x ln x 的切线，则实数m 的值为________．3.函数f (x )＝ln x ＋ax 存在与直线2x －y ＝0平行的切线，则实数a 的取值范围是( ) A ．(－∞，2] B ．(－∞，2) C ．(2，＋∞) D ．(0，＋∞)类型三：公切线问题1 (2016·高考全国卷Ⅱ)若直线y ＝kx ＋b 是曲线y ＝ln x ＋2的切线，也是曲线y ＝ln(x ＋1)的切线，则b ＝________.2．若曲线f (x )＝a cos x 与曲线g (x )＝x 2＋bx ＋1在交点(0，m )处有公切线，则a ＋b ＝( ) A ．－1 B ．0 C ．1D ．2 3．(2018·南昌模拟)已知f (x )＝ln x ，g (x )＝12x 2＋mx ＋72(m ＜0)，直线l 与函数f (x )，g (x )的图象都相切，且与f (x )图象的切点为(1，f (1))，则m 的值为( )A ．－1B ．－3C ．－4D ．－24．(2018·潍坊模拟)若存在过点O (0,0)的直线l 与曲线y ＝x 3－3x 2＋2x 和y ＝x 2＋a 都相切，则a 的值是________．类型一：在型切线方程1．(2017·高考全国卷Ⅰ)曲线y ＝x 2＋1x 在点(1,2)处的切线方程为________．解析：∵y ＝x 2＋1x ，∴y ′＝2x －1x 2，∴y ′|x ＝1＝2－1＝1，∴所求切线方程为y －2＝x －1，即x －y ＋1＝0. 答案：x －y ＋1＝02．(2017·高考天津卷)已知a ∈R ，设函数f (x )＝ax －ln x 的图象在点(1，f (1))处的切线为l ，则l 在y 轴上的截距为________．解析：由题意可知f ′(x )＝a －1x ，所以f ′(1)＝a －1，因为f (1)＝a ，所以切点坐标为(1，a )，所以切线l 的方程为y －a ＝(a －1)(x －1)，即y ＝(a －1)x ＋1.令x ＝0，得y ＝1，即直线l 在y 轴上的截距为1. 答案：13：2016考全国卷Ⅲ)已知f (x )为偶函数，当x ＜0时，f (x )＝ln(－x )＋3x ，则曲线y ＝f (x )在点(1，－3)处的切线方程是________．解析：令x ＞0，则－x ＜0，f (－x )＝ln x －3x ，又f (－x )＝f (x )， ∴f (x )＝ln x －3x (x ＞0)，则f ′(x )＝1x－3(x ＞0)，∴f ′(1)＝－2，∴在点(1，－3)处的切线方程为y ＋3＝－2(x －1)，则y ＝－2x －1. 答案：y ＝－2x －14．曲线y ＝a ln x (a ＞0)在x ＝1处的切线与两坐标轴围成的三角形的面积为4，则a ＝________.解析：∵y ＝a ln x ，∴y ′＝ax，∴在x ＝1处的切线的斜率k ＝a ，而f (1)＝a ln 1＝0，故切点为(1,0)，∴切线方程为y ＝a (x －1)．令y ＝0，得x ＝1；令x ＝0，得y ＝－a . ∴三角形面积S ＝12×a ×1＝4，∴a ＝8.答案：85．(2018·山师附中质检)已知直线y ＝kx ＋b 与曲线y ＝ax 2＋2＋ln x 相切于点P (1,4)，则b 的值为( )A ．3B ．1C ．－3D ．－1解析：选D.法一：因为点P (1,4)在曲线y ＝ax 2＋2＋ln x 上，所以a ＋2＝4，解得a ＝2，故y ′＝2ax ＋1x ＝4x ＋1x，所以y ′|x ＝1＝5＝k ，将点P (1,4)代入y ＝5x ＋b ，得b ＝－1.故选D.法二：由题意得y ′＝2ax ＋1x ，所以在点P (1,4)处的切线方程为y －4＝(2a ＋1)(x －1)，即y ＝(2a ＋1)x －2a ＋3，故⎩⎪⎨⎪⎧2a ＋1＝k ，－2a ＋3＝b ，a ＋2＝4，解得⎩⎪⎨⎪⎧a ＝2，k ＝5，b ＝－1.6．(2018·福州质检)如图，y ＝f (x )是可导函数，直线l ：y ＝kx ＋2是曲线y ＝f (x )在x ＝3处的切线，令g (x )＝xf (x )，g ′(x )是g (x )的导函数，则g ′(3)＝( )A ．－1B ．0C ．2D ．4解析：选B.依题意得f (3)＝k ×3＋2＝1，k ＝－13，则f ′(3)＝k ＝－13，g ′(3)＝f (3)＋3f ′(3)＝1－1＝0，故选B.7．(2018·赣中南五校联考)已知函数f n (x )＝x n ＋1，n ∈N 的图象与直线x ＝1交于点P ，若图象在点P 处的切线与x 轴交点的横坐标为x n ，则log 2 019x 1＋log 2 019x 2＋…＋log 2 019x 2 018的值为( )A ．－1B ．1－log 2 0192 018C ．－log 2 0192 018D ．1解析：选A.由题意可得点P 的坐标为(1,1)，f ′n (x )＝(n ＋1)·x n ，所以f n (x )图象在点P 处的切线的斜率为n ＋1，故可得切线的方程为y －1＝(n ＋1)(x －1)，所以切线与x 轴交点的横坐标为x n ＝nn ＋1，则log 2 019x 1＋log 2 019x 2＋…＋log 2 019x 2 018＝log 2 019(x 1x 2…x 2 018)＝log 2019⎝⎛⎭⎫12×23×34×…×2 0182 019＝log 2 01912 019＝－1，故选A.8．(2018·兰州模拟)已知函数f (x )，g (x )满足f (5)＝5，f ′(5)＝3，g (5)＝4，g ′(5)＝1，则函数y ＝f (x )＋2g (x )的图象在x ＝5处的切线方程为________．解析：由y ＝f (x )＋2g (x )＝h (x )知y ′＝h ′(x )＝f ′(x )g (x )－(f (x )＋2)g ′(x )g 2(x )得h ′(5)＝f ′(5)g (5)－(f (5)＋2)g ′(5)g 2(5)＝3×4－(5＋2)×142＝516.又h (5)＝f (5)＋2g (5)＝5＋24＝74，所以切线方程为y －74＝516(x －5)，即5x －16y ＋3＝0. 答案：5x －16y ＋3＝09．设函数f (x )＝ax －bx ，曲线y ＝f (x )在点(2，f (2))处的切线方程为7x －4y －12＝0.则f (x )的解析式为________．解析：方程7x －4y －12＝0可化为y ＝74x －3.当x ＝2时，y ＝12.又f ′(x )＝a ＋bx2，于是⎩⎨⎧2a －b 2＝12，a ＋b 4＝74，解得⎩⎪⎨⎪⎧a ＝1，b ＝3.故f (x )＝x －3x .答案：f (x )＝x －3x类型二：过型切线方程1. 已知函数f (x )＝x ln x ，若直线l 过点(0，－1)，并且与曲线y ＝f (x )相切，则直线l 的方程为( )A ．x ＋y －1＝0B ．x －y －1＝0C ．x ＋y ＋1＝0D ．x －y ＋1＝0解析：∵点(0，－1)不在曲线f (x )＝x ln x 上， ∴设切点为(x 0，y 0)．又∵f ′(x )＝1＋ln x ，∴⎩⎪⎨⎪⎧y 0＝x 0ln x 0，y 0＋1＝(1＋ln x 0)x 0，解得x 0＝1，y 0＝0.∴切点为(1,0)，∴f ′(1)＝1＋ln 1＝1.∴直线l 的方程为y ＝x －1，即x －y －1＝0.故选B. 答案：B2 若直线y ＝2x ＋m 是曲线y ＝x ln x 的切线，则实数m 的值为________．解析：设切点为(x 0，x 0ln x 0)，由y ′＝(x ln x )′＝ln x ＋x ·1x ＝ln x ＋1，得切线的斜率k ＝ln x 0＋1，故切线方程为y －x 0ln x 0＝(ln x 0＋1)(x －x 0)，整理得y ＝(ln x 0＋1)x －x 0，与y ＝2x ＋m 比较得⎩⎪⎨⎪⎧ln x 0＋1＝2，－x 0＝m ，解得x 0＝e ，故m ＝－e. 答案：－e3.函数f (x )＝ln x ＋ax 存在与直线2x －y ＝0平行的切线，则实数a 的取值范围是( ) A ．(－∞，2] B ．(－∞，2) C ．(2，＋∞)D ．(0，＋∞)解析：直线2x －y ＝0的斜率为2，且f ′(x )＝1x ＋a (x ＞0)，令1x ＋a ＝2得a ＝2－1x .因为x＞0，则1x＞0，所以a ＜2.故选B.答案：B类型三：公切线问题1 (2016·高考全国卷Ⅱ)若直线y ＝kx ＋b 是曲线y ＝ln x ＋2的切线，也是曲线y ＝ln(x ＋1)的切线，则b ＝________.解析：直线y ＝kx ＋b 与曲线y ＝ln x ＋2，y ＝ln(x ＋1)均相切，设切点分别为A (x 1，y 1)，B (x 2，y 2)，由y ＝ln x ＋2得y ′＝1x ，由y ＝ln(x ＋1)得y ′＝1x ＋1，∴k ＝1x 1＝1x 2＋1，∴x 1＝1k ，x 2＝1k －1，∴y 1＝－ln k ＋2，y 2＝－ln k .即A ⎝⎛⎭⎫1k ，－ln k ＋2， B ⎝⎛⎭⎫1k －1，－ln k ， ∵A 、B 在直线y ＝kx ＋b 上，∴⎩⎨⎧2－ln k ＝k ·1k＋b ，－ln k ＝k ·⎝⎛⎭⎫1k －1＋b ⇒⎩⎪⎨⎪⎧b ＝1－ln 2，k ＝2. 答案：1－ln 22．若曲线f (x )＝a cos x 与曲线g (x )＝x 2＋bx ＋1在交点(0，m )处有公切线，则a ＋b ＝( ) A ．－1 B ．0 C ．1D ．2解析：选C.依题意得，f ′(x )＝－a sin x ，g ′(x )＝2x ＋b ，于是有f ′(0)＝g ′(0)，即－a sin 0＝2×0＋b ，b ＝0， m ＝f (0)＝g (0)，即m ＝a ＝1，因此a ＋b ＝1.3．(2018·南昌模拟)已知f (x )＝ln x ，g (x )＝12x 2＋mx ＋72(m ＜0)，直线l 与函数f (x )，g (x )的图象都相切，且与f (x )图象的切点为(1，f (1))，则m 的值为( )A ．－1B ．－3C ．－4D ．－2解析：选D.∵f ′(x )＝1x，∴直线l 的斜率为k ＝f ′(1)＝1，又f (1)＝0， ∴切线l 的方程为y ＝x －1.g ′(x )＝x ＋m ，设直线l 与g (x )的图象的切点为(x 0，y 0)，则有⎩⎪⎨⎪⎧x 0＋m ＝1，y 0＝x 0－1，y 0＝12x 2＋mx 0＋72，m ＜0解得m ＝－2.4．(2018·潍坊模拟)若存在过点O (0,0)的直线l 与曲线y ＝x 3－3x 2＋2x 和y ＝x 2＋a 都相切，则a 的值是________．解析：易知点O (0,0)在曲线y ＝x 3－3x 2＋2x 上． ①当O (0,0)是切点时，由y ′＝3x 2－6x ＋2，得y ′|x ＝0＝2，即直线l 的斜率为2，故直线l 的方程为y ＝2x .由⎩⎪⎨⎪⎧y ＝2x ，y ＝x 2＋a ，得x 2－2x ＋a ＝0，依题意Δ＝4－4a ＝0，得a ＝1.②当O (0,0)不是切点时，设直线l 与曲线y ＝x 3－3x 2＋2x 相切于点P (x 0，y 0)，则y 0＝x 30－3x 20＋2x 0，且k ＝y ′|x ＝x 0＝3x 20－6x 0＋2，① 又k ＝y 0x 0＝x 20－3x 0＋2，②联立①②，得x 0＝32(x 0＝0舍去)，所以k ＝－14，故直线l 的方程为y ＝－14x .由⎩⎪⎨⎪⎧y ＝－14x ，y ＝x 2＋a ，得x 2＋14x ＋a ＝0，依题意，Δ＝116－4a ＝0，得a ＝164.综上，a ＝1或a ＝164.答案：1或164。

历年高考数学导数压轴题

历年高考数学导数压轴题
1. 2017年高考数学导数题：
①已知函数f(x)的导数是g(x)，若g(x)的导数等于函数f(x)的二阶导数，求f(x)的表达式。

解：令数列{y，y’，y”}表示函数f(x)的值与其一阶导数与二阶导数，
令数列{u，u’}表示函数g(x)的值与其一阶导数，那么依据题意有：
u’=y”，u=y’，由于积分的连续性，可得函数f(x)的表达式：f(x)=xu-
1/2∫udu+φ(x)，其中φ(x)是任意可导函数。

2. 2018年高考数学导数题：
①已知函数f(x)在(-1,1)上有关于x的二阶导数存在且满足f'(-1)=f'(1)，
求f(x)的一般形式。

解：由题意可知f'(-1)=f'(1)，即函数f(x)在(-1,1)处有极值，f”(x)存在于(-1,1)，根据可导多次函数的性质，在(-1,1)处函数f(x)可表示为：
f(x)=ax^3+bx^2+cx+d，其中a、b、c、d均为常数，求出常数a、b、c
值可得f(x)的一般形式。

3. 2019年高考数学导数题：
①已知函数f(x)的导数为2x-1，求f(x)的一般形式；
解：令y=f(x)，则有y’=2x-1，由积分的连续性，可得y=x^2-2ln|x|+C，其中C为任意常数，即f(x)=x^2-2ln|x|+C。

【K12高考数学】2017年高考真题分类汇编(理数)：专题2导数(解析版)

2017年高考真题分类汇编（理数）：专题2导数一、单选题（共3题；共6分）1、（2017•浙江）函数y=f（x）的导函数y=f′（x）的图象如图所示，则函数y=f（x）的图象可能是（）A、B、C、D、2、（2017•新课标Ⅱ）若x=﹣2是函数f（x）=（x2+ax﹣1）e x﹣1的极值点，则f（x）的极小值为（）A、﹣1B、﹣2e﹣3C、5e﹣3D、13、（2017•新课标Ⅲ）已知函数f（x）=x2﹣2x+a（e x﹣1+e﹣x+1）有唯一零点，则a=（）A、﹣B、C、D、1二、解答题（共8题；共50分）4、（2017•浙江）已知函数f（x）=（x﹣）e﹣x（x≥）．（Ⅰ）求f（x）的导函数；（Ⅱ）求f（x）在区间[，+∞）上的取值范围．5、（2017•山东）已知函数f（x）=x2+2cosx，g（x）=e x（cosx﹣sinx+2x﹣2），其中e≈2.17828…是自然对数的底数．（13分）（Ⅰ）求曲线y=f（x）在点（π，f（π））处的切线方程；（Ⅱ）令h（x）=g（x）﹣af（x）（a∈R），讨论h（x）的单调性并判断有无极值，有极值时求出极值．6、（2017•北京卷）已知函数f（x）=e x cosx﹣x．（13分）(1)求曲线y=f（x）在点（0，f（0））处的切线方程；(2)求函数f（x）在区间[0，]上的最大值和最小值．7、（2017·天津）设a∈Z，已知定义在R上的函数f（x）=2x4+3x3﹣3x2﹣6x+a在区间（1，2）内有一个零点x0，g（x）为f（x）的导函数．（Ⅰ）求g（x）的单调区间；（Ⅱ）设m∈[1，x0）∪（x0，2]，函数h（x）=g（x）（m﹣x0）﹣f（m），求证：h（m）h（x0）＜0；（Ⅲ）求证：存在大于0的常数A，使得对于任意的正整数p，q，且∈[1，x0）∪（x0，2]，满足|﹣x0|≥．8、（2017•江苏）已知函数f（x）=x3+ax2+bx+1（a＞0，b∈R）有极值，且导函数f′（x）的极值点是f（x）的零点．（极值点是指函数取极值时对应的自变量的值）（Ⅰ）求b关于a的函数关系式，并写出定义域；（Ⅱ）证明：b2＞3a；（Ⅲ）若f（x），f′（x）这两个函数的所有极值之和不小于﹣，求a的取值范围．9、（2017•新课标Ⅰ卷）已知函数f（x）=ae2x+（a﹣2）e x﹣x．（12分）(1)讨论f（x）的单调性；(2)若f（x）有两个零点，求a的取值范围．10、（2017•新课标Ⅱ）已知函数f（x）=ax2﹣ax﹣xlnx，且f（x）≥0．（Ⅰ）求a；（Ⅱ）证明：f（x）存在唯一的极大值点x0，且e﹣2＜f（x0）＜2﹣2．11、（2017•新课标Ⅲ）已知函数f（x）=x﹣1﹣alnx．（Ⅰ）若f（x）≥0，求a的值；（Ⅱ）设m为整数，且对于任意正整数n，（1+）（1+）…（1+）＜m，求m的最小值．答案解析部分一、单选题1、【答案】D【考点】函数的图象，函数的单调性与导数的关系【解析】【解答】解：由当f′（x）＜0时，函数f（x）单调递减，当f′（x）＞0时，函数f（x）单调递增，则由导函数y=f′（x）的图象可知：f（x）先单调递减，再单调递增，然后单调递减，最后单调递增，排除A，C，且第二个拐点（即函数的极大值点）在x轴上的右侧，排除B，故选D【分析】根据导数与函数单调性的关系，当f′（x）＜0时，函数f（x）单调递减，当f′（x）＞0时，函数f（x）单调递增，根据函数图象，即可判断函数的单调性，然后根据函数极值的判断，即可判断函数极值的位置，即可求得函数y=f（x）的图象可能2、【答案】A【考点】导数的运算，利用导数研究函数的单调性，利用导数研究函数的极值【解析】【解答】解：函数f（x）=（x2+ax﹣1）e x﹣1，可得f′（x）=（2x+a）e x﹣1+（x2+ax﹣1）e x﹣1，x=﹣2是函数f（x）=（x2+ax﹣1）e x﹣1的极值点，可得：﹣4+a+（3﹣2a）=0．解得a=﹣1．可得f′（x）=（2x﹣1）e x﹣1+（x2﹣x﹣1）e x﹣1，=（x2+x﹣2）e x﹣1，函数的极值点为：x=﹣2，x=1，当x＜﹣2或x＞1时，f′（x）＞0函数是增函数，x∈（﹣2，1）时，函数是减函数，x=1时，函数取得极小值：f（1）=（12﹣1﹣1）e1﹣1=﹣1．故选：A．【分析】求出函数的导数，利用极值点，求出a，然后判断函数的单调性，求解函数的极小值即可．3、【答案】C【考点】利用导数研究函数的单调性，导数在最大值、最小值问题中的应用，函数的零点与方程根的关系，函数的零点【解析】【解答】解：因为f（x）=x2﹣2x+a（e x﹣1+e﹣x+1）=﹣1+（x﹣1）2+a（e x﹣1+）=0，所以函数f（x）有唯一零点等价于方程1﹣（x﹣1）2=a（e x﹣1+）有唯一解，等价于函数y=1﹣（x﹣1）2的图象与y=a（e x﹣1+）的图象只有一个交点．①当a=0时，f（x）=x2﹣2x≥﹣1，此时有两个零点，矛盾；②当a＜0时，由于y=1﹣（x﹣1）2在（﹣∞，1）上递增、在（1，+∞）上递减，且y=a（e x﹣1+）在（﹣∞，1）上递增、在（1，+∞）上递减，所以函数y=1﹣（x﹣1）2的图象的最高点为A（1，1），y=a（e x﹣1+）的图象的最高点为B（1，2a），由于2a＜0＜1，此时函数y=1﹣（x﹣1）2的图象与y=a（e x﹣1+）的图象有两个交点，矛盾；③当a＞0时，由于y=1﹣（x﹣1）2在（﹣∞，1）上递增、在（1，+∞）上递减，且y=a（e x﹣1+）在（﹣∞，1）上递减、在（1，+∞）上递增，所以函数y=1﹣（x﹣1）2的图象的最高点为A（1，1），y=a（e x﹣1+）的图象的最低点为B（1，2a），由题可知点A与点B重合时满足条件，即2a=1，即a=，符合条件；综上所述，a=，故选：C．【分析】通过转化可知问题等价于函数y=1﹣（x﹣1）2的图象与y=a（e x﹣1+）的图象只有一个交点求a的值．分a=0、a＜0、a＞0三种情况，结合函数的单调性分析可得结论．二、解答题4、【答案】解：（Ⅰ）函数f（x）=（x﹣）e﹣x（x≥），导数f′（x）=（1﹣••2）e﹣x﹣（x﹣）e﹣x=（1﹣x+）e﹣x=（1﹣x）（1﹣）e﹣x；（Ⅱ）由f（x）的导数f′（x）=（1﹣x）（1﹣）e﹣x，可得f′（x）=0时，x=1或，当＜x＜1时，f′（x）＜0，f（x）递减；当1＜x＜时，f′（x）＞0，f（x）递增；当x＞时，f′（x）＜0，f（x）递减，且x≥⇔x2≥2x﹣1⇔（x﹣1）2≥0，则f（x）≥0．由f（）=e，f（1）=0，f（）=e，即有f（x）的最大值为e，最小值为f（1）=0．则f（x）在区间[，+∞）上的取值范围是[0，e]．【考点】简单复合函数的导数，利用导数研究函数的单调性，导数在最大值、最小值问题中的应用【解析】【分析】（Ⅰ）求出f（x）的导数，注意运用复合函数的求导法则，即可得到所求；（Ⅱ）求出f（x）的导数，求得极值点，讨论当＜x＜1时，当1＜x＜时，当x＞时，f（x）的单调性，判断f（x）≥0，计算f（），f（1），f（），即可得到所求取值范围．5、【答案】解：（Ⅰ）f（π）=π2﹣2．f′（x）=2x﹣2sinx，∴f′（π）=2π．∴曲线y=f（x）在点（π，f（π））处的切线方程为：y﹣（π2﹣2）=2π（x﹣π）．化为：2πx﹣y﹣π2﹣2=0．（Ⅱ）h（x）=g（x）﹣af（x）=e x（cosx﹣sinx+2x﹣2）﹣a（x2+2cosx）h′（x）=e x（cosx﹣sinx+2x﹣2）+e x（﹣sinx﹣cosx+2）﹣a（2x﹣2sinx）=2（x﹣sinx）（e x﹣a）=2（x﹣sinx）（e x﹣e lna）．令u（x）=x﹣sinx，则u′（x）=1﹣cosx≥0，∴函数u（x）在R上单调递增．∵u（0）=0，∴x＞0时，u（x）＞0；x＜0时，u（x）＜0．（i）a≤0时，e x﹣a＞0，∴x＞0时，h′（x）＞0，函数h（x）在（0，+∞）单调递增；x＜0时，h′（x）＜0，函数h（x）在（﹣∞，0）单调递减．∴x=0时，函数h（x）取得极小值，h（0）=﹣1﹣2a．（ii）a＞0时，令h′（x）=2（x﹣sinx）（e x﹣e lna）=0．解得x1=lna，x2=0．①0＜a＜1时，x∈（﹣∞，lna）时，e x﹣e lna＜0，h′（x）＞0，函数h（x）单调递增；x∈（lna，0）时，e x﹣e lna＞0，h′（x）＜0，函数h（x）单调递减；x∈（0，+∞）时，e x﹣e lna＞0，h′（x）＞0，函数h（x）单调递增．∴当x=0时，函数h（x）取得极小值，h（0）=﹣2a﹣1．当x=lna时，函数h（x）取得极大值，h（lna）=﹣a[ln2a﹣2lna+sin（lna）+cos（lna）+2]．②当a=1时，lna=0，x∈R时，h′（x）≥0，∴函数h（x）在R上单调递增．③1＜a时，lna＞0，x∈（﹣∞，0）时，e x﹣e lna＜0，h′（x）＞0，函数h（x）单调递增；x∈（0，lna）时，e x﹣e lna＜0，h′（x）＜0，函数h（x）单调递减；x∈（lna，+∞）时，e x﹣e lna＞0，h′（x）＞0，函数h（x）单调递增．∴当x=0时，函数h（x）取得极大值，h（0）=﹣2a﹣1．当x=lna时，函数h（x）取得极小值，h（lna）=﹣a[ln2a﹣2lna+sin（lna）+cos（lna）+2]．综上所述：a≤0时，函数h（x）在（0，+∞）单调递增；x＜0时，函数h（x）在（﹣∞，0）单调递减．x=0时，函数h（x）取得极小值，h（0）=﹣1﹣2a．0＜a＜1时，函数h（x）在x∈（﹣∞，lna）是单调递增；函数h（x）在x∈（lna，0）上单调递减．当x=0时，函数h（x）取得极小值，h（0）=﹣2a﹣1．当x=lna时，函数h（x）取得极大值，h（lna）=﹣a[ln2a﹣2lna+sin（lna）+cos（lna）+2]．当a=1时，lna=0，函数h（x）在R上单调递增．a＞1时，函数h（x）在（﹣∞，0），（lna，+∞）上单调递增；函数h（x）在（0，lna）上单调递减．当x=0时，函数h（x）取得极大值，h（0）=﹣2a﹣1．当x=lna时，函数h（x）取得极小值，h（lna）=﹣a[ln2a﹣2lna+sin（lna）+cos（lna）+2]．【考点】导数的加法与减法法则，导数的乘法与除法法则，函数的单调性与导数的关系，利用导数研究函数的单调性，利用导数研究函数的极值，利用导数研究曲线上某点切线方程【解析】【分析】（Ⅰ）f（π）=π2﹣2．f′（x）=2x﹣2sinx，可得f′（π）=2π即为切线的斜率，利用点斜式即可得出切线方程．（Ⅱ）h（x）=g（x）﹣af（x）=e x（cosx﹣sinx+2x﹣2）﹣a（x2+2cosx），可得h′（x）=2（x﹣sinx）（e x﹣a）=2（x﹣sinx）（e x﹣e lna）．令u（x）=x﹣sinx，则u′（x）=1﹣cosx≥0，可得函数u（x）在R上单调递增．由u（0）=0，可得x＞0时，u（x）＞0；x＜0时，u（x）＜0．对a分类讨论：a≤0时，0＜a＜1时，当a=1时，a＞1时，利用导数研究函数的单调性极值即可得出．6、【答案】（1）解：函数f（x）=e x cosx﹣x的导数为f′（x）=e x（cosx﹣sinx）﹣1，可得曲线y=f（x）在点（0，f（0））处的切线斜率为k=e0（cos0﹣sin0）﹣1=0，切点为（0，e0cos0﹣0），即为（0，1），曲线y=f（x）在点（0，f（0））处的切线方程为y=1；（2）解：函数f（x）=e x cosx﹣x的导数为f′（x）=e x（cosx﹣sinx）﹣1，令g（x）=e x（cosx﹣sinx）﹣1，则g（x）的导数为g′（x）=e x（cosx﹣sinx﹣sinx﹣cosx）=﹣2e x•sinx，当x∈[0，]，可得g′（x）=﹣2e x•sinx≤0，即有g（x）在[0，]递减，可得g（x）≤g（0）=0，则f（x）在[0，]递减，即有函数f（x）在区间[0，]上的最大值为f（0）=e0cos0﹣0=1；最小值为f（）=e cos﹣=﹣．【考点】利用导数求闭区间上函数的最值，利用导数研究曲线上某点切线方程【解析】【分析】（1.）求出f（x）的导数，可得切线的斜率和切点，由点斜式方程即可得到所求方程；（2.）求出f（x）的导数，再令g（x）=f′（x），求出g（x）的导数，可得g（x）在区间[0，]的单调性，即可得到f（x）的单调性，进而得到f（x）的最值．7、【答案】（Ⅰ）解：由f（x）=2x4+3x3﹣3x2﹣6x+a，可得g（x）=f′（x）=8x3+9x2﹣6x﹣6，进而可得g′（x）=24x2+18x﹣6．令g′（x）=0，解得x=﹣1，或x=．当x变化时，g′（x），g（x）的变化情况如下表：x（﹣∞，﹣1）（﹣1，）（，+∞）g′（x）+﹣+g（x）↗↘↗所以，g（x）的单调递增区间是（﹣∞，﹣1），（，+∞），单调递减区间是（﹣1，）．（Ⅱ）证明：由h（x）=g（x）（m﹣x0）﹣f（m），得h（m）=g（m）（m﹣x0）﹣f（m），h（x0）=g（x0）（m﹣x0）﹣f（m）．令函数H1（x）=g（x）（x﹣x0）﹣f（x），则H′1（x）=g′（x）（x﹣x0）．由（Ⅰ）知，当x∈[1，2]时，g′（x）＞0，故当x∈[1，x0）时，H′1（x）＜0，H1（x）单调递减；当x∈（x0，2]时，H′1（x）＞0，H1（x）单调递增．因此，当x∈[1，x0）∪（x0，2]时，H1（x）＞H1（x0）=﹣f（x0）=0，可得H1（m）＞0即h（m）＞0，令函数H2（x）=g（x0）（x﹣x0）﹣f（x），则H′2（x）=g′（x0）﹣g（x）．由（Ⅰ）知，g（x）在[1，2]上单调递增，故当x∈[1，x0）时，H′2（x）＞0，H2（x）单调递增；当x∈（x0，2]时，H′2（x）＜0，H2（x）单调递减．因此，当x∈[1，x0）∪（x0，2]时，H2（x）＞H2（x0）=0，可得得H2（m）＜0即h（x0）＜0，．所以，h（m）h（x0）＜0．（Ⅲ）对于任意的正整数p，q，且，令m=，函数h（x）=g（x）（m﹣x0）﹣f（m）．由（Ⅱ）知，当m∈[1，x0）时，h（x）在区间（m，x0）内有零点；当m∈（x0，2]时，h（x）在区间（x0，m）内有零点．所以h（x）在（1，2）内至少有一个零点，不妨设为x1，则h（x1）=g（x1）（﹣x0）﹣f（）=0．由（Ⅰ）知g（x）在[1，2]上单调递增，故0＜g（1）＜g（x1）＜g（2），于是|﹣x0|=≥=．因为当x∈[1，2]时，g（x）＞0，故f（x）在[1，2]上单调递增，所以f（x）在区间[1，2]上除x0外没有其他的零点，而≠x0，故f（）≠0．又因为p，q，a均为整数，所以|2p4+3p3q﹣3p2q2﹣6pq3+aq4|是正整数，从而|2p4+3p3q﹣3p2q2﹣6pq3+aq4|≥1．所以|﹣x0|≥．所以，只要取A=g（2），就有|﹣x0|≥．【考点】利用导数研究函数的单调性，利用导数研究函数的极值，不等式的证明，函数的零点【解析】【分析】（Ⅰ）求出函数的导函数g（x）=f′（x）=8x3+9x2﹣6x﹣6，求出极值点，通过列表判断函数的单调性求出单调区间即可．（Ⅱ）由h（x）=g（x）（m﹣x0）﹣f（m），推出h（m）=g（m）（m﹣x0）﹣f（m），令函数H1（x）=g（x）（x﹣x0）﹣f（x），求出导函数H′1（x）利用（Ⅰ）知，推出h（m）h（x0）＜0．（Ⅲ）对于任意的正整数p，q，且，令m=，函数h（x）=g（x）（m﹣x0）﹣f（m）．由（Ⅱ）知，当m∈[1，x0）时，当m∈（x0，2]时，通过h（x）的零点．转化推出|﹣x0|=≥=．推出|2p4+3p3q﹣3p2q2﹣6pq3+aq4|≥1．然后推出结果．8、【答案】（Ⅰ）解：因为f（x）=x3+ax2+bx+1，所以g（x）=f′（x）=3x2+2ax+b，g′（x）=6x+2a，令g′（x）=0，解得x=﹣．由于当x＞﹣时g′（x）＞0，g（x）=f′（x）单调递增；当x＜﹣时g′（x）＜0，g（x）=f′（x）单调递减；所以f′（x）的极小值点为x=﹣，由于导函数f′（x）的极值点是原函数f（x）的零点，所以f（﹣）=0，即﹣+﹣+1=0，所以b=+（a＞0）．因为f（x）=x3+ax2+bx+1（a＞0，b∈R）有极值，所以f′（x）=3x2+2ax+b=0有两个不等的实根，所以4a2﹣12b＞0，即a2﹣+＞0，解得a＞3，所以b=+（a＞3）．（Ⅱ）证明：由（1）可知h（a）=b2﹣3a=﹣+=（4a3﹣27）（a3﹣27），由于a＞3，所以h（a）＞0，即b2＞3a；（Ⅲ）解：由（1）可知f′（x）的极小值为f′（﹣）=b﹣，设x1，x2是y=f（x）的两个极值点，则x1+x2=，x1x2=，所以f（x1）+f（x2）=++a（+）+b（x1+x2）+2=（x1+x2）[（x1+x2）2﹣3x1x2]+a[（x1+x2）2﹣2x1x2]+b（x1+x2）+2=﹣+2，又因为f（x），f′（x）这两个函数的所有极值之和不小于﹣，所以b﹣+﹣+2=﹣≥﹣，因为a＞3，所以2a3﹣63a﹣54≤0，所以2a（a2﹣36）+9（a﹣6）≤0，所以（a﹣6）（2a2+12a+9）≤0，由于a＞3时2a2+12a+9＞0，所以a﹣6≤0，解得a≤6，所以a的取值范围是（3，6]．【考点】导数的运算，利用导数研究函数的单调性，利用导数研究函数的极值，导数在最大值、最小值问题中的应用【解析】【分析】（Ⅰ）通过对f（x）=x3+ax2+bx+1求导可知g（x）=f′（x）=3x2+2ax+b，进而再求导可知g′（x）=6x+2a，通过令g′（x）=0进而可知f′（x）的极小值点为x=﹣，从而f（﹣）=0，整理可知b=+（a＞0），结合f（x）=x3+ax2+bx+1（a ＞0，b∈R）有极值可知f′（x）=0有两个不等的实根，进而可知a＞3．（Ⅱ）通过（1）构造函数h（a）=b2﹣3a=﹣+=（4a3﹣27）（a3﹣27），结合a＞3可知h（a）＞0，从而可得结论；（Ⅲ）通过（1）可知f′（x）的极小值为f′（﹣）=b﹣，利用韦达定理及完全平方关系可知y=f（x）的两个极值之和为﹣+2，进而问题转化为解不等式b﹣+﹣+2=﹣≥﹣，因式分解即得结论．9、【答案】（1）解：由f（x）=ae2x+（a﹣2）e x﹣x，求导f′（x）=2ae2x+（a﹣2）e x ﹣1，当a=0时，f′（x）=2e x﹣1＜0，∴当x∈R，f（x）单调递减，当a＞0时，f′（x）=（2e x+1）（ae x﹣1）=2a（e x+）（e x﹣），令f′（x）=0，解得：x=ln，当f′（x）＞0，解得：x＞ln，当f′（x）＜0，解得：x＜ln，∴x∈（﹣∞，ln）时，f（x）单调递减，x∈（ln，+∞）单调递增；当a＜0时，f′（x）=2a（e x+）（e x﹣）＜0，恒成立，∴当x∈R，f（x）单调递减，综上可知：当a≤0时，f（x）在R单调减函数，当a＞0时，f（x）在（﹣∞，ln）是减函数，在（ln，+∞）是增函数；（2）由f（x）=ae2x+（a﹣2）e x﹣x=0，有两个零点，由（1）可知：当a＞0时，f（x）=0，有两个零点，则f（x）min=a+（a﹣2）﹣ln，=a（）+（a﹣2）×﹣ln，=1﹣﹣ln，由f（x）min＜0，则1﹣﹣ln＜0，整理得：a﹣1+alna＜0，设g（a）=alna+a﹣1，a＞0，g′（a）=lna+1+1=lna+2，令g′（a）=0，解得：a=e﹣2，当a∈（0，e﹣2），g′（a）＜0，g（a）单调递减，当a∈（e﹣2，+∞），g′（a）＞0，g（a）单调递增，g（a）min=g（e﹣2）=e﹣2lne﹣2+e﹣2﹣1=﹣﹣1，由g（1）=1﹣1﹣ln1=0，∴0＜a＜1，a的取值范围（0，1）．【考点】导数的运算，利用导数研究函数的单调性，利用导数求闭区间上函数的最值，函数零点的判定定理【解析】【分析】（1.）求导，根据导数与函数单调性的关系，分类讨论，即可求得f （x）单调性；（2.）由（1）可知：当a＞0时才有个零点，根据函数的单调性求得f（x）最小值，由f（x）min＜0，g（a）=alna+a﹣1，a＞0，求导，由g（a）min=g（e﹣2）=e﹣2lne﹣2+e﹣2﹣1=﹣﹣1，g（1）=0，即可求得a的取值范围．10、【答案】（Ⅰ）解：因为f（x）=ax2﹣ax﹣xlnx=x（ax﹣a﹣lnx）（x＞0），则f（x）≥0等价于h（x）=ax﹣a﹣lnx≥0，因为h′（x）=a﹣，且当0＜x＜时h′（x）＜0、当x＞时h′（x）＞0，所以h（x）min=h（），又因为h（1）=a﹣a﹣ln1=0，所以=1，解得a=1；（Ⅱ）证明：由（1）可知f（x）=x2﹣x﹣xlnx，f′（x）=2x﹣2﹣lnx，令f′（x）=0，可得2x﹣2﹣lnx=0，记t（x）=2x﹣2﹣lnx，则t′（x）=2﹣，令t′（x）=0，解得：x=，所以t（x）在区间（0，）上单调递减，在（，+∞）上单调递增，所以t（x）min=t（）=ln2﹣1＜0，从而t（x）=0有解，即f′（x）=0存在两根x0，x2，且不妨设f′（x）在（0，x0）上为正、在（x0，x2）上为负、在（x2，+∞）上为正，所以f（x）必存在唯一极大值点x0，且2x0﹣2﹣lnx0=0，所以f（x0）=﹣x0﹣x0lnx0=﹣x0+2x0﹣2=x0﹣，由x0＜可知f（x0）＜（x0﹣）max=﹣+=；由f′（）＜0可知x0＜＜，所以f（x）在（0，x0）上单调递增，在（x0，）上单调递减，所以f（x0）＞f（）=﹣+=＞；综上所述，f（x）存在唯一的极大值点x0，且e﹣2＜f（x0）＜2﹣2．【考点】导数的运算，利用导数研究函数的极值，利用导数求闭区间上函数的最值，导数在最大值、最小值问题中的应用，不等式的综合【解析】【分析】（Ⅰ）通过分析可知f（x）≥0等价于h（x）=ax﹣a﹣lnx≥0，进而利用h′（x）=a﹣可得h（x）min=h（），从而可得结论；（Ⅱ）通过（Ⅰ）可知f（x）=x2﹣x﹣xlnx，记t（x）=f′（x）=2x﹣2﹣lnx，解不等式可知t（x）min=t（）=ln2﹣1＜0，从而可知f′（x）=0存在两根x0，x2，利用f（x）必存在唯一极大值点x0及x0＜可知f（x0）＜，另一方面可知f（x0）＞f（）=﹣+=＞．11、【答案】解：（Ⅰ）因为函数f（x）=x﹣1﹣alnx，x＞0，所以f′（x）=1﹣=，且f（1）=0．所以当a≤0时f′（x）＞0恒成立，此时y=f（x）在（0，+∞）上单调递增，所以在（0,1）上f(x)<0,这与f（x）≥0矛盾；当a＞0时令f′（x）=0，解得x=a，所以y=f（x）在（0，a）上单调递减，在（a，+∞）上单调递增，即f（x）min=f（a），又因为f（x）min=f（a）≥0，所以a=1；（Ⅱ）由（Ⅰ）可知当a=1时f（x）=x﹣1﹣lnx≥0，即lnx≤x﹣1，所以ln（x+1）≤x当且仅当x=0时取等号，所以ln（1+）＜，k∈N*,所以，k∈N*．一方面，因为++…+=1﹣＜1，所以，（1+）（1+）…（1+）＜e；另一方面，（1+）（1+）…（1+）＞（1+）（1+）（1+）=＞2，同时当n≥3时，（1+）（1+）…（1+）∈（2，e）．因为m为整数，且对于任意正整数n（1+）（1+）…（1+）＜m，所以m的最小值为3．【考点】函数的单调性与导数的关系，利用导数研究函数的单调性，等比数列的前n项和，反证法与放缩法【解析】【分析】（Ⅰ）通过对函数f（x）=x﹣1﹣alnx（x＞0）求导，分a≤0、a＞0两种情况考虑导函数f′（x）与0的大小关系可得结论；（Ⅱ）通过（Ⅰ）可知lnx≤x﹣1，进而取特殊值可知ln（1+）＜，k∈N*．一方面利用等比数列的求和公式放缩可知（1+）（1+）…（1+）＜e；另一方面可知（1+）（1+）…（1+）＞2，且当n≥3时，（1+）（1+）…（1+）∈（2，e）．。

高考数学真题导数专题及答案

2017年高考真题导数专题一．解答题（共12小题）1．已知函数f（x）=ae2x+（a﹣2）e x﹣x．（1）讨论f（x）的单调性；（2）若f（x）有两个零点，求a的取值范围．2．已知函数f（x）=ax2﹣ax﹣xlnx，且f（x）≥0．（1）求a；（2）证明：f（x）存在唯一的极大值点x0，且e﹣2＜f（x0）＜2﹣2．3．已知函数f（x）=x﹣1﹣alnx．（1）若f（x）≥0，求a的值；（2）设m为整数，且对于任意正整数n，（1+）（1+）…（1+）＜m，求m的最小值．4．已知函数f（x）=x3+ax2+bx+1（a＞0，b∈R）有极值，且导函数f′（x）的极值点是f（x）的零点．（极值点是指函数取极值时对应的自变量的值）（1）求b关于a的函数关系式，并写出定义域；（2）证明：b2＞3a；（3）若f（x），f′（x）这两个函数的所有极值之和不小于﹣，求a的取值范围．5．设函数f（x）=（1﹣x2）e x．（1）讨论f（x）的单调性；（2）当x≥0时，f（x）≤ax+1，求a的取值范围．6．已知函数f（x）=（x﹣）e﹣x（x≥）．（1）求f（x）的导函数；（2）求f（x）在区间[，+∞）上的取值范围．7．已知函数f（x）=x2+2cosx，g（x）=e x（cosx﹣sinx+2x﹣2），其中e≈2.17828…是自然对数的底数．（Ⅰ）求曲线y=f（x）在点（π，f（π））处的切线方程；（Ⅱ）令h（x）=g （x）﹣a f（x）（a∈R），讨论h（x）的单调性并判断有无极值，有极值时求出极值．8．已知函数f（x）=e x cosx﹣x．（1）求曲线y=f（x）在点（0，f（0））处的切线方程；（2）求函数f（x）在区间[0，]上的最大值和最小值．9．设a∈Z，已知定义在R上的函数f（x）=2x4+3x3﹣3x2﹣6x+a在区间（1，2）内有一个零点x0，g（x）为f（x）的导函数．（Ⅰ）求g（x）的单调区间；（Ⅱ）设m∈[1，x0）∪（x0，2]，函数h（x）=g（x）（m﹣x0）﹣f（m），求证：h（m）h（x0）＜0；（Ⅲ）求证：存在大于0的常数A，使得对于任意的正整数p，q，且∈[1，x0）∪（x0，2]，满足|﹣x0|≥．10．已知函数f（x）=x3﹣ax2，a∈R，（1）当a=2时，求曲线y=f（x）在点（3，f（3））处的切线方程；（2）设函数g（x）=f（x）+（x﹣a）cosx﹣sinx，讨论g（x）的单调性并判断有无极值，有极值时求出极值．11．设a，b∈R，|a|≤1．已知函数f（x）=x3﹣6x2﹣3a（a﹣4）x+b，g（x）=e x f （x）．（Ⅰ）求f（x）的单调区间；（Ⅱ）已知函数y=g（x）和y=e x的图象在公共点（x0，y0）处有相同的切线，（i）求证：f（x）在x=x0处的导数等于0；（ii）若关于x的不等式g（x）≤e x在区间[x0﹣1，x0+1]上恒成立，求b的取值范围．12．已知函数f（x）=e x（e x﹣a）﹣a2x．（1）讨论f（x）的单调性；（2）若f（x）≥0，求a的取值范围．2017年高考真题导数专题参考答案与试题解析一．解答题（共12小题）1．（2017•新课标Ⅰ）已知函数f（x）=ae2x+（a﹣2）e x﹣x．（1）讨论f（x）的单调性；（2）若f（x）有两个零点，求a的取值范围．【解答】解：（1）由f（x）=ae2x+（a﹣2）e x﹣x，求导f′（x）=2ae2x+（a﹣2）e x ﹣1，当a=0时，f′（x）=﹣2e x﹣1＜0，∴当x∈R，f（x）单调递减，当a＞0时，f′（x）=（2e x+1）（ae x﹣1）=2a（e x+）（e x﹣），令f′（x）=0，解得：x=ln，当f′（x）＞0，解得：x＞ln，当f′（x）＜0，解得：x＜ln，∴x∈（﹣∞，ln）时，f（x）单调递减，x∈（ln，+∞）单调递增；当a＜0时，f′（x）=2a（e x+）（e x﹣）＜0，恒成立，∴当x∈R，f（x）单调递减，综上可知：当a≤0时，f（x）在R单调减函数，当a＞0时，f（x）在（﹣∞，ln）是减函数，在（ln，+∞）是增函数；（2）①若a≤0时，由（1）可知：f（x）最多有一个零点，当a＞0时，f（x）=ae2x+（a﹣2）e x﹣x，当x→﹣∞时，e2x→0，e x→0，∴当x→﹣∞时，f（x）→+∞，当x→∞，e2x→+∞，且远远大于e x和x，∴当x→∞，f（x）→+∞，∴函数有两个零点，f（x）的最小值小于0即可，由f（x）在（﹣∞，ln）是减函数，在（ln，+∞）是增函数，∴f（x）min=f（ln）=a×（）+（a﹣2）×﹣ln＜0，∴1﹣﹣ln＜0，即ln+﹣1＞0，设t=，则g（t）=lnt+t﹣1，（t＞0），求导g′（t）=+1，由g（1）=0，∴t=＞1，解得：0＜a＜1，∴a的取值范围（0，1）．方法二：（1）由f（x）=ae2x+（a﹣2）e x﹣x，求导f′（x）=2ae2x+（a﹣2）e x﹣1，当a=0时，f′（x）=2e x﹣1＜0，∴当x∈R，f（x）单调递减，当a＞0时，f′（x）=（2e x+1）（ae x﹣1）=2a（e x+）（e x﹣），令f′（x）=0，解得：x=﹣lna，当f′（x）＞0，解得：x＞﹣lna，当f′（x）＜0，解得：x＜﹣lna，∴x∈（﹣∞，﹣lna）时，f（x）单调递减，x∈（﹣lna，+∞）单调递增；当a＜0时，f′（x）=2a（e x+）（e x﹣）＜0，恒成立，∴当x∈R，f（x）单调递减，综上可知：当a≤0时，f（x）在R单调减函数，当a＞0时，f（x）在（﹣∞，﹣lna）是减函数，在（﹣lna，+∞）是增函数；（2）①若a≤0时，由（1）可知：f（x）最多有一个零点，②当a＞0时，由（1）可知：当x=﹣lna时，f（x）取得最小值，f（x）min=f（﹣lna）=1﹣﹣ln，当a=1，时，f（﹣lna）=0，故f（x）只有一个零点，当a∈（1，+∞）时，由1﹣﹣ln＞0，即f（﹣lna）＞0，故f（x）没有零点，当a∈（0，1）时，1﹣﹣ln＜0，f（﹣lna）＜0，由f（﹣2）=ae﹣4+（a﹣2）e﹣2+2＞﹣2e﹣2+2＞0，故f（x）在（﹣∞，﹣lna）有一个零点，假设存在正整数n0，满足n0＞ln（﹣1），则f（n0）=（a+a﹣2）﹣n0＞﹣n0＞﹣n0＞0，由ln（﹣1）＞﹣lna，因此在（﹣lna，+∞）有一个零点．∴a的取值范围（0，1）．2．（2017•新课标Ⅱ）已知函数f（x）=ax2﹣ax﹣xlnx，且f（x）≥0．（1）求a；（2）证明：f（x）存在唯一的极大值点x0，且e﹣2＜f（x0）＜2﹣2．【解答】（1）解：因为f（x）=ax2﹣ax﹣xlnx=x（ax﹣a﹣lnx）（x＞0），则f（x）≥0等价于h（x）=ax﹣a﹣lnx≥0，求导可知h′（x）=a﹣．则当a≤0时h′（x）＜0，即y=h（x）在（0，+∞）上单调递减，所以当x0＞1时，h（x0）＜h（1）=0，矛盾，故a＞0．因为当0＜x＜时h′（x）＜0、当x＞时h′（x）＞0，所以h（x）min=h（），又因为h（1）=a﹣a﹣ln1=0，所以=1，解得a=1；（2）证明：由（1）可知f（x）=x2﹣x﹣xlnx，f′（x）=2x﹣2﹣lnx，令f′（x）=0，可得2x﹣2﹣lnx=0，记t（x）=2x﹣2﹣lnx，则t′（x）=2﹣，令t′（x）=0，解得：x=，所以t（x）在区间（0，）上单调递减，在（，+∞）上单调递增，所以t（x）min=t（）=ln2﹣1＜0，从而t（x）=0有解，即f′（x）=0存在两根x0，x2，且不妨设f′（x）在（0，x0）上为正、在（x0，x2）上为负、在（x2，+∞）上为正，所以f（x）必存在唯一极大值点x0，且2x0﹣2﹣lnx0=0，所以f（x0）=﹣x0﹣x0lnx0=﹣x0+2x0﹣2=x0﹣，由x0＜可知f（x0）＜（x0﹣）max=﹣+=；由f′（）＜0可知x0＜＜，所以f（x）在（0，x0）上单调递增，在（x0，）上单调递减，所以f（x0）＞f（）=；综上所述，f（x）存在唯一的极大值点x0，且e﹣2＜f（x0）＜2﹣2．3．（2017•新课标Ⅲ）已知函数f（x）=x﹣1﹣alnx．（1）若f（x）≥0，求a的值；（2）设m为整数，且对于任意正整数n，（1+）（1+）…（1+）＜m，求m的最小值．【解答】解：（1）因为函数f（x）=x﹣1﹣alnx，x＞0，所以f′（x）=1﹣=，且f（1）=0．所以当a≤0时f′（x）＞0恒成立，此时y=f（x）在（0，+∞）上单调递增，这与f（x）≥0矛盾；当a＞0时令f′（x）=0，解得x=a，所以y=f（x）在（0，a）上单调递减，在（a，+∞）上单调递增，即f（x）min=f （a），又因为f（x）min=f（a）≥0，所以a=1；（2）由（1）可知当a=1时f（x）=x﹣1﹣lnx≥0，即lnx≤x﹣1，所以ln（x+1）≤x当且仅当x=0时取等号，所以ln（1+）＜，k∈N*．一方面，ln（1+）+ln（1+）+…+ln（1+）＜++…+=1﹣＜1，即（1+）（1+）…（1+）＜e；另一方面，（1+）（1+）…（1+）＞（1+）（1+）（1+）=＞2；从而当n≥3时，（1+）（1+）…（1+）∈（2，e），因为m为整数，且对于任意正整数n，（1+）（1+）…（1+）＜m成立，所以m的最小值为3．4．（2017•江苏）已知函数f（x）=x3+ax2+bx+1（a＞0，b∈R）有极值，且导函数f′（x）的极值点是f（x）的零点．（极值点是指函数取极值时对应的自变量的值）（1）求b关于a的函数关系式，并写出定义域；（2）证明：b2＞3a；（3）若f（x），f′（x）这两个函数的所有极值之和不小于﹣，求a的取值范围．【解答】（1）解：因为f（x）=x3+ax2+bx+1，所以g（x）=f′（x）=3x2+2ax+b，g′（x）=6x+2a，令g′（x）=0，解得x=﹣．由于当x＞﹣时g′（x）＞0，g（x）=f′（x）单调递增；当x＜﹣时g′（x）＜0，g（x）=f′（x）单调递减；所以f′（x）的极小值点为x=﹣，由于导函数f′（x）的极值点是原函数f（x）的零点，所以f（﹣）=0，即﹣+﹣+1=0，所以b=+（a＞0）．因为f（x）=x3+ax2+bx+1（a＞0，b∈R）有极值，所以f′（x）=3x2+2ax+b=0的实根，所以4a2﹣12b≥0，即a2﹣+≥0，解得a≥3，所以b=+（a≥3）．（2）证明：由（1）可知h（a）=b2﹣3a=﹣+=（4a3﹣27）（a3﹣27），由于a＞3，所以h（a）＞0，即b2＞3a；（3）解：由（1）可知f′（x）的极小值为f′（﹣）=b﹣，设x1，x2是y=f（x）的两个极值点，则x1+x2=，x1x2=，所以f（x1）+f（x2）=++a（+）+b（x1+x2）+2=（x1+x2）[（x1+x2）2﹣3x1x2]+a[（x1+x2）2﹣2x1x2]+b（x1+x2）+2=﹣+2，又因为f（x），f′（x）这两个函数的所有极值之和不小于﹣，所以b﹣+﹣+2=﹣≥﹣，因为a＞3，所以2a3﹣63a﹣54≤0，所以2a（a2﹣36）+9（a﹣6）≤0，所以（a﹣6）（2a2+12a+9）≤0，由于a＞3时2a2+12a+9＞0，所以a﹣6≤0，解得a≤6，所以a的取值范围是（3，6]．5．（2017•新课标Ⅱ）设函数f（x）=（1﹣x2）e x．（1）讨论f（x）的单调性；（2）当x≥0时，f（x）≤ax+1，求a的取值范围．【解答】解：（1）因为f（x）=（1﹣x2）e x，x∈R，所以f′（x）=（1﹣2x﹣x2）e x，令f′（x）=0可知x=﹣1±，当x＜﹣1﹣或x＞﹣1+时f′（x）＜0，当﹣1﹣＜x＜﹣1+时f′（x）＞0，所以f（x）在（﹣∞，﹣1﹣），（﹣1+，+∞）上单调递减，在（﹣1﹣，﹣1+）上单调递增；（2）由题可知f（x）=（1﹣x）（1+x）e x．下面对a的范围进行讨论：①当a≥1时，设函数h（x）=（1﹣x）e x，则h′（x）=﹣xe x＜0（x＞0），因此h（x）在[0，+∞）上单调递减，又因为h（0）=1，所以h（x）≤1，所以f（x）=（1﹣x）h（x）≤x+1≤ax+1；②当0＜a＜1时，设函数g（x）=e x﹣x﹣1，则g′（x）=e x﹣1＞0（x＞0），所以g（x）在[0，+∞）上单调递增，又g（0）=1﹣0﹣1=0，所以e x≥x+1．因为当0＜x＜1时f（x）＞（1﹣x）（1+x）2，所以（1﹣x）（1+x）2﹣ax﹣1=x（1﹣a﹣x﹣x2），取x0=∈（0，1），则（1﹣x0）（1+x0）2﹣ax0﹣1=0，所以f（x0）＞ax0+1，矛盾；③当a≤0时，取x0=∈（0，1），则f（x0）＞（1﹣x0）（1+x0）2=1≥ax0+1，矛盾；综上所述，a的取值范围是[1，+∞）．6．（2017•浙江）已知函数f（x）=（x﹣）e﹣x（x≥）．（1）求f（x）的导函数；（2）求f（x）在区间[，+∞）上的取值范围．【解答】解：（1）函数f（x）=（x﹣）e﹣x（x≥），导数f′（x）=（1﹣••2）e﹣x﹣（x﹣）e﹣x=（1﹣x+）e﹣x=（1﹣x）（1﹣）e﹣x；（2）由f（x）的导数f′（x）=（1﹣x）（1﹣）e﹣x，可得f′（x）=0时，x=1或，当＜x＜1时，f′（x）＜0，f（x）递减；当1＜x＜时，f′（x）＞0，f（x）递增；当x＞时，f′（x）＜0，f（x）递减，且x≥⇔x2≥2x﹣1⇔（x﹣1）2≥0，则f（x）≥0．由f（）=e，f（1）=0，f（）=e，即有f（x）的最大值为e，最小值为f（1）=0．则f（x）在区间[，+∞）上的取值范围是[0，e]．7．（2017•山东）已知函数f（x）=x2+2cosx，g（x）=e x（cosx﹣sinx+2x﹣2），其中e≈2.17828…是自然对数的底数．（Ⅰ）求曲线y=f（x）在点（π，f（π））处的切线方程；（Ⅱ）令h（x）=g （x）﹣a f（x）（a∈R），讨论h（x）的单调性并判断有无极值，有极值时求出极值．【解答】解：（I）f（π）=π2﹣2．f′（x）=2x﹣2sinx，∴f′（π）=2π．∴曲线y=f（x）在点（π，f（π））处的切线方程为：y﹣（π2﹣2）=2π（x﹣π）．化为：2πx﹣y﹣π2﹣2=0．（II）h（x）=g （x）﹣a f（x）=e x（cosx﹣sinx+2x﹣2）﹣a（x2+2cosx）h′（x）=e x（cosx﹣sinx+2x﹣2）+e x（﹣sinx﹣cosx+2）﹣a（2x﹣2sinx）=2（x﹣sinx）（e x﹣a）=2（x﹣sinx）（e x﹣e lna）．令u（x）=x﹣sinx，则u′（x）=1﹣cosx≥0，∴函数u（x）在R上单调递增．∵u（0）=0，∴x＞0时，u（x）＞0；x＜0时，u（x）＜0．（1）a≤0时，e x﹣a＞0，∴x＞0时，h′（x）＞0，函数h（x）在（0，+∞）单调递增；x＜0时，h′（x）＜0，函数h（x）在（﹣∞，0）单调递减．∴x=0时，函数h（x）取得极小值，h（0）=﹣1﹣2a．（2）a＞0时，令h′（x）=2（x﹣sinx）（e x﹣e lna）=0．解得x1=lna，x2=0．①0＜a＜1时，x∈（﹣∞，lna）时，e x﹣e lna＜0，h′（x）＞0，函数h（x）单调递增；x∈（lna，0）时，e x﹣e lna＞0，h′（x）＜0，函数h（x）单调递减；x∈（0，+∞）时，e x﹣e lna＞0，h′（x）＞0，函数h（x）单调递增．∴当x=0时，函数h（x）取得极小值，h（0）=﹣2a﹣1．当x=lna时，函数h（x）取得极大值，h（lna）=﹣a[ln2a﹣2lna+sin（lna）+cos （lna）+2]．②当a=1时，lna=0，x∈R时，h′（x）≥0，∴函数h（x）在R上单调递增．③1＜a时，lna＞0，x∈（﹣∞，0）时，e x﹣e lna＜0，h′（x）＞0，函数h（x）单调递增；x∈（0，lna）时，e x﹣e lna＜0，h′（x）＜0，函数h（x）单调递减；x∈（lna，+∞）时，e x﹣e lna＞0，h′（x）＞0，函数h（x）单调递增．∴当x=0时，函数h（x）取得极大值，h（0）=﹣2a﹣1．当x=lna时，函数h（x）取得极小值，h（lna）=﹣a[ln2a﹣2lna+sin（lna）+cos （lna）+2]．综上所述：a≤0时，函数h（x）在（0，+∞）单调递增；x＜0时，函数h（x）在（﹣∞，0）单调递减．x=0时，函数h（x）取得极小值，h（0）=﹣1﹣2a．0＜a＜1时，函数h（x）在x∈（﹣∞，lna）是单调递增；函数h（x）在x∈（lna，0）上单调递减．当x=0时，函数h（x）取得极小值，h（0）=﹣2a﹣1．当x=lna 时，函数h（x）取得极大值，h（lna）=﹣a[ln2a﹣2lna+sin（lna）+cos（lna）+2]．当a=1时，lna=0，函数h（x）在R上单调递增．a＞1时，函数h（x）在（﹣∞，0），（lna，+∞）上单调递增；函数h（x）在（0，lna）上单调递减．当x=0时，函数h（x）取得极大值，h（0）=﹣2a﹣1．当x=lna 时，函数h（x）取得极小值，h（lna）=﹣a[ln2a﹣2lna+sin（lna）+cos（lna）+2]．8．（2017•北京）已知函数f（x）=e x cosx﹣x．（1）求曲线y=f（x）在点（0，f（0））处的切线方程；（2）求函数f（x）在区间[0，]上的最大值和最小值．【解答】解：（1）函数f（x）=e x cosx﹣x的导数为f′（x）=e x（cosx﹣sinx）﹣1，可得曲线y=f（x）在点（0，f（0））处的切线斜率为k=e0（cos0﹣sin0）﹣1=0，切点为（0，e0cos0﹣0），即为（0，1），曲线y=f（x）在点（0，f（0））处的切线方程为y=1；（2）函数f（x）=e x cosx﹣x的导数为f′（x）=e x（cosx﹣sinx）﹣1，令g（x）=e x（cosx﹣sinx）﹣1，则g（x）的导数为g′（x）=e x（cosx﹣sinx﹣sinx﹣cosx）=﹣2e x•sinx，当x∈[0，]，可得g′（x）=﹣2e x•sinx≤0，即有g（x）在[0，]递减，可得g（x）≤g（0）=0，则f（x）在[0，]递减，即有函数f（x）在区间[0，]上的最大值为f（0）=e0cos0﹣0=1；最小值为f（）=e cos﹣=﹣．9．（2017•天津）设a∈Z，已知定义在R上的函数f（x）=2x4+3x3﹣3x2﹣6x+a在区间（1，2）内有一个零点x0，g（x）为f（x）的导函数．（Ⅰ）求g（x）的单调区间；（Ⅱ）设m∈[1，x0）∪（x0，2]，函数h（x）=g（x）（m﹣x0）﹣f（m），求证：h（m）h（x0）＜0；（Ⅲ）求证：存在大于0的常数A，使得对于任意的正整数p，q，且∈[1，x0）∪（x0，2]，满足|﹣x0|≥．【解答】（Ⅰ）解：由f（x）=2x4+3x3﹣3x2﹣6x+a，可得g（x）=f′（x）=8x3+9x2﹣6x﹣6，进而可得g′（x）=24x2+18x﹣6．令g′（x）=0，解得x=﹣1，或x=．当x变化时，g′（x），g（x）的变化情况如下表：x（﹣∞，﹣1）（﹣1，）（，+∞）g′（x）+﹣+g（x）↗↘↗所以，g（x）的单调递增区间是（﹣∞，﹣1），（，+∞），单调递减区间是（﹣1，）．（Ⅱ）证明：由h（x）=g（x）（m﹣x0）﹣f（m），得h（m）=g（m）（m﹣x0）﹣f（m），h（x0）=g（x0）（m﹣x0）﹣f（m）．令函数H1（x）=g（x）（x﹣x0）﹣f（x），则H′1（x）=g′（x）（x﹣x0）．由（Ⅰ）知，当x∈[1，2]时，g′（x）＞0，故当x∈[1，x0）时，H′1（x）＜0，H1（x）单调递减；当x∈（x0，2]时，H′1（x）＞0，H1（x）单调递增．因此，当x∈[1，x0）∪（x0，2]时，H1（x）＞H1（x0）=﹣f（x0）=0，可得H1（m）＞0即h（m）＞0，令函数H2（x）=g（x0）（x﹣x0）﹣f（x），则H′2（x）=g′（x0）﹣g（x）．由（Ⅰ）知，g（x）在[1，2]上单调递增，故当x∈[1，x0）时，H′2（x）＞0，H2（x）单调递增；当x∈（x0，2]时，H′2（x）＜0，H2（x）单调递减．因此，当x∈[1，x0）∪（x0，2]时，H2（x）＞H2（x0）=0，可得得H2（m）＜0即h（x0）＜0，．所以，h（m）h（x0）＜0．（Ⅲ）对于任意的正整数p，q，且，令m=，函数h（x）=g（x）（m﹣x0）﹣f（m）．由（Ⅱ）知，当m∈[1，x0）时，h（x）在区间（m，x0）内有零点；当m∈（x0，2]时，h（x）在区间（x0，m）内有零点．所以h（x）在（1，2）内至少有一个零点，不妨设为x1，则h（x1）=g（x1）（﹣x0）﹣f（）=0．由（Ⅰ）知g（x）在[1，2]上单调递增，故0＜g（1）＜g（x1）＜g（2），于是|﹣x0|=≥=．因为当x∈[1，2]时，g（x）＞0，故f（x）在[1，2]上单调递增，所以f（x）在区间[1，2]上除x0外没有其他的零点，而≠x0，故f（）≠0．又因为p，q，a均为整数，所以|2p4+3p3q﹣3p2q2﹣6pq3+aq4|是正整数，从而|2p4+3p3q﹣3p2q2﹣6pq3+aq4|≥1．所以|﹣x0|≥．所以，只要取A=g（2），就有|﹣x0|≥．10．（2017•山东）已知函数f（x）=x3﹣ax2，a∈R，（1）当a=2时，求曲线y=f（x）在点（3，f（3））处的切线方程；（2）设函数g（x）=f（x）+（x﹣a）cosx﹣sinx，讨论g（x）的单调性并判断有无极值，有极值时求出极值．【解答】解：（1）当a=2时，f（x）=x3﹣x2，∴f′（x）=x2﹣2x，∴k=f′（3）=9﹣6=3，f（3）=×27﹣9=0，∴曲线y=f（x）在点（3，f（3））处的切线方程y=3（x﹣3），即3x﹣y﹣9=0（2）函数g（x）=f（x）+（x﹣a）cosx﹣sinx=x3﹣ax2+（x﹣a）cosx﹣sinx，∴g′（x）=（x﹣a）（x﹣sinx），令g′（x）=0，解得x=a，或x=0，①若a＞0时，当x＜0时，g′（x）＞0恒成立，故g（x）在（﹣∞，0）上单调递增，当x＞a时，g′（x）＞0恒成立，故g（x）在（a，+∞）上单调递增，当0＜x＜a时，g′（x）＜0恒成立，故g（x）在（0，a）上单调递减，∴当x=a时，函数有极小值，极小值为g（a）=﹣a3﹣sina当x=0时，有极大值，极大值为g（0）=﹣a，②若a＜0时，当x＞0时，g′（x）＞0恒成立，故g（x）在（﹣∞，0）上单调递增，当x＜a时，g′（x）＞0恒成立，故g（x）在（﹣∞，a）上单调递增，当a＜x＜0时，g′（x）＜0恒成立，故g（x）在（a，0）上单调递减，∴当x=a时，函数有极大值，极大值为g（a）=﹣a3﹣sina当x=0时，有极小值，极小值为g（0）=﹣a③当a=0时，g′（x）=x（x+sinx），当x＞0时，g′（x）＞0恒成立，故g（x）在（0，+∞）上单调递增，当x＜0时，g′（x）＞0恒成立，故g（x）在（﹣∞，0）上单调递增，∴g（x）在R上单调递增，无极值．11．（2017•天津）设a，b∈R，|a|≤1．已知函数f（x）=x3﹣6x2﹣3a（a﹣4）x+b，g（x）=e x f（x）．（Ⅰ）求f（x）的单调区间；（Ⅱ）已知函数y=g（x）和y=e x的图象在公共点（x0，y0）处有相同的切线，（i）求证：f（x）在x=x0处的导数等于0；（ii）若关于x的不等式g（x）≤e x在区间[x0﹣1，x0+1]上恒成立，求b的取值范围．【解答】（Ⅰ）解：由f（x）=x3﹣6x2﹣3a（a﹣4）x+b，可得f'（x）=3x2﹣12x ﹣3a（a﹣4）=3（x﹣a）（x﹣（4﹣a）），令f'（x）=0，解得x=a，或x=4﹣a．由|a|≤1，得a＜4﹣a．当x变化时，f'（x），f（x）的变化情况如下表：x（﹣∞，a）（a，4﹣a）（4﹣a，+∞）f'（x）+﹣+f（x）↗↘↗∴f（x）的单调递增区间为（﹣∞，a），（4﹣a，+∞），单调递减区间为（a，4﹣a）；（Ⅱ）（i）证明：∵g'（x）=e x（f（x）+f'（x）），由题意知，∴，解得．∴f（x）在x=x0处的导数等于0；（ii）解：∵g（x）≤e x，x∈[x0﹣1，x0+1]，由e x＞0，可得f（x）≤1．又∵f（x0）=1，f'（x0）=0，故x0为f（x）的极大值点，由（I）知x0=a．另一方面，由于|a|≤1，故a+1＜4﹣a，由（Ⅰ）知f（x）在（a﹣1，a）内单调递增，在（a，a+1）内单调递减，故当x0=a时，f（x）≤f（a）=1在[a﹣1，a+1]上恒成立，从而g（x）≤e x在[x0﹣1，x0+1]上恒成立．由f（a）=a3﹣6a2﹣3a（a﹣4）a+b=1，得b=2a3﹣6a2+1，﹣1≤a≤1．令t（x）=2x3﹣6x2+1，x∈[﹣1，1]，∴t'（x）=6x2﹣12x，令t'（x）=0，解得x=2（舍去），或x=0．∵t（﹣1）=﹣7，t（1）=﹣3，t（0）=1，故t（x）的值域为[﹣7，1]．∴b的取值范围是[﹣7，1]．12．（2017•新课标Ⅰ）已知函数f（x）=e x（e x﹣a）﹣a2x．（1）讨论f（x）的单调性；（2）若f（x）≥0，求a的取值范围．【解答】解：（1）f（x）=e x（e x﹣a）﹣a2x=e2x﹣e x a﹣a2x，∴f′（x）=2e2x﹣ae x﹣a2=（2e x+a）（e x﹣a），①当a=0时，f′（x）＞0恒成立，∴f（x）在R上单调递增，②当a＞0时，2e x+a＞0，令f′（x）=0，解得x=lna，当x＜lna时，f′（x）＜0，函数f（x）单调递减，当x＞lna时，f′（x）＞0，函数f（x）单调递增，③当a＜0时，e x﹣a＞0，令f′（x）=0，解得x=ln（﹣），当x＜ln（﹣）时，f′（x）＜0，函数f（x）单调递减，当x＞ln（﹣）时，f′（x）＞0，函数f（x）单调递增，综上所述，当a=0时，f（x）在R上单调递增，当a＞0时，f（x）在（﹣∞，lna）上单调递减，在（lna，+∞）上单调递增，当a＜0时，f（x）在（﹣∞，ln（﹣））上单调递减，在（ln（﹣），+∞）上单调递增，（2）①当a=0时，f（x）=e2x＞0恒成立，②当a＞0时，由（1）可得f（x）min=f（lna）=﹣a2lna≥0，∴lna≤0，∴0＜a≤1，③当a＜0时，由（1）可得f（x）min=f（ln（﹣））=﹣a2ln（﹣）≥0，∴ln（﹣）≤，∴﹣2≤a＜0，综上所述a的取值范围为[﹣2，1]。

2017全国一卷数学导数题

2017全国一卷数学导数题天上的星星真多啊！数也数不清。

有的星星喜欢穿着一身黑色的衣服，那是因为它们害怕被太阳公公看到自己穿着的白衣服。

可我发现了一颗明亮的星星，它的身体呈黄色，它那乌黑的眼睛里闪烁着神奇的光芒，像是在对我说：“请问你需要什么帮助吗？”你猜我想对它说什么呢？(注意：写完后再仔细读一遍)(5分)一、下面两个命题，哪个与原命题等价？(4分)(1)小数的性质命题A： 1／ x=1／(x＋y)=1／ x+y(2)正数的性质命题B： 1／ x=1／(x＋y)=x(2分)1、1。

(4分)命题A：假设，并证明。

结论：假设：小数点右移两位，将得到假设命题：若y大于0，则x可以省略。

由假设知x>0，并且x是整数。

证明：∵ x^2+(y-1)(x-y)=0，∴(x^2+(y-1)(x-y))+((x-y)^2+(x^2+(y-1)(x-y)))=0，∴(x^2+(y-1)(x-y))+((x-y)^2+(x^2+(y-1)(x-y)))=0，∴x=y-1，∵x=y-1，∴x+y=y-1，综上，∴x>y-1，∴(x^2+(y-1)(x-y))+((x-y)^2+(x^2+(y-1)(x-y)))>0，即x>y-1。

二、比较，选择(6分) 1。

(6分)小数的性质和正数的性质。

命题A与原命题无关。

命题B与原命题有关。

证明：原命题为假设与结论均为整数，由小数的性质有小数点右移两位将得到小数，并且小数点左移两位将得到原小数的近似值，根据近似值的特点和定义可知，原命题为真，从而得到命题B为真。

3。

(4分)正数的性质与小数的性质。

命题A与原命题无关。

命题B与原命题有关。

17年高考真题—文科数学2：导数

2017高考真题分类汇编：导数1．【2017浙江 7】函数()y f x =的导函数()y f x '=的图像如图所示，则函数()y f x =的图像可能是（）2．【2017天津 10】已知a R ∈，设函数()ln f x ax x =-的图象在点()()1,1f 处的切线为l ，则l 在y 轴上的截距为__________。

3．【2017课标I 14】曲线21y x x=+在点()1,2处的切线方程为__________________。

4．【2017天津 19】设,a b R ∈，||1a ≤。

已知函数()()32634f x x x a a x b =---+，()()xg x e f x =。

⑴求()f x 的单调区间；⑵已知函数()y g x =和x y e =的图象在公共点()00,x y 处有相同的切线，①求证：()f x 在0x x =处的导数等于0；②若关于x 的不等式()x g x e ≤在区间[]001,1x x -+上恒成立，求b 的取值范围。

5．【2017北京 20】已知函数()cos xf x e x x =-。

⑴求曲线()y f x =在点()()0,0f 处的切线方程；⑵求函数()f x 在区间[]0,2π上的最大值和最小值。

6．【2017江苏 20】已知函数()()3210,f x x ax bx a b R =+++>∈有极值，且导函数()f x '的极值点是()f x 的零点（极值点是指函数取极值时对应的自变量的值）。

⑴求b 关于a 的函数关系式，并写出定义域；⑵证明：23b a >；⑶若()(),f x f x '这两个函数的所有极值之和不小于72-，求a 的取值范围。

7．【2017山东 20】已知函数()()321132f x x ax a R =-∈。

⑴当2a =时，求曲线()y f x =在点()()3,3f 处的切线方程；⑵设函数()()()cos sin g x f x x a x x =+--，讨论()g x 的单调性并判断有无极值，有极值时求出极值。

【精品】2017-2018年高考数学导数大题+答案(40页)

【精品】2017-2018年高考数学导数大题+答案一．解答题（共28小题）1．已知函数f（x）=e x（e x﹣a）﹣a2x．（1）讨论f（x）的单调性；（2）若f（x）≥0，求a的取值范围．2．已知函数f（x）=ae2x+（a﹣2）e x﹣x．（1）讨论f（x）的单调性；（2）若f（x）有两个零点，求a的取值范围．3．已知函数f（x）=lnx+ax2+（2a+1）x．（1）讨论f（x）的单调性；（2）当a＜0时，证明f（x）≤﹣﹣2．4．已知函数f（x）=x﹣1﹣alnx．（1）若f（x）≥0，求a的值；（2）设m为整数，且对于任意正整数n，（1+）（1+）…（1+）＜m，求m的最小值．5．设a，b∈R，|a|≤1．已知函数f（x）=x3﹣6x2﹣3a（a﹣4）x+b，g（x）=e x f （x）．（Ⅰ）求f（x）的单调区间；（Ⅱ）已知函数y=g（x）和y=e x的图象在公共点（x0，y0）处有相同的切线，（i）求证：f（x）在x=x0处的导数等于0；（ii）若关于x的不等式g（x）≤e x在区间[x0﹣1，x0+1]上恒成立，求b的取值范围．6．设a∈Z，已知定义在R上的函数f（x）=2x4+3x3﹣3x2﹣6x+a在区间（1，2）内有一个零点x0，g（x）为f（x）的导函数．（Ⅰ）求g（x）的单调区间；（Ⅱ）设m∈[1，x0）∪（x0，2]，函数h（x）=g（x）（m﹣x0）﹣f（m），求证：h（m）h（x0）＜0；（Ⅲ）求证：存在大于0的常数A，使得对于任意的正整数p，q，且∈[1，x0）∪（x0，2]，满足|﹣x0|≥．7．已知函数f（x）=x3﹣ax2，a∈R，（1）当a=2时，求曲线y=f（x）在点（3，f（3））处的切线方程；（2）设函数g（x）=f（x）+（x﹣a）cosx﹣sinx，讨论g（x）的单调性并判断有无极值，有极值时求出极值．8．设函数f（x）=（1﹣x2）e x．（1）讨论f（x）的单调性；（2）当x≥0时，f（x）≤ax+1，求a的取值范围．9．已知函数f（x）=x3+ax2+bx+1（a＞0，b∈R）有极值，且导函数f′（x）的极值点是f（x）的零点．（极值点是指函数取极值时对应的自变量的值）（1）求b关于a的函数关系式，并写出定义域；（2）证明：b2＞3a；（3）若f（x），f′（x）这两个函数的所有极值之和不小于﹣，求a的取值范围．10．已知函数f（x）=ax2﹣ax﹣xlnx，且f（x）≥0．（1）求a；（2）证明：f（x）存在唯一的极大值点x0，且e﹣2＜f（x0）＜2﹣2．11．已知函数f（x）=x2+2cosx，g（x）=e x（cosx﹣sinx+2x﹣2），其中e≈2.17828…是自然对数的底数．（Ⅰ）求曲线y=f（x）在点（π，f（π））处的切线方程；（Ⅱ）令h（x）=g （x）﹣a f（x）（a∈R），讨论h（x）的单调性并判断有无极值，有极值时求出极值．12．已知函数f（x）=e x cosx﹣x．（1）求曲线y=f（x）在点（0，f（0））处的切线方程；（2）求函数f（x）在区间[0，]上的最大值和最小值．13．已知函数f（x）=（x﹣）e﹣x（x≥）．（1）求f（x）的导函数；（2）求f（x）在区间[，+∞）上的取值范围．14．已知函数f（x）=（x+1）lnx﹣a（x﹣1）．（I）当a=4时，求曲线y=f（x）在（1，f（1））处的切线方程；（II）若当x∈（1，+∞）时，f（x）＞0，求a的取值范围．15．设f（x）=xlnx﹣ax2+（2a﹣1）x，a∈R．（Ⅰ）令g（x）=f′（x），求g（x）的单调区间；（Ⅱ）已知f（x）在x=1处取得极大值，求实数a的取值范围．16．已知函数f（x）=（x﹣2）e x+a（x﹣1）2．（Ⅰ）讨论f（x）的单调性；（Ⅱ）若f（x）有两个零点，求a的取值范围．17．设函数f（x）=xe a﹣x+bx，曲线y=f（x）在点（2，f（2））处的切线方程为y=（e﹣1）x+4，（Ⅰ）求a，b的值；（Ⅱ）求f（x）的单调区间．18．设函数f（x）=ax2﹣a﹣lnx，g（x）=﹣，其中a∈R，e=2.718…为自然对数的底数．（Ⅰ）讨论f（x）的单调性；（Ⅱ）证明：当x＞1时，g（x）＞0；（Ⅲ）确定a的所有可能取值，使得f（x）＞g（x）在区间（1，+∞）内恒成立．19．（Ⅰ）讨论函数f（x）=e x的单调性，并证明当x＞0时，（x﹣2）e x+x+2＞0；（Ⅱ）证明：当a∈[0，1）时，函数g（x）=（x＞0）有最小值．设g（x）的最小值为h（a），求函数h（a）的值域．20．设函数f（x）=lnx﹣x+1．（1）讨论f（x）的单调性；（2）证明当x∈（1，+∞）时，1＜＜x；（3）设c＞1，证明当x∈（0，1）时，1+（c﹣1）x＞c x．21．设函数f（x）=（x﹣1）3﹣ax﹣b，x∈R，其中a，b∈R．（1）求f（x）的单调区间；（2）若f（x）存在极值点x0，且f（x1）=f（x0），其中x1≠x0，求证：x1+2x0=3；（3）设a＞0，函数g（x）=|f（x）|，求证：g（x）在区间[0，2]上的最大值不小于．22．设函数f（x）=acos2x+（a﹣1）（cosx+1），其中a＞0，记|f（x）|的最大值为A．（Ⅰ）求f′（x）；（Ⅱ）求A；（Ⅲ）证明：|f′（x）|≤2A．23．设函数f（x）=ax2﹣a﹣lnx，其中a∈R．（Ⅰ）讨论f（x）的单调性；（Ⅱ）确定a的所有可能取值，使得f（x）＞﹣e1﹣x在区间（1，+∞）内恒成立（e=2.718…为自然对数的底数）．24．设函数f（x）=x3﹣ax﹣b，x∈R，其中a，b∈R．（1）求f（x）的单调区间；（2）若f（x）存在极值点x0，且f（x1）=f（x0），其中x1≠x0，求证：x1+2x0=0；（3）设a＞0，函数g（x）=|f（x）|，求证：g（x）在区间[﹣1，1]上的最大值不小于．25．已知函数f（x）=（x﹣2）e x+a（x﹣1）2有两个零点．（Ⅰ）求a的取值范围；（Ⅱ）设x1，x2是f（x）的两个零点，证明：x1+x2＜2．26．已知f（x）=a（x﹣lnx）+，a∈R．（I）讨论f（x）的单调性；（II）当a=1时，证明f（x）＞f′（x）+对于任意的x∈[1，2]成立．27．设函数f（x）=x3+ax2+bx+c．（1）求曲线y=f（x）在点（0，f（0））处的切线方程；（2）设a=b=4，若函数f（x）有三个不同零点，求c的取值范围；（3）求证：a2﹣3b＞0是f（x）有三个不同零点的必要而不充分条件．28．已知函数f（x）=a x+b x（a＞0，b＞0，a≠1，b≠1）．（1）设a=2，b=．①求方程f（x）=2的根；②若对于任意x∈R，不等式f（2x）≥mf（x）﹣6恒成立，求实数m的最大值；（2）若0＜a＜1，b＞1，函数g（x）=f（x）﹣2有且只有1个零点，求ab的值．导数大题-近两年高考题参考答案与试题解析一．解答题（共28小题）1．（2017•新课标Ⅰ）已知函数f（x）=e x（e x﹣a）﹣a2x．（1）讨论f（x）的单调性；（2）若f（x）≥0，求a的取值范围．【解答】解：（1）f（x）=e x（e x﹣a）﹣a2x=e2x﹣e x a﹣a2x，∴f′（x）=2e2x﹣ae x﹣a2=（2e x+a）（e x﹣a），①当a=0时，f′（x）＞0恒成立，∴f（x）在R上单调递增，②当a＞0时，2e x+a＞0，令f′（x）=0，解得x=lna，当x＜lna时，f′（x）＜0，函数f（x）单调递减，当x＞lna时，f′（x）＞0，函数f（x）单调递增，③当a＜0时，e x﹣a＞0，令f′（x）=0，解得x=ln（﹣），当x＜ln（﹣）时，f′（x）＜0，函数f（x）单调递减，当x＞ln（﹣）时，f′（x）＞0，函数f（x）单调递增，综上所述，当a=0时，f（x）在R上单调递增，当a＞0时，f（x）在（﹣∞，lna）上单调递减，在（lna，+∞）上单调递增，当a＜0时，f（x）在（﹣∞，ln（﹣））上单调递减，在（ln（﹣），+∞）上单调递增，（2）①当a=0时，f（x）=e2x＞0恒成立，②当a＞0时，由（1）可得f（x）min=f（lna）=﹣a2lna≥0，∴lna≤0，∴0＜a≤1，③当a＜0时，由（1）可得f（x）min=f（ln（﹣））=﹣a2ln（﹣）≥0，∴ln（﹣）≤，∴﹣2≤a＜0，综上所述a的取值范围为[﹣2，1]2．（2017•新课标Ⅰ）已知函数f（x）=ae2x+（a﹣2）e x﹣x．（1）讨论f（x）的单调性；（2）若f（x）有两个零点，求a的取值范围．【解答】解：（1）由f（x）=ae2x+（a﹣2）e x﹣x，求导f′（x）=2ae2x+（a﹣2）e x ﹣1，当a=0时，f′（x）=﹣2e x﹣1＜0，∴当x∈R，f（x）单调递减，当a＞0时，f′（x）=（2e x+1）（ae x﹣1）=2a（e x+）（e x﹣），令f′（x）=0，解得：x=ln，当f′（x）＞0，解得：x＞ln，当f′（x）＜0，解得：x＜ln，∴x∈（﹣∞，ln）时，f（x）单调递减，x∈（ln，+∞）单调递增；当a＜0时，f′（x）=2a（e x+）（e x﹣）＜0，恒成立，∴当x∈R，f（x）单调递减，综上可知：当a≤0时，f（x）在R单调减函数，当a＞0时，f（x）在（﹣∞，ln）是减函数，在（ln，+∞）是增函数；（2）①若a≤0时，由（1）可知：f（x）最多有一个零点，当a＞0时，f（x）=ae2x+（a﹣2）e x﹣x，当x→﹣∞时，e2x→0，e x→0，∴当x→﹣∞时，f（x）→+∞，当x→∞，e2x→+∞，且远远大于e x和x，∴当x→∞，f（x）→+∞，∴函数有两个零点，f（x）的最小值小于0即可，由f（x）在（﹣∞，ln）是减函数，在（ln，+∞）是增函数，∴f（x）min=f（ln）=a×（）+（a﹣2）×﹣ln＜0，∴1﹣﹣ln＜0，即ln+﹣1＞0，设t=，则g（t）=lnt+t﹣1，（t＞0），求导g′（t）=+1，由g（1）=0，∴t=＞1，解得：0＜a＜1，∴a的取值范围（0，1）．方法二：（1）由f（x）=ae2x+（a﹣2）e x﹣x，求导f′（x）=2ae2x+（a﹣2）e x﹣1，当a=0时，f′（x）=2e x﹣1＜0，∴当x∈R，f（x）单调递减，当a＞0时，f′（x）=（2e x+1）（ae x﹣1）=2a（e x+）（e x﹣），令f′（x）=0，解得：x=﹣lna，当f′（x）＞0，解得：x＞﹣lna，当f′（x）＜0，解得：x＜﹣lna，∴x∈（﹣∞，﹣lna）时，f（x）单调递减，x∈（﹣lna，+∞）单调递增；当a＜0时，f′（x）=2a（e x+）（e x﹣）＜0，恒成立，∴当x∈R，f（x）单调递减，综上可知：当a≤0时，f（x）在R单调减函数，当a＞0时，f（x）在（﹣∞，﹣lna）是减函数，在（﹣lna，+∞）是增函数；（2）①若a≤0时，由（1）可知：f（x）最多有一个零点，②当a＞0时，由（1）可知：当x=﹣lna时，f（x）取得最小值，f（x）min=f（﹣lna）=1﹣﹣ln，当a=1，时，f（﹣lna）=0，故f（x）只有一个零点，当a∈（1，+∞）时，由1﹣﹣ln＞0，即f（﹣lna）＞0，故f（x）没有零点，当a∈（0，1）时，1﹣﹣ln＜0，f（﹣lna）＜0，由f（﹣2）=ae﹣4+（a﹣2）e﹣2+2＞﹣2e﹣2+2＞0，故f（x）在（﹣∞，﹣lna）有一个零点，假设存在正整数n0，满足n0＞ln（﹣1），则f（n0）=（a+a﹣2）﹣n0＞﹣n0＞﹣n0＞0，由ln（﹣1）＞﹣lna，因此在（﹣lna，+∞）有一个零点．∴a的取值范围（0，1）．3．（2017•新课标Ⅲ）已知函数f（x）=lnx+ax2+（2a+1）x．（1）讨论f（x）的单调性；（2）当a＜0时，证明f（x）≤﹣﹣2．【解答】（1）解：因为f（x）=lnx+ax2+（2a+1）x，求导f′（x）=+2ax+（2a+1）==，（x＞0），①当a=0时，f′（x）=+1＞0恒成立，此时y=f（x）在（0，+∞）上单调递增；②当a＞0，由于x＞0，所以（2ax+1）（x+1）＞0恒成立，此时y=f（x）在（0，+∞）上单调递增；③当a＜0时，令f′（x）=0，解得：x=﹣．因为当x∈（0，﹣）f′（x）＞0、当x∈（﹣，+∞）f′（x）＜0，所以y=f（x）在（0，﹣）上单调递增、在（﹣，+∞）上单调递减．综上可知：当a≥0时f（x）在（0，+∞）上单调递增，当a＜0时，f（x）在（0，﹣）上单调递增、在（﹣，+∞）上单调递减；（2）证明：由（1）可知：当a＜0时f（x）在（0，﹣）上单调递增、在（﹣，+∞）上单调递减，所以当x=﹣时函数y=f（x）取最大值f（x）max=f（﹣）=﹣1﹣ln2﹣+ln（﹣）．从而要证f（x）≤﹣﹣2，即证f（﹣）≤﹣﹣2，即证﹣1﹣ln2﹣+ln（﹣）≤﹣﹣2，即证﹣（﹣）+ln（﹣）≤﹣1+ln2．令t=﹣，则t＞0，问题转化为证明：﹣t+lnt≤﹣1+ln2．…（*）令g（t）=﹣t+lnt，则g′（t）=﹣+，令g′（t）=0可知t=2，则当0＜t＜2时g′（t）＞0，当t＞2时g′（t）＜0，所以y=g（t）在（0，2）上单调递增、在（2，+∞）上单调递减，即g（t）≤g（2）=﹣×2+ln2=﹣1+ln2，即（*）式成立，所以当a＜0时，f（x）≤﹣﹣2成立．4．（2017•新课标Ⅲ）已知函数f（x）=x﹣1﹣alnx．（1）若f（x）≥0，求a的值；（2）设m为整数，且对于任意正整数n，（1+）（1+）…（1+）＜m，求m的最小值．【解答】解：（1）因为函数f（x）=x﹣1﹣alnx，x＞0，所以f′（x）=1﹣=，且f（1）=0．所以当a≤0时f′（x）＞0恒成立，此时y=f（x）在（0，+∞）上单调递增，这与f（x）≥0矛盾；当a＞0时令f′（x）=0，解得x=a，所以y=f（x）在（0，a）上单调递减，在（a，+∞）上单调递增，即f（x）min=f （a），又因为f（x）min=f（a）≥0，所以a=1；（2）由（1）可知当a=1时f（x）=x﹣1﹣lnx≥0，即lnx≤x﹣1，所以ln（x+1）≤x当且仅当x=0时取等号，所以ln（1+）＜，k∈N*．一方面，ln（1+）+ln（1+）+…+ln（1+）＜++…+=1﹣＜1，即（1+）（1+）…（1+）＜e；另一方面，（1+）（1+）…（1+）＞（1+）（1+）（1+）=＞2；从而当n≥3时，（1+）（1+）…（1+）∈（2，e），因为m为整数，且对于任意正整数n，（1+）（1+）…（1+）＜m成立，所以m的最小值为3．5．（2017•天津）设a，b∈R，|a|≤1．已知函数f（x）=x3﹣6x2﹣3a（a﹣4）x+b，g（x）=e x f（x）．（Ⅰ）求f（x）的单调区间；（Ⅱ）已知函数y=g（x）和y=e x的图象在公共点（x0，y0）处有相同的切线，（i）求证：f（x）在x=x0处的导数等于0；（ii）若关于x的不等式g（x）≤e x在区间[x0﹣1，x0+1]上恒成立，求b的取值范围．【解答】（Ⅰ）解：由f（x）=x3﹣6x2﹣3a（a﹣4）x+b，可得f'（x）=3x2﹣12x ﹣3a（a﹣4）=3（x﹣a）（x﹣（4﹣a）），令f'（x）=0，解得x=a，或x=4﹣a．由|a|≤1，得a＜4﹣a．当x变化时，f'（x），f（x）的变化情况如下表：∴f（x）的单调递增区间为（﹣∞，a），（4﹣a，+∞），单调递减区间为（a，4﹣a）；（Ⅱ）（i）证明：∵g'（x）=e x（f（x）+f'（x）），由题意知，∴，解得．∴f（x）在x=x0处的导数等于0；（ii）解：∵g（x）≤e x，x∈[x0﹣1，x0+1]，由e x＞0，可得f（x）≤1．又∵f（x0）=1，f'（x0）=0，故x0为f（x）的极大值点，由（I）知x0=a．另一方面，由于|a|≤1，故a+1＜4﹣a，由（Ⅰ）知f（x）在（a﹣1，a）内单调递增，在（a，a+1）内单调递减，故当x0=a时，f（x）≤f（a）=1在[a﹣1，a+1]上恒成立，从而g（x）≤e x在[x0﹣1，x0+1]上恒成立．由f（a）=a3﹣6a2﹣3a（a﹣4）a+b=1，得b=2a3﹣6a2+1，﹣1≤a≤1．令t（x）=2x3﹣6x2+1，x∈[﹣1，1]，∴t'（x）=6x2﹣12x，令t'（x）=0，解得x=2（舍去），或x=0．∵t（﹣1）=﹣7，t（1）=﹣3，t（0）=1，故t（x）的值域为[﹣7，1]．∴b的取值范围是[﹣7，1]．6．（2017•天津）设a∈Z，已知定义在R上的函数f（x）=2x4+3x3﹣3x2﹣6x+a在区间（1，2）内有一个零点x0，g（x）为f（x）的导函数．（Ⅰ）求g（x）的单调区间；（Ⅱ）设m∈[1，x0）∪（x0，2]，函数h（x）=g（x）（m﹣x0）﹣f（m），求证：h（m）h（x0）＜0；（Ⅲ）求证：存在大于0的常数A，使得对于任意的正整数p，q，且∈[1，x0）∪（x0，2]，满足|﹣x0|≥．【解答】（Ⅰ）解：由f（x）=2x4+3x3﹣3x2﹣6x+a，可得g（x）=f′（x）=8x3+9x2﹣6x﹣6，进而可得g′（x）=24x2+18x﹣6．令g′（x）=0，解得x=﹣1，或x=．当x变化时，g′（x），g（x）的变化情况如下表：（所以，g（x）的单调递增区间是（﹣∞，﹣1），（，+∞），单调递减区间是（﹣1，）．（Ⅱ）证明：由h（x）=g（x）（m﹣x0）﹣f（m），得h（m）=g（m）（m﹣x0）﹣f（m），h（x0）=g（x0）（m﹣x0）﹣f（m）．令函数H1（x）=g（x）（x﹣x0）﹣f（x），则H′1（x）=g′（x）（x﹣x0）．由（Ⅰ）知，当x∈[1，2]时，g′（x）＞0，故当x∈[1，x0）时，H′1（x）＜0，H1（x）单调递减；当x∈（x0，2]时，H′1（x）＞0，H1（x）单调递增．因此，当x∈[1，x0）∪（x0，2]时，H1（x）＞H1（x0）=﹣f（x0）=0，可得H1（m）＞0即h（m）＞0，令函数H2（x）=g（x0）（x﹣x0）﹣f（x），则H′2（x）=g′（x0）﹣g（x）．由（Ⅰ）知，g（x）在[1，2]上单调递增，故当x∈[1，x0）时，H′2（x）＞0，H2（x）单调递增；当x∈（x0，2]时，H′2（x）＜0，H2（x）单调递减．因此，当x∈[1，x0）∪（x0，2]时，H2（x）＞H2（x0）=0，可得得H2（m）＜0即h（x0）＜0，．所以，h（m）h（x0）＜0．（Ⅲ）对于任意的正整数p，q，且，令m=，函数h（x）=g（x）（m﹣x0）﹣f（m）．由（Ⅱ）知，当m∈[1，x0）时，h（x）在区间（m，x0）内有零点；当m∈（x0，2]时，h（x）在区间（x0，m）内有零点．所以h（x）在（1，2）内至少有一个零点，不妨设为x1，则h（x1）=g（x1）（﹣x0）﹣f（）=0．由（Ⅰ）知g（x）在[1，2]上单调递增，故0＜g（1）＜g（x1）＜g（2），于是|﹣x0|=≥=．因为当x∈[1，2]时，g（x）＞0，故f（x）在[1，2]上单调递增，所以f（x）在区间[1，2]上除x0外没有其他的零点，而≠x0，故f（）≠0．又因为p，q，a均为整数，所以|2p4+3p3q﹣3p2q2﹣6pq3+aq4|是正整数，从而|2p4+3p3q﹣3p2q2﹣6pq3+aq4|≥1．所以|﹣x0|≥．所以，只要取A=g（2），就有|﹣x0|≥．7．（2017•山东）已知函数f（x）=x3﹣ax2，a∈R，（1）当a=2时，求曲线y=f（x）在点（3，f（3））处的切线方程；（2）设函数g（x）=f（x）+（x﹣a）cosx﹣sinx，讨论g（x）的单调性并判断有无极值，有极值时求出极值．【解答】解：（1）当a=2时，f（x）=x3﹣x2，∴f′（x）=x2﹣2x，∴k=f′（3）=9﹣6=3，f（3）=×27﹣9=0，∴曲线y=f（x）在点（3，f（3））处的切线方程y=3（x﹣3），即3x﹣y﹣9=0（2）函数g（x）=f（x）+（x﹣a）cosx﹣sinx=x3﹣ax2+（x﹣a）cosx﹣sinx，∴g′（x）=（x﹣a）（x﹣sinx），令g′（x）=0，解得x=a，或x=0，①若a＞0时，当x＜0时，g′（x）＞0恒成立，故g（x）在（﹣∞，0）上单调递增，当x＞a时，g′（x）＞0恒成立，故g（x）在（a，+∞）上单调递增，当0＜x＜a时，g′（x）＜0恒成立，故g（x）在（0，a）上单调递减，∴当x=a时，函数有极小值，极小值为g（a）=﹣a3﹣sina当x=0时，有极大值，极大值为g（0）=﹣a，②若a＜0时，当x＞0时，g′（x）＞0恒成立，故g（x）在（﹣∞，0）上单调递增，当x＜a时，g′（x）＞0恒成立，故g（x）在（﹣∞，a）上单调递增，当a＜x＜0时，g′（x）＜0恒成立，故g（x）在（a，0）上单调递减，∴当x=a时，函数有极大值，极大值为g（a）=﹣a3﹣sina当x=0时，有极小值，极小值为g（0）=﹣a③当a=0时，g′（x）=x（x+sinx），当x＞0时，g′（x）＞0恒成立，故g（x）在（0，+∞）上单调递增，当x＜0时，g′（x）＞0恒成立，故g（x）在（﹣∞，0）上单调递增，∴g（x）在R上单调递增，无极值．8．（2017•新课标Ⅱ）设函数f（x）=（1﹣x2）e x．（1）讨论f（x）的单调性；（2）当x≥0时，f（x）≤ax+1，求a的取值范围．【解答】解：（1）因为f（x）=（1﹣x2）e x，x∈R，所以f′（x）=（1﹣2x﹣x2）e x，令f′（x）=0可知x=﹣1±，当x＜﹣1﹣或x＞﹣1+时f′（x）＜0，当﹣1﹣＜x＜﹣1+时f′（x）＞0，所以f（x）在（﹣∞，﹣1﹣），（﹣1+，+∞）上单调递减，在（﹣1﹣，﹣1+）上单调递增；（2）由题可知f（x）=（1﹣x）（1+x）e x．下面对a的范围进行讨论：①当a≥1时，设函数h（x）=（1﹣x）e x，则h′（x）=﹣xe x＜0（x＞0），因此h（x）在[0，+∞）上单调递减，又因为h（0）=1，所以h（x）≤1，所以f（x）=（1﹣x）h（x）≤x+1≤ax+1；②当0＜a＜1时，设函数g（x）=e x﹣x﹣1，则g′（x）=e x﹣1＞0（x＞0），所以g（x）在[0，+∞）上单调递增，又g（0）=1﹣0﹣1=0，所以e x≥x+1．因为当0＜x＜1时f（x）＞（1﹣x）（1+x）2，所以（1﹣x）（1+x）2﹣ax﹣1=x（1﹣a﹣x﹣x2），取x0=∈（0，1），则（1﹣x0）（1+x0）2﹣ax0﹣1=0，所以f（x0）＞ax0+1，矛盾；③当a≤0时，取x0=∈（0，1），则f（x0）＞（1﹣x0）（1+x0）2=1≥ax0+1，矛盾；综上所述，a的取值范围是[1，+∞）．9．（2017•江苏）已知函数f（x）=x3+ax2+bx+1（a＞0，b∈R）有极值，且导函数f′（x）的极值点是f（x）的零点．（极值点是指函数取极值时对应的自变量的值）（1）求b关于a的函数关系式，并写出定义域；（2）证明：b2＞3a；（3）若f（x），f′（x）这两个函数的所有极值之和不小于﹣，求a的取值范围．【解答】（1）解：因为f（x）=x3+ax2+bx+1，所以g（x）=f′（x）=3x2+2ax+b，g′（x）=6x+2a，令g′（x）=0，解得x=﹣．由于当x＞﹣时g′（x）＞0，g（x）=f′（x）单调递增；当x＜﹣时g′（x）＜0，g（x）=f′（x）单调递减；所以f′（x）的极小值点为x=﹣，由于导函数f′（x）的极值点是原函数f（x）的零点，所以f（﹣）=0，即﹣+﹣+1=0，所以b=+（a＞0）．因为f（x）=x3+ax2+bx+1（a＞0，b∈R）有极值，所以f′（x）=3x2+2ax+b=0的实根，所以4a2﹣12b≥0，即a2﹣+≥0，解得a≥3，所以b=+（a≥3）．（2）证明：由（1）可知h（a）=b2﹣3a=﹣+=（4a3﹣27）（a3﹣27），由于a＞3，所以h（a）＞0，即b2＞3a；（3）解：由（1）可知f′（x）的极小值为f′（﹣）=b﹣，设x1，x2是y=f（x）的两个极值点，则x1+x2=，x1x2=，所以f（x1）+f（x2）=++a（+）+b（x1+x2）+2=（x1+x2）[（x1+x2）2﹣3x1x2]+a[（x1+x2）2﹣2x1x2]+b（x1+x2）+2=﹣+2，又因为f（x），f′（x）这两个函数的所有极值之和不小于﹣，所以b﹣+﹣+2=﹣≥﹣，因为a＞3，所以2a3﹣63a﹣54≤0，所以2a（a2﹣36）+9（a﹣6）≤0，所以（a﹣6）（2a2+12a+9）≤0，由于a＞3时2a2+12a+9＞0，所以a﹣6≤0，解得a≤6，所以a的取值范围是（3，6]．10．（2017•新课标Ⅱ）已知函数f（x）=ax2﹣ax﹣xlnx，且f（x）≥0．（1）求a；（2）证明：f（x）存在唯一的极大值点x0，且e﹣2＜f（x0）＜2﹣2．【解答】（1）解：因为f（x）=ax2﹣ax﹣xlnx=x（ax﹣a﹣lnx）（x＞0），则f（x）≥0等价于h（x）=ax﹣a﹣lnx≥0，求导可知h′（x）=a﹣．则当a≤0时h′（x）＜0，即y=h（x）在（0，+∞）上单调递减，所以当x0＞1时，h（x0）＜h（1）=0，矛盾，故a＞0．因为当0＜x＜时h′（x）＜0、当x＞时h′（x）＞0，所以h（x）min=h（），又因为h（1）=a﹣a﹣ln1=0，所以=1，解得a=1；（2）证明：由（1）可知f（x）=x2﹣x﹣xlnx，f′（x）=2x﹣2﹣lnx，令f′（x）=0，可得2x﹣2﹣lnx=0，记t（x）=2x﹣2﹣lnx，则t′（x）=2﹣，令t′（x）=0，解得：x=，所以t（x）在区间（0，）上单调递减，在（，+∞）上单调递增，所以t（x）min=t（）=ln2﹣1＜0，从而t（x）=0有解，即f′（x）=0存在两根x0，x2，且不妨设f′（x）在（0，x0）上为正、在（x0，x2）上为负、在（x2，+∞）上为正，所以f（x）必存在唯一极大值点x0，且2x0﹣2﹣lnx0=0，所以f（x0）=﹣x0﹣x0lnx0=﹣x0+2x0﹣2=x0﹣，由x0＜可知f（x0）＜（x0﹣）max=﹣+=；由f′（）＜0可知x0＜＜，所以f（x）在（0，x0）上单调递增，在（x0，）上单调递减，所以f（x0）＞f（）=；综上所述，f（x）存在唯一的极大值点x0，且e﹣2＜f（x0）＜2﹣2．11．（2017•山东）已知函数f（x）=x2+2cosx，g（x）=e x（cosx﹣sinx+2x﹣2），其中e≈2.17828…是自然对数的底数．（Ⅰ）求曲线y=f（x）在点（π，f（π））处的切线方程；（Ⅱ）令h（x）=g （x）﹣a f（x）（a∈R），讨论h（x）的单调性并判断有无极值，有极值时求出极值．【解答】解：（I）f（π）=π2﹣2．f′（x）=2x﹣2sinx，∴f′（π）=2π．∴曲线y=f（x）在点（π，f（π））处的切线方程为：y﹣（π2﹣2）=2π（x﹣π）．化为：2πx﹣y﹣π2﹣2=0．（II）h（x）=g （x）﹣a f（x）=e x（cosx﹣sinx+2x﹣2）﹣a（x2+2cosx）h′（x）=e x（cosx﹣sinx+2x﹣2）+e x（﹣sinx﹣cosx+2）﹣a（2x﹣2sinx）=2（x﹣sinx）（e x﹣a）=2（x﹣sinx）（e x﹣e lna）．令u（x）=x﹣sinx，则u′（x）=1﹣cosx≥0，∴函数u（x）在R上单调递增．∵u（0）=0，∴x＞0时，u（x）＞0；x＜0时，u（x）＜0．（1）a≤0时，e x﹣a＞0，∴x＞0时，h′（x）＞0，函数h（x）在（0，+∞）单调递增；x＜0时，h′（x）＜0，函数h（x）在（﹣∞，0）单调递减．∴x=0时，函数h（x）取得极小值，h（0）=﹣1﹣2a．（2）a＞0时，令h′（x）=2（x﹣sinx）（e x﹣e lna）=0．解得x1=lna，x2=0．①0＜a＜1时，x∈（﹣∞，lna）时，e x﹣e lna＜0，h′（x）＞0，函数h（x）单调递增；x∈（lna，0）时，e x﹣e lna＞0，h′（x）＜0，函数h（x）单调递减；x∈（0，+∞）时，e x﹣e lna＞0，h′（x）＞0，函数h（x）单调递增．∴当x=0时，函数h（x）取得极小值，h（0）=﹣2a﹣1．当x=lna时，函数h（x）取得极大值，h（lna）=﹣a[ln2a﹣2lna+sin（lna）+cos （lna）+2]．②当a=1时，lna=0，x∈R时，h′（x）≥0，∴函数h（x）在R上单调递增．③1＜a时，lna＞0，x∈（﹣∞，0）时，e x﹣e lna＜0，h′（x）＞0，函数h（x）单调递增；x∈（0，lna）时，e x﹣e lna＜0，h′（x）＜0，函数h（x）单调递减；x∈（lna，+∞）时，e x﹣e lna＞0，h′（x）＞0，函数h（x）单调递增．∴当x=0时，函数h（x）取得极大值，h（0）=﹣2a﹣1．当x=lna时，函数h（x）取得极小值，h（lna）=﹣a[ln2a﹣2lna+sin（lna）+cos （lna）+2]．综上所述：a≤0时，函数h（x）在（0，+∞）单调递增；x＜0时，函数h（x）在（﹣∞，0）单调递减．x=0时，函数h（x）取得极小值，h（0）=﹣1﹣2a．0＜a＜1时，函数h（x）在x∈（﹣∞，lna）是单调递增；函数h（x）在x∈（lna，0）上单调递减．当x=0时，函数h（x）取得极小值，h（0）=﹣2a﹣1．当x=lna 时，函数h（x）取得极大值，h（lna）=﹣a[ln2a﹣2lna+sin（lna）+cos（lna）+2]．当a=1时，lna=0，函数h（x）在R上单调递增．a＞1时，函数h（x）在（﹣∞，0），（lna，+∞）上单调递增；函数h（x）在（0，lna）上单调递减．当x=0时，函数h（x）取得极大值，h（0）=﹣2a﹣1．当x=lna 时，函数h（x）取得极小值，h（lna）=﹣a[ln2a﹣2lna+sin（lna）+cos（lna）+2]．12．（2017•北京）已知函数f（x）=e x cosx﹣x．（1）求曲线y=f（x）在点（0，f（0））处的切线方程；（2）求函数f（x）在区间[0，]上的最大值和最小值．【解答】解：（1）函数f（x）=e x cosx﹣x的导数为f′（x）=e x（cosx﹣sinx）﹣1，可得曲线y=f（x）在点（0，f（0））处的切线斜率为k=e0（cos0﹣sin0）﹣1=0，切点为（0，e0cos0﹣0），即为（0，1），曲线y=f（x）在点（0，f（0））处的切线方程为y=1；（2）函数f（x）=e x cosx﹣x的导数为f′（x）=e x（cosx﹣sinx）﹣1，令g（x）=e x（cosx﹣sinx）﹣1，则g（x）的导数为g′（x）=e x（cosx﹣sinx﹣sinx﹣cosx）=﹣2e x•sinx，当x∈[0，]，可得g′（x）=﹣2e x•sinx≤0，即有g（x）在[0，]递减，可得g（x）≤g（0）=0，则f（x）在[0，]递减，即有函数f（x）在区间[0，]上的最大值为f（0）=e0cos0﹣0=1；最小值为f（）=e cos﹣=﹣．13．（2017•浙江）已知函数f（x）=（x﹣）e﹣x（x≥）．（1）求f（x）的导函数；（2）求f（x）在区间[，+∞）上的取值范围．【解答】解：（1）函数f（x）=（x﹣）e﹣x（x≥），导数f′（x）=（1﹣••2）e﹣x﹣（x﹣）e﹣x=（1﹣x+）e﹣x=（1﹣x）（1﹣）e﹣x；（2）由f（x）的导数f′（x）=（1﹣x）（1﹣）e﹣x，可得f′（x）=0时，x=1或，当＜x＜1时，f′（x）＜0，f（x）递减；当1＜x＜时，f′（x）＞0，f（x）递增；当x＞时，f′（x）＜0，f（x）递减，且x≥⇔x2≥2x﹣1⇔（x﹣1）2≥0，则f（x）≥0．由f（）=e，f（1）=0，f（）=e，即有f（x）的最大值为e，最小值为f（1）=0．则f（x）在区间[，+∞）上的取值范围是[0，e]．14．（2016•新课标Ⅱ）已知函数f（x）=（x+1）lnx﹣a（x﹣1）．（I）当a=4时，求曲线y=f（x）在（1，f（1））处的切线方程；（II）若当x∈（1，+∞）时，f（x）＞0，求a的取值范围．【解答】解：（I）当a=4时，f（x）=（x+1）lnx﹣4（x﹣1）．f（1）=0，即点为（1，0），函数的导数f′（x）=lnx+（x+1）•﹣4，则f′（1）=ln1+2﹣4=2﹣4=﹣2，即函数的切线斜率k=f′（1）=﹣2，则曲线y=f（x）在（1，0）处的切线方程为y=﹣2（x﹣1）=﹣2x+2；（II）∵f（x）=（x+1）lnx﹣a（x﹣1），∴f′（x）=1++lnx﹣a，∴f″（x）=，∵x＞1，∴f″（x）＞0，∴f′（x）在（1，+∞）上单调递增，∴f′（x）＞f′（1）=2﹣a．①a≤2，f′（x）＞f′（1）≥0，∴f（x）在（1，+∞）上单调递增，∴f（x）＞f（1）=0，满足题意；②a＞2，存在x0∈（1，+∞），f′（x0）=0，函数f（x）在（1，x0）上单调递减，在（x0，+∞）上单调递增，由f（1）=0，可得存在x0∈（1，+∞），f（x0）＜0，不合题意．综上所述，a≤2．15．（2016•山东）设f（x）=xlnx﹣ax2+（2a﹣1）x，a∈R．（Ⅰ）令g（x）=f′（x），求g（x）的单调区间；（Ⅱ）已知f（x）在x=1处取得极大值，求实数a的取值范围．【解答】解：（Ⅰ）∵f（x）=xlnx﹣ax2+（2a﹣1）x，∴g（x）=f′（x）=lnx﹣2ax+2a，x＞0，g′（x）=﹣2a=，当a≤0，g′（x）＞0恒成立，即可g（x）的单调增区间是（0，+∞）；当a＞0，当x＞时，g′（x）＜0，函数为减函数，当0＜x＜，g′（x）＞0，函数为增函数，∴当a≤0时，g（x）的单调增区间是（0，+∞）；当a＞0时，g（x）的单调增区间是（0，），单调减区间是（，+∞）；（Ⅱ）∵f（x）在x=1处取得极大值，∴f′（1）=0，①当a≤0时，f′（x）单调递增，则当0＜x＜1时，f′（x）＜0，f（x）单调递减，当x＞1时，f′（x）＞0，f（x）单调递增，∴f（x）在x=1处取得极小值，不合题意，②当0＜a＜时，＞1，由（1）知，f′（x）在（0，）内单调递增，当0＜x＜1时，f′（x）＜0，当1＜x＜时，f′（x）＞0，∴f（x）在（0，1）内单调递减，在（1，）内单调递增，即f（x）在x=1处取得极小值，不合题意．③当a=时，=1，f′（x）在（0，1）内单调递增，在（1，+∞）上单调递减，则当x＞0时，f′（x）≤0，f（x）单调递减，不合题意．④当a＞时，0＜＜1，当＜x＜1时，f′（x）＞0，f（x）单调递增，当x＞1时，f′（x）＜0，f（x）单调递减，∴当x=1时，f（x）取得极大值，满足条件．综上实数a的取值范围是a＞．16．（2016•新课标Ⅰ）已知函数f（x）=（x﹣2）e x+a（x﹣1）2．（Ⅰ）讨论f（x）的单调性；（Ⅱ）若f（x）有两个零点，求a的取值范围．【解答】解：（Ⅰ）由f（x）=（x﹣2）e x+a（x﹣1）2，可得f′（x）=（x﹣1）e x+2a（x﹣1）=（x﹣1）（e x+2a），①当a≥0时，由f′（x）＞0，可得x＞1；由f′（x）＜0，可得x＜1，即有f（x）在（﹣∞，1）递减；在（1，+∞）递增；②当a＜0时，若a=﹣，则f′（x）≥0恒成立，即有f（x）在R上递增；若a＜﹣时，由f′（x）＞0，可得x＜1或x＞ln（﹣2a）；由f′（x）＜0，可得1＜x＜ln（﹣2a）．即有f（x）在（﹣∞，1），（ln（﹣2a），+∞）递增；在（1，ln（﹣2a））递减；若﹣＜a＜0，由f′（x）＞0，可得x＜ln（﹣2a）或x＞1；由f′（x）＜0，可得ln（﹣2a）＜x＜1．即有f（x）在（﹣∞，ln（﹣2a）），（1，+∞）递增；在（ln（﹣2a），1）递减；（Ⅱ）①由（Ⅰ）可得当a＞0时，f（x）在（﹣∞，1）递减；在（1，+∞）递增，且f（1）=﹣e＜0，x→+∞，f（x）→+∞；x→﹣∞，f（x）→+∞．f（x）有两个零点；②当a=0时，f（x）=（x﹣2）e x，所以f（x）只有一个零点x=2；③当a＜0时，若a＜﹣时，f（x）在（1，ln（﹣2a））递减，在（﹣∞，1），（ln（﹣2a），+∞）递增，又当x≤1时，f（x）＜0，所以f（x）不存在两个零点；当a≥﹣时，f（x）在（1，+∞）单调递增，又x≤1时，f（x）＜0，所以f（x）不存在两个零点．综上可得，f（x）有两个零点时，a的取值范围为（0，+∞）．17．（2016•北京）设函数f（x）=xe a﹣x+bx，曲线y=f（x）在点（2，f（2））处的切线方程为y=（e﹣1）x+4，（Ⅰ）求a，b的值；（Ⅱ）求f（x）的单调区间．【解答】解：（Ⅰ）∵y=f（x）在点（2，f（2））处的切线方程为y=（e﹣1）x+4，∴当x=2时，y=2（e﹣1）+4=2e+2，即f（2）=2e+2，同时f′（2）=e﹣1，∵f（x）=xe a﹣x+bx，∴f′（x）=e a﹣x﹣xe a﹣x+b，则，即a=2，b=e；（Ⅱ）∵a=2，b=e；∴f（x）=xe2﹣x+ex，∴f′（x）=e2﹣x﹣xe2﹣x+e=（1﹣x）e2﹣x+e=（1﹣x+e x﹣1）e2﹣x，∵e2﹣x＞0，∴1﹣x+e x﹣1与f′（x）同号，令g（x）=1﹣x+e x﹣1，则g′（x）=﹣1+e x﹣1，由g′（x）＜0，得x＜1，此时g（x）为减函数，由g′（x）＞0，得x＞1，此时g（x）为增函数，则当x=1时，g（x）取得极小值也是最小值g（1）=1，则g（x）≥g（1）=1＞0，故f′（x）＞0，即f（x）的单调区间是（﹣∞，+∞），无递减区间．18．（2016•四川）设函数f（x）=ax2﹣a﹣lnx，g（x）=﹣，其中a∈R，e=2.718…为自然对数的底数．（Ⅰ）讨论f（x）的单调性；（Ⅱ）证明：当x＞1时，g（x）＞0；（Ⅲ）确定a的所有可能取值，使得f（x）＞g（x）在区间（1，+∞）内恒成立．【解答】（Ⅰ）解：由f（x）=ax2﹣a﹣lnx，得f′（x）=2ax﹣=（x＞0），当a≤0时，f′（x）＜0在（0，+∞）成立，则f（x）为（0，+∞）上的减函数；当a＞0时，由f′（x）=0，得x==，∴当x∈（0，）时，f′（x）＜0，当x∈（，+∞）时，f′（x）＞0，则f（x）在（0，）上为减函数，在（，+∞）上为增函数；综上，当a≤0时，f（x）为（0，+∞）上的减函数，当a＞0时，f（x）在（0，）上为减函数，在（，+∞）上为增函数；（Ⅱ）证明：要证g（x）＞0（x＞1），即﹣＞0，即证，也就是证，令h（x）=，则h′（x）=，∴h（x）在（1，+∞）上单调递增，则h（x）min=h（1）=e，即当x＞1时，h（x）＞e，∴当x＞1时，g（x）＞0；（Ⅲ）解：由f（x）＞g（x），得，设t（x）=，由题意知，t（x）＞0在（1，+∞）内恒成立，∵t（1）=0，∴有t′（x）=2ax=≥0在（1，+∞）内恒成立，令φ（x）=，则φ′（x）=2a=，当x≥2时，φ′（x）＞0，令h（x）=，h′（x）=，函数在[1，2）上单调递增，∴h（x）min=h（1）=﹣1．又2a≥1，e1﹣x＞0，∴1＜x＜2，φ′（x）＞0，综上所述，x＞1，φ′（x）＞0，φ（x）在区间（1，+∞）单调递增，∴t′（x）＞t′（1）≥0，即t（x）在区间（1，+∞）单调递增，∴a≥．19．（2016•新课标Ⅱ）（Ⅰ）讨论函数f（x）=e x的单调性，并证明当x＞0时，（x﹣2）e x+x+2＞0；（Ⅱ）证明：当a∈[0，1）时，函数g（x）=（x＞0）有最小值．设g （x）的最小值为h（a），求函数h（a）的值域．【解答】解：（1）证明：f（x）=f'（x）=e x（）=∵当x∈（﹣∞，﹣2）∪（﹣2，+∞）时，f'（x）＞0∴f（x）在（﹣∞，﹣2）和（﹣2，+∞）上单调递增∴x＞0时，＞f（0）=﹣1即（x﹣2）e x+x+2＞0（2）g'（x）===a∈[0，1）由（1）知，当x＞0时，f（x）=的值域为（﹣1，+∞），只有一解使得，只需•e t≤0恒成立，可得﹣2＜t≤2，由x＞0，可得t∈（0，2]当x∈（0，t）时，g'（x）＜0，g（x）单调减；当x∈（t，+∞），g'（x）＞0，g（x）单调增；h（a）===记k（t）=，在t∈（0，2]时，k'（t）=＞0，故k（t）单调递增，所以h（a）=k（t）∈（，]．20．（2016•新课标Ⅲ）设函数f（x）=lnx﹣x+1．（1）讨论f（x）的单调性；（2）证明当x∈（1，+∞）时，1＜＜x；（3）设c＞1，证明当x∈（0，1）时，1+（c﹣1）x＞c x．【解答】解：（1）函数f（x）=lnx﹣x+1的导数为f′（x）=﹣1，由f′（x）＞0，可得0＜x＜1；由f′（x）＜0，可得x＞1．即有f（x）的增区间为（0，1）；减区间为（1，+∞）；（2）证明：当x∈（1，+∞）时，1＜＜x，即为lnx＜x﹣1＜xlnx．由（1）可得f（x）=lnx﹣x+1在（1，+∞）递减，可得f（x）＜f（1）=0，即有lnx＜x﹣1；设F（x）=xlnx﹣x+1，x＞1，F′（x）=1+lnx﹣1=lnx，当x＞1时，F′（x）＞0，可得F（x）递增，即有F（x）＞F（1）=0，即有xlnx＞x﹣1，则原不等式成立；（3）证明：设G（x）=1+（c﹣1）x﹣c x，G′（x）=c﹣1﹣c x lnc，可令G′（x）=0，可得c x=，由c＞1，x∈（0，1），可得1＜c x＜c，即1＜＜c，由（1）可得c x=恰有一解，设为x=x0是G（x）的最大值点，且0＜x0＜1，由G（0）=G（1）=0，且G（x）在（0，x0）递增，在（x0，1）递减，可得G（x0）=1+（c﹣1）x0﹣c x0＞0成立，则c＞1，当x∈（0，1）时，1+（c﹣1）x＞c x．21．（2016•天津）设函数f（x）=（x﹣1）3﹣ax﹣b，x∈R，其中a，b∈R．（1）求f（x）的单调区间；（2）若f（x）存在极值点x0，且f（x1）=f（x0），其中x1≠x0，求证：x1+2x0=3；（3）设a＞0，函数g（x）=|f（x）|，求证：g（x）在区间[0，2]上的最大值不小于．【解答】解：（1）函数f（x）=（x﹣1）3﹣ax﹣b的导数为f′（x）=3（x﹣1）2﹣a，当a≤0时，f′（x）≥0，f（x）在R上递增；当a＞0时，当x＞1+或x＜1﹣时，f′（x）＞0，当1﹣＜x＜1+，f′（x）＜0，可得f（x）的增区间为（﹣∞，1﹣），（1+，+∞），减区间为（1﹣，1+）；（2）证明：f′（x0）=0，可得3（x0﹣1）2=a，由f（x0）=（x0﹣1）3﹣3x0（x0﹣1）2﹣b=（x0﹣1）2（﹣2x0﹣1）﹣b，f（3﹣2x0）=（2﹣2x0）3﹣3（3﹣2x0）（x0﹣1）2﹣b=（x0﹣1）2（8﹣8x0﹣9+6x0）﹣b=（x0﹣1）2（﹣2x0﹣1）﹣b，即为f（3﹣2x0）=f（x0）=f（x1），即有3﹣2x0=x1，即为x1+2x0=3；（3）证明：要证g（x）在区间[0，2]上的最大值不小于，即证在[0，2]上存在x1，x2，使得f（x1）﹣f（x2）≥．当a≥3时，f（x）在[0，2]递减，f（2）=1﹣2a﹣b，f（0）=﹣1﹣b，f（0）﹣f（2）=2a﹣2≥4＞，递减，成立；当0＜a＜3时，f（1﹣）=（﹣）3﹣a（1﹣）﹣b=﹣﹣a+a﹣b=﹣a﹣b，f（1+）=（）3﹣a（1+）﹣b=﹣a﹣a﹣b=﹣﹣a﹣b，f（2）=1﹣2a﹣b，f（0）=﹣1﹣b，f（2）﹣f（0）=2﹣2a，若0＜a≤时，f（2）﹣f（0）=2﹣2a≥成立；若a＞时，f（1﹣）﹣f（1+）=＞成立．综上可得，g（x）在区间[0，2]上的最大值不小于．22．（2016•新课标Ⅲ）设函数f（x）=acos2x+（a﹣1）（cosx+1），其中a＞0，记|f（x）|的最大值为A．（Ⅰ）求f′（x）；（Ⅱ）求A；（Ⅲ）证明：|f′（x）|≤2A．【解答】（I）解：f′（x）=﹣2asin2x﹣（a﹣1）sinx．（II）当a≥1时，|f（x）|=|acos2x+（a﹣1）（cosx+1）|≤a|cos2x|+（a﹣1）|（cosx+1）|≤a|cos2x|+（a﹣1）（|cosx|+1）|≤a+2（a﹣1）=3a﹣2=f（0），因此A=3a﹣2．当0＜a＜1时，f（x）等价为f（x）=acos2x+（a﹣1）（cosx+1）=2acos2x+（a﹣1）cosx﹣1，令g（t）=2at2+（a﹣1）t﹣1，则A是|g（t）|在[﹣1，1]上的最大值，g（﹣1）=a，g（1）=3a﹣2，且当t=时，g（t）取得极小值，极小值为g（）=﹣﹣1=﹣，（二次函数在对称轴处取得极值）令﹣1＜＜1，得a＜（舍）或a＞．因此A=3a﹣2①当0＜a≤时，g（t）在（﹣1，1）内无极值点，|g（﹣1）|=a，|g（1）|=2﹣3a，|g（﹣1）|＜|g（1）|，∴A=2﹣3a，②当＜a＜1时，由g（﹣1）﹣g（1）=2（1﹣a）＞0，得g（﹣1）＞g（1）＞g（），又|g（）|﹣|g（﹣1）|=＞0，∴A=|g（）|=，综上，A=．（III）证明：由（I）可得：|f′（x）|=|﹣2asin2x﹣（a﹣1）sinx|≤2a+|a﹣1|，当0＜a≤时，|f′（x）|≤1+a≤2﹣4a＜2（2﹣3a）=2A，当＜a＜1时，A==++≥1，∴|f′（x）|≤1+a≤2A，当a≥1时，|f′（x）|≤3a﹣1≤6a﹣4=2A，综上：|f′（x）|≤2A．23．（2016•四川）设函数f（x）=ax2﹣a﹣lnx，其中a∈R．（Ⅰ）讨论f（x）的单调性；（Ⅱ）确定a的所有可能取值，使得f（x）＞﹣e1﹣x在区间（1，+∞）内恒成立（e=2.718…为自然对数的底数）．【解答】解：（Ⅰ）由题意，f′（x）=2ax﹣=，x＞0，①当a≤0时，2ax2﹣1≤0，f′（x）≤0，f（x）在（0，+∞）上单调递减．②当a＞0时，f′（x）=，当x∈（0，）时，f′（x）＜0，当x∈（，+∞）时，f′（x）＞0，故f（x）在（0，）上单调递减，在（，+∞）上单调递增．（Ⅱ）原不等式等价于f（x）﹣+e1﹣x＞0在x∈（1．+∞）上恒成立，一方面，令g（x）=f（x）﹣+e1﹣x=ax2﹣lnx﹣+e1﹣x﹣a，只需g（x）在x∈（1．+∞）上恒大于0即可，又∵g（1）=0，故g′（x）在x=1处必大于等于0．令F（x）=g′（x）=2ax﹣+﹣e1﹣x，g′（1）≥0，可得a．另一方面，当a时，F′（x）=2a+≥1+=+e1﹣x，∵x∈（1，+∞），故x3+x﹣2＞0，又e1﹣x＞0，故F′（x）在a时恒大于0．∴当a时，F（x）在x∈（1，+∞）单调递增．∴F（x）＞F（1）=2a﹣1≥0，故g（x）也在x∈（1，+∞）单调递增．∴g（x）＞g（1）=0，即g（x）在x∈（1，+∞）上恒大于0．综上，a．24．（2016•天津）设函数f（x）=x3﹣ax﹣b，x∈R，其中a，b∈R．（1）求f（x）的单调区间；（2）若f（x）存在极值点x0，且f（x1）=f（x0），其中x1≠x0，求证：x1+2x0=0；（3）设a＞0，函数g（x）=|f（x）|，求证：g（x）在区间[﹣1，1]上的最大值不小于．【解答】解：（1）若f（x）=x3﹣ax﹣b，则f′（x）=3x2﹣a，分两种情况讨论：①、当a≤0时，有f′（x）=3x2﹣a≥0恒成立，此时f（x）的单调递增区间为（﹣∞，+∞），②、当a＞0时，令f′（x）=3x2﹣a=0，解得x=或x=，当x＞或x＜﹣时，f′（x）=3x2﹣a＞0，f（x）为增函数，当﹣＜x＜时，f′（x）=3x2﹣a＜0，f（x）为减函数，故f（x）的增区间为（﹣∞，﹣），（，+∞），减区间为（﹣，）；（2）若f（x）存在极值点x0，则必有a＞0，且x0≠0，由题意可得，f′（x）=3x2﹣a，则x02=，进而f（x0）=x03﹣ax0﹣b=﹣x0﹣b，又f（﹣2x0）=﹣8x03+2ax0﹣b=﹣x0+2ax0﹣b=f（x0），由题意及（Ⅰ）可得：存在唯一的实数x1，满足f（x1）=f（x0），其中x1≠x0，则有x1=﹣2x0，故有x1+2x0=0；（Ⅲ）设g（x）在区间[﹣1，1]上的最大值M，max{x，y}表示x、y两个数的最大值，下面分三种情况讨论：①当a≥3时，﹣≤﹣1＜1≤，由（I）知f（x）在区间[﹣1，1]上单调递减，所以f（x）在区间[﹣1，1]上的取值范围是[f（1），f（﹣1）]，因此M=max{|f（1）|，|f（﹣1）|}=max{|1﹣a﹣b|，|﹣1+a﹣b|}=max{|a﹣1+b|，|a﹣1﹣b|}=，所以M=a﹣1+|b|≥2②当a＜3时，，由（Ⅰ）、（Ⅱ）知，f（﹣1）≥=f（），f（1）≤=，所以f（x）在区间[﹣1，1]上的取值范围是[f（），f（﹣）]，因此M=max{|f（）|，|f（﹣）|}=max{||，||}=max{||，||}=，③当0＜a＜时，，由（Ⅰ）、（Ⅱ）知，f（﹣1）＜=f（），f（1）＞=，所以f（x）在区间[﹣1，1]上的取值范围是[f（﹣1），f（1）]，因此M=max{|f（﹣1）|，|f（1）|}=max{|﹣1+a﹣b|，|1﹣a﹣b|}=max{|1﹣a+b|，|1﹣a﹣b|}=1﹣a+|b|＞，综上所述，当a＞0时，g（x）在区间[﹣1，1]上的最大值不小于．25．（2016•新课标Ⅰ）已知函数f（x）=（x﹣2）e x+a（x﹣1）2有两个零点．（Ⅰ）求a的取值范围；（Ⅱ）设x1，x2是f（x）的两个零点，证明：x1+x2＜2．【解答】解：（Ⅰ）∵函数f（x）=（x﹣2）e x+a（x﹣1）2，∴f′（x）=（x﹣1）e x+2a（x﹣1）=（x﹣1）（e x+2a），①若a=0，那么f（x）=0⇔（x﹣2）e x=0⇔x=2，函数f（x）只有唯一的零点2，不合题意；②若a＞0，那么e x+2a＞0恒成立，当x＜1时，f′（x）＜0，此时函数为减函数；当x＞1时，f′（x）＞0，此时函数为增函数；此时当x=1时，函数f（x）取极小值﹣e，由f（2）=a＞0，可得：函数f（x）在x＞1存在一个零点；当x＜1时，e x＜e，x﹣2＜﹣1＜0，∴f（x）=（x﹣2）e x+a（x﹣1）2＞（x﹣2）e+a（x﹣1）2=a（x﹣1）2+e（x﹣1）﹣e，令a（x﹣1）2+e（x﹣1）﹣e=0的两根为t1，t2，且t1＜t2，则当x＜t1，或x＞t2时，f（x）＞a（x﹣1）2+e（x﹣1）﹣e＞0，故函数f（x）在x＜1存在一个零点；即函数f（x）在R是存在两个零点，满足题意；③若﹣＜a＜0，则ln（﹣2a）＜lne=1，当x＜ln（﹣2a）时，x﹣1＜ln（﹣2a）﹣1＜lne﹣1=0，e x+2a＜e ln（﹣2a）+2a=0，即f′（x）=（x﹣1）（e x+2a）＞0恒成立，故f（x）单调递增，当ln（﹣2a）＜x＜1时，x﹣1＜0，e x+2a＞e ln（﹣2a）+2a=0，即f′（x）=（x﹣1）（e x+2a）＜0恒成立，故f（x）单调递减，当x＞1时，x﹣1＞0，e x+2a＞e ln（﹣2a）+2a=0，即f′（x）=（x﹣1）（e x+2a）＞0恒成立，故f（x）单调递增，故当x=ln（﹣2a）时，函数取极大值，由f（ln（﹣2a））=[ln（﹣2a）﹣2]（﹣2a）+a[ln（﹣2a）﹣1]2=a{[ln（﹣2a）﹣2]2+1}＜0得：函数f（x）在R上至多存在一个零点，不合题意；④若a=﹣，则ln（﹣2a）=1，当x＜1=ln（﹣2a）时，x﹣1＜0，e x+2a＜e ln（﹣2a）+2a=0，即f′（x）=（x﹣1）（e x+2a）＞0恒成立，故f（x）单调递增，当x＞1时，x﹣1＞0，e x+2a＞e ln（﹣2a）+2a=0，即f′（x）=（x﹣1）（e x+2a）＞0恒成立，故f（x）单调递增，故函数f（x）在R上单调递增，函数f（x）在R上至多存在一个零点，不合题意；⑤若a＜﹣，则ln（﹣2a）＞lne=1，当x＜1时，x﹣1＜0，e x+2a＜e ln（﹣2a）+2a=0，即f′（x）=（x﹣1）（e x+2a）＞0恒成立，故f（x）单调递增，当1＜x＜ln（﹣2a）时，x﹣1＞0，e x+2a＜e ln（﹣2a）+2a=0，即f′（x）=（x﹣1）（e x+2a）＜0恒成立，故f（x）单调递减，当x＞ln（﹣2a）时，x﹣1＞0，e x+2a＞e ln（﹣2a）+2a=0，即f′（x）=（x﹣1）（e x+2a）＞0恒成立，故f（x）单调递增，故当x=1时，函数取极大值，由f（1）=﹣e＜0得：函数f（x）在R上至多存在一个零点，不合题意；综上所述，a的取值范围为（0，+∞）证明：（Ⅱ）∵x1，x2是f（x）的两个零点，∴f（x1）=f（x2）=0，且x1≠1，且x2≠1，∴﹣a==，令g（x）=，则g（x1）=g（x2）=﹣a，∵g′（x）=，∴当x＜1时，g′（x）＜0，g（x）单调递减；当x＞1时，g′（x）＞0，g（x）单调递增；设m＞0，则g（1+m）﹣g（1﹣m）=﹣=，设h（m）=，m＞0，则h′（m）=＞0恒成立，即h（m）在（0，+∞）上为增函数，h（m）＞h（0）=0恒成立，即g（1+m）＞g（1﹣m）恒成立，令m=1﹣x1＞0，则g（1+1﹣x1）＞g（1﹣1+x1）⇔g（2﹣x1）＞g（x1）=g（x2）⇔2﹣x1＞x2，即x1+x2＜2．26．（2016•山东）已知f（x）=a（x﹣lnx）+，a∈R．（I）讨论f（x）的单调性；（II）当a=1时，证明f（x）＞f′（x）+对于任意的x∈[1，2]成立．【解答】（Ⅰ）解：由f（x）=a（x﹣lnx）+，得f′（x）=a（1﹣）+==（x＞0）．若a≤0，则ax2﹣2＜0恒成立，∴当x∈（0，1）时，f′（x）＞0，f（x）为增函数，当x∈（1，+∞）时，f′（x）＜0，f（x）为减函数；当a＞0，若0＜a＜2，当x∈（0，1）和（，+∞）时，f′（x）＞0，f（x）为增函数，当x∈（1，）时，f′（x）＜0，f（x）为减函数；若a=2，f′（x）≥0恒成立，f（x）在（0，+∞）上为增函数；若a＞2，当x∈（0，）和（1，+∞）时，f′（x）＞0，f（x）为增函数，当x∈（，1）时，f′（x）＜0，f（x）为减函数；（Ⅱ）解：∵a=1，令F（x）=f（x）﹣f′（x）=x﹣lnx﹣1=x﹣lnx+．令g（x）=x﹣lnx，h（x）=．则F（x）=f（x）﹣f′（x）=g（x）+h（x），由，可得g（x）≥g（1）=1，当且仅当x=1时取等号；又，设φ（x）=﹣3x2﹣2x+6，则φ（x）在[1，2]上单调递减，且φ（1）=1，φ（2）=﹣10，∴在[1，2]上存在x0，使得x∈（1，x0）时φ（x0）＞0，x∈（x0，2）时，φ（x0）＜0，∴函数h（x）在（1，x0）上单调递增；在（x0，2）上单调递减，由于h（1）=1，h（2）=，因此h（x）≥h（2）=，当且仅当x=2取等号，∴f（x）﹣f′（x）=g（x）+h（x）＞g（1）+h（2）=，∴F（x）＞恒成立．即f（x）＞f′（x）+对于任意的x∈[1，2]成立．27．（2016•北京）设函数f（x）=x3+ax2+bx+c．（1）求曲线y=f（x）在点（0，f（0））处的切线方程；（2）设a=b=4，若函数f（x）有三个不同零点，求c的取值范围；（3）求证：a2﹣3b＞0是f（x）有三个不同零点的必要而不充分条件．【解答】解：（1）函数f（x）=x3+ax2+bx+c的导数为f′（x）=3x2+2ax+b，可得y=f（x）在点（0，f（0））处的切线斜率为k=f′（0）=b，切点为（0，c），可得切线的方程为y=bx+c；（2）设a=b=4，即有f（x）=x3+4x2+4x+c，由f（x）=0，可得﹣c=x3+4x2+4x，由g（x）=x3+4x2+4x的导数g′（x）=3x2+8x+4=（x+2）（3x+2），当x＞﹣或x＜﹣2时，g′（x）＞0，g（x）递增；当﹣2＜x＜﹣时，g′（x）＜0，g（x）递减．即有g（x）在x=﹣2处取得极大值，且为0；g（x）在x=﹣处取得极小值，且为﹣．由函数f（x）有三个不同零点，可得﹣＜﹣c＜0，解得0＜c＜，则c的取值范围是（0，）；（3）证明：若f（x）有三个不同零点，令f（x）=0，可得f（x）的图象与x轴有三个不同的交点．即有f（x）有3个单调区间，即为导数f′（x）=3x2+2ax+b的图象与x轴有两个交点，可得△＞0，即4a2﹣12b＞0，即为a2﹣3b＞0；若a2﹣3b＞0，即有导数f′（x）=3x2+2ax+b的图象与x轴有两个交点，当c=0，a=b=4时，满足a2﹣3b＞0，即有f（x）=x（x+2）2，图象与x轴交于（0，0），（﹣2，0），则f（x）的零点为2个．故a2﹣3b＞0是f（x）有三个不同零点的必要而不充分条件．28．（2016•江苏）已知函数f（x）=a x+b x（a＞0，b＞0，a≠1，b≠1）．（1）设a=2，b=．①求方程f（x）=2的根；②若对于任意x∈R，不等式f（2x）≥mf（x）﹣6恒成立，求实数m的最大值；（2）若0＜a＜1，b＞1，函数g（x）=f（x）﹣2有且只有1个零点，求ab的值．【解答】解：函数f（x）=a x+b x（a＞0，b＞0，a≠1，b≠1）．（1）设a=2，b=．①方程f（x）=2；即：=2，可得x=0．②不等式f（2x）≥mf（x）﹣6恒成立，即≥m（）﹣6恒成立．令t=，t≥2．不等式化为：t2﹣mt+4≥0在t≥2时，恒成立．可得：△≤0或即：m2﹣16≤0或m≤4，∴m∈（﹣∞，4]．实数m的最大值为：4．（2）g（x）=f（x）﹣2=a x+b x﹣2，g′（x）=a x lna+b x lnb=a x[+]lnb，0＜a＜1，b＞1可得，令h（x）=+，则h（x）是递增函数，而，lna＜0，lnb＞0，因此，x0=时，h（x0）=0，因此x∈（﹣∞，x0）时，h（x）＜0，a x lnb＞0，则g′（x）＜0．x∈（x0，+∞）时，h（x）＞0，a x lnb＞0，则g′（x）＞0，则g（x）在（﹣∞，x0）递减，（x0，+∞）递增，因此g（x）的最小值为：g（x0）．①若g（x0）＜0，x＜log a2时，a x＞=2，b x＞0，则g（x）＞0，因此x1＜log a2，且x1＜x0时，g（x1）＞0，因此g（x）在（x1，x0）有零点，则g（x）至少有两个零点，与条件矛盾．②若g（x0）＞0，函数g（x）=f（x）﹣2有且只有1个零点，g（x）的最小值为g（x0），可得g（x0）=0，由g（0）=a0+b0﹣2=0，因此x0=0，因此=0，﹣=1，即lna+lnb=0，ln（ab）=0，则ab=1．可得ab=1．。

专题02+导数+2017年高考数学(理)试题分项版分析+Word版含分析

专題02导数1.【2017课标II，理11】若x=—2是函数f (x) =(x2• ax-1)e x」的极值点，贝U f(x)的极小值为( )3 3A. -1B.-2e_C.5e_D.1【答案】A【解析】试题分析:由题可得八X)= (2x+ + (j? = [7 +(4+2)*+d—10"S^/V2> = 0,所臥“1, /(x) = (Y l-x-l)A1,故八© = 令广(功＞0,解得兀c-2或兀：＞1,所以才(力在()单调递増，在(-2J)单调递减所以/(劝极小值为于⑴= (1T—= T ,故选A【考点】函数的极值；函数的单调性【名师点睛】(1)可导函数y= f(x)在点x o处取得极值的充要条件是f'x0) = 0,且在x o左侧与右侧f'刈的符号不同。

⑵若f(x)在(a, b)内有极值，那么f(x)在(a, b)内绝不是单调函数，即在某区间上单调增或减的函数没有极值。

2.【2017课标3,理11】已知函数f (x) = x2「2x • a(e x‘ • e戏1)有唯一零点，则a=1 1 1A. B. — C. —D. 12 3 2【答案】C【解析】试题分析：函数的零点满足x2 -2x - -a e x4 - e^1, 设g x=e x4e"1，则g x =e xJ -e"^e x4当g x =0时，x =1，当x 1时，g x ： 0，函数g x单调递减, 当x 1时，g'x £,函数g x单调递增,当x =1时，函数取得最小值g 1 =2 ,设h x =x2-2x，当x =1时，函数取得最小值一1 , 2 x J1 _ e Tx-1 一x-4 e e若-a>0 ,函数丘(兀)与函数吆(x)没有交点，当-时，-觀⑴=人⑴时，止匕时函数加x)和觀(兀)有一个交点，即—Q2=-1,解得a = -•故选C.2【考点】函数的零点；导函数研究函数的单调性，分类讨论的数学思想【名师点睛】函数零点的应用主要表现在利用零点求参数范围，若方程可解，通过解方程即可得出参数的范围，若方程不易解或不可解，则将问题转化为构造两个函数，利用两个函数图象的关系求解，这样会使得问题变得直观、简单，这也体现了数形结合思想的应用.3.【2017浙江，7】函数y=f(x)的导函数y = f (x)的图像如图所示，则函数y=f(x)的图像可能是【答案】D【解析】试题分析：原函数先减再增，再减再增，且由增变减时，极值点大于0,因此选D.【考点】导函数的图象【名师点睛】本题主要考查导数图象与原函数图象的关系：若导函数图象与x轴的交点为x0，且图象在X。

2017高考试题分类汇编之函数导数(精校版)

2017年高考试题分类汇编之函数与导数一、选择题（在每小题给出的四个选项中，只有一项是符合题目要求的）1（2017北京文）已知函数，则（）.A是偶函数，且在R上是增函数.B是奇函数，且在R上是增函数.C是偶函数，且在R上是减函数.D是奇函数，且在R上是增函数2.（2017新课标Ⅱ文）函数2()ln(28)f x x x=--的单调递增区间是（）.A(,2)-∞-.B(,1)-∞.C(1,)+∞.D(4,)+∞3.（2017山东文）设()()121,1xf xx x<<=-≥⎪⎩,若()()1f a f a=+,则1fa⎛⎫=⎪⎝⎭（）2.A4.B6.C8.D4.（2017山东文）若函数()e xf x在()f x的定义域上单调递增,则称函数()f x具有M性质.下列函数中具有M性质的是（）xxfA-=2)(..B()2f x x=.C()3xf x-=.D()cosf x x=5.（2017新课标Ⅰ文数）函数sin21cosxyx=-的部分图像大致为（）6.（2017新课标Ⅰ文数）已知函数()ln ln(2)f x x x=+-，则（）.A)(xfy=在)2,0(单调递增.B)(xfy=在)2,0(单调递减.C)(xfy=的图像关于直线1=x对称.D)(xfy=的图像关于点)0,1(对称7.（2017天津文）已知奇函数()f x在R上是增函数.若0.8221(log),(log 4.1),(2)5a fb fc f=-==，则,,a b c的大小关系为（）.A a b c<<.B b a c<<.C c b a<<.D c a b<<1()3()3x xf x=-()f x8.（2017天津文）已知函数||2,1,()2, 1.x xf xx xx+<⎧⎪=⎨+≥⎪⎩设Ra∈，若关于x的不等式()||2xf x a≥+在R上恒成立，则a的取值范围是（）.A[2,2]-.B[-.C[-.D[-9.（2017新课标Ⅲ文数）函数2sin1xxxy++=的部分图像大致为（）.A.B.C.D10.（2017新课标Ⅲ文数）已知函数211()2()x xf x x x a e e--+=-++有唯一零点，则=a（）21.-A.B13.C121.D11.（2017新课标Ⅲ理数）已知函数211()2()x xf x x x a e e--+=-++有唯一零点，则=a（）21.-A31.B21.C1.D12.（2017新课标Ⅰ理数）函数()f x在(,)-∞+∞单调递减，且为奇函数．若(11)f=-，则满足21()1xf--≤≤的x的取值范围是（）.A[2,2]-.B[1,1]-.C[0,4].D[1,3]13.（2017新课标Ⅱ理）若2x=-是函数21()(1)e xf x x ax-=+-的极值点，则()f x的极小值为（）1.-A.B32e--.C35e-1.D14.（2017天津理）已知奇函数()f x在R上是增函数，()()g x xf x=.若2(log 5.1)a g=-，0.8(2)b g=，(3)c g=，则cba,,的大小关系为（）.A a b c<<.B c b a<<.C b a c<<.D b c a<<15.（2017天津理）已知函数23,1,()2, 1.x x xf xx xx⎧-+≤⎪=⎨+>⎪⎩设Ra∈，若关于x的不等式()||2xf x a ≥+在R 上恒成立，则a 的取值范围是（） ]2,1647.[-A ]1639,1647.[-B ]2,32.[-C ]1639,32.[-D 16.（2017山东理）已知当[]0,1x ∈时，函数()21y mx =-的图象与y m 的图象有且只有一个交点，则正实数m 的取值范围是（）.A (])0,1⎡+∞⎣ .B (][)0,13,+∞ .C()⎡+∞⎣.D ([)3,+∞17.（2017浙江）若函数b ax x x f ++=2)(在区间]1,0[上的最大值是M ，最小值是m ，则m M -（）.A 与a 有关，且与b 有关 .B 与a 有关，但与b 无关 .C 与a 无关，且与b 无关.D 与a 无关，但与b 有关18.（2017浙江）函数)(x f y =的导函数的图象如图所示，则函数)(x f y =的图象可能是（）二、填空题（将正确的答案填在题中横线上）19.（2017山东文）已知)(x f 是定义在R 上的偶函数,且)2()4(-=+x f x f .若当[3,0]x ∈-时,()6x f x -=,则=)919(f .20.（2017天津文）已知a ∈R ，设函数()ln f x ax x =-的图象在点))1(,1(f 处的切线为l ，则l 在y 轴上的截距为 .21.（2017新课标Ⅱ文）已知函数()f x 是定义在R 上的奇函数，当(,0)x ∈-∞时，32()2f x x x =+，则(2)f =.22.（2017新课标Ⅲ文数）设函数10()20x x x f x x +≤⎧=⎨>⎩，，，，则满足1()()12f x f x +->的x 的取值范围是__________.()y f x '=23.（2017新课标Ⅰ文数）曲线21y x x=+在点)2,1(处的切线方程为_______. 24.（2017新课标Ⅲ理数）设函数10()20xx x f x x +≤⎧=⎨>⎩，，，，则满足1()()12f x f x +->的x 的取值范围是_____________.25.（2017山东理）若函数()x e f x （ 2.71828e = 是自然对数的底数）在()f x 的定义域上单调递增，则称函数()f x 具有M 性质.下列函数中所有具有M 性质的函数的序号为. ①()2x f x -=②()3x f x -=③()3f x x = ④()22f x x =+26.（2017江苏）已知函数．若，则实数的取值范围是．27.（2017江苏）．设是定义在R 上且周期为1的函数，在区间上，其中集合，，则方程的解的个数是．三、解答题（应写出必要的文字说明、证明过程或演算步骤） 28.（2017北京文）已知函数．（Ⅰ）求曲线在点处的切线方程；（Ⅱ）求函数在区间上的最大值和最小值．29.（2017新课标Ⅱ文）设函数2()(1)e x f x x =-.（1）讨论()f x 的单调性；（2）当0x ≥时，()1f x ax ≤+，求a 的取值范围.31()2e exx f x x x =-+-2(1)(2)0f a f a -+≤a ()f x [0,1)2,,(),,x x D f x x x D ⎧∈⎪=⎨∉⎪⎩1{n D x x n-==*}n ∈N ()lg 0f x x -=()e cos x f x x x =-()y f x =(0,(0))f ()f x π[0,]230.（2017天津文））设,a b ∈R ，||1a ≤.已知32()63(4)f x x x a a x b =---+，()e ()x g x f x =. （Ⅰ）求()f x 的单调区间；（Ⅱ）已知函数()y g x =和e x y =的图象在公共点),(00y x 处有相同的切线，（i ）求证：()f x 在0x x =处的导数等于0；（ii ）若关于x 的不等式()e x g x ≤在区间00[1,1]x x -+上恒成立，求b 的取值范围.31.（2017新课标Ⅲ文数）已知函数.)12(ln )(2x a ax x x f +++=（1）讨论()f x 的单调性；（2）当0<a 时，证明3()24f x a≤--．32.（2017新课标Ⅰ文数）已知函数.)()(2x a a e e x f x x --=（1）讨论()f x 的单调性；（2）若()0f x ≥，求a 的取值范围．33.（2017山东文）已知函数()3211,32f x x ax a =-∈R . （Ⅰ）当2=a 时,求曲线()y f x =在点()()3,3f 处的切线方程；（Ⅱ）设函数()()()cos sin g x f x x a x x =+--,讨论()g x 的单调性并判断有无极值,有极值时求出极值.34.（2017新课标Ⅱ理）已知函数2()ln f ax a x x x x =--，且()0f x ≥．（1）求a ；（2）证明：()f x 存在唯一的极大值点0x ，且220e ()2f x --<<．35.（2017北京理）已知函数.cos )(x x e x f x -= （Ⅰ）求曲线)(x f y =在点))0(,0(f 处的切线方程；（Ⅱ）求函数)(x f 在区间[0，]上的最大值和最小值.π236.（2017浙江）已知函数).21()12()(≥--=-x e x x x f x（Ⅰ）求)(x f 的导函数；（Ⅱ）求)(x f 在区间上的取值范围．37.（2017山东理）已知函数()22cos f x x x =+，()()cos sin 22x g x e x x x =-+-. （Ⅰ）求曲线()y f x =在点()(),f x π处的切线方程；（Ⅱ）令()()()()h x g x af x a R =-∈，讨论()h x 单调性并判断有无极值，若有求出极值.38.（2017新课标Ⅰ理数）已知函数2()(2)x x f x ae a e x =+--.1[+)2∞，（1）讨论()f x 的单调性；（2）若()f x 有两个零点，求a 的取值范围.39.（2017江苏）已知函数有极值，且导函数的极值点是的零点．（1）求关于的函数关系式，并写出定义域；（2）证明：；（3）若，这两个函数的所有极值之和不小于，求的取值范围．40.（2017新课标Ⅲ理数）已知函数.ln 1)(x a x x f --=32()1(0,)f x x ax bx a b =+++>∈R ()f x '()f x b a 23b a >()f x ()f x '72-a()0f x ≥（1）若，求a 的值；（2）设m 为整数，且对于任意正整数n ，21111++1+)222n ()(1)(m <，求m 的最小值．41.（2017天津理）设a ∈Z ，已知定义在R 上的函数432()2336f x x x x x a =+--+在区间(1,2)内有一个零点0x ，()g x 为()f x 的导函数. （Ⅰ）求()g x 的单调区间；（Ⅱ）设00[1,)(,2]m x x ∈ ，函数0()()()()h x g x m x f m =--，求证：0()()0h m h x <；（Ⅲ）求证：存在大于0的常数A ，使得对于任意的正整数,p q ，且00[1,)(,2],px x q∈ 满足041||p x q Aq -≥.。

2017全国高考导数解答题文科

2017文(全国高考导数解答题) 科．高考如是考1、2017年全国一卷21．（12分）xx2xaa已知函数=e(e﹣)﹣．)f(x（1）讨论的单调性；)(xf a的取值范围．，求（2）若0?xf()2、2017全国二卷（21）（12分）x2xf(x). 设函数)e=(1-f(x) 1（）讨论的单调性；axf(x)ax. ）当0时，，求+1的取值范围2（??）（本小题20（文）数学北京卷（3、2017年分）13．已知函数x x ecos x??f(x)（Ⅰ）求曲线在点处的切线方程；(0)))(?yfx(0,fπ上的最大值和最小（Ⅱ）求函数在区间)(fx][0,2值．高考如是考参考答案年全国一卷21．（12分）1、2017xx2xaa )﹣﹣．已知函数=e(e)f(x（1）讨论的单调性；)f(x a）若，求的取值范围．（20f(x)?，为义域的解析】（1）函数定【),??(x)(??f，. ，在单调递增①若，则xx2xx2?)??ef?(x)2eea?aea?a)(?(2.x2e)?xf()(??,??0a?得，则由②若?0)f?(x ax?a?0ln，所时，当时，；当??0)?()?0?x(ln a,??)x?x(??,ln a)ff(x. 以在单调递减，在单调递增)a(x),(??,ln a)??(ln f a. ③若，则由得?)ln(?x?0f(x)?0a?2aa，当时，时，；当??)???x?(ln(?x?(??,ln(),))0f)(x?x0)f?(22aa单调递减，在在单调递增故. )),??))?(ln(??(,ln(?)f(x22（2）①若，则，所以.②若，则由（1）得，当时，取得最2x e?x)(f0(x)?f0a?小)xf(a ln xa?0?值，最小值为.从而当且仅当，.22a ln)f(ln a??a0?a ln a?时，即0?)x(f1?aa取得最时，）得，当，则由（③若1)?x?ln()(xf0?a2a3a 从而当且仅当.小值，最小值为2)]?ln(a[(ln(f??))?224.3a3，即时22e a??0?)]?ln(a[?0(fx)?4243的取值范围为综上，.a,1]e2[?42、2017全国二卷（21）（12分）2x xf(x). =(1-)e设函数f(x)的单调性； 1）讨论（xf(x)axa.时，）当（20的取值范围，求+1??．分））（本小题1320（（文）数学北京卷、32017年．已知函数x xx)?ecos x?(f在点（Ⅰ）求曲线处的切线方程；(0))(0,fxy?f()π[0,]上的最大值和最小（Ⅱ）求函数在区间)x(f2值．?. 1)(【答案】Ⅰ；最小值；（Ⅱ）最大值?1y?2。

2017年高考数学理试题分类汇编：导数及其应用

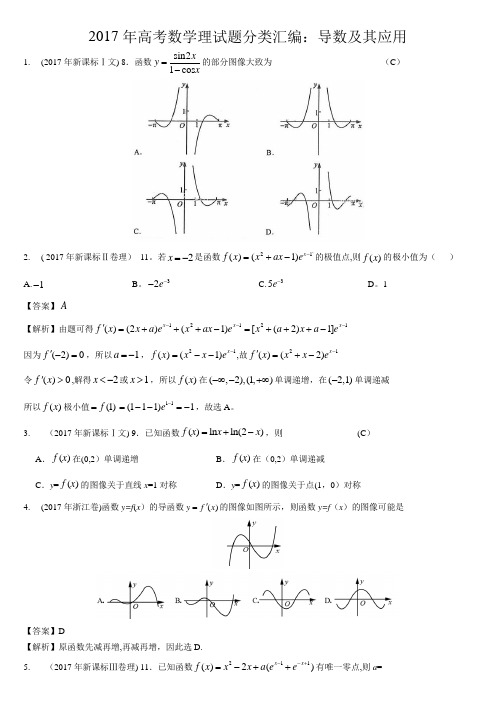
2017年高考数学理试题分类汇编：导数及其应用1. (2017年新课标Ⅰ文) 8．函数sin21cos xy x=-的部分图像大致为（C ）2. ( 2017年新课标Ⅱ卷理） 11。

若2x =-是函数21`()(1)x f x x ax e-=+-的极值点,则()f x 的极小值为（）A.1- B 。

32e -- C.35e - D 。

1 【答案】A【解析】由题可得12121()(2)(1)[(2)1]x x x f x x a ex ax e x a x a e ---'=+++-=+++-因为(2)0f '-=，所以1a =-，21()(1)x f x x x e-=--,故21()(2)x f x x x e -'=+-令()0f x '>,解得2x <-或1x >，所以()f x 在(,2),(1,)-∞-+∞单调递增，在(2,1)-单调递减所以()f x 极小值(1)f =11(111)1e-=--=-，故选A 。

3. （2017年新课标Ⅰ文) 9．已知函数()ln ln(2)f x x x =+-，则 (C ） A ．()f x 在(0,2）单调递增B ．()f x 在（0,2）单调递减C ．y =()f x 的图像关于直线x =1对称D ．y =()f x 的图像关于点(1，0）对称4. (2017年浙江卷)函数y=f (x ）的导函数()y f x '=的图像如图所示，则函数y=f （x ）的图像可能是【答案】D【解析】原函数先减再增,再减再增，因此选D.5. （2017年新课标Ⅲ卷理) 11．已知函数211()2()x x f x x x a ee --+=-++有唯一零点,则a =A ．12- B ．13C ．12D ．1【答案】C6. （ 2017年新课标Ⅱ卷理)21.已知函数()2ln f x ax ax x x =--,且()0f x ≥。

17年高考真题—理科数学2：导数

2017高考真题分类汇编：导数1．【2017浙江 7】函数()y f x =的导函数()y f x '=的图像如图所示，则函数()y f x =的图像可能是（）2．【2017课标II 11】若2x =-是函数()()211x f x x ax e -=+-的极值点，则()f x 的极小值为（）（A ）1- （B ）32e -- （C ）35e - （D ）13．【2017课标III 11】已知函数()()2112x x f x x x a e e --+=-++有唯一零点，则（）（A ）12-（B ）13 （C ）12（D ）1 4．【2017北京 19】已知函数()cos xf x e x x =-。

⑴求曲线()y f x =在点()()0,0f 处的切线方程；⑵求函数()f x 在区间[]0,2π上的最大值和最小值。

5．【2017天津 20】设a Z ∈，已知定义在R 上的函数()4322336f x x x x x a =+--+在区间()1,2内有一个零点0x ，()g x 为()f x 的导函数。

⑴求()g x 的单调区间；⑵设[)(]001,,2m x x ∈，函数()()()()0h x g x m x f m =--，求证：()()00h m h x <；⑶求证：存在大于0的常数A ，使得对于任意的正整数,p q ，且[)(]001,,2px x q∈，满足041||p x q Aq-≥。

6．【2017江苏 20】已知函数()()3210,f x x ax bx a b R =+++>∈有极值，且导函数()f x '的极值点是()f x 的零点（极值点是指函数取极值时对应的自变量的值）。

⑴求b 关于a 的函数关系式，并写出定义域；⑵证明：23b a >；⑶若()(),f x f x '这两个函数的所有极值之和不小于72-，求a 的取值范围。

2017年高考数学试题分项版—函数、导数应用(原卷版)

2017年高考数学试题分项版—函数、导数应用（原卷版）一、选择题1．(2017·全国Ⅰ文，8)函数y ＝sin 2x1－cos x的部分图象大致为( )2．(2017·全国Ⅰ文，9)已知函数f (x )＝ln x ＋ln(2－x )，则( ) A ．f (x )在(0,2)上单调递增 B ．f (x )在(0,2)上单调递减C ．y ＝f (x )的图象关于直线x ＝1对称D ．y ＝f (x )的图象关于点(1,0)对称3．(2017·全国Ⅱ文，8)函数f (x )＝ln(x 2－2x －8)的单调递增区间是( ) A ．(－∞，－2) B ．(－∞，1) C ．(1，＋∞)D ．(4，＋∞)4．(2017·全国Ⅲ文，7)函数y ＝1＋x ＋sin x x2的部分图象大致为( )5．(2017·全国Ⅲ文，12)已知函数f (x )＝x 2－2x ＋a (e x －1＋e－x ＋1)有唯一零点，则a 等于( )A ．－12B ．13C ．12D ．16．(2017·北京文，5)已知函数f (x )＝3x －⎝⎛⎭⎫13x，则f (x )( ) A ．是偶函数，且在R 上是增函数B ．是奇函数，且在R 上是增函数C ．是偶函数，且在R 上是减函数D ．是奇函数，且在R 上是减函数7．(2017·北京文，8)根据有关资料，围棋状态空间复杂度的上限M 约为3361，而可观测宇宙中普通物质的原子总数N 约为1080.则下列各数中与MN 最接近的是( )(参考数据：lg 3≈0.48)A ．1033B ．1053C ．1073D ．10938．(2017·天津文，6)已知奇函数f (x )在R 上是增函数．若a ＝－f ⎝⎛⎭⎫log 215，b ＝f ()log 24.1，c ＝f (20.8)，则a ，b ，c 的大小关系为( ) A ．a <b <c B ．b <a <c C ．c <b <aD ．c <a <b9．(2017·天津文，8)已知函数f (x )＝⎩⎪⎨⎪⎧|x |＋2，x <1，x ＋2x ，x ≥1.设a ∈R ，若关于x 的不等式f (x )≥⎪⎪⎪⎪x2＋a 在R 上恒成立，则a 的取值范围是( ) A ．[－2,2] B ．[－23，2] C ．[－2,23]D ．[－23，23]10．(2017·山东文，9)设f (x )＝⎩⎨⎧x ，0<x <1，2 x －1 ，x ≥1，若f (a )＝f (a ＋1)，则f ⎝⎛⎭⎫1a 等于( ) A ．2 B ．4 C ．6 D ．811．(2017·山东文，10)若函数e x f (x )(e ＝2.718 28…是自然对数的底数)在f (x )的定义域上单调递增，则称函数f (x )具有M 性质，下列函数中具有M 性质的是( ) A ．f (x )＝2－xB ．f (x )＝x 2C ．f (x )＝3－xD ．f (x )＝cos x12．(2017·浙江，5)若函数f (x )＝x 2＋ax ＋b 在区间[0,1]上的最大值是M ，最小值是m ，则M －m ( )A ．与a 有关，且与b 有关B ．与a 有关，但与b 无关C ．与a 无关，且与b 无关D ．与a 无关，但与b 有关13．(2017·浙江，7)函数y ＝f (x )的导函数y ＝f ′(x )的图象如图所示，则函数y ＝f (x )的图象可能是( )14．(2017·全国Ⅰ理，5)已知函数f (x )在(－∞，＋∞)上单调递减，且为奇函数．若f (1)＝－1，则满足－1≤f (x －2)≤1的x 的取值范围是( ) A ．[－2,2] B ．[－1,1] C ．[0,4] D ．[1,3]15．(2017·全国Ⅰ理，11)设x ，y ，z 为正数，且2x ＝3y ＝5z ，则( ) A ．2x <3y <5z B ．5z <2x <3y C ．3y <5z <2xD ．3y <2x <5z16．(2017·全国Ⅱ理，11)若x ＝－2是函数f (x )＝(x 2＋ax －1)e x －1的极值点，则f (x )的极小值为( ) A ．－1 B ．－2e －3C ．5e －3D ．117．(2017·全国Ⅲ理，11)已知函数f (x )＝x 2－2x ＋a (e x －1＋e－x ＋1)有唯一零点，则a 等于( )A ．－12B ．13C ．12D ．118．(2017·北京理，5)已知函数f (x )＝3x －⎝⎛⎭⎫13x，则f (x )( ) A ．是奇函数，且在R 上是增函数 B ．是偶函数，且在R 上是增函数 C ．是奇函数，且在R 上是减函数 D ．是偶函数，且在R 上是减函数19．(2017·北京理，8)根据有关资料，围棋状态空间复杂度的上限M 约为3361，而可观测宇宙中普通物质的原子总数N 约为1080.则下列各数中与MN 最接近的是( )(参考数据：lg 3≈0.48) A ．1033 B ．1053 C ．1073D ．109320．(2017·天津理，6)已知奇函数f (x )在R 上是增函数，g (x )＝xf (x )．若a ＝g (－log 25.1)，b ＝g (20.8)，c ＝g (3)，则a ，b ，c 的大小关系为( )A ．a <b <cB ．c <b <aC ．b <a <cD ．b <c <a21．(2017·天津理，8)已知函数f (x )＝⎩⎪⎨⎪⎧x 2－x ＋3，x ≤1，x ＋2x ，x >1.设a ∈R ，若关于x 的不等式f (x )≥⎪⎪⎪⎪x2＋a 在R 上恒成立，则a 的取值范围是( ) A.⎣⎡⎦⎤－4716，2 B.⎣⎡⎦⎤－4716，3916 C.[]－23，2D.⎣⎡⎦⎤－23，3916 22．(2017·山东理，10)已知当x ∈[0,1]时，函数y ＝(mx －1)2的图象与y ＝x ＋m 的图象有且只有一个交点，则正实数m 的取值范围是( ) A ．(0,1]∪[23，＋∞) B ．(0,1]∪[3，＋∞) C ．(0，2]∪[23，＋∞) D ．(0，2]∪[3，＋∞)二、填空题1．(2017·全国Ⅰ文，14)曲线y ＝x 2＋1x在点(1,2)处的切线方程为________．2．(2017·全国Ⅱ文，14)已知函数f (x )是定义在R 上的奇函数，当x ∈(－∞，0)时，f (x )＝2x 3＋x 2，则f (2)＝________.3．(2017·全国Ⅲ文，16)设函数f (x )＝⎩⎪⎨⎪⎧x ＋1，x ≤0，2x ，x >0，则满足f (x )＋f ⎝⎛⎭⎫x －12>1的x 的取值范围是________．4．(2017·天津文，10)已知a ∈R ，设函数f (x )＝ax －ln x 的图象在点(1，f (1))处的切线为l ，则l 在y 轴上的截距为________．5．(2017·山东文，14)已知f (x )是定义在R 上的偶函数，且f (x ＋4)＝f (x －2)．若当x ∈[－3,0]时，f (x )＝6－x ，则f (919)＝________.6．(2017·浙江，17)已知a ∈R ，函数f (x )＝|x ＋4x －a |＋a 在区间[1,4]上的最大值是5，则a 的取值范围是________．7.(2017·江苏，11)已知函数f (x )＝x 3－2x ＋e x －1e x ，其中e 是自然对数的底数，若f (a －1)＋f (2a 2)≤0，则实数a 的取值范围是________．8．(2017·江苏，14)设f (x )是定义在R 上且周期为1的函数，在区间[0,1)上，f (x )＝⎩⎪⎨⎪⎧x 2，x ∈D ，x ，x ∉D ，其中集合D ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪x ＝n －1n ，n ∈N *，则方程f (x )－lg x ＝0的解的个数是________．9.(2017·全国Ⅲ理，15)设函数f (x )＝⎩⎪⎨⎪⎧x ＋1，x ≤0，2x ，x >0，则满足f (x )＋f ⎝⎛⎭⎫x －12>1的x 的取值范围是________．10．(2017·山东理，15)若函数e x f (x )(e ＝2.718 28…是自然对数的底数)在f (x )的定义域上单调递增，则称函数f (x )具有M 性质，下列函数中所有具有M 性质的函数的序号为________． ①f (x )＝2－x ；②f (x )＝3－x ；③f (x )＝x 3；④f (x )＝x 2＋2.三、解答题1．(2017·全国Ⅰ文，21)已知函数f (x )＝e x (e x －a )－a 2x . (1)讨论f (x )的单调性；(2)若f (x )≥0，求a 的取值范围．2．(2017·全国Ⅱ文，21)设函数f (x )＝(1－x 2)e x . (1)讨论f (x )的单调性；(2)当x ≥0时，f (x )≤ax ＋1，求a 的取值范围．3．(2017·全国Ⅲ文，21)已知函数f (x )＝ln x ＋ax 2＋(2a ＋1)x . (1)讨论f (x )的单调性；(2)当a <0时，证明f (x )≤－34a －2.4．(2017·北京文，20)已知函数f (x )＝e x cos x －x . (1)求曲线y ＝f (x )在点(0，f (0))处的切线方程； (2)求函数f (x )在区间⎣⎡⎦⎤0，π2上的最大值和最小值．5．(2017·天津文，19)设a ，b ∈R ，|a |≤1.已知函数f (x )＝x 3－6x 2－3a (a －4)x ＋b ，g (x )＝e x f (x )． (1)求f (x )的单调区间；(2)已知函数y ＝g (x )和y ＝e x 的图象在公共点(x 0，y 0)处有相同的切线． ①求证：f (x )在x ＝x 0处的导数等于0；②若关于x 的不等式g (x )≤e x 在区间[x 0－1，x 0＋1]上恒成立，求b 的取值范围．6．(2017·山东文，20)已知函数f (x )＝13x 3－12ax 2，a ∈R .(1)当a ＝2时，求曲线y ＝f (x )在点(3，f (3))处的切线方程；(2)设函数g (x )＝f (x )＋(x －a )cos x －sin x ，讨论g (x )的单调性并判断有无极值，有极值时求出极值．7．(2017·浙江，20)已知函数f (x )＝(x －2x －1)e －x ⎝⎛⎭⎫x ≥12. (1)求f (x )的导函数；(2)求f (x )在区间⎣⎡⎭⎫12，＋∞上的取值范围．8．(2017·江苏，20)已知函数f (x )＝x 3＋ax 2＋bx ＋1(a >0，b ∈R )有极值，且导函数f ′(x )的极值点是f (x )的零点．(极值点是指函数取极值时对应的自变量的值) (1)求b 关于a 的函数关系式，并写出定义域； (2)证明：b 2>3a ；(3)若f (x )，f ′(x )这两个函数的所有极值之和不小于－72，求a 的取值范围．9．(2017·全国Ⅰ理，21)已知函数f (x )＝a e 2x ＋(a －2)e x －x . (1)讨论f (x )的单调性；(2)若f (x )有两个零点，求a 的取值范围．10．(2017·全国Ⅱ理，21)已知函数f (x )＝ax 2－ax －x ln x ，且f (x )≥0. (1)求a ；(2)证明：f (x )存在唯一的极大值点x 0，且e －2<f (x 0)<2－2.11．(2017·全国Ⅲ理，21)已知函数f (x )＝x －1－a ln x . (1)若f (x )≥0，求a 的值；(2)设m 为整数，且对于任意正整数n ，⎝⎛⎭⎫1＋12⎝⎛⎭⎫1＋122·…·⎝⎛⎭⎫1＋12n <m ，求m 的最小值．12．(2017·北京理，19)已知函数f (x )＝e x cos x －x . (1)求曲线y ＝f (x )在点(0，f (0))处的切线方程； (2)求函数f (x )在区间⎣⎡⎦⎤0，π2上的最大值和最小值．13．(2017·天津理，20)设a ∈Z ，已知定义在R 上的函数f (x )＝2x 4＋3x 3－3x 2－6x ＋a 在区间(1,2)内有一个零点x 0，g (x )为f (x )的导函数． (1)求g (x )的单调区间；(2)设m ∈[1，x 0)∪(x 0,2]，函数h (x )＝g (x )(m －x 0)－f (m )，求证：h (m )h (x 0)<0；(3)求证：存在大于0的常数A ，使得对于任意的正整数p ，q ，且p q ∈[1，x 0)∪(x 0,2]，满足⎪⎪⎪⎪p q －x 0≥1Aq 4.14．(2017·山东理，20)已知函数f (x )＝x 2＋2cos x ，g (x )＝e x (cos x －sin x ＋2x －2)，其中e ＝ 2.718 28…是自然对数的底数．(1)求曲线y ＝f (x )在点(π，f (π))处的切线方程；(2)令h (x )＝g (x )－af (x )(a ∈R )，讨论h (x )的单调性并判断有无极值，有极值时求出极值．。