静电场中的电介质
23. 静电场中的电介质

1 E dS 0S1 S2
S
P dS P dS PS2 S 2
S S2
0
1 1 E dS 0 S1
S
S
0 E P dS q0
0
0
四、电极化强度与极化电荷的关系 在均匀介质中, 极化电荷只出现在介质表面 或两种介质的分界面上。 设一均匀电介质薄片(S、l)置于电场(E) 中,表面将出现极化电荷。
p ql p ql P P V Sl 一般情形: P e P cos P n n
的q’为多少?
介质被均匀极化,介质内无净极化电荷。
介质内的场强: E E0 E
极化电荷产生的附加电场 实验表明: 对于各向同性的电介质,在E0不太大的 情况下,有:
P ( r 1) 0 E
上式表明P,E的简单比例关系,将比例系数写 成稍复杂的形式,是为了以后相对更重要的式子 表达方便。
en为薄片表面外法向单位矢量
例:
n
θ - - - - - + + + + +
- - - - - - + + + + +P +
P
思考:将介质从中分开,能否分离正、负
极化电荷?
§7-9 有电介质时的高斯定理 电位移
1 真空中的高斯定理: E dS qi
S
0
1 介质中的高斯定理: E dS
极化面电荷: P ·en
介质内表面(r =R1)处:
( r 1) q0 er P 0 ( r 1) E 2 4r r
1 P r R
学院14-2静电场中的电介质

电场中的电介质
1. 电介质对电场的影响 2. 电介质的极化 3. 电介质的高斯定理 电位移矢量
一
电介质对电场的影响
电介质: 绝缘体(insulator) 电介质: 绝缘体(insulator)
(放在电场中的)电介 放在电场中的)
+Q
+
+ + + + +
-Q
-
+
电场 质 实验 结论: 结论: 介质充满电场或介质表面为等势面时
σ σ = d1 + d2 εoεr1 εoεr 2
ε1ε2S C = q / ∆V = ε1d2 + ε2d1
• 各电介质层中的场强不同 • 相当于电容器的串联
平板电容器中充介质的另一种情况 由极板内为等势体
∆V1 = ∆V2
σ
σ1 ∆S1 ε1 A ε2
−σ
∆V 1 E1 = d
∆V2 E2 = d
+
+ +
v v v v 令: D = ε0εr E = ε E ε —介电常数 D ---电位移矢量 ---电位移矢量 v v 则: --电介质的高斯定理 D⋅ dS = ∑q0i --电介质的高斯定理 ∫
S i
εr v v ε0εr E⋅ dS =σ0∆S = q0 ∫
S
E=
E0
+σ '
- - - - - - - - - - - - - - - - -
S1
A
ε1
S2 d1
ε2
B
D ∆S1 = σ∆S1 1
D =σ 1
同理, 同理,做一个圆柱形高斯面 S2
v v ∫ D⋅ dS = ∑qi (S2内) D2 = σ
大学物理(6.2.1)--静电场中的电介质

d r
P
E
0 - -+- -+- -+- -+- -+-
E E0 0 r 0 r
'
(1
1 r
)
0
,
电极化率
10/13
电介质的击穿
理想电介质中没有自由电荷,但是实际的电 介质中总是存在一定的自由电荷。可以在电场作用 下产生微弱的电流。
加在电介质上的电场强度足够大时,电介质 中的电流迅速增加,其绝缘性能被破坏,甚至电介 质可能被烧毁。这叫电介质的击穿。
热释电性:温度的变化 表面产生极化电荷
电光效应:施加电场 晶体折射率发生变化
重要应用领域:
微电子学技术、超声波技术、电子光学、激光技术 、
新材料等
3/13
※ 电介质对电场的影响
( 电介质放在电场中)
U 0 E0
+
-
+
-
+
-
+
-
+
-
+
-
+
-
σ σ
电场
U E
+++++++
- - -εr- - - -
)
0
,
Q'
εr εr
1
Q0
9/13
※ 电极化强度与电场强度的关系
充满 r 的各向同性均匀电介质的平行板电容器
P
σ
'
r 1 r
0
,
P ( r 1)0E
P (r 1)0E
静电场中的电介质

C 与 d S 0 有关
S
C ; d C
插入介质
0S q C u A uB d
C
0 r S
d
C
(2)球形电容器 已知
设+q、-q 场强分布: E 电势差:
RB
RA RB
q
r q
B A
RA
q 4 0 r 2
q q
RB
1 1 u A uB dr ( ) 2 4 0 RA RB R A 4 0 r
f
pe
pe
3;
+ E + 外 + + + +
在外电场中有极分子的固有电 矩要受到一个力矩作用,电矩方 向趋于外电场方向。但由于热运 动的存在,不会完全一致。
有极分子的取向极化!
+ E + 外 + + + +
+
两端面出现极化电荷层
电介质被极化的宏观效果
①外电场越强,极化电荷越多; ②电介质不均匀,则不仅在电介质表面会出现极 化电荷,在电介质内部也会出现极化电荷; ③对均匀电介质,在其内部任一小区域内,正负 电荷数量仍然相等,因而仍然表现出电中性。
二、电极化强度和极化电荷
单位体积内分子电偶极矩的矢量和 P
1、电极化强度(矢量)
pi
V
物理意义:描述了电介质极化强弱,反映了电介质 内分子电偶极矩排列的有序或无序程度。
在各向同性的电介质中,P 0 E
称为电介质的电极化率,它取决于电介质的性质。
2、极化电荷和自由电荷 极化电荷
E E0
++++++ r + ------- C
静电场中的电介质(IV)

大小:DA 0
Q
R1 R2
DB Dc 4 r 2 D 0A 0
EB
Q
4 0
rr2
0
r
EC
Q
40r 2
U A
E dr
r
R1 r
EA
dr
R2 R1
EB
dr
R2 EC dr
Q
4 0
1 r R1
1
r R2
1 R2
U B
R2 r
EB
dr
R2 EC dr
E
0 0
0
1
0
( 0
)
E0
r
D
q'
0 0 r
-σ'
E
P S
+σ' -σ0
=01-1 r q'=q0 1-1 r
q0 q'=q0 / r
s
0
r
E
dS
q0
D= 0 r E E
D的高斯定理:
D dS
s
q0
例:金属球半径为R1 、带电+Q;均匀、 各向同性介 质层外半径R2 、相对介电常数 r ;求:D、E、U 分布 解:由对称性分析确定 E、D 沿矢径方向
15.2 电介质的极化
电介质的分类
有极分子:分子的正负电 荷中心在无电场时不重合 的,有固定的电偶极矩, 如H2O、HCl等。
无极分子:分子的正负 电荷中心在无电场时是 重合的,没有固定的电 偶极矩,如H2、HCl4、 CO2、N2、O2等。
几种极性分子的固有电矩
无极分子的极化 ——位移极化
有极分子的极化 ——取向极化
第15章 静电场中的电介质
2.静电场中的电介质
自由电荷 束缚电荷
1 E dS
S
0
q
S
0
1
0
P dS
S
( 0 E P) dS q0
S S
电位移矢量定义:
D 0E P
( 0 E P) dS q0
S S
自由电荷
3、极化(束缚)电荷与极化强度的关系: 对于均匀的电介质,极化电荷集中在它的表面。电介质 产生的一切宏观效果都是通过未抵消的束缚电荷来体现。
如图,在平板电容器两极板间的介 质内沿着方向取一长度为dl,横截面为 dS的小圆柱体,在其内部极化可视为 是均匀的。
dl
' dS
' dS
P
点的总场强为:
' 退极化场 是电介质中的总电场强度。 E E E 0 E0 是自由电荷产生的电场。
' E 是极化电荷产生的退极化场
E E0 E'
' '
2.电极化强度矢量
宏观上,电介质极化程度用电极化强度矢量来描述, 其定义式为:
P lim
pi
S S S in
Pn '
P dS dS
'
极化强度力线
在任一曲面内极化电荷的负值等于极化强度的通量。
四、电介质中的高斯定理
根据介质极化和 真空中高斯定律 ' P d S q
S S
S
电位移矢量
0
' ( q q 0 ) S
1 E dS
(2)对各向同性电介质( P e 0 E)
静电场中 的电介质

静电场中的电介质 , ,
1.2 电介质的极化
1.电介质极化的机理
对于无极分子,在外电场的作用下,正、负电荷的中心被电场力拉开,使得正、负电荷中心产 生相对位移(这种极化称为位移极化),形成电偶极子。
在此力偶矩的作用下,有极分子的电偶极矩方向将转向与外电场基本一致的方向,这种极化称 为转向极化,其结果是电介质的两端出现等量异号的电荷.
真空中 r 1,空气中 r 1.005 ,可认为近似等于 1,其他电介质的 r 都大于 1。电介质的相对电容
率 r 和真空中电容率 0 的乘积称为电介质的电容率 ,即 r0
静电场中的电介质 , ,
1.2 电介质的极化
3.电介质的击穿
如果外电场足够大,电介质分子就会摆脱分子的束缚成为自由电子,电介质的绝缘性被破坏而 成为导体,这个过程称为电介质的击穿,这个外电场的场强称为击穿场强。
大学物理
静电场中的电介质 , ,
1.1 电介质的分类
电介质又称绝缘体。我们通常把气体、油类、蜡脂、玻璃、云母、陶瓷、橡胶等这些基本不导 电的物质称为电介质。
对于各向同性的电介质可分为无极分子和有极分子两类。
静电场中的电介质 , ,
1.2 电介质的极化
电介质的极化是指在外电场作用下电介质表面产生极化电荷的现象。 其中,极化电荷又称束缚电荷,是指在外电场中,均匀介质内部各处仍成电中性,但在介质表 面出现的不能离开电介质到其他带电体,也不能在电介质内部自由移动的电荷。
静电场中的电介质 , ,
1.2 电介质的极化
2.电介质对电场的影响
如果不存在电介质(真空),自由电荷激发的场强大小为 E0 ,引入均匀电介质后,当均匀电介质充
满电场不为零的空间,或几种均匀电介质分区充满电场且分界面都是等势面时,电介质的场强大小 E 将
静电场中的电介质

SD dS Q0
选半径为r,长度为L的高斯圆柱 面
r
R2 R1
SD dS l
D2 π rl l D
2πr
E D
ε0εr 2 π ε0εrr
(R1 r R2 )
P
0 E
( r
1) 0 E
r 1 2 πrr
r
R2 R1
(2) E
2π
0
r
r
E1 2 π 0 r R1 (r R1)
q0 有关.
s内
特例: 真空——特别介质
特例: 真空——特别介质
q' 0 , P 0 , D 0E P 0E
回到:
1
E
s
dS
0
(
q0
S内 )
3. 如何求解介质中电场?
本课程只要 求特殊情况
各向同性电介质 q0 ,q' 分布具有某些对称性
(1)各向同性电介质:
P
0E
为常数
D 0E P 0E 0E 0(1 )E
模型 “电子气”
与电场的 相互作用
静电感应
电偶极子
无极分子电介质: 位移极化 有极分子电介质: 转向极化
宏观 效果
静电平衡
导体内 E 导体表面
0, 0 E表面
内部:分子偶极矩矢量
和不为零
pi 0
i
感应电荷 0E 出现束缚电荷(极化电荷)
4.极化现象的描述
1) 从分子偶极矩角度
单位体积内分子偶极矩矢量和——极化强度.
R2的薄导体圆筒组成,其间充
以相对电容率为r的电介质. 设
直导体和圆筒单位长度上的电
荷分别为+和- . 求(1)电介 质中的电场强度、电位移矢量
6-静电场中的电介质

v v 1 q E⋅ dS = ∑ = 1 ( ∫
S
ε0
S内
ε0
∑q +∑q′)
0 S内 S内
式中的 ∑q 为闭合曲面内一切正、负电荷的代数和 为闭合曲面内一切正、 即自由电荷q 极化电荷q (即自由电荷q0、极化电荷q’)
v v 1 ∫ E⋅dS = (∑q0 +∑q′)
S
ε0
------ 有源场
分析电场所具有的对称性质 巧作高斯面, 巧作高斯面,即选择适当形状的闭合曲面为高斯面 计算通过高斯面的电位移通量
v v dS ΦD = ∫ D⋅ dS = ∫ D
S
计算高斯面内所包围的自由电荷的代数和 由电介质中的高斯定理求出电位移 D
∑q0
D∫dS = ∑q0
D=
∑q0
∫dS
由电位移 D 求出场强 E
4 0εr1r2 πε r r Br r ∞r r ∞ UA = ∫ E⋅ dl = ∫ E⋅ dl +∫ E⋅ dl Q A B A A r r E3 = ∞ 2 4 0εr2r πε =UAB +∫ E4 ⋅ dr
S内
S内
v v 1 Q∫ E0 ⋅ dS = ∑q0
S
v v ∴∫ ε0E0 ⋅ dS = ∑ 0 q
S S内
ε0 S内
v v ∴∫ ε0εr E⋅ dS = ∑ 0 q
S S内
v v v 令 D=ε ε E =εE ----电位移矢量 ----电位移矢量 0 r v v 自由电荷 电位移通量 ∴ D⋅ d = ∑ 0 S q ∫
§2
静电场中的电介质
H+ H C−+ H −
电介质:内部几乎没有可以自由运动电荷的物体, 电介质:内部几乎没有可以自由运动电荷的物体,又称为 绝缘体 电偶极子模型 正负电荷
静电场中的电介质特性

(1) 无极分子的位移极化 在外加电场作用下, 在外加电场作用下,无极分子原本重合的 正负电荷“重心”错开了, 正负电荷“重心”错开了,形成了一个电 偶极子, 偶极子,分子电偶极矩的方向沿外电场方 向。这种在外电场作用下产生的电偶极矩 称为感生电矩。 称为感生电矩。 在外电场的作用下电介质出现极化电荷的 现象,就是电介质的极化。 现象,就是电介质的极化。 在外场作用下,主要是电子位移, 在外场作用下,主要是电子位移,因而无 极分子的极化机制通常称为电子位移极化。 极分子的极化机制通常称为电子位移极化。
电介质体内一般没有自由电荷, 具有良好的绝缘性能 特点:具有极化能力和其中能够长期存在
电场的性质是电介质的基本属性
电介质的四大基本常数
介电常数:综合反映介质内部电极化行为的一个 介电常数 综合反映介质内部电极化行为的一个 主要的宏观物理量;以电极化的方式传递、 主要的宏观物理量;以电极化的方式传递、存 贮或记录电的作用与影响 电导是指电介质在电场作用下存在泄露电流 电导是指电介质在电场作用下存在泄露电流 介电损耗是电介质在电场作用下存在电能的损耗 介电损耗是电介质在电场作用下存在电能的损耗 击穿是指在强电场下可能导致电介质的破坏 击穿是指在强电场下可能导致电介质的破坏
1.无电场时 1.无电场时 有极分子 无极分子
分子热运动,各分子电偶极矩的取向杂乱无章, 分子热运动,各分子电偶极矩的取向杂乱无章, 整个电介质宏观上对外呈电中性 整个电介质宏观上对外呈电中性 2. 有电场时 有极分子介质-----取向极化 (orientation polarization) 有极分子介质 取向极化 orientation 无极分子介质-----位移极化(displacement polarization) 位移极化(displacement 无极分子介质 位移极化 边缘出现电荷 电荷分布 电介质的极化共同效果 电介质的极化共同效果 -----边缘出现电荷分布 极化 极化电荷( Polarization charges) 束缚电荷( bound charges)
电磁学 第3章静电场中的电介质

∫∫ ρ′ = −
v v P ds
∆V
注意: 注意:均匀极化时电介质内部的极化电荷体密度为零
20
4.电介质表面(外)极化电荷面密度 电介质表面( 电介质表面 内
r dS
θ
dS
r r v ˆ dq ′ = P ⋅ d s = P ⋅ dsn = Pnds 面外
dq ′ v ˆ σ′= = P ⋅ n = Pn dS
16
约定: 约定:
q ', ρ ',σ q0, ρ
0
'
,λ ,λ
'
,σ
0
0
表示极化电荷; 表示极化电荷; 表示自由电荷
二、极化强度与极化电荷的关系 在已极化的介质内任意作一闭合面S 在已极化的介质内任意作一闭合面 基本认识: 基本认识: 1)S 把位于S 附近的电介质分子分为两部分 ) 把位于 附近的电介质分子分为两部分 一部分在 S 内 一部分在 S 外 2)只有电偶极矩穿过 的分子对 )只有电偶极矩穿过S 电偶极矩穿过 S内外的极化电荷才有贡献 内外的极化电荷 内外的极化电荷才
S
17
1.小面元 附近分子对面 内极化电荷的贡献 小面元dS附近分子对面 小面元 附近分子对面S内极化电荷的贡献 在dS附近薄层内认为介质均匀极化 附近薄层内认为介质均匀极化 薄层: 为底、 的圆柱。 薄层:以dS为底、长为 的圆柱。 为底 长为l的圆柱 只有中心落在薄层内的分子 才对面S内电荷有贡献 内电荷有贡献。 才对面 内电荷有贡献。 所以, 所以,
∫L
s
E ⋅dL = 0
v v
v
v
∫∫ s E ⋅ d s =
q ε0
媒质中{
导体感应电荷, 导体感应电荷,感应电场又反过来影响原 电场,静电平衡。 电场,静电平衡 电介质:即绝缘体,不导电物体, 电介质:即绝缘体,不导电物体,在电场 中怎样? 中怎样?
第三章静电场中的电介质
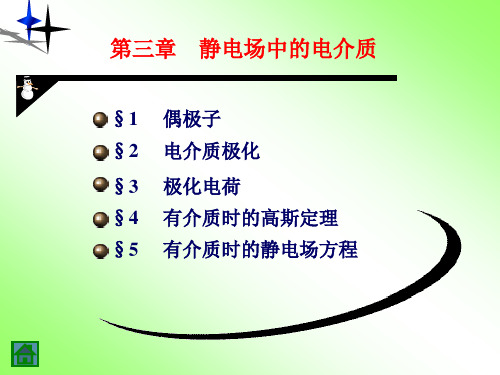
1 E ds ( q0 q)
s
0
s内
s内
q P ds
s内 s
1 1 E dS q0 q q0 P dS 0 0 S S
0 E P dS q0
四、 有介质时的高斯定理应用
令D 0 E P
S
引入辅助物理量:电位移矢量(electric displacement)
D 0E P
介质存在时高斯定理:
D ds q0
s s内
电位移矢量对任意闭合曲面的通量等于该曲面内所有自由 电荷的代数和。 二、电位移矢量D 1、定义:
(S )
_
E0
内
ds
l
P dS q
( S内)
V
S
外
V 内的极化电荷总量 q P ds s P d s 该点的极化电荷体密度 ' s V
'
P ds / V
' s
* 此式为各点极化电荷体密度和该点极化强度的关系。
q' , ' , ' 分别表示极化电荷、体密度、面密度 • q0 , 0 , 0 分别表示自由电荷、体密度、面密度
•
二、极化电荷体密度与极化强度的关系:
1、以位移极化为例 极化分子电矩
p分子
ql
S
E0
ds
单位体积有 n 个分子 极化强度矢量
l
0
P np分子 nql
D E
6 静电场中的电介质.

E
E0
E
'
E0
r
E
E0
E
'
E0
r
r :电介质的相对电容率(相对介电常数)
真空(空气) r 1 其它电介质: r 1
0 :真空电容率(真空介电常数)
0 r :电介质的(绝对)电容率(绝对介电常数)
3. 电极化强度
定义:
P
p
V
p :每个分子的电偶
E
'
εr 1 εr
E0
①
'
+-+
+-+
+-+
+
-+
+
+-
+
0
E0
0
ε0
同理
代入①式,有
E' '
ε0
'
r E E' E -+- -+- -+- - +- - +- - 0
σ
'
εr εr
1
σ0
(1
1 εr
)σ0
'
+-+
+-+
+-+
+
-+
+
-+Q+0
0
r E E' E
' -+- -+- -+- - +- - +-Q-' 0
大学物理_4静电场中的电介质

S
i
自由电荷
各向同性 线性介质
P 0r 1E
D 0r E E 介质方程
r 0 称介质的介电常数(电容率)
在 斯具 定有 理某出种发对解称出性D的情况下,可以首先由高
即 D E P q
说明:
1.电位移在闭合面上的通量只和闭合面内的自
第十五章 静电场中的电介质
(Dielectric In Electrostatic Field)
§15.1 电介质对电场的影响 §15.2 电介质的极化 §15.3 D的高斯定律 §15.4 电容器及其电容 §15.5 电容器的能量
§15.1 电介质对电场的影响 电介质的特点:无自由电荷,不导电。 电场中置入各向同性均匀电介质时的影响
定义 C Q 单位:法拉 F
U
电容只与几何因素和介质有关 固有的容电本领
【例1】求真空中孤立导体球的电容
解:设球带电为 Q
导体球电势 U Q
4 0 R
导体球电容 C Q
U
4 0 R
问题
欲得到 1F的电容, 孤立导体球的半径R
由孤立导体球电容公式知
R
1
4 0
9109 m
R3
4π 0r 2
(r (r
R) R)
q2r2
we
0E2
2
32π2
q2
0
R
6
32π2 0 r 4
(r R) (r R)
静电能:We
V wedV
0
we
4πr
2dr
9-7 电介质

一.电介质
电介质是指在通常条件电阻率超过108.m 的物质下导电性能极差的物质。
电工学中一般认为电阻率超过108.m的物 质就属于电介质。 电介质可以作为绝缘材料使用,同时,在电 场作用下,电介质会被极化,某些固体电介质具 有许多与极化相关的特殊性能,如电致伸缩、压 电性、铁电性等等。
r
R2
R1
r R1
r R2 E q0
E 0
4 0r 2
R1 r R2
E
4 0 r r 2
q0
r
r
r
R2
R1
UO Edr Edr Edr Edr
0 0 R1 R2
R1
R2
R2
R1
0 r r
q0
2
dr
R2
σ ' -
E 2 2 0 0
σ ' - - - - - - - - - - - - - - - - +
+
+ +
0
适用于各向同性的 0 E0 0 E E0 E 均匀电介质充满整个电 0 0 r 0 r
0 0
+ + +
+ +
+ + + + + + + + + + + + + + + + +
r
S
D d S q 0
S
通过高斯面的电位移通量等于高斯面所包围
《静电场中的电介质》课件

电介质的极化机制可以分为电子式极化、离子式极化和取向式极化三种。电子式极化是由于电介质中的电子受到 电场作用而产生的位移;离子式极化是由于电介质中的离子受到电场作用而产生的位移;取向式极化是由于电介 质中的分子或分子的取向受到电场作用而产生的改变。
02 静电场中的电介质
电介质在静电场中的表现
压电材料的研究涉及晶体、陶瓷、复合材料等多个领域,研究者通过优化材料成分、结 构及制备工艺,提高压电材料的性能,如压电常数、机电耦合系数等,以拓展其应用范
围。
新型电介质材料的研究
总结词
新型电介质材料在能源、环保、医疗等领域 具有广阔的应用前景。
详细描述
随着科技的发展,新型电介质材料不断涌现 ,如铁电材料、弛豫铁电体、多铁性材料等 。这些材料在储能、传感、信息处理等方面 展现出独特的优势,为相关领域的技术创新
VS
详细描述
压电材料中的电介质在受到外力作用时, 会发生形变导致分子间的电荷重新分布, 产生电压。这种现象称为压电效应。利用 压电效应可以制作传感器和换能器等器件 ,广泛应用于声学、电子学和物理学等领 域。
05 电介质在静电场中的研究进展
高介电常数材料的研究
总结词
高介电常数材料在静电场中表现出优异的电 学性能,是当前研究的热点之一。
电介质的极化机制包括电子极化、离子极化和取向极化等,这些机制在不同频率和 强度的电场中表现不同。
电介质的极化状态会影响其在静电场中的行为,如介电常数和电导率等,这些性质 在电子设备和电磁波传播等领域有重要应用。
电介质极化对电场的影响
01
电介质的极化状态会改变静电场的分布,因为电介质的存在会 导致电场畸变。
02
电介质在静电场中的行为可以用Maxwell方程组描述,通过求
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
静电场中的电介质
(一)要求
1、了解电介质极化的微观机制,掌握极化强度矢量的物理意义
2、理解极化电荷的含义,掌握极化电荷、极化电荷面密度与极化强度矢量P 之间的关系
3、掌握有介质时场的讨论方法,会用介质中的高斯定理来计算静电场;明确E 、P 、D 的联系和区别
4、了解静电场的能量及能量密度
5、演示实验:介质对电容器电容的影响
(二)要点
1、电介质的极化
(1)电介质的电结构
(2)电介质的极化
2、极化强度矢量
(1)极化强度矢量
(2)极化电荷
(3)极化电荷体密度与面密度
3、有介质时的静电场方程
(1)电位移矢量
(2)介质中的高斯定理
(3)介质中的电场方程
*4、静电场的边值关系
5、静电场的能量和能量密度
(三)难点
求解介质中静电场的具体问题,如极化电荷的分布,介质中电场的分布等
§ 3-1电介质的极化
一、介质中的电场强度
实验表明,电容器中填充介质后电容增大,增大程度由填充介质的相对介电常数£决定。
由于引入外电场后,电介质表面出现电荷,产生附加电场比方向与外电场方向相反,削
弱了电介质内部的外电场,这样
f f f 4
E=E^ + E f
但
E t丰E‘,辰工On
二、电介质的极化
在外电场作用下电介质表面出现电荷的现象叫做电介质的极化,在表面出现的这种电荷叫极化电荷(束缚电荷)。
由于极化电荷比自由电荷少得多,极化电场比感应电场也小得多,因此介质内部合场强不为零但要注意极化电荷与自由电荷、极化电场与感应电场的区别。
§3-2极化强度矢量
一、极化的微观机制1无极分子的位移极化
在外电场作用下,无极分子正负电荷“中心”发生相对位移而出现极化电荷的现象,称为位移极化。
2、有极分子的取向极化
在外电场作用下,有极分子的电偶极矩受到电场的力矩而转向外电
场,在垂直于外电场方向的两端面上也出现极化电荷的现象,称为取向极化。
二、极化强度矢量
1定义
在介质中取一无限小体积元A L ,设△ I
内分子电偶极矩的矢量和为,则定义极化强度矢量为
也就是说,极化强度矢量等于单位体积内所有分子电偶极矩的矢量和。
它是描述介质内部极化程度的物理量。
单位:库/米2 ( C/m 2 )。
若介质内部各点“的大小、方向均相同,则称为均匀极化。
在真空和处于静电平衡状态的导体中,没有极化电荷,所以—°。
2、P与极化电荷的关系
在介质中取一个长为/底面积为的圆柱截面
由于圆柱体体积A r很小,其内可看作常数。
整个圆柱体内电偶极矩的总和为
=,PAK=P(S/)cos0 = (o<S)/
所以,圆柱体表面极化电荷面密度为
y = PCO30
写成矢量形式,得
* f 貝
u f= Pn
A
介为介质表面法线的单位矢量。
若与眩之间夹角2,则CT'
〜只0>^
若P与刃之间夹角'2,则c"—尸<k osZ) V °
f 尺
g = —.
若P与/之间夹角2,则- Pros/? 0
$-3介质中的电场
亠、基本关系式
有介质存在时,无论介质内、外或空间任一点的
反,极化电荷面密度为 C ,自由电荷面密度为
E = S —色
二、与丄;的关系
实验表明,在各向同性介质中,任一点的极化强 度矢量与该点的总场强大小成正比,方向相同,可写 为"―2‘1厂,Z 称为介质的极化率,它是一个大 于零的纯数,由介质本身性质决定。
所谓均匀介质, 就是上处处相同的介质。
例:设一平行板电容器上下两极板的自由电荷面度为 士 01其中充
满极化率为乂 的介质,讨论其电场。
总场强为丘二+ F
,由于片方向与方向相
,介质内的总场强为
1、求介质中的总场强
由于自由电荷场强为
极化电荷场强为
£' = —
所以,总场强为
E = E il-E t=^~ —
窃 %
则广刃,这样
E =比—%E
1+Z (1 十Z)禺
令耳;「十2,匚7称为相对介电常数。
介质中的总场强为
而极化电荷面密度
2、充满介质后的电容
充满介质后,电容器的电容比原来增大了八「倍
3、极化电荷面密度
夕=土(1 一 丄)5
®"o
式中,
上称为绝对介电常数,简称介电常数
§3-4介质中的高斯定理
一、介质中的高斯定理
1、数学表达式
有介质存在时,咼斯定理仍然成立。
但在计算咼
斯面内包围的电荷时,应包括自由电荷和极化电荷q,即
甘丘-ds = —(X条+工
(I)$0
而
甘戸•力二一工
(5)
两式整理后,得
甘(矶丘+戶).石二艺务
(I)
如果定义一点的电位移矢量D为
D = + P
则有
(O
上式称为有介质存在时的高斯定理。
因为() 是电位移矢量的通量,所以它可以表述为:通过任一闭合曲面的电位移通量,等于包围在该闭合面内自由电荷的代数和。
2、关于定理的几点说明
(1)有介质存在时的咼斯定理是更普遍的规律,它概括了真空中的高斯定理。
(2)在万的高斯定理中,@和P不直接出现,在电荷和介质分布具有一定对称性的情况下,可以由自由电荷9(1的分布,求出万的分布。
(3)高斯面上任一点的D是由空间总的自由电荷的分布决定,不能认为只与面内自由电荷有关。
二、电位移矢量
1、物理意义
D 是复合量,它既描述电场,同时也描述介质极 化。
引进D 的目的是为了使有介质存在时高斯定理的 形式简化。
2、与上;的关系
—* —►
因为"―才时]戶,所以
=£©E +光£占—(1 +才)左洱
1 * Z - £,
£ - 所以 &占丘=匣
三、应用举例
半径为j?的金属球,电荷为q 〔I ,放在均匀无限
大介质中,介质的介电常数为匕。
求介质中的电 场强度。
■卜 而,
解:在金属球外的介质中 取一点/\ P 距球心的距离为 尸。
以U 为球心、厂为半径作一 同心球面为高斯面,则由介质中的 高斯定理,得
介质中的场强为
E 丄=二 %
£ 4冗# 4兀£岛尸
若金属球放在真空中,则场强为
E = — 4冗£輕
§3-5静电场的能量
,、电容器的能量
^Dds =
电位移矢量
b
将一电池与电容器
相连,电池给电容器充电。
在某一瞬间,电容器带电量@、极板间电位差为孔时,将电量
由电容器的负极移到正极时,电源克
服电场力作功为
dA = iidq
这也是移动电荷时外力所作的功。
而c?在电量由°T Q的整个充电
这功应转变为电容器所储存的能量,用W
表示。
利用电容的定义我们可以把丄面的结果
改写为
过程中,外力所作的总功为
所以,电容f也是反映电容器储存能量本领大小的物
理量。
二、电场的能量
以平行板电容器为例
设平行板电容器的极板面积为极板间的距
离为",两极板间充满绝对介电常数为£的
均匀电介质,则其电容为
d
而两极板间的电位差
U= Ed
所以平行板电容器电场的能量为
V 2 2
式中I 是极板间存在电场的空
间的体积。
在平行板电容器中,电场是均匀场,所以能量也是均匀分布的。
在单位体积内的能量,即能流密度为
IV 1 “ 1 —
tu ——= —DE = —E£
V 2 2
上式虽然是从平行板电容器推导出来的,但却是普遍成立的。
对于任意电场,总的电场能量是能流密度的体积分,即
W = \(jaV^-\DEdV =丄\sE2dV
y 2 Y 2 Y
<£) ——£^E
在真空中,由于丄,所以。
