MATLAB实现无约束求解
用Matlab实现非线性无约束优化的几种方法比较

用Matlab实现非线性无约束优化的几种方法比较王娜;朱逸夫【摘要】在实际规划问题的求解过程中,优化解的真值具有不可预知性,为了寻找可用的稳定解,往往需要用不同的算法进行试算,并对所有计算结果进行甄别,这需要应用者具备良好的经验.为此,利用Matlab工具箱中的fminunc和fminsearch命令格式,并根据牛顿法、拟牛顿法、最速下降法、阻尼牛顿法和修正牛顿法等方法,分别编程实现在经典算例中求解无约束非线性优化问题,并对计算结果进行了比较和分析.【期刊名称】《长春工程学院学报(自然科学版)》【年(卷),期】2018(019)004【总页数】5页(P95-99)【关键词】非线性规划;Matlab;无约束优化;一维搜索;搜索方向【作者】王娜;朱逸夫【作者单位】长春工程学院教务处 ,长春 130012;长春工程学院计算机技术与工程学院 ,长春 130012【正文语种】中文【中图分类】TP3910 引言非线性无约束最优化技术是一门实践性很强的方法,应用者往往要在实践中不断地总结[1-4]。
对有些应用者来说,不必要浪费了大量的时间和精力,系统而深入地学习优化算法及公式,他们只希望能够快速地找到有效的解法、合适的优化软件,并能在计算机上尽快地求出问题的解[5]。
为此本文针对非线性无约束优化模型,利用几种不同的Matlab求解非线性无约束优化问题的调用格式,或根据无约束优化的算法编程进行求解,并进行解的比较和分析,提高非线性规划模型的应用效果和能力。
1 非线性无约束优化的基本理论设无约束非线性规划的模型为minf(x),x=(x1,x2,…,xn)T∈Rn,(1)求解无约束优化问题的主要思想是下降算法:每一步都要求函数值有所下降,其迭代格式为x(k+1)=x(k)+αkd(k),即对应于点列{xk}上的函数值列{f(xk)}必须是逐渐减小的,或者至少是不增加的,因而有f(x0)≥f(x1)≥…≥f(xk)≥f(xk+1)≥…(2)我们还要求这些点列收敛于全局最优解。
数学实验——无约束优化
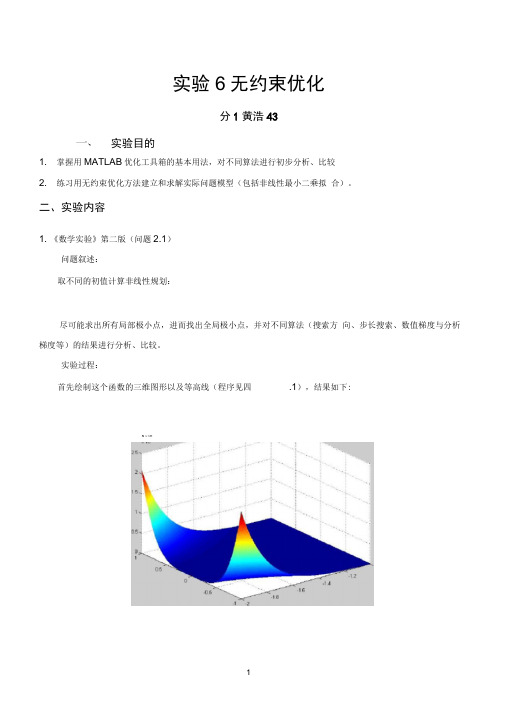
实验6无约束优化分1黄浩43实验目的1. 掌握用MATLAB优化工具箱的基本用法,对不同算法进行初步分析、比较2. 练习用无约束优化方法建立和求解实际问题模型(包括非线性最小二乘拟合)。
二、实验内容1. 《数学实验》第二版(问题2.1)问题叙述:取不同的初值计算非线性规划:尽可能求出所有局部极小点,进而找出全局极小点,并对不同算法(搜索方向、步长搜索、数值梯度与分析梯度等)的结果进行分析、比较。
实验过程:首先绘制这个函数的三维图形以及等高线(程序见四.1),结果如下:s M tn0-”19 A8 A1G \ 5 -14 -13 \ 2 A1通过观察这两幅图,可以得到,x2确定时,x1越负,函数值越大,x1确定时,x2绝对值越大,函数值越大。
但对于x1正向偏离0的情况,并没有很好的反映,于是扩大绘图范围,做出下图(程序见四.2):-1 -10由上面两幅图可见,方程像是一个四角被捏起的花布,而且z的最小值为0< 因此只要求解该方程的零点,即得到了方程的局部极小点,且若将原方程变形为:我们容易发现,该方程的零点为:x2=0或x1=0或x1=1或在求解零点之前,先针对一个零点,不妨用x1=1, x2=1,分析不同算法的优劣。
在matlab的无约束优化中,可以使用fminumc和fminsearch两种函数,搜索方向的算法有BFGS 公式、DFP公式和最速下降法三种(书中还提到的Gill-Murray 公式在matlab中已经不再使用),步长的一维搜索有混合二次三次多项式插值和三次多项式插值两种方法,另外,在求解函数梯度是也有数值方法和分析方法两种。
在对上述四类算法因素进行分析时,我们采用控制变量法,每次只保持一种或两种算法因素改变,分析它的精度及效率。
(一)分析fminumc与fminsearch两种方法的精度及效率选择初值为x1=0.8,x2=0.8,使用fminunc和fminsearch的默认算法及控制参数,输出结果如下(程序见四.3、四.4):因为精确解为x1=1, z=0,我们便可以比较出不同算法的精度。
用MATLAB求解无约束优化问题-电子科技大学

-218.0000
注:有些实际问题可能会有一个约束条件:决策变量
只能取整数,如x1、x2取整数。这类问题实际上是整数线 性规划问题。如果把它当成一个线性规划来解,求得其最 优解刚好是整数时,故它就是该整数规划的最优解。若用 线性规划解法求得的最优解不是整数,将其取整后不一定 是相应整数规划的最优解,这样的整数规划应用专门的方 法求解(如割平面法、分支定界法)。
S.t.
0.4 0
1.1 0
1 0
0 0.5
0 1.2
10.3X 890000
x1
1 0 0
0 1 0
0 0 1
1 0 0
0 1 0
0 400 0X 600 1 500
x2
,X
x3
最速下降法是一种最基本的算法,它在最优化方法中占有重要地位.最
速下降法的优点是工作量小,存储变量较少,初始点要求不高;缺点是收敛
慢,最速下降法适用于寻优过程的前期迭代或作为间插步骤,当接近极值
点时,宜选用别种收敛快的算法.
2.牛顿法算法步骤:
(1) 选定初始点 X 0 E n ,给定允许误差 0 ,令 k=0;
s.t. AX b
命令:x=linprog(c,A,b)
2、模型:min z=cX
s.t. AX b Aeq X beq
命令:x=linprog(c,A,b,Aeq,beq)
注意:若没有不等式:AX b 存在,则令A=[ ],b=[ ].
3、模型:min z=cX
s.t. AX b Aeq X beq
x1 0, x2 0
解: 编写M文件如下:
如何在Matlab中进行约束优化和约束求解

如何在Matlab中进行约束优化和约束求解在科学研究和工程应用中,经常会遇到优化问题。
而在实际问题中,往往会涉及到各种约束条件。
为了得到最优解,我们需要在考虑约束的情况下进行优化。
在本文中,我们将介绍如何在Matlab中进行约束优化和约束求解。
一、优化问题的基本概念在开始具体介绍Matlab中的约束优化和约束求解方法之前,让我们先了解一些基本的概念。
1.1 目标函数目标函数是优化问题中需要最小化或最大化的函数。
在Matlab中,我们可以使用符号表达式或函数句柄来表示目标函数。
1.2 约束条件约束条件是在优化过程中需要满足的条件。
约束条件可以分为等式约束和不等式约束。
等式约束要求某些变量之间的关系满足特定的等式,而不等式约束要求某些变量满足特定的不等式。
1.3 优化变量优化变量是在优化问题中需要找到最优解的变量。
在Matlab中,我们可以使用符号表达式或变量来表示优化变量。
二、约束优化的实现方法在Matlab中,有多种方法可以求解带有约束条件的优化问题。
下面我们将介绍几种常见的方法。
2.1 内点法内点法是一种求解约束优化问题的常用方法。
该方法通过将约束问题转化为无约束的问题,然后使用内点算法在约束域内求解最优解。
在Matlab中,我们可以使用fmincon函数来实现内点法。
该函数通过指定目标函数、约束条件和初始点等参数,来求解带有约束的优化问题。
2.2 逐步二次规划法逐步二次规划法是一种求解约束优化问题的有效方法。
该方法通过逐步迭代,不断缩小可行域并得到更优的解。
在Matlab中,我们可以使用fmincon函数的'interior-point'选项来实现逐步二次规划法。
该选项使用了内点法和二次规划的思想,来求解约束优化问题。
2.3 遗传算法遗传算法是一种模拟自然进化过程的优化方法。
该方法通过不断演化和选择适应度较高的个体,来搜索最优解。
在Matlab中,我们可以使用ga函数来实现遗传算法。
实验五:无约束优化

实验五:无约束优化班级 姓名 学号一、实验目的:学会用matlab 软件求解单变量和多变量无约束优化问题。
二、实验要求:1. 熟悉一维搜索的方法:进退法、黄金分割法、抛物线插值法、Armijo 准则;2. 熟悉求解多变量无约束问题的方法:变量轮换法、最速下降法、牛顿法、共轭梯度法;3. 会用matlab 软件求解无约束优化问题。
三、实验内容:1、试用matlab 优化工具箱中的fmincon 函数求解下列非线性规划问题:2221232212323123212223123m in ()8020..2023,,0f x x x x x x x x x x s t x x x x x x x =+++⎧-+≥⎪++≤⎪⎪--+=⎨⎪+=⎪⎪≥⎩(1)给出matlab 源代码; (2)求解结果粘贴.2、(精确一维搜索) 用0.618法求函数2()sin f x x x =-在[]0,1上的极小点,取自变量的允许误差为410δ-=,函数变量的允许误差为510ε-=。
3、(不精确一维搜索) Armijo 准则是许多非线性规划算法求步长时都必须执行的步骤。
Armijo 准则是指给定()0,1,(0,0.5),βσ∈∈令步长因子km k αβ=,其中km 是满足下列不等式的最小非负整数()()()mmTk k k k k f x d f x g d βσβ+≤+*这里k g 是函数()f x 在当前迭代点k x 处的梯度函数,k d 是当前迭代点k x 处的搜索方向. 可以证明()f x 若是连续可微的且满足0T k k g d <,则准则是有限终止的,即存在正数σ,使得对于充分大的正整数m ,()*成立.为了程序实现的方便,我们把Armijo 准则描述成下列详细的算法步骤: 算法1(Armijo 准则)步0:给定()0,1,(0,0.5),βσ∈∈令:0m =;步1:若不等式()()m m T k k k k k f x d f x g d βσβ+≤+成立, 置:,k m m = 1:km k k k x x d β+=+,停止.否则,转步2;步2:令:1m m =+,转步1.(1)试将上述的Armijo 准则编制成可重复利用的matlab 程序模块。
无约束优化方法与MATLAB实现

例4-1 MA TLAB实现,用M函数文件形式求解:syms s t;f=s^2+3*t^2-2*t*s+4*t+3*s;[x,minf]=minZBLH(f,[-2 6],[0.2 0.2],1.5,[t s],0.0001,0.0001) 坐标轮换minZBLH函数文件如下:function [x,minf] = minconPS2(f,x0,delta,u,var,eps1,eps2)%目标函数:f;%初始点:x0;%收缩系数:u;%自变量向量:var;%步长精度:eps1;%自变量精度:eps2;if nargin == 7eps2 = 1.0e-6;endn = length(var);y = x0;bmainCon = 1;while bmainConyf = subs(f,var,y);yk_1 = y;for i=1:ntmpy = zeros(size(y));tmpy(i) = delta(i);tmpf = subs(f, var,y+tmpy);if tmpf < yfbcon = 1;while bcontmpy(i) = 2*tmpy(i);tmpf_i = subs(f, var,y+tmpy);if tmpf_i <yfy_res = y + tmpy;elsebcon = 0;endendelsetmpy(i) = delta(i);tmpf = subs(f, var,y-tmpy);if tmpf < yfbcon = 1;while bcontmpy(i) = 2*tmpy(i);tmpf_i = subs(f, var,y-tmpy);if tmpf_i <yfy_res = y - tmpy;elsebcon = 0;endendelsey_res = y ;delta = delta/u;endendy = y_res;endif norm(y - yk_1) <= eps2if max(abs(delta)) <= eps1x = y;bmainCon = 0;elsedelta = delta / u;endendendminf =subs(f,var,x);M函数文件的运行结果如下:x = -1.7499-3.2499minf = -8.3750======================================================= 例4-2 MA TLAB实现,用M函数文件形式求解:syms t s;f=t^2+s^2-t*s-10*t-4*s+60;[x,mf]=minFD(f,[0 0],[t s])梯度法函数文件minFD如下:function [x,minf] = minFD(f,x0,var,eps)%目标函数:f;%初始点:x0;%自变量向量:var;%精度:eps;%目标函数取最小值时的自变量值:x;%目标函数的最小值:minfformat long;if nargin == 3eps = 1.0e-6;endsyms l;tol = 1;gradf = - jacobian(f,var);while tol>epsv = subs(gradf,var,x0);tol = norm(v);y = x0 + l*v;yf = subs(f,var,y);[a,b] = minJT(yf,0,0.1);xm = minHJ(yf,a,b); %用黄金分割法进行一维搜索x1 = x0 + xm*v;x0 = x1;endx = x1;minf = subs(subs(f,x(1)),x(2));format short;M函数文件的运行结果如下:x = 8.0000 6.0000mf =8.0000======================================================================= 例4-3 MA TLAB实现,用M函数文件形式求解:syms t s;f=t^2-4*s^2;[x,mf]=minNT(f,[1 1],[t s])牛顿法函数文件minNT如下function [x,minf] = minNT(f,x0,var,eps)%目标函数:f;%初始点:x0;%自变量向量var;%精度:eps;%目标函数取最小时的自变量值:x;%目标函数最小值:minf;format long;if nargin == 3eps = 1.0e-6;endtol = 1;x0 = transpose(x0);gradf = jacobian(f,var); %梯度方向jacf = jacobian(gradf,var); %雅克比矩阵while tol>epsv = subs(gradf,var,x0);tol = norm(v);pv = subs(jacf,var,x0);p = -inv(pv)*transpose(v); %搜索方向p = double(p);x1 = x0 + p;x0 = x1;endx = x1;minf = subs(f,var,x);format short;M函数文件的运行结果如下:x = 0mf = 0============================================================================ 例4-4 MA TLAB实现,用M函数文件形式求解:syms t s z;f=(t-s+z)^2+(-t+s+z)^2+(t+s+z)^2[x,mf]=minMNT(f,[0.5 1 0.5],[t s z])阻尼牛顿法函数文件minNT如下function [x,minf] = minMNT(f,x0,var,eps)format long;if nargin == 3eps = 1.0e-6;endtol = 1;x0 = transpose(x0);syms l;gradf = jacobian(f,var);jacf = jacobian(gradf,var);while tol>epsv = subs(gradf,var,x0);tol = norm(v);pv = subs(jacf,var,x0);p = -inv(pv)*transpose(v);y = x0 + l*p;[a,b] = minJT(yf,0,0.1); %进退法求单峰区间xm = minHJ(yf,a,b); %黄金分割法进行一维搜素x1 = x0 + xm*p;x0 = x1;endx = x1;minf = subs(f,var,x);format short;M函数文件的运行结果如下:x = 1.0e-015 *-0.3468-0.6936-0.3468mf =2.4053e-030=================================================================== 例4-5 MA TLAB实现,用M函数文件形式求解:syms t s;f=t^2+4*s^2;[x,mf]=minGETD(f,[1 1],[t s])共轭梯度法函数文件minGETD如下x0 = transpose(x0);n = length(var);syms l;gradf = jacobian(f,var);v0 = subs(gradf,var,x0);p = -transpose(v0);k = 0;while 1v = subs(gradf,var,x0);tol = norm(v);if tol<=epsx = x0;break;endy = x0 + l*p;yf = subs(f,var,y);[a,b] = minJT(yf,0,0.1); %进退法确定单峰区间xm = minPWX(yf,a,b); %二次插值一维搜素x1 = x0 + xm*p;vk = subs(gradf,var,x1);if tol<=epsx = x1;break;endif k+1==nx0 = x1;continue;elselamda = dot(vk,vk)/dot(v,v);p = -transpose(vk) + lamda*p;k = k+1;x0 = x1;endendminf = subs(f,var,x);format short;M函数文件的运行结果如下:x = 1.0e-015 *0.33310.0971mf = 1.4868e-031=================================================================== 例4-6 MA TLAB实现,用M函数文件形式求解:syms t s;f=4*(t-5)^2+(s-6)^2;X=[8 10 11;9 11 11];[x,mf]=minSimpSearch(f,X,1.2,0.5,2.0,0.3,[t s])单纯形法函数文件minGETD如下function [x,minf] = minSimpSearch(f,X,alpha,sita,gama,beta,var,eps)%:f;%反射系数:alpha;%紧缩系数:sita;%扩展系数:gama;%收缩系数:beta;%自变量向量:var;%精度:eps;%目标函数取最小值时的自变量值:x;%目标函数最小值:minf;format long;if nargin == 7eps = 1.0e-6;endN = size(X);n = N(2);FX = zeros(1,n);while 1for i=1:nFX(i) = subs(f,var,X(:,i));end[XS,IX] = sort(FX); %将单纯形的顶点按目标函数值的大小重新编号Xsorted = X(:,IX); %排序后的编号px = sum(Xsorted(:,1:(n-1)),2)/(n-1); %单纯形的中心Fpx = subs(f,var,px);SumF = 0;for i=1:nSumF = SumF + (FX(IX(i)) - Fpx)^2;endSumF = sqrt(SumF/n);if SumF <= epsx = Xsorted(:,1);break;elsex2 = px + alpha*(px - Xsorted(:,n)); %将中心点向单纯形外反射fx2 = subs(f,var,x2);if fx2 < XS(1)x3 = px + gama*(x2 - px); %中心点的扩展fx3 = subs(f,var,x3);if fx3 < XS(1)Xsorted(:,n) = x3;X = Xsorted;continue;elseXsorted(:,n) = x2;X = Xsorted;continue;endelseif fx2 < XS(n-1)Xsorted(:,n) = x2;X = Xsorted;continue;elseif fx2 < XS(n)Xsorted(:,n) = x2;endx4 = px + beta*(Xsorted(:,n) - px); %中心点压缩fx4 = subs(f,var,x4);FNnew = subs(f,var,Xsorted(:,n));if fx4 < FNnewXsorted(:,n) = x4;X = Xsorted;continue;elsex0 = Xsorted(:,1);for i=1:nXsorted(:,j) = x0 + sita*(Xsorted(:,j) - x0);endendendendendX = Xsorted;endminf = subs(f,var,x);format short;M函数文件的运行结果如下:x = 5.00025.9999mf =1.8370e-007================================================================= 例4-7 MA TLAB实现,用M函数文件形式求解:syms t s;f=t^2+2*s^2-4*t-2*t*s;p=[-1 0; 0 1];[x,mf]=minPowell(f,[1 1],p,[t s])Powell法函数文件minPowell如下function [x,minf] = minPowell(f,x0,P,var,eps)%目标函数:f;%初始搜索点:x0;%线性无关的初始向量组:p;%自变量向量:var;%精度:eps;%目标函数取最小值时的自变量:x;%目标函数的最小值:minf:format long;if nargin == 4eps = 1.0e-6;endn = length(var)+1;syms l;while 1y = zeros(size(P));y(:,1) = x0;for i=1:n-1 %在每个搜索方向上进行一维搜索yv = y(:,i) + l*P(:,i);fy = subs(f, var,yv);[a,b] = minJT(fy,0,0.1);tl = minPWX(fy,a,b);y(:,i+1) = y(:,i) + tl*P(:,i);endP(:,n) = y(:,n) - y(:,1);if norm(P(:,n)) <= eps %精度判断x = y(:,n);break;elsefor j=1:nFY(j) = subs(f, var,y(:,j));endmaxDF = -inf;m = 0;for j=1:n-1 %求出算法中对应的m df = FY(j) - FY(j+1);if df > maxDFmaxDF = df;m = j+1;endendtmpF = subs(f, var,2*y(:,n)-y(:,1));fl = FY(1) - 2*FY(n) + tmpF;if fl<2*maxDFyv = y(:,n) + l*P(:,n);fy = subs(f, var,yv);[a,b] = minJT(fy,0,0.1);tl = minPWX(fy,a,b);x0 = y(:,n) + tl*P(:,n);P(:,m:(n-1)) = P(:,(m+1):n); %重新设置搜索方向elsex0 = y(:,n);endendendminf = subs(f,var,x);format short;M函数文件的运行结果如下:x = 4.00002.0000mf = -8.0000====================================================================== 例4-8 MA TLAB实现,用M函数文件形式求解:syms x1 x2f=x1^2+4*x2^2;[x,mf]=minDFP(f,[1 1],[x1 x2])DF P法函数文件minDFP如下function [x,minf] = minDFP(f,x0,var,eps)%目标函数:f:%初始点:x0;%自变量向量:var;%精度:eps;%目标函数取最小值时的自变量:x;%目标函数的最小值:minf;format long;if nargin == 3eps = 1.0e-6;endx0 = transpose(x0);n = length(var);syms l;H = eye(n,n);gradf = jacobian(f,var);v0 = subs(gradf,var,x0);p = -H*transpose(v0);k = 0;while 1v = subs(gradf,var,x0);tol = norm(v);if tol<=epsx = x0;break;endy = x0 + l*p;yf = subs(f,var,y);[a,b] = minJT(yf,0,0.1);xm = minPWX(yf,a,b); %用抛物线法进行一维搜索 x1 = x0 + xm*p;vk = subs(gradf,var,x1);tol = norm(vk);if tol<=epsx = x1;break;endif k+1==n %重新迭代x0 = x1;continue;elsedx = x1 - x0;dgf = vk - v;dgf = transpose(dgf);dxT = transpose(dx);dgfT = transpose(dgf);mdx = dx*dxT;mdgf = dgf*dgfT;fz = H*(dgf*(dgfT*H));H = H + mdx/(dxT*dgf)-inv(dgfT*(H*dgf))*fz; %校正公式 p = -H*transpose(vk);k = k+1;x0 = x1;endendminf = subs(f,var,x);format short;M 函数文件的运行结果如下:x = 1.0e-015 *⎪⎪⎭⎫ ⎝⎛-0555.01110.0 mf = 2.4652e-032==============================例4-10 用fminsearch 函数求解函数5)1(213)2(1)(2221-+-+--=x x X f 的极值。
第九讲 最优化问题的MATLAB求解

得:x = 0.6111 -0.3055 可事先绘制图像,来获得初始搜索点。 可事先绘制图像,来获得初始搜索点。首先较为随意 地给出一个绘图区域: 地给出一个绘图区域: >>x=0:0.2:5;y=0:0.2:5;[xx,yy]=meshgrid(x,y); >>zz=(xx.^2-2*xx).*exp(-xx.^2-yy.^2-xx.*yy);mesh(xx,yx —— 自变量,是由若干分量组成的列向量; 自变量,是由若干分量组成的列向量; f —— x的各分量前的系数构成的向量; 的各分量前的系数构成的向量; 的各分量前的系数构成的向量 f﹒x —— 目标函数(即求该函数的最小值),是 f 与 x 目标函数(即求该函数的最小值), ),是 ﹒ 的数量积。 数量积。
0.2
0
-0.2
-0.4
-0.6 6 4 2 0 1 0 3 2 5 4
根据上图,重新确定一个更为合理的绘图区域: 根据上图,重新确定一个更为合理的绘图区域: >>x=-3:0.2:3;y=-3:0.2:3;[xx,yy]=meshgrid(x,y); >>zz=(xx.^2-2*xx).*exp(-xx.^2-yy.^2-xx.*yy);mesh(xx,yy,zz)
反映求解过程中的迭代次数等信息 该值若为正,说明求解成功, 该值若为正,说明求解成功,否则表明求解 出现问题。 出现问题。 目标函数的最优解 求解结果(令目标函数取得最优解的 ) 求解结果(令目标函数取得最优解的x)
最简形式: 最简形式: x=linprog (f, A,B,C,D, xm, xM, x0) 注意:各参数的参数名可以变, 注意:各参数的参数名可以变,但位置必须 跟上述格式对牢。若相应的约束不存在, 跟上述格式对牢。若相应的约束不存在,应该用 空矩阵[ 占位 占位。 空矩阵 ]占位。 由于输入变量较多且往往较复杂, 由于输入变量较多且往往较复杂,一般需事 先定义。 先定义。
利用MATLAB求解无约束优化问题 ppt课件

[3] fminunc为中型优化算法的步长一维搜索提供了两种算法,
由options中参数LineSearchType控制:
LineSearchType=’quadcubic’(缺省值),
混合的二次和三次多项式插值;
LineSearchType=’cubicpoly’,三次多项式插值
利用MATLAB求解无约束
优化问题
3
例1 min f(x)=(4x12+2x22+4x1x2+2x2+1)*ex1
1、编写M-文件 fun.m: function f = fun (x) f = exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1);
2、输入M文件wliti.m如下: x0 = [-1, 1]; x=fminunc(‘fun’,x0); y=fun(x)
[2] fminunc为中型优化算法的搜索方向提供了3种算法,
由 options中的参数HessUpdate控制: HessUpdate=’bfgs’(默认值),拟牛顿法的BFGS公式; HessUpdate=’dfp’,拟牛顿法的DFP公式; HessUpdate=’steepdesc’,最速下降法
利用MATLAB求解无约束优化问题
matlab解多元函数无约束优化问题
标准型为:min F(X)
命令格式为: [x,fval,exitflag,output]= fminunc(fun, x0 ,options);
或 [x,fval,exitflag,output]= fminsearch(fun, x0 ,options);
(3)比较各种算法主程序compare.m
matlab无约束最优化函数有约束最优化函数

有约束最优化问题的一般描述为 min f (x),其中 xs.t.G ( x)0
x [x1, x2,L , xn ],该数学表示的含义即求取一组x,使得目标 函数f (x)为最小,且满足约束条件G(x) 0.记号s.t.是英文 suject to的缩写,表示x要满足后面的约束条件。 约束条件可以进一步细化为: 1.线性约束不等式:Ax b 2.线性等式约束:Aeq x beq 3.非线性不等式约束:Cx 0 4.非线性等式约束:Ceq 0 5.x的下界和上界:Lbnd x Ubnd
无约束最优化函数 有约束最优化函数
1 无约束最优化问题 2 有约束最优化问题 3 注意
1 无约束最优化问题 2 有约束最后化问题 3 注意
无约束优化问题的一般描述为:min f (x) x
其中x [x1, x2,L xn ]T ,该数学表达式的含义即求一组x, 使目标函数f (x)为最小。
fminunc命令与fminsearch都只能用于解决实数问题,求 得的结果也为局部最小值。
不同之处在于fminunc求极值目标函数必须连续; fminsearch求解的效率较低,但其可以求解非连续函数 极值。
1 无约束最优化问题最优化问题的一般描述为 min f (x),其中 xs.t.G ( x)0
1 无约束最优化问题 2 有约束最优化问题 3 注意
1 无约束最优化问题 2 有约束最优化问题 3 注意
fminsearch fminunc fminbnd fmincon
最大值问题 极小值问题
谢谢观赏
x [x1, x2,L , xn ],该数学表示的含义即求取一组x,使得目标 函数f (x)为最小,且满足约束条件G(x) 0.记号s.t.是英文 suject to的缩写,表示x要满足后面的约束条件。 约束条件可以进一步细化为: 1.线性约束不等式:Ax b 2.线性等式约束:Aeq x beq 3.非线性不等式约束:Cx 0 4.非线性等式约束:Ceq 0 5.x的下界和上界:Lbnd x Ubnd
用Matlab求解非线性规划

用Matlab 求解非线性规划1.无约束优化问题)(min x f n Rx ∈,其中向量x 的n 个分量i x 都是决策变量,称)(x f 目标函数。
用Matlab 求解:先建立函数文件mbhs.m ,内容是)(x f 的表达式;再回到Matlab 命令区输入决策变量初值数据x0,再命令[x,fmin]=fminunc(@mbhs,x0) 如:)32(m in 22212x x R x +∈的最优解是.)0,0(T x = 用Matlab 计算,函数文件为 function f=mbhs(x)f=2*x(1)^2+3*x(2)^2;再输入初值 x0=[1;1]; 并执行上述命令,结果输出为 x =? fmin =? 略。
2.约束优化问题.),,...,2,1(,0)(),,...,2,1(,0)(..)(min U x L m i x h p i x g t s x f i i Rx n ≤≤===≤∈其中:向量x 的n 个分量i x 都是决策变量,称)(x f 目标函数、)(x g i 等式约束函数、)(x h i 不等式约束函数、L 下界、U 上界。
用Matlab 求解:先把模型写成适用于Matlab 的标准形式.,0)(,0)(,,..)(min U x L x h x g beq x Aeq b Ax t s x f n Rx ≤≤=≤=≤∈ 约束条件中:把线性的式子提炼出来得前两个式子;后三个式子都是列向量。
(如:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡===⨯⨯)()()([],[],,,11262x g x g x g beq Aeq b A p )再建立两个函数文件:目标函数mbhs.m ;约束函数yshs.m再回到Matlab 命令区,输入各项数据及决策变量初值数据x0,执行命令[x,fmin]=fmincon(@mbhs,x0,A,b,Aeq,beq,L,U,@yshs)例:单位球1222≤++z y x 内,曲面xy y x z 1.05.022--+=的上方,平面008.0=-++z y x 之上(不是上面),满足上述三个条件的区域记为D ,求函数)1cos()sin(2-+-+-z e z y x e xy xyz 在D 上的最大值、最大值点。
matlab的minimize 函数

matlab的minimize 函数
`minimize` 函数是 MATLAB 优化工具箱中的函数,用于求解无约束优化问题。
这个函数尝试找到函数的最小值,基于提供的初始点、梯度或Hessian 矩阵。
基本语法是:
```matlab
x = minimize(fun,x0)
```
其中:
`fun` 是要最小化的目标函数。
`x0` 是初始点。
返回的 `x` 是最优解。
如果你想使用梯度或Hessian矩阵,你可以使用以下语法:
```matlab
x = minimize(fun,x0,options)
```
其中 `options` 是一个结构体,可以包含梯度函数和Hessian矩阵。
为了使用 `minimize` 函数,你需要安装并加载 MATLAB 的优化工具箱。
你可以使用以下命令检查是否已安装该工具箱:
```matlab
ver('optimtool')
```
如果没有安装,你可以通过 MATLAB 的 "Add-Ons" 菜单来安装。
用Matlab解无约束优化问题
返回
用Matlab解无约束优化问题
1. 一元函数无约束优化问题:
min f(x)
x1 ≤ x ≤ x 2
常用格式如下: (1)x= fminbnd (fun,x1,x2) (2)x= fminbnd (fun,x1,x2 ,options) (3)[x,fval]= fminbnd(...) (4)[x,fval,exitflag]= fminbnd(...) (5)[x,fval,exitflag,output]= fminbnd(...) 其中(3)、(4)、(5)的等式右边可选用(1)或 (2)的等式右边。 函数fminbnd的算法基于黄金分割法和二次插值法,它 要求目标函数必须是连续函数,并可能只给出局部最优 解。
fval
exitflag
output
所
Options中常用的几个参数的名称、含义、取值如下:
(1) Display: 显示水平.取值为’off’时,不显示输出; 取值为’iter’时,显示每次迭代的信息;取值为’final’时, 显示最终结果.默认值为’final’. (2) MaxFunEvals: 允许进行函数评价的最大次数,取 值为正整数. (3) MaxIter: 允许进行迭代的最大次数,取值为正整数.
3. 优化函数的输出变量下表:
变量 x 描 述 由优化函数求得的值.若exitflag>0,则x 为解;否则,x不是最终解,它只是迭代制止 时优化过程的值 解x处的目标函数值 描述退出条件: exitflag>0,表目标函数收敛于解x处 exitflag=0,表已达到函数评价或迭代 的最大次数 exitflag<0,表目标函数不收敛 包含优化结果信息的输出结构. Iterations:迭代次数 Algorithm:所采用的算法 FuncCount:函数评价次数 调用函数 所有优化函数 linprog,quadprog,fgoalattain, fmincon,fminimax,lsqcurvefit, lsqnonlin, fminbnd
用Matlab解无约束优化问题24页PPT

36、如果我们国家的法律中只有某种 神灵, 而不是 殚精竭 虑将神 灵揉进 宪法, 总体上 来说, 法律就 会更好 。—— 马克·吐 温 37、纲纪废弃之日,便是暴政兴起之 时。— —威·皮 物特
38、若是没有公众舆论的支持,法律 是丝毫 没有力 量的。 ——菲 力普斯 39、一个判例造出另一个判例,它们 迅速累 聚,进 而变成 法律。 ——朱 尼厄斯
40、人类法律,事物有规律,这是不 远躺在泥坑里的人,才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭,生活刹那间变成了一片黑暗。——普列姆昌德 33、希望是人生的乳母。——科策布 34、形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍,就是一下子不要学很多。——洛克
工程计算MATLAB_优化设计_方法函数无约束最优化

(2)梯度法 在函数的导数可求的情况下,梯度法是一种更 优的方法。 常见的梯度法有最速下降法、Newton法、 Marquart法、共轭梯度法和拟牛顿法(QuasiNewton method)等。 在所有这些方法中,用的最多的是拟牛顿法
33/45
5.2 无约束最优化问题
5.2 无约束最优化问题
5.2.2 单变量最小化问题 2. 相关函数
(1)fminbnd 功能:找到固定区间内单变量函数的最小值。 语法: [x,fval] = fminbnd(...) 返回解x处目标函数的值。 [x,fval,exitflag] = fminbnd(...) 返回exitflag值描述fminbnd函数的退出条件。 [x,fval,exitflag,output] = fminbnd(...) 返回包含优化信息的结构输出。
13/45
5.1 优化函数
5.1.3 @(函数句柄)函数
>> x=0:0.001:1; >> y=humps(x); >> plot(x,y); >> .1.3 @(函数句柄)函数
>> x=fminbnd(@humps,0.3,1) x= 0.6370
15/45
28/45
2. 相关函数
5.2 无约束最优化问题
5.2.2 单变量最小化问题 2. 相关函数
(2)实例 例1:在区间(0,2π)上求函数sin(x)的最小值
>> x=fminbnd(@sin,0,2*pi)
x= 4.7124 >> y=sin(x) y= -1.0000
29/45
5.2 无约束最优化问题
