立体几何中的最值问题(一)

合集下载

高中数学立体几何中的最值问题专题辅导

高中数学立体几何中的最值问题海红楼立体几何主要研究空间中点、线、面之间的位置关系，与空间图形有关的线段、角、体积等最值问题常常在试题中出现。

下面举例说明解决这类问题的常用方法。

一、运用变量的相对性求最值例1. 在正四棱锥S-ABCD 中，SO ⊥平面ABCD 于O ，SO=2，底面边长为2，点P 、Q 分别在线段BD 、SC 上移动，则P 、Q 两点的最短距离为（）A. 55B. 552C. 2D. 1解析：如图1，由于点P 、Q 分别在线段BD 、SC 上移动，先让点P 在BD 上固定，Q 在SC 上移动，当OQ 最小时，PQ 最小。

过O 作OQ ⊥SC ，在Rt △SOC 中，552=OQ 中。

又P 在BD 上运动，且当P 运动到点O 时，PQ 最小，等于OQ 的长为552，也就是异面直线BD 和SC 的公垂线段的长。

故选B 。

图1二、定性分析法求最值例2. 已知平面α//平面β，AB 和CD 是夹在平面α、β之间的两条线段。

AB ⊥CD ，AB=3，直线AB 与平面α成30°角，则线段CD 的长的最小值为______。

解析：如图2，过点B 作平面α的垂线，垂足为O ，连结AO ，则∠BAO=30°。

过B 作BE//CD 交平面α于E ，则BE=CD 。

连结AE ，因为AB ⊥CD ，故AB ⊥BE 。

则在Rt △ABE 中，BE=AB ·tan ∠BAE ≥AB ·tan ∠BAO=3·tan30°=3。

故3≥CD 。

图2三、展成平面求最值例3. 如图3-1，四面体A-BCD 的各面都是锐角三角形，且AB=CD=a ，AC=BD=b ，AD=BC=c 。

平面α分别截棱AB 、BC 、CD 、DA 于点P 、Q 、R 、S ，则四边形PQRS 的周长的最小值是（）A. 2aB. 2bC. 2cD. a+b+c图3-1解析：如图3-2，将四面体的侧面展开成平面图形。

几何中的最值问题

几何中的最值问题作为一门重要的数学学科，几何中有许多重要的概念和方法，其中最值问题是一个广泛研究的内容。

在几何中，最值问题是指在某些条件下，某个几何量（如长度、面积、体积等）的最大值或最小值问题。

本文将从不同角度介绍几何中的最值问题及其应用。

一、最值问题的基础概念在几何问题中，最值问题最常见的便是一些面积、长度和体积的最值问题。

最常见的方法是使用微积分的极值定理，通过计算导数为0的点来找到函数的最大值和最小值。

此外，还有最大和最小的边界问题。

这些问题需要考虑的是给定条件下的最大可行解或最小可行解。

例如，给定一个面积固定的矩形，我们需要求出其长度和宽度的最大或最小值。

这些问题与微积分密切相关，但在解决这些问题时需要更多的几何知识和直觉。

二、平面几何中的最值问题在平面几何中，最值问题通常涉及三角形、四边形和圆形等形状。

这些形状的特性可以用来求解最值问题，通常需要使用各种几何知识和技巧。

例如，对于一个给定面积的三角形，在其周长恒定的情况下，需要求出该三角形的最大或最小长度。

为解决这类问题，我们可以利用三角形的海涅定理或余弦定理，通过微积分的极值定理得到最优解。

对于圆形，最值问题可能涉及到面积和周长问题，这些需要用到圆相关的特点和公式，如半径、直径、周长和面积等，通常需要通过微积分的方法求解。

另一方面，对于四边形最值问题，我们需要利用它们的对角线和相邻边的关系来解决，这通常需要将四边形划分为三角形或矩形来计算。

三、空间几何中的最值问题在空间几何中，最值问题通常涉及立体体积，包括长方体、正方体、棱锥和棱柱等。

这些问题需要利用空间几何的特点和公式来求解，常用的方法包括微积分的极值定理和立体几何的体积计算公式。

例如，对于一个矩形长方体，在其表面积固定的情况下，需要求出其有最大或最小的体积。

如果我们设该矩形长方体的长、宽和高分别为x、y和z，那么该矩形长方体的体积可以表示为V(x,y,z)=xyz。

通过微积分的方法，可以证明只有当x=y=z时，该方体的体积最大。

立体几何中线段长度的最值问题

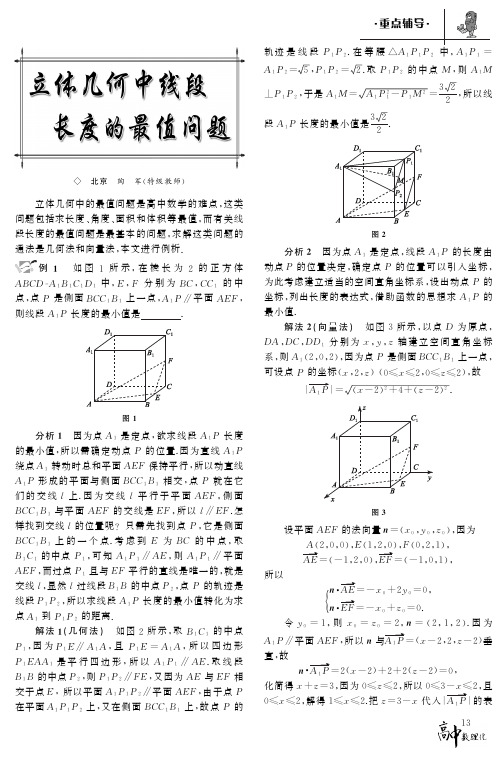
重点辅导Җ㊀北京㊀陶㊀军(特级教师)㊀㊀立体几何中的最值问题是高中数学的难点,这类问题包括求长度㊁角度㊁面积和体积等最值,而有关线段长度的最值问题是最基本的问题,求解这类问题的通法是几何法和向量法,本文进行例析．例１㊀如图１所示,在棱长为２的正方体A B C D ＧA １B １C １D １中,E ,F 分别为B C ,C C １的中点,点P 是侧面B C C １B １上一点,A １P ʊ平面A E F ,则线段A １P 长度的最小值是．图１分析１㊀因为点A １是定点,欲求线段A １P 长度的最小值,所以需确定动点P 的位置．因为直线A １P 绕点A １转动时总和平面A E F 保持平行,所以动直线A １P 形成的平面与侧面B C C １B １相交,点P 就在它们的交线l 上．因为交线l 平行于平面A E F ,侧面B C C １B １与平面A E F 的交线是E F ,所以l ʊE F ．怎样找到交线l 的位置呢?只需先找到点P ,它是侧面B C C １B １上的一个点．考虑到E 为B C 的中点,取B １C １的中点P １,可知A １P １ʊA E ,则A １P １ʊ平面A E F ,而过点P １且与E F 平行的直线是唯一的,就是交线l ,显然l 过线段B １B 的中点P ２,点P 的轨迹是线段P １P ２,所以求线段A １P 长度的最小值转化为求点A １到P １P ２的距离．解法１(几何法)㊀如图２所示,取B １C １的中点P １,因为P １E ʊA １A ,且P １E ＝A １A ,所以四边形P １E A A １是平行四边形,所以A １P １ʊA E ．取线段B １B 的中点P ２,则P １P ２ʊF E ,又因为A E 与E F 相交于点E ,所以平面A １P １P ２ʊ平面A E F ,由于点P 在平面A １P １P ２上,又在侧面B C C １B １上,故点P 的轨迹是线段P １P ２．在等腰әA １P １P ２中,A １P １＝A １P ２＝５,P １P ２＝２．取P １P ２的中点M ,则A １M ʅP １P ２,于是A １M ＝A １P ２１－P １M ２＝３２２,所以线段A １P 长度的最小值是３２２．图２分析２㊀因为点A １是定点,线段A １P 的长度由动点P 的位置决定,确定点P 的位置可以引入坐标,为此考虑建立适当的空间直角坐标系,设出动点P 的坐标,列出长度的表达式,借助函数的思想求A １P 的最小值．解法２(向量法)㊀如图３所示,以点D 为原点,D A ,D C ,D D １分别为x ,y ,z 轴建立空间直角坐标系,则A １(２,０,２),因为点P 是侧面B C C １B １上一点,可设点P 的坐标(x ,２,z )(０ɤx ɤ２,０ɤz ɤ２),故|A １P ң|(x －２)２＋４＋(z －２)２．图３设平面A E F 的法向量n ＝(x ０,y ０,z ０),因为A (２,０,０),E (１,２,０),F (０,２,１),A E ң＝(－１,２,０),E F ң＝(－１,０,１),所以n A E ң＝－x ０＋２y ０＝０,n E F ң＝－x ０＋z ０＝０．{令y ０＝１,则x ０＝z ０＝２,n ＝(２,１,２)．因为A １P ʊ平面A E F ,所以n 与A １P ң＝(x －２,２,z －２)垂直,故n A １P ң＝２(x －２)＋２＋２(z －２)＝０,化简得x ＋z ＝３,因为０ɤz ɤ２,所以０ɤ３－x ɤ２,且０ɤx ɤ２,解得１ɤx ɤ２．把z ＝３－x 代入|A １P ң|的表３１重点辅导达式,整理得|A １P ң|＝２(x －３２)２＋９２,x ɪ[１,２],故当x ＝３２时,|A １P ң|取得最小值３２２．例２㊀如图４所示,在棱长为２的正方体A B C D ＧA １B １C １D １中,E 为B C 的中点,点P 在线段D １E 上,点P 到直线C C １的距离的最小值为．图４分析１㊀求点P 到直线C C １的距离的最小值,就是找点P 到直线C C １的垂线段P Q 长度的最小值．求线段P Q 的长度涉及空间上两个动点长度的距离问题,不易处理．注意到C C １ʅ平面A B C D ,P Q ʅC C １,则P Q ʊ平面A B C D ．因此,我们可以把P Q 正投影在平面A B C D 上,点P 在平面A B C D 上的正投影H 落在线段D E 上,点Q 在平面A B C D 上的正投影是点C ,于是P Q ＝H C ,求P Q 的最小值转化为在平面A B C D 上求定点C 与线段D E 上的动点H 之间距离的最小值,就是求定点C 到D E 的距离．解法１(几何法)㊀如图５所示,过点P 作P Q ʅC C １,Q 为垂足,因为C C １ʅ平面A B CD ,所以P Q ʊ平面A B C D ,过点P 作PH ʅDE ,H 为垂足,则PH ʅ平面A B C D ,所以PH ʊQ C ,且P Q ʊH C ,Q C ʅH C ,故四边形P Q C H 是矩形,P Q ＝H C ,在R t әC D E 中,当C H ʅD E 时,C H 长度最小,因为C E ＝１,C D ＝２,D E ＝５,所以C H ＝１ˑ２５＝２５５,故点P 到直线C C １的距离的最小值为２５５．图５分析２㊀设点P 到直线C C １的距离为P Q ,因为P ,Q 分别在线段D １E 和C C １上,故可以引入两个变量控制点P ,Q 的位置．设E P ң＝λE D １ң(０ɤλɤ１),C Q ң＝μC C １ң(０ɤμɤ１),根据正方体的特殊性建立适当的空间直角坐标系,利用向量的坐标运算推出点P ,Q 的坐标,进而用λ,μ表示P Q ң,利用P Q ң C C １ң＝０找出λ,μ的关系式,代入P Q 长度的表达式,转化为一元函数求最值．解法２(向量法)㊀如图６所示,以D 为原点,D A ,D C ,D D １分别为x ,y ,z 轴建立空间直角坐标系,则D １(０,０,２),E (１,２,０),C １(０,２,２),C (０,２,０),E D １ң＝(－１,－２,２),由于点P 在线段D １E 上,可设E P ң＝λE D １ң(０ɤλɤ１),即E P ң＝(－λ,－２λ,２λ),由此得点P 的坐标为(,,)．图６过点P 作P Q 垂直于C C １,Q 为垂足,设点Q 的坐标(０,２,m ),P Q ң＝(λ－１,２λ,m －２λ),C C １ң＝(０,０,２),因为P Q ңʅC C １ң,所以P Q ң C C １ң＝０,即２(m －２λ)＝０,m ＝２λ,P Q ң＝(λ－１,２λ,０),|P Q ң|＝(λ－１)２＋(２λ)２＋０２＝５(λ－１５)２＋４５,λɪ[０,１]．当λ＝１５,P Q 取得最小值２５５．综上所述,利用几何法求线段长度的最值,要点是先用立体几何知识确定动点的轨迹,再用平面几何知识求最值;利用向量法求线段长度的最值,要点是建立适当的坐标系,设出动点坐标,建立线段长度的表达式,借助向量知识把题目中的几何条件合理转化为代数条件,找到动点坐标的关系,把线段长度的表达式转化为一元函数,用函数的思想求最值．(作者单位:北京市怀柔区第一中学)４１。

高数140招之71-立体几何中的最值问题的解题策略

一、与线段长有关的最值问题【典例1】在直三棱柱ABC A 1B 1C 1中，底面为直角三角形， ∠ACB ＝90°，AC ＝6，BC ＝CC 1＝2，P 是BC 1上一动点，如图所示，则CP ＋PA 1的最小值为________．[解析]PA 1在平面A 1BC 1内，PC 在平面BCC 1内，将其铺平后转化为平面上的问题．铺平平面A 1BC 1，平面BCC 1，如图所示，计算得A 1B ＝AB 1＝210，BC 1＝2.又A 1C 1＝6，故△A 1BC 1是∠A 1C 1B ＝90°的直角三角形．设P 是BC 1上任一点，CP ＋PA 1≥A 1C ，即当A 1，P ，C 三点共线时，CP ＋PA 1有最小值．在△A 1C 1C 中，由余弦定理得A 1C ＝62＋ 2 2－2×6×2×cos 135°＝52，故(CP ＋PA 1)min ＝52.【变式练习】1.如图所示，在棱长为1的正方体ABCD A 1B 1C 1D 1的面对角线A 1B 上存在一点P ，使得AP ＋D 1P 取得最小值，则此最小值为()A ．2B.6＋22C ．2＋2 D.2＋2解析：选D将△A 1AB 与△A 1BD 1放在同一平面内，如图所示．连接AD 1，则AD 1为AP ＋D 1P 的最小值．因为AA 1＝A 1D 1＝1，∠AA 1D 1＝90°＋45°＝135°，所以由余弦定理得AD 1＝AA 21＋A 1D 21－2×AA 1×A 1D 1×cos 135°＝2＋2. 2．某三棱锥的三视图如图所示，且三个三角形均为直角三角形，则xy 的最大值为________．解析：由三视图知三棱锥如图所示，底面ABC 是直角三角形，AB ⊥BC ， PA ⊥平面ABC ，BC ＝27， PA 2＋y 2＝102，(27)2＋PA 2＝x 2，因此xy ＝x 102－[x 2－ 27 2] ＝x128－x 2≤x 2＋ 128－x 22＝64，当且仅当x 2＝128－x 2，即x ＝8时取等号，因此xy 的最大值是64.3．已知直三棱柱ABC A 1B 1C 1的侧棱长为6，且底面是边长为2的正三角形，用一平面截此棱柱，与侧棱AA 1，BB 1，CC 1分别交于三点M ，N ，Q ，若△MNQ 为直角三角形，则该直角三角形斜边长的最小值为()A ．22B ．3C ．23D ．4解析：选C 如图，不妨设N 在B 处，设AM ＝h ，CQ ＝m ，则MB 2＝h 2＋4，BQ 2＝m 2＋4，MQ 2＝(h －m )2＋4，由MB 2＝BQ 2＋MQ 2，得m 2－hm ＋2＝0.Δ＝h 2－8≥0⇒h 2≥8，该直角三角形斜边MB ＝4＋h 2≥23，故该直角三角形斜边长的最小值为23.故选C.二、与面积有关的最值问题【典例2】已知正四面体S ABC 的棱长为1，如果一个高为36的长方体能在该正四面体内任意转动，则该长方体的长和宽形成的长方形的面积的最大值为________．解析：如图，易知正四面体S ABC 的内切球的球心O 必在高线SH 上，延长AH 交BC 于点D ，则D 为BC 的中点，连接SD ，设内切球切SD 于点E ，连接AO .因为H 是正三角形ABC 的中心，所以AH ∶DH ＝2∶1.易得Rt △OAH ∽Rt △DSH ，所以OA OH ＝DSDH＝3，可得OA ＝3OH ＝SO ，因此SH ＝4OH ，可得内切球的半径R ＝OH ＝14SH .因为正四面体S ABC 的棱长为1，所以在Rt △DSH中，DS ＝SH 2＋DH 2＝ 4R 2＋(13×32)2＝32，解得R 2＝124.要满足一个高为36的长方体能在该正四面体内任意转动，则长方体的体对角线长不超过正四面体内切球的直径，设该长方体的长和宽分别为x ，y ，其长和宽形成的长方形的面积为S ，则4R 2≥(36)2＋x 2＋y 2，所以x 2＋y 2≤112，所以S ＝xy ≤x 2＋y 22≤124，当且仅当x ＝y ＝612时等号成立，即该长方体的长和宽形成的长方形的面积的最大值为124. 【变式练习】1.(2018·全国卷Ⅰ)已知正方体的棱长为1，每条棱所在直线与平面α所成的角都相等，则α截此正方体所得截面面积的最大值为() A ．334B ．233C ．324D ．32【答案】A【解析】如图所示，在正方体ABCD A 1B 1C 1D 1中，平面AB 1D 1与棱A 1A ，A 1B 1，A 1D 1所成的角都相等，又正方体的其余棱都分别与A 1A ，A 1B 1，A 1D 1平行，故正方体ABCD A 1B 1C 1D 1的每条棱所在直线与平面AB 1D 1所成的角都相等．如图所示，取棱AB ，BB 1，B 1C 1，C 1D 1，D 1D ，DA 的中点E ，F ，G ，H ，M ，N ，则正六边形EFGHMN 所在平面与平面AB 1D 1平行且面积最大，此截面面积为S 正六边形EFGHMN ＝6×12×22×22×sin 60°＝334.故选A.2．已知球O 是正三棱锥A BCD 的外接球，BC ＝3，AB ＝23，点E 在线段BD 上，且BD ＝3BE ，过点E 作球O 的截面，则所得截面中面积最小的截面圆的面积是________．【答案】2π【解析】如图，设△BCD 的中心为点O 1，球O 的半径为R ，则A ，O ，O 1三点共线．连接O 1D ，O 1E ，OD ，OE ，则O 1D ＝3，AO 1＝AD 2－O 1D 2＝3.在Rt △OO 1D 中，R 2＝3＋(3－R )2，即R ＝2，所以OO 1＝1.在△O 1DE 中，DE ＝23BD ＝2，∠O 1DE ＝30°，所以由余弦定理得O 1E ＝3＋4－2×3×2× cos 30°＝1.所以OE ＝2.过点E 作圆O 的截面，当截面与OE 垂直时，截面的面积最小，此时截面圆的半径为22－（2）2＝2，所以截面圆的面积为2π.3．在长方体ABCD A 1B 1C 1D 1中，AB ＝AD ＝4，AA 1＝2.过点A 1作平面α与AB ，AD 分别交于M ，N 两点，若AA 1与平面α所成的角为45°，则截面A 1MN 面积的最小值是________．【答案】2π【解析】如图，过点A 作AE ⊥MN ，连接A 1E ，因为A 1A ⊥平面ABCD ，所以A 1A ⊥MN ，所以MN ⊥平面A 1AE ，所以A 1E ⊥MN ，平面A 1AE ⊥平面A 1MN ，所以∠AA 1E 为AA 1与平面A 1MN 所成的角，所以∠AA 1E ＝45°，在Rt △A 1AE 中，因为AA 1＝2，所以AE ＝2，A 1E ＝22，在Rt △MAN 中，由射影定理得ME ·EN ＝AE 2＝4，由基本不等式得MN ＝ME ＋EN ≥2ME ·EN ＝4，当且仅当ME ＝EN ，即E 为MN 的中点时等号成立，所以截面A 1MN 面积的最小值为12×4×22＝42.三、与体积有关的最值问题【典例3】(2017·全国卷Ⅰ)如图，圆形纸片的圆心为O ，半径为5 cm ，该纸片上的等边三角形ABC 的中心为O .D ，E ，F 为圆O 上的点，△DBC ，△ECA ，△FAB 分别是以BC ，CA ，AB 为底边的等腰三角形．沿虚线剪开后，分别以BC ，CA ，AB 为折痕折起△DBC ，△ECA ，△FAB ，使得D ，E ，F 重合，得到三棱锥．当△ABC 的边长变化时，所得三棱锥体积(单位：cm 3)的最大值为________．【答案】415【解析】如图，连接OD 交BC 于点G ，由题意知，OD ⊥BC .易得OG ＝36BC ，设OG ＝x ，则BC ＝23x ，DG ＝5－x ， S △ABC ＝12×23x ×3x ＝33x 2，故所得三棱锥的体积V ＝13×33x 2× 5－x 2－x 2＝3x 2×25－10x ＝3×25x 4－10x 5.令f (x )＝25x 4－10x 5，x ∈(0，52)，则f ′(x )＝100x 3－50x 4，令f ′(x )＞0，即x 4－2x 3＜0，得0＜x ＜2；令f ′(x )＜0，得2＜x ＜52，则当x ∈(0，52)时，f (x )≤f (2)＝80， ∴V ≤3×80＝415.∴所求三棱锥的体积的最大值为415.【变式练习】1．(2018·全国卷Ⅲ)设A ，B ，C ，D 是同一个半径为4的球的球面上四点，△ABC 为等边三角形且其面积为93，则三棱锥D ABC 体积的最大值为()A ．123B ．183C ．243D ．543【答案】B【解析】由等边△ABC 的面积为93，可得34AB 2＝93，所以AB ＝6，所以等边△ABC的外接圆的半径为r ＝33AB ＝23.设球的半径为R ，球心到等边△ABC 的外接圆圆心的距离为d ，则d ＝R 2－r 2＝16－12＝2.所以三棱锥D ABC 高的最大值为2＋4＝6，所以三棱锥D ABC 体积的最大值为13×93×6＝183.2．已知圆锥的侧面展开图是半径为3的扇形，则该圆锥体积的最大值为________．【答案】23π【解析】由题意得圆锥的母线长为3，设圆锥的底面半径为r ，高为h ，则h ＝9－r 2，所以圆锥的体积V ＝13πr 2h ＝13πr 29－r 2＝13π9r 4－r 6.设f (r )＝9r 4－r 6(r ＞0)，则f ′(r )＝36r 3－6r 5，令f ′(r )＝36r 3－6r 5＝6r 3(6－r 2)＝0，得r ＝6，所以当0＜r ＜6时，f ′(r )＞0，f (r )单调递增；当r ＞6时，f ′(r )＜0，f (r )单调递减，所以f (r )max ＝f (6)＝108，所以V max ＝13π×108＝23π.3．已知A ，B ，C 是球O 的球面上三点，且AB ＝AC ＝3，BC ＝33，D 为该球面上的动点，球心O 到平面ABC 的距离为球半径的一半，则三棱锥D ABC 体积的最大值为________．【答案】274【解析】如图，在△ABC 中， ∵AB ＝AC ＝3，BC ＝33， ∴由余弦定理可得cos A ＝32＋32－ 33 22×3×3＝－12，∴sin A ＝32.设△ABC 外接圆O ′的半径为r ，则3332＝2r ，得r ＝3.设球的半径为R ，连接OO ′，BO ′，OB ，则R 2＝(R 2)2＋32，解得R ＝23.由图可知，当点D 到平面ABC 的距离为32R 时，三棱锥D ABC 的体积最大，∵S △ABC ＝12×3×3×32＝934，∴三棱锥D ABC 体积的最大值为13×934×33＝274.4．如图，等腰梯形ABCD 中，AB ∥CD ，AD ＝AB ＝BC ＝1，CD ＝2，E 为CD 的中点，将△ADE 沿AE 折到△APE 的位置．(1)证明：AE ⊥PB ；(2)当四棱锥P ABCE 的体积最大时，求二面角A PE C 的余弦值．解：(1)证明：在等腰梯形ABCD 中，连接BD ，交AE 于点O ， ∵AB ∥CE ，AB ＝CE ，∴四边形ABCE 为平行四边形， ∴AE ＝BC ＝AD ＝DE ，∴△ADE 为等边三角形， ∴在等腰梯形ABCD 中，∠C ＝∠ADE ＝π3，BD ⊥BC ，∴BD ⊥AE .如图，翻折后可得OP ⊥AE ，OB ⊥AE ，又OP ⊂平面POB ，OB ⊂平面POB ，OP ∩OB ＝O ，∴AE ⊥平面POB ，∵PB ⊂平面POB ，∴AE ⊥PB .(2)当四棱锥P ABCE 的体积最大时，平面PAE ⊥平面ABCE .又平面PAE ∩平面ABCE ＝AE ，PO ⊂平面PAE ，PO ⊥AE ，∴OP ⊥平面ABCE .以O 为坐标原点，OE所在的直线为x 轴，OB 所在的直线为y 轴，OP 所在的直线为z轴，建立空间直角坐标系，由题意得，P(0，0，32)，E(12，0，0)，C(1，32，0)，∴PE―→＝(12，0，－32)，EC―→＝(12，32，0)，设平面PCE的法向量为n1＝(x，y，z)，则{·n1＝0，·n1＝0，)即{12x－32z＝0，12x＋32y＝0，)设x＝3，则y＝－1，z＝1，∴n1＝(3，－1，1)为平面PCE的一个法向量，易知平面PAE的一个法向量为n2＝(0，1，0)，cos n1，n2 ＝n1·n2|n1||n2|＝－11×5＝－55.由图知所求二面角APEC为钝角，∴二面角APEC的余弦值为－5 5 .[解题技法]立体几何中的最值问题的解题策略空间几何体中的某些对象，如点、线、面，在约束条件下运动，带动相关的线段长度、体积等发生变化，进而就有了面积与体积的最值问题.定性分析：在空间几何体的变化过程中，通过观察运动点的位置变化，确定其相关量的变化规律，进而发现相关面积或体积的变化规律，求得其最大值或最小值.定量分析：将所求问题转化为某一个相关量的问题，即转化为关于其中一个量的函数，求其最大值或最小值的问题．根据具体情况，有函数法、不等式法、三角函数法等多种方法可供选择.。

高中数学立体几何中的最值问题

高中数学立体几何中的最值问题在高中数学的学习中，立体几何一直是一个重点和难点，而其中的最值问题更是让许多同学感到头疼。

这类问题往往需要我们综合运用空间想象力、几何知识以及数学方法来求解。

接下来，让我们一起深入探讨立体几何中的最值问题。

一、常见类型及解法1、距离最值问题（1）两点间距离最值在立体几何中，求两点间距离的最值，常常需要我们将空间中的两点转化到同一平面内。

例如，在长方体中，求异面直线上两点的最短距离，就需要通过平移将其转化为共面直线，然后利用平面几何中的知识求解。

（2）点到直线距离最值求点到直线的距离最值时，通常要找到点在直线上的投影。

如果直线是某一平面的斜线，那么可以通过作垂线找到投影，再利用勾股定理计算距离。

（3）点到平面距离最值对于点到平面的距离最值，一般可以利用空间向量法。

先求出平面的法向量，然后通过向量的数量积来计算点到平面的距离。

2、面积最值问题（1）三角形面积最值在立体几何中，涉及三角形面积的最值问题，可能需要考虑三角形的边长关系或者角度大小。

例如，已知三角形的两边及其夹角，当夹角为直角时，面积最大。

（2）四边形面积最值对于四边形，如平行四边形，其面积可以表示为底边乘以高。

当底边长度固定时，高取得最大值时面积最大；或者当四边形的对角线相互垂直时，面积等于对角线乘积的一半。

3、体积最值问题（1）柱体体积最值对于柱体，如圆柱、棱柱，其体积等于底面积乘以高。

当底面积不变时，高最大则体积最大；反之，高最小时体积最小。

（2）锥体体积最值锥体体积为三分之一底面积乘以高。

在求解锥体体积最值时，需要关注底面积和高的变化。

二、例题分析例 1：在棱长为 2 的正方体 ABCD A1B1C1D1 中，E、F 分别是棱AB、BC 的中点，求点 A1 到直线 EF 的距离。

解：连接 A1C1、C1F、EF，因为 A1C1 平行于 EF，所以点 A1 到直线 EF 的距离等于点 A1 到直线 C1F 的距离。

立体几何的最值问题

立体几何最值问题立体几何是数学中的一个重要分支，它研究的是空间图形的性质和数量关系。

在立体几何中，我们经常遇到最值问题，即寻找某个量的最大值或最小值。

本文将介绍立体几何中最值问题的几个方面：1.立体几何位置关系立体几何中的位置关系是指空间中点、线、面之间的相对位置。

解决位置关系问题需要运用空间想象和逻辑推理。

在立体几何中最值问题中，位置关系往往与距离、角度等问题交织在一起，需要综合考虑多种因素。

2.立体几何中的距离立体几何中的距离是指空间中两点之间的直线距离，或者是点与线、线与面之间的距离。

在解决最值问题时，我们需要考虑如何利用距离公式来计算最短路径、最大距离等。

3.立体几何中的体积立体几何中的体积是指空间中封闭图形的体积，或者是两个平面图形之间的距离。

计算体积需要运用体积公式，而解决最大或最小面积问题则需要考虑如何调整图形的形状和大小。

4.立体几何中的最短路径立体几何中的最短路径问题是指寻找空间中两点之间的最短距离。

解决这类问题需要运用距离公式和几何定理，有时还需要借助对称、旋转等技巧。

5.立体几何中的最大/最小面积立体几何中的最大/最小面积问题通常涉及到平面图形在空间中的展开和折叠。

解决这类问题需要运用面积公式和平面几何定理，同时要注意图形的对称性和边长之间的关系。

6.立体几何中的角度问题立体几何中的角度问题是指空间中两条直线或两个平面之间的夹角。

解决这类问题需要运用角度公式和空间向量，同时要注意图形的对称性和边长之间的关系。

7.立体几何中的轨迹问题立体几何中的轨迹问题是指一个点或一条线在空间中按照一定规律移动所形成的轨迹。

解决这类问题需要运用轨迹方程和运动学原理，同时要注意轨迹的形状和大小随时间的变化情况。

立体几何中体积与面积最值问题的解法

1 声明本文首先以体积最大和面积最小的物体为例，讨论它们的最大/小值的解决方案。

接下来，给定指定的条件，通过拉格朗日型最优化技术对最大化体积最小化面积问题进行剖析。

最后，在说明了结果及其分析之后，讨论此类问题的求解思路及扩展性。

2 体积最大和面积最小的物体体积最大和面积最小的物体是立体几何的典型问题，它可以被看作是一种拉格朗日型优化问题，即在完成最大化体积和最小化面积的条件下寻求平衡点。

典型的体积最大和面积最小物体有球形、柱形、长方体等，也可以拓展到多边形，例如三角形等。

2.1 球形球形是一种立体几何体，其体积最大，面积最小，可以通过满足一定条件解决最大体积最小面积问题。

大体积最小面积问题的解法主要有两种：1) 根据体积最大的物体的方程，可以求出球的半径r，其中`V=4/3πr^3`；2) 因为球的周长是最长，周长和平面面积是相关的，因此可以求出球的周长C，从而计算球的面积`S=4πr^2`；这两个方程使用上面的公式，可以求出球的体积和面积。

根据拉格朗日型优化例子求出：当半径r=1时，体积最大，体积V=4/3πr^3=4.19，面积最小，面积S=4πr^2=12.57；当半径r=2时，体积最小，体积V=33.51，面积最大，面积S=50.27。

2.2 柱形柱形也是一种常用的立体几何物体，它的体积最大，面积最小的条件也可以满足。

柱的体积的最大/小值可以利用柱体的内切球的半径r求出，其中`V=πr²h`; 柱的面积最大/小值可以求出其元表面积`S=(2πrh+2πr²)`。

根据拉格朗日型优化例子求出：当半径r=1时，体积最大，体积V=πr²h=2.14，面积最小，面积S=2πr²+2πrh=10.30；当半径r=2时，体积最小，体积V=12.56，面积最大，面积S=18.85。

2.3 长方体长方体也是常用的立体几何物体，其体积最大，面积最小的条件也可以满足。

长方体的体积的最大/小值可以利用它的公式`V=a*b*c`进行求解，其中a,b,c分别为直角坐标三边的长度；长方体的表面积最大/小值可以求出其元表面积`S=2(a*b+b*c+a*c)`。

高三数学选择填空难题突破立体几何中最值问题

高三数学选择填空难题突破立体几何中最值问题高三数学选择填空难题突破——立体几何中的最值问题一、方法综述高考试题将趋于关注那些考查学生运用运动变化观点处理问题的题目，而几何问题中的最值与范围类问题，既可以考查学生的空间想象能力，又考查运用运动变化观点处理问题的能力，因此，将是有中等难度的考题。

此类问题，可以充分考查图形推理与代数推理，同时往往也需要将问题进行等价转化，比如求一些最值时，向平面几何问题转化，这些常规的降维操作需要备考时加强关注与训练。

立体几何中的最值问题一般涉及到距离、面积、体积、角度等四个方面，此类问题多以规则几何体为载体，涉及到几何体的结构特征以及空间线面关系的逻辑推理、空间角与距离的求解等，题目较为综合。

解决此类问题一般可从三个方面思考：一是函数法，即利用传统方法或空间向量的坐标运算，建立所求的目标函数，转化为函数的最值问题求解；二是根据几何体的结构特征，变动态为静态，直观判断在什么情况下取得最值；三是将几何体平面化，如利用展开图，在平面几何图中直观求解。

二、解题策略类型一：距离最值问题例1：如图，矩形ADFE，矩形CDFG，正方形ABCD两两垂直，且AB=2，若线段DE上存在点P使得GP⊥BP，则边CG长度的最小值为（）解：建立空间直角坐标系，设CG长度为a及点P的坐标，求BP与GP的坐标，得到函数关系式，利用函数求其最值。

举一反三：如图，在棱长为1的正方体ABCD-A中，点E、F分别是棱BC、CC'的中点，P是侧面BCC'B内一点，若A'P⊥平面AEF，则线段A'P长度的取值范围是_____。

二、改写后的文章高三数学选择填空难题突破——立体几何中的最值问题一、方法综述高考试题将趋于关注那些考查学生运用运动变化观点处理问题的题目。

而几何问题中的最值与范围类问题，不仅可以考查学生的空间想象能力，还可以考查运用运动变化观点处理问题的能力，因此这类问题将是有中等难度的考题。

立体几何中的最值问题【解析版】

第四章立体几何专题17 立体几何中的最值问题【压轴综述】在立体几何中，判定和证明空间的线线、线面以及面面之间的位置关系(主要是平行与垂直的位置关系)，计算空间图形中的几何量(主要是角与距离)是两类基本问题．在涉及最值的问题中主要有三类，一是距离（长度）的最值问题；二是面（体）积的最值问题；三是在最值已知的条件下，确定参数（其它几何量）的值.从解答思路看，有几何法（利用几何特征）和代数法(应用函数思想、应用基本不等式等)两种，都需要我们正确揭示空间图形与平面图形的联系，并有效地实施空间图形与平面图形的转换．要善于将空间问题转化为平面问题：这一步要求我们具备较强的空间想象能力，对几何体的结构特征要牢牢抓住，有关计算公式熟练掌握.一、涉及几何体切接问题最值计算求解与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径等.通过作截面，把空间问题转化为平面图形与圆的接、切问题，再利用平面几何知识寻找几何中元素间的关系求解．这样才能进一步将空间问题转化为平面内的问题；二.涉及角的计算最值问题1. 二面角的平面角及其求法有：定义法、三垂线定理及其逆定理、找公垂面法、射影公式、向量法等，依据题目选择方法求出结果．2.求异面直线所成角的步骤:一平移,将两条异面直线平移成相交直线．二定角,根据异面直线所成角的定义找出所成角．三求角,在三角形中用余弦定理或正弦定理或三角函数求角．四结论．3.线面角的计算：（1）利用几何法：原则上先利用图形“找线面角”或者遵循“一做----二证----三计算”. （2）利用向量法求线面角的方法(i分别求出斜线和它在平面内的射影直线的方向向量，转化为求两个方向向量的夹角(或其补角)；(ii)通过平面的法向量来求，即求出斜线的方向向量与平面的法向量所夹的锐角(钝角时取其补角)，取其余角就是斜线和平面所成的角.下面通过例题说明应对这类问题的方法与技巧.【压轴典例】例1.（2018·全国高考真题（理））已知正方体的棱长为1，每条棱所在直线与平面所成的角都相等，则α截此正方体所得截面面积的最大值为（）A B C ．4D 【答案】A 【解析】根据相互平行的直线与平面所成的角是相等的，所以在正方体1111ABCD A B C D -中，平面11AB D 与线11111,,AA A B A D 所成的角是相等的，所以平面11AB D 与正方体的每条棱所在的直线所成角都是相等的，同理平面1C BD 也满足与正方体的每条棱所在的直线所成角都是相等，要求截面面积最大，则截面的位置为夹在两个面11AB D 与1C BD 中间的，且过棱的中点的正六边形，且边长为2，所以其面积为26(2S ==，故选A. 例2.（2018·全国高考真题（文））设A B C D ，，，是同一个半径为4的球的球面上四点，ABC △为等边三角形且其面积为D ABC -体积的最大值为（）A ．B ．C ．D ．【答案】B 【解析】如图所示，点M 为三角形ABC 的中心，E 为AC 中点，当DM ⊥平面ABC 时，三棱锥D ABC -体积最大此时，OD OB R 4===2393ABCSAB == AB 6∴=,点M 为三角形ABC 的中心2BM 233BE ∴==Rt OMB ∴中，有22OM 2OB BM =-=DM OD OM 426∴=+=+=()max 19361833D ABC V -∴=⨯=故选B.例3.（2017·全国高考真题（理））a ，b 为空间中两条互相垂直的直线，等腰直角三角形ABC 的直角边AC 所在直线与a ，b 都垂直，斜边AB 以直线AC 为旋转轴旋转，有下列结论： ①当直线AB 与a 成60°角时，AB 与b 成30°角； ②当直线AB 与a 成60°角时，AB 与b 成60°角； ③直线AB 与a 所成角的最小值为45°； ④直线AB 与a 所成角的最大值为60°.其中正确的是________.（填写所有正确结论的编号）【答案】②③ 【解析】由题意知，a 、b 、AC 三条直线两两相互垂直，画出图形如图，不妨设图中所示正方体边长为1，故|AC |＝1，|AB|=斜边AB 以直线AC 为旋转轴，则A 点保持不变，B 点的运动轨迹是以C 为圆心，1为半径的圆，以C 坐标原点，以CD 为x 轴，CB 为y 轴，CA 为z 轴，建立空间直角坐标系，则D （1，0，0），A （0，0，1），直线a 的方向单位向量a =（0，1，0），|a |＝1，直线b 的方向单位向量b =（1，0，0），|b |＝1，设B 点在运动过程中的坐标中的坐标B ′（cosθ，sinθ，0），其中θ为B ′C 与CD 的夹角，θ∈[0，2π），∴AB ′在运动过程中的向量，'AB =（cosθ，sinθ，﹣1），|'AB|=设'AB 与a 所成夹角为α∈[0，2π]，则cosα()()10102'cos sin a AB θθ--⋅==⋅，，，，， ∴α∈[4π，2π]，∴③正确，④错误．设'AB 与b 所成夹角为β∈[0，2π]，cosβ()()'11002''AB b cossin AB bbAB θθ⋅-⋅===⋅⋅，，，，|cosθ|，当'AB 与a 夹角为60°时，即α3π=，|sinθ|3πα===， ∵cos 2θ+sin 2θ＝1，∴cosβ2=|cosθ|12=，∵β∈[0，2π]，∴β3π=，此时'AB 与b 的夹角为60°， ∴②正确，①错误．故答案为：②③．例4.（2017·全国高考真题（理））如图，圆形纸片的圆心为O ，半径为5 cm ，该纸片上的等边三角形ABC 的中心为O .D ，E ，F 为圆O 上的点，△DBC ，△ECA ，△FAB 分别是以BC ，CA ，AB 为底边的等腰三角形．沿虚线剪开后，分别以BC ，CA ，AB 为折痕折起△DBC ，△ECA ，△FAB ，使得D ，E ，F 重合，得到三棱锥．当△ABC 的边长变化时，所得三棱锥体积(单位：cm 3)的最大值为______．【答案】15【解析】如下图，连接DO 交BC 于点G ，设D ，E ，F 重合于S 点，正三角形的边长为x (x >0)，则133OG x =3x =. ∴35FG SG x ==-，222233566SO h SG GO x x ⎛⎫⎛⎫==-=-- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭3553x ⎛⎫=- ⎪ ⎪⎝⎭， ∴三棱锥的体积2113355333ABC V S h x x ⎛⎫=⋅=- ⎪ ⎪⎝⎭451535123x x =-. 设()4535n x x x =-，x >0，则()345320n x x x '=，令()0n x '=，即43403x =，得43x ，易知()n x 在43x 处取得最大值. ∴max 154854415V =-=例5.（2016·浙江高考真题（理））如图，在ABC中，AB=BC=2，∠ABC=120°.若平面ABC外的点P和线段AC上的点D，满足PD=DA，PB=BA，则四面体PBCD的体积的最大值是 .【答案】【解析】中，因为，所以.由余弦定理可得，所以.设，则，.在中，由余弦定理可得.故.在中，，.由余弦定理可得，所以.由此可得，将ABD沿BD翻折后可与PBD重合，无论点D在任何位置，只要点D的位置确定，当平面PBD⊥平面BDC时，四面体PBCD的体积最大（欲求最大值可不考虑不垂直的情况）.过作直线的垂线，垂足为.设，则，即，解得.而的面积.当平面PBD⊥平面BDC 时：四面体的体积.观察上式，易得，当且仅当，即时取等号，同时我们可以发现当时，取得最小值，故当时，四面体的体积最大，为例6.（2019·安徽芜湖一中高三开学考试）在Rt AOB ∆中，6OAB π∠=，斜边4AB =．Rt AOC ∆可以通过Rt AOB ∆以直线AO 为轴旋转得到，且二面角B AO C --是直二面角．动点D 的斜边AB 上．（1）求证：平面COD ⊥平面AOB ；（2）求直线CD 与平面AOB 所成角的正弦的最大值．【答案】（1）详见解析；（2277【解析】（1）AOB ∆为直角三角形，且斜边为AB ，2AOB π∴∠=.将Rt AOB ∆以直线AO 为轴旋转得到Rt AOC ∆，则2AOC π∠=，即OC AO ⊥.二面角B AO C --是直二面角，即平面AOC ⊥平面AOB . 又平面AOC平面AOB AO =，OC ⊂平面AOC ，OC ∴⊥平面AOB .OC ⊂平面COD ，因此，平面COD ⊥平面AOB ；（2）在Rt AOB ∆中，6OAB π∠=，斜边4AB =，122OB AB ∴==且3OBA π∠=. 由（1）知，OC ⊥平面AOB ，所以，直线CD 与平面AOB 所成的角为ODC ∠. 在Rt OCD ∆中，2COD π∠=，2OC OB ==，2224CD OD OC OD =+=+，22sin 4OC ODC CD OD ∴∠==+，当⊥OD AB 时，OD 取最小值，此时sin ODC ∠取最大值，且sin33OD OB π==.因此，22227sin 774OC ODC CD OD ∠==≤=+，即直线CD 与平面AOB 所成角的正弦的最大值为277. 例7.（2019·深圳市高级中学高三月考（文））如图，AB 是圆O 的直径，点C 是圆O 上异于A ，B 的点，PO 垂直于圆O 所在的平面，且PO ＝OB ＝1.(1)若D 为线段AC 的中点，求证：AC⊥平面PDO ； (2)求三棱锥P －ABC 体积的最大值； (3)若，点E 在线段PB 上，求CE ＋OE 的最小值．【答案】（1）见解析；（2）；（3）【解析】(1)证明：在△AOC中，因为OA＝OC，D为AC的中点，所以AC⊥DO.又PO垂直于圆O所在的平面，所以PO⊥AC.因为DO∩PO＝O，所以AC⊥平面PDO.(2)解：因为点C在圆O上，所以当CO⊥AB时，C到AB的距离最大，且最大值为1.又AB＝2，所以△ABC面积的最大值为.又因为三棱锥P－ABC的高PO＝1，故三棱锥P－ABC体积的最大值为.(3)解：在△POB中，PO＝OB＝1，∠POB＝90°，所以.同理，所以PB＝PC＝BC.在三棱锥P－ABC中，将侧面BCP绕PB旋转至平面BC′P，使之与平面ABP共面，如图所示．当O，E，C′共线时，CE＋OE取得最小值．又因为OP＝OB，，所以垂直平分PB，即E为PB的中点．从而，即CE＋OE的最小值为.例8.（2016·江苏高考真题）现需要设计一个仓库，它由上下两部分组成，上部分的形状是正四棱锥，下部分的形状是正四棱柱（如图所示），并要求正四棱柱的高是正四棱锥的高的4倍.（1）若则仓库的容积是多少？（2）若正四棱锥的侧棱长为，则当为多少时，仓库的容积最大？【答案】（1）312（2）【解析】（1）由PO 1=2知OO 1=4PO 1=8. 因为A 1B 1=AB=6，所以正四棱锥P-A 1B 1C 1D 1的体积正四棱柱ABCD-A 1B 1C 1D 1的体积所以仓库的容积V=V 锥+V 柱=24+288=312（m 3）.（2）设A 1B 1=a （m ），PO 1=h （m ），则0<h<6，OO 1=4h.连结O 1B 1. 因为在中，所以，即于是仓库的容积，从而. 令，得或（舍）.当时，，V 是单调增函数；当时，，V 是单调减函数.故时，V 取得极大值，也是最大值.因此，当m 时，仓库的容积最大.【压轴训练】1．（2019·四川石室中学高三开学考试（文））在ABC △中，已知23AB =6BC =045ABC ∠=，D 是边AC 上一点，将ABD △沿BD 折起，得到三棱锥A BCD -．若该三棱锥的顶点A 在底面BCD 的射影M 在线段BC 上，设BM x =，则x 的取值范围为（） A.()23,26 B.()6,23C.()3,6D.()0,23【答案】B 【解析】由将ABD △沿BD 折起，得到三棱锥A BCD -，且A 在底面BCD 的射影M 在线段BC 上，如图2所示，AM ⊥平面BCD ，则AM BD ⊥，在折叠前图1中，作AM BD ⊥，垂足为N ，在图1中过A 作1AM BC ⊥于点1M ，当运动点D 与点C 无限接近时，折痕BD 接近BC ，此时M 与点1M 无限接近，在图2中，由于AB 是直角ABM ∆的斜边，BM 为直角边，所以BM AB <，由此可得1BM BM AB <<,因为ABC ∆中，023,26,45ABC AB BC ∠===，由余弦定理可得23AC =,所以221(23)(6)6BM =-=，所以623BM <<由于BM x =，所以实数x 的取值范围是()6,23，故选B ．2．（2019·四川高三月考（文））已知球O 表面上的四点A ，B ，C ，P 满足2AC BC ==2AB =．若四面体PABC 体积的最大值为23，则球O 的表面积为（） A ．254πB ．254π C ．2516π D ．8π【答案】A 【解析】当平面ABP 与平面ABC 垂直时，四面体ABCP 的体积最大．由AC BC ==2AB =，得90ACB ︒∠=．设点Р到平面ABC 的距离为h，则112323h ⨯=，解得2h =．设四面体ABCP 外接球的半径为R ，则()22221R R =-+，解得5R=4．所以球O 的表面积为2525444ππ⎛⎫⨯= ⎪⎝⎭．故选：A ．3．（2019·湖南雅礼中学高三月考（理））圆锥的母线长为2，其侧面展开图的中心角为θ弧度，过圆锥顶点的截面中，面积的最大值为2，则θ的取值范围是（） A．),2π B．π⎡⎤⎣⎦C．}D．,2π⎫⎪⎪⎣⎭【答案】A 【解析】设轴截面的中心角为α，过圆锥顶点的截面的顶角为β，且βα≤ 过圆锥顶点的截面的面积为：122sin β2sin β2⨯⨯⨯=，又过圆锥顶点的截面中，面积的最大值为2，故此时β2π=，故απ2π≤＜圆锥底面半径r )2sin22α=∈ ∴侧面展开图的中心角为θ弧度2sin222πsin22απα⨯⨯==∈),2π 故选：A.4．（2019·安徽高考模拟（理））如图，已知四面体ABCD 为正四面体，1AB ＝，E ，F 分别是AD ，BC 中点．若用一个与直线EF 垂直，且与四面体的每一个面都相交的平面α去截该四面体，由此得到一个多边形截面，则该多边形截面面积最大值为（）A ．14B ．24C ．34D ．1【答案】A 【解析】将正四面体补成正方体，如下图所示：EF α⊥ ∴截面为平行四边形MNKL ，可得1NK KL +=又//KL BC ，//KN AD ，且AD BC ⊥ KN KL ∴⊥ 可得2124MNKLNK KL S NK KL +⎛⎫=⋅≤=⎪⎝⎭四边形（当且仅当NK KL =时取等号）本题正确选项：A5．（2019·湖北高三月考（理））若一个四棱锥底面为正方形，顶点在底面的射影为正方形的中心，且该四棱锥的体积为9，当其外接球表面积最小时，它的高为( ) A ．3 B ．2C ．3D ．33【答案】A 【解析】设正方形的边长为a ，则四棱锥的高为227h a =2a ，则其外接圆的半径22r a =.设球的半径为R ，则()222h R r R -+=，解得44222272727210844108a a R a a a =+=++4322272793441084a a a ≥⋅⋅=，当且仅当42274108a a =，即3a =时等号成立，此时，四棱锥的高为2272739h a ===.故选A. 6．（2019·四川雅安中学高三开学考试（文））已知三棱锥D ABC -四个顶点均在半径为R 的球面上，且2AB BC ==，2AC =，若该三棱锥体积的最大值为1，则这个球的表面积为（）A.50081πB.1009πC.259πD.4π【答案】B 【解析】2AB BC ==，2AC = 222AB BC AC ∴+= AB BC ∴⊥112ABC S AB BC ∆∴=⋅= 如下图所示：若三棱锥D ABC -体积最大值为1，则点D 到平面ABC 的最大距离：3d = 即：3DO '=设球的半径为R ，则在Rt OAO '∆中：()22213R R =+-，解得：53R =∴球的表面积：210049S R ππ==本题正确选项：B7．（2017·山西高三（理））两球1O 和2O 在棱长为1的正方体1111ABCD A B C D -的内部，且互相外切，若球1O 与过点A 的正方体的三个面相切，球2O 与过点1C 的正方体的三个面相切，则球1O 和2O 的表面积之和的最小值为( ) A ．(323p B ．(423pC ．(323p +D ．(423p【答案】A 【解析】设球1O 与球2O 的半径分别为r 1,r 2,∴r 1+r 23r 1+r 2)= 3 r 1+r 2313+=332-， r 1+r 2⩾12r r 球1O 与球2O 的面积之和为： S =4π(21r+21r)=4π(r 1+r 2)2−8π12r r ⩾()212π13+−2π()2313+=(6−3)π,当且仅当r 1=r 2时取等号其面积最小值为(6−3π. 故选A.8．（2019·广东高考模拟（理））平面四边形ABCD 中，2AD AB ==5CD CB ==且AD AB ⊥，现将ABD ∆沿对角线BD 翻折成A BD '∆，则在A BD '∆折起至转到平面BCD 的过程中，直线A C '与平面BCD 所成最大角的正切值为（）A ．2B ．12C 3D 3【答案】D 【解析】取BD 的中点O,则,,,A B A D BC CD A O BD CO BD '''==∴⊥⊥即BD ⊥平面A OC ',从而平面BCD ⊥平面A OC ',因此A '在平面BCD 的射影在直线OC 上，即A CO '∠为直线A C '与平面BCD 所成角，因为2AD AB ==5CD CB ==AD AB ⊥，所以111,2sin sin sin 22A O A O OC A CO OA C OA C OC '''''==∴∠=∠=∠≤,即A CO '∠最大值为π6，因此直线A C '与平面BCD 所成最大角的正切值为π3tan63=，选D.9．（2019·云南省玉溪第一中学高二月考（理））已知底面边长为42，侧棱长为25的正四棱锥S ABCD -内接于球1O ．若球2O 在球1O 内且与平面ABCD 相切，则球2O 的直径的最大值为__________．【答案】8 【解析】如图所示，正四棱锥S ABCD -内接于球1O ，1SO 与平面ABCD 交于点O ，正方形ABCD 中，42,4AB AO ==，在直角三角形SAO 中，2222(25)42SO SA OA =-=-=，设球1O 的半径为R ，则在直角三角形1OAO 中，222(2)4R R -+=，解得5R =，所以球1O 的直径为10，当求2O 与平面ABCD 相切且与球1O 相切时，球2O 的直径最大，又因为球2SO =，所以球2O 的直径的最大值为1028-=.10．（2019·山西高三月考）已知三棱锥P ABC -的四个顶点都在半径为3的球面上，AB AC ⊥，则该三棱锥体积的最大值是__．【答案】323【解析】如图所示，设,AB m AC n ==，则12ABCS mn ∆=，ABC ∆22m n +22934m n +-，三棱锥P ABC -的体积公式为222222111(93)(93)324344m n m n m n mn +++⨯-≤⨯-，设224m n t +=，则1()(93)3f t t t =-+，1()93329f t t t '⎫=-+⎪-⎭，令()0f t '=，解得8t =，()f t 在()0,8单增，[]8,9单减，max 32()(8)3f t f ∴==，所以三棱锥P ABC -体积最大值为32311．（2019·云南师大附中高三月考）在直三棱柱111ABC A B C -中，90BAC ∠=︒且14BB =，设其外接球的球心为O ，已知三棱锥O -ABC 的体积为2，则球O 的表面积的最小值是_____________. 【答案】28π 【解析】如图，在Rt ABC △中，设AB c =，=AC b ，则22BC b c =+，取BC ，11B C 的中点分别为2O ，1O ，则2O ，1O 分别为Rt ABC △和111Rt A B C △的外接圆的圆心，连接2O 1O ，又直三棱柱111ABC A B C -的外接球的球心为O ，则O 为2O 1O 的中点，连接OB ，则OB 为三棱柱外接球的半径．设半径为R ，因为直三棱柱111ABC A B C -，所以1214BB O O ==，所以三棱锥O ABC -的高为2，即22OO =，又三棱锥O ABC -体积为2，所以1122632O ABC V bc bc -=⨯⨯=⇒=．在2Rt OO B △中，2222222221()4424b c b c R BC OO ++⎛⎫=+=+=+ ⎪⎝⎭⎝⎭，所以2=4πS R =球表22224π4π()16π2π16π12π16π28π4b c b c bc ⎛⎫++=+++=+= ⎪⎝⎭≥，当且仅当b c =时取“=”，所以球O 的表面积的最小值是28π，故答案为28π.12．（2019·湖南高三月考（文））已知三棱锥A BCD -满足3AB BD DC CA ====，则该三棱锥体积的最大值为________. 【答案】3【解析】取AD 中点E ，连接BE ，CE ，因为3AB BD DC CA ====，所以BE AD ⊥，CE AD ⊥，且BE CE =，由题意可得，当平面⊥BAD 平面CAD 时，棱锥的高最大，等于BE ，此时体积也最大；所以此时该三棱锥体积为113sin sin 362-∆=⋅⋅=⋅⋅⋅∠⋅=⋅∠A BCD ACD V S BE CA CD ACD BE CE ACD ，设ACD θ∠=，则sin 3cos 22πθθ-⎛⎫=⋅=⎪⎝⎭CE CD ，所以239cos sin 9sin cos 9sin sin 222222θθθθθθ-⎛⎫=⋅=⋅=- ⎪⎝⎭A BCD V ，令sin2θ=x ，因为0θπ<<，所以0sin12θ<<，设3()=-f x x x ，01x <<，则2()13'=-f x x ，由2()130'=->f x x 得303x <<；由2()130'=-<f x x 得313x <<；所以函数3()=-f x x x 在30,3⎛⎫ ⎪ ⎪⎝⎭上单调递增，在3,13⎛⎫⎪ ⎪⎝⎭上单调递减；所以max 333323()33279⎛⎫==-= ⎪ ⎪⎝⎭f x f ，因此三棱锥体积的最大值为239239-=⋅=A BCD V . 故答案为2313．（2019·河南高三月考（文））已知三棱锥P ABC -的四个顶点均在同一个球面上，底面ABC ∆满足6BA BC ==，2ABC π∠=，若该三棱锥体积的最大值为3．则其外接球的体积为________.【答案】323π 【解析】如图所示：设球心为O ，ABC △所在圆面的圆心为1O ，则1OO ⊥平面ABC ；因为6BA BC ==2ABC π∠=，所以ABC △是等腰直角三角形，所以1O 是AC 中点；所以当三棱锥体积最大时，P 为射线1O O 与球的交点，所以113p ABC ABC V PO S -=⋅⋅；因为16632ABCS==，设球的半径为R ，所以2221113PO PO OO R R AO R R =+=-=+-(213333R R ⋅-⋅=，解得：2R =，所以球的体积为：343233R ππ=.14．（2019·四川双流中学高三月考（文））已知球的直径4DC =，A ，B 是该球面上的两点，6ADC BDC π∠=∠=，则三棱锥A BCD -的体积最大值是______.【答案】2 【解析】因为球的直径4DC =，且6ADC BDC π∠=∠=，所以2AC BC ==，23AD BD ==13A BCD BCD V S h -∆=⨯⨯（其中h 为点A 到底面BCD 的距离），故当h 最大时，A BCD V -的体积最大，即当面ADC ⊥面BDC 时，h 最大且满足4223h =⨯3h =112233232A BCD V -=⨯⨯⨯=.15．（2019·河北高三月考）在四棱锥P ABCD -中，PD AC ⊥，AB ⊥平面PAD ，底面ABCD 为正方形，且3CD PD +=，若四棱锥P ABCD -的每个顶点都在球O 的球面上，则球O 的表面积的最小值为_____. 【答案】6π 【解析】∵AB ⊥平面PAD ，∴AB PD ⊥，又PD AC ⊥，∴PD ⊥平面ABCD ，则四棱锥P ABCD -可补形成一个长方体，球O 的球心为PB 的中点，设()03CD x x =<<，则3PD x =-.从而球O 的表面积为()()222223431262x x x x πππ⎛⎫++- ⎪⎡⎤=-+≥⎣⎦ ⎪⎝⎭. 故答案为6π 16.（2016·浙江高考真题（文））如图，已知平面四边形ABCD ，AB=BC=3，CD=1，AD=5，∠ADC=90°.沿直线AC 将ACD 翻折成ACD'，直线AC 与BD' 所成角的余弦的最大值是______.6 【解析】试题分析：如图，连接BD′，设直线AC 与'BD 所成的角为θ．O 是AC 的中点.由已知得6AC =，以OB 为x 轴， OA 为y 轴，过O 与平面ABC 垂直的直线为z 轴，建立空间直角坐标系，则60,2A ⎛⎫ ⎪ ⎪⎝⎭， 302B ⎛⎫ ⎪ ⎪⎝⎭， 60,2C ⎛⎫- ⎪ ⎪⎝⎭.作DH AC ⊥于H ，连接D′H 翻折过程中， 'D H 始终与AC 垂直，则266CD CH CA ===则63OH = 15306DH ⨯==因此30630'cos ,sin 636D αα⎛⎫-- ⎪ ⎪⎝⎭（设∠DHD′=α），则3030630'BD αα⎛⎫= ⎪ ⎪⎝⎭，与CA 平行的单位向量为()0,1,0n =，所以cos cos ',BD n θ= ''BD n BD n⋅=＝6395cos α+，所以cos 1α=-时， cos θ取得最大值，为66． 17．（2019·重庆一中高三开学考试（理））已知正方形ABCD 的边长为22，将ABC ∆沿对角线AC 折起，使平面ABC ⊥平面ACD ，得到如图所示的三棱锥B-ACD .若O 为AC 的中点，点M ，N 分别为DC ，BO 上的动点（不包括端点），且BN CM =，则当三棱锥N-AMC 的体积取得最大值时，点N 到平面ACD 的距离为______.【答案】1【解析】由题意知，BO AC ⊥，而平面ABC ⊥平面ACD ，所以BO ⊥平面ACD ，易知BO ＝2，设BN x =，三棱锥N AMC -的高为NO ，则2NO x =-，由三棱锥体积公式得21122=22(2)(1)3233N AMC V y x x x -=⨯⨯⨯-=--+，∴x ＝1时，y max ＝23.此时，211NO =-=. 故本题正确答案为1.18．（2019·浙江高三开学考试）如图，在棱长为2的正方体1111ABCD A B C D -中，点M 是AD 中点，动点P 在底面ABCD 内（不包括边界），使四面体1A BMP 体积为23，则1C P 的最小值是___________．【答案】2305【解析】由已知得四面体1A BMP 体积1122,33A MBP MBP V S -∆=⨯⨯= 所以1,MBPS ∆=设P 到BM 的距离为h ，则151,2MBP S h ∆=⨯⨯= 解得25,5h =所以P 在底面ABCD 内（不包括边界）与BM 平行且距离为255的线段l 上，要使1C P 的最小，则此时P 是过C 作BM 的垂线的垂足.点C 到BM 的距离为45,5所以25,5CP = 此时()221min 252302.55C P ⎛⎫=+= ⎪ ⎪⎝⎭故答案为2305. 19．（2019·安徽合肥一中高考模拟（文））如图，在棱长为 1 的正方体1111ABCD A B C D -中，点M 是AD 的中点，动点P 在底面ABCD 内（不包括边界），若1//B P 平面1A BM ，则1C P 的最小值是____．【答案】305 【解析】取BC 中点N ，连结11,,B D B N DN ，作CO DN ⊥，连1C O ，因为面1//B DN 面面1A BM ，所以动点P 在底面ABCD 内的轨迹为线段DN ，当点P 与点O 重合时，1C P 取得最小值，因为1115222552DN CO DC NC CO ⋅=⋅⇒==，所以221min 11130()155C P C O CO CC ==+=+=. 20．（2019·湖南高三期末（文））点P 在正方体1111ABCD A B C D -的侧面11BCC B 及其边界上运动，并保持1AP BD ⊥，若正方体边长为2，则PB 的取值范围是__________．【答案】2,2⎡⎤⎣⎦【解析】连结1AB ，AC ，1CB ，易知平面11ACB BD ⊥，故P 点的轨道为线段1CB ，当P 在1CB 当P 与C 或1B 重合时：最大值为2则PB 的取值范围是2⎤⎦.故答案为：2⎤⎦。

立体几何最值问题-高考数学一题多解

立体几何最值问题-高考数学一题多解一、攻关方略事物的空间形成，总是表现为不同维数且遵循由低维到高维的发展规律，所谓升维策略，就是把维数、抽象水平较低的或局部的问题转化为维数、抽象水平较高或整体性较强的整体间的关系问题，通过对整体性质或关系的考虑，使原问题获得解决的策略，如平面图形通过翻折或旋转成为空间图形就是二维向三维的转化与变换．在解题时，考虑把高维空间的问题转化为低维空间的问题，这种处理问题的方法叫降维法，也可称之为降维策略，如将立体几何问题转化为平面几何问题．实际上，许多立体几何问题如求空间角、空间距离等，通常总是转化为平面内的问题，通过计算来解决的，当然将空间角、空间距离转变为平面角、平面上点线距离这一步是需要证明的．在立体几何学习中经常碰到几何体中有变角或变动的线段，此时必须根据题意列出沟通已知量与变量之间的关系，运用函数与方程的思想来处理，立体几何中由于动点的变化引起的最值，通常建立关于与动点相关的角度的目标函数，转化为函数最值问题求解．若在空间图形中建立空间直角坐标系，利用向量坐标法，结合条件得到方程（组），则可用解方程（组）求出结果，利用函数与方程的思想方法还可以解空间图形中涉及线面关系、面面关系的探究性问题．真可谓：翻折旋转二维升三，空间问题降维处理．点动角变牵动图形，立几最值函数搞定．1．如图所示，圆形纸片的圆心为O ，半径为5cm ，该纸片上的等边三角形ABC 的中心为O ．D 、E 、F 为圆O 上的点，DBC △、ECA △、FAB 分别是以BC 、CA 、AB 为底边的等腰三角形，沿虚线剪开后，分别以BC 、CA 、AB 为折痕折起DBC △、ECA △、FAB ，使得D 、E 、F 重合，得到三棱锥．当ABC 的边长变化时，所得三棱锥体积（单位：cm 3）的最大值为______．【针对训练】2．点P 在ABC 所在平面α外，PA α⊥，PB PC ==，3tan 2PBC ∠=，则点A 到平面PBC 的距离的最大值是______．3．如图所示，在ABC 中，2AB BC ==，120ABC ∠=︒．若平面ABC 外的点P 和线段AC 上的点D ，满足PD DA =，PB BA =，则四面体P BCD -的体积的最大值是______．4．已知底面边长为2的正三棱锥-P ABC ，其表面展开图是123PP P ，如图所示，求123PP P 的各边长及此三棱锥的体积V ．5．已知球的直径4SC =，A 、B 是该球面上的两点，30ASC BSC ∠=∠=︒，则三棱锥S ABC -的体积的最大值为______．（2021全国新高考Ⅰ卷19）6．已知直三棱柱111ABC A B C -中，侧面11AA B B 为正方形，2AB BC ==，E ，F 分别为AC 和1CC 的中点，D 为棱11A B 上的点．11BF A B ⊥（1）证明：BF DE ⊥；（2）当1B D 为何值时，面11BB C C 与面DFE 所成的二面角的正弦值最小?（2022新高考1卷）7．已知正四棱锥的侧棱长为l ，其各顶点都在同一球面上.若该球的体积为36π，且333l ≤≤）A ．8118,4⎡⎤⎢⎥⎣⎦B ．2781,44⎡⎤⎢⎥⎣⎦C ．2764,43⎡⎤⎢⎥⎣⎦D ．[18,27]（2022年全国乙卷（文数）第12题）8．已知球O 的半径为1，四棱锥的顶点为O ，底面的四个顶点均在球O 的球面上，则当该四棱锥的体积最大时，其高为（）A ．13B ．12C D ．2（2022年全国乙卷（文数）第18题）9．如图，四面体ABCD 中，AD CD ⊥，AD CD =，ADB BDC ∠=∠，E 为AC 的中点．(1)证明：平面BED ⊥平面ACD ；(2)设2AB BD ==，60ACB ∠=︒，点F 在BD 上，当AFC △的面积最小时，求三棱锥F ABC -的体积．10．如图，已知平面四边形ABCD ，AB=BC=3，CD=1，ADC=90°．沿直线AC 将ACD 翻折成ACD '△，直线AC 与BD '所成角的余弦的最大值是________.11．已知四边形ABCD ，2AB BD DA ===，BC CD ==ABD △沿BD 折起，使二面角A BD C --的大小在5,66ππ⎡⎤⎢⎥⎣⎦内，则直线AB 与CD 所成角的余弦值取值范围是（）A ．08⎡⎢⎣⎦，B ．08⎡⎢⎣⎦，C ．01⎡⎫⎪⎢⎪⎣⎦⎣⎭ D ．88⎢⎣⎦，参考答案：1．3【分析】先求得所求三棱锥体积的表达式，然后利用导数或基本不等式求得体积的最大值.【详解】解法一：由题意可知，折起后所得三棱锥为正三棱锥，当ABC 的边长变化时，设ABC 的边长为()0a a >cm ，则ABC 的面积为24a ．DBC △的高为56a -，则正三棱锥的高为=∴2503->，∴0a <<．∴所得三棱锥的体积213412V a =⨯=．令45253t a a =-，则34100t a ='，由0t '=，得a =此时所得三棱锥的体积最大，为3．解法二：如图所示，连接OD 交BC 于点G ，由题意知，OD BC ⊥，OG 是等边三角形ABC 内切圆半径，21π1sin 3232BC BC OG ⨯⨯=⨯⨯，解得OG =，∴OG 的长度与BC 的长度成正比．设OG x =，则BC =，5DG x =-，2132ABC S x =⨯=△，则所得三棱锥的体积2213V =⨯=令()452510f x x x =-，50,2x ⎛⎫∈ ⎪⎝⎭．则()3410050f x x x '=-，令()0f x '≥，即4320x x -≤，得02x <≤．则当50,2x ⎛⎫∈ ⎪⎝⎭时，()()280f x f =≤，∴V ≤．∴所求三棱锥的体积的最大值为3．解法三：如图所示，连接OE 交AC 于点H ，连接AO 、OC ，设OH x =．则AC =，5EH x =-，三棱锥D ABC -2ABC S = ，D ABC V -=2≤=，当且仅当104x x =-，即2x =时取等号．∴所求三棱锥的体积的最大值为3．【点睛】本题为平面图形折叠成空间图形，当折叠终止时，几何体是一个正三棱锥，这个正三棱锥底面边长是一个变元，从而导致三棱锥体积的变化，特别要提醒的是，在折叠问题中，必须注意到折叠过程中哪些要素在变化，哪些要素始终保持不变，其中不变要素见核心要素．根据平面图形的性质，寻找不变的数量关系以及直线与直线平行和垂直的位置关系，是解决折叠问题的突破口，因此折叠问题要通过变图、想图、构图、用图的过程，积极思考，体会解题程序方向性，直击问题的本质，折叠问题既要看清平面转化为空间的过程，又要了解三维空间图形问题的平面化处理，两者是互通的．在建立体积表达式的函数模型之后，结合函数思想求最值，通常用导数法，也可考虑运用基本不等式的方法．策略一:以动正三角形AEC 的边长为变元建立函数关系式，运用导数法求其最大值.策略二:以动正三角形ABC 的中心到边的距离为变元建立函数关系式，运用导数法求其最大值.策略三:以动正三角形ABC 的中心到边的距离为变元建立函数关系式，运用基本不等式求最大值，注意等号成立的条件.2【分析】法一，取BC 的中点D ，连接AD 、PD ，设ADP θ∠=，用θ的正余弦表示AD ，PD ，再利用等体积法求解作答.法二，作PD BC ⊥于点D ，连接AD ，作AF PD ⊥于点F ，证明AF ⊥平面PBC ，再利用均值不等式求解作答.【详解】解法一，取BC 的中点D ，连接AD 、PD ，如图，因PB PC =，则PD BC ⊥，而3tan2PBC ∠=，有sin PBC ∠=则有sin PD PB PBC =⋅∠=PA ⊥平面ABC ，,AD BC ⊂平面ABC ，则PA AD ⊥，PA BC ⊥，又,,PA PD P PA PD ⋂=⊂平面PAD ，因此BC ⊥平面PAD ，AD ⊂平面PAD ，则AD BC ⊥，在Rt PAD △中，令(0,)2ADP πθ∠=∈，sin ,cos PA PD AD PD θθ==，设点A 到平面PBC 的距离为h ，11,22PBC ABC S BC PD S BC AD =⋅=⋅ ，由A PBC P ABC V V --=得：1133PBC ABC S h S PA ⋅=⋅ ，即1122BC PD h BC AD PA ⋅⋅=⋅⋅，于是得cos sin 2AD PA PD PD h PD PD θθθ⋅⋅==，当且仅当22=πθ，即4πθ=时取等号，所以点A 到平面PBC解法二，在PBC 中，作PD BC ⊥于点D ，连接AD ，作AF PD ⊥于点F，如图，PA ⊥平面ABC ，BC ⊂平面ABC ，则PA BC ⊥，又,,PA PD P PA PD ⋂=⊂平面PAD ，因此BC ⊥平面PAD ，而BC ⊂平面PBC ，则有平面PAD ⊥平面PBC ，又平面PAD ⋂平面PBC PD =，AF ⊂平面PAD ，因此AF ⊥平面PBC ，即AF 就是点A 到平面PBC 的距离，而3tan 2PBC ∠=，有sin PBD ∠=sin PD PB PBD =⋅∠=，在Rt PAD △中，22211()1222PA AD PD PA AD AF PD PD PD PD +⋅=≤==当且仅当3PA AD ==时取等号，所以点A 到平面PBC3．12##0.5【分析】先求得四面体P BCD -体积的表达式，利用基本不等式或函数的单调性求得体积的最大值.【详解】解法一：由2AB BC ==，120ABC ∠=︒，可得AC =要求四面体P BCD -的体积，关键是寻找底面三角形BCD 的面积BCD S △和点P 到平面BCD 的距离h ，易知2h ≤．设AD x =，则DP x =，DC x =，()12sin 3022DBC xS x =⨯⨯⨯︒=△，其中(0,x ∈，且h x ≤．∴2111366622P BCDBCD x x x x V S h h x -⎛⎫-+=⨯=≤≤= ⎪ ⎪⎝⎭△．当且仅当x x =，即x =P BCD -的体积的最大值是12．解法二：设PD AD x ==，∵PB PA =，PBD ABD ≌△△，1133P BCD BCD V S h -=⨯=△（h 为三棱锥P BCD -的高）．当平面PBD ⊥平面BDC 时，使四面体PBCD 的体积较大．作PH BD ⊥，垂足为H ，则PH ⊥平面BCD ，sin sin h PH PD PDB x ADB ==⋅∠=⋅∠．此时，()211sin sin sin 662P BCDx x V ADB ADB ADB -=⋅∠≤∠=∠⎝⎭，当且仅当x =1sin 2P BCD V ADB -=∠，当90ADB ∠=︒，即AD BD ⊥时，P BCD V -最大值为12．解法三：∵13P BCD BCD V S h -=⨯△（h 为三棱锥P BCD -的高），在ABC 中，2AB BC ==，120ABC ∠=︒，则AC =30BAC BCA ∠=∠=︒，设(0PD DA x x ==<<，则DC x =-，1sin 22BCD xS BC CD BCA =⨯⋅∠=△．在ABD △中，由余弦定理，有2222cos BD AD AB AD AB BAC =+-⋅∠．代入整理得BD =PBD △中，由余弦定理，有222cos 2PB BD PD PBD PB BD+-∠=⋅，代值整理得cos PBD ∠∴sin PBD ∠=．过P 作PM BD ⊥，垂足为M ，则PM 为四面体P BCD -的高．∴sin h PM PB PBM ==∠故111336P BCDBCD V S h -===△，t =，∵0x <<12t ≤<，∴224x t -=-．2141466P BCDt V t t t--⎛⎫=⨯=- ⎪⎝⎭在[)1,2t ∈上单调递减．∴当1t =，即x =P BCD -的体积最大为1411612P BCD V --=⨯=．4．1213234PP PP P P ===，3【分析】由12APB CBP ≌△△，分析可得123PP P 是边长为4的正三角形，再由13P ABC ABC S PO V -=⋅ 结合题干数据求解即可.【详解】由题图可知1P 、B 、2P 三点共线，∴12APBCBP ≌△△．∵60ABC ∠=︒，∴1260ABP CBP ∠=∠=︒，1APB △和2CBP △都是正三角形．∴124PP =．同理可知其他两边长也是4，∴123PP P 是边长为4的正三角形．折叠后是棱长为2的正四面体-P ABC ，如图所示．设顶点P 在底面内的投影为O ，连结BO 并延长，交AC 于点D ，则D 为AC 的中点，O 为ABC 的重心，PO ⊥底面ABC ．AO AB ==，PO ==．故133P ABC ABC V S PO -=⋅=△．5．2【分析】过AB 作与SC 垂直的截面ABM ．通过13S ABC ABM V SC S -=⋅△，分析即得解.【详解】过AB 作平面ABM SC ⊥且SC 平面ABM M =，如图所示，由题意知SAC 、SBC △均为直角三角形．∵4SC =，30ASC BSC ∠=∠=︒，故SAC SBC ≅ ，∴SA =，2CA =，∴SA ACAM BM SC⋅==．∴2141sin 2sin 2332S ABCABM V SC S AMB AMB -=⋅=⨯⨯∠=∠≤△．∴三棱锥S ABC -体积的最大值为2．故答案为：26．（1）证明见解析；（2）112B D =【分析】（1）方法二：通过已知条件，确定三条互相垂直的直线，建立合适的空间直角坐标系，借助空间向量证明线线垂直；（2）方法一：建立空间直角坐标系，利用空间向量求出二面角的平面角的余弦值最大，进而可以确定出答案；【详解】（1）[方法一]：几何法因为1111,//BF AB AB AB ⊥，所以BF AB ⊥．又因为1AB BB ⊥，1BF BB B ⋂=，所以AB ⊥平面11BCC B ．又因为2AB BC ==，构造正方体1111ABCG A B C G -，如图所示，过E 作AB 的平行线分别与AG BC ，交于其中点,M N ，连接11,AM BN ，因为E ，F 分别为AC 和1CC 的中点，所以N 是BC 的中点，易证1Rt Rt BCF B BN ≅ ，则1CBF BBN ∠=∠．又因为1190BBN BNB ∠+∠=︒，所以1190CBF BNB BF BN ∠+∠=︒⊥，．又因为111111,BF AB BN AB B ⊥= ，所以BF ⊥平面11A MNB ．又因为ED ⊂平面11A MNB ，所以BF DE ⊥．[方法二]【最优解】：向量法因为三棱柱111ABC A B C -是直三棱柱，1BB ∴⊥底面ABC ，1B B AB ∴⊥11//A B AB ，11BF A B ⊥，BF AB ∴⊥，又1BB BF B ⋂=，AB ∴⊥平面11BCC B ．所以1,,BA BC BB 两两垂直．以B 为坐标原点，分别以1,,BA BC BB 所在直线为,,x y z 轴建立空间直角坐标系，如图．()()()0,0,0,2,0,0,0,2,0,B A C ∴()()()1110,0,2,2,0,2,0,2,2B A C ，()()1,1,0,0,2,1E F ．由题设(),0,2D a （02a ≤≤）．因为()()0,2,1,1,1,2BF DE a ==--，所以()()0121120BF DE a ⋅=⨯-+⨯+⨯-=，所以BF DE ⊥．[方法三]：因为11BF A B ⊥，11//A B AB ，所以BF AB ⊥，故110BF A B ⋅= ，0BF AB ⋅=，所以()11BF ED BF EB BB B D ⋅=⋅++ ()11=BF B D BF EB BB ⋅+⋅+ 1BF EB BF BB =⋅+⋅ 11122BF BA BC BF BB ⎛⎫=--+⋅ ⎪⎝⎭11122BF BA BF BC BF BB =-⋅-⋅+⋅ 112BF BC BF BB =-⋅+⋅111cos cos 2BF BC FBC BF BB FBB =-⋅∠+⋅∠1=2202-⨯⨯，所以BF ED ⊥．（2）[方法一]【最优解】：向量法设平面DFE 的法向量为(),,m x y z =，因为()()1,1,1,1,1,2EF DE a =-=--，所以00m EF m DE ⎧⋅=⎨⋅=⎩ ，即()0120x y z a x y z -++=⎧⎨-+-=⎩．令2z a =-，则()3,1,2m a a =+-因为平面11BCC B 的法向量为()2,0,0BA =，设平面11BCC B 与平面DEF 的二面角的平面角为θ，则cos m BA m BA θ⋅=⋅==当12a =时，2224a a -+取最小值为272，此时cos θ=所以()minsin θ=112B D =．[方法二]：几何法如图所示，延长EF 交11A C 的延长线于点S ，联结DS 交11B C 于点T ，则平面DFE 平面11B BCC FT =．作1BH FT ⊥，垂足为H ，因为1DB ⊥平面11BB C C ，联结DH ，则1D H B ∠为平面11BB C C 与平面DFE 所成二面角的平面角．设1,B D t =[0,2],t ∈1B T s =，过1C 作111//CG AB 交DS 于点G ．由111113C S C G SA A D ==得11(2)3C G t =-．又1111B D BT C G C T=，即12(2)3t s s t =--，所以31t s t =+．又111B H BT C F FT =，即11B H =，所以1B H =所以DH ==则11sin B D DHB DH∠===所以，当12t =时，()1min 3sin 3DHB ∠=．[方法三]：投影法如图，联结1,FB FN，DEF 在平面11BB C C 的投影为1BN F ，记面11BB C C 与面DFE 所成的二面角的平面角为θ，则1cos B NF DEFS S θ=．设1(02)BD t t =≤≤，在1Rt DB F中，DF ==在Rt ECF中，EF =D 作1B N 的平行线交EN 于点Q ．在Rt DEQ △中，DE ==在DEF 中，由余弦定理得222cos 2DF EF DE DFE DF EF+-∠=⋅=，sin DFE ∠1sin 2DFE S DF EF DFE =⋅∠ =13,2B NF S = 1cos B NF DFES S θ==，sin θ，当12t =，即112B D =，面11BB C C与面DFE 所成的二面角的正弦值最小，最小值为3．【整体点评】第一问，方法一为常规方法，不过这道题常规方法较为复杂，方法二建立合适的空间直角坐标系，借助空间向量求解是最简单，也是最优解；方法三利用空间向量加减法则及数量积的定义运算进行证明不常用，不过这道题用这种方法过程也很简单，可以开拓学生的思维.第二问：方法一建立空间直角坐标系，利用空间向量求出二面角的平面角是最常规的方法，也是最优方法；方法二：利用空间线面关系找到，面11BB C C 与面DFE 所成的二面角，并求出其正弦值的最小值，不是很容易找到；方法三：利用面DFE 在面11BB C C 上的投影三角形的面积与DFE △面积之比即为面11BB C C 与面DFE 所成的二面角的余弦值，求出余弦值的最小值，进而求出二面角的正弦值最小，非常好的方法，开阔学生的思维．7．C【分析】设正四棱锥的高为h ，根据题意求出正四棱锥的底面边长与高的关系，再利用导数求解即可.【详解】设球体的半径为R ，由题知：34363R ππ=，所以球的半径3R =.设正四棱锥的底面边长为2a ，高为h ，则222222l h a h =+=+，22232(3)a h =+-,所以26h l =，2222a l h =-所以正四棱锥的体积42622411214()=333366936l l l V Sh a h l l ⎛⎫==⨯⨯=⨯-⨯- ⎪⎝⎭，设()641=936x f x x ⎛⎫- ⎪⎝⎭，3x ≤≤，所以()5233112449696x x f x x x ⎛⎫⎛⎫-'=-= ⎪⎝⎭⎝⎭，当3x ≤≤()0f x ¢>，()f x 为增函数，当x <≤()0f x '<，()f x 为减函数，所以当l =时，正四棱锥的体积V 取最大值，最大值为643，又3l =时，274V =，l =814V =,所以正四棱锥的体积V 的最小值为274，所以该正四棱锥体积的取值范围是276443⎡⎤⎢⎥⎣⎦，.故选：C 8．C【分析】令四棱锥底面四边形外接圆半径为r ，用r 表示四棱锥的高及底面四边形面积最大值，再借助导数求解作答.【详解】设该四棱锥底面四边形为ABCD ，平面ABCD 截球O 所得小圆半径为r ，则球心O到平面ABCD 的距离h =设四边形ABCD 对角线,AC BD 的夹角为α，则1sin 2ABCD S AC BD α=⋅，于是得该四棱锥的体积：12sin 22sin 36623ABCD V S h BD r r rπα=⋅=⋅≤⋅⋅=当且仅当对角线,AC BD 是截面小圆互相垂直的两条直径，即四边形ABCD 为正方形时取等号，令2(0,1)r x =∈，有23r =23(),(0,1)f x x x x =-∈，求导得：22()233()3f x x x x x '=-=-，当203x <<时，()0f x '>，当213x <<时，()0f x '<，因此函数()f x 在2(0,)3上单调递增，在2(,1)3上单调递减，当23x =时，23max 224()(()3327f x =-=，从而当223r =时，max 222(333r =⨯⨯max V =，此时3h ==，故选：C9．(1)证明见解析；【分析】（1）利用线面垂直的判定定理可得AC ⊥平面BED ，然后根据面面垂直的判定定理可得平面BED ⊥平面ACD ；（2）首先判断出三角形AFC 的面积最小时F 点的位置，然后求得F 到平面ABC 的距离，从而求得三棱锥F ABC -的体积或利用等积法及锥体的体积公式即得.【详解】（1）AD CD = ，ADB BDC ∠=∠，BD BD =，ADB CDB ∴≅ ，AB BC ∴=，又E 为AC 的中点．AC BE ∴⊥，AD CD = ，E 为AC 的中点．AC DE ∴⊥，又BE DE E = ，BE ⊂平面BED ，DE ⊂平面BED ，AC ∴⊥平面BED ，又AC ⊂ 平面ACD ，∴平面BED ⊥平面ACD ；（2）方法一：依题意2AB BD BC ===，60ACB ∠=︒，三角形ABC 是等边三角形，所以2,1,AC AE CE BE ====由于,AD CD AD CD =⊥，所以三角形ACD 是等腰直角三角形，所以1DE =，所以222DE BE BD +=，即DE BE ⊥，由于AC BE E ⋂=，,AC BE ⊂平面ABC ，所以DE ⊥平面ABC ，由于ADB CDB ≅△△，所以FBA FBC ∠=∠，由于BF BFFBA FBC AB CB =⎧⎪∠=∠⎨⎪=⎩，所以FBA FBC ≅ ，所以AF CF =，所以EF AC ⊥，由于12AFC S AC EF =⋅⋅ ，所以当EF 最短时，三角形AFC 的面积最小，过E 作EF BD ⊥，垂足为F ，在Rt BED △中，1122BE DE BD EF ⋅⋅=⋅⋅，解得2EF =，所以13,222DF BF DF ===-=，所以34BF BD =，过F 作FH BE ⊥，垂足为H ，则//FH DE ，又DE ⊥平面ABC ，所以FH ⊥平面ABC ，且34FH BF DE BD ==，所以34FH =，所以111323324F ABC ABC V S FH -=⋅⋅=⨯⨯=方法二：AB BC = ，60ACB ∠=︒，2AB =ABC ∴ 是边长为2的等边三角形，BE ∴=连接EF ，由于ADB CDB ≅△△，所以FBA FBC ∠=∠，由于BF BFFBA FBC AB CB =⎧⎪∠=∠⎨⎪=⎩，所以FBA FBC ≅ ，所以AF CF =，所以EF AC ⊥，由于12AFC S AC EF =⋅⋅ ，所以当EF 最短时，三角形AFC 的面积最小，即EF BD ⊥时，AFC △的面积最小，,,2AD CD AD CD AC ⊥== ，E 为AC 的中点，∴1DE =，222DE BE BD +=，BE ED ∴⊥，在Rt BED △中，1122BE DE BD EF ⋅⋅=⋅⋅，解得2EF =，∴32BF ，113222BEF S BF EF ∴=⋅=⋅11233F ABC A BEF C BEF BEF V V V S AC ---∴=+=⋅=⋅= .10．6【分析】取AC 中点O ，连接OB ，过点O 作Oz ⊥平面ABC ，以点O 为原点建立空间直角坐标系，设二面角D AC B '--的大小为α，把直线A C 与BD '所成角的余弦表示为α的函数，求出函数最大值作答.【详解】在ACD 中，90ADC ∠= ，1,CD AD ==则AC =，过D 作DH AC ⊥于H ，连接D H '，如图，显然D H AC '⊥，ACD 绕直线AC 旋转过程中，线段DH 绕点H 在垂直于直线AC 的平面γ内旋转到D H '，取AC 中点O ，连接OB ，因3AB BC ==，有OB AC ⊥，OB =，,663CD ADD H DH CH OH AC⋅'=====，过点O 作Oz ⊥平面ABC ，以点O 为原点，射线,,OB OA Oz 分别为,,x y z 轴非负半轴，建立空间直角坐标系，则A ，B ，(0,2C -，显然有//Oz 平面γ，设二面角D AC B '--的大小为[0,]απ∈，有(,,sin )636D αα'-，则有(,sin )6236BD αα=--' ，CA的方向向量为(0,1,0)n = ，设直线AC 与BD '所成的角为θ，于是得||cos |cos ,|||||n BD n BD n BD θ'⋅'=〈〉=='因[0,]απ∈，则1cos 1α-≤≤，于是得cos 6θ=，当且仅当cos 1α=取等号，所以直线AC 与BD '11．A【分析】取BD 中点O ，连接AO ，CO ，以O 为原点建立空间直角坐标系，利用二面角A BD C --的大小θ的正余弦表示,AB CD的坐标，利用空间向量建立函数关系求解作答.【详解】取BD 中点O ，连接AO ，CO ，而AB =BD =DA =2，BC =CD，则CO ⊥BD ，AO ⊥BD ，且CO =1，AOAOC ∠是二面角A BD C --的平面角，令5[,]66AOC ππθ∠=∈，显然有BD ⊥平面AOC ，BD ⊂平面BCD ，则平面AOC ⊥平面BCD ，在平面AOC 内过O 作Oz OC ⊥，而平面AOC I 平面BCD OC =，因此Oz ⊥平面BCD ，即射线,,OC OD Oz 两两垂直，以O 为原点，射线,,OC OD Oz 分别为,,x y z轴非负半轴，建立空间直角坐标系，如图，则(0,1,0),(1,0,0),(0,1,0)B C D -，)A θθ，,1,),(1,1,0)BA CD θθ==-，设直线AB 与CD 所成的角为α，则||cos |cos ,|||||AB CD AB CD AB CD α⋅=〈〉==，由5[,66ππθ∈得：cos [,]22θ∈，15122θ-≤≤，则5|1|[0,2θ∈，于是得cos[0,]α∈，8.所以直线AB与CD 所成角的余弦值取值范围是[0,]8故选：A答案第18页，共18页。

空间几何体中最值问题的常用求法

ʏ廖子宜立体几何中的最值问题主要与空间图形的距离㊁角㊁面积㊁体积有关,是高考命题的热点㊂此类问题涉及知识面较广,灵活性较大,常用的求法有:二次函数性质法㊁基本不等式法㊁射影法㊁两点之间线段最短法㊁垂线段最短法㊁三角函数性质法等㊂一㊁二次函数性质法例1 如图1,一个圆锥的底面半径为2c m ,高为6c m ,其中有一个高为x c m 的内接圆柱㊂当x 取何值时,圆柱的侧面积最大?图1解:依题意得S 圆柱侧=2πr x =2π2-x 3x =4πx -2π3x 2,x ɪ(0,6)㊂当x =-4π2-2π3=3时,这个二次函数有最大值6π,故当圆柱的高为3c m 时,圆柱的侧面积最大,其最大值为6πc m 2㊂评注:二次函数y =a x 2+b x +c (a ʂ0),当a >0时,有最小值;当a <0时,有最大值㊂二㊁基本不等式法例2 已知圆柱的轴截面的周长L 为定值,则圆柱侧面积的最大值是㊂解:设圆柱的底面直径和高分别为d ,h ,则d +h =L 2,所以S 圆柱侧=πd h ɤπd +h 22=πL216(当且仅当d =h 时取等号)㊂故圆柱侧面积的最大值为πL216㊂评注:基本不等式为:a ,b ɪR +,a +b ȡ2a b ,当且仅当a =b 时等号成立㊂基本不等式逆用为:a ,b ɪR +,a b ɤa +b 22,当且仅当a =b 时等号成立㊂三㊁射影法例3 如图2,棱长为1的正方体A B C D -A 1B 1C 1D 1中,若G ,E 分别是B B 1,C 1D 1的中点,点F 是正方形A D D 1A 1的中心,则四边形B GEF 在正方体侧面及底面共6个面内的射影图形的面积的最大值是㊂图2解:显然,四边形B G E F 在前后侧面上的射影图形的面积相等㊂易知点E 在前面平面上的射影是A 1B 1的中点E 1,点F 在前面平面上的射影是A A 1的中点F 1,可得四边形B G E 1F 1的面积为12㊂同理可得,四边形B G E F 在左右侧面上的射影图形的面积相等且等于18;在上下底面上的射影图形的面积相等且等于38㊂故四边形B G E F 在前后侧面上的射影图形的面积最大,其最大值为12㊂评注:解题的关键是找到四边形B G E F 四个顶点在各个面上的射影点的位置,再根据正方体的性质计算其面积㊂四㊁两点之间线段最短法例4 如图3所示,已知圆柱的高为80c m ,底面半径为10c m ,轴截面上有P ,Q 两点,且P A =40c m ,B 1Q =30c m ,若一只蚂蚁沿着侧面从P 点爬到Q 点,则蚂蚁爬过的最短路径长为㊂91知识结构与拓展高一数学 2023年4月Copyright ©博看网. All Rights Reserved.图3解:将圆柱侧面沿母线A A 1展开,得到如图4所示的矩形㊂图4易得A 1B 1=10π㊂过点Q 作Q S ʅA A 1于点S ,在R tәP Q S 中,P S =80-40-30=10,Q S =A 1B 1=10π,所以P Q =P S 2+Q S 2=10π2+1,即蚂蚁爬过的最短路径长是10π2+1cm ㊂评注:求几何体表面上两点间的最小距离,可将几何体沿着某棱(母线)剪开后展开,画出其侧面展开图,把求曲线长问题转化为求平面上的线段长问题㊂五㊁垂线段最短法例5 如图5,在棱长为2的正方体A B C D -A 1B 1C 1D 1中,E 为B C 的中点,点P 在线段D 1E 上,则点P 到直线C C 1的距离的最小值为㊂图5解:过E 作E E 1ʅ底面A 1B 1C 1D 1交B 1C 1于E 1,过P 作P H ʅD 1E 1于H ㊂连接C 1H ,作P P 1ʅC C 1于P 1㊂易知四边形P P 1C 1H 是矩形,点P 在线段E D 1上运动,点P 到直线C C 1的距离是C 1H ㊂当C 1H 为R t әC 1D 1E 1的底边D 1E 1上的高时,C 1H 最小,记高为h ㊂依题意得C 1D 1=2,C 1E 1=1,所以D 1E 1=5㊂由12C 1D 1㊃C 1E 1=12D 1E 1㊃h ,可得h =255㊂故点P 到直线C C 1的距离的最小值为255㊂评注:当点P 在D 1E 上移动时(不含端点),四边形P P 1C 1H 一定是矩形;当点P 与D 1或E 重合时,点P 到直线C C 1的距离的最小值为C 1D 1或CE ,此时显然不是最小值㊂六㊁三角函数性质法例6 如图6所示,边长A C =3,B C =4,A B =5的三角形简易遮阳棚,其A ,B 是地面上南北方向两个定点,正西方向射出的太阳光线与地面成30ʎ角,当遮阳棚A B C 与地面的夹角等于时,才能保证所遮影面A B D 的面积最大㊂图6解:易知әA B C 为直角三角形㊂在平面A B C 内,由C 向A B 引垂线,垂足为Q ,则D Q 为C D 在地面上的射影,且A B ʅ平面C QD ㊂因为太阳光与地面成30ʎ角,所以øC D Q =30ʎ㊂在әC D Q 中,C Q =125,由正弦定理得C Q s i n 30ʎ=Q D s i nøQ C D ,所以Q D =245s i nøQ C D ㊂为使面A B D 的面积最大,需Q D 最大即可,只有当øQ C D =90ʎ时才可达到最大,从而øC Q D =60ʎ㊂故当遮阳棚A B C 与地面成60ʎ角时,才能保证所遮影面A B D 面积最大㊂评注:正弦函数y =s i n x 在0,π2上单调递增,在π2,π上单调递减㊂作者单位:福建省泉州市外国语学校(责任编辑郭正华)2 知识结构与拓展高一数学 2023年4月Copyright ©博看网. All Rights Reserved.。

立体几何解析几何最值问题

立体几何解析几何最值问题立体几何和解析几何都是数学中的分支领域，它们在研究物体的形状、位置和运动等方面有着不同的方法和应用。

在解析几何中，最值问题是其中一个重要的问题类型，它涉及到找到函数在特定区域内的最大值或最小值。

在立体几何中，我们研究的是空间中的物体，比如点、线、面、体等。

解析几何则是研究平面几何与坐标系统之间的关系，通常使用坐标点来表示点、线、曲线等。

解析几何中最值问题的解决方法通常是通过求导来进行。

我们可以将问题转化为一个函数，然后求该函数的导数，找到导数为0的点，再通过比较得出最大值或最小值。

这种方法在求解平面最值问题时非常有效。

而在立体几何中，最值问题通常涉及到体积、面积或长度等量的最大化或最小化。

解决这类问题可以利用几何性质和定理来进行推导和求解。

比如，要求一个几何体的体积的最大值，我们可以通过寻找几何体的特定形状的体积公式以及几何性质来得出最优解。

具体地说，在立体几何中，最值问题的解决方法可以归纳如下：1.求解体积最大问题：对于已知形状的几何体，我们可以通过推导体积公式，并利用一些方法来求解体积的最大值。

例如，求解一个长方体在给定表面积约束条件下的最大体积，我们可以设长方体的长、宽、高分别为x、y、z，然后利用约束条件和体积公式写出等式，最后通过求解方程组可得到最优解。

2.求解表面积最小问题：类似地，我们可以通过推导表面积公式，并利用一些方法来求解表面积的最小值。

例如，求解一个包含给定体积的圆柱体的表面积最小值，我们可以设圆柱体的底面半径为r、高度为h，然后通过体积公式将h表示为r的函数，并利用表面积公式得到表面积的表达式，最后求解表面积的最小值。

3.求解长度最短问题：有时候我们需要找到连接两个点的最短路径，可以利用几何性质和定理求解。

例如，求解从一个点到直线的最短距离，我们可以利用点到直线的距离公式，并通过求导的方法求解最短距离的点。

总而言之，立体几何和解析几何最值问题的求解方法有所不同，但都可以通过推导公式、利用几何性质和定理以及求导等方法来解决。

高三数学立体几何中的最值问题四则

立体几何中的最值问题四则1. 用配方法求距离的最值例1. 如图1，正方形ABCD 、ABEF 边长都是1，且平面ABCD 、ABEF 互相垂直，点M 在AC 上移动，点N 在BF 上移动，若CM BN a a ==<<()02。

试求当a 为何值时，MN 的值最小。

图1分析：此题的解题关键是想用含a 的代数式表示距离，再用配方法求最值。

解：过M 作MH AB ⊥，垂足为H ，连结NH ，如图1所示。

在正方形ABCD 中，AB CB ⊥，所以BC MH //，因为平面AC ⊥平面AE ，所以MH ⊥平面AE ，即MH NH ⊥。

因为CM BN a AB CB BE =====,1，所以AC BF ==2 即AM a =-2， MH AH a BH a ==-=12222,，由余弦定理求得NH a =22。

所以MN MH NH =+22=-+=-+=-+<<()()()()12222212212022222a a a a a a当a =22时，MN =22，即M 、N 分别移到AC 、BF 的中点时，MN 的值最小，最小值为222. 结合实际找最值位置例2. 在一X 硬纸上，抠去一个半径为3的圆洞，然后把此洞套在一个底面边长为4，高为6的正三棱锥A —BCD 上，并使纸面与锥面平行，则能穿过这X 纸面的棱锥的高的最大值是________。

图2解：如图2所示，假设硬纸上的圆洞刚好卡在B'C'D'处。

设正三棱锥A BCD -的顶点A 在平面BCD 上的射影为A'，在平面B'C'D'上的射影为O 。

连结BA'、B'O 并延长分别交CD 、C'D'于E 、E'点，则平面B C D '''//平面BCD ，所以B E BE BC BC''''=， B E B O BE BA ''''==3232，，即B O BA B C BC ''''=。

立体几何中的最值问题

如图５所示，了制作一个圆为
例２三棱锥ＳＡＢＣ－中，条棱长为，余棱长一其均为１求ａ为何值时，
最大，求最大值．并如图３设ｓ，ｃ—ｎ，
ቤተ መጻሕፍቲ ባይዱ形灯笼，要制作４个全等的先
形骨架，总计耗用９６ｍ铁丝，．用ＳＩ塑料片制成圆柱的侧ＩＴ
１）利用一次、次、比例函数性质求最值二反
■ｒ’，－
何性质．比较常用的性质如：１）两点之间以直线段最
短；）垂线段最短等．２
■■ ＿
例３（０９全国卷）已知二面角ｚ的大小２０年
为６。动点Ｐ、分别在平面ａＪ内，０，Ｑ、９Ｐ到ｐ的距离为
）．
Ｂ２；Ｃ２；Ｄ４
的侧面绕行２周到达Ａ点的最短路线的长为
．
如图４分别作Ｑ，Ａ一
析ａ于Ａ，ＡＣ￣Ｚ于ＣＰＢｊ口于Ｂ，＿ＰＤ－Ｚ于Ｄ，ｌ－
ＣＢ则ＡＣＱ、Ｄ，Ｑ＝ＰＤＢ
Ｃ
。ｃ
和下底面（安装上底面）不．当
析
其余棱长均为１取，
柱底面半径ｒ取何值时，Ｓ取得最大值？并求出该最大值（果结图５
罐
ＡＢ中点Ｈ，接ＨＳＨＣ，连、
图３
精确到００）．１ｍ。．

立体几何动点最值问题

立体几何动点最值问题
立体几何动点最值问题是指在立体几何空间中，给定一些特定条件下，求一个动点的某个值的最大或最小值。

这类问题广泛应用于建筑设计、机械工程、地理测量等领域。

在解决立体几何动点最值问题时，通常需要利用几何性质和数学方法进行分析和求解。

下面以两个典型的问题为例进行拓展说明。

问题一：在一个正方体中，找到离一个定点最远的顶点。

解答：首先，我们找到这个正方体的中心点，然后根据对称性可以知道，离中心点最远的顶点就是通过连接中心点和一个面的对角线的顶点。

因此，我们可以通过计算这个对角线的长度，并找出最长的对角线来确定离定点最远的顶点。

问题二：在一个球体上，找到离球心最远的点。

解答：根据球体的几何性质，离球心最远的点是球体表面上的点。

因此，我们可以通过计算球心到球面上各点的距离，并找出最大距离的点来确定离球心最远的点。

在实际应用中，立体几何动点最值问题的解决往往需要结合具体的条件和约束条件进行分析和求解。

这些问题可能涉及到线段、面积、体积等几何量的计算，以及最优化等数学方法的运用。

因此，解决这类
问题需要理解立体几何的基本概念和性质，并熟练掌握相关的计算和求解技巧。

专题4.4 立体几何中最值问题(解析版)

一．方法综述高考试题将趋于关注那些考查学生运用运动变化观点处理问题的题目，而几何问题中的最值与范围类问题，既可以考查学生的空间想象能力，又考查运用运动变化观点处理问题的能力，因此，将是有中等难度的考题．此类问题，可以充分考查图形推理与代数推理，同时往往也需要将问题进行等价转化，比如求一些最值时，向平面几何问题转化，这些常规的降维操作需要备考时加强关注与训练．立体几何中的最值问题一般涉及到距离、面积、体积、角度等四个方面,此类问题多以规则几何体为载体,涉及到几何体的结构特征以及空间线面关系的逻辑推理、空间角与距离的求解等,题目较为综合,解决此类问题一般可从三个方面思考：一是函数法,即利用传统方法或空间向量的坐标运算,建立所求的目标函数,转化为函数的最值问题求解；二是根据几何体的结构特征，变动态为静态，直观判断在什么情况下取得最值；三是将几何体平面化，如利用展开图，在平面几何图中直观求解.二．解题策略类型一距离最值问题【例1】【河南省焦作市2019届高三三模】在棱长为4的正方体ABCD﹣A1B1C1D1中，点E、F分别在棱AA1和AB上，且C1E⊥EF，则|AF|的最大值为（）A．B．1 C．D．2【答案】B【解析】以AB，AD，AA1所在直线为x，y，z轴，建立空间直角坐标系如图所示，则C1（4，4，4），设E（0，0，z），z∈[0，4]，F（x，0，0），x∈[0，4]，则|AF|＝x．＝（4，4，4﹣z），＝（x，0，﹣z）．因为C1E⊥EF，所以，即：z2+4x﹣4z＝0，x＝z﹣．当z＝2时，x取得最大值为1．|AF|的最大值为1．故选：B．【指点迷津】建立空间直角坐标系，求出坐标，利用C 1E⊥EF，求出|AF|满足的关系式，然后求出最大值即可．利用向量法得到|AF|的关系式是解题的关键，故选D.【举一反三】1、【江西省吉安市2019届高三上学期期末】若某几何体的三视图如图所示，则该几何体的最长棱的棱长为A．B．C．D．【答案】A【解析】解：根据三视图知，该几何体是一个正四棱锥，画出图形如图所示；则，，底面CDEB，结合图形中的数据，求得，在中，由勾股定理得，同理求得，．故选：A ．2、【河南省顶级名校2019届高三第四次联合测评】在侧棱长为的正三棱锥中，侧棱OA ，OB ，OC 两两垂直，现有一小球P 在该几何体内，则小球P 最大的半径为 A ． B ． C ．D ．【答案】B 【解析】当小球与三个侧面，，及底面都相切时，小球的体积最大此时小球的半径最大，即该小球为正三棱锥的内切球设其半径为由题可知因此本题正确选项：3、如右图所示，在棱长为2的正方体1111ABCD A B C D 中， E 为棱1CC 的中点，点,P Q 分别为面1111A B C D和线段1B C 上的动点，则PEQ ∆周长的最小值为_______．【解析】将面1111A B C D 与面11BB C C 折成一个平面，设E 关于11B C 的对称点为M ，E 关于1B C 对称点为N,则PEQ ∆周长的最小值为MN ==类型二面积的最值问题【例2】【河南省郑州市2019年高三第二次质量检测】在长方体中，，，分别是棱的中点，是底面内一动点，若直线与平面没有公共点，则三角形面积的最小值为（）A ．B ．C ．D ．【答案】C 【解析】补全截面EFG 为截面EFGHQR 如图，其中H 、Q 、R 分别为、的中点，易证平面ACD 1∥平面EFGHQR ，∵直线D 1P 与平面EFG 不存在公共点， ∴D 1P∥面ACD 1，∴D 1P 面ACD 1，∴P ∈AC ，∴过P 作AC 的垂线，垂足为K ，则BK=,此时BP 最短，△PBB 1的面积最小，∴三角形面积的最小值为，故选：C．【指点迷津】截面问题，往往涉及线面平行，面面平行定义的应用等，考查空间想象能力、逻辑思维能力及计算求解能力.解题的关键是注意明确截面形状，确定几何量.本题由直线与平面没有公共点可知线面平行，补全所给截面后，易得两个平行截面，从而确定点P所在线段，得解．【举一反三】1、【湖南省衡阳市2019届高三二模】如图，直角三角形，，，将绕边旋转至位置，若二面角的大小为，则四面体的外接球的表面积的最小值为（）A．B．C．D．【答案】B【解析】如图，，，分别为，，的中点，作面，作面，连，，易知点即为四面体的外接球心，，，.设，，则，，，.【处理一】消元化为二次函数..【处理二】柯西不等式..所以.2、如图，在正四棱柱1111D C B A ABCD -中，2,11==AA AB ，点P 是平面1111D C B A 内的一个动点，则三棱锥ABC P -的正视图与俯视图的面积之比的最大值为（）A ．1B ．2C ．21D ．41 【答案】BABC P -的正视图与俯视图的面积之比的最大值为2；故选B ．3、【福建省2019届高三模拟】若某几何体的三视图如图所示，则该几何体的所有侧面和底面中，面积的最大值为（）A ．2B ．C ．3D ．【答案】C【解析】由三视图可得，该几何体的直观图如图所示，其中，为的中点，平面，，.所以，，.又因为，，所以，故，所以.故选C.类型三体积的最值问题【例3】如图，已知平面平面，，、是直线上的两点，、是平面内的两点，且，，，，，是平面上的一动点，且有，则四棱锥体积的最大值是（）A. B. C. D.【答案】A【指点迷津】本题主要考查面面垂直的性质，棱锥的体积公式以及求最值问题. 求最值的常见方法有①配方法：若函数为一元二次函数，常采用配方法求函数求值域，其关键在于正确化成完全平方式，并且一定要先确定其定义域；②换元法；③不等式法；④单调性法；⑤图像法，本题首先根据线面关系将体积最值转化为函数求最值问题，然后应用方法①解答的. 【举一反三】1、已知AD 与BC 是四面体ABCD 中相互垂直的棱，若6AD BC ==，且60ABD ACD ∠=∠=，则四面体ABCD 的体积的最大值是A. B. C. 18 D. 36 【答案】A2、如图，已知平面l αβ=，A 、B 是l 上的两个点，C 、D 在平面β内，且,,DA CB αα⊥⊥4AD =，6,8AB BC ==，在平面α上有一个动点P ，使得APD BPC ∠=∠，则P ABCD -体积的最大值是（）A. B.16 C.48 D.144 【答案】C 【解析】,,DA DA βααβ⊂⊥∴⊥面.,,DA CB αα⊥⊥PAD ∴∆和PBC ∆均为直角三角形．,APD BPC PAD ∠=∠∴∆∽PBC ∆.4,8,2AD BC PB PA ==∴=.学科&网过P 作PM AB ⊥,垂足为M .则PM β⊥.令AM t =,()t R ∈.则2222PA AM PB BM -=-,即()222246PA t PA t -=--,2124,PA t PM ∴=-∴=底面四边形ABCD 为直角梯形面积为()1486362S =+⨯=.学科&网136483P ABCD V -∴=⨯=.故C 正确.3.【河南省八市重点高中联盟“领军考试”2019届高三第三次测评】已知一个高为l 的三棱锥，各侧棱长都相等，底面是边长为2的等边三角形，内有一个体积为的球，则的最大值为（） A ． B ．C ．D ．【答案】A 【解析】依题意，当球与三棱锥的四个面都相切时，球的体积最大，该三棱锥侧面的斜高为，，，所以三棱锥的表面积为，设三棱锥的内切球半径为，则三棱锥的体积，所以，所以，所以，故选A.类型四角的最值问题【例4】如图，四边形ABCD 和ADPQ 均为正方形，它们所在的平面互相垂直，动点M 在线段PQ 上，E 、F 分别为AB 、BC 的中点.设异面直线EM 与AF 所成的角为θ，则θcos 的最大值为.【答案】25【解析】建立坐标系如图所示.设1AB =，则11(1,,0),(,0,0)22AF E =.设(0,,1)(01)M y y ≤≤，则1(,,1)2EM y =-，由于异面直线所成角的范围为(0,]2π，所以cos θ==.2281145y y +=-+，令81,19y t t +=≤≤，则281161814552y y t t+=≥++-，当1t =时取等号.所以2cos 5θ==≤=，当0y =时，取得最大值.C【指点迷津】空间的角的问题，只要便于建立坐标系均可建立坐标系，然后利用公式求解.解本题要注意，空间两直线所成的角是不超过90度的.几何问题还可结合图形分析何时取得最大值.当点M 在点P 处时，EM 与AF 所成角为直角，此时余弦值为0（最小），当点M 向左移动时，.EM 与AF 所成角逐渐变小，点M 到达点Q 时，角最小，余弦值最大. 【举一反三】1、矩形ABCD 中，，，将△ABC 与△ADC 沿AC 所在的直线进行随意翻折，在翻折过程中直线AD 与直线BC 成的角范围（包含初始状态）为（）A.B.C.D.【答案】C2、在正方体1111D C B A ABCD -中，O 是BD 中点，点P 在线段11D B 上，直线OP 与平面BD A 1所成的角为α，则αsin 的取值范围是（） A ．]33,32[B ．]21,31[C ．]33,43[D ．]31,41[ 【答案】A3.【云南省昆明市云南师范大学附属中学2019届高三上学期第四次月考】如图，在正方体中，点P为AD的中点，点Q为上的动点，给出下列说法：可能与平面平行；与BC所成的最大角为；与PQ一定垂直；与所成的最大角的正切值为；．其中正确的有______写出所有正确命题的序号【答案】【解析】解：由在棱长为1的正方体中点P为AD的中点，点Q为上的动点，知：在中，当Q为的中点时，，由线面平行的判定定理可得PQ与平面平行，故正确；在中，当Q为的中点时，，，，可得，故错误；在中，由，可得平面，即有，故正确；在中，如图，点M为中点，PQ与所成的角即为PQ与所成的角，当Q与，或重合时，PQ与所成的角最大，其正切值为，故正确；在中，当Q 为的中点时，PQ 的长取得最小值，且长为，故正确．故答案为：．4、在正四面体P ABC -中，点M 是棱PC 的中点，点N 是线段AB 上一动点，且AN AB λ=，设异面直线NM 与AC 所成角为α，当1233λ≤≤时，则cos α的取值范围是__________．【答案】,3838⎡⎢⎣⎦ 【解析】设P 到平面ABC 的射影为点O ,取BC 中点D ,以O 为原点，在平面ABC 中，以过O 作DB 的平行线为x 轴，以OD 为y 轴，以OP 为z 轴，建立空间直角坐标系，如图，设正四面体P −ABC的棱长为则()()(((0,4,0,,,,A B C P M --，由AN AB λ=,得(),64,0N λ-，∴((),56,NM AC λ=--→-=-，∵异面直线NM 与AC 所成角为α, 1233λ≤≤，∴2NM AC cos NM AC α⋅==⋅，设32t λ-=，则5733t 剟∴222111124626()41t cos t t t tα==-+-⋅+，∵1313375t <剟cos α.∴cos α的取值范围是⎣⎦.三．强化训练一、选择题1、【甘肃省2019届高三第一次高考诊断】四棱锥的顶点均在一个半径为3的球面上，若正方形的边长为4，则四棱锥的体积最大值为（）A．B．C．D．【答案】D【解析】设正方形的中心为，当在于球心的连线上时，四棱锥高最高，由于底面面积固定，则高最高时，四棱锥体积取得最大值.设高为，，球的半径为，故，解得.故四棱锥的体积的最大值为.故选D.2．【广东省东莞市2019届高三第二次调研】已知一个四棱锥的正主视图和俯视图如图所示，其中，则该四棱锥的高的最大值为A．B．C．4 D．2【答案】A【解析】解：如图所示，由题意知，平面平面ABCD，设点P到AD的距离为x，当x最大时，四棱锥的高最大，因为，所以点P的轨迹为一个椭圆，由椭圆的性质得，当时，x取得最大值，即该四棱锥的高的最大值为．故选：A．3．【四川省教考联盟2019届高三第三次诊断】已知四棱锥的底面四边形的外接圆半径为3，且此外接圆圆心到点距离为2，则此四棱锥体积的最大值为（）A．12 B．6 C．32 D．24【答案】A【解析】由锥体的体积公式v=，可知，当s和h都最大时，体积最大.由题得顶点P到底面ABCD的距离h≤2.当点P在底面上的射影恰好为圆心O时，即PO⊥底面ABCD时，PO最大=2，即,此时,即四边形ABCD为圆内接正方形时，四边形ABCD的面积最大，所以此时四边形ABCD的面积的最大值=,所以.故选：A4．【安徽省蚌埠市2019届高三第一次检查】某三棱锥的三视图如图所示，网格纸上小正方形的边长为1，三棱锥表面上的点M在俯视图上的对应点为A，三棱锥表面上的点N在左视图上的对应点为B，则线段MN的长度的最大值为A ．B ．C ．D ．【答案】D 【解析】由三视图可知，该三棱锥的底面是直角三角形，一条侧棱与底面垂直（平面），为几何体的直观图如图，在上，重合，当与重合时，线段的长度的最大值为．故选D ．5．如图，在矩形ABCD 中， 2,1AB AD ==,点E 为CD 的中点， F 为线段CE （端点除外）上一动点现将DAF ∆沿AF 折起，使得平面ABD ⊥平面ABC 设直线FD 与平面ABCF 所成角为θ，则sin θ的最大值为（）A.13 B. 4 C. 12 D. 23【答案】C 【解析】如图：在矩形中，过点作的垂线交于点，交于点设，6．【2019年4月2019届高三第二次全国大联考】已知正四面体的表面积为，点在内（不含边界）. 若，且，则实数的取值范围为（） A ． B ． C ．D ．【答案】A 【解析】设正四面体的棱长为则，解得则正四面体的高为记点到平面、、的距离分别为则因为，所以，则故又，故即实数的取值范围为本题正确选项：二、填空题7．【山东省青岛市2019届高三3月一模】在四棱锥中，底面是边长为2的正方形，面，且，若在这个四棱锥内有一个球，则此球的最大表面积为__________．【答案】【解析】在这个四棱锥内有一个球，则此球的最大表面积时，对应的球应该是内切球，此时球的半径最大，设内切球的球心为O半径为R，连接球心和ABCD四个点，构成五个小棱锥，根据体积分割得到，五个小棱锥的体积之和即为大棱锥的体积，，根据AB垂直于AD，PD垂直于AB 可得到AB垂直于面PDA，故得到AB垂直于PA，同理得到BC垂直于PC，表面积为：，此时球的表面积为：.故答案为：.8．【陕西省西安地区陕师大附中、西安高级中学、高新一中、铁一中学、西工大附中等八校2019届高三3月联考】如图，已知正四棱柱和半径为的半球O，底面ABCD在半球O底面所在平面上，，，，四点均在球面上，则该正四棱柱的体积的最大值为______．【答案】4【解析】设正四棱柱的高为h，底面棱长为a，则正四棱柱的底面外接圆直径为，所以，．由勾股定理得，即，得，其中，所以，正四棱柱的体积为，其中，构造函数，其中，则，令，得．当时，；当时，．所以，函数在处取得极大值，亦即最大值，则．因此，该正四棱柱的体积的最大值为4．9．【陕西省西安地区陕师大附中、西安高级中学、高新一中、铁一中学、西工大附中等八校2019届高三3月联考】如图，已知圆柱和半径为的半球O，圆柱的下底面在半球O底面所在平面上，圆柱的上底面内接于球O，则该圆柱的体积的最大值为_____．【答案】2π【解析】解：设圆柱的底面圆半径为r，高为h；则h2+r2＝R2＝3；所以圆柱的体积为V＝πr2h＝π（3﹣h2）h＝π（3h﹣h3）；则V′（h）＝π（3﹣3h2），令V′（h）＝0，解得h＝1；所以h∈（0，1）时，V′（h）＞0，V（h）单调递增；h∈（1，）时，V′（h）＜0，V（h）单调递减；所以h＝1时，V（h）取得最大值为V（1）＝2π．故答案为：2π．10．【江西省上饶市2019届高三二模】一个棱长为的正方体形状的铁盒内放置一个正四面体，且能使该正四面体在铁盒内任意转动，则该正四面体的体积的最大值是_____.【答案】【解析】由题该正四面体在铁盒内任意转动，故其能在正方体的内切球内任意转动，内切球半径为6，设正四面体棱长为a, 将此正四面体镶嵌在棱长为x的正方体内，如图所示：则x=，外接球的球心和正方体体心O重合，∴外接球的球半径为：=6,a=4又正四面体的高为∴该正四面体的体积为故答案为11．【河北省衡水市第二中学2019届高三上期中】已知体积为的正四棱锥外接球的球心为，其中在四棱锥内部.设球的半径为，球心到底面的距离为.过的中点作球的截面，则所得截面圆面积的最小值是___________.【答案】【解析】如图取底面的中心为，连接平面，且球心在上，由条件知，，连接，，则，于是底面的边长为.又，故四棱锥的高是，所以，即，从而，，于是，过的中点的最小截面圆是以点为圆心的截面圆，该截面圆的半径是，故所求面积为.12．【江西省临川第一中学等九校2019届高三3月联考】如图所示，三棱锥的顶点，，，都在同一球面上，过球心且，是边长为2等边三角形，点、分别为线段，上的动点（不含端点），且，则三棱锥体积的最大值为__________．【答案】【解析】过球心，又是边长为的等边三角形，，,三角形是等腰直角三角形，，，又因为,在平面内，由线面垂直的判定定理可得平面,即平面，设，，则三棱锥体积，当且仅当，即时取等号，故答案为.13．【安徽省蚌埠市2019届高三下学期第二次检查】正三棱锥中，，点在棱上，且.正三棱锥的外接球为球，过点作球的截面，截球所得截面面积的最小值为__________．【答案】【解析】因为，所以，所以，同理，故可把正三棱锥补成正方体（如图所示），其外接球即为球，直径为正方体的体对角线，故，设的中点为，连接，则且，所以，当平面时，平面截球的截面面积最小，此时截面为圆面，其半径为，故截面的面积为．填．14．【江西师范大学附属中学2019高三上学期期末】若一个四棱锥的底面为正方形，顶点在底面的射影为正方形的中心，且该四棱锥的体积为9，当其外接球的体积最小时，它的高为_________．【答案】【解析】设四棱锥底面边长为a，高为h，底面对角线交于O，由条件四棱锥P-ABCD为正四棱锥，其外接球的球心M在高PO上，设外接球半径为R，在直角三角形MAO中，，又该四棱锥的体积为9，所以所以，，，时，时，所以时R极小即R最小，此时体积最小.故答案为3.15．【江西省上饶市2019届高三二模】已知正方体的棱长为，平面与对角线垂直且与每个面均有交点，若截此正方体所得的截面面积为，周长为，则的最大值为______.【答案】【解析】因为平面与对角线垂直，所以平面与对角面平行，作出图象，为六边形,设则,所以，由对称性得平面过对角线中点时截面面积取最大值为，则的最大值为.16．【河南省洛阳市2019届高三第二次统考】正四面体中，是的中点，是棱上一动点，的最小值为，则该四面体内切球的体积为_____.【答案】【解析】如下图，正方体中作出一个正四面体将正三角形和正三角形沿边展开后使它们在同一平面内，如下图：要使得最小，则三点共线，即：，设正四面体的边长为，在三角形中，由余弦定理可得：，解得：，所以正方体的边长为2，正四面体的体积为：，设四正面体内切球的半径为，由等体积法可得：，整理得：，解得：，所以该四面体内切球的体积为.17．【2019届湘赣十四校高三联考第二次考试】如图，正三棱锥的高，底面边长为4，，分别在和上，且，当三棱锥体积最大时，三棱锥的内切球的半径为________．【答案】【解析】设，，当时，取得最大值，此时为中点，经过点，且，，所以可求，，因此易求，，，，又∵，∴.。

巧借平面三点共线求解立体几何最值

㊃题根研究㊃Җ㊀江苏㊀陆海琴㊀㊀空间几何体是由点㊁线㊁面构成的,在处理立体几何问题时,巧用平面几何性质,可使问题简洁求解.本文利用三点共线原理,探究一类立体几何最值问题.题根㊀平面四边形A B C D 中,在对角线A C 上寻找一点P ,使其到点B ㊁D 距离之和最小.利用三点共线原理易知B D 与A C 的交点,即为所求的点P .下面就此性质的应用,进行变式探究.1㊀直接应用求最值㊀㊀图1例1㊀(2015年福建卷)如图1所示,A B 是圆O 的直径,点C 是圆O 上异于A ㊁B 的点,P O 垂直于圆O 所在平面,且P O =O B =1.(1)若D 为线段A C的中点,求证A C ʅ平面P D O ;(2)求三棱锥P -A B C 体积的最大值;(3)若B C =2,点E 在线段P B 上,求C E +O E 的最小值.(1)㊁(2)略.(3)在әP O B 中,P O =O B =1,øP O B =90ʎ,所以P B =12+12=2.同理P C =2,所以P B =P C =B C .㊀㊀图2在三棱锥P -A B C 中,将侧面B C P 绕P B 旋转至平面B C ᶄP ,使之与平面A B P 共面,如图2所示.当O ㊁E ㊁C ᶄ共线时,C E +O E 取得最小值.又因为P O =O B ,C ᶄP =C ᶄB ,所以O C ᶄ垂直平分P B ,故O C ᶄ=O E+E C ᶄ=22+62=2+62,即C E +O E 的最小值为2+62.将面P B C 旋转至与面P A B 共面的位置时,即可直接应用题根的形式求此最值.2㊀多角度展开求最值例2㊀如图3所示,在直三棱柱A B C -㊀㊀图3A 1B 1C 1中,A B =B C =2,B B 1=2,øA BC =90ʎ,M ㊁N 分别为A A 1㊁C 1B 1的中点,求沿棱柱的表面从点M 到N 的最短路径.最短路径可按如下3种展开方式求解.1)沿棱B B 1展开,如图4.所以MN =1+(322)2=222.2)沿棱A 1B 1展开,如图5.过点M 作MP ʅB B 1于点P ,故MN =(2)2+(1+22)2=72+2.3)沿棱A 1C 1展开,如图6所示.图4㊀㊀㊀㊀㊀㊀㊀图5㊀㊀㊀㊀㊀㊀㊀图6过点M 作A A 1的垂线,过点N 作A 1C 1的垂线,2线交于点Q ,所以MN =(32)2+(32)2=322.综上可知MN 的最小值为322.本题通过运用平面化策略将几何体展开后利用题根求最值,但展开的方式并不唯一,因此应就其可能情况分别求最值,再将所得结果进行比较得出最小值.3㊀借助共线原理确定点的位置例3㊀(2012年福建卷)在长方体A B C D -A 1B 1C 1D 1中,A B =A D =1,A A 1=2,M 为棱D D 1上的一点.(1)求三棱锥A -M C C 1的体积;(2)当A 1M +M C 取得最小值时,求证:B 1M ʅ平面MA C .(1)略.(2)证明:将侧面C D D 1C 1绕DD 1逆时针转90ʎ展开,与侧面A D D 1A 1共面(如图7).当A 1㊁M ㊁C ᶄ共线时,A 1M +M C 取得最小值.由A D =C D =1,A A 1=2,得M 为D D 1中点.连接C 1M ,在әC 1M C 中,M C 1=2,M C =2,C C 1=2,故C C 21=3㊃通法研究㊃㊀图7M C 21+M C 2,得øC M C 1=90ʎ,即C M ʅM C 1.又由长方体A B C D -A 1B 1C 1D 1可知B 1C 1ʅ平面C D D 1C 1,所以B 1C 1ʅC M .又B 1C 1ɘC 1M =C 1,所以C M ʅ平面B 1C 1M ,得C M ʅB 1M .同理可证B 1M ʅAM .又AM ɘM C =M ,所以B 1Mʅ平面MA C .本题将最值问题作为条件来确定点的位置,从而利用题根将侧面展开后,由3点共线原理得到了点M 的位置,为后续解题创造了条件.4㊀变化应用到点面距例4㊀在长方体A B C D -A 1B 1C 1D 1中,A B =2,B C =A A 1=1,点P 为对角线A C 1上的动点,点Q 为底面A B C D 上的动点(点P ㊁Q 可以重合),则B 1P +P Q 的最小值为(㊀㊀).A㊀2;㊀㊀B ㊀3;㊀㊀C ㊀32;㊀㊀D㊀2如图8所示,求B 1P +P Q 的最小值,易知当点Q 位于A C 上时,P Q 可取到最小值.连接A B 1,将面A B 1C 旋转至与面A C C 1在同一平面(如图9),过点B 1作A C 的垂线,交A C 于点Q ,则B 1即为所求最小距离.㊀图8㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀图9由题目条件知A C ʅC C 1,A B 1ʅB 1C 1,A B 1=3,øC A C 1=øB 1A C 1=30ʎ,所以øA B 1Q =30ʎ,所以A Q =32,由勾股定理得B 1Q =32,即为所求.故正确选项为C .本题将点到点的距离变化为点到面的距离,同样利用平面化策略,将问题转化为点到线的最小值问题.综上,空间问题平面化是处理立体几何问题常用策略,平面化后再利用平面图形的性质原理解题.当然问题的考查形式不仅局限于本文所述,请同学们不断进行归纳总结,进而提高解题能力.(作者单位:江苏省海安县实验中学)Җ㊀河北㊀王崇艳㊀㊀空间向量的引入,利用点的坐标将几何问题代数化处理,降低了立体几何问题求解的难度,特别是空间角问题的求解.空间角主要包括2条异面直线所成的角㊁直线与平面所成的角㊁2个平面所成的角.本文引例说明向量法在求解空间问题中的理论基础及注意事项,以期对同学们复习此部分内容有所帮助㊀图1引例㊀(2015年天津卷)如图1所示,在四棱柱A B C D -A 1B 1C 1D 1中,侧棱A 1A ʅ面A B C D ,A B ʅA C ,A B =1,A C =A A 1=2,A D =C D =5,且点M ㊁N 分别为B 1C ㊁D 1D 的中点.(1)求直线MN 与C D 1夹角的余弦值(改编);(2)求二面角D 1-A C -B 1的正弦值;(3)设E 为棱A 1B 1上的点,若直线N E 和平面A B C D 所成角的正弦值为1/3,求线段A 1E 的长.1㊀恰当建系㊀准确找坐标建立坐标系是利用向量法求解立体几何问题的出发点.建系以充分利用题目条件中直接或间接给出的垂直关系为依据,尽可能使更多的点落在坐标轴上.间接的垂直关系常存在于特殊的平面几何图形中,如菱形㊁等腰三角形等.本题直接给出侧棱A 1A ʅ面A B C D ,A B ʅA C 为坐标系的建立奠定了基础.图如图2,以A 为原点建立空间直角坐标系,依题意可得A (0,0,0)㊁B (0,1,0)㊁C (2,0,0)㊁D (1,-2,0)㊁A 1(0,0,2)㊁B 1(0,1,2)㊁C 1(2,0,2)㊁D 1(1,-2,2).因为M ㊁N 分别为B 1C ㊁D 1D 的中点,得M (1,1/2,1)㊁N (1,-2,1).2㊀把握空间角求解的理论基础1)异面直线所成的角用传统方法求异面直线所成的角,首先需找到所成的角或其补角再求解,难度大,易出错.利用直线上4。

例谈立体几何最值问题的几种解法

思路探寻立体几何最值问题侧重于考查同学们的空间想象、逻辑推理和数学运算等能力.常见的立体几何最值问题是求立体几何图形中某条线段、某个角、体积、表面积的最值，那么如何求解呢？一、利用函数思想在大多数情况下，我们可以把与动点有关的立体几何问题看作函数问题来求解.以其中某一个量，如动点的坐标、线段的长、角的大小为变量，建立关于该变量的关系式，并将其视为函数式，即可利用一次函数、二次函数、三角函数的性质和图象求得最值.例1.如图1，正方体ABCD-A1B1C1D1的棱长为1，P为AA1的中点，M在侧面AA1B1B上，若D1M⊥CP，则ΔBCM）.C.5D.2图1图2解：过M作MG⊥平面ABCD，垂足为G，作GH⊥BC于点H，连接MH，以D为坐标原点，建立如图2所示的空间直角坐标系，可得D()0,0,0，C()0,1,0，A()1,0,0，P()1,0,12，D1(0,0,1)，B()1,1,0.设M()1,a,b，则D1M=()1,a,b-1，CP=()1,-1,12，∵D1M⊥CP，∴ D1M⋅ CP=12b-a+12=0，∴b=2a-1，∴CH=1-a，MG=2a-1，∴MH=()1-a2+()2a-12=5a2-6a+2，∴SΔBCM=12BC⋅MH=1=可知当a=35时，ΔBCM面积取最小值，为SΔBCM=12×=故选B.在建立空间直角坐标系后，设出点M的坐标，以a、b为变量，构建关于a的函数式SΔBCM=然后将5a2-6a+2看作二次函数式，对其配方，根据二次函数的性质即可知函数在a=35时取最小值.二、运用基本不等式在解答立体几何最值问题时，我们往往可以先根据立体几何中的性质、定义、定理求得目标式；然后将其进行合理的变形，采用拆项、凑系数、补一次项，去掉常数项等方式，配凑出两式的和或积，就可以直接运用基本不等式来求得最值.在运用基本不等式求最值时，要把握三个条件：一正、二定、三相等.例2.已知三棱锥P-ABC的4个顶点均在球心为O、直径为23的球面上，PA=2，且PA,PB,PC两两垂直.当PC+AB取最大值时，三棱锥O-PAB的体积为（）.A. C.6解：∵PA,PB,PC两两互相垂直，∴三棱锥P-ABC可补全为如图3所示的长方体.则长方体的外接球即为三棱锥P-ABC的外接球，∴PA2+PB2+PC2=()232=12，又PA=2，∴PB2+PC2=10，∵AB2=PA2+PB2=2+PB2，∴PC2+AB2=2+PB2+PC2=12，∴()PC+AB2-2PC⋅AB=12，又PC⋅AB≤()PC+AB22，∴12=()PC+AB2-2PC⋅AB≥()PC+AB2-2()PC+AB22=12()PC+AB2，当且仅当PC=AB时取等号，∴()PC+AB max=26，此时PC=AB=6，PB=图347思路探寻AB 2-PA 2=2，∴V O -PAB =12V C -PAB =16S △PAB ⋅PC =112PA ⋅PB⋅PC =112×2×2×6故选B.根据长方体的性质得到()PC +AB 2-2PC ⋅AB =10后，可发现该式中含有PC 、AB 的和与积，根据基本不等式a +b ≥2ab 求解，即可得到三棱锥O -PAB 的体积.三、转化法运用转化法求解立体几何最值问题有两种思路.一是将问题转化为平面几何问题.先将几何体的表面展开，或将几何体内部满足条件的某些面展开成平面；再在平面内利用平面几何知识，如正余弦定理、两点间的距离最短、三角形的两边之和大于第三边等求解，这样问题就变得十分直观，容易求解了.另一种思路是根据题意和几何图形中的点、线、面的位置关系，明确其中改变的量和不变的量及其关系，根据简单几何体的性质、表面积公式、体积公式，将问题转化为求某些线段或角的最值.再结合简单几何体的性质，几何图形中点、线、面的位置关系求得最值例3.如图4，在正三棱柱ABC -A 1B 1C 1中，AA 1=AB =2，D 在A 1C 上，E 是A 1B 的中点，则()AD +DE 2的最小值是（）.A.6-7 B.27 C.3+7 D.5+7图4图5解：将平面A 1BC 与平面A 1AC 翻折到同一平面上，连接AE ，如图5所示，设AE ⋂A 1C =F ．由题意可知A 1A =AC =BC =2，A 1C =A 1B =22，所以AA 21+AC 2=A 1C 2，所以AA 1⊥AC ，则∠AA 1C =45°，由余弦定理可得cos∠BA 1C =A 1B 2+A 1C 2-BC 22A 1B ⋅A 1C=8+8-42×22×22=34，则sin∠BA 1C =1-cos 2∠BA 1C =故cos∠AA 1B =cos ()∠AA 1C +∠BA 1C =cos ∠AA 1C cos ∠BA 1C -sin ∠AA 1C sin ∠BA 1C =32-148．因为E 是A 1B 的中点，所以A 1E =2，由余弦定理可得AE 2=AA 21+A 1E 2-2AA 1⋅A 1E cos∠BA 1A=4+2-2×2×2×32-148=3+7．因为D 在A 1C 上，所以AD +DE ≥AE ，当A 、E 、D 三点共线时，等号成立，则()AD +DE 2≥3+7.故选C .将平面A 1BC 与平面A 1AC 翻折到同一平面上，就可以把立体几何问题转化为平面几何问题，即可根据勾股定理和余弦定理求得A 1E 以及AE 的值.分析图形可知当A 、E 、D 三点共线时，AD +DE 取得最大值，再结合余弦定理求解即可.例4.已知球O 的表面积为60π，四面体P -ABC 内接于球O ，ΔABC 是边长为6的正三角形，平面PBC ⊥平面ABC ，则四面体P -ABC 体积的最大值为（）.A.18B.27C.32D.81解：因为球O 的表面积为60π，所以球的半径R ==15，由题意知四面体P -ABC 底面三角形的面积为定值，要使四面体的体积最大，只须使顶点P 到底面的距离最大，又因为平面PBC ⊥平面ABC ，所以当PB =PC 时，点P 到底面的距离最大，而ΔABC 外接圆的半径r =62sin60°=23，则O 到面ABC 的距离为d =R 2-r 2=3，且O 到面PBC 的距离为h =12r =3，设点P 到平面ABC 的距离为H ，则R 2=()H -d 2+h 2，解得H =33，此时体积最大值为V max =13×12×6×6×sin60°×33=27.故选B.解答本题，首先根据球的表面积求得球的半径；再根据题意和几何体的特征明确当PB =PC 时，点P 到底面的距离最大；最后根据外接圆的性质、勾股定理求出点P 到底面的距离，即可求出最大值.除了上述三种方法外，有时还可采用定义法、构造法来求立体几何最值问题的答案.总之，同学们在解题时，要先根据题意和几何体的结构特征寻找取得最值的情形，求得目标式；然后根据目标式的特征，选用合适的方法求最值.（作者单位：贵州省江口中学）48。