三角形的角及倒角模型

合集下载

三角形角度计算模型

三角形角度计算模型1. 三角形的角三角形的内角与外角：三角形的相邻两条边所组成的角叫做三角形的内角．三角形的任意一边与另一边的反向延长线所组成的角叫做三角形的外角．2. 三角形内角和定理三角形内角和定理：三角形三个内角和等于180°，即在△ABC 中，180A B C ∠+∠+∠=°．三角形内角和定理的推论：推论：三角形的一个外角等于和它不相邻的两个内角的和．利用三角形内角和定理及其推论的关键是：根据图形特点，将若干个分散的角集中到一个三角形中．3. 三角形常见角度计算模型（1）“A ”字型：如图1，D 、E 分别为AB 、AC 上的点，则B C ADE AED ∠+∠=∠+∠．如图2，180BDE CED A ∠+∠=°+∠．（2）“8”字型：如图3，AD 、BC 相交于点O ，则A B C D ∠+∠=∠+∠．（3）燕尾型：如图4，BOC A B C ∠=∠+∠+∠．如图5，A O BDO CEO ∠+∠=∠+∠．（4）两个内角平分线所成的角与第三个角之间的关系：如图6，∠ABC 、∠ACB 的内角平分线相交于点P ，则1902P A ∠=°+∠．DCABO图3 BOA图4 图7图8ABC FPEBCDE A 图1C PBA 图6B 图5CDE A O BCDE A图2（5）一个内角平分线与一个外角平分线所成的角与第三个角之间的关系：如图7，∠ACE 与∠ABC 的平分线相交于点P ，则12P A ∠=∠．（6）两个外角平分线所成的角与第三个角之间的关系：如图8，∠CBF 与∠BCE 的平分线相交于点P ，则1902P A ∠=°−∠．（7）同角或等角的余角相等在两个直角三角形中，如果题中隐含着一个直角三角形的一个锐角与另一个直角三角形的锐角相等（同角或对顶角），则剩下的另一组锐角也相等．如图9，在Rt △ABC 和Rt △CDE 中，B 、C 、D 在一条直线上，则A DCE ∠=∠，ACB E ∠=∠．如图10，在Rt △ABC 中，90C ∠=°，DE ⊥AB ，由于C C ∠=∠（公共角），则B AED ∠=∠．如图11，在Rt △ABC 和Rt △ACD 中，由于C C ∠=∠（公共角），所以DAC B ∠=∠．如图12，在Rt △ABC 和Rt △CDE 中，由于C C ∠=∠（公共角），所以B E ∠=∠．如图12，在Rt △AEF 和Rt △BDF 中，由于AFE BFD ∠=∠（对顶角），所以B E ∠=∠．图11EDCBA 图12FAB C D E 图9AB C D 图10E。

三角形倒角8个基本型

三角形倒角8个基本型
三角形倒角8个基本型
一、直角三角形型
指三角形的三条边均为直线，作工时采ユ直角三角形的两个外角倒角。

该型可分为正直角三角形和倒直角三角形两种型型。

二、锐角三角形型
指三角形的三条边均为直线，作工时采ユ锐角三角形的两个外角倒角。

该型可分为正锐角三角形和倒锐角三角形两种型型。

三、圆角三角形型
指三角形的三条边均为弧线，作工时采ユ圆角三角形的两个外角倒角。

该型可分为正圆角三角形和倒圆角三角形两种型型。

四、菱形型
指四条边均为直线的多边形，作工时采ユ菱形的两个外角倒角。

该型可分为正菱形和倒菱形两种型型。

五、六边形型
指六条边均为直线的多边形，作工时采ユ六边形的四个外角倒角。

该型可分为正六边形和倒六边形两种型型。

六、椭圆型
指四条边均为椭圆的多边形，作工时采ユ椭圆的两个外角倒角。

该型可分为正椭圆和倒椭圆两种型型。

七、不规则四边形型
指由不同正方形、长方形或多边形组成的不规则四边形，作工时
采ユ不规则四边形的四个外角倒角。

该型可分为正不规则四边形和倒不规则四边形两种型型。

八、五角形型
指五条边均为直线的多边形，作工时采ユ五角形的五个外角倒角。

该型可分为正五角形和倒五角形两种型型。

2024中考数学常见几何模型归纳总结—三角形中的倒角模型-高分线模型、双(三)垂直模型

2024中考数学常见几何模型归纳总结—三角形中的倒角模型-高分线模型、双（三）垂直模型近年来各地考试中常出现一些几何倒角模型，该模型主要涉及高线、角平分线及角度的计算（内角和定理、外角定理等）。

熟悉这些模型可以快速得到角的关系，求出所需的角。

本专题高分线模型、双垂直模型、子母型双垂直模型（射影定理模型）进行梳理及对应试题分析，方便掌握。

模型1：高分线模型条件：AD 是高，AE 是角平分线结论：∠DAE=2B C∠∠-例1．（2023秋·浙江·八年级专题练习）如图，在ABC 中，30A ∠=︒，50B ∠=︒，CD 为ACB ∠的平分线，CE AB ⊥于点E ，则ECD ∠度数为（）A ．5︒B ．8︒C ．10︒D ．12︒【答案】C 【分析】依据直角三角形，即可得到40BCE ∠=︒，再根据30A ∠=︒,CD 平分ACB ∠,即可得到BCD ∠的度数,再根据DCE BCD BCE ∠=∠-∠进行计算即可．【详解】解：50,B CE AB ∠=︒⊥ ,40BCE ∴∠=︒,又30A ∠=︒ ,CD 平分ACB ∠,1118050305022()BCD BCA ∴∠=∠=⨯︒-︒-︒=︒，504010DCE BCD BCE ∴∠=∠-∠=︒-︒=︒,故选：C ．【点睛】本题考查的是三角形内角和定理，熟知三角形内角和是180︒是解答此题的关键．例2．（2023春·河南南阳·七年级统考期末）如图，在△ABC 中，∠1＝∠2，G 为AD 的中点，BG 的延长线交AC 于点E ，F 为AB 上的一点，CF 与AD 垂直，交AD 于点H ，则下面判断正确的有（）①AD 是△ABE 的角平分线；②BE 是△ABD 的边AD 上的中线；③CH 是△ACD 的边AD 上的高；④AH 是△ACF 的角平分线和高A ．1个B ．2个C ．3个D ．4个【答案】B【详解】解：①根据三角形的角平分线的概念，知AG 是△ABE 的角平分线，故此说法错误；②根据三角形的中线的概念，知BG 是△ABD 的边AD 上的中线，故此说法错误；③根据三角形的高的概念，知CH 为△ACD 的边AD 上的高，故此说法正确；④根据三角形的角平分线和高的概念，知AH 是△ACF 的角平分线和高线，故此说法正确．故选：B ．【点睛】本题考查了三角形的角平分线、三角形的中线、三角形的高的概念，注意：三角形的角平分线、中线、高都是线段，且都是顶点和三角形的某条边相交的交点之间的线段．透彻理解定义是解题的关键．例3．（2023·安徽合肥·七年级统考期末）如图，已知AD 、AE 分别是Rt △ABC 的高和中线，AB ＝9cm ，AC ＝12cm ，BC ＝15cm ，试求：（1）AD 的长度；（2）△ACE 和△ABE 的周长的差．【答案】（1）AD 的长度为365cm ；（2）△ACE 和△ABE 的周长的差是3cm ．【分析】（1）利用直角三角形的面积法来求线段AD 的长度；（2）由于AE 是中线，那么BE ＝CE ，再表示△ACE 的周长和△ABE 的周长，化简可得△ACE 的周长﹣△ABE 的周长＝AC ﹣AB 即可．【详解】解：（1）∵∠BAC ＝90°，AD 是边BC 上的高，∴S △ACB =12AB•AC ＝12BC•AD ，∵AB ＝9cm ，AC ＝12cm ，BC ＝15cm ，∴AD ＝AB AC CB ⋅＝91215⨯＝365（cm ），即AD 的长度为365cm ；（2）∵AE 为BC 边上的中线，∴BE ＝CE ，∴△ACE 的周长﹣△ABE 的周长＝AC+AE+CE ﹣（AB+BE+AE ）＝AC ﹣AB ＝12﹣9＝3（cm ），即△ACE 和△ABE 的周长的差是3cm ．【点睛】此题主要考查了三角形的面积，关键是掌握直角三角形的面积求法．例4．（2023·广东东莞·八年级校考阶段练习）如图，在ABC 中，AD ，AE 分别是ABC 的高和角平分线，若30B ∠=︒，50C ∠=︒．(1)求DAE ∠的度数．(2)试写出DAE ∠与C B ∠-∠关系式，并证明．(3)如图，F 为AE 的延长线上的一点，FD BC ⊥于D ，这时AFD ∠与C B ∠-∠的关系式是否变化，说明理由．【答案】(1)10︒(2)()12DAE C B ∠=∠-∠(3)不变，理由见解析【分析】（1）根据三角形内角和求出BAC ∠，根据角平分线的定义得到50BAE ∠=︒，根据高线的性质得到90ADE ∠=︒，从而求出60BAD ∠=︒，继而根据角的和差得到结果；（2）根据角平分线的定义得到12BAE BAC ∠=∠，根据三角形内角和求出119022EAC B C ∠=︒-∠-∠，根据角的和差得到结果；（3）过A 作AG BC ⊥于G ，结合（2）知1()2EAG C B ∠=∠-∠，证明FD AG ∥，得到AFD EAG ∠=∠，即可证明．【详解】（1）解：∵30B ∠=︒，50C ∠=︒，∴1805030100BAC ∠=︒-︒-︒=︒，∵AE 平分BAC ∠，∴1502BAE CAE BAC ∠=∠=∠=︒，∵AD 是高，∴90ADE ∠=︒，∵30B ∠=︒，∴60BAD ∠=︒，∴10DAE BAD BAE ∠=∠-∠=︒；（2）()12DAE C B ∠=∠-∠，证明如下：∵AE 平分BAC ∠，∴12EAC BAC ∠=∠，∵180BAC B C ∠=︒-∠-∠，∴()11101902822B C B C EAC ︒-∠-∠-∠︒-==∠∠，∴EAD EAC DAC ∠=∠-∠()11090922B C C =︒∠---∠︒-∠()12C B =∠-∠；（3）不变，理由是：如图，过A 作AG BC ⊥于G ，由（2）可知：1()2EAG C B ∠=∠-∠，AG BC ⊥ ，90AGB ∠=︒，FD BC ⊥ ，90FDC ∴∠=︒，AGD FDC ∴∠=∠，FD AG ∴∥，AFD EAG ∴∠=∠，1()2AFD C B ∴∠=∠-∠．【点睛】本题主要考查三角形的内角和定理、角平分线的性质、直角三角形的性质和平行线的判定与性质，熟练掌握三角形的内角和定理和角平分线的性质是解题的关键．模型2：双垂直模型结论：①∠A =∠C ；②∠B =∠AFD =∠CFE ；③AB CD AE BC ⋅=⋅。

三角形倒角模型2024

引言：在三维建模中，倒角模型是一种常用的技术，用于给几何体的尖锐边缘添加平滑的圆角效果。

在本文中，我们将继续探讨三角形倒角模型的相关内容。

首先我们会简要回顾前文介绍的方法，然后深入讨论另外五个方面的内容，包括：双曲线倒角、坡度倒角、螺旋倒角、圆柱倒角和体积倒角。

通过详细的阐述，我们希望读者能够更好地理解和应用这些倒角模型技术。

概述：三角形的倒角模型是指给三角形的边缘或角度添加圆角效果。

倒角模型可以使模型更显真实，同时也能够消除尖锐边缘的刺眼感。

在之前的文章中，我们介绍了一种基本的三角形倒角模型方法，即通过增加额外的顶点来切割原始三角形，然后连接这些顶点以形成圆角效果。

在本文中，我们将深入讨论更多的三角形倒角模型技术。

正文内容：1.双曲线倒角1.1定义双曲线倒角1.2双曲线倒角的计算方法1.3双曲线倒角的应用实例1.4双曲线倒角的优缺点1.5双曲线倒角与其他倒角方法的比较2.坡度倒角2.1坡度倒角的原理2.2坡度倒角的计算方法2.3坡度倒角的应用实例2.4坡度倒角的优缺点2.5坡度倒角与其他倒角方法的比较3.螺旋倒角3.1螺旋倒角的原理3.2螺旋倒角的计算方法3.3螺旋倒角的应用实例3.4螺旋倒角的优缺点3.5螺旋倒角与其他倒角方法的比较4.圆柱倒角4.1圆柱倒角的定义4.2圆柱倒角的计算方法4.3圆柱倒角的应用实例4.4圆柱倒角的优缺点4.5圆柱倒角与其他倒角方法的比较5.体积倒角5.1体积倒角的概念5.2体积倒角的计算方法5.3体积倒角的应用实例5.4体积倒角的优缺点5.5体积倒角与其他倒角方法的比较总结：通过本文的讨论，我们详细了解了五种不同的三角形倒角模型技术。

双曲线倒角、坡度倒角、螺旋倒角、圆柱倒角和体积倒角都是常用的倒角方法。

它们各自具有不同的原理、计算方法、应用实例和优缺点。

通过比较不同的倒角方法，我们可以根据具体需求选择最适合的方法来创建高质量的倒角模型。

文末400字，请将前文正文段落补足至1300字。

2024中考数学常见几何模型归纳总结—三角形中的倒角模型-双角平分线(三角形)模型

2024中考数学常见几何模型归纳总结—三角形中的倒角模型-双角平分线（三角形）模型模型1、双角平分线模型图1图2图31）两内角平分线的夹角模型条件：如图1，在△ABC 中，∠ABC 和∠ACB 的平分线BE ，CF 交于点G ；结论：1902BGC A ∠=︒+∠．2）两外角平分线的夹角模型条件：如图2，在△ABC 中，BO ，CO 是△ABC 的外角平分线；结论：1902O A ∠=︒-∠．3）一个内角一个外角平分线的夹角模型条件：如图3，在△ABC 中，BP 平分∠ABC ，CP 平分∠ACB 的外角，两条角平分线相交于点P ；结论：12P A ∠=∠．图4图5图64）凸多边形双内角平分线的夹角模型条件：如图4，BP 、CP 平分∠ABC 、∠DCB ，两条角平分线相交于点P ；结论：2P A D ∠=∠+∠5）两内角平分线的夹角模型条件：如图5，BP 、DP 平分∠BCD 、∠CDE ，两条角平分线相交于点P ；结论：2180P A B E ∠=∠+∠+∠-︒6）一个内角一个外角平分线的夹角模型（累计平分线）条件：如图6，A α∠=，,ABC ACD ∠∠的平分线相交于点1P ，11,PBC PCD ∠∠的平分线相交于点2P ，2P BC ∠，2P CD ∠的平分线相交于点3P ……以此类推；结论：n P ∠的度数是2n α．7）旁心模型旁心：三角形的一条内角平分线与其他两个角的外角平分线交于一点条件：如图，BD 平分∠ABC ，CD 平分∠ACB 的外角，两条角平分线相交于点D ；结论：AD 平分∠CAD 例1．（2022秋·安徽阜阳·八年级统考期中）如图，在ABC 中，点P 是ABC 内一点，且点P 到ABC 三边的距离相等，若124BPC ∠=︒，则A ∠=．【答案】68︒【分析】由条件可知BP CP 、平分ABC ∠和ACB ∠，利用三角形内角和可求得A ∠．【详解】解：∵点P 到ABC 三边的距离相等，∴BP 平分ABC ∠，CP 平分ACB ∠，∴180A ABC ACB ∠=︒-∠+∠（），1802PBC PCB =︒-∠+∠（）1802180BPC =︒-⨯︒-∠（）1802180124=︒-⨯︒-︒（）68=︒故答案为：68︒．【点睛】本题考查角平分线的性质与判定，掌握角平分线的交点到三角形三边的距离相等是解题的关键．例2．（2022·湖北十堰·八年级统考期末）如图，在五边形ABCDE 中，A B E a ∠+∠+∠=，DP ，CP 分别平分EDC ∠，BCD ∠，则P ∠的度数是．【答案】1902α- 【分析】利用多边形内角和公式、三角形内角和定理和角平分线的定义即可求解．【详解】解：∵五边形的内角和为()52180540-⨯︒=︒，∴540EDC BCD α∠+∠=︒-，∵,DP CP 分别为EDC ∠、BCD ∠的平分线，∴12PDC EDC ∠=∠，12PCD BCD ∠=∠，∴()()1154022PDC PCD EDC BCD α∠+∠=∠+∠=︒-，∴()111805409022P αα∠=︒-︒-=-︒，故答案为：1902α-︒．【点睛】本题考查了多边形的内角和公式，牢记n 边形的内角和为()2180n -⨯︒是解题关键．例3．（2023·山东济南·校考模拟预测）如图1，在△ABC 中，∠BAC 的平分线AD 与∠BCA 的平分线CE 交于点O ．(1)求证：∠AOC ＝90°＋12∠ABC ；(2)当∠ABC ＝90°时，且AO ＝3OD （如图2），判断线段AE ，CD ，AC 之间的数量关系，并加以证明．【答案】(1)见解析(2)43AE +CD =AC ，证明见解析【分析】（1）求出∠BAC +∠BCA =180°-∠ABC ，根据角平分线定义求出∠OAC =12∠BAC ，∠OCA =12∠BCA ，即可求出∠OAC +∠OCA 的度数，根据三角形内角和定理求出即可；（3）在AC 上分别截取AM 、CN ，使AM =AE ，CN =CD ，连接OM ，ON ，证△AEO ≌△AMO ，△DCO ≌△NCO ，推出∠EOA =∠MOA ，∠CON =∠COD ，OD =ON ，求出∠MON =∠MOA =45°，根据角平分线性质求出MK =ML ，据此计算即可求解．【详解】（1）证明：∵∠ABC +∠ACB +∠BAC =180°，∴∠BAC +∠BCA =180°-∠ABC ，∵∠BAC 的平分线AD 与∠BCA 的平分线CE 交于点O ．∴∠OAC =12∠BAC ，∠OCA =12∠BCA ，∴∠OAC +∠OCA =12（∠BAC +∠BCA ）=12（180°-∠ABC ）=90°-12∠ABC ，∴∠AOC =180°-（∠OAC +∠OCA ）=180°-（90°-12∠ABC ），即∠AOC =90°+12∠ABC ；（2）解：43AE +CD =AC ，证明：如图2，∵∠AOC =90°+12∠ABC =135°，∴∠EOA =45°，在AC 上分别截取AM 、CN ，使AM =AE ，CN =CD ，连接OM ，ON ，则在△AEO 和△AMO 中，AE AM EAO MAO AO AO =⎧⎪∠=∠⎨⎪=⎩，∴△AEO ≌△AMO ，同理△DCO ≌△NCO ，∴∠EOA =∠MOA ，∠CON =∠COD ，OD =ON ，∴∠EOA =∠MOA =∠CON =∠COD =45°，∴∠MON =∠MOA =45°，过M 作MK ⊥AD 于K ，ML ⊥ON 于L，∴MK =ML ，S △AOM =12AO ×MK ，S △MON =12ON ×ML ，∴AOM MON S AO ON S ∆∆=，∵AOM MON S AM S MN ∆∆=，∴AO AM ON MN =，∵AO =3OD ，∴31AO OD =，∴31AO AM ON MN ==，∴AN =43AM =43AE ，∵AN +NC =AC ，∴43AE +CD =AC ．【点睛】本题考查了全等三角形的性质和判定，角平分线定义和性质，三角形的面积，三角形内角和定理的应用，熟练掌握各性质定理是解答此题的关键．例4．（2023秋·成都市·八年级专题练习）如图，在ABC 中，58B ∠=︒，三角形两外角的角平分线交于点E ，则AEC ∠=．【答案】61°【分析】先根据三角形的内角和定理和平角定义求得∠DAC +∠ACF 的度数，再根据角平分线的定义求得∠EAC +∠ECA 的度数，即可解答．【详解】解：∵∠B +∠BAC +∠BCA =180°，∠B =58°，∴∠BAC +∠BCA =180°﹣∠B =180°﹣58°=122°，∵∠BAC +∠DAC =180°，∠BCA +∠ACF =180°，∴∠DAC +∠ACF =360°﹣（∠BAC +∠BCA ）=360°﹣122°=238°，∵AE 平分∠DAC ，CE 平分∠ACF ，∴∠EAC =12∠DAC ，∠ECA =12∠ACF ，∴∠EAC +∠ECA =12（∠DAC +∠ACF ）=119°，∵∠EAC +∠ECA +∠AEC =180°，∴∠AEC =180°﹣（∠EAC +∠ECA ）=180°﹣119°=61°，故答案为：61°．【点睛】本题考查三角形的内角和定理、角平分线的定义、平角定义，熟练掌握三角形的内角和定理和角平分线的定义是解答的关键．例5．（2023·湖北·八年级专题练习）如图，已知在ABC ∆中，B ∠、C ∠的外角平分线相交于点G ，若ABC m ∠=︒，ACB n ∠=︒，求BGC ∠的度数.【答案】()12BGC m n ∠=+ 【分析】运用角平分线的知识列出等式求解即可．解答过程中要注意代入与之有关的等量关系．【详解】解：∠B 、∠C 的外角平分线相交于点G ，在BCG ∆中，∠BGC=180°-（12∠EBC+12∠BCF ）=180°-12（∠EBC+∠BCF ）=180°-12（180°-∠ABC+180°-∠ACB ）=180°-12（180°-m°+180°-n°）；=()12+ m n 【点睛】本题考查的是三角形内角和定理以及角平分线的知识．此类题的关键是找出与之相关的等量关系简化计算得出．例6．（2023·辽宁葫芦岛·八年级统考期中）如图，CD 、BD 分别平分∠ACE 、∠ABC ，∠A ＝70°，则∠BDC ＝（）A ．35°B ．25°C ．70°D ．60°【答案】A 【分析】根据角平分线的定义可得∠CBD ＝12∠ABC ，∠DCE ＝12∠ACE ，再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠DCE ＝∠D ＋∠CBD ，∠ACE ＝∠A ＋∠ABC ，然后整理求出∠D ＝12∠A ．【详解】解：∵CD 、BD 分别平分∠ACE 、∠ABC ，∴∠CBD ＝12∠ABC ，∠DCE ＝12∠ACE ，由三角形的外角性质得，∠DCE ＝∠D ＋∠CBD ，∠ACE ＝∠A ＋∠ABC ，∴∠D ＋∠CBD ＝12（∠A ＋∠ABC ）∴∠D ＝12∠A ，∵∠A ＝70°，∴∠D ＝12×70°＝35°．故选：A ．【点睛】本题考查了三角形的外角性质，角平分线的定义，注意整体思想的利用是解答的关键．例7．（2022秋·八年级课时练习）如图，1BA 和1CA 分别是ABC 的内角平分线和外角平分线，2BA 是1A BD ∠的平分线，2CA 是1A CD ∠的平分线，3BA 是2A BD ∠的平分线，3CA 是2A CD ∠的平分线，……以此类推，若A α∠=，则2020A ∠=．【答案】20202α【分析】根据角平分线的定义可得∠A 1BC =12∠ABC ，∠A 1CD =12∠ACD ，再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD =∠A +∠ABC ，∠A 1CD =∠A 1BC +∠A 1，整理即可得解112A A ∠=∠，同理求出∠A 2，∠A 3，可以发现后一个角等于前一个角的12，根据此规律即可得解．【详解】∵A 1B 是∠ABC 的平分线，A 1C 是∠ACD 的平分线，∴∠A 1BC =12∠ABC ，∠A 1CD =12∠ACD ，又∵∠ACD =∠A +∠ABC ，∠A 1CD =∠A 1BC +∠A 1，∴12（∠A +∠ABC ）=12∠ABC +∠A 1，∴∠A 1=12∠A ，∵∠A =α．∠A 1=12∠A =12α，同理可得∠A 2=12∠A 1=212α，根据规律推导，∴2020A ∠=20202α，故答案为20202α．【点睛】本题主要考查的是三角形外角性质，角平分线定理，熟知三角形的一个外角等于与它不相邻的两个内角的和的性质，角平分线的定义是解题的关键．例8．（2023春·成都市七年级课时练习）如图在△ABC 中，BO ，CO 分别平分∠ABC ，∠ACB ，交于O ，CE为外角∠ACD 的平分线，交BO 的延长线于点E ，记1BAC ∠=∠，2BEC ∠=∠，则以下结论①122∠=∠，②32BOC ∠=∠，③901BOC ∠=︒+∠，④902BOC ∠=︒+∠，正确的是．（把所有正确的结论的序号写在横线上）【答案】①④【分析】依据角平分线的性质以及三角形外角性质，即可得到∠1＝2∠2，∠BOC ＝90°＋12∠1，∠BOC ＝90°＋∠2，再分析判断．【详解】∵CE 为外角∠ACD 的平分线，BE 平分∠ABC ，∴∠DCE ＝12∠ACD ，∠DBE ＝12∠ABC ，又∵∠DCE 是△BCE 的外角，∴∠2＝∠DCE−∠DBE ＝12（∠ACD−∠ABC ）＝12∠1，故①正确；∵BO ，CO 分别平分∠ABC ，∠ACB ，∴∠OBC ＝12ABC ，∠OCB ＝12∠ACB ，∴∠BOC ＝180°−（∠OBC ＋∠OCB ）＝180°−12（∠ABC ＋∠ACB ）＝180°−12（180°−∠1）＝90°＋12∠1，故②、③错误；∵OC 平分∠ACB ，CE 平分∠ACD ，∴∠ACO ＝12∠ACB ，∠ACE ＝12∠ACD ，∴∠OCE ＝12（∠ACB ＋∠ACD ）＝12×180°＝90°，∵∠BOC 是△COE 的外角，∴∠BOC ＝∠OCE ＋∠2＝90°＋∠2，故④正确；故答案为：①④．【点睛】本题考查了三角形的内角和定理，三角形的一个外角等于与它不相邻的两个内角的和的性质，以及角平分线的定义．例9．（2023秋·广东佛山·八年级校考期末）（1）如图1所示，在ABC 中，ABC ∠和ACB ∠的平分线将于点O ，则有1902BOC A ∠=+∠︒，请说明理由．（2）如图2所示，在ABC 中，内角的平分线ABC ∠和外角ACD ∠的平分线交于点O ，请直接写出BOC∠与BAC ∠之间的关系，不必说明理由．（3）如图3所示，AP ，BP 分别平分CAD ∠，CBD ∠，则有1()2P C D ∠=∠+∠，请说明理由．（4）如图4所示，AP ，BP 分别平分CAM ∠，CBD ∠，请直接写出P ∠与C ∠，D ∠之间的关系，不必说明理由．【答案】(1)理由见解析；(2)∠BAC=2∠BOC ；(3)理由见解析；(4)11+9022P D C ∠=∠∠+︒【分析】(1)根据OB 是∠ABC 的角平分线，OC 是∠ACB 的角平分线，利用三角形的内角和等于180°即可得出结果；(2)根据OB 是∠ABC 的角平分线，OC 是∠ACD 的角平分线，利用三角形的外角性质即可得出结果；(3)根据AP 是∠DAC 的角平分线，BP 是∠DBC 的角平分线，利用三角形的外角性质列出等式∠D+∠DAP=∠P+∠DBP ，∠P+∠PAC=∠PBC+∠C ，分析等式即可得出结果；(4)AP 是∠MAC 的角平分线，BP 是∠DBC 的角平分线，设∠DBP=∠PBC=x ，∠MAP=∠PAC=y ，利用三角形外角性质和内角和性质即可得出结果．【详解】解：(1)∵OB 是∠ABC 的角平分线，OC 是∠ACB 的角平分线∴∠ABO=OBC ，∠ACO=∠OCB∵∠A+∠ABC+∠ACB=180°∴∠OCB+∠OBC=()11802902A A ︒-∠÷=︒-∠∴∠BOC=11=180909022A A ⎛⎫︒-︒-∠=︒+∠ ⎪⎝⎭(2)∵OB 是∠ABC 的角平分线，OC 是∠ACD 的角平分线∴∠ABO=∠OBC ，∠ACO=∠OCD∵∠BAC +∠ABC=∠ACD ，∠OBC+∠BOC =∠OCD ∴2∠OBC+2∠BOC =2∠OCD∴∠ABC+2∠BOC =∠ACD ∴∠BAC=2∠BOC(3)∵AP 是∠DAC 的角平分线，BP 是∠DBC 的角平分线∴∠DAP=∠PAC ，∠DBP=∠PBC∵∠D+∠DAP=∠P+∠DBP ，∠P+∠PAC=∠PBC+∠C∴∠D-∠P=∠P-∠C ∴1()2P C D ∠=∠+∠(4)∵AP 是∠MAC 的角平分线，BP 是∠DBC 的角平分线∴∠MAP=∠PAC ，∠DBP=∠PBC 设∠DBP=∠PBC=x ，∠MAP=∠PAC=y∴∠AGB=∠C+2x ∴∠BEP=∠AEG=180°-（∠C+2x ）-y∴∠P=180°-∠BEP-∠DBP=∠C+x+y ∵∠D+∠AEG=∠MAP ∴∠D+180°-（∠C+2x ）-y=y∴x+y=119022D C ∠-∠+︒∴119022P D C C ∠=∠-∠+︒+∠∴11+9022P D C ∠=∠∠+︒【点睛】本题主要考查的是角平分线性质的综合运用，正确的掌握角平分线的性质以及运用是解题的关键．例9．（2023·江苏八年级课时练习）（1）如图所示，在ABC 中，,BO CO 分别是ABC ∠和ACB ∠的平分线，证明：1902BOC A ∠=+∠︒．（2）如图所示，ABC 的外角平分线BD 和CD 相交于点D ，证明：1902BDC A -︒∠=∠．（3）如图所示，ABC 的内角平分线BD 和外角平分线CD 相交于点D ，证明：12D A ∠=∠．【答案】（1）见解析；（2）见解析；（3）见解析【详解】（1）设,ABO OBC x ACO BCO y ∠=∠=∠=∠=．由ABC 的内角和为180︒，得22180A x y ︒∠++=．①由BOC 的内角和为180︒，得180BOC x y ∠++=︒．②由②得180x y BOC +=-∠︒．③把③代入①，得()2180180A BOC ∠+-∠=︒︒，即2180BOC A ∠=︒+∠，即1902BOC A ∠=+∠︒（2）∵BD 、CD 为△ABC 两外角∠ABC 、∠ACB 的平分线，∴()()1122BCD A ABC DBC A ACB ∠=∠+∠∠=∠+∠、，由三角形内角和定理得，180BDC BCD DBC ∠=︒-∠-∠，=180°-12[∠A +（∠A +∠ABC +∠ACB ）]，=180°-12（∠A +180°），=90°-12∠A ；（3）如图：∵BD 为△ABC 的角平分线，交AC 与点E ，CD 为△ABC 外角∠ACE 的平分线，两角平分线交于点D ∴∠1=∠2，∠5=12（∠A +2∠1），∠3=∠4，在△ABE 中，∠A =180°-∠1-∠3∴∠1+∠3=180°-∠A ①在△CDE 中，∠D =180°-∠4-∠5=180°-∠3-12（∠A +2∠1），即2∠D =360°-2∠3-∠A -2∠1=360°-2（∠1+∠3）-∠A ②，把①代入②得∠D =12∠A ．【点睛】此题考查的是三角形内角与外角的关系，角平分线的性质，三角形内角和定理，属中学常规题．课后专项训练1．（2023·成都·八年级月考）如图，ABC ∆的外角ACD ∠的平分线CP 与内角ABC ∠的平分线BP 交于点P ，若40BPC ∠=︒，则(CAP ∠=)A ．40︒B ．45︒C ．50︒D ．60︒【解答】解：延长BA ，作PN BD ⊥，PF BA ⊥，PM AC ⊥，设PCD x ∠=︒，CP 平分ACD ∠，ACP PCD x ∴∠=∠=︒，PM PN =，BP 平分ABC ∠，ABP PBC ∴∠=∠，PF PN =，PF PM ∴=，40BPC ∠=︒ ，(40)ABP PBC PCD BPC x ∴∠=∠=∠-∠=-︒，2(40)(40)80BAC ACD ABC x x x ∴∠=∠-∠=︒-︒-︒-︒-︒=︒，100CAF ∴∠=︒，在Rt PFA ∆和Rt PMA ∆中，PA PA PM PF=⎧⎨=⎩，Rt PFA Rt PMA(HL)∴∆≅∆，50FAP PAC ∴∠=∠=︒．故选：C ．2．（2023秋·绵阳市·八年级专题练习）如图，在ABC 中，50ABC ∠=︒，60ACB ∠=︒，点E 在BC 的延长线上，ABC ∠的平分线BD 与ACE ∠的平分线CD 相交于点D ，连接AD ，下列结论中不正确的是（）A ．70BAC ∠=︒B ．90DOC ∠=︒C ．35BDC ∠=︒D ．55DAC ∠=︒【答案】B 【分析】根据三角形的内角和定理列式计算即可求出BAC ∠，即可判断A 选项；根据角平分线的定义求出ABO ∠，再利用三角形的内角和定理求出AOB ∠，然后利用对顶角，即可判断B 选项；根据邻补角的定义和角平分线的定义求出DCO ∠，再利用三角形的内角和定理求出BDC ∠，即可判断C 选项；利用角平分线的性质，推出AD 为ABC 的外角平分线，然后列式计算求出DAC ∠，即可判断D 选项．【详解】解：50ABC ∠=︒ ，60ACB ∠=︒，180180506070BAC ABC ACB ∴∠=︒-∠-∠=︒-︒-︒=︒，故A 选项正确，不符合题意；BD Q 平分ABC ∠，11502522ABO ABC ∴∠=∠=⨯︒=︒，在ABO 中，180180702585AOB BAC ABO ∠=︒-∠-∠=︒-︒-︒=︒，85DOC AOB ∴∠=∠=︒，故B 选项错误，符合题意；CD 平分ACE ∠，()()1111801806060222ACD ACE ACB ∴∠=∠=︒-∠=︒-︒=︒，在COD △中，180180856035BDC COD ACD ∠=︒-∠-∠=︒-︒-︒=︒，故C 选项正确，不符合题意；BD Q 、CD 分别是ABC ∠和ACE ∠的平分线，D ∴到AB 、AC 、BC 的距离相等，AD ∴是ABC 的外角平分线，()()11180180705522DAC BAC ∴∠=︒-∠=︒-︒=︒，故D 选项正确，不符合题意．故选：B ．【点睛】本题考查角平分线的性质，三角形的内角和定理，角平分线的定义，熟记定理和概念是解题关键．3．（2022春·北京海淀·七年级校考期中）如图，在平面直角坐标系中，直线AB 与y 轴在正半轴、x 轴正半轴分别交A 、B 两点，点C 在BA 的延长线上，AD 平分∠CAO ，BD 平分∠ABO ，则∠D 的度数是（）A ．30°B ．45°C ．55°D ．60°【答案】B 【分析】由OA ⊥OB 即可得出∠OAB +∠ABO =90°、∠AOB =90°，再根据角平分线的定义以及三角形内角和定理即可求出∠D 的度数．【详解】解：∵OA ⊥OB ，∴∠OAB +∠ABO =90°，∠AOB =90°．∵DA 平分∠CAO ，∴∠DAO =12∠OAC =12（180°-∠OAB ）．∵DB 平分∠ABO ，∴∠ABD =12∠ABO ，∴∠D =180°-∠DAO -∠OAB -∠ABD =180°-12（180°-∠OAB ）-∠OAB -12∠ABO =90°-12（∠OAB +∠ABO ）=45°．故选：B ．【点睛】本题考查了三角形内角和定理，解题的关键是找出∠D =90°-12（∠OAB +∠ABO ）．本题属于基础题，难度不大，解决该题型题目时，熟练运用三角形内角和定理解决问题是关键．4．（2022秋·河北张家口·八年级统考阶段练习）如图，点O 在ABC 内，且到三边的距离相等，连接,OB OC ．若120BOC ∠=︒，则A ∠的度数是（）A ．30︒B ．45︒C ．60︒D ．70︒【答案】C 【分析】由点O 在ABC 内，且到三边的距离相等，可知O 是角平分线的交点，则12OBC ABC ∠=∠，12OCB ACB ∠=∠，由180OBC OCB BOC ∠+∠+∠=︒，可得120ABC ACB ∠+∠=︒，根据180A ABC ACB ∠+∠+∠=︒，计算求解即可．【详解】解：∵点O 在ABC 内，且到三边的距离相等，∴O 是角平分线的交点，∴12OBC ABC ∠=∠，12OCB ACB ∠=∠，∵180OBC OCB BOC ∠+∠+∠=︒，∴1112018022ABC ACB ∠+∠+︒=︒，即120ABC ACB ∠+∠=︒，∵180A ABC ACB ∠+∠+∠=︒，∴60A ∠=︒，故选：C ．【点睛】本题考查了角平分线的判定定理，三角形内角和定理．解题的关键在于明确角度之间的数量关系．5．（2022秋·四川绵阳·八年级统考期末）如图，在△ABC 中，∠A ＝30°，E 为BC 延长线上一点，∠ABC 与∠ACE 的平分线相交于点D ，则∠D 等于（）A ．10°B ．15°C ．20°D ．30°【答案】B【分析】先根据角平分线的定义得到12∠=∠，34∠=∠，再根据三角形外角性质得1234A ∠+∠=∠+∠+∠，13D ∠=∠+∠，则2123A ∠=∠+∠，利用等式的性质得到12D A ∠=∠，然后把A ∠的度数代入计算即可．【详解】解答：解：∵ABC ∠的平分线与ACE ∠的平分线交于点D ，∴12∠=∠，34∠=∠，∵ACE A ABC ∠=∠+∠，即1234A ∠+∠=∠+∠+∠，∴2123A ∠=∠+∠，∵13D ∠=∠+∠，∴11301522D A ∠=∠=⨯︒=︒．故选：B ．【点睛】本题考查了三角形内角和定理和三角形外角性质、角平分线的性质等，根据三角形内角和是180°和三角形外角性质进行分析是解题关键．6．（2023春·福建漳州·七年级统考期末）如图，在ABC 中，,ACB A BD ∠∠<是角平分线，BE 是边AC 上的高，延长BD 与外角ACF ∠的平分线交于点G ．以下四个结论：①ABD CBD ∠=∠；②90ABE A ∠+∠=︒；③45G ∠=︒；④2A ACB EBD ∠∠∠-=．其中结论正确的个数是（）A ．1B ．2C ．3D ．4【答案】C 【分析】由三角形的角平分线的含义可判断①，由三角形的高的含义可判断②，证明2ABC GBC ∠=∠，2ACF GCF ∠=∠，ACF ABC A ∠=∠+∠，GCF GBC G ∠=∠+∠，可判断③，由()2290BED ADB ∠=︒-∠，ADB DBC ACB ∠=∠+∠，可得()218022BED DBC ACB ∠=︒-∠+∠，从而可判断④，从而可得答案．【详解】解：∵BD 是ABC 角平分线，∴ABD CBD ∠=∠，故①符合题意；∵BE 是边AC 上的高，∴90ABE A ∠+∠=︒，故②符合题意；∵BD 是ABC 角平分线，CG 平分ACF ∠，∴2ABC GBC ∠=∠，2ACF GCF∠=∠∵ACF ABC A ∠=∠+∠，GCF GBC G ∠=∠+∠，∴22GCF GBC A ∠=∠+∠，∴12G A ∠=∠，∵90A ∠<︒，∴45G ∠<︒，故③不符合题意；∵()2290BED ADB ∠=︒-∠，ADB DBC ACB ∠=∠+∠，∴()218022BED DBC ACB ∠=︒-∠+∠()1802ABC ACB =︒-∠+∠()180180A ACB =︒-︒-∠+∠A ACB =∠-∠，故④符合题意；故选C 【点睛】本题考查的是三角形的内角和定理的应用，三角形的角平分线与高的含义，三角形的外角的性质，灵活运用三角形的外角的性质解决问题是关键．7．（2022秋·贵州遵义·八年级校考阶段练习）如图，Rt ABC 中，90ACB ∠=︒，16BAC ∠=︒，ACB ∠的平分线与外角ABD ∠的平分线交于点E ，连接AE ，则AEC ∠的度数为．【答案】37︒/37度【分析】由角平分线的性质可得EF EH EG ==，进而可证明EA 是BAC ∠的外角平分线，再利用三角形的内角和定理解答即可．【详解】解：过E 点分别作EF AC ⊥于F ，作EG AB ⊥于点G ，作EH CD ⊥于H ，∵EC 是ACB ∠的平分线，EB 是ABD ∠的平分线，∴EF EH =，EG EH =，∴EF EG =，∴EA 是BAC ∠的外角平分线，∵90ACB ∠=︒，16BAC ∠=︒，∴45ACE ∠=︒，∴180168222FAB EAB ∠︒-︒∠===︒，∴()()18018082164518014337AEC EAC ACE ∠=︒-∠+∠=︒-︒+︒+︒=︒-︒=︒．故答案为：37︒．【点睛】本题考查了三角形内角平分线和外角平分线的定义，掌握角平分线的定义是解题的关键．8．（2023春·江苏南通·七年级统考阶段练习）如图，1BA 和1CA 分别是ABC 的内角平分线和外角平分线，2BA 是1A BD ∠的平分线，2CA 是1A CD ∠的平分线，3BA 是2A BD ∠的平分线，3CA 是2A CD ∠的平分线，若A α∠=，则999A ∠=．【答案】9992α【分析】根据角平分线的定义可得112BD ABC A =∠∠，112ACD ACD ∠=∠，再根据三角形外角的性质可得()11122ABC A ABC A ∠+∠=∠+∠，化简可得112A A ∠=∠，进一步找出其中的规律，即可求出999A ∠的度数．【详解】解：1BA 和1CA 分别是ABC 的内角平分线和外角平分线，112A BD ABC ∠∠∴=，112ACD ACD ∠=∠，又ACD ABC A ∠=∠+∠Q ，111A CD A BD A ∠∠∠=+，()11122ABC A ABC A ∠∠∠∠∴+=+，11122A A α∴∠=∠=，同理可得：21211112222A A αα∠=∠=⨯=，23131122A A ∠∠α==，......则999999999122A A α∠==，故答案为：9992α．【点睛】本题考查了三角形的内角和定理，三角形外角的性质，角平分线的定义等，找出1A ∠，2A ∠，3A ∠与A ∠的规律是解题的关键．9．（2022秋·北京大兴·八年级统考期末）如图，在ABC 中，AB AC <，BAC ∠的平分线与外角BCD ∠的平分线相交于点M ，作AB 的延长线得到射线AE ，作射线BM ，有下面四个结论：①MCD MAB ∠>∠；②BM CM =；③射线BM 是EBC ∠的角平分线；④1902BMC BAC ∠=︒-∠．所有正确结论的序号是．【答案】①③④【分析】由角平分线的定义可知MAB MAC ∠=∠．再根据三角形外角的性质得出MCD MAC AMC ∠=∠+∠，即可确定MCD MAB ∠>∠，故①正确；过点M 作MF AD ⊥于点F ，MG BC ⊥于点G ，MH AE ⊥于点H ，由角平分线的性质定理可得出MF MG MH ==．即易证Rt Rt (HL)BMG BMH ≌，得出MBG MBH ∠=∠，即说明射线BM 是EBC ∠的角平分线，故③正确；利用反证法，假设BM CM =，易证CBE BCD ∠=∠，即得出A ABC CB =∠∠．由AB AC <，可知ABC ACB ∠≠∠，即说明BM CM =不成立，故②错误；由BMC BMG CMG ∠=∠+∠，即得出(90)(90)BMC MBG MCG ∠=︒-∠+︒-∠．再根据角平分线的定义即得出11(90)(90)22BMC CBE BCD ∠=︒-∠+︒-∠，最后结合三角形内角和定理即可求出结论，可判断④正确．【详解】解：∵AM 为BAC ∠的平分线，∴MAB MAC ∠=∠．∵MCD MAC AMC ∠=∠+∠，∴MCD MAC ∠>∠，∴MCD MAB ∠>∠，故①正确；如图，过点M 作MF AD ⊥于点F ，MG BC ⊥于点G ，MH AE ⊥于点H ，∵AM 为BAC ∠的平分线，CM 为BCD ∠的平分线，∴MF MG MH ==．又∵BM BM =，∴Rt Rt (HL)BMG BMH ≌，∴MBG MBH ∠=∠，即射线BM 是EBC ∠的角平分线，故③正确；假设BM CM =，∴MBC MCB ∠=∠．∵CM 为BCD ∠的平分线，BM 是EBC ∠的角平分线，∴MBE MBC ∠=∠，MCB MCD ∠=∠，∴MBE MBC MCB MCD ∠+∠=∠+∠，即CBE BCD ∠=∠，∴180180CBE BCD ︒-∠=︒-∠，即A ABC CB =∠∠．∵AB AC <，∴ABC ACB ∠≠∠，∴假设不成立，故②错误；∵BMC BMG CMG ∠=∠+∠，∴(90)(90)BMC MBG MCG ∠=︒-∠+︒-∠．∵1122MBG CBE MCG BCD ∠=∠∠=∠，，∴11(90)(90)22BMC CBE BCD ∠=︒-∠+︒-∠，∴11(90)(90)22BMC CBE BCD ∠=︒-∠+︒-∠1118022CBE BCD =︒-∠-∠11180(180)(180)22ABC ACB =︒-︒-∠-︒-∠1()2ABC ACB =∠+∠1(180)2BAC =︒-∠1902BAC =︒-∠，∴④正确．综上可知所有正确结论的序号是①③④．故答案为：①③④．【点睛】本题考查角平分线的定义，角平分线的性质定理，三角形全等的判定和性质，三角形外角的性质及三角形内角和的应用等知识．正确作出辅助线构造全等三角形，并利用数形结合的思想是解题关键．10．（2023春·河北·七年级专题练习）如图，在△ABC 中，∠ABC 和∠ACB 的角平分线交于点O ，延长BO 与∠ACB 的外角平分线交于点D ，若∠BOC ＝130°，则∠D ＝【答案】40°【分析】根据角平分线的定义结合三角形外角的性质即可得到结论．【详解】解：∵∠ABC 和∠ACB 的角平分线交于点O ，∴∠ACO=12∠ACB ，∵CD 平分∠ACE ，∴∠ACD=12∠ACE ，∵∠ACB+∠ACE=180°，∴∠OCD=∠ACO+∠ACD=12（∠ACB+∠ACE ）=12×180°=90°，∵∠BOC ＝130°，∴∠D=∠BOC-∠OCD=130°-90°=40°，故答案为：40°．【点睛】本题考查了三角形的外角性质，角平分线的定义，熟练掌握相关性质和概念正确推理计算是解题的关键．11．（2023·浙江杭州·八年级期末）如图，在四边形ABCD 中，A D m ∠+∠=︒，ABC ∠的平分线与BCD ∠的平分线交于点P ，则P ∠=．（用含字母m 的代数式表示）【答案】12m ︒【分析】根据四边形的内角和是360°，求出∠ABC+∠BCD 的度数，然后根据角平分线的定义及三角形的内角和定理求出∠P 的度数即可．【详解】解：∵∠A+∠D=m°，且四边形内角和为360°，∴∠ABC+∠BCD=360°-m°，∵PB 、PC 是∠ABC 、∠BCD 的角平分线，∴∠PBC=12ABC ∠，∠BCP=12BCD ∠，∴∠PBC+∠BCP=1111+=(+)(360) 2222ABC BCD ABC BCD m ∠∠∠∠=︒-︒∴∠P=180°-（∠PBC+∠BCP）=11180(360)22m m︒-︒-︒=︒故答案为：12m︒．【点睛】本题考查了四边形的内角和及三角形的内角和与角平分线相关的角度计算问题，解题的关键是表达出∠PBC+∠BCP的度数．12．（2023春·河南·七年级专题练习）如图，点M是△ABC两个内角平分线的交点，点N是△ABC两外角平分线的交点，如果∠CMB：∠CNB＝3：2，那么∠CAB＝．【答案】36°【分析】由角平分线的定义得∠NCM=∠MBN=12×180°=90°，再比的关系可求得∠CMB=108°，再由内角平分线及三角形内角和即可求得结果．【详解】由题意得：∠NCM=∠MBN=12×180°=90°，∴∠CMB+∠CNB=180°，又∠CMB：∠CNB=3：2，∴∠CMB=108°，∴12（∠ACB+∠ABC）=180°-∠CMB=72°，∴∠ACB+∠ABC=144°，∴∠CAB=180°-（∠ACB+∠ABC）=36°．【点睛】本题考查了三角形内角和定理、三角形角平分线的定义等知识，由条件得到∠NCM=∠MBN=90°是关键．13．（2023·黑龙江八年级课时练习）（1）如图（1）所示，已知在△ABC中，O为∠ABC和∠ACB的平分线BO，CO的交点．试猜想∠BOC和∠A的关系，并说明理由．（2）如图（2）所示，若O为∠ABC的平分线BO和∠ACE的平分线CO的交点，则∠BOC与∠A的关系又该怎样？为什么？【答案】(1)∠BOC=12∠A+90°；理由见解析；(2)∠BOC=12∠A；理由见解析【分析】(1)根据三角形内角和定理得出∠A+∠ABC+∠ACB=180°，∠BOC+∠OBC+∠OCB=180°，根据角平分线的性质得出∠ABC=2∠OBC，∠ACB=2∠OCB，然后得出∠BOC+12∠ABC+12∠ACB=180°，最后得出结论；(2)根据外角的性质得出∠A+∠ABC=∠ACE，∠OBC+∠BOC=∠OCE，然后根据角平分线的性质得出∠ABC=2∠OBC，∠ACE=2∠OCE，最后根据∠BOC=∠OCE-∠OBC得出答案．【详解】(1)∠BOC=12∠A+90°．在△ABC中，∠A+∠ABC+∠ACB=180°，在△BOC中，∠BOC+∠OBC+∠OCB=180°，又∵BO，CO分别是∠ABC，∠ACB的平分线，∴∠ABC=2∠OBC，∠ACB=2∠OCB．∴∠BOC+12∠ABC+12∠ACB=180°．∴∠BOC=180°﹣12(∠ABC+∠ACB)=180°-12(180°-∠A)=90°+12∠A．(2)∠BOC=12∠A．∵∠A+∠ABC=∠ACE，∠OBC+∠BOC=∠OCE，∴∠A=∠ACE-∠ABC，∠BOC=∠OCE-∠OBC 又∵BO，CO分别是∠ABC和∠ACE的平分线，∴∠ABC=2∠OBC，∠ACE=2∠OCE．∴∠BOC=∠OCE-∠OBC=12∠ACE-12∠ABC=12(∠ACE-∠ABC)=12∠A．【点睛】本题考查了角平分线的性质和三角形外角的性质，熟练掌握外角性质并能正确计算是解题关键．14．（2023·北京昌平·八年级校考阶段练习）认真阅读下面关于三角形内外角平分线所夹角的探究片段，完成所提出的问题.探究1：如图l，在△ABC中，O是∠ABC与∠ACB的平分线BO和CO的交点，通过分析发现∠BOC=90 +12∠A,理由如下：∵BO 和CO 分别是∠ABC 和∠ACB 的角平分线∴∠1=12∠ABC,∠2=12∠ACB ∴∠l+∠2=12(∠ABC+∠ACB)=12(180︒-∠A)=90︒-12∠A ∴∠BOC=180︒-(∠1+∠2)=180︒-(90︒-12∠A)=90︒+12∠A (1)探究2；如图2中，O 是12∠ABC 与外角12∠ACD 的平分线BO 和CO 的交点，试分析∠BOC 与∠A 有怎样的关系？请说明理由．(2)探究3：如图3中,O 是外角∠DBC 与外角∠ECB 的平分线BO 和CO 的交点，则∠BOC 与∠A 有怎样的关系？（直接写出结论）(3)拓展：如图4，在四边形ABCD 中，O 是∠ABC 与∠DCB 的平分线BO 和CO 的交点，则∠BOC 与∠A+∠D 有怎样的关系？（直接写出结论）【答案】（1）探究2结论：∠BOC=12A ∠；（2）探究3：结论∠BOC=90°－12A ∠；（3）拓展：结论()12BOC A D ∠=∠+∠【分析】（1）根据角平分线的定义可得∠1=12∠ABC ，∠2=12∠ACD ，再根据三角形的一个外角等于与它不相邻的两个内角的和和角平分线的定义可得∠2=12∠ACD=12（∠A+∠ABC ），∠BOC=∠2-∠1，然后整理即可得解；（2）根据三角形的外角性质以及角平分线的定义表示出∠OBC 和∠OCB ，再根据三角形的内角和定理解答；（3）同（1）的求解思路．【详解】（1）探究2结论：∠BOC=12∠A ．理由如下：如图，∵BO和CO分别是∠ABC和∠ACD的角平分线，∴∠1=12∠ABC，∠2=12∠ACD，又∵∠ACD是△ABC的一个外角，∴∠2=12∠ACD=12（∠A+∠ABC）=12∠A+∠1，∵∠2是△BOC的一个外角，∴∠BOC=∠2-∠1=12∠A+∠1-∠1=12∠A，即∠BOC=12∠A；（2）由三角形的外角性质和角平分线的定义，∠OBC=12（∠A+∠ACB），∠OCB=12（∠A+∠ABC），在△BOC中，∠BOC=180°-∠OBC-∠OCB=180°-12（∠A+∠ACB）-12（∠A+∠ABC），=180°-12（∠A+∠ACB+∠A+∠ABC），=180°-12（180°+∠A），=90°-12∠A；故答案为∠BOC=90°-12∠A．（3）∠OBC+∠OCB=12（360°-∠A-∠D），在△BOC中，∠BOC=180°-12（360°-∠A-∠B）=12（∠A+∠D）．故答案为∠BOC=12（∠A+∠D）．【点睛】本题考查了三角形的外角性质，角平分线的定义，三角形的内角和定理，熟记性质并准确识图，整体思想的利用是解题的关键．15．（2023春·江苏无锡·七年级校考阶段练习）如图1，点A、B分别在射线OM、ON上运动（不与点O重合），AC、BC分别是∠BAO和∠ABO的角平分线，BC延长线交OM于点G．（1）若∠MON＝60°，则∠ACG＝°；若∠MON＝90°，则∠ACG＝°；（2）若∠MON＝n°，请求出∠ACG的度数；（用含n的代数式表示）（3）如图2，若∠MON＝n°，过C 作直线与AB交于F，若CF∥OA时，求∠BGO－∠ACF的度数．（用含n的代数式表示）．【答案】（1）60°；45°；（2）90°－12n；（3）90°－12n．【分析】（1）根据三角形的内角和求出∠ABO+∠BAO的度数，再根据角平分线的定义及外角的性质即可得到∠ACG的度数；（2）根据（1）中的结论即可求出答案；（3）根据角平分线的性质，平行线的性质得到∠ACF=∠CAO=∠BAC，利用外角的性质得到∠BGO－∠ACF=∠ACG，由此得到答案.【详解】（1）∵∠MON+∠ABO+∠BAO＝180°，∴∠ABO+∠BAO=180°-∠MON，∵AC、BC分别是∠BAO和∠ABO的角平分线，∴∠ABC=12∠ABO，∠BAC=12∠BAO，当∠MON＝60°，∠ACG=∠ABC+∠BAC=12(∠ABO+∠BAO)=12（180°-∠MON）=60°，当∠MON＝90°，∠ACG=∠ABC+∠BAC=12(∠ABO+∠BAO)=12（180°-∠MON）=45°，故答案为：60°，45°；（2）由（1）知∠ACG=12（180°-∠MON），∵∠MON＝n°，∴∠ACG=12（180°-∠MON）=90°－12n；（3）∵AC平分∠BAO，∴∠BAC=∠CAO∵CF∥OA，∴∠ACF=∠CAO=∠BAC，∵∠BGO=∠ABG+∠BAO=∠ABG+2∠ACF,∴∠BGO－∠ACF=∠ABG+2∠ACF-∠ACF=∠ABG+∠ACF=∠ABG+∠BAC=∠ACG,∵∠MON＝n°时∠ACG=90°－12n，∴∠BGO－∠ACF=90°－12n.【点睛】此题考查三角形的内角和定理，外角的性质定理，平行线的性质定理，解题时注意共性思想的理解和利用.16．（2023·山西晋城·七年级统考期末）在△ABC中，已知∠A＝α．（1）如图1，∠ABC、∠ACB的平分线相交于点D．①当α＝70°时，∠BDC度数＝度（直接写出结果）；②∠BDC的度数为（用含α的代数式表示）；（2）如图2，若∠ABC的平分线与∠ACE角平分线交于点F，求∠BFC的度数（用含α的代数式表示）．（3）在（2）的条件下，将△FBC以直线BC为对称轴翻折得到△GBC，∠GBC的角平分线与∠GCB的角平分线交于点M（如图3），求∠BMC的度数（用含α的代数式表示）．【答案】（1）（1）①125°；②1902α︒+，（2）1BFC2α∠=；（3）1BMC904α︒∠=+【分析】（1）①由三角形内角和定理易得∠ABC+∠ACB=110°，然后根据角平分线的定义，结合三角形内角和定理可求∠BDC；②由三角形内角和定理易得∠ABC+∠ACB=180°-∠A，采用①的推导方法即可求解；（2）由三角形外角性质得BFC FCE FBC∠=∠-∠，然后结合角平分线的定义求解；（3）由折叠的对称性得BGC BFC∠=∠，结合（1）②的结论可得答案．【详解】解：（1）①∵12DBC∠=∠ABC，∠DCB＝12∠ACB，∴∠BDC＝180°﹣∠DBC﹣∠DCB＝180°﹣12（∠ABC+∠ACB）＝180°﹣12（180°﹣70°）＝125°②∵12DBC∠=∠ABC，∠DCB＝12∠ACB，∴∠BDC＝180°﹣∠DBC﹣∠DCB＝180°﹣12（∠ABC +∠ACB ）＝180°﹣12（180°﹣∠A ）＝90°+12∠A＝90°+12α．故答案分别为125°，90°+12α．（2）∵BF 和CF 分别平分∠ABC 和∠ACE ∴1FBC ABC 2∠=∠，1FCE ACE 2∠=∠，∴BFC FCE FBC ∠=∠-∠＝11(ACE ABC)A 22∠-∠=∠即1BFC 2α∠=．（3）由轴对称性质知：1BGC BFC 2α∠=∠=，由（1）②可得1BMC 90BGC 2∠=︒+∠，∴1BMC 904α∠=︒+．【点睛】本题考查三角形中与角平分线有关的角度计算，熟练掌握三角形内角和定理，以及三角形的外角性质是解题的关键．17．（2023·江苏连云港·七年级统考期中）在数学学习过程中，对有些具有特殊结构，且结论又具有一般性的数学问题我们常将其作为一个数学模型加以识记，以积累和丰富自己的问题解决经验．【结论发现】小明在处理教材第43页第21题后发现：三角形的一个内角平分线与另一内角的外角平分线的夹角的度数是三角形第三内角度数的一半．【结论探究】（1）如图1，在ABC 中，点E 是ABC 内角ACB ∠平分线CE 与外角ABD ∠的平分线BE 的交点，则有12∠=∠E A ．请补齐下方的说理过程．理由如下：因为180EBC EBD ∠+∠=°，又因为在EBC 中，180EBC E ECB ∠+∠+∠=°，所以EBC EBD EBC E ECB ∠+∠=∠+∠+∠．所以EBD E ∠=∠+∠______．（理由是：等式性质）同理可得：ABD A ∠=∠+∠______．又因为BE 和CE 分别是ABD ∠和ACB ∠的角平分线，所以12EBD ABD ∠=∠，∠______12ACB =∠．所以1122ABD E ACB ∠=∠+∠．即111222E ABD ACB ∠=∠-∠=（ABD ACB ∠-∠）．所以12∠=∠E A ．请直接应用上面的“结论发现”解决下列问题：【简单应用】（2）如图2，在ABC 中，40ABC ∠=︒．延长BA 至G ，延长AC 至H ，已知BAC ∠、CAG ∠的角平分线与BCH ∠的角平分线及其反向延长线交于E 、F ，求F ∠的度数；【变式拓展】（3）如图3，四边形ABCD 的内角BCD ∠与外角ABG ∠的平分线形成如图所示形状．①已知150A ∠=︒，80D ∠=︒，求E F ∠+∠的度数；②直接写出E F ∠+∠与A D ∠+∠的关系．【答案】（1）ECB ，ACB ，ECB ；（2）70°；（3）①205°；②E F ∠+∠=12（A D ∠+∠）+90°【分析】（1）根据三角形外角的性质以及角平分线的定义，即可得到答案；（2）先推出∠AEC =12∠ABC =20°，再推出∠EAC +∠FAC ==90°，进而即可求解；（3）①延长BA 、CD 交于点M ，延长CE 、BF 交于点N ，可得∠N =12∠M ，进而即可求解；②根据∠N =12∠M ，结合平角的意义以及三角形内角和定理，即可得到结论．【详解】解：（1）因为180EBC EBD ∠+∠=°，又因为在EBC 中，180EBC E ECB ∠+∠+∠=°，所以EBC EBD EBC E ECB ∠+∠=∠+∠+∠．所以EBD E ∠=∠+∠ECB ．（理由是：等式性质）同理可得：ABD A ∠=∠+∠_ACB_．又因为BE 和CE 分别是ABD ∠和ACB ∠的角平分线，所以12EBD ABD ∠=∠，∠__ECB____12ACB =∠．所以1122ABD E ACB ∠=∠+∠．即111222E ABD ACB ∠=∠-∠=（ABD ACB ∠-∠）．所以12∠=∠E A ．故答案是：ECB ，ACB ，ECB ；（2）∵40ABC ∠=︒，∴∠AEC =12∠ABC =20°，∵BAC ∠、CAG ∠的角平分线与BCH ∠的角平分线及其反向延长线交于E 、F ，∴∠EAC +∠FAC =12∠ABC +12CAG ∠=12(∠ABC +CAG ∠)=12×180°=90°，∴∠F=180°-90°-20°=70°；（3）①延长BA 、CD 交于点M ，延长CE 、BF 交于点N ，∵BF ，CE 平分∠ABG 、∠DCB ，∴∠N =12∠M ，∵150=︒∠BAD ，80ADC ∠=︒，∴∠M =180°-（180°-150°）-（180°-80°）=50°，∴∠N =25°，∴AEF BFE ∠+∠=360°-（180°-25°）=205°；②∵AEF BFE ∠+∠=360°-（180°-∠N ）=180°+∠N ，BAD ∠+ADC ∠=180°+∠M ，又∵∠N =12∠M ，∴AEF BFE ∠+∠-180°=12（BAD ∠+ADC ∠-180°），即：E F ∠+∠=12（A D ∠+∠）+90°．【点睛】本题主要考查三角形的内角和定理，三角形的外角的性质，角平分线的定义，掌握三角形外角的性质，是解题的关键．18．（2023春·江苏南京·七年级期中）（1）问题发现：如图1，在ABC 中，40A ∠=︒，ABC ∠和ACB ∠的平分线交于P ，则BPC ∠的度数是______（2）类比探究：如图2，在ABC 中，ABC ∠的平分线和ACB ∠的外角ACE ∠的角平分线交于P ，则BPC ∠与A ∠的关系是______，并说明理由．（3）类比延伸：如图3，在ABC 中，ABC ∠外角FBC ∠的角平分线和ACB ∠的外角BCE ∠的角平分线交于P ，请直接写出BPC ∠与A ∠的关系是______．【答案】（1）110°；（2）12BPC A ∠=∠；（3）1902BPC A ∠=︒-∠【分析】（1）根据三角形内角和定理求出∠ABC+∠ACB ，根据角平分线的定义、三角形内角和定理计算即可；（2）根据三角形外角的性质得到∠ACE=∠ABC+∠A 、∠PCE=∠PBC+∠BPC ，根据角平分线的定义解答；（3）根据（1）的结论然后用角分线的定义，计算即可．【详解】解：（1）∵40A ∠=︒，。

三角形中的倒角模型——飞镖模型、风筝模型以及翻角模型学生版

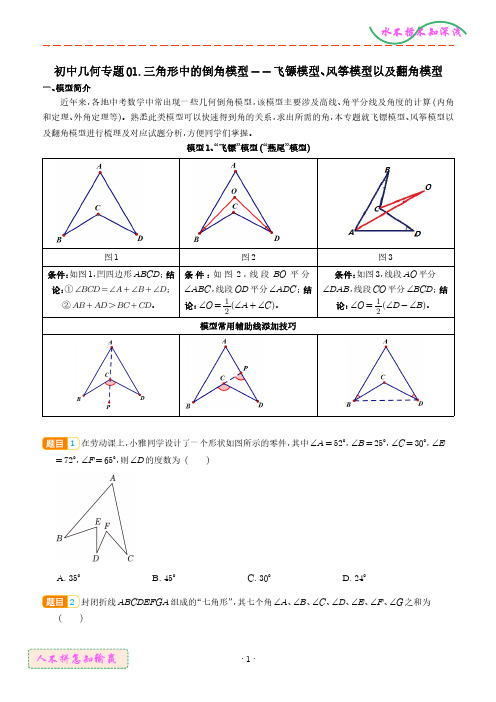
初中几何专题01.三角形中的倒角模型--飞镖模型、风筝模型以及翻角模型一、模型简介近年来，各地中考数学中常出现一些几何倒角模型，该模型主要涉及高线、角平分线及角度的计算(内角和定理、外角定理等)。

熟悉此类模型可以快速得到角的关系，求出所需的角，本专题就飞镖模型、风筝模型以及翻角模型进行梳理及对应试题分析，方便同学们掌握。

模型1、“飞镖”模型(“燕尾”模型)图1图2图3条件：如图1，凹四边形ABCD；结论：①∠BCD=∠A+∠B+∠D；②AB+AD>BC+CD。

条件：如图2，线段BO平分∠ABC，线段OD平分∠ADC；结论：∠O=12(∠A+∠C)。

条件：如图3，线段AO平分∠DAB，线段CO平分∠BCD；结论：∠O=12(∠D-∠B)。

模型常用辅助线添加技巧1在劳动课上，小雅同学设计了一个形状如图所示的零件，其中∠A=52°，∠B=25°，∠C=30°，∠E =72°，∠F=65°，则∠D的度数为()A.35°B.45°C.30°D.24°2封闭折线ABCDEFGA组成的“七角形”，其七个角∠A、∠B、∠C、∠D、∠E、∠F、∠G之和为()A.180°B.270°C.360°D.720°3请阅读下列材料，并完成相应的任务：有趣的“飞镖图”如图，这种形似飞镖的四边形，可以形象地称它为“飞镖图”．当我们仔细观察后发现，它实际上就是凹四边形．那么它具有哪些性质呢？又将怎样应用呢？下面我们进行认识与探究：凹四边形通俗地说，就是一个角“凹”进去的四边形，其性质有：凹四边形中最大内角外面的角等于其余三个内角之和．(即如图1．∠ADB=∠A+∠B+∠C)理由如下：方法一：如图2，连结AB，则在△ABC中，∠C+∠CAB+∠CBA=180°，即∠1+∠2+∠3+∠4+∠C=180°，又∵在△ABD中，∠1+∠2+∠ADB=180°，∴∠ADB=∠3+∠4+∠C，即∠ADB=∠CAD+∠CBD+∠C．方法二：如图3，连结CD并延长至F，∵∠1和∠3分别是△ACD和△BCD的一个外角，⋯大家在探究的过程中，还发现有很多方法可以证明这一结论．任务：(1)填空：“方法一”主要依据的一个数学定理是；(2)探索及应用：根据“方法二”中辅助线的添加方式，写出该证明过程的剩余部分．2、风筝模型(鹰爪模型)或角内翻模型图1图21)风筝(鹰爪)模型：结论：∠A+∠O=∠1+∠2；2)风筝(鹰爪)模型(变形)：结论：∠A+∠O=∠2-∠1。

初中数学倒角模型

初中数学中的倒角模型通常指的是涉及两个或多个直线或者线段在相交处形成90度角的情况，这种特殊的角度组合在解决与直角三角形、相似性、勾股定理以及面积计算等相关几何问题时非常常见。

以下是几个常见的倒角模型及其相关性质和应用：
1. 直角三角形模型：
直角三角形的基本性质：直角三角形斜边上的高线将斜边分为两个等腰直角三角形，因此，高等于两直角边的乘积除以斜边。

勾股定理：直角三角形的两条直角边满足a² + b² = c²，其中c为斜边的长度。

2. 两直线垂直模型：
当两条直线在同一平面上且互相垂直时，它们的斜率之积为1，即m₁
m₂ = 1，这里m₁和m₂分别为两条直线的斜率。

或者说，在坐标系中，如果一条直线经过点A(x₁, y₁)，斜率为k，则与其垂直的直线过点B(x₂, y₂)且斜率为k，即y y₂ = k(x x₂) 和 y y₁ = k(x x₁)。

3. 倒角直角梯形模型：
若一个直角梯形的两个底角均为90度，则它的高线同时也是中位线，与上底和下底分别垂直，此时可以用分割法求得面积，即面积=上底长×高/2 + 下底长×高/2。

4. 猪蹄模型：
这是一种描述两个图形相切且其中一个图形内部有一个90度角的模型，例如圆与正方形或矩形相切，圆心到相切直线的距离等于半径。

在这种情况下，可以通过构建直角三角形来解决问题，如半径、内切圆的半径和外切圆半径之间的关系等。

初中数学——三角形的内外角和倒角模型

飞镖模型
A
12
D
B
34
C
结论：∠BDC=∠A+∠B+∠C
A
D B
连接BC
∵三角形内角和180°
∴∠A+∠ABC+ ∠ACB =180°
∠DBC+∠D+ ∠DCB=180°
C
∴∠A+∠ABC+ ∠ACB= ∠DBC+∠D+ ∠DCB 又∵ ∠ABC= ∠ABD+ ∠DBC
∠ACB= ∠ACD+ ∠DCB
∠A+∠B+∠F=∠BOF
在飞镖模型EDCO中
∠D+∠E+∠C=∠EOC
∠BOF=∠EOC=105 °(对顶角相等)
O
∴ ∠A+∠B+∠C +∠D+∠E+∠F=210°
“8”字模型
∵三角形内角和180°
∴∠A+∠B+ ∠1 =180° ∠C+∠D+ ∠2=180°
∠A+∠B+ ∠1 =∠C+∠D+ ∠2
∴∠A+∠ABC+∠ACB=∠BDC
飞镖模型
A
D
B
C
实现角的数量转换
飞镖模型
连接BD 在飞镖模型ABDN中 ∠A+∠ABD+∠NDB=∠AND=100 ° 在飞镖模型BDCM中 ∠C+∠BDA+∠DBM=∠CMB=130 ° ∴ ∠A+∠ABM+∠C+∠NDC=230 °
M N
在飞镖模型ABOF中
∵∠1=∠2（对顶角相等）
∴∠A+∠B=∠C+∠D

初中数学三角形中的倒角模型-“8”字模型、“A”字模型与三角板模型及参考答案

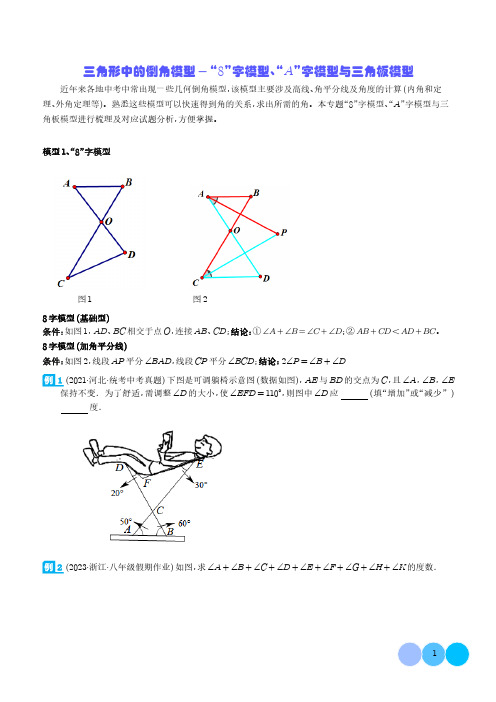
三角形中的倒角模型-“8”字模型、“A”字模型与三角板模型近年来各地中考中常出现一些几何倒角模型，该模型主要涉及高线、角平分线及角度的计算(内角和定理、外角定理等)。

熟悉这些模型可以快速得到角的关系，求出所需的角。

本专题“8”字模型、“A”字模型与三角板模型进行梳理及对应试题分析，方便掌握。

模型1、“8”字模型图1图28字模型(基础型)条件：如图1，AD、BC相交于点O，连接AB、CD；结论：①∠A+∠B=∠C+∠D；②AB+CD<AD+BC。

8字模型(加角平分线)条件：如图2，线段AP平分∠BAD，线段CP平分∠BCD；结论：2∠P=∠B+∠D1(2021·河北·统考中考真题)下图是可调躺椅示意图(数据如图)，AE与BD的交点为C，且∠A，∠B，∠E 保持不变．为了舒适，需调整∠D的大小，使∠EFD=110°，则图中∠D应(填“增加”或“减少”)度．2(2023·浙江·八年级假期作业)如图，求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠K的度数．3(2023·山东德州·八年级校考阶段练习)如图1，已知线段AB,CD相交于点O，连接AC,BD，则我们把形如这样的图形称为“8字型”．(1)求证：∠A+∠C=∠B+∠D；(2)如图2，若∠CAB和∠BDC的平分线AP和DP相交于点P，且与CD,AB分别相交于点M、N．①若∠B=100°,∠C=120°，求∠P的度数；②若角平分线中角的关系改为“∠CAP=13∠CAB,∠CDP=13∠CDB”，试探究∠P与∠B,∠C之间的数量关系．4(2023春·广东深圳·七年级统考期末)定理：三角形任意两边之和大于第三边．(1)如图1，线段AD，BC交于点E，连接AB，CD，判断AD+BC与AB+CD的大小关系，并说明理由；(2)如图2，OC平分∠AOB，P为OC上任意一点，在OA，OB上截取OE=OF，连接PE，PF．求证：PE=PF；(3)如图3，在△ABC中，AB>AC，P为角平分线AD上异于端点的一动点，求证：PB-PC>BD-CD．5(2023春·江苏苏州·七年级校联考期中)阅读：基本图形通常是指能够反映一个或几个定理，或者能够反映图形基本规律的几何图形．这些图形以基本概念、基本事实、定理、常用的数学结论和基本规律为基础，图形简单又具有代表性．在几何问题中，熟练把握和灵活构造基本图形，能更好地帮助我们解决问题．我们将图1①所示的图形称为“8字形”．在这个“8字形”中，存在结论∠A+∠B=∠C+∠D．我们将图1②所示的凹四边形称为“飞镖形”．在这个“飞镖形”中，存在结论∠AOC=∠A+∠C+∠P．(1)直接利用上述基本图形中的任意一种，解决问题：如图2，AP、CP分别平分∠BAD、∠BCD，说明：∠P=12∠B+∠D．(2)将图2看作基本图形，直接利用(1)中的结论解决下列问题：①如图3，直线AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，若∠B=30°，∠D=20°，求∠P的度数．②在图4中，AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，猜想∠P与∠B、∠D的关系(直接写出结果，无需说明理由)．③在图5中，AP平分∠BAD，CP平分∠BCD的外角∠BCE，猜想∠P与∠B、∠D的关系(直接写出结果，无需说明理由)．模型2、“A”字模型结论：①∠3+∠4=∠D+∠E；②∠1+∠2=∠A+180°。

三角形倒角模型结论和证明

三角形倒角模型结论和证明1. 引言好啦，今天咱们聊聊三角形倒角模型！这个名字听起来挺高大上的，但其实说白了就是把一个三角形的角给“修整”一下，让它看起来更柔和，更圆润。

就像我们在生活中总是希望把事情搞得圆滑一点，避免那些尖锐的冲突一样，倒角模型的主要目的是为了优化、提高效率，简直是“顺其自然”的典范嘛。

接下来，我会跟大家细说这个模型的结论和证明，保证你听完后，不仅会觉得有趣，还能带点干货回家。

2. 三角形倒角模型的基本概念2.1 什么是倒角？首先，咱得弄明白啥叫“倒角”。

通俗点说，就是把三角形的角切掉，留下一个小平面。

你可以想象一下，如果你有一个三角形的饼干，把那尖尖的角削平，这样就不会刮到嘴巴，吃起来也更爽口了。

倒角的目的是为了降低尖锐的边界，给人一种更加温和、亲切的感觉。

这就像我们在社交场合中，总是希望用更柔和的方式与人交流，不让人觉得不适。

2.2 倒角的应用在很多地方，倒角都是一个关键的设计元素。

比如说，在工业设计中，很多产品的边角都是经过倒角处理的，这样既好看，又能提高安全性。

想象一下，家里的家具如果都有尖角，那可真是个安全隐患。

小孩玩耍时不小心撞到，家长可就要心疼得直叫唤了！而且，倒角还可以让产品在生产时更容易加工，减少磨损，简直是一举两得，聪明得不得了。

3. 三角形倒角模型的结论3.1 模型的结论通过对三角形倒角模型的分析，我们得出一个结论：倒角处理可以有效提升结构的稳定性，同时降低受力集中现象。

这听起来可能有点抽象，简单来说，就是给三角形的角“减负”，让它在受到外力时不容易崩溃。

就像一个团队，大家都团结一致，才能更好地面对外部挑战，毕竟“团结就是力量”嘛！3.2 生活中的反思再说说这个模型在生活中的启示吧。

我们每个人都是一座小小的三角形，在生活中不可避免地会遇到各种冲突和挑战。

如果我们能够像倒角那样，适度地“软化”自己的态度，处理问题时就会更有智慧，减少不必要的摩擦。

比如说，当朋友之间有误会时，咱不妨先放下架子，真诚沟通，总比剑拔弩张要强得多。

第二讲三角形的角及倒角模型

第二讲三角形的角及倒角模型1、如图1，求证：A B＋AE＞BC＋CD＋DE1AB＞（求证：AC＋BD，BD是四边形ABCD的对角线，且AC、BD相交于点O2、如图2，AC、2。

CD＋AD）＋BC＋，BAD＝∠BCF＝∠BAC＝∠BCA＝45°又有∠＝∠如图3、3，⊿ADE和⊿ABC中，∠EADAED ＋∠ECA的度数；）1 求∠ECF＋∠DAC（ FC的位置关系，并对你的结论加以证明。

与2）判断ED（D＋∠E的度数。

＝，∠A30°，求∠B＋∠C＋∠、如图求∠4、a的度数。

55，6-4、6-2D（点A、除外）向下拖动，依次可得图、图6-3图EAD6-1、6将图中线段上一点）之间有什么关系？AED（∠E、∠D、∠C、∠B、∠A中∠6-4、图6-3、图6-2分别探究图。

AB＋AC＞BE＋EC试说明：D7、如图7，在⊿ABC中是BC上任意一点，E是AD上任意一点，＝C 。

＝，BM平分∠ABC，且∠A27°，∠M＝33°，则∠平分∠、如图88，已知DMADCACBBA和CA的延长线上，CF、EF分别平分∠的边和点99、如图所示，点ED分别在⊿ABC D的关系：。

，∠，试探索∠和∠AEDF与∠B10、如图10，⊿ABC的一条外角平分线是CE，F是CA延长线上一点，FG∥EC交AB于点G，已知∠DCE＝50°，∠ABC＝40°，求∠FGA的度数。

EDF＝⊥AB，∠AFD＝158°，则∠、如图11，在⊿ABC中，∠B＝∠C，FD⊥BC，ED11的角平分线。

B、∠CBP、CP是任意⊿ABC的∠12、如图12-1，（1）探求∠BPC与∠A的数量关系。

（2）∠BPC能等于90度吗？说明理由。

（3）当∠A为多少度时，∠BPC＝2∠A？（4）把图12-1中的⊿ABC变成图12-2中的四边形ABCD，BP、CP仍然是∠B、∠C的角平分线，猜想∠BPC与∠A，∠D有何数量关系？（只写出猜想结果，不写说理过程）。

三角形中角度计算相关的模型(飞镖模型、8字模型、角分线模型)

三角形中与角度计算相关的模型两个定理：一、平面内，三角形的三个内角和为180°。

二、平面内，三角形的一个外角等于其不相邻的两个外角和。

由上述两个定理可导出本文如下说要讲述的相关模型：8字模型、飞镖模型、两内角角平分线模型、两外角角平分线模型、内外角角平分线模型、共顶点的角平分线与高线夹角模型。

下面一一推导证明。

条件：AD、BC相交于点O。

结论：∠A+∠B=∠C+∠D。

(上面两角之和等于下面两角之和)证明：在∠ABO中，由内角和定理：∠A+∠B+∠BOA=180°在∠CDO中，∠C+∠D+∠COD=180°，∠∠A+∠B+∠BOA=180°=∠C+∠D+∠COD，由对顶角相等：∠BOA=∠COD故有∠A+∠B=∠C+∠D应用：如下左图所示，五角星中，∠A+∠B+∠C+∠D+∠E=180°条件：四边形ABDC如上左图所示。

结论：∠D=∠A+∠B+∠C。

(凹四边形凹外角等于三个内角和)证明：如上右图，连接AD并延长到E，则：∠BDC=∠BDE+∠CDE=(∠B+∠1)+(∠2+∠C)=∠B+∠BAC+∠C。

本质为两个三角形外角和定理证明。

应用：如下左图，则∠A+∠B+∠C+∠D+∠E+∠F=260°(下右图中两个飞镖)。

条件：△ABC 中，BI 、CI 分别是∠ABC 和∠ACB 的角平分线，且相交于点I 。

结论：A I ∠+︒=∠2190 证明： ∵BI 是∠ABC 平分线，∴ABC ∠=∠212 ∵CI 是∠ACB 平分线，∴ACB ∠=∠213由A →B →I →C →A 的飞镖模型可知： ∠I =∠A +∠2+∠3=∠A +ABC ∠21+ACB ∠21=∠A +)180(21A ∠-︒=A ∠+︒2190. 应用：如上图，BI 、CI 分别是∠ABC 和∠ACB 的角平分线，且相交于点I 。

(1) 若∠A =60° ，则∠I =120° (2) 若∠I =110°，则∠A =40° (3) 若∠A =α，则∠I =α2190+︒。

【方法总结】几何证明中的倒角技巧大全

【方法总结】几何证明中的倒角技巧大全
常用几何倒角方法技巧：
1.三角形内角和：三角形的内角和为180°
2.三角形外角定理：三角形的外角等于与之不相邻的两个内角之和
3.角平分线：角的角平分线把这个角分为两个完全相等的角
4.直角三角形：直角三角形两锐角互余
5.平行线：平行线的性质
6等腰三角形：三角形等边对等角，底角相等
7.四边形内角和：四边形内角和为360°
8.三角形两大基本模型：“8字”模型和“飞镖”模型的角度关系
9.圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半。

10.方程思想：设角度为未知数，利用上述倒角技巧找出等量关系
一、用到平行线性质，外角
二、用到八字形和飞镖形
线.
三、用到方程思想
∴∠ECF=25°
四、用到三角形内角和，外角定理等
五、用互余倒角
40°
六、通过计算证明相等
七、用圆周角定理倒角
心角的一半，∠A=25°。

专题三角形中的倒角模型之平行线+拐点模型(学生版)-2025年中考数学常见几何模型

三角形中的倒角模型之平行线+拐点模型近年来各地中考中常出现一些几何倒角模型，该模型主要涉及高线、角平分线及角度的计算(内角和定理、外角定理等)。

平行线+拐点模型在初中数学几何模块中属于基础工具类问题，也是学生必须掌握的一块内容，熟悉这些模型可以快速得到角的关系，求出所需的角。

本专题就平行线+拐点模型(猪蹄模型(M型)、铅笔头模型、牛角模型、羊角模型、“5”字模型)进行梳理及对应试题分析，方便掌握。

拐点(平行线)模型的核心是一组平行线与一个点，然后把点与两条线分别连起来，就构成了拐点模型，这个点叫做拐点，两条线的夹角叫做拐角。

通用解法：见拐点作平行线；基本思路：和差拆分与等角转化。

目录例题讲模型模型1.猪蹄模型(M型与锯齿型)模型2.铅笔头模型模型3.牛角模型模型4.羊角模型模型5.蛇形模型(“5”字模型)习题练模型例题讲模型模型1.猪蹄模型(M型与锯齿型)先说说这个名字的由来，为什么叫猪蹄模型呢？因为它长得像猪蹄，也有叫M模型或锯齿模型的，都是根据外形来取的，只要你喜欢，叫什么都无所谓，掌握其中的核心才是关键。

①注意：拐角为左右依次排列；②若出现不是依次排列的，应进行拆分。

图1图2图3条件：如图1，①已知：AM∥BN，结论：∠APB=∠A+∠B；②条件：∠APB=∠A+∠B，结论：AM∥BN.证明：如图1，过点P作PQ∥AM，∵PQ∥AM，AM∥BN，∴PQ∥AM∥BN，∴∠A=∠APQ，∠B=∠BPQ，∴∠A+∠B=∠APQ+∠BPQ=∠APB，即：∠APB=∠A+∠B．条件：如图2，已知：AM∥BN，结论：∠P1+∠P3=∠A+∠B+∠P2.证明：根据图1中结论可得，∠A+∠B+∠P2=∠P1+∠P3，条件：如图3，已知：AM∥BN，结论：∠P1+∠P3+...+∠P2n+1=∠A+∠B+∠P2+...+∠P2n.证明：由图2的规律得，∠A+∠B+∠P2+⋯+P2n=∠P1+∠P3+∠P5+⋯+∠P2n+11.(2024·山西·二模)如图是一种卫星接收天线的轴截面示意图，卫星波束AB与DC平行射入接收天线，经反射聚集到焦点O处，若∠ABO=38°，∠DCO=45°，则∠BOC的度数为()A.90°B.83°C.76°D.73°2.(2024九年级下·辽宁·学业考试)如图，AB∥CD，AE=EF,∠A=25°,∠EFC=130°，则∠C的度数为．3.(2023春·河南驻马店·九年级专题练习)已知AB∥CD，∠EAF=13∠EAB，∠ECF=13∠ECD，若∠E=66°，则∠F为()A.23°B.33°C.44°D.46°4.(2023·广东深圳·校联考模拟预测)北京冬奥会掀起了滑雪的热潮，谷爱凌的励志故事也激励着我们青少年，很多同学纷纷来到滑雪场，想亲身感受一下奥运健儿在赛场上风驰电掣的感觉，但是第一次走进滑雪场的你，如果不想体验人仰马翻的感觉，学会正确的滑雪姿势是最重要的，正确的滑雪姿势是上身挺直略前倾，与小腿平行，使脚的根部处于微微受力的状态，如图所示，AB∥CD，当人脚与地面的夹角∠CDE=60°时，求出此时上身AB与水平线的夹角∠BAF的度数为()A.60°B.45°C.50°D.55°5.(23-24七年级下·广东云浮·期末)小明学习了角平分线的定义以及平行线的判定与性质的相关知识后，对角之间的关系进行了拓展探究．如图，直线AB∥CD，直线AC是直线AB，CD的第三条截线，AK，CK分别是∠BAC，∠DCA的平分线，并且相交于点K．问题解决：(1)∠BAC，∠DCA的平分线AK，CK所夹的∠K的度数为；问题探究：(2)如图2，∠BAK，∠DCK的平分线相交于点K1，请写出∠AK1C与∠AKC之间的等量关系，并说明理由；拓展延伸：(3)在图3中作∠BAK1，∠DCK1的平分线相交于点K，作∠BAK2，∠DCK2的平分线相交于点K3，依此类推，作∠BAK2023，∠DCK2023的平分线相交于点K2024，求出∠K2024的度数．6.(2024·上海·八年级校考期中)已知，直线AB∥CD。

翻折倒角的结论

翻折倒角的结论一、倒角的数学原理与一般方法【数学原理】倒角的数学原理，本质上只有一条，即为三角形的内角和定理及其推论——三角形外角的性质。

由于三角形的外角性质是加和的形式，会使得运算更简洁。

【计算方法】倒角的计算方法，其实就只有一条：利用内角和或外角性质找等量关系，列方程！不过，列方程也是有讲究的，总体思路是宁可多设几个字母，也要尽可能地使方程简洁，进而降低角度计算过程的复杂度。

二、倒角的四个重要模型倒角的模型主要有四个：①平行线与拐点模型②字与飞镖模型③双角平分线模型④折角模型前两个模型已经在上一篇文章中说明，继续介绍后两个模型，重点介绍“双角平分线模型”。

（一）平行线与拐点模型（三）字与飞镖模型（三）双角平分线模型1、模型条件&结论2、应用场景在应对与多条角平分线相关的角度问题时，“双角平分线模型”非常好用，所求夹角∠BPC的大小只有∠A有关！3、证明思路或方法（以双内角平分线图形为例）模型的证明依然是朴素的，即为最基本的方法：“根据三角形的内角和定理或外角性质列方程”。

其它两个图形对应的结论也可类似证明。

整个证明过程，只有朴素的数学原理，没有太多需要动脑筋的地方，便可轻松地把问题解决。

这也是我一贯的解题方法，我希望我的学生是更富有逻辑思考能力的，而不是记住一堆华丽的技巧，正所谓“大道至简”。

4、经典例题（四）折角模型1、模型条件&结论2、应用场景在三角形的翻折问题求解角度时使用。

以上两个图形的唯一区别仅在于翻折后的点A'是落在△ABC的内部还是外部。

如果点A'是落在△ABC的内部，则为左边的模型；如果点A'是落在△ABC的外部，则为右边的模型。

3、证明思路或方法（以右边图形为例）4、经典例题（五）其它常见模型1、四边形的双角平分线模型区别：唯一之处就在于所求角是四边形的相邻两角的平分线所构成角（适用于左边模型）还是相对两角的角平分线所构成的角（适用于右边模型）。