浮力专题液面变化及其解题技巧(很全面很详尽)
浮力液面升降问题的类型及解题技巧

液面升降问题的分析冰浮于液面的问题是生活中的常见问题,在各类试卷中经常出现,但由于这类问题的现象不太明显,观察需要的时间较长,不为一般的学生所重视.即使一部分学生有意识地去进行观察,出会现因为问题类型比较多,而结论只有“升”和“降”两种,常常出现而把现象和条件的对应关系混淆的现象,导致认识的偏差。
为了更深刻地理解引起液面“升”、“降”的原因,准确把握条件和现象之间的关系。
可以将各类问题进行分类处理,从最基本的漂浮在液面上的冰熔化成水后液面的升降问题为基点,逐步展开思考形成系统的认识。
更重要的是可以通过这些问题的讨论和思考,把许多有关物体浮沉和液面变化问题连成一个整体。
对于液体中的物体由于某种变化而引起的液面升降问题的形式出现,本文介绍一种简便快捷的判断方法——“状态法”.(一)、什么叫状态法所谓“状态法”,就是对变化前后液体中的物体所处的状态进行比较来判断液面的升降.(二)、如何用“状态法”速断液面升降若变化前后液体中的物体都处于漂浮、悬浮状态,而无沉体出现,则液面不变;若液体中的物体,在变化前无沉体,而变化后有沉体出现,则液面下降;若液体中的物体,在变化前有沉体,而变化后无沉体出现,则液面升高.说明:变化前后液体中物体的总质量保持不变;容器中液体的密度不变.(三)、证明设液体中的物体的总重为G,变化前后在液体中所受的总浮力分别为F浮、F浮′.若变化前后均无沉体出现,由浮沉条件知F浮′=F浮=G,ρ液gV排′=ρ液gV排,则V排′=V排,液面不变.若变化前无沉体,变化后有沉体,由浮沉条件知F浮=G,F浮′<G,则F浮′<F浮,即V排′<V排,故液面下降.若变化前有沉体,变化后无沉体,由浮沉条件知F浮<G,F浮′=G,则F浮′>F浮,即V排′>V排,故液面上升.一、液面升降的主要类型有:类型一:纯冰浸于液体,熔化后判断液面升降1、纯冰在纯水中熔化;2、纯冰在盐水(或其它密度比水大的液体)中熔化;3、纯冰在密度比水小的液体中熔化;类型二:冰块中含有其它杂质,冰块熔化后判断水面升降。
浮力整体法分析液面变化及冰化水问题

浮力整体法分析液面变化及冰化水问题第一篇:浮力整体法分析液面变化及冰化水问题捞放货物问题1、一艘船漂浮在湖面上,将船上的货物扔进湖里,请问船体将沉一些),湖面将(上升、下降或不变)。
2、一艘船漂浮在湖面上,将船上的货物用钢丝吊在船下,请问船体将(上浮一些或下沉一些),湖面将(上升、下降或不变)。
冰化水问题3、容器里装满水,水面上漂浮着一块冰,问,并在融化后水面将或不变)。
冰包物问题1、容器里盛满水,一块冰包木块浮在水面上,溶化后液面怎么变化降或不变)。
2、容器里盛满水,一块冰包铁块浮在水面上,溶化后液面怎么变化降或不变)。
3、容器里盛满水,一块冰包气泡浮在水面上,溶化后液面怎么变化降或不变)。
1.有一个烧杯,烧杯中的冰块漂浮在水中,烧杯中的水面恰好与烧杯口相平。
待这些冰全部融化后,水是否会溢出,或水面是否会下降?解析:因为冰块处于漂浮状态,故有G冰=F浮,∴ρ冰V冰g=ρ水V排g化解得ρ冰V冰=ρ水V排∵冰融化成水后质量不变,故有m冰=m水融∴ρ冰V冰=ρ水V 水融综合两式:ρ冰V冰=ρ水V排,ρ冰V冰=ρ水V水融可得ρ水V排=ρ水V水融∴V排=V水融,∴水面既不会升高也不会降低答:。
还有以下的几种类型的浮冰问题:1.冰在果汁中浮着,叫你判断冰融化后液面的变化,其实这时冰融化后水面时会变化的。
2.冰中含有杂质小石块,冰此时可能悬浮也可能漂浮,然后让你计算一些数据,比如压强,密度(石块的),等等!我在举个例子:2.一杯浓橘汁加了冰块后,刚好不会溢出,如果冰块融化,则液面将怎么变化?解析:(我要偷懒了)和上面那个题一样的方法,可以得出如下结论ρ冰V冰=ρ汁V 排,ρ冰V冰=ρ水V水融综合可得:ρ汁V排=ρ水V水融因为ρ汁>ρ水所以V排<V水融所以会溢出。
答:.........浮冰问题种种冰、水是同种物质的不同状态,冰可由水凝固而成,水由冰熔化可得。
由于冰、水密度不等,带来了一些需要我们探究的问题。
1、冰山一角到底是冰山的多少?解析:设冰山体积为V,浮在水面上的冰山体积为V1,因为冰漂浮在水面上,F浮=G冰,即ρ水g(V-V1)= ρ冰 gV1化简得V1=V冰(ρ水-ρ冰)/ρ水=V冰/10,即浮于水面的冰山一角是冰山的十分之一。
中考物理复习《浮力液面高度变化量计算方法与技巧》
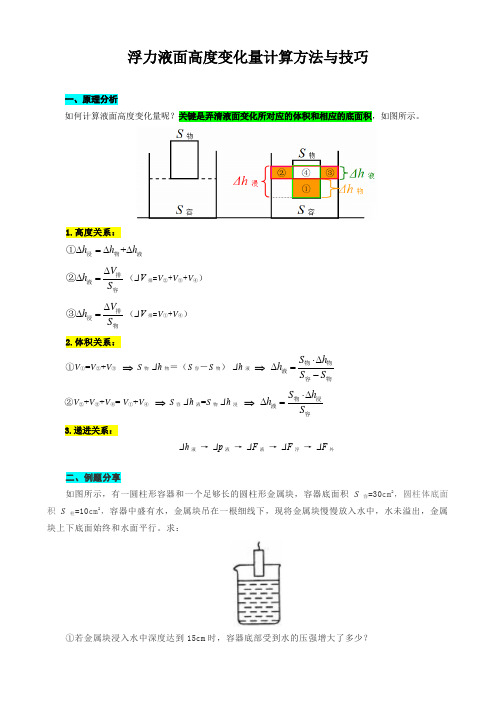
浮力液面高度变化量计算方法与技巧一、原理分析如何计算液面高度变化量呢?关键是弄清液面变化所对应的体积和相应的底面积,如图所示。
1.高度关系:+h h h ∆=∆∆浸物液①V h S ∆∆=排液容②(ΔV 排=V ②+V ③+V ④)V h S ∆∆=排浸物③(ΔV 排=V ①+V ④)2.体积关系:①V ①=V ②+V ③ ⇒ S 物·Δh 物=(S 容-S 物)·Δh 液 ⇒ S h h S S ⋅∆∆=-物物液物容②V ②+V ③+V ④= V ①+V ④ ⇒ S 容·Δh 液=S 物·Δh 浸 ⇒ S h h S ⋅∆∆=浸物液容3.递进关系:Δh 液 → Δp 液 → ΔF 液 → ΔF 浮 → ΔF 外二、例题分享如图所示,有一圆柱形容器和一个足够长的圆柱形金属块,容器底面积S 容=30cm 2,圆柱体底面积S柱=10cm 2,容器中盛有水,金属块吊在一根细线下,现将金属块慢慢放入水中,水未溢出,金属块上下底面始终和水面平行。
求:①若金属块浸入水中深度达到15cm 时,容器底部受到水的压强增大了多少?②若绳子从金属块底部刚好接触到水面时开始向下放下15cm时,容器底部受到水的压强增了多少?1.第1小问分析过程:要求水对容器底部增加的压强,也就是求水位增加的高度。
如何求水位增加的高度呢?思维过程如下:当圆柱体浸入水中15cm时,实际上是一个动态过程,圆柱体一边下降,水位一边上升,圆柱体下降的深度加上水位上升的高度刚好为15cm。
由此可见,如何将动态变化过程转化为静态过程才是解题关键。
多数同学可能有这样的思维过程:假设原来水位不变,我们把圆柱体浸入水中后排开的水用容器接到,然后将排开的水再倒回容器中。
这个时候有两种思考:(1)倒入圆柱体两边的空白处,这样水位上升的高度,Δh=V排/(S容-S柱)。
显然,圆柱体浸入水中的深度就是15cm+Δh,跟题意矛盾。
(完整版)浮力解题技巧

一、对浮力的认识1. 在液体中,无论是上浮还是下沉的物体,无论形状规则或不规则,无论运动或静止,也无论浸在哪种液体中,只要物体底部有液体,就会受到液体给物体向上的托力,也就是浮力。
2.浸在气体中的物体也会受到气体的浮力3.一切浸在液体中的物体,都受到液体对它竖直向上的浮力,既包括上浮,下沉的物体,也包括漂浮、沉入液体底部的物体,但不包括浸在液体中或与容器下表面结合紧密的物体,如桥墩、插入泥中的木桩等4.两种特殊情况下的浮力要分清:1)、当物体部分浸入液体中时,上表面受到的向下的液体压力为零,则浮力大小等于下表面受到的压力的大小。
2)、当浸在液体中的物体下表面和容器底部紧密接触时,则液体对物体向上的压力为零,物体将不受浮力的作用,只受向下的压力。
二、掌握计算浮力大小的四种方法.1.称重法:利用弹簧测力计两次读数不等来计算浮力.基本公式F浮=G-F拉(式中的G和F拉分别为称在空气中的物体和称在液体中的同一物体时弹簧测力计的读数。
即两次弹簧测力计示数之差)适用范围:此式适用于液体中下沉的物体.常用于题中已知用弹簧测力计称物体重的情况.2.压力差法.利用浮力产生的原因来计算浮力.基本公式F浮=F向上-F向下.适用范围:此法用于判断物体是否受到浮力或计算浸没深度已知的规则物体所受的浮力.3.原理法——利用阿基米德原理来计算浮力.基本公式:F浮=G排液=M排液g=ρ液gV排液.适用范围:普遍适用.4.平衡法:利用物体漂浮或悬浮的条件来计算浮力.基本公式:F浮=G物(物体漂浮或悬浮)、F浮+N支=G物(物体沉底)、F浮=G物+F拉.(用绳子拉住)适用范围:漂浮体、悬浮体、沉底、连接体等.其中称重法、原理法、平衡法是常用的计算浮力的方法.其它方法一般都要与原理法联合使用,才能顺利完成浮力问题的解答.三、求解浮力问题的一般步骤1. 明确研究对象(受力物体)2. 明确研究对象所处的运动状态.(漂浮、悬浮、沉底、上浮或下沉等)3. 对研究对象进行受力分析,并画出受力示意图.(除分析重力、浮力外,还要注意是否有其它相关联的物体对它是否有拉力、压力等)3. 列出物体处于平衡状态下的力的平衡方程(在展开方程时,应注意抓住题中的关键字“全浸”、“部分浸”、“漂浮”、“沉底”、“露出水面”等)4列等式、解方程求出未知量.四.例题讲解1.如图所示,是小鹰同学测量某种液体密度的过程,请你根据实验数据,求:(1)小石块的质量;(2)小石块的体积;(3)液体的密度.(g 取10N/kg)2、如图所示,将边长为5cm的实心正方体木块轻轻放入装满水的溢水杯中,木块静止时,从杯中溢出水的质量为0.1kg(g取10N/kg)。
浮力培补之“液面变化问题”

浮力培补之“液面变化问题”一、冰熔化问题——判断液面的变化例题1:(冰化水)一冰块漂浮在水面上,当冰完全熔化后,容器中的水面高度将。
变式1:(冰化水)一冰块漂浮在盐水上,当冰完全熔化后,容器中的液面将。
变式2:(冰化水)一冰块放入某液体中(密度为0.95g/cm3),如图所示。
当冰完全熔化后,容器中的液面将。
总结:(冰化水)一冰块在某液体中时,当冰完全熔化冰后,容器中的液面将。
二、组合的漂浮物体之液面的变化例题2:(船中抛物)若一池塘里漂浮有一只小船,船中有一木球。
当将木球抛入水中,池塘的水面高度将。
变式1:(船中抛物)若一池塘里漂浮有一只小船,船中有一铁球。
当将铁球抛入水中,池塘的水面高度将。
(船中抛物)若一池塘里漂浮有一只小船,船中有一球。
当将球抛入水中,池塘的水面高度将。
变式2:如图所示,在盛有某种液体的圆柱形容器内放有一木块A,在木块A的下方用轻质细线悬挂一体积相同的金属块B.金属块B浸没在液体内,而木块A部分露出液面,此时细线有弹力,液面正好与容器口齐平。
细线突然断开,待稳定后液面(选填“下降”、“上升”或“不变”)练习:1.如圏1所示,容器中装有一定质量的水,先后按甲、乙两种方式使物体A和小玻璃杯漂浮在水面上(图中细线重力及体积均不计)。
设甲、乙两图中物体A和小玻璃杯共同受到的浮力分别为F甲和F乙,水对容器底的压强分别为P甲和P乙,则(()A.F甲<F乙,P甲=P乙B.F甲=F乙,P甲=P乙C.F甲=F乙,P甲﹥P乙D.F甲>F乙,P甲<P乙2如图2将一个实心铁球A和一个密度小于水的木球B放在小盒中再将小盒放在水槽中,漂浮在水面上,那么下列说法正确的是()A将A从盒中拿出放到水的水中,水槽中水面高度不变B将A从盒中拿出放到水的水中,水槽中水面高度下降C.将B从盒中章出放到水的水中,水槽中水面高度下降D将B从盒中拿出放到水的水中,水槽中水面高度上升3.如图3所示,在未盛满水的容器中漂浮着一只小船,船中装有一个铁球,铁球与小船质量相等,现将铁球取出放入容器中,小船仍浮在水面上,铁球沉底,下列说法正确的是()A.水对小船的浮力小于水对铁球的浮力B.水对小船所减小的浮力等于水对铁球的浮力C.甲图容器对地面压强大于乙图容器对地面压强D.乙图中水对容器底的压强小于甲图中水对容器底的压强4.如图4所示,烧杯内装有适量水,有一塑料试管下面一小铁块,浮在水面上。
浮力计算题型及解题技巧

浮力是物理学中的重要概念,其在计算题中的应用也比较广泛。
以下是一些常见的浮力计算题型和解题技巧:1.计算物体所受的浮力大小这种题型通常会给出物体的体积、密度、重力加速度等参数,要求计算物体在液体中所受的浮力大小。
解题技巧如下:•首先,根据物体的密度和液体的密度,判断物体是否完全浸没在液体中,还是只有一部分浸在液体中。
•对于完全浸没的物体,可以根据阿基米德原理计算物体所受的浮力大小:F浮=ρgV排,其中ρ为液体的密度,g为重力加速度,V排为物体的排开液体的体积。
•对于只有一部分浸在液体中的物体,可以根据物体的密度和液体的密度,计算物体所受的浮力大小:F浮=ρgV浸/V物,其中V浸为物体浸在液体中的体积,V物为物体的总体积。
2.计算物体在液体中所受的浮力变化量这种题型通常会给出物体在液体中所受的浮力大小的变化量,要求计算物体所受的浮力变化量。
解题技巧如下:•首先,根据物体的体积、密度、重力加速度等参数,计算物体在液体中所受的浮力大小。
•然后,根据物体所受的浮力变化量,可以计算物体在液体中所受的浮力变化量:ΔF浮=ΔρgVΔV排,其中Δρ为液体的密度变化量,g为重力加速度,ΔV排为物体的排开液体的体积变化量。
3.计算物体在液体中所受的浮力对运动状态的影响这种题型通常会给出物体在液体中所受的浮力大小和物体的运动状态,要求计算浮力对物体的运动状态的影响。
解题技巧如下:•首先,根据物体的体积、密度、重力加速度等参数,计算物体在液体中所受的浮力大小。
•然后,根据牛顿第二定律,可以计算出物体的加速度:a=F合/m,其中F合为物体所受的合力,m为物体的质量。
•最后,根据加速度的大小和方向,可以判断物体是加速上升、减速上升、加速下降、减速下降等运动状态。
需要注意的是,在计算浮力的过程中,要遵循阿基米德原理和牛顿第三定律等物理原理,避免出现错误。
同时,在解题过程中要灵活运用各种物理公式和解题方法,避免思维定势。
除了上述提到的浮力计算题型和解题技巧,还有一些其他的浮力计算问题需要我们注意:1.计算浮力对物体的运动状态的影响这种题型通常会给出物体在液体中所受的浮力大小和物体的运动状态,要求计算浮力对物体的运动状态的影响。
浮力专题:浮力习题中的液面变化问题(有答案)

浮力专题:浮力习题中的液面变化问题【例1】(纯冰熔于液体)容器内分别装有水和盐水,在液面上浮着一块冰,问:(1)冰在水中熔化后,水面如何变化?(2)冰在盐水中熔化后,液面如何变化?【答案】(1)不变;(2)上升【解析】液面是否变化,关键是看V排是否等于V化水。
(1)①当冰漂浮时,依漂浮条件知,F浮=G冰即ρ水ɡV排= G冰= m冰g ∴V排=m冰/ρ水②冰化成水后,冰的质量与水的质量没有变化即m化水= m冰∴V化水=m冰/ρ水③所以V排=V化水即冰块完全熔化后水面高度不变。
(2)同理:纯冰浮在盐水液面上,当冰熔化后液面将上升。
练习1:若一冰块在水中,冰块与容器底部相接触并相互间有压力,则当冰块完全熔化后,容器内的水面将怎样变化?【答案】上升【解析】冰块没有漂浮在水面上,冰块所受浮力小于冰块所受重力,∴熔化前F浮<G冰,即ρ水g V排<G冰,故得V排<m冰/ρ水。
熔化为水的体积V化水=m水/ρ水= m冰/ρ水,∴V排<V化水,即熔化后水面要上升。
【例2】(冰中有杂质)在盛水的烧杯中漂浮着一块冰,冰中夹着一小木块,问:(1)当冰完全熔化为水时,水面将如何变化?(2)若冰中夹杂着一小石块,冰熔化后液面如何变化?【答案】(1)不变;(2)下降【解析】方法一:比较体积变化法①冰块漂浮时:F浮=G冰+G木即ρ水gV排= G冰+G木,V前排= (m冰+m木)/ ρ水=m冰/ρ水+m木/ρ水②当冰块化成水时:m化水= m冰∴V化水=m冰/ρ水又因为木块仍漂浮,F木浮= G木即ρ水gV木排= m木g ∴V木排=m木/ρ水V后排=V化水+V木排= m冰/ρ水+ m木/ρ水 (2)由(1)(2)得:V前排= V后排故当冰完全熔化成水时,水面不变。
方法二:比较浮力变化法熔化前冰块和木块都漂浮∴F前浮= G冰+ G木熔化后熔化成的水悬浮,木块仍漂浮∴F后浮= G化水+ G木又G化水= G冰所以F前浮=F后浮,即熔化前后所受浮力不变,所以液面将不变。
(浮力)液面变化与压强—(疑难解读+解题技巧)2021届九年级物理中考复习(优等生)专题讲义

微专题10-5 液面变化与压强知识· 解读一,常用公式:①压力压强②浮力③液面高度变化量(适用于粗细均匀地柱形容器)。
二,基本步骤:①作图,帮助思路问题。
②找等量关系(通常为液面变化量h △或排开液体体积变化量V △)。
③列方程,计算。
典例·解读即。
培优· 训练一,选择题1,一种液体地密度随深度而增加,它地变化规律是ρ=ρ0+kh,式中ρ0,k 是常数,h 表示深度。
设深度足够,有一只密度为ρ',地实心小球投入此液体中,且ρ'>ρ0,则下面判断中正确地是( )A.小球将一沉到底,不再运动B.小球将漂浮在液面上,不能下沉C.小球经过一段运动过程,最终悬浮在深h =处D.小球经过一段运动过程,最终悬浮在深h =处2,在一装满水地容器中,放入一质量为20克地物体,从容器中溢出15克地水,则该物块在水中地浮沉情况和水对容器底部地压强应该是 ( )A.下沉,压强不变B.上浮,压强增大C.漂浮,压强减小D.悬浮,压强减小3,(多选)粗试管甲和细试管乙中都装有一些沙子,二者地总重量相等,试管地底部是平地,它们都竖直地,静止地浮在水面上。
对两个试管来讲,下面表述中正确地是 ( )A .排开水地体积相等B .水对管底地压力相等C .水对管底地压强相等D .水对管地浮力相等除了上述体积等量关系,我们还可以从水地体积前后不变地角度列出等式求出h △。
即:下面看具体计算过程:4,气象探测气球在充满氢气后,所受浮力远远大于重力.将该气球放出后,若气球不破裂,其运动情况将是( )A.一直不停地上升B.匀速向上升C.只能升到一定地高度,并将停留在这一高度D.升到一定高度后会下降, 下降到一定高度后又会上升5,如图所示,在容器里盛有一部分水银,在水银面上浮着一铁球.若在容器里再轻轻地注入一定量水,则铁球相对于原来地位置要 ( )A.上升些B.下降些C.既不上升,也不下降D.无法判断6,(多选)如图所示,在四只相同地杯子中都盛了水,甲杯中漂浮着一木块,乙杯中漂浮着一冰块,丙杯中悬浮着一空心塑料球,丁杯地底部有一小铁球.此时,四只杯子中地水面等高,且木块,冰块,塑料球和小铁球地体积相等。
]与浮力有关的液面变化类问题
![]与浮力有关的液面变化类问题](https://img.taocdn.com/s3/m/a3e54c9b0029bd64783e2c75.png)
底受到水的压力为F2,此时水槽底部受到水的压强与捞起金属球前的变 化量为p,水的密度为ρ水。根据上述条件可知金属球捞起放入烧杯后
A.烧杯受到的浮力为F2 –F1 B.烧杯排开水的体积增大了 C.金属球受的支持力为F2 –F1–pS D.水槽底部受到水的压力变化了 pS 4.(10顺二)如图10(a)所示,装有部h,试管壁粗细均匀、厚度不 计;现将某物块放入试管内,物块漂浮在试管内的水面上,试管仍漂浮
(2)先后两次水对容器底的压强差
甲
乙
10.如图所示、一圆柱形平底容器底面积为
,把它平放在水平桌面上,在容器内放入一个底面积为
,高为0.15m的圆柱形物块,且与容器底不完全密合,物块的平均密度 为
求:(1)物块对容器底的压强? (2)向容器内缓慢注入重量为多少千克的水时,物块对容器底的压强 恰好为零?
5.一块0℃的冰放在盛有0℃的水的容器中。已知冰块与容器底部相接 触并相互间有压力,则当冰完全融化为0℃的水后.容器中水面的位置 将( ) A.上升; B.下降; C.保持不变; D.水面的升或降决定于冰和容器内水的体积。 6.如图所示,装有金属球的小盆漂浮在圆柱形水槽的水面上。此时小 盆受浮力F1。若把金属球从盆中拿出并投入水槽中,球沉到水槽的底 部。此时小盆受浮力F2,水槽底对金属球的支持力为N。那么( )
A.hA ׃hB =3 1 ׃B. hB =0.04m C. pA- pB =200Pa ; D.GA+GB= 1.52N ; F2 =F1
图7
图9 乙 甲
3.(09朝一)如图7所示,在底面积为S的圆柱形水槽底部有一个金属 球,圆柱型的烧杯漂浮在水面上,此时烧杯底受到水的压力为F1。若把 金属球从水中捞出放在烧杯里使其底部保持水平漂浮在水中,此时烧杯
初中物理学习中如何解决浮力问题中液面的升降问题精选全文完整版

可编辑修改精选全文完整版初中物理学习中如何解决浮力问题中液面的升降问题[日期:2010-10-22] 来源:北小营中学作者:李立清[字体:大中小] 在学习浮力时,大多学生认为不好学,尤其是在一些特殊题型的解法上有些学生感到很头疼,不知道解题的思路,就更不知道从何下手,在考试中影响了自己的成绩。
下面就浮力中有关这种特殊题型的解决谈谈自己的解题体会。
首先是冰融化后考虑容器中液面升降的问题:题目1 在一个盛有水的烧杯中放入一个冰块,水不溢出,过一段时间冰融化后,问杯中液面上升、下降还是不变?解析根据阿基米德原理和浮沉条件列出关系式(1)F浮=G排水, 经整理得到V排=m排水/ρ水(2)F浮=G冰,G化水=G冰→m化水=m冰→V化水=m冰/ρ水由于F浮相等,G排水=G冰→m排水=m冰,所以V排=V化水,即液面不变。
注意:液面上升也好、下降也好,这类问题关键在于我们比较的问题是什么,确立好问题就知道如何下手。
实际上我们要比较的是冰融化前在水中的排水体积和冰融化后的水的体积的大小关系。
冰块可以放在水中,那将它放在其他液体中会怎样呢题目2 在一个盛有盐水的烧杯中放入一个冰块,水不溢出,过一段时间冰融化后,问杯中液面上升、下降还是不变?解析根据阿基米德原理和浮沉条件列出关系式(1)F浮=G排盐水, 经整理得到V排=m排盐水/ρ盐水(2)F浮=G冰,G化水=G冰→m化水=m冰→V化水=m冰/ρ水由于F浮相等,G排盐水=G冰→m排盐水=m冰,但是ρ盐水>ρ水所以V排<V化水,即液面上升。
注意:题目2与1的区别是烧杯中盛放的液体不同。
在考虑(1)和(2)中最后V排与V化水时,要考虑到液体密度的不同。
题目3 在一个盛有酒精的烧杯中放入一个冰块,水不溢出,过一段时间冰融化后,问杯中液面上升、下降还是不变?解析在拿到这个题目时,大部分学生如果掌握了上面两个题的解题过程,很快的就会列出阿基米德原理和浮沉条件关系式,但是他没有考虑到酒精的密度和水密度的关系,冰块不会漂浮怎么办?但是如果考虑到冰会沉到杯子的底部,冰融化体积减小,自然答案就会出来,液面下降。
浮力专题课液面变化

★若液体中的物体,在变化前有沉底物体,
而变化后无沉底物体出现,则液面升高。
课堂小结
解决浮力变化问题的方法: ① 比较V排 ② 比较F浮
有三个实心小球甲、乙、丙,甲球在水中悬浮,乙球在水中下沉,丙球漂 浮在水面上.现将甲、乙、丙三球同时放在一只敞口的小铁盒里,然后将 小铁盒漂浮在盛水的容器中(如图1所示),下列判断正确的是 ( ABD ) A.只将小球甲从盒中取出放入水中后,容器中水面高度不变 B.只将小球乙从盒中取出放入水中后,容器中水面高度下降 C.只将小球丙从盒中取出放入水中后,容器中水面高度上升 D.将甲、乙、丙三球同时放入水中后,容器中水面下降 .
图D
图E
图F
结论:液面降低
例1:如图,在盛水的容器内漂浮一木 盆,木盆内有一个铁球。试想, 若把铁球拿出放入水中,液面高 度将如何变化?
如图所示,在盛水的容器底部有一 铁球,上面漂浮着一个木盆,若将铁 球捞出放入盆里,盆仍漂浮在水面, 容器中水面将如何变化?
例2:如图,在盛水的容器内漂浮一木 盆,木盆内有一个木球。试想, 若把木球拿出放入水中,液面高 度将如何变化?
例3: 如图,在盛水的容器内漂浮一木 盆,木盆内有一个空心金属球。
(球 水)试想,若把金属球拿出 放入水中,液面高度将如何变化?
变化前 变化后
液面变化 下降 上升 不变 不变
总结
★若变化前后液体中的物体都处于漂浮、悬
浮状态,而无沉底物体出现,则液面不变;
★若液体中的物体,在变化前无沉底物体,
液面上升下降
1、漂浮在水面上的冰融化,液面如何变 化?
冰
水
分析:
冰
水
图A
水
浮力专题_液面变化和解题技巧(很全面、很详尽)

液面升降问题的分析..各种情况都包含,配有详图2018年2月11日对于液体中的物体由于某种变化而引起的液面升降问题的形式出现,本文介绍一种简便快捷的判断方法——“状态法”.(一)、状态法:就是对液体变化前、后的物体所处的状态进行比较来判断液面的上升、下将、不变的方法.(二)、状态法迅速判断液面升降方法:①若变化前后液体中的物体都处于漂浮、悬浮状态,而无沉体出现,则液面不变;②若液体中的物体,在变化前无沉体,而变化后有沉体出现,则液面下降;③若液体中的物体,在变化前有沉体,而变化后无沉体出现,则液面升高;说明:变化前后液体中物体的总质量保持不变;容器中液体的密度不变.(三)、证明设液体中的物体的总重为G,变化前后在液体中所受的总浮力分别为F浮、F浮′.若变化前后均无沉体出现,由浮沉条件知①F浮′=F浮=G,ρ液gV排′=ρ液gV排,则V排′=V排,液面不变.②若变化前无沉体,变化后有沉体,由浮沉条件知F浮=G,F浮′<G,则F浮′<F浮,即V排′<V排,故液面下降.③若变化前有沉体,变化后无沉体,由浮沉条件知F浮<G,F浮′=G,则F浮′>F浮,即V排′>V排,故液面上升.一、液面升降的主要类型有:类型Ⅰ:纯冰浸于液体,熔化后判断液面升降①、纯冰在纯水中熔化;②、纯冰在盐水(或其它密度比水大的液体)中熔化;③、纯冰在密度比水小的液体中熔化;类型Ⅱ:冰块中含有其它杂质,冰块熔化后判断水面升降。
①、含有木块(或其它密度比水小的固体)的冰块在纯水中熔化;②、含有石块(或其它密度比水大的固体)的冰块在纯水中熔化;③、含有煤油(或其它密度比水小的液体)的冰块在纯水中熔化;类型Ⅲ:冰块中含有一定质量的气体,冰块熔化后判断水面升降。
类型Ⅳ:容器中的固态物质投入水中后判断液面升降①、固态物质的密度小于水的密度②、固态物质的密度等于水的密度③、固态物质的密度大于水的密度二、解题关键:无论液面上升或者下降,关键在比较的问题是什么,确立好问题就知道如何下手。
(完整版)浮力液面升降问题的类型及解题技巧

液面升降问题的分析冰浮于液面的问题是生活中的常见问题,在各类试卷中经常出现,但由于这类问题的现象不太明显,观察需要的时间较长,不为一般的学生所重视.即使一部分学生有意识地去进行观察,出会现因为问题类型比较多,而结论只有“升”和“降”两种,常常出现而把现象和条件的对应关系混淆的现象,导致认识的偏差。
为了更深刻地理解引起液面“升”、“降”的原因,准确把握条件和现象之间的关系。
可以将各类问题进行分类处理,从最基本的漂浮在液面上的冰熔化成水后液面的升降问题为基点,逐步展开思考形成系统的认识。
更重要的是可以通过这些问题的讨论和思考,把许多有关物体浮沉及液面变化问题连成一个整体。
一、液面升降的主要类型有:类型一:纯冰浸于液体,熔化后判断液面升降1、纯冰在纯水中熔化;2、纯冰在盐水(或其它密度比水大的液体)中熔化;3、纯冰在密度比水小的液体中熔化;类型二:冰块中含有其它杂质,冰块熔化后判断水面升降。
1、含有木块(或其它密度比水小的固体)的冰块在纯水中熔化;2、含有石块(或其它密度比水大的固体)的冰块在纯水中熔化;3、含有煤油(或其它密度比水小的液体)的冰块在纯水中熔化;类型三:冰块中含有一定质量的气体,冰块熔化后判断水面升降。
类型四:容器中的固态物质投入水中后判断液面升降1、固态物质的密度小于水的密度2、固态物质的密度等于水的密度3、固态物质的密度大于水的密度二、解题关键:液面上升也好、下降也好,关键在于我们比较的问题是什么,确立好问题就知道如何下手。
实际上我们要比较的是冰熔化前(或物体投放前)在液体中排开液体的体积和冰熔化成水后的体积(或物体投放后液体体积)的大小关系:若前体积大于后体积,液面下降;若前体积等于后体积,液面不变;若前体积小于后体积,液面上升。
三、判断方法1、比较体积变化法:比较的是冰熔化前(或物体投放前)在液体中排开液体的体积和冰熔化成水后的体积(或物体投放后液体体积)的大小关系:若前体积大于后体积,液面下降;若前体积等于后体积,液面不变;若前体积小于后体积,液面上升。
浮力的解题方法和思路汇总,配例题,有干货,不白看

浮力的解题方法和思路汇总,配例题,有干货,不白看
展开全文
浮力是初中物理的重难点,难倒了一大批小伙伴,今天我来给大家做一下梳理。
浮力的4种计算方法:
1.浮力的产生原因:F浮=F向上-F向下
若物体漂浮,则F向下=0 F浮=F向上(即物体下表面所受压力=浮力)
2.称重法:F浮=G-F拉
3.阿基米德原理:F浮=G排=m排g=ρ液gV排
4.漂浮/悬浮:F浮=G物
物体的浮沉条件
1.上浮:F浮>G物ρ液>ρ物
2.漂浮:F浮=G物ρ液>ρ物(平衡态)
3.悬浮:F浮=G物ρ液=ρ物(平衡态)
4.下沉:F浮<G物ρ液<ρ物
5.沉底:F浮<G物ρ液<ρ物(平衡态)
我们来看两道例题,大家先自己完成,再核对我的答案。
核对一下答案:
第1题的关键入手点就是“悬浮”,利用我刚才讲的:悬浮:F浮=G物ρ液=ρ物就可以解决了
第2题要学会看图,有5个考点:
(1)开始物体还未入水,拉力不变,大小等于重力;
(2)之后物体从下表面接触水到完全浸没,V排变大,F浮变大,所以拉力变小;
(3)拉力变化的过程正好是物体入水的过程,下降的距离就是物体的高度;
(4)完全浸没后,F浮不变,拉力也不变;
(5)物体密度的求解思路:通过重力得到质量、通过浸没后的浮力得到体积、再利用ρ=m/V得到物体的体积,这个思路很常用,一定要掌握。
今天讲到这里,大家可以关注我,看我之前发的《浮力经典题》视频合集,更好的掌握浮力的计算方法,希望能够帮助到大家。
浮力知识-液面变化

用“状态法”速断液面升降对于液体中的物体由于某种变化而引起的液面升降问题,经常困惑着学生.考虑到这类问题在各种考试中多以填空、选择题的形式出现,现介绍一种简便快捷的判断方法——“状态法”一、什么叫状态法所谓“状态法”,就是对变化前后液体中的物体所处的状态进行比较来判断液面的升降.二、如何用“状态法”速断液面升降(1)若变化前后液体中的物体都处于漂浮、悬浮状态,而无沉体出现,则液面不变;(2)若液体中的物体,在变化前无沉体,而变化后有沉体出现,则液面下降;(3)若液体中的物体,在变化前有沉体,而变化后无沉体出现,则液面升高.说明:变化前后液体中物体的总质量保持不变;容器中液体的密度不变.三、证明设液体中的物体的总重为G,变化前后在液体中所受的总浮力分别为F浮、F浮′.若变化前后均无沉体出现,由浮沉条件知F浮′=F浮=G,ρ液gV排′=ρ液gV排,则V排′=V排,液面不变.若变化前无沉体,变化后有沉体,由浮沉条件知F浮=G,F浮′<G,则F浮′<F浮,即V排′<V排,故液面下降.若变化前有沉体,变化后无沉体,由浮沉条件知F浮<G,F浮′=G,则F浮′>F浮,即V排′>V排,故液面上升.四、应用举例例1(1996年贵阳)有三个实心小球甲、乙、丙,甲球在水中悬浮,乙球在水中下沉,丙球漂浮在水面上.现将甲、乙、丙三球同时放在一只敞口的小铁盒里,然后将小铁盒漂浮在盛水的容器中(如图1所示),下列判断正确的是()A.只将小球甲从盒中取出放入水中后,容器中水面不变B.只将小球乙从盒中取出放入水中后,容器中水面下降C.只将小球丙从盒中取出放入水中后,容器中水面上升D.将甲、乙、丙三球同时放入水中后,容器中水面下降解析原来的铁盒在水中漂浮,将小球从盒中取出放入水中后,铁盒仍漂浮,甲球悬浮,乙球下沉,丙球漂浮.显然,只要不将乙球取出放入水中,就无沉体出现,容器中的水面不变;当将乙球取出放入水中时,因有沉体出现,容器中的水面下降,故答案应选A、B、D.例2(1997年北京)如图2所示,在一较大容器的水面上放一木块,木块面放一个体积为1分米3、重7.84牛的物体,此时木块漂浮.如果将物体从木块上拿下并放入水中,当木块和物体都静止时,容器中的水面将()A.上升B.下降C.不变D.无法判断解析将物体从木块上拿下后,木块仍漂浮在水面,容器中水面的变化取决于物体放入水中静止时所处的状态.因为ρ物=G物/gV物=0.8×103 千克/米3<ρ水,所以物体在水中静止呈漂浮状态,容器中水面不变.故答案应选C.例3如图3所示,在盛水的缸底有一个实心铁球,水面上漂浮着一个脸盆.若将铁球捞出放入盆中,盆仍漂浮在水面上,则缸底所受水的压强()A.变大B.变小C.不变D.无法判断解析此题虽然是液体压强大小问题,但根据液体压强公式p=ρgh知,水的密度不变,压强大小取决于水的深度,即此题实质仍是判断水面变化问题.原来水中的铁球沉底,脸盆漂浮:当将铁球捞出放入盆中后,脸盆和铁球呈漂浮状态.由“状态法”可判断缸里的水面上升,则缸底受到水的压强变大,故答案应选A.例4(1998年广东)桶里水面漂浮着一块冰,当冰溶化成水时,水面的高度与原来相比()A.上升B.下降C.不变D.三种情况都有可能解析假想冰化成的水集中为一水团,则水团应悬浮在水中.浮在水面上的冰块,溶化后变为悬浮在水中的水团,无沉体出现,则桶里的水面不变,故答案应选C.例5在上述例4中,若浮冰中间夹有小木块,则冰溶化后,桶里的水面____;若浮冰中间夹有小石块,则冰溶化后,桶里的水面____.解析若浮冰中间有小木块,当冰溶化后,变为悬浮的水团和漂浮的木块,无沉体出现,则桶里水面不变;若浮冰中间夹有小石块,当冰溶化后,变为悬浮的水团和沉底的石块,则桶里水面下降.在学习浮力时,大多学生认为不好学,尤其是在一些特殊题型的解法上有些学生感到很头疼,不知道解题的思路,就更不知道从何下手,在考试中影响了自己的成绩。
浮力专题:液面变化及其解题技巧(很全面、很详尽)

学习好资料欢迎下载液面升降问题的分析各种情况都包含,配有详图2018年2月11日对于液体中的物体由于某种变化而引起的液面升降问题的形式出现,本文介绍一种简便快捷的判断方法——“状态法”.(一)、状态法:就是对液体变化前、后的物体所处的状态进行比较来判断液面的上升、下将、不变的方法.(二)、状态法迅速判断液面升降方法:①若变化前后液体中的物体都处于漂浮、悬浮状态,而无沉体出现,则液面不变;②若液体中的物体,在变化前无沉体,而变化后有沉体出现,则液面下降;③若液体中的物体,在变化前有沉体,而变化后无沉体出现,则液面升高;说明:变化前后液体中物体的总质量保持不变;容器中液体的密度不变.(三)、证明设液体中的物体的总重为G,变化前后在液体中所受的总浮力分别为F浮、F浮′.若变化前后均无沉体出现,由浮沉条件知①F浮′=F浮=G,ρ液gV排′=ρ液gV排,则V排′=V排,液面不变.②若变化前无沉体,变化后有沉体,由浮沉条件知F浮=G,F浮′<G,则F浮′<F浮,即V排′<V排,故液面下降.③若变化前有沉体,变化后无沉体,由浮沉条件知F浮<G,F浮′=G,则F浮′>F浮,即V排′>V排,故液面上升.一、液面升降的主要类型有:类型Ⅰ:纯冰浸于液体,熔化后判断液面升降①、纯冰在纯水中熔化;②、纯冰在盐水(或其它密度比水大的液体)中熔化;③、纯冰在密度比水小的液体中熔化;类型Ⅱ:冰块中含有其它杂质,冰块熔化后判断水面升降。
①、含有木块(或其它密度比水小的固体)的冰块在纯水中熔化;②、含有石块(或其它密度比水大的固体)的冰块在纯水中熔化;③、含有煤油(或其它密度比水小的液体)的冰块在纯水中熔化;类型Ⅲ:冰块中含有一定质量的气体,冰块熔化后判断水面升降。
类型Ⅳ:容器中的固态物质投入水中后判断液面升降①、固态物质的密度小于水的密度②、固态物质的密度等于水的密度③、固态物质的密度大于水的密度二、解题关键:无论液面上升或者下降,关键在比较的问题是什么,确立好问题就知道如何下手。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
液面升降问题的分析各种情况都包含,配有详图2018年2月11日对于液体中的物体由于某种变化而引起的液面升降问题的形式出现,本文介绍一种简便快捷的判断方法——“状态法”.(一)、状态法:就是对液体变化前、后的物体所处的状态进行比较来判断液面的上升、下将、不变的方法.(二)、状态法迅速判断液面升降方法:①若变化前后液体中的物体都处于漂浮、悬浮状态,而无沉体出现,则液面不变②若液体中的物体,在变化前无沉体,而变化后有沉体出现,则液面下降③若液体中的物体,在变化前有沉体,而变化后无沉体出现,则液面升高;说明变化前后液体中物体的总质量保持不变容器中液体的密度不变.(三)、证明设液体中的物体的总重为G,变化前后在液体中所受的总浮力分别为F浮、F浮′.若变化前后均无沉体出现,由浮沉条件知①F浮′=F浮=G,ρ液gV排′=ρ液gV排,则V排′=V排,液面不变.②若变化前无沉体,变化后有沉体,由浮沉条件知F浮=G,F浮′<G,则F浮′<F浮,即V排′<V排,故液面下降.③若变化前有沉体,变化后无沉体,由浮沉条件知F浮<G,F浮′=G,则F浮′>F浮,即V排′>V排,故液面上升.一、液面升降的主要类型有:类型Ⅰ:纯冰浸于液体,熔化后判断液面升降①、纯冰在纯水中熔化;②、纯冰在盐水(或其它密度比水大的液体)中熔化;③、纯冰在密度比水小的液体中熔化;类型Ⅱ:冰块中含有其它杂质,冰块熔化后判断水面升降。
①、含有木块(或其它密度比水小的固体)的冰块在纯水中熔化;②、含有石块(或其它密度比水大的固体)的冰块在纯水中熔化;③、含有煤油(或其它密度比水小的液体)的冰块在纯水中熔化;类型Ⅲ:冰块中含有一定质量的气体,冰块熔化后判断水面升降。
类型Ⅳ:容器中的固态物质投入水中后判断液面升降①、固态物质的密度小于水的密度②、固态物质的密度等于水的密度③、固态物质的密度大于水的密度二、解题关键:无论液面上升或者下降,关键在比较的问题是什么,确立好问题就知道如何下手。
关键问题:比较冰熔化前(或物体投放前)在液体中排开液体的体积和冰熔化成水后的体积(或物体投放后液体体积)的大小关系:⑴若前体积大于后体积,液面下降;若前体积等于后体积,液面不变;⑵若前体积小于后体积,液面上升。
三、判断方法1、比较体积变化法:比较冰熔化前(或物体投放前)在液体中排开液体的体积和冰熔化成水后的体积(或物体投放后液体体积)的大小关系:⑴若前体积大于后体积,液面下降;若前体积等于后体积,液面不变;⑵若前体积小于后体积,液面上升。
2、比较压力变化法:比较前后容器底部受到压力的变化。
①F前=P前×S底=ρ液gh前S底②F后=P后×S底=ρ液gh后S底根据前后压力的大小关系得出液体前后深度的关系,再判断液面的升降情况。
3、比较浮力变化法:比较前后浮力的变化判断液面的升降。
①若F前浮>F后浮,则液面下降;②若F前浮<F后浮,则液面上升;③若F前浮=F后浮,则液面不变。
四、各类型问题的分析解答类型一:1、纯冰在纯水中熔化——液面高度不变例1:有一块冰浮在容器的水面上,当冰块完全熔化后,水面高度将怎样变化?结论:纯冰浮在水面上.当冰熔化后液面将不变。
解析:这是一道最典型最基础的题型,我们理解后,可作为其它类型题解决的知识点直接分析。
液面升降取决于冰融化后这部分水的体积与冰漂浮时排开水的体积变化,所以方法Ⅰ比较体积变化法⒈当冰漂浮时,依漂浮条件可知,F浮=G冰即ρ水ɡV排= G冰= m冰g ∴V排=m冰/ρ水⒉冰化成水后,冰的质量与水的质量没有变化即m化水= m冰∴V化水=m冰/ρ水⒊所以V排=V化水即冰块完全熔化后水面高度不变。
方法Ⅱ变化前后总压力不变※冰熔化前后,冰与水总重量没有变化,所以熔化前后对容器底部的压力没有变化F前=F后即ρ前S器底=P后S器底ρ水ɡh前S器底=ρ水ɡh后S器底∴h前=h后即液面不变。
方法Ⅲ比较浮力变化法※浮力F浮= ρ液•g•V排,对于液体密度ρ液不变情况,浮力大小取决于物体排开液体的体积V排,而V排的大小就决定了液面的高度。
这样,对这类问题只须比较前后两种情况下物体所受浮力的大小,①如果浮力变小,即F前浮>F后浮,则物体排开液体的体积变小,液面下降。
②如果浮力不变则液面高度不变,③如果浮力变大则液面上升。
对这道题:熔化前冰漂浮F前浮= G物熔化后,冰化为水属于悬浮状态,则:F后浮= G物所以F 前浮= F后浮,液面高度不变。
比较上述三种解法可见,第二、三种解法简单易懂,学生容易掌握,适应于课堂教学。
我们在物理教学中还可以将这种方法推广到其它情况下液面升降问题的讨论中去,培养学生思维能力,做到举一反三。
结论:纯冰浮在水面上.当冰熔化后液面将不变。
例2:若一冰块在水中,冰块与容器底部相接触并相互间有压力,则当冰块完全熔化后,容器内的水面将怎样变化?解析:冰块没有漂浮在水面上,冰块所受浮力小于冰块所受重力,∴熔化前F浮<G冰,即ρ水g V排<G冰,故得V排<m冰/ρ水熔化为水的体积 V化水=m水/ρ水= m冰/ρ水∴V排<V化水,即熔化后水面要上升。
结论:纯冰压在水底.当冰熔化后液面将上升。
类型一:2、纯冰在盐水(或其它密度比水大的液体)中熔化——液面高度上升例3:有一块冰漂浮在一杯浓盐水中(冰的密度是0.9×103千克/米3;浓盐水的密度是1.1×103千克/米3).如果冰块全部熔化后,则 ( )A.液面不变 B.液面上升 C.液面下降 D.无法判断解析:冰块熔化前,在盐水中处于漂浮状态.则有F浮=G冰,即ρ盐水g V排=m冰g ∴V排=m冰/ρ盐水化成水后,冰的质量与水的质量没有变化即m化水= m冰∴V化水=m冰/ρ水∵ρ水<ρ盐水。
∴V化水>V排,冰块在浓盐水中熔化后液面上升.结论:纯冰浮在密度比水大的液面上.当冰熔化后液面将上升。
类型一:3、纯冰在密度比水小的液体中熔化——液面高度下降例4:有一块冰漂浮在一杯酒精(或煤油等)中,当冰块完全熔化后,液面高度将怎样变化?解析:冰块熔化前,在酒精中处于漂浮状态.则有F浮=G冰,即ρ酒g V排=m冰g ∴V排=m冰/ρ酒化成水后,冰的质量与水的质量没有变化即m化水= m冰∴V化水=m冰/ρ水∵ρ酒<ρ水。
∴V化水<V排,冰块在浓盐水中熔化后液面下降.结论:纯冰浮在密度比水小的液面上.当冰熔化后液面将下降。
类型二:1、含有木块(或其它密度比水小的固体)的冰块在纯水中熔化;例5:在盛水的烧杯中漂浮着一块冰,冰中夹着一小木块,当冰完全熔化为水时,水面将如何变化?方法一比较体积变化法①冰块漂浮时:F浮=G冰+G木即ρ水gV排= G冰+G木,V前排= (m冰+m木)/ ρ水=m冰/ρ水+m木/ρ水 (1)②当冰块化成水时:m化水= m冰∴V化水=m冰/ρ水又因为木块仍漂浮,F木浮= G木即ρ水gV木排= m木g ∴V木排=m木/ρ水V后排=V化水+V木排= m冰/ρ水+ m木/ρ水 (2)由(1) .(2)得:V前排= V后排故当冰完全熔化成水时,水面不变。
方法二比较浮力变化法熔化前冰块和木块都漂浮∴F前浮= G冰+ G木熔化后熔化成的水悬浮,木块仍漂浮∴F后浮= G化水+ G木又G化水= G冰所以F前浮=F后浮,即熔化前后所受浮力不变,所以液面将不变。
推论:当冰块中含有密度比水小的固体(如小蜡块)或将密度比水小的固体放在冰块上浮于容器内水面上,则冰熔化后,仿照上述方法推算可知,水面将保持不变。
类型二:2、含有石块(或其它密度比水大的固体)的冰块在纯水中熔化;例6.:有一块冰中含有小石块,浮在容器的水面上,当冰块完全熔化后,水面高度怎样变化?解:方法一比较体积变化法①冰块熔化前排开水的体积为:V排=F浮/ρ水g=G总/ρ水g=(G冰+G石)/ρ水g=(m冰+m水)/ρ水①②熔化后的体积为冰化成的水的体积加上沉在容器底的石块的体积,即:V后=V水+V石=m水/ρ水+m石/ρ石=m冰/ρ水+m石/ρ石②比较①②式,∵ρ石>ρ水,∴V后<V排所以液面下降。
方法二比较浮力变化法①熔化前冰块和含有的小石块漂浮∴F前浮 = G冰 + G石②熔化后熔化成的水悬浮,F化水浮=G化水;而石块沉底,F石浮<G石∴F后浮 = F化水浮+F石浮=G化水 + F石浮,又G化水= G冰所以F前浮>F后浮,即熔化后所受浮力减小,所以液面将下降。
推论:当冰块中含有密度比水大的物体(如小铁块、盐水等)或将密度比水大的物体放在冰块上浮于容器内水面上,则冰熔化后,物体沉入水底,水面将下降。
类型二:3、含有煤油(或其它密度比水小的液体)的冰块在纯水中熔化;例7:有一块冰中含有液态的煤油,浮在容器内的水面上,当冰块完全熔化后,液面高度将怎样变化?①冰块熔化前排开水的体积为:V排=F浮/ρ水g=G总/ρ水g=(G冰+G油)/ρ水g=(m冰+m油)/ρ水①②熔化后的体积为冰化成的水的体积加上煤油的体积,即:V=V水+V油=m水/ρ水+m油/ρ油=m冰/ρ水+m油/ρ油②比较①②式,∵ρ油<ρ水,∴V>V排所以液面上升。
类型三:冰块中含有一定质量的气体,冰块熔化后判断水面升降。
例8:一块冰漂浮在容器的水面上,冰块中含有一定质量的气体(空气、氢气、二氧化碳),当冰完全熔化后,容器中的水面如何变化?①冰块熔化前排开水的体积为:V排=F浮/ρ水g=G总/ρ水g=(G冰+G气体)/ρ水g=(m冰+m气体)/ρ水①㈡熔化后的体积为冰化成的水的体积等于冰排开水的体积,但气体挥发,总体积减少,V排′<V排,所以液面下降。
变化:若漂浮在水面上的冰块中有一气泡,当冰块融化后水面将怎么变化?冰块里的气泡的质量可以忽略不计,冰熔化后水面保持不变.类型四:1、固态物质的密度小于水的密度例9:盆内水面上有一塑料碗,碗内有木块,若将木块投入水中,盆内水面将(填“上升”、“下降”或“保持不变”)。
解析:①投入前,碗与木块漂浮在水面上,所以F浮=G碗+G木据阿基米德原理,得F浮=G排=ρ水gV排所以ρ水gV排=G碗+G球,故得V排=G碗/ρ水g+G木/ρ水g ⑴②木块投入水中后,盆漂浮在水面上,分析得V盆排=G盆/ρ水g木块漂浮在水面上,则V木排=G木/ρ水g因此,后来碗与木块排开水的总体积V总排=V盆排+V木排=G盆/ρ水g +G木/ρ水g ⑵由⑴⑵得V总排=V排,所以液面保持不变。
类型四:2、固态物质的密度等于水的密度当ρ物=ρ水时,物体悬浮。
物体投入水中后物体排开水的体积为:V物排=m物/ρ物= m物/ ρ水=⊿V排,即水面高度无变化。
类型四:3、固态物质的密度大于水的密度例10:盆内水面上有一塑料碗,碗内是实心铁块,将铁块投入水中,盆内水面将(填“上升”、“下降”或“保持不变”)。
