2017年10月十七中高三月考试卷及答案
湖北省江汉2017届高三上学期10月月考试题数学文Word版含答案

湖北省江汉平原高级中学2017届高三年级上学期10月月考数学(文科)试题★祝考试顺利★时间:120分钟 分值150分_第I 卷(选择题共60分)一、选择题(本大题12小题,每小题5分,共60分)1.若函数)1,0(),1(log )(≠>+=a a x x f a 且的定义域和值域都是[0,1],则a=( )A.21B. 2C.22 D. 22.已知{}(,)1,1x y x y Ω=≤≤,A 是由曲线y x =与2y x =围成的封闭区域,若向Ω上随机投一点p ,则点p 落入区域A 的概率为( ) A.16 B. 18 C. 112 D.1243.某人从甲地去乙地共走了500m ,途经一条宽为x m 的河流,该人不小心把一件物品丢在途中,若物品掉在河里就找不到,物品不掉在河里,则能找到,已知该物品能被找到的概率为45,则河宽为( )80m B.100m C.40m D.50m4.设1,0()2,0xx x f x x ⎧≥⎪=⎨<⎪⎩,则((2))f f -=( ) A .1- B .14 C .12 D .325.函数2211()31x x f x x x x ⎧-⎪=⎨-->⎪⎩,,,,≤则))2((f f 的值为A .-1B .-3C .0D .-86.已知函数()f x 是定义在R 上的奇函数,它的图象关于直线1x =对称,且()(01)f x x x =<≤,则当(5,7]x ∈时,()y f x =的解析式是( )A .()2f x x =-B .()4f x x =-C .()6f x x =-D .()8f x x =- 7.已知f(x)=14x 2+sin(2π+x),f′(x)为f(x)的导函数,则f′(x)的图象是( )8.函数2()34lg(1)f x x x x=-+++-的定义域是()A.[-1,4] B.(]1,4-C.[1,4] D.(]1,49.函数2()lg2xf xx-=+的定义域为()A.(),2(2,)-∞-+∞B.(,2)-∞C.(2,2)- D.()2,-+∞10.某几何体三视图如图所示,则该几何体的体积为()A.82π- B.8π- C.82π- D.84π-11.一个直棱柱的对角线长是9 cm和15 cm,高是5 cm,若它的底面是菱形,则这个直棱柱的侧面积是( )A.160 cm2B.320 cm2C.cm2 D. cm212.如图,是CCTV 青年歌手大奖赛上某位选手得分的茎叶图,去掉一个最高分和一个最低分后,所剩数据的方差为 A .647B .9C .738D .780第II 卷(非选择题)二、填空题(本大题共4个小题,每题5分,满分20分) 13.若函数()11x mf x a =+-是奇函数,则m 为__________。
陕西省西安市2017届高三10月月考数学文试题Word版含答案

2016—2017学年第一学期9月月考数学文科试题(2016.10. 04)分值150分 考试时间120分钟一 选择题(共十二个小题,每小题5分,每小题只有一个正确答案)1 .已知集合P ={y =x 2+1}, Q ={y|y =x 2+1,x ∈R},S ={x|y =x 2+1,x∈ R},T ={(x , y)|y =x 2+1,x ∈R},M ={x|x ≥1},则( )A .P =MB .Q =SC .S =TD .Q =M2.已知集合A =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x -2x≤0,x ∈N ,B ={x|x ≤2,x ∈Z},则满足条件A ⊆C ⊆B 的集合C 的个数为( ) A .1 B .2 C .4 D .83 给定两个命题p ,q ,若⌝p 是q 的必要而不充分条件, 则p 是⌝q 的A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件4. 设命题p :函数y =sin 2x 的最小正周期为π2;命题q :函数y =cos x的图象关于直线x =π2对称.则下列判断正确的是( )A .p 为真B .q 为真C .p ∧q 为假D .p ∨q 为真 5.函数f(x)=1-2x +1x +3的定义域为( ) A .(-3,0] B .(-3,1]C .(-∞,-3)∪(-3,0]D .(-∞,-3)∪(-3,1]6.已知函数f (x )为R 上的减函数,则满足f ⎝ ⎛⎭⎪⎫⎪⎪⎪⎪⎪⎪1x <f (1)的实数x 的取值范围 是( )A .(-1,1)B .(0,1)C .(-1,0)∪(0,1)D .(-∞,-1)∪(1,+∞) 7.如右图,已知正四棱锥S -ABCD 所有棱长都为1,点E 是侧棱SC 上一动点,过点E 垂直于SC 的截面将正四棱锥分成上、下两部分.记SE =x (0<x <1),截面下面部分的体积为V (x ),则函数y =V (x )的图象大致为 ( ).8、点P 在曲线y =x 3-x +23上移动,设点P 处切线的倾斜角为α,则角α的取值范围是( )A.⎣⎢⎡⎦⎥⎤0,π2B.⎣⎢⎡⎭⎪⎫0,π2∪⎣⎢⎡⎭⎪⎫3π4,π C.⎣⎢⎡⎭⎪⎫3π4,π D.⎝ ⎛⎦⎥⎤π2,3π49 已知函数若a 、b 、c 互不相等,且f(a) =f(b)=f(c), 则abc 的取值范围是( )(A)(1,10) (B)(5,6) (C)(10,12) (D)(20,24)10.函数f (x )=⎩⎪⎨⎪⎧-x +3a , x <0,a x, x ≥0,(a >0且a ≠1)是R 上的减函数,则a 的取值范围是( )A .(0,1)B .[13,1)C .(0,13]D .(0,23]11、4cos 50°-tan 40°=( )A. 2B.2+32C. 3 D .22-1 12.给出下列结论:①当a <0时,(a 2) 32 =a 3; ②n a n =|a |(n >1,n ∈N +,n 为偶数);③函数f (x )=(x -2)12 -(3x -7)0的定义域是{x |x ≥2且x ≠73}; ④若2x=16,3y=127,则x +y =7. 其中正确的是( )A .①②B .②③C .③④D .②④二 填空题(每小题题5分,共20分) 13.|1+lg 0.001|+ lg 213-4lg 3+4+lg 6-lg 0.02的值为______.14, 已知函数f (x )=⎩⎪⎨⎪⎧|x 2+5x +4|,x ≤0,2|x -2|,x >0.若函数y =f (x )-a |x |恰有4个零点,则实数a 的取值范围为_______.15. 设集合A ={ (x ,y)|(x -4)2+y 2=1},B ={(x ,y)|(x -t)2+(y -at+2)2=1},如果命题“∃t ∈R ,A ∩B ≠∅”是真命题,则实数a 的取值范围是______.16. 若函数f (x )(x ∈R)是周期为4的奇函数,且在[0,2]上的解析式为f (x )= ⎩⎪⎨⎪⎧x (1-x ),0≤x ≤1,sin πx ,1<x ≤2,则f ⎝ ⎛⎭⎪⎫294+f ⎝ ⎛⎭⎪⎫416=______.三 解答题(17题10分,18到22每小题12分)17.设集合A ={x|-1≤x ≤2},B ={x|x 2-(2m +1)x +2m<0}.(1)当m<12时,化简集合B ;(2)若A ∪B =A ,求实数m 的取值范围.18 已知命题p :方程2x 2+ax -a 2=0在[-1,1]上有解;命题q :只有一个实数x 0满足不等式x 202+2ax 0+2a ≤0,若命题“p ∨q ”是假命题,求a的取值范围.19. 已知函数f(x)=(2cos 2x -1)sin 2x +12cos 4x.(1)求f(x)的最小正周期及最大值;(2)若α∈⎝ ⎛⎭⎪⎫π2,π,且f(α)=22,求α的值.20 设二次函数f (x )=ax 2+bx +c (a ≠0)在区间[-2,2]上的最大值、最小值分别是M ,m ,集合A ={x |f (x )=x }.(1)若A ={1,2},且f (0)=2,求M 和m 的值;(2)若A ={1},且a ≥1,记g (a )=M +m ,求g (a )的最小值. 21.已知函数f (x )=e x +e -x ,其中e 是自然对数的底数.(1)证明:f (x )是R 上的偶函数.(2)若关于x 的不等式mf (x )≤e -x +m -1在(0,+∞)上恒成立,求实数m 的取值范围.(3)已知正数a 满足:存在x 0∈[1,+∞),使得f (x 0)<a (-x 30+3x 0)成立.试比较e a -1与a e -1的大小,并证明你的结论.22、已知函数f (x )=ax sin x +cos x ,且f (x )在x =π4处的切线斜率为2π8.(1)求a 的值,并讨论f (x )在[-π,π]上的单调性; (2)设函数g (x )=ln(mx +1)+1-x1+x ,x ≥0,其中m >0,若对任意的x 1∈[0,+∞)总存在x 2∈[0,π2],使得g (x 1)≥f (x 2)成立,求m 的取值范围.2016—2017学年第一学期9月月考数学文科试题(2016.10.04)分值150分 考试时间120分钟一 选择题(共十二个小题,每小题5分,每小题只有一个正确答案)二 填空题(每小题题5分,共20分) 13.____6____. 14, ___(1,2)_____. 15 __[0,4/3]______. 16 ___5/16___.三 解答题(17题10分,其余小题12分)17.设集合A ={x|-1≤x ≤2},B ={x|x 2-(2m +1)x +2m<0}.(1)当m<12时,化简集合B ;(2)若A ∪B =A ,求实数m 的取值范围.题号12 3 4 5 6 7 8 9 10 11 12 答案 DDACACABCBCB18. 已知命题p :方程2x 2+ax -a 2=0在[-1,1]上有解;命题q :只有一个实数x 0满足不等式x 202+2ax 0+2a ≤0,若命题“p ∨q ”是假命题,求a的取值范围.19. 已知函数f(x)=(2cos 2x -1)sin 2x +12cos 4x.(1)求f(x)的最小正周期及最大值;(2)若α∈⎝ ⎛⎭⎪⎫π2,π,且f(α)=22,求α的值.20. 设二次函数f (x )=ax 2+bx +c (a ≠0)在区间[-2,2]上的最大值、最小值分别是M ,m ,集合A ={x |f (x )=x }.(1)若A ={1,2},且f (0)=2,求M 和m 的值;(2)若A ={1},且a ≥1,记g (a )=M +m ,求g (a )的最小值.21.已知函数f(x)=e x+e-x,其中e是自然对数的底数.(1)证明:f(x)是R上的偶函数.(2)若关于x的不等式mf(x)≤e-x+m-1在(0,+∞)上恒成立,求实数m的取值范围.(3)已知正数a满足:存在x0∈[1,+∞),使得f(x0)<a(-x30+3x0)成立.试比较e a-1与a e-1的大小,并证明你的结论.22、已知函数f (x )=ax sin x +cos x ,且f (x )在x =π4处的切线斜率为2π8. (1)求a 的值,并讨论f (x )在[-π,π]上的单调性;(2)设函数g (x )=ln(mx +1)+1-x 1+x,x ≥0,其中m >0,若对任意的x 1∈[0,+∞)总存在x 2∈[0,π2],使得g (x 1)≥f (x 2)成立,求m 的取值范围.。
莆田十七中2017届高三上学期第一次月考数学试卷(文科) 含解析

2016—2017学年福建省莆田十七中高三(上)第一次月考数学试卷(文科)一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.设函数y=的定义域为M,集合N={y|y=x2,x∈R},则M∩N=()A.∅B.N C.[1,+∞)D.M2.函数y=的定义域为()A.(,1) B.(,∞) C.(1,+∞)D.(,1)∪(1,+∞)3.设x∈R,则“|x﹣2|<1"是“x2+x﹣2>0”的()A.充分而不必要条件 B.必要而不充分条件C.充要条件 D.既不充分也不必要条件4.函数f(x)=lnx﹣的零点所在的大致区间是()A.(1,2)B.(2,3) C.(1,)D.(e,+∞)5.下列函数中,既是奇函数又在区间(0,+∞)上单调递增的函数为()A.y=x﹣1B.y=lnx C.y=x3D.y=|x|6.函数f(x﹣)=x2+,则f(3)=()A.8 B.9 C.11 D.107.已知f(x)是R上的偶函数,且在(﹣∞,0)上是增函数,设,b=f(log43),c=f(0.4﹣1。
2)则a,b,c的大小关系为()A.a<c<b B.b<a<c C.c<a<b D.c<b<a8.已知lga+lgb=0,函数f(x)=a x与函数g(x)=﹣log b x的图象可能是()A. B. C. D.9.已知函数f(x)=a x﹣1+log a x在区间[1,2]上的最大值和最小值之和为a,则实数a为()A.B.C.2 D.410.已知函数f(x)满足f(x)=f(π﹣x),且当x∈(﹣,)时,f(x)=e x+sinx,则()A.B.C.D.11.己知y=f(x)是定义在R上的奇函数,当x<0时,f(x)=x+2,那么不等式2f(x)﹣1<0的解集是()A.B.或C. D.或12.设偶函数f(x)在(0,+∞)上为减函数,且f(2)=0,则不等式>0的解集为()A.(﹣2,0)∪(2,+∞)B.(﹣∞,﹣2)∪(0,2) C.(﹣∞,﹣2)∪(2,+∞)D.(﹣2,0)∪(0,2)二、填空题:(本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置) 13.函数f(x)=log(x2﹣2x﹣3)的单调递增区间为.14.已知f(x)=,则f(﹣)+f()等于.15.当a>0,a≠1时,函数f(x)=log a(x﹣1)+1的图象恒过定点A,若点A在直线mx﹣y+n=0上,则4m+2n的最小值是.16.定义在(﹣∞,+∞)上的偶函数f(x)满足f(x+1)=﹣f(x),且f(x)在[﹣1,0]上是增函数,下面五个关于f(x)的命题中:①f(x)是周期函数;②f(x)的图象关于x=1对称;③f(x)在[0,1]上是增函数;④f(x)在[1,2]上为减函数;⑤f(2)=f(0).正确命题的个数是.三、解答题:(共6小题,70分,须写出必要的解答过程)17.已知函数f(x)=的定义域为A,集合B是不等式x2﹣(2a+1)x+a2+a>0的解集.(Ⅰ)求A,B;(Ⅱ)若A∪B=B,求实数a的取值范围.18.已知p:x∈A={x|x2﹣2x﹣3≤0,x∈R},q:x∈B={x|x2﹣2mx+m2﹣4≤0,x∈R,m ∈R}(1)若A∩B=[0,3],求实数m的值;(2)若p是¬q的充分条件,求实数m的取值范围.19.命题p:关于x的不等式x2+2ax+4>0对一切x∈R恒成立,q:函数f(x)=(3﹣2a)x是增函数.若p∨q为真,p∧q为假.求实数a的取值范围.20.已知函数f(x)=(log2x﹣2)(log4x﹣)(1)当x∈[2,4]时,求该函数的值域;(2)若f(x)>mlog2x对于x∈[4,16]恒成立,求m的取值范围.21.已知f(x)是定义在[﹣1,1]上的奇函数,f(1)=1,且若∀a、b∈[﹣1,1],a+b≠0,恒有>0,(1)证明:函数f(x)在[﹣1,1]上是增函数;(2)解不等式;(3)若对∀x∈[﹣1,1]及∀a∈[﹣1,1],不等式f(x)≤m2﹣2am+1恒成立,求实数m 的取值范围.22.定义在R上的增函数y=f(x)对任意x,y∈R都有f(x+y)=f(x)+f(y),则(1)求f(0);(2)证明:f(x)为奇函数;(3)若f(k•3x)+f(3x﹣9x﹣2)<0对任意x∈R恒成立,求实数k的取值范围.2016-2017学年福建省莆田十七中高三(上)第一次月考数学试卷(文科)参考答案与试题解析一、选择题(本大题共12小题,每小题5分,满分60分。
2017届高三第三次月考试题 数学理(含答案)word版

南昌一中2017届高三第三次月考数学试题(理)时间:8:00-10:00 总分:150分一、选择题:(本大题共10小题,每小题5分,共50分。
在各题所给出的四个选项中,有且只有一个是正确的) 1.对于函数()cos f x x x =+,下列命题中正确的是( )A .,()2x R f x ∀∈=B .,()2x R f x ∃∈=C .,()2x R f x ∀∈>D .,()2x R f x ∃∈>2.设,l m 是两条不同的直线,α是一个平面,则下列命题正确的是( )A .若,,m l l m αα⊥⊂⊥则B .若//,,//m l m l αα⊂则C .若//,,l m l m αα⊥⊥则D .若,,//l m m l αα⊥⊥则3.在等差数列{}n a 中,若23102π=+a a ,则)32sin(6π-a =( )A .23B .21C .23-D .21-4.已知向量(2,1)=--a ,10⋅=a b,||-a b ||=b ( )A.B.C .20D .40 5.函数()sin()(0)3f x x πωω=+>的最小正周期为π,则该函数图象( )A .关于直线4x π=对称 B .关于直线3x π=对称C .关于点(,0)4π对称D .关于点(,0)3π对称6.△ABC 的外接圆的圆心为O ,半径为1,20OA AB AC ++= 且OA AB =,则向量CA 在CB 方向上的投影为( )A .21B.2C .32D.2-7.使函数()sin(2))f x x x θθ=++()x R ∈是奇函数,且在[0,]4π上是减函数的θ的一个值是( )A .3πB .23π C .43πD .53π 8.一个几何体的三视图及长度数据如图, 则该几何体的表面积与体积分别为 ( ) A.7 B.8C.372 D.382+ 9.已知数列{a n }和{b n } 满足11=a ,且n a ,1+n a 是函数n n x b x x f 2)(2+-=的两个零点,则=10b ( )A .24B .32C .48D .6410.等差数列{}n a 的前n项和为n S ,已知32011s i n )1(2011)1232π=-+-a a (,62011cos)1(2011)1201032010π=-+-a a (,则2011S =( )A .0B .2011C .4022D .32011二、填空题(本大题共5小题,每小题5分,共25分.将答案填在题后的横线上.)11.已知)3,1(=a ,)6,2(--=b ,10||=c ,若5)(=⋅+c b a ,则a 与c 的夹角为_______ 12.在等比数列{}n a 中,m n a 2=,n m a 2=)(n m ≠,则n m a +=________13.棱长为1的正方体1111D C B A ABCD -的8个顶点都在球O 的表面上,E 、F 分别是棱1AA 、1DD 的中点,则直线EF 被球O 截得的线段长为_________14.设)6s in ,6(co s ππn n a n =,*N n ∈,)3,1(=,则 ++++=2221||||a a y 210||a ++的值为_________15.已知函数x x x 23)(f 2-=,数列{}n a 的前n 项和为n S ,点),(n S n (*N n ∈)均在函数f (x )的图象上,13+=n n n a a b , n T 是数列{}n b 的前n 项和,则使得20n m T <对所有n N *∈都成立的最小正整数m =_______三、解答题:(本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.) 16.(本小题满分12分)数列{}n a 的前n 项和记为n S ,()111,211n n a a S n +==+≥ (1)求{}n a 的通项公式;(2)等差数列{b n }的各项为正,其前n 项和为n T ,且153=T ,又112233,,a b a b a b +++成等比数列,求n T .17.(本小题满分12分)已知向量m ,1)4x =,n 2(cos ,cos )44x x=,函数()f x =m ·n . (1)若()1f x =,求2cos()3x π-的值; (2)在△ABC 中,角A ,B ,C 的对边分别是,,a b c ,且满足1cos 2a C cb +=,求()f B 的取值范围.18.(本小题满分12分)如图,在长方体ABCD —A 1B 1C 1D 1,中,AD=AA 1=1,AB=2,点E 在棱AB 上移动. (1)当E 为AB 的中点时,求点E 到面ACD 1的距离; (2)AE 等于何值时,二面角D 1—EC —D 的大小为4π. 19.(本小题满分12分)已知向量33(cos ,sin )22x x a = ,(cos ,sin )22x x b =- ,且[,]2x ππ∈.(1)求a b ⋅ 及a b +;(2)若函数||2)(x f ++⋅=λ的最小值为23-,求λ的值.1A C20.(本小题满分13分)已知数列{}n a 满足1*115,32()n n n a a a n N ++==+∈;(1)证明:数列1{2}n n a ++是等比数列,并求出数列{}n a 的通项公式; (2)若121,3n n nn b a ++=-求数列{}n b 的前n 项和为n S ; (3)令1nn n a c a +=,数列{}n c 的前n 项和为n T ,求证:3493n n n T -<<.21.(本小题满分14分)已知函数2()ln f x x x =+.(1)若函数()()g x f x ax =-在定义域内为增函数,求实数a 的取值范围;(2)在(1)的条件下,若1a >,3()3x x h x e ae =-,[0,ln 2]x ∈,求()h x 的极小值;(3)设2()2()3()F x f x x kx k R =--∈,若函数()F x 存在两个零点,(0)m n m n <<,且满足02x m n =+,问:函数()F x 在00(,())x F x 处的切线能否平行于x 轴?若能,求出该切线方程,若不能,请说明理由.参考答案一、选择题(本大题共10小题,每小题5分,共50分。
【月考试卷】四川省成都市2017届高三10月月考数学(文)试题 Word版含答案

高2014级第五期10月阶段性考试数学试题(文)一. 选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知全集U =Z ,集合{}1,6A =,{}2,0,1,6A B = ,那么=⋂B A C U )(( ) A .∅ B .{}3,4,5 C .{}2,0 D .{}1,62. 复数iiZ 212+-=(i 为虚数单位)所对应复平面内的点在( ) A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 3. 已知b a ,是平面α内的两条不同直线,直线l 在平面α外,则b l a l ⊥⊥,是α⊥l 的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件 D . 既不充分也不必要条件4.若[x]表示不超过x 的最大整数,如[2.6]2,[ 2.6]3=-=-,执行如图所示的程序框图,记输出的值为0S ,则103log S =( )A. -1B. 0C. 1D. 25. 函数)2)(2sin(3)(πϕϕ<+=x x f 的图像向左平移6π个单位后关于原点对称, 则ϕ等于( )A.6π B. 6π- C.3π D.3π- 6. 若等差数列{}n a 的公差0d ≠, 前n 项和为n S , 若*n N ∀∈, 都有10n S S ≤, 则( ) A. *n N ∀∈,1n n a a -< B. 9100a a ⋅> C. 217S S > D. 190S ≥ 7.函数1x y e--=的图象大致形状是( )8. 已知点P 在直线320x y +-=上, 点Q 在直线360x y ++=上, 线段PQ 的中点为00(,)M x y , 且002y x <+, 则y x 的取值范围是( ) A.1[,0)3- B. 1(,0)3- C. 1(,)3-+∞ D. 1(,)(0,)3-∞-+∞ 9. 已知某几何体的三视图如图所示, 三视图是边长为1的等腰直角三角形和 边长为1的正方形, 则该几何体的体积为( )A.16 B. 13 C. 12 D. 2310. 已知函数||1211()()21log (1)x f x x =-++, 则使得()(21)f x f x >-成立的x 的取值范围是( )A. 1(,1)3B. 1(,)(1,)3-∞+∞ C. 1(,1)3-1(0,)(1,)3+∞D. ()1,11,(1,)3⎛⎫-∞--+∞ ⎪⎝⎭11. 设12,e e 分别为具有公共焦点12,F F 的椭圆和双曲线的离心率, P 是椭圆和双曲线的一个公共点, 且满足1212||||PF PF F F +=,=( )A.B. 2C. D. 112.在锐角ABC ∆中, ,,A B C 所对边分别为,,a b c , 且22b a ac -=, 则11tan tan A B-的取值范围为( ) A. (1,)+∞B.C.D. 正视侧视俯视二. 填空题(每小题5分,共20分)13. 若sin 2x =-cos 2x = . 14. 已知正数y x ,满足0=-+xy y x ,则y x 23+的最小值为 .15.过直线y x =上的一点作圆22(5)(1)2x y -+-=的两条切线12l l ,, 当直线12l l ,关于y x =对称时,它们之间的夹角为__________.16. 已知函数2()244f x x tx t =---, 21()(2)g x t x=-+, 两个函数图象的公切线恰为3条, 则实数t 的取值范围为 .三. 解答题(共70分)17. (12分)已知数列{}n a 的前n 项和n S 满足,132-=n n a S 其中*∈N n(1)求数列{}n a 的通项公式;(2)设,32nn b a nn n +=求数列{}n b 的前n 项的和n T 。
【月考试卷】山东省2017届高三实验班10月月考数学理试题 Word版含答案

数学(理A )试题一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项 是符合题目要求的.1.设集合2|11A x x ⎧⎫=≥⎨⎬+⎩⎭,集合{}|2,0x B y y x ==<,则A B = ( ) A .(]1,1- B .[]1,1- C .(],1-∞ D .[)1,-+∞ 2.已知a b >,则下列不等式中恒成立的是( ) A .ln ln a b > B .11a b< C .2a ab > D .222a b ab +> 3. ,,m n l 为不重合的直线,,,αβγ为不重合的平面,则下列说法正确的是( ) A .,m l n l ⊥⊥,则//m n B . ,αγβγ⊥⊥,则αβ⊥ C .//,//m n αα,则//m n D .//,//αγβγ,则//αβ 4.在复平面内,复数()212z i =+对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限5.三棱锥的三视图中俯视图是等腰直角三角形,三棱锥的外接球的体积记为1V ,俯视图绕斜边所在直线旋转一周形成的几何体的体积记为2V ,则12V V =( )A. B. C .12 D.6.已知点(),M a b 在由不等式组002x y x y ≥⎧⎪≥⎨⎪+≤⎩确定的平面区域内,则点(),N a b a b +-所在平面区域的面积是( ) A .1 B .2 C .4 D .87.已知A B P 、、是双曲线22221x y a b -=上的不同三点,且A B 、关于坐标原点对称,若直线PA PB 、的斜率乘积23PA PB k k =,则该双曲线的离心率等于( ) ABCD8.如图,在棱长为1的正方体1111ABCD A BC D -中,点,E F 分别是棱1,BC CC 的中点,P 是椭圆11BCC B 内一点,若1//A P 平面AEF ,则线段1A P 长度的取值范围是( )A.⎡⎢⎣⎦ B.⎣ C.⎣⎦ D. 9.如图,12F F 、是双曲线()222210,0x y a b a b-=>>的左、右焦点,过1F 的直线l 与双曲线的左右两支分别交于点A B 、. 若2ABF ∆为等边三角形,则双曲线的离心率为( )A .4BC .3D 10.设函数()f x '是函数()()f x x R ∈的导函数,()01f =,且()()33f x f x '=-,则()()4f x f x '>的解集为( )A .ln 4,3⎛⎫+∞⎪⎝⎭ B .ln 2,3⎛⎫+∞ ⎪⎝⎭ C .⎫+∞⎪⎪⎝⎭ D .⎫+∞⎪⎪⎝⎭二、填空题(本大题共5个小题,每小题5分,满分25分,将答案填在答题纸上)11.过抛物线()220y px p =>的焦点F 作直线l ,交抛物线于,A B 两点,交其准线于C 点,若3CB BF =,则直线l 的斜率为___________.12.已知F 是双曲线221412x y -=的左焦点,()1,4,A P 是双曲线右支上的动点PF PA +的最小值为___________.13.若函数()222f x x x a =++与()1g x x x a =-++有相同的最小值,则不等式()5g x ≥的解集为__________.14.半径为R 的球O 中有一内接圆柱,当圆柱的侧面积最大时,圆柱的侧面积与球的表面积之比是____________.15.设1,1a b >>,若2ab e =,则ln 2aS b e =-的最大值为___________.三、解答题 (本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.)16.(本题满分12分)已知命题:p 函数()()2lg 6f x ax x a =-+的定义域为R ,命题:q 关于x 的方程223210x ax a -++=的两个实根均大于3,若“p 或q ”为真,“p 且q ”为假,求实数a的取值范围. 17.(本题满分12分)如图,在梯形ABCD 中,0//,1,60AB CD AD DC CB ABC ===∠=,四边形ACFE 为矩形,平面ACFE ⊥平面ABCD ,1CF =. (1)求证:BC ⊥平面ACFE ;(2)点M 在线段EF 上运动,设平面MAB 与平面FCB 所成二面角的平面角为()090θθ≤,试求cos θ的取值范围.18.(本题满分12分)等差数列{}n a 中,13a =,其前n 项和为n S ,等比数列{}n b 中各项均为正数,11b =,且2212b S +=,数列{}n b 的公比22S q b =. (1)求数列{}n a 与{}n b 的通项公式; (2)证明:121111233n S S S ≤+++< . 19.(本题满分12分)首届世界低碳经济大会在南昌召开,本届大会以“节能减排,绿色生态”为主题,某单位在国家科研部门的支持下,进行技术攻关,采用了新式艺,把二氧化碳转化为一种可利用的化工产品,已知该单位每月的处理量最少为300吨,最多为600吨,月处理成本y (元)与月处理量x (吨)之间的函数关系可近似地表示为21200450002y x x =-+,且每处理一吨二氧化碳得到可利用的化工产品价值为200元.(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则需要国家至少补贴多少元才能使该单位不亏损? 20.(本题满分13分)已知动圆P 与圆()221:381F x y ++=相切,且与圆()222:31F x y -+=相内切,记圆心P的轨迹为曲线C ;设Q 为曲线C 上的一个不在x 轴上的动点,O 为坐标原点,过点2F 作OQ的平行线交曲线C 于,M N 两个不同的点. (1)求曲线C 的方程;(2)试探究MN 和2OQ 的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;(3)记2QF M ∆的面积为1S ,2OF N ∆的面积为2S ,令12S S S =+,求S 的最大值. 21.(本题满分14分) 已知函数()()()21212ln 2f x ax a x x a R =-++∈. (1) 若曲线()y f x =在1x =和3x =处的切线互相平行,求a 的值; (2) 求()f x 的单调区间;(3) 设()22g x x x =-,若对任意(]10,2x ∈,均存在(]20,2x ∈,使得()()12f x g x <,求a 的取值范围.参考答案一、选择题二、填空题11.k =± 12.9 13.(][),32,-∞-+∞ 14.1:2 15.e - 三、解答题16.解:若p 真,则00a >⎧⎨∆<⎩,∴3a >,......................2分若q 真,令()22321f x x ax a =-++,则应满足()()()22234210399210a a f a a ⎧∆=--+≥⎪⎨=-++>⎪⎩......................4分∴222522a a a a a ⎧⎪≥≤-⎪>⎨⎪⎪<>⎩或或∴52a >..............................6分 又由题意可得p 真q 假或p 假q 真.............................7分(1) 若p 真q 假,则352a a >⎧⎪⎨≤⎪⎩,∴a 无解.........................9分17.解:(1)证明:在梯形ABCD 中, ∵//,1AB CD AD DC CB ===,060ABC ∠=,∴2AB =................................2分∴22202cos6031AC AB BC AB BC =+-=, ∴222AB AC BC =+,∴BC AC ⊥.........................4分∵平面ACFE ⊥平面ABCD ,平面ACFE 平面ABCD AC =,BC ⊂平面ABCD ,∴BC ⊥平面ACFE .......................6分(2) 由(1)可建立分别以直线,,CA CB CF 为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系,令(0FM λλ=≤≤,则())()()0,0,0,,0,1,0,,,0,1C AB M λ,∴{}{},,1,1AB BM λ==-.设()1,,n x y z =为平面MAB 的一个法向量, 由110,0n AB n BM ==,联立得00y x y z λ⎧+=⎪⎨-+=⎪⎩,联1x =,则()1n λ=...........................8分 ∵()21,0,0n =是平面FCB 的一个法向量, ∴1212cos n n n n θ== .............................10分∵0λ≤≤0λ=时,cos θλ=cos θ有最大值12.∴1cos 2θ⎤∈⎥⎣⎦.............................12分 18.解:(1)由于221212S b q =-=-,可得12qq q-=................2分 解得:3q =或4q =-(舍去)..........................3分 221219,23S d a a S a ==-=-=..........................4分 ∴()3133n a n n =+-=.......................5分13n n b +=..............................................6分 (2)证明:由3n a n =,得()332n n n S +=..........................7分∴()122113331n S n n n n ⎛⎫==- ⎪++⎝⎭∴12111211111112111322334131n S S S n n n ⎛⎫⎛⎫+++=-+-+-++-=- ⎪ ⎪++⎝⎭⎝⎭...............9分 ∵1n ≥,∴11012n <≤+,∴121213313n ⎛⎫≤-< ⎪+⎝⎭...........................11分 故121111233n S S S ≤+++< ......................................12分 19.解:(1)由题意可知,二氧化碳每吨的平均处理成本为1450002002001002y x x x =+-≥=....................4分 当且仅当1450002x x=,即300x =时等号成立,.............................5分 故该单位月处理量为300吨时,才能使每吨的平均处理成本最低,最低成本为100元..............6分(2)获利,设该单位每月获利为S 元,则()2211200400450004003500022S x y x x x =-=-+-=--+,...................9分因为[]300,600x ∈,所以[]15000,35000S ∈.............................11分 故该单位每月获利,最大利润为35000元...............................12分 20.解:(1)设圆心P 的坐标为(),x y ,半径为R ,由于动圆P 一圆()221:381F x y ++=相切,且与圆()222:31F x y -+=相内切,所以动圆P 与圆()221:381F x y ++=只能内切.∴1121229=861PF RPF PF F F PF R ⎧=-⎪⇒+>=⎨=-⎪⎩........................2分∴圆心P 的轨迹为以12,F F 为焦点的椭圆,其中28,26a c ==,∴2224,3,7a c b a c ===-=故圆心P 的轨迹22:1167x y C +=............................4分 (2)设()()()112233,,,,,M x y N x y Q x y ,直线:OQ x my =,则直线:3MN x my =+,由221167x my x y=⎧⎪⎨+=⎪⎩可得:22222112716112716m x m y m ⎧=⎪⎪+⎨⎪=⎪+⎩,∴2232232112716112716m x m y m ⎧=⎪⎪+⎨⎪=⎪+⎩, ∴()22222332221121112112716716716m m OQ x y m m m +=+=+=+++........................ 4分由2231167x my x y =+⎧⎪⎨+=⎪⎩可得:()2271642490m y my ++-=,∴121224249,716716m y y y y m m +=-=-++, ∴21MN y ===-()22561716m m +===+...................8分∴()()22222561171621121716m MNm m OQm ++==++ ∴MN 和2OQ 的比值为一个常数,这个常数为12...................9分 (3)∵//MN OQ ,∴2QF M ∆的面积2OF M =∆的面积,∴12OMN S S S S ∆=+=, ∵O 到直线:3MN x my =+的距离d =∴()2225611122716716m S MN d m m +==⨯=++ ...................11分t =,则()2211m t t =-≥,()2284848497971167t t S t t t t===+-++,∵97t t +≥=97t t =,即t =7m =±时取等号)∴当m =时,S取最大值........................13分 21.解:()()()2210f x ax a x x=-++>...............1分 (1)由题意知()()13f f =,即()()22123213a a a a -++=-++,解得23a =,..................3分 (2)()()()()120ax x f x x x--=>...................4分 ①当0a ≤时,∵0x >,∴10ax -<,在区间()0,2上,()0f x '>;在区间()2,+∞上,()0f x '<,故()f x 的单调递增区间是()0,2,单调递减区间是()2,+∞........................5分 ②当102a <<时,12a >,在区间()0,2和1,a ⎛⎫+∞ ⎪⎝⎭上,()0f x '>; 在区间12,a ⎛⎫ ⎪⎝⎭上,()0f x '<,故()f x 的单调递增区间是()0,2和1,a ⎛⎫+∞ ⎪⎝⎭, 单调递减区间是12,a ⎛⎫⎪⎝⎭....................6分 ③当12a =时,()()2202x f x x-'=≥,故()f x 的单调递增区间是()0,+∞,................7分④当12a >时,102a <<,在区间10,a ⎛⎫ ⎪⎝⎭和()2,+∞上,()0f x '>; 在区间1,2a ⎛⎫ ⎪⎝⎭上,()0f x '<,故()f x 的单调递增区间是10,a ⎛⎫ ⎪⎝⎭和()2,+∞,单调递减区间是1,2a ⎛⎫ ⎪⎝⎭................................8分 (3)由题意知,在(]0,2上有()()max max f x g x <,........................9分由已知得()max 0g x =,由(2)可知, ①当12a ≤时,()f x 在(]0,2上单调递增, 故()()()max 222212ln2222ln2f x f a a a ==-++=--+,所以222ln 20a --+<,解得ln 21a >-, 故1ln 212a -<≤..............11分 ②当12a >时,()f x 在10,a ⎛⎤ ⎥⎝⎦上单调递增; 在1,2a⎡⎤⎢⎥⎣⎦的单调递减, 故()max 1122ln 2f x f a a a ⎛⎫==---⎪⎝⎭, 由12a >可知11ln ln ln 12a e>>=-, 所以2ln 2a >-,即2ln 2a -<,所以,22ln 0a --<,..................... 13分 所以()max 0f x <,综上所述,ln 21a >-...................14分。
福建莆田第十七中学2017届新高三语文第一次月考试题

2016-2017年莆田十七中高三第一次月考语文试题本试卷分第Ⅰ卷(阅读题)和第Ⅱ卷(表达题)两部分。
考生作答时,将答案写在答题卡上,在本试卷上答题无效。
考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷阅读题甲必考题一、现代文阅读(9分,每小题3分)《论语》说:“礼之用,和为贵。
”“君子和而不同,小人同而不和。
”前句是根本的价值观,后句是待人做事的根本态度;总的是在承认差别的基础上求各得其所。
以和为贵不是单纯的美好愿望,是以对宇宙的根本认识为基础而提出的根本价值观。
两千多年前,中国人就提出了“和实生物”的观点。
指出宇宙万物都是不同成分和因素和谐共存的统一体。
从自然到人类社会,从家庭、单位、社区、社会、国家、国际,以至生态,都是如此。
世界是和的世界;万物以和为基础,存在于和的状态中。
以和为贵是在这一根本认识基础上提出的,就是以和为最高的价值。
和的实质是各得其所,以和为贵就是要在承认差别的前提和基础上求各得其所。
孔子说“政者正也”,又说如果有机会当政,一定以“正名”为当务之急,做到君君臣臣,父父子子。
“正”是他治国的根本理念。
《子罕》篇又有“子曰:‘吾自卫反鲁,然后乐正,雅颂各得其所。
’”以各得其所释“正”。
“正名”,“君君臣臣,父父子子”也就是要使君臣父子各得其所。
程子说:“万物庶事莫不各有其所,得其所则安,失其所则悖。
圣人所以能使天下顺治,非能为物作则也,唯止于各于其所而已。
”“和为贵”,就是以各得其所为最高的目标。
“君子和而不同,小人同而不和。
”和而不同就是要承认差别,在承认差别的基础上求和谐,而不是取消差别求统一、和谐。
达到和谐的基本方法是中庸、中道。
各得其所的基础是中。
只有各个部分、各种因素都无过无不及,达到中的要求,才有整体的和。
程子说:“使万物无一失所者,斯天理,中而已。
”各得其所是目标,和而不同是原则,中庸、中道是途径。
和与中是从不同的角度说,和是总体的状态和目标,中是各局部应处的状态和要求,二者相合,就是中和,也就是各得其所。
【湖北省黄冈中学】2017届高三上学期10月月考数学(理科)试卷(附答案与解析)
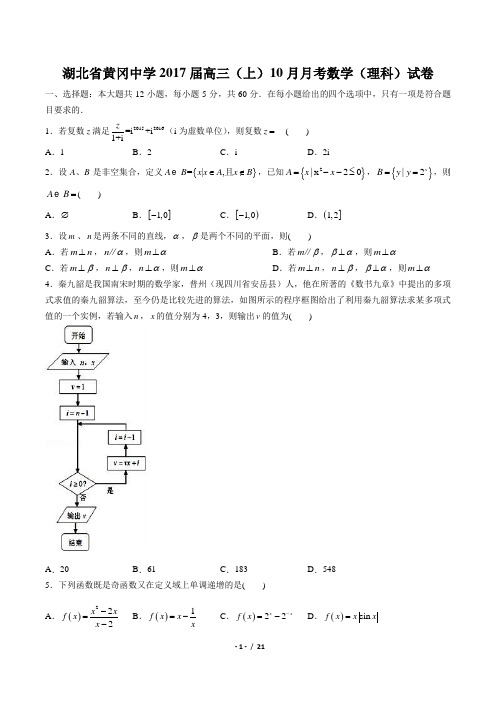
{=|A B x x∈A B=(.∅.设m、n2x y 的最大值是20162016b x ++.已知向量(cos ,sin a α=(cos ,sin b β=,则a 与a b +的夹角为 B .61na ++,则,1AF AB =,1CE CA =,1BD BC =,则D E D F 的12n na +++=12n n a +++=1222n na n +++=+,12n n a -++=12n +=⇒2n n +++⨯()21n ++-,12n +++-)2124n ++.)证明:设FC 的中点为GI IH I =,∴GIH 面GH ABC ∥面)解:连接OO 故()(2,2,0,0,1,BC BF =--=-设(),,n x y z =是平面BCF 的一个法向量,则2n BC x n BF y ⎧=-⎪⎨=-+⎪⎩,则(3,n =-又平面ABC 的一个法向量(OO'0,0,='7,'7'n OO n OO n OO ==, O 的余弦值为()1e ln 2ln3ln 2ln 1ln nn n n ++>++-+++-{A B=x|x ∈,{|B y =AB A =⋂故选:B .【考点】空间中直线与平面之间的位置关系.n α,则m m α,故A m β,βα⊥α或m ⊂αm α,故B 错误. β⊥,n ⊥,则m α⊥,正确.n ⊥,n ⊥⊂α或m α,故D7.【考点】简单线性规划.,解得:,即赋值为即可.20162016b x ++【考点】平面向量数量积的运算.【分析】设向量与的夹角为【解答】解:∵向量(cos ,sin a α=,(cos ,sin b β=,设向量a 与b 的夹角为∴()2a ab a a b 1cos +=+=+θ,222222cos a b a a b b θ+=++=+()1cos cos ,22cos a a ba a ba ab ++++==+0π, ∴a 与a b +的夹角3π. . 【考点】余弦函数的对称性.11a ⎛++ -⎝11n a ⎛++ -⎝,1AF AB =,1CE CA =,1BD BC =,所以:1,DE ⎛=- ,1,DF ⎛=- 所以:311DE DF ⋅=-+=- 故答案为:14-1612n n a +++=122n n a +++=, 12n n a -++=12n +=⇒2n n +++⨯()21n ++-,12n +++-2+故()(2,2,0,0,1,BC BF =--=-设(),,n x y z =是平面BCF 的一个法向量,则2n BC x n BF y ⎧⋅=-⎪⎨⋅=-+⎪⎩,则(3,n =-又平面ABC 的一个法向量(OO'0,0,='7,'7'n OO n OO n OO ==, O 的余弦值为71,2,,由累加法﹣在(()1ln 2ln3ln 2ln 1ln ne n n n ++>++-+++-。
2017届高三上学期10月月考数学试卷(文科) Word版含解析

2017届高三上学期10月月考试卷数学(文科)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的,把答案填在答题卷的相应位置.1.集合A={x|﹣1≤x≤2},B={x|x<1},则A∩B=()A.{x|x<1} B.{x|﹣1≤x≤2} C.{x|﹣1≤x≤1} D.{x|﹣1≤x<1}2.复数等于()A.1+i B.1﹣i C.﹣1+i D.﹣1﹣i3.若a,b∈R,且a>b,则下列不等式中恒成立的是()A.B.a2>b2C.2a>2b D.4.函数的值域是()A.[0,+∞)B.(0,+∞)C.[﹣1,+∞)D.(﹣1,+∞)5.“a>0”是“|a|>0”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6.下列命题中的假命题是()A.∃x∈R,lgx=0 B.∃x∈R,tanx=1 C.∀x∈R,x3>0 D.∀x∈R,2x>07.某种豆类生长枝数随时间增长,前6月数据如下:则下列函数模型中能较好地反映豆类枝数在第x月的数量y与x之间的关系的是()A.y=2x B.y=x2﹣x+2 C.y=2x D.y=logx+228.设f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x+2x+b,则b为()A.﹣1 B.0 C.1 D.无法确定9.设点P对应的复数为﹣3+3i,以原点为极点,实轴正半轴为极轴建立极坐标系,则点P的极坐标为()A.(,)B.(,) C.(3,) D.(﹣3,)10.函数f(x)=e x+x﹣2的零点所在的一个区间是()A.(﹣2,﹣1)B.(﹣1,0)C.(0,1)D.(1,2)11.给定函数①y=x,②y=log(x+1),③y=|x﹣1|,④y=2x+1,其中在区间(0,1)上单调递减的函数的序号是()A.①②B.②③C.③④D.①④12.已知a>0,函数f(x)=x3﹣ax在[﹣1,1]上是单调减函数,则a的最小值是()A.﹣3 B.﹣1 C.1 D.3二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卷的相应位置.13.命题“∀x∈R,x2≥0”的否定是.14.某校有老师200人,男学生1400人,女学生1200人,现用分层抽样的方法从所有师生中抽取一个容量为n的样本;已知从女学生中抽取的人数为90人,则n= .15.设x>0,则的最小值是.16.设f(x)=则使f(x)=11成立的实数x的集合为.三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.17.已知集合A={x|4≤x<8},B={x|2<x<10},C={x|x<a}.(1)求A∪B;(∁A)∩B;R(2)若A∩C≠∅,求a的取值范围.18.近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机的对入院50人进行了问卷调查得到了如下的列联表:(Ⅰ)用分层抽样的方法在患心肺疾病的人群中抽6人,其中男性抽多少人?(Ⅱ)在上述抽取的6人中选2人,求恰有一名女性的概率;(Ⅲ)为了研究心肺疾病是否与性别有关,请计算出统计量K2,你有多大的把握认为心肺疾病与性别有关?下面的临界值表供参考:(参考公式,其中n=a+b+c+d)19.已知直线l经过点P(1,1),倾斜角α=,(1)写出直线l的参数方程.(2)设l与圆x2+y2=4相交于点A、B,求点P到A、B两点的距离之积.20.设函数f(x)=|x+|+|x﹣a|(a>0).(Ⅰ)证明:f(x)≥2;(Ⅱ)若f(3)<5,求a的取值范围.21.已知函数f(x)=x3﹣3ax+b的图象在(1,f(1))处与y=2相切.(1)求a,b的值;(2)求f(x)的单调递减区间.22.设函数,a为常数,且f(3)=(1)求a值;(2)求使f(x)≥4的x值的取值范围;(3)设g(x)=﹣x+m,对于区间[3,4]上每一个x值,不等式f(x)>g(x)恒成立,求实数m的取值范围.2017届高三上学期10月月考数学试卷(文科)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的,把答案填在答题卷的相应位置.1.集合A={x|﹣1≤x≤2},B={x|x<1},则A∩B=()A.{x|x<1} B.{x|﹣1≤x≤2} C.{x|﹣1≤x≤1} D.{x|﹣1≤x<1}【考点】交集及其运算.【分析】利用交集和数轴即可求出A∩B.【解答】解:A∩B={x|﹣1≤x≤2}∩{x|x<1}={x|﹣1≤x≤2,且x<1}={x|﹣1≤x<1}.故选D.2.复数等于()A.1+i B.1﹣i C.﹣1+i D.﹣1﹣i【考点】复数代数形式的乘除运算.【分析】利用复数的运算法则即可得出.【解答】解:原式==1+i.故选A.3.若a,b∈R,且a>b,则下列不等式中恒成立的是()A.B.a2>b2C.2a>2b D.【考点】命题的真假判断与应用.【分析】举出反例a=1,b=﹣2,可判断A,B,D均不成立,进而得到答案.【解答】解:当a=1,b=﹣2时,a>b,但,故A中不等式不恒成立,a2<b2,故B中不等式不恒成立,,故D中不等式不恒成立,而2a>2b恒成立,故选:C.4.函数的值域是()A.[0,+∞)B.(0,+∞)C.[﹣1,+∞)D.(﹣1,+∞)【考点】函数的值域.【分析】根据幂函数的值域即可求解.【解答】解:函数y=的定义域为{x|x≥0},其值域是[0,+∞),那么:函数的值域是[﹣1,+∞),故选:C.5.“a>0”是“|a|>0”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【考点】必要条件.【分析】本题主要是命题关系的理解,结合|a|>0就是{a|a≠0},利用充要条件的概念与集合的关系即可判断.【解答】解:∵a>0⇒|a|>0,|a|>0⇒a>0或a<0即|a|>0不能推出a>0,∴a>0”是“|a|>0”的充分不必要条件故选A6.下列命题中的假命题是()A.∃x∈R,lgx=0 B.∃x∈R,tanx=1 C.∀x∈R,x3>0 D.∀x∈R,2x>0【考点】命题的真假判断与应用.【分析】A、B、C可通过取特殊值法来判断;D、由指数函数的值域来判断.【解答】解:A、x=1成立;B、x=成立;D、由指数函数的值域来判断.对于C选项x=﹣1时,(﹣1)3=﹣1<0,不正确.故选C7.某种豆类生长枝数随时间增长,前6月数据如下:则下列函数模型中能较好地反映豆类枝数在第x月的数量y与x之间的关系的是()x+2A.y=2x B.y=x2﹣x+2 C.y=2x D.y=log2【考点】线性回归方程.【分析】本题要选择合适的模型,从所给数据可以看出图象大约过(1,2)和(2,4),把这两个点代入所给的四个解析式发现只有y=2t最合适,再考查四个选项,找出正确选项即可.【解答】解:从所给数据可以看出图象大约过(1,2)和(2,4)把这两个点代入所给的四个解析式发现只有y=2t最合适,故选:C.8.设f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x+2x+b,则b为()A.﹣1 B.0 C.1 D.无法确定【考点】函数奇偶性的性质.【分析】根据奇函数的性质,可得f(0)=0,代入构造关于b的方程,解得答案.【解答】解:∵f(x)为定义在R上的奇函数,∴f(0)=0,∵当x≥0时,f(x)=2x+2x+b,∴f(0)=1+b=0,解得:b=﹣1.故选:A9.设点P对应的复数为﹣3+3i,以原点为极点,实轴正半轴为极轴建立极坐标系,则点P的极坐标为()A.(,)B.(,) C.(3,) D.(﹣3,)【考点】极坐标刻画点的位置.【分析】先求出点P的直角坐标,P到原点的距离r,根据点P的位置和极角的定义求出极角,从而得到点P的极坐标.【解答】解:∵点P对应的复数为﹣3+3i,则点P的直角坐标为(﹣3,3),点P到原点的距离r=3,且点P第二象限的平分线上,故极角等于,故点P的极坐标为(,),故选 A.10.函数f(x)=e x+x﹣2的零点所在的一个区间是()A.(﹣2,﹣1)B.(﹣1,0)C.(0,1)D.(1,2)【考点】函数零点的判定定理.【分析】将选项中各区间两端点值代入f(x),满足f(a)•f(b)<0(a,b为区间两端点)的为答案.【解答】解:因为f(0)=﹣1<0,f(1)=e﹣1>0,所以零点在区间(0,1)上,故选C.11.给定函数①y=x,②y=log(x+1),③y=|x﹣1|,④y=2x+1,其中在区间(0,1)上单调递减的函数的序号是()A.①②B.②③C.③④D.①④【考点】函数单调性的判断与证明.【分析】根据一次函数及指数函数,对数函数的性质,判断函数的单调性,从而得出答案.【解答】解:y=x,k=1,递增,y=,底数是,递减,y=|x﹣1|=1﹣x,递减,y=2x+1,底数是2,递增,故选:B.12.已知a>0,函数f(x)=x3﹣ax在[﹣1,1]上是单调减函数,则a的最小值是()A.﹣3 B.﹣1 C.1 D.3【考点】利用导数研究函数的单调性.【分析】求出函数的导数,问题转化为a≥3x2在[﹣1,1]恒成立,根据二次函数的性质求出a的最小值即可.【解答】解:若函数f(x)=x3﹣ax在[﹣1,1]上是单调减函数,即f′(x)=3x2﹣a≤0在[﹣1,1]恒成立,即a≥3x2在[﹣1,1]恒成立,故a≥3,a的最大值是3,故选:D.二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卷的相应位置.13.命题“∀x∈R,x2≥0”的否定是∃x∈R,x2<0 .【考点】命题的否定.【分析】根据一个命题的否定定义解决.【解答】解:由命题的否定义知:要否定结论同时改变量词故答案是∃x∈R,x2<014.某校有老师200人,男学生1400人,女学生1200人,现用分层抽样的方法从所有师生中抽取一个容量为n的样本;已知从女学生中抽取的人数为90人,则n= 210 .【考点】分层抽样方法.【分析】先求出每个个体被抽到的概率,用每层的个体数乘以每个个体被抽到的概率等于该层应抽取的个体数,再把各层抽取的样本数相加可得样本容量 n的值.【解答】解:每个个体被抽到的概率等于=,应抽取的男学生人数为1400×=105,应抽取的老师人数为200×=15,故样本容量 n=90+105+15=210.故答案为210.15.设x>0,则的最小值是.【考点】基本不等式.【分析】依题意,利用基本不等式即可.【解答】解:∵x>0,∴y=3x+≥2(当且仅当x=时取等号).故答案为:16.设f(x)=则使f(x)=11成立的实数x的集合为{1,7,13} .【考点】函数的值.【分析】当x≥10时,f(x)=x﹣2=11;当1≤x<10时,f(x)=f(x+6),由1≤x<10,得7≤x+6<16,当7≤x+6<10时,f(x)=f(x+6)=f(x+12);当10≤x+6<16时,f(x)=f (x+6).由此能求出使f(x)=11成立的实数x的集合.【解答】解:∵f(x)=,f(x)=11,∴当x≥10时,f(x)=x﹣2=11,解得x=11;当1≤x<10时,f(x)=f(x+6),由1≤x<10,得7≤x+6<16,当7≤x+6<10时,13≤x+12<16,f(x)=f(x+6)=f(x+12)=x+12﹣2=11,解得x=1;当10≤x+6<16时,f(x)=f(x+6)=x+6﹣2=11,解得x=7.综上,使f(x)=11成立的实数x的集合为{1,7,13}.故答案为:{1,7,13}.三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.17.已知集合A={x|4≤x<8},B={x|2<x<10},C={x|x<a}.A)∩B;(1)求A∪B;(∁R(2)若A∩C≠∅,求a的取值范围.【考点】交、并、补集的混合运算;交集及其运算.【分析】本题考查集合的交、并、补运算,对于(1)求出A的补集是关键,对于(2)利用A ∩C≠∅确定参数a的取值范围【解答】解:(1)∵集合A={x|4≤x<8},B={x|2<x<10},∴A∪B={x|2<x<10},∵CA={x|x<4或x≥8}RA)∩B={x|8≤x<10或2<x<4}∴(CR(2)∵若A∩C≠∅,A={x|4≤x<8},C={x|x<a}.∴a的取值范围是a>4∴a∈(4,+∞)18.近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机的对入院50人进行了问卷调查得到了如下的列联表:(Ⅰ)用分层抽样的方法在患心肺疾病的人群中抽6人,其中男性抽多少人?(Ⅱ)在上述抽取的6人中选2人,求恰有一名女性的概率;(Ⅲ)为了研究心肺疾病是否与性别有关,请计算出统计量K2,你有多大的把握认为心肺疾病与性别有关?下面的临界值表供参考:(参考公式,其中n=a+b+c+d)【考点】独立性检验的应用;分层抽样方法.【分析】(I)根据分层抽样的方法,在患心肺疾病的人群中抽6人,先计算了抽取比例,再根据比例即可求出男性应该抽取人数.(II)在上述抽取的6名学生中,女性的有2人,男性4人.女性2人记A,B;男性4人为c,d,e,f,列出其一切可能的结果组成的基本事件个数,通过列举得到满足条件事件数,求出概率.(III)根据所给的公式,代入数据求出临界值,把求得的结果同临界值表进行比较,看出有多大的把握认为心肺疾病与性别有关.【解答】解:(I )在患心肺疾病的人群中抽6人,则抽取比例为 =,∴男性应该抽取20×=4人….(II )在上述抽取的6名学生中,女性的有2人,男性4人.女性2人记A ,B ;男性4人为c ,d ,e ,f ,则从6名学生任取2名的所有情况为:(A ,B )、(A ,c )、(A ,d )、(A ,e )、(A ,f )、(B ,c )、(B ,d )、(B ,e )、(B ,f )、(c ,d )、(c ,e )、(c ,f )、(d ,e )、(d ,f )、(e ,f )共15种情况,其中恰有1名女生情况有:(A ,c )、(A ,d )、(A ,e )、(A ,f )、(B ,c )、(B ,d )、(B ,e )、(B ,f ),共8种情况,故上述抽取的6人中选2人,恰有一名女性的概率概率为P=.….(III )∵K 2≈8.333,且P (k 2≥7.879)=0.005=0.5%,那么,我们有99.5%的把握认为是否患心肺疾病是与性别有关系的.….19.已知直线l 经过点P (1,1),倾斜角α=,(1)写出直线l 的参数方程.(2)设l 与圆x 2+y 2=4相交于点A 、B ,求点P 到A 、B 两点的距离之积. 【考点】直线的参数方程.【分析】对第(1)问,由过点(x 0,y 0),且倾斜角为α的直线的参数方程可得l 的参数方程;对第(2)问,根据l 的参数方程,可设A ,B,再将l 的参数方程代入圆的方程中,得到一个关于t 的一元二次方程,由韦达定理可得点P 到A 、B 两点的距离之积.【解答】解:(1)因为过点(x 0,y 0),且倾斜角为α的直线的参数方程,由题意,将x 0=1,y 0=1,α=代入上式得直线l 的参数方程为(t 为参数).(2)因为A ,B 都在直线l 上,故可设它们对应的参数分别为t 1,t 2,则点A,B的坐标分别为A,B,将直线l的参数方程代入圆的方程x2+y2=4中,整理得,则t1,t2是此方程的两根,由韦达定理得t1t2=﹣2,所以|PA|•|PB|=|t1t2|=2.即点P到A、B两点的距离之积为2.20.设函数f(x)=|x+|+|x﹣a|(a>0).(Ⅰ)证明:f(x)≥2;(Ⅱ)若f(3)<5,求a的取值范围.【考点】绝对值不等式的解法.【分析】(Ⅰ)由a>0,f(x)=|x+|+|x﹣a|,利用绝对值三角不等式、基本不等式证得f (x)≥2成立.(Ⅱ)由f(3)=|3+|+|3﹣a|<5,分当a>3时和当0<a≤3时两种情况,分别去掉绝对值,求得不等式的解集,再取并集,即得所求.【解答】解:(Ⅰ)证明:∵a>0,f(x)=|x+|+|x﹣a|≥|(x+)﹣(x﹣a)|=|a+|=a+≥2=2,故不等式f(x)≥2成立.(Ⅱ)∵f(3)=|3+|+|3﹣a|<5,∴当a>3时,不等式即a+<5,即a2﹣5a+1<0,解得3<a<.当0<a≤3时,不等式即 6﹣a+<5,即 a2﹣a﹣1>0,求得<a≤3.综上可得,a的取值范围(,).21.已知函数f(x)=x3﹣3ax+b的图象在(1,f(1))处与y=2相切.(1)求a,b的值;(2)求f(x)的单调递减区间.【考点】利用导数研究函数的单调性;利用导数研究曲线上某点切线方程.【分析】(1)求出函数的导数,根据f(1)=2,f′(1)=0,求出a,b的值即可;(2)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可.【解答】解:(1)f′(x)=3x2﹣3a,由题意,解得:;(2)由(1)得:f′(x)=3x2﹣3,令f′(x)<0,解得:﹣1<x<1,所以f(x)的单调递减区间为(﹣1,1).22.设函数,a为常数,且f(3)=(1)求a值;(2)求使f(x)≥4的x值的取值范围;(3)设g(x)=﹣x+m,对于区间[3,4]上每一个x值,不等式f(x)>g(x)恒成立,求实数m的取值范围.【考点】函数恒成立问题;其他不等式的解法.【分析】(1),可得,利用指数函数的单调性可得10﹣3a=1解出即可.(2)由已知,利用指数函数的单调性即可得出10﹣3x≤﹣2.(3)由题意f(x)>g(x)化为恒成立.即在[3,4]恒成立.设,上述问题等价于m<h(x)min,利用函数与在[3,4]为增函数,可得h(x)在[3,4]为增函数,即可得到h(x)的最小值.【解答】解:(1),即,∴10﹣3a=1,解得a=3.(2)由已知,∴10﹣3x≤﹣2.解得x≥4故f(x)≥4解集为{x|x≥4}.(3)依题意f(x)>g(x)化为恒成立即在[3,4]恒成立设则m<h(x)min,∵函数与在[3,4]为增函数,可得h(x)在[3,4]为增函数,∴,∴m<2.。
山东省武城县2017届高三10月月考数学(理)试题

高三数学(理)月考试题2016.10第I 卷(共50分)一、选择题(本大题共10小题,每小题5分,共50分) 1.已知集合2{|450}A x x x =--<,{|24}B x x =<<,则AB =( )A.(1,3)B.(1,4)C.(2,3)D.(2,4)2.已知向量(1,2),(0,1),(2,)a b c k ===-,若(2)//a b c +,则k =( )A.8B.12C.12-D.-83.下列说法正确的是( )A.命题“若21x =,则1x =”的否命题为:“若21x =,则1x ≠”B.若命题2:,10p x R x x ∃∈-+<,则命题2:,10p x R x x ⌝∀∈-+>C.命题“若x y =,则sin sin x y =”的逆否命题为真命题D.“2560x x --=”的必要不充分条件是“1x =-”4.已知指数函数()y f x =的图象过点1(,)22,则2log (2)f 的值为( )A.12B.12-C.-2D.25.已知:sin()3cos()sin()2πθπθθ++-=-,则2sin cos cos θθθ+=( )A.15B.25D.356.不等式|5||1|8x x -++<的解集为( )A.(,2)-∞B.(2,6)-C.(6,)+∞D.(1,5)-7.函数ln ||||x x y x =的图象是( )8.下列四个命题, 其中正确命题的个数( )①若||a b >,则22a b > ②若,a b c d >>,则a c b d ->- ③若,a b c d >>,则ac bd > ④若0a b >>,则c c a b> A.3个B.2个C.1个D.0个9.已知定义在R 上的函数||()21x m f x -=-(m 为实数)为偶函数,记3(2),(3)m a f b f -==,0.5(log 3)c f =,则( )A.a b c <<B.a c b <<C.c a b <<D.c b a <<10.已知定义在R 上的函数()y f x =对任意的x 都满足(2)()f x f x +=,当11x -≤<时,()sin2f x x π=,若函数()()log ||a g x f x x =-至少6个零点,则a 取值范围是( ) A.1(0,](5,)5+∞ B.1(0,)[5,)5+∞C.11(,](5,7)75D.11(,)[5,7)75第II 卷(共100分)二、填空题:本大题共5小题,每小题5分,共25分.11.已知1233,3()log (6),3x e x f x x x -⎧<⎪=⎨-≥⎪⎩,则(f f 的值为 .12.曲线2sin (0)y x x π=≤≤与x 轴围成的封闭图形的面积为.13.若,x y 满足20449x y y x x y -≥⎧⎪≥⎨⎪+≤⎩,则2z x y =+的最大值为.14.在ABC ∆中,角,,A B C 所对边的长分别为,,a b c,已知b =,sin A C2sin B =,则cos A = .15.如图,点P 从点O 出发,分别按逆时针方向沿周长均为12的正三角形、正方形运动一周,,O P 两点连线的距离y 与点P 走过的路程x 的函数关系分别记为()y f x =,()y g x =,定义函数(),()()()(),()()f x f x g x h x g x f x g x ≤⎧=⎨>⎩,对于函数()y h x =,下列结论正确的是.①(4)h = ②函数()h x 的图象关于直线6x =对称;③函数()h x值域为; ④函数()h x 的单调增区间为(0,5).三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.16.(本小题满分12分)在ABC ∆中,角A B C 、、对边分别是a b c 、、,且满足222()AB AC a b c ⋅=--. (I )求角A 的大小;(II )若4a =,ABC ∆的面积为,b c .17.(本小题满分12分)已知向量,m n 的夹角为60°,且||1,||2m n ==,又2,3a m n b m n =+=-+. (I )求a 与b 的夹角的余弦;(II )设,c ta b d m n =-=-,若c d ⊥,求实数t 的值.18. (本小题满分12分)已知函数()sin(2))63f x x x ππ=++-. (I )求()f x 的单调递增区间;(II )将函数()y f x =的图象向左平移3π个单位,再将得到的图象上各点的横坐标伸长到原来的2倍(纵坐标不变)得到函数()y g x =的图象,求函数()y g x =在2[,]33ππ-上的值域.19. (本小题满分12分)设函数3()3(1),(0)f x x a x b a =-++≠.(I )若曲线()y f x =在点(2,(2))f 处与直线8y =相切,求,a b 的值; (II )求函数()()3g x f x x =+的单调区间与极值.20. (本小题满分13分)某厂家举行大型的促销活动,经测算某产品当促销费用为x 万元时,销售量t 万件满足952(1)t x =-+(其中0x a ≤≤,a 为正常数).现假定生产量与销售量相等,已知生产该产品t 万件还需投入成本(102)t +万元(不含促销费用),产品的销售价格定为20(4)t+万元/万件.(I )将该产品的利润y 万元表示为促销费用x 万元的函数; (II )促销费用投入多少万元时,厂家的利润最大.21.(本小题满分14分)已知函数()xlnx f x =和2()(1)()g x m x m R =-∈. (I )1m =时,求方程()()f x g x =的实根;(II )若对于任意的(1,)x ∈+∞,函数()y g x =的图象总在函数()y f x =图象的上方,求m 的取值范围;(III )求证:*2224424ln(21)()41142141n n n N n ⨯⨯++⋅⋅⋅+>+∈⨯-⨯-⨯-.。
高2017级10月数学月考试题(理、文)(含答案)

1平昌县得胜中学高2017级10月月考试题一、选择题:(共12题 每题5分 共60分)1(理).已知集合A={3|),(x y y x =},A={x y y x =|),(},则B A 的元素个数是 ( ) A. 4B. 3C. 2D. 11(文).已知集合A={1,2,3,4},B={2,4,6,8},则A ⋂B 中元素的个数为 ( ) A .1B .2C .3D .42.设复数z 满足(2)(2)5z i i --=,则z 等于 ( )A.2+3iB. 2-3iC. 3+2iD. 3-2i 3.已知向量a=(l ,0),b=(-3,4)的夹角为θ,则θ2sin 等于 ( )A. 257-B. 257C. 2524-D. 25244.已知命题p:0,x ∀>总有(1)1,xx e +>则p ⌝为 ( )A.00,x ∃≤使得00(1)1x x e+≤ B. 00,x ∃>使得00(1)1x x e +≤C.0,x ∀>总有(1)1xx e +≤ D. 0,x ∀≤总有(1)1xx e +≤5.设Sn 为等差数列{an }的前n 项和,837=4,2S a a =-,则a 9等于( ) A.-6 B.-4 C.-2 D.26.已知函数()2log ,01,02x x x f x x >⎧⎪=⎨⎛⎫≤⎪⎪⎝⎭⎩ 若()2f a =,则a 等于( )A .1-B .4C .1-或4D .1或4-7.函数||lg )33()(x x f xx-+=的图象大致为( )8.设函数f (x )=cos(x +3π),则下列结论错误的是 ( ) A .f (x )的一个周期为−2π B .y =f (x )的图像关于直线x =83π对称C .f (x +π)的一个零点为x =6πD .f (x )在(2π,π)单调递减29.设x ,y 满足约束条件326000x y x y +-≤⎧⎪≥⎨⎪≥⎩,则z =x -y 的取值范围是( ) A .[–3,0]B .[–3,2]C .[0,2]D .[0,3]10.执行如图程序框图,如果输入的x,t 均为2,则输出的S 等于 ( ) A.4 B.5 C.6 D.711. 已知椭圆C :22221x y a b+=(a >b >0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为 ( )A.3B.3C.3D .1312.已知函数211()2()x x f x x x a ee --+=-++有唯一零点,则a = ( )A .12-B .13C .12D .1二、填空题:(共4题 每题5分 共20分)13(文)从进入决赛的6名选手中决出1名一等奖,2名二等奖,3名三等奖,则可能的决赛结果共有 种.(用数字作答)13(理) ()()342211+x y x y +的展开式中的系数是14.若数列}{n a 的前n 项和3132+=n n a S ,则}{n a 的通项公式是 =n a15.已知△ABC 的面积为32,AC =3,∠ABC =π3,则△ABC 的周长等于16.过抛物线y 2=4x 的焦点F ,作相互垂直的两条焦点弦AB 和CD ,则|AB|+|CD|的最小值是__________.三、解答题:( 17-21题各12分;22-24题选做一题,各10分 ,共70分)17.设数列{}n a 满足123(21)2n a a n a n +++-=.(1)求{}n a 的通项公式; (2)求数列21n a n ⎧⎫⎨⎬+⎩⎭的前n 项和 18.某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任3务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人。
福建省莆田第十七中学2017届新高三第一次月考数学(文)试题 含答案

2016-2017年莆田十七中高三第一次月考数学试卷(文科)第Ⅰ卷一、选择题(本大题共12小题,每小题5分,满分60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
) 1.设函数y=1+x 的定义域为M ,集合N={y|y=x 2,x ∈R},则M ∩N=( )A .φB .NC .[1,+∞)D .M 2.函数y=)34(log 15.0-x 的定义域为( )A .(43,1)B .(43,+∞)C .(1,+∞)D .(43,1)∪(1,+∞)3.设x R ∈ ,则“21x -< "是“220x x +-> "的( ) A .充分而不必要条件 B .必要而不充分条件 C .充要条件 D .既不充分也不必要条件4.函数xx x f 2ln )(-=零点所在的大致区间为( )A .)2,1(B .)3,2(C .)1,1(e 和)4,3(D .),(∞+e5.下列函数中,既是奇函数又在区间),0(+∞上单调递增的函数为( )A 。
1y x -= B 。
l n y x = C .3y x =D .||y x =6。
函数,则( )A .8B .9C .11D .107 。
已知是定义在上的偶函数,且在上是增函数,设,则、、的大小关系是 ( )A.B 。
C .D .8. 已知,函数与函数的图象可能是( )9.函数xa x f ax log )(1+=-在区间上的最大值和最小值之和为a ,则实数a 为( )A .21B .2C .2D .410.已知函数()f x 满足()()f x f x π=-,且当(,)22x ππ∈-时,()s i n xf x e x =+,则( ) A .5()()()346f f f πππ<< B .5()()()436f f f πππ<<C .5()()()463f f f πππ<<D .5()()()643f f f πππ<<11.己知是定义在R 上的奇函数,当时,,那么不等式的解集是( )A .B .或C .D .或12.设偶函数在上为减函数,且,则不等式的解集为( )A .(-2,2)B .(0,2)C ,D (0,2) ∪( -∞,—2)第Ⅱ卷(非选择题 共90分)二、填空题:(本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置) 13. 函数f (x )=(x 2-2x -3)的单调递增区间是_________14.已知2,(0)()(1),(0)x x f x f x x >⎧=⎨+≤⎩,则44()()33f f -+等于______________15.当0,1a a >≠时,函数()l o g (1)1afx x =-+的图象恒过定点A ,若点A 在直线mx -y +n =0上,则42mn +的最小值是 .16。
17级第三次月考文综答案

36.【答案】(1)依云水发源于阿尔卑斯山高山冰雪融水和山地降水;水下渗至山地岩层和土层当中经过15年缓慢的过滤,使其水质良好;经15年缓慢矿化使其富含矿物质。
(6分)(2)依云小镇位于(欧非)板块交界处,拥有丰富的地热资源;依云温泉具有较多保健功能,发展温泉产业资源优势明显;位于欧洲中部,周边居民消费水平高,温泉产业市场广阔;资金充足有利于完善基础设施,发展相关产业,增加温泉产业的吸引力。
(8分)(3)APM协会成员主要是包括水源地周围的村民,其生产生活直接关系到依云水的品质;由协会出资可以鼓励当地居民造林和少施化肥等措施,减少环境破坏;协会成员负责可以加强对水源地的监督,保证其品质。
(6分)(4)因地制宜发展特色产业;保护环境打造宜居空间;以政府为主导企业为主体,鼓励全社会共同参与小镇建设。
(4分)37.【答案】(1)该段山地纬度较低,基带热量充足;(2分)山体相对高度大,气候垂直差异明显;(2分)坡向(迎风坡和背风坡)及局部地形(干热河谷)对气候条件影响大,气候条件复杂多样。
(2分)(2)该地夏季因地势海拔高,气温较低,气候凉爽;冬季纬度较低,且北部山地阻挡冬季风南下,温度较高,气候温和。
(4分)(3)西坡为迎风坡,降水较丰富;(2分)河流较多,且有水库,灌溉用水稳定;(2分)地形相对平坦,多河谷及山间盆地,宜农耕地较多。
(2分)(4)差异:各农业气候层的分布上限,东坡均高于西坡,因此东坡热量条件更好。
(2分)原因:东北坡为背风坡,降水少,太阳辐射更强;东北坡气流下沉增温。
(4分)38.(1)①贯彻开放、共享的新发展理念,搭建贸易合作新平台,推动形成陆海内外联动、东西双向互济的开放格局。
(4分)②进一步降低关税,加快跨境电子商务发展,更大程度满足消费者需求。
(4分)③要实行高水平的贸易自由化便利化政策,放宽市场准入,提升通关便利化水平。
(3分)④采取更加积极有效的政策措施,促进居民收入增加、消费能力增强,持续释放国内市场潜力,扩大进口空间。
福建省莆田第十七中学2017届新高三第一次月考物理试题 含答案

2016—2017年莆田十七中高三第一次月考物理试卷本试卷分为第I卷(选择题)和第II卷(非选择题)两部分,共110分,考试时间120分钟第Ⅰ卷选择题(共48分)一、选择题:本题共12小题,每小题4分,共计48分.1——8每小题只有一个选项符合题意.9—-12每小题有多个选项符合题意.全部选对的得分,选对但不全的得2分,错选或不答的得0分.1汽车进行刹车试验,若速率从8 m/s匀减速至零,需用时间1 s,按规定速率为8 m/s的汽车刹车后拖行路程不得超过5.9 m,那么上述刹车试验的拖行路程是否符合规定( )A.拖行路程为8 m,符合规定B.拖行路程为8 m,不符合规定C.拖行路程为4 m,符合规定D.拖行路程为4 m,不符合规定2.从同一地点同时开始沿同一直线运动的两个物体Ⅰ、Ⅱ的v-t 图象如图所示,在0~t0时间内,下列说法中正确的是:()A.Ⅰ、Ⅱ两个物体所受的合外力都在不断减小B.Ⅰ物体的加速度不断增大,Ⅱ物体的加速度不断减小C.Ⅰ、Ⅱ两个物体在t1时刻相遇D.Ⅰ、Ⅱ两个物体的平均速度大小都是221vv3.如图所示,两物体A 、B 的质量分别为M 和m ,用跨过定滑轮的轻绳相连,物体A 静止在粗糙水平面上,细线与水平方向的夹角为θ,B 悬停于空中。
若不计细线与滑轮间的摩擦,重力加速度为g 。
则A .地面对物体A 的支持力大小等于θsin mg Mg -B .物体A 对地面的压力大小等于MgC .物体A 与地面之间的动摩擦因数等于θθsin cos mg Mg mg -D .物体A 所受摩擦力大小等于04.如图所示,质量为M 的斜面体A 放在粗糙水平面上,用轻绳拴住质量为m 的小球B 置于斜面上,轻绳与斜面平行且另一端固定在竖直墙面上,不计小球与斜面间的摩擦,斜面体与墙不接触,整个系统处于静止状态。
则A .水平面对斜面体没有摩擦力作用 B .水平面对斜面体有向左的摩擦力作用C .斜面体对水平面的压力等于(M +m )gD .斜面体对水平面的压力小于(M +m)g5.某物体以30 m/s 的初速度竖直上抛,不计空气阻力,g 取,5 s 内物体的A.路程为60mB.位移大小为25 m,方向向上C.速度改变量的大小为10m/sD.平均速度大小为13 m/s,方向向上6.两个物体M、m 用跨过光滑定滑轮的轻绳相连,如图所示放置,OA、OB与水平面的夹角分别为30°、60°,物体M的重力大小为20 N,M、m均处于静止状态.则A.绳OA对M的拉力大小为103NB.绳OB对M的拉力大小为10 NC.m受到水平面的静摩擦力大小为103ND.m受到水平面的静摩擦力的方向水平向左7.如图所示,木块b放在一固定斜面上,其上表面水平,木块a放在b上.用平行于斜面向上的力F作用于aα,、b均保持静止。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
十七中34级高三第一次月考语文试题一、阅读下面的文言文,完成1-4题。
(19分)赵鼎,字元镇,解州闻喜人。
生四岁而孤,母樊教之,通经义百家之书。
登崇宁五年进士第,对策斥章惇误国。
累官为河南洛阳令,宰相吴敏知其能,擢为开封士曹。
金人陷太原,朝廷议割三镇地,鼎曰:“祖宗之地不可以与人,何庸议?”已而京师失守,二帝北行。
金人议立张邦昌,鼎与胡寅、张浚逃太学中,不书议状。
高宗即位,除权户部员外郎。
擢右司谏。
刘光世部将王德擅杀韩世忠之将,而世忠亦率部曲夺建康守府廨。
鼎言:“德总兵在外,专杀无忌,此而不治,孰不可为?”命鼎鞫德。
鼎又请下诏切责世忠,而指取其将吏付有司治罪,诸将肃然。
上曰:“肃宗兴灵武得一李勉,朝廷始尊。
今朕得卿,无愧昔人矣。
”中丞范宗尹言,故事无自司谏迁殿中者,上曰:“鼎在言路极举职,所言四十事,已施行三十有六。
”遂迁侍御史。
鼎上疏言:“顷张浚出使川、陕,国势百倍于今。
浚有补天浴日之功,陛下有砺山带河之誓,君臣相信,古今无二,而终致物议,以被窜逐。
今臣无浚之功而当其任,远去朝廷,其能免于纷纷乎?”又言:“臣所请兵不满数千半皆老弱所赍金帛至微荐举之人除命甫下弹墨已行。
臣日侍宸衷,所陈已艰难,况在千里之外乎?”时人士皆惜其去,台谏有留行者。
会边报沓至,鼎每陈用兵大计,及朝辞,上曰:“卿岂可远去,当遂相卿。
”九月,拜尚书右仆射、同中书门下平章事兼知枢密院事,制下,朝士相庆。
在吉阳三年,潜居深处,门人故吏皆不敢通问,惟广西帅张宗元时馈醪米。
桧知之,令本军月具存亡申。
鼎遣人语其子汾曰:“桧必欲杀我,我死,汝曹无患;不尔,祸及一家矣。
”遗言属其子归葬,遂不食而死,时绍兴十七年也,天下闻而悲之。
(选自《宋史·赵鼎传》,有删改)1.下列对文中画波浪线部分的断句,正确的一项是(3分)A.臣所请兵/不满数千/半皆老弱/所赍金帛至微/荐举之人除/命甫下/弹墨已行B.臣所请兵不满数千/半皆老弱/所赍金帛至微/荐举之人除命甫下/弹墨已行C.臣所请兵不满数千/半皆老弱所赍/金帛至微/荐举之人除命甫下/弹墨已行D.臣所请兵/不满数千/半皆老弱所赍/金帛至微/荐举之人除/命甫下/弹墨已行2.下列对文中加点词语的相关内容的解说,不正确的一项是(3分)A.对策,在中国古代科举中是殿试考试的主要内容。
“策问”与“对策”分别指应试与出题两个部分,内容主要是治国安邦、国计民生的政治大事。
B.太学,中国古代的国立大学。
上古的大学,称为成均、上庠。
汉武帝时,采纳董仲舒的建议,于京师长安设立。
C.除权,古代用来表示官职任免的术语,指除去旧职,授予新职,在这里指让赵鼎暂时代理户部员外郎。
D.宸衷,皇帝的心意。
宸,北极星(北辰)的所在、星天之枢。
后借指帝王所居,又引申为王位、帝王的代称。
3.下列对原文有关内容的概括和分析,不正确的一项是(3分)A.赵鼎忠君爱国,反对割地求和,金人掳获徽钦二帝后,准备立张邦昌为帝,赵鼎拒绝书写文书,躲进太学。
B.赵鼎正直敢言,参加进士考试时批评章惇误国,王德擅杀韩世忠手下将领,他直接将其抓捕和审讯。
C.赵鼎深得高宗信任,他的建议基本被采纳实行。
皇上力排众议,从谏官破格提拔为侍御史。
D.赵鼎晚景凄凉,被贬到吉阳之后,门人故吏均不敢与他来往。
当他得知秦桧有意置自己于死地时,为不牵连家人,绝食而亡。
4.把文中画横线的句子翻译成现代汉语。
(10分)(1)德总兵在外,专杀无忌,此而不治,孰不可为?(5分)(2)君臣相信,古今无二,而终致物议,以被窜逐。
(5分)参考答案:1.B (金帛是朝廷赏赐的,故不能与“所赍”断开,“除命甫下”是指对荐举的人的任命刚刚公布,也应与“荐举之人”连在一起。
)2.A (A“策问”与“对策”分别指出题与应试两个部分。
)3. B (“命鼎鞫德”,省略了主语“上”,他是在皇上命令下审讯王德的。
)4(1)王德在外统领军队,擅自杀人没有顾忌,这样如果不进行治理,还有什么不能做呢(或:还有谁不敢做呢)?(得分点“总兵”“专杀”“而”各1分,句意2分)(2)君臣互相信任,古今没有第二,(张浚如今)却最终遭到别人非议,以致被放逐。
(得分点“相信”“物议”“窜逐”各1分,句意2分)译文:赵鼎字元稹,解州闻喜人。
长到四岁的时候失去了父亲,母亲樊氏教育他,(他)通晓儒家经典要旨和诸子百家的作品。
崇宁五年考取进士,回答策问时斥责章淳误国。
多次升迁后出任河南洛阳令,宰相吴敏知道他有才能,提拔他担任开封士曹。
金兵攻占太原,朝廷准备议和并割让三镇地给金人。
赵鼎说:“祖宗留下的土地不可以给别人,有什么可以商量的?”不久京城失守,徽钦二帝被金兵掳走,带到北方。
金人商量立张邦昌为皇帝,赵鼎与胡寅、张浚逃到太学中,不肯书写议状。
高宗即位,任命赵鼎代理户部员外郎,不久又提拔为右司谏。
刘光世的部将王德擅自杀死韩世忠的将领,而韩世忠也率领部下夺取建康府衙。
赵鼎说:“王德在外统领军队,专权杀人没有顾忌,这样如果不进行治理,什么不能做呢?”皇上命令赵鼎审讯王德。
赵鼎又请求皇上下令严词斥责韩世忠,而且下令抓捕韩世忠的将领并交给有关部门治罪,各位将领都肃然无声。
皇上说:“肃宗复兴时在灵武得到一个李勉,朝廷才开始受到尊敬,现在我得到你,就没有什么愧对古人了。
”中丞范宗尹说,旧例没有从司谏升为殿中侍御史的,高宗说:“赵鼎在担任谏官时非常尽职,他提出的四十件事,已经施行了三十六件。
”不久迁为侍御史。
赵鼎上疏说:“当年张浚出使川陕,国势比今天强盛百倍。
张浚有补天浴日伟大的功劳,陛下有砺山带河永远不变的誓言。
君臣互相信任,古今没有第二,(张浚现在)却最终遭到别人非议,以致被放逐。
如今我没有张浚那样的功劳却担任了他的官职,(如果我)迅速远离朝廷,是不是就能避开别人的议论呢?”又说:“我请求带领士兵,数量不满一千,一半都是老弱病残,所赐给的财物又很少,推荐人的任命书刚刚下达,弹劾人的文书已经到来。
我每天按皇上的心意行事,想要陈述我的观点还是很艰难,何况远在千里之外的人呢?”当时的人们都为他的离去惋惜,御史台有人上谏留下他。
这时刚好有边疆报告送来,赵鼎常常陈述用兵的大计。
等到他上朝辞行时,高宗说:“你怎么能离去呢?我将要任命你作宰相。
”九月,任命赵鼎为尚书右仆射、同中书门下平章事兼知枢密院事,诏书一下,满朝大臣都来祝贺他。
在吉阳三年,深居简出,门人和旧日同僚都不敢来往来问候。
只有广西帅张宗元不时给他送米。
秦桧知道这件事后,命令吉阳军每月开具存亡的报告。
赵鼎派人告诉他的儿子赵汾说:“秦桧一定要杀我,我死了,你们就没有忧患,不这样的话,灾祸会降临到我们一家人身上。
”留下遗言叫他的儿子把他送回家安葬,于是绝食而死。
当时是绍兴十七年。
天下人听说这件事都为他悲伤。
二、阅读下面的文言文,完成5-8题。
(19分)陈韡,字子华,福州候官人。
父孔硕,为朱熹、吕祖谦门人。
登开禧元年进士第,嘉定十四年,辟京东、河北干官。
韡谓:“山东、河北遗民,宜使归耕其土,给耕牛农具。
然后括淮甸闲田,募民为兵,给田而薄征之;盐丁又别廪为一军,此第二重藩篱也。
”十五年,淮西告捷,韡策金人必专向安丰,使卞整、张惠各以其兵屯卢州以待之。
其后金人果犯安丰,韡调诸军应援捣虚,遂有堂门之捷,俘其四驸马者。
绍定二年冬,盗起闽中,帅王居安属韡提举四隅保甲,韡有亲丧,辞之。
明年,起复,知南剑州。
时有议当招不当捕者,韡言:“始者贼仅百计,招而不捕,养之至千,又养之至万,今复养之,将至于无算。
”韡亲提兵督捕,所至克捷。
四年二月,躬往邵武督捕余寇,贼首迎降,韡以其力屈乃降,卒诛之。
赣寇陈三枪据松梓山砦出没江西广东所至屠残韡遣官吏谕降贼辄杀之乃谓盗贼起于贪吏劾其尤者二人韡亲督诸将,乘春瘴未生,薄松梓山。
士皆攀厓上,贼巢荡为烟埃,端平二年,入奏事,帝称其平寇功,韡顿首言曰:“臣不佞,徒有孤忠,仗陛下威灵,苟逃旷败耳,何功之有。
”景定元年,援福建安抚大使知福州。
明年卒,年八十有三。
崔福者,故群盗,尝为官军所捕,逸去。
因隶军籍,收李全有功,名重江、淮,又累从韡捕贼,积功至刺史、大将军。
会淮兵有警,步帅王鉴出师,鉴请福行,韡因厚遣之。
福不乐为鉴用,遇敌不击,托以葬女擅归,亦不闻于制置司。
鉴怒,请必正其慢令之罪。
会韡亦厌忌之,遂坐以军法。
(节选自《宋史·陈韡传》)5、下列对文中划波浪线部分的断句,正确的一项是(3分)A、赣寇陈三枪据松梓山砦/出没江西/广东/所至屠残/韡遣官吏谕降贼/辄杀之/乃谓盗贼起于贪/吏劾其尤者二人/B、赣寇陈三枪据松梓山砦/出没江西/广东/所至屠残/韡遣官吏谕降/贼辄杀之/乃谓盗贼起于贪吏劾其尤者二人/C、赣寇陈三枪据松梓山砦/出没江西/广东/所至屠残/韡遣官吏谕降贼/辄杀之/乃谓盗贼起于贪吏/劾其尤者二人/D、赣寇陈三枪据松梓山砦/出没江西/广东/所至屠残/韡遣官吏谕降/贼辄杀之/乃谓盗贼起于贪吏/劾其尤者二人/6、下列对文中加点词语的相关内容的解说,不正确的一项(3分)A、门人的意思可以是门客,也可以是弟子(即求学者),本文中的意思是后者。
B、遗民这个词有多重含义,在这里是指躲避金人的劫掠,逃到南方的地方百姓。
C、保甲是一种户籍编制制度,几户联保,设保长一名;文中意即推举陈韡为保长。
D、中国古代帝王的女婿称作“驸马”。
辽、金等少数民族王朝的帝婿也用此称谓。
7、下列对原文有关内容的概括和分析,不正确的一项是(3分)A、陈韡开始为官,便倡议屯田御边。
他任职后提出,官府可以给百姓提供土地、耕牛和农具,再把百姓武装起来,以此作为抵挡金兵南下的屏障。
B、陈韡思路清晰,平贼寇立场坚定。
他常常亲自督率军队,四方征战,深得皇帝信任;对待贼寇态度强硬,对有的投降的盗贼也找理由杀掉。
C、陈韡足智多谋,作战中善出奇兵。
他深得用兵之道,战略上能准确地判断敌人的进攻方向,战术上注重协调保障、出其不意,所以总能出奇制胜。
D、陈韡以己好恶,对崔福先斩后奏。
崔福早年为寇,但从军后屡立战功;而陈韡接到王鉴的报告后,恰好自己也不喜欢他,就将崔福军法处置,实为不妥。
8、把文中划横线的句子翻译成现代汉语。
(10分)(1)臣不佞,徒有孤忠,仗陛下威灵,苟逃旷败耳,何功之有。
(2)福不乐为鉴用,遇敌不击,托以葬女擅归,亦不闻于制置司。
5、D6、C(提举四隅保甲是官职名,负责管理各地的保甲组织。
保长由联保的几户推举即可,不需要大帅举荐。
)7、A(文中“宜使归耕其土”意思是让百姓返回各自的土地上耕种,并非官府提供土地。
)8、(1)我并没有什么才能,所有的只是一片忠心,仰仗着陛下的神威,暂且免于失败罢了,哪有什么功劳。
(“不佞”“逃旷败”,宾语前置各一分,句意2分)(2)崔福不乐意被王鉴调用,遇到敌人也不出击,以给女儿下葬为理由擅自回来,也不向制置司报告。
(“乐为”“托”“闻”各1分,句意2分)三、阅读下面这首宋诗,完成9-10题(11分)弈棋二首呈任公渐(其一)黄庭坚偶无公事客休时,席上谈兵校两棋。
