静力学基础习题及答案
(完整版)静力学基础习题及答案

静力学基础一、判断题1.外力偶作用的刚结点处,各杆端弯矩的代数和为零。
(×)2.刚体是指在外力的作用下大小和形状不变的物体。
(√)3.在刚体上加上(或减)一个任意力,对刚体的作用效应不会改变。
(×)4.一对等值、反向,作用线平行且不共线的力组成的力称为力偶。
(√)5.固定端约束的反力为一个力和一个力偶。
(×)6.力的可传性原理和加减平衡力系公理只适用于刚体。
(√)7.在同一平面内作用线汇交于一点的三个力构成的力系必定平衡。
(×)8.力偶只能使刚体转动,而不能使刚体移动。
(√)9.表示物体受力情况全貌的简图叫受力图。
(√)10.图1中F对 O点之矩为m0 (F) = FL 。
(×)图 1二、选择题1. 下列说法正确的是( C )A、工程力学中我们把所有的物体都抽象化为变形体。
B、在工程力学中我们把所有的物体都抽象化为刚体。
C、稳定性是指结构或构件保持原有平衡状态。
D、工程力学是在塑性范围内,大变形情况下研究其承截能力。
2.下列说法不正确的是( A )A、力偶在任何坐标轴上的投形恒为零。
B、力可以平移到刚体内的任意一点。
C、力使物体绕某一点转动的效应取决于力的大小和力作用线到该点的垂直距离。
D、力系的合力在某一轴上的投形等于各分力在同一轴上投形的代数和。
3.依据力的可传性原理,下列说法正确的是( D )A、力可以沿作用线移动到物体内的任意一点。
B、力可以沿作用线移动到任何一点。
C、力不可以沿作用线移动。
D、力可以沿作用线移动到刚体内的任意一点。
4.两直角刚杆AC、CB支承如图,在铰C处受力F作用,则A、B两处约束力与x轴正向所成的夹角α、β分别为:α=___B___,β=___D___。
A、30°;B、45°;C、90°;D、135°。
5.下列正确的说法是。
( D )图 2A、工程力学中,将物体抽象为刚体。
B、工程力学中,将物体抽象为变形体。
《理论力学》静力学典型习题+答案
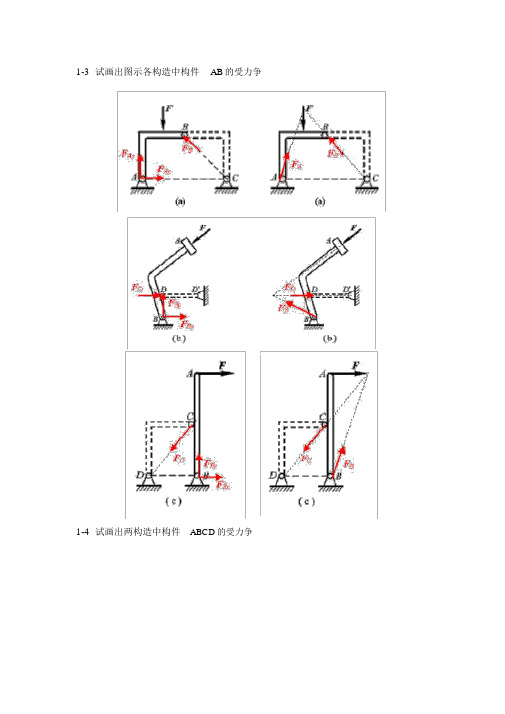
1-3 试画出图示各构造中构件AB的受力争1-4 试画出两构造中构件ABCD的受力争1-5 试画出图 a 和 b 所示刚系统整体各个构件的受力争1-5a1-5b1- 8 在四连杆机构的ABCD的铰链 B 和 C上分别作用有力F1和 F2,机构在图示位置均衡。
试求二力F1和 F2之间的关系。
解:杆 AB,BC, CD为二力杆,受力方向分别沿着各杆端点连线的方向。
解法 1( 分析法 )假定各杆受压,分别选用销钉 B 和 C 为研究对象,受力以下图:yyFBCC xB Fo45BCx30o o F60F2CDF AB F1由共点力系均衡方程,对 B 点有:F x0F2F BC cos4500对 C点有:F x0FBC F1 cos3000解以上二个方程可得:F12 6F2 1.63F23解法 2( 几何法 )分别选用销钉 B 和 C 为研究对象,依据汇交力系均衡条件,作用在 B 和C 点上的力构成关闭的力多边形,以下图。
F F2BCF AB o30o45CD60oFF BC F1对 B 点由几何关系可知:F2F BC cos450对 C 点由几何关系可知:F BC F1 cos300解以上两式可得:F1 1.63F22-3 在图示构造中,二曲杆重不计,曲杆AB 上作用有主动力偶 M。
试求 A 和 C 点处的拘束力。
解: BC为二力杆 ( 受力以下图 ) ,故曲杆 AB 在 B 点处遇到拘束力的方向沿BC 两点连线的方向。
曲杆AB遇到主动力偶M的作用, A 点和 B 点处的拘束力一定构成一个力偶才能使曲杆AB保持均衡。
AB受力以下图,由力偶系作用下刚体的均衡方程有(设力偶逆时针为正):M0 F A10a sin(450 )M 0F A0.354Ma此中:tan 1。
对 BC杆有:F C FB F A0.354M 3aA,C两点拘束力的方向以下图。
2-4解:机构中 AB杆为二力杆,点A,B 出的拘束力方向即可确立。
静力学习题课答案

【1】 梁AB 一端为固定端支座,另一端无约束,这样的梁称为悬臂梁。
它承受均布荷载q 和一集中力P 的作用,如图4-9(a )所示。
已知P =10kN , q =2kN/m ,l =4m ,︒=45α,梁的自重不计,求支座A 的反力。
【解】:取梁AB 为研究对象,其受力图如图4-9(b )所示。
支座反力的指向是假定的,梁上所受的荷载和支座反力组成平面一般力系。
在计算中可将线荷载q 用作用其中心的集中力2qlQ =来代替。
选取坐标系,列平衡方程。
)(kN 07.7707.010cos 0cos - 0A A →=⨯====∑ααP X P X X)(kN 07.11707.010242sin 2 0sin 2 0A A ↑=⨯+⨯=+==--=∑ααP ql Y P qlY Y )( m kN 28.404707.0108423sin 83 0sin 422ql 022A A ⋅=⨯⨯+⨯⨯=⋅+==⋅-⎪⎭⎫⎝⎛+-=∑l P ql m l P l l m M A αα力系既然平衡,则力系中各力在任一轴上的投影代数和必然等于零,力系中各力对任一点之矩的代数和也必然为零。
因此,我们可以列出其它的平衡方程,用来校核计算有无错误。
校核028.40407.114424242A A B =+⨯-⨯⨯=+⋅-⨯=∑m l Y l ql M 可见,Y A 和m A 计算无误。
【2】 钢筋混凝土刚架,所受荷载及支承情况如图4-12(a )所示。
已知kN 20 m,kN 2 kN,10 kN/m,4=⋅===Q m P q ,试求支座处的反力。
【解】:取刚架为研究对象,画其受力图如图4-12(b )所示,图中各支座反力指向都是假设的。
本题有一个力偶荷载,由于力偶在任一轴上投影为零,故写投影方程时不必考虑力偶,由于力偶对平面内任一点的矩都等于力偶矩,故写力矩方程时,可直接将力偶矩m 列入。
设坐标系如图4-12(b )所示,列三个平衡方程)(kN 3446106 06 0A A ←-=⨯--=--==++=∑q P X q P X X)(kN 296418220310461834 036346 0B B A ↑=⨯++⨯+⨯=+++==⨯--⨯-⨯-⨯=∑q m Q P Y q m Q P Y M)(kN 92920 00B A B A ↓-=-=-==-+=∑Y Q Y Q Y Y Y校核3462203102)9(6)34(6363266 C=⨯⨯+-⨯+⨯+-⨯--⨯=⨯+-++-=∑qmQPYXMAA说明计算无误。
静力学习题及答案

04
平面任意力系
平面任意力系简化及结果分析
主矢和主矩的概念及计算 简化结果的判断方法
简化中心的选取原则
举例分析平面任意力系的 简化过程
平面任意力系平衡条件及方程
平面任意力系平衡的必要与 充分条件
平衡方程的应用举例
平衡方程的建立及求解方法
特殊情况下平衡方程的应用
平面任意力系平衡问题解法举例
01
力偶性质
力偶没有合力,所以力偶不能用一个力来代替,也不能与一个力来平衡;力偶对其作用面内任一点之矩恒等于力 偶矩,且与矩心位置无关;在同一平面内的两个力偶,如果它们的力偶矩大小相等,转向相同,则这两个力偶等 效。
平面力偶系合成与平衡条件
平面力偶系合成
若干个在同一平面内的力偶组成平面力偶系,可依次用矢量合成的方法求出各力偶的合力偶矩,再求 出这些合力偶矩的矢量和。
80%
解法一
几何法。通过作力多边形或力三 角形,利用几何关系求解未知力 。
100%
解法二
解析法。根据平衡方程列出方程 组,通过求解方程组得到未知量 。
80%
解法三
图解法。在图上按比例作出各力 的图示,利用平行四边形法则或 三角形法则求解未知力。
03
平面力偶系
力偶及其性质
力偶定义
由两个大小相等、方向相反且不共线的平行力组成的力系。
力的单位
在国际单位制中,力的单位是牛顿(N)。
静力学公理及其推论
01
02
静力学公理:作用于刚体 的两个力,使刚体保持平 衡的必要和充分条件是: 这两个力大小相等、方向 相反,且作用在同一直线 上。
静力学公理的推论
03
04
05
二力平衡条件:作用在刚 体上的两个力平衡的必要 和充分条件是:这两个力 的大小相等、方向相反, 且作用在同一直线上。
(完整版)工程力学课后习题答案

工程力学练习册学校学院专业学号教师姓名第一章静力学基础 1第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)2 第一章静力学基础(d)(e)(f)(g)第一章静力学基础 3 1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)4 第一章静力学基础1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)第一章静力学基础 5 (b)(c)(d)6 第一章静力学基础(e)第一章静力学基础7 (f)(g)8 第二章 平面力系第二章 平面力系2-1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如第二章 平面力系 9图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F AB BC 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
工程力学(第二版)习题册答案

一、填空题
1. 相 对 滑 动 相 对 滑 动 趋 势 接触面的切线 相反 2. 10N 20N 30N 30N 30N 3. 100N 竖直向上 平衡 4. 平稳无冲击 自锁
阻碍物体相对滑动
相对滑动趋势
二、选择题
1. A
三、简答题
1. ①问题中含有可能发生相对滑动的摩擦面,因此,存在摩擦力; ②受力图中要画出摩擦力,摩擦力总是沿着接触面的切线方向并与物体相对滑
7.
8.
9.
第二章 平面力系
第一节 共线力系的合成与平衡
一、填空题
1. 在同一条直线上
2. FR Fi FR 0
二、计算题
设向右为正方向。 则 FR=120+40-80-200=-120N 方向:水平向左
第二节 平面汇交力系的合成
一、填空题
1. 作用于同一平面内且各力作用线相交于一点的力系 共线力系 力的作用点 2. -F 或 F 0 0 -F 或 F 3. 合力在任一坐标轴上的投影 各分力在同一轴上投影的代数和 4. F4 F3 5. 自行封闭 6. 所有各力在 x 轴上投影的代数和为零 所有各力在 y 轴上投影的代数和为零 Fx 0 Fy 0
3. 后轮:摩擦力向前 前轮:摩擦力向后
4. 不下滑,处于自锁状态
四、计算题
FT 60 18 3N
五、应用题
1. (提示)从摩擦力与 F 对 B 点的力矩大小的比较进行考虑
第三章 空间力系 第一节 力在空间坐标轴上的投影与合成
一、填空题
1. 力的作用线不都在同一平面内呈空间分布的力系 2. 一次投影法 二次投影法
二、选择题
1. A 2.B
它所限制物体
三、简答题
1.柔性体约束只能承受拉力,不能承受压力。 2.被约束物体可以沿约束的水平方向自由滑动,也可以向离开约束的方向运动, 但不能向垂直指向约束的方向运动。 3.剪刀的两半部分可以绕销钉轴线相对转动,但不能在垂直销钉轴线的平面内沿 任意方向做相对移动。 4.木条不能沿圆柱销半径方向移动,但可以绕销轴做相对转动。 5.固定端约束既限制物体在约束处沿任何方向的移动,也限制物体在约束处的转 动。
理论力学习题及答案(全)

第一章静力学基础一、是非题1.力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
()2.在理论力学中只研究力的外效应。
()3.两端用光滑铰链连接的构件是二力构件。
()4.作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
()5.作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
()6.三力平衡定理指出:三力汇交于一点,则这三个力必然互相平衡。
()7.平面汇交力系平衡时,力多边形各力应首尾相接,但在作图时力的顺序可以不同。
()8.约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
()二、选择题1.若作用在A点的两个大小不等的力F1和F2,沿同一直线但方向相反。
则其合力可以表示为。
①F1-F2;②F2-F1;③F1+F2;2.作用在一个刚体上的两个力F A、F B,满足F A=-F B的条件,则该二力可能是。
①作用力和反作用力或一对平衡的力;②一对平衡的力或一个力偶。
③一对平衡的力或一个力和一个力偶;④作用力和反作用力或一个力偶。
3.三力平衡定理是。
①共面不平行的三个力互相平衡必汇交于一点;②共面三力若平衡,必汇交于一点;③三力汇交于一点,则这三个力必互相平衡。
4.已知F1、F2、F3、F4为作用于刚体上的平面共点力系,其力矢关系如图所示为平行四边形,由此。
①力系可合成为一个力偶;②力系可合成为一个力;③力系简化为一个力和一个力偶;④力系的合力为零,力系平衡。
5.在下述原理、法则、定理中,只适用于刚体的有。
①二力平衡原理;②力的平行四边形法则;③加减平衡力系原理;④力的可传性原理;⑤作用与反作用定理。
三、填空题1.二力平衡和作用反作用定律中的两个力,都是等值、反向、共线的,所不同的是。
2.已知力F沿直线AB作用,其中一个分力的作用与AB成30°角,若欲使另一个分力的大小在所有分力中为最小,则此二分力间的夹角为度。
(完整版)工程力学课后习题答案

工程力学练习册学校学院专业学号教师姓名第一章静力学基础 1第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)2 第一章静力学基础(d)(e)(f)(g)第一章静力学基础 3 1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)4 第一章静力学基础1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)第一章静力学基础 5 (b)(c)(d)6 第一章静力学基础(e)第一章静力学基础7 (f)(g)8 第二章 平面力系第二章 平面力系2-1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如第二章 平面力系 9图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F AB BC 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
静力学练习题及参考答案

静力学练习题及参考答案1. 问题描述:一根长度为L的均质杆以一端固定在墙上,另一端悬挂一重物。
重物造成的杆的弯曲应力最大为σ。
杆的质量可以忽略不计。
计算重物的质量m。
解答:根据静力学原理,杆的弯曲应力可以用公式计算:σ = M / S,其中M是杆的弯矩,S是杆的截面横截面积。
因为杆是均质杆,所以它的截面横截面积在整个杆上都是相等的。
设杆的截面横截面积为A。
杆的弯矩M可以通过杆的长度L和重物的力矩T计算得到:M = T * (L/2)。
代入上面的公式,我们可以得到:σ = (T * (L/2)) / A。
根据题目的描述,我们可以得到如下等式:σ = (m * g * (L/2)) / A,其中g是重力加速度。
我们可以将这个等式转换成求解未知质量m的方程。
将等式两边的A乘以m,并将等式两边的m乘以g,我们可以得到如下方程:m^2 = (2 * σ * A) / (g * L)解这个方程,我们可以求得未知质量m。
2. 问题描述:一根均质杆的长度为L,质量为M。
杆的一端固定在墙上,另一端悬挂一重物。
杆与地面的夹角为θ。
重物造成的杆的弯曲应力最大为σ。
求重物的质量m。
解答:在这个问题中,除了重物的力矩,还需要考虑到重力对杆的力矩。
由于杆是均质杆,其质量可以均匀分布在整个杆上。
假设杆上的每个微小质量元都受到与其距离一致的力矩。
重物造成的力矩可以用公式计算:M1 = m * g * (L/2) * sinθ,其中g 是重力加速度。
由于杆是均质杆,它的质心位于杆的中点。
因此重力对杆的力矩可以用公式计算:M2 = M * g * (L/2) * cosθ。
根据静力学的原理,杆的弯曲应力可以用公式计算:σ = M / S,其中M是杆的弯矩,S是杆的截面横截面积。
在这个问题中,我们可以将弯曲应力的计算公式推广到杆的中点(也就是质心):σ = (M1 + M2) / S代入上面的公式,我们可以得到:σ = ((m * g * (L/2) * sinθ) + (M *g * (L/2) * cosθ)) / S根据题目的描述,我们可以得到如下等式:σ = ((m * g * (L/2) * sinθ) + (M * g * (L/2) * cosθ)) / (A / 2),其中A是杆的横截面积。
静力学习题及答案

静力学习题及答案静力学习题及答案静力学是力学的一个重要分支,研究物体在静止状态下的平衡条件和力的作用。
在学习静力学的过程中,我们常常会遇到一些练习题,通过解答这些问题可以帮助我们更好地理解和掌握静力学的基本原理和方法。
本文将给出一些常见的静力学学习题及其答案,希望对大家的学习有所帮助。
1. 简支梁上的均匀物体问题:一根质量为m、长度为L的均匀杆,两端分别简支在两个支点上,杆的中点处有一个质量为M的物体悬挂在上面。
求支点对杆的反力。
解答:首先我们可以根据杆的对称性得出,两个支点对杆的反力大小相等,记为R。
然后我们可以根据力的平衡条件得出以下方程:在x方向上:0 = R + R在y方向上:0 = Mg + 2R解方程得到:R = Mg/2所以支点对杆的反力大小为Mg/2。
2. 斜面上的物体问题:一个质量为m的物体静止放置在一个倾斜角为θ的光滑斜面上,斜面的倾角方向与水平方向的夹角为α。
求物体受到的斜面支持力和重力的合力大小。
解答:首先我们可以将物体的重力分解为斜面方向和垂直斜面方向的分力。
重力沿斜面方向的分力为mg*sin(α),垂直斜面方向的分力为mg*cos(α)。
根据力的平衡条件,物体在斜面上的合力应该为零。
所以斜面支持力的大小等于物体在斜面方向上的重力分力大小,即斜面支持力的大小为mg*sin(α)。
3. 悬挂物体的倾斜角问题:一个质量为m的物体悬挂在两个长度分别为L1和L2的绳子上,绳子的另一端分别固定在两个点上,两个点之间的距离为L。
求物体的倾斜角θ。
解答:首先我们可以根据力的平衡条件得出以下方程:在x方向上:0 = T1*sin(θ) - T2*sin(θ)在y方向上:0 = T1*cos(θ) +T2*cos(θ) - mg其中T1和T2分别为两条绳子的张力。
解方程得到:T1 = T2 = mg/(2*cos(θ))根据三角函数的定义,我们可以得到:L1/L = sin(θ) 和L2/L = cos(θ)将上面的方程代入,解方程得到:θ = arctan(L1/L2)通过解答这些静力学学习题,我们可以更好地理解和应用静力学的基本原理和方法。
静力学和动力学练习题(含答案)

静力学和动力学练习题(含答案)静力学和动力学练题 (含答案)静力学练题1. 一个质量为10kg的物体置于水平面上。
一个力F = 50N施加在物体上,使其保持静止。
求摩擦力的大小。
解答:根据静力学的条件,物体保持静止时,合力为零。
我们可以设置以下方程:ΣF = F - F_f = 0其中,ΣF为合力,F为施加在物体上的力,F_f为摩擦力。
代入已知数据,得到:50N - F_f = 0解方程得到 F_f = 50N,因此摩擦力的大小为50N。
2. 一个质量为5kg的物体沿斜面下滑,斜面的倾角为30度。
在不考虑摩擦的情况下,求物体的加速度。
解答:根据静力学的条件,物体在斜面上保持平衡时,合力沿着斜面的方向为零。
我们可以设置以下方程:ΣF = m * g * sinθ - m * g * cosθ = 0其中,ΣF为合力,m为物体的质量,g为重力加速度,θ为斜面的倾角。
代入已知数据,得到:5kg * 9.8m/s^2 * sin30° - 5kg * 9.8m/s^2 * cos30° = 0解方程得到加速度 a = 4.9m/s^2,因此物体的加速度为4.9m/s^2。
动力学练题1. 一个质量为2kg的物体以速度4m/s沿着水平方向运动。
一个恒力F = 6N施加在物体上,与运动方向垂直。
求物体在3秒后的速度。
解答:根据动力学的条件,物体在受到恒力作用时,速度的变化可以通过牛顿第二定律来计算。
我们可以使用以下公式:F = m * a其中,F为力的大小,m为物体的质量,a为物体的加速度。
根据题目已提供的数据,可以计算出物体的加速度:6N = 2kg * a解方程得到 a = 3m/s^2。
然后,我们可以使用以下公式来计算物体的速度变化:v = u + a * t其中,v为物体的最终速度,u为物体的初始速度,a为物体的加速度,t为时间间隔。
代入已知数据,计算得到:v = 4m/s + 3m/s^2 * 3s = 4m/s + 9m/s = 13m/s因此,物体在3秒后的速度为13m/s。
《工程力学》详细版习题参考答案

∑ Fx
=FAx
+
FBx
+
FCx
=− 1 2
F
+
F
−
1 2
F
=0
∑ Fy
= FAy
+
FBy
+
FCy
= − 3 2
F
+
3 F = 0 2
∑ M B= FBy ⋅ l=
3 Fl 2
因此,该力系的简化结果为一个力偶矩 M = 3Fl / 2 ,逆时针方向。
题 2-2 如图 2-19(a)所示,在钢架的 B 点作用有水平力 F,钢架重力忽 略不计。试求支座 A,D 的约束反力。
(a)
(b)
图 2-18
解:(1)如图 2-18(b)所示,建立直角坐标系 xBy。 (2)分别求出 A,B,C 各点处受力在 x,y 轴上的分力
思考题与练习题答案
FAx
= − 12 F ,FAy
= − 3 F 2
= FBx F= ,FBy 0
FCx
= − 12 F ,FCy
= 3 F 2
(3)求出各分力在 B 点处的合力和合力偶
(3)根据力偶系平衡条件列出方程,并求解未知量
∑ M =0 − aF + 2aFD =0
《工程力学》
可解得 F=Ay F=D F /2 。求得结果为正,说明 FAy 和 FD 的方向与假设方向相同。 题 2-3 如 图 2-20 ( a ) 所 示 , 水 平 梁 上 作 用 有 两 个 力 偶 , 分 别 为
3-4 什么是超静定问题?如何判断问题是静定还是超静定?请说明图 3-12 中哪些是静定问题,哪些是超静定问题?
(a)
工程力学课后习题答案(静力学和材料力学)
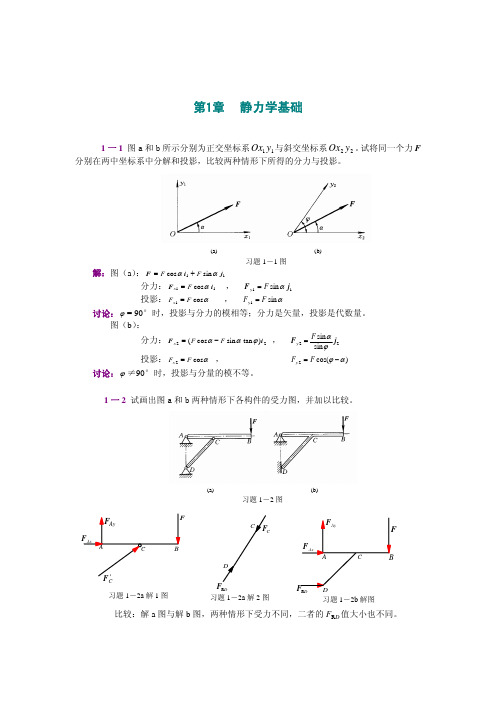
1 一 3 试画出图示各构件的受力图。
F
D
习题 1-3 图
C
F
D
C
A
B
FA
FB
习题 1-3a 解 1 图
F Ax
A
B
FAy
FB
习题 1-3a 解 2 图
C
BF
B
D
FB
FD
C
A
FA 习题 1-3b 解 2 图
W
FAx
FAy
习题 1-3c 解图
F
A
A
F
α
B C
FA
D
FAFD 习题 1-3d 解 2 图
FB2 x
B
FDy
C FB2 y
F Dx D
W
习题 1-4b 解 2 图
F'B1
B
F'B2x
F'B2 y F1
A B
F'B2x
习题 1-4c 解 1 图
F1 F'B2 y
FDx D FDy
F'B2x B
C
F'B2 y
W
F'B2 B
习题 1-4c 解 2 图
习题 1-4b 解 3 图
FA
A
B
F B1
习题 1-4d 解 1 图
可推出图(b)中 FAB = 10FDB = 100F = 80 kN。
FED αD
FDB FD′ B
FCB
α
B
F 习题 1-12 解 1 图
F AB 习题 1-12 解 2 图
1—13 杆 AB 及其两端滚子的整体重心在 G 点,滚子搁置在倾斜的光滑刚性平面上,如
理论力学 静力学 习题答案

习题:1-1(b)、(c)、(d),1-2(a)、(l)1-1 画出下列各图中物体A,ABC 或构件AB,AC 的受力图。
未画重力的各物体的自重不计,所有接触处均为光滑接触。
1-2 画出下列每个标注字符的物体的受力图。
题图中未画重力的各物体的自重不计,所有接触处均为光滑接触。
习题:2-3,2-5,2-6,2-8,2-12,2-14,2-18,2-10,2-402-3 如图示刚架的点B 作用一水平力F,刚架重量略去不计。
求支座A,D 的约束力F A和F D。
解:一、取刚架为研究对象,画受力图,如图(b)。
二、列平衡方程,求支座 A,D 的约束力 F A 和F D。
由三力平衡汇交定理,支座A 的约束力F A 必通过点C,方向如图(b)所示。
取坐标系Cxy ,由平衡理论得式(1)、(2)联立,解得2-5 图所示为一拨桩装置。
在木桩的点 A上系一绳,将绳的另一端固定在点C,在绳的点B 系另一绳BE,将它的另一端固定在点 E。
然后在绳的点 D 用力向下拉,使绳的 BD 段水平,AB 段铅直,DE 段与水平线、CB 段与铅直线间成等角θ= 0.1 rad(当 θ很小时,tanθ≈θ)。
如向下的拉力 F =800 N,求绳 AB 作用于桩上的拉力。
解:一、研究节点D,坐标及受力如图(b)二、列平衡方程,求 F DB解得讨论:也可以向垂直于F DE 方向投影,直接得三、研究节点 B ,坐标及受力如图(c) 四、列平衡方程,求 F AB0xF =∑,'sin 0BC DB F F θ-=0yF=∑,cos 0BC AB F F θ-=解得 80kN AB F =2-6 在图示结构中,各构件的自重略去不计,在构件BC 上作用一力偶矩为M 的力偶,各尺寸如图。
求支座A 的约束力。
解:一、研究对象:BC ,受力如图(b ) 二、列平衡方程,求F B 、F C 为构成约束力偶,有三、研究对象:ADC ,受力如图(c ) 四、列平衡方程,求 F A(方向如图)2-8 已知梁AB 上作用一力偶,力偶矩为M,梁长为l ,梁重不计。
理论力学练习册及答案同济

理论力学练习册及答案同济一、静力学基础1. 题目:一个均匀的木杆,长度为2m,重量为50kg,一端固定在墙上,另一端自由。
求木杆的重心位置。
答案:木杆的重心位于其几何中心,即木杆的中点。
由于木杆均匀,其重心距离固定端1m。
2. 题目:一个质量为10kg的物体,受到三个力的作用:F1=20N向右,F2=30N向上,F3=15N向左。
求物体的合力大小和方向。
答案:合力F = F1 + F2 + F3 = (20N, 0) + (0, 30N) + (-15N, 0) = (5N, 30N)。
合力大小F = √(5² + 30²) = √(25 + 900) = √925 ≈30.41N。
合力方向与水平线的夹角θ满足tanθ = 30N / 5N = 6,所以θ ≈ 80.53°。
二、动力学基础1. 题目:一个质量为2kg的物体,从静止开始沿直线运动,加速度为5m/s²。
求物体在第3秒末的速度和位移。
答案:速度v = at = 5m/s² × 3s = 15m/s。
位移s = 0.5at² = 0.5 × 5m/s² × (3s)² = 22.5m。
2. 题目:一个质量为5kg的物体,以20m/s的初速度沿直线运动,受到一个恒定的阻力,大小为10N。
求物体在第5秒末的速度。
答案:加速度a = F/m = -10N / 5kg = -2m/s²。
速度v = v0 + at = 20m/s - 2m/s² × 5s = 0m/s。
三、转动动力学1. 题目:一个半径为0.5m的均匀圆盘,质量为10kg,绕通过其中心的轴旋转。
若圆盘的角加速度为10rad/s²,求圆盘的转动惯量。
答案:转动惯量I = mr² = 10kg × (0.5m)² = 2.5kg·m²。
《理论力学》静力学典型习题+答案
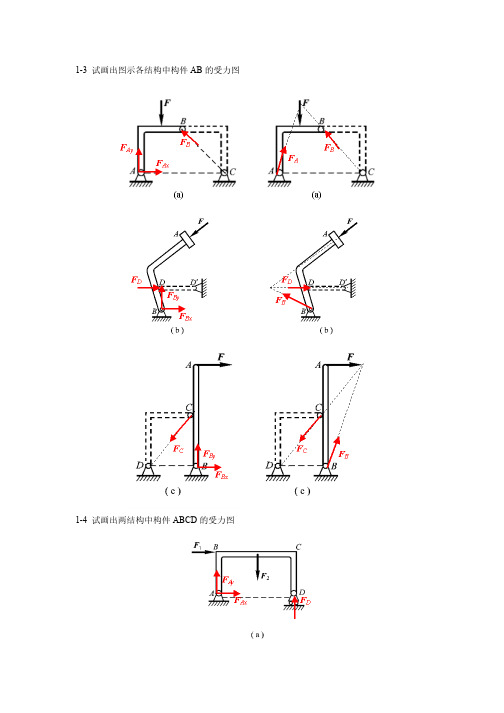
1-3 试画出图示各结构中构件AB的受力图的受力图1-4 试画出两结构中构件ABCD的受力图的受力图1-5 试画出图a和b所示刚体系整体各个构件的受力图所示刚体系整体各个构件的受力图1-5a 1-5b 在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
为二力杆,受力方向分别沿着各杆端点连线的方向。
为二力杆,受力方向分别沿着各杆端点连线的方向。
6F 2 F BCF ABB45oy x F BCF CD C60o F 130ox y 力构成封闭的力多边形,如图所示。
力构成封闭的力多边形,如图所示。
为二力杆为二力杆((受力如图所示受力如图所示)),故曲杆10a F BC60o F 130o F 2 F BCAB45o 解:机构中AB杆为二力杆,点A,B出的约束力方向即可确定。
由力偶系作用下刚体的平衡条件,点O,C处的约束力方向也可确定,各杆的受力如图所示。
对BC杆有:0=åM30sin20=-××MCBFB对AB杆有:杆有:ABFF=对OA杆有:杆有: 0=åM01=×-AOFMA求解以上三式可得:mNM×=31,NFFFCOAB5===,方向如图所示。
,方向如图所示。
////2-6求最后简化结果。
解:解:2-6a2-6a坐标如图所示,各力可表示为坐标如图所示,各力可表示为: :j Fi FF23211+=,i FF=2,j Fi FF23213+-=先将力系向A点简化得(红色的):j Fi FFR3+=,kFaMA23=方向如左图所示。
由于AR MF^,可进一步简化为一个不过A点的力点的力((绿色的绿色的)),主矢不变,其作用线距A点的距离ad43=,位置如左图所示。
,位置如左图所示。
2-6b同理如右图所示,可将该力系简化为一个不过A点的力(绿色的),主矢为:,主矢为:i F F R2-= 其作用线距A 点的距离a d43=,位置如右图所示。
静力学习题及答案

1 2 q 2 =0
2
D
C
D ND1 NC ND1′
NC-ND1-q×2=0
ND1=-2kN, NC=2kN
M
A B
ND2′
2、取D点为研究对象 ∑Y=0, ND2′+ND1′-P=0 ND2′=7kN 3、取AD杆为研究对象 ∑MA=0, ∑Y=0,
D
YA
XB B YA M A XA YB
对BD杆,有 ∑M B= 0 , P· cos45°-ND· cos45°+F· sin45°= 0 L/2· L· L· ∑Y = 0, P /2-ND+F = 0 ND -P-Y B′= 0 Fmax =μs· D N 所以 (1) (2) (3)
P F YB′ B XB′
取abbd杆为研究对象对ab杆有ma0mybl0ybml2002100kn对bd杆对bd杆有m有pdbybxbndfb0pl2cos45ndlcos45flsin450p2ndf01y0ndpyb02fmaxsnd3所以p2pybspyb0p0410001400knp400kn四图示结构由丁字梁abc直梁ce与支杆dh组成cd点为铰接均不计自重
MA M q XC q M E 45° D SD YC SD C P 30 ° B A C XA
E
45° D
解: 1、取CE杆为研究对象 ∑MC=0, SD=(M+ M+
1 2 q2 1 2
2
q2
2
-SDsin45°×2=0
50 200 2 2 sin 45
)÷sin45°×2=
=225
一、在图示平面力系中,已知:F1 = 10N,F2 =40N,F3 = 40N,M = 30N· m。 试求其合力,并画在图上(图中长度单位为米) 解:将力系向O点简化 主矢: R x = F2-F1 = 40-10 = 30N R y = -F3 = -40N 2 R ′= R x 2 R y=50N 主矩: MO =(F1 +F2 +F3)×3+M = (10+40+40)×3+30 = 300N· m 合力的作用线至O点的距离 d = MO / R′=6m=OO′ 合力的方向: cos(R,i )= R x / R =0.6 ∠(R,i )=53.13°=β cos(R,j )= R y / R =-0.8 ∠(R,j)=143.13=γ
理论力学静力学典型习题+答案

1-3试画出图示各结构中构件AB的受力图1-4试画出两结构中构件ABCD勺受力图1-5试画出图a和b所示刚体系整体各个构件的受力图1-5a1-5b1- 8在四连杆机构的ABCD勺铰链B和C上分别作用有力F i和F2,机构在图示位置平衡。
试求二力F1和F2之间的关系。
解:杆AB BC CD为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B和C为研究对象,受力如图所示:由共点力系平衡方程,对B点有:F x 0 F2F BC COS45°0对C点有:F x 0 F BC F1COS300 0解以上二个方程可得:F12 6F 1.63F2解法2(几何法)分别选取销钉B和C为研究对象,根据汇交力系平衡条件,作用在B和C点上的力构成封闭的力多边形,如图所示。
对B点由几何关系可知:F2F BC COS450对C点由几何关系可知:F BC F1 COS300解以上两式可得:F1 1.63F22-3在图示结构中,二曲杆重不计,曲杆AB上作用有主动力偶M试求A和C 点处的约束力。
解:BC为二力杆(受力如图所示),故曲杆AB在B点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB受到主动力偶M的作用,A点和B点处的约束力必须构成一个力偶才能使曲杆AB保持平衡。
AB受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正):M 0 F A 10a sin(450) M 0 F A 0.354M其中:tan -。
对BC杆有:F C F B F A 0.354M3 aA,C两点约束力的方向如图所示。
2-4解:机构中AB 杆为二力杆,点A,B 出的约束力方向即可确定。
由力偶系作用下 刚体的平衡条件,点 0,C 处的约束力方向也可确定,各杆的受力如图所示。
对1313 -6aFFi FjF 2 FiF 3- F i - —Fj2 222F RFi3Fj M A■-3 Fak F R M A V3 d a F R2Fi24d3 a F X 0 PsinFB X0 F y 0 F By P P cos0 F X 04F A X F B X 0F y 0F AyF By0 M A 0 MA F Byl 0求解以上三式可得:M 1 3N m , F ABF OF C 5N ,方向如图所示Psi nAF BxF AxBC 杆有:M 0对AB 杆有: F B F AF B BC sin300 M 2对OA 杆有:M 0 M i F AOA 0F By , MFA X,FAy, FBX, M A 0 N D aG -cos F l coscos2F y 0 N D cosG F 0N D ,arccosf 2(F (2FG)a 卡G)l ]F Ay F By P(1 COS ) M A P(1 cos )1M y O p eta n F BC cos c F BC sin eta n 0 F BC60.6N 2M x' 0 P 1 aF B c F BC S in2a 0 F B100N F y 0 F Z0F Ay,F A;z M x 0 M DE 0 F2COS4500 F20 M AO 0 F6COS45° a F COS450 COS450 a 0 F6 2 F M BH 02F4COS450 a F6COS450 a 0 F4 2F M AD 02F1 a F6COS450 a F sin450 a 0 £ 1 2 F M CD 02F1 a F3 a F sin45°a 0 F3 1F M BC 02F x 0F3 a F5 a F4COS450 a 0 F50 M 1500N cm Fy 0M O0以下几题可看一看!FA , F NA , FB , F NB ,tan3( f sif s2)FNB 0ta n 6002aM cf s2f si2 3F By 2a 0 F ByM H 0 F D y a Fa 0 F Dy FM BF DX a F 2a 0 F DX2FF y 0F AyF DyF By 0F AyF M A0 FD X a FB X 2aFB XFM BF AX 2aFD Xa0 FA XFM c 0 F D bF XF D-F M A0 F B bF XbF i F 2 (F i2Mpcos45° psin45° F 2)DF N 2 N iF i F 2f s N i f s N 2F i ,N i ,F 2,N 2, f s:s 2p D F e f 2M0 f siF By0.223, f s2 4.49 FB x N iP(i _f s2) _2( i —f ;2)f s%.223450F xF yM AT cosAC sinF N T sinF s T cos pT sin AC cosAB . sin 2FN , F s , T, fsf s 0.646a l . a几F NB a Pcos-Psi n 022 3F NA a P cos-Psin a 小 —— 02 2、3 F AF BPsi nM A 0M B 0 F x 0F A F Bf si F NAS 2F NBS24.49 i2MF D )b F ACAyD 2MF (bF 2x)F B F I F AAa b F A F 3 FxAy F i F 3 cos450F 1M2qa F yF 2aF2 Z M r ( 2qa) F x 0 FAXF 3 cos45(F AX(MaaF AyF 2 F 3si n450 P 4qa 0F AyP 4qa M A F 2 a P 2a 4qa 2a F 3S in450 '3aMM A 24qa 2 Pa M M A0 F By 2a F2a 0 F ByF Ay 2a F 2a 0 F A 『FF x 0 F AXFBx FF 32qa) F 0 F EF2 M C 0 F Bx a F By aV 2(MF AX2q x a) a F E sin450 a 0 F BxM eM BF By FF NDF 3 sin450F yM AM B0F BXM AN 13r P 3rcos60020 N i 6.93(N)F xFA XN 1 sin 60°F AX 6(N) F y 0F AyN 1cos600P 0 F Ay 12.5'(N) FN 1cos300 Tcos300 6.93(N)M A F N 2Lsin2P -cos2 M BF N LsinP Lcos F s Lcos2F S P F SFNtan100 F RC ,F RD F RC , F RD F RC , F RD2 2M A 0 F ND aI 0F ND44M A0F NC a F l 0F NC -FF NDaM O 0 F SC R F SD R 0FNCF X 0sinF — ----------- F----- FS D NCN D1 cos 1 cossin 1 costan —, f SD tanFRC,F2 221 cosF RCSDF NDF SD 0tan — 2 I FaFla cos —2PF RCsi n[180°(1800 2,sin ] ftanFl sinISD (Pa Fl )(1 cos )F yF NDP F SC sin F ND PFl ( (cosasin tan —)2f SD tanFl sin(Pa Fl )(1 cos )F B F ACFBF AC tan1 F3(F ND P) R MDF B \M E (P F NE )1RtanF NDM D M E!FRM DF NDBPL FaM AM EF yF x 4 f sP 4f sP } f s ,1 3f s }F SC%F X0 F NC costa nFl sin (Pa Fl )(1 cos )F NCsinF SC cos F SD 0FNDFSDM E 1FFNE F NE F SD tan2FNDF min{ —P,」 P,R R 3 1 F SD F NE F SE F 02P R M DF SE RF SD 3FFSDf s F ND M FM GF SE;FF SE f s F NEF max 0.362.该系统的位置可通过杆OA 与水平方向的夹角B 完全确定,有一个自由度。
工程力学(静力学答案)
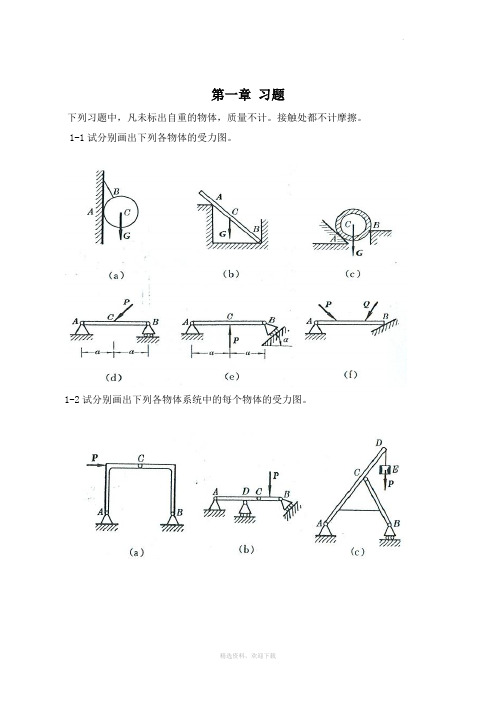
第一章习题下列习题中,凡未标出自重的物体,质量不计。
接触处都不计摩擦。
1-1试分别画出下列各物体的受力图。
1-2试分别画出下列各物体系统中的每个物体的受力图。
1-3试分别画出整个系统以及杆BD,AD,AB(带滑轮C,重物E和一段绳索)的受力图。
1-4构架如图所示,试分别画出杆HED,杆BDC及杆AEC的受力图。
1-5构架如图所示,试分别画出杆BDH,杆AB,销钉A及整个系统的受力图。
1-6构架如图所示,试分别画出杆AEB,销钉A及整个系统的受力图。
1-7构架如图所示,试分别画出杆AEB,销钉C,销钉A及整个系统的受力图。
1-8结构如图所示,力P作用在销钉C上,试分别画出AC,BCE及DEH部分的受力图。
参考答案1-1解:1-2解:1-3解:1-4解:1-5解:1-6解:1-7解:1-8解:第二章 习题参考答案2-1解:由解析法,23cos 80RX F X P P Nθ==+=∑12sin 140RY F Y P P Nθ==+=∑故: 22161.2R RX RY F F F N=+=1(,)arccos2944RYR RF F P F '∠==2-2解:即求此力系的合力,沿OB 建立x 坐标,由解析法,有123cos45cos453RX F X P P P KN==++=∑13sin 45sin 450RY F Y P P ==-=∑故: 223R RX RY F F F KN=+=方向沿OB 。
2-3解:所有杆件均为二力杆件,受力沿直杆轴线。
(a ) 由平衡方程有:0X =∑sin 300ACAB FF -=0Y =∑cos300ACFW -=联立上二式,解得:0.577AB F W =(拉力)1.155AC F W=(压力)(b ) 由平衡方程有:0X =∑cos 700ACAB F F -=0Y =∑sin 700ABFW -=联立上二式,解得:1.064AB F W =(拉力)0.364AC F W=(压力)(c ) 由平衡方程有:0X =∑cos 60cos300ACAB FF -=0Y =∑sin 30sin 600ABAC FF W +-=联立上二式,解得:0.5AB F W=(拉力)0.866AC F W=(压力)(d ) 由平衡方程有:0X =∑sin 30sin 300ABAC FF -=0Y =∑cos30cos300ABAC FF W +-=联立上二式,解得:0.577AB F W =(拉力)0.577AC F W=(拉力)2-4解:(a)受力分析如图所示:由x=∑224cos45042RAF P⋅-=+15.8RAF KN∴=由Y=∑222sin45042RA RBF F P⋅+-=+7.1RBF KN∴=(b)解:受力分析如图所示:由0x =∑3cos 45cos 45010RA RB F F P ⋅--=Y =∑1sin 45sin 45010RA RB F F P ⋅+-=联立上二式,得:22.410RA RB F KN F KN==2-5解:几何法:系统受力如图所示三力汇交于点D ,其封闭的力三角形如图示所以: 5RA F KN=(压力)5RB F KN=(与X 轴正向夹150度)2-6解:受力如图所示:已知,1R F G = ,2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-⋅=--2-7解:受力分析如图所示,取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=0Y =∑sin 45sin 450CBRA F F '-=联立后,解得:0.707RA F P=0.707RB F P=由二力平衡定理 0.707RB CB CBF F F P '===2-8解:杆AB ,AC 均为二力杆,取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=0Y =∑sin 30sin 600ABAC FF W +-=联立上二式,解得:7.32AB F KN =-(受压)27.3AC F KN=(受压)2-9解:各处全为柔索约束,故反力全为拉力,以D ,B 点分别列平衡方程(1)取D 点,列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==(2)取B 点列平衡方程由0Y =∑sin cos 0BDT T αα'-=230BDT T ctg Wctg KN αα'∴===2-10解:取B 为研究对象:由0Y =∑sin 0BC F P α-=sin BC PF α∴=取C 为研究对象:由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑sin cos cos 0BC DC CE F F F ααα--+=联立上二式,且有BCBC F F '= 解得:2cos 12sin cos CE P F ααα⎛⎫=+ ⎪⎝⎭取E 为研究对象:由0Y =∑cos 0NH CEF F α'-=CECE F F '=故有:22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解:取A 点平衡:0x =∑sin 75sin 750ABAD FF -=0Y =∑cos 75cos 750ABAD FF P +-=联立后可得:2cos 75AD AB PF F ==取D 点平衡,取如图坐标系:0x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD PF F F KN'∴===⋅=2-12解:整体受力交于O 点,列O 点平衡由x=∑cos cos300RA DCF F Pα+-=Y=∑sin sin300RAF Pα-=联立上二式得:2.92RAF KN=1.33DCF KN=(压力)列C点平衡x=∑405DC ACF F-⋅=Y=∑305BC ACF F+⋅=联立上二式得:1.67ACF KN=(拉力)1.0BCF KN=-(压力)2-13解:(1)取DEH 部分,对H 点列平衡0x =∑205RD REF F '⋅-= 0Y =∑105RD F Q ⋅-=联立方程后解得: 5RD F Q =2REF Q '=(2)取ABCE 部分,对C 点列平衡0x =∑cos 450RERA FF -= 0Y =∑sin 450RBRA FF P --=且RE REF F '=联立上面各式得: 22RA F Q =2RB F Q P=+(3)取BCE 部分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
静力学基础
一、判断题
1.外力偶作用的刚结点处,各杆端弯矩的代数和为零。
(× )
2.刚体是指在外力的作用下大小和形状不变的物体。
(√ )
3.在刚体上加上(或减)一个任意力,对刚体的作用效应不会改变。
(× )
4.一对等值、反向,作用线平行且不共线的力组成的力称为力偶。
(√ )
5.固定端约束的反力为一个力和一个力偶。
(× )
6.力的可传性原理和加减平衡力系公理只适用于刚体。
(√ )
7.在同一平面内作用线汇交于一点的三个力构成的力系必定平衡。
(× )
8.力偶只能使刚体转动,而不能使刚体移动。
(√ )
9.表示物体受力情况全貌的简图叫受力图。
(√ )
10.图1中F对O点之矩为m0 (F) = FL 。
(× )
图 1
二、选择题
1. 下列说法正确的是(C )
A、工程力学中我们把所有的物体都抽象化为变形体。
B、在工程力学中我们把所有的物体都抽象化为刚体。
C、稳定性是指结构或构件保持原有平衡状态。
D、工程力学是在塑性范围内,大变形情况下研究其承截能力。
2.下列说法不正确的是(A )
A、力偶在任何坐标轴上的投形恒为零。
B、力可以平移到刚体内的任意一点。
C、力使物体绕某一点转动的效应取决于力的大小和力作用线到该点的垂直距离。
D、力系的合力在某一轴上的投形等于各分力在同一轴上投形的代数和。
3.依据力的可传性原理,下列说法正确的是(D )
A、力可以沿作用线移动到物体内的任意一点。
B、力可以沿作用线移动到任何一点。
C、力不可以沿作用线移动。
D、力可以沿作用线移动到刚体内的任意一点。
4.两直角刚杆AC、CB支承如图,在铰C处受力F作用,则A、B两处约束力与x轴正向所成的夹角α、β分别为:
α=___B___,β=___D___。
A、30°;
B、45°;
C、90°;
D、135°。
5.下列正确的说法是。
(D )
图2
A、工程力学中,将物体抽象为刚体。
B、工程力学中,将物体抽象为变形体。
C、工程力学中,研究外效应时,将物体抽象为刚体。
而研究内效应时,则抽象为变形体。
D、以上说法都不正确。
6.关于约束的说法是(D )
A、柔体约束,沿柔体轴线背离物体。
B、光滑接触面约束,约束反力沿接触面公法线,指向物体。
C、固定端支座,反力可以正交分解为两个力方向假设。
D、以上A B正确。
7.力偶的特点,下列说法正确的是(B )
A、力偶可以用力来维持平衡
B、力偶的合成结果仍为一力偶
C、力偶矩大小相等,方向相反的二力偶,互为等效力偶
D、力偶不可以任意搬动
8.构件的刚度是指构件(C )
A、抵抗破坏的能力
B、不产生变形的能力
C、抵抗变形的能力
D、保持平衡的能力
9.构件的强度是指构件(A )
A、抵抗破坏的能力
B、不产生变形的能力
C、抵抗变形的能力
D、保持平衡的能力。
