高中数学人教A版必修四1.4.1正弦函数、余弦函数的图像同步测试【有答案】
人教A版数学必修四1.4.1正弦函数、余弦函数的图象.doc

高中数学学习材料马鸣风萧萧*整理制作[精练精析]1.4.1正弦函数、余弦函数的图象素能综合检测一、选择题(每题4分,共16分)1.以下对正弦函数y=sinx的图象描述不正确的是( )(A)在x∈[2kπ,2kπ+2π](k∈Z)上的图象形状相同,只是位置不同(B)介于直线y=1与直线y=-1之间(C)关于x轴对称(D)与y轴仅有一个交点【解析】选C.根据诱导公式一可知A正确,结合y=sinx的图象,可知B、D均正确,C不正确.3.(2008·福建高考)函数y=cosx(x∈R)的图象向左平移个单位后,得到函数y=g(x)的图象,则g(x)的解析式为( )(A)-sinx (B)sinx(C)-cosx (D)cosx【解析】选A.由y=cosx(x∈R)的图象向左平移个单位得,y=g(x)=cos(x+)=-sinx.二、填空题(每题4分,共8分)5.(思维拓展题)方程x2=cosx的实根个数有______个. 【解析】如图所示,可知方程有2个实根.答案:26.下列函数图象相同的序号是______.①y=cosx与y=cos(π+x);②y=sin(x-)与y=sin(-x);③y=sinx与y=sin(-x);④y=sin(2π+x)与y=sinx.【解析】y=cos(π+x)=-cosx,与y=cosx图象不同;y=sin(x-)=-cosx,y=sin(-x)=cosx,故图象同;y=sin(-x)=-sinx与y=sinx图象不同;y=sin(2π+x)=sinx与y=sinx图象相同.答案:④[探究创新]9.(10分)若函数y=2cosx(0≤x≤2π)的图象和直线y=2围成一个封闭的平面图形,求这个封闭图形的面积.【解析】观察图可知:图形S1与S2,S3与S4都是两个对称图形,有S1=S2,S3=S4,因此函数y=2cosx的图象与直线y=2所围成的图形面积,可以等积的转化为求矩形OABC的面积.∵|OA|=2,|OC|=2π,∴S矩形OABC=2×2π=4π.。
高一数学人教A版必修4学案:141正弦函数、余弦函数的图象含答案1.doc

1.4三角函数的图象与性质1. 4.1正弦函数、余弦函数的图象[学习目标]1.了解利用单位圆中的正眩线画正弦曲线的方法.2.掌握“五点法”画正弦曲线和余弦曲线的步骤和方法,能用“五点法”作出简单的正弦、余弦曲线.3.理解正弦曲线与余眩曲线之I'可的联系.戸预习导学 /挑战自我,点点落实_____________________________________________________________[知识链接]1.在如图单位圆中,角G的正弦线、余弦线分别是什么?答sin a = MP;cosa = OM.2.设实数x对应的角的正弦值为y,则对应关系y=sinx就是一个函数,称为正弦函数;同样y=cosx也是一个函数,称为余弦函数,这两个函数的定义域是什么?答正弦函数和余弦函数的定义域都是R3.作函数图象最基本的方法是什么?其步骤是什么?答作函数图象最基本的方法是描点法,其步骤是列表、描点、连线.[预习导引]1.正弦曲线、余弦曲线正弦函数)^=sinx(xWR)和余弦函数y=cos x(x R)的图象分别叫正弦曲线和余弦曲线.2.“五点法”画图画正弦函数y=sin x, xe[0,2n]的图象,五个关键点是(0,0),(申,1),(兀,。
),(器,一1),(2兀,0);画余弦函数);=cosx, X W[0,2TT]的图象,五个关键点是(0,1), (J, 0),(兀,—1), (|兀,0),(2n, 1).3.正弦、余弦曲线的联系依据诱导公式cosx=sin(x+¥),要得到y=cosx的图彖,只需把y=sinx的图彖向左平移乡个单位长度即可.戸课堂讲义重点难点,个个击破__________________________________________________________ 要点一“五点法”作正弦、余弦函数的图象例1用“五点法”作出下列函数的简图.(1)y=sinx— 1, [0,2n];(2)y=2+cosx, x 曰0,2TT].解⑴列表:X0兀27132兀sinx010-10sinx— 1-10-1-2-1描点连线,如图(2)列表:X0712兀 3 尹2兀COSX10-1012+cosx32123描点连线,如图规律方法作正弦、余弦曲线要理解几何法作图,掌握五点法作图.“五点、”即y=sinx或y=cosx 的图象在一个最小正周期内的最高点、最低点和与x轴的交点."五点法”是作简图的常用方法. 跟踪演练1⑴作出函数y=—sinx(0WxW27t)的简图;(2)作出函数y=yj 1 —cos~x的图彖. 解⑴列表:X07T2兀3兀T271sinx010-10—sinx0-1010⑵将y=y[\—co?x化为^=|sinx|,sin x(2kn WxW兀+2kn, Z:EZ),.—sin X(TI+2kjt<x W 2兀+2kn, A W Z)・其图象如图要点二正弦、余弦函数图象的应用例2⑴方程x2—cosx=0的实数解的个数是___________⑵方程sinx=lgx的解的个数是__________ .答案(1)2 (2)3解析(1)作函数y=cosx与歹=< 的图象,如图所示,由图象,可知原方程有两个实数解.(2)用五点法画岀函数y=sin x, x^[0,2n]的图象,再依次向左、右连续平移2兀个单位,得到y=sinx 的图象.描出点(寻,-1), (1,0), (10,1)并用光滑曲线连接得到y=]gx^J图象,如图所示.由图象可知方程sinx=lgx的解有3个.规律方法利用三角函数图象能解决求方程解的个数问题,也可利用方程解的个数(或两函数图象的交点个数)求字母参数的范围问题.跟踪演练2函数/(x) = sin x+2|sin x|, X W [0,2TT ]的图象与直线y=k 有.R 仅有两个不同的交 点,求《的取值范围.3sinx,炸[0,兀], 解,/(x) = sinx+2|sinx|=1 . u —sinx, xt (7T, 2疋|・图象如图, 若使/(x)的图象与直线y=k 有且仅有两个不同的交点,根据图可得 «的取值范围是(1,3).要点三利用三角函数图象求函数的定义域 例3求函数夕=yj log2sin^— 1的定义域. 解为使函数有意义,需满足 呃佥TN 。
人教a版必修4学案:1.4.1正弦函数、余弦函数的图象(含答案)
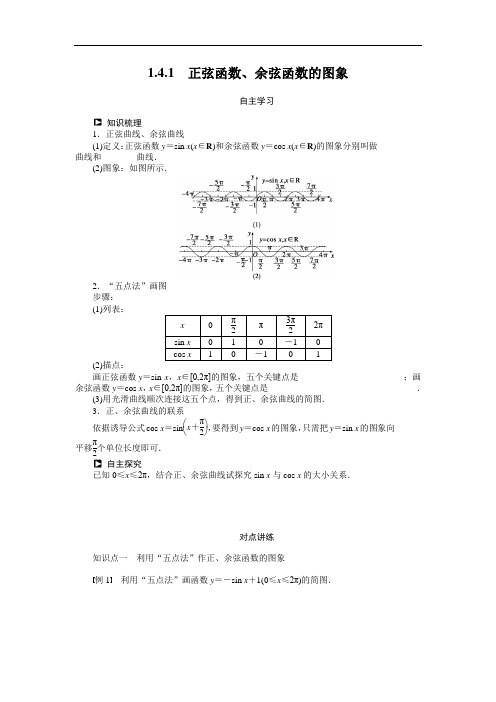
1.4.1 正弦函数、余弦函数的图象自主学习知识梳理1.正弦曲线、余弦曲线 (1)定义:正弦函数y =sin x (x ∈R )和余弦函数y =cos x (x ∈R )的图象分别叫做__________曲线和________曲线.(2)图象:如图所示.2.“五点法”画图 步骤: (1)列表:x 0 π2 π 3π2 2π sin x 0 1 0 -1 0 cos x1-11(2)描点:画正弦函数y =sin x ,x ∈[0,2π]的图象,五个关键点是________________________;画余弦函数y =cos x ,x ∈[0,2π]的图象,五个关键点是__________________________________.(3)用光滑曲线顺次连接这五个点,得到正、余弦曲线的简图. 3.正、余弦曲线的联系依据诱导公式cos x =sin ⎝⎛⎭⎫x +π2,要得到y =cos x 的图象,只需把y =sin x 的图象向______平移π2个单位长度即可.自主探究已知0≤x ≤2π,结合正、余弦曲线试探究sin x 与cos x 的大小关系.对点讲练知识点一 利用“五点法”作正、余弦函数的图象例1 利用“五点法”画函数y =-sin x +1(0≤x ≤2π)的简图.回顾归纳作正弦、余弦曲线要理解几何法作图,掌握五点法作图.“五点”即y=sin x或y=cos x的图象在一个最小正周期内的最高点、最低点和与x轴的交点.“五点法”是作简图的常用方法.变式训练1利用“五点法”画函数y=-1-cos x,x∈[0,2π]的简图.知识点二利用三角函数图象求定义域例2求函数f(x)=lg sin x+16-x2的定义域.回顾归纳一些三角函数的定义域可以借助函数图象直观地观察得到,同时要注意区间端点的取舍.变式训练2求函数f(x)=cos x+lg(8x-x2)的定义域.知识点三利用三角函数的图象判断方程解的个数例3在同一坐标系中,作函数y=sin x和y=lg x的图象,根据图象判断出方程sin x =lg x的解的个数.回顾归纳三角函数的图象是研究函数的重要工具,通过图象可较简便的解决问题,这正是数形结合思想方法的应用.变式训练3求方程x2=cos x的实数解的个数.1.正、余弦曲线在研究正、余弦函数的性质中有着非常重要的应用,是运用数形结合思想解决三角函数问题的基础.2.五点法是画三角函数图象的基本方法,要熟练掌握,与五点法作图有关的问题是高考常考知识点之一.课时作业一、选择题1.函数y =sin x (x ∈R )图象的一条对称轴是( ) A .x 轴 B .y 轴C .直线y =xD .直线x =π22.函数y =-cos x 的图象与余弦函数y =cos x 的图象( ) A .只关于x 轴对称 B .关于原点对称 C .关于原点、x 轴对称 D .关于原点、坐标轴对称 3.如果x ∈[0,2π],则函数y =sin x +-cos x 的定义域为( )A .[0,π] B.⎣⎡⎦⎤π2,3π2C.⎣⎡⎦⎤π2,πD.⎣⎡⎦⎤3π2,2π 4.在(0,2π)内使sin x >|cos x |的x 的取值范围是( ) A.⎝⎛⎭⎫π4,3π4 B.⎝⎛⎦⎤π4,π2∪⎝⎛⎦⎤5π4,3π2 C.⎝⎛⎭⎫π4,π2 D.⎝⎛⎭⎫5π4,7π4 5.已知函数y =2sin x ⎝⎛⎭⎫π2≤x ≤5π2的图象与直线y =2围成一个封闭的平面图形,那么此封闭图形的面积( )A .4B .8C .4πD .2π二、填空题6.函数y =cos x1+sin x的定义域为____________.7.函数y =2cos x +1的定义域是______________.8.设0≤x ≤2π,且|cos x -sin x |=sin x -cos x ,则x 的取值范围为________.三、解答题9.利用“五点法”作出下列函数的简图:(1)y =-sin x (0≤x ≤2π);(2)y =1+cos x (0≤x ≤2π).10.分别作出下列函数的图象.(1)y =|sin x |,x ∈R ;(2)y =sin|x |,x ∈R .§1.4 三角函数的图象与性质 1.4.1 正弦函数、余弦函数的图象答案知识梳理1.(1)正弦 余弦2.(2)(0,0),⎝⎛⎭⎫π2,1,(π,0),⎝⎛⎭⎫3π2,-1,(2π,0) (0,1),⎝⎛⎭⎫π2,0,(π,-1),⎝⎛⎭⎫3π2,0,(2π,1) 3.左 自主探究解 正、余弦曲线如图所示.由图象可知①当x =π4或x =5π4时,sin x =cos x ,②当π4<x <5π4时,sin x >cos x .③当0≤x <π4或5π4<x ≤2π时,sin x <cos x .对点讲练例1 解 利用“五点法”作图 取值列表:x 0 π2π3π2 2π sin x 0 1 0 -1 0 1-sin x 1 0 121变式训练1 x0 π2 π 3π2 2π cos x 1 0 -1 0 1 -1-cos x-2-1-1-2例2 解 由题意,x 满足不等式组⎩⎨⎧sin x >016-x 2≥0, 即⎩⎨⎧-4≤x ≤4sin x >0,作出y =sin x 的图象,如图所示.结合图象可得:x ∈[-4,-π)∪(0,π).变式训练2 解 由⎩⎪⎨⎪⎧8x -x 2>0cos x ≥0,得⎩⎨⎧0<x <8cos x ≥0.画出y =cos x ,x ∈[0,3π]的图象,如图所示.结合图象可得:x ∈⎝⎛⎦⎤0,π2∪⎣⎡3π2,5π2.例3 解 建立坐标系xOy ,先用五点法画出函数y =sin x ,x ∈[0,2π]的图象,再依次向左、右连续平移2π个单位,得到y =sin x 的图象.描出点⎝⎛⎭⎫1101,(1,0),(10,1)并用光滑曲线连接得到y =lg x 的图象,如图所示.由图象可知方程sin x =lg x 的解有3个.变式训练3 解 作函数y =cos x 与y =x 2的图象,如图所示, 由图象,可知原方程有两个实数解.课时作业 1.D2.C [结合图象易知.]3.C [∵sin x ≥0且-cos x ≥0,∴x ∈⎣⎡⎦⎤π2π.] 4.A[∵sin x >|cos x |,∴sin x >0,∴x ∈(0,π),在同一坐标系中画出y =sin x ,x ∈(0,π)与y =|cos x |,x ∈(0,π)的图象,观察图象易得x ∈⎝⎛⎭⎫π4,3π4.]5.C [数形结合,如图所示.y =2sin x ,x ∈⎣⎡⎦⎤π2,5π2的图象与直线y =2围成的封闭平面图形面积相当于由x =π2,x =5π2, y =0,y =2围成的矩形面积,即S =⎝⎛⎭⎫5π2-π2×2=4π.]6.⎝⎛⎦⎤-π22k π,π2+2k π (k ∈Z ) 解析 x 应满足:⎩⎪⎨⎪⎧1+sin x ≠0⇒sin x ≠-1,cos x ≥0,综合正、余弦函数图象可知:-π2+2k π<x ≤π2+2k π. 7.⎣⎡⎦⎤2k π-2π3,2k π+2π3 ,(k ∈Z ) 解析 由2cos x +1≥0,得cos x ≥-12,∴2k π-2π3x ≤2k π+2π3,k ∈Z .8.⎣⎡⎦⎤π4,5π4 解析 由题意知sin x -cos x ≥0,即cos x ≤sin x ,在同一坐标系画出y =sin x ,x ∈[0,2π] 与y =cos x ,x ∈[0,2π]的图象,如图所示:观察图象得:π4≤x ≤5π4.9.解 利用“五点法”作图. (1)列表:(2)列表:10.解 (1)y =|sin x |=⎩⎪⎨⎪⎧sin x (2k π≤x ≤2k π+π)-sin x (2k π+π<x ≤2k π+2π)(k ∈Z ).其图象如图所示,(2)y =sin|x |=⎩⎪⎨⎪⎧sin x (x ≥0)-sin x (x <0),其图象如图所示,。
高中数学人教A版必修四1.4.1正弦函数、余弦函数的图像同步练习

《1.4.1正弦函数、余弦函数的图像》同步练习1. 满足sin x≥12的x的集合为()A.{x|2kπ+π6≤x≤2kπ+5π6, k∈Z}B.{x|2kπ+5π6≤x≤2kπ+7π6, k∈Z}C.{x|2kπ−π6≤x≤2kπ+π6, k∈Z}D.{x|2kπ−π3≤x≤2kπ+2π3, k∈Z}2. 已知f(x)=sin(2x+π2),g(x)=cos(2x−π2),则下列结论中不正确的是()A.将函数f(x)的图象向右平移π4个单位后得到函数g(x)的图象B.函数y=f(x)⋅g(x)的图象关于(π8,0)对称C.函数y=f(x)⋅g(x)的最大值为12D.函数y=f(x)⋅g(x)的最小正周期为π23. 函数y=|sin x|的一个单调增区间是()A.[−π4, π4] B.[π, 3π2] C.[π4, 3π4] D.[3π2, 2π]4. 给出的下列函数中在(π2, π)上是增函数的是________.A.y=sin2xB.y=cos2x.5. 若函数f(x)=sinωx(ω>0)的图象的相邻两对称轴间的距离为2,则ω的值为()A.2πB.π2C.πD.2π6. y=cos x,x∈[0, 5π2]的图象与直线y=13的交点的个数为()A.0B.1C.2D.37. 设函数f(x)=cos(x+π3),则下列结论错误的是( )A.f(x)的一个周期为−2πB.y=f(x)的图像关于直线x=8π3对称C.f(x+π)的一个零点为x=π6D.f(x)在(π2, π)单调递减8. 函数f(x)=sin(ωx+φ)(ω>0, |φ|<π2)的最小正周期是π,若其图象向右平移π6个单位,得到的函数为偶函数,则函数f(x)的图象()A.关于直线x=5π12对称 B.关于点(7π12, 0)对称C.关于点(5π12, 0)对称 D.关于直线x=π12对称9. 函数y=ln1|x−1|与函数y=cosπx图象所有交点的横坐标之和为( )A.3B.4C.8D.610. 已知直线x=x1,x=x2分别是曲线f(x)=2sin(x+π3)与g(x)=−cos x的对称轴,则f(x1−x2)=()A.2B.0C.±2D.±111. 函数y=2sin x−cos x在区间[0,5π]上的零点个数为________.12. 若a=sin46∘,b=cos46∘,c=cos36∘,则a、b、c由小到大的顺序为________.13. 不等式cos x≥12的解集是________.14. 函数y =a −sin xx ∈(0, 5π2)的图象与过点(0, 1)且平行于x 轴的直线有两个交点,则实数a 的取值范围是________.15. 根据正弦函数、余弦函数的图象,写出使下列不等式成立的x 的取值集合: (1)sin x ≥√32(x ∈R);(2)√2+2cos x ≥0(x ∈R).16. 已知函数f(x)=cos (ωx +φ)(ω>0, 0<φ≤π)为奇函数,且其图象上相邻的一个最高点与一个最低点之间的距离为2. (1)求f(x)的解析式;(2)若f(α+π3)=−23(−π3<α<0),求sin (2α−π3)的值.17. 已知函数f(x)=A sin (wx +φ)(x ∈R, w >0, 0<φ<π2)的部分图象如图所示.(1)求函数f(x)的解析式; (2)求函数g(x)=f(x −π12)−f(x +π12)的单调递增区间.18. 已知函数f(x)=cos (2x +π3)+cos (2x +23π),g(x)=cos 2x . (1)若α∈(π4,π2),且f(α)=−35√3,求g(α)的值;(2)若x∈[−π6,π3],求f(x)+g(x)的最大值.参考答案1.【答案】A2.【答案】B3.【答案】B4.【答案】B5.【答案】B6.【答案】D7.【答案】D8.【答案】B9.【答案】D10.【答案】C11.【答案】512.【答案】b<a<c13.【答案】{x|2kπ−π3≤x≤2kπ+π3, k∈Z.}14.【答案】(0, 1]15.【答案】由sin x≥√32(x∈R),结合正弦函数在一个周期上的图象,如图(1)所示,可得x的范围为{x|2kπ+π3≤x≤2kπ+2π3, k∈z}.由√2+2cos x≥0(x∈R),可得cos x≥−√22,结合余弦函数在一个周期上的图象如图(2)所示,可得x的范围为{x|2kπ−3π4≤x≤2kπ+3π4, k∈z}.16.【答案】解:(1)由函数f(x)=cos(ωx+φ)(ω>0, 0<φ≤π)为奇函数,可得φ=π2,f(x)=cos(ωx+π2)=−sinωx.又其图象上相邻的一个最高点与一个最低点之间的距离为√4+π2,可得√22+(πω)2=√4+π2,∴ ω=1,f(x)=−sin x.(2)∴ f(α+π3)=−sin(α+π3)=−23(−π3<α<0),∴ sin(α+π3)=23,即23=cos[π2−(α+π3)]=cos(π6−α)=cos(α−π6),∴ sin(α−π6)=−√1−cos2(α−π6)=−√53,∴ sin(2α−π3)=2sin(α−π6)⋅cos(α−π6)=−4√59.17.【答案】由图可知T2=11π12−5π12,可得T=π,则2πω=π,则ω=2,又图象经过(5π12, 0),故有2×5π12+φ=kπ,k∈Z,得φ=−5π6+kπ,又0<φ<π2,取φ=π6.过(0, 1)点,所以A sinφ=1,可得A=2.得f(x)=2sin(2x+π6).g(x)=f(x −π12)−f(x +π12)=2sin [2(x −π12)+π6]−2sin [2(x +π12)+π6]=2sin 2x −2sin (2x +π3)=2sin 2x −2sin 2x cos π3−2cos 2x sin π3=sin 2x −√3cos 2x =2sin (2x −π3),由2kπ−π2≤2x −π3≤2kπ+π2,k ∈Z , 得kπ−π12≤x ≤kπ+5π12,k ∈Z ,所以g(x)的单调递增区间为[kπ−π12, kπ+5π12],k ∈Z . 18.【答案】解:(1)由f(x)=cos (2x +π3)+cos (2x +23π) 得f(x)=12cos 2x −√32sin 2x −12cos 2x −√32sin 2x =−√3sin 2x .因为f(α)=−35√3,即−√3sin 2α=−35√3,所以sin 2α=35.又因为α∈(π4,π2), 所以2α∈(π2,π).故cos 2α=−45,即g(α)=−45.(2)f(x)+g(x)=−√3sin 2x +cos 2x =2cos (2x +π3). 因为x ∈[−π6,π3], 所以2x +π3∈[0,π]. 所以当2x +π3=0,即x =−π6时,f(x)+g(x)有最大值,最大值为2.。
高中数学 第一章 三角函数 1.4.1 正弦函数、余弦函数的图象课时训练(含解析)新人教A版必修4

高中数学第一章三角函数1.4.1 正弦函数、余弦函数的图象课时训练(含解析)新人教A版必修4编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(高中数学第一章三角函数1.4.1 正弦函数、余弦函数的图象课时训练(含解析)新人教A版必修4)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为高中数学第一章三角函数1.4.1 正弦函数、余弦函数的图象课时训练(含解析)新人教A 版必修4的全部内容。
1.4。
1 正弦函数、余弦函数的图象课时目标 1.了解正弦函数、余弦函数的图象.2。
会用“五点法”画出正弦函数、余弦函数的图象.1.正弦曲线、余弦曲线2.“五点法”画图画正弦函数y=sin x,x∈[0,2π]的图象,五个关键点是_________________________;画余弦函数y=cos x,x∈[0,2π]的图象,五个关键点是__________________________.3.正、余弦曲线的联系依据诱导公式cos x=sin错误!,要得到y=cos x的图象,只需把y=sin x的图象向________平移错误!个单位长度即可.一、选择题1.函数y=sin x (x∈R)图象的一条对称轴是()A.x轴B.y轴C.直线y=x D.直线x=错误!2.函数y=cos x(x∈R)的图象向右平移错误!个单位后,得到函数y=g(x)的图象,则g(x)的解析式为( )A.-sin x B.sin xC.-cos x D.cos x3.函数y=-sin x,x∈[-错误!,错误!]的简图是( )4.在(0,2π)内使sin x>|cos x|的x的取值范围是()A。
高中数学人教A版必修4第一章三角函数1.4.1正弦函数、余弦函数的图象(1) 答案和解析

高中数学人教A版必修4第一章三角函数1.4.1正弦函数、余弦函数的图象(1)学校:___________姓名:___________班级:___________考号:___________ 一、单选题1.点π,2M m⎛⎫-⎪⎝⎭在函数y=sin x的图象上,则m等于( )A.0B.1C.-1D.22.在同一坐标系中函数y=sin x,x∈[0,2π]与y=sin x,x∈[2π,4π]的图象( ) A.重合B.形状相同,位置不同C.形状不同,位置相同D.形状不同,位置不同3.函数y=-sin x,x∈π3,22π⎡⎤-⎢⎥⎣⎦的简图是( )A.B. C.D.4.y=1+sinx,x∈[0,2π]的图象与直线y=2交点的个数是( ) A.0B.1C.2D.3 5.不等式cos x<0,x∈[0,2π]的解集为( )A.π3,22π⎛⎫⎪⎝⎭B.π3,22π⎡⎤⎢⎥⎣⎦C.π0,2⎛⎫⎪⎝⎭D.π,22π⎛⎫⎪⎝⎭6.方程lg x=sin x的解的个数为( )A.0B.1C.2D.3二、填空题7.用“五点法”画出y=2sin x在[0,2π]内的图象时,应取的五个点为________________.8.若sin x =2m +1且x ∈R,则m 的取值范围是________.9.函数y =的定义域是__________.10.直线x sin α+y +2=0的倾斜角的取值范围是________________.三、解答题11.用“五点法”作函数y =-2cos x +3(0≤x ≤2π)的简图. 12.判断方程10xsinx =的根的个数. 13.方程sin x =12a -在x ∈π,3π⎡⎤⎢⎥⎣⎦上有两个实数根,求a 的取值范围.参考答案1.C 【解析】 ∵点π,2M m ⎛⎫-⎪⎝⎭在函数y =sin x 的图象上, ∴sin12m π-==,解得1m =-.选C . 2.B【解析】由题意得,两函数的解析式相同,定义域不同. 所以两函数的图象相同,但位置不同. 选B . 3.D 【解析】 用排除法求解.当x =0时,y =-sin 0=0,故可排除A 、C ; 当x =32π时,y =-sin32π=1,故可排除B . 选D . 4.B 【解析】 方法一:由函数y =1+sin x ,x ∈[0,2π]的图象(如图所示),可知其与直线y =2只有1个交点.选B .方法二:由x ∈[0,2π]可得1sin 1x -≤≤,所以01sin 2x ≤+≤,故函数y =1+sin x 的最大值为2,所以直线y =2与函数y =1+sin x 的图象只有1个交点.选B . 5.A 【解析】方法一:由函数y =cos x 的图象知,在[0,2π]内使cos x <0的x 的范围是π3,22π⎛⎫⎪⎝⎭. 故不等式的解集为π3,22π⎛⎫⎪⎝⎭.选A 方法二: 由0cosx <得,322,22k x k k Z ππππ+<<+∈, 又02x π≤≤, 所以322x ππ<<. 故不等式的解集为π3,22π⎛⎫⎪⎝⎭.选A . 6.D 【解析】在同一坐标系内作出函数y =lg x 与函数y =sin x 的图象如图所示,由图知两函数的图象有三个交点,所以方程有三个解.选D .点睛:判断方程根的个数的方法 (1)通过解方程的方法判断.(2)当方程不容易求解时,可构造两个函数,并在同一坐标系内画出两个函数的图象,通过观察两函数图象公共点的个数来判断方程解的个数,这种方法为数形结合在解题中的运用.用图象法判断方程根的个数时,有时要用函数的奇偶性进行判断. 7.(0,0),π,22⎛⎫ ⎪⎝⎭,(π,0),3π,22⎛⎫- ⎪⎝⎭,(2π,0) 【解析】画函数y =sin x 在[0,2π]内的图象时五个关键点为3(0,0),(,1),(,0),(,1),(2,0)22ππππ-, 因此画y =2sin x 在[0,2π]内的图象时,应取的五个点即把相应的五个关键点的纵坐标变为原来的2倍即可,即为3(0,0),(,2),(,0),(,2),(2,0)22ππππ-. 答案:3(0,0),(,2),(,0),(,2),(2,0)22ππππ- 8.[-1,0]【解析】因为-1≤sin x ≤1,sin x =2m +1, 所以-1≤2m +1≤1, 解得-1≤m ≤0.故实数m 的取值范围是[-1,0]. 答案:[-1,0]9.{}x |2(21),k x k k Z ππ<<+∈ 【详解】 由120log sinx ≥得0<sin x ≤1,由正弦函数图象得22,k x k k Z πππ<<∈+, 所以函数的定义域为{|22,}x k x k k Z πππ<<∈+答案:{|22,}x k x k k Z πππ<<∈+10.π30,,π44π⎡⎤⎡⎫⋃⎪⎢⎥⎢⎣⎦⎣⎭【解析】因为sin α∈[-1,1], 所以-sin α∈[-1,1],所以已知直线的斜率范围为[-1,1],由倾斜角与斜率关系得倾斜角范围是π30,,π44π⎡⎤⎡⎫⋃⎪⎢⎥⎢⎣⎦⎣⎭. 答案:π30,,π44π⎡⎤⎡⎫⋃⎪⎢⎥⎢⎣⎦⎣⎭11.见解析 【解析】 试题分析:根据描点法作图的步骤:列表、描点、连线的步骤求解即可. 试题解析: 由条件列表如下:描点、连线得出函数y =-2cos x +3(0≤x ≤2π)的图象如图所示.点睛:(1)画正弦函数y =cos x 在[0,2π]上的图象时,起关键作用的五个点是(0,1),(,0),(,1)2ππ-,3(,0),(2,1)2ππ. (2)用五点法画cos()y A x ωϕ=+的图象时,五个关键点的横坐标不再是30,,,,222ππππ,而是令x ωϕ+取上述五个值,得到的相应x 的值. 12.方程根的个数为7 【解析】 试题分析:在同一坐标系内画出函数sin y x =和函数10xy =在y 轴右侧的图象,通过两函数图象公共点的个数,并结合函数为奇函数来判断出方程10xsinx =根的个数.试题解析:由题意得,当x =3π时,311010x y π==<;当x =4π时,411010x y π==>. 在同一坐标系内分别作出函数sin y x =和函数10xy =在y 轴右侧的图象,如图所示.由图象知,直线y =10x在y 轴右侧与函数y =sinx 的图象有且只有3个公共点, 又由函数为奇函数的性质可知,在y 轴左侧两函数的图象也有3个公共点,加上原点O (0,0),共有7个公共点. 所以方程10xsinx =根的个数为7.13.11a <≤-【解析】试题分析:根据正弦函数的单调性,得到当[,]3x ππ∈时,在区间[,]3ππ上且2x π≠时,存在两个自变量x 对应同一个sin x .由此得到若()f x 有两个零点,即1sin 2ax -=,在[,]3x ππ∈上有两个零点,由此建立关于a 的不等式,解之即可得到实数a 的取值范围.试题解析:首先作出sin y x =,[,]3x ππ∈的图象,然后再作出12ay -=的图象,如果sin y x =,[,]3x ππ∈与12a y -=的图象有两个交点,方程1sin 2a x -=,[,]3x ππ∈就有两个实数根. 设1sin y x =,[,]3x ππ∈,212ay -=. 1sin y x =,[,]3x ππ∈的图象如图.112a-≤<,即11a -<≤sin y x =,[,]3x ππ∈的图象与1 2ay-=的图象有两个交点,即方程1sin2ax-=在[,]3xππ∈上有两个实根.点睛:本题给出三角函数式,求满足函数在指定区间上有两个零点的参数a的取值范围,着重考查了三角函数的单调性与函数的图象与性质等知识,属于中档题.。
人教新课标版数学 高一人教A版必修4 1.4.1 正弦函数、余弦函数的图象 作业

[A.基础达标]1.以下对于正弦函数y =sin x 的图象描述不正确的是( )A .在x ∈[2k π,2k π+2π],k ∈Z 上的图象形状相同,只是位置不同B .关于x 轴对称C .介于直线y =1和y =-1之间D .与y 轴仅有一个交点解析:选B.观察y =sin x 图象可知A 、C 、D 正确,且关于原点中心对称,故选B. 2.用“五点法”作函数y =cos 2x ,x ∈R 的图象时,首先应描出的五个点的横坐标是( )A .0,π2,π,3π2,2πB .0,π4,π2,3π4,πC .0,π,2π,3π,4πD .0,π6,π3,π2,2π3解析:选B.令2x =0,π2,π,3π2和2π,得x =0,π4,π2,3π4,π,故选B.3.函数y =-sin x ,x ∈⎣⎡⎦⎤-π2,3π2的简图是( )解析:选D.可以用特殊点来验证.x =0时,y =-sin 0=0,排除A 、C.当x =3π2时,y=-sin 3π2=1,排除B.4.函数y =1+sin x ,x ∈[0,2π]的图象与直线y =32的交点个数为( )A .1B .2C .3D .0解析:选B.作出两个函数的图象如图所示,可知交点的个数为2.5.(2015·舒城中学调研)如图所示,函数y =cos x ·|sin x ||cos x |⎝⎛⎭⎫0≤x <3π2且x ≠π2的图象是( )解析:选C.y =⎩⎨⎧sin x ,0≤x <π2或π≤x <32π,-sin x ,π2<x <π,结合选项知C 正确.6.用五点法画出y =2sin x 在[0,2π]内的图象时,应取的五个点为________.解析:可结合函数y =sin x 的五个关键点寻找,即把相应的五个关键点的纵坐标变为原来的2倍即可.答案:(0,0),(π2,2),(π,0),(3π2,-2),(2π,0)7.若sin x =2m +1且x ∈R ,则m 的取值范围是________. 解析:由正弦函数图象得-1≤sin x ≤1, 所以-1≤2m +1≤1,所以m ∈[-1,0]. 答案:[-1,0]8.在[0,2π]上满足cos ⎝⎛⎭⎫π2+x ≤-32的x 的取值范围是________. 解析:因为cos ⎝⎛⎭⎫π2+x ≤-32,所以-sin x ≤-32,所以sin x ≥32.又因为0≤x ≤2π,结合如图所示的图象可得π3≤x ≤2π3.答案:⎣⎡⎦⎤π3,2π39.用“五点法”画出y =cos(7π2-x ),x ∈[0,2π]的简图.解:由诱导公式得y =cos(7π2-x )=-sin x ,(1)列表:x 0 π2 π 3π22πy =-sin x-11 0(2)描点:在坐标系内描出点(0,0),(π2,-1),(π,0),(3π2,1),(2π,0).(3)作图:将上述五点用平滑的曲线顺次连接起来.10.用“五点法”作出函数y =cos(x +π6),x ∈[-π6,11π6]的图象.解:找出五点,列表如下:u =x +π60 π2 π 3π2 2π x -π6 π3 5π6 4π3 11π6 y =cos u1-11描点连线,其图象如图所示:[B.能力提升]1.在[0,2π]内,不等式sin x <-32的解集是( ) A .(0,π) B.⎝⎛⎭⎫π3,4π3 C.⎝⎛⎭⎫4π3,5π3D.⎝⎛⎭⎫5π3,2π解析:选C.画出y =sin x ,x ∈[0,2π]的草图如下:因为sin π3=32,所以sin ⎝⎛⎭⎫π+π3=-32, sin ⎝⎛⎭⎫2π-π3=-32. 即在[0,2π]内,满足sin x =-32的是x =4π3或x =5π3.可知不等式sin x <-32的解集是⎝⎛⎭⎫4π3,5π3. 2.将余弦函数y =cos x 的图象向右至少平移m 个单位,可以得到函数y =-sin x 的图象,则m =( ) A.π2 B .π C.3π2D.3π4解析:选C.根据诱导公式得,y =-sin x =cos(3π2-x )=cos(x -3π2),故欲得到y =-sin x的图象,需将y =cos x 的图象向右至少平移3π2个单位长度.3.用五点法作函数y =-cos(x +π2)+1,x ∈[0,2π]的图象时应取的五个关键点是________.解析:因为y =-cos(x +π2)+1=sin x +1,x ∈[0,2π],所以应取的五个关键点分别为(0,1),(π2,2),(π,1),(32π,0),(2π,1). 答案:(0,1),(π2,2),(π,1),(32π,0),(2π,1)4.方程cos(π2-x )=1100x 2有________个正实根.解析:方程cos(π2-x )=1100x 2,即sin x =1100x 2.在同一直角坐标系中作出函数y =sin x 与y =1100x 2的大致图象,如图所示:由图可知在y 轴右侧函数y =sin x 与y =1100x 2的图象有3个交点,故原方程有3个正实根.答案:35.求函数y =1-2cos x +lg(2sin x -1)的定义域. 解:要使函数有意义,只要⎩⎪⎨⎪⎧1-2cos x ≥0,2sin x -1>0,即⎩⎨⎧cos x ≤12,sin x >12.分别作出y =cos x ,y =sin x ,x ∈[0,2π]的草图,如图所示.cos x ≤12的解集为⎩⎨⎧⎭⎬⎫x π3+2k π≤x ≤53π+2k π,k ∈Z ;sin x >12的解集为⎩⎨⎧⎭⎬⎫x π6+2k π<x <5π6+2k π,k ∈Z ,它们的交集为 ⎩⎨⎧⎭⎬⎫x π3+2k π≤x <5π6+2k π,k ∈Z ,即为函数的定义域.6.(选做题)用“五点法”作出函数y =1-2sin x ,x ∈[-π,π]的简图,并回答下列问题:(1)观察函数图象,写出满足下列条件的x的区间.①y>1;②y<1.(2)若直线y=a与y=1-2sin x,x∈[-π,π]有两个交点,求a的取值范围.解:列表如下:x -π-π20π2πsin x 0-10101-2sin x 131-1 1描点连线得:(1)由图象可知图象在y=1上方部分时y>1,在y=1下方部分时y<1,所以①当x∈(-π,0)时,y>1;②当x∈(0,π)时,y<1.(2)如图所示,当直线y=a与y=1-2sin x有两个交点时,1<a<3或-1<a<1,所以a的取值范围是{a|1<a<3或-1<a<1}.。
人教A版高中数学必修4课后习题 第一章 1.4.1 正弦函数、余弦函数的图象

第一章三角函数1.4 三角函数的图象与性质1.4.1 正弦函数、余弦函数的图象课后篇巩固探究1.函数y=sin(-x),x∈[0,2π]的简图是( )∈[0,2π]的图象可看作是由y=sinx,x∈[0,2π]的图象关于x轴对称得到的,故选B.2.已知cos x=-12,且x∈[0,2π],则角x等于( )A.2π3或4π3B.π3或2π3C.π6或5π6D.5π6或11π6:由图象可知,x=2π3或4π3.3.已知f(x)=sin(x+π2),g(x)=cos(x-π2),则f(x)的图象( )A.与g(x)的图象相同B.与g(x)的图象关于y轴对称C.向左平移π2个单位,得g(x)的图象D.向右平移π2个单位,得g(x)的图象,得f(x)=sin(x+π2)=cosx,所以f(x)=sin(x+π2)=cosx的图象向右平移π2个单位,得到g(x)的图象.4.函数y=-xcos x的部分图象是( )解析令y=f(x),因为f(x)的定义域为R,f(-x)=-(-x)cos(-x)=xcosx=-f(x),所以函数y=-xcosx是奇函数,它的图象关于原点对称,所以排除A,C选项;因为当x∈0,π2时,y=-xcosx<0,所以排除B选项.5.当x ∈[0,2π]时,满足sin (π2-x)≥-12的x 的取值范围是( )A.[0,2π3]B.[4π3,2π]C.[0,2π3]∪[4π3,2π]D.[2π3,4π3]sin (π2-x)≥-12,得cosx≥-12.画出y=cosx,x ∈[0,2π],y=-12的图象,如图所示.∵cos 2π3=cos 4π3=-12,∴当x ∈[0,2π]时,由cosx≥-12,可得x ∈[0,2π3]∪[4π3,2π].6.在(0,2π)内使sin x>|cos x|的x 的取值范围是( ) A.(π4,3π4) B.(π4,π2]∪(5π4,3π2]C.(π4,π2)D.(5π4,7π4)x=π2时,sin π2=1>|cos π2|=0,故排除选项C,D,当5π4<x<3π2时,sinx<0,|cosx|>0,故排除选项B.7.方程sin x=x10的根的个数是( )A.7B.8C.9D.10y=sinx与y=x10的图象(如图所示),由图象,得两函数的图象有7个不同交点,即方程sinx=x10的根的个数是7,故选A.8.函数y=√2cosx-√2的定义域是.,只需2cosx-√2≥0,即cosx≥√22.由余弦函数图象知(如图),所求定义域为[-π4+2kπ,π4+2kπ],k∈Z.-π4+2kπ,π4+2kπ],k∈Z9.利用正弦曲线,写出函数y=2sin x(π6≤x≤2π3)的值域是.的部分图象如图.当ax=2,当in=1,故y ∈[1,2].10.设0≤x≤2π,且|cos x-sin x|=sin x-cos x,则x 的取值范围为 .|cosx-sinx|=sinx-cosx,所以sinx≥cosx,由y=sinx,y=cosx 在[0,2π]上的图象,得π4≤x≤5π4.[π4,5π4]11.函数y=2sin x 与函数y=x 图象的交点有 个.y=2sinx 与y=x 的图象可见有3个交点.12.函数f(x)=sin x+2|sin x|,x ∈[0,2π]的图象与直线y=k 有且仅有两个不同的交点,则实数k 的取值范围为 .f(x)={3sinx ,0≤x ≤π,-sinx ,π<x ≤2π的图象如图所示,故由图象知1<k<3.13.利用“五点法”画出函数y=2-sin x,x∈[0,2π]的简图.取值列表如下:(2)描点连线,图象如图所示:14.作出函数y=1-2sin x,x∈[-π,π]的简图,并回答下列问题:(1)观察函数图象,写出满足下列条件的x的区间.①y>1;②y<1.(2)若直线y=a与y=1-2sin x,x∈[-π,π]的图象有两个交点,求a的取值范围.:描点,连线得:(1)由图象可知图象在直线y=1上方部分时y>1,在直线y=1下方部分时y<1,所以,①当x∈(-π,0)时,y>1;②当x∈(0,π)时,y<1.(2)如图所示,当直线y=a与y=1-2sinx有两个交点时,1<a<3或-1<a<1,所以a的取值范围是{a|1<a<3或-1<a<1}.。
人教A版高中数学必修四+141+正弦函数、余弦函数的图像+测试(教师版)+Word版含答案.docx

1.4. 1正弦函数、余弦函数的图像(检测教师版)班级:、选择题(共6小题,每题5分,共30分)*=葺■时,y= —sin 苧=1,排除B.【答案】D在[0, 2兀]内,不等式sin 水一¥的解集是()因为sin +=¥,所以sin (JT +专【答案】C3. 将余眩函数y=cos x 的图象向右至少平移刃个单位,可以得到函数尸一 sin x 的图象,则m时间:40分钟总分:60分姓名:1. 函数 y= —sin x,【解析】可以用特殊点來验证.y= —sin 0 = 0,排除 A 、C ;2.A. (0, Ji) C.R (- — 乩(3' 3丿"5兀门 厂2 H D.【解析】 画出y=sin x, [0, 2肌]的草图如下:即在[0, 2 Ji ]内,满足sin /=— 可知不等式sin 水一当的解集是4 兀5 nA T ,〒丿•的简图是()JI 3JTx=0 时, 4兀小 5 n 比=飞一或才=飞一.需将y=cos x 的图象向右至少平移芋个单位长度.【答案】4.函数尸sin x,圧[0, 2 n ]的图象与直线尸一*的交点有(/5兀y=0, y=2围成的矩形面积,即5=(^—【答案】CJIA ・TB-兀【解析】根据诱导公式得,y= —sin x=cos3 Ji~~x= cos x3 Ji,故欲得到y= —sin/的图象,A. 1个B. 2个C. 3个D. 4个【解析】 在[0, 2 口]内使sin|的角/为平■和丄卩,所以y=sin x, [0, 2兀]的图象与直线y=2个交点,故选B.【答案】5.已知函数y=2sin守W 点冷T 的图象与直线尸2围成一个封闭的平面图形,那么此封闭图形的血积()A. 4B. 8【解析】数形结合,如图所示.■ Ji 5 Ji"y=2sin x 、xe —,刁一 的图象与直线y=2围成的封闭平而图形而积相当于由5兀【答案】D二.填空题(共2小题,每题5分,共10分)7.利用余弦曲线,写出满足cos Q0,圧[0,2叮的/的区间是三、解答题(共2小题,每题10分,共20分)9. 用五点法作出函数y=l-cos x (0WxW2ir )的简图.【解析】列表:一1 -2y21O 7T n 3m 2*TT 云2 2D【解析】由题意得2cos X,显然只有D 合适.门 113 [o,訂<尹【解析】 画出y=cos x,胆[0, 2兀]上的图象如图所示.cos Q0的区间为0,【答案】3HT' 2兀8.函数y=logisin 才的定义域是2【解析】 由loglsin *20知0〈sin xWl,由正眩函数图象知2斤兀〈*〈2力兀+兀,【答案】 {x\2k^ <x<2kn + n , kwZ} yX,2兀U描点连线,如图.10.作出函数y= — si nx,乳丘[—兀,兀]的简图,并回答下列问题:(1)观察函数图象,写出满足下列条件的/的区间:①sin %>0;②sin %<0.(2)直线尸丄与y= —sin x的图象有儿个交点?2⑴根据图象可知图象在x轴上方的部分sin x>0,在/轴下方的部分sin ^<0. 所以①当用(一兀,0)时,sin 乂>0;②当(0,兀)时,sin %<0.⑵画出直线尸?得知有两个交点.。
人教版必修4正弦函数、余弦函数的图象检测卷附答案ME

第一章 三角函数(必修4)1.4.1 正弦函数、余弦函数的图象A 级 基础巩固一、选择题1.函数y =3sin ⎝ ⎛⎭⎪⎫π2x +π4的振幅和周期分别为( )A .3,4B .3,π2 C.π2,4 D.π2,3解析:由于函数y =3sin ⎝ ⎛⎭⎪⎫π2x +π4,所以振幅是3,周期是T =2ππ2=4.答案:A2.如图,2弧度的圆心角所对的弦长为2,这个圆心角所对应的扇形面积是()A.1sin 1 B.1sin21 C.1cos21 D .tan 1解析:作OC ⊥AB ,垂足为C ,在△AOC 中,sin 1=1r ,所以r =1sin 1,所以S =12r 2α=12×1sin21×2=1sin21,故选B.答案:B3.下列函数中,既是偶函数又存在零点的是( ) A .y =cos x B .y =sin x C .y =ln x D .y =x 2+1 解析:由函数是偶函数,排除选项B 、C ,又选项D 中函数没有零点,排除D.答案:A4.已知ω>0,函数f (x )=cos ⎝⎛⎭⎪⎫ωx +π3的一条对称轴为x =π3,一个对称中心为⎝ ⎛⎭⎪⎫π12,0,则ω有( ) A .最小值2 B .最大值2 C .最小值1 D .最大值1解析:由题意知π3-π12≥T 4,故T =2πω≤π,ω≥2. 答案:A5.将函数f (x )=sin ⎝⎛⎭⎪⎫2x +π6的图象分别向左、向右平移φ个单位后,所得的图象都关于y 轴对称,则φ的最小值分别为( )A.π6,π3B.π3,π6C.2π3,5π6D.π6,π12解析:函数f (x )的图象向左平移φ个单位得到函数g (x )=sin ⎝⎛⎭⎪⎫2x +2φ+π6的图象,向右平移φ个单位得函数h (x )=sin ⎝⎛⎭⎪⎫2x -2φ+π6的图象,于是,2φ+π6=π2+k π,k ∈Z ,-2φ+π6=π2+k π,k ∈Z ,于是φ的最小值分别为π6,π3. 答案:A6.已知a =tan ⎝⎛⎭⎪⎫-7π6,b =cos 23π4,c =sin ⎝ ⎛⎭⎪⎫-334π,则a 、b 、c 的大小关系是( )A .b >a >cB .a >b >cC .b >c >aD .a >c >b解析:a =tan ⎝⎛⎭⎪⎫-π-π6=-tan π6=-33,b =cos 234π=cos ⎝⎛⎭⎪⎫6π-π4=cos π4=22,c =sin ⎝ ⎛⎭⎪⎫-334π=sin ⎝⎛⎭⎪⎫-8π-π4=-sin π4=-22,所以b >a >c . 答案:A7.设g (x )的图象是由函数f (x )=cos 2x 的图象向左平移π3个单位得到的,则g ⎝ ⎛⎭⎪⎫π6等于( ) A .1 B .-12C .0D .-1解析:由f (x )=cos 2x 的图象向左平移π3个单位得到的是g (x )=cos ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x +π3的图象,则g ⎝ ⎛⎭⎪⎫π6=cos ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫π6+π3=cos π=-1.故选D.答案:D8.如果函数y =3cos(2x +φ)的图象关于点⎝ ⎛⎭⎪⎫4π3,0中心对称,那么|φ|的最小值为( )A.π6B.π4C.π3D.π2解析:由y =3cos(2x +φ)的图象关于点⎝ ⎛⎭⎪⎫4π3,0中心对称,知f ⎝ ⎛⎭⎪⎫4π3=0,即3cos ⎝ ⎛⎭⎪⎫8π3+φ=0,所以8π3+φ=k π+π2(k ∈Z),所以φ=k π+π2-8π3(k ∈Z),|φ|的最小值为π6.答案:A9.已知函数f (x )=⎪⎪⎪⎪⎪⎪sin ⎝⎛⎭⎪⎫2x -π6,则下列说法中正确的是( )A .函数f (x )的周期是π4B .函数f (x )的图象的一条对称轴方程是x =π3C .函数f (x )在区间⎣⎢⎡⎦⎥⎤2π3,5π6上为减函数 D .函数f (x )是偶函数解析:当x =π3时,f (x )=1,所以x =π3是函数图象的一条对称轴.答案:B10.设f (n )=cos ⎝ ⎛⎭⎪⎫n π2+π4,则f (1)+f (2)+f (3)+…+f (2 015)等于( )A. 2 B .- 22 C .0 D.22解析:f (n )=cos ⎝ ⎛⎭⎪⎫n π2+π4的周期T =4;且f (1)=cos ⎝ ⎛⎭⎪⎫π2+π4=cos 3π4=-22,f (2)=cos ⎝ ⎛⎭⎪⎫π+π4=-22,f (3)=cos ⎝ ⎛⎭⎪⎫3π2+π4=22,f (4)=cos ⎝⎛⎭⎪⎫2π+π4=22.所以f (1)+f (2)+f (3)+f (4)=0,所以f (1)+f (2)+…+f (2 015)=f (2 013)+f (2 014)+f (2 015)=f (1)+f (2)+f (3)=-22.答案:B 11.函数y =sin(2x +φ)⎝ ⎛⎭⎪⎫0<φ<π2图象的一条对称轴在区间⎝ ⎛⎭⎪⎫π6,π3内,则满足此条件的一个φ值为( )A.π12B.π6C.π3D.5π6解析:令2x +φ=k π+π2(k ∈Z),解得x =k π2+π4-φ2(k ∈Z),因为函数y =sin(2x +φ)⎝ ⎛⎭⎪⎫0<φ<π2图象的一条对称轴在区间⎝ ⎛⎭⎪⎫π6,π3内,所以令π6<k π2+π4-φ2<π3(k ∈Z),解得k π-π6<φ<k π+π6(k ∈Z),四个选项中只有A 符合,故选A.答案:A12.函数y =1+sin x ,x ∈[0,2π]的图象与直线y =2交点的个数是( ) A .0 B .1 C .2 D .3解析:由函数y =1+sin x ,x ∈[0,2π]的图象(如图所示),可知其与直线y =2只有1个交点.答案:B二、填空题13.函数y =6sin ⎝ ⎛⎭⎪⎫14x -π6的振幅是________,周期是________,频率是_______,初相是_______,图象最高点的坐标是___________.解析:由题意,得A =6,T =2π14=8π,f =1T =18π,φ=-π6.当14x -π6=2k π+π2(k ∈Z),即x =8k π+8π3(k ∈Z)时,函数取得最大值6.答案:6 8π 18π -π6 ⎝ ⎛⎭⎪⎫8k π+8π3,6(k ∈Z) 14.在函数y =-2sin ⎝ ⎛⎭⎪⎫4x +23π的图象与x 轴的交点中,离原点最近的交点坐标是________.解析:当y =0时,sin ⎝⎛⎭⎪⎫4x +2π3=0,所以4x +2π3=k π,k ∈Z ,所以x =k4π-π6,k ∈Z ,取k =0,则x =-π6,取k =1,则x =π12,所以离原点最近的交点坐标是⎝ ⎛⎭⎪⎫π12,0.答案:⎝ ⎛⎭⎪⎫π12,0 15.已知f (x )=3sin(ωx +φ)对任意x 都有f ⎝ ⎛⎭⎪⎫π3+x =f ⎝ ⎛⎭⎪⎫π3-x ,则f ⎝ ⎛⎭⎪⎫π3等于________.解析:由f ⎝ ⎛⎭⎪⎫π3+x =f ⎝ ⎛⎭⎪⎫π3-x 知x =π3是f (x )的一条对称轴,故f ⎝ ⎛⎭⎪⎫π3=±3.答案:±316.若sin x =2m +1且x ∈R ,则m 的取值范围是________. 解析:因为-1≤sin x ≤1,sin x =2m +1,所以-1≤2m +1≤1,解得-1≤m ≤0.答案:[-1,0] 三、解答题17.用“五点法”作函数y =-2cos x +3(0≤x ≤2π)的简图. 解:列表:18.判断方程sin x =x10的根的个数.解:当x =3π时,y =x 10=3π10<1;当x =4π时,y =x 10=4π10>1.分别作出函数y =sin x 及y =x10的简图在y 轴的右侧图象,如下图所示.观察图象知,直线y =x10在y 轴右侧与曲线y =sin x 有且只有3个交点,又由对称性可知,在y 轴左侧也有3个交点,加上原点O(0,0),一共有7个交点.所以方程根的个数为7.19.设函数f (x )=sin(2x +φ)(-π<φ<0),已知它的一条对称轴是直线x =π8. (1)求φ;(2)求函数f (x )的单调递减区间. 解:(1)函数的一条对称轴是直线x =π8,2×π8+φ=k π+π2,k ∈Z ,因为-π<φ<0,所以φ=-3π4.(2)由(1)知,f (x )=sin ⎝⎛⎭⎪⎫2x -3π4,π2+2k π≤2x -3π4≤3π2+2k π,k ∈Z ,即5π8+k π≤x ≤9π8+k π,k ∈Z ,所以函数f (x )的单调递减区间为⎣⎢⎡⎦⎥⎤5π8+k π,9π8+k π(k ∈Z).20.函数f (x )=A sin(ωx -π6)+1(A >0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为π2.(1)求函数f (x )的解析式;(2)设α∈⎝ ⎛⎭⎪⎫0,π2,则f ⎝ ⎛⎭⎪⎫α2=2,求α的值. 解:(1)因为函数f (x )的最大值为3,所以A +1=3,即A =2.因为函数图象的相邻两条对称轴之间的距离为π2,所以最小正周期T =π,所以ω=2,故函数f (x )的解析式为y =2sin ⎝ ⎛⎭⎪⎫2x -π6+1. (2)因为f ⎝ ⎛⎭⎪⎫α2=2sin ⎝ ⎛⎭⎪⎫α-π6+1=2, 所以sin ⎝ ⎛⎭⎪⎫α-π6=12, 因为0<α<π2,所以-π6<α-π6<π3,所以α-π6=π6,故α=π3.B 级 能力提升1.方程lg x =sin x 的解的个数为( ) A .0 B .1 C .2 D .3解析:作出y =lg x 与y =sin x 的图象,如下图所示,由图知有三个交点,所以方程有三个解.答案:D2.不等式cos x <0,x ∈[0,2π]的解集为( ) A.⎝ ⎛⎭⎪⎫π2,3π2 B.⎣⎢⎡⎦⎥⎤π2,3π2 C.⎝ ⎛⎭⎪⎫0,π2 D.⎝ ⎛⎭⎪⎫π2,2π 解析:由y =cos x 的图象知,在[0,2π]内使cos x <0的x 的范围是⎝ ⎛⎭⎪⎫π2,3π2.答案:A3.直线xsin α+y +2=0的倾斜角的取值范围是________________. 解析:因为sin α∈[-1,1],所以-sin α∈[-1,1],所以已知直线的斜率范围为[-1,1],由倾斜角与斜率关系得倾斜角范围是⎣⎢⎡⎦⎥⎤0,π4∪⎣⎢⎡⎭⎪⎫3π4,π.答案:⎣⎢⎡⎦⎥⎤0,π4∪⎣⎢⎡⎭⎪⎫3π4,π4.函数y =log 12sin x 的定义域是______________.解析:由log 12sin x ≥0知0<sin x ≤1,由正弦函数图象知2k π<x<2k π+π,k∈Z.答案:{x|2k π<x<2k π+π,k ∈Z}5.已知θ是第四象限角,且sin ⎝ ⎛⎭⎪⎫θ+π4=35,则tan ⎝ ⎛⎭⎪⎫θ-π4=________.解析:由题意知sin ⎝ ⎛⎭⎪⎫θ+π4=35,θ是第四象限角,所以cos ⎝ ⎛⎭⎪⎫θ+π4>0,所以cos ⎝ ⎛⎭⎪⎫θ+π4=1-sin2⎝ ⎛⎭⎪⎫θ+π4=45.tan ⎝ ⎛⎭⎪⎫θ-π4=tan ⎝ ⎛⎭⎪⎫θ+π4-π2=-1tan ⎝ ⎛⎭⎪⎫θ+π4= -cos ⎝ ⎛⎭⎪⎫θ+π4sin ⎝ ⎛⎭⎪⎫θ+π4=-4535=-43. 答案:-436.已知sin α+2cos α=0,则2sin αcos α-cos 2α的值是________. 解析:由sin α+2cos α=0,得tan α=-2. 所以2sin αcos α-cos 2α= 2sin αcos α-cos 2αsin 2α+cos 2α=2tan α-1tan 2α+1=-4-14+1=-1. 答案:-17.已知f (x )=2sin ⎝ ⎛⎭⎪⎫2x -π6-m 在x ∈⎣⎢⎡⎦⎥⎤0,π2上有两个不同的零点,则m的取值范围是________.解析:f (x )有两个零点,即m =2sin ⎝ ⎛⎭⎪⎫2x -π6,在⎣⎢⎡⎦⎥⎤0,π2上有两个不同的实根.当x ∈⎣⎢⎡⎦⎥⎤0,π2时,2x -π6∈⎣⎢⎡⎦⎥⎤-π6,56π,结合正弦曲线知m ∈[1,2).答案:[1,2)8.方程sin x =1-a 2在x ∈⎣⎢⎡⎦⎥⎤π3,π上有两个实数根,求α的取值范围.解:在同一直角坐标系中作出y =sin x ,x ∈⎣⎢⎡⎦⎥⎤π3,π的图象,y =1-a 2的图象,由图象可知,当32≤1-a 2<1,即-1<a ≤1-3时,y =sin x ,x ∈⎣⎢⎡⎦⎥⎤π3,π的图象与y =1-a 2的图象有两个交点,即方程sin x =1-a 2在x ∈⎝ ⎛⎭⎪⎫π3,π上有两个实数根.故所求a 的取值范围为(-1,1- 3 ].9.已知函数y =A sin(ωx +φ)+m 的最大值是4,最小值是0,最小正周期是π2,直线x =π3是其图象的一条对称轴,则下面各解析式符合条件的是( ) A .y =4sin ⎝ ⎛⎭⎪⎫4x +π6+2 B .y =2sin ⎝ ⎛⎭⎪⎫2x +π3+2C .y =2sin ⎝ ⎛⎭⎪⎫4x +π3+2D .y =2sin ⎝ ⎛⎭⎪⎫4x +π6+2解析:因为最大值是4,故选项A 不符合题意.又因为T =2πω=π2,所以ω=4,故排除选项B.令4x +π3=π2+k π,k ∈Z ⇒4x =π6+k π,k ∈Z ⇒x =π24+k π4,k ∈Z ,令π24+k π4=π3,得k =π6∉Z ,排除选项C ,故选D. 答案:D10.已知函数y =sin(ωx +φ)(ω>0,-π<φ≤π)的图象如图所示,则φ=________.解析:由题意得T2=2π-34π,所以T =52π,ω=45.由x =34π时y =-1得-1=sin ⎝ ⎛⎭⎪⎫35π+φ,又-2π5<35π+φ<85π,所以35π+φ=32π ,所以φ=910π.答案:910π11.(本小题满分10分)已知0<α<π2,sin α=45.(1)求tan α的值;(2)求sin (α+π)-2cos ⎝ ⎛⎭⎪⎫π2+α-sin (-α)+cos (π+α)的值.解:(1)因为0<α<π2,sin α=45,所以cos α=35,故tan α=43.(2)sin (α+π)-2cos ⎝ ⎛⎭⎪⎫π2+α-sin (-α)+cos (π+α)=-sin α+2sin αsin α-cos α= sin αsin α-cos α=tan αtan α-1=4.12.(本小题满分12分)已知函数f (x )=2sin ⎝ ⎛⎭⎪⎫2x -π6+a ,a 为常数.(1)求函数f (x )的最小正周期;(2)若x ∈⎣⎢⎡⎦⎥⎤0,π2时,f (x )的最小值为-2,求a 的值.解:(1)f (x )=2sin ⎝ ⎛⎭⎪⎫2x -π6+a .所以f (x )的最小正周期T =2π2=π.(2)当x ∈⎣⎢⎡⎦⎥⎤0,π2时,2x -π6∈⎣⎢⎡⎦⎥⎤-π6,5π6,所以x =0时,f (x )取得最小值,即2sin ⎝ ⎛⎭⎪⎫-π6+a =-2,故a =-1.13.已知函数f (x )=3sin ⎝ ⎛⎭⎪⎫12x -π4,x ∈R.(1)利用“五点法”画出函数f (x )在一个周期⎣⎢⎡⎦⎥⎤π2,9π2上的简图; (2)先把f (x )的图象上所有点向左平移π2个单位长度,得到f 1(x )的图象;然后把f 1(x )的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到f 2(x )的图象;再把f 2(x )的图象上所有点的纵坐标缩短到原来的13倍(横坐标不变),得到g (x )的图象,求g (x )的解析式.解:(1)列表取值,描出五个关键点并用光滑曲线连接,得到一个周期的简图.3 0(2)将f (x )=3sin ⎝ ⎛⎭⎪⎫12x -π4图象上所有点向左平移π2个单位长度得到f 1(x )=3sin ⎣⎢⎡⎦⎥⎤12⎝⎛⎭⎪⎫x +π2-π4=3sin 12x 的图象.把f 1(x )=3sin 12x 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)得到f 2(x )=3sin 14x 的图象,把f 2(x )=3sin 14x 的图象上所有点的纵坐标缩短到原来的13(横坐标不变)得到g (x )=sin 14x 的图象.14.(本小题满分12分)(2015·湖北卷)某同学用“五点法”画函数f (x )=A sin(ωx +φ)⎝⎛⎭⎪⎫ω>0,||φ<π2在某一个周期内的图象时,列表并填入了部分数据,如下表:(1)(2)将y =f (x )图象上所有点向左平行移动π6个单位长度,得到y =g (x )的图象,求y =g (x )的图象离原点O 最近的对称中心.解:(1)根据表中已知数据,解得A =5,ω=2,φ=-π6.数据补全如下表:且函数表达式为f (x )=5sin ⎝ ⎭⎪⎫2x -6.(2)由(1)知f (x )=5sin ⎝⎛⎭⎪⎫2x -π6,因此g (x )=5sin ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫x +π6-π6=5sin ⎝ ⎛⎭⎪⎫2x +π6.因为y =sin x 的对称中心为(k π,0),k ∈Z ,令2x +π6=k π,k ∈Z ,解得x =k π2-π12,k ∈Z ,即y =g (x )图象的对称中心为⎝ ⎛⎭⎪⎫k π2-π12,0,k ∈Z ,其中离原点O 最近的对称中心为⎝ ⎛⎭⎪⎫-π12,0.15.(本小题满分12分)函数f (x )=A sin ⎝⎛⎭⎪⎫ωx -π6+1(A >0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为π2.(1)求函数f (x )的解析式;(2)设α∈⎝⎛⎭⎪⎫0,π2,f ⎝ ⎛⎭⎪⎫α2=2,求α的值.解:(1)因为函数f (x )的最大值为3,所以A +1=3,即A =2,因为函数图象的相邻两条对称轴之间的距离为π2, 所以最小正周期T =π,所以ω=2,故函数f (x )的解析式为y =2sin ⎝⎛⎭⎪⎫2x -π6+1.(2)因为f ⎝ ⎛⎭⎪⎫α2=2sin ⎝ ⎛⎭⎪⎫α-π6+1=2,即sin ⎝ ⎛⎭⎪⎫α-π6=12,因为0<α<π2,所以-π6<α-π6<π3, 所以α-π6=π6,故α=π3.16.(本小题满分12分)已知函数y =A sin(ωx +φ)(A >0,ω>0,|ω|<π)的一段图象如图所示.(1)求此函数的解析式;(2)求此函数在(-2π,2π)上的递增区间. 解:(1)由图可知,其振幅为A =23,由于T2=6-(-2)=8,所以周期为T =16,所以ω=2πT =2π16=π8,此时解析式为y =23sin ⎝ ⎛⎭⎪⎫π8x +φ.因为点(2,-23)在函数y =23sin ⎝ ⎛⎭⎪⎫π8x +φ的图象上,所以π8×2+φ=2k π-π2,所以φ=2k π-3π4(k ∈Z).又|φ|<π,所以φ=-3π4.故所求函数的解析式为y =23sin ⎝ ⎛⎭⎪⎫π8x -3π4. (2)由2k π-π2≤π8x -3π4≤2k π+π2(k ∈Z),得16k +2≤x ≤16k +10(k ∈Z),所以函数y =23sin ⎝ ⎛⎭⎪⎫π8x -3π4的递增区间是[16k +2,16k +10](k ∈Z). 当k =-1时,有递增区间[-14,-6],当k =0时,有递增区间[2,10], 与定义区间求交集得此函数在(-2π,2π)上的递增区间为(-2π,-6]和[2,2π].17.(本小题满分12分)设函数f (x )=sin(2x +φ)(-π<φ<0),y =f (x )的图象的一条对称轴是直线x =π8.(1)求φ;(2)求函数y =f (x )的单调增区间;(3)画出函数y =f (x )在区间[0,π]上的图象.解:(1)因为x =π8是函数y =f (x )的图象的对称轴,所以sin ⎝ ⎛⎭⎪⎫2×π8+φ=±1,即π4+φ=k π+π2,k ∈Z.因此-π<φ<0,所以当k =-1时得φ=-3π4.(2)由(1)知φ=-3π4,因此y =sin ⎝⎛⎭⎪⎫2x -3π4.由题意得2k π-π2≤2x -3π4≤2k π+π2,k ∈Z ,解得k π+π8≤x ≤k π+58π,(k ∈Z)所以函数y =sin ⎝⎛⎭⎪⎫2x -3π4的单调增区间为: ⎣⎢⎡⎦⎥⎤k π+π8,k π+5π8,k ∈Z.(3)由y =sin ⎝⎛⎭⎪⎫2x -3π4知: 令z =2x -34π,x ∈[0,π]①列表如下:。
高中数学 第一章 1.4.1 正弦函数、余弦函数的图象检测 新人教A版必修4

亲爱的同学:这份试卷将再次记录你的自信、沉着、智慧和收获,我们一直投给你信任的目光……学 习 资 料 专 题第一章 1.4 1.4.1 正弦函数、余弦函数的图象A 级 基础巩固一、选择题1.对于正弦函数y =sin x 的图象,下列说法错误的是( D ) A .向左右无限伸展B .与y =cos x 的图象形状相同,只是位置不同C .与x 轴有无数个交点D .关于y 轴对称2.从函数y =cos x ,x ∈[0,2π)的图象来看,对应于cos x =12的x 有( B )A .1个值B .2个值C .3个值D .4个值[解析] 如图所示,y =cos x ,x ∈[0,2π]与y =12的图象,有2个交点,∴方程有2个解.3.在[0,2π]上,满足sin x ≥22的x 的取值范围是( B ) A .[0,π4]B .[π4,3π4]C .[π4,π2]D .[3π4,π][解析] 由图象得:x 的取值范围是[π4,34π].4.函数y =-cos x (x >0)的图象中与y 轴最近的最高点的坐标为( B ) A .(π2,1)B .(π,1)C .(0,1)D .(2π,1)[解析] 用五点法作出函数y =-cos x ,x >0的图象如图所示.5.函数y =|sin x |的图象( B ) A .关于x 轴对称 B .关于y 轴对称 C .关于原点对称 D .关于坐标轴对称[解析] y =|sin x |=⎩⎪⎨⎪⎧sin x , k π≤x <2k π+π-sin x , k π+π≤x <2k π+2πk ∈Z ,其图象如图:6.函数y =1sin x 的定义域为( B )A .RB .{x |x ≠k π,k ∈Z }C .[-1,0)∪(0,1]D .{x |x ≠0}[解析] 由sin x ≠0,得x ≠k π(k ∈Z ),故选B . 二、填空题7.已知函数f (x )=3+2cos x 的图象经过点(π3,b ),则b =__4__.[解析] b =f (π3)=3+2cos π3=4.8.下列各组函数中,图象相同的是__(4)__. (1)y =cos x 与y =cos(π+x ); (2)y =sin(x -π2)与y =sin(π2-x );(3)y =sin x 与y =sin(-x ); (4)y =sin(2π+x )与y =sin x .[解析] 本题所有函数的定义域是R . cos(π+x )=-cos x ,则(1)不同; sin(x -π2)=-sin(π2-x )=-cos x ,sin(π2-x )=cos x ,则(2)不同;sin(-x )=-sin x ,则(3)不同; sin(2π+x )=sin x ,则(4)相同. 三、解答题9.在[0,2π]内用五点法作出y =-sin x -1的简图. [解析] (1)按五个关键点列表(2)描点并用光滑曲线连接可得其图象,如图所示.10.判断方程x 2-cos x =0的根的个数.[解析] 设f (x )=x 2,g (x )=cos x ,在同一直角坐标系中画出f (x )和g (x )的图象,如图所示.由图知f (x )和g (x )的图象有两个交点,则方程x 2-cos x =0有两个根.B 级 素养提升一、选择题1.若cos x =0,则角x 等于( B ) A .k π(k ∈Z ) B .π2+k π(k ∈Z )C .π2+2k π(k ∈Z )D .-π2+2k π(k ∈Z )2.当x ∈[0,2π]时,满足sin(π2-x )≥-12的x 的取值范围是( C )A .[0,2π3]B .[4π3,2π]C .[0,2π3]∪[4π3,2π]D .[2π3,4π3][解析] 由诱导公式化简可得cos x ≥-12,结合余弦函数的图象可知选C .3.函数y =cos x +|cos x | x ∈[0,2π]的大致图象为( D)[解析] y =cos x +|cos x |=⎩⎪⎨⎪⎧2cos x x ∈[0,π2]∪[3π2,2π]0 x ∈π2,3π2,故选D .4.在(0,2π)上使cos x >sin x 成立的x 的取值范围是( A ) A .(0,π4)∪(5π4,2π)B .(π4,π2)∪(π,5π4)C .(π4,5π4)D .(-3π4,π4)[解析] 第一、三象限角平分线为分界线,终边在下方的角满足cos x >sin x . ∵x ∈(0,2π),∴cos x >sin x 的x 范围不能用一个区间表示,必须是两个区间的并集. 二、填空题5.若sin x =2m +1,则m 的取值范围是__{m |-1≤m ≤0}__. [解析] 由-1≤2m +1≤1,解得-1≤m ≤0. 6.函数f (x )=⎩⎪⎨⎪⎧sin x ,x ≥0,x +2,x <0,则不等式f (x )>12的解集是 ⎩⎨⎧⎭⎬⎫x |-32<x <0,或π6+2k π<x <5π6+2k π,k ∈N .[解析] 在同一平面直角坐标系中画出函数f (x )和函数y =12的图象,如图所示,当f (x )>12时,函数f (x )的图象位于函数y =12的图象上方,此时有-32<x <0或π6+2k π<x <5π6+2k π(k ∈N ).三、解答题7.若集合M ={θ|sin θ≥12},N ={θ|cos θ≤12},θ∈[0,2π],求M ∩N .[解析] 首先作出正弦函数,余弦函数在[0,2π]上的图象以及直线y =12,如图所示.由图象可知,在[0,2π]内, sin θ≥12,π6≤θ≤5π6,cos θ≤12时,π3≤θ≤4π3.所以在[0,2π]内,同时满足sin θ≥12与cos θ≤12时,π3≤θ≤5π6.所以M ∩N ={θ|π3≤θ≤5π6}.8.已知函数f (x )=⎩⎪⎨⎪⎧sin x x ≤cos x ,cos xx >sin x ,试画出f (x )的图象.[解析] 在同一坐标系内分别画出正、余弦曲线,再比较两个函数的图象,上方的画成实线,下方的画面虚线,则实线部分即为f (x )的图象.C级能力拔高若函数y=2cos x(0≤x≤2π)的图象和直线y=2围成一个封闭的平面图形,求这个封闭图形的面积.[解析]观察图可知:图形S1与S2,S3与S4是两个对称图形,有S1=S2,S3=S4,因此函数y=2cos x的图象与直线y=2所围成的图形面积可以转化为求矩形OABC的面积.因为|OA|=2,|OC|=2π,所以S矩形OABC=2×2π=4π.故所求封闭图形的面积为4π.。
高中数学人教版必修四课后练习(含解析):1.4.1正弦函数、余弦函数的图象.docx

高中数学学习材料马鸣风萧萧*整理制作1.4.1正弦函数、余弦函数的图象班级:__________姓名:__________设计人:__________日期:__________课后练习基础过关1.函数y=-sin x,的简图是A. B.C. D.2.下列说法不正确的是A.y=sin x的图象与y=cos x的图象的形状完全一样,只是在坐标系中的位置不同B.y=sin x的图象介于直线y=±1之间C.y=cos x(0≤x≤2π)的图象的五个关键点是(0,0),,(π,0),,(2π,0)D.y=sin x与y=cos x的图象与x轴都有无数个公共点3.方程的解的个数是马鸣风萧萧马鸣风萧萧A.5B.6C.7D.84.若0≤sin α≤,且α∈[-2π,0),则α的取值范围是A.[-2π,-]∪[-,-π]B.[-2π+2kπ,-+2kπ]∪[-+2kπ,-π+2kπ](k∈Z)C.[0,]∪[,π]D.[2kπ,2kπ+]∪[2kπ+,2kπ+π](k∈Z)5.方程cos x=lg x的实根的个数是____.6.不等式2sin x-1≥0的解集为.7.若,且x∈R,则m的取值范围是 .8.根据y=cos x的图象解不等式:,x∈[0,2π].能力提升1.若函数f(x)=sin x+2|sin x|,x∈[0,2π]的图象与直线y=k有且只有两个不同的交点,求k 的取值范围.2.画出函数在一个周期内的图像.马鸣风萧萧1.4.1正弦函数、余弦函数的图象详细答案【基础过关】 1.D 2.C【解析】A 、B 、D 正确.如图, 的图象的五个关键点应是(0,1),,(π,−1),(2π,1).故选C.3.C【解析】在同一坐标系中分别作出函数: ,的图象,如图,当 时,,故由图可知函数 ,的图象在y 轴左边有3个交点、右边有3个交点,再加上原点,共计7个交点,即方程的解的个数是7.故选C.4.A【解析】根据题意结合正弦函数图象可知,α满足[2kπ,2kπ+]∪[2k π+,2kπ+π](k ∈Z),∵α∈[-2π,0),∴α的取值范围是[-2π,-]∪[-,-π].故选A.5.3【解析】求方程cos x =lg x 的实根的个数等价于求函数y =cos x 与y =lg x 的图象的交点个数.如图所示,可得两图象的交点个数为3,即方程cos x =1g x 的实根的个数是3.马鸣风萧萧6.[2k π+,2k π+](k ∈Z )【解析】不等式等价于sin x ≥,由正弦函数的图象可知,不等式的解集为[2k π+,2k π+](k ∈Z ).【备注】要解决此类问题,应先找出不等式在一个周期内的解,然后再加上周期的整数倍即可.7.(]1,3,5⎡⎫--⋃-+⎪⎢⎣⎭∞∞【解析】由cosx ∈[―1,1],x ∈R , 得211132m m --≤≤+,即211,32211,32m m m m -⎧≥-⎪⎪+⎨-⎪≤⎪+⎩510,3230,32m m m m +⎧≥⎪⎪+⎨+⎪≥⎪+⎩12,532m 3,3m m m ⎧≥-<-⎪⎪⎨⎪≤->-⎪⎩或或所以m≤−3或15m ≥-. 8.函数cos y x =,[0,2]x π∈的图像 如图所示:根据图像可得不等式的解集为:5753663xx x ππππ⎧⎫≤≤≤≤⎨⎬⎩⎭或.【能力提升】1.3sin (0),()sin (2),x x f x x x πππ≤≤⎧=⎨-<≤⎩作出函数的图像如图:马鸣风萧萧由图可知当13k <<时函数()sin 2sin f x x x =+,[0,2]x π∈的图像与直线y k =有且只有两个不同的交点. 2.(1)列表如下:-(2)描点、连线如下图【解析】本题考查“五点法”作函数 的简图.先作变量代换,令 再用方程思想由 取来确定对应 的值,最后根据 的值描点,连线画出函数的图象.。
人教版高中数学高一A版必修4同步优化训练 1.4.1正弦函数、余弦函数的图象

1.4 三角函数的图象与性质 1.4.1 正弦函数、余弦函数的图象5分钟训练(预习类训练,可用于课前)1.以下对正弦函数y=sinx 的图象描述不正确的是( )A.在x ∈[2kπ,2(k+1)π](k ∈Z )上的图象形状相同,只是位置不同B.介于直线y=1与直线y=-1之间C.关于x 轴对称D.与y 轴仅一个交点解析:画出y=sinx 的图象,根据图象可知A 、B 、D 三项都正确. 答案:C2.设M 和m 分别是函数y=31cosx-1的最大值和最小值,则M+m=_____________. 解析:M=31-1=32-,m=-31-1=34-,∴M+m=32-34-=-2.答案:-23.利用五点法,在[0,2π]上画出下列函数的简图: (1)y=sinx-1;(2)y=2cosx.解析:画函数的简图,可以采用“五点法”,关键是找出五个关键点,所以,最好利用列表整理数据,使问题既清晰又准确. (1)第一步:按五个关键点列表;x 0 2π π 23π 2π sinx1-1 0 sinx-1 -1 0 -1 -2-1第二步:描点;第三步:画图,即用光滑的曲线将五个点连接起来.(2)第一步:按五个关键点列表;x 0 2π π 23π 2π cosx1-10 1 2cosx 2 0 -2 02第二步:描点;第三步:画图,即用光滑的曲线将五个点连接起来.10分钟训练(强化类训练,可用于课中)1.函数y=2sin(3x+4π)的对称轴为________________,对称中心为______________. 解析:观察y=sinx 的图象,x=kπ+2π(k ∈Z )是其对称轴,(kπ,0)是其对称中心.由3x+4π=kπ+2π(k ∈Z ),得x=3πk +12π(k ∈Z )为对称轴;由3x+4π=kπ(k ∈Z ),得(3πk -12π,0)(k∈Z )为对称中心. 答案:x=3πk +12π(k ∈Z ) (3πk -12π,0)(k ∈Z ) 2.分析y=sinx-1及y=2sinx 的图象在[0,2π]上与y=sinx 的图象的位置关系.解:(1)在同一坐标系中画出y=sinx-1与y=sinx 的图象.通过图象比较,可知y=sinx-1的图象是将y=sinx 的图象整个向下平行移动了1个单位得到的.(2)在同一坐标系中,画出y=2sinx 与y=sinx 的图象.通过图象很容易看出,将y=sinx 的图象上所有的点的纵坐标扩大到原来的2倍,横坐标保持不变,就可以得到y=2sinx 的图象.3.作出函数y=-sinx ,x ∈[-π,π]的简图,并回答下列问题: (1)观察函数图象,写出满足下列条件的x 的区间: ①sinx >0;②sinx<0. (2)直线y=21与y=-sinx 的图象有几个交点? 解:利用五点法作图,(1)根据图象可知图象在x 轴上方的部分sinx >0,在x 轴下方的部分sinx <0,所以当x ∈(-π,0)时,sinx >0;当x ∈(0,π)时,sinx <0. (2)画出直线y=21,得知有两个交点. 30分钟训练(巩固类训练,可用于课后)1.对于余弦函数y=cosx 的图象,有以下描述:①向左向右无限伸展;②与y=sinx 的形状完全一样,只是位置不同; ③与x 轴有无数多个交点;④关于y 轴对称. 其中正确的描述有( )A.1项B.2项C.3项D.4项 解析:由函数y=cosx 的图象可知①②③④都正确. 答案:D2.在(0,2π)上,使sinx >cosx 成立的x 的取值范围是( )A.(4π,2π)∪(π,45π) B.(4π,π)C.(4π,45π)D.(4π,π)∪(45π,23π)解法一:作出在(0,2π)区间上正弦和余弦函数的图象,解出两交点的横坐标为4π和45π,由图(1)可得答案C.(1) (2)解法二:在单位圆中作出第一、三象限的角平分线如图(2),由正弦线、余弦线可知应选C. 答案:C3.方程sinx=lgx 的实根的个数有( )A.1个B.2个C.3个D.无穷多个 解析:如图,在同一直角坐标系中作函数y=sinx 与y=lgx 的图象.由图中看出两函数图象有三个交点(x i ,y i ),其中x i ∈(1,10)(i=1,2,3)是方程sinx=lgx 的解,此方程再无别的解. 答案:C4.y=1+cosx ,x ∈[0,2π]与直线y=23的图象交点个数为___________. 解析:分别画出y=1+cosx 与y=23的图象,确定交点. 答案:25.(2005高考上海卷,理10)函数f(x)=sinx+2|sinx |,x ∈[0,2π]的图象与直线y=k 有且仅有两个不同的交点,则k 的取值范围是_________________. 解析:∵f(x)=⎩⎨⎧∈-∈],2,[,sin ),,0[,sin 3πππx x x x∴y=f(x)的图象如下图.故若y=f(x)与y=k 的图象有且仅有两个交点,则k 的范围是1<k <3. 答案:1<k <3 6.方程sinx=10x的根的个数为______________. 解析:这是一个超越方程,无法直接求解,考虑数形结合思想,转化为函数y=10x与函数y=sinx 的图象交点个数,借助图形直观求解.当x≥4π时,10x ≥104π>1≥sinx;当0<x <4π时,sin 25π=1>205π=10x ,从而x >0时,有3个交点,由对称性x <0时,也有3个交点,加上原点,一共有7个交点.答案:77.作出函数y=x tan 1sinx 的图象. 解析:函数y=x tan 1sinx 的图象即是y=cosx(x≠kπ且x≠kπ+2π,k ∈Z )的图象,因此作出y=cosx的图象后,要把x=kπ和x=kπ+2π,k ∈Z 的这些点去掉.首先将函数的解析式变形,化为最简形式,然后作函数的图象. 当sinx≠0且tanx 有意义,即x≠kπ且x≠kπ+2π(k ∈Z )时,有y=x tan 1sinx=cosx ,即y=cosx(x≠kπ且x≠kπ+2π,k ∈Z ). 其图象如下图.8.画出下列函数的简图:(1)y=3+sinx ,x ∈[0,2π]; (2)y=2-sinx ,x ∈[0,2π]; (3)y=-cosx+3,x ∈[-π,π].解析:可以采用“五点法”,关键是找出五个关键点,整理数据,描点画图. 解:(画法略)快乐时光代词语法课上,约翰的思想开了小差.突然老师问道:“约翰,你能说出两个代词吗?”约翰站起来,摇摇头说:“谁?我!”。
人教A版高中数学必修四同步测试1.4.1正弦函数、余弦函数的图像(教师版)

1.4.1 正弦函数、余弦函数的图像(检测教师版)时间:40分钟 总分:60分班级: 姓名:一、 选择题(共6小题,每题5分,共30分)1.函数y =-sin x ,x ∈⎣⎢⎡⎦⎥⎤-π2,3π2的简图是( )【解析】 可以用特殊点来验证.x =0时,y =-sin 0=0,排除A 、C ;当x =3π2时,y =-sin 3π2=1,排除B .【答案】 D2.在[0,2π]内,不等式sin x <-32的解集是( ) A .(0,π) B .⎝ ⎛⎭⎪⎫π3,4π3C .⎝⎛⎭⎪⎫4π3,5π3D .⎝⎛⎭⎪⎫5π3,2π【解析】 画出y =sin x ,x ∈[0,2π]的草图如下:因为sin π3=32,所以sin ⎝ ⎛⎭⎪⎫π+π3=-32,sin ⎝ ⎛⎭⎪⎫2π-π3=-32. 即在[0,2π]内,满足sin x =-32的是x =4π3或x =5π3. 可知不等式sin x <-32的解集是⎝ ⎛⎭⎪⎫4π3,5π3.【答案】 C3.将余弦函数y =cos x 的图象向右至少平移m 个单位,可以得到函数y =-sin x 的图象,则m=( )A .π2B .πC .3π2D .3π4【解析】 根据诱导公式得,y =-sin x =cos ⎝⎛⎭⎪⎫3π2-x =cos ⎝⎛⎭⎪⎫x -3π2,故欲得到y =-sinx 的图象,需将y =cos x 的图象向右至少平移3π2个单位长度.【答案】 C4.函数y =sin x ,x ∈[0,2π]的图象与直线y =-12的交点有( )A .1个B .2个C .3个D .4个【解析】 在[0,2π]内使sin x =-12的角x 为7π6和11π6,所以y =sin x ,x ∈[0,2π]的图象与直线y =-12有2个交点,故选B .【答案】 B5.已知函数y =2sin x ⎝ ⎛⎭⎪⎫π2≤x ≤5π2的图象与直线y =2围成一个封闭的平面图形,那么此封闭图形的面积( )A .4B .8C .4πD .2π【解析】数形结合,如图所示.y =2sin x ,x ∈⎣⎢⎡⎦⎥⎤π2,5π2的图象与直线y =2围成的封闭平面图形面积相当于由x =π2,x =5π2, y =0,y =2围成的矩形面积,即S =⎝⎛⎭⎪⎫5π2-π2×2=4π.【答案】 C6.函数y =cos x +|cos x |,x ∈[0,2π]的大致图象为( )【解析】 由题意得y =⎩⎪⎨⎪⎧2cos x ,0≤x ≤π2或32π≤x ≤2π,0,π2<x <32π.显然只有D 合适.【答案】 D二、填空题(共2小题,每题5分,共10分)7.利用余弦曲线,写出满足cos x >0,x ∈[0,2π]的x 的区间是_________.【解析】 画出y =cos x ,x ∈[0,2π]上的图象如图所示.cos x >0的区间为⎣⎢⎡⎭⎪⎫0,π2∪⎝⎛⎦⎥⎤3π2,2π.【答案】 ⎣⎢⎡⎭⎪⎫0,π2∪⎝ ⎛⎦⎥⎤3π2,2π 8.函数y =log 12sin x 的定义域是__________.【解析】 由log 12sin x ≥0知0<sin x ≤1,由正弦函数图象知2k π<x <2k π+π,k ∈Z .【答案】 {x |2k π<x <2k π+π,k ∈Z }三、解答题(共2小题,每题10分,共20分) 9.用五点法作出函数y =1-cos x (0≤x ≤2π)的简图.【解析】 列表:描点连线,如图.10.作出函数y=-sin x,x∈[-π,π]的简图,并回答下列问题:(1)观察函数图象,写出满足下列条件的x的区间:①sin x>0;②sin x<0.(2)直线y=12与y=-sin x的图象有几个交点?【解析】:利用五点法作图.(1)根据图象可知图象在x轴上方的部分sin x>0,在x轴下方的部分sin x<0.所以①当x∈(-π,0)时,sin x>0;②当x∈(0,π)时,sin x<0.(2)画出直线y=12,得知有两个交点.。
人教A版高中数学高一必修4练习 1.4.1正弦函数、余弦函数的图象

A 级 基础巩固一、选择题1.点M ⎝⎛⎭⎫π2,-m 在函数y =sin x 的图象上,则m 等于( ) A .0B .1C .-1D .2解析:由题意-m =sin π2,所以-m =1,所以m =-1.答案:C2.在同一坐标系中函数y =sin x ,x ∈[0,2π]与y =sin x ,x ∈[2π,4π]的图象( ) A .重合B .形状相同,位置不同C .形状不同,位置相同D .形状不同,位置不同解析:解析式相同,定义域不同. 答案:B3.函数y =sin (-x ),x ∈[0,2π]的简图是( )解析:由y =sin (-x )=-sin x 可知,其图象和y =sin x 的图象关于x 轴对称. 答案:B4.函数y =1+sin x ,x ∈[0,2π]的图象与直线y =2交点的个数是( ) A .0B .1C .2D .3解析:由函数y =1+sin x ,x ∈[0,2π]的图象(如图所示),可知其与直线y =2只有1个交点.答案:B5.在[0,2π]内,不等式sin x <-32的解集是( ) A .(0,π)B.⎝⎛⎭⎫π3,4π3C.⎝⎛⎭⎫4π3,5π3D.⎝⎛⎭⎫5π3,2π 解析:画出y =sin x ,x ∈[0,2π]的草图如下.因为sin π3=32,所以sin ⎝⎛⎭⎫π+π3=-32,sin ⎝⎛⎭⎫2π-π3=-32.即在[0,2π]内,满足sin x =-32的x =4π3或5π3.可知不等式sin x <-32的解集是⎝⎛⎭⎫4π3,5π3. 答案:C 二、填空题6.用“五点法”画出y =2sin x 在[0,2π]内的图象时,应取的五个点为________________.解析:可结合函数y =sin x 的五个关键点寻找,即把相应的五个关键点的纵坐标变为原来的2倍即可.答案:(0,0),⎝⎛⎭⎫π2,2,(π,0),⎝⎛⎭⎫3π2,-2,(2π,0) 7.若sin x =2m +1且x ∈R ,则m 的取值范围是________. 解析:因为-1≤sin x ≤1,sin x =2m +1, 所以-1≤2m +1≤1,解得-1≤m ≤0. 答案:[-1,0] 8.函数y =log 12sin x 的定义域是______________. 解析:由log 12sin x ≥0知0<sin x ≤1,由正弦函数图象知2k π<x <2k π+π,k ∈Z.答案:{x |2k π<x <2k π+π,k ∈Z} 三、解答题9.用“五点法”作函数y =-2cos x +3(0≤x ≤2π)的简图. 解:列表:xπ2π3π22π-2cos x -2 0 2 0 -2 -2cos x +313531描点、连线得出函数y =-2cos x +3(0≤x ≤2π)的图象:10.判断方程sin x =x10的根的个数.解:当x =3π时,y =x 10=3π10<1;当x =4π时,y =x 10=4π10>1.分别作出函数y =sin x 及y =x10的简图在y 轴的右侧图象,如下图所示.观察图象知,直线y =x10在y 轴右侧与曲线y =sin x 有且只有3个交点,又由对称性可知,在y 轴左侧也有3个交点,加上原点O (0,0),一共有7个交点.所以方程根的个数为7.B 级 能力提升1.已知函数f (x )=|sin x |,x ∈[-2π,2π],则方程f (x )=12的所有根的和等于( )A .0B .πC .-πD .-2π解析:若f (x )=12,即|sin x |=12,则sin x =12或sin x =-12.因为x ∈[-2π,2π],所以方程sin x =12的4个根关于x =-π2对称,则对称的2个根之和为-π,则4个根之和为-2π,由对称性可得sin x =-12的四个根之和为2π.综上,方程f (x )=12的所有根的和等于0.答案:A2.直线x sin α+y +2=0的倾斜角的取值范围是___________. 解析:因为sin α∈[-1,1],所以-sin α∈[-1,1],所以已知直线的斜率范围为[-1,1],由倾斜角与斜率关系得倾斜角范围是⎣⎡⎦⎤0,π4∪⎣⎡⎭⎫3π4,π.答案:⎣⎡⎦⎤0,π4∪⎣⎡⎭⎫3π4,π 3.若函数f (x )=sin x +2|sin x |,x ∈[0,2π]的图象与直线y =k 有且仅有两个不同的交点,求k 的范围.解:原函数可化为分段函数f (x )=⎩⎪⎨⎪⎧3sin x , x ∈[0,π),-sin x , x ∈[π,2π],如图所示,由图象可得k ∈(1,3).。
高中数学人教A版必修四1.4.1正弦函数、余弦函数的图像同步练习

«1.4.1正弦函数、余弦函数的图像》同步练习1.满足Si" >势恢的集合为()A.{X|2/C7T +-<%<2kn+ ―, k E Z]6 6S.{x\2kn + — < x < 2kn + —f k E Z]6 6C.{x\2kn — -< % < 2kn + -f kEZ]6 6D.{%| 2kn — - < % < 2kn + k E Z}3 32.已知f(x) = sin(2x +扌),g(x) = cos(2x - £),则下列结论中不正确的是()A.将函数f(x)的图象向右平移扌个单位后得到函数g(x)的图象B.函数y = f(x) • g(x)的图象关于G,0)对称C.函数y = f(x) • g(x)的最大值为扌D.函数y = /(%) • g(x)的最小正周期为f3.函数y=|sinx|的一个单调增区间是()A・〔U] B.[7T,乎] C.R,芋] D.[y, 2n]4.给出的下列函数中在G,TF)上是增函数的是_________ •A.y = sin2xB.y = cos2x ・5.若函数/(%) = sina)%(60 > 0)的图象的相邻两对称轴间的距离为2,则s的值为()A.-B.-C.TTD.2/Tn 26.y = cosx, x E [0,夢]的图象与直线y =扌的交点的个数为()试卷第7页,总7贞7.设函数f(E = cos(% +》则下列结论错误的是()SA./(x)的一个周期为一2兀B.y = 的图像关于直线咒=竽对称SC./(x +疋)的一个零点为兀=£D・f(X)在(£ 7T)单调递减8.函数/'(x) = sin(3x + e)(3 > 0, lei <夕)的最小正周期是7T,若其图象向右平移£个单位,得到的函数为偶函数,则函数/'(X)的图象()A.关于直线% =誇对称B.关于点(磊,0)对称C.关于点(菩,0)对称D.关于直线x =令对称9.函数y = In击与函数y = COSTTX图象所有交点的横坐标之和为()A.3B.4C.8D.610.已知直线x =心,x =勺分别是曲线fCO = 2sin (x +扌)与= 一® x的对称轴, 则f (心)=()~x2A.2B.OC.±2D.±l11.函数y = 2sinx - cosx在区间[0,5n]上的零点个数为_______ .12.若a = sin46\ b =cos46°> c= cos36°» 则a、b> c由小到大的顺序为___________ ・13.不等式cosx>|的解集是__________ •14. 函数y = a - sin%% G (0,为的图象与过点(0, 1)且平行于兀轴的直线有两个交点,则 实数a 的取值范围是 _______ .15. 根据正弦函数、余弦函数的图彖,写出使下列不等式成立的x 的取值集合:(1) sinx >^(x G/?);(2) V2 + 2cosx > 0(% 6 R).16.已知函数f(x) = cos(wx + <p)(w > 0, 0 < <兀)为奇函数,且英图象上相邻的一个 最髙点与一个最低点之间的距离为、还齐.(1)求产仗)的解析式;(2)若f (a + 扌)=一扌(一彳 V a V 0).求sin(2a -扌)的值.S S S S18.已知函数/*(%) = cos(2x + 韦)+ cos(2x + 評),g(x) = cos2x.(2)若aG(f, f),且f(a)=-£\^,求g(a)的值:w > 0, 0 < < 3的部分图象如图所示.(2 )若兀G ,扌],求f W + 9(兀)的最大值.6 3参考答案1.【答案】A2.【答案】B3.【答案】B4.【答案】B5.【答案】B6.【答案】D7.【答案】D8.【答案】B9.【答案】D10.【答案】C11.【答案】512.【答案】b<a<c13.【答案】[x\2kn --< x < 2kn + k E Z. }3 314.【答案】(0, 1]15.【答案】Fhsinx >害(x G R),结合正弦函数在一个周期上的图象, 如图(1)所示,可得尤的范围为{x\2kn + ^<x < 2kn + ^-, k G z}.由逅 + 2cosx > 0(x E可得COSX >结合余弦函数在一个周期上的图象如图(2)所示,可得X的范用为{x\2kn - y < x < 2kn + 乎,k G z}.解:(1)由函= COS(O>X + <p)(w > 0, 0 < < 7F)为奇函数,可得(P = /(%)= cos(cox +匚)=—sincox ・又英图象上相邻的一个最高点与一个最低点之间的距离为何〒,可得(22 + (?)2 = 丁4 + 沪,目 3 = 1, /(%) = —sinx・(2) □ /(a + 亍)=—sin(a + 扌)=一;(—扌 < a V 0), E sin(a + 扌)=話即;=cos[F _ (a + £)] = cos(f _ a) = cos(a _ {),回sin(a _ £)= _Jl_cos2(a_m = _晋,□ sin(2a —亍)=2sin(a —f) • cos(a 一f)= 一芋.17.【答案】由图可知£ =詈一兽可得T=n,2 12 12则竺=充,则3=2,3又图象经过(菩,0),故有2 X —+(p = kn^ k e Zt得卩=——+ Zc7r,12 6又0 V e V Z取e =巴.过(0, 1)点,所以i4sin<p = l,可得月=2.得f(x) = 2sin(2x + 9 ・6(x -自一f(x + ^)=2sin[2(x 一寻)+ f] - 2sin[2(x + 寻)+ £]= 2sin2x — 2sin(2x + =2sin2x — 2sin2%cosf— 2cos2xsin^-= sin2x — V^cos2x = 2sin(2x-^)»由2/C7T -- S 2% ---- S 2Z C7T H—, k G Z,2 3 2得花7T--- < X < /C7T H -- , k G Z t12 12所以g(x)的单调递增区间为[心一扫,心+菩],kez.18.【答案】解:(1)由f(x) = cos(2x + 7) + cos(2x +s s得f(x) = 7cos2x — 7^sin2x — |cos2x — ^-sin2x = —x/3sin2x ・因为f(a) =—-V3» 即—V5sin2a = — - V3»5 S所以sin2a =又因为f),所以2a G G,TT).故cos2a =—,5即g(a) = _右(2) /(%) + g(x) = —V3sin2x + cos2x = 2cos(2x +扌)・因为%G ,自,6 3所以2x + £ G [0,7r].s所以当2x+f=0,即X = 时,/(%) + g(x)有最大值,最大值为2・6。
高中数学人教A版必修4练习1.4.1 正弦函数、余弦函数的图像 课下检测 Word版含解析

一、选择题.用“五点法”作=的图像时,首先描出的五个点的横坐标是( ).,,π,π,π .,,,π,π.,π,π,π,π .,,,,π解析:由=,,π,π,π知五个点的横坐标是,,,π,π.答案:.下列函数图像相同的是( ).=与=(π+).=(-)与=(-).=与=(-).=(π+)与=解析:根据诱导公式知=与=(π+)的图像相同.答案:.不等式 <,∈[π]的解集为( ).(,) .[,].(,) .(,π)解析:由=的图像知,在[π]内使<的的范围是(,π).答案:.对余弦函数=的图像,有以下描述:①向左向右无限延伸;②与=的图像形状完全一样,只是位置不同;③与轴有无数多个交点;④关于轴对称.其中正确的描述有( ).个.个.个.个解析:由余弦函数的图像知①②③④均正确.答案:二、填空题.当∈[-π,π]时,=与=的图像交点的个数为.解析:如图,有个交点.答案:.函数=,∈[π]的图像和直线=围成的一个封闭的平面图形的面积是.解析:如下图所示,将余弦函数的图像在轴下方的部分补到轴的上方,可得一个矩形,其面积为π×=π.答案:π.先将=-的图像向左平移个单位长度,再向上平行移动个单位长度,得到函数()的图像,则()=.解析:由=(+)-+知=,即()= .答案:.函数=的定义域为.解析:由>结合=的图像知π<<π+π(∈).答案:(π,π+π)(∈)三、解答题.作出函数=-,∈[-π,π]的简图,并回答下列问题:()观察函数图像,写出满足下列条件的的区间:①>,②<.()直线=与=-的图像有几个交点?解:利用五点法作图.()根据图像,可知图像在轴上方时,->,在轴下方时,-<,所以当∈(-π,)时,->,<;当∈(,π)时,-<,>.()画出直线=,由图像可知有两个交点..方程=在∈[,π]上有两个实数根,求的取值范围.解:首先作出=,∈[,π]上的图像,然后再作出=的图像,由图像知,如果=与=的图像有两个交点,方程=,∈[,π]就有两个实数根.设=,∈[,π],=.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《1.4.1正弦函数、余弦函数的图像》同步检测
1. 满足sin x≥1
2
的x的集合为()
A.{x|2kπ+π
6≤x≤2kπ+5π
6
, k∈Z}
B.{x|2kπ+5π
6≤x≤2kπ+7π
6
, k∈Z}
C.{x|2kπ−π
6≤x≤2kπ+π
6
, k∈Z}
D.{x|2kπ−π
3≤x≤2kπ+2π
3
, k∈Z}
2. 已知f(x)=sin(2x+π
2),g(x)=cos(2x−π
2
),则下列结论中不正确的是()
A.将函数f(x)的图象向右平移π
4
个单位后得到函数g(x)的图象
B.函数y=f(x)⋅g(x)的图象关于(π
8
,0)对称
C.函数y=f(x)⋅g(x)的最大值为1
2
D.函数y=f(x)⋅g(x)的最小正周期为π
2
3. 函数y=|sin x|的一个单调增区间是()
A.[−π
4, π
4
] B.[π, 3π
2
] C.[π
4
, 3π
4
] D.[3π
2
, 2π]
4. 给出的下列函数中在(π
2
, π)上是增函数的是________.
A.y=sin2x
B.y=cos2x.
5. 若函数f(x)=sinωx(ω>0)的图象的相邻两对称轴间的距离为2,则ω的值为()
A.2π
B.π
2
C.π
D.2π
6. y=cos x,x∈[0, 5π
2]的图象与直线y=1
3
的交点的个数为()
A.0
B.1
C.2
D.3
7. 设函数f(x)=cos(x+π
3
),则下列结论错误的是( ) A.f(x)的一个周期为−2π
B.y=f(x)的图像关于直线x=8π
3
对称
C.f(x+π)的一个零点为x=π
6
D.f(x)在(π
2
, π)单调递减
8. 函数f(x)=sin(ωx+φ)(ω>0, |φ|<π
2)的最小正周期是π,若其图象向右平移π
6
个
单位,得到的函数为偶函数,则函数f(x)的图象()
A.关于直线x=5π
12对称 B.关于点(7π
12
, 0)对称
C.关于点(5π
12, 0)对称 D.关于直线x=π
12
对称
9. 函数y=ln1
|x−1|
与函数y=cosπx图象所有交点的横坐标之和为( )
A.3
B.4
C.8
D.6
10. 已知直线x=x1,x=x2分别是曲线f(x)=2sin(x+π
3
)与g(x)=−cos x的对称轴,则f(x1−x2)=()
A.2
B.0
C.±2
D.±1
11. 函数y=2sin x−cos x在区间[0,5π]上的零点个数为________.
12. 若a=sin46∘,b=cos46∘,c=cos36∘,则a、b、c由小到大的顺序为________.
13. 不等式cos x≥1
2
的解集是________.
14. 函数y=a−sin xx∈(0, 5π
2
)的图象与过点(0, 1)且平行于x轴的直线有两个交点,则实数a的取值范围是________.
15. 根据正弦函数、余弦函数的图象,写出使下列不等式成立的x的取值集合:
(1)sin x≥√3
2
(x∈R);
(2)√2+2cos x≥0(x∈R).
16. 已知函数f(x)=cos (ωx +φ)(ω>0, 0<φ≤π)为奇函数,且其图象上相邻的一个最高点与一个最低点之间的距离为√4+π2. (1)求f(x)的解析式;
(2)若f(α+π
3
)=−2
3
(−π
3
<α<0),求sin (2α−π
3
)的值.
17. 已知函数f(x)=A sin (wx +φ)(x ∈R, w >0, 0<φ<π
2)的部分图象如图所示.
(1)求函数f(x)的解析式;
(2)求函数g(x)=f(x −π
12)−f(x +π
12)的单调递增区间.
18. 已知函数f(x)=cos (2x +π
3)+cos (2x +2
3π),g(x)=cos 2x . (1)若α∈(π
4,π
2),且f(α)=−35√3,求g(α)的值;
(2)若x ∈[−π
6,π
3],求f(x)+g(x)的最大值.
参考答案
1.【答案】A
2.【答案】B
3.【答案】B
4.【答案】B
5.【答案】B
6.【答案】D
7.【答案】D
8.【答案】B
9.【答案】D
10.【答案】C
11.【答案】5
12.【答案】b<a<c
13.【答案】{x|2kπ−π
3≤x≤2kπ+π
3
, k∈Z.}
14.【答案】(0, 1]
15.【答案】
由sin x≥√3
2
(x∈R),结合正弦函数在一个周期上的图象,如图(1)所示,
可得x的范围为{x|2kπ+π
3≤x≤2kπ+2π
3
, k∈z}.。
