几何五大模型一
小学数学五大几何模型

小学数学五大几何模型知识框架一、等积模型DC BA①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比;③夹在一组平行线之间的等积变形,如右图ACDBCD S S =△△;反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.二、共角定理(鸟头定理)两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.:():()ABC ADE S S AB AC AD AE =⨯⨯△△(1)(2)(3)(4)三、蝴蝶定理任意四边形中的比例关系(“蝴蝶定理”): ①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.S 4S 3S 2S 1O DC BA梯形中比例关系(“梯形蝴蝶定理”):①2213::S S a b =②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +.A BC DO baS 3S 2S 1S 4四、相似模型(一)金字塔模型 (二) 沙漏模型GF E ABCD ABCDEF G①AD AE DE AFAB AC BC AG ===; ②22:ADE ABC S S AF AG =△△:.所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方; ⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半. 相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具. 在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形.五、共边定理(燕尾定理)有一条公共边的三角形叫做共边三角形。
几何的五大模型

几何的五大模型一、等积变换模型(1)等底等高的两个三角形面积相等(2)两个三角形高相等,面积比等于它们的底之比(3)两个三角形底相等,面积比等于它们的高之比如左图S1:S2=a:b(4)夹在一组平行线之间的等积变形,如右上图,S△ABC= S△BAD反之,如果S△ABC= S△BCD,则可知直线AB平行于CD (AB∥CD)二、鸟头定理(共角定理)模型(1)两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
(2)共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
如图在△ABC中,D,E分别是AB,AC上的点如图.(或D在BA的延长线上,E在AC上),则S△ABC:S△ADE=(AB×AC):(AD×AE)推理过程连接BE,再利用等积变换模型即可。
证明:图(1)中设:过顶点D做底边AE的高为H1;过顶点B做底边AC的高为H2△ABE中S△ADE:S△ABE=AD:AB同理S△ADE:S△ABE=H1:H2 AD:AB= H1:H2又因S△ADE=AE*H1*1/2S△ABC=AC*H2*1/2 得出S△ADE:S△ABC=AE*H1:AC*H2 所以S△ADE:S△ABC=(AB×AC):(AD×AE)图(2)中设过顶点D作底边AE的高为H1,过顶点B做底边AC的高为H2△DBE中,S△ADE:S△ABE=AD:ABS△ADE:S△ABE= H1:H2 AD:AB= H1:H2又因S△ADE=AE*H1*1/2S△ABC=AC*H2*1/2 得出S△ADE:S△ABC=AE*H1:AC*H2所以S△ADE:S△ABC=(AB×AC):(AD×AE)三、蝴蝶定理模型任意四边形中的比例关系(“蝴蝶定理”)①S1:S2=S4:S3 或者 S1×S3=S2×S4②AO:OC=(S1+S2):(S4+S3)证明(1):在△ABD中,S1:S2=DO:OB在△DCB中,S4:S3=DO:OB 得到S1:S2=S4:S3或者 S1×S3=S2×S4(十字相乘法)证明(2):设过D点作底边AC的高为H1,过B点作底边AC的高为H2(S1+S2):(S4+S3)=(AO*H1*1/2+AO*H2*1/2):(OC*H1*1/2+ OC*H2*1/2)约分得到:(S1+S2):(S4+S3)=AO:OC蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径。
小学奥数几何五大模型
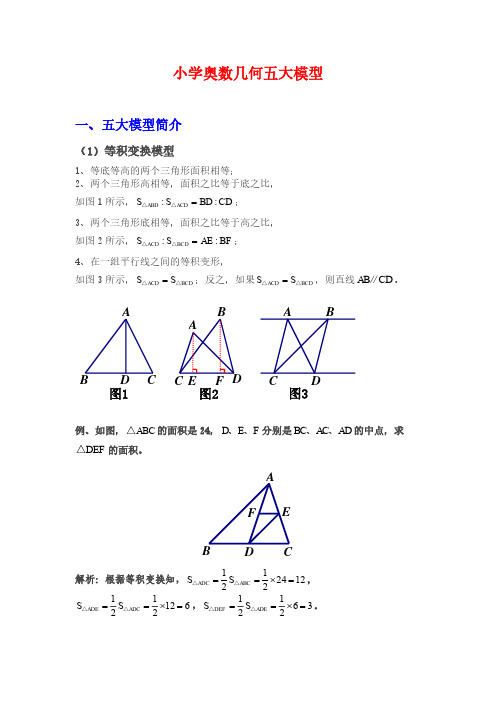
(4)相似模型1、相似三角形:形状相同、大小不相等的两个三角形相似;2、寻找相似模型的大前提是平行线:平行于三角形一边的直线和其他两边或两边延长线相交,所构成的三角形与原三角形相似。
3、相似三角形性质:①相似三角形的一切对应线段(对应高、对应边)的比等于相似比;②相似三角形周长的比等于相似比;③相似三角形面积的比等于相似比的平方。
相似模型大致分为金字塔模型、沙漏模型这两大类,注意这两大类中都含有DE BC ∥。
(一)金字塔模型 (二) 沙漏模型结论:因为DE BC ∥,所以ADE ABC △∽△,则①AD AE DE==;②22::ADE ABC S S AD AB =△△。
②::ABO BCO S S AE EC =△△;ED C BA E DCB A③::ACO BCO S S AF FB =△△。
二、五大模型经典例题详解 (1)等积变换模型例1、图中的E F G 、、分别是正方形ABCD 三条边的三等分点,如果正方形的边长是12,那么阴影部分的面积是多少?GFE D CBA解析:把另外三个三等分点标出之后,正方形的3条边AB BC CD 、、就被分成了相等的三段。
把点H 和这些分点、正方形的顶点连接,这样就把整个正方形分割成了9个形状各不相同的三角形,同时我们把空白部分的6个三角形按顺时针标记1~6。
这9个三角形的底边都是正方形边长的三分之一;阴影部分被分割成了其中的3个三角形。
根据等积变换模型可知,CD 边上的阴影三角形的面积与第1、2个三角形相等;BC 边上的阴影三角形与第3、4个三角形相等;AB 边上的阴影三角形与第5、6个三角形相等。
因此,阴影面积是空白面积的二分之一,是正方形面积的三分之一,即:12×12÷3=48。
例2、如图所示,Q E P M 、、、分别为直角梯形ABCD 两边AB CD 、上的点,且DQ CP ME 、、彼此平行,已知5753AD BC AE EB ====、、、,求阴影部分三角形PQM 的面积。
几何的五大模型

几何的五大模型一、等积变换模型1、等底等高的两个三角形面积相等。
2、两个三角形高相等,面积比等于它们的底之比。
3、两个三角形底相等,面积比等于它的的高之比。
二、共角定理模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等到于对应角(相等角或互补角)两夹边的乘积之比。
三、蝴蝶定理模型(说明:任意四边形与四边形、长方形、梯形,连接对角线所成四部的比例关系是一样的。
)四、相似三角形模型相似三角形:是形状相同,但大小不同的三角形叫相似三角形。
相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比。
相似三角形的面积比等于它们相似比的平方。
五、燕尾定理模型解析: 因为阴影部分比三角形EFG 的面积大10厘米2,都加上梯形FGCB 后,根据差不变性质,所得的两个新图形的面积差不变,即平行四边行ABCD 比直角三角形ECB 的面积大10厘米2,所以平行四边形ABCD 的面积等于10×8÷2+10=50厘米2 。
解析:利用燕尾定理,连接FC ,BFD 面积 /BFC 面积=DE/EC=1/2,如果BFD 面积为1份的话,BFC 为2份;又DF=FG ,所以BFG 面积与BFD 面积相等也是1份,故FGC 面积是2-1=1份,那么BG=GC ;再利用燕尾定理,DFC 的面积与DFB 相等也是1份,BDC 的面积是4份=6,故一份面积是6/4=1.5,阴影部分是1+2/3=5/3份,面积是1.5×5/3=2.5 EF=(=。
所以阴影部分如图,长方形ABCD 的面积是12,CE = 2DE ,F 是DG 的中点,那么图中阴影部分面积是________。
中,与平行,,、分别是的中点,已知阴影四边形则梯形在右图中,平行四边形ABCD 的边BC 长10厘米,直角三角形ECB 的直角边EC 长8厘米。
已知阴影部分的总面积比三角形EFG 的面积大10厘米2,求平行四边形ABCD 的面积。
小学数学几何必考五大模型

今天就为大家推荐一篇小学数学几何五大模型的内容。
一、等积 模①型等底等高的两个三角形面积相等;
AB
②两个三角形高相等,面积比等于它们的底之比;
两个三角形底相等,面积比等于它们的高之S比1 ;S2
典型例题
【例1】如图,正方形ABCD的边长为6,AE= 1.5,CF= 2.长
方形EFGH的面积为?
H
H
A
D
A
D
E
E
G
G
B FC
B
FC
【解析】连接DE,DF,则长方形EFGH的面积是三角形DEF面 积的二倍.
三角形DEF的面积等于正方,所形以的长面方积形减E去FG三H面个积三为角33. 形的面积,
【巩固】如图所示,正方形ABCD的边长为8厘米,长方形EBGF 的长BG为10厘米,那么长方形的宽为几厘米?
【解析】本题主要是让学生会运用等底等高的两个平行四边形面积 相等(长方形和正方形可以看作特殊的平行四边形).三角形面积等 于与它等底等高的平行四边形面积的一半.
【巩固】如图所示,正方形ABCD的边长为8厘米,长方形EBGF 的长BG为10厘米,那么长方形的宽为几厘米?
证明:连接AG(我们通过△ABG把这两个长方形和正方形联系在一起)
∴ 正方形ABCD与长方形EFGB面积相等。长方形的宽=8 ×8÷10=6.4(厘
【例2】长方形ABCD的面积为36cm2,E 、F、G为各边 中点,H为AD边上任意一点,问阴影部分面积是多少 ?
【解析解,】H法C 一,:如寻下找图可:利用的条件,连接BH
如右图
几何的五大模型

几何的五大模型一、等积变换模型(1)等底等高的两个三角形面积相等(2)两个三角形高相等,面积比等于它们的底之比(3)两个三角形底相等,面积比等于它们的高之比如左图S1: S2=a:b(4)夹在一组平行线之间的等积变形,如右上图,SAABC= S △ BAD反之,如果S △ BCD则可知直线AB平行于CD (AB// CDSAABC=二、鸟头定理(共角定理)模型(1)两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
(2)共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
如图在△ ABC中,D, E分别是AB AC上的点如图•(或D在BA的延长线上,E 在AC 上),贝s S ABO :S AADE=(AB X AC):(AD X AE)T D图CoJI/u//\//(B・....................推理过程连接BE再利用等积变换模型即可。
证明:图(1)中设:过顶点D做底边AE的高为H1 ;过顶点B做底边AC的高为H2△ ABE 中SA ADE SA ABE=AD AB同理SAADE SAABE=HI H2 AD : AB= HI: H2 }又因SAADE=AE*H1*1^ AA S AABC=AC*H2*V2 得出SAADE SAABC=AE*H1 AC*H2所以SAADE SA ABC=(Ax AC):(AD x AE)图(2)中设过顶点D作底边AE的高为H1,过顶点B做底边AC的高为H2ADBE 中,SA ADE SA ABE=AD ABS A ADE SA ABE= H1: H2 AD : AB= H1: H2又因SAADE=AE*H1*V2S AABC=AC*H2*V2 得岀SAADE SAABC=AE*H1 AC*H2所以SA ADE SA ABC=(Ax AC):(ADx AE)三、蝴蝶定理模型任意四边形中的比例矢系(“蝴蝶定理”)①S1 :S2=S4:S3 或者S1 X S3=S2x S4②AO:OC=(S1+S2):(S4+S3)证明(1):在乂 ABD 中,S1: S2=DO:OB在厶DCB 中,S4: S3=DO OB 得至(J S1 :S2=S4:S3 或者S1 x S3=S2X S4(十字相乘法)证明(2): 设过D点作底边AC的高为H1,过B点作底边AC的高为H2(S1+S2):(S4+S3)= ( AO*H1*1^+AO*H2*V2) : ( OC*H1*1^+ OC*H2*V2)约分得到:(S1+S2):(S4+S3)=AO : OC蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径。
几何的五大模型

5、 想想?正方形ABCD中,还有哪些没有包块进去,及与份数之间旳关系
6、SΔADE =S2+S3,S ΔBCF =S4+S3 想想?为何,用了什么模型
7、∴正方形ABCD被提成了24份 S阴影=S2+S4=6÷24×12=3cm2
例题:相同模型
例题4:如图,长方形ABCD中,E为AD旳中点,AF与BE、BD分别交于
例题:二分之一模型
例题3:如图ABFE和CDEF都是矩形,AB旳长是4厘米,BC旳长是3厘 米,那么图中阴影部分旳面积是多少平方厘米。
分析:阴影部分是一种个三角形,矩形CDEF中阴影 A
B
部分旳三角形底边长度为矩形旳长,高与矩 E
F
形宽相等,根据面积公式可知S阴影=SEDCF÷2
D
C
思索:二分之一模型是什么意思?
分析:SΔ黄+SΔ绿=S长方形÷2(=宽×长÷2)
黄色三角形面积21cm2,占长方形面积百分比
黄
50%-15%=35% 所以,长方形面积=21÷35%=60cm2
红
红
绿
例题:等积变换
例题2:图中ABCD是个直角梯形,以AD为一边向外作长方形ADEF, 其面积为6.36平方厘米,连接BE交AD于P,再连接PC,则图 中阴影部分旳面积是多少平方厘米?
AB
S1 S2
a
b
图1
CD 图2
概念
2、鸟头定理(共角定理)模型
1)两个三角形中有一种角相等或互补,这两个三角形叫做共角三角形
2)共角三角形旳面积比等于相应交(相等或互补角)两夹边旳乘积之比
D
E
A
D
A
A
E D
BC
小升初数学几何奥赛几何五大模型

小升初几何五大模型一、五大模型简介1 等积变换①、等底等高的两个三角形面积相等②、两个三角形高相等,面积之比等于底之比,如图1③、两个三角形底相等,面积在之比等于高之比,如图2④、在一组平行线之间的等积变形,如图3图1 图2 图3例、如图,三角形ABC的面积是24,D、E、F分别是BC、AC、AD的中点,求三角形DEF 的面积。
解:S△ADC=12S△ABC=12×24=12S△ADE=12S△ADC=12×12=6;S△DEF=12S△ADE=12×6=32 鸟头共角定理模型①、两个三角形中有一个角相等或互补,这两个三角形叫共角三角形;②、共角三角形的面积之比等于对应角相等角或互补角两夹边的乘积之比。
如图下图三角形ABC中,D、E分别是AB、AC上或AB、AC延长线上的点S△ABC S△ADE =SS×AC SS×AE例、如图在ΔABC中,D在BA的延长线上,E在AC上,且AB:AD=5:2,AE:EC=3:2,△ADE的面积为12平方厘米,求ΔABC的面积。
解:由题意知:S△ABCS△ADE =AB×ACAD×AE=52×53=256∴S△ABC=256×S△ADE=256×12=50(平方厘米)3 蝴蝶模型1、梯形中比例关系“梯形蝴蝶定理”①S2=S4(梯形两翼相等)②S1:S3:S2:S4=a2:b2:ab:ab③梯形S对应的分数为(a+b)2例、如图,梯形ABCD,AB与CD平行,对角线AC、BD交于点O,已知△AOB、△BOC的面积分别为25平方厘米、35平方厘米,求梯形ABCD的面积。
解:S△AOB:S△BOC=25:35=5:7S△AOB:S△DOC=SS2:SS2=52:72=25:49∴S△DOC=49又S△AOD=S△BOC=35∴S SSSS=25+35+35+49=144(平方厘米)2、任意四边形中的比例关系“蝴蝶定理”:①S1:S2=S4:S3或S1×S3=S2×S4②AO:OC=S1:S4=S2:S3=(S1+S2):(S4+S3)例、如图,四边形ABCD的对角线AC、BD交于点O,如果三角形ABD的面积等于三角形BCD面积的1/3,且AO=2,求OC解:AO:OC=S△ABD:S△BCD=1:3OC=2×3=64 相似模型1、相似三角形:形状相同,大小不相等的两个三角形相似;2、寻找相似模型的大前提是平行线:平行于三角形一边的直线和其他两边或两边延长线相交,所构成的三角形与原三角形相似。
小学奥数几何五大模型
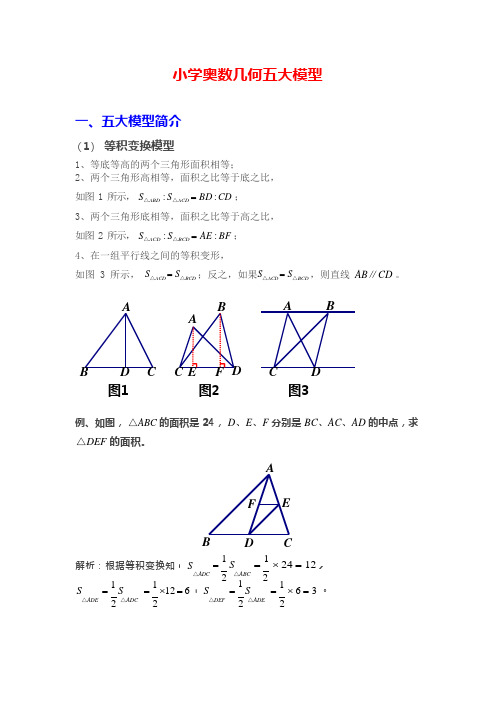
小学奥数几何五大模型一、五大模型简介(1) 等积变换模型1、等底等高的两个三角形面积相等;2、两个三角形高相等,面积之比等于底之比, 如图 1 所示, S △ABD : S △ACD = BD : CD ;3、两个三角形底相等,面积之比等于高之比, 如图 2 所示, S △ACD : S △BCD = AE : BF ;4、在一组平行线之间的等积变形,如图 3 所示, S △ACD = S △BCD ;反之,如果S △ACD = S △BCD ,则直线 AB ∥CD 。
图1图2图3例、如图, △ABC 的面积是 24, D 、E 、F 分别是 BC 、AC 、AD 的中点,求 △DEF 的面积。
解析:根据等积变换知, S = 1 S = 1 ⨯ 24 = 12 , S = 1S △ADC= 1 ⨯12 = 6 , S 2 △ABC = 1 S 2= 1 ⨯ 6 = 3 。
△ADE2 △ADC2 △DEF2 △ADE 2(2)鸟头模型(共角定理)1、两个三角形中有一个角相等或互补,这两个三角形叫共角三角形;2、共角三角形的面积之比等于对应角(相等或互补)两夹边的乘积之比。
如下图△ABC 中,D、E 分别是AB、AC 上或AB、AC 延长线上的点。
则有:S△ADES△ABC=AD ⨯AE。
AB ⨯AC我们现在以互补为例来简单证明一下共角定理!证明:如图,连接BE ,根据等积变换模型知,S△ADE: S△ABE=AD : AB 、S△ABE: S△CBE=AE : CE ,所以S△ABE:S△ABC=S△ABE:(S△ABE+S△CBE)=AE:AC。
因此S△ADE =S△ADE ⨯S△ABE =AD⨯AE=AD ⨯AE。
S△ABCS△ABES△ABCAB AC AB ⨯AC例、如图,在△ABC 中,点D 在BA 的延长线上,点E 在AC 上,且AB : AD = 5 : 2,AE : EC = 3: 2 ,△ADE 的面积为 12 平方厘米,求△ABC 的面积。
1数学几何五大模型

数 学 几 何 五 大 模 型一、等积变换模型⑴等底等高的两个三角形面积相等;其它常见的面积相等的情况⑵两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比。
如上图12::S S a b =⑶夹在一组平行线之间的等积变形,如下图ACD BCD S S =△△;反之,如果ACDBCD S S =△△,则可知直线AB 平行于CD 。
⑷正方形的面积等于对角线长度平方的一半;⑸三角形面积等于与它等底等高的平行四边形面积的一半; 二、鸟头定理(共角定理)模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
如图,在ABC △中,,D E 分别是,AB AC 上的点(如图1)或D 在BA 的延长线上,E 在AC 上(如图2),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△1S 2S 1S 2S ab图1 图2三、蝴蝶定理模型任意四边形中的比例关系(“蝴蝶定理”):(1) 1243::S S S S =或者1324S S S S ⨯=⨯(2)()()1243::AO OC S S S S =++ 蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
梯形中比例关系(“梯形蝴蝶定理”)(1)2213::S S a b =(2)221324::::::S S S S a b ab ab =;(3)梯形S 的对应份数为()2a b +。
四、相似模型相似三角形性质:金字塔模型 沙漏模型(1)AD AE DE AFAB AC BC AG===; (2)22::ADE ABCS S AF AG =△△。
所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比;⑵相似三角形的面积比等于它们相似比的平方。
几何的五大模型

利用燕尾定理,连接FC,BFD面积/BFC面积=DE/EC=1/2,如果BFD面积为1份的话,BFC为2份;又DF=FG,所以BFG面积与BFD面积相等也是1份,故FGC面积是2-1=1份,那么BG=GC;再利用燕尾定理,DFC的面积与DFB相等也是1份,BDC的面积是4份=6,故一份面积是6/4=1.5,阴影部分是1+2/3=5/3份,面积是1.5×5/3=2关系是一样的。)
四、相似三角形模型
相似三角形:是形状相同,但大小不同的三角形叫相似三角形。
相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比。
相似三角形的面积比等于它们相似比的平方。
五、燕尾定理模型
解析:
因为阴影部分比三角形EFG的面积大10厘米2,都加上梯形FGCB后,根据差不变性质,所得的两个新图形的面积差不变,即平行四边行ABCD比直角三角形ECB的面积大10厘米2,所以平行四边形ABCD的面积等于10×8÷2+10=50厘米2。
几何的五大模型
一、等积变换模型
1、等底等高的两个三角形面积相等。
2、两个三角形高相等,面积比等于它们的底之比。
3、两个三角形底相等,面积比等于它的的高之比。
二、共角定理模型
两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等到于对应角(相等角或互补角)两夹边的乘积之比。
三、蝴蝶定理模型
显然,最大的三角形的面积为21公顷.
解析:
如图所示,设上底为a,则下底为2a,梯形的高为h,则EF= (a+2a)= ,所以,
。所以
阴影部分
= 即 ,梯形 ABCD的面积=
如下图所示,为了方便叙述,将某些点标上字母.
小升初-数学-几何-五大几何模型

高之比.① 12:S S 蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.梯形中比例关系(“梯形蝴蝶定理”): ①2213::S S a b =②221324::::::S S S S a b ab ab =; 知识框架五大几何模型③ S 的对应份数为()2a b +. 四、相似模型(一)金字塔模型(二)沙漏模型 ①AD AE DE AFAB AC BC AG===; ②22:ADE ABC S S AF AG =△△:.所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:【例 1】 米?【巩固】 如图,四边形ABCD 和EFGH 都是平行四边形,四边形ABCD 的面积是16,:3:1BG GC =,则四边形EFGH 的面积=________.【例 2】 已知三角形ABC 的面积为a ,:2:1AF FC =,E 是BD 的中点,且EF ∥BC ,交CD 于G ,求阴影部分的面积.【巩固】图中ABCD 是边长为12cm 的正方形,从G 到正方形顶点C 、D 连成一个三角形,已知这个三角形在AB 上截得的EF 长度为4cm ,那么三角形GDC 的面积是多少?例题精讲【例 3】 如图,O 是矩形一条对角线的中点,图中已经标出两个三角形的面积为3和4,那么阴影部分的一块直角三角形的面积是多少?【巩固】 ABCD 是平行四边形,面积为72平方厘米,E 、F 分别为AB 、BC 的中点,则图中阴影部分的面积为平方厘米.二、蝴蝶模型【例 4】 如图所示,长方形ABCD 内的阴影部分的面积之和为70,AB=8,AD=15四边形EFGO 的面积为______.【巩固】 如图5所示,矩形ABCD 的面积是24平方厘米,、三角形ADM 与三角形BCN 的面积之【例 5】 【巩固】 27.那么【例 6】 【巩固】 CD ,DA()m n +的【例 7】 ,那么平【巩固】 ,6B 分别是正六边形各边的中点;那么图中阴影六边形的面积是平方厘米.【例 8】 已知四边形ABCD ,CHFG 为正方形,:1:8S S =乙甲,a 与b 是两个正方形的边长,求:?a b = 【巩固】 如图,三角形ABC 的面积是1,BD DE EC ==,CF FG GA ==,三角形ABC 被分成9部分,请写出这9部分的面积各是多少?【例 9】 如右图,面积为1的ABC △中,::1:2:1BD DE EC =,::1:2:1CF FG GA =,::1:2:1AH HI IB =,求阴影部分面积.【巩固】 如图,ABC ∆的面积为1,点D 、E 是BC 边的三等分点,点F 、G 是AC 边的三等分点,那么四边形JKIH 的面积是多少?【例 10】 如图,面积为l 的三角形ABC 中,D 、E 、F 、G 、H 、I 分别是AB 、BC 、CA 的三等分点,求阴影部分面积.【巩固】 如图,面积为l 的三角形ABC 中,D 、E 、F 、G 、H 、I 分别是AB 、BC 、CA 的三等分点,求中心六边形面积.【随练1】BF 、MGQA 的【随练2】【作业1】【作业2】6【作业3】BC 的中【作业4】【作业5】、CD 、DA 的重点,如果左图中阴影部分与右图中阴影部分的面积之比是最简分数mn,那么,m +n 的值等于__________。
小学奥数-几何五大模型(等高线模型)

小学奥数-几何五大模型(等高线模型)一、引言本文档将介绍小学奥数中的几何五大模型之一:等高线模型。
等高线模型是一个有趣而重要的几何模型,它不仅可以帮助学生理解空间中的形状和结构,还能培养学生的观察力和空间想象能力。
二、等高线模型的基本概念等高线模型是通过连接相同高度的点所得到的曲线或曲面。
在地理中,等高线模型常用于表示山脉、山丘和河流等地形特征。
在几何学中,等高线模型是一个重要的图形展示方法,它可以用来表示并描述三维物体的形状、轮廓和高度变化。
三、等高线模型的应用等高线模型在现实生活和工程领域中有广泛的应用。
以下是等高线模型的一些应用案例:1. 地理学:用于绘制地图和描绘地形。
2. 工程学:用于设计山区公路、水坝和建筑物等。
3. 农业学:用于规划农田排水、灌溉和排污系统。
4. 水资源管理:用于分析和预测水流和洪水情况。
5. 生物学:用于模拟生物栖息地和物种分布情况。
四、如何绘制等高线模型绘制等高线模型需要掌握一些基本的技巧和规则,以下是一些建议:1. 根据所绘制的物体选择适当的比例尺。
2. 使用直尺和铅笔绘制基本轮廓。
3. 根据高度信息确定等高线的间距和密度。
4. 使用曲线工具或自由手绘法绘制等高线。
5. 将等高线逐渐升高或降低以绘制出真实的高度变化。
五、等高线模型的注意事项在绘制等高线模型时需要注意以下事项:1. 保持准确性和规范性,尽量避免绘制错误的轮廓。
2. 根据需要使用不同的线型和颜色来表示不同的高度变化。
3. 在绘制过程中要注意比例和尺寸的准确性。
4. 考虑地图或图纸上的标尺尺寸,以确保其他观看者可以正确理解模型。
结论等高线模型是一种重要的几何模型,它可以帮助学生理解空间中的形状和结构。
通过绘制等高线模型,学生可以培养观察力和空间想象能力,并应用于实际生活和工程领域。
希望本文对小学奥数学习者对等高线模型的理解有所帮助。
几何五大模型一

几何五大模型一、等积变换模型1、等底等高的两个三角形面积相等.2、两个三角形高相等,面积比等于它们的底之比。
3、两个三角形底相等,面积比等于它的的高之比.二、共角定理模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等到于对应角(相等角或互补角)两夹边的乘积之比。
三、蝴蝶定理模型(说明:任意四边形与四边形、长方形、梯形,连接对角线所成四部的比例关系是一样的.)四、相似三角形模型相似三角形:是形状相同,但大小不同的三角形叫相似三角形。
相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比。
相似三角形的面积比等于它们相似比的平方。
五、燕尾定理模等积变形: 等积变形是小学几何里面一个非常重要的思想,小学所以的几何题,或多或少的都会用到等积变形的思想,几何五大模型也都是依托等积变形思想变化而成的。
一半模型平行四边形、梯形、任意四边形中的一些一半模型.一、模型归纳总结1、等面积变换模型(1)直线平行于,可知;反之,如果,则可知直线平行于.如图A(2)两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比;如图B图A 图B(3)一半面积关系【例1】、如图,每一个正方形四边中点的连线构成另一内接小正方形,则阴影部分面积为原正方形面积的几分之几?【例2】、如右图,过平行四边形内的一点作边的平行线、,若的面积为8平方分米,求平行四边形的面积比平行四边形的面积大多少平方分米?【例4】、如图1,一个长方形被切成8块,其中三块的面积分别为12,23,32,则图中阴影部分的面积为_____二、不规则图形求面积的常用方法【例5】、右图中两个半径为1的圆扇形与叠放在一起,是正方形,则整个阴影图形的面积是 .()点睛:求正方形面积还可以有新的方法呀家庭作业1、图中是两个正方形,边长分别为8厘米和4厘米,那么阴影部分的面积是平方厘米.2、(★★)右图是一块长方形耕地,它由四个小长方形拼合而成,其中三个小长方形的面积分别为15、18、30公顷,问图中阴影部分的面积是多少?3、如图所示,正方形的边长为厘米,长方形的长为厘米,那么长方形的宽为几厘米?_ A _ B_ G_ C _ E _ F_ D_ A _ B_ G_ C_ E_ F_ D。
几何的五大模型

几何的五大模型一、等积变换模型(1) 等底等高的两个三角形面积相等(2) 两个三角形高相等,面积比等于它们的底之比(3) 两个三角形底相等,面积比等于它们的高之比如左图S1: S2=a:b⑷夹在一组平行线之间的等积变形,如右上图,S^ABc= S △ BAD 反之,如果SΔABc= S △ BCD)则可知直线AB平行于CD (AB// CD二、鸟头定理(共角定理)模型(1) 两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
(2) 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
如图在△ ABC中,D, E分别是AB AC上的点如图.(或D在BA的延长线上,E在AC上),贝S S ABC: S△ADE=(AB × AC):(AD × AE)T DJI/U/ / \/ / \B ・ ------------------图(2)推理过程连接BE再利用等积变换模型即可。
证明:图(1)中设:过顶点D做底边AE的高为H1;过顶点B做底边AC的图Co高为H2△ ABE中S A ADE S A ABE=AD AB同理S A ADE S A ABE=HI H2 AD : AB= HI: H2 }又因S A ADE=AE*H1*1∕2^^ S A ABC=AC*H2*1∕2 得出S A ADE S A ABC=AE*H1 AC*H2所以S A ADE S A ABC=(A× AC):(AD × AE)图(2)中设过顶点D作底边AE的高为H1,过顶点B做底边AC的高为H2A DBE中, S A ADE S A ABE=AD ABS A ADE S A ABE= H1: H2 AD : AB= H1: H2又因S A ADE=AE*H1*1∕2S A ABC=AC*H2*1∕2得出S A ADE S A ABC=AE*H1 AC*H2 所以S A ADE S A ABC=(A× AC):(AD × AE)三、蝴蝶定理模型任意四边形中的比例关系(“蝴蝶定理”)①S1:S2=S4:S3 或者S1 × S3=S2× S4②AO:OC=(S1+S2):(S4+S3)证明(1):在乂 ABD中,S1: S2=DO:OB在厶DCB中,S4: S3=DO OB 得到S1:S2=S4:S3 或者S1 × S3=S2 × S4(十字相乘法)证明(2):设过D点作底边AC的高为H1,过B点作底边AC的高为H2(S1+S2):(S4+S3)= ( AO*H1*1∕2+AO*H2*1∕2):( OC*H1*1∕2+ OC*H2*1∕2)约分得到:(S1+S2):(S4+S3)=AO : OC蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几何五大模型
一、等积变换模型
1、等底等高的两个三角形面积相等。
2、两个三角形高相等,面积比等于它们的底之比。
3、两个三角形底相等,面积比等于它的的高之比。
二、共角定理模型
两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等到于对应角(相等角或互补角)两夹边的乘积之比。
三、蝴蝶定理模型
(说明:任意四边形与四边形、长方形、梯形,连接对角线所成四部的比例关系是一样的。
)
四、相似三角形模型
相似三角形:是形状相同,但大小不同的三角形叫相似三角形。
相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比。
相似三角形的面积比等于它们相似比的平方。
五、燕尾定理模
等积变形: 等积变形是小学几何里面一个非常重要的思想,小学所以的几何题,或多或少的都会用到等积变形的思想,几何五大模型也都是依托等积变形思想变化而成的。
一半模型
平行四边形、梯形、任意四边形中的一些一半模型。
一、 模型归纳总结
1、等面积变换模型
(1)直线AB 平行于CD ,可知BCD ACD S S ∆∆=;
反之,如果BCD ACD S S ∆∆=,则可知直线AB 平行于CD .如图A
(2)两个三角形高相等,面积比等于它们的底之比;
两个三角形底相等,面积比等于它们的高之比;
::ABD ACD S S BD CD =△△如图
B
D
C B
A
D
C
B A
图A 图B
(3)一半面积关系
S 4
S 3
S 2S 1
A
B
C
D
D
C
A
1
2
S S =阴影长方形 1324
S S S S +=+
【例1】、如图,每一个正方形四边中点的连线构成另一接小正方形,则阴影部分面积为原正方形面积的几分之几?
第8题
【例2】、如右图,过平行四边形ABCD 的一点P 作边的平行线EF 、GH ,若PBD 的面积为8平方分米,求平行四边形PHCF 的面积比平行四边形PGAE 的面积大多少平方分米?
B
C
G
H
【例4】、如图1,一个长方形被切成8块,其中三块的面积分别为12,23,32,则图中阴影部分的面积为_____
D
C B
F
二、不规则图形求面积的常用方法
【例5】、右图中两个半径为1的1
4圆扇形'
A O B
''与AOB叠放在一起,POQO'是
正方形,则整个阴影图形的面积是。
( 3.14
π=)
点睛:求正方形面积还可以有新的方法呀
A
家庭作业
1、图中是两个正方形,边长分别为8厘米和4厘米,那么阴影部分的面积是平方厘米.
2、(★★)右图是一块长方形耕地,它由四个小长方形拼合而成,其中三个小长方形的面积分别为15、18、30公顷,问图中阴影部分的面积是多少?
3、如图所示,正方形ABCD的边长为8厘米,长方形EBGF的长BG为10厘米,那么长方形的宽为几厘米?
_A_B
_G_C
_E
_F
_D
_A_B
_G_C
_E
_F
_D。
