多项式拟合与插值的计算方法

合集下载

数值计算方法插值与拟合

数值计算方法插值与拟合数值计算方法在科学计算和工程应用中起着重要的作用，其中插值和拟合是其中两个常用的技术。

插值是指通过已知的离散数据点来构造出连续函数或曲线的过程，拟合则是找到逼近已知数据的函数或曲线。

本文将介绍插值和拟合的基本概念和常见的方法。

一、插值和拟合的基本概念插值和拟合都是通过已知数据点来近似表达未知数据的方法，主要区别在于插值要求通过已知数据点的函数必须经过这些数据点，而拟合则只要求逼近这些数据点。

插值更加精确，但是可能会导致过度拟合；拟合则更加灵活，能够通过调整参数来平衡拟合精度和模型复杂度。

二、插值方法1. 线性插值线性插值是一种简单的插值方法，通过已知数据点构造出线段，然后根据插值点在线段上进行线性插值得到插值结果。

2. 拉格朗日插值拉格朗日插值是一种基于多项式插值的方法，通过已知数据点构造出一个多项式，并根据插值点求解插值多项式来得到插值结果。

3. 分段线性插值分段线性插值是一种更加灵活的插值方法，通过将插值区间分成若干小段，然后在每个小段上进行线性插值。

三、拟合方法1. 最小二乘法拟合最小二乘法是一种常用的拟合方法，通过最小化实际观测点和拟合函数之间的残差平方和来确定拟合函数的参数。

2. 多项式拟合多项式拟合是一种基于多项式函数的拟合方法，通过选择合适的多项式次数来逼近已知数据点。

3. 曲线拟合曲线拟合是一种更加灵活的方法，通过选择合适的曲线函数来逼近已知数据点，常见的曲线包括指数曲线、对数曲线和正弦曲线等。

四、插值与拟合的应用场景插值和拟合在实际应用中具有广泛的应用场景，比如图像处理中的图像重建、信号处理中的滤波器设计、金融中的风险评估等。

五、插值与拟合的性能评价插值和拟合的性能可以通过多种指标进行评价，常见的评价指标包括均方根误差、相关系数和拟合优度等。

六、总结插值和拟合是数值计算方法中常用的技术，通过已知数据点来近似表达未知数据。

插值通过已知数据点构造出连续函数或曲线，拟合则找到逼近已知数据的函数或曲线。

三次样条插值与多项式拟合的关系

三次样条插值与多项式拟合的关系《三次样条插值与多项式拟合的关系》一、简介在数学建模和数据分析中，插值和拟合是非常重要的方法。

三次样条插值和多项式拟合是其中常见且有效的技术。

它们之间有着密切的关系，对于理解它们的原理、特点和应用是很有帮助的。

二、三次样条插值的原理与方法三次样条插值是一种通过对给定的一组点进行插值，得到一个分段三次插值多项式的方法。

它的原理是将整个插值区间划分为多个小区间，每个小区间内都使用一个三次多项式来插值。

这样可以保证整个插值曲线在每个小区间内都是光滑的，并且两个相邻的插值多项式在连接点处有相同的函数值和导数值。

三次样条插值不仅可以实现较高的插值精度，还可以很好地避免龙格现象和振荡问题。

三、多项式拟合的原理与方法多项式拟合是一种通过多项式来逼近已知数据点的方法。

常见的拟合方法包括最小二乘法和最小二乘多项式拟合等。

多项式拟合的原理是使用一个n次多项式函数来逼近n个数据点，使得这个多项式函数在这n个数据点处的函数值与给定数据点的函数值尽可能接近，并且可以用于对其他数据点的预测。

四、三次样条插值与多项式拟合的关系在实际应用中，三次样条插值和多项式拟合有着密切的关系。

可以将三次样条插值看作是一种特殊的分段多项式拟合，只不过它要求在每个小区间上都使用三次多项式来进行拟合。

多项式拟合可以被认为是三次样条插值的一种特殊情况，当插值区间只有一个小区间时，三次样条插值就变成了普通的三次多项式拟合。

可以说三次样条插值和多项式拟合是在不同层次上对数据进行逼近的方法，它们之间有着内在的联系和相互影响。

五、个人观点和理解在实际工程和科学领域中，三次样条插值和多项式拟合都有着广泛的应用。

对于一些特定的数据集，三次样条插值可以提供更加精确和光滑的插值结果，而对于一些简单的数据集，多项式拟合可能会更加高效和简便。

了解它们之间的关系和特点，可以帮助我们在实际应用中选择合适的技术来处理数据，并且更好地理解其原理和局限性。

第二章插值与拟合

1 不为零。
xn
n xn xn
实用测量数据处理方法
中南大学
三、线性插值
假定已知区间[xk, xk+1] 的端点处的函数值 yk=f(xk), yk+1=f(xk+1),要求线性插值多项式 L1(x),使它满足 L1(xk)=yk
L1(xk+1)=yk+1
则L1(x)的表达式可按下式给出：
实用测量数据处理方法
中南大学
l k 1 ( x k 1 ) 1, l k 1 ( x j ) 0( j k , k 1) l k ( x k ) 1, l k ( x j ) 0( j k 1, k 1) (28) l k 1 ( x k 1 ) 1, l k 1 ( x j ) 0( j k 1, k ) 满足（28 ）式的插值基函数很容易求出的，例如求 l k 1 ( x)，因为它有两个零点 k 和x k 1，故可表达为： x l k 1 ( x) A( x x k )(x x k 1 ) 其中A为待定系数可由 k 1 ( x k 1 ) 1定出： l 1 A ( x k 1 x k )(x k 1 x k 1 ) ( x x k )(x x k 1 ) 于是l k 1 ( x)＝，同理可得 ( x k 1 x k )(x k 1 x k 1 ) ( x x k－1 )(x x k 1 ) ( x x k 1 )(x x k ) l k ( x)＝，l k 1 ( x)＝ ( x k x k－1 )(x k x k 1 ) ( x k＋1 x k 1 )(x k 1 x k )
解：2、抛物插值

插值与拟合方法

插值与拟合方法在实际中，常常要处理由实验或测量所得到的一批离散数据．插值与拟合方法就是要通过这些数据去确定某一类已知函数的参数或寻找某个近似函数，使所得到的近似函数与已知数据有较高的拟合精度．插值问题:要求这个近似函数（曲线或曲面）经过所已知的所有数据点．通常插值方法一般用于数据较少的情况．数据拟合：不要求近似函数通过所有数据点，而是要求它能较好地反映数据的整体变化趋势。

共同点：插值与拟合都是根据实际中一组已知数据来构造一个能够反映数据变化规律的近似函数的方法，由于对近似要求的准则不同，因此二者在数学方法上有很大的差异．插值问题的一般提法：已知某函数)(x f y =（未知）的一组观测（或试验）数据),,2,1)(,(n i y x ii⋅⋅⋅=，要寻求一个函数)(x φ，使iiy x =)(φ),,2,1(n i ⋅⋅⋅=，则)()(x f x ≈φ．实际中,常常在不知道函数)(x f y =的具体表达式的情况下，对于i x x =有实验测量值iy y =),,2,1,0(n i ⋅⋅⋅=，寻求另一函数)(x φ使满足：)()(i i i x f y x ==φ),,2,1,0(n i ⋅⋅⋅=称此问题为插值问题，并称函数)(x φ为)(x f 的插值函数，nx x x x ,,,,21⋅⋅⋅称为插值节点，),,2,1,0()(n i y x ii⋅⋅⋅==φ称为插值条件，即)()(iiix f y x ==φ),,2,1,0(n i ⋅⋅⋅=，则)()(x f x ≈φ．（1）拉格朗日（Lagrange ）插值设函数)(x f y =在1+n 个相异点nx x x x ,,,,21⋅⋅⋅上的函数值为ny y y y ,,,,21⋅⋅⋅，要求一个次数不超过n 的代数多项式nnnx a x a x a a x P +⋅⋅⋅+++=221)(使在节点i x 上有),,2,1,0()(n i y x P ii n ⋅⋅⋅==成立，称之为n 次代数插值问题，)(x P n称为插值多项式．可以证明n 次代数插值是唯一的．事实上: 可以得到j n j n i i j in y x x xx x P j i ∑∏==⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫⎝⎛--=≠00)()( 当1=n 时，有二点一次（线性）插值多项式：101001011)(y x x x x y x x x x x P --+--=当n =2时，有三点二次（抛物线）插值多项式：2120210121012002010212))(())(())(())(())(())(()(y x x x x x x x x y x x x x x x x x y x x x x x x x x x P ----+----+----=（2）牛顿（Newton ）插值牛顿插值的基本思想：由于)(x f y =关于二节点10,x x 的线性插值为)()()()()()()()()(00101000010101x x x x x f x f x p x x x x x f x f x f x p ---+=---+= 假设满足插值条件)2,1,0()()(2===i x p y x f iii的二次插值多项式一般形式为))(()()(1212x x x x c x x c c x p --+-+= 由插值条件可得⎪⎩⎪⎨⎧=--+-+=-+=)())(()()()()(21202202101011000x f x x x x c x x c c x f x x c c x f c 可以解出⎪⎪⎪⎩⎪⎪⎪⎨⎧------=--==020101121220101100)()()()()()(),(x x x x x f x f x x x f x f c x x x f x f c x f c所以))(()())(()()(10211020102x x x x c x p x x x x c x x c c x p --+=--+-+=类似的方法，可以得到三次插值多项式等，按这种思想可以得到一般的牛顿插值公式．函数的差商及其性质对于给定的函数)(x f ，用),,,(10n x x x f ⋅⋅⋅表示关于节点nx x x ,,,1⋅⋅⋅的n 阶差商，则有一阶差商：01011)()(),(x x x f x f x x f --=，121221)()(),(x x x f x f x x f --= 二阶差商：021021210),(),(),,(x x x x f x x f xx x f --=n 阶差商：0110211),,,(),,,(),,,(x x x x x f x x x f x x x f n n n n -⋅⋅⋅-⋅⋅⋅=⋅⋅⋅-差商有下列性质：（1）差商的分加性：∑∏=≠=-=⋅⋅⋅nk nk j j j kk n x xx f xx x f 0)(01)()(),,,(．（2）差商的对称性：在),,,(1nx x x f ⋅⋅⋅中任意调换jix x ,的次序其值不变．牛顿插值公式：一次插值公式为))(,()()(01001x x x x f x f x p -+=二次插值公式为))()(,,()())()(,,())(,()()(1021011021001002x x x x x x x f x p x x x x x x x f x x x x f x f x p --+=--+-+=于是有一般的牛顿插值公式为)())()(,,,()()())()(,,,())()(,,())(,()()(11010111010102100100----⋅⋅⋅--⋅⋅⋅+=-⋅⋅⋅--⋅⋅⋅+⋅⋅⋅+--+-+=n n n n n n x x x x x x x x x f x p x x x x x x x x x f x x x x x x x f x x x x f x f x p可以证明：其余项为))(())()(,,,,()(11010n n n x x x x x x x x x x x x f x R --⋅⋅⋅--⋅⋅⋅=-实际上，牛顿插值公式是拉格朗日插值公式的一种变形，二者是等价的．另外还有著名的埃尔米特（Hermite ）插值等．（3）样条函数插值方法样条，实质上就是由分段多项式光滑连接而成的函数，一般称为多项式样条．由于样条函数的特殊性质，决定了样条函数在实际中有着重要的应用．样条函数的一般概念定义设给定区间],[b a 的一个分划b x x x a n=<⋅⋅⋅<<=∆1:，如果函数)(x s 满足条件：(1) 在每个子区间),,2,1](,[1n i x x ii ⋅⋅⋅=-上是k 次多项式； (2) )(x s 及直到k -1阶的导数在],[b a 上连续．则称)(x s 是关于分划△的一个k 次多项式样条函数，nx x x ,,,1⋅⋅⋅称为样条节点，121,,,-⋅⋅⋅n x x x 称为内节点，nx x ,0称为边界节点，这类样条函数的全体记作),(k S P∆，称为k 次样条函数空间．若),()(k S x s P∆∈，则)(x s 是关于分划△的k 次多项式样条函数．k 次多项式样条函数的一般形式为∑∑=-=+-+=ki n j k j jii k x x k i x x s 011)(!!)(βα其中),,1,0(k i i=α和)1,,2,1(-=n j jβ均为任意常数，而)1,,2,1(,0,)()(-=⎪⎩⎪⎨⎧<≥-=-+n j x x x x x x x x jj kj kj在实际中最常用的是2=k 和３的情况，即为二次样条函数和三次样条函数．二次样条函数：对于],[b a 上的分划b x x x a n=<⋅⋅⋅<<=∆1:,则)2,()(!2!2)(11222102∆βαααP n j j jS x x x x x s ∈-+++=∑-=+其中)1,2,1(,0,)()(22-=⎪⎩⎪⎨⎧<≥-=-+n j x x x x x x x x j j j j ．三次样条函数：对于],[b a 上的分划b x x xa n =<⋅⋅⋅<<=∆10:,则)3,()(!3!3!2)(1133322103∆βααααP n j j jS x x x x x x s ∈-++++=∑-=+其中)1,2,1(,0,)()(33-=⎪⎩⎪⎨⎧<≥-=-+n j x x x x x x x x jjj j ．1 二次样条函数插值)2,()(2∆∈P S x s 中含有2+n 个待定常数，故应需要2+n 个插值条件，因此，二次样条插值问题可分为两类：问题(1)：已知插值节点ix 和相应的函数值),,2,1,0(n i y i⋅⋅⋅=，以及端点0x (或n x )处的导数值0'y (或ny ')，求)2,()(2∆∈PS x s 使得⎩⎨⎧'=''='⋅⋅⋅==))(()(),,2,1,0()(20022n n i i y x s y x s n i y x s 或（5.1）问题(2)：已知插值节点ix 和相应的导数值),,2,1,0(n i y i⋅⋅⋅='，以及端点0x (或n x )处的函数值0y (或ny )，求)2,()(2∆∈P S x s 使得⎩⎨⎧==⋅⋅⋅='='))(()(),,2,1,0()(20022n n i i y x s y x s n i y x s 或(5.2)事实上，可以证明这两类插值问题都是唯一可解的．对于问题(1)，由条件(5.1)⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧'=+='==-+++==++==++=∑-=00210211222102121211112020201002)(,,3,2,)(2121)(21)(21)(y x x s n j y x x x x x s yx x x s y x x x s j j i i j i jj j ααβααααααααα 引入记号T n ),,,,,(11210-=ββααα X 为未知向量，T nn y y y y ),,,,(10'= C 为已知向量， ⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡---=-0010)(21)(21211)(212110211211021212212222211200x x x x x x x x x x x x x x x n n n n n A 于是，问题转化为求方程组C AX =的解Tn ),,,,,(1121-=ββααα X 的问题，即可得到二次样条函数的)(2x s 的表达式．对于问题(2)的情况类似．２．三次样条函数插值由于)3,()(3∆∈P S x s 中含有3+n 个待定系数，故应需要3+n 个插值条件，因此可将三次样条插值问题分为三类：问题(1)：已知插值节点jx 和相应的函数值),,2,1,0(n j y j⋅⋅⋅=，以及两个端点0x ，n x 处的导数值0'y ，ny '，求)3,()(3∆∈PS x s 使满足条件⎪⎩⎪⎨⎧='='⋅⋅⋅==),0()(),,1,0()(33n j y x s n j y x s j j j j(5.3)问题(2)：已知插值节点jx 和相应的函数值),,2,1,0(n j y j⋅⋅⋅=，以及两个端点0x ，nx 处的二阶导数值0y ''，n y ''，求)3,()(3∆∈PS x s 使满足条件⎪⎩⎪⎨⎧=''=''⋅⋅⋅==),0()(),,1,0()(33n j y x s n j y x s j j j j(5.4)问题(3)：类似地，求)3,()(3∆∈PSx s 使满足条件⎪⎩⎪⎨⎧=+=-==)2,1,0)(0()0(),,1,0()(0)(3)(33k x s x s n j y x s k n k j j(5.5)这三类插值问题的条件都是3+n 个，可以证明其解都是唯一的〔8〕．一般的求解方法可以仿照二次样条的情况处理方法，在这里给出一种更简单的方法．仅依问题(1)为例，问题(2)和问题(3)的情况类似处理．由于在)3,()(3∆PS x s ∈区间],[b a 上是一个分段光滑，且具有二阶连续导数的三次多项式，则在子区间],[1+j jx x 上)(3x s ''是线性函数，记),,,1,0)((3n j x s d jj =''=为待定常数．由拉格朗日插值公式可得nj x x h h x x d h x x d x s j j j jj j jj j ,,1,0,,)(1113=-=-+-=''+++显然jjj h d dx s -='''+13)(在],[1+j jx x上为常数．于是在],[1+j j x x 上有31233)(6)(2))(()(j jjj j j j j j x x h d d x x d x x x s y x s --+-+-'+=+(5.6)则当1+=j x x 时，由(5.6)式和问题(1)的条件得121231362)()(+++=-++'+=j j jj j j j j j j y h d d h d h x s y x s故可解得)2(6)(113+++--='j j j jjj j d d h h y y x s（5.7）将(5.7)式代入(5.6)式得)1,,1,0](,[,)(6)(2)()2(6)(1312113-=∈--+-+-⎥⎥⎦⎤⎢⎢⎣⎡+--+=++++n j x x x x x h d d x x d x x d d h h y y y x s j j j jj j j jj j j j j j j j(5.8) 在],[1j j x x-上同样的有),,2,1](,[,)(6)(2)()2(6)(131112111111113n j x x x x x h d d x x d x x d d h h y y y x s j j j j j j j j j j j j j j j j =∈--+-+-⎥⎥⎦⎤⎢⎢⎣⎡+--+=------------(5.9) 根据)(3x s的一阶导数连续性，由(5.9)式得)()2(6)0(311113j j j j j j j j x s d d h h y y x s '=++-=-'---- 结合(5.7)式整理得⎪⎪⎭⎫ ⎝⎛---+=++++--+-+----11111111162j j j j j j j j j j j j j j j j j h y y h y y h h d h h h d d h h h 引入记号⎪⎪⎭⎫ ⎝⎛---+=+=--+--111116,j j j j j j j j j j j j j h y y h y y h h c h h h a ，111--+=-j j j j h h h a ．则)1,,2,1(,2)1(11-==++-+-n j c d a d d a j j j j j j（5.10）再由边界条件：nny x s y x s '=''=')(,)(33得⎪⎪⎩⎪⎪⎨⎧⎪⎪⎭⎫ ⎝⎛--'=+⎪⎪⎭⎫ ⎝⎛'--=+----111100010106262n n n n n n n h y y y h d d y h y y h d d(5.11)联立(5.10),(5.11)式得方程组C D A =⋅（5.12）其中⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡---=----2121212112112200n n n n a a a a a aA ，⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=-n n d d d d 110 D ，⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛--'⎪⎪⎭⎫ ⎝⎛'--=----111110001066n n n n n n hy y y h c c y h y y h C 由方程组(6.12)可以唯一解出),,1,0(n j d j=，代入（5.8）式就可以得三次样条函数)(3x s 的表达式．Ｂ样条函数插值方法磨光函数实际中的许多问题，往往是既要求近似函数（曲线或曲面）有足够的光滑性，又要求与实际函数有相同的凹凸性，一般插值函数和样条函数都不具有这种性质．如果对于一个特殊函数进行磨光处理生成磨光函数（多项式），则用磨光函数构造出样条函数作为插值函数，既有足够的光滑性，而且也具有较好的保凹凸性，因此磨光函数在一维插值（曲线）和二维插值（曲面）问题中有着广泛的应用．由积分理论可知，对于可积函数通过积分会提高函数的光滑度，因此，我们可以利用积分方法对函数进行磨光处理．定义若)(x f 为可积函数，对于0>h ，则称积分⎰+-=22,1)(1)(hx h x h dt t f h x f为)(x f 的一次磨光函数，h 称为磨光宽度．同样的，可以定义)(x f 的k 次磨光函数为)1()(1)(22,1,>=⎰+--k dt t f h x f hx h x h k h k事实上，磨光函数)(,x f h k 比)(x f 的光滑程度要高，且当磨光宽度h 很小时)(,x f h k 很接近于)(x f ．等距Ｂ样条函数对于任意的函数)(x f ，定义其步长为１的中心差分算子δ如下：⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛+=2121)(x f x f x f δ在此取0)(+=x x f ，则002121+++⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛+=x x x δ是一个单位方波函数（如图5-1），记0)(+=Ωx x δ．并取1=h ，对)(0x Ω进行一次磨光得++++-+++-+++--+-+=-=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛+==⎰⎰⎰⎰)1(2)1(2121)()(11212100212101x x x dt t dt t dt t t dt t x x xx x x x x x ΩΩ显然)(1x Ω是连续的（如图5-2）．)(1x Ωo1-1/2 0 1/2 x -1 0 1 x 图5-1图5-2类似地可得到k 次磨光函数为kk j jk j k j k x k C x ++=+⎪⎭⎫ ⎝⎛-++-=Ω∑21!)1()(11 实际上,可以证明：)(x kΩ是分段k 次多项式，且具有1-k 阶连续导数，其k 阶导数有2+k个间断点，记为)1,,2,1,0(21+⋅⋅⋅=+-=k j k j x j．从而可知)(x kΩ是对应于分划+∞<<⋅⋅⋅<<<-∞∆+110:k x x x 的k 次多项式样条函数，称之为基本样条函数，简称为k 次Ｂ样条．由于样条节点为)1,,2,1,0(21+⋅⋅⋅=+-=k j k j xj是等距的，故)(x k Ω又称为k 次等距Ｂ样条函数．对于任意函数)(x f 的k 次磨光函数，由归纳法可以得到 [4,8] ：⎪⎭⎫⎝⎛+≤≤--Ω=⎰∞+∞--22)()(1)(1,h x t h x dt t f htx h x f k h k 特别地，当1)(=x f 时，有1)(11⎰+∞∞--=-dt htx hk Ω，从而1)(⎰+∞∞-=dx x k Ω，且当k ≥1时有递推关系⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-Ω⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛+Ω⎪⎭⎫ ⎝⎛++=Ω--212121211)(11x x k x k x k x k k k一维等距Ｂ样条函数插值等距Ｂ样条函数与通常的样条如下的关系：定理设有区间],[b a 的均匀分划nab h n j jh x x j -=⋅⋅⋅=+=),,,1,0(:0∆，则对任意 k 次样条函数),()(k S x S p k ∆∈都可以表示为Ｂ样条函数族1021-=-=⎭⎬⎫⎩⎨⎧⎪⎭⎫⎝⎛+---n j k j k k j h x x Ω的线性组合[14]．根据定理 5.1,如果已知曲线上一组点()jjy x ,，其中),,1,0,0(0n j h jh x x j⋅⋅⋅=>+=，则可以构造出一条样条磨光曲线（即为Ｂ样条函数族的线性组合）⎪⎭⎫⎝⎛--=∑--=j h x x c x S n kj k j k 01)(Ω 其中)1,,1,(-⋅⋅⋅+--=n k k j c j为待定常数．用它来逼近曲线，既有较好的精度，又有良好的保凸性．实际中，最常用的是3=k 的情况，即一般形式为⎪⎭⎫ ⎝⎛--=∑+-=j h x x c x S n j j 01133)(Ω 其中3+n 个待定系数)1,,0,1(+⋅⋅⋅-=n j c j可以由三类插值条件确定．由插值条件(5.3)得()()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧'=-'='==-='=-'='∑∑∑+-=+-=+-=n n j j n i n j j i n j j y j n c h x S ni y j i c x S y j c h x S 113311330113031)(,,1,0,)(1)(ΩΩΩ(5.13)注意到)(3x Ω的局部非零性及其函数值：61)1(,32)0(33=±=ΩΩ，当2≥x 时0)(3=x Ω；且由)21()21()(223--+='x x x ΩΩΩ知，21)1(,0)0(33=±'='ΩΩ，当2≥x 时0)(3='x Ω．则(5.13)中的每一个方程中只有三个非零系数，具体的为⎪⎩⎪⎨⎧'=+-==++'=+-+-+--n n n i i i i y h c c n i y c c c y h c c 2,,1,0,6421111011(5.14)由方程组(5.14)容易求解出)1,,0,1(+⋅⋅⋅-=n j c j，即可得到三次样条函数)(3x S 表达式．类似地，由插值条件(5.4)得待定系数的)1,,0,1(+⋅⋅⋅-=n j c j所满足的方程组为⎪⎩⎪⎨⎧''=+-==++''=+-+-+--nn n n i i i i y h c c c n i y c c c y h c c c 21111021012,,1,0,642（5.15）由插值条件(5.5)得待定系数的)1,,0,1(+⋅⋅⋅-=n j cj所满足的方程组为⎪⎪⎩⎪⎪⎨⎧==++=-+---=-++-=-+-+-+-+--+--+--ni y c c c c c c c c c c c c c c c c c c c i i i i n n n n n n n n ,,1,0,640)()(2)(0)(0)(0)()(4)(1111011111111011（5.16）方程组(5.15),(5.16)也都是容易求解的．注：上述等距Ｂ样条插值公式也适用于近似等距的情形，但在端点0x 和n x 处误差可能较大，实际应用时，为了提高在端点0x 和nx 处的精度，可以适当向左右延拓几个节点．二维等距Ｂ样条函数插值设有空间曲面),(y x f z =(未知),如果已知二维等距节点()()τj y ih x y x ji++=0,,)0,(>τh 上的值为),,2,1,0;,,2,1,0(m j n i z ij⋅⋅⋅=⋅⋅⋅=，则相应的Ｂ样条磨光曲面的一般形式为⎪⎭⎫ ⎝⎛--⎪⎭⎫⎝⎛--=∑∑--=--=j y y i h x x c y x s l m lj k ij n ki τΩΩ0011),( 其中),,2,1,0;,,2,1,0(m j n i c ij⋅⋅⋅=⋅⋅⋅=为待定常数，l k ,可以取不同值，常用的也是2,=l k 和３的情形．这是一种具有良好保凸性的光滑曲面(函数)，在工程设计中是常用的，但只能使用于均匀分划或近似均匀分划的情况．（4）最小二乘拟合方法最小二乘拟合方法的思想：由于一般插值问题并不总是可解的（即当插值条件多于待定系数的个数时，其问题无解），同时，问题的插值条件本身一般是近似的，为此，只要求在节点上近似地满足插值条件，并使它们的整体误差最小，这就是最小二乘拟合法．最小二乘拟合方法可以分为线性最小二乘拟合方法和非线性最小二乘拟合方法．线性最小二乘拟合方法设{}m k kx 0)(=φ是一个线性无关的函数系，则称线性组合∑==mk k k x a x 0)()(φφ为广义多项式．如三角多项式：∑∑==+=mk k mk kkx b kx ax 0sin cos )(φ．设由给定的一组测量数据),(iiy x 和一组正数),,2,1(n i w i⋅⋅⋅=，求一个广义多项式∑==mk k k x a x 0)()(φφ使得目标函数[]21)(∑=-=ni i i i y x w S φ(5.17)达到最小，则称函数)(x φ为数据),,2,1)(,(n i y x ii⋅⋅⋅=关于权系数),,2,1(n i w i⋅⋅⋅=的最小二乘拟合函数，由于)(x φ关于待定系数ia 是线性的，故此问题又称为线性最小二乘问题．注意：这里{}m k kx 0)(=φ可根据实际来选择，权系数iw 的选取更是灵活多变的，有时可选取1=i w ，或nw i 1=，对于nw i1=，则相应问题称为均方差的极小化问题．最小二乘拟合函数的求解要使最小二乘问题的目标函数(5.17)达到最小，则由多元函数取得极值的必要条件得),,2,1,0(0m k a Sk==∂∂ 即),,2,1,0(0)()(10m k x y x a w i k ni i m k i k k i ⋅⋅⋅⋅==⎥⎦⎤⎢⎣⎡-∑∑==φφ 亦即),,2,1,0()()()(001m k x y w a x x w n i i k i i j mj n i i k i j i ⋅⋅⋅⋅==⎥⎦⎤⎢⎣⎡∑∑∑===φφφ(5.18)是未知量为ma a a a ,,,,21⋅⋅⋅的线性方程组，称(5.18)式为正规方程组．实际中可适当选择函数系{}m k kx 0)(=φ，由正规方程组解出ma a a a ,,,,210⋅⋅⋅，于是可得最小二乘拟合函数∑==mk kk x a x 0)()(φφ．一般线性最小二乘拟合方法将上面一元函数的最小二乘拟合问题推广到多元函数，即为多维线性最小二乘拟合问题．假设已知多元函数),,,(21nx x x f y ⋅⋅⋅=的一组测量数据);,,,(21iniiiy x x x ⋅⋅⋅),,2,1(m i ⋅⋅⋅=和一组线性无关的函数系{}N k nk x x x 021),,,(=⋅⋅⋅φ，求函数∑=⋅⋅⋅=⋅⋅⋅Nk n k k n x x x a x xx 02121),,,(),,,(φφ对于一组正数mw w w ,,,21⋅⋅⋅，使得目标函数[]2121),,,(∑=⋅⋅⋅-=mi ni i i i i x x x y w S φ达到最小．其中待定系数N a a a a,,,,210⋅⋅⋅由正规方程组),,2,1,0(),(),(0N k y a Nj k j k j⋅⋅⋅==∑=φφφ确定，此处ini i i k mi i k ni i i k mi ni i i j i k j y x x x w y x x x x x x w ),,,(),(),,,(),,,(),(21121121⋅⋅⋅=⋅⋅⋅⋅⋅⋅=∑∑==φφφφφφ注：上面的函数φ关于ia 都是线性的，这就是线性最小二乘拟合问题，对于这类问题的正规组总是容易求解的．如果φ关于ia 是非线性的，则相应的问题称为非线性最小二乘拟合问题．非线性最小二乘拟合方法假设已知多元函数),,,(21nx x x f y ⋅⋅⋅=的一组测量数据);,,,(21iniiiy x x x ⋅⋅⋅),,2,1(m i ⋅⋅⋅=，要求一个关于参数),,2,1,0(N j a j⋅⋅⋅=是非线性的函数),,,;,,,(1021Nn a a a x x x ⋅⋅⋅⋅⋅⋅=φφ对一组正数mw w w ,,,21⋅⋅⋅使得目标函数[]21102110),,,;,,,(),,,(∑=⋅⋅⋅⋅⋅⋅-=⋅⋅⋅mi N ni i i i i N a a a x x x y w a a a S φ达到最小，则称之为非线性最小二乘问题．这类问题属于无约束的最优化问题，一般问题的求解是很复杂的，通常情况下，可以采用共轭梯度法、最速下降法、拟牛顿法和变尺度法等方法求解．实例：黄河小浪底调水调沙问题问题的提出2004年６月至７月黄河进行了第三次调水调沙试验，特别是首次由小浪底、三门峡和万家寨三大水库联合调度，采用接力式防洪预泄放水，形成人造洪峰进行调沙试验获得成功．整个试验期为20多天，小浪底从６月19日开始预泄放水，直到７月13日恢复正常供水结束．小浪底水利工程按设计拦沙量为75.5亿立方米，在这之前，小浪底共积泥沙达14.15亿吨．这次调水调试验一个重要目的就是由小浪底上游的三门峡和万家寨水库泄洪，在小浪底形成人造洪峰，冲刷小浪底库区沉积的泥沙．在小浪底水库开闸泄洪以后，从6月27日开始三门峡水库和万家寨水库陆续开闸放水，人造洪峰于29日先后到达小浪底，7月3日达到最大流量2700立方米/每秒，使小浪底水库的排沙量也不断地增加．下面是由小浪底观测站从6月29日到7月10日检测到的试验数据：表5-1: 试验观测数据单位：水流为立方米/每秒，含沙量为公斤/立方米·84··85·注：以上数据主要是根据媒体公开报道的结果整理而成的，不一定与真实数据完全相符．现在，根据试验数据建立数学模型研究下面的问题：(1) 给出估算任意时刻的排沙量及总排沙量的方法；(2) 确定排沙量与水流量的变化关系．模型的建立与求解对于问题（１），根据所给问题的试验数据，要计算任意时刻的排沙量，就要确定出排沙量随时间变化的规律，可以通过插值来实现．考虑到实际中排沙量应该是随时间连续变化的，为了提高精度，我们采用三次Ｂ样条函数进行插值．下面构造三次Ｂ样条函数)(x S y =．由试验数据，时间是每天的早８点和晚８点，间隔都是12个小时，共24个点)24,,2,1(⋅⋅⋅=i t i．为了计算方便，令)23,,,1,0(122128⋅⋅⋅=+⎥⎦⎤⎢⎣⎡⋅+-=i i t x i i(5.19)则it 对应于)23,,1,0(1⋅⋅⋅=+=i i x i．于是以)23,,1,0(⋅⋅⋅=i x i为插值节点（等距），步长1=h ．其相应的排沙量为)23,,1,0(⋅⋅⋅=i y i 对应关系如下表：·86·表5-2: 插值数据对应关系单位：排沙量为公斤函数)(x S y =所满足的条件为 (1)23,,1,0,)(⋅⋅⋅==i y x S ii；(2) 3500)(,56400)(2223222323231212-=--≈'='=--≈'='x x y y x S y x xy yx S y .取)(x S 的三次Ｂ样条函数一般形式为∑-=⎪⎭⎫⎝⎛--=24103)(j j j h x x c x S Ω·87·其中)24,,1,0,1(⋅⋅⋅-=j cj为待定常数，1=h ．在这里⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<<+-+-≤+-=Ω2,021,342611,3221)(23233x x x x x x x x x且易知⎪⎪⎪⎩⎪⎪⎪⎨⎧≥±===Ω2,01,610,32)(3x x x x和⎪⎪⎩⎪⎪⎨⎧≥±===Ω'2,01,210,0)(3x x x x 根据Ｂ样条函数的性质，)(x S ''在[]23,x x 上连续，则有()∑-=--'='='2413)(j jj xx c x S y Ω由插值条件(1),(2)可得到下列方程组()()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧'=-'=''=-'='⋅⋅⋅==-=∑∑∑-=-=-=23241323024130241323)()(23,,1,0,)(y j c x S y j c x S i y j i c x S j j j j i j j i ΩΩΩ 即⎪⎩⎪⎨⎧'=+-'=+-⋅⋅⋅==++-+-23242311112223,,1,0,64y c c y c c i y c c c i i i i 将232324112,2y c c y c c '+='-=-代入前24个方程中的第一个和最后一个，便可得到方程组F AC =，其中·88·⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⋅⋅⋅⋅⋅⋅=⨯232102424,421410141014124c c c c C A ，⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡'-'+=3400048000684000458400266626232322100 y y y y y y F显然A 为满秩阵，方程组F AC =一定有解，用消元法求解可得问题的解为56044.39830=c , 4117111.2031=c , 2159510.7882=c , 9189845.6433=c ,1203106.6364=c , 8239727.8115=c ,8249182.1166=c , 1263543.7217=c ,9287842.9988=c , 2302284.2839=c ,4317419.86810=c , 1304836.24311=c ,3307635.15912=c ,6305423.11913=c ,2270672.36214=c ,4240287.43115=c ,0154177.91216=c ,4103000.92017=c ,99818.406218=c , 43725.454719=c ,49279.775020=c ,32155.445221=c , 2098.444222=c ,7450.777923=c ,-450.777924311.2034,2232324011='+=='-=-y c c y c c . 将)24,,1,0,1(⋅⋅⋅-=j c j代入()∑-=--==24131)(j jj x c x S y Ω(5.20)即得排沙量的变化规律．由（5.19）和(5.20)式可得到第i 时间段（12小时为一段）内，任意时刻]12,0[∈t 的排沙量．则总的排沙量为()dt j t c dx x S Y j j⎰∑⎰-=--Ω==284824132411)(经计算可得1110844.1⨯=Y 吨，即从6月29日至7月10日小浪底水库排沙总量大约为1.844亿吨,此与媒体报道的排沙量基本相符.对于问题(2),研究排沙量与水量的关系，从试验数据可以看出，开始排沙量是随着水流量的增加而增长，而后是随着水流量的减少而减少．显然，变化规律并非是线性的关系，为此，我们问题分为两部分，从开始水流量增加到最大值2720立方米/每秒（即增长的过程）为一段，从水流量的最大值到结束为第二段，分别来研究水流量与排沙量的关系．具体数据如表5-3和5-4.表5-3: 第一阶段试验观测数据单位：水流为立方米/每秒，含沙量为公斤/立方米表5-4: 第二阶段试验观测数据单位：水流为立方米/每秒，含沙量为公斤/立方米对于第一阶段，由表5-3用Matlab作图（如图5-3）可以看出其变化趋势，我们用多项式作最小二乘拟合．·90··91·图5-3设拟合函数为∑==mk kk x a x 1)(φ确定待定常数),,1,0(m k ak=使得211111102])([∑∑∑===⎥⎦⎤⎢⎣⎡-=-=i i i m k k i k i i y x a y x S φ有最小值．于是可以得到正规方程组为m k x y a x mj i k i i j i j k i ,,1,0,0111111 ==⎪⎭⎫⎝⎛∑∑∑===+ 当3=m 时，即取三次多项式拟合，则3,2,1,0,1113111321112111110111==⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛∑∑∑∑∑==+=+=+=k x y a x a x a x a x i k i i i k i i k i i k i i k i求解可得73321108423.1,103172.1,3.1784,-2492.9318--⨯=⨯-===a a a a ．于是可得拟合多项式为332213)(x a x a x a a x +++=φ，最小误差为847.72=S ，拟合效果如图所示．·92·图:三次拟合效果，带*号的为拟合曲线．类似地，当4=m 时，即取四次多项式拟合，则正规方程组为4,3,2,1,0111411143111321112111110111==⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛∑∑∑∑∑∑==+=+=+=+=k x y a x a x a x a x a x i ki i i k i i k i i k i i k i i k i求解可得104633210109312.1,1094.1,102626.7,12.0624,-7434.6557---⨯-=⨯=⨯-===a a a a a 于是可得拟合多项式为443322104)(x a x a x a x a a x ++++=φ，最小误差为102.66=S ，拟合效果如图5-5所示．图5-5:四次拟合效果，带*号的为拟合曲线．从上面的三次多项式拟合和四次多项拟合效果来看，差别不大．基本可以看出排沙量与水流量的关系．图5-6:第二段三·93··94· 次多项式拟合效果对于第二阶段，由表5-4可以类似地处理．我们用线性最小二乘法作三次和四多项式拟合．拟合效果如图5-6和5-7所示，最小误差分别为5.459=S 和1.236=S ．从拟合效果来看，显然四次多项式拟合要比三次多项式拟合好的多．图5-7:第二段四次多项式拟合效果。

插值与拟合算法分析

插值与拟合算法分析在数学与计算机科学领域，插值与拟合算法是两种常用的数据处理技术。

插值算法通过已知数据点之间的内插来估算未知数据点的值，而拟合算法则通过求取最佳拟合曲线或函数来逼近已知数据点。

本文将对插值与拟合算法进行详细分析，并比较它们在不同应用中的优缺点。

一、插值算法插值算法主要用于通过已知数据点之间的内插来估算未知数据点的值。

常用的插值算法包括拉格朗日插值、牛顿插值、样条插值等。

这些算法根据插值函数的不同特点，适用于不同类型的数据处理。

1. 拉格朗日插值拉格朗日插值是一种基于代数多项式的插值方法。

它通过构造一个全局多项式函数来拟合已知数据点，并推导出未知数据点的估算值。

拉格朗日插值算法具有简单易懂、计算效率高等优点，但在处理大量数据点时可能会出现龙格现象，导致插值结果有一定误差。

2. 牛顿插值牛顿插值是一种基于差商的插值方法。

它通过计算差商的递推关系，构造一个分段多项式函数来拟合已知数据点。

相比于拉格朗日插值，牛顿插值算法具有更高的数值稳定性和精度，并且可以方便地进行动态插值。

3. 样条插值样条插值是一种基于分段函数的插值方法。

它将整个数据区间划分为若干小段，并使用不同的插值函数对每一段进行插值。

样条插值算法通过要求插值函数的高阶导数连续，能够更好地逼近原始数据的曲线特征，因此在光滑性较强的数据处理中常被使用。

二、拟合算法拟合算法主要用于通过最佳拟合曲线或函数来逼近已知数据点。

常用的拟合算法包括最小二乘拟合、多项式拟合、非线性拟合等。

这些算法可以使拟合曲线与已知数据点尽可能地接近，从而进行更精确的数据分析和预测。

1. 最小二乘拟合最小二乘拟合是一种通过最小化残差平方和来求取最佳拟合曲线的方法。

它利用数据点与拟合曲线的差异来评估拟合效果，并通过求取最小残差平方和的参数值来确定拟合曲线的形状。

最小二乘拟合算法广泛应用于线性回归和曲线拟合等领域。

2. 多项式拟合多项式拟合是一种通过多项式函数来逼近已知数据点的方法。

多项式插值计算方法

多项式插值计算方法引言：在数学和计算机科学中，插值是一种常见的数值计算方法，用于通过已知的数据点来估计未知的数据点。

多项式插值是插值方法中的一种，通过构造一个多项式函数来逼近数据点，从而实现插值的目的。

本文将介绍多项式插值的基本概念、计算方法和应用领域。

一、多项式插值的基本概念多项式插值是指通过已知的n个数据点(x1, y1), (x2, y2), ..., (xn, yn)，构造一个n次多项式函数P(x)来逼近这些数据点。

通过将P(x)代入已知的数据点，可以满足P(xi) = yi，即多项式函数经过已知数据点。

二、多项式插值的计算方法1. 拉格朗日插值法拉格朗日插值法是一种常用的多项式插值计算方法。

通过构造一个满足已知数据点的n次多项式函数P(x)，可以使用拉格朗日插值公式来计算多项式的系数。

具体步骤如下：- 构造插值多项式P(x) = L1(x)y1 + L2(x)y2 + ... + Ln(x)yn，其中Li(x)为拉格朗日基函数。

- 拉格朗日基函数的计算公式为Li(x) = Π(j=1 to n, j ≠ i)(x-xj)/(xi-xj)，即除了第i个数据点外，其他数据点的插值基函数的乘积。

- 将已知数据点代入插值多项式，可以得到相应的系数，进而得到插值多项式P(x)。

2. 牛顿插值法牛顿插值法是另一种常用的多项式插值计算方法。

通过构造一个满足已知数据点的n次多项式函数P(x)，可以使用牛顿插值公式来计算多项式的系数。

具体步骤如下：- 构造插值多项式P(x) = c0 + c1(x-x0) + c2(x-x0)(x-x1) + ... + cn(x-x0)(x-x1)...(x-xn-1)，其中ci为差商。

- 差商的计算公式为ci = f[x0, x1, ..., xi]/(xi-x0)(xi-x1)...(xi-xi-1)，即已知数据点的函数值的差商。

- 使用差商递推公式可以计算出所有的差商，进而得到插值多项式P(x)。

c++三次多项式拟合_数学建模_003_插值和拟合_2020_9_3

c++三次多项式拟合_数学建模_003_插值和拟合_2020_9_3插值问题：有限个已知数据点，构造⼀个解析表达式，由此计算数据点之间的函数值，称之为插值。

当数据量不够，需要补充,且认定已有数据可信时,通常利⽤函数插值⽅法。

常见插值⽅法：拉格朗⽇插值(lagrange插值)分段线性插值Hermite三次样条插值克⾥⾦插值(地理学)反距离权重插值算法(地理学)拉格朗⽇插值(⾼次多项式插值)：(次数太⾼有Runge现象)1. 曲线光滑；误差估计有表达式2. 收敛性不能保证(振荡现象)3. ⽤于理论分析，实际意义不⼤matlab中没有分段线性插值：1. 收敛性良好2. 只⽤两个节点，且线性，简单实⽤3. 曲线不光滑三次样条插值:1. 曲线2阶光滑，收敛性有保证2. 实际中应⽤⼴泛3. 误差估计较难拟合：已知有限个数据点，求近似函数，可不过已知数据点，只要求在某种意义下它在这些点上的总偏差最⼩。

曲线拟合要解决的两个问题：1. 线型的选择(关键点，⼀般根据散点图)2. 线型中参数的计算参数的求解：1. 线性拟合----最⼩⼆乘法2. ⾮线性拟合----Gauss-Newton迭代法最⼩⼆乘法:函数表达式：其中 , k=[1,n],是线性⽆关的函数，是待定系数，⽬的找⼀组适当的，使得与的距离平⽅和最⼩。

这种准则称为最⼩⼆乘准则，求系数的⽅法称为最⼩⼆乘拟合法。

MATLAB拟合：线性拟合：polyfit(x,y,n)函数x,y被拟合数据的⾃变量和应变量，n为拟合多项式的次数polyval()函数多项式在 x 处的值 y 可⽤polyval函数计算⾮线性拟合：[b,r] = polyfit(x ,y ,fun,bo, option)fun: 拟合函数 b0：拟合参数初始化迭值option: 拟合选项 b:拟合参数 r:拟合残差MATLAB拟合⼯具箱： cftool(⾹)插值和拟合的异同联系都是根据实际中⼀-组已知数据来构造⼀个能够反映数据变化规律的近似函数的⽅法。

多项式插值与拟合

多项式插值与拟合多项式插值与拟合技术是数学领域中一种常用的数据处理方法。

它可以有效地根据给定的数据点集，通过构造一个多项式函数，来近似描述数据的整体趋势。

本文将介绍多项式插值与拟合的基本原理、方法和应用。

一、多项式插值的原理和方法多项式插值是一种通过已知数据点集来构造与之完全吻合的多项式函数的方法。

它基于一个重要的数学定理：给定n+1个不同的数据点，存在一个n次多项式可以通过这些数据点。

在多项式插值中，最常用的插值方法是拉格朗日插值和牛顿插值。

拉格朗日插值使用一个n次多项式来逼近给定的数据点，使得多项式通过所有数据点；而牛顿插值则利用了差商的概念，使用一个n次多项式来逼近数据点，从而构造插值多项式。

二、多项式拟合的原理和方法多项式拟合是一种通过已知数据点集来找到一个次数较低的多项式函数，以最佳拟合数据的方法。

与多项式插值不同，多项式拟合不要求多项式经过所有数据点，而是通过最小化误差函数来找到最优解。

最常见的多项式拟合方法是最小二乘拟合，也称为线性最小二乘拟合。

该方法通过最小化数据点到拟合曲线的垂直距离之和，来得到最优的拟合曲线。

经过最小二乘拟合后，可以得到一个最佳的多项式函数，以最小化误差。

三、多项式插值与拟合的应用多项式插值与拟合广泛应用于各个领域的数据处理和分析中。

以下列举几个典型的应用场景：1. 数据重建：当给定一组具有缺失数据点的数据集时，通过多项式插值可以估计出缺失数据点的数值，从而恢复完整的数据集。

2. 数据平滑：多项式拟合可以通过将原始数据点拟合为平滑的曲线或者曲面，从而更好地展示数据的整体趋势，去除数据的噪声干扰。

3. 数据预测：基于已知的数据点，可以使用多项式拟合方法预测未来或未知的数据点的数值，为决策和规划提供依据。

4. 图像处理：多项式插值和拟合在图像处理中也有广泛应用，例如图像修复、数字图像放大等。

总结：多项式插值与拟合是一种有效的数据处理方法，可以用于数据重建、数据平滑、数据预测和图像处理等领域。

数值分析实验插值与拟合

数值分析实验插值与拟合插值是指根据已知的数据点，通过其中一种数学方法来构造一个函数，使得该函数在已知的数据点上与被插值函数相等。

插值方法可以分为两类：基于多项式的插值和非多项式插值。

基于多项式的插值方法中，最常用的是拉格朗日插值和牛顿插值。

拉格朗日插值方法通过一个n次多项式来逼近被插值函数，该多项式通过n个已知数据点中的所有点。

牛顿插值方法则通过一个n次多项式来逼近被插值函数，该多项式通过n个已知数据点中的前m+1个点。

非多项式插值方法中，最常用的是分段线性插值和样条插值。

分段线性插值方法将插值区间划分为多个小段，在每一段内使用线性函数来逼近被插值函数。

样条插值方法则使用分段低阶多项式来逼近被插值函数，保证了插值函数和原函数在插值区间内的连续性、光滑性。

拟合是指在给定的离散数据点集合上，通过选取一个函数，使得该函数与数据点之间的误差最小化。

拟合方法可以分为两类：线性拟合和非线性拟合。

线性拟合方法中，最简单的是最小二乘法。

最小二乘法拟合是通过最小化观测数据与拟合函数的残差平方和来选择最佳函数参数。

在实验中，最小二乘法常用于线性回归问题，例如估计一个直线或者平面来拟合数据。

非线性拟合方法中，最常用的是非线性最小二乘法和局部加权回归。

非线性最小二乘法通过将非线性拟合问题转化为线性问题，使用最小二乘法来寻找最佳参数。

局部加权回归方法则通过给予不同数据点不同的权重，以更好地逼近数据点。

在数值分析实验中，插值与拟合可以应用于各种实际问题。

例如，在地理信息系统中，通过已知的地理坐标点来插值出未知点的地理信息。

在气象学中，通过已知的气象数据点来插值出未知点的气象信息。

在工程学中，通过已知的测量数据点来拟合出一个最佳的拟合函数来预测未来的测量值。

需要注意的是，插值和拟合的精度在很大程度上取决于数据的分布和拟合函数的选择。

如果数据点过于稀疏或者数据点中存在异常值，可能导致插值和拟合结果不准确。

因此，在进行插值和拟合之前，需要对数据进行预处理，例如去除异常值、平滑数据等。

数值计算中的插值和拟合方法

在数值计算中，插值和拟合是两种常用的方法，用于通过已知数据点推测未知数据点的数值。

插值是一种通过已知数据点构建一个函数，以便在这些数据点之间进行预测。

而拟合是一种将一个函数与已知数据点进行匹配，以便预测未知数据点的数值。

插值的目标是通过经过已知数据点的连续函数来准确地估计未知数据点的数值。

最简单的插值方法是线性插值，它假设两个相邻数据点之间的函数值是线性变化的。

线性插值可以用于计算两个已知数据点之间的任何位置的函数值。

如果我们有更多的数据点，可以使用更高阶的插值方法，如二次插值或三次插值。

这些方法使用多项式来表示数据点之间的函数，以便更准确地预测未知数据点。

然而，插值方法并不总是最理想的选择。

在某些情况下，通过已知数据点精确地构建一个连续函数是不可能的。

这可能是因为数据点之间的差异太大，或者数据点的数量太少。

在这种情况下，拟合方法可以提供更好的预测结果。

拟合的目标是找到一个函数，使其与已知数据点的误差最小。

最常用的拟合方法是最小二乘拟合，它通过最小化数据点的残差的平方和来找到最佳拟合函数。

最小二乘拟合可以用于各种不同的函数类型，如线性拟合、多项式拟合、指数拟合等。

根据数据点的分布和特性，我们可以选择适当的拟合函数来获得最准确的预测结果。

在实际应用中，插值和拟合方法经常同时使用。

例如，在地理信息系统中，我们可能需要通过已知地点的气温数据来估计未知地点的气温。

我们可以使用插值方法来构建一个连续函数，以便在已知地点之间预测未知地点的气温。

然后，我们可以使用拟合方法来匹配这个连续函数与其他已知数据点，以提高预测的准确性。

插值和拟合方法在科学、工程、金融等各个领域都有广泛的应用。

在科学研究中，它们可以用于数据分析和预测，以帮助我们理解和解释实验结果。

在工程中，它们可以用于控制系统设计、信号处理和机器学习等领域。

在金融领域，它们可以用于市场预测和风险管理等重要任务。

总而言之，插值和拟合是数值计算中常用的方法，用于通过已知数据点推测未知数据点的数值。

数值分析中的插值与拟合

数值分析中的插值与拟合插值和拟合是数值分析中常用的技术，用于估计或预测数据集中缺失或未知部分的数值。

在本文中，我们将讨论插值和拟合的概念、方法和应用。

一、插值插值是通过已知数据点之间的连续函数来估计中间数据点的数值。

插值方法可以根据不同的数据和需求选择合适的插值函数，常用的插值方法包括拉格朗日插值、牛顿插值和埃尔米特插值。

1.1 拉格朗日插值拉格朗日插值是一种基于多项式的插值方法。

通过已知的n个数据点，可以构建一个n-1次的插值多项式。

这个多项式通过已知数据点上的函数值来准确地经过每一个点。

1.2 牛顿插值牛顿插值方法也是一种多项式插值方法，通过差商的概念来构建插值多项式。

差商是一个递归定义的系数，通过已知数据点的函数值计算得出。

牛顿插值可以通过递推的方式计算出插值多项式。

1.3 埃尔米特插值埃尔米特插值是一种插值方法，适用于已知数据点和导数值的情况。

它基于拉格朗日插值的思想，通过引入导数信息来逼近数据的真实分布。

埃尔米特插值可以更准确地估计数据点之间的值，并且可以保持导数的连续性。

二、拟合拟合是通过一个模型函数来逼近已知数据点的数值。

拟合方法旨在找到最适合数据集的函数形式，并通过最小化误差来确定函数的参数。

常见的拟合方法包括最小二乘法、多项式拟合和曲线拟合。

2.1 最小二乘法最小二乘法是一种常用的拟合方法，通过最小化数据点到拟合函数的误差平方和来确定最佳拟合曲线或曲面。

最小二乘法适用于线性和非线性拟合问题，可以用于拟合各种类型的非线性函数。

2.2 多项式拟合多项式拟合是一种基于多项式函数的拟合方法。

通过多项式的线性组合来近似已知数据集的数值。

多项式拟合可以通过最小二乘法或其他优化算法来确定拟合函数的系数。

2.3 曲线拟合曲线拟合是一种用曲线函数来逼近已知数据点的拟合方法。

曲线函数可以是非线性的，并且可以根据数据的特点进行选择。

曲线拟合可以通过优化算法来确定拟合函数的参数。

三、应用插值和拟合在数值分析中有广泛的应用。

插值与拟合方法

插值与拟合方法插值和拟合是数学中常用的方法，用于根据已知数据点的信息，推断出未知数据点的数值或函数的形式。

插值和拟合方法是经典的数学问题，应用广泛，特别是在数据分析、函数逼近和图像处理等领域。

1.插值方法：插值方法是通过已知数据点的信息，推断出两个已知数据点之间的未知数据点的数值。

插值方法的目的是保证插值函数在已知数据点处与实际数据值一致，并且两个已知数据点之间的连续性良好。

最常用的插值方法是拉格朗日插值法和牛顿插值法。

拉格朗日插值法根据已知数据点的横纵坐标，构造一个多项式函数，满足通过这些数据点。

拉格朗日插值法可以用于任意次数的插值。

牛顿插值法是使用差商的概念进行插值。

差商是指一个多项式在两个数据点之间的斜率。

牛顿插值法通过迭代计算得到与已知数据点一致的多项式。

插值方法的优点是可以精确地经过已知数据点，但是在两个已知数据点之间的插值部分可能会出现震荡现象，从而导致插值结果不准确。

2.拟合方法：拟合方法是通过已知数据点的信息，找出一个函数或曲线，使其能够最好地拟合已知数据点。

拟合方法的目标是寻找一个函数或曲线，尽可能地逼近已知数据点，并且能够在未知数据点处进行预测。

最常用的拟合方法是最小二乘法。

最小二乘法是通过求解最小化残差平方和的问题来进行拟合。

残差是指已知数据点与拟合函数的差异。

最小二乘法的目标是找到一个函数，使得所有数据点的残差平方和最小。

拟合方法的优点是可以得到一个光滑的函数或曲线，从而可以预测未知数据点的数值。

但是拟合方法可能会导致过拟合问题，即过度拟合数据点，导致在未知数据点处的预测结果不准确。

除了最小二乘法，还有其他的拟合方法，如局部加权回归和样条插值等。

局部加权回归是一种基于最小二乘法的拟合方法，它通过赋予不同的数据点不同的权重，来实现对未知数据点的预测。

样条插值是一种基于多项式插值的拟合方法，它将整个数据集分段拟合，并且在分段部分保持连续性和光滑性。

总结：插值和拟合方法是数学中的经典方法，用于根据已知数据点的信息，推断出未知数据点的数值或函数的形式。

数值分析实验报告插值与拟合

解：（1）
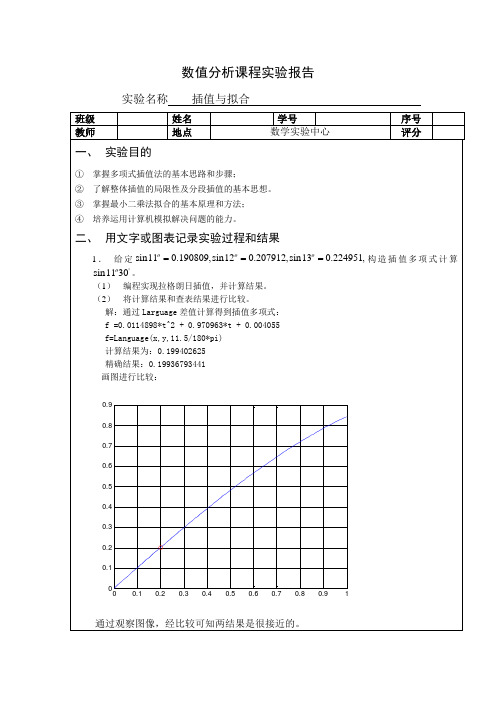
结果分析：高次插值稳定性差，而低次插值对于较大区间逼近精度又不够，而且，随着节点的加密，采用高次插值，插值函数两端会发生激烈震荡。解决这一矛盾的有效方法就是采用分段低次代数插值。
（2）
通过采用分段线性插值得到以下结果：
结果分析：通过采用分段线性插值，发现随着插值节点增多，插值计算结果的误差越来越小，而且分段线性插值的优点是计算简单，曲线连续和一致收敛，但是不具有光滑性。
拟合是指通过观察或测量得到一组离散数据序列，i=1,2，…，m，构造插值函数逼近客观存在的函数，使得向量与的误差或距离最小。
可知当基函数的选择不同时，拟合函数的误差也会不同，所以在对数据进行拟合时应选择适合的基函数。
三、练习思考
整体插值有何局限性？如何避免？
答：整体插值的过程中，若有无效数据则整体插值后插值曲线的平方误差会比较大，即在该数据附近插值曲线的震动幅度较大。在插值处理前，应对原始数据进行一定的筛选，剔除无效数据。
②相同点：通过已知一些离散点集M上的约束，求取一个定义在连续集合S(M包含于S)的未知连续函数，从而达到获取整体规律目的
四、本次实验的重点难点分析
答:加强了对插值和拟合的认识，了解了其算法思想，并使用matlab将其实现。学会了观察插值拟合后的图形，并分析其问题。
画图进行比较：
通过观察图像，经比较可知两结果是很接近的。
2．区间作等距划分：，以（）为节点对函数进行插值逼近。（分别取）
（1）用多项式插值对进行逼近，并在同一坐标系下作出函数的图形，进行比较。写出插值函数对的逼近程度与节点个数的关系，并分析原因。
（2）试用分段插值（任意选取）对进行逼近，在同一坐标下画出图形，观察分段插值函数对的逼近程度与节点个数的关系。

等距多项式插值公式计算法

等距多项式插值公式计算法
等距多项式插值公式是一种用于实现等距插值的多项式插值方法。

它利用多项式拟合，把
一组离散的点连接起来，进行插值来估计中间的数据。

换句话说，等距多项式插值法就是
将相同距离的单个点连接起来形成一个多项式，以便用多项式函数来表示它。

采用分奇格拉德拉夫多项式的插值公式的表达式为：P(x)=A0+A1(x-x0)+A2[(x-x0)(x-
x1)]+...+An[(x-x0)(x-x1)...(x-xn-1)]。

其中，A0、A1...An分别是多项式插值中各项
系数，而x0、x1...xn-1则是插值中已知点的位置。

根据公式可以看出，通过求解多项式
插值公式中的系数，就可以计算出一条单条函数，该函数就可以将给定的离散数据连接起来。

等距多项式插值公式的优点是可以计算出定义域上的任何点的值。

它具有很好的拟合能力，有助于更好地拟合给定数据。

如果选取多项式次数足够高，可以精确插值，使结果非常接
近实际结果。

但是，等距多项式插值公式也有一定的缺点。

例如，如果拟合的数据量比较少，多项式的
次数就不能太高，否则会使插值的误差变大；另外，多项式的拟合也会受到原始数据的影响，如果数据不足或缺失，拟合的结果可能是不正确的。

综上所述，等距多项式插值公式是一种实现等距插值的方法，它具有对给定数据进行拟合
的优势，但会随着原始数据的数量而产生偏差，因此需要在合理选择拟合次数的情况下使用。

多项式插值计算方法

多项式插值计算方法一、引言多项式插值是数值分析中常用的一种方法，它可以通过已知的数据点来构造一个多项式函数，从而在数据点之间进行插值。

多项式插值方法在实际应用中具有广泛的用途，例如图像处理、数据拟合、信号处理等领域。

本文将介绍多项式插值的基本原理和几种常用的计算方法。

二、基本原理多项式插值的基本原理是通过已知的数据点来构造一个多项式函数，使得该函数经过这些数据点。

假设已知的数据点为(x1, y1), (x2, y2), ..., (xn, yn)，其中xi和yi分别表示自变量和因变量的取值。

我们希望找到一个多项式函数P(x)，使得P(xi) = yi。

根据插值定理，只要选取足够多的数据点，就可以找到一个唯一的多项式函数满足插值条件。

三、拉格朗日插值法拉格朗日插值法是一种常用的多项式插值方法。

它基于拉格朗日插值多项式的思想，通过构造一个n次多项式来实现插值。

具体步骤如下：1. 根据已知的n+1个数据点，构造拉格朗日插值多项式的基函数Li(x)，其中i表示第i个数据点。

2. 将基函数Li(x)与对应的因变量yi相乘，得到Li(x)*yi。

3. 将所有的Li(x)*yi相加，得到最终的插值多项式P(x)。

4. 将自变量x代入插值多项式P(x)中，即可得到对应的插值结果。

拉格朗日插值法的优点是简单易懂，计算量较小。

但当数据点较多时，计算复杂度会增加，同时在边界处的插值结果可能会出现较大误差。

四、牛顿插值法牛顿插值法是另一种常用的多项式插值方法。

它基于差商的概念，通过构造一个n次多项式来实现插值。

具体步骤如下：1. 根据已知的n+1个数据点，计算差商表。

2. 根据差商表的值，构造牛顿插值多项式。

3. 将自变量x代入插值多项式中，即可得到对应的插值结果。

牛顿插值法的优点是计算效率高，尤其适用于数据点较多的情况。

但在插值区间较大时，插值结果可能会出现振荡现象。

五、埃尔米特插值法埃尔米特插值法是一种基于导数信息的多项式插值方法。

三次样条插值与多项式拟合的关系

三次样条插值与多项式拟合的关系1. 介绍在数学和计算机科学领域里，三次样条插值和多项式拟合都是常用的数据拟合方法。

它们都可以根据一系列的数据点来估计出一个函数，并在一定程度上能够描述数据的特征和趋势。

在本文中，我们将探讨三次样条插值和多项式拟合之间的关系，以及它们各自的优缺点。

2. 三次样条插值的基本概念三次样条插值是一种通过在相邻的数据点之间使用三次多项式来逼近数据的方法。

其基本思想是在相邻两个数据点之间构造一个三次多项式，并要求这些三次多项式在相邻数据点处拥有相同的函数值和导数值。

这样可以保证拟合的曲线在每个数据点处都能够平滑地连接，并且能够较好地反映数据的特征。

3. 多项式拟合的基本概念多项式拟合是一种通过使用一个多项式函数来逼近数据的方法。

其基本思想是找到一个多项式函数，使得它在给定的数据点处能够最好地拟合已有的数据。

通常情况下，我们会选择低阶的多项式函数，如线性函数或二次函数，以避免过拟合的问题。

4. 三次样条插值与多项式拟合的关系从数学原理上来讲，三次样条插值其实也可以看作是一种多项式拟合的方法。

因为在每个相邻的数据点之间，我们都使用了一个三次多项式来逼近数据。

所以可以说，三次样条插值是一种局部的多项式拟合方法。

5. 优缺点比较在实际应用中，三次样条插值和多项式拟合各有其优缺点。

三次样条插值能够保证拟合曲线在每个数据点处的平滑连接，能够比较好地反映数据的特征。

然而，它在整体拟合的时候可能会出现振荡的问题，特别是在数据点比较稀疏的情况下。

而多项式拟合则可以灵活地通过选择不同阶数的多项式来逼近数据，能够较好地拟合整体趋势。

但是，它容易出现过拟合的问题，特别是在数据点较多的情况下。

6. 个人观点和理解在我看来，三次样条插值和多项式拟合都是非常有用的数据拟合方法。

在实际应用中，我们可以根据具体的数据特点和需求来选择合适的方法。

如果需要保证拟合曲线在每个数据点处平滑连接，同时又能较好地反映整体趋势，可以选择三次样条插值。

多项式插值计算方法

多项式插值计算方法引言：多项式插值是数值分析中常用的一种方法，用于通过已知数据点构造一个多项式函数，以逼近或插值这些数据点。

本文将介绍多项式插值的基本概念、插值多项式的计算方法以及应用场景。

一、多项式插值的基本概念在实际问题中，我们经常需要通过有限个数据点来近似或还原一个函数。

多项式插值是一种常见的数值方法，通过构造一个多项式函数来逼近或插值已知的数据点。

多项式插值的基本思想是：假设我们有n+1个数据点(x0, y0), (x1, y1), ..., (xn, yn)，其中xi为已知的节点，yi为对应的函数值。

我们希望找到一个次数不超过n的多项式P(x)，使得P(xi)=yi。

这个多项式P(x)就是我们要求解的插值多项式。

二、拉格朗日插值多项式的计算方法拉格朗日插值多项式是多项式插值的一种常用方法。

它的基本思想是构造n次多项式，使得多项式在每个节点上都满足插值条件。

具体计算步骤如下：1. 根据已知的n+1个数据点(x0, y0), (x1, y1), ..., (xn, yn)，构造n 次拉格朗日基函数：Li(x) = Π[j=0, j≠i]^(n) (x-xj) / (xi-xj)，其中i=0,1,...,n。

2. 构造拉格朗日插值多项式：P(x) = Σ[i=0]^(n) yi * Li(x)，其中i=0,1,...,n。

三、牛顿插值多项式的计算方法牛顿插值多项式是另一种常用的多项式插值方法。

它的基本思想是通过差商来递推计算插值多项式的系数。

具体计算步骤如下：1. 根据已知的n+1个数据点(x0, y0), (x1, y1), ..., (xn, yn)，计算差商表：f[x0] = y0，f[x1] = (y1-y0) / (x1-x0)，f[x2] = (f[x2]-f[x1]) / (x2-x1)，...f[xn] = (f[xn]-f[xn-1]) / (xn-xn-1)。

2. 构造牛顿插值多项式：P(x) = f[x0] + Σ[i=1]^(n) f[x0, x1, ..., xi] * Π[j=0]^(i-1) (x-xj)，其中i=1,2,...,n。