第四章 相平衡习题教学内容
第四章相平衡思考题.doc

第四章相平衡思考题1.纯氮气和空气算一个相吗?【解】纯氮气和空气各算一个相。
2.当两个相的温度相同但压力不同时,两个相能达到平衡吗?如果两相的压力相同而温度不同,两相能达到平衡吗?【解】一般而言,当系统达到热力学平衡时,系统将同时满足热平衡、力平衡、相平衡和化学平衡。
具体到相平衡,其条件是各物质在两相屮的化学势相同。
影响化学势的因素有温度和压力,达到相平衡时一般温度和压力亦相等。
如果温度相同,而压力不等同样有达到相平衡的可能,如渗透系统;同样地,在压力相同而温度不同的情况下,也应该有达到相平衡的可能性。
3.在抽空的真空容器中,有一定量的NH.HS ( s),加热后NH-HS ( s)分解,试说明组分数和自由度。
【解】分解反应为NHHS ( s) - NH ( g) +HS ( g),组分数K = 3・1 - 1 = 1 ,自由度f = 1・2 + 2=1 o4.恒温恒压下,某葡萄糖和氯化钠同时溶于水屮,用一张只允许水通过的半透膜将此溶液与纯水分开。
当系统达到平衡后,系统的自由度为多少?【解】广=3-2+1 =2 o5.说明物系点和相点的区别,什么时候物系点和相点是统一的?【解】物系点表示系统的组成,而相点表示系统相的组成。
当系统是单相的时候,两者是重合的。
6.图4・2屮,当系统处于临界点C时,自由度是多少?【解】自由度等于零。
7.如用二氧化碳超临界流体作萃取剂,最低的工作压力是多少?能在室温下进行此操作吗?【解】二氧化碳的临界参数是tc = 31.26°C、p c =7.2 MPa,因此最低压力是7.2 MPa o因为to =31.26 °C 十分接近典型的室温值25°C,因此C02超临界流体萃取可以在近室温下操作。
8.在一高压容器屮有足够量的水,向容器屮充入氮气压力到10 MPa,这时还能用Clausius-Clapeyron 方程计算水的沸点吗?【解】当压力达到10 MPa时,而水的临界压力为22.129 MPa,几乎接近一半,此时水的体积不能忽略,水蒸气也不能视为理想气体,所以不能用Clausius-Clapeyron 方程计算水的沸点。
相平衡课后解答.docx

第四章相平衡复习题1.判断下列说法是否正确,为什么?(1)在一个密封的容器内,装满了 373.2K 的水,一点空隙也不留,这时水的蒸气压等于零;(2)在室温和大气压力下,纯水的蒸气压为P*, 若在水面上充入 N2( g)以增加外压,则纯水的蒸气压下降;(3)小水滴与水汽混在一起成雾状,因为它们都有相同的化学组成和性质,所以是一个相;(4)面粉和米粉混合得十分均匀,肉眼已无法分清彼此,所以它们已成为一相;(5)将金粉和银粉混合加热至熔融,再冷却至固态它们已成为一相;(6) 1molNaCl (s)溶于一定量的水中,在298K 时,只有一个蒸气压;(7) 1molNaCl (s)溶于一定量的水中,再加少量的KNO 3( S),在一定的外压下,当达到气—液平衡时,温度必有定值;(8)纯水在三相点和冰点时,都是三相共存,根据相律,这两点的自由度都应该等于零。
答( 1)不对(2)不对(3)不对,两相——气相与液相(4)不对,两相(5)正确。
(6)正确(7)冰点时,两相共存, f=1 。
2.指出下列平衡系统中的物种数、组分数、相数和自由度数。
(1) NH 4Cl ( s)在真空容器中,分解成NH 3( g)和 HCl ( g)达平衡;(2) NH 4Cl ( s)在含有一定量 NH 3( g)的容器中,分解成NH 3( g)和 HCl ( g)达平衡;(3) CaCO3( s)在真空容器中,分解成CO2( g)和 CaO( s)达平衡;(4) NH 4 HCO 3( s)在真空容器中,分解成NH3(g), CO2( g)和 H 2O(g) 达平衡;(5) NaCl 水溶液与纯水分置于某半透膜两边,达渗透平衡;(6) NaCl ( s)与其饱和溶液达平衡;(7)过量的 NH 4Cl ( s), NH 4I( s)在真空容器中达成如下的分解平衡;NH4 Cl (s)NH 3( g) +HCl ( g)i.含有 Na+ ,K + ,SO42- ,NO 3-四种离子的均匀水溶液。
相平衡习题教学提纲

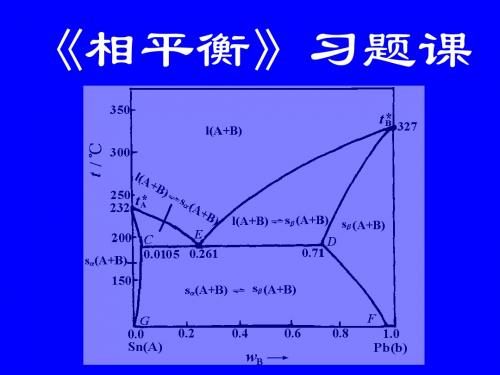
二、计算题 1. 已知A、B二组分体系的气液平衡相图如下
图所示:
(1)指出I、II、III区域内各有哪些相共存
(2)若xB=0.33的A、B混合液用精馏方法,能 否得到两个纯组分?得到的产物是什么?
(3)由140gB与30gA组成的混合液,将其蒸馏加 热到90℃,试问馏出液的组成如何?残留液的 组成如何?馏出液与残液各为多少摩尔?(A和 B的摩尔质量分别为100g和200g)
(1)指明各区域的相 和自由度数
(2) 420K时气液平衡 两相的组成各为多少?
( 3 ) 在 含 32kg 甲 醇 与 88kg乙烯乙二醇的体系 中,计算在420K时平衡 液相和气相各为多少? 已知甲醇和乙烯乙二醇 的摩尔质量分别为32 g, 88g
此课件下载可自行编辑修改,仅供参考! 感谢您的支持,我们努力做得更好!谢谢
4、硅-镁体系的相图如右所示, (1)根据相图确定镁-硅间形成化合物
的化学式,并分析相图。已知镁和硅的 摩尔质量分别为24.3g和28.1g (2)将含90%(质量 分数)硅的溶液5kg 冷却到1512K时,可 得到纯硅多少?溶液 组成如何?
3. 如图为乙烯乙二醇 与甲醇的T-x图
2、练习:HAc及C 6H6的相图如下图 (1)指出各区域所存在的相和自由度数 (2)从图中可见最低共熔温度为-8 ℃,
最低共熔混合物的质量分数为0.64,试问 将含苯0.75和0.25的溶液各100g,由20 ℃冷却时,首先析出的固体为何物,计算 最多能析出固体的质量。
例题:正庚烷和2,3,4-三甲基戊烷为一 具有最低共熔点的系统。实验测得最低 共熔温度为-114.4 ℃。最低共熔混合物 的组成为含正庚烷0.24(物质的量分数)。 今有含正庚烷为 0.80,0.90,0.95的溶 液,试分别计算将上述溶液冷却时,最多 能结晶出正庚烷的物质的量分数。
第四章 相平衡

• 例 :在某温度下 , 体系中 PCl5(g)部分分解产生了一定量的 PCl3(g)
和Cl2(g) 并达到了化学平衡, 体系中独立的化学反应数R为多少?
组分数K是多少?
• 体系中只存在下面一个化学反应:
PCl5(g)= PCl3(g) + Cl2(g) • 该体系中独立的化学反应数R=1
• 该体系中物种数S=3
• 解: 有反应: S=3 R=1 R’= 1 分解反应平衡 [p(NH3)=p(H2S)] NH4HS(s) = NH3(g) + H2S(g)
∴
K=3-1-1=1
f = K- + 2=1-2 + 2=1
• 即此体系的温度和压力两变量中只有一个是独立的 . 体系的温度 固定时, NH4HS的分解压力一定,故体系的压力恒定; 反之,若体系 的压力一定,体系的温度必也被确定.
吉布斯相律
• 相律的物理含义是:
体系的自由度等于体系的独立组分数 K 减去相数 再加上环境变量数2(温度和压力).
• 在某些特殊条件下, 环境变量不仅仅为温度和压力, 可能 存在其它变量, 故相律更一般的可表达为:
f=K– +n
• 式中: f为体系的自由度;
K为组分数;
为相数;
n为环境变量数, 一般情况下n=2(T, p).
• 独立组分数(K), 简称为组分数, 指确定体系组成所必须
的变量数.
• 定义:
K=S-R-R’
• S:物种数, R:独立的化学反应数, R’:浓度限制数
• 独立的化学反应数 (R): 一个多相系统存在多个反应时 ,
• 浓度限制数(R’): 同一相中存在的浓度之间的关系。
独立的化学反应指不能由其他反应组合推导出来的反应.
物理化学(第三版)第4章相平衡

R=1 NH4HCO3(s) ƒ NH3(g) CO2 (g) H2O(g) R'=2 p(NH3)=p(CO2)
p(NH3)=p(H2O) p(CO2)=p(H2O) C=4-1-2=1
练习 : ⑴ 将PCl3(g)和Cl2(g)放在一真空容器中,达平衡后, C=?
答:容器内有PCl5(g)=PCl3(g)+Cl2(g) S=3,R=1,R’=0,C=3– 1– 0=2。
冰水混合物 P=2
PCl5 (g) ƒ PCl3(g) Cl2 (g) P=1
CaCO3(s) ƒ CaO(s) CO2 (g)
P=3
NH4Cl(s) ƒ NH3(g) HCl(g)
P=2
水、冰和水蒸气组成的系统
P=3
2. 物种数(S)和组分数(C)
(1)物种数 系统中所包含的化学物质的种类数。用S表示 例如, 系统中含有PCl3、PCl5、和Cl2三种物质 S=3
均匀混合
P=1
分为两层
P=2
分为三层
P=3
液体:P=1,2, 3 (视其互溶程度而定)
(3)固体 P=1,2,…
固溶体(固体溶液): P =1
铈锆固溶体
碳化钛-碳化钨固溶体粉末
固体:除固溶体之外,有几种物质就有几相 P=1,2…
注意:相数与数量无关,与破碎程度无关。 P =1
相和相数(P)
气体:P=1 无论包括多少中气体都是一相 液体:P=1,2, 3 (视其互溶程度而定) 固体:P=1,2,…,有几种物质就有几相(固溶体除外)
C(s)
1 2
O2
(
g)
ƒ
CO( g )
⑴
C(s) O2 (g) ƒ CO2 (g)
物理化学课件-相平衡

水的相图
E p B 冰 水
A C D T 气
水的相图
dp/dT=∆fusHm/∆fusVm ∆ ∆ E p
-20oC, 2.×108Pa × 临界点 374oC, × B 2.23×107Pa
冰
水
A C D T1 0.0098oC T 气
水的相图
AB 是气 液两相平衡线,即水的蒸气压曲线。它不能任意 是气-液两相平衡线 即水的蒸气压曲线。 液两相平衡线, 延长,终止于临界点 临界点p=2.2×107Pa,T=647K,这时 临界点。 延长,终止于临界点。临界点 × , , 液界面消失。 气-液界面消失。高于临界温度,不能用加压的方法使气体 液界面消失 高于临界温度, 液化。 液化。
f=K-Φ +2
相律是由吉布斯(Gibbs)1876年得到 1876年得到 相律是由吉布斯 1876 是自然界的普遍规律之一. 的,是自然界的普遍规律之一
相律推导
个组分, 个相.每个相中每种物质都存在 并没有化学反应. 每个相中每种物质都存在,并没有化学反应 设平衡系统中有K个组分 Φ 个相 每个相中每种物质都存在 并没有化学反应
µB(β) =µB θ(β)+ห้องสมุดไป่ตู้Tlna B(β) β β β
f=Φ(K-1)+2-K(Φ-1) 1 = KΦ-Φ+2-KΦ+K=K-Φ+2 Φ Φ
相律
如果指定了温度或压力: 如果指定了温度或压力 f*=K- Φ +1 1 f*称为条件自由度 如果考虑到 个因素的影响 则相 称为条件自由度,如果考虑到 个因素的影响,则相 如果考虑到n个因素的影响 律应写为: 律应写为 f*=K- Φ +n 在上述推导中假设每个组分在每个相中都有分配,如 在上述推导中假设每个组分在每个相中都有分配 如 中不含B 总变量中应减去一个变量,相 果某一相( 中不含 物质,总变量中应减去一个变量 果某一相 α)中不含B物质 总变量中应减去一个变量 相 应的化学势相等的等式中也减少一个,因此 因此,不影响相律的 应的化学势相等的等式中也减少一个 因此 不影响相律的 表达式. 表达式
第四章 相平衡

① 面:固相区、液相区、气相区,f = 1 - 1 + 2 = 2 ② 线:固-气平衡线、固-液平衡线、 液-气平衡线、过冷水-气平衡线 f = 1 - 2 + 2 = 1 ③ A:三相点,273.16 K,0.611 kPa 固-水(纯)-气(水蒸汽)三相平衡共存, f = 1 - 3 + 2 = 0 热力学温标:0和A之间分为273.16格,每一格为1 K, 1 K(Kelvin) = 1/273.16 冰点:101.325 kPa、273.15 K(0℃) 固-液(饱和空气的水溶液)-气(潮湿空气)三相平衡共存。 凝固点:一定外压下,固-液两相平衡时的温度。 B:临界点,647 K,2.2 × 104 kPa
蒸气压-组成图 沸点-组成图 熔点-组成图
一、单组分系统的相图 K = 1,f = 1 - Φ + 2 = 3 – Φ f = 0,Φ = 3;f = 2,Φ = 1
第二节 单组分系统
0.6106
0.6106
0.6106
0.0098
2.338
20
101.325
若B为易挥发组分: (1) B在气相中的浓度大于它在液相中的浓度。 (2) A在液相中的浓度大于它在气相中的浓度。
二、杠杆规则 物系点:表示系统状态的点。 相点:表示平衡系统中某一相状态的点。 (1) 单相区,物系点与相点重合;两相区,物系点与 相点分离。 (2) 自物系点做水平线与 气、液相线的交点为 相点。物系点垂直组 成轴变化,相点则沿 相线变化。
水的相图应用: 冷冻干燥:通过升华从冻结的样品中去除水分或溶剂。 优点:① 在较低温度下进行。 ② 可保留样品的化学结构、 营养成分、生物活性。 ③ 产品的复水性和速溶性好。 ④ 脱水彻底,利于长时间保 存和运输。 设备:生化用冷冻干燥设备。
高中物理第四章 物体的平衡

第四章物体的平衡这一主要学习共点力的平衡和力矩的平衡及其简单应用,属于力学的基本内容。
其中平衡条件的理解与运用是本章的重点。
这一章以前三章学习的基本知识为基础(特别是物体的受力分析和牛顿运动定律),学习物体运动的一种特殊状态-平衡态。
前两节学习共点力作用下物体的平衡,掌握力的平衡条件(不涉及转动问题);三四两节研究物体的转动平衡问题,学习力矩的概念,掌握有固定转动轴物体的平衡条件。
通过最后一节对物体的平衡状态进一步学习,知道物体平衡有稳定和不稳定之分。
物体的平衡问题在实际中有很多应用,因此在学习时要注意联系实际,对学好本章很有好处。
第一节共点力作用下物体的平衡【教学要求】1.了解共点力作用下物体平衡的概念。
2.知道共点力作用下物体平衡的条件。
【知识要点】一.共点力:_____________________________________________的力称之为共点力。
二.共点力作用下物体的平衡一个物体在共点力作用下,如果保持________________________________,那么该物体则处于平衡状态。
注意:(1)正确理解“保持”两字。
例如竖直上抛的物体运动到最高点时,虽然速度为零,但这个状态不能保持,故不属于平衡状态。
(2)正确理解“一个”两字。
只有作用在同一个物体上的力才有平衡的可能,作用在两个物体上的力是不可能平衡的。
比如作用力和反作用力,尽管大小相等,方向相反,作用在同一直线上,但由于它们分别作用在两个物体上,故达到平衡是不可能的。
三.共点力作用下物体的平衡条件共点力作用下物体的平衡条件:_____________________________。
特例:(1)两个力互相平衡,则必须是两力的大小_____、方向_____,作用在______________上。
(2)三个力互相平衡,则其中任意两个力的合力必与第三个力大小______、方向______、作用在同一直线上。
四.三个共点力作用下物体平衡的特点物体在三个共点力作用下处于平衡状态,在把表示这三个力的有向线段首尾相接,必组成一个封闭的三角形。
第四章 相平衡(第二节)

相点与冰点区别的原因
冰点温度比三相点温度低 0.01 K 是由两种因素造成的: (1)外压增加 点下降0.00748 K 使凝固
(2) 水中溶有空气 使凝
固点下降 0.00241 K。
复习思考题
1. 在水的三相点时,自由度为零,而冰点的自由度 是否也为零? 2. 克-克方程的意义?适用条件? 作业:P129,11,12
C
T/K
水相图的静态分析
①面:f=2,Ф=1,单相区 面AOB:s 相 面BOC:g 相 面AOC:l 相 OA线:气-液平衡线 ②线:f=1,Ф=2,两相平衡线
OB线:气-固平衡线
OC线:固-液平衡线
OD线:过冷水-气的 亚稳平衡线 ③点:O点,f=0,Ф=3,三相共存点 温度为 273.16 K,压力为610.62 Pa
单组分体系
史竞艳
2010.12.25
第四 第二节 单组分体系
教学目的和要求
1、掌握描述单组分体系的克拉贝龙-克劳修斯方程;
2、掌握水的相图中点、线、面的含义和应用。
重点 1、掌握克拉贝龙-克劳修斯方程;
2、掌握水的相图。
难点 如何分析和使用相图?
本节要点
1 . 单组分体系相图的特点 2 . 克拉贝龙方程
N 点:汽,水两相平衡,f=1
O
B
NQ 段:水蒸气温度不断升高, f=2
0
T/K
5. 水的三相点与冰点的区别
三相点 是物质自身的特性,不能加以改变,如 H2O的三相点 T 273.16 K , p 610.62 Pa 冰点 是在大气压力 下,水、冰、气三相 共存的点。当大气压 力为 105 Pa 时,冰点 温度为 273.15 K ,改 变外压,冰点也随之 改变。
第四章 多相平衡系统的热力学

p
2 H 2O
p pO 2
2 H2
C = S-R=3-1=2
R表示的是独立的化学平衡数。
20
f =C–P+2
需要注意的是,R表示的是独立的化学平衡数。
例如:化学反应
CO(g) + H2O(g) ===CO2 (g)+ H2 (g) (1)
C(s) +CO2(g)===2CO(g)
C(s) + H2O(g) === CO(g)+H2(g)
d ln p vap H m 2 dT RT
这就是Clausius-Clapeyron 方程, vap H m 是摩尔气化热。 假定 vap H m 的值与温度无关,积分得:
p2 vap H m 1 1 ln ( ) p1 R T1 T2
这公式可用来计算不同温度下的蒸气压或摩尔蒸发热。
O点: 三相点 p/Pa
22.12MPa C
三相点与冰点是否 是一回事?
≈
超临界流体 A ●
水的冰点
pθ
B D
O
A点:临界点
超临界流体的特 点及技术
610.62Pa
≈
647.4K
273.15K
273.16K
T/K
35
超临界流体萃取的实例
• • • • • 萃取化工产品之中的萘 从咖啡豆萃取咖啡因 茶叶中脱除茶碱 烟草中脱除尼古丁 辣椒中提取辣椒色素
30
例题2 碳酸钠和水可以组成下列化合物: Na2CO3.H2O,Na2CO3.7H2O,Na,与碳酸钠水溶液及冰共存的含水盐最
多可有几种?
(2)30℃时,与水蒸气平衡共存的含水盐最多可
相平衡习题课

《物理化学》
相平衡习题课
基本要求
• 相、组分数、自由度的意义; 组分数、自由度的意义; • 应用相律分析平衡体系中的组分数、自由度数; 应用相律分析平衡体系中的组分数、自由度数; • 克拉贝龙、克劳修斯 克拉贝龙方程; 克拉贝龙方程; 克拉贝龙、克劳修斯-克拉贝龙方程 • 单组分相图的分析; 单组分相图的分析; • 相图分离提纯物质的基本原理。 相图分离提纯物质的基本原理。
• 某反应体系中有 某反应体系中有C(s)、 H2O(g)、 CO(g)、 CO2(g)、 H2(g)5种物质 , 、 种物质, 、 、 、 种物质 建立了如下三个平衡: 在1200 K建立了如下三个平衡: 建立了如下三个平衡 H2O(g)+C(s)=H2(g)+CO(g); ; CO2(g)+H2(g)=H2O(g)+CO(g) ; CO2(g)+C(s)=2CO(g), , • 则此体系的独立组分数K= 3 、自由度 自由度f= 2 、相数 相数Φ= 2 则此体系的独立组分数 • 某平衡体系内存在以下化学平衡: 某平衡体系内存在以下化学平衡: C(s) +O2(g) =CO2(g); ; CO(g)+0.5O2(g)=CO2(g); ; C(s)+ 0.5O2(g)=CO(g), , • 则此体系的独立组分数 则此体系的独立组分数K= 2 、自由度f= 2 自由度 、相数Φ= 2 。 相数 。
• 在低温下,将某种盐溶于水并析出氢氧化物,该体系的独立组分 在低温下,将某种盐溶于水并析出氢氧化物, 数为 ( C ) A. 1;B. 2;C. 3;D. 4 ; ; ; • 将N2、H2、NH3三种气体通入 三种气体通入773 K、32423 kPa的合成塔中,在 的合成塔中, 、 的合成塔中 催化剂存在下发生反应并达到平衡, 催化剂存在下发生反应并达到平衡,则该体系的自由度为 ( A ) A. 1;B. 3;C. 0;D. 2 1; 3; 0; • 一个 组分体系,最多可以有 ( B )相共存。 一个2组分体系, 相共存。 组分体系 相共存 A. 3相;B. 4相 ;C. 5相 ; D. 6相 相 相 相 相 • 定温下,水、苯、苯甲酸平衡体系中可以同时共存的最大相数为 定温下, ( B ) A. 3相;B. 4相 ;C. 5相 ; D. 6相 相 相 相 相
第四章-相平衡习题

第四章相平衡习题1.指出下列平衡系统的组分数、自由度数各为多少?(1)NH4Cl(S)部分分解为NH3(g)和HCl(g)物种数S=3,化学平衡关系式数目R=1,浓度限制条件数目R’=1[NH3(g)和HCl(g)〕浓度相等]组分数K=S-R-R’=3-1-1=1相数Ø=2〔固相和气相两相〕自由度f=k-Ø+2=1-2+2=1(2)若上述体系中额外再加入少量的NH3〔g〕物种数S=3,化学平衡关系式数目R=1,浓度限制条件数目R’=0[NH3(g)和HCl(g)〕不能建立浓度关系]组分数K=S-R-R’=3-1-0=2相数Ø=2〔固相和气相两相〕自由度f=k-Ø+2=2-2+2=2(3)NH4HS(S)和任意量的NH3(g)与H2S〔g〕平衡;物种数S= 3, 化学平衡式R=1,R’ = 0组分数K= S–R- R’ = 3 – 1 – 0 = 2相数Ø=2〔固相和气相两相〕自由度f=k–Ø+2= 2 –2+2= 2(4)C(S)、CO〔g〕、CO2(g)、O2(g)在373K时达到平衡。
物种数S=4,存在下面的化学平衡式:C+O2↔CO22C+O2↔2CO 2CO+O2↔2CO2CO2+C↔2CO实际上后面两个化学式都可以通过前面两个平衡式获得,则R= 2,而不是等于4。
无浓度限制条件,R’ = 0,则:K = S–R - R’ = 4 – 2 = 2相数Ø=2〔固相和气相两相〕由于有温度条件限制,所以自由度为f=K–Ø+1=2–2+1=12.在水、苯和苯甲酸的体系中,若指定了下列事项,试问系统中最多可能有几个相,并各举一例。
〔1〕指定温度;K =S–R–R’,S = 3, R = R’ = 0, 则K = 3f = K–Φ + 1 = 4–Φf = 0时,Φ= 4, 体系最多有四相,如气相、苯甲酸固体、苯甲酸饱和水溶液和苯甲酸饱和苯溶液。
物理化学4章_多相平衡-习题课

413
D D' E
G
M
熔化物+Cd(s)
G E 413 Bi(s)+熔化物 D B Bi(s)+Cd(s)
M
t/s
上一页 下一页
0 Bi
0.2
0.4
0.6
0.8
wCd
1 Cd
相平衡习题课
水-盐体系 溶解度法
E:冰、盐、溶液三相共存及 三相共存所能达到的最低温 度。两相共存区,杠杆规则 适用。
上一页
形成不稳定化合物
上一页
下一页
相平衡习题课
(1)步冷曲线法 (2)分析
L
(3)冷却过程中 相变化的情况
E (SA) (SB)
上一页
下一页
Cd-Bi二元相图的绘制
1.0Bi
a
A
0.4Cd 1.0Cd 0.2Cd 0.7Cd b c d e H A'
F
p
A
H 596
熔化物(单相)
546
C
F
T /K
C
B
j
等压
熔液(单相)
T /K
I
固溶体Ⅰ (单相)
k
E
B
C
固溶体Ⅱ
J
D
0 KNO3 (A)
423
H
F
x(TiNO3 )
G (单相) 1.0 TiNO3 (B)
AJ是固溶体Ⅰ的组成曲线; JEC线为三相共存线 BC是固溶体Ⅱ的组成曲线; 下一页 上一页
相平衡习题课
1.指出下列平衡体系的组分数,自由度(或条件 自由度)各为多少? a. NH4Cl(g)部分分解为NH3(g)和HCl(g) NH4Cl==NH3+HCl
相平衡习题课
-1
1 1 T 405 . 55 K tri
p tri =2274.5Pa; T =444.4K tri
③当氢醌在500K沸腾时,pex=p*(l),
ln p ( l) 5332 . 7
70840 J mol 8 . 314 J mol
-1
-1 -1
K
1 1 465 . 15 K 500 K
pex=p*(l)=19173.2Pa
三、下图是碳的相图,试根据该图回答下列问题:
①说明曲线OA、OB、OC三条线的物理意义;②说明O点 的物理意义; ③碳在25℃、100kPa下以什么状态稳定存在? ④在2000K时,增加压力,使石墨转变成金刚石是一个放 热反应,试从相图判断两者的摩尔体积Vm哪个大? ⑤试从相图上估计2000K时,将石墨转变成金刚石需要多 大压力?
解:①C=3;P=2;F=3 ②C=1; P =2; F =1 ③C=2; P =2; F =2 ④C=2; P =3; F =1
二、氢醌的饱和蒸气压与ห้องสมุดไป่ตู้度的数据如下:
l t/℃ p * /P a 1 9 2 .0 5 3 3 2 .7 g 2 1 6 .5 1 3 3 3 4 .4
s g
1 3 2 .4 1 3 3 .3
相平衡习题课习题课动能定理习题课数学分析习题课讲义习题课教案习题课怎么上杠杆习题课物理习题课教案机械能守恒定律习题课如何上好习题课
《相平衡》习题课
一、指出下列几个系统的组分数C、相数P和 自由度数F: ①N2(g)和O2(g)溶于水,且达到气液平衡; ②NH4Cl(s)在一个容器中部分分解且达到化 学平衡; ③同②,但在容器中原来已有HCl(g); ④固态CaCO3在一个预先抽空的容器中部分 分解且达到化学平衡。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章相平衡习题第四章相平衡习题1.指出下列平衡系统的组分数、自由度数各为多少?(1)NH4Cl(S)部分分解为NH3(g)和HCl(g)物种数S=3,化学平衡关系式数目R=1,浓度限制条件数目R’=1[NH3(g)和HCl(g))浓度相等]组分数K=S-R-R’=3-1-1=1相数Ø=2(固相和气相两相)自由度f=k-Ø+2=1-2+2=1(2)若上述体系中额外再加入少量的NH3(g)物种数S=3,化学平衡关系式数目R=1,浓度限制条件数目R’=0[NH3(g)和HCl(g))不能建立浓度关系] 组分数K=S-R-R’=3-1-0=2相数Ø=2(固相和气相两相)自由度f=k-Ø+2=2-2+2=2(3)NH4HS(S)和任意量的NH3(g)及H2S(g)平衡;物种数S = 3, 化学平衡式R =1,R’ = 0组分数K = S –R - R’ = 3 – 1 – 0 = 2相数Ø=2(固相和气相两相)自由度f = k –Ø + 2 = 2 – 2 + 2 = 2(4)C(S)、CO(g)、CO2(g)、O2(g)在373K时达到平衡。
物种数S=4,存在下面的化学平衡式:C+O2↔CO2 2C+O2↔2CO 2CO+O2↔2CO2 CO2+C↔2CO 实际上后面两个化学式都可以通过前面两个平衡式获得,则R = 2,而不是等于4。
无浓度限制条件,R’ = 0,则:K = S–R - R’ = 4 – 2 = 2相数Ø=2(固相和气相两相)由于有温度条件限制,所以自由度为f = K–Ø + 1 = 2 – 2 + 1 = 12.在水、苯和苯甲酸的体系中,若指定了下列事项,试问系统中最多可能有几个相,并各举一例。
(1)指定温度;K = S–R–R’,S = 3, R = R’ = 0, 则K = 3f = K–Φ + 1 = 4 –Φf = 0时,Φ= 4, 体系最多有四相,如气相、苯甲酸固体、苯甲酸饱和水溶液和苯甲酸饱和苯溶液。
(2)指定温度和水中苯甲酸的浓度;K = S–R–R’,S = 3, R = 1,R’ = 0, 则K = 2f = K–Φ + 1 = 3 –Φf = 0时,Φ= 3, 体系最多有三相,如气相、苯甲酸饱和水溶液和苯甲酸饱和苯溶液。
(3)指定温度、压力和苯中苯甲酸的浓度。
K = S–R–R’,S = 3, R =1,R’ = 0, 则K = 2f = K–Φ = 2 –Φf = 0时,Φ= 2 , 体系最多有两相,如苯甲酸饱和水溶液和苯甲酸饱和苯溶液。
3.试指出下述系统的自由度数、如f ≠ 0,则指出变量是什么?(1)在标准压力下,水与水蒸气平衡组分数K = S = 1,相数Ø= 2,指定压力,则f = K–Ø + 1=1 – 2 + 1=0体系为无变量体系(2)水与水蒸气平衡组分数K = S = 1,相数Ø=2,则f = K–Ø + 2 =1 – 2 + 2=1体系为单变量体系,变量是温度或压力中的任一个(3)在标准压力下,I2在水中和CCl4中分配已达平衡,无I2(S)存在组分数K = S = 3相数Ø=2,指定压力,则:f = K–Ø + 1=3 – 2 + 1=2体系为双组分变量,变量为温度和I2在水或CCl4中的任一个浓度。
(4)NH3、H2、N2三种气体已达平衡组分数K = S–R - R’ = 3 – 1 = 2f = K–Ø + 2=2 – 1 + 2 = 3体系为多变量体系,变量为温度、压力和某种物质浓度。
(5)在标准压力pθ下,NaOH水溶液与H3PO4水溶液混合后;S = 6, R = 3, R’ = 0, K = S–R–R’ = 3, Ø = 1f = K–Ø + 1=3 – 1 + 1=3体系为多变量体系,变量为温度、NaOH浓度和H3PO4浓度。
(6)在标准压力下,H2SO4水溶液与H2SO4∙H2O(S)已达平衡。
物种数S = 3(水、H2SO4、H2SO4∙H2O(S)),化学平衡关系式R = 1(生成H2SO4∙H2O(S)的反应),R’ = 0,则K = S–R - R’ = 3 – 1 = 2相数Ø=2,硫酸水溶液和固体H2SO4∙H2O,指定压力,则f = K–Ø +1=2 – 2 + 1=1体系为单变量体系,变量为温度。
4.图为硫的相图(1)写出图中各线和点代表哪些相的平衡;(2)叙述体系的状态由X在恒压下加热至Y所发生的变化。
答:硫有单斜硫(固)和正交硫(固)二种晶型,及液态硫与气态硫四种相态,由于单组分只能三相共存,因而在硫的相图中出现了四个三相点:B、C、F、E。
(1)三相点:B,正交、单斜和气相;C,单斜、气相和液相;F,正交、单斜和液相;E,正交、液相和气相。
两相平衡线:AB,正交和气相;BC,单斜和气相;CD,气相和液相;FC,单斜和液相;GF,正交和液相;BF,正交和单斜;BE,正交和单斜;CE,液相和单斜;EF,正交和液相。
(2)从X 到Y ,先正交硫的恒压升温过程至BF 两相平衡线上,然后为单斜硫的恒压升温过程至CF 两相平衡线上,最后为液相硫的恒压升温过程。
5.氯仿的正常沸点为334.6K (外压为101.325kPa ),试求氯仿的摩尔蒸汽热及313K 时的饱和蒸汽压。
解:由特鲁顿规则知:2112228888334.629.445/11ln ()2944511ln()101.3258.314334.631349m b m H T kJ mol H p p R T T p p kPa∆==⨯=∆=-=-=6.今把一批装有注射液的安培放入高压消毒锅内加热消毒,若用151.99 kPa 的水蒸气进行加热,问锅内的温度有多少度?(已知Δvap H m = 40.67 kJ/mol ) 解:122211()4067011()8.314373.15385112vap m O H R T T T T K C∆=-=-=≈21根据克-克方程:p ln p 151.99ln101.3257. 某有机物的正常沸点为530K ,从文献查得:压力减至0.267 kPa 时,它的沸点为313K ,问此有机物在1.33 kPa 时的沸点是多少?(假定363-503K 范围内温度对气化热的影响可以忽略 )解:注:正常沸点时对应的饱和蒸汽压为p θ.8.氢醌的蒸汽压实验数据如下:固 =气液 =气温度/K 405.5 436.6 465.1 489.6 压力/kPa0.1333 1.33345.3327 13.334求(1)氢醌的升华热、蒸发热、熔化热(设它们均不随温度而变); (2)气、液、固三相共存时的温度与压力; (3)在500K 沸腾时的外压。
解:121211()11()8.314405.5436.6109.0/11()11()8.314465.1489.670.83/38.17/m m m m m m m m m H R T T H H kJ mol H R T T H H kJ molH H H kJ mol∆=-∆=-∆=∆=-∆=-∆=∆∆∆升华21升华升华蒸发21蒸发蒸发熔化升华蒸发(1)根据克-克方程:p ln p 1.3334ln0.1333p lnp 13.334ln 5.3327=-=2211213222()ln 0.267(363503)ln101.3258.31436350364.4/64.410(503)1.33ln 101.3258.314503392.6p H T T p RT T H H kJ molT T T K∆-=∆-=⨯⨯∆=⨯-=⨯=1111()10901811()()8.314405.511()7083311()()8.314465.1m m H R T T I T H R T T II T ∆=-=-∆=-=-升华1蒸发1(2)设三相共存时的温度为T ,压力为p,则:p ln p p ln 0.1333p ln p p ln5.3327联合(I )和(II )式得:p=2.316kPa, T=444.9K1211()7083311()8.314465.1500m H R T T ∆=-=-蒸发1p (3)ln p p ln5.3327得:p=19.1kPa9. 为了降低空气的湿度,让压力为p θ的潮湿空气通过一冷却至248K 的管道,试用下列数据,估计在管道出口处空气中水蒸气的分压。
水在283K 和273K 时的蒸汽压分别为1.228和0.6106KPa ,273K 时冰的熔化热为333.5kJ/kg (假定所涉及的热效应都不随温度而变)。
当此空气的温度回升到293K 时(压力仍为p θ),问这时空气的相对湿度为若干?解:潮湿空气中的水蒸气,先从气相变为液相,再由液相变为固相,知道冰的熔化热,不知水的相变热,由克克方程:1.22811ln()0.61068.31427328344.93/44.93333.50.01850.93/vap m vap m sub m vap m fus mH H kJ mol H H H kJ mol∆=-∆=∆=∆+∆=+⨯=设248K 时冰的饱和蒸汽压为p 2,则根据克克方程:225093011ln()0.61068.3142732480.064p p kPa=-= 设293K 时水的饱和蒸汽压为p 2’,则根据克克方程:'2'24493011ln ()0.61068.3142732932.350.064100% 2.72%2.35p p kPa=-=⨯=相对湿度为:10.两个挥发性液体A 和B 构成一理想溶液,在某温度时溶液的蒸汽压为54.1kPa ,在气相中A 的摩尔分数为0.45,液相中为0.65,求此温度下纯A 和纯B 的蒸汽压。
解:****0.4554.137.450.65(10.45)54.185.0110.65A A A A A A AB B B B B B B y p p p x y p p kPa x y p p p x y p p kPa x ⨯==⇒-⨯==⇒-总总总总根据道尔顿分压定律和拉乌尔定律:======11.由甲苯和苯组成的某一溶液含30%(W/W )的甲苯,在303K 时纯甲苯和纯苯的蒸汽压分别为4.89和15.76 kPa ,设该溶液为理想溶液,问303K 时溶液的总蒸汽压和分压各为若干? 解:0.3920.2670.30.792784.870.267 1.30.73311.5512.85x x x kPa x kPa p kPa⨯⨯甲苯苯*甲苯甲苯甲苯*苯苯苯总甲苯苯==,=1-0.267=0.733+p =p ==p =p =15.76==p +p =14. 已知液体A 与液体B 可形成理想溶液,液体A 的正常沸点为338K ,其汽化热为35 kJ.mol -1。
